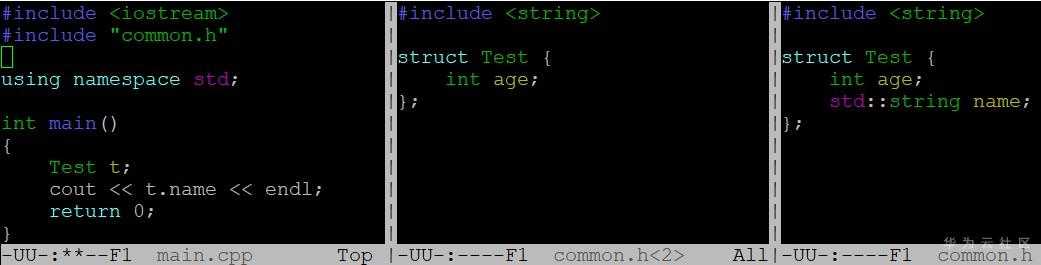
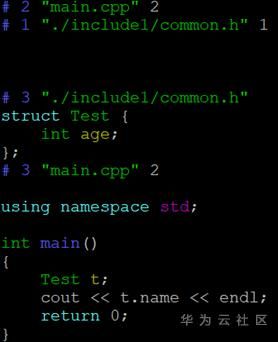
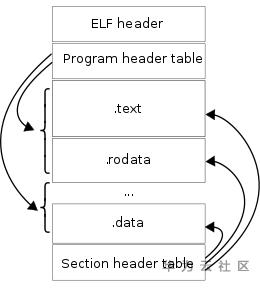
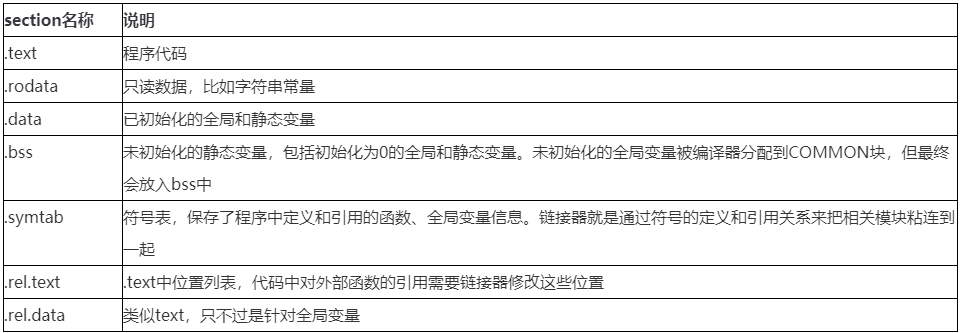
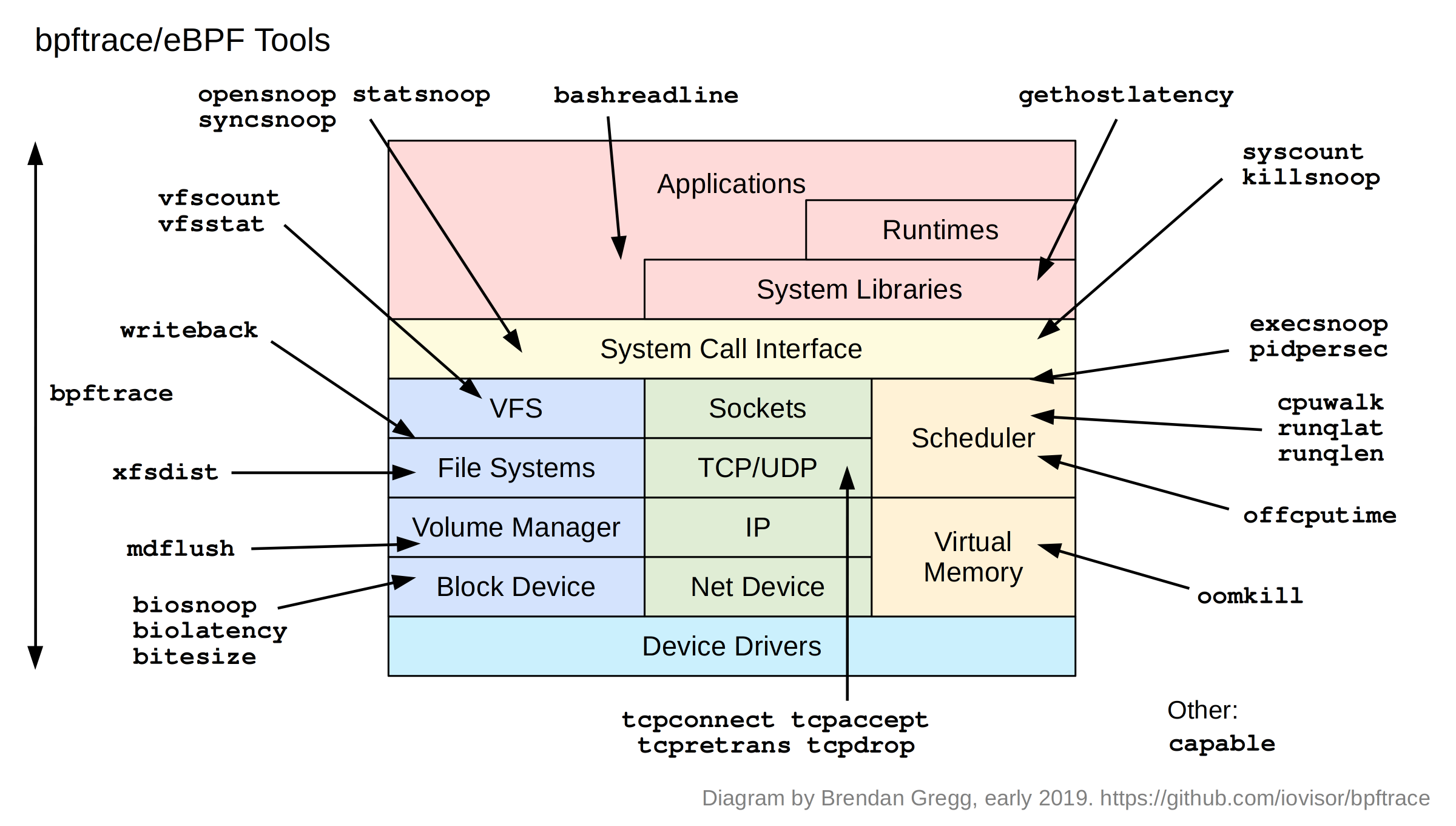
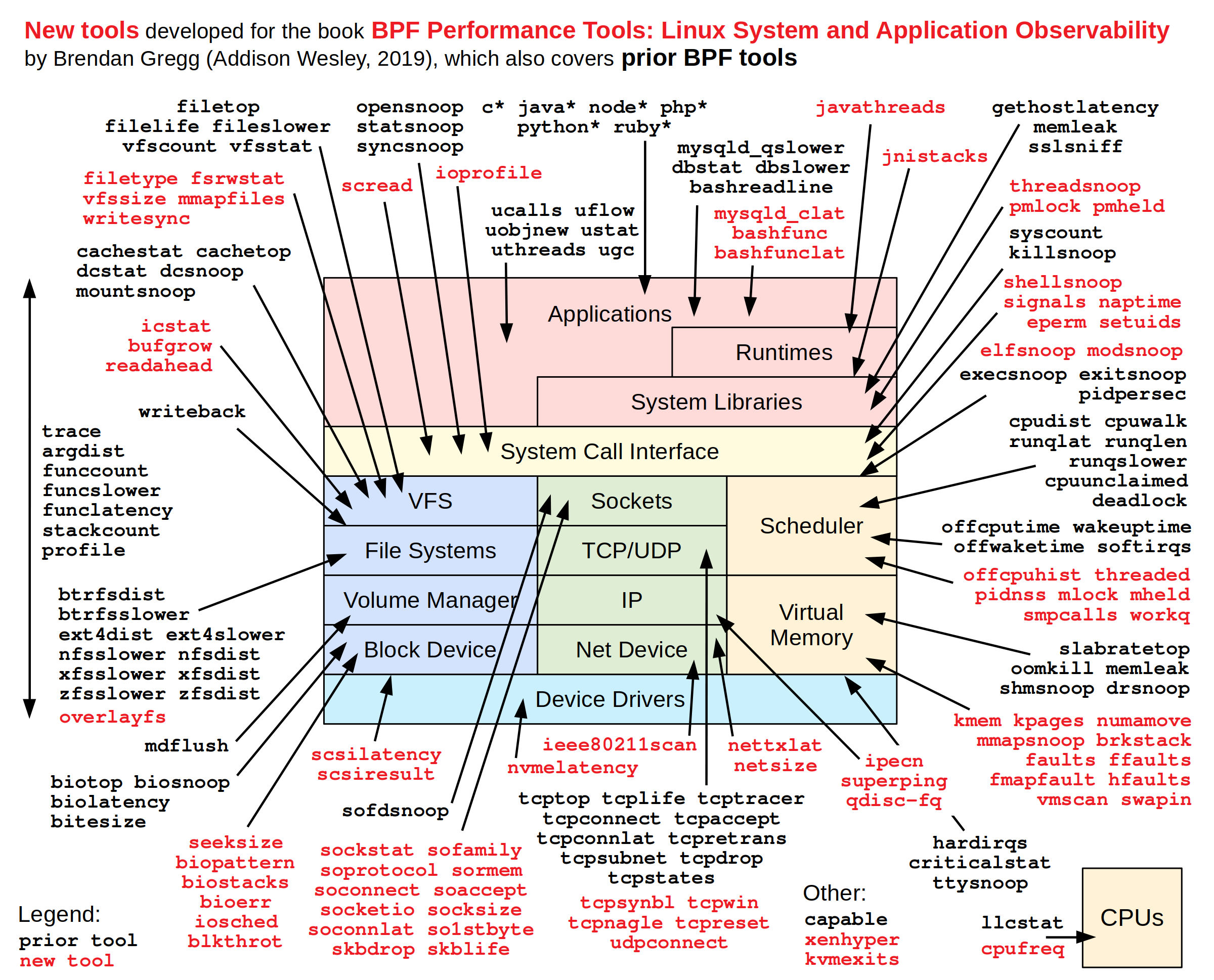
系统调用
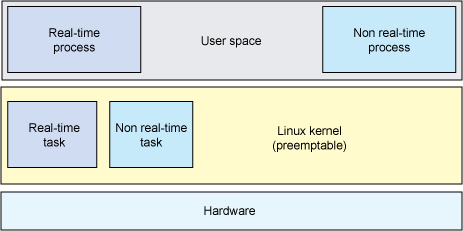
一般情况下进程不能访问内核所占内存空间也不能调用内核函数。为了和用户空间上运行的进程进行交互,内核提供了一组接口。透过该接口,应用程序可以访问硬件设备和其他操作系统资源。这组接口在应用程序和内核之间扮演了使者的角色,应用程序发送各种请求,而内核负责满足这些请求(或者让应用程序暂时搁置)。系统调用就是用户空间应用程序和内核提供的服务之间的一个接口。
系统调用在用户空间进程和硬件设备之间添加了一个中间层,其为用户空间提供了一种统一的硬件的抽象接口,保证了系统的稳定和安全,使用户程序具有可移植性。例如fork(),read(),write()等用户程序可以使用的函数都是系统调用。
用户空间的程序无法直接执行内核代码。它们不能直接调用内核空间中的函数,因为内核驻留在受保护的地址空间上。所以,应用程序应该以某种方式通知系统,告诉内核自己需要执行一个系统调用,希望系统切换到内核态,这样内核就可以代表应用程序来执行该系统调用了。那么应用程序应该以何种方式通知系统,系统如何切换到内核态?
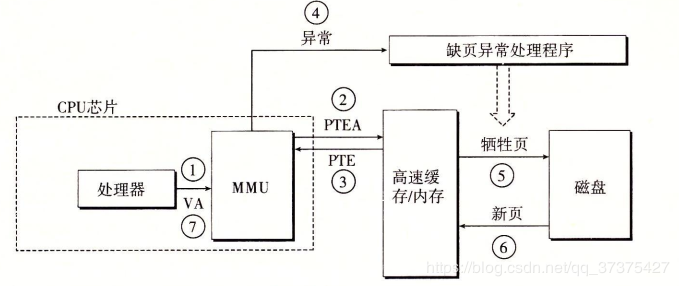
其实这种改变是通过软中断来实现。首先,用户程序为系统调用设置参数。其中一个参数是系统调用编号。参数设置完成后,程序执行“系统调用”指令。x86系统上的软中断由int产生。这个指令会导致一个异常:产生一个事件,这个事件会致使处理器切换到内核态并执行0x80号异常处理程序。此时的异常处理程序实际上就是系统调用处理程序,该处理程序的名字为system_call,它与硬件体系结构紧密相关。对于x86-32系统来说,该处理程序位于arch/x86/kernel/entry_32.S`文件中,代码为:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26......
ENTRY(system_call)
RING0_INT_FRAME
t miss an interrupt
TRACE_IRQS_OFF
movl TI_flags(%ebp), %ecx
testl $_TIF_ALLWORK_MASK, %ecx
jne syscall_exit_work
......
在Linux中,每个系统调用被赋予一个系统调用号。这样,通过这个独一无二的号就可以关联系统调用。当用户空间的进程执行一个系统调用的时候,这个系统调用号就被用来指明到底是要执行哪个系统调用。进程不会提及系统调用的名称。系统调用号定义文件以及形式如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14$ cat ./arch/x86/include/asm/unistd.h
1 | # cat arch/x86/include/asm/unistd_32.h |
系统调用号相当关键,一旦分配就不能再有任何变更,否则编译好的应用程序就会崩溃。Linux有一个“未实现”系统调用sys_ni_syscall(),它除了返回一ENOSYS外不做任何其他工作,这个错误号就是专门针对无效的系统调用而设的。
因为所有的系统调用陷入内核的方式都一样,所以仅仅是陷入内核空间是不够的。因此必须把系统调用号一并传给内核。在x86上,系统调用号是通过eax寄存器传递给内核的。在陷人内核之前,用户空间就把相应系统调用所对应的号放入eax中了。这样系统调用处理程序一旦运行,就可以从eax中得到数据。其他体系结构上的实现也都类似。
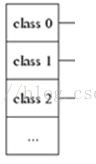
内核记录了系统调用表中的所有已注册过的系统调用的列表,存储在sys_call_table中。它与体系结构有关,32位x86一般定义在arch/x86/kernel/syscall_table_32.s文件中。这个表中为每一个有效的系统调用指定了惟一的系统调用号。sys_call_table是一张由指向实现各种系统调用的内核函数的函数指针组成的表。syscall_table_32.s文件如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26ENTRY(sys_call_table)
.long sys_restart_syscall /* 0 - old "setup()" system call, used for restarting */
.long sys_exit
.long ptregs_fork
.long sys_read
.long sys_write
.long sys_open /* 5 */
.long sys_close
.long sys_waitpid
.long sys_creat
.long sys_link
.long sys_unlink /* 10 */
.long ptregs_execve
......
.long sys_timerfd_settime /* 325 */
.long sys_timerfd_gettime
.long sys_signalfd4
.long sys_eventfd2
.long sys_epoll_create1
.long sys_dup3 /* 330 */
.long sys_pipe2
.long sys_inotify_init1
.long sys_preadv
.long sys_pwritev
.long sys_rt_tgsigqueueinfo /* 335 */
.long sys_perf_event_open
system_call()函数通过将给定的系统调用号与NR_syscalls做比较来检查其有效性。如果它大于或者等于NR syscalls,该函数就返回一ENOSYS。否则,就执行相应的系统调用。1
call *sys_call_table(,%eax, 4)
由于系统调用表中的表项是以32位(4字节)类型存放的,所以内核需要将给定的系统调用号乘以4,然后用所得的结果在该表中查询其位置。
除了系统调用号以外,大部分系统调用都还需要一些外部的参数输入。所以,在发生异常的时候,应该把这些参数从用户空间传给内核。最简单的办法就是像传递系统调用号一样把这些参数也存放在寄存器里。在x86系统上,ebx,ecx,edx,esi和edi按照顺序存放前五个参数。需要六个或六个以上参数的情况不多见,此时,应该用一个单独的寄存器存放指向所有这些参数在用户空间地址的指针。给用户空间的返回值也通过寄存器传递。在x86系统上,它存放在eax寄存器中。
下面我们看看用中断的方式如何完成系统调用功能:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int main(int argc, const char *argv[])
{
pid_t pid;
asm volatile (
"mov $0, %%ebx\n\t"
"mov $20, %%eax\n\t" //把系统调用号20放入`eax`寄存器中,20对应于`SYS_getpid()系统调用
"int $0x80\n\t" //0x80中断
"mov %%eax, %0\n\t" //将执行结果存放在`pid`变量中
:"=m"(pid)
);
printf("int PID: %d\n", pid);
printf("api PID: %d\n", getpid());
return 0;
}
此处没有传递参数,因为getpid不需要参数。本实例执行结果为:1
2
3$ ./target_bin
int PID: 4911
api PID: 4911
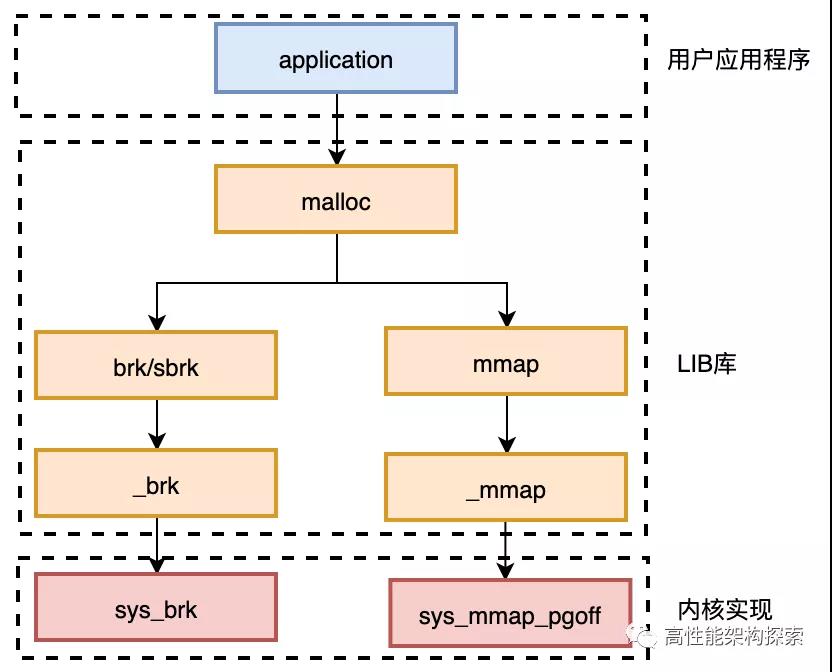
一般情况下,应用程序通过在用户空间实现的应用编程接口(API)而不是系统调用来编程。API是一个函数定义,说明了如何获得一个给定的服务,比如read()、malloc()、free()、abs()等。它有可能和系统调用形式上一致,比如read()接口就和read系统调用对应,但这种对应并非一一对应,往往会出现几种不同的API内部用到统一个系统调用,比如malloc()、free()内部利用brk()系统调用来扩大或缩小进程的堆;或一个API利用了好几个系统调用组合完成服务。更有些API甚至不需要任何系统调用——因为它不必需要内核服务,如计算整数绝对值的abs()接口。
Linux的用户编程接口遵循了在Unix世界中最流行的应用编程界面标准——POSIX标准,这套标准定义了一系列API。在Linux中(Unix也如此)这些API主要是通过C库(libc)实现的,它除了定义的一些标准的C函数外,一个很重要的任务就是提供了一套封装例程将系统调用在用户空间包装后供用户编程使用。不过封装并非必须的,如果你愿意直接调用,内核也提供了一个syscall()函数来实现调用。如下示例为使用C库调用和直接调用分别来获取当前进程ID:1
2
3
4
5
6
7
8
9
10
11
12
13
int main(int argc, const char *argv[])
{
pid_t pid, pidt;
pid = getpid();
pidt = syscall(SYS_getpid);
printf("getpid: %d\n", pid);
printf("SYS_getpid: %d\n", pidt);
return 0;
}
系统调用在内核有一个实现函数,以getpid为例,其在内核实现为:1
2
3
4
5
6
7
8
9
10
11
12
13/**
* sys_getpid - return the thread group id of the current process
*
* Note, despite the name, this returns the tgid not the pid. The tgid and
* the pid are identical unless CLONE_THREAD was specified on clone() in
* which case the tgid is the same in all threads of the same group.
*
* This is SMP safe as current->tgid does not change.
*/
SYSCALL_DEFINE0(getpid)
{
return task_tgid_vnr(current);
}
其中SYSCALL_DEFINE0为一个宏,它定义一个无参数(尾部数字代表参数个数)的系统调用,展开后代码如下:1
2
3
4asmlinkage long sys_getpid(void)
{
return current->tpid;
}
其中asmlinkage是一个编译指令,通知编译器仅从栈中提取该函数参数,所有系统调用都需要这个限定词。系统调用getpid()在内核中被定义成sys_getpid(),这是Linux所有系统调用都应该遵守的命名规则。
Linux中实现系统调用利用了0x86体系结构中的软件中断,也就是调用int $0x80汇编指令,这条汇编指令将产生向量为128的编程异常,此时处理器切换到内核态并执行0x80号异常处理程序。此时的异常处理程序实际上就是系统调用处理程序,该处理程序的名字为system_call(),对于x86-32系统来说,该处理程序位于arch/x86/kernel/entry_32.S文件中,使用汇编语言编写。那么所有的系统调用都会转到这里。在执行int 0x80前,系统调用号被装入eax寄存器(相应参数也会传递到其它寄存器中),这个系统调用号被用来指明到底是要执行哪个系统调用,这样系统调用处理程序一旦运行,就从eax中得到系统调用号,然后根据系统调用号在系统调用表中寻找相应服务例程(例如sys_getpid()函数)。当服务例程结束时,system_call()从eax获得系统调用的返回值,并把这个返回值存放在曾保存用户态eax寄存器栈单元的那个位置上,最后该函数再负责切换到用户空间,使用户进程继续执行。
硬中断及中断处理
操作系统负责管理硬件设备,为了使系统和硬件设备的协同工作不降低机器性能,系统和硬件的通信使用中断的机制,也就是让硬件在需要的时候向内核发出信号,这样使得内核不用去轮询设备而导致做很多无用功。
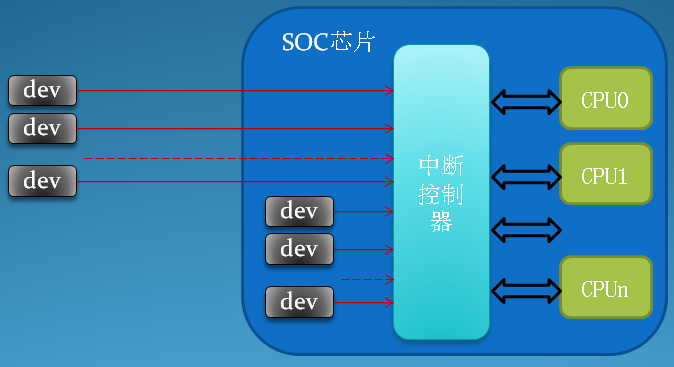
中断使得硬件可以发出通知给处理器,硬件设备生成中断的时候并不考虑与处理器的时钟同步,中断可以随时产生。也就是说,内核随时可能因为新到来的中断而被打断。当接收到一个中断后,中断控制器会给处理器发送一个电信号,处理器检测到该信号便中断自己当前工作而处理中断。
在响应一个中断时,内核会执行一个函数,该函数叫做中断处理程序或中断服务例程(ISR)。中断处理程序运行与中断上下文,中断上下文中执行的代码不可阻塞,应该快速执行,这样才能保证尽快恢复被中断的代码的执行。中断处理程序是管理硬件驱动的驱动程序的组成部分,如果设备使用中断,那么相应的驱动程序就注册一个中断处理程序。
在驱动程序中,通常使用request_irq()来注册中断处理程序。该函数在文件<include/linux/interrupt.h>中声明:1
2
3extern int __must_check
request_irq(unsigned int irq, irq_handler_t handler, unsigned long flags,
const char *name, void *dev);
第一个参数为要分配的中断号;第二个参数为指向中断处理程序的指针;第三个参数为中断处理标志。该函数实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82static inline int __must_check
request_irq(unsigned int irq, irq_handler_t handler, unsigned long flags,
const char *name, void *dev)
{
return request_threaded_irq(irq, handler, NULL, flags, name, dev);
}
int request_threaded_irq(unsigned int irq, irq_handler_t handler,
irq_handler_t thread_fn, unsigned long irqflags,
const char *devname, void *dev_id)
{
struct irqaction *action;
struct irq_desc *desc;
int retval;
/*
* handle_IRQ_event() always ignores IRQF_DISABLED except for
* the _first_ irqaction (sigh). That can cause oopsing, but
* the behavior is classified as "will not fix" so we need to
* start nudging drivers away from using that idiom.
*/
if ((irqflags & (IRQF_SHARED|IRQF_DISABLED)) == (IRQF_SHARED|IRQF_DISABLED)) {
pr_warning("IRQ %d/%s: IRQF_DISABLED is not guaranteed on shared IRQs\n",
irq, devname);
}
/*
* Lockdep wants atomic interrupt handlers:
*/
irqflags |= IRQF_DISABLED;
/*
* Sanity-check: shared interrupts must pass in a real dev-ID,
* otherwise we'll have trouble later trying to figure out
* which interrupt is which (messes up the interrupt freeing
* logic etc).
*/
if ((irqflags & IRQF_SHARED) && !dev_id)
return -EINVAL;
desc = irq_to_desc(irq);
if (!desc)
return -EINVAL;
if (desc->status & IRQ_NOREQUEST)
return -EINVAL;
if (!handler) {
if (!thread_fn)
return -EINVAL;
handler = irq_default_primary_handler;
}
//分配一个irqaction
action = kzalloc(sizeof(struct irqaction), GFP_KERNEL);
if (!action)
return -ENOMEM;
action->handler = handler;
action->thread_fn = thread_fn;
action->flags = irqflags;
action->name = devname;
action->dev_id = dev_id;
chip_bus_lock(irq, desc);
//将创建并初始化完在的action加入desc
retval = __setup_irq(irq, desc, action);
chip_bus_sync_unlock(irq, desc);
if (retval)
kfree(action);
if (irqflags & IRQF_SHARED) {
/*
* It's a shared IRQ -- the driver ought to be prepared for it
* to happen immediately, so let's make sure....
* We disable the irq to make sure that a 'real' IRQ doesn't
* run in parallel with our fake.
*/
unsigned long flags;
disable_irq(irq);
local_irq_save(flags);
handler(irq, dev_id);
local_irq_restore(flags);
enable_irq(irq);
}
return retval;
}
下面看一下中断处理程序的实例,以rtc驱动程序为例,代码位于<drivers/char/rtc.c>中。当RTC驱动装载时,rtc_init()函数会被调用来初始化驱动程序,包括注册中断处理函数:1
2
3
4
5
6
7
8
9
10/*
* XXX Interrupt pin #7 in Espresso is shared between RTC and
* PCI Slot 2 INTA# (and some INTx# in Slot 1).
*/
if (request_irq(rtc_irq, rtc_interrupt, IRQF_SHARED, "rtc",
(void *)&rtc_port)) {
rtc_has_irq = 0;
printk(KERN_ERR "rtc: cannot register IRQ %d\n", rtc_irq);
return -EIO;
}
处理程序函数rtc_interrupt():1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42/*
* A very tiny interrupt handler. It runs with IRQF_DISABLED set,
* but there is possibility of conflicting with the set_rtc_mmss()
* call (the rtc irq and the timer irq can easily run at the same
* time in two different CPUs). So we need to serialize
* accesses to the chip with the rtc_lock spinlock that each
* architecture should implement in the timer code.
* (See ./arch/XXXX/kernel/time.c for the set_rtc_mmss() function.)
*/
static irqreturn_t rtc_interrupt(int irq, void *dev_id)
{
/*
* Can be an alarm interrupt, update complete interrupt,
* or a periodic interrupt. We store the status in the
* low byte and the number of interrupts received since
* the last read in the remainder of rtc_irq_data.
*/
spin_lock(&rtc_lock); //保证`rtc_irq_data`不被`SMP`机器上其他处理器同时访问
rtc_irq_data += 0x100;
rtc_irq_data &= ~0xff;
if (is_hpet_enabled()) {
/*
* In this case it is HPET RTC interrupt handler
* calling us, with the interrupt information
* passed as arg1, instead of irq.
*/
rtc_irq_data |= (unsigned long)irq & 0xF0;
} else {
rtc_irq_data |= (CMOS_READ(RTC_INTR_FLAGS) & 0xF0);
}
if (rtc_status & RTC_TIMER_ON)
mod_timer(&rtc_irq_timer, jiffies + HZ/rtc_freq + 2*HZ/100);
spin_unlock(&rtc_lock);
/* Now do the rest of the actions */
spin_lock(&rtc_task_lock); //避免`rtc_callback`出现系统情况,RTC`驱动允许注册一个回调函数在每个`RTC`中断到来时执行。
if (rtc_callback)
rtc_callback->func(rtc_callback->private_data);
spin_unlock(&rtc_task_lock);
wake_up_interruptible(&rtc_wait);
kill_fasync(&rtc_async_queue, SIGIO, POLL_IN);
return IRQ_HANDLED;
}
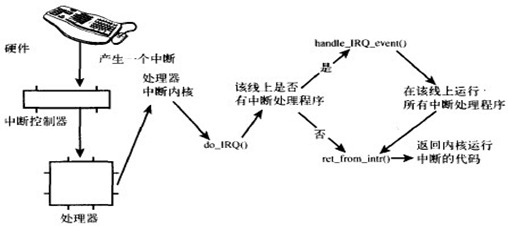
在内核中,中断的旅程开始于预定义入口点,这类似于系统调用。对于每条中断线,处理器都会跳到对应的一个唯一的位置。这样,内核就可以知道所接收中断的IRQ号了。初始入口点只是在栈中保存这个号,并存放当前寄存器的值(这些值属于被中断的任务);然后,内核调用函数do_IRQ()。从这里开始,大多数中断处理代码是用C写的。do_IRQ()的声明如下:1
unsigned int do_IRQ(struct pt_regs regs)
因为C的调用惯例是要把函数参数放在栈的顶部,因此pt_regs结构包含原始寄存器的值,这些值是以前在汇编入口例程中保存在栈上的。中断的值也会得以保存,所以,do_IRQ()可以将它提取出来,X86的代码为:1
int irq = regs.orig_eax & 0xff
计算出中断号后,do_IRQ()对所接收的中断进行应答,禁止这条线上的中断传递。在普通的PC机器上,这些操作是由mask_and_ack_8259A()来完成的,该函数由do_IRQ()调用。接下来,do_IRQ()需要确保在这条中断线上有一个有效的处理程序,而且这个程序已经启动但是当前没有执行。如果这样的话,do_IRQ()就调用handle_IRQ_event()来运行为这条中断线所安装的中断处理程序,函数位于<kernel/irq/handle.c>:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70/**
* handle_IRQ_event - irq action chain handler
* @irq: the interrupt number
* @action: the interrupt action chain for this irq
*
* Handles the action chain of an irq event
*/
irqreturn_t handle_IRQ_event(unsigned int irq, struct irqaction *action)
{
irqreturn_t ret, retval = IRQ_NONE;
unsigned int status = 0;
//如果没有设置`IRQF_DISABLED,将CPU中断打开,应该尽量避免中断关闭情况,本地中断关闭情况下会导致中断丢失。
if (!(action->flags & IRQF_DISABLED))
local_irq_enable_in_hardirq();
do { //遍历运行中断处理程序
trace_irq_handler_entry(irq, action);
ret = action->handler(irq, action->dev_id);
trace_irq_handler_exit(irq, action, ret);
switch (ret) {
case IRQ_WAKE_THREAD:
/*
* Set result to handled so the spurious check
* does not trigger.
*/
ret = IRQ_HANDLED;
/*
* Catch drivers which return WAKE_THREAD but
* did not set up a thread function
*/
if (unlikely(!action->thread_fn)) {
warn_no_thread(irq, action);
break;
}
/*
* Wake up the handler thread for this
* action. In case the thread crashed and was
* killed we just pretend that we handled the
* interrupt. The hardirq handler above has
* disabled the device interrupt, so no irq
* storm is lurking.
*/
if (likely(!test_bit(IRQTF_DIED,
&action->thread_flags))) {
set_bit(IRQTF_RUNTHREAD, &action->thread_flags);
wake_up_process(action->thread);
}
/* Fall through to add to randomness */
case IRQ_HANDLED:
status |= action->flags;
break;
default:
break;
}
retval |= ret;
action = action->next;
} while (action);
if (status & IRQF_SAMPLE_RANDOM)
add_interrupt_randomness(irq);
local_irq_disable();//关中断
return retval;
}
前面说到中断应该尽快执行完,以保证被中断代码可以尽快的恢复执行。但事实上中断通常有很多工作要做,包括应答、重设硬件、数据拷贝、处理请求、发送请求等。为了求得平衡,内核把中断处理工作分成两半,中断处理程序是上半部——接收到中断就开始执行。能够稍后完成的工作推迟到下半部操作,下半部在合适的时机被开中段执行。例如网卡收到数据包时立即发出中断,内核执行网卡已注册的中断处理程序,此处工作就是通知硬件拷贝最新的网络数据包到内存,然后将控制权交换给系统之前被中断的任务,其他的如处理和操作数据包等任务被放到随后的下半部中去执行。下一节我们将了解中断处理的下半部。
下半部机制之软中断
中断处理程序以异步方式执行,其会打断其他重要代码,其运行时该中断同级的其他中断会被屏蔽,并且当前处理器上所有其他中断都有可能会被屏蔽掉,还有中断处理程序不能阻塞,所以中断处理需要尽快结束。由于中断处理程序的这些缺陷,导致了中断处理程序只是整个硬件中断处理流程的一部分,对于那些对时间要求不高的任务,留给中断处理流程的另外一部分,也就是本节要讲的中断处理流程的下半部。
那哪些工作由中断处理程序完成,哪些工作留给下半部来执行呢?其实上半部和下半部的工作划分不存在某种严格限制,这主要取决于驱动程序开发者自己的判断,一般最好能将中断处理程序执行时间缩短到最小。中断处理程序几乎都需要通过操作硬件对中断的到达进行确认,有时还会做对时间非常敏感的工作(如拷贝数据),其余的工作基本上留给下半部来处理,下半部就是执行与中断处理密切相关但中断处理程序本身不执行的工作。一般对时间非常敏感、和硬件相关、要保证不被其它中断(特别是相同的中断)打断的这些任务放在中断处理程序中执行,其他任务考虑放在下半部执行。
那下半部什么时候执行呢?下半部不需要指定明确执行时间,只要把任务推迟一点,让它们在系统不太忙且中断恢复后执行就可以了,而且执行期间可以相应所有中断。
上半部只能通过中断处理程序实现,而下半部可以有多种机制来实现,在2.6.32版本中,有三种不同形式的下半部实现机制:软中断、tasklet、工作队列。下面来看一下这三种下半部的实现。
软中断
在start_kernerl()函数中,系统初始化软中断。1
2
3
4
5
6
7
8
9
10
11
12
13asmlinkage void __init start_kernel(void)
{
char * command_line;
extern struct kernel_param __start___param[], __stop___param[];
smp_setup_processor_id();
......
softirq_init();//初始化软中断
......
/* Do the rest non-__init'ed, we're now alive */
rest_init();
}
在softirq_init()中会注册两个常用类型的软中断,具体代码如下(位于kernel/softirq.c):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21void __init softirq_init(void)
{
int cpu;
for_each_possible_cpu(cpu) {
int i;
per_cpu(tasklet_vec, cpu).tail =
&per_cpu(tasklet_vec, cpu).head;
per_cpu(tasklet_hi_vec, cpu).tail =
&per_cpu(tasklet_hi_vec, cpu).head;
for (i = 0; i < NR_SOFTIRQS; i++)
INIT_LIST_HEAD(&per_cpu(softirq_work_list[i], cpu));
}
register_hotcpu_notifier(&remote_softirq_cpu_notifier);
//此处注册两个软中断
open_softirq(TASKLET_SOFTIRQ, tasklet_action);
open_softirq(HI_SOFTIRQ, tasklet_hi_action);
}
注册函数open_softirq()参数含义:
nr:软中断类型action:软中断处理函数
1 | void open_softirq(int nr, void (*action)(struct softirq_action *)) |
softirq_action结构表示软中断,定义在<include/linux/interrupt.h>1
2
3
4struct softirq_action
{
void (*action)(struct softirq_action *);
}
文件<kernel/softirq.c>中定义了32个该结构体的数组:1
static struct softirq_action softirq_vec[NR_SOFTIRQS] __cacheline_aligned_in_smp;
每注册一个软中断都会占该数组一个位置,因此系统中最多有32个软中断。从上面的代码中,我们可以看到open_softirq()中。其实就是对softirq_vec数组的nr项赋值。softirq_vec是一个32元素的数组,实际上Linux内核只使用了几项:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21/* PLEASE, avoid to allocate new softirqs, if you need not _really_ high
frequency threaded job scheduling. For almost all the purposes
tasklets are more than enough. F.e. all serial device BHs et
al. should be converted to tasklets, not to softirqs.
*/
enum
{
HI_SOFTIRQ=0,
TIMER_SOFTIRQ,
NET_TX_SOFTIRQ,
NET_RX_SOFTIRQ,
BLOCK_SOFTIRQ,
BLOCK_IOPOLL_SOFTIRQ,
TASKLET_SOFTIRQ,
SCHED_SOFTIRQ,
HRTIMER_SOFTIRQ,
RCU_SOFTIRQ, /* Preferable RCU should always be the last softirq */
NR_SOFTIRQS
};
那么软中断注册完成之后,什么时候触发软中断处理函数执行呢?通常情况下,软中断会在中断处理程序返回前标记它,使其在稍后合适的时候被执行。在下列地方,待处理的软中断会被检查和执行:
- 处理完一个硬件中断以后;
- 在
ksoftirqd内核线程中; - 在那些显示检查和执行待处理的软中断的代码中,如网络子系统中。
无论如何,软中断会在do_softirq()(位于<kernel/softirq.c>中)中执行,如果有待处理的软中断,do_softirq会循环遍历每一个,调用他们的软中断处理程序。1
2
3
4
5
6
7
8
9
10
11
12
13asmlinkage void do_softirq(void) {
__u32 pending;
unsigned long flags;
//如果在硬件中断环境中就退出,软中断不可以在硬件中断上下文或者是在软中断环境中使用,使用`in_interrupt()来防止软中断嵌套,和抢占硬中断环境。
if (in_interrupt())
return; //禁止本地中断
local_irq_save(flags);
pending = local_softirq_pending();
//如果有软中断要处理,则进入__do_softirq()
if (pending)
__do_softirq();
local_irq_restore(flags);
}
下面看一下__do_softirq()的实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59asmlinkage void __do_softirq(void)
{
struct softirq_action *h;
__u32 pending;
int max_restart = MAX_SOFTIRQ_RESTART;
int cpu;
pending = local_softirq_pending(); //pending`用于保留待处理软中断32位位图
account_system_vtime(current);
__local_bh_disable((unsigned long)__builtin_return_address(0));
lockdep_softirq_enter();
cpu = smp_processor_id();
restart:
/* Reset the pending bitmask before enabling irqs */
set_softirq_pending(0);
local_irq_enable();
h = softirq_vec;
do {
if (pending & 1) { //如果`pending`第`n`位被设置为1,那么处理第`n`位对应类型的软中断
int prev_count = preempt_count();
kstat_incr_softirqs_this_cpu(h - softirq_vec);
trace_softirq_entry(h, softirq_vec);
h->action(h); //执行软中断处理函数
trace_softirq_exit(h, softirq_vec);
if (unlikely(prev_count != preempt_count())) {
printk(KERN_ERR "huh, entered softirq %td %s %p"
"with preempt_count %08x,"
" exited with %08x?\n", h - softirq_vec,
softirq_to_name[h - softirq_vec],
h->action, prev_count, preempt_count());
preempt_count() = prev_count;
}
rcu_bh_qs(cpu);
}
h++;
pending >>= 1; //pending`右移一位,循环检查其每一位
} while (pending); //直到`pending`变为0,pending`最多32位,所以循环最多执行32次。
local_irq_disable();
pending = local_softirq_pending();
if (pending && --max_restart)
goto restart;
if (pending)
wakeup_softirqd();
lockdep_softirq_exit();
account_system_vtime(current);
_local_bh_enable();
}
使用软中断必须要在编译期间静态注册,一般只有像网络这样对性能要求高的情况才使用软中断,文章前面我们也看到,系统中注册的软中断就那么几个。大部分时候,使用下半部另外一种机制tasklet的情况更多一些,tasklet可以动态的注册,可以被看作是一种性能和易用性之间寻求平衡的一种产物。事实上,大部分驱动程序都是用tasklet来实现他们的下半部。
下半部机制之tasklet
tasklet是利用软中断实现的一种下半部机制。tasklet相比于软中断,其接口更加简单方便,锁保护要求较低。tasklet由tasklet_struct结构体表示:1
2
3
4
5
6
7
8struct tasklet_struct
{
struct tasklet_struct *next; //链表中下一个tasklet
unsigned long state; //tasklet状态
atomic_t count; //引用计数
void (*func)(unsigned long); //tasklet处理函数
unsigned long data; //给tasklet处理函数的参数
};
tasklet还分为了高优先级tasklet与一般tasklet,前面分析软中断时softirq_init()注册的两个tasklet软中断。1
2
3
4
5
6
7
8void __init softirq_init(void)
{
......
//此处注册两个软中断
open_softirq(TASKLET_SOFTIRQ, tasklet_action);
open_softirq(HI_SOFTIRQ, tasklet_hi_action);
......
}
其处理函数分别为tasklet_action()和tasklet_hi_action()。
tasklet_action()函数实现为:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35static void tasklet_action(struct softirq_action *a)
{
struct tasklet_struct *list;
local_irq_disable();
list = __get_cpu_var(tasklet_vec).head;
__get_cpu_var(tasklet_vec).head = NULL;
__get_cpu_var(tasklet_vec).tail = &__get_cpu_var(tasklet_vec).head;
local_irq_enable();
while (list) {
struct tasklet_struct *t = list;
list = list->next;
if (tasklet_trylock(t)) {
if (!atomic_read(&t->count)) { //t->count`为零才会调用`task_struct`里的函数
if (!test_and_clear_bit(TASKLET_STATE_SCHED, &t->state))
BUG();
t->func(t->data); //设置了`TASKLET_STATE_SCHED`标志才会被遍历到链表上对应的函数
tasklet_unlock(t);
continue;
}
tasklet_unlock(t);
}
local_irq_disable();
t->next = NULL;
*__get_cpu_var(tasklet_vec).tail = t;
__get_cpu_var(tasklet_vec).tail = &(t->next);
__raise_softirq_irqoff(TASKLET_SOFTIRQ);
local_irq_enable();
}
}
tasklet_hi_action函数实现类似1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34static void tasklet_hi_action(struct softirq_action *a)
{
struct tasklet_struct *list;
local_irq_disable();
list = __get_cpu_var(tasklet_hi_vec).head;
__get_cpu_var(tasklet_hi_vec).head = NULL;
__get_cpu_var(tasklet_hi_vec).tail = &__get_cpu_var(tasklet_hi_vec).head;
local_irq_enable();
while (list) {
struct tasklet_struct *t = list;
list = list->next;
if (tasklet_trylock(t)) {
if (!atomic_read(&t->count)) {
if (!test_and_clear_bit(TASKLET_STATE_SCHED, &t->state))
BUG();
t->func(t->data);
tasklet_unlock(t);
continue;
}
tasklet_unlock(t);
}
local_irq_disable();
t->next = NULL;
*__get_cpu_var(tasklet_hi_vec).tail = t;
__get_cpu_var(tasklet_hi_vec).tail = &(t->next);
__raise_softirq_irqoff(HI_SOFTIRQ);
local_irq_enable();
}
}
这两个函数主要是做了如下动作:
- 禁止中断,并为当前处理器检索
tasklet_vec或tasklet_hi_vec链表。 - 将当前处理器上的该链表设置为`NULL,达到清空的效果。
- 运行相应中断。
- 循环遍历获得链表上的每一个待处理的`tasklet。
- 如果是多处理器系统,通过检查
TASKLET_STATE_RUN来判断这个tasklet是否正在其他处理器上运行。如果它正在运行,那么现在就不要执行,跳到下一个待处理的tasklet去。 - 如果当前这个
tasklet没有执行,将其状态设置为TASKLETLET_STATE_RUN,这样别的处理器就不会再去执行它了。 - 检查
count值是否为0,确保tasklet没有被禁止。如果tasklet被禁止,则跳到下一个挂起的tasklet去。 - 现在可以确定这个
tasklet没有在其他地方执行,并且被我们设置为执行状态,这样它在其他部分就不会被执行,并且引用计数器为0,现在可以执行tasklet的处理程序了。 - 重复执行下一个
tasklet,直至没有剩余的等待处理的tasklets。
一般情况下,都是用tasklet来实现下半部,tasklet可以动态创建、使用方便、执行速度快。下面来看一下如何创建自己的tasklet呢?
第一步,声明自己的tasklet。既可以静态也可以动态创建,这取决于选择是想有一个对tasklet的直接引用还是间接引用。静态创建方法(直接引用),可以使用下列两个宏的一个(在Linux/interrupt.h中定义):1
2DECLARE_TASKLET(name,func,data)
DECLARE_TASKLET_DISABLED(name,func,data)
这两个宏的实现为:1
2
3
4
5
这两个宏之间的区别在于引用计数器的初始值不同,前面一个把创建的tasklet的引用计数器设置为0,使其处于激活状态,另外一个将其设置为1,处于禁止状态。而动态创建(间接引用)的方式如下:1
tasklet_init(t,tasklet_handler,dev);
其实现代码为:1
2
3
4
5
6
7
8
9void tasklet_init(struct tasklet_struct *t,
void (*func)(unsigned long), unsigned long data)
{
t->next = NULL;
t->state = 0;
atomic_set(&t->count, 0);
t->func = func;
t->data = data;
}
第二步,编写tasklet处理程序。tasklet处理函数类型是void tasklet_handler(unsigned long data)。因为是靠软中断实现,所以tasklet不能休眠,也就是说不能在tasklet中使用信号量或者其他什么阻塞式的函数。由于tasklet运行时允许响应中断,所以必须做好预防工作,如果新加入的tasklet和中断处理程序之间共享了某些数据额的话。两个相同的tasklet绝不能同时执行,如果新加入的tasklet和其他的tasklet或者软中断共享了数据,就必须要进行适当地锁保护。
第三步,调度自己的tasklet。调用tasklet_schedule()(或tasklet_hi_schedule())函数,tasklet就会进入挂起状态以便执行。如果在还没有得到运行机会之前,如果有一个相同的tasklet又被调度了,那么它仍然只会运行一次。如果这时已经开始运行,那么这个新的tasklet会被重新调度并再次运行。一种优化策略是一个tasklet总在调度它的处理器上执行。
调用tasklet_disable()来禁止某个指定的tasklet,如果该tasklet当前正在执行,这个函数会等到它执行完毕再返回。调用tasklet_disable_nosync()也是来禁止的,只是不用在返回前等待tasklet执行完毕,这么做不太安全,因为没法估计该tasklet是否仍在执行。tasklet_enable()激活一个tasklet。可以使用tasklet_kill()函数从挂起的对列中去掉一个tasklet。这个函数会首先等待该tasklet执行完毕,然后再将其移去。当然,没有什么可以阻止其他地方的代码重新调度该tasklet。由于该函数可能会引起休眠,所以禁止在中断上下文中使用它。
下面来看一下函数tasklet_schedule的实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24static inline void tasklet_schedule(struct tasklet_struct *t)
{
//检查tasklet的状态是否为TASKLET_STATE_SCHED.如果是,说明tasklet已经被调度过了,函数返回。
if (!test_and_set_bit(TASKLET_STATE_SCHED, &t->state))
__tasklet_schedule(t);
}
void __tasklet_schedule(struct tasklet_struct *t)
{
unsigned long flags;
//保存中断状态,然后禁止本地中断。在执行tasklet代码时,这么做能够保证处理器上的数据不会弄乱。
local_irq_save(flags);
//把需要调度的tasklet加到每个处理器一个的tasklet_vec链表或task_hi_vec链表的表头上去。
t->next = NULL; *__get_cpu_var(tasklet_vec).tail = t;
__get_cpu_var(tasklet_vec).tail = &(t->next);
//唤起TASKLET_SOFTIRQ或HI_SOFTIRQ软中断,这样在下一次调用do_softirq()时就会执行该tasklet。
raise_softirq_irqoff(TASKLET_SOFTIRQ);
//恢复中断到原状态并返回。
local_irq_restore(flags);
}
tasklet_hi_schedule()函数的实现细节类似。
对于软中断,内核会选择几个特殊的实际进行处理(常见的是中 断处理程序返回时)。软中断被触发的频率有时会很好,而且还可能会自行重复触发,这带来的结果就是用户空间的进程无法获得足够的处理器时间,因为处于饥饿 状态。同时,如果单纯的对重复触发的软中断采取不立即处理的策略也是无法接受的。
内核选中的方案是不会立即处理重新触发的软中断,作为改进,当大量软中断出现的时候,内核会唤醒一组内核线程来处理这些负载。这些线程在最低优先级上运行(nice值为19)。这种这种方案能够保证在软中断负担很 重的时候用户程序不会因为得不到处理时间而处理饥饿状态。相应的,也能保证“过量”的软中断终究会得到处理。最后,在空闲系统上,这个方案同样表现良好,软中断处理得非常迅速(因为仅存的内存线程肯定会马上调度)。为了保证只要有空闲的处理器,它们就会处理软中断,所以给每个处理器都分配一个这样的线程。 所有线程的名字都叫做ksoftirad/n,区别在于n,它对应的是处理器的编号。一旦该线程被初始化,它就会执行类似下面这样的死循环:1
2
3
4
5
6
7
8
9
10
11
12
13for(;;){
if(!softirq_pending(cpu))//softirq_pending()负责发现是否有待处理的软中断
schedule(); //没有待处理软中断就唤起调度程序选择其他可执行进程投入运行
set_current_state(TASK_RUNNING);
while(softirq_pending(cpu)){
do_softirq();//有待处理的软中断,ksoftirq调用do_softirq()去处理他。
if(need_resched()) //如果有必要的话,每次软中断完成之后调用schedule函数让其他重要进程得到处理机会
schedule();
}
//当所有需要执行的操作都完成以后,该内核线程将自己设置为 TASK_INTERRUPTIBLE状态
set_current_state(TASK_INTERRUPTIBLE);
}
下半部机制之工作队列及几种机制的选择
工作队列是下半部的另外一种将工作推后执行形式。和软中断、tasklet不同,工作队列将工作推后交由一个内核线程去执行,并且该下半部总会在进程上下文中执行。这样,工作队列允许重新调度甚至是睡眠。
所以,如果推后执行的任务需要睡眠,就选择工作队列。如果不需要睡眠,那就选择软中断或`tasklet。工作队列是唯一能在进程上下文中运行的下半部实现机制,也只有它才可以睡眠。
工作队列子系统是一个用于创建内核线程的接口,通过它创建的进程负责执行由内核其他部分排到队列里的任务。它创建的这些内核线程称作工作者线程。工作队列可以让你的驱动程序创建一个专门的工作者线程来处理需要推后的工作。不过,工作队列子系统提供了一个缺省的工作者线程来处理这些工作。因此,工作队列最基本的表现形式就转变成一个把需要推后执行的任务交给特定的通用线程这样一种接口。缺省的工作线程叫做event/n。每个处理器对应一个线程,这里的n代表了处理器编号。除非一个驱动程序或者子系统必须建立一个属于自己的内核线程,否则最好还是使用缺省线程。
使用下面命令可以看到默认event工作者线程,每个处理器对应一个线程:1
2
3# ps x | grep event | grep -v grep
9 ? S 0:00 [events/0]
10 ? S 0:00 [events/1]
工作者线程使用workqueue_struct结构表示(位于<kernel/workqueue.c>中):1
2
3
4
5
6
7
8
9
10
11struct workqueue_struct {
struct cpu_workqueue_struct *cpu_wq; //该数组每一项对应系统中的一个处理器
struct list_head list;
const char *name;
int singlethread;
int freezeable; /* Freeze threads during suspend */
int rt;
struct lockdep_map lockdep_map;
}
每个处理器,每个工作者线程对应对应一个cpu_workqueue_struct结构体(位于<kernel/workqueue.c>中):1
2
3
4
5
6
7
8
9
10struct cpu_workqueue_struct {
spinlock_t lock; //保护该结构
struct list_head worklist; //工作列表
wait_queue_head_t more_work; //等待队列,其中的工作者线程因等待而处于睡眠状态
struct work_struct *current_work;
struct workqueue_struct *wq; //关联工作队列结构
struct task_struct *thread; // 关联线程,指向结构中工作者线程的进程描述符指针
} ____cacheline_aligned;
每个工作者线程类型关联一个自己的workqueue_struct,在该结构体里面,给每个线程分配一个cpu_workqueue_struct,因而也就是给每个处理器分配一个,因为每个处理器都有一个该类型的工作者线程。
所有的工作者线程都是使用普通的内核线程实现的,他们都要执行worker_thread()函数。在它初始化完以后,这个函数执行一个死循环执行一个循环并开始休眠,当有操作被插入到队列的时候,线程就会被唤醒,以便执行这些操作。当没有剩余的时候,它又会继续休眠。工作由work_struct(位于<kernel/workqueue.c>中)结构表示:1
2
3
4
5
6
7struct work_struct {
atomic_long_t data;
......
struct list_head entry;//连接所有链表
work_func_t func;
.....
};
当一个工作线程被唤醒时,它会执行它的链表上的所有工作。工作一旦执行完毕,它就将相应的work_struct对象从链表上移去,当链表不再有对象时,它就继续休眠。woker_thread()函数如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29static int worker_thread(void *__cwq)
{
struct cpu_workqueue_struct *cwq = __cwq;
DEFINE_WAIT(wait);
if (cwq->wq->freezeable)
set_freezable();
for (;;) {
//线程将自己设置为休眠状态并把自己加入等待队列
prepare_to_wait(&cwq->more_work, &wait, TASK_INTERRUPTIBLE);
if (!freezing(current) &&
!kthread_should_stop() &&
list_empty(&cwq->worklist))
schedule();//如果工作对列是空的,线程调用`schedule()函数进入睡眠状态
finish_wait(&cwq->more_work, &wait);
try_to_freeze();
//如果链表有对象,线程就将自己设为运行态,脱离等待队列
if (kthread_should_stop())
break;
//再次调用`run_workqueue()执行推后的工作
run_workqueue(cwq);
}
return 0;
}
之后由run_workqueue()函数来完成实际推后到此的工作:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32static void run_workqueue(struct cpu_workqueue_struct *cwq)
{
spin_lock_irq(&cwq->lock);
while (!list_empty(&cwq->worklist)) {
//链表不为空时,选取下一个节点对象
struct work_struct *work = list_entry(cwq->worklist.next,
struct work_struct, entry);
//获取希望执行的函数`func`及其参数`data
work_func_t f = work->func;
......
trace_workqueue_execution(cwq->thread, work);
cwq->current_work = work;
//把该结点从链表上解下来
list_del_init(cwq->worklist.next);
spin_unlock_irq(&cwq->lock);
BUG_ON(get_wq_data(work) != cwq);
//将待处理标志位`pending`清0
work_clear_pending(work);
lock_map_acquire(&cwq->wq->lockdep_map);
lock_map_acquire(&lockdep_map);
//执行函数
f(work);
lock_map_release(&lockdep_map);
lock_map_release(&cwq->wq->lockdep_map);
......
spin_lock_irq(&cwq->lock);
cwq->current_work = NULL;
}
spin_unlock_irq(&cwq->lock);
}
系统允许有多种类型工作者线程存在,默认情况下内核只有event这一种类型的工作者线程,每个工作者线程都由一个cpu_workqueue_struct结构体表示,大部分情况下,驱动程序都使用现存的默认工作者线程。
工作队列的使用很简单。可以使用缺省的events任务队列,也可以创建新的工作者线程。
第一步、创建需要推后完成的工作。1
2DECLARE_WORK(name,void (*func)(void *),void *data); //编译时静态创建
INIT_WORK(struct work_struct *work, void (*func)(void *)); //运行时动态创建
第二步、编写队列处理函数,处理函数会由工作者线程执行,因此,函数会运行在进程上下文中,默认情况下,允许相应中断,并且不持有锁。如果需要,函数可以睡眠。需要注意的是,尽管处理函数运行在进程上下文中,但它不能访问用户空间,因为内核线程在用户空间没有相应的内存映射。函数原型如下:1
void work_hander(void *data);
第三步、调度工作队列。调用schedule_work(&work);work马上就会被调度,一旦其所在的处理器上的工作者线程被唤醒,它就会被执行。当然如果不想快速执行,而是想延迟一段时间执行,调用schedule_delay_work(&work,delay),delay是要延迟的时间节拍。
默认工作者线程的调度函数其实就是做了一层封装,减少了 默认工作者线程的参数输入,如下:1
2
3
4
5
6
7
8
9int schedule_work(struct work_struct *work)
{
return queue_work(keventd_wq, work);
}
int schedule_delayed_work(struct delayed_work *dwork, unsigned long delay)
{
return queue_delayed_work(keventd_wq, dwork, delay);
}
第四步、刷新操作,插入队列的工作会在工作者线程下一次被唤醒的时候执行。有时,在继续下一步工作之前,你必须保证一些操作已经执行完毕等等。由于这些原因,内核提供了一个用于刷新指定工作队列的函数:1
void flush_scheduled_work(void);
这个函数会一直等待,直到队列中所有的对象都被执行后才返回。在等待所有待处理的工作执行的时候,该函数会进入休眠状态,所以只能在进程上下文中使用它。需要说明的是,该函数并不取消任何延迟执行的工作。取消延迟执行的工作应该调用:int cancel_delayed_work(struct work_struct *work);这个函数可以取消任何与work_struct相关挂起的工作。
下面为一个示例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//struct work_struct ws;
struct delayed_work dw;
void workqueue_func(struct work_struct *ws) //处理函数
{
printk(KERN_ALERT"Hello, this is shallnet!\n");
}
static int __init kwq_init(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
//INIT_WORK(&ws, workqueue_func); //建需要推后完成的工作
//schedule_work(&ws); //调度工作
INIT_DELAYED_WORK(&dw, workqueue_func);
schedule_delayed_work(&dw, 10000);
return 0;
}
static void __exit kwq_exit(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
flush_scheduled_work();
}
module_init(kwq_init);
module_exit(kwq_exit);
MODULE_LICENSE("GPL");
MODULE_AUTHOR("shallnet");
MODULE_DESCRIPTION("blog.csdn.net/shallnet");
上面的操作是使用缺省的工作队列,下面来看一下创建一个新的工作队列是如何操作的?
创建一个新的工作队列和与之相应的工作者线程,方法很简单,使用如下函数:1
struct workqueue_struct *create_workqueue(const char *name);
name是新内核线程的名字。比如缺省events队列的创建是这样使用的:1
2struct workqueue_struct *keventd_wq;
kevent_wq = create_workqueue("event");
这样就创建了所有的工作者线程,每个处理器都有一个。然后调用如下函数进行调度:1
2int queue_work(struct workqueue_struct *wq, struct work_struct *work);
int queue_delayed_work(struct workqueue_struct *wq,struct delayed_work *work,unsigned long delay);
最后可以调用flush_workqueue(struct workqueue_struct *wq);刷新指定工作队列。
下面为自定义新的工作队列的示例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
struct workqueue_struct *sln_wq = NULL;
//struct work_struct ws;
struct delayed_work dw;
void workqueue_func(struct work_struct *ws)
{
printk(KERN_ALERT"Hello, this is shallnet!\n");
}
static int __init kwq_init(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
sln_wq = create_workqueue("sln_wq"); //创建名为`sln_wq`的工作队列
//INIT_WORK(&ws, workqueue_func);
//queue_work(sln_wq, &ws);
INIT_DELAYED_WORK(&dw, workqueue_func); //
queue_delayed_work(sln_wq, &dw, 10000); //
return 0;
}
static void __exit kwq_exit(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
flush_workqueue(sln_wq);
}
module_init(kwq_init);
module_exit(kwq_exit);
MODULE_LICENSE("GPL");
MODULE_AUTHOR("shallnet");
MODULE_DESCRIPTION("blog.csdn.net/shallnet");
使用ps可以查看到名为sln_wq的工作者线程。
在当前2.6.32版本中,我们讲了三种下半部机制:软中断、tasklet、工作队列。其中tasklet基于软中断,而工作队列靠内核线程实现。
使用软中断必须要确保共享数据的安全,因为相同类别的软中断可能在不同处理器上同时执行。在对于时间要求是否严格和执行频率很高的应用,或准备利用每一处理器上的变量或类型情形,可以考虑使用软中断,如网络子系统。
tasklet接口简单,可以动态创建,且两个通知类型的tasklet不能同时执行,所以实现起来较简单。驱动程序应该尽量选择tasklet而不是软中断。
工作队列工作于进程上下文,易于使用。由于牵扯到内核线程或上下文的切换,可能开销较大。如果你需要把任务推后到进程上下文中,或你需要休眠,那就只有使用工作队列了。
内核时钟中断
内核中很多函数是基于时间驱动的,其中有些函数需要周期或定期执行。比如有的每秒执行100次,有的在等待一个相对时间之后执行。除此之外,内核还必须管理系统运行的时间日期。
周期性产生的时间都是有系统定时器驱动的,系统定时器是一种可编程硬件芯片,它可以以固定频率产生中断,该中断就是所谓的定时器中断,其所对应的中断处理程序负责更新系统时间,也负责执行需要周期性运行的任务。
系统定时器以某种频率自行触发时钟中断,该频率可以通过编程预定,称作节拍率。当时钟中断发生时,内核就通过一种特殊的中断处理器对其进行处理。内核知道连续两次时钟中断的间隔时间,该间隔时间就称为节拍。内核就是靠这种已知的时钟中断间隔来计算实际时间和系统运行时间的。内核通过控制时钟中断维护实际时间,另外内核也为用户提供一组系统调用获取实际日期和实际时间。时钟中断对才操作系统的管理来说十分重要,系统更新运行时间、更新实际时间、均衡调度程序中个处理器上运行队列、检查进程是否用尽时间片等工作都利用时钟中断来周期执行。
内核有一个全局变量jiffies,该变量用来记录系统起来以后产生的节拍总数。系统启动是,该变量被设置为0,此后每产生一次时钟中断就增加该变量的值。jiffies每一秒增加的值就是HZ。jiffies定义于头文件<include/linux/jiffies.h>中:1
extern unsigned long volatile __jiffy_data jiffies;
对于32位unsigned long,可以存放最大值为4294967295,所以当节拍数达到最大值后还要继续增加的话,它的值就会回到0值。内核提供了四个宏(位于文件<include/linux/jiffies.h>中)来比较节拍数,这些宏可以正确处理节拍计数回绕情况。1
2
3
4
5
6
7
8
9
10
下面示例来打印出当前系统启动后经过的jiffies以及秒数:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
static int __init jiffies_init(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
printk(KERN_ALERT"Current ticks is: %lu, seconds: %lu\n", jiffies, jiffies/HZ);
return 0;
}
static void __exit jiffies_exit(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
}
module_init(jiffies_init);
module_exit(jiffies_exit);
MODULE_LICENSE("GPL");
MODULE_AUTHOR("shallnet");
MODULE_DESCRIPTION("blog.csdn.net/shallnet");
执行输出结果为:1
2
3# insmod jfs.ko
===jiffies_init===
Current ticks is: 10106703, seconds: 10106
时钟中断发生时,会触发时钟中断处理程序,始终中断处理程序部分和体系结构相关,下面简单分析一下x86体系的处理:
时钟的初始化在time_init()中,在start_kernel()中调用time_init(),如下:1
2
3
4
5
6asmlinkage void __init start_kernel(void)
{
......
time_init();
......
}
下面分析一下time_init()的实现,该函数位于文件<arch/x86/kernel/time.c>中:1
2
3
4
5
6
7
8
9
10void __init time_init(void)
{
late_time_init = x86_late_time_init;
}
static __init void x86_late_time_init(void)
{
x86_init.timers.timer_init(); //
tsc_init();
}
结构体x86_init位于arch/x86/kernel/x86_init.c中1
2
3
4
5
6
7
8struct x86_init_ops x86_init __initdata = {
......
.timers = {
.setup_percpu_clockev>--= setup_boot_APIC_clock,
.tsc_pre_init = x86_init_noop,
.timer_init = hpet_time_init,
}
}
默认timer初始化函数为:1
2
3
4
5
6void __init hpet_time_init(void)
{
if (!hpet_enable())
setup_pit_timer();
setup_default_timer_irq();
}
函数setup_default_timer_irq();注册中断处理函数:1
2
3
4
5
6
7
8
9
10void __init setup_default_timer_irq(void)
{
setup_irq(0, &irq0);
}
static struct irqaction irq0 = {
.handler = timer_interrupt,
.flags = IRQF_DISABLED | IRQF_NOBALANCING | IRQF_IRQPOLL | IRQF_TIMER,
.name = "timer"
};
对应的中断处理函数为:timer_interrupt():1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28static irqreturn_t timer_interrupt(int irq, void *dev_id)
{
/* Keep nmi watchdog up to date */
inc_irq_stat(irq0_irqs);
/* Optimized out for !IO_APIC and x86_64 */
if (timer_ack) {
/*
* Subtle, when I/O APICs are used we have to ack timer IRQ
* manually to deassert NMI lines for the watchdog if run
* on an 82489DX-based system.
*/
spin_lock(&i8259A_lock);
outb(0x0c, PIC_MASTER_OCW3);
/* Ack the IRQ; AEOI will end it automatically. */
inb(PIC_MASTER_POLL);
spin_unlock(&i8259A_lock);
}
//在此处调用体系无关的时钟处理例程
global_clock_event->event_handler(global_clock_event);
/* MCA bus quirk: Acknowledge irq0 by setting bit 7 in port 0x61 */
if (MCA_bus)
outb_p(inb_p(0x61)| 0x80, 0x61);
return IRQ_HANDLED;
}
时钟例程在系统启动时start_kernel()函数中调用tick_init()初始化:1
2
3
4void __init tick_init(void)
{
clockevents_register_notifier(&tick_notifier);
}
tick_notifier定义如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78static struct notifier_block tick_notifier = {
.notifier_call = tick_notify,
};
static int tick_notify(struct notifier_block *nb, unsigned long reason, void *dev)
{
switch (reason) {
case CLOCK_EVT_NOTIFY_RESUME:
tick_resume();
break;
default:
break;
}
return NOTIFY_OK;
}
static void tick_resume(void)
{
struct tick_device *td = &__get_cpu_var(tick_cpu_device);
unsigned long flags;
int broadcast = tick_resume_broadcast();
spin_lock_irqsave(&tick_device_lock, flags);
clockevents_set_mode(td->evtdev, CLOCK_EVT_MODE_RESUME);
if (!broadcast) {
if (td->mode == TICKDEV_MODE_PERIODIC)
tick_setup_periodic(td->evtdev, 0);
else
tick_resume_oneshot();
}
spin_unlock_irqrestore(&tick_device_lock, flags);
}
/*
* Setup the device for a periodic tick
*/
void tick_setup_periodic(struct clock_event_device *dev, int broadcast)
{
tick_set_periodic_handler(dev, broadcast);
......
}
/*
* 根据broadcast设置周期性的处理函数(kernel/time/tick-broadcast.c),这里就设置了始终中断函数timer_interrupt中调用的时钟处理例程
*/
void tick_set_periodic_handler(struct clock_event_device *dev, int broadcast)
{
if (!broadcast)
dev->event_handler = tick_handle_periodic;
else
dev->event_handler = tick_handle_periodic_broadcast;
}
/*
* ,以tick_handle_periodic为例,每一个始终节拍都调用该处理函数,而该处理过程中,主要处理工作处于tick_periodic()函数中。
*/
void tick_handle_periodic(struct clock_event_device *dev)
{
int cpu = smp_processor_id();
ktime_t next;
tick_periodic(cpu);
if (dev->mode != CLOCK_EVT_MODE_ONESHOT)
return;
next = ktime_add(dev->next_event, tick_period);
for (;;) {
if (!clockevents_program_event(dev, next, ktime_get()))
return;
if (timekeeping_valid_for_hres())
tick_periodic(cpu);
next = ktime_add(next, tick_period);
}
}
tick_periodic()函数主要有以下工作:
下面来看分析一下该函数:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18/*
* Periodic tick
*/
static void tick_periodic(int cpu)
{
if (tick_do_timer_cpu == cpu) {
write_seqlock(&xtime_lock);
/* 记录下一个节拍事件 */
tick_next_period = ktime_add(tick_next_period, tick_period);
do_timer(1);
write_sequnlock(&xtime_lock);
}
update_process_times(user_mode(get_irq_regs()));//更新所耗费的各种节拍数
profile_tick(CPU_PROFILING);
}
其中函数do_timer()(位于kernel/timer.c中)对jiffies_64做增加操作:1
2
3
4
5
6void do_timer(unsigned long ticks)
{
jiffies_64 += ticks;
update_wall_time(); //更新墙上时钟
calc_global_load(); //更新系统平均负载统计值
}
update_process_times更新所耗费的各种节拍数。1
2
3
4
5
6
7
8
9
10
11
12
13void update_process_times(int user_tick)
{
struct task_struct *p = current;
int cpu = smp_processor_id();
/* Note: this timer irq context must be accounted for as well. */
account_process_tick(p, user_tick);
run_local_timers();
rcu_check_callbacks(cpu, user_tick);
printk_tick();
scheduler_tick();
run_posix_cpu_timers(p);
}
函数run_local_timers()会标记一个软中断去处理所有到期的定时器。1
2
3
4
5
6void run_local_timers(void)
{
hrtimer_run_queues();
raise_softirq(TIMER_SOFTIRQ);
softlockup_tick();
}
在时钟中断处理函数time_interrupt()函数调用体系结构无关的时钟处理例程完成之后,返回到与体系结构的相关的中断处理函数中。以上所有的工作每一次时钟中断都会运行,也就是说如果HZ=100,那么时钟中断处理程序每一秒就会运行100次。
内核定时器和定时执行
前面章节说到了把工作推后到除现在以外的时间执行的机制是下半部机制,但是当你需要将工作推后到某个确定的时间段之后执行,使用定时器是很好的选择。
上一节内核时间管理中讲到内核在始终中断发生执行定时器,定时器作为软中断在下半部上下文中执行。时钟中断处理程序会执行update_process_times函数,在该函数中运行run_local_timers()函数来标记一个软中断去处理所有到期的定时器。如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18void update_process_times(int user_tick)
{
struct task_struct *p = current;
int cpu = smp_processor_id();
/* Note: this timer irq context must be accounted for as well. */
account_process_tick(p, user_tick);
run_local_timers();
rcu_check_callbacks(cpu, user_tick);
printk_tick();
scheduler_tick();
run_posix_cpu_timers(p);
}
void run_local_timers(void)
{
hrtimer_run_queues();
raise_softirq(TIMER_SOFTIRQ);
softlockup_tick();
}
在分析定时器的实现之前我们先来看一看使用内核定时器的一个实例,示例如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct timer_list sln_timer;
void sln_timer_do(unsigned long l)
{
mod_timer(&sln_timer, jiffies + HZ);
printk(KERN_ALERT"param: %ld, jiffies: %ld\n", l, jiffies);
}
void sln_timer_set(void)
{
init_timer(&sln_timer);
sln_timer.expires = jiffies + HZ; //1s
sln_timer.function = sln_timer_do;
sln_timer.data = 9527;
add_timer(&sln_timer);
}
static int __init sln_init(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
sln_timer_set();
return 0;
}
static void __exit sln_exit(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
del_timer(&sln_timer);
}
module_init(sln_init);
module_exit(sln_exit);
MODULE_LICENSE("GPL");
MODULE_AUTHOR("allen");
该示例作用是每秒钟打印出当前系统jiffies的值。
内核定时器由结构timer_list表示,定义在文件<include/linux/timer.h>中。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15struct timer_list {
struct list_head entry;
unsigned long expires;
void (*function)(unsigned long);
unsigned long data;
struct tvec_base *base;
void *start_site;
char start_comm[16];
int start_pid;
struct lockdep_map lockdep_map;
};
如示例,内核提供部分操作接口来简化管理定时器,
第一步、定义一个定时器:struct timer_list sln_timer;
第二步、初始化定时器数据结构的内部值。1
init_timer(&sln_timer);//初始化定时器
1 |
|
第三步、填充timer_list结构中需要的值:1
2
3sln_timer.expires = jiffies + HZ; //1s`后执行
sln_timer.function = sln_timer_do; //执行函数
sln_timer.data = 9527;
sln_timer.expires表示超时时间,它以节拍为单位的绝对计数值。如果当前jiffies计数等于或大于sln_timer.expires的值,那么sln_timer.function所指向的处理函数sln_timer_do就会执行,并且该函数还要使用长整型参数sln_timer.dat。1
void sln_timer_do(unsigned long l);
第四步、激活定时器:1
add_timer(&sln_timer); //向内核注册定时器
这样定时器就可以运行了。
add_timer()的实现如下:1
2
3
4
5void add_timer(struct timer_list *timer)
{
BUG_ON(timer_pending(timer));
mod_timer(timer, timer->expires);
}
add_timer()调用了mod_timer()。mod_timer()用于修改定时器超时时间。1
mod_timer(&sln_timer, jiffies + HZ);
由于add_timer()是通过调用mod_timer()来激活定时器,所以也可以直接使用mod_timer()来激活定时器,如果定时器已经初始化但没有激活,mod_timer()也会激活它。
如果需要在定时器超时前停止定时器,使用del_timer()函数来完成。1
del_timer(&sln_timer);
该函数实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29int del_timer(struct timer_list *timer)
{
struct tvec_base *base;
unsigned long flags;
int ret = 0;
timer_stats_timer_clear_start_info(timer);
if (timer_pending(timer)) {
base = lock_timer_base(timer, &flags);
if (timer_pending(timer)) {
detach_timer(timer, 1);
if (timer->expires == base->next_timer &&
!tbase_get_deferrable(timer->base))
base->next_timer = base->timer_jiffies;
ret = 1;
}
spin_unlock_irqrestore(&base->lock, flags);
}
return ret;
}
static inline void detach_timer(struct timer_list *timer,
int clear_pending)
{
struct list_head *entry = &timer->entry;
debug_deactivate(timer);
__list_del(entry->prev, entry->next);
if (clear_pending)
entry->next = NULL;
entry->prev = LIST_POISON2;
}
当使用del_timer()返回后,定时器就不会再被激活,但在多处理器机器上定时器上定时器中断可能已经在其他处理器上运行了,所以删除定时器时需要等待可能在其他处理器上运行的定时器处理I程序都退出,这时就要使用del_timer_sync()函数执行删除工作:1
del_timer_sync(&sln_timer);
该函数不能在中断上下文中使用。
该函数详细实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36int del_timer_sync(struct timer_list *timer)
{
unsigned long flags;
local_irq_save(flags);
lock_map_acquire(&timer->lockdep_map);
lock_map_release(&timer->lockdep_map);
local_irq_restore(flags);
for (;;) { //一直循环,直到删除`timer`成功再退出
int ret = try_to_del_timer_sync(timer);
if (ret >= 0)
return ret;
cpu_relax();
}
}
int try_to_del_timer_sync(struct timer_list *timer)
{
struct tvec_base *base;
unsigned long flags;
int ret = -1;
base = lock_timer_base(timer, &flags);
if (base->running_timer == timer)
goto out;
ret = 0;
if (timer_pending(timer)) {
detach_timer(timer, 1);
if (timer->expires == base->next_timer &&
!tbase_get_deferrable(timer->base))
base->next_timer = base->timer_jiffies;
ret = 1;
}
out:
spin_unlock_irqrestore(&base->lock, flags);
return ret;
}
一般情况下应该使用del_timer_sync()函数代替del_timer()函数,因为无法确定在删除定时器时,他是否在其他处理器上运行。为了防止这种情况的发生,应该调用del_timer_sync()函数而不是del_timer()函数。否则,对定时器执行删除操作后,代码会继续执行,但它有可能会去操作在其它处理器上运行的定时器正在使用的资源,因而造成并发访问,所有优先使用删除定时器的同步方法。
除了使用定时器来推迟任务到指定时间段运行之外,还有其他的方法处理延时请求。有的方法会在延迟任务时挂起处理器,有的却不会。实际上也没有方法能够保证实际的延迟时间刚好等于指定的延迟时间。
- 最简单的 延迟方法是忙等待,该方法实现起来很简单,只需要在循环中不断旋转直到希望的时钟节拍数耗尽。比如:
1
2
3unsigned long delay = jiffies+10; //延迟10个节拍
while(time_before(jiffies,delay))
;
这种方法当代码等待时,处理器只能在原地旋转等待,它不会去处理其他任何任务。最好在任务等待时,允许内核重新调度其它任务执行。将上面代码修改如下:1
2
3unsigned long delay = jiffies+10; //10个节拍
while(time_before(jiffies,delay))
cond_resched();
看一下cond_resched()函数具体实现代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int __sched _cond_resched(void)
{
if (should_resched()) {
__cond_resched();
return 1;
}
return 0;
}
static void __cond_resched(void)
{
add_preempt_count(PREEMPT_ACTIVE);
schedule(); //最终还是调用`schedule()函数来重新调度其它程序运行
sub_preempt_count(PREEMPT_ACTIVE);
}
函数cond_resched()将重新调度一个新程序投入运行,但它只有在设置完need_resched标志后才能生效。换句话说,就是系统中存在更重要的任务需要运行。再由于该方法需要调用调度程序,所以它不能在中断上下文中使用——只能在进程上下文中使用。事实上,所有延迟方法在进程上下文中使用,因为中断处理程序都应该尽可能快的执行。另外,延迟执行不管在哪种情况下都不应该在持有锁时或者禁止中断时发生。
有时内核需要更短的延迟,甚至比节拍间隔还要短。这时可以使用内核提供的
ms、ns、us级别的延迟函数。1
2
3void udelay(unsigned long usecs); //arch/x86/include/asm/delay.h
void ndelay(unsigned long nsecs); //arch/x86/include/asm/delay.h
void mdelay(unsigned long msecs);udelay()使用忙循环将任务延迟指定的ms后执行,其依靠执行数次循环达到延迟效果,mdelay()函数是通过udelay()函数实现,如下:1
2
3
4
(__builtin_constant_p(n) && (n)<=MAX_UDELAY_MS) ? udelay((n)*1000) : \
({unsigned long __ms=(n); while (__ms--) udelay(1000);}))udelay()函数仅能在要求的延迟时间很短的情况下执行,而在高速机器中时间很长的延迟会造成溢出。对于较长的延迟,mdelay()工作良好。schedule_timeout()函数是更理想的延迟执行方法。该方法会让需要延迟执行的任务睡眠到指定的延迟时间耗尽后再重新运行。但该方法也不能保证睡眠时间正好等于指定的延迟时间,只能尽量是睡眠时间接近指定的延迟时间。当指定的时间到期后,内核唤醒被延迟的任务并将其重新放回运行队列。用法如下:1
2set_current_state(TASK_INTERRUPTIBLE); //将任务设置为可中断睡眠状态
schedule_timeout(s*HZ); //小睡一会儿,“s”秒后唤醒
唯一的参数是延迟的相对时间,单位是jiffies,上例中将相应的任务推入可中断睡眠队列,睡眠s秒。在调用函数schedule_timeout之前,不要要将任务设置成可中断或不和中断的一种,否则任务不会休眠。这个函数需要调用调度程序,所以调用它的代码必须保证能够睡眠,简而言之,调用代码必须处于进程上下文中,并且不能持有锁。
事实上schedule_timeout()函数的实现就是内核定时器的一个简单应用。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55signed long __sched schedule_timeout(signed long timeout)
{
struct timer_list timer;
unsigned long expire;
switch (timeout)
{
case MAX_SCHEDULE_TIMEOUT:
/*
* These two special cases are useful to be comfortable
* in the caller. Nothing more. We could take
* MAX_SCHEDULE_TIMEOUT from one of the negative value
* but I' d like to return a valid offset (>=0) to allow
* the caller to do everything it want with the retval.
*/
schedule();
goto out;
default:
/*
* Another bit of PARANOID. Note that the retval will be
* 0 since no piece of kernel is supposed to do a check
* for a negative retval of schedule_timeout() (since it
* should never happens anyway). You just have the printk()
* that will tell you if something is gone wrong and where.
*/
if (timeout < 0) {
printk(KERN_ERR "schedule_timeout: wrong timeout "
"value %lx\n", timeout);
dump_stack();
current->state = TASK_RUNNING;
goto out;
}
}
expire = timeout + jiffies;
//下一行代码设置了超时执行函数`process_timeout()。
setup_timer_on_stack(&timer, process_timeout, (unsigned long)current);
__mod_timer(&timer, expire, false, TIMER_NOT_PINNED); //激活定时器
schedule(); //调度其他新任务
del_singleshot_timer_sync(&timer);
/* Remove the timer from the object tracker */
destroy_timer_on_stack(&timer);
timeout = expire - jiffies;
out:
return timeout < 0 ? 0 : timeout;
}
当定时器超时时,process_timeout()函数被调用:
static void process_timeout(unsigned long __data)
{
wake_up_process((struct task_struct *)__data);
}
当任务被重新调度时,将返回代码进入睡眠前的位置继续执行,位置正好在schedule()处。
进程上下文的代码为了等待特定时间发生,可以将自己放入等待队列。但是,等待队列上的某个任务可能既在等待一个特定事件到来,又在等待一个特定时间到期,就看谁来得更快。这种情况下,代码可以简单的使用scedule_timeout()函数代替schedule()函数,这样一来,当希望指定时间到期后,任务都会被唤醒,当然,代码需要检查被唤醒的原因,有可能是被事件唤醒,也有可能是因为延迟的时间到期,还可能是因为接收到了信号,然后执行相应的操作。
进程管理分析
进程其实就是程序的执行时的实例,是处于执行期的程序。在Linux内核中,进程列表被存放在一个双向循环链表中,链表中每一项都是类型为task_struct的结构,该结构称作进程描述符,进程描述符包含一个具体进程的所有信息,这个结构就是我们在操作系统中所说的PCB(Process Control Block)。该结构定义于<include/linux/sched.h>文件中:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22struct task_struct {
volatile long state; /* -1 unrunnable, 0 runnable, >0 stopped */
void *stack;
atomic_t usage;
unsigned int flags; /* per process flags, defined below */
unsigned int ptrace;
int lock_depth; /* BKL lock depth */
......
int prio, static_prio, normal_prio;
unsigned int rt_priority;
const struct sched_class *sched_class;
struct sched_entity se;
struct sched_rt_entity rt;
......
struct task_struct *parent; /* recipient of SIGCHLD, wait4() reports */
struct list_head children; /* list of my children */
struct list_head sibling; /* linkage in my parent's children list */
......
};
该结构体中包含的数据可以完整的描述一个正在执行的程序:打开的文件、进程的地址空间、挂起的信号、进程的状态、以及其他很多信息。
在系统运行过程中,进程频繁切换,所以我们需要一种方式能够快速获得当前进程的task_struct,于是进程内核堆栈底部存放着struct thread_info。该结构中有一个成员指向当前进程的task_struct。在x86上,struct thread_info在文件<arch/x86/include/asm/thread_info.h>中定义:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18struct thread_info {
struct task_struct *task; /* 该指针存放的是指向该任务实际`task_struct`的指针 */
struct exec_domain *exec_domain; /* execution domain */
__u32 flags; /* low level flags */
__u32 status; /* thread synchronous flags */
__u32 cpu; /* current CPU */
int preempt_count; /* 0 => preemptable, <0 => BUG */
mm_segment_t addr_limit;
struct restart_block restart_block;
void __user *sysenter_return;
unsigned long previous_esp; /* ESP of the previous stack in
case of nested (IRQ) stacks
*/
__u8 supervisor_stack[0];
int uaccess_err;
};
使用current宏就可以获得当前进程的进程描述符。
每一个进程都有一个父进程,每个进程管理自己的子进程。每个进程都是init进程的子进程,init进程在内 核系统启动的最后阶段启动init进程,该进程读取系统的初始化脚本并执行其他相关程序,最终完成系统启动的整个过程。每个进程有0个或多个子进程,进程间的关系存放在进程描述符中。task_struct中有一个parent的指针,指向其父进程;还有个children的指针指向其子进程的链表。所以,对于当前进程,可以通过current宏来获得父进程和子进程的进程描述符。
下面程序打印当前进程、父进程信息和所有子进程信息:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
void sln_taskstruct_do(void)
{
struct task_struct *cur,
*parent,
*task;
struct list_head *first_child,
*child_list,
*cur_chd;
//获取当前进程信息
cur = current;
printk(KERN_ALERT"Current: %s[%d]\n",
cur->comm, cur->pid);
//获取父进程信息
parent = current->parent;
printk(KERN_ALERT"Parent: %s[%d]\n",
parent->comm, parent->pid);
//获取所有祖先进程信息
for (task = cur; task != &init_task; task = task->parent) {
printk(KERN_ALERT"ancestor: %s[%d]\n",
task->comm, task->pid);
}
//获取所有子进程信息
child_list = &cur->children;
first_child = &cur->children;
for (cur_chd = child_list->next;
cur_chd != first_child;
cur_chd = cur_chd->next) {
task = list_entry(child_list, struct task_struct, sibling);
printk(KERN_ALERT"Children: %s[%d]\n",
task->comm, task->pid);
}
}
static int __init sln_init(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
sln_taskstruct_do();
return 0;
}
static void __exit sln_exit(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
}
module_init(sln_init);
module_exit(sln_exit);
MODULE_LICENSE("GPL");
MODULE_AUTHOR("shallnet");
MODULE_DESCRIPTION("blog.csdn.net/shallnet");
执行结果如下:1
2
3
4
5
6
7
8 # insmod task.ko
===sln_init===
Current: insmod[4315]
Parent: bash[4032]
ancestor: insmod[4315]
ancestor: bash[4032]
ancestor: login[2563]
ancestor: init[1]
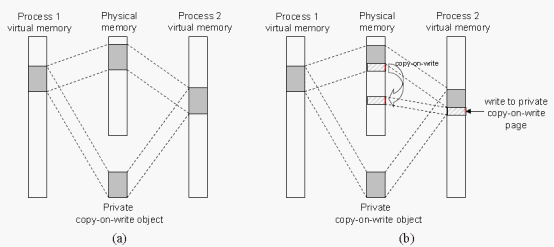
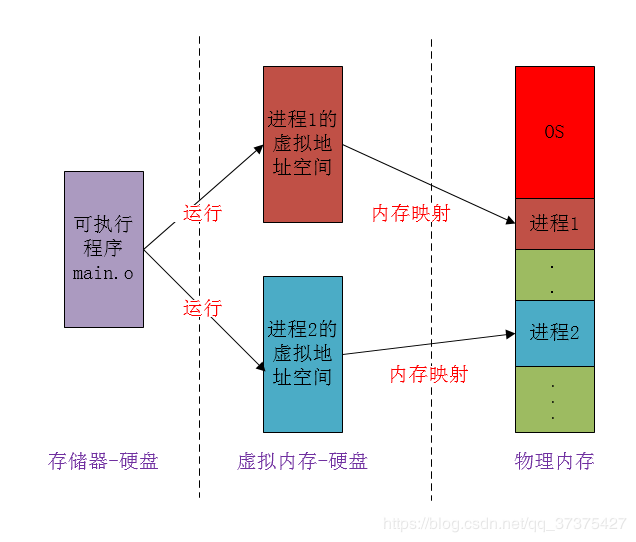
Linux操作系统提供产生进程的机制,在Linux下的fork()使用写时拷贝(copy-on-write)页实现。这种技术原理是:内存并不复制整个进程地址空间,而是让父进程和子进程共享同一拷贝,只有在需要写入的时候,数据才会被复制。也就是资源的复制只是发生在需要写入的时候才进行,在此之前都是以只读的方式共享。
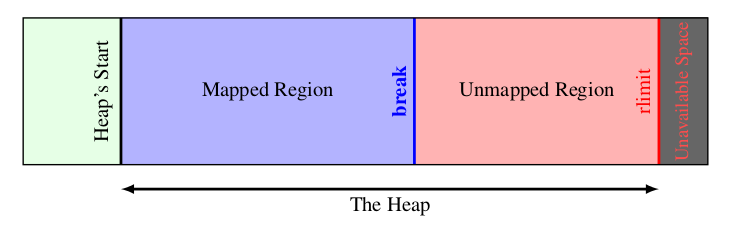
Linux通过clone()系统调用实现fork(),然后clone()去调用do_fork(),do_fork()完成创建中大部分工作。库函数vfork()、__clone()都根据各自需要的参数标志去调用clone()。fork()的实际开销就是复制父进程的页表以及给子进程创建唯一的进程描述符。
用户空间的fork()经过系统调用进入内核,在内核中对应的处理函数为sys_fork(),定义于<arch/x86/kernel/process.c>文件中。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354int sys_fork(struct pt_regs *regs)
{
return do_fork(SIGCHLD, regs->sp, regs, 0, NULL, NULL);
}
long do_fork(unsigned long clone_flags,
unsigned long stack_start,
struct pt_regs *regs,
unsigned long stack_size,
int __user *parent_tidptr,
int __user *child_tidptr)
{
struct task_struct *p;
int trace = 0;
long nr;
......
p = copy_process(clone_flags, stack_start, regs, stack_size,
child_tidptr, NULL, trace);
......
return nr;
}
static struct task_struct *copy_process(unsigned long clone_flags,
unsigned long stack_start,
struct pt_regs *regs,
unsigned long stack_size,
int __user *child_tidptr,
struct pid *pid,
int trace)
{
int retval;
struct task_struct *p;
int cgroup_callbacks_done = 0;
if ((clone_flags & (CLONE_NEWNS|CLONE_FS)) == (CLONE_NEWNS|CLONE_FS))
return ERR_PTR(-EINVAL);
/*
* Thread groups must share signals as well, and detached threads
* can only be started up within the thread group.
*/
if ((clone_flags & CLONE_THREAD) && !(clone_flags & CLONE_SIGHAND))
return ERR_PTR(-EINVAL);
/*
* Shared signal handlers imply shared VM. By way of the above,
* thread groups also imply shared VM. Blocking this case allows
* for various simplifications in other code.
*/
if ((clone_flags & CLONE_SIGHAND) && !(clone_flags & CLONE_VM))
return ERR_PTR(-EINVAL);
/*
* Siblings of global init remain as zombies on exit since they are
* not reaped by their parent (swapper). To solve this and to avoid
* multi-rooted process trees, prevent global and container-inits
* from creating siblings.
*/
if ((clone_flags & CLONE_PARENT) &&
current->signal->flags & SIGNAL_UNKILLABLE)
return ERR_PTR(-EINVAL);
retval = security_task_create(clone_flags);
if (retval)
goto fork_out;
retval = -ENOMEM;
p = dup_task_struct(current);
if (!p)
goto fork_out;
ftrace_graph_init_task(p);
rt_mutex_init_task(p);
DEBUG_LOCKS_WARN_ON(!p->hardirqs_enabled);
DEBUG_LOCKS_WARN_ON(!p->softirqs_enabled);
retval = -EAGAIN;
if (atomic_read(&p->real_cred->user->processes) >=
p->signal->rlim[RLIMIT_NPROC].rlim_cur) {
if (!capable(CAP_SYS_ADMIN) && !capable(CAP_SYS_RESOURCE) &&
p->real_cred->user != INIT_USER)
goto bad_fork_free;
}
retval = copy_creds(p, clone_flags);
if (retval < 0)
goto bad_fork_free;
/*
* If multiple threads are within copy_process(), then this check
* triggers too late. This doesn't hurt, the check is only there
* to stop root fork bombs.
*/
retval = -EAGAIN;
if (nr_threads >= max_threads)
goto bad_fork_cleanup_count;
if (!try_module_get(task_thread_info(p)->exec_domain->module))
goto bad_fork_cleanup_count;
p->did_exec = 0;
delayacct_tsk_init(p); /* Must remain after dup_task_struct() */
copy_flags(clone_flags, p);
INIT_LIST_HEAD(&p->children);
INIT_LIST_HEAD(&p->sibling);
rcu_copy_process(p);
p->vfork_done = NULL;
spin_lock_init(&p->alloc_lock);
init_sigpending(&p->pending);
p->utime = cputime_zero;
p->stime = cputime_zero;
p->gtime = cputime_zero;
p->utimescaled = cputime_zero;
p->stimescaled = cputime_zero;
p->prev_utime = cputime_zero;
p->prev_stime = cputime_zero;
p->default_timer_slack_ns = current->timer_slack_ns;
task_io_accounting_init(&p->ioac);
acct_clear_integrals(p);
posix_cpu_timers_init(p);
p->lock_depth = -1; /* -1 = no lock */
do_posix_clock_monotonic_gettime(&p->start_time);
p->real_start_time = p->start_time;
monotonic_to_bootbased(&p->real_start_time);
p->io_context = NULL;
p->audit_context = NULL;
cgroup_fork(p);
p->mempolicy = mpol_dup(p->mempolicy);
if (IS_ERR(p->mempolicy)) {
retval = PTR_ERR(p->mempolicy);
p->mempolicy = NULL;
goto bad_fork_cleanup_cgroup;
}
mpol_fix_fork_child_flag(p);
p->irq_events = 0;
p->hardirqs_enabled = 1;
p->hardirqs_enabled = 0;
p->hardirq_enable_ip = 0;
p->hardirq_enable_event = 0;
p->hardirq_disable_ip = _THIS_IP_;
p->hardirq_disable_event = 0;
p->softirqs_enabled = 1;
p->softirq_enable_ip = _THIS_IP_;
p->softirq_enable_event = 0;
p->softirq_disable_ip = 0;
p->softirq_disable_event = 0;
p->hardirq_context = 0;
p->softirq_context = 0;
p->lockdep_depth = 0; /* no locks held yet */
p->curr_chain_key = 0;
p->lockdep_recursion = 0;
p->blocked_on = NULL; /* not blocked yet */
p->bts = NULL;
p->stack_start = stack_start;
/* Perform scheduler related setup. Assign this task to a CPU. */
sched_fork(p, clone_flags);
retval = perf_event_init_task(p);
if (retval)
goto bad_fork_cleanup_policy;
if ((retval = audit_alloc(p)))
goto bad_fork_cleanup_policy;
/* copy all the process information */
if ((retval = copy_semundo(clone_flags, p)))
goto bad_fork_cleanup_audit;
if ((retval = copy_files(clone_flags, p)))
goto bad_fork_cleanup_semundo;
if ((retval = copy_fs(clone_flags, p)))
goto bad_fork_cleanup_files;
if ((retval = copy_sighand(clone_flags, p)))
goto bad_fork_cleanup_fs;
if ((retval = copy_signal(clone_flags, p)))
goto bad_fork_cleanup_sighand;
if ((retval = copy_mm(clone_flags, p)))
goto bad_fork_cleanup_signal;
if ((retval = copy_namespaces(clone_flags, p)))
goto bad_fork_cleanup_mm;
if ((retval = copy_io(clone_flags, p)))
goto bad_fork_cleanup_namespaces;
retval = copy_thread(clone_flags, stack_start, stack_size, p, regs);
if (retval)
goto bad_fork_cleanup_io;
if (pid != &init_struct_pid) {
retval = -ENOMEM;
pid = alloc_pid(p->nsproxy->pid_ns);
if (!pid)
goto bad_fork_cleanup_io;
if (clone_flags & CLONE_NEWPID) {
retval = pid_ns_prepare_proc(p->nsproxy->pid_ns);
if (retval < 0)
goto bad_fork_free_pid;
}
}
p->pid = pid_nr(pid);
p->tgid = p->pid;
if (clone_flags & CLONE_THREAD)
p->tgid = current->tgid;
if (current->nsproxy != p->nsproxy) {
retval = ns_cgroup_clone(p, pid);
if (retval)
goto bad_fork_free_pid;
}
p->set_child_tid = (clone_flags & CLONE_CHILD_SETTID) ? child_tidptr : NULL;
/*
* Clear TID on mm_release()?
*/
p->clear_child_tid = (clone_flags & CLONE_CHILD_CLEARTID) ? child_tidptr: NULL;
p->robust_list = NULL;
p->compat_robust_list = NULL;
INIT_LIST_HEAD(&p->pi_state_list);
p->pi_state_cache = NULL;
/*
* sigaltstack should be cleared when sharing the same VM
*/
if ((clone_flags & (CLONE_VM|CLONE_VFORK)) == CLONE_VM)
p->sas_ss_sp = p->sas_ss_size = 0;
/*
* Syscall tracing should be turned off in the child regardless
* of CLONE_PTRACE.
*/
clear_tsk_thread_flag(p, TIF_SYSCALL_TRACE);
clear_tsk_thread_flag(p, TIF_SYSCALL_EMU);
clear_all_latency_tracing(p);
/* ok, now we should be set up.. */
p->exit_signal = (clone_flags & CLONE_THREAD) ? -1 : (clone_flags & CSIGNAL);
p->pdeath_signal = 0;
p->exit_state = 0;
/*
* Ok, make it visible to the rest of the system.
* We dont wake it up yet.
*/
p->group_leader = p;
INIT_LIST_HEAD(&p->thread_group);
/* Now that the task is set up, run cgroup callbacks if
* necessary. We need to run them before the task is visible
* on the tasklist. */
cgroup_fork_callbacks(p);
cgroup_callbacks_done = 1;
/* Need tasklist lock for parent etc handling! */
write_lock_irq(&tasklist_lock);
/*
* The task hasn't been attached yet, so its cpus_allowed mask will
* not be changed, nor will its assigned CPU.
*
* The cpus_allowed mask of the parent may have changed after it was
* copied first time - so re-copy it here, then check the child's CPU
* to ensure it is on a valid CPU (and if not, just force it back to
* parent's CPU). This avoids alot of nasty races.
*/
p->cpus_allowed = current->cpus_allowed;
p->rt.nr_cpus_allowed = current->rt.nr_cpus_allowed;
if (unlikely(!cpu_isset(task_cpu(p), p->cpus_allowed) ||
!cpu_online(task_cpu(p))))
set_task_cpu(p, smp_processor_id());
/* CLONE_PARENT re-uses the old parent */
if (clone_flags & (CLONE_PARENT|CLONE_THREAD)) {
p->real_parent = current->real_parent;
p->parent_exec_id = current->parent_exec_id;
} else {
p->real_parent = current;
p->parent_exec_id = current->self_exec_id;
}
spin_lock(¤t->sighand->siglock);
/*
* Process group and session signals need to be delivered to just the
* parent before the fork or both the parent and the child after the
* fork. Restart if a signal comes in before we add the new process to
* it's process group.
* A fatal signal pending means that current will exit, so the new
* thread can't slip out of an OOM kill (or normal SIGKILL).
*/
recalc_sigpending();
if (signal_pending(current)) {
spin_unlock(¤t->sighand->siglock);
write_unlock_irq(&tasklist_lock);
retval = -ERESTARTNOINTR;
goto bad_fork_free_pid;
}
if (clone_flags & CLONE_THREAD) {
atomic_inc(¤t->signal->count);
atomic_inc(¤t->signal->live);
p->group_leader = current->group_leader;
list_add_tail_rcu(&p->thread_group, &p->group_leader->thread_group);
}
if (likely(p->pid)) {
list_add_tail(&p->sibling, &p->real_parent->children);
tracehook_finish_clone(p, clone_flags, trace);
if (thread_group_leader(p)) {
if (clone_flags & CLONE_NEWPID)
p->nsproxy->pid_ns->child_reaper = p;
p->signal->leader_pid = pid;
tty_kref_put(p->signal->tty);
p->signal->tty = tty_kref_get(current->signal->tty);
attach_pid(p, PIDTYPE_PGID, task_pgrp(current));
attach_pid(p, PIDTYPE_SID, task_session(current));
list_add_tail_rcu(&p->tasks, &init_task.tasks);
__get_cpu_var(process_counts)++;
}
attach_pid(p, PIDTYPE_PID, pid);
nr_threads++;
}
total_forks++;
spin_unlock(¤t->sighand->siglock);
write_unlock_irq(&tasklist_lock);
proc_fork_connector(p);
cgroup_post_fork(p);
perf_event_fork(p);
return p;
bad_fork_free_pid:
if (pid != &init_struct_pid)
free_pid(pid);
bad_fork_cleanup_io:
put_io_context(p->io_context);
bad_fork_cleanup_namespaces:
exit_task_namespaces(p);
bad_fork_cleanup_mm:
if (p->mm)
mmput(p->mm);
bad_fork_cleanup_signal:
if (!(clone_flags & CLONE_THREAD))
__cleanup_signal(p->signal);
bad_fork_cleanup_sighand:
__cleanup_sighand(p->sighand);
bad_fork_cleanup_fs:
exit_fs(p); /* blocking */
bad_fork_cleanup_files:
exit_files(p); /* blocking */
bad_fork_cleanup_semundo:
exit_sem(p);
bad_fork_cleanup_audit:
audit_free(p);
bad_fork_cleanup_policy:
perf_event_free_task(p);
mpol_put(p->mempolicy);
bad_fork_cleanup_cgroup:
cgroup_exit(p, cgroup_callbacks_done);
delayacct_tsk_free(p);
module_put(task_thread_info(p)->exec_domain->module);
bad_fork_cleanup_count:
atomic_dec(&p->cred->user->processes);
exit_creds(p);
bad_fork_free:
free_task(p);
fork_out:
return ERR_PTR(retval);
}
上面执行完以后,回到do_fork()函数,如果copy_process()函数成功返回。新创建的子进程被唤醒并让其投入运行。内核有意选择子进程先运行。因为一般子进程都会马上调用exec()函数,这样可以避免写时拷贝的额外开销。如果父进程首先执行的话,有可能会开始向地址空间写入。
线程机制提供了在同一程序内共享内存地址空间运行的一组线程。线程机制支持并发程序设计技术,可以共享打开的文件和其他资源。如果你的系统是多核心的,那多线程技术可保证系统的真正并行。在Linux中,并没有线程这个概念,Linux中所有的线程都当作进程来处理,换句话说就是在内核中并没有什么特殊的结构和算法来表示线程。在Linux中,线程仅仅是一个使用共享资源的进程。每个线程都拥有一个隶属于自己的task_struct。所以说线程本质上还是进程,只不过该进程可以和其他一些进程共享某些资源信息。
内核有时需要在后台执行一些操作,这种任务可以通过内核线程完成,内核线程独立运行在内核空间的标准进程。内核线程和普通的进程间的区别在于内核线程没有独立的地址空间。它们只在讷河空间运行,从来不切换到用户空间去。内核进程和普通进程一样,可以被调度,也可以被抢占。内核线程也只能由其它内核线程创建,内核是通过从kthreadd内核进程中衍生出所有新的内核线程来自动处理这一点的。在内核中创建一个的内核线程方法如下:1
2
3struct task_struct *kthread_create(int (*threadfn)(void *data),
void *data,
const char namefmt[], ...)
该函数实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28struct task_struct *kthread_create(int (*threadfn)(void *data),
void *data,
const char namefmt[],
...)
{
struct kthread_create_info create;
create.threadfn = threadfn;
create.data = data;
init_completion(&create.done);
spin_lock(&kthread_create_lock);
list_add_tail(&create.list, &kthread_create_list);
spin_unlock(&kthread_create_lock);
wake_up_process(kthreadd_task);
wait_for_completion(&create.done);
if (!IS_ERR(create.result)) {
struct sched_param param = { .sched_priority = 0 };
va_list args;
va_start(args, namefmt);
vsnprintf(create.result->comm, sizeof(create.result->comm),
namefmt, args);
va_end(args);
/*
* root may have changed our (kthreadd's) priority or CPU mask.
* The kernel thread should not inherit these properties.
*/
sched_setscheduler_nocheck(create.result, SCHED_NORMAL, ¶m);
set_cpus_allowed_ptr(create.result, cpu_all_mask);
}
新的任务是由kthread内核进程通过clone()系统调用而创建的。新的进程将运行threadfn函数,给其传递参数data,新的进程名称为namefmt,新创建的进程处于不可运行状态,需要调用wake_up_process()明确的唤醒它,否则它不会主动运行。也可以通过调用kthread_run()来创建一个进程并让它运行起来。1
2
3
4
5
6
7
8
({ \
struct task_struct *__k \
= kthread_create(threadfn, data, namefmt, ## __VA_ARGS__); \
if (!IS_ERR(__k)) \
wake_up_process(__k); \
__k; \
})
kthread_run其实就是创建了一个内核线程并且唤醒了。内核线程启动后就一直运行直到调用do_exit()退出或者内核的其他部分调用kthread_stop()退出。1
int kthread_stop(struct task_struct *k);
下面为一个使用内核线程的示例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
struct task_struct *sln_task;
int sln_kthread_func(void *arg)
{
while (!kthread_should_stop()) {
printk(KERN_ALERT"===%s===\n", __func__);
set_current_state(TASK_INTERRUPTIBLE);
schedule_timeout(2*HZ);
}
return 0;
}
void sln_init_do(void)
{
int data = 9527;
sln_task = kthread_create(sln_kthread_func,
&data,
"sln_kthread_task");
if (IS_ERR(sln_task)) {
printk(KERN_ALERT"kthread_create() failed!\n");
return;
}
wake_up_process(sln_task);
}
void sln_exit_do(void)
{
if (NULL != sln_task) {
kthread_stop(sln_task);
sln_task = NULL;
}
}
static int __init sln_init(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
sln_init_do();
return 0;
}
static void __exit sln_exit(void)
{
printk(KERN_ALERT"===%s===\n", __func__);
sln_exit_do();
}
module_init(sln_init);
module_exit(sln_exit);
MODULE_LICENSE("GPL");
MODULE_AUTHOR("shallnet");
MODULE_DESCRIPTION("blog.csdn.net/shallnet");
既然有进程的创建,那就有进程的终结,终结时内核必须释放它所占有的资源。内核终结时,大部分任务都是靠do_exit()来完成。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109NORET_TYPE void do_exit(long code)
{
struct task_struct *tsk = current;
int group_dead;
profile_task_exit(tsk);
WARN_ON(atomic_read(&tsk->fs_excl));
//不可在中断上下文中使用该函数
if (unlikely(in_interrupt()))
panic("Aiee, killing interrupt handler!");
if (unlikely(!tsk->pid))
panic("Attempted to kill the idle task!");
tracehook_report_exit(&code);
validate_creds_for_do_exit(tsk);
/*
* We're taking recursive faults here in do_exit. Safest is to just
* leave this task alone and wait for reboot.
*/
if (unlikely(tsk->flags & PF_EXITING)) {
printk(KERN_ALERT
"Fixing recursive fault but reboot is needed!\n");
//设置PF_EXITING:表示进程正在退出
tsk->flags |= PF_EXITPIDONE;
set_current_state(TASK_UNINTERRUPTIBLE);
schedule();
}
exit_irq_thread();
exit_signals(tsk); /* sets PF_EXITING */
/*
* tsk->flags are checked in the futex code to protect against
* an exiting task cleaning up the robust pi futexes.
*/
smp_mb();
spin_unlock_wait(&tsk->pi_lock);
if (unlikely(in_atomic()))
printk(KERN_INFO "note: %s[%d] exited with preempt_count %d\n",
current->comm, task_pid_nr(current),
preempt_count());
acct_update_integrals(tsk);
group_dead = atomic_dec_and_test(&tsk->signal->live);
if (group_dead) {
hrtimer_cancel(&tsk->signal->real_timer);
exit_itimers(tsk->signal);
if (tsk->mm)
setmax_mm_hiwater_rss(&tsk->signal->maxrss, tsk->mm);
}
acct_collect(code, group_dead);
if (group_dead)
tty_audit_exit();
if (unlikely(tsk->audit_context))
audit_free(tsk);
tsk->exit_code = code;
taskstats_exit(tsk, group_dead);
//调用__exit_mm()函数放弃进程占用的mm_struct,如果没有别的进程使用它们即没被共享,就彻底释放它们
exit_mm(tsk);
if (group_dead)
acct_process();
trace_sched_process_exit(tsk);
exit_sem(tsk); //调用sem_exit()函数。如果进程排队等候IPC信号,它则离开队列
//分别递减文件描述符,文件系统数据等的引用计数。当引用计数的值为0时,就代表没有进程在使用这些资源,此时就释放
exit_files(tsk);
exit_fs(tsk);
check_stack_usage();
exit_thread();
cgroup_exit(tsk, 1);
if (group_dead && tsk->signal->leader)
disassociate_ctty(1);
module_put(task_thread_info(tsk)->exec_domain->module);
proc_exit_connector(tsk);
/*
* Flush inherited counters to the parent - before the parent
* gets woken up by child-exit notifications.
*/
perf_event_exit_task(tsk);
//调用exit_notify()向父进程发送信号,将子进程的父进程重新设置为线程组中的其他线程或init进程,并把进程状态设为TASK_ZOMBIE.
exit_notify(tsk, group_dead);
mpol_put(tsk->mempolicy);
tsk->mempolicy = NULL;
if (unlikely(current->pi_state_cache))
kfree(current->pi_state_cache);
/*
* Make sure we are holding no locks:
*/
debug_check_no_locks_held(tsk);
/*
* We can do this unlocked here. The futex code uses this flag
* just to verify whether the pi state cleanup has been done
* or not. In the worst case it loops once more.
*/
tsk->flags |= PF_EXITPIDONE;
if (tsk->io_context)
exit_io_context();
if (tsk->splice_pipe)
__free_pipe_info(tsk->splice_pipe);
validate_creds_for_do_exit(tsk);
preempt_disable();
exit_rcu();
/* causes final put_task_struct in finish_task_switch(). */
tsk->state = TASK_DEAD;
schedule(); //调用`schedule()切换到其他进程
BUG();
/* Avoid "noreturn function does return". */
for (;;)
cpu_relax(); /* For when BUG is null */
}
进程终结时所需的清理工作和进程描述符的删除被分开执行,这样尽管在调用了do_exit()之后,线程已经僵死不能允许情况下,系统还是保留了它的进程描述符。在父进程获得已经终结的子进程信息后,子进程的task_struct结构才被释放。Linux中有一系列wait()函数,这些函数都是基于系统调用wait4()实现的。它的动作就是挂起调用它的进程直到其中的一个子进程退出,此时函数会返回该退出子进程的PID。 最终释放进程描述符时,会调用release_task()。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33void release_task(struct task_struct * p)
{
struct task_struct *leader;
int zap_leader;
repeat:
tracehook_prepare_release_task(p);
/* don't need to get the RCU readlock here - the process is dead and
* can't be modifying its own credentials */
atomic_dec(&__task_cred(p)->user->processes);
proc_flush_task(p);
write_lock_irq(&tasklist_lock);
tracehook_finish_release_task(p);
__exit_signal(p); //释放目前僵死进程所使用的所有剩余资源,并进行统计记录
zap_leader = 0;
leader = p->group_leader;
//如果进程是线程组最后一个进程,并且领头进程已经死掉,那么就通知僵死的领头进程的父进程
if (leader != p && thread_group_empty(leader) && leader->exit_state == EXIT_ZOMBIE)
{
BUG_ON(task_detached(leader));
do_notify_parent(leader, leader->exit_signal);
zap_leader = task_detached(leader);
if (zap_leader)
leader->exit_state = EXIT_DEAD;
}
write_unlock_irq(&tasklist_lock);
release_thread(p);
call_rcu(&p->rcu, delayed_put_task_struct);
p = leader;
if (unlikely(zap_leader))
goto repeat;
}
子进程不一定能保证在父进程前边退出,所以必须要有机制来保证子进程在这种情况下能找到一个新的父进程。否则的话,这些成为孤儿的进程就会在退出时永远处于僵死状态,白白的耗费内存。解决这个问题的办法,就是给子进程在当前线程组内找一个线程作为父亲。一旦系统给进程成功地找到和设置了新的父进程,就不会再有出现驻留僵死进程的危险了,init进程会例行调用wait()来等待子进程,清除所有与其相关的僵死进程。
进程调度
Linux为多任务系统,正常情况下都存在成百上千个任务。由于Linux提供抢占式的多任务模式,所以Linux能同时并发地交互执行多个进程,而调度程序将决定哪一个进程投入运行、何时运行、以及运行多长时间。调度程序是像Linux这样的多任务操作系统的基础,只有通过调度程序的合理调度,系统资源才能最大限度地发挥作用,多进程才会有并发执行的效果。当系统中可运行的进程数目比处理器的个数多,就注定在某一时刻有一些进程不能执行,这些不能执行的进程在等待执行。调度程序的基本工作就是停止一个进程的运行,再在这些等待执行的进程中选择一个来执行。
调度程序停止一个进程的运行,再选择一个另外进程的动作开始运行的动作被称作抢占(preemption)。一个进程在被抢占之前能够运行的时间是预先设置好的,这个预先设置好的时间就是进程的的时间片(timeslice)。时间片就是分配给每个可运行进程的处理器时间段,它表明进程在被抢占前所能持续运行时间。
处理器的调度策略决定调度程序在何时让什么进程投入运行。调度策略通常需要在进程响应迅速(相应时间短)和进程吞吐量高之间寻找平衡。所以调度程序通常采用一套非常复杂的算法来决定最值得运行的进程投入运行。调度算法中最基本的一类当然就是基于优先级的调度,也就是说优先级高的先运行,相同优先级的按轮转式进行调度。优先级高 的进程使用的时间片也长。调度程序总是选择时间片未用尽且优先级最高的进程运行。这句话就是说用户和系统可以通过设置进程的优先级来响应系统的调度。基于此,Linux设计上一套动态优先级的调度方法。一开始,先为进程设置一个基本的优先级,然而它允许调度程序根据需要来加减优先级。Linux内核提供了两组独立的优先级范围。第一种是nice值,范围从-20到19,默认为0。nice值越大优先级越小。另外nice值也用来决定分配给进程时间片的长短。Linux下通过命令可以查看进程对应nice值,如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19$ ps -el
F S UID PID PPID C PRI NI ADDR SZ WCHAN TTY TIME CMD
4 S 0 1 0 0 80 0 - 725 ? ? 00:00:01 init
1 S 0 2 0 0 80 0 - 0 ? ? 00:00:00 kthreadd
1 S 0 3 2 0 -40 - - 0 ? ? 00:00:01 migration/0
1 S 0 4 2 0 80 0 - 0 ? ? 00:00:00 ksoftirqd/0
1 S 0 9 2 0 80 0 - 0 ? ? 00:00:00 ksoftirqd/1
......
1 S 0 39 2 0 85 5 - 0 ? ? 00:00:00 ksmd
......
1 S 0 156 2 0 75 -5 - 0 ? ? 00:00:00 kslowd000
1 S 0 157 2 0 75 -5 - 0 ? ? 00:00:00 kslowd001
......
4 S 499 2951 1 0 81 1 - 6276 ? ? 00:00:00 rtkit-daemon
......
第二种范围是实时优先级,默认范围是从0到99。任何实时的优先级都高于普通优先级。
进程执行时,它会根据具体情况改变状态,进程状态是调度和对换的依据。Linux 将进程状态分为五种: TASK_RUNNING 、TASK_INTERRUPTIBLE 、TASK_UNINTERRUPTIBLE、TASK_STOPPED和TASK_ZOMBILE。进程的状态随着进程的调度发生改变 。
| 状态 | |
|---|---|
| TASK_RUNNING | 可运行 |
| TASK_INTERRUPTIBLE | 可中断的等待状态 |
| TASK_UNINTERRUPTIBLE | 不可中断的等待状态 |
| TASK_STOPPED | 停止状态 |
| TASK_TRACED | 被跟踪状态 |
TASK_RUNNING (运行):无论进程是否正在占用 CPU ,只要具备运行条件,都处于该状态。 Linux 把处于该状态的所有 PCB 组织成一个可运行队列 run_queue ,调度程序从这个队列中选择进程运行。事实上,Linux 是将就绪态和运行态合并为了一种状态。
TASK_INTERRUPTIBLE (可中断阻塞): Linux 将阻塞态划分成 TASK_INTERRUPTIBLE 、 TASK_UNINTERRUPTIBLE 、 TASK_STOPPED 三种不同的状态。处于 TASK_INTERRUPTIBLE 状态的进程在资源有效时被唤醒,也可以通过信号或定时中断唤醒。
TASK_UNINTERRUPTIBLE (不可中断阻塞):另一种阻塞状态,处于该状态的进程只有当资源有效时被唤醒,不能通过信号或定时中断唤醒。在执行ps命令时,进程状态为D且不能被杀死。
TASK_STOPPED (停止):第三种阻塞状态,处于该状态的进程只能通过其他进程的信号才能唤醒。
TASK_TRACED (被跟踪):进程正在被另一个进程监视,比如在调试的时候。
我们在设置这些状态的时候是可以直接用语句进行的比如:p—>state = TASK_RUNNING。同时内核也会使用set_task_state()和set_current_state()函数来进行。
Linux调度器是以模块方式提供的,这样允许不同类型的进程可以有针对性地选择调度算法。完全公平调度(CFS)是针对普通进程的调度类,CFS采用的方法是对时间片分配方式进行根本性的重新设计,完全摒弃时间片而是分配给进程一个处理器使用比重。通过这种方式,CFS确保了进程调度中能有恒定的公平性,而将切换频率置于不断变动之中。
与Linux 2.6之前调度器不同,2.6版本内核的CFS没有将任务维护在链表式的运行队列中,它抛弃了active/expire数组,而是对每个CPU维护一个以时间为顺序的红黑树。该树方法能够良好运行的原因在于:
- 红黑树可以始终保持平衡,这意味着树上没有路径比任何其他路径长两倍以上。
- 由于红黑树是二叉树,查找操作的时间复杂度为`O(log n)。但是除了最左侧查找以外,很难执行其他查找,并且最左侧的节点指针始终被缓存。
- 对于大多数操作(插入、删除、查找等),红黑树的执行时间为
O(log n),而以前的调度程序通过具有固定优先级的优先级数组使用O(1)。O(log n)行为具有可测量的延迟,但是对于较大的任务数无关紧要。 - 红黑树可通过内部存储实现,即不需要使用外部分配即可对数据结构进行维护。
要实现平衡,CFS使用“虚拟运行时”表示某个任务的时间量。任务的虚拟运行时越小,意味着任务被允许访问服务器的时间越短,其对处理器的需求越高。CFS还包含睡眠公平概念以便确保那些目前没有运行的任务(例如,等待 I/O)在其最终需要时获得相当份额的处理器。
对于实时进程,Linux 采用了两种调度策略,即先来先服务调度( First-In, First-Out , FIFO )和时间片轮转调度( Round Robin , RR )。因为实时进程具有一定程度的紧迫性,所以衡量一个实时进程是否应该运行,Linux 采用了一个比较固定的标准。
下面是调度相关的一些数据结构:调度实体:struct sched_entity1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64struct sched_entity {
struct load_weight load; /* for load-balancing */
struct rb_node run_node;
struct list_head group_node;
unsigned int on_rq;
u64 exec_start;
u64 sum_exec_runtime;
u64 vruntime;
u64 prev_sum_exec_runtime;
u64 last_wakeup;
u64 avg_overlap;
u64 nr_migrations;
u64 start_runtime;
u64 avg_wakeup;
u64 avg_running;
u64 wait_start;
u64 wait_max;
u64 wait_count;
u64 wait_sum;
u64 iowait_count;
u64 iowait_sum;
u64 sleep_start;
u64 sleep_max;
s64 sum_sleep_runtime;
u64 block_start;
u64 block_max;
u64 exec_max;
u64 slice_max;
u64 nr_migrations_cold;
u64 nr_failed_migrations_affine;
u64 nr_failed_migrations_running;
u64 nr_failed_migrations_hot;
u64 nr_forced_migrations;
u64 nr_forced2_migrations;
u64 nr_wakeups;
u64 nr_wakeups_sync;
u64 nr_wakeups_migrate;
u64 nr_wakeups_local;
u64 nr_wakeups_remote;
u64 nr_wakeups_affine;
u64 nr_wakeups_affine_attempts;
u64 nr_wakeups_passive;
u64 nr_wakeups_idle;
struct sched_entity *parent;
/* rq on which this entity is (to be) queued: */
struct cfs_rq *cfs_rq;
/* rq "owned" by this entity/group: */
struct cfs_rq *my_q;
};
该结构在./linux/include/linux/sched.h中,表示一个可调度实体(进程,进程组,等等)。它包含了完整的调度信息,用于实现对单个任务或任务组的调度。调度实体可能与进程没有关联。这里包括负载权重load、对应的红黑树结点run_node、虚拟运行时vruntime(表示进程的运行时间,并作为红黑树的索引)、开始执行时间、最后唤醒时间、各种统计数据、用于组调度的CFS运行队列信息cfs_rq,等等。
调度类:struct sched_class。该调度类也在sched.h中,是对调度器操作的面向对象抽象,协助内核调度程序的各种工作。调度类是调度器管理器的核心,每种调度算法模块需要实现struct sched_class建议的一组函数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51struct sched_class {
const struct sched_class *next;
void (*enqueue_task) (struct rq *rq, struct task_struct *p, int wakeup);
void (*dequeue_task) (struct rq *rq, struct task_struct *p, int sleep);
void (*yield_task) (struct rq *rq);
void (*check_preempt_curr) (struct rq *rq, struct task_struct *p, int flags);
struct task_struct * (*pick_next_task) (struct rq *rq);
void (*put_prev_task) (struct rq *rq, struct task_struct *p);
int (*select_task_rq)(struct task_struct *p, int sd_flag, int flags);
unsigned long (*load_balance) (struct rq *this_rq, int this_cpu,
struct rq *busiest, unsigned long max_load_move,
struct sched_domain *sd, enum cpu_idle_type idle,
int *all_pinned, int *this_best_prio);
int (*move_one_task) (struct rq *this_rq, int this_cpu,
struct rq *busiest, struct sched_domain *sd,
enum cpu_idle_type idle);
void (*pre_schedule) (struct rq *this_rq, struct task_struct *task);
void (*post_schedule) (struct rq *this_rq);
void (*task_wake_up) (struct rq *this_rq, struct task_struct *task);
void (*set_cpus_allowed)(struct task_struct *p,
const struct cpumask *newmask);
void (*rq_online)(struct rq *rq);
void (*rq_offline)(struct rq *rq);
void (*set_curr_task) (struct rq *rq);
void (*task_tick) (struct rq *rq, struct task_struct *p, int queued);
void (*task_new) (struct rq *rq, struct task_struct *p);
void (*switched_from) (struct rq *this_rq, struct task_struct *task,
int running);
void (*switched_to) (struct rq *this_rq, struct task_struct *task,
int running);
void (*prio_changed) (struct rq *this_rq, struct task_struct *task,
int oldprio, int running);
unsigned int (*get_rr_interval) (struct task_struct *task);
void (*moved_group) (struct task_struct *p);
};
其中的主要函数:
enqueue_task:当某个任务进入可运行状态时,该函数将得到调用。它将调度实体(进程)放入红黑树中,并对nr_running变量加 1。从前面“Linux进程管理”的分析中可知,进程创建的最后会调用该函数。dequeue_task:当某个任务退出可运行状态时调用该函数,它将从红黑树中去掉对应的调度实体,并从nr_running变量中减 1。yield_task:在compat_yield sysctl关闭的情况下,该函数实际上执行先出队后入队;在这种情况下,它将调度实体放在红黑树的最右端。check_preempt_curr:该函数将检查当前运行的任务是否被抢占。在实际抢占正在运行的任务之前,CFS 调度程序模块将执行公平性测试。这将驱动唤醒式(wakeup)抢占。pick_next_task:该函数选择接下来要运行的最合适的进程。load_balance:每个调度程序模块实现两个函数,load_balance_start()和load_balance_next(),使用这两个函数实现一个迭代器,在模块的load_balance例程中调用。内核调度程序使用这种方法实现由调度模块管理的进程的负载平衡。set_curr_task:当任务修改其调度类或修改其任务组时,将调用这个函数。task_tick:该函数通常调用自 time tick 函数;它可能引起进程切换。这将驱动运行时(running)抢占。
调度类的引入是接口和实现分离的设计典范,你可以实现不同的调度算法(例如普通进程和实时进程的调度算法就不一样),但由于有统一的接口,使得调度策略 被模块化,一个Linux调度程序可以有多个不同的调度策略。调度类显著增强了内核调度程序的可扩展性。每个任务都属于一个调度类,这决定了任务将如何调 度。 调度类定义一个通用函数集,函数集定义调度器的行为。例如,每个调度器提供一种方式,添加要调度的任务、调出要运行的下一个任务、提供给调度器等等。每个 调度器类都在一对一连接的列表中彼此相连,使类可以迭代(例如,要启用给定处理器的禁用)。注意,将任务函数加入队列或脱离队列只需从特定调度结构中加入或移除任务。 核心函数 pick_next_task 选择要执行的下一个任务(取决于调度类的具体策略)。
sched_rt.c,sched_fair.c,sched_idletask.c等(都在kernel/目录下)就是不同的调度算法实现。不要忘了调度类是任务结构本身的一部分(参见 task_struct)。这一点简化了任务的操作,无论其调度类如何。因为进程描述符中有sched_class引用,这样就可以直接通过进程描述符来 调用调度类中的各种操作。在调度类中,随着调度域的增加,其功能也在增加。 这些域允许您出于负载平衡和隔离的目的将一个或多个处理器按层次关系分组。 一个或多个处理器能够共享调度策略(并在其之间保持负载平衡),或实现独立的调度策略。
可运行队列:struct rq。调度程序每次在进程发生切换时,都要从可运行队列中选取一个最佳的进程来运行。Linux内核使用rq数据结构(以前的内核中该结构为 runqueue)表示一个可运行队列信息(也就是就绪队列),每个CPU都有且只有一个这样的结构。该结构在kernel/sched.c中,不仅描述了每个处理器中处于可运行状态(TASK_RUNNING),而且还描述了该处理器的调度信息。如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34struct rq {
/* runqueue lock: */
spinlock_t lock;
unsigned long nr_running;
unsigned long cpu_load[CPU_LOAD_IDX_MAX];
/* capture load from *all* tasks on this cpu: */
struct load_weight load;
unsigned long nr_load_updates;
u64 nr_switches;
u64 nr_migrations_in;
struct cfs_rq cfs;
struct rt_rq rt;
unsigned long nr_uninterruptible;
struct task_struct *curr, *idle;
unsigned long next_balance;
struct mm_struct *prev_mm;
u64 clock;
atomic_t nr_iowait;
/* calc_load related fields */
unsigned long calc_load_update;
long calc_load_active;
......
};
进程调度的入口点是函数schedule(),该函数调用pick_next_task(),pick_next_task()会以优先级为序,从高到低,一次检查每一个调度类,且从最高优先级的调度类中,选择最高优先级的进程。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99asmlinkage void __sched schedule(void)
{
struct task_struct *prev, *next;
unsigned long *switch_count;
struct rq *rq;
int cpu;
need_resched:
preempt_disable();
cpu = smp_processor_id();
rq = cpu_rq(cpu);
rcu_sched_qs(cpu);
prev = rq->curr;
switch_count = &prev->nivcsw;
release_kernel_lock(prev);
need_resched_nonpreemptible:
schedule_debug(prev);
if (sched_feat(HRTICK))
hrtick_clear(rq);
spin_lock_irq(&rq->lock);
update_rq_clock(rq);
clear_tsk_need_resched(prev);
if (prev->state && !(preempt_count() & PREEMPT_ACTIVE)) {
if (unlikely(signal_pending_state(prev->state, prev)))
prev->state = TASK_RUNNING;
else
deactivate_task(rq, prev, 1);
switch_count = &prev->nvcsw;
}
pre_schedule(rq, prev);
if (unlikely(!rq->nr_running))
idle_balance(cpu, rq);
put_prev_task(rq, prev);
<strong>next = pick_next_task(rq); //<span><span><span style="font-size:14px;">//挑选最高优先级别的任务</span></span></span></strong>
if (likely(prev != next)) {
sched_info_switch(prev, next);
perf_event_task_sched_out(prev, next, cpu);
rq->nr_switches++;
rq->curr = next;
++*switch_count;
context_switch(rq, prev, next); /* unlocks the rq */
/*
* the context switch might have flipped the stack from under
* us, hence refresh the local variables.
*/
cpu = smp_processor_id();
rq = cpu_rq(cpu);
} else
spin_unlock_irq(&rq->lock);
post_schedule(rq);
if (unlikely(reacquire_kernel_lock(current) < 0))
goto need_resched_nonpreemptible;
preempt_enable_no_resched();
if (need_resched())
goto need_resched;
}
static inline struct task_struct *
pick_next_task(struct rq *rq)
{
const struct sched_class *class;
struct task_struct *p;
/*
* Optimization: we know that if all tasks are in
* the fair class we can call that function directly:
*/
if (likely(rq->nr_running == rq->cfs.nr_running)) {
p = fair_sched_class.pick_next_task(rq);
if (likely(p))
return p;
}
//从最高优先级类开始,遍历每一个调度类。每一个调度类都实现了pick_next_task,他会返回指向下一个可运行进程的指针,没有时返回NULL。
class = sched_class_highest;
for ( ; ; ) {
p = class->pick_next_task(rq);
if (p)
return p;
/*
* Will never be NULL as the idle class always
* returns a non-NULL p:
*/
class = class->next;
}
}
被阻塞(休眠)的进程处于不可执行状态,是不能被调度的。进程休眠一般是由于等待一些事件,内核首先把自己标记成休眠状态,从可执行红黑树中移出,放入等待队列,然后调用schedule()选择和执行一个其他进程。唤醒的过程刚好相反,进程设置为可执行状态,然后从等待队列中移到可执行红黑树中。
等待队列是由等待某些事件发生的进程组成的简单链表。内核用wake_queue_head_t来代表队列。进程把自己放入等待队列中并设置成不可执状态。当等待队列相关事件发生时,队列上进程会被唤醒。函数inotify_read()是实现等待队列的一个典型用法:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52static ssize_t inotify_read(struct file *file, char __user *buf,
size_t count, loff_t *pos)
{
struct fsnotify_group *group;
struct fsnotify_event *kevent;
char __user *start;
int ret;
DEFINE_WAIT(wait);
start = buf;
group = file->private_data;
while (1) {
//进程的状态变更为`TASK_INTERRUPTIBLE`或`TASK_UNINTERRUPTIBLE。
prepare_to_wait(&group->notification_waitq, &wait, TASK_INTERRUPTIBLE);
mutex_lock(&group->notification_mutex);
kevent = get_one_event(group, count);
mutex_unlock(&group->notification_mutex);
if (kevent) {
ret = PTR_ERR(kevent);
if (IS_ERR(kevent))
break;
ret = copy_event_to_user(group, kevent, buf);
fsnotify_put_event(kevent);
if (ret < 0)
break;
buf += ret;
count -= ret;
continue;
}
ret = -EAGAIN;
if (file->f_flags & O_NONBLOCK)
break;
ret = -EINTR;
if (signal_pending(current))
break;
if (start != buf)
break;
schedule();
}
finish_wait(&group->notification_waitq, &wait);
if (start != buf && ret != -EFAULT)
ret = buf - start;
return ret;
}
唤醒是通过wake_up()进行。她唤醒指定的等待队列上 的所有进程。它调用try_to_wake_up,该函数负责将进程设置为TASK_RUNNING状态,调用active_task()将此进程放入可 执行队列,如果被唤醒进程的优先级比当前正在执行的进程的优先级高,还要设置need_resched标志。
上下文切换,就是从一个可执行进程切换到另一个可执行进程,由定义在kernel/sched.c的context_switch函数负责处理。每当一个新的进程被选出来准备投入运行的时候,schedule`就会调用该函数。它主要完成如下两个工作:
- 调用定义在
include/asm/mmu_context.h中的switch_mm()。该函数负责把虚拟内存从上一个进程映射切换到新进程中。 - 调用定义在
include/asm/system.h的switch_to(),该函数负责从上一个进程的处理器状态切换到新进程的处理器状态,这包括保存,恢复栈信息和寄存器信息。
内核也必须知道什么时候调用schedule(),单靠用户代码显示调用schedule(),他们可能就会永远地执行下去,相反,内核提供了一个need_resched标志来表明是否需要重新执行一次调度。当 某个进程耗尽它的时间片时,scheduler_tick()就会设置这个标志,当一个优先级高的进程进入可执行状态的时候,try_to_wake_up()也会设置这个标志。内核检查该标志,确认其被设置,调用schedule()来切换到一个新的进程。该标志对内核来讲是一个信息,它表示应当有其他进程应当被运行了。
用于访问和操作need_resched的函数:
set_tsk_need_resched(task):设置指定进程中的need_resched标志clear_tsk_need_resched(task):清除指定进程中的nedd_resched标志need_resched():检查need_resched标志的值,如果被设置就返回真,否则返回
在返回用户空间以及从中断返回的时候,内核也会检查need_resched标志,如果已被设置,内核会在继续执行之前调用该调度程序。最后,每个进程都包含一个need_resched标志,这是因为访 问进程描述符内的数值要比访问一个全局变量要快(因为current宏速度很快并且描述符通常都在高速缓存中)。在2.6内核中,他被移到了thread_info结构体里。
用户抢占发生在:
- 从系统调用返回时;
- 从终端处理程序返回用户空间时。
内核抢占发生在:
- 中断处理正在执行,且返回内核空间前;
- 内核代码再一次具有可抢占性的时候;
- 内核任务显式调用
schedule()函数; - 内核中的任务阻塞的时候。
内核同步
如同Linux应用一样,内核的共享资源也要防止并发,因为如果多个执行线程同时访问和操作数据有可能发生各个线程之间相互覆盖共享数据的情况。
在Linux只是单一处理器的时候,只有在中断发生或内核请求重新调度执行另一个任务时,数据才可能会并发访问。但自从内核开始支持对称多处理器之后,内核代码可以同时运行在多个处理器上,如果此时不加保护,运行在多个处理器上的代码完全可能在同一时刻并发访问共享数据。
一般把访问和操作共享数据的代码段称作临界区,为了避免在临界区中发生并发访问,程序员必须保证临界区代码原子执行,也就是要么全部执行,要么不执行。如果两个执行线程在同一个临界区同时执行,就发生了竞态(race conditions),避免并发防止竞态就是所谓的同步。
在Linux内核中造成并发的原因主要有如下:
- 中断 — 中断几乎可以在任何时刻异步发生,也就可能随时打断当前正在执行的代码。
- 软中断和
tasklet— 内核能在任何时刻唤醒或调度软中断和tasklet,打断当前正在执行的代码。 - 内核抢占 — 因为内核具有抢占性,所以内核中的任务可能会被另一任务抢占。
- 睡眠及与用户空间的同步 — 在内核执行的进程可能会睡眠,这就会唤醒调度程序,从而导致调度一个新的用户进程执行。
- 对称多处理 — 两个或多个处理器可以同时执行代码。(真并发)
通过锁可以防止并发执行,并且保护临界区不受竞态影响。任何执行线程要访问临界区代码时首先先获得锁,这样当后面另外的执行线程要访问临界区时就不能再获得该锁,这样临界区就禁止后来执行线程访问。Linux自身实现了多种不同的锁机制,各种锁各有差别,区别主要在于当锁被争用时,有些会简单地执行等待,而有些锁会使当前任务睡眠直到锁可用为止。本节将会分析各锁的使用和实现。但是使用锁也会带来副作用,锁使得线程按串行方式对资源进行访问,所以使用锁无疑会降低系统性能;并且锁使用不当还会造成死锁。
下面来看一下Linux下同步的方法,包括原子操作、自旋锁、信号量等方式。
原子操作
该操作是其它同步方法的基础,原子操作可以保证指令以原子的方式执行,执行过程不会被打断。Linux内核提供了两组原子操作接口:原子整数操作和原子位操作。
针对整数的原子操作只能对atomic_t类型的数据进行处理。该类类型定义与文件<include/linux/types.h>:1
2
3typedef struct {
volatile int counter;
} atomic_t;
下面举例说明原子操作的用法:
定义一个atomic_c类型的数据很简单,还可以定义时给它设定初值:1
2
3
4atomic_t u;
/* 定义 u */
atomic_t v = ATOMIC_INIT(0) /*定义 v 并把它初始化为0*/
对其操作:1
2
3
4
5
6
7
8
9atomic_set(&v,4)
/* v = 4 ( 原子地)*/
atomic_add(2,&v)
/* v = v + 2 = 6 (原子地) */
atomic_inc(&v)
/* v = v + 1 =7(原子地)*/
如果需要将atomic_t转换成int型,可以使用atomic_read()来完成:1
printk("%d\n", atomic_read(&v)); /* 会打印7*/
原子整数操作最常见的用途就是实现计数器。使用复杂的锁机制来保护一个单纯的计数器是很笨拙的,所以,开发者最好使用atomic_inc()和atomic_dec()这两个相对来说轻便一点的操作。
还可以用原子整数操作原子地执行一个操作并检查结果。一个常见的例子是原子的减操作和检查。1
int atomic_dec_and_test(atomic_t *v)
这个函数让给定的原子变量减1,如果结果为0,就返回1;否则返回0。特定体系结构的所有原子整数操作可以在文件<arch/x86/include/asm/atomic.h>中找到。如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
static inline int atomic_read(const atomic_t *v)
{
return v->counter;
}
static inline void atomic_set(atomic_t *v, int i)
{
v->counter = i;
}
static inline void atomic_add(int i, atomic_t *v)
{
asm volatile(LOCK_PREFIX "addl %1,%0"
: "+m" (v->counter)
: "ir" (i));
}
static inline void atomic_sub(int i, atomic_t *v)
{
asm volatile(LOCK_PREFIX "subl %1,%0"
: "+m" (v->counter)
: "ir" (i));
}
static inline int atomic_sub_and_test(int i, atomic_t *v)
{
unsigned char c;
asm volatile(LOCK_PREFIX "subl %2,%0; sete %1"
: "+m" (v->counter), "=qm" (c)
: "ir" (i) : "memory");
return c;
}
......
除了原子整数之外,内核还提供了一组针对位操作的函数,这些操作也是和体系结构相关的。例如在x86下set_bit实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13static __always_inline void
set_bit(unsigned int nr, volatile unsigned long *addr)
{
if (IS_IMMEDIATE(nr)) {
asm volatile(LOCK_PREFIX "orb %1,%0"
: CONST_MASK_ADDR(nr, addr)
: "iq" ((u8)CONST_MASK(nr))
: "memory");
} else {
asm volatile(LOCK_PREFIX "bts %1,%0"
: BITOP_ADDR(addr) : "Ir" (nr) : "memory");
}
}
原子操作是对普通内存地址指针进行的操作,只要指针指向了任何你希望的数据,你就可以对它进行操作。原子位操作(以x86为例)相关函数定义在文件<arch/x86/include/asm/bitops.h>中。
自旋锁
不是所有的临界区都是像增加或减少变量这么简单,有的时候临界区可能会跨越多个函数,这这时就需要使用更为复杂的同步方法——锁。Linux内核中最常见的锁是自旋锁,自旋锁最多只能被一个可执行线程持有,如果一个可执行线程视图获取一个已经被持有的锁,那么该线程将会一直进行忙循环等待锁重新可用。在任意时候,自旋锁都可以防止多余一个执行线程同时进入临界区。由于自旋忙等过程是很费时间的,所以自旋锁不应该被长时间持有。
自旋锁相关方法如下:
| 方法 | spinlock中的定义 |
|---|---|
定义spin lock并初始化 |
DEFINE_SPINLOCK() |
动态初始化spin lock |
spin_lock_init() |
获取指定的spin lock |
spin_lock() |
获取指定的spin lock同时disable本CPU中断 |
spin_lock_irq() |
保存本CPU当前的irq状态,disable本CPU中断并获取指定的spin lock |
spin_lock_irqsave() |
获取指定的spin lock同时disable本CPU的`bottom half |
spin_lock_bh() |
释放指定的spin lock |
spin_unlock() |
释放指定的spin lock同时enable本CPU中断 |
spin_lock_irq() |
释放指定的spin lock同时恢复本CPU的中断状态 |
spin_lock_irqsave() |
获取指定的spin lock同时enable本CPU的bottom half |
spin_unlock_bh() |
尝试去获取spin lock,如果失败,不会spin,而是返回非零值 |
spin_trylock() |
判断spin lock是否是locked,如果其他的thread已经获取了该lock,那么返回非零值,否则返回0 |
spin_is_locked() |
自旋锁的实现和体系结构密切相关,代码通常通过汇编实现。与体系结构相关的部分定义在<asm/spinlock.h>,实际需要用到的接口定义在文件<linux/spinlock.h>中。一个实际的锁的类型为spinlock_t,定义在文件<include/linux/spinlock_types.h>中:1
2
3
4
5
6
7
8
9
10
11
12
13typedef struct {
raw_spinlock_t raw_lock;
unsigned int break_lock;
unsigned int magic, owner_cpu;
void *owner;
struct lockdep_map dep_map;
} spinlock_t;
自旋锁基本使用形式如下:1
2
3
4DEFINE_SPINLOCK(lock);
spin_lock(&lock);
/* 临界区 */
spin_unlock(&lock);
实际上有 4 个函数可以加锁一个自旋锁:1
2
3
4
5void spin_lock(spinlock_t *lock);
void spin_lock_irq(spinlock_t *lock); //相当于`spin_lock() + local_irq_disable()。
void spin_lock_irqsave(spinlock_t *lock, unsigned long flags);
//禁止中断(只在本地处理器)在获得自旋锁之前; 之前的中断状态保存在flags里。相当于spin_lock() + local_irq_save()。
void spin_lock_bh(spinlock_t *lock); //获取锁之前禁止软件中断,但是硬件中断留作打开的,相当于spin_lock() + local_bh_disable()。
也有 4 个方法来释放一个自旋锁; 你用的那个必须对应你用来获取锁的函数。1
2
3
4void spin_unlock(spinlock_t *lock);
void spin_unlock_irqrestore(spinlock_t *lock, unsigned long flags);
void spin_unlock_irq(spinlock_t *lock);
void spin_unlock_bh(spinlock_t *lock);
下面看一下DEFINE_SPINLOCK()、spin_lock_init()、spin_lock()、spin_lock_irqsave()的实现:1
2
3
4
5
spin_lock:1
2
3
4
5
6
7
8
9
10
11
12
13
void __lockfunc _spin_lock(spinlock_t *lock)
{
__spin_lock(lock);
}
static inline void __spin_lock(spinlock_t *lock)
{
preempt_disable();
spin_acquire(&lock->dep_map, 0, 0, _RET_IP_);
LOCK_CONTENDED(lock, _raw_spin_trylock, _raw_spin_lock);
}
spin_lock_irqsave:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
unsigned long __lockfunc _spin_lock_irqsave(spinlock_t *lock)
{
return __spin_lock_irqsave(lock);
}
static inline unsigned long __spin_lock_irqsave(spinlock_t *lock)
{
unsigned long flags;
local_irq_save(flags); //spin_lock的实现没有禁止本地中断这一步
preempt_disable();
spin_acquire(&lock->dep_map, 0, 0, _RET_IP_);
LOCK_CONTENDED(lock, _raw_spin_trylock, _raw_spin_lock);
_raw_spin_lock_flags(lock, &flags);
return flags;
}
读写自旋锁一种比自旋锁粒度更小的锁机制,它保留了“自旋”的概念,但是在写操作方面,只能最多有1个写进程,在读操作方面,同时可以有多个读执行单元。当然,读和写也不能同时进行。读者写者锁有一个类型rwlock_t,在<linux/spinlokc.h>中定义。 它们可以以 2 种方式被声明和被初始化:
静态方式:1
rwlock_t my_rwlock = RW_LOCK_UNLOCKED;
动态方式:1
2rwlock_t my_rwlock;
rwlock_init(&my_rwlock);
可用函数的列表现在应当看来相当类似。 对于读者,有下列函数可用:1
2
3
4
5
6
7
8void read_lock(rwlock_t *lock);
void read_lock_irqsave(rwlock_t *lock, unsigned long flags);
void read_lock_irq(rwlock_t *lock);
void read_lock_bh(rwlock_t *lock);
void read_unlock(rwlock_t *lock);
void read_unlock_irqrestore(rwlock_t *lock, unsigned long flags);
void read_unlock_irq(rwlock_t *lock);
void read_unlock_bh(rwlock_t *lock);
对于写存取的函数是类似的:1
2
3
4
5
6
7
8
9void write_lock(rwlock_t *lock);
void write_lock_irqsave(rwlock_t *lock, unsigned long flags);
void write_lock_irq(rwlock_t *lock);
void write_lock_bh(rwlock_t *lock);
int write_trylock(rwlock_t *lock);
void write_unlock(rwlock_t *lock);
void write_unlock_irqrestore(rwlock_t *lock, unsigned long flags);
void write_unlock_irq(rwlock_t *lock);
void write_unlock_bh(rwlock_t *lock);
在与下半部配合使用时,锁机制必须要小心使用。由于下半部可以抢占进程上下文的代码,所以当下半部和进程上下文共享数据时,必须对进程上下文的共享数据进行保护,所以需要加锁的同时还要禁止下半部执行。同样的,由于中断处理器可以抢占下半部,所以如果中断处理器程序和下半部共享数据,那么就必须在获取恰当的锁的同时还要禁止中断。 同类的tasklet不可能同时运行,所以对于同类tasklet中的共享数据不需要保护,但是当数据被两个不同种类的tasklet共享时,就需要在访问下半部中的数据前先获得一个普通的自旋锁。由于同种类型的两个软中断也可以同时运行在一个系统的多个处理器上,所以被软中断共享的数据必须得到锁的保护。
信号量
一个被占有的自旋锁使得请求它的线程循环等待而不会睡眠,这很浪费处理器时间,所以自旋锁使用段时间占有的情况。Linux提供另外的同步方式可以在锁争用时让请求线程睡眠,直到锁重新可用时在唤醒它,这样处理器就不必循环等待,可以去执行其它代码。这种方式就是即将讨论的信号量。
信号量是一种睡眠锁,如果有一个任务试图获得一个已经被占用的信号量时,信号量会将其放入一个等待队列,然后睡眠。当持有的信号量被释放后,处于等待队列中的那个任务将被唤醒,并获得信号量。信号量比自旋锁提供了更好的处理器利用率,因为没有把时间花费在忙等带上。但是信号量也会有一定的开销,被阻塞的线程换入换出有两次明显的上下文切换,这样的开销比自旋锁要大的多。
如果需要在自旋锁和信号量中做出选择,应该根据锁被持有的时间长短做判断,如果加锁时间不长并且代码不会休眠,利用自旋锁是最佳选择。相反,如果加锁时间可能很长或者代码在持有锁有可能睡眠,那么最好使用信号量来完成加锁功能。信号量一个有用特性就是它可以同时允许任意数量的锁持有者,而自旋锁在一个时刻最多允许一个任务持有它。信号量同时允许的持有者数量可以在声明信号量时指定,当为1时,成为互斥信号量,否则成为计数信号量。
信号量的实现与体系结构相关,信号量使用struct semaphore类型用来表示信号量,定义于文件<include/linux/semaphore.h>中:1
2
3
4
5struct semaphore {
spinlock_t lock;
unsigned int count;
struct list_head wait_list;
};
信号量初始化方法有如下:
方法一:1
2
3
4
5
6
7
8struct semaphore sem;
void sema_init(struct semaphore *sem, int val);//初始化信号量,并设置信号量 sem 的值为 val。
static inline void sema_init(struct semaphore *sem, int val)
{
static struct lock_class_key __key;
*sem = (struct semaphore) __SEMAPHORE_INITIALIZER(*sem, val);
lockdep_init_map(&sem->lock.dep_map, "semaphore->lock", &__key, 0);
}
方法二:1
DECLARE_MUTEX(name);
定义一个名为 name 的信号量并初始化为1。
其实现为:1
2
方法三:1
2
3
4
5
6
7
//以不加锁状态动态创建信号量
//以加锁状态动态创建信号量
信号量初始化后就可以使用了,使用信号量主要有如下方法:1
2
3
4
5
6
7
8
9
10void down(struct semaphore * sem);
//该函数用于获得信号量 sem,它会导致睡眠,因此不能在中断上下文使用;
int down_interruptible(struct semaphore * sem);
//该函数功能与 down 类似,不同之处为,因为 down()而进入睡眠状态的进程不能被信号打断,但因为 down_interruptible()而进入睡眠状态的进程能被信号打断,信号也会导致该函数返回,这时候函数的返回值非 0;
int down_trylock(struct semaphore * sem);
//该函数尝试获得信号量`sem,如果能够立刻获得,它就获得该信号量并返回0, 否则,返回非0值。它不会导致调用者睡眠,可以在中断上下文使用。
up(struct semaphore * sem);
//释放指定信号量,如果睡眠队列不空,则唤醒其中一个队列。
信号量一般这样使用:1
2
3
4
5
6
7
8/* 定义信号量
DECLARE_MUTEX(mount_sem);
//down(&mount_sem);/* 获取信号量,保护临界区,信号量被占用之后进入不可中断睡眠状态
down_interruptible(&mount_sem);/* 获取信号量,保护临界区,信号量被占用之后进入不可中断睡眠状态
. . .
critical section /* 临界区
. . .
up(&mount_sem);/* 释放信号量
下面看一下这些函数的实现:
down():1
2
3
4
5
6
7
8
9
10
11
12
13
14
15void down(struct semaphore *sem)
{
unsigned long flags;
spin_lock_irqsave(&sem->lock, flags);
if (likely(sem->count > 0))
sem->count--;
else
__down(sem);
spin_unlock_irqrestore(&sem->lock, flags);
}
static noinline void __sched __down(struct semaphore *sem)
{
__down_common(sem, TASK_UNINTERRUPTIBLE, MAX_SCHEDULE_TIMEOUT);
}
down_interruptible():1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18int down_interruptible(struct semaphore *sem)
{
unsigned long flags;
int result = 0;
spin_lock_irqsave(&sem->lock, flags);
if (likely(sem->count > 0))
sem->count--;
else
result = __down_interruptible(sem);
spin_unlock_irqrestore(&sem->lock, flags);
return result;
}
static noinline int __sched __down_interruptible(struct semaphore *sem)
{
return __down_common(sem, TASK_INTERRUPTIBLE, MAX_SCHEDULE_TIMEOUT);
}
down_trylock():1
2
3
4
5
6
7
8
9
10
11
12
13int down_trylock(struct semaphore *sem)
{
unsigned long flags;
int count;
spin_lock_irqsave(&sem->lock, flags);
count = sem->count - 1;
if (likely(count >= 0))
sem->count = count;
spin_unlock_irqrestore(&sem->lock, flags);
return (count < 0);
}
up():1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19void up(struct semaphore *sem)
{
unsigned long flags;
spin_lock_irqsave(&sem->lock, flags);
if (likely(list_empty(&sem->wait_list)))
sem->count++;
else
__up(sem);
spin_unlock_irqrestore(&sem->lock, flags);
}
static noinline void __sched __up(struct semaphore *sem)
{
struct semaphore_waiter *waiter = list_first_entry(&sem->wait_list,
struct semaphore_waiter, list);
list_del(&waiter->list);
waiter->up = 1;
wake_up_process(waiter->task);
}
正如自旋锁一样,信号量也有区分读写访问的可能,读写信号量在内核中使用rw_semaphore结构表示,x86体系结构定义在<arch/x86/include/asm/rwsem.h>文件中:1
2
3
4
5
6
7
8struct rw_semaphore {
signed long count;
spinlock_t wait_lock;
struct list_head wait_list;
struct lockdep_map dep_map;
};
读写信号量的使用方法和信号量类似,其操作函数有如下:1
2
3
4
5
6
7
8
9DECLARE_RWSEM(name) //声明名为name的读写信号量,并初始化它。
void init_rwsem(struct rw_semaphore *sem); //对读写信号量`sem`进行初始化。
void down_read(struct rw_semaphore *sem); //读者用来获取`sem,若没获得时,则调用者睡眠等待。
void up_read(struct rw_semaphore *sem); //读者释放`sem。
int down_read_trylock(struct rw_semaphore *sem); //读者尝试获取sem,如果获得返回1,如果没有获得返回0。可在中断上下文使用。
void down_write(struct rw_semaphore *sem); //写者用来获取`sem,若没获得时,则调用者睡眠等待。
int down_write_trylock(struct rw_semaphore *sem); //写者尝试获取sem,如果获得返回1,如果没有获得返回0。可在中断上下文使用
void up_write(struct rw_semaphore *sem); //写者释放sem。
void downgrade_write(struct rw_semaphore *sem); //把写者降级为读者。
互斥体
除了信号量之外,内核拥有一个更简单的且可睡眠的锁,那就是互斥体。互斥体的行为和计数是1的信号量类似,其接口简单,实现更高效。 互斥体在内核中使用mutex表示,定义于<include/linux/mutex.h>:1
2
3
4
5
6
7struct mutex {
/* 1: unlocked, 0: locked, negative: locked, possible waiters */
atomic_t count;
spinlock_t wait_lock;
struct list_head wait_list;
......
};
静态定义mutex:1
DEFINE_MUTEX(name);
实现如下:1
2
3
4
5
6
7
8
9
动态定义mutex:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18mutex_init(&mutex);
void
__mutex_init(struct mutex *lock, const char *name, struct lock_class_key *key)
{
atomic_set(&lock->count, 1);
spin_lock_init(&lock->wait_lock);
INIT_LIST_HEAD(&lock->wait_list);
mutex_clear_owner(lock);
debug_mutex_init(lock, name, key);
}
锁定和解锁如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31mutex_lock(&mutex);
/* 临界区 */
mutex_unlock(&mutex);
void __sched mutex_lock(struct mutex *lock)
{
might_sleep();
/*
* The locking fastpath is the 1->0 transition from
* 'unlocked' into 'locked' state.
*/
__mutex_fastpath_lock(&lock->count, __mutex_lock_slowpath);
mutex_set_owner(lock);
}
void __sched mutex_unlock(struct mutex *lock)
{
/*
* The unlocking fastpath is the 0->1 transition from 'locked'
* into 'unlocked' state:
*/
/*
* When debugging is enabled we must not clear the owner before time,
* the slow path will always be taken, and that clears the owner field
* after verifying that it was indeed current.
*/
mutex_clear_owner(lock);
__mutex_fastpath_unlock(&lock->count, __mutex_unlock_slowpath);
}
其他mutex方法:1
2int mutex_trylock(struct mutex *); //视图获取指定互斥体,成功返回1;否则返回0。
int mutex_is_locked(struct mutex *lock); //判断锁是否被占用,是返回1,否则返回0。
使用mutex时,要注意一下:
mutex的使用技术永远是1;在同一上下文中上锁解锁;- 当进程持有一个
mutex时,进程不可退出; mutex不能在中断或下半部中使用。
抢占禁止
在前面章节讲进程管理的时候听到过内核抢占,由于内核可抢占,内核中的进程随时都可能被另外一个具有更高优先权的进程打断,这也就意味着一个任务与被抢占的任务可能会在同一个临界区运行。所以才有本节前面自旋锁来避免竞态的发生,自旋锁有禁止内核抢占的功能。但像每CPU变量的数据只能被一个处理器访问,可以不需要使用锁来保护,如果没有使用锁,内核又是抢占式的,那么新调度的任务就可能访问同一个变量。这个时候就可以通过禁止内核抢占来避免竞态的发生,禁止内核抢占使用preetmpt_disable()函数,这是一个可以嵌套调用的函数,可以使用任意次。每次调用都必须有一个相应的preempt_enable()调用,当最后一次preempt_enable()被调用时,内核抢占才重新启用。内核抢占相关函数如下:1
2
3
4
5
6
7
8
9
10
11
12preempt_enable()
//内核抢占计数preempt_count减1
preempt_disable()
//内核抢占计数preempt_count加1,当该值降为0时检查和执行被挂起的需要调度的任务
preempt_enable_no_resched()
//内核抢占计数preempt_count减1,但不立即抢占式调度
preempt_check_resched ()
//如果必要进行调度
preempt_count()
//返回抢占计数
preempt_schedule()
//内核抢占时的调度程序的入口点
以preempt_enable()为例,看一下其实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
asmlinkage void __sched preempt_schedule(void)
{
struct thread_info *ti = current_thread_info();
/*
* If there is a non-zero preempt_count or interrupts are disabled,
* we do not want to preempt the current task. Just return..
*/
if (likely(ti->preempt_count || irqs_disabled()))
return;
do {
add_preempt_count(PREEMPT_ACTIVE);
schedule();
sub_preempt_count(PREEMPT_ACTIVE);
/*
* Check again in case we missed a preemption opportunity
* between schedule and now.
*/
barrier();
} while (need_resched());
内存管理之页的分配与回收
内存管理单元(MMU)负责将管理内存,在把虚拟地址转换为物理地址的硬件的时候是按页为单位进行处理,从虚拟内存的角度来看,页就是内存管理中的最小单位。页的大小与体系结构有关,在 x86 结构中一般是4KB(32位)或者8KB(64位)。
通过 getconf 命令可以查看系统的page的大小:1
2
3
4
5# getconf -a | grep PAGE
PAGESIZE 4096
PAGE_SIZE 4096
_AVPHYS_PAGES 230873
_PHYS_PAGES 744957
内核中的每个物理页用struct page结构表示,结构定义于文件<include/linux/mm_types.h>:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39struct page {
unsigned long flags; /*页的状态*/
atomic_t _count; /* 页引用计数 */
union {
atomic_t _mapcount; /* 已经映射到mms的pte的个数*/
struct { /* */
u16 inuse;
u16 objects;
};
};
union {
struct {
unsigned long private;
struct address_space *mapping;
};
spinlock_t ptl;
struct kmem_cache *slab; /* 指向slab层 */
struct page *first_page; /* Compound tail pages */
};
union {
pgoff_t index; /* Our offset within mapping. */
void *freelist; /* SLUB: freelist req. slab lock */
};
struct list_head lru; /* 将页关联起来的链表项 */
void *virtual; /* Kernel virtual address (NULL if
not kmapped, ie. highmem) */
unsigned long debug_flags; /* Use atomic bitops on this */
void *shadow;
};
内核使用这一结构来管理系统中所有的页,因为内核需要知道一个该页是否被分配,是被谁拥有的等信息。
由于ISA总线的DMA处理器有严格的限制,只能对物理内存前16M寻址,内核线性地址空间只有1G,CPU不能直接访问所有的物理内存。这样就导致有一些内存不能永久地映射在内核空间上。所以在Linux中,把页分为不同的区,使用区来对具有相似特性的页进行分组。分组如下(以x86-32为例):
| 区域 | 用途 |
|---|---|
| ZONE_DMA | 小于16M内存页框,这个区包含的页用来执行DMA操作。 |
| ZONE_NORMAL | 16M~896M内存页框,个区包含的都是能正常映射的页。 |
| ZONE_HIGHMEM | 大于896M内存页框,这个区包”高端内存”,其中的页能不永久地映射到内核地址空间。 |
linux 把系统的页划分区,形成不同的内存池,这样就可以根据用途进行分配了。
每个区都用struct zone表示,定义于<include/linux/mmzone.h>中。该结构体较大,详细结构体信息可以查看源码文件。
Linux提供了几个以页为单位分配释放内存的接口,定义于<include/linux/gfp.h>中。分配内存主要有以下方法:
| 函数 | 用途 |
|---|---|
| alloc_page(gfp_mask) | 只分配一页,返回指向页结构的指针 |
| alloc_pages(gfp_mask, order) | 分配 2^order 个页,返回指向第一页页结构的指针 |
| __get_free_page(gfp_mask) | 只分配一页,返回指向其逻辑地址的指针 |
| __get_free_pages(gfp_mask, order) | 分配 2^order 个页,返回指向第一页逻辑地址的指针 |
| get_zeroed_page(gfp_mask) | 只分配一页,让其内容填充为0,返回指向其逻辑地址的指针 |
alloc_*函数返回的是内存的物理地址,get_*函数返回内存物理地址映射后的逻辑地址。如果无须直接操作物理页结构体的话,一般使用 get_*函数。
释放页的函数有:1
2
3extern void __free_pages( struct page *page, unsignedintorder);
extern void free_pages(unsigned longaddr, unsigned intorder);
extern void free_hot_page( struct page *page);
当需要以页为单位的连续物理页时,可以使用上面这些分配页的函数,对于常用以字节为单位的分配来说,内核提供来kmalloc()函数。
kmalloc()函数和用户空间一族函数类似,它可以以字节为单位分配内存,对于大多数内核分配来说,kmalloc函数用得更多。1
void *kmalloc(size_t size, gfp_t gfp_mask);
参数中有个gfp_mask标志,这个标志是控制分配内存时必须遵守的一些规则。
gfp_mask标志有3类:
- 行为标志 :控制分配内存时,分配器的一些行为,如何分配所需内存。
- 区标志 :控制内存分配在那个区(ZONE_DMA, ZONE_NORMAL, ZONE_HIGHMEM 之类)。
- 类型标志 :由上面2种标志组合而成的一些常用的场景。
行为标志主要有以下几种:
| 行为标志 | 描述 |
|---|---|
| __GFP_WAIT | 分配器可以睡眠 |
| __GFP_HIGH | 分配器可以访问紧急事件缓冲池 |
| __GFP_IO | 分配器可以启动磁盘`I/O |
| __GFP_FS | 分配器可以启动文件系统`I/O |
| __GFP_COLD | 分配器应该使用高速缓存中快要淘汰出去的页 |
| __GFP_NOWARN | 分配器将不打印失败警告 |
| __GFP_REPEAT | 分配器在分配失败时重复进行分配,但是这次分配还存在失败的可能 |
| __GFP_NOFALL | 分配器将无限的重复进行分配。分配不能失败 |
| __GFP_NORETRY | 分配器在分配失败时不会重新分配 |
| __GFP_NO_GROW | 由slab层内部使用 |
| __GFP_COMP | 添加混合页元数据,在 hugetlb 的代码内部使用 |
标志主要有以下3种:
| 区标志 | 描述 |
|---|---|
__GFP_DMA |
从 ZONE_DMA 分配 |
__GFP_DMA32 |
只在 ZONE_DMA32 分配 ,和 ZONE_DMA 类似,该区包含的页也可以进行DMA操作 |
__GFP_HIGHMEM |
从 ZONE_HIGHMEM 或者 ZONE_NORMAL 分配,优先从 ZONE_HIGHMEM 分配,如果 ZONE_HIGHMEM 没有多余的页则从ZONE_NORMAL 分配 |
类型标志是编程中最常用的,在使用标志时,应首先看看类型标志中是否有合适的,如果没有,再去自己组合 行为标志和区标志。
| 类型标志 | 描述 | 实际标志 |
|---|---|---|
| GFP_ATOMIC | 这个标志用在中断处理程序,下半部,持有自旋锁以及其他不能睡眠的地方 | __GFP_HIGH |
| GFP_NOWAIT | 与 GFP_ATOMIC 类似,不同之处在于,调用不会退给紧急内存池。这就增加了内存分配失败的可能性 | 0 |
| GFP_NOIO | 这种分配可以阻塞,但不会启动磁盘I/O。这个标志在不能引发更多磁盘I/O时能阻塞I/O代码,可能会导致递归 |
__GFP_WAIT |
| GFP_NOFS | 这种分配在必要时可能阻塞,也可能启动磁盘I/O,但不会启动文件系统操作。这个标志在你不能再启动另一个文件系统的操作时,用在文件系统部分的代码中 |
(__GFP_WAIT| __GFP_IO) |
| GFP_KERNEL | 这是常规的分配方式,可能会阻塞。这个标志在睡眠安全时用在进程上下文代码中。为了获得调用者所需的内存,内核会尽力而为。这个标志应当为首选标志 | (__GFP_WAIT| __GFP_IO | __GFP_FS ) |
| GFP_USER | 这是常规的分配方式,可能会阻塞。用于为用户空间进程分配内存时 | (__GFP_WAIT| __GFP_IO | __GFP_FS ) |
| GFP_HIGHUSER | 从 ZONE_HIGHMEM 进行分配,可能会阻塞。用于为用户空间进程分配内存 | (__GFP_WAIT| __GFP_IO | __GFP_FS |__GFP_HIGHMEM) |
| GFP_DMA | 从 ZONE_DMA 进行分配。需要获取能供DMA使用的内存的设备驱动程序使用这个标志。通常与以上的某个标志组合在一起使用。 |
__GFP_DMA |
以上各种类型标志的使用场景总结:
| 场景 | 相应标志 |
|---|---|
| 进程上下文,可以睡眠 | 使用 GFP_KERNEL |
| 进程上下文,不可以睡眠 | 使用 GFP_ATOMIC,在睡眠之前或之后以 GFP_KERNEL 执行内存分配 |
| 中断处理程序 | 使用 GFP_ATOMIC |
| 软中断 | 使用 GFP_ATOMIC |
| tasklet | 使用 GFP_ATOMIC |
需要用于DMA的内存,可以睡眠 |
使用 (GFP_DMA|GFP_KERNEL) |
需要用于DMA的内存,不可以睡眠 |
使用 (GFP_DMA|GFP_ATOMIC),或者在睡眠之前执行内存分配 |
kmalloc 所对应的释放内存的方法为:1
void kfree(const void *);
vmalloc()也可以按字节来分配内存。1
void *vmalloc(unsigned long size)
和kmalloc是一样的作用,不同在于前者分配的内存虚拟地址是连续的,而物理地址则无需连续。kmalloc()可以保证在物理地址上都是连续的,虚拟地址当然也是连续的。vmalloc()函数只确保页在虚拟机地址空间内是连续的。它通过分配非联系的物理内存块,再“修正”页表,把内存映射到逻辑地址空间的连续区域中,就能做到这点。但很显然这样会降低处理性能,因为内核不得不做“拼接”的工作。所以这也是为什么不得已才使用vmalloc()的原因 。vmalloc()可能睡眠,不能从中断上下文中进行调用,也不能从其他不允许阻塞的情况下进行调用。释放时必须使用vfree()。1
void vfree(const void *);
对于内存页面的管理,通常是先在虚存空间中分配一个虚存区间,然后才根据需要为此区间分配相应的物理页面并建立起映射,也就是说,虚存区间的分配在前,而物理页面的分配在后。但由于频繁的请求和释放不同大小的连续页框,必然导致在已分配页框的块内分散了许多小块的空闲页框,由此产生的问题是:即使有足够的空闲页框可以满足请求,但当要分配一个大块的连续页框时,无法满足请求。这就是著名的内存管理问题:外碎片问题。Linux采用著名的伙伴(Buddy)系统算法来解决外碎片问题。
把所有的空闲页框分组为11个块链表。每个块链表包含大小为1,2,4,8,16,32,64,128,256,512,1024个的页框。伙伴系统算法原理为:
假设请求一个256个页框的块,先在256个页框的链表内检查是否有一个空闲的块。如果没有这样的块,算法会查找下一个更大的块,在512个页框的链表中找一个空闲块。如果存在这样的块,内核就把512的页框分成两半,一半用作满足请求,另一半插入256个页框的链表中。如果512个页框的块链表也没有空闲块,就继续找更大的块,1024个页框的块。如果这样的块存在,内核把1024个页框的256个页框用作请求,然后从剩余的768个中拿出512个插入512个页框的链表中,把最后256个插入256个页框的链表中。
页框块的释放过程如下:
如果两个块具有相同的大小:a,并且他们的物理地址连续那么这两个块成为伙伴,内核就会试图把大小为a的一对空闲伙伴块合并为一个大小为2a的单独块。该算法还是迭代的,如果合并成功的话,它还会试图合并2a的块。
管理分区数据结构struct zone_struct中,涉及到空闲区数据结构。1
2
3
4
5
6struct free_area free_area[MAX_ORDER];
struct free_area {
struct list_head free_list[MIGRATE_TYPES];
unsigned long nr_free;
};
采用伙伴算法分配内存时,每次至少分配一个页面。但当请求分配的内存大小为几十个字节或几百个字节时应该如何处理?如何在一个页面中分配小的内存区,小内存区的分配所产生的内碎片又如何解决?slab的分配模式可以解决该问题。
内存管理之slab分配器
上一节最后说到对于小内存区的请求,如果采用伙伴系统来进行分配,则会在页内产生很多空闲空间无法使用,因此产生slab分配器来处理对小内存区(几十或几百字节)的请求。Linux中引入slab的主要目的是为了减少对伙伴算法的调用次数。
内核经常反复使用某一内存区。例如,只要内核创建一个新的进程,就要为该进程相关的数据结构(task_struct、打开文件对象等)分配内存区。当进程结束时,收回这些内存区。因为进程的创建和撤销非常频繁,Linux把那些频繁使用的页面保存在高速缓存中并重新使用。
slab分配器基于对象进行管理,相同类型的对象归为一类(如进程描述符就是一类),每当要申请这样一个对象,slab分配器就分配一个空闲对象出去,而当要释放时,将其重新保存在slab分配器中,而不是直接返回给伙伴系统。对于频繁请求的对象,创建适当大小的专用对象来处理。对于不频繁的对象,用一系列几何分布大小的对象来处理(详见通用对象)。
slab分配模式把对象分组放进缓冲区,为缓冲区的组织和管理与硬件高速缓存的命中率密切相关,因此,slab缓冲区并非由各个对象直接构成,而是由一连串的“大块(Slab)”构成,而每个大块中则包含了若干个同种类型的对象,这些对象或已被分配,或空闲。实际上,缓冲区就是主存中的一片区域,把这片区域划分为多个块,每块就是一个slab,每个slab由一个或多个页面组成,每个slab中存放的就是对象。
slab相关数据结构:
缓冲区数据结构使用kmem_cache结构来表示。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74struct kmem_cache {
/* 1) per-cpu data, touched during every alloc/free */
struct array_cache *array[NR_CPUS];
/* 2) Cache tunables. Protected by cache_chain_mutex */
unsigned int batchcount;
unsigned int limit;
unsigned int shared;
unsigned int buffer_size;
u32 reciprocal_buffer_size;
/* 3) touched by every alloc & free from the backend */
unsigned int flags; /* constant flags */
unsigned int num; /* # of objs per slab */
/* 4) cache_grow/shrink */
/* order of pgs per slab (2^n) */
unsigned int gfporder;
/* force GFP flags, e.g. GFP_DMA */
gfp_t gfpflags;
size_t colour; /* cache colouring range */
unsigned int colour_off; /* colour offset */
struct kmem_cache *slabp_cache;
unsigned int slab_size;
unsigned int dflags; /* dynamic flags */
/* constructor func */
void (*ctor)(void *obj);
/* 5) cache creation/removal */
const char *name;
struct list_head next;
/* 6) statistics */
unsigned long num_active;
unsigned long num_allocations;
unsigned long high_mark;
unsigned long grown;
unsigned long reaped;
unsigned long errors;
unsigned long max_freeable;
unsigned long node_allocs;
unsigned long node_frees;
unsigned long node_overflow;
atomic_t allochit;
atomic_t allocmiss;
atomic_t freehit;
atomic_t freemiss;
/*
* If debugging is enabled, then the allocator can add additional
* fields and/or padding to every object. buffer_size contains the total
* object size including these internal fields, the following two
* variables contain the offset to the user object and its size.
*/
int obj_offset;
int obj_size;
/*
* We put nodelists[] at the end of kmem_cache, because we want to size
* this array to nr_node_ids slots instead of MAX_NUMNODES
* (see kmem_cache_init())
* We still use [MAX_NUMNODES] and not [1] or [0] because cache_cache
* is statically defined, so we reserve the max number of nodes.
*/
struct kmem_list3 *nodelists[MAX_NUMNODES];
/*
* Do not add fields after nodelists[]
*/
};
其中struct kmem_list3结构体链接slab,共享高速缓存,其定义如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16/*
* The slab lists for all objects.
*/
struct kmem_list3 {
struct list_head slabs_partial; /* partial list first, better asm code */
struct list_head slabs_full;
struct list_head slabs_free;
unsigned long free_objects;
unsigned int free_limit;
unsigned int colour_next; /* Per-node cache coloring */
spinlock_t list_lock;
struct array_cache *shared; /* shared per node */
struct array_cache **alien; /* on other nodes */
unsigned long next_reap; /* updated without locking */
int free_touched; /* updated without locking */
};
该结构包含三个链表:slabs_partial、slabs_full、slabs_free,这些链表包含缓冲区所有slab,slab描述符struct slab用于描述每个slab:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15/*
* struct slab
*
* Manages the objs in a slab. Placed either at the beginning of mem allocated
* for a slab, or allocated from an general cache.
* Slabs are chained into three list: fully used, partial, fully free slabs.
*/
struct slab {
struct list_head list;
unsigned long colouroff;
void *s_mem; /* including colour offset */
unsigned int inuse; /* num of objs active in slab */
kmem_bufctl_t free;
unsigned short nodeid;
};
一个新的缓冲区使用如下函数创建:1
struct kmem_cache *kmem_cache_create (const char *name, size_t size, size_t align, unsigned long flags, void (*ctor)(void *));
函数创建成功会返回一个指向所创建缓冲区的指针;撤销一个缓冲区调用如下函数:1
void kmem_cache_destroy(struct kmem_cache *cachep);
上面两个函数都不能在中断上下文中使用,因为它可能睡眠。
在创建来缓冲区之后,可以通过下列函数获取对象:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17/**
* kmem_cache_alloc - Allocate an object
* @cachep: The cache to allocate from.
* @flags: See kmalloc().
*
* Allocate an object from this cache. The flags are only relevant
* if the cache has no available objects.
*/
void *kmem_cache_alloc(struct kmem_cache *cachep, gfp_t flags)
{
void *ret = __cache_alloc(cachep, flags, __builtin_return_address(0));
trace_kmem_cache_alloc(_RET_IP_, ret,
obj_size(cachep), cachep->buffer_size, flags);
return ret;
}
该函数从给点缓冲区cachep中返回一个指向对象的指针。如果缓冲区的所有slab中都没有空闲对象,那么slab层必须通过kmem_getpages()获取新的页,参数flags传递给_get_free_pages()。1
static void *kmem_getpages(struct kmem_cache *cachep, gfp_t flags, int nodeid);
释放对象使用如下函数:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21/**
* kmem_cache_free - Deallocate an object
* @cachep: The cache the allocation was from.
* @objp: The previously allocated object.
*
* Free an object which was previously allocated from this
* cache.
*/
void kmem_cache_free(struct kmem_cache *cachep, void *objp)
{
unsigned long flags;
local_irq_save(flags);
debug_check_no_locks_freed(objp, obj_size(cachep));
if (!(cachep->flags & SLAB_DEBUG_OBJECTS))
debug_check_no_obj_freed(objp, obj_size(cachep));
__cache_free(cachep, objp);
local_irq_restore(flags);
trace_kmem_cache_free(_RET_IP_, objp);
}
如果你要频繁的创建很多相同类型的对象,就要当考虑使用slab高速缓存区。
实际上上一节所讲kmalloc()函数也是使用slab分配器分配的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36static __always_inline void *kmalloc(size_t size, gfp_t flags)
{
struct kmem_cache *cachep;
void *ret;
if (__builtin_constant_p(size)) {
int i = 0;
if (!size)
return ZERO_SIZE_PTR;
return NULL;
found:
if (flags & GFP_DMA)
cachep = malloc_sizes[i].cs_dmacachep;
else
cachep = malloc_sizes[i].cs_cachep;
ret = kmem_cache_alloc_notrace(cachep, flags);
trace_kmalloc(_THIS_IP_, ret,
size, slab_buffer_size(cachep), flags);
return ret;
}
return __kmalloc(size, flags);
}
kfree函数实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26/**
* kfree - free previously allocated memory
* @objp: pointer returned by kmalloc.
*
* If @objp is NULL, no operation is performed.
*
* Don't free memory not originally allocated by kmalloc()
* or you will run into trouble.
*/
void kfree(const void *objp)
{
struct kmem_cache *c;
unsigned long flags;
trace_kfree(_RET_IP_, objp);
if (unlikely(ZERO_OR_NULL_PTR(objp)))
return;
local_irq_save(flags);
kfree_debugcheck(objp);
c = virt_to_cache(objp);
debug_check_no_locks_freed(objp, obj_size(c));
debug_check_no_obj_freed(objp, obj_size(c));
__cache_free(c, (void *)objp);
local_irq_restore(flags);
}
最后,结合上一节,看看分配函数的选择:
- 如果需要连续的物理页,就可以使用某个低级页分配器或
kmalloc()。 - 如果想从高端内存进行分配,使用
alloc_pages()。 - 如果不需要物理上连续的页,而仅仅是虚拟地址上连续的页,那么就是用
vmalloc。 - 如果要创建和销毁很多大的数据结构,那么考虑建立slab高速缓存。
内存管理之进程地址空间
进程地址空间由进程可寻址的虚拟内存组成,Linux 的虚拟地址空间为0~4G字节(注:本节讲述均以32为为例)。Linux内核将这 4G 字节的空间分为两部分。将最高的 1G 字节(从虚拟地址0xC0000000到0xFFFFFFFF),供内核使用,称为“内核空间”。而将较低的 3G 字节(从虚拟地址 0x00000000 到 0xBFFFFFFF),供各个进程使用,称为“用户空间” 。因为每个进程可以通过系统调用进入内核。因此,Linux 内核由系统内的所有进程共享。于是,从具体进程的角度来看,每个进程可以拥有 4G 字节的虚拟空间。
尽管一个进程可以寻址4G的虚拟内存,但就不代表它就有权限访问所有的地址空间,虚拟内存空间必须映射到某个物理存储空间(内存或磁盘空间),才真正地可以被使用。进程只能访问合法的地址空间,如果一个进程访问了不合法的地址空间,内核就会终止该进程,并返回“段错误”。虚拟内存的合法地址空间在哪而呢?我们先来看看进程虚拟地址空间的划分:
其中堆栈安排在虚拟地址空间顶部,数据段和代码段分布在虚拟地址空间底部,空洞部分就是进程运行时可以动态分布的空间,包括映射内核地址空间内容、动态申请地址空间、共享库的代码或数据等。在虚拟地址空间中,只有那些映射到物理存储空间的地址才是合法的地址空间。每一片合法的地址空间片段都对应一个独立的虚拟内存区域(VMA,virtual memory areas ),而进程的进程地址空间就是由这些内存区域组成。
Linux 采用了复杂的数据结构来跟踪进程的虚拟地址,进程地址空间使用内存描述符结构体来表示,内存描述符由mm_struct结构体表示,该结构体表示在<include/linux/mm_types.h>文件中:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86struct mm_struct {
struct vm_area_struct * mmap; /* list of VMAs */
struct rb_root mm_rb;
struct vm_area_struct * mmap_cache; /* last find_vma result */
unsigned long (*get_unmapped_area) (struct file *filp,
unsigned long addr, unsigned long len,
unsigned long pgoff, unsigned long flags);
void (*unmap_area) (struct mm_struct *mm, unsigned long addr);
unsigned long mmap_base; /* base of mmap area */
unsigned long task_size; /* size of task vm space */
unsigned long cached_hole_size; /* if non-zero, the largest hole below free_area_cache */
unsigned long free_area_cache; /* first hole of size cached_hole_size or larger */
pgd_t * pgd;
atomic_t mm_users; /* How many users with user space? */
atomic_t mm_count; /* How many references to "struct mm_struct" (users count as 1) */
int map_count; /* number of VMAs */
struct rw_semaphore mmap_sem;
spinlock_t page_table_lock; /* Protects page tables and some counters */
struct list_head mmlist; /* List of maybe swapped mm's. These are globally strung together off init_mm.mmlist, and are protected by mmlist_lock */
/* Special counters, in some configurations protected by the
* page_table_lock, in other configurations by being atomic.
*/
mm_counter_t _file_rss;
mm_counter_t _anon_rss;
unsigned long hiwater_rss; /* High-watermark of RSS usage */
unsigned long hiwater_vm; /* High-water virtual memory usage */
unsigned long total_vm, locked_vm, shared_vm, exec_vm;
unsigned long stack_vm, reserved_vm, def_flags, nr_ptes;
unsigned long start_code, end_code, start_data, end_data;
unsigned long start_brk, brk, start_stack;
unsigned long arg_start, arg_end, env_start, env_end;
unsigned long saved_auxv[AT_VECTOR_SIZE]; /* for /proc/PID/auxv */
struct linux_binfmt *binfmt;
cpumask_t cpu_vm_mask;
/* Architecture-specific MM context */
mm_context_t context;
/* Swap token stuff */
/*
* Last value of global fault stamp as seen by this process.
* In other words, this value gives an indication of how long
* it has been since this task got the token.
* Look at mm/thrash.c
*/
unsigned int faultstamp;
unsigned int token_priority;
unsigned int last_interval;
unsigned long flags; /* Must use atomic bitops to access the bits */
struct core_state *core_state; /* coredumping support */
spinlock_t ioctx_lock;
struct hlist_head ioctx_list;
/*
* "owner" points to a task that is regarded as the canonical
* user/owner of this mm. All of the following must be true in
* order for it to be changed:
*
* current == mm->owner
* current->mm != mm
* new_owner->mm == mm
* new_owner->alloc_lock is held
*/
struct task_struct *owner;
/* store ref to file /proc/<pid>/exe symlink points to */
struct file *exe_file;
unsigned long num_exe_file_vmas;
struct mmu_notifier_mm *mmu_notifier_mm;
};
该结构体中第一行成员mmap就是内存区域,用结构体struct vm_area_struct来表示:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62/*
* This struct defines a memory VMM memory area. There is one of these
* per VM-area/task. A VM area is any part of the process virtual memory
* space that has a special rule for the page-fault handlers (ie a shared
* library, the executable area etc).
*/
struct vm_area_struct {
struct mm_struct * vm_mm; /* The address space we belong to. */
unsigned long vm_start; /* Our start address within vm_mm. */
unsigned long vm_end; /* The first byte after our end address
within vm_mm. */
/* linked list of VM areas per task, sorted by address */
struct vm_area_struct *vm_next;
pgprot_t vm_page_prot; /* Access permissions of this VMA. */
unsigned long vm_flags; /* Flags, see mm.h. */
struct rb_node vm_rb;
/*
* For areas with an address space and backing store,
* linkage into the address_space->i_mmap prio tree, or
* linkage to the list of like vmas hanging off its node, or
* linkage of vma in the address_space->i_mmap_nonlinear list.
*/
union {
struct {
struct list_head list;
void *parent; /* aligns with prio_tree_node parent */
struct vm_area_struct *head;
} vm_set;
struct raw_prio_tree_node prio_tree_node;
} shared;
/*
* A file's MAP_PRIVATE vma can be in both i_mmap tree and anon_vma
* list, after a COW of one of the file pages. A MAP_SHARED vma
* can only be in the i_mmap tree. An anonymous MAP_PRIVATE, stack
* or brk vma (with NULL file) can only be in an anon_vma list.
*/
struct list_head anon_vma_node; /* Serialized by anon_vma->lock */
struct anon_vma *anon_vma; /* Serialized by page_table_lock */
/* Function pointers to deal with this struct. */
const struct vm_operations_struct *vm_ops;
/* Information about our backing store: */
unsigned long vm_pgoff; /* Offset (within vm_file) in PAGE_SIZE
units, *not* PAGE_CACHE_SIZE */
struct file * vm_file; /* File we map to (can be NULL). */
void * vm_private_data; /* was vm_pte (shared mem) */
unsigned long vm_truncate_count;/* truncate_count or restart_addr */
struct vm_region *vm_region; /* NOMMU mapping region */
struct mempolicy *vm_policy; /* NUMA policy for the VMA */
};vm_area_struct结构体描述了进程地址空间内连续区间上的一个独立内存范围,每一个内存区域都使用该结构体表示,每一个结构体以双向链表的形式连接起来。除链表结构外,Linux 还利用红黑树mm_rb来组织 vm_area_struct。通过这种树结构,Linux 可以快速定位某个虚拟内存地址。
该结构体中成员vm_start和vm_end表示内存区间的首地址和尾地址,两个值相减就是内存区间的长度。
成员vm_mm则指向其属于的进程地址空间结构体。所以两个不同的进程将同一个文件映射到自己的地址空间中,他们分别都会有一个vm_area_struct结构体来标识自己的内存区域。两个共享地址空间的线程则只有一个vm_area_struct结构体来标识,因为他们使用的是同一个进程地址空间。
vm_flags标识内存区域所包含的页面的行为和信息,反映内核处理页面所需要遵守的行为准则。
可以使用cat /proc/PID/maps命令和pmap命令查看给定进程空间和其中所含的内存区域。以笔者系统上进程号为17192的进程为例。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16# cat /proc/17192/maps //显示该进程地址空间中全部内存区域
001e3000-00201000 r-xp 00000000 fd:00 789547 /lib/ld-2.12.so
00201000-00202000 r--p 0001d000 fd:00 789547 /lib/ld-2.12.so
00202000-00203000 rw-p 0001e000 fd:00 789547 /lib/ld-2.12.so
00209000-00399000 r-xp 00000000 fd:00 789548 /lib/libc-2.12.so
00399000-0039a000 ---p 00190000 fd:00 789548 /lib/libc-2.12.so
0039a000-0039c000 r--p 00190000 fd:00 789548 /lib/libc-2.12.so
0039c000-0039d000 rw-p 00192000 fd:00 789548 /lib/libc-2.12.so
0039d000-003a0000 rw-p 00000000 00:00 0
08048000-08049000 r-xp 00000000 fd:00 1191771 /home/allen/Myprojects/blog/conn_user_kernel/test/a.out
08049000-0804a000 rw-p 00000000 fd:00 1191771 /home/allen/Myprojects/blog/conn_user_kernel/test/a.out
b7755000-b7756000 rw-p 00000000 00:00 0
b776d000-b776e000 rw-p 00000000 00:00 0
b776e000-b776f000 r-xp 00000000 00:00 0 [vdso]
bfc9f000-bfcb4000 rw-p 00000000 00:00 0 [stack]
# 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17# pmap 17192
17192: ./a.out
001e3000 120K r-x-- /lib/ld-2.12.so //本行和下面两行为动态链接程序ld.so的代码段、数据段、bss段
00201000 4K r---- /lib/ld-2.12.so
00202000 4K rw--- /lib/ld-2.12.so
00209000 1600K r-x-- /lib/libc-2.12.so //本行和下面为C库中libc.so的代码段、数据段和bss段
00399000 4K ----- /lib/libc-2.12.so
0039a000 8K r---- /lib/libc-2.12.so
0039c000 4K rw--- /lib/libc-2.12.so
0039d000 12K rw--- [ anon ]
08048000 4K r-x-- /home/allen/Myprojects/blog/conn_user_kernel/test/a.out //可执行对象的代码段
08049000 4K rw--- /home/allen/Myprojects/blog/conn_user_kernel/test/a.out //可执行对象的数据段
b7755000 4K rw--- [ anon ]
b776d000 4K rw--- [ anon ]
b776e000 4K r-x-- [ anon ]
bfc9f000 84K rw--- [ stack ] //堆栈段
total 1860K
结构体中vm_ops域指定内存区域相关操作函数表,内核使用表中方法操作VMA,操作函数表由vm_operations_struct结构体表示,定义在<include/linux/mm.h>文件中:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23/*
* These are the virtual MM functions - opening of an area, closing and
* unmapping it (needed to keep files on disk up-to-date etc), pointer
* to the functions called when a no-page or a wp-page exception occurs.
*/
struct vm_operations_struct {
void (*open)(struct vm_area_struct * area); //指定内存区域被加载到一个地址空间时函数被调用
void (*close)(struct vm_area_struct * area); //指定内存区域从地址空间删除时函数被调用
int (*fault)(struct vm_area_struct *vma, struct vm_fault *vmf); //没有出现在物理内存中的页面被访问时,页面故障处理调用该函数
/* notification that a previously read-only page is about to become
* writable, if an error is returned it will cause a SIGBUS */
int (*page_mkwrite)(struct vm_area_struct *vma, struct vm_fault *vmf);
/* called by access_process_vm when get_user_pages() fails, typically
* for use by special VMAs that can switch between memory and hardware
*/
int (*access)(struct vm_area_struct *vma, unsigned long addr,
void *buf, int len, int write);
......
};
在内核中,给定一个属于某个进程的虚拟地址,要求找到其所属的区间以及vma_area_struct结构,这通过find_vma()来实现,这种搜索通过红-黑树进行。该函数定义于<mm/mmap.c>中:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35/* Look up the first VMA which satisfies addr < vm_end, NULL if none. */
struct vm_area_struct *find_vma(struct mm_struct *mm, unsigned long addr)
{
struct vm_area_struct *vma = NULL;
if (mm) {
/* 首先检查最近使用的内存区域,看缓存的VMA是否包含所需地址 */
/* (命中率接近35%.) */
vma = mm->mmap_cache;
//如果缓存中不包含未包含希望的VMA,该函数搜索红-黑树。
if (!(vma && vma->vm_end > addr && vma->vm_start <= addr)) {
struct rb_node * rb_node;
rb_node = mm->mm_rb.rb_node;
vma = NULL;
while (rb_node) {
struct vm_area_struct * vma_tmp;
vma_tmp = rb_entry(rb_node, struct vm_area_struct, vm_rb);
if (vma_tmp->vm_end > addr) {
vma = vma_tmp;
if (vma_tmp->vm_start <= addr)
break;
rb_node = rb_node->rb_left;
} else
rb_node = rb_node->rb_right;
}
if (vma)
mm->mmap_cache = vma;
}
}
return vma;
}
当某个程序的映像开始执行时,可执行映像必须装入到进程的虚拟地址空间。如果该进程用到了任何一个共享库,则共享库也必须装入到进程的虚拟地址空间。由此可看出,Linux并不将映像装入到物理内存,相反,可执行文件只是被连接到进程的虚拟地址空间中。随着程序的运行,被引用的程序部分会由操作系统装入到物理内存,这种将映像链接到进程地址空间的方法被称为“内存映射”。
当可执行映像映射到进程的虚拟地址空间时,将产生一组vm_area_struct结构来描述虚拟内存区间的起始点和终止点,每个vm_area_struct结构代表可执行映像的一部分,可能是可执行代码,也可能是初始化的变量或未初始化的数据,这些都是在函数do_mmap()中来实现的。随着vm_area_struct结构的生成,这些结构所描述的虚拟内存区间上的标准操作函数也由 Linux 初始化。1
2
3
4
5
6
7
8
9
10
11
12static inline unsigned long do_mmap(struct file *file, unsigned long addr,
unsigned long len, unsigned long prot,
unsigned long flag, unsigned long offset)
{
unsigned long ret = -EINVAL;
if ((offset + PAGE_ALIGN(len)) < offset)
goto out;
if (!(offset & ~PAGE_MASK))
ret = do_mmap_pgoff(file, addr, len, prot, flag, offset >> PAGE_SHIFT);
out:
return ret;
}
该函数会将一个新的地址区间加入到进程的地址空间中。定义于<include/linux/mm.h>。
函数中参数的含义:
file:表示要映射的文件。offset:文件内的偏移量,因为我们并不是一下子全部映射一个文件,可能只是映射文件的一部分,off 就表示那部分的起始位置。len:要映射的文件部分的长度。addr:虚拟空间中的一个地址,表示从这个地址开始查找一个空闲的虚拟区。prot:这个参数指定对这个虚拟区所包含页的存取权限。可能的标志有PROT_READ、PROT_WRITE、PROT_EXEC、PROT_NONE。前 3 个标志与标志VM_READ、VM_WRITE、VM_EXEC的意义一样。PROT_NONE表示进程没有以上 3 个存取权限中的任意一个。- flag`:这个参数指定虚拟区的其他标志。
该函数调用do_mmap_pgoff()函数,该函数做内存映射的主要工作,该函数比较长,详细实现可查看<mm/mmap.c>文件。
由于文件到虚存的映射仅仅是建立了一种映射关系,虚存页面到物理页面之间的映射还没有建立。当某个可执行映象映射到进程虚拟内存中并开始执行时,因为只有很少一部分虚拟内存区间装入到了物理内存,很可能会遇到所访问的数据不在物理内存。这时,处理器将向 Linux 报告一个页故障及其对应的故障原因,
内核必须从磁盘映像或交换文件(此页被换出)中将其装入物理内存,这就是请页机制。