Hexo

Posted on Edited on

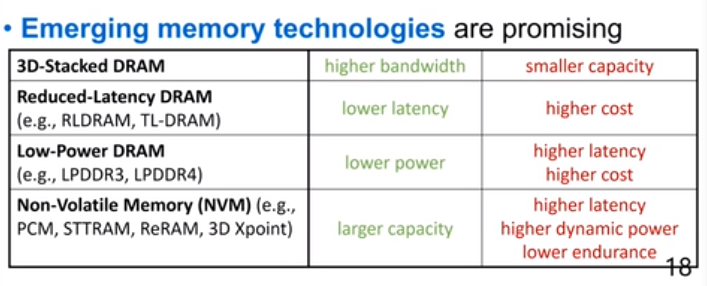
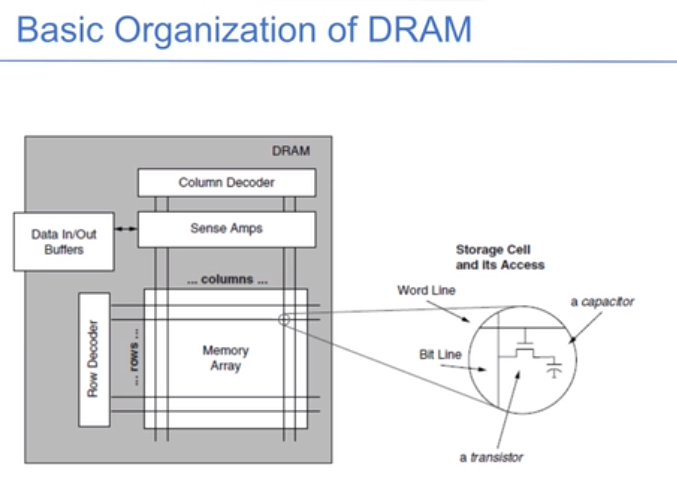
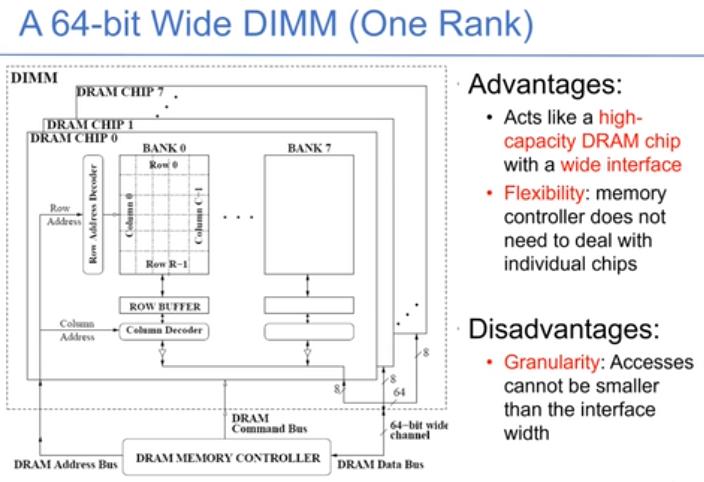
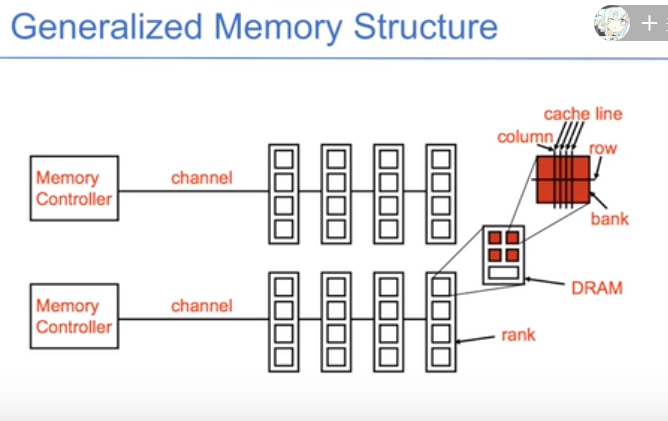
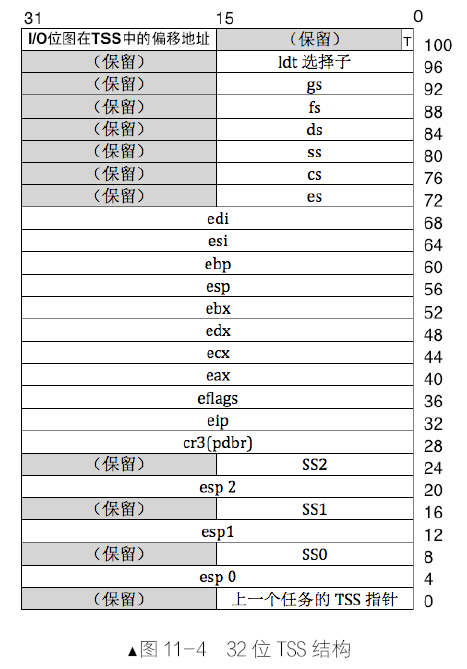
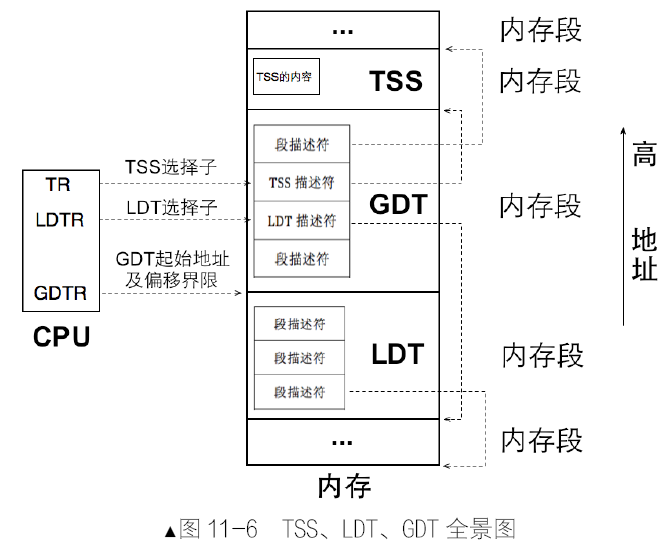
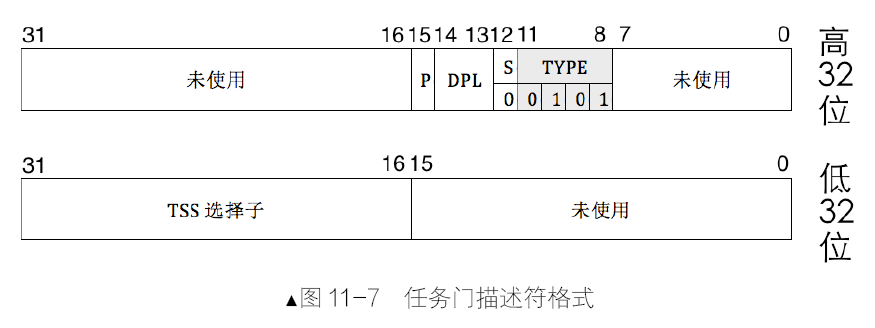
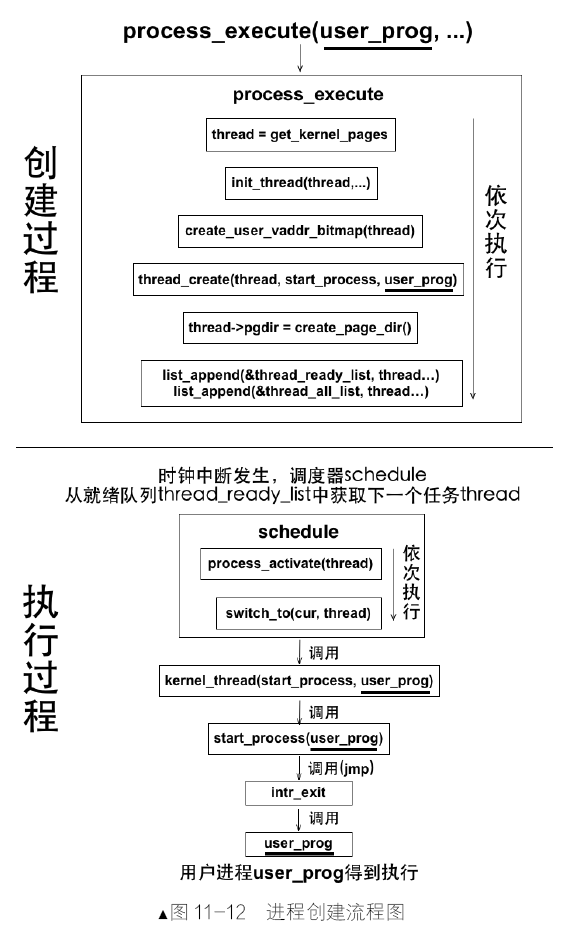
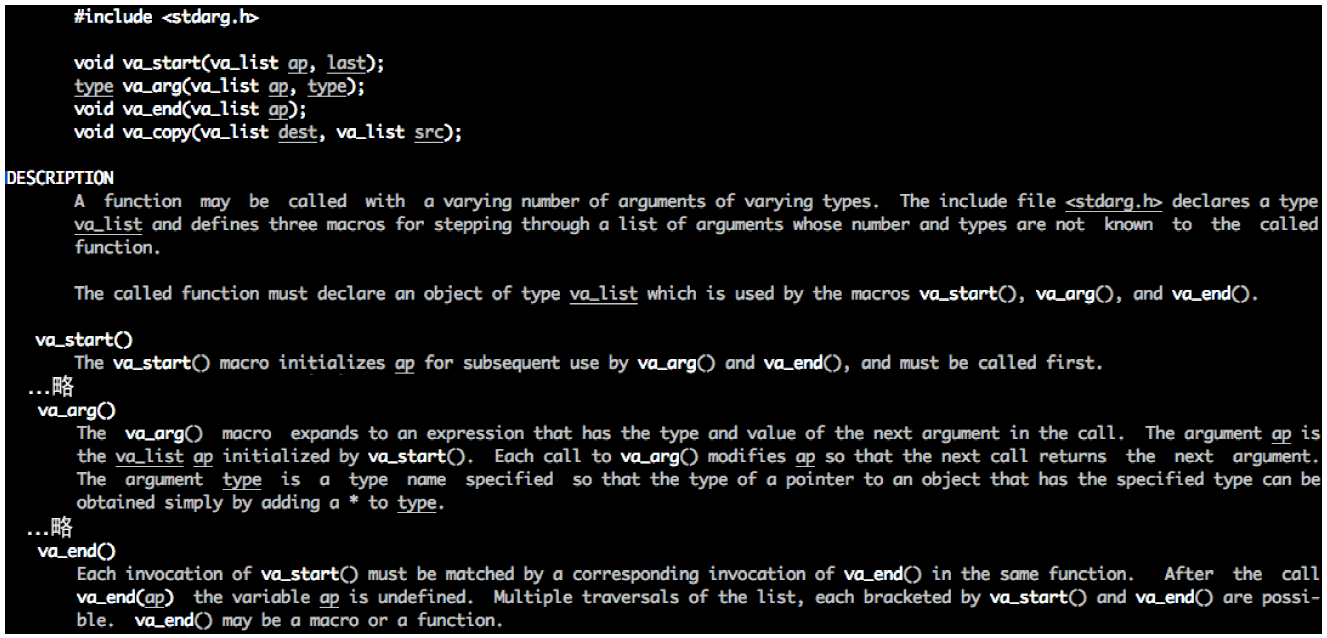
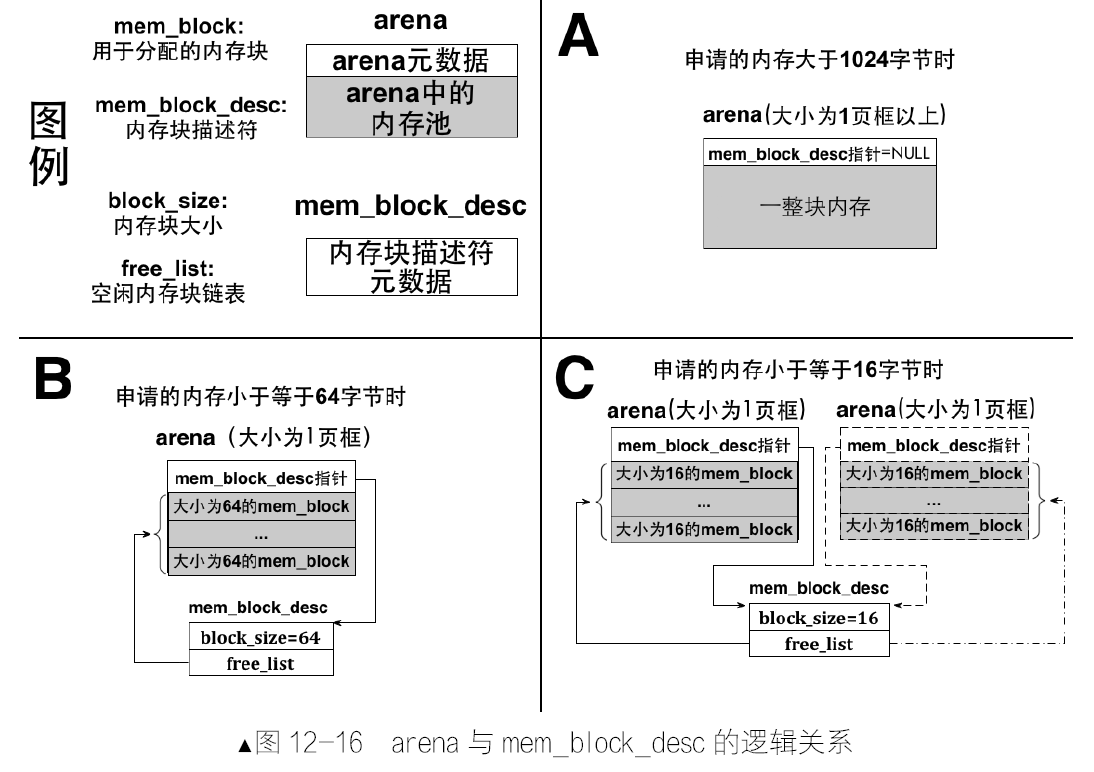
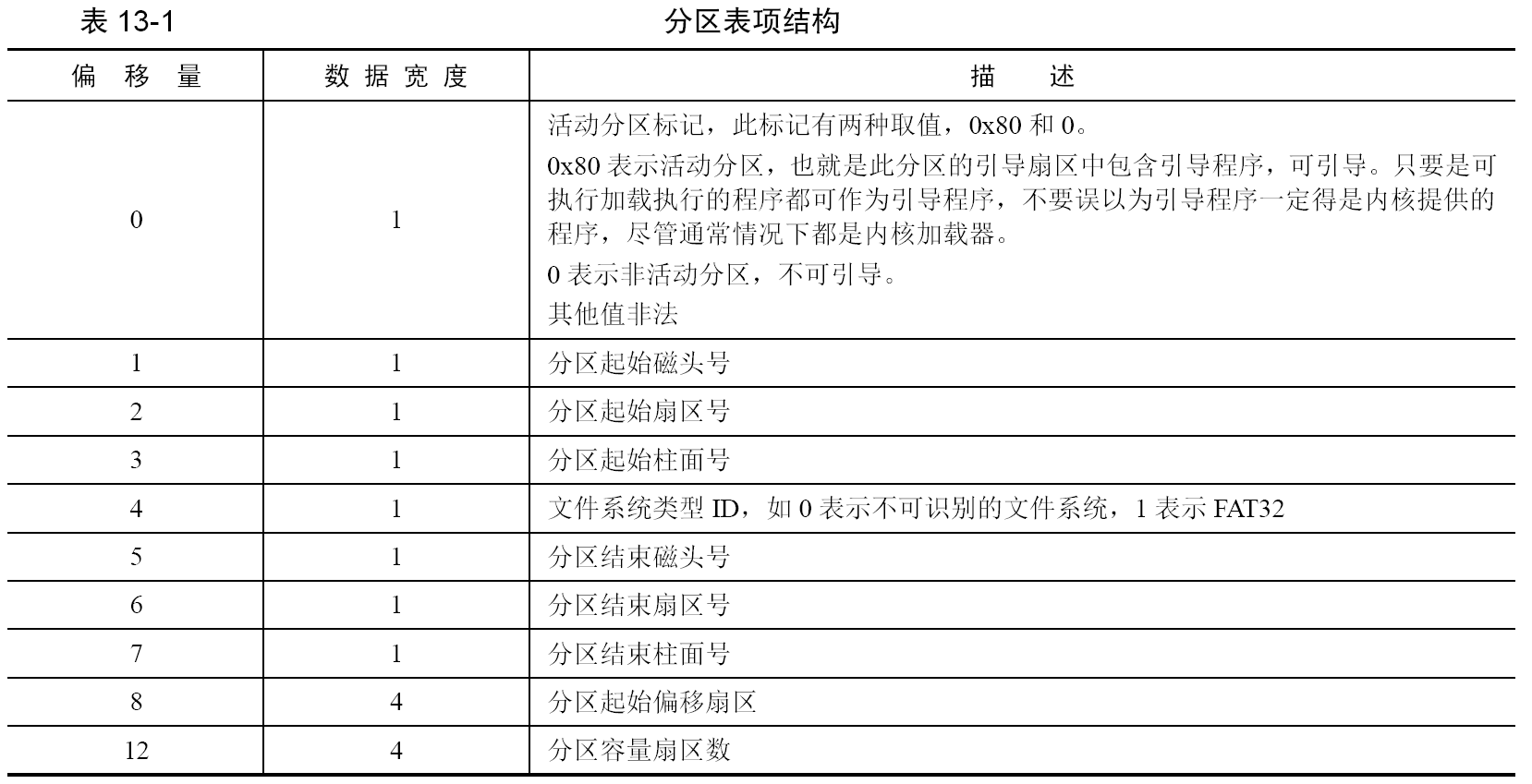
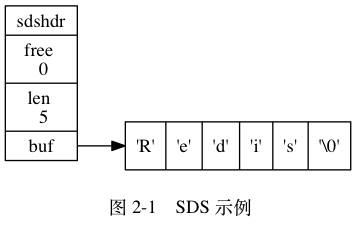
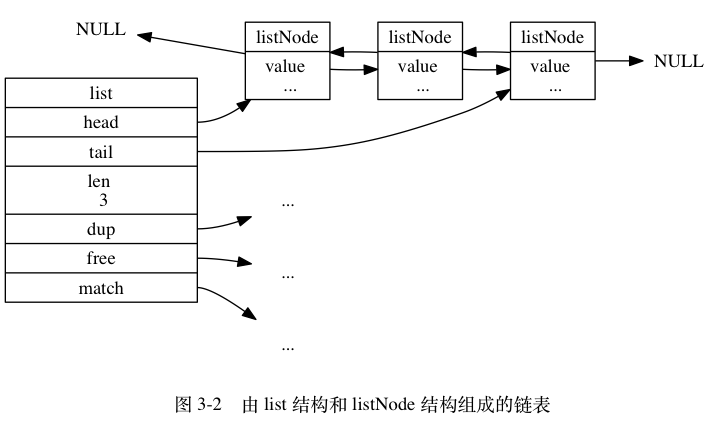
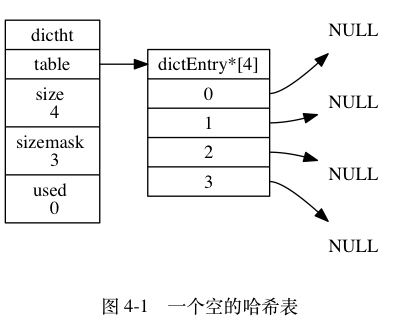
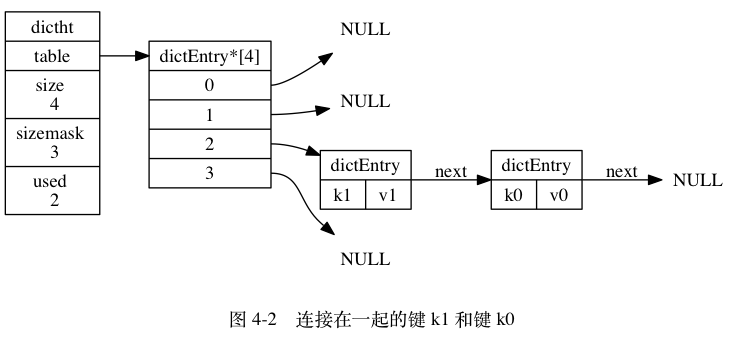
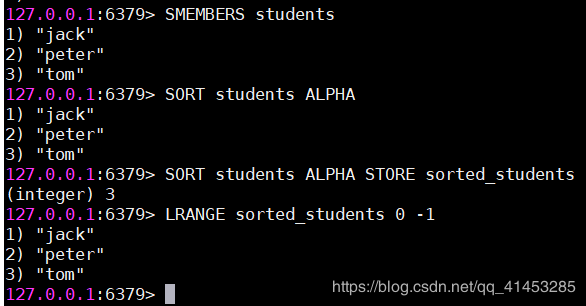
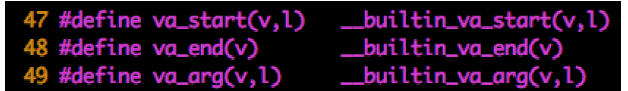Leetcode101. Symmetric Tree

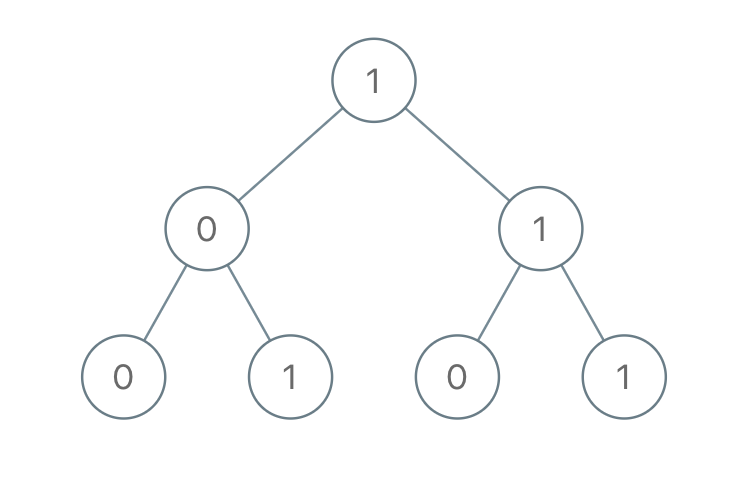
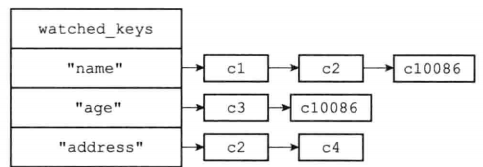
Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).

For example, this binary tree [1,2,2,3,4,4,3] is symmetric:

1
2
3
4
5
    1
   / \
  2   2
 / \ / \
3  4 4  3

But the following [1,2,2,null,3,null,3] is not:

1
2
3
4
5
  1
 / \
2   2
 \   \
 3    3

判断一个树是不是镜像的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    
    bool digui(TreeNode* left, TreeNode* right) {
        if(left == NULL && right == NULL)
            return true;
        if(left == NULL || right == NULL)
            return false;
        if(left->val != right->val)
            return false;
        return digui(left->left, right->right) && digui(left->right, right->left);
    }
    
    bool isSymmetric(TreeNode* root) {
        if(root == NULL)
            return true;
        return digui(root->left, root->right);
    }
};

Leetcode102. Binary Tree Level Order Traversal

Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).

For example:

1
2
3
4
5
6
7
8
9
10
11
12
Given binary tree [3,9,20,null,null,15,7],
    3
   / \
  9  20
    /  \
   15   7
return its level order traversal as:
[
  [3],
  [9,20],
  [15,7]
]

给定一个二叉树，返回其按层序遍历得到的节点值。层序遍历即逐层地、从左到右访问所有结点。在每一层遍历开始前，先记录队列中的结点数量 n（也就是这一层的结点数量），然后一口气处理完这一层的 n 个结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q;
        vector<vector<int>> result;
        if(root!=NULL)
            q.push(root);
        while(!q.empty()) {
            int n = q.size();
            vector<int> result_temp;
            for(int i=0;i<n;i++) {
                TreeNode* temp = q.front();
                q.pop();
                result_temp.push_back(temp->val);
                if(temp->left != NULL)
                    q.push(temp->left);
                if(temp->right != NULL)
                    q.push(temp->right);
            }
            result.push_back(result_temp);
        }
        return result;
    }
};

Leetcode103. Binary Tree Zigzag Level Order Traversal

Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).

For example:

1
2
3
4
5
6
7
8
9
10
11
12
Given binary tree [3,9,20,null,null,15,7],
    3
   / \
  9  20
    /  \
   15   7
return its zigzag level order traversal as:
[
  [3],
  [20,9],
  [15,7]
]

层次遍历，正序逆序分别输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        if(root == NULL)
            return {};
        vector<vector<int>> res;
        queue<TreeNode*> q;
        q.push(root);
        int rev = 1, lenn = 0;
        while(!q.empty()) {
            vector<TreeNode*> temp;
            int len = q.size();
            while(len --) {
                TreeNode* tt = q.front();
                temp.push_back(tt);
                q.pop();
                if(tt->left)
                    q.push(tt->left);
                if(tt->right)
                    q.push(tt->right);
            }
            res.push_back({});
            for(auto a : temp) {
                res[lenn].push_back(a->val);
            }
            
            if(rev == -1) 
                reverse(res[lenn].begin(), res[lenn].end());
            lenn ++;
            rev = rev * -1;
        }
        return res;
    }
};

Leetcode104. Maximum Depth of Binary Tree

Given a binary tree, find its maximum depth. The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Note: A leaf is a node with no children.

Example:

1
2
3
4
5
6
7
8
Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
return its depth = 3.

找到二叉树的最大深度。

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL)
            return 0;
        if(root->left == NULL && root->right == NULL)
            return 1;
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    }
};

Leetcode105. Construct Binary Tree from Preorder and Inorder Traversal

Given preorder and inorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

1
2
3
4
5
6
7
8
9
preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]
Return the following binary tree:

    3
   / \
  9  20
    /  \
   15   7

从前序和中序恢复一棵二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    
    TreeNode* dfs(vector<int>& preorder, int pLeft, int pRight, vector<int> &inorder, int iLeft, int iRight) {
        if(pLeft > pRight || iLeft > iRight)
            return NULL;
        int i;
        for(i = iLeft; i <= iRight; i ++) {
            if(preorder[pLeft] == inorder[i])
                break;
        }
        TreeNode *cur = new TreeNode(preorder[pLeft]);
        cur->left = dfs(preorder, pLeft+1, pLeft+i-iLeft, inorder, iLeft, i-1);
        cur->right = dfs(preorder, pLeft+i-iLeft+1, pRight, inorder, i+1, iRight);
        return cur;
    }
    
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return dfs(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1);
        
    }
};

Leetcode106. Construct Binary Tree from Inorder and Postorder Traversal

Given inorder and postorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

1
2
3
4
5
6
7
8
9
inorder = [9,3,15,20,7]
postorder = [9,15,7,20,3]
Return the following binary tree:

    3
   / \
  9  20
    /  \
   15   7

从中序和后序恢复一棵二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    
    TreeNode* dfs(vector<int>& inorder, int iLeft, int iRight, vector<int> &postorder, int pLeft, int pRight) {
        if(pLeft > pRight || iLeft > iRight)
            return NULL;
        int i;
        for(i = iLeft; i <= iRight; i ++) {
            if(postorder[pRight] == inorder[i])
                break;
        }
        TreeNode *cur = new TreeNode(postorder[pRight]);
        cur->left = dfs(inorder, iLeft, i-1, postorder, pLeft, pLeft+i-iLeft-1);
        cur->right = dfs(inorder, i+1, iRight, postorder, pLeft+i-iLeft, pRight-1);
        return cur;
    }
    
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return dfs(inorder, 0, inorder.size()-1, postorder, 0, postorder.size()-1);
    }
};

Leetcode107. Binary Tree Level Order Traversal II

Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).

For example:

1
2
3
4
5
6
7
8
9
10
11
12
Given binary tree [3,9,20,null,null,15,7],
    3
   / \
  9  20
    /  \
   15   7
return its bottom-up level order traversal as:
[
  [15,7],
  [9,20],
  [3]
]

用BFS简单做做就ok

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        if(root == NULL)
            return {};
        vector<vector<int>> res;
        
        queue<TreeNode*> q;
        q.push(root);
        vector<TreeNode*> vec;
        while(!q.empty()) {
            vector<int> ress;
            vec.clear();
            ress.clear();
            int n = q.size();
            while(n--) {
                TreeNode* temp = q.front();
                q.pop();
                vec.push_back(temp);
                if(temp->left)
                    q.push(temp->left);
                if(temp->right)
                    q.push(temp->right);
            }
            
            for(int i = 0; i < vec.size(); i++) {
                ress.push_back(vec[i]->val);
            }
            res.insert(res.begin(), ress);
        }
        // reverse(res.begin(), res.end());如果不是之前在最前边插入而是在最后翻转的话，会更快。
        return res;
    }
};

下边这个更快：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<TreeNode *> aa;
        vector<TreeNode *> ak;
        vector<int> al;
        vector<vector<int>> zero;
        if(root == NULL){
            return zero;
        }
        al.push_back(root->val);
        aa.push_back(root);
        zero.push_back(al);
        while(aa.size() != 0){
            ak.clear();
            al.clear();
            for(TreeNode* k:aa){
                if(k->left != NULL){
                    al.push_back(k->left->val);
                    ak.push_back(k->left);
                }
                if(k->right != NULL){
                    al.push_back(k->right->val);
                    ak.push_back(k->right);
                }
            }
            aa = ak;
            if(al.size() !=0){
                zero.push_back(al);
            }
        }
        reverse(zero.begin(),zero.end());
        return zero;
        
    }
};

Leetcode108. Convert Sorted Array to Binary Search Tree

Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

1
2
3
4
5
6
7
8
9
Given the sorted array: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

将有序数组或有序链表转成平衡二叉排序树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    
    TreeNode* bst(vector<int>& nums, int left, int right) {
        TreeNode* root;
        if(left > right) {
            root = NULL;
        } else if(left == right) {
            root = new TreeNode(nums[left]);
        } else {
            int mid = (left + right) / 2;
            root = new TreeNode(nums[mid]);
            root->left = bst(nums, left, mid - 1);
            root->right = bst(nums, mid+1, right); 
        }
        return root;
    }
    
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        int n = nums.size();
        if(n == 0)
            return NULL;
        TreeNode* root = bst(nums, 0, n - 1);
        return root;
    }
};

Leetcode109. Convert Sorted List to Binary Search Tree

Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

1
2
3
4
5
6
7
8
9
Given the sorted linked list: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

将链表转化为平衡的二叉排序树，将中间的点作为根节点，左边的为左子树，右边的为右子树。依次递归即可。由于链表统计长度比较麻烦，先转化为数组即可。也可以使用一个指针走一步，另一个指针走两步来获得中间的结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    TreeNode* sortedListToBST(ListNode* head) {
        if(head == NULL)
            return NULL;
        return dfs(head, NULL);
    }
    
    TreeNode* dfs(ListNode* head, ListNode* tail) {
        if(head == tail) {
            return NULL;
        }
        ListNode *fast = head, *slow = head;
        while(fast != tail && fast->next != tail) {
            fast = fast->next->next;
            slow = slow->next;
        }
        
        TreeNode *root = new TreeNode(slow->val);
        root->left = dfs(head, slow);
        root->right = dfs(slow->next, tail);
        return root;
    }
};

Leetcode110. Balanced Binary Tree

Given a binary tree, determine if it is height-balanced. For this problem, a height-balanced binary tree is defined as:

  • a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Example 1:

1
2
3
4
5
6
7
8
Given the following tree [3,9,20,null,null,15,7]:

    3
   / \
  9  20
    /  \
   15   7
Return true.

Example 2:

1
2
3
4
5
6
7
8
9
10
Given the following tree [1,2,2,3,3,null,null,4,4]:

       1
      / \
     2   2
    / \
   3   3
  / \
 4   4
Return false.

求二叉树是否平衡，根据题目中的定义，高度平衡二叉树是每一个结点的两个子树的深度差不能超过1，那么我们肯定需要一个求各个点深度的函数，然后对每个节点的两个子树来比较深度差，时间复杂度为O(NlgN)，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(!root) return true;
        if(abs(getLength(root->left) - getLength(root->right)) > 1) return false;
        return isBalanced(root->left)&&isBalanced(root->right);
    }
    int getLength(TreeNode* root) {
        if(!root) return 0;
        return 1 + max(getLength(root->left), getLength(root->right));
    }
};

Leetcode111. Minimum Depth of Binary Tree

Given a binary tree, find its minimum depth. The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example:

1
2
3
4
5
6
7
8
Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
return its minimum depth = 2.

如果说有个单支树 那么返回的高度 是 1+不为空子树的长度！在这里翻车了。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root == NULL)
            return 0;
        if(root->left == NULL && root->right == NULL)
            return 1;
        if(root->left == NULL) return 1+minDepth(root->right);
        if(root->right == NULL) return 1+minDepth(root->left);
        return 1 + min(minDepth(root->left), minDepth(root->right));
    }
};

Leetcode112. Path Sum

Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.

Note: A leaf is a node with no children.

Example:

1
2
3
4
5
6
7
8
9
10
Given the below binary tree and sum = 22,

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1
return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

简单dfs。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool dfs(TreeNode* root, int sum, int cur) {
        if(root == NULL)
            return false;
        if(root->left == NULL && root->right == NULL) {
            return sum == cur + root->val;
        }
        return dfs(root->left, sum, cur + root->val) || dfs(root->right, sum, cur + root->val);
    }
    
    bool hasPathSum(TreeNode* root, int sum) {
        if(root == NULL)
            return false;
        return dfs(root, sum, 0);
    }
};

Leetcode113. Path Sum II

Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum.

Note: A leaf is a node with no children.

Example:

1
2
3
4
5
6
7
8
9
Given the below binary tree and sum = 22,

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

Return:

1
2
3
4
[
   [5,4,11,2],
   [5,8,4,5]
]

路径可能不止一条，所以必须要把整棵树遍历。所谓的路径是一个root-to-leaf path。所以从根节点开始，先保证有一个数组来存放路径。但是我们把这个数组当作栈来用，也就是使用push_back、pop_back。每进入一个节点就push，离开以这个节点为根的树就pop，到达叶子节点就判断是否是所求路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    
    void dfs(TreeNode* root, int sum, int cur_sum, vector<int> cur, vector<vector<int>>& res) {
        if(root == NULL)
            return;
        cur_sum += root->val;
        cur.push_back(root->val);
        if(!root->left && !root->right) {
            if(sum == cur_sum)
                res.push_back(cur);
            return;
        }
        dfs(root->left, sum, cur_sum, cur, res);
        dfs(root->right, sum, cur_sum, cur, res);
        cur_sum -= root->val;
        cur.pop_back();
    }
    
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
        if(root == NULL)
            return {};
        vector<int> temp;
        vector<vector<int> > res;
        dfs(root, sum, 0, temp, res);
        return res;
    }
};

Leetcode114. Flatten Binary Tree to Linked List

Given a binary tree, flatten it to a linked list in-place.

For example, given the following tree:

1
2
3
4
5
    1
   / \
  2   5
 / \   \
3   4   6

The flattened tree should look like:

1
2
3
4
5
6
7
8
9
10
11
1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6

这道题要求把二叉树展开成链表，根据展开后形成的链表的顺序分析出是使用先序遍历，递归版本的先利用 DFS 的思路找到最左子节点，然后回到其父节点，把其父节点和右子节点断开，将原左子结点连上父节点的右子节点上，然后再把原右子节点连到新右子节点的右子节点上，然后再回到上一父节点做相同操作。举例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1
    / \
   2   5
  / \   \
 3   4   6

     1
    / \
   2   5
    \   \
     3   6
      \    
       4

   1
    \
     2
      \
       3
        \
         4
          \
           5
            \
             6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    
    void flatten(TreeNode* root) {
        if(root == NULL)
            return;
        if(root->left)
            flatten(root->left);
        if(root->right)
            flatten(root->right);
        TreeNode* tmp = root->right;
        root->right = root->left;
        root->left = NULL;
        
        while(root->right)
            root = root->right;
        root->right = tmp;
        
    }
};

Leetcode116. Populating Next Right Pointers in Each Node

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

  • You may only use constant extra space.
  • Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

1
2
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]

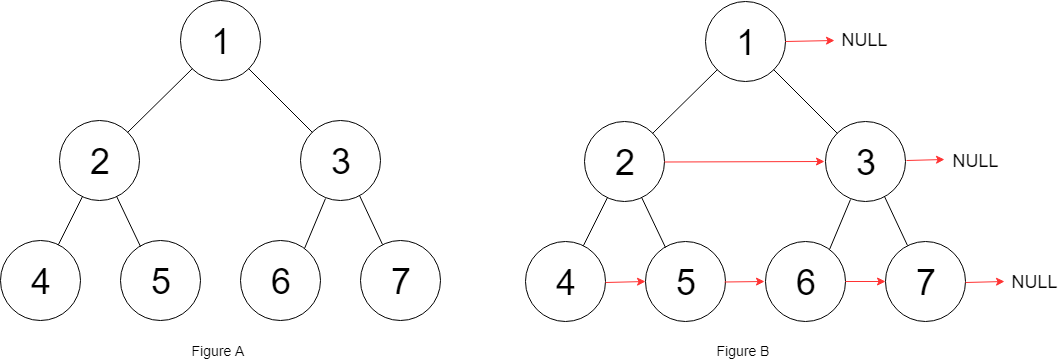
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with ‘#’ signifying the end of each level.

层次遍历即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    Node* connect(Node* root) {
        if(root == NULL)
            return NULL;
        queue<Node*> q;
        q.push(root);
        int rev = 1, lenn = 0;
        while(!q.empty()) {
            vector<Node*> temp;
            int len = q.size();
            while(len --) {
                Node* tt = q.front();
                temp.push_back(tt);
                q.pop();
                if(tt->left)
                    q.push(tt->left);
                if(tt->right)
                    q.push(tt->right);
            }
            
            for(int i = 0; i < temp.size()-1; i ++) {
                temp[i]->next = temp[i+1];
            }
            temp[temp.size()-1]->next = NULL;
        }
        return root;
    }
};

或者说，若节点的左子结点存在的话，其右子节点必定存在，所以左子结点的 next 指针可以直接指向其右子节点，对于其右子节点的处理方法是，判断其父节点的 next 是否为空，若不为空，则指向其 next 指针指向的节点的左子结点，若为空则指向 NULL。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    Node* connect(Node* root) {
        if(!root)
            return root;
        if(root->left)
            root->left->next = root->right;
        if(root->right)
            root->right->next = root->next ? root->next->left : NULL;
        connect(root->left);
        connect(root->right);
        return root;

    }
};

Leetcode117. Populating Next Right Pointers in Each Node II

Given a binary tree

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL. Initially, all next pointers are set to NULL.

原本的完全二叉树的条件不再满足，但是整体的思路还是很相似，由于子树有可能残缺，故需要平行扫描父节点同层的节点，找到他们的左右子节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    Node* connect(Node* root) {
        if(root == NULL) return root;
        Node *ne = root->next;
        while(ne) {
            if(ne->left) {
                ne = ne->left;
                break;
            }
            if(ne->right) {
                ne = ne->right;
                break;
            }
            ne = ne->next;
        }
        
        if(root->right) root->right->next = ne;
        if(root->left)  root->left->next = root->right ? root->right : ne;
        connect(root->right);
        connect(root->left);
        return root;
    }
};

Leetcode118. Pascal’s Triangle

Given a non-negative integer numRows, generate the first numRows of Pascal’s triangle. In Pascal’s triangle, each number is the sum of the two numbers directly above it.

Example: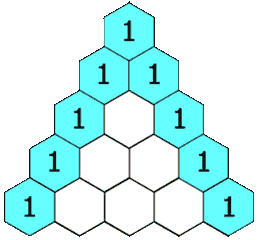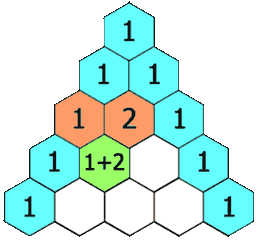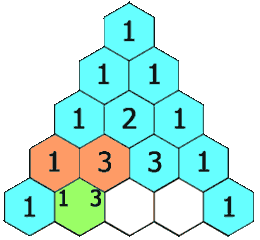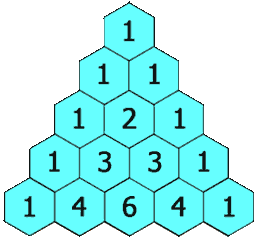

1
2
3
4
5
6
7
8
9
Input: 5
Output:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

杨辉三角，简单。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> res;
        for(int i = 0; i < numRows; i ++) {
            vector<int> temp(i+1);
            temp[0] = temp[i] = 1;
            res.push_back(temp);
        }
        if(numRows == 0 || numRows == 1)
            return res;
        for(int i = 2; i < numRows; i ++) {
            for(int j = 1; j < i; j ++ ) {
                res[i][j] = res[i-1][j-1] + res[i-1][j];
            }
        }
        
        return res;
    }
};

Leetcode119. Pascal’s Triangle II

Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal’s triangle.

Note that the row index starts from 0.（图跟上一个题一样）
是一个简单的dp，但是注意不能从前往后，因为从前往后的话就会覆盖掉之前迭代的结果。！！！！！！！

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> dp(rowIndex+1, 1);
        for(int i = 2; i <= rowIndex; i ++) {
            for(int j = i - 1; j >= 1; j --)
                dp[j] = dp[j] + dp[j - 1];
        }
        return dp;
    }
};

Leetcode120. Triangle

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below. For example, given the following triangle

1
2
3
4
5
6
[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
简单dp，注意从后向前就行。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        vector<vector<int>> result = triangle;
        for(int i = triangle.size()-2; i >= 0; i --) {
            for(int j = 0; j < triangle[i].size(); j ++) {
                result[i][j] = min(result[i+1][j], result[i+1][j+1]) + result[i][j];
            }
        }
        return result[0][0];
    }
};

Leetcode121. Best Time to Buy and Sell Stock

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Example 1:

1
2
Input: [7,1,5,3,6,4]
Output: 5

Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Not 7-1 = 6, as selling price needs to be larger than buying price.
Example 2:

1
2
Input: [7,6,4,3,1]
Output: 0

Explanation: In this case, no transaction is done, i.e. max profit = 0.

我们按照动态规划的思想来思考这道问题。

状态

有 买入（buy） 和 卖出（sell） 这两种状态。

转移方程

对于买来说，买之后可以卖出（进入卖状态），也可以不再进行股票交易（保持买状态）。

对于卖来说，卖出股票后不在进行股票交易（还在卖状态）。

只有在手上的钱才算钱，手上的钱购买当天的股票后相当于亏损。也就是说当天买的话意味着损失-prices[i]，当天卖的话意味着增加prices[i]，当天卖出总的收益就是 buy+prices[i] 。

所以我们只要考虑当天买和之前买哪个收益更高，当天卖和之前卖哪个收益更高。

buy = max(buy, -price[i]) （注意：根据定义 buy 是负数）
sell = max(sell, prices[i] + buy)
边界

第一天 buy = -prices[0], sell = 0，最后返回 sell 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()<=1)
            return 0;
        int buy = prices[0],sell=0;
        for(int i=1;i<prices.size();i++){
            buy = min(prices[i],buy);
            sell = max(sell,prices[i]-buy);
        }
        return sell;
    }
};

Leetcode122. Best Time to Buy and Sell Stock II

Say you have an array prices for which the ith element is the price of a given stock on day i. Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

1
2
3
4
Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
             Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.

Example 2:
Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
engaging multiple transactions at the same time. You must sell before buying again.

1
2
3
4
Example 3:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

这道题由于可以无限次买入和卖出。我们都知道炒股想挣钱当然是低价买入高价抛出，那么这里我们只需要从第二天开始，如果当前价格比之前价格高，则把差值加入利润中，因为我们可以昨天买入，今日卖出，若明日价更高的话，还可以今日买入，明日再抛出。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
	public:
    int maxProfit(vector<int>& prices) {
        int res = 0;
        for(int i = 1; i < prices.size();i ++) {
            if(prices[i] > prices[i - 1]) {
                res += (prices[i] - prices[i - 1]);
            }
        }
        return res;
    }
};

Leetcode123. Best Time to Buy and Sell Stock III

Say you have an array for which the i th element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most two transactions.

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

1
2
3
4
Input: [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
             Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.

Example 2:

1
2
3
4
5
Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
             Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
             engaging multiple transactions at the same time. You must sell before buying again.

Example 3:

1
2
3
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

这道是要求最多交易两次，找到最大利润，还是需要用动态规划Dynamic Programming来解，而这里我们需要两个递推公式来分别更新两个变量local和global，我们其实可以求至少k次交易的最大利润，找到通解后可以设定 k = 2，即为本题的解答。我们定义local[i][j]为在到达第i天时最多可进行j次交易并且最后一次交易在最后一天卖出的最大利润，此为局部最优。然后我们定义global[i][j]为在到达第i天时最多可进行j次交易的最大利润，此为全局最优。它们的递推式为：

1
2
3
local[i][j] = max(global[i - 1][j - 1] + max(diff, 0), local[i - 1][j] + diff)

global[i][j] = max(local[i][j], global[i - 1][j])

其中局部最优值是比较前一天并少交易一次的全局最优加上大于0的差值，和前一天的局部最优加上差值中取较大值，而全局最优比较局部最优和前一天的全局最优，代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxProfit(vector<int> &prices) {
        if (prices.empty()) return 0;
        int n = prices.size(), g[n][3] = {0}, l[n][3] = {0};
        for (int i = 1; i < prices.size(); ++i) {
            int diff = prices[i] - prices[i - 1];
            for (int j = 1; j <= 2; ++j) {
                l[i][j] = max(g[i - 1][j - 1] + max(diff, 0), l[i - 1][j] + diff);
                g[i][j] = max(l[i][j], g[i - 1][j]);
            }
        }
        return g[n - 1][2];
    }
};

Leetcode124. Binary Tree Maximum Path Sum

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example 1:

1
2
3
4
5
Input: [1,2,3]
       1
      / \
     2   3
Output: 6

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
Input: [-10,9,20,null,null,15,7]
     -10
     / \
    9  20
	  /  \
	 15   7
Output: 42
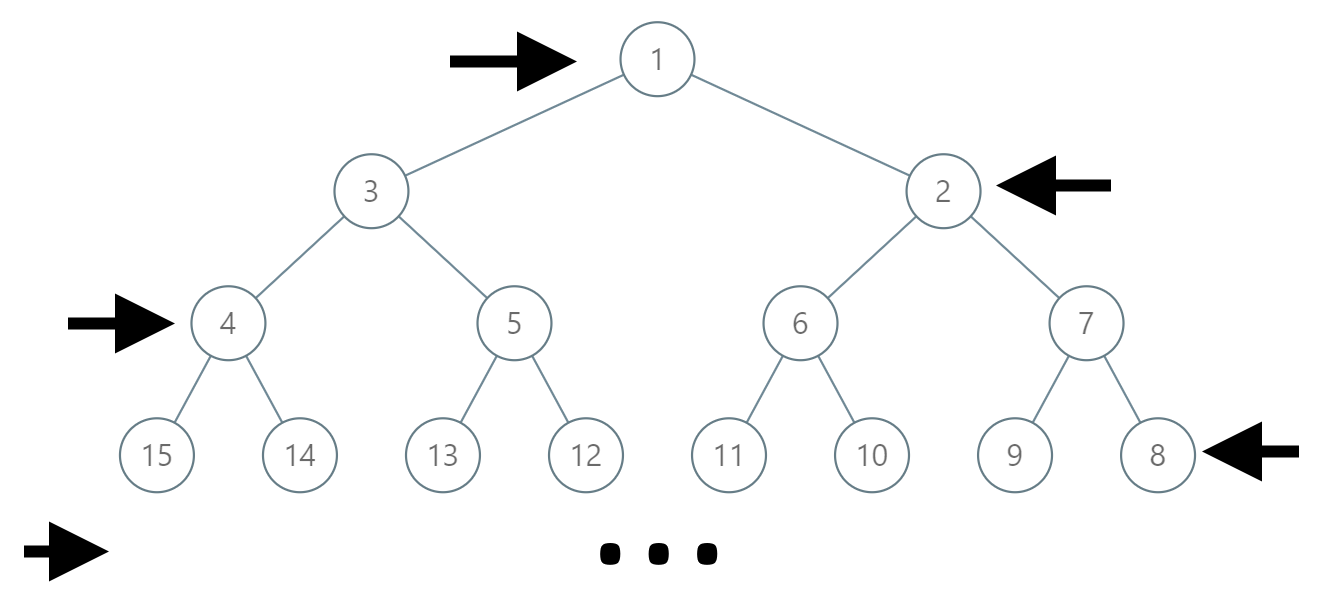
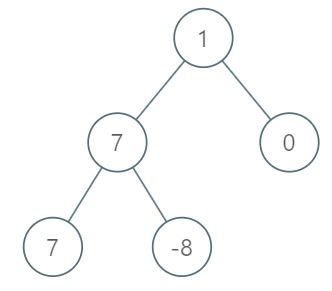
    4
   / \
  11 13
 / \
7   2

由于这是一个很简单的例子，很容易就能找到最长路径为 7->11->4->13，那么怎么用递归来找出正确的路径和呢？根据以往的经验，树的递归解法一般都是递归到叶节点，然后开始边处理边回溯到根节点。这里就假设此时已经递归到结点7了，其没有左右子节点，如果以结点7为根结点的子树最大路径和就是7。然后回溯到结点 11，如果以结点 11 为根结点的子树，最大路径和为 7+11+2=20。但是当回溯到结点4的时候，对于结点 11 来说，就不能同时取两条路径了，只能取左路径，或者是右路径，所以当根结点是4的时候，那么结点 11 只能取其左子结点7，因为7大于2。所以，对于每个结点来说，要知道经过其左子结点的 path 之和大还是经过右子节点的 path 之和大。递归函数返回值就可以定义为以当前结点为根结点，到叶节点的最大路径之和，然后全局路径最大值放在参数中，用结果 res 来表示。

在递归函数中，如果当前结点不存在，直接返回0。否则就分别对其左右子节点调用递归函数，由于路径和有可能为负数，这里当然不希望加上负的路径和，所以和0相比，取较大的那个，就是要么不加，加就要加正数。然后来更新全局最大值结果 res，就是以左子结点为终点的最大 path 之和加上以右子结点为终点的最大 path 之和，还要加上当前结点值，这样就组成了一个条完整的路径。而返回值是取 left 和 right 中的较大值加上当前结点值，因为返回值的定义是以当前结点为终点的 path 之和，所以只能取 left 和 right 中较大的那个值，而不是两个都要，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int maxPathSum(TreeNode* root) {
        int res = INT_MIN;
        helper(root, res);
        return res;
    }
    int helper(TreeNode* node, int& res) {
        if (!node) return 0;
        int left = max(helper(node->left, res), 0);
        int right = max(helper(node->right, res), 0);
        res = max(res, left + right + node->val);
        return max(left, right) + node->val;
    }
};

Leetcode125. Valid Palindrome

Given a string, determine if it is a palindrome, considering only alphanumeric characters and ignoring cases.

Note: For the purpose of this problem, we define empty string as valid palindrome.

Example 1:

1
2
Input: "A man, a plan, a canal: Panama"
Output: true

Example 2:

1
2
Input: "race a car"
Output: false

这道题只考虑数字和字母（字母有大小写之分），所以遇到其它符号时，自动跳过。具体来说就是，分别从字符串两边向中间遍历，遇到非数字和字母的符号就跳过，直至左右两个指针遇到。这题有些隐藏的小细节需要注意。

  1. 字母有大小写之分，比较之前应该先统一转变为小写或大写。
  2. 如果输入的字符串没有数字或字母，该字符串仍然看做是回文。
  3. 在指针向中间靠拢的过程中，若指针一直没有遇到数字或字母，就会一直加加或减减，此时应注意判断指针是否越界。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    
    bool islegal(char s) {
        if ('A'<=s && s<='Z' || 'a'<=s && s<='z' || '0'<=s && s<='9')
            return true;
        return false;
    }
    
    bool isPalindrome(string s) {
        if(s == "" || s.length()==1 || s.length()==0)
            return true;
        int left = 0, cur = 0, right = s.size();
        while(left < right) {
            while(left < right && !islegal(s[left]))
                left ++;
            while(left < right && !islegal(s[right]))
                right --;
            if('A'<=s[left] && s[left]<='Z')
                s[left] += 32;
            if('A'<=s[right] && s[right]<='Z')
                s[right] += 32;
            
            if(s[left] != s[right])
                return false;
            left ++;
            right --;
        }
        return true;
    }
};

Leetcode126. Word Ladder II

Given two words ( beginWord and endWord ), and a dictionary’s word list, find all shortest transformation sequence(s) from beginWord to endWord , such that:

  • Only one letter can be changed at a time
  • Each transformed word must exist in the word list. Note that beginWord is not a transformed word.

Note:

  • Return an empty list if there is no such transformation sequence.
  • All words have the same length.
  • All words contain only lowercase alphabetic characters.
  • You may assume no duplicates in the word list.
  • You may assume beginWord and endWord are non-empty and are not the same.

Example 1:

1
2
3
4
5
6
7
8
9
10
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

Output:
 [
   ["hit","hot","dot","dog","cog"],
   ["hit","hot","lot","log","cog"]
 ]

Example 2:

1
2
3
4
5
6
7
8
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

Output: []

Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.

下面这种解法的核心思想是 BFS，大概思路如下：目的是找出所有的路径，这里建立一个路径集 paths，用以保存所有路径，然后是起始路径p，在p中先把起始单词放进去。然后定义两个整型变量 level，和 minLevel，其中 level 是记录循环中当前路径的长度，minLevel 是记录最短路径的长度，这样的好处是，如果某条路径的长度超过了已有的最短路径的长度，那么舍弃，这样会提高运行速度，相当于一种剪枝。还要定义一个 HashSet 变量 words，用来记录已经循环过的路径中的词，然后就是 BFS 的核心了，循环路径集 paths 里的内容，取出队首路径，如果该路径长度大于 level，说明字典中的有些词已经存入路径了，如果在路径中重复出现，则肯定不是最短路径，所以需要在字典中将这些词删去，然后将 words 清空，对循环对剪枝处理。然后取出当前路径的最后一个词，对每个字母进行替换并在字典中查找是否存在替换后的新词，这个过程在之前那道 Word Ladder 里面也有。如果替换后的新词在字典中存在，将其加入 words 中，并在原有路径的基础上加上这个新词生成一条新路径，如果这个新词就是结束词，则此新路径为一条完整的路径，加入结果中，并更新 minLevel，若不是结束词，则将新路径加入路径集中继续循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
      vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
          vector<vector<string>> res;
          unordered_set<string> dict(wordList.begin(), wordList.end());
          vector<string> p{beginWord};
          queue<vector<string>> paths;
          paths.push(p);
          int level = 1, minLevel = INT_MAX;
          unordered_set<string> words;
          while (!paths.empty()) {
              auto t = paths.front(); paths.pop();
              if (t.size() > level) {
                  for (string w : words) dict.erase(w);
                  words.clear();
                  level = t.size();
                  if (level > minLevel) break;
              }
              string last = t.back();
              for (int i = 0; i < last.size(); ++i) {
                  string newLast = last;
                  for (char ch = 'a'; ch <= 'z'; ++ch) {
                      newLast[i] = ch;
                      if (!dict.count(newLast)) continue;
                      words.insert(newLast);
                      vector<string> nextPath = t;
                      nextPath.push_back(newLast);
                      if (newLast == endWord) {
                           res.push_back(nextPath);
                           minLevel = level;
                      } else paths.push(nextPath);
                  }
              }
          }
          return res;
      }
};

先建图，再使用bfs建立最短路，因为在建立最短路时f[v] = f[u] + 1，所以在之后用dfs找到相差1的点就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
class Solution {
public:
    unordered_map<string, int> data;
    vector<vector<int>> g;
    vector<int> f;
    vector<vector<string>> res;
    vector<string> wl;
    
    void dfs(int u, int ed, vector<string>& ans){
        ans.push_back(wl[u]);
        if (u == ed) {
            res.push_back(ans);
            return;
        }
        for (int v : g[u]) {
            if (f[v] + 1 == f[u]) {
                dfs(v, ed, ans);
                ans.pop_back();
            }
        }
    }
    vector<vector<string>> findLadders(string bw, string ew, vector<string>& wl) {
        wl.push_back(bw);
        for (int i = 0; i < wl.size(); i ++)
            data[wl[i]] = i;

        if (!data.count(ew))
            return {};
        int ed = data[ew];
        int st = wl.size()-1;
        
        g.assign(wl.size(), {});
        for (int i = 0; i < wl.size(); i ++) {
            int m = wl[i].length();
            for (int j = 0; j < m; j ++) {
                char c = wl[i][j];
                for (int k = 0; k < 26; k ++) {
                    if (c - 'a' != k) {
                        wl[i][j] = k + 'a';
                        if (!data.count(wl[i]))
                            continue;
                        int v = data[wl[i]];
                        g[i].push_back(v);
                    }
                }
                wl[i][j] = c;
            }
        }

        f.assign(wl.size(), 1e9);
        queue<int> q;
        f[ed] = 0;
        q.push(ed);
        while(!q.empty()) {
            int t = q.front();
            q.pop();
            for (int v : g[t]) {
                if (f[t] + 1 < f[v]) {
                    f[v] = f[t] + 1;
                    q.push(v);
                }
            }
        }

        this->wl = wl;  
        vector<string> ans;
        dfs(st, ed, ans);
        return res;
    }
};

Leetcode127. Word Ladder

Given two words (beginWord and endWord), and a dictionary’s word list, find the length of shortest transformation sequence from beginWord to endWord, such that:

  • Only one letter can be changed at a time.
  • Each transformed word must exist in the word list.

Note:

  • Return 0 if there is no such transformation sequence.
  • All words have the same length.
  • All words contain only lowercase alphabetic characters.
  • You may assume no duplicates in the word list.
  • You may assume beginWord and endWord are non-empty and are not the same.

Example 1:

1
2
3
4
5
6
7
8
9
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

Output: 5

Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.

不太懂啊……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        unordered_set<string> S;
        for (auto& word: wordList) S.insert(word);
        unordered_map<string, int> dist;
        dist[beginWord] = 0;
        queue<string> q;
        q.push(beginWord);

        while (q.size()) {
            auto t = q.front();
            q.pop();

            string r = t;
            for (int i = 0; i < t.size(); i ++ ) {
                t = r;
                for (char j = 'a'; j <= 'z'; j ++ ) {
                    t[i] = j;
                    if (S.count(t) && !dist.count(t)) {
                        dist[t] = dist[r] + 1;
                        if (t == endWord) return dist[t] + 1;
                        q.push(t);
                    }
                }
            }
        }
        return 0;
    }
};

Leetcode128. Longest Consecutive Sequence

Given an unsorted array of integers nums, return the length of the longest consecutive elements sequence.

You must write an algorithm that runs in O(n) time.

Example 1:

1
2
3
Input: nums = [100,4,200,1,3,2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.

这道题要求求最长连续序列，并给定了O(n)复杂度限制，我们的思路是，使用一个集合HashSet存入所有的数字，然后遍历数组中的每个数字，如果其在集合中存在，那么将其移除，然后分别用两个变量pre和next算出其前一个数跟后一个数，然后在集合中循环查找，如果pre在集合中，那么将pre移除集合，然后pre再自减1，直至pre不在集合之中，对next采用同样的方法，那么next-pre-1就是当前数字的最长连续序列，更新res即可。这里再说下，为啥当检测某数字在集合中存在当时候，都要移除数字。这是为了避免大量的重复计算，就拿题目中的例子来说吧，我们在遍历到4的时候，会向下遍历3，2，1，如果都不移除数字的话，遍历到1的时候，还会遍历2，3，4。同样，遍历到3的时候，向上遍历4，向下遍历2，1，等等等。如果数组中有大量的连续数字的话，那么就有大量的重复计算，十分的不高效，所以我们要从HashSet中移除数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> s(nums.begin(), nums.end());
        int res = 0;
        int local_res;
        for(int i : nums) {
            if (!s.count(i))
                continue;
            int res1 = 1;
            int prev = i-1, next = i+1;
            s.erase(i);
            while(s.count(prev)) s.erase(prev--);
            while(s.count(next)) s.erase(next++);
            res = max(res, next-prev-1);
        }
        return res;
    }
};

Leetcode129. Sum Root to Leaf Numbers

Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.

An example is the root-to-leaf path 1->2->3 which represents the number 123.

Find the total sum of all root-to-leaf numbers.

Note: A leaf is a node with no children.

Example:

1
2
3
4
5
6
7
8
9
Input: [1,2,3]
    1
   / \
  2   3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
Input: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

跟1022一样的代码，只是变成了十进制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int result;
    void dfs(TreeNode* root ,int now){
        if(!root)
            return;
        if(!root->left && !root->right){
            result += (now*10) + root->val;
        }
        int val = (now*10) + root->val;
        if(root->left)
            dfs(root->left, val);
        if(root->right)
            dfs(root->right, val);
    }

    int sumNumbers(TreeNode* root) {
        result=0;
        dfs(root,0);
        return result;        
    }
};

Leetcode130. Surrounded Regions

Given a 2D board containing ‘X’ and ‘O’ (the letter O), capture all regions surrounded by ‘X’. A region is captured by flipping all ‘O’s into ‘X’s in that surrounded region.

Example:

1
2
3
4
5
6
7
8
9
10
X X X X
X O O X
X X O X
X O X X
After running your function, the board should be:

X X X X
X X X X
X X X X
X O X X

Explanation: Surrounded regions shouldn’t be on the border, which means that any ‘O’ on the border of the board are not flipped to ‘X’. Any ‘O’ that is not on the border and it is not connected to an ‘O’ on the border will be flipped to ‘X’. Two cells are connected if they are adjacent cells connected horizontally or vertically.

将包住的O都变成X，但不同的是边缘的O不算被包围，都可以用 DFS 来解。在网上看到大家普遍的做法是扫矩阵的四条边，如果有O，则用 DFS 遍历，将所有连着的O都变成另一个字符，比如 A，这样剩下的O都是被包围的，然后将这些O变成X，把A变回O就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    void solve(vector<vector<char>>& board) {
        int m = board.size(), n = board[0].size();
        for(int i = 0; i < m; i ++) 
            for(int j = 0; j < n; j ++)
                if((i == 0 || i == m-1 || j == 0 || j == n - 1) && board[i][j] == 'O')
                    dfs(board, i, j);
        for(int i = 0; i < m; i ++) 
            for(int j = 0; j < n; j ++)
                if(board[i][j] == 'O')
                    board[i][j] = 'X';
                else if(board[i][j] == 'A')
                    board[i][j] = 'O';
        
    }
    
    void dfs(vector<vector<char>>& board, int i, int j) {
        if(board[i][j] == 'O') {
            board[i][j] = 'A';
            int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
            for(int ii = 0; ii < 4; ii ++) {
                int xx = i + dir[ii][0];
                int yy = j + dir[ii][1];
                if(xx >= 0 && xx < board.size() && yy >= 0 && yy < board[0].size())
                    dfs(board, xx, yy);
            }
        }
    }
    
};

Leetcode131. Palindrome Partitioning

Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.

Example:

1
2
3
4
5
6
Input: "aab"
Output:
[
  ["aa","b"],
  ["a","a","b"]
]

搜索题，用dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<vector<string>> partition(string s) {
        if(s.length() == 0)
            return {};
        vector<vector<string>> res;
        vector<string> cur;
        int index = 0;
        dfs(res, cur, s, index);
        return res;
    }
    void dfs(vector<vector<string>>& res, vector<string> cur, string s, int index) {
        if(index >= s.length()) {
            res.push_back(cur);
            return;
        }
        for(int i = index; i < s.length(); i ++) {
            string su = s.substr(index, i - index + 1);
            if(isPalidrome(su)) {
                cur.push_back(su);
                dfs(res, cur, s, i + 1);
                cur.pop_back();
            }
        }
    }
    bool isPalidrome(string su) {
        int len = su.length();
        for(int i = 0; i < len / 2; i ++) 
            if(su[i] != su[len - 1 - i])
                return false;
        return true;
    }
};

Leetcode132. Palindrome Partitioning II

Given a string s, partition s such that every substring of the partition is a palindrome.

Return the minimum cuts needed for a palindrome partitioning of s.

Example 1:

1
2
3
Input: s = "aab"
Output: 1
Explanation: The palindrome partitioning ["aa","b"] could be produced using 1 cut.

Example 2:

1
2
Input: s = "a"
Output: 0

Example 3:

1
2
Input: s = "ab"
Output: 1

Constraints:

  • 1 <= s.length <= 2000
  • s consists of lower-case English letters only.

这道题是让找到把原字符串拆分成回文串的最小切割数，如果首先考虑用 brute force 来做的话就会十分的复杂，因为不但要判断子串是否是回文串，而且还要找出最小切割数，情况会非常的多，不好做。所以对于这种玩字符串且是求极值的题，就要祭出旷古神器动态规划 Dynamic Programming 了，秒天秒地秒空气，DP 在手天下我有。好，吹完一波后，开始做题。DP 解法的两个步骤，定义 dp 数组和找状态转移方程。首先来定义 dp 数组，这里使用最直接的定义方法，一维的 dp 数组，其中 dp[i] 表示子串 [0, i] 范围内的最小分割数，那么最终要返回的就是 dp[n-1] 了，这里先加个 corner case 的判断，若s串为空，直接返回0，OJ 的 test case 中并没有空串的检测，但博主认为还是加上比较好，毕竟空串也算是回文串的一种，所以最小分割数为0也说得过去。接下来就是大难点了，如何找出状态转移方程。

如何更新 dp[i] 呢，前面说过了其表示子串 [0, i] 范围内的最小分割数。那么这个区间的每个位置都可以尝试分割开来，所以就用一个变量j来从0遍历到i，这样就可以把区间 [0, i] 分为两部分，[0, j-1] 和 [j, i]，那么 suppose 已经知道区间 [0, j-1] 的最小分割数 dp[j-1]，因为是从前往后更新的，而 j 小于等于 i，所以 dp[j-1] 肯定在 dp[i] 之前就已经算出来了。这样就只需要判断区间 [j, i] 内的子串是否为回文串了，是的话，dp[i] 就可以用 1 + dp[j-1] 来更新了。判断子串的方法用的是之前那道 Palindromic Substrings 一样的方法，使用一个二维的 dp 数组p，其中 p[i][j] 表示区间 [i, j] 内的子串是否为回文串，其状态转移方程为 p[i][j] = (s[i] == s[j]) && p[i+1][j-1]，其中 p[i][j] = true if [i, j]为回文。这样的话，这道题实际相当于同时用了两个 DP 的方法，确实难度不小呢。

第一个 for 循环遍历的是i，此时先将 dp[i] 初始化为 i，因为对于区间 [0, i]，就算每个字母割一刀（怎么听起来像凌迟？！），最多能只用分割 i 次，不需要再多于这个数字。但是可能会变小，所以第二个 for 循环用 j 遍历区间 [0, j]，根据上面的解释，需要验证的是区间 [j, i] 内的子串是否为回文串，那么只要 s[j] == s[i]，并且 i-j < 2 或者 p[j+1][i-1] 为 true 的话，先更新 p[j][i] 为 true，然后在更新 dp[i]，这里需要注意一下 corner case，当 j=0 时，直接给 dp[i] 赋值为0，因为此时能运行到这，说明 [j, i] 区间是回文串，而 j=0， 则说明 [0, i] 区间内是回文串，这样根本不用分割啊。若 j 大于0，则用 dp[j-1] + 1 来更新 dp[i]，最终返回 dp[n-1] 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int minCut(string s) {
        if (s.empty()) return 0;
        int n = s.size();
        vector<vector<bool>> p(n, vector<bool>(n));
        vector<int> dp(n);
        for (int i = 0; i < n; ++i) {
            dp[i] = i;
            for (int j = 0; j <= i; ++j) {
                if (s[i] == s[j] && (i - j < 2 || p[j + 1][i - 1])) {
                    p[j][i] = true;
                    dp[i] = (j == 0) ? 0 : min(dp[i], dp[j - 1] + 1);
                }
            }
        }
        return dp[n - 1];
    }
};

我们也可以反向推，这里的dp数组的定义就刚好跟前面反过来了，dp[i] 表示区间 [i, n-1] 内的最小分割数，所以最终只需要返回 dp[0] 就是区间 [0, n-1] 内的最喜哦啊分割数了，极为所求。然后每次初始化 dp[i] 为 n-1-i 即可，j 的更新范围是 [i, n)，此时就只需要用 1 + dp[j+1] 来更新 dp[i] 了，为了防止越界，需要对 j == n-1 的情况单独处理一下，整个思想跟上面的解法一模一样，请参见之前的讲解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int minCut(string s) {
       if (s.empty()) return 0;
       int n = s.size();
       vector<vector<bool>> p(n, vector<bool>(n));
       vector<int> dp(n);
       for (int i = n - 1; i >= 0; --i) {
           dp[i] = n - i - 1;
           for (int j = i; j < n; ++j) {
               if (s[i] == s[j] && (j - i <= 1 || p[i + 1][j - 1])) {
                   p[i][j] = true;
                   dp[i] = (j == n - 1) ? 0 : min(dp[i], dp[j + 1] + 1);
               }
           }
       }
       return dp[0];
    }
};

下面这种解法是论坛上的高分解法，没用使用判断区间 [i, j] 内是否为回文串的二维dp数组，节省了空间。但写法上比之前的解法稍微有些凌乱，也算是个 trade-off 吧。这里还是用的一维 dp 数组，不过大小初始化为了 n+1，这样其定义就稍稍发生了些变化，dp[i] 表示由s串中前 i 个字母组成的子串的最小分割数，这样 dp[n] 极为最终所求。接下来就要找状态转移方程了。这道题的更新方式比较特别，跟之前的都不一样，之前遍历 i 的时候，都是更新的 dp[i]，这道题更新的却是 dp[i+len+1] 和 dp[i+len+2]，其中 len 是以i为中心，总长度为 2len + 1 的回文串，比如 bob，此时 i=1，len=1，或者是i为中心之一，总长度为 2len + 2 的回文串，比如 noon，此时 i=1，len=1。中间两个for循环就是分别更新以 i 为中心且长度为 2len + 1 的奇数回文串，和以 i 为中心之一且长度为 2len + 2 的偶数回文串的。i-len 正好是奇数或者偶数回文串的起始位置，由于我们定义的 dp[i] 是区间 [0, i-1] 的最小分割数，所以 dp[i-len] 就是区间 [0, i-len-1] 范围内的最小分割数，那么加上奇数回文串长度2*len + 1，此时整个区间为 [0, i+len]，即需要更新 dp[i+len+1]。如果是加上偶数回文串的长度2*len + 2，那么整个区间为 [0, i+len+1]，即需要更新 dp[i+len+2]。这就是分奇偶的状态转移方程，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int minCut(string s) {
        if (s.empty()) return 0;
        int n = s.size();
        vector<int> dp(n + 1, INT_MAX);
        dp[0] = -1;
        for (int i = 0; i < n; ++i) {
            for (int len = 0; i - len >= 0 && i + len < n && s[i - len] == s[i + len]; ++len) {
                dp[i + len + 1] = min(dp[i + len + 1], 1 + dp[i - len]);
            }
            for (int len = 0; i - len >= 0 && i + len + 1 < n && s[i - len] == s[i + len + 1]; ++len) {
                dp[i + len + 2] = min(dp[i + len + 2], 1 + dp[i - len]);
            }
        }
        return dp[n];
    }
};

Leetcode133. Clone Graph

Given a reference of a node in a connected undirected graph. Return a deep copy (clone) of the graph. Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.

1
2
3
4
class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:

  • For simplicity sake, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

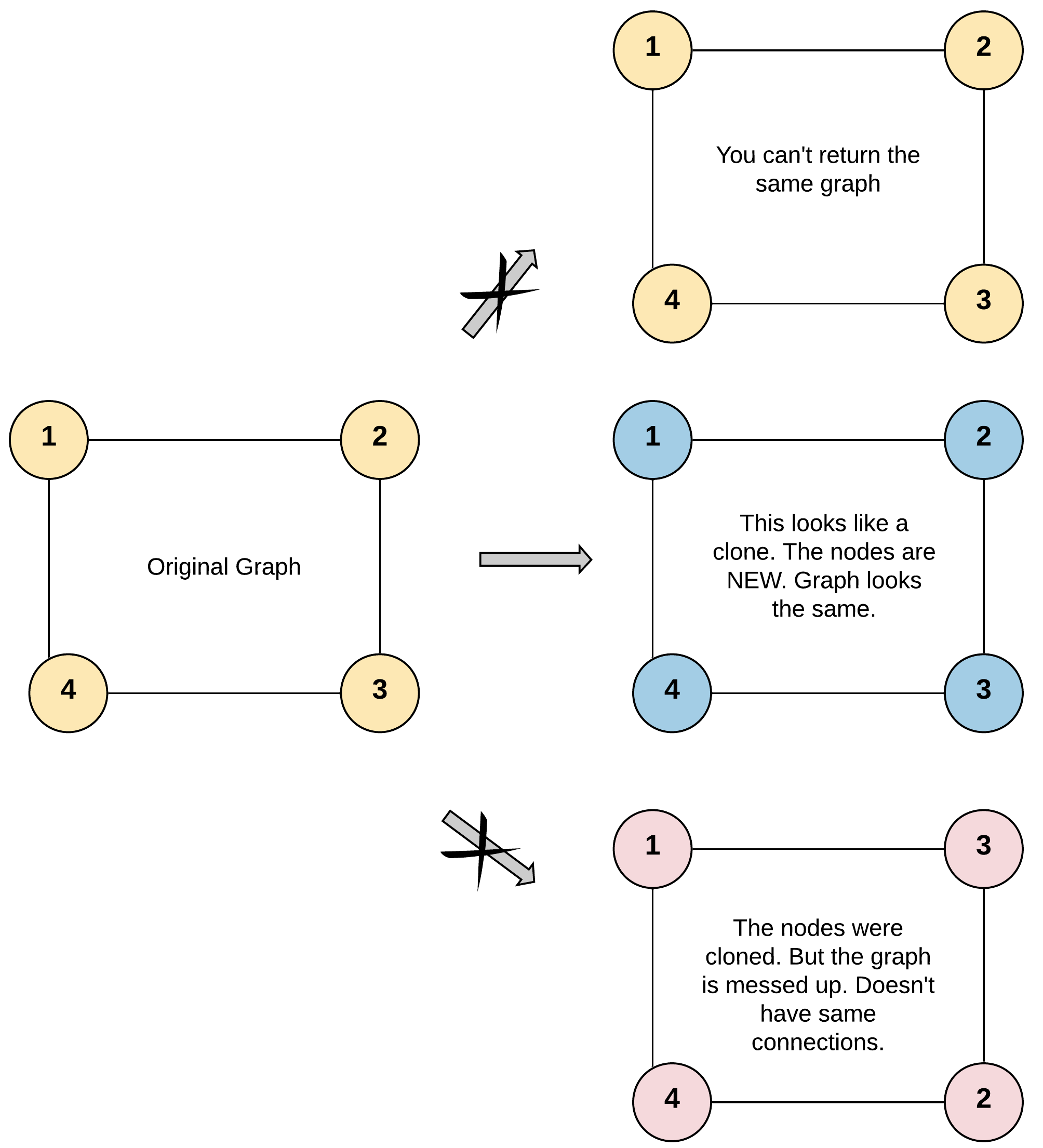
Example 1:

1
2
3
4
5
6
7
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

这道题目的难点在于如何处理每个结点的 neighbors，由于在深度拷贝每一个结点后，还要将其所有 neighbors 放到一个 vector 中，而如何避免重复拷贝呢？这道题好就好在所有结点值不同，所以我们可以使用 HashMap 来对应原图中的结点和新生成的克隆图中的结点。对于图的遍历的两大基本方法是深度优先搜索 DFS 和广度优先搜索 BFS，这里我们先使用深度优先搜索DFS来解答此题，在递归函数中，首先判空，然后再看当前的结点是否已经被克隆过了，若在 HashMap 中存在，则直接返回其映射结点。否则就克隆当前结点，并在 HashMap 中建立映射，然后遍历当前结点的所有 neihbor 结点，调用递归函数并且加到克隆结点的 neighbors 数组中即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:

    Node* dfs(Node* node, unordered_map<Node*, Node*>& ma) {
        if(!node)
            return NULL;
        if(ma.count(node))
            return ma[node];
        Node* new_node = new Node(node->val);
        ma[node] = new_node;
        for(Node* t : node->neighbors) 
            new_node->neighbors.push_back(dfs(t, ma));
        return new_node;
    }
    
    Node* cloneGraph(Node* node) {
        unordered_map<Node*, Node*> ma;
        return dfs(node, ma);
    }
};

Leetcode134. Gas Station

There are N gas stations along a circular route, where the amount of gas at station i is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1). You begin the journey with an empty tank at one of the gas stations.

Return the starting gas station’s index if you can travel around the circuit once in the clockwise direction, otherwise return -1.

Note:

  • If there exists a solution, it is guaranteed to be unique.
  • Both input arrays are non-empty and have the same length.
  • Each element in the input arrays is a non-negative integer.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Input: 
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

Output: 3

Explanation:
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.

思路: 累加在每个位置的left += gas[i] - cost[i], 就是在每个位置剩余的油量, 如果left一直大于0, 就可以一直走下取. 如果left小于0了, 那么就从下一个位置重新开始计数, 并且将之前欠下的多少记录下来, 如果最终遍历完数组剩下的燃料足以弥补之前不够的, 那么就可以到达, 并返回最后一次开始的位置.否则就返回-1.

证明这种方法的正确性: 

  1. 如果从头开始, 每次累计剩下的油量都为整数, 那么没有问题, 他可以从头开到结束.
  2. 如果到中间的某个位置, 剩余的油量为负了, 那么说明之前累积剩下的油量不够从这一站到下一站了. 那么就从下一站从新开始计数. 为什么是下一站, 而不是之前的某站呢? 因为第一站剩余的油量肯定是大于等于0的, 然而到当前一站油量变负了, 说明从第一站之后开始的话到当前油量只会更少而不会增加. 也就是说从第一站之后, 当前站之前的某站出发到当前站剩余的油量是不可能大于0的. 所以只能从下一站重新出发开始计算从下一站开始剩余的油量, 并且把之前欠下的油量也累加起来, 看到最后剩余的油量是不是大于欠下的油量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int start = 0, lack = 0, left = 0;
        for(int i = 0; i < gas.size(); i++)
        {
            left += gas[i] - cost[i];
            if(left < 0)
            {
                start = i+1;
                lack += left;
                left = 0;
            }
        }
        return left+lack>=0?start:-1;
    }
};

Leetcode135. Candy

There are N children standing in a line. Each child is assigned a rating value.

You are giving candies to these children subjected to the following requirements:

  • Each child must have at least one candy.
  • Children with a higher rating get more candies than their neighbors.
  • What is the minimum candies you must give?

这道题看起来很难，其实解法并没有那么复杂，当然我也是看了别人的解法才做出来的，先来看看两遍遍历的解法，首先初始化每个人一个糖果，然后这个算法需要遍历两遍，第一遍从左向右遍历，如果右边的小盆友的等级高，等加一个糖果，这样保证了一个方向上高等级的糖果多。然后再从右向左遍历一遍，如果相邻两个左边的等级高，而左边的糖果又少的话，则左边糖果数为右边糖果数加一。最后再把所有小盆友的糖果数都加起来返回即可。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int candy(vector<int>& ratings) {
        int res = 0, n = ratings.size();
        vector<int> nums(n, 1);
        for (int i = 0; i < n - 1; ++i) {
            if (ratings[i + 1] > ratings[i]) nums[i + 1] = nums[i] + 1;
        }
        for (int i = n - 1; i > 0; --i) {
            if (ratings[i - 1] > ratings[i]) nums[i - 1] = max(nums[i - 1], nums[i] + 1);
        }
        for (int num : nums) res += num;
        return res;
    }
};

下面来看一次遍历的方法，相比于遍历两次的思路简单明了，这种只遍历一次的解法就稍有些复杂了。首先我们给第一个同学一个糖果，那么对于接下来的一个同学就有三种情况：

  1. 接下来的同学的rating等于前一个同学，那么给接下来的同学一个糖果就行。
  2. 接下来的同学的rating大于前一个同学，那么给接下来的同学的糖果数要比前一个同学糖果数加1。
  3. 接下来的同学的rating小于前一个同学，那么我们此时不知道应该给这个同学多少个糖果，需要看后面的情况。

对于第三种情况，我们不确定要给几个，因为要是只给1个的话，那么有可能接下来还有rating更小的同学，总不能一个都不给吧。也不能直接给前一个同学的糖果数减1，有可能给多了，因为如果后面再没人了的话，其实只要给一个就行了。还有就是，如果后面好几个rating越来越小的同学，那么前一个同学的糖果数可能还得追加，以保证最后面的同学至少能有1个糖果。来一个例子吧，四个同学，他们的rating如下：

1
1 3 2 1

先给第一个rating为1的同学一个糖果，然后从第二个同学开始遍历，第二个同学rating为3，比1大，所以多给一个糖果，第二个同学得到两个糖果。下面第三个同学，他的rating为2，比前一个同学的rating小，如果我们此时给1个糖果的话，那么rating更小的第四个同学就得不到糖果了，所以我们要给第四个同学1个糖果，而给第三个同学2个糖果，此时要给第二个同学追加1个糖果，使其能够比第三个同学的糖果数多至少一个。那么我们就需要统计出多有个连着的同学的rating变小，用变量cnt来记录，找出了最后一个减小的同学，那么就可以往前推，每往前一个加一个糖果，这就是个等差数列，我们可以直接利用求和公式算出这些rating减小的同学的糖果之和。然后我们还要看第一个开始减小的同学的前一个同学需不需要追加糖果，只要比较cnt和pre的大小，pre是之前同学得到的最大糖果数，二者做差加1就是需要追加的糖果数，加到结果res中即可，参见代码如下：

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int candy(vector<int>& ratings) {
        if (ratings.empty()) return 0;
        int res = 1, pre = 1, cnt = 0;
        for (int i = 1; i < ratings.size(); ++i) {
            if (ratings[i] >= ratings[i - 1]) {
                if (cnt > 0) {
                    res += cnt * (cnt + 1) / 2;
                    if (cnt >= pre) res += cnt - pre + 1;
                    cnt = 0;
                    pre = 1;
                }
                pre = (ratings[i] == ratings[i - 1]) ? 1 : pre + 1;
                res += pre;
            } else {
                ++cnt;
            }
        }     
        if (cnt > 0) {
            res += cnt * (cnt + 1) / 2;
            if (cnt >= pre) res += cnt - pre + 1;
        }
        return res;
    }
};

Leetcode136. Single Number

Given a non-empty array of integers, every element appears twice except for one. Find that single one.

Note:

  • Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?
1
2
3
4
Example 1:

Input: [2,2,1]
Output: 1
1
2
3
4
Example 2:

Input: [4,1,2,1,2]
Output: 4

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。算法应该具有线性时间复杂度。且可以不使用额外空间来实现。

我的：

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int a=0;
        for(int i=0;i<nums.size();i++){
            a ^= nums[i];
        }
        return a;
    }
};

复杂些的：
有一个 n 个元素的数组，除了两个数只出现一次外，其余元素都出现两次，让你找出这两个只出现一次的数分别是几，要求时间复杂度为 O(n) 且再开辟的内存空间固定(与 n 无关)。

示例 :
输入: [1,2,2,1,3,4]
输出: [3,4]

根据前面找一个不同数的思路算法，在这里把所有元素都异或，那么得到的结果就是那两个只出现一次的元素异或的结果。然后，因为这两个只出现一次的元素一定是不相同的，所以这两个元素的二进制形式肯定至少有某一位是不同的，即一个为 0 ，另一个为 1 ，现在需要找到这一位。根据异或的性质 任何一个数字异或它自己都等于 0，得到这个数字二进制形式中任意一个为 1 的位都是我们要找的那一位。再然后，以这一位是 1 还是 0 为标准，将数组的 n 个元素分成两部分。将这一位为 0 的所有元素做异或，得出的数就是只出现一次的数中的一个，将这一位为 1 的所有元素做异或，得出的数就是只出现一次的数中的另一个。这样就解出题目。忽略寻找不同位的过程，总共遍历数组两次，时间复杂度为O(n)。

Leetcode137. Single Number II

Given a non-empty array of integers, every element appears three times except for one, which appears exactly once. Find that single one.

Note: Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Example 1:

1
2
Input: [2,2,3,2]
Output: 3

这道题就是除了一个单独的数字之外，数组中其他的数字都出现了三次，还是要利用位操作 Bit Manipulation 来解。可以建立一个 32 位的数字，来统计每一位上1出现的个数，如果某一位上为1的话，那么如果该整数出现了三次，对3取余为0，这样把每个数的对应位都加起来对3取余，最终剩下来的那个数就是单独的数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int sum = 0;
        int res = 0;
        for(int i = 0; i < 32; i ++) {
            sum = 0;
            for(int j = 0; j < nums.size(); j ++) {
                sum += (nums[j] >> i) & 1;
            }
            res |= ((sum % 3) << i);
        }
        return res;
    }
};

Leetcode138. Copy List with Random Pointer

A linked list is given such that each node contains an additional random pointer which could point to any node in the list or null. Return a deep copy of the list.

The Linked List is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:

  • val: an integer representing Node.val
  • random_index: the index of the node (range from 0 to n-1) where random pointer points to, or null if it does not point to any node.

Example 1:

1
2
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]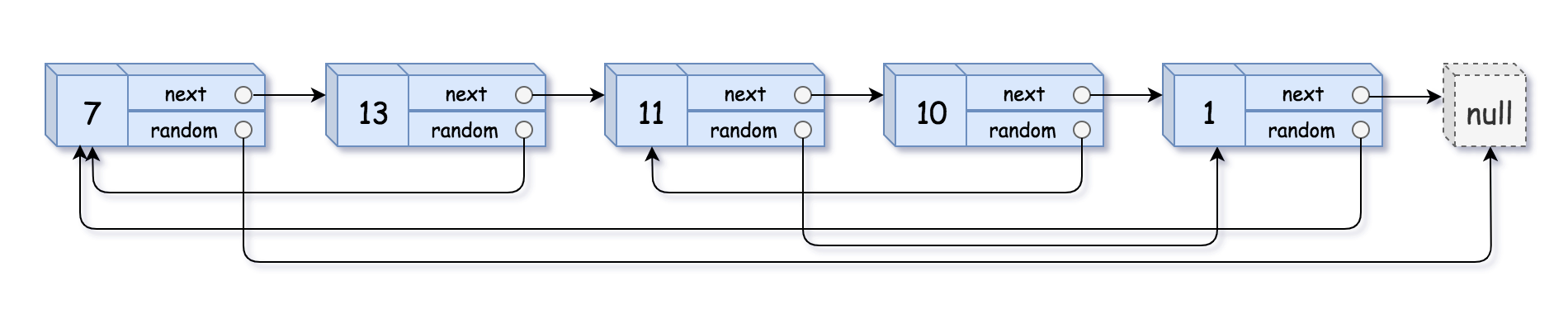

Example 2:

1
2
Input: head = [[1,1],[2,1]]
Output: [[1,1],[2,1]]

这道链表的深度拷贝题的难点就在于如何处理随机指针的问题，由于每一个节点都有一个随机指针，这个指针可以为空，也可以指向链表的任意一个节点，如果在每生成一个新节点给其随机指针赋值时，都要去遍历原链表的话，OJ 上肯定会超时，所以可以考虑用 HashMap 来缩短查找时间，第一遍遍历生成所有新节点时同时建立一个原节点和新节点的 HashMap，第二遍给随机指针赋值时，查找时间是常数级。

教训就是别想着省空间用unordered_map<int, Node*>，碰上重复的真没法处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(!head)
            return NULL;
        Node* cur = head, *res = new Node(-1), *res_head = res;
        unordered_map<Node*, Node*> ma;
        while(cur != NULL) {
            Node *new_cur = new Node(cur->val);
            res->next = new_cur;
            res = res->next;
            ma[cur] = new_cur;
            cur = cur->next;
        }
        
        cur = head;
        res = res_head->next;
        while(cur != NULL) {
            if(cur->random != NULL)
                res->random = ma[cur->random];
            res = res->next;
            cur = cur->next;
        }
        return res_head->next;
        
    }
};

Leetcode139. Word Break

Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words.

Note:

  • The same word in the dictionary may be reused multiple times in the segmentation.
  • You may assume the dictionary does not contain duplicate words.

Example 1:

1
2
3
Input: s = "leetcode", wordDict = ["leet", "code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".

Example 2:

1
2
3
4
Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
             Note that you are allowed to reuse a dictionary word.

这道题其实还是一道经典的 DP 题目，也就是动态规划 Dynamic Programming。博主曾经说玩子数组或者子字符串且求极值的题，基本就是 DP 没差了，虽然这道题没有求极值，但是玩子字符串也符合 DP 的状态转移的特点。把一个人的温暖转移到另一个人的胸膛… 咳咳，跑错片场了，那是爱情转移～ 强行拉回，DP 解法的两大难点，定义 dp 数组跟找出状态转移方程，先来看 dp 数组的定义，这里我们就用一个一维的 dp 数组，其中 dp[i] 表示范围 [0, i) 内的子串是否可以拆分，注意这里 dp 数组的长度比s串的长度大1，是因为我们要 handle 空串的情况，我们初始化 dp[0] 为 true，然后开始遍历。注意这里我们需要两个 for 循环来遍历，因为此时已经没有递归函数了，所以我们必须要遍历所有的子串，我们用j把 [0, i) 范围内的子串分为了两部分，[0, j) 和 [j, i)，其中范围 [0, j) 就是 dp[j]，范围 [j, i) 就是 s.substr(j, i-j)，其中 dp[j] 是之前的状态，我们已经算出来了，可以直接取，只需要在字典中查找 s.substr(j, i-j) 是否存在了，如果二者均为 true，将 dp[i] 赋为 true，并且 break 掉，此时就不需要再用j去分 [0, i) 范围了，因为 [0, i) 范围已经可以拆分了。最终我们返回 dp 数组的最后一个值，就是整个数组是否可以拆分的布尔值了，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        vector<int> dp(s.length() + 1, false);
        unordered_set<string> se(wordDict.begin(), wordDict.end());
        
        dp[0] = true;
        for(int i = 1; i <= s.length(); i ++) {
            bool temp = false;
            int j;
            for(j = 0; j < i; j ++) {
                temp = se.count(s.substr(j, i - j)) != 0;
                if(temp && dp[j])
                    break;
            }
            if(j == i)
                dp[i] = false;
            else
                dp[i] = true;
        }
        
        return dp[s.length()];
    }
};

Leetcode140. Word Break II

Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, add spaces in s to construct a sentence where each word is a valid dictionary word. Return all such possible sentences.

Note:

  • The same word in the dictionary may be reused multiple times in the segmentation.
  • You may assume the dictionary does not contain duplicate words.

Example 1:

1
2
3
4
5
6
7
8
Input:
s = "catsanddog"
wordDict = ["cat", "cats", "and", "sand", "dog"]
Output:
[
  "cats and dog",
  "cat sand dog"
]

Example 2:

1
2
3
4
5
6
7
8
9
10
Input:
s = "pineapplepenapple"
wordDict = ["apple", "pen", "applepen", "pine", "pineapple"]
Output:
[
  "pine apple pen apple",
  "pineapple pen apple",
  "pine applepen apple"
]
Explanation: Note that you are allowed to reuse a dictionary word.

Example 3:

1
2
3
4
5
Input:
s = "catsandog"
wordDict = ["cats", "dog", "sand", "and", "cat"]
Output:
[]

这道题是之前那道Word Break 拆分词句的拓展，那道题只让我们判断给定的字符串能否被拆分成字典中的词，而这道题加大了难度，让我们求出所有可以拆分成的情况，就像题目中给的例子所示。

如果就给你一个s和wordDict，不看Output的内容，你会怎么找出结果。比如对于例子1，博主可能会先扫一遍wordDict数组，看有没有单词可以当s的开头，那么我们可以发现cat和cats都可以，比如我们先选了cat，那么此时s就变成了 “sanddog”，我们再在数组里找单词，发现了sand可以，最后剩一个dog，也在数组中，于是一个结果就出来了。然后回到开头选cats的话，那么此时s就变成了 “anddog”，我们再在数组里找单词，发现了and可以，最后剩一个dog，也在数组中，于是另一个结果也就出来了。那么这个查询的方法很适合用递归来实现，因为s改变后，查询的机制并不变，很适合调用递归函数。再者，我们要明确的是，如果不用记忆数组做减少重复计算的优化，那么递归方法跟brute force没什么区别，大概率无法通过OJ。所以我们要避免重复计算，如何避免呢，还是看上面的分析，如果当s变成 “sanddog”的时候，那么此时我们知道其可以拆分成sand和dog，当某个时候如果我们又遇到了这个 “sanddog”的时候，我们难道还需要再调用递归算一遍吗，当然不希望啦，所以我们要将这个中间结果保存起来，由于我们必须要同时保存s和其所有的拆分的字符串，那么可以使用一个HashMap，来建立二者之间的映射，那么在递归函数中，我们首先检测当前s是否已经有映射，有的话直接返回即可，如果s为空了，我们如何处理呢，题目中说了给定的s不会为空，但是我们递归函数处理时s是会变空的，这时候我们是直接返回空集吗，这里有个小trick，我们其实放一个空字符串返回，为啥要这么做呢？我们观察题目中的Output，发现单词之间是有空格，而最后一个单词后面没有空格，所以这个空字符串就起到了标记当前单词是最后一个，那么我们就不要再加空格了。接着往下看，我们遍历wordDict数组，如果某个单词是s字符串中的开头单词的话，我们对后面部分调用递归函数，将结果保存到rem中，然后遍历里面的所有字符串，和当前的单词拼接起来，这里就用到了我们前面说的trick。for循环结束后，记得返回结果res之前建立其和s之间的映射，方便下次使用，参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<string> wordBreak(string s, vector<string>& wordDict) {
        unordered_map<string, vector<string>> m;
        return helper(s, wordDict, m);
    }
    vector<string> helper(string s, vector<string>& wordDict, unordered_map<string, vector<string>>& m) {
        if (m.count(s)) return m[s];
        if (s.empty()) return {""};
        vector<string> res;
        for (string word : wordDict) {
            if (s.substr(0, word.size()) != word) continue;
            vector<string> rem = helper(s.substr(word.size()), wordDict, m);
            for (string str : rem) {
                res.push_back(word + (str.empty() ? "" : " ") + str);
            }
        }
        return m[s] = res;
    }
};

Leetcode141. Linked List Cycle

Given a linked list, determine if it has a cycle in it.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Example 1:

1
2
3
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where tail connects to the second node.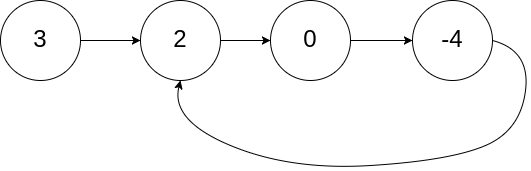


Example 2:

1
2
3
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where tail connects to the first node.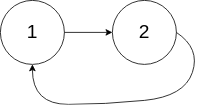


Example 3:

1
2
3
Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

快慢指针判断链表是否有环。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *fast = head, *slow = head;
        while(slow && fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
            if(slow == fast) 
                return true;
        }
        return false;
    }
};

Leetcode142. Linked List Cycle II

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Note: Do not modify the linked list.

Example 1:

1
2
3
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.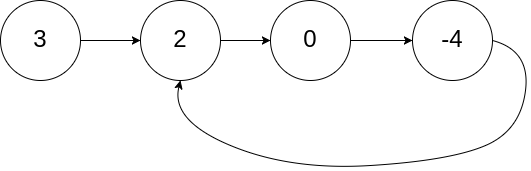

Example 2:

1
2
3
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.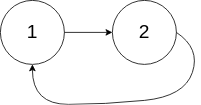

这个求单链表中的环的起始点是之前那个判断单链表中是否有环的延伸，可参之前那道 Linked List Cycle。这里还是要设快慢指针，不过这次要记录两个指针相遇的位置，当两个指针相遇了后，让其中一个指针从链表头开始，此时再相遇的位置就是链表中环的起始位置，为啥是这样呢，因为快指针每次走2，慢指针每次走1，快指针走的距离是慢指针的两倍。而快指针又比慢指针多走了一圈。所以 head 到环的起点+环的起点到他们相遇的点的距离 与 环一圈的距离相等。现在重新开始，head 运行到环起点 和 相遇点到环起点 的距离也是相等的，相当于他们同时减掉了 环的起点到他们相遇的点的距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast = head, *slow = head;
        int count = 0;
        while(fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow)
                break;
        }
        
        if(!fast || !fast->next)
            return NULL;
        
        slow = head;
        while(slow != fast) {
            slow = slow->next;
            fast = fast->next;
        }
        
        return fast;
    }
};

分析

复杂度O(n^2)的方法，使用两个指针a, b。a从表头开始一步一步往前走，遇到null则说明没有环，返回false；a每走一步，b从头开始走，如果遇到b==a.next，则说明有环true，如果遇到b==a，则说明暂时没有环，继续循环。

后来找到了复杂度O(n)的方法，使用两个指针slow,fast。两个指针都从表头开始走，slow每次走一步，fast每次走两步，如果fast遇到null，则说明没有环，返回false；如果slow==fast，说明有环，并且此时fast超了slow一圈，返回true。

为什么有环的情况下二者一定会相遇呢？因为fast先进入环，在slow进入之后，如果把slow看作在前面，fast在后面每次循环都向slow靠近1，所以一定会相遇，而不会出现fast直接跳过slow的情况。

扩展问题

在网上搜集了一下这个问题相关的一些问题，思路开阔了不少，总结如下：

  1. 环的长度是多少？
  2. 如何找到环中第一个节点（即Linked List Cycle II）？
  3. 如何将有环的链表变成单链表（解除环）？
  4. 如何判断两个单链表是否有交点？如何找到第一个相交的节点？

首先我们看下面这张图：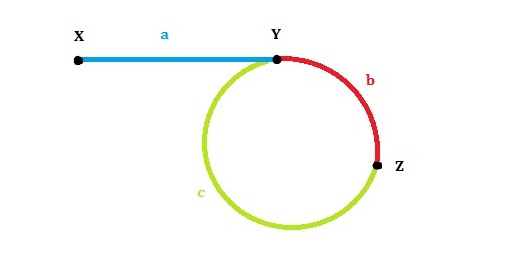

设：链表头是X，环的第一个节点是Y，slow和fast第一次的交点是Z。各段的长度分别是a,b,c，如图所示。环的长度是L。slow和fast的速度分别是qs,qf。下面我们来挨个问题分析。

  • 1.
    • 方法一（网上都是这个答案）：第一次相遇后，让slow,fast继续走，记录到下次相遇时循环了几次。因为当fast第二次到达Z点时，fast走了一圈，slow走了半圈，而当fast第三次到达Z点时，fast走了两圈，slow走了一圈，正好还在Z点相遇。
    • 方法二：第一次相遇后，让fast停着不走了，slow继续走，记录到下次相遇时循环了几次。
    • 方法三（最简单）： 第一次相遇时slow走过的距离：a+b，fast走过的距离：a+b+c+b。因为fast的速度是slow的两倍，所以fast走的距离是slow的两倍，有 2(a+b) = a+b+c+b，可以得到a=c（这个结论很重要！）。我们发现L=b+c=a+b，也就是说，从一开始到二者第一次相遇，循环的次数就等于环的长度。
    1. 我们已经得到了结论a=c，那么让两个指针分别从X和Z开始走，每次走一步，那么正好会在Y相遇！也就是环的第一个节点。
    1. 在上一个问题的最后，将c段中Y点之前的那个节点与Y的链接切断即可。
    1. 如何判断两个单链表是否有交点？先判断两个链表是否有环，如果一个有环一个没环，肯定不相交；如果两个都没有环，判断两个列表的尾部是否相等；如果两个都有环，判断一个链表上的Z点是否在另一个链表上。
    • 如何找到第一个相交的节点？求出两个链表的长度L1,L2（如果有环，则将Y点当做尾节点来算），假设L1<L2，用两个指针分别从两个链表的头部开始走，长度为L2的链表先走(L2-L1)步，然后两个一起走，直到二者相遇。

Leetcode 143. Reorder List

Given a singly linked list L: L0→L1→…→Ln-1→Ln, reorder it to: L0→Ln→L1→Ln-1→L2→Ln-2→…. You may not modify the values in the list’s nodes, only nodes itself may be changed.

Example 1:

1
Given 1->2->3->4, reorder it to 1->4->2->3.

Example 2:

1
Given 1->2->3->4->5, reorder it to 1->5->2->4->3.

分为三步：

  1. 找中点 （快慢指针）
  2. 将中点之后的部分链表反转
  3. 反转的部分挨个拼接
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    
    ListNode* reverse(ListNode *head){
        ListNode *prev = NULL, *cur = head;
        while(cur != NULL) {
            ListNode *tmp = cur->next;
            cur->next = prev;
            prev = cur;
            cur = tmp;
        }
        return prev;
    }
    
    void reorderList(ListNode* head) {
        if(head == NULL)
            return;
        ListNode *slow = head, *fast = head;
        while(fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
        }
        // fast is tail, slow is 1/2 of list
        ListNode *head2 = reverse(slow->next);
        slow->next = NULL;
        while(head != NULL && head2 != NULL) {
            ListNode *tmp1 = head->next;
            ListNode *tmp2 = head2->next;
            head2->next = head->next;
            head->next = head2;
            head = tmp1;
            head2 = tmp2;
        }
    }
};

Leetcode144. Binary Tree Preorder Traversal

Given a binary tree, return the preorder traversal of its nodes’ values.

Example:

1
2
3
4
5
6
7
8
Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [1,2,3]

题目的要求是不能使用递归求解，于是只能考虑到用非递归的方法，这就要用到stack来辅助运算。由于先序遍历的顺序是”根-左-右”, 算法为：

  1. 把根节点 push 到栈中
  2. 循环检测栈是否为空，若不空，则取出栈顶元素，保存其值，然后看其右子节点是否存在，若存在则 push 到栈中。再看其左子节点，若存在，则 push 到栈中。

这道题不配为medium，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if(root == NULL)
            return {};
        stack<TreeNode*> s;
        s.push(root);
        vector<int> res;
        while(!s.empty()) {
            TreeNode* tmp = s.top();
            s.pop();
            res.push_back(tmp->val);
            if(tmp->right)
                s.push(tmp->right);
            if(tmp->left)
                s.push(tmp->left);
        }
        return res;
    }
};

Leetcode145. Binary Tree Postorder Traversal

Given the root of a binary tree, return the postorder traversal of its nodes’ values.

后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    
    void add(vector<int>& res, TreeNode* root) {
        if (root == NULL)
            return ;
        if (root->left)
            add(res, root->left);
        if (root->right)
            add(res, root->right);
        res.push_back(root->val);
    }
    
    vector<int> postorderTraversal(TreeNode* root) {
        if (root == NULL)
            return {};
        vector<int> res;
        add(res, root);
        return res;
    }
};

Leetcode146. LRU Cache

Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and put.

  • get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.
  • put(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.

The cache is initialized with a positive capacity.

Follow up:
Could you do both operations in O(1) time complexity?

Example:

1
2
3
4
5
6
7
8
9
10
11
LRUCache cache = new LRUCache( 2 /* capacity */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // returns 1
cache.put(3, 3);    // evicts key 2
cache.get(2);       // returns -1 (not found)
cache.put(4, 4);    // evicts key 1
cache.get(1);       // returns -1 (not found)
cache.get(3);       // returns 3
cache.get(4);       // returns 4

这道题让我们实现一个 LRU 缓存器，LRU 是 Least Recently Used 的简写，就是最近最少使用的意思。那么这个缓存器主要有两个成员函数，get 和 put，其中 get 函数是通过输入 key 来获得 value，如果成功获得后，这对 (key, value) 升至缓存器中最常用的位置（顶部），如果 key 不存在，则返回 -1。而 put 函数是插入一对新的 (key, value)，如果原缓存器中有该 key，则需要先删除掉原有的，将新的插入到缓存器的顶部。如果不存在，则直接插入到顶部。若加入新的值后缓存器超过了容量，则需要删掉一个最不常用的值，也就是底部的值。具体实现时我们需要三个私有变量，cap, l和m，其中 cap 是缓存器的容量大小，l是保存缓存器内容的列表，m是 HashMap，保存关键值 key 和缓存器各项的迭代器之间映射，方便我们以 O(1) 的时间内找到目标项。

然后我们再来看 get 和 put 如何实现，get 相对简单些，我们在 HashMap 中查找给定的 key，若不存在直接返回 -1。如果存在则将此项移到顶部，这里我们使用 C++ STL 中的函数 splice，专门移动链表中的一个或若干个结点到某个特定的位置，这里我们就只移动 key 对应的迭代器到列表的开头，然后返回 value。这里再解释一下为啥 HashMap 不用更新，因为 HashMap 的建立的是关键值 key 和缓存列表中的迭代器之间的映射，get 函数是查询函数，如果关键值 key 不在 HashMap，那么不需要更新。如果在，我们需要更新的是该 key-value 键值对儿对在缓存列表中的位置，而 HashMap 中还是这个 key 跟键值对儿的迭代器之间的映射，并不需要更新什么。

对于 put，我们也是现在 HashMap 中查找给定的 key，如果存在就删掉原有项，并在顶部插入新来项，然后判断是否溢出，若溢出则删掉底部项(最不常用项)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class LRUCache{
public:
    LRUCache(int capacity) {
        cap = capacity;
    }
    
    int get(int key) {
        auto it = m.find(key);
        if (it == m.end()) return -1;
        l.splice(l.begin(), l, it->second);
        return it->second->second;
    }
    
    void put(int key, int value) {
        auto it = m.find(key);
        if (it != m.end()) l.erase(it->second);
        l.push_front(make_pair(key, value));
        m[key] = l.begin();
        if (m.size() > cap) {
            int k = l.rbegin()->first;
            l.pop_back();
            m.erase(k);
        }
    }
    
private:
    int cap;
    list<pair<int, int>> l;
    unordered_map<int, list<pair<int, int>>::iterator> m;
};

Leetcode147. Insertion Sort List

Sort a linked list using insertion sort.

A graphical example of insertion sort. The partial sorted list (black) initially contains only the first element in the list.
With each iteration one element (red) is removed from the input data and inserted in-place into the sorted list

Algorithm of Insertion Sort:

  • Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list.
  • At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there.
  • It repeats until no input elements remain.

Example 1:

1
2
Input: 4->2->1->3
Output: 1->2->3->4

Example 2:

1
2
Input: -1->5->3->4->0
Output: -1->0->3->4->5

使用插入排序来排序链表。可以按照数组中的思路来做，先将创建一个新的链表，然后每次将原来的链表中的第一个节点拿出来与新的链表做对比，需要比较head的值和新建链表中每个值，直到找到合适的位置插入即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        if(!head || !head->next) 
            return head;
        ListNode* ress = new ListNode(-1);
        while(head != NULL) {
            ListNode *res = ress;
            ListNode *tmp = head->next;
            while(res->next && res->next->val <= head->val) {
                res = res->next;
            }
            head->next = res->next;
            res->next = head;
            head = tmp;
        }
        return ress->next;
    }
};

Leetcode148. Sort List

Sort a linked list in O(n log n) time using constant space complexity.

Example 1:

1
2
Input: 4->2->1->3
Output: 1->2->3->4

Example 2:

1
2
Input: -1->5->3->4->0
Output: -1->0->3->4->5

常见排序方法有很多，插入排序，选择排序，堆排序，快速排序，冒泡排序，归并排序，桶排序等等。。它们的时间复杂度不尽相同，而这里题目限定了时间必须为O(nlgn)，符合要求只有快速排序，归并排序，堆排序，而根据单链表的特点，最适于用归并排序。为啥呢？这是由于链表自身的特点决定的，由于不能通过坐标来直接访问元素，所以快排什么的可能不太容易实现（但是被评论区的大神们打脸，还是可以实现的），堆排序的话，如果让新建结点的话，还是可以考虑的，若只能交换结点，最好还是不要用。而归并排序（又称混合排序）因其可以利用递归来交换数字，天然适合链表这种结构。归并排序的核心是一个 merge() 函数，其主要是合并两个有序链表，这个在 LeetCode 中也有单独的题目 Merge Two Sorted Lists。由于两个链表是要有序的才能比较容易 merge，那么对于一个无序的链表，如何才能拆分成有序的两个链表呢？我们从简单来想，什么时候两个链表一定都是有序的？就是当两个链表各只有一个结点的时候，一定是有序的。而归并排序的核心其实是分治法 Divide and Conquer，就是将链表从中间断开，分成两部分，左右两边再分别调用排序的递归函数 sortList()，得到各自有序的链表后，再进行 merge()，这样整体就是有序的了。因为子链表的递归函数中还是会再次拆成两半，当拆到链表只有一个结点时，无法继续拆分了，而这正好满足了前面所说的“一个结点的时候一定是有序的”，这样就可以进行 merge 了。然后再回溯回去，每次得到的都是有序的链表，然后进行 merge，直到还原整个长度。这里将链表从中间断开的方法，采用的就是快慢指针，大家可能对快慢指针找链表中的环比较熟悉，其实找链表中的中点同样好使，因为快指针每次走两步，慢指针每次走一步，当快指针到达链表末尾时，慢指针正好走到中间位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if (!head || !head->next) 
            return head;
        ListNode *slow = head, *fast = head, *prev = head;
        while(fast && fast->next) {
            prev = slow;
            slow = slow->next;
            fast = fast->next->next;
        }
        prev->next = NULL;
        return merge(sortList(head), sortList(slow));
    }
    
    ListNode* merge(ListNode *first, ListNode *second) {
        ListNode *prev = new ListNode(-1);
        ListNode *cur = prev;
        while(first && second) {
            if(first->val < second->val) {
                cur->next = first;
                first = first->next;
            }
            else {
                cur->next = second;
                second = second->next;
            }
            cur = cur->next;
        }
        if(first)
            cur->next = first;
        if(second)
            cur->next = second;
        return prev->next;
    }
    
};

Leetcode 150. Evaluate Reverse Polish Notation

Evaluate the value of an arithmetic expression in Reverse Polish Notation. Valid operators are +, -, *, /. Each operand may be an integer or another expression.

Note:

  • Division between two integers should truncate toward zero.
  • The given RPN expression is always valid. That means the expression would always evaluate to a result and there won’t be any divide by zero operation.

Example 1:

1
2
3
Input: ["2", "1", "+", "3", "*"]
Output: 9
Explanation: ((2 + 1) * 3) = 9

Example 2:

1
2
3
Input: ["4", "13", "5", "/", "+"]
Output: 6
Explanation: (4 + (13 / 5)) = 6

Example 3:

1
2
3
4
5
6
7
8
9
10
Input: ["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
Output: 22
Explanation: 
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

逆波兰表达式就是把操作数放前面，把操作符后置的一种写法，从前往后遍历数组，遇到数字则压入栈中，遇到符号，则把栈顶的两个数字拿出来运算，把结果再压入栈中，直到遍历完整个数组，栈顶数字即为最终答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        if(tokens.size() == 1) 
            return stoi(tokens[0]);
        stack<int> s;
        for(int i = 0; i < tokens.size(); i ++) {
            if (tokens[i] != "+" && tokens[i] != "-" && tokens[i] != "*" && tokens[i] != "/") {
                s.push(stoi(tokens[i]));
            }
            else {
                int a1 = s.top(); s.pop();
                int a2 = s.top(); s.pop();
                if (tokens[i] == "+") s.push(a2 + a1);
                if (tokens[i] == "-") s.push(a2 - a1);
                if (tokens[i] == "*") s.push(a2 * a1);
                if (tokens[i] == "/") s.push(a2 / a1);
            }
        }
        return s.top();
    }
};

Leetcode151. Reverse Words in a String

Given an input string, reverse the string word by word.

Example 1:

1
2
Input: "the sky is blue"
Output: "blue is sky the"

Example 2:

1
2
3
Input: "  hello world!  "
Output: "world! hello"
Explanation: Your reversed string should not contain leading or trailing spaces.

Example 3:

1
2
3
Input: "a good   example"
Output: "example good a"
Explanation: You need to reduce multiple spaces between two words to a single space in the reversed string.

我自己的复杂度超级高：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    string reverseWords(string s) {
        if(s == "")
            return "";
        string ans = "";
        int p2 = s.length()-1;
        while(p2 >= 0) {
            string temp;
            while(p2 >= 0 && s[p2] == ' ') {
                p2 --;
            }
            while(p2 >= 0 && s[p2] != ' ')
                temp = s[p2--] + temp;
            ans = ans + temp + " ";
            p2 --;
        }
        int i, j;
        for(i = ans.length()-1, j = 0; i >= 0; i --)
            if(ans[i] == ' ')
                j ++;
            else
                break;
        ans = ans.substr(0, ans.length()-j);
        return ans;
    }
};

先反转，然后逐个单词反转。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Solution {
    public String reverseWords(String s) {
        StringBuilder sb = new StringBuilder(" " + s + " ");
        sb.reverse();
        StringBuilder result = new StringBuilder();
        int begin = 0;
        for (int i = 0; i < sb.length() - 1; i++) {
            char c1 = sb.charAt(i);
            char c2 = sb.charAt(i + 1);
            if (c1 == ' ' && c2 != ' ') {
                begin = i;
            } else if (c1 != ' ' && c2 == ' ') {
                for (int j = i; j >= begin; j--) {
                    result.append(sb.charAt(j));
                }
            }
        }
        
        return result.toString().trim();
    }
}

Leetcode152. Maximum Product Subarray

Given an integer array nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.

Example 1:

1
2
3
Input: [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.

Example 2:

1
2
3
Input: [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.

这道题属于动态规划的题型，之前常见的是Maximum SubArray，现在是Product Subarray，不过思想是一致的。
当然不用动态规划，常规方法也是可以做的，但是时间复杂度过高（TimeOut），像下面这种形式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 思路：用两个指针来指向字数组的头尾
int maxProduct(int A[], int n)
{
    assert(n > 0);
    int subArrayProduct = -32768; 
    
    for (int i = 0; i != n; ++ i) {
        int nTempProduct = 1;
        for (int j = i; j != n; ++ j) {
            if (j == i)
                nTempProduct = A[i];
            else
                nTempProduct *= A[j];
            if (nTempProduct >= subArrayProduct)
                 subArrayProduct = nTempProduct;
        }
    }
    return subArrayProduct;
}

用动态规划的方法，就是要找到其转移方程式，也叫动态规划的递推式，动态规划的解法无非是维护两个变量，局部最优和全局最优，我们先来看Maximum SubArray的情况，如果遇到负数，相加之后的值肯定比原值小，但可能比当前值大，也可能小，所以，对于相加的情况，只要能够处理局部最大和全局最大之间的关系即可，对此，写出转移方程式如下：

1
2
local[i + 1] = Max(local[i] + A[i], A[i]);
global[i + 1] = Max(local[i + 1], global[i]);

对应代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int maxSubArray(int A[], int n)
{
    assert(n > 0);
    if (n <= 0)
        return 0;
    int global = A[0];
    int local = A[0];
    
    for(int i = 1; i != n; ++ i) {
        local = MAX(A[i], local + A[i]);
        global = MAX(local, global);
    }
    return global;
}

而对于Product Subarray，要考虑到一种特殊情况，即负数和负数相乘：如果前面得到一个较小的负数，和后面一个较大的负数相乘，得到的反而是一个较大的数，如{2，-3，-7}，所以，我们在处理乘法的时候，除了需要维护一个局部最大值，同时还要维护一个局部最小值，由此，可以写出如下的转移方程式：

1
2
3
max_copy[i] = max_local[i]
max_local[i + 1] = Max(Max(max_local[i] * A[i], A[i]),  min_local * A[i])
min_local[i + 1] = Min(Min(max_copy[i] * A[i], A[i]),  min_local * A[i])

对应代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#define MAX(x,y) ((x)>(y)?(x):(y))
#define MIN(x,y) ((x)<(y)?(x):(y))

int maxProduct1(int A[], int n)
{
    assert(n > 0);
    if (n <= 0)
        return 0;

    if (n == 1)
        return A[0];
    int max_local = A[0];
    int min_local = A[0];

    int global = A[0];
    for (int i = 1; i != n; ++ i) {
        int max_copy = max_local;
        max_local = MAX(MAX(A[i] * max_local, A[i]), A[i] * min_local);
        min_local = MIN(MIN(A[i] * max_copy, A[i]), A[i] * min_local);
        global = MAX(global, max_local);
    }
    return global;
}

总结：动态规划题最核心的步骤就是要写出其状态转移方程，但是如何写出正确的方程式，需要我们不断的实践并总结才能达到。

Leetcode153. Find Minimum in Rotated Sorted Array

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

Find the minimum element.

You may assume no duplicate exists in the array.

Example 1:

1
2
Input: [3,4,5,1,2] 
Output: 1

Example 2:

1
2
Input: [4,5,6,7,0,1,2]
Output: 0

没有固定的 target 值比较，而是要跟数组中某个特定位置上的数字比较，决定接下来去哪一边继续搜索。这里用中间的值 nums[mid] 和右边界值 nums[right] 进行比较，若数组没有旋转或者旋转点在左半段的时候，中间值是一定小于右边界值的，所以要去左半边继续搜索，反之则去右半段查找，最终返回 nums[right] 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int findMin(vector<int>& nums) {
        int m = 0, n = nums.size()-1;
        while(m < n) {
            int mid = m + (n - m) / 2;
            if(nums[mid] > nums[n])
                m = mid + 1;
            else
                n = mid;
        }
        return nums[n];
    }
};

Leetcode154. Find Minimum in Rotated Sorted Array II

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

Find the minimum element.

The array may contain duplicates.

Example 1:

1
2
Input: [1,3,5]
Output: 1

Example 2:

1
2
Input: [2,2,2,0,1]
Output: 0

当数组中存在大量的重复数字时，就会破坏二分查找法的机制，将无法取得 O(lgn) 的时间复杂度，又将会回到简单粗暴的 O(n)，比如这两种情况：{2, 2, 2, 2, 2, 2, 2, 2, 0, 1, 1, 2} 和 {2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2}，可以发现，当第一个数字和最后一个数字，还有中间那个数字全部相等的时候，二分查找法就崩溃了，因为它无法判断到底该去左半边还是右半边。这种情况下，将右指针左移一位（或者将左指针右移一位），略过一个相同数字，这对结果不会产生影响，因为只是去掉了一个相同的，然后对剩余的部分继续用二分查找法，在最坏的情况下，比如数组所有元素都相同，时间复杂度会升到 O(n)，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int findMin(vector<int>& nums) {
        int left = 0, right = (int)nums.size() - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > nums[right]) left = mid + 1;
            else if (nums[mid] < nums[right]) right = mid;
            else --right;
        }
        return nums[right];
    }
};

还是可以用分治法 Divide and Conquer 来解，只有在 nums[start] < nums[end] 的时候，才能返回 nums[start]，等于的时候不能返回，比如 [3, 1, 3] 这个数组，或者当 start 等于 end 成立的时候，也可以直接返回 nums[start]，后面的操作跟之前那道题相同，每次将区间 [start, end] 从中间 mid 位置分为两段，分别调用递归函数，并比较返回值，每次取返回值较小的那个即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int findMin(vector<int>& nums) {
        return helper(nums, 0, (int)nums.size() - 1);
    }
    int helper(vector<int>& nums, int start, int end) {
        if (start == end) return nums[start];
        if (nums[start] < nums[end]) return nums[start];
        int mid = (start + end) / 2;
        return min(helper(nums, start, mid), helper(nums, mid + 1, end));
    }
};

Leecode155. Min Stack

Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.

  • push(x) – Push element x onto stack.
  • pop() – Removes the element on top of the stack.
  • top() – Get the top element.
  • getMin() – Retrieve the minimum element in the stack.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Input
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

Output
[null,null,null,null,-3,null,0,-2]

Explanation
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top();    // return 0
minStack.getMin(); // return -2

Constraints: Methods pop, top and getMin operations will always be called on non-empty stacks.

这道最小栈跟原来的栈相比就是多了一个功能，可以返回该栈的最小值。使用两个栈来实现，一个栈来按顺序存储 push 进来的数据，另一个用来存出现过的最小值。代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class MinStack {
public:
    stack<int> s;
    stack<int> s_min;
    
    MinStack() { }
    
    void push(int x) {
        s.push(x);
        if(s_min.empty() || s_min.top() >= x)
            s_min.push(x);
    }
    
    void pop() {
        int temp = s.top();
        s.pop();
        if(!s_min.empty() && temp == s_min.top())
            s_min.pop();
    }
    
    int top() {
        return s.top();
    }
    
    int getMin() {
        return s_min.top();
    }
};

Leetcode157. read N Characters Given Read4

因为是付费的题目，所以只贴一下题解就算了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
/********************************************************************************** 
 * 
 * The API: int read4(char *buf) reads 4 characters at a time from a file.
 * 
 * The return value is the actual number of characters read. 
 * For example, it returns 3 if there is only 3 characters left in the file.
 * 
 * By using the read4 API, implement the function int read(char *buf, int n) 
 * that reads n characters from the file.
 * 
 * Note:
 *   The read function will only be called once for each test case.
 * 
 **********************************************************************************/

// Forward declaration of the read4 API.
int read4(char *buf);

class Solution {
    public:
        /**
         * @param buf Destination buffer
         * @param n   Maximum number of characters to read
         * @return    The number of characters read
         */
        int read(char *buf, int n) {
            srand(time(0));
            if (rand()%2){
                return read1(buf, n);
            }
            return read2(buf, n);
        }

        //read the data in-place. potential out-of-boundary issue
        int read1(char *buf, int n) {
            int len = 0;
            int size = 0;

            // `buf` could be accessed out-of-boundary 
            while(len <=n && (size = read4(buf))>0){
                size = len + size > n ?  n - len : size;
                len += size;
                buf += size;
            }
            return  len;
        }

        //using a temp-buffer to avoid peotential out-of-boundary issue
        int read2(char *buf, int n) {
            char _buf[4];   // the buffer for read4()
            int _n = 0;     // the return for read4()
            int len = 0;    // total buffer read from read4()
            int size = 0;   // how many bytes need be copied from `_buf` to `buf`
            while((_n = read4(_buf)) > 0){
                //check the space of `buf` whether full or not
                size = len + _n > n ? n-len : _n;
                strncpy(buf+len, _buf, size);
                len += size;
                //buffer is full
                if (len>=n){
                    break;
                }
            }
            return len;
        }
};

Leetcode159. Longest Substring with At Most Two Distinct Characters

Given a string s , find the length of the longest substring t that contains at most 2 distinct characters.

Example 1:

1
2
3
Input: "eceba"
Output: 3
Explanation: _t_ is "ece" which its length is 3.

Example 2:

1
2
3
Input: "ccaabbb"
Output: 5
Explanation: _t_ is "aabbb" which its length is 5.

这道题给我们一个字符串，让求最多有两个不同字符的最长子串。那么首先想到的是用 HashMap 来做，HashMap 记录每个字符的出现次数，然后如果 HashMap 中的映射数量超过两个的时候，这里需要删掉一个映射，比如此时 HashMap 中e有2个，c有1个，此时把b也存入了 HashMap，那么就有三对映射了，这时 left 是0，先从e开始，映射值减1，此时e还有1个，不删除，left 自增1。这时 HashMap 里还有三对映射，此时 left 是1，那么到c了，映射值减1，此时e映射为0，将e从 HashMap 中删除，left 自增1，然后更新结果为 i - left + 1，以此类推直至遍历完整个字符串，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
	public:
    int lengthOfLongestSubstringTwoDistinct(string s) {
        int res = 0, left = 0;
        unordered_map<char, int> m;
        for (int i = 0; i < s.size(); ++i) {
            ++m[s[i]];
            while (m.size() > 2) {
                if (--m[s[left]] == 0) m.erase(s[left]);
	                ++left;
            }
            res = max(res, i - left + 1);
        }
        return res;
    }
};

我们除了用 HashMap 来映射字符出现的个数，还可以映射每个字符最新的坐标，比如题目中的例子 “eceba”，遇到第一个e，映射其坐标0，遇到c，映射其坐标1，遇到第二个e时，映射其坐标2，当遇到b时，映射其坐标3，每次都判断当前 HashMap 中的映射数，如果大于2的时候，那么需要删掉一个映射，还是从 left=0 时开始向右找，看每个字符在 HashMap 中的映射值是否等于当前坐标 left，比如第一个e，HashMap 此时映射值为2，不等于 left 的0，那么 left 自增1，遇到c的时候，HashMap 中c的映射值是1，和此时的 left 相同，那么我们把c删掉，left 自增1，再更新结果，以此类推直至遍历完整个字符串，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
	public:
    int lengthOfLongestSubstringTwoDistinct(string s) {
        int res = 0, left = 0;
        unordered_map<char, int> m;
        for (int i = 0; i < s.size(); ++i) {
            m[s[i]] = i;
            while (m.size() > 2) {
                if (m[s[left]] == left) m.erase(s[left]);
                ++left;
            }
            res = max(res, i - left + 1);
        }
        return res;
    }
};

后来又在网上看到了一种解法，这种解法是维护一个 sliding window，指针 left 指向起始位置，right 指向 window 的最后一个位置，用于定位 left 的下一个跳转位置，思路如下：

  • 若当前字符和前一个字符相同，继续循环。
  • 若不同，看当前字符和 right 指的字符是否相同
    • 若相同，left 不变，右边跳到 i - 1
    • 若不同，更新结果，left 变为 right+1，right 变为 i - 1

最后需要注意在循环结束后，还要比较结果 res 和 s.size() - left 的大小，返回大的，这是由于如果字符串是 “ecebaaa”，那么当 left=3 时，i=5,6 的时候，都是继续循环，当i加到7时，跳出了循环，而此时正确答案应为 “baaa” 这4个字符，而我们的结果 res 只更新到了 “ece” 这3个字符，所以最后要判断 s.size() - left 和结果 res 的大小。

另外需要说明的是这种解法仅适用于于不同字符数为2个的情况，如果为k个的话，还是需要用上面两种解法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
	public:
    int lengthOfLongestSubstringTwoDistinct(string s) {
        int left = 0, right = -1, res = 0;
        for (int i = 1; i < s.size(); ++i) {
            if (s[i] == s[i - 1]) continue;
            if (right >= 0 && s[right] != s[i]) {
                res = max(res, i - left);
                left = right + 1;
            }
            right = i - 1;
        }
        return max(s.size() - left, res);
    }
};

Leetcode160. Intersection of Two Linked Lists

Write a program to find the node at which the intersection of two singly linked lists begins.

Example 1:

1
2
3
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
Output: Reference of the node with value = 8
Input Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,0,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.


Example 2:

1
2
3
Input: intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Reference of the node with value = 2
Input Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [0,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.


Example 3:

1
2
3
4
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: null
Input Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.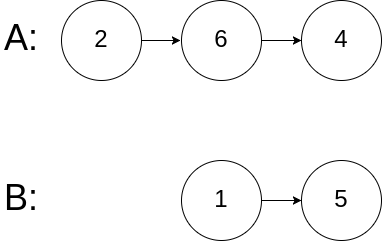

简单做了做，没明白题意，就是求两个链表的交。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode *pa = headA, *pb = headB;
        while(pa != pb) {
            if(pa != NULL)
                pa = pa->next;
            else
                pa = headB;
            if(pb != NULL)
                pb = pb->next;
            else
                pb = headA;
        }
        return pa;
    }
};

解题思路：

方法一

先统计两个链表的长度，再遍历较长的链表，使两个链表等长，之后同时遍历两个链表，如果遍历某个结点时相等，则返回结点值，全部结点遍历完成之后如果未找到交叉结点，则返回NULL

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    if(headA==NULL||headB==NULL)return NULL;
    struct ListNode *p=headA,*q=headB;
    int nA=0,nB=0;//统计两链表长度。
    int i=0;
    while(p!=NULL){
        nA++;
        p=p->next;    
    }
    while(q!=NULL){
        nB++;
        q=q->next;
    }
    p=headA;q=headB;
    if(nA>nB){
        while(i<(nA-nB)){
            i++;
            p=p->next;
        }
    }
    else if(nB>nA){
        while(i<(nB-nA)){
            i++;
            q=q->next;
        }
    }
 
    while(p!=NULL&&q!=NULL){
        if(p==q)return p;
        p=p->next;
        q=q->next;
    }
    return NULL;
}

方法二

将B链表表头链接到A链表表尾，如果A和B有交叉点则形成环形链表，否则是单链表。此时题目就变为环形链表找第一个进入环形的结点(思想方法见142.环形链表)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    
    if(headA == NULL || headB == NULL){
        return NULL;
    }
    struct ListNode* aListTail = headA;//指向A链表尾
    struct ListNode* p = headA->next;//工作指针
    
    while(p != NULL){
        aListTail = aListTail->next;
        p = p->next;
    }
    aListTail->next = headB;
    //使用"142.环形链表II"的思想和方法
    struct ListNode* slow = headA,*fast = headA;
    p = headA;
    while(fast != NULL && fast->next != NULL){
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast){
            while(p != slow){
                p = p->next;
                slow = slow->next;
            }
            aListTail->next = NULL;
            return p;
        }
    }
    aListTail->next = NULL;
    return NULL;
}

方法三

此方法可以想象成是把A链表链接到B链表之后，并且B链表连接到A链表之后，此时A与B变成两个长度相等的大链表，同时遍历两个大链表，第一个相同结点就是交叉结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    if(headA == NULL || headB == NULL){
        return NULL;
    }
    //工作指针
    struct ListNode* p = headA;
    struct ListNode* q = headB;
    
    while(p != q){
        p = p == NULL ? headB : p->next;
        q = q == NULL ? headA : q->next;
    }
    
    return p;
}

Leetcode162. Find Peak Element

A peak element is an element that is greater than its neighbors. Given an input array nums, where nums[i] ≠ nums[i+1], find a peak element and return its index. The array may contain multiple peaks, in that case return the index to any one of the peaks is fine.

You may imagine that nums[-1] = nums[n] = -∞.

Example 1:

1
2
3
Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.

Example 2:

1
2
3
4
Input: nums = [1,2,1,3,5,6,4]
Output: 1 or 5 
Explanation: Your function can return either index number 1 where the peak element is 2, 
             or index number 5 where the peak element is 6.

由于题目中提示了要用对数级的时间复杂度，那么我们就要考虑使用类似于二分查找法来缩短时间，由于只是需要找到任意一个峰值，那么我们在确定二分查找折半后中间那个元素后，和紧跟的那个元素比较下大小，如果大于，则说明峰值在前面，如果小于则在后面。这样就可以找到一个峰值了，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int left = 0, right = nums.size()-1;
        while(left < right) {
            int mid = left + (right - left) / 2;
            if(nums[mid] >= nums[mid+1])
                right = mid;
            else
                left = mid + 1;
        }
        return right;
    }
};

leetcode165. Compare Version Numbers

Given two version numbers, version1 and version2, compare them.

Version numbers consist of one or more revisions joined by a dot ‘.’. Each revision consists of digits and may contain leading zeros. Every revision contains at least one character. Revisions are 0-indexed from left to right, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example 2.5.33 and 0.1 are valid version numbers.

To compare version numbers, compare their revisions in left-to-right order. Revisions are compared using their integer value ignoring any leading zeros. This means that revisions 1 and 001 are considered equal. If a version number does not specify a revision at an index, then treat the revision as 0. For example, version 1.0 is less than version 1.1 because their revision 0s are the same, but their revision 1s are 0 and 1 respectively, and 0 < 1.

Return the following:

  • If version1 < version2, return -1.
  • If version1 > version2, return 1.
  • Otherwise, return 0.

Example 1:

1
2
3
Input: version1 = "1.01", version2 = "1.001"
Output: 0
Explanation: Ignoring leading zeroes, both "01" and "001" represent the same integer "1".

Example 2:

1
2
3
Input: version1 = "1.0", version2 = "1.0.0"
Output: 0
Explanation: version1 does not specify revision 2, which means it is treated as "0".

Example 3:

1
2
3
Input: version1 = "0.1", version2 = "1.1"
Output: -1
Explanation: version1's revision 0 is "0", while version2's revision 0 is "1". 0 < 1, so version1 < version2.

Example 4:

1
2
Input: version1 = "1.0.1", version2 = "1"
Output: 1

Example 5:

1
2
Input: version1 = "7.5.2.4", version2 = "7.5.3"
Output: -1

由于两个版本号所含的小数点个数不同，有可能是1和1.1.1比较，还有可能开头有无效0，比如01和1就是相同版本，还有可能末尾无效0，比如1.0和1也是同一版本。对于没有小数点的数字，可以默认为最后一位是小数点，而版本号比较的核心思想是相同位置的数字比较，比如题目给的例子，1.2和13.37比较，我们都知道应该显示1和13比较，13比1大，所以后面的不用再比了，再比如1.1和1.2比较，前面都是1，则比较小数点后面的数字。那么算法就是每次对应取出相同位置的小数点之前所有的字符，把他们转为数字比较，若不同则可直接得到答案，若相同，再对应往下取。如果一个数字已经没有小数点了，则默认取出为0，和另一个比较，这样也解决了末尾无效0的情况。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int compareVersion(string version1, string version2) {
        int len1 = version1.length(), len2 = version2.length();
        int i1 = 0, i2 = 0;
        int temp1, temp2;
        while(i1 < len1 || i2 < len2) {
            temp1 = 0;
            while(i1 < len1 && version1[i1] != '.') {
                temp1 = temp1 * 10 + (version1[i1] - '0');
                i1 ++;
            }
            temp2 = 0;
            while(i2 < len2 && version2[i2] != '.') {
                temp2 = temp2 * 10 + (version2[i2] - '0');
                i2 ++;
            }
            printf("%d %d\n", temp1, temp2);
            if(temp1 > temp2)
                return 1;
            else if(temp1 < temp2)
                return -1;
            i1 ++;
            i2 ++;    
        }
        if(temp1 > temp2)
            return 1;
        else if(temp1 < temp2)
            return -1;
        else
            return 0;
    }
};

由于这道题我们需要将版本号以’.’分开，那么我们可以借用强大的字符串流stringstream的功能来实现分段和转为整数，使用这种方法写的代码很简洁，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int compareVersion(string version1, string version2) {
        istringstream v1(version1 + "."), v2(version2 + ".");
        int d1 = 0, d2 = 0;
        char dot = '.';
        while (v1.good() || v2.good()) {
            if (v1.good()) v1 >> d1 >> dot;
            if (v2.good()) v2 >> d2 >> dot;
            if (d1 > d2) return 1;
            else if (d1 < d2) return -1;
            d1 = d2 = 0;
        }
        return 0;
    }
};

最后我们来看一种用C语言的字符串指针来实现的方法，这个方法的关键是用到将字符串转为长整型的strtol函数，关于此函数的用法可以参见我的另一篇博客strtol 函数用法。参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int compareVersion(string version1, string version2) {
        int res = 0;
        char *v1 = (char*)version1.c_str(), *v2 = (char*)version2.c_str();
        while (res == 0 && (*v1 != '\0' || *v2 != '\0')) {
            long d1 = *v1 == '\0' ? 0 : strtol(v1, &v1, 10);
            long d2 = *v2 == '\0' ? 0 : strtol(v2, &v2, 10);
            if (d1 > d2) return 1;
            else if (d1 < d2) return -1;
            else {
                if (*v1 != '\0') ++v1;
                if (*v2 != '\0') ++v2;
            }
        }
        return res;
    }
};

Leetcode166. Fraction to Recurring Decimal

Given two integers representing the numerator and denominator of a fraction, return the fraction in string format.

If the fractional part is repeating, enclose the repeating part in parentheses.

If multiple answers are possible, return any of them.

Example 1:

1
2
Input: numerator = 1, denominator = 2
Output: "0.5"

Example 2:

1
2
Input: numerator = 2, denominator = 1
Output: "2"

Example 3:

1
2
Input: numerator = 2, denominator = 3
Output: "0.(6)"

Example 4:

1
2
Input: numerator = 4, denominator = 333
Output: "0.(012)"

Example 5:

1
2
Input: numerator = 1, denominator = 5
Output: "0.2"

由于还存在正负情况，处理方式是按正数处理，符号最后在判断，那么我们需要把除数和被除数取绝对值，那么问题就来了：由于整型数INT的取值范围是-2147483648～2147483647，而对-2147483648取绝对值就会超出范围，所以我们需要先转为long long型再取绝对值。那么怎么样找循环呢，肯定是再得到一个数字后要看看之前有没有出现这个数。为了节省搜索时间，我们采用哈希表来存数每个小数位上的数字。还有一个小技巧，由于我们要算出小数每一位，采取的方法是每次把余数乘10，再除以除数，得到的商即为小数的下一位数字。等到新算出来的数字在之前出现过，则在循环开始出加左括号，结束处加右括号。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    string fractionToDecimal(int numerator, int denominator) {
        string res = "";
        int l1 = numerator >= 0 ? 1 : -1;
        int l2 = denominator >= 0 ? 1 : -1;
        long long num = abs((long long)numerator);
        long long den = abs((long long)denominator);
        long long out = num / den;
        long long remain = num % den;
        if(numerator == 0)
            return "0";
        if(l1 * l2 == -1)
            res = "-";
        res = res + to_string(out);
        if(remain == 0)
            return res;
        res = res + ".";
        string s = "";
        unordered_map<int, int> m;
        int pos = 0;
        while(remain != 0) {
            if(m.find(remain) != m.end()) {
                s.insert(m[remain], "(");
                s = s + ")";
                return res + s;
            }
            m[remain] = pos;
            out = (remain * 10) / den;
            remain = (remain * 10) % den;
            s = s + to_string(out);
            
            pos ++;
        }
        return res + s;
    }
};

Leetcode167. Two Sum II - Input array is sorted

Given an array of integers that is already sorted in ascending order, find two numbers such that they add up to a specific target number.

The function twoSum should return indices of the two numbers such that they add up to the target, where index1 must be less than index2.

Note:

Your returned answers (both index1 and index2) are not zero-based.
You may assume that each input would have exactly one solution and you may not use the same element twice.

Example:

1
2
3
Input: numbers = [2,7,11,15], target = 9
Output: [1,2]
Explanation: The sum of 2 and 7 is 9. Therefore index1 = 1, index2 = 2.

乍一看来，Two Sum II 这道题和 Two Sum 问题一样平平无奇。然而，这道题实际上内藏玄机，加上了数组有序的变化之后，它就换了一套解法。

如果你直接翻答案的话，会发现这就是一道普通的双指针解法。两个指针，O(n)的时间。但是，如果你只看答案，没有理解背后的道理，就会陷入一看就会，一做就跪的困境。

实际上，在这个双指针解法背后蕴含的是缩减搜索空间的通用思想。那么，这篇文章将会为你细细讲述这个解法背后的道理，让你能真正地理解这道经典题目。同时，要做到下次遇到同类题目时，可以快速想到这种解法。

看到有序这个条件，你可能首先想到的是二分查找。但是仔细一想，需要固定一个数，对另一个数进行二分查找，这样时间复杂度是O(nlogn) ，显然不行。在不排序的情况下都做得到O(n)时间、O(n)空间。那么我们的目标只可能是：O(n)的时间、O(1)的空间！

代码的逻辑很简单，就轻轻巧巧地使用了两个指针，一个只向左移动，一个只向右移动。走完一趟，就得到了答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int left=0,right=numbers.size()-1;
        vector<int> result;
        while(left != right) {
            if(numbers[left] + numbers[right] > target) {
                right --;
            }
            else if(numbers[left] + numbers[right] < target) {
                left ++;
            }
            else {
                result.push_back(left+1);
                result.push_back(right+1);
                break;
            }
        }
        return result;
    }
};

双指针解法的正确性解释
我们考虑两个指针指向的数字，A[i] 和 A[j]。由于数组是有序的，在一开始，A[i] 是数组中最小的数字，A[j] 是最大的数字。我们将 A[i] + A[j] 与目标和 t`Arget 进行比较，则可能有两种情况：

A[i] + A[j] 大了。这时候，我们应该去找更小的两个数。由于 A[i] 已经是最小的元素了，将任何 A[i] 以外的数跟 A[j] 相加的话，和只会更大。因此 A[j] 一定不能构成正确的解，于是将 j 向左移动一格，排除 A[j]。
A[i] + A[j] 小了。这时候，我们应该去找更大的两个数。由于 A[j] 已经是最大的元素了，将任何 A[j] 以外的数跟 A[i] 相加的话，和只会更小。因此 A[i] 一定不能构成正确的解，于是将 i 向右移动一格，排除 A[i]。
而第一步排除掉最左或最后的一个数后，我们再看子数组 A[i..j] ，其中 A[i] 又是最小的数字，A[j] 又是最大的数字。我们可以继续进行这样的排除。以此类推，进行 步，就可以排除掉所有可能的情况。

可以看到，无论 A[i] + A[j] 的结果是大了还是小了，我们都可以排除掉其中一个数。这样的排除法和二分搜索很相似。二分搜索通过每次排除一半的元素来减少比较的次数；而这道题的方法通过每次排除一个元素来减少比较的次数。两者又恰好都是利用了数组有序这个性质。

说到这里，这个解法的原理已经揭开一半了。接下来，我们再用更直观的方式，从搜索空间的角度真正地理解这道题。

在这道题中，我们要寻找的是符合条件的一对下标(i, j)，它们需要满足的约束条件是：

  • i、j都是合法的下标
  • i < j（题目要求）

而我们希望从中找到满足 A[i] + A[j] == target 的下标。以n=8为例，这时候全部的搜索空间是：

由于i、j的约束条件的限制，搜索空间是白色的倒三角部分。可以看到，搜索空间的大小是O(n^2)数量级的。如果用暴力解法求解，一次只检查一个单元格，那么时间复杂度一定是O(n^2)。而更优的算法，则可以在一次操作内排除掉多个不合格的单元格，从而快速削减搜索空间，定位问题的解。

那么我们来看看，本题的双指针解法是如何削减搜索空间的。一开始，我们检查右上方单元格 ，即计算 A[0] + A[7] ：

假设A[0] + A[7]小于目标和，由于 A[7] 已经是最大的数，我们可以推出 A[0] + A[6] 、A[0] + A[5]、……、A[0] + A[1] 也都小于目标和，这些都是不合要求的解，可以一次排除，如下图所示。这相当于排除i=0的全部解，削减了一行的搜索空间，对应双指针解法中的 i++。

以此类推，每次会削减一行或一列的搜索空间，经过n步以后，一定能检查完所有的可能性。

这种方法的运行还是较慢， 只比10.34%的C++要快。

Leetcode168. Excel Sheet Column Title

Given a positive integer, return its corresponding column title as appear in an Excel sheet.

For example:

1
2
3
4
5
6
7
8
1 -> A
2 -> B
3 -> C
...
26 -> Z
27 -> AA
28 -> AB 
...

Example 1:

1
2
Input: 1
Output: "A"

Example 2:

1
2
Input: 28
Output: "AB"

Example 3:

1
2
Input: 701
Output: "ZY"

Excel序是这样的：AZ, AAZZ, AAA~ZZZ, ……本质上就是将一个10进制数转换为一个26进制的数。注意：由于下标从1开始而不是从0开始，因此要减一操作。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    string convertToTitle(int n) {
        string result = "";
        while(n>0) {
            result = (char)('A'+ (n-1)%26) + result;
            n = (n-1) / 26;
        }
        return result;
    }
};

Leetcode169. Majority Element

Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times.

You may assume that the array is non-empty and the majority element always exist in the array.

Example 1:

1
2
Input: [3,2,3]
Output: 3

Example 2:

1
2
Input: [2,2,1,1,1,2,2]
Output: 2

最简单的做法就是先排序，然后返回（n / 2）个元素，但是这样太慢了。

1
2
3
4
5
6
7
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        return nums[nums.size()/2];
    }
};

有一种比较巧妙的做法，用的是Boyer-Moore’s Algorithm，用count记录当前的m的个数，如果m为0了说明这个数不是出现最多的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int m = nums[0], i, count = 1;
        int numsSize = nums.size();
        for (i = 1; i < numsSize; i ++)
        {
            if (count == 0){ 
                m = nums[i];
                count ++;
            }
            else if (m == nums[i])
                count++;
            else 
                count--;
        }
    return m;
    }
};

Leetcode170. Two Sum III - Data structure design

Design and implement a TwoSum class. It should support the following operations: add and find.

add - Add the number to an internal data structure.
find - Find if there exists any pair of numbers which sum is equal to the value.

Example 1:

1
2
3
add(1); add(3); add(5);
find(4) -> true
find(7) -> false

Example 2:

1
2
3
add(3); add(1); add(2);
find(3) -> true
find(6) -> false

让我们设计一个 Two Sum 的数据结构。先来看用 HashMap 的解法，把每个数字和其出现的次数建立映射，然后遍历 HashMap，对于每个值，先求出此值和目标值之间的差值t，然后需要分两种情况来看，如果当前值不等于差值t，那么只要 HashMap 中有差值t就返回 True，或者是当差值t等于当前值时，如果此时 HashMap 的映射次数大于1，则表示 HashMap 中还有另一个和当前值相等的数字，二者相加就是目标值，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class TwoSum {
public:
    void add(int number) {
        ++m[number];
    }
    bool find(int value) {
        for (auto a : m) {
            int t = value - a.first;
            if ((t != a.first && m.count(t)) || (t == a.first && a.second > 1)) {
                return true;
            }
        }
        return false;
    }
private:
    unordered_map<int, int> m;
};

Leetcode171. Excel Sheet Column Number

Given a column title as appear in an Excel sheet, return its corresponding column number.

Example 1:

1
2
Input: "A"
Output: 1

Example 2:

1
2
Input: "AB"
Output: 28

Example 3:

1
2
Input: "ZY"
Output: 701

给一个excel表中的列标，把它转换成十进制的数，简单，但是要用long才能过。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int titleToNumber(string s) {
        int length = s.length();
        long result = 0;
        long temp = 1;
        for(int i = length - 1; i >= 0; i--) {
            result += (s[i] - 'A' + 1) * temp;
            temp *= 26;
        }
        return result;
    }
};

简单做法:

1
2
3
4
5
6
7
8
9
public int titleToNumber(String s) {
        if (s.length() == 0 || s == null)
            return 0;
        int sum = 0;
        for (int i = 0; i < s.length(); i++) {
            sum = sum * 26 + (s.charAt(i) - 'A' + 1);
        }
        return sum;
    }

Leetcode172. Factorial Trailing Zeroes

Given an integer n, return the number of trailing zeroes in n!.

Example 1:

1
2
3
Input: 3
Output: 0
Explanation: 3! = 6, no trailing zero.

Example 2:

1
2
3
Input: 5
Output: 1
Explanation: 5! = 120, one trailing zero.

让求一个数的阶乘末尾0的个数，也就是要找乘数中 10 的个数，而 10 可分解为2和5，而2的数量又远大于5的数量（比如1到 10 中有2个5，5个2），那么此题即便为找出5的个数。仍需注意的一点就是，像 25，125，这样的不只含有一个5的数字需要考虑进去

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int trailingZeroes(int n) {
        int res = 0;
        while(n) {
            res += n/5;
            n /= 5;
        }
        return res;
    }
};

Leetcode173. Binary Search Tree Iterator

Implement an iterator over a binary search tree (BST). Your iterator will be initialized with the root node of a BST.

Calling next() will return the next smallest number in the BST.

Example:

1
2
3
4
5
6
7
8
9
10
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // return 3
iterator.next();    // return 7
iterator.hasNext(); // return true
iterator.next();    // return 9
iterator.hasNext(); // return true
iterator.next();    // return 15
iterator.hasNext(); // return true
iterator.next();    // return 20
iterator.hasNext(); // return false

关键在于理解inorder的stack代表了什么含义，为什么要用到这个stack：stack的存在是为了我们找回来时的路。但是不一定立刻就去找到successor，如果call到了，再沿着栈顶元素去找。而做法就是首先将最左边的路径一路推进栈，每次从栈中pop来提取next。提取之后还要保证，如果栈顶有right，那么一路将top -> right 的left推入栈；如果没有right，栈顶本身就是successor。这样做完这一系列检查后，栈顶元素就可以保证是successor。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class BSTIterator {
public:
    stack<TreeNode*> s;
    
    BSTIterator(TreeNode* root) {
        //s = new stack<TreeNode*>();
        while(root != NULL) {
            s.push(root);
            root = root->left;
        }
    }
    
    /** @return the next smallest number */
    int next() {
        TreeNode* cur = s.top();
        s.pop();
        TreeNode *temp = cur->right;
        while(temp) {
            s.push(temp);
            temp = temp->left;
        }
        return cur->val;
    }
    
    /** @return whether we have a next smallest number */
    bool hasNext() {
        return !s.empty();
    }
};

Leetcode175. Combine Two Tables

Table: Person
+————-+———+
| Column Name | Type |
+————-+———+
| PersonId | int |
| FirstName | varchar |
| LastName | varchar |
+————-+———+
PersonId is the primary key column for this table.

Table: Address
+————-+———+
| Column Name | Type |
+————-+———+
| AddressId | int |
| PersonId | int |
| City | varchar |
| State | varchar |
+————-+———+
AddressId is the primary key column for this table.

Write a SQL query for a report that provides the following information for each person in the Person table, regardless if there is an address for each of those people:

1
FirstName, LastName, City, State

Person表左连接 Address表查询,不能用条件查询,因为不管该人是否有地址

1
2
3
# Write your MySQL query statement below
select FirstName, LastName, City, State
from Person left join Address on Person.PersonId=Address.PersonId

Leetcode176. Second Highest Salary

Write a SQL query to get the second highest salary from the Employee table.

1
2
3
4
5
6
7
+----+--------+
| Id | Salary |
+----+--------+
| 1  | 100    |
| 2  | 200    |
| 3  | 300    |
+----+--------+

For example, given the above Employee table, the query should return 200 as the second highest salary. If there is no second highest salary, then the query should return null.

1
2
3
4
5
+---------------------+
| SecondHighestSalary |
+---------------------+
| 200                 |
+---------------------+

刚开始的想法是使用ORDER BY指令排序，然后通过LIMIT输出第二行数据就可以了，但是这样做会有两个bug，一个是如果存在两个Id有相同的Salary并且都为最高，则我们的输出还是最高Salary；另一个就是这样无法满足题目要求的If there is no second highest salary, then the query should return null。这是因为SELECT指令会在没有满足条件的输出时，会输出空。

所以我们应该使用MAX()函数，其满足没有记录时输出null的条件。

题解：

1
2
3
# Write your MySQL query statement below
SELECT MAX(Salary) AS SecondHighestSalary FROM Employee 
WHERE Salary < (SELECT MAX(Salary) FROM Employee);

Leetcode177. Nth Highest Salary

Write a SQL query to get the nth highest salary from the Employee table.

1
2
3
4
5
6
7
+----+--------+
| Id | Salary |
+----+--------+
| 1  | 100    |
| 2  | 200    |
| 3  | 300    |
+----+--------+

For example, given the above Employee table, the nth highest salary where n = 2 is 200. If there is no nth highest salary, then the query should return null.

1
2
3
4
5
+------------------------+
| getNthHighestSalary(2) |
+------------------------+
| 200                    |
+------------------------+

找出表中工资第n高的

order by,limit 及变量的使用

1
2
3
4
5
6
7
8
9
CREATE FUNCTION getNthHighestSalary(N INT) RETURNS INT
BEGIN
      declare m int;
      set m = n - 1;
  RETURN (
      # Write your MySQL query statement below.
      select distinct salary from Employee order by salary desc limit m, 1
  );
END

Leetcode178. Rank Scores

Write a SQL query to rank scores. If there is a tie between two scores, both should have the same ranking. Note that after a tie, the next ranking number should be the next consecutive integer value. In other words, there should be no “holes” between ranks.

1
2
3
4
5
6
7
8
9
10
+----+-------+
| Id | Score |
+----+-------+
| 1  | 3.50  |
| 2  | 3.65  |
| 3  | 4.00  |
| 4  | 3.85  |
| 5  | 4.00  |
| 6  | 3.65  |
+----+-------+

For example, given the above Scores table, your query should generate the following report (order by highest score):

1
2
3
4
5
6
7
8
9
10
+-------+------+
| Score | Rank |
+-------+------+
| 4.00  | 1    |
| 4.00  | 1    |
| 3.85  | 2    |
| 3.65  | 3    |
| 3.65  | 3    |
| 3.50  | 4    |
+-------+------+

这道题给了我们一个分数表，让我们给分数排序，要求是相同的分数在相同的名次，下一个分数在相连的下一个名次，中间不能有空缺数字，解题的思路是对于每一个分数，找出表中有多少个大于或等于该分数的不同的分数，然后按降序排列即可，参见代码如下：

1
2
3
SELECT Score, 
(SELECT COUNT(DISTINCT Score) FROM Scores WHERE Score >= s.Score) Rank 
FROM Scores s ORDER BY Score DESC;

Leetcode179. Largest Number

Given a list of non negative integers, arrange them such that they form the largest number.

Example 1:

1
2
Input: [10,2]
Output: "210"

Example 2:

1
2
Input: [3,30,34,5,9]
Output: "9534330"

Note: The result may be very large, so you need to return a string instead of an integer.

这道题给了我们一个数组，让将其拼接成最大的数，那么根据题目中给的例子来看，主要就是要给数组进行排序，但是排序方法不是普通的升序或者降序，因为9要排在最前面，而9既不是数组中最大的也不是最小的，所以要自定义排序方法。对于两个数字a和b来说，如果将其都转为字符串，如果 ab > ba，则a排在前面，比如9和34，由于 934>349，所以9排在前面，再比如说 30 和3，由于 303<330，所以3排在 30 的前面。按照这种规则对原数组进行排序后，将每个数字转化为字符串再连接起来就是最终结果。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    string largestNumber(vector<int>& nums) {
        string res;
        sort(nums.begin(), nums.end(), [](int a, int b) {
           return to_string(a) + to_string(b) > to_string(b) + to_string(a); 
        });
        for (int i = 0; i < nums.size(); ++i) {
            res += to_string(nums[i]);
        }
        return res[0] == '0' ? "0" : res;
    }
};

Leetcode180. Consecutive Numbers

Table: Logs

1
2
3
4
5
6
+-------------+---------+
| Column Name | Type    |
+-------------+---------+
| id          | int     |
| num         | varchar |
+-------------+---------+

id is the primary key for this table.

Write an SQL query to find all numbers that appear at least three times consecutively.

Return the result table in any order.

The query result format is in the following example:

Logs table:

1
2
3
4
5
6
7
8
9
10
11
+----+-----+
| Id | Num |
+----+-----+
| 1  | 1   |
| 2  | 1   |
| 3  | 1   |
| 4  | 2   |
| 5  | 1   |
| 6  | 2   |
| 7  | 2   |
+----+-----+

Result table:

1
2
3
4
5
+-----------------+
| ConsecutiveNums |
+-----------------+
| 1               |
+-----------------+

1 is the only number that appears consecutively for at least three times.

1
2
3
4
5
6
7
8
# Write your MySQL query statement below

select distinct l1.num as ConsecutiveNums
from logs l1, logs l2, logs l3
where l1.id = l2.id-1 
and l2.id = l3.id-1
and l1.num = l2.num 
and l2.num = l3.num;

Leetcode181. Employees Earning More Than Their Managers

The Employee table holds all employees including their managers. Every employee has an Id, and there is also a column for the manager Id.

1
2
3
4
5
6
7
8
+----+-------+--------+-----------+
| Id | Name  | Salary | ManagerId |
+----+-------+--------+-----------+
| 1  | Joe   | 70000  | 3         |
| 2  | Henry | 80000  | 4         |
| 3  | Sam   | 60000  | NULL      |
| 4  | Max   | 90000  | NULL      |
+----+-------+--------+-----------+

Given the Employee table, write a SQL query that finds out employees who earn more than their managers. For the above table, Joe is the only employee who earns more than his manager.

1
2
3
4
5
+----------+
| Employee |
+----------+
| Joe      |
+----------+

自连接，找出比其上司挣得更多的员工。

1
2
3
# Write your MySQL query statement below
select r1.Name as Employee from Employee as r1, Employee as r2 
where r1.ManagerId = r2.Id and r1.Salary > r2.Salary

Leetcode182. Duplicate Emails

Write a SQL query to find all duplicate emails in a table named Person.

1
2
3
4
5
6
7
+----+---------+
| Id | Email   |
+----+---------+
| 1  | a@b.com |
| 2  | c@d.com |
| 3  | a@b.com |
+----+---------+

For example, your query should return the following for the above table:

1
2
3
4
5
+---------+
| Email   |
+---------+
| a@b.com |
+---------+

在表中，可能会包含重复值。这并不成问题，不过，有时您也许希望仅仅列出不同（distinct）的值。关键词 DISTINCT 用于返回唯一不同的值。

1
2
3
# Write your MySQL query statement below
select distinct  r1.Email as Email from Person as r1, Person as r2 
where r1.Email = r2.Email and r1.Id != r2.Id

Leetcode183. Customers Who Never Order

Suppose that a website contains two tables, the Customers table and the Orders table. Write a SQL query to find all customers who never order anything.

Table: Customers.

1
2
3
4
5
6
7
8
+----+-------+
| Id | Name  |
+----+-------+
| 1  | Joe   |
| 2  | Henry |
| 3  | Sam   |
| 4  | Max   |
+----+-------+

Table: Orders.

1
2
3
4
5
6
+----+------------+
| Id | CustomerId |
+----+------------+
| 1  | 3          |
| 2  | 1          |
+----+------------+

Using the above tables as example, return the following:

1
2
3
4
5
6
+-----------+
| Customers |
+-----------+
| Henry     |
| Max       |
+-----------+

使用NOT IN

1
2
3
select Name as Customers
from Customers
where Id not in (select CustomerId from Orders)

使用左外连接 然后使用条件语句

1
2
3
4
5
SELECT C.Name Customers
    FROM Customers C
    LEFT JOIN Orders O
    ON C.Id=O.CustomerId
    WHERE O.CustomerId IS NULL;

Leetcode184. Department Highest Salary

The Employee table holds all employees. Every employee has an Id, a salary, and there is also a column for the department Id.

1
2
3
4
5
6
7
8
9
+----+-------+--------+--------------+
| Id | Name  | Salary | DepartmentId |
+----+-------+--------+--------------+
| 1  | Joe   | 70000  | 1            |
| 2  | Jim   | 90000  | 1            |
| 3  | Henry | 80000  | 2            |
| 4  | Sam   | 60000  | 2            |
| 5  | Max   | 90000  | 1            |
+----+-------+--------+--------------+

The Department table holds all departments of the company.

1
2
3
4
5
6
+----+----------+
| Id | Name     |
+----+----------+
| 1  | IT       |
| 2  | Sales    |
+----+----------+

Write a SQL query to find employees who have the highest salary in each of the departments. For the above tables, your SQL query should return the following rows (order of rows does not matter).

1
2
3
4
5
6
7
+------------+----------+--------+
| Department | Employee | Salary |
+------------+----------+--------+
| IT         | Max      | 90000  |
| IT         | Jim      | 90000  |
| Sales      | Henry    | 80000  |
+------------+----------+--------+

可以将Employee表先按DepartmentId分组然后SELECT出部门id和最大工资作为子查询，然后再两个表JOIN起来查询出需要的信息。代码如下：

1
2
3
4
5
6
SELECT Department.name `Department`, Employee.name `Employee`, Salary
FROM Employee JOIN Department 
ON Employee.DepartmentId = Department.Id
WHERE (Employee.DepartmentId, Salary) IN 
(SELECT DepartmentId, MAX(Salary) 
FROM Employee GROUP BY DepartmentId)

Leetcode185. Department Top Three Salaries

Table: Employee

1
2
3
4
5
6
7
8
+--------------+---------+
| Column Name  | Type    |
+--------------+---------+
| Id           | int     |
| Name         | varchar |
| Salary       | int     |
| DepartmentId | int     |
+--------------+---------+

Id is the primary key for this table.Each row contains the ID, name, salary, and department of one employee.

Table: Department

1
2
3
4
5
6
+-------------+---------+
| Column Name | Type    |
+-------------+---------+
| Id          | int     |
| Name        | varchar |
+-------------+---------+

Id is the primary key for this table. Each row contains the ID and the name of one department.

A company’s executives are interested in seeing who earns the most money in each of the company’s departments. A high earner in a department is an employee who has a salary in the top three unique salaries for that department.

Write an SQL query to find the employees who are high earners in each of the departments.

Return the result table in any order.

The query result format is in the following example:

Employee table:

1
2
3
4
5
6
7
8
9
10
11
+----+-------+--------+--------------+
| Id | Name  | Salary | DepartmentId |
+----+-------+--------+--------------+
| 1  | Joe   | 85000  | 1            |
| 2  | Henry | 80000  | 2            |
| 3  | Sam   | 60000  | 2            |
| 4  | Max   | 90000  | 1            |
| 5  | Janet | 69000  | 1            |
| 6  | Randy | 85000  | 1            |
| 7  | Will  | 70000  | 1            |
+----+-------+--------+--------------+

Department table:

1
2
3
4
5
6
+----+-------+
| Id | Name  |
+----+-------+
| 1  | IT    |
| 2  | Sales |
+----+-------+

Result table:

1
2
3
4
5
6
7
8
9
10
+------------+----------+--------+
| Department | Employee | Salary |
+------------+----------+--------+
| IT         | Max      | 90000  |
| IT         | Joe      | 85000  |
| IT         | Randy    | 85000  |
| IT         | Will     | 70000  |
| Sales      | Henry    | 80000  |
| Sales      | Sam      | 60000  |
+------------+----------+--------+

In the IT department:

  • Max earns the highest unique salary
  • Both Randy and Joe earn the second-highest unique salary
  • Will earns the third-highest unique salary

In the Sales department:

  • Henry earns the highest salary
  • Sam earns the second-highest salary
  • There is no third-highest salary as there are only two employees
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Write your MySQL query statement below
select t2.name  as Department, t1.Employee , t1.salary from 
(
    select e1.id, e1.name as employee, e1.salary, e1.departmentid from Employee  e1
    inner join  Employee e2
    on e1.departmentid = e2.departmentid
    and e1.salary<=e2.salary
    group by e1.id
    having count(distinct(e2.salary))<=3
)
t1
inner join
(select * from Department )t2
on t1.DepartmentId  = t2.id

Leetcode187. Repeated DNA Sequences

The DNA sequence is composed of a series of nucleotides abbreviated as ‘A’, ‘C’, ‘G’, and ‘T’.

For example, “ACGAATTCCG” is a DNA sequence.
When studying DNA, it is useful to identify repeated sequences within the DNA.

Given a string s that represents a DNA sequence, return all the 10-letter-long sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in any order.

Example 1:

1
2
Input: s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
Output: ["AAAAACCCCC","CCCCCAAAAA"]

Example 2:

1
2
Input: s = "AAAAAAAAAAAAA"
Output: ["AAAAAAAAAA"]

哈希表。直接把每个长度为10的字符串的count记下来，然后看计数大于1的子串有哪些。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<string> findRepeatedDnaSequences(string s) {
        map<string, int> m;
        if (s.length() < 10)
            return {};
        for(int i = 0; i <= s.length()-10;i ++) {
            string tmp = s.substr(i, 10);
            if (!m.count(tmp))
                m[tmp] = 1;
            else 
                m[tmp] ++;
        }
        vector<string> v;
        for(pair<string, int> p : m) {
            if (p.second > 1)
                v.push_back(p.first);
        }
        return v;
    }
};

此题由于构成输入字符串的字符只有四种，分别是 A, C, G, T，下面来看下它们的 ASCII 码用二进制来表示：

A: 0100 0001　　C: 0100 0011　　G: 0100 0111　　T: 0101 0100

由于目的是利用位来区分字符，当然是越少位越好，通过观察发现，每个字符的后三位都不相同，故而可以用末尾三位来区分这四个字符。而题目要求是 10 个字符长度的串，每个字符用三位来区分，10 个字符需要30位，在 32 位机上也 OK。为了提取出后 30 位，还需要用个 mask，取值为 0x7ffffff，用此 mask 可取出后27位，再向左平移三位即可。算法的思想是，当取出第十个字符时，将其存在 HashMap 里，和该字符串出现频率映射，之后每向左移三位替换一个字符，查找新字符串在 HashMap 里出现次数，如果之前刚好出现过一次，则将当前字符串存入返回值的数组并将其出现次数加一，如果从未出现过，则将其映射到1。为了能更清楚的阐述整个过程，就用题目中给的例子来分析整个过程：

首先取出前九个字符 AAAAACCCC，根据上面的分析，用三位来表示一个字符，所以这九个字符可以用二进制表示为 001001001001001011011011011，然后继续遍历字符串，下一个进来的是C，则当前字符为 AAAAACCCCC，二进制表示为 001001001001001011011011011011，然后将其存入 HashMap 中，用二进制的好处是可以用一个 int 变量来表示任意十个字符序列，比起直接存入字符串大大的节省了内存空间，然后再读入下一个字符C，则此时字符串为 AAAACCCCCA，还是存入其二进制的表示形式，以此类推，当某个序列之前已经出现过了，将其存入结果 res 中即可，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<string> findRepeatedDnaSequences(string s) {
        if (s.length() <= 10)
            return {};
        vector<string> v;
        int mask = 0x7ffffff, cur = 0;
        unordered_map<int, int> m;
        for (int i = 0; i < 9; i ++)
            cur = (cur << 3) | (s[i] & 7);
        for (int i = 9; i < s.length(); i ++) {
            cur = ((cur & mask)<<3) | (s[i] & 7);
            if (m.count(cur)) {
                if (m[cur] == 1)
                    v.push_back(s.substr(i-9, 10));
                m[cur] ++;
            }
            else
                m[cur] = 1;
        }
        return v;
    }
};

Leetcode189. Rotate Array

Given an array, rotate the array to the right by k steps, where k is non-negative.

Follow up: Try to come up as many solutions as you can, there are at least 3 different ways to solve this problem.
Could you do it in-place with O(1) extra space?

Example 1:

1
2
3
4
5
6
Input: nums = [1,2,3,4,5,6,7], k = 3
Output: [5,6,7,1,2,3,4]
Explanation:
rotate 1 steps to the right: [7,1,2,3,4,5,6]
rotate 2 steps to the right: [6,7,1,2,3,4,5]
rotate 3 steps to the right: [5,6,7,1,2,3,4]

Example 2:

1
2
3
4
5
Input: nums = [-1,-100,3,99], k = 2
Output: [3,99,-1,-100]
Explanation: 
rotate 1 steps to the right: [99,-1,-100,3]
rotate 2 steps to the right: [3,99,-1,-100]

由于提示中要求我们空间复杂度为 O(1)，所以我们不能用辅助数组，上面的思想还是可以使用的，但是写法就复杂的多，而且需要用到很多的辅助变量，我们还是要将 nums[idx] 上的数字移动到 nums[(idx+k) % n] 上去，为了防止数据覆盖丢失，我们需要用额外的变量来保存，这里用了 pre 和 cur，其中 cur 初始化为了数组的第一个数字，然后当然需要变量 idx 标明当前在交换的位置，还需要一个变量 start，这个是为了防止陷入死循环的，初始化为0，一旦当 idx 变到了 strat 的位置，则 start 自增1，再赋值给 idx，这样 idx 的位置也改变了，可以继续进行交换了。举个例子，假如 [1, 2, 3, 4], K=2 的话，那么 idx=0，下一次变为 idx = (idx+k) % n = 2，再下一次又变成了 idx = (idx+k) % n = 0，此时明显 1 和 3 的位置还没有处理过，所以当我们发现 idx 和 start 相等，则二者均自增1，那么此时 idx=1，下一次变为 idx = (idx+k) % n = 3，就可以交换完所有的数字了。

因为长度为n的数组只需要更新n次，所以我们用一个 for 循环来处理n次。首先 pre 更新为 cur，然后计算新的 idx 的位置，然后将 nums[idx] 上的值先存到 cur 上，然后把 pre 赋值给 nums[idx]，这相当于把上一轮的 nums[idx] 赋给了新的一轮，完成了数字的交换，然后 if 语句判断是否会变到处理过的数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        if (nums.empty() || (k %= nums.size()) == 0) return;
        int temp;
        int length = nums.size();
        int idx = 0, start = 0, cur = nums[0], pre = -1;
        for(int i = 0; i < length; i ++) {
            pre = cur;
            idx = (idx + k) % length;
            cur = nums[idx];
            nums[idx] = pre;
            if (idx == start) {
                idx = ++start;
                cur = nums[idx];
            }
        }
    }
};

这道题其实还有种类似翻转字符的方法，思路是先把前 n-k 个数字翻转一下，再把后k个数字翻转一下，最后再把整个数组翻转一下:

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        if (nums.empty() || (k %= nums.size()) == 0) return;
        int n = nums.size();
        reverse(nums.begin(), nums.begin() + n - k);
        reverse(nums.begin() + n - k, nums.end());
        reverse(nums.begin(), nums.end());
    }
};

Leetcode190. Reverse Bits

Reverse bits of a given 32 bits unsigned integer.

Example 1:

1
2
3
Input: 00000010100101000001111010011100
Output: 00111001011110000010100101000000
Explanation: The input binary string 00000010100101000001111010011100 represents the unsigned integer 43261596, so return 964176192 which its binary representation is 00111001011110000010100101000000.

Example 2:

1
2
3
Input: 11111111111111111111111111111101
Output: 10111111111111111111111111111111
Explanation: The input binary string 11111111111111111111111111111101 represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is 10111111111111111111111111111111.

把要翻转的数从右向左一位位的取出来，如果取出来的是1，将结果 res 左移一位并且加上1；如果取出来的是0，将结果 res 左移一位，然后将n右移一位即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    uint32_t reverseBits(uint32_t n) {
        int res = 0;
        for(int i = 0; i < 32; i ++) {
            if(n & 1)
                res = (res << 1) + 1;
            else 
                res = res << 1;
            n = n >> 1;
        }
        return res;
    }
};

Leetcode191. Number of 1 Bits

Write a function that takes an unsigned integer and return the number of ‘1’ bits it has (also known as the Hamming weight).

Example 1:

1
2
3
Input: 00000000000000000000000000001011
Output: 3
Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits.

Example 2:

1
2
3
Input: 00000000000000000000000010000000
Output: 1
Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit.

Example 3:

1
2
3
Input: 11111111111111111111111111111101
Output: 31
Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits.

同样的位操作

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int res = 0;
        for(int i = 0; i < 32; i ++) {
            if(n & 1)
                res ++;
            n = n >> 1;
        }
        return res;
    }
};

Leetcode192. Word Frequency

Write a bash script to calculate the frequency of each word in a text file words.txt.

For simplicity sake, you may assume:

  • words.txt contains only lowercase characters and space ‘ ‘ characters.
  • Each word must consist of lowercase characters only.
  • Words are separated by one or more whitespace characters.

Example:

Assume that words.txt has the following content:

1
2
the day is sunny the the
the sunny is is

Your script should output the following, sorted by descending frequency:

1
2
3
4
the 4
is 3
sunny 2
day 1
1
cat words.txt | tr -s ' ' '\n' | sort | uniq -c | sort -r | awk '{ print $2, $1 }'
  • tr -s: 通过目标字符串截取字符串，只保留一个实例（多个空格只算和一个空格等效）
  • sort: 排序，将相同的字符串连续在一起，以便统计相同字符串
  • uniq -c: 过滤重复行，并统计相同的字符串
  • sort -r：逆序排序
  • awk '{print $2,$1}'：格式化输出

Leetcode193. Valid Phone Numbers

Given a text file file.txt that contains list of phone numbers (one per line), write a one liner bash script to print all valid phone numbers.

You may assume that a valid phone number must appear in one of the following two formats: (xxx) xxx-xxxx or xxx-xxx-xxxx. (x means a digit)

You may also assume each line in the text file must not contain leading or trailing white spaces.

Example: Assume that file.txt has the following content:

1
2
3
987-123-4567
123 456 7890
(123) 456-7890

Your script should output the following valid phone numbers:

1
2
987-123-4567
(123) 456-7890

写一个bash命令，用grep加上正则表达式：

1
2
# Read from the file file.txt and output all valid phone numbers to stdout.
grep -e '^[0-9]\{3\}-[0-9]\{3\}-[0-9]\{4\}$' -e '^([0-9]\{3\}) [0-9]\{3\}-[0-9]\{4\}$' file.txt

Leetcode194. Transpose File

Given a text file file.txt, transpose its content.

You may assume that each row has the same number of columns, and each field is separated by the ‘ ‘ character.

Example:

If file.txt has the following content:

1
2
3
name age
alice 21
ryan 30

Output the following:

1
2
name alice ryan
age 21 30

这道题让我们转置一个文件，其实感觉就是把文本内容当做了一个矩阵，每个单词空格隔开看做是矩阵中的一个元素，然后将转置后的内容打印出来。那么我们先来看使用awk关键字的做法，关于awk的介绍可以参见这个帖子。其中NF表示当前记录中的字段个数，就是有多少列，NR表示已经读出的记录数，就是行号，从1开始。那么在这里NF是2，因为文本只有两列，这里面这个for循环还跟我们通常所熟悉for循环不太一样，通常我们以为i只能是1和2，然后循环就结束了，而这里的i实际上遍历的数字为1,2,1,2,1,2，我们可能看到实际上循环了3遍1和2，而行数正好是3，可能人家就是这个机制吧。知道了上面这些，那么下面的代码就不难理解了，遍历过程如下：

i = 1, s = [name]

i = 2, s = [name; age]

i = 1, s = [name alice; age]

i = 2, s = [name alice; age 21]

i = 1, s = [name alice ryan; age 21]

i = 2, s = [name alice ryan; age 21 30]

然后我们再将s中的各行打印出来即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
awk '{
    for (i = 1; i <= NF; ++i) {
        if (NR == 1) s[i] = $i;
        else s[i] = s[i] " " $i;
    }
} END {
    for (i = 1; s[i] != ""; ++i) {
        print s[i];
    }
}' file.txt

Leetcode195. Tenth Line

Given a text file file.txt, print just the 10th line of the file.

Example: Assume that file.txt has the following content:

1
2
3
4
5
6
7
8
9
10
Line 1
Line 2
Line 3
Line 4
Line 5
Line 6
Line 7
Line 8
Line 9
Line 10

Your script should output the tenth line, which is:

1
Line 10

Shell分类的题全部都可以使用awk或者sed等linux命令来完成的，并且使用起来较为简单

awk：

1
awk 'NR == 10' file.txt

NR是awk的一个内置变量，可以理解为第几行。显然这个是非常简单的，输出第10行的内容。

sed：

1
sed -n '10p' file.txt

至于sed和awk其实都一样，不过是换了一种表达方式而已。

也可以使用bash风格来解决。

1
2
3
4
5
6
7
8
9
10
#!/bin/bash
lines=0
while read -r line
do
    let lines=lines+1
    echo "$line"
    if(($lines == 10));then
        echo "$line"
    fi
done<file.txt

由于本身这道题就比较简单，所以也容易理解这段代码。定义一个变量lines用来计算行数，然后使用while read line的一种方法，该方法可以参考while read line 介绍。然后就是每次读取一行内容对lines进行+1，判断是否等于10，等于的话就直接输出。

Leetcode196. Delete Duplicate Emails

Write a SQL query to delete all duplicate email entries in a table named Person, keeping only unique emails based on its smallest Id.

1
2
3
4
5
6
7
+----+------------------+
| Id | Email            |
+----+------------------+
| 1  | john@example.com |
| 2  | bob@example.com  |
| 3  | john@example.com |
+----+------------------+

Id is the primary key column for this table.
For example, after running your query, the above Person table should have the following rows:

1
2
3
4
5
6
+----+------------------+
| Id | Email            |
+----+------------------+
| 1  | john@example.com |
| 2  | bob@example.com  |
+----+------------------+

Note: Your output is the whole Person table after executing your sql. Use delete statement.

1
2
# Write your MySQL query statement below
delete p1 from Person as p1, Person as p2 where p1.Email = p2.Email and p1.Id > p2.Id

Leetcode197. Rising Temperature

Given a Weather table, write a SQL query to find all dates’ Ids with higher temperature compared to its previous (yesterday’s) dates.

1
2
3
4
5
6
7
8
+---------+------------------+------------------+
| Id(INT) | RecordDate(DATE) | Temperature(INT) |
+---------+------------------+------------------+
|       1 |       2015-01-01 |               10 |
|       2 |       2015-01-02 |               25 |
|       3 |       2015-01-03 |               20 |
|       4 |       2015-01-04 |               30 |
+---------+------------------+------------------+

For example, return the following Ids for the above Weather table:

1
2
3
4
5
6
+----+
| Id |
+----+
|  2 |
|  4 |
+----+
1
2
3
4
select a.Id 
from Weather a inner join Weather b 
on b.Date+interval 1 day =a.Date
    where a.Temperature>b.Temperature;
1
2
3
4
select a.Id 
from Weather a inner join Weather b 
on datediff(a.RecordDate, b.RecordDate) = 1 
    where a.Temperature>b.Temperature;

Leetcode198. House Robber

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.

Example 1:

Input: [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
Example 2:

Input: [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.

根据这道题的条件特点：
如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警（即相邻的数字不能同时作为最终求和的有效数字）。

分析
这个条件如果精简掉其他内容，很容易让人联想到奇偶数。这个解法就是从这点出发。
设置两个变量，sumOdd 和 sumEven 分别对数组的奇数和偶数元素求和。

最后比较这两个和谁更大，谁就是最优解。

接下来要解决的就是最优解不是纯奇数和或者偶数和的情况。
这种情况下，最优解可能前半段出现在这边，后半段出现在另一边。
那么只要找到一个时机，当这一段的最优解没有另一边好时，就复制对面的最优解过来。

其实就是比较每个步骤内的奇数偶数和谁大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int rob(vector<int>& nums) {
        int sumEven=0;
        int sumOdd=0;
        for (int i = 0; i < nums.size(); i++)
        {
            if (i % 2 == 0)
            {
                sumEven += nums[i];
                sumEven = max(sumEven,sumOdd);
            }
            else
            {
                sumOdd += nums[i];
                sumOdd = max(sumEven,sumOdd);
            }
        }
        return max(sumOdd, sumEven);
    }
};

Leetcode199. Binary Tree Right Side View

Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.

Example 1:

1
2
Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]

Example 2:

1
2
Input: root = [1,null,3]
Output: [1,3]

这道题要求我们打印出二叉树每一行最右边的一个数字，实际上是求二叉树层序遍历的一种变形，我们只需要保存每一层最右边的数字即可，可以参考我之前的博客 Binary Tree Level Order Traversal 二叉树层序遍历，这道题只要在之前那道题上稍加修改即可得到结果，还是需要用到数据结构队列queue，遍历每层的节点时，把下一层的节点都存入到queue中，每当开始新一层节点的遍历之前，先把新一层最后一个节点值存到结果中，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> rightSideView(TreeNode *root) {
        vector<int> res;
        if (!root) return res;
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            res.push_back(q.back()->val);
            int size = q.size();
            for (int i = 0; i < size; ++i) {
                TreeNode *node = q.front();
                q.pop();
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        return res;
    }
};

Leetcode200. Number of Islands

Given a 2d grid map of ‘1’s (land) and ‘0’s (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:

1
2
3
4
5
6
7
Input:
11110
11010
11000
00000

Output: 1

Example 2:

1
2
3
4
5
6
7
Input:
11000
11000
00100
00011

Output: 3

这道题的主要思路是深度优先搜索。每次走到一个是 1 的格子，就搜索整个岛屿。

网格可以看成是一个无向图的结构，每个格子和它上下左右的四个格子相邻。如果四个相邻的格子坐标合法，且是陆地，就可以继续搜索。

在深度优先搜索的时候要注意避免重复遍历。我们可以把已经遍历过的陆地改成 2，这样遇到 2 我们就知道已经遍历过这个格子了，不进行重复遍历。

每遇到一个陆地格子就进行深度优先搜索，最终搜索了几次就知道有几个岛屿。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    void dfs(vector<vector<char>>& grid, int i, int j) {
        if ( i < 0 || i > grid.size()-1 || j < 0 || j > grid[0].size()-1 || grid[i][j] != '1') 
            return;
        grid[i][j] = '0';
        dfs(grid, i+1, j);
        dfs(grid, i-1, j);
        dfs(grid, i, j+1);
        dfs(grid, i, j-1);
    }
    int numIslands(vector<vector<char>>& grid) {
        if (grid.size() == 0 || grid[0].size() == 0)
            return 0;
        int count = 0;
        for( int i = 0; i < grid.size(); i ++)
            for( int j = 0; j < grid[0].size(); j ++) {
                if (grid[i][j] == '1') {
                    dfs(grid, i, j);
                    count ++;
                }
            }
        return count;
    }
};

Posted on Edited on

Leetcode1002. Find Common Characters

Given an array A of strings made only from lowercase letters, return a list of all characters that show up in all strings within the list (including duplicates). For example, if a character occurs 3 times in all strings but not 4 times, you need to include that character three times in the final answer.

You may return the answer in any order.

Example 1:

Input: [“bella”,”label”,”roller”]
Output: [“e”,”l”,”l”]
Example 2:

Input: [“cool”,”lock”,”cook”]
Output: [“c”,”o”]

Note:

  • 1 <= A.length <= 100
  • 1 <= A[i].length <= 100
  • A[i][j] is a lowercase letter

这个打表要二维打表，第一次的时候没有注意，用了一维的，所以错了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<string> commonChars(vector<string>& A) {
        string s;
        int vis[102][27]={0};
        vector<string> res;
        for(int i=0;i<A.size();i++){
            s = A[i];
            for(int j=0;j<A[i].length();j++){
                vis[i][s[j]-'a']++;
            }
        }
        // 打表，记下来每个string中每个字母出现的次数
        
        for(int i=0;i<26;i++){
            int minn=1000;
            for(int j=0;j<A.size();j++)
		    {
			    if(vis[j][i]<minn)
				    minn=vis[j][i];
    	    }
    	    //看这个字母在每个string中出现的最少次数，
            for(int j=0;j<minn;j++){
		        string s1;
		        s1+=char('a'+i);
                res.push_back(s1);
            }
        }
        return res;
    }
};

Leetcode1003. Check If Word Is Valid After Substitutions

We are given that the string “abc” is valid.

From any valid string V, we may split V into two pieces X and Y such that X + Y (X concatenated with Y) is equal to V. (X or Y may be empty.) Then, X + “abc” + Y is also valid.

If for example S = “abc”, then examples of valid strings are: “abc”, “aabcbc”, “abcabc”, “abcabcababcc”. Examples of invalid strings are: “abccba”, “ab”, “cababc”, “bac”.

Return true if and only if the given string S is valid.

Example 1:

1
2
3
4
5
Input: "aabcbc"
Output: true
Explanation: 
We start with the valid string "abc".
Then we can insert another "abc" between "a" and "bc", resulting in "a" + "abc" + "bc" which is "aabcbc".

Example 2:

1
2
3
4
5
Input: "abcabcababcc"
Output: true
Explanation: 
"abcabcabc" is valid after consecutive insertings of "abc".
Then we can insert "abc" before the last letter, resulting in "abcabcab" + "abc" + "c" which is "abcabcababcc".

Example 3:

1
2
Input: "abccba"
Output: false

Example 4:

1
2
Input: "cababc"
Output: false

Note:

  • 1 <= S.length <= 20000
  • S[i] is ‘a’, ‘b’, or ‘c’

使用 vector 来模拟栈, 当遍历访问到 c 时, 需要判断 stack 中是否已经有 a 和 b 的存在.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool isValid(string s) {
        vector<char> v;
        v.resize(20000);
        int p = 0;
        for (char c : s) {
            if (c == 'c') {
                if (!(p > 0 && v[p-1] == 'b') || !(p > 1 && v[p-2] == 'a'))  
                    return false;
                p -= 2;
            }
            else {
                v[p] = c;
                p ++;
            }
        }
        return p == 0;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    bool isValid(string s) {
        stack<char> st;
        int n = s.size();
        for(int i = 0; i < n; i++)
        {
            if(s[i] == 'c')
            {
                if(st.empty() || st.top() != 'b')
                    return false;
                st.pop();
                if(st.empty() || st.top() != 'a')
                    return false;
                st.pop();   
            }
            else if(s[i] == 'b')
            {
                if(st.empty() || st.top() != 'a')
                    return false;
                st.push(s[i]);
            }
            else
                st.push(s[i]);
        }
        return st.empty();
    }
};

Leetcode1004. Max Consecutive Ones III

Given an array A of 0s and 1s, we may change up to K values from 0 to 1.

Return the length of the longest (contiguous) subarray that contains only 1s.

Example 1:

1
2
3
4
5
Input: A = [1,1,1,0,0,0,1,1,1,1,0], K = 2
Output: 6
Explanation:
[1,1,1,0,0,1,1,1,1,1,1]
Bolded numbers were flipped from 0 to 1.  The longest subarray is underlined.

Example 2:

1
2
3
4
5
Input: A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
Output: 10
Explanation:
[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
Bolded numbers were flipped from 0 to 1.  The longest subarray is underlined.

Note:

  • 1 <= A.length <= 20000
  • 0 <= K <= A.length
  • A[i] is 0 or 1

一个由0和1组成的数组，最多反转k个元素，问能够形成的最长的1序列是多长。这个是滑动窗口的题。对数组进行遍历，如果遇到0，就先把它反转，统计被反转的0的个数，如果反转了0之后，发现反转多了，就移动窗口（left++），直到反转的0小于等于k个，再计算窗口的大小。

用个变量 cnt 记录当前将0变为1的个数，在遍历数组的时候，若遇到了0，则 cnt 自增1。若此时 cnt 大于K了，说明该缩小窗口了，用个 while 循环，若左边界为0，移除之后，此时 cnt 应该自减1，left 自增1，每次用窗口大小更新结果 res 即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int longestOnes(vector<int>& nums, int k) {
        int left = 0;
        int cnt = 0, res = 0, len = nums.size();
        for(int i = 0; i < len; i ++) {
            if (nums[i] == 0)
                cnt ++;
            while(cnt > k) {
                if (nums[left] == 0)
                    cnt --;
                left ++;
            }
            res = max(res, i - left + 1);
        }
        return res;
    }
};

我们也可以写的更简洁一些，不用 while 循环，但是还是用的滑动窗口的思路，其中i表示左边界，j为右边界。在遍历的时候，若遇到0，则K自减1，若K小于0了，且 A[i] 为0，则K自增1，且i自增1，最后返回窗口的大小即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int longestOnes(vector<int>& A, int K) {
        int n = A.size(), i = 0, j = 0;
        for (; j < n; ++j) {
            if (A[j] == 0) --K;
            if (K < 0 && A[i++] == 0) ++K;
        }
        return j - i;
    }
};

Leetcode1005. Maximize Sum Of Array After K Negations

Given an array A of integers, we must modify the array in the following way: we choose an i and replace A[i] with -A[i], and we repeat this process K times in total. (We may choose the same index i multiple times.) Return the largest possible sum of the array after modifying it in this way.

Example 1:

1
2
3
Input: A = [4,2,3], K = 1
Output: 5
Explanation: Choose indices (1,) and A becomes [4,-2,3].

Example 2:

1
2
3
Input: A = [3,-1,0,2], K = 3
Output: 6
Explanation: Choose indices (1, 2, 2) and A becomes [3,1,0,2].

Example 3:

1
2
3
Input: A = [2,-3,-1,5,-4], K = 2
Output: 13
Explanation: Choose indices (1, 4) and A becomes [2,3,-1,5,4].

题目的意思是将A中的数进行取反（正变负，负变正）K次，可以重复对一个元素取反，最后求A中元素总和的最大值。取反可以分为两种情况：当A中都是正数的时候，比如{1,2,4,6}，如果K是偶数，那么可以不用进行取反操作，因为负负得正；如果K是奇数，则只需要对最小的数取反一次即可。当A中有正数也有负数的时候，比如{-4,-3,-1,2,5}，此时对负数元素进行取反操作，直到当前元素大于0或者K次转换已用完，此时针对K中剩余的转换次数，又可以细分为两种情况：

  1. K中剩余的转换次数为偶数，即A中元素全是正数，依据负负得正，不用再进行额外的转换了。
  2. K中剩余的转换次数为奇数，即还需要再将某个元素转换一次，而为了元素总和最大，需要比较当前元素（正数）和前一个元素（负数）的绝对值大小，对较小的元素进行取反。

最后使用一个for循环，计算A中所有元素总和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int largestSumAfterKNegations(vector<int>& A, int K) {
        int b = 0, s = 0, length = A.size();
        int i = 0, sum = 0;
        sort(A.begin(), A.end());
        if(A[0] >= 0) {
            if(K % 2)
                A[0] = -A[0];
        }
        else {
            i = 0;
            while(i < length && A[i] < 0 && K --) {
                A[i] = -A[i];
                i++;
            }
            if (K > 0 && K%2 != 0) {
                 abs(A[i]) < abs(A[i-1]) ? A[i] = -A[i] : A[i-1] = -A[i-1];
            }
        }
        for(i = 0; i < length; i ++)
            sum += A[i];
        return sum;
    }
};

Leetcode1006. Clumsy Factorial

Normally, the factorial of a positive integer n is the product of all positive integers less than or equal to n. For example, factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1.

We instead make a clumsy factorial: using the integers in decreasing order, we swap out the multiply operations for a fixed rotation of operations: multiply (*), divide (/), add (+) and subtract (-) in this order.

For example, clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1. However, these operations are still applied using the usual order of operations of arithmetic: we do all multiplication and division steps before any addition or subtraction steps, and multiplication and division steps are processed left to right.

Additionally, the division that we use is floor division such that 10 * 9 / 8 equals 11. This guarantees the result is an integer.

Implement the clumsy function as defined above: given an integer N, it returns the clumsy factorial of N.

Example 1:

1
2
3
Input: 4
Output: 7
Explanation: 7 = 4 * 3 / 2 + 1

Example 2:

1
Input: 10 Output: 12 Explanation: 12 = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1

Note:

  • 1 <= N <= 10000
  • -2^31 <= answer <= 2^31 - 1 (The answer is guaranteed to fit within a 32-bit integer.)

这道题定义了一种笨拙的阶乘，与正常的连续相乘不同的是，这里按顺序使用乘除加减号来计算，这里要保持乘除的优先级，现在给了一个正整数N，让求这种笨拙的阶乘是多少。由于需要保持乘除的优先级，使得问题变的稍微复杂了一些，否则直接按顺序一个个的计算就好。根据题目中的例子2分析，刚开始的乘和除可以直接计算，紧跟其后的加法，也可以直接累加，但是之后的减号，就不能直接计算，而是要先计算后面的乘和除，所以遇到了减号，是需要特殊处理一下的。

把算式进行分割，注意到算符是循环的，除了第一组是+、*、/、+以外，其他的-、*、/、+，所以用一个临时变量来记下当前组的符号即可，剩下的就按照循环来做。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int clumsy(int n) {
        int sum = 0, i = n, j = 0;
        while(i > 0) {
            int tmp = 1;
            if (i != n)
                tmp = -1;
            for (j = 0; j < 4 && i > 0; j ++) {
                if (j == 0) tmp *= (i --);
                if (j == 1) tmp *= (i --);
                if (j == 2) tmp /= (i --);
                if (j == 3) tmp += (i --);
            }
            sum += tmp;
            if (i == 0)
                break;
        }
        return sum;
    }
};

其他的做法：用个变量j来循环遍历这个数组，从而知道当前该做什么操作。还需要一个变量 cur 来计算乘和除优先级的计算，初始化为N，此时从 N-1 遍历到1，若遇到乘号，则 cur 直接乘以当前数字，若遇到除号，cur 直接除以当前数字，若遇到加号，可以直接把当前数字加到结果 res 中，若遇到减号，此时需要判断一下，因为只有第一个乘和除后的结果是要加到 res 中的，后面的都是要减去的，所以要判断一下若当前数字等于 N-4 的时候，加上 cur，否者都是减去 cur，然后 cur 更新为当前数字，因为减号的优先级小于乘除，不能立马运算。之后j自增1并对4取余，最终返回的时候也需要做个判断，因为有可能数字比较小，减号还没有出来，且此时的最后面的乘除结果还保存在 cur 中，那么是加是减还需要看N的大小，若小于等于4，则加上 cur，反之则减去 cur，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int clumsy(int N) {
        int res = 0, cur = N, j = 0;
        vector<char> ops{'*', '/', '+', '-'};
        for (int i = N - 1; i >= 1; --i) {
            if (ops[j] == '*') {
                cur *= i;
            } else if (ops[j] == '/') {
                cur /= i;
            } else if (ops[j] == '+') {
                res += i;
            } else {
                res += (i == N - 4) ? cur : -cur;
                cur = i;
            }
            j = (j + 1) % 4;
        }
        return res + ((N <= 4) ? cur : -cur);
    }
};

再来看一种比较简洁的写法，由于每次遇到减号时，优先级会被改变，而前面的乘除加是可以提前计算的，所以可以每次处理四个数字，即首先处理 N, N-1, N-2, N-3 这四个数字，这里希望每次可以得到乘法计算时的第一个数字，可以通过N - i*4得到，这里需要满足i*4 < N，知道了这个数字，然后可以立马算出乘除的结果，只要其大于等于3。然后需要将乘除之后的结果更新到 res 中，还是需要判断一下，若是第一个乘除的结果，需要加上，后面的都是减去。乘除后面跟的是加号，所以要加上 num-3 这个数字，前提是 num 大于3，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int clumsy(int N) {
        int res = 0;
        for (int i = 0; i * 4 < N; ++i) {
            int num = N - i * 4, t = num;
            if (num >= 3) t = num * (num - 1) / (num - 2);
            res += (i == 0) ? t : -t;
            if (num > 3) res += (num - 3);
        }
        return res;
    }
};

Leetcode1007. Minimum Domino Rotations For Equal Row

In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the ith domino, so that tops[i] and bottoms[i] swap values.

Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.

If it cannot be done, return -1.

Example 1:

1
2
3
4
5
Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
Output: 2
Explanation: 
The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

1
2
3
4
Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
Output: -1
Explanation: 
In this case, it is not possible to rotate the dominoes to make one row of values equal.

Constraints:

  • 2 <= tops.length <= 2 * 104
  • bottoms.length == tops.length
  • 1 <= tops[i], bottoms[i] <= 6

这道题说是有长度相等的两个数组A和B，分别表示一排多米诺的上边数字和下边数字，多米诺的个数和数组的长度相同，数字为1到6之间，问最少旋转多少次多米诺，可以使得上边或下边的数字全部相同。例子1中给了图解，很好的帮我们理解题意，实际上出现次数越多的数字越可能就是最终全部相同的数字，所以统计A和B中每个数字出现的次数就变的很重要了，由于A和B中有可能相同位置上的是相同的数字，则不用翻转，要使得同一行变为相同的数字，翻转的地方必须是不同的数字，如何才能知道翻转后可以使同一行完全相同呢？需要某个数字在A中出现的次数加上在B中出现的次数减去A和B中相同位置出现的次数后正好等于数组的长度，这里就需要用三个数组 cntA，cntB，和 same 来分别记录某个数字在A中，B中，A和B相同位置上出现的个数，然后遍历1到6，只要符合上面提到的条件，就可以直接返回数组长度减去该数字在A和B中出现的次数中的较大值。

总结就是：tops中某种大小的个数，加上bottoms中某种大小的个数，减去tops和bottoms里这种大小相同的个数，需要等于总个数，这样才能实现一排相同的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int minDominoRotations(vector<int>& tops, vector<int>& bottoms) {
        int n = tops.size(), res = 0;
        vector<int> cnt1(7, 0), cnt2(7, 0), same(7, 0);
        for (int i = 0; i < n; i ++) {
            cnt1[tops[i]] ++;
            cnt2[bottoms[i]] ++;
            if (tops[i] == bottoms[i])
                same[tops[i]] ++;
        }

        for (int i = 1; i < 7; i ++) {
            if (cnt1[i] + cnt2[i] - same[i] == n)
                return n - max(cnt1[i], cnt2[i]);
        }
        return -1;
    }
};

Leetcode1008. Construct Binary Search Tree from Preorder Traversal

Return the root node of a binary search tree that matches the given preorder traversal.

(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)

Example 1:

Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
	public:
    
    TreeNode* build(vector<int>& preorder,int i,int j){
        if(i>=j){
            return NULL;
        }
        int temp=preorder[i];
        int ii;
        for(ii=i+1;ii<j;ii++)
            if(temp<preorder[ii])
                break;
        TreeNode* root = new TreeNode(preorder[i]);
        root->left = build(preorder,i+1,ii);
        root->right = build(preorder,ii,j);
        return root;
    }
   
    TreeNode* bstFromPreorder(vector<int>& preorder) {
        if(preorder.empty())
            return NULL;
        return build(preorder,0,preorder.size());
    }
};

一道简单的中序遍历题竟然做了这么久。。。

Leetcode1009. Complement of Base 10 Integer

Every non-negative integer N has a binary representation. For example, 5 can be represented as “101” in binary, 11 as “1011” in binary, and so on. Note that except for N = 0, there are no leading zeroes in any binary representation.

The complement of a binary representation is the number in binary you get when changing every 1 to a 0 and 0 to a 1. For example, the complement of “101” in binary is “010” in binary.

For a given number N in base-10, return the complement of it’s binary representation as a base-10 integer.

Example 1:

1
2
3
Input: 5
Output: 2
Explanation: 5 is "101" in binary, with complement "010" in binary, which is 2 in base-10.

Example 2:

1
2
3
Input: 7
Output: 0
Explanation: 7 is "111" in binary, with complement "000" in binary, which is 0 in base-10.

Example 3:

1
2
3
Input: 10
Output: 5
Explanation: 10 is "1010" in binary, with complement "0101" in binary, which is 5 in base-10.

将十进制变成二进制然后取反加和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
	public:
    int bitwiseComplement(int N) {
        if(N == 0)
            return 1;
        if(N == 1)
            return 0;
        vector<int> re;
        while(N) {
            re.push_back(N & 1);
            N = N >> 1;
        }
        reverse(re.begin(), re.end());
        int res = 0;
        for(int i = 0; i < re.size(); i ++) {
            res = res * 2 + (~re[i] & 1);
        }
        return res;
    }
};

方法二，利用位运算直接取反。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
	public:
    int bitwiseComplement(int N) {
        int i = 0;
        if(!N)
            return 1;
        while(N > pow(2, i))
            i ++;
        return (~N) & ((int)pow(2, i) - 1);
    }
};

Leetcode1010. Pairs of Songs With Total Durations Divisible by 60

In a list of songs, the i-th song has a duration of time[i] seconds.

Return the number of pairs of songs for which their total duration in seconds is divisible by 60. Formally, we want the number of indices i, j such that i < j with (time[i] + time[j]) % 60 == 0.

Example 1:

1
2
3
4
5
6
Input: [30,20,150,100,40]
Output: 3
Explanation: Three pairs have a total duration divisible by 60:
(time[0] = 30, time[2] = 150): total duration 180
(time[1] = 20, time[3] = 100): total duration 120
(time[1] = 20, time[4] = 40): total duration 60

Example 2:

1
2
3
Input: [60,60,60]
Output: 3
Explanation: All three pairs have a total duration of 120, which is divisible by 60.

一开始的思路，是暴力枚举，枚举第一首歌，然后第二首歌是枚举在第一首歌之后的所有情况，判断条件成立就 ans++ 。但这样子的时间复杂度是 O(n^2) 。题目中，数组长度 n<=6e+4，所以时间复杂度是 3.6e+9，这样子会超时。

因此上述暴力枚举的方法行不通。

如果两首歌时间之和要能被60整除，说明余数为0，那么假设第一首歌对60的余数是 a ，那么另一首歌的对60的余数为 60-a 才行。所以我们可以用一个长度为60的数组，下标刚好对应求余后的数，每次找到一个新的歌余数为 a，就看它前面对应余数为 60-a 的有多少首歌，即可以匹配为多少对。最后这首歌的余数对应的下标数组值 ++。

这样解决之后，我们只用遍历一次数组即可，所以时间复杂度是 O(n) ，但是需要了额外的空间开销。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
	public:
    int numPairsDivisibleBy60(vector<int>& time) {
        int length = time.size();
        int res = 0;
        vector<int> yushu(60, 0);
        for(int i = 0; i < length; i ++) {
            res += yushu[(60 - time[i]%60)%60];
            yushu[ time[i]%60 ] ++;
        }
        return res;
    }
};

Leetcode1011. Capacity To Ship Packages Within D Days

A conveyor belt has packages that must be shipped from one port to another within D days.

The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.

Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within D days.

Example 1:

1
2
3
4
5
6
7
8
Input: weights = [1,2,3,4,5,6,7,8,9,10], D = 5
Output: 15
Explanation: A ship capacity of 15 is the minimum to ship all the packages in 5 days like this:
1st day: 1, 2, 3, 4, 5
2nd day: 6, 7
3rd day: 8
4th day: 9
5th day: 10

Note that the cargo must be shipped in the order given, so using a ship of capacity 14 and splitting the packages into parts like (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) is not allowed.

Example 2:

1
2
3
4
5
6
Input: weights = [3,2,2,4,1,4], D = 3
Output: 6
Explanation: A ship capacity of 6 is the minimum to ship all the packages in 3 days like this:
1st day: 3, 2
2nd day: 2, 4
3rd day: 1, 4

Example 3:

1
2
3
4
5
6
7
Input: weights = [1,2,3,1,1], D = 4
Output: 3
Explanation:
1st day: 1
2nd day: 2
3rd day: 3
4th day: 1, 1

Constraints:

  • 1 <= D <= weights.length <= 5 * 104
  • 1 <= weights[i] <= 500

这道题说是有一条传送带在运送包裹货物，每个包裹有各自的重量，每天要把若干包裹运送到货轮上，货轮有特定的承载量，要求在给定的D天内将所有货物装上货轮，问船的最小载重量是多少。

首先来分析，由于船的载重量是固定的，而包裹在传送带上又只能按照顺序上传，并不能挑拣，所以一旦加上当前包裹超过了船的载重量，则必须要放弃这个包裹，比较极端的例子就是，假如船的载重量是 50，现在船上已经装了一个重量为1的包裹，而下一个包裹重量是 50，那么这个包裹只能装在下一条船上。知道了这一点后，再来分析一下，船的载重量的范围，先来分析一下最小值，由于所有的包裹都要上船，所以最小的船载重量至少应该是最重的那个包裹，不然上不了船了，而最大的载重量就是包裹的总重量，一条船就能拉走了。所以正确的答案就在这两个边界范围之内，挨个遍历的话实在有些太不高效了。

这里就要祭出二分搜索法了，当算出了中间值 mid 后，利用这个载重量去算需要多少天能运完，然后去和D做比较，如果大于D，说明需要增加载重量，否则减少载重量，最终会终止到正确的结果。具体来看代码，left 初始化为最大的包裹重量，right 初始化为所有的包裹重量总和。然后进行 while 循环，求出 mid，同时使用两个变量 cnt 和 cur，分别用来计算需要的天数，和当前货物的重量，其中 cnt 初始化为1，至少需要一天来运货物。然后遍历所有的包裹重量，每次加到 cur，若此时 cur 大于 mid 了，说明当前包裹不能加了，将 cur 重置为当前包裹重量，为下条船做准备，然后 cnt 自增1。遍历完了之后，判断若 cnt 大于D，则 left 赋值为 mid+1，否则 right 赋值为 mid，最终返回 left 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int shipWithinDays(vector<int>& weights, int days) {
        int sum = 0, size = weights.size(), max_val = -1, need;
        for (int i = 0; i < size; i ++) {
            max_val = max(max_val, weights[i]);
            sum += weights[i];
        }
        int left = max_val, right = sum, mid;
        while(left < right) {
            mid = left + (right - left) / 2;
            int cur = 0;
            need = 1;
            for (int i = 0; i < size; i ++) {
                if (cur + weights[i] > mid) {
                    need ++;
                    cur = 0;
                }
                cur += weights[i];
            }
            if (need > days)
                left = mid+1;
            else
                right = mid;
        }
        return right;
    }
};

Leetcode1013. Partition Array Into Three Parts With Equal Sum

Given an array A of integers, return true if and only if we can partition the array into three non-empty parts with equal sums.

Formally, we can partition the array if we can find indexes i+1 < j with (A[0] + A[1] + … + A[i] == A[i+1] + A[i+2] + … + A[j-1] == A[j] + A[j-1] + … + A[A.length - 1])

Example 1:

1
2
3
Input: A = [0,2,1,-6,6,-7,9,1,2,0,1]
Output: true
Explanation: 0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1

Example 2:

1
2
Input: A = [0,2,1,-6,6,7,9,-1,2,0,1]
Output: false

Example 3:

1
2
3
Input: A = [3,3,6,5,-2,2,5,1,-9,4]
Output: true
Explanation: 3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4

1、检查总数是否能被3整除;
2、循环遍历数组A，计算和的一部分;如果找到平均值，则将该部分重置为0，并增加计数器;
3、到最后，如果平均可以看到至少3次，返回true;否则返回假。
注意:如果在数组结束前找到2次平均值(sum / 3)，那么剩下的部分也等于平均值。因此，计数器达到3后无需继续。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
	public:
    bool canThreePartsEqualSum(vector<int>& A) {
        int sum = 0, part_sum = 0, i;
        for(int i = 0; i < A.size(); i ++) 
            sum += A[i];
        if(sum % 3 != 0)
            return false;
        sum /= 3;
        for(i = 0; i < A.size(); i ++) {
            part_sum += A[i];
            if(part_sum == sum)
                break;
        }
        for(part_sum = 0, i = i + 1; i < A.size(); i++) {
            part_sum += A[i];
            if(part_sum == sum)
                break;
        }
        if(i < A.size() - 1)
            return true;
        return false;
    }
};

Leetcode1014. Best Sightseeing Pair

Given an array A of positive integers, A[i] represents the value of the i-th sightseeing spot, and two sightseeing spots i and j have distance j - i between them.

The score of a pair (i < j) of sightseeing spots is (A[i] + A[j] + i - j) : the sum of the values of the sightseeing spots, minus the distance between them.

Return the maximum score of a pair of sightseeing spots.

Example 1:

1
2
3
Input: [8,1,5,2,6]
Output: 11
Explanation: i = 0, j = 2, A[i] + A[j] + i - j = 8 + 5 + 0 - 2 = 11

Note:

  • 2 <= A.length <= 50000
  • 1 <= A[i] <= 1000

这道题给了一个正整数的数组A，定义了一种两个数字对儿的记分方式，为A[i] + A[j] + i - j，现在让找出最大的那组的分数。利用加法的分配律，可以得到A[i] + i + A[j] - j，为了使这个表达式最大化，A[i] + i自然是越大越好，这里可以使用一个变量 mx 来记录之前出现过的A[i] + i的最大值，则当前的数字就可以当作数对儿中的另一个数字，其减去当前坐标值再加上 mx 就可以更新结果 res 了，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int maxScoreSightseeingPair(vector<int>& values) {
        int maxx = INT_MIN, res = INT_MIN;
        for (int i = 0; i < values.size(); i ++) {
            res = max(res, maxx + values[i] - i);
            maxx = max(maxx, values[i] + i);
        }
        return res;
    }
};

Leetcode1015. Smallest Integer Divisible by K

Given a positive integer K, you need to find the length of the smallest positive integer N such that N is divisible by K, and N only contains the digit 1.

Return *the length of *N. If there is no such N, return -1.

Note: N may not fit in a 64-bit signed integer.

Example 1:

1
2
3
Input: K = 1
Output: 1
Explanation: The smallest answer is N = 1, which has length 1.

Example 2:

1
2
3
Input: K = 2
Output: -1
Explanation: There is no such positive integer N divisible by 2.

Example 3:

1
2
3
Input: K = 3
Output: 3
Explanation: The smallest answer is N = 111, which has length 3.

Constraints:

  • 1 <= K <= 105

这道题说是给了一个正整数K，让找到一个长度最短且只由1组成的正整数N，可以整除K，问最短的长度是多少，若没有，则返回 -1。关于整除的一些性质，博主记得小学就应该学过，比如能被2整除的数字必须是偶数，能被3整除的数字各个位加起来必须能被3整除，能被5整除的数字的末尾数字必须是0或者5。由于N都是由1组成的，所以一定不可能整除2或者5，所以只要K中包含2或者5，直接返回 -1。其实有一个定理，若K不能被2或5整除，则一定有一个长度小于等于K且均由1组成的数，可以整除K。这里只要找到那个最短的长度即可。

从1开始检查，每次乘以 10 再加1，就可以得到下一个数字，但是由于K可能很大，则N就会超出整型数的范围，就算是长整型也不一定 hold 的住，所以不能一直变大，而是每次累加后都要对 K 取余，若余数为0，则直接返回当前长度，若不为0，则用余数乘以 10 再加1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int smallestRepunitDivByK(int k) {
        if (k % 2 == 0 || k % 5 == 0)
            return -1;
        int r = 0;
        for (int i = 1; i <= k; i ++) {
            r = r * 10 + 1;
            if (r % k == 0)
                return i;
            r = r % k;
        }
        return -1;
    }
};

Leetcode1016. Binary String With Substrings Representing 1 To N

Given a binary string S (a string consisting only of ‘0’ and ‘1’s) and a positive integer N, return true if and only if for every integer X from 1 to N, the binary representation of X is a substring of S.

Example 1:

1
2
Input: S = "0110", N = 3
Output: true

Example 2:

1
2
Input: S = "0110", N = 4
Output: false

Note:

  • 1 <= S.length <= 1000
  • 1 <= N <= 10^9

这道题给了一个二进制的字符串S，和一个正整数N，问从1到N的所有整数的二进制数的字符串是否都是S的子串。

验证从N到1之间所有的数字，先求出其二进制数的字符串，在 C++ 中可以利用 bitset 来做，将其转为字符串即可。由于定义了 32 位的 bitset，转为字符串后可能会有许多 leading zeros，所以首先要移除这些0，通过在字符串中查找第一个1，然后通过取子串的函数就可以去除所有的起始0了。然后在S中查找是否存在这个二进制字符串，若不存在，直接返回 false，遍历完成后返回 true 即可，参见代码如下：

学到了，bitset还可以这么用，转成二进制字符串确实很方便。

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    bool queryString(string S, int N) {
        for (int i = N; i > 0; --i) {
            string b = bitset<32>(i).to_string();
            if (S.find(b.substr(b.find("1"))) == string::npos) return false;
        }
        return true;
    }
};

Leetcode1017. Convert to Base -2

Given an integer n, return a binary string representing its representation in base -2.

Note that the returned string should not have leading zeros unless the string is “0”.

Example 1:

1
2
3
Input: n = 2
Output: "110"
Explantion: (-2)2 + (-2)1 = 2

Example 2:

1
2
3
Input: n = 3
Output: "111"
Explantion: (-2)2 + (-2)1 + (-2)0 = 3

Example 3:

1
2
3
Input: n = 4
Output: "100"
Explantion: (-2)2 = 4

这道题给了一个十进制的非负数N，让转为以负二进制的数。我们对于十进制数转二进制的数字应该比较熟悉，就是每次N%2或者N&1，然后再将N右移一位，即相当于除以2，直到N为0为止。对于转为负二进制的数字，也是同样的做法，唯一不同的是，每次要除以 -2，即将N右移一位之后，要变为相反数，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    string baseNeg2(int N) {
        string res;
        while (N != 0) {
            res = to_string(N & 1) + res;
            N = -(N >> 1);
        }
        return res == "" ? "0" : res;
    }
};

由于转二进制数是要对2取余，则转负二进制就要对 -2 取余，然后N要除以 -2，但是有个问题是，取余操作可能会得到负数，但我们希望只得到0或1，这样就需要做些小调整，使其变为正数，变化方法是，余数加2，N加1，证明方法如下所示：

1
2
3
-1 = (-2) * 0 + (-1)
-1 = (-2) * 0 + (-2) + (-1) - (-2)
-1 = (-2) * (0 + 1) + (-1) - (-2)

先加上一个 -2，再减去一个 -2，合并后就是N加1，余数加2，这样就可以把余数加到结果字符串中了，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    string baseNeg2(int N) {
        string res;
        while (N != 0) {
            int rem = N % (-2);
            N /= -2;
            if (rem < 0) {
                rem += 2;
                N += 1;
            }
            res = to_string(rem) + res;
        }
        return res == "" ? "0" : res;
    }
};

Leetcode1018. Binary Prefix Divisible By 5

Given an array A of 0s and 1s, consider N_i: the i-th subarray from A[0] to A[i] interpreted as a binary number (from most-significant-bit to least-significant-bit.)

Return a list of booleans answer, where answer[i] is true if and only if N_i is divisible by 5.

Example 1:

1
2
3
Input: [0,1,1]
Output: [true,false,false]
Explanation: The input numbers in binary are 0, 01, 011; which are 0, 1, and 3 in base-10.  Only the first number is divisible by 5, so answer[0] is true.

Example 2:

1
2
Input: [1,1,1]
Output: [false,false,false]

Example 3:

1
2
Input: [0,1,1,1,1,1]
Output: [true,false,false,false,true,false]

Example 4:

1
2
Input: [1,1,1,0,1]
Output: [false,false,false,false,false]

假设当前访问 A[i - 1], 表示的数为 old_number, 那么当访问 A[i] 时, 所表示的数 new_number = old_number * 2 + A[i];

  • 如果直接判断 new_number 是否能被 5 整除, 容易出现溢出的问题, 因为按照上面遍历的方式, C++ 只能保存 32-bit 的数据, 但是题目中说明 1 <= A.length <= 30000.
  • 我们不需要知道具体的 new_number 数值大小, 而只需要它与 5 的余数;
    -发现一个数学公式: (a*b + c) % d = ((a%d)*(b%d) + c%d) % d, 因此 new_number % 5 可以表示为 ((old_number % 5) * 2 + A[i]) % 5.
  • 由第 4 点, 可以将 number % 5 作为一个整体, 更新公式为 a = (a * 2 + A[i]) % 5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
	public:
    vector<bool> prefixesDivBy5(vector<int>& A) {
        vector<bool> res;
        int ans = 0, temp = 1;
        for(int i = 0; i < A.size(); i ++) {
            ans = ((ans * 2)%5 + A[i])%5;
            if(ans % 5 == 0)
                res.push_back(true);
            else
                res.push_back(false);
        }
        return res;
    }
};

Leetcode1019. Next Greater Node In Linked List

You are given the head of a linked list with n nodes.

For each node in the list, find the value of the next greater node. That is, for each node, find the value of the first node that is next to it and has a strictly larger value than it.

Return an integer array answer where answer[i] is the value of the next greater node of the ith node (1-indexed). If the ith node does not have a next greater node, set answer[i] = 0.

Example 1:

1
2
Input: head = [2,1,5]
Output: [5,5,0]

Example 2:

1
2
Input: head = [2,7,4,3,5]
Output: [7,0,5,5,0]

这道题给了一个链表，让找出每个结点值的下一个较大的结点值，跟之前的 Next Greater Element I，Next Greater Element II，和 Next Greater Element III 很类似，不同的是这里不是数组，而是链表，就稍稍的增加了一些难度，因为链表无法直接根据下标访问元素，在遍历链表之前甚至不知道总共有多少个结点。基本上来说，为了达到线性的时间复杂度，这里需要维护一个单调递减的栈，若当前的数字小于等于栈顶元素，则加入栈，若当前数字大于栈顶元素，非常棒，说明栈顶元素的下一个较大数字找到了，标记上，且把栈顶元素移除，继续判断下一个栈顶元素和当前元素的关系，直到当前数字小于等于栈顶元素为止。通过这种方法，就可以在线性的时间内找出所有数字的下一个较大的数字了。

这里新建两个数组，res 和 nums 分别保存要求的结果和链表的所有结点值，还需要一个栈 st 和一个变量 cnt（记录当前的数组坐标），然后开始遍历链表，首先把当前结点值加入数组 nums，然后开始循环，若栈不空，且当前结点值大于栈顶元素（注意这里单调栈存的并不是结点值，而是该值在 nums 数组中的坐标值，这是为了更好的在结果 res 中定位），此时用该结点值来更新结果 res 中的对应的位置，然后将栈顶元素移除，继续循环直到条件不满足位置。然后把当前的坐标加入栈中，此时还要更新结果 res 的大小，因为由于链表的大小未知，无法直接初始化 res 的大小，当然我们可以在开头的时候先遍历一遍链表，得到结点的个数也是可以的，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<int> nextLargerNodes(ListNode* head) {
        vector<int> res;
        stack<int> s;
        int cnt = 0;
        ListNode* cur = head;
        while(cur) {
            cnt ++;
            res.push_back(cur->val);
            cur = cur->next;
        }
        vector<int> res2(cnt, 0);
        cnt = 0;
        
        while(head != NULL) {
            while (!s.empty() && res[s.top()] < head->val) {
                res2[s.top()] = head->val;
                s.pop();
            }
            s.push(cnt);
            head = head->next;
            cnt ++;
        }
        return res2;
    }
};

这个人写的方法需要经常resize，不一定更快。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> nextLargerNodes(ListNode* head) {
        vector<int> res, nums;
        stack<int> st;
        int cnt = 0;
        while (head) {
            nums.push_back(head->val);
            while (!st.empty() && head->val > nums[st.top()]) {
                res[st.top()] = head->val;
                st.pop();
            }
            st.push(cnt);
            res.resize(++cnt);
            head = head->next;
        }
        return res;
    }
};

再看一种方法，首先把链表反转，也是用单调栈的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
    ListNode* reverseList(ListNode* head)
    {
        if (head->next == nullptr)
            return head;
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }

public:
    vector<int> nextLargerNodes(ListNode* head) {
        if (head == nullptr)
            return {};
        ListNode* revHead = reverseList(head);
        ListNode* curr = revHead;
        
        std::vector<int> result;
        std::stack<int> st;
        
        while (curr != nullptr)
        {
            if (st.empty())
            {
                result.push_back(0);
                st.push(curr->val);
                curr = curr->next;
            }
            else
            {
                while (!st.empty() && curr->val >= st.top())
                    st.pop();
                if (!st.empty())
                    result.push_back(st.top());
                else
                    result.push_back(0);
                st.push(curr->val);
                curr = curr->next;
            }
        }
        std::reverse(result.begin(), result.end());
        return result;
    }
};

Leetcode1020. Number of Enclaves

Given a 2D array A, each cell is 0 (representing sea) or 1 (representing land)

A move consists of walking from one land square 4-directionally to another land square, or off the boundary of the grid.

Return the number of land squares in the grid for which we cannot walk off the boundary of the grid in any number of moves.

Example 1:

1
2
3
4
Input: [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
Output: 3
Explanation:
There are three 1s that are enclosed by 0s, and one 1 that isn't enclosed because its on the boundary.

Example 2:

1
2
3
4
Input: [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
Output: 0
Explanation:
All 1s are either on the boundary or can reach the boundary.

Note:

  • 1 <= A.length <= 500
  • 1 <= A[i].length <= 500
  • 0 <= A[i][j] <= 1
  • All rows have the same size.

这道题给了一个只有0和1的二维数组A，其中0表示海洋，1表示陆地，每次只能从一块陆地走到和其相连的另一块陆地上，问有多少块陆地可以不用走到边界上。其实这道题就是让找出被0完全包围的1的个数，反过来想，如果有1在边界上，那么和其相连的所有1都是不符合题意的，所以只要以边界上的1为起点，遍历所有和其相连的1，并且标记，则剩下的1一定就是被0完全包围的。遍历的方法可以用 BFS 或者 DFS，先来看 BFS 的解法，使用一个队列 queue，遍历数组A，现将所有1的个数累加到结果 res，然后将边界上的1的坐标加入队列中。然后开始 while 循环，去除队首元素，若越界了，或者对应的值不为1，直接跳过。否则标记当前位置值为0，并且 res 自减1，然后将周围四个位置都排入队列中，最后返回结果 res 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int numEnclaves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size(), num1 = 0;
        queue<pair<int, int>> q;
        for (int i = 0; i < m; i ++)
            for (int j = 0; j < n; j ++) {
                num1 += grid[i][j];
                if (i == 0 || i == m-1 || j == 0 || j == n-1)
                    q.push(make_pair(i, j));
            }
        while(!q.empty()) {
            int x = q.front().first, y = q.front().second;
            q.pop();
            if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] != 1) 
                continue;
            if (grid[x][y] == 1) {
                grid[x][y] = 0;
                num1 --;
            }
            q.push(make_pair(x, y+1));
            q.push(make_pair(x, y-1));
            q.push(make_pair(x+1, y));
            q.push(make_pair(x-1, y));
        }
        return num1;
    }
};

用深度优先确实能快一点点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    
    void dfs(vector<vector<int>>& grid, int i, int j) {
        if (i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || grid[i][j] != 1)
            return;
        grid[i][j] = 0;
        dfs(grid, i, j+1);
        dfs(grid, i, j-1);
        dfs(grid, i+1, j);
        dfs(grid, i-1, j);
    }
    
    int numEnclaves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size(), num1 = 0;
        
        for (int i = 0; i < m; i ++) {
            if (grid[i][0] == 1)
                dfs(grid, i, 0);
            if (grid[i][n-1] == 1)
                dfs(grid, i, n-1);
        }
        
        for (int i = 0; i < n; i ++) {
            if (grid[0][i] == 1)
                dfs(grid, 0, i);
            if (grid[m-1][i] == 1)
                dfs(grid, m-1, i);
        }
        
        for (int i = 0; i < m; i ++)
            for (int j = 0; j < n; j ++)
                if (grid[i][j] == 1)
                    num1 ++;
        return num1;
    }
};

Leetcode1021. Remove Outermost Parentheses

A valid parentheses string is either empty (“”), “(“ + A + “)”, or A + B, where A and B are valid parentheses strings, and + represents string concatenation. For example, “”, “()”, “(())()”, and “(()(()))” are all valid parentheses strings.

A valid parentheses string S is primitive if it is nonempty, and there does not exist a way to split it into S = A+B, with A and B nonempty valid parentheses strings.

Given a valid parentheses string S, consider its primitive decomposition: S = P_1 + P_2 + … + P_k, where P_i are primitive valid parentheses strings.

Return S after removing the outermost parentheses of every primitive string in the primitive decomposition of S.

Example 1:

1
2
3
4
5
Input: "(()())(())"
Output: "()()()"
Explanation: 
The input string is "(()())(())", with primitive decomposition "(()())" + "(())".
After removing outer parentheses of each part, this is "()()" + "()" = "()()()".

Example 2:

1
2
3
4
5
Input: "(()())(())(()(()))"
Output: "()()()()(())"
Explanation: 
The input string is "(()())(())(()(()))", with primitive decomposition "(()())" + "(())" + "(()(()))".
After removing outer parentheses of each part, this is "()()" + "()" + "()(())" = "()()()()(())".

Example 3:

1
2
3
4
5
Input: "()()"
Output: ""
Explanation: 
The input string is "()()", with primitive decomposition "()" + "()".
After removing outer parentheses of each part, this is "" + "" = "".

Note:

  1. S.length <= 10000
  2. S[i] is “(“ or “)”
  3. S is a valid parentheses string

比较简单，把最外边的一层括号移走，可以用栈，也可以用计数器。如果遇到左括号且栈不空说明这个左括号不是外边的括号，加到结果中，再把这个左括号压栈；如果是右括号，就先弹出栈，再判断如果栈不空则说明这个右括号也不是外边的括号，加到结果中。

不知道为啥我这个这么慢，反正过了就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    string removeOuterParentheses(string S) {
        string result="";
        int length = S.length();
        int ss=0;
        for(int i=0;i<length;i++){
            if(S[i]=='('){
                if(ss!=0)
                    result=result+'(';
                ss++;
            }
            else if(S[i]==')'){
                ss--;
                if(ss!=0)
                    result=result+")";
            }
        }
        return result;
    }
};

Leetcode1022. Sum of Root To Leaf Binary Numbers

Given a binary tree, each node has value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit. For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.

For all leaves in the tree, consider the numbers represented by the path from the root to that leaf.

Return the sum of these numbers.

深度优先遍历一波，因为好久没写dsf了，所以特地写一写。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int result;
    void dfs(TreeNode* root ,int now){
        if(!root->left && !root->right){
            result += (now<<1) + root->val;
        }
        int val = (now<<1) + root->val;
        if(root->left)
            dfs(root->left, val);
        if(root->right)
            dfs(root->right, val);
    }
    
    int sumRootToLeaf(TreeNode* root) {
        result=0;
        dfs(root,0);
        return result;
    }
};

Leetcode1023. Camelcase Matching

A query word matches a given pattern if we can insert lowercase letters to the pattern word so that it equals the query. (We may insert each character at any position, and may insert 0 characters.)

Given a list of queries, and a pattern, return an answer list of booleans, where answer[i] is true if and only if queries[i] matches the pattern.

Example 1:

1
2
3
4
5
6
Input: queries = ["FooBar","FooBarTest","FootBall","FrameBuffer","ForceFeedBack"], pattern = "FB"
Output: [true,false,true,true,false]
Explanation: 
"FooBar" can be generated like this "F" + "oo" + "B" + "ar".
"FootBall" can be generated like this "F" + "oot" + "B" + "all".
"FrameBuffer" can be generated like this "F" + "rame" + "B" + "uffer".

Example 2:

1
2
3
4
5
Input: queries = ["FooBar","FooBarTest","FootBall","FrameBuffer","ForceFeedBack"], pattern = "FoBa"
Output: [true,false,true,false,false]
Explanation: 
"FooBar" can be generated like this "Fo" + "o" + "Ba" + "r".
"FootBall" can be generated like this "Fo" + "ot" + "Ba" + "ll".

Example 3:

1
2
3
4
Input: queries = ["FooBar","FooBarTest","FootBall","FrameBuffer","ForceFeedBack"], pattern = "FoBaT"
Output: [false,true,false,false,false]
Explanation: 
"FooBarTest" can be generated like this "Fo" + "o" + "Ba" + "r" + "T" + "est".

Note:

  • 1 <= queries.length <= 100
  • 1 <= queries[i].length <= 100
  • 1 <= pattern.length <= 100
  • All strings consists only of lower and upper case English letters.

给一个字符串和一个模式串，看能不能在模式串里加小写字母来转换成字符串，比较简单。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<bool> camelMatch(vector<string>& queries, string pattern) {
        vector<bool> ans;
        for(int i=0;i<queries.size();i++){
            bool succ=true;
            int index=0;
            for(int j=0;j<queries[i].size();j++){
                while(islower(queries[i][j])&& pattern[index]!=queries[i][j]){
                    j++;
                }
                if(pattern[index]==queries[i][j])
                    index++;
                else{
                    succ=false;
                    break;
                }
            
            }
            ans.push_back(succ);
        }
        return ans;
    }
};

我的代码比较慢，可以看看大佬们怎么写的。

Solution 1, Find
For each query, find all letters in pattern left-to-right. If we found all pattern letters, check that the rest of the letters is in the lower case.

对每个查询，从左到右找pattern里的字幕，如果找到了，检查剩余的是否是小写字母。感觉跟我的类似。

For simplicity, we can replace the found pattern letter in query with a lowercase ‘a’.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<bool> camelMatch(vector<string>& qs, string pattern, vector<bool> res = {}) {
  for (auto i = 0; i < qs.size(); ++i) {
    for (auto p = -1, j = 0; j < pattern.size(); ++j) {
      p = qs[i].find(pattern[j], p + 1);
      if (p == string::npos) {
        res.push_back(false);
        break;
      }
      qs[i][p] = 'a';
    }
    if (res.size() <= i) res.push_back(all_of(begin(qs[i]), end(qs[i]), [](char ch) { return islower(ch); }));
  }
  return res;
}

Solution 2, Simple Scan
Instead of using the find function, we can just check all characters in the query. If a character matches the pattern pointer (pattern[p]), we advance that pointer (++p). Otherwise, we check that the query character is in the lower case.

检查查询的字符串，如果一个字符与pattern[p]匹配了，就继续，如果不匹配，看是不是小些

With this solution, it’s also easer to realize that the complexity is O(n), where n is the total number of query characters.

1
2
3
4
5
6
7
8
9
10
vector<bool> camelMatch(vector<string>& qs, string pattern, vector<bool> res = {}) {
  for (auto i = 0, j = 0, p = 0; i < qs.size(); ++i) {
    for (j = 0, p = 0; j < qs[i].size(); ++j) {
      if (p < pattern.size() && qs[i][j] == pattern[p]) ++p;
      else if (!islower(qs[i][j])) break;
    }
    res.push_back(j == qs[i].size() && p == pattern.size());
  }
  return res;
}

Complexity Analysis

  • Runtime: O(n), where n is all letters in all queries. We process each letter only once.
  • Memory: O(m), where m is the number of queries (to store the result).
  • 时间复杂度O(n)，空间复杂度O(m)

Leetcode1024. Video Stitching

You are given a series of video clips from a sporting event that lasted T seconds. These video clips can be overlapping with each other and have varied lengths.

Each video clip clips[i] is an interval: it starts at time clips[i][0] and ends at time clips[i][1]. We can cut these clips into segments freely: for example, a clip [0, 7] can be cut into segments [0, 1] + [1, 3] + [3, 7].

Return the minimum number of clips needed so that we can cut the clips into segments that cover the entire sporting event ([0, T]). If the task is impossible, return -1.

寻找最少的可以覆盖[0, T]区间的区间数量，一开始没搞定，看答案搞定的。总体思路就是一开始先排序，并且记下来两个end，一个是当前的end，一个是之前一次的end，如果现在这个小区间的end比之前的pre_end还小，直接不考虑了。我做的时候忽略了这一点，如果不记下来之前的per_end的话，可能有区间是重复的（现在这个小区间如果加进去了，就跟上次加进去的那个小区间有重复的部分或者重合）

Example 1:

1
2
3
4
5
6
7
Input: clips = [[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]], T = 10
Output: 3
Explanation: 
We take the clips [0,2], [8,10], [1,9]; a total of 3 clips.
Then, we can reconstruct the sporting event as follows:
We cut [1,9] into segments [1,2] + [2,8] + [8,9].
Now we have segments [0,2] + [2,8] + [8,10] which cover the sporting event [0, 10].

Example 2:

1
2
3
4
Input: clips = [[0,1],[1,2]], T = 5
Output: -1
Explanation: 
We can't cover [0,5] with only [0,1] and [0,2].

Example 3:

1
2
3
4
Input: clips = [[0,1],[6,8],[0,2],[5,6],[0,4],[0,3],[6,7],[1,3],[4,7],[1,4],[2,5],[2,6],[3,4],[4,5],[5,7],[6,9]], T = 9
Output: 3
Explanation: 
We can take clips [0,4], [4,7], and [6,9].

Example 4:

1
2
3
4
Input: clips = [[0,4],[2,8]], T = 5
Output: 2
Explanation: 
Notice you can have extra video after the event ends.

Note:

1 <= clips.length <= 100
0 <= clips[i][0], clips[i][1] <= 100
0 <= T <= 100

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    
    static bool comp(const vector<int> &a, const vector<int> &b) {
        if(a[0]==b[0])
            return a[1] > b[1];
        return a[0] < b[0];
    }
    
    int videoStitching(vector<vector<int>>& clips, int T) {
        sort(clips.begin(), clips.end(), comp);
        int count=0, cur_end=0, pre_end=-1;
        for(int i = 0; i < clips.size(); i ++){
            if(clips[i][1] <= cur_end)
                continue;
            if(clips[i][0] > cur_end)
                return -1;
            if(clips[i][0] > pre_end){
                pre_end = cur_end;
                count++;
            }
            cur_end = clips[i][1];
            if(cur_end >= T)
                return count;
        }
        return -1;
    }
};

Leetcode1025. Divisor Game

Alice and Bob take turns playing a game, with Alice starting first.

Initially, there is a number N on the chalkboard. On each player’s turn, that player makes a move consisting of:

Choosing any x with 0 < x < N and N % x == 0.
Replacing the number N on the chalkboard with N - x.
Also, if a player cannot make a move, they lose the game.

Return True if and only if Alice wins the game, assuming both players play optimally.

Example 1:

1
2
3
Input: 2
Output: true
Explanation: Alice chooses 1, and Bob has no more moves.

Example 2:

1
2
3
Input: 3
Output: false
Explanation: Alice chooses 1, Bob chooses 1, and Alice has no more moves.

Note:

  • 1 <= N <= 1000

两个人玩游戏，给一个数字N，先轮到A走，A选一个数字x使得0 < x < N且N % x == 0，之后N变为N-x，如果谁选不出来x，那就输了，A遇见偶数赢，奇数输。

如果A看见偶数，就选x=1，则N变成奇数，B只能再选一个奇数，又把N变成偶数，由于1是奇数且1没法再选，故A遇见偶数一定赢，反之则输。

1
2
3
4
5
6
class Solution {
public:
    bool divisorGame(int N) {
        return (N%2)==0;
    }
};

Leetcode1026. Maximum Difference Between Node and Ancestor

Given the root of a binary tree, find the maximum value V for which there exists different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.

(A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.)

Example 1:

1
2
3
4
5
6
7
8
9
Input: [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: 
We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Note:

  • The number of nodes in the tree is between 2 and 5000.
  • Each node will have value between 0 and 100000.

给一棵树，找到最大值v，这个v是节点和祖先的值的差的绝对值。dfs里一定要有一个最大一个最小，这样才能算出来绝对值最大的一个，之前考虑只放一个值，没有搞定。

一个dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int val=0;
    
    void dfs(TreeNode* root,int maxval,int minval){
        val = max(val, abs(root->val - maxval));
        val = max(val, abs(root->val - minval));
        maxval = max(maxval, root->val);
        minval = min(minval, root->val);
        if(root->right) dfs(root->right,maxval,minval);
        if(root->left) dfs(root->left,maxval,minval);
    }
    
    int maxAncestorDiff(TreeNode* root) {
        dfs(root,root->val,root->val);
        return val;
    }
};

Leetcode1027. Longest Arithmetic Sequence

Given an array A of integers, return the length of the longest arithmetic subsequence in A.

Recall that a subsequence of A is a list A[i_1], A[i_2], …, A[i_k] with 0 <= i_1 < i_2 < … < i_k <= A.length - 1, and that a sequence B is arithmetic if B[i+1] - B[i] are all the same value (for 0 <= i < B.length - 1).

Example 1:

1
2
3
4
Input: A = [3,6,9,12]
Output: 4
Explanation:
The whole array is an arithmetic sequence with steps of length = 3.

Example 2:

1
2
3
4
Input: A = [9,4,7,2,10]
Output: 3
Explanation:
The longest arithmetic subsequence is [4,7,10].

Example 3:

1
2
3
4
Input: A = [20,1,15,3,10,5,8]
Output: 4
Explanation:
The longest arithmetic subsequence is [20,15,10,5].

Constraints:

  • 2 <= A.length <= 1000
  • 0 <= A[i] <= 500

这道题给了一个数组，让找最长的等差数列的长度，首先来考虑如何定义 DP 数组，最直接的就是用一个一维数组，其中dp[i]表示区间 [0, i] 中的最长等差数列的长度，但是这样定义的话，很难找出状态转移方程。因为有些隐藏信息被我们忽略了，就是等差数列的相等的差值，不同的等差数列的差值可以是不同的，所以不包括这个信息的话将很难更新 dp 值。所以这里就需要一个二维数组，dp[i][j]表示在区间 [0, i] 中的差值为j的最长等差数列的长度减1，这里减1是因为起始的数字并没有被算进去，不过不要紧，最后再加回来就行了。

还有一个需要注意的地方，由于等差数列的差值有可能是负数，而数组的下标不能是负数，所以需要处理一下，题目中限定了数组中的数字范围为0到 500 之间，所以差值的范围就是 -500 到 500 之间，可以给差值加上个 1000，这样差值范围就是 500 到 1500 了，二维 dp 数组的大小可以初始化为 nx2000。更新 dp 值的时候，先遍历一遍数组，对于每个遍历到的数字，再遍历一遍前面的所有数字，算出差值 diff，再加上 1000，然后此时的dp[i][diff]可以赋值为dp[j][diff]+1，然后用这个新的 dp 值来更新结果 res，最后别忘了 res 加1后返回，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int longestArithSeqLength(vector<int>& A) {
        int res = 0, n = A.size();
        vector<vector<int>> dp(n, vector<int>(2000));
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                int diff = A[i] - A[j] + 1000;
                dp[i][diff] = dp[j][diff] + 1;
                res = max(res, dp[i][diff]);
            }
        }
        return res + 1;
    }
};

Leetcode1028. Recover a Tree From Preorder Traversal

We run a preorder depth-first search (DFS) on the root of a binary tree.

At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node. If the depth of a node is D, the depth of its immediate child is D + 1. The depth of the root node is 0.

If a node has only one child, that child is guaranteed to be the left child.

Given the output traversal of this traversal, recover the tree and return its root.

Example 1:

1
2
Input: traversal = "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]

Example 2:

1
2
Input: traversal = "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]

Example 3:

1
2
Input: traversal = "1-401--349---90--88"
Output: [1,401,null,349,88,90]

这道题让我们根据一棵二叉树的先序遍历的结果来重建这棵二叉树。这里为了能够只根据先序遍历的结果来唯一的重建出二叉树，提供了每个结点值的深度，用短杠的个数来表示，根结点的深度为0，前方没有短杠，后面的数字前方只有一个短杠的就是根结点的左右子结点，然后紧跟在一个短杠后面的两个短杠的数字就是根结点左子结点的左子结点，以此类推。

遍历输入字符串，先提取短杠的个数，因为除了根结点之外，所有的深度值都是在结点值前面的，所有用一个 for 循环先提取出短杠的个数 level，然后提取结点值，也是用一个 for 循环，因为结点值可能是个多位数，有了结点值之后我们就可以新建一个结点了。下一步就比较 tricky 了，因为先序遍历跟 DFS 搜索一样有一个回到先前位置的过程，比如例子1中，当我们遍历到结点5的时候，此时是从叶结点4回到了根结点的右子结点5，现在栈中有4个结点，而当前深度为1的结点5是要连到根结点的，所以栈中的无关结点就要移除，需要把结点 2，3，4 都移除，就用一个 while 循环，假如栈中元素个数大于当前的深度 level，就移除栈顶元素。那么此时栈中就只剩根结点了，就可以连接了。此时我们的连接策略是，假如栈顶元素的左子结点为空，则连在左子结点上，否则连在右子结点上，因为题目中说了，假如只有一个子结点，一定是左子结点。然后再把当前结点压入栈即可，字符串遍历结束后，栈中只会留有一个结点（题目中限定了树不为空），就是根结点，直接返回即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    TreeNode* recoverFromPreorder(string S) {
        vector<TreeNode*> st;
        int i = 0, level = 0, val = 0, n = S.size();
        while (i < n) {
            for (level = 0; i < n && S[i] == '-'; ++i) {
                ++level;
            }
            for (val = 0; i < n && S[i] != '-'; ++i) {
                val = 10 * val + (S[i] - '0');
            }
            TreeNode *node = new TreeNode(val);
            while (st.size() > level) st.pop_back();
            if (!st.empty()) {
                if (!st.back()->left) st.back()->left = node;
                else st.back()->right = node;
            }
            st.push_back(node);
        }
        return st[0];
    }
};

我自己的方法是根据-的数量得到层数，判断这是到第几层了，如果超过了当前的层数，就说明到底了，返回就行。但是不知道为什么很慢。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    TreeNode* dfs(string s, int& cur, int depth) {
        if (cur == s.length())
            return NULL;
        
        int i = cur, len = s.length();
        while(i < len && i < cur+depth) {
            if (s[i] != '-')
                break;
            i ++;
        }
        if (i != cur+depth)
            return NULL;
        
        int val = 0;
        while(i < len)
            if ('0' <= s[i] && s[i] <= '9')
                val = val * 10 + s[i++] - '0';
            else
                break;
        TreeNode* res = new TreeNode(val);
        
        cur = i;
        res->left = dfs(s, cur, depth+1);
        res->right = dfs(s, cur, depth+1);
        
        return res;
    }
    
    TreeNode* recoverFromPreorder(string s) {
        int pos = 0;
        return dfs(s, pos, 0);
    }
};

Leetcode1029. Two City Scheduling

There are 2N people a company is planning to interview. The cost of flying the i-th person to city A is costs[i][0], and the cost of flying the i-th person to city B is costs[i][1].

Return the minimum cost to fly every person to a city such that exactly N people arrive in each city.

Example 1:

1
2
3
4
5
6
7
Input: [[10,20],[30,200],[400,50],[30,20]]
Output: 110
Explanation: 
The first person goes to city A for a cost of 10.
The second person goes to city A for a cost of 30.
The third person goes to city B for a cost of 50.
The fourth person goes to city B for a cost of 20.

The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.

Note:

  • 1 <= costs.length <= 100
  • It is guaranteed that costs.length is even.
  • 1 <= costs[i][0], costs[i][1] <= 1000

公司计划面试 2N 人。第 i 人飞往 A 市的费用为 costs[i][0]，飞往 B 市的费用为 costs[i][1]。
返回将每个人都飞到某座城市的最低费用，要求每个城市都有 N 人抵达。

由于人数是偶数个，一半的人去A,一半的人去B，换个角度，每个人要么去A，要么去B。如果他去A比去B的路程短，而且，这个节省的路程比一半的人还多，那么他就去A。所以，以去A和去B的路程差作为Key进行升序排序，前面一半人去A，后面去B。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    static bool comp(vector<int>&a, vector<int>&b) {
        return a[0]-a[1] < b[0]-b[1];
    }
    int twoCitySchedCost(vector<vector<int>>& costs) {
        int result=0;
        if(costs.size()==0)
            return result;
        sort(costs.begin(), costs.end(), comp);
        int ii=costs.size();
        int i;
        for(i=0;i<ii/2;i++)
            result += costs[i][0];
        for(;i<ii;i++)
            result+=costs[i][1];
        return result;
    }
};

Leetcode1030. Matrix Cells in Distance Order

We are given a matrix with R rows and C columns has cells with integer coordinates (r, c), where 0 <= r < R and 0 <= c < C.

Additionally, we are given a cell in that matrix with coordinates (r0, c0).

Return the coordinates of all cells in the matrix, sorted by their distance from (r0, c0) from smallest distance to largest distance. Here, the distance between two cells (r1, c1) and (r2, c2) is the Manhattan distance, |r1 - r2| + |c1 - c2|. (You may return the answer in any order that satisfies this condition.)

Example 1:

1
2
3
Input: R = 1, C = 2, r0 = 0, c0 = 0
Output: [[0,0],[0,1]]
Explanation: The distances from (r0, c0) to other cells are: [0,1]

Example 2:

1
2
3
4
Input: R = 2, C = 2, r0 = 0, c0 = 1
Output: [[0,1],[0,0],[1,1],[1,0]]
Explanation: The distances from (r0, c0) to other cells are: [0,1,1,2]
The answer [[0,1],[1,1],[0,0],[1,0]] would also be accepted as correct.

Example 3:

1
2
3
4
Input: R = 2, C = 3, r0 = 1, c0 = 2
Output: [[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]]
Explanation: The distances from (r0, c0) to other cells are: [0,1,1,2,2,3]
There are other answers that would also be accepted as correct, such as [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]].

Note:

  • 1 <= R <= 100
  • 1 <= C <= 100
  • 0 <= r0 < R
  • 0 <= c0 < C

根据与给定的点的顺序排序。

看到一种比较辣鸡的做法，就是先把所有点都加进去，再排序，顺便学习了一个新的写法，如下的lambda表达式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
      
    vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {
        auto comp = [r0,c0](vector<int> &a, vector<int> &b){
            return abs(a[0]-r0) + abs(a[1]-c0) < abs(b[0]-r0) + abs(b[1]-c0);
        };
        vector<vector<int>> res;
        for(int i=0;i<R;i++)
            for(int j=0;j<C;j++)
                res.push_back({i,j});
        
        sort(res.begin(),res.end(),comp);
        return res;
    }
};

用bfs做也行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    
    vector<vector<int> > allCellsDistOrder(int R, int C, int r0, int c0) {
        int visit[R][C];
        memset(visit,0,sizeof(int)*R*C);
        int direction[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
        queue< pair<int, int> > qu;
        vector< vector<int> > res;
        qu.push({r0,c0});
        while(!qu.empty()){
            pair<int ,int> temp = qu.front();
            qu.pop();
            int x = temp.first;
            int y = temp.second;
            if(visit[x][y]==1)
                continue;
            res.push_back({x,y});
            visit[x][y]=1;
            for(int i=0;i<4;i++){
                int xx = x + direction[i][0];
                int yy = y + direction[i][1];
                if ( xx>= 0 && xx < R && yy >=0 && yy < C && visit[xx][yy] == 0){
                     qu.push({xx,yy});
                }
            }
            
        }
        return res;
    }
};

更新一种做法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    
    static bool comp(vector<int>& a, vector<int>& b) {
        return a[2] < b[2];
    }
    
    vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {
        int k = 0;
        vector<vector<int>> v(R*C, vector<int>(3));
        for (int i = 0; i < R; i ++) {
            for(int j = 0; j < C; j ++) {
                v[k][0] = i;
                v[k][1] = j;
                v[k][2] = abs(i - r0) + abs(j - c0);
                k ++;
            }
        }
        sort(v.begin(), v.end(), comp);
	        
        for(int kk = 0; kk < R*C; kk ++) {
            v[kk].pop_back();
        }
        return v;
    }
};

Leetcode1031. Maximum Sum of Two Non-Overlapping Subarrays

Given an integer array nums and two integers firstLen and secondLen, return the maximum sum of elements in two non-overlapping subarrays with lengths firstLen and secondLen.

The array with length firstLen could occur before or after the array with length secondLen, but they have to be non-overlapping.

A subarray is a contiguous part of an array.

Example 1:

1
2
3
Input: nums = [0,6,5,2,2,5,1,9,4], firstLen = 1, secondLen = 2
Output: 20
Explanation: One choice of subarrays is [9] with length 1, and [6,5] with length 2.

Example 2:

1
2
3
Input: nums = [3,8,1,3,2,1,8,9,0], firstLen = 3, secondLen = 2
Output: 29
Explanation: One choice of subarrays is [3,8,1] with length 3, and [8,9] with length 2.

Example 3:

1
2
3
Input: nums = [2,1,5,6,0,9,5,0,3,8], firstLen = 4, secondLen = 3
Output: 31
Explanation: One choice of subarrays is [5,6,0,9] with length 4, and [3,8] with length 3.

题意：给你一个数组，再给你一个L，M，求在这个数组里面，两个不重合的长度分别为L，M的最的最大和。

思路：先预处理一个dp[i][2]，dp[i][0]表示以i为开头，长度为L的值；dp[i][1]表示以i为开头，长度为M的值。再两层for，遍历i，j分别表示两个数组的头，只要两个数组不重合，就是合适的数组。最后求个最大值就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int maxSumTwoNoOverlap(vector<int>& nums, int l, int m) {
        int n = nums.size(), res = 0;
        vector<int> sum(n, 0);
        vector<vector<int>> dp(n, vector<int>(2, 0));
        
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < l && i+j < n; j ++)
                dp[i][0] += nums[i+j];
            for (int j = 0; j < m && i+j < n; j ++)
                dp[i][1] += nums[i+j];
        }
        
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < n; j ++) {
                if (i + l <= j)
                    res = max(res, dp[i][0]+dp[j][1]);
                if (j + m <= i)
                    res = max(res, dp[i][0]+dp[j][1]);
            }
        }
        return res;
    }
};

这道题给了一个非负数组A，还有两个长度L和M，说是要分别找出不重叠且长度分别为L和M的两个子数组，前后顺序无所谓，问两个子数组最大的数字之和是多少。来看论坛上的高分解法吧，首先建立累加和数组，这里可以直接覆盖A数组，然后定义Lmax为在最后M个数字之前的长度为L的子数组的最大数字之和，同理，Mmax表示在最后L个数字之前的长度为M的子数组的最大数字之和。结果res初始化为前 L+M 个数字之和，然后遍历数组，从 L+M 开始遍历，先更新Lmax和Mmax，其中Lmax用A[i - M] - A[i - M - L]来更新，Mmax用A[i - L] - A[i - M - L]来更新。然后取Lmax + A[i] - A[i - M]和Mmax + A[i] - A[i - L]之间的较大值来更新结果 res 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxSumTwoNoOverlap(vector<int>& A, int L, int M) {
        for (int i = 1; i < A.size(); ++i) {
            A[i] += A[i - 1];
        }
        int res = A[L + M - 1], Lmax = A[L - 1], Mmax = A[M - 1];
        for (int i = L + M; i < A.size(); ++i) {
            Lmax = max(Lmax, A[i - M] - A[i - M - L]);
            Mmax = max(Mmax, A[i - L] - A[i - M - L]);
            res = max(res, max(Lmax + A[i] - A[i - M], Mmax + A[i] - A[i - L]));
        }
        return res;
    }
};

Leetcode1033. Moving Stones Until Consecutive

Three stones are on a number line at positions a, b, and c. Each turn, you pick up a stone at an endpoint (ie., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let’s say the stones are currently at positions x, y, z with x < y < z. You pick up the stone at either position x or position z, and move that stone to an integer position k, with x < k < z and k != y. The game ends when you cannot make any more moves, ie. the stones are in consecutive positions.

When the game ends, what is the minimum and maximum number of moves that you could have made? Return the answer as an length 2 array: answer = [minimum_moves, maximum_moves]

Example 1:

1
2
3
Input: a = 1, b = 2, c = 5
Output: [1,2]
Explanation: Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.

Example 2:

1
2
3
Input: a = 4, b = 3, c = 2
Output: [0,0]
Explanation: We cannot make any moves.

Example 3:

1
2
3
Input: a = 3, b = 5, c = 1
Output: [1,2]
Explanation: Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.

a,b,c表示三个位置，在三个位置上各有一个石头。现在要移动三个石头中的若干个，每次移动都必须选两端石头的里面的位置，最终使得它们三个放在连续的位置。问最少需要多少次移动，最多需要多少次移动。

如果三个石头本来就连续，则不用移动。例：1，2，3

如果三个石头本来不连续，则：
最少移动次数：

  1. 有两个石头之间的距离小于等于2，则最少只需要一次移动。例：1，2，4，把4移动到3即可；或者例1，3，5，把5移到2即可。
  2. 所有石头之间的最小距离>2，则最少需要移动两个石头。例：1，4，7，需要把两个石头移动到另一个的旁边。

最多移动次数：
题目说了，只能像两端石头里面的那些位置上放，所以最多移动的次数就是本来两端石头中间包含的点（并且去掉中间的石头），策略是每次向内移动一步。例：1，3，5，在1和5中间之间共有2个可以放的点（分别为2，4），所以最多只能有max_ - min_ - 2次移动。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
	public:
    vector<int> numMovesStones(int a, int b, int c) {
        int sum_ = a + b + c;
        int min_ = min(a, min(b, c));
        int max_ = max(a, max(b, c));
        int mid_ = sum_ - min_ - max_;
	        
        if (max_ - min_ == 2)
            return {0, 0};
	        
        int min_move = min(mid_ - min_, max_ - mid_) <= 2 ? 1 : 2;
        int max_move = max_ - min_ - 2;
        return {min_move, max_move};
    }
};

Leetcode1034. Coloring A Border

Given a 2-dimensional grid of integers, each value in the grid represents the color of the grid square at that location.

Two squares belong to the same connected component if and only if they have the same color and are next to each other in any of the 4 directions.

The border of a connected component is all the squares in the connected component that are either 4-directionally adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).

Given a square at location (r0, c0) in the grid and a color, color the border of the connected component of that square with the given color, and return the final grid.

Example 1:

1
2
Input: grid = [[1,1],[1,2]], r0 = 0, c0 = 0, color = 3
Output: [[3, 3], [3, 2]]

Example 2:

1
2
Input: grid = [[1,2,2],[2,3,2]], r0 = 0, c0 = 1, color = 3
Output: [[1, 3, 3], [2, 3, 3]]

Example 3:

1
2
Input: grid = [[1,1,1],[1,1,1],[1,1,1]], r0 = 1, c0 = 1, color = 2
Output: [[2, 2, 2], [2, 1, 2], [2, 2, 2]]

Note:

  • 1 <= grid.length <= 50
  • 1 <= grid[0].length <= 50
  • 1 <= grid[i][j] <= 1000
  • 0 <= r0 < grid.length
  • 0 <= c0 < grid[0].length
  • 1 <= color <= 1000

这道题给了一个二维数组 grid，和一个起始位置 (r0, c0)，格子里的数字代表不同的颜色，又给了一个新的颜色 color，现在让给起始位置所在的连通区域的边缘填充这种新的颜色。这道题的难点就是如何找出连通区域的边缘，找连通区域并不难，因为有了起始点，可以用 DFS 或者 BFS 来找出所有相连的位置，而边缘位置需要进一步判断，一种情况是当前位置是二维矩阵的边缘，那么其一定也是连通区域的边缘，另一种情况是若四个相邻位置有其他的颜色，则当前位置也一定是边缘。下面先来看 BFS 的解法，主体还是经典的 BFS 写法不变，使用队列 queue，和一个 TreeSet 来记录已经遍历过的位置。将起始位置先放入 queue 和 visited 集合，然后进行 while 循环，取出队首元素，然后判断当前位置是否是二维数组的边缘，是的话直接将颜色更新 color。然后遍历周围四个位置，若越界了或者访问过了直接跳过，然后看若颜色和起始位置的颜色相同，则加入 visited 和 queue，否则将当前位置的颜色更新为 color，因为周围有不同的颜色了，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<vector<int>> colorBorder(vector<vector<int>>& grid, int row, int col, int color) {
        int m = grid.size(), n = grid[0].size(), ori_color = grid[row][col];
        vector<vector<int>> visited(m, vector<int>(n, 0));
        vector<vector<int>> dirs{{-1, 0}, {0, 1}, {1, 0}, {0, -1}}  ;
        queue<int> q;
        q.push(row*n + col);
        visited[row][col] = 1;
        while(!q.empty()) {
            int x = q.front() / n;
            int y = q.front() % n;
            q.pop();
            if (x == 0 || x == m-1 || y == 0 || y == n-1)
                grid[x][y] = color;
            for (int i = 0; i < 4; i ++) {
                int xx = x + dirs[i][0];
                int yy = y + dirs[i][1];
                if (xx < 0 || xx >= m || yy < 0 || yy >= n || visited[xx][yy] == 1)
                    continue;
                if (grid[xx][yy] == ori_color) {
                    q.push(xx * n + yy);
                    visited[xx][yy] = 1;
                }
                else 
                    grid[x][y] = color;
            }
        }
        return grid;
    }
};

Leetcode1035. Uncrossed Lines

We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw connecting lines : a straight line connecting two numbers A[i] and B[j] such that:A[i] == B[j];

The line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.

Return the maximum number of connecting lines we can draw in this way.

Example 1:

1
2
3
4
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Example 2:

1
2
Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Example 3:

1
2
Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

Note:

  • 1 <= A.length <= 500
  • 1 <= B.length <= 500
  • 1 <= A[i], B[i] <= 2000

这道题给了A和B两个数字数组，并且上下并列排放，说是可以用线来连接相同的数字，问最多能连多少根线而且不会发生重叠。首先来想一下，什么情况下两条连线会相交，可以观察下例子1给的图，发现若把4和2分别连上会交叉，这是因为在A数组中是 4，2，而且在B数组中是 2，4，顺序不一样。再来看例子2，分别连 5，1，2 或者 2，1，2，或者 5，2，5 都是可以的，仔细观察，可以发现这些其实就是最长公共子序列 Longest Common Subsequence。使用一个二维数组dp，其中dp[i][j]表示数组A的前i个数字和数组B的前j个数字的最长相同的子序列的数字个数，这里大小初始化为 (m+1)x(n+1)，这里的m和n分别是数组A和数组B的长度。接下来就要找状态转移方程了，如何来更新dp[i][j]，若二者对应位置的字符相同，表示当前的 LCS 又增加了一位，所以可以用dp[i-1][j-1] + 1来更新dp[i][j]。否则若对应位置的字符不相同，由于是子序列，还可以错位比较，可以分别从数组A或者数组B去掉一个当前数字，那么其dp值就是dp[i-1][j]和dp[i][j-1]，取二者中的较大值来更新dp[i][j]即可，最终的结果保存在了dp[m][n]中，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int maxUncrossedLines(vector<int>& A, vector<int>& B) {
        int m = A.size(), n = B.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (A[i - 1] == B[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
};

Leetcode1037. Valid Boomerang

A boomerang is a set of 3 points that are all distinct and not in a straight line. Given a list of three points in the plane, return whether these points are a boomerang.

Example 1:

1
2
Input: [[1,1],[2,3],[3,2]]
Output: true

Example 2:

1
2
Input: [[1,1],[2,2],[3,3]]
Output: false

Note:

points.length == 3
points[i].length == 2
0 <=points[i][j]<= 100

判断三个点是不是互异且不共线的，简单

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool isBoomerang(vector<vector<int>>& points) {
        for(int i=0;i<points.size();i++)
            for(int j=i+1;j<points.size();j++)
                if(points[i][0]==points[j][0] && points[i][1]==points[j][1])
                    return false;
        int dx1 = points[1][0] - points[0][0];
        int dx2 = points[1][1] - points[0][1];
        int dx3 = points[2][0] - points[1][0];
        int dx4 = points[2][1] - points[1][1];
        if(dx1*dx4-dx2*dx3==0)
            return false;
        return true;
    }
};

Leetcode1038. Binary Search Tree to Greater Sum Tree

Given the root of a binary search tree with distinct values, modify it so that every node has a new value equal to the sum of the values of the original tree that are greater than or equal to node.val.

As a reminder, a binary search tree is a tree that satisfies these constraints:

The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.

Example 1:

Input: [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

典型的中序遍历，先遍历右子树，再把root赋值，最后看左子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int sum=0;
    void houxu(TreeNode* root){
        if(root->right)
            houxu(root->right);
        sum+=root->val;
        root->val = sum;
        if(root->left)
            houxu(root->left);
        
    }
    TreeNode* bstToGst(TreeNode* root) {
        houxu(root);
        return root;
    }
};

Leetcode1039. Minimum Score Triangulation of Polygon

You have a convex n-sided polygon where each vertex has an integer value. You are given an integer array values where values[i] is the value of the ith vertex (i.e., clockwise order).

You will triangulate the polygon into n - 2 triangles. For each triangle, the value of that triangle is the product of the values of its vertices, and the total score of the triangulation is the sum of these values over all n - 2 triangles in the triangulation.

Return the smallest possible total score that you can achieve with some triangulation of the polygon.

Example 1:

1
2
3
Input: values = [1,2,3]
Output: 6
Explanation: The polygon is already triangulated, and the score of the only triangle is 6.

Example 2:

1
2
3
4
Input: values = [3,7,4,5]
Output: 144
Explanation: There are two triangulations, with possible scores: 3*7*5 + 4*5*7 = 245, or 3*4*5 + 3*4*7 = 144.
The minimum score is 144.

Example 3:

1
2
3
Input: values = [1,3,1,4,1,5]
Output: 13
Explanation: The minimum score triangulation has score 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13.

Constraints:

  • n == values.length
  • 3 <= n <= 50
  • 1 <= values[i] <= 100

这道题说有一个N边形，让我们连接不相邻的顶点，从而划分出三角形，最多可以划分出 N-2 个三角形，每划分出一个三角形，得分是三个顶点的乘积，问最小的得分是多少。首先要来定义 DP 数组，这里一维数组肯定是不够用的，因为需要保存区间信息，所以这里用个二维数组，其中dp[i][j]表示从顶点i到顶点j为三角形的一条边，可以组成的所有的三角形的最小得分。接下来推导状态转移方程，由于三角形的一条边已经确定了，接下来就要找另一个顶点的位置，这里需要遍历所有的情况，使用一个变量k，遍历区间 (i, j) 中的所有的顶点，由顶点i，j，和k组成的三角形的得分是A[i] * A[k] * A[j]可以直接算出来，这个三角形将整个区间分割成了两部分，分别是 (i, k) 和 (k, j)，这两个区间的最小得分值可以直接从 dp 数组中取得，分别是dp[i][k]和dp[k][j]，这样状态转移方程就有了，用dp[i][k] + A[i] * A[k] * A[j] + dp[k][j]来更新dp[i][j]，为了防止整型越界，不能直接将 dp 数组都初始化为整型最大值INT_MAX，而是在更新的时候，判断若dp[i][j]为0时，用INT_MAX，否则用其本身值，最终的结果保存在dp[0][n-1]中，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int minScoreTriangulation(vector<int>& A) {
        int n = A.size();
        vector<vector<int>> dp(n, vector<int>(n));
        for (int i = n - 1; i >= 0; --i) {
            for (int j = i + 1; j < n; ++j) {
                for (int k = i + 1; k < j; ++k) {
                    dp[i][j] = min(dp[i][j] == 0 ? INT_MAX : dp[i][j], dp[i][k] + A[i] * A[k] * A[j] + dp[k][j]);
                }
            }
        }
        return dp[0][n - 1];
    }
};

再来看一种同样的 DP 解法，和上面的区别是 dp 数组更新的顺序不同，之前说过了更新大区间的 dp 值需要用到小区间的 dp 值，这里是按照区间的大小来更新的，从2更新到n，然后确定区间 (i, j) 的大小为 len，再遍历中间所有的k，状态转移方程还是跟上面一样的。这种更新方法在其他的题目也有用到，最典型的就是那道 Burst Balloons，参见代码如下：

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int minScoreTriangulation(vector<int>& A) {
        int n = A.size();
        vector<vector<int>> dp(n, vector<int>(n));
        for (int len = 2; len < n; ++len) {
            for (int i = 0; i + len < n; ++i) {
                int j = i + len;
                dp[i][j] = INT_MAX;
                for (int k = i + 1; k < j; ++k) {
                    dp[i][j] = min(dp[i][j], dp[i][k] + A[i] * A[k] * A[j] + dp[k][j]);
                }
            }
        }
        return dp[0][n - 1];
    }
};

Leetcode1041. Robot Bounded In Circle

On an infinite plane, a robot initially stands at (0, 0) and faces north. The robot can receive one of three instructions:

  • “G”: go straight 1 unit;
  • “L”: turn 90 degrees to the left;
  • “R”: turn 90 degrees to the right.

The robot performs the instructions given in order, and repeats them forever.

Return true if and only if there exists a circle in the plane such that the robot never leaves the circle.

Example 1:

1
2
3
4
Input: instructions = "GGLLGG"
Output: true
Explanation: The robot moves from (0,0) to (0,2), turns 180 degrees, and then returns to (0,0).
When repeating these instructions, the robot remains in the circle of radius 2 centered at the origin.

Example 2:

1
2
3
Input: instructions = "GG"
Output: false
Explanation: The robot moves north indefinitely.

Example 3:

1
2
3
Input: instructions = "GL"
Output: true
Explanation: The robot moves from (0, 0) -> (0, 1) -> (-1, 1) -> (-1, 0) -> (0, 0) -> ...

Constraints:

  • 1 <= instructions.length <= 100
  • instructions[i] is ‘G’, ‘L’ or, ‘R’.

这道题说是在一个无限大的区域，有个机器人初始化站在原点 (0, 0) 的位置，面朝北方。该机器人有三种指令可以执行，G表示朝当前方向前进一步，L表示向左转 90 度，R表示向右转 90 度，现在给了一些连续的这样的指令，若一直重复的按顺序循环执行下去，问机器人是否会在一个固定的圆圈路径中循环。首先我们需要执行一遍所有的指令，然后根据最后的状态（包括位置和朝向）来分析机器人是否之后会一直走循环路线。若执行过一遍所有指令之后机器人还在原点上，则一定是在一个圆圈路径上（即便是机器人可能就没移动过，一个点也可以看作是圆圈路径）。若机器人偏离了起始位置，只要看此时机器人的朝向，只要不是向北，则其最终一定会回到起点。

知道了最终状态和循环路径的关系，现在就是如何执行这些指令了。也不难，用一个变量表示当前的方向，0表示北，1为东，2为南，3为西，按这个顺序写出偏移量数组 dirs，就是在迷宫遍历的时候经常用到的那个数组。然后记录当前位置 cur，初始化为 (0, 0)，然后就可以执行指令了，若遇到G指令，根据 idx 从 dirs 数组中取出偏移量加到 cur 上即可。若遇到L指令，idx 是要减1的，为了避免负数，先加上个4，再减1，再对4取余。同理，若遇到R指令，idx 加1之后对4取余。最后判断若还在原点，或者朝向不为北的时候，返回 true 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    bool isRobotBounded(string instructions) {
        vector<vector<int>> dirs{{0, 1}, {-1, 0}, {0, -1}, {1, 0}};
        int xx = 0, yy = 0;
        int direction = 0;
        for (int i = 0; i < instructions.size(); i ++) {
            if (instructions[i] == 'G') {
                xx += dirs[direction][0];
                yy += dirs[direction][1];
            }
            else if (instructions[i] == 'L')
                direction = (direction + 1 ) % 4;
            else if (instructions[i] == 'R')
                direction = (direction + 4 - 1) % 4;
        }
        return (xx == 0 && yy == 0) || direction != 0;
    }
};

Leetcode1042. Flower Planting With No Adjacent

You have N gardens, labelled 1 to N. In each garden, you want to plant one of 4 types of flowers. paths[i] = [x, y] describes the existence of a bidirectional path from garden x to garden y. Also, there is no garden that has more than 3 paths coming into or leaving it.

Your task is to choose a flower type for each garden such that, for any two gardens connected by a path, they have different types of flowers.

Return any such a choice as an array answer, where answer[i] is the type of flower planted in the (i+1)-th garden. The flower types are denoted 1, 2, 3, or 4. It is guaranteed an answer exists.

Example 1:

1
2
Input: N = 3, paths = [[1,2],[2,3],[3,1]]
Output: [1,2,3]

Example 2:

1
2
Input: N = 4, paths = [[1,2],[3,4]]
Output: [1,2,1,2]

Example 3:

1
2
Input: N = 4, paths = [[1,2],[2,3],[3,4],[4,1],[1,3],[2,4]]
Output: [1,2,3,4]

Note:

  • 1 <= N <= 10000
  • 0 <= paths.size <= 20000
  • No garden has 4 or more paths coming into or leaving it.
  • It is guaranteed an answer exists.

有 N 个花园，按从 1 到 N 标记。在每个花园中，你打算种下四种花之一。 paths[i] = [x, y] 描述了花园 x 到花园 y 的双向路径。另外，没有花园有 3 条以上的路径可以进入或者离开。你需要为每个花园选择一种花，使得通过路径相连的任何两个花园中的花的种类互不相同。以数组形式返回选择的方案作为答案 answer，其中 answer[i] 为在第 (i+1) 个花园中种植的花的种类。花的种类用 1, 2, 3, 4 表示。保证存在答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> gardenNoAdj(int N, vector<vector<int>>& paths) {
        vector<int> res(N, 0);
        vector<vector<int>> graph(N);
        for(int i = 0 ; i < paths.size(); i ++) {
            graph[paths[i][0]-1].push_back(paths[i][1]-1);
            graph[paths[i][1]-1].push_back(paths[i][0]-1);
        }
        for (int i = 0; i < N; ++i) {      
            int mask = 0;
            for (const auto& j : graph[i])
                mask |= (1 << res[j]);
            for (int c = 1; c <= 4 && res[i] == 0; ++c)
                if (!(mask & (1 << c))) res[i] = c;
        }
        return res;
    }
};

Leetcode1043. Partition Array for Maximum Sum

Given an integer array arr, you should partition the array into (contiguous) subarrays of length at most k. After partitioning, each subarray has their values changed to become the maximum value of that subarray.

Return the largest sum of the given array after partitioning.

Example 1:

1
2
3
Input: arr = [1,15,7,9,2,5,10], k = 3
Output: 84
Explanation: arr becomes [15,15,15,9,10,10,10]

Example 2:

1
2
Input: arr = [1,4,1,5,7,3,6,1,9,9,3], k = 4
Output: 83

Example 3:

1
2
Input: arr = [1], k = 1
Output: 1

Constraints:

  • 1 <= arr.length <= 500
  • 0 <= arr[i] <= 109
  • 1 <= k <= arr.length

这道题给了一个数组 arr，和一个正整数k，说是将数组分成若干个长度不超过k的子数组，分割后的子数组所有的数字都变成该子数组中的最大值，让求分割后的所有子数组数字之和。由于分割的子数组长度不固定，用暴力搜索的话将会有很多很多种情况，不出意外的话会超时。对于这种玩子数组，又是求极值的题，刷题老司机们应该立马就能想到用动态规划 Dynamic Programming 来做。先来定义 dp 数组，先从最简单的考虑，使用一个一维的 dp 数组，其中dp[i]就表示分割数组中的前i个数字组成的数组可以得到的最大的数字之和。下面来考虑状态转移方程怎么求，对于dp[i]来说，若把最后k个数字分割出来，那么前i个数字就被分成了两个部分，前 i-k 个数字，其数字之和可以直接由dp[i-k]来取得，后面的k个数字，则需要求出其中最大的数字，然后乘以k，用这两部分之和来更新dp[i]即可。由于题目中说了分割的长度不超过k，那么就是说小于k的也是可以的，则需要遍历 [1, k] 区间所有的长度，均进行分割。接下来看代码，建立一个大小为 n+1 的 dp 数组，然后i从1遍历到n，此时新建一个变量 curMax 记录当前的最大值，然后用j从1遍历到k，同时要保证 i-j 是大于等于0的，因为需要前半部分存在，实际上这是从第i个数字开始往前找j个数字，然后记录其中最大的数字 curMax，并且不断用dp[i-j] + curMax * j来更新dp[i]即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxSumAfterPartitioning(vector<int>& arr, int k) {
        int n = arr.size();
        vector<int> dp(n + 1);
        for (int i = 1; i <= n; ++i) {
            int curMax = 0;
            for (int j = 1; j <= k && i - j >= 0; ++j) {
                curMax = max(curMax, arr[i - j]);
                dp[i] = max(dp[i], dp[i - j] + curMax * j);
            }
        }
        return dp[n];
    }
};

Leetcode1046. Last Stone Weight

We have a collection of stones, each stone has a positive integer weight.

Each turn, we choose the two heaviest stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:

  • If x == y, both stones are totally destroyed;
  • If x != y, the stone of weight x is totally destroyed, and the stone of weight y has new weight y-x.
  • At the end, there is at most 1 stone left. Return the weight of this stone (or 0 if there are no stones left.)

Example 1:

1
2
3
4
5
6
7
Input: [2,7,4,1,8,1]
Output: 1
Explanation: 
We combine 7 and 8 to get 1 so the array converts to [2,4,1,1,1] then,
we combine 2 and 4 to get 2 so the array converts to [2,1,1,1] then,
we combine 2 and 1 to get 1 so the array converts to [1,1,1] then,
we combine 1 and 1 to get 0 so the array converts to [1] then that's the value of last stone.

堆排序解法，主要是看看人家的堆排序怎么写。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
	public:
    int lastStoneWeight(vector<int>& stones) {
        int p, q;
        if(stones.size() == 1)
            return stones[0];
        while(stones.size() >= 2) {
            heapsort(stones);
            p = stones.back(); stones.pop_back();
            q = stones.back(); stones.pop_back();
            int diff = p - q;
            if(diff)    stones.push_back(diff);
        }
        if(stones.empty())   
            return 0;
        return stones[0];
    }
    
    void heapsort(vector<int>& stones) {
        if(stones.size() <= 1)  return;
        build_heap(stones);
        int heap_size = stones.size();
        while(heap_size >= 2) {
            swap(stones[0], stones[heap_size - 1]);
            heap_size --;
            max_heapify(stones, 0, heap_size);
        }
    }
    
    void build_heap(vector<int>& stones) {
        for(int i=stones.size()/2; i>=0; i--){
            max_heapify(stones, i, stones.size());
        }
    }
   
    void max_heapify(vector<int>& stones, int i, int heap_size){
        int large = i;
        if(2*i+1<heap_size && stones[i]<stones[2*i+1])  large = 2*i+1;
        if(2*i+2<heap_size && stones[large]<stones[2*i+2])  large = 2*i+2;
        if(large != i){
            swap(stones[i], stones[large]);
            max_heapify(stones, large, heap_size);
        }
    }
    
    void swap(int &a, int &b){
        int temp;
        temp = a; a = b; b = temp;
    } 
};

Leetcode1047. Remove All Adjacent Duplicates In String

Given a string S of lowercase letters, a duplicate removal consists of choosing two adjacent and equal letters, and removing them.

We repeatedly make duplicate removals on S until we no longer can.

Return the final string after all such duplicate removals have been made. It is guaranteed the answer is unique.

Example 1:

1
2
3
4
Input: "abbaca"
Output: "ca"
Explanation: 
For example, in "abbaca" we could remove "bb" since the letters are adjacent and equal, and this is the only possible move.  The result of this move is that the string is "aaca", of which only "aa" is possible, so the final string is "ca".

Note:

  • 1 <= S.length <= 20000
  • S consists only of English lowercase letters.

借用了栈的思想，但是这么做会超内存。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
string removeDuplicates(string S) {
        stack<char> st;
        for(int i=S.length()-1;i>=0;i--){
            if(!st.empty() && st.top()==S[i]){
                st.pop();
                continue;
            }
            else
                st.push(S[i]);
        }
        string res;
        while(!st.empty()){
            res = res + st.top();
            st.pop();
        }
        return res;
    }
};

借鉴了大佬的做法：

1
2
3
4
5
6
7
8
9
string removeDuplicates(string S) {
    string res = "";
    for (char& c : S)
        if (res.size() && c == res.back())
            res.pop_back();
        else
            res.push_back(c);
    return res;
}
1
2
3
4
5
6
7
8
9
10
class Solution {
	public:
    string removeDuplicates(string S) {
        string a;
        for (auto& c : S) 
            if (a.size() && a.back() == c) a.pop_back();
            else a.push_back(c);
        return a;
    }
};

这里a.size()是返回字符数量，a.back()返回最后一个字符，pop_back和push_back和vector一样了。

把我自己的超时的代码改了一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
	public:
    string removeDuplicates(string S) {
        string res="";
        int len = 0;
        int S_len = S.size();
        for(int i=0;i<S_len;i++){
            if( len>0 && res[len-1]==S[i]){
                res.pop_back();
                len--;
            }
            else{
                res += S[i];
                len++;
            }
        }
        return res;
    }
};

Leetcode1048. Longest String Chain

Given a list of words, each word consists of English lowercase letters.

Let’s say word1 is a predecessor of word2 if and only if we can add exactly one letter anywhere in word1 to make it equal to word2. For example, “abc” is a predecessor of “abac”.

A *word chain *is a sequence of words [word_1, word_2, …, word_k] with k >= 1, where word_1 is a predecessor of word_2, word_2 is a predecessor of word_3, and so on.

Return the longest possible length of a word chain with words chosen from the given list of words.

Example 1:

1
2
3
Input: words = ["a","b","ba","bca","bda","bdca"]
Output: 4
Explanation: One of the longest word chain is "a","ba","bda","bdca".

Example 2:

1
2
Input: words = ["xbc","pcxbcf","xb","cxbc","pcxbc"]
Output: 5

Constraints:

  • 1 <= words.length <= 1000
  • 1 <= words[i].length <= 16
  • words[i] only consists of English lowercase letters.

这道题给了一个单词数组，定义了一种前任关系，说是假如在 word1 中任意位置加上一个字符，能变成 word2 的话，那么 word1 就是 word2 的前任，实际上 word1 就是 word2 的一个子序列。现在问在整个数组中最长的前任链有多长，暴力搜索的话会有很多种情况，会产生大量的重复计算，所以会超时。这种玩数组求极值的题十有八九都是用动态规划 Dynamic Programming 来做的，这道题其实跟之前那道 Longest Arithmetic Subsequence 求最长的等差数列的思路是很像的。首先来定义 dp 数组，这里用一个一维的数组就行了，其中 dp[i] 表示 [0, i] 区间的单词的最长的前任链。下面来推导状态转移方程，对于当前位置的单词，需要遍历前面所有的单词，这里需要先给单词按长度排个序，因为只有长度小1的单词才有可能是前任，所以只需要遍历之前所有长度正好小1的单词，若是前任关系，则用其 dp 值加1来更新当前 dp 值即可。判断前任关系可以放到一个子数组中来做，其实就是检测是否是子序列，没啥太大的难度，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int longestStrChain(vector<string>& words) {
        int n = words.size(), res = 1;
        sort(words.begin(), words.end(), [](string& a, string &b){
            return a.size() < b.size();
        });
        vector<int> dp(n, 1);
        for (int i = 1; i < n; ++i) {
            for (int j = i - 1; j >= 0; --j) {
                if (words[j].size() + 1 < words[i].size()) break;
                if (words[j].size() == words[i].size()) continue;
                if (helper(words[j], words[i])) {
                    dp[i] = max(dp[i], dp[j] + 1);
                    res = max(res, dp[i]);
                }
            }
        }
        return res;
    }
    bool helper(string word1, string word2) {
        int m = word1.size(), n = word2.size(), i = 0;
        for (int j = 0; j < n; ++j) {
            if (word2[j] == word1[i]) ++i;
        }
        return i == m;
    }
};

论坛上的高分解法在检验是否是前任时用了一种更好的方法，不是检测子序列，而是将当前的单词，按顺序每次去掉一个字符，然后看剩下的字符串是否在之前出现过，是的话就说明有前任，用其 dp 值加1来更新当前 dp 值，这是一种更巧妙且简便的方法。这里由于要快速判断前任是否存在，所以不是用的 dp 数组，而是用了个 HashMap，对于每个遍历到的单词，按顺序移除掉每个字符，若剩余的部分在 HashMap 中，则更新 dp 值和结果 res，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int longestStrChain(vector<string>& words) {
        int n = words.size(), res = 1;
        sort(words.begin(), words.end(), [](string& a, string& b){ return a.size() < b.size(); });
        unordered_map<string, int> dp;
        for (string word : words) {
            dp[word] = 1;
            for (int i = 0; i < word.size(); ++i) {
                string pre = word.substr(0, i) + word.substr(i + 1);
                if (dp.count(pre)) {
                    dp[word] = max(dp[word], dp[pre] + 1);
                    res = max(res, dp[word]);
                }
            }
        }
        return res;
    }
};

Leetcode1049. Last Stone Weight II

You are given an array of integers stones where stones[i] is the weight of the ith stone.

We are playing a game with the stones. On each turn, we choose any two stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:

If x == y, both stones are destroyed, and
If x != y, the stone of weight x is destroyed, and the stone of weight y has new weight y - x.
At the end of the game, there is at most one stone left.

Return the smallest possible weight of the left stone. If there are no stones left, return 0.

Example 1:

1
2
3
4
5
6
7
Input: stones = [2,7,4,1,8,1]
Output: 1
Explanation:
We can combine 2 and 4 to get 2, so the array converts to [2,7,1,8,1] then,
we can combine 7 and 8 to get 1, so the array converts to [2,1,1,1] then,
we can combine 2 and 1 to get 1, so the array converts to [1,1,1] then,
we can combine 1 and 1 to get 0, so the array converts to [1], then that's the optimal value.

Example 2:

1
2
Input: stones = [31,26,33,21,40]
Output: 5

Example 3:

1
2
Input: stones = [1,2]
Output: 1

Constraints:

  • 1 <= stones.length <= 30
  • 1 <= stones[i] <= 100

这道题是之前那道 Last Stone Weight 的拓展，之前那道题说是每次取两个最大的进行碰撞，问最后剩下的重量。而这里是可以任意取两个石头进行碰撞，并且需要最后剩余的重量最小，这种玩数组求极值的题十有八九都是用动态规划 Dynamic Programming 来做的。首先来考虑 dp 数组该如何定义，若是直接用 dp[i] 来表示区间 [0, i] 内的石头碰撞后剩余的最小重量，状态转移方程将十分难推导，因为石子是任意选的，当前的 dp 值和之前的没有太大的联系。这里需要重新考虑 dp 数组的定义，这道题的解法其实挺难想的，需要转换一下思维，虽说是求碰撞后剩余的重量，但实际上可以看成是要将石子分为两堆，且尽可能让二者的重量之和最接近。若分为的两堆重量相等，则相互碰撞后最终将直接湮灭，剩余为0；若不相等，则剩余的重量就是两堆石子的重量之差。这道题给的数据范围是石子个数不超过 30 个，每个的重量不超过 100，这样的话总共的石子重量不超过 3000，分为两堆的话，每堆的重量不超过 1500。我们应该将 dp[i] 定义为数组中的石子是否能组成重量为i的一堆，数组大小设为 1501 即可，且 dp[0] 初始化为 true。这里的状态转移的思路跟之前那道 Coin Change 是很相似的，遍历每个石头，累加当前石头重量到 sum，然后从 1500 和 sum 中的较小值开始遍历（因为每堆的总重量不超过 1500），且i要大于 stone，小于当前石头的i不需要更新，由于当前的石头重量 stone 知道了，那么假如 i-stone 的 dp 值为 true 的话，则 dp[i] 也一定为 true。更新完成之后，从 sum/2 开始遍历，假如其 dp 值为 true，则用总重量 sum 减去当前重量的2倍，就是二堆石头重量的差值了，也就是碰撞后的剩余重量了，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        vector<bool> dp(1501);
        dp[0] = true;
        int sum = 0;
        for (int stone : stones) {
            sum += stone;
            for (int i = min(1500, sum); i >= stone; --i) {
                dp[i] = dp[i] || dp[i - stone];
            }
        }
        for (int i = sum / 2; i >= 0; --i) {
            if (dp[i]) return sum - 2 * i;
        }
        return 0;
    }
};

Leetcode1051. Height Checker

Students are asked to stand in non-decreasing order of heights for an annual photo.

Return the minimum number of students not standing in the right positions. (This is the number of students that must move in order for all students to be standing in non-decreasing order of height.)

Example 1:

1
2
Input: [1,1,4,2,1,3]
Output: 3

Explanation:
Students with heights 4, 3 and the last 1 are not standing in the right positions.

Note:

  • 1 <= heights.length <= 100
  • 1 <= heights[i] <= 100

看上去比较简单的题，找到没有按照顺序排列的数，想用一种不需要排序的方法来做，但是失败了，因为如果其他数字有序，只有一个无序，是要移动很多的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    /*int heightChecker(vector<int>& heights) {
        int res=0;
        for(int i=1;i<heights.size()-1;i++){
            if(!(heights[i]>=heights[i-1] && heights[i]<=heights[i+1]))
                res++;
        }
        return res;
    }
	*/
    int heightChecker(vector<int>& h) {
        int res = 0
        vector<int> s = h;
        sort(begin(s), end(s));
        for (auto i = 0; i < h.size(); ++i) 
            res += h[i] != s[i];
        return res;
    }
};

Leetcode1052. Grumpy Bookstore Owner

Today, the bookstore owner has a store open for customers.length minutes. Every minute, some number of customers (customers[i]) enter the store, and all those customers leave after the end of that minute.

On some minutes, the bookstore owner is grumpy. If the bookstore owner is grumpy on the i-th minute, grumpy[i] = 1, otherwise grumpy[i] = 0. When the bookstore owner is grumpy, the customers of that minute are not satisfied, otherwise they are satisfied.

The bookstore owner knows a secret technique to keep themselves not grumpy for X minutes straight, but can only use it once.

Return the maximum number of customers that can be satisfied throughout the day.

Example 1:

1
2
3
4
Input: customers = [1,0,1,2,1,1,7,5], grumpy = [0,1,0,1,0,1,0,1], X = 3
Output: 16
Explanation: The bookstore owner keeps themselves not grumpy for the last 3 minutes. 
The maximum number of customers that can be satisfied = 1 + 1 + 1 + 1 + 7 + 5 = 16.

Note:

  • 1 <= X <= customers.length == grumpy.length <= 20000
  • 0 <= customers[i] <= 1000
  • 0 <= grumpy[i] <= 1

滑动窗口. 统计在大小为 X 的窗口中, 有多少顾客刚好处在店主脾气不好的时刻, 即grumpy[i] == 1。其中grumpy[i] == 0对应的顾客始终是满意的, 使用 base 来统计. 而对于那些grumpy[i] == 1的顾客, 只有在他们刚好在滑动窗口中, 才能满意, 用 new_satisfied 统计在滑动窗口中新满意的顾客, 在窗口滑动过程中使用 max_satisfied 来记录最大值. 最后返回 base + max_satisfied.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int maxSatisfied(vector<int>& customers, vector<int>& grumpy, int minutes) {
        int res = 0, len = grumpy.size();
        int sat = 0, new_sat = 0, max_sat = 0;
        for (int i = 0; i < len; i ++) {
            if (grumpy[i] == 0)
                sat += customers[i];
            else
                new_sat += customers[i];
            if (i >= minutes)
                new_sat -= (customers[i-minutes] * grumpy[i-minutes]);
            max_sat = max(max_sat, new_sat);
        }
        return sat + max_sat;
    }
};

Leetcode1053. Previous Permutation With One Swap

Given an array of positive integers arr (not necessarily distinct), return the lexicographically largest permutation that is smaller than arr, that can be made with exactly one swap (A swap exchanges the positions of two numbers arr[i] and arr[j]). If it cannot be done, then return the same array.

Example 1:

1
2
3
Input: arr = [3,2,1]
Output: [3,1,2]
Explanation: Swapping 2 and 1.

Example 2:

1
2
3
Input: arr = [1,1,5]
Output: [1,1,5]
Explanation: This is already the smallest permutation.

Example 3:

1
2
3
Input: arr = [1,9,4,6,7]
Output: [1,7,4,6,9]
Explanation: Swapping 9 and 7.

Example 4:

1
2
3
Input: arr = [3,1,1,3]
Output: [1,3,1,3]
Explanation: Swapping 1 and 3.

Constraints:

  • 1 <= arr.length <= 104
  • 1 <= arr[i] <= 104

这道题给了一个正整数的数组，说是让任意交换两个数字，使得变成字母顺序最大的一种全排列，但是需要小于原先的排列，若无法得到这样的全排列（说明当前已经是最小的全排列），则返回原数组。通过分析题目中给的例子不难理解题意，根据例子2来看，若给定的数组就是升序排列的，则无法得到更小的全排列，说明只有遇到降序的位置的时候，才有可能进行交换。但是假如有多个可以下降的地方呢，比如例子1，3到2下降，2到1下降，这里是需要交换2和1的，所以最好是从后往前检验，遇到前一个数字比当前数字大的情况时，前一个数字必定是交换方之一，而当前数字并不是。比如例子3，数字4的前面是9，正确结果是9和7交换，所以还要从4往后遍历一下，找到一个仅次于9的数字交换才行，而且数字相同的话，取坐标较小的那个，比如例子4就是这种情况。

首先从后往前遍历，假如当前数字大于等于前一个数字，直接跳过，否则说明需要交换的。从当前位置再向后遍历一遍，找到第一个仅次于拐点的数字交换即可，注意下面的代码虽然嵌套了两个 for 循环，其实是线性的时间复杂度，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> prevPermOpt1(vector<int>& arr) {
        int n = arr.size(), mx = 0, idx = -1;
        for (int i = n - 1; i > 0; --i) {
            if (arr[i] >= arr[i - 1]) continue;
            for (int j = i; j < n; ++j) {
                if (arr[j] < arr[i - 1] && mx < arr[j]) {
                    mx = arr[j];
                    idx = j;
                }
            }
            swap(arr[i - 1], arr[idx]);
            break;
        }
        return arr;
    }
};

Leetcode1054. Distant Barcodes

In a warehouse, there is a row of barcodes, where the ith barcode is barcodes[i].

Rearrange the barcodes so that no two adjacent barcodes are equal. You may return any answer, and it is guaranteed an answer exists.

Example 1:

1
2
Input: barcodes = [1,1,1,2,2,2]
Output: [2,1,2,1,2,1]

Example 2:

1
2
Input: barcodes = [1,1,1,1,2,2,3,3]
Output: [1,3,1,3,1,2,1,2]

Constraints:

  • 1 <= barcodes.length <= 10000
  • 1 <= barcodes[i] <= 10000

这道题说在一个仓库，有一排条形码，这里用数字表示，现在让给数字重新排序，使得相邻的数字不相同，并且说了一定会有合理的答案。意思就是说最多的重复个数不会超过数组长度的一半，否则一定会有相邻的重复数字。那么来分析一下题目，既然是为了避免重复数字被排在相邻的位置，肯定是要优先关注出现次数多的数字，因为它们更有可能出现在相邻的位置。这道题是可以用贪婪算法来做的，每次取出出现次数最多的两个数字，将其先排列起来，然后再取下一对出现次数最多的两个数字，以此类推直至排完整个数组。这里为了快速知道出现次数最多的数字，可以使用优先队列来做，里面放一个 pair 对儿，由频率和数字组成，这样优先队列就可以根据频率由高到低来自动排序了。统计频率的话就使用一个 HashMap，然后将频率和数字组成的 pair 对儿加入优先队列。进行 while 循环，条件是队列中的 pair 对儿至少两个，这样才能每次取出两个，将其加入结果 res 中，然后其频率分别减1，只要没减到0，就都加回优先队列中。最后可能队列还有一个剩余，有的话将数字加入结果 res 中即可，参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> rearrangeBarcodes(vector<int>& barcodes) {
        vector<int> res;
        priority_queue<pair<int, int>> pq;
        unordered_map<int, int> numCnt;
        for (int num : barcodes) ++numCnt[num];
        for (auto &a : numCnt) {
            pq.push({a.second, a.first});
        }
        while (pq.size() > 1) {
            auto a = pq.top(); pq.pop();
            auto b = pq.top(); pq.pop();
            res.push_back(a.second);
            res.push_back(b.second);
            if (--a.first > 0) pq.push(a);
            if (--b.first > 0) pq.push(b);
        }
        if (!pq.empty()) 
            res.push_back(pq.top().second);
        return res;
    }
};

论坛上的高分解法貌似没有用到优先队列，不过整个思路还是大体相同的，还是用 HashMap 来统计频率，这里将组成的频率和数字的 pair 对儿放到一个数组中，然后给数组按照从大到小的顺序来排列。接下里就要填充 res 数组了，方法是先填偶数坐标的位置，将频率最大的数字分别填进去，当偶数坐标填完了之后，再填奇数坐标的位置，这样保证不会有相连的重复数字。使用一个变量 pos，表示当前要填的坐标，初始化为0，之后来遍历这个频率和数字的 pair 对儿，从高到低，先填充所有偶数，若 pos 大于数组长度了，则切换为填充奇数即可，参见代码如下：

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> rearrangeBarcodes(vector<int>& barcodes) {
        int n = barcodes.size(), pos = 0;
        vector<int> res(n);
        vector<pair<int, int>> vec;
        unordered_map<int, int> numCnt;
        for (int num : barcodes) ++numCnt[num];
        for (auto &a : numCnt) {
            vec.push_back({a.second, a.first});
        }
        sort(vec.rbegin(), vec.rend());
        for (auto &a : vec) {
            for (int i = 0; i < a.first; ++i, pos += 2) {
                if (pos >= n) pos = 1;
                res[pos] = a.second;
            }
        }
        return res;
    }
};

Leetcode1055. Shortest Way to Form String

From any string, we can form a subsequence of that string by deleting some number of characters (possibly no deletions).

Given two strings source and target, return the minimum number of subsequences of source such that their concatenation equals target. If the task is impossible, return -1.

Example 1:

1
2
3
Input: source = "abc", target = "abcbc"
Output: 2
Explanation: The target "abcbc" can be formed by "abc" and "bc", which are subsequences of source "abc".

Example 2:

1
2
3
Input: source = "abc", target = "acdbc"
Output: -1
Explanation: The target string cannot be constructed from the subsequences of source string due to the character "d" in target string.

Example 3:

1
2
3
Input: source = "xyz", target = "xzyxz"
Output: 3
Explanation: The target string can be constructed as follows "xz" + "y" + "xz".

Constraints:

  • Both the source and target strings consist of only lowercase English letters from “a”-“z”.
  • The lengths of source and target string are between 1 and 1000.

这道题说我们可以通过删除某些位置上的字母从而形成一个新的字符串，现在给了两个字符串 source 和 target，问最少需要删除多个字母，可以把 source 字母串拼接成为 target。注意这里的 target 字符串可能会远长于 source，所以需要多个 source 字符串 concatenate 到一起，然后再进行删除字母。对于 target 中的每个字母，都需要在 source 中匹配到，所以最外层循环肯定是遍历 target 中的每个字母，可以使用一个指针j，初始化赋值为0，接下来就要在 source 中匹配这个 target[j]，所以需要遍历一下 source 字符串，如果匹配上了 target[j]，则j自增1，继续匹配下一个，当循环退出后，此时有一种情况需要考虑，就是对于这个 target[j] 字母，整个 source 字符串都无法匹配，说明 target 中存在 source 中没有的字母，这种情况下是要返回 -1 的，如何判定这种情况呢？当然可以在最开始把 source 中所有的字母放到一个 HashSet 中，然后对于 target 中每个字母都检测看是否在集合中。但这里可以使用更简便的方法，就是在遍历 source 之前，用另一个变量 pre 记录当前j的位置，然后当遍历完 source 之后，若j没有变化，则说明有其他字母存在，直接返回 -1 即可，参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int shortestWay(string source, string target) {
        int res = 0, j = 0, m = source.size(), n = target.size();
        while (j < n) {
            int pre = j;
            for (int i = 0; i < m; ++i) {
                if (j < n && source[i] == target[j]) ++j;
            }
            if (j == pre) return -1;
            ++res;
        }
        return res;
    }
};

下面这种方法思路和上面基本一样，就是没有直接去遍历 source 数组，而是使用了 STL 的 find 函数。开始还是要遍历 target 字符串，对于每个字母，首先在 source 中调用 find 函数查找一下，假如找不到，直接返回 -1。有的话，就从 pos+1 位置开始再次查找该字母，且其位置赋值为 pos，注意这里 pos+1 的原因是因为其初始化为了 -1，需要从0开始找，或者 pos 已经赋值为上一个匹配位置了，所以要从下一个位置开始查找。假如 pos 为 -1 了，说明当前剩余字母中无法匹配了，需要新的一轮循环，此时将 res 自增1，并将 pos 赋值为新的 source 串中的第一个匹配位置，参见代码如下：

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int shortestWay(string source, string target) {
        int res = 1, pos = -1, n = target.size();
        for (int i = 0; i < n; ++i) {
            if (source.find(target[i]) == -1) return -1;
            pos = source.find(target[i], pos + 1);
            if (pos == -1) {
                ++res;
                pos = source.find(target[i]);
            }
        }
        return res;
    }
};

Leetcode1056. Confusing Number

Given a number N, return true if and only if it is a confusing number , which satisfies the following condition:

We can rotate digits by 180 degrees to form new digits. When 0, 1, 6, 8, 9 are rotated 180 degrees, they become 0, 1, 9, 8, 6 respectively. When 2, 3, 4, 5 and 7 are rotated 180 degrees, they become invalid. A confusing number is a number that when rotated 180 degrees becomes a different number with each digit valid.

Example 1:

1
2
3
4
Input: 6
Output: true
Explanation:
We get `9` after rotating `6`, `9` is a valid number and `9!=6`.

Example 2:

1
2
3
4
Input: 89
Output: true
Explanation:
We get `68` after rotating `89`, `86` is a valid number and `86!=89`.

Example 3:

1
2
3
4
Input: 11
Output: false
Explanation:
We get `11` after rotating `11`, `11` is a valid number but the value remains the same, thus `11` is not a confusing number.

Example 4:

1
2
3
4
Input: 25
Output: false
Explanation:
We get an invalid number after rotating `25`.

Note:

  • 0 <= N <= 10^9
  • After the rotation we can ignore leading zeros, for example if after rotation we have 0008 then this number is considered as just 8.

这道题定义了一种迷惑数，将数字翻转 180 度，其中 0, 1, 8 旋转后保持不变，6变成9，9变成6，数字 2, 3, 4, 5, 和 7 旋转后变为非法数字。若能将某个数翻转后成为一个合法的新的数，就说这个数是迷惑数。这道题的难度并不大，就是考察的是遍历整数各个位上的数字，使用一个 while 循环，然后用 mod10 取出当前最低位上的数字，将不合法的数字放入一个 HashSet 中，这样直接在 HashSet 中查找一下当前数字是否存在，存在直接返回 false。不存在的话，则要进行翻转，因为只有6和9两个数字翻转后会得到不同的数字，所以单独判断一下，然后将当前数字拼到 num 的最低位即可，最终拼成的 num 就是原数字 N 的翻转，最后别忘了比较一下是否相同，参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool confusingNumber(int N) {
        int num = 0, oldN = N;
        unordered_set<int> invalid{{2, 3, 4, 5, 7}};
        while (N > 0) {
            int digit = N % 10;
            if (invalid.count(digit)) return false;
            if (digit == 6) digit = 9;
            else if (digit == 9) digit = 6;
            num = num * 10 + digit;
            N /= 10;
        }
        return num != oldN;
    }
};

这也可以用一个 HashMap 来建立所有的数字映射，然后还是用一个变量 oldN 来记录原来的数字，然后遍历N上的每一位数字，若其不在 HashMap 中，说明有数字无法翻转，直接返回 false，否则就把翻转后的数字加入 res，最后只要看 res 和 oldN 是否相等即可，参见代码如下：

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool confusingNumber(int N) {
        unordered_map<int, int> m{{0, 0}, {1, 1}, {6, 9}, {8, 8}, {9, 6}};
        long oldN = N, res = 0;
        while (N > 0) {
            if (!m.count(N % 10)) return false;
            res = res * 10 + m[N % 10];
            N /= 10;
        }
        return res != oldN;
    }
};

下面来看一种双指针的解法，这里先用一个数组 rotate 来按位记录每个数字翻转后得到的数字，用 -1 来表示非法情况，然后将数字 N 转为字符串，用两个指针 left 和 right 分别指向开头和末尾。用 while 循环进行遍历，假如此时 left 和 right 中有任何一个指向的数字翻转后是非法，直接返回 false。然后看 left 指向的数字翻转后跟 right 指向的数字是否相同，若不同，则将 res 标记为 true，然后移动 left 和 right 指针，最终返回 res 即可，参见代码如下：

解法三：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    bool confusingNumber(int N) {
        bool res = false;
        vector<int> rotate{0, 1, -1, -1, -1, -1, 9, -1, 8, 6};
        string str = to_string(N);
        int n = str.size(), left = 0, right = n - 1;
        while (left <= right) {
            if (rotate[str[left] - '0'] == -1 || rotate[str[right] - '0'] == -1) return false;
            if (rotate[str[left] - '0'] != (str[right] - '0')) res = true;
            ++left; --right;
        }
        return res;
    }
};

Leetcode1057. Campus Bikes

On a campus represented as a 2D grid, there are N workers and M bikes, with N <= M. Each worker and bike is a 2D coordinate on this grid.

Our goal is to assign a bike to each worker. Among the available bikes and workers, we choose the (worker, bike) pair with the shortest Manhattan distance between each other, and assign the bike to that worker. (If there are multiple (worker, bike) pairs with the same shortest Manhattan distance, we choose the pair with the smallest worker index; if there are multiple ways to do that, we choose the pair with the smallest bike index). We repeat this process until there are no available workers.

The Manhattan distance between two points p1 and p2 is Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|.

Return a vector ans of length N, where ans[i] is the index (0-indexed) of the bike that the i-th worker is assigned to.

Example 1:

1
2
3
4
Input: workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]]
Output: [1,0]
Explanation:
Worker 1 grabs Bike 0 as they are closest (without ties), and Worker 0 is assigned Bike 1. So the output is [1, 0].

Example 2:

1
2
3
4
Input: workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]]
Output: [0,2,1]
Explanation:
Worker 0 grabs Bike 0 at first. Worker 1 and Worker 2 share the same distance to Bike 2, thus Worker 1 is assigned to Bike 2, and Worker 2 will take Bike 1. So the output is [0,2,1].

Note:

  • 0 <= workers[i][j], bikes[i][j] < 1000
  • All worker and bike locations are distinct.
  • 1 <= workers.length <= bikes.length <= 1000

这道题用一个二维数组来表示一个校园坐标，上面有一些人和共享单车，人的数量不多余单车的数量，现在要让每一个人都分配一辆单车，人和单车的距离是用曼哈顿距离表示的。这里的分配方法其实是有一些 confuse 的，并不是每个人要拿离其距离最近的单车，也不是每辆单车要分配给距离其最近的人，而是要从所有的 单车-人 对儿中先挑出距离最短的一对儿，然后再挑出距离第二短的组合，以此类推，直到所有的人都被分配到单车了为止。这样的话就需要求出每一对人车距离，将所有的人车距离，和对应的人和车的标号都存到一个二维数组中。然后对这个二维数组进行排序，这里需要重写排序规则，将人车距离小的排前面，假如距离相等，则将人标号小的放前面，假如人的标号也相同，则就将车标号小的放前面。对人车距离数组排好序之后，此时需要两个数组来分别标记每个人被分配的车标号，和每个车的主人标号。现在从最小的人车距离开始取，若此时的人和车都没有分配，则进行分配，遍历完所有的人车距离之后，最终的结果就存在了标记每个人分配的车标号的数组中，参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {
        int m = workers.size(), n = bikes.size();
        vector<int> assignedWorker(m, -1), assignedBike(n, -1);
        vector<vector<int>> dist;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int d = abs(workers[i][0] - bikes[j][0]) + abs(workers[i][1] - bikes[j][1]);
                dist.push_back({d, i, j});
            }
        }
        sort(dist.begin(), dist.end(), [](vector<int>& a, vector<int>& b) {
                return a[0] < b[0] || (a[0] == b[0] && a[1] < b[1]) || (a[0] == b[0] && a[1] == b[1] && a[2] < b[2]);
            });
        for (auto &a : dist) {
            if (assignedWorker[a[1]] == -1 && assignedBike[a[2]] == -1) {
                assignedWorker[a[1]] = a[2];
                assignedBike[a[2]] = a[1];
            }
        }
        return assignedWorker;
    }
};

上面的解法虽然可以通过 OJ，但是并不是很高效，应该是排序的部分拖慢了速度。其实这道题的范围是有限的，因为车和人的坐标是有限的，最大的人车距离也不会超过 2000，那么利用桶排序来做就是个不错的选择，只需要 2001 个桶就行了，桶中放的是 pair 对儿，其中　buckets[i] 表示距离是i的人和车的标号组成的 pair 对儿。这样当计算出每个人车距离后，将其放入对应的桶中即可，就自动排好了序。然后开始遍历每个桶，由于每个桶中可能不止放了一个 pair 对儿，所以需要遍历每个桶中所有的组合，然后的操作就和上面的相同了，若此时的人和车都没有分配，则进行分配，遍历完所有的人车距离之后，最终的结果就存在了标记每个人分配的车标号的数组中，参见代码如下：

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {
        int m = workers.size(), n = bikes.size();
        vector<int> assignedWorker(m, -1), assignedBike(n, -1);
        vector<vector<pair<int, int>>> buckets(2001);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int dist = abs(workers[i][0] - bikes[j][0]) + abs(workers[i][1] - bikes[j][1]);
                buckets[dist].push_back({i, j});
            }
        }
        for (int dist = 0; dist <= 2000; ++dist) {
            for (int k = 0; k < buckets[dist].size(); ++k) {
                if (assignedWorker[buckets[dist][k].first] == -1 && assignedBike[buckets[dist][k].second] == -1) {
                    assignedWorker[buckets[dist][k].first] = buckets[dist][k].second;
                    assignedBike[buckets[dist][k].second] = buckets[dist][k].first;
                }
            }
        }
        return assignedWorker;
    }
};

Leetcode1058. Minimize Rounding Error to Meet Target

Given an array of prices [p1,p2…,pn] and a target, round each price pi to Roundi(pi) so that the rounded array [Round1(p1),Round2(p2)…,Roundn(pn)] sums to the given target. Each operation Roundi(pi) could be either Floor(pi) or Ceil(pi).

Return the string “-1” if the rounded array is impossible to sum to target. Otherwise, return the smallest rounding error, which is defined as Σ |Roundi(pi) - (pi)| for i from 1 to n, as a string with three places after the decimal.

Example 1:

1
2
3
4
Input: prices = [“0.700”,”2.800”,”4.900”], target = 8
Output: “1.000”
Explanation: 
Use Floor, Ceil and Ceil operations to get (0.7 - 0) + (3 - 2.8) + (5 - 4.9) = 0.7 + 0.2 + 0.1 = 1.0 .

Example 2:

1
2
3
4
Input: prices = [“1.500”,”2.500”,”3.500”], target = 10
Output: “-1”
Explanation: 
It is impossible to meet the target.

Note:

  • 1 <= prices.length <= 500.
  • Each string of prices prices[i] represents a real number which is between 0 and 1000 and has exactly 3 decimal places.
    target is between 0 and 1000000.

如果一个数字是一个整数， 那么我们只能取floor，不能取ceil。这相当于一个无法调整的数字，否则就是一个可调整的数字。我们把所有可调整的数字的小数部分放入一个priority queue中，把priority queue的size记为pqsize。

然后我们先判断什么情况下无法得到target：

  • 如果取最小的可能的和，那么所有数字都要取floor。如果这个和仍然比target大，或者比target-pqsize小，那么就说明无论如何也不可能得到target。这样我们就返回 “-1”
  • 若满足上述条件，我们一定可以取到满足题目条件的和。我们需要知道调整多少个数字，即把floor操作变成ceil操作。需要调整的数字个数等于target-pqsize。
  • 为了的达到最小的rounding error，对于每个调整的操作，我们希望它们小数尽可能大，这可以由之前的priority queue得到。取那个数字的ceil。最后把所有不需要调整的小数也加上，就是最小的rounding error了。
  • 注意最后返回字符串是，需要做些特殊处理，只保留最后3位小数即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    string minimizeError(vector<string>& prices, int target) {
        priority_queue<double> pq;
        int sum = 0;
        for (auto price : prices) {
            sum += floor(stod(price));
            double diffPrice = stod(price) - floor(stod(price));
            if (diffPrice != 0) {
                pq.push(diffPrice);
            }
        }
        if (sum > target || sum < target - pq.size()) {
            return "-1";
        }
        int diff = target - sum;
        double error = 0;
        while (!pq.empty()) {
            double fl = pq.top();
            pq.pop();
            error += diff > 0 ? 1 - fl : fl;
            diff--;
        }        
        string ans = to_string(error);
        return ans.substr(0, ans.find('.') + 4);
    }
};

Leetcode1059. 从始点到终点的所有路径

给定有向图的边 edges，以及该图的始点 source 和目标终点 destination，确定从始点 source 出发的所有路径是否最终结束于目标终点 destination，即：

  • 从始点 source 到目标终点 destination 存在至少一条路径
  • 如果存在从始点 source 到没有出边的节点的路径，则该节点就是路径终点。
  • 从始点source到目标终点 destination 可能路径数是有限数字
  • 当从始点 source 出发的所有路径都可以到达目标终点 destination 时返回 true，否则返回 false。
1
2
3
输入：n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
输出：false
说明：节点 1 和节点 2 都可以到达，但也会卡在那里。
1
2
3
输入：n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
输出：false
说明：有两种可能：在节点 3 处结束，或是在节点 1 和节点 2 之间无限循环。
1
2
输入：n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
输出：true

简单dfs，搜索时不能搜索到非end的断头路或者有end在中间的路。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution{
    public:
    bool leadToDestination(int n,std::vector<std::vector<int>>& edge,int start,int end){
        std::vector<std::vector<int>> m(m);
        std::vector<bool> visited(n,false);
        for(auto e:edge){
            m[e[0]].push_back(e[1]);
        }
        if(!m[end].empty()){
            return false;
        }
        return DFS(m,visited,start,end);
    }
    bool DFS(std::vector<std::vector<int>>& m,std::vector<bool>& visitd,int cur,int end){
        if(!m[cur].size()==0&&cur!=end){
            return false;
        }
        for(auto next:m[cur]){
            if(visitd[next]){
                return false;
            }
            visitd[next]=true;
            if(!DFS(m,visitd,cur,end)){
                return false;
            }
            visitd[next]=false;
        }
    }
};

Leetcode1060. Missing Element in Sorted Array

Given a sorted array A of unique numbers, find the K-th missing number starting from the leftmost number of the array.

Example 1:

1
2
3
4
Input: A = [4,7,9,10], K = 1
Output: 5
Explanation: 
The first missing number is 5.

Example 2:

1
2
3
4
Input: A = [4,7,9,10], K = 3
Output: 8
Explanation: 
The missing numbers are [5,6,8,...], hence the third missing number is 8.

Example 3:

1
2
3
4
Input: A = [1,2,4], K = 3
Output: 6
Explanation: 
The missing numbers are [3,5,6,7,...], hence the third missing number is 6.

Note:

  • 1 <= A.length <= 50000
  • 1 <= A[i] <= 1e7
  • 1 <= K <= 1e8

给出一个有序数组 A，数组中的每个数字都是 独一无二的，找出从数组最左边开始的第 K 个缺失数字。

拿到这个题之后，看了下Note中取值范围都比较大，因此如果想一个数字一个数字去判断的话肯定会超时。所以需要使用一个点小技巧，即跳过不需要判断的数字。直接计算出每两个相邻数字之间能满足多少个，从而更新k。

先对nums排序。然后开始遍历，计算nums相邻两个元素之间的数字数即nums[i] - pre - 1个，是否可以满足需要的k。如果能满足，那么直接找出要返回的数字pre+k。如果不能满足，把k去掉已能满足的数字nums[i] - pre - 1。最后如果所有的nums数字都已经用完，但是还不能满足k，则需要返回nums[nums.size() - 1] + k。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int missingElement(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end());
        int pre = nums[0];
        for (int i = 1; i < nums.size(); ++i) {
            if (k < nums[i] - pre) {
                return pre + k;
            } else {
                k -= nums[i] - pre - 1;
            }
            pre = nums[i];
        }
        return pre + k;
    }
};

Leetcode1061. 按字典序排列最小的等效字符串

给出长度相同的两个字符串：A 和 B，其中 A[i] 和 B[i] 是一组等价字符。举个例子，如果 A = “abc” 且 B = “cde”，那么就有 ‘a’ == ‘c’, ‘b’ == ‘d’, ‘c’ == ‘e’。

等价字符遵循任何等价关系的一般规则：

  • 自反性：’a’ == ‘a’
  • 对称性：’a’ == ‘b’ 则必定有 ‘b’ == ‘a’
  • 传递性：’a’ == ‘b’ 且 ‘b’ == ‘c’ 就表明 ‘a’ == ‘c’

例如，A 和 B 的等价信息和之前的例子一样，那么 S = “eed”, “acd” 或 “aab”，这三个字符串都是等价的，而 “aab” 是 S 的按字典序最小的等价字符串。利用 A 和 B 的等价信息，找出并返回 S 的按字典序排列最小的等价字符串。

示例 1：

1
2
3
4
5
输入：A = "parker", B = "morris", S = "parser"
输出："makkek"
解释：根据 A 和 B 中的等价信息，
我们可以将这些字符分为 [m,p], [a,o], [k,r,s], [e,i] 共 4 组。
每组中的字符都是等价的，并按字典序排列。所以答案是 "makkek"。

示例 2：

1
2
3
4
5
输入：A = "hello", B = "world", S = "hold"
输出："hdld"
解释：根据 A 和 B 中的等价信息，
我们可以将这些字符分为 [h,w], [d,e,o], [l,r] 共 3 组。
所以只有 S 中的第二个字符 'o' 变成 'd'，最后答案为 "hdld"。

示例 3：

1
2
3
4
5
输入：A = "leetcode", B = "programs", S = "sourcecode"
输出："aauaaaaada"
解释：我们可以把 A 和 B 中的等价字符分为 
[a,o,e,r,s,c], [l,p], [g,t] 和 [d,m] 共 4 组，
因此 S 中除了 'u' 和 'd' 之外的所有字母都转化成了 'a'，最后答案为 "aauaaaaada"。

并查集merge的时候，让祖先字符更小的作为代表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class dsu
{
	vector<int> f;
public:
	dsu(int n)
	{
		f.resize(n);
		for(int i = 0; i < n; ++i)
			f[i] = i;
	}
	void merge(int a, int b)
	{
		int fa = find(a), fb = find(b);
        if(fa > fb)//字母小的当代表，关键点
		    f[fa] = fb;
        else
            f[fb] = fa;
	}
	int find(int a)
	{
		int origin = a;
		while(a != f[a])
			a = f[a];
		return f[origin] = a;
	}
};
class Solution {
public:
    string smallestEquivalentString(string A, string B, string S) {
    	dsu u(26);
    	for(int i = 0; i < A.size(); ++i)
    		u.merge(A[i]-'a', B[i]-'a');
    	for(int i = 0; i < S.size(); ++i)
    		S[i] = u.find(S[i]-'a')+'a';
    	return S;
    }
};

Leetcode1062. Longest Repeating Substring

Given a string S, find out the length of the longest repeating substring(s). Return 0 if no repeating substring exists.

Example 1:

1
2
3
Input: “abcd”
Output: 0
Explanation: There is no repeating substring.

Example 2:

1
2
3
Input: “abbaba”
Output: 2
Explanation: The longest repeating substrings are “ab” and “ba”, each of which occurs twice.

Example 3:

1
2
3
Input: “aabcaabdaab”
Output: 3
Explanation: The longest repeating substring is “aab”, which occurs 3 times.

Example 4:

1
2
3
Input: “aaaaa”
Output: 4
Explanation: The longest repeating substring is “aaaa”, which occurs twice.

Constraints:

  • The string S consists of only lowercase English letters from ‘a’ - ‘z’.
  • 1 <= S.length <= 1500

解题思路：这题我们采用动态规划的方法。我们先定义dp[i][j]为分别以第i个字符和第j个字符结尾的substring有相同共同后缀的最大长度。因此，我们也要求i>j。我们注意到，当S[i] != S[j]，那么dp[i][j] = 0，否则dp[i][j] = dp[i-1][j-1] + 1。这就是我们的状态转移方程。

1
2
dp[i][j] = dp[i-1][j-1] + 1 ----------- S[i] == S[j]
dp[i][j] = 0 -------------------------- S[i] != S[j]

我们更新dp[i][j]的最大值，就可以得到最后的答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int longestRepeatingSubstring(string S) {
        int ans = INT_MIN;
        vector<vector<int>> dp(S.size() + 1, vector<int>(S.size() + 1, 0));
        for (auto i = 1; i <= S.size(); i++) {
            for (auto j = 1; j < i; j++) {
                if (S[i-1] == S[j-1]) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
                ans = max(ans, dp[i][j]);
            }
        }
        return ans;
    }
};

复杂度分析

  • N是字符串的长度。
  • 时间复杂度: O(N^2)
  • 空间复杂度: O(N^2)

Leetcode 1064. Fixed Point

Given an array A of distinct integers sorted in ascending order, return the smallest index i that satisfies A[i] == i. Return -1 if no such i exists.

Example 1:

1
2
3
4
Input: [-10,-5,0,3,7]
Output: 3
Explanation: 
For the given array, A[0] = -10, A[1] = -5, A[2] = 0, A[3] = 3, thus the output is 3.

Example 2:

1
2
3
4
Input: [0,2,5,8,17]
Output: 0
Explanation: 
A[0] = 0, thus the output is 0.

Example 3:

1
2
3
4
Input: [-10,-5,3,4,7,9]
Output: -1
Explanation: 
There is no such i that A[i] = i, thus the output is -1.

Note:

  • 1 <= A.length < 10^4
  • -10^9 <= A[i] <= 10^9

因为给出的是一个排序的array，而index也是自然从0到n-1的排序数组，因此本题采用二分法来查找A[i] == i的index。当 i < A[i]，我们往左边查找，当i >= A[i]时， 我们往右边查找。需要注意的因为要求最小的index，我们更新右端点时，需要i >= A[i]。如果是最大的index， 则应该是i > A[i]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int fixedPoint(vector<int>& A) {
        int left = 0;
        int right = A.size() - 1;
        while (left + 1 < right) {
            int mid = left + (right - left) / 2;
            if (A[mid] >= mid) {
                right = mid;
            }
            else {
                left = mid;
            }
        }
        if (left == A[left]) {
            return left;
        }
        if (right == A[right]) {
            return right;
        }
        return -1;
    }
};

Leetcode1065. Index Pairs of a String

Given a text string and words (a list of strings), return all index pairs [i, j] so that the substring text[i]…text[j] is in the list of words.

Example 1:

1
2
Input: text = “thestoryofleetcodeandme”, words = [“story”,”fleet”,”leetcode”]
Output: [[3,7],[9,13],[10,17]]

Example 2:

1
2
3
4
Input: text = “ababa”, words = [“aba”,”ab”]
Output: [[0,1],[0,2],[2,3],[2,4]]
Explanation: 
Notice that matches can overlap, see “aba” is found in [0,2] and [2,4].

Note:

  • All strings contains only lowercase English letters.
  • It’s guaranteed that all strings in words are different.
  • 1 <= text.length <= 100
  • 1 <= words.length <= 20
  • 1 <= words[i].length <= 50

Return the pairs [i,j] in sorted order (i.e. sort them by their first coordinate in case of ties sort them by their second coordinate).

这道题可以直接用string find函数来做，但是需要分析一下时间复杂度。取决于具体的函数实现，比如CPP的find函数没有用KMP实现，所以最坏的情况复杂度是O(M * N)，这样带入本题，时间复杂度是O(M * sum(len(word)))。其中M是text的长度，sum(len(word))是words中word的长度之和。

如果用字典树Trie来实现，则当M < sum(len(word))时，时间复杂度可以优化。首先建立基于words的字典树trie，然后在text中以每一个位置i为起点向后遍历，并判断往后每一个位置j是否在字典树中，若在则加入要返回的结果rets中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
struct Trie {
    vector<Trie*> children = vector<Trie*>(26, nullptr);
    bool is_find = false;
};
class Solution {
    Trie* constructTrie(const vector<string>& words) {
        Trie* trie = new Trie();
        for (const auto& word : words) {
            Trie* cur = trie;
            for (const auto ch : word) {
                if (cur->children[ch - 'a'] == nullptr) {
                    cur->children[ch - 'a'] = new Trie();
                }
                cur = cur->children[ch - 'a'];
            }
            cur->is_find = true;
        }
        return trie;
    }
public:
    vector<vector<int>> indexPairs(string text, vector<string>& words) {
        const Trie* const trie = constructTrie(words);
        vector<vector<int>> rets;
        for (int i = 0; i < text.size(); ++i) {
            const Trie* cur = trie;           
            for (int j = i; j < text.size() && cur != nullptr; ++j) {
                cur = cur->children[text[j] - 'a'];
                if (cur && cur->is_find) {
                    rets.push_back({i, j});
                }
            }
        }
        return rets;
    }
};

Leetcode1071. Greatest Common Divisor of Strings

For strings S and T, we say “T divides S” if and only if S = T + … + T (T concatenated with itself 1 or more times)

Return the largest string X such that X divides str1 and X divides str2.

Example 1:

1
2
Input: str1 = "ABCABC", str2 = "ABC"
Output: "ABC"

Example 2:

1
2
Input: str1 = "ABABAB", str2 = "ABAB"
Output: "AB"

Example 3:

1
2
Input: str1 = "LEET", str2 = "CODE"
Output: ""

最长公共重复子串重复若干次之后能分别得到str1和str2，那么最明显地，该子串的长度一定是str1和str2长度的公因数。看了一下字符串的长度最多只有1000，所以我们完全可以对长度进行遍历，判断每个公因数是不是构成最长公共重复子串。因为要找最长的，所以找到最长之后，直接返回即可。时间复杂度O(N^2)。外部循环找到公因数，时间复杂度O(N)；内部要创建新的字符串和原先的字符串进行比较，时间复杂度也是O(N)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    string gen(string str, int i) {
        string res;
        while (i--) {
            res += str;
        }
        return res;
    }
    
    string gcdOfStrings(string str1, string str2) {
        int l1 = str1.length(), l2 = str2.length();
        int length = min(l1, l2);
        string res;
        for(int i = length; i > 0; i --) {
            if(l1 % i == 0 && l2 % i == 0) {
                int t1 = l1 / i;
                int t2 = l2 / i;
                string gcd = str1.substr(0, i);
                string s1 = gen(gcd, t1);
                string s2 = gen(gcd, t2);
                if ((s1 == str1) && (s2 == str2)) {
                    res = gcd;
                    break;
                }
            }
        }
        return res;
    }
};

题目要求 X 能除尽 str1 且 X 能除尽 str2，且 X 为最长。那么可以理解为 str1 由 m 个 X 连接而成， str2 由 n 个 X 连接而成。由此可知 str1 + str2 由 m + n 个 X 拼接而成，而且 str1 + str2 与 str2 + str1 在值上是相等的。然后此题就转化为了求最大公约数。str1 和 str2 长度的最大公约数，就是所求 X 的长度。

辗转相除法是递归算法，一句话概括这个算法就是：两个整数的最大公约数，等于其中较小的数 和两数相除余数 的最大公约数。比如 10 和 25，25 除以 10 商 2 余 5，那么 10 和 25 的最大公约数，等同于 10 和 5 的最大公约数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public String gcdOfStrings(String str1, String str2) {
        // 如果 (str1 + str2) 和 (str2 + str1) 的值不相等
        if (!(str1 + str2).equals(str2 + str1)) {
            return "";
        }
        // 两个字符串长度的最大公约数
        int maxCommonDivisor = gcd(str1.length(), str2.length());
        return str1.substring(0, maxCommonDivisor);
    }
    
    // 辗转相除法求最大公约数
    private int gcd(int a, int b) {
        return (a % b == 0) ? b : gcd(b, a % b);
    }
}

Leetcode1072. Flip Columns For Maximum Number of Equal Rows

You are given an m x n binary matrix matrix.

You can choose any number of columns in the matrix and flip every cell in that column (i.e., Change the value of the cell from 0 to 1 or vice versa).

Return the maximum number of rows that have all values equal after some number of flips.

Example 1:

1
2
3
Input: matrix = [[0,1],[1,1]]
Output: 1
Explanation: After flipping no values, 1 row has all values equal.

Example 2:

1
2
3
Input: matrix = [[0,1],[1,0]]
Output: 2
Explanation: After flipping values in the first column, both rows have equal values.

Example 3:

1
2
3
Input: matrix = [[0,0,0],[0,0,1],[1,1,0]]
Output: 2
Explanation: After flipping values in the first two columns, the last two rows have equal values.

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 300
  • matrix[i][j] is either 0 or 1.

其实按照列翻转没有什么用，把0开头的或者1开头的，选一种，全部翻转，用哈希表计数，找到最多出现的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int maxEqualRowsAfterFlips(vector<vector<int>>& matrix) {
        unordered_map<string, int> m;
        for (auto& mat : matrix) {
            int length = mat.size();
            string str(length, ' ');
            if (mat[0] == 0){
                for(int i = 0; i < length; i ++) {
                    mat[i] ^= 1;
                    str[i] = mat[i] == 1 ? '1': '0';
                }
            }
            else {
                for(int i = 0; i < length; i ++) {
                    str[i] = mat[i] == 1 ? '1' : '0';
                }
            }
            m[str] ++;
        }
        int res = 0;
        for (auto it = m.begin(); it != m.end(); it ++)
            res = max(res, it->second);
        return res;
    }
};

Leetcode1073. Adding Two Negabinary Numbers

Given two numbers arr1 and arr2 in base -2, return the result of adding them together.

Each number is given in array format: as an array of 0s and 1s, from most significant bit to least significant bit. For example, arr = [1,1,0,1] represents the number (-2)^3 + (-2)^2 + (-2)^0 = -3. A number arr in array, format is also guaranteed to have no leading zeros: either arr == [0] or arr[0] == 1.

Return the result of adding arr1 and arr2 in the same format: as an array of 0s and 1s with no leading zeros.

Example 1:

1
2
3
Input: arr1 = [1,1,1,1,1], arr2 = [1,0,1]
Output: [1,0,0,0,0]
Explanation: arr1 represents 11, arr2 represents 5, the output represents 16.

Example 2:

1
2
Input: arr1 = [0], arr2 = [0]
Output: [0]

Example 3:

1
2
Input: arr1 = [0], arr2 = [1]
Output: [1]

Constraints:

  • 1 <= arr1.length, arr2.length <= 1000
  • arr1[i] and arr2[i] are 0 or 1
  • arr1 and arr2 have no leading zeros

这道题说是有两个负二进制数是用数组来表示的，现在让返回它们相加后的结果，还是放在数组中来表示。这道题其实利用的方法跟那道很像，都是一位一位的处理的，直接加到结果 res 数组中的。这里使用两个指针i和j，分别指向数组 arr1 和 arr2 的末尾，然后用个变量 carry 表示进位，当i大于等于0时，carry 加上i指向的数字，并且i自减1，同理，当j大于等于0时，carry 加上j指向的数字，并且j自减1。由于数组中当每位上只能放一个数字，所以让 carry ‘与’上1，并加入到结果 res 数组后。然后需要再填充更高一位上的数字，对于二进制来说，直接右移1位即可，这里由于是负二进制，所以右移1位之后再取负。之后要移除所有的 leading zeros，因为这里高位是加到了 res 的后面，所以要去除末尾的零，使用个 while 去除。最后别忘了将 res 翻转一下返回即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {
        vector<int> res;
        int carry = 0, i = (int)arr1.size() - 1, j = (int)arr2.size() - 1;
        while (i >= 0 || j >= 0 || carry) {
            if (i >= 0) carry += arr1[i--];
            if (j >= 0) carry += arr2[j--];
            res.push_back(carry & 1);
            carry = -(carry >> 1);
        }
        while (res.size() > 1 && res.back() == 0) 
            res.pop_back();
        reverse(res.begin(), res.end());
        return res;
    }
};

Leetcode1078. Occurrences After Bigram

Given words first and second, consider occurrences in some text of the form “first second third”, where second comes immediately after first, and third comes immediately after second.

For each such occurrence, add “third” to the answer, and return the answer.

Example 1:

1
2
Input: text = "alice is a good girl she is a good student", first = "a", second = "good"
Output: ["girl","student"]

Example 2:

1
2
Input: text = "we will we will rock you", first = "we", second = "will"
Output: ["we","rock"]

Note:

  • 1 <= text.length <= 1000
  • text consists of space separated words, where each word consists of lowercase English letters.
  • 1 <= first.length, second.length <= 10
  • first and second consist of lowercase English letters.

第一种是先split，然后对比，运行时间较长但是内存占用小：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    
    vector<string> split(string text){
        vector<string> res;
        int begin=0;
        string temp="";
        for(int i=0;i<text.length();i++){
            if(text[i]==' '){
                res.push_back(temp); 
                temp="";
            }
            else{
                temp = temp + text[i];
            }
        }
        res.push_back(temp);
        return res;
    }
    
    vector<string> findOcurrences(string text, string first, string second) {
        int n;
        vector<string> res;
        vector<string> split_string = split(text);
        for(int i=0;i<split_string.size()-2;i++){
            if(split_string[i]==first && split_string[i+1]==second)
                res.push_back(split_string[i+2]);
        }
        return res;
    }
};

人家有的大佬是用了流做的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<string> findOcurrences(string text, string first, string second) {
        vector<string>rst;
        stringstream ss(text);
        string s1,s2,cand;
        ss>>s1>>s2;
        while(ss>>cand){
            if(s1==first && s2==second)rst.push_back(cand);
            s1=s2;
            s2=cand;
        }
        return rst;
    }
};

Leetcode1079. Letter Tile Possibilities

You have a set of tiles, where each tile has one letter tiles[i] printed on it. Return the number of possible non-empty sequences of letters you can make.

Example 1:

1
2
3
Input: "AAB"
Output: 8
Explanation: The possible sequences are "A", "B", "AA", "AB", "BA", "AAB", "ABA", "BAA".

Example 2:

1
2
Input: "AAABBC"
Output: 188

Note:

  • 1 <= tiles.length <= 7
  • tiles consists of uppercase English letters.

求一个字符串的所有子串。第一想法优先使用全排列，即深度优先，但有一个核心问题：子串怎么办？全排列无法解决，子串的检索问题，这是我一开始苦思而不得解的地方。

解法一：

这是本题区别于普通全排列中，最隐蔽而又最有趣的一个点：字符串的全排列出来了，那字符串的所有不同子串，还会远吗？答案就是，全排列字符串的所有前缀子串里！检索全排列的全部不同子串（包含全排列本身），即为所求。

解法二：

因为问题的规模在7个字符内，解法一在时间和内存上均可接受。但当问题规模快速扩大时，基于解法一，如何优化？优化核心是，首先将字符串排序（排序大法好），一旦发生不同字符间的交换，则自字符串起始位置至交换发生的位置为前缀的子串，均发生变化！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int res=0;
    void dfs(string tiles, int i){
        res++;
        for (int j = i; j < tiles.size(); j++){
            if(i!=j && tiles[i]==tiles[j])
                continue;
            swap(tiles[i], tiles[j]);
            dfs(tiles, i+1);
        }
    }
    
    int numTilePossibilities(string tiles) {
        sort(tiles.begin(),tiles.end());
        dfs(tiles,0);
        return res-1;
    }
};

Leetcode1080. Insufficient Nodes in Root to Leaf Paths

Given the root of a binary tree, consider all root to leaf paths: paths from the root to any leaf. (A leaf is a node with no children.)

A node is insufficient if every such root to leaf path intersecting this node has sum strictly less than limit.

Delete all insufficient nodes simultaneously, and return the root of the resulting binary tree.

Example 1:

1
2
Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
Output: [1,2,3,4,null,null,7,8,9,null,14]

Example 2:

1
2
Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
Output: [5,4,8,11,null,17,4,7,null,null,null,5]

Example 3:

1
2
Input: root = [1,2,-3,-5,null,4,null], limit = -1
Output: [1,null,-3,4]

Note:

  • The given tree will have between 1 and 5000 nodes.
  • -10^5 <= node.val <= 10^5
  • -10^9 <= limit <= 10^9

这道题定义了一种不足结点，就是说经过该结点的所有根到叶路径之和的都小于给定的 limit，现在让去除所有的这样的不足结点，返回剩下的结点组成的二叉树。这题好就好在给的例子都配了图，能够很好的帮助我们理解题意，给的例子很好的覆盖了大多数的情况，博主能想到的唯一没有覆盖的情况就是可能根结点也是不足结点，这样的话有可能会返回空树。这里首先处理一下 corner case，即根结点是叶结点的情况，这样只需要看根结点值是否小于 limit，是的话直接返回空指针，因为此时的根结点是个不足结点，需要被移除，否则直接返回根结点。一个比较快速的判断是否是叶结点的方法是看其左右子结点是否相等，因为只有均为空的时候才会相等。若根结点不为叶结点，且其左子结点存在的话，就对其左子结点调用递归，此时的 limit 需要减去根结点值，将返回的结点赋值给左子结点。同理，若其右子结点存在的话，就对其右子结点调用递归，此时的 limit 需要减去根结点值，将返回的结点赋值给右子结点。最后还需要判断一下，若此时的左右子结点都被赋值为空了，则当前结点也需要被移除，因为经过其左右子结点的根到叶路径就是经过该结点的所有路径，若其和均小于 limit，则当前结点也需要被移除，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        if (root->left == root->right) {
            return root->val < limit ? nullptr : root;
        }
        if (root->left) {
            root->left = sufficientSubset(root->left, limit - root->val);
        }
        if (root->right) {
            root->right = sufficientSubset(root->right, limit - root->val);
        }
        return root->left == root->right ? nullptr : root;
    }
};

Leetcode1081. Smallest Subsequence of Distinct Characters

Given a string s, return the lexicographically smallest subsequence of s that contains all the distinct characters of s exactly once.

Example 1:

1
2
Input: s = "bcabc"
Output: "abc"

Example 2:

1
2
Input: s = "cbacdcbc"
Output: "acdb"

找出字典序最小的子序列。一次遍历，维护一个stack，存一个降序排列的堆，堆底是最小值，如果是之前出现过的字符，则跳过；否则遇到当前字符字典序小于之前最大值，并且最大值之后还会出现，那么就pop掉，直到之前的stack没有值或者比当前小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    string smallestSubsequence(string s) {
        string res;
        stack<int> st;
        int* record = (int*)malloc(sizeof(int)*128);
        int* visited = (int*)malloc(sizeof(int)*128);
        for (int i = 0; i < 128; i ++) {
            record[i] = 0;
            visited[i] = 0;
        }
        for (char c : s) 
            record[c] ++;
        for (char c : s) {
            -- record[c];

            if (visited[c])
                continue;
            
            while(!st.empty() && st.top() > c && record[st.top()] > 0) {
                visited[st.top()] = 0;
                st.pop();
            }
            st.push(c);
            visited[c] = 1;
        }
        
        while(!st.empty()) {
            res += (char)(st.top());
            st.pop();
        }
        reverse(res.begin(), res.end());
        return res;
    }
};

这道题实际上需要用单调栈的思路来做，首先需要统计每个字母出现的次数，这里可以使用一个大小为 128 的数组 cnt 来表示，还需要一个数组 visited 来记录某个字母是否出现过。先遍历一遍字符串，统计每个字母出现的次数到 cnt 中。再遍历一遍给定的字符串，对于遍历到的字母，在 cnt 数组中减去一个，然后看该字母是否已经在 visited 数组中出现过，是的话直接跳过。否则需要进行一个 while 循环，这里的操作实际上是为了确保得到的结果是字母顺序最小的，若当前字母小于结果 res 中的最后一个字母，且该最后的字母在 cnt 中还存在，说明之后还会遇到这个字母，则可以在 res 中先去掉这个字母，以保证字母顺序最小，并且 visited 数组中标记为0，表示未访问。这里是尽可能的将 res 打造成单调递增的，但如果后面没有这个字母了，就不能移除，所以说并不能保证一定是单调递增的，但可以保证得到的结果是字母顺序最小的。while 循环退出后，将该字母加到结果 res 后，并且 visited 标记为1。这里还有个小 trick，结果 res 在初始化给个0，这样就不用判空了，而且0是小于所有字母的，不会影响这个逻辑，最后返回的时候去掉首位0就行了，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    string smallestSubsequence(string s) {
        string res = "0";
        vector<int> cnt(128), visited(128);
        for (char c : s) ++cnt[c];
        for (char c : s) {
            --cnt[c];
            if (visited[c]) continue;
            while (c < res.back() && cnt[res.back()]) {
                visited[res.back()] = 0;
                res.pop_back();
            }
            res += c;
            visited[c] = 1;
        }
        return res.substr(1);
    }
};

Leetcode1089. Duplicate Zeros

Given a fixed length array arr of integers, duplicate each occurrence of zero, shifting the remaining elements to the right. Note that elements beyond the length of the original array are not written. Do the above modifications to the input array in place, do not return anything from your function.

Example 1:

1
2
3
Input: [1,0,2,3,0,4,5,0]
Output: null
Explanation: After calling your function, the input array is modified to: [1,0,0,2,3,0,0,4]

Example 2:

1
2
3
Input: [1,2,3]
Output: null
Explanation: After calling your function, the input array is modified to: [1,2,3]

双指针也许是本题的最优解法。具体思路是维护一个快指针和一个慢指针。快指针是遇到0就多进一步。这样遍历一遍数据后，快指针和慢指针会有一个差值。这个差值就是需要填充0的个数。

接下来，我们需要从后向前遍历数组。如果慢指针指向的元素不为0，则把快指针指向的元素替换为慢指针指向的元素；如果慢指针指向的元素为0，则把快指针和快指针之前指向的元素替换为0。

你可能会发现对于不同的数组，第一遍遍历之后fast指针的值是不一样的。区别在于数组末尾是否为0，如果末尾为0，则fast指针的值(数组索引)为数组长度+1。如果末尾不是0，则fast指针的值是数组长度。其实数组最后一位是0的话，其实是不用复制这个值的。因此从后向前遍历的时候需要判断fast指针的值是否小于n，这样就可以把数组末尾为0的时候就不会复制了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
	public:
    void duplicateZeros(vector<int>& arr) {
        int n = arr.size();
        int slow = 0, fast = 0;
        while(fast < n) {
            if(arr[slow] == 0)
                fast ++;
            fast ++;
            slow ++;
        }
        fast --;
        slow --;
        while(slow >= 0) {
            if(fast < n)
                arr[fast] = arr[slow];
            if(arr[slow] == 0)
                arr[--fast] = arr[slow];
            fast --;
            slow --;
        }
    }
};

Leetcode1090. Largest Values From Labels

We have a set of items: the i-th item has value values[i] and label labels[i].

Then, we choose a subset S of these items, such that:

  • |S| <= num_wanted
  • For every label L, the number of items in S with label L is <= use_limit.

Return the largest possible sum of the subset S.

Example 1:

1
2
3
Input: values = [5,4,3,2,1], labels = [1,1,2,2,3], `num_wanted` = 3, use_limit = 1
Output: 9
Explanation: The subset chosen is the first, third, and fifth item.

Example 2:

1
2
3
Input: values = [5,4,3,2,1], labels = [1,3,3,3,2], `num_wanted` = 3, use_limit = 2
Output: 12
Explanation: The subset chosen is the first, second, and third item.

Example 3:

1
2
3
Input: values = [9,8,8,7,6], labels = [0,0,0,1,1], `num_wanted` = 3, use_limit = 1
Output: 16
Explanation: The subset chosen is the first and fourth item.

Example 4:

1
2
3
Input: values = [9,8,8,7,6], labels = [0,0,0,1,1], `num_wanted` = 3, use_limit = 2
Output: 24
Explanation: The subset chosen is the first, second, and fourth item.

Note:

  • 1 <= values.length == labels.length <= 20000
  • 0 <= values[i], labels[i] <= 20000
  • 1 <= num_wanted, use_limit <= values.length

这道题说是给了一堆物品，每个物品有不同的价值和标签，分别放在 values 和 labels 数组中，现在让选不超过 num_wanted 个物品，且每个标签类别的物品不超过 use_limit，问能得到的最大价值是多少。说实话这道题博主研究了好久才弄懂题意，而且主要是看例子分析出来的，看了看踩比赞多，估计许多人跟博主一样吧。这道题可以用贪婪算法来做，因为需要尽可能的选价值高的物品，但同时要兼顾到物品的标签种类。所以可以将价值和标签种类组成一个 pair 对儿，放到一个优先队列中，这样就可以按照价值从高到低进行排列了。同时，由于每个种类的物品不能超过 use_limit 个，所以需要统计每个种类被使用了多少次，可以用一个 HashMap 来建立标签和其使用次数之间的映射。先遍历一遍所有物品，将价值和标签组成 pair 对儿加入优先队列中。然后进行循环，条件是 num_wanted 大于0，且队列不为空，此时取出队顶元素，将其标签映射值加1，若此时仍小于 use_limit，说明当前物品可以入选，将其价值加到 res 中，并且 num_wanted 自减1即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int largestValsFromLabels(vector<int>& values, vector<int>& labels, int num_wanted, int use_limit) {
        int res = 0, n = values.size();
        priority_queue<pair<int, int>> pq;
        unordered_map<int, int> useMap;
        for (int i = 0; i < n; ++i) {
            pq.push({values[i], labels[i]});
        }
        while (num_wanted > 0 && !pq.empty()) {
            int value = pq.top().first, label = pq.top().second; pq.pop();
            if (++useMap[label] <= use_limit) {
                res += value;
                --num_wanted;
            }
        }
        return res;
    }
};

Leetcode1091. Shortest Path in Binary Matrix

Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

  • All the visited cells of the path are 0.
  • All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).
  • The length of a clear path is the number of visited cells of this path.

Example 1:

1
2
Input: grid = [[0,1],[1,0]]
Output: 2

Example 2:

1
2
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Example 3:

1
2
Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1

Constraints:

  • n == grid.length
  • n == grid[i].length
  • 1 <= n <= 100
  • grid[i][j] is 0 or 1

这道题给了一个 nxn 的二维数组，里面都是0和1，让找出一条从左上角到右下角的干净路径，所谓的干净路径就是均由0组成，并且定义了相邻的位置是八个方向，不仅仅是通常的上下左右。例子中还给了图帮助理解，但是也有一丢丢的误导，博主最开始以为只需要往右，下，和右下三个方向走就行了，其实并不一定，任何方向都是可能的，说白了还是一道迷宫遍历的问题。既然是迷宫遍历求最少步数，那么广度优先遍历 Breadth-First Search 就是不二之选了，还是使用一个队列 queue 来做，初识时将 (0, 0) 放进去，再用一个 TreeSet 来标记访问过的位置。注意这里的方向数组要用到八个方向，while 循环中用的还是经典的层序遍历的写法，就是经典的写法，没有啥特殊的地方，博主感觉已经写了无数次了，在进行这一切之前，先判断一下起始点，若为1，直接返回 -1 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        if (grid[0][0] == 1) return -1;
        int res = 0, n = grid.size();
        set<vector<int>> visited;
        visited.insert({0, 0});
        queue<vector<int>> q;
        q.push({0, 0});
        vector<vector<int>> dirs{{-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}};
        while (!q.empty()) {
            ++res;
            for (int i = q.size(); i > 0; --i) {
                auto t = q.front(); q.pop();
                if (t[0] == n - 1 && t[1] == n - 1) return res;
                for (auto dir : dirs) {
                    int x = t[0] + dir[0], y = t[1] + dir[1];
                    if (x < 0 || x >= n || y < 0 || y >= n || grid[x][y] == 1 || visited.count({x, y})) continue;
                    visited.insert({x, y});
                    q.push({x, y});
                }
            }
        }
        return -1;
    }
};

Leetcode1093. Statistics from a Large Sample

You are given a large sample of integers in the range [0, 255]. Since the sample is so large, it is represented by an array count where count[k] is the number of times that k appears in the sample.

Calculate the following statistics:

  • minimum: The minimum element in the sample.
  • maximum: The maximum element in the sample.
  • mean: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
  • median:
    • If the sample has an odd number of elements, then the median is the middle element once the sample is sorted.
    • If the sample has an even number of elements, then the median is the average of the two middle elements once the sample is sorted.
  • mode: The number that appears the most in the sample. It is guaranteed to be unique.

Return the statistics of the sample as an array of floating-point numbers [minimum, maximum, mean, median, mode]. Answers within 10-5 of the actual answer will be accepted.

Example 1:

1
2
3
4
5
6
7
Input: count = [0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
Output: [1.00000,3.00000,2.37500,2.50000,3.00000]
Explanation: The sample represented by count is [1,2,2,2,3,3,3,3].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.

Example 2:

1
2
3
4
5
6
7
Input: count = [0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
Output: [1.00000,4.00000,2.18182,2.00000,1.00000]
Explanation: The sample represented by count is [1,1,1,1,2,2,2,3,3,4,4].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.

Constraints:

  • count.length == 256
  • 0 <= count[i] <= 109
  • 1 <= sum(count) <= 109
  • The mode of the sample that count represents is unique.

这道题说是有很多在0到 255 中的整数，由于重复的数字太多了，所以这里采用的是统计每个数字出现的个数的方式，用数组 count 来表示，其中 count[i] 表示数字i出现的次数。现在让统计原始数组中的最大值，最小值，平均值，中位数，和众数。这里面的最大最小值很好求，最小值就是 count 数组中第一个不为0的位置，最大值就是 count 数组中最后一个不为0的位置。最小值 mn 初始化为 256，在遍历 count 数组的过程中，遇到不为0的数字时，若此时 mn 为 256，则更新为坐标i。最大值 mx 直接每次更新为值不为0的坐标i即可。平均值也好求，只要求出所有的数字之和，跟数字的个数相除就行了，注意由于数字之和可能很大，需要用 double 来表示。众数也不难求，只要找出 count 数组中的最大值，则其坐标就是众数。比较难就是中位数了，由于数组的个数可奇可偶，中位数的求法不同，这里为了统一，采用一个小 trick，比如数组 1，2，3 和 1，2，3，4，可以用坐标为 (n-1)/2 和 n/2 的两个数字求平均值得到，对于长度为奇数的数组，这两个坐标表示的是相同的数字。这里由于是统计数组，所以要找的两个位置是 (cnt+1)/2 和 (cnt+2)/2，其中 cnt 是所有数字的个数。再次遍历 count 数组，使用 cur 来累计当前经过的数字个数，若 cur 小于 first，且 cur 加上 count[i] 大于等于 first，说明当前数字i即为所求，加上其的一半到 median。同理，若 cur 小于 second，cur 加上 count[i] 大于等于 second，说明当前数字i即为所求，加上其的一半到 median 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<double> sampleStats(vector<int>& count) {
        double mn = 256, mx = 0, mean = 0, median = 0, sum = 0;
        int cnt = 0, mode = 0;
        for (int i = 0; i < count.size(); ++i) {
            if (count[i] == 0) continue;
            if (mn == 256) mn = i;
            mx = i;
            sum += (double)i * count[i];
            cnt += count[i];
            if (count[i] > count[mode]) mode = i;
        }
        mean = sum / cnt;
        int first = (cnt + 1) / 2, second = (cnt + 2) / 2, cur = 0;
        for (int i = 0; i < count.size(); ++i) {
            if (cur < first && cur + count[i] >= first) median += i / 2.0;
            if (cur < second && cur + count[i] >= second) median += i / 2.0;
            cur += count[i];
        }
        return {mn, mx, sum / cnt, median, (double)mode};
    }
};

Leetcode1094. Car Pooling

You are driving a vehicle that has capacity empty seats initially available for passengers. The vehicle only drives east (ie. it cannot turn around and drive west.)

Given a list of trips, trip[i] = [num_passengers, start_location, end_location] contains information about the i-th trip: the number of passengers that must be picked up, and the locations to pick them up and drop them off. The locations are given as the number of kilometers due east from your vehicle’s initial location.

Return true if and only if it is possible to pick up and drop off all passengers for all the given trips.

Example 1:

1
2
Input: trips = [[2,1,5],[3,3,7]], capacity = 4
Output: false

Example 2:

1
2
Input: trips = [[2,1,5],[3,3,7]], capacity = 5
Output: true

Example 3:

1
2
Input: trips = [[2,1,5],[3,5,7]], capacity = 3
Output: true

Example 4:

1
2
Input: trips = [[3,2,7],[3,7,9],[8,3,9]], capacity = 11
Output: true

Constraints:

  • trips.length <= 1000
  • trips[i].length == 3
  • 1 <= trips[i][0] <= 100
  • 0 <= trips[i][1] < trips[i][2] <= 1000
  • 1 <= capacity <= 100000

这道题说的是拼车的那些事儿，给了一个数组，里面是很多三元对儿，分别包含乘客个数，上车时间和下车时间，还给了一个变量 capacity，说是任何时候的乘客总数不超过 capacity 的话，返回 true，否则就返回 false。这道题其实跟之前的 Meeting Rooms II 是一样，只不过那道题是求需要的房间的总个数，而这里是限定了乘客的总数，问是否会超载。使用的解题思想都是一样的，主要是需要将上车时间点和下车时间点拆分开，然后按时间顺序排列在同一条时间轴上，上车的时候就加上这些人数，下车的时候就减去这些人数。若某个时间点上的总人数超过了限定值，就直接返回 false 就行了，这里博主没有用 TreeMap，而是直接都放到一个数组中，然后对该数组按时间点进行排序，再遍历排序后的数组，进行累加元素之和即可，参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        int cur = 0;
        vector<vector<int>> data;
        for (auto trip : trips) {
            data.push_back({trip[1], trip[0]});
            data.push_back({trip[2], -trip[0]});
        }
        sort(data.begin(), data.end());
        for (auto &a : data) {
            cur += a[1];
            if (cur > capacity) return false;
        }
        return true;
    }
};

接下来看一种更加高效的解法，并不用进行排序，那个太耗时了。题目限定了时间点不会超过 1000，所以这里就建立一个大小为 1001 的 cnt 数组，然后遍历 trips 数组，将对应的上车时间点加上乘客人数，下车时间点减去乘客人数，这样的话就相当于排序完成了，有点计数排序的感觉。之后再遍历这个 cnt 数组，累加当前的值，只要超过 capacity 了，就返回 false，否则最终返回 true 即可，参见代码如下：

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        int cur = 0;
        vector<int> cnt(1001);
        for (auto &trip : trips) {
            cnt[trip[1]] += trip[0];
            cnt[trip[2]] -= trip[0];
        }
        for (int i = 1; i <= 1000; ++i) {
            cur += cnt[i];
            if (cur > capacity) return false;
        }
        return true;
    }
};

Posted on Edited on

Http和Https

HTTP 是一种 超文本传输协议(Hypertext Transfer Protocol)，HTTP 是一个在计算机世界里专门在两点之间传输文字、图片、音频、视频等超文本数据的约定和规范。
HTTP 主要内容分为三部分，超文本（Hypertext）、传输（Transfer）、协议（Protocol）。

超文本就是不单单只是本文，它还可以传输图片、音频、视频，甚至点击文字或图片能够进行超链接的跳转。上面这些概念可以统称为数据，传输就是数据需要经过一系列的物理介质从一个端系统传送到另外一个端系统的过程。通常我们把传输数据包的一方称为请求方，把接到二进制数据包的一方称为应答方。

而协议指的就是是网络中(包括互联网)传递、管理信息的一些规范。如同人与人之间相互交流是需要遵循一定的规矩一样，计算机之间的相互通信需要共同遵守一定的规则，这些规则就称为协议，只不过是网络协议。说到 HTTP，不得不提的就是 TCP/IP 网络模型，一般是五层模型。如下图所示

但是也可以分为四层，就是把链路层和物理层都表示为网络接口层

还有一种就是 OSI 七层网络模型，它就是在五层协议之上加了表示层和会话层

而 HTTPS 的全称是 Hypertext Transfer Protocol Secure，从名称我们可以看出 HTTPS 要比 HTTPS 多了 secure 安全性这个概念，实际上， HTTPS 并不是一个新的应用层协议，它其实就是 HTTP + TLS/SSL 协议组合而成，而安全性的保证正是 TLS/SSL 所做的工作。也就是说，HTTPS 就是身披了一层 SSL 的 HTTP。

那么，HTTP 和 HTTPS 的主要区别是什么呢？

最简单的，HTTP 在地址栏上的协议是以 http:// 开头，而 HTTPS 在地址栏上的协议是以 https:// 开头

1
2
http://www.cxuanblog.com/
https://www.cxuanblog.com/

HTTP 是未经安全加密的协议，它的传输过程容易被攻击者监听、数据容易被窃取、发送方和接收方容易被伪造；而 HTTPS 是安全的协议，它通过 密钥交换算法 - 签名算法 - 对称加密算法 - 摘要算法 能够解决上面这些问题。

HTTP 的默认端口是 80，而 HTTPS 的默认端口是 443。

HTTP Get 和 Post 区别

HTTP 中包括许多方法，Get 和 Post 是 HTTP 中最常用的两个方法，基本上使用 HTTP 方法中有 99% 都是在使用 Get 方法和 Post 方法，所以有必要我们对这两个方法有更加深刻的认识。

get 方法一般用于请求，比如你在浏览器地址栏输入 www.cxuanblog.com 其实就是发送了一个 get 请求，它的主要特征是请求服务器返回资源，而 post 方法一般用于
表单的提交，相当于是把信息提交给服务器，等待服务器作出响应，get 相当于一个是 pull/拉的操作，而 post 相当于是一个 push/推的操作。get 方法是不安全的，因为你在发送请求的过程中，你的请求参数会拼在 URL 后面，从而导致容易被攻击者窃取，对你的信息造成破坏和伪造；/test/demo_form.asp?name1=value1&name2=value2而 post 方法是把参数放在请求体 body 中的，这对用户来说不可见。

1
2
3
POST /test/demo_form.asp HTTP/1.1
Host: w3schools.com
name1=value1&name2=value2
  • get 请求的 URL 有长度限制，而 post 请求会把参数和值放在消息体中，对数据长度没有要求。
  • get 请求会被浏览器主动 cache，而 post 不会，除非手动设置。
  • get 请求在浏览器反复的 回退/前进 操作是无害的，而 post 操作会再次提交表单请求。
  • get 请求在发送过程中会产生一个 TCP 数据包；post 在发送过程中会产生两个 TCP 数据包。对于 get 方式的请求，浏览器会把 http header 和 data 一并发送出去，服务器响应 200（返回数据）；而对于 post，浏览器先发送 header，服务器响应 100 continue，浏览器再发送 data，服务器响应 200 ok（返回数据）。

什么是无状态协议，HTTP 是无状态协议吗，怎么解决

无状态协议(Stateless Protocol) 就是指浏览器对于事务的处理没有记忆能力。举个例子来说就是比如客户请求获得网页之后关闭浏览器，然后再次启动浏览器，登录该网站，但是服务器并不知道客户关闭了一次浏览器。

HTTP 就是一种无状态的协议，他对用户的操作没有记忆能力。可能大多数用户不相信，他可能觉得每次输入用户名和密码登陆一个网站后，下次登陆就不再重新输入用户名和密码了。这其实不是 HTTP 做的事情，起作用的是一个叫做 小甜饼(Cookie) 的机制。它能够让浏览器具有记忆能力。

当你向服务端发送请求时，服务端会给你发送一个认证信息，服务器第一次接收到请求时，开辟了一块 Session 空间（创建了Session对象），同时生成一个 sessionId ，并通过响应头的 Set-Cookie：JSESSIONID=XXXXXXX 命令，向客户端发送要求设置 Cookie 的响应；客户端收到响应后，在本机客户端设置了一个 JSESSIONID=XXXXXXX 的 Cookie 信息，该 Cookie 的过期时间为浏览器会话结束；

接下来客户端每次向同一个网站发送请求时，请求头都会带上该 Cookie信息（包含 sessionId ）， 然后，服务器通过读取请求头中的 Cookie 信息，获取名称为 JSESSIONID 的值，得到此次请求的 sessionId。这样，你的浏览器才具有了记忆能力。

还有一种方式是使用 JWT 机制，它也是能够让你的浏览器具有记忆能力的一种机制。与 Cookie 不同，JWT 是保存在客户端的信息，它广泛的应用于单点登录的情况。JWT 具有两个特点

  • JWT 的 Cookie 信息存储在客户端，而不是服务端内存中。也就是说，JWT 直接本地进行验证就可以，验证完毕后，这个 Token 就会在 Session 中随请求一起发送到服务器，通过这种方式，可以节省服务器资源，并且 token 可以进行多次验证。
  • JWT 支持跨域认证，Cookies 只能用在单个节点的域或者它的子域中有效。如果它们尝试通过第三个节点访问，就会被禁止。使用 JWT 可以解决这个问题，使用 JWT 能够通过多个节点进行用户认证，也就是我们常说的跨域认证。

UDP 和 TCP 的区别

TCP 和 UDP 都位于计算机网络模型中的运输层，它们负责传输应用层产生的数据。下面我们就来聊一聊 TCP 和 UDP 分别的特征和他们的区别

UDP 的全称是 User Datagram Protocol，用户数据报协议。它不需要所谓的握手操作，从而加快了通信速度，允许网络上的其他主机在接收方同意通信之前进行数据传输。数据报是与分组交换网络关联的传输单元。UDP 的特点主要有

  • UDP 能够支持容忍数据包丢失的带宽密集型应用程序
  • UDP 具有低延迟的特点
  • UDP 能够发送大量的数据包
  • UDP 能够允许 DNS 查找，DNS 是建立在 UDP 之上的应用层协议。

TCP 的全称是Transmission Control Protocol ，传输控制协议。它能够帮助你确定计算机连接到 Internet 以及它们之间的数据传输。通过三次握手来建立 TCP 连接，三次握手就是用来启动和确认 TCP 连接的过程。一旦连接建立后，就可以发送数据了，当数据传输完成后，会通过关闭虚拟电路来断开连接。TCP 的主要特点有

  • TCP 能够确保连接的建立和数据包的发送
  • TCP 支持错误重传机制
  • TCP 支持拥塞控制，能够在网络拥堵的情况下延迟发送
  • TCP 能够提供错误校验和，甄别有害的数据包。
  • TCP 和 UDP 的不同

下面为你罗列了一些 TCP 和 UDP 的不同点，方便理解，方便记忆。

TCP 三次握手和四次挥手

TCP 三次握手和四次挥手也是面试题的热门考点，它们分别对应 TCP 的连接和释放过程。下面就来简单认识一下这两个过程。在了解具体的流程前，我们需要先认识几个概念

  • SYN：它的全称是 Synchronize Sequence Numbers，同步序列编号。是 TCP/IP 建立连接时使用的握手信号。在客户机和服务器之间建立 TCP 连接时，首先会发送的一个信号。客户端在接受到 SYN 消息时，就会在自己的段内生成一个随机值 X。
  • SYN-ACK：服务器收到 SYN 后，打开客户端连接，发送一个 SYN-ACK 作为答复。确认号设置为比接收到的序列号多一个，即 X + 1，服务器为数据包选择的序列号是另一个随机数 Y。
  • ACK：Acknowledge character, 确认字符，表示发来的数据已确认接收无误。最后，客户端将 ACK 发送给服务器。序列号被设置为所接收的确认值即 Y + 1。

如果用现实生活来举例的话就是：小明 - 客户端 小红 - 服务端

  • 小明给小红打电话，接通了后，小明说喂，能听到吗，这就相当于是连接建立。
  • 小红给小明回应，能听到，你能听到我说的话吗，这就相当于是请求响应。
  • 小明听到小红的回应后，好的，这相当于是连接确认。在这之后小明和小红就可以通话/交换信息了。

在连接终止阶段使用四次挥手，连接的每一端都会独立的终止。下面我们来描述一下这个过程。

  • 首先，客户端应用程序决定要终止连接(这里服务端也可以选择断开连接)。这会使客户端将 FIN 发送到服务器，并进入 FIN_WAIT_1 状态。当客户端处于 FIN_WAIT_1 状态时，它会等待来自服务器的 ACK 响应。
  • 然后第二步，当服务器收到 FIN 消息时，服务器会立刻向客户端发送 ACK 确认消息。
  • 当客户端收到服务器发送的 ACK 响应后，客户端就进入 FIN_WAIT_2 状态，然后等待来自服务器的 FIN 消息
  • 服务器发送 ACK 确认消息后，一段时间（可以进行关闭后）会发送 FIN 消息给客户端，告知客户端可以进行关闭。
  • 当客户端收到从服务端发送的 FIN 消息时，客户端就会由 FIN_WAIT_2 状态变为 TIME_WAIT 状态。处于 TIME_WAIT 状态的客户端允许重新发送 ACK 到服务器为了防止信息丢失。客户端在 TIME_WAIT 状态下花费的时间取决于它的实现，在等待一段时间后，连接关闭，客户端上所有的资源（包括端口号和缓冲区数据）都被释放。

还是可以用上面那个通话的例子来进行描述

  • 小明对小红说，我所有的东西都说完了，我要挂电话了。
  • 小红说，收到，我这边还有一些东西没说。
  • 经过若干秒后，小红也说完了，小红说，我说完了，现在可以挂断了
  • 小明收到消息后，又等了若干时间后，挂断了电话

简述 HTTP1.0/1.1/2.0 的区别

HTTP 1.0

HTTP 1.0 是在 1996 年引入的，从那时开始，它的普及率就达到了惊人的效果。

  • HTTP 1.0 仅仅提供了最基本的认证，这时候用户名和密码还未经加密，因此很容易收到窥探。
  • HTTP 1.0 被设计用来使用短链接，即每次发送数据都会经过 TCP 的三次握手和四次挥手，效率比较低。
  • HTTP 1.0 只使用 header 中的 If-Modified-Since 和 Expires 作为缓存失效的标准。
  • HTTP 1.0 不支持断点续传，也就是说，每次都会传送全部的页面和数据。
  • HTTP 1.0 认为每台计算机只能绑定一个 IP，所以请求消息中的 URL 并没有传递主机名（hostname）。

HTTP 1.1

HTTP 1.1 是 HTTP 1.0 开发三年后出现的，也就是 1999 年，它做出了以下方面的变化

  • HTTP 1.1 使用了摘要算法来进行身份验证
  • HTTP 1.1 默认使用长连接，长连接就是只需一次建立就可以传输多次数据，传输完成后，只需要一次切断连接即可。长连接的连接时长可以通过请求头中的 keep-alive 来设置
  • HTTP 1.1 中新增加了 E-tag，If-Unmodified-Since, If-Match, If-None-Match 等缓存控制标头来控制缓存失效。
  • HTTP 1.1 支持断点续传，通过使用请求头中的 Range 来实现。
  • HTTP 1.1 使用了虚拟网络，在一台物理服务器上可以存在多个虚拟主机（Multi-homed Web Servers），并且它们共享一个IP地址。

HTTP 2.0

HTTP 2.0 是 2015 年开发出来的标准，它主要做的改变如下

  • 头部压缩，由于 HTTP 1.1 经常会出现 User-Agent、Cookie、Accept、Server、Range 等字段可能会占用几百甚至几千字节，而 Body 却经常只有几十字节，所以导致头部偏重。HTTP 2.0 使用 HPACK 算法进行压缩。
  • 二进制格式，HTTP 2.0 使用了更加靠近 TCP/IP 的二进制格式，而抛弃了 ASCII 码，提升了解析效率
  • 强化安全，由于安全已经成为重中之重，所以 HTTP2.0 一般都跑在 HTTPS 上。
  • 多路复用，即每一个请求都是是用作连接共享。一个请求对应一个id，这样一个连接上可以有多个请求。

HTTP 常见的请求头

这个问题比较开放，因为 HTTP 请求头有很多，这里只简单举出几个例子。HTTP 标头会分为四种，分别是 通用标头、实体标头、请求标头、响应标头。分别介绍一下

通用标头

通用标头主要有三个，分别是 Date、Cache-Control 和 Connection

Date 是一个通用标头，它可以出现在请求标头和响应标头中，表示的是格林威治标准时间，这个时间要比北京时间慢八个小时

Cache-Control 是一个通用标头，他可以出现在请求标头和响应标头中，Cache-Control 的种类比较多，虽然说这是一个通用标头，但是有一些特性是请求标头具有的，有一些是响应标头才有的。主要大类有 可缓存性、阈值性、 重新验证并重新加载 和其他特性

Connection 决定当前事务（一次三次握手和四次挥手）完成后，是否会关闭网络连接。Connection 有两种，一种是持久性连接，即一次事务完成后不关闭网络连接；另一种是非持久性连接，即一次事务完成后关闭网络连接

HTTP1.1 其他通用标头如下

实体标头

实体标头是描述消息正文内容的 HTTP 标头。实体标头用于 HTTP 请求和响应中。头部Content-Length、 Content-Language、 Content-Encoding 是实体头。

Content-Length 实体报头指示实体主体的大小，以字节为单位，发送到接收方。

Content-Language 实体报头描述了客户端或者服务端能够接受的语言。

Content-Encoding 这又是一个比较麻烦的属性，这个实体报头用来压缩媒体类型。Content-Encoding 指示对实体应用了何种编码。

常见的内容编码有这几种： gzip、compress、deflate、identity ，这个属性可以应用在请求报文和响应报文中

1
2
Accept-Encoding: gzip, deflate //请求头
Content-Encoding: gzip  //响应头

下面是一些实体标头字段

请求标头

Host 请求头指明了服务器的域名（对于虚拟主机来说），以及（可选的）服务器监听的 TCP 端口号。如果没有给定端口号，会自动使用被请求服务的默认端口（比如请求一个 HTTP 的 URL 会自动使用 80 作为端口）。

1
Host: developer.mozilla.org

上面的 Accpet、 Accept-Language、Accept-Encoding 都是属于内容协商的请求标头。

HTTP Referer 属性是请求标头的一部分，当浏览器向 web 服务器发送请求的时候，一般会带上 Referer，告诉服务器该网页是从哪个页面链接过来的，服务器因此可以获得一些信息用于处理。

1
Referer: https://developer.mozilla.org/testpage.html

If-Modified-Since 通常会与 If-None-Match 搭配使用，If-Modified-Since 用于确认代理或客户端拥有的本地资源的有效性。获取资源的更新日期时间，可通过确认首部字段 Last-Modified 来确定。大白话说就是如果在 Last-Modified 之后更新了服务器资源，那么服务器会响应 200，如果在 Last-Modified 之后没有更新过资源，则返回 304。

1
If-Modified-Since: Mon, 18 Jul 2016 02:36:04 GMT

If-None-Match HTTP 请求标头使请求成为条件请求。对于 GET 和 HEAD 方法，仅当服务器没有与给定资源匹配的 ETag 时，服务器才会以 200 状态发送回请求的资源。对于其他方法，仅当最终现有资源的ETag与列出的任何值都不匹配时，才会处理请求。

1
If-None-Match: "c561c68d0ba92bbeb8b0fff2a9199f722e3a621a"

Accept：接受请求 HTTP 标头会通告客户端其能够理解的 MIME 类型

Accept-Charset：属性规定服务器处理表单数据所接受的字符集。常用的字符集有：UTF-8 - Unicode 字符编码 ；ISO-8859-1 - 拉丁字母表的字符编码

首部字段 Accept-Language 用来告知服务器用户代理能够处理的自然语言集（指中文或英文等），以及自然语言集的相对优先级。可一次指定多种自然语言集。

请求标头我们大概就介绍这几种，后面会有一篇文章详细深挖所有的响应头的，下面是一个响应头的汇总，基于 HTTP 1.1

响应标头

Access-Control-Allow-Origin：一个返回的 HTTP 标头可能会具有 Access-Control-Allow-Origin ，Access-Control-Allow-Origin 指定一个来源，它告诉浏览器允许该来源进行资源访问。

Keep-Alive：Keep-Alive 表示的是 Connection 非持续连接的存活时间，可以进行指定。

Server：服务器标头包含有关原始服务器用来处理请求的软件的信息。应该避免使用过于冗长和详细的 Server 值，因为它们可能会泄露内部实施细节，这可能会使攻击者容易地发现并利用已知的安全漏洞。例如下面这种写法

1
Server: Apache/2.4.1 (Unix)

Set-Cookie 用于服务器向客户端发送 sessionID。

Transfer-Encoding：首部字段 Transfer-Encoding 规定了传输报文主体时采用的编码方式。HTTP /1.1 的传输编码方式仅对分块传输编码有效。

X-Frame-Options：HTTP 首部字段是可以自行扩展的。所以在 Web 服务器和浏览器的应用上，会出现各种非标准的首部字段。首部字段 X-Frame-Options 属于 HTTP 响应首部，用于控制网站内容在其他 Web 网站的 Frame 标签内的显示问题。其主要目的是为了防止点击劫持（clickjacking）攻击。

下面是一个响应头的汇总，基于 HTTP 1.1

地址栏输入 URL 发生了什么

首先，你需要在浏览器中的 URL 地址上，输入你想访问的地址。然后，浏览器会根据你输入的 URL 地址，去查找域名是否被本地 DNS 缓存，不同浏览器对 DNS 的设置不同，如果浏览器缓存了你想访问的 URL 地址，那就直接返回 ip。如果没有缓存你的 URL 地址，浏览器就会发起系统调用来查询本机 hosts 文件是否有配置 ip 地址，如果找到，直接返回。如果找不到，就向网络中发起一个 DNS 查询。

首先来看一下 DNS 是啥，互联网中识别主机的方式有两种，通过主机名和 IP 地址。我们人喜欢用名字的方式进行记忆，但是通信链路中的路由却喜欢定长、有层次结构的 IP 地址。所以就需要一种能够把主机名到 IP 地址的转换服务，这种服务就是由 DNS 提供的。DNS 的全称是 Domain Name System 域名系统。DNS 是一种由分层的 DNS 服务器实现的分布式数据库。DNS 运行在 UDP 上，使用 53 端口。

DNS 是一种分层数据库，它的主要层次结构如下

一般域名服务器的层次结构主要是以上三种，除此之外，还有另一类重要的 DNS 服务器，它是 本地 DNS 服务器(local DNS server)。严格来说，本地 DNS 服务器并不属于上述层次结构，但是本地 DNS 服务器又是至关重要的。每个 ISP(Internet Service Provider) 比如居民区的 ISP 或者一个机构的 ISP 都有一台本地 DNS 服务器。当主机和 ISP 进行连接时，该 ISP 会提供一台主机的 IP 地址，该主机会具有一台或多台其本地 DNS 服务器的 IP地址。通过访问网络连接，用户能够容易的确定 DNS 服务器的 IP地址。当主机发出 DNS 请求后，该请求被发往本地 DNS 服务器，它起着代理的作用，并将该请求转发到 DNS 服务器层次系统中。

首先，查询请求会先找到本地 DNS 服务器来查询是否包含 IP 地址，如果本地 DNS 无法查询到目标 IP 地址，就会向根域名服务器发起一个 DNS 查询。

注意：DNS 涉及两种查询方式：一种是递归查询(Recursive query) ，一种是迭代查询(Iteration query)。《计算机网络：自顶向下方法》竟然没有给出递归查询和迭代查询的区别，找了一下网上的资料大概明白了下。

  • 如果根域名服务器无法告知本地 DNS 服务器下一步需要访问哪个顶级域名服务器，就会使用递归查询；
  • 如果根域名服务器能够告知 DNS 服务器下一步需要访问的顶级域名服务器，就会使用迭代查询。
  • 在由根域名服务器 -> 顶级域名服务器 -> 权威 DNS 服务器后，由权威服务器告诉本地服务器目标 IP 地址，再有本地 DNS 服务器告诉用户需要访问的 IP 地址。

第三步，浏览器需要和目标服务器建立 TCP 连接，需要经过三次握手的过程，具体的握手过程请参考上面的回答。

  • 在建立连接后，浏览器会向目标服务器发起 HTTP-GET 请求，包括其中的 URL，HTTP 1.1 后默认使用长连接，只需要一次握手即可多次传输数据。
  • 如果目标服务器只是一个简单的页面，就会直接返回。但是对于某些大型网站的站点，往往不会直接返回主机名所在的页面，而会直接重定向。返回的状态码就不是 200 ，而是 301,302 以 3 开头的重定向码，浏览器在获取了重定向响应后，在响应报文中 Location 项找到重定向地址，浏览器重新第一步访问即可。
  • 然后浏览器重新发送请求，携带新的 URL，返回状态码 200 OK，表示服务器可以响应请求，返回报文。

HTTPS 的工作原理

我们上面描述了一下 HTTP 的工作原理，下面来讲述一下 HTTPS 的工作原理。因为我们知道 HTTPS 不是一种新出现的协议，而是HTTP+SSL。所以，我们探讨 HTTPS 的握手过程，其实就是 SSL/TLS 的握手过程。

TLS 旨在为 Internet 提供通信安全的加密协议。TLS 握手是启动和使用 TLS 加密的通信会话的过程。在 TLS 握手期间，Internet 中的通信双方会彼此交换信息，验证密码套件，交换会话密钥。每当用户通过 HTTPS 导航到具体的网站并发送请求时，就会进行 TLS 握手。除此之外，每当其他任何通信使用HTTPS（包括 API 调用和在 HTTPS 上查询 DNS）时，也会发生 TLS 握手。TLS 具体的握手过程会根据所使用的密钥交换算法的类型和双方支持的密码套件而不同。我们以RSA 非对称加密来讨论这个过程。整个 TLS 通信流程图如下：

  • 在进行通信前，首先会进行 HTTP 的三次握手，握手完成后，再进行 TLS 的握手过程
  • ClientHello：客户端通过向服务器发送 hello 消息来发起握手过程。这个消息中会夹带着客户端支持的 TLS 版本号(TLS1.0 、TLS1.2、TLS1.3) 、客户端支持的密码套件、以及一串 客户端随机数。
  • ServerHello：在客户端发送 hello 消息后，服务器会发送一条消息，这条消息包含了服务器的 SSL 证书、服务器选择的密码套件和服务器生成的随机数。
  • 认证(Authentication)：客户端的证书颁发机构会认证 SSL 证书，然后发送 Certificate 报文，报文中包含公开密钥证书。最后服务器发送 ServerHelloDone 作为 hello 请求的响应。第一部分握手阶段结束。
  • 加密阶段：在第一个阶段握手完成后，客户端会发送 ClientKeyExchange 作为响应，这个响应中包含了一种称为 The premaster secret 的密钥字符串，这个字符串就是使用上面公开密钥证书进行加密的字符串。随后客户端会发送 ChangeCipherSpec，告诉服务端使用私钥解密这个 premaster secret 的字符串，然后客户端发送 Finished 告诉服务端自己发送完成了。Session key 其实就是用公钥证书加密的公钥。
  • 实现了安全的非对称加密：然后，服务器再发送 ChangeCipherSpec 和 Finished 告诉客户端解密完成，至此实现了 RSA 的非对称加密。

Posted on Edited on

Leetcode1304. Find N Unique Integers Sum up to Zero

Given an integer n, return any array containing n unique integers such that they add up to 0.

Example 1:

1
2
3
Input: n = 5
Output: [-7,-1,1,3,4]
Explanation: These arrays also are accepted [-5,-1,1,2,3] , [-3,-1,2,-2,4].

Example 2:

1
2
Input: n = 3
Output: [-1,0,1]

Example 3:

1
2
Input: n = 1
Output: [0]

偶数关于原点对称，奇数加上一个0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<int> sumZero(int n) {
        if(n == 1)
            return {0};
        vector<int> res;
        int sum = 0;
        for(int i = 0; i < n-1; i ++){
            sum += i;
            res.push_back(i);
        }
        res.push_back(-sum);
        return res;
    }
};

Leetcode1309. Decrypt String from Alphabet to Integer Mapping

Given a string s formed by digits (‘0’ - ‘9’) and ‘#’ . We want to map s to English lowercase characters as follows:

  • Characters (‘a’ to ‘i’) are represented by (‘1’ to ‘9’) respectively.
  • Characters (‘j’ to ‘z’) are represented by (‘10#’ to ‘26#’) respectively.

Return the string formed after mapping. It’s guaranteed that a unique mapping will always exist.

Example 1:

1
2
3
Input: s = "10#11#12"
Output: "jkab"
Explanation: "j" -> "10#" , "k" -> "11#" , "a" -> "1" , "b" -> "2".

Example 2:

1
2
Input: s = "1326#"
Output: "acz"

Example 3:

1
2
Input: s = "25#"
Output: "y"

Example 4:

1
2
Input: s = "12345678910#11#12#13#14#15#16#17#18#19#20#21#22#23#24#25#26#"
Output: "abcdefghijklmnopqrstuvwxyz"

简单的模拟题，但是很麻烦：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    string freqAlphabets(string s) {
        string res = "";
        for(int i = 0; i < s.length(); ) {
            char c = s[i];
            if(i+2 < s.length() && s[i+2] == '#') {
                char cc = s[i+1];
                int temp = (c - '0') * 10 + (cc - '0') - 1;
                res += ('a' + temp);
                i += 3;
            }
            else {
                char cc = 'a' + (c - '0' - 1);
                res += cc;
                i += 1;
            }
        }
        return res;
    }
};

Leetcode1313. Decompress Run-Length Encoded List

We are given a list nums of integers representing a list compressed with run-length encoding.

Consider each adjacent pair of elements [freq, val] = [nums[2i], nums[2i+1]] (with i >= 0). For each such pair, there are freq elements with value val concatenated in a sublist. Concatenate all the sublists from left to right to generate the decompressed list.

Return the decompressed list.

Example 1:

1
2
3
4
5
Input: nums = [1,2,3,4]
Output: [2,4,4,4]
Explanation: The first pair [1,2] means we have freq = 1 and val = 2 so we generate the array [2].
The second pair [3,4] means we have freq = 3 and val = 4 so we generate [4,4,4].
At the end the concatenation [2] + [4,4,4] is [2,4,4,4].

Example 2:

1
2
Input: nums = [1,1,2,3]
Output: [1,3,3]

Constraints:

  • 2 <= nums.length <= 100
  • nums.length % 2 == 0
  • 1 <= nums[i] <= 100
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    vector<int> decompressRLElist(vector<int>& nums) {
        vector<int> result;
        for(int i=0;i<nums.size();i+=2) {
            for(int j=0;j<nums[i];j++) {
                result.push_back(nums[i+1]);
            }
        }
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> decompressRLElist(vector<int>& nums) {
        vector<int> res;
        int i=0;
        while(i+1<nums.size()-i){
            int a=nums[2*i],b=nums[2*i+1];
            while(a--)
                res.push_back(b);
            i+=1;
        }
        return res;
    }
};

Leetcode1314. Matrix Block Sum

Given a m x n matrix mat and an integer k, return a matrix answer where each answer[i][j] is the sum of all elements mat[r][c] for:

  • i - k <= r <= i + k,
  • j - k <= c <= j + k, and
  • (r, c) is a valid position in the matrix.

Example 1:

1
2
Input: mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[12,21,16],[27,45,33],[24,39,28]]

Example 2:

1
2
Input: mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
Output: [[45,45,45],[45,45,45],[45,45,45]]

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n, k <= 100
  • 1 <= mat[i][j] <= 100

二维前缀和求一个矩形区域的和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> dp(m+1, vector<int>(n+1, 0));
        vector<vector<int>> ret(m, vector<int>(n, 0));
        for (int i = 1; i <= m; i ++) {
            for (int j = 1; j <= n; j ++)
                dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];
        }
        
        for (int i = 1; i <= m; i ++) {
            for (int j = 1; j <= n; j ++) {
                int r1 = max(1, i-k), c1 = max(1, j-k);
                int r2 = min(m, i+k), c2 = min(n, j+k);
                
                ret[i-1][j-1] = dp[r2][c2] - dp[r2][c1-1] - dp[r1-1][c2] + dp[r1-1][c1-1];
            }
        }
        return ret;
    }
};

Leetcode1317. Convert Integer to the Sum of Two No-Zero Integers

Given an integer n. No-Zero integer is a positive integer which doesn’t contain any 0 in its decimal representation.

Return a list of two integers [A, B] where:

  • A and B are No-Zero integers.
  • A + B = n

It’s guarateed that there is at least one valid solution. If there are many valid solutions you can return any of them.

Example 1:

1
2
Input: n = 2 : [1,1]
Explanation: A = 1, B = 1. A + B = n and both A and B don't contain any 0 in their decimal representation.

把一个数分解成两个不含有0的数的和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    
    bool have0(int nn) {
        while(nn) {
            int temp = nn % 10;
            if(temp == 0)
                return true;
            nn = nn / 10;
        }
        return false;
    }
    
    vector<int> getNoZeroIntegers(int n) {
        for(int i = 1; i <= n/2; i ++) {
            if(!have0(i) && !have0(n-i))
                return {i, n-i};
        }
        return {};
    }
};

Leetcode1323. Maximum 69 Number

Given a positive integer num consisting only of digits 6 and 9. Return the maximum number you can get by changing at most one digit (6 becomes 9, and 9 becomes 6).

Example 1:

1
2
3
4
5
6
7
8
Input: num = 9669
Output: 9969
Explanation: 
Changing the first digit results in 6669.
Changing the second digit results in 9969.
Changing the third digit results in 9699.
Changing the fourth digit results in 9666. 
The maximum number is 9969.

Example 2:

1
2
3
Input: num = 9996
Output: 9999
Explanation: Changing the last digit 6 to 9 results in the maximum number.

Example 3:

1
2
3
Input: num = 9999
Output: 9999
Explanation: It is better not to apply any change.

翻转一位数（6变9）找到最大的，只要找到从头到尾第一个6就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maximum69Number (int num) {
        string numm = to_string(num);
        for(int i =0; i < numm.size(); i ++) {
            if(numm[i] == '6'){
                numm[i] = '9';
                return stoi(numm);
            }
        }
        return num;
    }
};

Leetcode1331. Rank Transform of an Array

Given an array of integers arr, replace each element with its rank. The rank represents how large the element is. The rank has the following rules:

Rank is an integer starting from 1.
The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
Rank should be as small as possible.

Example 1:

1
2
3
Input: arr = [40,10,20,30]
Output: [4,1,2,3]
Explanation: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.

把一个数组中的数字用排序后这个数字的rank来替换，注意没有跨越rank的那种情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> arrayRankTransform(vector<int>& arr) {
        map<int, int> mp;
        vector<int> rr(arr);
        sort(rr.begin(), rr.end());
        int rank = 1;
        for(int i = 0; i < rr.size(); i ++) {
            if(mp[rr[i]] == 0)
                mp[rr[i]] = rank ++;
        }
        for(int i = 0; i < arr.size(); i ++) {
            arr[i] = mp[arr[i]];
        }
        return arr;
    }
};

Leetcode1332. Remove Palindromic Subsequences

Given a string s consisting only of letters ‘a’ and ‘b’. In a single step you can remove one palindromic subsequence from s.

Return the minimum number of steps to make the given string empty.

A string is a subsequence of a given string, if it is generated by deleting some characters of a given string without changing its order.

A string is called palindrome if is one that reads the same backward as well as forward.

Example 1:

1
2
3
Input: s = "ababa"
Output: 1
Explanation: String is already palindrome

Example 2:

1
2
3
4
Input: s = "abb"
Output: 2
Explanation: "abb" -> "bb" -> "". 
Remove palindromic subsequence "a" then "bb".

Example 3:

1
2
3
4
Input: s = "baabb"
Output: 2
Explanation: "baabb" -> "b" -> "". 
Remove palindromic subsequence "baab" then "b".

Example 4:

1
2
Input: s = ""
Output: 0

由于只有 a 和 b 两个字符。其实最多的消除次数就是 2。因为我们无论如何都可以先消除全部的 1 再消除全部的 2（先消除 2 也一样），这样只需要两次即可完成。 我们再看一下题目给的一次消除的情况，题目给的例子是“ababa”，我们发现其实它本身就是一个回文串，所以才可以一次全部消除。那么思路就有了：

如果 s 是回文，则我们需要一次消除；否则需要两次，一定要注意特殊情况， 对于空字符串，我们需要 0 次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int removePalindromeSub(string s) {
        if(s.length() == 0)
            return 0;
        int ii = 0, jj = s.length()-1;
        while(ii < jj) {
            if(s[ii] != s[jj])
                break;
            ii ++;
            jj --;
        }
        if(ii < jj)
            return 2;
        else
            return 1;
    }
};

Leetcode1337. The K Weakest Rows in a Matrix

Given a m * n matrix mat of ones (representing soldiers) and zeros (representing civilians), return the indexes of the k weakest rows in the matrix ordered from the weakest to the strongest.

A row i is weaker than row j, if the number of soldiers in row i is less than the number of soldiers in row j, or they have the same number of soldiers but i is less than j. Soldiers are always stand in the frontier of a row, that is, always ones may appear first and then zeros.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Input: mat = 
[[1,1,0,0,0],
 [1,1,1,1,0],
 [1,0,0,0,0],
 [1,1,0,0,0],
 [1,1,1,1,1]], 
k = 3
Output: [2,0,3]
Explanation: 
The number of soldiers for each row is: 
row 0 -> 2 
row 1 -> 4 
row 2 -> 1 
row 3 -> 2 
row 4 -> 5 
Rows ordered from the weakest to the strongest are [2,0,3,1,4]

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Input: mat = 
[[1,0,0,0],
 [1,1,1,1],
 [1,0,0,0],
 [1,0,0,0]], 
k = 2
Output: [0,2]
Explanation: 
The number of soldiers for each row is: 
row 0 -> 1 
row 1 -> 4 
row 2 -> 1 
row 3 -> 1 
Rows ordered from the weakest to the strongest are [0,2,3,1]

在mat的2维阵列中，算出每一个row当中，1的数量。利用1的数量进行排序，并返回前k名。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {
        vector<int> weak;
        for(int i = 0; i < mat.size(); i ++) {
            weak.push_back(0);
            int count = 0;
            for(int j = 0; j < mat[i].size(); j ++) {
                count += mat[i][j];
            }
            weak[i] = count;
        }
        map<int, vector<int>> mp;
        for(int i = 0; i < mat.size(); i ++) {
            mp[weak[i]].push_back(i);
        }
        sort(weak.begin(), weak.end());
        vector<int> res;
        int kk = 0;
        for(auto i = mp.begin(); i != mp.end() ; i ++) {
            for(int ii = 0; ii < (i->second).size(); ii ++) {
                res.push_back((i->second)[ii]);
                kk ++;
                if(kk == k)
                    break;
            }
            if(kk == k)
                break;
        }
        return res;
    }
};

Leetcode1340. Jump Game V

Given an array of integers arr and an integer d. In one step you can jump from index i to index:

  • i + x where: i + x < arr.length and 0 < x <= d.
  • i - x where: i - x >= 0 and 0 < x <= d.

In addition, you can only jump from index i to index j if arr[i] > arr[j] and arr[i] > arr[k] for all indices k between i and j (More formally min(i, j) < k < max(i, j)).

You can choose any index of the array and start jumping. Return the maximum number of indices you can visit.

Notice that you can not jump outside of the array at any time.

Example 1:

1
2
3
4
5
Input: arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
Output: 4
Explanation: You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.

Example 2:

1
2
3
Input: arr = [3,3,3,3,3], d = 3
Output: 1
Explanation: You can start at any index. You always cannot jump to any index.

Example 3:

1
2
3
Input: arr = [7,6,5,4,3,2,1], d = 1
Output: 7
Explanation: Start at index 0. You can visit all the indicies.

Constraints:

  • 1 <= arr.length <= 1000
  • 1 <= arr[i] <= 105
  • 1 <= d <= arr.length

给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到：

  • i + x ，其中 i + x < arr.length 且 0 < x <= d 。
  • i - x ，其中 i - x >= 0 且 0 < x <= d 。

除此以外，你从下标 i 跳到下标 j 需要满足：arr[i] > arr[j] 且 arr[i] > arr[k] ，其中下标 k 是所有 i 到 j 之间的数字（更正式的，min(i, j) < k < max(i, j)）。

你可以选择数组的任意下标开始跳跃。请你返回你 最多 可以访问多少个下标。请注意，任何时刻你都不能跳到数组的外面。

相当于是在有向无环图中找到一条最长路，因为是从一个柱子一直不停的跳到另外的柱子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
public:
    
    vector<vector<int>> g;
    vector<int> dp;
    
    int dfs(int u) {
        if (dp[u] != -1)
            return dp[u];
        
        dp[u] = 0;
        for (int v : g[u]) {
            int dist = dfs(v);  // f[v]
            dp[u] = max(dp[u], dist); // 取最大的f[v]
        }
        
        dp[u] ++;
        // 这个++表示u到v的这条边
        
        return dp[u];
    }
    
    
    int maxJumps(vector<int>& arr, int d) {
        int n = arr.size();
        g.assign(n, vector<int>());
        
        for (int i = 0; i < n; i ++) {
            // 在两个方向上，构图
            for (int j = 1; j <= d && i - j >= 0 && arr[i-j] < arr[i]; j ++)
                // 最远不能超过d，高度小过a[i]，不能跑出去边界
                g[i].push_back(i - j);
            for (int j = 1; j <= d && i + j < n && arr[i+j] < arr[i]; j ++)
                // 最远不能超过d，高度小过a[i]，不能跑出去边界
                g[i].push_back(i + j);
        }
        
        dp.assign(n, -1);
        // 从一个点出发能走的最长路径
        
        for (int i = 0; i < n; i ++)
            dfs(i);

        int res = -1;
        for (int i = 0; i < n; i ++)
            res = max(res, dp[i]);
        
        return res;
    }
};

Leetcode1346. Check If N and Its Double Exist

Given an array arr of integers, check if there exists two integers N and M such that N is the double of M ( i.e. N = 2 * M).

More formally check if there exists two indices i and j such that :

  • i != j
  • 0 <= i, j < arr.length
  • arr[i] == 2 * arr[j]

Example 1:

1
2
3
Input: arr = [10,2,5,3]
Output: true
Explanation: N = 10 is the double of M = 5,that is, 10 = 2 * 5.

Example 2:

1
2
3
Input: arr = [7,1,14,11]
Output: true
Explanation: N = 14 is the double of M = 7,that is, 14 = 2 * 7.

Example 3:

1
2
3
Input: arr = [3,1,7,11]
Output: false
Explanation: In this case does not exist N and M, such that N = 2 * M.

注意0的问题，只有有两个0的时候返回true

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool checkIfExist(vector<int>& arr) {
        map<int, int> mp;
        for(int i = 0; i < arr.size(); i ++)
            mp[arr[i]] ++;
        for(int i = 0; i < arr.size(); i ++) {
            if(mp[arr[i]*2] && arr[i] != 0 || arr[i] == 0 && mp[arr[i]] > 1  )
                return true;
        }
        return false;
    }
};

Leetcode1349. Maximum Students Taking Exam

Given a m * n matrix seats that represent seats distributions in a classroom. If a seat is broken, it is denoted by ‘#’ character otherwise it is denoted by a ‘.’ character.

Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the maximum number of students that can take the exam together without any cheating being possible..

Students must be placed in seats in good condition.

Example 1:

1
2
3
4
5
Input: seats = [["#",".","#","#",".","#"],
                [".","#","#","#","#","."],
                ["#",".","#","#",".","#"]]
Output: 4
Explanation: Teacher can place 4 students in available seats so they don't cheat on the exam.

Example 2:

1
2
3
4
5
6
7
Input: seats = [[".","#"],
                ["#","#"],
                ["#","."],
                ["#","#"],
                [".","#"]]
Output: 3
Explanation: Place all students in available seats.

Example 3:

1
2
3
4
5
6
7
Input: seats = [["#",".",".",".","#"],
                [".","#",".","#","."],
                [".",".","#",".","."],
                [".","#",".","#","."],
                ["#",".",".",".","#"]]
Output: 10
Explanation: Place students in available seats in column 1, 3 and 5.

状态压缩dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
class Solution {
public:
    
    bool check2(int s, int ss, int m) {
        for (int k = 0; k < m; k ++) {
            int b = (s >> k) & 1;
            if (!b)
                continue;
            int bss0 = 0, bss2 = 0;
            if (k)
                bss0 = (ss >> (k-1)) & 1;
            if (k != m-1)
                bss2 = (ss >> (k+1)) & 1;
            if (bss0 || bss2)
                return false;
        }
        return true;
    }
    
    bool check(int s, const vector<char>& line, int m) {
        int preb = 0;
        for (int k = 0; k < m; k ++) {
            int b = (s >> k) & 1;
            if (b && line[k] == '#')
                return false;
            if (preb && b)
                return false;
            preb = b;
        }
        return true;
    }
    
    
    int maxStudents(vector<vector<char>>& seats) {
        int n = seats.size(), m = seats[0].size();
        
        int maxseats = 1 << m;
        vector<int> y(maxseats, 0);
        vector<int> x(maxseats, 0);
        vector<bool> oky(maxseats, true);
        vector<bool> okx(maxseats, true);
        
        for (int i = 0; i < n; i ++) {
            x.assign(maxseats, 0);
            okx.assign(maxseats, false);
            
            for (int s = 0; s < maxseats; s ++) {
                okx[s] = check(s, seats[i], m);
                if (!okx[s])
                    continue;
                
                int cnt = 0;
                for (int k = 0; k < m; k ++)
                    cnt += ( s >> k) & 1;
                
                for (int ss = 0; ss < maxseats; ss ++)
                    if (oky[ss]) {
                        if (!check2(s, ss, m))
                            continue;
                        x[s] = max(x[s], y[ss] + cnt);
                    }
            }
            swap(x, y);
            swap(okx, oky);
        }
        
        int maxv = 0;
        for (int v : y)
            maxv = max(maxv, v);
        return maxv;
    }
};

Leetcode1351. Count Negative Numbers in a Sorted Matrix

Given a m * n matrix grid which is sorted in non-increasing order both row-wise and column-wise. Return the number of negative numbers in grid.

Example 1:

1
2
3
Input: grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
Output: 8
Explanation: There are 8 negatives number in the matrix.

统计一个矩阵中有多少个负数？有毛病，这么简单。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int countNegatives(vector<vector<int>>& grid) {
        int res = 0;
        for(int i = 0; i < grid.size(); i ++)
            for(int j = 0; j < grid[0].size(); j ++)
                if(grid[i][j] < 0)
                    res ++;
        return res;
    }
};

Leetcode1356. Sort Integers by The Number of 1 Bits

Given an integer array arr. You have to sort the integers in the array in ascending order by the number of 1’s in their binary representation and in case of two or more integers have the same number of 1’s you have to sort them in ascending order.

Return the sorted array.

Example 1:

1
2
3
4
5
6
7
Input: arr = [0,1,2,3,4,5,6,7,8]
Output: [0,1,2,4,8,3,5,6,7]
Explantion: [0] is the only integer with 0 bits.
[1,2,4,8] all have 1 bit.
[3,5,6] have 2 bits.
[7] has 3 bits.
The sorted array by bits is [0,1,2,4,8,3,5,6,7]

Example 2:

1
2
3
Input: arr = [1024,512,256,128,64,32,16,8,4,2,1]
Output: [1,2,4,8,16,32,64,128,256,512,1024]
Explantion: All integers have 1 bit in the binary representation, you should just sort them in ascending order.

根据数字二进制下 1 的数目排序，简单。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    
    static int bitnum(int a) {
        int res = 0;
        while(a) {
            res += a & 1;
            a = a >> 1;
        }
        return res;
    }
    
    static bool cmp(int a, int b) {
        if(bitnum(a) < bitnum(b))
            return true;
        else if(bitnum(a) == bitnum(b))
            return a < b;
        else
            return false;
    }
    
    vector<int> sortByBits(vector<int>& arr) {
        sort(arr.begin(), arr.end(), cmp);
        return arr;
    }
};

Leetcode1360. Number of Days Between Two Dates

Write a program to count the number of days between two dates. The two dates are given as strings, their format is YYYY-MM-DD as shown in the examples.

Example 1:

1
2
Input: date1 = "2019-06-29", date2 = "2019-06-30"
Output: 1

Example 2:

1
2
Input: date1 = "2020-01-15", date2 = "2019-12-31"
Output: 15

计算时间间隔，无聊。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int daysBetweenDates(string date1, string date2) {
        tm time1, time2; //tm是表示日期的结构体
        memset(&time1, 0, sizeof(tm));
        memset(&time2, 0, sizeof(tm)); //初始化
        time1.tm_year = stoi(date1.substr(0, 4)) - 1900; //year表示与1900年的差值
        time1.tm_mon = stoi(date1.substr(5, 2)) - 1;
        time1.tm_mday = stoi(date1.substr(8, 2));
        time2.tm_year = stoi(date2.substr(0, 4)) - 1900;
        time2.tm_mon = stoi(date2.substr(5, 2)) - 1; //mon从0开始取值
        time2.tm_mday = stoi(date2.substr(8, 2));
        time_t t1 = mktime(&time1), t2 = mktime(&time2); //mktime用于将struct tm转化为time_t类型
        return abs(t1 - t2) / (3600 * 24);  //time_t就是天数
    }
};

Leetcode1365. How Many Numbers Are Smaller Than the Current Number

Given the array nums, for each nums[i] find out how many numbers in the array are smaller than it. That is, for each nums[i] you have to count the number of valid j’s such that j != i and nums[j] < nums[i].

Return the answer in an array.

Example 1:

1
2
3
4
5
6
7
8
Input: nums = [8,1,2,2,3]
Output: [4,0,1,1,3]
Explanation: 
For nums[0]=8 there exist four smaller numbers than it (1, 2, 2 and 3). 
For nums[1]=1 does not exist any smaller number than it.
For nums[2]=2 there exist one smaller number than it (1). 
For nums[3]=2 there exist one smaller number than it (1). 
For nums[4]=3 there exist three smaller numbers than it (1, 2 and 2).

这个算法用的是map，为什么能管用呢，因为map内部已经把数字排好序了，用iterator遍历的时候相当于是有序的了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    
    vector<int> smallerNumbersThanCurrent(vector<int>& nums) {
        vector<int> res;
        map<int, int> mp;
        for(int i = 0; i < nums.size(); i ++) {
            mp[nums[i]] ++;
        }
        int presum = 0;
        for(auto a = mp.begin(); a != mp.end(); a ++) {
            int sec = a->second;
            mp[a->first] = presum;
            presum = presum + sec;
        }
        for(int i = 0; i < nums.size(); i ++){
            res.push_back(mp[nums[i]]);
        }
        return res;
    }
};

Leetcode1370. Increasing Decreasing String

Given a string s. You should re-order the string using the following algorithm:

  • Pick the smallest character from s and append it to the result.
  • Pick the smallest character from s which is greater than the last appended character to the result and append it.
  • Repeat step 2 until you cannot pick more characters.
  • Pick the largest character from s and append it to the result.
  • Pick the largest character from s which is smaller than the last appended character to the result and append it.
  • Repeat step 5 until you cannot pick more characters.
  • Repeat the steps from 1 to 6 until you pick all characters from s.
  • In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.

Return the result string after sorting s with this algorithm.

Example 1:

1
2
3
4
5
6
7
Input: s = "aaaabbbbcccc"
Output: "abccbaabccba"
Explanation: After steps 1, 2 and 3 of the first iteration, result = "abc"
After steps 4, 5 and 6 of the first iteration, result = "abccba"
First iteration is done. Now s = "aabbcc" and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc"
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba"

没看懂题意，因为踩的人比较多，所以简单看看就过了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    string sortString(string s) {
        string res;
        vector<int> ma(26, 0);
        int i = 0, len = s.length();
        for(int i = 0; i < len; i ++)
            ma[s[i] - 'a'] ++;
        int count = 0;
        while(count < len) {
            for(int i = 0; i < 26; i ++)
                if(ma[i]) {
                    res += ('a' + i);
                    ma[i] --;
                    count ++;
                }
            for(int i = 25; i >= 0; i --)
                if(ma[i]) {
                    res += ('a' + i);
                    ma[i] --;
                    count ++;
                }
        }
        return res;
    }
};

Leetcode1374. Generate a String With Characters That Have Odd Counts

Given an integer n, return a string with n characters such that each character in such string occurs an odd number of times. The returned string must contain only lowercase English letters. If there are multiples valid strings, return any of them.

Example 1:

1
2
3
Input: n = 4
Output: "pppz"
Explanation: "pppz" is a valid string since the character 'p' occurs three times and the character 'z' occurs once. Note that there are many other valid strings such as "ohhh" and "love".

Example 2:

1
2
3
Input: n = 2
Output: "xy"
Explanation: "xy" is a valid string since the characters 'x' and 'y' occur once. Note that there are many other valid strings such as "ag" and "ur".

返回一个字符串，每个字母都只出现过奇数次。神经病题，要处理奇数和偶数的不同情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    string generateTheString(int n) {
        string res;
        if(n % 2 == 0) {
            for(int i = 0; i < n-1; i ++)
                res += 'a';
            res += 'b';
        }
        if(n % 2 == 1) {
            for(int i = 0; i < n; i ++)
                res += 'a';
        }
        return res;
    }
};

Leetcode1380. Lucky Numbers in a Matrix

Given a m * n matrix of distinct numbers, return all lucky numbers in the matrix in any order. A lucky number is an element of the matrix such that it is the minimum element in its row and maximum in its column.

Example 1:

1
2
3
Input: matrix = [[3,7,8],[9,11,13],[15,16,17]]
Output: [15]
Explanation: 15 is the only lucky number since it is the minimum in its row and the maximum in its column

Example 2:

1
2
3
Input: matrix = [[1,10,4,2],[9,3,8,7],[15,16,17,12]]
Output: [12]
Explanation: 12 is the only lucky number since it is the minimum in its row and the maximum in its column.

找到行最小，列最大的数，做法简单直白，但是有好的做法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> luckyNumbers (vector<vector<int>>& matrix) {
        vector<int> res;
        int row = matrix.size(), col = matrix[0].size();
        for(int i = 0; i < row; i ++) {
            int j = 0, minn = 999999, minn_j = -1;
            for(; j < col; j ++) {
                if(minn > matrix[i][j]) {
                    minn = matrix[i][j];
                    minn_j = j;
                    }
            }
            int ii;
            for(ii = 0; ii < row; ii ++)
                if(matrix[ii][minn_j] > minn)
                    break;
            if(ii == row)
                res.push_back(minn);
        }
        return res;
    }
};

Leetcode1385. Find the Distance Value Between Two Arrays

Given two integer arrays arr1 and arr2, and the integer d, return the distance value between the two arrays. The distance value is defined as the number of elements arr1[i] such that there is not any element arr2[j] where |arr1[i]-arr2[j]| <= d.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Input: arr1 = [4,5,8], arr2 = [10,9,1,8], d = 2
Output: 2
Explanation: 
For arr1[0]=4 we have: 
|4-10|=6 > d=2 
|4-9|=5 > d=2 
|4-1|=3 > d=2 
|4-8|=4 > d=2 
For arr1[1]=5 we have: 
|5-10|=5 > d=2 
|5-9|=4 > d=2 
|5-1|=4 > d=2 
|5-8|=3 > d=2
For arr1[2]=8 we have:
|8-10|=2 <= d=2
|8-9|=1 <= d=2
|8-1|=7 > d=2
|8-8|=0 <= d=2

计算一行中没有差的绝对值大于d的行数。「距离值」 定义为符合此描述的元素数目：对于元素 arr1[i] ，不存在任何元素 arr2[j] 满足 |arr1[i]-arr2[j]| <= d 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findTheDistanceValue(vector<int>& arr1, vector<int>& arr2, int d) {
        int res = 0;
        for(int i = 0; i < arr1.size(); i ++) {
            int j;
            for(j = 0; j < arr2.size(); j ++) {
                if(abs(arr1[i] - arr2[j]) <= d)
                    break;
            }
            if(j == arr2.size())
                res ++;
        }
        return res;
    }
};

Leetcode1389. Create Target Array in the Given Order

Given two arrays of integers nums and index. Your task is to create target array under the following rules:

  • Initially target array is empty.
  • From left to right read nums[i] and index[i], insert at index index[i] the value nums[i] in target array.
  • Repeat the previous step until there are no elements to read in nums and index.
  • Return the target array.

It is guaranteed that the insertion operations will be valid.

Example 1:

1
2
3
4
5
6
7
8
9
Input: nums = [0,1,2,3,4], index = [0,1,2,2,1]
Output: [0,4,1,3,2]
Explanation:
nums       index     target
0            0        [0]
1            1        [0,1]
2            2        [0,1,2]
3            2        [0,1,3,2]
4            1        [0,4,1,3,2]

目标数组 target 最初为空。按从左到右的顺序依次读取 nums[i] 和 index[i]，在 target 数组中的下标 index[i] 处插入值 nums[i] 。重复上一步，直到在 nums 和 index 中都没有要读取的元素。

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    vector<int> createTargetArray(vector<int>& nums, vector<int>& index) {
        vector<int> res;
        for(int i = 0; i < nums.size(); i ++) {
            res.insert(res.begin()+index[i], nums[i]);
        }
        return res;
    }
};

没用insert函数也行，但是效率好低

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:

    void move(vector<int>& nums, int i) {
        int ii;
        for(ii = i + 1; ii < nums.size() && nums[ii] != -1; ii ++);
        for(int k = ii; k > i; k --) {
            nums[k] = nums[k-1];
        }
    }
    vector<int> createTargetArray(vector<int>& nums, vector<int>& index) {
        vector<int> res(nums.size(), -1);
        for(int i = 0; i < nums.size(); i ++) {
            if(res[index[i]] == -1)
                res[index[i]] = nums[i];
            else {
                move(res, index[i]);
                res[index[i]] = nums[i];
            }
        }
        return res;
    }
};

Leetcode1394. Find Lucky Integer in an Array

Given an array of integers arr, a lucky integer is an integer which has a frequency in the array equal to its value. Return a lucky integer in the array. If there are multiple lucky integers return the largest of them. If there is no lucky integer return -1.

Example 1:

1
2
3
Input: arr = [2,2,3,4]
Output: 2
Explanation: The only lucky number in the array is 2 because frequency[2] == 2.

Example 2:

1
2
3
Input: arr = [1,2,2,3,3,3]
Output: 3
Explanation: 1, 2 and 3 are all lucky numbers, return the largest of them.

找一个数量是它自身的元素，如果有多个，则返回最大的那个，如果没有就返回-1。别忘了排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int findLucky(vector<int>& arr) {
        sort(arr.begin(), arr.end());
        int prev = arr[0], count = 1, res = -1;
        for(int i = 1; i < arr.size(); i ++) {
            if(prev != arr[i]) {
                if(count == prev)
                    res = prev;
                prev = arr[i];
                count = 1;
            }
            else {
                count ++;
            }
        }
        if(count == prev)
            res = prev;
        return res;
    }
};

Leetcode1399. Count Largest Group

Given an integer n. Each number from 1 to n is grouped according to the sum of its digits. Return how many groups have the largest size.

Example 1:

1
2
3
4
Input: n = 13
Output: 4
Explanation: There are 9 groups in total, they are grouped according sum of its digits of numbers from 1 to 13:
[1,10], [2,11], [3,12], [4,13], [5], [6], [7], [8], [9]. There are 4 groups with largest size.

把数字按照各位和分组，找到个数最多的那些组，输出个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    
    int get(int n) {
        int sum = 0;
        while(n) {
            sum += (n % 10);
            n /= 10;
        }
        return sum;
    }
    
    int countLargestGroup(int n) {
        map<int, int> mp;
        for(int i = 1; i <= n; i ++)
            mp[get(i)] ++;
        int maxx = -1, res = 0;
        for(auto i = mp.begin(); i != mp.end(); i ++) {
            if(maxx < i->second) {
                maxx = i->second;
                res = 1;
            }
            else if(maxx == i->second)
                res ++;
        }
        
        return res;
    }
};

Posted on Edited on

磁盘

磁盘结构：

寻址方式：

每个磁头用来读track的数据，每个track是一个圈，每个盘片有很多个track，不同盘片的同一位置的track组成一个柱面。

编址方式：CHS，属于哪个柱面（cylinder）、属于哪个盘面上（header）、属于哪个部分（sector）。右边是逻辑地址。

既是电子式的设备、又是机械式的设备，它的性能评价由时间决定：seek time + rotational latency + data transfer rate。

seek time是磁头来回移动的时间，如果seek time变短了则IO越快，取决于磁头和块之间的距离。如果要读数据只能等转轴转到这个块，这个时间就是rotational speed。data transfer rate主要分为内部的传输速率（数据从track传到磁盘内部的buffer）和外部的传输速率（从接口到主机）。

数据传输量越大，则数据传输花的时间越多，磁盘访问的效率越高，每次访问数据量越大，才能均摊掉另外两部份的时间。

来的请求越来越多的时候，延迟会更大。如果利用率大于70%上，那么延迟时间就会呈指数增加，这是排队论中说明的。

第一个指标是在容量上要多少盘，第二个指标是要达到一定的性能指标需要提供多少盘。第三个指标则是考虑了所有指标的访问服务时间。需要盘的数量由Dc和Dp两个的最大值决定。

传输速率：数据在里圈和外圈是不一样的，里圈比较小，如果在每英寸放的比特数是相同的，则外圈放更多的数据量，如果放相同的数据量的话，外圈的密度就更小，所以可以在外圈放更多的数据。角速度相同，则外圈的转动速度要考虑。提出zone的概念，外圈有更多的sector。外圈传输的速率比里圈更高。

磁盘固件调度：地址转换。图中200在盘片的背面，一个磁盘两个面。

1到5个盘片相当于1到10个盘面，每个盘面上有不同个数的track，每个柱面cylinder有track，一个track上有不同个数的sector。从一个逻辑地址找到其物理地址。

在每个track中留一个sector，用于把坏的sector映射过来，但是还要防止不连续，所以做一定的调整，不把坏的块直接映射到备用块，而是做一定的映射。

如果在track之间进行访问的话呢，注意不能浪费转，加一个skew偏移，让他在读完一个track之后继续读另一个track，不浪费。

disk cache为硬件做一个缓冲。做预读，预先放在缓冲中；写缓冲。

磁盘调度：磁盘控制器基于磁头当前位置选择完成下一个请求，实现更短的响应时间，更高的吞吐和对所有块更均等的访问延迟。主要有：

  • 先来先服务FCFS
  • 最短寻道时间SSTF：根据离当前磁头位置最近的块选择服务，有的请求会被饿死
  • SCAN：像是电梯，从磁盘的开头开始移动，直到走到最后，移动过程中一直服务请求。为了避免SSTF算法（最短寻道时间算法）来的“饥饿”现象，SCAN要求磁头每轮朝一个固定方向移动来服务访问请求（如果该方向有自请求），当磁头走到尽头后这个时候百寻道方向会发生调转。所以SCAN可以看作规定了磁头移动方向的SSTF算法。
  • C-SCAN：等待时间更可能均衡。一直都是从某个起点开始扫描。加了一个Circle规定的SCAN算法，也就是磁头移动方向始终固定，到尽头后直接返回到另度一端的开始位置，继续沿着这个方向扫描。
  • Look和C-LOOK：对应SCAN和C-SCAN的改进算法。因为SCAN和C-SCAN中每次磁头都要走到磁道尽头，问而实际过程中并不需要要求磁头走到尽头，而是到达该方向的答最后一个请求后即可返回，这样可以避免一些不必要的磁头移动。

SSD

非易失性存储器NVM提供了高速的访问和持久性。下图是不同存储层次。

闪存是电子非易失可重写的介质。闪存最基本的单元是floating gage transistor。通过横着的wordline和竖着的bitline读取，当读取到之后，放进sense amplifiers中，这叫做行选中。page是一行，block是这一块。

这是读的原理图。闪存不可覆盖写，需要擦除操作，读写粒度与擦除粒度不同。而且是有限次擦除的。

闪存中的块分为三种状态：live、dead（这两个是写过的）、free（没写过的）。引出垃圾回收，选择一些块去回收。根据数据的“年龄”和是否有效判断是否需要对其进行移动和垃圾回收。在为数据分配空间时尽量把数据写到写次数比较少的块上。

FTL：FTL简单来说就是系统维护了一个逻辑Block地址（LBA，logical block addresses ）和物理Block地址（PBA, physical block addresses）的对应关系，有了这层映射关系，我们需要修改时就不需要改动原来的物理块，只需要标记原块为废块，同时找一个没用的新物理块对应到原来的逻辑块上就好了。使用更小更快的SRAM来存储这个映射。

page-level FTL：维护页到页的映射关系。可以把任意逻辑页映射到任意的物理页。但是页表很大。

block-level FTL：维护块的映射关系，会更小，因为块会更大，所需要的项更少。逻辑页地址用块地址加偏移来表示。

LBA/PBA的映射本身会对寿命均衡产生正面影响。就如我们SD卡上的FAT文件系统，文件分配表会被经常修改，但由于修改的是逻辑块，我们可以让每次物理块不同而避免经常擦写相同的物理块，这本身就保证不会有物理块被经常擦写。但是有一种情况它没有办法处理，即冷的数据块（cold block），它们被写入后没有更改，就一直占据某些物理块，而这些物理块寿命还很长，而别的热的块却在飞速损耗中。这种情况怎么办呢？我们只有在合适的时机帮它们换个位置了，如何选择这个时机很重要，而且这个搬家动作本身也会损耗寿命本身。这些策略也是各个FTL算法的精华了。

block-base FTL：存放数据的block+存放新数据的block+存映射表的block+保留的block

c图中，如果d-block中的数据都是invalid的，u-block中的数据都是合法刚写入的，那d-block中的数据就要擦除，且变成u-block；而且u-block要变成d-block，这种overhead是最小的。b图中，把d-block的valid块移动到u-block中，d-block中的数据就要擦除，且变成u-block；而且u-block要变成d-block，这种开销是中等的。a图中，d-block和u-block中的valid块位置不一样，要新找一个free block拷贝过去，然后把这两个块变成free的。

main memory

以CPU插座为北的话，靠近CPU插座的一个起连接作用的芯片称为“北桥芯片”。北桥芯片就是主板上离CPU最近的芯片，这主要是考虑到北桥芯片与处理器之间的通信最密切，为了提高通信性能而缩短传输距离。北桥与外存进行通信。从外存中取出来，放到DRAM里。

ALU中只有有限个寄存器，数据需要放到主存中，主存也负责信息的交换。FPGA和GPU都需要memory的参与，让数据更快地参与计算。

南桥芯片（South Bridge）是主板芯片组的重要组成部分，一般位于主板上离CPU插槽较远的下方，PCI的前面，即靠主机箱前的一面，这种布局是考虑到它所连接的I/O总线较多，离处理器远一点有利于布线。

现在有更多的数据密集型的程序，需要更快和更高的带宽，能耗的要求也是重要的考虑，DRAM技术上很难变得更好。很多的数据库都会移动到内存中，放到外存上会延迟很高。图计算有很强的随机性，图越来越大的时候，从外存中随机IO会很慢，大数据处理也放到内存中来。大于40%的功耗放到了DRAM中，隔一段时间就要把DRAM中的数据重写一遍。

几种新的DRAM，3D-stacked DRAM把二维变成三维。

40-35nm的DRAM的制造会变得很困难，因为在刷新和提供足够存储数据的能力上会有问题。

CPU会连接DRAM上很多的channel，channel会连接DIMM，DIMM分成rank，rank中是一个一个的chip，chip中有bank，bank中有row/col。

DRAM逻辑上是一个大二维数组，每一行叫wordline，行列交点叫做cell单元。先使用行解码器找到行号，把数据读取到sense amps中，相当于是row buffer，在使用列解码器找到数据块。

每个地址都是一个行列对，读取一个数据时，在二维矩阵中找：

  • 选中这一行，再放到row buffer中
  • 在row buffer中使用列选择器进行读写，如果第二次读取的跟上一次读取的row相同，则为hit状态。
  • precharge：在DRAM中加电压读取是破坏性的，这一步是从row buffer中恢复之前的数据。

DRAM的chip连接着很多的bank，这些bank共享地址/数据/指令总线，每个chip有自己的数据通路，每次只能读取几个bit。下图中把不同的chip组织起来，能够实现更大的数据通路。

channel是通道，不同通道的数据互不干扰，有不同的内存控制器。下图是一个简单的层次结构图。DIMM之间分时共享。

从CPU的角度看，它提供了两个memory channel，同一个channel可以连接多个DIMM条，正面和反面都是芯片。正面是rank0，背面是rank1，rank的结构层次是就是这样的，通过address把数据读取出来。每个rank的64bit通过每个chip的8bit输出的，每个chip的8bit通过任意一个bank输出，在一个bank中选择row和col：

在每个bank中，并行操作row buffer，实现多个bank并行操作的流水线。

地址映射：把2Gb的memory编址，把31个bit进行划分，以下两种，第二种把col进行分割，有利于并行，第一个bank放64bit，第二个bank放第二个64bit，这样可以并行起来。不同的排布导致了不同的并行性。

DRAM的refresh：电容中的电子会慢慢泄露，控制器会发出请求，每一行在64毫秒之后会被写入到row buffer中并被写回到row中，只要机器是开着的，每一行都要刷新，所以DRAM一直在工作。DRAM不能扩展也是因为这一个原因。在refresh时不能响应相应的请求。有两种refresh的方法：每隔一段时间刷新一个（burst），或者是每隔一段时间把所有的都刷新一下（distribute）。

减少refresh的次数：每次refresh几行，既减少了等待时间，又提高了效率。DRAM容量越大则refresh的时间越长，越影响读写效率。

很多row没有必要每隔一段很短的时间（64ms）就刷新，使用64ms是为了考虑worst case。如果256ms做一次的话，只有小于1000个cell失效，采用适合refersh的频率。

如何控制DRAM的时序：需要controller来控制时序，每一个channel都有一个controller。主要有以下几个功能：

  • 确保正确操作，refresh和计时
  • 在满足DRAM请求的同时要满足一定的时序条件，把请求翻译为DRAM指令序列。
  • 指令调度，优先调度某些请求，提高性能。
  • 管理电源、能耗，选择性的开关DRAM芯片。

DRAM conroller放在CPU的chip中，直接对memory controller进行设置，方便且带宽高。图中，左边是CPU发过来的请求，中间的方框是memory controller，把请求发送到不同的队列中，在进入队列前进行地址翻译，

从memory发过来的请求先缓存在不同的buffer中，然后到DRAM的bank中去，再发送到实体芯片中。

调度算法：

  • FCFS：先来先服务
  • FR-FCFS：first ready指的是如果在buffer中有已经就绪的数据，就先服务，而且不能让先来的等很久。
  • 主要目标是实现最大的row buffer命中率。

调度的策略实际上是给每个请求一个优先级：

  • 请求时间
  • 是否命中row buffer
  • 请求种类（prefetch，read，write），程序在等待读的操作时比store的操作优先级高
  • 已经miss很久的操作优先级肯定高，被很多指令依赖的请求优先级高

row buffer管理策略：

  • 第一步active这个row，读取到row buffer中，第二步读取响应数据，最后再写回到对应row中。下文中的两种策略指的是precharge什么时候做。
  • open row：不做precharge，即不写回，保持读的这个row在row buffer中，这个好处是命中简单，坏处是如果不命中的话需要很麻烦
  • closed row：完全遵循顺序。
  • 如何自适应的选择？



DRAM时序控制：选中row，读取到row buffer中，保持一段时间做IO，再写回。下图是时序控制图：

功耗管理：DRAM提供了不同的功耗管理模式。

Multi-Disk System

多盘系统中最重要的是容错。如果错误已经体现在系统了，找到这个错误再去repair。

  • reliability：持续提供服务，对应MTTF

  • maintainability：服务中断，对应MTTR

  • availability：对外服务的时间占比，对应EA=MTTF/(MTTF+MTTR)

  • MTBF: Mean Time Between Failure

  • MTTR: Mean Time To Recover

  • MTTF: Mean Time To Failure

  • MTBF = MTTR + MTTF


RAID的分类

file system

文件系统：用户直接操作和管理外存上的信息，繁琐复杂，易于出错，可靠性差；多道程序、分时系统的出现要求以方便可靠的方式共享大容量外存储器。

  • program: 转成<File name, offset>
  • file system: 转成<partition, block #>
  • device driver: 转成<disk #, sector #>
  • I/O controller: 转成<cylinder, track, sector>
  • disk media

文件系统的功能:

  • 命名空间：实现按名存取，文件目录的建立、维护、检索
  • 存储管理：存储空间的分配与管理；文件块管理，实现逻辑地址与存储物理地址的映射。
  • 数据保护（灾备）与可靠性

下图是一段程序，将一个文件的内容传到另一个文件中。用create创建一个新的文件。

文件操作：

文件夹操作：

文件是一连串的数据，和文件控制块（inode），存放着描述文件的信息。文件夹是一种特殊的文件，也有inode，但是content是子文件夹的目录项。

两个程序都打开了同一个文件，生成两个file handler，或者只打开一次共享给两个程序用。每个handler有不同的offset给每个打开文件的程序使用。

ext2的inode组成：

目录是特殊文件，它其中的内容是directory entry。目录项要记录父目录、当前目录和子目录。下图是目录树，右图中是inode和entry的结构。用户拿到pathname，从根目录开始查，先找到inode，判断权限，再继续向下查找。

在这个过程中，要注意：

  • 权限检查。access control list。
  • 软链接。两个inode指向同一个文件，万一出现环的话？
  • 挂载点。一个文件名可能是一个挂载文件系统，查找过程需要继续进入新的文件系统进行查找。

读取过程：

文件系统内部

简单的文件系统：

进行文件写的时候的时序操作图

目录树就是一个树形的结构，对大部分文件系统适用。通过filename找到inode，如果一个目录下有三个文件的话，如图所示:

一个系统里可能有多个文件系统，需要挂载到系统上。如何找到根目录：找到特定的地点写入根目录的位置。一个目录中有成千上万的目录时，这时缓存一部分目录，用树的结构，分为子目录。下图是硬链接：

下图是软链接，修改时要再跳一步去修改。

文件内存分配策略：

  • 连续分配：保证每个文件都是连续的。容易形成空洞。

    • 改进：部分连续的分配

  • 链式分配：分配的时候简单，但是读取的时候难，通过循环遍历

    • 一个变种是FAT：不是把链表存在块中，而是把所有的链接存在表中，索引表放到内存中。

  • 索引分配：用一个单独的块来索引空间，在分配空间上比较灵活，读取也方便。

可以把索引分配方式和链式分配结合：每个数据块的分配采用索引方式，这样会生成一些索引块，把索引块用链式连接起来。可以支持更大的文件。下图中我们有索引块、二级索引块，等。

缓存：把相关的数据放到一起，需要比较大的传输IO，传输较大的块，均摊开销。

Fast File System：把一个数据组放到一个柱面上，不需要做seek的操作，直接在这个柱面读取。分配的时候尽可能连续分配；实现预取。重新分配空间，把不连续的文件变为连续；预先分配，提前留出空间。

一致性的存在：如果存放的指针没有保持一致性，文件的完整性就会损失。如果两个文件引用了同一个文件但是ref_count为1，会出错。出现一致性问题的原因有：

  • 并发修改。两个进程并发访问文件。
  • 盘坏掉了。
  • 偶然出错。数据传输过程中的错误
  • 系统崩溃。系统突然掉电，易失性数据丢失。

real multi-write atomicity：

  • write-ahead logging：如果直接往正常的数据写的话，可能会终端，先把A’，B’，C’写到log中，如果没问题了再真正写。

  • shadow paging：先把数据写到新的位置，再把指针指过来。只要保证更新指针是原子性操作就行。

Posted on Edited on

一些你可能正感到迷惑的问题

软件是如何访问硬件的

硬件在输入输出上大体分为串行和并行，相应的接口也就是串行接口和并行接口。CPU通过串行接口与串行设备数据传输。并行设备的访问类似，只不过
是通过并行接口进行的。访问外部硬件有两个方式：

  • 将某个外设的内存映射到一定范围的地址空间中，CPU通过地址总线访问该内存区域时会落到外设的内存中，这种映射让CPU 访问外设的内存就如同访问主板上的物理内存一样。
  • 外设是通过IO接口与CPU通信的，CPU访问外设，就是访问IO接口，由IO接口将信息传递给另一端的外设。

应用程序操作系统是如何配合到一起的

编译器提供了一套库函数，库函数中又有封装的系统调用，这样的代码集合称之为运行库。C 语言的运行库称为C 运行库，就是所谓的CRT（C Runtime Library）。

用户态与内核态是对CPU 来讲的，是指CPU 运行在用户态（特权3 级）还是内核态（特权0 级）。用户进程陷入内核态是指：由于内部或外部中断发生，当前进程被暂时终止执行，其上下文被内核的中断程序保存起来后，开始执行一段内核的代码，所以“用户态与内核态”是对CPU 来说的。

为什么称为“陷入”内核

应用程序处于特权级3，操作系统内核处于特权级0。当用户程序欲访问系统资源时（无论是硬件，还是内核数据结构），它需要进行系统调用。这样CPU 便进入了内核态，也称管态。

内存访问为什么要分段

内存是随机读写设备，即访问其内部任何一处，不需要从头开始找，只要直接给出其地址便可。CPU 采用“段基址+段内偏移地址”的方式来访问任意内存。这
样的好处是程序可以重定位了，尽管程序指令中给的是绝对物理地址，但终究可以同时运行多个程序了。重定位就是将程序中指令的地址改写成另外一个地址，但该地址处的内容还是原地址处的内容。

只要程序分了段，把整个段平移到任何位置后，段内的地址相对于段基址是不变的，无论段基址是多少，只要给出段内偏移地址，CPU 就能访问到正确的指令。于是加载用户程序时，只要将整个段的内容复制到新的位置，再将段基址寄存器中的地址改成该地址，程序便可准确无误地运行，因为程序中用的是段内偏移地址，相对于新的段基址，该偏移地址处的内存内容还是一样的。

代码中为什么分为代码段、数据段？

分段只是为了使程序更加优美。如果是在平坦模型下编程，操作系统将整个4GB 内存都放在同一个段中，我们就不需要来回切换段寄存器所指向的段。对于代码中是否要分段，这取决于操作系统是否在平坦模型下。

指令间不存在空隙，下一条指令的地址是按照前面指令的尺寸大小排下来的，这就是Intel 处理器的程序计数器cs：eip能够自动获得下一条指令的原理，即将当前eip 中的地址加上当前指令机器码的大小便是内存中下一条指令的起始地址。为了让程序内指令接连不断地执行，要把指令全部排在一起，形成一片连续的指令区域，这就是代码段。把数据连续地并排在一起存储形成的段落，就称为数据段。

只要指令逻辑上是连续的就可以，没必要一定得是物理上连续。所以，明确一点，即使数据和代码在物理上混在一起，程序也是可以运行的，这并不意味
着指令被数据“断开”了。只要程序中有指令能够跨过这些数据就行啦，最典型的就是用jmp 跳过数据区。

在保护模式下，有这样一个数据结构，它叫全局描述符表（Global Descriptor Table，GDT），这个表中的每一项称为段描述符。编译器负责挑选出数据具备的属性，从而根据属性将程序片段分类，比如，划分出了只读属性的代码段和可写属性的数据段。操作系统通过设置GDT 全局描述符表来构建段描述符，在段描述符中指定段的位置、大小及属性（包括S 字段和TYPE 字段）。CPU 中的段寄存器提前被操作系统赋予相应的选择子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
section my_code vstart=0
;通过远跳转的方式给代码段寄存器CS 赋值0x90
jmp 0x90:start
start: ;标号start 只是为了jmp 跳到下一条指令
;初始化数据段寄存器DS
mov ax,section.my_data.start
add ax,0x900 ;加0x900 是因为本程序会被mbr 加载到内存0x900 处
shr ax,4 ;提前右移4 位,因为段基址会被CPU 段部件左移4 位
mov ds,ax

;初始化栈段寄存器SS
mov ax,section.my_stack.start
add ax,0x900 ;加0x900 是因为本程序会被mbr 加载到内存0x900 处
shr ax,4 ;提前右移4 位,因为段基址会被CPU 段部件左移4 位
mov ss,ax
mov sp,stack_top ;初始化栈指针

;此时CS､DS､SS 段寄存器已经初始化完成,下面开始正式工作
push word [var2] ;变量名var2 编译后变成0x4
jmp $

;自定义的数据段
section my_data align=16 vstart=0
var1 dd 0x1
var2 dd 0x6

;自定义的栈段
section my_stack align=16 vstart=0
times 128 db 0
stack_top: ;此处用于栈顶,标号作用域是当前section,
;以当前section 的vstart 为基数

代码是实模式下运行的程序，其中自定义了三个段，代码段取名为my_code，数据段取名为my_data，栈段取名为my_stack。用“jmp 0x90：0”初始化了程序计数器CS 和IP。这样段寄存器CS 就是程序中咱们自己划分的代码段了。各section 中的定义都有align=16 和vstart=0，这是用来指定各section 按16 位对齐的，第 6～10 行是初始化数据段寄存器DS，是用程序中自已划分的段my_data 的地址来初始化的。第 12～17 行是初始化栈段寄存器，原理和数据段差不多，唯一区别是栈段初始化多了个针指针SP，为它初始化的值stack_top 是最后一行，因为栈指针在使用过程中指向的地址越来越低，所以初始化时一
定得是栈段的最高地址。

物理地址、逻辑地址、有效地址、线性地址、虚拟地址的区别

物理地址就是物理内存真正的地址，相当于内存中每个存储单元的门牌号，具有唯一性。在实模式下，“段基址+段内偏移地址”经过段部件的处理，直接输出的就是物理地址，CPU 可以直接用此地址访问内存。

而在保护模式下，“段基址+段内偏移地址”称为线性地址，不过，此时的段基址已经不再是真正的地址了，而是一个称为选择子的东西。它本质是个索引，类似于数组下标，通过这个索引便能在GDT 中找到相应的段描述符，在该描述符中记录了该段的起始、大小等信息，这样便得到了段基址。

若没有开启地址分页功能，此线性地址就被当作物理地址来用，可直接访问内存。若开启了分页功能，此线性地址又多了一个名字，就是虚拟地址（虚拟地址、线性地址在分页机制下都是一回事）。虚拟地址要经过CPU 页部件转换成具体的物理地址，这样CPU 才能将其送上地址总线去访问内存。

无论在实模式或是保护模式下，段内偏移地址又称为有效地址，也称为逻辑地址。线性地址或称为虚拟地址，这都不是真实的内存地址。它们都用来描述程序或任务的地址空间。

什么是段重叠

CPU 的内存寻址方式是：给我一个段基址，再给我一个相对于该段起始位置的偏移地址，我就能访问到相应内存。它并不要求一个内存地址只隶属于某一个段。用段A 去访问，其偏移为5，用段B 去访问，其偏移量为3。这样一来，用段B 和段A 在地址0xC02 之后，一直到段B偏移地址为0xfffe 的部分，像是重叠在一起了，这就是段重叠了。

什么是平坦模型

所以说平坦模型指的就是一个段。段的大小可以是地址总线能够到达的范围。

cs、ds 这类sreg 段寄存器，位宽是多少

CPU 内部的段寄存器（Segment reg）如下：

  1. CS—代码段寄存器（Code Segment Register），其值为代码段的段基值。
  2. DS—数据段寄存器（Data Segment Register），其值为数据段的段基值。
  3. ES—附加段寄存器（Extra Segment Register），其值为附加数据段的段基值，称为“附加”是因为此段寄存器用途不像其他sreg 那样固定，可以额外做他用。
  4. FS—附加段寄存器（Extra Segment Register），其值为附加数据段的段基值，同上，用途不固定，使用上灵活机动。
  5. GS—附加段寄存器（Extra Segment Register），其值为附加数据段的段基值。
  6. SS—堆栈段寄存器（Stack Segment Register），其值为堆栈段的段值。

在实模式下，CS、DS、ES、SS 中的值为段基址，是具体的物理地址，内存单元的逻辑地址仍为“段基值：段内偏移量”的形式。在保护模式下，装入段寄存器的不再是段地址，而是“段选择子”（Selector），当然，选择子也是数值，其依然为16 位宽度。

什么是工程，什么是协议

软件中的工程是指开发一套软件所需要的全部文件，包括配置环境。

协议是一种大家共同遵守的规约，主要用来实现通信、共享、协作，给大家统一一种接口、一组数据调用或者分析的约定。

局部变量和函数参数为什么要放在栈中

局部变量只是自己在用，放在数据段中纯属浪费空间，没有必要，故将其放在自己的栈中，随时可以清理，真正体现了局部的意义。

堆是程序运行过程中用于动态内存分配的内存空间，是操作系统为每个用户进程规划的，属于软件范畴。栈是处理器运行必备的内存空间，是硬件必需的，但又是由软件（操作系统）提供的。

栈从高地址往低地址发展，堆是从低地址往高地址发展，堆和栈早晚会碰头，它们各自的大小取决于实际的使用情况，界限并不明朗。

编译型程序与解释型程序的区别

解释型语言，也称为脚本语言，本身是文本文件，是某个应用程序的输入，这个应用程序是脚本解释器。由于只是文本，这些脚本中的代码在脚本解释器看来和字符串无异。也就是说，脚本中的代码从来没真正上过CPU 去执行，CPU 的cs：ip 寄存器从来没指向过它们，在CPU 眼里只看得到脚本解释器

本质上是脚本解释器在时时分析这个脚本，动态根据关键字和语法来做出相应的行为。因此脚本中若出现错误，先前正确的部分也会被正常执行，这和编译型程序有很大区别。

编译型语言编译出来的程序，运行时本身就是一个进程。它是由操作系统直接调用的。也就是由操作系统加载到内存后，操作系统将CS：IP 寄存器指向这个程序的入口，使它直接上CPU 运行。

什么是大端字节序、小端字节序

  1. 小端：因为低位在低字节，强制转换数据型时不需要再调整字节了。
  2. 大端：有符号数，其字节最高位不仅表示数值本身，还起到了符号的作用。符号位固定为第一字节，也就是最高位占据最低地址，符号直接可以取出来，容易判断正负。

简要说明一下小端的优势。因为在做强制数据类型转换时，如果转换是由低精度转向高精度，这数值本身没什么变化，如short 是2 字节，将其转换为4 字节的int 类型，无非是由0x1234 变成了0x00001234，数值上是不变的，只是存储形式上变了。如果转换是高精度转向低精度，也就是多个字节的数值要减少一
些存储字节，这必然是要丢弃一部分数值。编译器的转换原则是强制转换到低精度类型，丢弃数值的高字节位，只保留数值的低字节。

对于大端的优势，就硬件而言，就是符号位的判断变得方便了。最高位在最低地址，也就是直接就可以取到了，不用再跨越几个字节，减少了时钟周期。

BIOS 中断、DOS 中断、Linux 中断的区别

BIOS 和DOS 都是存在于实模式下的程序，由它们建立的中断调用都是建立在中断向量表（Interrupt Vector Table，IVT）中的。它们都是通过软中断指令int 中断号来调用的。

中断向量表中的每个中断向量大小是4 字节。这4 字节描述了一个中断处理例程（程序）的段基址和段内偏移地址。BIOS 中断调用的主要功能是提供了硬件访问的方法，该方法使对硬件的操作变得简单易行。BIOS 中断程序处理是用来操作硬件的，故该处理程序中一定到处都是in/out 指令。

DOS 是运行在实模式下的，故其建立的中断调用也建立在中断向量表中，只不过其中断向量号和BIOS的不能冲突。

而 Linux 内核是在进入保护模式后才建立中断例程的，不过在保护模式下，中断向量表已经不存在了，取而代之的是中断描述符表（Interrupt Descriptor Table，IDT）。所以在Linux 下执行的中断调用，访问的中断例程是在中断描述符表中，已不在中断向量表里了。Linux 的系统调用和DOS 中断调用类似，不过Linux 是通过int 0x80 指令进入一个中断程序后再根据eax 寄存器的值来调用不同的子功能函数的。

Section 和Segment 的区别

在汇编源码中，通常用语法关键字 section 或segment 来表示一段区域，它们是编译器提供的伪指令，作用是相同的，都是在程序中“逻辑地”规划一段区域，此区域便是节。操作系统在加载程序时，不需要对逐个节进行加载，只要给出相同权限的节的集合就行了，这样操作系统就能为它们分配不同的段选择子，从而指向不同段描述符，实现不同的访问权限了。

section 称为节，是指在汇编源码中经由关键字section 或segment 修饰、逻辑划分的指令或数据区域，汇编器会将这两个关键字修饰的区域在目标文件中编译成节，也就是说“节”最初诞生于目标文件中。

segment 称为段，是链接器根据目标文件中属性相同的多个section 合并后的section 集合，这个集合称为segment，也就是段，链接器把目标文件链接成可执行文件，因此段最终诞生于可执行文件中。我们平时所说的可执行程序内存空间中的代码段和数据段就是指的segment。

Program Headers 部分，此处一共有两个段，第一个段是我们的代码段，通过其Flg 值为RE 便可推断，只读（Readonly）可执行（Execute）。第二个段便是我们的数据段，但此数据段中只包含.bss 节（section），它用于存储全局未初始化数据故其Flg 必然可读写，其属性为RW。

操作系统是如何识别文件系统的

各分区都有超级块，一般位于本分区的第2 个扇区，比如若各分区的扇区以0 开始索引，其第1 个扇区便是超级块的起始扇区。超级块里面记录了此分区的信息，其中就有文件系统的魔数，一种文件系统对应一个魔数。

如何控制 CPU 的下一条指令

我们常说的用于存放下一条指令地址的寄存器称为程序计数器PC。在 x86 体系结构的CPU 中程序计数器PC 并不是单一的某种寄存器，它是一种寄存器组合，指的段寄存器CS 和指令寄存器IP。CS 和IP 是CPU 待执行的下一条指令的段基址和段内偏移地址，不能直接用mov 指令去改变它们。有专门改变执行流的指令，如jmp、call、int、ret，这些指令可以同时修改cs 和ip，它们在硬件级别上实现了原子操作。

库函数是用户进程与内核的桥梁

例如对printf的声明：

1
extern int printf (__const char *__restrict __format,...);

头文件被包含进来后，其内容也是原样被展开到include 所在的位置，就是把整个头文件中的内容挪了过来。头文件中一般仅仅有函数声明，这个声明告诉编译器至少两件事。

  1. 函数返回值类型、参数类型及个数，用来确定分配的栈空间。
  2. 该函数是外部函数，定义在其他文件，现在无法为其分配地址，需要在链接阶段将该函数体所在的目标文件一同链接时再安排地址。

如果预处理后，主调函数所在的文件中找不到所调用函数的函数体，一定要在链接阶段把该函数体所在的目标文件链接进来。编译器提供的C 运行库中已经为我们准备好了这些标准函数的函数体所在的目标文件，在链接时默默帮我们链接上了。这些目标文件都是待重定位文件，重定位文件意思是文件中的函数是没有地址的，用file 命令查看它们时会显示relocatable，它们中的地址是在与用户程序的目标文件链接成一个可执行文件时由链接器统一分配的。

MBR、EBR、DBR 和OBR 各是什么

MBR 是主引导记录，Master 或Main Boot Record，它存在于整个硬盘最开始的那个扇区，即0盘0道1扇区，这个扇区便称为MBR 引导扇区。在 MBR 引导扇区中存储引导程序，为的是从BIOS 手中接过系统的控制权，。BIOS 知道MBR 在0 盘0 道1 扇区，这是约定好的，因此它会将0 盘0 道1 扇区中的MBR 引
导程序加载到物理地址0x7c00，然后跳过去执行，这样BIOS 就把处理器使用权移交给MBR 了。在 MBR 引导扇区中的内容是：

  1. 446 字节的引导程序及参数；
  2. 64 字节的分区表；
  3. 2 字节结束标记0x55 和0xaa。

MBR 的作用相当于下一棒的引导程序总入口，BIOS 把控制权交给MBR 就行了，由MBR 从众多可能的接力选手中挑出合适的人选并交出系统控制权，这个过程就是由“主引导程序”去找“次引导程序”。MBR 引导程序的任务就是把控制权交给操作系统加载器，由该加载器完成操作系统的自举，最终使控制权交付给操作系统内核。

为了让 MBR 知道哪里有操作系统，我们在分区时，如果想在某个分区中安装操作系统，就用分区工具将该分区设置为活动分区，设置活动分区的本质就是把分区表中该分区对应的分区表项中的活动标记为0x80。

“控制权交接”是处理器从“上一棒选手”跳到“下一棒选手”来完成的，内核加载器的入口地址是这里所说的“下一棒选手”，为了MBR 方便找到活动分区上的内核加载器，内核加载器的入口地址也必须在固定的位置，这个位置就是各分区最开始的扇区，这也是约定好的。这个“各分区起始的扇区”中存放的是操作系统
引导程序—内核加载器，因此该扇区称为操作系统引导扇区，其中的引导程序（内核加载器）称为操作系统引导记录OBR，即OS Boot Record，此扇区也称为OBR 引导扇区。在OBR 扇区的前3 个字节存放了跳转指令，这同样是约定，因此MBR 找到活动分区后，就大胆主动跳到活动分区OBR 引导扇区的起始处，该起始处的跳转指令马上将处理器带入操作系统引导程序，从此MBR 完成了交接工作，以后便是内核的天下了。

DBR 是DOS Boot Record，也就是DOS 操作系统的引导记录（程序）。在 DOS 时代只有4 个分区，不存在扩展分区，这4 个分区都相当于主分区，所以各主分区最开始的扇区称为DBR 引导扇区。

这里提到了扩展分区就不得不提到EBR。当初为了解决分区数量限制的问题才有了扩展分区，EBR是扩展分区中为了兼容MBR 才提出的概念，主要是兼容MBR 中的分区表。为扩展分区存储分区表的扇区称为EBR，即Expand Boot Record，

MBR 和EBR 是分区工具创建维护的，不属于操作系统管理的范围，因此操作系统不可以往里面写东西。OBR 是各分区（主分区或逻辑分区）最
开始的扇区，因此属于操作系统管理。DBR、OBR、MBR、EBR 都包含引导程序，因此它们都称为引导扇区，只要该扇区中存在可执行的程序，该扇区就是可引导扇区。若该扇区位于整个硬盘最开始的扇区，并且以0x55 和0xaa 结束，BIOS就认为该扇区中存在MBR，该扇区就是MBR 引导扇区。

部署工作环境

我们需要哪些编译器

NASM 是一个为可移植性与模块化而设计的一个80x86的汇编器。它支持相当多的目标文件格式，包括’Linux’和’NetBSD/FreeBSD’，’a.out’，’ELF’，’COFF’，微软16位的’OBJ’和’Win32’。它还可以输出纯二进制文件。它的语法设计得相当的简洁易懂，和Intel语法相似但更简单。它支持’Pentium’，’P6’，’MMX’，’3DNow!’，’SSE’和’SSE2’指令集。

编写MBR 主引导记录，让我们开始掌权

计算机的启动过程

CPU 的硬件电路被设计成只能运行处于内存中的程序。因此，OS需要被载入内存中，大概上分两部分。

  1. 程序被加载器（软件或硬件）加载到内存某个区域。
  2. CPU 的cs：ip 寄存器被指向这个程序的起始地址。

操作系统在加载程序时，是需要某个加载器来将用户程序存储到内存中的。其实“加载器”本质上它就是一堆函数组成的模块。

软件接力第一棒，BIOS

BIOS全称叫Base Input & Output System，即基本输入输出系统。

实模式下的1MB内存布局

Intel 8086有20条地址线，故其可以访问1MB的内存空间，即2的20次方=1048576=1MB，地址范围是0x00000到0xFFFFF。下表是实模式下1MB内存布局。

地址0～0x9FFFF处是DRAM（Dynamic Random Access Memory），即动态随机访问内存，我们所装的物理内存就是DRAM，如DDR、DDR2 等。动态指此种存储介质需要定期地刷新，它的空间范围是640KB，这片地址对应到了DRAM，也就是插在主板上的内存条。

地址总线宽度决定了可以访问的内存空间大小，如16位机的地址总线为20位，其地址范围是1MB，但是并不是只有内存条需要通过地址总线访问，需要在地址总线上提前预留出来一些地址空间给其他外设用，留够了以后，地址总线上其余的可用地址再指向DRAM，也就是指插在主板上的内存条，所以地址总线的长度与DRAM的大小不同。

顶部的0xF0000～0xFFFFF，这64KB的内存是ROM，这里面存的就是BIOS的代码。BIOS还建立了中断向量表，这样就可以通过int 中断号来实现相关的硬件调用，当然BIOS建立的这些功能就是对硬件的IO操作，也就是输入输出，加上一些重要的、保证计算机能运行的那些硬件的基本IO操作，就行了。这就是BIOS称为基本输入输出系统的原因。

BIOS被写进ROM。ROM也是块内存，内存就需要被访问。此ROM被映射在低端1MB内存的顶部，即地址0xF0000～0xFFFFF处。**只要访问此处的地址便是访问了BIOS，这个映射是由硬件完成的。**BIOS本身是个程序，程序要执行，就要有个入口地址才行，此入口地址便是0xFFFF0。

CPU访问内存是用段地址+偏移地址来实现的，由于在实模式之下，段地址需要乘以16后才能与偏移地址相加，求出的和便是物理地址，CPU便拿此地址直接用了。在接电的一瞬间，CPU的cs:ip寄存器被强制初始化为0xF000:0xFFF0。由于开机的时候处于实模式，在实模式下的段基址要乘以16，也就是左移4位，于是0xF000:0xFFF0的等效地址将是0xFFFF0，此地址便是BIOS的入口地址。物理地址0xFFFF0处应该是指令，否则会出错，里面有条指令jmp far f000:e05b，这是条跳转指令，也就是证明了在内存物理地址0xFFFF0处的内容是一条跳转指令。

BIOS最后一项工作校验启动盘中位于0盘0道1扇区的内容。0盘0道1扇区本质上就相当于0盘0道0扇区。CHS方法（即柱面Cylinder磁头Header扇区Sector，另外一种是LBA 方式，暂不关心），0盘说的是0磁头，因为一张盘是有上下两个盘面的，一个盘面上对应一个磁头，所以用磁头Header来表示盘面。0道是指0柱面，柱面Cylinder指的是所有盘面上、编号相同的磁道的集合。在CHS方式中扇区的编号是从1开始的，它就是磁盘上最开始的那个扇区。如果此扇区末尾的两个字节分别是魔数0x55和0xaa，BIOS便认为此扇区中确实存在可执行的程序，便加载到物理地址0x7c00，随后跳转到此地址，继续执行。

8086CPU要求物理地址0x0～0x3FF存放中断向量表，所以此处不能动了；按 DOS 1.0 要求的最小内存32KB来说，MBR希望给人家尽可能多的预留空间，所以MBR只能放在32KB的末尾；MBR本身也是程序，是程序就要用到栈，估计1KB内存够用了。结合以上三点，选择32KB中的最后1KB最为合适，32KB换算为十六进制为0x8000，减去1KB(0x400)的话，等于0x7c00。这就是倍受质疑的0x7c00 的由来。

让 MBR 先飞一会儿

$和$$是编译器NASM 预留的关键字，用来表示当前行和本section的地址，起到了标号的作用。汇编语言中的标号是程序员“显式地”写在明处的，如：

1
2
code_start：
mov ax， 0

code_start这个标号被nasm认为是一个地址，此地址便是mov ax, 0这条指令所在的地址，即其指令机器码存放的内存位置是code_start。code_start只是个标记，CPU并不认识，nasm会用为其安排的地址来替换标号code_start，到了CPU手中，已经被替换为有意义的数字形式的地址了。

$属于“隐式地”藏在本行代码前的标号，也就是编译器给当前行安排的地址，看不到却又无处不在，$在每行都有。如果上面的例子改为：

1
2
code_start：
jmp $

这就和jmp code_start是等效的。$和code_start是同一个值。

$$指代本section的起始地址，此地址同样是编译器给安排的。默认情况下，它们的值是相对于本文件开头的偏移量。如果该section用了vstart=xxxx修饰，$$的值则是此section的虚拟起始地址xxxx。$的值是以xxxx为起始地址的顺延。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
;主引导程序
;------------------------------------------------------------
SECTION MBR vstart=0x7c00
mov ax,cs
mov ds,ax
mov es,ax
mov ss,ax
mov fs,ax
mov sp,0x7c00

; 清屏利用0x06号功能,上卷全部行,则可清屏｡
; -----------------------------------------------------------
;INT 0x10 功能号:0x06 功能描述:上卷窗口
;------------------------------------------------------
;输入:
;AH 功能号= 0x06
;AL = 上卷的行数(如果为0,表示全部)
;BH = 上卷行属性
;(CL,CH) = 窗口左上角的(X,Y)位置
;(DL,DH) = 窗口右下角的(X,Y)位置
;无返回值:
mov ax, 0x600
mov bx, 0x700
mov cx, 0 ; 左上角: (0, 0)
mov dx, 0x184f ; 右下角: (80,25),
; VGA 文本模式中,一行只能容纳80个字符,共25行｡
; 下标从0 开始,所以0x18=24,0x4f=79
int 0x10 ; int 0x10

;;;;;;;;; 下面这三行代码获取光标位置 ;;;;;;;;;
;.get_cursor 获取当前光标位置,在光标位置处打印字符｡
mov ah, 3 ; 输入: 3 号子功能是获取光标位置,需要存入ah 寄存器
mov bh, 0 ; bh 寄存器存储的是待获取光标的页号

int 0x10 ; 输出: ch=光标开始行,cl=光标结束行
; dh=光标所在行号,dl=光标所在列号

;;;;;;;;; 获取光标位置结束 ;;;;;;;;;;;;;;;;

;;;;;;;;; 打印字符串 ;;;;;;;;;;;
;还是用10h 中断,不过这次调用13 号子功能打印字符串
mov ax, message
mov bp, ax ; es:bp 为串首地址,es 此时同cs 一致,
; 开头时已经为sreg 初始化

; 光标位置要用到dx 寄存器中内容,cx 中的光标位置可忽略
mov cx, 5 ; cx 为串长度,不包括结束符0 的字符个数
mov ax, 0x1301 ;子功能号13 显示字符及属性,要存入ah 寄存器,
; al 设置写字符方式 ah=01: 显示字符串,光标跟随移动
mov bx, 0x2 ; bh 存储要显示的页号,此处是第0 页,
; bl 中是字符属性,属性黑底绿字(bl = 02h)
int 0x10 ; 执行BIOS 0x10 号中断
;;;;;;;;; 打字字符串结束 ;;;;;;;;;;;;;;;

jmp $ ; 使程序悬停在此

message db "1 MBR"
times 510-($-$$) db 0
db 0x55,0xaa

代码功能为：在屏幕上打印字符串“1 MBR”，背景色为黑色，前景色为绿色。

  • 第3行的vstart=0x7c00表示本程序在编译时，告诉编译器，把我的起始地址编译为0x7c00。
  • 第4～8行是用cs寄存器的值去初始化其他寄存器。由于BIOS是通过jmp 0:0x7c00跳转到MBR的，故cs此时为0。对于ds、es、fs、gs这类sreg，CPU中不能直接给它们赋值，没有从立即数到段寄存器的电路实现，只有通过其他寄存器来中转，这里我们用的是通用寄存器ax来中转。
  • 第9行是初始化栈指针，在CPU上运行的程序得遵从CPU的规则，mbr也是程序，是程序就要用到栈。目前0x7c00以下暂时是安全的区域，就把它当作栈来用。
  • 第11～28行是清屏。这里也演示了BIOS中断int 0x10的用法。
  • 第30～35行是做打印前的工作，先获取光标位置，目的是避免打印字符混乱，覆盖别人的输出。这里还用到了页的概念，往bh寄存器中写入了0，这是告诉BIOS例程，我要获取第0页当前的光标。
  • 第38～52行是往光标处打印字符。说一下第48行的mov ax, 0x1301，13对应的是ah寄存器，这是调用0x13号子功能。01对应的是al寄存器，表示的是写字符方式，其低2位才有意义，各位功能描述如下：
    • al=0，显示字符串，并且光标返回起始位置。
    • al=1，显示字符串，并且光标跟随到新位置。
    • al=2，显示字符串及其属性，并且光标返回起始位置。
    • al=3，显示字符串及其属性，光标跟随到新位置。
  • 第55行执行了个死循环，$是本行指令的地址，这属于伪指令，是汇编器在编译期间分配的地址。在最终编译出来的程序中，$会被替换为指令实际所在行的地址。jmp是个近跳转，$是jmp自己的地址，于是跳到自己所在的地址再执行自己，又是跳到自己所在的地址再继续执行跳转
  • 第57行是定义打印的字符串。
  • 第58行的$$是指本section的起始地址，上面说过了$是本行所在的地址，故$-$$是本行到本section的偏移量。由于MBR的最后两个字节是固定的内容，分别是0x55和0xaa，要预留出这2个字节，故本扇区内前512-2=510字节要填满，第50行的times 510-($-$$) db 0是在用0将本扇区剩余空间填充。

完善MBR

地址、section、vstart 浅尝辄止

本质上，程序中各种数据结构的访问，就是通过该数据结构的起始地址＋该数据结构所占内存的大小来实现的。数据的地址，其实就是该数据相对整个程序开头的距离，即偏移量。

  • 第1行的mov指令，$$表示的是所在的section的起始地址，由于这6 行代码中没有定义section，故nasm 默认把全体文件当成一个大的section，全体文件自然偏移地址为0，所以在反汇编代码那列中，起始地址$$被置换为0。
  • 第2行代码是真指令，不牵涉到符号转换，所以反汇编后的代码同源码一致。
  • 第3行引用了var变量的值，[]符号是取所在地址处的内容。在相应的反汇编代码中，相应的第三行中var这个符号地址被编译器替换为0xd。结合地址列查看一下内容列，地址为0xd 的内容为99，这正是var 的值。
  • 第4行源码为label: mov ax, $，label是个标号，代表指令mov ax, $所在地址。$是个隐式的标号，表示当前行地址。
  • 第5行的jmp label编译后被替换为jmp short 0x8，这是短跳转指令，地址为8处的内容是第4行的mov ax, $，同样吻合。
  • 第 6 行的便是数据定义了，定义了双字节变量var，其值为99。在内容处的第6行可知，内容为99，与源码定义吻合。

“地址”列中的数字和“内容”列中的内容有这样一种关系：地址等于上一个地址+上一个地址处的内容的长度。例如地址列第二行的3等于“上一个地址0”+“上一个地址 0 处的内容：B80000 的长度3”，以此类推。编译器给程序中各符号（变量名或函数名等）分配的地址，就是各符号相对于文件开头的偏移量。

CPU 的实模式

实模式是指8086 CPU 的寻址方式、寄存器大小、指令用法等，是用来反应CPU 在该环境下如何工作的概念。CPU 大体上可以划分为3 个部分，它们是控制单元、运算单元、存储单元。控制单元是 CPU 的控制中心，CPU 需要经过它的帮忙才知道自己下一步要做什么。而控制单元大致由指令寄存器IR（Instruction Register）、指令译码器ID（Instruction Decoder）、操作控制器OC（Operation Controller）组成。

程序被加载到内存后，指令指针寄存器IP指向内存中下一条待执行指令的地址，控制单元根据IP寄存器的指向，将位于内存中的指令逐个装载到指令寄存器中。然后指令译码器将位于指令寄存器中的指令按照指令格式来解码，分析出操作码是什么，操作数在哪里之类的。

存储单元是指CPU内部的L1、L2缓存及寄存器，待处理的数据就存放在这些存储单元中。寄存器可分为两大类，程序员可以使用的寄存器称为程序可见寄存器，如通用寄存器、段寄存器。程序不可见寄存器是指程序员不可使用，也无法访问到它们，系统运行期间可能要用到寄存器。

运算单元负责算术运算（加减乘除）和逻辑运算（比较、移位），它从控制单元那里接收命令（信号）并执行，它没有自主意识，只是个执行部件。

CPU 中的寄存器大致上分为两大类。

  • 一类是其内部使用的，程序员不能使用。我们无法使用一些寄存器，比如全局描述符表寄存器GDTR、中断描述符表寄存器IDTR、局部描述符表寄存器LDTR、
    任务寄存器TR、控制寄存器CR0～3、指令指针寄存器IP、标志寄存器flags、调试寄存器DR0～7。
  • 另一类是对程序员可见的寄存器。我们进行汇编语言程序设计时，能够直接操作的就是这些寄存器，如段寄存器、通用寄存器。

上面提到的“段基址：段内偏移地址”中的段基址，就是用段寄存器来存储的，段寄存器的作用就是指定一片内存的起始地址，故也称为段基址寄存器。尽管段基址在实模式下要乘以16，在保护模式下只是个选择子（保护模式中会讲），但其作用就是指定一片内存的起始地址。而段内偏移地址，顾名思义，仅仅相对于此起始地址的偏移量。

访问内存就要提供地址，初次访问内存时，该地址肯定不能用内存本身来存，用寄存器来存储内存地址。由于要指定的是内存中的一段区域的起始地址，所以称之为段基址寄存器，也称段寄存器，无论是在实模式下，还是保护模式下，它们都是16位宽。

  • 代码段把所有指令都连续排放在一起，形成了一个全部都是指令的区域，里面存储的是指令的操作码及寻址方式等。代码段寄存器CS就是用来指向内存中这段指令区域的起始地址。

  • 数据段和代码段类似，只是这段区域存储的是程序运行所需要的数据，属于指令的操作数。数据段寄存器DS便是用来指向此数据区域的起始地址。

  • 栈段是在内存中，硬盘文件中可真没有。一般的栈段是由操作系统分配指定的，所以是属于被加载到内存后才有的。栈段寄存器SS 就是用来指向此区域的起始地址。

  • 值得说明的是在16 位CPU 中，只有一个附加段寄存器ES。而FS和GS附加段寄存器是在32 位CPU 中增加的。

  • IP寄存器是不可见寄存器，CS寄存器是可见寄存器。这两个配合在一起后就是CPU的罗盘。访问内存就要用“段：段内偏移”的形式，所以CS 寄存器用来存代码段段基址，IP 寄存器用来存储代码段段内偏移地址，同CS 寄存器一样都是16 位宽。

  • flags 寄存器是计算机的窗口，展示了CPU 内部各项设置、指标。任何一个指令的执行、其执行过程的细节、对计算机造成了哪些影响，都在flags 寄存器中通过一些标志位反映出来。

  • 无论是实模式，还是保护模式，通用寄存器有8 个，分别是AX、BX、CX、DX、SI、DI、BP、SP。

拿AX寄存器举例，根据图3-6可知，AX寄存器是由AH寄存器和AL寄存器组成的，它们都是8位寄存器，AX寄存器的低8位是AL寄存器。高8位是AH寄存器。由于某种原因，16位AX寄存器不够用了，将其扩展（Extend）为32位，在AX原有的基础上，增加16位作为高16位便是扩展的AX，即EAX。所以EAX归根结底也是由AL、AH组成的，AL或AH值变了直接影响EAX。

以上的这8个寄存器实际上是通用寄存器，通用是说每个寄存器的功能不单一，可以有多种用途，不像段寄存器SS那样只能用来放栈段基址，通用寄存器可以用来保存任何数据。一般情况下，cx寄存器用作循环的次数控制，bx寄存器用于存储起始地址。

实模式下内存分段的由来

有了保护模式后，为了与老的模式区别开来，所以称老的模式为实模式。实模式的“实”体现在：程序中用到的地址都是真实的物理地址，“段基址：段内偏移”产生的逻辑地址就是物理地址，也就是程序员看到的完全是真实的内存。

为了让16位的寄存器寻址能够访问20位的地址空间，CPU 工程师定位到根本瓶颈是在段寄存器，它要是能提供20位的段地址，哪怕偏移地址是1也照样可以访问到内存的各个角落。于是，通过先把16位的段基址左移4位后变成20位，再加段内偏移地址，这样便形成了20位地址，只要保证了段基址是20位的，偏移地址是多少位都不关心了，从而突破了16位寄存器作为偏移地址而无法访问1MB空间的限制。

拿 0xFFFF 来说，现在能访问的最大的地址是0xFFFF：0xFFFF，经过左移段基址4位后得到的最大地址是：0xFFFF * 16 + 0xFFFF = 0xFFFF0 + 0xFFFF = 0xFFFFF + 0xFFF0 = 1M + 16 * 4KB - 16 - 1 = 0x10FFEF。得到的最大地址是1MB+64KB-16字节，因为这是空间范围，所以要减去1得到地址范围。多出来64K-16 字节，这部分内存就是传说中的高端内存区，但是这部分内存不存在。所以由于超过了20位而产生的进位，就给丢掉了。其作用相当于把地址对1MB取模了。

实模式下CPU 内存寻址方式

下面把8086的寻址模式和大家说说。寻址方式，从大方向来看可以分为三大类：

  • 寄存器寻址；
  • 立即数寻址；
  • 内存寻址。
    • 直接寻址；
    • 基址寻址；
    • 变址寻址；
    • 基址变址寻址。

寄存器寻址：最直接的寻址方式就是寄存器寻址，它是指“数”在寄存器中，直接从寄存器中拿数据就行了。例如下面用mul 指令实现0x10*0x9。

1
2
3
mov ax, 0x10
mov dx, 0x9
mul dx

以上三条指令都是寄存器寻址。第一条命令是将0x10存入ax寄存器，第二条命令是将0x9存入dx，第三条指令是求ax和dx的乘积，乘积的高16位在dx寄存器，低16位在ax寄存器。只要牵扯到寄存器的操作，无论其是源操作数，还是目的操作数，都是寄存器寻址。上面的第一、二条指令，它们的源操作数都是立即数，所以也属于立即数寻址。

立即数寻址：如果操作数“直接”存在指令中，直接拿过来，立即就能用了。为了突显“立即就能用”的高效率，此数便称为立即数。立即数免去了找数的过程。如：

1
2
mov ax,0x18
mov ds, ax

第一条指令中的源操作数0x18是立即数，目的操作数ax是寄存器，所以它既是立即数寻址，也是寄存器寻址。第二条指令中，源操作数和目的操作数都是寄存器，所以纯粹是寄存器寻址。提醒一下，像这样的寻址也是立即数寻址：

1
2
mov ax, macro_selector
mov ax, label_start

第一条指令的源操作数macro_selector是个宏，第二条指令的源操作数label_start是个标号，这两个在编译阶段会转换为数字，最终可执行文件中的依然是立即数。

内存寻址：操作数在内存中的寻址方式称为内存寻址。大多数时候操作数位于内存中的某个位置，只知道操作数所在的内存地址，不知道操作数的值，更谈不上将其变成立即数用在指令中了，这就更加有理由让内存寻址成为“应该”。由于访问内存是用“段基址：偏内偏移地址”的形式，此形式只用在内存访问中。默认情况下数据段寄存器是DS，即段基址已经有了，只要再给出段内偏移地址就可以访问内存了，最终起决定作用的、有效的是段内偏移地址，所以段内偏移地址称为有效地址。以下所说的寻址方法都是在内存中寻址的方法。

直接寻址，就是将直接在操作数中给出的数字作为内存地址，通过中括号的形式告诉CPU，取此地址中的值作为操作数。如：

1
2
mov ax, [0x1234]
mov ax, [fs:0x5678]

0x1234 是段内偏移地址，默认的段地址是DS。这条指令是将内存地址DS:0x1234处的值写入ax寄存器。第二条指令中，由于使用了段跨越前缀fs, 0x5678的段基址则变成了gs寄存器。最终的内存地址是gs寄存器的值*16+0x5678，CPU到此内存地址取值再存入ax寄存器。

基址寻址，就是在操作数中用bx寄存器或寄存器作为地址的起始，地址的变化以它为基础。这里说的是只能用bx 或bp 作为基址寄存器。用寄存器作为内存寻址，到了保护模式下就没这个限制了，基址寄存器可选择的很多。说明一下，bx 寄存器的默认段寄存器是DS，而bp 寄存器的默认段寄存器是SS，即bp 和sp 都是栈的有效地址。

sp寄存器作为栈顶指针，相当于栈中数据的游标，这是专门给push 指令和pop 指令做导航用的寄存器，push 指令往哪个内存压入数据，popd 将哪个地址的数据弹出栈，都要看sp 的值是多少。在实模式下，CPU 字长是16，所以实模式下的push 指令默认情况下是压入2 字节的数据，其工作原理可以分为两步，假如执行push ax：

1
2
sub sp，2 先将sp 的值减去
mov sp，ax 再将ax 的值mov 加到新的sp 指向的内存

实模式下 pop 指令，其工作原理也分为两步，假如执行pop ax：

1
2
mov ax， [sp] 先将sp 指向的值mov 到
add sp，2 再将sp 的指针+2

访问栈有两种方式，一种是把栈当成“栈”来使用，也就是用push 和pop 指令操作栈，但这样我们只能访问到栈顶，即sp 指向的地址，没有办法直接访问到栈底和栈顶之间的数据。很多时候，我们需要读写栈中的数据，即需要把栈当成普通数据段那样访问。举个需要直接写栈的例子，比如标志寄存器eflags 无法直接修改，只能用pushf指令把eflags寄存器的内容压到栈中，我们在栈中修改完后，再用popf 把它弹回到eflags 中。处理器为了让开发人员方便控制栈中数据，提供了这种把栈当成数据段来访问的方式，可以用寄存器bp 来给出栈中偏移量，所以bp 默认的段寄存器就是SS，这样就可通过SS：bp 的方式把栈当成普通的数据段来访问。

在32 位环境下，ebp寄存器应用在堆栈框架中，堆栈框架是编译器在栈中为局部变量分配内存空间的方式，局部变量存在于函数中，因此有关堆栈框架的汇编指令是在函数的开头和结尾处。下面通过这段代码了解堆栈框架的原理。

1
2
3
4
5
int a = 0；
function(int b, int c) {
    int d；
}
a++；
  1. 调用function(1,2)；按照C语言调用规范，参数入栈的顺序从右到左：会先压入2，再压入1。每个参数在栈中各占4字节。
  2. 栈中再压入function的返回地址，此时栈顶的值是执行“a++”相关指令的地址。

下面是堆栈框架的指令。
3. push ebp；将ebp 压入栈，栈中备份ebp 的值，占用4 字节。
4. mov ebp, esp；将esp 的值复制到ebp，ebp 作为堆栈框架的基址，可用于对栈中的局部变量和其他参数寻址。此时的 ebp 便是栈中局部变量的分界线。在这之后，esp 将自减一定的值为局部变量在栈中分配空间，该值取决于所有局部变量空间大小的总和。
5. sub esp, 4；由于函数function 中有局部变量d，局部变量是在栈中存放的，故esp 要预留出4 字节，专门给变量d 使用。

终于到了应用 ebp 指针的时候，以ebp 为基址对栈中数据寻址。

  • [ebp-4]是局部变量d，对应上面的第（5）步。
  • [ebp]是ebp 在栈中的备份，对应上面的第（3）步。
  • [ebp+4]是函数的返回地址，对应上面的第（2）步。
  • 函数中的参数b是用[ebp+8]访问，参数c用[ebp+12]访问，对应上面的第（1）步。

栈中数据的布局如图 3-8 所示。

  • 函数结束后跳过局部变量的空间：mov esp, ebp。
  • 恢复ebp 的值：pop ebp。
  • 至此函数中堆栈框架的指令结束了，然后是返回指令ret，接着主调函数中执行add esp, 8来回收参数b 和c 的空间。

堆栈框架的工作是为函数分配局部变量空间，因此应该在刚刚进入函数时就进行为局部变量分配空间的工作，离开函数时再回收局部变量的空间。
数时进行的。

变址寻址其实和基址寻址类似，只是寄存器由bx、bp 换成了si 和di。si 是指源索引寄存器（source index），di 是指目的索引寄存器（destination index）。两个寄存器的默认段寄存器也是ds。mov [di]，ax ：将寄存器ax的值存入ds：di 指向的内存；mov [si+0x1234], ax ：变址中也可以加个偏移量。变址寻址主要是用于字符搬运方面的指令，这两个寄存器在很多指令中都要成对使用，如movsb，movsw，movsd等。

基址变址寻址；从名字上看，这是基址寻址和变址寻址的结合，即基址寄存器bx或bp加一个变址寄存器si或di。如：

1
2
mov [bx+di], ax
add [bx+si], ax

第一条指令是将ax中的值送入以ds为段基址，bx+di 为偏移地址的内存。第二条指令是将ax与[ds：bx+si]处的值相加后存入内存[ds：bx+si]。

栈

给栈指定一片内存区域，区域的起始地址作为栈基址，存入栈基址寄存器SS中，另一端是动态变化的，用栈指针寄存器SP来指定，栈顶地址肯定小于栈底地址。栈中的内存地址用段基址SS的值*16+栈指针SP（段内偏移地址）形成的20位地址访问到的。硬件提供了相应的方法来存取栈，即push 和pop 指令。push 指令负责把数据压入栈，pop 指令功能相反，将其从栈中取出。

栈指针寄存器SP中的值是段内偏移地址，是栈顶相对于栈底的偏移量。push压入数据的过程是：先将SP减去字长，目的是避免将栈顶的数据破坏，所得的差再存入SP，栈顶在此被更新，这样栈顶就指向了栈中下一个存储单元的位置。再将数据压入SP（新的栈顶）指向的新的内存地址。pop指令相反，栈指针寄存器SP的值增大一个数据单位。由于要弹出的数据就在当前栈顶，所以在弹出数据后，才将SP加上字长，所得的和再存入SP，从而更新了栈顶。

即使是这里的硬件栈，咱们也可以自己维护指针，如push ax可以这样代替：

1
2
3
mov bp,sp
sub bp, 2
mov [bp],ax

push 和pop 操作是要成对出现的，这样才能维护栈平衡。

实模式下的call/ret

经过代码段段基址寄存器CS*16后再加上代码段的段内偏移地址寄存器IP的值，所得的和就是指令存放的内存地址。CPU 在此内存地址处获得指令并执行。所以说，CPU 前进的方向永远是CS：IP 这两个寄存器。call指令用来执行一段新的代码，需要返回指令ret来帮忙。ret（return）指令的功能是在栈顶（寄存器ss：sp 所指向的地址）弹出2 字节的内容来替换IP寄存器。retf（return far）是从栈顶取得4 字节，栈顶处的2 字节用来替换IP 寄存器，另外的2 字节用来替换CS 寄存器。retf指令会使sp指针+4。，call和ret是一对配合，用于近调用和近返回，call far和retf是一对配合，用于远调用和远返回。

在 8086 处理器中，也就是我们所说的实模式下，call 指令调用函数有四种方式。

  • 16 位实模式相对近调用：call 指令所调用目标函数和当前代码段是同一个段，所以只给出段内偏移地址。和“近”有关的调用就可以用关键字near来修饰，由于是在同一个代码段中，所以只要给出目标函数的相对地址即可。指令格式是call near 立即数地址。。此指令是个3字节指令，0xe8是此操作的操作码，占1 字节，剩下2 字节便是操作数。
    • 此操作数并不是目标函数的绝对地址，只是相对于目标函数地址的相对增量，所以此操作数并不能直接被CPU使用。CPU在实际执行中还要将此增量还原成绝对地址。所以此相对近调用并不能称为“直接”相对近调用。
    • near 的意思同数据类型伪指令word 一样，是指在内存地址处取2 字节内容，或者将操作数强制转换为2 字节。可以认为像near、short、far，这些用在调用或转移中的修饰符（后面会说到），其意义就是数据类型转换。
  • 16 位实模式间接绝对近调用。“间接”是指目标函数的地址并没有直接给出，地址要么在寄存器中，要么在内存中，总之不以立即数的形式出现。“绝对”是指目标函数的地址是绝对地址，不像“16 位相对近调用”中的那样是相对地址。指令的一般形式是call 寄存器寻址或call 内存寻址，如call ax，call [0x1234]。
  • 16 位实模式直接绝对远调用。凡是包含“远”，就意指要跨段啦，目标函数和当前指令不在同一个段中。由于是远调用，所以CS 和IP 都要用新的，call 指令将来还是要回来的，所以要在栈中保留回来的路，即先把老的CS 寄存器压入栈，再把老的IP 寄存器压入栈后，用新的CS 和IP 寄存器替换，从此开启新
    的旅途。call far 段基址（立即数）：段内偏移地址（立即数）
  • 16 位实模式间接绝对远调用。这和第 3 种的区别就是“直接”变“间接”了。也就是说，段基址和段内偏移地址，都不是立即数。16 位间接绝对远调用指令格式是：call far 内存寻址，如call far [bx],call far [0x1234]

实模式下的jmp

jmp 转移指令只要更新CS：IP 寄存器或只更新IP 寄存器就好了，不需要保存它们的值，所以跳到新的地址后没办法再回来，它属于“一去不回头”地去执行新指令。和 call 一样，按远近（是否跨段）来划分，大致分为两类，近转移、远转移。不过在转移方式中，还有个更近的，叫短转移。相对近转移和相对短转移相比，就是操作数范围增大了，由8 位宽度变成了16 位宽度，操作数依然是地址相对量，可正可负，范围是-32768～32767。间接，是指操作数并不直接给出，而是存储在寄存器或内存中。绝对地址顾名思义，就是段内偏移地址，指的是“CS：IP”中的IP 值，偏移地址是16位。

标志寄存器flags

实模式下标志寄存器是16 位的flags，在32 位保护模式下，扩展（extend）了标志寄存器，成为32位的eflags。

  • 第0位为CF位，即Carry Flag，意为进位。因为CF 为1 时，也就是最高位有进位或借位，肯定是溢出。
  • 第2位为PF位，即Parity Flag，意为奇偶位。用于标记结果低8 位中1 的个数。
  • 第4位为AF位，即Auxiliary carry Flag，意为辅助进位标志，用来记录运算结果低4 位的进、借位情况。
  • 第6位为ZF位，即Zero Flag，意为零标志位。若计算结果为0，此标志为1，否则为0。
  • 第7位为SF位，即Sign Flag，意为符号标志位。若运算结果为负，则SF 位为1，否则为0。
  • 第8位为TF位，即Trap Flag，意为陷阱标志位。此位若为1，用于让CPU 进入单步运行方式，若为0，则为连续工作的方式。
  • 第9位为IF位，即Interrupt Flag，意为中断标志位。若IF 位为1，表示中断开启，CPU 可以响应外部可屏蔽中断。
  • 第10位为DF位，即Direction Flag，意为方向标志位。此标志位用于字符串操作指令中，当DF 为1 时，指令中的操作数地址会自动减少一个单位。
  • 第11位为OF位，即Overflow Flag，意为溢出标志位。用来标识计算的结果是否超过了数据类型可表示的范围

有条件转移

如果条件满足，jxx 将会跳转到指定的位置去执行，否则继续顺序地执行下一条指令。其格式为 jxx 目标地址。若条件满足则跳转到目标地址，否则顺序执行下一条指令。其中，目标地址只能是段内偏移地址。在实模式下，由编译器根据当前指令与目标地址的偏移量，自行将其编译成短转移或近转移。条件转移指令一定得在某个能够影响标志位的指令之后进行。

让我们直接对显示器说点什么吧

为了简化CPU 访问外部设备的工作，能够轻松地同任何硬件通信，约定好IO 接口的功能:

  1. 设置数据缓冲，解决CPU 与外设的速度不匹配
  2. 设置信号电平转换电路
  3. 设置数据格式转换
  4. 设置时序控制电路来同步CPU 和外部设备
  5. 提供地址译码

同一时刻，CPU 只能和一个IO 接口通信。使用一个芯片仲裁IO 接口的竞争，还要连接各种内部总线。由于它的使命，它的名字就叫做输入输出控制中心（I/O control hub，ICH），也就是南桥芯片。南桥用于连接pci、pci-express、AGP 等低速设备，北桥用于连接高速设备，如内存。南桥提供了专门用于扩展的接口，这就是PCI 接口。

IO 接口是连接CPU和硬件的桥梁，一端是CPU，另一端是硬件。端口是IO接口开放给CPU的接口。端口也是寄存器，寄存器就有数据宽度，有8位、16位、32位。CPU 提供了专门的指令来干这事，in和out。

in指令用于从端口中读取数据，其一般形式是：

  1. in al, dx；
  2. in ax, dx。

其中al 和ax 用来存储从端口获取的数据，dx 是指端口号。这是固定用法，只要用in指令，源操作数（端口号）必须是dx，而目的操作数是用al，还是ax，取决于dx 端口指代的寄存器是8 位宽度，还是16 位宽度。

out 指令用于往端口中写数据，其一般形式是：

  1. out dx, al
  2. out dx,ax
  3. out 立即数, al
  4. out 立即数, ax

注意啦，这和 in 指令相反，in 指令的源操作数是端口号，而out 指令中的目的操作数是端口号。

硬盘介绍

通过读写硬盘控制器的端口让硬盘工作，端口就是位于IO控制器上的寄存器，此处的端口是指硬盘控制器上的寄存器。

端口可以被分为两组，Command Block registers和Control Block registers。Command Block registers
用于向硬盘驱动器写入命令字或者从硬盘控制器获得硬盘状态，Control Block registers 用于控制硬盘工作状态。下面重点介绍Command Block registers 组中的寄存器。

  • data寄存器是负责管理数据的，其作用是读取或写入数据。数据的读写还是越快越好，所以此寄存器较其他寄存器宽一些，16 位；
  • 读硬盘时，端口0x171或0x1F1的寄存器名字叫Error寄存器，只在读取硬盘失败时有用，里面才会记录失败的信息，尚未读取的扇区数在Sector count 寄存器中；在写硬盘时，此寄存器有了别的用途，用来存储额外参数，叫Feature 寄存器。
  • Sector count 寄存器用来指定待读取或待写入的扇区数；
  • 用28位比特来描述一个扇区的地址，最大可寻址范围是2的28次方，称为LBA方法，与之对应的LBA low、LBA mid、LBA high三个寄存器都是8位宽度的。
    • LBA low 寄存器用来存储28位地址的第0～7位，LBA mid寄存器用来存储第8～15位，LBA high寄存器存储第16～23位。
  • device寄存器是个杂项，它的宽度是8位。
    • 在此寄存器的低4位用来存储LBA地址的第24～27 位。
    • 第4位用来指定通道上的主盘或从盘，0代表主盘，1代表从盘。
    • 第6位用来设置是否启用LBA方式，1代表启用LBA模式，0代表启用CHS模式。
    • 另外的两位：第5位和第7位是固定为1的，称为MBS位。
  • 端口0x1F7或0x177的寄存器名称是Status，它是8位宽度的寄存器，用来给出硬盘的状态信息；在写硬盘时，端口0x1F7或0x177的寄存器名称是command。

一般硬盘操作的基本顺序：

  1. 先选择通道，往该通道的sector count 寄存器中写入待操作的扇区数。
  2. 往该通道上的三个LBA 寄存器写入扇区起始地址的低24 位。
  3. 往device 寄存器中写入LBA 地址的24～27 位，并置第6 位为1，使其为LBA 模式，设置第4位，选择操作的硬盘（master 硬盘或slave 硬盘）。
  4. 往该通道上的command 寄存器写入操作命令。
  5. 读取该通道上的status 寄存器，判断硬盘工作是否完成。
  6. 如果以上步骤是读硬盘，进入下一个步骤。否则，完工。
  7. 将硬盘数据读出。

硬盘工作完成后，它已经准备好了数据，咱们该怎么获取呢？一般常用的数据传送方式如下。

  1. 无条件传送方式。数据源设备一定是随时准备好了数据。
  2. 查询传送方式。称为程序I/O、PIO（Programming Input/Output Model），是指传输之前，由程序先去检测设备的状态。数据源设备在一定的条件下才能传送数据
  3. 中断传送方式。也称为中断驱动I/O。通知CPU 可以采用中断的方式，当数据源设备准备好数据后，它通过发中断来通知CPU 来拿数据
  4. 直接存储器存取方式（DMA）。完全由数据源设备和内存直接传输，CPU 直接到内存中拿数据就好了
  5. I/O 处理机传送方式。

让 MBR 使用硬盘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
;主引导程序
;------------------------------------------------------------
%include "boot.inc"
SECTION MBR vstart=0x7c00
mov ax,cs
mov ds,ax
mov es,ax
mov ss,ax
mov fs,ax
mov sp,0x7c00
mov ax,0xb800
mov gs,ax
;清屏
;利用0x06 号功能，上卷全部行，则可清屏
; -----------------------------------------------------------
;INT 0x10 功能号：0x06 功能描述：上卷窗口
;------------------------------------------------------
;输入：
;AH 功能号= 0x06
;AL = 上卷的行数（如果为0，表示全部）
;BH = 上卷行属性
;(CL,CH) = 窗口左上角的(X,Y)位置
;(DL,DH) = 窗口右下角的(X,Y)位置
;无返回值：

mov ax, 0600h
mov bx, 0700h
mov cx, 0 ; 左上角: (0, 0)
mov dx, 184fh ; 右下角: (80,25),
; 因为VGA 文本模式中，一行只能容纳80 个字符，共25 行
; 下标从0 开始，所以0x18=24，0x4f=79
int 10h ; int 10h
; 输出字符串:MBR
mov byte [gs:0x00],'1'
mov byte [gs:0x01],0xA4
mov byte [gs:0x02],' '
mov byte [gs:0x03],0xA4
mov byte [gs:0x04],'M'
mov byte [gs:0x05],0xA4
;表示绿色背景闪烁,4 表示前景色为红色
mov byte [gs:0x06],'B'
mov byte [gs:0x07],0xA4
mov byte [gs:0x08],'R'
mov byte [gs:0x09],0xA4
mov eax,LOADER_START_SECTOR ; 起始扇区lba 地址
mov bx,LOADER_BASE_ADDR ; 写入的地址
mov cx,1 ; 待读入的扇区数
call rd_disk_m_16 ; 以下读取程序的起始部分(一个扇区)
jmp LOADER_BASE_ADDR
;-------------------------------------------------------------------------------
;功能:读取硬盘n 个扇区
rd_disk_m_16:
;-------------------------------------------------------------------------------
; eax=LBA 扇区号
; bx=将数据写入的内存地址
; cx=读入的扇区数
mov esi,eax ;备份eax
mov di,cx ;备份cx
;读写硬盘:
;第1 步:设置要读取的扇区数
mov dx,0x1f2
mov al,cl
out dx,al ;读取的扇区数
mov eax,esi ;恢复ax
;第2 步:将LBA 地址存入0x1f3 ～ 0x1f6
;LBA 地址7～0 位写入端口0x1f3
mov dx,0x1f3
out dx,al
;LBA 地址15～8 位写入端口0x1f4
mov cl,8
shr eax,cl
mov dx,0x1f4
out dx,al
;LBA 地址23～16 位写入端口0x1f5
shr eax,cl
mov dx,0x1f5
out dx,al
shr eax,cl
and al,0x0f ;lba 第24～27 位
or al,0xe0 ; 设置7～4 位为1110,表示lba 模式
mov dx,0x1f6
out dx,al

;第3 步:向0x1f7 端口写入读命令,0x20
mov dx,0x1f7
mov al,0x20
out dx,al
;第4 步:检测硬盘状态
.not_ready:
;同一端口,写时表示写入命令字,读时表示读入硬盘状态
nop
in al,dx
and al,0x88 ;第4 位为1 表示硬盘控制器已准备好
; 第7 位为1 表示硬盘忙
cmp al,0x08
jnz .not_ready ;若未准备好,继续等
;第5 步:从0x1f0 端口读数据
mov ax, di
mov dx, 256
mul dx
mov cx, ax
; di 为要读取的扇区数,一个扇区有512 字节,每次读入一个字
; 共需di*512/2 次,所以di*256
mov dx, 0x1f0
.go_on_read:
in ax,dx
mov [bx],ax
add bx,2
loop .go_on_read
ret
times 510-($-$$) db 0
db 0x55,0xaa

程序最开始的%include “boot.inc”，这个%include 是nasm 编译器中的预处理指令，意思是让编译器在编译之前把boot.inc 文件包含进来。

第 50～52 行为函数rd_disk_m_16 传递参数。在此说明一下，汇编语言中定义的函数（或者称为例程，proc），由于汇编语言能够直接操作寄存器，所以其传递参数可以用寄存器，也可以用栈。用寄存器传参数，没有固定的形式，原则上用哪个寄存器都行，此函数需要三个参数，我们选择用eax、bx、cx 寄存器来传递参数。

寄存器 cx 是读入的扇区数，cx 其值为1。到底读入几个扇区，是由实际文件大小来决定的。由于将来会写一个简单的loader，其大小肯定不会超过512 字节，所以此处读入的扇区数置为1 即可。

函数名rd_disk_m_16 的意思是“在16 位模式下读硬盘”。第 64 行的“mov esi，eax”是把eax 中的值先备份到esi 中。因为al 在out 指令中会被用到，这会影响到eax 的低8 位。第 65 行是备份读取的扇区数到di 寄存器，di 寄存器是16 位的，和cx 大小一致。cx 的值会在读取数据时用到，所以在此提前备份。第 67～70 行，按照咱们操作硬盘的约定，先选定一个通道，再往sector count 寄存器中写扇区数。往端口中写入数据用out 指令，注意out 指令中dx 寄存器是用来存储端口号的。其操作格式可见3.3.1 节的结尾部分。

第 74～95 行是将LBA 地址写入三个LBA 寄存器和device 寄存器的低4 位。端口0x1f3 是寄存器LBAlow，端口0x1f4 是寄存器LBA mid，端口0x1f5 是寄存器LBA high。shr 指令是逻辑右移指令，这里主要通过此指令置换出地址的相应部分，写入相应的LBA 寄存器。第93 行的“or al，0xe0”，用了or“或”指令和0xe0 做或运算，拼出device 寄存器的值。高4 位为e，即高4 位的二进制表示为1110，其第5 位和第7 位固定为1，第6 位为1 表示启用LBA。第 97～100 行便是写入命令啦，因为我们这里是读操作，所以读扇区的命令是0x20。通过out 指令写入command 端口0x1f7 后，硬盘就开始工作了。

第 102～109 行检测status 寄存器的BSY 位。由于status 寄存器依然是0x1f7 端口，所以不需要再为dx 重新赋值。105 行的nop 表示空操作，即什么也不做，只是为了增加延迟，相当于sleep 了一小下，目的是减少打扰硬盘的工作。第 111～122 行是从硬盘取数据的过程。由于data 寄存器是16 位，即每次in 操作只读入2 字节，根据读入的数据总量（扇区数*512 字节）来求得执行in 指令的次数。第 123 行返回指令ret，它用来从函数中返回。

保护模式入门

保护模式概述

为什么要有保护模式

实模式的缺点：

  1. 实模式下操作系统和用户程序属于同一特权级，这哥俩平起平坐，没有区别对待。
  2. 用户程序所引用的地址都是指向真实的物理地址，也就是说逻辑地址等于物理地址，实实在在地指哪打哪。
  3. 用户程序可以自由修改段基址，可以不亦乐乎地访问所有内存，没人拦得住。

以上 3 个原因属于安全缺陷，没有安全可言的CPU 注定是不可依赖的，这决定了用户程序乃至操作系统的数据都可以被随意地删改，一旦出事往往都是灾难性的，而且不容易排查。

  1. 访问超过64KB 的内存区域时要切换段基址，转来转去容易晕乎。
  2. 一次只能运行一个程序，无法充分利用计算机资源。
  3. 共20 条地址线，最大可用内存为1MB，这即使在20 年前也不够用。

保护模式下，物理内存地址不能直接被程序访问，程序内部的地址（虚拟地址）需要被转化为物理地址后再去访问。

我们说实模式时，指的是32 位的CPU 运行在16 位模式下的状态，不是CPU 变身成纯粹的16位啦，大家不要感到迷惑。

初见保护模式

保护模式之寄存器扩展

为了让一个寄存器就能访问 4GB 空间，需要寄存器宽度提升到32 位。除段寄存器外，通用寄存器、指令指针寄存器、标志寄存器都由原来的16 位扩展到了32 位。注意段寄存器用16位就够用了。

寄存器要保持向下兼容，不能推翻之前的方案从头再来，必须在原有的基础上扩展（extend），各寄存器在原有16 位的基础上，再次向高位扩展了16 位，成为了32 位寄存器。经过extend 后的寄存器，统一在名字前加了e 表示扩展，

左边已经标注名字的寄存器有通用寄存器组，名字前统一加了字符E表示扩展，同样，EFLAGS寄存器和EIP分别在FLAGS和IP基础上扩展而成。图下边的6个段寄存器，依然是16 位。寄存器中低16位的部分可以单独使用。高16位没办法单独使用，只能在用32位寄存器时才有机会用到它们。

偏移地址与实模式下的一样，但段基址可不是简单的一个地址的事了，专门找了个数据结构—全局描述符表，其中每一个表项称为段描述符，其大小为64字节，用来描述各个内存段的起始地址、大小、权限等信息。该全局描述符表很大，所以放在了内存中，由GDTR寄存器指向它就行。

这样，段寄存器中保存的内容叫“选择子”，selector，该选择子其实就是个数，用这个数来索引全局描述符表中的段描述符，把全局描述符表当成数组，选择子就像数组下标一样。对段寄存器应用了缓存技术，将段信息用一个寄存器来缓存，这就是段描述符缓冲寄存器。以后每次访问相同的段时，就直接读取该段寄存器对应的段描述符缓冲寄存器。

段描述符缓冲寄存器也可以用在实模式下，在实模式下时，段基址左移4位后的结果就被放入段描述符缓冲寄存器中，以后每次引用一个段时，就直接走段描述符缓冲寄存器，直到该段寄存器被重新赋值。

80286虽然有了保护模式，但其依然是16位的CPU，其通用寄存器还是16位宽。但其与8086不同的是其地址线由20位变为了24位，即寻址空间变成了2的24次方，等于16MB大小。

有了保护模式，之前的实模式下的程序还得兼容，所以便有了个“过渡模式”，即虚拟8086 模式。因为80286是首款具备保护模式的CPU，而之前的CPU都是只有实模式，最有代表性的、应用最广的CPU 是8086。综上所述，CPU 有三种模式：实模式、虚拟8086 模式、保护模式。

保护模式之寻址扩展

在保护模式下的内存寻址中，基址寄存器不再只是bx、bp，而是所有32位的通用寄存器，变址寄存器也是一样，不再只是si、di，而是除esp 之外的所有32 位通用寄存器，偏移量由实模式的16位变成了32位。并且，还可以对变址寄存器乘以一个比例因子，注意比例因子，只能是1、2、4、8。

具体形式如下代码。

1
2
3
mov eax，[eax+edx*8+0x12345678]
mov eax，[eax+edx*2+0x8]
mov eax，[ecx*4+0x1234]

虽然esp 无法用作变址寄存器，但其可用于基址寄存器。所以，如下代码是正确的。

1
2
mov eax，[esp]
mov eax，[esp+2]

保护模式之运行模式反转

编译器提供了伪指令bits，用它来向编译器传达：我下面的指令都要编译成xx位的，因为我知道下面的代码的运行环境是xx 模式。比如在实模式下，运行的指令都是16 位的，所以编译器要将代码编译成16 位的指令。在实模式下准备好了保护模式所需要的环境后，进入保护模式后的代码就应该是32 位指令。也就是，同一段程序要经历两种模式，所以同一段程序中有两种模式的机器码。bits 指令的范围是从当前bits 标签直到下一个bits 标签的范围，这个范围中的代码将被编译成相应字长的机器码。

bits 的指令格式是[bits 16]或[bits 32]。

  • [bits 16]是告诉编译器，下面的代码帮我编译成16 位的机器码。
  • [bits 32]是告诉编译器，下面的代码帮我编译成32 位的机器码。

如果要用另一模式下的操作数大小，需要在指令前添加指令前缀0x66，将当前模式临时改变成另一模式。这就是反转的意义，不管是当前模式是什么，总是转变成相反的运行模式。比如，在指令中添加了 0x66 反转前缀之后：

  • 假设当前运行模式是 16 位实模式，操作数大小将变为32 位。
  • 假设当前运行模式是 32 位保护模式，操作数大小将变为16 位。
  • 这个转换只是临时的，只在当前指令有效。


第 5 行是16 位指令，但当前已在32 位模式下，所以要用操作数反转前缀0x66 来临时将当前模式的32 位操作数反转成16 位大小的操作数，故机器码是66B83412。最前面的0x66 正是反转前缀，b8、3412分别是操作码和操作数。

寻址方式反转前缀0x67：不同模式之间不仅可以使用对方模式下的操作数，还可以使用对方模式下的寻址方式。第3行把eax 寄存器作为基址寻址，eax 寄存器不属于实模式，所以在机器码前添加了寻址方式反转前缀0x67。

保护模式之指令扩展

mul 指令是无符号数相乘指令，指令格式是mul 寄存器/内存。其中“寄存器/内存”是乘数。

  • 如果乘数是 8 位，则把寄存器al 当作另一个乘数，结果便是16 位，存入寄存器ax。
  • 如果乘数是 16 位，则把寄存器ax 当作另一个乘数，结果便是32 位，存入寄存器eax。
  • 如果乘数是32 位，则把寄存器eax 当作另一个乘数，结果便是64 位，存入edx：eax，其中edx 是积的高32 位，eax 是积的低32 位。

对于无符号数除法指令div，其格式是div 寄存器/内存，其中的“寄存器/内存”是除法计算中的除数。

  • 如果除数是8 位，被除数就是16 位，位于寄存器ax。所得的结果，商在寄存器al，余数在寄存器ah。
  • 如果除数是16 位，被除数就是32 位，被除数的高16 位则位于寄存器dx，被除数的低16 位则位于寄存器ax。所得的结果，商在寄存器ax，余数在寄存器dx。
  • 如果除数是32 位，被除数就是64 位，被除数的高32 位则位于寄存器edx，被除数的低32 位则位于寄存器eax，所得的结果，商在寄存器eax，余数在寄存器edx。

对于 push 指令，需要根据其操作数的类型，分别讨论，操作数类型如下。

  1. 立即数。
  2. 寄存器。
  3. 内存。

第 1 种情况，对于立即数来说，可以分别压入8 位、16 位、32 位数据。指令格式是：

  • push 8 位立即数
  • push 16 位立即数
  • push 32 位立即数

虽说可以压入8位立即数，但实际上，对于CPU 来说，出于对齐的考虑，操作数要么是16 位，要么是32 位，所以8 位立即数会被扩展成各模式下的默认操作数宽度，即实模式下8 位立即数扩展成为16 位后再入栈，保护模式下扩展成为32 位后再入栈。

在实模式环境下：

  • 当压入 8 位立即数时，由于实模式下默认操作数是16 位，CPU 会将其扩展为16 位后再将其入栈，sp-2。
  • 当压入 16 位立即数时，CPU 会将其直接入栈，sp-2。
  • 当压入 32 位立即数时，CPU 会将其直接入栈，sp-4。

在保护模式下，同样是这些压入立即数的指令，栈指针会有怎样的变化呢？

  • 当压入 8 位立即数时，由于保护模式下默认操作数是32 位，CPU 将其扩展为32 位后入栈，esp 指针减4。
  • 当压入 16 位立即数时，CPU 直接压入2 字节，esp 指针减2。
  • 当压入 32 位立即数时，CPU 直接压入4 字节，esp 指针减4。

实模式下每次压入一个段寄存器，栈指针sp 都会减2。保护模式下每次压入一个段寄存器，栈指针esp 都会减4。对于通用寄存器和内存，无论是在实模式或保护模式：

  • 如果压入的是 16 位数据，栈指针减2。
  • 如果压入的是 32 位数据，栈指针减4。

全局描述符表

全局描述符表（Global Descriptor Table，GDT）是保护模式下内存段的登记表，这是不同于实模式的显著特征之一。

段描述符

用来描述内存段的属性被放到了一个称为段描述符的结构中，该结构专门用来描述一个内存段，该结构是8字节大小。

保护模式下地址总线宽度是 32 位，段基址需要用32 位地址来表示。段界限表示段边界的扩展最值，即最大扩展到多少或最小扩展到多少。扩展方向只有上下两种。对于数据段和代码段，段的扩展方向是向上，即地址越来越高，此时的段界限用来表示段内偏移的最大值。对于栈段，段的扩展方向是向下，即地址越来越低，此时的段界限用来表示段内偏移的最小值。

段界限用20 个二进制位来表示。只不过此段界限只是个单位量，它的单位要么是字节，要么是4KB，这是由描述符中的G位来指
定的。最终段的边界是此段界限值*单位，故段的大小要么是2的20次方等于1MB，要么是2的32次方（4KB 等于2 的12 次方，12+20=32）等于4GB。

上面所说的1MB 和4GB 只是个范围，并不是具体的边界值。由于段界限只是个偏移量，是从0 算起的，所以实际的段界限边界值=（描述符中段界限+1）*（段界限的粒度大小：4KB 或者1）-1。

如果 G 位为0，表示段界限粒度大小为1 字节，根据上面的公式，*实际段界限=（描述符中段界限+1）1 -1=描述符中段界限，段界限实际大小就等于描述符中的段界限值。

如果 G 位为1，表示段界限粒度大小为4KB 字节，故实际段界限=（描述符中段界限+1）*4k-1。举个例子，如果是平坦模型，段界限为0xFFFFF，G位为1，套用上面公式，段界限边界值=0x100000*0x1000-1=0xFFFFFFFF。

段描述符的低32位分为两部分，前16位用来存储段的段界限的前0～15位，后16位用来存储段基址的0～15位。主要的属性都在段描述符的高32位。

  • 0～7位是段基址的16～23，24～31位是段基址的24～31位，加上在段描述符低32位中的段基址0～15位，这下32位基地址才算齐全了。
  • 8～11 位是type字段，共4位，用来指定本描述符的类型。
    • 一个段描述符，分为系统段/数据段，这是由段描述符中的S位决定的，用它指示是否是系统段。S为0时表示系统段，S为1时表示数据段。
    • type字段是要和S字段配合在一起才能确定段描述符的确切类型
    • 称为“门”的结构便是系统段，也就是硬件系统需要的结构。门的意思就是入口，它通往一段程序。
    • 该字段共4 位，用于表示内存段或门的子类型。

  • 表中的 A 位表示Accessed位，这是由CPU来设置的，每当该段被CPU访问过后，CPU 就将此位置1。

  • C 表示一致性代码段，也称为依从代码段。一致性代码段是指如果自己是转移的目标段，并且自己是一致性代码段，自己的特权级一定要高于当前特权级，转移后的特权级不与自己的DPL 为主，而是与转移前的低特权级一致，也就是听从、依从转移前的低特权级。C 为1 时则表示该段是一致性代码段，C 为0 时则表示该段为非一致性代码段。

  • R 表示可读，R 为1 表示可读，R 为0 表示不可读。这个属性一般用来限制代码段的访问。如果指令执行过程中，CPU 发现某些指令对R 为0 的段进行访问，如使用段超越前缀CS 来访问代码段，CPU 将抛出异常。

  • X 表示该段是否可执行，EXecutable。我们所说的指令和数据，在CPU 眼中是没有任何区别的，都是010101 这样类似的二进制。所以要用type 中的X 位来标识出是否是可执行的代码。代码段是可执行的，即X 为1。而数据段是不可执行的，即X 为0。

  • E 是用来标识段的扩展方向，Extend。E 为0 表示向上扩展，即地址越来越高，通常用于代码段和数据段。E 为1 表示向下扩展，地址越来越低，通常用于栈段。

  • W 是指段是否可写，Writable。W 为1 表示可写，通常用于数据段。W 为0表示不可写入，通常用于代码段。对于W 为0 的段有写入行为，同样会引发CPU 抛出异常。

  • 段描述符的第12位是S字段，用来指出当前描述符是否是系统段。S为0表示系统段，S为1表示非系统段。

  • 段描述符的第13～14位是DPL字段，Descriptor Privilege Level，即描述符特权级，这是保护模式提供的安全解决方案，将计算机世界按权力划分成不同等级，每一种等级称为一种特权级。由于段描述符用来描述一个内存段或一段代码的情况（若描述符类型为“门”），所以描述符中的DPL是指所代表的内存段的特权级。

    • 这两位能表示4 种特权级，分别是0、1、2、3 级特权，数字越小，特权级越大。
    • 某些指令只能在0 特权级下执行，从而保证了安全。

  • 段描述符的第15 位是P 字段，Present，即段是否存在。如果段存在于内存中，P 为1，否则P 为0。P 字段是由CPU 来检查的，如果为0，CPU 将抛出异常。

  • 段描述符的第 20 位为AVL 字段，从名字上看它是AVaiLable，可用的。不过这“可用的”是对用户来说的，也就是操作系统可以随意用此位。

  • 段描述符的第21 位为L 字段，用来设置是否是64 位代码段。L 为1 表示64 位代码段，否则表示32位代码段。

  • 段描述符的第22 位是D/B字段，用来指示有效地址（段内偏移地址）及操作数的大小。与指令相关的内存段是代码段和栈段，所以此字段是D 或B。

    • 对于代码段来说，此位是D 位，若D为0，表示指令中的有效地址和操作数是16位，指令有效地址用IP寄存器。
    • 若D为1，表示指令中的有效地址及操作数是32 位，指令有效地址用EIP 寄存器。
    • 对于栈段来说，此位是B 位，用来指定操作数大小，若B为0用sp寄存器；若B为1用esp寄存器。

  • 段描述符的第23位是G 字段，Granularity，粒度，用来指定段界限的单位大小。所以此位是用来配合段界限的。

    • 若G为0，表示段界限的单位是1 字节，这样段最大是2的20次方*1字节，即1MB。
    • 若G为1，表示段界限的单位是4KB，这样段最大是2 的20次方*4KB字节，即4GB。

全局描述符表GDT、局部描述符表LDT 及选择子

一个段描述符只用来描述一个内存段。代码段要占用一个段描述符、数据段和栈段等，多个内存段也要各自占用一个段描述符，放在全局描述符表，它相当于是描述符的数组，数组中的每个元素都是8 字节的描述符。可以用选择子（马上会讲到）中提供的下标在GDT中索引描述符。

全局描述符表位于内存中，需要用专门的寄存器指向它后，CPU 才知道它在哪里。这个专门的寄存器便是GDTR，即GDT Register，专门用来存储GDT 的内存地址及大小。GDTR 是个48位的寄存器。lgdt为gdtr初始化。

为了进入保护模式才讲述lgdt，因此看上去此指令是在实模式下执行的，但实际上，此指令在保护模式下也能够执行。言外之意便是进入保护模式需要有GDT，但进入保护模式后，还可以再重新换个GDT 加载。在保护模式下重新换个GDT 的原因是实模式下只能访问低端1MB空间，所以GDT只能位于1MB之内。在进入保护模式后，访问的内存空间突破了1MB，可以将GDT 放在合适的位置后再重新加载进来。

lgdt的指令格式是：lgdt 48位内存数据。这 48 位内存数据划分为两部分，其中前16位是GDT以字节为单位的界限值，所以这16位相当于GDT的字节大小减1。后32位是GDT的起始地址。由于GDT的大小是16位二进制，其表示的范围是2
的16次方等于65536字节。每个描述符大小是8字节，GDT中最多可容纳的描述符数量是65536/8=8192个，即GDT 中可容纳8192 个段或门。

段寄存器 CS、DS、ES、FS、GS、SS，在实模式下时，段中存储的是段基地址，即内存段的起始地址。而在保护模式下时，由于段基址已经存入了段描述符中，所以段寄存器中再存放段基址是没有意义的，在段寄存器中存入的是一个叫作选择子的东西。用此索引值在段描述符表中索引相应的段描述符，这样，便在段描述符中得到了内存段的起始地址和段界限值等相关信息。

由于段寄存器是16位，所以选择子也是16位：

  • 在其低2位即第0～1位，用来存储RPL，即请求特权级，可以表示0、1、2、3 四种特权级。
  • 在选择子的第2位是TI位，即Table Indicator，用来指示选择子是在GDT中，还是LDT中。
  • 选择子的高13 位，即第3～15 位是描述符的索引值，用此值在GDT中索引描述符。前面说过GDT相当于一个描述符数组，所以此选择子中的索引值就是GDT 中的下标

选择子的作用主要是确定段描述符，确定描述符的目的，一是为了特权级、界限等安全考虑，最主要的还是要确定段的基地址。

保护模式下的段寄存器中已经是选择子，不再是直接的段基址。段基址在段描述符中，用给出的选择子索引到描述符后，CPU 自动从段描述符中取出段基址，这样再加上段内偏移地址，便凑成了“段基址：段内偏移地址”的形式。

局部描述符表，叫LDT，Local Descriptor Table，它是CPU厂商为在硬件一级原生支持多任务而创造的表，按照CPU 的设想，一个任务对应一个LDT。LDT 也位于内存中，其地址需要先被加载到某个寄存器后，CPU 才能使用LDT，该寄存器是LDTR，即LDT Register。同样也有专门的指令用于加载LDT，即lldt。以后每切换任务时，都要用lldt 指令重新加载任务的私有内存段。

段描述符是需要用选择子去访问的。故，lldt 的指令格式为：lldt 16 位寄存器/16 位内存，无论是寄存器，还是内存，其内容一定是个选择子，该选择子用来在GDT 中索引LDT 的段描述符。

实模式下寄存器都是16位的，如果段基址和段内偏移地址都为16位的最大值，即0xFFFF：0xFFFF，最大地址是0xFFFF0+0xFFFF，即0x10FFEF。由于实模式下的地址线是20位，最大寻址空间0x00000～0xFFFFF。超出1MB内存的部分在逻辑上也是正常的，将超过1MB 的部分自动回绕到0地址，继续从0地址开始映射。相当于把地址对1MB 求模。超过1MB 多余出来的内存被称为高端内存区HMA。

地址（Address）线从0开始编号，在8086/8088 中，20 位地址线表示的内存是2 的20 次方即0x0～0xFFFFF。若地址进位到1MB 以上，如0x100000，由于没有第21 位地址线，相当于丢掉了进位1，变成了0x00000。用某根输出线来控制第21 根地址线（A20）的有效性，故被称为A20Gate。

  • 如果 A20Gate 被打开，当访问到0x100000～0x10FFEF 之间的地址时，CPU 将真正访问这块物理内存。
  • 如果 A20Gate 被禁止，当访问0x100000～0x10FFEF 之间的地址时，CPU 将采用8086/8088 的地址回绕。

其实打开A20Gate 的方式是极其简单的，将端口0x92 的第1 位置1 就可以了：

1
2
3
in al，0x92
or al，0000_0010B
out 0x92，al

保护模式的开关，CR0 寄存器的PE 位

控制寄存器是CPU 的窗口，既可以用来展示CPU的内部状态，也可用于控制CPU 的运行机制。这次我们要用到的是CR0 寄存器。更准确地说，我们要用到CR0寄存器的第0 位，即PE 位，Protection Enable，此位用于启用保护模式，是保护模式的开关。

处理器微架构简介

流水线

乱序执行

乱序执行，是指在CPU 中运行的指令并不按照代码中的顺序执行，而是按照一定的策略打乱顺序执行，也许后面的指令先执行，当然，得保证指令之间不具备相关性。

x86 发展到后来，虽然还是CISC 指令集，但其内部已经采用RISC 内核，译码对于x86 体系来说，除了按照指令格式分析机器码外，还要将CISC 指令分解成多个RISC 指令。当一个“大”操作被分解成多个“微”操作时，它们之间通常独立无关联，所以非常适合乱序执行。

缓存

根据程序的局部性原理采取缓存策略。

分支预测

对于无条件跳转，直接跳过去就是了。所谓的预测是针对有条件跳转来说的，因为不知道条件成不成立。最简单的统计是根据上一次跳转的结果来预测本次，如果上一次跳转啦，这一次也预测为跳转，否则不跳。

最简单的方法是2 位预测法。用2 位bit 的计数器来记录跳转状态，每跳转一次就加1，直到加到最大值3 就不再加啦，如果未跳转就减1，直到减到最小值0 就不再减了。当遇到跳转指令时，如果计数器的值大于1 则跳转，如果小于等于1 则不跳。

Intel 的分支预测部件中用了分支目标缓冲器（Branch Target Buffer，BTB）。

BTB 中记录着分支指令地址，CPU 遇到分支指令时，先用分支指令的地址在BTB 中查找，若找到相同地址的指令，根据跳转统计信息判断是否把相应的预测分支地址上的指令送上流水线。在真正执行时，根据实际分支流向，更新BTB 中跳转统计信息。

如果 BTB 中没有相同记录该怎么办呢？这时候可以使用Static Predictor，静态预测器，存储在里面的预测策略是固定写死的。比如，转移目标的地址若小于当前转移指令的地址，则认为转移会发生。静态预测器的策略是：若向上跳转则转移会发生，若向下跳转则转移不发生。

如果分支预测错了，也就是说，当前指令执行结果与预测的结果不同，需要将流水线清空。因为处于执行阶段的是当前指令，即分支跳转指令。处于“译码”“取指”的是尚未执行的指令，即错误分支上的指令。

使用远跳转指令清空流水线，更新段描述符缓冲寄存器

段描述符缓冲寄存器在CPU 的实模式和保护模式中都同时使用，在不重新引用一个段时，段描述符缓冲寄存器中的内容是不会更新的，无论是在实模式，还是保护模式下，CPU 都以段描述符缓冲寄存器中的内容为主。实模式进入保护模式时，由于段描述符缓冲寄存器中的内容仅仅是实模式下的20 位的段基址，很多属性位都是错误的值，这对保护模式来说必然会造成错误，所以需要马上更新段描述符缓冲寄存器，也就是要想办法往相应段寄存器中加载选择子。

CPU 为了提高效率而采用了流水线，这样，指令间是重叠执行的。某一行之前的指令都是16 位指令，自此行之后，CPU 便进入了保护模式，但它依然还是16 位的指令，相当于处于16 位保护模式下。为了让其使用32 位偏移地址，所以添加了伪指
令dword，故其机器码前会加0x66 反转前缀。

流水线的工作是这样的：在16位指令代码执行的同时，32位指令及其之后的部分指令已经被送上流水线了，但是，段描述符缓冲寄存器在实模式下时已经在使用了，其低20位是段基址，但其他位默认为0，也就是描述符中的D 位为0，这表示当前的操作数大小是16 位。流水线上的指令全是按照16 位操作数来译码的，所以需要加入一个无条件跳转指令。综上所述，解决问题的关键就是既要改变代码段描述符缓冲寄存器的值，又要清空流水线。

代码段寄存器cs，只有用远过程调用指令call、远转移指令jmp、远返回指令retf 等指令间接改变，没有直接改变cs 的方法，如直接mov cs，xx 是不行的。另外，之前介绍过了流水线原理，CPU 遇到jmp指令时，之前已经送上流水线上的指令只有清空，所以jmp 指令有清空流水线的神奇功效。

保护模式之内存段的保护

向段寄存器加载选择子时的保护

当引用一个内存段时，实际上就是往段寄存器中加载选择子，为了避免出现非法引用内存段的情况，在这时候，处理器会在以下几方面做出检查。

首先根据选择子的值验证段描述符是否超越界限。选择子的高13位是段描述符的索引值，第0～1位是RPL，第2 位是TI 位。首先选择子的索引值一定要小于等于描述符表（GDT 或LDT）中描述符的个数。在往段寄存器中加载选择子时，处理器要求选择子中的索引值要满足下面表达式：描述符表基地址+选择子中的索引值*8+7 <=描述符表基地址+描述符表界限值。

检查过程如下：处理器先检查TI 的值，如果TI 是0，则从全局描述符表寄存器gdtr 中拿到GDT基地址和GDT 界限值。如果TI 是1，则从局部描述符表寄存器ldtr 中拿到LDT 基地址和LDT 界限值。有了描述符表基地址和描述符表界限值后，把选择子的高13 位代入上面的表达式，若不成立，处理器则抛出异常。

段描述符中还有个type 字段，这用来表示段的类型，也就是不同的段有不同的作用。在选择子检查过后，就要检查段的类型了。这里主要是检查段寄存器的用途和段类型是否匹配。大的原则如下。

  • 只有具备可执行属性的段（代码段）才能加载到 CS 段寄存器中。
  • 只具备执行属性的段（代码段）不允许加载到除 CS 外的段寄存器中。
  • 只有具备可写属性的段（数据段）才能加载到 SS 栈段寄存器中。
  • 至少具备可读属性的段才能加载到 DS、ES、FS、GS 段寄存器中。
  • 如果 CPU 发现有任意上述规则不符，检查就不会通过。

**检查完 type 后，还会再检查段是否存在。**CPU 通过段描述符中的P 位来确认内存段是否存在，如果P 位为1，则表示存在，这时候就可以将选择子载入段寄存器了，同时段描述符缓冲寄存器也会更新为选择子对应的段描述符的内容，随后处理器将段描述符中的A 位置为1，表示已经访问过了。如果P 位为0，则表示该内存段不存在，不存在的原因可能是由于内存不足，操作系统将该段移出内存转储到硬盘上了。这时候处理器会抛出异常，自动转去执行相应的异常处理程序，异常处理程序将段从硬盘加载到内存后并将P 位置为1，随后返回。CPU 继续执行刚才的操作，判断P 位。

代码段和数据段的保护

代码段既然也是内存中的区域，所以对于代码段的访问也要用“段基址：段内偏移地址”的形式，在32 位保护模式下，段基址存放在CS 寄存器中，段内偏移地址，即有效地址，存放在EIP 寄存器中。CS：EIP 只是指令的起始地址，指令本身也是有长度的，之前我们见过各种各样的机器码，它们的长度有2 字节的、3 字节的等，如jmp .-2，其机器码为ebfe，大小就是2 字节。CPU 得确保指令“完全、完整”地任意一部分都在当前的代码段内，也就是要满足以下条件：

  • EIP 中的偏移地址+指令长度-1≤实际段界限大小
  • 如果不满足条件，指令未完整地落在本段内，CPU 则会抛出异常。

数据地址也要遵循此原则：偏移地址+数据长度-1≤实际段界限大小。

栈段的保护

虽然段描述符type 中的e 位用来表示段的扩展方向，但它和别的描述符属性一样，仅仅是用来描述段的性质，即使e 等于1 向下扩展，依然可以引用不断向上递增的内存地址，即使e 等于0 向上扩展，也依然可以引用不断向下递减的内存地址。栈顶指针[e]sp 的值逐渐降低，这是push 指令的作用，与描述符是否向下扩展无关，也就是说，是数据段就可以用作栈。

CPU 对数据段的检查，其中一项就是看地址是否超越段界限。如果将向上扩展的数据段用作栈，那CPU 将按照上一节提到的数据段的方式检查该段。如果用向下扩展的段做栈的话，情况有点复杂，这体现在段界限的意义上。

  • 对于向上扩展的段，实际的段界限是段内可以访问的最后一字节。
  • 对于向下扩展的段，实际的段界限是段内不可以访问的第一个字节。

栈的段界限是以栈段的基址为基准的，并不是以栈底，因此栈的段界限肯定是位于栈顶之下。地址本身由低向高发展，段界限也是个地址，而栈的扩展方向是由高地址向低地址，与段界限有个碰撞的趋势。为了避免碰撞，将段界限地址+1 视为栈可以访问的下限。段界限+1，才是栈指针可达的下边界。

32 位保护模式下栈的栈顶指针是esp 寄存器，栈的操作数大小是由B 位决定的，我们这里假设B 为1，即操作数是32 位。栈段也是位于内存中，所以它也要受控于段描述符中的G 位。

  • 如果 G 为0，实际的段界限大小=描述符中的段界限。
  • 如果 G 为1，实际的段界限大小=描述符中段界限*0x1000+0xFFF。

同代码段的操作数一样，用于压栈的操作数也有其长度，push 指令每向栈中压入操作数时，实际上就是将esp 指针减去操作数的大小（2 字节或4 字节）后，再将操作数复制到esp 减4 后的新地址。栈指针可访问的最低地址是由实际段界限决定的，但栈段最大可访问的地址是由B 位决定的，我们这里B 位为1，表示32 位操作数，所以栈指针最大可访问地址是0xFFFFFFFF。综上所述，每次向栈中压入数据时就是CPU 检查栈段的时机，它要求必须满足以下条件。

  • 实际段界限+1≤esp-操作数大小≤ 0xFFFFFFFF
    • 假设现在esp 指针为0xFFFFE002，段描述符的G 位为1，描述符中的段界限为0xFFFFD。故实际段界限为0x1000*FFFFD+0xFFF=0xFFFFDFFF。当执行push ax，压入2 字节的操作数，即esp-2=0xFFFFE000，新的esp 值≥实际段界限0xFFFFDFFF +1。如果执行push eax，压入4 字节的数据，esp-4=0xFFFFDFFE，小于实际段界限0xFFFFDFFF，故CPU 会抛出异常。
  • 由于 esp 只是栈段内的偏移地址，其真正物理地址还要加上段基址。假设段基址为0，故该栈段：
    • 最大可访问地址为 0+0xFFFFFFFF=0xFFFFFFFF。
    • 最小可访问地址为 0+0xFFFFDFFF+1=0xFFFFE000。
    • 栈段空间大小为 0xFFFFFFFF-0xFFFFE000=8KB。

保护模式进阶，向内核迈进

获取物理内存容量

在Linux 中有多种方法获取内存容量，如果一种方法失败，就会试用其他方法。比如在Linux 2.6 内核中，是用detect_memory函数来获取内存容量的。其函数在本质上是通过调用BIOS中断0x15 实现的，分别是BIOS 中断0x15 的3 个子功能，子功能号要存放到寄存器EAX 或AX 中，如下。

  • EAX=0xE820：遍历主机上全部内存。
  • AX=0xE801：分别检测低 15MB 和16MB～4GB 的内存，最大支持4GB。
  • AH=0x88：最多检测出64MB 内存，实际内存超过此容量也按照64MB 返回。

BIOS 中断是实模式下的方法，只能在进入保护模式前调用。获取内存信息，其内部是通过连续调用硬件的应用程序接口来获取内存信息的。BIOS 0x15 中断提供了丰富的功能，具体要调用的功能，需要在寄存器ax 中指定。其中0xE8xx系列的子功能较为强大，0x15 中断的子功能0xE820 和0xE801 都可以用来获取内存，区别是0xE820 返回的是内存布局；而0xE801 直接返回的是内存容量。

BIOS 中断 0x15 的子功能0xE820 能够获取系统的内存布局，BIOS按照类型属性来划分这片系统内存，所以这种查询呈迭代式，每次BIOS 只返回一种类型的内存信息，直到将所有内存类型返回完毕。子功能0xE820 的强大之处是返回的内存信息较丰富，包括多个属性字段，内存信息的内容是用地址范围描述符来描述的，用于存储这种描述符的结构称之为地址范围描述符ARDS。。每次int 0x15 之后，BIOS就返回这样一个20个字节的数据。

其中的 Type 字段用来描述这段内存的类型，这里所谓的类型是说明这段内存的用途：

  • AddressRangeMemory 这段内存可以被操作系统使用
  • AddressRangeReserved 内存使用中或者被系统保留，操作系统不可以用此内存
  • 其他 将来会用到，目前保留。

BIOS 中断只是一段函数例程，调用它就要为其提供参数：

  • 调用前输入
    • EAX 子功能号：EAX 寄存器用来指定子功能号，此处输入为0xE820
    • EBX ARDS 后续值：内存信息需要按类型分多次返回，由于每次执行一次中断都只返回一种类型内存的ARDS 结构，所以要记录下一个待返回的内存ARDS，在下一次中断调用时通过此值告诉BIOS 该返回哪个ARDS，这就是后续值的作用。第一次调用时一定要置为0，EBX具体值我们不用关注，字取决于具体BIOS 的实现。每次中断返回后，BIOS 会更新此值
    • ES：DI ARDS缓冲区：BIOS 将获取到的内存信息写入此寄存器指向的内存，每次都以ARDS 格式返回
    • ECX ARDS 结构的字节大小：用来指示BIOS 写入的字节数。调用者和BIOS 都同时支持的大小是20 字节，将来也许会扩展此结构
    • EDX 固定为签名标记0x534d4150，此十六进制数字是字符串SMAP 的ASCII 码：BIOS 将调用者正在请求的内存信息写入ES：DI 寄存器所指向的ARDS 缓冲区后，再用此签名校验其中的信息
  • 返回后输出：
    • CF 位若 CF 位为0 表示调用未出错，CF 为1，表示调用出错
    • EAX 字符串SMAP 的ASCII 码0x534d4150
    • ES:DI ARDS 缓冲区地址，同输入值是一样的，返回时此结构中已经被BIOS 填充了内存信息
    • CX BIOS 写入到ES:DI 所指向的ARDS 结构中的字节数，BIOS 最小写入20 字节
    • EBX 后续值：下一个ARDS 的位置。每次中断返回后，BIOS 会更新此值，BIOS 通过此值可以找到下一个待返回的ARDS 结构，咱们不需要改变EBX 的值，下一次中断调用时还会用到它。在CF 位为0 的情况下，若返回后的EBX 值为0，表示这是最后一个ARDS 结构

另一个获取内存容量的方法是BIOS0x15 中断的子功能0xE801。此方法最大只能识别4GB内存，此方法检测到的内存是分别存放到两组寄存器中的。低于15MB 的内存以1KB 为单位大小来记录，单位数量在寄存器AX 和CX 中记录，所以15MB 空间以下的实际内存容量=AX*1024。AX、CX 最大值为0x3c00，即0x3c00*1024=15MB。16MB～4GB是以64KB 为单位大小来记录的，单位数量在寄存器BX 和DX 中记录，所以16MB 以上空间的内存实际大小=BX*64*1024。

  • 调用前输入
    • AX：Function Code，子功能号：0xE801
    • CF位：Carry Flag， 若CF 位为0 表示调用未出错，CF 为1，表示调用出错
    • AX：Extended 1， 以1KB 为单位，只显示15MB 以下的内存容量，故最大值为0x3c00，即AX 表示的最大内存为0x3c00*1024=15MB
    • BX： Extended 2， 以64KB 为单位，内存空间16MB～4GB 中连续的单位数量，即内存大小为BX641024 字节
    • CX： Configured 1， 同AX
  • 返回后输出
    • DX： Configured 2， 同BX

最后一个获取内存的方法也同样是BIOS 0x15 中断，子功能号是0x88。该方法简单到只能识别最大64MB 的内存。即使内存容量大于64MB，也只会显示63MB，只会显示1MB之上的内存，不包括这1MB。

启用内存分页机制，畅游虚拟空间

CPU 在引用一个段时，都要先查看段描述符。CPU 允许在描述符表中已注册的段不在内存中存在，这就是它提供给软件使用的策略，我们利用它实现段式内存管理。

  • 如果该描述符中的P 位为1，表示该段在内存中存在。访问过该段后，CPU 将段描述符中的A 位置1，表示近来刚访问过该段。
  • 相反，如果P 位为0，说明内存中并不存在该段，CPU将会抛出异常，转而去执行中断处理程序将相应的段从外存中载入到内存，并将段描述符的P 位置1，中断处理函数结束后返回，CPU 重复执行这个检查，继续查看该段描述符的P 位，此时已经为1 了，在检查通过后，将段描述符的A 位置1。

首先要做的是解除线性地址与物理地址一一对应的关系，然后将它们的关系重新建立。通过某种映射关系，可以将线性地址映射到任意物理地址。对于地址转换这种实时性较高的需求，通过一张表来实现，该表就是我们所说的页表。

将段基址和段内偏移地址相加求和的工作是由CPU 的段部件自动完成的。整个访问内存的过程如图5-6 所示。分页机制要建立在分段机制的基础上。图 5-7 说明，CPU 在不打开分页机制的情况下，是按照默认的分段方式进行的，段基址和段内偏移地址经过段部件处理后所输出的线性地址，CPU 就认为是物理地址。如果打开了分页机制，段部件输出的线性地址就不再等同于物理地址了，我们称之为虚拟地址，CPU 必须要拿到物理地址才行，此虚拟地址对应的物理地址需要在页表中查找，这项查找工作是由页部件自动完成的。

**分页机制的思想是：通过映射，可以使连续的线性地址与任意物理内存地址相关联，逻辑上连续的线性地址其对应的物理地址可以不连续。**分页机制的作用有两方面。

  • 将线性地址转换成物理地址。
  • 用大小相等的页代替大小不等的段。

上图表示的是一个进程的地址转换过程，从线性空间到虚拟空间再到物理地址空间，每个空间大小都是4GB。图上的4GB 物理地址空间属于所有进程包括操作系统在内的共享资源，其中标注为已分配页的内存块被分配给了其他进程，当前进程只能使用未分配页。此转换过程对任意一个进程都是一样的，也就是说，每个进程都有自己的4GB 虚拟空间。

在分页机制下，分配情形如图中所示的虚拟地址空间中的代码段和数据段。代码段和数据段在逻辑上被拆分成以页为单位的小内存块。这时的虚拟地址虚如其名，不能存放任何数据。接着操作系统开始为这些虚拟内存页分配真实的物理内存页，它查找物理内存中可用的页，然后在页表中登记这些物理页地址，这样就完成了虚拟页到物理页的映射，每个进程都以为自己独享4GB 地址空间。

线性地址对应物理地址的这种映射关系需要用页表（Page Table）存储。页表中的每一行（只有一个单元格）称为页表项（Page Table Entry，PTE），其大小是4字节，页表项的作用是存储内存物理地址。当访问一个线性地址时，实际上就是在访问页表项中所记录的物理内存地址。

页是地址空间的计量单位，线性地址的一页也要对应物理地址的一页。一页大小为4KB，这样一来，4GB地址空间被划分成4GB/4KB=1M 个页，也就是4GB 空间中可以容纳1048576 个页，页表中自然也要有1048576个页表项，这就是我们要说的一级页表。

经以上分析，虚拟地址的高20 位可用来定位一个物理页，低12 位可用来在该物理页内寻址。这是如何实现的呢？物理地址写在页表的页表项中，段部件输出的只是线性地址，所以问题就变成了：怎样用线性地址找到页表中对应的页表项。

分页机制打开前要将页表地址加载到控制寄存器cr3中。一个页表项对应一个页，所以，用线性地址的高20 位作为页表项的索引，每个页表项要占用4 字节大小，所以这高20 位的索引乘以4 后才是该页表项相对于页表物理地址的字节偏移量。用cr3 寄存器中的页表物理地址加上此偏移量便是该页表项的物理地址，从该页表项中得到映射的物理页地址，然后用线性地址的低12 位与该物理页地址相加，所得的地址之和便是最终要访问的物理地址。拿mov ax，[0x1234]来说：

段基址为0，段内偏移地址为0x1234，经过段部件处理后，输出的线性地址是0x1234。页部件分析0x1234 的高20 位，用十六进制表示高20 位是0x00001。将此项作为页表项索引，再将该索引乘以4 后加上cr3 寄存器中页表的物理地址，这样便得到索引所指代的页表项的物理地址，从该物理地址处（页表项中）读取所映射的物理页地址：0x9000。线性地址的低12 位是0x234，它作为物理页的页内偏移地址与物理页地址0x9000 相加，和为0x9234，这就是线性地址0x1234 最终转换成的物理地址。

每个页表的物理地址在页目录表中都以页目录项（Page Directory Entry，PDE）的形式存储，页目录项大小同页表项一
样，都用来描述一个物理页的物理地址，其大小都是4字节，而且最多有1024 个页表，所以页目录表也是4KB 大小，同样也是标准页的大小。

页目录表中共1024 个页表，也就是有1024 个页目录项。一个页目录项中记录一个页表物理页地址，物理页地址是指页的物理地址，在页目录项及页表项中记录的都是页的物理地址。每个页表中有1024 个页表项，每个页表项中是一个物理页地址，最终数据写在这页表项中指定的物理页中。图中最粗的线存放页目录表物理页，稍细一点的线指向的是用来存放页表的物理页，其他最细的线是页表项中分配的物理页。

每个页表中可容纳1024个物理页，故每个页表可表示的内存容量是1024*4KB=4MB，所有页表可表示的内存容量是1024*4MB=4GB。页目录中1024 个页表，只需要10 位二进制就能够表示了，所以，虚拟地址的高10 位（第31～22 位）用来在页目录中定位一个页表，也就是这高10 位用于定位页目录中的页目录项PDE，PDE 中有页表物理页地址。由于页表中可容纳1024 个物理页，故只需要10 位二进制就能够表示了。所以虚拟地址的中间10 位（第21～12 位）用来在页表中定位具体的物理页。由于标准页都是4KB，12 位二进制便可以表达4KB 之内的任意地址，故线性地址中余下的12 位（第11～0 位）用于页内偏移量。二级页表地址转换原理是将32 位虚拟地址拆分成高10 位、中间10 位、低12 位三部分，

同一级页表一样，访问任何页表内的数据都要通过物理地址。由于页目录项PDE 和页表项PTE 都是4 字节大小，给出了PDE 和PTE 索引后，还需要在背后悄悄乘以4，再加上页表物理地址，这才是最终要访问的绝对物理地址。转换过程背后的具体步骤如下。

  • 用虚拟地址的高10 位乘以4，作为页目录表内的偏移地址，加上页目录表的物理地址，所得的和，便是页目录项的物理地址。读取该页目录项，从中获取到页表的物理地址。
  • 用虚拟地址的中间10 位乘以4，作为页表内的偏移地址，加上在第1 步中得到的页表物理地址，所得的和，便是页表项的物理地址。读取该页表项，从中获取到分配的物理页地址。
  • 虚拟地址的高10 位和中间10 位分别是PDE 和PTE 的索引值，所以它们需要乘以4。但低12 位就不是索引值啦，其表示的范围是0～0xfff，作为页内偏移最合适，所以虚拟地址的低12 位加上第2 步中得到的物理页地址，所得的和便是最终转换的物理地址。

比如 mov ax，[0x1234567]：

指令mov ax，[0x1234567]经过段部件处理，输出的线性地址为0x1234567，页部件首先要把地址拆分成高10位、中间10 位、低12 位三部分。其实低12 位最容易得出，十六进制的每1 位代表4 位二进制，所以低12 位直接就是0x567。

  • 高 10 位是0000 0001 00，十六进制为0x4。

  • 中间 10 位是10 0011 0100，十六进制为0x234。

  • 低 12 位是0101 0110 0111，十六进制为0x567。

  • 第一步：为了得到页表物理地址，页部件用虚拟地址高 10 位乘以4 的积与页目录表物理地址相加，所得的和便是页目录项地址，读取该页目录项，获取页表物理地址。这里是0x4*4=0x10，页表物理地址存储在cr3寄存器中。要找的页表位于物理地址0x1000。

  • 第二步：为了得到具体的物理页，需要找到页表中对应的页表项。页部件用虚拟地址中间 10 位的值乘以4 的积与第一步中得到的页表地址相加，所得的和便是页表项物理地址。这里是0x234*4=0x8d0，页表项物理地址是0x8d0+0x1000=0x18d0。在该页表项中的值是0xfa000，这意味着分配的物理页地址是0xfa000。

  • 第三步：为了得到最终的物理地址，用虚拟地址低12 位作为页内偏移地址与第二步中得到的物理页地址相加，所得的和便是最终的物理地址。这里是0xfa000+0x567=0xfa567。

页目录项和页表项是4 字节大小，用来存储物理页地址，只有第12～31位才是物理地址，地址的低12位是0，所以只需要记录物理地址高20 位。其他位：

  • P，Present，意为存在位。若为1 表示该页存在于物理内存中，若为0 表示该表不在物理内存中。
  • RW，Read/Write，意为读写位。若为1 表示可读可写，若为0 表示可读不可写。
  • US，User/Supervisor，意为普通用户/超级用户位。若为1 时，表示处于User 级，任意级别（0、1、2、3）特权的程序都可以访问该页。若为0，表示处于Supervisor 级，特权级别为3 的程序不允许访问该页，该页只允许特权级别为0、1、2 的程序可以访问。
  • PWT，Page-level Write-Through，意为页级通写位，也称页级写透位。若为1 表示此项采用通写方式，表示该页不仅是普通内存，还是高速缓存。
  • PCD，Page-level Cache Disable，意为页级高速缓存禁止位。若为1 表示该页启用高速缓存，为0 表示禁止将该页缓存。这里咱们将其置为0。
  • A，Accessed，意为访问位。若为1 表示该页被CPU 访问过，A 位也可以用来记录某一内存页的使用频率
  • D，Dirty，意为脏页位。当CPU 对一个页面执行写操作时，就会设置对应页表项的D 位为1。此项仅针对页表项有效，并不会修改页目录项中的D 位。
  • PAT，Page Attribute Table，意为页属性表位，能够在页面一级的粒度上设置内存属性。比较复杂，将此位置0 即可。
  • G，Global，意为全局位。将虚拟地址与物理地址转换结果存储在TLB（Translation Lookaside Buffer）中。此G 位用来指定该页是否为全局页，为1 表示是全局页，为0 表示不是全局页。若为全局页，该页将在高速缓存TLB 中一直保存，给出虚拟地址直接就出物理地址。
  • AVL，意为Available 位，表示可用，谁可以用？当然是软件，操作系统可用该位，CPU 不理会该位的值，那咱们也不理会吧。

控制寄存器cr3 用于存储页表物理地址，所以cr3 寄存器又称为页目录基址寄存器（Page Directory Base Register，PDBR）。只要在cr3 寄存器的第31～12 位中写入物理地址的高20 位就行了。另外，cr3 寄存器的低12 位中，除第3 位的PWT 位和第4 位的PCD 位外，其余位都没用。启动分页机制的开关是将控制寄存器cr0 的PG 位置1，PG 位是cr0 寄存器的最后一位：第31 位。

处理器准备了一个高速缓存，可以匹配高速的处理器速率和低速的内存访问速度，它专门用来存放虚拟地址页框与物理地址页框的映射关系，这个调整缓存就是TLB，即Translation Lookaside Buffer，俗称快表。TLB 中的条目是虚拟地址的高20 位到物理地址高20 位的映射结果，实际上就是从虚拟页框到物理页框的映射。除此之外TLB中还有一些属性位，比如页表项的RW 属性。

有两种方法可以间接更新TLB，一个是针对TLB 中所有条目的方法—重新加载CR3，比如将CR3 寄存器的数据读出来后再写入CR3，这会使整个TLB 失效。另一个方法是针对TLB 中某个条目的更新。处理器提供了指令invlpg（invalidate page），它用于在TLB 中刷新某个虚拟地址对应的条目，处理器是用虚拟地址来检索TLB 的，因此很自然地，指令invlpg 的操作数也是虚拟地址，其指令格式为invlpg m。

加载内核

ELF 目标文件归纳见:

程序中最重要的部分就是段（segment）和节（section），它们是真正的程序体，程序中有很多段，如代码段和数据段等，同样也有很多节，段是由节来组成的，多个节经过链接之后就被合并成一个段了，段和节的信息也是用 header 来描述的，程序头是program header，节头是section header。程序中段的大小和数量是不固定的，节的大小和数量也不固定，用程序头表（program header table）和节头表（section header table）描述。这两个表相当于数组，数组元素分别是程序头program header 和节头section header。在表中，每个成员（数组元素）都统称为条目，即 entry，一个条目代表一个段或一个节的头描述信息。对于程序头表，它本质上就是用来描述段（segment）的，所以您也可以称它为段头表。ELF header 是个用来描述各种“头”的“头”，程序头表和节头表中的元素也是程序头和节头。

无论是在待重定位文件，还是可执行文件中，文件最开头的部分必须是elf header。在ELF header之后紧挨着的是程序头表，这对于可执行文件是必须存在的，而对于待重定位文件是可选的。其他成员的位置要取决于各头表中的说明。

一些重要的数据结构中用到了自定义的数据类型：

C 语言中的结构体能够很直观地表示物理内存结构：

  • e_ident[16]是16 字节大小的数组，用来表示elf 字符等信息，开头的4 个字节是固定不变的，是elf 文件的魔数，它们分别是0x7f，以及字符串ELF 的ascii码：0x45, 0x4c, 0x46。

  • e_type 占用2 字节，是用来指定elf 目标文件的类型，，ET_LOPROC和ET_HIPROC 这两个类型的取值跨度好大，显得似乎有些怪异，其实把它们搞得如此怪异，是为了突显它们的“与众不同”，它们是与硬件相关的参数，在它们之间的取值用来标识与处理器相关的文件格式。

  • e_machine 占用2 字节，用来描述elf 目标文件的体系结构类型，也就是说该文件要在哪种硬件平台（哪种机器）上才能运行。

  • e_version 占用4 字节，用来表示版本信息。

  • e_entry 占用4 字节，用来指明操作系统运行该程序时，将控制权转交到的虚拟地址。

  • e_phoff 占用4 字节，用来指明程序头表（program header table）在文件内的字节偏移量。如果没有程序头表，该值为0。

  • e_shoff 占用4 字节，用来指明节头表（section header table）在文件内的字节偏移量。若没有节头表，该值为0。

  • e_flags 占用4 字节，用来指明与处理器相关的标志

  • e_ehsize 占用2 字节，用来指明elf header 的字节大小。

  • e_phentsize 占用2 字节，用来指明程序头表（program header table）中每个条目（entry）的字节大小，即每个用来描述段信息的数据结构的字节大小，该结构是后面要介绍的struct Elf32_Phdr。

  • e_phnum 占用2 字节，用来指明程序头表中条目的数量。实际上就是段的个数。

  • e_shentsize 占用2 字节，用来指明节头表（section header table）中每个条目（entry）的字节大小，即每个用来描述节信息的数据结构的字节大小。

  • e_shnum 占用2 字节，用来指明节头表中条目的数量。实际上就是节的个数。

  • e_shstrndx 占用2 字节，用来指明string name table 在节头表中的索引index。

程序头表中的条目的数据结构，这是用来描述各个段的信息用的，此段是指程序中的某个数据或代码的区域段落：

  • p_type 占用4 字节，用来指明程序中该段的类型。
  • p_offset 占用4 字节，用来指明本段在文件内的起始偏移字节。
  • p_vaddr 占用4 字节，用来指明本段在内存中的起始虚拟地址。
  • p_paddr 占用4 字节，仅用于与物理地址相关的系统中，因为System V 忽略用户程序中所有的物理地址，所以此项暂且保留，未设定。
  • p_filesz 占用4 字节，用来指明本段在文件中的大小。
  • p_memsz 占用4 字节，用来指明本段在内存中的大小。
  • p_flags 占用4 字节，用来指明与本段相关的标志，本段具有可执行权限、可写权限、可读权限、与操作系统相关、处理器相关
  • p_align 占用4 字节，用来指明本段在文件和内存中的对齐方式。如果值为0 或1，则表示不对齐。否则p_align 应该是2 的幂次数。

通过 dd 命令往磁盘上写，命令如下。dd if= kernel.bin of=/your_path/hd60M.img bs=512 count=200 seek=9 conv=notrunc，seek 为9，目的是跨过前9 个扇区（第0～8 个扇区），我们在第9 个扇区写入。count 为200，目的是一次往参数of 指定的文件中写入200 个扇区。

特权级深入浅出

操作系统位于最内环的0 级特权，它要直接控制硬件，掌控各种核心数据，所以它的权利必须最大。系统程序分别位于
1 级特权和2 级特权，运行在这两层的程序一般是虚拟机、驱动程序等系统服务。在最外层的是3 级特权，我们的用户程序
就运行在此层，用户程序被设计为“有需求时找操作系统”，所以它不需要太大的能力，能完成一般工作即可，因此它的权利最弱。

TSS，即Task State Segment，意为任务状态段，它是处理器在硬件上原生支持多任务的一种实现方式，TSS 是一种数据结构，它用于存储任务的环境。TSS 是每个任务都有的结构，它用于一个任务的标识，程序拥有此结构才能运行。

任务在特权级变换时，本质上是处理器的当前特权级在变换，由一个特权级变成了另外一个特权级。处理器在不同特权级下，应该用不同特权级的栈，原因是如果在同一个栈中容纳所有特权级的数据时，这种交叉引用会使栈变得非常混乱，并且，用一个栈容纳多个特权级下的数据，栈容量有限，这很容易溢出。

特权级转移分为两类，一类是由中断门、调用门等手段实现低特权级转向高特权级，另一类则相反，是由调用返回指令从高特权级返回到低特权级，这是唯一一种能让处理器降低特权级的情况。

  • 对于特权级由低到高的情况，由于不知道目标特权级对应的栈地址在哪里，所以要提前把目标栈的地址记录在某个地方，当处理器向高特权级转移时再从中取出来加载到SS 和ESP 中以更新栈，这个保存的地方就是TSS。处理器会自动地从TSS 中找到对应的高特权级栈地址。也就是说，除了调用返回外，处理器只能由低特权级向高特权级转移，TSS 中所记录的栈是转移后的高特权级目标栈，所以它一定比当前使用的栈特权级要高，只用于向更高特权级转移时提供相应特权的栈地址。

所以，TSS 中不需要记录3 特权级的栈，因为3 特权级是最低的，没有更低的特权级会向它转移。不是每个任务都有4 个栈，一个任务可有拥有的栈的数量取决于当前特权级是否还有进一步提高的可能，即取决于它最低的特权级别。比如3 特权级的程序，它是最低的特权级，还能提升三级，所以可额外拥有2、1、0 特权级栈，用于将特权分别转移到2、1、0 级时使用。

对于由高特权返回到低特权级的情况，处理器是不需要在TSS 中去寻找低特权级目标栈的。TSS 中只记录2、1、0 特权级的栈，而且，低特权级栈的地址其实已经存在了，这是由处理器的向高特权级转移指令（如int、call 等）实现的机制决定的。

当处理器由低向高特权级转移时，它自动地把当时低特权级的栈地址（SS 和ESP）压入了转移后的高特权级所在的栈中，所以，当用返回指令如retf 或iret 从高特权级向低特权级返回时，处理器可以从当前使用的高特权级的栈中获取低特权级的栈段选择子及偏移量。当下次处理器再进入到高特权级时，它依然会在 TSS 中寻找对应的高特权级栈，而TSS 中栈指针值都是固定的，每次进入高特权级都会重复使用它们。

TSS 是硬件支持的系统数据结构，它和GDT 等一样，由软件填写其内容，由硬件使用。GDT 也要加载到寄存器GDTR 中才能被处理器找到，TSS 也是一样，它是由TR（Task Register）寄存器加载的，每次处理器执行不同任务时，将TR 寄存器加载不同任务的TSS 就成了。

计算机特权级的标签体现在DPL、CPL 和RPL，在 CPU 中运行的是指令，其运行过程中的指令总会属于某个代码段，该代码段的特权级，也就是代码段描述符中的DPL，便是当前CPU 所处的特权级，这个特权级称为当前特权级，即CPL（Current Privilege Level），它表示处理器正在执行的代码的特权级别。当前特权级实际上是指处理器当前所处的特权级，是指处理器的特权角色，在任意时刻，当前特权级CPL 保存在CS 选择子中的RPL 部分。

代码是资源的请求者，代码段寄存器CS所指向的是处理器中当前运行的指令，所以代码段寄存器CS 中选择子的RPL 位称为当前特权级CPL，只是代码段寄存器CS 中的RPL 是CPL，其他段寄存器中选择子的RPL 与CPL 无关，因为CPL 是针对具有“能动性”的访问者（执行者）来说的，代码是执行者，它表示访问的请求者，所以CPL 只存放在代码段寄存器CS 中低2 位的RPL 中。

DPL，即Descriptor Privilege Level，描述符特权级，DPL 字段在段描述符中占2位，表示4 个组合，00b、01b、10b、11b，所有特权级都齐了。DPL 是段描述符所代表的内存区域的“门槛”权限，访问者能否迈过此门槛访问到本描述符所代表的资源，其特权级至少要等于这个门槛。

对于受访者为数据段（段描述符中 type 字段中未有X 可执行属性）来说：只有访问者的权限大于等于该DPL 表示的最低权限才能够继续访问，否则连这个门槛都迈不过去。对于受访者为代码段（段描述符中 type 字段中含有X 可执行属性）来说：只有访问者的权限等于该DPL 表示的最低权限才能够继续访问，CPU 没有理由先自降等级后再去做某事。

处理器从中断处理程序中返回到用户态的时候是唯一一种处理器会从高特权降到低特权运行的情况。中断处理都是在 0 特权级下进行的，因为中断的发生多半是外部硬件发生了某种状况或发生了某种不可抗力事件而必须要通知CPU 导致的，所以，在中断的处理过程中需要具备访问硬件的能力。再者，有些中断处理中需要的指令只能在0 特权级下使用，这部分指令称为特权指令。除了从中断处理过程返回外，任何时候CPU 都不允许从高特权级转移到低特权级。比目标代码段特权级低的访问者也会被拒绝访问目标代码段。综上所述，对于受访问者为代码段的情况，只能是平级访问。

一致性代码段也称为依从代码段，Conforming，用来实现从低特权级的代码向高特权级的代码转移。一致性代码段是指如果自己是转移后的目标段，自己的特权级（DPL）一定要大于等于转移前的CPL，即数值上CPL≥DPL，也就是一致性代码段的DPL 是权限的上限，任何在此权限之下的特权级都可以转到此代码段上执行。

该关系用公式表示如下：在数值上，CPL≥一致性代码段的DPL，一致性代码段的一大特点是转移后的特权级不与自己的特权级（DPL）为主，而是与转移前的低特权级一致，听从、依从转移前的低特权级，这就是它称为“依从、一致”的原因。

顺便说一句，代码段可以有一致性和非一致性之分，但所有的数据段总是非一致的，即数据段不允许被比本数据段特权级更低的代码段访问。

处理器只有通过“门结构”才能由低特权级转移到高特权级，是记录一段程序起始地址的描述符。门结构是记录一段程序起始地址的描述符。有一种称为“门描述符”的结构，用来描述一段程序。进入这种神奇的“门”，处理器便能转移到更高的特权级上。
门描述符同段描述符类似，都是 8 字节大小的数据结构，用来描述门中通向的代码。

除了任务门外，其他三种门都是对应到一段例程，即对应一段函数，而不是像段描述符对应的是一片内存区域。任务门描述符可以放在GDT、LDT 和IDT中，调用门可以位于GDT、LDT 中，中断门和陷阱门仅位于IDT 中。

任务门、调用门都可以用call 和jmp 指令直接调用，原因是这两个门描述符都位于描述符表中，要么是GDT，要么是LDT，访问它们同普通的段描述符是一样的，也必须要通过选择子，因此只要在call 或jmp 指令后接任务门或调用门的选择子便可调用它们了。陷阱门和中断门只存在于IDT 中，因此不能主动调用，只能由中断信号来触发调用。任务门有点特殊，它用任务TSS 的描述符选择子来描述一个任务。

  1. 调用门：call 和jmp 指令后接调用门选择子为参数，以调用函数例程的形式实现从低特权向高特权转移，可用来实现系统调用。call 指令使用调用门可以实现向高特权代码转移，jmp 指令使用调用门只能实现向平级代码转移。
  2. 中断门：以 int 指令主动发中断的形式实现从低特权向高特权转移，Linux 系统调用便用此中断门实现，就是那个著名的int 0x80。中断门只允许存在于IDT 中。
  3. 陷阱门：以 int3 指令主动发中断的形式实现从低特权向高特权转移，这一般是编译器在调试时用
  4. 任务门：任务以任务状态段TSS 为单位，用来实现任务切换，它可以借助中断或指令发起。当中断发生时，如果对应的中断向量号是任务门，则会发起任务切换。也可以像调用门那样，用call 或jmp 指令后接任务门的选择子或任务TSS 的选择子。

门的“门槛”是访问者特权级的下限，访问者的特权级再低也不能比门描述符的特权级DPL 低，否则访问者连门都进不去，更谈不上使用调用门。门描述符的DPL 特权级要低于或等于当前特权级CPL，即数值上CPL≤门的DPL，此处可见，门描述符相当于数据段描述符一样，只允许比自己特权级高或相同特权级的程序访问。

门的“门框”是访问者特权级的上限，访问者的特权级再高也不能比门描述符中目标程序所在代码段的DPL 高。门中包含的目标程序所在的段的特权级DPL 要高于或等于当前特权级CPL，即数值上CPL≥目标代码段DPL，进门之后，处理器将以目标代码段DPL 为当前特权级CPL。

各种门结构存在的目的就是为了让处理器提升特权级，这样处理器才能够做一些低特权级下无法完成的工作。调用门是一个描述符，称为门描述符，其中记录的是内核服务程序所在代码段的选择子及在代码段中的偏移地址。门描述符定义在全局描述符表GDT 和局部描述符表LDT 中，所以，要想使用调用门，就要通过门描述符的选择子。

  • 在用户程序中有一句代码call 调用门选择子，call 指令可以使用调用门，参数就是调用门的选择子，该选择子指向GDT 或LDT 中的某个门描述符，不管选择子中的TI 位是0，还是1，我们暂且认为它是指向GDT 中的调用门。处理器用门描述符选择子的高13 位（索引位）乘以8 作为该描述符在GDT 中的偏移量，再加上寄存器GDTR 中的GDT 基地址，最终找到了门描述符的地址，它位于GDT中从0 起的第3 个描述符位置。
  • 在该描述符中记录的是内核例程的地址。我们知道，在保护模式下描述某个内存地址是离不开选择子和偏移量的，所以，门描述符中记录的是内核例程所在代码段的选择子及偏移量。处理器再用代码段选择子，重复之前的步骤，用选择子中高13位的索引值乘以8，再加上GDT 基址，所得到的地址为该代码段选择子所指向的内核代码段描述符地址，在该内核代码段描述符中找到内核代码段基址，用它加上门描述符中记录的内核例程在代码段中的偏移量，最终得到内核例程的起始地址。

为了方便软件开发人员，处理器在固件上实现参数的自动复制，即，将用户进程压在3 特权级栈中的参数自动复制到0 特权级栈中。所以，在图中，其高32 位的起始处有个参数个数，这是处理器将用户提供的参数复制给内核时需要用到的，参数在栈中的顺序是挨着的，所以处理器只需要知道复制几个参数就行了，这就是调用门描述符中“参数个数”的作用，它是专门给处理器准备的。该位是用5 个BIT 来表示的，所以最多可传递31 个参数。

调用门可以用call 指令和jmp 指令调用，jmp 属于一去不回头的指令，基本上用在不需要从调用门返回的场合。call 指令由于会在栈中留下返回地址，所以在执行retf 指令时还能返回。

调用门的过程保护

假设用户进程要调用某个调用门，该门描述符中参数的个数是2，也就是用户进程需要为该调用门提供2 个参数才行。调用前的当前特权级为3，调用后的新特权级为0，所以调用门转移前用的是3 特权级栈，调用后用的是0 特权级栈。

  • 现在为此调用门提供2个参数，这是在使用调用门前完成的，目前是在3 特权级，所以要在特权级栈中压入参数，分别是参数1 和参数2
  • 在这一步骤中要确定新特权级使用的栈，新特权级就是未来的CPL，它就是转移后的目标代码段的DPL。所以，根据门描述符中选择子对应的目标代码段的DPL，处理器自动在TSS 中找到合适的栈段选择子SS 和栈指针ESP，它们作为转移后新的栈，记作SS_new、ESP_new。
  • 检查新栈段选择子对应的描述符的DPL 和TYPE，如果未通过检查则处理器引发异常。
  • 如果转移后的目标代码段DPL 比CPL 要高，说明栈段选择子SS_new 是特权级更高的栈，这说明需要特权级转换，需要切换到新栈，将旧栈段选择子记作SS_old，旧栈指针记作ESP_old。由于转移前的旧栈段选择子SS_old 及指针ESP_old 得保存到新栈中，这样在高特权级的目标程序执行完成后才能通过retf 指令恢复旧栈。将SS_new 加载到栈段寄存器SS，esp_new 加载到栈指针寄存器esp，这样便启用了新栈。
  • 在使用新栈后，将上一步中临时保存的SS_old 和ESP_old 压入到当前新栈中，也就是0 特权级栈。由于咱们讨论的是32 位模式，故栈操作数也是32 位，SS_old 只是16 位数据，将其高16 位用0 填充后入栈保存。

  • 在这一步中要将用户栈中的参数复制到转移后的新栈中，根据调用门描述符中的“参数个数”决定复制几个参数。
  • 由于调用门描述符中记录的是目标程序所在代码段的选择子及偏移地址，这意味着代码段寄存器CS要用该选择子重新加载，只要段寄存器被加载，段描述符缓冲寄存器就会被刷新，从而相当于切换到了新段上运行，这是段间远转移，所以需要将当前代码段CS 和EIP 都备份在栈中，这两个值分别记作CS_old 和EIP_old，由于CS_old 只是16 位数据，在32 位模式下栈操作数大小是32 位，故将其高16 位用0 填充后再入栈。这两个值是将来恢复用户进程的关键，也就是从内核进程中返回时用的地址。
  • 一切就绪，只差运行调用门中指向的程序啦，于是，把门描述符中的代码段选择子装载到代码段寄存器CS，把偏移量装载到指令指针寄存器EIP。

下面是利用 retf 指令从调用门返回的过程：

  • 当处理器执行到retf 指令时，它知道这是远返回，所以需要从栈中返回旧栈的地址及返回到低特权级的程序中。这时候它要进行特权级检查。先检查栈中CS选择子，根据其RPL位，即未来的CPL，判断在返回过程中是否要改变特权级。
  • 此时栈顶应该指向栈中的EIP_old。在此步骤中获取栈中CS_old 和EIP_old，根据该CS_old 选择子对应的代码段的DPL 及选择子中的RPL 做特权级检查，规则不再赘述。如果检查通过，先从栈中弹出32 位数据，即EIP_old 到寄存器EIP，然后再弹出32 位数据CS_old，此时要临时处理一下，由于所有的段寄存器都是16 位的，当然包括CS，所以丢弃CS_old 的高16 位，将低16 位加载到CS 寄存器。此时栈指针ESP_new 指向最后一个参数。
  • 如果返回指令retf 后面有参数，则增加栈指针ESP_new 的值，以跳过栈中参数，retf 后面的参数应该等于参数个数*参数大小。此时，栈指针ESP_new 便指向ESP_old。
  • 如果在第1 步中判断出需要改变特权级，从栈中弹出32 位数据ESP_old 到寄存器ESP。同样寄存器 SS 也是16 位的，故再弹出32 位的SS_old，只将其低16 位加载到寄存器SS，此时恢复了旧栈。相当于丢弃寄存器SS 和ESP 中原有的SS_new 和ESP_new。

RPL，Request Privilege Level，请求特权级，代表真正请求者的特权级，其实是代表真正资源需求者的CPL。在请求某特权级为DPL 级别的资源时，参与特权检查的不只是CPL，还要加上RPL，CPL 和RPL的特权必须同时大于等于受访者的特权DPL，即：数值上 CPL≥DPL 并且RPL≤DPL

RPL 引入的目的是避免低特权级的程序访问高特权级的资源。DPL 相当于权限的门槛，它代表进入本描述符所对应内存区域的最低权限，任何想迈过这个门槛的人，它的RPL 和CPL 权限必须都要大于等于DPL，即数值上CPL≤DPL && RPL≤DPL。用来检查当前请求者和真正的资源需求方是否都具有访问受访者的资格。处理器的特权检查，都是只发生在往段寄存器中加载选择子访问描述符的那一瞬间，所以，RPL 放在选择子中是多么的合理。

总结下不通过调用门、直接访问一般数据和代码时的特权检查规则，

  • 对于受访者为代码段时：
    • 如果目标为非一致性代码段，要求：数值上 CPL=RPL=目标代码段DPL
    • 如果目标为一致性代码段，要求：数值上（CPL≥目标代码段DPL && RPL≥目标代码段DPL）
    • 受访者若为代码，只有在特权级转移时才会被用到，所以有关代码的特权检查都发生在能够改变代码段寄存器CS 和指令指针寄存器EIP 的指令中，即这些指令要么改变EIP，要么改变CS 和EIP。例如call、jmp、int、ret、sysexit 等能改变程序执行流的指令。
  • 对于受访者为数据段时：
    • 数值上（CPL ≤目标数据段DPL && RPL ≤ 目标数据段 DPL）
  • 栈段的特权级检查比较特殊，因为在各个特权级下，处理器都要有相应的栈（后面会说到），也就是说栈的特权等级要和CPL 相同。所以往段寄存器SS 中赋予数据段选择子时，处理器要求CPL 等于栈段选择子对应的数据段的DPL，即数值上CPL = RPL = 用作栈的目标数据段DPL。
  • 受访者若为数据，特权级检查会发生在往数据段寄存器中加载段选择子的时候，数据段寄存器包括DS 和附加段寄存器ES、FS、GS。

RPL 是位于选择子中的，所以，要看当前运行的程序在访问数据或代码时用的是谁提供的选择子，如果用的
是自己提供的选择子，那肯定CPL 和RPL 都出自同一个程序；如果选择子是别人提供的，那就有可能RPL和CPL 出自两段程序。CPL 是对当前正在运行的程序而言的，而RPL 有可能是正在运行的程序。

在保护模式下，处理器中的“阶级”不仅体现在数据和代码的访问，还体现在指令中。

  • 一方面将指令分级的原因是有些指令的执行对计算机有着严重的影响，它们只有在0 特权级下被执行，因此被称为特权指令（Privilege Instruction）。
  • 另一方面体现在I/O 读写控制上。IO 读写特权是由标志寄存器eflags 中的IOPL 位和TSS 中的IO 位图决定的，它们用来指定执行IO 操作的最小特权级。IO 相关的指令只有在当前特权级大于等于IOPL 时才能执行，所以它们称为IO 敏感指令（I/O Sensitive Instruction），如果当前特权级小于IOPL 时执行这些指令会引发处理器异常。这类指令有in、out、cli、sti。

在eflags 寄存器中第12～13 位便是IOPL（I/O Privilege Level），即IO 特权级，它除了限制当前任务进行IO 敏感指令的最低特权级外，还用来决定任务是否允许操作所有的IO 端口，IOPL 位是打开所有IO 端口的开关。每个任务（内核进程或用户进程）都有自己的eflags 寄存器，所以每个任务都有自己的IOPL，它表示当前任务要想执行全部IO 指令的最低特权级，也就是处理器最低的CPL，只有任务的当前特权级大于等于IOPL才允许执行全部IO 指令，即数值上CPL≤IOPL。通过IO 位图来设置部分端口的访问权限。

I/O 位图是位于TSS 中的，它可以存在，也可以不存在，它只是用来设置对某些特定端口的访问，没有它的话便默认为禁止访问所有端口。有一项是“I/O 位图在TSS 中的偏移地址”，它在TSS 中偏移102 字节的地方，占2 个字节空间，就是图5-47 的左上角，此处用来存储I/O 位图的偏移地址，即此地址是I/O 位图在TSS 中以0 为起始的偏移量。如果某个TSS 存在I/O 位图的话，此处用来保存它的偏移地址。

TSS 中如果有I/O 位图的话，它将位于TSS 的顶端，这就是TSS 的实际尺寸并不固定的原因，当包括I/O 位图时，其大小是“I/O 位图偏移地址”+8192+1 字节，结尾这个1 字节是I/O 位图中最后的0xff。此字节有两个作用。

  • 第一，处理器允许I/O 位图中不映射所有的端口，即I/O 位图长度可以不足8KB，但位图的最后一字节必须为0xFF。如果在位图范围外的端口，处理器一律默认禁止访问。这样一来，如果位图最后一字节的0xFF 属于全部65536 个端口范围之内，字节各位全为1 表示禁止访问此字节代表的全部端口，这并没什么过错。
  • 第二，如果该字节已经超过了全部端口的范围，它并不用来映射端口，只是用来作为位图的边界标记，用于跨位图最后一个字节时的“余量字节”。避免越界访问TSS 外的内存。

完善内核

函数调用约定简介

在栈中保存、来传递参数：

  1. 首先，每个进程都有自己的栈，这就是每个内存自己的专用内存空间。
  2. 其次，保存参数的内存地址不用再花精力维护，已经有栈机制来维护地址变化了，参数在栈中的位置可以通过栈顶的偏移量来得到。

我们要解决的是参数压栈顺序问题，和栈空间的清理工作呢。我们按照由谁来清理栈空间分类，目前的调用约定见表

stdcall 的调用约定意味着：

  1. 调用者将所有参数从右向左入栈。
  2. 被调用者清理参数所占的栈空间。

主调用者：

1
2
3
4
; 从右到左将参数入栈
 push 2 ;压入参数b
 push 3 ;压入参数a
 call subtract ;调用函数subtract

以上是主调函数，现在看下被调函数 subtract 中做了什么。
被调用者：

1
2
3
4
5
6
7
8
9
10
11
 push ebp ;压入ebp 备份
 mov ebp,esp ;将esp 赋值给ebp
;用ebp 作为基址来访问栈中参数
 mov eax,[ebp+0x8] ;偏移8 字节处为第1 个参数a
 add eax,[ebp+0xc] ;偏移0xc 字节处是第2 个参数b
;参数a 和b 相加后存入eax
 mov esp,ebp ;为防止中间有入栈操作,用ebp 恢复esp
;本句在此例子中可有可无,属于通用代码
 pop ebp ;将ebp 恢复
 ret 8 ;数字8 表示返回后使esp+8
;函数返回时由被调函数清理了栈中参数

stdcall 是被调用者负责清理栈空间，subtract需要在返回前或返回时完成。在返回前清理栈相对困难一些，清理栈是指将栈顶回退到参数之前。因为返回地址在参数之下，ret 指令执行时必须保证当前栈顶是返回地址。所以通常在返回时“顺便”完成。于是ret 指令便有了这样的变体，其格式为：ret 16 位立即数，这是允许在返回时顺便再将栈指针 esp 修改的指令。

cdecl 调用约定由于起源于C 语言，所以又称为C 调用约定，是C 语言默认的调用约定，最大的亮点是它允许函数中参数的数量不固定。cdecl 的调用约定意味着。

  1. 调用者将所有参数从右向左入栈。
  2. 调用者清理参数所占的栈空间。
1
2
int subtract(int a, int b); //被调用者
int sub = subtract (3,2); // 主调用者

主调用者：

1
2
3
4
5
; 从右到左将参数入栈
push 2 ;压入参数b
push 3 ;压入参数a
call subtract ;调用函数subtract
add esp, 8 ;回收（清理）栈空间

被调用者：

1
2
3
4
5
6
7
8
9
10
push ebp ;压入ebp 备份
mov ebp,esp ;将esp 赋值给ebp
;用ebp 作为基址来访问栈中参数
mov eax,[ebp+0x8] ;偏移8 字节处为第1 个参数a
add eax,[ebp+0xc] ;偏移0xc 字节处是第2 个参数b
;参数a 和b 相加后存入eax
mov esp,ebp ;为防止中间有入栈操作，用ebp 恢复esp
;本句在此例子中可有可无,属于通用代码
pop ebp ;将ebp 恢复
ret

通过将esp 加上8 字节的方式回收了参数a 和参数b，本例中的其他代码都和stdcall 一样。

汇编语言和 C 语言混合编程

BIOS 中断走的是中断向量表，所以有很多中断号给它用，而系统调用走的是中断描述符表中的一项而已，所以只用了第0x80 项中断。系统调用的子功能要用eax 寄存器来指定。我们要看看系统调用输入参数的传递方式：

  • 当输入的参数小于等于5 个时，Linux 用寄存器传递参数。当参数个数大于5 个时，把参数按照顺序放入连续的内存区域，并将该区域的首地址放到ebx 寄存器。这里我们只演示参数小于等于5 个的情况。
  • eax 寄存器用来存储子功能号（寄存器eip、ebp、esp 是不能使用的）。5 个参数存放在以下寄存器中，
    传送参数的顺序如下。
    • ebx 存储第1 个参数。
    • ecx 存储第2 个参数。
    • edx 存储第3 个参数。
    • esi 存储第4 个参数。
    • edi 存储第5 个参数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
section .data
str_c_lib: db "c library says: hello world!", 0xa ;0xa 为LF ASCII 码
str_c_lib_len equ $-str_c_lib
str_syscall: db "syscall says: hello world!", 0xa
str_syscall_len equ $-str_syscall
section .text
global _start

_start:
;;;;;;;;;;;;; 方式1: 模拟C 语言中系统调用库函数write ;;;;;;;;;;;;;
push str_c_lib_len ;按照C 调用约定压入参数
push str_c_lib
push 1
call simu_write ;调用下面定义的simu_write
add esp,12 ;回收栈空间

;;;;;;;;;;;;; 方式2: 跨过库函数，直接进行系统调用 ;;;;;;;;;;;;;
mov eax, 4 ;第4 号子功能是write 系统调用（不是C 库函数write）
mov ebx, 1
mov ecx, str_syscall
mov edx, str_syscall_len
int 0x80 ;发起中断，通知Linux 完成请求的功能
;;;;;;;;;;;;; 退出程序 ;;;;;;;;;;;
mov eax,1 ;第1 号子功能是exit
int 0x80 ;发起中断，通知Linux 完成请求的功能
;;;;;;;下面自定义的simu_write 用来模拟C 库中系统调用函数write

;;;;;;这里模拟它的实现原理
simu_write:
push ebp ;备份ebp
mov ebp,esp
mov eax,4 ;第4 号子功能是write 系统调用（不是C 库函数write）
mov ebx, [ebp+8] ;第1 个参数
mov ecx, [ebp+12] ;第2 个参数
mov edx, [ebp+16] ;第3 个参数
int 0x80 ;发起中断，通知Linux 完成请求的功能
pop ebp ;恢复ebp
ret

第 11～17 行是在模拟调用C 库函数write 的方式。这里是按照C 调用约定将参数从右到左依次入栈，随后调用simu_write 实现字符串打印功能。
第 19～24 行是在演示第2 种系统调用的方式，这是最简单直接可依赖的方式。第0～24 行是在eax中赋予子功能号，参数按照顺序依次写入对应的寄存器。第 31～40 行是simu_write 的实现，它内部在本质上和第2 种方式一样，都是在内部调用int 指令直接和系统通信实现系统调用。

内联汇编

内联汇编称为inline assembly，GCC 支持在C 代码中直接嵌入汇编代码，所以称为GCC inline assembly。GCC只支持AT&T汇编，下表是AT&T汇编和Intel汇编的区别：

在 Intel 语法中，立即数就是普通的数字，如果让立即数成为内存地址，需要将它用中括号括起来，[立即数]这样才表示以“立即数”为地址的内存。而 AT&T 认为，内存地址既然是数字，那数字也应该被当作内存地址，所以，数字被优先认为是内存
地址，也就是说，操作数若为数字，则统统按以该数字为地址的内存来访问。这样，立即数的地位比较次要了，如果想表示成单纯的立即数，需要额外在前面加个前缀$。

在 AT&T 中的内存寻址有固定的格式。segreg（段基址）：base_address(offset_address,index,size)。该格式对应的表达式为：segreg（段基址）：base_address+ offset_address+ index*size。此表达式的格式和 Intel 32 位内存寻址中的基址变址寻址类似，Intel 的格式：segreg:[base+index*size+offset]

不过与Intel 不同的是AT&T 地址表达式的值是内存地址，直接被当作内存来读写，而不是普通数字。看上去格式有些怪异，但其实这是一种“通用”格式，格式中短短的几个成员囊括了它所有内存寻址的方式，任意一种内存寻址方式，其格式都是这个通用格式的子集，都是格式中各种成员的组合。下面介绍下这些成员项。

  • base_address 是基地址，可以为整数、变量名，可正可负。
  • offset_address 是偏移地址，index 是索引值，这两个必须是那8 个通用寄存器之一。
  • size 是个长度，只能是1、2、4、8（Intel 语法中也是只能乘以这4 个数）。

基本内联汇编是最简单的内联形式，其格式为：asm [volatile] ("assembly code")，各关键字之间可以用空格或制表符分隔，也可以紧凑挨在一起不分隔，各部分意义如下：

  • 关键字 asm 用于声明内联汇编表达式，这是内联汇编固定的部分，不可少。
  • asm 和__asm__是一样的，是由gcc 定义的宏：#define __asm__ asm。
  • 关键字volatile 是可选项，它告诉gcc：“不要修改我写的汇编代码，请原样保留”。volatile和__volatile__是一样的，是由gcc 定义的宏：#define __volatile__ volatile。
  • 汇编代码必须位于圆括号中，而且必须用双引号引起来。
    • 指令必须用双引号引起来，无论双引号中是一条指令或多条指令。
    • 一对双引号不能跨行，如果跨行需要在结尾用反斜杠’'转义。
    • 指令之间用分号’；’、换行符’\n’或换行符加制表符’\n’’\t’分隔。

asm [volatile] (“assembly code”:output : input : clobber/modify)和前面的基本内联汇编相比，扩展内联汇编在圆括号中变成了4 部分，多了output、input 和clobber/modify 三项。其中的每一部分都可以省略，甚至包括assembly code。省略的部分要保留冒号分隔符来占位，如果省略的是后面的一个或多个连续的部分，分隔符也不用保留，比如省略了clobber/modify，不需要保留input 后面的冒号。

  • assembly code：还是用户写入的汇编指令，和基本内联汇编一样。
  • output：output 用来指定汇编代码的数据如何输出给C 代码使用。内嵌的汇编指令运行结束后，如果想将运行结果存储到c 变量中，就用此项指定输出的位置。output 中每个操作数的格式为：操作数修饰符约束名（C 变量名）
  • input：input 用来指定C 中数据如何输入给汇编使用。input 中每个操作数的格式为：[操作数修饰符] 约束名
    • 单独强调一下，以上的output()和input()括号中的是C 代码中的变量，output(c 变量)和input(c 变量)就像C 语言中的函数，将C 变量转换成汇编代码的操作数。
  • clobber/modify：汇编代码执行后会破坏一些内存或寄存器资源，通过此项通知编译器，可能造成寄存器或内存数据的破坏，这样gcc 就知道哪些寄存器或内存需要提前保护起来。

上面所说的“要求”，在扩展内联汇编中称为“约束”，它所起的作用就是把C 代码中的操作数（变量、立即数）映射为汇编中所使用的操作数，实际就是描述C 中的操作数如何变成汇编操作数。这些约束的作用域是input 和output 部分，约束分为四种：

  • 寄存器约束就是要求gcc 使用哪个寄存器，将input 或output 中变量约束在某个寄存器中。常见的寄存器约束有：
    • a：表示寄存器eax/ax/al
    • b：表示寄存器ebx/bx/bl
    • c：表示寄存器ecx/cx/cl
    • d：表示寄存器edx/dx/dl

先看下基本内联汇编，见文件 base_asm.c。

1
2
3
4
5
6
7
8
9
10
11
#include<stdio.h>
int in_a = 1, in_b = 2, out_sum;
void main() {
    asm(" pusha; \
    movl in_a, %eax; \
    movl in_b, %ebx; \
    addl %ebx, %eax; \
    movl %eax, out_sum; \
    popa");
    printf("sum is %d\n",out_sum);
}

加法指令的两个输入操作数是in_a 和in_b，输出和存储在变量out_sum 中。在基本内联汇编中的寄存器用单个%做前缀，在扩展内联汇编中，单个%有了新的用途，用来表示占位符，所以在扩展内联汇编中的寄存器前面用两个%做前缀。再看下用扩展内联汇编是怎么做的，见文件 reg_constraint.c。

1
2
3
4
5
6
#include<stdio.h>
void main() {
    int in_a = 1, in_b = 2, out_sum;
    asm("addl %%ebx, %%eax":"=a"(out_sum):"a"(in_a),"b"(in_b));
    printf("sum is %d\n",out_sum);
}

in_a 和in_b 是在input 部分中输入的，用约束名a 为c 变量in_a 指定了用寄存器eax，用约束名b 为c 变量in_b 指定了用寄存器ebx。addl 指令的结果存放到了寄存器eax 中，在output 中用约束名a 指定了把寄存器eax 的值存储到c 变量out_sum 中。output 中的’=’号是操作数类型修饰符，表示只写，其实就是out_sum=eax的意思。

  • 内存约束是要求gcc 直接将位于input 和output 中的C 变量的内存地址作为内联汇编代码的操作数，不需要寄存器做中转，直接进行内存读写，也就是汇编代码的操作数是C 变量的指针。
    • m：表示操作数可以使用任意一种内存形式。
    • o：操作数为内存变量，但访问它是通过偏移量的形式访问，即包含offset_address 的格式。

下面的文件 mem.c 用约束m 为例。

1
2
3
4
5
6
7
#include<stdio.h>
void main() {
    int in_a = 1, in_b = 2;
    printf("in_b is %d\n", in_b);
    asm("movb %b0, %1;"::"a"(in_a),"m"(in_b));
    printf("in_b now is %d\n", in_b);
}

mem.c 的作用是变量in_b 用in_a 的值替换。in_b 最终变成1。第 5 行是内联汇编，把in_a 施加寄存器约束a，告诉gcc 把变量in_a 放到寄存器eax 中，对in_b 施加内存约束m，告诉gcc 把变量in_b 的指针作为内联代码的操作数。第 5 行对寄存器eax 的引用：%b0，这是用的32 位数据的低8 位，在这里就是指al 寄存器。

立即数即常数，此约束要求gcc 在传值的时候不通过内存和寄存器，直接作为立即数传给汇编代码。由于立即数不是变量，只能作为右值，所以只能放在input 中。

  • i：表示操作数为整数立即数

  • F：表示操作数为浮点数立即数

  • I：表示操作数为0～31 之间的立即数

  • J：表示操作数为0～63 之间的立即数

  • N：表示操作数为0～255 之间的立即数

  • O：表示操作数为0～32 之间的立即数

  • X：表示操作数为任何类型立即数

  • 通用约束：0～9：此约束只用在input 部分，但表示可与output 和input 中第n 个操作数用相同的寄存器或内存。

为方便对操作数的引用，扩展内联汇编提供了占位符，它的作用是代表约束指定的操作数（寄存器、内存、立即数），我们更多的是在内联汇编中使用占位符来引用操作数。占位符分为序号占位符和名称占位符两种。

  • 序号占位符：序号占位符是对在output 和input 中的操作数，按照它们从左到右出现的次序从0 开始编号，一直到9，也就是说最多支持10 个序号占位符。操作数用在 assembly code 中，引用它的格式是%0～9。
%%ebx, %%eax":"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
- "=a"(out_sum)序号为0，%0 对应的是eax。
- "a"(in_a)序号为1，%1 对应的是eax。
- "b"(in_b)序号为2，%2 对应的是ebx。

必须要人为显式地告诉gcc 我们动了寄存器和内存，只要在clobber/modify部分明确写出来就行了，记得要用双引号把寄存器名称引起来，多个寄存器之间用逗号'，'分隔，这里的寄存器不用再加两个'%'啦，只写名称即可，如：```asm("movl %%eax, %0;movl %%eax,%%ebx":"=m" (ret_value)::"bx")```

**机器模式**用来在机器层面上指定数据的大小及格式。GCC 支持内联汇编，由于各种约束均不能确切地表达具体的操作数对象，所以引用了机器模式，用来从更细的粒度上描述数据对象的大小及其指定部分。GCC 根据不同的硬件平台，将机器模式定义在多个文件中，其中所有平台都通用的机器模式定义在gcc/machmode.def 文件中，其他与具体平台相关的机器模式定义在自己的平台路径下。

操作码就是**指定操作数为寄存器中的哪个部分**。寄存器按是否可单独使用，可分成几个部分，拿 eax 举例。
- 低部分的一字节：al
- 高部分的一字节：ah
- 两字节部分：ax
- 四字节部分：eax
- h：输出寄存器高位部分中的那一字节对应的寄存器名称，如ah、bh、ch、dh。
- b：输出寄存器中低部分1 字节对应的名称，如al、bl、cl、dl。
- w：输出寄存器中大小为2 个字节对应的部分，如ax、bx、cx、dx。
- k：输出寄存器的四字节部分，如eax、ebx、ecx、edx。

# 中断
操作系统是中断驱动的

## 中断分类
把中断按事件来源分类，来自CPU 外部的中断就称为外部中断，来自CPU 内部的中断称为内部中断。

### 外部中断
外部中断是指来自CPU 外部的中断，而外部的中断源必须是某个硬件，所以外部中断又称为硬件中断。**所以一种可行的方案是CPU 提供统一的接口作为中断信号的公共线路，所有来自外设的中断信号都共享公共线路连接到CPU**。CPU 为大家提供了两条信号线。外部硬件的中断是通过两根信号线通知CPU 的，这两根信号线就是INTR（INTeRrupt）和NMI（Non Maskable Interrupt）。
![](/img/1593968345.jpg)

CPU 为了区分两种中断类型，**通过不同的引脚加以区分**，同一种类型的中断共用同一根信号线进入CPU，这样CPU 就不需要在每次收到中断时再辨析是哪种类型了。**只要从INTR 引脚收到的中断都是不影响系统运行的**，可以随时处理；而只要从NMI 引脚收到的中断，CPU 都没有运行下去的必要了。

可屏蔽的意思是此外部设备发出的中断，CPU 可以不理会，因为它不会让系统宕机，所以可以通过eflags寄存器的IF 位将所有这些外部设备的中断屏蔽。**把中断处理程序分为上半部和下半部两部分，把中断处理程序中需要立即执行的部分划分到上半部，中断处理程序中那些不紧急的部分则被推迟到下半部中去完成**。当上半部执行完成后就把中断打开了，下半部也属于中断处理程序，所以中断处理程序下半部则是在开中断的情况下执行的。**不可屏蔽中断是通过NMI 引脚进入CPU 的，它表示系统中发生了致命的错误**。不可屏蔽中断可以理解成“即将宕机”中断。

CPU 收到中断后，通过中断向量表或中断描述符表（中断向量表是实模式下的中断处理程序数组，在保护模式下已经被中断描述符表代替）来实现的：
- **首先为每一种中断分配一个中断向量号，中断向量号就是一个整数**，它就是中断向量表或中断描述符表中的索引下标，用来索引中断项。
- 中断发起时，**相应的中断向量号通过NMI 或INTR引脚被传入CPU**，CPU 根据此中断向量号在中断向量表或中断描述符表中检索对应的中断处理程序并去执行。

### 内部中断
内部中断可分为**软中断**和**异常**。
- 软中断，就是**由软件主动发起的中断**，它是主观上的，并不是客观上的某种内部错误。以下是可以发起中断的指令。
    - `int 8位立即数`。8位立即数可表示256种中断，这与处理器所支持的中断数是相吻合的。
    - `int3`。`int3`是调试断点指令，其所触发的中断向量号是3。
        - 我们用gdb 或bochs 调试程序时，实际上就是调试器fork 了一个子进程，**子进程用于运行被调试的程序**。
        - 调试器中经常要设置断点，其原理就是**父进程修改了子进程的指令，将其用int3指令替换**，从而子进程调用了int3 指令触发中断。
        - 用此指令实现调试的原理是int3 指令的机器码是0xcc，断点本质上是指令的地址，**调试器（父进程）将被调试进程（子进程）断点起始地址的第1 个字节备份好之后，在原地将该指令的第1 字节修改为0xcc**。
        - 这样指令执行到断点处时，会去执行机器码为0xcc 的int3 指令，该指令会触发3 号中断，从而会去执行3 号中断对应的中断处理程序。
        - 中断处理程序将当前的寄存器和相关内存单元压栈保存，用户在查看寄存器和变量时就是从栈中获取的。
        - 当恢复执行所调试的进程时，中断处理程序需要将之前备份的1 字节还原至断点处，然后恢复各寄存器和内存单元的值，修改返回地址为断点地址，用iret 指令退出中断，返回到用户进程继续执行。
    - **into**。这是中断溢出指令，它所触发的中断向量号是4。不过，能否引发4 号中断是要看eflags 标志寄存器中的OF 位是否为1，如果是1 才会引发中断。
    - **bound**。这是检查数组索引越界指令，它可以触发5 号中断，用于检查数组的索引下标是否在上下边界之内。该指令格式是`bound 16/32位寄存器, 16/32位内存`。目的操作数是用寄存器来存储的，其内容是待检测的数组下标值。源操作数是内存，其内容是数组下标的下边界和上边界。当执行bound 指令时，若**下标处于数组索引的范围之外，则会触发5 号中断**。
    - **ud2**。未定义指令，这会触发第6 号中断。该指令表示指令无效，CPU 无法识别。
    

异常是另一种内部中断，是指令执行期间CPU 内部产生的错误引起的。由于是运行时错误，所以它不受标志寄存器eflags 中的IF 位影响，无法向用户隐瞒。对于中断是否无视eflags 中的IF 位，可以这么理解：
- 首先，只要是导致运行错误的中断类型都会无视IF 位，不受IF 位的管束，如NMI、异常。
- 其次，由于int n 型的软中断用于实现系统调用功能，不能因为IF 位为0 就不顾用户请求，所以为了用户功能正常，软中断必须也无视IF 位。
- 总结：只要中断关系到“正常”运行，就不受IF 位影响。

并不是所有的异常都很致命，按照轻重程度，可以分为以下三种。
- **Fault，也称为故障**。这种错误是可以被修复的一种类型。当发生此类异常时CPU 将机器状态恢复到异常之前的状态，之后调用中断处理程序时，**CPU 将返回地址依然指向导致fault 异常的那条指令**。如操作系统课程中所说的缺页异常page fault，
- **Trap，也称为陷阱**。此异常通常用在调试中，比如int3 指令便引发此类异常，为了让中断处理程序返回后能够继续向下执行，CPU将中断处理程序的返回地址指向导致异常指令的下一个指令地址。
- **Abort，也称为终止**，这是最严重的异常类型，一旦出现，程序将无法继续运行。导致此异常的错误通常是硬件错误，或者某些系统数据结构出错。

![](/img/1593969804.jpg)

**中断机制的本质是来了一个中断信号后，调用相应的中断处理程序**。为了统一中断管理，把来自外部设备、内部指令的各种中断类型统统归结为一种管理方式，即**为每个中断信号分配一个整数，用此整数作为中断的ID，而这个整数就是所谓的中断向量**，然后用此ID 作为中断描述符表中的索引，这样就能找到对应的表项，进而从中找到对应的中断处理程序。

## 中断描述符表
**中断描述符表（Interrupt Descriptor Table，IDT）是保护模式下用于存储中断处理程序入口的表**，当CPU 接收一个中断时，需要用中断向量在此表中检索对应的描述符，在该描述符中找到中断处理程序的起始地址，然后执行中断处理程序。实模式下用于存储中断处理程序入口的表叫**中断向量表（Interrupt Vector Table，IVT）**。

**位于地址0～0x3ff 的是中断向量表IVT，它是实模式下用于存储中断处理程序入口的表**。对比中断向量表，中断描述符表有两个区别。
- 中断描述符表地址不限制，在哪里都可以。
- 中断描述符表中的每个描述符用8 字节描述。

在CPU 内部有个**中断描述符表寄存器**（IDTR），该寄存器分为两部分：**第0～15 位是表界限**，即IDT 大小减1，第16～47 位是**IDT 的基地址**，只有寄存器IDTR指向了IDT，当CPU 接收到中断向量号时才能找到中断向量处理程序，这样中断系统才能正常运作。同加载GDTR 一样，加载IDTR 也有个专门的指令—lidt，其用法是：`lidt 48 位内存数据`，在这48 位内存数据中，前16 位是IDT 表界限，后32 位是IDT 线性基地址。

完整的中断过程分为CPU 外和CPU 内两部分。
- CPU 外：外部设备的中断由中断代理芯片接收，处理后将该中断的中断向量号发送到CPU。
- CPU 内：CPU 执行该中断向量号对应的中断处理程序。

- **处理器根据中断向量号定位中断门描述符**，然后再去执行该中断描述符中的中断处理程序。**由于中断描述符是8 个字节，所以处理器用中断向量号乘以8 后，再与IDTR 中的中断描述符表地址相加**，所求的地址之和便是该中断向量号对应的中断描述符。
- **处理器进行特权级检查**。中断门的特权检查同调用门类似，对于软件主动发起的软中断，**当前特权级CPL 必须在门描述符DPL 和门中目标代码段DPL 之间**。这是为了防止位于3 特权级下的用户程序主动调用某些只为内核服务的例程。
    - 如果是由软中断`int n`、`int3`和`into`引发的中断，这些是用户进程中主动发起的中断，**处理器要检查当前特权级CPL 和门描述符DPL**，这是检查进门的特权下限，如果`CPL 权限大于等于DPL`，即`数值上CPL≤门描述符DPL`，特权级“门槛”检查通过，进入下一步的“门框”检查。否则，处理器抛出异常。
    - 这一步**检查特权级的上限**（门框）：**处理器要检查当前特权级CPL 和门描述符中所记录的选择子对应的目标代码段DPL**，如果CPL 权限小于目标代码段DPL，即**数值上CPL>目标代码段DPL**，检查通过。否则CPL 若大于等于目标代码段DPL，处理器将引发异常，也就是说，**除了用返回指令从高特权级返回，特权转移只能发生在由低向高**。
    - 若中断是由外部设备和异常引起的，只直接检查CPL 和目标代码段的DPL，要求CPL 权限小于目标代码段DPL，即**数值上CPL >目标代码段DPL**，否则处理器引发异常。
- 执行中断处理程序。特权级检查通过后，**将门描述符目标代码段选择子加载到代码段寄存器CS 中，把门描述符中中断处理程序的偏移地址加载到EIP**，开始执行中断处理程序。

![](/img/1594002593.jpg)

**指令cli 使IF 位为0，这称为关中断，指令sti 使IF 位为1，这称为开中断。**

**进入中断时要把NT 位和TF 位置为0**。TF 表示Trap Flag，也就是陷阱标志位，这用在调试环境中，**当TF 为0 时表示禁止单步执行**；NT 位表示Nest Task Flag，即**任务嵌套标志位**，也就是用来标记任务嵌套调用的情况。**任务嵌套调用是指CPU 将当前正执行的旧任务挂起，转去执行另外的新任务，待新任务执行完后，CPU 再回到旧任务继续执行**。
- 将旧任务TSS 选择子写到了新任务TSS 中的“上一个任务TSS 的指针”字段中。
- 将新任务标志寄存器eflags 中的NT 位置1，表示新任务之所以能够执行，是因为有别的任务调用了它。

当CPU 执行iret 时，它会去检查NT 位的值，**如果NT 位为1，这说明当前任务是被嵌套执行的**，因此会从自己TSS 中“上一个任务TSS 的指针”字段中获取旧任务，然后去执行该任务。如果NT 位的值为0，这表示当前是在中断处理环境下，于是就执行正常的中断退出流程。

处理器根据中断向量号在中断描述符表中**找到相应的中断门描述符**，**门描述符中保存的是中断处理程序所在代码段的选择子及在段内偏移量**，处理器从该描述符中加载目标代码段选择子到代码段寄存器CS 及偏移量到指令指针寄存器EIP。当前进程被中断打断后，为了从中断返回后能继续运行该进程，**处理器自动把CS 和EIP 的当前值保存到中断处理程序使用的栈中**。不同特权级别下处理器使用不同的栈，至于中断处理程序使用的是哪个栈，要视它当时所在的特权级别，因为中断是可以在任何特权级别下发生的。

**除了要保存CS、EIP 外，还需要保存标志寄存器EFLAGS**，如果涉及到特权级变化，还要压入SS 和ESP 寄存器。
- **处理器根据中断向量号找到对应的中断描述符后，拿CPL 和中断门描述符中选择子对应的目标代码段的DPL 比对**：
    - 若CPL 权限比DPL 低，即数值上CPL > DPL，这表示要向高特权级转移，需要切换到高特权级的栈。这也意味着当执行完中断处理程序后，若要正确返回到当前被中断的进程，同样需要将栈恢复为此时的旧栈。保存当前旧栈SS 和ESP 的值，TSS 中找到同目标代码段DPL 级别相同的栈加载到寄存器SS 和ESP 中。
    - 在新栈中压入EFLAGS 寄存器；
    - 由于要切换到目标代码段，**对于这种段间转移，要将CS 和EIP 保存到当前栈中备份**，
    - 某些异常会有错误码，此错误码用于报告异常是在哪个段上发生的，错误码会紧跟在EIP 之后入栈，记作ERROR_CODE。

![](/img/1594007235.jpg)

如果在第1 步中判断未涉及到特权级转移，便不会到TSS 中寻找新栈，而是继续使用当前旧栈，因此也谈不上恢复旧栈，此时中断发生时栈中数据不包括SS_old 和ESP_old。
![](/img/1594007310.jpg)

中断返回是用`iret`指令实现的，即interrupt ret，**此指令专用于从中断处理程序返回**，iret 指令并不清楚栈中数据的正确性，它只负责把栈顶处往上的数据，每次4 字节，**一定要保证从栈顶往上的顺序是EIP、CS、EFLAGS**，根据特权级是否有变化，还有ESP、SS。若处理器发现返回后特权级会变化，还会继续将两个双字数据返回到ESP、SS，其中SS也是16 位寄存器，所以同样也是弹出32 位数据后，只将其中的低16 位加载到SS。**16 位模式下用iretw，32 位模式下用iretd**。

假设栈顶已位于EIP_old：
- 当处理器执行到iret 指令时，它知道要执行远返回，**首先需要从栈中返回被中断进程的代码段选择子CS_old 及指令指针EIP_old**。这时候它要进行特权级检查。先检查栈中CS 选择子CS_old，根据其RPL 位，即未来的CPL，判断在返回过程中是否要改变特权级。
- 栈中CS 选择子是CS_old，根据CS_old 对应的代码段的DPL 及CS_old 中的RPL 做特权级检查。**如果检查通过，随即需要更新寄存器CS 和EIP**。如果进入中断时未涉及特权级转移，此时栈指针是ESP_old，否则栈指针是ESP_new
- **将栈中保存的EFLAGS 弹出到标志寄存器EFLAGS**。如果在第1 步中判断返回后要改变特权级，此时栈指针是ESP_new，它指向栈中的ESP_old。否则进入中断时属于平级转移，用的是旧栈，此时栈指针是ESP_old，栈中已无因此次中断发生而入栈的数据，栈指针指向中断发生前的栈顶。
- 如果在第1 步中判断出返回时需要改变特权级，此时便需要**将ESP_old和SS_old 分别加载到寄存器ESP 及SS**

错误码的低2位不再是RPL，而**是EXT和IDT**。总之，**错误码本质上就是个描述符选择子**，通过低3 位属性来修饰此选择子指向是哪个表中的哪个描述符。
- EXT 表示EXTernal event，即外部事件，**用来指明中断源是否来自处理器外部**，如果中断源是不可屏蔽中断NMI 或外部设备，EXT 为1，否则为0。
- IDT 表示**选择子是否指向中断描述符表IDT**，IDT 位为1，则表示此选择子指向中断描述符表，否则指向全局描述符表GDT 或局部描述符表LDT。
- **TI为0时用来指明选择子是从GDT 中检索描述符，为1 时是从LDT 中检索描述符**。

![](/img/1594009669.jpg)

中断返回时，iret 指令并不会把错误码从栈中弹出，所以在中断处理程序中需要手动用栈指针跨过错误码或将其弹出。否则栈顶处若不是EIP（EIP_old）的话，iret 返回时将会载入错误的值到后续寄存器。

## 可编程中断控制器 8259A
8259A 的作用是负责所有来自外设的中断。8259A 用于管理和控制可屏蔽中断，它表现在屏蔽外设中断，对它们实行优先级判决，向CPU 提供中断向量号等功能。将多个8259A级联，每一个8259A 就被称为1 片。**n 片8259A 通过级联可支持7n+1 个中断源**，级联时只能有一片8259A为主片master，其余的均为从片slave。来自从片的中断只能传递给主片，再由主片向上传递给CPU，也就是说**只有主片才会向CPU 发送INT 中断信号**。，8259A 在收到了中断后，对中断判优，将优先级最高的中断转发给CPU 处理。8259A 在收到了中断后，对中断判优，将优先级最高的中断转发给CPU 处理。
![](/img/1594017978.jpg)

- INT：8259A 选出优先级最高的中断请求后，发信号通知CPU。
- INTA：INT Acknowledge，中断响应信号。位于8259A 中的INTA 接收来自CPU 的INTA 接口的中断响应信号。
- IMR：Interrupt Mask Register，中断屏蔽寄存器，宽度是8 位，用来屏蔽某个外设的中断。
- IRR：Interrupt Request Register，中断请求寄存器，宽度是8 位。它的作用是接受经过IMR 寄存器过滤后的中断信号并锁存，此寄存器中全是等待处理的中断，“相当于”5259A 维护的未处理中断信号队列。
- PR：Priority Resolver，优先级仲裁器。当有多个中断同时发生，或当有新的中断请求进来时，将
它与当前正在处理的中断进行比较，找出优先级更高的中断。
- ISR：In-Service Register，中断服务寄存器，宽度是8 位。当某个中断正在被处理时，保存在此寄存器中。

![](/img/1594018210.jpg)
寄存器都是8 位，8259A 共8 个IRQ 接口，可以用8 位寄存器中的每一位代表8259A 的每个IRQ 接口。


# 内存管理系统
## makefile 简介
makefile 基本语法包括三部分，这三部分加在一起称为一组规则：
1. 目标文件是指此规则中想要生成的文件，可以是.o 结尾的目标文件，也可以是可执行文件，也可以是个伪目标，后面会介绍伪目标。
2. 依赖文件是指要生成此规则中的目标文件，需要哪些文件。通常依赖文件不是1 个，所以此处是个依赖文件的列表。
3. 命令是指此规则中要执行的动作，这些动作是指各种shell 命令，一个命令要单独占用一行，在行首必须以Tab 开头。

make 程序分别获取依赖文件和目标文件的mtime，对比依赖文件的mtime 是否比目标文件的mtime 新，就知道是否要执行规则中的命令。在Linux 中，文件分为属性和数据两部分，每个文件有三种时间，分别用于记录与文件属性和文件数据相关的时间，这三个时间分别是：
1. atime，即access time，表示访问文件数据部分时间，每次读取文件数据部分时就会更新atime，强调下，
是读取文件数据（内容）时改变atime。
2. ctime，即change time，表示文件属性或数据的改变时间，每当文件的属性或数据被修改时，就会更新ctime，也就是说ctime 同时跟踪文件属性和文件数据变化的时间。
3. mtime，即modify time，表示文件数据部分的修改时间，每次文件的数据被修改时就会更新mtime。

**规则中的命令并不总是被执行**，**当规则中不存在依赖文件时，这个目标文件名就称为—伪目标**。伪目标所在的规则纯粹地执行命令，只要给make 指定该伪目标名做参数，就能让伪目标规则中的命令直接执行。

all:
@echo “test ok”

1
2
3
4
5
6
7
8
由于makefile 中仅有这一个目标all，所以如果此时执行make all 或make，程序只会输出test ok。为了避免伪目标和真实目标文件同名的情况，可以**用关键字“.PHONY”来修饰伪目标**，格式为`.PHONY:伪目标名`，

伪目标的命名并没有固定的规则，用户可以按照自己的意愿定义成自己喜欢的名字。
![](/img/20200727181600.png)

在makefile 中的目标，是以递归的方式逐层向上查找目标的，就好像是从迷宫的出口往回找来时的路一样，由果寻因，逐个向上推导。

写个makefile：

test2.o:test2.c
gcc -c -o test2.o test2.c
test1.o:test1.c
gcc -c -o test1.o test1.c
test.bin:test1.o test2.o
gcc -o test.bin test1.o test2.o
all:test.bin
@echo “compile done”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
第1～4 行都是在准备.o 目标文件，第5～6 行是将.o 文件生成二进制文件test.bin。第7 行的目标all 是为了编译test.bin:
1. make 未找到文件GNUmakefile，便继续找文件makefile，找到后，根据命令的参数all，从文件中找到all 所在的规则。
2. make 发现all 的依赖文件test.bin 不存在，于是就去找以test.bin 为目标文件的规则。
3. 第5 行终于找到了test.bin 的规则，但make 发现，test.bin 的依赖文件test1.o 和test2.o 都不存在，于是先去找以test1.o 为目标文件的规则。
4. 同样经过千辛万苦，在第3 行找到了生成test1.o 的规则，但它的依赖文件是test1.c，由于test1.o本身不存在，所以不用再查看test1.c 的mtime，直接执行此规则的命令，即第4 行的`gcc -c -o test1.o test1.c`，用test1.c 来编译test1.o。
5. 生成test1.o 后，执行流程返回到test.bin 所在的规则，即第5 行，此时make 发现test2.o 也不存在，于是继续递归查找目标test2.o。
6. 同样，在第1 行发现test2.o 所在的规则，由于test2.o 本身不存在，也不再检查其所依赖文件test2.c的mtime，直接执行规则中的编译命令`gcc -c -o test2.o test2.c` 生成test2.o。
7. 生成test2.o 后，此时执行流程又回到了第5 行，make 发现两个依赖文件test1.o 和test2.o 都准备齐了，于是执行本规则的命令，即第6 行的`gcc -o test.bin test1.o test2.o`，将这两个目标文件生成可执行文件test.bin。
8. test.bin 终于生成了，此时回到了第2 步目标all 所在的规则，于是执行所在规则中的命令`@echo"compile done"`，打印字符串表示编译完成。

可以在makefile 中定义变量。变量定义的格式：`变量名=值（字符串）`，多个值之间用空格分开。make 程序在处理时会用空格将值打散，然后遍历每一个值。另外，值仅支持字符串类型，即使是数字也被当作字符串来处理。变量引用的格式：`$(变量名)`。这样，每次引用变量时，变量名就会被其值（字符串）替换。

![](/img/1595845452.jpg)

makefile 中另一个必须的功能是注释，如同shell 脚本一样，makefile 中用#来单行注释，只要各行第一个非空字符（除空格、tab）是’#’，本行内容便被注释了。如果在行尾是反斜杠字符’\’，这表示下一行也应被处理为当前行，所以，连同下一行也被注释掉。

下面列出了常见的部分语言程序的隐含规则。
- C 程序：“x.o”的生成依赖于“x.c”，生成x.o 的命令为：`$(CC) -c $(CPPFLAGS) $(CFLAGS)`。
- C++程序：“x.o”的生成依赖于“x.cc”或者“x.C”，生成x.o 的命令为：`$(CXX) -c $(CPPFLAGS) $(CFLAGS)`

make 还支持一种**自动化变量**，此变量**代表一组文件名，无论是目标文件名，还是依赖文件名，此变量值的范围属于这组文件名集合**，也就是说，自动化变量相当于对文件名集合循环遍历一遍。对于不同的文件名集合，有不同的自动化变量名，下面列举一些。
- `$@`，表示**规则中的目标文件名集合**，如果存在多个目标文件，`$@`则表示其中每一个文件名。
- `$<`，表示规则中依赖文件中的第1个文件。助记，‘<’很像是集合的最左边，也就是第1 个。
- `$^`，表示规则中所有依赖文件的集合，如果集合中有重复的文件，`$^`会自动去重。
- `$?`，表示规则中，所有比目标文件 mtime 更新的依赖文件集合。

`%`用来匹配任意多个非空字符。比如`%.o`代表所有以.o 为结尾的文件，`g%s.o`是以字符g 开头的所有以.o为结尾的文件，make 会拿这个字符串模式去文件系统上查找文件，默认为当前路径下。`%`通常用在规则中的目标文件中，以**用来匹配所有目标文件**，%也可以用在规则中的依赖文件中，因为目标文件才是要生成的文件，所以当%用在依赖文件中时，其所匹配的文件名要以目标文件为准。现将makefile 更新如下。

%.o:%.c
gcc -c -o $@ $^
objfiles = test1.o test2.o
test.bin:$(objfiles)
gcc -o $@ $^
all:test.bin
@echo “compile done”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

## 实现 assert 断言
在我们系统中，我们实现两种断言，一种是为内核系统使用的ASSERT，另一种是为用户进程使用的assert。一方面，当内核运行中出现问题时，多属于严重的错误，着实没必要再运行下去了。另一方面，断言在输出报错信息时，屏幕输出不应该被其他进程干扰。综上两点原因，ASSERT 排查出错误后，最好在关中断的情况下打印报错信息。

之前咱们已经建立好了文件interrupt.c，更新:（project/c8/a/kernel/interrupt.c）
```C++
#define EFLAGS_IF 0x00000200 // eflags 寄存器中的if 位为1
#define GET_EFLAGS(EFLAG_VAR) asm volatile("pushfl; popl %0" : "=g" (EFLAG_VAR))

/* 开中断并返回开中断前的状态*/
enum intr_status intr_enable() {
    enum intr_status old_status;
    if (INTR_ON == intr_get_status()) {
        old_status = INTR_ON;
        return old_status;
    } else {
        old_status = INTR_OFF;
        asm volatile("sti"); // 开中断，sti 指令将IF 位置1
        return old_status;
    }
}
/* 关中断，并且返回关中断前的状态 */
enum intr_status intr_disable() {
    enum intr_status old_status;
    if (INTR_ON == intr_get_status()) {
        old_status = INTR_ON;
        asm volatile("cli" : : : "memory"); // 关中断，cli 指令将IF 位置0
        return old_status;
    } else {
        old_status = INTR_OFF;
        return old_status;
    }
}
/* 将中断状态设置为status */
enum intr_status intr_set_status(enum intr_status status) {
    return status & INTR_ON ? intr_enable() : intr_disable();
}
/* 获取当前中断状态 */
enum intr_status intr_get_status() {
    uint32_t eflags = 0;
    GET_EFLAGS(eflags);
    return (EFLAGS_IF & eflags) ? INTR_ON : INTR_OFF;
}

定义了两个宏，用来获取中断状态。其中EFLAGS_IF 表示开中断时eflags 寄存器中的IF 的值，由于IF 位于eflags 中的第9 位，故EFLAGS_IF 的值为0x00000200。宏 GET_EFLAGS 用来获取 eflags 寄存器的值。它就是段内嵌汇编代码，其中EFLAG_VAR是C 代码中用来存储eflags 值的变量，它用寄存器约束g 来约束EFLAG_VAR 可以放在内存中或寄存器中，之后用pushfl 将eflags 寄存器的值压入栈，然后再用popl 指令将其弹出到与EFLAG_VAR 关联的约束中，最后C 变量EFLAG_VAR 获得eflags 的值。

intr_get_status 函数作用是获取当前的中断状态。intr_enable功能是把中断打开，这就是所谓的“开中断”，再把执行开中断前的中断状态返回。开中断的原理就是执行sti 指令将eflags 中的IF 位置1。

在C 语言中ASSERT 是用宏来定义的，其原理是判断传给ASSERT 的表达式是否成立，若表达式成立则什么都不做，否则打印出错信息并停止执行。__VA_ARGS__是预处理器所支持的专用标识符。代表所有与省略号相对应的参数。”…”表示定义的宏其参数可变。我们传给panic_spin 的其中一个参数是__VA_ARGS__。同样作为参数的还有__FILE__，__LINE__，__func__，这三个是预定义的宏，分别表示被编译的文件名、被编译文件中的行号、被编译的函数名。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#ifndef __KERNEL_DEBUG_H
#define __KERNEL_DEBUG_H
void panic_spin(char* filename, int line, const char* func, const char* condition);

#define PANIC(...) panic_spin (__FILE__, __LINE__, __func__, __VA_ARGS__)

#ifdef NDEBUG
    #define ASSERT(CONDITION) ((void)0)
#else
    #define ASSERT(CONDITION)\
        if(CONDITION){

        }else{ \
        /* 符号#让编译器将宏的参数转化为字符串字面量 */ \
            PANIC(#CONDITION); \
        }
 #endif /*__NDEBUG */

 #endif /*__KERNEL_DEBUG_H*/

我们给出了让宏等于空的条件，用预处理指令#ifdef 判断，如果定义了宏NDEBUG，就执行上面说过的第13 行，使ASSERT 等于 (void)0。此宏NDEBUG 可以在gcc 编译时指定，方法很简单，只要用gcc 的参数-D 来定义NDEBUG 就行了，如gcc –DNDEBUG，不过我们通常将“–DNDEBUG”定义在makefile 中。

1
2
3
4
5
6
7
8
9
10
/* 打印文件名、行号、函数名、条件并使程序悬停 */
void panic_spin(char* filename, int line, const char* func, const char* condition) {
    intr_disable(); // 因为有时候会单独调用panic_spin，所以在此处关中断
    put_str("\n\n\n!!!!! error !!!!!\n");
    put_str("filename:"); put_str(filename); put_str("\n");
    put_str("line:0x"); put_int(line); put_str("\n");
    put_str("function:"); put_str((char*)func); put_str("\n");
    put_str("condition:"); put_str((char*)condition); put_str("\n");
    while(1);
}

实现字符串操作函数

按照C 代码的字符串函数名编写自己的函数。为此，咱们在lib 目录下建立了string.c 文件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/* 将dst_起始的size 个字节置为value */
void memset(void* dst_, uint8_t value, uint32_t size) {
    ASSERT(dst_ != NULL);
    uint8_t* dst = (uint8_t*)dst_;
    while (size-- > 0)
        *dst++ = value;
}

/* 将src_起始的size 个字节复制到dst_ */
void memcpy(void* dst_, const void* src_, uint32_t size) {
    ASSERT(dst_ != NULL && src_ != NULL);
    uint8_t* dst = dst_;
    const uint8_t* src = src_;
    while (size-- > 0)
        *dst++ = *src++;
}

/* 连续比较以地址a_和地址b_开头的size 个字节，若相等则返回0，
若a_大于b_，返回+1，否则返回−1 */
int memcmp(const void* a_, const void* b_, uint32_t size) {
    const char* a = a_;
    const char* b = b_;
    ASSERT(a != NULL || b != NULL);
    while (size-- > 0) {
        if(*a != *b) {
            return *a > *b ? 1 : −1;
        }
        a++;
        b++;
    }
    return 0;
}
  • memset 函数用于内存区域的数据初始化，原理是逐字节地把value 写入起始内存地址为dst_的size 个空间，在本系统中通常用于内存分配时的数据清0。
  • memcpy 函数用于内存数据拷贝，原理是将src_起始的size 个字节复制到dst_，逐字节拷贝。
  • memcmp 函数用于一段内存数据比较，分别以两个地址a_和b_为起始，如果在size 个字节内，a_中的某个内存字节的数值（或ASCII 码）大于b_中同一相对位置的内存数值，此时返回1，如果这两个地址中，同一位置的所有值都相等，则返回0，否则返回−1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/* 将字符串从src_复制到dst_ */
char* strcpy(char* dst_, const char* src_) {
    ASSERT(dst_ != NULL && src_ != NULL);
    char* r = dst_;       // 用来返回目的字符串起始地址
    while((*dst_++ = *src_++));
    return r;
}

/* 返回字符串长度 */
uint32_t strlen(const char* str) {
   ASSERT(str != NULL);
   const char* p = str;
   while(*p++);
   return (p - str - 1);
}

/* 比较两个字符串,若a_中的字符大于b_中的字符返回1,相等时返回0,否则返回-1. */
int8_t strcmp (const char* a, const char* b) {
   ASSERT(a != NULL && b != NULL);
   while (*a != 0 && *a == *b) {
      a++;
      b++;
   }
/* 如果*a小于*b就返回-1,否则就属于*a大于等于*b的情况。在后面的布尔表达式"*a > *b"中,
 * 若*a大于*b,表达式就等于1,否则就表达式不成立,也就是布尔值为0,恰恰表示*a等于*b */
   return *a < *b ? -1 : *a > *b;
}

/* 从左到右查找字符串str中首次出现字符ch的地址(不是下标,是地址) */
char* strchr(const char* str, const uint8_t ch) {
   ASSERT(str != NULL);
   while (*str != 0) {
      if (*str == ch) {
	 return (char*)str;	    // 需要强制转化成和返回值类型一样,否则编译器会报const属性丢失,下同.
      }
      str++;
   }
   return NULL;
}
  • strcpy 函数用于把起始于地址src_的字符串复制到地址dst_，这和memcpy 原理相同，只不过strcpy以src_处的字符’0’作为终止条件，memcpy 以拷贝的字节数size 为终止条件。
  • strlen 函数用于返回字符串的长度，即字符数。
  • strcmp 函数用于比较起始地址分别为a 和b 的两个字符串是否相等，若a 中某个字符的ASCII 值大于b 中同一相对位置字符的ASCII 值，此时返回1，若字符都相同，则返回0，否则返回−1。同memcpy的原理相同，区别就是strcmp 以地址a 处的字符串的长度，也就是直到字符0 为终止条件，memcpy 的终止条件是size 个比对的字节。
  • strchr 返回的是字符ch 在字符串str 中，从左到右最先出现的所在地址，并不是下标，这一点请注意。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/* 从后往前查找字符串str中首次出现字符ch的地址(不是下标,是地址) */
char* strrchr(const char* str, const uint8_t ch) {
    ASSERT(str != NULL);
    const char* last_char = NULL;
    /* 从头到尾遍历一次,若存在ch字符,last_char总是该字符最后一次出现在串中的地址(不是下标,是地址)*/
    while (*str != 0) {
        if (*str == ch) {
            last_char = str;
        }
        str++;
   }
   return (char*)last_char;
}

/* 将字符串src_拼接到dst_后,将回拼接的串地址 */
char* strcat(char* dst_, const char* src_) {
    ASSERT(dst_ != NULL && src_ != NULL);
    char* str = dst_;
    while (*str++);
        --str;      // 别看错了，--str是独立的一句，并不是while的循环体
    while((*str++ = *src_++));	 // 当*str被赋值为0时,此时表达式不成立,正好添加了字符串结尾的0.
    return dst_;
}

/* 在字符串str中查找指定字符ch出现的次数 */
uint32_t strchrs(const char* str, uint8_t ch) {
    ASSERT(str != NULL);
    uint32_t ch_cnt = 0;
    const char* p = str;
    while(*p != 0) {
        if (*p == ch) {
            ch_cnt++;
        }
        p++;
    }
    return ch_cnt;
}

  • strrchr 函数返回的是从后往前查找字符串str 中首次出现字符ch 的地址，注意，是字符在字符串中的地址，并不是下标值。此函数虽然是从后往前找，但原理上是通过从前往后（从左到右）的顺序查找的，这样的好处是无需事先知道字符串的结束字符’\0’的地址。
  • strcat 函数的功能是字符串拼接，将src_处的字符串接在dst_的结尾处，并将dst_返回。实现原理是将src_处的字符串拷贝到dst_的结束处。
  • strchrs 函数用于返回字符ch 在字符串str 中出现的次数。

位图 bitmap 及其函数的实现

二进制位中的每一位与其他资源中的数据单位都是一对一的关系，这实际就成了一种映射，即map，于是这组二进制位就有了更恰当的名字—位图。对于它的实现，用字节型数组还是比较方便的，数组中的每一个元素都是一字节，每1 字节含有8 位，因此位图的1 字节对等表示8 个资源单位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#ifndef __LIB_KERNEL_BITMAP_H
#define __LIB_KERNEL_BITMAP_H
#include "global.h"
#define BITMAP_MASK 1
struct bitmap {
   uint32_t btmp_bytes_len;
/* 在遍历位图时,整体上以字节为单位,细节上是以位为单位,所以此处位图的指针必须是单字节 */
   uint8_t* bits;
};

void bitmap_init(struct bitmap* btmp);
bool bitmap_scan_test(struct bitmap* btmp, uint32_t bit_idx);
int bitmap_scan(struct bitmap* btmp, uint32_t cnt);
void bitmap_set(struct bitmap* btmp, uint32_t bit_idx, int8_t value);
#endif

struct bitmap中只定义了两个成员：位图的指针bits 和位图的字节长度btmp_bytes_len。一种“乐观”的解决方案是在struct bitmap 中提供位图的指针，就是uint8_t* bits。用指针bits 来记录位图的地址，真正的位图由上一级模块提供，并由上一级模块把位图的地址赋值给bits。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
/* 将位图btmp初始化 */
void bitmap_init(struct bitmap* btmp) {
   memset(btmp->bits, 0, btmp->btmp_bytes_len);   
}

/* 判断bit_idx位是否为1,若为1则返回true，否则返回false */
bool bitmap_scan_test(struct bitmap* btmp, uint32_t bit_idx) {
   uint32_t byte_idx = bit_idx / 8;    // 向下取整用于索引数组下标
   uint32_t bit_odd  = bit_idx % 8;    // 取余用于索引数组内的位
   return (btmp->bits[byte_idx] & (BITMAP_MASK << bit_odd));
}

/* 在位图中申请连续cnt个位,成功则返回其起始位下标，失败返回-1 */
int bitmap_scan(struct bitmap* btmp, uint32_t cnt) {
   uint32_t idx_byte = 0; // 用于记录空闲位所在的字节
/* 先逐字节比较,蛮力法 */
   while (( 0xff == btmp->bits[idx_byte]) && (idx_byte < btmp->btmp_bytes_len)) {
/* 1表示该位已分配,所以若为0xff,则表示该字节内已无空闲位,向下一字节继续找 */
      idx_byte++;
   }

   ASSERT(idx_byte < btmp->btmp_bytes_len);
   if (idx_byte == btmp->btmp_bytes_len) {  // 若该内存池找不到可用空间		
      return -1;
   }

 /* 若在位图数组范围内的某字节内找到了空闲位，
  * 在该字节内逐位比对,返回空闲位的索引。*/
   int idx_bit = 0;
 /* 和btmp->bits[idx_byte]这个字节逐位对比 */
   while ((uint8_t)(BITMAP_MASK << idx_bit) & btmp->bits[idx_byte]) { 
	 idx_bit++;
   }
	 
   int bit_idx_start = idx_byte * 8 + idx_bit;    // 空闲位在位图内的下标
   if (cnt == 1) {
      return bit_idx_start;
   }

   uint32_t bit_left = (btmp->btmp_bytes_len * 8 - bit_idx_start);   // 记录还有多少位可以判断
   uint32_t next_bit = bit_idx_start + 1;
   uint32_t count = 1;	      // 用于记录找到的空闲位的个数

   bit_idx_start = -1;	      // 先将其置为-1,若找不到连续的位就直接返回
   while (bit_left-- > 0) {
      if (!(bitmap_scan_test(btmp, next_bit))) {	 // 若next_bit为0
	 count++;
      } else {
	 count = 0;
      }
      if (count == cnt) {	    // 若找到连续的cnt个空位
	 bit_idx_start = next_bit - cnt + 1;
	 break;
      }
      next_bit++;          
   }
   return bit_idx_start;
}

/* 将位图btmp的bit_idx位设置为value */
void bitmap_set(struct bitmap* btmp, uint32_t bit_idx, int8_t value) {
   ASSERT((value == 0) || (value == 1));
   uint32_t byte_idx = bit_idx / 8;    // 向下取整用于索引数组下标
   uint32_t bit_odd  = bit_idx % 8;    // 取余用于索引数组内的位

/* 一般都会用个0x1这样的数对字节中的位操作,
 * 将1任意移动后再取反,或者先取反再移位,可用来对位置0操作。*/
   if (value) {		      // 如果value为1
      btmp->bits[byte_idx] |= (BITMAP_MASK << bit_odd);
   } else {		      // 若为0
      btmp->bits[byte_idx] &= ~(BITMAP_MASK << bit_odd);
   }
}

bitmap_init 函数只有一个参数，即位图指针btmp，此函数功能是初始化位图btmp，它是用memset函数根据位图的字节大小btmp_bytes_len 将位图的每一个字节用0 来填充。bitmap_scan_test 函数接受两个参数，分别是位图指针btmp 和位索引bit_idx。其功能是判断位图btmp中的第bit_idx 位是否为1，若为1，则返回true，否则返回false。bitmap_scan 函数接受两个参数，分别是位图指针btmp 及位的个数cnt。此函数的功能是在位图btmp 中找到连续的cnt 个可用位，返回起始空闲位下标，若没找到cnt 个空闲位，返回−1。

内存管理系统

一种可行的方案是将物理内存划分成两部分，一部分只用来运行内核，另一部分只用来运行用户进程，将内存规划出不同的部分，专项专用。我们把物理内存分成两个内存池，一部分称为用户物理内存池，此内存池中的物理内存只用来分配给用户进程。另一部分就是内核物理内存池，此内存池中的物理内存只给操作系统使用。内存池中的内存按单位大小来获取，这个单位大小是4KB，称为页，故，内存池中管理的是一个个大小为4KB 的内存块，从内存池中获取的内存大小至少为4KB 或者为4KB 的倍数

我们让内核也通过内存管理系统申请内存，为此，它也要有个虚拟地址池，当它申请内存时，从内核自己的虚拟地址池中分配虚拟地址，再从内核物理内存池（内核专用）中分配物理内存，然后在内核自己的页表将这两种地址建立好映射关系。

两个文件memory.h 和memory.c，有关内存管理的代码都写在其中。在头文件中定义了虚拟地址结构，定义了struct virtual_addr，此结构就是虚拟地址池，用于虚拟地址管理。struct virtual_addr 包含两个成员，一个是vaddr_bitmap，它的类型是位图结构体struct bitmap，用来以页为单位管理虚拟地址的分配情况。vaddr_start 用来记录虚拟地址的起始值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#ifndef __KERNEL_MEMORY_H
#define __KERNEL_MEMORY_H
#include "stdint.h"
#include "bitmap.h"

/* 用于虚拟地址管理 */
struct virtual_addr {
   struct bitmap vaddr_bitmap; // 虚拟地址用到的位图结构 
   uint32_t vaddr_start;       // 虚拟地址起始地址
};

extern struct pool kernel_pool, user_pool;
void mem_init(void);
#endif

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include "memory.h"
#include "stdint.h"
#include "print.h"

#define PG_SIZE 4096

/***************  位图地址 ********************
 * 因为0xc009f000是内核主线程栈顶，0xc009e000是内核主线程的pcb.
 * 一个页框大小的位图可表示128M内存, 位图位置安排在地址0xc009a000,
 * 这样本系统最大支持4个页框的位图,即512M */
#define MEM_BITMAP_BASE 0xc009a000
/*************************************/

/* 0xc0000000是内核从虚拟地址3G起. 0x100000意指跨过低端1M内存,使虚拟地址在逻辑上连续 */
#define K_HEAP_START 0xc0100000

/* 内存池结构,生成两个实例用于管理内核内存池和用户内存池 */
struct pool {
   struct bitmap pool_bitmap;	 // 本内存池用到的位图结构,用于管理物理内存
   uint32_t phy_addr_start;	 // 本内存池所管理物理内存的起始地址
   uint32_t pool_size;		 // 本内存池字节容量
};

struct pool kernel_pool, user_pool;      // 生成内核内存池和用户内存池
struct virtual_addr kernel_vaddr;	 // 此结构是用来给内核分配虚拟地址

/* 初始化内存池 */
static void mem_pool_init(uint32_t all_mem) {
   put_str("   mem_pool_init start\n");
   uint32_t page_table_size = PG_SIZE * 256;	  // 页表大小= 1页的页目录表+第0和第768个页目录项指向同一个页表+
                                                  // 第769~1022个页目录项共指向254个页表,共256个页框
   uint32_t used_mem = page_table_size + 0x100000;	  // 0x100000为低端1M内存
   uint32_t free_mem = all_mem - used_mem;
   uint16_t all_free_pages = free_mem / PG_SIZE;		  // 1页为4k,不管总内存是不是4k的倍数,
								  // 对于以页为单位的内存分配策略，不足1页的内存不用考虑了。
   uint16_t kernel_free_pages = all_free_pages / 2;
   uint16_t user_free_pages = all_free_pages - kernel_free_pages;

/* 为简化位图操作，余数不处理，坏处是这样做会丢内存。
好处是不用做内存的越界检查,因为位图表示的内存少于实际物理内存*/
   uint32_t kbm_length = kernel_free_pages / 8;			  // Kernel BitMap的长度,位图中的一位表示一页,以字节为单位
   uint32_t ubm_length = user_free_pages / 8;			  // User BitMap的长度.

   uint32_t kp_start = used_mem;				  // Kernel Pool start,内核内存池的起始地址
   uint32_t up_start = kp_start + kernel_free_pages * PG_SIZE;	  // User Pool start,用户内存池的起始地址

   kernel_pool.phy_addr_start = kp_start;
   user_pool.phy_addr_start   = up_start;

   kernel_pool.pool_size = kernel_free_pages * PG_SIZE;
   user_pool.pool_size	 = user_free_pages * PG_SIZE;

   kernel_pool.pool_bitmap.btmp_bytes_len = kbm_length;
   user_pool.pool_bitmap.btmp_bytes_len	  = ubm_length;

/*********    内核内存池和用户内存池位图   ***********
 *   位图是全局的数据，长度不固定。
 *   全局或静态的数组需要在编译时知道其长度，
 *   而我们需要根据总内存大小算出需要多少字节。
 *   所以改为指定一块内存来生成位图.
 *   ************************************************/
// 内核使用的最高地址是0xc009f000,这是主线程的栈地址.(内核的大小预计为70K左右)
// 32M内存占用的位图是2k.内核内存池的位图先定在MEM_BITMAP_BASE(0xc009a000)处.
   kernel_pool.pool_bitmap.bits = (void*)MEM_BITMAP_BASE;
							       
/* 用户内存池的位图紧跟在内核内存池位图之后 */
   user_pool.pool_bitmap.bits = (void*)(MEM_BITMAP_BASE + kbm_length);
   /******************** 输出内存池信息 **********************/
   put_str("      kernel_pool_bitmap_start:");put_int((int)kernel_pool.pool_bitmap.bits);
   put_str(" kernel_pool_phy_addr_start:");put_int(kernel_pool.phy_addr_start);
   put_str("\n");
   put_str("      user_pool_bitmap_start:");put_int((int)user_pool.pool_bitmap.bits);
   put_str(" user_pool_phy_addr_start:");put_int(user_pool.phy_addr_start);
   put_str("\n");

   /* 将位图置0*/
   bitmap_init(&kernel_pool.pool_bitmap);
   bitmap_init(&user_pool.pool_bitmap);

   /* 下面初始化内核虚拟地址的位图,按实际物理内存大小生成数组。*/
   kernel_vaddr.vaddr_bitmap.btmp_bytes_len = kbm_length;      // 用于维护内核堆的虚拟地址,所以要和内核内存池大小一致

  /* 位图的数组指向一块未使用的内存,目前定位在内核内存池和用户内存池之外*/
   kernel_vaddr.vaddr_bitmap.bits = (void*)(MEM_BITMAP_BASE + kbm_length + ubm_length);

   kernel_vaddr.vaddr_start = K_HEAP_START;
   bitmap_init(&kernel_vaddr.vaddr_bitmap);
   put_str("   mem_pool_init done\n");
}

/* 内存管理部分初始化入口 */
void mem_init() {
   put_str("mem_init start\n");
   uint32_t mem_bytes_total = (*(uint32_t*)(0xb00));
   mem_pool_init(mem_bytes_total);	  // 初始化内存池
   put_str("mem_init done\n");
}

定义了宏MEM_BITMAP_BASE，用以表示内存位图的基址，其值为0xc009a000，PCB 要占用4KB 大小的内存空间，不过要注意的是PCB 所占用的内存必须是自然页，完整、单独地占用一个物理页框。

对memory.h进行修改

1
2
3
4
5
6
7
8
9
10
11
/* 内存池标记,用于判断用哪个内存池 */
enum pool_flags {
   PF_KERNEL = 1,    // 内核内存池
   PF_USER = 2	     // 用户内存池
};  
#define	 PG_P_1	  1	// 页表项或页目录项存在属性位
#define	 PG_P_0	  0	// 页表项或页目录项存在属性位
#define	 PG_RW_R  0	// R/W 属性位值, 读/执行
#define	 PG_RW_W  2	// R/W 属性位值, 读/写/执行
#define	 PG_US_S  0	// U/S 属性位值, 系统级
#define	 PG_US_U  4	// U/S 属性位值, 用户级

内存管理中，必不可少的操作就是修改页表，这势必涉及到页表项及页目录项的操作，memory.h 中定义了一些PG_开头的宏，这是页表项或页目录项的属性，memory.c 中的函数会用到它们。PG 前缀表示页表项或页目录项，US 表示第2 位的US 位，RW 表示第1 位的RW 位，P 表示第0 位的P 位。

  • PG_P_1 表示P 位的值为1，表示此页内存已存在。
  • PG_P_0 表示P 位的值为0，表示此页内存不存在。
  • PG_RW_W表示RW 位的值为W，即RW=1，表示此页内存允许读、写、执行。
  • PG_RW_R 表示RW 位的值为R，即RW=0，表示此页内存允许读、执行。
  • PG_US_S 表示US 位的值为S，即US=0，表示只允许特权级别为0、1、2 的程序访问此页内存，3 特权级程序不被允许。
  • PG_US_U 表示US 位的值为U，即US=1，表示允许所有特权级别程序访问此页内存。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
#include "memory.h"
#include "bitmap.h"
#include "stdint.h"
#include "global.h"
#include "debug.h"
#include "print.h"
#include "string.h"

#define PG_SIZE 4096

/***************  位图地址 ********************
 * 因为0xc009f000是内核主线程栈顶，0xc009e000是内核主线程的pcb.
 * 一个页框大小的位图可表示128M内存, 位图位置安排在地址0xc009a000,
 * 这样本系统最大支持4个页框的位图,即512M */
#define MEM_BITMAP_BASE 0xc009a000
/*************************************/

#define PDE_IDX(addr) ((addr & 0xffc00000) >> 22)
#define PTE_IDX(addr) ((addr & 0x003ff000) >> 12)

/* 0xc0000000是内核从虚拟地址3G起. 0x100000意指跨过低端1M内存,使虚拟地址在逻辑上连续 */
#define K_HEAP_START 0xc0100000

/* 内存池结构,生成两个实例用于管理内核内存池和用户内存池 */
struct pool {
   struct bitmap pool_bitmap;	 // 本内存池用到的位图结构,用于管理物理内存
   uint32_t phy_addr_start;	 // 本内存池所管理物理内存的起始地址
   uint32_t pool_size;		 // 本内存池字节容量
};

struct pool kernel_pool, user_pool;      // 生成内核内存池和用户内存池
struct virtual_addr kernel_vaddr;	 // 此结构是用来给内核分配虚拟地址

/* 在pf表示的虚拟内存池中申请pg_cnt个虚拟页,
 * 成功则返回虚拟页的起始地址, 失败则返回NULL */
static void* vaddr_get(enum pool_flags pf, uint32_t pg_cnt) {
   int vaddr_start = 0, bit_idx_start = -1;
   uint32_t cnt = 0;
   if (pf == PF_KERNEL) {
      bit_idx_start  = bitmap_scan(&kernel_vaddr.vaddr_bitmap, pg_cnt);
      if (bit_idx_start == -1) {
	 return NULL;
      }
      while(cnt < pg_cnt) {
	 bitmap_set(&kernel_vaddr.vaddr_bitmap, bit_idx_start + cnt++, 1);
      }
      vaddr_start = kernel_vaddr.vaddr_start + bit_idx_start * PG_SIZE;
   } else {	
   // 用户内存池,将来实现用户进程再补充
   }
   return (void*)vaddr_start;
}

/* 得到虚拟地址vaddr对应的pte指针*/
uint32_t* pte_ptr(uint32_t vaddr) {
   /* 先访问到页表自己 + \
    * 再用页目录项pde(页目录内页表的索引)做为pte的索引访问到页表 + \
    * 再用pte的索引做为页内偏移*/
   uint32_t* pte = (uint32_t*)(0xffc00000 + \
	 ((vaddr & 0xffc00000) >> 10) + \
	 PTE_IDX(vaddr) * 4);
   return pte;
}

/* 得到虚拟地址vaddr对应的pde的指针 */
uint32_t* pde_ptr(uint32_t vaddr) {
   /* 0xfffff是用来访问到页表本身所在的地址 */
   uint32_t* pde = (uint32_t*)((0xfffff000) + PDE_IDX(vaddr) * 4);
   return pde;
}

/* 在m_pool指向的物理内存池中分配1个物理页,
 * 成功则返回页框的物理地址,失败则返回NULL */
static void* palloc(struct pool* m_pool) {
   /* 扫描或设置位图要保证原子操作 */
   int bit_idx = bitmap_scan(&m_pool->pool_bitmap, 1);    // 找一个物理页面
   if (bit_idx == -1 ) {
      return NULL;
   }
   bitmap_set(&m_pool->pool_bitmap, bit_idx, 1);	// 将此位bit_idx置1
   uint32_t page_phyaddr = ((bit_idx * PG_SIZE) + m_pool->phy_addr_start);
   return (void*)page_phyaddr;
}

/* 页表中添加虚拟地址_vaddr与物理地址_page_phyaddr的映射 */
static void page_table_add(void* _vaddr, void* _page_phyaddr) {
   uint32_t vaddr = (uint32_t)_vaddr, page_phyaddr = (uint32_t)_page_phyaddr;
   uint32_t* pde = pde_ptr(vaddr);
   uint32_t* pte = pte_ptr(vaddr);

/************************   注意   *************************
 * 执行*pte,会访问到空的pde。所以确保pde创建完成后才能执行*pte,
 * 否则会引发page_fault。因此在*pde为0时,*pte只能出现在下面else语句块中的*pde后面。
 * *********************************************************/
   /* 先在页目录内判断目录项的P位，若为1,则表示该表已存在 */
   if (*pde & 0x00000001) {	 // 页目录项和页表项的第0位为P,此处判断目录项是否存在
      ASSERT(!(*pte & 0x00000001));

      if (!(*pte & 0x00000001)) {   // 只要是创建页表,pte就应该不存在,多判断一下放心
	 *pte = (page_phyaddr | PG_US_U | PG_RW_W | PG_P_1);    // US=1,RW=1,P=1
      } else {			    //应该不会执行到这，因为上面的ASSERT会先执行。
	 PANIC("pte repeat");
	 *pte = (page_phyaddr | PG_US_U | PG_RW_W | PG_P_1);      // US=1,RW=1,P=1
      }
   } else {			    // 页目录项不存在,所以要先创建页目录再创建页表项.
      /* 页表中用到的页框一律从内核空间分配 */
      uint32_t pde_phyaddr = (uint32_t)palloc(&kernel_pool);

      *pde = (pde_phyaddr | PG_US_U | PG_RW_W | PG_P_1);

      /* 分配到的物理页地址pde_phyaddr对应的物理内存清0,
       * 避免里面的陈旧数据变成了页表项,从而让页表混乱.
       * 访问到pde对应的物理地址,用pte取高20位便可.
       * 因为pte是基于该pde对应的物理地址内再寻址,
       * 把低12位置0便是该pde对应的物理页的起始*/
      memset((void*)((int)pte & 0xfffff000), 0, PG_SIZE);
         
      ASSERT(!(*pte & 0x00000001));
      *pte = (page_phyaddr | PG_US_U | PG_RW_W | PG_P_1);      // US=1,RW=1,P=1
   }
}

/* 分配pg_cnt个页空间,成功则返回起始虚拟地址,失败时返回NULL */
void* malloc_page(enum pool_flags pf, uint32_t pg_cnt) {
   ASSERT(pg_cnt > 0 && pg_cnt < 3840);
/***********   malloc_page的原理是三个动作的合成:   ***********
      1通过vaddr_get在虚拟内存池中申请虚拟地址
      2通过palloc在物理内存池中申请物理页
      3通过page_table_add将以上得到的虚拟地址和物理地址在页表中完成映射
***************************************************************/
   void* vaddr_start = vaddr_get(pf, pg_cnt);
   if (vaddr_start == NULL) {
      return NULL;
   }

   uint32_t vaddr = (uint32_t)vaddr_start, cnt = pg_cnt;
   struct pool* mem_pool = pf & PF_KERNEL ? &kernel_pool : &user_pool;

   /* 因为虚拟地址是连续的,但物理地址可以是不连续的,所以逐个做映射*/
   while (cnt-- > 0) {
      void* page_phyaddr = palloc(mem_pool);
      if (page_phyaddr == NULL) {  // 失败时要将曾经已申请的虚拟地址和物理页全部回滚，在将来完成内存回收时再补充
	 return NULL;
      }
      page_table_add((void*)vaddr, page_phyaddr); // 在页表中做映射 
      vaddr += PG_SIZE;		 // 下一个虚拟页
   }
   return vaddr_start;
}

/* 从内核物理内存池中申请pg_cnt页内存,成功则返回其虚拟地址,失败则返回NULL */
void* get_kernel_pages(uint32_t pg_cnt) {
   void* vaddr =  malloc_page(PF_KERNEL, pg_cnt);
   if (vaddr != NULL) {	   // 若分配的地址不为空,将页框清0后返回
      memset(vaddr, 0, pg_cnt * PG_SIZE);
   }
   return vaddr;
}

/* 初始化内存池 */
static void mem_pool_init(uint32_t all_mem) {
   put_str("   mem_pool_init start\n");
   uint32_t page_table_size = PG_SIZE * 256;	  // 页表大小= 1页的页目录表+第0和第768个页目录项指向同一个页表+
                                                  // 第769~1022个页目录项共指向254个页表,共256个页框
   uint32_t used_mem = page_table_size + 0x100000;	  // 0x100000为低端1M内存
   uint32_t free_mem = all_mem - used_mem;
   uint16_t all_free_pages = free_mem / PG_SIZE;		  // 1页为4k,不管总内存是不是4k的倍数,
								  // 对于以页为单位的内存分配策略，不足1页的内存不用考虑了。
   uint16_t kernel_free_pages = all_free_pages / 2;
   uint16_t user_free_pages = all_free_pages - kernel_free_pages;

/* 为简化位图操作，余数不处理，坏处是这样做会丢内存。
好处是不用做内存的越界检查,因为位图表示的内存少于实际物理内存*/
   uint32_t kbm_length = kernel_free_pages / 8;			  // Kernel BitMap的长度,位图中的一位表示一页,以字节为单位
   uint32_t ubm_length = user_free_pages / 8;			  // User BitMap的长度.

   uint32_t kp_start = used_mem;				  // Kernel Pool start,内核内存池的起始地址
   uint32_t up_start = kp_start + kernel_free_pages * PG_SIZE;	  // User Pool start,用户内存池的起始地址

   kernel_pool.phy_addr_start = kp_start;
   user_pool.phy_addr_start   = up_start;

   kernel_pool.pool_size = kernel_free_pages * PG_SIZE;
   user_pool.pool_size	 = user_free_pages * PG_SIZE;

   kernel_pool.pool_bitmap.btmp_bytes_len = kbm_length;
   user_pool.pool_bitmap.btmp_bytes_len	  = ubm_length;

/*********    内核内存池和用户内存池位图   ***********
 *   位图是全局的数据，长度不固定。
 *   全局或静态的数组需要在编译时知道其长度，
 *   而我们需要根据总内存大小算出需要多少字节。
 *   所以改为指定一块内存来生成位图.
 *   ************************************************/
// 内核使用的最高地址是0xc009f000,这是主线程的栈地址.(内核的大小预计为70K左右)
// 32M内存占用的位图是2k.内核内存池的位图先定在MEM_BITMAP_BASE(0xc009a000)处.
   kernel_pool.pool_bitmap.bits = (void*)MEM_BITMAP_BASE;
							       
/* 用户内存池的位图紧跟在内核内存池位图之后 */
   user_pool.pool_bitmap.bits = (void*)(MEM_BITMAP_BASE + kbm_length);
   /******************** 输出内存池信息 **********************/
   put_str("      kernel_pool_bitmap_start:");put_int((int)kernel_pool.pool_bitmap.bits);
   put_str(" kernel_pool_phy_addr_start:");put_int(kernel_pool.phy_addr_start);
   put_str("\n");
   put_str("      user_pool_bitmap_start:");put_int((int)user_pool.pool_bitmap.bits);
   put_str(" user_pool_phy_addr_start:");put_int(user_pool.phy_addr_start);
   put_str("\n");

   /* 将位图置0*/
   bitmap_init(&kernel_pool.pool_bitmap);
   bitmap_init(&user_pool.pool_bitmap);

   /* 下面初始化内核虚拟地址的位图,按实际物理内存大小生成数组。*/
   kernel_vaddr.vaddr_bitmap.btmp_bytes_len = kbm_length;      // 用于维护内核堆的虚拟地址,所以要和内核内存池大小一致

  /* 位图的数组指向一块未使用的内存,目前定位在内核内存池和用户内存池之外*/
   kernel_vaddr.vaddr_bitmap.bits = (void*)(MEM_BITMAP_BASE + kbm_length + ubm_length);

   kernel_vaddr.vaddr_start = K_HEAP_START;
   bitmap_init(&kernel_vaddr.vaddr_bitmap);
   put_str("   mem_pool_init done\n");
}

/* 内存管理部分初始化入口 */
void mem_init() {
   put_str("mem_init start\n");
   uint32_t mem_bytes_total = (*(uint32_t*)(0xb00));
   mem_pool_init(mem_bytes_total);	  // 初始化内存池
   put_str("mem_init done\n");
}

定义了两个宏，PDE_IDX 用于返回虚拟地址的高10 位，即pde 索引部分，此部分用于在页目录表中定位pde。PTE_IDX 用于返回虚拟地址的中间10 位，即pte 索引部分，此部分用于在页表中定位pte。函数中定义的变量vaddr_start 用于存储分配的起始虚拟地址，bit_idx_start 用于存储位图扫描函数bitmap_scan 的返回值，默认为−1。

如果pf等于PF_KERNEL，便认为是在内核虚拟地址池中申请地址，于是调用bitmap_scan 函数扫描内核虚拟地址池中的位图。若bitmap_scan 返回−1，则vaddr_get 函数返回NULL。用while 循环，根据申请的页数量，即pg_cnt 的值，逐次调用bitmap_set 函数将相应位置1。

将位图置 1 之后，工作基本上完成了，现在需要将 bit_idx_start 转换为虚拟地址，如代码vaddr_start = kernel_vaddr.vaddr_start + bit_idx_start * PG_SIZE，因为位图中的一位代表实际1 页大小的内存，所以转换原理还是很简单的，就是用虚拟内存池的起始地址kernel_vaddr. vaddr_start 加上起始位索引bit_idx_start 相对于内存池的虚拟页偏移地址bit_idx_start * PG_SIZE。

处理器处理32 位地址的三个步骤如下：

  1. 首先处理高10 位的pde 索引，从而处理器得到页表物理地址。
  2. 其次处理中间10 位的pte 索引，进而处理器得到普通物理页的物理地址。
  3. 最后是把低12 位作为普通物理页的页内偏移地址，此偏移地址加上物理页的物理地址，得到的地址之和便是最终的物理地址，处理器到此物理地址上进行读写操作。

函数pte_ptr，它接受一个参数vaddr，功能是得到地址vaddr 所在pte 的指针。要想获取pte 的地址，必须先访问到页目录表，再通过其中的页目录项pde，找到相应的页表，在页表中才是页表项pte。因此，我们需要分别在地址的高10 位、中间10 位和低12 位中填入合适的数，拼凑出满足此要求的新的32 位地址new_vaddr。

由于最后一个页目录项中存储的是页目录表物理地址，故当32 位地址中高20 位为0xfffff 时，这就表示访问到的是最后一个页目录项，即获得了页目录表物理地址。这也很容易理解，0xfffffxxx 的高10 位是0x3ff，中间10 位也是0x3ff，也就是处理pde索引时得到的是页目录表的物理地址，此时处理器以为此页目录表就是页表，继续用pte 索引在该页表（页目录表）找到最后一个页表项pte（其实是页目录项pde），所以再次获得了页目录表物理地址（当然处理器以为获得的是普通物理页的物理地址）。

新虚拟地址new_vaddr 等于0xfffff000 再加上vaddr 的页目录项索引乘以4 的积，即(0xfffff000) + PDE_IDX(vaddr) * 4。此时的new_vaddr 便落到vaddr 所在的页目录项pde 的物理地址上。由于此结果仅仅是个整型数值，需要将其通过强制类型转换成32 位整型指针。最终的新虚拟地址new_vaddr 保存在指针变量pde 中，因此pde = (uint32_t*)((0xfffff000) + PDE_IDX(vaddr) * 4)，此时指针变量pde 指向了vaddr 所在的pde，最后通过return pde 将指针返回。

pte_ptr 和pde_ptr 这两个函数返回的是能够访问到vaddr 所在pte 及pde 的新虚拟地址new_vaddr，new_vaddr 经过处理器处理32 位地址的三个步骤，最终指向vaddr 的pte 及pde 所在的物理地址。因此，这两个函数的功能等同于：给我一个新的虚拟地址new_vaddr，让它指向vaddr 所在的pde 及pte，也就是让new_vaddr 指向pde 及pte 所在的物理地址。

这两个函数中的参数 vaddr，可以是已经分配、在页表中存在的，也可以是尚未分配，目前页表中不存在的虚拟地址，pte_ptr 和pde_ptr 这两个函数只是根据虚拟地址转换的规则计算出vaddr 对应的pte 及pde 的虚拟地址，与vaddr 所在的pte 及pde 是否存在无关。

palloc函数只接受一个参数m_pool，功能是在m_pool 指向的物理内存池中分配1 个物理页，成功时则返回页框的物理地址，失败时则返回NULL。定义的变量bit_idx 用于存储bitmap_scan 函数的返回值，bitmap_scan 函数在物理内存池的位图中查找可用位，如果失败，则返回−1，因此函数palloc 也将返回NULL，宣告失败。若bitmap_scan 的返回值不为−1，也就是找到了可用位，接下来再通过函数bitmap_set将bit_idx 位设置为1，也就是代码bitmap_set(&m_pool->pool_bitmap, bit_idx, 1)。变量 page_phyaddr 用于保存分配的物理页地址，它的值是物理内存池的起始地址m_pool->phy_addr_start+ 物理页在内存池中的偏移地址（bit_idx * PG_SIZE）。最后通过return (void*) page_phyaddr将物理页地址转换成空指针后返回。

数page_table_add，它接受两个参数，虚拟地址_vaddr 和物理地址_page_phyaddr，功能是添加虚拟地址_vaddr 与物理地址_page_phyaddr 的映射。本质上是在页表中添加此虚拟地址对应的页表项pte，并把物理页的物理地址写入此页表项pte 中。

在4MB（0x0～0x3ff000）的范围内新增pte 时，只要申请个物理页并将此物理页的物理地址写入新的pte 即可，无需再做额外操作。可是，当我们访问的虚拟地址超过了此范围时，比如0x400000，还要申请个物理页来新建页表，同时将用作页表的物理页地址写入页目录表中的第1个页目录项pde 中。也就是说，只要新增的虚拟地址是4MB 的整数倍时，就一定要申请两个物理页，一个物理页作为新的页表，同时在页目录表中创建个新的pde，并把此物理页的物理地址写入此pde。另一个物理页作为普通的物理页，同时在新建的页表中添加个新的pte，并把此物理页的物理地址写入此pte。

如果pte 不存在，就将物理页的物理地址及相关属性写到此pte 中，即代码*pte = (page_phyaddr | PG_US_U | PG_RW_W | PG_P_1)，这样vaddr 对应的pte 就被映射到物理地址page_phyaddr 上，并添加了属性US=1，RW=1，P=1。

如果发现pde 不存在时，需要申请个新的物理页来创建新的页表，因此调用palloc(&kernel_pool)申请新的物理页并将地址保存在变量pde_phyaddr 中。随后将新物理页的物理地址pde_phyaddr 和相关属性写入此pde 中，即代码*pde = (pde_phyaddr | PG_US_U | PG_RW_W | PG_P_1)，属性同样是US=1，RW=1，P=1。

线程

实现内核线程

任务调度器就是操作系统中用于把任务轮流调度上处理器运行的一个软件模块，它是操作系统的一部分。调度器在内核中维护一个任务表（也称进程表、线程表或调度表），然后按照一定的算法，从任务表中选择一个任务，然后把该任务放到处理器上运行，当任务运行的时间片到期后，再从任务表中找另外一个任务放到处理器上运行，周而复始，让任务表中的所有任务都有机会运行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<stdio.h>
#include<pthread.h>

void* thread_func(void* _arg) {
   unsigned int * arg = _arg;
   printf(" new thread: my tid is %u\n", *arg);
}

void main() {
   pthread_t new_thread_id;
   pthread_create(&new_thread_id, NULL, thread_func, &new_thread_id);
   printf("main thread: my tid is %u\n", pthread_self());
   usleep(100);
}

我们在第2 行包含了pthread.h，这是POSIX 版本线程库。第11 行利用了pthread_create 函数创建线程，此函数的原型是：

1
2
3
4
int pthread_create (pthread_t *__restrict __newthread,
__const pthread_attr_t *__restrict __attr,
void *(*__start_routine) (void *),
void *__restrict __arg) __THROW __nonnull ((1, 3));
  • 第 1 个参数__newthread用于存储新创建线程的id，也就是tid，这里保存在pthread_t 类型的变量new_thread_id 中。
  • 第 2 个参数__attr用于指定线程的类型，我们这里就用默认类型就好，因此实参是NULL。
  • 第 3 个参数__start_routine是个函数指针，确切地说是个返回值为void*、参数为void的函数指针，用来指定线程中所调用的函数的地址，或者说是在线程中运行的函数的地址。这里的实参就是在上面定义的函数thread_func，也就是说*让新创建的线程去调用执行thread_func 函数。
  • 第 4 个参数__arg，它是用来配合第3 个参数的，是给在线程中运行的函数__start_routine 的参数，我们此处把new_thread_id 传给thread_func。注意，由于给__start_routine 函数做参数的只有这一个形参，当参数多于一个时，最好把参数封装为一个结构体，把此结构体地址传给__arg，然后在__start_routine 指向的函数体中再去解析参数。
  • pthread_create 函数的返回值若为0，则表示创建线程成功，否则就表示出错码。

进程与线程的关系、区别简述

程序是指静态的、存储在文件系统上、尚未运行的指令代码，它是实际运行时程序的映像。进程是指正在运行的程序，即进行中的程序，程序必须在获得运行所需要的各类资源后才能成为进程，资源包括进程所使用的栈，使用的寄存器等。

进程是一种控制流集合，集合中至少包含一条执行流，执行流之间是相互独立的，但它们共享进程的所有资源，它们是处理器的执行单位，或者称为调度单位，它们就是线程。

线程和进程比，进程拥有整个地址空间，从而拥有全部资源，线程没有自己的地址空间，因此没有任何属于自己的资源，需要借助进程的资源“生存”，所以线程被称为轻量级进程。线程是最小的执行单元。纯粹的进程实际上就相当于单一线程的进程，也就是单线程进程。进程中若显式创建了多个线程时，就会有多个执行流，也就是多线程进程。

线程是纯粹的执行部分，它运行所需要的资源存储在进程这个大房子中，进程中包含此进程中所有线程使用的资源，因此线程依赖于进程，存在于进程之中，用表达式来表示：进程=线程+资源。进程拥有整个地址空间，其中包括各种资源，而进程中的所有线程共享同一个地址空间，原因很简单，因为这个地址空间中有线程运行所需要的资源。

只有线程才具备能动性，它才是处理器的执行单元，因此它是调度器眼中的调度单位。进程只是个资源整合体，它将进程中所有线程运行时用到资源收集在一起，供进程中的所有线程使用，真正上处理器上运行的其实都叫线程，进程中的线程才是一个个的执行实体、执行流。

进程独自拥有整个地址空间，在这个空间中装有线程运行所需的资源，所以地址空间相当于资源容器。因此，进程与线程的关系是进程是资源容器，线程是资源使用者。进程与线程的区别是线程没有自己独享的资源，因此没有自己的地址空间，它要依附在进程的地址空间中从而借助进程的资源运行。

把需要等待外界条件的状态称为“阻塞态”，把外界条件成立时，进程可以随时准备运行的状态称为“就绪态”，把正在处理器上运行的进程的状态称为“运行态”。

操作系统为每个进程提供了一个PCB，Process Control Block，即程序控制块，用它来记录与此进程相关的信息，比如进程状态、PID、优先级等。每个进程都有自己的PCB，所有PCB 放到一张表格中维护，这就是进程表，PCB 又可称为进程表项。“寄存器映像”用来保存进程的“现场”，进程在处理器上运行时，所有寄存器的值都将保存到此处。

线程仅仅是个执行流，在用户空间，还是在内核空间实现它，最大的区别就是线程表在哪里，由谁来调度它上处理器。如果线程在用户空间中实现，线程表就在用户进程中，用户进程就要专门写个线程用作线程调度器，由它来调度进程内部的其他线程。如果线程在内核空间中实现，线程表就在内核中，该线程就会由操作系统的调度器统一调度，无论该线程属于内核，还是用户进程。

实现线程的两种方式——内核或用户进程

在用户空间中实现线程的好处是可移植性强，由于是用户级的实现，所以在不支持线程的操作系统上也可以写出完美支持线程的用户程序。如果在用户空间中实现线程，用户线程就要肩负起调度器的责任，因此除了要实现进程内的线程调度器外，还要自己在进程内维护线程表。

在用户进程中实现线程有以下优/缺点。

  • 线程的调度算法是由用户程序自己实现的，可以根据实现应用情况为某些线程加权调度。
  • 将线程的寄存器映像装载到CPU 时，可以在用户空间完成，即不用陷入到内核态，这样就免去了进入内核时的入栈及出栈操作。
  • 进程中的某个线程若出现了阻塞（通常是由于系统调用造成的），操作系统不知道进程中存在线程，它以为此进程是传统型进程（单线程进程），因此会将整个进程挂起，即进程中的全部线程都无法运行。
  • 线程在用户空间实现，由于整个进程占据处理器的时间片是有限的，这有限的时间片还要再分给内部的线程，所以每个线程执行的时间片非常非常短暂。

相比在用户空间中实现线程，内核提供的线程相当于让进程多占了处理器资源，另一方面的优点是当进程中的某一线程阻塞后，由于线程是由内核空间实现的，操作系统认识线程，所以就只会阻塞这一个线程，此线程所在进程内的其他线程将不受影响，这又相当于提速了。缺点是用户进程需要通过系统调用陷入内核，这多少增加了一些现场保护的栈操作。

在内核空间实现线程

先构造PCB 及其相关的基础部分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#ifndef __THREAD_THREAD_H
#define __THREAD_THREAD_H
#include "stdint.h"

/* 自定义通用函数类型,它将在很多线程函数中做为形参类型 */
typedef void thread_func(void*);

/* 进程或线程的状态 */
enum task_status {
   TASK_RUNNING,
   TASK_READY,
   TASK_BLOCKED,
   TASK_WAITING,
   TASK_HANGING,
   TASK_DIED
};

/***********   中断栈intr_stack   ***********
 * 此结构用于中断发生时保护程序(线程或进程)的上下文环境:
 * 进程或线程被外部中断或软中断打断时,会按照此结构压入上下文
 * 寄存器,  intr_exit中的出栈操作是此结构的逆操作
 * 此栈在线程自己的内核栈中位置固定,所在页的最顶端
********************************************/
struct intr_stack {
    uint32_t vec_no;	 // kernel.S 宏VECTOR中push %1压入的中断号
    uint32_t edi;
    uint32_t esi;
    uint32_t ebp;
    uint32_t esp_dummy;	 // 虽然pushad把esp也压入,但esp是不断变化的,所以会被popad忽略
    uint32_t ebx;
    uint32_t edx;
    uint32_t ecx;
    uint32_t eax;
    uint32_t gs;
    uint32_t fs;
    uint32_t es;
    uint32_t ds;

/* 以下由cpu从低特权级进入高特权级时压入 */
    uint32_t err_code;		 // err_code会被压入在eip之后
    void (*eip) (void);
    uint32_t cs;
    uint32_t eflags;
    void* esp;
    uint32_t ss;
};

/***********  线程栈thread_stack  ***********
 * 线程自己的栈,用于存储线程中待执行的函数
 * 此结构在线程自己的内核栈中位置不固定,
 * 用在switch_to时保存线程环境。
 * 实际位置取决于实际运行情况。
 ******************************************/
struct thread_stack {
   uint32_t ebp;
   uint32_t ebx;
   uint32_t edi;
   uint32_t esi;

/* 线程第一次执行时,eip指向待调用的函数kernel_thread 
其它时候,eip是指向switch_to的返回地址*/
   void (*eip) (thread_func* func, void* func_arg);

/*****   以下仅供第一次被调度上cpu时使用   ****/

/* 参数unused_ret只为占位置充数为返回地址 */
   void (*unused_retaddr);
   thread_func* function;   // 由Kernel_thread所调用的函数名
   void* func_arg;    // 由Kernel_thread所调用的函数所需的参数
};

/* 进程或线程的pcb,程序控制块 */
struct task_struct {
   uint32_t* self_kstack;	 // 各内核线程都用自己的内核栈
   enum task_status status;
   uint8_t priority;		 // 线程优先级
   char name[16];
   uint32_t stack_magic;	 // 用这串数字做栈的边界标记,用于检测栈的溢出
};

void thread_create(struct task_struct* pthread, thread_func function, void* func_arg);
void init_thread(struct task_struct* pthread, char* name, int prio);
struct task_struct* thread_start(char* name, int prio, thread_func function, void* func_arg);
#endif

用typedef 定义了thread_func，它用来指定在线程中运行的函数类型。我们在线程中打算运行某段代码（函数）时，需要一个参数来接收该函数的地址。接下来用enum task_status结构定义了线程的状态，当然这也是进程的状态，进程与线程的区别是它们是否独自拥有地址空间，也就是是否拥有页表，程序的状态都是通用的，因此enum task_status结构同样也是进程的状态。

结构体 struct thread_stack 定义了线程栈，此栈有2个作用，主要就是体现在第5 个成员eip 上。首次执行某个函数时，这个栈就用来保存待运行的函数，其中eip 便是该函数的地址；任务切换时，此eip 用于保存任务切换后的新任务的返回地址。

5个寄存器ebp、ebx、edi、esi、和esp 归主调函数所用，其余的寄存器归被调函数所用。换句话说，不管被调函数中是否使用了这5 个寄存器，在被调函数执行完后，这5 个寄存器的值不该被改变。因此被调函数必须为主调函数保护好这5 个寄存器的值，在被调函数运行完之后，这5 个寄存器的值必须和运行前一样，它必须在自己的栈中存储这些寄存器的值。

1
2
3
void (*unused_retaddr);
thread_func* function;
void* func_arg;

其中，unused_retaddr 用来充当返回地址，在返回地址所在的栈帧占个位置，因此unused_retaddr 中的值并不重要，仅仅起到占位的作用。function 是由函数kernel_thread 所调用的函数名，即function 是在线程中执行的函数。func_arg 是由kernel_thread 所调用的函数所需的参数，即function 的参数，因此最终的情形是：在线程中调用的是function(func_arg)。

在线程中待执行的函数function 及其参数func_arg 是由kernel_thread 去调用执行的，它们两个作为kernel_thread 的参数，形如这样的形式：

1
2
3
kernel_thread(thread_func* func, void* func_arg) {
func(func_arg);
}

进入到函数kernel_thread 时，栈顶处是返回地址，因此栈顶+4 的位置保存的是function，栈顶+8 保存的是func_arg。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include "thread.h"
#include "stdint.h"
#include "string.h"
#include "global.h"
#include "memory.h"

#define PG_SIZE 4096

/* 由kernel_thread去执行function(func_arg) */
static void kernel_thread(thread_func* function, void* func_arg) {
   function(func_arg); 
}

/* 初始化线程栈thread_stack,将待执行的函数和参数放到thread_stack中相应的位置 */
void thread_create(struct task_struct* pthread, thread_func function, void* func_arg) {
   /* 先预留中断使用栈的空间,可见thread.h中定义的结构 */
   pthread->self_kstack -= sizeof(struct intr_stack);

   /* 再留出线程栈空间,可见thread.h中定义 */
   pthread->self_kstack -= sizeof(struct thread_stack);
   struct thread_stack* kthread_stack = (struct thread_stack*)pthread->self_kstack;
   kthread_stack->eip = kernel_thread;
   kthread_stack->function = function;
   kthread_stack->func_arg = func_arg;
   kthread_stack->ebp = kthread_stack->ebx = kthread_stack->esi = kthread_stack->edi = 0;
}

/* 初始化线程基本信息 */
void init_thread(struct task_struct* pthread, char* name, int prio) {
   memset(pthread, 0, sizeof(*pthread));
   strcpy(pthread->name, name);
   pthread->status = TASK_RUNNING; 
   pthread->priority = prio;
/* self_kstack是线程自己在内核态下使用的栈顶地址 */
   pthread->self_kstack = (uint32_t*)((uint32_t)pthread + PG_SIZE);
   pthread->stack_magic = 0x19870916;	  // 自定义的魔数
}

/* 创建一优先级为prio的线程,线程名为name,线程所执行的函数是function(func_arg) */
struct task_struct* thread_start(char* name, int prio, thread_func function, void* func_arg) {
/* pcb都位于内核空间,包括用户进程的pcb也是在内核空间 */
   struct task_struct* thread = get_kernel_pages(1);

   init_thread(thread, name, prio);
   thread_create(thread, function, func_arg);

   asm volatile ("movl %0, %%esp; pop %%ebp; pop %%ebx; pop %%edi; pop %%esi; ret" : : "g" (thread->self_kstack) : "memory");
   return thread;
}

thread_start函数接受4 个参数，name 为线程名，prio 为线程的优先级，要执行的函数是function，func_arg 是函数function 的参数。thread_start 的功能是创建一优先级为prio的线程，线程名为name，线程所执行的函数是function(func_arg)。

在函数体内，先通过get_kernel_pages(1)在内核空间中申请一页内存，即4096 字节，将其赋值给新创建的PCB 指针thread，即struct task_struct* thread。注意，由于get_kernel_page 返回的是页的起始地址，故thread 指向的是PCB 的最低地址。

接下来调用init_thread（thread, name, prio）来初始化刚刚创建的thread 线程。它接受3 个参数，pthread 是待初始化线程的指针，name 是线程名称，prio 是线程的优先级，此函数功能是将3 个参数写入线程的PCB，并且完成PCB 一级的其他初始化。在 init_thread 中，先调用memset(pthread, 0, sizeof(*pthread))将pthread 所在的PCB 清0，即清0一页。再通过strcpy(pthread->name, name)将线程名写入PCB 中的name 数组中。接下来为线程的状态pthread->status 赋值。pthread->self_kstack 是线程自己在0 特权级下所用的栈，在线程创建之初，它被初始化为线程PCB 的最顶端，即(uint32_t)pthread + PG_SIZE。

thread_create 接受3 个参数，pthread 是待创建的线程的指针，function 是在线程中运行的函数，func_arg是function 的参数。函数的功能是初始化线程栈thread_stack，将待执行的函数和参数放到thread_stack 中相应的位置。在 thread_create 中，pthread->self_kstack -= sizeof（struct intr_stack）是为了预留线程所使用的中断栈struct intr_stack 的空间，这有两个目的。

  1. 将来线程进入中断后，位于kernel.S 中的中断代码会通过此栈来保存上下文。
  2. 将来实现用户进程时，会将用户进程的初始信息放在中断栈中。

因此，必须要事先把struct intr_stack的空间留出来。pthread->self_kstack在init_thread 中已经被指向了PCB 的最顶端，所以现在要减去中断栈的大小。此时pthread->self_kstack指向PCB 中的中断栈下面的地址。

kernel_thread 接受两个参数，function 是kernel_thread 中调用的函数，func_arg 是function 的参数，因此kernel_thread 函数的功能就是调用function(func_arg)。，kernel_thread通过ret 来执行，因此无法按照正常的函数调用形式传递kernel_thread 所需要的参数，只能将参数放在kernel_thread 所用的栈中，即处理器进入kernel_thread 函数体时，栈顶为返回地址，栈顶+4 为参数function，栈顶+8 为参数func_arg。

汇编代码在输出部分，"g" (thread->self_kstack)使thread->self_kstack的值作为输入，采用通用约束g，即内存或寄存器都可以。在汇编语句部分， movl %0, %%esp，也就是使thread->self_kstack的值作为栈顶，此时thread->self_kstack指向线程栈的最低处，这是我们在函数thread_create中设定的。接下来的这连续4 个弹栈操作：pop %%ebp; pop %%ebx; pop %%edi; pop %%esi使之前初始化的0 弹入到相应寄存器中。

在执行ret 后，处理器会去执行kernel_thread函数。接着在kernel_thread 函数中会调用传给函数function(func_arg)。

核心数据结构，双向链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#ifndef __LIB_KERNEL_LIST_H
#define __LIB_KERNEL_LIST_H
#include "global.h"

#define offset(struct_type,member) (int)(&((struct_type*)0)->member)
#define elem2entry(struct_type, struct_member_name, elem_ptr) \
	 (struct_type*)((int)elem_ptr - offset(struct_type, struct_member_name))

/**********   定义链表结点成员结构   ***********
*结点中不需要数据成元,只要求前驱和后继结点指针*/
struct list_elem {
   struct list_elem* prev; // 前躯结点
   struct list_elem* next; // 后继结点
};

/* 链表结构,用来实现队列 */
struct list {
/* head是队首,是固定不变的，不是第1个元素,第1个元素为head.next */
   struct list_elem head;
/* tail是队尾,同样是固定不变的 */
   struct list_elem tail;
};

/* 自定义函数类型function,用于在list_traversal中做回调函数 */
typedef bool (function)(struct list_elem*, int arg);

void list_init (struct list*);
void list_insert_before(struct list_elem* before, struct list_elem* elem);
void list_push(struct list* plist, struct list_elem* elem);
void list_iterate(struct list* plist);
void list_append(struct list* plist, struct list_elem* elem);  
void list_remove(struct list_elem* pelem);
struct list_elem* list_pop(struct list* plist);
bool list_empty(struct list* plist);
uint32_t list_len(struct list* plist);
struct list_elem* list_traversal(struct list* plist, function func, int arg);
bool elem_find(struct list* plist, struct list_elem* obj_elem);
#endif

结构体struct list_elem是链表中结点的结构，这是链表的核心。一般的链表结点中除了前驱或后继结点的指针外，还包括数据成员，即链表结点是数据的存储单元。，它最主要的功能是“链”，咱们的链表单纯是为了将已有的数据以一定的时序链起来，因此不是为了存储，所以结点中不需要数据成员。

head 和tail 这两个成员是固定不变的，它们是链表固定的两个入口。新插入的结点不会替代它们的位置，只是会插入在head 和tail 之间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#include "list.h"
#include "interrupt.h"

/* 初始化双向链表list */
void list_init (struct list* list) {
   list->head.prev = NULL;
   list->head.next = &list->tail;
   list->tail.prev = &list->head;
   list->tail.next = NULL;
}

/* 把链表元素elem插入在元素before之前 */
void list_insert_before(struct list_elem* before, struct list_elem* elem) { 
   enum intr_status old_status = intr_disable();

/* 将before前驱元素的后继元素更新为elem, 暂时使before脱离链表*/ 
   before->prev->next = elem; 

/* 更新elem自己的前驱结点为before的前驱,
 * 更新elem自己的后继结点为before, 于是before又回到链表 */
   elem->prev = before->prev;
   elem->next = before;

/* 更新before的前驱结点为elem */
   before->prev = elem;

   intr_set_status(old_status);
}

/* 添加元素到列表队首,类似栈push操作 */
void list_push(struct list* plist, struct list_elem* elem) {
   list_insert_before(plist->head.next, elem); // 在队头插入elem
}

/* 追加元素到链表队尾,类似队列的先进先出操作 */
void list_append(struct list* plist, struct list_elem* elem) {
   list_insert_before(&plist->tail, elem);     // 在队尾的前面插入
}

/* 使元素pelem脱离链表 */
void list_remove(struct list_elem* pelem) {
   enum intr_status old_status = intr_disable();
   
   pelem->prev->next = pelem->next;
   pelem->next->prev = pelem->prev;

   intr_set_status(old_status);
}

/* 将链表第一个元素弹出并返回,类似栈的pop操作 */
struct list_elem* list_pop(struct list* plist) {
   struct list_elem* elem = plist->head.next;
   list_remove(elem);
   return elem;
} 

/* 从链表中查找元素obj_elem,成功时返回true,失败时返回false */
bool elem_find(struct list* plist, struct list_elem* obj_elem) {
   struct list_elem* elem = plist->head.next;
   while (elem != &plist->tail) {
      if (elem == obj_elem) {
	 return true;
      }
      elem = elem->next;
   }
   return false;
}

/* 把列表plist中的每个元素elem和arg传给回调函数func,
 * arg给func用来判断elem是否符合条件.
 * 本函数的功能是遍历列表内所有元素,逐个判断是否有符合条件的元素。
 * 找到符合条件的元素返回元素指针,否则返回NULL. */
struct list_elem* list_traversal(struct list* plist, function func, int arg) {
   struct list_elem* elem = plist->head.next;
/* 如果队列为空,就必然没有符合条件的结点,故直接返回NULL */
   if (list_empty(plist)) { 
      return NULL;
   }

   while (elem != &plist->tail) {
      if (func(elem, arg)) {		  // func返回ture则认为该元素在回调函数中符合条件,命中,故停止继续遍历
	 return elem;
      }					  // 若回调函数func返回true,则继续遍历
      elem = elem->next;	       
   }
   return NULL;
}

/* 返回链表长度 */
uint32_t list_len(struct list* plist) {
   struct list_elem* elem = plist->head.next;
   uint32_t length = 0;
   while (elem != &plist->tail) {
      length++; 
      elem = elem->next;
   }
   return length;
}

/* 判断链表是否为空,空时返回true,否则返回false */
bool list_empty(struct list* plist) {		// 判断队列是否为空
   return (plist->head.next == &plist->tail ? true : false);
}

list_init 只接受一个参数list，功能是初始化双向链表list。此时钟表是空的，因此函数内部的初始化工作就是把表头head 和表尾tail 连接起来，即list->head.next = &list->tail和list->tail.prev = &list->head。head.prev 和tail.next 的值无意义，因此被置为NULL。

函数 list_insert_before 接受两个参数，before 和elem，它们皆为链表结点的指针，此函数功能是把链表元素elem 插入在元素before 之前。通过intr_disable将中断关闭，旧中断状态用变量old_status 保存，以此保证下面的4 个操作的原子性（不可拆分、连续性）。通过intr_set_status(old_status)将中断恢复。

list_push 接受两个参数，plist 是链表，elem 是链表结点，功能是添加元素elem 到列表plist 的队首，其实这就是栈的特性，后进先出，因此相当于用链表实现了栈。其内部是调用list_insert_before(plist->head.next, elem)实现的，即在队头head.next 的前面插入elem。函数 list_append 接受两个参数，plist 是链表，elem 是链表结点，功能是添加元素elem 到列表plist的队尾，其实这就是队列的特性，先进先出，因此相当于用链表实现了线性队列。其内部是调用list_insert_before(&plist->tail, elem)实现的，就是在队尾tail 的前面插入elem。

多线程调度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

/* 进程或线程的pcb,程序控制块 */
struct task_struct {
   uint32_t* self_kstack;	 // 各内核线程都用自己的内核栈
   enum task_status status;
   char name[16];
   uint8_t priority;
   uint8_t ticks;	   // 每次在处理器上执行的时间嘀嗒数

/* 此任务自上cpu运行后至今占用了多少cpu嘀嗒数,
 * 也就是此任务执行了多久*/
   uint32_t elapsed_ticks;

/* general_tag的作用是用于线程在一般的队列中的结点 */
   struct list_elem general_tag;				    

/* all_list_tag的作用是用于线程队列thread_all_list中的结点 */
   struct list_elem all_list_tag;

   uint32_t* pgdir;              // 进程自己页表的虚拟地址
   uint32_t stack_magic;	 // 用这串数字做栈的边界标记,用于检测栈的溢出
};

ticks是任务每次被调度到处理器上执行的时间嘀嗒数，也就是我们所说的任务的时间片，每次时钟中断都会将当前任务的ticks 减1，当减到0时就被换下处理器。priority 表示任务的优先级。当ticks 递减为0 时，就要被时间中断处理程序和调度器换下处理器，调度器把priority 重新赋值给ticks，这样当此线程下一次又被调度时，将再次在处理器上运行ticks 个时间片。

elapsed_ticks 用于记录任务在处理器上运行的时钟嘀嗒数，从开始执行，到运行结束所经历的总时钟数。general_tag 的类型是struct list_elem，也就是general_tag 是双向链表中的结点。它是线程的标签，当线程被加入到就绪队列thread_ready_list 或其他等待队列中时，就把该线程PCB 中general_tag 的地址加入队列。

pgdir 是任务自己的页表。线程与进程的最大区别就是进程独享自己的地址空间，即进程有自己的页表，而线程共享所在进程的地址空间，即线程无页表。如果该任务为线程，pgdir 则为NULL，否则pgdir会被赋予页表的虚拟地址。

调度器主要任务就是读写就绪队列，增删里面的结点，结点是线程PCB 中的general_tag，“相当于”线程的PCB，从队列中将其取出时一定要还原成PCB 才行。调度器是从就绪队列thread_ready_list中“取出”上处理器运行的线程，所有待执行的线程都在thread_ready_list中，我们的调度机制很简单，就是Round-Robin Scheduling，俗称RR，即轮询调度，按先进先出的顺序始终调度队头的线程。就绪队列thread_ready_list 中的线程都属于运行条件已具备，但还在等待被调度运行的线程，因此thread_ready_list中的线程的状态都是TASK_READY。而当前运行线程的状态为TASK_RUNNING，它仅保存在全部队列 thread_all_list 当中。

调度器按照队列先进先出的顺序，把就绪队列中的第1 个结点作为下一个要运行的新线程，将该线程的状态置为TASK_RUNNING，之后通过函数switch_to 将新线程的寄存器环境恢复，这样新线程便开始执行。

  1. 时钟中断处理函数。
  2. 调度器schedule。
  3. 任务切换函数switch_to。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

/* 实现任务调度 */
void schedule() {

   ASSERT(intr_get_status() == INTR_OFF);

   struct task_struct* cur = running_thread(); 
   if (cur->status == TASK_RUNNING) { // 若此线程只是cpu时间片到了,将其加入到就绪队列尾
      ASSERT(!elem_find(&thread_ready_list, &cur->general_tag));
      list_append(&thread_ready_list, &cur->general_tag);
      cur->ticks = cur->priority;     // 重新将当前线程的ticks再重置为其priority;
      cur->status = TASK_READY;
   } else { 
      /* 若此线程需要某事件发生后才能继续上cpu运行,
      不需要将其加入队列,因为当前线程不在就绪队列中。*/
   }

   ASSERT(!list_empty(&thread_ready_list));
   thread_tag = NULL;	  // thread_tag清空
/* 将thread_ready_list队列中的第一个就绪线程弹出,准备将其调度上cpu. */
   thread_tag = list_pop(&thread_ready_list);   
   struct task_struct* next = elem2entry(struct task_struct, general_tag, thread_tag);
   next->status = TASK_RUNNING;
   switch_to(cur, next);
}

schedule的功能是将当前线程换下处理器，并在就绪队列中找出下个可运行的程序，将其换上处理器。schedule 主要内容就是读写就绪队列，因此它不需要参数。通过running_thread()获取了当前运行线程的PCB，将其存入PCB 指针cur 中。接下来分两种情况来考虑：

  • 如果当前线程cur 的时间片到期了，就将其通过list_append 函数重新加入到就绪队列thread_ready_list。由于此时它的时间片ticks 已经为0，为了下次运行时不至于马上被换下处理器，将ticks 的值再次赋值为它的优先级prio，最后将cur 的状态status 置为TASK_READY。
  • 如果当前线程cur 并不是因为时间片到期而被换下处理器，肯定是由于某种原因被阻塞了，这时候不需要处理就绪队列，因为当前运行线程并不在就绪队列中。

有可能就绪队列为空，为避免无线程可调度的情况，暂时用ASSERT (!list_empty(&thread_ready_list))来保障。通过thread_tag = list_pop(&thread_ready_list)从就绪队列中弹出一个可用线程并存入thread_tag。thread_tag 并不是线程，它仅仅是线程PCB 中的general_tag 或all_list_tag，要获得线程的信息，必须将其转换成PCB 才行，因此我们用到了宏elem2entry，elem2entry 定义在list.h 中：

1
2
3
#define offset(struct_type,member) (int)(&((struct_type*)0)->member)
#define elem2entry(struct_type, struct_member_name, elem_ptr) \
(struct_type*)((int)elem_ptr - offset(struct_type, struct_member_name))

参数 elem_ptr 是待转换的地址，它属于某个结构体中某个成员的地址，参数struct_member_name 是elem_ptr所在结构体中对应地址的成员名字，也就是说参数struct_member_name 是个字符串，参数struct_type 是elem_ptr所属的结构体的类型。宏elem2entry 的作用是将指针elem_ptr 转换成struct_type 类型的指针，其原理是用elem_ptr 的地址减去elem_ptr 在结构体struct_type 中的偏移量，此地址差便是结构体struct_type 的起始地址，最后再将此地址差转换为struct_type 指针类型。

从队列中弹出的结点元素并不能直接用，因为咱们链表中的结点并不是PCB，而是PCB 中的general_tag 或all_list_tag，需要将它们转换成所在的PCB 的地址。所以，整个转换过程要分为两步，先完成地址转换，再完成类型转换。

&PCB 相当于基址。general_tag 在PCB 中的偏移量 = &(PCB.general_tag)–&PCB = n，这里的&PCB恰恰是咱们最终要求解的，令基址&PCB的值等于0，&(PCB.general_tag)就等于偏移量n。宏offset接受两个参数，struct_type是结构体类型，member 是结构体成员的名字，其核心代码&((struct_type*)0)->member则为结构体成员member 在结构体中的偏移量。

通过elem2entry获得了新线程的PCB 地址，将其赋值给next，紧接着通过next-> status = TASK_RUNNING将新线程的状态置为TASK_RUNNING，这表示新线程next 可以上处理器了，于是准备切换寄存器映像，这是通过调用switch_to 函数完成的，调用形式为switch_to(cur, next)，意为将线程cur 的上下文保护好，再将线程next 的上下文装载到处理器，从而完成了任务切换。

系统中的任务调度，过程中需要保护好任务两层执行流的上下文，这分两部分来完成。第一部分是进入中断时的保护，这保存的是任务的全部寄存器映像，也就是进入中断前任务所属第一层的状态，这些寄存器映像相当于任务中用户代码的上下文。第二部分是保护内核环境上下文，保护esi、edi、ebx 和ebp 这4 个寄存器就够了。这4 个寄存器映像相当于任务中的内核代码的上下文，也就是第二层执行流。这几个寄存器的值会让处理器把程序执行到内核代码的结束处，用第一部分中保护的全部寄存器映像来恢复任务，从而退出中断，使任务彻底恢复为进入中断前的状态。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
[bits 32]
section .text
global switch_to
switch_to:
   ;栈中此处是返回地址	       
   push esi
   push edi
   push ebx
   push ebp

   mov eax, [esp + 20]		 ; 得到栈中的参数cur, cur = [esp+20]
   mov [eax], esp                ; 保存栈顶指针esp. task_struct的self_kstack字段,
				 ; self_kstack在task_struct中的偏移为0,
				 ; 所以直接往thread开头处存4字节便可。
;------------------  以上是备份当前线程的环境，下面是恢复下一个线程的环境  ----------------
   mov eax, [esp + 24]		 ; 得到栈中的参数next, next = [esp+24]
   mov esp, [eax]		 ; pcb的第一个成员是self_kstack成员,用来记录0级栈顶指针,
				 ; 用来上cpu时恢复0级栈,0级栈中保存了进程或线程所有信息,包括3级栈指针
   pop ebp
   pop ebx
   pop edi
   pop esi
   ret				 ; 返回到上面switch_to下面的那句注释的返回地址,
				 ; 未由中断进入,第一次执行时会返回到kernel_thread

switch_to函数接受两个参数，第1 个参数是当前线程cur，第2 个参数是下一个上处理器的线程，此函数的功能是保存cur 线程的寄存器映像，将下一个线程next 的寄存器映像装载到处理器。

最下面的4 个寄存器是咱们进入switch_to 时压入的。为了恢复寄存器映像，先得知道寄存器映像被保存在哪个栈中，也就是咱们得在切换前把当前的栈指针保存在某个地方，下次再被调度上处理器前，再从相同的地方恢复栈指针，这个地方就选PCB 中的成员self_kstack。

在switch_to 中self_kstack 已被固定引用为偏移PCB 0 字节的地方，因此必须要把self_kstack 放在PCB 的起始处，即task_struct 的开头。第 11 行的mov eax, [esp + 20]中[esp + 20]是为了获取栈中cur 的值，也就是当前线程的PCB 地址，再将它mov 到寄存器eax 中，因为self_kstack 在PCB 中偏移为0，所以此时eax 可以认为是当前线程PCB 中self_kstack 的地址。第 12 行mov [eax], esp将当前栈顶指针esp 保存到当前线程PCB 中的self_kstack 成员中。

第 16 行mov eax, [esp + 24]中[esp + 24]是为了获取栈中的next 的值，也就是next 线程的PCB 地址，之后将它mov 到寄存器eax，同样此时eax 可以认为是next 线程PCB 中self_kstack的地址。因此，[eax]中保存的是next 线程的栈指针。第 17 行mov esp, [eax]是将next 线程的栈指针恢复到esp 中，经过这一步后便找到了next 线程的栈，从而可以从栈中恢复之前保存过的寄存器映像。

输入输出系统

同步机制——锁

互斥也可称为排他，是指某一时刻公共资源只能被1 个任务独享，即不允许多个任务同时出现在自己的临界区中。竞争条件是指多个任务以非互斥的方式同时进入临界区，公共资源的最终状态依赖于这些任务的临界区中的微操作执行次序。

在计算机中，信号量就是个0 以上的整数值，当为0 时表示已无可用信号，或者说条件不再允许，因此它表示某种信号的累积“量”，故称为信号量。P 是指Proberen，表示减少，V 是指单词Verhogen，表示增加。增加操作up 包括两个微操作：

  1. 将信号量的值加1。
  2. 唤醒在此信号量上等待的线程。

减少操作down 包括三个子操作。

  1. 判断信号量是否大于0。
  2. 若信号量大于0，则将信号量减1。
  3. 若信号量等于0，当前线程将自己阻塞，以在此信号量上等待。

信号量是个全局共享变量，up 和down 又都是读写这个全局变量的操作，而且它们都包含一系列的子操作，因此它们必须都是原子操作。信号量的初值代表是信号资源的累积量，也就是剩余量，若初值为1 的话，它的取值就只能为0 和1，这便称为二元信号量，我们可以利用二元信号量来实现锁。在二元信号量中，down 操作就是获得锁，up 操作就是释放锁。我们可以让线程通过锁进入临界区，可以借此保证只有一个线程可以进入临界区，从而做到互斥。大致流程为：

  • 线程A 进入临界区前先通过down 操作获得锁（我们有强制通过锁进入临界区的手段），此时信号量的值便为0。
  • 后续线程B 再进入临界区时也通过down 操作获得锁，由于信号量为0，线程B 便在此信号量上等待，也就是相当于线程B 进入了睡眠态。
  • 当线程A 从临界区出来后执行up 操作释放锁，此时信号量的值重新变成1，之后线程A 将线程B唤醒。
  • 线程B 醒来后获得了锁，进入临界区。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/* 当前线程将自己阻塞,标志其状态为stat. */
void thread_block(enum task_status stat) {
/* stat取值为TASK_BLOCKED,TASK_WAITING,TASK_HANGING,也就是只有这三种状态才不会被调度*/
   ASSERT(((stat == TASK_BLOCKED) || (stat == TASK_WAITING) || (stat == TASK_HANGING)));
   enum intr_status old_status = intr_disable();
   struct task_struct* cur_thread = running_thread();
   cur_thread->status = stat; // 置其状态为stat 
   schedule();		      // 将当前线程换下处理器
/* 待当前线程被解除阻塞后才继续运行下面的intr_set_status */
   intr_set_status(old_status);
}

/* 将线程pthread解除阻塞 */
void thread_unblock(struct task_struct* pthread) {
   enum intr_status old_status = intr_disable();
   ASSERT(((pthread->status == TASK_BLOCKED) || (pthread->status == TASK_WAITING) || (pthread->status == TASK_HANGING)));
   if (pthread->status != TASK_READY) {
      ASSERT(!elem_find(&thread_ready_list, &pthread->general_tag));
      if (elem_find(&thread_ready_list, &pthread->general_tag)) {
	 PANIC("thread_unblock: blocked thread in ready_list\n");
      }
      list_push(&thread_ready_list, &pthread->general_tag);    // 放到队列的最前面,使其尽快得到调度
      pthread->status = TASK_READY;
   } 
   intr_set_status(old_status);
}

thread_block，它接受一个参数stat，stat 是线程的状态，它的取值为“不可运行态”，函数功能是将当前线程的状态置为stat，从而实现了线程的阻塞。stat 取值范围是TASK_BLOCKED、TASK_WAITING 和TASK_HANGING，这三个就是上面所说的“不可运行态”。只有status 为TASK_RUNNING 的线程才可以被添加到就绪队列thread_ready_list。当前运行线程的status 必然是TASK_RUNNING。在调用schedule 之后，下面的中断状态恢复代码intr_set_status(old_status)本次便没机会执行了，只有在当前线程被唤醒后才会被执行到。

函数thread_unblock 与thread_block 的功能相反，它将某线程解除阻塞，唤醒某线程。被阻塞的线程已无法运行，无法自己唤醒自己，必须被其他线程唤醒，因此参数pthread 指向的是目前已经被阻塞，又希望被唤醒的线程。通过list_push 将阻塞的线程重新添加到就绪队列，这里用list_push 是将线程添加到就绪队列的队首，因此保证这个睡了很久的线程能被优先调度。最后再将线程的status 置为TASK_READY，至此，线程重新回到了就绪队列，它有再被调度的机会了，也就是实现了唤醒。

1
2
3
4
5
6
7
8
9
10
11
12
/* 信号量结构 */
struct semaphore {
   uint8_t  value;
   struct   list waiters;
};

/* 锁结构 */
struct lock {
   struct   task_struct* holder;	    // 锁的持有者
   struct   semaphore semaphore;	    // 用二元信号量实现锁
   uint32_t holder_repeat_nr;		    // 锁的持有者重复申请锁的次数
};

锁结构中必须包含一个信号量成员，这里就是semaphore，它就是信号量结构体struct semaphore实例。此信号量的初值会被赋值为1，也就是用二元信号量实现锁。成员holder_repeat_nr 用来累积锁的持有者重复申请锁的次数，释放锁的时候会参考此变量的值。为了避免内外层函数在释放锁时会对同一个锁释放两次，用此变量来累积重复申请的次数，释放锁时会根据变量holder_repeat_nr 的值来执行具体动作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/* 初始化信号量 */
void sema_init(struct semaphore* psema, uint8_t value) {
   psema->value = value;       // 为信号量赋初值
   list_init(&psema->waiters); //初始化信号量的等待队列
}

/* 初始化锁plock */
void lock_init(struct lock* plock) {
   plock->holder = NULL;
   plock->holder_repeat_nr = 0;
   sema_init(&plock->semaphore, 1);  // 信号量初值为1
}

/* 信号量down操作 */
void sema_down(struct semaphore* psema) {
/* 关中断来保证原子操作 */
   enum intr_status old_status = intr_disable();
   while(psema->value == 0) {	// 若value为0,表示已经被别人持有
      ASSERT(!elem_find(&psema->waiters, &running_thread()->general_tag));
      /* 当前线程不应该已在信号量的waiters队列中 */
      if (elem_find(&psema->waiters, &running_thread()->general_tag)) {
	 PANIC("sema_down: thread blocked has been in waiters_list\n");
      }
/* 若信号量的值等于0,则当前线程把自己加入该锁的等待队列,然后阻塞自己 */
      list_append(&psema->waiters, &running_thread()->general_tag); 
      thread_block(TASK_BLOCKED);    // 阻塞线程,直到被唤醒
   }
/* 若value为1或被唤醒后,会执行下面的代码,也就是获得了锁。*/
   psema->value--;
   ASSERT(psema->value == 0);	    
/* 恢复之前的中断状态 */
   intr_set_status(old_status);
}

/* 信号量的up操作 */
void sema_up(struct semaphore* psema) {
/* 关中断,保证原子操作 */
   enum intr_status old_status = intr_disable();
   ASSERT(psema->value == 0);	    
   if (!list_empty(&psema->waiters)) {
      struct task_struct* thread_blocked = elem2entry(struct task_struct, general_tag, list_pop(&psema->waiters));
      thread_unblock(thread_blocked);
   }
   psema->value++;
   ASSERT(psema->value == 1);	    
/* 恢复之前的中断状态 */
   intr_set_status(old_status);
}

/* 获取锁plock */
void lock_acquire(struct lock* plock) {
/* 排除曾经自己已经持有锁但还未将其释放的情况。*/
   if (plock->holder != running_thread()) { 
      sema_down(&plock->semaphore);    // 对信号量P操作,原子操作
      plock->holder = running_thread();
      ASSERT(plock->holder_repeat_nr == 0);
      plock->holder_repeat_nr = 1;
   } else {
      plock->holder_repeat_nr++;
   }
}

/* 释放锁plock */
void lock_release(struct lock* plock) {
   ASSERT(plock->holder == running_thread());
   if (plock->holder_repeat_nr > 1) {
      plock->holder_repeat_nr--;
      return;
   }
   ASSERT(plock->holder_repeat_nr == 1);

   plock->holder = NULL;	   // 把锁的持有者置空放在V操作之前
   plock->holder_repeat_nr = 0;
   sema_up(&plock->semaphore);	   // 信号量的V操作,也是原子操作
}

sema_init 函数接受两个参数，psema 是待初始化的信号量，value 是信号量的初值，函数功能是将信号量psema 初值初始化为value。锁是用信号量来实现的，因此锁的初始化中会调用sema_init。函数lock_init 接受一个参数，plock 是待初始化的锁。函数功能是将锁的持有者holder 置为空，将持有者重复申请次数累积变量holder_repeat_nr 置为0，并调用sema_init(&plock->semaphore, 1)将锁使用的信号量初值赋值为1，这样锁中的信号量就成为了二元信号量。

函数sema_down接受一个参数，psema 是待执行down 操作的信号量。函数功能就是在信号量psema 上执行个down 操作。为保证down 操作的原子性，在函数开头便通过intr_disable 关了中断。这里通过while(psema->value == 0)判断信号量是否为0，如果为0，就进入while 的循环体做两件事。

  1. 将自己添加到该信号量的等待队列中。对应的代码为list_append(&psema->waiters, &running_thread()->general_tag);
  2. 将自己阻塞，状态为TASK_BLOCKED。对应的代码为：thread_block(TASK_BLOCKED);

如果信号量不为0，也就是为1，则将信号量减1，即psema->value--。

函数sema_up 接受一个参数，psema 是待执行up 操作的信号量。函数功能是将信号量的值加1。函数内部的操作也要保证原子性，因此在函数的开头也执行了intr_disable 函数关中断。其他线程可以申请锁了，因此在信号量的等待队列psema->waiters 中通过list_pop 弹出队首的第一个线程，并通过宏elem2entry 将其转换成PCB，存储到thread_blocked 中。然后通过thread_unblock(thread_blocked)将此线程唤醒。在将线程唤醒后，接下来将信号量值加1，即代码psema->value++。

提醒一下，所谓的唤醒并不是指马上就运行，而是重新加入到就绪队列，将来可以参与调度，运行是将来的事。最后通过intr_set_status(old_status)恢复之前的中断状态。

函数lock_acquire 接受一个参数，plock 是所要获得的锁，函数功能是获取锁plock。在函数开头先判断自己是否已经是该锁的持有者，即代码if (plock->holder != running_thread())。如果自己尚未持有此锁的话，通过sema_down(&plock->semaphore)将锁的信号量减1。成功后将当前线程记为锁的持有者，即plock->holder = running_thread()，然后将holder_repeat_nr 置为1，表示第1 次申请了该锁。

函数lock_release 只接受一个参数，plock 指向待释放的锁，函数功能是释放锁plock。如果持有者的变量holder_repeat_nr大于1，这说明自已多次申请该锁，此时还不能真正将锁释放，因此只是将holder_repeat_nr--，随后返回。如果锁持有者的变量holder_repeat_nr 为1，说明现在可以释放锁了，通过代码plock->holder = NULL 将持有者置空，随后将holder_repeat_nr 置为0，最后通过sema_up(&plock->semaphore)将信号量加1，自此，锁被真正释放。

环形缓冲区的实现

只要我们能够设计出合理的缓冲区操作方式，就能够解决生产者与消费者问题。环形缓冲区本质上依然是线性缓冲区，但其使用方式像环一样，没有固定的起始地址和终止地址，环内任何地址都可以作为起始和结束。缓冲区相当于一个队列，数据在队列头被写入，在队尾处被读出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

/* 环形队列 */
struct ioqueue {
// 生产者消费者问题
    struct lock lock;
 /* 生产者,缓冲区不满时就继续往里面放数据,
  * 否则就睡眠,此项记录哪个生产者在此缓冲区上睡眠。*/
    struct task_struct* producer;

 /* 消费者,缓冲区不空时就继续从往里面拿数据,
  * 否则就睡眠,此项记录哪个消费者在此缓冲区上睡眠。*/
    struct task_struct* consumer;
    char buf[bufsize];			    // 缓冲区大小
    int32_t head;			    // 队首,数据往队首处写入
    int32_t tail;			    // 队尾,数据从队尾处读出
};
  • struct ioqueue 结构便是咱们定义的环形缓冲区，它包括六个成员，其中：
  • lock 是本缓冲区的锁，每次对缓冲区操作时都要先申请这个锁，从而保证缓冲区操作互斥。
  • producer 是生产者，此项来记录当缓冲区满时，在此缓冲区睡眠的生产者线程。
  • consumer 是消费者，此项来记录当缓冲区空时，在此缓冲区睡眠的消费者线程。
  • buf[bufsize]是定义的缓冲区数组，其大小为bufsize，在上面用define 定义为64。
  • head 是缓冲区队列的队首地址，tail 是队尾地址。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
/* 初始化io队列ioq */
void ioqueue_init(struct ioqueue* ioq) {
   lock_init(&ioq->lock);     // 初始化io队列的锁
   ioq->producer = ioq->consumer = NULL;  // 生产者和消费者置空
   ioq->head = ioq->tail = 0; // 队列的首尾指针指向缓冲区数组第0个位置
}

/* 返回pos在缓冲区中的下一个位置值 */
static int32_t next_pos(int32_t pos) {
   return (pos + 1) % bufsize; 
}

/* 判断队列是否已满 */
bool ioq_full(struct ioqueue* ioq) {
   ASSERT(intr_get_status() == INTR_OFF);
   return next_pos(ioq->head) == ioq->tail;
}

/* 判断队列是否已空 */
static bool ioq_empty(struct ioqueue* ioq) {
   ASSERT(intr_get_status() == INTR_OFF);
   return ioq->head == ioq->tail;
}

/* 使当前生产者或消费者在此缓冲区上等待 */
static void ioq_wait(struct task_struct** waiter) {
   ASSERT(*waiter == NULL && waiter != NULL);
   *waiter = running_thread();
   thread_block(TASK_BLOCKED);
}

/* 唤醒waiter */
static void wakeup(struct task_struct** waiter) {
   ASSERT(*waiter != NULL);
   thread_unblock(*waiter); 
   *waiter = NULL;
}

/* 消费者从ioq队列中获取一个字符 */
char ioq_getchar(struct ioqueue* ioq) {
   ASSERT(intr_get_status() == INTR_OFF);

/* 若缓冲区(队列)为空,把消费者ioq->consumer记为当前线程自己,
 * 目的是将来生产者往缓冲区里装商品后,生产者知道唤醒哪个消费者,
 * 也就是唤醒当前线程自己*/
   while (ioq_empty(ioq)) {
      lock_acquire(&ioq->lock);	 
      ioq_wait(&ioq->consumer);
      lock_release(&ioq->lock);
   }

   char byte = ioq->buf[ioq->tail];	  // 从缓冲区中取出
   ioq->tail = next_pos(ioq->tail);	  // 把读游标移到下一位置

   if (ioq->producer != NULL) {
      wakeup(&ioq->producer);		  // 唤醒生产者
   }

   return byte; 
}

/* 生产者往ioq队列中写入一个字符byte */
void ioq_putchar(struct ioqueue* ioq, char byte) {
   ASSERT(intr_get_status() == INTR_OFF);

/* 若缓冲区(队列)已经满了,把生产者ioq->producer记为自己,
 * 为的是当缓冲区里的东西被消费者取完后让消费者知道唤醒哪个生产者,
 * 也就是唤醒当前线程自己*/
   while (ioq_full(ioq)) {
      lock_acquire(&ioq->lock);
      ioq_wait(&ioq->producer);
      lock_release(&ioq->lock);
   }
   ioq->buf[ioq->head] = byte;      // 把字节放入缓冲区中
   ioq->head = next_pos(ioq->head); // 把写游标移到下一位置

   if (ioq->consumer != NULL) {
      wakeup(&ioq->consumer);          // 唤醒消费者
   }
}

ioqueue_init 函数接受一个缓冲区参数ioq，用于初始化缓冲区ioq。此函数负责三样工作，先通过初始化io 队列的锁，再将生产者和消费者置为NULL，最后再将缓冲区的队头和队尾置为下标0。next_pos 函数接受一个参数pos，功能是返回pos 在缓冲区中的下一个位置值，它是将pos+1 后再对bufsize 求模得到的，这保证了缓冲区指针回绕着数组buf，从而实现了环形缓冲区。ioq_full 函数接受一个缓冲区参数ioq。功能是返回队列是否已满，若已满则返回true，否则返回false。原理是next_pos(ioq->head) == ioq->tail。ioq_empty 函数接受一个缓冲区参数ioq。功能是返回队列是否为空，若空则返回true。原理是判断ioq->head 是否等于ioq->tail，若头尾相等则为空。

ioq_wait 函数接受一个参数waiter，函数功能是使当前线程睡眠，并在缓冲区中等待。估计大伙儿都猜到了，传给waiter 的实参一定是缓冲区中的成员producer 或consumer。在函数体内就做了两件事，将当前线程记录在waiter 指向的指针中，也就是缓冲区中的producer 或consumer，因此*waiter 相当于ioq->consumer 或ioq->producer。随后调用thread_block(TASK_BLOCKED)将当前线程阻塞。wakeup 函数接受一个参数waiter，它同样也是pcb 类型的二级指针，因此传给它的实参也是缓冲区中的成员producer 或consumer。函数功能就是通过thread_unblock(*waiter)唤醒*waiter（生产者或消费者），随后将*waiter置空。

ioq_getchar 函数接受一个缓冲区参数ioq，函数功能是从ioq 的队尾处返回一个字节，这属于从缓冲区中取数据，因此ioq_getchar 是由消费者线程调用的。函数体中，先通过while(ioq_empty(ioq))循环判断缓冲区ioq 是否为空，如果为空就表示没有数据可取，只好先在此缓冲区上睡眠，直到有生产者将数据添加到此缓冲区后再被叫醒重新取数据。while 循环体中先通过lock_acquire(&ioq->lock)申请缓冲区的锁，持有锁后，通过ioq_ wait(&ioq->consumer)将自己阻塞，也就是在此缓冲区上休眠。在while 循环判断中，如果缓冲区不为空的话，通过代码byte = ioq->buf[ioq->tail]从缓冲区队尾获取1 字节的数据，接着通过ioq->tail = next_pos(ioq->tail)将队尾更新为下一个位置。如果现在缓冲区已被当前消费者线程腾出一个数据单位的空间了，此时应该叫醒生产者继续往缓冲区中添加数据。因此调用wakeup(&ioq->producer)唤醒生产者。之后通过return byte 返回获取数据。

ioq_putchar 函数接受两个参数，一个是缓冲区参数ioq，另一个是待加入字节数据byte，函数功能是往缓冲区ioq 中添加byte，这是由生产者线程调用的。在函数体中也是先通过while 循环判断缓冲区ioq 是否为满，如果满了的话，先申请缓冲区的锁ioq->lock，然后通过调用ioq_wait(&ioq->producer)将自己阻塞并登记在缓冲区ioq 的成员producer 中，这样消费者便知道唤醒哪个生产者了。随后释放锁。如果缓冲区不满的话，通过ioq->buf[ioq->head] = byte，将数据byte 写入缓冲区的队首ioq->head。随后通过ioq->head = next_pos(ioq->head)将队首更新为下一位置。

用户进程

为什么要有任务状态段 TSS

TSS 是Task State Segment 的缩写。LDT 是Local Descriptor Table 的缩写，即局部描述符表，为每个程序单独赋予一个结构来存储其私有的资源。LDT 属于任务私有的结构，LDT 必须像其他描述符那样在GDT 注册，之后便能够用选择子找到它。描述符的作用是描述一段内存区域的属性，其中最重要的属性是内存区域的起始地址及偏移大小。

LDT 虽然是描述符“表”，为了在GDT 中注册，必须也得为它找个描述符，用此描述符来描述某任务的LDT 的起始地址及偏移大小，此描述符便称为LDT 描述符。

在LDT 中，描述符的D 位和L 位固定为0。LDT 描述符属于系统段描述符，因此S 为0。在S 为0 的前提下，若TYPE 的值为0010，这表示此描述符是LDT 描述符。CPU 专门准备了个寄存器来存储其位置及偏移量，想必您又猜到了，对，这就是LDTR。CPU 同样也准备了配套的指令，就是lldt，用此指令能够将ldt 加载到LDTR 寄存器。lldt 的指令格式为lldt 16 位通用寄存器或16位内存单元。

对比一下，加载 GDT 的指令是lgdt，其格式是：lgdt 16 位内存单元 & 32 位内存单元 ，前 16 位表示GDT 的偏移大小，后32 位表示GDT 的起始地址。区别是，lgdt 的操作数是GDT 表的偏移量及起始地址，而lldt 的操作数是ldt 在GDT 中的选择子。

LDTR 寄存器结构如图。LDTR 分为两个部分，选择器是中16 位的LDT 选择子，描述符缓冲器中是LDT 的起始地址及偏移大小等属性。LDT 中的描述符全部用于指向任务自己的内存段。

选择子的高 13 位表示可索引的描述符范围，2 的13 次方等于8192，也就是说一个任务最多可定义8192个内存段。由于LDT 描述符放在GDT 中，如果任务是用LDT 来实现的话，最多可同时创建8192 个任务。当前运行的任务，其LDT 位于LDTR 指向的地址，这样CPU 才能从中拿到任务运行所需要的资源（指令和数据）。因此，每切换一个任务时，需要用lldt 指令重新加载新任务的LDT 到LDTR。

当加载新任务时，CPU 自动把当前任务（旧任务）的状态存入当前任务的TSS，然后将新任务TSS 中的数据载入到对应的寄存器中，这就实现了任务
切换。TSS 就是任务的代表，CPU 用不同的TSS 区分不同的任务，因此任务切换的本质就是TSS 的换来换去。TSS 描述符也要在GDT 中注册，这样才能“找到它”。

TSS 描述符属于系统段描述符，因此S为0，在S 为0 的情况下，TYPE 的值为10B1。B 表示busy 位，B 位为0 时，表示任务不繁忙，B 位为1 时，表示任务繁忙。任务繁忙有两方面的含义，一方面就是指此任务是否为当前正在CPU 上运行的任务。另一方面是指此任务嵌套调用了新的任务，CPU 正在执行新任务，此任务暂时挂起。新老任务的调用关系形成了调用关系链。给当前任务打个标记，目的是避免当前任务调用自己，当前任务只能调用其他任务，不能自己调用自己。CPU 利用B 位来判断被调用的任务是否是当前任务，若被调用任务的B 位为1，这就表示当前任务自己在调用自己。因此，B 位主要是用来给CPU 做重入判断用的。

TSS 同其他普通段一样，是位于内存中的区域，TSS 中的数据是按照固定格式来存储的，所以TSS 是个数据结构。

TSS 中有三组栈：SS0 和esp0，SS1 和esp1，SS2 和esp2。这三组栈是用来由低特权级往高特权级跳转时用的，最低的特权级是3，没有更低的特权级会跳入3 特权级，因此，TSS 中没有SS3 和esp3。当任务被换下CPU 时，CPU 会自动将当前寄存器中的值存储到TSS 中的对应位置，当有新任务上CPU 运行时，CPU会自动从新任务的TSS 中找到相应的寄存器值加载到对应的寄存器中。

TSS 和LDT 一样，必须要在GDT 中注册才行，这也是为了在引用描述符的阶段做安全检查。因此TSS 是通过选择子来访问的，将tss 加载到寄存器TR 的指令是ltr，其指令格式为：ltr 16 位通用寄存器或16位内存单元，有了 TSS 后，任务在被换下CPU 时，由CPU 自动地把当前任务的资源状态（所有寄存器、必要的内存结构，如栈等）保存到该任务对应的TSS 中（由寄存器TR 指定）。CPU 通过新任务的TSS 选择子加载新任务时，会把该TSS 中的数据载入到CPU 的寄存器中，同时用此TSS 描述符更新寄存器TR。

总结；

  • TSS 由用户提供，由CPU 自动维护。
  • TSS 与其他普通段一样，也有自己的描述符，即TSS 描述符，用它来描述一个TSS 的信息，此描述符需要定义在GDT 中。寄存器TR 始终指向当前任务的
    TSS。任务切换就是改变TR 的指向，CPU 自动将当前寄存器组的值（快照）写入TR 指向的TSS，同时将新任务TSS 中的各寄存器的值载入CPU 中对应的寄存器，从而实现了任务切换。
  • TSS 和LDT 都只能且必须在GDT 中注册描述符，TR 寄存器中存储的是TSS 的选择子，LDTR 寄存器中存储的是LDT 的选择子，GDTR 寄存器中存储的是GDT 的起始地址及界限偏移（大小减1）

CPU 原生支持的任务切换方式

进行任务切换的方式有中断+任务门，call 或jmp+任务门和iretd，下面分别介绍。

通过中断+任务门进行任务切换。中断是定时发生的，因此用中断进行任务切换的好处是明显的：实现简单，抢占式多任务调度，所有任务都有运行的机会。若想通过中断的方式进行任务切换，该中断对应的描述符中必须要包含TSS选择子，唯一包含TSS 选择子的描述符便是任务门描述符。CPU 为原生支持多任务做了很多努力，最直接实现任务切换的方式是任务门。

任务门描述符中的内容是TSS 选择子，任务门描述符也是系统段，因此S 的值为0，在S 为0的情况下，TYPE 的值为0101 时，就表示此描述符是任务门描述符。当中断发生时，处理器通过中断向量号在IDT 中找到描述符后，通过分析描述符中字段S 和字段TYPE的组合，发现此中断对应的描述符是中断门描述符，则转而去执行此中断门描述符中指定的中断处理例程。在中断处理程序的最后，通过iretd 指令返回到被中断任务的中断前的代码处。若发现中断对应的是门描述符，此时便进行任务切换。

当中断发生时，假设当前任务A 被中断，CPU 进入中断后，它有可能的动作是：

  • 假设是中断门或陷阱门，执行完中断处理例程后是用iretd 指令返回到任务A 中断前的指令部分。
  • 假设是任务门，进行任务切换，此时是嵌套调用任务B，任务B 在执行期间又发生了中断，进入了对应的中断门，当执行完对应的中断处理程序后，用iretd 指令返回。
  • 同样假设是任务门，任务A 调用任务B 执行，任务B 执行完成后要通过iretd 指令返回到任务A，使任务A 继续完成后续的指令。

标志寄存器eflags 中的NT 位和TSS 中的上一个任务的TSS 指针字段用于区分这几种情况。NT 位是eflags 中的第14 位，1bit 的宽度，它表示Nest Task Flag，任务嵌套。任务嵌套是指当前任务是被前一个任务调用后才执行的，也就是当前任务嵌套于另一个任务中，相当于另一个任务的子任务，在
此任务执行完成后还要回到前一个任务，使其继续执行。TSS 的字段上一个任务的TSS 指针，用于记录是哪个任务调用了当前任务，此字段中的值是TSS 的地址，因此它就形成了任务嵌套关系的单向链表，每个TSS 属于链表中的结点，CPU用此链表来记录任务的嵌套调用关系。

当调用一个新任务时，处理器做了两件准备工作。

  • 自动将新任务 eflags 中的NT 位置为1，这就表示新任务能够执行的原因是被别的任务调用，也就是嵌套调用。
  • 随后处理器将旧任务的TSS 选择子写入新任务TSS 的“上一个任务的TSS 指针”字段中。

当CPU 执行iretd 指令时，始终要判断NT 位的值。如果NT 等于1，这表示是从新任务返回到旧任务，于是CPU 到当前任务（新任务）TSS 的“上一个任务的TSS 指针”字段中获取旧任务的TSS，转而去执行旧任务。如果NT 等于0，这表示要回到当前任务中断前的指令部分。

中断发生时，通过任务门进行任务切换的过程如下。

  1. 从该任务门描述符中取出任务的TSS 选择子。
  2. 用新任务的TSS 选择子在GDT 中索引TSS 描述符。
  3. 判断该TSS 描述符的P 位是否为1，为1 表示该TSS 描述符对应的TSS 已经位于内存中TSS 描述符指定的位置，可以访问。否则P 不为1 表示该TSS 描述符对应的TSS 不在内存中，这会导致异常。
  4. 从寄存器TR 中获取旧任务的TSS 位置，保存旧任务（当前任务）的状态到旧TSS 中。其中，任务状态是指CPU 中寄存器的值，这仅包括TSS 结构中列出的寄存器：8 个通用寄存器，6 个段寄存器，指令指针eip，栈指针寄存器esp，页表寄存器cr3 和标志寄存器eflags 等。
  5. 把新任务的TSS 中的值加载到相应的寄存器中。
  6. 使寄存器TR 指向新任务的TSS。
  7. 将新任务（当前任务）的TSS 描述符中的B 位置1。
  8. 将新任务标志寄存器中eflags 的NT 位置1。
  9. 将旧任务的TSS 选择子写入新任务TSS 中“上一个任务的TSS 指针”字段中。
  10. 开始执行新任务。

当新任务执行完成后，调用iretd 指令返回到旧任务，此时处理器检查NT 位，若其值为1，便进行返回工作，步骤如下。

  1. 将当前任务（新任务）标志寄存器中eflags 的NT 位置0。
  2. 将当前任务TSS 描述符中的B 位置为0。
  3. 将当前任务的状态信息写入TR 指向的TSS。
  4. 获取当前任务TSS 中“上一个任务的TSS 指针”字段的值，将其加载到TR 中，恢复上一个任务的状态。
  5. 执行上一个任务（当前任务），从而恢复到旧任务。

call、jmp 切换任务

call 是有去有回的指令，jmp 是一去不回的指令，它们在调用新任务时的区别也在于此。call 指令以任务嵌套的方式调用新任务，当以call 指令调用新任务时，我们以操作数为TSS 选择子为例，比如call 0x0018:0x1234，任务切换的步骤如下。

  1. CPU 忽略偏移量0x1234，拿选择子0x0018 在GDT 中索引到第3 个描述符。
  2. 检查描述符中的P 位，若P 为0，表示该描述符对应的段不存在，这将引发异常。同时检查该描述符的S 与TYPE 的值，判断其类型，如果是TSS 描述符，检查该描述符的B 位，B 位若为1 将抛出GP异常，即表示调用不可重入。
  3. 进行特权级检查，数值上“CPL 和TSS 选择子中的RPL”都要小于等于TSS 描述符的DPL，否则抛出GP 异常。
  4. 特权检查完成后，将当前任务的状态保存到寄存器TR 指向的TSS 中。
  5. 加载新任务TSS 选择子到TR 寄存器的选择器部分，同时把TSS 描述符中的起始地址和偏移量等属性加载到TR 寄存器中的描述符缓冲器中。
  6. 将新任务TSS 中的寄存器数据载入到相应的寄存器中，同时进行特权级检查，如果检查未通过，则抛出GP 异常。
  7. CPU 会把新任务的标志寄存器eflags 中的NT 位置为1。
  8. 将旧任务TSS 选择子写入新任务TSS 中的字段“上一个任务的TSS 指针”中，这表示新任务是被旧任务调用才执行的。
  9. 然后将新任务TSS 描述符中的B 位置为1 以表示任务忙。旧任务TSS 描述符中的B 位不变，依然保持为1，旧任务的标志寄存器eflags 中的NT 位的值保持不变，之前是多少就是多少。
  10. 开始执行新任务，完成任务切换。

jmp 指令以非嵌套的方式调用新任务，新任务和旧任务之间不会形成链式关系。当以jmp 指令调用新任务时，新任务TSS 描述符中的B 位会被CPU 置为1 以表示任务忙，旧任务TSS 描述符中的B 位会被CPU 清0。

Linux 为每个CPU 创建一个TSS，在各个CPU 上的所有任务共享同一个TSS，各CPU 的TR 寄存器保存各CPU 上的TSS，在用ltr指令加载TSS 后，该TR 寄存器永远指向同一个TSS，之后再也不会重新加载TSS。在进程切换时，只需要把TSS 中的SS0 及esp0 更新为新任务的内核栈的段地址及栈指针。

当CPU 由低特权级进入高特权级时，CPU 会“自动”从TSS 中获取对应高特权级的栈指针，CPU 自动从当前任务的TSS 中获取SS0 和esp0 字段的值作为0 特权级的栈，然后Linux执行一系列的push 指令将任务的状态的保存在0 特权级栈中，也就是TSS 中SS0 和esp0 所指向的栈。任务切换的开销更小了。

定义并初始化 TSS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

// ----------------  GDT描述符属性  ----------------

#define	DESC_G_4K    1
#define	DESC_D_32    1
#define DESC_L	     0	// 64位代码标记，此处标记为0便可。
#define DESC_AVL     0	// cpu不用此位，暂置为0  
#define DESC_P	     1
#define DESC_DPL_0   0
#define DESC_DPL_1   1
#define DESC_DPL_2   2
#define DESC_DPL_3   3
/* 
   代码段和数据段属于存储段，tss和各种门描述符属于系统段
   s为1时表示存储段,为0时表示系统段.
*/
#define DESC_S_CODE	1
#define DESC_S_DATA	DESC_S_CODE
#define DESC_S_SYS	0
#define DESC_TYPE_CODE	8	// x=1,c=0,r=0,a=0 代码段是可执行的,非依从的,不可读的,已访问位a清0.  
#define DESC_TYPE_DATA  2	// x=0,e=0,w=1,a=0 数据段是不可执行的,向上扩展的,可写的,已访问位a清0.
#define DESC_TYPE_TSS   9	// B位为0,不忙

#define	 RPL0  0
#define	 RPL1  1
#define	 RPL2  2
#define	 RPL3  3

#define TI_GDT 0
#define TI_LDT 1

#define SELECTOR_K_CODE	   ((1 << 3) + (TI_GDT << 2) + RPL0)
#define SELECTOR_K_DATA	   ((2 << 3) + (TI_GDT << 2) + RPL0)
#define SELECTOR_K_STACK   SELECTOR_K_DATA 
#define SELECTOR_K_GS	   ((3 << 3) + (TI_GDT << 2) + RPL0)
/* 第3个段描述符是显存,第4个是tss */
#define SELECTOR_U_CODE	   ((5 << 3) + (TI_GDT << 2) + RPL3)
#define SELECTOR_U_DATA	   ((6 << 3) + (TI_GDT << 2) + RPL3)
#define SELECTOR_U_STACK   SELECTOR_U_DATA

#define GDT_ATTR_HIGH		 ((DESC_G_4K << 7) + (DESC_D_32 << 6) + (DESC_L << 5) + (DESC_AVL << 4))
#define GDT_CODE_ATTR_LOW_DPL3	 ((DESC_P << 7) + (DESC_DPL_3 << 5) + (DESC_S_CODE << 4) + DESC_TYPE_CODE)
#define GDT_DATA_ATTR_LOW_DPL3	 ((DESC_P << 7) + (DESC_DPL_3 << 5) + (DESC_S_DATA << 4) + DESC_TYPE_DATA)


//---------------  TSS描述符属性  ------------
#define TSS_DESC_D  0 

#define TSS_ATTR_HIGH ((DESC_G_4K << 7) + (TSS_DESC_D << 6) + (DESC_L << 5) + (DESC_AVL << 4) + 0x0)
#define TSS_ATTR_LOW ((DESC_P << 7) + (DESC_DPL_0 << 5) + (DESC_S_SYS << 4) + DESC_TYPE_TSS)
#define SELECTOR_TSS ((4 << 3) + (TI_GDT << 2 ) + RPL0)

struct gdt_desc {
   uint16_t limit_low_word;
   uint16_t base_low_word;
   uint8_t  base_mid_byte;
   uint8_t  attr_low_byte;
   uint8_t  limit_high_attr_high;
   uint8_t  base_high_byte;
}; 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

/* 任务状态段tss结构 */
struct tss {
    uint32_t backlink;
    uint32_t* esp0;
    uint32_t ss0;
    uint32_t* esp1;
    uint32_t ss1;
    uint32_t* esp2;
    uint32_t ss2;
    uint32_t cr3;
    uint32_t (*eip) (void);
    uint32_t eflags;
    uint32_t eax;
    uint32_t ecx;
    uint32_t edx;
    uint32_t ebx;
    uint32_t esp;
    uint32_t ebp;
    uint32_t esi;
    uint32_t edi;
    uint32_t es;
    uint32_t cs;
    uint32_t ss;
    uint32_t ds;
    uint32_t fs;
    uint32_t gs;
    uint32_t ldt;
    uint32_t trace;
    uint32_t io_base;
}; 
static struct tss tss;

/* 更新tss中esp0字段的值为pthread的0级线 */
void update_tss_esp(struct task_struct* pthread) {
   tss.esp0 = (uint32_t*)((uint32_t)pthread + PG_SIZE);
}

/* 创建gdt描述符 */
static struct gdt_desc make_gdt_desc(uint32_t* desc_addr, uint32_t limit, uint8_t attr_low, uint8_t attr_high) {
   uint32_t desc_base = (uint32_t)desc_addr;
   struct gdt_desc desc;
   desc.limit_low_word = limit & 0x0000ffff;
   desc.base_low_word = desc_base & 0x0000ffff;
   desc.base_mid_byte = ((desc_base & 0x00ff0000) >> 16);
   desc.attr_low_byte = (uint8_t)(attr_low);
   desc.limit_high_attr_high = (((limit & 0x000f0000) >> 16) + (uint8_t)(attr_high));
   desc.base_high_byte = desc_base >> 24;
   return desc;
}

/* 在gdt中创建tss并重新加载gdt */
void tss_init() {
   put_str("tss_init start\n");
   uint32_t tss_size = sizeof(tss);
   memset(&tss, 0, tss_size);
   tss.ss0 = SELECTOR_K_STACK;
   tss.io_base = tss_size;

/* gdt段基址为0x900,把tss放到第4个位置,也就是0x900+0x20的位置 */

  /* 在gdt中添加dpl为0的TSS描述符 */
  *((struct gdt_desc*)0xc0000920) = make_gdt_desc((uint32_t*)&tss, tss_size - 1, TSS_ATTR_LOW, TSS_ATTR_HIGH);

  /* 在gdt中添加dpl为3的数据段和代码段描述符 */
  *((struct gdt_desc*)0xc0000928) = make_gdt_desc((uint32_t*)0, 0xfffff, GDT_CODE_ATTR_LOW_DPL3, GDT_ATTR_HIGH);
  *((struct gdt_desc*)0xc0000930) = make_gdt_desc((uint32_t*)0, 0xfffff, GDT_DATA_ATTR_LOW_DPL3, GDT_ATTR_HIGH);
   
  /* gdt 16位的limit 32位的段基址 */
   uint64_t gdt_operand = ((8 * 7 - 1) | ((uint64_t)(uint32_t)0xc0000900 << 16));   // 7个描述符大小
   asm volatile ("lgdt %0" : : "m" (gdt_operand));
   asm volatile ("ltr %w0" : : "r" (SELECTOR_TSS));
   put_str("tss_init and ltr done\n");
}

在 tss.c 的开头第8～36行定义了TSS 的结构体struct tss，第 40 行定义的函数update_tss_esp用来更新TSS 中的esp0，只修改TSS 中的特权级0 对应的栈。此函数将TSS 中esp0 修改为参数pthread 的0 级栈地址，也就是线程pthread的PCB 所在页的最顶端—(uint32_t)pthread + PG_SIZE。

在第 45 行创建了函数make_gdt_desc，专门生成描述符结构。此函数的实现是按照段描述符的格式来拼数据，在内部生成一局部描述符结构体变量struct gdt_desc desc，后面把此结构体变量中的属性填充好后通过return 返回其值。第 58 行是函数tss_init，此函数除了用来初始化tss 并将其安装到GDT 中外，还另外在GDT 中安装两个供用户进程使用的描述符，一个是DPL 为3 的数据段，另一个是DPL 为3 的代码段。第 61 行将全局变量tss 清0 后，在第62 行为其ss0 字段赋0 级栈段的选择子SELECTOR_ K_STACK。第 63 行代码tss.io_base = tss_size，将tss 的io_base 字段置为tss 的大小tss_size，这表示此TSS 中并没有IO 位图。在第 68 行，我们在GDT 中安装TSS 描述符。在调用make_gdt_desc后，其返回的描述符是安装在0xc0000920 的地址，即*((struct gdt_desc*)0xc0000920)，

接下来在第71 行和第72 行安装了两个DPL 为3 的段描述符，分别是代码段和数据段，这是为用户进程提前做的准备，它们在GDT 中的位置基于TSS 描述符顺延，分别是偏移GDT0x28 和0x30 的位置。在第 75 行，定义了变量gdt_operand 作为lgdt 指令的操作数。

操作数中的高32 位是GDT 起始地址，在这里我们把GDT 线性地址0xc0000900 先转换成uint32_t 后，再将其转换成uint64_t 位，最后通过按位或运算符’|’拼合在一起。通过内联汇编，第76 行将新的GDT 重新加载，第77 行将tss 加载到TR。至此，新的GDT 和TSS已经生效。

实现用户进程

在 thread_start（…,function,…）的调用中，function 是我们最终在线程中执行的函数。在thread_start 内部，先是通过get_kernel_pages(1)在内核内存池中获取1 个物理页做线程的pcb，即thread，接着调用init_thread 初始化该线程pcb 中的信息，然后再用thread_create 创建线程运行的栈，实际上是将栈中的返回地址指向了kernel_thread 函数，因此相当于调用了kernel_thread，在kernel_thread 中通过调用function 的方式使function 得到执行。如果要基于线程实现进程，我们把function 替换为创建进程的新函数就可以啦。

进程是基于线程实现的，因此它和线程一样使用相同的pcb 结构，即struct task_struct，我们要做的就是在此结构中增加一个成员，用它来跟踪用户空间虚拟地址的分配情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

/* 进程或线程的pcb,程序控制块 */
struct task_struct {
   uint32_t* self_kstack;	 // 各内核线程都用自己的内核栈
   enum task_status status;
   char name[16];
   uint8_t priority;
   uint8_t ticks;	   // 每次在处理器上执行的时间嘀嗒数

/* 此任务自上cpu运行后至今占用了多少cpu嘀嗒数,
 * 也就是此任务执行了多久*/
   uint32_t elapsed_ticks;

/* general_tag的作用是用于线程在一般的队列中的结点 */
   struct list_elem general_tag;				    

/* all_list_tag的作用是用于线程队列thread_all_list中的结点 */
   struct list_elem all_list_tag;

   uint32_t* pgdir;              // 进程自己页表的虚拟地址

   struct virtual_addr userprog_vaddr;   // 用户进程的虚拟地址
   uint32_t stack_magic;	 // 用这串数字做栈的边界标记,用于检测栈的溢出
};

其中第 95 行的struct virtual_addr userprog_vaddr 便是每个用户进程的虚拟地址池。第93 行的pgdir 用于存放进程页目录表的虚拟地址，这将在为进程创建页表时为其赋值。

页表虽然用于管理内存，但它本身也要用内存来存储，所以要为每个进程单独申请存储页目录项及页表项的虚拟内存页。除此之外，我们还要为用户进程创建在3 特权级的栈。鉴于以上两点原因，这必然涉及到内存分配的工作，咱们的内存管理是在 memory.c 中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150

/* 在pf表示的虚拟内存池中申请pg_cnt个虚拟页,
 * 成功则返回虚拟页的起始地址, 失败则返回NULL */
static void* vaddr_get(enum pool_flags pf, uint32_t pg_cnt) {
   int vaddr_start = 0, bit_idx_start = -1;
   uint32_t cnt = 0;
   if (pf == PF_KERNEL) {     // 内核内存池
      bit_idx_start  = bitmap_scan(&kernel_vaddr.vaddr_bitmap, pg_cnt);
      if (bit_idx_start == -1) {
	 return NULL;
      }
      while(cnt < pg_cnt) {
	 bitmap_set(&kernel_vaddr.vaddr_bitmap, bit_idx_start + cnt++, 1);
      }
      vaddr_start = kernel_vaddr.vaddr_start + bit_idx_start * PG_SIZE;
   } else {	     // 用户内存池	
      struct task_struct* cur = running_thread();
      bit_idx_start  = bitmap_scan(&cur->userprog_vaddr.vaddr_bitmap, pg_cnt);
      if (bit_idx_start == -1) {
	 return NULL;
      }

      while(cnt < pg_cnt) {
	 bitmap_set(&cur->userprog_vaddr.vaddr_bitmap, bit_idx_start + cnt++, 1);
      }
      vaddr_start = cur->userprog_vaddr.vaddr_start + bit_idx_start * PG_SIZE;

   /* (0xc0000000 - PG_SIZE)做为用户3级栈已经在start_process被分配 */
      ASSERT((uint32_t)vaddr_start < (0xc0000000 - PG_SIZE));
   }
   return (void*)vaddr_start;
}


/* 在用户空间中申请4k内存,并返回其虚拟地址 */
void* get_user_pages(uint32_t pg_cnt) {
   lock_acquire(&user_pool.lock);
   void* vaddr = malloc_page(PF_USER, pg_cnt);
   memset(vaddr, 0, pg_cnt * PG_SIZE);
   lock_release(&user_pool.lock);
   return vaddr;
}

/* 将地址vaddr与pf池中的物理地址关联,仅支持一页空间分配 */
void* get_a_page(enum pool_flags pf, uint32_t vaddr) {
   struct pool* mem_pool = pf & PF_KERNEL ? &kernel_pool : &user_pool;
   lock_acquire(&mem_pool->lock);

   /* 先将虚拟地址对应的位图置1 */
   struct task_struct* cur = running_thread();
   int32_t bit_idx = -1;

/* 若当前是用户进程申请用户内存,就修改用户进程自己的虚拟地址位图 */
   if (cur->pgdir != NULL && pf == PF_USER) {
      bit_idx = (vaddr - cur->userprog_vaddr.vaddr_start) / PG_SIZE;
      ASSERT(bit_idx > 0);
      bitmap_set(&cur->userprog_vaddr.vaddr_bitmap, bit_idx, 1);

   } else if (cur->pgdir == NULL && pf == PF_KERNEL){
/* 如果是内核线程申请内核内存,就修改kernel_vaddr. */
      bit_idx = (vaddr - kernel_vaddr.vaddr_start) / PG_SIZE;
      ASSERT(bit_idx > 0);
      bitmap_set(&kernel_vaddr.vaddr_bitmap, bit_idx, 1);
   } else {
      PANIC("get_a_page:not allow kernel alloc userspace or user alloc kernelspace by get_a_page");
   }

   void* page_phyaddr = palloc(mem_pool);
   if (page_phyaddr == NULL) {
      return NULL;
   }
   page_table_add((void*)vaddr, page_phyaddr); 
   lock_release(&mem_pool->lock);
   return (void*)vaddr;
}

/* 得到虚拟地址映射到的物理地址 */
uint32_t addr_v2p(uint32_t vaddr) {
   uint32_t* pte = pte_ptr(vaddr);
/* (*pte)的值是页表所在的物理页框地址,
 * 去掉其低12位的页表项属性+虚拟地址vaddr的低12位 */
   return ((*pte & 0xfffff000) + (vaddr & 0x00000fff));
}

/* 初始化内存池 */
static void mem_pool_init(uint32_t all_mem) {
   put_str("   mem_pool_init start\n");
   uint32_t page_table_size = PG_SIZE * 256;	  // 页表大小= 1页的页目录表+第0和第768个页目录项指向同一个页表+
                                                  // 第769~1022个页目录项共指向254个页表,共256个页框
   uint32_t used_mem = page_table_size + 0x100000;	  // 0x100000为低端1M内存
   uint32_t free_mem = all_mem - used_mem;
   uint16_t all_free_pages = free_mem / PG_SIZE;		  // 1页为4k,不管总内存是不是4k的倍数,
							  // 对于以页为单位的内存分配策略，不足1页的内存不用考虑了。
   uint16_t kernel_free_pages = all_free_pages / 2;
   uint16_t user_free_pages = all_free_pages - kernel_free_pages;

/* 为简化位图操作，余数不处理，坏处是这样做会丢内存。
好处是不用做内存的越界检查,因为位图表示的内存少于实际物理内存*/
   uint32_t kbm_length = kernel_free_pages / 8;			  // Kernel BitMap的长度,位图中的一位表示一页,以字节为单位
   uint32_t ubm_length = user_free_pages / 8;			  // User BitMap的长度.

   uint32_t kp_start = used_mem;				  // Kernel Pool start,内核内存池的起始地址
   uint32_t up_start = kp_start + kernel_free_pages * PG_SIZE;	  // User Pool start,用户内存池的起始地址

   kernel_pool.phy_addr_start = kp_start;
   user_pool.phy_addr_start   = up_start;

   kernel_pool.pool_size = kernel_free_pages * PG_SIZE;
   user_pool.pool_size	 = user_free_pages * PG_SIZE;

   kernel_pool.pool_bitmap.btmp_bytes_len = kbm_length;
   user_pool.pool_bitmap.btmp_bytes_len	  = ubm_length;

/*********    内核内存池和用户内存池位图   ***********
 *   位图是全局的数据，长度不固定。
 *   全局或静态的数组需要在编译时知道其长度，
 *   而我们需要根据总内存大小算出需要多少字节。
 *   所以改为指定一块内存来生成位图.
 *   ************************************************/
// 内核使用的最高地址是0xc009f000,这是主线程的栈地址.(内核的大小预计为70K左右)
// 32M内存占用的位图是2k.内核内存池的位图先定在MEM_BITMAP_BASE(0xc009a000)处.
   kernel_pool.pool_bitmap.bits = (void*)MEM_BITMAP_BASE;
							       
/* 用户内存池的位图紧跟在内核内存池位图之后 */
   user_pool.pool_bitmap.bits = (void*)(MEM_BITMAP_BASE + kbm_length);
   /******************** 输出内存池信息 **********************/
   put_str("      kernel_pool_bitmap_start:");put_int((int)kernel_pool.pool_bitmap.bits);
   put_str(" kernel_pool_phy_addr_start:");put_int(kernel_pool.phy_addr_start);
   put_str("\n");
   put_str("      user_pool_bitmap_start:");put_int((int)user_pool.pool_bitmap.bits);
   put_str(" user_pool_phy_addr_start:");put_int(user_pool.phy_addr_start);
   put_str("\n");

   /* 将位图置0*/
   bitmap_init(&kernel_pool.pool_bitmap);
   bitmap_init(&user_pool.pool_bitmap);

   lock_init(&kernel_pool.lock);
   lock_init(&user_pool.lock);

   /* 下面初始化内核虚拟地址的位图,按实际物理内存大小生成数组。*/
   kernel_vaddr.vaddr_bitmap.btmp_bytes_len = kbm_length;      // 用于维护内核堆的虚拟地址,所以要和内核内存池大小一致

  /* 位图的数组指向一块未使用的内存,目前定位在内核内存池和用户内存池之外*/
   kernel_vaddr.vaddr_bitmap.bits = (void*)(MEM_BITMAP_BASE + kbm_length + ubm_length);

   kernel_vaddr.vaddr_start = K_HEAP_START;
   bitmap_init(&kernel_vaddr.vaddr_bitmap);
   put_str("   mem_pool_init done\n");
}

在内存池struct pool 中新增了锁struct lock lock，用它来在内存申请时做互斥，避免公共资源的竞争。在接下来的vaddr_get函数中，我们新增了在用户内存池分配内存的功能，即代码第48～62 行。get_user_pages用来在用户内存池中以整页为单位分配内存，返回分配的虚拟地址。另一个新增的函数是 get_a_page，它用来在某个内存池中获取一个页，功能是申请一页内存，并用vaddr映射到该页。

最后一个要介绍的新函数是 addr_v2p，此函数返回虚拟地址vaddr 所映射的物理地址。addr_v2p 的原理是根据页表映射原理，先得到虚拟地址vaddr 最终所映射到的物理页框起始地址，也就是在页表中vaddr 所在的pte 中记录的那个物理页地址，然后再将vaddr 的低12 位与此值相加，所得的地址和便是vaddr 映射的物理地址。

该函数实现中的uint32_t*pte = pte_ptr(vaddr)，在指针变量pte中得到vaddr 的所在pte 的地址，此时*pte 的内容是vaddr 所在pte 的内容，也就是vaddr 最终所映射到的物理页框的32 位地址中的高20 位和12 位的页表项属性，因为页框都是自然页，低12 位地址是0，所以页表项pte（和页目录项pde）中只需要记录页框的高20 位地址即可，(*pte & 0xfffff000)。另外的代码(vaddr& 0x00000fff)就是获取原虚拟地址vaddr 的低12 位。

最后要说明的是由于我们在内存池 struct pool 中增加了锁，在内存池初始化函数mem_pool_init 中，我们增加了锁的初始化：lock_init(&kernel_pool.lock);和lock_init(&user_pool.lock);。

退出中断的出口是汇编语言函数intr_exit，此函数用来恢复中断发生时、被中断的任务的上下文状态，并且退出中断。从中断返回，必须要经过intr_exit，即使是“假装”。必须提前准备好用户进程所用的栈结构，在里面填装好用户进程的上下文信息，借一系列pop 出栈的机会，将用户进程的上下文信息载入CPU 的寄存器，为用户进程的运行准备好环境。

我们要在栈中存储的CS 选择子，其RPL必须为3。操作系统会将选择子的RPL 置为用户进程的CPL，只有CPL 和RPL 在数值上同时小于等于选择子所指向的内存段的DPL 时，CPU 的安全检测才通过，既然用户进程的特权级为3，用户进程所有段选择子的RPL 都置为3，因此，在RPL=CPL=3 的情况下，用户进程只能访问DPL 为3 的内存段，即代码段、数据段、栈段。

栈中段寄存器的选择子必须指向DPL 为3 的内存段。必须使栈中eflags 的IF 位为1，继续响应新的中断。必须使栈中eflags 的IOPL 位为0，不允许用户进程直接访问硬件。

用户进程创建的流程

在process_execute中，先调用函数get_kernel_pages申请1 页内存创建进程的pcb，这里的pcb就是thread，接下来调用函数init_thread对thread 进行初始化。随后调用函数create_user_vaddr_bitmap为用户进程创建管理虚拟地址空间的位图。接着调用thread_create创建线程，此函数的作用是将函数start_process和用户进程user_prog作为kernel_thread的参数，以使kernel_thread能够调用start_proces(user_prog)。接下来是调用函数create_page_dir为进程创建页表，随后通过函数list_append将进程pcb，加入就绪队列和全部队列，至此用户进程的创建部分完成。

在schedule中，调用了process_activate来激活进程或线程的相关资源（页表等），随后通过switch_to函数调度进程，根据先前进程创建时函数thread_create的工作，已经将kernel_thread作为函数switch_to的返回地址，即在switch_to中退出后，处理器会执行kernel_thread函数。

函数start_process主要用来构建用户进程的上下文，它会将user_prog作为进程“从中断返回”的地址，由于是从0 特权级的中断返回，故返回地址user_prog被iretd指令使用，为了复用中断退出的代码，现在需要跳转到中断出口intr_exit处，利用那里的iretd指令使返回地址user_prog作为EIP 寄存器的值以使user_prog得到执行，故相当于start_process调用intr_exit，intr_exit调用user_prog，最终用户进程user_prog在3 特权级下执行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

extern void intr_exit(void);

/* 构建用户进程初始上下文信息 */
void start_process(void* filename_) {
   void* function = filename_;
   struct task_struct* cur = running_thread();
   cur->self_kstack += sizeof(struct thread_stack);
   struct intr_stack* proc_stack = (struct intr_stack*)cur->self_kstack;	 
   proc_stack->edi = proc_stack->esi = proc_stack->ebp = proc_stack->esp_dummy = 0;
   proc_stack->ebx = proc_stack->edx = proc_stack->ecx = proc_stack->eax = 0;
   proc_stack->gs = 0;		 // 用户态用不上,直接初始为0
   proc_stack->ds = proc_stack->es = proc_stack->fs = SELECTOR_U_DATA;
   proc_stack->eip = function;	 // 待执行的用户程序地址
   proc_stack->cs = SELECTOR_U_CODE;
   proc_stack->eflags = (EFLAGS_IOPL_0 | EFLAGS_MBS | EFLAGS_IF_1);
   proc_stack->esp = (void*)((uint32_t)get_a_page(PF_USER, USER_STACK3_VADDR) + PG_SIZE) ;
   proc_stack->ss = SELECTOR_U_DATA; 
   asm volatile ("movl %0, %%esp; jmp intr_exit" : : "g" (proc_stack) : "memory");
}

/* 击活页表 */
void page_dir_activate(struct task_struct* p_thread) {
/********************************************************
 * 执行此函数时,当前任务可能是线程。
 * 之所以对线程也要重新安装页表, 原因是上一次被调度的可能是进程,
 * 否则不恢复页表的话,线程就会使用进程的页表了。
 ********************************************************/

/* 若为内核线程,需要重新填充页表为0x100000 */
   uint32_t pagedir_phy_addr = 0x100000;  // 默认为内核的页目录物理地址,也就是内核线程所用的页目录表
   if (p_thread->pgdir != NULL)	{    // 用户态进程有自己的页目录表
      pagedir_phy_addr = addr_v2p((uint32_t)p_thread->pgdir);
   }

   /* 更新页目录寄存器cr3,使新页表生效 */
   asm volatile ("movl %0, %%cr3" : : "r" (pagedir_phy_addr) : "memory");
}

/* 击活线程或进程的页表,更新tss中的esp0为进程的特权级0的栈 */
void process_activate(struct task_struct* p_thread) {
   ASSERT(p_thread != NULL);
   /* 击活该进程或线程的页表 */
   page_dir_activate(p_thread);

   /* 内核线程特权级本身就是0,处理器进入中断时并不会从tss中获取0特权级栈地址,故不需要更新esp0 */
   if (p_thread->pgdir) {
      /* 更新该进程的esp0,用于此进程被中断时保留上下文 */
      update_tss_esp(p_thread);
   }
}

函数start_process接收一个参数filename_，此参数表示用户程序的名称，此函数用来创建用户进程filename_的上下文，也就是填充
用户进程的struct intr_stack，通过假装从中断返回的方式，间接使filename_运行。

start_process 的函数体中第一句是void* function = filename_;。用户进程上下文保存在struct intr_stack栈中。在函数init_thread中pthread->self_kstack = (uint32_t*)((uint32_t)pthread + PG_SIZE);，目的是初始化线程所用的栈的基址，后面的两个栈struct intr_stack和struct thread_stack的布局及所占的空间以此基地址往下顺延，这个布局操作是在函数thread_create中完成的，相关代码是：pthread->self_kstack -= sizeof(struct intr_stack);和pthread->self_kstack -= sizeof(struct thread_stack);

struct intr_stack栈用来存储进入中断时任务的上下文，struct thread_stack用来存储在中断处理程序中、任务切换（switch_to）前后的上下文。这两个栈的布局情况如图。

为了引用struct intr_stack 栈，我们通过代码cur->self_ kstack += sizeof(struct thread_stack);使指针self_kstack跨过struct thread_stack栈，最终指向struct intr_stack栈的最低处，此时PCB 中栈的情况如图。

程序能上 CPU 运行，原因就是CS:[E]IP 指向了程序入口地址。通过proc_stack->eip = function;，先对栈中eip 赋值为function，这是start_process的参数filename_的值。通过proc_stack->cs = SELECTOR_U_CODE将栈中代码段寄存器cs 赋值为先前我们已在GDT 中安装好的用户级代码段。接下来对栈中eflags 赋值，EFLAGS_IOPL_0表示IOPL 位为0，EFLAGS_IF_1表示IF 位为1，EFLAGS_MBS固定为1，它们在eflags 中的位置如图。


用户程序内存空间的最顶端用来存储命令行参数及环境变量，接着是栈空间和堆空间，栈向下扩展，堆向上扩展，栈与堆在空间上是相接的，最下面的未初始化数据段bss、初始化数据段data 及代码段text由链接器和编译器负责。在 4GB 的虚拟地址空间中，(0xc0000000-1)是用户空间的最高地址，0xc0000000～0xffffffff 是内核空间。

由于在申请内存时，内存管理模块返回的地址是内存空间的下边界，所以我们为栈申请的地址应该是（0xc0000000-0x1000），此地址是用户栈空间栈顶的下边界。这里我们用宏来定义此地址，即USER_STACK3_VADDR，#define USER_STACK3_VADDR (0xc0000000 - 0x1000)，用第27 行的get_a_page(PF_USER, USER_STACK3_VADDR)先获取特权级3 的栈的下边界地址，将此地址再加上PG_SIZE，所得的和就是栈的上边界，即栈底，将此栈底赋值给proc_stack->esp。

在进程创建部分，有一项工作是create_page_dir，这是提前为用户进入创建了页目录表，在进程执行部分，有一项工作是process_activate，这是使任务自己的页表生效。我们是在函数start_process中为用户进程创建了3 特权级栈，start_process是在执行任务页表激活之后执行的，也就是在process_activate之后运行，那时已经把页表更新为用户进程的页表了，所以3 特权级栈是安装在用户进程自己的页表中的。

第 29 行通过内联汇编，将栈esp 替换为我们刚刚填充好的proc_stack，然后通过jmp intr_exit使程序流程跳转到中断出口地址intr_exit，通过那里的一系列pop 指令和iretd 指令，将proc_stack 中的数据载入CPU 的寄存器，从而使程序“假装”退出中断，进入特权级3。

page_dir_activate接受一个参数p_thread，用来激活p_thread 的页表，p_thread可能是进程，也可能是线程。process_activate的功能有两个，一是激活线程或进程的页表，二是更新tss 中的esp0 为进程的特权级0 的栈。进程或线程在被中断信号打断时，处理器会进入0 特权级，并会在0 特权级栈中保存进程或线程的上下文环境。如果被中断的是0 特权级的内核线程，由于内核线程已经是0 特权级，进入中断后不涉及特权级的改变，所以处理器并不会到tss 中获取esp0，所以，用if (p_thread->pgdir)来判断：如果是用户进程的话才去更新tss 中的esp0。

bss 简介

链接器将目标文件中属性相同的节（section）合并成段（segment），因此一个段是由多个节组成的，我们平时所说的C 程序内存空间中的数据段、代码段就是指合并后的segment。一是为了保护模式下的安全检查，二是为了操作系统在加载程序时省事。按照属性来划分节，大致上有三种类型。

  • 可读写的数据，如数据节.data 和未初始化节.bss。
  • 只读可执行的代码，如代码节.text 和初始化代码节.init。
  • 只读数据，如只读数据节.rodata，一般情况下字符串就存储在此节。

经过这样的划分，所有节都可归并到以上三种之一，这样方便了操作系统加载程序时的内存分配。由链接器把目标文件中相同属性的节归并之后的节的集合，便称为segment，它存在于二进制可执行文件中。

bss 并不存在于程序文件中，它仅存在于内存中，其实际内容是在程序运行过程中才产生的，程序文件中仅在elf 头中有bss 节的虚拟地址、大小等相关记录，bss 中的数据是未初始化的全局变量和局部静态变量，程序运行后才会为它们赋值，bss 区域的目的是提前为这些未初始化数据预留内存空间。由于bss 中的内容是变量，其属性为可读写，这和数据段属性一致，故链接器将bss 占用的内存空间大小合并到数据段占用的内存中，这样便在数据段中预留出bss 的空间以供程序在将来运行时使用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/* 创建页目录表,将当前页表的表示内核空间的pde复制,
 * 成功则返回页目录的虚拟地址,否则返回-1 */
uint32_t* create_page_dir(void) {

   /* 用户进程的页表不能让用户直接访问到,所以在内核空间来申请 */
   uint32_t* page_dir_vaddr = get_kernel_pages(1);
   if (page_dir_vaddr == NULL) {
      console_put_str("create_page_dir: get_kernel_page failed!");
      return NULL;
   }

/************************** 1  先复制页表  *************************************/
   /*  page_dir_vaddr + 0x300*4 是内核页目录的第768项 */
   memcpy((uint32_t*)((uint32_t)page_dir_vaddr + 0x300*4), (uint32_t*)(0xfffff000+0x300*4), 1024);
/*****************************************************************************/

/************************** 2  更新页目录地址 **********************************/
   uint32_t new_page_dir_phy_addr = addr_v2p((uint32_t)page_dir_vaddr);
   /* 页目录地址是存入在页目录的最后一项,更新页目录地址为新页目录的物理地址 */
   page_dir_vaddr[1023] = new_page_dir_phy_addr | PG_US_U | PG_RW_W | PG_P_1;
/*****************************************************************************/
   return page_dir_vaddr;
}

/* 创建用户进程虚拟地址位图 */
void create_user_vaddr_bitmap(struct task_struct* user_prog) {
   user_prog->userprog_vaddr.vaddr_start = USER_VADDR_START;
   uint32_t bitmap_pg_cnt = DIV_ROUND_UP((0xc0000000 - USER_VADDR_START) / PG_SIZE / 8 , PG_SIZE);
   user_prog->userprog_vaddr.vaddr_bitmap.bits = get_kernel_pages(bitmap_pg_cnt);
   user_prog->userprog_vaddr.vaddr_bitmap.btmp_bytes_len = (0xc0000000 - USER_VADDR_START) / PG_SIZE / 8;
   bitmap_init(&user_prog->userprog_vaddr.vaddr_bitmap);
}

/* 创建用户进程 */
void process_execute(void* filename, char* name) { 
   /* pcb内核的数据结构,由内核来维护进程信息,因此要在内核内存池中申请 */
   struct task_struct* thread = get_kernel_pages(1);
   init_thread(thread, name, default_prio); 
   create_user_vaddr_bitmap(thread);
   thread_create(thread, start_process, filename);
   thread->pgdir = create_page_dir();
   
   enum intr_status old_status = intr_disable();
   ASSERT(!elem_find(&thread_ready_list, &thread->general_tag));
   list_append(&thread_ready_list, &thread->general_tag);

   ASSERT(!elem_find(&thread_all_list, &thread->all_list_tag));
   list_append(&thread_all_list, &thread->all_list_tag);
   intr_set_status(old_status);
}

我们目前使用的是二级页表，加载到页目录表寄存器CR3 中的是页目录表的物理地址，页目录表中一共包含1024 个页目录项（pde），页目录项大小为4B，故页目录表大小为4KB。每个页表本身占用4KB。每个页表可表示的地址空间为1024*4KB=4MB，一个页目录表中可包含1024 个页表，因此可表示1024*4MB=4GB 大小的地址空间。目前我们的内核位于0xc0000000 以上的地址空间，也就是位于页目录表中第768～1023 个页目录项所
指向的页表中，这一共是256 个页目录项，即1GB 空间，目前页表与内核的关系如图。

图 11-20 是任意进程的页目录表，其中，用户进程占据页目录表中第0～767 个页目录项，内核占据页目录表中第768～1023 个页目录项。

为用户进程创建虚拟内存池的函数是create_user_vaddr_bitmap，它接受一个参数user_prog，表示用户进程，函数功能是创建用户进程的虚拟地址位图user_prog->userprog_vaddr，也就是按照用户进程的虚拟内存信息初始化位图结构体struct virtual_addr。user_prog->userprog_vaddr.vaddr_start是位图中所管理的内存空间的起始地址，我们为用户进程定的起始地址是USER_VADDR_START，该值定义在process.h中，其值为0x8048000，这是Linux 用户程序入口地址。

变量bitmap_pg_cnt用来记录位图需要的内存页框数，计算过程中用到了宏DIV_ROUND_UP，它用来实现除法的向上取整，此宏定义在global.h 中，原型是：#define DIV_ROUND_UP(X, STEP) ((X + STEP - 1) / (STEP))。

接下来通过get_kernel_pages(bitmap_pg_cnt)为位图分配内存，返回的地址记录在位图指针user_prog->userprog_vaddr.vaddr_bitmap.bits 中。然后将位图长度记录在user_prog->userprog_vaddr. vaddr_bitmap.btmp_bytes_len中。最后调用函数bitmap_init(&user_prog->userprog_vaddr.vaddr_bitmap)进行位图初始化，至此用户虚拟地址位图创建完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/* 实现任务调度 */
void schedule() {

   ASSERT(intr_get_status() == INTR_OFF);

   struct task_struct* cur = running_thread(); 
   if (cur->status == TASK_RUNNING) { // 若此线程只是cpu时间片到了,将其加入到就绪队列尾
      ASSERT(!elem_find(&thread_ready_list, &cur->general_tag));
      list_append(&thread_ready_list, &cur->general_tag);
      cur->ticks = cur->priority;     // 重新将当前线程的ticks再重置为其priority;
      cur->status = TASK_READY;
   } else { 
      /* 若此线程需要某事件发生后才能继续上cpu运行,
      不需要将其加入队列,因为当前线程不在就绪队列中。*/
   }

   ASSERT(!list_empty(&thread_ready_list));
   thread_tag = NULL;	  // thread_tag清空
/* 将thread_ready_list队列中的第一个就绪线程弹出,准备将其调度上cpu. */
   thread_tag = list_pop(&thread_ready_list);   
   struct task_struct* next = elem2entry(struct task_struct, general_tag, thread_tag);
   next->status = TASK_RUNNING;

   /* 激活任务页表等 */
   process_activate(next);
   switch_to(cur, next);
}

在 thread.c 中需要修改schedule，修改的内容也很简单，就是在第126 行增加了代码process_activate(next);，process_activate除了用来更新任务的页表外，还要根据任务是否为进程，修改tss 中的esp0，此函数之前已经介绍了。

进一步完善内核

Linux 系统调用浅析

Linux 系统调用是用中断门来实现的，通过软中断指令int来主动发起中断信号。Linux只占用一个中断向量号，即0x80，处理器执行指令int 0x80 时便触发了系统调用。在系统调用之前，Linux在寄存器eax中写入子功能号，通过int 0x80进行系统调用时，对应的中断处理例程会根据
eax 的值来判断用户进程申请哪种系统调用。syscall 的原型是int syscall(int number, …)，其中的number是int 型，这是系统调用号。number 后面的“…”表示此函数支持变参。函数syscall并不是由操作系统提供的，它是由C运行库glibc提供的，因此syscall实际上是库函数。

直接的做法是利用操作系统提供的_syscall[X]，它是一系列的宏。_syscall 是系统调用“族”，所以图中用_syscallX来表示它们，其中的X 表示系统调用中的参数个数，其原型是_syscallX(type,name,type1,arg1,type2,arg2,…)。_syscallX是用宏来实现的，根据系统调用中参数个数、类型及返回值的不同，这里共有7 个不同的宏，分别是_syscall[0-6]，因此，对于参数个数不同的系统调用，需要调用不同的宏来完成。

Linux 中的系统调用是用寄存器来传递参数的，这些参数需要依次存入到不同的通用寄存器（除esp）中。其中，寄存器eax用来保存子功能号，ebx保存第1 个参数，ecx保存第2 个参数，edx保存第3 个参数，esi保存第4 个参数，edi 保存第5 个参数。

传递参数还可以用栈（内存），用户进程执行int 0x80时还处于用户态，编译器根据C调用约定，系统调用所用的参数会被压到用户栈中，这是3 特权级栈。当int 0x80执行后，任务陷入内核态，此时进入了0 特权级，因此需要用到0 特权级栈，但系统调用的参数还在3 特权级的栈中，为了获取用户栈地址，还得在0 特权级栈中获取处理器自动压入的用户栈的SS 和esp 寄存器的值，然后再次从用户栈中获取参数。

_syscall3 举例，如下所示：

1
2
3
4
5
6
7
8
9
#define _syscall3(type, name, type1, arg1, type2, arg2, type3, arg3) \
type name(type1 arg1, type2 arg2, type3 arg3) { \
long __res; \
__asm__ volatile ("push %%ebx; movl %2,%%ebx; int $0x80; pop %%ebx" \
        : "=a" (__res) \
        : "0" (__NR_##name),"ri" ((long)(arg1)),"c" ((long)(arg2)), \
        "d" ((long)(arg3)) : "memory"); \
__syscall_return(type,__res); \
}

第2～9行是宏体，第2 行的type是函数的返回值类型，name是函数名，也就是系统调用名，函数名后面括号中是一系列的形参，用的是宏_syscall3中的参数。第3 行是函数体的开始，__res是返回值。跨过第4 行先说下第5～7 行，第5 行的"=a" (__res)位于输出部output，这表明变量__res 由寄存器eax赋值。我们知道，根据abi 约定，eax 作为函数调用的返回值，这里是用变量__res来存储从中断返回后的返回值。第6 行是参数输入部input，"0" (__NR_##name)中的_NR_##name 是系统调用的字符串名，即__NR_系统调用名，然后变成数值型的子功能号，其中##表示联结字符串，"0" (__NR_##name)中的0 是通用约束，表示__NR_##name使用的寄存器或内存与第0 个约束表达式使用的寄存器或内存一致，这里指的是和第5行的"=a" (__res)一致，也就是寄存器eax 既做子功能号输入，又做返回值的输出。后面"ri" ((long)(arg1))是将变量arg1 约束到通用寄存器中，"c" ((long)(arg2))是将变量约束到ecx寄存器中，第7 行的"d"((long)(arg3))是将变量约束到edx 中。第4行是内联汇编代码，其中push %%ebx的作用是在用户空间的栈中提前保护好ebx的值，movl %2,%%ebx将arg1 的值写入寄存器ebx，%2是序号占位符，表示第2 个约束，即arg1 对应的寄存器或内存。int $0x80触发软中断，进行系统调用，完成后通过pop %%ebx恢复ebx的值。

第8 行是__syscall_return(type,__res);，对返回值__res判断后返回，其中__syscall_return也是个宏，实现如下，不再说明。

1
2
3
4
5
6
7
8
#define __syscall_return(type, res) \
    do { \
        if ((unsigned long)(res) >= (unsigned long)(-125)) { \
            errno = -(res); \
            res = -1; \
        } \
    return (type) (res); \
} while (0)

当参数多于5 个时，可以用内存来传递，注意啦，此时在内存中存储的参数仅是第1 个参数及第6 个以上的所有参数，不包括第2～5 个参数，第2～5 个参数依然要顺序放在寄存器ecx、edx、esi 及edi 中，eax 始终是子功能号。我们看下宏_syscall6的实现就清楚了，如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#define _syscall6(type,name, type1,arg1, type2,arg2, type3,arg3,
                  type4,arg4, type5,arg5, type6,arg6) \
type name (type1 arg1,type2 arg2,type3 arg3,\
           type4 arg4,type5 arg5,type6 arg6) { \
    long __res; \
    struct { long __a1; long __a6; } __s = { (long)arg1, (long)arg6 }; \
    __asm__ volatile ("push %%ebp ; push %%ebx ; movl 4(%2),%%ebp ; " \
                      "movl 0(%2),%%ebx ; movl %1,%%eax ; int $0x80 ; " \
                      "pop %%ebx ; pop %%ebp" \
    : "=a" (__res) \
    : "i" (__NR_##name),"0" ((long)(&__s)),"c" ((long)(arg2)), \
    "d" ((long)(arg3)),"S" ((long)(arg4)),"D" ((long)(arg5)) \
    : "memory"); \
    __syscall_return(type,__res); \
}

系统调用的实现

系统调用的实现思路:

  1. 用中断门实现系统调用，效仿Linux 用0x80 号中断作为系统调用的入口。
  2. 在IDT 中安装0x80 号中断对应的描述符，在该描述符中注册系统调用对应的中断处理例程。
  3. 建立系统调用子功能表syscall_table，利用eax 寄存器中的子功能号在该表中索引相应的处理函数。
  4. 用宏实现用户空间系统调用接口_syscall，最大支持3 个参数的系统调用，故只需要完成_syscall[0-3]。寄存器传递参数，eax 为子功能号，ebx保存第1 个参数，ecx 保存第2 个参数，edx 保存第3 个参数。

首先我们要修改interrupt.c，在其中安装0x80 对应的中断描述符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
…略
#define IDT_DESC_CNT 0x81 // 目前总共支持的中断数
…略
extern uint32_t syscall_handler(void);
…略
/*初始化中断描述符表*/
static void idt_desc_init(void) {
    int i, lastindex = IDT_DESC_CNT - 1;
    for (i = 0; i < IDT_DESC_CNT; i++) {
        make_idt_desc(&idt[i], IDT_DESC_ATTR_DPL0, intr_entry_table[i]);
}
/* 单独处理系统调用，系统调用对应的中断门dpl 为3，
* 中断处理程序为单独的syscall_handler */
    make_idt_desc(&idt[lastindex], IDT_DESC_ATTR_DPL3, syscall_handler);
    put_str(" idt_desc_init done\n");
}

宏IDT_DESC_CNT修改为0x81，这表示我们最大支持0x81个中断，即0～0x80，0x80是我们系统调用对应的中断向量。声明了外部函数syscall_handler，我们将在kernel.S 中定义它，syscall_handler就是系统调用对应的中断入口例程。在后面的idt_desc_init函数中，我们在增加了0x80号中断向量对应的中断描述符，在描述符中注册的中断处理例程为syscall_handler。这里要注意的是记得给此描述符的dpl 指定为用户级IDT_DESC_ATTR_DPL3，若指定为0 级，则在3 级环境下执行int 指令会产生GP 异常。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/* 无参数的系统调用 */
#define _syscall0(NUMBER) ({				       \
   int retval;					               \
   asm volatile (					       \
   "int $0x80"						       \
   : "=a" (retval)					       \
   : "a" (NUMBER)					       \
   : "memory"						       \
   );							       \
   retval;						       \
})

/* 一个参数的系统调用 */
#define _syscall1(NUMBER, ARG1) ({			       \
   int retval;					               \
   asm volatile (					       \
   "int $0x80"						       \
   : "=a" (retval)					       \
   : "a" (NUMBER), "b" (ARG1)				       \
   : "memory"						       \
   );							       \
   retval;						       \
})

/* 两个参数的系统调用 */
#define _syscall2(NUMBER, ARG1, ARG2) ({		       \
   int retval;						       \
   asm volatile (					       \
   "int $0x80"						       \
   : "=a" (retval)					       \
   : "a" (NUMBER), "b" (ARG1), "c" (ARG2)		       \
   : "memory"						       \
   );							       \
   retval;						       \
})

/* 三个参数的系统调用 */
#define _syscall3(NUMBER, ARG1, ARG2, ARG3) ({		       \
   int retval;						       \
   asm volatile (					       \
      "int $0x80"					       \
      : "=a" (retval)					       \
      : "a" (NUMBER), "b" (ARG1), "c" (ARG2), "d" (ARG3)       \
      : "memory"					       \
   );							       \
   retval;						       \
})

咱们打算最多支持3 个参数的系统调用，它们是_syscall[0-3]，代码中列出了无参数版本和3 个参数的版本。

修改kernel.S，在里面安装中断向量0x80 对应的中断处理程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
;;;;;;;;;;;;;;;;   0x80号中断   ;;;;;;;;;;;;;;;;
[bits 32]
extern syscall_table
section .text
global syscall_handler
syscall_handler:
;1 保存上下文环境
   push 0			    ; 压入0, 使栈中格式统一

   push ds
   push es
   push fs
   push gs
   pushad			    ; PUSHAD指令压入32位寄存器，其入栈顺序是:
				        ; EAX,ECX,EDX,EBX,ESP,EBP,ESI,EDI 
				 
   push 0x80			; 此位置压入0x80也是为了保持统一的栈格式

;2 为系统调用子功能传入参数
   push edx			    ; 系统调用中第3个参数
   push ecx			    ; 系统调用中第2个参数
   push ebx			    ; 系统调用中第1个参数

;3 调用子功能处理函数
   call [syscall_table + eax*4]	    ; 编译器会在栈中根据C函数声明匹配正确数量的参数
   add esp, 12			    ; 跨过上面的三个参数

;4 将call调用后的返回值存入待当前内核栈中eax的位置
   mov [esp + 8*4], eax	
   jmp intr_exit		    ; intr_exit返回,恢复上下文

声明了外部数据结构syscall_table，syscall_table是个数组，数组成员是系统调用中子功能对应的处理函数（以后将在新文件中定义它），这里我们用子功能号在此数组中索引子功能号对应的处理函数。由于只支持3 个参数的系统调用，故只压入了三个参数，按照C调用约定，最右边的参数先入栈，因此先把edx 中的第3 个参数入栈，其次是ecx 中的第2 个参数、ebx 中的第1 个参数。

寄存器 eax 中是系统调用子功能号，用它在数组syscall_table中索引对应的子功能处理函数。syscall_table中存储的是函数地址，每个成员是4 字节大小，因此在第122 行中，要用eax*4 做syscall_table的偏移量，这样代码call [syscall_table + eax*4]便去调用子功能处理函数。调用之后，在第123 行通过add esp, 12跨过这三个参数。

通过mov [esp + 8*4], eax将返回值写到了栈（此时是内核栈）中保存eax的那个内存空间。这里解释一下[esp+8*4]，这是寄存器相对寻址，esp 就是当前栈顶，8*4就是相对栈顶，往栈中高地址方向的偏移量，其实把8*4拆分成(1+7)*4更好，其中的1 是指上面的push 0x80所占的4 字节，另外的7 是指pushad指令会将eax 最先压入，故要跨过7 个4 字节，总共是8 个4 字节，即[esp+8*4]是对应栈中eax 的“藏身之所”。

要实现的第一个系统调用是getpid，getpid 的功能是获取任务自己的pid，getpid 是给用户进程使用的接口函数，它在内核中对应的处理函数是sys_getpid。定义了syscall_table相关参数，syscall_nr表示最大支持的系统调用子功能个数，其值为32。第8 行用typedef自定义syscall类型为空指针void*，第9 行syscall是数组syscall_table的元素类型，也就是syscall_table为函数指针数组。第12 行是sys_getpid的定义，它的实现很简单，就是将当前任务pcb 中的pid 返回。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#define syscall_nr 32 
typedef void* syscall;
syscall syscall_table[syscall_nr];

/* 返回当前任务的pid */
uint32_t sys_getpid(void) {
   return running_thread()->pid;
}

/* 初始化系统调用 */
void syscall_init(void) {
   put_str("syscall_init start\n");
   syscall_table[SYS_GETPID] = sys_getpid;
   put_str("syscall_init done\n");
}

在系统中安装第一个系统调用—getpid：

1
2
3
4
5
6
7
8
#ifndef __LIB_USER_SYSCALL_H
#define __LIB_USER_SYSCALL_H
#include "stdint.h"
enum SYSCALL_NR {
    SYS_GETPID
};
uint32_t getpid(void);
#endif

主要定义了枚举结构enum SYSCALL_NR，此结构用来存放系统调用子功能号，目前里面只有SYS_GETPID，默认值为0，以后再增加新的系统调用后还需要把新的子功能号添加到此结构中。

getpid放在syscall.c 中比较合适：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include "syscall.h"

/* 无参数的系统调用 */
#define _syscall0(NUMBER) ({ \
    int retval; \
    asm volatile ( \
    "int $0x80" \
    : "=a" (retval) \
    : "a" (NUMBER) \
    : "memory" \
    ); \
    retval; \
})

/* 返回当前任务pid */
uint32_t getpid() {
    return _syscall0(SYS_GETPID);
}

总结下增加系统调用的步骤。

  1. 在syscall.h中的结构enum SYSCALL_NR里添加新的子功能号。
  2. 在syscall.c中增加系统调用的用户接口。
  3. 在syscall-init.c中定义子功能处理函数并在syscall_table中注册。

printf的实现

C调用约定规定：由调用者把参数以从右向左的顺序压入栈中，并且由调用者清理堆栈中的参数。printf(char* format, arg1, arg2，…)中的参数format 就是包含%类型字符的字符串，其调用后栈中布局如图。无论函数的参数个数是否固定，采用 C 调用约定，调用者都能完好地回收栈空间

为方便引用函数中的可变参数，编译器gcc 的头文件stdarg.h 中定义了3 个宏。这3 个宏va_start、va_end 和va_arg 都以va（Variable Argument）开头，表示可变参数，但这里它们的值都是以_builtin为开头的内建符号，va_start(v,l)的值为_builtin_va_start(v,l)，gcc 的内建函数都放在其源码文件builtins.c 中用函数static rtxexpand_builtin_va_start (tree exp)来处理__builtin_va_start。

执行man 3 stdarg 后回车：

ap（argument pointer）是个指针变量，表示参数的指针，用来指向可变参数在栈中的地址。ap 的类型为va_list，本质上是指针类型，类型是char*。下面是3 个宏的说明。

  1. va_start(ap,v)，参数ap是用于指向可变参数的指针变量，参数v 是支持可变参数的函数的第1 个参数。此宏的功能是使指针ap 指向v 的地址，它的调用必须先于其他两个宏，相当于初始化ap 指针的作用。
  2. va_arg(ap,t)，参数ap 是用于指向可变参数的指针变量，参数t 是可变参数的类型，此宏的功能是使指针ap 指向栈中下一个参数的地址并返回其值。
  3. va_end(ap)，将指向可变参数的变量ap 置为null，也就是清空指针变量ap。

实现printf

函数vsprintf原型是int vsprintf(char *str, const char *format, va_list ap);。此函数的功能是把ap 指向的可变参数，以字符串格式format 中的符号’%’为替换标记，不修改原格式字符串format，将format 中除“%类型字符”以外的内容复制到str，把“%类型字符”替换成具体参数后写入str 中对应“%类型字符”的位置，vsprintf 执行完成后返回字符串str 的长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#define va_start(ap, v) ap = (va_list)&v  // 把ap指向第一个固定参数v
#define va_arg(ap, t) *((t*)(ap += 4))	  // ap指向下一个参数并返回其值
#define va_end(ap) ap = NULL		  // 清除ap

/* 将整型转换成字符(integer to ascii) */
static void itoa(uint32_t value, char** buf_ptr_addr, uint8_t base) {
   uint32_t m = value % base;	    // 求模,最先掉下来的是最低位   
   uint32_t i = value / base;	    // 取整
   if (i) {			    // 如果倍数不为0则递归调用。
      itoa(i, buf_ptr_addr, base);
   }
   if (m < 10) {      // 如果余数是0~9
      *((*buf_ptr_addr)++) = m + '0';	  // 将数字0~9转换为字符'0'~'9'
   } else {	      // 否则余数是A~F
      *((*buf_ptr_addr)++) = m - 10 + 'A'; // 将数字A~F转换为字符'A'~'F'
   }
}

/* 将参数ap按照格式format输出到字符串str,并返回替换后str长度 */
uint32_t vsprintf(char* str, const char* format, va_list ap) {
   char* buf_ptr = str;
   const char* index_ptr = format;
   char index_char = *index_ptr;
   int32_t arg_int;
   while(index_char) {
      if (index_char != '%') {
	 *(buf_ptr++) = index_char;
	 index_char = *(++index_ptr);
	 continue;
      }
      index_char = *(++index_ptr);	 // 得到%后面的字符
      switch(index_char) {
	 case 'x':
	    arg_int = va_arg(ap, int);
	    itoa(arg_int, &buf_ptr, 16); 
	    index_char = *(++index_ptr); // 跳过格式字符并更新index_char
	    break;
      }
   }
   return strlen(str);
}

/* 格式化输出字符串format */
uint32_t printf(const char* format, ...) {
   va_list args;
   va_start(args, format);	       // 使args指向format
   char buf[1024] = {0};	       // 用于存储拼接后的字符串
   vsprintf(buf, format, args);
   va_end(args);
   return write(buf); 
}

va_list定义在stdio.h中，代码是typedef char* va_list;，因此va_list是字符指针。va_start(ap, v)的作用是初始化指针ap，即把ap 指向栈中可变参数中的第一个参数v，ap = (va_list)&v。va_arg(ap, t)的作用是使指针ap 指向栈中下一个参数，并根据下一个参数的类型t 返回下一个参数的值，其实现是*((t*)(ap += 4))。va_arg(ap, t)必须在va_start(ap, v)之后调用，否则指针ap未初始化将导致错误。ap 已经指向了栈中可变参数中的第1 个参数，(ap+=4)将指向下一个参数在栈中的地址，而后将其强制转换成t 型指针(t*)，最后再用*号取值，即*((t*)(ap += 4))是下一个参数的值。va_end(ap)的作用就是回收指针ap，清空，其实现为ap = NULL。

itoa作用是将整型转换为字符串。其原型是void itoa(uint32_t value, char** buf_ptr_addr, uint8_t base)，iota 的任务有两个：一个是数制转换，另一个是将转换后的数值转换成字符，即第20 行的代码*((*buf_ptr_addr)++) = m + '0'。

vsprint的功能是将参数ap按照格式format 输出到字符串str 并返回替换后str 的长度。printf支持可变参数，因此它的函数声明为uint32_t printf(const char* format, ...)，其中的“…”表示可变参数。定义了变量args用它来指向参数，并调用宏va_start(args, format)对其初始化。定义了1024 字节大小的数组buf，用它来存储由vsprintf处理的结果，也就是str，完成之后宏va_end(args)使args 清空。最后执行系统调用write(buf)将处理后的字符串输出。

完善堆内存管理

arena是很多开源项目中都会用到的内存管理概念，将一大块内存划分成多个小内存块，每个小内存块之间互不干涉，可以分别管理，这样众多的小内存块就称为arena。arena 的一大块内存也是通过malloc_page获得的以4KB 为粒度的内存，按内存块的大小，可以划分出多种不同规格的arena，特定大小的arena只响应相应大小的请求。为支持多种容量内存块的分配，我们要提前建立好多种不同容量内存块的arena。arena分为两部分，一部分是元信息，用来描述自己内存池中空闲内存块数量，此部分占用的空间是固定的，约为12 字节。另一部分就是内存池区域，这里面有无数的内存块mem_block，此部分占用arena 大量的空间。

arena 也是一样的，起始为某一类型内存块的arena只有1 个，分配完时系统再创建一个同规格的arena，又被分配完时再创建。为了跟踪每个arena中的空闲内存块，分别为每一种规格的内存块建立一个内存块描述符，即mem_block_desc，在其中记录内存块规格大小，以及位于所有同类arena 中的空闲内存块链表。

在内存管理系统中，arena 为任意大小内存的分配提供了统一的接口，它既支持 1024 字节以下的小块内存的分配，又支持大于1024 字节以上的大块内存，malloc 函数实际上就是通过arena 申请这些内存块。arena 是个内存仓库，并不直接对外提供内存分配，只有内存块描述符才对外提供内存块，内存块描述符将同类arena 中的空闲内存块汇聚到一起，作为某一规格内存块的分配入口。因此，内存块描述符与arena 是一对多的关系，每个arena 都要与唯一的内存块描述符关联起来，多个同一规格的arena 为同一规格的内存块描述符供应内存块，它们各自的元信息中用内存块描述符指针指向同一个内存块描述符。

右上角的A 图是用于处理大于1024 字节的大内存的arena，其大小是1 页框以上，其中的内存池部分并没有划分成多个小内存块，因此arena 元信息中，内存块描述符指针mem_block_desc值为NULL。左下角的图B 是被拆分成64KB 小内存块的arena，其指针mem_block_desc指向规格为64 字节的内存块描述符，内存块描述符的空闲内存块链表free_list将arena 中可用内存块汇总。C中当一个arena 中的内存块不够用时，需要用多个arena 为同一规格内存块“供货”。此例的内存块描述符规格是16 字节，因此与其关联“供货”的arena 规格也必须是16 字节。起初是左边那个arena 为其提供内存块，当它的内存块分配耗尽时，系统又创建右边的arena（虚线表示的），从而保证该规格的内存块“货源充足”。

构建7种规格的内存块描述符：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
…略
/* 内存块 */
struct mem_block {
   struct list_elem free_elem;
};

/* 内存块描述符 */
struct mem_block_desc {
   uint32_t block_size; // 内存块大小
   uint32_t blocks_per_arena; // 本arena 中可容纳此mem_block 的数量
   struct list free_list; // 目前可用的mem_block 链表
};

#define DESC_CNT 7 // 内存块描述符个数
…略

在memory.h 中最先定义的是内存块结构struct mem_block，只有一个成员struct list_elem，用来添加到同规格内存块描述符的free_list中。内存块mem_block所占用的内存是从arena 中拆分出来的，其相关属性用mem_block_desc来描述，有3 个成员，free_list是空闲内存块链表，block_size是本描述符的规格，它的free_list中只能添加规格为block_size的内存块。blocks_per_arena是告诉本arena 中可容纳规格为block_size的内存块的数量。最后的宏DESC_CNT表示内存块描述符的数量，其值为7，从16 字节起，分别是16、32、64、128、256、512、1024 字节，共有7 种规格的内存块。

新的memory.c：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/* 内存仓库arena元信息 */
struct arena {
   struct mem_block_desc* desc;	 // 此arena关联的mem_block_desc
/* large为ture时,cnt表示的是页框数。
 * 否则cnt表示空闲mem_block数量 */
   uint32_t cnt;
   bool large;		   
};

struct mem_block_desc k_block_descs[DESC_CNT];	// 内核内存块描述符数组
struct pool kernel_pool, user_pool;      // 生成内核内存池和用户内存池
struct virtual_addr kernel_vaddr;	 // 此结构是用来给内核分配虚拟地址

/* 为malloc做准备 */
void block_desc_init(struct mem_block_desc* desc_array) {				   
   uint16_t desc_idx, block_size = 16;

   /* 初始化每个mem_block_desc描述符 */
   for (desc_idx = 0; desc_idx < DESC_CNT; desc_idx++) {
      desc_array[desc_idx].block_size = block_size;

      /* 初始化arena中的内存块数量 */
      desc_array[desc_idx].blocks_per_arena = (PG_SIZE - sizeof(struct arena)) / block_size;	  

      list_init(&desc_array[desc_idx].free_list);

      block_size *= 2;         // 更新为下一个规格内存块
   }
}

/* 内存管理部分初始化入口 */
void mem_init() {
   put_str("mem_init start\n");
   uint32_t mem_bytes_total = (*(uint32_t*)(0xb00));
   mem_pool_init(mem_bytes_total);	  // 初始化内存池
/* 初始化mem_block_desc数组descs,为malloc做准备 */
   block_desc_init(k_block_descs);
   put_str("mem_init done\n");
}

给arena 结构体指针赋予1 个页框以上的内存，页框中除了此结构体外的部分都将作为arena 的内存池区域，该区域会被平均拆分成多个规格大小相等的内存块，即mem_block，这些mem_block会被添加到内存块描述符的free_list。结构中第1个成员是desc，它指向本arena中的内存块被关联到哪个内存块描述符，同一规格的arena 只能关联到同一规格的内存块描述符，desc只能指向规格为64 字节的内存块描述符。第2个成员是cnt，它的意义要取决于第3 个成员large的值。当large 为ture 时，cnt 表示的是本arena 占用的页框数，否则large 为false 时，cnt 表示本arena 中还有多少空闲内存块可用，将来释放内存时要用到此项。

内核内存块描述符数组k_block_descs[DESC_CNT]，共有7 种描述符规格。通过for循环将7 种规格的内存块描述符初始化，分别初始化内核内存块描述符的block_size、blocks_per_arena和free_list。block_size 起始值为16，desc_idx 起始值为0，循环体的最后会将其乘以2，因此下标desc_idx越低，block_size越小，也就是说，内核和用户内存块描述符数组中，下标越低的内存块描述符，其表示的内存块容量越小。对blocks_per_arena 初始化时，减去arena 的大小后再向下整除，这样保证内存块数量不会越过此arena 占用的页框边界，不过会浪费一部分内存。最后调用list_init 初始化内存块描述符的free_list。

sys_malloc 的功能是分配并维护内存块资源，动态创建arena 以满足内存块的分配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
/* 返回arena中第idx个内存块的地址 */
static struct mem_block* arena2block(struct arena* a, uint32_t idx) {
  return (struct mem_block*)((uint32_t)a + sizeof(struct arena) + idx * a->desc->block_size);
}

/* 返回内存块b所在的arena地址 */
static struct arena* block2arena(struct mem_block* b) {
   return (struct arena*)((uint32_t)b & 0xfffff000);
}

/* 在堆中申请size字节内存 */
void* sys_malloc(uint32_t size) {
   enum pool_flags PF;
   struct pool* mem_pool;
   uint32_t pool_size;
   struct mem_block_desc* descs;
   struct task_struct* cur_thread = running_thread();

/* 判断用哪个内存池*/
   if (cur_thread->pgdir == NULL) {     // 若为内核线程
      PF = PF_KERNEL; 
      pool_size = kernel_pool.pool_size;
      mem_pool = &kernel_pool;
      descs = k_block_descs;
   } else {				      // 用户进程pcb中的pgdir会在为其分配页表时创建
      PF = PF_USER;
      pool_size = user_pool.pool_size;
      mem_pool = &user_pool;
      descs = cur_thread->u_block_desc;
   }

   /* 若申请的内存不在内存池容量范围内则直接返回NULL */
   if (!(size > 0 && size < pool_size)) {
      return NULL;
   }
   struct arena* a;
   struct mem_block* b;	
   lock_acquire(&mem_pool->lock);

/* 超过最大内存块1024, 就分配页框 */
   if (size > 1024) {
      uint32_t page_cnt = DIV_ROUND_UP(size + sizeof(struct arena), PG_SIZE);    // 向上取整需要的页框数

      a = malloc_page(PF, page_cnt);

      if (a != NULL) {
	 memset(a, 0, page_cnt * PG_SIZE);	 // 将分配的内存清0  

      /* 对于分配的大块页框,将desc置为NULL, cnt置为页框数,large置为true */
	 a->desc = NULL;
	 a->cnt = page_cnt;
	 a->large = true;
	 lock_release(&mem_pool->lock);
	 return (void*)(a + 1);		 // 跨过arena大小，把剩下的内存返回
      } else { 
	 lock_release(&mem_pool->lock);
	 return NULL; 
      }
   } else {    // 若申请的内存小于等于1024,可在各种规格的mem_block_desc中去适配
      uint8_t desc_idx;
      
      /* 从内存块描述符中匹配合适的内存块规格 */
      for (desc_idx = 0; desc_idx < DESC_CNT; desc_idx++) {
	 if (size <= descs[desc_idx].block_size) {  // 从小往大后,找到后退出
	    break;
	 }
      }

   /* 若mem_block_desc的free_list中已经没有可用的mem_block,
    * 就创建新的arena提供mem_block */
      if (list_empty(&descs[desc_idx].free_list)) {
	 a = malloc_page(PF, 1);       // 分配1页框做为arena
	 if (a == NULL) {
	    lock_release(&mem_pool->lock);
	    return NULL;
	 }
	 memset(a, 0, PG_SIZE);

    /* 对于分配的小块内存,将desc置为相应内存块描述符, 
     * cnt置为此arena可用的内存块数,large置为false */
	 a->desc = &descs[desc_idx];
	 a->large = false;
	 a->cnt = descs[desc_idx].blocks_per_arena;
	 uint32_t block_idx;

	 enum intr_status old_status = intr_disable();

	 /* 开始将arena拆分成内存块,并添加到内存块描述符的free_list中 */
	 for (block_idx = 0; block_idx < descs[desc_idx].blocks_per_arena; block_idx++) {
	    b = arena2block(a, block_idx);
	    ASSERT(!elem_find(&a->desc->free_list, &b->free_elem));
	    list_append(&a->desc->free_list, &b->free_elem);	
	 }
	 intr_set_status(old_status);
      }    

   /* 开始分配内存块 */
      b = elem2entry(struct mem_block, free_elem, list_pop(&(descs[desc_idx].free_list)));
      memset(b, 0, descs[desc_idx].block_size);

      a = block2arena(b);  // 获取内存块b所在的arena
      a->cnt--;		   // 将此arena中的空闲内存块数减1
      lock_release(&mem_pool->lock);
      return (void*)b;
   }
}

arena2block接受两个参数，arena指针a 和内存块mem_block 在arena 中的索引，函数功能是返回arena中第idx 个内存块的首地址。arena 结构体struct arena 并不是全部arena 的大小，结构体中仅有3 个成员，它就是我们所说的arena的元信息。在arena 指针指向的页框中，除去元信息外的部分才被用于内存块的平均拆分，每个内存块都是相等的大小且连续挨着，因此arena2block 的原理是在arena 指针指向的页框中，跳过元信息部分，即struct arena 的大小，再用idx 乘以该arena 中内存块大小，最终的地址便是arena 中第idx 个内存块的首地址，最后将其转换成mem_block 类型后返回。内存块大小记录在由desc 指向的内存块描述符的block_size 中。转换过程对应的代码是return (struct mem_block*)((uint32_t)a + sizeof(struct arena) + idx * a->desc->block_size)。

block2arena接受一个参数，内存块指针b。用于将7 种规格的内存块转换为内存块所在的arena，内存块的高20 位地址便是arena 所在的地址，将此地址转换成struct arena*后返回即可，对应代码return (struct arena*)((uint32_t)b & 0xfffff000)。

sys_malloc 只有一个参数size是申请的内存字节数。针对内核线程和用户进程两种情况为PF、mem_pool、pool_size 和descs赋值。定义了arena 指针a 和mem_block 指针b，指针a 用来指向新创建的arena，指针b 用来指向arena中的mem_block。如前介绍原理时所述，arena 既可处理大于1024 字节的大内存分配，也支持1024 字节以内的小内存分配。

如果申请的内存量大于1024 字节，先计算页框数，存入变量page_cnt。a = malloc_page(PF,page_cnt)把malloc_page返回的页框地址赋值给arena指针a。内存中并没有struct arena和struct mem_block静态实例，只有指向堆中的指针。对大内存的处理我们直接返回arena 的内存区，没有对应的内存块描述符，故a->desc = NULL。a->cnt此时的意义是此arena占用的页框数，因此a->cnt = page_cnt。a->large = true表示此arena 用于处理大于1024 字节以上的内存分配。用(a+1)跨过arena 元信息，也就是跨过一个struct arena的大小。最后通过return (void*)(a + 1)把arena 中的内存池起始地址返回。

内存小于1024 字节的情况：用for循环排查所有的内存块描述符，下标越低，其block_size 的值越小，从低容量的内存块向上找，遍历7种block_size，找到desc_idx。if (list_empty (&descs[desc_idx].free_list))判断是否有可用的内存块，如果没有则用a = malloc_page(PF, 1)分配1页内存来创建新的arena，之后用memset(a, 0, PG_SIZE)清0。a->desc = &descs[desc_idx];使desc 指向上面找到的内存块描述符。a->large置为false，表示此arena 不用于处理大于1024 字节的大内存。a->cnt置为descs[desc_idx].blocks_per_arena，表示此arena 现在具有的空闲内存块数量。

在创建新的arena 后，下一步是将它拆分成内存块，循环次数是descs[desc_idx].blocks_per_arena，通过arena2block完成，新拆分出来的内存块添加到内存块描述符的free_list中。用list_pop从free_list中弹出一个内存块，此时得到的仅仅是内存块mem_block中list_elem的地址，因此要用到elem2entry宏将其转换成mem_block的地址。

分配内存时的一般步骤如下。

  1. 在虚拟地址池中分配虚拟地址，相关的函数是vaddr_get，此函数操作的是内核虚拟内存池位图kernel_vaddr.vaddr_bitmap或用户虚拟内存池位图pcb->userprog_vaddr.vaddr_bitmap。
  2. 在物理内存池中分配物理地址，相关的函数是palloc，此函数操作的是内核物理内存池位图kernel_pool->pool_bitmap或用户物理内存池位图user_pool->pool_bitmap。
  3. 在页表中完成虚拟地址到物理地址的映射，相关的函数是page_table_add。

释放内存是与分配内存相反的过程，咱们对照着设计一套释放内存的方法。

  1. 在物理地址池中释放物理页地址，相关的函数是pfree，操作的位图同palloc。
  2. 在页表中去掉虚拟地址的映射，原理是将虚拟地址对应pte 的P 位置0，CPU 就认为该虚拟地址未做映射，从而达到删除虚拟地址的目的。相关的函数是page_table_pte_remove。
  3. 在虚拟地址池中释放虚拟地址，相关的函数是vaddr_remove，操作的位图同vaddr_get。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/* 将物理地址pg_phy_addr回收到物理内存池 */
void pfree(uint32_t pg_phy_addr) {
   struct pool* mem_pool;
   uint32_t bit_idx = 0;
   if (pg_phy_addr >= user_pool.phy_addr_start) {     // 用户物理内存池
      mem_pool = &user_pool;
      bit_idx = (pg_phy_addr - user_pool.phy_addr_start) / PG_SIZE;
   } else {	  // 内核物理内存池
      mem_pool = &kernel_pool;
      bit_idx = (pg_phy_addr - kernel_pool.phy_addr_start) / PG_SIZE;
   }
   bitmap_set(&mem_pool->pool_bitmap, bit_idx, 0);	 // 将位图中该位清0
}

/* 去掉页表中虚拟地址vaddr的映射,只去掉vaddr对应的pte */
static void page_table_pte_remove(uint32_t vaddr) {
   uint32_t* pte = pte_ptr(vaddr);
   *pte &= ~PG_P_1;	// 将页表项pte的P位置0
   asm volatile ("invlpg %0"::"m" (vaddr):"memory");    //更新tlb
}

/* 在虚拟地址池中释放以_vaddr起始的连续pg_cnt个虚拟页地址 */
static void vaddr_remove(enum pool_flags pf, void* _vaddr, uint32_t pg_cnt) {
   uint32_t bit_idx_start = 0, vaddr = (uint32_t)_vaddr, cnt = 0;

   if (pf == PF_KERNEL) {  // 内核虚拟内存池
      bit_idx_start = (vaddr - kernel_vaddr.vaddr_start) / PG_SIZE;
      while(cnt < pg_cnt) {
	 bitmap_set(&kernel_vaddr.vaddr_bitmap, bit_idx_start + cnt++, 0);
      }
   } else {  // 用户虚拟内存池
      struct task_struct* cur_thread = running_thread();
      bit_idx_start = (vaddr - cur_thread->userprog_vaddr.vaddr_start) / PG_SIZE;
      while(cnt < pg_cnt) {
	 bitmap_set(&cur_thread->userprog_vaddr.vaddr_bitmap, bit_idx_start + cnt++, 0);
      }
   }
}

函数pfree接受一个参数，即物理页框地址pg_phy_addr，功能是将物理页框回收到相应的物理内存池。根据物理地址池的起始地址判断pg_phy_addr属于哪个物理内存池，用变量mem_pool指向物理内存池，bit_idx为物理地址在相应物理内存池中的偏移量，最后通过代码bitmap_set(&mem_pool->pool_bitmap, bit_idx, 0)在位图中回收该位。

函数page_table_pte_remove接受虚拟地址vaddr，功能是将pte中的P 位置0。函数体中，先调用pte_ptr(vaddr)获取虚拟地址所在的pte 指针，通过代码*pte &= ~PG_P_1使pte中的P位取反为0。之后更新TLB，有两种方式，一是用invlpg 指令更新单条虚拟地址条目，另外一个是重新加载cr3 寄存器，这将直接清空TLB。采用invlpg指令去单独更新vaddr 对应的缓存。invlpg的指令格式为invlpg m，其中m是操作数，表示虚拟地址内存，invalpg是汇编指令，asm volatile ("invlpg %0"::"m" (vaddr):"memory")来更新虚拟地址vaddr 在tlb 缓存中的条目，

vaddr_remove接受3个参数，pf 是虚拟内存池标志，_vaddr 是待释放的虚拟地址，pg_cnt 是连续的虚拟页框数。函数功能是在虚拟地址池中释放以_vaddr 起始的连续pg_cnt 个虚拟页地址。先根据pf 判断是处理哪个虚拟内存池，然后再用位图函数bitmap_set将虚拟地址在虚拟内存池位图中相应的位清0。如果是内核，就针对内核的虚拟内存池kernel_vaddr操作，计算虚拟地址vaddr在位图kernel_vaddr中的偏移量，存入变量bit_idx_start中，然后循环pg_cnt次，依次将虚拟内存池位图中的相应位清0。针对用户虚拟内存池的处理与此同理，只是虚拟内存池位图是当前用户进程pcb->userprog_vaddr，不再赘述。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

/* 释放以虚拟地址vaddr为起始的cnt个物理页框 */
void mfree_page(enum pool_flags pf, void* _vaddr, uint32_t pg_cnt) {
   uint32_t pg_phy_addr;
   uint32_t vaddr = (int32_t)_vaddr, page_cnt = 0;
   ASSERT(pg_cnt >=1 && vaddr % PG_SIZE == 0); 
   pg_phy_addr = addr_v2p(vaddr);  // 获取虚拟地址vaddr对应的物理地址

/* 确保待释放的物理内存在低端1M+1k大小的页目录+1k大小的页表地址范围外 */
   ASSERT((pg_phy_addr % PG_SIZE) == 0 && pg_phy_addr >= 0x102000);
   
/* 判断pg_phy_addr属于用户物理内存池还是内核物理内存池 */
   if (pg_phy_addr >= user_pool.phy_addr_start) {   // 位于user_pool内存池
      vaddr -= PG_SIZE;
      while (page_cnt < pg_cnt) {
	 vaddr += PG_SIZE;
	 pg_phy_addr = addr_v2p(vaddr);

	 /* 确保物理地址属于用户物理内存池 */
	 ASSERT((pg_phy_addr % PG_SIZE) == 0 && pg_phy_addr >= user_pool.phy_addr_start);

	 /* 先将对应的物理页框归还到内存池 */
	 pfree(pg_phy_addr);

         /* 再从页表中清除此虚拟地址所在的页表项pte */
	 page_table_pte_remove(vaddr);

	 page_cnt++;
      }
   /* 清空虚拟地址的位图中的相应位 */
      vaddr_remove(pf, _vaddr, pg_cnt);

   } else {	     // 位于kernel_pool内存池
      vaddr -= PG_SIZE;	      
      while (page_cnt < pg_cnt) {
	 vaddr += PG_SIZE;
	 pg_phy_addr = addr_v2p(vaddr);
      /* 确保待释放的物理内存只属于内核物理内存池 */
	 ASSERT((pg_phy_addr % PG_SIZE) == 0 && \
	       pg_phy_addr >= kernel_pool.phy_addr_start && \
	       pg_phy_addr < user_pool.phy_addr_start);
	
	 /* 先将对应的物理页框归还到内存池 */
	 pfree(pg_phy_addr);

         /* 再从页表中清除此虚拟地址所在的页表项pte */
	 page_table_pte_remove(vaddr);

	 page_cnt++;
      }
   /* 清空虚拟地址的位图中的相应位 */
      vaddr_remove(pf, _vaddr, pg_cnt);
   }
}

mfree_page接受3 个参数，pf 是内存池标志，_vaddr 是待释放的虚拟地址，pg_cnt 是连续的页框数，此函数的功能是释放以虚拟地址vaddr 为起始的cnt 个物理页框。先调用pfree 清空物理地址位图中的相应位，再调用page_table_pte_remove 删除页表中此地址的pte，最后调用vaddr_remove 清除虚拟地址位图中的相应位。

sys_free 针对页框级别的内存和小内存块的处理有各自的方法，对于大内存的处理称之为释放，就是把页框在虚拟内存池和物理内存池的位图中将相应位置0。对于小内存的处理称之为回收，是将arena 中的内存块重新放回到内存块描述符中的空闲块链表free_list。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

/* 回收内存ptr */
void sys_free(void* ptr) {
   ASSERT(ptr != NULL);
   if (ptr != NULL) {
      enum pool_flags PF;
      struct pool* mem_pool;

   /* 判断是线程还是进程 */
      if (running_thread()->pgdir == NULL) {
	 ASSERT((uint32_t)ptr >= K_HEAP_START);
	 PF = PF_KERNEL; 
	 mem_pool = &kernel_pool;
      } else {
	 PF = PF_USER;
	 mem_pool = &user_pool;
      }

      lock_acquire(&mem_pool->lock);   
      struct mem_block* b = ptr;
      struct arena* a = block2arena(b);	     // 把mem_block转换成arena,获取元信息
      ASSERT(a->large == 0 || a->large == 1);
      if (a->desc == NULL && a->large == true) { // 大于1024的内存
	 mfree_page(PF, a, a->cnt); 
      } else {				 // 小于等于1024的内存块
	 /* 先将内存块回收到free_list */
	 list_append(&a->desc->free_list, &b->free_elem);

	 /* 再判断此arena中的内存块是否都是空闲,如果是就释放arena */
	 if (++a->cnt == a->desc->blocks_per_arena) {
	    uint32_t block_idx;
	    for (block_idx = 0; block_idx < a->desc->blocks_per_arena; block_idx++) {
	       struct mem_block*  b = arena2block(a, block_idx);
	       ASSERT(elem_find(&a->desc->free_list, &b->free_elem));
	       list_remove(&b->free_elem);
	    }
	    mfree_page(PF, a, 1); 
	 } 
      }   
      lock_release(&mem_pool->lock); 
   }
}

sys_free 只接受1 个参数，内存指针ptr，函数功能是释放ptr 指向的内存。将ptr赋值给内存块指针b，然后通过struct arena* a = block2arena(b)获取内存块b 所在的arena 指针，此目的是获取arena 中的元信息，通过元信息中的变量desc 和large 的值分别进行下一步处理。如果a->desc的值为NULL 并且a->large的值为true，这说明待释放的内存（也就是ptr 指向的内存）并不是在arena 中的小内存块，而是大于1024 字节的大内存，其大小是1 个或多个页框。如果待释放的内存是小内存块，流程就进入了list_append(&a->desc-> free_list, &b->free_elem)，将此内存块回收到此内存块描述符的free_list 中。如果++a->cnt与内存块描述符中的blocks_per_arena相等，则此arena 中的空闲内存块已经达到最大数，说明可以释放。

先在syscall.h 中添加malloc 和free 的系统调用号及接口:

1
2
3
4
5
6
7
8
9
10
enum SYSCALL_NR {
   SYS_GETPID,
   SYS_WRITE,
   SYS_MALLOC,
   SYS_FREE
};
uint32_t getpid(void);
uint32_t write(char* str);
void* malloc(uint32_t size);
void free(void* ptr);

接着在syscall.c 中完成malloc 和free 的实现：

1
2
3
4
5
6
7
8
9
/* 申请size 字节大小的内存，并返回结果 */
void* malloc(uint32_t size) {
   return (void*)_syscall1(SYS_MALLOC, size);
}

/* 释放ptr 指向的内存 */
void free(void* ptr) {
   _syscall1(SYS_FREE, ptr);
}

最后在syscall-init.c 中完成系统调用号与子功能处理函数的关联，也就是更新数组syscall_table。

1
2
3
4
5
6
7
8
9
/* 初始化系统调用 */
void syscall_init(void) {
   put_str("syscall_init start\n");
   syscall_table[SYS_GETPID] = sys_getpid;
   syscall_table[SYS_WRITE] = sys_write;
   syscall_table[SYS_MALLOC] = sys_malloc;
   syscall_table[SYS_FREE] = sys_free;
   put_str("syscall_init done\n");
}

编写硬盘驱动程序

硬盘及分区表

磁盘分区表（Disk Partition Table）简称DPT，是由多个分区元信息汇成的表，表中每一个表项都对应一个分区，主要记录各分区的起始扇区地址，大小界限等。磁盘分区表就是个数组，此数组长度固定为4，数组元素是分区元信息的结构。最初的磁盘分区表位于** MBR 引导扇区中。MBR（Main Boot Record）即主引导记录，它是一段引导程序，其所在的扇区称为主引导扇区**，该扇区位于0 盘0 道1 扇区（物理扇区编号从1 开始，逻辑扇区地址LBA 从0 开始），也就是硬盘最开始的扇区，扇区大小为512 字节，这512 字节内容由三部分组成。

  1. 主引导记录MBR。MBR 引导程序位于主引导扇区中偏移0～0x1BD 的空间，共计446 字节大小，这其中包括硬盘参数及部分指令（由BIOS 跳入执行），它是由分区工具产生的，独立于任何操作系统。
  2. 磁盘分区表DPT。磁盘分区表位于主引导扇区中偏移0x1BE～0x1FD 的空间，总共64 字节大小，每个分区表项是16字节，因此磁盘分区表最大支持4 个分区。
  3. 结束魔数55AA，表示此扇区为主引导扇区，里面包含控制程序。位于扇区偏移0x1FE～0x1FF，也就是最后2 个字节。
  4. 位于引导扇区后有多个空闲的扇区：对于不够一个柱面的剩余的空间一般不再利用，并不参与分区。除去MBR 引导扇区占用的1 扇区，这部分剩余空间是62 个扇区。

扩展分区被划分出多个子扩展分区，每个子扩展分区都有自己的分区表，所以子扩展分区在逻辑上相当于单独的硬盘，各分区表在各个子扩展分区最开始的扇区中，该扇区同MBR 引导扇区结构相同，称为EBR，即扩展引导记录。MBR 和EBR 所在的扇区统称为引导扇区。由于扩展分区采用了链式分区表，理论上支持无限个逻辑分区。EBR 中分区表的第一分区表项用来描述所包含的逻辑分区的元信息，第二分区表项用来描述下一个子扩展分区的地址。位于EBR 中的分区表相当于链表中的结点，第一个分区表项存的是分区数据，第二个分区表项存的是后继分区的指针。

分区表项的结构：

活动分区是指引导程序所在的分区，这个引导程序通常是操作系统内核加载器，故此引导程序通常被称为操作系统引导记录，即OBR（OS Boot Record）。如果MBR 发现该分区表项的活动分区标记为0x80，这就表示该分区的引导扇区中有引导程序，MBR 就将CPU 使用权交给此引导程序，此扇区被称为操作系统引导扇区，也就是OBR 引导扇区。而 OBR 引导扇区是分区中最开始的扇区，归操作系统的文件系统管理，因此操作系统通常往OBR 引导扇区中添加内核加载器的代码，供MBR 调用以实现操作系统自举，

分区起始偏移扇区是个相对量，它表示各分区的起始扇区地址是相对于某“基准”的偏移扇区数，各分区的绝对扇区LBA 地址=“基准”的绝对扇区起始LBA 地址+各分区的起始偏移扇区，分区容量扇区数就是表示分区的容量扇区数。以上两项用来确定一个分区的位置和大小。

文件系统

文件系统概念简介

块是文件系统的读写单位，因此文件至少要占据一个块，在FAT文件系统中存储的文件，其所有的块被用于链式结构来组织，在每个块的最后存储下一个块的地址，从而块与块之间串联到一起，文件中的块可以分布在各个零散的空间中。算法效率低下，而且每访问一个结点，就要涉及一次硬盘寻道。

UNIX 文件系统将文件以索引结构来组织，文件中的块依然可以分散到不连续的零散空间中，保留了磁盘高利用率的优点，更重要的是文件系统为每个文件的所有块建立了一个索引表，索引表就是块地址数组，每个数组元素就是块的地址，数组元素下标是文件块的索引，第n 个数组元素指向文件中的第n 个块，这样访问任意一个块的时候，只要从索引表中获得块地址就可以了，速度大大提升。包含此索引表的索引结构称为inode，即index node，索引结点，用来索引、跟踪一个文件的所有块。在UINX文件系统中，一个文件必须对应一个inode。

每个索引表中共15 个索引项，前 12 个索引项是文件的前12个块的地址，它们是可直接获得地址的块。若文件大于 12 个块，那就再建立个新的块索引表，新索引表称为一级间接块索引表，表中可容纳256 个块的地址，该物理块的地址存储到老索引表的第13 个索引项中。有了一级间接块索引表，文件最大可达12+256=268 个块。再建立二级间接块索引表，此表中各表项存储的是一级间接块索引表，有了二级间接块索引表，文件最大可达12+256+256*256个块。三级间接块索引表所在块的地址记录在老索引表的第15 个索引项中，文件最大可达12+256+256*256+256*256*256个块，

i 结点编号是指此inode 的序号，这通常是指它在inode 数组中的下标。权限是指读、写、执行。属主是指文件的拥有者，时间是指创建时间、修改时间、访问时间等。文件大小是指文件的字节尺寸。下面这些连续的各种块指针及索引表指针是文件所有块的索引，也就是指向文件的实体部分。inode 是文件实体数据块的描述符。Linux 中每分区的inode 数量是固定的，可以用tune2fs 命令查看inode 数量。inode 的数量等于文件的数量，分区中所有文件的inode 通过inode_table表格来维护。一个分区的利用率分为inode的利用率和磁盘空间利用率两种，在Linux 中可以通过df –i 命令查看inode 利用率，不加参数执行df 时，查看的是空间利用率。

在Linux 中，目录和文件都用inode 来表示，目录是包含文件的文件。如果该inode 表示的是普通文件，此inode指向的数据块中的内容应该是普通文件自己的数据。如果该inode表示的是目录文件，此inode 指向的数据块中的内容应该是该目录下的目录项。目录相当于个文件列表（或者是表格），每个文件在目录中都是一个entry（条目、项），这个entry 是目录中各个文件的描述，它称为目录项，目录项中至少要包括文件名、文件类型及文件对应的inode 编号。有了目录项后，通过文件名找文件实体数据块的流程是。

  1. 在目录中找到文件名所在的目录项。
  2. 从目录项中获取inode 编号。
  3. 用inode 编号作为inode 数组的索引下标，找到inode。
  4. 从该inode 中获取数据块的地址，读取数据块。


查找任意文件时，都直接到根目录的数据块中找相关的目录项，然后递归查找，最终可以找到任意子目录中的文件。

超级块是保存文件系统元信息的元信息。用位图来管理inode 的使用情况，也要为这些空闲块准备个位图。一个简单的超级块结构如图。

魔数用来确定文件系统的类型的标志，超级块是在为分区创建文件系统时创建的，所有有关文件系统元信息的配置都在超级块中，因此它被固定存储在各分区的第2 个扇区，通常是占用一个扇区的大小。

图是一个典型的inode结构的文件系统布局。操作系统引导块就是操作系统引导记录OBR 所在的地址，即操作系统引导扇区，它位于各分区最开始的扇区。在操作系统引导块后面的依次是超级块、空闲块的位图、inode 位图、inode 数组、根目录、空闲块区域。根目录和空闲块区域是真正用于存储数据的区域。

创建文件系统

创建超级块、i 结点、目录项

有关文件操作的代码我们定义在fs 目录下，本节咱们新建这个目录，超级块所在的文件位于fs/super_block.h中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/* 超级块 */
struct super_block {
   uint32_t magic;		    // 用来标识文件系统类型,支持多文件系统的操作系统通过此标志来识别文件系统类型
   uint32_t sec_cnt;		    // 本分区总共的扇区数
   uint32_t inode_cnt;		    // 本分区中inode数量
   uint32_t part_lba_base;	    // 本分区的起始lba地址

   uint32_t block_bitmap_lba;	    // 块位图本身起始扇区地址
   uint32_t block_bitmap_sects;     // 扇区位图本身占用的扇区数量

   uint32_t inode_bitmap_lba;	    // i结点位图起始扇区lba地址
   uint32_t inode_bitmap_sects;	    // i结点位图占用的扇区数量

   uint32_t inode_table_lba;	    // i结点表起始扇区lba地址
   uint32_t inode_table_sects;	    // i结点表占用的扇区数量

   uint32_t data_start_lba;	    // 数据区开始的第一个扇区号
   uint32_t root_inode_no;	    // 根目录所在的I结点号
   uint32_t dir_entry_size;	    // 目录项大小

   uint8_t  pad[460];		    // 加上460字节,凑够512字节1扇区大小
} __attribute__ ((packed));

超级块连1扇区都不到，但磁盘操作要以扇区为单位在超级块的最后定义了460字节的pad 数组填充扇区，凑够512字节。为了保证编译后的超级块实例大小为512 字节，添加了__attribute__ ((packed));。

inode 定义在fs/inode.h中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* inode结构 */
struct inode {
   uint32_t i_no;    // inode编号

/* 当此inode是文件时,i_size是指文件大小,
若此inode是目录,i_size是指该目录下所有目录项大小之和*/
   uint32_t i_size;

   uint32_t i_open_cnts;   // 记录此文件被打开的次数
   bool write_deny;	   // 写文件不能并行,进程写文件前检查此标识

/* i_sectors[0-11]是直接块, i_sectors[12]用来存储一级间接块指针 */
   uint32_t i_sectors[13];
   struct list_elem inode_tag;
};

inode 结构中：

  • i_no是inode编号，它是在inode 数组中的下标。
  • i_size是此inode 指向的文件的大小。
    • inode 指向的是普通文件时，i_size表示普通文件的大小，
    • inode 指向的是目录时，i_size 表示目录中所有目录项的大小之和。
    • i_size 是以字节为单位的大小，并不是以数据块为单位
  • i_open_cnts表示此文件被打开的次数。
  • write_deny用于限制文件的并行写操作，必须保证文件在执行写操作时，该文件不能再有其他并行的写操作
  • i_sectors是数据块的指针，
    • 数据的前12 个块i_sectors[0-11]是直接块，也就是它们中记录的是数据块的扇区地址
    • i_sectors[12]用来存储一级间接块索引表的扇区地址
  • inode_tag 是此inode 的标识，用于加入已打开的inode 列表作为缓存。

目录项的定义在fs/dir.h中，如代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#define MAX_FILE_NAME_LEN  16	 // 最大文件名长度

/* 目录结构 */
struct dir {
   struct inode* inode;   
   uint32_t dir_pos;	  // 记录在目录内的偏移
   uint8_t dir_buf[512];  // 目录的数据缓存
};

/* 目录项结构 */
struct dir_entry {
   char filename[MAX_FILE_NAME_LEN];  // 普通文件或目录名称
   uint32_t i_no;		      // 普通文件或目录对应的inode编号
   enum file_types f_type;	      // 文件类型
};

宏MAX_FILE_NAME_LEN便是文件名的最大长度，其值为16。struct dir是目录结构，它并不在磁盘上存在，只用于与目录相关的操作时，在内存中创建。其成员inode 是指针，用于指向内存中inode，该inode 必然是在已打开的inode 队列；成员dir_pos用于遍历目录时记录“游标”在目录中的偏移，也就是目录项的偏移量，所以dir_pos大小应为目录项大小的整数倍。成员dir_buf用于目录的数据缓存，如读取目录时，用来存储返回的目录项，这是后话了。

下面是目录项结构struct dir_entry，它是连接文件名与inode 的纽带，成员filename是文件名，这里只支持最大16 个字符的文件名。成员i_no是文件filename 对应的inode 编号。成员f_type是指filename 的类型，具体类型定义在fs/fs.h 中。

1
2
3
4
5
6
7
8
9
10
#define MAX_FILES_PER_PART 4096	    // 每个分区所支持最大创建的文件数
#define BITS_PER_SECTOR 4096	    // 每扇区的位数
#define SECTOR_SIZE 512		    // 扇区字节大小
#define BLOCK_SIZE SECTOR_SIZE	    // 块字节大小

enum file_types {
   FT_UNKNOWN,	  // 不支持的文件类型
   FT_REGULAR,	  // 普通文件
   FT_DIRECTORY	  // 目录
};

完成格式化分区的函数是partition_format。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/* 格式化分区,也就是初始化分区的元信息,创建文件系统 */
static void partition_format(struct partition* part) {
/* 为方便实现,一个块大小是一扇区 */
   uint32_t boot_sector_sects = 1;	  
   uint32_t super_block_sects = 1;
   uint32_t inode_bitmap_sects = DIV_ROUND_UP(MAX_FILES_PER_PART, BITS_PER_SECTOR);	   // I结点位图占用的扇区数.最多支持4096个文件
   uint32_t inode_table_sects = DIV_ROUND_UP(((sizeof(struct inode) * MAX_FILES_PER_PART)), SECTOR_SIZE);
   uint32_t used_sects = boot_sector_sects + super_block_sects + inode_bitmap_sects + inode_table_sects;
   uint32_t free_sects = part->sec_cnt - used_sects;  

/************** 简单处理块位图占据的扇区数 ***************/
   uint32_t block_bitmap_sects;
   block_bitmap_sects = DIV_ROUND_UP(free_sects, BITS_PER_SECTOR);
   /* block_bitmap_bit_len是位图中位的长度,也是可用块的数量 */
   uint32_t block_bitmap_bit_len = free_sects - block_bitmap_sects; 
   block_bitmap_sects = DIV_ROUND_UP(block_bitmap_bit_len, BITS_PER_SECTOR); 
/*********************************************************/
   
   /* 超级块初始化 */
   struct super_block sb;
   sb.magic = 0x19590318;
   sb.sec_cnt = part->sec_cnt;
   sb.inode_cnt = MAX_FILES_PER_PART;
   sb.part_lba_base = part->start_lba;

   sb.block_bitmap_lba = sb.part_lba_base + 2;	 // 第0块是引导块,第1块是超级块
   sb.block_bitmap_sects = block_bitmap_sects;

   sb.inode_bitmap_lba = sb.block_bitmap_lba + sb.block_bitmap_sects;
   sb.inode_bitmap_sects = inode_bitmap_sects;

   sb.inode_table_lba = sb.inode_bitmap_lba + sb.inode_bitmap_sects;
   sb.inode_table_sects = inode_table_sects; 

   sb.data_start_lba = sb.inode_table_lba + sb.inode_table_sects;
   sb.root_inode_no = 0;
   sb.dir_entry_size = sizeof(struct dir_entry);

   printk("%s info:\n", part->name);
   printk("   magic:0x%x\n   part_lba_base:0x%x\n   all_sectors:0x%x\n   inode_cnt:0x%x\n   block_bitmap_lba:0x%x\n   block_bitmap_sectors:0x%x\n   inode_bitmap_lba:0x%x\n   inode_bitmap_sectors:0x%x\n   inode_table_lba:0x%x\n   inode_table_sectors:0x%x\n   data_start_lba:0x%x\n", sb.magic, sb.part_lba_base, sb.sec_cnt, sb.inode_cnt, sb.block_bitmap_lba, sb.block_bitmap_sects, sb.inode_bitmap_lba, sb.inode_bitmap_sects, sb.inode_table_lba, sb.inode_table_sects, sb.data_start_lba);

函数partition_format接受1 个参数，待创建文件系统的分区part。创建文件系统就是创建文件系统所需要的元信息，这包括超级块位置及大小、空闲块位图的位置及大小、inode 位图的位置及大小、inode 数组的位置及大小、空闲块起始地址、根目录起始地址。创建步骤如下：

  1. 根据分区part 大小，计算分区文件系统各元信息需要的扇区数及位置。
  2. 在内存中创建超级块，将以上步骤计算的元信息写入超级块。
  3. 将超级块写入磁盘。
  4. 将元信息写入磁盘上各自的位置。
  5. 将根目录写入磁盘。

为引导块和超级块占用的扇区数赋值，简单起见，它们均占用1 扇区大小。inode_bitmap_sects表示inode位图占用的扇区数，MAX_FILES_PER_PART定义在fs.h中，表示分区可创建的最大文件数，也就是inode数量，它的值为4096。BITS_PER_SECTOR同样定义在fs.h中，其值也为4096，经过宏DIV_ROUND_UP计算后inode_bitmap_sects的值为1，inode 位图占用1 扇区。

inode_table_sects表示inode 数组占用的扇区数，这是由inode 的尺寸和数量决定的。先用**空闲块数free_sects**除以每扇区的位数，这样便得到了空闲块位图block_bitmap占用的扇区数block_bitmap_sects。空闲块位图占用了一部分空闲扇区，因此现在真正的空闲块数得把lock_bitmap_sects从free_sets中减去，其结果也是位图中位的个数，把结果写入变量block_bitmap_bit_len，然后再用变量lock_bitmap_bit_len重新除以BITS_PER_SECTOR，这便是空闲块位图最终占用的扇区数block_bitmap_sects。

代码sb.root_inode_no = 0表示根目录的inode 编号为0，也就是说inode 数组中第0 个inode 我们留给了根目录。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
   struct disk* hd = part->my_disk;
/*******************************
 * 1 将超级块写入本分区的1扇区 *
 ******************************/
   ide_write(hd, part->start_lba + 1, &sb, 1);
   printk("   super_block_lba:0x%x\n", part->start_lba + 1);

/* 找出数据量最大的元信息,用其尺寸做存储缓冲区*/
   uint32_t buf_size = (sb.block_bitmap_sects >= sb.inode_bitmap_sects ? sb.block_bitmap_sects : sb.inode_bitmap_sects);
   buf_size = (buf_size >= sb.inode_table_sects ? buf_size : sb.inode_table_sects) * SECTOR_SIZE;
   uint8_t* buf = (uint8_t*)sys_malloc(buf_size);	// 申请的内存由内存管理系统清0后返回
   
/**************************************
 * 2 将块位图初始化并写入sb.block_bitmap_lba *
 *************************************/
   /* 初始化块位图block_bitmap */
   buf[0] |= 0x01;       // 第0个块预留给根目录,位图中先占位
   uint32_t block_bitmap_last_byte = block_bitmap_bit_len / 8;
   uint8_t  block_bitmap_last_bit  = block_bitmap_bit_len % 8;
   uint32_t last_size = SECTOR_SIZE - (block_bitmap_last_byte % SECTOR_SIZE);	     // last_size是位图所在最后一个扇区中，不足一扇区的其余部分

   /* 1 先将位图最后一字节到其所在的扇区的结束全置为1,即超出实际块数的部分直接置为已占用*/
   memset(&buf[block_bitmap_last_byte], 0xff, last_size);
   
   /* 2 再将上一步中覆盖的最后一字节内的有效位重新置0 */
   uint8_t bit_idx = 0;
   while (bit_idx <= block_bitmap_last_bit) {
      buf[block_bitmap_last_byte] &= ~(1 << bit_idx++);
   }
   ide_write(hd, sb.block_bitmap_lba, buf, sb.block_bitmap_sects);

获取分区part 自己所属的硬盘hd，hd 将作为后续参数。超级块已经构建完成，将其写到本分区开始的扇区加1 的地方，即part->start_lba + 1，也就是跨过引导扇区，把超级块写入引导扇区后面的扇区中。选出占用空间最大的元信息，使其尺寸作为申请的缓冲区大小，申请内存返回给指针buf，buf 是通用的缓冲区，接下来往磁盘中的数据写入操作都将buf 作为数据源，通过不同的类型转换，使buf 变成合适的缓冲区类型。

我们把第0 个空闲块作为根目录，因此我们需要在空闲块位图中将第0 位置1。把块位图最后一个扇区中不属于空闲块的位初始为1。在将位图持久化到硬盘之前，一定要将位图最后一扇区中的多余位初始为1，表示它们已被占用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/***************************************
 * 3 将inode位图初始化并写入sb.inode_bitmap_lba *
 ***************************************/
   /* 先清空缓冲区*/
   memset(buf, 0, buf_size);
   buf[0] |= 0x1;      // 第0个inode分给了根目录
   /* 由于inode_table中共4096个inode,位图inode_bitmap正好占用1扇区,
    * 即inode_bitmap_sects等于1, 所以位图中的位全都代表inode_table中的inode,
    * 无须再像block_bitmap那样单独处理最后一扇区的剩余部分,
    * inode_bitmap所在的扇区中没有多余的无效位 */
   ide_write(hd, sb.inode_bitmap_lba, buf, sb.inode_bitmap_sects);

/***************************************
 * 4 将inode数组初始化并写入sb.inode_table_lba *
 ***************************************/
 /* 准备写inode_table中的第0项,即根目录所在的inode */
   memset(buf, 0, buf_size);  // 先清空缓冲区buf
   struct inode* i = (struct inode*)buf; 
   i->i_size = sb.dir_entry_size * 2;	 // .和..
   i->i_no = 0;   // 根目录占inode数组中第0个inode
   i->i_sectors[0] = sb.data_start_lba;	     // 由于上面的memset,i_sectors数组的其它元素都初始化为0 
   ide_write(hd, sb.inode_table_lba, buf, sb.inode_table_sects);
   
/***************************************
 * 5 将根目录初始化并写入sb.data_start_lba
 ***************************************/
   /* 写入根目录的两个目录项.和.. */
   memset(buf, 0, buf_size);
   struct dir_entry* p_de = (struct dir_entry*)buf;

   /* 初始化当前目录"." */
   memcpy(p_de->filename, ".", 1);
   p_de->i_no = 0;
   p_de->f_type = FT_DIRECTORY;
   p_de++;

   /* 初始化当前目录父目录".." */
   memcpy(p_de->filename, "..", 2);
   p_de->i_no = 0;   // 根目录的父目录依然是根目录自己
   p_de->f_type = FT_DIRECTORY;

   /* sb.data_start_lba已经分配给了根目录,里面是根目录的目录项 */
   ide_write(hd, sb.data_start_lba, buf, 1);

   printk("   root_dir_lba:0x%x\n", sb.data_start_lba);
   printk("%s format done\n", part->name);
   sys_free(buf);

将inode 位图（buf）中第0 个inode 置为1，原因是我们把inode 数组中第0 个inode 分配给了根目录。接下来准备把inode数组写入sb.inode_table_lba。inode_table_sects是通过宏DIV_ROUND_UP除法向上取整得到的结果，因此inode_table最终在磁盘上占据的全部扇区中，并不是所有空间都是inode_table的内容。

我们把第0 个inode 已经分配给了根目录，因此现在要初始化第0 个inode 为根目录的信息。将buf转换为inode结构struct inode型指针后，通过i->i_size = sb.dir_entry_ size * 2将i_size赋值为两个目录项的大小。i->i_no = 0为inode 编号赋值为0，表示此inode 自己是inode 数组中第0 个inode。i->i_sectors[0] = sb.data_start_lba使此inode 的第0 个数据块指向sb.data_start_lba，也就是我们把根目录安排在最开始的空闲块中。

memset清0 工作使i_sectors数组的其他元素也都被初始化为0。最后一项工作是在根目录中写目录项”.”和”..”。任何目录都有这两个目录项，”.”表示当前目录，”..”表示上一级目录。将buf转换为目录项struct dir_entry型指针，此时p_de指向buf，接下来先对第1 个目录项.初始化。通过memcpy函数把.写入目录项的filename成员，接下来分别为目录项的i_no赋值为0，使其指向根目录自己，为目录项的f_type赋值为FT_DIRECTORY，使其类型为目录。p_de++执行过后，p_de指向下一目录项..。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/* 在磁盘上搜索文件系统,若没有则格式化分区创建文件系统 */
void filesys_init() {
   uint8_t channel_no = 0, dev_no, part_idx = 0;

   /* sb_buf用来存储从硬盘上读入的超级块 */
   struct super_block* sb_buf = (struct super_block*)sys_malloc(SECTOR_SIZE);

   if (sb_buf == NULL) {
      PANIC("alloc memory failed!");
   }
   printk("searching filesystem......\n");
   while (channel_no < channel_cnt) {
      dev_no = 0;
      while(dev_no < 2) {
	 if (dev_no == 0) {   // 跨过裸盘hd60M.img
	    dev_no++;
	    continue;
	 }
	 struct disk* hd = &channels[channel_no].devices[dev_no];
	 struct partition* part = hd->prim_parts;
	 while(part_idx < 12) {   // 4个主分区+8个逻辑
	    if (part_idx == 4) {  // 开始处理逻辑分区
	       part = hd->logic_parts;
	    }
	 
	 /* channels数组是全局变量,默认值为0,disk属于其嵌套结构,
	  * partition又为disk的嵌套结构,因此partition中的成员默认也为0.
	  * 若partition未初始化,则partition中的成员仍为0. 
	  * 下面处理存在的分区. */
	    if (part->sec_cnt != 0) {  // 如果分区存在
	       memset(sb_buf, 0, SECTOR_SIZE);

	       /* 读出分区的超级块,根据魔数是否正确来判断是否存在文件系统 */
	       ide_read(hd, part->start_lba + 1, sb_buf, 1);   

	       /* 只支持自己的文件系统.若磁盘上已经有文件系统就不再格式化了 */
	       if (sb_buf->magic == 0x19590318) {
		  printk("%s has filesystem\n", part->name);
	       } else {			  // 其它文件系统不支持,一律按无文件系统处理
		  printk("formatting %s`s partition %s......\n", hd->name, part->name);
		  partition_format(part);
	       }
	    }
	    part_idx++;
	    part++;	// 下一分区
	 }
	 dev_no++;	// 下一磁盘
      }
      channel_no++;	// 下一通道
   }
   sys_free(sb_buf);
}

这里只支持partition_format创建的文件系统，其魔数等于0x19590318，如果未发现魔数为0x19590318的文件系统就调用partition_format去创建。

文件描述符简介

Linux 提供了称为文件结构的数据结构，专门用于记录与文件操作相关的信息，每次打开一个文件就会产生一个文件结构，多次打开该文件就为该文件生成多个文件结构，各自文件操作的偏移量分别记录在不同的文件结构中，从而实现了即使同一个文件被同时多次打开，各自操作的偏移量也互不影响的灵活性。Linux 把所有的“文件结构”组织到一起形成数组统一管理，该数组称为文件表。

在Linux 中每个进程都有单独的、完全相同的一套文件描述符，为避免文件表占用过大的内存空间，进程可打开的最大文件数有限。文件描述符数组中
的前3 个都是标准的文件描述符，如文件描述符0 表示标准输入，1 表示标准输出，2 表示标准错误。

文件结构中包含进程执行文件操作的偏移量，它属于与各个任务单独绑定的资源。当用户进程打开文件时，文件系统给用户进程返回的是该进程PCB 中文件描述符数组下标值，也就是文件描述符。

这涉及到以下三个数据结构，它们都是位于内存中的。

  1. PCB 中的文件描述符数组。
  2. 存储所有文件结构的文件表。
  3. inode 队列，也就是inode 缓存。

某进程把文件描述符作为参数提交给文件系统时，文件系统用此文件描述符在该进程的PCB 中的文件描述符数组中索引对应的元素，从该元素中获取对应的文件结构的下标，用该下标在文件表中索引相应的文件结构，从该文件结构中获取文件的inode，最终找到了文件的数据块。

其实open 操作的本质就是创建相应文件描述符的过程，创建文件描述符的过程就是逐层在这三个数据结构中找空位，在该空位填充好数据后返回该位置的地址，比如：

  1. 在全局的inode 队列中新建一inode（这肯定是在空位置处新建），然后返回该inode 地址。
  2. 在全局的文件表中找一空位，在该位置填充文件结构，使其fd_inode 指向上一步中返回的inode地址，然后返回本文件结构在文件表中的下标值。
  3. 在PCB 中的文件描述符数组中找一空位，使该位置的值指向上一步中返回的文件结构下标，并返回本文件描述符在文件描述符数组中的下标值。

我们不仅要添加单独的文件处理模块，还需要改进pcb。

1
2
3
4
5
6
7
8
9
#define MAX_FILES_OPEN_PER_PROC 8

/* 进程或线程的pcb，程序控制块 */
struct task_struct {
   uint32_t elapsed_ticks;
   int32_t fd_table[MAX_FILES_OPEN_PER_PROC]; // 文件描述符数组
   /* general_tag 的作用是用于线程在一般的队列中的结点 */
   struct list_elem general_tag;
};

fd_table 是任务的文件描述符数组，其类型是int32_t，即每个成员都是int32_t整数，其长度是宏MAX_FILES_OPEN_PER_PROC，此宏的值是8，也就是每个任务可以打开的文件数是8。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 初始化线程基本信息 */
void init_thread(struct task_struct* pthread, char* name, int prio) {

   /* 预留标准输入输出*/
   pthread->fd_table[0] = 0;
   pthread->fd_table[1] = 1;
   pthread->fd_table[2] = 2;
   /* 其余的全置为-1 */
   uint8_t fd_idx = 3;
   while (fd_idx < MAX_FILES_OPEN_PER_PROC) {
      pthread->fd_table[fd_idx] = -1;
      fd_idx++;
   }

   pthread->stack_magic = 0x19870916; // 自定义的魔数

三个标准的文件描述符，0 是标准输入，1 是标准输出，2 是标准错误。

文件操作相关的基础函数

inode 操作有关的函数

与inode 实现相关的代码在fs/inode.c中，这是新创建的文件：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
/* 用来存储inode位置 */
struct inode_position {
   bool	 two_sec;	// inode是否跨扇区
   uint32_t sec_lba;	// inode所在的扇区号
   uint32_t off_size;	// inode在扇区内的字节偏移量
};

/* 获取inode所在的扇区和扇区内的偏移量 */
static void inode_locate(struct partition* part, uint32_t inode_no, struct inode_position* inode_pos) {
   /* inode_table在硬盘上是连续的 */
   ASSERT(inode_no < 4096);
   uint32_t inode_table_lba = part->sb->inode_table_lba;

   uint32_t inode_size = sizeof(struct inode);
   uint32_t off_size = inode_no * inode_size;	    // 第inode_no号I结点相对于inode_table_lba的字节偏移量
   uint32_t off_sec  = off_size / 512;		    // 第inode_no号I结点相对于inode_table_lba的扇区偏移量
   uint32_t off_size_in_sec = off_size % 512;	    // 待查找的inode所在扇区中的起始地址

   /* 判断此i结点是否跨越2个扇区 */
   uint32_t left_in_sec = 512 - off_size_in_sec;
   if (left_in_sec < inode_size ) {	  // 若扇区内剩下的空间不足以容纳一个inode,必然是I结点跨越了2个扇区
      inode_pos->two_sec = true;
   } else {				  // 否则,所查找的inode未跨扇区
      inode_pos->two_sec = false;
   }
   inode_pos->sec_lba = inode_table_lba + off_sec;
   inode_pos->off_size = off_size_in_sec;
}

/* 将inode写入到分区part */
void inode_sync(struct partition* part, struct inode* inode, void* io_buf) {	 // io_buf是用于硬盘io的缓冲区
   uint8_t inode_no = inode->i_no;
   struct inode_position inode_pos;
   inode_locate(part, inode_no, &inode_pos);	       // inode位置信息会存入inode_pos
   ASSERT(inode_pos.sec_lba <= (part->start_lba + part->sec_cnt));
   
   /* 硬盘中的inode中的成员inode_tag和i_open_cnts是不需要的,
    * 它们只在内存中记录链表位置和被多少进程共享 */
   struct inode pure_inode;
   memcpy(&pure_inode, inode, sizeof(struct inode));

   /* 以下inode的三个成员只存在于内存中,现在将inode同步到硬盘,清掉这三项即可 */
   pure_inode.i_open_cnts = 0;
   pure_inode.write_deny = false;	 // 置为false,以保证在硬盘中读出时为可写
   pure_inode.inode_tag.prev = pure_inode.inode_tag.next = NULL;

   char* inode_buf = (char*)io_buf;
   if (inode_pos.two_sec) {	    // 若是跨了两个扇区,就要读出两个扇区再写入两个扇区
   /* 读写硬盘是以扇区为单位,若写入的数据小于一扇区,要将原硬盘上的内容先读出来再和新数据拼成一扇区后再写入  */
      ide_read(part->my_disk, inode_pos.sec_lba, inode_buf, 2);	// inode在format中写入硬盘时是连续写入的,所以读入2块扇区

   /* 开始将待写入的inode拼入到这2个扇区中的相应位置 */
      memcpy((inode_buf + inode_pos.off_size), &pure_inode, sizeof(struct inode));
   
   /* 将拼接好的数据再写入磁盘 */
      ide_write(part->my_disk, inode_pos.sec_lba, inode_buf, 2);
   } else {			    // 若只是一个扇区
      ide_read(part->my_disk, inode_pos.sec_lba, inode_buf, 1);
      memcpy((inode_buf + inode_pos.off_size), &pure_inode, sizeof(struct inode));
      ide_write(part->my_disk, inode_pos.sec_lba, inode_buf, 1);
   }
}

程序开头定义的struct inode_position用于记录inode 所在的扇区地址及在扇区内的偏移量，two_sec用于标识inode 是否跨扇区。sec_lba是inode 的扇区地址，off_size是inode在扇区内的偏移字节。

函数inode_locate接受3 个参数，分区part、inode编号inode_no及inode_pos，inode_pos类型是上面提到的struct inode_position，用于记录inode 在硬盘上的位置，函数功能是定位inode 所在的扇区和扇区内的偏移量，将其写入inode_pos 中。

获取编号为inode_no 对应的inode 的位置，off_sec是该inode偏移扇区地址，off_size_in_sec是该inode 在扇区中的偏移字节，off_sec是相
对于inode_table_lba的扇区偏移量。off_sec是相对于inode_table的扇区偏移量，因此inode的绝对扇区地址inode_pos->sec_lba等于inode_table_lba加上off_sec，而inode 扇区内的字节偏移量inode_pos->off_size仍然等于off_size_in_sec。

下面是函数inode_sync，它接受3 个参数，分区part、待同步的inode 指针、操作缓冲区io_buf，函数功能是将inode 写入到磁盘分区part。io_buf 是主调函数提供的缓冲区。先通过函数inode_locate定位该inode 的位置，位置信息在inode_pos中保存。inode 中的三个成员i_open_cnts、write_deny和inode_tag，它们用于统计inode 操作状态，只在内存中有意义。io_buf转换为inode_buf，此缓冲区用于拼接同步的inode 数据；判断inode 是否跨扇区，如果inode_pos.two_sec为true，说明该inode 横跨两个扇区，因此读入2 个扇区到inode_buf；memcpy函数将pure_inode 拷贝到inode_buf 中的相应位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

/* 根据i结点号返回相应的i结点 */
struct inode* inode_open(struct partition* part, uint32_t inode_no) {
   /* 先在已打开inode链表中找inode,此链表是为提速创建的缓冲区 */
   struct list_elem* elem = part->open_inodes.head.next;
   struct inode* inode_found;
   while (elem != &part->open_inodes.tail) {
      inode_found = elem2entry(struct inode, inode_tag, elem);
      if (inode_found->i_no == inode_no) {
	 inode_found->i_open_cnts++;
	 return inode_found;
      }
      elem = elem->next;
   }

   /*由于open_inodes链表中找不到,下面从硬盘上读入此inode并加入到此链表 */
   struct inode_position inode_pos;

   /* inode位置信息会存入inode_pos, 包括inode所在扇区地址和扇区内的字节偏移量 */
   inode_locate(part, inode_no, &inode_pos);

/* 为使通过sys_malloc创建的新inode被所有任务共享,
 * 需要将inode置于内核空间,故需要临时
 * 将cur_pbc->pgdir置为NULL */
   struct task_struct* cur = running_thread();
   uint32_t* cur_pagedir_bak = cur->pgdir;
   cur->pgdir = NULL;
   /* 以上三行代码完成后下面分配的内存将位于内核区 */
   inode_found = (struct inode*)sys_malloc(sizeof(struct inode));
   /* 恢复pgdir */
   cur->pgdir = cur_pagedir_bak;

   char* inode_buf;
   if (inode_pos.two_sec) {	// 考虑跨扇区的情况
      inode_buf = (char*)sys_malloc(1024);

   /* i结点表是被partition_format函数连续写入扇区的,
    * 所以下面可以连续读出来 */
      ide_read(part->my_disk, inode_pos.sec_lba, inode_buf, 2);
   } else {	// 否则,所查找的inode未跨扇区,一个扇区大小的缓冲区足够
      inode_buf = (char*)sys_malloc(512);
      ide_read(part->my_disk, inode_pos.sec_lba, inode_buf, 1);
   }
   memcpy(inode_found, inode_buf + inode_pos.off_size, sizeof(struct inode));

   /* 因为一会很可能要用到此inode,故将其插入到队首便于提前检索到 */
   list_push(&part->open_inodes, &inode_found->inode_tag);
   inode_found->i_open_cnts = 1;

   sys_free(inode_buf);
   return inode_found;
}

/* 关闭inode或减少inode的打开数 */
void inode_close(struct inode* inode) {
   /* 若没有进程再打开此文件,将此inode去掉并释放空间 */
   enum intr_status old_status = intr_disable();
   if (--inode->i_open_cnts == 0) {
      list_remove(&inode->inode_tag);	  // 将I结点从part->open_inodes中去掉
   /* inode_open时为实现inode被所有进程共享,
    * 已经在sys_malloc为inode分配了内核空间,
    * 释放inode时也要确保释放的是内核内存池 */
      struct task_struct* cur = running_thread();
      uint32_t* cur_pagedir_bak = cur->pgdir;
      cur->pgdir = NULL;
      sys_free(inode);
      cur->pgdir = cur_pagedir_bak;
   }
   intr_set_status(old_status);
}

/* 初始化new_inode */
void inode_init(uint32_t inode_no, struct inode* new_inode) {
   new_inode->i_no = inode_no;
   new_inode->i_size = 0;
   new_inode->i_open_cnts = 0;
   new_inode->write_deny = false;

   /* 初始化块索引数组i_sector */
   uint8_t sec_idx = 0;
   while (sec_idx < 13) {
   /* i_sectors[12]为一级间接块地址 */
      new_inode->i_sectors[sec_idx] = 0;
      sec_idx++;
   }
}

函数inode_open 接受两个参数，分区part及inode编号inode_no，函数功能是根据inode_no 返回相应的i 结点指针。在内存中为各分区创建了inode 队列，即part->open_inodes，这个队列为已打开的inode的缓存。如果找到后就执行return inode_found返回找到的inode 指针。如果inode 队列中没有该inode，先创建inode_pos，调用inode_locate定位该inode，位置存储到inode_pos 中。

我们从硬盘上获取到的inode，其所占的内存是我们用sys_malloc从堆中分配的。为了使inode 置于内核空间被所有任务共享，需要临时将当前任务pcb->pgdir置为NULL，待为inode 完成内存分配后再将任务的pgdir 恢复。先将当前任务的页表地址备份到变量cur_pagedir_bak中，将pgdir 置为NULL 后，接着调用sys_malloc分配1个inode 大小的内存，指针存入变量inode_found，它是我们为磁盘上的inode 所分配的内存变量。然后将pgdir恢复为cur_pagedir_bak。根据程序局部性原理，通常情况下此inode 会被再次使用到，因此通过list_push将它插入到inode 队列的最前面，以便下次更快被找到。将它的i_open_cnts置为1，表示目前此inode 仅被打开1 次。然后释放缓冲区inode_buf，返回inode_found 指针，至此inode_open 函数结束。

接下来是函数inode_close，它接受1 个参数，inode 指针inode，功能是关闭inode。关闭inode 的思路是将inode 的i_open_cnts 减1，若其值为0，则说明此inode 未被打开，此时可以将其从inode 队列中去掉并回收空间了。又将页表置为NULL，使sys_free正确释放内核中的inode。sys_free之后，再把页表换回来。

最后一个函数是inode_init，它接受2 个参数，inode编号inode_no及待初始化的inode指针new_inode，功能是初始化new_inode。初始化inode中的i_no为参数inode_no，i_size和i_open_cnt为0，write_deny为false。接下来是初始化i_sectors数组，该数组大小是13 个元素，前12 个是直接块地址，第13 个一级间接块索引表地址，在此统统置为0。

文件操作相关的函数我们定义在fs/file.c和fs/file.h中，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/* 文件结构 */
struct file {
   uint32_t fd_pos;      // 记录当前文件操作的偏移地址,以0为起始,最大为文件大小-1
   uint32_t fd_flag;
   struct inode* fd_inode;
};

/* 标准输入输出描述符 */
enum std_fd {
   stdin_no,   // 0 标准输入
   stdout_no,  // 1 标准输出
   stderr_no   // 2 标准错误
};

/* 位图类型 */
enum bitmap_type {
   INODE_BITMAP,     // inode位图
   BLOCK_BITMAP	     // 块位图
};

#define MAX_FILE_OPEN 32    // 系统可打开的最大文件数

struct file就是所说的文件结构，其中的fd_pos用于记录当前文件操作的偏移地址，该值最小是0，最大为文件大小减1。fd_flag是文件操作标识，如O_RDONLY，fd_inode是inode 指针，用来指向inode 队列part-> open_inodes中的inode。enum std_fd是标准文件描述符，enum bitmap_type是位图类型，包括INODE_BITMAP和BLOCK_BITMAP，宏MAX_FILE_OPEN的值是32，这是系统可打开的最大文件数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
/* 文件表 */
struct file file_table[MAX_FILE_OPEN];

/* 从文件表file_table中获取一个空闲位,成功返回下标,失败返回-1 */
int32_t get_free_slot_in_global(void) {
   uint32_t fd_idx = 3;
   while (fd_idx < MAX_FILE_OPEN) {
      if (file_table[fd_idx].fd_inode == NULL) {
	 break;
      }
      fd_idx++;
   }
   if (fd_idx == MAX_FILE_OPEN) {
      printk("exceed max open files\n");
      return -1;
   }
   return fd_idx;
}

/* 将全局描述符下标安装到进程或线程自己的文件描述符数组fd_table中,
 * 成功返回下标,失败返回-1 */
int32_t pcb_fd_install(int32_t globa_fd_idx) {
   struct task_struct* cur = running_thread();
   uint8_t local_fd_idx = 3; // 跨过stdin,stdout,stderr
   while (local_fd_idx < MAX_FILES_OPEN_PER_PROC) {
      if (cur->fd_table[local_fd_idx] == -1) {	// -1表示free_slot,可用
	 cur->fd_table[local_fd_idx] = globa_fd_idx;
	 break;
      }
      local_fd_idx++;
   }
   if (local_fd_idx == MAX_FILES_OPEN_PER_PROC) {
      printk("exceed max open files_per_proc\n");
      return -1;
   }
   return local_fd_idx;
}

/* 分配一个i结点,返回i结点号 */
int32_t inode_bitmap_alloc(struct partition* part) {
   int32_t bit_idx = bitmap_scan(&part->inode_bitmap, 1);
   if (bit_idx == -1) {
      return -1;
   }
   bitmap_set(&part->inode_bitmap, bit_idx, 1);
   return bit_idx;
}
   
/* 分配1个扇区,返回其扇区地址 */
int32_t block_bitmap_alloc(struct partition* part) {
   int32_t bit_idx = bitmap_scan(&part->block_bitmap, 1);
   if (bit_idx == -1) {
      return -1;
   }
   bitmap_set(&part->block_bitmap, bit_idx, 1);
   /* 和inode_bitmap_malloc不同,此处返回的不是位图索引,而是具体可用的扇区地址 */
   return (part->sb->data_start_lba + bit_idx);
} 

/* 将内存中bitmap第bit_idx位所在的512字节同步到硬盘 */
void bitmap_sync(struct partition* part, uint32_t bit_idx, uint8_t btmp_type) {
   uint32_t off_sec = bit_idx / 4096;  // 本i结点索引相对于位图的扇区偏移量
   uint32_t off_size = off_sec * BLOCK_SIZE;  // 本i结点索引相对于位图的字节偏移量
   uint32_t sec_lba;
   uint8_t* bitmap_off;

/* 需要被同步到硬盘的位图只有inode_bitmap和block_bitmap */
   switch (btmp_type) {
      case INODE_BITMAP:
	 sec_lba = part->sb->inode_bitmap_lba + off_sec;
	 bitmap_off = part->inode_bitmap.bits + off_size;
	 break;

      case BLOCK_BITMAP: 
	 sec_lba = part->sb->block_bitmap_lba + off_sec;
	 bitmap_off = part->block_bitmap.bits + off_size;
	 break;
   }
   ide_write(part->my_disk, sec_lba, bitmap_off, 1);
}

代码中的file_table是文件结构数组，长度是MAX_FILE_OPEN，也就是最多可同时打开MAX_FILE_OPEN次文件，函数get_free_slot_in_global功能是从文件表file_table中获取一个空闲位，成功则返回空闲位下标，失败则返回−1。实现原理是遍历file_table，找出fd_inode为null 的数组元素，该元素表示为空，将其下标返回即可，file_table中的前3 个成员预留给标准输入、标准输出及标准错误。

函数pcb_fd_install接受1 个参数，全局描述符下标globa_fd_idx。函数功能是将globa_fd_idx安装到进程或线程自己的文件描述符数组fd_table 中，成功则返回fd_table 中空位的下标，失败则返回−1。函数inode_bitmap_alloc，功能是分配一个i 结点，返回i 结点号。函数block_bitmap_alloc功能是分配1 个扇区，返回其扇区地址。函数bitmap_sync功能是将内存中bitmap第bit_idx位所在的512 字节同步到硬盘。

有关目录操作的函数我们定义在fs/dir.c：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

struct dir root_dir;             // 根目录

/* 打开根目录 */
void open_root_dir(struct partition* part) {
   root_dir.inode = inode_open(part, part->sb->root_inode_no);
   root_dir.dir_pos = 0;
}

/* 在分区part上打开i结点为inode_no的目录并返回目录指针 */
struct dir* dir_open(struct partition* part, uint32_t inode_no) {
   struct dir* pdir = (struct dir*)sys_malloc(sizeof(struct dir));
   pdir->inode = inode_open(part, inode_no);
   pdir->dir_pos = 0;
   return pdir;
}

/* 在part分区内的pdir目录内寻找名为name的文件或目录,
 * 找到后返回true并将其目录项存入dir_e,否则返回false */
bool search_dir_entry(struct partition* part, struct dir* pdir, \
		     const char* name, struct dir_entry* dir_e) {
   uint32_t block_cnt = 140;	 // 12个直接块+128个一级间接块=140块

   /* 12个直接块大小+128个间接块,共560字节 */
   uint32_t* all_blocks = (uint32_t*)sys_malloc(48 + 512);
   if (all_blocks == NULL) {
      printk("search_dir_entry: sys_malloc for all_blocks failed");
      return false;
   }

   uint32_t block_idx = 0;
   while (block_idx < 12) {
      all_blocks[block_idx] = pdir->inode->i_sectors[block_idx];
      block_idx++;
   }
   block_idx = 0;

   if (pdir->inode->i_sectors[12] != 0) {	// 若含有一级间接块表
      ide_read(part->my_disk, pdir->inode->i_sectors[12], all_blocks + 12, 1);
   }
/* 至此,all_blocks存储的是该文件或目录的所有扇区地址 */

   /* 写目录项的时候已保证目录项不跨扇区,
    * 这样读目录项时容易处理, 只申请容纳1个扇区的内存 */
   uint8_t* buf = (uint8_t*)sys_malloc(SECTOR_SIZE);
   struct dir_entry* p_de = (struct dir_entry*)buf;	    // p_de为指向目录项的指针,值为buf起始地址
   uint32_t dir_entry_size = part->sb->dir_entry_size;
   uint32_t dir_entry_cnt = SECTOR_SIZE / dir_entry_size;   // 1扇区内可容纳的目录项个数

   /* 开始在所有块中查找目录项 */
   while (block_idx < block_cnt) {		  
   /* 块地址为0时表示该块中无数据,继续在其它块中找 */
      if (all_blocks[block_idx] == 0) {
	 block_idx++;
	 continue;
      }
      ide_read(part->my_disk, all_blocks[block_idx], buf, 1);

      uint32_t dir_entry_idx = 0;
      /* 遍历扇区中所有目录项 */
      while (dir_entry_idx < dir_entry_cnt) {
	 /* 若找到了,就直接复制整个目录项 */
	 if (!strcmp(p_de->filename, name)) {
	    memcpy(dir_e, p_de, dir_entry_size);
	    sys_free(buf);
	    sys_free(all_blocks);
	    return true;
	 }
	 dir_entry_idx++;
	 p_de++;
      }
      block_idx++;
      p_de = (struct dir_entry*)buf;  // 此时p_de已经指向扇区内最后一个完整目录项了,需要恢复p_de指向为buf
      memset(buf, 0, SECTOR_SIZE);	  // 将buf清0,下次再用
   }
   sys_free(buf);
   sys_free(all_blocks);
   return false;
}

程序开头定义了root_dir，它是分区的根目录。函数open_root_dir接受一个参数，分区part，功能是打开分区part 的根目录。函数dir_open，它接受两个参数，分区part和inode 编号inode_no，功能是在分区part 上打开i 结点为inode_no 的目录并返回目录指针。

函数search_dir_entry接受4个参数，分区part、目录指针pdir、文件名name、目录项指针dir_e，函数功能是在part 分区内的pdir 目录内寻找名为name 的文件或目录，找到后返回true 并将其目录项存入dir_e，否则返回false。函数开头定义了变量block_cnt，表示inode 总的块数，其值为140，即12 个直接块+128 个一级间接块。为这140 个扇区地址申请内存，返回地址赋值给all_blocks。往目录中写目录项的时候，写入的都是完整的目录项，避免了目录项跨扇区的情况，因此在实际搜索目录项的时候每次只从硬盘读取一扇区就好了，所以我们为缓冲区buf 申请的内存大小是SECTOR_SIZE，即1 扇区。将缓冲区转换为目录项struct dir_entry类型，赋值给p_de，若判断all_blocks[block_idx]不为0，这表示已分配扇区地址了，于是从该扇区地址all_blocks[block_idx]读入1 扇区数据到buf，用目录项指针p_de遍历该扇区内的所有目录项，比较目录项的p_de->filename是否和待查找的文件名name 相等，若相等则表示找到该文件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/* 关闭目录 */
void dir_close(struct dir* dir) {
/*************      根目录不能关闭     ***************
 *1 根目录自打开后就不应该关闭,否则还需要再次open_root_dir();
 *2 root_dir所在的内存是低端1M之内,并非在堆中,free会出问题 */
   if (dir == &root_dir) {
   /* 不做任何处理直接返回*/
      return;
   }
   inode_close(dir->inode);
   sys_free(dir);
}

/* 在内存中初始化目录项p_de */
void create_dir_entry(char* filename, uint32_t inode_no, uint8_t file_type, struct dir_entry* p_de) {
   ASSERT(strlen(filename) <=  MAX_FILE_NAME_LEN);

   /* 初始化目录项 */
   memcpy(p_de->filename, filename, strlen(filename));
   p_de->i_no = inode_no;
   p_de->f_type = file_type;
}

函数dir_close接受1 个参数，目录指针dir，功能是关闭目录dir。关闭目录的本质是关闭目录的inode并释放目录占用的内存，根目录不能被真正地关闭，不做任何处理直接返回。原因是首先根目录始终应该是打开的，它是所有目录的父目录，查找文件时必须要从根目录开始找。其次是根目录root_dir 占用的是静态内存，它位于低端1MB 之内，并非是在堆中申请的，不能将其释放。函数create_dir_entry功能是在内存中创建目录项p_de。函数的实现就是在初始化目录项p_de：将文件名拷贝到目录项p_de->filename中，用inode_no为p_de->i_no赋值，用file_type 为p_de->f_type 赋值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
/* 将目录项p_de写入父目录parent_dir中,io_buf由主调函数提供 */
bool sync_dir_entry(struct dir* parent_dir, struct dir_entry* p_de, void* io_buf) {
   struct inode* dir_inode = parent_dir->inode;
   uint32_t dir_size = dir_inode->i_size;
   uint32_t dir_entry_size = cur_part->sb->dir_entry_size;

   ASSERT(dir_size % dir_entry_size == 0);	 // dir_size应该是dir_entry_size的整数倍

   uint32_t dir_entrys_per_sec = (512 / dir_entry_size);       // 每扇区最大的目录项数目
   int32_t block_lba = -1;

   /* 将该目录的所有扇区地址(12个直接块+ 128个间接块)存入all_blocks */
   uint8_t block_idx = 0;
   uint32_t all_blocks[140] = {0};	  // all_blocks保存目录所有的块

   /* 将12个直接块存入all_blocks */
   while (block_idx < 12) {
      all_blocks[block_idx] = dir_inode->i_sectors[block_idx];
      block_idx++;
   }

   struct dir_entry* dir_e = (struct dir_entry*)io_buf;	       // dir_e用来在io_buf中遍历目录项
   int32_t block_bitmap_idx = -1;

   /* 开始遍历所有块以寻找目录项空位,若已有扇区中没有空闲位,
    * 在不超过文件大小的情况下申请新扇区来存储新目录项 */
   block_idx = 0;
   while (block_idx < 140) {  // 文件(包括目录)最大支持12个直接块+128个间接块＝140个块
      block_bitmap_idx = -1;
      if (all_blocks[block_idx] == 0) {   // 在三种情况下分配块
	 block_lba = block_bitmap_alloc(cur_part);
	 if (block_lba == -1) {
	    printk("alloc block bitmap for sync_dir_entry failed\n");
	    return false;
	 }

      /* 每分配一个块就同步一次block_bitmap */
	 block_bitmap_idx = block_lba - cur_part->sb->data_start_lba;
	 ASSERT(block_bitmap_idx != -1);
	 bitmap_sync(cur_part, block_bitmap_idx, BLOCK_BITMAP);

	 block_bitmap_idx = -1;
	 if (block_idx < 12) {	    // 若是直接块
	    dir_inode->i_sectors[block_idx] = all_blocks[block_idx] = block_lba;
	 } else if (block_idx == 12) {	  // 若是尚未分配一级间接块表(block_idx等于12表示第0个间接块地址为0)
	    dir_inode->i_sectors[12] = block_lba;       // 将上面分配的块做为一级间接块表地址
	    block_lba = -1;
	    block_lba = block_bitmap_alloc(cur_part);	       // 再分配一个块做为第0个间接块
	    if (block_lba == -1) {
	       block_bitmap_idx = dir_inode->i_sectors[12] - cur_part->sb->data_start_lba;
	       bitmap_set(&cur_part->block_bitmap, block_bitmap_idx, 0);
	       dir_inode->i_sectors[12] = 0;
	       printk("alloc block bitmap for sync_dir_entry failed\n");
	       return false;
	    }

	 /* 每分配一个块就同步一次block_bitmap */
	    block_bitmap_idx = block_lba - cur_part->sb->data_start_lba;
	    ASSERT(block_bitmap_idx != -1);
	    bitmap_sync(cur_part, block_bitmap_idx, BLOCK_BITMAP);

	    all_blocks[12] = block_lba;
	    /* 把新分配的第0个间接块地址写入一级间接块表 */
	    ide_write(cur_part->my_disk, dir_inode->i_sectors[12], all_blocks + 12, 1);
	 } else {	   // 若是间接块未分配
	    all_blocks[block_idx] = block_lba;
	    /* 把新分配的第(block_idx-12)个间接块地址写入一级间接块表 */
	    ide_write(cur_part->my_disk, dir_inode->i_sectors[12], all_blocks + 12, 1);
	 }

	 /* 再将新目录项p_de写入新分配的间接块 */
	 memset(io_buf, 0, 512);
	 memcpy(io_buf, p_de, dir_entry_size);
	 ide_write(cur_part->my_disk, all_blocks[block_idx], io_buf, 1);
	 dir_inode->i_size += dir_entry_size;
	 return true;
      }

   /* 若第block_idx块已存在,将其读进内存,然后在该块中查找空目录项 */
      ide_read(cur_part->my_disk, all_blocks[block_idx], io_buf, 1); 
      /* 在扇区内查找空目录项 */
      uint8_t dir_entry_idx = 0;
      while (dir_entry_idx < dir_entrys_per_sec) {
	 if ((dir_e + dir_entry_idx)->f_type == FT_UNKNOWN) {	// FT_UNKNOWN为0,无论是初始化或是删除文件后,都会将f_type置为FT_UNKNOWN.
	    memcpy(dir_e + dir_entry_idx, p_de, dir_entry_size);    
	    ide_write(cur_part->my_disk, all_blocks[block_idx], io_buf, 1);

	    dir_inode->i_size += dir_entry_size;
	    return true;
	 }
	 dir_entry_idx++;
      }
      block_idx++;
   }   
   printk("directory is full!\n");
   return false;
}

sync_dir_entry接受3 个参数，父目录parent_dir、目录项p_de、缓冲区io_buf，功能是将目录项p_de写入父目录parent_dir 中，其中io_buf 由主调函数提供。当inode 是目录时，其i_size是目录中目录项的大小之和，父目录的大小是dir_inode->i_size，获取了超级块的大小，存入变量dir_entry_size。计算1 扇区可容纳的完整的目录项数，结果写入变量dir_entrys_per_sec，使目录项指针dir_e指向缓冲区io_buf。

由于删除文件时会造成目录中存在空洞，所以在写入文件时，要逐个目录项查找空位，所以从头在这12 个扇区中找空闲目录项位置。之后先判断扇区是否分配，若未分配，通过函数block_bitmap_alloc为其分配一扇区，扇区地址写入变量block_lba。由于block_bitmap_alloc仅是操作内存中的块位图，为保持数据同步，现在要将块位图同步到硬盘，于是计算block_lba相对于data_start_lba的偏移，调用bitmap_sync将块位图同步到硬盘。判断当前为空的块是直接块，还是间接块，若块索引小于12，则属于直接块，故将分配的扇区地址写入i_sectors[block_idx]和all_blocks[block_idx]。若正好是第12 个块，即一级间接块索引表地址为空，该创建间接块，将刚才分配的扇区地址block_lba作为一级间接块索引表的地址写入i_sectors[12]，重新再分配一扇区，此时block_lba更新为新分配的扇区地址，该扇区地址将作为第0 个间接块，将新分配的
扇区地址更新到all_blocks[12]，这是第0 个间接块的地址，随后调用ide_write将间接块地址写入一级间接块索引表所在的扇区。处理块已存在，不需要分配块的情况也就是要在该扇区中寻找空闲的目录项，先将该扇区读到io_buf中，接着通过while 循环遍历dir_entrys_per_sec个目录项，判断若目录项的f_type为FT_UNKNOWN，这表示该目录项未分配，将目录项p_de写入io_buf，接着调用ide_write将目录项同步到硬盘，最后使目录的i_size加上1 个目录项大小dir_entry_size。

继续完善fs.c，在其中添加文件搜索的功能，函数search_file。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#define MAX_PATH_LEN 512	    // 路径最大长度

/* 文件类型 */
enum file_types {
   FT_UNKNOWN,	  // 不支持的文件类型
   FT_REGULAR,	  // 普通文件
   FT_DIRECTORY	  // 目录
};

/* 打开文件的选项 */
enum oflags {
   O_RDONLY,	  // 只读
   O_WRONLY,	  // 只写
   O_RDWR,	  // 读写
   O_CREAT = 4	  // 创建
};

/* 用来记录查找文件过程中已找到的上级路径,也就是查找文件过程中"走过的地方" */
struct path_search_record {
   char searched_path[MAX_PATH_LEN];	    // 查找过程中的父路径
   struct dir* parent_dir;		    // 文件或目录所在的直接父目录
   enum file_types file_type;		    // 找到的是普通文件还是目录,找不到将为未知类型(FT_UNKNOWN)
};

宏MAX_PATH_LEN 表示路径名最大的长度，这里其值为512。枚举结构enum oflags是打开文件时的选项，可选的值一般有O_RDONLY、O_WRONLY、O_RDWR、O_CREAT、O_EXCL等，它们是定义在文件/usr/include/asm-generic/fcntl.h中的宏，如图：

定义了struct path_search_record，它是路径搜索记录，此结构用来记录查找文件过程中已处理过的上级路径，也就是查找文件过程中”走过的地方”。用此结构的目的是想获取路径中“断链”的部分，其中成员searched_path就是查找过程中不存在的路径。成员parent_dir用于记录文件或目录所在的直接父目录，成员file_type是找到的文件类型，若找不到文件的话，该值为未知类型FT_UNKNOWN。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
/* 搜索文件pathname,若找到则返回其inode号,否则返回-1 */
static int search_file(const char* pathname, struct path_search_record* searched_record) {
   /* 如果待查找的是根目录,为避免下面无用的查找,直接返回已知根目录信息 */
   if (!strcmp(pathname, "/") || !strcmp(pathname, "/.") || !strcmp(pathname, "/..")) {
      searched_record->parent_dir = &root_dir;
      searched_record->file_type = FT_DIRECTORY;
      searched_record->searched_path[0] = 0;	   // 搜索路径置空
      return 0;
   }

   uint32_t path_len = strlen(pathname);
   /* 保证pathname至少是这样的路径/x且小于最大长度 */
   ASSERT(pathname[0] == '/' && path_len > 1 && path_len < MAX_PATH_LEN);
   char* sub_path = (char*)pathname;
   struct dir* parent_dir = &root_dir;	
   struct dir_entry dir_e;

   /* 记录路径解析出来的各级名称,如路径"/a/b/c",
    * 数组name每次的值分别是"a","b","c" */
   char name[MAX_FILE_NAME_LEN] = {0};

   searched_record->parent_dir = parent_dir;
   searched_record->file_type = FT_UNKNOWN;
   uint32_t parent_inode_no = 0;  // 父目录的inode号
   
   sub_path = path_parse(sub_path, name);
   while (name[0]) {	   // 若第一个字符就是结束符,结束循环
      /* 记录查找过的路径,但不能超过searched_path的长度512字节 */
      ASSERT(strlen(searched_record->searched_path) < 512);

      /* 记录已存在的父目录 */
      strcat(searched_record->searched_path, "/");
      strcat(searched_record->searched_path, name);

      /* 在所给的目录中查找文件 */
      if (search_dir_entry(cur_part, parent_dir, name, &dir_e)) {
	 memset(name, 0, MAX_FILE_NAME_LEN);
	 /* 若sub_path不等于NULL,也就是未结束时继续拆分路径 */
	 if (sub_path) {
	    sub_path = path_parse(sub_path, name);
	 }

	 if (FT_DIRECTORY == dir_e.f_type) {   // 如果被打开的是目录
	    parent_inode_no = parent_dir->inode->i_no;
	    dir_close(parent_dir);
	    parent_dir = dir_open(cur_part, dir_e.i_no); // 更新父目录
	    searched_record->parent_dir = parent_dir;
	    continue;
	 } else if (FT_REGULAR == dir_e.f_type) {	 // 若是普通文件
	    searched_record->file_type = FT_REGULAR;
	    return dir_e.i_no;
	 }
      } else {		   //若找不到,则返回-1
	 /* 找不到目录项时,要留着parent_dir不要关闭,
	  * 若是创建新文件的话需要在parent_dir中创建 */
	 return -1;
      }
   }

   /* 执行到此,必然是遍历了完整路径并且查找的文件或目录只有同名目录存在 */
   dir_close(searched_record->parent_dir);	      

   /* 保存被查找目录的直接父目录 */
   searched_record->parent_dir = dir_open(cur_part, parent_inode_no);	   
   searched_record->file_type = FT_DIRECTORY;
   return dir_e.i_no;
}

函数search_file接受2 个参数，被检索的文件pathname和路径搜索记录指针searched_record，功能是搜索文件pathname，若找到则返回其inode 号，否则返回−1。判断如果待查找的是根目录，为避免后续无用的查找工作，直接在searched_record中写入根目录信息后返回。用指针sub_path指向路径名pathname，声明目录指针parent_dir指向根目录，我们要从根目录开始往下查找文件，然后声明了目录项dir_e。声明了数组name[MAX_FILE_NAME_LEN]，它用来存储路径解析中的各层路径名。从根目录开始解析路径，因此初始化parent_inode_no为根目录的inode 编号0。

下面开始搜索文件。搜索文件的原理是路径解析，也就是把路径按照分隔符’/‘拆分，每解析出一层路径名就去目录中确认相应的目录项，与目录项中的filename 比对，找到后继续路径解析，直到路径解析完成或找不到某个中间目录就返回。执行sub_path = path_parse(sub_path, name)开始路径解析，path_parse 返回后，最上层的路径名会存储在name 中，返回值存入sub_path，此时的sub_path 已经剥去了最上层的路径。使用while 循环处理各层路径，其判断条件是name[0]，只要name[0]不等于字符串结束符’\0’路径解析尚未结束。每次解析过的路径都会追加到searched_record->searched_path中，searched_path用于记录已解析的路径，由于是先调用path_parse 解析路径，再调用search_dir_entry去验证路径是否存在，因此searched_record->searched_path中的最后一级目录未必存在，其前的所有路径都是存在的。调用search_dir_entry判断解析出来的上层路径name 是否在父目录parent_dir 中存在，再次执行sub_path = path_parse(sub_path, name)进行下一步的路径解析。

dir_e中已经是目录项的信息了，通过if(FT_DIRECTORY == dir_e.f_type)来判断解析出的最上层路径name 是否为目录，若是目录，就将父目录的inode 编号赋值给变量parent_inode_no，此变量用于备份父目录的inode 编号，它会在最后一级路径为目录的情况下用到。接下来把目录name打开，重新为parent_dir赋值，parent_dir = dir_open(cur_part, dir_e.i_no)。searched_record->parent_dir = parent_dir更新搜索记录中的父目录。

程序若能执行到dir_close，这说明两件事。

  1. 路径pathname 已经被完整地解析过了，各级都存在。
  2. pathname 的最后一层路径不是普通文件，而是目录。

结论是待查找的目标是目录，如“/a/b/c”，c 是目录，不是普通文件。此时searched_record-> parent_dir是路径pathname 中的最后一级目录c，并不是倒数第二级的父目录b，我们在任何时候都应该使searched_record->parent_dir是被查找目标的直接父目录。因此我们需要把searched_record->parent_dir重新更新为父目录b。在重新打开父目录之前，为避免内存溢出，先调用dir_close 关闭目录searched_record->parent_dir。接下来是重新打开父目录，打开父目录并为searched_record->parent_dir赋值。然后在下一行更新成员file_type为FT_DIRECTORY，最后返回目录的inode 编号。

创建文件

创建文件需要考虑：

  1. 创建文件的inode。这就涉及到向inode_bitmap申请位图来获得inode号，因此inode_bitmap会被更新，inode_table数组中的某项也会由新的inode 填充。
  2. inode->i_sectors是文件具体存储的扇区地址，这需要向block_bitmap申请可用位来获得可用的块，因此block_bitmap会被更新，分区的数据区data_start_lba以后的某个扇区会被分配。
  3. 新增加的文件必然存在于某个目录，所以该目录的inode->i_size会增加个目录项的大小。此新增加的文件对应的目录项需要写入该目录的inode->i_sectors[]中的某个扇区，原有扇区可能已满，所以有可能要申请新扇区来存储目录项。
  4. 若其中某步操作失败，需要回滚之前已成功的操作。
  5. inode_bitmap、block_bitmap、新文件的 inode 及文件所在目录的 inode，这些位于内存中已经被改变的数据要同步到硬盘。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
/* 创建文件,若成功则返回文件描述符,否则返回-1 */
int32_t file_create(struct dir* parent_dir, char* filename, uint8_t flag) {
   /* 后续操作的公共缓冲区 */
   void* io_buf = sys_malloc(1024);
   if (io_buf == NULL) {
      printk("in file_creat: sys_malloc for io_buf failed\n");
      return -1;
   }

   uint8_t rollback_step = 0;	       // 用于操作失败时回滚各资源状态

   /* 为新文件分配inode */
   int32_t inode_no = inode_bitmap_alloc(cur_part); 
   if (inode_no == -1) {
      printk("in file_creat: allocate inode failed\n");
      return -1;
   }

/* 此inode要从堆中申请内存,不可生成局部变量(函数退出时会释放)
 * 因为file_table数组中的文件描述符的inode指针要指向它.*/
   struct inode* new_file_inode = (struct inode*)sys_malloc(sizeof(struct inode)); 
   if (new_file_inode == NULL) {
      printk("file_create: sys_malloc for inode failded\n");
      rollback_step = 1;
      goto rollback;
   }
   inode_init(inode_no, new_file_inode);	    // 初始化i结点

   /* 返回的是file_table数组的下标 */
   int fd_idx = get_free_slot_in_global();
   if (fd_idx == -1) {
      printk("exceed max open files\n");
      rollback_step = 2;
      goto rollback;
   }

   file_table[fd_idx].fd_inode = new_file_inode;
   file_table[fd_idx].fd_pos = 0;
   file_table[fd_idx].fd_flag = flag;
   file_table[fd_idx].fd_inode->write_deny = false;

   struct dir_entry new_dir_entry;
   memset(&new_dir_entry, 0, sizeof(struct dir_entry));

   create_dir_entry(filename, inode_no, FT_REGULAR, &new_dir_entry);	// create_dir_entry只是内存操作不出意外,不会返回失败

/* 同步内存数据到硬盘 */
   /* a 在目录parent_dir下安装目录项new_dir_entry, 写入硬盘后返回true,否则false */
   if (!sync_dir_entry(parent_dir, &new_dir_entry, io_buf)) {
      printk("sync dir_entry to disk failed\n");
      rollback_step = 3;
      goto rollback;
   }

   memset(io_buf, 0, 1024);
   /* b 将父目录i结点的内容同步到硬盘 */
   inode_sync(cur_part, parent_dir->inode, io_buf);

   memset(io_buf, 0, 1024);
   /* c 将新创建文件的i结点内容同步到硬盘 */
   inode_sync(cur_part, new_file_inode, io_buf);

   /* d 将inode_bitmap位图同步到硬盘 */
   bitmap_sync(cur_part, inode_no, INODE_BITMAP);

   /* e 将创建的文件i结点添加到open_inodes链表 */
   list_push(&cur_part->open_inodes, &new_file_inode->inode_tag);
   new_file_inode->i_open_cnts = 1;

   sys_free(io_buf);
   return pcb_fd_install(fd_idx);

/*创建文件需要创建相关的多个资源,若某步失败则会执行到下面的回滚步骤 */
rollback:
   switch (rollback_step) {
      case 3:
	 /* 失败时,将file_table中的相应位清空 */
	 memset(&file_table[fd_idx], 0, sizeof(struct file)); 
      case 2:
	 sys_free(new_file_inode);
      case 1:
	 /* 如果新文件的i结点创建失败,之前位图中分配的inode_no也要恢复 */
	 bitmap_set(&cur_part->inode_bitmap, inode_no, 0);
	 break;
   }
   sys_free(io_buf);
   return -1;
}

函数file_create接受3 个参数，父目录partent_dir、文件名filename、创建标识flag，功能是在目录parent_dir中以模式flag 去创建普通文件filename，若成功则返回文件描述符，即pcb->fd_table 中的下标，否则返回−1。一般情况下硬盘操作都是一次读写一个扇区，考虑到有数据会跨扇区的情况，故申请2 个扇区大小的缓冲区，因此在函数开头就先申请了1024 字节的缓冲区io_buf。

创建文件包括多个修改资源的步骤，我们创建新文件的顺序是：创建文件i结点->文件描述符fd->目录项。这种“从后往前”创建步骤的好处是每一步创建失败时回滚操作少。用于回滚的代码在标签rollback处，从上到下依次是case 3、case2、case1，各case 之间没有break，它们是一种累加的回滚。调用inode_bitmap_alloc为新文件分配inode，为新文件的inode—new_file_inode申请内存，如果内存分配成功的话，执行inode_init初始化new_file_inode。调用get_free_slot_in_global从file_talbe中获取空闲文件结构的下标，写入变量fd_idx中。如果file_table中没有空闲位则返回−1。初始化文件表中的文件结构，为文件创建新目录项new_dir_entry，并将其清0，调用create_dir_entry用filename、inode_no 和FT_REGULAR填充new_dir_entry。函数sync_dir_entry(parent_dir, &new_dir_entry, io_buf)将其写入到父目录
parent_dir 中。sync_dir_entry会改变父目录inode 中的信息，因此调用函数inode_sync将父目录inode 同步到硬盘。

分别将新文件的inode 同步到硬盘，将inode_bitmap位图同步到硬盘，新文件的inode 添加到inode 列表，也就是cur_part->open_inodes，随后在其i_open_cnts 置为1。将io_buf释放，然后调用pcb_fd_install(fd_idx)，在数组pcb->fd_table中找个空闲位安装fd_idx，若成功则返回空闲位的下标，若失败则返回−1，用return 将其返回值返回。

系统交互

fork 的原理与实现

fork 函数原型是pid_t fork(void)，返回值是数字，该数字有可能是子进程的pid，有可能是0，也有可能是−1，fork 的任务就是克隆一个一模一样的进程出来，该进程拥有独立完整的程序体，是个独立的执行流。此fork 就是把某个进程的全部资源复制了一份，，然后让处理器的cs:eip寄存器指向新进程的指令部分。

在真正编写fork 代码之前，首先在thread.h的task_struct中增加了成员int16_t parent_pid，它位于cwd_inode_nr之后，表示父进程的pid。然后在thread.c中的init_thread函数中增加一句pthread->parent_pid = −1;。另外在thread.c中还为fork专门增加了个分配pid 的函数，其声明为pid_t fork_pid(void)，其实现是return allocate_pid();。

在fork.c中实现了fork的内核部分，sys_fork：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
extern void intr_exit(void);

/* 将父进程的pcb、虚拟地址位图拷贝给子进程 */
static int32_t copy_pcb_vaddrbitmap_stack0(struct task_struct* child_thread, struct task_struct* parent_thread) {
/* a 复制pcb所在的整个页,里面包含进程pcb信息及特级0极的栈,里面包含了返回地址, 然后再单独修改个别部分 */
   memcpy(child_thread, parent_thread, PG_SIZE);
   child_thread->pid = fork_pid();
   child_thread->elapsed_ticks = 0;
   child_thread->status = TASK_READY;
   child_thread->ticks = child_thread->priority;   // 为新进程把时间片充满
   child_thread->parent_pid = parent_thread->pid;
   child_thread->general_tag.prev = child_thread->general_tag.next = NULL;
   child_thread->all_list_tag.prev = child_thread->all_list_tag.next = NULL;
   block_desc_init(child_thread->u_block_desc);
/* b 复制父进程的虚拟地址池的位图 */
   uint32_t bitmap_pg_cnt = DIV_ROUND_UP((0xc0000000 - USER_VADDR_START) / PG_SIZE / 8 , PG_SIZE);
   void* vaddr_btmp = get_kernel_pages(bitmap_pg_cnt);
   if (vaddr_btmp == NULL) return -1;
   /* 此时child_thread->userprog_vaddr.vaddr_bitmap.bits还是指向父进程虚拟地址的位图地址
    * 下面将child_thread->userprog_vaddr.vaddr_bitmap.bits指向自己的位图vaddr_btmp */
   memcpy(vaddr_btmp, child_thread->userprog_vaddr.vaddr_bitmap.bits, bitmap_pg_cnt * PG_SIZE);
   child_thread->userprog_vaddr.vaddr_bitmap.bits = vaddr_btmp;
   /* 调试用 */
   ASSERT(strlen(child_thread->name) < 11);	// pcb.name的长度是16,为避免下面strcat越界
   strcat(child_thread->name,"_fork");
   return 0;
}

/* 复制子进程的进程体(代码和数据)及用户栈 */
static void copy_body_stack3(struct task_struct* child_thread, struct task_struct* parent_thread, void* buf_page) {
   uint8_t* vaddr_btmp = parent_thread->userprog_vaddr.vaddr_bitmap.bits;
   uint32_t btmp_bytes_len = parent_thread->userprog_vaddr.vaddr_bitmap.btmp_bytes_len;
   uint32_t vaddr_start = parent_thread->userprog_vaddr.vaddr_start;
   uint32_t idx_byte = 0;
   uint32_t idx_bit = 0;
   uint32_t prog_vaddr = 0;

   /* 在父进程的用户空间中查找已有数据的页 */
   while (idx_byte < btmp_bytes_len) {
      if (vaddr_btmp[idx_byte]) {
	 idx_bit = 0;
	 while (idx_bit < 8) {
	    if ((BITMAP_MASK << idx_bit) & vaddr_btmp[idx_byte]) {
	       prog_vaddr = (idx_byte * 8 + idx_bit) * PG_SIZE + vaddr_start;
	 /* 下面的操作是将父进程用户空间中的数据通过内核空间做中转,最终复制到子进程的用户空间 */

	       /* a 将父进程在用户空间中的数据复制到内核缓冲区buf_page,
	       目的是下面切换到子进程的页表后,还能访问到父进程的数据*/
	       memcpy(buf_page, (void*)prog_vaddr, PG_SIZE);

	       /* b 将页表切换到子进程,目的是避免下面申请内存的函数将pte及pde安装在父进程的页表中 */
	       page_dir_activate(child_thread);
	       /* c 申请虚拟地址prog_vaddr */
	       get_a_page_without_opvaddrbitmap(PF_USER, prog_vaddr);

	       /* d 从内核缓冲区中将父进程数据复制到子进程的用户空间 */
	       memcpy((void*)prog_vaddr, buf_page, PG_SIZE);

	       /* e 恢复父进程页表 */
	       page_dir_activate(parent_thread);
	    }
	    idx_bit++;
	 }
      }
      idx_byte++;
   }
}

函数copy_pcb_vaddrbitmap_stack0接受2 个参数，子进程child_thread、父进程parent_thread，功能是将父进程的pcb、虚拟地址位图拷贝给子进程。通过memcpy把父进程的pcb 及其内核栈一同复制给子进程。通过fork_pid函数为子进程分配新的pid。置子进程的status为TASK_READY，目的是让调试器schedule 安排其上CPU。还有将子进程时间片ticks 置为child_thread->priority，为其加满时间片，以及将parent_pid置为parent_thread->pid等。用child_thread->userprog_vaddr.vaddr_bitmap.bits来管理进程的虚拟地址空间，子进程不能和父进程共用同一个虚拟地址位图，通过block_desc_init(child_thread->u_block_desc)初始化进程自己的内存块描述符，计算虚拟地址位图需要的页框数bitmap_pg_cnt，申请bitmap_pg_cnt一个内核页框来存储位图。

函数copy_body_stack3功能是复制子进程的进程体及用户栈。用户使用的内存是用虚拟内存池来管理的，也就是pcb中的 userprog_vaddr。这包括用户进程体占用的内存、堆中申请的内存和用户栈内存。堆从低地址往高地址发展，栈从USER_STACK3_VADDR，即0xc0000000 - 0x1000处往低地址发展。它们的分布不连续，因此我们要遍历虚拟地址位图中的每一位，这样才能找出进程正在使用的内存。

要想把数据从一个进程拷贝到另一个进程，必须要借助内核空间作为数据中转，即先将父进程用户空间中的数据复制到内核的buf_page中，然后再将buf_page 复制到子进程的用户空间中。在父进程虚拟地址空间中每找到一页占用的内存，就在子进程的虚拟地址空间中分配一页内存，然后将buf_page 中父进程的数据复制到为子进程新分配的虚拟地址空间页。在将buf_page的数据拷贝到子进程之前，一定要将页表替换为子进程的页表。

在父进程虚拟地址位图字节长度btmp_bytes_len的范围内逐字节查看位图，如果该字节不为0，也就是某位为1，即某个位有效，已分配，下面开始逐位查看该字节。通过if 判断，如果某位的值为1，就在第53 行将该位转换为虚拟地址prog_vaddr，接下来通过memcpy将prog_vaddr处的1 页复制到buf_page。下面在为子进程分配内存之前，先调用page_dir_activate(child_thread)激活子进程的页表，然后再调用get_a_page_without_opvaddrbitmap(PF_USER, prog_vaddr)为子进程分配1 页，接着再调用memcpy((void*)prog_vaddr,buf_page, PG_SIZE);完成内核空间到子进程空间的复制，最后再调用page_dir_activate(parent_thread)将父进程的页表恢复。然后进入下一循环，继续寻找父进程占用的虚拟空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
/* 为子进程构建thread_stack和修改返回值 */
static int32_t build_child_stack(struct task_struct* child_thread) {
/* a 使子进程pid返回值为0 */
   /* 获取子进程0级栈栈顶 */
   struct intr_stack* intr_0_stack = (struct intr_stack*)((uint32_t)child_thread + PG_SIZE - sizeof(struct intr_stack));
   /* 修改子进程的返回值为0 */
   intr_0_stack->eax = 0;

/* b 为switch_to 构建 struct thread_stack,将其构建在紧临intr_stack之下的空间*/
   uint32_t* ret_addr_in_thread_stack  = (uint32_t*)intr_0_stack - 1;

   /***   这三行不是必要的,只是为了梳理thread_stack中的关系 ***/
   uint32_t* esi_ptr_in_thread_stack = (uint32_t*)intr_0_stack - 2; 
   uint32_t* edi_ptr_in_thread_stack = (uint32_t*)intr_0_stack - 3; 
   uint32_t* ebx_ptr_in_thread_stack = (uint32_t*)intr_0_stack - 4; 
   /**********************************************************/

   /* ebp在thread_stack中的地址便是当时的esp(0级栈的栈顶),
   即esp为"(uint32_t*)intr_0_stack - 5" */
   uint32_t* ebp_ptr_in_thread_stack = (uint32_t*)intr_0_stack - 5; 

   /* switch_to的返回地址更新为intr_exit,直接从中断返回 */
   *ret_addr_in_thread_stack = (uint32_t)intr_exit;

   /* 下面这两行赋值只是为了使构建的thread_stack更加清晰,其实也不需要,
    * 因为在进入intr_exit后一系列的pop会把寄存器中的数据覆盖 */
   *ebp_ptr_in_thread_stack = *ebx_ptr_in_thread_stack =\
   *edi_ptr_in_thread_stack = *esi_ptr_in_thread_stack = 0;
   /*********************************************************/

   /* 把构建的thread_stack的栈顶做为switch_to恢复数据时的栈顶 */
   child_thread->self_kstack = ebp_ptr_in_thread_stack;	    
   return 0;
}

/* 更新inode打开数 */
static void update_inode_open_cnts(struct task_struct* thread) {
   int32_t local_fd = 3, global_fd = 0;
   while (local_fd < MAX_FILES_OPEN_PER_PROC) {
      global_fd = thread->fd_table[local_fd];
      ASSERT(global_fd < MAX_FILE_OPEN);
      if (global_fd != -1) {
	 file_table[global_fd].fd_inode->i_open_cnts++;
      }
      local_fd++;
   }
}

/* 拷贝父进程本身所占资源给子进程 */
static int32_t copy_process(struct task_struct* child_thread, struct task_struct* parent_thread) {
   /* 内核缓冲区,作为父进程用户空间的数据复制到子进程用户空间的中转 */
   void* buf_page = get_kernel_pages(1);
   if (buf_page == NULL) {
      return -1;
   }

   /* a 复制父进程的pcb、虚拟地址位图、内核栈到子进程 */
   if (copy_pcb_vaddrbitmap_stack0(child_thread, parent_thread) == -1) {
      return -1;
   }

   /* b 为子进程创建页表,此页表仅包括内核空间 */
   child_thread->pgdir = create_page_dir();
   if(child_thread->pgdir == NULL) {
      return -1;
   }

   /* c 复制父进程进程体及用户栈给子进程 */
   copy_body_stack3(child_thread, parent_thread, buf_page);

   /* d 构建子进程thread_stack和修改返回值pid */
   build_child_stack(child_thread);

   /* e 更新文件inode的打开数 */
   update_inode_open_cnts(child_thread);

   mfree_page(PF_KERNEL, buf_page, 1);
   return 0;
}

/* fork子进程,内核线程不可直接调用 */
pid_t sys_fork(void) {
   struct task_struct* parent_thread = running_thread();
   struct task_struct* child_thread = get_kernel_pages(1);    // 为子进程创建pcb(task_struct结构)
   if (child_thread == NULL) {
      return -1;
   }
   ASSERT(INTR_OFF == intr_get_status() && parent_thread->pgdir != NULL);

   if (copy_process(child_thread, parent_thread) == -1) {
      return -1;
   }

   /* 添加到就绪线程队列和所有线程队列,子进程由调试器安排运行 */
   ASSERT(!elem_find(&thread_ready_list, &child_thread->general_tag));
   list_append(&thread_ready_list, &child_thread->general_tag);
   ASSERT(!elem_find(&thread_all_list, &child_thread->all_list_tag));
   list_append(&thread_all_list, &child_thread->all_list_tag);
   
   return child_thread->pid;    // 父进程返回子进程的pid
}

函数build_child_stack接受1 个参数，子进程child_thread。功能是为子进程构建thread_stack和修改返回值。为了让子进程也能继续fork 之后的代码运行，必须也从中断退出，也就是要经过intr_exit。子进程是由调试器schedule 调度执行的，它要用到switch_to 函数，而switch_to函数要从栈thread_stack中恢复上下文，因此我们要想办法构建出合适的thread_stack。根据abi 约定，eax 寄存器中是函数返回值，因此intr_stack栈中的eax 置为0。下面构建一个thread_stack，把它的栈底放在intr_stack栈顶的下面，即(uint32_t*)intr_0_stack - 1，此地址是thread_stack栈中eip的位置，分别为thread_stack中的esi、edi、ebx、ebp安排位置，指针ebp_ptr_in_thread_stack是thread_stack的栈顶，我们必须把它的值存放在pcb 中偏移为0 的地方，即task_struct中的self_kstack处。将地址ret_addr_in_thread_stack处的值赋值为intr_exit的地址，也就是thread_stack中的eip是intr_exit，这就保证了子进程被调度时，可以直接从中断返回，也就是实现了从fork 之后的代码处继续执行的目的。最后把ebp_ptr_in_thread_stack的值，也就是thread_stack的栈顶记录在pcb 的self_ kstack处，这样switch_to便获得了thread_stack栈顶，从而使程序迈向intr_exit。

函数update_inode_open_cnts接受1个参数，线程thread，功能是fork 之后，更新线程thread的inode 打开数。遍历fd_table中所有文件描述符，从中获得全局文件表file_table的下标global_fd找到对应的文件结构，使相应文件结构中fd_inode的i_open_cnts加1。

copy_process函数接受2个参数，子进程child_thread和父进程parent_thread，功能是拷贝父进程本身所占资源给子进程。函数开头申请了1 页的内核空间作为内核缓冲区，即buf_page。调用函数copy_pcb_vaddrbitmap_stack0把父进程子的pcb、虚拟地址位图及内核栈复制给子进程，接着调用create_page_dir函数为子进程创建页表。然后调用函数copy_body_stack3复制父进程进程体及用户栈给子进程，接着调用函数build_child_stack为子进程构建thread_stack，随后调用update_inode_open_cnts更新inode 的打开数，最后释放buf_page。

下面是函数sys_fork。功能是克隆当前进程。函数先调用get_kernel_pages(1)获得1 页内核空间作为子进程的pcb。接下来调用copy_process复制父进程的信息到子进程，将其加入到就绪队列和全部队列，最后返回子进程的pid。

添加fork 系统调用与实现init 进程

在Linux 中，init 是用户级进程，它是第一个启动的程序，因此它的pid是1，后续的所有进程都是它的孩子，故init 是所有进程的父进程，所以它还负责所有子进程的资源回收，要先完成fork 系统调用。系统调用的3 个步骤：

  1. 在syscall.h中的enum SYSCALL_NR 结构中添加SYS_FORK。
  2. 在syscall.c中添加fork()，原型是pid_t fork(void)，实现是return _syscall0(SYS_FORK);。
  3. 在syscall-init.c中的函数syscall_init中，添加代码syscall_table[SYS_FORK] = sys_fork;。

init定义在main.c中

1
2
3
4
5
6
7
8
9
10
/* init 进程 */
void init(void) {
   uint32_t ret_pid = fork();
   if(ret_pid) {
      printf("i am father, my pid is %d, child pid is %d\n", getpid(), ret_pid);
   } else {
      printf("i am child, my pid is %d, ret pid is %d\n", getpid(), ret_pid);
   }
   while(1);
}

init是用户级进程，因此咱们要调用process_execute创建进程，在创建主线程的函数make_main_thread之前创建init，也就是在函数thread_init中完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/* 初始化线程环境 */
void thread_init(void) {
   put_str("thread_init start\n");

   list_init(&thread_ready_list);
   list_init(&thread_all_list);
   lock_init(&pid_lock);

 /* 先创建第一个用户进程:init */
   process_execute(init, "init");         // 放在第一个初始化,这是第一个进程,init进程的pid为1

/* 将当前main函数创建为线程 */
   make_main_thread();

   /* 创建idle线程 */
   idle_thread = thread_start("idle", 10, idle, NULL);

   put_str("thread_init done\n");
}

添加 read 系统调用，获取键盘输入

Linux 中从键盘获取输入是利用read 系统调用，要改进sys_read，让其支持键盘。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/* 从文件描述符fd指向的文件中读取count个字节到buf,若成功则返回读出的字节数,到文件尾则返回-1 */
int32_t sys_read(int32_t fd, void* buf, uint32_t count) {
   ASSERT(buf != NULL);
   int32_t ret = -1;
   if (fd < 0 || fd == stdout_no || fd == stderr_no) {
      printk("sys_read: fd error\n");
   } else if (fd == stdin_no) {
      char* buffer = buf;
      uint32_t bytes_read = 0;
      while (bytes_read < count) {
	 *buffer = ioq_getchar(&kbd_buf);
	 bytes_read++;
	 buffer++;
      }
      ret = (bytes_read == 0 ? -1 : (int32_t)bytes_read);
   } else {
      uint32_t _fd = fd_local2global(fd);
      ret = file_read(&file_table[_fd], buf, count);   
   }
   return ret;
}

加入了标准输入stdin_no的处理。若发现fd是stdin_no，下面就通过while和ioq_getchar(&kbd_buf)，每次从键盘缓冲区kbd_buf中获取1 个字符，直到获取了count 个字符为止。

下面syscall.c中添加read 的系统调用，Linux 中read 函数的原型是：ssize_t read(int fd, void *buf, size_t count);，这和sys_read接口是一样的，在syscall.h的enum SYSCALL_NR中添加SYS_READ后，在syscall.c中添加系统调用read 的实现

1
2
3
4
/* 从文件描述符fd 中读取count 个字节到buf */
int32_t read(int32_t fd, void* buf, uint32_t count) {
   return _syscall3(SYS_READ, fd, buf, count);
}

最后在syscall_init.c的syscall_init函数中添加代码syscall_table[SYS_READ] = sys_read，在syscall_table数组中把read 与sys_read绑定到一起就行了。

添加 putchar、clear 系统调用

系统调用putchar的原型是int putchar(int c)，若成功输出，则返回值为(unsigned int)c，若失败则返回EOF，EOF 通常为−1。清屏命令clear对应的内核部分叫cls_screen。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
global cls_screen
cls_screen:
   pushad
   ;;;;;;;;;;;;;;;
	; 由于用户程序的cpl为3,显存段的dpl为0,故用于显存段的选择子gs在低于自己特权的环境中为0,
	; 导致用户程序再次进入中断后,gs为0,故直接在put_str中每次都为gs赋值. 
   mov ax, SELECTOR_VIDEO	       ; 不能直接把立即数送入gs,须由ax中转
   mov gs, ax

   mov ebx, 0
   mov ecx, 80*25
 .cls:
   mov word [gs:ebx], 0x0720		  ;0x0720是黑底白字的空格键
   add ebx, 2
   loop .cls 
   mov ebx, 0

 .set_cursor:				  ;直接把set_cursor搬过来用,省事
;;;;;;; 1 先设置高8位 ;;;;;;;;
   mov dx, 0x03d4			  ;索引寄存器
   mov al, 0x0e				  ;用于提供光标位置的高8位
   out dx, al
   mov dx, 0x03d5			  ;通过读写数据端口0x3d5来获得或设置光标位置 
   mov al, bh
   out dx, al

;;;;;;; 2 再设置低8位 ;;;;;;;;;
   mov dx, 0x03d4
   mov al, 0x0f
   out dx, al
   mov dx, 0x03d5 
   mov al, bl
   out dx, al
   popad
   ret

下面是系统调用putchar 和clear 的实现

1
2
3
4
5
6
7
8
9
/* 输出一个字符 */
void putchar(char char_asci) {
   _syscall1(SYS_PUTCHAR, char_asci);
}

/* 清空屏幕 */
void clear(void) {
   _syscall0(SYS_CLEAR);
}

这两个函数完成之后，还要在syscall.h的enum SYSCALL_NR结构中添加SYS_PUTCHAR和SYS_CLEAR，最后在syscall-init.c中增加初始化代码syscall_table[SYS_PUTCHAR] = sys_putchar;和syscall_table[SYS_CLEAR] = cls_screen;。

实现一个简单的 shell

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#define cmd_len 128	   // 最大支持键入128个字符的命令行输入
#define MAX_ARG_NR 16	   // 加上命令名外,最多支持15个参数

/* 存储输入的命令 */
static char cmd_line[cmd_len] = {0};

/* 用来记录当前目录,是当前目录的缓存,每次执行cd命令时会更新此内容 */
char cwd_cache[64] = {0};

/* 输出提示符 */
void print_prompt(void) {
   printf("[rabbit@localhost %s]$ ", cwd_cache);
}

/* 从键盘缓冲区中最多读入count个字节到buf。*/
static void readline(char* buf, int32_t count) {
   assert(buf != NULL && count > 0);
   char* pos = buf;
   while (read(stdin_no, pos, 1) != -1 && (pos - buf) < count) { // 在不出错情况下,直到找到回车符才返回
      switch (*pos) {
       /* 找到回车或换行符后认为键入的命令结束,直接返回 */
	 case '\n':
	 case '\r':
	    *pos = 0;	   // 添加cmd_line的终止字符0
	    putchar('\n');
	    return;

	 case '\b':
	    if (buf[0] != '\b') {		// 阻止删除非本次输入的信息
	       --pos;	   // 退回到缓冲区cmd_line中上一个字符
	       putchar('\b');
	    }
	    break;

	 /* 非控制键则输出字符 */
	 default:
	    putchar(*pos);
	    pos++;
      }
   }
   printf("readline: can`t find enter_key in the cmd_line, max num of char is 128\n");
}

/* 简单的shell */
void my_shell(void) {
   cwd_cache[0] = '/';
   while (1) {
      print_prompt(); 
      memset(cmd_line, 0, cmd_len);
      readline(cmd_line, cmd_len);
      if (cmd_line[0] == 0) {	 // 若只键入了一个回车
	 continue;
      }
   }
   panic("my_shell: should not be here");
}

第11 行的cmd_len表示命令字符串最大的长度，其值为128，下一行的MAX_ARG_NR表示最大支持的参数个数。数组cmd_line用来存储键入的命令。数组cwd_cache用来存储当前目录名。函数print_prompt用于输出命令提示符，用printf函数输出[rabbit@localhost %s]$，函数readline接受2 个参数，缓冲区buf 和读入的字符数，功能是从键盘缓冲区中最多读入count 个字节到buf。字符指针pos 指向缓冲区buf，通过pos 往buf 中写数据。

函数体每次通过read 系统调用读入1 个字符到buf中。通过switch结构判断读入的字符*pos的值，前三个case 是处理控制键，分别是回车换行符及退格键。函数my_shell就是所实现的简单shell，函数中先将当前工作目录缓存cwd_cache 置为根目录’/‘，然后通过while 语句，循环调用print_prompt 输出命令提示符，然后调用readline 获取用户输入。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int main(void) {
   put_str("I am kernel\n");
   init_all();
   cls_screen();
   console_put_str("[rabbit@localhost /]$ ");
   while(1);
   return 0;
}
/* init进程 */
void init(void) {
   uint32_t ret_pid = fork();
   if(ret_pid) {  // 父进程
      while(1);
   } else {	  // 子进程
      my_shell();
   }
   panic("init: should not be here");
}

在键盘驱动中：

1
2
3
4
5
6
7
8
9
   /*****************  快捷键ctrl+l和ctrl+u的处理 *********************
    * 下面是把ctrl+l和ctrl+u这两种组合键产生的字符置为:
    * cur_char的asc码-字符a的asc码, 此差值比较小,
    * 属于asc码表中不可见的字符部分.故不会产生可见字符.
    * 我们在shell中将ascii值为l-a和u-a的分别处理为清屏和删除输入的快捷键*/
if ((ctrl_down_last && cur_char == 'l') || (ctrl_down_last && cur_char == 'u')) {
   cur_char -= 'a';
}
    /****************************************************************/

变量cur_char中存储的是按键的ASCII 码，在keyboard.c将ctrl+l和ctrl+u组合键也转换为ASCII 码，不过此时cur_char中存储的是字符l 或字符u 的ASCII 码值减去字符a 的ASCII 码值的差。在ASCII 码表中，ASCII 码值为十进制0～31 和127 的字符是控制字符，它们不可见，因此字符l 和字符u 的ASCII 码值减去a 的ASCII 后的差会落到控制字符中，但并不是所有的控制字符都可占用，对于系统中已经处理的控制字符必须要保留。比如退格键‘\b’、换行符‘\n’和回车符‘\r’的ASCII 码分别是8、10 和13，咱们已经在shell.c 中针对它们做出了处理，因此要定义其他快捷键的话，要将这三个控制键的ASCII 码跨过去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/* 从键盘缓冲区中最多读入count个字节到buf。*/
static void readline(char* buf, int32_t count) {
   assert(buf != NULL && count > 0);
   char* pos = buf;

   while (read(stdin_no, pos, 1) != -1 && (pos - buf) < count) { // 在不出错情况下,直到找到回车符才返回
      switch (*pos) {
       /* 找到回车或换行符后认为键入的命令结束,直接返回 */
	 case '\n':
	 case '\r':
	    *pos = 0;	   // 添加cmd_line的终止字符0
	    putchar('\n');
	    return;

	 case '\b':
	    if (cmd_line[0] != '\b') {		// 阻止删除非本次输入的信息
	       --pos;	   // 退回到缓冲区cmd_line中上一个字符
	       putchar('\b');
	    }
	    break;

	 /* ctrl+l 清屏 */
	 case 'l' - 'a': 
	    /* 1 先将当前的字符'l'-'a'置为0 */
	    *pos = 0;
	    /* 2 再将屏幕清空 */
	    clear();
	    /* 3 打印提示符 */
	    print_prompt();
	    /* 4 将之前键入的内容再次打印 */
	    printf("%s", buf);
	    break;

	 /* ctrl+u 清掉输入 */
	 case 'u' - 'a':
	    while (buf != pos) {
	       putchar('\b');
	       *(pos--) = 0;
	    }
	    break;

	 /* 非控制键则输出字符 */
	 default:
	    putchar(*pos);
	    pos++;
      }
   }
   printf("readline: can`t find enter_key in the cmd_line, max num of char is 128\n");
}

把ctrl+l键处理为清屏操作，这分为四步来完成。

  • 先将pos 指向的字符置为0，也就是字符串结束符‘\0’。
  • 调用clear 系统调用清屏。
  • 然后调用print_prompt 函数重新输出命令提示符。
  • 把buf 中的字符串通过printf 打印出来。

处理快捷键“ctrl+u”的实现原理是通过while循环连续输出退格符，然后使指针pos逐步递减，并将对应位置为0，直到pos 指向了buf 的起始处。

解析键入的字符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
/* 分析字符串cmd_str中以token为分隔符的单词,将各单词的指针存入argv数组 */
static int32_t cmd_parse(char* cmd_str, char** argv, char token) {
   assert(cmd_str != NULL);
   int32_t arg_idx = 0;
   while(arg_idx < MAX_ARG_NR) {
      argv[arg_idx] = NULL;
      arg_idx++;
   }
   char* next = cmd_str;
   int32_t argc = 0;
   /* 外层循环处理整个命令行 */
   while(*next) {
      /* 去除命令字或参数之间的空格 */
      while(*next == token) {
	 next++;
      }
      /* 处理最后一个参数后接空格的情况,如"ls dir2 " */
      if (*next == 0) {
	 break; 
      }
      argv[argc] = next;

     /* 内层循环处理命令行中的每个命令字及参数 */
      while (*next && *next != token) {	  // 在字符串结束前找单词分隔符
	 next++;
      }

      /* 如果未结束(是token字符),使tocken变成0 */
      if (*next) {
	 *next++ = 0;	// 将token字符替换为字符串结束符0,做为一个单词的结束,并将字符指针next指向下一个字符
      }
   
      /* 避免argv数组访问越界,参数过多则返回0 */
      if (argc > MAX_ARG_NR) {
	 return -1;
      }
      argc++;
   }
   return argc;
}

char* argv[MAX_ARG_NR];    // argv必须为全局变量，为了以后exec的程序可访问参数
int32_t argc = -1;
/* 简单的shell */
void my_shell(void) {
   cwd_cache[0] = '/';
   while (1) {
      print_prompt(); 
      memset(final_path, 0, MAX_PATH_LEN);
      memset(cmd_line, 0, MAX_PATH_LEN);
      readline(cmd_line, MAX_PATH_LEN);
      if (cmd_line[0] == 0) {	 // 若只键入了一个回车
	 continue;
      }
      argc = -1;
      argc = cmd_parse(cmd_line, argv, ' ');
      if (argc == -1) {
	 printf("num of arguments exceed %d\n", MAX_ARG_NR);
	 continue;
      }
      
      int32_t arg_idx = 0;
      while(arg_idx < argc) {
	 printf("%s ", argv[arg_idx]); 
	 arg_idx++;
      }
      printf("\n");
   }
   panic("my_shell: should not be here");
}

函数cmd_parse接受3 个参数，用户键入的原始命令串cmd_str、参数字符串数组argv、分隔符token。功能是分析字符串cmd_str 中以token 为分隔符的单词，将解析出来的单词的指针存入argv 数组。指针next 指向cmd_str，next 用于处理每一个字符，while 外层循环处理整个命
令行cmd_str。argv[argc] = next，每找出一个字符串就将其在cmd_str 中的起始next 存储到argv 数组。

添加系统调用

按照添加系统调用的三个步骤：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
enum SYSCALL_NR {
   SYS_GETPID,
   SYS_WRITE,
   SYS_MALLOC,
   SYS_FREE,
   SYS_FORK,
   SYS_READ,
   SYS_PUTCHAR,
   SYS_CLEAR,
   SYS_GETCWD,
   SYS_OPEN,
   SYS_CLOSE,
   SYS_LSEEK,
   SYS_UNLINK,
   SYS_MKDIR,
   SYS_OPENDIR,
   SYS_CLOSEDIR,
   SYS_CHDIR,
   SYS_RMDIR,
   SYS_READDIR,
   SYS_REWINDDIR,
   SYS_STAT,
   SYS_PS
};

以上定义的enum SYSCALL_NR是咱们系统中目前所支持的所有系统调用。下面是新增的系统调用实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
/* 获取当前工作目录 */
char* getcwd(char* buf, uint32_t size) {
   return (char*)_syscall2(SYS_GETCWD, buf, size);
}

/* 以flag方式打开文件pathname */
int32_t open(char* pathname, uint8_t flag) {
   return _syscall2(SYS_OPEN, pathname, flag);
}

/* 关闭文件fd */
int32_t close(int32_t fd) {
   return _syscall1(SYS_CLOSE, fd);
}

/* 设置文件偏移量 */
int32_t lseek(int32_t fd, int32_t offset, uint8_t whence) {
   return _syscall3(SYS_LSEEK, fd, offset, whence);
}

/* 删除文件pathname */
int32_t unlink(const char* pathname) {
   return _syscall1(SYS_UNLINK, pathname);
}

/* 创建目录pathname */
int32_t mkdir(const char* pathname) {
   return _syscall1(SYS_MKDIR, pathname);
}

/* 打开目录name */
struct dir* opendir(const char* name) {
   return (struct dir*)_syscall1(SYS_OPENDIR, name);
}

/* 关闭目录dir */
int32_t closedir(struct dir* dir) {
   return _syscall1(SYS_CLOSEDIR, dir);
}

/* 删除目录pathname */
int32_t rmdir(const char* pathname) {
   return _syscall1(SYS_RMDIR, pathname);
}

/* 读取目录dir */
struct dir_entry* readdir(struct dir* dir) {
   return (struct dir_entry*)_syscall1(SYS_READDIR, dir);
}

/* 回归目录指针 */
void rewinddir(struct dir* dir) {
   _syscall1(SYS_REWINDDIR, dir);
}

/* 获取path属性到buf中 */
int32_t stat(const char* path, struct stat* buf) {
   return _syscall2(SYS_STAT, path, buf);
}

/* 改变工作目录为path */
int32_t chdir(const char* path) {
   return _syscall1(SYS_CHDIR, path);
}

/* 显示任务列表 */
void ps(void) {
   _syscall0(SYS_PS);
}

这些系统调用要在syscall_table 中注册：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/* 初始化系统调用 */
void syscall_init(void) {
   put_str("syscall_init start\n");
   syscall_table[SYS_GETPID]     = sys_getpid;
   syscall_table[SYS_WRITE]      = sys_write;
   syscall_table[SYS_MALLOC]     = sys_malloc;
   syscall_table[SYS_FREE]       = sys_free;
   syscall_table[SYS_FORK]       = sys_fork;
   syscall_table[SYS_READ]       = sys_read;
   syscall_table[SYS_PUTCHAR]    = sys_putchar;
   syscall_table[SYS_CLEAR]      = cls_screen;
   syscall_table[SYS_GETCWD]     = sys_getcwd;
   syscall_table[SYS_OPEN]       = sys_open;
   syscall_table[SYS_CLOSE]      = sys_close;
   syscall_table[SYS_LSEEK]	 = sys_lseek;
   syscall_table[SYS_UNLINK]	 = sys_unlink;
   syscall_table[SYS_MKDIR]	 = sys_mkdir;
   syscall_table[SYS_OPENDIR]	 = sys_opendir;
   syscall_table[SYS_CLOSEDIR]   = sys_closedir;
   syscall_table[SYS_CHDIR]	 = sys_chdir;
   syscall_table[SYS_RMDIR]	 = sys_rmdir;
   syscall_table[SYS_READDIR]	 = sys_readdir;
   syscall_table[SYS_REWINDDIR]	 = sys_rewinddir;
   syscall_table[SYS_STAT]	 = sys_stat;
   syscall_table[SYS_PS]	 = sys_ps;
   put_str("syscall_init done\n");
}

加载用户进程

exec 函数定义在userprog/exec.c 中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
extern void intr_exit(void);
typedef uint32_t Elf32_Word, Elf32_Addr, Elf32_Off;
typedef uint16_t Elf32_Half;

/* 32位elf头 */
struct Elf32_Ehdr {
   unsigned char e_ident[16];
   Elf32_Half    e_type;
   Elf32_Half    e_machine;
   Elf32_Word    e_version;
   Elf32_Addr    e_entry;
   Elf32_Off     e_phoff;
   Elf32_Off     e_shoff;
   Elf32_Word    e_flags;
   Elf32_Half    e_ehsize;
   Elf32_Half    e_phentsize;
   Elf32_Half    e_phnum;
   Elf32_Half    e_shentsize;
   Elf32_Half    e_shnum;
   Elf32_Half    e_shstrndx;
};

/* 程序头表Program header.就是段描述头 */
struct Elf32_Phdr {
   Elf32_Word p_type;		 // 见下面的enum segment_type
   Elf32_Off  p_offset;
   Elf32_Addr p_vaddr;
   Elf32_Addr p_paddr;
   Elf32_Word p_filesz;
   Elf32_Word p_memsz;
   Elf32_Word p_flags;
   Elf32_Word p_align;
};

/* 段类型 */
enum segment_type {
   PT_NULL,            // 忽略
   PT_LOAD,            // 可加载程序段
   PT_DYNAMIC,         // 动态加载信息 
   PT_INTERP,          // 动态加载器名称
   PT_NOTE,            // 一些辅助信息
   PT_SHLIB,           // 保留
   PT_PHDR             // 程序头表
};

定义了elf相关的数据结构和一些以前缀Elf32_开头的变量，这是为了在名称上与elf 相关结构中的变量类型吻合，其实变量类型只是存储数值的空间大小而已，ELF 结构字段中的变量大小分别是4 字节和2 字节。结构体struct Elf32_Ehdr定义的是32 位elf 文件头。接下来是结构体struct Elf32_Phdr，它表示程序头表，也就是段头表。枚举类型enum segment_type表示可识别的段的类型，这里咱们只关注类型为PT_LOAD的段就可以了，它是可加载的段，也就是程序本身的程序体。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/* 将文件描述符fd指向的文件中,偏移为offset,大小为filesz的段加载到虚拟地址为vaddr的内存 */
static bool segment_load(int32_t fd, uint32_t offset, uint32_t filesz, uint32_t vaddr) {
   uint32_t vaddr_first_page = vaddr & 0xfffff000;    // vaddr地址所在的页框
   uint32_t size_in_first_page = PG_SIZE - (vaddr & 0x00000fff);     // 加载到内存后,文件在第一个页框中占用的字节大小
   uint32_t occupy_pages = 0;
   /* 若一个页框容不下该段 */
   if (filesz > size_in_first_page) {
      uint32_t left_size = filesz - size_in_first_page;
      occupy_pages = DIV_ROUND_UP(left_size, PG_SIZE) + 1;	     // 1是指vaddr_first_page
   } else {
      occupy_pages = 1;
   }

   /* 为进程分配内存 */
   uint32_t page_idx = 0;
   uint32_t vaddr_page = vaddr_first_page;
   while (page_idx < occupy_pages) {
      uint32_t* pde = pde_ptr(vaddr_page);
      uint32_t* pte = pte_ptr(vaddr_page);

      /* 如果pde不存在,或者pte不存在就分配内存.
       * pde的判断要在pte之前,否则pde若不存在会导致
       * 判断pte时缺页异常 */
      if (!(*pde & 0x00000001) || !(*pte & 0x00000001)) {
	 if (get_a_page(PF_USER, vaddr_page) == NULL) {
	    return false;
	 }
      } // 如果原进程的页表已经分配了,利用现有的物理页,直接覆盖进程体
      vaddr_page += PG_SIZE;
      page_idx++;
   }
   sys_lseek(fd, offset, SEEK_SET);
   sys_read(fd, (void*)vaddr, filesz);
   return true;
}

函数segment_load接受4 个参数，文件描述符fd、段在文件中的字节偏移量offset、段大小filesz、段被加载到的虚拟地址vaddr，函数功能是将文件描述符fd 指向的文件中，偏移为offset，大小为filesz 的段加载到虚拟地址为vaddr 的内存空间。变量vaddr_first_page用于获取虚拟地址vaddr 所在的页框起始地址。变量size_in_first_page就表示文件在第一个页框中占用的字节大小，变量occupy_pages表示该段占用的总页框数，如果段大小filesz 大于size_in_first_page，这表示一个页框容不下该段，计算该段占用的页框数并赋值给occupy_pages，如果段比较小，一个页框可以容纳该段，就将occupy_pages置为1。

下面是从文件系统上加载用户进程到刚刚分配好的内存中，先通过sys_lseek函数将文件指针定位到段在文件中的偏移地址，然后将该段读入到虚拟地
址vaddr 处。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
/* 从文件系统上加载用户程序pathname,成功则返回程序的起始地址,否则返回-1 */
static int32_t load(const char* pathname) {
   int32_t ret = -1;
   struct Elf32_Ehdr elf_header;
   struct Elf32_Phdr prog_header;
   memset(&elf_header, 0, sizeof(struct Elf32_Ehdr));

   int32_t fd = sys_open(pathname, O_RDONLY);
   if (fd == -1) {
      return -1;
   }

   if (sys_read(fd, &elf_header, sizeof(struct Elf32_Ehdr)) != sizeof(struct Elf32_Ehdr)) {
      ret = -1;
      goto done;
   }

   /* 校验elf头 */
   if (memcmp(elf_header.e_ident, "\177ELF\1\1\1", 7) \
      || elf_header.e_type != 2 \
      || elf_header.e_machine != 3 \
      || elf_header.e_version != 1 \
      || elf_header.e_phnum > 1024 \
      || elf_header.e_phentsize != sizeof(struct Elf32_Phdr)) {
      ret = -1;
      goto done;
   }

   Elf32_Off prog_header_offset = elf_header.e_phoff; 
   Elf32_Half prog_header_size = elf_header.e_phentsize;

   /* 遍历所有程序头 */
   uint32_t prog_idx = 0;
   while (prog_idx < elf_header.e_phnum) {
      memset(&prog_header, 0, prog_header_size);
      
      /* 将文件的指针定位到程序头 */
      sys_lseek(fd, prog_header_offset, SEEK_SET);

     /* 只获取程序头 */
      if (sys_read(fd, &prog_header, prog_header_size) != prog_header_size) {
	 ret = -1;
	 goto done;
      }

      /* 如果是可加载段就调用segment_load加载到内存 */
      if (PT_LOAD == prog_header.p_type) {
	 if (!segment_load(fd, prog_header.p_offset, prog_header.p_filesz, prog_header.p_vaddr)) {
	    ret = -1;
	    goto done;
	 }
      }

      /* 更新下一个程序头的偏移 */
      prog_header_offset += elf_header.e_phentsize;
      prog_idx++;
   }
   ret = elf_header.e_entry;
done:
   sys_close(fd);
   return ret;
}

/* 用path指向的程序替换当前进程 */
int32_t sys_execv(const char* path, const char* argv[]) {
   uint32_t argc = 0;
   while (argv[argc]) {
      argc++;
   }
   int32_t entry_point = load(path);     
   if (entry_point == -1) {	 // 若加载失败则返回-1
      return -1;
   }
   
   struct task_struct* cur = running_thread();
   /* 修改进程名 */
   memcpy(cur->name, path, TASK_NAME_LEN);
   cur->name[TASK_NAME_LEN-1] = 0;

   struct intr_stack* intr_0_stack = (struct intr_stack*)((uint32_t)cur + PG_SIZE - sizeof(struct intr_stack));
   /* 参数传递给用户进程 */
   intr_0_stack->ebx = (int32_t)argv;
   intr_0_stack->ecx = argc;
   intr_0_stack->eip = (void*)entry_point;
   /* 使新用户进程的栈地址为最高用户空间地址 */
   intr_0_stack->esp = (void*)0xc0000000;

   /* exec不同于fork,为使新进程更快被执行,直接从中断返回 */
   asm volatile ("movl %0, %%esp; jmp intr_exit" : : "g" (intr_0_stack) : "memory");
   return 0;
}

函数load接受1个参数，可执行文件的绝对路径pathname，功能是从文件系统上加载用户程序pathname，成功则返回程序的起始地址，否则返回−1。先定义了elf头elf_header和程序头prog_header，读取可执行文件的elf头到elf_header。开始校验elf 头，判断加载的文件是否是elf 格式的。elf 头的e_ident字段是elf 格式的魔数，它是个16 字节的数组：

  • e_ident[7～15]暂时未用；

  • 开头的4 个字节是固定不变的，它们分别是0x7f和字符串ELF的asc码0x45 0x4c 0x46。

  • 成员e_ident[4]表示elf 是32 位，还是64 位，值为1 表示32 位，值为2 表示64 位。

  • e_ident[5]表示字节序，值为1 表示小端字节序，值为2 表示大端字节序。

  • e_ident[6]表示elf 版本信息，默认为1。

  • e_ident[0-6]应该分别等于十六进制0x7F、0x45、0x4C、0x46、0x1、0x1 和0x1。

  • e_type表示目标文件类型，其值应该为ET_EXEC，即等于2。

  • e_machine表示体系结构，其值应该为EM_386，即等于3。

  • e_version表示版本信息，其值应该为1。

  • e_phnum用来指明程序头表中条目的数量，也就是段的个数，基值应该小于等于1024。

  • e_phentsize用来指明程序头表中每个条目的字节大小，也就是每个用来描述段信息的数据结构的字节大小，该结构就是struct Elf32_Phdr，因此值应该为sizeof (struct Elf32_Phdr)。

  • 程序头的起始地址记录在e_phoff中，将其获取到变量prog_header_offset。程序头条目大小记录在e_phentsize中，将其获取到变量prog_header_size中。

  • 程序头即段头，段的数量在e_phnum中记录，while 循环处理e_phnum 个段信息。

使用户进程支持参数

C 运行库也称为CRT（C RunTime library），它的实现也基于C 标准库，因此CRT 属于C 标准库的扩展。CRT 多是补充C 标准库中没有的功能，为适配本操作系统环境而定制开发的。因此CRT 并不通用，只适用于在本操作系统上运行的程序。其实CRT 代码才是用户程序的第一部分，我们的main 函数实质上是被夹在CRT 中执行的，它只是用户程序的中间部分，编译后的二进制可执行程序中还包括了 CRT 的指令。

1
2
3
4
5
6
7
8
9
[bits 32]
extern main
section .text
global _start
_start:
;下面这两个要和execv 中load 之后指定的寄存器一致
   push ebx ;压入argv
   push ecx ;压入argc
   call main

第2行通过extern main声明了外部函数main，即用户程序中的主函数main。第5行是标号_start，它是链接器默认的入口符号，如果ld 命令链接时未使用链接脚本或-e 参数指定入口符号的话，默认会以符号_start为程序入口。在文件exec.c中我们已经把新进程的参数压入内核栈中相应的寄存器，sys_execv执行完成从intr_exit返回后，寄存器ebx 是参数数组argv 的地址，寄存器ecx 是参数个数argc。因此将它们压入栈，此时的栈是用户栈，通过call 指令调用外部函数main，也就是用户程序开发人员所负责的主函数main。

系统调用 wait 和exit

exit 的作用很直白，就是使进程“主动”退出。wait 的作用是阻塞父进程自己，直到任意一个子进程结束运行。wait 通常是由父进程调用的。尽管某个进程没有子进程，但只要它调用了wait 系统调用，该进程就被认为是父进程，内核就要去查找它的子进程，由于它没有子进程，此时wait会返回−1，表示其没有子进程。如果有子进程，这时候该进程就被阻塞，不再运行，内核就要去遍历其所有的子进程，查找哪个子进程退出了，并将子进程退出时的返回值传递给父进程，随后将父进程唤醒。

C 运行库中调用exit的形式就是exit(子进程的返回值)，那子进程直接调用exit(返回值)就可以了。wait的原型是pid_t wait(int *status)，其中status 是父进程用于存储子进程返回值的地址，父进程调用它之后，内核就会把子进程的返回值存储到status 指向的内存空间。

当父进程提前退出时，它所有的子进程还在运行，这些进程就称为孤儿进程。这时init 进程会成为这些子进程的新父亲，当子进程退出时会由init 负责为其“收尸”。僵尸进程也称为zombie。如果父进程在派生出子进程后并没有调用wait 等待接收子进程的返回值，这时某个子进程调用exit 退出了，其pcb 所占的空间不能释放，僵尸进程就是针对子进程的返回值是否成功提交给父进程而提出的，父进程不调用wait，就无法获知子进程的返回值，从而内核就无法回收子进程pcb 所占的空间，因此就会在队列中占据一个进程表项。僵尸进程是没有进程体的，因为其进程体已在调用exit 时被内核回收了，现在只剩下一个pcb还在进程队列中，它并不占太多的资源。

管道

管道是进程间通信的方式之一，管道也被视为文件，只是该文件并不存在于文件系统上，而是只存在于内存中，也要使用open、close、read、write 等方法来操作管道。管道通常被多个进程共享，而且存在于内存之中，因此共享的原理是所有进程在地址空间中都可以访问到它，其实就是内核空间中的内存缓冲区，指环形缓冲区。管道有两端，一端用于从管道中读入数据，另一端用于往管道中写入数据。这两端使用文件描述符的
方式来读取，故进程创建管道实际上是内核为其返回了用于读取管道缓冲区的文件描述符，一个描述符用于读，另一个描述符用于写。

通常情况下是用户进程为内核提供一个长度为2的文件描述符数组，内核会在该数组中写入管道操作的两个描述符，假设数组名为fd，那么fd[0] 用于读取管道，fd[1]用于写入管道，进程与管道的读写关系如图。

通常的用法是进程在创建管道之后，马上调用fork，克隆出一个子进程，子进程完全继承了父进程的一切，父子进程都可以通过文件描述符fd[1] 向管道中写数据，通过文件描述符fd[0]从管道中读取数据*。

管道分为两种：匿名管道和命名管道，匿名管道在创建之后只能通过内核为其返回的文件描述符来访问，此管道只对创建它的进程及其子进程可见，对其他进程不可见，因此除父子进程之外的其他进程便不知道此管道的存在，故匿名管道只能局限用于父子进程间的通信。有名管道是专门为解决匿名管道的局限性而生的，在Linux 中可以通过命令mkfifo 来创建命名管道。

管道的设计

管道对于Linux 来说也是文件，因此它也需要用文件相关的数据结构来处理管道，Linux 是利用现有的文件结构和VFS 索引结点的inode 共同完成
管道的，并没有单独为管道创建新的数据结构，结构示意如图。

文件结构中的f_inode指向VFS 的inode，该inode指向1 个页框大小的内存区域，该区域便是管道用于存储数据的内存空间。也就是说，Linux 的管道大小是4096 字节。f_op用于指向操作（OPeration）方法。对于管道来说，f_op会指向pipe_read和pipe_write，pipe_read会从管道的 1 页内存中读取数据，pipe_write会往管道的1 页内存中写入数据。管道不需要inode，fd_flags的值将是0xFFFF，不再是O_RDONLY、O_WRONLY等值。把文件结构中的fd_inode指向管道的内存缓冲区。

无论进程的文件描述符是多少，只要使任意进程的文件描述符所指向的、位于file_table中的文件结构是同一个就行了。

为避免进程无限休眠的情况，我们让生产者和消费者每次只读写“适量”的数据，避免环形缓冲区满或空的情况，这样生产者或消费者进程就不会阻塞了。

在Linux 中创建管道的方法是系统调用pipe，其原型是int pipe(int pipefd[2])，成功返回0，失败返回−1，其中pipefd[2]是长度为2的整型数组，用来存储系统返回的文件描述符，文件描述符fd[0]用于读取管道，fd[1]用于写入管道。

1
2
3
4
5
6
7
8
9
10
/* 返回环形缓冲区中的数据长度 */
uint32_t ioq_length(struct ioqueue* ioq) {
   uint32_t len = 0;
   if (ioq->head >= ioq->tail) {
      len = ioq->head - ioq->tail;
   } else {
      len = bufsize - (ioq->tail - ioq->head);     
   }
   return len;
}

函数ioq_length 接受1 个参数，环形缓冲区ioq，功能是返回环形缓冲区中的数据长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
/* 判断文件描述符local_fd是否是管道 */
bool is_pipe(uint32_t local_fd) {
   uint32_t global_fd = fd_local2global(local_fd); 
   return file_table[global_fd].fd_flag == PIPE_FLAG;
}

/* 创建管道,成功返回0,失败返回-1 */
int32_t sys_pipe(int32_t pipefd[2]) {
   int32_t global_fd = get_free_slot_in_global();

   /* 申请一页内核内存做环形缓冲区 */
   file_table[global_fd].fd_inode = get_kernel_pages(1); 

   /* 初始化环形缓冲区 */
   ioqueue_init((struct ioqueue*)file_table[global_fd].fd_inode);
   if (file_table[global_fd].fd_inode == NULL) {
      return -1;
   }
  
   /* 将fd_flag复用为管道标志 */
   file_table[global_fd].fd_flag = PIPE_FLAG;

   /* 将fd_pos复用为管道打开数 */
   file_table[global_fd].fd_pos = 2;
   pipefd[0] = pcb_fd_install(global_fd);
   pipefd[1] = pcb_fd_install(global_fd);
   return 0;
}

/* 从管道中读数据 */
uint32_t pipe_read(int32_t fd, void* buf, uint32_t count) {
   char* buffer = buf;
   uint32_t bytes_read = 0;
   uint32_t global_fd = fd_local2global(fd);

   /* 获取管道的环形缓冲区 */
   struct ioqueue* ioq = (struct ioqueue*)file_table[global_fd].fd_inode;

   /* 选择较小的数据读取量,避免阻塞 */
   uint32_t ioq_len = ioq_length(ioq);
   uint32_t size = ioq_len > count ? count : ioq_len;
   while (bytes_read < size) {
      *buffer = ioq_getchar(ioq);
      bytes_read++;
      buffer++;
   }
   return bytes_read;
}

/* 往管道中写数据 */
uint32_t pipe_write(int32_t fd, const void* buf, uint32_t count) {
   uint32_t bytes_write = 0;
   uint32_t global_fd = fd_local2global(fd);
   struct ioqueue* ioq = (struct ioqueue*)file_table[global_fd].fd_inode;

   /* 选择较小的数据写入量,避免阻塞 */
   uint32_t ioq_left = bufsize - ioq_length(ioq);
   uint32_t size = ioq_left > count ? count : ioq_left;

   const char* buffer = buf;
   while (bytes_write < size) {
      ioq_putchar(ioq, *buffer);
      bytes_write++;
      buffer++;
   }
   return bytes_write;
}

先看下代码第二个函数sys_pipe，它接受1个参数，存储管道文件描述符的数组pipefd，功能是创建管道，成功后描述符pipefd[0] 可用于读取管道，pipefd[1] 可用于写入管道，然后返回值为0，否则返回−1。函数先调用get_free_slot_in_global从file_table中获得可用的文件结构空位下标，记为global_fd，然后为该文件结构中的fd_inode分配一页内核内存做管道的环形缓冲区。接着调用ioqueue_init初始化环形缓冲区。将该文件结构的fd_flag置为宏PIPE_FLAG，宏PIPE_FLAG定义在pipe.h中，代码是#define PIPE_FLAG 0xFFFF，正如我们在设计阶段所说的，复用了文件结构中的fd_flag成员，把该值置为0xFFFF来表示此文件结构对应的是管道。把fd_pos置为2，表示有两个文件描述符对应这个管道，描述符分别存储到pipefd[0]和pipefd[1]中，我们分别用它们来读取和写入管道。

函数is_pipe接受1 个参数，文件描述符local_fd，功能是判断文件描述符local_fd是否是管道。判断的原理是先找出local_fd对应的file_table中的下标global_fd，然后判断文件表file_talbe[global_fd]的fd_flag的值是否为PIPE_FLAG。函数pipe_read接受3 个参数，文件描述符fd、存储数据的缓冲区buf、读取数据的数量count，功能是从文件描述符fd 中读取count 字节到buf。函数pipe_write功能是把缓冲区buf 中的count 个字节写入管道对应的文件描述符fd。

在shell 中支持管道

管道利用了输入输出重定向。如果命令的输入并不来自于键盘，而是来自于文件，这就称为输入重定向，如果命令的输出并不是屏幕，而是想写入到文件，这就称为输出重定向。利用输入输出重定向的原理，可以将一个命令的输出作为另一个命令的输入。因此命令行中若包括管道符，则将管道符左边
命令的输出作为管道符右边命令的输入。

1
2
3
4
5
6
7
8
9
10
11
/* 将文件描述符old_local_fd重定向为new_local_fd */
void sys_fd_redirect(uint32_t old_local_fd, uint32_t new_local_fd) {
   struct task_struct* cur = running_thread();
   /* 针对恢复标准描述符 */
   if (new_local_fd < 3) {
      cur->fd_table[old_local_fd] = new_local_fd;
   } else {
      uint32_t new_global_fd = cur->fd_table[new_local_fd];
      cur->fd_table[old_local_fd] = new_global_fd;
   }
}

函数sys_fd_redirect接受2 个参数，旧文件描述符old_local_fd、新文件描述符new_local_fd，功能是**将文件描述符old_local_fd重定向为new_local_fd。将数组fd_table中下标为old_local_fd的元素的值用下标为new_local_fd的元素的值替换。另外，pcb 中文件描述符表fd_table和全局文件表file_table中的前3 个元素都是预留的，它们分别作为标准输入、标准输出和标准错误，因此，如果new_local_fd小于3 的话，不需要从fd_table中获取元素值，可以直接把new_local_fd赋值给fd_table[old_local_fd]，而这通常用于将输入输出恢复为标准的输入输出。获取了当前线程cur，对标准输入输出做了特殊处理，如果new_local_fd小于3，直接将new_local_fd给cur->fd_table[old_local_fd]赋值，否则先获得new_local_fd对应的file_table下标new_global_fd，然后将new_global_fd赋值给cur->fd_table[old_local_fd]，至此完成了重定向。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
/* 执行命令 */
static void cmd_execute(uint32_t argc, char** argv) {
   if (!strcmp("ls", argv[0])) {
      buildin_ls(argc, argv);
   } else if (!strcmp("cd", argv[0])) {
      if (buildin_cd(argc, argv) != NULL) {
	 memset(cwd_cache, 0, MAX_PATH_LEN);
	 strcpy(cwd_cache, final_path);
      }
   } else if (!strcmp("pwd", argv[0])) {
      buildin_pwd(argc, argv);
   } else if (!strcmp("ps", argv[0])) {
      buildin_ps(argc, argv);
   } else if (!strcmp("clear", argv[0])) {
      buildin_clear(argc, argv);
   } else if (!strcmp("mkdir", argv[0])){
      buildin_mkdir(argc, argv);
   } else if (!strcmp("rmdir", argv[0])){
      buildin_rmdir(argc, argv);
   } else if (!strcmp("rm", argv[0])) {
      buildin_rm(argc, argv);
   } else if (!strcmp("help", argv[0])) {
      buildin_help(argc, argv);
   } else {      // 如果是外部命令,需要从磁盘上加载
      int32_t pid = fork();
      if (pid) {	   // 父进程
	 int32_t status;
	 int32_t child_pid = wait(&status);          // 此时子进程若没有执行exit,my_shell会被阻塞,不再响应键入的命令
	 if (child_pid == -1) {     // 按理说程序正确的话不会执行到这句,fork出的进程便是shell子进程
	    panic("my_shell: no child\n");
	 }
	 printf("child_pid %d, it's status: %d\n", child_pid, status);
      } else {	   // 子进程
	 make_clear_abs_path(argv[0], final_path);
	 argv[0] = final_path;

	 /* 先判断下文件是否存在 */
	 struct stat file_stat;
	 memset(&file_stat, 0, sizeof(struct stat));
	 if (stat(argv[0], &file_stat) == -1) {
	    printf("my_shell: cannot access %s: No such file or directory\n", argv[0]);
	    exit(-1);
	 } else {
	    execv(argv[0], argv);
	 }
      }
   }
}

char* argv[MAX_ARG_NR] = {NULL};
int32_t argc = -1;
/* 简单的shell */
void my_shell(void) {
   cwd_cache[0] = '/';
   while (1) {
      print_prompt(); 
      memset(final_path, 0, MAX_PATH_LEN);
      memset(cmd_line, 0, MAX_PATH_LEN);
      readline(cmd_line, MAX_PATH_LEN);
      if (cmd_line[0] == 0) {	 // 若只键入了一个回车
	 continue;
      }

      /* 针对管道的处理 */
      char* pipe_symbol = strchr(cmd_line, '|');
      if (pipe_symbol) {
   /* 支持多重管道操作,如cmd1|cmd2|..|cmdn,
    * cmd1的标准输出和cmdn的标准输入需要单独处理 */

   /*1 生成管道*/
	 int32_t fd[2] = {-1};	    // fd[0]用于输入,fd[1]用于输出
	 pipe(fd);
	 /* 将标准输出重定向到fd[1],使后面的输出信息重定向到内核环形缓冲区 */
	 fd_redirect(1,fd[1]);

   /*2 第一个命令 */
	 char* each_cmd = cmd_line;
	 pipe_symbol = strchr(each_cmd, '|');
	 *pipe_symbol = 0;

	 /* 执行第一个命令,命令的输出会写入环形缓冲区 */
	 argc = -1;
	 argc = cmd_parse(each_cmd, argv, ' ');
	 cmd_execute(argc, argv);

	 /* 跨过'|',处理下一个命令 */
	 each_cmd = pipe_symbol + 1;

	 /* 将标准输入重定向到fd[0],使之指向内核环形缓冲区*/
	 fd_redirect(0,fd[0]);
   /*3 中间的命令,命令的输入和输出都是指向环形缓冲区 */
	 while ((pipe_symbol = strchr(each_cmd, '|'))) { 
	    *pipe_symbol = 0;
	    argc = -1;
	    argc = cmd_parse(each_cmd, argv, ' ');
	    cmd_execute(argc, argv);
	    each_cmd = pipe_symbol + 1;
	 }

   /*4 处理管道中最后一个命令 */
	 /* 将标准输出恢复屏幕 */
         fd_redirect(1,1);

	 /* 执行最后一个命令 */
	 argc = -1;
	 argc = cmd_parse(each_cmd, argv, ' ');
	 cmd_execute(argc, argv);

   /*5  将标准输入恢复为键盘 */
         fd_redirect(0,0);

   /*6 关闭管道 */
	 close(fd[0]);
	 close(fd[1]);
      } else {		// 一般无管道操作的命令
	 argc = -1;
	 argc = cmd_parse(cmd_line, argv, ' ');
	 if (argc == -1) {
	    printf("num of arguments exceed %d\n", MAX_ARG_NR);
	    continue;
	 }
	 cmd_execute(argc, argv);
      }
   }
   panic("my_shell: should not be here");
}

把shell.c中原本判断内建、外部命令的一堆if else 封装到函数cmd_execute中。通过strchr函数在cmd_line中寻找管道字符’|’，如果找到，pipe_symbol的值则为字符’|’的地址。

除cmd1 的标准输入和cmdn 的标准输出不变外，其他命令的标准输入和输出都要重定向到管道。下面分六步来完成管道操作。

  • 第一步，生成管道，这是调用pipe系统调用完成的。调用fd_redirect(1,fd[1])将标准输出重定向到用于写管道的文件描述符fd[1]，至此程序的输出都写到管道中。
  • 第二步，解析第1 个命令并执行。命令行中的各个命令是用指针each_cmd记录的，它指向各命令在cmd_line中的地址。解析出命令后调用cmd_execute执行，然后使pipe_symbol加1，跨过cmd_line 中的相应的’|’。在执行第2个命令之前，执行fd_redirect(0,fd[0])将标准输入重定向到管道，这样第2 个命令才能获得第1 个命令的输出。
  • 第三步，循环处理cmd2~cmdn-1，此时它们的标准输入和输出都已指向管道，继续解析命令并执行。
  • 第四步，调用fd_redirect(1,1)将标准输出恢复为屏幕，然后执行最后一个命令，此时命令的输出信息会在屏幕上显示。
  • 第五步，调用fd_redirect(0,0)将标准输入恢复为键盘。
  • 第六步，将管道关闭。

Posted on Edited on

什么是一致性

多个节点之间不能产生矛盾。

CAP

对一个分布式系统，不能同时满足以下三点：

  • 一致性
  • 可用性
  • 分区容错性

要在一致性和可用性之间进行取舍。

一致性模型

弱一致性：最终一致性，向数据库中写数据，如果立即读取的话不保证能读取到，但是保证你最终读取到。例如DNS服务器，Cassandra的通信协议Gossip。

强一致性：分布式系统希望数据不能存在单个节点上，分布式系统对fault tolerance主要解决方案是state machine replication的共识算法。paxos其实是一个共识算法，系统的最终一致性不仅需要达成共识，还会取决于client。

强一致性算法

主从同步复制：

  • Master接受写请求
  • Master复制日志到slave
  • Master等到，直至所有从库返回，所有从库返回之前系统不可用

强一致性算法的主要思想是多数派，每次写都保证写入大于N/2个节点，每次读保证从大于N/2个节点中读。但是在并发的时候无法保证系统的正确性，顺序非常重要，如下图的例子。

Paxos

Basic Paxos算法中的角色：

  • Client：系统外部角色，请求发起者，像民众。
  • Proposer：接受Clinet请求，向集群发出提议，并在冲突发生时，起到冲突调节的作用。像议员提出提案。
  • Acceptor：提议投票和接收者，只有在形成法定人数（Quorum，多数派）的时候，提案才会被接受，像国会。
  • Learner：提议接收者，备份，对集群一致性没什么影响。

Basic Paxos的阶段：

  • prepare：一个client通过proposer提出一个提案，编号为N，此N大于这个proposer之前提出的提案编号，请求接受这个提案。
  • promise：如果N大于此acceptor之前接受的任何提案编号则接受，否则拒绝。
  • accept：如果达到了多数派，proposer会发出accept请求，此请求包含提案编号N以及提案内容。
  • accepted：如果此acceptor在此期间没有收到任何编号大于N的提案，则接受此提案内容，否则忽略。

假如proposer失败：

client发起请求，但是接受请求的proposer失败了，proposer准备1号提案，acceptor接受，但是让proposer接受时宕机，另外一个proposer启动起来，接替上一个proposer继续向acceptor发送请求，最终返回到client。即使第一次没有完成的话，也有接续的proposer继续完成。

活锁：两个议员同时提出议案，先讨论提案号大的，但是提案号小的那个会重新更新提案号再提交，这样一直争论，其实都是两个相同的提案，只是因为同时提交了。用一个random的时间，把两个矛盾的提案隔开，避免冲突的发生。

basic paxos难以实现，角色很多。使用multi paxos。multi提出了leader的概念，所有的提案都要经过这个leader，就是唯一一个proposer，不管client请求来不来，proposer之间先竞选，选出一个leader，只能这个leader提出提案，其他的proposer提出的都不予理会。在一个server的任期之内，任何请求只需要一轮请求即可。

资料

Paxos将系统中的角色分为提议者 (Proposer)，决策者 (Acceptor)，和最终决策学习者 (Learner):

  • Proposer: 提出提案 (Proposal)。Proposal信息包括提案编号 (Proposal ID) 和提议的值 (Value)。
  • Acceptor：参与决策，回应Proposers的提案。收到Proposal后可以接受提案，若Proposal获得多数Acceptors的接受，则称该Proposal被批准。
  • Learner：不参与决策，从Proposers/Acceptors学习最新达成一致的提案（Value）。
  • 在多副本状态机中，每个副本同时具有Proposer、Acceptor、Learner三种角色。

Paxos算法中的角色

Paxos算法通过一个决议分为两个阶段（Learn阶段之前决议已经形成）：

  • 第一阶段：Prepare阶段。Proposer向Acceptors发出Prepare请求，Acceptors针对收到的Prepare请求进行Promise承诺。
  • 第二阶段：Accept阶段。Proposer收到多数Acceptors承诺的Promise后，向Acceptors发出Propose请求，Acceptors针对收到的Propose请求进行Accept处理。
  • 第三阶段：Learn阶段。Proposer在收到多数Acceptors的Accept之后，标志着本次Accept成功，决议形成，将形成的决议发送给所有Learners。

Paxos算法流程

Paxos算法流程中的每条消息描述如下：

  • Prepare: Proposer生成全局唯一且递增的Proposal ID (可使用时间戳加Server ID)，向所有Acceptors发送Prepare请求，这里无需携带提案内容，只携带Proposal ID即可。
  • Promise: Acceptors收到Prepare请求后，做出“两个承诺，一个应答”。

两个承诺：

  1. 不再接受Proposal ID小于等于（注意：这里是<= ）当前请求的Prepare请求。
  2. 不再接受Proposal ID小于（注意：这里是< ）当前请求的Propose请求。

一个应答：

不违背以前作出的承诺下，回复已经Accept过的提案中Proposal ID最大的那个提案的Value和Proposal ID，没有则返回空值。

Propose: Proposer 收到多数Acceptors的Promise应答后，从应答中选择Proposal ID最大的提案的Value，作为本次要发起的提案。如果所有应答的提案Value均为空值，则可以自己随意决定提案Value。然后携带当前Proposal ID，向所有Acceptors发送Propose请求。
Accept: Acceptor收到Propose请求后，在不违背自己之前作出的承诺下，接受并持久化当前Proposal ID和提案Value。
Learn: Proposer收到多数Acceptors的Accept后，决议形成，将形成的决议发送给所有Learners。

Paxos算法伪代码描述如下：

  • 获取一个Proposal ID n，为了保证Proposal ID唯一，可采用时间戳+Server ID生成；
  • Proposer向所有Acceptors广播Prepare(n)请求；
  • Acceptor比较n和minProposal，如果n>minProposal，minProposal=n，并且将 acceptedProposal 和 acceptedValue 返回；
  • Proposer接收到过半数回复后，如果发现有acceptedValue返回，将所有回复中acceptedProposal最大的acceptedValue作为本次提案的value，否则可以任意决定本次提案的value；
  • 到这里可以进入第二阶段，广播Accept (n,value) 到所有节点；
  • Acceptor比较n和minProposal，如果n>=minProposal，则acceptedProposal=minProposal=n，acceptedValue=value，本地持久化后，返回；否则，返回minProposal。
  • 提议者接收到过半数请求后，如果发现有返回值result >n，表示有更新的提议，跳转到1；否则value达成一致。

原始的Paxos算法（Basic Paxos）只能对一个值形成决议，决议的形成至少需要两次网络来回，在高并发情况下可能需要更多的网络来回，极端情况下甚至可能形成活锁。如果想连续确定多个值，Basic Paxos搞不定了。因此Basic Paxos几乎只是用来做理论研究，并不直接应用在实际工程中。

实际应用中几乎都需要连续确定多个值，而且希望能有更高的效率。Multi-Paxos正是为解决此问题而提出。Multi-Paxos基于Basic Paxos做了两点改进：

针对每一个要确定的值，运行一次Paxos算法实例（Instance），形成决议。每一个Paxos实例使用唯一的Instance ID标识。
在所有Proposers中选举一个Leader，由Leader唯一地提交Proposal给Acceptors进行表决。这样没有Proposer竞争，解决了活锁问题。在系统中仅有一个Leader进行Value提交的情况下，Prepare阶段就可以跳过，从而将两阶段变为一阶段，提高效率。

Multi-Paxos首先需要选举Leader，Leader的确定也是一次决议的形成，所以可执行一次Basic Paxos实例来选举出一个Leader。选出Leader之后只能由Leader提交Proposal，在Leader宕机之后服务临时不可用，需要重新选举Leader继续服务。在系统中仅有一个Leader进行Proposal提交的情况下，Prepare阶段可以跳过。

Multi-Paxos通过改变Prepare阶段的作用范围至后面Leader提交的所有实例，从而使得Leader的连续提交只需要执行一次Prepare阶段，后续只需要执行Accept阶段，将两阶段变为一阶段，提高了效率。为了区分连续提交的多个实例，每个实例使用一个Instance ID标识，Instance ID由Leader本地递增生成即可。

Multi-Paxos允许有多个自认为是Leader的节点并发提交Proposal而不影响其安全性，这样的场景即退化为Basic Paxos。

Raft

把达到共识、日志复制这个问题划分成3个子问题，怎么选leader，怎么把log同步到其他节点，怎么保证集群的共识是一致的。重定义了角色，把server分成三个角色，leader，follower(从其中选择leader)，candidate(follower竞选leader时的中间角色)。

多个节点中，follower只能从leader处获得命令，所有节点都是从follower状态开始的，有一个follower想要成为leader，则进入candidate状态，开始投票，同意了则称为leader。所有的请求都会经过leader，由leader向这些节点公布。leader自己先写入，再告诉其他的节点写入，这个过程叫log replication。Raft用timeout控制选举，如果经过一段时间，节点还没有收到leader的心跳信息，这时认为集群中是没有leader的，开始竞选。如果一个节点成为candidate，则另外节点的时钟被刷新，就不会参与竞选，除非经过一段时间后没有收到leader节点的心跳。两个节点同时成为candidate，并且选票相等，然后这两个节点会随机等待一个timeout，如果时间短的timeout会成为leader。所有的写请求都会经过leader，leader会把log发送给所有节点。

资料

不同于Paxos算法直接从分布式一致性问题出发推导出来，Raft算法则是从多副本状态机的角度提出，用于管理多副本状态机的日志复制。Raft实现了和Paxos相同的功能，它将一致性分解为多个子问题：Leader选举（Leader election）、日志同步（Log replication）、安全性（Safety）、日志压缩（Log compaction）、成员变更（Membership change）等。同时，Raft算法使用了更强的假设来减少了需要考虑的状态，使之变的易于理解和实现。

Raft将系统中的角色分为领导者（Leader）、跟从者（Follower）和候选人（Candidate）：

Leader：接受客户端请求，并向Follower同步请求日志，当日志同步到大多数节点上后告诉Follower提交日志。
Follower：接受并持久化Leader同步的日志，在Leader告之日志可以提交之后，提交日志。
Candidate：Leader选举过程中的临时角色。

Raft要求系统在任意时刻最多只有一个Leader，正常工作期间只有Leader和Followers。

Raft算法角色状态转换如下：

Follower只响应其他服务器的请求。如果Follower超时没有收到Leader的消息，它会成为一个Candidate并且开始一次Leader选举。收到大多数服务器投票的Candidate会成为新的Leader。Leader在宕机之前会一直保持Leader的状态。

Raft算法将时间分为一个个的任期（term），每一个term的开始都是Leader选举。在成功选举Leader之后，Leader会在整个term内管理整个集群。如果Leader选举失败，该term就会因为没有Leader而结束。

Leader选举

Raft 使用心跳（heartbeat）触发Leader选举。当服务器启动时，初始化为Follower。Leader向所有Followers周期性发送heartbeat。如果Follower在选举超时时间内没有收到Leader的heartbeat，就会等待一段随机的时间后发起一次Leader选举。

Follower将其当前term加一然后转换为Candidate。它首先给自己投票并且给集群中的其他服务器发送 RequestVote RPC （RPC细节参见八、Raft算法总结）。结果有以下三种情况：

赢得了多数的选票，成功选举为Leader；

  • 收到了Leader的消息，表示有其它服务器已经抢先当选了Leader；
  • 没有服务器赢得多数的选票，Leader选举失败，等待选举时间超时后发起下一次选举。

选举出Leader后，Leader通过定期向所有Followers发送心跳信息维持其统治。若Follower一段时间未收到Leader的心跳则认为Leader可能已经挂了，再次发起Leader选举过程。

Raft保证选举出的Leader上一定具有最新的已提交的日志，这一点将在四、安全性中说明。

日志同步

Leader选出后，就开始接收客户端的请求。Leader把请求作为日志条目（Log entries）加入到它的日志中，然后并行的向其他服务器发起 AppendEntries RPC （RPC细节参见八、Raft算法总结）复制日志条目。当这条日志被复制到大多数服务器上，Leader将这条日志应用到它的状态机并向客户端返回执行结果。

某些Followers可能没有成功的复制日志，Leader会无限的重试 AppendEntries RPC直到所有的Followers最终存储了所有的日志条目。

日志由有序编号（log index）的日志条目组成。每个日志条目包含它被创建时的任期号（term），和用于状态机执行的命令。如果一个日志条目被复制到大多数服务器上，就被认为可以提交（commit）了。

Raft日志同步保证如下两点：

如果不同日志中的两个条目有着相同的索引和任期号，则它们所存储的命令是相同的。
如果不同日志中的两个条目有着相同的索引和任期号，则它们之前的所有条目都是完全一样的。
第一条特性源于Leader在一个term内在给定的一个log index最多创建一条日志条目，同时该条目在日志中的位置也从来不会改变。

第二条特性源于 AppendEntries 的一个简单的一致性检查。当发送一个 AppendEntries RPC 时，Leader会把新日志条目紧接着之前的条目的log index和term都包含在里面。如果Follower没有在它的日志中找到log index和term都相同的日志，它就会拒绝新的日志条目。

一般情况下，Leader和Followers的日志保持一致，因此 AppendEntries 一致性检查通常不会失败。然而，Leader崩溃可能会导致日志不一致：旧的Leader可能没有完全复制完日志中的所有条目。

上图阐述了一些Followers可能和新的Leader日志不同的情况。一个Follower可能会丢失掉Leader上的一些条目，也有可能包含一些Leader没有的条目，也有可能两者都会发生。丢失的或者多出来的条目可能会持续多个任期。

Leader通过强制Followers复制它的日志来处理日志的不一致，Followers上的不一致的日志会被Leader的日志覆盖。

Leader为了使Followers的日志同自己的一致，Leader需要找到Followers同它的日志一致的地方，然后覆盖Followers在该位置之后的条目。

Leader会从后往前试，每次AppendEntries失败后尝试前一个日志条目，直到成功找到每个Follower的日志一致位点，然后向后逐条覆盖Followers在该位置之后的条目。

安全性

Raft增加了如下两条限制以保证安全性：

拥有最新的已提交的log entry的Follower才有资格成为Leader。
这个保证是在RequestVote RPC中做的，Candidate在发送RequestVote RPC时，要带上自己的最后一条日志的term和log index，其他节点收到消息时，如果发现自己的日志比请求中携带的更新，则拒绝投票。日志比较的原则是，如果本地的最后一条log entry的term更大，则term大的更新，如果term一样大，则log index更大的更新。

Leader只能推进commit index来提交当前term的已经复制到大多数服务器上的日志，旧term日志的提交要等到提交当前term的日志来间接提交（log index 小于 commit index的日志被间接提交）。
之所以要这样，是因为可能会出现已提交的日志又被覆盖的情况：

在阶段a，term为2，S1是Leader，且S1写入日志（term, index）为(2, 2)，并且日志被同步写入了S2；

在阶段b，S1离线，触发一次新的选主，此时S5被选为新的Leader，此时系统term为3，且写入了日志（term, index）为（3， 2）;

S5尚未将日志推送到Followers就离线了，进而触发了一次新的选主，而之前离线的S1经过重新上线后被选中变成Leader，此时系统term为4，此时S1会将自己的日志同步到Followers，按照上图就是将日志（2， 2）同步到了S3，而此时由于该日志已经被同步到了多数节点（S1, S2, S3），因此，此时日志（2，2）可以被提交了。；

在阶段d，S1又下线了，触发一次选主，而S5有可能被选为新的Leader（这是因为S5可以满足作为主的一切条件：1. term = 5 > 4，2. 最新的日志为（3，2），比大多数节点（如S2/S3/S4的日志都新），然后S5会将自己的日志更新到Followers，于是S2、S3中已经被提交的日志（2，2）被截断了。

增加上述限制后，即使日志（2，2）已经被大多数节点（S1、S2、S3）确认了，但是它不能被提交，因为它是来自之前term（2）的日志，直到S1在当前term（4）产生的日志（4， 4）被大多数Followers确认，S1方可提交日志（4，4）这条日志，当然，根据Raft定义，（4，4）之前的所有日志也会被提交。此时即使S1再下线，重新选主时S5不可能成为Leader，因为它没有包含大多数节点已经拥有的日志（4，4）。

日志压缩

在实际的系统中，不能让日志无限增长，否则系统重启时需要花很长的时间进行回放，从而影响可用性。Raft采用对整个系统进行snapshot来解决，snapshot之前的日志都可以丢弃。

每个副本独立的对自己的系统状态进行snapshot，并且只能对已经提交的日志记录进行snapshot。

Snapshot中包含以下内容：

日志元数据。最后一条已提交的 log entry的 log index和term。这两个值在snapshot之后的第一条log entry的AppendEntries RPC的完整性检查的时候会被用上。
系统当前状态。
当Leader要发给某个日志落后太多的Follower的log entry被丢弃，Leader会将snapshot发给Follower。或者当新加进一台机器时，也会发送snapshot给它。发送snapshot使用InstalledSnapshot RPC（RPC细节参见八、Raft算法总结）。

做snapshot既不要做的太频繁，否则消耗磁盘带宽， 也不要做的太不频繁，否则一旦节点重启需要回放大量日志，影响可用性。推荐当日志达到某个固定的大小做一次snapshot。

做一次snapshot可能耗时过长，会影响正常日志同步。可以通过使用copy-on-write技术避免snapshot过程影响正常日志同步。

成员变更

成员变更是在集群运行过程中副本发生变化，如增加/减少副本数、节点替换等。

成员变更也是一个分布式一致性问题，既所有服务器对新成员达成一致。但是成员变更又有其特殊性，因为在成员变更的一致性达成的过程中，参与投票的进程会发生变化。

如果将成员变更当成一般的一致性问题，直接向Leader发送成员变更请求，Leader复制成员变更日志，达成多数派之后提交，各服务器提交成员变更日志后从旧成员配置（Cold）切换到新成员配置（Cnew）。

因为各个服务器提交成员变更日志的时刻可能不同，造成各个服务器从旧成员配置（Cold）切换到新成员配置（Cnew）的时刻不同。

成员变更不能影响服务的可用性，但是成员变更过程的某一时刻，可能出现在Cold和Cnew中同时存在两个不相交的多数派，进而可能选出两个Leader，形成不同的决议，破坏安全性。

由于成员变更的这一特殊性，成员变更不能当成一般的一致性问题去解决。

为了解决这一问题，Raft提出了两阶段的成员变更方法。集群先从旧成员配置Cold切换到一个过渡成员配置，称为共同一致（joint consensus），共同一致是旧成员配置Cold和新成员配置Cnew的组合Cold U Cnew，一旦共同一致Cold U Cnew被提交，系统再切换到新成员配置Cnew。

Raft两阶段成员变更过程如下：

  • Leader收到成员变更请求从Cold切成Cnew；
  • Leader在本地生成一个新的log entry，其内容是Cold∪Cnew，代表当前时刻新旧成员配置共存，写入本地日志，同时将该log entry复制至Cold∪Cnew中的所有副本。在此之后新的日志同步需要保证得到Cold和Cnew两个多数派的确认；
  • Follower收到Cold∪Cnew的log entry后更新本地日志，并且此时就以该配置作为自己的成员配置；
  • 如果Cold和Cnew中的两个多数派确认了Cold U Cnew这条日志，Leader就提交这条log entry；
  • 接下来Leader生成一条新的log entry，其内容是新成员配置Cnew，同样将该log entry写入本地日志，同时复制到Follower上；
  • Follower收到新成员配置Cnew后，将其写入日志，并且从此刻起，就以该配置作为自己的成员配置，并且如果发现自己不在Cnew这个成员配置中会自动退出；
  • Leader收到Cnew的多数派确认后，表示成员变更成功，后续的日志只要得到Cnew多数派确认即可。Leader给客户端回复成员变更执行成功。

异常分析：

  • 如果Leader的Cold U Cnew尚未推送到Follower，Leader就挂了，此后选出的新Leader并不包含这条日志，此时新Leader依然使用Cold作为自己的成员配置。
  • 如果Leader的Cold U Cnew推送到大部分的Follower后就挂了，此后选出的新Leader可能是Cold也可能是Cnew中的某个Follower。
  • 如果Leader在推送Cnew配置的过程中挂了，那么同样，新选出来的Leader可能是Cold也可能是Cnew中的某一个，此后客户端继续执行一次改变配置的命令即可。
  • 如果大多数的Follower确认了Cnew这个消息后，那么接下来即使Leader挂了，新选出来的Leader肯定位于Cnew中。

两阶段成员变更比较通用且容易理解，但是实现比较复杂，同时两阶段的变更协议也会在一定程度上影响变更过程中的服务可用性，因此我们期望增强成员变更的限制，以简化操作流程。

两阶段成员变更，之所以分为两个阶段，是因为对Cold与Cnew的关系没有做任何假设，为了避免Cold和Cnew各自形成不相交的多数派选出两个Leader，才引入了两阶段方案。

如果增强成员变更的限制，假设Cold与Cnew任意的多数派交集不为空，这两个成员配置就无法各自形成多数派，那么成员变更方案就可能简化为一阶段。

那么如何限制Cold与Cnew，使之任意的多数派交集不为空呢？方法就是每次成员变更只允许增加或删除一个成员。

可从数学上严格证明，只要每次只允许增加或删除一个成员，Cold与Cnew不可能形成两个不相交的多数派。

一阶段成员变更：

  • 成员变更限制每次只能增加或删除一个成员（如果要变更多个成员，连续变更多次）。
  • 成员变更由Leader发起，Cnew得到多数派确认后，返回客户端成员变更成功。
  • 一次成员变更成功前不允许开始下一次成员变更，因此新任Leader在开始提供服务前要将自己本地保存的最新成员配置重新投票形成多数派确认。
  • Leader只要开始同步新成员配置，即可开始使用新的成员配置进行日志同步。

Raft算法总结

Raft算法各节点维护的状态：

Leader选举：

日志同步：

Raft状态机：

ZAB

ZAB(ZooKeeper Atomic Broadcast)则是为ZooKeeper设计的一种支持崩溃恢复的原子广播协议。

在看ZAB之前我们先复习一下两阶段提交协议

两阶段提交顾名思义主要分为两个阶段

  • 第一阶段（请求阶段）:协调者首先会发送某个事务的执行请求给其它所有的参与者，当参与者收到perpare请求时会检查自身并告诉协调者自己的决策是同意还是取消
  • 第二阶段（提交阶段）:协调者将根据第一阶段的投票结果发送提交或回滚请求（一般是所有参与者都返回同意就发送提交请求，否则发送回滚请求）。

当然两阶段提交协议并不完美，而且存在数据不一致、同步阻塞、单点等问题，这里不在本文的讨论范围

协议介绍

好了，复习完两阶段提交协议，接下来我们继续来分析ZAB协议。

很多人会误以为ZAB协议是Paxos的一种特殊实现，事实上他们是两种不同的协议。ZAB和Paxos最大的不同是，ZAB主要是为分布式主备系统设计的，而Paxos的实现是一致性状态机(state machine replication)尽管ZAB不是Paxos的实现，但是ZAB也参考了一些Paxos的一些设计思想，比如：

  • leader向follows提出提案(proposal)
  • leader 需要在达到法定数量(半数以上)的follows确认之后才会进行commit
  • 每一个proposal都有一个纪元(epoch)号，类似于Paxos中的选票(ballot)

ZAB特性

一致性保证

  • 可靠提交(Reliable delivery) -如果一个事务 A 被一个server提交(committed)了，那么它最终一定会被所有的server提交
  • 全局有序(Total order) - 假设有A、B两个事务，有一台server先执行A再执行B，那么可以保证所有server上A始终都被在B之前执行
  • 因果有序(Causal order) - 如果发送者在事务A提交之后再发送B,那么B必将在A之前执行

只要大多数（法定数量）节点启动，系统就行正常运行。当节点下线后重启，它必须保证能恢复到当前正在执行的事务。

ZAB的具体实现

ZooKeeper由client、server两部分构成

  • client可以在任何一个server节点上进行读操作
  • client可以在任何一个server节点上发起写请求，非leader节点会把此次写请求转发到leader节点上。由leader节点执行
  • ZooKeeper使用改编的两阶段提交协议来保证server节点的事务一致性

ZXID


ZooKeeper会为每一个事务生成一个唯一且递增长度为64位的ZXID,ZXID由两部分组成：低32位表示计数器(counter)和高32位的纪元号(epoch)。epoch为当前leader在成为leader的时候生成的，且保证会比前一个leader的epoch大

实际上当新的leader选举成功后，会拿到当前集群中最大的一个ZXID，并去除这个ZXID的epoch,并将此epoch进行加1操作，作为自己的epoch。

历史队列(history queue)

每一个follower节点都会有一个先进先出（FIFO)的队列用来存放收到的事务请求，保证执行事务的顺序

可靠提交由ZAB的事务一致性协议保证
全局有序由TCP协议保证
因果有序由follower的历史队列(history queue)保证

ZAB工作模式

  • 广播(broadcast)模式
  • 恢复(recovery)模式

广播(broadcast)模式

  • leader从客户端收到一个写请求
  • leader生成一个新的事务并为这个事务生成一个唯一的ZXID，
  • leader将这个事务发送给所有的follows节点
  • follower节点将收到的事务请求加入到历史队列(history queue)中,并发送ack给ack给leader
  • 当leader收到大多数follower（超过法定数量）的ack消息，leader会发送commit请求
  • 当follower收到commit请求时，会判断该事务的ZXID是不是比历史队列中的任何事务的ZXID都小，如果是则提交，如果不是则等待比它更小的事务的commit

恢复模式

恢复模式大致可以分为四个阶段

  • 选举

  • 发现

  • 同步

  • 广播

  • 当leader崩溃后，集群进入选举阶段，开始选举出潜在的新leader(一般为集群中拥有最大ZXID的节点)

  • 进入发现阶段，follower与潜在的新leader进行沟通，如果发现超过法定人数的follower同意，则潜在的新leader将epoch加1，进入新的纪元。新的leader产生

  • 集群间进行数据同步，保证集群中各个节点的事务一致

  • 集群恢复到广播模式，开始接受客户端的写请求

当 leader在commit之后但在发出commit消息之前宕机，即只有老leader自己commit了，而其它follower都没有收到commit消息 新的leader也必须保证这个proposal被提交.(新的leader会重新发送该proprosal的commit消息)

当 leader产生某个proprosal之后但在发出消息之前宕机，即只有老leader自己有这个proproal，当老的leader重启后(此时左右follower),新的leader必须保证老的leader必须丢弃这个proprosal.(新的leader会通知上线后的老leader截断其epoch对应的最后一个commit的位置)

Posted on Edited on

Introduction

Programming Languages三个部分：

  • 理论Theory：怎么设计语言Language design、类型系统Type system、形式语言semantics and logics
  • 环境Environment：编译器、运行时
  • 应用Application：程序分析（静态程序分析）、程序验证、程序合成

过去十多年，语言的核心部分变化得很小，语言主要三类：命令式语言、函数式语言、逻辑式语言；但是程序变得很复杂，如何确保程序可靠性、安全性和性能。

静态分析作用：

  • 对提高程序可靠性很有必要：空指针异常、内存泄漏等，静态分析减少这些bug；
  • 程序安全性：私有信息泄露、注入攻击等；
  • 编译优化：死代码删除；
  • 理解程序。

静态分析：在运行一个程序P之前，就要分析它的行为和聊起是否满足某些特性。

  • P是否有一些信息泄露问题
  • P是否有一些空指针
  • 所有类型转换都是安全的么
  • 两个指针指向同一块地址么
  • 一些assert是可能fail的么

莱斯定理：并不存在准确判断程序的方法。一个递归可枚举（recursively enumerable）的语言的所有不那么简单（non-trivial）的性质都是不可预测（undecidable）的。正常的语言的一些比较感兴趣的性质都不能给一个准确的答案。noon-trivial的性质约等于一些有趣（interesting）的性质。总之，一个完美的静态分析是不存在的。

将任意程序看作一个Partial Function，它描述了程序的行为，关于程序行为的任何非平凡属性，都不存在可以检查该属性的通用算法，即不可判定 。

这里平凡属性是指对所有程序都为真或者都为假的属性，非平凡就是对有些为真有些为假。特别注意莱斯定理的适用条件是关于程序行为而不是结构，并且不适用莱斯定理的也未必可判定。例如程序使用了多少个变量，就是涉及程序结构的问题，所以像[确定程序使用的变量是否多于50个]这样的问题无法用莱斯定义来说明它是不是不可判定的。

完美的静态分析满足sound和complete的。Sound > Truth > Complete，Truth是说所有可能的行为，Sound说的是包含Truth且有其他的，Complete只有Truth中所有可能行为的一部分，Complete中爆出来的一定是Truth中的，而Sound中爆出来的不一定是Truth中的。

不存在既Sound又Complete的，只需要Useful的就好了，Useful包括：

  • Compromise Soundness：漏报
  • Compromise Completeness：误报

在静态分析中绝大多数都是Sound且不是那么准确的。但是Sound是很重要的，对其中一类的分析（编译优化）是很重要的。Sound可以翻译为全面

1
2
3
4
5
6
7
8
if (...) {
    B b = new B();
    a.fld = b;
} else {
    C c = new C();
    a.fld = c;
}
B b' = (B) a.fld;

上述程序是not safe的，这个结论需要通过分析两条指令得到，所以是Sound的，如果只分析了一个if段，则可能得到safe的结论，这个结论就是Unsound的。

越Sound越好，就越能检测出潜在的问题，力争保证Sound再提高精度。

对下面一段程序：

1
2
3
4
if(input)
    x = 1;
else
    x = 0;

两个分析结果：

  • input是true的时候，x = 1；否则x = 0。Sound、precise、expensive，通过上下文确定分析结果
  • x = 1 or x = 0。Sound、imprecise、cheap，

两个结果都是对的，只要结果包含了x = 1 或 x = 0，结论就是Sound的。在分析的时候确保Sound，同时也要做好分析的精度和速度的权衡。

抽象：用一些符号来归纳近似程序中的行为。一个例子：判断所有变量的正负（+、-、0），检查是否会除0，或者数组下标是否非法。v=e?1:-1是未知的，v=w/0是非法的，用两个符号表示。

近似（over-approximation）：针对程序中每一个语句，给这些抽象值，定义转换规则。根据分析目标和程序中每一个语句的语义，在抽象值的基础上设计转换函数。

假设程序中有这些抽象语句，正数+正数、负数+负数、等等类似的，通过分析就可以得到下边的表，而且能找到程序中的一些错误：

但是上边的分析可能会造成误报，报出来的错误比真正的错误多了。

对控制流也可进行分析，但由于输入很多种，产生控制流爆炸问题，需要对控制流进行merge。

Intermediate Representation

静态分析器需要一种程序表示格式（IR）。

编译器和静态分析器都是分析一个程序。编译器是将高级代码转换成机器能理解的机器码，类似一个翻译器，同时可以在翻译过程中报错。首先，通过Scanner做词法分析；通过Parser做语法分析，语法规则通过上下文无关文法描述，形成抽象语法树；用Type checker做语义分析；通过转换器转换为三地址码的中间表示形式（IR）；最后生成机器码进行执行。通过前端将源码转换成IR中间表现形式之后才能进行静态分析。

对于：do i = i + 1; while(a[i]<v);它的AST为：

1
2
3
4
5
6
7
8
9
     do-while
  /           \
body            <
  |            /  \
assign        []   v
 /  \         /\
i    +       a  i
     /\
    i  1

树型结构转化为三地址码IR为：

1
2
3
1: i = i + 1
2: t1 = a[ i ]
3: if t1 < v goto 1

AST是高级语言结构，与语法结构很相似；基本是基于语言的，对于快速类型检查很有利，缺乏控制流信息；而IR是低级语言，与低级机器码很相似，一般是独立于语言的，包含了控制流信息，但是没有冗余信息，基本被认为是静态分析的基础。

中间表示Intermediate Representation(IR)

3-Address Code(3AC)：在表达式的右边最多只有一个操作符。如：
a + b + 3 ---> t1 = a + b; t2 = t1 + 3。

地址可以是以下几种：变量名（a、b）、常量值（3）、编译器生成的临时变量（t1、t2），不仅仅指的是内存地址。

每种指令都有特定的三地址码形式，也有一些特定形式的3AC：

  • x = y bop z：bop指的是二元操作符或者逻辑操作符
  • x = uop y：uop是一元操作符
  • x = y：赋值语句
  • goto L：跳转语句
  • if x goto L：有条件判断跳转语句
  • if x rop y goto L：有关系判断跳转语句

针对一个for循环：

1
2
3
4
5
6
7
8
public class ForLoop3AC {
    public static void main(String[] args) {
        int x = 0; 
        for( int i = 0; i < 10; i ++) {
            x = x + 1;
        }
    }
}

三地址码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static void main(java.lang.String[] args) {
    java.lang.String[] r0;
    int i1;
    r0 := @parameter0: java.lang.String[]; // 这是一种标记，r0是那个传进来的参数，这种赋值符号不是真实的赋值，作为特殊的赋值标记出来。

    i1 = 0;

label:
    if i1 >= 10 goto label2;
    i1 = i1 + 1;
    goto label1;
    // 三地址码中有一些label作为程序的标记
    // i和x做了优化，被合并了
label2:
    return;
}

然后是do-while loop：

$i0是生成的临时变量，访问的数组元素被赋值给临时变量。

调用函数：

Static Single Asssignment(SSA)

静态单赋值(static single assignment, SSA)使得3地址码(3-address code, 3AC)中的变量只有唯一一个定义，即每条语句中的变量都用不同的名字表示。在有分支控制流的情况，可以使用一个特殊的合并函数（Φ，phi-function），在控制流通过不同代码块时会有相应的取值。当考虑分支操作时，SSA引入Phi函数。比如x0=0和x1=1汇聚，引入x2=phi(x0,x1)，再进行之后的操作，确保单赋值。

为什么用SSA：把流控制信息通过独特的变量名引入到程序执行中，这可能帮助设计一些分析。定义-使用组更加地明显，当要使用一些特殊的优化算法时更方便，也引入了更有效的数据存储整合。

为什么不用SSA：可能会引入很多的Φ函数。

Control Flow Analysis

通常是说构建Control Flow Graph。如下图所示：

这个图是之后的静态分析的基础，CFG的节点是一个独立的三地址码命令，或者是一个代码块（Basic Block）。基本块是最大连续的三地址码指令，满足：

  • 只能在第一条指令进入
  • 只能在最后一条指令出去

对下图的代码段，1，2满足代码块的定义，但是加上3之后可能会从从其他地方跳到3，所以1，2是一个代码块。所以如果一句代码如果作为jump的目标，则作为代码块的开始。3，4组成的代码段如果再加上5的话，就有两个出口了，所以3，4组成一个代码段。一个语句有goto的话，作为代码段的出口。

算法：

  • INPUT: A sequence of three-address instructions of P
  • OUTPUT: A list of basic blocks of P
  • METHOD:
    • (1) Determine the leaders in P
      • The first instruction in P is a leader
      • Any target instruction of a conditional or unconditional jump is a leader
      • Any instruction that immediately follows a conditional or unconditional jump is a leader
    • (2) Build BBs for P
      • A BB consists of a leader and all its subsequent instructions until the next leader

对上文中的三地址码序列，首先找出每个BB的leader，第一句是一个入口，所有jump的目标是leader，3，7，12都是leader，jump指令后边的指令是一个leader，5，11，12是leader。一个leader及其后续的直到下一个leader的所有指令是一个BB。

leader有：1，3，5，7，11，12。所以代码块有：

  • B1 {1, 2}
  • B2 {3, 4}
  • B3 {5, 6}
  • B4 {7, 8, 9, 10}
  • B5 {11}
  • B6 {12}

接下来添边，进一步构建CFG。如果从A到B有一个条件或无条件跳转，两个块AB之间有一条边。如果A紧接着就是B块，而且A最后一条指令不是无条件跳转的话，也需要添一条边。

通常再添加两个节点，Entry和Exit。与IR无关，从Entry到第一个BB的边包含第一条IR指令，从BB到Exit的边包含可能的最后一条指令。

Data Flow Analysis

数据是如何在CFG中流动的？

何种data在CFG中流动？（应用程序特定数据）首先对data做抽象（对一些operator抽象），之后做近似（对表达式抽象），数据近似在代码块、CFG中运行。

  • may analysis：最常见的静态分析，输出可能正确的信息（over-approximation，最安全，可以被称为safe-approximation）；
  • must analysis：输出一定正确的信息（under-approximation）
  • 二者都是为了分析的正确性。

不同的数据流分析应用有不同的数据抽象和不同的近似策略（flow safe-approximation strategies），也有不同的转换函数和不同的控制流处理方法。

Input and Output states

每个IR指令s1的将一个input state（IN[s1]）转换成一个output state（OUT[s1]），每一个input(output) state与程序的一个点（program point）关联。s2的input就是s1的output，如果有分支的话，那OUT[s1]=IN[s2]=IN[s3]。如果有汇聚，那么IN[s2]=OUT[s1] ^ OUT[s3]

在每个数据流分析应用中，将每一个程序点（program point）关联一个数据流的值（data-flow value），这个值代表了，在这个点上所有能观察到的程序状态（program states）的一个抽象（abstraction）。

换句话说，数据流分析就是对程序中所有语句的IN和OUT，通过解析一系列safe-approximation约束规则（transfer function和控制流信息），找到一个方法，给它关联一个data-flow value。

data-flow value存在一个值域，这个值域就是之前说的“正、负、零、未定义、非法”等。

transfer function：正常的分析是按照程序执行的顺序分析。语句s对应的transfer function用fs来表示，则OUT[s] = fs(IN[s])，这句话是说，输入是执行s之前的value=IN[s]，转化为s执行完之后状态OUT[s]。另一种是反向分析，逆向程序执行的顺序，则IN[s] = fs(OUT[s])。

控制流的约束（control flow’s constraints）：一共是n条语句，在一个代码块中的控制流，IN[s(s+1)] = OUT[s(i)], for all i = 1, 2, ..., n-1，每一个语句的IN都是上一个语句的OUT。代码块的关系：IN[B]=IN[s1] OUT[B]=OUT[sn]。

一个基本块的transfer function，是其中所有语句的transfer function，即OUT[B]=fb(IN[B]), fb=fsn*...*fs2*fs1，IN[B]=∩ (P: a predecessor of B) OUT[P]

Reaching Definitions Analysis定义可达性

所有data-flow都基于CFG内部过程，不涉及函数调用；不涉及别名，变量都没有别名。

程序点p中的一个定义d，如果有一条路径能够从p到达点q，且在路径上d没有被“killed”。

变量的定义definition：是对变量复制的语句。上一句可以变为，程序点p中定义v的地方称为definition d，如果能从p走到q，且v不能被重新定义，否则走到q的v就不是d定义的v了。可以用于检测可能的未定义/未初始化。

如果存在一条路径使得程序点p上的定义d能够不被阻塞/不被重定义地到达q，则称定义d可达(reaches)q。

D: v = x op y这个语句生成v的一个definition，然后‘kills’其他所有对v的定义，但是保留了对其他变量的定义。transfer function为OUT[B]=(gen B)∪(IN[B]-kill(B))，去掉其他所有定义这个变量的语句。

control flow：IN[B]=∪ (P: a predecessor of B) OUT[P]，就是B所有的前驱P的OUT的并，一条结果都不放过，都考虑成B的IN。

定义可达性分析算法：

1
2
3
4
5
6
7
8
9
10
11
INPUT: CFG（kill(B) and gen(B) computed for each basic block B）
OUTPUT: IN[B] and OUT[B] for each basic block B
METHOD: 
    OUT[entry] = Φ
    for (each basic block B\entry)
        OUT[B] = Φ
    while(changes to any OUT occur)
        for(each basic block B\entry) {
            IN[B] = ∪ (P: a predecessor of B) OUT[P]
            OUT[B] = gen(B) ∪ (IN[B] - kill(B))
        }

算法的输入是控制流图，输出每一个基本块B的IN和OUT。算法的第一步是把所有的OUT变为空，入口的OUT也为空。但是在for里为什么排除entry呢？因为需要对一些特殊情况适用，考虑一些边界情况。如果所有的BB中有一个BB的OUT变化了，就要执行这个while，给每一个BB执行这个约束。


有8个definition，定义不同的变量颜色不同。8个定义每个定义用一个bit表示，0表示在这一某点这个definition不可以reach到，1表示在某一点这个definition可以reach到它，一开始当然每个BB上的8个bit都是0，没有一个definition可以reach到。

B1的IN是0000 0000，根据transfer function生成B1的OUTPUT，gen(B)是对D1和D2，所以00变成11，执行完BB1之后，这个OUTPUT变成1100 0000，B2的IN是所有B2的前驱的UNION（B1和B4），所以就是（11000000）∪（00000000），所以是1100 0000作为B2的IN，输出是kill掉所有定义y的地方，所以是10110000，第一次迭代执行完结果如下：

第二次迭代执行完之后：

因为第二次遍历之后还有变化，所以还需要第三次遍历，继续迭代，第三次迭代之后就不变了，这个OUT的结果就是final result，在一个基本块的OUT，哪一位为1则哪一个definition能够到哪个基本块。

不停地使用transfer function，直到算法停止，找到一个solution。transfer function中的gen(s)和kill(s)都是不变的，这里当一些facts加入到OUT中，就不会离开了，即0只会变成1，1也只会变成1而不会变成0。因为所有的facts是有限的，所以OUT的增长是有限的，直到没有facts可以加入到OUT为止。

算法最后到达了一个fixed point，也与单调性相关。如果OUT不变，IN不会变；如果IN不变，OUT也不会变，二者相互制衡。

live variables analysis

活变量分析指明了在程序点p上的变量值v，是否可以在以p为起点的CFG路径中被使用，如果是的话，说v在p上是活的，否则是死的。如果从p到q，v被使用到了但是没有被重新定义redefined（比如一开始等于0然后在某个点等于3了），这样v就是活的。

活变量的信息可以用于寄存器分配，如果所有寄存器都满了，就要选择一个变量进行替换，这时可以通过静态分析选择一个死变量进行替换。

data应该怎么抽象：把所有的数据用bit vector记录，第i个bit表示第i个变量，如果是0表示这个变量是死的，如果是1表示这个变量是活的。

通过forward来检测这个变量v是否是存活的：如果从p点开始向下走，经过很多statement，直到走到最后才知道这个变量v是否被使用了；如果使用backward，则更方便。


对于上图，B有两个后继，如果采用backward方法进行分析，则OUT[B]=∪ (S a successor of B) IN[B]，B的OUT是B的所有后继的IN的并集。v在S1中使用了。

假设在一些寄存器R中的变量v是活的，或者是否需要删掉值为3的变量v，是的话IN[B]={v}，不是的话IN[B]={}。

在图中，如果k=n则IN[B]={v}，如果k=v则IN[B]={v}，如果v=2则IN[B]={}，如果v=v-1则IN[B]={v}，如果v=2;k=v则IN[B]={}，如果k=v;v=2则IN[B]={v}。

由上，可以得到IN[B]=use(B) ∪ (OUT[B]-def(B))，前边已经知道OUT[B]了。如果变量被redefined了，就不应该在IN[B]里，如果在define之前就被use了，那就直接加进来。

定义活变量分析算法：

1
2
3
4
5
6
7
8
9
10
11
INPUT: CFG（def(B) and use(B) computed for each basic block B）
OUTPUT: IN[B] and OUT[B] for each basic block B
METHOD: 
    IN[exit] = Φ
    for (each basic block B\entry)
        IN[B] = Φ
    while(changes to any IN occur)
        for(each basic block B\exit) {
            OUT[B] = ∪ (P: a successor of B) IN[P]
            IN[B] = use(B) ∪ (OUT[B] - def(B))
        }

对一个程序进行分析，跟上边的分析类似，只是是从下向上的分析。

Available Expressions Analysis可用表达式分析

一个表达式x op y，如果所有路径从入口到p都一定要计算表达式x op y，且在计算x op y之后没有x和y的重定义，则称表达式x op y在点p是活的。

  • 这个定义也说明了在程序p中，可以用x op y的结果替换掉这个表达式。
  • 这个可以用于检测全局的通用表达式

抽象：表达式可以用bit vector来表示。

对于a = x op y，使用forward分析方法，它的IN={a+b}，它的OUT中应该加上x op y，因为x op y是刚执行的，被看成是gen；然后从IN中删掉所有涉及a的语句，这被看成是kill。所以，OUT[B]=gen(B)∪(IN[B]-kill(B))，IN[B]=∩(P a predecessor of B)OUT[P]。这里使用了交集，因为所有从入口到p点的路径都需要通过x op y这个函数。

因为表达式是否可重用涉及到程序的正确性，因此需要under-approximation，报少，但一定要对，确保safe。

1
2
3
4
5
6
7
8
9
10
11
INPUT: CFG（kill(B) and gen(B) computed for each basic block B）
OUTPUT: IN[B] and OUT[B] for each basic block B
METHOD: 
    OUT[entry] = Φ
    for (each basic block B\entry)
        OUT[B] = Φ
    while(changes to any OUT occur)
        for(each basic block B\entry) {
            IN[B] = ∩ (P: a predecessor of B) OUT[P]
            OUT[B] = gen(B) ∪ (IN[B] - kill(B))
        }

一个例子：

本节课的总结表：

foundation

假设一个有k个节点的CFG（一个程序的执行流），且这里的一个节点是一个statement，算法在每次迭代时都会更新每个节点的OUT信息。假设数据流分析中domain（所有程序里的definition作为数据流分析的值域）的值为V，可以定义一个k元组，每个node的OUT值作为这个k元组的值，(OUT[n1],OUT[n2],OUT[n3],…OUT[nk])，作为一个集合（V1×V2×…Vk）中的元素，这个集合定义为V^k，代表的是每次迭代遍历之后的分析值。所以说V^k存的是每次迭代之后每个节点分析的临时结果。每次迭代都可以作为使用函数F:V^k -> V^k，通过转换函数和控制流处理建立V^k之间的映射关系。算法输出一系列的k元组，直到两次输出的k元组相同。这是从另一个角度观察之前的算法。

每一个OUT初始化为空，之后开始遍历，第一次遍历结束之后产生一个OUT集，上标1表示第一次迭代，下标表示每个节点。一直迭代直到两次相同。每个k元组用Xi表示，每次遍历都可以表示成一个函数，比如X0作为F的输入，输出第一次迭代的结果X1，Xi=F[x(i-1)]，X(i)=X(i+1)=F(xi)，所以X(i)=F(xi)。

这里的Xi就是函数F的fixed point不动点，X=F(X)，迭代算法达到了一个不动点Xi。

迭代算法生成了数据流分析的方案，那：

  • 算法保证能停止或者能到达一个不动点么？或者总是能找到一个解么？
  • 如果上述成立，那算法只能找到一个不动点么？我们找到的不动点是最好的么？
  • 何时能找到不动点？

偏序partial order：我们定义一个偏序集(poset)为(P,⊑)，其中⊑在P上定义了一个二元偏序关系，满足：

  • 自反性(reflexivity)：∀x∈P,x⊑x
  • 反对称性(antisymmetry)：∀x,y∈P,x⊑y∧y⊑x ⟹ x=y
  • 传递性(transitivity)：∀x,y,z∈P,x⊑y∧y⊑z ⟹ x⊑z

偏序意味着有些在P内的有些元素对是没有办法比较的。

S是整数集合，⊑是小于等于关系，S满足偏序关系：

  • 1 ≤ 1，2 ≤ 2，所以满足自反性
  • x ≤ y ∩ y ≤ x，则x = y，所以满足反对称性
  • 1 ≤ 2 ∩ 2 ≤ 3，则1 ≤ 3，所以满足传递性

上下界：给定(P,⊑)和子集S⊂P，若u∈P是S的上界，则∀x∈S,x⊑u；类似地，若l∈P是S的下界，则∀x∈S,l⊑x，如下。

最小上界/上确界(lub/join)、最大下界/下确界(glb/meet)：所有S上界中最小的一个称为S的上确界，记为⊔S；所有S下界中最大的一个称为S的下确界，记为⊓S。通常，如果S只含两个元素a,b，那么上确界可被写成a⊔b(join)，下确界可被写成a⊓b(meet)

一些性质:

  • 并不是所有偏序集都有上确界或下确界；
  • 如果有的话一定唯一（反证法）；
  • 界不一定在子集S中。

格(lattice)：如果偏序集是格，则任两个元素对都有lub和glb。

半格(semilattice)：如果任两个元素对只有一侧的确界，则称其为join/meet半格。

完全格(complete lattice)：对于格的任意子集都有上下确界，那么该格称为完全格。完全格中的最大元素⊤=⊔P称为top，最小元素⊥=⊓P称为bottom。幂集依然是个完全格。结论：有限的格都是完全格。

乘积格(product lattice)：如果对于格L1=(P1,⊑1),L2=(P2,⊑2),…Ln=(Pn,⊑n)，如果对于所有的i，Li=(Pi,⊑i)有上下确界，那么定义乘积格L^n=(P,⊑)：

  • P = P1 × P2 × … × Pn
  • (x1, …, xn) ⊑ (y1, …, yn)，(x1⊑y1)∩…∩(xn⊑yn)
  • (x1, …, xn) ⊔ (y1, …, yn)，(x1⊔y1, …. xn⊔yn)
  • (x1, …, xn) ⊓ (y1, …, yn)，(x1⊓y1, …, xn⊓yn)

数据流分析框架(D, L, F)：

  • D：数据流的方向，正向或反向
  • L：一个格，包括V的值域和上下界操作符
  • F：从V到V的一个transfer function族

左右两边建立关联，OUT[s1]={a}和OUT[s3]={b}并之后作为s2的IN={a, b}，实际上就是在这个格上，数据流进行流动，OUT[s2]={a, b, c}。数据流分析可以被认为是在一个格的值域上迭代执行转换函数和meet/join操作。

对之前的三个问题：

  • 算法保证能停止或者能到达一个不动点么？或者总是能找到一个解么？这是格函数的单调性问题。
  • 如果上述成立，那算法只能找到一个不动点么？我们找到的不动点是最好的么？函数可能会有多个不动点，我们这个迭代过程是不是最精确的？
  • 何时能找到不动点？

单调性(monotonicity)：定义在格上的函数f:L↦L是单调的，若∀x,y∈L,x⊑y⟹f(x)⊑f(y)。

不动点定理(fixed-point theorem)：给定完全格(L,⊑)，若满足：(a) f:L↦L是单调的，(b) L是有限的(finite)，则最小不动点可以通过迭代f(⊥), f(f(⊥)), …, fk(⊥)迭代得到，最大不动点可通过f(⊤), f(f(⊤)), …, fk(⊤)迭代得到，直到到达一个不动点。

证明：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
根据f:L↦L和⊥，有⊥⊑f(⊥)。
因为f是单调的，所以：f(⊥)⊑f(f(⊥))=f^2(⊥)
同样的，不停使用这个性质，⊥⊑f(⊥)⊑f^2(⊥)⊑...⊑f^i(⊥)
因为L是有限的，对于一个特定的k，我们有：f^fix = f^k(⊥) = f^(k+1)(⊥)
因此不动点存在。

假定有另一个不动点x，x=f(x)
因为⊥的定义，⊥⊑x

因为f是单调的，f(⊥)⊑f(x)
假定f^i(⊥)⊑f^i(x)
因为f是单调的，我们有f^(i+1)(⊥)⊑f^(i+1)(x)
通过归纳，f^i(⊥)⊑f^i(x)
因此^i(⊥)⊑f^i(x)=x，f^fix=f^k(⊥)⊑x
因此不动点是最小的。

需要把迭代算法跟不动点定理相关联，一旦关联上就可以解释上述三个问题。把整个数据流分析算法看成CFG中节点OUT的更新，直到两次迭代的OUT都一样。

每一个迭代中，定义一个函数F，给每一个节点执行这个节点上的转换函数，然后沿着CFG应用meet/join。F包括：

  • 转换函数 fi: L↦L
  • meet/join函数：⊓/⊔: L × L ↦ L

证明函数F是单调的（monotonic）。transfer function一般都是monotonic的。对于meet/join函数，只要证二元关系是单调的就行。

1
2
3
4
5
Proof:
    在L上取三个元素x，y，z，x⊑y，我们希望证明 x ⊔ z ⊑ y ⊔ z，那这样的话这个关系就是单调的。y ⊑ y ⊔ z
    通过⊑的传递性，x ⊑ y ⊔ z
    因此y ⊔ z是x的上界，也是z的上界
    x ⊔ z是x和z的最小上界，因此x ⊔ z ⊑ y ⊔ z

以上说明⊔关系是单调的。

格的高度h是从顶到底的最长的路径，这个格的高度h=3。

假设每一次迭代，只能在格上走一步（即一个node里的一位0变成1），假定一共有k个node，格的高度是h，计算最坏情况下迭代次数是i=h*k。这也是能找到不动点的最坏次数。

May and Must Analyses, a Lattice View

图中的上下界确定，假定这个格是一个乘积格

May Analyses是一个bottom，代表一个不安全的结果，算是一个下界；另外有一个上界，是安全但是不完全/没用的结果。这里中间有一个Truth，将safe和unsafe隔开。如何知道分析一定是safe的？这是由单调性决定的。May Analyses从底部一直向上走，我们向上走先接触到的是最小不动点。从最底部走到最顶部，是从精度最高走到精度最低的。所以May Analyses一般都首先初始化为空。

Must从上向下走。代表最安全的结果，也有一个Truth代表安全和不安全的分界。上边的那些存在一些不安全的结果，越向下是越安全的。同样也有一些不动点，我们求解的结果一定是最好的不动点。

已经证明过不动点原理，一定达到最小/大不动点，may为什么是最小不动点呢？每一次走一步就按照transfer function向上走，达到一个least bound，每次迭代都是一个min step，最终达到最小上界。

How Precise is our solution

Meet-Over-All-Paths Solution(MOP)：用着一个meet把meet/join合并，所有的path合并到一点的时候，用meet/join合并。一个Path是从entry到Si的路径，P=Entry->S1->S2->…->Si。路径P的的transfer function记作FP，是这个路径上所有节点的transfer function的组合。

MOP就是枚举从Entry到Si所有的Path，然后把三条路径的FP结果join/meet起来，公式是：MOP[Si] = ⊔/⊓ FP(OUT[Entry]), A path P from Entry to Si，所有path应用transfer function之后进行meet/join，找到确界。有一些path是不可能走到的，所以这是不精确的。

我们的迭代算法和MOP：对于这样一个CFG：

使用迭代算法：

内部的join是S3的输入。如果用MOP的话，不是每个节点算完之后取join，而是一条path算完之后取一个join，是两个S3的OUT进行join：

如果用x和y进行替代，则Ours=F(x⊔y), MOP=F(x)⊔F(y)，这两个function之间有什么关系：

1
2
3
4
5
6
7
8
因为x ⊑ x ⊔ y 且 y ⊑ x ⊔ y
且transfer function是单调的，有：
F(x) ⊑ F(x⊔y)且F(y) ⊑ F(x⊔y)
这就意味着F(x⊔y)是一个F(x)和F(y)的上界

因为F(x) ⊔ F(y)是F(x)和F(y)的上确界(lub)，我们有：
F(x) ⊔ F(y) ⊑ F(x⊔y)
MOP ⊑ Ours

满足一个偏序关系，所以MOP更准，Ours比MOP更不准。

当F是可分配的（distributive），F(x) ⊔ F(y) = F(x⊔y)，则两个相同。位向量（bit-vector）或者Gen/kill问题都是distributive的。

Constant Propagation

在程序某点p，给定变量x，判断x在p点是不是保证指向一个常量。

在CFG中每个节点的OUT是一组pair(x, v)，x是一个变量，v是在这个节点之后x所拥有的值。这个分析是一个forward形式的。他的格：值V的定义域很简单：

越往下走越都不是常量，越安全但是越不精确。它的meet操作符（NAC表示not a constant）：

  • NAC ⊓ v = NAC
  • UNDEF ⊓ v = v
  • c(常量) ⊓ v(任意一个值)
    • c ⊓ c = c
    • c1 ⊓ c2 = NAC

transfer function：给定一个语句s: x=...，定义transfer function F为：F: OUT[s] = gen ∪ (IN[s] - {(x, _)})，其中
_是通配符，x无论值是什么，都有一个新的值，就把原来的值干掉。我们使用val(x)代表变量x指向的值。

  • s: x = c; // c is a constant gen = {(x, c)}
  • s: x = y; gen = {(x, val(y))}
  • s: x = y op z; gen = {(x, f(y, z))}

如果y和z的值都是常量的话，x就是val(y) op val(z)，如果val(y)或val(z)有一个是NAC，则x是NAC，其他情况下都是UNDEF。

但是它不是distributivity的，比如：

通过constant propagation求c，因为F(x) ⊓ F(y) = {(a, NAC), (b, NAC), (c, 10)}，这里c已经通过path算出来了，但是F(x⊓y) = {(a, NAC), (b, NAC), (c, NAC)}，所以是不一样的，F(x⊓y) ⊑ F(x) ⊓ F(y)。

worklist algorithm

是对迭代算法的优化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
INPUT: CFG（kill(B) and gen(B) computed for each basic block B）
OUTPUT: IN[B] and OUT[B] for each basic block B
METHOD: 
    OUT[entry] = Φ
    for (each basic block B\entry)
        OUT[B] = Φ
    Worklist <- all basic blocks
    while(worklist is not empty)
        Pick a basic block B from Worklist
        old_OUT = OUT[B]
        IN[B] = ∪ (P: a predecessor of B) OUT[P]
        OUT[B] = gen(B) ∪ (IN[B] - kill(B))
        if (old_OUT ≠ OUT[B])
            Add all successors of B to Worklist

如果B的OUT变了，那么所有的后继的输入IN就变了，那么只把IN变了的basic block加进worklist中。这样避免了大量的重复计算。

Inter-procedural Analysis

目前的分析都是过程内的分析，不处理函数调用。过程间分析会顺着call graph传递数据流，避免过于保守的假设造成的损失。做过程间分析需要的必要的是call graph。如何构造程序调用图？调用图是调用关系的表示，每个调用边从调用点指向调用的函数。对程序的优化、理解都有作用。

四个比较有代表性的算法，越往下就精度越高，越往上速度越快：

  • class hierarchy analysis(CHA)
  • rapid type analysis
  • variable type analysis
  • pointer analysis(k-CFA)


上图是Java的函数调用的种类，只有virtual call比较特殊，在执行的时候才知道调用的具体位置。virtual call中有个method dispatch，在执行使，一个virtual call取决于：

  • 方法的签名signature，通过签名可以唯一的确定一个标识符。
  • 调用者的类型。

定义一个函数dispatch(c, m)，来模拟这个调用过程，如果c包含了一个非抽象方法m’，且与m有相同的签名和名字，则返回m’，否则的话，返回的是dispatch(c', m)，这里c’是c的父类。

下图中dispatch的结果是Dispatch(B, A.foo()) = A.foo()，Dispatch(C, A.foo()) = C.foo()。

class hierarchy analysis(CHA)

需要整个程序的类的继承信息，根据类型求解目标方法。假定变量a可以指向所有的类A及其所有子类。

定义函数Resolve(cs)，其中cs表示call site，来求解所有可能的目标方法。如果是static call，就是写在调用中的方法。如果是special call，则需要处理构造函数、私有方法、父类方法三种情况，构造函数和私有方法两种情况就是写在调用中的方法，但是为了兼容父类方法这种情况，所以统一使用dispatch函数。如果是virtual call，首先取出变量c的声明类型C，对C和C继承树上所有的子类都调用dispatch，把它加入到目标方法中。

取出C和C所有的子类，这里对B及其子类C、D做dispatch，而且B没有foo方法，所以要去A中找foo方法，所以就是A.foo(), C.foo(), D.foo()。根据声明类型去找子类。

CHA很快，只考虑了声明类型及其继承关系，忽略了数据流和控制流信息。它的不足是很不精确。在IDE中很常用。

用CHA构造call graph，对每个可到达的方法m，解所有的可调用方法。直到没有方法可达。生成调用图之后有的方法可能是不可达的。

第一行算法做了初始化，WL是worklist，存了需要被处理的方法，CG是调用边，RM是可达方法的集合，进入RM之后就不需要被处理了。整个算法是一个大的while循环，循环内部从WL去一个方法，如果在RM中就不处理；否则对于这个方法m，执行Resolve方法，把每个方法加入到CG中，把新发现的方法加入到WL中，后边把新发现的方法继续处理，最后返回CG。

下图是个例子：

interprocedural control-flow graph

ICFG表示整个程序的结构，可以做过程间的分析，由每个方法的CFG和两种额外的边组成：

  • call edges: 从call sites到被调用者的入口
  • return edges: 从被调用者的返回语句指回向call sites
1
2
3
4
void foo() {
    bar(...); // call site
    int n = 3; // return site
}

ICFG的例子，整个程序的控制流图，需要保留call edge和return edge之间的边：

我们需要edge transfer，进行数据流的转换，这个转换是顺着边的。call edge transfer传参数，return edge transfer传返回值。node transfer要处理等式运算。对于一个调用节点中的式子的左边的值，要把它kill掉，因为它的值回通过return edge流到下边的返回点。

对于调用，要把左值去掉，否则会与函数返回值冲突，因此b不在流中；接下来处理call edge，处理传参，参数传过来之后，x=6, y=7，最后return edge传输的是b=val(y)。

图中可以发现，call site到return site的边叫做call-to-return edge，使得可以传播本地数据流（函数内部的数据流，在这里a=6是可以通过这个边传递的，如果没有的话，就不能传播了）。如果删掉了，则要把调用者自己的数据再传输到被调用函数中，如第二张图


Pointer Analysis

motivation

CHA建立call graph，foo中调用了get方法，以下三个类实现了接口Number中的get方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void foo() {
    Number n = new One();
    int x = n.get();
}

interface Number {
    int get();
}
class Zero implements Number {
    public int get() {return 0;}
}
class One implements Number {
    public int get() {return 1;}
}
class Two implements Number {
    public int get() {return 2;}
}

如果用CHA解n的get方法的话，有3个目标函数，根据变量的类型，有三个子类。如果做constant propagation的话，有三个函数会返回给x，x就会被赋值为NAC，但是实际上根据类型，n只会指向One类型的变量，只有一个可能。

指针分析会根据变量指向的对象建图，只会对One类型做dispatch，得到的调用图是更准确的，解决了CHA引入更多可能的问题。

introduction

指针分析解决了程序中的指针可以指向哪个变量地址的问题，一个指针指向程序中的哪些对象，计算出来的结果会比实际上指向的对象更多。

1
2
3
4
5
6
7
8
9
10
11
void foo() {
    A a = new A();
    B x = new B();
    a.setB(x);
    B y = a.getB();
}
class A {
    B b;
    void setB(B b) { this.b = b; }
    B getB() { return this.b; }
}

创建了两个对象，调用了set方法和get方法，对其进行指针分析，得到指向关系。setB方法中的this是A类型，b是B类型。getB方法左边的y指向B类型。

别名分析与指针分析关系紧密但是有区别，指针分析回答了程序中的指针可以指向哪个对象；而别名分析指明了两个指针是否可以指向同一个对象。两个指针指向了同一个对象，则是别名：q和p是别名，x和y不是别名。别名可以通过指针分析得到，对于优化、调bug的基础。

1
2
3
4
p = new C();
q = p;
x = new X();
y = new Y();

key factors of pointer analysis

指针分析的要素：

  • 是一个复杂系统
  • 许多要素会影响精度和效率，下图是最关键的四个要素
    • 堆内存、上下文、控制流等

堆抽象

执行时堆内存的数量理论上是无限的，把程序动态分配出来的无穷无尽的堆对象抽象成为有限的抽象对象，这样使指针分析能够结束，限制静态分析处理对象的个数，下图中把左图中堆内存中分配的多个对象或有某些共性的对象合并成一个对象。

堆分析有很多内容，有两大流派，一个是store based model，一个是store less model。

只学习allocation-site abstraction，这种技术在分配点进行给动态对象建模的方式，用抽象的对象表示所有在这个创建点创建的对象。

1
2
3
for (i = 0; i < 3; i ++) {
    a = new A();
}

这里的程序在第二行有一个创建点，动态创建三个对象，o2表示创建点，在这个创建点创建了三个对象，使用这个方法创建的话，只会创建一个抽象的对象来表示这三个具体的对象。有几个new就会创建几个抽象点。

上下文敏感

它回答了指针分析中如何对上下文进行建模，通常有上下文敏感，上下文不敏感两种方式。每次调用都会产生不同的上下文，相应的形参也会不一样，是否将两次不同上下文的调用分开，上下不敏感会把不同的调用混合到一处，会降低精度。因此以上下文敏感为主。

流敏感

如何对程序的控制流进行建模，有两大类做法：敏感or不敏感。目前学到的所有分析方法都是敏感的。对一段程序做流敏感/不敏感的指针分析。

敏感的分析在程序的每一点都维护指向关系映射，都会检查指针指向的变化。不敏感的分析只维护一个指向映射，会保存所有的可能结果，为了保证结果的正确性，必须把所有可能的结果都保存下来，下图中右侧的s结果说明了这一点，它把x和y都放到了结果中，因为不知道c.f可能会指向什么。

analysis scope

回答了指针分析过程中需要分析哪些部分，全程序分析或者需求驱动的分析。全程序分析计算了所有指针指向的所有信息，如果感兴趣的只是第五行，那么可能只需要分析z就好了，这时需求驱动的分析更好。

concerned statements

只关注直接影响指针指向的语句，有一些类型的指针。

  • 局部变量指针
  • static field：类、class的指针，可以是global variable
  • instance field：建模为一个x指向的object；
  • array element：忽略数组的下标，看作一个对象；

pointer-affecting statements：能够影响指针的语句

  • New: x = new T();
  • assign: x = y;
  • store: x.f = y;
  • load: y = x.f;
  • call: r = x.k(a, …);

额外的：

  • 如果有复杂的调用，如a.b.c.d，可以分解为三地址码
  • 指针分析中virtual call是最复杂的，首先关注这个

pointer analysis Rules

指针分析中的域及其记法：

instance fields用O和F的乘积表示。pointer-to关系是一个映射，吧指针映射到指针集（O的幂集，原集合中所有的子集），就是方框中表示的。

对于new语句，创建一个对象，用oi表示创建出来的对象，让x指向oi。只要碰到这个语句，就把oi加入到pt(x)中。

assign的话，如果oi属于pt(y)的话，也让它属于pt(x)。

store：如果x指向一个语句oi，y指向另一个语句oj：

load：x.f指向oi了，oi的f域指向oj了，则让y指向oj

下图可以看到，对每一条Rule，横线上边的是前提，横线下边的是结论，下下图是汇总：

how to implement pointer analysis

指针分析用来生成指针的指向信息。类似下图中红线箭头的指向性信息，而且当指针变了的时候，指向性信息也会跟着变化。我们使用图将相关的指针联系起来，当pt(x)改变了的时候，将改变的部分同x的后继联系起来，将变化传播到x的后继。

pointer analysis algorithms

Pointer Flow Graph(PFG)是一个有向图，指明了对象间的指针指向关系。节点n代表了一个抽象对象或者变量，边e: x -> y表示指针x指向的对象可能会流向指针y（也由指针y指向），如下表所示，如果把y的值赋值给了x，那么就有一条边是从y指向x的。

下图便是一个画PFG的图，根据上边的定义，应该很好懂。通过PFG可以计算一个传递闭包，从而进行指针分析，比如e可以通过b到达，即e指向的对象也可以通过b指向。顺便加上了对b的初始化，这样更容易看出，pt(b)={oj}=pt(e)。

实现指针分析算法有两个步骤：

  • 构建PFG
  • 将指针指向信息整合进PFG

下图是算法，可以看到也使用了worklist算法。worklist中包含了需要被处理的指针指向信息，WL∈<Pointer, P(0)>，每个worklist入口<n, pts>，是“指针，指向集”对。

下图将分析整个算法：



这里使用了一个差分的方法，解决了冗余的存在。

对于下面的程序：

1
2
3
4
5
6
7
1: b = new C();
2: a = b;
3: c = new C();
4: c.f = a;
5: d = c;
6: c.f = d;
7: e = d.f;

第一步对于其中所有的x = new T()，把[<b, {o1}>, <c, {o3}>]加入到WL中，然后对于所有的x = y形式的语句，构造边，加入PFG。

对于WL中的所有元素，首先把其中一个元素从WL中移除，第一个处理的是<b, {o1}>，调用Propagate函数，对b，pt(b)加入pts中的元素，再在WL中加上<a, {o1}>。对于c也是如此。

之后再处理c.f相关的边，直接加上。生成的PFG如下：

pointer analysis with methods calls

过程间分析需要call graph，对于函数调用的Rule：

调用图call graph构成了一个“reachable world”，从一开始入口函数就是可达的，其他的可达方法在分析的时候被逐步发现，只有可达的方法会被分析。总体算法：

addReachable方法扩展了reachable world。

ProcessCall的调用：

例子：对以下程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class A {
    static void main() {
        A a = new A();
        A b = new B();
        A c = b.foo(a);
    }
    A foo(A x) { ... }
}
class B extends A {
    A foo(A y) {
        A r = new A();
        return r;
    }
}

一开始的时候WL为空，RM为空，CG为空。首先调用AddReachable函数把入口函数加入到可达图中，此时RM为{A.main()}，在AddReachable仍需把main函数中的x = new T()形式的语句加入到WL中，WL中变为[<a, {o3}>, <b, {o4}>]，再根据上边的指针分析算法进行分析。

CFL-Reachability and IFDS

Soundness and Soundines

Modern Pointer Analysis

Static Analysis for Security

Datalog-Based Analysis

Abstract Interpretation

Posted on Edited on

Redis数据库中的每个键值对都是由对象组成的：

  • 数据库键总是一个字符串对象；
  • 数据库键的值可以是字符串对象、列表对象、哈希对象、集合对象、有序集合对象这五种对象中的一种。

数据结构与对象

简单动态字符串

Redis自己构建了一种名叫“简单动态字符串”（SDS）的类型，当Redis需要的不仅仅是一个字符串字面量，而是一个可以被修改的字符串值时，使用SDS用作默认字符串表示。如果执行了：

1
2
redis> SET msg "hello world" 
OK

那么Redis将在数据库中建立一个新的键值对，其中：

  • 键值对的键是一个字符串对象，对象底层实现是一个保存着字符串的SDS
  • 键值对的值也是一个字符串对象，对象的底层实现也是一个保存着字符串的SDS

sds的定义

每个 sds.h/sdshdr 结构表示一个 SDS 值：

1
2
3
4
5
6
7
8
9
10
11
struct sdshdr {
    // 记录 buf 数组中已使用字节的数量
    // 等于 SDS 所保存字符串的长度
    int len;

    // 记录 buf 数组中未使用字节的数量
    int free;

    // 字节数组，用于保存字符串
    char buf[];
};

free属性的值为0，表示这个SDS没有分配任何未使用空间。
len属性的值为5，表示这个SDS保存了一个五字节长的字符串。
buf属性是一个char类型的数组，数组的前五个字节分别保存了’R’、’e’、’d’、’i’、’s’五个字符，而最后一个字节则保存了空字符’\0’。

SDS遵循C字符串以空字符结尾的惯例，保存空字符的1字节空间不计算在SDS的len属性里面，并且为空字符分配额外的1字节空间，以及添加空字符到字符串末尾等操作都是由SDS函数自动完成的，所以这个空字符对于SDS的使用者来说是完全透明的。

SDS与C字符串的区别

C语言使用长度为N+1的字符数组来表示长度为N的字符串，并且字符数组的最后一个元素总是空字符’\0’。C语言使用的这种简单的字符串表示方式，并不能满足Redis对字符串在安全性、效率、以及功能方面的要求。

Redis中使用SDS的优势：

  • 常数复杂度获取字符串长度：因为C字符串并不记录自身的长度信息，所以为了获取一个C字符串的长度，程序必须遍历整个字符串，这个操作的复杂度为O(N)。因为SDS在len属性中记录了SDS本身的长度，所以获取一个SDS长度的复杂度仅为O(1)。设置和更新SDS长度的工作是由SDS的API在执行时自动完成的，使用SDS无须进行任何手动修改长度的工作。
  • 杜绝缓冲区溢出：strcat函数执行字符串拼接时假定用户在执行这个函数时，已经为dest分配了足够多的内存，可以容纳src字符串中的所有内容，而一旦这个假定不成立时，就会产生缓冲区溢出。与C字符串不同，SDS的空间分配策略完全杜绝了发生缓冲区溢出的可能性：当SDSAPI需要对SDS进行修改时，API会先检查SDS的空间是否满足修改所需的要求，如果不满足的话，API会自动将SDS的空间扩展至执行修改所需的大小，然后才执行实际的修改操作，所以使用SDS既不需要手动修改SDS的空间大小，也不会出现前面所说的缓冲区溢出问题。
  • 减少内存分配次数，因为C字符串的长度和底层数组的长度之间存在着这种关联性，所以每次增长或者缩短一个C字符串，程序都总要对保存这个C字符串的数组进行一次内存重分配操作：
    • 如果程序执行的是增长字符串的操作，那么在执行这个操作之前，程序需要先通过内存重分配来扩展底层数组的空间大小——如果忘了这一步就会产生缓冲区溢出。
    • 如果程序执行的是缩短字符串的操作，那么在执行这个操作之后，程序需要通过内存重分配来释放字符串不再使用的那部分空间——如果忘了这一步就会产生内存泄漏。
    • 为了避免C字符串的这种缺陷，SDS通过未使用空间解除了字符串长度和底层数组长度之间的关联：在SDS中，buf数组的长度不一定就是字符数量加一，数组里面可以包含未使用的字节，而这些字节的数量就由SDS的free属性记录。通过未使用空间，SDS实现了空间预分配和惰性空间释放两种优化策略。
    • 空间预分配：空间预分配用于优化SDS的字符串增长操作：当SDS的API对一个SDS进行修改，并且需要对SDS进行空间扩展的时候，程序不仅会为SDS分配修改所必须要的空间，还会为SDS分配额外的未使用空间。其中，额外分配的未使用空间数量由以下公式决定：
      • 如果对SDS进行修改之后，SDS的长度（也即是len属性的值）将小于1MB，那么程序分配和len属性同样大小的未使用空间，这时SDSlen属性的值将和free属性的值相同。
      • 如果对SDS进行修改之后，SDS的长度将大于等于1MB，那么程序会分配1MB的未使用空间。举个例子，如果进行修改之后，SDS的len将变成30MB，那么程序会分配1MB的未使用空间，SDS的buf数组的实际长度将为30MB+1MB+1byte。
    • 惰性空间释放：惰性空间释放用于优化SDS的字符串缩短操作：当SDS的API需要缩短SDS保存的字符串时，程序并不立即使用内存重分配来回收缩短后多出来的字节，而是使用free属性将这些字节的数量记录起来，并等待将来使用。通过惰性空间释放策略，SDS避免了缩短字符串时所需的内存重分配操作，并为将来可能有的增长操作提供了优化。
  • 二进制安全：虽然数据库一般用于保存文本数据，但使用数据库来保存二进制数据的场景也不少见，因此，为了确保Redis可以适用于各种不同的使用场景，SDS的API都是二进制安全的（binary-safe）：所有SDS API都会以处理二进制的方式来处理SDS存放在buf数组里的数据，程序不会对其中的数据做任何限制、过滤、或者假设。
  • 兼容部分C字符串函数：虽然SDS的API都是二进制安全的，但它们一样遵循C字符串以空字符结尾的惯例：这些API总会将SDS保存的数据的末尾设置为空字符，并且总会在为buf数组分配空间时多分配一个字节来容纳这个空字符，这是为了让那些保存文本数据的SDS可以重用一部分<string.h>库定义的函数。

SDS API

函数 作用 时间复杂度
sdsnew 创建一个包含给定 C 字符串的 SDS 。 O(N) ， N 为给定 C 字符串的长度。
sdsempty 创建一个不包含任何内容的空 SDS 。 O(1)
sdsfree 释放给定的 SDS 。 O(1)
sdslen 返回 SDS 的已使用空间字节数。 这个值可以通过读取 SDS 的 len 属性来直接获得， 复杂度为 O(1) 。
sdsavail 返回 SDS 的未使用空间字节数。 这个值可以通过读取 SDS 的 free 属性来直接获得， 复杂度为 O(1) 。
sdsdup 创建一个给定 SDS 的副本（copy）。 O(N) ， N 为给定 SDS 的长度。
sdsclear 清空 SDS 保存的字符串内容。 因为惰性空间释放策略，复杂度为 O(1) 。
sdscat 将给定 C 字符串拼接到 SDS 字符串的末尾。 O(N) ， N 为被拼接 C 字符串的长度。
sdscatsds 将给定 SDS 字符串拼接到另一个 SDS 字符串的末尾。 O(N) ， N 为被拼接 SDS 字符串的长度。
sdscpy 将给定的 C 字符串复制到 SDS 里面， 覆盖 SDS 原有的字符串。 O(N) ， N 为被复制 C 字符串的长度。
sdsgrowzero 用空字符将 SDS 扩展至给定长度。 O(N) ， N 为扩展新增的字节数。
sdsrange 保留 SDS 给定区间内的数据， 不在区间内的数据会被覆盖或清除。 O(N) ， N 为被保留数据的字节数。
sdstrim 接受一个 SDS 和一个 C 字符串作为参数， 从 SDS 左右两端分别移除所有在 C 字符串中出现过的字符。 O(M*N) ， M 为 SDS 的长度， N 为给定C字符串的长度。
sdscmp 对比两个 SDS 字符串是否相同。 O(N) ， N 为两个 SDS 中较短的那个 SDS 的长度。

链表

链表提供了高效的节点重排能力， 以及顺序性的节点访问方式， 并且可以通过增删节点来灵活地调整链表的长度。
每个链表节点使用一个 adlist.h/listNode 结构来表示：

1
2
3
4
5
6
7
8
9
10
typedef struct listNode {
    // 前置节点
    struct listNode *prev;

    // 后置节点
    struct listNode *next;

    // 节点的值
    void *value;
} listNode;


多个 listNode 可以通过 prev 和 next 指针组成双端链表。虽然仅仅使用多个 listNode 结构就可以组成链表， 但使用 adlist.h/list 来持有链表的话， 操作起来会更方便：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
typedef struct list {
    // 表头节点
    listNode *head;

    // 表尾节点
    listNode *tail;

    // 链表所包含的节点数量
    unsigned long len;

    // 节点值复制函数
    void *(*dup)(void *ptr);

    // 节点值释放函数
    void (*free)(void *ptr);

    // 节点值对比函数
    int (*match)(void *ptr, void *key);
} list;

list结构为链表提供了表头指针head、表尾指针tail，以及链表长度计数器len，而dup、free和match成员则是用于实现多态链表所需的类型特定函数：

  • dup函数用于复制链表节点所保存的值；
  • free函数用于释放链表节点所保存的值；
  • match函数则用于对比链表节点所保存的值和另一个输入值是否相等。

Redis的链表实现的特性可以总结如下：

  • 双端：链表节点带有prev和next指针，获取某个节点的前置节点和后置节点的复杂度都是O(1)。
  • 无环：表头节点的prev指针和表尾节点的next指针都指向NULL，对链表的访问以NULL为终点。
  • 带表头指针和表尾指针：通过list结构的head指针和tail指针，程序获取链表的表头节点和表尾节点的复杂度为O(1)。
  • 带链表长度计数器：程序使用list结构的len属性来对list持有的链表节点进行计数，程序获取链表中节点数量的复杂度为O(1)。
  • 多态：链表节点使用void*指针来保存节点值，并且可以通过list结构的dup、free、match三个属性为节点值设置类型特定-函数，所以链表可以用于保存各种不同类型的值。

Redis 链表和链表节点的 API

函数 作用 时间复杂度
listSetDupMethod 将给定的函数设置为链表的节点值复制函数。 O(1) 。
listGetDupMethod 返回链表当前正在使用的节点值复制函数。 复制函数可以通过链表的 dup 属性直接获得， O(1)
listSetFreeMethod 将给定的函数设置为链表的节点值释放函数。 O(1) 。
listGetFree 返回链表当前正在使用的节点值释放函数。 释放函数可以通过链表的 free 属性直接获得， O(1)
listSetMatchMethod 将给定的函数设置为链表的节点值对比函数。 O(1)
listGetMatchMethod 返回链表当前正在使用的节点值对比函数。 对比函数可以通过链表的 match 属性直接获得，O(1)
listLength 返回链表的长度（包含了多少个节点）。 链表长度可以通过链表的 len 属性直接获得， O(1) 。
listFirst 返回链表的表头节点。 表头节点可以通过链表的 head 属性直接获得， O(1) 。
listLast 返回链表的表尾节点。 表尾节点可以通过链表的 tail 属性直接获得， O(1) 。
listPrevNode 返回给定节点的前置节点。 前置节点可以通过节点的 prev 属性直接获得， O(1) 。
listNextNode 返回给定节点的后置节点。 后置节点可以通过节点的 next 属性直接获得， O(1) 。
listNodeValue 返回给定节点目前正在保存的值。 节点值可以通过节点的 value 属性直接获得， O(1) 。
listCreate 创建一个不包含任何节点的新链表。 O(1)
listAddNodeHead 将一个包含给定值的新节点添加到给定链表的表头。 O(1)
listAddNodeTail 将一个包含给定值的新节点添加到给定链表的表尾。 O(1)
listInsertNode 将一个包含给定值的新节点添加到给定节点的之前或者之后。 O(1)
listSearchKey 查找并返回链表中包含给定值的节点。 O(N) ， N 为链表长度。
listIndex 返回链表在给定索引上的节点。 O(N) ， N 为链表长度。
listDelNode 从链表中删除给定节点。 O(1) 。
listRotate 将链表的表尾节点弹出，然后将被弹出的节点插入到链表的表头， 成为新的表头节点。 O(1)
listDup 复制一个给定链表的副本。 O(N) ， N 为链表长度。
listRelease 释放给定链表，以及链表中的所有节点。 O(N) ， N 为链表长度。

字典

字典， 又称符号表（symbol table）、关联数组（associative array）或者映射（map）， 是一种用于保存键值对（key-value pair）的抽象数据结构。

在字典中， 一个键（key）可以和一个值（value）进行关联（或者说将键映射为值）， 这些关联的键和值就被称为键值对。

字典中的每个键都是独一无二的， 程序可以在字典中根据键查找与之关联的值， 或者通过键来更新值， 又或者根据键来删除整个键值对， 等等。

字典经常作为一种数据结构内置在很多高级编程语言里面， 但 Redis 所使用的 C 语言并没有内置这种数据结构， 因此 Redis 构建了自己的字典实现。

字典在 Redis 中的应用相当广泛， 比如 Redis 的数据库就是使用字典来作为底层实现的， 对数据库的增、删、查、改操作也是构建在对字典的操作之上的。

Redis 字典的实现

Redis 的字典使用哈希表作为底层实现， 一个哈希表里面可以有多个哈希表节点， 而每个哈希表节点就保存了字典中的一个键值对。

哈希表

Redis 字典所使用的哈希表由 dict.h/dictht 结构定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef struct dictht {
    // 哈希表数组
    dictEntry **table;

    // 哈希表大小
    unsigned long size;

    // 哈希表大小掩码，用于计算索引值
    // 总是等于 size - 1
    unsigned long sizemask;

    // 该哈希表已有节点的数量
    unsigned long used;
} dictht;

解释如下：

  • table 属性是一个数组， 数组中的每个元素都是一个指向 dict.h/dictEntry 结构的指针， 每个 dictEntry 结构保存着一个键值对。
  • size 属性记录了哈希表的大小， 也即是 table 数组的大小， 而 used 属性则记录了哈希表目前已有节点（键值对）的数量。
  • sizemask 属性的值总是等于 size - 1 ， 这个属性和哈希值一起决定一个键应该被放到 table 数组的哪个索引上面。

哈希表节点

哈希表节点使用 dictEntry 结构表示， 每个 dictEntry 结构都保存着一个键值对：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef struct dictEntry {
    // 键
    void *key;

    // 值
    union {
        void *val;
        uint64_t u64;
        int64_t s64;
    } v;

    // 指向下个哈希表节点，形成链表
    struct dictEntry *next;
} dictEntry;

解释：

  • key 属性保存着键值对中的键， 而 v 属性则保存着键值对中的值， 其中键值对的值可以是一个指针， 或者是一个 uint64_t 整数， 又或者是一个 int64_t 整数。
  • next 属性是指向另一个哈希表节点的指针， 这个指针可以将多个哈希值相同的键值对连接在一次， 以此来解决键冲突（collision）的问题。

字典

Redis 中的字典由 dict.h/dict 结构表示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef struct dict {
    // 类型特定函数
    dictType *type;

    // 私有数据
    void *privdata;

    // 哈希表
    dictht ht[2];

    // rehash 索引
    // 当 rehash 不在进行时，值为 -1
    int rehashidx; /* rehashing not in progress if rehashidx == -1 */
} dict;

type 属性和 privdata 属性是针对不同类型的键值对， 为创建多态字典而设置的：

  • type 属性是一个指向 dictType 结构的指针， 每个 dictType 结构保存了一簇用于操作特定类型键值对的函数， Redis 会为用途不同的字典设置不同的类型特定函数。
  • privdata 属性则保存了需要传给那些类型特定函数的可选参数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
typedef struct dictType {
    // 计算哈希值的函数
    unsigned int (*hashFunction)(const void *key);

    // 复制键的函数
    void *(*keyDup)(void *privdata, const void *key);

    // 复制值的函数
    void *(*valDup)(void *privdata, const void *obj);

    // 对比键的函数
    int (*keyCompare)(void *privdata, const void *key1, const void *key2);

    // 销毁键的函数
    void (*keyDestructor)(void *privdata, void *key);

    // 销毁值的函数
    void (*valDestructor)(void *privdata, void *obj);
} dictType;

解释：

  • ht 属性是一个包含两个项的数组， 数组中的每个项都是一个 dictht 哈希表， 一般情况下， 字典只使用 ht[0] 哈希表， ht[1] 哈希表只会在对 ht[0] 哈希表进行 rehash 时使用。
  • 另一个和 rehash 有关的属性就是 rehashidx ： 它记录了 rehash 目前的进度， 如果目前没有在进行 rehash ， 那么它的值为 -1 。

Redis 哈希算法

当要将一个新的键值对添加到字典里面时， 程序需要先根据键值对的键计算出哈希值和索引值， 然后再根据索引值， 将包含新键值对的哈希表节点放到哈希表数组的指定索引上面。

Redis 计算哈希值和索引值的方法如下：

1
2
3
4
5
6
# 使用字典设置的哈希函数，计算键 key 的哈希值
hash = dict->type->hashFunction(key);

# 使用哈希表的 sizemask 属性和哈希值，计算出索引值
# 根据情况不同， ht[x] 可以是 ht[0] 或者 ht[1]
index = hash & dict->ht[x].sizemask;

如果我们要将一个键值对 k0 和 v0 添加到字典里面， 那么程序会先使用语句：

1
hash = dict->type->hashFunction(k0);

计算键 k0 的哈希值。假设计算得出的哈希值为 8 ， 那么程序会继续使用语句：

1
index = hash & dict->ht[0].sizemask = 8 & 3 = 0;

计算出键 k0 的索引值 0 ， 这表示包含键值对 k0 和 v0 的节点应该被放置到哈希表数组的索引 0 位置上

Redis 解决键冲突

当有两个或以上数量的键被分配到了哈希表数组的同一个索引上面时， 我们称这些键发生了冲突（collision）。

Redis 的哈希表使用链地址法（separate chaining）来解决键冲突： 每个哈希表节点都有一个 next 指针， 多个哈希表节点可以用 next 指针构成一个单向链表， 被分配到同一个索引上的多个节点可以用这个单向链表连接起来， 这就解决了键冲突的问题。

举个例子， 假设程序要将键值对 k2 和 v2 添加到图 4-6 所示的哈希表里面， 并且计算得出 k2 的索引值为 2 ， 那么键 k1 和 k2 将产生冲突， 而解决冲突的办法就是使用 next 指针将键 k2 和 k1 所在的节点连接起来。

Redis rehash

为了让哈希表的负载因子（load factor）维持在一个合理的范围之内， 当哈希表保存的键值对数量太多或者太少时， 程序需要对哈希表的大小进行相应的扩展或者收缩。

扩展和收缩哈希表的工作可以通过执行 rehash （重新散列）操作来完成， Redis 对字典的哈希表执行 rehash 的步骤如下：

  • 为字典的 ht[1] 哈希表分配空间， 这个哈希表的空间大小取决于要执行的操作， 以及 ht[0] 当前包含的键值对数量 （也即是ht[0].used 属性的值）：
    • 如果执行的是扩展操作， 那么 ht[1] 的大小为第一个大于等于 ht[0].used * 2 的 2^n （2 的 n 次方幂）；
    • 如果执行的是收缩操作， 那么 ht[1] 的大小为第一个大于等于 ht[0].used 的 2^n 。
  • 将保存在 ht[0] 中的所有键值对 rehash 到 ht[1] 上面： rehash 指的是重新计算键的哈希值和索引值， 然后将键值对放置到 ht[1] 哈希表的指定位置上。
  • 当 ht[0] 包含的所有键值对都迁移到了 ht[1] 之后 （ht[0] 变为空表）， 释放 ht[0] ， 将 ht[1] 设置为 ht[0] ， 并在 ht[1] 新创建一个空白哈希表， 为下一次 rehash 做准备。

举个例子， 假设程序要对图 4-8 所示字典的 ht[0] 进行扩展操作， 那么程序将执行以下步骤：

  • ht[0].used 当前的值为 4 ， 4 * 2 = 8 ， 而 8 （2^3）恰好是第一个大于等于 4 的 2 的 n 次方， 所以程序会将 ht[1] 哈希表的大小设置为 8 。 图 4-9 展示了 ht[1] 在分配空间之后， 字典的样子。
  • 将 ht[0] 包含的四个键值对都 rehash 到 ht[1] ， 如图 4-10 所示。
  • 释放 ht[0] ，并将 ht[1] 设置为 ht[0] ，然后为 ht[1] 分配一个空白哈希表，如图 4-11 所示。
  • 至此， 对哈希表的扩展操作执行完毕， 程序成功将哈希表的大小从原来的 4 改为了现在的 8 。




当以下条件中的任意一个被满足时， 程序会自动开始对哈希表执行扩展操作：

服务器目前没有在执行 BGSAVE 命令或者 BGREWRITEAOF 命令， 并且哈希表的负载因子大于等于 1 ；
服务器目前正在执行 BGSAVE 命令或者 BGREWRITEAOF 命令， 并且哈希表的负载因子大于等于 5 ；
其中哈希表的负载因子可以通过公式：

1
2
# 负载因子 = 哈希表已保存节点数量 / 哈希表大小
load_factor = ht[0].used / ht[0].size

根据 BGSAVE 命令或 BGREWRITEAOF 命令是否正在执行， 服务器执行扩展操作所需的负载因子并不相同， 这是因为在执行 BGSAVE 命令或BGREWRITEAOF 命令的过程中， Redis 需要创建当前服务器进程的子进程， 而大多数操作系统都采用写时复制（copy-on-write）技术来优化子进程的使用效率， 所以在子进程存在期间， 服务器会提高执行扩展操作所需的负载因子， 从而尽可能地避免在子进程存在期间进行哈希表扩展操作， 这可以避免不必要的内存写入操作， 最大限度地节约内存。

Redis 渐进式 rehash

扩展或收缩哈希表需要将 ht[0] 里面的所有键值对 rehash 到 ht[1] 里面， 但是， 这个 rehash 动作并不是一次性、集中式地完成的， 而是分多次、渐进式地完成的。这样避免了 rehash 对服务器性能造成影响。服务器不是一次性将 ht[0] 里面的所有键值对全部 rehash 到 ht[1] ， 而是分多次、渐进式地将 ht[0] 里面的键值对慢慢地 rehash 到 ht[1] 。

以下是哈希表渐进式 rehash 的详细步骤：

  • 为 ht[1] 分配空间， 让字典同时持有 ht[0] 和 ht[1] 两个哈希表。
  • 在字典中维持一个索引计数器变量 rehashidx ， 并将它的值设置为 0 ， 表示 rehash 工作正式开始。
  • 在 rehash 进行期间， 每次对字典执行添加、删除、查找或者更新操作时， 程序除了执行指定的操作以外， 还会顺带将 ht[0] 哈希表在 rehashidx 索引上的所有键值对 rehash 到 ht[1] ， 当 rehash 工作完成之后， 程序将 rehashidx 属性的值增一。
  • 随着字典操作的不断执行， 最终在某个时间点上， ht[0] 的所有键值对都会被 rehash 至 ht[1] ， 这时程序将 rehashidx 属性的值设为 -1 ， 表示 rehash 操作已完成。

渐进式 rehash 的好处在于它采取分而治之的方式， 将 rehash 键值对所需的计算工作均滩到对字典的每个添加、删除、查找和更新操作上， 从而避免了集中式 rehash 而带来的庞大计算量。

因为在进行渐进式 rehash 的过程中， 字典会同时使用 ht[0] 和 ht[1] 两个哈希表， 所以在渐进式 rehash 进行期间， 字典的删除（delete）、查找（find）、更新（update）等操作会在两个哈希表上进行： 比如说， 要在字典里面查找一个键的话， 程序会先在 ht[0] 里面进行查找， 如果没找到的话， 就会继续到 ht[1] 里面进行查找， 诸如此类。

另外， 在渐进式 rehash 执行期间， 新添加到字典的键值对一律会被保存到 ht[1] 里面， 而 ht[0] 则不再进行任何添加操作： 这一措施保证了 ht[0] 包含的键值对数量会只减不增， 并随着 rehash 操作的执行而最终变成空表。

Redis 字典 API

函数 作用 时间复杂度
dictCreate 创建一个新的字典。 O(1)
dictAdd 将给定的键值对添加到字典里面。 O(1)
dictReplace 将给定的键值对添加到字典里面， 如果键已经存在于字典，那么用新值取代原有的值。 O(1)
dictFetchValue 返回给定键的值。 O(1)
dictGetRandomKey 从字典中随机返回一个键值对。 O(1)
dictDelete 从字典中删除给定键所对应的键值对。 O(1)
dictRelease 释放给定字典，以及字典中包含的所有键值对。 O(N) ， N 为字典包含的键值对数量。

跳跃表

跳跃表（skiplist）是一种有序数据结构， 它通过在每个节点中维持多个指向其他节点的指针， 从而达到快速访问节点的目的。

跳跃表支持平均 O(logN) 最差 O(N) 复杂度的节点查找， 还可以通过顺序性操作来批量处理节点。

在大部分情况下， 跳跃表的效率可以和平衡树相媲美， 并且因为跳跃表的实现比平衡树要来得更为简单， 所以有不少程序都使用跳跃表来代替平衡树。

Redis 使用跳跃表作为有序集合键的底层实现之一： 如果一个有序集合包含的元素数量比较多， 又或者有序集合中元素的成员（member）是比较长的字符串时， Redis 就会使用跳跃表来作为有序集合键的底层实现。

跳跃表的实现

Redis 的跳跃表由 redis.h/zskiplistNode 和 redis.h/zskiplist 两个结构定义， 其中 zskiplistNode 结构用于表示跳跃表节点， 而 zskiplist结构则用于保存跳跃表节点的相关信息， 比如节点的数量， 以及指向表头节点和表尾节点的指针， 等等。

位于图片最左边的是 zskiplist 结构， 该结构包含以下属性：

  • header ：指向跳跃表的表头节点。
  • tail ：指向跳跃表的表尾节点。
  • level ：记录目前跳跃表内，层数最大的那个节点的层数（表头节点的层数不计算在内）。
  • length ：记录跳跃表的长度，也即是，跳跃表目前包含节点的数量（表头节点不计算在内）。

位于 zskiplist 结构右方的是四个 zskiplistNode 结构， 该结构包含以下属性：

  • 层（level）：节点中用 L1 、 L2 、 L3 等字样标记节点的各个层， L1 代表第一层， L2 代表第二层，以此类推。每个层都带有两个属性：前进指针和跨度。前进指针用于访问位于表尾方向的其他节点，而跨度则记录了前进指针所指向节点和当前节点的距离。在上面的图片中，连线上带有数字的箭头就代表前进指针，而那个数字就是跨度。当程序从表头向表尾进行遍历时，访问会沿着层的前进指针进行。
  • 后退（backward）指针：节点中用 BW 字样标记节点的后退指针，它指向位于当前节点的前一个节点。后退指针在程序从表尾向表头遍历时使用。
  • 分值（score）：各个节点中的 1.0 、 2.0 和 3.0 是节点所保存的分值。在跳跃表中，节点按各自所保存的分值从小到大排列。
  • 成员对象（obj）：各个节点中的 o1 、 o2 和 o3 是节点所保存的成员对象。

注意表头节点和其他节点的构造是一样的： 表头节点也有后退指针、分值和成员对象， 不过表头节点的这些属性都不会被用到， 所以图中省略了这些部分， 只显示了表头节点的各个层。

跳跃表节点的实现由 redis.h/zskiplistNode 结构定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
typedef struct zskiplistNode {
    // 后退指针
    struct zskiplistNode *backward;

    // 分值
    double score;

    // 成员对象
    robj *obj;

    // 层
    struct zskiplistLevel {

        // 前进指针
        struct zskiplistNode *forward;

        // 跨度
        unsigned int span;

    } level[];

} zskiplistNode;

跳跃表节点的 level 数组可以包含多个元素， 每个元素都包含一个指向其他节点的指针， 程序可以通过这些层来加快访问其他节点的速度， 一般来说， 层的数量越多， 访问其他节点的速度就越快。

每次创建一个新跳跃表节点的时候， 程序都根据幂次定律 （power law，越大的数出现的概率越小） 随机生成一个介于 1 和 32 之间的值作为 level 数组的大小， 这个大小就是层的“高度”。

图 5-2 分别展示了三个高度为 1 层、 3 层和 5 层的节点， 因为 C 语言的数组索引总是从 0 开始的， 所以节点的第一层是 level[0] ， 而第二层是 level[1] ， 以此类推。

每个层都有一个指向表尾方向的前进指针（level[i].forward 属性）， 用于从表头向表尾方向访问节点。

图 5-3 用虚线表示出了程序从表头向表尾方向， 遍历跳跃表中所有节点的路径：

迭代程序首先访问跳跃表的第一个节点（表头）， 然后从第四层的前进指针移动到表中的第二个节点。
在第二个节点时， 程序沿着第二层的前进指针移动到表中的第三个节点。
在第三个节点时， 程序同样沿着第二层的前进指针移动到表中的第四个节点。
当程序再次沿着第四个节点的前进指针移动时， 它碰到一个 NULL ， 程序知道这时已经到达了跳跃表的表尾， 于是结束这次遍历。

层的跨度（level[i].span 属性）用于记录两个节点之间的距离：

  • 两个节点之间的跨度越大， 它们相距得就越远。
  • 指向 NULL 的所有前进指针的跨度都为 0 ， 因为它们没有连向任何节点。
    初看上去， 很容易以为跨度和遍历操作有关， 但实际上并不是这样 —— 遍历操作只使用前进指针就可以完成了， 跨度实际上是用来计算排位（rank）的： 在查找某个节点的过程中， 将沿途访问过的所有层的跨度累计起来， 得到的结果就是目标节点在跳跃表中的排位。

举个例子， 图 5-4 用虚线标记了在跳跃表中查找分值为 3.0 、 成员对象为 o3 的节点时， 沿途经历的层： 查找的过程只经过了一个层， 并且层的跨度为 3 ， 所以目标节点在跳跃表中的排位为 3 。

通过一个zskiplist结构来持有节点，可以更方便的进行处理。

1
2
3
4
5
6
7
8
typedef struct zskiplist {
    // 表头节点和表尾节点
    struct zskiplistNode *header, *tailer;
    // 表中节点的数量
    unsigned long length;
    // 表中层数最大的节点的层数
    ine level;
} zskiplist;

Redis 跳跃表 API

函数 作用 时间复杂度
zslCreate 创建一个新的跳跃表。 O(1)
zslFree 释放给定跳跃表，以及表中包含的所有节点。 O(N) ， N 为跳跃表的长度。
zslInsert 将包含给定成员和分值的新节点添加到跳跃表中。 平均 O(N) ， N 为跳跃表长度。
zslDelete 删除跳跃表中包含给定成员和分值的节点。 平均 O(N) ， N 为跳跃表长度。
zslGetRank 返回包含给定成员和分值的节点在跳跃表中的排位。 平均 O(N) ， N 为跳跃表长度。
zslGetElementByRank 返回跳跃表在给定排位上的节点。 平均 O(N) ， N 为跳跃表长度。
zslIsInRange 给定一个分值范围（range）， 比如 0 到 15 ， 20 到 28，诸如此类， 如果给定的分值范围包含在跳跃表的分值范围之内， 那么返回 1 ，否则返回 0 。 通过跳跃表的表头节点和表尾节点， 这个检测可以用 O(1) 复杂度完成。
zslFirstInRange 给定一个分值范围， 返回跳跃表中第一个符合这个范围的节点。 平均 O(N) 。 N 为跳跃表长度。
zslLastInRange 给定一个分值范围， 返回跳跃表中最后一个符合这个范围的节点。 平均 O(N) 。 N 为跳跃表长度。
zslDeleteRangeByScore 给定一个分值范围， 删除跳跃表中所有在这个范围之内的节点。 O(N) ， N 为被删除节点数量。
zslDeleteRangeByRank 给定一个排位范围， 删除跳跃表中所有在这个范围之内的节点。 O(N) ， N 为被删除节点数量。

整数集合

整数集合（intset）是集合键的底层实现之一： 当一个集合只包含整数值元素， 并且这个集合的元素数量不多时， Redis 就会使用整数集合作为集合键的底层实现。

举个例子， 如果我们创建一个只包含五个元素的集合键， 并且集合中的所有元素都是整数值， 那么这个集合键的底层实现就会是整数集合：

1
2
3
4
5
redis> SADD numbers 1 3 5 7 9
(integer) 5

redis> OBJECT ENCODING numbers
"intset"

Redis 整数集合的实现

整数集合（intset）是 Redis 用于保存整数值的集合抽象数据结构， 它可以保存类型为 int16_t 、 int32_t 或者 int64_t 的整数值， 并且保证集合中不会出现重复元素。每个 intset.h/intset 结构表示一个整数集合：

1
2
3
4
5
6
7
8
9
10
typedef struct intset {
    // 编码方式
    uint32_t encoding;

    // 集合包含的元素数量
    uint32_t length;

    // 保存元素的数组
    int8_t contents[];
} intset;

解释：

  • contents 数组是整数集合的底层实现： 整数集合的每个元素都是 contents 数组的一个数组项（item）， 各个项在数组中按值的大小从小到大有序地排列， 并且数组中不包含任何重复项。
  • length 属性记录了整数集合包含的元素数量， 也即是 contents 数组的长度。

虽然 intset 结构将 contents 属性声明为 int8_t 类型的数组， 但实际上 contents 数组并不保存任何 int8_t 类型的值 —— contents 数组的真正类型取决于 encoding 属性的值：

  • encoding = INTSET_ENC_INT16 ， contents 是 int16_t 类型的数组（最小值为 -32,768 ，最大值为 32,767 ）。
  • encoding = INTSET_ENC_INT32 ， contents 是 int32_t 类型的数组（最小值为 -2,147,483,648 ，最大值为 2,147,483,647 ）。
  • encoding = INTSET_ENC_INT64 ， contents 是 int64_t 类型的数组（最小值为 -9,223,372,036,854,775,808 ，最大值为 9,223,372,036,854,775,807 ）。

Redis升级

每当我们要将一个新元素添加到整数集合里面， 并且新元素的类型比整数集合现有所有元素的类型都要长时， 整数集合需要先进行升级（upgrade）， 然后才能将新元素添加到整数集合里面。

升级整数集合并添加新元素共分为三步进行：

  • 根据新元素的类型， 扩展整数集合底层数组的空间大小， 并为新元素分配空间。
  • 将底层数组现有的所有元素都转换成与新元素相同的类型， 并将类型转换后的元素放置到正确的位上， 而且在放置元素的过程中， 需要继续维持底层数组的有序性质不变。
  • 将新元素添加到底层数组里面。

假设现在有一个 INTSET_ENC_INT16 编码的整数集合， 集合中包含三个 int16_t 类型的元素， 如图 6-3 所示。

因为每个元素都占用 16 位空间， 所以整数集合底层数组的大小为 3 * 16 = 48 位， 图 6-4 展示了整数集合的三个元素在这 48 位里的位置。

现在， 假设我们要将类型为 int32_t 的整数值 65535 添加到整数集合里面， 因为 65535 的类型 int32_t 比整数集合当前所有元素的类型都要长， 所以在将 65535 添加到整数集合之前， 程序需要先对整数集合进行升级。升级首先要做的是， 根据新类型的长度， 以及集合元素的数量（包括要添加的新元素在内）， 对底层数组进行空间重分配。整数集合目前有三个元素， 再加上新元素 65535 ， 整数集合需要分配四个元素的空间， 因为每个 int32_t 整数值需要占用 32 位空间， 所以在空间重分配之后， 底层数组的大小将是 32 * 4 = 128 位， 如图 6-5 所示。

虽然程序对底层数组进行了空间重分配， 但数组原有的三个元素 1 、 2 、 3 仍然是 int16_t 类型， 这些元素还保存在数组的前 48 位里面， 所以程序接下来要做的就是将这三个元素转换成 int32_t 类型， 并将转换后的元素放置到正确的位上面， 而且在放置元素的过程中， 需要维持底层数组的有序性质不变。

首先， 因为元素 3 在 1 、 2 、 3 、 65535 四个元素中排名第三， 所以它将被移动到 contents 数组的索引 2 位置上， 也即是数组 64 位至 95 位的空间内， 如图 6-6 所示。

接着， 因为元素 2 在 1 、 2 、 3 、 65535 四个元素中排名第二， 所以它将被移动到 contents 数组的索引 1 位置上， 也即是数组的 32位至 63 位的空间内， 如图 6-7 所示。

之后， 因为元素 1 在 1 、 2 、 3 、 65535 四个元素中排名第一， 所以它将被移动到 contents 数组的索引 0 位置上， 也即是数组的 0 位至 31 位的空间内， 如图 6-8 所示。

然后， 因为元素 65535 在 1 、 2 、 3 、 65535 四个元素中排名第四， 所以它将被添加到 contents 数组的索引 3 位置上， 也即是数组的96 位至 127 位的空间内， 如图 6-9 所示。

最后， 程序将整数集合 encoding 属性的值从 INTSET_ENC_INT16 改为 INTSET_ENC_INT32 ， 并将 length 属性的值从 3 改为 4 ，因为每次向整数集合添加新元素都可能会引起升级， 而每次升级都需要对底层数组中已有的所有元素进行类型转换， 所以向整数集合添加新元素的时间复杂度为 O(N) 。

其他类型的升级操作， 比如从 INTSET_ENC_INT16 编码升级为 INTSET_ENC_INT64 编码， 或者从 INTSET_ENC_INT32 编码升级为 INTSET_ENC_INT64 编码， 升级的过程都和上面展示的升级过程类似。

因为引发升级的新元素的长度总是比整数集合现有所有元素的长度都大， 所以这个新元素的值要么就大于所有现有元素， 要么就小于所有现有元素：

  • 在新元素小于所有现有元素的情况下， 新元素会被放置在底层数组的最开头（索引 0 ）；
  • 在新元素大于所有现有元素的情况下， 新元素会被放置在底层数组的最末尾（索引 length-1 ）。

Redis 升级的好处

整数集合的升级策略有两个好处， 一个是提升整数集合的灵活性， 另一个是尽可能地节约内存。

  • 提升灵活性：通常不会将两种不同类型的值放在同一个数据结构里面。但是， 因为整数集合可以通过自动升级底层数组来适应新元素， 所以我们可以随意地将 int16_t 、 int32_t 或者 int64_t 类型的整数添加到集合中， 而不必担心出现类型错误， 这种做法非常灵活。
  • 节约内存：当然， 要让一个数组可以同时保存 int16_t 、 int32_t 、 int64_t 三种类型的值， 最简单的做法就是直接使用 int64_t 类型的数组作为整数集合的底层实现。但是会出现浪费内存的情况。而整数集合现在的做法既可以让集合能同时保存三种不同类型的值， 又可以确保升级操作只会在有需要的时候进行， 这可以尽量节省内存。

Redis 降级

整数集合不支持降级操作， 一旦对数组进行了升级， 编码就会一直保持升级后的状态。

举个例子， 对于一个整数集合来说， 即使我们将集合里唯一一个真正需要使用 int64_t 类型来保存的元素 4294967295 删除了， 整数集合的编码仍然会维持 INTSET_ENC_INT64 ， 底层数组也仍然会是 int64_t 类型的。

Redis 整数集合 API

函数 作用 时间复杂度
intsetNew 创建一个新的整数集合。 O(1)
intsetAdd 将给定元素添加到整数集合里面。 O(N)
intsetRemove 从整数集合中移除给定元素。 O(N)
intsetFind 检查给定值是否存在于集合。 因为底层数组有序，查找可以通过二分查找法来进行， 所以复杂度为 O(\log N) 。
intsetRandom 从整数集合中随机返回一个元素。 O(1)
intsetGet 取出底层数组在给定索引上的元素。 O(1)
intsetLen 返回整数集合包含的元素个数。 O(1)
intsetBlobLen 返回整数集合占用的内存字节数。 O(1)

压缩列表

压缩列表（ziplist）是列表键和哈希键的底层实现之一。当一个列表键只包含少量列表项， 并且每个列表项要么就是小整数值， 要么就是长度比较短的字符串， 那么 Redis 就会使用压缩列表来做列表键的底层实现。

比如说， 执行以下命令将创建一个压缩列表实现的列表键：

1
2
3
4
5
redis> RPUSH lst 1 3 5 10086 "hello" "world"
(integer) 6

redis> OBJECT ENCODING lst
"ziplist"

因为列表键里面包含的都是 1 、 3 、 5 、 10086 这样的小整数值， 以及 “hello” 、 “world” 这样的短字符串。

另外， 当一个哈希键只包含少量键值对， 并且每个键值对的键和值要么就是小整数值， 要么就是长度比较短的字符串， 那么 Redis 就会使用压缩列表来做哈希键的底层实现。

举个例子， 执行以下命令将创建一个压缩列表实现的哈希键：

1
2
3
4
5
redis> HMSET profile "name" "Jack" "age" 28 "job" "Programmer"
OK

redis> OBJECT ENCODING profile
"ziplist"

因为哈希键里面包含的所有键和值都是小整数值或者短字符串。

Redis 压缩列表的构成

压缩列表是 Redis 为了节约内存而开发的， 由一系列特殊编码的连续内存块组成的顺序型（sequential）数据结构。一个压缩列表可以包含任意多个节点（entry）， 每个节点可以保存一个字节数组或者一个整数值。图 7-1 展示了压缩列表的各个组成部分， 表 7-1 则记录了各个组成部分的类型、长度、以及用途。

压缩列表各个组成部分的详细说明

|属性|类型|长度|用途|
|—|—|—|
|zlbytes|uint32_t|4 字节|记录整个压缩列表占用的内存字节数：在对压缩列表进行内存重分配， 或者计算 zlend 的位置时使用。|
|zltail|uint32_t|4 字节|记录压缩列表表尾节点距离压缩列表的起始地址有多少字节： 通过这个偏移量，程序无须遍历整个压缩列表就可以确定表尾节点的地址。|
|zllen|uint16_t|2 字节|记录了压缩列表包含的节点数量： 当这个属性的值小于 UINT16_MAX （65535）时， 这个属性的值就是压缩列表包含节点的数量； 当这个值等于 UINT16_MAX 时， 节点的真实数量需要遍历整个压缩列表才能计算得出。|
|entryX|列表节点|不定|压缩列表包含的各个节点，节点的长度由节点保存的内容决定。|
|zlend|uint8_t|1 字节|特殊值 0xFF （十进制 255 ），用于标记压缩列表的末端。|

图 7-2 展示了一个压缩列表示例：

  • 列表 zlbytes 属性的值为 0x50 （十进制 80）， 表示压缩列表的总长为 80 字节。
  • 列表 zltail 属性的值为 0x3c （十进制 60）， 这表示如果我们有一个指向压缩列表起始地址的指针 p ， 那么只要用指针 p 加上- 偏移量 60 ， 就可以计算出表尾节点 entry3 的地址。
  • 列表 zllen 属性的值为 0x3 （十进制 3）， 表示压缩列表包含三个节点。

Redis 压缩列表节点的构成

每个压缩列表节点可以保存一个字节数组或者一个整数值， 其中， 字节数组可以是以下三种长度的其中一种：

  • 长度小于等于 63 （2^{6}-1）字节的字节数组；
  • 长度小于等于 16383 （2^{14}-1） 字节的字节数组；
  • 长度小于等于 4294967295 （2^{32}-1）字节的字节数组；

而整数值则可以是以下六种长度的其中一种：

  • 4 位长，介于 0 至 12 之间的无符号整数；
  • 1 字节长的有符号整数；
  • 3 字节长的有符号整数；
  • int16_t 类型整数；
  • int32_t 类型整数；
  • int64_t 类型整数。

每个压缩列表节点都由 previous_entry_length 、 encoding 、 content 三个部分组成。

previous_entry_length：节点的 previous_entry_length 属性以字节为单位， 记录了压缩列表中前一个节点的长度。
previous_entry_length 属性的长度可以是 1 字节或者 5 字节；如果前一节点的长度小于 254 字节， 那么 previous_entry_length 属性的长度为 1 字节；前一节点的长度就保存在这一个字节里面。
如果前一节点的长度大于等于 254 字节， 那么 previous_entry_length 属性的长度为 5 字节： 其中属性的第一字节会被设置为 0xFE（十进制值 254）， 而之后的四个字节则用于保存前一节点的长度。

压缩列表的从表尾向表头遍历操作就是使用这一原理实现的： 只要我们拥有了一个指向某个节点起始地址的指针， 那么通过这个指针以及这个节点的 previous_entry_length 属性， 程序就可以一直向前一个节点回溯， 最终到达压缩列表的表头节点。

一个从表尾节点向表头节点进行遍历的完整过程：

  • 首先，我们拥有指向压缩列表表尾节点 entry4 起始地址的指针 p1 （指向表尾节点的指针可以通过指向压缩列表起始地址的指针加上zltail 属性的值得出）；
  • 通过用 p1 减去 entry4 节点 previous_entry_length 属性的值， 我们得到一个指向 entry4 前一节点 entry3 起始地址的指针 p2 ；
  • 通过用 p2 减去 entry3 节点 previous_entry_length 属性的值， 我们得到一个指向 entry3 前一节点 entry2 起始地址的指针 p3 ；
  • 通过用 p3 减去 entry2 节点 previous_entry_length 属性的值， 我们得到一个指向 entry2 前一节点 entry1 起始地址的指针 p4 ， entry1为压缩列表的表头节点；
  • 最终， 我们从表尾节点向表头节点遍历了整个列表。

encoding：节点的 encoding 属性记录了节点的 content 属性所保存数据的类型以及长度：

  • 一字节、两字节或者五字节长， 值的最高位为 00 、 01 或者 10 的是字节数组编码： 这种编码表示节点的 content 属性保存着字节数组， 数组的长度由编码除去最高两位之后的其他位记录；
  • 一字节长， 值的最高位以 11 开头的是整数编码： 这种编码表示节点的 content 属性保存着整数值， 整数值的类型和长度由编码除去最高两位之后的其他位记录；

content：节点的 content 属性负责保存节点的值， 节点值可以是一个字节数组或者整数， 值的类型和长度由节点的 encoding 属性决定。

Redis 连锁更新

Redis 将在特殊情况下产生的连续多次空间扩展操作称之为“连锁更新”（cascade update）

除了添加新节点可能会引发连锁更新之外， 删除节点也可能会引发连锁更新。

如果 e1 至 eN 都是大小介于 250 字节至 253 字节的节点， big 节点的长度大于等于 254 字节（需要 5 字节的 previous_entry_length 来保存）， 而 small 节点的长度小于 254 字节（只需要 1 字节的 previous_entry_length 来保存）， 那么当我们将 small 节点从压缩列表中删除之后， 为了让 e1 的 previous_entry_length 属性可以记录 big 节点的长度， 程序将扩展 e1 的空间， 并由此引发之后的连锁更新。

因为连锁更新在最坏情况下需要对压缩列表执行 N 次空间重分配操作， 而每次空间重分配的最坏复杂度为 O(N^2) 。

要注意的是， 尽管连锁更新的复杂度较高， 但它真正造成性能问题的几率是很低的：

  • 首先， 压缩列表里要恰好有多个连续的、长度介于 250 字节至 253 字节之间的节点， 连锁更新才有可能被引发， 在实际中， 这种情况并不多见；
  • 其次， 即使出现连锁更新， 但只要被更新的节点数量不多， 就不会对性能造成任何影响： 比如说， 对三五个节点进行连锁更新是绝对不会影响性能的；

因为以上原因， ziplistPush 等命令的平均复杂度仅为 O(N) ， 在实际中， 我们可以放心地使用这些函数， 而不必担心连锁更新会影响压缩列表的性能。

Redis 压缩列表 API

函数 作用 算法复杂度
ziplistNew 创建一个新的压缩列表。 O(1)
ziplistPush 创建一个包含给定值的新节点， 并将这个新节点添加到压缩列表的表头或者表尾。 平均 O(N^2) 。
ziplistInsert 将包含给定值的新节点插入到给定节点之后。 平均 O(N^2) 。
ziplistIndex 返回压缩列表给定索引上的节点。 O(N)
ziplistFind 在压缩列表中查找并返回包含了给定值的节点。 因为节点的值可能是一个字节数组， 所以检查节点值和给定值是否相同的复杂度为 O(N^2) 。
ziplistNext 返回给定节点的下一个节点。 O(1)
ziplistPrev 返回给定节点的前一个节点。 O(1)
ziplistGet 获取给定节点所保存的值。 O(1)
ziplistDelete 从压缩列表中删除给定的节点。 平均 O(N^2) 。
ziplistDeleteRange 删除压缩列表在给定索引上的连续多个节点。 平均 O(N^2) 。
ziplistBlobLen 返回压缩列表目前占用的内存字节数。 O(1)
ziplistLen 返回压缩列表目前包含的节点数量。 节点数量小于 65535 时 O(N) 。

因为 ziplistPush 、 ziplistInsert 、 ziplistDelete 和 ziplistDeleteRange 四个函数都有可能会引发连锁更新， 所以它们的最坏复杂度都是 O(N^2) 。

对象

Redis 并没有直接使用上述数据结构来实现键值对数据库， 而是基于这些数据结构创建了一个对象系统， 这个系统包含字符串对象、列表对象、哈希对象、集合对象和有序集合对象这五种类型的对象， 每种对象都用到了至少一种我们前面所介绍的数据结构。

通过这五种不同类型的对象， Redis 可以在执行命令之前， 根据对象的类型来判断一个对象是否可以执行给定的命令。 使用对象的另一个好处是， 我们可以针对不同的使用场景， 为对象设置多种不同的数据结构实现， 从而优化对象在不同场景下的使用效率。

除此之外， Redis 的对象系统还实现了基于引用计数技术的内存回收机制： 当程序不再使用某个对象的时候， 这个对象所占用的内存就会被自动释放； 另外， Redis 还通过引用计数技术实现了对象共享机制， 这一机制可以在适当的条件下， 通过让多个数据库键共享同一个对象来节约内存。

最后， Redis 的对象带有访问时间记录信息， 该信息可以用于计算数据库键的空转时长， 在服务器启用了 maxmemory 功能的情况下， 空转时长较大的那些键可能会优先被服务器删除。

Redis 对象的类型与编码

Redis 使用对象来表示数据库中的键和值， 每次当我们在 Redis 的数据库中新创建一个键值对时， 我们至少会创建两个对象， 一个对象用作键值对的键（键对象）， 另一个对象用作键值对的值（值对象）。

Redis 中的每个对象都由一个 redisObject 结构表示， 该结构中和保存数据有关的三个属性分别是 type 属性、 encoding 属性和 ptr 属性：

1
2
3
4
5
6
7
8
9
10
typedef struct redisObject {
    // 类型
    unsigned type:4;

    // 编码
    unsigned encoding:4;

    // 指向底层实现数据结构的指针
    void *ptr;
} robj;

对象的 type 属性记录了对象的类型， 这个属性的值可以是表中列出的常量的其中一个。

类型常量 对象的名称
REDIS_STRING 字符串对象
REDIS_LIST 列表对象
REDIS_HASH 哈希对象
REDIS_SET 集合对象
REDIS_ZSET 有序集合对象

对于 Redis 数据库保存的键值对来说， 键总是一个字符串对象， 而值则可以是字符串对象、列表对象、哈希对象、集合对象或者有序集合对象的其中一种， 因此：

  • 当我们称呼一个数据库键为“字符串键”时， 我们指的是“这个数据库键所对应的值为字符串对象”；
  • 当我们称呼一个键为“列表键”时， 我们指的是“这个数据库键所对应的值为列表对象”，

TYPE 命令的实现方式也与此类似， 当我们对一个数据库键执行 TYPE 命令时， 命令返回的结果为数据库键对应的值对象的类型， 而不是键对象的类型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 键为字符串对象，值为字符串对象
redis> SET msg "hello world"
OK

redis> TYPE msg
string

# 键为字符串对象，值为列表对象
redis> RPUSH numbers 1 3 5
(integer) 6

redis> TYPE numbers
list

# 键为字符串对象，值为哈希对象
redis> HMSET profile name Tome age 25 career Programmer
OK

redis> TYPE profile
hash

# 键为字符串对象，值为集合对象
redis> SADD fruits apple banana cherry
(integer) 3

redis> TYPE fruits
set

# 键为字符串对象，值为有序集合对象
redis> ZADD price 8.5 apple 5.0 banana 6.0 cherry
(integer) 3

redis> TYPE price
zset

表中列出了 TYPE 命令在面对不同类型的值对象时所产生的输出。

对象 对象 type 属性的值 TYPE 命令的输出
字符串对象 REDIS_STRING “string”
列表对象 REDIS_LIST “list”
哈希对象 REDIS_HASH “hash”
集合对象 REDIS_SET “set”
有序集合对象 REDIS_ZSET “zset”

编码和底层实现

对象的 ptr 指针指向对象的底层实现数据结构， 而这些数据结构由对象的 encoding 属性决定。

encoding 属性记录了对象所使用的编码， 也即是说这个对象使用了什么数据结构作为对象的底层实现， 这个属性的值可以是表 8-3 列出的常量的其中一个。

编码常量 编码所对应的底层数据结构
REDIS_ENCODING_INT long 类型的整数
REDIS_ENCODING_EMBSTR embstr 编码的简单动态字符串
REDIS_ENCODING_RAW 简单动态字符串
REDIS_ENCODING_HT 字典
REDIS_ENCODING_LINKEDLIST 双端链表
REDIS_ENCODING_ZIPLIST 压缩列表
REDIS_ENCODING_INTSET 整数集合
REDIS_ENCODING_SKIPLIST 跳跃表和字典

每种类型的对象都至少使用了两种不同的编码， 表中列出了每种类型的对象可以使用的编码。

类型 编码 对象
REDIS_STRING REDIS_ENCODING_INT 使用整数值实现的字符串对象。
REDIS_STRING REDIS_ENCODING_EMBSTR 使用 embstr 编码的简单动态字符串实现的字符串对象。
REDIS_STRING REDIS_ENCODING_RAW 使用简单动态字符串实现的字符串对象。
REDIS_LIST REDIS_ENCODING_ZIPLIST 使用压缩列表实现的列表对象。
REDIS_LIST REDIS_ENCODING_LINKEDLIST 使用双端链表实现的列表对象。
REDIS_HASH REDIS_ENCODING_ZIPLIST 使用压缩列表实现的哈希对象。
REDIS_HASH REDIS_ENCODING_HT 使用字典实现的哈希对象。
REDIS_SET REDIS_ENCODING_INTSET 使用整数集合实现的集合对象。
REDIS_SET REDIS_ENCODING_HT 使用字典实现的集合对象。
REDIS_ZSET REDIS_ENCODING_ZIPLIST 使用压缩列表实现的有序集合对象。
REDIS_ZSET REDIS_ENCODING_SKIPLIST 使用跳跃表和字典实现的有序集合对象。

使用 OBJECT ENCODING 命令可以查看一个数据库键的值对象的编码：

1
2
3
4
5
redis> SET msg "hello wrold"
OK

redis> OBJECT ENCODING msg
"embstr"

表中列出了不同编码的对象所对应的 OBJECT ENCODING 命令输出。

对象所使用的底层数据结构 编码常量 OBJECT ENCODING 命令输出
整数 REDIS_ENCODING_INT “int”
embstr 编码的简单动态字符串（SDS） REDIS_ENCODING_EMBSTR “embstr”
简单动态字符串 REDIS_ENCODING_RAW “raw”
字典 REDIS_ENCODING_HT “hashtable”
双端链表 REDIS_ENCODING_LINKEDLIST “linkedlist”
压缩列表 REDIS_ENCODING_ZIPLIST “ziplist”
整数集合 REDIS_ENCODING_INTSET “intset”
跳跃表和字典 REDIS_ENCODING_SKIPLIST “skiplist”

通过 encoding 属性来设定对象所使用的编码， 而不是为特定类型的对象关联一种固定的编码， 极大地提升了 Redis 的灵活性和效率， 因为 Redis 可以根据不同的使用场景来为一个对象设置不同的编码， 从而优化对象在某一场景下的效率。

Redis 字符串对象

字符串对象的编码可以是 int 、 raw 或者 embstr 。

如果一个字符串对象保存的是整数值， 并且这个整数值可以用 long 类型来表示， 那么字符串对象会将整数值保存在字符串对象结构的 ptr属性里面（将 void* 转换成 long ）， 并将字符串对象的编码设置为 int 。

如果字符串对象保存的是一个字符串值， 并且这个字符串值的长度大于 32 字节， 那么字符串对象将使用一个简单动态字符串（SDS）来保存这个字符串值， 并将对象的编码设置为 raw 。

如果字符串对象保存的是一个字符串值， 并且这个字符串值的长度小于等于 32 字节， 那么字符串对象将使用** embstr 编码**的方式来保存这个字符串值。

embstr 编码是专门用于保存短字符串的一种优化编码方式， 这种编码和 raw 编码一样， 都使用 redisObject 结构和 sdshdr 结构来表示字符串对象， 但 raw 编码会调用两次内存分配函数来分别创建 redisObject 结构和 sdshdr 结构， 而 embstr 编码则通过调用一次内存分配函数来分配一块连续的空间， 空间中依次包含 redisObject 和 sdshdr 两个结构。

embstr 编码的字符串对象在执行命令时， 产生的效果和 raw 编码的字符串对象执行命令时产生的效果是相同的， 但使用 embstr 编码的字符串对象来保存短字符串值有以下好处：

  • embstr 编码将创建字符串对象所需的内存分配次数从 raw 编码的两次降低为一次。
  • 释放 embstr 编码的字符串对象只需要调用一次内存释放函数， 而释放 raw 编码的字符串对象需要调用两次内存释放函数。
  • 因为 embstr 编码的字符串对象的所有数据都保存在一块连续的内存里面， 所以这种编码的字符串对象比起 raw 编码的字符串对象能够更好地利用缓存带来的优势。

可以用 long double 类型表示的浮点数在 Redis 中也是作为字符串值来保存的： 如果我们要保存一个浮点数到字符串对象里面， 那么程序会先将这个浮点数转换成字符串值， 然后再保存起转换所得的字符串值。

因为 Redis 没有为 embstr 编码的字符串对象编写任何相应的修改程序 （只有 int 编码的字符串对象和 raw 编码的字符串对象有这些程序）， 所以 embstr 编码的字符串对象实际上是只读的： 当我们对 embstr 编码的字符串对象执行任何修改命令时， 程序会先将对象的编码从 embstr 转换成 raw ， 然后再执行修改命令； 因为这个原因， embstr 编码的字符串对象在执行修改命令之后， 总会变成一个 raw 编码的字符串对象。

字符串命令的实现

因为字符串键的值为字符串对象， 所以用于字符串键的所有命令都是针对字符串对象来构建的， 表中列举了其中一部分字符串命令， 以及这些命令在不同编码的字符串对象下的实现方法。

命令 int 编码的实现方法 embstr 编码的实现方法 raw 编码的实现方法
SET 使用 int 编码保存值。 使用 embstr 编码保存值。 使用 raw 编码保存值。
GET 拷贝对象所保存的整数值， 将这个拷贝转换成字符串值， 然后向客户端返回这个字符串值。 直接向客户端返回字符串值。 直接向客户端返回字符串值。
APPEND 将对象转换成 raw 编码， 然后按raw 编码的方式执行此操作。 将对象转换成 raw 编码， 然后按raw 编码的方式执行此操作。 调用 sdscatlen 函数， 将给定字符串追加到现有字符串的末尾。
INCRBYFLOAT 取出整数值并将其转换成 longdouble 类型的浮点数， 对这个浮点数进行加法计算， 然后将得出的浮点数结果保存起来。 取出字符串值并尝试将其转换成long double 类型的浮点数， 对这个浮点数进行加法计算， 然后将得出的浮点数结果保存起来。 如果字符串值不能被转换成浮点数， 那么向客户端返回一个错误。 取出字符串值并尝试将其转换成 longdouble 类型的浮点数， 对这个浮点数进行加法计算， 然后将得出的浮点数结果保存起来。 如果字符串值不能被转换成浮点数， 那么向客户端返回一个错误。
INCRBY 对整数值进行加法计算， 得出的计算结果会作为整数被保存起来。 embstr 编码不能执行此命令， 向客户端返回一个错误。 raw 编码不能执行此命令， 向客户端返回一个错误。
DECRBY 对整数值进行减法计算， 得出的计算结果会作为整数被保存起来。 embstr 编码不能执行此命令， 向客户端返回一个错误。 raw 编码不能执行此命令， 向客户端返回一个错误。
STRLEN 拷贝对象所保存的整数值， 将这个拷贝转换成字符串值， 计算并返回这个字符串值的长度。 调用 sdslen 函数， 返回字符串的长度。 调用 sdslen 函数， 返回字符串的长度。
SETRANGE 将对象转换成 raw 编码， 然后按raw 编码的方式执行此命令。 将对象转换成 raw 编码， 然后按raw 编码的方式执行此命令。 将字符串特定索引上的值设置为给定的字符。
GETRANGE 拷贝对象所保存的整数值， 将这个拷贝转换成字符串值， 然后取出并返回字符串指定索引上的字符。 直接取出并返回字符串指定索引上的字符。 直接取出并返回字符串指定索引上的字符。

Redis 列表对象

列表对象的编码可以是 ziplist 或者 linkedlist 。ziplist 编码的列表对象使用压缩列表作为底层实现， 每个压缩列表节点（entry）保存了一个列表元素。举个例子， 如果我们执行以下 RPUSH 命令， 那么服务器将创建一个列表对象作为 numbers 键的值：

1
2
redis> RPUSH numbers 1 "three" 5
(integer) 3

如果 numbers 键的值对象使用的是 ziplist 编码， 这个这个值对象将会是图 8-5 所展示的样子：

另一方面， linkedlist 编码的列表对象使用双端链表作为底层实现， 每个双端链表节点（node）都保存了一个字符串对象， 而每个字符串对象都保存了一个列表元素。举个例子， 如果前面所说的 numbers 键创建的列表对象使用的不是 ziplist 编码， 而是 linkedlist 编码， 那么 numbers 键的值对象将是图 8-6 所示的样子。

为了简化字符串对象的表示， 我们在图 8-6 使用了一个带有 StringObject 字样的格子来表示一个字符串对象， 而 StringObject 字样下面的是字符串对象所保存的值。 图 8-7 代表的就是一个包含了字符串值 “three” 的字符串对象， 它是 8-8 的简化表示。

编码转换

当列表对象可以同时满足以下两个条件时， 列表对象使用 ziplist 编码：

  • 列表对象保存的所有字符串元素的长度都小于 64 字节；
  • 列表对象保存的元素数量小于 512 个；
  • 不能满足这两个条件的列表对象需要使用 linkedlist 编码。

以上两个条件的上限值是可以修改的， 具体请看配置文件中关于 list-max-ziplist-value 选项和 list-max-ziplist-entries 选项的说明。

对于使用 ziplist 编码的列表对象来说， 当使用 ziplist 编码所需的两个条件的任意一个不能被满足时， 对象的编码转换操作就会被执行： 原本保存在压缩列表里的所有列表元素都会被转移并保存到双端链表里面， 对象的编码也会从 ziplist 变为 linkedlist 。

以下代码展示了列表对象因为保存了长度太大的元素而进行编码转换的情况：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 所有元素的长度都小于 64 字节
redis> RPUSH blah "hello" "world" "again"
(integer) 3

redis> OBJECT ENCODING blah
"ziplist"

# 将一个 65 字节长的元素推入列表对象中
redis> RPUSH blah "wwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwww"
(integer) 4

# 编码已改变
redis> OBJECT ENCODING blah
"linkedlist"

列表命令的实现

因为列表键的值为列表对象， 所以用于列表键的所有命令都是针对列表对象来构建的， 表 8-8 列出了其中一部分列表键命令， 以及这些命令在不同编码的列表对象下的实现方法。

命令 ziplist 编码的实现方法 linkedlist 编码的实现方法
LPUSH 调用 ziplistPush 函数， 将新元素推入到压缩列表的表头。 调用 listAddNodeHead 函数， 将新元素推入到双端链表的表头。
RPUSH 调用 ziplistPush 函数， 将新元素推入到压缩列表的表尾。 调用 listAddNodeTail 函数， 将新元素推入到双端链表的表尾。
LPOP 调用 ziplistIndex 函数定位压缩列表的表头节点， 在向用户返回节点所保存的元素之后， 调用ziplistDelete 函数删除表头节点。 调用 listFirst 函数定位双端链表的表头节点， 在向用户返回节点所保存的元素之后， 调用 listDelNode 函数删除表头节点。
RPOP 调用 ziplistIndex 函数定位压缩列表的表尾节点， 在向用户返回节点所保存的元素之后， 调用ziplistDelete 函数删除表尾节点。 调用 listLast 函数定位双端链表的表尾节点， 在向用户返回节点所保存的元素之后， 调用 listDelNode 函数删除表尾节点。
LINDEX 调用 ziplistIndex 函数定位压缩列表中的指定节点， 然后返回节点所保存的元素。 调用 listIndex 函数定位双端链表中的指定节点， 然后返回节点所保存的元素。
LLEN 调用 ziplistLen 函数返回压缩列表的长度。 调用 listLength 函数返回双端链表的长度。
LINSERT 插入新节点到压缩列表的表头或者表尾时， 使用ziplistPush 函数； 插入新节点到压缩列表的其他位置时， 使用 ziplistInsert 函数。 调用 listInsertNode 函数， 将新节点插入到双端链表的指定位置。
LREM 遍历压缩列表节点， 并调用 ziplistDelete 函数删除包含了给定元素的节点。 遍历双端链表节点， 并调用 listDelNode 函数删除包含了给定元素的节点。
LTRIM 调用 ziplistDeleteRange 函数， 删除压缩列表中所有不在指定索引范围内的节点。 遍历双端链表节点， 并调用 listDelNode 函数删除链表中所有不在指定索引范围内的节点。
LSET 调用 ziplistDelete 函数， 先删除压缩列表指定索引上的现有节点， 然后调用 ziplistInsert 函数， 将一个包含给定元素的新节点插入到相同索引上面。 调用 listIndex 函数， 定位到双端链表指定索引上的节点， 然后通过赋值操作更新节点的值。

Redis 哈希对象

哈希对象的编码可以是 ziplist 或者 hashtable 。

ziplist 编码的哈希对象使用压缩列表作为底层实现， 每当有新的键值对要加入到哈希对象时， 程序会先将保存了键的压缩列表节点推入到压缩列表表尾， 然后再将保存了值的压缩列表节点推入到压缩列表表尾， 因此：

  • 保存了同一键值对的两个节点总是紧挨在一起， 保存键的节点在前， 保存值的节点在后；
  • 先添加到哈希对象中的键值对会被放在压缩列表的表头方向， 后添加到哈希对象中的键值对会被放在压缩列表的表尾方向。

如果我们执行以下 HSET 命令， 那么服务器将创建一个列表对象作为 profile 键的值：

1
2
3
4
5
6
7
8
redis> HSET profile name "Tom"
(integer) 1

redis> HSET profile age 25
(integer) 1

redis> HSET profile career "Programmer"
(integer) 1

如果 profile 键的值对象使用的是 ziplist 编码， 那么这个值对象将会是图 8-9 所示的样子， 其中对象所使用的压缩列表如图 8-10 所示。

另一方面， hashtable 编码的哈希对象使用字典作为底层实现， 哈希对象中的每个键值对都使用一个字典键值对来保存：

  • 字典的每个键都是一个字符串对象， 对象中保存了键值对的键；
  • 字典的每个值都是一个字符串对象， 对象中保存了键值对的值。

编码转换：当哈希对象可以同时满足以下两个条件时， 哈希对象使用 ziplist 编码：

  • 哈希对象保存的所有键值对的键和值的字符串长度都小于 64 字节；
  • 哈希对象保存的键值对数量小于 512 个；
  • 不能满足这两个条件的哈希对象需要使用 hashtable 编码。

对于使用 ziplist 编码的列表对象来说， 当使用 ziplist 编码所需的两个条件的任意一个不能被满足时， 对象的编码转换操作就会被执行： 原本保存在压缩列表里的所有键值对都会被转移并保存到字典里面， 对象的编码也会从 ziplist 变为 hashtable 。

Redis 集合对象

集合对象的编码可以是 intset 或者 hashtable 。intset 编码的集合对象使用整数集合作为底层实现， 集合对象包含的所有元素都被保存在整数集合里面。举个例子， 以下代码将创建一个如图 8-12 所示的 intset 编码集合对象：

1
2
redis> SADD numbers 1 3 5
(integer) 3

另一方面， hashtable 编码的集合对象使用字典作为底层实现， 字典的每个键都是一个字符串对象， 每个字符串对象包含了一个集合元素， 而字典的值则全部被设置为 NULL 。举个例子， 以下代码将创建一个如图 8-13 所示的 hashtable 编码集合对象：

1
2
redis> SADD fruits "apple" "banana" "cherry"
(integer) 3

编码的转换:当集合对象可以同时满足以下两个条件时， 对象使用 intset 编码：

  • 集合对象保存的所有元素都是整数值；
  • 集合对象保存的元素数量不超过 512 个；
  • 不能满足这两个条件的集合对象需要使用 hashtable 编码。

对于使用 intset 编码的集合对象来说， 当使用 intset 编码所需的两个条件的任意一个不能被满足时， 对象的编码转换操作就会被执行： 原本保存在整数集合中的所有元素都会被转移并保存到字典里面， 并且对象的编码也会从 intset 变为 hashtable 。

Redis 有序集合对象

有序集合的编码可以是 ziplist 或者 skiplist 。ziplist 编码的有序集合对象使用压缩列表作为底层实现， 每个集合元素使用两个紧挨在一起的压缩列表节点来保存， 第一个节点保存元素的成员（member）， 而第二个元素则保存元素的分值（score）。

压缩列表内的集合元素按分值从小到大进行排序， 分值较小的元素被放置在靠近表头的方向， 而分值较大的元素则被放置在靠近表尾的方向。举个例子， 如果我们执行以下 ZADD 命令， 那么服务器将创建一个有序集合对象作为 price 键的值：

1
2
redis> ZADD price 8.5 apple 5.0 banana 6.0 cherry
(integer) 3

如果 price 键的值对象使用的是 ziplist 编码， 那么这个值对象将会是图 8-14 所示的样子， 而对象所使用的压缩列表则会是 8-15 所示的样子。

skiplist 编码的有序集合对象使用zset结构作为底层实现， 一个 zset 结构同时包含一个字典和一个跳跃表：

1
2
3
4
typedef struct zset {
    zskiplist *zsl;
    dict *dict;
} zset;

zset 结构中的 zsl 跳跃表按分值从小到大保存了所有集合元素， 每个跳跃表节点都保存了一个集合元素： 跳跃表节点的 object 属性保存了元素的成员， 而跳跃表节点的 score 属性则保存了元素的分值。 通过这个跳跃表， 程序可以对有序集合进行范围型操作， 比如 ZRANK 、ZRANGE 等命令就是基于跳跃表 API 来实现的。

除此之外， zset 结构中的 dict 字典为有序集合创建了一个从成员到分值的映射， 字典中的每个键值对都保存了一个集合元素： 字典的键保存了元素的成员， 而字典的值则保存了元素的分值。 通过这个字典， 程序可以用 O(1) 复杂度查找给定成员的分值， ZSCORE 命令就是根据这一特性实现的， 而很多其他有序集合命令都在实现的内部用到了这一特性。

有序集合每个元素的成员都是一个字符串对象， 而每个元素的分值都是一个 double 类型的浮点数。 值得一提的是， 虽然 zset 结构同时使用跳跃表和字典来保存有序集合元素， 但这两种数据结构都会通过指针来共享相同元素的成员和分值， 所以同时使用跳跃表和字典来保存集合元素不会产生任何重复成员或者分值， 也不会因此而浪费额外的内存。

为什么有序集合需要同时使用跳跃表和字典来实现？在理论上来说， 有序集合可以单独使用字典或者跳跃表的其中一种数据结构来实现， 但无论单独使用字典还是跳跃表， 在性能上对比起同时使用字典和跳跃表都会有所降低。另一方面， 如果我们只使用跳跃表来实现有序集合， 那么跳跃表执行范围型操作的所有优点都会被保留， 但因为没有了字典， 所以根据成员查找分值这一操作的复杂度将从 O(log N) 。

有序集合命令的实现

因为有序集合键的值为有序集合对象， 所以用于有序集合键的所有命令都是针对有序集合对象来构建的， 列出了其中一部分有序集合键命令， 以及这些命令在不同编码的有序集合对象下的实现方法。

命令 ziplist 编码的实现方法 zset 编码的实现方法
ZADD 调用 ziplistInsert 函数， 将成员和分值作为两个节点分别插入到压缩列表。 先调用 zslInsert 函数， 将新元素添加到跳跃表， 然后调用 dictAdd 函数， 将新元素关联到字典。
ZCARD 调用 ziplistLen 函数， 获得压缩列表包含节点的数量， 将这个数量除以 2 得出集合元素的数量。 访问跳跃表数据结构的 length 属性， 直接返回集合元素的数量。
ZCOUNT 遍历压缩列表， 统计分值在给定范围内的节点的数量。 遍历跳跃表， 统计分值在给定范围内的节点的数量。
ZRANGE 从表头向表尾遍历压缩列表， 返回给定索引范围内的所有元素。 从表头向表尾遍历跳跃表， 返回给定索引范围内的所有元素。
ZREVRANGE 从表尾向表头遍历压缩列表， 返回给定索引范围内的所有元素。 从表尾向表头遍历跳跃表， 返回给定索引范围内的所有元素。
ZRANK 从表头向表尾遍历压缩列表， 查找给定的成员， 沿途记录经过节点的数量， 当找到给定成员之后， 途经节点的数量就是该成员所对应元素的排名。 从表头向表尾遍历跳跃表， 查找给定的成员， 沿途记录经过节点的数量， 当找到给定成员之后， 途经节点的数量就是该成员所对应元素的排名。
ZREVRANK 从表尾向表头遍历压缩列表， 查找给定的成员， 沿途记录经过节点的数量， 当找到给定成员之后， 途经节点的数量就是该成员所对应元素的排名。 从表尾向表头遍历跳跃表， 查找给定的成员， 沿途记录经过节点的数量， 当找到给定成员之后， 途经节点的数量就是该成员所对应元素的排名。
ZREM 遍历压缩列表， 删除所有包含给定成员的节点， 以及被删除成员节点旁边的分值节点。 遍历跳跃表， 删除所有包含了给定成员的跳跃表节点。 并在字典中解除被删除元素的成员和分值的关联。
ZSCORE 遍历压缩列表， 查找包含了给定成员的节点， 然后取出成员节点旁边的分值节点保存的元素分值。 直接从字典中取出给定成员的分值。

Redis 类型检查与命令多态

Redis 中用于操作键的命令基本上可以分为两种类型。其中一种命令可以对任何类型的键执行， 比如说 DEL 命令、 EXPIRE 命令、 RENAME 命令、 TYPE 命令、 OBJECT 命令， 等等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 字符串键
redis> SET msg "hello"
OK

# 列表键
redis> RPUSH numbers 1 2 3
(integer) 3

# 集合键
redis> SADD fruits apple banana cherry
(integer) 3

redis> DEL msg
(integer) 1

redis> DEL numbers
(integer) 1

redis> DEL fruits
(integer) 1

而另一种命令只能对特定类型的键执行， 比如说：

  • SET 、 GET 、 APPEND 、 STRLEN 等命令只能对字符串键执行；
  • HDEL 、 HSET 、 HGET 、 HLEN 等命令只能对哈希键执行；
  • RPUSH 、 LPOP 、 LINSERT 、 LLEN 等命令只能对列表键执行；
  • SADD 、 SPOP 、 SINTER 、 SCARD 等命令只能对集合键执行；
  • ZADD 、 ZCARD 、 ZRANK 、 ZSCORE 等命令只能对有序集合键执行；

类型检查的实现

从上面发生类型错误的代码示例可以看出， 为了确保只有指定类型的键可以执行某些特定的命令， 在执行一个类型特定的命令之前， Redis 会先检查输入键的类型是否正确， 然后再决定是否执行给定的命令。

类型特定命令所进行的类型检查是通过 redisObject 结构的 type 属性来实现的：在执行一个类型特定命令之前， 服务器会先检查输入数据库键的值对象是否为执行命令所需的类型， 如果是的话， 服务器就对键执行指定的命令；否则， 服务器将拒绝执行命令， 并向客户端返回一个类型错误。

多态命令的实现

Redis 除了会根据值对象的类型来判断键是否能够执行指定命令之外， 还会根据值对象的编码方式， 选择正确的命令实现代码来执行命令。举个例子， 在前面介绍列表对象的编码时我们说过， 列表对象有 ziplist 和 linkedlist 两种编码可用， 其中前者使用压缩列表 API 来实现列表命令， 而后者则使用双端链表 API 来实现列表命令。

现在， 考虑这样一个情况， 如果我们对一个键执行 LLEN 命令， 那么服务器除了要确保执行命令的是列表键之外， 还需要根据键的值对象所使用的编码来选择正确的 LLEN 命令实现：

  • 如果列表对象的编码为 ziplist ， 那么说明列表对象的实现为压缩列表， 程序将使用 ziplistLen 函数来返回列表的长度；
  • 如果列表对象的编码为 linkedlist ， 那么说明列表对象的实现为双端链表， 程序将使用 listLength 函数来返回双端链表的长度；

Redis 内存回收

因为 C 语言并不具备自动的内存回收功能， 所以 Redis 在自己的对象系统中构建了一个引用计数（reference counting）技术实现的内存回收机制， 通过这一机制， 程序可以通过跟踪对象的引用计数信息， 在适当的时候自动释放对象并进行内存回收。

每个对象的引用计数信息由 redisObject 结构的 refcount 属性记录：

1
2
3
4
5
6
typedef struct redisObject {
    // 引用计数
    int refcount;

    // ...
} robj;

对象的引用计数信息会随着对象的使用状态而不断变化：

  • 在创建一个新对象时， 引用计数的值会被初始化为 1 ；
  • 当对象被一个新程序使用时， 它的引用计数值会被增一；
  • 当对象不再被一个程序使用时， 它的引用计数值会被减一；
  • 当对象的引用计数值变为 0 时， 对象所占用的内存会被释放。
函数 作用
incrRefCount 将对象的引用计数值增一。
decrRefCount 将对象的引用计数值减一， 当对象的引用计数值等于 0 时， 释放对象。
resetRefCount 将对象的引用计数值设置为 0 ， 但并不释放对象， 这个函数通常在需要重新设置对象的引用计数值时使用。

对象的整个生命周期可以划分为创建对象、操作对象、释放对象三个阶段。

作为例子， 以下代码展示了一个字符串对象从创建到释放的整个过程：

1
2
3
4
5
6
7
8
// 创建一个字符串对象 s ，对象的引用计数为 1
robj *s = createStringObject(...)

// 对象 s 执行各种操作 ...

// 将对象 s 的引用计数减一，使得对象的引用计数变为 0
// 导致对象 s 被释放
decrRefCount(s)

其他不同类型的对象也会经历类似的过程。

Redis 对象共享

除了用于实现引用计数内存回收机制之外， 对象的引用计数属性还带有对象共享的作用。举个例子， 假设键 A 创建了一个包含整数值 100 的字符串对象作为值对象， 如图 8-20 所示。

图 8-21 就展示了包含整数值 100 的字符串对象同时被键 A 和键 B 共享之后的样子， 可以看到， 除了对象的引用计数从之前的 1 变成了 2 之外， 其他属性都没有变化。

共享对象机制对于节约内存非常有帮助， 数据库中保存的相同值对象越多， 对象共享机制就能节约越多的内存。

为什么 Redis 不共享包含字符串的对象？验证操作消耗的 CPU 时间会越来越多：

  • 如果共享对象是保存整数值的字符串对象， 那么验证操作的复杂度为 O(1) ；
  • 如果共享对象是保存字符串值的字符串对象， 那么验证操作的复杂度为 O(N) ；

如果共享对象是包含了多个值（或者对象的）对象， 比如列表对象或者哈希对象， 那么验证操作的复杂度将会是 O(N^2) 。
因此， 尽管共享更复杂的对象可以节约更多的内存， 但受到 CPU 时间的限制， Redis 只对包含整数值的字符串对象进行共享。

Redis 对象的空转时长

除了前面介绍过的 type 、 encoding 、 ptr 和 refcount 四个属性之外， redisObject 结构包含的最后一个属性为 lru 属性， 该属性记录了对象最后一次被命令程序访问的时间：

1
2
3
4
5
typedef struct redisObject {
    unsigned lru:22;

    // ...
} robj;

OBJECT IDLETIME 命令可以打印出给定键的空转时长， 这一空转时长就是通过将当前时间减去键的值对象的 lru 时间计算得出的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
redis> SET msg "hello world"
OK

# 等待一小段时间
redis> OBJECT IDLETIME msg
(integer) 20

# 等待一阵子
redis> OBJECT IDLETIME msg
(integer) 180

# 访问 msg 键的值
redis> GET msg
"hello world"

# 键处于活跃状态，空转时长为 0
redis> OBJECT IDLETIME msg
(integer) 0

OBJECT IDLETIME 命令的实现是特殊的， 这个命令在访问键的值对象时， 不会修改值对象的 lru 属性。

除了可以被 OBJECT IDLETIME 命令打印出来之外， 键的空转时长还有另外一项作用： 如果服务器打开了 maxmemory 选项， 并且服务器用于回收内存的算法为 volatile-lru 或者 allkeys-lru ， 那么当服务器占用的内存数超过了 maxmemory 选项所设置的上限值时， 空转时长较高的那部分键会优先被服务器释放， 从而回收内存。

单机数据库的实现

数据库

Redis服务器将所有数据库保存在服务器状态redis.h/redisServer结构的db数组中，db数组中的每个项都是一个redis.h/redisDb结构，代表一个数据库：

1
2
3
struct redisServer {
    redisDb* db;
}

每个Redis客户端都有自己的目标数据库，每当客户端执行数据库读写命令时，目标数据库就会成为这些命令的操作对象。服务器内部客户端状态redisClient结构的db属性记录了客户端当前的目标数据库，这个属性是一个指向redisServer.db数组中的其中一个元素的指针：

1
2
3
typedef struct redisClient {
    redisDb* db;
}

如果客户端执行SELECT命令，则会指向不同的数据库，这一操作是通过修改redisClient.db指针实现的。

Redis 数据库键空间

Redis 是一个键值对（key-value pair）数据库服务器， 服务器中的每个数据库都由一个 redis.h/redisDb 结构表示， 其中， redisDb 结构的dict字典保存了数据库中的所有键值对，我们将这个字典称为键空间（key space）：

1
2
3
4
5
6
typedef struct redisDb {
    // ...

    // 数据库键空间，保存着数据库中的所有键值对
    dict *dict;
} redisDb;

键空间和用户所见的数据库是直接对应的：

  • 键空间的键也就是数据库的键， 每个键都是一个字符串对象。
  • 键空间的值也就是数据库的值， 每个值可以是字符串对象、列表对象、哈希表对象、集合对象和有序集合对象在内的任意一种 Redis 对象。

举个例子， 如果我们在空白的数据库中执行以下命令：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
redis> SET message "hello world"
OK

redis> RPUSH alphabet "a" "b" "c"
(integer) 3

redis> HSET book name "Redis in Action"
(integer) 1

redis> HSET book author "Josiah L. Carlson"
(integer) 1

redis> HSET book publisher "Manning"
(integer) 1

那么在这些命令执行之后， 数据库的键空间将会是图 IMAGE_DB_EXAMPLE 所展示的样子：

  • alphabet 是一个列表键， 键的名字是一个包含字符串 “alphabet” 的字符串对象， 键的值则是一个包含三个元素的列表对象。
  • book 是一个哈希表键， 键的名字是一个包含字符串 “book” 的字符串对象， 键的值则是一个包含三个键值对的哈希表对象。
  • message 是一个字符串键， 键的名字是一个包含字符串 “message” 的字符串对象， 键的值则是一个包含字符串 “hello world” 的字符串对象。

添加新键

添加一个新键值对到数据库， 实际上就是将一个新键值对添加到键空间字典里面， 其中键为字符串对象， 而值则为任意一种类型的 Redis 对象。举个例子， 如果键空间当前的状态如图 IMAGE_DB_EXAMPLE 所示， 那么在执行以下命令之后：

1
2
redis> SET date "2013.12.1"
OK

键空间将添加一个新的键值对， 这个新键值对的键是一个包含字符串 “date” 的字符串对象， 而键值对的值则是一个包含字符串 “2013.12.1”的字符串对象， 如图 IMAGE_DB_AFTER_ADD_NEW_KEY 所示。

删除键

删除数据库中的一个键， 实际上就是在键空间里面删除键所对应的键值对对象。举个例子， 如果键空间当前的状态如图 IMAGE_DB_EXAMPLE 所示， 那么在执行以下命令之后：

1
2
redis> DEL book
(integer) 1

键 book 以及它的值将从键空间中被删除， 如图 IMAGE_DB_AFTER_DEL 所示。

更新键

对一个数据库键进行更新， 实际上就是对键空间里面键所对应的值对象进行更新， 根据值对象的类型不同， 更新的具体方法也会有所不同。举个例子， 如果键空间当前的状态如图 IMAGE_DB_EXAMPLE 所示， 那么在执行以下命令之后：

1
2
redis> SET message "blah blah"
OK

键 message 的值对象将从之前包含 “hello world” 字符串更新为包含 “blah blah” 字符串， 如图 IMAGE_DB_UPDATE_CAUSE_SET 所示。

对键取值

对一个数据库键进行取值， 实际上就是在键空间中取出键所对应的值对象， 根据值对象的类型不同， 具体的取值方法也会有所不同。举个例子， 如果键空间当前的状态如图 IMAGE_DB_EXAMPLE 所示， 那么当执行以下命令时：

1
2
redis> GET message
"hello world"

GET 命令将首先在键空间中查找键 message ， 找到键之后接着取得该键所对应的字符串对象值， 之后再返回值对象所包含的字符串 “helloworld” ， 取值过程如图 IMAGE_FETCH_VALUE_VIA_GET 所示。

其他键空间操作

很多针对数据库本身的 Redis 命令， 也是通过对键空间进行处理来完成的。比如说， 用于清空整个数据库的 FLUSHDB 命令， 就是通过删除键空间中的所有键值对来实现的。用于随机返回数据库中某个键的 RANDOMKEY 命令， 就是通过在键空间中随机返回一个键来实现的。

读写键空间时的维护操作

当使用 Redis 命令对数据库进行读写时， 服务器不仅会对键空间执行指定的读写操作， 还会执行一些额外的维护操作， 其中包括：

  • 在读取一个键之后（读操作和写操作都要对键进行读取）， 服务器会根据键是否存在， 以此来更新服务器的键空间命中（hit）次数或键空间不命中（miss）次数，
  • 在读取一个键之后， 服务器会更新键的 LRU （最后一次使用）时间， 这个值可以用于计算键的闲置时间，
  • 如果服务器在读取一个键时， 发现该键已经过期， 那么服务器会先删除这个过期键， 然后才执行余下的其他操作，
  • 如果有客户端使用 WATCH 命令监视了某个键， 那么服务器在对被监视的键进行修改之后， 会将这个键标记为脏（dirty）， 从而让事务程序注意到这个键已经被修改过，
  • 服务器每次修改一个键之后， 都会对脏（dirty）键计数器的值增一， 这个计数器会触发服务器的持久化以及复制操作执行，
  • 如果服务器开启了数据库通知功能， 那么在对键进行修改之后， 服务器将按配置发送相应的数据库通知。

设置键的生存时间或过期时间

通过EXPIRE命令或者PEXPIRE命令，客户端可以以秒或者毫秒精度为数据库中的某个键设置生存时间TTL，在经过指定时间后，服务器自动删除生存时间为0的键。

1
EXPIRE key 5

客户通过EXPIREAT或者PEXPIREAT以秒或毫秒精度给数据库中某个键设置过期时间（Linux时间戳），当键的过期时间到了，服务器自动从数据库中删除这个键。

Redis有四个不同命令用于设置键的生存时间或过期时间：

  • EXPIRE 将键key的生存时间设置为ttl秒。
  • PEXPIRE 将键key的生存时间设置为ttl毫秒。
  • EXPIREAT 将键key的过期时间设置为timestamp秒时间戳。
  • PEXPIREAT 将键key的过期时间设置为timestamp毫秒时间戳。

在redisDb结构体的expires字典用来保存数据库中所有键的过期时间，叫做过期字典：

  • 过期字典的键是一个指针，指向键空间中的某个键对象，
  • 值是一个long long类型的整数，保存间所指向的数据库键的过期时间（精确的UNIX毫秒时间戳）

图中是一个带有过期字典的数据库例子，键空间保存了数据库中的所有键值对，而过期字典保存了数据库键的过期时间。

PERSIST命令可以移除一个键的过期时间，在过期字典中找到一个给定的键，并解除键和值在过期字典中的关联。

TTL命令以秒为单位饭会键的剩余生存时间，而PTTL命令则以毫秒为单位饭会键的剩余生存时间。

通过过期字典，程序可以检查一个给定键是否过期：

  1. 检查给定键是否存在于过期字典，如果存在，那么取得键的过期时间；
  2. 检查当前UNIX时间戳是否大于键的过期时间，如果是的话则已过期，否则没过期。

过期键删除策略

如果一个键被删除了，什么时候会被删除：

  • 定时删除：设置过期时间同时，创建一个定时器，让定时器在键的过期时间到来时，立即执行对键的删除操作。
    • 优点：对内存友好，保证过期键尽可能快的删除，并释放过期键所占用的内存。
    • 缺点：对cpu时间是最不友好的，若过期键过多，会占用相当多cpu时间。
  • 惰性删除(被动删除)：放任过期键不管，当获取键时expireIfNeeded函数检查是否过期，过期就删除该键。
    • 优点：对cpu时间友好，只会操作键做过期检查，而不会删除其他无关过期键
    • 缺点：对内存不友好，过期键占用内存不释放，如果一个键再也不被访问到，那就造成内存一直占用，类似内存泄漏
  • 定期删除：每过一段时间，程序对数据库检查，然后删除过期键。
    • 如果删除操作执行得太频繁，或者执行时间太长，定期删除策略就会退化成定时删除策略，CPU消耗在删除过期键上
    • 如果删除操作执行太少，则退化为惰性删除

Redis的过期键删除策略

过期键的惰性删除策略由db.c/expireIfNeeded函数实现，所有读写数据库的Redis命令执行前都会调用expireIfNeeded函数对输入键进行检查，expireIfNeeded像是一个过滤器，它可以在命令真正执行前过滤掉过期的输入键。每个被访问的键都可能因为过期而被expireIfNeeded函数删除，所以每个命令的实现函数都必须同时能处理键存在或不存在的情况。

过期键的定期删除由redis.c/activeExpireCycle实现，它在规定的时间内分多次遍历服务器中的各个数据库，从数据库的expires字典中随机检查一部分键的过期时间，并删除其中的过期键。

AOF、RDB和复制功能对过期键的处理

生成RDB文件

在执行SAVE或者BGSAVE命令创建一个新的RDB文件时，程序会对数据库中的键进行检查，已过期的键不会被保存到新建的RDB文件中。

载入RDB文件

在启动Redis服务器时，如果服务器开启了RDB功能，那么服务器将对RDB文件进行载入：

  • 如果服务器以主服务器模式运行，那么在载入RDB文件时，程序会对文件中保存的键进行检查，未过期的键会被载入到数据库中，而过期键则会被忽略，所以过期键对载入RDB文件的主服务器不会造成影响。
  • 如果服务器以从服务器模式运行，那么在载入RDB文件时，文件中保存的所有键，不论是否过期，都会被载入到数据库中。不过，因为主从服务器在进行数据同步的时候，从服务器的数据库就会被清空，所以一般来讲，过期键对载入RDB文件的从服务器也不会造成影响。

AOF文件写入

当服务器以AOF持久化模式运行时，如果数据库中的某个键已经过期，但它还没有被惰性删除或者定期删除，那么AOF文件不会因为这个过期键而产生任何影响。当过期键被惰性删除或者定期删除之后，程序会向AOF文件追加一条DEL命令，来显式地记录该键已被删除。

举个例子，如果客户端使用GETmessage命令，试图访问过期的message键，那么服务器将执行以下三个动作：

  1. 从数据库中删除message键
  2. 追加一条DELmessage命令到AOF文件
  3. 向执行GE丆命令的客户端返回空回复。

AOF重写

和生成RDB文件时类似，在执行AOF重写的过程中，程序会对数据库中的键进行检查，已过期的键不会被保存到重写后的AOF文件中。

复制

服务器运行在复制模式下，从服务器的过期键删除动作由主服务器控制：

  • 主服务器在删除一个过期键之后，会显式地向所有从服务器发送一个DEL命令，告知从服务器删除这个过期键。
  • 从服务器在执行客户端发送的读命令时，即使碰到过期键也不会将过期键删除，而是继续像处理未过期的键一样来处理过期键。
  • 从服务器只有在接到主服务器发来的DEL命令之后，才会删除过期键

通过由主服务器来控制从服务器统一地删除过期键，可以保证主从服务器数据的一致性，也正是因为这个原因，当一个过期键仍然存在于主服务器的数据库时，这个过期键在从服务器里的复制品也会继续存在。

数据库通知

让客户通过订阅给定的频道或者模式，来获知数据库中键的变化，以及数据库中命令的执行情况，有两类：

  • 一类关注某个键执行了什么命令的通知称为键空间通知。
  • 一类关注某个命令被什么健执行了，称为键事件通知。

发送通知

发送数据库通知的功能由notify.c/notifyKeyspaceEvent函数实现：

1
void notifyKeyspaceEvent(int type, char* event, robj* key, int dbid);

type参数是当前想要发送的通知类型，其余三个是事件的名称、产生事件的键，以及产生事件的数据库号码。

流程：

  1. server.notify_keyspace_events属性就是服务器配置notify—keyspace—events选项所设置的值，如果给定的通知类型type不是服务器允许发送的通知类型，那么函数会直接返回，不做任何动作。
  2. 如果给定的通知是服务器允许发送的通知，那么下一步函数会检测服务器是否允许发送键空间通知，如果允许的话，程序就会构建并发送事件通知。
  3. 最后，函数检测服务器是否允许发送键事件通知，如果允许的话，程序就会构建并发送事件通知。

重点回顾

内容较多，回顾一下：

  • Redis服务器的所有数据库都保存在redisServer.db数组中，而数据库的数量则由redisServer.dbnum属性保存
  • 客户端通过修改目标数据库指针，让它指向redisServer.db数组中的不同元素来切换不同的数据库。
  • 数据库主要由dict和expires两个字典构成，其中dict字典负责保存键值对，而expires字典则负责保存键的过期时间
  • 因为数据库由字典构成，所以对数据库的操作都是建立在字典操作之上的
  • 数据库的键总是一个字符串对象，而值则可以是任意一种Redis对象类型，包括字符串对象、哈希表对象、集合对象、列表对象和有序集合对象，分别对应字符串键、哈希表键、集合键、列表键和有序集合键。
  • expires字典的键指向数据库中的某个键，而值则记录了数据库键的过期时间，过期时间是一个以毫秒为单位的UNIX时间戳
  • Redis使用惰性删除和定期删除两种策略来删除过期的键：惰性删除策略只在碰到过期键时才进行删除操作，定期删除策略则每隔一段时间主动查找并删除过期键。
  • 执行SAVE命令或者BGSAVE命令所产生的新RDB文件不会包含己经过期的键
  • 执行BGREWRITEAOF命令所产生的重写AOF文件不会包含已经过期的键
  • 当一个过期键被删除之后，服务器会追加一条DEL命令到现有AOF文件的末尾，显式地删除过期键。
  • 当主服务器删除一个过期键之后，它会向所有从服务器发送一条DEL命令，显式地删除过期键。
  • 从服务器即使发现过期键也不会自作主张地删除它，而是等待主节点发来DEL命令，这种统一、中心化的过期键删除策略可以保证主从服务器数据的一致性。
  • 当Redis命令对数据库进行修改之后，服务器会根据配置向客户端发送数据库通知。

RDB持久化

Redis是一个键值对数据库服务器，服务器中通常包含任意个非空数据库，而每个非空数据库中又可以包含任意个键值对，服务器中的非空数据库以及它们的键值对统称为数据库状态

Redis提供了RDB持久化功能，这个功能可以将Redis在内存中的数据库状态保存到磁盘中，避免数据意外丢失，产生的RDB文件是一个经过压缩的二进制文件，该文件可以还原生成RDB文件时的数据库状态。

RDB文件的创建与载入

两个Redis命令可以用于生成RDB文件，一个是SAVE，一个是BGSAVE。SAVE命令会阻塞Redis服务器进程，直到RDB文件创建完毕为止才重新处理命令请求。BGSAVE则会派生一个子进程，然后由子进程负责创建RDB文件，服务器进程可以继续处理命令请求，但是不能再处理一个SAVE和BGSAVE命令。

RDB文件的载入是在服务器启动时自动执行的，且会阻塞进程，所以RDB没有专门用于载入RDB文件的命令，如果Redis在启动时检测到了RDB文件存在，则会自动载入。

AOF文件的更新频率比RDB文件高，所以：

  • 如果服务器开启了AOF持久化功能，那么服务器优先使用AOF文件来还原数据库状态。
  • 只有在AOF持久化功能处于关闭状态时，服务器才会使用RDB文件来还原数据库状态。

自动间隔性保存

用户可以通过save选项设置多个保存条件，但只要任意一个条件被满足，服务器就可以执行BGSAVE命令，如：

1
2
3
save 900 1
save 300 10
save 60 10000

表示，在900秒内进行了至少一次修改，在300秒内至少10次修改，或在60秒内至少10000次修改

接着，根据save选项所设置的保存条件，设置服务器状态redisServer结构的saveparams属性：

1
2
3
struct redisServer {
    struct saveparam *saveparams;
}

saveparams属性是一个数组，每个saveparam结构都保存了一个save选项设置的保存条件。

服务器状态还维持着一个dirty计数器，以及一个lastsave属性：

  • dirty计数器记录距离上一次成功执行SAVE命令后，服务器对服务器状态进行了多少次修改。
  • lastsave是一个UNIX时间戳，记录上一次成功执行SAVE命令时的时间。

Redis的服务器周期性操作函数serverCron默认每隔100毫秒会执行一次，用于对正在运行的服务器进行维护，其中一项工作就是遍历saveparams数组中的所有保存条件，检查保存条件是否满足，如果满足则执行BGSAVE命令。

RDB文件结构

RDB 文件的最开头是 REDIS 部分， 这个部分的长度为 5 字节， 保存着 “REDIS” 五个字符。 通过这五个字符， 程序可以在载入文件时， 快速检查所载入的文件是否 RDB 文件。

db_version 长度为 4 字节， 它的值是一个字符串表示的整数， 这个整数记录了 RDB 文件的版本号， 比如 “0006” 就代表 RDB 文件的版本为第六版。

databases 部分包含着零个或任意多个数据库， 以及各个数据库中的键值对数据：

  • 如果服务器的数据库状态为空（所有数据库都是空的）， 那么这个部分也为空， 长度为 0 字节。
  • 如果服务器的数据库状态为非空（有至少一个数据库非空）， 那么这个部分也为非空， 根据数据库所保存键值对的数量、类型和内容不同， 这个部分的长度也会有所不同。

EOF 常量的长度为 1 字节， 这个常量标志着 RDB 文件正文内容的结束， 当读入程序遇到这个值的时候， 它知道所有数据库的所有键值对都已经载入完毕了。

check_sum 是一个 8 字节长的无符号整数， 保存着一个校验和， 这个校验和是程序通过对 REDIS 、 db_version 、 databases 、 EOF 四个部分的内容进行计算得出的。 服务器在载入 RDB 文件时， 会将载入数据所计算出的校验和与 check_sum 所记录的校验和进行对比， 以此来检查 RDB 文件是否有出错或者损坏的情况出现。

databases 部分

一个 RDB 文件的 databases 部分可以保存任意多个非空数据库。

比如说， 如果服务器的 0 号数据库和 3 号数据库非空， 那么服务器将创建一个如图 IMAGE_RDB_WITH_TWO_DB 所示的 RDB 文件， 图中的database 0 代表 0 号数据库中的所有键值对数据， 而 database 3 则代表 3 号数据库中的所有键值对数据。

每个非空数据库在 RDB 文件中都可以保存为 SELECTDB 、 db_number 、 key_value_pairs 三个部分， 如图 IMAGE_DATABASE_STRUCT_OF_RDB 所示。

SELECTDB 常量的长度为 1 字节， 当读入程序遇到这个值的时候， 它知道接下来要读入的将是一个数据库号码。

db_number 保存着一个数据库号码， 根据号码的大小不同， 这个部分的长度可以是 1 字节、 2 字节或者 5 字节。 当程序读入 db_number 部分之后， 服务器会调用 SELECT 命令， 根据读入的数据库号码进行数据库切换， 使得之后读入的键值对可以载入到正确的数据库中。

key_value_pairs 部分保存了数据库中的所有键值对数据， 如果键值对带有过期时间， 那么过期时间也会和键值对保存在一起。 根据键值对的数量、类型、内容、以及是否有过期时间等条件的不同， key_value_pairs 部分的长度也会有所不同。

key_value_pairs 部分

RDB 文件中的每个 key_value_pairs 部分都保存了一个或以上数量的键值对， 如果键值对带有过期时间的话， 那么键值对的过期时间也会被保存在内。不带过期时间的键值对在 RDB 文件中对由 TYPE 、 key 、 value 三部分组成。

TYPE 记录了 value 的类型， 长度为 1 字节， 值可以是以下常量的其中一个：

  • REDIS_RDB_TYPE_STRING
  • REDIS_RDB_TYPE_LIST
  • REDIS_RDB_TYPE_SET
  • REDIS_RDB_TYPE_ZSET
  • REDIS_RDB_TYPE_HASH
  • REDIS_RDB_TYPE_LIST_ZIPLIST
  • REDIS_RDB_TYPE_SET_INTSET
  • REDIS_RDB_TYPE_ZSET_ZIPLIST
  • REDIS_RDB_TYPE_HASH_ZIPLIST
    以上列出的每个 TYPE 常量都代表了一种对象类型或者底层编码， 当服务器读入 RDB 文件中的键值 对数据时， 程序会根据 TYPE 的值来决定如何读入和解释 value 的数据。

key 和 value 分别保存了键值对的键对象和值对象：

  • key 总是一个字符串对象， 它的编码方式和 REDIS_RDB_TYPE_STRING 类型的 value 一样。 根据内容长度的不同， key 的长度也会有所不同。
  • 根据 TYPE 类型的不同， 以及保存内容长度的不同， 保存 value 的结构和长度也会有所不同， 本节稍后会详细说明每种 TYPE 类型的value 结构保存方式。

带有过期时间的键值对在 RDB 文件中对由EXPIRETIME_MS、ms、 TYPE 、 key 、 value 五部分组成。

  • TYPE 、 key 、 value 三个部分的意义完全相同。
  • EXPIRETIME_MS 常量的长度为 1 字节， 它告知读入程序， 接下来要读入的将是一个以毫秒为单位的过期时间。
  • ms 是一个 8 字节长的带符号整数， 记录着一个以毫秒为单位的 UNIX 时间戳， 这个时间戳就是键值对的过期时间。

value的编码

RDB 文件中的每个 value 部分都保存了一个值对象， 每个值对象的类型都由与之对应的 TYPE 记录， 根据类型的不同， value 部分的结构、长度也会有所不同。

字符串对象

如果 TYPE 的值为 REDIS_RDB_TYPE_STRING ， 那么 value 保存的就是一个字符串对象， 字符串对象的编码可以是 REDIS_ENCODING_INT 或者REDIS_ENCODING_RAW 。如果字符串对象的编码为 REDIS_ENCODING_INT ， 那么说明对象中保存的是长度不超过 32 位的整数， 这种编码的对象将以ENCODING integer所示的结构保存，其中， ENCODING 的值可以是 REDIS_RDB_ENC_INT8 、 REDIS_RDB_ENC_INT16 或者 REDIS_RDB_ENC_INT32 三个常量的其中一个， 它们分别代表 RDB 文件使用 8 位（bit）、 16 位或者 32 位来保存整数值 integer。

如果字符串对象的编码为 REDIS_ENCODING_RAW ， 那么说明对象所保存的是一个字符串值， 根据字符串长度的不同， 有压缩和不压缩两种方法来保存这个字符串：

  • 如果字符串的长度小于等于 20 字节， 那么这个字符串会直接被原样保存len string。
  • 如果字符串的长度大于 20 字节， 那么这个字符串会被压缩之后再保存REDIS_RDB_ENC_LZF compressed_len origin_len compressed_string。REDIS_RDB_ENC_LZF 常量标志着字符串已经被 LZF 算法（http://liblzf.plan9.de）压缩过了， 读入程序在碰到这个常量时， 会对字符串进行解压缩： 其中 compressed_len 记录的是字符串被压缩之后的长度， 而 origin_len 记录的是字符串原来的长度， compressed_string 记录的则是被压缩之后的字符串。
列表对象

如果 TYPE 的值为 REDIS_RDB_TYPE_LIST ， 那么 value 保存的就是一个 REDIS_ENCODING_LINKEDLIST 编码的列表对象， RDB 文件保存这种对象的结构如list_length item1 item2 ... itemN所示。list_length 记录了列表的长度， 它记录列表保存了多少个项（item）。以 item 开头的部分代表列表的项，程序会以处理字符串对象的方式来保存和读入列表项。

集合对象

如果 TYPE 的值为 REDIS_RDB_TYPE_SET ， 那么 value 保存的就是一个 REDIS_ENCODING_HT 编码的集合对象， RDB 文件保存这种对象的结构如set_size elem1 elem2 ... elemN所示。set_size 是集合的大小， 它记录集合保存了多少个元素。图中以 elem 开头的部分代表集合的元素，程序会以处理字符串对象的方式来保存和读入集合元素。

哈希表对象

如果 TYPE 的值为 REDIS_RDB_TYPE_HASH ， 那么 value 保存的就是一个 REDIS_ENCODING_HT 编码的集合对象， RDB 文件保存这种对象的结构如 hash_size key_value_pair1 key_value_pair2 ... key_value_pairN 所示。hash_size 记录了哈希表保存了多少键值对，以 key_value_pair 开头的部分代表哈希表中的键值对， 结构中的每个键值对都以键紧挨着值的方式排列在一起，键值对的键和值都是字符串对象， 所以程序会以处理字符串对象的方式来保存和读入键值对。

有序集合对象

如果 TYPE 的值为 REDIS_RDB_TYPE_ZSET ， 那么 value 保存的就是一个 REDIS_ENCODING_SKIPLIST 编码的有序集合对象， RDB 文件保存这种对象的结构如sorted_set_size elem1 elem2 ... elemN所示。

sorted_set_size 记录了有序集合的大小， 也即是这个有序集合保存了多少元素。以 element 开头的部分代表有序集合中的元素， 每个元素又分为成员（member）和分值（score）两部分， 成员是一个字符串对象， 分值则是一个 double 类型的浮点数， 程序在保存 RDB 文件时会先将分值转换成字符串对象， 然后再用保存字符串对象的方法将分值保存起来。

INTSET 编码的集合

如果 TYPE 的值为 REDIS_RDB_TYPE_SET_INTSET ， 那么 value 保存的就是一个整数集合对象， RDB 文件保存这种对象的方法是， 先将整数集合转换为字符串对象， 然后将这个字符串对象保存到 RDB 文件里面。

ZIPLIST 编码的列表、哈希表或者有序集合

如果 TYPE 的值为 REDIS_RDB_TYPE_LIST_ZIPLIST 、 REDIS_RDB_TYPE_HASH_ZIPLIST 或者 REDIS_RDB_TYPE_ZSET_ZIPLIST ， 那么 value 保存的就是一个压缩列表对象， RDB 文件保存这种对象的方法是：

  • 将压缩列表转换成一个字符串对象。
  • 将转换所得的字符串对象保存到 RDB 文件。

如果程序在读入 RDB 文件的过程中， 碰到由压缩列表对象转换成的字符串对象， 那么程序会根据 TYPE 值的指示， 执行以下操作：

  • 读入字符串对象，并将它转换成原来的压缩列表对象。
  • 根据 TYPE 的值，设置压缩列表对象的类型： REDIS_RDB_TYPE_LIST_ZIPLIST 对应列表；REDIS_RDB_TYPE_HASH_ZIPLIST 对应哈希表； REDIS_RDB_TYPE_ZSET_ZIPLIST 对应有序集合。

分析RDB文件

使用od命令分析RDB文件。

不包含任何键值对的RDB文件

1
2
3
4
5
6
7
8
9
10
redis> FLUSHALL
OK

redis> SAVE
OK

$od -c dump.rdb
0000000 R E D I S 0 0 0 6 377 334 263 C 360 Z 334
0000020 362 V
0000022

这个RDB文件由一下四个部分组成：

  • 五个字节的”REDIS”字符串
  • 四个字节的版本号（db_version）0006
  • 一个字节的EOF常量（377）
  • 八个字节的校验和（377 334 263 C 360 Z 334 362 V）

包含字符串键的RDB文件

1
2
3
4
5
6
7
8
9
10
11
12
redis> FLUSHALL
OK

redis> SET MSG "HELLO"

redis> SAVE
OK

$od -c dump.rdb
0000000 R E D I S 0 0 0 6 376 \0 \0 003 M S G
0000020 005 H E L L O 377 207 z = 304 f T L 343
0000037

当一个数据库被保存到RDB文件时，这个数据块由一下三部分组成：

  • 一个一字节长度的特殊值SELECTDB（376）
  • 一个数据库号码（\0，0号数据库）
  • 一个或以上数量的键值对，在这里是（\0 003 M S G 005 H E L L O），\0是字符串类型的TYPE值REDIS_RDB_TYPE_STRING，003是键长度，005是值长度。

AOF持久化

AOF（Append Only File）通过保存Redis服务器所执行的写命令来记录数据库状态，被写入AOF文件的所有命令都是以Redis的命令请求协议格式保存的，因为Redis的命令请求协议是纯文本格式，所以可以直接打开一个AOF文件。

Redis AOF持久化的实现

AOF 持久化功能的实现可以分为命令追加（append）、文件写入、文件同步（sync）三个步骤。

命令追加

当 AOF 持久化功能处于打开状态时， 服务器在执行完一个写命令之后， 会以协议格式将被执行的写命令追加到服务器状态的 aof_buf 缓冲区的末尾：

1
2
3
4
5
6
struct redisServer {
    // AOF 缓冲区
    sds aof_buf;

    // ...
};

举个例子， 如果客户端向服务器发送以下命令：

1
2
redis> SET KEY VALUE
OK

那么服务器在执行这个 SET 命令之后， 会将以下协议内容追加到 aof_buf 缓冲区的末尾：

1
*3\r\n$3\r\nSET\r\n$3\r\nKEY\r\n$5\r\nVALUE\r\n

AOF 文件的写入与同步

Redis 的服务器进程就是一个事件循环（loop）， 这个循环中的文件事件负责接收客户端的命令请求， 以及向客户端发送命令回复， 而时间事件则负责执行像 serverCron 函数这样需要定时运行的函数。

在服务器每次结束一个事件循环之前， 它都会调用 flushAppendOnlyFile 函数， 考虑是否需要将 aof_buf 缓冲区中的内容写入和保存到 AOF 文件里面， 这个过程可以用以下伪代码表示：

1
2
3
4
5
6
7
8
9
10
11
12
13
def eventLoop():

    while True:

        # 处理文件事件，接收命令请求以及发送命令回复
        # 处理命令请求时可能会有新内容被追加到 aof_buf 缓冲区中
        processFileEvents()

        # 处理时间事件
        processTimeEvents()

        # 考虑是否要将 aof_buf 中的内容写入和保存到 AOF 文件里面
        flushAppendOnlyFile()

flushAppendOnlyFile 函数的行为由服务器配置的 appendfsync 选项的值来决定， 各个不同值产生的行为如表 TABLE_APPENDFSYNC 所示。

appendfsync 选项的值 flushAppendOnlyFile 函数的行为
always 将 aof_buf 缓冲区中的所有内容写入并同步到 AOF 文件。
everysec 将 aof_buf 缓冲区中的所有内容写入到 AOF 文件， 如果上次同步 AOF 文件的时间距离现在超过一秒钟， 那么再次对 AOF 文件进行同步， 并且这个同步操作是由一个线程专门负责执行的。
no 将 aof_buf 缓冲区中的所有内容写入到 AOF 文件， 但并不对 AOF 文件进行同步， 何时同步由操作系统来决定。

如果用户没有主动为 appendfsync 选项设置值， 那么 appendfsync 选项的默认值为 everysec 。

举个例子， 假设服务器在处理文件事件期间， 执行了以下三个写入命令：

1
2
3
SADD databases "Redis" "MongoDB" "MariaDB"
SET date "2013-9-5"
INCR click_counter 10086

那么 aof_buf 缓冲区将包含这三个命令的协议内容：

1
2
3
*5\r\n$4\r\nSADD\r\n$9\r\ndatabases\r\n$5\r\nRedis\r\n$7\r\nMongoDB\r\n$7\r\nMariaDB\r\n
*3\r\n$3\r\nSET\r\n$4\r\ndate\r\n$8\r\n2013-9-5\r\n
*3\r\n$4\r\nINCR\r\n$13\r\nclick_counter\r\n$5\r\n10086\r\n

如果这时 flushAppendOnlyFile 函数被调用， 假设服务器当前 appendfsync 选项的值为 everysec ， 并且根据 server.aof_last_fsync 属性显示， 距离上次同步 AOF 文件已经超过一秒钟， 那么服务器会先将 aof_buf 中的内容写入到 AOF 文件中， 然后再对 AOF 文件进行同步。

AOF 持久化的效率和安全性

服务器配置 appendfsync 选项的值直接决定 AOF 持久化功能的效率和安全性。

  • always 的效率是最慢的一个， 但lways 也是最安全的， 因为即使出现故障停机， AOF 持久化也只会丢失一个事件循环中所产生的命令数据。
  • 当 appendfsync 的值为 everysec 时，每隔超过一秒就要在子线程中对 AOF 文件进行一次同步： 从效率上来讲， everysec 模式足够快， 并且就算出现故障停机， 数据库也只丢失一秒钟的命令数据。
  • 当 appendfsync 的值为 no 时， 何时对 AOF 文件进行同步， 由操作系统控制。

AOF文件的载入与数据还原

服务器只要读取并重新执行一遍AOF文件里边保存的写命令就可以还原服务器关闭之前的数据库状态。步骤如下：

  1. 创建一个不带网络连接的伪客户端，因为Redis的命令只能在客户端上下文中执行，而载入AOF文件时没有客户端上下文；
  2. 从AOF文件中读取写命令；
  3. 使用伪客户端执行写命令；
  4. 直到AOF文件中的所有写命令被读取完。

AOF重写

AOF文件的体积不能无限增大，Redis服务器可以创建一个新的AOF文件来替代现有的AOF文件，但新AOF文件不会包含任何浪费空间的冗余命令，如对一条记录的重复修改。

AOF文件重写的实现

这个功能通过读取服务器当前数据库状态实现的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def AOF_REWRITE(tmp_tile_name):

  f = create(tmp_tile_name)

  # 遍历所有数据库
  for db in redisServer.db:

    # 如果数据库为空，那么跳过这个数据库
    if db.is_empty(): continue

    # 写入 SELECT 命令，用于切换数据库
    f.write_command("SELECT " + db.number)

    # 遍历所有键
    for key in db:
      # 如果键带有过期时间，并且已经过期，那么跳过这个键
      if key.have_expire_time() and key.is_expired(): continue
      if key.type == String:
        # 用 SET key value 命令来保存字符串键
        value = get_value_from_string(key)
        f.write_command("SET " + key + value)
      elif key.type == List:
        # 用 RPUSH key item1 item2 ... itemN 命令来保存列表键
        item1, item2, ..., itemN = get_item_from_list(key)
        f.write_command("RPUSH " + key + item1 + item2 + ... + itemN)
      elif key.type == Set:
        # 用 SADD key member1 member2 ... memberN 命令来保存集合键
        member1, member2, ..., memberN = get_member_from_set(key)
        f.write_command("SADD " + key + member1 + member2 + ... + memberN)
      elif key.type == Hash:
        # 用 HMSET key field1 value1 field2 value2 ... fieldN valueN 命令来保存哈希键
        field1, value1, field2, value2, ..., fieldN, valueN =\
        get_field_and_value_from_hash(key)
        f.write_command("HMSET " + key + field1 + value1 + field2 + value2 +\
                       ... + fieldN + valueN)
      elif key.type == SortedSet:
        # 用 ZADD key score1 member1 score2 member2 ... scoreN memberN
        # 命令来保存有序集键
        score1, member1, score2, member2, ..., scoreN, memberN = \
        get_score_and_member_from_sorted_set(key)
        f.write_command("ZADD " + key + score1 + member1 + score2 + member2 +\
                        ... + scoreN + memberN)
      else:
        raise_type_error()
      # 如果键带有过期时间，那么用 EXPIREAT key time 命令来保存键的过期时间
      if key.have_expire_time():
        f.write_command("EXPIREAT " + key + key.expire_time_in_unix_timestamp())
    # 关闭文件
    f.close()

因为新AOF文件只包含还原当前数据库状态所必须的命令，因此新AOF文件不会浪费硬盘空间。

AOF后台重写

调用aof_rewrite函数可以很好地完成创建一个新AOF文件的任务，但是因为这个函数会进行大量的写入操作，所以调用这个函数的线程将被长时间阻塞，所以需要将AOF重写程序放到子进程里实现。

使用子进程也要注意新的命令可能会对现有的数据库状态进行修改从而使得服务器当前的数据库状态和重写后的AOF文件所保存的状态不一致。为了解决不一致，Redis设置了一个AOF重写缓冲区，当Redis服务器执行完一个写命令后，会同时将这个写命令发送给AOF缓冲区和AOF重写缓冲区，这样可以保证：

  • AOF缓冲区的内容会定期被写入和同步到AOF文件中，对现有的AOF文件的处理工作会正常进行；
  • 从创建子进程开始，服务器执行的所有写操作都会被记录到AOF重写缓冲区中；

当子进程完成对AOF文件重写之后，它会向父进程发送一个完成信号，父进程接到该完成信号之后，会调用一个信号处理函数，该函数完成以下工作：

  • 将AOF重写缓存中的内容全部写入到新的AOF文件中；这个时候新的AOF文件所保存的数据库状态和服务器当前的数据库状态一致；
  • 对新的AOF文件进行改名，原子地（atomic）覆盖原有的AOF文件；完成新旧两个AOF文件的替换。

当这个信号处理函数执行完毕之后，主进程就可以继续像往常一样接收命令请求了。在整个AOF后台重写过程中，只有最后的“主进程写入命令到AOF缓存”和“对新的AOF文件进行改名，覆盖原有的AOF文件”这两个步骤（信号处理函数执行期间）会造成主进程阻塞，在其他时候，AOF后台重写都不会对主进程造成阻塞，这将AOF重写对性能造成的影响降到最低。

触发AOF后台重写的条件

AOF重写可以由用户通过调用BGREWRITEAOF手动触发。
服务器在AOF功能开启的情况下，会维持以下三个变量：

  • 记录当前AOF文件大小的变量aof_current_size。
  • 记录最后一次AOF重写之后，AOF文件大小的变量aof_rewrite_base_size。
  • 增长百分比变量aof_rewrite_perc。

每次当serverCron（服务器周期性操作函数）函数执行时，它会检查以下条件是否全部满足，如果全部满足的话，就触发自动的AOF重写操作：

  • 没有BGSAVE命令（RDB持久化）/AOF持久化在执行；
  • 没有BGREWRITEAOF在进行；
  • 当前AOF文件大小要大于server.aof_rewrite_min_size（默认为1MB），或者在redis.conf配置了auto-aof-rewrite-min-size大小；
  • 当前AOF文件大小和最后一次重写后的大小之间的比率等于或者等于指定的增长百分比（在配置文件设置了auto-aof-rewrite-percentage参数，不设置默认为100%）

如果前面三个条件都满足，并且当前AOF文件大小比最后一次AOF重写时的大小要大于指定的百分比，那么触发自动AOF重写。

重点回顾

  • AOF重写的目的是为了解决AOF文件体积膨胀的问题，使用更小的体积来保存数据库状态，整个重写过程基本上不影响Redis主进程处理命令请求；
  • AOF重写其实是一个有歧义的名字，实际上重写工作是针对数据库的当前状态来进行的，重写过程中不会读写、也不适用原来的AOF文件；
  • AOF可以由用户手动触发，也可以由服务器自动触发。

事件

Redis服务器是一个事件驱动程序，服务器需要处理以下两类事件：

  • 文件事件：Redis服务器通过套接字与客户端进行连接，而文件事件就是服务器对套接字操作的抽象。服务器与客户端的通信产生相应文件事件，而服务器通过监听并处理这些事件来完成一系列网络通信。
  • 时间事件：Redis服务器中的一些操作需要在给定时间点执行。

文件事件

Redis 基于 Reactor 模式开发了自己的网络事件处理器： 这个处理器被称为文件事件处理器（file event handler）。文件事件处理器使用 I/O 多路复用（multiplexing）程序来同时监听多个套接字， 并根据套接字目前执行的任务来为套接字关联不同的事件处理器。当被监听的套接字准备好执行连接应答（accept）、读取（read）、写入（write）、关闭（close）等操作时， 与操作相对应的文件事件就会产生， 这时文件事件处理器就会调用套接字之前关联好的事件处理器来处理这些事件。

文件事件处理器以单线程方式运行，通过使用 I/O 多路复用程序来监听多个套接字， 既实现了高性能的网络通信模型， 又可以很好地与 Redis 服务器中其他同样以单线程方式运行的模块进行对接， 这保持了 Redis 内部单线程设计的简单性。

文件事件处理器的构成

下图展示了文件事件处理器的四个组成部分， 它们分别是套接字、 I/O 多路复用程序、 文件事件分派器（dispatcher）、 以及事件处理器。

文件事件是对套接字操作的抽象，每当一个套接字准备好执行连接应答 (accept)、写入、读取、关闭等操作时，就会产生一个文件事件。I/O 多路复用程序负责监听多个套接字， 并向文件事件分派器传送那些产生了事件的套接字。

尽管多个文件事件可能会并发地出现， 但 I/O 多路复用程序通过一个队列以有序、同步、每次一个套接字的方式向文件事件分派器传送套接字： 当上一个套接字产生的事件被处理完毕之后， I/O 多路复用程序才会继续向文件事件分派器传送下一个套接字。文件事件分派器接收 I/O 多路复用程序传来的套接字， 并根据套接字产生的事件的类型， 调用相应的事件处理器。

I/O 多路复用程序的实现

Redis 的 I/O 多路复用程序的所有功能都是通过包装常见的 select 、 epoll 、 evport 和 kqueue 这些 I/O 多路复用函数库来实现的。因为 Redis 为每个 I/O 多路复用函数库都实现了相同的 API ， 所以 I/O 多路复用程序的底层实现是可以互换的

事件的类型

I/O 多路复用程序可以监听多个套接字的 ae.h/AE_READABLE 事件和 ae.h/AE_WRITABLE 事件， 这两类事件和套接字操作之间的对应关系如下：

  • 当套接字变得可读时（客户端对套接字执行 write 操作，或者执行 close 操作）， 或者有新的可应答（acceptable）套接字出现时（客户端对服务器的监听套接字执行 connect 操作）， 套接字产生 AE_READABLE 事件。
  • 当套接字变得可写时（客户端对套接字执行 read 操作）， 套接字产生 AE_WRITABLE 事件。

I/O 多路复用程序允许服务器同时监听套接字的 AE_READABLE 事件和 AE_WRITABLE 事件， 如果一个套接字同时产生了这两种事件， 那么文件事件分派器会优先处理 AE_READABLE 事件， 等到 AE_READABLE 事件处理完之后， 才处理 AE_WRITABLE 事件。

API

如下：

  • ae.c/aeCreateFileEvent 函数将给定套接字的给定事件加入到 I/O 多路复用程序的监听范围之内， 并对事件和事件处理器进行关联。
  • ae.c/aeDeleteFileEvent 函数让 I/O 多路复用程序取消对给定套接字的给定事件的监听， 并取消事件和事件处理器之间的关联。
  • ae.c/aeGetFileEvents 函数返回该套接字正在被监听的事件类型：
    • 如果套接字没有任何事件被监听， 那么函数返回 AE_NONE 。
    • 如果套接字的读事件正在被监听， 那么函数返回 AE_READABLE 。
    • 如果套接字的写事件正在被监听， 那么函数返回 AE_WRITABLE 。
    • 如果套接字的读事件和写事件正在被监听， 那么函数返回 AE_READABLE | AE_WRITABLE 。
  • ae.c/aeWait 函数在给定的时间内阻塞并等待套接字的给定类型事件产生， 当事件成功产生， 或者等待超时之后， 函数返回。
  • ae.c/aeApiPoll 函数在指定的时间內， 阻塞并等待所有被 aeCreateFileEvent 函数设置为监听状态的套接字产生文件事件， 当有至少一个事件产生， 或者等待超时后， 函数返回。
  • ae.c/aeProcessEvents 函数是文件事件分派器， 它先调用 aeApiPoll 函数来等待事件产生， 然后遍历所有已产生的事件， 并调用相应的事件处理器来处理这些事件。
  • ae.c/aeGetApiName 函数返回 I/O 多路复用程序底层所使用的 I/O 多路复用函数库的名称： 返回 “epoll” 表示底层为 epoll 函数库， 返回”select” 表示底层为 select 函数库， 诸如此类。

文件事件的处理器

Redis 为文件事件编写了多个处理器， 这些事件处理器分别用于实现不同的网络通讯需求， 比如说：

  • 为了对连接服务器的各个客户端进行应答， 服务器要为监听套接字关联连接应答处理器。程序会将这个连接应答处理器和服务器监听套接字的 AE_READABLE 事件关联起来， 当有客户端用sys/socket.h/connect 函数连接服务器监听套接字的时候， 套接字就会产生 AE_READABLE 事件， 引发连接应答处理器执行。
  • 为了接收客户端传来的命令请求， 服务器要为客户端套接字关联命令请求处理器。当一个客户端通过连接应答处理器成功连接到服务器之后， 服务器会将客户端套接字的 AE_READABLE 事件和命令请求处理器关联起来， 当客户端向服务器发送命令请求的时候， 套接字就会产生 AE_READABLE 事件， 引发命令请求处理器执行。
  • 为了向客户端返回命令的执行结果， 服务器要为客户端套接字关联命令回复处理器。当服务器有命令回复需要传送给客户端的时候， 服务器会将客户端套接字的 AE_WRITABLE 事件和命令回复处理器关联起来， 当客户端准备好接收服务器传回的命令回复时， 就会产生 AE_WRITABLE 事件， 引发命令回复处理器执行。
  • 当主服务器和从服务器进行复制操作时， 主从服务器都需要关联特别为复制功能编写的复制处理器。

一次完整的客户端与服务器连接事件示例

一次 Redis 客户端与服务器进行连接并发送命令的整个过程：

  • 假设一个 Redis 服务器正在运作， 那么这个服务器的监听套接字的 AE_READABLE 事件应该正处于监听状态之下， 而该事件所对应的处理器为连接应答处理器。
  • 如果这时有一个 Redis 客户端向服务器发起连接， 那么监听套接字将产生 AE_READABLE事件， 触发连接应答处理器执行： 处理器会对客户端的连接请求进行应答， 然后创建客户端套接字， 以及客户端状态， 并将客户端套接字的 AE_READABLE 事件与命令请求处理器进行关联， 使得客户端可以向主服务器发送命令请求。
  • 之后， 假设客户端向主服务器发送一个命令请求， 那么客户端套接字将产生 AE_READABLE 事件， 引发命令请求处理器执行， 处理器读取客户端的命令内容， 然后传给相关程序去执行。
  • 执行命令将产生相应的命令回复， 为了将这些命令回复传送回客户端， 服务器会将客户端套接字的 AE_WRITABLE 事件与命令回复处理器进行关联： 当客户端尝试读取命令回复的时候， 客户端套接字将产生 AE_WRITABLE 事件， 触发命令回复处理器执行， 当命令回复处理器将命令回复全部写入到套接字之后， 服务器就会解除客户端套接字的 AE_WRITABLE 事件与命令回复处理器之间的关联。

时间事件

Redis时间事件分为以下两类：

  1. 定时事件：程序在指定的时间之后执行一次。
  2. 周期性事件：程序每隔指定时间执行一次。

时间事件的属性：

  1. id：服务器为时间事件创建的全局唯一ID，ID号从小到大递增。
  2. when：毫秒精度的unix时间戳，记录时间事件的到达时间。
  3. timeProc：时间事件处理器，一个函数。当时间事件到达事，执行此函数。

时间事件的返回值决定了时间事件类型：如返回ae.h/AE_NOMORE，表示事件为定时事件，到达一次后则删除；如返回一个非AE_NOMORE的整数，表示事件为周期性事件，当事件到达之后，服务器会根据返回值更新时间事件的when属性，并以这种方式一直更新下去。当前Redis版本中只有周期性事件，没有使用定时事件。

实现

服务器将所有时间事件都存放在一个无序链表中，每当时间事件执行器执行时，它就遍历整个链表，找到所有已到达的时间事件并调用相应事件处理器。这里的的无序链表，指的是不按when属性大小排序，其实是按ID排序了，新的时间事件总是插入链表的表头。当前Redis版本中，服务器只使用serverCron一个时间事件，而在benchmark模式下，服务器也只使用2个时间事件，所以使用无序链表来保存时间事情，并不影响性能。

API

如下：

  • ae.c/aeCreateTimeEvent函数：接受一个毫秒数milliseconds和一个时间事件处理器proc作为参数，将一个新的时间事件添加到服务器，这个新的时间事件将在当前时间的milliseconds毫 秒之后到达，而事件的处理器为proc。
  • ae.c/aeDeleteFileEvent函数：数接受一个时间事件ID作为参数，然后从服务器中删除该ID所对应的时间事件。
  • ae.c/aeSearchNearestTimer函数：返回到达时间距离当前时间最接近的那个时间事件。
  • ae.c/processTimeEvents函数是时间事件的执行器，这个函数会遍历所有已到达的时间事件，并调用这些事件的处理器。已到达指的是，时间事件的when属性记录的UNIX时间戳等于或小于当前时间的UNIX时间戳。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def processTimeEvents():
    # 遍历服务器中的所有时间事件
    for time_event in all_time_event():
        # 检查事件是否已经到达
        if time_event.when <= unix_ts_now():
            # 事件已到达
            # 执行事件处理器，并获取返回值
            retval = time_event.timeProc()
            
            # 如果这是一个定时事件
            if retval == AE_NOMORE:
                # 那么将该事件从服务器中删除
                delete_time_event_from_server(time_event)
        # 如果这是一个周期性事件
        else:
            # 那么按照事件处理器的返回值更新时间事件的 when 属性
            # 让这个事件在指定的时间之后再次到达
            update_when(time_event, retval)

时间事件应用实例：serverCron函数

持续运行的Redis服务器需要定期对自身的资源和状态进行检查和调整，从而确保服务器可以长期、稳定地运行，这些定期操作由redis.c/serverCron函数负责执行，它的主要工作包括：

  • 更新服务器的各类统计信息，比如时间、内存占用、数据库占用情况等
  • 清理数据库中的过期键值对。
  • 关闭和清理连接失效的客户端
  • 尝试进行AOF或RDB持久化操作
  • 如果服务器是主服务器，那么对从服务器进行定期同步
  • 如果处于集群模式，对集群进行定期同步和连接测

事件调度与执行

因为服务器中同时存在文件事件和时间事件两种事件类型，所以服务器必须对这两种事件进行调度。事件的调度和执行由ae.c/aeProcessEvents函数负责，以下是该函数的伪代码表示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def aeProcessEvents():
    # 获取到达时间离当前时间最接近的时间事件
    time_event = aeSearchNearestTimer()
 
    # 计算最接近的时间事件距离到达还有多少毫秒
    remaind_ms = time_event.when - unix_ts_now()
 
    # 如果事件已到达，那么remaind_ms 的值可能为负数，将它设定为0
    if remaind_ms < 0:
        remaind_ms = 0
 
    # 根据remaind_ms 的值，创建timeval 结构
    timeval = create_timeval_with_ms(remaind_ms)
 
    # 阻塞并等待文件事件产生，最大阻塞时间由传入的timeval 结构决定
    # 如果remaind_ms 的值为0 ，那么aeApiPoll 调用之后马上返回，不阻塞
    aeApiPoll(timeval)
 
    # 处理所有已产生的文件事件
    processFileEvents()
 
    # 处理所有已到达的时间事件
    processTimeEvents()

将aeProcessEvents函数置于一个循环里面，加上初始化和清理函数，这就构成了Redis服务器的主函数，以下是该函数的伪代码表示：

1
2
3
4
5
6
7
8
9
10
def main():
    # 初始化服务器
    init_server()
    
    # 一直处理事件，直到服务器关闭为止
    while server_is_not_shutdown():
        aeProcessEvents()
    
    # 服务器关闭，执行清理操作
    clean_server()

事件的调度和执行规则：

  • aeApiPoll函数的最大阻塞时间由到达时间最接近当前时间的时间事件决定，这个方法既可以避免服务器对时间事件进行频繁的轮询（忙等待），也可以确保aeApiPoll函数不会阻塞过长时间。
  • 因为文件事件是随机出现的，如果等待并处理完一次文件事件之后，仍未有任何时间事件到达，那么服务器将再次等待并处理文件事件。随着文件事件的不断执行，时间会逐 渐向时间事件所设置的到达时间逼近，并最终来到到达时间，这时服务器就可以开始处理到 达的时间事件了。
  • 对文件事件和时间事件的处理都是同步、有序、原子地执行的，服务器不会中途中断事件处理，也不会对事件进行抢占，因此，不管是文件事件的处理器，还是时间事件的处理器，它们都会尽可地减少程序的阻塞时间，并在有需要时主动让出执行权，从而降低造成事件饥饿的可能性。
  • 因为时间事件在文件事件之后执行，并且事件之间不会出现抢占，所以时间事件的实际处理时间，通常会比时间事件设定的到达时间稍晚一些。

客户端

Redis服务器是典型的一对多服务器程序：一个服务器可以与多个客户端建立网络连接， 每个客户端可以向服务器发送命令请求，而服务器则接收并处理客户端发送的命令请求，并向客户端返回命令回复。
Redis服务器通过使用由I/O多路复用技术实现的文件事件处理器，Redis服务器使用单线程单进程的方式来处理命令请求，并与多个客户端进行网络通信。对每个客户端都会建立redisClient结构。Redis服务器状态结构的clients属性是一个链表，这个链表保存了所有与服务器连接的客户端的状态结构，对客户端执行批量操作，或者查找某个指定的客户端，都可以通过遍历clients链表来完成。

1
2
3
4
5
struct redisServer {
    // ...
    list *clients;// 一个链表，保存了所有客户端状态
    // ...
};

客户端属性

对于每个与服务器进行连接的客户端，服务器都为这些客户端建立了相应的redis.h/redisClient结构（客户端状态）。这个结构保存了客户端当前的状态信息，以及执行相关功能时需要用到的数据结构，其中包括：

  • 客户端的套接字描述符fd，记录了客户端正在使用的套接字描述符。如果是伪客户端，则为-1，否则为大于-1的整数。
  • 客户端的名字，默认时没有名字，使用CLIENT setname命令可以为客户端设置一个名字。
  • 客户端的标志值（flag）记录了客户端的角色，以及客户端目前的状态。flags属性的值可以是单个标志，也可以是多个标志的二进制或。
    • 一部分标志记录了客户端的角色：
      • REDIS_MASTER标志表示客户端代表的是一个主服务器， REDIS_SLAVE标志表示客户端代表的是一个从服务器
      • REDIS_PRE_PSYNC标志表示客户端代表的是一个版本低于Redis2.8的从服务器，主服务器不能使用PSYNC命令与这个从服务器进行同步。
      • REDIS_LUA_CLIENT标识表示客户端是专门用于处理Lua脚本里面包含的Redis命令的伪客户端
    • 而另外一部分标志则记录了客户端目前所处的状态：
      • REDIS_MONITOR标志表示客户端正在执行MONITOR命令
      • REDIS_UNIX_SOCKET标志表示服务器使用UNIX套接字来连接客户端
      • REDIS_BLOCKED标志表示客户端正在被BRPOP、BLPOP等命令阻塞
      • REDIS_UNBLOCKED标志表示客户端已经从REDIS_BLOCKED标志所表示的阻塞状态中脱离出来，只能在REDIS_BLOCKED标志打开的情况下使用
      • REDIS_MULTI标志表示客户端正在执行事务
      • REDIS_DIRTY_CAS标志表示事务使用WATCH命令监视的数据库键已经被修改。
      • REDIS_DIRTY_EXEC标志表示事务在命令入队时出现了错误，以上两个标志都表示事务的安全性已经被破坏
      • REDIS_CLOSE_ASAP标志表示客户端的输出缓冲区大小超出了服务器允许的范围，服务器会在下一次执行serverCron函数时关闭这个客户端，以免服务器的稳定性受到这个客户端影响。
      • REDIS_CLOSE_AFTER_REPLY标志表示有用户对这个客户端执行了CLIENT KILL命令，或者客户端发送给服务器的命令请求中包含了错误的协议内容。服务器会将客户端积存在输出缓冲区中的所有内容发送给客户端，然后关闭客户端。
      • REDIS_ASKING标志表示客户端向集群节点发送了 ASKING命令
      • REDIS_FORCE_AOF标志强制服务器将当前执行的命令写入到AOF文件里面， REDIS_FORCE_REPL标志强制主服务器将当前执行的命令复制给所有从服务器。
      • 在主从服务器进行命令传播期间，从服务器需要向主服务器发送REPLICATION ACK命令，在发送这个命令之前，从服务器必须打开主服务器对应的客户端的REDIS_MASTER_FORCE_REPLY标志，否则发送操作会被拒绝执行。
  • 指向客户端正在使用的数据库的指针，以及该数据库的号码
  • 客户端当前要执行的命令、命令的参数、命令参数的个数，以及指向命令实现函数的指针。
    • 在服务器将客户端发送的命令请求保存到客户端状态的querybuf属性之后，服务器将得到的命令参数以及命令参数的个数分别保存到客户端状态的argv属性和argc属性：
      • argv属性是一个数组，数组中的每个项都是一个字符串对象，其中argv[0]是要执行的命令，而之后的其他项则是传给命令的参数
      • argc属性则负责记录argv数组的长度
    • 分析出argv和argc之后，根据argv[0]的值找到命令所对应的实现函数，之后就可以调用并执行函数。
  • 客户端的输入缓冲区和输出缓冲区，用于保存客户端发送的命令请求，最大大小超过1GB则关闭这个客户端
    • 两个输出缓冲区；
    • 一个缓冲区固定大小，保存长度比较小的回复，如OK等
    • 另一个缓冲区可变大小，用于保存长度比较大的回复，由链表实现
  • 客户端的复制状态信息，以及进行复制所需的数据结构
  • 客户端执行BRPOP、BLPOP等列表阻塞命令时使用的数据结构
  • 客户端的事务状态，以及执行WATCH命令时用到的数据结构
  • 客户端执行发布与订阅功能时用到的数据结构
  • 客户端的身份验证标志，用于记录客户端是否通过了身份验证，当客户端未通过身份验证时，所有的命令（除了AUTH）都会被拒绝执行
  • 客户端的创建时间，客户端和服务器最后一次互动的时间，以及客户端的输出缓冲区大小超出软性限制（soft limit）的时间

客户端状态包含的属性可以分为两类：

  • 一类是比较通用的属性，这些属性很少与特定功能相关，无论客户端执行的是什么工 作，它们都要用到这些属性
  • 另外一类是和特定功能相关的属性，比如操作数据库时需要用到的db属性和dictid属性，执行事务时需要用到的mstate属性，以及执行WATCH命令时需要用到的watched_key s属性等等

客户端的创建与关闭

普通客户端的创建

如果客户端是通过网络连接与服务器进行连接的普通客户端，那么在客户端使用 connect 函数连接到服务器时，服务器就会调用连接事件处理器，为客户端创建相应的客户端状态，并将这个新的客户端状态添加到服务器状态结构clients链表的末尾

普通客户端的关闭

一个普通客户端可以因为多种原因而被关闭：

  • 客户端进程退出或者被杀死
  • 客户端向服务器发送了带有不符合协议格式的命令请求
  • 客户端成为了CLIENT KILL命令的目标
  • 用户为服务器设置了timeout配置选项，那么当客户端的空转时间超过timeout选项设置的值时，客户端将被关闭
  • 客户端发送的命令请求的大小超过了输入缓冲区的限制大小（默认为1 GB）
  • 要发送给客户端的命令回复的大小超过了输出缓冲区的限制大小

服务器使用两种模式来限制客户端输出缓冲区的大小：

  • 硬性限制（hard limit）：如果输出缓冲区的大小超过了硬性限制所设置的大小，那么服务器立即关闭客户端
  • 软性限制（soft limit）：如果输出缓冲区的大小超过了软性限制所设置的大小，但还没超过硬性限制，那么服务器将使用客户端状态结构的obuf_soft_limit_reached_time属性记录下客户端到达软性限制的起始时间；之后服务器会继续监视客户端，
    • 如果输出缓冲区的大小 一直超出软性限制，并且持续时间超过服务器设定的时长，那么服务器将关闭客户端
    • 相反地，如果输出缓冲区的大小在指定时间之内，不再超出软性限制，那么客户端就不会被关闭

使用client-output-buffer-limit选项可以为普通客户端、从服务器客户端、执行发布与订阅功能的客户端分别设置不同的软性限制和硬性限制，该选项的格式为：

1
2
3
4
client-output-buffer-limit <class> <hard limit> <soft limit> <soft seconds>
client-output-buffer-limit normal 0 0 0
client-output-buffer-limit slave 256mb 64mb 60
client-output-buffer-limit pubsub 32mb 8mb 60

以下是三个设置示例：
第一行设置将普通客户端的硬性限制和软性限制都设置为0，表示不限制客户端的输出缓冲区大小
第二行设置将从服务器客户端的硬性限制设置为256MB，而软性限制设置为64MB，软 性限制的时长为60秒
第三行设置将执行发布与订阅功能的客户端的硬性限制设置为32MB，软性限制设置为 8MB，软性限制的时长为60秒

Lua脚本的伪客户端

服务器会在初始化时创建负责执行Lua脚本中包含的Redis命令的伪客户端，并将这个伪 客户端关联在服务器状态结构的lua_client属性中

lua_client伪客户端在服务器运行的整个生命期中会一直存在，只有服务器被关闭时，这个客户端才会被关闭

AOF文件的伪客户端

服务器在载入AOF文件时，会创建用于执行AOF文件包含的Redis命令的伪客户端，并在载入完成之后，关闭这个伪客户端

服务器

Redis服务器负责与多个客户端建立网络连接，处理客户端发送的命令请求，在数据库中保存客户端执行命令产生的数据，并通过资源管理来维持服务器自身的运转。

命令请求的执行过程

从客户端发送SET KEY VALUE命令到获得回复OK期间，客户端和服务器共需要执行以下操作：

  • 客户端向服务器发送命令请求SET KEY VALUE
  • 服务器接收并处理客户端发来的命令请求SET KEY VALUE，在数据库中进行设置操作，并产生命令回复OK
  • 服务器将命令回复OK发送给客户端
  • 客户端接收服务器返回的命令回复OK，并将这个回复打印给用户观看

发送命令请求

Redis服务器的命令请求来自Redis客户端，当用户在客户端中键入一个命令请求时，客户端会将这个命令请求转换成协议格式，然后通过连接到服务器的套接字，将协议格式的命令请求发送给服务器。

读取命令请求

服务器将调用命令请求处理器来执行以下操作：

  • 读取套接字中协议格式的命令请求，并将其保存到客户端状态的输入缓冲区里面
  • 对输入缓冲区中的命令请求进行分析，提取出命令请求中包含的命令参数，以及命令参数的个数，然后分别将参数和参数个数保存到客户端状态的argv属性和argc属性里面
  • 调用命令执行器，执行客户端指定的命令

下图展示了程序将命令请求保存到客户端状态的输入缓冲区之后，客户端状态的样子:

之后，分析程序将对输入缓冲区中的协议进行分析，并将得出的分析结果保存到客户端状态的argv属性和argc属性里面，如下图所示：

命令执行器(1)：查找命令实现

命令执行器要做的第一件事就是根据客户端状态的argv[0]参数，在命令表（command table）中查找参数所指定的命令，并将找到的命令保存到客户端状态的cmd属性里面，命令表将返回”set”键所对应的redisCommand结构，客户端状态的cmd指针会指向这个redisCommand结构。

命令表是一个字典，字典的键是一个个命令名字，比如”set”、”get”、”del”等等；而字典的值则是一个个redisCommand结构，每个redisCommand结构记录了一个Redis命令的实现信息：

下表列出了sflags属性可以使用的标识值，以及这些标识的意义：

命令执行器(2)：执行预备操作

到目前为止，服务器已经将执行命令所需的命令实现函数（保存在客户端状态的cmd属性）、参数（保存在客户端状态的argv属性）、参数个数（保存在客户端状态的argc属性）都收集齐了。程序还需要进行一些预备操作：

  1. 检查客户端状态的cmd指针是否指向NULL，如果是的话，那么说明用户输入的命令名字找不到相应的命令实现，服务器返回一个错误；
  2. 根据客户端cmd属性指向的redisCommand结构的arity属性，检查参数个数是否正确，当参数个数不正确时直接返回一个错误；
  3. 检查客户端是否已经通过了身份验证，未通过身份验证的客户端只能执行AUTH命令；
  4. 如果服务器打开了maxmemory功能，那么在执行命令之前，先检查服务器的内存占用情况，并在有需要时进行内存回收；
  5. 如果服务器上一次执行BGSAVE命令时出错，并且服务器打开了stop-writes-on-bgsaveerror功能，而且服务器即将要执行的命令是一个写命令，那么服务器将向客户端返回一个错误；
  6. 如果客户端当前正在用SUBSCRIBE命令订阅频道，或者正在用PSUBSCRIBE命令订阅模式，那么服务器只会执行SUBSCRIBE、PSUBSCRIBE、UNSUBSCRIBE、 PUNSUBSCRIBE四个命令；
  7. 如果服务器正在进行数据载入，那么客户端发送的命令必须带有l标识才会被服务器执行；
  8. 如果服务器因为执行Lua脚本而超时并进入阻塞状态，那么服务器只会执行客户端发来的SHUTDOWN nosave命令和SCRIPT KILL命令；
  9. 如果客户端正在执行事务，那么服务器只会执行客户端发来的EXEC、DISCARD、 MULTI、WATCH四个命令，其他命令都会被放进事务队列中；
  10. 如果服务器打开了监视器功能，那么服务器会将要执行的命令和参数等信息发送给监视器。当完成了以上预备操作之后，服务器就可以开始真正执行命令了；

命令执行器(3)：调用命令的实现函数

服务器决定要执行命令时，它只要执行以下语句就可以了：

1
2
//client 是指向客户端状态的指针
client->cmd->proc(client);

被调用的命令实现函数会执行指定的操作，并产生相应的命令回复，这些回复会被保存在客户端状态的输出缓冲区里面（buf属性和reply属性），之后实现函数还会为客户端的套接字关联命令回复处理器。

命令执行器(4)：执行后续工作

在执行完实现函数之后，服务器还需要执行一些后续工作：

  1. 如果服务器开启了慢查询日志功能，那么慢查询日志模块会检查是否需要为刚刚执行完的命令请求添加一条新的慢查询日志；
  2. 根据刚刚执行命令所耗费的时长，更新被执行命令的redisCommand结构的milliseconds属性，并将命令的redisCommand结构的calls计数器的值增一；
  3. 如果服务器开启了AOF持久化功能，那么AOF持久化模块会将刚刚执行的命令请求写入到AOF缓冲区里面；
  4. 如果有其他从服务器正在复制当前这个服务器，那么服务器会将刚刚执行的命令传播给所有从服务器；

将命令回复发送给客户端

当客户端套接字变为可写状态时，服务器就会执行命令回复处理器，将保存在客户端输出缓冲区中的命令回复发送给客户端。当命令回复发送完毕之后，回复处理器会清空客户端状态的输出缓冲区，为处理下一个命令请求做好准备。

serverCron函数

Redis服务器中的serverCron函数默认每隔100毫秒执行一次，这个函数负责管理服务器的资源，并保持服务器自身的良好运转。

更新服务器时间缓存

为了减少系统调用的执行次数，服务器状态中的unixtime属性和mstime属性被用作当前时间的缓存：

1
2
3
4
5
6
7
8
struct redisServer {
    // ...
    //保存了秒级精度的系统当前UNIX 时间戳
    time_t unixtime;
    //保存了毫秒级精度的系统当前UNIX 时间戳
    long long mstime;
    // ...
};

这两个属性记录的时间的精确度并不高。

更新LRU时钟（lruclock属性、lru属性）

服务器状态中的lruclock属性保存了服务器的LRU时钟，这个属性和上面介绍的unixtime 属性、mstime属性一样，都是服务器时间缓存的一种：

1
2
3
4
5
6
7
struct redisServer {
    // ...
    //默认每10 秒更新一次的时钟缓存，
    //用于计算键的空转（idle ）时长。
    unsigned lruclock:22;
    // ...
};

每个Redis对象都会有一个lru属性，这个lru属性保存了对象最后一次被命令访问的时间，当服务器要计算一个数据库键的空转时间（也即是数据库键对应的值对象的空转时间），程序会用服务器的lruclock属性记录的时间减去对象的lru属性记录的时间，得出的计算结果就是这个对象的空转时间。

更新服务器每秒执行命令次数（ops_sec_开头的属性）

serverCron函数中的trackOperationsPerSecond函数会以每100毫秒一次的频率执行，这个函数的功能是以抽样计算的方式，估算并记录服务器在最近一秒钟处理的命令请求数量，这个值可以通过INFO status命令的instantaneous_ops_per_sec域查看。

trackOperationsPerSecond函数和服务器状态中四个ops_sec_开头的属性有关：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
struct redisServer {
    //上一次进行抽样的时间
    long long ops_sec_last_sample_time;
    
    //上一次抽样时，服务器已执行命令的数量
    long long ops_sec_last_sample_ops;
    
    // REDIS_OPS_SEC_SAMPLES 大小（默认值为16 ）的环形数组，
    //数组中的每个项都记录了一次抽样结果。
    long long ops_sec_samples[REDIS_OPS_SEC_SAMPLES];
    
    // ops_sec_samples 数组的索引值，
    //每次抽样后将值自增一，
    //在值等于16 时重置为0 ，
    //让ops_sec_samples 数组构成一个环形数组。
    int ops_sec_idx;
    // ...
};

trackOperationsPerSecond函数每次运行，都会：- 根据ops_sec_last_sample_time记录的上一次抽样时间和服务器的当前时间，以及ops_sec_last_sample_ops记录的上一次抽样的已执行命令数量和服务器当前的已执行命令数量，计算出服务器在一秒钟内能处理多少个命令请求的估计值，这个估计值会被作为一个新的数组项被放进 ops_sec_samples环形数组里面。

更新服务器内存峰值记录（stat_peak_memory属性）

服务器状态中的stat_peak_memory属性记录了服务器的内存峰值大小：每次serverCron函数执行时，程序都会查看服务器当前使用的内存数量，并与 stat_peak_memory保存的数值进行比较，如果当前使用的内存数量比stat_peak_memory属性记录的值要大，那么程序就将当前使用的内存数量记录到stat_peak_memory属性里面。

处理SIGTERM信号（sigtermHandler函数）

Redis会为服务器进程的SIGTERM信号关联sigtermHandler函数，这个信号处理器负责在服务器接到SIGTERM信号时，打开服务器状态的shutdown_asap标识：

1
2
3
4
5
6
7
// SIGTERM 信号的处理器
static void sigtermHandler(int sig) {
    //打印日志
    redisLogFromHandler(REDIS_WARNING,"Received SIGTERM, scheduling shutdown...");
    //打开关闭标识
    server.shutdown_asap = 1;
}

每次serverCron函数运行时，程序都会对服务器状态的shutdown_asap属性进行检查，并根据属性的值决定是否关闭服务器，服务器在关闭自身之前会进行RDB持久化操作，这也是服务器拦 截SIGTERM信号的原因，如果服务器一接到SIGTERM信号就立即关闭，那么它就没办法执 行持久化操作了。

管理客户端资源（clientsCron函数）

serverCron函数调用clientsCron函数，clientsCron函数会对客户端进行检查：

  • 如果客户端与服务器之间的连接已经超时，那么程序释放这个客户端
  • 如果客户端输入缓冲区的大小过长，那么程序会释放输入缓冲区，并重新创建一个，从而防止客户端的输入缓冲区耗费了过多的内存

管理数据库资源（databasesCron函数）

serverCron函数每次执行都会调用databasesCron函数，这个函数会对服务器中的一部分数据库进行检查，删除其中的过期键，并在有需要时，对字典进行收缩操作。

执行被延迟的BGREWRITEAOF（aof_rewrite_scheduled标记）

在服务器执行BGSAVE命令的期间，如果客户端向服务器发来BGREWRITEAOF命令， 那么服务器会将BGREWRITEAOF命令的执行时间延迟到BGSAVE命令执行完毕之后。
服务器的aof_rewrite_scheduled标识记录了服务器是否延迟了BGREWRITEAOF命令：

1
2
3
4
5
6
struct redisServer {
    // ...
    //如果值为1 ，那么表示有 BGREWRITEAOF 命令被延迟了。
    int aof_rewrite_scheduled;
    // ...
};

每次serverCron函数执行时，函数都会检查BGSAVE命令或者BGREWRITEAOF命令是否正在执行，如果这两个命令都没在执行，并且aof_rewrite_scheduled属性的值为1，那么服务器就会执行之前被推延的BGREWRITEAOF命令。

检查持久化操作的运行状态（rdb_child_pid属性、aof_child_pid属性）

服务器状态使用rdb_child_pid属性和aof_child_pid属性记录执行BGSAVE命令和BGREWRITEAOF命令的子进程的ID，这两个属性也可以用于检查BGSAVE命令或者BGREWRITEAOF命令是否正在执行。

每次serverCron函数执行时，程序都会检查rdb_child_pid和aof_child_pid两个属性的值， 只要其中一个属性的值不为-1，程序就会执行一次wait3函数，检查子进程是否有信号发来服务器进程：

  • 如果有信号到达，那么表示新的RDB文件已经生成完毕（对于BGSAVE命令来说），或者AOF文件已经重写完毕（对于BGREWRITEAOF命令来说），服务器需要进行相应命令的后续操作，比如用新的RDB文件替换现有的RDB文件，或者用重写后的AOF文件替换现有的 AOF文件。
  • 如果没有信号到达，那么表示持久化操作未完成，程序不做动作

如果rdb_child_pid和aof_child_pid两个属性的值都为-1，那么表示服务器没有在进行持久化操作，执行以下三个检查：

  • 查看是否有BGREWRITEAOF被延迟了，如果有的话，那么开始一次新的 BGREWRITEAOF操作；
  • 检查服务器的自动保存条件是否已经被满足，如果条件满足，并且服务器没有在执行其他持久化操作，那么服务器开始一次新的BGSAVE操作；
  • 检查服务器设置的AOF重写条件是否满足，如果条件满足，并且服务器没有在执行 其他持久化操作，那么服务器将开始一次新的BGREWRITEAOF操作；

将AOF缓冲区中的内容写入AOF文件

如果服务器开启了AOF持久化功能，并且AOF缓冲区里面还有待写入的数据，那么 serverCron函数将AOF缓冲区中的内容写入到AOF文件里面

关闭异步客户端

服务器会关闭那些输出缓冲区大小超出限制的客户端。

增加cronloops计数器的值（cronloops属性）

服务器状态的cronloops属性记录了serverCron函数执行的次数。cronloops属性目前在服务器中的唯一作用，就是在复制模块中实现“每执行serverCron函数N次就执行一次指定代码”的功能。

初始化服务器

初始化服务器状态结构（initServerConfig函数）

初始化服务器的第一步就是创建一个struct redisServer类型的实例变量server作为服务器的状态，并为结构中的各个属性设置默认值
初始化server变量的工作由redis.c/initServerConfig函数完成，以下是initServerConfig函数完成的主要工作：

  • 设置服务器的运行ID
  • 设置服务器的默认运行频率。
  • 设置服务器的默认配置文件路径
  • 设置服务器的运行架构
  • 设置服务器的默认端口号
  • 设置服务器的默认RDB持久化条件和AOF持久化条件
  • 初始化服务器的LRU时钟
  • 创建命令表

载入配置选项（initServerConfig函数）

在启动服务器时，用户可以通过给定配置参数或者指定配置文件来修改服务器的默认配置。

服务器在用initServerConfig函数初始化完server变量之后，就会开始载入用户给定的配置参数和配置文件，并根据用户设定的配置，对server变量相关属性的值进行修改。

初始化服务器数据结构（initServer函数）

在之前执行initServerConfig函数初始化server状态时，程序只创建了命令表一个数据结构，不过除了命令表之外，服务器状态还包含其他数据结构，比如：

  • server.clients链表，这个链表记录了所有与服务器相连的客户端的状态结构；
  • server.db数组，数组中包含了服务器的所有数据库；
  • 用于保存频道订阅信息的server.pubsub_channels字典，以及用于保存模式订阅信息的server.pubsub_patterns链表；
  • 用于执行Lua脚本的Lua环境server.lua。
  • 用于保存慢查询日志的server.slowlog属性；

当初始化服务器进行到这一步，服务器将调用initServer函数，为以上提到的数据结构分配内存，并在有需要时，为这些数据结构设置或者关联初始化值；

除了初始化数据结构之外，initServer还进行了一些非常重要的设置操作，其中包括：

  • 为服务器设置进程信号处理器
  • 创建共享对象：这些对象包含Redis服务器经常用到的一些值，服务器通过重用共享对象来避免反复创建相同的对象
  • 打开服务器的监听端口，并为监听套接字关联连接应答事件处理器，等待服务器正式运行时接受客户端的连接
  • 为serverCron函数创建时间事件，等待服务器正式运行时执行serverCron函数
  • 如果AOF持久化功能已经打开，那么打开现有的AOF文件，如果AOF文件不存在，那么 创建并打开一个新的AOF文件，为AOF写入做好准备。
  • 初始化服务器的后台I/O模块（bio），为将来的I/O操作做好准备

还原数据库状态

在完成了对服务器状态server变量的初始化之后，服务器需要载入RDB文件或者AOF文件，并根据文件记录的内容来还原服务器的数据库状态
根据服务器是否启用了AOF持久化功能，服务器载入数据时所使用的目标文件会有所不同：

  • 如果服务器启用了AOF持久化功能，那么服务器使用AOF文件来还原数据库状态
  • 相反地，如果服务器没有启用AOF持久化功能，那么服务器使用RDB文件来还原数据库状态

当服务器完成数据库状态还原工作之后，服务器将在日志中打印出载入文件并还原数据库状态所耗费的时长：

执行事件循环

在初始化的最后一步，开始执行服务器的事件循环（loop）

多机数据库的实现

复制

在Redis中，用户可以通过执行SLAVEOF命令或者设置slaveof选项，让一个服务器去复制（replicate）另一个服务器。我们称呼被复制的服务器为主服务器（master），而对主服务器进行复制的服务器则被称为从服务器（slave）。进行复制中的主从服务器双方的数据库将保存相同的数据，概念上将这种现象称作“数据库状态一致”，或者简称“一致”

有两个Redis服务器，地址分别为127.0.0.1:6379和127.0.0.1:12345，如果向127.0.0.1:12345发送如下命令：

1
2
127.0.0.1:12345> SLAVEOF 127.0.0.1 6379
OK

服务器127.0.0.1:12345将成为127.0.0.1:6379的从服务器，而服务器127.0.0.1:6379则会成为127.0.0.1:12345的主服务器。

旧版复制功能的实现

Redis的复制功能分为下面两个操作：

  • 同步操作（sync）：用于将从服务器的数据库状态更新至主服务器当前所处的数据库状态
  • 命令传播操作（command propagate）：则用于在主服务器的数据库状态被修改，导致主从服务器的数据库状态出现不一致时，让主从服务器的数据库重新回到一致状态

同步（SYNC命令）

当客户端向从服务器发送SLAVEOF命令，要求从服务器复制主服务器时，从服务器首先需要执行同步操作，也即是，将从服务器的数据库状态更新至主服务器当前所处的数据库状态

SYNC命令：从服务器对主服务器的同步操作需要通过向主服务器发送SYNC命令来完成，以下是SYNC命令的执行步骤：

  • 从服务器向主服务器发送SYNC命令
  • 收到SYNC命令的主服务器执行BGSAVE命令，在后台生成一个RDB文件，并使用一个缓冲区记录从现在开始执行的所有写命令
  • 当主服务器的BGSAVE命令执行完毕时，主服务器会将BGSAVE命令生成的RDB文件发送给从服务器，从服务器接收并载入这个RDB文件，将自己的数据库状态更新至主服务器 执行BGSAVE命令时的数据库状态
  • 主服务器将记录在缓冲区里面的所有写命令发送给从服务器，从服务器执行这些写命令，将自己的数据库状态更新至主服务器数据库当前所处的状态

下表展示了一个主从服务器进行同步的例子

命令传播

为了让主从服务器再次回到一致状态，主服务器需要对从服务器执行命令传播操作：主服务器会将自己执行的写命令发送给从服务器执行，当从服务器执行了相同的写命令之后，主从服务器将再次回到一致状态。

旧版复制功能的缺陷

在Redis中，从服务器对主服务器的复制可以分为以下两种情况：

  • 初次复制：从服务器以前没有复制过任何主服务器，或者从服务器当前要复制的主服务器和上一次复制的主服务器不同。
  • 断线后重复制：处于命令传播阶段的主从服务器因为网络原因而中断了复制，但从服务器通过自动重连接重新连上了主服务器，并继续复制主服务器

对于初次复制来说，旧版复制功能能够很好地完成任务，但对于断线后重复制来说，旧版复制功能虽然也能让主从服务器重新回到一致状态，但效率却非常低，因为需要重新执行SYNC命令，从服务器重新接收RDB文件进行同步。

新版复制功能

Redis从2.8版本开始，使用PSYNC命令代替SYNC命令来执行复制时的同步操作。
PSYNC命令具有完整重同步（full resy nchronization）和部分重同步（partial resynchronization）两种模式：

  • 完整重同步：用于处理初次复制情况：完整重同步的执行步骤和SYNC命令的执行步骤基本一样，它们都是通过让主服务器创建并发送RDB文件，以及向从服务器发送保存在缓冲区里面的写命令来进行同步；
  • 部分重同步：则用于处理断线后重复制情况：当从服务器在断线后重新连接主服务器时，如果条件允许，主服务器可以将主从服务器连接断开期间执行的写命令发送给从服务器，从服务器只要接收并执行这些写命令，就可以将数据库更新至主服务器当前所处的状态。
    PSYNC命令的部分重同步模式解决了旧版复制功能在处理断线后重复制时出现的低效情况。

部分重同步的实现

部分同步功能由以下三个部分构成：

  • 主服务器的复制偏移量（replication offset）和从服务器的复制偏移量
  • 主服务器的复制积压缓冲区（replication backlog）
  • 服务器的运行ID（run ID）

复制偏移量

执行复制的双方——主服务器和从服务器——会分别维护一个复制偏移量：

  • 主服务器每次向从服务器传播N个字节的数据时，就将自己的复制偏移量的值加上N
  • 从服务器每次收到主服务器传播来的N个字节的数据时，就将自己的复制偏移量的值加上N

通过对比主从服务器的复制偏移量，程序可以很容易地知道主从服务器是否处于一致状态：

  • 如果主从服务器处于一致状态，那么主从服务器两者的偏移量总是相同的
  • 相反，如果主从服务器两者的偏移量并不相同，那么说明主从服务器并未处于一致状态

复制积压缓冲区

复制积压缓冲区是由主服务器维护的一个固定长度（fixed-size）先进先出（FIFO）队列，默认大小为1MB。当主服务器进行命令传播时，它不仅会将写命令发送给所有从服务器，还会将写命令入队到复制积压缓冲区里面，如下图所示：

主服务器的复制积压缓冲区里面会保存着一部分最近传播的写命令，并且复制积压缓冲区会为队列中的每个字节记录相应的复制偏移量。

当从服务器重新连上主服务器时，从服务器会通过PSYNC命令将自己的复制偏移量offset发送给主服务器，主服务器会根据这个复制偏移量来决定对从服务器执行何种同步操作：

  • 如果offset偏移量之后的数据（也即是偏移量offset+1开始的数据）仍然存在于复制积压缓冲区里面，那么主服务器将对从服务器执行部分重同步操作，于是主服务器向从服务器发送+CONTINUE回复，表示数据同步将以部分重同步模式来进行；
  • 相反，如果offset偏移量之后的数据已经不存在于复制积压缓冲区，那么主服务器将对从服务器执行完整重同步操作

服务器运行ID

每个Redis服务器，不论主服务器还是从服务，都会有自己的运行ID；运行ID在服务器启动时自动生成，由40个随机的十六进制字符组成。当从服务器对主服务器进行初次复制时，主服务器会将自己的运行ID传送给从服务器， 而从服务器则会将这个运行ID保存起来。当从服务器断线并重新连上一个主服务器时，从服务器将向当前连接的主服务器发送之前保存的运行ID：

  • 如果从服务器保存的运行ID和当前连接的主服务器的运行ID相同，那么说明从服务器断线之前复制的就是当前连接的这个主服务器，主服务器可以继续尝试执行部分重同步操作；
  • 相反地，如果从服务器保存的运行ID和当前连接的主服务器的运行ID并不相同，那么说明从服务器断线之前复制的主服务器并不是当前连接的这个主服务器，主服务器将对从服务器执行完整重同步操作；

PSYNC命令的实现

PSYNC命令的调用方法有两种：

  • 如果从服务器以前没有复制过任何主服务器，或者之前执行过SLAVEOF no one命令：那么从服务器在开始一次新的复制时将向主服务器发送PSYNC ? -1命令，主动请求主服务器进行完整重同步
  • 如果从服务器已经复制过某个主服务器，那么从服务器在开始一次新的复制时将向主服务器发送PSYNC <runid> <offset>命令：
    • 其中runid是上一次复制的主服务器的运行 ID，而offset则是从服务器当前的复制偏移量，接收到这个命令的主服务器会通过这两个参数来判断应该对从服务器执行哪种同步操作。

接收到PSYNC命令的主服务器会向从服务器返回以下三种回复的其中一种：

  • 如果主服务器返回+FULLRESYNC <runid> <offset>回复，那么表示主服务器将与从服务器执行完整重同步操作：
    • 其中runid是这个主服务器的运行ID，从服务器会将这个ID保存起来，在下一次发送PSYNC命令时使用；而offset则是主服务器当前的复制偏移量，从服务器会将这个值作为自己的初始化偏移量
    • 如果主服务器返回+CONTINUE回复，那么表示主服务器将与从服务器执行部分重同步操作，从服务器只要等着主服务器将自己缺少的那部分数据发送过来就可以了
    • 如果主服务器返回-ERR回复，那么表示主服务器的版本低于Redis 2.8，它识别不了PSYNC命令，从服务器将向主服务器发送SYNC命令，并与主服务器执行完整同步操作

复制的实现

通过向从服务器发送SLAVEOF命令，我们可以让一个从服务器去复制一个主服务器：SLAVEOF <master_ip> <master_port>

步骤1：设置主服务器的地址和端口（masterhost、masterport属性）

当客户端向从服务器发送以下命令时：

1
127.0.0.1:12345> SLAVEOF 127.0.0.1 6479

从服务器首先要做的就是将客户端给定的主服务器IP地址127.0.0.1以及端口6379保存到服务器状态的masterhost属性和masterport属性里面。

SLAVEOF命令是一个异步命令，在完成masterhost属性和masterport属性的设置工作之后，从服务器将向发送SLAVEOF命令的客户端返回OK，表示复制指令已经被接收，而实际的复制工作将在OK返回之后才真正开始执行

步骤2：建立套接字连接（connect、accept）

在SLAVEOF命令执行之后，从服务器将根据命令所设置的IP地址和端口，创建连向主服务器的套接字连接。

如果从服务器创建的套接字能成功连接（connect）到主服务器，那么从服务器将为这个套接字关联一个专门用于处理复制工作的文件事件处理器，这个处理器将负责执行后续的复制工作。

而主服务器在接受（accept）从服务器的套接字连接之后，将为该套接字创建相应的客户端状态，并将从服务器看作是一个连接到主服务器的客户端来对待，这时从服务器将同时具有服务器（server）和客户端（client）两个身份：从服务器可以向主服务器发送命令请求，而主服务器则会向从服务器返回命令回复。

从服务器是主服务器的客户端。

步骤3：发送PING命令

从服务器成为主服务器的客户端之后，做的第一件事就是向主服务器发送一个PING命令。这个PING命令有两个作用：

  • 发送PING命令可以检查套接字的读写状态是否正常
  • 发送PING命令可以检查主服务器能否正常处理命令请求

从服务器在发送PING命令之后将遇到以下三种情况的其中一种：

  • 如果主服务器向从服务器返回了一个命令回复，但从服务器却不能在规定的时限 （timeout）内读取出命令回复的内容，那么表示主从服务器之间的网络连接状态不佳，不能继续执行复制工作的后续步骤。当出现这种情况时，从服务器断开并重新创建连向主服务器的套接字。
  • 如果主服务器向从服务器返回一个错误，那么表示主服务器暂时没办法处理从服务器的命令请求，不能继续执行复制工作的后续步骤。当出现这种情况时，从服务器断开并重新创建连向主服务器的套接字。
  • 如果从服务器读取到”PONG”回复，那么表示主从服务器之间的网络连接状态正常，并且主服务器可以正常处理从服务器（客户端）发送的命令请求，在这种情况下，从服务器可以继续执行复制工作的下个步骤。

步骤4：身份验证（AUTH命令、masterauth选项）

从服务器在收到主服务器返回的”PONG”回复之后，下一步要做的就是决定是否进行身份验证：

  • 如果从服务器设置了masterauth选项，那么进行身份验证
  • 如果从服务器没有设置masterauth选项，那么不进行身份验证

在需要进行身份验证的情况下，从服务器将向主服务器发送一条AUTH命令，命令的参数为从服务器masterauth选项的值。

从服务器在身份验证阶段可能遇到的情况有以下几种：

  1. 如果主服务器没有设置requirepass选项，并且从服务器也没有设置masterauth选项，那么主服务器将继续执行从服务器发送的命令，复制工作可以继续进行
  2. 如果从服务器通过AUTH命令发送的密码和主服务器requirepass选项所设置的密码相同，那么主服务器将继续执行从服务器发送的命令，复制工作可以继续进行。与此相反，如果主从服务器设置的密码不相同，那么主服务器将返回一个invalid password错误
  3. 如果主服务器设置了requirepass选项，但从服务器却没有设置masterauth选项，那么主服务器将返回一个NOAUTH错误。另一方面，如果主服务器没有设置requirepass选项，但从服务器却设置了masterauth选项，那么主服务器将返回一个no password is set错误

步骤5：发送端口信息（REPLCONF命令、slave_listening_port属性）

在身份验证步骤之后，从服务器将执行命令REPLCONF listening-port <port-number>， 向主服务器发送从服务器的监听端口号。

步骤6：同步（PSYNC命令）

在这一步，从服务器将向主服务器发送PSYNC命令，执行同步操作，并将自己的数据库更新至主服务器数据库当前所处的状态。值得一提的是，在同步操作执行之前，只有从服务器是主服务器的客户端，但是在执行同步操作之后，主服务器也会成为从服务器的客户端：

  • 如果PSYNC命令执行的是完整重同步操作，那么主服务器需要成为从服务器的客户端，才能将保存在缓冲区里面的写命令发送给从服务器执行。
  • 如果PSYNC命令执行的是部分重同步操作，那么主服务器需要成为从服务器的客户端，才能向从服务器发送保存在复制积压缓冲区里面的写命令

因此，在同步操作执行之后，主从服务器双方都是对方的客户端，它们可以互相向对方发送命令请求，或者互相向对方返回命令回复，如下图所示：

正因为主服务器成为了从服务器的客户端，所以主服务器才可以通过发送写命令来改变从服务器的数据库状态，不仅同步操作需要用到这一点，这也是主服务器对从服务器执行命令传播操作的基础。

步骤7：命令传播

当完成了同步之后，主从服务器就会进入命令传播阶段，这时主服务器只要一直将自己执行的写命令发送给从服务器，而从服务器只要一直接收并执行主服务器发来的写命令，就可以保证主从服务器一直保持一致了。

心跳检测

在命令传播阶段，从服务器默认会以每秒一次的频率，向主服务器发送命令：

1
2
REPLCONF ACK <replication_offset>
//其中replication_offset是从服务器当前的复制偏移量

发送REPLCONF ACK命令对于主从服务器有三个作用：

  • 检测主从服务器的网络连接状态
  • 辅助实现min-slaves选项
  • 检测命令丢失

检测主从服务器的网络连接状态（lag标志）

主从服务器可以通过发送和接收REPLCONF ACK命令来检查两者之间的网络连接是否正常：如果主服务器超过一秒钟没有收到从服务器发来的REPLCONF ACK命令，那么主服务器就知道主从服务器之间的连接出现问题了。
通过向主服务器发送INFO replication命令，在列出的从服务器列表的lag一栏中，我们可以看到相应从服务器最后一次向主服务器发送REPLCONF ACK命令距离现在过了多少秒：

在一般情况下，lag的值应该在0秒或者1秒之间跳动，如果超过1秒的话，那么说明主从服务器之间的连接出现了故障。

辅助实现min-slaves配置选项

Redis的min-slaves-to-write和min-slaves-max-lag两个选项可以防止主服务器在不安全的情况下执行写命令。

1
2
min-slaves-to-write 3
min-slaves-max-lag 10

那么在从服务器的数量少于3个，或者三个从服务器的延迟（lag）值都大于或等于10秒时，主服务器将拒绝执行写命令，这里的延迟值就是上面提到的INFO replication命令的lag值。

检测命令丢失

如果因为网络故障，主服务器传播给从服务器的写命令在半路丢失，那么当从服务器向主服务器发送REPLCONF ACK命令时，主服务器将发觉从服务器当前的复制偏移量少于自己的复制偏移量，然后主服务器就会根据从服务器提交的复制偏移量，在复制积压缓冲区里 面找到从服务器缺少的数据，并将这些数据重新发送给从服务器。

Sentinel（哨岗、哨兵）

Sentinel（哨岗、哨兵）是Redis的高可用性（high availability）解决方案：由一个或多个Sentinel实例（instance）组成的Sentinel系统（system）可以监视任意多个主服务器，以及这些主服务器属下的所有从服务器，并在被监视的主服务器进入下线状态时，自动将下线主服务器属下的某个从服务器升级为新的主服务器，然后由新的主服务器代替已下线的主服务器继续处理命令请求。

下图中：

  • 用双环图案表示的是当前的主服务器server1
  • 用单环图案表示的是主服务器的三个从服务器server2、server3以及server4
  • server2、server3、server4三个从服务器正在复制主服务器server1，而Sentinel系统则在监视所有四个服务器
  • 主服务器server1进入下线状态，那么从服务器server2、server3、server4对主服务器的复制操作将被中止，并且Sentinel系统会察觉到server1已下线
  • 当server1的下线时长超过用户设定的下线时长上限时，Sentinel系统就会对server1执行故障转移操作：
    • 首先，Sentinel系统会挑选server1属下的其中一个从服务器，并将这个被选中的从服务器升级为新的主服务器
    • 之后，Sentinel系统会向server1属下的所有从服务器发送新的复制指令，让它们成为新的主服务器的从服务器，当所有从服务器都开始复制新的主服务器时，故障转移操作执行完毕
    • 系统将server2升级为新的主服务器，并让服务器server3和server4成为server2的从服务器的过程
  • 另外，Sentinel还会继续监视已下线的server1，并在它重新上线时，将它设置为新的主服务器的从服务器
  • 如果server1重新上线的话，它将被Sentinel系统降级为server2的从服务器


Sentinel服务器的启动与初始化

启动一个Sentinel可以使用命令：

1
redis-sentinel /path/to/your/sentinel.conf

或者命令：

1
redis-server /path/to/your/sentinel.conf --sentinel

当一个Sentinel启动时，它需要执行以下步骤：

  • 初始化服务器
  • 将普通Redis服务器使用的代码替换成Sentinel专用代码
  • 初始化Sentinel状态
  • 根据给定的配置文件，初始化Sentinel的监视主服务器列表
  • 创建连向主服务器的网络连接

初始化Sentinel服务器

首先，因为Sentinel本质上只是一个运行在特殊模式下的Redis服务器，所以启动Sentinel的第一步，就是初始化一个普通的Redis服务器。
初始化Sentinel服务器与普通服务器的区别：
不过，因为Sentinel执行的工作和普通Redis服务器执行的工作不同，所以Sentinel的初始化过程和普通Redis服务器的初始化过程并不完全相同，下表展示了Redis服务器在Sentinel模式下运行时，服务器各个主要功能的使用情况：

使用Sentinel专用代码

启动Sentinel的第二个步骤就是将一部分普通Redis服务器使用的代码替换成Sentinel专用代码
比如说：普通Redis服务器使用redis.h/REDIS_SERVERPORT常量的值作为服务器端口#define REDIS_SERVERPORT 6379， 而Sentinel则使用sentinel.c/REDIS_SENTINEL_PORT常量的值作为服务器端口#define REDIS_SENTINEL_PORT 26379。

普通Redis服务器使用redis.c/redisCommandTable作为服务器的命令表，而Sentinel则使用sentinel.c/sentinelcmds作为服务器的命令表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
struct redisCommand redisCommandTable[] = {
    {"get",getCommand,2,"r",0,NULL,1,1,1,0,0},
    {"set",setCommand,-3,"wm",0,noPreloadGetKeys,1,1,1,0,0},
    {"setnx",setnxCommand,3,"wm",0,noPreloadGetKeys,1,1,1,0,0},
    // ...
    {"script",scriptCommand,-2,"ras",0,NULL,0,0,0,0,0},
    {"time",timeCommand,1,"rR",0,NULL,0,0,0,0,0},
    {"bitop",bitopCommand,-4,"wm",0,NULL,2,-1,1,0,0},
    {"bitcount",bitcountCommand,-2,"r",0,NULL,1,1,1,0,0}
}

struct redisCommand sentinelcmds[] = {
    {"ping",pingCommand,1,"",0,NULL,0,0,0,0,0},
    {"sentinel",sentinelCommand,-2,"",0,NULL,0,0,0,0,0},
    {"subscribe",subscribeCommand,-2,"",0,NULL,0,0,0,0,0},
    {"unsubscribe",unsubscribeCommand,-1,"",0,NULL,0,0,0,0,0},
    {"psubscribe",psubscribeCommand,-2,"",0,NULL,0,0,0,0,0},
    {"punsubscribe",punsubscribeCommand,-1,"",0,NULL,0,0,0,0,0},
    {"info",sentinelInfoCommand,-1,"",0,NULL,0,0,0,0,0}
};

sentinelcmds命令表也解释了为什么在Sentinel模式下，Redis服务器不能执行诸如SET、 DBSIZE、EVAL等等这些命令，因为服务器根本没有在命令表中载入这些命令。PING、 SENTINEL、INFO、SUBSCRIBE、UNSUBSCRIBE、PSUBSCRIBE和PUNSUBSCRIBE这七个命令就是客户端可以对Sentinel执行的全部命令了。

初始化Sentinel状态（struct sentinelState）

服务器会初始化一个sentinel.c/sentinelState结构（后面简称“Sentinel状态”），这个结构保存了服务器中所有和Sentinel功能有关的状态：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
struct sentinelState {
    //当前纪元，用于实现故障转移
    uint64_t current_epoch;

    //保存了所有被这个sentinel 监视的主服务器
    //字典的键是主服务器的名字
    //字典的值则是一个指向sentinelRedisInstance 结构的指针
    dict *masters;

    //是否进入了TILT 模式？
    int tilt;

    //目前正在执行的脚本的数量
    int running_scripts;

    //进入TILT 模式的时间
    mstime_t tilt_start_time;

    //最后一次执行时间处理器的时间
    mstime_t previous_time;

    // 一个FIFO 队列，包含了所有需要执行的用户脚本
    list *scripts_queue;
} sentinel;

初始化Sentinel状态的masters属性（struct sentinelRedisInstance）

Sentinel状态中的masters字典记录了所有被Sentinel监视的主服务器的相关信息，其中：

  • 字典的键是被监视主服务器的名字
  • 字典的值则是被监视主服务器对应的sentinel.c/sentinelRedisInstance结构

每个sentinelRedisInstance结构（后面简称“实例结构”）代表一个被Sentinel监视的Redis服务器实例（instance），这个实例可以是主服务器、从服务器，或者另外一个Sentinel。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
typedef struct sentinelRedisInstance {
    //标识值，记录了实例的类型，以及该实例的当前状态
    int flags;

    //实例的名字
    //主服务器的名字由用户在配置文件中设置
    //从服务器以及Sentinel 的名字由Sentinel 自动设置
    //格式为ip:port ，例如"127.0.0.1:26379"
    char *name;

    //实例的运行ID
    char *runid;

    //配置纪元，用于实现故障转移
    uint64_t config_epoch;

    //实例的地址
    sentinelAddr *addr;

    // SENTINEL down-after-milliseconds 选项设定的值
    //实例无响应多少毫秒之后才会被判断为主观下线（subjectively down ）
    mstime_t down_after_period;

    // SENTINEL monitor <master-name> <IP> <port> <quorum> 选项中的quorum 参数
    //判断这个实例为客观下线（objectively down ）所需的支持投票数量
    int quorum;

    // SENTINEL parallel-syncs <master-name> <number> 选项的值
    //在执行故障转移操作时，可以同时对新的主服务器进行同步的从服务器数量
    int parallel_syncs;

    // SENTINEL failover-timeout <master-name> <ms> 选项的值
    //刷新故障迁移状态的最大时限
    mstime_t failover_timeout;
    // ...
} sentinelRedisInstance;

sentinelRedisInstance.addr属性是一个指向sentinel.c/sentinelAddr结构的指针，这个结构保存着实例的IP地址和端口号：

1
2
3
4
typedef struct sentinelAddr {
    char *ip;
    int port;
} sentinelAddr;

对Sentinel状态的初始化将引发对masters字典的初始化，而masters字典的初始化是根据被载入的Sentinel配置文件来进行的。

Sentinel为主服务器master1创建如下第1张图所示的实例结构，并为主服务器master2创建如下第2张图所示的实例结构，而这两个实例结构又会被保存到Sentinel状态的masters字典中，

创建连向主服务器的网络连接

初始化Sentinel的最后一步是创建连向被监视主服务器的网络连接，Sentinel将成为主服务器的客户端，它可以向主服务器发送命令，并从命令回复中获取相关的信息。Sentinel会创建两个连向主服务器的异步网络连接：

  • 一个是命令连接，这个连接专门用于向主服务器发送命令，并接收命令回复
  • 另一个是订阅连接，这个连接专门用于订阅主服务器的__sentinel__:hello频道

为什么有两个连接？

在Redis目前的发布与订阅功能中，被发送的信息都不会保存在Redis服务器里面， 如果在信息发送时，想要接收信息的客户端不在线或者断线，那么这个客户端就会丢失这条信息。因此，为了不丢失__sentinel__:hello频道的任何信息，Sentinel必须专门用一 个订阅连接来接收该频道的信息
另一方面，除了订阅频道之外，Sentinel还必须向主服务器发送命令，以此来与主服务器进行通信，所以Sentinel还必须向主服务器创建命令连接
因为Sentinel需要与多个实例创建多个网络连接，所以Sentinel使用的是异步连接

获取主服务器信息

Sentinel默认会以每十秒一次的频率，通过命令连接向被监视的主服务器发送INFO命令，并通过分析INFO命令的回复来获取主服务器的当前信息。回复如下：

Sentinel可以获取以下两方面的信息：

  • 一方面是关于主服务器本身的信息，包括run_id域记录的服务器运行ID，以及role域记录的服务器角色。根据run_id域和role域记录的信息，Sentinel将对主服务器的实例结构进行更新；
  • 另一方面是关于主服务器属下所有从服务器的信息：
    • 每个从服务器都由一个”slave”字符串开头的行记录；
    • 每行的ip=域记录了从服务器的IP地址；
    • port=域则记录了从服务器的端口号。
    • 从服务器信息则会被用于更新主服务器实例结构的slaves字典， 这个字典记录了主服务器属下从服务器的名单。

获取从服务器信息

当Sentinel发现主服务器有新的从服务器出现时，Sentinel除了会为这个新的从服务器创建相应的实例结构之外，Sentinel还会创建连接到从服务器的命令连接和订阅连接。

Sentinel在默认情况下，会以每十秒一次的频率通过命令连接向从服务器发送INFO命令，并获得类似于以下内容的回复：

根据INFO命令的回复，Sentinel会提取出以下信息：

  • 从服务器的运行ID run_id
  • 从服务器的角色role
  • 主服务器的IP地址master_host，以及主服务器的端口号master_port
  • 主从服务器的连接状态master_link_status
  • 从服务器的优先级slave_priority
  • 从服务器的复制偏移量slave_repl_offset

向主服务器和从服务器发送消息

在默认情况下，Sentinel会以每两秒一次的频率，通过命令连接向所有被监视的主服务器和从服务器发送以下格式的命令：

1
PUBLISH __sentinel__:hello "<s_ip>,<s_port>,<s_runid>,<s_epoch>,<m_name>,<m_ip>,<m_port>,<m_epoch>"

这条命令向服务器的__sentinel__:hello频道发送了一条信息，信息的内容由多个参数组成：
其中以s_开头的参数记录的是Sentinel本身的信息，而m_开头的参数记录的则是主服务器的信息

  • 如果Sentinel正在监视的是主服务器，那么这些参数记录的就是主服务器的信息
  • 如果Sentinel正在监视的是从服务器，那么这些参数记录的就是从服务器正在复制的主服务器的信息

接收服务器和从服务器的频道消息

当Sentinel与一个主服务器或者从服务器建立起订阅连接之后，Sentinel就会通过订阅连接，向服务器发送以下命令：

1
SUBSCRIBE __sentinel__:hello

Sentinel对__sentinel__:hello频道的订阅会一直持续到Sentinel与服务器的连接断开为止。对于每个与Sentinel连接的服务器，Sentinel既通过命令连接向服务器的__sentinel__:hello频道发送信息，又通过订阅连接从服务器的__sentinel__:hello频道接收信息。

对于监视同一个服务器的多个Sentinel来说，一个Sentinel发送的信息会被其他Sentinel接收到，这些信息会被用于更新其他Sentinel对发送信息Sentinel的认知，也会被用于更新其他Sentinel对被监视服务器的认知。

举个例子，假设现在有sentinel1、sentinel2、sentinel3三个Sentinel在监视同一个服务器， 那么当sentinel1向服务器的__sentinel__:hello频道发送一条信息时，所有订阅了__sentinel__:hello频道的Sentinel（包括sentinel1自己在内）都会收到这条信息，如下图所示：

当一个Sentinel从__sentinel__:hello频道收到一条信息时，Sentinel会对这条信息进行分析，提取出信息中的Sentinel IP地址、Sentinel端口号、Sentinel运行ID等八个参数，并进行以下检查：

  • 如果信息中记录的Sentinel运行ID和接收信息的Sentinel的运行ID相同，那么说明这条信息是Sentinel自己发送的，Sentinel将丢弃这条信息，不做进一步处理
  • 相反地，如果信息中记录的Sentinel运行ID和接收信息的Sentinel的运行ID不相同，那么说明这条信息是监视同一个服务器的其他Sentinel发来的，接收信息的Sentinel将根据信息中的各个参数，对相应主服务器的实例结构进行更新

更新sentinels字典

Sentinel为主服务器创建的实例结构（struct sentinelRedisInstance）中的sentinels字典保存了除Sentinel本身之外，所有同样监视这个主服务器的其他Sentinel的资料：

  • sentinels字典的键是其中一个Sentinel的名字，格式为ip:port；
  • sentinels字典的值则是键所对应Sentinel的实例结构，比如对于键”127.0.0.1:26379”来说，这个键在sentinels字典中的值就是IP为127.0.0.1，端口号为26379的Sentinel的实例结构

当一个Sentinel接收到其他Sentinel发来的信息时，目标Sentinel会从信息中分析并提取出以下两方面参数：

  • 与Sentinel有关的参数：源Sentinel的IP地址、端口号、运行ID和配置纪元
  • 与主服务器有关的参数：源Sentinel正在监视的主服务器的名字、IP地址、端口号和配 置纪元

根据信息中提取出的主服务器参数，目标Sentinel会在自己的Sentinel状态的masters字典中查找相应的主服务器实例结构，然后根据提取出的Sentinel参数，检查主服务器实例结构的sentinels字典中，源Sentinel的实例结构是否存在：

  • 如果源Sentinel的实例结构已经存在，那么对源Sentinel的实例结构进行更新
  • 如果源Sentinel的实例结构不存在，那么说明源Sentinel是刚刚开始监视主服务器的新Sentinel，目标Sentinel会为源Sentinel创建一个新的实例结构，并将这个结构添加到sentinels字典里面

创建连向其他Sentinel的命令连接

当Sentinel通过频道信息发现一个新的Sentinel时，它不仅会为新Sentinel在sentinels字典中创建相应的实例结构，还会创建一个连向新Sentinel的命令连接，而新Sentinel也同样会创建连向这个Sentinel的命令连接，最终监视同一主服务器的多个Sentinel将形成相互连接的网络。

Sentinel之间不会创建订阅连接：Sentinel在连接主服务器或者从服务器时，会同时创建命令连接和订阅连接，但是在连接其他Sentinel时，却只会创建命令连接，而不创建订阅连接。这是因为Sentinel需要通过接收主服务器或者从服务器发来的频道信息来发现未知的新Sentinel，所以才需要建立订阅连接，而相互已知的Sentinel只要使用命令连接来进行通信就足够。

检测主观下线状态

在默认情况下，Sentinel会以每秒一次的频率向所有与它创建了命令连接的实例（包括主服务器、从服务器、其他Sentinel在内）发送PING命令，并通过实例返回的PING命令回复来判断实例是否在线。

实例对PING命令的回复可以分为以下两种情况：

  • 有效回复：实例返回+PONG、-LOADING、-MASTERDOWN三种回复的其中一种
  • 无效回复：实例返回除+PONG、-LOADING、-MASTERDOWN三种回复之外的其他 回复，或者在指定时限内没有返回任何回复

Sentinel配置文件中的down-after-milliseconds选项指定了Sentinel判断实例进入主观下线所需的时间长度：如果一个实例在down-after-milliseconds毫秒内，连续向Sentinel返回无效回复，那么Sentinel会修改这个实例所对应的实例结构，在结构的flags属性中打开SRI_S_DOWN标识，以此来表示这个实例已经进入主观下线状态

检测客观下线状态

当Sentinel将一个主服务器判断为主观下线之后，为了确认这个主服务器是否真的下线了，它会向同样监视这一主服务器的其他Sentinel进行询问，看它们是否也认为主服务器已经进入了下线状态（可以是主观下线或者客观下线）。当Sentinel从其他Sentinel那里接收到足够数量的已下线判断之后，Sentinel就会将从服务器判定为客观下线，并对主服务器执行故障转移操作。

发送SENTINEL is-master-down-byaddr <ip> <port> <current_epoch> <runid>命令询问其他Sentinel是否同意主服务器已下线。

当一个Sentinel（目标Sentinel）接收到另一个Sentinel（源Sentinel）发来的SENTINEL ismaster-down-by命令时，目标Sentinel会分析并取出命令请求中包含的各个参数，并根据其中的主服务器IP和端口号，检查主服务器是否已下线，然后向源Sentinel返回一条包含三个参数的Multi Bulk回复作为SENTINEL is-master-down-by命令的回复：

  1. down_state
  2. leader_runid
  3. leader_epoch

回复含义如下：

根据其他Sentinel发回的SENTINEL is-master-down-by-addr命令回复，Sentinel将统计其他Sentinel同意主服务器已下线的数量，当这一数量达到配置指定的判断客观下线所需的数量时，Sentinel会将主服务器实例结构flags属性的SRI_O_DOWN标识打开，表示主服务器已经进入客观下线状态。

选取领头Sentinel

当一个主服务器被判断为客观下线时，监视这个下线主服务器的各个Sentinel会进行协商，选举出一个领头Sentinel，并由领头Sentinel对下线主服务器执行故障转移操作。

以下是选举领头Sentinel的规则和方法：

  1. 所有在线的Sentinel都有被选为领头Sentinel的资格，换句话说，监视同一个主服务器的多个在线Sentinel中的任意一个都有可能成为领头Sentinel
  2. 每次进行领头Sentinel选举之后，不论选举是否成功，所有Sentinel的配置纪元 （configuration epoch）的值都会自增一次。配置纪元实际上就是一个计数器，并没有什么特别的
  3. 在一个配置纪元里面，所有Sentinel都有一次将某个Sentinel设置为局部领头Sentinel的机会，并且局部领头一旦设置，在这个配置每个发现主服务器进入客观下线的Sentinel都会要求其他Sentinel将自己设置为局部领头Sentinel
  4. 当一个Sentinel（源Sentinel）向另一个Sentinel（目标Sentinel）发送SENTINEL ismaster-down-by-addr命令，并且命令中的runid参数不是*符号而是源Sentinel的运行ID时，这表示源Sentinel要求目标Sentinel将前者设置为后者的局部领头Sentinel
  5. Sentinel设置局部领头Sentinel的规则是先到先得：最先向目标Sentinel发送设置要求的源Sentinel将成为目标Sentinel的局部领头Sentinel，而之后接收到的所有设置要求都会被目标Sentinel拒绝
  6. 目标Sentinel在接收到SENTINEL is-master-down-by-addr命令之后，将向源Sentinel返回一条命令回复，回复中的leader_runid参数和leader_epoch参数分别记录了目标Sentinel的局部领头Sentinel的运行ID和配置纪元
  7. 源Sentinel在接收到目标Sentinel返回的命令回复之后，会检查回复中leader_epoch参数的值和自己的配置纪元是否相同，如果相同的话，那么源Sentinel继续取出回复中的leader_runid参数，如果leader_runid参数的值和源Sentinel的运行ID一致，那么表示目标Sentinel将源Sentinel设置成了局部领头Sentinel
  8. 如果有某个Sentinel被半数以上的Sentinel设置成了局部领头Sentinel，那么这个Sentinel成为领头Sentinel。举个例子，在一个由10个Sentinel组成的Sentinel系统里面，只要有大于等于10/2+1=6个Sentinel将某个Sentinel设置为局部领头Sentinel，那么被设置的那个Sentinel就会成 为领头Sentine
  9. 因为领头Sentinel的产生需要半数以上Sentinel的支持，并且每个Sentinel在每个配置纪元里面只能设置一次局部领头Sentinel，所以在一个配置纪元里面，只会出现一个领头 Sentinel
  10. 如果在给定时限内，没有一个Sentinel被选举为领头Sentinel，那么各个Sentinel将在一段时间之后再次进行选举，直到选出领头Sentinel为止

假设现在有三个Sentinel正在监视同一个主服务器，并且这三个Sentinel之前已经通过 SENTINEL is-master-down-by -addr命令确认主服务器进入了客观下线状态，如下图所示

那么为了选出领头Sentinel，三个Sentinel将再次向其他Sentinel发送SENTINEL is-masterdown-by-addr命令，如下图所示

和检测客观下线状态时发送的SENTINEL is-master-down-by-addr命令不同，Sentinel这次发送的命令会带有Sentinel自己的运行ID，例如：SENTINEL is-master-down-byaddr 127.0.0.1 6379 0 e955b4c85598ef5b5f055bc7ebfd5e828dbed4fa

如果接收到这个命令的Sentinel还没有设置局部领头Sentinel的话，它就会将运行ID为e955b4c85598ef5b5f055bc7ebfd5e828dbed4fa的Sentinel设置为自己的局部领头Sentinel，并返 回类似以下的命令回复：

1
2
3
1) 1
2) e955b4c85598ef5b5f055bc7ebfd5e828dbed4fa
3) 0

然后接收到命令回复的Sentinel就可以根据这一回复，统计出有多少个Sentinel将自己设置成了局部领头Sentinel
根据命令请求发送的先后顺序不同，可能会有某个Sentinel的SENTINEL is-master-downby -addr命令比起其他Sentinel发送的相同命令都更快到达，并最终胜出领头Sentinel的选举， 然后这个领头Sentinel就可以开始对主服务器执行故障转移操作了

故障转移

在选举产生出领头Sentinel之后，领头Sentinel将对已下线的主服务器执行故障转移操作
该操作包含下面3个步骤：

  • 在已下线主服务器属下的所有从服务器里面，挑选出一个从服务器，并将其转换为主服务器
  • 让已下线主服务器属下的所有从服务器改为复制新的主服务器
  • 将已下线主服务器设置为新的主服务器的从服务器，当这个旧的主服务器重新上线 时，它就会成为新的主服务器的从服务器

选出新的主服务器

故障转移操作第一步要做的就是在已下线主服务器属下的所有从服务器中，挑选出一个状态良好、数据完整的从服务器，然后向这个从服务器发送SLAVEOF no one命令，将这个从服务器转换为主服务器

领头Sentinel会将已下线主服务器的所有从服务器保存到一个列表里面，然后按照以下规则，一项一项地对列表进行过滤：

  • 删除列表中所有处于下线或者断线状态的从服务器，保证列表中剩余的从服务器都是正常在线的
  • 删除列表中所有最近五秒内没有回复过领头Sentinel的INFO命令的从服务器，保证列表中剩余的从服务器都是最近成功进行过通信的
  • 删除所有与已下线主服务器连接断开超过down-after-milliseconds*10毫秒的从服务器：down-after-milliseconds选项指定了判断主服务器下线所需的时间，而删除断开时长超过down-after-milliseconds*10毫秒的从服务器，列表中剩余的从服务器都没有过早地与主服务器断开连接，换句话说，列表中剩余的从服务器保存的数据都是比较新的

之后，领头Sentinel将根据从服务器的优先级，对列表中剩余的从服务器进行排序，并选出其中优先级最高的从服务器。如果有多个具有相同最高优先级的从服务器，那么领头Sentinel将按照从服务器的复制偏移量，对具有相同最高优先级的所有从服务器进行排序，并选出其中偏移量最大的从服务器（复制偏移量最大的从服务器就是保存着最新数据的从服务器）

最后，如果有多个优先级最高、复制偏移量最大的从服务器，那么领头Sentinel将按照运行ID对这些从服务器进行排序，并选出其中运行ID最小的从服务器

领头Sentinel向被选中的从服务器server2发送SLAVEOF no one命令的情形：

在发送SLAVEOF no one命令之后，领头Sentinel会以每秒一次的频率（平时是每十秒一次），向被升级的从服务器发送INFO命令，并观察命令回复中的角色（role）信息，当被升级服务器的role从原来的slave变为master时，领头Sentinel就知道被选中的从服务器已经顺利升级为主服务器了。
例如，在上图所展示的例子中，领头Sentinel会一直向server2发送INFO命令，当server2返回的命令回复从：

1
2
3
4
5
# Replication
role:slave
...
# Other sections
...

变为：

1
2
3
4
5
# Replication
role:master
...
# Other sections
...

的时候，领头Sentinel就知道server2已经成功升级为主服务器了。

修改从服务器的复制目标

当新的主服务器出现之后，领头Sentinel下一步要做的就是，让已下线主服务器属下的所有从服务器去复制新的主服务器，这一动作可以通过向从服务器发送SLAVEOF命令来实现。下图展示了在故障转移操作中，领头Sentinel向已下线主服务器server1的两个从服务器server3和server4发送SLAVEOF命令，让它们复制新的主服务器server2的例子。

下图展示了server3和server4成为server2的从服务器之后，各个服务器以及领头Sentinel的样子：

将旧的主服务器变为从服务器

故障转移操作最后要做的是，将已下线的主服务器设置为新的主服务器的从服务器。比如说，下图就展示了被领头Sentinel设置为从服务器之后，服务器server1的样子。

因为旧的主服务器已经下线，所以这种设置是保存在server1对应的实例结构里面的，当 server1重新上线时，Sentinel就会向它发送SLAVEOF命令，让它成为server2的从服务器。例如，下图就展示了server1重新上线并成为server2的从服务器的例子

集群

集群通过分片（sharding）来进行数据共享，并提供复制和故障转移功能

集群节点

一个Redis集群通常由多个节点（node）组成。可以将各个独立的节点连接起来，构成一个包含多个节点的集群。连接各个节点的工作可以使用CLUSTER MEET命令来完成，该命令的格式如下：

1
CLUSTER MEET <ip> <port>

向一个节点node发送CLUSTER MEET命令，可以让node节点与ip和port所指定的节点进行握手，当握手成功时，node节点就会将ip和port所指定的节点添加到node节点当前所在的集群中。

假设现在有三个独立的节点127.0.0.1:7000、127.0.0.1:7001、 127.0.0.1:7002，我们首先使用客户端连上节点7000，通过发送CLUSTER NODE命令可以看到，集群目前只包含7000自己一个节点：

通过向节点7000发送以下命令，我们可以将节点7001添加到节点7000所在的集群里面：

继续向节点7000发送以下命令，我们可以将节点7002也添加到节点7000和节点7001所在 的集群里面：

启动节点

一个节点就是一个运行在集群模式下的Redis服务器，Redis服务器在启动时会根据cluster-enabled配置选项是否为yes来决定是否开启服务器的集群模式。

  • 节点（运行在集群模式下的Redis服务器）会继续使用所有在单机模式中使用的服务器组件，比如说：
  • 节点会继续使用文件事件处理器来处理命令请求和返回命令回复
  • 节点会继续使用时间事件处理器来执行serverCron函数，而serverCron函数又会调用集 群模式特有的clusterCron函数clusterCron函数负责执行在集群模式下需要执行的常规操 作，例如向集群中的其他节点发送Gossip消息，检查节点是否断线，或者检查是否需要对下 线节点进行自动故障转移等
  • 节点会继续使用数据库来保存键值对数据，键值对依然会是各种不同类型的对象
  • 节点会继续使用RDB持久化模块和AOF持久化模块来执行持久化工作
  • 节点会继续使用发布与订阅模块来执行PUBLISH、SUBSCRIBE等命令
  • 节点会继续使用复制模块来进行节点的复制工作
  • 节点会继续使用Lua脚本环境来执行客户端输入的Lua脚本

除此之外，节点会继续使用redisServer结构来保存服务器的状态，使用redisClient结构来 保存客户端的状态，至于那些只有在集群模式下才会用到的数据，节点将它们保存到了 cluster.h/clusterNode结构、cluster.h/clusterLink结构，以及cluster.h/clusterState结构里面。

集群数据结构

clusterNode结构保存了一个节点的当前状态，比如节点的创建时间、节点的名字、节点当前的配置纪元、节点的IP地址和端口号等等。每个节点都会使用一个clusterNode结构来记录自己的状态，并为集群中的所有其他节点 （包括主节点和从节点）都创建一个相应的clusterNode结构，以此来记录其他节点的状态：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
struct clusterNode {
    //创建节点的时间
    mstime_t ctime;
 
    //节点的名字，由40 个十六进制字符组成
    //例如68eef66df23420a5862208ef5b1a7005b806f2ff
    char name[REDIS_CLUSTER_NAMELEN];
 
    //节点标识
    //使用各种不同的标识值记录节点的角色（比如主节点或者从节点），
    //以及节点目前所处的状态（比如在线或者下线）。
    int flags;
 
    //节点当前的配置纪元，用于实现故障转移
    uint64_t configEpoch;
 
    //节点的IP 地址
    char ip[REDIS_IP_STR_LEN];
 
    //节点的端口号
    int port;
 
    //保存连接节点所需的有关信息
    clusterLink *link;
    // ...
};

clusterNode结构的link属性是一个clusterLink结构，该结构保存了连接节点所需的有关信息，比如套接字描述符，输入缓冲区和输出缓冲区：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
typedef struct clusterLink {
    //连接的创建时间
    mstime_t ctime;
 
    // TCP 套接字描述符
    int fd;
 
    //输出缓冲区，保存着等待发送给其他节点的消息（message ）。
    sds sndbuf;
 
    //输入缓冲区，保存着从其他节点接收到的消息。
    sds rcvbuf;
 
    //与这个连接相关联的节点，如果没有的话就为NULL
    struct clusterNode *node;
} clusterLink;

redisClient结构和clusterLink结构都有自己的套接字描述符和输入、输出缓冲区，这两个结构的区别在于，redisClient结构中的套接字和缓冲区是用于连接客户端的，而clusterLink结构中的套接字和缓冲区则是用于连接节点的

最后，每个节点都保存着一个clusterState结构，这个结构记录了在当前节点的视角下， 集群目前所处的状态，例如集群是在线还是下线，集群包含多少个节点，集群当前的配置纪元，诸如此类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
typedef struct clusterState {
    //指向当前节点的指针
    clusterNode *myself;
 
    //集群当前的配置纪元，用于实现故障转移
    uint64_t currentEpoch;
 
    //集群当前的状态：是在线还是下线
    int state;
 
    //集群中至少处理着一个槽的节点的数量
    int size;
 
    //集群节点名单（包括myself 节点）
    //字典的键为节点的名字，字典的值为节点对应的clusterNode 结构
    dict *nodes;
    // ...
} clusterState;

下图展示了节点7000创建的clusterState结构，这个结构从节点7000的角度记录了集群以及集群包含的三个节点的当前状态

  • 结构的currentEpoch属性的值为0，表示集群当前的配置纪元为0
  • 结构的size属性的值为0，表示集群目前没有任何节点在处理槽，因此结构的state属性的 值为REDIS_CLUSTER_FAIL，这表示集群目前处于下线状态
  • 结构的nodes字典记录了集群目前包含的三个节点，
  • 三个节点的clusterNode结构的flags属性都是REDIS_NODE_MASTER，说明三个节点都是主节点
  • 在节点7001创建的clusterState结构中，my self指针将指向代表节点7001的 clusterNode结构，而节点7000和节点7002则是集群中的其他节点

CLUSTER MEET命令的实现

通过向节点A发送CLUSTER MEET命令，客户端可以让接收命令的节点A将另一个节点B添加到节点A当前所在的集群里面：

1
CLUSTER MEET <ip> <port>

收到命令的节点A将与节点B进行握手（handshake），以此来确认彼此的存在，并为将来的进一步通信打好基础：

  • 节点A会为节点B创建一个clusterNode结构，并将该结构添加到自己的 clusterState.nodes字典里面
  • 之后，节点A将根据CLUSTER MEET命令给定的IP地址和端口号，向节点B发送一条 MEET消息（message）
  • 如果一切顺利，节点B将接收到节点A发送的MEET消息，节点B会为节点A创建一个 clusterNode结构，并将该结构添加到自己的clusterState.nodes字典里面
  • 之后，节点B将向节点A返回一条PONG消息
  • 如果一切顺利，节点A将接收到节点B返回的PONG消息，通过这条PONG消息节点A 可以知道节点B已经成功地接收到了自己发送的MEET消息
  • 之后，节点A将向节点B返回一条PING消息
  • 如果一切顺利，节点B将接收到节点A返回的PING消息，通过这条PING消息节点B可以知道节点A已经成功地接收到了自己返回的PONG消息，握手完成
  • 之后，节点A会将节点B的信息通过Gossip协议传播给集群中的其他节点，让其他节点也与节点B进行握手

槽指派

Redis集群通过分片的方式来保存数据库中的键值对：集群的整个数据库被分为16384个槽（slot），数据库中的每个键都属于这16384个槽的其中一个，集群中的每个节点可以处理0个或最多16384个槽。

当数据库中的16384个槽都有节点在处理时，集群处于上线状态（ok）；相反地，如果数据库中有任何一个槽没有得到处理，那么集群处于下线状态（fail）。通过向节点发送CLUSTER ADDSLOTS命令，我们可以将一个或多个槽指派（assign）给节点负责：

1
CLUSTER ADDSLOTS <slot> [slot ...]

执行以下命令可以将槽0至槽5000指派给节点7000负责：

1
127.0.0.1:7000> CLUSTER ADDSLOTS 0 1 2 3 4 ... 5000

记录节点的槽指派信息

clusterNode结构的slots属性和numslot属性记录了节点负责处理哪些槽。slots属性是一个二进制位数组（bit array），这个数组的长度为16384/8=2048个字节，共包含16384个二进制位。
Redis根据索引i上的二进制位的值来判断节点是否负责处理槽i：i上的二进制位的值为1则处理槽i，为0则不处理槽i。

numslots属性则记录节点负责处理的槽的数量，也即是slots数组中值为1的二进制位的数量。

传播节点的槽指派信息

一个节点除了会将自己负责处理的槽记录在clusterNode结构的slots属性和numslots属性之 外，它还会将自己的slots数组通过消息发送给集群中的其他节点，以此来告知其他节点自己目前负责处理哪些槽。集群中的每个节点都会知道数据库中的16384个槽分别被指派给了集群中的哪些节点。

记录集群所有槽的指派信息

clusterState结构中的slots数组记录了集群中所有16384个槽的指派信息：

1
2
3
4
5
typedef struct clusterState {
    // ...
    clusterNode *slots[16384];
    // ...
} clusterState;

slots数组包含16384个项，每个数组项都是一个指向clusterNode结构的指针：

  • 如果slots[i]指针指向NULL，那么表示槽i尚未指派给任何节点
  • 如果slots[i]指针指向一个clusterNode结构，那么表示槽i已经指派给了clusterNode结构所 代表的节点。

如果只将槽指派信息保存在各个节点的clusterNode.slots数组里，会出现一些无法高效地解决的问题，而clusterState.slots数组的存在解决了这些问题：

  • 如果节点只使用clusterNode.slots数组来记录槽的指派信息，那么为了知道槽i是否已经被指派，或者槽i被指派给了哪个节点，程序需要遍历clusterState.nodes字典中的所有clusterNode结构，检查这些结构的slots数组，直到找到负责处理槽i的节点为止，这个过程的复杂度为O（N），其中N为clusterState.nodes字典保存的clusterNode结构的数量
  • 所有槽的指派信息保存在clusterState.slots数组里面，程序要检查槽i是否已经被指派，又或者取得负责处理槽i的节点，只需要访问clusterState.slots[i]的值即可，这个操作的复杂度仅为O（1）

虽然clusterState.slots数组记录了集群中所有槽的指派信息，但使用clusterNode结构的slots数组来记录单个节点的槽指派信息仍然是有必要的：因为当程序需要将某个节点的槽指派信息通过消息发送给其他节点时，程序只需要将相应节点的clusterNode.slots数组整个发送出去就可以了。clusterState.slots数组记录了集群中所有槽的指派信息，而clusterNode.slots数组只记录了clusterNode结构所代表的节点的槽指派信息，这是两个slots数组的关键区别所在。

CLUSTER ADDSLOTS命令的实现

CLUSTER ADDSLOTS命令接受一个或多个槽作为参数，并将所有输入的槽指派给接收该命令的节点负责：

1
CLUSTER ADDSLOTS <slot> [slot ...]

CLUSTER ADDSLOTS命令的实现可以用以下伪代码来表示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def CLUSTER_ADDSLOTS(*all_input_slots):
    # 遍历所有输入槽，检查它们是否都是未指派槽
    for i in all_input_slots:
        # 如果有哪怕一个槽已经被指派给了某个节点
        # 那么向客户端返回错误，并终止命令执行
        if clusterState.slots[i] != NULL:
            reply_error()
            return

    # 如果所有输入槽都是未指派槽
    # 那么再次遍历所有输入槽，将这些槽指派给当前节点
    for i in all_input_slots:
        # 设置clusterState 结构的slots 数组
        # 将slots[i]的指针指向代表当前节点的clusterNode 结构
        clusterState.slots[i] = clusterState.myself

        # 访问代表当前节点的clusterNode 结构的slots 数组
        # 将数组在索引i 上的二进制位设置为1
        setSlotBit(clusterState.myself.slots, i)

下图展示了一个节点的clusterState结构，clusterState.slots数组中的所有指针都指向NULL，并且clusterNode.slots数组中的所有二进制位的值都是0，这说明当前节点没有被指派任何槽，并且集群中的所有槽都是未指派的：

当客户端对上图所示的节点执行命令：CLUSTER ADDSLOTS 1 2将槽1和槽2指派给节点之后，节点的clusterState结构将被更新成下图所示的样子：

在集群中执行命令

当客户端向节点发送与数据库键有关的命令时，接收命令的节点会计算出命令要处理的数据库键属于哪个槽，并检查这个槽是否指派给了自己：

  • 如果键所在的槽正好就指派给了当前节点，那么节点直接执行这个命令
  • 如果键所在的槽并没有指派给当前节点，那么节点会向客户端返回一个MOVED错误， 指引客户端转向（redirect）至正确的节点，并再次发送之前想要执行的命令。

计算键所属槽

节点使用以下伪代码算法来计算给定键key属于哪个槽：

1
2
def slot_number(key):
    return CRC16(key) & 16383

其中CRC16(key)语句用于计算键key的CRC-16校验和，而& 16383语句则用于计算出一个介于0至16383之间的整数作为键key的槽号

使用CLUSTER KEYSLOT <key>可以查看一个给定键属于哪个槽

判断槽是否由当前节点负责处理

当节点计算出键所属的槽i之后，节点就会检查自己在clusterState.slots数组中的项i，判断键所在的槽是否由自己负责：

  • 如果clusterState.slots[i]等于clusterState.myself，那么说明槽i由当前节点负责，节点可以执行客户端发送的命令
  • 如果clusterState.slots[i]不等于clusterState.myself，那么说明槽i并非由当前节点负责，节点会根据clusterState.slots[i]指向的clusterNode结构所记录的节点IP和端口号，向客户端返回MOVED错误，指引客户端转向至正在处理槽i的节点

MOVED错误

当节点发现键所在的槽并非由自己负责处理的时候，节点就会向客户端返回一个 MOVED错误，指引客户端转向至正在负责槽的节点。

MOVED错误的格式为：MOVED <slot> <ip>:<port>，其中slot为键所在的槽，而ip和port则是负责处理槽slot的节点的IP地址和端口号。当客户端接收到节点返回的MOVED错误时，客户端会根据MOVED错误中提供的IP地址和端口号，转向至负责处理槽slot的节点，并向该节点重新发送之前想要执行的命令。

一个集群客户端通常会与集群中的多个节点创建套接字连接，而所谓的节点转向实际上就是换一个套接字来发送命令
如果客户端尚未与想要转向的节点创建套接字连接，那么客户端会先根据MOVED错误提供的IP地址和端口号来连接节点，然后再进行转向。

集群模式的redis-cli客户端在接收到MOVED错误时，并不会打印出MOVED错误， 而是根据MOVED错误自动进行节点转向，并打印出转向信息，所以我们是看不见节点返回的MOVED错误的。

节点数据库的实现

节点只能使用0号数据库，而单机Redis服务器则没有这一限制。

除了将键值对保存在数据库里面之外，节点还会用clusterState结构中的 slots_to_keys跳跃表来保存槽和键之间的关系：

1
2
3
4
5
typedef struct clusterState {
    // ...
    zskiplist *slots_to_keys;
    // ...
} clusterState;

slots_to_keys跳跃表每个节点的分值（score）都是一个槽号，而每个节点的成员 （member）都是一个数据库键：

  • 每当节点往数据库中添加一个新的键值对时，节点就会将这个键以及键的槽号关联到slots_to_keys跳跃表
  • 当节点删除数据库中的某个键值对时，节点就会在slots_to_keys跳跃表解除被删除键与槽号的关联

举例：

重新分片

Redis集群的重新分片操作可以将任意数量已经指派给某个节点（源节点）的槽改为指派给另一个节点（目标节点），并且相关槽所属的键值对也会从源节点被移动到目标节点。重新分片操作可以在线（online）进行，在重新分片的过程中，集群不需要下线，并且源节点和目标节点都可以继续处理命令请求。

Redis集群的重新分片操作是由Redis的集群管理软件redis-trib负责执行的，Redis提供了进行重新分片所需的所有命令，而redis-trib则通过向源节点和目标节点发送命令来进行重新分片操作，redis-trib对集群的单个槽slot进行重新分片的步骤如下：

  1. redis-trib对目标节点发送CLUSTER SETSLOT <slot> IMPORTING <source_id>命令， 让目标节点准备好从源节点导入（import）属于槽slot的键值对
  2. redis-trib对源节点发送CLUSTER SETSLOT <slot> MIGRATING <target_id>命令，让源节点准备好将属于槽slot的键值对迁移（migrate）至目标节点
  3. redis-trib向源节点发送CLUSTER GETKEYSINSLOT <slot> <count>命令，获得最多count个属于槽slot的键值对的键名（key name）
  4. 对于步骤3获得的每个键名，redis-trib都向源节点发送一个MIGRATE <target_ip> <target_port> <key_name> 0 <time out>命令，将被选中的键原子地从源节点迁移至目标节点
  5. 重复执行步骤3和步骤4，直到源节点保存的所有属于槽slot的键值对都被迁移至目标节点为止。每次迁移键的过程如下图所示
  6. redis-trib向集群中的任意一个节点发送CLUSTER SETSLOTNODE 命令，将槽slot指派给目标节点，这一指派信息会通过消息发送至整个集群，最终集群中的所 有节点都会知道槽slot已经指派给了目标节点

ASK错误

在进行重新分片期间，源节点向目标节点迁移一个槽的过程中，可能会出现这样一种情况：属于被迁移槽的一部分键值对保存在源节点里面，而另一部分键值对则保存在目标节点里面。这时当客户端向源节点发送一个与数据库键有关的命令，并且命令要处理的数据库键恰好就属于正在被迁移的槽时：

  • 源节点会先在自己的数据库里面查找指定的键，如果找到的话，就直接执行客户端发送的命令（底层实现：如果节点收到一个关于键key的命令请求，并且键key所属的槽i正好就指派给了这个节点，那么节点会尝试在自己的数据库里查找键key，如果找到了的话，节点就直接执行客户端发送的命令）
  • 相反地，如果源节点没能在自己的数据库里面找到指定的键，那么这个键有可能已经被迁移到了目标节点，源节点将向客户端返回一个ASK错误，指引客户端转向正在导入槽的目标节点，并再次发送之前想要执行的命令（底层实现：如果节点没有在自己的数据库里找到键key，那么节点会检查自己的 clusterState.migrating_slots_to[i]，看键key所属的槽i是否正在进行迁移，如果槽i的确在进行 迁移的话，那么节点会向客户端发送一个ASK错误，引导客户端到正在导入槽i的节点去查找键key）

CLUSTER SETSLOT IMPORTING命令的实现

clusterState结构的importing_slots_from数组记录了当前节点正在从其他节点导入的槽：
如果importing_slots_from[i]的值不为NULL，而是指向一个clusterNode结构，那么表示当前节点正在从clusterNode所代表的节点导入槽i

1
2
3
4
5
typedef struct clusterState {
    // ...
    clusterNode *importing_slots_from[16384];
    // ...
} clusterState;

在对集群进行重新分片的时候，向目标节点发送命令，可以将目标节点clusterState.importing_slots_from[i]的值设置为source_id所代表节点的clusterNode结构：CLUSTER SETSLOT <i> IMPORTING <source_id>

CLUSTER SETSLOT MIGRATING命令的实现

clusterState结构的migrating_slots_to数组记录了当前节点正在迁移至其他节点的槽：
如果migrating_slots_to[i]的值不为NULL，而是指向一个clusterNode结构，那么表示当前 节点正在将槽i迁移至clusterNode所代表的节点

1
2
3
4
5
typedef struct clusterState {
    // ...
    clusterNode *migrating_slots_to[16384];
    // ...
} clusterState;

在对集群进行重新分片的时候，向源节点发送命令，可以将源节点clusterState.migrating_slots_to[i]的值设置为target_id所代表节点的 clusterNode结构：CLUSTER SETSLOT <i> MIGRATING <target_id>

ASKING命令

ASKING命令功能：唯一要做的就是打开发送该命令的客户端的REDIS_ASKING标识。在一般情况下，如果客户端向节点发送一个关于槽i的命令，而槽i又没有指派给这个节点的话，那么节点将向客户端返回一个MOVED错误；但是，如果节点的clusterState.importing_slots_from[i]显示节点正在导入槽i，并且发送命令的客户端带有REDIS_ASKING标识，那么节点将破例执行这个关于槽i的命令一次。

当客户端接收到ASK错误并转向至正在导入槽的节点时，客户端会先向节点发送一个 ASKING命令，然后才重新发送想要执行的命令，这是因为如果客户端不发送ASKING命令，而直接发送想要执行的命令的话，那么客户端发送的命令将被节点拒绝执行，并返回 MOVED错误；
另外要注意的是，客户端的REDIS_ASKING标识是一个一次性标识，当节点执行了一个带有REDIS_ASKING标识的客户端发送的命令之后，客户端的REDIS_ASKING标识就会被移除。

ASK错误和MOVED错误的区别

ASK错误和MOVED错误都会导致客户端转向，它们的区别在于：

  • MOVED错误代表槽的负责权已经从一个节点转移到了另一个节点：在客户端收到关于槽i的MOVED错误之后，客户端每次遇到关于槽i的命令请求时，都可以直接将命令请求发送 至MOVED错误所指向的节点，因为该节点就是目前负责槽i的节点
  • ASK错误只是两个节点在迁移槽的过程中使用的一种临时措施：在客户端收到关于槽i的ASK错误之后，客户端只会在接下来的一次命令请求中将关于槽i的命令请求发送至ASK错误所指示的节点，但这种转向不会对客户端今后发送关于槽i的命令请求产生任何影响，客户端仍然会将关于槽i的命令请求发送至目前负责处理槽i的节点，除非ASK错误再次出现。

复制与故障转移

Redis集群中的节点分为主节点（master）和从节点（slave）：

  • 主节点用于处理槽
  • 从节点则用于复制某个主节点，并在被复制的主节点下线时，代替下线主节点继续处理命令请求

对于包含7000、7001、7002、7003四个主节点的集群来说，我们可以将7004、7005两个节点添加到集群里面，并将这两个节点设定为节点7000的从节点，如下图所示（图中以双圆形表示主节点，单圆形表示从节点）

下表记录了集群各个节点的当前状态，以及它们正在做的工作

如果这时，节点7000进入下线状态，那么集群中仍在正常运作的几个主节点将在节点7000的两个从节点中选出一个节点作为新的主节点，这个新的主节点将接管原来节点7000负责处理的槽，并继续处理客户端发送的命令请求。

设置从节点

向一个节点发送命令，可以让接收命令的节点成为node_id所指定节点的从节点，并开始对主节点进行复制：CLUSTER REPLICATE <node_id>：

  • 接收到该命令的节点首先会在自己的clusterState.nodes字典中找到node_id所对应节点的clusterNode结构，并将自己的clusterState.myself.slaveof指针指向这个结构，以此来记录这个节点正在复制的主节点 
    1
    2
    3
    4
    5
    6
    struct clusterNode {
        // ...
        //如果这是一个从节点，那么指向主节点
        struct clusterNode *slaveof;
        // ...
    };
  • 然后节点会修改自己在clusterState.myself.flags中的属性，关闭原本的REDIS_NODE_MASTER标识，打开REDIS_NODE_SLAVE标识，表示这个节点已经由原来 的主节点变成了从节点；
  • 最后，节点会调用复制代码，并根据clusterState.myself.slaveof指向的clusterNode结构所保存的IP地址和端口号，对主节点进行复制。因为节点的复制功能和单机Redis服务器的复制功能使用了相同的代码，所以让从节点复制主节点相当于向从节点发送命令SLAVEOF。
  • 一个节点成为从节点，并开始复制某个主节点这一信息会通过消息发送给集群中的其他节点，最终集群中的所有节点都会知道某个从节点正在复制某个主节点
  • 集群中的所有节点都会在代表主节点的clusterNode结构的slaves属性和numslaves属性中记录正在复制这个主节点的从节点名单： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    struct clusterNode {
        // ...
        //正在复制这个主节点的从节点数量
        int numslaves;

        // 一个数组
        //每个数组项指向一个正在复制这个主节点的从节点的clusterNode 结构
        struct clusterNode **slaves;
        // ...
    };

故障检测

集群中的每个节点都会定期地向集群中的其他节点发送PING消息，以此来检测对方是否在线，如果接收PING消息的节点没有在规定的时间内，向发送PING消息的节点返回 PONG消息，那么发送PING消息的节点就会将接收PING消息的节点标记为疑似下线，在结构的flags属性中打开REDIS_NODE_PFAIL标识，以此表示节点进入了疑似下线状态。

如果在一个集群里面，半数以上负责处理槽的主节点都将某个主节点x报告为疑似下线，那么这个主节点x将被标记为已下线（FAIL），将主节点x标记为已下线的节点会向集群广播一条关于主节点x的FAIL消息，所有收到这条FAIL消息的节点都会立即将主节点x标记为已下线。

故障转移

当一个从节点发现自己正在复制的主节点进入了已下线状态时，从节点将开始对下线主节点进行故障转移，以下是故障转移的执行步骤：

  • 复制下线主节点的所有从节点里面，会有一个从节点被选中
  • 被选中的从节点会执行SLAVEOF no one命令，成为新的主节点
  • 新的主节点会撤销所有对已下线主节点的槽指派，并将这些槽全部指派给自己
  • 新的主节点向集群广播一条PONG消息，这条PONG消息可以让集群中的其他节点立 即知道这个节点已经由从节点变成了主节点，并且这个主节点已经接管了原本由已下线节点 负责处理的槽
  • 新的主节点开始接收和自己负责处理的槽有关的命令请求，故障转移完成

选举新的主节点

以下是集群选举新的主节点的方法：

  1. 集群的配置纪元是一个自增计数器，它的初始值为0
  2. 当集群里的某个节点开始一次故障转移操作时，集群配置纪元的值会被增一
  3. 对于每个配置纪元，集群里每个负责处理槽的主节点都有一次投票的机会，而第一个向主节点要求投票的从节点将获得主节点的投票
  4. 当从节点发现自己正在复制的主节点进入已下线状态时，从节点会向集群广播一条CLUSTERMSG_TYPE_FAILOVER_AUTH_REQUEST消息，要求所有收到这条消息、并且具有投票权的主节点向这个从节点投票
  5. 如果一个主节点具有投票权（它正在负责处理槽），并且这个主节点尚未投票给其他从节点，那么主节点将向要求投票的从节点返回一条 CLUSTERMSG_TYPE_FAILOVER_AUTH_ACK消息，表示这个主节点支持从节点成为新的 主节点
  6. 每个参与选举的从节点都会接收CLUSTERMSG_TYPE_FAILOVER_AUTH_ACK消 息，并根据自己收到了多少条这种消息来统计自己获得了多少主节点的支持
  7. 如果集群里有N个具有投票权的主节点，那么当一个从节点收集到大于等于N/2+1张支持票时，这个从节点就会当选为新的主节点
  8. 因为在每一个配置纪元里面，每个具有投票权的主节点只能投一次票，所以如果有N 个主节点进行投票，那么具有大于等于N/2+1张支持票的从节点只会有一个，这确保了新的 主节点只会有一个
  9. 如果在一个配置纪元里面没有从节点能收集到足够多的支持票，那么集群进入一个新的配置纪元，并再次进行选举，直到选出新的主节点为止

消息

集群中的各个节点通过发送和接收消息（message）来进行通信，我们称发送消息的节点为发送者（sender），接收消息的节点为接收者（receiver）。

节点发送的消息主要有以下五种：

  • MEET消息：当发送者接到客户端发送的CLUSTER MEET命令时，发送者会向接收者 发送MEET消息，请求接收者加入到发送者当前所处的集群里面
  • PING消息：集群里的每个节点默认每隔一秒钟就会从已知节点列表中随机选出五个节点，然后对这五个节点中最长时间没有发送过PING消息的节点发送PING消息，以此来检测被选中的节点是否在线。
  • PONG消息：当接收者收到发送者发来的MEET消息或者PING消息时，为了向发送者确认这条MEET消息或者PING消息已到达，接收者会向发送者返回一条PONG消息。另外， 一个节点也可以通过向集群广播自己的PONG消息来让集群中的其他节点立即刷新关于这个节点的认识。
  • FAIL消息：当一个主节点A判断另一个主节点B已经进入FAIL状态时，节点A会向集群广播一条关于节点B的FAIL消息，所有收到这条消息的节点都会立即将节点B标记为已下线
  • PUBLISH消息：当节点接收到一个PUBLISH命令时，节点会执行这个命令，并向集群广播一条PUBLISH消息，所有接收到这条PUBLISH消息的节点都会执行相同的PUBLISH命令

消息的结构

一条消息由消息头（header）和消息正文（data）组成

节点发送的所有消息都由一个消息头包裹，每个消息头都由一个cluster.h/clusterMsg结构表示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
typedef struct {
    //消息的长度（包括这个消息头的长度和消息正文的长度）
    uint32_t totlen;
    //消息的类型
    uint16_t type;
    //消息正文包含的节点信息数量
    //只在发送MEET 、PING 、PONG 这三种Gossip 协议消息时使用
    uint16_t count;
    //发送者所处的配置纪元
    uint64_t currentEpoch;
    //如果发送者是一个主节点，那么这里记录的是发送者的配置纪元
    //如果发送者是一个从节点，那么这里记录的是发送者正在复制的主节点的配置纪元
    uint64_t configEpoch;
    //发送者的名字（ID ）
    char sender[REDIS_CLUSTER_NAMELEN];
    //发送者目前的槽指派信息
    unsigned char myslots[REDIS_CLUSTER_SLOTS/8];
    //如果发送者是一个从节点，那么这里记录的是发送者正在复制的主节点的名字
    //如果发送者是一个主节点，那么这里记录的是REDIS_NODE_NULL_NAME
    //（一个40 字节长，值全为0 的字节数组）
    char slaveof[REDIS_CLUSTER_NAMELEN];
    //发送者的端口号
    uint16_t port;
    //发送者的标识值
    uint16_t flags;
    //发送者所处集群的状态
    unsigned char state;
    //消息的正文（或者说，内容）
    union clusterMsgData data;
} clusterMsg;

clusterMsg.data属性指向联合cluster.h/clusterMsgData，这个联合就是消息的正文：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
union clusterMsgData {
    // MEET 、PING 、PONG 消息的正文
    struct {
        //每条MEET 、PING 、PONG 消息都包含两个
        // clusterMsgDataGossip 结构
        clusterMsgDataGossip gossip[1];
    } ping;
    // FAIL 消息的正文
    struct {
        clusterMsgDataFail about;
    } fail;
    // PUBLISH 消息的正文
    struct {
        clusterMsgDataPublish msg;
    } publish;
    //其他消息的正文...
};

clusterMsg结构的currentEpoch、sender、myslots等属性记录了发送者自身的节点信息， 接收者会根据这些信息，在自己的clusterState.nodes字典里找到发送者对应的clusterNode结 构，并对结构进行更新。

MEET、PING、PONG消息的实现（Gossip协议）

Redis集群中的各个节点通过Gossip协议来交换各自关于不同节点的状态信息，其中Gossip协议由MEET、PING、PONG三种消息实现，这三种消息的正文都由两个cluster.h/clusterMsgDataGossip结构组成：

1
2
3
4
5
6
7
8
9
10
union clusterMsgData {
    // ...
    // MEET 、PING 和PONG 消息的正文
    struct {
        //每条MEET 、PING 、PONG 消息都包含两个
        // clusterMsgDataGossip 结构
        clusterMsgDataGossip gossip[1];
    } ping;
    //其他消息的正文...
};

因为MEET、PING、PONG三种消息都使用相同的消息正文，所以节点通过消息头clusterMsg结构的type属性来判断一条消息是MEET消息、PING消息还是PONG消息。

每次发送MEET、PING、PONG消息时，发送者都从自己的已知节点列表中随机选出两个节点（可以是主节点或者从节点），并将这两个被选中节点的信息分别保存到两个clusterMsgDataGossip结构里面
clusterMsgDataGossip结构记录了被选中节点的名字，发送者与被选中节点最后一次发送和接收PING消息和PONG消息的时间戳，被选中节点的IP地址和端口号，以及被选中节点的标识值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef struct {
    //节点的名字
    char nodename[REDIS_CLUSTER_NAMELEN];
    //最后一次向该节点发送PING 消息的时间戳
    uint32_t ping_sent;
    //最后一次从该节点接收到PONG 消息的时间戳
    uint32_t pong_received;
    //节点的IP 地址
    char ip[16];
    //节点的端口号
    uint16_t port;
    //节点的标识值
    uint16_t flags;
} clusterMsgDataGossip;

当接收者收到MEET、PING、PONG消息时，接收者会访问消息正文中的两个clusterMsgDataGossip结构，并根据自己是否认识clusterMsgDataGossip结构中记录的被选中节点来选择进行哪种操作：

  • 如果被选中节点不存在于接收者的已知节点列表，那么说明接收者是第一次接触到被选中节点，接收者将根据结构中记录的IP地址和端口号等信息，与被选中节点进行握手
  • 如果被选中节点已经存在于接收者的已知节点列表，那么说明接收者之前已经与被选中节点进行过接触，接收者将根据clusterMsgDataGossip结构记录的信息，对被选中节点所对应的clusterNode结构进行更新

举个发送PING消息和返回PONG消息的例子，假设在一个包含A、B、C、D、E、F六个节点的集群里：

  • 节点A向节点D发送PING消息，并且消息里面包含了节点B和节点C的信息，当节点D收到这条PING消息时，它将更新自己对节点B和节点C的认识
  • 之后，节点D将向节点A返回一条PONG消息，并且消息里面包含了节点E和节点F的消息，当节点A收到这条PONG消息时，它将更新自己对节点E和节点F的认识

FAIL消息的实现

当集群里的主节点A将主节点B标记为已下线（FAIL）时，主节点A将向集群广播一条关于主节点B的FAIL消息，所有接收到这条FAIL消息的节点都会将主节点B标记为已下线
在集群的节点数量比较大的情况下，单纯使用Gossip协议来传播节点的已下线信息会给节点的信息更新带来一定延迟，而发送FAIL消息可以让集群里的所有节点立即知道某个主节点已下线，从而尽快判断是否需要将集群标记为下线，又或者对下线主节点进行故障转移。

FAIL消息的正文由cluster.h/clusterMsgDataFail结构表示，这个结构只包含一个nodename属性，该属性记录了已下线节点的名字，因为集群里的所有节点都有一个独一无二的名字，所以FAIL消息里面只需要保存下线节点的名字，接收到消息的节点就可以根据这个名字来判断是哪个节点下线了

1
2
3
typedef struct {
    char nodename[REDIS_CLUSTER_NAMELEN];
} clusterMsgDataFail;

PUBLISH消息的实现

当客户端向集群中的某个节点发送命令：PUBLISH <channel> <message>，接收到PUBLISH命令的节点不仅会向channel频道发送消息message，它还会向集群广播一条PUBLISH消息，所有接收到这条PUBLISH消息的节点都会向channel频道发送 message消息。换句话说，向集群中的某个节点发送PUBLISH命令，将导致集群中的所有节点都向channel频道发送message消息
为什么不直接向节点广播PUBLISH命令：实际上，要让集群的所有节点都执行相同的PUBLISH命令，最简单的方法就是向所有节点广播相同的PUBLISH命令，这也是Redis在复制PUBLISH命令时所使用的方法， 不过因为这种做法并不符合Redis集群的“各个节点通过发送和接收消息来进行通信”这一 规则，所以节点没有采取广播PUBLISH命令的做法

PUBLISH消息的正文由cluster.h/clusterMsgDataPublish结构表示：

1
2
3
4
5
6
7
typedef struct {
    uint32_t channel_len;
    uint32_t message_len;
    //定义为8 字节只是为了对齐其他消息结构
    //实际的长度由保存的内容决定
    unsigned char bulk_data[8];
} clusterMsgDataPublish;

解释:

  • bulk_data属性是一个字节数组，这个字节数组保存了客户端通过PUBLISH命令发送给节点的channel参数和message参数
  • channel_len和 message_len则分别保存了channel参数的长度和message参数的长度
    • 其中bulk_data的0字节至channel_len-1字节保存的是channel参数
    • 而bulk_data的channel_len字节至channel_len+message_len-1字节保存的则是message参数

例如：如果节点收到的PUBLISH命令为：
PUBLISH “news.it” “hello”
那么节点发送的PUBLISH消息的clusterMsgDataPublish结构将如下图所示：其中 bulk_data数组的前七个字节保存了channel参数的值”news.it”，而bulk_data数组的后五个字节 则保存了message参数的值”hello”

独立功能的实现

发布与订阅

Redis的发布与订阅功能由PUBLISH、SUBSCRIBE、PSUBSCRIBE等命令组成。通过执行SUBSCRIBE命令，客户端可以订阅一个或多个频道，从而成为这些频道的订阅者（subscriber）：每当有其他客户端使用PUBLISH命令向被订阅的频道发送消息（message）时，频道的所有订阅者都会收到这条消息

客户端还可以通过执行PSUBSCRIBE命令订阅一个或多个模式，从 而成为这些模式的订阅者：每当有其他客户端向某个频道发送消息时，消息不仅会被发送给 这个频道的所有订阅者，它还会被发送给所有与这个频道相匹配的模式的订阅者。

举个例子，假设如下图所示：
客户端A正在订阅频道news.it。
客户端B正在订阅频道news.et。
客户端C和客户端D正在订阅与”news.it”频道和”news.et”频道相匹配的模式news.[ie]t

如果这时某个客户端执行PUBLISH命令，向”news.it”频道发送消息”hello”，那么不仅正在订阅”news.it”频道的客户端A会收到消息，客户端C和客户端D也同样会收到消息，因为这两个客户端正在订阅匹配”news.it”频道 的news.[ie]t模式，如下图所示：
PUBLISH "news.it" "hello"

与此类似，如果某个客户端执行下面的命令，向”news.et”频道发送消息”world”，那么不仅正在订阅”news.et”频道的客户端B会收到消 息，客户端C和客户端D也同样会收到消息，因为这两个客户端正在订阅匹配”news.et”频道 的”news.[ie]t”模式，如下图所示：
PUBLISH "news.et" "world"

频道的订阅与退订

Redis将所有频道的订阅关系都保存在服务器状态的pubsub_channels字典里面，这个字典的键是某个被订阅的频道，而键的值则是一个链表，链表里面记录了所有订阅这个频道的客户端：

1
2
3
4
5
6
struct redisServer {
    // ...
    //保存所有频道的订阅关系
    dict *pubsub_channels;
    // ...
};

通过执行SUBSCRIBE命令，客户端可以订阅一个或多个频道，从而成为这些频道的订阅者（subscriber）：每当有其他客户端使用PUBLISH命令向被订阅的频道发送消息（message）时，频道的所有订阅者都会收到这条消息。根据频道是否已经有其他订阅者，关联操作分为两种情况执行：

  • 如果频道已经有其他订阅者，那么它在pubsub_channels字典中必然有相应的订阅者链 表，程序唯一要做的就是将客户端添加到订阅者链表的末尾
  • 如果频道还未有任何订阅者，那么它必然不存在于pubsub_channels字典，程序首先要在 pubsub_channels字典中为频道创建一个键，并将这个键的值设置为空链表，然后再将客户端 添加到链表，成为链表的第一个元素
1
2
3
4
5
6
7
8
9
def subscribe(*all_input_channels):
    # 遍历输入的所有频道
    for channel in all_input_channels:
        # 如果channel 不存在于pubsub_channels 字典（没有任何订阅者）
        # 那么在字典中添加channel 键，并设置它的值为空链表
        if channel not in server.pubsub_channels:
            server.pubsub_channels[channel] = []
        # 将订阅者添加到频道所对应的链表的末尾
        server.pubsub_channels[channel].append(client)

频道的退订（UNSUBSCRIBE命令）

UNSUBSCRIBE命令的行为和SUBSCRIBE命令的行为正好相反，当一个客户端退订某个或某些频道的时候，服务器将从pubsub_channels中解除客户端与被退订频道之间的关联：

  • 程序会根据被退订频道的名字，在pubsub_channels字典中找到频道对应的订阅者链表， 然后从订阅者链表中删除退订客户端的信息
  • 如果删除退订客户端之后，频道的订阅者链表变成了空链表，那么说明这个频道已经没有任何订阅者了，程序将从pubsub_channels字典中删除频道对应的键
1
2
3
4
5
6
7
8
9
10
11

def unsubscribe(*all_input_channels):
    #遍历要退订的所有频道
    for channel in all_input_channels:
        # 在订阅者链表中删除退订的客户端
        server.pubsub_channels[channel].remove(client)
 
        # 如果频道已经没有任何订阅者了（订阅者链表为空）
        # 那么将频道从字典中删除
        if(len(server.pubsub_channels[channel])==0:
            server.pubsub_channels.remove(channel)

模式的订阅与退订

服务器将所有频道的订阅关系都保存在服务器状态的pubsub_channels属性里面，与此类似，服务器也将所有模式的订阅关系都保存在服务器状态的pubsub_patterns属性里面：

1
2
3
4
5
6
struct redisServer {
    // ...
    //保存所有模式订阅关系
    list *pubsub_patterns;
    // ...
};

pubsub_patterns属性是一个链表，链表中的每个节点都包含着一个pubsubPattern结构， 这个结构的pattern属性记录了被订阅的模式，而client属性则记录了订阅模式的客户端：

1
2
3
4
5
6
7
typedef struct pubsubPattern {
    //订阅模式的客户端
    redisClient *client;
 
    //被订阅的模式
    robj *pattern;
} pubsubPattern;

下图展示了一个pubsub_patterns链表示例，这个链表记录了以下信息：

  • 客户端client-7正在订阅模式”music.*”
  • 客户端client-8正在订阅模式”book.*”
  • 客户端client-9正在订阅模式”news.*”

订阅模式

每当客户端执行PSUBSCRIBE命令订阅某个或某些模式的时候，服务器会对每个被订阅的模式执行以下两个操作：

  1. 新建一个pubsubPattern结构，将结构的pattern属性设置为被订阅的模式，client属性设置为订阅模式的客户端
  2. 将pubsubPattern结构添加到pubsub_patterns链表的表尾

PSUBSCRIBE命令的实现原理可以用以下伪代码来描述：

1
2
3
4
5
6
7
8
9
10
11
def psubscribe(*all_input_patterns):
    # 遍历输入的所有模式
    for pattern in all_input_patterns:
        # 创建新的pubsubPattern 结构
        # 记录被订阅的模式，以及订阅模式的客户端
        pubsubPattern = create_new_pubsubPattern()
        pubsubPattern.client = client
        pubsubPattern.pattern = pattern
        
        # 将新的pubsubPattern追加到pubsub_patterns 链表末尾
        server.pubsub_patterns.append(pubsubPattern)

模式的退订

模式的退订命令PUNSUBSCRIBE是PSUBSCRIBE命令的反操作：当一个客户端退订某个或某些模式的时候，服务器将在pubsub_patterns链表中查找并删除那些pattern属性为被退订模式，并且client属性为执行退订命令的客户端的pubsubPattern结构。PUNSUBSCRIBE命令的实现原理可以用以下伪代码来描述：

1
2
3
4
5
6
7
8
9
10
11
def punsubscribe(*all_input_patterns):
        # 遍历所有要退订的模式
        for pattern in all_input_patterns:
            # 遍历pubsub_patterns 链表中的所有pubsubPattern 结构
            for pubsubPattern in server.pubsub_patterns:
                #如果当前客户端和pubsubPattern 记录的客户端相同
                # 并且要退订的模式也和pubsubPattern 记录的模式相同
                if client == pubsubPattern.client and \
                        pattern == pubsubPattern.pattern:
                    # 那么将这个pubsubPattern 从链表中删除
                    server.pubsub_patterns.remove(pubsubPattern)

消息的发送

命令格式如下：PUBLISH <channel> <message>。当一个客户端执行PUBLISH命令的时候，会将消息message发送给频道channel。服务器执行以下两个动作：

  • 将消息message发送给channel频道的所有订阅者
  • 如果有一个或多个模式pattern与频道channel相匹配，那么将消息message发送给 pattern模式的订阅者

将消息发送给频道订阅者

PUBLISH命令要做的就是在pubsub_channels字典里找到频道channel的订阅者名单（一个链表），然后将消息发送给名单上的所有客户端。PUBLISH命令将消息发送给频道订阅者的方法可以用以下伪代码来描述：

1
2
3
4
5
6
7
8
9
10
11
def channel_publish(channel, message):
    # 如果channel键不存在于pubsub_channels 字典中
    # 那么说明channel 频道没有任何订阅者
    # 程序不做发送动作，直接返回
    if channel not in server.pubsub_channels:
        return
    # 运行到这里，说明channel 频道至少有一个订阅者
    # 程序遍历channel 频道的订阅者链表
    # 将消息发送给所有订阅者
    for subscriber in server.pubsub_channels[channel]:
        send_message(subscriber, message)

将消息发送给模式订阅者

为了将消息发送给所有与channel频道相匹配的模式的订阅者，PUBLISH命令要做的就是遍历整个pubsub_patterns链表，查找那些与channel频道相匹配的模式，并将消息发送给订阅了这些模式的客户端。PUBLISH命令将消息发送给模式订阅者的方法可以用以下伪代码来描述：

1
2
3
4
5
6
7
def pattern_publish(channel, message):
    # 遍历所有模式订阅消息
    for pubsubPattern in server.pubsub_patterns:
        # 如果频道和模式相匹配
        if match(channel, pubsubPattern.pattern):
            # 那么将消息发送给订阅该模式的客户端
            send_message(pubsubPattern.client, message)

查看订阅信息

PUBSUB命令是Redis 2.8新增加的命令之一，客户端可以通过这个命令来查看频道或者模式的相关信息，比如某个频道目前有多少订阅者，又或者某个模式目前有多少订阅者。

PUBSUB CHANNELS命令

功能：用于返回服务器当前被订阅的频道
命令格式如下：PUBSUB CHANNELS [pattern]

  • 其中pattern参数是可选的：
    • 如果不给定pattern参数，那么命令返回服务器当前被订阅的所有频道
    • 如果给定pattern参数，那么命令返回服务器当前被订阅的频道中那些与pattern模式相匹配的频道

这个子命令是通过遍历服务器pubsub_channels字典的所有键（每个键都是一个被订阅的频道），然后记录并返回所有符合条件的频道来实现的。这个过程可以用以下伪代码来描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def pubsub_channels(pattern=None):
    # 一个列表，用于记录所有符合条件的频道
    channel_list = []
 
    # 遍历服务器中的所有频道
    # （也即是pubsub_channels 字典的所有键）
    for channel in server.pubsub_channels:
        # 当以下两个条件的任意一个满足时，将频道添加到链表里面：
        #1 ）用户没有指定pattern 参数
        #2 ）用户指定了pattern 参数，并且channel 和pattern 匹配
        if (pattern is None) or match(channel, pattern):
            channel_list.append(channel)
    #向客户端返回频道列表
    return channel_list

PUBSUB NUMSUB命令

功能：接受任意多个频道作为输入参数，并返回这些频道的订阅者数量，命令格式如下：PUBSUB NUMSUB [channel-1 channel-2...channel-n]

这个子命令是通过在pubsub_channels字典中找到频道对应的订阅者链表，然后返回订阅 者链表的长度来实现的（订阅者链表的长度就是频道订阅者的数量）
这个过程可以用以下 伪代码来描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def pubsub_numsub(*all_input_channels):
    # 遍历输入的所有频道
    for channel in all_input_channels:
        # 如果pubsub_channels 字典中没有channel 这个键
        # 那么说明channel 频道没有任何订阅者
        if channel not in server.pubsub_channels:
            # 返回频道名
            reply_channel_name(channel)
            # 订阅者数量为0
            reply_subscribe_count(0)
        # 如果pubsub_channels 字典中存在channel 键
        # 那么说明channel 频道至少有一个订阅者
        else:
            # 返回频道名
            reply_channel_name(channel)
            # 订阅者链表的长度就是订阅者数量
            reply_subscribe_count(len(server.pubsub_channels[channel])

PUBSUB NUMPAT命令

功能：用于返回服务器当前被订阅模式的数量。命令格式如下：PUBSUB NUMPAT

这个子命令是通过返回pubsub_patterns链表的长度来实现的，因为这个链表的长度就是 服务器被订阅模式的数量。这个过程可以用以下伪代码来描述：

1
2
3
def pubsub_numpat():
    # pubsub_patterns 链表的长度就是被订阅模式的数量
    reply_pattern_count(len(server.pubsub_patterns))

事务

Redis通过MULTI、EXEC、WATCH等命令来实现事务（transaction）功能。事务提供了一种将多个命令请求打包，然后一次性、按顺序地执行多个命令的机制，并且在事务执行期间，服务器不会中断事务而改去执行其他客户端的命令请求，它会将事务中的所有命令都执行完毕，然后才去处理其他客户端的命令请求。

Redis事务不支持回滚机制，如果事务中的命令是在执行期间出现了错误，事务的后续命令也会继续执行下去，并且之前执行的命令也不会有任何影响
事务因为命令入队出错而被服务器拒绝执行，事务中的所有命令都不会被执行。

以下是一个事务执行的过程，该事务首先以一个MULTI命令为开始，接着将多个命令放入事务当中，最后由EXEC命令将这个事务提交（commit）给服务器执行：

事务的实现

三个阶段：

  • 事务开始
  • 命令入队
  • 事务执行

事务开始（MULTI命令）

MULTI命令的执行标志着事务的开始。MULTI命令可以将执行该命令的客户端从非事务状态切换至事务状态，这一切换是通过在客户端状态的flags属性中打开REDIS_MULTI标识来完成的，MULTI命令的实现可以用以 下伪代码来表示：

1
2
3
4
5
def MULTI():
    # 打开事务标识
    client.flags |= REDIS_MULTI
    # 返回OK 回复
    replyOK()

命令入队

当一个客户端处于非事务状态时，这个客户端发送的命令会立即被服务器执行。当一个客户端切换到事务状态之后，服务器会根据这个客户端发来的不同命令执行不同的操作：

  • 如果客户端发送的命令为EXEC、DISCARD、WATCH、MULTI四个命令的其中一个， 那么服务器立即执行这个命令
  • 与此相反，如果客户端发送的命令是EXEC、DISCARD、WATCH、MULTI四个命令以外的其他命令，那么服务器并不立即执行这个命令，而是将这个命令放入一个事务队列里面，然后向客户端返回QUEUED回复

事务队列（mstate属性）

每个Redis客户端都有自己的事务状态，这个事务状态保存在客户端状态的mstate属性里面：

1
2
3
4
5
6
typedef struct redisClient {
    // ...
    //事务状态
    multiState mstate; /* MULTI/EXEC state */
    // ...
} redisClient;

事务状态包含一个事务队列，以及一个已入队命令的计数器（也可以说是事务队列的长度）：

1
2
3
4
5
6
7
typedef struct multiState {
    //事务队列，FIFO 顺序
    multiCmd *commands;
 
    //已入队命令计数
    int count;
} multiState;

事务队列是一个multiCmd类型的数组，数组中的每个multiCmd结构都保存了一个已入队命令的相关信息，包括指向命令实现函数的指针、命令的参数，以及参数的数量：

1
2
3
4
5
6
7
8
9
10
typedef struct multiCmd {
    //参数
    robj **argv;
 
    //参数数量
    int argc;
 
    //命令指针
    struct redisCommand *cmd;
} multiCmd;

事务队列以先进先出（FIFO）的方式保存入队的命令，较先入队的命令会被放到数组的 前面，而较后入队的命令则会被放到数组的后面

执行事务

当一个处于事务状态的客户端向服务器发送EXEC命令时，这个EXEC命令将立即被服务器执行。服务器会遍历这个客户端的事务队列，执行队列中保存的所有命令，最后将执行命令所得的结果全部返回给客户端。EXEC命令的实现原理可以用以下伪代码来描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def EXEC():
    # 创建空白的回复队列
    reply_queue = []
 
    # 遍历事务队列中的每个项
    # 读取命令的参数，参数的个数，以及要执行的命令
    for argv, argc, cmd in client.mstate.commands:
        # 执行命令，并取得命令的返回值
        reply = execute_command(cmd, argv, argc)
 
        # 将返回值追加到回复队列末尾
        reply_queue.append(reply)
 
    # 移除REDIS_MULTI 标识，让客户端回到非事务状态
    client.flags & = ~REDIS_MULTI
 
    # 清空客户端的事务状态，包括：
    #1 ）清零入队命令计数器
    #2 ）释放事务队列
    client.mstate.count = 0
    release_transaction_queue(client.mstate.commands)
    # 将事务的执行结果返回给客户端
    send_reply_to_client(client, reply_queue)

WATCH命令

WATCH命令是一个乐观锁（optimistic locking），它可以在EXEC命令执行之前，监视任意数量的数据库键，并在EXEC命令执行时，检查被监视的键是否至少有一个已经被修改过了，如果是的话，服务器将拒绝执行事务，并向客户端返回代表事务执行失败的空回复。

使用WATCH命令监视数据库键（watched_keys字典）

每个Redis数据库都保存着一个watched_keys字典，字典的键是某个被WATCH命令监视的数据库键，字典的值则是一个链表，链表中记录了所有监视相应数据库键的客户端：

1
2
3
4
5
6
typedef struct redisDb {
    // ...
    //正在被WATCH 命令监视的键
    dict *watched_keys;
    // ...
} redisDb;

通过watched_keys字典，服务器可以清楚地知道哪些数据库键正在被监视，以及哪些客户端正在监视这些数据库键。

监视机制的触发（touchWatchKey函数、REDIS_DIRTY_CAS标识）

所有对数据库进行修改的命令，比如SET、LPUSH、SADD、ZREM、DEL、FLUSHDB等等，在执行之后都会调用multi.c/touchWatchKey函数对watched_keys字典进行检查，查看是否有客户端正在监视刚刚被命令修改过的数据库键，如果有的话，那么touchWatchKey函数会将监视被修改键的客户端的REDIS_DIRTY_CAS标识打开，表示该客户端的事务安全性已经被破坏。

touchWatchKey函数的定义可以用以下伪代码来描述：

1
2
3
4
5
6
7
8
def touchWatchKey(db, key):
    # 如果键key 存在于数据库的watched_keys 字典中
    # 那么说明至少有一个客户端在监视这个key
    if key in db.watched_keys:
        # 遍历所有监视键key 的客户端
        for client in db.watched_keys[key]:
            # 打开标识
            client.flags |= REDIS_DIRTY_CAS

举个例子，对于下图所示的watched_keys字典来说：

  • 如果键”name”被修改，那么c1、c2、c10086三个客户端的REDIS_DIRTY_CAS标识将被打开
  • 如果键”age”被修改，那么c3和c10086两个客户端的REDIS_DIRTY_CAS标识将被打开
  • 如果键”address”被修改，那么c2和c4两个客户端的REDIS_DIRTY_CAS标识将被打开

判断事务是否安全

当服务器接收到一个客户端发来的EXEC命令时，服务器会根据这个客户端是否打开了REDIS_DIRTY_CAS标识来决定是否执行事务：

  • 如果REDIS_DIRTY_CAS打开，那么说明客户端所监视的键当中，至少有一个键已经被修改过了，服务器会拒绝执行客户端提交的事务
  • 如果REDIS_DIRTY_CAS没有打开，那么说明客户端监视的所有键都没有被修改过，事务仍然是安全的，服务器将执行客户端提交的这个事务

事务的ACID性质

在传统的关系式数据库中，常常用ACID性质来检验事务功能的可靠性和安全性。在Redis中，事务总是具有以下的特性：

  • 原子性（Atomicity）
  • 一致性（Consistency）
  • 隔离性 （Isolation）
  • 当Redis运行在某种特定的持久化模式下时，事务也具有耐久性 （Durability）

原子性

事务具有原子性指的是，数据库将事务中的多个操作当作一个整体来执行，服务器要么就执行事务中的所有操作，要么就一个操作也不执行。对于Redis的事务功能来说，事务队列中的命令要么就全部都执行，要么就一个都不执行，因此，Redis的事务是具有原子性的

Redis不支持事务回滚机制 （rollback），即使事务队列中的某个命令在执行期间出现了错误，整个事务也会继续执行下去，直到将事务队列中的所有命令都执行完毕为止。

一致性

事务具有一致性指的是，如果数据库在执行事务之前是一致的，那么在事务执行之后， 无论事务是否执行成功，数据库也应该仍然是一致的。“一致”指的是数据符合数据库本身的定义和要求，没有包含非法或者无效的错误数据。

Redis通过谨慎的错误检测和简单的设计来保证事务的一致性，下面将分别介绍三个Redis事务可能出错的地方，并说明Redis是如何妥善地处理这些错误，从而确保事务的一致性的。

  • 入队错误：如果一个事务在入队命令的过程中，出现了命令不存在，或者命令的格式不正确等情况，那么Redis将拒绝执行这个事务
  • 执行错误：事务还可能在执行的过程中发生错误，关于这种错误有两个需要说明的地方：
    • 执行过程中发生的错误都是一些不能在入队时被服务器发现的错误，这些错误只会在命令实际执行时被触发
    • 即使在事务的执行过程中发生了错误，服务器也不会中断事务的执行，它会继续执行事务中余下的其他命令，并且已执行的命令（包括执行命令所产生的结果）不会被出错的命令影响
  • 服务器停机：如果Redis服务器在执行事务的过程中停机，那么根据服务器所使用的持久化模式，可能有以下情况出现：
    • 如果服务器运行在无持久化的内存模式下，那么重启之后的数据库将是空白的，因此数据总是一致的
    • 如果服务器运行在RDB模式下，那么在事务中途停机不会导致不一致性，因为服务器可以根据现有的RDB文件来恢复数据，从而将数据库还原到一个一致的状态。如果找不到可供使用的RDB文件，那么重启之后的数据库将是空白的，而空白数据库总是一致的
    • 如果服务器运行在AOF模式下，那么在事务中途停机不会导致不一致性，因为服务器可以根据现有的AOF文件来恢复数据，从而将数据库还原到一个一致的状态。如果找不到可供使用的AOF文件，那么重启之后的数据库将是空白的，而空白数据库总是一致的

隔离性

事务的隔离性指的是，即使数据库中有多个事务并发地执行，各个事务之间也不会互相影响，并且在并发状态下执行的事务和串行执行的事务产生的结果完全相同。因为Redis使用单线程的方式来执行事务（以及事务队列中的命令），并且服务器保证， 在执行事务期间不会对事务进行中断，因此，Redis的事务总是以串行的方式运行的，并且事务也总是具有隔离性的

耐久性（持久性）

事务的耐久性指的是，当一个事务执行完毕时，执行这个事务所得的结果已经被保存到永久性存储介质（比如硬盘）里面了，即使服务器在事务执行完毕之后停机，执行事务所得的结果也不会丢失。因为Redis的事务不过是简单地用队列包裹起了一组Redis命令，Redis并没有为事务提供任何额外的持久化功能，所以Redis事务的耐久性由Redis所使用的持久化模式决定。

Lua脚本

创建并修改Lua环境

为了在Redis服务器中执行Lua脚本，Redis在服务器内嵌了一个Lua环境，并对这个Lua环境进行了一系列修改，从而确保这个Lua环境可以满足Redis服务器的需要。Redis服务器创建并修改Lua环境的整个过程由以下步骤组成：

  • 创建一个基础的Lua环境，之后的所有修改都是针对这个环境进行的。服务器首先调用Lua的C API函数lua_open，创建一个新的Lua环境。
  • 载入多个函数库到Lua环境里面，让Lua脚本可以使用这些函数库来进行数据操作
    • 基础库（base library）：这个库包含Lua的核心（core）函数；
    • 表格库（table library）：这个库包含用于处理表格的通用函数；
    • 字符串库（string library）：这个库包含用于处理字符串的通用函数；
    • 数学库（math library）：这个库是标准C语言数学库的接口；
    • 调试库（debug library）：这个库提供了对程序进行调试所需的函数；
    • Lua CJSON库：这个库用于处理UTF-8编码的JSON格式；
    • Struct库：这个库用于在Lua值和C结构 （struct）之间进行转换；
    • Lua cmsgpack库：这个库用于处理 MessagePack格式的数据；
  • 创建全局表格redis，并将它设为全局变量。这个表格包含了对Redis进行操作的函数，比如用于在Lua脚本中 执行Redis命令的redis.call函数
  • 使用Redis自制的随机函数来替换Lua原有的带有副作用的随机函数，从而避免在脚本中引入副作用
  • 创建排序辅助函数__redis__compare_helper，Lua环境使用这个辅佐函数来对一部分Redis命令的结果进行排序，从而消除这些命令的不确定性
  • 创建redis.pcall函数的错误报告辅助函数，这个函数可以提供更详细的出错信息
  • 对Lua环境中的全局环境进行保护，防止用户在执行Lua脚本的过程中，将额外的全 局变量添加到Lua环境中
  • 将完成修改的Lua环境保存到服务器状态的lua属性中，等待执行服务器传来的Lua脚本

Lua环境协作组件

伪客户端

因为执行Redis命令必须有相应的客户端状态，所以为了执行Lua脚本中包含的Redis命令，Redis服务器专门为Lua环境创建了一个伪客户端，并由这个伪客户端负责处理Lua脚本中包含的所有Redis命令。Lua脚本使用redis.call函数或者redis.pcall函数执行一个Redis命令，需要完成以下步骤：

  1. Lua环境将redis.call函数或者redis.pcall函数想要执行的命令传给伪客户端
  2. 伪客户端将脚本想要执行的命令传给命令执行器
  3. 命令执行器执行伪客户端传给它的命令，并将命令的执行结果返回给伪客户端
  4. 伪客户端接收命令执行器返回的命令结果，并将这个命令结果返回给Lua环境
  5. Lua环境在接收到命令结果之后，将该结果返回给redis.call函数或者redis.pcall函数
  6. 接收到结果的redis.call函数或者redis.pcall函数会将命令结果作为函数返回值返回给 脚本中的调用者

lua_scripts字典

除了伪客户端之外，Redis服务器为Lua环境创建的另一个协作组件是lua_scripts字典：字典的键为某个Lua脚本的SHA1校验和（checksum），字典的值则是SHA1校验和对应的Lua脚本

1
2
3
4
5
struct redisServer {
    // ...
    dict *lua_scripts;
    // ...
};

Redis服务器会将所有被EVAL命令执行过的Lua脚本，以及所有被SCRIPT LOAD命令载入过的Lua脚本都保存到lua_scripts字典里面，lua_scripts字典有两个作用：一个是实现SCRIPT EXISTS命令，另一个是实现脚本复制功能。

EVAL命令的实现

EVAL命令可以直接执行Lua脚本，执行过程可以分为以下三个步骤：

  • 根据客户端给定的Lua脚本，在Lua环境中定义一个Lua函数
  • 将客户端给定的脚本保存到lua_scripts字典，等待将来进一步使用
  • 执行刚刚在Lua环境中定义的函数，以此来执行客户端给定的Lua脚本

定义脚本函数

当客户端向服务器发送EVAL命令，要求执行某个Lua脚本的时候，服务器首先要做的就是在Lua环境中，为传入的脚本定义一个与这个脚本相对应的Lua函数，其中：

  • Lua函数的名字由f_前缀加上脚本的SHA1校验和（四十个字符长）组成
  • 函数的体（body）则是脚本本身

使用函数来保存客户端传入的脚本有以下好处：

  • 执行脚本的步骤非常简单，只要调用与脚本相对应的函数即可
  • 通过函数的局部性来让Lua环境保持清洁，减少了垃圾回收的工作量，并且避免了使用全局变量
  • 如果某个脚本所对应的函数在Lua环境中被定义过至少一次，那么只要记得这个脚本的SHA1校验和，服务器就可以在不知道脚本本身的情况下，直接通过调用Lua函数来执行脚本

将脚本保存到lua_scripts字典

EVAL命令要做的第二件事是将客户端传入的脚本保存到服务器的lua_scripts字典里面

执行脚本函数

在为脚本定义函数，并且将脚本保存到lua_scripts字典之后，服务器还需要进行一些设置钩子、传入参数之类的准备动作，才能正式开始执行脚本。整个准备和执行脚本的过程如下：

  • 将EVAL命令中传入的键名（key name）参数和脚本参数分别保存到KEYS数组和ARGV数组，然后将这两个数组作为全局变量传入到Lua环境里面
  • 为Lua环境装载超时处理钩子（hook），这个钩子可以在脚本出现超时运行情况时， 让客户端通过SCRIPT KILL命令停止脚本，或者通过SHUTDOWN命令直接关闭服务器
  • 执行脚本函数
  • 移除之前装载的超时钩子
  • 将执行脚本函数所得的结果保存到客户端状态的输出缓冲区里面，等待服务器将结果返回给客户端
  • 对Lua环境执行垃圾回收操作

EVALSHA命令

使用EVALSHA命令则可以根据脚本的SHA1校验和来对脚本进行求值，但这个命令要求校验和对应的脚本必须至少被EVAL命令执行过一次，或者这个校验和对应的脚本曾经被SCRIPT LOAD命令载入过。

EVALSHA命令的实现：每个被EVAL命令成功执行过的Lua脚本，在Lua环境里面都有一个与这个脚本相对应的Lua函数，函数的名字由f_前缀加上40个字符长的 SHA1校验和组成，例如f_5332031c6b470dc5a0dd9b4bf2030dea6d65de91。只要脚本对应的函数曾经在Lua环境里面定义过，那么即使不知道脚本的内容本身，客户端也可以根据脚本的SHA1校验和来调用脚本对应的函数，从而达到执行脚本的目的，这就是EVALSHA命令的实现原理。可以用伪代码来描述这一原理：

1
2
3
4
5
6
7
8
9
10
11
12
def EVALSHA(sha1):
    # 拼接出函数的名字
    # 例如：f_5332031c6b470dc5a0dd9b4bf2030dea6d65de91
    func_name = "f_" + sha1
 
    # 查看这个函数在Lua 环境中是否存在
    if function_exists_in_lua_env(func_name):
        # 如果函数存在，那么执行它
        execute_lua_function(func_name)
    else:
        # 如果函数不存在，那么返回一个错误
        send_script_error("SCRIPT NOT FOUND")

脚本管理命令

SCRIPT FLUSH

SCRIPT FLUSH命令用于清除服务器中所有和Lua脚本有关的信息，这个命令会释放并重建lua_scripts字典，关闭现有的Lua环境并重新创建一个新的Lua环境。以下为SCRIPT FLUSH命令的实现伪代码：

1
2
3
4
5
6
7
8
9
def SCRIPT_FLUSH():
    # 释放脚本字典
    dictRelease(server.lua_scripts)
    # 重建脚本字典
    server.lua_scripts = dictCreate(...)
    # 关闭Lua 环境
    lua_close(server.lua)
    # 初始化一个新的Lua 环境
    server.lua = init_lua_env()

SCRIPT EXISTS

SCRIPT EXISTS命令根据输入的SHA1校验和，检查校验和对应的脚本是否存在于服务器中，SCRIPT EXISTS命令是通过检查给定的校验和是否存在于lua_scripts字典来实现的。以下是该命令的实现伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def SCRIPT_EXISTS(*sha1_list):
    # 结果列表
    result_list = []
    #遍历输入的所有SHA1 校验和
    for sha1 in sha1_list:
        # 检查校验和是否为lua_scripts 字典的键
        # 如果是的话，那么表示校验和对应的脚本存在
        # 否则的话，脚本就不存在
        if sha1 in server.lua_scripts:
            # 存在用1 表示
            result_list.append(1)
        else:
            # 不存在用0 表示
            result_list.append(0)
    # 向客户端返回结果列表
    send_list_reply(result_list)

SCRIPT LOAD

SCRIPT LOAD命令只加载/保存脚本，但是不执行脚本。命令首先在Lua环境中为脚本创建相对应的函数，然后再将脚本对应的键值对保存到lua_scripts字典里面。举个例子，如果我们执行以下命令：

那么服务器将在Lua环境中创建以下函数：

并将键为”2f31ba2bb6d6a0f42cc159d2e2dad55440778de3”，值为”return’hi’”的键值对添加 到服务器的lua_scripts字典里面。

SCRIPT KILL

如果服务器设置了lua-time-limit配置选项，那么在每次执行Lua脚本之前，服务器都会在Lua环境里面设置一个超时处理钩子（hook）。超时处理钩子在脚本运行期间，会定期检查脚本已经运行了多长时间，一旦钩子发现脚本的运行时间已经超过了lua-time-limit选项设置的时长，钩子将定期在脚本运行的间隙中， 查看是否有SCRIPT KILL命令或者SHUTDOWN命令到达服务器。
下图展示了带有超时处理钩子的脚本的运行过程：

如果超时运行的脚本未执行过任何写入操作，那么客户端可以通过SCRIPT KILL命令来指示服务器停止执行这个脚本，并向执行该脚本的客户端发送一个错误回复。处理完SCRIPT KILL命令之后，服务器可以继续运行。如果脚本已经执行过写入操作，那么客户端只能用SHUTDOWN nosave命令来停止服务器，从而防止不合法的数据被写入数据库中。

脚本的复制

与其他普通Redis命令一样，当服务器运行在复制模式之下时，具有写性质的脚本命令也会被复制到从服务器，这些命令包括EVAL命令、EVALSHA命令、SCRIPT FLUSH命令，以 及SCRIPT LOAD命令。

复制EVAL命令、SCRIPT FLUSH命令、SCRIPT LOAD命令

Redis复制EVAL、SCRIPT FLUSH、SCRIPT LOAD三个命令的方法和复制其他普通Redis 命令的方法一样，当主服务器执行完以上三个命令的其中一个时，主服务器会直接将被执行的命令传播（propagate）给所有从服务器，如下图所示：

复制EVALSHA命令

EVALSHA命令是所有与Lua脚本有关的命令中，复制操作最复杂的一个。对于一个在主服务器被成功执行的EVALSHA命令来说，相同的EVALSHA命令在从服务器执行时却可能会出现脚本未找到（not found）错误。

Redis要求主服务器在传播EVALSHA命令的时候，必须确保EVALSHA命令要执行的脚本已经被所有从服务器载入过，如果不能确保这一点的话， 主服务器会将EVALSHA命令转换成一个等价的EVAL命令，然后通过传播EVAL命令来代替EVALSHA命令。传播EVALSHA命令，或者将EVALSHA命令转换成EVAL命令，都需要用到服务器状态的lua_scripts字典和repl_scriptcache_dict字典，接下来的小节将分别介绍这两个字典的作用， 并最终说明Redis复制EVALSHA命令的方法。

①判断传播EVALSHA命令是否安全的方法（repl_scriptcache_dict字典）：主服务器使用服务器状态的repl_scriptcache_dict字典记录自己已经将哪些脚本传播给了所有从服务器：

1
2
3
4
5
struct redisServer {
    // ...
    dict *repl_scriptcache_dict;
    // ...
};

字典的键是一个个Lua脚本的SHA1校验和，字典的值则全部都是 NULL。当一个校验和出现在repl_scriptcache_dict字典时，说明这个校验和对应的Lua脚本已经传播给了所有从服务器，主服务器可以直接向从服务器传播包含这个SHA1校验和的 EVALSHA命令，而不必担心从服务器会出现脚本未找到错误。

②清空repl_scriptcache_dict字典：每当主服务器添加一个新的从服务器时，主服务器都会清空自己的repl_scriptcache_dict字典，这是因为：随着新从服务器的出现，repl_scriptcache_dict字典里面记录的脚本已经不再被所有从服务器载入过，所以要强制自己重新向所有从服务器传播脚本，从而确保新的从服务器不会出现脚本未找到错误。

③EVALSHA命令转换成EVAL命令的方法：通过使用EVALSHA命令指定的SHA1校验和，以及lua_scripts字典保存的Lua脚本，服务器总可以将一个EVALSHA命令：EVALSHA <sha1> <numkeys> [key ...] [arg ...]转换成一个等价的EVAL命令：EVAL <script> <numkeys> [key ...] [arg ...]。

具体的转换方法如下：

  • 根据SHA1校验和sha1，在lua_scripts字典中查找sha1对应的Lua脚本script
  • 将原来的EVALSHA命令请求改写成EVAL命令请求，并且将校验和sha1改成脚本script，至于numkeys、key、arg等参数则保持不变
  • 如果一个SHA1值所对应的Lua脚本没有被所有从服务器载入过，那么主服务器可以将EVALSHA命令转换成等价的EVAL命令，然后通过传播等价的EVAL命令来代替原本想要传播的EVALSHA命令，以此来产生相同的脚本执行效果，并确保所有从服务器都不会出现脚本未找到错误

④传播EVALSHA命令的方法：当主服务器成功在本机执行完一个EVALSHA命令之后，它将根据EVALSHA命令指定的SHA1校验和是否存在于repl_scriptcache_dict字典来决定是向从服务器传播EVALSHA命令还是EVAL命令：

  • 如果EVALSHA命令指定的SHA1校验和存在于repl_scriptcache_dict字典，那么主服务器直接向从服务器传播EVALSHA命令
  • 如果EVALSHA命令指定的SHA1校验和不存在于repl_scriptcache_dict字典，那么主服务器会将EVALSHA命令转换成等价的EVAL命令，然后传播这个等价的EVAL命令，并将 EVALSHA命令指定的SHA1校验和添加到repl_scriptcache_dict字典里面

SORT

Redis的SORT命令可以对列表键、集合键或者有序集合键的值进行排序。

SORT 命令

对键key进行排序，默认不带任何选项的SORT：只可以对包含数字键的键key进行排序，且默认是升序排序。例如下面对一个包含3个数字的列表进行排序：

1
2
3
4
5
6
7
redis> RPUSH numbers 3 1 2
(integer) 3

redis> SORT numbers
1) "1"
2) "2"
3) "3"

SORT命令的实现（struct redisSortObject）

  • SORT命令为每个被排序的键都创建一个与键长度相同的数组，数组的每个项都是一个redisSortObject结构；
  • 遍历数组，将各个数组项的obj指针分别指向numbers列表的各个项，构成obj指针和列表项之间的一对一关系，如下图所示
  • 遍历数组，将各个obj指针所指向的列表项转换成一个double类型的浮点数，并将这 个浮点数保存在相应数组项的u.score属性里面，如下图所示
  • 根据数组项u.score属性的值，对数组进行数字值排序，排序后的数组项按u.score属 性的值从小到大排列，如下图所示
  • 遍历数组，将各个数组项的obj指针所指向的列表项作为排序结果返回给客户端，程 序首先访问数组的索引0，返回u.score值为1.0的列表项”1”；然后访问数组的索引1，返回 u.score值为2.0的列表项”2”；最后访问数组的索引2，返回u.score值为3.0的列表项”3”

以下是redisSortObject结构的完整定义：

1
2
3
4
5
6
7
8
9
10
11
12
typedef struct _redisSortObject {
    //被排序键的值
    robj *obj;
 
    //权重
    union {
        //排序数字值时使用
        double score;
        //排序带有BY 选项的字符串值时使用
        robj *cmpobj;
    } u;
} redisSortObject;

ALPHA选项

命令格式：SORT <key> ALPHA

功能：默认的SORT只可以对包含数字的键进行排序，使用ALPHA选项可以对包含字符串值的键进行排序。例如下面对一个包含3个字符串值的集合键进行排序：

1
2
3
4
5
6
7
8
9
10
11
12
13
redis> SADD fruits apple banana cherry
(interger) 3

# 元素在集合中是乱序排放的
redis> SMEMBERS fruits
1) "apple"
2) "cherry"
3) "banana"

redis> SORT fruits ALPHA
1) "apple"
2) "banana"
3) "cherry"

过程:

  • 创建一个redisSortObject结构数组，数组的长度等于fruits集合的大小；
  • 遍历数组，将各个数组项的obj指针分别指向fruits集合的各个元素；
  • 根据obj指针所指向的集合元素，对数组进行字符串排序，排序后的数组项按集合元素的字符串值从小到大排列；
  • 遍历数组，依次将数组项的obj指针所指向的元素返回给客户端

ASC选项与DESC选项

命令格式：SORT <key> ASC、SORT <key> DESC。

功能：默认情况下SORT对排序结果进行升序结果（也就是ASC选项），但是使用DESC选项可以对排序的结果进行降序排序

BY选项

命令格式：SORT <key> BY <by-pattern>

功能：默认情况下SORT是根据键的元素的值作为权重来进行排序的，但是通过BY选项，SORT命令可以指定某些字符串键，或者某个哈希键所包含的某些域来作为元素的权重对一个键进行排序。例如，根据其他键的值作为权重来对fruits进行排序：

执行上面SORT fruits BY*-price命令的详细步骤如下：

  • 创建一个redisSortObject结构数组，数组的长度等于fruits集合的大小
  • 遍历数组，将各个数组项的obj指针分别指向fruits集合的各个元素，如下图所示
  • 遍历数组，根据各个数组项的obj指针所指向的集合元素，以及BY选项所给定的模式 *-price，查找相应的权重键：
    • 对于”apple”元素，查找程序返回权重键”apple-price”
    • 对于”banana”元素，查找程序返回权重键”banana-price”
    • 对于”cherry”元素，查找程序返回权重键”cherry-price”
  • 将各个权重键的值转换成一个double类型的浮点数，然后保存在相应数组项的u.score 属性里面，如下图所示
    • “apple”元素的权重键”apple-price”的值转换之后为8.0
    • “banana”元素的权重键”banana-price”的值转换之后为5.5
    • “cherry”元素的权重键”cherry-price”的值转换之后为7.0
  • 以数组项u.score属性的值为权重，对数组进行排序，得到一个按u.score属性的值从 小到大排序的数组，如下图所示
    • 权重为5.5的”banana”元素位于数组的索引0位置上
    • 权重为7.0的”cherry”元素位于数组的索引1位置上
    • 权重为8.0的”apple”元素位于数组的索引2位置上
  • 遍历数组，依次将数组项的obj指针所指向的集合元素返回给客户端

ALPHA选项与BY选项的配合使用

SORT <key> BY <by-pattern> ALPHA。在上面，我们介绍了BY选项可以根据其他权重键的值进行排序，但是其他权重键的值也是数字类型，如果其他权重键的值是字符串类型，那么就可以配合ALPHA选项来实现。

  • 创建一个redisSortObject结构数组，数组的长度等于fruits集合的大小
  • 遍历数组，将各个数组项的obj指针分别指向fruits集合的各个元素，如下图所示
  • 遍历数组，根据各个数组项的obj指针所指向的集合元素，以及BY选项所给定的模式 *-id，查找相应的权重键：
    • 对于”apple”元素，查找程序返回权重键”apple-id”
    • 对于”banana”元素，查找程序返回权重键”banana-id”
    • 对于”cherry “元素，查找程序返回权重键”cherry-id”
  • 将各个数组项的u.cmpobj指针分别指向相应的权重键（一个字符串对象），如下图所示
  • 以各个数组项的权重键的值为权重，对数组执行字符串排序，结果如下图所示
    • 权重为”FRUIT-13”的”cherry”元素位于数组的索引0位置上
    • 权重为”FRUIT-25”的”apple”元素位于数组的索引1位置上
    • 权重为”FRUIT-79”的”banana”元素位于数组的索引2位置上
  • 遍历数组，依次将数组项的obj指针所指向的集合元素返回给客户端

LIMIT选项

命令格式：SORT <key> LIMIT <offset> <count>。功能：使用LIMIT选项可以限制SORT命令返回的结果数量。从offset索引（索引从0开始）处开始返回count条结果。

GET选项

命令格式：SORT <key> GET <by-pattern>。功能：默认情况下SORT命令返回的是自己排序的结果，使用GET选项可以根据自己键的值来对别对的键进行排序。GET选项支持1个或多个，下面或依次介绍

STORE选项

命令格式：SORT <key> STORE <new_key>。功能：使用STORE选项，可以将排序的结果保存到一个新键中。

SORT命令选项的执行顺序

如果按照选项来划分的话，一个SORT命令的执行过程可以分为以下几步：

  • 排序：在这一步，命令会使用ALPHA、ASC或DESC、BY这几个选项，对输入键进 行排序，并得到一个排序结果集
  • 限制排序结果集的长度：在这一步，命令会使用LIMIT选项，对排序结果集的长度进 行限制，只有LIMIT选项指定的那部分元素会被保留在排序结果集中
  • 获取外部键：在这一步，命令会使用GET选项，根据排序结果集中的元素，以及 GET选项指定的模式，查找并获取指定键的值，并用这些值来作为新的排序结果集
  • 保存排序结果集：在这一步，命令会使用STORE选项，将排序结果集保存到指定的 键上面去
  • 向客户端返回排序结果集：在最后这一步，命令遍历排序结果集，并依次向客户端 返回排序结果集中的元素

二进制位数组操作

实现：Redis使用字符串对象来表示位数组，因为字符串对象使用的SDS数据结构是二进制安全的，所以程序可以直接使用SDS结构来保存位数组，并使用SDS结构的操作函数来处理位数组。

下图展示了用SDS表示的，一字节长的位数组：

  • redisObject.type的值为REDIS_STRING，表示这是一个字符串对象。
  • sdshdr.len的值为1，表示这个SDS保存了一个一字节长的位数组
  • buf数组中的buf[0]字节保存了一字节长的位数组
  • buf数组中的buf[1]字节保存了SDS程序自动追加到值的末尾的空字符’\0’

为了方便与表示二进制位，我们把buf[0]一字节表示为下面所示的状态（1字节8位）

备注（重点）：

  • buf数组保存二进制位与我们平时表示的二进制为顺序是相反的
    • 例如在上图中我们的buf数组第1字节表示的二进制为10110010，实质上其表示的是01001101
    • 使用逆序来保存位数组可以简化SETBIT命令的实现（后面介绍SETBIT命令会解释）

GETBIT命令

功能：用于获取位数组指定偏移量上的二进制位的值

因为GETBIT命令执行的所有操作都可以在常数时间内完成，所以该命令的算法复杂度 为O（1）
格式：GETBIT <bitarray> <offset>

  • bitarray：二进制数组的名称
  • offset：偏移量（索引从0开始）

GETBIT命令的执行过程:

  • 计算byte= [offset÷8]，byte值记录了offset偏移量指定的二进制位保存在位数组的哪个字节
  • 计算bit=（offset mod 8）+1，bit值记录了offset偏移量指定的二进制位是byte字节的 第几个二进制位
  • 根据byte值和bit值，在位数组bitarray中定位offset偏移量指定的二进制位，并返回这个位的值

举个例子，对于下图所示的位数组来说，执行以下命令：

1
GETBIT <bitarray> 3

将执行以下操作：

  • [3÷8]的值为0
  • （3 mod 8）+1的值为4
  • 定位到buf[0]字节上面，然后取出该字节上的第4个二进制位（从左向右数）的值
  • 向客户端返回二进制位的值1

SETBIT命令

功能：用于为位数组指定偏移量上的二进制位设置值，并将之前二进制位的旧值返回

因为SETBIT命令执行的所有操作都可以在常数时间内完成，所以该命令的时间复杂度为 O（1）
格式：SETBIE <bitarray> <offset> <value>

  • bitarray：二进制位数组
  • offset：偏移量（从0开始）
  • value：设置的值

SETBIT命令的执行过程：

  • 计算len=[offset÷8]+1，len值记录了保存offset偏移量指定的二进制位至少需 要多少字节
  • 检查bitarray键保存的位数组（也即是SDS）的长度是否小于len，如果是的话，将 SDS的长度扩展为len字节，并将所有新扩展空间的二进制位的值设置为0。
  • 计算byte=[offset÷8]，byte值记录了offset偏移量指定的二进制位保存在位数 组的哪个字节
  • 计算bit=（offset mod 8）+1，bit值记录了offset偏移量指定的二进制位是byte字节的 第几个二进制位
  • 根据byte值和bit值，在bitarray键保存的位数组中定位offset偏移量指定的二进制位， 首先将指定二进制位现在值保存在oldvalue变量，然后将新值value设置为这个二进制位的值
  • 向客户端返回oldvalue变量的值

演示案例
首先，如果我们对下图所示的位数组执行命令：SETBIT <bitarray> 1 1

那么服务器将执行以下操作：

  • 计算[1÷8]+1，得出值1，这表示保存偏移量为1的二进制位至少需要1字节长 位数组
  • 检查位数组的长度，发现SDS的长度不小于1字节，无须执行扩展操作
  • 计算[1÷8]，得出值0，说明偏移量为1的二进制位位于buf[0]字节
  • 计算（1 mod 8）+1，得出值2，说明偏移量为1的二进制位是buf[0]字节的第2个二进 制位
  • 定位到buf[0]字节的第2个二进制位上面，将二进制位现在的值0保存到oldvalue变 量，然后将二进制位的值设置为1
  • 向客户端返回oldvalue变量的值0

带有扩展操作的SETBIT命令演示案例

前面展示的SETBIT例子无须对位数组进行扩展，现在，让我们来看一个需要对位数组进行扩展的例子
假设我们对下图所示的位数组执行命令：SETBIT <bitarray> 12 1。

那么服务器将执行以下操作：

  • 计算[12÷8]+1，得出值2，这表示保存偏移量为12的二进制位至少需要2字节长的位数组
  • 对位数组的长度进行检查，得知位数组现在的长度为1字节，小于最小长度2字节，所以程序会要求将位数组的长度扩展为2字节。不过，尽管程序只要求2字节长的位数组，但SDS的空间预分配策略会为SDS额外多分配2字节的未使用空间，再加上 为保存空字符而额外分配的1字节，扩展之后buf数组的实际长度为5字节，如下图所示
  • 计算[12÷8]，得出值1，说明偏移量为12的二进制位位于buf[1]字节中
  • 计算（12 mod 8）+1，得出值5，说明偏移量为12的二进制位是buf[1]字节的第5个二进制位
  • 定位到buf[1]字节的第5个二进制位，将二进制位现在的值0保存到oldvalue变量，然 后将二进制位的值设置为1
  • 向客户端返回oldvalue变量的值0。 左图展示了SETBIT命令定位并设置指定二进制位的过程，而右图则展示了SETBIT 命令执行之后，位数组的样子

注意，因为buf数组使用逆序来保存位数组，所以当程序对buf数组进行扩展之后，写入操作可以直接在新扩展的二进制位中完成，而不必改动位数组原来已有的二进制位。相反地，如果buf数组使用和书写位数组时一样的顺序来保存位数组，那么在每次扩展 buf数组之后，程序都需要将位数组已有的位进行移动，然后才能执行写入操作，这比 SETBIT命令目前的实现方式要复杂，并且移位带来的CPU时间消耗也会影响命令的执行速度。

BITCOUNT命令

功能：用于统计位数组里面，值为1的二进制位的数量。

二进制位统计算法（1）：遍历算法

实现BITCOUNT命令最简单直接的方法，就是遍历位数组中的每个二进制位，并在遇到值为1的二进制位时，将计数器的值增一，遍历算法虽然实现起来简单，但效率非常低。

二进制位统计算法（2）：查表算法

优化检查操作的一个办法是使用查表法：对于一个有限集合来说，集合元素的排列方式是有限的，而对于一个有限长度的位数组来说，它能表示的二进制位排列也是有限的。根据这个原理，我们可以创建一个表，表的键为某种排列的位数组，而表的值则是相应位数组中，值为1的二进制位的数量。我们只需执行一次查表操作，就可以检查多个二进制位。

二进制位统计算法（3）：variable-precision SWAR算法

BITCOUNT命令要解决的问题——统计一个位数组中非0二进制位的数量，在数学上被称为“计算汉明重量（Hamming Weight）”。以下是一个处理32位长度位数组的variable-precision SWAR算法的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
uint32_t swar(uint32_t i) {
    //步骤1
    i = (i & 0x55555555) + ((i >> 1) & 0x55555555);
 
    //步骤2
    i = (i & 0x33333333) + ((i >> 2) & 0x33333333);
 
    //步骤3
    i = (i & 0x0F0F0F0F) + ((i >> 4) & 0x0F0F0F0F);
 
    //步骤4
    i = (i*(0x01010101) >> 24);
    
    return i;
}

以下是调用swar（bitarray）的执行步骤：

  • 步骤1计算出的值i的二进制表示可以按每两个二进制位为一组进行分组，各组的十进制表示就是该组的汉明重量
  • 步骤2计算出的值i的二进制表示可以按每四个二进制位为一组进行分组，各组的十进制表示就是该组的汉明重量
  • 步骤3计算出的值i的二进制表示可以按每八个二进制位为一组进行分组，各组的十进制表示就是该组的汉明重量
  • 步骤4的i*0x01010101语句计算出bitarray的汉明重量并记录在二进制位的最高八位，而 >>24语句则通过右移运算，将bitarray的汉明重量移动到最低八位，得出的结果就是bitarray 的汉明重量

举个例子，对于调用swar（0x3A70F21B），程序在第一步将计算出值0x2560A116，这 个值的每两个二进制位的十进制表示记录了0x3A70F21B每两个二进制位的汉明重量，如下表所示

之后，程序在第二步将计算出值0x22304113，这个值的每四个二进制位的十进制表示记 录了0x3A70F21B每四个二进制位的汉明重量，如下表所示

接下来，程序在第三步将计算出值0x4030504，这个值的每八个二进制位的十进制表示 记录了0x3A70F21B每八个二进制位的汉明重量，如下表所示

在第四步，程序首先计算0x4030504*0x01010101=0x100c0904，将汉明重量聚集到二进 制位的最高八位，如下表所示

之后程序计算0x100c0904 >> 24，将汉明重量移动到低八位，最终得出值0x10，也即是 十进制值16，这个值就是0x3A70F21B的汉明重量，如下表所示

swar函数每次执行可以计算32个二进制位的汉明重量，它比之前介绍的遍历算法要快32 倍，比键长为8位的查表法快4倍，比键长为16位的查表法快2倍，并且因为swar函数是单纯 的计算操作，所以它无须像查表法那样，使用额外的内存。
另外，因为swar函数是一个常数复杂度的操作，所以我们可以按照自己的需要，在一次循环中多次执行swar，从而按倍数提升计算汉明重量的效率：

  • 例如，如果我们在一次循环中调用两次swar函数，那么计算汉明重量的效率就从之前的 一次循环计算32位提升到了一次循环计算64位
  • 又例如，如果我们在一次循环中调用四次swar函数，那么一次循环就可以计算128个二 进制位的汉明重量，这比每次循环只调用一次swar函数要快四倍！
  • 当然，在一个循环里执行多个swar调用这种优化方式是有极限的：一旦循环中处理的位数组的大小超过了缓存的大小，这种优化的效果就会降低并最终消失

二进制位统计算法（4）：Redis的实现

BITCOUNT命令的实现用到了查表和variable-precisionSWAR两种算法：

  • 查表算法使用键长为8位的表，表中记录了从0000 0000到1111 1111在内的所有二进制位 的汉明重量
  • 至于variable-precision SWAR算法方面，BITCOUNT命令在每次循环中载入128个二进 制位，然后调用四次32位variable-precision SWAR算法来计算这128个二进制位的汉明重量

在执行BITCOUNT命令时，程序会根据未处理的二进制位的数量来决定使用那种算法：

  • 如果未处理的二进制位的数量大于等于128位，那么程序使用variable-precision SWAR算 法来计算二进制位的汉明重量
  • 如果未处理的二进制位的数量小于128位，那么程序使用查表算法来计算二进制位的汉 明重量

以下伪代码展示了BITCOUNT命令的实现原理：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#一个表，记录了所有八位长位数组的汉明重量
#程序将8 位长的位数组转换成无符号整数，并在表中进行索引
#例如，对于输入0000 0011 ，程序将二进制转换为无符号整数3
#然后取出weight_in_byte[3] 的值2
# 2 就是0000 0011 的汉明重量
weight_in_byte = [0,1,1,2,1,2,2,/*...*/,7,7,8]
 
def BITCOUNT(bits):
    # 计算位数组包含了多少个二进制位
    count = count_bit(bits)
 
    # 初始化汉明重量为零
    weight = 0
 
    # 如果未处理的二进制位大于等于128 位
    # 那么使用variable-precision SWAR 算法来处理
    while count >= 128:
        # 四个swar 调用，每个调用计算32 个二进制位的汉明重量
        # 注意：bits[i:j] 中的索引j 是不包含在取值范围之内的
        weight += swar(bits[0:32])
        weight += swar(bits[32:64])
        weight += swar(bits[64:96])
        weight += swar(bits[96:128])
 
        # 移动指针，略过已处理的位，指向未处理的位
        bits = bits[128:]
        # 减少未处理位的长度
        count -= 128
 
    # 如果执行到这里，说明未处理的位数量不足128 位
    # 那么使用查表法来计算汉明重量
    while count:
        # 将8 个位转换成无符号整数，作为查表的索引（键）
        index = bits_to_unsigned_int(bits[0:8])
        weight += weight_in_byte[index]
 
        # 移动指针，略过已处理的位，指向未处理的位
        bits = bits[8:]
        # 减少未处理位的长度
        count -= 8
    
    # 计算完毕，返回输入二进制位的汉明重量
    return weight

这个BITCOUNT实现的算法复杂度为O（n），其中n为输入二进制位的数量。更具体一点，我们可以用以下公式来计算BITCOUNT命令在处理长度为n的二进制位输入时，命令中的两个循环需要执行的次数：

  • 第一个循环的执行次数可以用公式loop 1=n÷128」计算得出
  • 第二个循环的执行次数可以用公式loop 2=n mod 128计算得出

BITOP命令

功能：可以对多个位数组进行按位与（and）、按位或（or）、按位异或（xor）、取反（not）。

复杂度：

  • BITOP AND、BITOP OR、BITOP XOR三个命令可以接受多个位数组作为输入， 程序需要遍历输入的每个位数组的每个字节来进行计算，所以这些命令的复杂度为 O（n^2）

  • 因为BITOP NOT命令只接受一个位数组输入，所以它的复杂度为 O（n）

  • 在执行BITOP AND命令时，程序用&操作计算出所有输入二进制位的逻辑与结果，然后保存在指定的键上面。

  • 在执行BITOP OR命令时，程序用|操作计算出所有输入二进制位的逻辑或结果，然后保存在指定的键上面

  • 在执行BITOP XOR命令时，程序用^操作计算出所有输入二进制位的逻辑异或结果，然后保存在指定的键上面

  • 在执行BITOP NOT命令时，程序用~操作计算出输入二进制位的逻辑非结果，然后保存在指定的键上面。

举个例子，假设客户端执行命令：BITOP AND result x y。其中，键x保存的位数组如左图所示，而键y保存的位数组如右图所示：

BITOP命令将执行以下操作：

  • 创建一个空白的位数组value，用于保存AND操作的结果
  • 对两个位数组的第一个字节执行buf[0] & buf[0]操作，并将结果保存到value[0]字节
  • 对两个位数组的第二个字节执行buf[1] & buf[1]操作，并将结果保存到value[1]字节
  • 对两个位数组的第三个字节执行buf[2] & buf[2]操作，并将结果保存到value[2]字节
  • 经过前面的三次逻辑与操作，程序得到了下图所示的计算结果，并将它保存在键 result上面

慢查询日志

Redis的慢查询日志功能用于记录执行时间超过给定时长的命令请求，用户可以通过这个功能产生的日志来监视和优化查询速度。

慢查询日志选项：

  • slowlog-log-slower-than选项：指定执行时间超过多少微秒（1秒等于1000 000微秒）的命令请求会被记录到日志上
  • slowlog-max-len选项：指定服务器最多保存多少条慢查询日志

服务器使用先进先出的方式保存多条慢查询日志，当服务器存储的慢查询日志数量等于slowlog-max-len选项的值时，服务器在添加一条新的慢查询日志之前，会先将最旧的一条慢查询日志删除

慢查询日志的格式，以下面的图片为例：

  1. 日志的唯一标识符
  2. 命令执行时的UNIX时间戳
  3. 命令执行的时常（单位微秒）
  4. 命令以及命令参数
  5. 命令执行的客户端IP与端口

慢查询记录的保存

服务器状态中有几个变量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct redisServer {
    // ...
    //下一条慢查询日志的ID
    long long slowlog_entry_id;

    //保存了所有慢查询日志的链表
    list *slowlog;

    //服务器配置slowlog-log-slower-than 选项的值
    long long slowlog_log_slower_than;

    //服务器配置slowlog-max-len 选项的值
    unsigned long slowlog_max_len;
    // ...
};
  • slowlog_entry_id属性的初始值为0，每当创建一条新的慢查询日志时，这个属性的值就会用作新日志的id值，之后程序会对这个属性的值增一
    例如，在创建第一条慢查询日志时，slowlog_entry_id的值0会成为第一条慢查询日志的 ID，而之后服务器会对这个属性的值增一；当服务器再创建新的慢查询日志的时候， slowlog_entry_id的值1就会成为第二条慢查询日志的ID，然后服务器再次对这个属性的值增一。
  • slowlog链表：保存了服务器中的所有慢查询日志，链表中的每个节点都保存了一个slowlogEntry结构，每个slowlogEntry结构代表一条慢查询日志
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
typedef struct slowlogEntry {
    //唯一标识符
    long long id;

    //命令执行时的时间，格式为UNIX 时间戳
    time_t time;

    //执行命令消耗的时间，以微秒为单位
    long long duration;

    //命令与命令参数
    robj **argv;

    //命令与命令参数的数量
    int argc;
} slowlogEntry;

每个slowlogEntry结构代表一条慢查询日志。举个例子：

下图展示了一个服务器状态中和慢查询功能有关的属性：

  • slowlog_entry_id的值为6，表示服务器下条慢查询日志的id值将为6
  • slowlog链表包含了id为5至1的慢查询日志，最新的5号日志排在链表的表头，而最旧的1 号日志排在链表的表尾，这表明slowlog链表是使用插入到表头的方式来添加新日志的
  • slowlog_log_slower_than记录了服务器配置slowlog-log-slower-than选项的值0，表示任何 执行时间超过0微秒的命令都会被慢查询日志记录
  • slowlog-max-len属性记录了服务器配置slowlog-max-len选项的值5，表示服务器最多储存五条慢查询日志

慢查询日志的阅览和删除

定义查看日志 的SLOWLOG GET命令：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def SLOWLOG_GET(number=None):
    # 用户没有给定number 参数
    # 那么打印服务器包含的全部慢查询日志
    if number is None:
        number = SLOWLOG_LEN()

    # 遍历服务器中的慢查询日志
    for log in redisServer.slowlog:
        if number <= 0:
            # 打印的日志数量已经足够，跳出循环
            break
        else:
            # 继续打印，将计数器的值减一
            number -= 1
        # 打印日志
        printLog(log)

查看日志数量的SLOWLOG LEN命令可以用以下伪代码来定义：

1
2
3
def SLOWLOG_LEN():
    # slowlog 链表的长度就是慢查询日志的条目数量
    return len(redisServer.slowlog)

另外，用于清除所有慢查询日志的SLOWLOG RESET命令可以用以下伪代码来定义：

1
2
3
4
5
def SLOWLOG_RESET():
    # 遍历服务器中的所有慢查询日志
    for log in redisServer.slowlog:
        # 删除日志
        deleteLog(log)

添加新日志（slowlogPushEntryIfNeeded函数）

在每次执行命令的之前和之后，程序都会记录微秒格式的当前UNIX时间戳，这两个时间戳之间的差就是服务器执行命令所耗费的时长，服务器会将这个时长作为参数之一传给slowlogPushEntryIfNeeded函数，而slowlogPushEntryIfNeeded函数则负责检查是否需要为这次执行的命令创建慢查询日志。以下伪代码展示了这一过程：

1
2
3
4
5
6
7
8
9
10
11
#记录执行命令前的时间
before = unixtime_now_in_us()

#执行命令
execute_command(argv, argc, client)

#记录执行命令后的时间
after = unixtime_now_in_us()

#检查是否需要创建新的慢查询日志
slowlogPushEntryIfNeeded(argv, argc, before-after)

slowlogPushEntryIfNeeded函数的作用有两个：

  • 检查命令的执行时长是否超过slowlog-log-slower-than选项所设置的时间，如果是的话，就为命令创建一个新的日志，并将新日志添加到slowlog链表的表头；
  • 检查慢查询日志的长度是否超过slowlog-max-len选项所设置的长度，如果是的话， 那么将多出来的日志从slowlog链表中删除掉

以下是slowlogPushEntryIfNeeded函数的实现代码，需要说明的是slowlogCreateEntry函数，该函数根据传入的参数，创建一个新的慢查询日志，并将redisServer.slowlog_entry_id的值增1

1
2
3
4
5
6
7
8
9
10
11
12
13
void slowlogPushEntryIfNeeded(robj **argv, int argc, long long duration) {
//慢查询功能未开启，直接返回
if (server.slowlog_log_slower_than < 0) return;

//如果执行时间超过服务器设置的上限，那么将命令添加到慢查询日志
if (duration >= server.slowlog_log_slower_than)
    //新日志添加到链表表头
    listAddNodeHead(server.slowlog,slowlogCreateEntry(argv,argc,duration));

    //如果日志数量过多，那么进行删除
    while (listLength(server.slowlog) > server.slowlog_max_len)
        listDelNode(server.slowlog,listLast(server.slowlog));
}

监视器

通过执行MONITOR命令，客户端可以将自己变为一个监视器，实时地接收并打印出服务器当前处理的命令请求的相关信息：

每当一个客户端向服务器发送一条命令请求时，服务器除了会处理这条命令请求之外， 还会将关于这条命令请求的信息发送给所有监视器，如下图所示：

成为监视器

发送MONITOR命令可以让一个普通客户端变为一个监视器，MONITOR命令的实现原理可以用 以下伪代码来实现：

1
2
3
4
5
6
7
def MONITOR():
    # 打开客户端的监视器标志
    client.flags |= REDIS_MONITOR
    # 将客户端添加到服务器状态的monitors 链表的末尾
    server.monitors.append(client)
    # 向客户端返回OK
    send_reply("OK")

举个例子，如果客户端c10086向服务器发送MONITOR命令，那么这个客户端的REDIS_MONITOR标志会被打开，并且这个客户端本身会被添加到monitors链表的表尾。

向监视器发送命令信息

服务器在每次处理命令请求之前，都会调用replicationFeedMonitors函数，由这个函数将被处理的命令请求的相关信息发送给各个监视器，以下是replicationFeedMonitors函数的伪代码定义，函数首先根据传入的参数创建信息， 然后将信息发送给所有监视器：

1
2
3
4
5
6
7
8
def replicationFeedMonitors(client, monitors, dbid, argv, argc):
    # 根据执行命令的客户端、当前数据库的号码、命令参数、命令参数个数等参数
    # 创建要发送给各个监视器的信息
    msg = create_message(client, dbid, argv, argc)
    # 遍历所有监视器
    for monitor in monitors:
        # 将信息发送给监视器
        send_message(monitor, msg)

举个例子，假设服务器在时间1378822257.329412，根据IP为127.0.0.1、端口号为56604 的客户端发送的命令请求，对0号数据库执行命令KEYS*，那么服务器将创建以下信息：

如果服务器monitors链表的当前状态如上图所示，那么服务器会分别将信息发送给c128、c256、c512和c10086四个监视器，如下图所示

Posted on Edited on

3.数组中重复的数字

题目描述

在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是第一个重复的数字2。

解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    # 这里要特别注意~找到任意重复的一个值并赋值到duplication[0]
    # 函数返回True/False
    def duplicate(self, numbers, duplication):
        if not numbers:
            return False
        for _, v in enumerate(numbers):
            if v >= len(numbers) or v < 0:
                return False
        for i in range(len(numbers)):
            while numbers[i] != i:
                if numbers[i] == numbers[numbers[i]]:
                    duplication[0] = numbers[i]
                    return True
                else:
                    idx = numbers[i]
                    numbers[i], numbers[idx] = numbers[idx], numbers[i]
        return False

使用 O(1) 空间的解法: 但条件一定要明确，存在重复数字。思维类似于寻找链表环的入口。

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def duplicateInArray(self, nums):
        f = s = 0
        while f == 0 or f != s:
            f = nums[nums[f]]
            s = nums[s]
        f = 0
        while f != s:
            f = nums[f]
            s = nums[s]
        return s

回到目录

4.二维数组中的查找

题目描述

在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    def Find(self, target, array):
        if not array:
            return False
        row = len(array)                # 数组的行数
        col = len(array[0])             # 数组的列数
        i， j = row - 1, 0                           # i, j这样规定是从左下开始查找，也可以从右上
        while i >= 0 and j < col:       # 双指针来判断是否在array中
            if array[i][j] == target:
                return True             # 如果等于输出True
            elif array[i][j] > target:
                i -= 1                  # 如果大于则往上移一格
            else:
                j += 1                  # 如果小于则往右移一格
        return False                    #如果最后走到了边界仍没有，则输出False

回到目录

5.替换空格

题目描述

请实现一个函数，将一个字符串中的每个空格替换成“%20”。例如，当字符串为 We Are Happy .则经过替换之后的字符串为 We%20Are%20Happy 。

解法：

1
2
3
4
5
6
7
8
9
10
class Solution:
    # s 源字符串
    def replaceSpace(self, s):
        res = []
        for i in s:
            if i == ' ':
                res.extend(['%', '2', '0'])
            else:
                res.append(i)
        return ''.join(res)

回到目录

6.从尾到头打印链表

题目描述

输入一个链表，按链表从尾到头的顺序返回一个ArrayList。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    # 返回从尾部到头部的列表值序列，例如[1,2,3]
    def printListFromTailToHead(self, head):
        res = []
        while head:
            res.append(head.val)
            head = head.next
        return res[::-1]

还可以递归实现：

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def printListReversingly(self, head):
        self.res = []

        def helper(p):
            if p:
                helper(p.next)
                self.res.append(p.val)

        helper(head)
        return self.res

回到目录

7.重建二叉树

题目描述

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    # 返回构造的TreeNode根节点
    def reConstructBinaryTree(self, pre, tin):
        if not pre or not tin:
            return None
        root = TreeNode(0)
        root.val = pre[0]
        idx = tin.index(pre[0])
        root.left = self.reConstructBinaryTree(pre[1: idx + 1], tin[:idx])
        root.right = self.reConstructBinaryTree(pre[idx + 1:], tin[idx + 1:])
        return root
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def buildTree(self, preorder, inorder):

        def dfs(stop):
            if preorder and inorder[-1] != stop:
                root = TreeNode(preorder.pop())
                root.left = dfs(root.val)
                inorder.pop()
                root.right = dfs(stop)
                return root

        preorder, inorder = preorder[::-1], inorder[::-1]
        return dfs(None)

回到目录

8.二叉树的下一个节点

题目描述

给定一个二叉树和其中的一个节点，请找出中序遍历顺序的下一个节点并且返回。注意，树中的节点不仅包含左右子节点，同时包含指向父节点的指针。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
#         self.father = None
class Solution:
    def inorderSuccessor(self, q):
        if not q: return None
        if q.right:
            q = q.right
            while q.left:
                q = q.left
            return q
        while q.father and q.father.right == q:
            q = q.father
        return q.father

回到目录

9.用两个栈实现队列

题目描述

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def __init__(self):
        self.s1 = []
        self.s2 = []
    def push(self, node):
        while self.s1:
            self.s2.append(self.s1.pop())
        self.s1.append(node)
        while self.s2:
            self.s1.append(self.s2.pop())
    def pop(self):
        return self.s1.pop()

回到目录

10.斐波那契数列

题目描述

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。
n<=39

解法：

1
2
3
4
5
class Solution:
    def Fibonacci(self, n):
        if n <= 1:
            return n
        return self.Fibonacci(n - 1) + self.Fibonacci(n - 2)
1
2
3
4
5
6
class Solution:
    def Fibonacci(self, n):
        res=[0, 1, 1]
        for _ in range(n):
            res[0], res[1], res[2] = res[1], res[2], res[1] + res[2]
        return res[0] if n > 2 else res[n]
1
2
3
4
5
6
class Solution:
    def Fibonacci(self, n):
        a, b = 1, 0
        for _ in range(n):
            a, b = a+b, a
        return b

回到目录

11.旋转数组中的最小数字

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。
NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def findMin(self, nums):
        if not nums: return -1
        l, r = 0, len(nums) - 1
        while l < r:
            mid = (l + r) >> 1
            if nums[mid] > nums[r]:
                l = mid + 1
            elif nums[mid] == nums[r]:
                r -= 1
            else:
                r = mid
        return nums[l]

回到目录

12.矩阵中的路径

题目描述

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则之后不能再次进入这个格子。

注意：

输入的路径不为空；
所有出现的字符均为大写英文字母；

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution(object):
    def hasPath(self, matrix, string):
        if not matrix or not matrix[0] or not string:
            return False
        m, n = len(matrix), len(matrix[0])
        state = [[True] * n for _ in range(m)]

        def dfs(i, j, pos):
            if 0 <= i < m and 0 <= j < n and state[i][j]:
                state[i][j] = ret = False
                if matrix[i][j] == string[pos]:
                    if pos == len(string) - 1:
                        return True
                    ret = dfs(i, j-1, pos+1) or dfs(i, j+1, pos+1) or dfs(i-1, j, pos+1) or dfs(i+1, j, pos+1)
                if not ret:
                    state[i][j] = True
                return ret

        for i in range(m):
            for j in range(n):
                if matrix[i][j] == string[0]:
                    if dfs(i, j, 0):
                        return True
        return False

回到目录

13.机器人的运动范围

题目描述

地上有一个 m 行和 n 列的方格，横纵坐标范围分别是 0∼m−1 和 0∼n−1。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格。但是不能进入行坐标和列坐标的数位之和大于 k 的格子。请问该机器人能够达到多少个格子？

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def movingCount(self, threshold, rows, cols):

        def dfs(x, y):
            if 0<=x<rows and 0<=y<cols and not dp[x][y]:
                dp[x][y] = 1
                if threshold >= sum(map(int, list(str(x)) + list(str(y)))):
                    self.res += 1
                    for dx, dy in delta:
                        dfs(x+dx, y+dy)

        dp = [[0] * cols for _ in range(rows)]
        self.res = 0
        delta = ((-1, 0), (0, 1), (1, 0), (0, -1))
        dfs(0, 0)
        return self.res

回到目录

14.剪绳子

题目描述

给你一根长度为 n 绳子，请把绳子剪成 m 段（m、n 都是整数，2≤n≤58 并且 m≥2）。每段的绳子的长度记为k[0]、k[1]、……、k[m]。k[0]k[1] … k[m] 可能的最大乘积是多少？例如当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到最大的乘积18。

解法：

1
2
3
4
5
6
7
class Solution:
    def maxProductAfterCutting(self,n):
        dp = [0]*(n+1)
        for i in range(2,n+1):
            for j in range(1,i):
                dp[i] = max(dp[i], max(dp[j]*(i-j), j*(i-j)))
        return dp[n]
1
2
3
class Solution:
    def maxProductAfterCutting(self,n):
        return n - 1 if n < 4 else 3 ** ((n-2) // 3) * ((n-2) % 3 + 2)

回到目录

15.二进制中 1 的个数

题目描述

输入一个整数，输出该数二进制表示中1的个数。其中负数用补码表示。

解法：

1
2
3
4
5
6
7
8
9
class Solution:
    def NumberOf1(self, n):
        count = 0
        if n < 0:
            n &= 0xffffffff
        while n:
            count += 1
            n &= (n - 1)
        return count

回到目录

16.数值的整数次方

题目描述

实现函数double Power(double base, int exponent)，求base的 exponent次方。不得使用库函数，同时不需要考虑大数问题。

解法：

1
2
3
4
5
6
7
8
9
10
class Solution:  # 简单快速幂解法
    def Power(self, base, exponent):
        exp = abs(exponent)
        r = 1
        while exp:
            if exp & 1:
                r *= base
            base *= base
            exp >>= 1
        return r if exponent >= 0 else 1/r

回到目录

18.删除列表中重复的节点

题目描述

在一个排序的链表中，存在重复的节点，请删除该链表中重复的节点，重复的节点不保留，返回链表头指针。 例如，链表1->2->3->3->4->4->5 处理后为 1->2->5

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def deleteDuplication(self, pHead):
        dummy = tmp = ListNode(0)
        tmp.next = pHead
        while pHead and pHead.next:
            if pHead.val == pHead.next.val:
                while pHead.next and pHead.val == pHead.next.val:
                    pHead = pHead.next
                tmp.next = pHead.next
            else:
                tmp = tmp.next
            pHead = pHead.next
        return dummy.next

回到目录

19.正则表达式匹配

题目描述

请实现一个函数用来匹配包括’.’和’‘的正则表达式。模式中的字符’.’表示任意一个字符，而’‘表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串”aaa”与模式”a.a”和”abaca”匹配，但是与”aa.a”和”ab*a”均不匹配。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def isMatch(self, s, p):
        dp = [[False] * (len(p)+1) for _ in range(len(s)+1)]
        dp[0][0] = True
        for j in range(1, len(p)+1):
            if p[j-1] == '*':
                dp[0][j] = dp[0][j-2]
        for i in range(1, len(s)+1):
            for j in range(1, len(p)+1):
                if p[j-1] != '*':
                    dp[i][j] = dp[i-1][j-1] and p[j-1] in (s[i-1], '.')
                else:
                    dp[i][j] = dp[i][j-2] or dp[i-1][j] and p[j-2] in (s[i-1], '.')
        return dp[-1][-1]

回到目录

20.表示数值的字符串

题目描述

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串”+100”,”5e2”,”-123”,”3.1416”和”-1E-16”都表示数值。但是”12e”,”1a3.14”,”1.2.3”,”+-5”和”12e+4.3”都不是。

解法：

两种写法： 第一种是一次遍历所有条件判断，第二种就好理解很多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution(object):
    def isNumber(self, s):
        s = s.strip()
        met_dot = met_e = met_digit = False
        for i, char in enumerate(s):
            if char in '+-':
                if i > 0 and s[i-1] not in 'eE':
                    return False
            elif char == '.':
                if met_dot or met_e: return False
                met_dot = True
            elif char == 'e' or char == 'E':
                if met_e or not met_digit:
                    return False
                met_e, met_digit = True, False
            elif char.isdigit():
                met_digit = True
            else:
                return False
        return met_digit
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:
    def isNumber(self, s: str) -> bool:
        s = s.strip()
        validList = set(['+', '-', '.', 'e', 'E'])
        isFirst = True

        for c in s:
            if c.isdigit():
                isFirst = False
                continue
            if c not in validList:
                return False
            if c == 'e' or c == 'E':
                if isFirst:
                    return False
                isFirst = True
                validList = set(['+', '-'])
            if c == '.':
                validList = set(['e', 'E'])
            if c == '+' or c == '-':
                if not isFirst:
                    return False
                validList.remove('+')
                validList.remove('-')

        return True and not isFirst

回到目录

21.调整数组顺序使奇数位于偶数前面

题目描述

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def reOrderArray(self, array):
        if not array:
            return None
        i, j = 0, len(array) - 1
        while i <= j:
            while i <= len(array) - 1 and array[i] % 2 == 1:
                i += 1
            while j >= 0 and array[j] % 2 == 0:
                j -= 1
            array[i], array[j] = array[j], array[i]
        return array

回到目录

22.链表中倒数第 k 个节点

题目描述

输入一个链表，输出该链表中倒数第k个节点。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def findKthToTail(self, head, k):
        if not head or k <= 0:
            return None
        fast = slow = head
        for _ in range(k): # 快慢指针来走，之所以先判断是为了防止 k 等于链表长度的情况。
            if not fast: return None
            fast = fast.next
        while fast:
            fast, slow = fast.next, slow.next
        return slow

回到目录

23.链表中环的入口节点

题目描述

给一个链表，若其中包含环，请找出该链表的环的入口节点，否则，输出null。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def EntryNodeOfLoop(self, pHead):
        pre = post = pHead
        while pre and pre.next:       # 确保快指针有意义没有到头
            post = post.next          # 慢指针走一步
            pre = pre.next.next       # 快指针走两步
            if pre == post:           # 相遇的时候即是有环
                post = pHead          # 慢指针再从头走
                while pre != post:    # 两个指针都是每次一步直到相遇
                    pre = pre.next
                    post = post.next
                return post           # 相遇的地方即是环的入口
        return None

回到目录

24.反转链表

题目描述

输入一个链表，反转链表后，输出新链表的表头。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    # 返回ListNode
    def ReverseList(self, pHead):
        pre, cur = None, pHead
        while cur:
            tmp = cur.next
            cur.next = pre
            pre = cur
            cur = tmp
        return pre
# 简化如下
class Solution:
    # 返回ListNode
    def ReverseList(self, pHead):
        pre, cur = None, pHead
        while cur:
            pre, pre.next, cur = cur, pre, cur.next
        return pre
# 递归法
class Solution:
    # 返回ListNode
    def ReverseList(self, pHead):
        if not pHead or not pHead.next:
            return pHead
        else:
            newHead = self.ReverseList(pHead.next)
            pHead.next.next = pHead
            pHead.next = None
            return newHead
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        if not head or not head.next:
            return head
        dummy = ListNode(0)
        dummy.next = head
        while head.next:
            cur = head.next
            head.next = cur.next
            cur.next = dummy.next
            dummy.next = cur
        return dummy.next

回到目录

25.合并两个排序的链表

题目描述

输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    # 返回合并后列表
    def Merge(self, pHead1, pHead2):
        dummy = tmp = ListNode(-1)  # 创建一个新链表来合并两个旧链表
        p1, p2 = pHead1, pHead2
        while p1 and p2:            # 都不为空的情况
            if p1.val <= p2.val:
                tmp.next = p1
                p1 = p1.next
            else:
                tmp.next = p2
                p2 = p2.next
            tmp = tmp.next
        tmp.next = p1 or p2         # 一开始都为空或者其中一个为空或者经过while循环后其中一个为空的情况都包含了
        return dummy.next

回到目录

26.树的子结构

题目描述

输入两棵二叉树A，B，判断B是不是A的子结构。我们规定空树不是任何树的子结构。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def hasSubtree(self, p1, p2):
        if not p1 or not p2:
            return False
        if self.isPart(p1, p2):
            return True
        return self.hasSubtree(p1.left, p2) or self.hasSubtree(p1.right, p2)

    def isPart(self, p1, p2):
        if not p2:
            return True
        if not p1 or p1.val != p2.val:
            return False
        return self.isPart(p1.left, p2.left) and self.isPart(p1.right, p2.right)

回到目录

27.二叉树的镜像

题目描述

操作给定的二叉树，将其变换为源二叉树的镜像。

输入描述

1
2
3
4
5
6
7
8
9
10
11
12
二叉树的镜像定义：源二叉树
    	    8
    	   /  \
    	  6   10
    	 / \  / \
    	5  7 9 11
    	镜像二叉树
    	    8
    	   /  \
    	  10   6
    	 / \  / \
    	11 9 7  5

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    # 返回镜像树的根节点
    def Mirror(self, root):
        if not root:
            return None
        root.left, root.right = root.right, root.left
        if root.left:                # 简洁的话可以不加下面这两个判断，
            self.Mirror(root.left)   # 因为递归调用后第一个判断和这个等效，
        if root.right:               # 但是涉及函数调用，会让速度更慢
            self.Mirror(root.right)
        return root

回到目录

28.对称的二叉树

题目描述

请实现一个函数，用来判断一棵二叉树是不是对称的。

如果一棵二叉树和它的镜像一样，那么它是对称的。

输入描述

1
2
3
4
5
6
7
8
9
10
11
12
13
如下图所示二叉树[1,2,2,3,4,4,3,null,null,null,null,null,null,null,null]为对称二叉树：
    1
   / \
  2   2
 / \ / \
3  4 4  3

如下图所示二叉树[1,2,2,null,4,4,3,null,null,null,null,null,null]不是对称二叉树：
    1
   / \
  2   2
   \ / \
   4 4  3

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSymmetric(self, root):
        if not root: return True

        def isSym(p, q):
            if p and q:
                return p.val == q.val and isSym(p.left, q.right) and isSym(p.right, q.left)
            return p is q

        return isSym(root.left, root.right)

回到目录

29.顺时针打印矩阵

题目描述

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def printMatrix(self, matrix):
        res = []
        if not matrix: return res
        x = y = i = 0
        delta = ((0, 1), (1, 0), (0, -1), (-1, 0))
        pos = [0, 0, len(matrix[0])-1, len(matrix)-1] # 左、上、右、下。后面懒得判断推出来的。
        while pos[0] <= pos[2] and pos[1] <= pos[3]:
            while pos[0] <= y <= pos[2] and pos[1] <= x <= pos[3]:
                res.append(matrix[x][y])
                x, y = x+delta[i][0], y+delta[i][1]
            x, y = x-delta[i][0], y-delta[i][1]
            i = (i+1) % 4
            pos[i] += sum(delta[i])
            x, y = x+delta[i][0], y+delta[i][1]
        return res

动用了hin多空间

1
2
3
4
5
6
7
class Solution:
    def printMatrix(self, matrix):
        res = []
        while matrix:
            res += matrix[0]
            matrix = list(zip(*matrix[1:]))[::-1]
        return res

回到目录

30.包含min函数的栈

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数（时间复杂度应为O（1））。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class MinStack:

    def __init__(self):
        self.stack = []
        self.stkmin = []

    def push(self, x: int) -> None:
        if not self.stkmin or self.getMin() > x:
            self.stkmin.append(x)
        else:
            self.stkmin.append(self.getMin())
        self.stack.append(x)

    def pop(self) -> None:
        if self.stack:
            self.stkmin.pop()
            return self.stack.pop()

    def top(self) -> int:
        if self.stack:
            return self.stack[-1]

    def getMin(self) -> int:
        if self.stkmin:
            return self.stkmin[-1]

进阶牛逼版 O(1)空间复杂度 O(1)时间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class MinStack:

    def __init__(self):
        self.stack = []
        self.mins = 0

    def push(self, x: int) -> None:
        if not self.stack:
            self.mins = x
            self.stack.append(0)
        else:
            compare = x - self.mins
            self.stack.append(compare)
            self.mins = x if compare < 0 else self.mins            

    def pop(self) -> None:
        top1 = self.stack.pop()
        if top1 < 0:
            self.mins = self.mins - top1

    def top(self) -> int:
        if self.stack[-1] > 0:
            return self.mins + self.stack[-1]
        else:
            return self.mins

    def getMin(self) -> int:
        return self.mins

回到目录

31.栈的压入弹出序列

题目描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。

假设压入栈的所有数字均不相等。

例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。

注意：若两个序列长度不等则视为并不是一个栈的压入、弹出序列。若两个序列都为空，则视为是一个栈的压入、弹出序列。

解法：

1
2
3
4
5
6
7
8
9
10
class Solution:
    def isPopOrder(self, pushV, popV):
        if len(pushV) != len(popV): return False
        stack, i = [], 0       # 用 stack 来模拟进出栈。
        for v in pushV:
            stack.append(v)
            while stack and stack[-1] == popV[i]:
                stack.pop()
                i += 1
        return not stack

回到目录

32.从上到下打印二叉树

题目描述

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    # 返回从上到下每个节点值列表，例：[1,2,3]
    def PrintFromTopToBottom(self, root):
        res = []
        if root:
            level = [root]
            while level:
                res.extend([x.val for x in level])
                level = [leaf for node in level for leaf in (node.left, node.right) if leaf]
        return res

回到目录

33.二叉搜索树的后序遍历序列

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true，否则返回false.假设输入的数组的任意两个数字都互不相同。

解法：

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def verifySequenceOfBST(self, sequence):
        if not sequence:
            return True  # 看 OJ 要求 True or False
        def dfs(Max, stop):
            if sequence and Max >= sequence[-1] >= stop:
                x = sequence.pop()
                dfs(Max, x)
                dfs(x, stop)
        dfs(float('inf'), float('-inf'))
        return not sequence

回到目录

34.二叉树中和为某一值的路径

题目描述

输入一棵二叉树和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。
从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

解法：

分析： 分为两个解法，一种是递归的做法，另外一种是迭代的做法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def pathSum(self, root: TreeNode, tsum: int) -> List[List[int]]:
        if not root :
            return []

        temp, res = [], []

        def DFTS(root):
            temp.append(root.val)
            if not root.left and not root.right and sum(temp) == tsum:
                res.append(temp.copy())
            if root.left:
                DFTS(root.left)
            if root.right:
                DFTS(root.right)
            temp.pop()

        DFTS(root)
        return res

迭代法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def pathSum(self, root: TreeNode, Psum: int) -> List[List[int]]:
        if not root:
            return []
        stack, res = [(root, [root.val])], []
        while stack:
            node, cur = stack.pop()
            if not node.left and not node.right and sum(cur) == Psum:
                res.append(cur)
            if node.left:
                stack.append((node.left, cur + [node.left.val]))
            if node.right:
                stack.append((node.right, cur + [node.right.val]))
        return res

返回目录

35.复杂链表的复制

题目描述

输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针指向任意一个节点），返回结果为复制后复杂链表的head。（注意，输出结果中请不要返回参数中的节点引用，否则判题程序会直接返回空）

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# class RandomListNode:
#     def __init__(self, x):
#         self.label = x
#         self.next = None
#         self.random = None
class Solution:
    # 返回 RandomListNode
    def Clone(self, pHead):
        if not pHead:
            return None
        p1 = p2 = p3 = pHead
        while p1:
            tmp = RandomListNode(p1.label)
            tmp.next = p1.next
            tmp.random = None
            p1.next = tmp
            p1 = p1.next.next
        while p2:
            tmp = p2.next
            tmp.random = p2.random.next if p2.random else None
            p2 = p2.next.next
        dummy = tmp = p3.next
        while p3:
            p3.next = p3.next.next
            tmp.next = p3.next.next if p3.next else None
            p3, tmp = p3.next, tmp.next
        return dummy

回到目录

36.二叉搜索树与双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。
注意：需要返回双向链表最左侧的节点。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def convert(self, root):
        if not root: return None
        prev = None
        stack = []
        while stack or root:
            while root:
                stack.append(root)
                root = root.left
            node = stack.pop()
            node.left = prev
            if prev:
                prev.right = node
            root = node.right
            prev = node
        cur = prev
        while cur.left:
            cur = cur.left
        return cur

回到目录

37.序列化二叉树

题目描述

请实现两个函数，分别用来序列化和反序列化二叉树。
您需要确保二叉树可以序列化为字符串，并且可以将此字符串反序列化为原始树结构。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:

    def serialize(self, root):
        def doit(node):
            if node:
                vals.append(str(node.val))
                doit(node.left)
                doit(node.right)
            else:
                vals.append('#')
        vals = []
        doit(root)
        return ','.join(vals)


    def deserialize(self, data):
        def doit():
            val = next(vals)
            if val == '#':
                return None
            node = TreeNode(int(val))
            node.left = doit()
            node.right = doit()
            return node
        vals = iter(data.split(','))
        return doit()

返回目录

38.字符串的排列

题目描述

输入一组数字（可能包含重复数字），输出其所有的排列方式。

解法：

1
2
3
4
5
6
7
8
9
class Solution:
    def permutation(self, nums):
        perms = [[]]
        for n in nums:
            perms = [
                p[:i] + [n] + p[i:]
                for p in perms
                for i in range((p+[n]).index(n)+1)]
        return perms

回到目录

39.数组中出现次数超过一半的数字

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def MoreThanHalfNum_Solution(self, numbers):
        if not numbers:
            return 0
        candidate = numbers[0]
        count = 1
        for i in range(1,len(numbers)):
            if numbers[i] == candidate:
                count += 1
            else:
                count -= 1
                if count == 0:
                    candidate = numbers[i]
                    count = 1
        # 上面是摩尔投票法，下面为验证，这样可以保证时间复杂度在 O(n) 。
        if numbers.count(candidate) * 2 > len(numbers):
            return candidate
        else:
            return 0

回到目录

40.最大的k个数

题目描述

在未排序的数组中找到前k个大的元素。 请注意，它们是排序顺序中前k个大的元素，而不是前k个不同的元素。

解法：

1

回到目录

41.数据流的中位数

题目描述

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from heapq import *
class Solution:

    def __init__(self):
        self.heaps = [], []

    def insert(self, num):
        small, large = self.heaps
        heappush(small, -heappushpop(large, num))
        if len(large) < len(small):
            heappush(large, -heappop(small))

    def getMedian(self):
        small, large = self.heaps
        if len(large) > len(small):
            return float(large[0])
        return (large[0] - small[0]) / 2.0

回到目录

42.连续子数组的最大和

题目描述

一个整数数组中的元素有正有负，在该数组中找出一个连续子数组，要求该连续子数组中各元素的和最大，这个连续子数组便被称作最大连续子数组。比如数组{2,4,-7,5,2,-1,2,-4,3}的最大连续子数组为{5,2,-1,2}，最大连续子数组的和为5+2-1+2=8。

解法：

1
2
3
4
5
6
7
class Solution:
    def FindGreatestSumOfSubArray(self, array):
        best = cur = array[0]
        for i in range(1, len(array)):
            cur = max(array[i], array[i] + cur)
            best = max(best, cur)
        return best

回到目录

43.1~n整数中1出现的次数

题目描述

输入一个整数n，求从1到n这n个整数的十进制表示中1出现的次数。例如输入12，从1到12这些整数中包含“1”的数字有1，10，11和12，其中“1”一共出现了5次。

解法：

1
2
3
4
5
6
7
8
class Solution:
    def numberOf1Between1AndN_Solution(self, n):
        count, i = 0, 1
        while i <= n:
            a, b = n // i, n % i
            count += (a+8) // 10 * i + (a%10 == 1) * (b+1)
            i *= 10
        return count

回到目录

44.数字序列中某一位的数字

题目描述

数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中，第5位（从0开始计数）是5，第13位是1，第19位是4，等等。请写一个函数求任意位对应的数字。

解法：

1
2
3
4
5
6
7
8
class Solution(object):    # 快速跳过不用检查的位数，确定区间。
    def digitAtIndex(self, n):
        n -= 1
        for digit in range(1, 11):
            first = 10 ** (digit - 1)
            if n < 9 * first * digit:
                return int(str(first + n // digit)[n % digit])
            n -= 9 * first * digit

回到目录

45.把数组排成最小的数

题目描述

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组[3, 32, 321]，则打印出这3个数字能排成的最小数字321323。

解法：

1
2
3
4
5
6
class Solution:
    def printMinNumber(self, nums):
        if not nums: return ''
        if set(nums) == {0}: return "0"
        diff = len(str(max(nums))) - len(str(min(nums))) + 1
        return "".join(sorted(map(str,nums),key= lambda x: x*diff))

回到目录

46.把数字翻译成字符串

题目描述

给定一个数字，我们按照如下规则把它翻译为字符串：
0翻译成”a”，1翻译成”b”，……，11翻译成”l”，……，25翻译成”z”。
一个数字可能有多个翻译。例如12258有5种不同的翻译，它们分别是”bccfi”、”bwfi”、”bczi”、”mcfi”和”mzi”。
请编程实现一个函数用来计算一个数字有多少种不同的翻译方法。

解法：

1
2
3
4
5
6
7
8
9
class Solution:
    def getTranslationCount(self, s):
        if not s: return 0
        dp = [1] * len(s)
        for i in range(len(s)-2, -1, -1):
            dp[i] = dp[i+1]
            if s[i] == '1' or s[i] == '2' and s[i+1] < '6':
                dp[i] += dp[i+2]
        return dp[0]

可简化为 O(1) 空间

1
2
3
4
5
6
7
8
9
10
class Solution:
    def getTranslationCount(self, s):
        if not s: return 0
        l = r = 1
        for i in range(len(s)-2, -1, -1):
            if s[i] == '1' or s[i] == '2' and s[i+1] < '6':
                l, r = l + r, l
            else:
                r = l
        return l

回到目录

47.礼物的最大价值

题目描述

在一个m×n的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于0）。
你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格直到到达棋盘的右下角。
给定一个棋盘及其上面的礼物，请计算你最多能拿到多少价值的礼物？

解法：

1
2
3
4
5
6
7
8
9
10
class Solution:
    def getMaxValue(self, grid):
        dp = [0] * len(grid[0])
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if j > 0:
                    dp[j] = grid[i][j] + max(dp[j-1], dp[j])
                else:
                    dp[j] = grid[i][j] + dp[j]
        return dp[-1]

回到目录

48.最长不含重复字符的子字符串

题目描述

给定一个字符串，找到最长子字符串的长度而不重复字符。

解法：

分析： 滑动窗口解决问题，如果遍历一遍 s，如果遍历到没有出现的元素，窗口右端立马扩张，并计算最大长度。如果遍历到之前出现的元素，则将窗口左端置为上次出现的位置的后一位。只有出现没有遍历过的元素才会计算最大长度。因为一旦是遍历过的元素，只有可能是保持不变或者缩小。

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def lengthOfLongestSubstring(self, s):
        start = maxLength = 0
        used = {}
        for i, c in enumerate(s):
            if c in used and start <= used[c]:
                start = used[c] + 1
            else:
                maxLength = max(maxLength, i - start + 1)
            used[c] = i
        return maxLength

返回目录

49.丑数

题目描述

我们把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。求第n个丑数的值。

解法：

1
2
3
4
5
6
7
8
9
10
class Solution:
    def nthUglyNumber(self, n):
        ugly = [1]
        i2 = i3 = i5 = 0
        while len(ugly) < n:
            while ugly[i2] * 2 <= ugly[-1]: i2 += 1
            while ugly[i3] * 3 <= ugly[-1]: i3 += 1
            while ugly[i5] * 5 <= ugly[-1]: i5 += 1
            ugly.append(min(ugly[i2] * 2, ugly[i3] * 3, ugly[i5] * 5))
        return ugly[-1]
1
2
3
4
5
class Solution:
    ugly = sorted(2**a * 3**b * 5**c
                  for a in range(32) for b in range(20) for c in range(14))
    def nthUglyNumber(self, n):
        return self.ugly[n-1]

回到目录

50.第一个只出现一次的字符

题目描述

在字符串中找出第一个只出现一次的字符。如输入”abaccdeff”，则输出b。如果字符串中不存在只出现一次的字符，返回#字符。

解法：

1
2
3
4
5
6
7
8
9
class Solution:
    def firstNotRepeatingChar(self, s):
        if not s: return '#'
        import collections
        count = collections.Counter(s)
        for i in set(s):
            if count[i] == 1:
                return i
        return '#'

回到目录

52.两个链表的第一个公共节点

题目描述

输入两个链表，找出它们的第一个公共节点。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def FindFirstCommonNode(self, pHead1, pHead2):
        if not pHead1 or not pHead2:
            return None
        l1, l2 = 0, 0
        p1, p2 = pHead1, pHead2
        while p1:
            p1 = p1.next
            l1 += 1
        while p2:
            p2 = p2.next
            l2 += 1
        p1, p2 = pHead1, pHead2
        if l1 >= l2:
            while l1 - l2:
                p1 = p1.next
                l1 -= 1
        else:
            while l2 - l1:
                p2 = p2.next
                l2 -= 1
        while p1 and p2:
            if p1 == p2:
                return p1
            p1 = p1.next
            p2 = p2.next
        return None
1
2
3
4
5
6
7
class Solution:
    def FindFirstCommonNode(self, pHead1, pHead2):
        p1, p2 = pHead1, pHead2
        while p1 != p2:          # 1.判断是否为同一个相交处 2.判断是否走完了一整遍
            p1 = p1.next if p1 else pHead2
            p2 = p2.next if p2 else pHead1
        return p1

回到目录

53.在排序数组中查找数字

题目描述

统计一个数字在排序数组中出现的次数。如果不存在返回 0。
例如输入排序数组[1, 2, 3, 3, 3, 3, 4, 5]和数字3，由于3在这个数组中出现了4次，因此输出4。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def getNumberOfK(self, nums, k):
        if not nums: return 0
        def search(lo, hi):
            if nums[lo] == k == nums[hi]:
                return [lo, hi]
            if nums[lo] <= k <= nums[hi]:
                mid = (lo + hi) // 2
                l, r = search(lo, mid), search(mid+1, hi)
                return max(l, r) if -1 in l+r else [l[0], r[1]]
            return [-1, -1]
        l, r = search(0, len(nums)-1)
        return 0 if l == -1 else r - l + 1

回到目录

54.二叉搜索树的第k个结点

题目描述

给定一棵二叉搜索树，请找出其中的第k小的结点。

你可以假设树和k都存在，并且1≤k≤树的总结点数。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def kthNode(self, root, k):
        stack = []
        while stack or root:
            while root:
                stack.append(root)
                root = root.left
            node = stack.pop()
            k -= 1
            if not k: return node
            root = node.right
          return None

回到目录

55.二叉树的深度

题目描述

输入一棵二叉树，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def TreeDepth(self, pRoot):
        if not pRoot:
            return 0
        depthleft = self.TreeDepth(pRoot.left)
        depthright = self.TreeDepth(pRoot.right)
        return max(depthleft, depthright) + 1

回到目录

56.数组中数字出现的次数

56-1.数组中只出现一次的两个数字

题目描述

一个整型数组里除了两个数字之外，其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。你可以假设这两个数字一定存在。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
import functools
class Solution:
    def findNumsAppearOnce(self, nums):
        if len(nums) < 2: return []
        diff = functools.reduce(lambda r, x: r ^ x, nums)
        idx = len(bin(diff)) - bin(diff).rfind('1') - 1
        num1 = num2 = 0
        for num in nums:
            if (num >> idx) & 1:
                num1 ^= num
            else:
                num2 ^= num
        return [num1, num2]

回到目录

56-2.数组中唯一只出现一次的数字

题目描述

在一个数组中除了一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。你可以假设满足条件的数字一定存在。
思考题：
如果要求只使用 O(n) 的时间和额外 O(1) 的空间，该怎么做呢？

解法：

1
2
3
4
5
6
7
class Solution:  # 面试用装x解法
    def findNumberAppearingOnce(self, nums):
        a = b = 0
        for n in nums:
            a = (a ^ n) & ~b
            b = (b ^ n) & ~a
        return a
1
2
3
4
5
6
7
8
9
10
11
class Solution:  # 常规解法
    def findNumberAppearingOnce(self, nums):
        ans = 0
        for i in range(32):
            cnt = 0
            for n in nums:
                if (n >> i) & 1:
                    cnt += 1
            if cnt % 3:
                ans |= 1 << i
        return ans if ans < 2**31 else ans - 2**32

回到目录

57.和为S的两个数

题目描述

输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def FindNumbersWithSum(self, array, tsum):
        if not array:
            return []
        i = 0
        j = len(array) - 1
        while i < j:
            if array[i] + array[j] > tsum:
                j -= 1
            elif array[i] + array[j] < tsum:
                i += 1
            else:
                return array[i], array[j]
        return []
57 - 1.和为S的连续正数序列
题目描述

输入一个正数s,打印出所有和为s的连续正数序列（至少含有两个数）。例如输入15，由于1+2+3+4+5=4+5+6=7+8=15；所以打印出三个连续序列1 ~ 5, 4 ~ 6, 7 ~ 8

解法：
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def FindContinuousSequence(self, tsum):
        low, high = 1, 2
        res = []
        while low <= tsum // 2:
            if sum(range(low, high + 1)) == tsum:
                res.append(list(range(low, high + 1)))
                low += 1
            elif sum(range(low, high + 1)) < tsum:
                high += 1
            else:
                low += 1
        return res

回到目录

58.翻转字符串

题目描述

输入一个英文句子，翻转句子中单词的顺序，但单词内字符的顺序不变。为简单起见，标点符号和普通字母一样处理。例如输入字符串“I am a student.”，则输出“student. a am I”

解法：

1
2
3
class Solution:
    def ReverseSentence(self, s):
        return ' '.join(s.split(' ')[::-1])

回到目录

59.队列的最大值

题目描述

给定一个数组和滑动窗口的大小，请找出所有滑动窗口的最大值。例如，输入数组{2,3,4,2,6,2,5,1}和数字3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        dq = collections.deque()             # 使用双向队列解决本题
        res = []
        for i, v in enumerate(nums):
            while dq and nums[dq[-1]] < v:   # dq中如果存在多个元素
                dq.pop()                     # 一定是降序排列的
            dq += i,
            if dq[0] == i - k:               # 判断dq中第一位是否有效
                dq.popleft()
            if i >= k - 1:                   # 满足滑动窗口长度才有输出
                res += nums[dq[0]],
        return res

回到目录

60.n个骰子的点数

题目描述

将一个骰子投掷n次，获得的总点数为s，s的可能范围为n6n。掷出某一点数，可能有多种掷法，例如投掷2次，掷出3点，共有[1,2],[2,1]两种掷法。请求出投掷n次，掷出n6n点分别有多少种掷法。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution(object):
    def numberOfDice(self, n):
        dp = [0] * (6 * n)
        dp[0:6] = [1] * 6
        for time in range(2,n+1): # time 是次数，从 2 开始是因为下一行要计算本次的上限索引。
            for i in range(6*time-1, -1, -1):
                dp[i]=0     # 因为上一轮的计算到这没有用了，因为点不为 0，所以清空重新计算。
                for j in range(6, 0, -1):
                    if i < j:
                        continue
                    dp[i] += dp[i - j]
        return dp[n-1:]

回到目录

61.扑克牌中的顺子

题目描述

从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的。2～10为数字本身，A为1，J为11，Q为12，K为13，大小王可以看做任意数字。为了方便，大小王均以0来表示，并且假设这副牌中大小王均有两张。

解法：

1
2
3
4
5
class Solution:
    def isContinuous(self, numbers):
        if not numbers: return False
        nums = [x for x in numbers if x]
        return max(nums) - min(nums) < 5 if len(nums) == len(set(nums)) else False

回到目录

62.圆圈中最后剩下的数字

题目描述

题目：0,1,…,n-1这n个数字拍成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里身下的最后一个数字。

解法：

递归法 代码不好理解并且递归深度大，不推荐。在牛客网上无法 AC 。但思路正确。

1
2
3
4
5
class Solution:
    def LastRemaining_Solution(self, n, m):
        if n < 1 or m < 1:
            return -1
        return 0 if n == 1 else (self.LastRemaining_Solution(n - 1, m) + m) % n

循环迭代法

1
2
3
4
5
6
7
8
class Solution:
    def LastRemaining_Solution(self, n, m):
        if n < 1 or m < 1:
            return -1
        last = 0
        for i in range(2,n + 1):
            last = (last + m) % i
        return last

回到目录

63.股票的最大利润

题目描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

解法：

1
2
3
4
5
6
7
class Solution:
    def maxProfit(self, prices):
        min_p, max_p = float('inf'), 0
        for i in range(len(prices)):
            min_p = min(min_p, prices[i])
            max_p = max(max_p, prices[i] - min_p)
        return max_p

回到目录

64.求 1+2+3+…+n

题目描述

求1+2+…+n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

解法：

1
2
3
4
5
class Solution:
    def getSum(self, n):  # 递归也可以实现，但是数大了以后会超出递归栈的上限，所以 reduce 很棒。
        import functools
        return functools.reduce(lambda x, y: x+y, range(n+1))

回到目录

65.不用加减乘除做加法

题目描述

写一个函数，求两个整数之和，要求在函数体内不得使用四则运算符号。

解法：

1
2
3
4
5
6
class Solution:
    def Add(self, num1, num2):
        mask = 0xffffffff    # 因为 Python 没有整型溢出，所以需要规定个范围掩码
        while num2 & mask:   # 当 num2 超过 mask 时，num1 也要和 mask 做 与
            num1, num2 = num1 ^ num2, (num1 & num2) << 1
        return num1 & mask if num2 > mask else num1

回到目录

66.构建乘积数组

题目描述

给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0]* A[1]* …* A[i-1]* A[i+1]* …* A[n-1]。不能使用除法。

解法：

1
2
3
4
5
6
7
8
9
10
class Solution:
    def multiply(self, A):
        B = [1] * len(A)
        for i in range(1, len(A)):
            B[i] = B[i - 1] * A[i- 1]
        tmp = 1
        for j in range(len(A) - 2, -1, -1):
            tmp *= A[j + 1]
            B[j] *= tmp
        return B

回到目录

0%