机器学习中的高性能计算

CPU优化

为什么需要高性能编程

简单谈一下我们为什么需要高性能编程。其实原因很简单，那就是我们希望计算尽量快。

在机器学习领域，模型训练和推理过程中都有大量的计算，尤其是大量的向量和矩阵计算。比如矩阵乘法（GEMM），卷积（Conv），类似Polling/Filter的算子等，这些计算有一个共同的特点就是可以利用并行编程加块计算的速度。

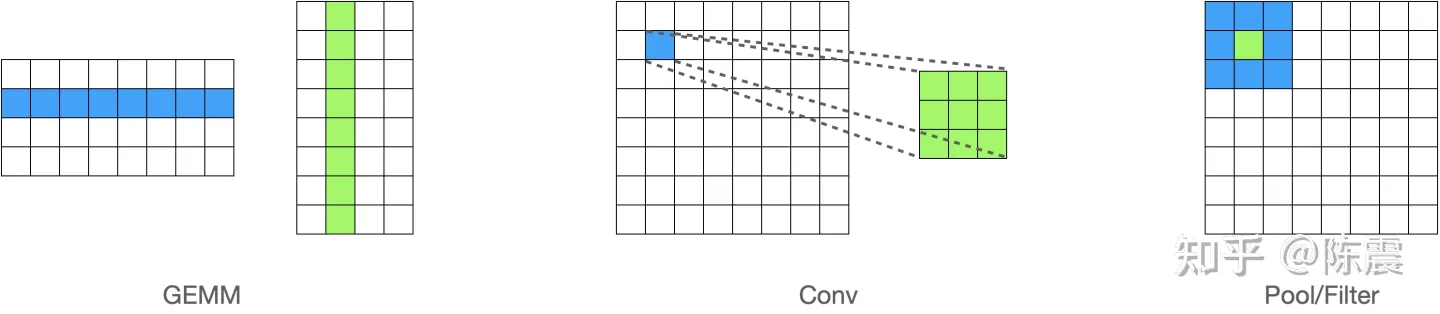
机器学习中常见的计算，都可以利用并行计算加速

举一个最简单的例子。如果我们要对一张图片（简化为一个矩阵）进行模糊处理（Blur），最简单的一种算法就是均值模糊，又叫标准盒式过滤器（Normalized Box Filter），其方法就是对每一个元素和围绕它周围的元素求均值，周围的元素可以组成一个“盒子”或者叫“核”。

这个“盒子”的选择方法一般有两种，要么当前元素作为盒子的左上角元素（如图中浅蓝色的盒子）；要么作为盒子的中间元素（如图中灰色的盒子）。在实际编程中，还要考虑处理边界的情况（如同中深蓝色的盒子）。选择哪一种方法这里并不重要，为了简化编程，我们在接下来的编程中选择第一种。

其实，均值模糊在实现中还可以利用深度神经网络中很常用的卷积（Conv）操作，即如果我们用一个值全都是1的卷积核对每个元素进行卷积操作，可以得到相同的结果。或者从另外一个角度，卷积就是一种Filter。本文为了简单，我们接下来还是用最朴素的求和方法。

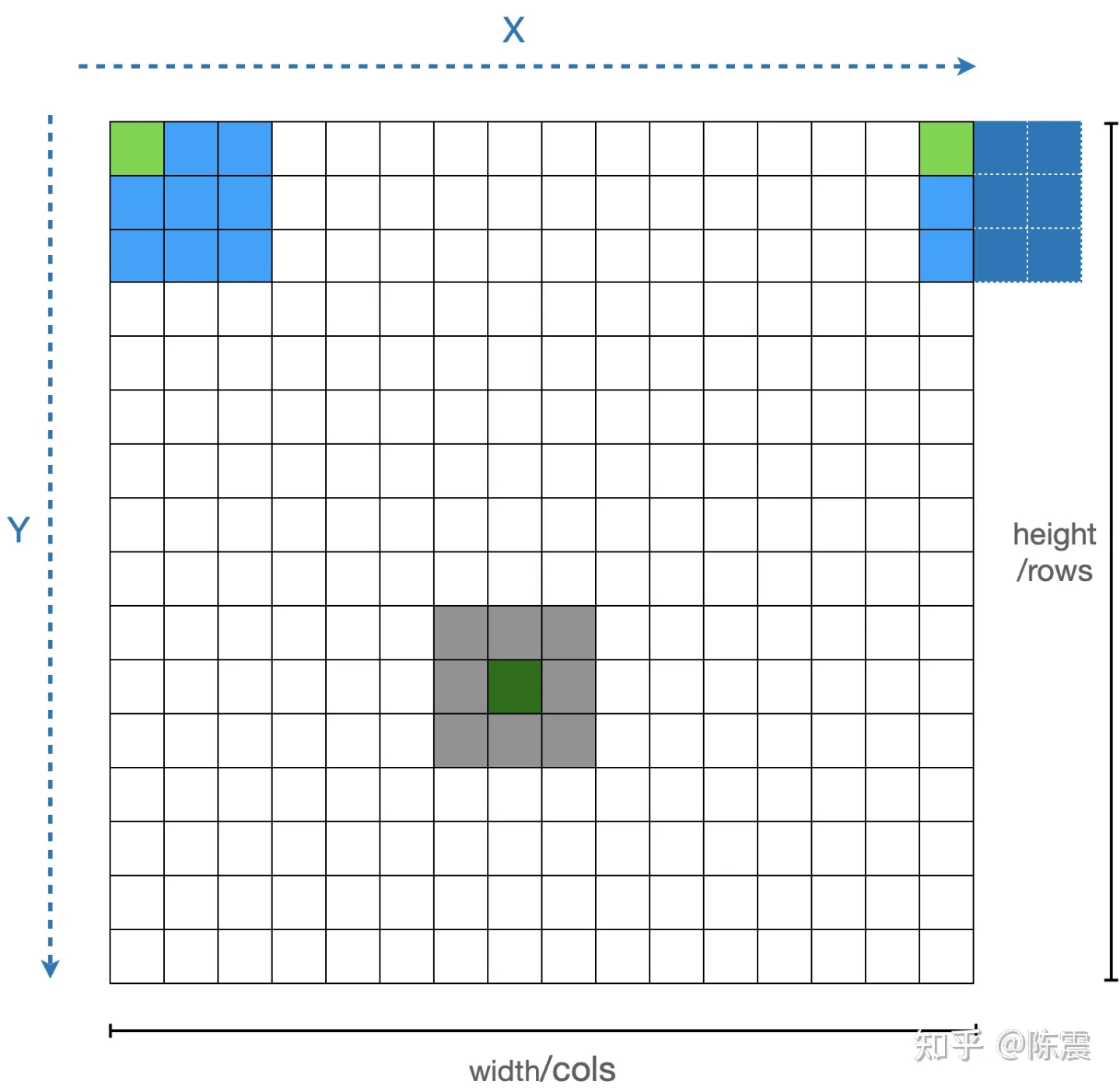
对图片进行均值模糊

算法的朴素实现

对于上面这个问题，最简单的实现就是一个两层嵌套的循环，对每一个元素分别进行计算。这个代码相信计算机专业大学一年级的同学就能很快的写出来，这里不多解释了。

void blur_mat_original(const vector<vector<float>> &input,
                       vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  int right, right_right, below, below_below;
  for (int x = 0; x < width; ++x) {
    right = x + 1 >= width ? width - 1 : x + 1;
    right_right = x + 2 >= width ? width - 1 : x + 2;
    for (int y = 0; y < height; ++y) {
      below = y + 1 >= height ? height - 1 : y + 1;
      below_below = y + 2 >= height ? height - 1 : y + 2;
      output[y][x] =
          ((input[y][x] + input[y][right] + input[y][right_right]) +
           (input[below][x] + input[below][right] + input[below][right_right]) +
           (input[below_below][x] + input[below_below][right] +
            input[below_below][right_right])) / 9;
    }
  }
}

我们选择的测试矩阵大小为 81924096，核大小为33，数据类型为float32。 使用gcc编译并运行，这段代码在我的机器上的执行时间是3914ms

$ g++ cpu.cpp -O0 -o cpu -std=c++11 && ./cpu

消除重复计算

如果这是一道程序员面试题，上面的这个答案显然不能拿到高分，因为这里面有肉眼可见的重复计算。由于我们是遍历每一个元素，对其“盒子”内的元素求均值时，我们计算了9个元素的和，在遍历过程中，由于盒子间会有重叠，因此有些元素的和被重复计算了。如下图中浅绿色和深绿色的两个元素的计算，橙色部分的计算就是重复的。

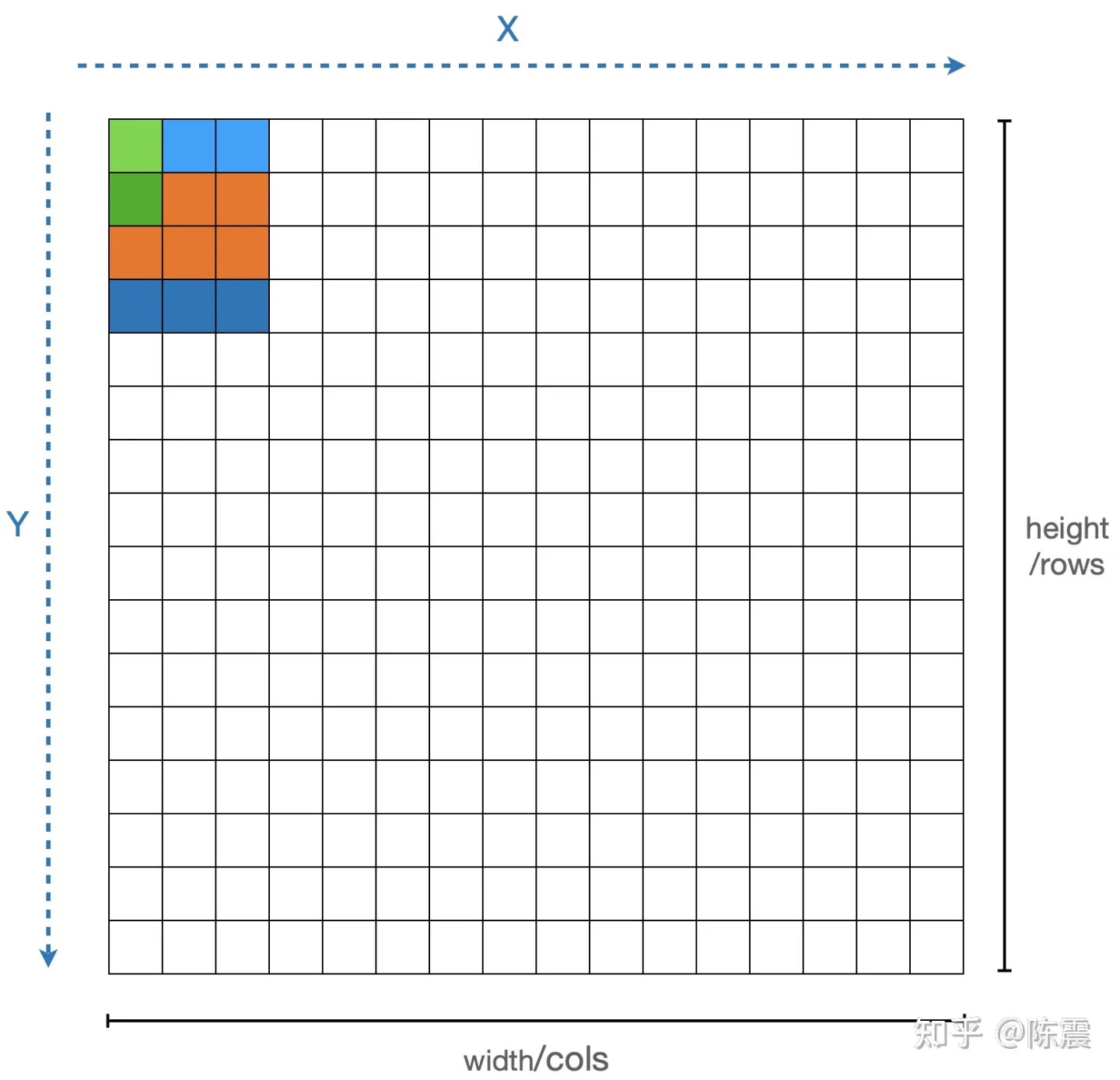
深绿色和浅绿色两个元素的计算过程中存在重复计算

如何优化呢？

我们可以把这个计算分成两个阶段，两次遍历。第一次遍历，如左图，对每一个元素和其右边两个元素求均值并保存下来，如左图的黄色部分。等所有元素都变成黄色之后，我们进行第二次遍历，对每一个元素和其下方的两个元素求和并求均值，从而得到最终的解。

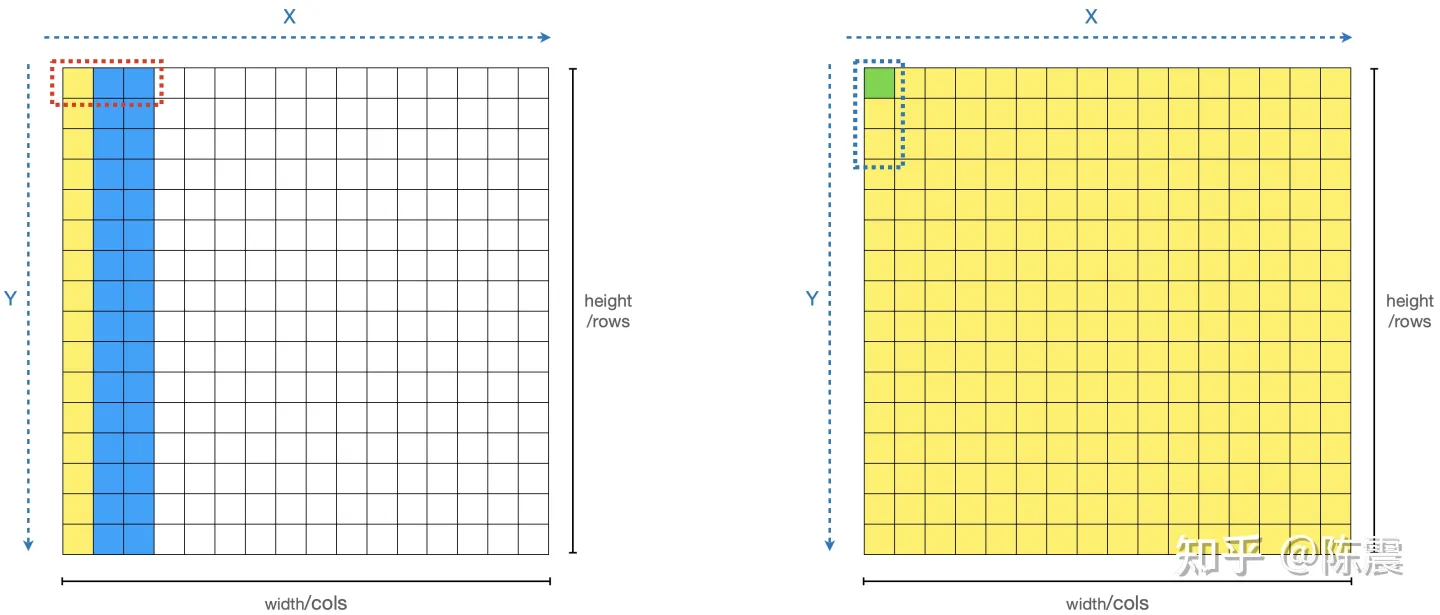
两阶段计算，消除重复计算

void blur_mat_redup(const vector<vector<float>> &input,
                    vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  int right, right_right, below, below_below;
  for (int x = 0; x < width; ++x) {
    for (int y = 0; y < height; ++y) {
      right = x + 1 >= width ? width - 1 : x + 1;
      right_right = x + 2 >= width ? width - 1 : x + 2;
      output[y][x] =
          (input[y][x] + input[y][right] + input[y][right_right]) / 3;
    }
  }
 
  for (int x = 0; x < width; ++x) {
    for (int y = 0; y < height; ++y) {
      below = y + 1 >= height ? height - 1 : y + 1;
      below_below = y + 2 >= height ? height - 1 : y + 2;
      output[y][x] =
          (output[y][x] + output[below][x] + output[below_below][x]) / 3;
    }
  }
}

上面是具体的代码实现，就是把原来的一个循环改成了两个循环，并充分利用了output变量的空间缓存中间结果，是一种典型的“空间换时间”的方法。再使用同样的参数和硬件配置，编译并运行后，性能果然有所提升，总时间从3914ms下降到3281ms。

如果有应届生同学在面试中写出了上面的答案，我觉得有比较大的概率会通过第一轮面试：）

内存优化

上面的优化我们通过减少重复计算从而提升了代码的性能。但是，了解计算机组成原理和体系结构的同学会知道，如今的CPU的主频非常高，制约计算机性能的主要方面往往是IO的性能，尤其是内存的性能。大多数时候CPU都在等内存的数据，因此我们才会有L1缓存，L2缓存等硬件和非阻塞机制来减少CPU等待IO的时间。下图展示了从CPU到寄存器、缓存、物理内存、固态硬盘、机械硬盘等不同硬件的速度。基本上每差一级，速度都有数量级上的降低。

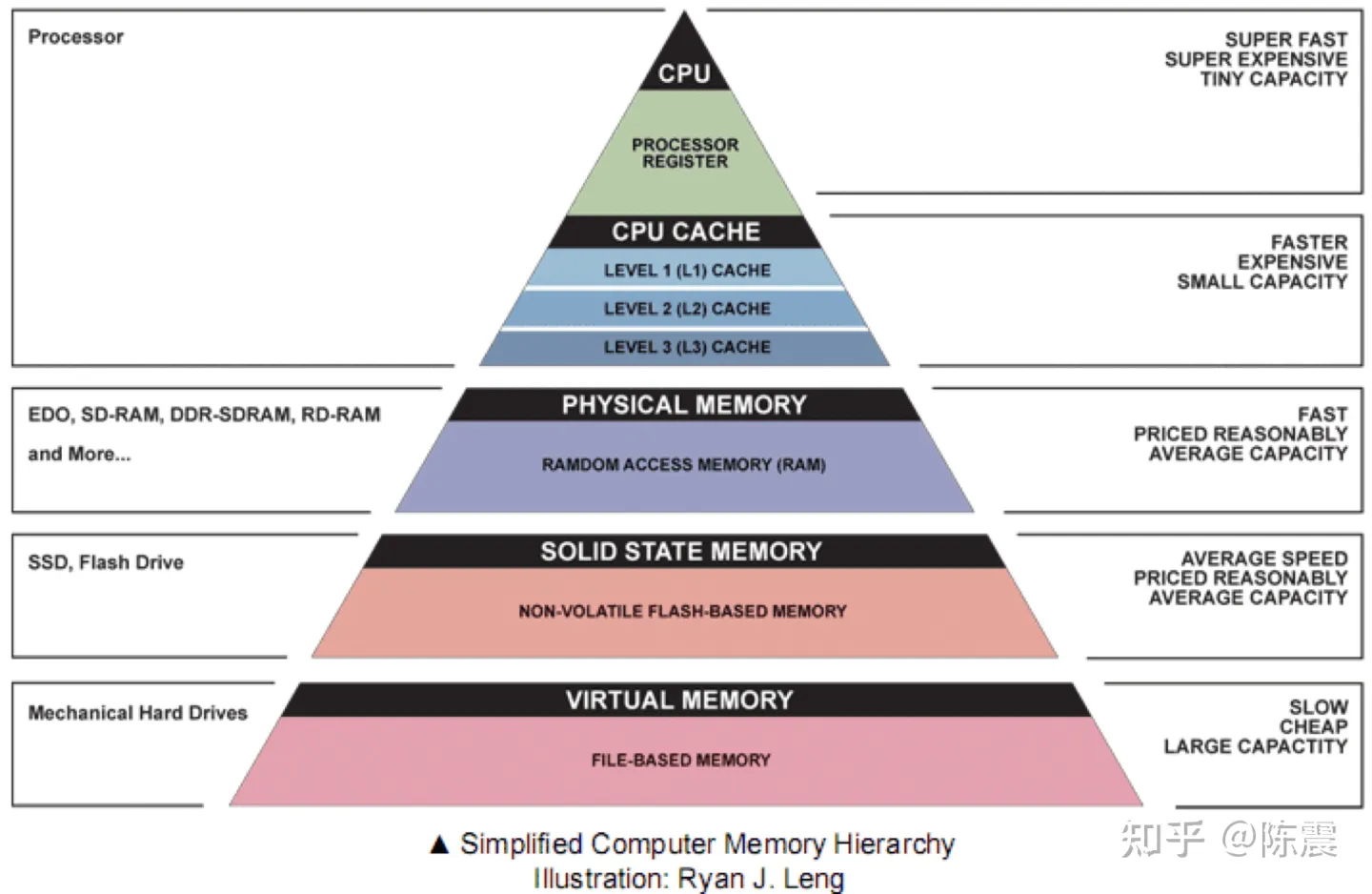
那么从内存的角度，我们能优化哪些？首先我们总结几个知识点：

• IO远远慢于计算，数量级上的慢
• 内存的随机读写远远慢于顺序读写，即便是RAM
• 在大多数编程语言中，都是“行优先”。也就是说我们代码中如果用了二维数组，其在内存中的真实分布是一行一行顺序拼起来的

这三个知识点跟上面的代码有什么关系？如果你观察的足够仔细就会发现，由于我们编程的习惯问题，我们的两层循环中，外层循环是X，内层循环是Y。虽然这样写代码看起来“很舒服”，但是我们的内存就“很不舒服”了，这会导致比较严重的内存随机读写的问题，如下图左边所示。

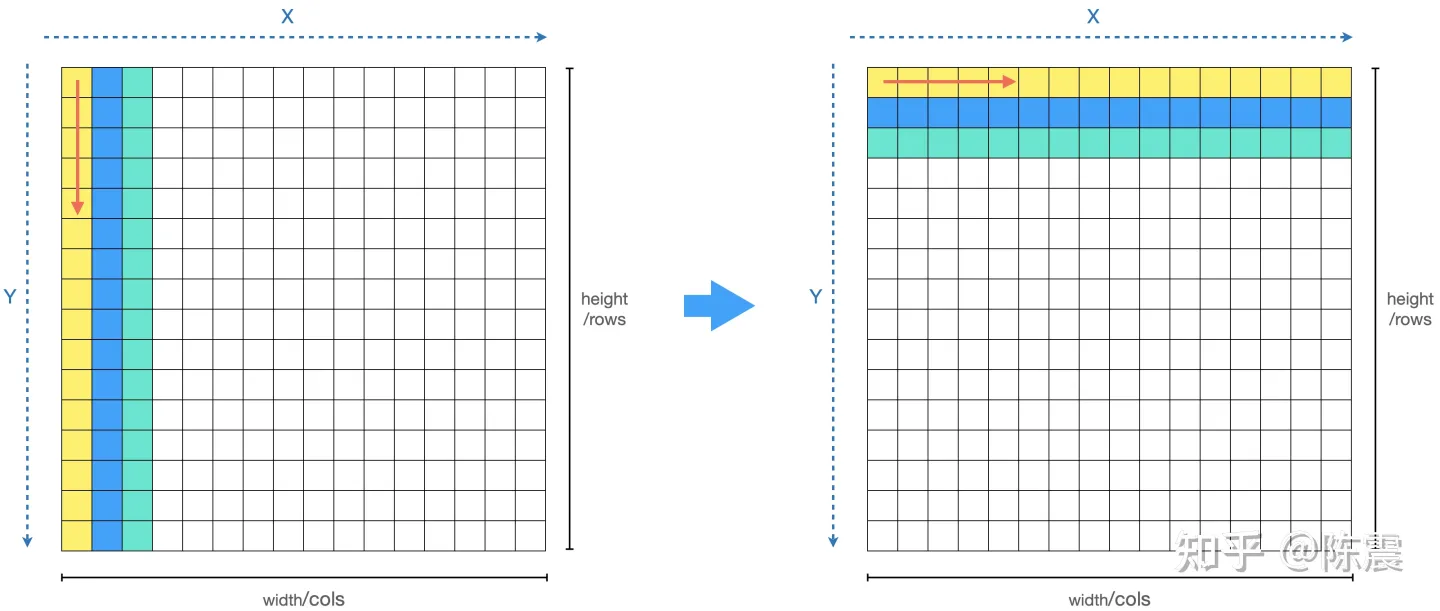
其优化方法也非常简单，我们只需要把两层循环交换一下位置。

void blur_mat_locality(const vector<vector<float>> &input,
                       vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  int right, right_right, below, below_below;
  // 交换位置
  for (int y = 0; y < height; ++y) {
    for (int x = 0; x < width; ++x) {
      right = x + 1 >= width ? width - 1 : x + 1;
      right_right = x + 2 >= width ? width - 1 : x + 2;
      output[y][x] =
          (input[y][x] + input[y][right] + input[y][right_right]) / 3;
    }
  }
  // 交换位置
  for (int y = 0; y < height; ++y) {
    for (int x = 0; x < width; ++x) {
      below = y + 1 >= height ? height - 1 : y + 1;
      below_below = y + 2 >= height ? height - 1 : y + 2;
      output[y][x] =
          (output[y][x] + output[below][x] + output[below_below][x]) / 3;
    }
  }
}

这么一个简单的操作，会有多大的性能提升呢？这次的运行时间从3281ms大幅下降到2057ms， 性能提升了37%，相较于最原始的做法，几乎提升了一倍！

如果一个应届生同学的面试能优化到这个程度，应该可以拿到Offer了吧：）

注意：为了简化编程，代码中用vector<vector<float>>表示矩阵，因此，矩阵的两行数据之前，在内存中可能并不是顺序排列，这更加剧了内存随机访问的开销

CPU并行

其实到上面，我们还没进入并行编程的部分。那么如何利用并行编程对上面的代码继续优化？我们在遍历和计算每个元素时，他们之间是“独立”的，也就是说我们可以利用CPU的多个核心，同时对多个元素进行计算，这就是并行编程最朴素思想。

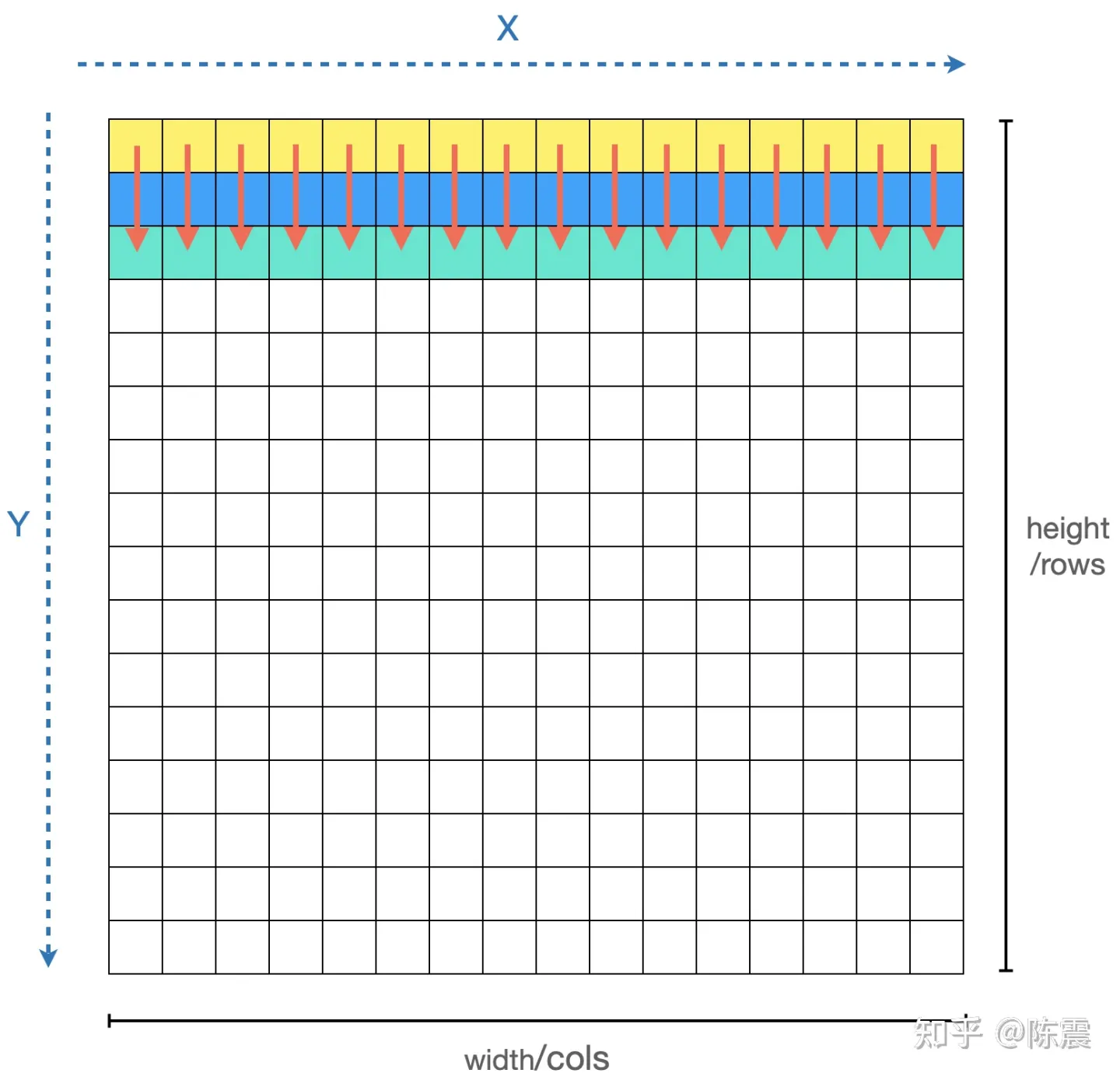
利用多线程同时处理

实际的编程中，我们可以利用多线程机制。如果CPU有16个核，那么我们可以同时启动16个线程，每个线程负责矩阵中的一列或者一行数据的计算（应该优先用列还是行？大家可以思考一下）。多线程编程不是本文的重点，我们直接介绍一种更简单的方法：OpenMP。

OpenMP是一个开源的并行计算模型和接口，通过提供一系列的编译级别的指令，大大简化了CPU上并行编程的难度。关于OpenMP的详细介绍，大家可以关注官网或者其他资料，这里不再赘述。回到我们的问题本身，我们只需要在代码中增加一行，就可以利用CPU的多核实现并行计算：

void blur_mat_parallel(const vector<vector<float>> &input,
                       vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  #pragma omp parallel for
  for (int y = 0; y < height; ++y) {
    int below = y + 1 >= height ? height - 1 : y + 1;
    int below_below = y + 2 >= height ? height - 1 : y + 2;
    for (int x = 0; x < width; ++x) {
      int right = x + 1 >= width ? width - 1 : x + 1;
      int right_right = x + 2 >= width ? width - 1 : x + 2;
      output[y][x] =
          ((input[y][x] + input[y][right] + input[y][right_right]) +
           (input[below][x] + input[below][right] + input[below][right_right]) +
           (input[below_below][x] + input[below_below][right] +
            input[below_below][right_right])) / 9;
    }
  }
}

这里我们使用了OpenMP中的指令#pragma omp parallel for，这条指令告诉编译器，接下来的这个for循环，请帮我使用多线程进行并行计算。由于使用了编译指令，因此gcc在编译这段代码的时候，对会循环中y的每一个值在一个线程中运行从而实现并行加速。当然，OpenMP假设接下来的这些循环之间是“独立”的，且不会保证多个循环之间的执行顺序问题，这些都需要程序员自己去保证。

为了能成功编译，需要额外添加一个编译选项-fopenmp。

$ g++ cpu.cpp -O0 -o cpu -std=c++11 -fopenmp && ./cpu

经过这样的优化，我们这段代码的运行时间是多少呢？182ms！相较于最朴素的实现，我们整整提升了21.5倍，这就是并行编程的威力。

细心的同学可能发现了，上面的这段代码中仍然有重复计算的部分，我们为什么没有把第三章中的优化方法也用上呢？我们试试看。

void blur_mat_parallel_redup(const vector<vector<float>> &input,
                             vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  #pragma omp parallel for
  for (int y = 0; y < height; ++y) {
    for (int x = 0; x < width; ++x) {
      int right = x + 1 >= width ? width - 1 : x + 1;
      int right_right = x + 2 >= width ? width - 1 : x + 2;
      output[y][x] =
          (input[y][x] + input[y][right] + input[y][right_right]) / 3;
    }
  }
  // can not parallel here ！！！
  for (int y = 0; y < height; ++y) {
    for (int x = 0; x < width; ++x) {
      int below = y + 1 >= height ? height - 1 : y + 1;
      int below_below = y + 2 >= height ? height - 1 : y + 2;
      output[y][x] =
          (output[y][x] + output[below][x] + output[below_below][x]) / 3;
    }
  }
}

由于把一个循环变成两个循环，我们需要用两次OpenMP的编译指令。但是仔细观察就会发现，第二个循环体在计算过程中，需要同时读output和写output矩阵且多个线程之间的读写操作存在交集。当多个线程同时且随机地对output进行操作时，由于这里没有锁机制，会出现严重的不一致问题，从而影响计算结果的正确性。那上面的这种写法实际效率如何？大约在1115ms左右，远远慢于刚刚的182ms。

如果一个应届生同学能回答到这个程度，应该会拿到一个不错的 Offer了：）

分片执行

那有没有什么方法，可以同时利用多线程加速并且消除重复计算呢？肯定有，那就是Tiling分片计算方法。上一章节的实现之所以会出现错误主要有两个因素。一是因为存在了两个循环，因此不得不两次使用OpenMP的编译指令；二则是因为output变量在多个线程之前存在了同时读写的问题。Tilling的中文含义是“瓷砖”，也就是说，我们把原始数据像铺瓷砖一样“一大片一大片”的处理。

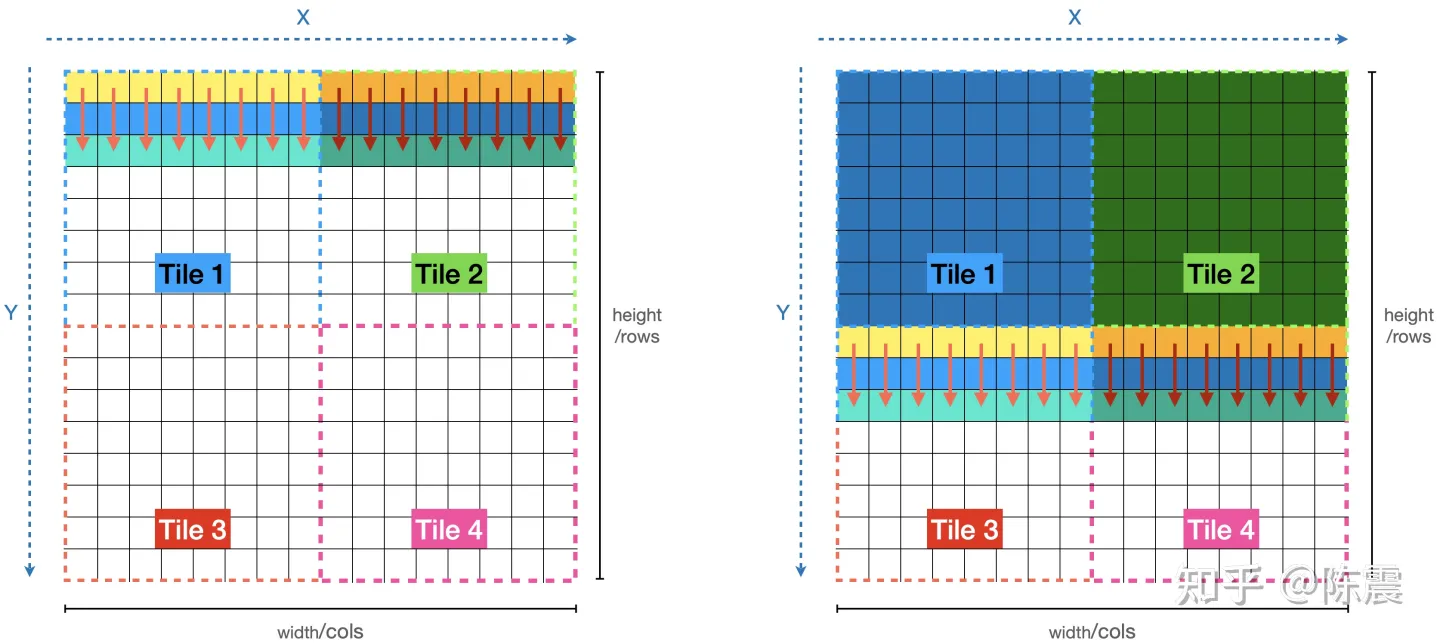
分片计算Tiling

如上图所示，我们可以把原始数据分片成四份，四个分片可以并行，分片内部也可以按照之前的方法并行。看代码：

void blur_mat_tiling_parallel(const vector<vector<float>> &input,
                              vector<vector<float>> &output, int tile_width, int tile_height) {
  int height = input.size();
  int width = input[0].size();
  #pragma omp parallel for
  for (int tile_y = 0; tile_y < height / tile_height; ++tile_y) {
    int t_y = tile_y * tile_height;
    for (int tile_x = 0; tile_x < width / tile_width; ++tile_x) {
      int t_x = tile_x * tile_width;
      vector<vector<float>> tile_tmp(tile_height, vector<float>(tile_width, 0));
      for (int y = 0; y < tile_height; ++y) {
        int target_y = t_y + y;
        for (int x = 0; x < tile_width; ++x) {
          int target_x = t_x + x;
          int right = target_x + 1 >= width ? width - 1 : target_x + 1;
          int right_right = target_x + 2 >= width ? width - 1 : target_x + 2;
          tile_tmp[y][x] = (input[target_y][target_x] + input[target_y][right] +
                            input[target_y][right_right]) / 3;
        }
      }
 
      for (int y = 0; y < tile_height; ++y) {
        int target_y = t_y + y;
        int below = y + 1 >= tile_height ? tile_height - 1 : y + 1;
        int below_below = y + 2 >= tile_height ? tile_height - 1 : y + 2;
        for (int x = 0; x < tile_width; ++x) {
          int target_x = t_x + x;
          output[target_y][target_x] =
              (tile_tmp[y][x] + tile_tmp[below][x] + tile_tmp[below_below][x]) / 3;
        }
      }
    }
  }
}

现在，代码貌似变得复杂了一点，别慌。改动就两点：

1. 把原来的两次循环改成了四层循环，从而可以在分片维度实现并行，比如在第5行，我们可以在最外层的循环使用OpenMP的编译指令
2. 在第10行，我们为每个分片增加了一个临时存储空间，在减少重复计算的同时，避免上一章中提到的多线程同步的问题

经过这样的优化，性能是多少呢？同样的参数和硬件配置下，这个实现是231ms，貌似并没有比之前的更好。至于为什么，我没做深入的profile所以不好确认。我猜测是更复杂的循环和临时空间的使用，都影响了实际执行的性能。这也告诉我们性能优化在很多时候并不是把“十八般武艺”都用上就会更好。

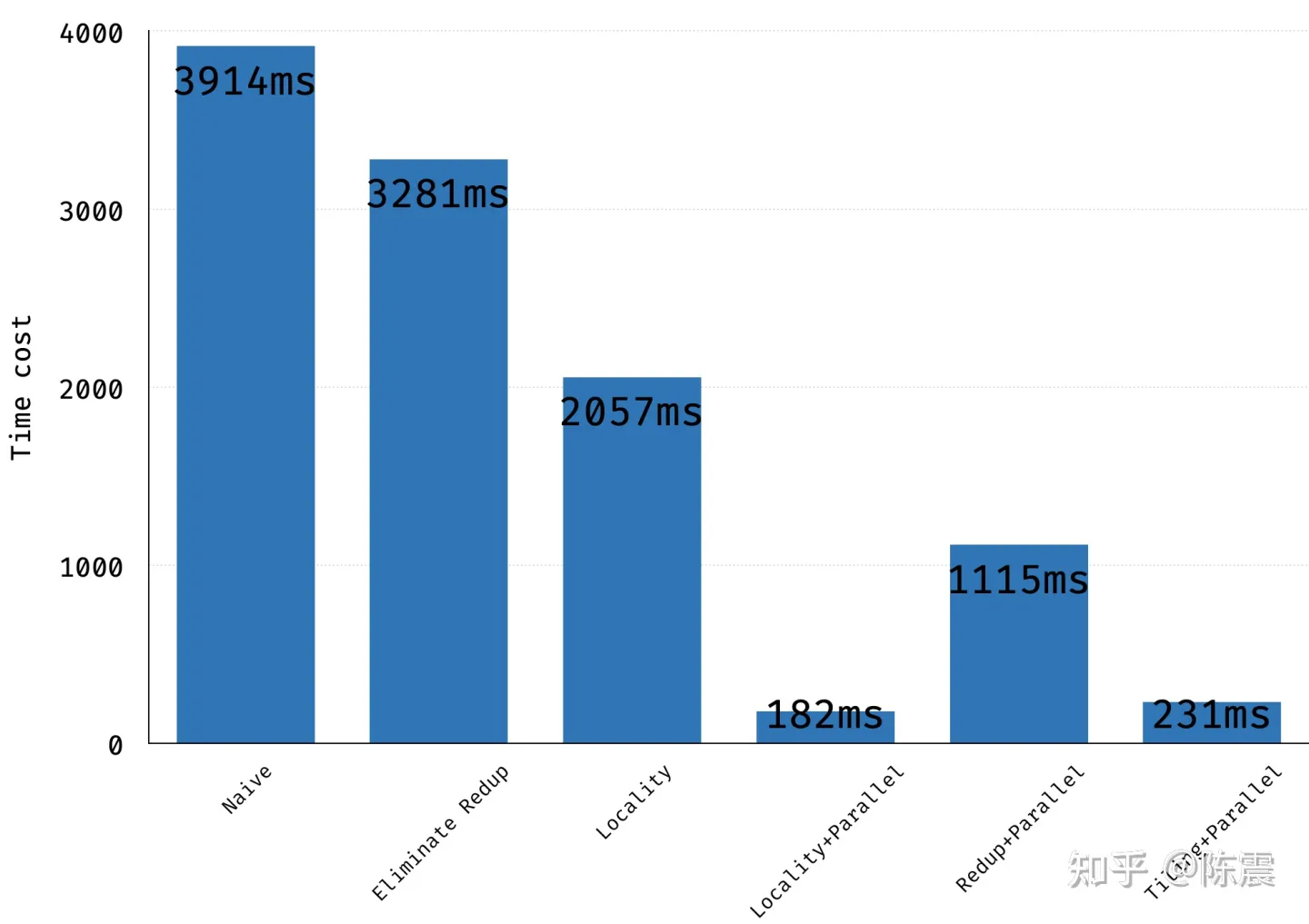
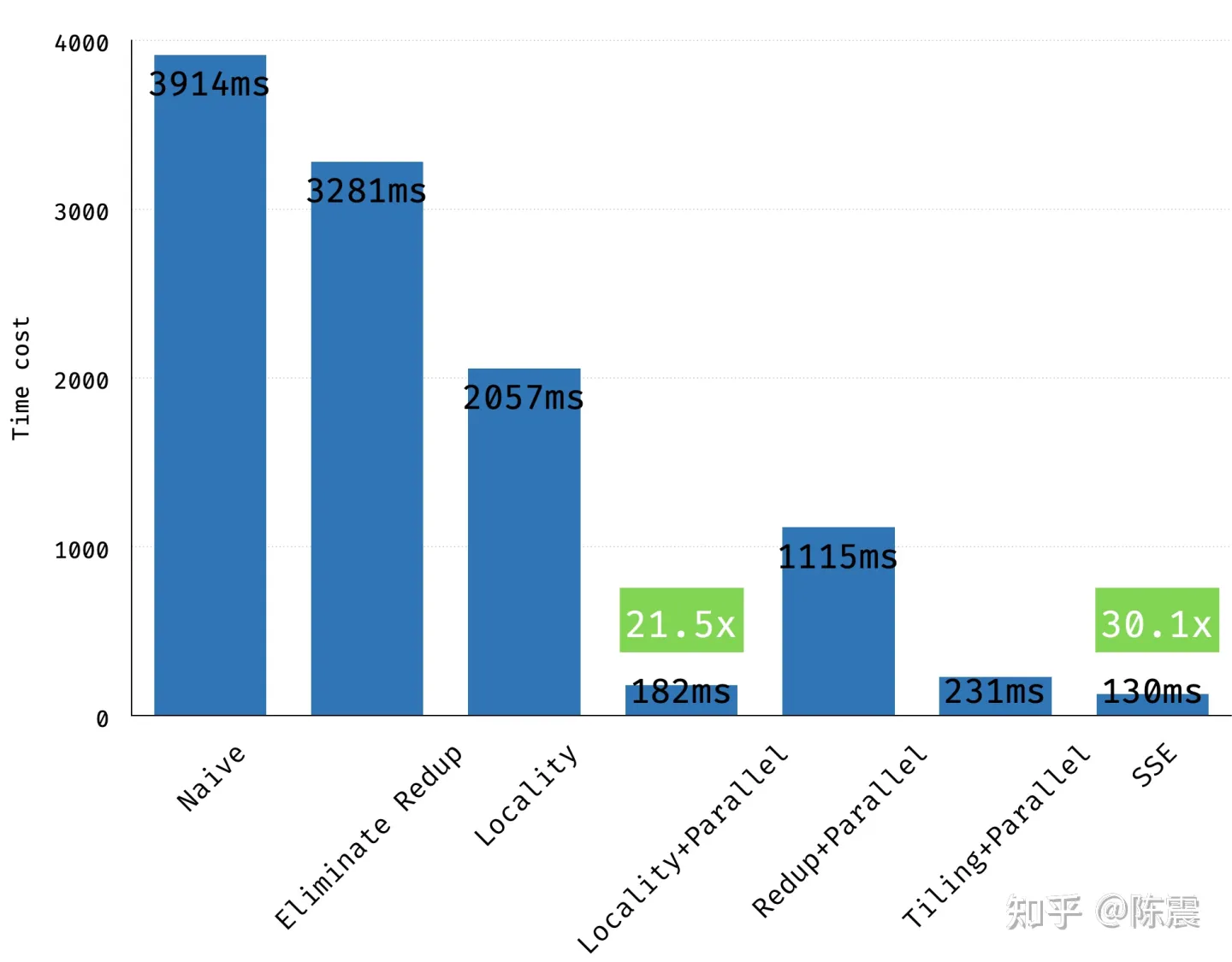
不同优化方法的性能对比

到这里，我们从消除重复计算；内存连续性和并行计算三个方面对代码进行了优化，执行时间从3914ms大幅下降到200ms一下，提升了近20倍。

指令集优化SIMD

除了上面提到的三种优化，还有没有其他手段？该轮到大杀器“指令集优化”出场了。

我们知道，CPU的计算都被抽象成了一系列的CPU指令集，有些指令集负责从内存加载数据到寄存器，有些指令集则从寄存器读取数据执行具体的计算操作，然后再由另外一些指令集把寄存器中的数据更新回内存。不同的CPU架构和指令集能操作的数据大小是不同的，从16bit，32bit到64bit。在同样的计算精度下，能操作的数据量越大就代表了计算的“吞吐”越大，也就表示更快的计算速度。这正是SIMD的初衷。

Single Instruction Multiple Data指的就是CPU在硬件上，支持一个指令读写一个向量(128bit)，更重要的是，可以对两个向量同时执行计算且计算是可分割的。也就是说可以把128bit看成4个32bit的float分别对4个float执行同样的计算。举个例子，如果我们要计算四对数的和：

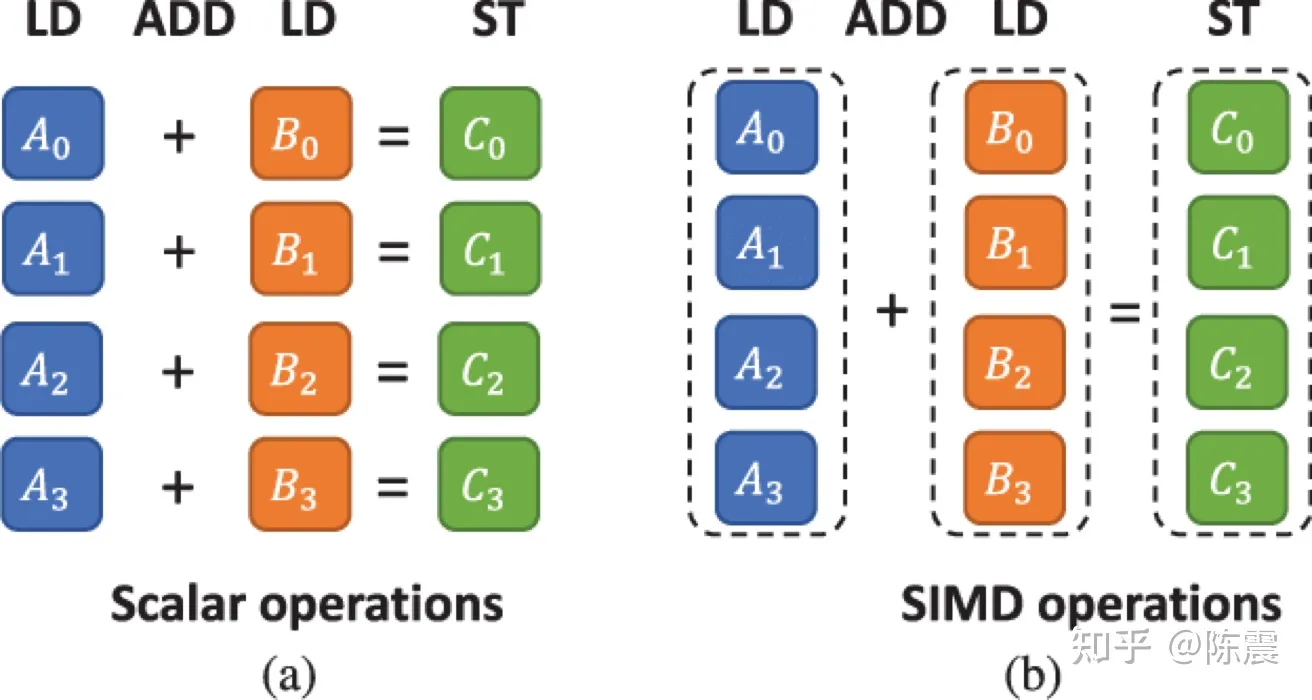
单指令集和SIMD的区别

在没有用SIMD时，我们首先需要八次LD操作用来从内存把数据加载到寄存器；然后用四次ADD操作执行加法计算；最后再用四次ST操作，把计算结果存储到内存中，故共需要16次CPU指令操作。

如果用SIMD，我们首先需要一次LD操作一次性把四个数据加载到寄存器；然后执行一次ADD操作完成加法计算；最后用一次ST操作把数据更新回内存，这样只需要3次CPU指令操作。相较于第一种方法性能提升了5倍之多，下图则从另外两个角度展示了SIMD的优势。

SIMD可同时操作一个向量，从而大大减少指令数量

目前绝大多数的CPU都支持SIMD，那如何使用SIMD能力？不同的CPU架构和厂商提供了不同的SIMD指令集来支持，以我们常用的x86架构来说，我们可以通过SSE指令集来使用x86架构下的SIMD能力。

SSE优化

SSE指令集介绍

目前，绝大多数的CPU都支持SIMD，不同的CPU架构和厂商提供了不同的SIMD指令集来支持，以常用的x86架构来说，我们可以通过SSE指令集来使用x86架构下的SIMD能力。

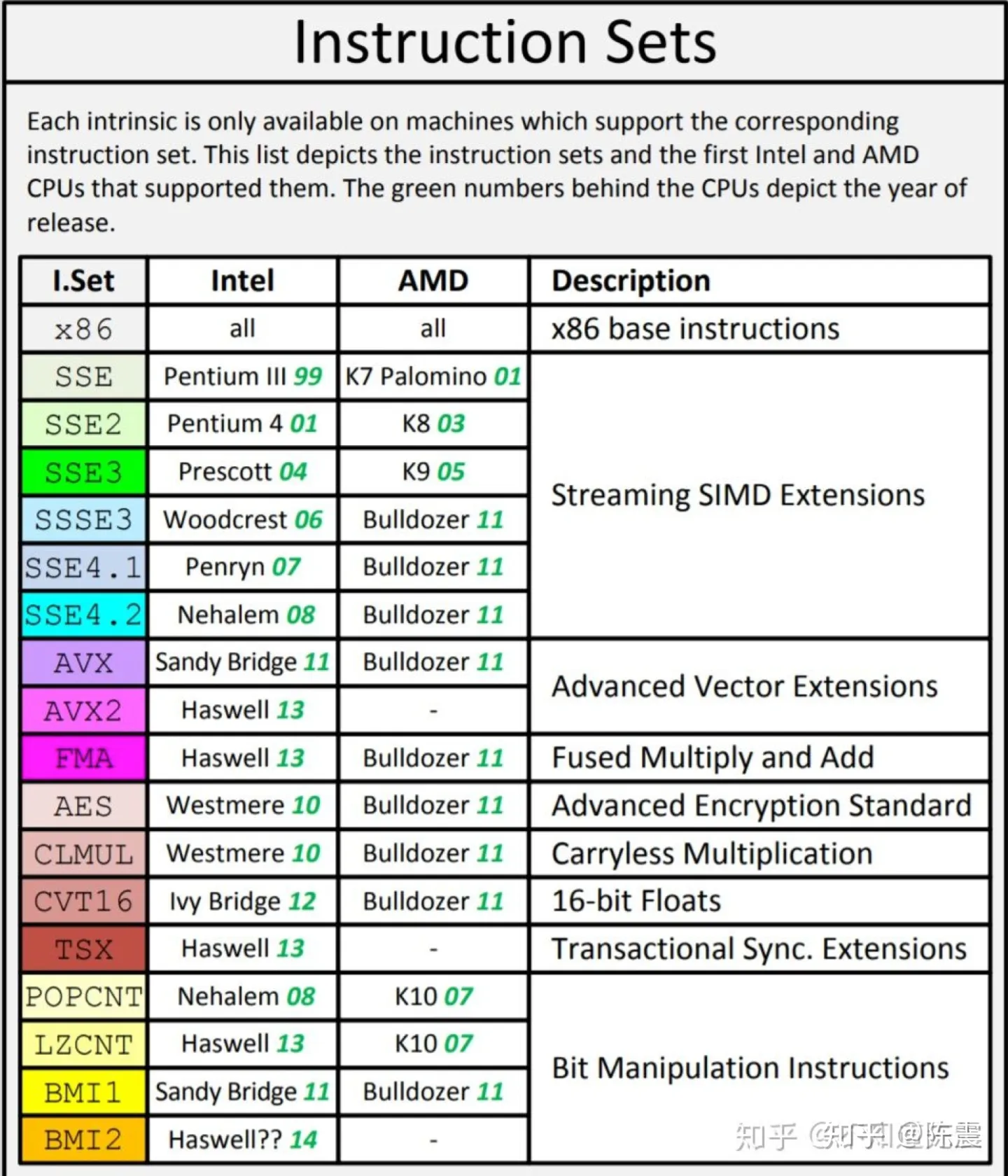
以SSE为代表的多种SIMD指令集

SSE指令集是对普通指令集的扩充，其使用方法可以归纳为：“接-化-发”，即：

1. 使用SSE专门的LOAD指令从内存加载一个向量到寄存器。
2. 使用SSE专门的OP指令对两个向量进行某种计算
3. 使用SSE专门的STORE指令把计算结果从寄存机写回到内存

在实际写代码中，我们可以直接使用汇编调用SSE相关的指令，但是更常见的方式还是用Intel提供的C/C++的指令集内联函数intrinsics，详细的文档见：Intel® Intrinsics Guide。比如跟LOAD指令相关的内联函数就有这么多，主要功能是从内存地址mem_addr处，加载128bit的数据到寄存器。

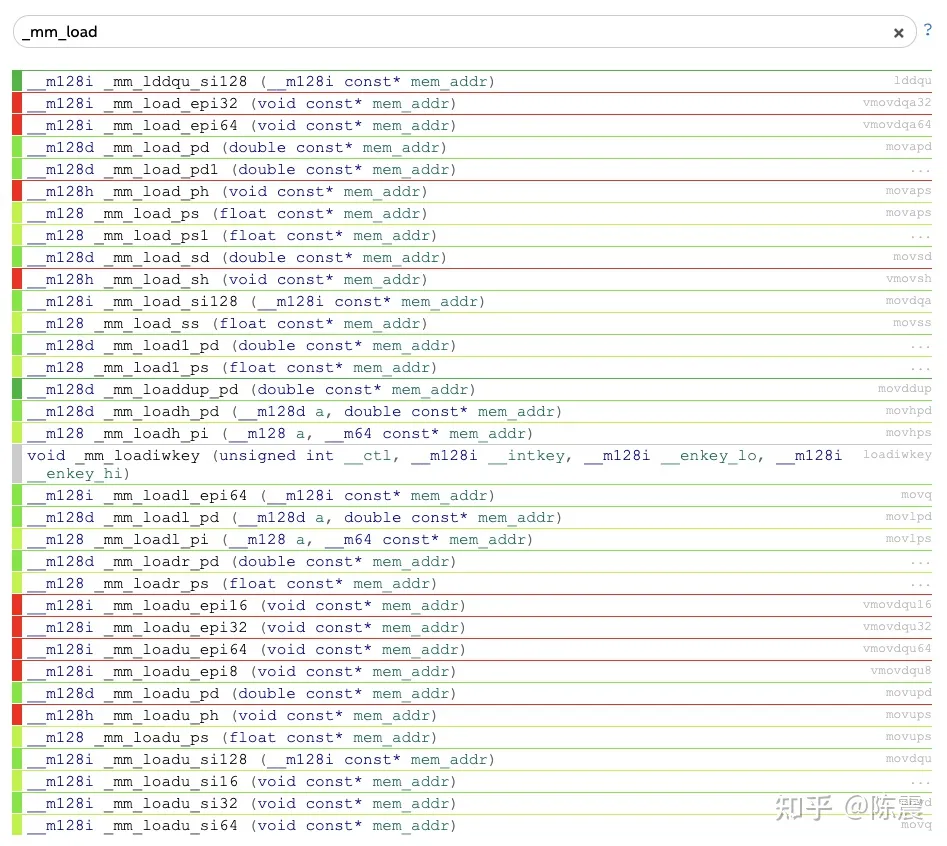
Intel intrinsics中与load相关的指令集函数

之所以有这么多种，首先由于支持的数据类型不同。其中m128表示128bit的单精度浮点数；m128h表示半精度；128d表示128bit的双精度浮点数；m128i表示128bit的整数型。

其次，函数签名不同。SSE指令的函数从命名上，主要分成三部分，以_mm_loadu_pd为例：

1. 第一部分均以_mm开头，表示属于SSE指令集;
2. 第二部分表明操作类型，比如load，add，store等。但部分指令后面跟有[l|h|u|r]等字母，比如u表示mem_addr不需要内存对齐，r表示反向读取等；
3. 第三部分主要包括两个字母，大部分以[p|s]开头，p表示packed即对128bits的数据全部执行相同的操作，s表示scalar，只对128bit中的第一组数据执行操作，如下图所示。而第二个字母往往和数据类型相关，比如[d|h|s]等，分别表示双精度、半精度、单精度等。

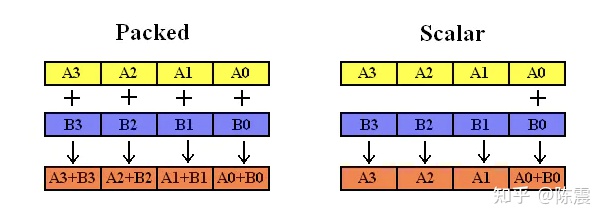
由于SSE指令集发展多年，有SSE、SSE2、SSE3、SSEE3、SSE4.1、AVX等众多版本，但是命名上主要遵循上面的规则。在真正使用时可以查阅Intel® Intrinsics Guide 了解细节。

SSE指令集优化

接下来尝试使用SSE指令集对原来的代码进行优化。由于SSE指令集操作的单位都是128bit，即可同时操作四个32bit的单精度float数据，为了编程方便，我们修改blur操作的kernel大小，从33修改为34，代码执行的流程如下图：

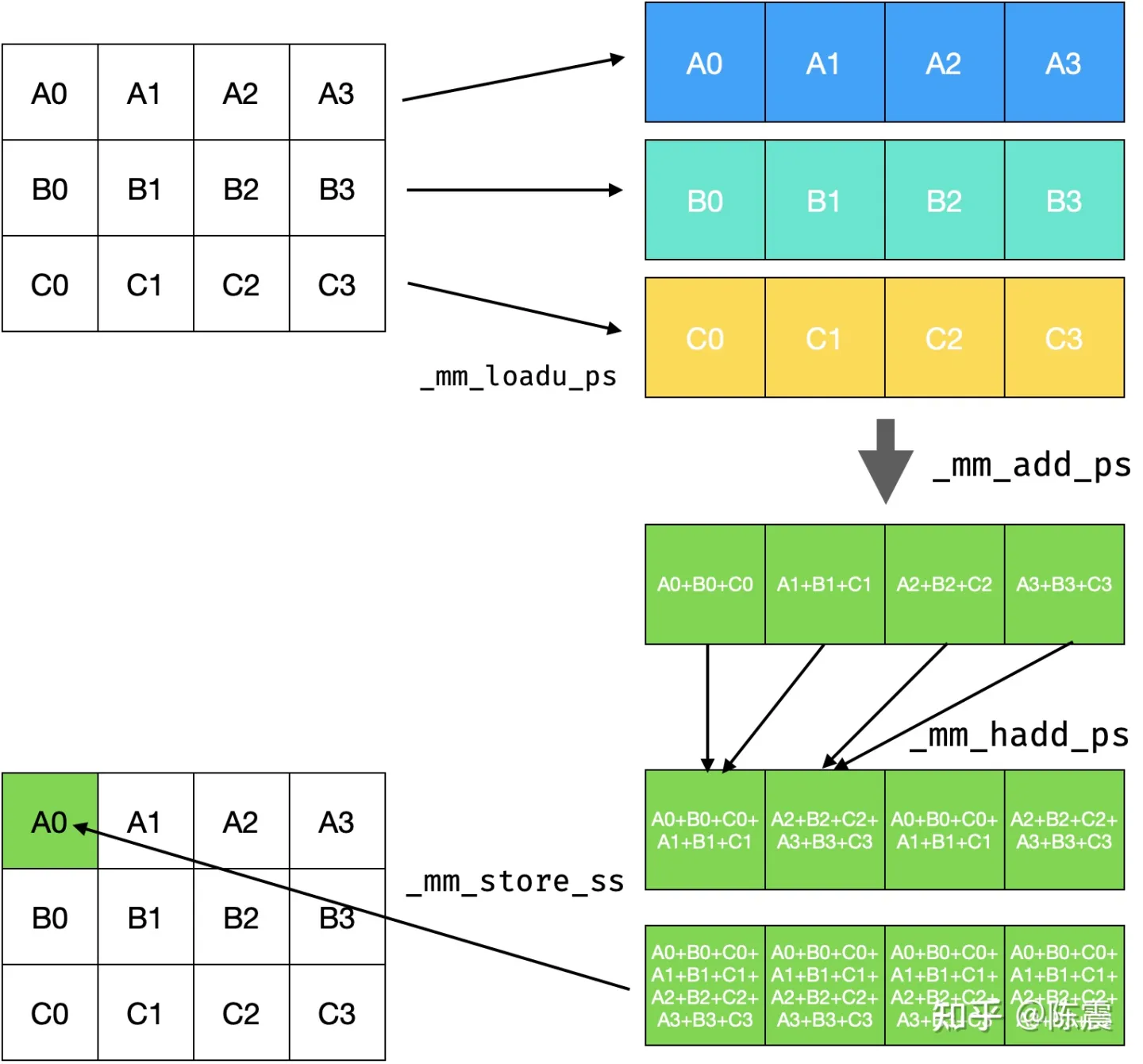
利用SSE指令集修改计算流程

1. 通过三次_mm_loadu_ps操作，分别内存加载3*4个元素到寄存器。
2. 通过两次_mm_add_ps操作，对寄存器中的数据执行packed加法操作，执行完成后寄存器中每一小部分都累积了结果。（类似于Ring AllReduce中的ScatterReduce操作）
3. 接下来通过两次_mm_hadd_ps操作把集群器中的四个结果再次累加，_mm_hadd_ps操作比较特别，它会把相邻的两个数相加，然后把结果写到最高两位。（类似于Tree Reduce操作）
4. 最后通过一次_mm_store_ss操作，把结果写回内存。由于寄存器中的四个元素的值都是最终的结果，因此只需要执行一次scalar操作即可。

此外，我们仍然可以用openmp，在循环的最外层进行并行计算加速，详细代码如下：

// 导入SSE指令集的头文件
#include <pmmintrin.h>
 
void blur_mat_sse(const vector<vector<float>> &input,
                  vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
#pragma omp parallel for
  for (int y = 0; y < height; ++y) {
    for (int x = 0; x < width; ++x) {
      int below = y + 1 >= height ? height - 1 : y + 1;
      int below_below = y + 2 >= height ? height - 1 : y + 2;
      // 三次数据加载
      __m128 vdata_1 = _mm_loadu_ps(&input[y][x]);
      __m128 vdata_2 = _mm_loadu_ps(&input[below][x]);
      __m128 vdata_3 = _mm_loadu_ps(&input[below_below][x]);
      // 两次逐元素相加，packed操作
      __m128 vres = _mm_add_ps(vdata_1, vdata_2);
      vres = _mm_add_ps(vres, vdata_3);
      // 两次相邻元素相加，packed操作
      vres = _mm_hadd_ps(vres, vres);
      vres = _mm_hadd_ps(vres, vres);
      // 写回内存，scalar操作
      _mm_store_ss(&output[y][x], vres);
      output[y][x] /= 12;
    }
  }
}

看一下动图：

实际编译运行看一下效果。由于使用了SSE指令集，在编译时需要显示指定编译选项-msse3：

$ g++ cpu.cpp -O0 -o cpu -std=c++11 -fopenmp -msse3 && ./cpu

经过SSE指令集的优化，我们代码的性能进一步提升到了130ms，相较于最原始的版本，加速了30倍。

小结

这篇文章里，我们通过实现一个blur滤波器，把原来需要执行3.9秒的一段代码逐步优化到只需要0.13秒，加速比超过了30倍。其背后的原理并不复杂，主要是

• 消除重复计算
• 考虑内存/缓存的本地性
• 利用多核CPU并行计算
• 利用Tiling机制
• 使用SIMD SSE指令

等几个技术。其中加速效果最好，显而易见的，就是多核并行计算和SIMD机制。

在机器学习、深度学习应用中，主要的计算类型包括GEMM（通用矩阵乘法）、Conv（卷积）、Pooling、Activation等，这些计算本质上都满足并行计算和SIMD的前提，因此基于并行计算的优化方法被大量应用到机器学习领域中。

另一方面，如今的通用CPU发展越来越受制于物理定律的限制，即CPU的核数、L1/L2的缓存大小都难以有数量级上的增长，而计算的需求却在指数级增长，单纯靠CPU已经难以满足计算的需求。此时，以GPGPU为代表的专用加速器以拯救者的身姿出现在我们面前，成为推动深度学习发展的功臣。如何利用GPGPU继续优化我们的代码，我们放到下一篇中介绍。

GPU和CUDA优化

GPGPU简介

在上两篇中，我们使用多种技术提高了Blur算子的速度，效果最好的技术是利用多核和SIMD指令集，通过并行计算来提升速度。这给我们一个很大的启发，如果我们的CPU能扩展到数百数千甚至数万的核，不就能进一步加速了吗？事实上，传统超算就是这么干的。但是传统超算的做法是一种分布式计算的思路，即用数十个机柜，每个机柜内放置数百个计算单元（看成一台服务器），每个计算单元有几个CPU，以此组成一个巨大的CPU集群。集群间通过高速网络，配合上分布式的编程来使用整个集群的数以万记的CPU执行计算任务。

之所以用分布式计算的思路提高整个系统的并行计算的能力，主要原因是CPU的发展已面临物理定律的限制，人们无法在有限的成本下创造出核心数更多的CPU。此时人们发现，原本用来做图形渲染的专用硬件，GPU（Graphic Processing Unit），非常适合用于并行计算。

我个人认为原因有三点：首先，GPU在渲染画面时需要同时渲染数以百万记的顶点或三角形，因此GPU硬件设计时就利用多种技术优化并行计算/渲染的效率；第二，GPU作为专用的硬件，只负责并行计算/并行渲染这一类任务，不承担复杂的逻辑控制和分时切换等任务，可更专注于计算本身，通过专用指令集和流水线等技术，优化计算效率和吞吐；最后，GPU作为一类外插设备，在尺寸、功率、散热、兼容性等方面的限制远远小于CPU，让GPU可以有更大的缓存、显存和带宽，可以放置更多的计算核心，而这进一步体现到成本上的优势（成本对于技术的普及非常重要）。

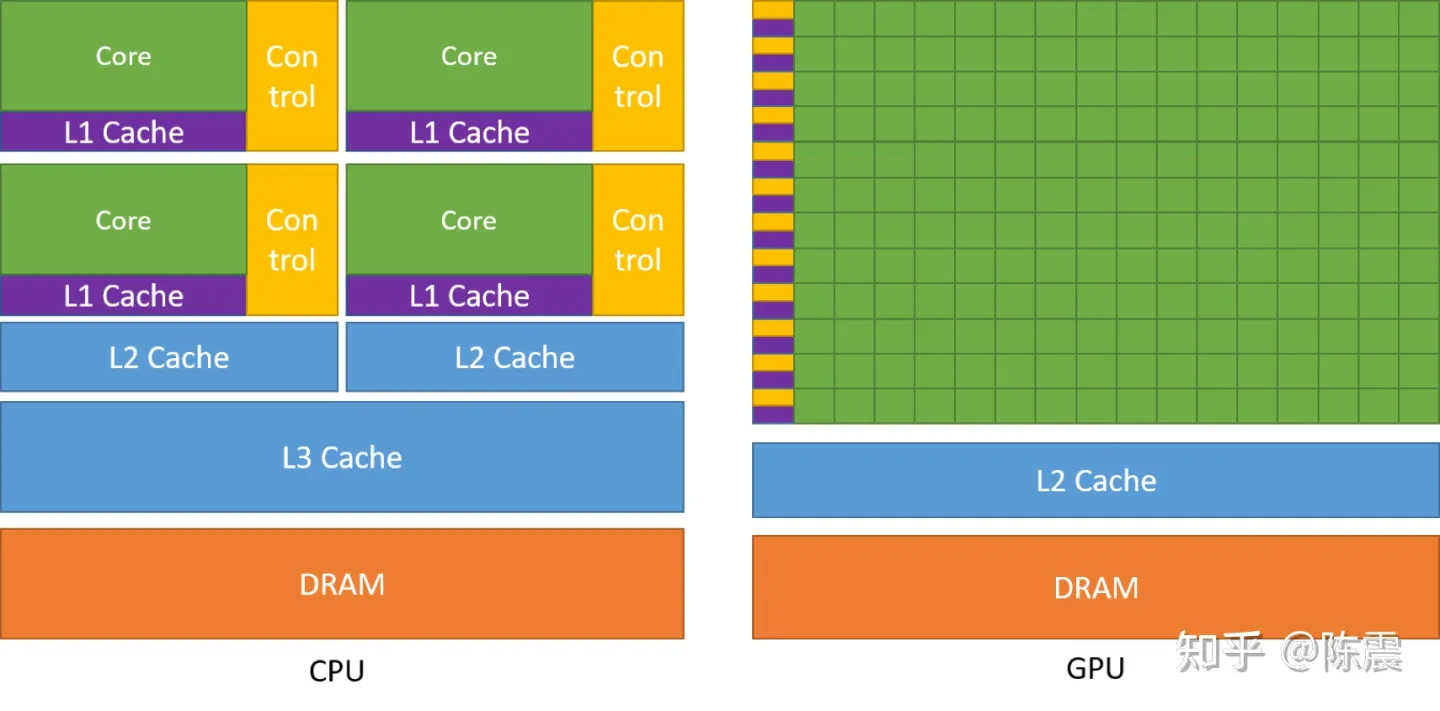
CPU和GPU对比示意图

上图是CPU和GPU的一个对比示意图。由于CPU除了计算任务外，还需要负责大量的逻辑控制，分时调度，兼容多种指令集等等“包袱”，真正用来计算的部分其实很少。而GPU则不然，GPU可以在更大的自由度下，放置更多的计算核心。

其实从最本质的角度来讲，GPU之所以适合并行计算场景，是因为GPU使用的是SIMT（Single Instruction Multiple Threads）模型。SIMT可以看成是SIMD（Single Instruction Multiple Data）模型的一种增强。

Nvidia公司在2000年推出第一款GPU，但是直到2006年才把GPU用于通用计算任务，其转折点就是CUDA（Compute Unified Device Architecture）的出现。CUDA是一整套软件技术，把Nvidia GPU的计算能力封装成一套编程规范和编程语言接口，同时提供相应的编译器、调试器等工具，这使得程序员能方便的使用GPU并行计算能力，执行通用的计算任务，因此又被称为GPGPU（General-purpose computing on graphics processing units）。在CUDA出现6年之后，Alex Krizhevsky和其老师Geoffrey Hinton在CUDA的帮助下成功地实现了AlexNet深度神经网络，一举打开了此轮人工智能浪潮的大门。AlexNet论文中提到：模型的深度对于提高算法性能至关重要，但是其计算成本很高，GPU的使用让深度神经网络的训练具有可行性。

甚至可以武断地说，如果没有GPU和CUDA，尤其是后者，以深度神经网络为主要代表的人工智能算法很可能是另外一种命运。当然，Nvidia并不是唯一一家生产GPU和提供上层编程框架的公司，除了Nvidia GPU和CUDA之外，Intel、AMD和最近几年爆火的如寒武纪、海思等公司，也推出了不同的硬件和软件平台，但是无论完善度、丰富性尤其是生态上，Nvidia仍然是毫无疑问的王者。因此这篇文章介绍的还是Nvidia的GPU，下文中提到的GPU，没有特殊说明都代指Nvidia GPU。

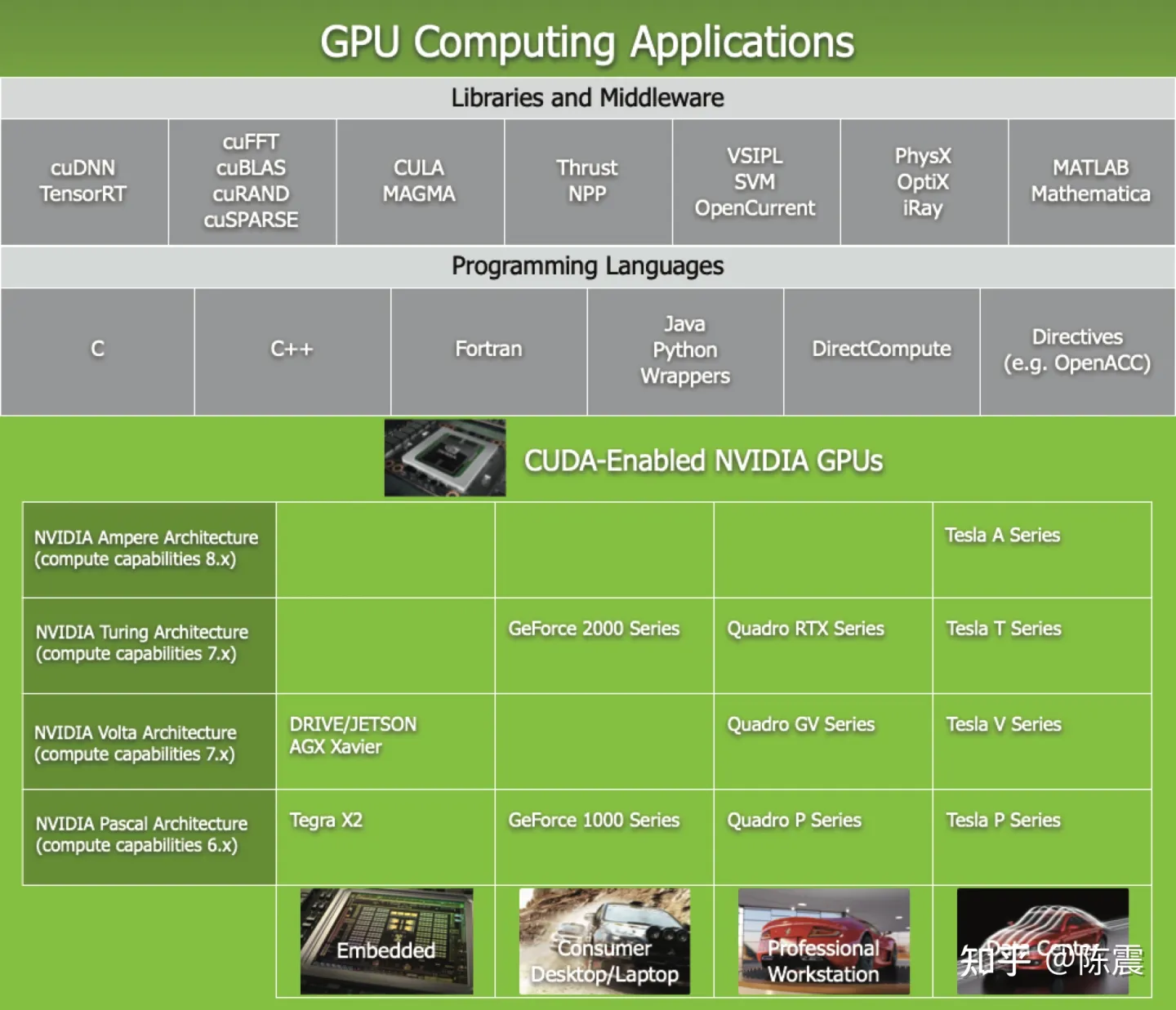
Nvidia的软硬件生态

上图是Nvidia提供的一整套软硬件平台。Nvidia针对嵌入式端，桌面级消费卡、专业工作站和数据中心提供了不同的硬件产品，但是在软件层，通过CUDA抽象成了统一的编程接口并提供C/C++/Python/Java等多种编程语言的支持。CUDA的这一层抽象非常重要，因为有了这层抽象，向下开发者的代码可在不同的硬件平台上快速迁移；向上，在CUDA基础上封装了用于科学计算的cuBLAS（兼容BLAS接口），用于深度学习的cuDNN等中间件和代码库。这些中间件对于Tensorflow，PyTorch这一类的深度学习框架非常重要，可以更容易地使用CUDA和底层硬件进行机器学习的计算任务。

GPU硬件架构

对于一般开发者而言，大多数情况下接触到的都是CUDA层。但是由于GPU的特殊性，为了能正确高效使用CUDA，非常有必要学习一下GPU的硬件架构。由于Nvidia的GPU发展非常迅速，平均1-2年就会推出一款新GPU或核心架构，因此这里简单介绍下，不涉及硬件细节（主要是我也不太懂硬件）。

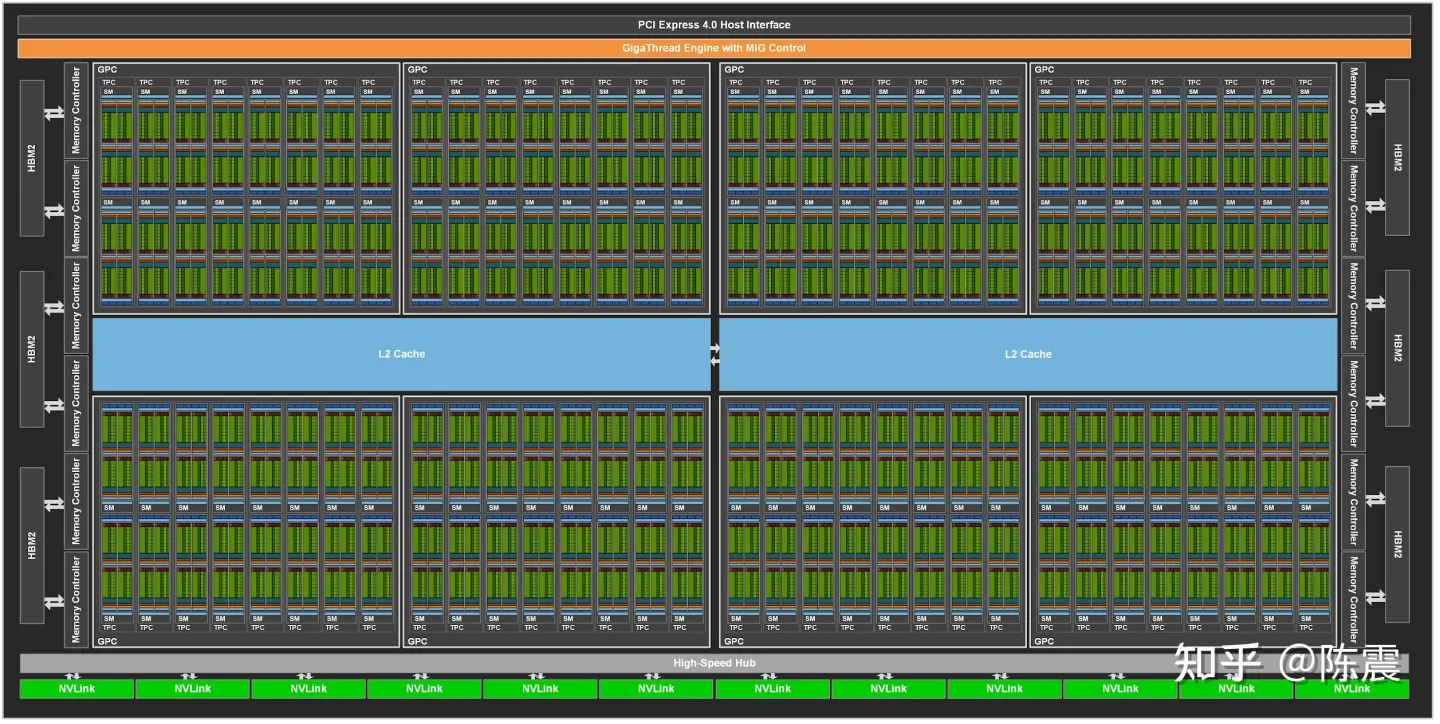
Nvidia A100 GPU的硬件架构

我们以Nvidia 2020年推出的Ampere架构和A100 GPU为例（A10、A30、RTX3090等型号也是Ampere架构）为例。上图是整个A100的硬件架构，从上到下，其主要组成部分：

• PCIe接口层，目前大部分GPU都是通过PCIe以外部设备的方式集成到服务器上；
• GigaThread Engine with MIG是GPU用于调度资源的引擎，Ampere架构还支持了MIG（Multiple Instance GPU）控制即允许对GPU进行硬件隔离切分；
• 中间占据面积最大的绿色部分是GPU的核心计算单元，共有6912个CUDA Cores，这是重点部分，我们在后面详细介绍；
• 中间蓝色部分是L2缓存，在GPU层面提供大于40MB的共享缓存；
• 最下层的NVLink是用于多个GPU间快速通信的模块（在分布式训练中非常重要）；
• 两侧的HBM2（High Bandwidth Memory）即我们通常说的显存。A100提供了高达1.56TB带宽，40GB/80GB的显存；

其中最重要的绿色部分是计算核心，在A100中这些计算单元又进一步被“分组”成了GPC（Graphic Processing Cluster）- TPC（Texture Processing Cluster） - SM（Streaming Multiprocessor）几个概念。最需要了解的是SM的架构，把其中一个SM放大：

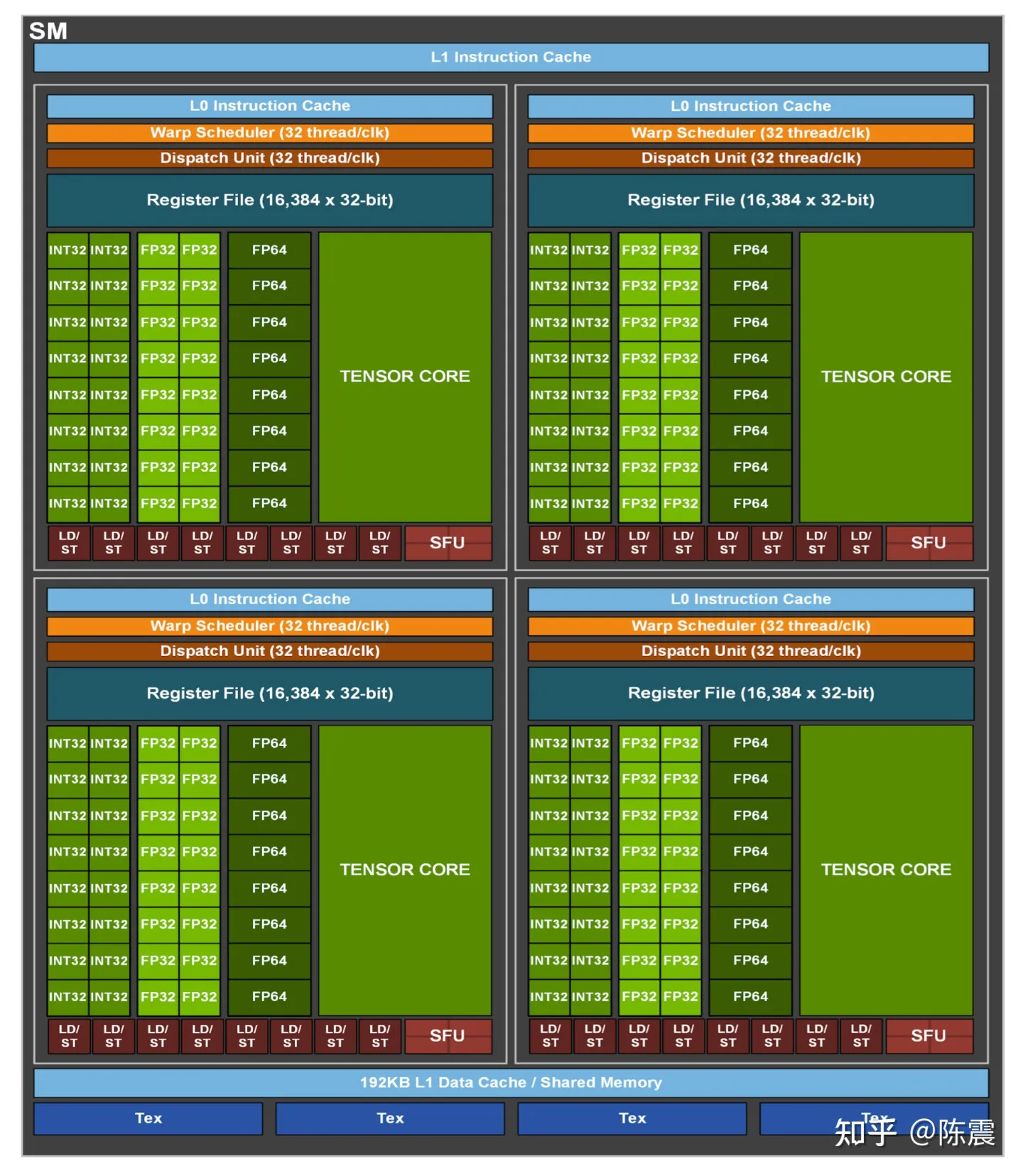
Nvidia A100的SM硬件架构

SM可以看成是GPU计算调度的一个基本单位，只有对其架构和硬件规格有一定认识，才能更高效地利用GPU的硬件能力。SM中自上而下分别有：

• L1 Shared Memory，在SM层面提供192KB的共享缓存
• 接下来是四个PB（Process Block），每个PB内部分别有
• • L0缓存
    • Warp Scheduler用于计算任务调度
    • Dispatch Unit用于计算任务发射
    • Register File寄存器
    • 16个专用于INT32计算的核心
    • 16个专用于FP32计算的核心
    • 8个专用于FP64计算的核心
    • 4个Tensor Core，这是受Google TPU的影响，专门设计用于执行A*B+C这类矩阵计算的硬件单元，甚至还支持稀疏矩阵计算，Tensor Core对深度学习的加速非常明显
    • 8个用于LOAD/STORE数据的硬件单元
    • 4个SFU（Special Function Unit）用于执行超越函数、插值等特殊计算

因此一个SM内就有64个用于计算的核心，Nvidia称之为CUDA Core（但是我没搞明白64是怎么算出来的）。而一整块A100 GPU则密密麻麻地放置了108个SM，总计6912个CUDA Core，可以简单理解成这是一个拥有6912个核心的巨型CPU！

至此，我们应该能搞懂为什么GPU比CPU更适合执行并行计算了，就是“专业人干专业事，大力就会出奇迹“嘛。

CUDA基本概念

为了方便地使用GPU的硬件能力，Nvidia在软件层做了抽象，形成软件上的一系列逻辑概念，这些逻辑概念跟GPU的硬件有一定的对应关系。

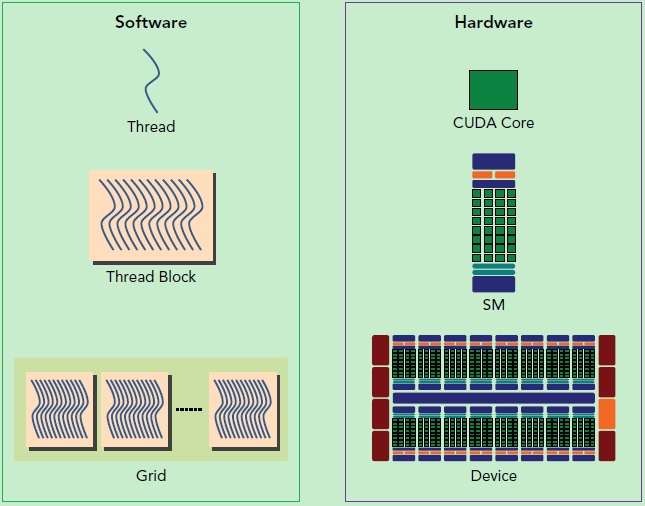
GPU软件和硬件的对应关系

如上图，CUDA编程中的最小单元称之为Thread，可以简单认为一个软件Thread会在一个硬件CUDA Core中执行，而Thread中执行的内容或函数称之为Kernel。多个相同的Thread组成一个Thread Block，软件Thread Block会被调度到一个硬件SM上执行，同一个Thread Block内的多个Thread执行相同的kernel并共享SM内的硬件资源。而多个Thread Block又可以进一步组成一个Grid，一个软件Grid可以看成一次GPU的计算任务，被提交到一整个GPU硬件中执行。这几个概念非常重要，简单总结下：

• kernel：Thread执行的内容/代码/函数
• Thread：执行kernel的最小单元，被SM调度到CUDA Core中执行（其实还有一个Warp的概念，为了简单，这里先略过）
• Thread Block：多个Thread组合，GPU任务调度的最小单元（这个描述不太准确，应该是Warp，为了简单暂时先不细究），被调度到SM中执行。一个SM可以同时执行多个Thread Block，但是一个Thread Block只能被调度到一个SM上。
• Grid：多个Thread Block的组合，被调度到整个GPU中执行

同时，Thread、Thread Block和Grid由于所处层次不同，他们可以访问的存储资源也不同。如Thread只能访问自身的寄存器，Thread Block可以访问SM中的L1缓存，而Grid则可以访问L2缓存和更大的HBM显存。在第一篇文章中我们就介绍过不同层次的存储其访问速度往往是数量级的差别，GPU也不例外，在后续的文章中我们会看到，针对CUDA的优化很大一部分就是如何正确高效的使用GPU中的多级存储来提高GPU的方寸比，从而进一步提高GPU的计算效率。

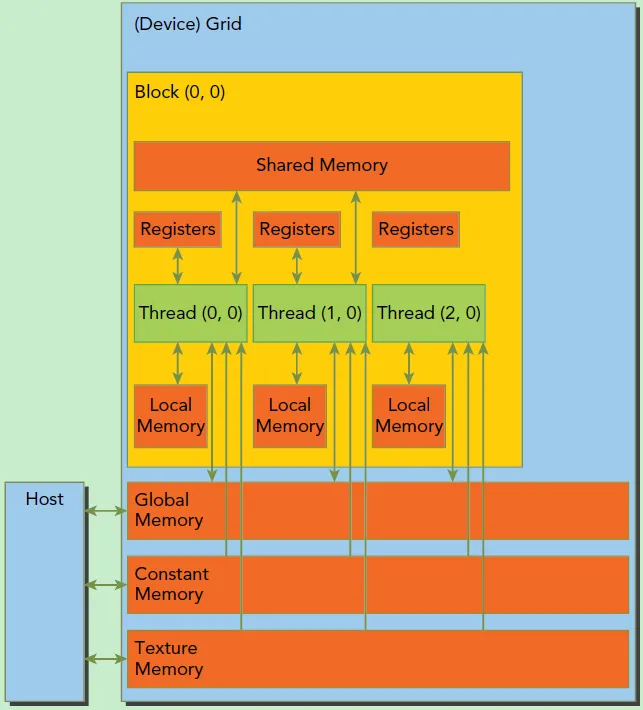
Nvidia GPU的内存模型

到底如何使用CUDA？由于GPU是作为一类外挂设备，通过PCIe之类的接口插到服务器上，因此在CUDA编程中，称GPU为Device，而服务器上的CPU和内存统称为Host。在编写CUDA代码时，最主要的工作就是编写kernel函数，然后利用CUDA提供的接口，把kernel函数从Host发射到Device中执行，Device则从 Grid → Thread Block → Warp → Thread 一层层的调度下最终完成kernel的计算。

在计算开始前，还需要用CUDA接口把计算要用到的数据从Host拷贝到Device中。Device完成计算后，则需要利用CUDA接口把计算结果从Device拷贝回Host中，因此总结下来，CUDA编程分为三步：

1. 从Host拷贝数据到Device
2. 把需要Device执行的kernel函数发射给Device
3. 从Device拷贝计算结果到Host

如果有点抽象，我们看个例子。

CUDA HelloWorld

CUDA HelloWorld代码很简单，求两个数组A和B的和。代码分两部分，首先实现上面介绍的三步流程。

#include <cuda.h>
 
// Host code
int main() {
  int N = 1024;
  size_t size = N * sizeof(float);
 
  // Host端申请内存
  float* h_A = (float*)malloc(size);
  float* h_B = (float*)malloc(size);
  float* h_C = (float*)malloc(size);
 
  // Device端申请显存，分别用来存放A、B和结果C
  float* d_A, d_B, d_C;
  cudaMalloc(&d_A, size);
  cudaMalloc(&d_B, size);
  cudaMalloc(&d_C, size);
 
  // 把需要计算的结果从Host拷贝到Device
  cudaMemcpy(d_A, h_A, size, cudaMemcpyHostToDevice);
  cudaMemcpy(d_B, h_B, size, cudaMemcpyHostToDevice);
 
  // 执行kernel，需要指定两个参数
  int threadsPerBlock = 256;
  int blocksPerGrid = (N + threadsPerBlock - 1) / threadsPerBlock;
  VecAdd<<<blocksPerGrid, threadsPerBlock>>>(d_A, d_B, d_C, N);
 
  // 把计算结果拷贝回Host
  cudaMemcpy(h_C, d_C, size, cudaMemcpyDeviceToHost);
 
  // 释放Device中的显存
  cudaFree(d_A);
  cudaFree(d_B);
  cudaFree(d_C);
 
  // 释放Host的内存
  ...
}

代码比较直白，其中cuda开头的函数都是CUDA库中提供的，比如cudaMalloc会在Device中申请一段显存，cudaMemcpy则可以在Host和Device之间进行数据拷贝等，不再赘述。

核心是kernel函数部分，先看看kernel函数的实现：

__global__ void VecAdd(float* A, float* B, float* C, int N) {
  int i = blockDim.x * blockIdx.x + threadIdx.x;
  if (i < N) C[i] = A[i] + B[i];
}

Kernel函数只有两行并不复杂，但是需要好好解释。

这个kernel函数把数组A和数组B逐元素相加，结果写到数组C中。即C[i] = A[i] + B[i]。如果在CPU上编程，一个循环遍历就搞定了。但是当用CUDA编程时，我们希望利用GPU中数千个计算核心同时计算，每个核心只负责A和B的一个元素。但是，如何分配任务？

如果GPU中的每个核心都有唯一的ID，比如0号核心执行C[0] = A[0] + B[0]，127号核心执行C[127] = A[127] + B[127]就好了。但是如果我们要操作的数据大于GPU的核心数怎么办？因此CUDA做了一层逻辑抽象。当一个计算任务在GPU中执行时，这个任务相关的Grid、Thread Block和Thread都有一系列的身份标识，即几个全局变量：

• blockDim：表明kernel所在的Thread Block的尺寸，包含x, y, z三个维度
• blockIdx：表明kernel所在的Thread Block的index，包含x, y, z三个维度
• threadIdx：表明kernel在在的Thead在Thread Block内的idx，包括x, y, z三个维度

只要引入了cuda.h的头文件，在代码中可以直接使用上面几个全局变量，这几个全局变量的值会在执行时由CUDA自动维护更新。因此，kernel函数 i 的计算方法就是用blockDim.x乘以blockIdx.x再加上threadIdx.x，就可以算出当前一个唯一的、逻辑ID被当前的thread使用。那为什么只用到了x维度，没有用到y和z维度？

答案在于Host端代码中，在启动kernel时，代码中指定了两个模板类参数：blocksPerGrid和threadsPerBlock。其含义通过名字就能看懂。这两个参数被我们指定成两个int型数字。

int threadsPerBlock = 256;
int blocksPerGrid = (N + threadsPerBlock - 1) / threadsPerBlock;
 
VecAdd<<<blocksPerGrid, threadsPerBlock>>>(d_A, d_B, d_C, N);

其实这两个参数还可以是dim2或dim3类型。如果是dim2类型，那么逻辑ID可以通过逻辑x和逻辑y唯一确定，其计算方法如下。

int y = blockIdx.y * blockDim.y + threadIdx.y;
int x = blockIdx.x * blockDim.x + threadIdx.x;
int i = blockDim.y * y + x;

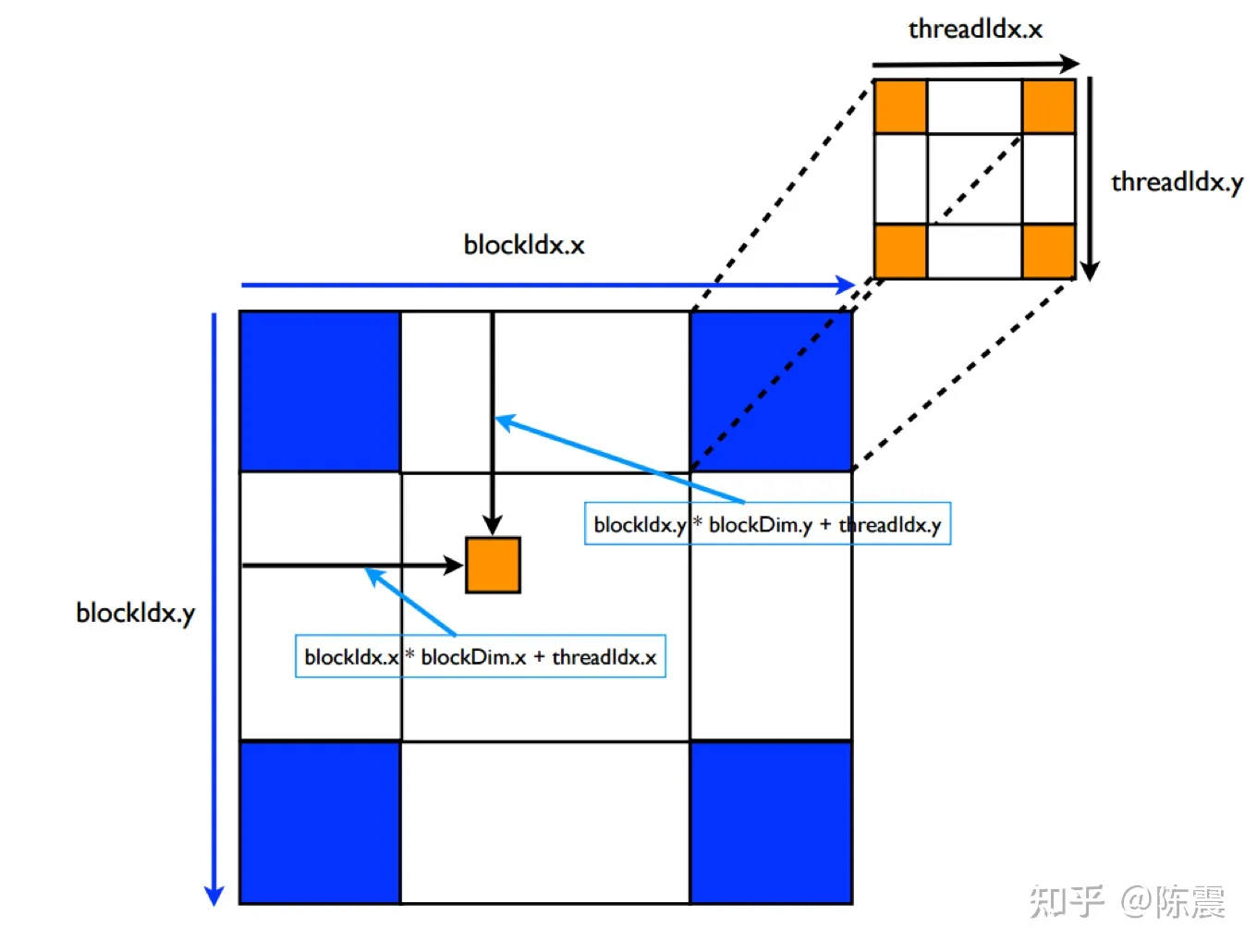
原理可以参考上图。这与二维数组索引转换成一维数组索引的过程是类似的，相信有基本编程经验的同学很快就能搞懂。