Leetcode901 - 1000

Posted on

Leetcode901. Online Stock Span

Write a class StockSpanner which collects daily price quotes for some stock, and returns the span of that stock’s price for the current day.

The span of the stock’s price today is defined as the maximum number of consecutive days (starting from today and going backwards) for which the price of the stock was less than or equal to today’s price.

For example, if the price of a stock over the next 7 days were [100, 80, 60, 70, 60, 75, 85], then the stock spans would be [1, 1, 1, 2, 1, 4, 6].

Example 1:

1
2
3
4
5
6
7
8
9
10
11
Input: ["StockSpanner","next","next","next","next","next","next","next"], [[],[100],[80],[60],[70],[60],[75],[85]]
Output: [null,1,1,1,2,1,4,6]
Explanation:
First, S = StockSpanner() is initialized.  Then:
S.next(100) is called and returns 1,
S.next(80) is called and returns 1,
S.next(60) is called and returns 1,
S.next(70) is called and returns 2,
S.next(60) is called and returns 1,
S.next(75) is called and returns 4,
S.next(85) is called and returns 6.

Note that (for example) S.next(75) returned 4, because the last 4 prices (including today’s price of 75) were less than or equal to today’s price.

Note:

  • Calls to StockSpanner.next(int price)will have 1 <= price <= 10^5.
  • There will be at most 10000 calls to StockSpanner.next per test case.
  • There will be at most 150000 calls to StockSpanner.next across all test cases.
  • The total time limit for this problem has been reduced by 75% for C++, and 50% for all other languages.

这道题定义了一个 StockSpanner 的类，有一个 next 函数，每次给当天的股价，让我们返回之前连续多少天都是小于等于当前股价。

可以找连续递增的子数组的长度么，其实也是不行的，就拿题目中的例子来说吧 [100, 80, 60, 70, 60, 75, 85]，数字 75 前面有三天是比它小的，但是这三天不是有序的，是先增后减的，那怎么办呢？我们先从简单的情况分析，假如当前的股价要小于前一天的，那么连续性直接被打破了，所以此时直接返回1就行了。但是假如大于等于前一天股价的话，情况就比较 tricky 了，因为此时所有小于等于前一天股价的天数肯定也是小于等于当前的，那么我们就需要知道是哪一天的股价刚好大于前一天的股价，然后用这一天的股价跟当前的股价进行比较，若大于当前股价，说明当前的连续天数就是前一天的连续天数加1，而若小于当前股价，我们又要重复这个过程，去比较刚好大于之前那个的股价。所以我们需要知道对于每一天，往前推刚好大于当前股价的是哪一天，用一个数组 pre，其中 pre[i] 表示从第i天往前推刚好大于第i天的股价的是第 pre[i] 天。接下来看如何实现 next 函数，首先将当前股价加入 nums 数组，然后前一天在数组中的位置就是 (int)nums.size()-2。再来想想 corner case 的情况，假如当前是数组中的第0天，前面没有任何股价了，我们的 pre[0] 就赋值为 -1 就行了，怎么知道当前是否是第0天，就看 pre 数组是否为空。再有就是由于i要不断去 pre 数组中找到之前的天数，所以最终i是有可能到达 pre[0] 的，那么就要判断当i为 -1 时，也要停止循环。循环的最后一个条件就是当之前的股价小于等当前的估计 price 时，才进行循环，这个前面讲过了，循环内部就是将 pre[i] 赋值给i，这样就完成了跳到之前天的操作。while 循环结束后要将i加入到 pre 数组，因为这个i就是从当前天往前推，一个大于当前股价的那一天，有了这个i，就可以计算出连续天数了，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class StockSpanner {
public:
    StockSpanner() {}

    int next(int price) {
        nums.push_back(price);
        int i = (int)nums.size() - 2;
        while (!pre.empty() && i >= 0 && nums[i] <= price) {
            i = pre[i];
        }
        pre.push_back(i);
        return (int)pre.size() - 1 - i;
    }

private:
    vector<int> nums, pre;
};

我们还可以使用栈来做，里面放一个 pair 对儿，分别是当前的股价和之前比其小的连续天数。在 next 函数中，使用一个 cnt 变量，初始化为1。还是要个 while 循环，其实核心的本质都是一样的，循环的条件首先是栈不能为空，并且栈顶元素的股价小于等于当前股价，那么 cnt 就加上栈顶元素的连续天数，可以感受到跟上面解法在这里的些许不同之处了吧，之前是一直找到第一个大于当前股价的天数在数组中的位置，然后相减得到连续天数，这里是在找的过程中直接累加连续天数，最终都可以得到正确的结果，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class StockSpanner {
public:
    StockSpanner() {}

    int next(int price) {
        int cnt = 1;
        while (!st.empty() && st.top().first <= price) {
            cnt += st.top().second; st.pop();
        }
        st.push({price, cnt});
        return cnt;
    }

private:
    stack<pair<int, int>> st;
};

Leetcode904. Fruit Into Baskets

In a row of trees, the i-th tree produces fruit with type tree[i].

You start at any tree of your choice, then repeatedly perform the following steps:

Add one piece of fruit from this tree to your baskets. If you cannot, stop.
Move to the next tree to the right of the current tree. If there is no tree to the right, stop.
Note that you do not have any choice after the initial choice of starting tree: you must perform step 1, then step 2, then back to step 1, then step 2, and so on until you stop.

You have two baskets, and each basket can carry any quantity of fruit, but you want each basket to only carry one type of fruit each.

What is the total amount of fruit you can collect with this procedure?

Example 1:

1
2
3
Input: [1,2,1]
Output: 3
Explanation: We can collect [1,2,1].

Example 2:

1
2
3
Input: [0,1,2,2]
Output: 3 Explanation: We can collect [1,2,2].
If we started at the first tree, we would only collect [0, 1].

Example 3:

1
2
3
Input: [1,2,3,2,2]
Output: 4 Explanation: We can collect [2,3,2,2].
If we started at the first tree, we would only collect [1, 2].

Example 4:

1
2
3
Input: [3,3,3,1,2,1,1,2,3,3,4]
Output: 5  Explanation: We can collect [1,2,1,1,2].
If we started at the first tree or the eighth tree, we would only collect 4 fruits.

Note:

  • 1 <= tree.length <= 40000
  • 0 <= tree[i] < tree.length

这道题说是给了我们一排树，每棵树产的水果种类是 tree[i]，说是现在有两种操作，第一种是将当前树的水果加入果篮中，若不能加则停止；第二种是移动到下一个树，若没有下一棵树，则停止。现在我们有两个果篮，可以从任意一个树的位置开始，但是必须按顺序执行操作一和二，问我们最多能收集多少个水果。说实话这道题的题目描述确实不太清晰，博主看了很多遍才明白意思，论坛上也有很多吐槽的帖子，但实际上这道题的本质就是从任意位置开始，若最多只能收集两种水果，问最多能收集多少个水果。那么再进一步提取，其实就是最多有两个不同字符的最长子串的长度，跟之前那道 Longest Substring with At Most Two Distinct Characters 一模一样，只不过换了一个背景，代码基本都可以直接使用的，博主感觉这样出题有点不太好吧，完全重复了。之前那题的四种解法这里完全都可以使用，先来看第一种，使用一个 HashMap 来记录每个水果出现次数，当 HashMap 中当映射数量超过两个的时候，我们需要删掉一个映射，做法是滑动窗口的左边界 start 的水果映射值减1，若此时减到0了，则删除这个映射，否则左边界右移一位。当映射数量回到两个的时候，用当前窗口的大小来更新结果 res 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int totalFruit(vector& tree) {
        int res = 0, start = 0, n = tree.size();
        unordered_map<int, int> fruitCnt;
        for (int i = 0; i < n; ++i) {
            ++fruitCnt[tree[i]];
            while (fruitCnt.size() > 2) {
                if (--fruitCnt[tree[start]] == 0) {
                    fruitCnt.erase(tree[start]);
                }
                ++start;
            }
            res = max(res, i - start + 1);
        }
        return res;
    }
};

我们除了用 HashMap 来映射字符出现的个数，我们还可以映射每个数字最新的坐标，比如题目中的例子 [0,1,2,2]，遇到第一个0，映射其坐标0，遇到1，映射其坐标1，当遇到2时，映射其坐标2，每次我们都判断当前 HashMap 中的映射数，如果大于2的时候，那么需要删掉一个映射，我们还是从 start=0 时开始向右找，看每个字符在 HashMap 中的映射值是否等于当前坐标 start，比如0，HashMap 此时映射值为0，等于 left 的0，那么我们把0删掉，start 自增1，再更新结果，以此类推直至遍历完整个数组，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int totalFruit(vector& tree) {
        int res = 0, start = 0, n = tree.size();
        unordered_map<int, int> fruitPos;
        for (int i = 0; i < n; ++i) {
            fruitPos[tree[i]] = i;
            while (fruitPos.size() > 2) {
                if (fruitPos[tree[start]] == start) {
                    fruitPos.erase(tree[start]);
                }
                ++start;
            }
            res = max(res, i - start + 1);
        }
        return res;
    }
};

后来又在网上看到了一种解法，这种解法是维护一个滑动窗口 sliding window，指针 left 指向起始位置，right 指向 window 的最后一个位置，用于定位 left 的下一个跳转位置，思路如下：

  • 若当前字符和前一个字符相同，继续循环。
  • 若不同，看当前字符和 right 指的字符是否相同：
  • 若相同，left 不变，右边跳到 i - 1。
  • 若不同，更新结果，left 变为 right+1，right 变为 i - 1。

最后需要注意在循环结束后，我们还要比较结果 res 和 n - left 的大小，返回大的，这是由于如果数组是 [5,3,5,2,1,1,1]，那么当 left=3 时，i=5,6 的时候，都是继续循环，当i加到7时，跳出了循环，而此时正确答案应为 [2,1,1,1] 这4个数字，而我们的结果 res 只更新到了 [5,3,5] 这3个数字，所以我们最后要判断 n - left 和结果 res 的大小。

另外需要说明的是这种解法仅适用于于不同字符数为2个的情况，如果为k个的话，还是需要用上面两种解法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int totalFruit(vector<int>& tree) {
        int res = 0, left = 0, right = -1, n = tree.size();
        for (int i = 1; i < n; ++i) {
            if (tree[i] == tree[i - 1]) continue;
            if (right >= 0 && tree[right] != tree[i]) {
                res = max(res, i - left);
                left = right + 1;
            }
            right = i - 1;
        }
        return max(n - left, res);
    }
};

还有一种不使用 HashMap 的解法，这里我们使用若干个变量，其中 cur 为当前最长子数组的长度，a和b为当前候选的两个不同的水果种类，cntB 为水果b的连续个数。我们遍历所有数字，假如遇到的水果种类是a和b中的任意一个，那么 cur 可以自增1，否则 cntB 自增1，因为若是新水果种类的话，默认已经将a种类淘汰了，此时候选水果由类型b和这个新类型水果构成，所以当前长度是 cntB+1。然后再来更新 cntB，假如当前水果种类是b的话，cntB 自增1，否则重置为1，因为 cntB 统计的就是水果种类b的连续个数。然后再来判断，若当前种类不是b，则此时a赋值为b， b赋值为新种类。最后不要忘了用 cur 来更新结果 res，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int totalFruit(vector<int>& tree) {
        int res = 0, cur = 0, cntB = 0, a = 0, b = 0;
        for (int fruit : tree) {
            cur = (fruit == a || fruit == b) ? cur + 1 : cntB + 1;
            cntB = (fruit == b) ? cntB + 1 : 1;
            if (b != fruit) {
                a = b; b = fruit;
            }
            res = max(res, cur);
        }
        return res;
    }
};

Leetcode905. Sort Array By Parity

Given an array A of non-negative integers, return an array consisting of all the even elements of A, followed by all the odd elements of A.

You may return any answer array that satisfies this condition.

Example 1:

1
2
3
Input: [3,1,2,4]
Output: [2,4,3,1]
The outputs [4,2,3,1], [2,4,1,3], and [4,2,1,3] would also be accepted.

Note:

1 <= A.length <= 5000
0 <= A[i] <= 5000

将奇数和偶数分类。。。简单

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> sortArrayByParity(vector<int>& A) {
        for(int i = 0; i < A.size(); i ++){
            if(A[i] % 2){
                for(int j = i + 1; j < A.size(); j++){
                    if(A[j] % 2 == 0){
                        int temp = A[j];
                        A[j] = A[i];
                        A[i] = temp;
                    }
                }
            }
        }
        return A;
    }
};

Leetcode907. Sum of Subarray Minimums

Given an array of integers A, find the sum of min(B), where B ranges over every (contiguous) subarray of A.

Since the answer may be large, return the answer modulo 10^9 + 7.

Example 1:

1
2
3
4
Input: [3,1,2,4]
Output: 17
Explanation: Subarrays are [3], [1], [2], [4], [3,1], [1,2], [2,4], [3,1,2], [1,2,4], [3,1,2,4].
Minimums are 3, 1, 2, 4, 1, 1, 2, 1, 1, 1.  Sum is 17.

Note:

  • 1 <= A.length <= 30000
  • 1 <= A[i] <= 30000

这道题给了一个数组，对于所有的子数组，找到最小值，并返回累加结果，并对一个超大数取余。由于我们只关心子数组中的最小值，所以对于数组中的任意一个数字，需要知道其是多少个子数组的最小值。就拿题目中的例子 [3,1,2,4] 来分析，开始遍历到3的时候，其本身就是一个子数组，最小值也是其本身，累加到结果 res 中，此时 res=3，然后看下个数1，是小于3的，此时新产生了两个子数组 [1] 和 [3,1]，且最小值都是1，此时在结果中就累加了 2，此时 res=5。接下来的数字是2，大于之前的1，此时会新产生三个子数组，其本身单独会产生一个子数组 [2]，可以先把这个2累加到结果 res 中，然后就是 [1,2] 和 [3,1,2]，可以发现新产生的这两个子数组的最小值还是1，跟之前计算数字1的时候一样，可以直接将以1结尾的子数组最小值之和加起来，那么以2结尾的子数组最小值之和就是 2+2=4，此时 res=9。对于最后一个数字4，其单独产生一个子数组 [4]，还会再产生三个子数组 [3,1,2,4], [1,2,4], [2,4]，其并不会对子数组的最小值产生影响，所以直接加上以2结尾的子数组最小值之和，总共就是 4+4=8，最终 res=17。

分析到这里，就知道我们其实关心的是以某个数字结尾时的子数组最小值之和，可以用一个一维数组 dp，其中dp[i]表示以数字A[i]结尾的所有子数组最小值之和，将dp[0]初始化为A[0]，结果res也初始化为A[0]。然后从第二个数字开始遍历，若大于等于前一个数字，则当前dp[i]赋值为dp[i-1]+A[i]，前面的分析已经解释了，当前数字A[i]组成了新的子数组，同时由于A[i]不会影响最小值，所以要把之前的最小值之和再加一遍。假如小于前一个数字，就需要向前遍历，去找到第一个小于A[i]的位置j，假如j小于0，表示前面所有的数字都是小于A[i]的，那么A[i]是前面i+1个以A[i]结尾的子数组的最小值，累加和为(i+1) x A[i]，若j大于等于0，则需要分成两部分累加，dp[j] + (i-j)xA[i]，这个也不难理解，前面有i-j个以A[i]为结尾的子数组的最小值是A[i]，而再前面的子数组的最小值就不是A[i]了，但是还是需要加上一遍其本身的最小值之和，因为每个子数组末尾都加上A[i]均可以组成一个新的子数组，最终的结果res就是将dp数组累加起来即可，别忘了对超大数取余，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int sumSubarrayMins(vector<int>& A) {
        int res = A[0], n = A.size(), M = 1e9 + 7;
        vector<int> dp(n);
        dp[0] = A[0];
        for (int i = 1; i < n; ++i) {
            if (A[i] >= A[i - 1]) dp[i] = dp[i - 1] + A[i];
            else {
                int j = i - 1;
                while (j >= 0 && A[i] < A[j]) --j;
                dp[i] = (j < 0) ? (i + 1) * A[i] : (dp[j] + (i - j) * A[i]);
            }
            res = (res + dp[i]) % M;
        }
        return res;
    }
};

上面的方法虽然 work，但不是很高效，原因是在向前找第一个小于当前的数字，每次都要线性遍历一遍，造成了平方级的时间复杂度。而找每个数字的前小数字或是后小数字，正是单调栈擅长的，可以参考博主之前的总结贴 LeetCode Monotonous Stack Summary 单调栈小结。这里我们用一个单调栈来保存之前一个小的数字的位置，栈里先提前放一个 -1，作用会在之后讲解。还是需要一个 dp 数组，跟上面的定义基本一样，但是为了避免数组越界，将长度初始化为 n+1，其中 dp[i] 表示以数字 A[i-1] 结尾的所有子数组最小值之和。对数组进行遍历，当栈顶元素不是 -1 且 A[i] 小于等于栈顶元素，则将栈顶元素移除。这样栈顶元素就是前面第一个比 A[i] 小的数字，此时 dp[i+1] 更新还是跟之前一样，分为两个部分，由于知道了前面第一个小于 A[i] 的数字位置，用当前位置减去栈顶元素位置再乘以 A[i]，就是以 A[i] 为结尾且最小值为 A[i] 的子数组的最小值之和，而栈顶元素之前的子数组就不受 A[i] 影响了，直接将其 dp 值加上即可。将当前位置压入栈，并将 dp[i+1] 累加到结果 res，同时对超大值取余，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int sumSubarrayMins(vector<int>& A) {
        int res = 0, n = A.size(), M = 1e9 + 7;
        stack<int> st{{-1}};
        vector<int> dp(n + 1);
        for (int i = 0; i < n; ++i) {
            while (st.top() != -1 && A[i] <= A[st.top()]) {
                st.pop();
            }
            dp[i + 1] = (dp[st.top() + 1] + (i - st.top()) * A[i]) % M;
            st.push(i);
            res = (res + dp[i + 1]) % M;
        }
        return res;
    }
};

再来看一种解法，由于对于每个数字，只要知道了其前面第一个小于其的数字位置，和后面第一个小于其的数字位置，就能知道当前数字是多少个子数组的最小值，直接相乘累加到结果 res 中即可。这里我们用两个单调栈 st_pre 和 st_next，栈里放一个数对儿，由数字和其在原数组的坐标组成。还需要两个一维数组 left 和 right，其中 left[i] 表示以 A[i] 为结束为止且 A[i] 是最小值的子数组的个数，right[i] 表示以 A[i] 为起点且 A[i] 是最小值的子数组的个数。对数组进行遍历，当 st_pre 不空，且栈顶元素大于 A[i]，移除栈顶元素，这样剩下的栈顶元素就是 A[i] 左边第一个小于其的数字的位置，假如栈为空，说明左边的所有数字都小于 A[i]，则 left[i] 赋值为 i+1，否则赋值为用i减去栈顶元素在原数组中的位置的值，然后将 A[i] 和i组成数对儿压入栈 st_pre。对于 right[i] 的处理也很类似，先将其初始化为 n-i，然后看若 st_next 不为空且栈顶元素大于 A[i]，然后取出栈顶元素t，由于栈顶元素t是大于 A[i]的，所以 right[t.second] 就可以更新为 i-t.second，然后将 A[i] 和i组成数对儿压入栈 st_next，最后再遍历一遍原数组，将每个 A[i] x left[i] x right[i] 算出来累加起来即可，别忘了对超大数取余，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int sumSubarrayMins(vector<int>& A) {
        int res = 0, n = A.size(), M = 1e9 + 7;
        stack<pair<int, int>> st_pre, st_next;
        vector<int> left(n), right(n);
        for (int i = 0; i < n; ++i) {
            while (!st_pre.empty() && st_pre.top().first > A[i]) {
                st_pre.pop();
            }
            left[i] = st_pre.empty() ? (i + 1) : (i - st_pre.top().second);
            st_pre.push({A[i], i});
            right[i] = n - i;
            while (!st_next.empty() && st_next.top().first > A[i]) {
                auto t = st_next.top(); st_next.pop();
                right[t.second] = i - t.second;
            }
            st_next.push({A[i], i});
        }
        for (int i = 0; i < n; ++i) {
            res = (res + A[i] * left[i] * right[i]) % M;
        }
        return res;
    }
};

我们也可以对上面的解法进行空间上的优化，只用一个单调栈，用来记录当前数字之前的第一个小的数字的位置，然后遍历每个数字，但是要多遍历一个数字，i从0遍历到n，当 i=n 时，cur 赋值为0，否则赋值为 A[i]。然后判断若栈不为空，且 cur 小于栈顶元素，则取出栈顶元素位置 idx，由于是单调栈，那么新的栈顶元素就是 A[idx] 前面第一个较小数的位置，由于此时栈可能为空，所以再去之前要判断一下，若为空，则返回 -1，否则返回栈顶元素，用 idx 减去栈顶元素就是以 A[idx] 为结尾且最小值为 A[idx] 的子数组的个数，然后用i减去 idx 就是以 A[idx] 为起始且最小值为 A[idx] 的子数组的个数，然后 A[idx] x left x right 就是 A[idx] 这个数字当子数组的最小值之和，累加到结果 res 中并对超大数取余即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int sumSubarrayMins(vector<int>& A) {
        int res = 0, n = A.size(), M = 1e9 + 7;
        stack<int> st;
        for (int i = 0; i <= n; ++i) {
            int cur = (i == n) ? 0 : A[i];
            while (!st.empty() && cur < A[st.top()]) {
                int idx = st.top(); st.pop();
                int left = idx - (st.empty() ? -1 : st.top());
                int right = i - idx;
                res = (res + A[idx] * left * right) % M;
            }
            st.push(i);
        }
        return res;
    }
};

Leetcode908. Smallest Range I

Given an array A of integers, for each integer A[i] we may choose any x with -K <= x <= K, and add x to A[i]. After this process, we have some array B. Return the smallest possible difference between the maximum value of B and the minimum value of B.

Example 1:

1
2
3
Input: A = [1], K = 0
Output: 0
Explanation: B = [1]

Example 2:
1
2
3
Input: A = [0,10], K = 2
Output: 6
Explanation: B = [2,8]

Example 3:
1
2
3
Input: A = [1,3,6], K = 3
Output: 0
Explanation: B = [3,3,3] or B = [4,4,4]

Note:

  • 1 <= A.length <= 10000
  • 0 <= A[i] <= 10000
  • 0 <= K <= 10000

给了一个非负数的数组，和一个非负数K，说是数组中的每一个数字都可以加上 [-K, K] 范围内的任意一个数字，问新数组的最大值最小值之间的差值最小是多少。这道题的难度是 Easy，理论上应该是可以无脑写代码的，但其实很容易想的特别复杂。本题的解题标签是 Math，这种类型的题目基本上就是一种脑筋急转弯的题目，有时候一根筋转不过来就怎么也做不出来。首先来想，既然是要求新数组的最大值和最小值之间的关系，那么肯定是跟原数组的最大值最小值有着某种联系，原数组的最大值最小值我们可以很容易的得到，只要找出了跟新数组之间的联系，问题就能迎刃而解了。题目中说了每个数字都可以加上 [-K, K] 范围内的数字，当然最大值最小值也可以，如何让二者之间的差值最小呢？当然是让最大值尽可能变小，最小值尽可能变大了，所以最大值 mx 要加上 -K，而最小值 mn 要加上K，然后再做减法，即 (mx-K)-(mn+K) = mx-mn+2K，这就是要求的答案啦。

只要找到数组A 最大值和最小值的差，然后和2k比较即可得到结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int smallestRangeI(vector<int>& A, int K) {
        // find max and min
        int maxx = INT_MIN;
        int minn = INT_MAX;
        for(int i=0;i<A.size();i++){
            if(A[i]>maxx)
                maxx = A[i];
            if(A[i]<minn)
                minn = A[i];
        }
        if(minn+K >= maxx-K)
            return 0;
        else
            return maxx - minn - 2 * K;
    }
};

Leetcode909. Snakes and Ladders

On an N x N board, the numbers from 1 to N*N are written boustrophedonically starting from the bottom left of the board, and alternating direction each row. For example, for a 6 x 6 board, the numbers are written as follows:

You start on square 1 of the board (which is always in the last row and first column). Each move, starting from square x, consists of the following:

  • You choose a destination square S with number x+1, x+2, x+3, x+4, x+5, or x+6, provided this number is <= N*N.
    (This choice simulates the result of a standard 6-sided die roll: ie., there are always at most 6 destinations, regardless of the size of the board.)
  • If S has a snake or ladder, you move to the destination of that snake or ladder. Otherwise, you move to S.

A board square on row r and column c has a “snake or ladder” if board[r][c] != -1. The destination of that snake or ladder is board[r][c].

Note that you only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving. (For example, if the board is [[4,-1],[-1,3]], and on the first move your destination square is 2, then you finish your first move at 3, because you do notcontinue moving to 4.)

Return the least number of moves required to reach square N*N. If it is not possible, return -1.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: [
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]]
Output: 4
Explanation:
At the beginning, you start at square 1 [at row 5, column 0].
You decide to move to square 2, and must take the ladder to square 15.
You then decide to move to square 17 (row 3, column 5), and must take the snake to square 13.
You then decide to move to square 14, and must take the ladder to square 35.
You then decide to move to square 36, ending the game.
It can be shown that you need at least 4 moves to reach the N*N-th square, so the answer is 4.

这道题给了一个 NxN 大小的二维数组，从左下角从1开始，蛇形游走，到左上角或者右上角到数字为 NxN，中间某些位置会有梯子，就如同传送门一样，直接可以到达另外一个位置。现在就如同玩大富翁 Big Rich Man 一样，有一个骰子，可以走1到6内的任意一个数字，现在奢侈一把，有无限个遥控骰子，每次都可以走1到6以内指定的步数，问最小能用几步快速到达终点 NxN 位置。博主刚开始做这道题的时候，看是求极值，以为是一道动态规划 Dynamic Programming 的题，结果发现木有办法重现子问题，没法写出状态转移方程，只得作罢。但其实博主忽略了一点，求最小值还有一大神器，广度优先搜索 BFS，最直接的应用就是在迷宫遍历的问题中，求从起点到终点的最少步数，也可以用在更 general 的场景，只要是存在确定的状态转移的方式，可能也可以使用。这道题基本就是类似迷宫遍历的问题，可以走的1到6步可以当作六个方向，这样就可以看作是一个迷宫了，唯一要特殊处理的就是遇见梯子的情况，要跳到另一个位置。这道题还有另一个难点，就是数字标号和数组的二维坐标的转换，这里起始点是在二维数组的左下角，且是1，而代码中定义的二维数组的 (0, 0) 点是在左上角，需要转换一下，还有就是这道题的数字是蛇形环绕的，即当行号是奇数的时候，是从右往左遍历的，转换的时候要注意一下。

初始时将数字1放入，然后还需要一个 visited 数组，大小为 nxn+1。在 while 循环中进行层序遍历，取出队首数字，判断若等于 nxn 直接返回结果 res。否则就要遍历1到6内的所有数字i，则 num+i 就是下一步要走的距离，需要将其转为数组的二维坐标位置，这个操作放到一个单独的子函数中，后边再讲。有了数组的坐标，就可以看该位置上是否有梯子，有的话，需要换成梯子能到达的位置，没有的话还是用 num+i。有了下一个位置，再看 visited 中的值，若已经访问过了直接跳过，否则标记为 true，并且加入队列 queue 中即可，若 while 循环退出了，表示无法到达终点，返回 -1。将数字标号转为二维坐标位置的子函数也不算难，首先应将数字标号减1，因为这里是从1开始的，而代码中的二维坐标是从0开始的，然后除以n得到横坐标，对n取余得到纵坐标。但这里得到的横纵坐标都还不是正确的，因为前面说了数字标记是蛇形环绕的，当行号是奇数的时候，列数需要翻转一下，即用 n-1 减去当前列数。又因为代码中的二维数组起点位置在左上角，同样需要翻转一样，这样得到的才是正确的横纵坐标，返回即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int snakesAndLadders(vector<vector<int>>& board) {
        int len = board.size(), res = 0;
        len = len*len;
        queue<int> q{{1}};
        vector<bool> visited(len + 1);
        
        while (!q.empty()) {
            int s = q.size();
            for (int i = 0; i < s; i ++) {
                int num = q.front(); q.pop();
                if (num == len)
                    return res;
                for (int i = 1; i <= 6 && num + i <= len; ++i) {
                    int next = getBoardValue(board, num + i);
                    if (next == -1) next = num + i;
                    if (visited[next]) continue;
                    visited[next] = true;
                    q.push(next);
                }
            }
            res ++;
        }
        return -1;
    }
    
    int getBoardValue(vector<vector<int>>& board, int i) {
        int len = board.size(), x = (i - 1) / len, y = (i - 1) % len;
        if (x % 2 == 1) y = len - 1 - y;
        x = len - 1 - x;
        return board[x][y];
    }
};

Leetcode911. Online Election

In an election, the i-th vote was cast for persons[i] at time times[i].

Now, we would like to implement the following query function: TopVotedCandidate.q(int t) will return the number of the person that was leading the election at time t.

Votes cast at time t will count towards our query. In the case of a tie, the most recent vote (among tied candidates) wins.

Example 1:

1
2
3
4
5
6
7
Input: ["TopVotedCandidate","q","q","q","q","q","q"], [[[0,1,1,0,0,1,0],[0,5,10,15,20,25,30]],[3],[12],[25],[15],[24],[8]]
Output: [null,0,1,1,0,0,1]
Explanation:
At time 3, the votes are [0], and 0 is leading.
At time 12, the votes are [0,1,1], and 1 is leading.
At time 25, the votes are [0,1,1,0,0,1], and 1 is leading (as ties go to the most recent vote.)
This continues for 3 more queries at time 15, 24, and 8.

Note:

  • 1 <= persons.length = times.length <= 5000
  • 0 <= persons[i] <= persons.length
  • times is a strictly increasing array with all elements in [0, 10^9].
  • TopVotedCandidate.q is called at most 10000 times per test case.
  • TopVotedCandidate.q(int t) is always called with t >= times[0].

这道题是关于线上选举的问题，这里给了两个数组 persons 和 times，表示在某个时间点times[i]，i这个人把选票投给了 persons[i]，现在有一个q函数，输入时间点t，让返回在时间点t时得票最多的人，当得票数相等时，返回最近得票的人。因为查询需求的时间点是任意的，在某个查询时间点可能并没有投票发生，但需要知道当前的票王，当然最傻的办法就是每次都从开头统计到当前时间点，找出票王，但这种方法大概率会超时，正确的方法实际上是要在某个投票的时间点，都统计出当前的票王，然后在查询的时候，查找刚好大于查询时间点的下一个投票时间点，返回前一个时间点的票王即可，所以这里可以使用一个 TreeMap 来建立投票时间点和当前票王之间的映射。如何统计每个投票时间点的票王呢，可以使用一个 count 数组，其中count[i]就表示当前i获得的票数，还需要一个变量 lead，表示当前的票王。现在就可以开始遍历所有的投票了，对于每个投票，将票数加到 count 中对应的人身上，然后跟 lead 比较，若当前人的票数大于等于 lead 的票数，则 lead 更换为当前人，同时建立当前时间点和票王之间的映射。在查询的时候，由于时间点是有序的，所以可以使用二分搜索法，由于使用的是 TreeMap，具有自动排序的功能，可以直接用upper_bound来查找第一个比t大的投票时间，然后再返回上一个投票时间点的票王即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class TopVotedCandidate {
public:
    TopVotedCandidate(vector& persons, vector& times) {
        int n = persons.size(), lead = 0;
        vector<int> count(n + 1);
        for (int i = 0; i < n; ++i) {
            if (++count[persons[i]] >= count[lead]) {
                lead = persons[i];
            }
            m[times[i]] = lead;
        }
    }
    int q(int t) {
        return (--m.upper_bound(t))->second;
    }

private:
    map<int, int> m;
};

我们也可以用 HashMap 来取代 TreeMap，但因为 HashMap 无法进行时间点的排序，不好使用二分搜索法了，所以就需要记录投票时间数组 times，保存在一个私有变量中。在查询函数中自己来写二分搜索法，查找第一个大于目标值的数。由于要返回上一个投票时间点，所以要记得减1，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class TopVotedCandidate {
public:
    TopVotedCandidate(vector& persons, vector& times) {
        int n = persons.size(), lead = 0;
        vector<int> count(n + 1);
        this->times = times;
        for (int i = 0; i < n; ++i) {
            if (++count[persons[i]] >= count[lead]) {
                lead = persons[i];
            }
            m[times[i]] = lead;
        }
    }
    int q(int t) {
        int left = 0, right = times.size();
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (times[mid] <= t) left = mid + 1;
            else right = mid;
        }
        return m[times[right - 1]];
    }

private:
    unordered_map<int, int> m;
    vector times;
};

Leetcode912. Sort an Array

Given an array of integers nums, sort the array in ascending order.

Example 1:

1
2
Input: [5,2,3,1]
Output: [1,2,3,5]

Example 2:

1
2
Input: [5,1,1,2,0,0]
Output: [0,0,1,1,2,5]

Note:

  • 1 <= A.length <= 10000
  • -50000 <= A[i] <= 50000

这道题让我们给数组排序，常见排序方法有很多，插入排序，选择排序，堆排序，快速排序，冒泡排序，归并排序，桶排序等等。它们的时间复杂度不尽相同，这道题貌似对于平方级复杂度的排序方法会超时，所以只能使用那些速度比较快的排序方法啦。题目给定了每个数字的范围是 [-50000, 50000]，并不是特别大，这里可以使用记数排序 Count Sort，建立一个大小为 100001 的数组 count，然后统计 nums 中每个数字出现的个数，然后再从0遍历到 100000，对于每个遍历到的数字i，若个数不为0，则加入 count 数组中对应个数的 i-50000 到结果数组中，这里的 50000 是 offset，因为数组下标不能为负数，在开始统计个数的时候，每个数字都加上了 50000，那么最后组成有序数组的时候就要减去，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector sortArray(vector& nums) {
        int n = nums.size(), j = 0;
        vector<int> res(n), count(100001);
        for (int num : nums) ++count[num + 50000];
        for (int i = 0; i < count.size(); ++i) {
            while (count[i]-- > 0) {
                res[j++] = i - 50000;
            }
        }
        return res;
    }
};

下面是快速排序。快排的精髓在于选一个 pivot，然后将所有小于 pivot 的数字都放在左边，大于 pivot 的数字都放在右边，等于的话放哪边都行。但是此时左右两边的数组各自都不一定是有序的，需要再各自调用相同的递归，直到细分到只有1个数字的时候，再返回的时候就都是有序的了，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        quick(nums, 0, (int)nums.size()-1);
        return nums;
    }
    
    void quick(vector<int>& nums, int start, int end) {
        if (start >= end)
            return;
        int pivot = nums[(start+end)/2], i = start, j = end;
        while(i <= j) {
            while(i <= j && nums[i] < pivot)
                i ++;
            while(i <= j && nums[j] > pivot)
                j --;
            if (i <= j) {
                swap(nums[i], nums[j]);
                i ++;
                j --;
            }
        }
        quick(nums, start, j);
        quick(nums, i, end);
    }
};

Leetcode914. X of a Kind in a Deck of Cards

In a deck of cards, each card has an integer written on it.

Return true if and only if you can choose X >= 2 such that it is possible to split the entire deck into 1 or more groups of cards, where:

Each group has exactly X cards.
All the cards in each group have the same integer.

Example 1:

1
2
3
Input: deck = [1,2,3,4,4,3,2,1]
Output: true
Explanation: Possible partition [1,1],[2,2],[3,3],[4,4].

Example 2:
1
2
3
Input: deck = [1,1,1,2,2,2,3,3]
Output: false´
Explanation: No possible partition.

Example 3:
1
2
3
Input: deck = [1]
Output: false
Explanation: No possible partition.

Example 4:
1
2
3
Input: deck = [1,1]
Output: true
Explanation: Possible partition [1,1].

Example 5:
1
2
3
Input: deck = [1,1,2,2,2,2]
Output: true
Explanation: Possible partition [1,1],[2,2],[2,2].

Constraints:

  • 1 <= deck.length <= 10^4
  • 0 <= deck[i] < 10^4

1、这道题给定一个vector，vector中存放着卡牌的数字，比如1、2、3、4这样子，你需要把这些卡牌分成多组。要求同一组中的卡牌数字一致，并且每一组中的卡牌张数一样。比如123321，你就可以分成[1,1]，[2,2]，[3,3]。如果可以这样分组，并且组中卡牌张数大于等于2，那么返回true，否则返回false。限制卡牌数字在[0,10000)，vector中的卡牌张数在[1,10000]。

2、我们最开始可以用vector也可以用map，来存放各个数字的卡牌各有多少张。（笔者一开始的错误想法：这里用先排序后遍历的做法，有点傻，因为排序O(nlogn)的时间复杂度太高了，还不如直接遍历。）得到各个数字卡牌的张数之后，我们需要看一下是否可以分组。这里有个地方要注意下，比如卡牌1有4张，卡牌2有6张，是否可以分组呢？可以的，每组2张就可以了，卡牌1有2组，卡牌2有3组。也就是说，我们要求各种数字卡牌的张数的最大公约数，看一下最大公约数是否大于等于2。而不能简单地看各种数字卡牌的张数是否一致。

但是求集体的最大公约数太麻烦了，还不如直接从2开始，判断所有数字可不可以整除2。如果可以，那么返回true。如果不行，看一下是否可以整除3……继续判断，一直到最小的张数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    bool hasGroupsSizeX(vector<int>& deck) {
        unordered_map<int, int> mapp;
        for(int i = 0; i < deck.size(); i ++)
            mapp[deck[i]] ++;
        int minn = 9999999;
        for(auto it = mapp.begin(); it != mapp.end(); it ++)
            minn = min(minn, it->second);
        int flag;
        for(int i = 2; i <= minn; i ++) {
            flag = 0;
            for(auto it = mapp.begin(); it != mapp.end(); it ++) {
                if(it->second % i != 0) {
                    flag = 1;
                    break;
                }
            }
            if(flag == 0)
                return true;
        }
        return false;
    }
};

Leetcode915. Partition Array into Disjoint Intervals

Given an array A, partition it into two (contiguous) subarrays left and right so that:

  • Every element in left is less than or equal to every element in right.
  • left and right are non-empty.
  • left has the smallest possible size.

Return the length of left after such a partitioning. It is guaranteed that such a partitioning exists.

Example 1:

1
2
3
Input: [5,0,3,8,6]
Output: 3
Explanation: left = [5,0,3], right = [8,6]

Example 2:

1
2
3
Input: [1,1,1,0,6,12]
Output: 4
Explanation: left = [1,1,1,0], right = [6,12]

Note:

  • 2 <= A.length <= 30000
  • 0 <= A[i] <= 10^6
  • It is guaranteed there is at least one way to partition A as described.

这道题说是给了一个数组A，让我们分成两个相邻的子数组 left 和 right，使得 left 中的所有数字小于等于 right 中的，并限定了每个输入数组必定会有这么一个分割点，让返回数组 left 的长度。这道题并不算一道难题，当然最简单并暴力的方法就是遍历所有的分割点，然后去验证左边的数组是否都小于等于右边的数，这种写法估计会超时，这里就不去实现了。直接来想优化解法吧，由于分割成的 left 和 right 数组本身不一定是有序的，只是要求 left 中的最大值要小于等于 right 中的最小值，只要这个条件满足了，一定就是符合题意的分割。left 数组的最大值很好求，在遍历数组的过程中就可以得到，而 right 数组的最小值怎么求呢？其实可以反向遍历数组，并且使用一个数组 backMin，其中 backMin[i] 表示在范围 [i, n-1] 范围内的最小值，有了这个数组后，再正向遍历一次数组，每次更新当前最大值 curMax，这就是范围 [0, i] 内的最大值，通过 backMin 数组快速得到范围 [i+1, n-1] 内的最小值，假如 left 的最大值小于等于 right 的最小值，则 i+1 就是 left 的长度，直接返回即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int partitionDisjoint(vector& A) {
        int n = A.size(), curMax = INT_MIN;
        vector<int> backMin(n, A.back());
        for (int i = n - 2; i >= 0; --i) {
            backMin[i] = min(backMin[i + 1], A[i]);
        }
        for (int i = 0; i < n - 1; ++i) {
            curMax = max(curMax, A[i]);
            if (curMax <= backMin[i + 1]) return i + 1;
        }
        return 0;
    }
};

下面来看论坛上的主流解法，只需要一次遍历即可，并且不需要额外的空间，这里使用三个变量，partitionIdx 表示分割点的位置，preMax 表示 left 中的最大值，curMax 表示当前的最大值。思路是遍历每个数字，更新当前最大值 curMax，并且判断若当前数字 A[i] 小于 preMax，说明这个数字也一定是属于 left 数组的，此时整个遍历到的区域应该都是属于 left 的，所以 preMax 要更新为 curMax，并且当前位置也就是潜在的分割点，所以 partitionIdx 更新为i。由于题目中限定了一定会有分割点，所以这种方法是可以得到正确结果的，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int partitionDisjoint(vector& A) {
        int partitionIdx = 0, preMax = A[0], curMax = preMax;
        for (int i = 1; i < A.size(); ++i) {
            curMax = max(curMax, A[i]);
            if (A[i] < preMax) {
                preMax = curMax;
                partitionIdx = i;
            }
        }
        return partitionIdx + 1;
    }
};

Leetcode916. Word Subsets

We are given two arrays A and B of words. Each word is a string of lowercase letters.

Now, say that word b is a subset of word a if every letter in b occurs in a, including multiplicity. For example, “wrr” is a subset of “warrior”, but is not a subset of “world”.

Now say a word a from A is universal if for every b in B, b is a subset of a.

Return a list of all universal words in A. You can return the words in any order.

Example 1:

1
2
Input: A = ["amazon","apple","facebook","google","leetcode"], B = ["e","o"]
Output: ["facebook","google","leetcode"]

Example 2:

1
2
Input: A = ["amazon","apple","facebook","google","leetcode"], B = ["l","e"]
Output: ["apple","google","leetcode"]

Example 3:

1
2
Input: A = ["amazon","apple","facebook","google","leetcode"], B = ["e","oo"]
Output: ["facebook","google"]

Example 4:

1
2
Input: A = ["amazon","apple","facebook","google","leetcode"], B = ["lo","eo"]
Output: ["google","leetcode"]

Example 5:

1
2
Input: A = ["amazon","apple","facebook","google","leetcode"], B = ["ec","oc","ceo"]
Output: ["facebook","leetcode"]

Note:

  • 1 <= A.length, B.length <= 10000
  • 1 <= A[i].length, B[i].length <= 10
  • A[i] and B[i] consist only of lowercase letters.
  • All words in A[i] are unique: there isn’t i != j with A[i] == A[j].

这道题定义了两个单词之间的一种子集合关系，就是说假如单词b中的每个字母都在单词a中出现了（包括重复字母），就说单词b是单词a的子集合。现在给了两个单词集合A和B，让找出集合A中的所有满足要求的单词，使得集合B中的所有单词都是其子集合。配合上题目中给的一堆例子，意思并不难理解，根据子集合的定义关系，其实就是说若单词a中的每个字母的出现次数都大于等于单词b中每个字母的出现次数，单词b就一定是a的子集合。现在由于集合B中的所有单词都必须是A中某个单词的子集合，那么其实只要对于每个字母，都统计出集合B中某个单词中出现的最大次数，比如对于这个例子，B=[“eo”,”oo”]，其中e最多出现1次，而o最多出现2次，那么只要集合A中有单词的e出现不少1次，o出现不少于2次，则集合B中的所有单词一定都是其子集合。这就是本题的解题思路，这里使用一个大小为 26 的一维数组 charCnt 来统计集合B中每个字母的最大出现次数，而将统计每个单词的字母次数的操作放到一个子函数 helper 中，当 charCnt 数组更新完毕后，下面就开始检验集合A中的所有单词了。对于每个遍历到的单词，还是要先统计其每个字母的出现次数，然后跟 charCnt 中每个位置上的数字比较，只要均大于等于 charCnt 中的数字，就可以加入到结果 res 中了，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<string> wordSubsets(vector<string>& words1, vector<string>& words2) {
        vector<int> char_num(26, 0);
        vector<string> res;
        for (int i = 0; i < words2.size(); i ++) {
            vector<int> t = helper(words2[i]);
            for (int j = 0; j < 26; j ++)
                char_num[j] = max(char_num[j], t[j]);   
        }
        
        for (int i = 0; i < words1.size(); i ++) {
            vector<int> t = helper(words1[i]);
            int j = 0;
            for (j = 0; j < 26; j ++)
                if (t[j] < char_num[j])
                    break;
            if (j == 26)
                res.push_back(words1[i]);
        }
        return res;
    }
    
    vector<int> helper(string a) {
        vector<int> res(26, 0);
        for (int i = 0; i < a.length(); i ++)
            res[a[i] - 'a'] ++;
        return res;
    }
};

Leetcode917. Reverse Only Letters

Given a string S, return the “reversed” string where all characters that are not a letter stay in the same place, and all letters reverse their positions.

Example 1:

1
2
Input: "ab-cd"
Output: "dc-ba"

Example 2:
1
2
Input: "a-bC-dEf-ghIj"
Output: "j-Ih-gfE-dCba"

Example 3:
1
2
Input: "Test1ng-Leet=code-Q!"
Output: "Qedo1ct-eeLg=ntse-T!"

Note:

  • S.length <= 100
  • 33 <= S[i].ASCIIcode <= 122
  • S doesn’t contain \ or “

给定一个字符串 S，返回 “反转后的” 字符串，其中不是字母的字符都保留在原地，而所有字母的位置发生反转。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    
    bool isletter(char b) {
        if ((b >= 'a' && b <= 'z') || (b >= 'A' && b <= 'Z'))
            return true;
        else
            return false;
    }
    
    string reverseOnlyLetters(string S) {
        int i = 0, j = S.length();
        while(i < j) {
            if(!isletter(S[i]))
                i ++;
            else if(!isletter(S[j]))
                j --;
            else {
                char c = S[i];
                S[i] = S[j];
                S[j] = c;
                i ++;
                j --;
            }
        }
        return S;
    }
};

Leetcode918. Maximum Sum Circular Subarray

Given a circular array C of integers represented by A, find the maximum possible sum of a non-empty subarray of C.

Here, a circular array means the end of the array connects to the beginning of the array. (Formally, C[i] = A[i]when 0 <= i < A.length, and C[i+A.length] = C[i] when i >= 0.)

Also, a subarray may only include each element of the fixed buffer A at most once. (Formally, for a subarray C[i], C[i+1], ..., C[j], there does not exist i <= k1, k2 <= j with k1 % A.length = k2 % A.length.)

Example 1:

1
2
3
Input: [1,-2,3,-2]
Output: 3
Explanation: Subarray [3] has maximum sum 3

Example 2:

1
2
Input: [5,-3,5]
Output: 10 Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10

Example 3:

1
2
3
Input: [3,-1,2,-1]
Output: 4
Explanation: Subarray [2,-1,3] has maximum sum 2 + (-1) + 3 = 4

Example 4:

1
2
Input: [3,-2,2,-3]
Output: 3 Explanation: Subarray [3] and [3,-2,2] both have maximum sum 3

Example 5:

1
2
Input: [-2,-3,-1]
Output: -1 Explanation: Subarray [-1] has maximum sum -1

Note:

  • -30000 <= A[i] <= 30000
  • 1 <= A.length <= 30000

这道题让求环形子数组的最大和，既然是子数组，则意味着必须是相连的数字，而由于环形数组的存在，说明可以首尾相连，这样的话，最长子数组的范围可以有两种情况，一种是正常的，数组中的某一段子数组，另一种是分为两段的，即首尾相连的。对于第一种情况，其实就是之前那道题 Maximum Subarray 的做法，对于第二种情况，需要转换一下思路，除去两段的部分，中间剩的那段子数组其实是和最小的子数组，只要用之前的方法求出子数组的最小和，用数组总数字和一减，同样可以得到最大和。两种情况的最大和都要计算出来，取二者之间的较大值才是真正的和最大的子数组。但是这里有个 corner case 需要注意一下，假如数组中全是负数，那么和最小的子数组就是原数组本身，则求出的差值是0，而第一种情况求出的和最大的子数组也应该是负数，那么二者一比较，返回0就不对了，所以这种特殊情况需要单独处理一下，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int maxSubarraySumCircular(vector& A) {
        int sum = 0, mn = INT_MAX, mx = INT_MIN, curMax = 0, curMin = 0;
        for (int num : A) {
            curMin = min(curMin + num, num);
            mn = min(mn, curMin);
            curMax = max(curMax + num, num);
            mx = max(mx, curMax);
            sum += num;
        }
        return (sum - mn == 0) ? mx : max(mx, sum - mn);
    }
};

Leetcode921. Minimum Add to Make Parentheses Valid

Given a string S of ‘(‘ and ‘)’ parentheses, we add the minimum number of parentheses ( ‘(‘ or ‘)’, and in any positions ) so that the resulting parentheses string is valid.

Formally, a parentheses string is valid if and only if:

It is the empty string, or
It can be written as AB (A concatenated with B), where A and B are valid strings, or
It can be written as (A), where A is a valid string.
Given a parentheses string, return the minimum number of parentheses we must add to make the resulting string valid.

Example 1:

1
2
Input: "())"
Output: 1

Example 2:
1
2
Input: "((("
Output: 3

Example 3:
1
2
Input: "()"
Output: 0

Example 4:
1
2
Input: "()))(("
Output: 4

Note:

S.length <= 1000
S only consists of ‘(‘ and ‘)’ characters.

一道变形的括号匹配，这里注意如果res为负数的话，要及时纠正成正的且也要在最终结果加一，如上边的Example4的样子，如果只是按照栈的做法，结果是0，是错的，其实要加4个。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int minAddToMakeValid(string S) {
        int res=0,result=0;
        for(int i=0;i<S.size();i++)
            if(S[i]=='(')
                res++;
            else{
                res--;
                if(res<0){
                    res=0;
                    result++;
                }
            }
        return result+res;
    }
};

Leetcode922. Sort Array By Parity II

Given an array A of non-negative integers, half of the integers in A are odd, and half of the integers are even.

Sort the array so that whenever A[i] is odd, i is odd; and whenever A[i] is even, i is even.

You may return any answer array that satisfies this condition.

Example 1:

1
2
Input: [4,2,5,7]
Output: [4,5,2,7]

Explanation: [4,7,2,5], [2,5,4,7], [2,7,4,5] would also have been accepted.

Note:

2 <= A.length <= 20000
A.length % 2 == 0
0 <= A[i] <= 1000

首先，将所有偶数元素放在正确的位置就足够了，因为所有奇数元素也都在正确的位置。 所以我们只关注A [0]，A [2]，A [4]，……

理想情况下，我们希望有一些分区，左边的所有内容都已经正确，右边的所有内容都是未定的。
实际上，如果我们把它分成两个切片，即偶数= A [0]，A [2]，A [4]，……和奇数= A [1]，A [3]，A [5]，这个想法是有效的， ….我们的不变量将是偶数切片中的所有小于i的位置都是正确的，并且奇数切片中小于j的所有位置都是正确的。

对于每个偶数，让我们使A[i]也为偶数。 为此，我们将从奇数切片中提取一个元素。 我们将j传递到奇数切片，直到找到偶数元素，然后交换。 我们的不变量得以维持，因此算法是正确的。

就是说对每一个偶数位置的奇数，在奇数位置找一个偶数，然后交换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> sortArrayByParityII(vector<int>& A) {
        int j = 1;
        for(int i = 0; i < A.size(); i += 2){
            if(A[i] % 2 == 1){
                while(A[j] % 2 == 1)
                    j += 2;
                int temp = A[i];
                A[i] = A[j];
                A[j] = temp;
            }
        }
        return A;
    }
};

Leetcode925. Long Pressed Name

Your friend is typing his name into a keyboard. Sometimes, when typing a character c, the key might get long pressed, and the character will be typed 1 or more times.

You examine the typed characters of the keyboard. Return True if it is possible that it was your friends name, with some characters (possibly none) being long pressed.

Example 1:

1
2
3
Input: name = "alex", typed = "aaleex"
Output: true
Explanation: 'a' and 'e' in 'alex' were long pressed.

Example 2:
1
2
3
Input: name = "saeed", typed = "ssaaedd"
Output: false
Explanation: 'e' must have been pressed twice, but it wasn't in the typed output.

Example 3:
1
2
Input: name = "leelee", typed = "lleeelee"
Output: true

Example 4:
1
2
3
Input: name = "laiden", typed = "laiden"
Output: true
Explanation: It's not necessary to long press any character.

Constraints:

  • 1 <= name.length <= 1000
  • 1 <= typed.length <= 1000
  • The characters of name and typed are lowercase letters.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    bool isLongPressedName(string name, string typed) {
        if(name[0] != typed[0])
            return false;
        int count1, count2, i, j;
        int length1 = name.length(), length2 = typed.length();
        for(i = 1, j = 1; i < length1 || j < length2; i ++, j ++) {
            if(name[i-1] != typed[j-1])
                return false;
            count1 = 1;
            count2 = 1;
            while(name[i] == name[i-1]) {
                count1 ++;
                i ++;
            }
            while(typed[j] == typed[j-1]) {
                count2 ++;
                j ++;
            }
             cout<< count1 << " " << count2 << endl;
            if(count2 < count1)
                return false;  
        }
        if(name[length1-1] != typed[length2-1])
            return false;
        return true;
    }
};

不简单……边界条件很多，而且很麻烦。

Leetcode926. Flip String to Monotone Increasing

A string of ‘0’s and ‘1’s is monotone increasing if it consists of some number of ‘0’s (possibly 0), followed by some number of ‘1’s (also possibly 0.)

We are given a string S of ‘0’s and ‘1’s, and we may flip any ‘0’ to a ‘1’ or a ‘1’ to a ‘0’.

Return the minimum number of flips to make S monotone increasing.

Example 1:

1
2
3
Input: "00110"
Output: 1
Explanation: We flip the last digit to get 00111.

Example 2:

1
2
3
Input: "010110"
Output: 2
Explanation: We flip to get 011111, or alternatively 000111.

Example 3:

1
2
3
Input: "00011000"
Output: 2
Explanation: We flip to get 00000000.

Note:

  • 1 <= S.length <= 20000
  • S only consists of ‘0’ and ‘1’ characters.

这道题给了我们一个只有0和1的字符串，现在说是可以将任意位置的数翻转，即0变为1，或者1变为0，让组成一个单调递增的序列，即0必须都在1的前面，博主刚开始想的策略比较直接，就是使用双指针分别指向开头和结尾，开头的指针先跳过连续的0，末尾的指针向前跳过连续的1，然后在中间的位置分别记录0和1的个数，返回其中较小的那个。这种思路乍看上去没什么问题，但是实际上是有问题的，比如对于这个例子 “10011111110010111011”，如果按这种思路的话，就应该将所有的0变为1，从而返回6，但实际上更优的解法是将第一个1变为0，将后4个0变为1即可，最终可以返回5，这说明了之前的解法是不正确的。这道题可以用动态规划 Dynamic Programming 来做，需要使用两个 dp 数组，其中 cnt1[i] 表示将范围是 [0, i-1] 的子串内最小的将1转为0的个数，从而形成单调字符串。同理，cnt0[j] 表示将范围是 [j, n-1] 的子串内最小的将0转为1的个数，从而形成单调字符串。这样最终在某个位置使得 cnt0[i]+cnt1[i] 最小的时候，就是变为单调串的最优解，这样就可以完美的解决上面的例子，子串 “100” 的最优解是将1变为0，而后面的 “11111110010111011” 的最优解是将4个0变为1，总共加起来就是5，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int minFlipsMonoIncr(string S) {
        int n = S.size(), res = INT_MAX;
        vector<int> cnt1(n + 1), cnt0(n + 1);
        for (int i = 1, j = n - 1; j >= 0; ++i, --j) {
            cnt1[i] += cnt1[i - 1] + (S[i - 1] == '0' ? 0 : 1);
            cnt0[j] += cnt0[j + 1] + (S[j] == '1' ? 0 : 1);
        }
        for (int i = 0; i <= n; ++i) res = min(res, cnt1[i] + cnt0[i]);
        return res;
    }
};

我们可以进一步优化一下空间复杂度，用一个变量 cnt1 来记录当前位置时1出现的次数，同时 res 表示使到当前位置的子串变为单调串的翻转次数，用来记录0的个数，因为遇到0就翻1一定可以组成单调串，但不一定是最优解，每次都要和 cnt1 比较以下，若 cnt1 较小，就将 res 更新为 cnt1，此时保证了到当前位置的子串变为单调串的翻转次数最少，并不关心到底是把0变为1，还是1变为0了，其实核心思想跟上面的解法很相近，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int minFlipsMonoIncr(string S) {
        int n = S.size(), res = 0, cnt1 = 0;
        for (int i = 0; i < n; ++i) {
            (S[i] == '0') ? ++res : ++cnt1;
            res = min(res, cnt1);
        }
        return res;
    }
};

Leetcode929. Unique Email Addresses

Every email consists of a local name and a domain name, separated by the @ sign. For example, in alice@leetcode.com, alice is the local name, and leetcode.com is the domain name. Besides lowercase letters, these emails may contain ‘.’s or ‘+’s.

If you add periods (‘.’) between some characters in the local name part of an email address, mail sent there will be forwarded to the same address without dots in the local name. For example, “alice.z@leetcode.com” and “alicez@leetcode.com” forward to the same email address. (Note that this rule does not apply for domain names.)

If you add a plus (‘+’) in the local name, everything after the first plus sign will be ignored. This allows certain emails to be filtered, for example m.y+name@email.com will be forwarded to my@email.com. (Again, this rule does not apply for domain names.)

It is possible to use both of these rules at the same time.

Given a list of emails, we send one email to each address in the list. How many different addresses actually receive mails?

Example 1:

1
2
3
Input: ["test.email+alex@leetcode.com","test.e.mail+bob.cathy@leetcode.com","testemail+david@lee.tcode.com"]
Output: 2
Explanation: "testemail@leetcode.com" and "testemail@lee.tcode.com" actually receive mails

Note:

  • 1 <= emails[i].length <= 100
  • 1 <= emails.length <= 100
  • Each emails[i] contains exactly one ‘@’ character.
  • All local and domain names are non-empty.
  • Local names do not start with a ‘+’ character.

字符串处理，如果一个email地址里有点(‘.’)的话，就忽略这个点，如果有加号(‘+’)，忽略这个加号到(‘@’)之间的字符。判断一共有几个一样的email地址。不难，但是涉及字符串处理的话总归有些麻烦的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int numUniqueEmails(vector<string>& emails) {
        char result[100][100];
        memset(result,'\0',sizeof(result));
        int result_len=0;
        for(unsigned int i=0; i<emails.size(); i++)
        {
            char temp[100];
            memset(temp,'\0',100);
            int temp_len = 0, k=0;
            unsigned int j;
            for(j=0; j<emails[i].length(); j++)
            {
                if(emails[i][j]=='.')
                    continue;
                else if(emails[i][j]=='+' || emails[i][j]=='@' )
                    break;
                else
                    temp[temp_len++]=emails[i][j];
            }
            for(j=emails[i].find('@'); j<emails[i].length(); j++)
                temp[temp_len++]=emails[i][j];

            for(k=0; k<result_len; k++)
                if(strcmp(result[k],temp)==0)
                    break;
            if(k==result_len)
                memcpy(result[result_len++], temp, sizeof(temp));
            memset(temp,'\0',100);
        }
        return result_len;
    }
};

我的另一种做法，用set去重

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
	public:
    int numUniqueEmails(vector<string>& emails) {
        set<string> result;
        for(int i = 0; i < emails.size(); i ++) {
            string temp;
            int j;
            for(j = 0; j < emails[i].size(); j ++) {
                if(emails[i][j] == '+' || emails[i][j] == '@')
                    break;
                if(emails[i][j] == '.')
                    continue;
                temp += emails[i][j];
            }
            while(emails[i][j] != '@')
                j ++;
            for(; j < emails[i].size(); j ++) {
                temp += emails[i][j];
            }
            result.insert(temp);
        }
        return result.size();
    }
};

解析：
For each email address, convert it to the canonical address that actually receives the mail. This involves a few steps:

  • Separate the email address into a local part and the rest of the address.
  • If the local part has a ‘+’ character, remove it and everything beyond it from the local part.
  • Remove all the zeros from the local part.
  • The canonical address is local + rest.

After, we can count the number of unique canonical addresses with a Set structure.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int numUniqueEmails(String[] emails) {
        Set<String> seen = new HashSet();
        for (String email: emails) {
            int i = email.indexOf('@');
            String local = email.substring(0, i);
            String rest = email.substring(i);
            if (local.contains("+")) {
                local = local.substring(0, local.indexOf('+'));
            }
            local = local.replaceAll(".", "");
            seen.add(local + rest);
        }

        return seen.size();
    }
}

Leetcode930. Binary Subarrays With Sum

In an array A of 0s and 1s, how many non-empty subarrays have sum S?

Example 1:

1
2
3
4
5
6
7
8
Input: A = [1,0,1,0,1], S = 2
Output: 4
Explanation:
The 4 subarrays are bolded below:
[1,0,1]
[1,0,1,0]
[0,1,0,1]
[1,0,1]

Note:

  • A.length <= 30000
  • 0 <= S <= A.length
  • A[i] is either 0 or 1.

这道题给了我们一个只由0和1组成的数组A，还有一个整数S，问数组A中有多少个子数组使得其和正好为S。博主最先没看清题意，以为是按二进制数算的，但是看了例子之后才发现，其实只是单纯的求和而已。那么马上就想着应该是要建立累加和数组的，然后遍历所有的子数组之和，但是这个遍历的过程还是平方级的复杂度，这道题的 OJ 卡的比较严格，只放行线性的时间复杂度。所以这种遍历方式是不行的，但仍需要利用累加和的思路，具体的方法是在遍历的过程中使用一个变量 curSum 来记录当前的累加和，同时使用一个 HashMap，用来映射某个累加出现的次数，初始化需要放入 {0,1} 这个映射对儿，后面会讲解原因。在遍历数组的A的时候，对于每个遇到的数字 num，都加入累加和 curSum 中，然后看若 curSum-S 这个数有映射值的话，那么说明就存在 m[curSum-S] 个符合题意的子数组，应该加入到结果 res 中，假如 curSum 正好等于S，即 curSum-S=0 的时候，此时说明从开头到当前位置正好是符合题目要求的子数组，现在明白刚开始为啥要加入 {0,1} 这个映射对儿了吧，就是为了处理这种情况。然后此时 curSum 的映射值自增1即可。其实这道题的解法思路跟之前那道 Contiguous Array 是一样的，那道题是让找0和1个数相同的子数组，这里让找和为S的子数组，都可以用一个套路来解题，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int numSubarraysWithSum(vector<int>& A, int S) {
        int res = 0, curSum = 0;
        unordered_map<int, int> m{{0, 1}};
        for (int num : A) {
            curSum += num;
            res += m[curSum - S];
            ++m[curSum];
        }
        return res;
    }
};

我们也可以使用滑动窗口 Sliding Window 来做，也是线性的时间复杂度，其实还是利用到了累计和的思想，不过这个累加和不是从开头到当前位置之和，而是这个滑动窗口内数字之和，这 make sense 吧，因为只要这个滑动窗口内数字之和正好等于S了，即是符合题意的一个子数组。遍历数组A，将当前数字加入 sum 中，然后看假如此时 sum 大于S了，则要进行收缩窗口操作，左边界 left 右移，并且 sum 要减去这个移出窗口的数字，当循环退出后，假如此时 sum 小于S了，说明当前没有子数组之和正好等于S，若 sum 等于S了，则结果 res 自增1。此时还需要考虑一种情况，就是当窗口左边有连续0的时候，因为0并不影响 sum，但是却要算作不同的子数组，所以要统计左起连续0的个数，并且加到结果 res 中即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int numSubarraysWithSum(vector<int>& A, int S) {
        int res = 0, sum = 0, left = 0, n = A.size();
        for (int i = 0; i < n; ++i) {
            sum += A[i];
            while (left < i && sum > S) sum -= A[left++];
            if (sum < S) continue;
            if (sum == S) ++res;
            for (int j = left; j < i && A[j] == 0; ++j) {
                ++res;
            }
        }
        return res;
    }
};

Leetcode931. Minimum Falling Path Sum

Given a square array of integers A, we want the minimum sum of a falling path through A.

A falling path starts at any element in the first row, and chooses one element from each row. The next row’s choice must be in a column that is different from the previous row’s column by at most one.

Example 1:

1
2
3
4
5
6
7
8
9
Input: [[1,2,3],[4,5,6],[7,8,9]]
Output: 12
Explanation:
The possible falling paths are:

-   `[1,4,7], [1,4,8], [1,5,7], [1,5,8], [1,5,9]`
-   `[2,4,7], [2,4,8], [2,5,7], [2,5,8], [2,5,9], [2,6,8], [2,6,9]`
-   `[3,5,7], [3,5,8], [3,5,9], [3,6,8], [3,6,9]`
The falling path with the smallest sum is [1,4,7], so the answer is 12.

Note:

  • 1 <= A.length == A[0].length <= 100
  • -100 <= A[i][j] <= 100

这道题给了一个长宽相等的二维数组，说是让找一个列路径，使得相邻两个位置的数的距离不超过1，可以通过观察题目中给的例子来理解题意。由于每个位置上的累加值是由上一行的三个位置中较小的那个决定的，所以这就是一道典型的动态规划 Dynamic Programming 的题，为了节省空间，直接用数组A本身当作 dp 数组，其中 A[i][j] 就表示最后一个位置在 (i, j) 的最小的下降路径，则最终只要在最后一行中找最小值就是所求。由于要看上一行的值，所以要从第二行开始遍历，那么首先判断一下数组是否只有一行，是的话直接返回那个唯一的数字即可。否则从第二行开始遍历，一定存在的是 A[i-1][j] 这个数字，而它周围的两个数字需要判断一下，存在的话才进行比较取较小值，将最终的最小值加到当前的 A[i][j] 上即可。为了避免重新开一个 for 循环，判断一下，若当前是最后一行，则更新结果 res，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& A) {
        if (A.size() == 1) return A[0][0];
        int n = A.size(), res = INT_MAX;
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                int pre = A[i - 1][j];
                if (j > 0) pre = min(pre, A[i - 1][j - 1]);
                if (j < n - 1) pre = min(pre, A[i - 1][j + 1]);
                A[i][j] += pre;
                if (i == n - 1) res = min(res, A[i][j]);
            }
        }
        return res;
    }
};

Leetcode932. Beautiful Array

For some fixed N, an array A is beautiful if it is a permutation of the integers 1, 2, …, N, such that:

For every i < j, there is no k with i < k < j such that A[k] * 2 = A[i] + A[j].

Given N, return any beautiful array A. (It is guaranteed that one exists.)

Example 1:

1
2
Input: 4
Output: [2,1,4,3]

Example 2:

1
2
Input: 5
Output: [3,1,2,5,4]

Note:

  • 1 <= N <= 1000

这道题定义了一种漂亮数组，说的是在任意两个数字之间，不存在一个正好是这两个数之和的一半的数字，现在让返回长度是N的一个漂亮数组，注意这里长度是N的漂亮数组一定是由1到N之间的数字组成的，每个数字都会出现，而且一定存在这样的漂亮数组。博主刚开始时是没什么头绪的，想着总不会是要遍历所有的排列情况，然后对每个情况去验证是否是漂亮数组的吧，想想都觉得很不高效，于是就放弃挣扎，直接逛论坛了。不出意外，最高票的还是你李哥，居然提出了逆天的线性时间的解法，献上膝盖，怪不得有网友直接要 Venmo 号立马打钱，LOL～ 这道题给了提示说是要用分治法来做，但是怎么分是这道题的精髓，若只是普通的对半分，那么在 merge 的时候还是要验证是否是漂亮数组，麻烦！但若按奇偶来分的话，那就非常的叼了，因为奇数加偶数等于奇数，就不会是任何一个数字的2倍了。这就是奇偶分堆的好处，这时任意两个数字肯定不能分别从奇偶堆里取了，那可能你会问，奇数堆会不会有三个奇数打破这个规则呢？只要这个奇数堆是从一个漂亮数组按固定的规则变化而来的，就能保证一定也是漂亮数组，因为对于任意一个漂亮数组，若对每个数字都加上一个相同的数字，或者都乘上一个相同的数字，则一定还是漂亮数组，因为数字的之间的内在关系并没有改变。明白了上面这些，基本就可以解题了，假设此时已经有了一个长度为n的漂亮数组，如何将其扩大呢？可以将其中每个数字都乘以2并加1，就都会变成奇数，并且这个奇数数组还是漂亮的，然后再将每个数字都乘以2，那么都会变成偶数，并且这个偶数数组还是漂亮的，两个数组拼接起来，就会得到一个长度为 2n 的漂亮数组。就是这种思路，可以从1开始，1本身就是一个漂亮数组，然后将其扩大，注意这里要卡一个N，不能让扩大的数组长度超过N，只要在变为奇数和偶数时加个判定就行了，将不大于N的数组加入到新的数组中，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> beautifulArray(int N) {
        vector<int> res{1};
        while (res.size() < N) {
            vector<int> t;
            for (int num : res) {
                if (num * 2 - 1 <= N) t.push_back(num * 2 - 1);
            }
            for (int num : res) {
                if (num * 2 <= N) t.push_back(num * 2);
            }
            res = t;
        }
        return res;
    }
};

Leetcode933. Number of Recent Calls

Write a class RecentCounter to count recent requests. It has only one method: ping(int t), where t represents some time in milliseconds. Return the number of pings that have been made from 3000 milliseconds ago until now. Any ping with time in [t - 3000, t] will count, including the current ping. It is guaranteed that every call to ping uses a strictly larger value of t than before.

Example 1:

1
2
Input: inputs = ["RecentCounter","ping","ping","ping","ping"], inputs = [[],[1],[100],[3001],[3002]]
Output: [null,1,2,3,3]

Note:

  • Each test case will have at most 10000 calls to ping.
  • Each test case will call ping with strictly increasing values of t.
  • Each call to ping will have 1 <= t <= 10^9.

行吧，我是没看懂这个题是什么意思。。。只是判断t和3000的关系。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class RecentCounter {
public:
    queue<int> q;
    RecentCounter() {
        
    }
    
    int ping(int t) {
        q.push(t);
        while(q.front()<t-3000)
            q.pop();
        return q.size();
    }
};

Leetcode934. Shortest Bridge

In a given 2D binary array A, there are two islands. (An island is a 4-directionally connected group of 1s not connected to any other 1s.)

Now, we may change 0s to 1s so as to connect the two islands together to form 1 island.

Return the smallest number of 0s that must be flipped. (It is guaranteed that the answer is at least 1.)

Example 1:

1
2
Input: [[0,1],[1,0]]
Output: 1

Example 2:

1
2
Input: [[0,1,0],[0,0,0],[0,0,1]]
Output: 2

Example 3:

1
2
Input: [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]]
Output: 1

Note:

  • 1 <= A.length = A[0].length <= 100
  • A[i][j] == 0 or A[i][j] == 1

这道题说是有一个只有0和1的二维数组，其中连在一起的1表示岛屿，现在假定给定的数组中一定有两个岛屿，问最少需要把多少个0变成1才能使得两个岛屿相连。在 LeetCode 中关于岛屿的题目还不少，但是万变不离其宗，核心都是用 DFS 或者 BFS 来解，有些还可以用联合查找 Union Find 来做。这里要求的是最小值，首先预定了一个 BFS，这就相当于洪水扩散一样，一圈一圈的，用的就是 BFS 的层序遍历。好，现在确定了这点后，再来想，这里并不是从某个点开始扩散，而是要从一个岛屿开始扩散，那么这个岛屿的所有的点都是 BFS 的起点，都是要放入到 queue 中的，所以要先来找出一个岛屿的所有点。找的方法就是遍历数组，找到第一个1的位置，然后对其调用 DFS 或者 BFS 来找出所有相连的1，先来用 DFS 的方法，对第一个为1的点调用递归函数，将所有相连的1都放入到一个队列 queue 中，并且将该点的值改为2，然后使用 BFS 进行层序遍历，每遍历一层，结果 res 都增加1，当遇到1时，直接返回 res 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
class Solution {
public:
    int shortestBridge(vector<vector>& A) {
        int res = 0, n = A.size(), startX = -1, startY = -1;
        queue<int> q;
        vector<int> dirX{-1, 0, 1, 0}, dirY = {0, 1, 0, -1};
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (A[i][j] == 0) continue;
                startX = i; startY = j;
                break;
            }
            if (startX != -1) break;
        }
        helper(A, startX, startY, q);
        while (!q.empty()) {
            for (int i = q.size(); i > 0; --i) {
                int t = q.front(); q.pop();
                for (int k = 0; k < 4; ++k) {
                    int x = t / n + dirX[k], y = t % n + dirY[k];
                    if (x < 0 || x >= n || y < 0 || y >= n || A[x][y] == 2) continue;
                    if (A[x][y] == 1) return res;
                    A[x][y] = 2;
                    q.push(x * n + y);
                }
            }
            ++res;
        }
        return res;
    }
    void helper(vector<vector>& A, int x, int y, queue& q) {
        int n = A.size();
        if (x < 0 || x >= n || y < 0 || y >= n || A[x][y] == 0 || A[x][y] == 2) return;
        A[x][y] = 2;
        q.push(x * n + y);
        helper(A, x + 1, y, q);
        helper(A, x, y + 1, q);
        helper(A, x - 1, y, q);
        helper(A, x, y - 1, q);
    }
};

我们也可以使用 BFS 来找出所有相邻的1，再加上后面的层序遍历的 BFS，总共需要两个 BFS，注意这里第一个 BFS 不需要是层序遍历的，而第二个 BFS 是必须层序遍历，可以对比一下看一下这两种写法有何不同，参见代码如下：

``C++
class Solution {
public:
    int shortestBridge(vector<vector>& A) {
        int res = 0, n = A.size();
        queue<int> q, que;
        vector<int> dirX{-1, 0, 1, 0}, dirY = {0, 1, 0, -1};
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (A[i][j] == 0) continue;
                A[i][j] = 2;
                que.push(i * n + j);
                break;
            }
            if (!que.empty()) break;
        }
        while (!que.empty()) {
            int t = que.front(); que.pop();
            q.push(t);
            for (int k = 0; k < 4; ++k) {
                int x = t / n + dirX[k], y = t % n + dirY[k];
                if (x < 0 || x >= n || y < 0 || y >= n || A[x][y] == 0 || A[x][y] == 2) continue;
                A[x][y] = 2;
                que.push(x * n + y);
            }
        }
        while (!q.empty()) {
            for (int i = q.size(); i > 0; --i) {
                int t = q.front(); q.pop();
                for (int k = 0; k < 4; ++k) {
                    int x = t / n + dirX[k], y = t % n + dirY[k];
                    if (x < 0 || x >= n || y < 0 || y >= n || A[x][y] == 2) continue;
                    if (A[x][y] == 1) return res;
                    A[x][y] = 2;
                    q.push(x * n + y);
                }
            }
            ++res;
        }
        return res;
    }
};

LeetCode] 935. Knight Dialer 骑士拨号器

The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:

A chess knight can move as indicated in the chess diagram below:

We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

Given an integer n, return how many distinct phone numbers of length n we can dial.

You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

As the answer may be very large, return the answer modulo 109 + 7.

Example 1:

1
2
3
Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

Example 2:

1
2
3
Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

1
2
Input: n = 3
Output: 46

Example 4:

1
2
Input: n = 4
Output: 104

Example 5:

1
2
3
Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod.

Constraints:

  • 1 <= n <= 5000

这道题说是有一种骑士拨号器，在一个电话拨号盘上跳跃，其跳跃方式是跟国际象棋中的一样，不会国际象棋的童鞋可以将其当作中国象棋中的马，马走日象飞田。这个骑士可以放在 10 个数字键上的任意一个，但其跳到的下一个位置却要符合其在国际象棋中的规则，也就是走日。现在给了一个整数N，说是该骑士可以跳N次，问能拨出多个不同的号码，并且提示了结果要对一个超大数字取余。这里使用一个二维数组 dp，其中 dp[i][j] 表示骑士第i次跳到数字j时组成的不同号码的个数，那么最终所求的就是将 dp[N-1][j] 累加起来，j的范围是0到9。接下来看状态转移方程怎么写，当骑士在第i次跳到数字j时，考虑其第 i-1 次是在哪个位置，可能有多种情况，先来分析拨号键盘的结构，找出从每个数字能到达的下一个位置，可得如下关系：

1
2
3
4
5
6
7
8
9
10
0 -> 4, 6
1 -> 6, 8
2 -> 7, 9
3 -> 4, 8
4 -> 3, 9, 0
5 ->
6 -> 1, 7, 0
7 -> 2, 6
8 -> 1, 3
9 -> 4, 2

可以发现，除了数字5之外，每个数字都可以跳到其他位置，其中4和6可以跳到三个不同位置，其他都只能取两个位置。反过来想，可以去的位置，就表示也可能从该位置回来，所以根据当前的位置j，就可以在数组中找到上一次骑士所在的位置，并将其的 dp 值累加上即可，这就是状态转移的方法，由于第一步是把骑士放到任意一个数字上，就要初始化 dp[0][j] 为1，然后进行状态转移就行了，记得每次累加之后要对超大数取余，最后将 dp[N-1][j] 累加起来的时候，也要对超大数取余，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int knightDialer(int N) {
        int res = 0, M = 1e9 + 7;
        vector<vector<int>> dp(N, vector<int>(10));
        vector<vector<int>> path{{4, 6}, {6, 8}, {7, 9}, {4, 8}, {3, 9, 0}, {}, {1, 7, 0}, {2, 6}, {1, 9}, {4, 2}};
        for (int i = 0; i < 10; ++i) dp[0][i] = 1;
        for (int i = 1; i < N; ++i) {
            for (int j = 0; j <= 9; ++j) {
                for (int idx : path[j]) {
                    dp[i][j] = (dp[i][j] + dp[i - 1][idx]) % M;
                }
            }
        }
        for (int i = 0; i < 10; ++i) res = (res + dp.back()[i]) % M;
        return res;
    }
};

我们也可以用递归+记忆数组的方式来写，整体思路和迭代的方法并没有什么区别，之前类似的题目也不少，就不多解释了，可以对照上面的讲解和代码来理解，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int knightDialer(int N) {
        int res = 0, M = 1e9 + 7;
        vector<vector<int>> memo(N + 1, vector<int>(10));
        vector<vector<int>> path{{4, 6}, {6, 8}, {7, 9}, {4, 8}, {3, 9, 0}, {}, {1, 7, 0}, {2, 6}, {1, 9}, {4, 2}};
        for (int i = 0; i < 10; ++i) {
        	res = (res + helper(N - 1, i, path, memo)) % M;
        }
        return res;
    }
    int helper(int n, int cur, vector<vector<int>>& path, vector<vector<int>>& memo) {
    	if (n == 0) return 1;
    	if (memo[n][cur] != 0) return memo[n][cur];
    	int res = 0, M = 1e9 + 7;
    	for (int idx : path[cur]) {
    		res = (res + helper(n - 1, idx, path, memo)) % M;
    	}
    	return memo[n][cur] = res;
    }
};

Leetcode937. Reorder Data in Log Files

You have an array of logs. Each log is a space delimited string of words.

For each log, the first word in each log is an alphanumeric identifier. Then, either:

  • Each word after the identifier will consist only of lowercase letters, or;
  • Each word after the identifier will consist only of digits.
    We will call these two varieties of logs letter-logs and digit-logs. It is guaranteed that each log has at least one word after its identifier.

Reorder the logs so that all of the letter-logs come before any digit-log. The letter-logs are ordered lexicographically ignoring identifier, with the identifier used in case of ties. The digit-logs should be put in their original order.

Return the final order of the logs.

Example 1:

1
2
Input: logs = ["dig1 8 1 5 1","let1 art can","dig2 3 6","let2 own kit dig","let3 art zero"]
Output: ["let1 art can","let3 art zero","let2 own kit dig","dig1 8 1 5 1","dig2 3 6"]

对于每条日志，其第一个字为字母数字标识符。然后，要么：标识符后面的每个字将仅由小写字母组成，或标识符后面的每个字将仅由数字组成。

将这两种日志分别称为字母日志和数字日志。保证每个日志在其标识符后面至少有一个字。将日志重新排序，使得所有字母日志都排在数字日志之前。字母日志按字母顺序排序，忽略标识符，标识符仅用于表示关系。数字日志应该按原来的顺序排列。返回日志的最终顺序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    
    static bool cmp(string a,string b) {
        int ii = 0, jj = 0;
        while(a[ii ++] != ' ') ;
        while(b[jj ++] != ' ') ;
        return a.substr(ii, a.length() - ii + 1) <= b.substr(jj, b.length() - jj + 1);
        // 这里要比较后边所有的，不能比较一个字符
    }
    
    vector<string> reorderLogFiles(vector<string>& logs) {
        vector<string> res;
        int len = logs.size();
        vector<bool> flag(len, 0);
        for(int i = 0; i < len; i ++) {
            int ii = 0;
            while(logs[i][ii ++] != ' ') ;
            cout << logs[i][ii] << endl;
            if('a' <= logs[i][ii] && logs[i][ii] <= 'z') {
                res.push_back(logs[i]);
                flag[i] = 1;
            }
        }
        sort(res.begin(), res.end(), cmp);
        for(string t : res)
            cout << t << endl;
        for(int i = 0; i < len; i ++) {
            if(!flag[i])
                res.push_back(logs[i]);
        }
        return res;
    }
};

Leetcode938. Range Sum of BST

Given the root node of a binary search tree, return the sum of values of all nodes with value between L and R (inclusive).

The binary search tree is guaranteed to have unique values.
一棵树，给定了根节点，再给一个范围（L，R），求这棵二叉树中在这个范围内的数的和，太简单了。。。直接递归查找，没难度，还奇怪呢这么简单的题还标着个medium。。。

1
2
3
4
Example 1:

Input: root = [10,5,15,3,7,null,18], L = 7, R = 15
Output: 32
1
2
3
4
Example 2:

Input: root = [10,5,15,3,7,13,18,1,null,6], L = 6, R = 10
Output: 23
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int rangeSumBST(TreeNode* root, int L, int R) {
        if(root){
            if(root->val >= L && root->val <= R)
                return root->val + rangeSumBST(root->left,L,R)+rangeSumBST(root->right,L,R);
            else
                return rangeSumBST(root->left,L,R)+rangeSumBST(root->right,L,R);            
        }
        return 0;
    }
};

Leetcode939. Minimum Area Rectangle

Given a set of points in the xy-plane, determine the minimum area of a rectangle formed from these points, with sides parallel to the x and y axes.

If there isn’t any rectangle, return 0.

Example 1:

1
2
Input: [[1,1],[1,3],[3,1],[3,3],[2,2]]
Output: 4

Example 2:

1
2
Input: [[1,1],[1,3],[3,1],[3,3],[4,1],[4,3]]
Output: 2

Note:

  • 1 <= points.length <= 500
  • 0 <= points[i][0] <= 40000
  • 0 <= points[i][1] <= 40000
  • All points are distinct.

这道题给了我们一堆点的坐标，问能组成的最小的矩形面积是多少，题目中限定了矩形的边一定是平行于主轴的，不会出现旋转矩形的形状。如果知道了矩形的两个对角顶点坐标，求面积就非常的简单了，但是随便取四个点并不能保证一定是矩形，不过这四个点坐标之间是有联系的，相邻的两个顶点要么横坐标，要么纵坐标，一定有一个是相等的，这个特点先记下。策略是，先找出两个对角线的顶点，一但两个对角顶点确定了，其实这个矩形的大小也就确定了，另外的两个点其实就是分别在跟这两个点具有相同的横坐标或纵坐标的点中寻找即可，为了优化查找的时间，可以事先把所有具有相同横坐标的点的纵坐标放入到一个 HashSet 中，使用一个 HashMap，建立横坐标和所有具有该横坐标的点的纵坐标的集合之间的映射。然后开始遍历任意两个点的组合，由于这两个点必须是对角顶点，所以其横纵坐标均不能相等，若有一个相等了，则跳过该组合。否则看其中任意一个点的横坐标对应的集合中是否均包含另一个点的纵坐标，均包含的话，说明另两个顶点也是存在的，就可以计算矩形的面积了，更新结果 res，若最终 res 还是初始值，说明并没有能组成矩形，返回0即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int minAreaRect(vector<vector<int>>& points) {
        int res = INT_MAX, n = points.size();
        unordered_map<int, unordered_set<int>> m;
        for (auto point : points) {
            m[point[0]].insert(point[1]);
        }
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (points[i][0] == points[j][0] || points[i][1] == points[j][1]) continue;
                if (m[points[i][0]].count(points[j][1]) && m[points[j][0]].count(points[i][1])) {
                    res = min(res, abs(points[i][0] - points[j][0]) * abs(points[i][1] - points[j][1]));
                }   
            }
        }
        return res == INT_MAX ? 0 : res;
    }
};

Leetcode941. Valid Mountain Array

Given an array A of integers, return true if and only if it is a valid mountain array.

Recall that A is a mountain array if and only if:

  • A.length >= 3
  • There exists some i with 0 < i < A.length - 1 such that:
    • A[0] < A[1] < … A[i-1] < A[i]
    • A[i] > A[i+1] > … > A[A.length - 1]

Example 1:

1
2
Input: [2,1]
Output: false

Example 2:
1
2
Input: [3,5,5]
Output: false

Example 3:
1
2
Input: [0,3,2,1]
Output: true

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
	public:
    bool validMountainArray(vector<int>& A) {
        bool flag = false;
        if(A.size() < 3)
            return false;
        int i = 0;
        for(; i < A.size()-1; i ++)
            if(A[i] >= A[i+1])
                break;
        if(i == 0 || i == A.size()-1)
            return false;
        for(; i < A.size()-1; i ++)
            if(A[i] <= A[i+1])
                break;
        if(i != A.size() - 1)
            return false;
        return true;
    }
};

Leetcode942. DI String Match

Given a string S that only contains “I” (increase) or “D” (decrease), letN = S.length.

Return any permutation A of [0, 1, …, N] such that for alli = 0, ..., N-1:

If S[i] == “I”, then A[i] < A[i+1]
If S[i] == “D”, then A[i] > A[i+1]

Example 1:

1
2
Input: "IDID"
Output: [0,4,1,3,2]

Example 2:
1
2
Input: "III"
Output: [0,1,2,3]

Example 3:
1
2
Input: "DDI"
Output: [3,2,0,1]

Note:

1 <= S.length <= 10000
S only contains characters “I” or “D”.

题目的意思是，将字符串与数组一一对应，因为数组多一位，不考虑这一位。剩下的位置，如果字符串写的是‘I’，那么该位置上的数应该比右边所有的数都小。而如果是‘D’，则是比右边的都大。现在需要找到其中任意一组。

其实这个题是一个贪心，并且有点dp的感觉。感觉这个题解不唯一，其实还是比较简单能够证明反例。评论有人提出了解法证明，可以看一下：

只需要证明，对于任何 > 或者 < , 算法的规则都能满足。
△N = max-min; 由于每次遇到一个符号，△N-1。
当符号为“ < < <”: max—可以保证符号的正确性。
当符号为“ > > >”: min++可以保住符号的正确性。
当符号为“ ……< > < “: 任意时刻max和min开始比较，是否满足 min < max?
答案是：YES! 由于符号的数量为N，最开始△N = N。由于至少出现一对大于号和小于号 , min(△N)= 1，仍然满足min < max;
综上，得证。

因为每一位对应的数字只有两种情况：比右边所有数都大，或者都小。那么我们可以设定两个值，初始的话：low = 0，high = N。这样，从左开始遍历字符串，碰见一个字符，如果是‘I’，那么就直接赋值low，同时low++。这样，‘I’右边所有的数，一定是都比这个位置大的。因为此时low>a[i]，同时high > low。

反而言之，碰见‘D’，直接赋值hight，同时high—。这样所有的数就一定比这个小了。大概就是这样，在O(n)的时间复杂度下就能构造出答案数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<int> diStringMatch(string S) {
        vector<int> res = vector<int>(S.size()+1);
        int low = 0,high=S.size();
        for(int i=0;i<S.size();i++){
            if(S[i]=='I')
                res[i]=low++;
            else
                res[i]=high--;
        }
        res[S.size()]=low;
        return res;
    }
};

Leetcode944. Delete Columns to Make Sorted

We are given an array A of N lowercase letter strings, all of the same length.

Now, we may choose any set of deletion indices, and for each string, we delete all the characters in those indices.

For example, if we have an array A = [“abcdef”,”uvwxyz”] and deletion indices {0, 2, 3}, then the final array after deletions is [“bef”, “vyz”], and the remaining columns of A are [“b”,”v”], [“e”,”y”], and [“f”,”z”]. (Formally, the c-th column is [A[0][c], A[1][c], …, A[A.length-1][c]].)

Suppose we chose a set of deletion indices D such that after deletions, each remaining column in A is in non-decreasing sorted order.

Return the minimum possible value of D.length.

Example 1:

1
2
Input: ["cba","daf","ghi"]
Output: 1

Explanation:
After choosing D = {1}, each column [“c”,”d”,”g”] and [“a”,”f”,”i”] are in non-decreasing sorted order.
If we chose D = {}, then a column [“b”,”a”,”h”] would not be in non-decreasing sorted order.
Example 2:
1
2
Input: ["a","b"]
Output: 0

Explanation: D = {}
Example 3:
1
2
Input: ["zyx","wvu","tsr"]
Output: 3

Explanation: D = {0, 1, 2}

Note:

1 <= A.length <= 100
1 <= A[i].length <= 1000

字符串数组 A 中的每个字符串元素的长度相同，统计index个数，这个index 的要求是 A[i].charAt(index)，i=0,1,2,3,4 组成的 字符序列 不是严格递增。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int minDeletionSize(vector<string>& A) {
        int isize=A.size();
        int jsize=A[0].size();
        int ans=0;
        for(int j=0;j<jsize;j++){
            for(int i=0;i<isize-1;i++){
                if(A[i][j]>A[i+1][j]){
                    ans++;
                    break;
                }
            }
        }
        return ans;
    }
};

Leetcode945. Minimum Increment to Make Array Unique

Given an array of integers A, a move consists of choosing any A[i], and incrementing it by 1.

Return the least number of moves to make every value in A unique.

Example 1:

1
2
3
Input: [1,2,2]
Output: 1
Explanation:  After 1 move, the array could be [1, 2, 3].

Example 2:

1
2
3
4
Input: [3,2,1,2,1,7]
Output: 6
Explanation:  After 6 moves, the array could be [3, 4, 1, 2, 5, 7].
It can be shown with 5 or less moves that it is impossible for the array to have all unique values.

Note:

  • 0 <= A.length <= 40000
  • 0 <= A[i] < 40000

这道题给了一个数组，说是每次可以将其中一个数字增加1，问最少增加多少次可以使得数组中没有重复数字。给的两个例子可以帮助我们很好的理解题意，这里主要参考了 lee215 大神的帖子，假如数组中没有重复数字的话，则不需要增加，只有当重复数字存在的时候才需要增加。比如例子1中，有两个2，需要将其中一个2增加到3，才能各不相同。但有时候只增加一次可能并不能解决问题，比如例子2中，假如要处理两个1，增加其中一个到2并不能解决问题，因此2也是有重复的，甚至增加到3还是有重复，所以一直得增加到4才行，但此时如何知道后面是否还有1，所以需要一个统一的方法来增加，最好是能从小到大处理数据，则先给数组排个序，然后用一个变量 need 表示此时需要增加到的数字，初始化为0，由于是从小到大处理，这个 need 会一直变大，而且任何小于 need 的数要么是数组中的数，要么是某个数字增后的数，反正都是出现过了。然后开始遍历数组，对于遍历到的数字 num，假如 need 大于 num，说明此时的 num 是重复数字，必须要提高到 need，则将 need-num 加入结果 res 中，反之若 need 小于 num，说明 num 并未出现过，不用增加。然后此时更新 need 为其和 num 之间的较大值并加1，因为 need 不能有重复，所以要加1，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int minIncrementForUnique(vector<int>& A) {
        int res = 0, need = 0;
        sort(A.begin(), A.end());
        for (int num : A) {
        	res += max(need - num, 0);
        	need = max(num, need) + 1;
        }
        return res;
    }
};

假如数组中有大量的重复数字的话，那么上面的方法还是需要一个一个的来处理，来看一种能同时处理大量的重复数字的方法。这里使用了一个 TreeMap 来统计每个数字和其出现的次数之间的映射。由于 TreeMap 可以对 key 自动排序，所以就没有必要对原数组进行排序了，这里还是要用变量 need，整体思路和上面的解法很类似。建立好了 TreeMap 后开始遍历，此时单个数字的增长还是 max(need - num, 0)，这个已经在上面解释过了，由于可能由多个，所以还是要乘以个数 a.second，到这里还没有结束，因为 a.second 这多么多个数字都被增加到了同一个数字，而这些数字应该彼此再分开，好在现在没有比它们更大的数字，那么问题就变成了将k个相同的数字变为不同，最少的增加次数，答案是 k*(k-1)/2，这里就不详细推导了，其实就是个等差数列求和，这样就可以知道将 a.second 个数字变为不同总共需要增加的次数，下面更新 need，在 max(need, num) 的基础上，还要增加个数 a.second，从而到达一个最小的新数字，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int minIncrementForUnique(vector<int>& A) {
        int res = 0, need = 0;
        map<int, int> numCnt;
        for (int num : A) ++numCnt[num];
        for (auto &a : numCnt) {
        	res += a.second * max(need - a.first, 0) + a.second * (a.second - 1) / 2;
        	need = max(need, a.first) + a.second;
        }
        return res;
    }
};

再来看一种联合查找 Union Find 的方法，这是一种并查集的方法，在岛屿群组类的问题上很常见，可以搜搜博主之前关于岛屿类题目的讲解，很多都使用了这种方法。但是这道题乍一看好像跟群组并没有明显的关系，但其实是有些很微妙的联系的。这里的 root 使用一个 HashMap，而不是用数组，因为数字不一定是连续的，而且可能跨度很大，使用 HashMap 会更加省空间一些。遍历原数组，对于每个遍历到的数字 num，调用 find 函数，这里实际上就是查找上面的方法中的 need，即最小的那个不重复的新数字，而 find 函数中会不停的更新 root[x]，而只要x存在，则不停的自增1，直到不存在时候，则返回其本身，那么实际上从 num 到 need 中所有的数字的 root 值都标记成了 need，就跟它们是属于一个群组一样，这样做的好处在以后的查询过程中可以更快的找到 need 值，这也是为啥这种方法不用给数组排序的原因，若还是不理解的童鞋可以将例子2代入算法一步一步执行，看每一步的 root 数组的值是多少，应该不难理解，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int minIncrementForUnique(vector<int>& A) {
        int res = 0;
        unordered_map<int, int> root;
        for (int num : A) {
        	res += find(root, num) - num;
        }
        return res;
    }
    int find(unordered_map<int, int>& root, int x) {
    	return root[x] = root.count(x) ? find(root, root[x] + 1) : x;
    }
};

LeetCode946. Validate Stack Sequences

Given two sequences pushed and popped with distinct values, return true if and only if this could have been the result of a sequence of push and pop operations on an initially empty stack.

Example 1:

1
2
3
4
5
Input: pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
Output: true
Explanation: We might do the following sequence:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1

Example 2:

1
2
3
Input: pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
Output: false
Explanation: 1 cannot be popped before 2.

Note:

  • 0 <= pushed.length == popped.length <= 1000
  • 0 <= pushed[i], popped[i] < 1000
  • pushed is a permutation of popped.
  • pushed and popped have distinct values.

这道题给了两个序列 pushed 和 popped，让判断这两个序列是否能表示同一个栈的压入和弹出操作，由于栈是后入先出的顺序，所以并不是任意的两个序列都是满足要求的。比如例子2中，先将 1，2，3，4 按顺序压入栈，此时4和3出栈，接下来压入5，再让5出栈，接下来出栈的是2而不是1，所以例子2会返回 false。而这道题主要就是模拟这个过程，使用一个栈，和一个变量i用来记录弹出序列的当前位置，此时遍历压入序列，对遍历到的数字都压入栈，此时要看弹出序列当前的数字是否和栈顶元素相同，相同的话就需要移除栈顶元素，并且i自增1，若下一个栈顶元素还跟新位置上的数字相同，还要进行相同的操作，所以用一个 while 循环来处理。直到最终遍历完压入序列后，若此时栈为空，则说明是符合题意的，否则就是 false，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
        stack<int> st;
        int i = 0;
        for (int num : pushed) {
        	st.push(num);
        	while (!st.empty() && st.top() == popped[i]) {
        		st.pop();
        		++i;
        	}
        }
        return st.empty();
    }
};

Leetcode947. Most Stones Removed with Same Row or Column

On a 2D plane, we place n stones at some integer coordinate points. Each coordinate point may have at most one stone.

A stone can be removed if it shares either the same row or the same column as another stone that has not been removed.

Given an array stones of length n where stones[i] = [xi, yi] represents the location of the ith stone, return the largest possible number of stones that can be removed.

Example 1:

1
2
3
4
5
6
7
8
9
Input: stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]]
Output: 5
Explanation: One way to remove 5 stones is as follows:
Remove stone [2,2] because it shares the same row as [2,1].
Remove stone [2,1] because it shares the same column as [0,1].
Remove stone [1,2] because it shares the same row as [1,0].
Remove stone [1,0] because it shares the same column as [0,0].
Remove stone [0,1] because it shares the same row as [0,0].
Stone [0,0] cannot be removed since it does not share a row/column with another stone still on the plane.

Constraints:

  • 1 <= stones.length <= 1000
  • 0 <= xi, yi <= 104
  • No two stones are at the same coordinate point.

给一个2D数组，其中的元素代表2D的位置，同一位置只会有一个石头，同行或同列的石头能被移走（前提是存在与它同行或同列的石头，如果只有它自己就不能移走），问最多可移走多少个石头。

思路

问题转换：同行同列的石头阵可以被移走直到只剩下一个石头。那么把同行同列的石头全都归到一个group，这个group的个数就是最后剩下的石头数量。则被移走的石头数量=石头总数量 - group个数

任务就变成了把同行同列的石头归到一个group里，两种方法，DFS和Union-Find

DFS

可把 (row, col) 看作一条边，建立无向图。但是注意一个问题，就是(1,2) 和 (2,1)是两个位置，但会被认为是同一条边，这时需要把这两种边区分开，题中有这样一个限制条件0 <= xi, yi <= 104 ，所以可定义0～10000是row的区间，10001～20001是col的范围。也就是把col + 10001，但是实际上col+10000也通过了。

这样做就可以访问一个位置（row，col）时，把row行和col列的位置全都标记为访问过，再递归标记它们关联的行和列，为一个组。下一次再从未访问过的位置重新标记新的一组。这样就可找出一共有多少个组。

可能行和列的概念容易混淆，可以认为列也是要遍历的“行”，只不过列的index是从10000开始的。

这里标记访问过不是一个位置一个位置地标，而是标整行整列，表示这一行或列已经访问过（可把列理解为index从10000开始的“行”）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//19ms
    public int removeStones(int[][] stones) {
        int groups = 0;
        HashMap<Integer, List<Integer>> graph = new HashMap<>();
        boolean[] visited = new boolean[20001];
        
        for(int[] stone : stones) {
            int row = stone[0];
            int col = stone[1] + 10000;
            if(!graph.containsKey(row)) {
                graph.put(row, new ArrayList<Integer>());
            }
            graph.get(row).add(col);
            
            if(!graph.containsKey(col)) {
                graph.put(col, new ArrayList<Integer>());
            }
            graph.get(col).add(row);
        }
        
        for(Integer key : graph.keySet()) {
            if(visited[key]) continue;
            dfs(key, graph, visited);
            groups ++;
        }
        return stones.length - groups;
    }
    
    void dfs(int rowCol, HashMap<Integer, List<Integer>> graph, boolean[] visited) {
        if(visited[rowCol]) return;
        visited[rowCol] = true;
        //行的话找同一列，列的话找同一行的stone，把同行或同列的标记为访问，为同一group
        for(Integer next : graph.get(rowCol)) {
            if(visited[next]) continue;
            dfs(next, graph, visited);
        }
    }

如果DFS深度过深，担心StackOverflowError，可用stack版DFS，和BFS差不多，只不过BFS用的queue储存节点，先进先访问。DFS用stack储存节点，后进的先访问，直到到达尽头。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public int removeStones(int[][] stones) {
    int groups = 0;
    HashMap<Integer, List<Integer>> graph = new HashMap<>();
    boolean[] visited = new boolean[20001];
    
    for(int[] stone : stones) {
        int row = stone[0];
        int col = stone[1] + 10000;
        if(!graph.containsKey(row)) {
            graph.put(row, new ArrayList<Integer>());
        }
        graph.get(row).add(col);
        
        if(!graph.containsKey(col)) {
            graph.put(col, new ArrayList<Integer>());
        }
        graph.get(col).add(row);
    }
    
    for(Integer key : graph.keySet()) {
        if(visited[key]) continue;
        Stack<Integer> stack = new Stack<>();
        stack.push(key);
        visited[key] = true;
        while(!stack.isEmpty()) {
            int rowCol = stack.pop();
            for(Integer next : graph.get(rowCol)) {
                if(visited[next]) continue;
                visited[next] = true;
                stack.push(next);
            }
        }
        groups ++;
    }
    return stones.length - groups;
}

Union-Find

思路和上面一样，也是把同行同列的归为一个group，最后用石头总数-group个数。

还是把(row, col）看成一条边，也可理解为它们是关联的数字。还是row是0～10000区间，col是10001～20001区间。但是这里加了一个情况，就是一个点还没有被访问的时候，它的parent是0，访问过的点要么parent是它自己，要么是其他点。所以为了和0区别开，row的范围移到1～10001，col移到10002～20002。所以row要加1，col要加10002。

  • parent：上面还有其他parent。
  • root：parent是它自己（最上层parent）。

统一把col的root设为row的root。这样做有什么用处？row和col有同一个root，当同一列的位置来的时候，可通过col找到这个root，当同一行的位置来的时候，可通过row找到同一root，这样就可达到把同行和同列的石头都归为一个group的效果。

当row和col未访问过，即parent==0时，把row的parent标记为它自己，col的parent标记为row。一个访问过一个没访问过时，标记root为访问过的root。

当有不同的root时，把col的root，重点强调是root，而不是简单的parent，标记为row的root

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    int removeStones(vector<vector<int>>& stones) {
        vector<int> parent(20003, 0);
        int res = 0;
        for (auto stone : stones)
            uni(parent, stone[0]+1, stone[1]+10002, res);
        return stones.size() - res;
    }
    
    void uni(vector<int>& parent, int st1, int st2, int& res) {
        int pr = find(parent, st1);
        int pc = find(parent, st2);
        if (pr == pc) {
            if (pr == 0) {
                res ++;
                parent[st1] = st1;
                parent[st2] = st1;
            }
        }
        else {
            if (pr == 0)
                parent[st1] = pc;
            else if (pc == 0)
                parent[st2] = pr;
            else {
                res --;
                parent[pc] = pr;
            }
        }
    }
    
    int find(vector<int>& parent, int st) {
        int sp = parent[st];
        while(sp != parent[sp])
            sp = parent[st] = find(parent, sp);
        return sp;
    }
};

Leetcode948. Bag of Tokens

You have an initial power P, an initial score of 0 points, and a bag of tokens.

Each token can be used at most once, has a value token[i], and has potentially two ways to use it.

  • If we have at least token[i] power, we may play the token face up, losing token[i] power, and gaining 1 point.
  • If we have at least 1 point, we may play the token face down, gaining token[i] power, and losing 1 point.

Return the largest number of points we can have after playing any number of tokens.

Example 1:

1
2
Input: tokens = [100], P = 50
Output: 0

Example 2:

1
2
Input: tokens = [100,200], P = 150
Output: 1

Example 3:

1
2
Input: tokens = [100,200,300,400], P = 200
Output: 2

Note:

  • tokens.length <= 1000
  • 0 <= tokens[i] < 10000
  • 0 <= P < 10000

这道题说是给了一个初始力量值P，然后有一个 tokens 数组，有两种操作可以选择，一种是减去 tokens[i] 的力量，得到一分，但是前提是减去后剩余的力量不能为负。另一种是减去一分，得到 tokens[i] 的力量，前提是减去后的分数不能为负，问一顿操作猛如虎后可以得到的最高分数是多少。这道题其实题意不是太容易理解，而且例子也没给解释，博主也是读了好几遍题目才明白的。比如例子3，开始有 200 的力量，可以先花 100，得到1个积分，此时还剩 100 的力量，但由于剩下的 token 值都太大，没法换积分了，只能用积分来换力量，既然都是花一个1个积分，肯定是要换最多的力量，于是换来 400 力量，此时总共有 500 的力量，积分还是0，但是一顿操作后，白嫖了 400 的力量，岂不美哉？！这 500 的力量刚好可以换两个积分，所以最后返回的就是2。通过上述分析，基本上可以知道策略了，从最小的 token 开始，用力量换积分，当力量不够时，就用基本换最大的力量，如果没有积分可以换力量，就结束，或者所有的 token 都使用过了，也结束，这就是典型的贪婪算法 Greedy Algorithm，也算对得起其 Medium 的身价。这里先给 tokens 数组排个序，然后使用双指针i和j，分别指向开头和末尾，当 i<=j 进行循环，从小的 token 开始查找，只要力量够，就换成积分，不能换的时候，假如 i>j 或者此时积分为0，则退出；否则用一个积分换最大的力量，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int bagOfTokensScore(vector<int>& tokens, int P) {
        int res = 0, cur = 0, n = tokens.size(), i = 0, j = n - 1;
        sort(tokens.begin(), tokens.end());
        while (i <= j) {
            while (i <= j && tokens[i] <= P) {
                P -= tokens[i++];
                res = max(res, ++cur);
            }
            if (i > j || cur == 0) break;
            --cur;
            P += tokens[j--];
        }
        return res;
    }
};

我们也可以换一种写法，不用 while 套 while，而是换成赏心悦目的 if … else 语句，其实也没差啦，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int bagOfTokensScore(vector<int>& tokens, int P) {
        int res = 0, cur = 0, n = tokens.size(), i = 0, j = n - 1;
        sort(tokens.begin(), tokens.end());
        while (i <= j) {
            if (P >= tokens[i]) {
                P -= tokens[i++];
                res = max(res, ++cur);
            } else if (cur > 0) {
                --cur;
                P += tokens[j--];
            } else {
                break;
            }
        }
        return res;
    }
};

我们也可以使用递归来做，使用一个子函数 helper，将i和j当作参数输入，其实原理跟上的方法一摸一样，不难理解，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int bagOfTokensScore(vector<int>& tokens, int P) {
        sort(tokens.begin(), tokens.end());
        return helper(tokens, P, 0, (int)tokens.size() - 1, 0);
    }
    int helper(vector<int>& tokens, int P, int i, int j, int cur) {
        if (i > j) return cur;
        int res = cur;
        if (tokens[i] <= P) {
            res = max(res, helper(tokens, P - tokens[i], i + 1, j, cur + 1));
        } else if (cur > 0) {
            res = max(res, helper(tokens, P + tokens[j], i, j - 1, cur - 1));
        }
        return res;
    }
};

Leetcode949. Largest Time for Given Digits

Given an array of 4 digits, return the largest 24 hour time that can be made. The smallest 24 hour time is 00:00, and the largest is 23:59. Starting from 00:00, a time is larger if more time has elapsed since midnight. Return the answer as a string of length 5. If no valid time can be made, return an empty string.

Example 1:

1
2
Input: [1,2,3,4]
Output: "23:41"

Example 2:
1
2
Input: [5,5,5,5]
Output: ""

使用STL中的全排列生成：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
	public:
    string largestTimeFromDigits(vector<int>& A) {
        string res = "";
        sort(A.begin(), A.end(), greater<int>());
        do {
            if( (A[0] <= 1 || (A[0] == 2 && A[1] < 4)) && A[2] < 6) {
                stringstream ss;
                ss << A[0] << A[1] << ":" << A[2] << A[3];
                return ss.str();
            }
        } while(prev_permutation(A.begin(), A.end()));
        return "";
    }
};

Leetcode950. Reveal Cards In Increasing Order

In a deck of cards, every card has a unique integer. You can order the deck in any order you want.

Initially, all the cards start face down (unrevealed) in one deck.

Now, you do the following steps repeatedly, until all cards are revealed:

Take the top card of the deck, reveal it, and take it out of the deck.
If there are still cards in the deck, put the next top card of the deck at the bottom of the deck.
If there are still unrevealed cards, go back to step 1. Otherwise, stop.
Return an ordering of the deck that would reveal the cards in increasing order.

The first entry in the answer is considered to be the top of the deck.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
Input: [17,13,11,2,3,5,7]
Output: [2,13,3,11,5,17,7]
Explanation: 
We get the deck in the order [17,13,11,2,3,5,7] (this order doesn't matter), and reorder it.
After reordering, the deck starts as [2,13,3,11,5,17,7], where 2 is the top of the deck.
We reveal 2, and move 13 to the bottom.  The deck is now [3,11,5,17,7,13].
We reveal 3, and move 11 to the bottom.  The deck is now [5,17,7,13,11].
We reveal 5, and move 17 to the bottom.  The deck is now [7,13,11,17].
We reveal 7, and move 13 to the bottom.  The deck is now [11,17,13].
We reveal 11, and move 17 to the bottom.  The deck is now [13,17].
We reveal 13, and move 17 to the bottom.  The deck is now [17].
We reveal 17.
Since all the cards revealed are in increasing order, the answer is correct.

Note:

1 <= A.length <= 1000
1 <= A[i] <= 10^6
A[i] != A[j] for all i != j

woc什么乱七八糟的题，这个确实没懂。

从牌组顶部抽一张牌，显示它，然后将其从牌组中移出。
如果牌组中仍有牌，则将下一张处于牌组顶部的牌放在牌组的底部。
如果仍有未显示的牌，那么返回步骤 1。否则，停止行动。
得到的序列要求是递增序列。

例如 1 3 2 通过上述变换，可以得到1 2 3，满足题目要求。

解法是：1 2 3 通过上述变换，可以得到 1 3 2，即这道题的解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> deckRevealedIncreasing(vector<int>& deck) {
        queue<int> q;
        vector<int> res(deck.size());
        sort(deck.begin(),deck.end());
        for(int i=0;i<deck.size();i++)
            q.push(i);
        for(int i=0;i<deck.size();i++)
        {
            int temp = q.front();
            res[temp]=deck[i];
            q.pop();
            
            temp = q.front();
            q.push(temp);
            q.pop();
        }
        return res;
    }
};

Leetcode951. Flip Equivalent Binary Trees

For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.

A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.

Write a function that determines whether two binary trees are flip equivalent. The trees are given by root nodes root1 and root2.

Example 1:

Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.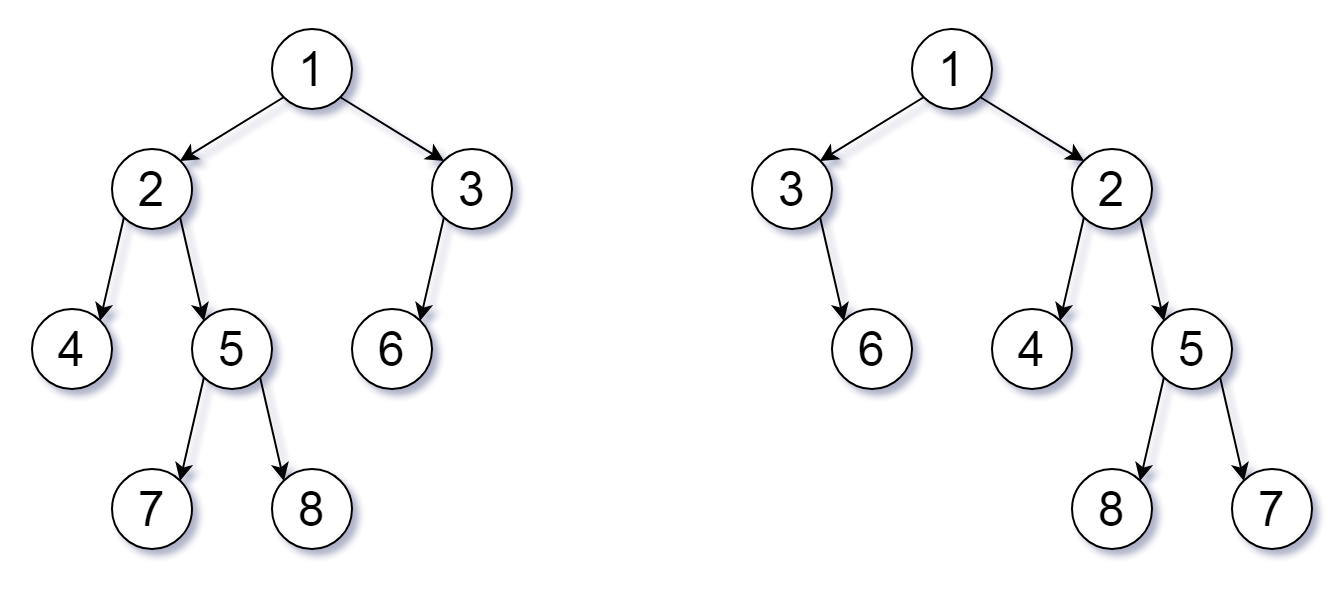

这种做法好复杂啊。。。有太多情况需要考虑了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
class Solution {
public:
    
    bool compare(TreeNode* root1, TreeNode* root2){
        if( root1->left == NULL && root1->right == NULL && root2->left == NULL && root2->right == NULL ) {
            return true;
        }
        else if( root1->left != NULL && root1->right != NULL && root2->left != NULL && root2->right != NULL ) {
             if(root1->left->val == root2->left->val && root1->right->val == root2->right->val) {
                return true;
            } else if(root1->right->val == root2->left->val && root1->left->val == root2->right->val) {
                TreeNode* temp = root1->right;
                root1->right = root1->left;
                root1->left = temp;
                return true;
            } else {
                return false;
            }
        } else if ( root1->left == NULL && root1->right != NULL && root2->left == NULL && root2->right != NULL ){
            if(root1->right->val == root2->right->val) {
                return true;
            } else {
                return false;
            }
        } else if ( root1->left != NULL && root1->right == NULL && root2->left != NULL && root2->right == NULL ) {
            if(root1->left->val == root2->left->val) {
                return true;
            } else {
                return false;
            }
        } else if ( root1->left == NULL && root1->right != NULL && root2->left != NULL && root2->right == NULL ){
            if(root1->right->val == root2->left->val) {
                root1->left = root1->right;
                root1->right = NULL;
                return true;
            } else {
                return false;
            }
        } else if ( root1->left != NULL && root1->right == NULL && root2->left == NULL && root2->right != NULL ) {
            if(root1->left->val == root2->right->val) {
                root1->right = root1->left;
                root1->left = NULL;
                return true;
            } else {
                return false;
            }
        }
        return false;
    }

    bool order(TreeNode* root1, TreeNode* root2){
        if (root1 == NULL && root2 == NULL) {
            return true;
        }
        if (root1 == NULL || root2 == NULL) {
            return false;
        }
        if( root1 != NULL && root2 != NULL ) {
            if(root1->val == root2->val)
                compare(root1, root2);
            else
                return false;
            return order(root1->left, root2->left) && order(root1->right, root2->right);
        }
        return false;
        
        
    }
    
    bool flipEquiv(TreeNode* root1, TreeNode* root2) {
        return order(root1, root2);
    }
};

另一种做法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool flipEquiv(TreeNode* root1, TreeNode* root2) {
        // Two null trees are flip equivalent
        // A non-null and null tree are NOT flip equivalent
        // Two non-null trees with different root values are NOT flip equivalent
        // Two non-null trees are flip equivalent if
        //      The left subtree of tree1 is flip equivalent with the left subtree of tree2 and the right subtree of tree1 is   
        //      flipequivalent with the right subtree of tree2 (no flip case)
        //      OR
        //      The right subtree of tree1 is flip equivalent with the left subtree of tree2 and the left subtree of tree1 is
        //      flipequivalent with the right subtree of tree2 (flip case)
        if ( !root1 && !root2 ) return true;
        if ( !root1 && root2 || root1 &&!root2 || root1->val != root2->val ) return false;
        return flipEquiv( root1->left, root2->left ) && flipEquiv( root1->right, root2->right )
            || flipEquiv( root1->right, root2->left ) && flipEquiv( root1->left, root2->right );
    }
};

Leetcode953. Verifying an Alien Dictionary

In an alien language, surprisingly they also use english lowercase letters, but possibly in a different order. The order of the alphabet is some permutation of lowercase letters.

Given a sequence of words written in the alien language, and the order of the alphabet, return true if and only if the given words are sorted lexicographicaly in this alien language.

Example 1:

1
2
3
Input: words = ["hello","leetcode"], order = "hlabcdefgijkmnopqrstuvwxyz"
Output: true
Explanation: As 'h' comes before 'l' in this language, then the sequence is sorted.

Example 2:
1
2
3
Input: words = ["word","world","row"], order = "worldabcefghijkmnpqstuvxyz"
Output: false
Explanation: As 'd' comes after 'l' in this language, then words[0] > words[1], hence the sequence is unsorted.

Example 3:
1
2
3
Input: words = ["apple","app"], order = "abcdefghijklmnopqrstuvwxyz"
Output: false
Explanation: The first three characters "app" match, and the second string is shorter (in size.) According to lexicographical rules "apple" > "app", because 'l' > '∅', where '∅' is defined as the blank character which is less than any other character (More info).

从一个新的字母序判断是不是有序的字符串数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
	public:
    bool isAlienSorted(vector<string>& words, string order) {
        map<char, int> mp;
        for(int i = 0; i < order.length(); i ++)
            mp[order[i]] = i;
        int size = words.size();
        for(int i = 0; i < size-1; i ++) {
            int j = i + 1;
            int min_size = min(words[i].length(), words[j].length());
            int k;
            for(k = 0; k < min_size; k ++)
                if(mp[words[i][k]] > mp[words[j][k]])
                    return false;
                else if (mp[words[i][k]] < mp[words[j][k]])
                    break;
	            if(k == min_size && words[i].length() > words[j].length())
	                return false;
	        }
        return true;
    }
};

Leetcode955. Delete Columns to Make Sorted II

We are given an array A of N lowercase letter strings, all of the same length.

Now, we may choose any set of deletion indices, and for each string, we delete all the characters in those indices.

For example, if we have an array A = [“abcdef”,”uvwxyz”] and deletion indices {0, 2, 3}, then the final array after deletions is [“bef”,”vyz”].

Suppose we chose a set of deletion indices D such that after deletions, the final array has its elements in lexicographic order (A[0] <= A[1] <= A[2] … <= A[A.length - 1]).

Return the minimum possible value of D.length.

Example 1:

1
2
3
4
5
6
Input: ["ca","bb","ac"]
Output: 1
Explanation:
After deleting the first column, A = ["a", "b", "c"].
Now A is in lexicographic order (ie. A[0] <= A[1] <= A[2]).
We require at least 1 deletion since initially A was not in lexicographic order, so the answer is 1.

Example 2:

1
2
3
4
5
6
Input: ["xc","yb","za"]
Output: 0
Explanation:
A is already in lexicographic order, so we don't need to delete anything.
Note that the rows of A are not necessarily in lexicographic order:
ie. it is NOT necessarily true that (A[0][0] <= A[0][1] <= ...)

Example 3:

1
2
3
4
Input: ["zyx","wvu","tsr"]
Output: 3
Explanation:
We have to delete every column.

Note:

  • 1 <= A.length <= 100
  • 1 <= A[i].length <= 100

这道题说是给了一个字符串数组，里面的字符串长度均相同，这样如果将每个字符串看作一个字符数组的话，于是就可以看作的一个二维数组，题目要求数组中的字符串是按照字母顺序的，问最少需要删掉多少列。我们知道比较两个长度相等的字符串的字母顺序时，就是从开头起按照两两对应的位置比较，只要前面的字符顺序已经比出来了，后面的字符的顺序就不用管了，比如 “bx” 和 “ea”，因为 b 比 e 小，所以 “bx” 比 “ea” 小，后面的 x 和 a 的顺序无关紧要。如果看成二维数组的话，在比较A[i][j]和A[i+1][j]时，假如 [0, j-1] 中的某个位置k，已经满足了A[i][k] < A[i+1][k]的话，这里就不用再比了，所以用一个数组 sorted 来标记某相邻的两个字符串之间是否已经按照字母顺序排列了。然后用两个 for 循环，外层是遍历列，内层是遍历行，然后看若sorted[i]为 false，且A[i][j] > A[i + 1][j]的话，说明当前列需要被删除，结果 res 自增1，且 break 掉内层 for 循环。当内层 for 循环 break 掉或者自己结束后，此时看 i 是否小于 m-1，是的话说明是 break 掉的，直接 continue 外层循环。若是自己退出的，则在遍历一遍所有行，更新一下 sorted 数组即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int minDeletionSize(vector<string>& A) {
        int res = 0, m = A.size(), n = A[0].size(), i = 0, j = 0;
        vector<int> sorted(m - 1);
        for (j = 0; j < n; ++j) {
            for (i = 0; i < m - 1; ++i) {
                if (!sorted[i] && A[i][j] > A[i + 1][j]) {
                    ++res;
                    break;
                }
            }
            if (i < m - 1) continue;
            for (i = 0; i < m - 1; ++i) {
                sorted[i] |= A[i][j] < A[i + 1][j];
            }
        }
        return res;
    }
};

Leetcode957. Prison Cells After N Days

There are 8 prison cells in a row, and each cell is either occupied or vacant.

Each day, whether the cell is occupied or vacant changes according to the following rules:

If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
Otherwise, it becomes vacant.
(Note that because the prison is a row, the first and the last cells in the row can’t have two adjacent neighbors.)

We describe the current state of the prison in the following way: cells[i] == 1 if the i-th cell is occupied, else cells[i] == 0.

Given the initial state of the prison, return the state of the prison after N days (and N such changes described above.)

Example 1:

1
2
3
4
5
6
7
8
9
10
11
Input: cells = [0,1,0,1,1,0,0,1], N = 7
Output: [0,0,1,1,0,0,0,0]
Explanation: The following table summarizes the state of the prison on each day:
Day 0: [0, 1, 0, 1, 1, 0, 0, 1]
Day 1: [0, 1, 1, 0, 0, 0, 0, 0]
Day 2: [0, 0, 0, 0, 1, 1, 1, 0]
Day 3: [0, 1, 1, 0, 0, 1, 0, 0]
Day 4: [0, 0, 0, 0, 0, 1, 0, 0]
Day 5: [0, 1, 1, 1, 0, 1, 0, 0]
Day 6: [0, 0, 1, 0, 1, 1, 0, 0]
Day 7: [0, 0, 1, 1, 0, 0, 0, 0]

Example 2:

1
2
Input: cells = [1,0,0,1,0,0,1,0], N = 1000000000
Output: [0,0,1,1,1,1,1,0]

Note:

  • cells.length == 8
  • cells[i] is in {0, 1}
  • 1 <= N <= 10^9

这道题给了一个只由0和1构成的数组，数组长度固定为8，现在要进行N步变换，变换的规则是若一个位置的左右两边的数字相同，则该位置的数字变为1，反之则变为0，让求N步变换后的数组的状态。需要注意的数组的开头和结尾的两个位置，由于一个没有左边，一个没有右边，默认其左右两边的数字不相等，所以不管首尾数字初始的时候是啥，在第一次变换之后一定会是0，而且一直会保持0的状态。可能是有一个周期循环的，这样就完全没有必要每次都算一遍。正确的做法的应该是建立状态和当前N值的映射，一旦当前计算出的状态在 HashMap 中出现了，说明周期找到了，这样就可以通过取余来快速的缩小N值。为了使用 HashMap 而不是 TreeMap，这里首先将数组变为字符串，然后开始循环N，将当前状态映射为 N-1，然后新建了一个长度为8，且都是0的字符串。更新的时候不用考虑首尾两个位置，因为前面说了，首尾两个位置一定会变为0。更新完成了后，便在 HashMap 查找这个状态是否出现过，是的话算出周期，然后N对周期取余。最后再把状态字符串转为数组即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<int> prisonAfterNDays(vector<int>& cells, int N) {
        vector<int> res;
        string str;
        for (int num : cells) str += to_string(num);
        unordered_map<string, int> m;
        while (N > 0) {
            m[str] = N--;
            string cur(8, '0');
            for (int i = 1; i < 7; ++i) {
                cur[i] = (str[i - 1] == str[i + 1]) ? '1' : '0';
            }
            str = cur;
            if (m.count(str)) {
                N %= m[str] - N;
            }
        }
        for (char c : str) res.push_back(c - '0');
        return res;
    }
};

Leetcode958. Check Completeness of a Binary Tree

Given a binary tree, determine if it is a complete binary tree.

Definition of a complete binary tree from Wikipedia:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

Example 1:

1
2
3
Input: [1,2,3,4,5,6]
Output: true
Explanation: Every level before the last is full (ie. levels with node-values {1} and {2, 3}), and all nodes in the last level ({4, 5, 6}) are as far left as possible.

Example 2:
1
2
3
Input: [1,2,3,4,5,null,7]
Output: false
Explanation: The node with value 7 isn't as far left as possible.

用BFS遍历二叉树，当遇到空节点时，如果队列中还有未遍历的节点则该二叉树不完整。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    bool isCompleteTree(TreeNode* root) {
        if(root == NULL)
            return true;
        queue<TreeNode*> q;
        q.push(root);
        TreeNode* temp;
        bool res = true;
        while(!q.empty()) {
            int size = q.size();
            temp = q.front();
            q.pop();
            if(temp == NULL)
                res = false;
            else {
                if(!res)
                    return false;
                q.push(temp->left);
                q.push(temp->right);
            }
        }
        return true;
    }
};

Leetcode959. Regions Cut By Slashes

In a N x N grid composed of 1 x 1 squares, each 1 x 1 square consists of a /, \, or blank space. These characters divide the square into contiguous regions.

(Note that backslash characters are escaped, so a \ is represented as “\“.)

Return the number of regions.

Example 1:

1
2
3
4
5
Input: [
  " /",
  "/ "
]
Output: 2

Explanation: The 2x2 grid is as follows:

Example 2:

1
2
3
4
5
Input: [
  " /",
  "  "
]
Output: 1

Explanation: The 2x2 grid is as follows:

Example 3:

1
2
3
4
5
6
Input: [
  "\\/",
  "/\\"
]
Output: 4
Explanation: (Recall that because \ characters are escaped, "\\/" refers to \/, and "/\\" refers to /\.)

The 2x2 grid is as follows:

Example 4:

1
2
3
4
5
6
Input: [
  "/\\",
  "\\/"
]
Output: 5
Explanation: (Recall that because \ characters are escaped, "/\\" refers to /\, and "\\/" refers to \/.)

The 2x2 grid is as follows:

Example 5:

1
2
3
4
5
6
Input: [
  "//",
  "/ "
]
Output: 3
Explanation: The 2x2 grid is as follows:

Note:

  • 1 <= grid.length == grid[0].length <= 30
  • grid[i][j] is either ‘/‘, ‘\’, or ‘ ‘.

这道题说是有个 NxN 个小方块，每个小方块里可能是斜杠，反斜杠，或者是空格。然后问这些斜杠能将整个区域划分成多少个小区域。这的确是一道很有意思的题目，虽然只是 Medium 的难度，但是博主拿到题目的时候是懵逼的，这尼玛怎么做？无奈只好去论坛上看大神们的解法，结果发现大神们果然牛b，巧妙的将这道题转化为了岛屿个数问题 Number of Islands，具体的做法将每个小区间化为九个小格子，这样斜杠或者反斜杠就是对角线或者逆对角线了，是不是有点图像像素化的感觉，就是当你把某个图片尽可能的放大后，到最后你看到也就是一个个不同颜色的小格子组成了这幅图片。这样只要把斜杠的位置都标记为1，而空白的位置都标记为0，这样只要找出分隔开的0的群组的个数就可以了，就是岛屿个数的问题啦。使用一个 DFS 来遍历即可，这个并不难，这道题难就难在需要想出来这种像素化得转化，确实需要灵光一现啊，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    int regionsBySlashes(vector<string>& grid) {
        int n = grid.size(), res = 0;
        vector<vector<int>> nums(3 * n, vector<int>(3 * n));
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == '/') {
                    nums[i * 3][j * 3 + 2] = 1;
                    nums[i * 3 + 1][j * 3 + 1] = 1;
                    nums[i * 3 + 2][j * 3] = 1;
                } else if (grid[i][j] == '\\') {
                    nums[i * 3][j * 3] = 1;
                    nums[i * 3 + 1][j * 3 + 1] = 1;
                    nums[i * 3 + 2][j * 3 + 2] = 1;
                }
            }
        }
        for (int i = 0; i < nums.size(); ++i) {
            for (int j = 0; j < nums.size(); ++j) {
                if (nums[i][j] == 0) {
                    helper(nums, i, j);
                    ++res;
                }
            }
        }
        return res;
    }
    void helper(vector<vector<int>>& nums, int i, int j) {
        if (i >= 0 && j >= 0 && i < nums.size() && j < nums.size() && nums[i][j] == 0) {
            nums[i][j] = 1;
            helper(nums, i - 1, j);
            helper(nums, i, j + 1);
            helper(nums, i + 1, j);
            helper(nums, i, j - 1);
        }
    }
};

Leetcode961. N-Repeated Element in Size 2N Array

In a array A of size 2N, there are N+1 unique elements, and exactly one of these elements is repeated N times.

Return the element repeated N times.

Example 1:

1
2
Input: [1,2,3,3]
Output: 3

Example 2:
1
2
Input: [2,1,2,5,3,2]
Output: 2

Example 3:
1
2
Input: [5,1,5,2,5,3,5,4]
Output: 5

Note:

4 <= A.length <= 10000
0 <= A[i] < 10000
A.length is even

一个桶排序搞定

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int repeatedNTimes(vector<int>& A) {
        int counter[10000];
        memset(counter, 0, sizeof(counter));
        for(int i = 0; i < A.size(); i ++){
            counter[A[i]] ++;
            if(counter[A[i]] >= A.size() / 2)
                return A[i];
        }
        return -1;
    }
};

看到了大佬的解法，跪了，如果有两个连续一样的元素，直接返回

The intuition here is that the repeated numbers have to appear either next to each other (A[i] == A[i + 1]), or alternated (A[i] == A[i + 2]).

The only exception is sequences like [2, 1, 3, 2]. In this case, the result is the last number, so we just return it in the end. This solution has O(n) runtime.

1
2
3
4
5
int repeatedNTimes(vector<int>& A) {
  for (auto i = 0; i < A.size() - 2; ++i)
    if (A[i] == A[i + 1] || A[i] == A[i + 2]) return A[i];
  return A[A.size() - 1]; 
}

Another interesting approach is to use randomization (courtesy of @lee215 ). If you pick two numbers randomly, there is a 25% chance you bump into the repeated number. So, in average, we will find the answer in 4 attempts, thus O(4) runtime.
1
2
3
4
int repeatedNTimes(vector<int>& A, int i = 0, int j = 0) {
  while (A[i = rand() % A.size()] != A[j = rand() % A.size()] || i == j);
  return A[i];
}

Leetcode962. Maximum Width Ramp

A ramp in an integer array nums is a pair (i, j) for which i < j and nums[i] <= nums[j]. The width of such a ramp is j - i.

Given an integer array nums, return the maximum width of a ramp in nums. If there is no ramp in nums, return 0.

Example 1:

1
2
3
Input: nums = [6,0,8,2,1,5]
Output: 4
Explanation: The maximum width ramp is achieved at (i, j) = (1, 5): nums[1] = 0 and nums[5] = 5.

Example 2:

1
2
3
Input: nums = [9,8,1,0,1,9,4,0,4,1]
Output: 7
Explanation: The maximum width ramp is achieved at (i, j) = (2, 9): nums[2] = 1 and nums[9] = 1.

Constraints:

  • 2 <= nums.length <= 5 * 104
  • 0 <= nums[i] <= 5 * 104

这道题说给了一个数组A，这里定义了一种叫做 Ramp 的范围 (i, j)，满足 i < j 且 A[i] <= A[j]，而 ramp 就是 j - i，这里让求最宽的 ramp，若没有，则返回0。其实就是让在数组中找一前一后的两个数字，前面的数字小于等于后面的数字，且两个数字需要相距最远，让求这个最远的距离。先想一下，什么时侯不存在这个 ramp，就是当数组是严格递减的时候，那么不存在前面的数字小于等于后面的数字的情况，于是 ramp 是0。这道题的优化解法应该是使用单调栈。这里用一个数组 idx，来记录一个单调递减数组中数字的下标，遍历原数组A，对于每个遍历到的数字 A[i]，判断若此时下标数组为空，或者当前数字 A[i] 小于该下标数组中最后一个坐标在A中表示的数字时，将当前坐标i加入 idx，继续保持单调递减的顺序。反之，若 A[i] 比较大，则可以用二分搜索法来找出单调递减数组中第一个小于 A[i] 的数字的坐标，这样就可以快速得到 ramp 的大小，并用来更新结果 res 即可，这样整体的复杂度就降到了 O(nlgn)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int maxWidthRamp(vector<int>& nums) {
        int res = 0;
        vector<int> s;
        for (int i = 0; i < nums.size(); i ++) {
            if (s.size() == 0 || nums[i] <= nums[s.back()])
                s.push_back(i);
            else {
                int left = 0, right = s.size()-1;
                while(left < right) {
                    int mid = left + (right - left) / 2;
                    if (nums[mid] > nums[i])
                        left = mid+1;
                    else
                        right = mid;
                }
                res = max(res, i - s[right]);
            }
        }
        return res;   
    }
};

或者：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int maxWidthRamp(vector<int>& A) {
        stack<int> s;
        int maxlen = 0, i;
        for(i = 0; i < A.size(); ++i)
        {
        	if(s.empty() || A[s.top()] > A[i])//单调递减栈
                s.push(i);
        }
        for(i = A.size()-1; i >= 0; --i)
        {
            while(!s.empty() && A[i] >= A[s.top()])
            {
                maxlen = max(maxlen, i-s.top());
                s.pop();
            }
        }
        return maxlen;
    }
};

Leetcode963. Minimum Area Rectangle II

Given a set of points in the xy-plane, determine the minimum area of any rectangle formed from these points, with sides not necessarily parallel to the x and y axes.

If there isn’t any rectangle, return 0.

Example 1:

1
2
3
Input: [[1,2],[2,1],[1,0],[0,1]]
Output: 2.00000
Explanation: The minimum area rectangle occurs at [1,2],[2,1],[1,0],[0,1], with an area of 2.

Example 2:

1
2
3
Input: [[0,1],[2,1],[1,1],[1,0],[2,0]]
Output: 1.00000 
Explanation: The minimum area rectangle occurs at [1,0],[1,1],[2,1],[2,0], with an area of 1.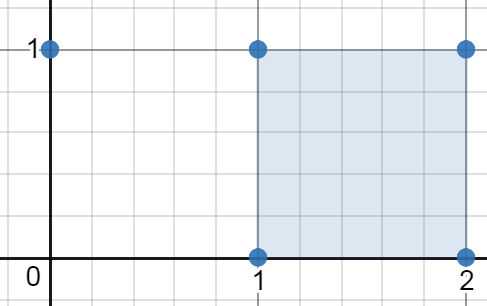

Example 3:

1
2
3
Input: [[0,3],[1,2],[3,1],[1,3],[2,1]]
Output: 0 
Explanation: There is no possible rectangle to form from these points.

Example 4:

1
2
3
Input: [[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]]
Output: 2.00000 
Explanation: The minimum area rectangle occurs at [2,1],[2,3],[3,3],[3,1], with an area of 2.

Note:

  • 1 <= points.length <= 50
  • 0 <= points[i][0] <= 40000
  • 0 <= points[i][1] <= 40000
  • All points are distinct.
  • Answers within 10^-5 of the actual value will be accepted as correct.

这道题是之前那道 Minimum Area Rectangle 的拓展，虽说是拓展，但是解题思想完全不同。那道题由于矩形不能随意翻转，所以任意两个相邻的顶点一定是相同的横坐标或者纵坐标，而这道题就不一样了，矩形可以任意翻转，就不能利用之前的特点了。那该怎么办呢，这里就要利用到矩形的对角线的特点了，我们都知道矩形的两条对角线长度是相等的，而且相交于矩形的中心，这个中心可以通过两个对顶点的坐标求出来。只要找到了两组对顶点，它们的中心重合，并且表示的对角线长度相等，则一定可以组成矩形。基于这种思想，可以遍历任意两个顶点，求出它们之间的距离，和中心点的坐标，将这两个信息组成一个字符串，建立和顶点在数组中位置之间的映射，这样能组成矩形的点就被归类到一起了。接下来就是遍历这个 HashMap 了，只能取出两组顶点及更多的地方，开始遍历，分别通过顶点的坐标算出两条边的长度，然后相乘用来更新结果 res 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    double minAreaFreeRect(vector<vector<int>>& points) {
        int n = points.size();
        if (n < 4) return 0.0;
        double res = DBL_MAX;
        unordered_map<string, vector<vector<int>>> m;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                long dist = getLength(points[i], points[j]);
                double centerX = (points[i][0] + points[j][0]) / 2.0;
                double centerY = (points[i][1] + points[j][1]) / 2.0;
                string key = to_string(dist) + "_" + to_string(centerX) + "_" + to_string(centerY);
                m[key].push_back({i, j});
            }
        }
        for (auto &a : m) {
            vector<vector<int>> vec = a.second;
            if (vec.size() < 2) continue;
            for (int i = 0; i < vec.size(); ++i) {
                for (int j = i + 1; j < vec.size(); ++j) {
                    int p1 = vec[i][0], p2 = vec[j][0], p3 = vec[j][1];
                    double len1 = sqrt(getLength(points[p1], points[p2]));
                    double len2 = sqrt(getLength(points[p1], points[p3]));
                    res = min(res, len1 * len2);
                }
            }
        }
        return res == DBL_MAX ? 0.0 : res;
    }
    long getLength(vector<int>& pt1, vector<int>& pt2) {
        return (pt1[0] - pt2[0]) * (pt1[0] - pt2[0]) + (pt1[1] - pt2[1]) * (pt1[1] - pt2[1]);
    }
};

Leetcode965. Univalued Binary Tree

A binary tree is univalued if every node in the tree has the same value.

Return true if and only if the given tree is univalued.

Example 1: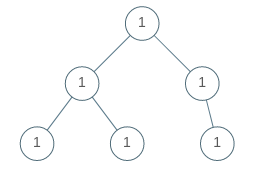

Input: [1,1,1,1,1,null,1]
Output: true

Example 2: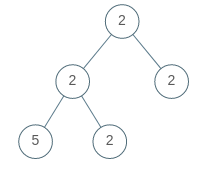

Input: [2,2,2,5,2]
Output: false

Note:

The number of nodes in the given tree will be in the range [1, 100].
Each node’s value will be an integer in the range [0, 99].

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool des(TreeNode* root,int val){
        if(root==NULL)
            return true;
        if(root->val != val)
            return false;
        return des(root->left,val)&&des(root->right,val);
        
        
    }
    bool isUnivalTree(TreeNode* root) {
        if(root==NULL)
            return true;
        return des(root,root->val);
    }
};

Leetcode966. Vowel Spellchecker

Given a wordlist, we want to implement a spellchecker that converts a query word into a correct word.

For a given query word, the spell checker handles two categories of spelling mistakes:

  • Capitalization: If the query matches a word in the wordlist (case-insensitive), then the query word is returned with the same case as the case in the wordlist.
    • Example: wordlist = [“yellow”], query = “YellOw”: correct = “yellow”
    • Example: wordlist = [“Yellow”], query = “yellow”: correct = “Yellow”
    • Example: wordlist = [“yellow”], query = “yellow”: correct = “yellow”
  • Vowel Errors: If after replacing the vowels (‘a’, ‘e’, ‘i’, ‘o’, ‘u’) of the query word with any vowel individually, it matches a word in the wordlist - (case-insensitive), then the query word is returned with the same case as the match in the wordlist.
    • Example: wordlist = [“YellOw”], query = “yollow”: correct = “YellOw”
    • Example: wordlist = [“YellOw”], query = “yeellow”: correct = “” (no match)
    • Example: wordlist = [“YellOw”], query = “yllw”: correct = “” (no match)

In addition, the spell checker operates under the following precedence rules:

  • When the query exactly matches a word in the wordlist (case-sensitive), you should return the same word back.
  • When the query matches a word up to capitlization, you should return the first such match in the wordlist.
  • When the query matches a word up to vowel errors, you should return the first such match in the wordlist.
  • If the query has no matches in the wordlist, you should return the empty string.

Given some queries, return a list of words answer, where answer[i] is the correct word for query = queries[i].

Example 1:

1
2
Input: wordlist = ["KiTe","kite","hare","Hare"], queries = ["kite","Kite","KiTe","Hare","HARE","Hear","hear","keti","keet","keto"]
Output: ["kite","KiTe","KiTe","Hare","hare","","","KiTe","","KiTe"]

Note:

  • 1 <= wordlist.length <= 5000
  • 1 <= queries.length <= 5000
  • 1 <= wordlist[i].length <= 7
  • 1 <= queries[i].length <= 7
  • All strings in wordlist and queries consist only of english letters.

这道题给了一组单词，让实现一个拼写检查器，把查询单词转换成一个正确的单词。这个拼写检查器主要有两种功能，一种是可以忽略大小写，另一种是忽略元音的错误，所谓元音是 a，e，i，o，u，这五个字母。另外题目中还制定了一些其他规则：假如有和查询单词一模一样的单词，考虑大小写，此时应该优先返回。第二个优先级是字母及顺序都一样，但大小写可能不同的，第三个优先级是有元音错误的单词也可以返回，最后都不满足的话返回空串。首先对于第一种情况，返回和查询单词一模一样的单词，很简单，将所有单词放入一个 HashSet 中，这样就可以快速确定一个查询单词是否在原单词数组中出现过。对于第二种情况，做法是将每个单词都转为小写，然后建立小写单词和原单词之间都映射，注意对于转为小写后相同都单词，我们只映射第一个出现该小写状态的单词，后面的不用管。对于第三种情况，对于每个单词，转为小写之后，然后把所有的元音字母用特殊字符替代，比如下划线，然后也是建立这种特殊处理后的状态和原单词之间的映射。当映射都建立好了之后，就可以遍历所有的查询单词了，首先是去 HashSet 中找，若有跟该查询单词一模一样的，直接加入结果 res 中。若没有，则先将查询单词变为小写，然后去第一个 HashMap 中查找，若存在，直接加入结果 res 中。若没有，再把所有的元音变为下划线，去第二个 HashMap 中查找，存在则直接加入结果 res 中。若没有，则将空串加入结果 res 中，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Solution {
public:
    
    char tolower(char c) {
        if ('A' <= c && c <= 'Z')
            return (char)(c + 32);
        return c;
    }
    
    vector<string> spellchecker(vector<string>& wordlist, vector<string>& queries) {
        vector<string> res;
        unordered_set<string> st;
        unordered_map<string, string> map;
        unordered_map<string, string> map_v;
        for (int i = 0; i < wordlist.size(); i ++) {
            string word = wordlist[i];
            st.insert(word);
            for (int j = 0; j < word.length(); j ++)
                word[j] = tolower(word[j]);
            if (!map.count(word))
                map[word] = wordlist[i];
            for (int j = 0; j < word.length(); j ++)
                if (word[j] == 'a' || word[j] == 'e' || word[j] == 'i' || word[j] == 'o' || word[j] == 'u')
                    word[j] = '_';
            if (!map_v.count(word))
                map_v[word] = wordlist[i];
        }
        
        for (string& query : queries) {
            if (st.count(query)) {
                res.push_back(query);
                continue;
            }
            
            for (int j = 0; j < query.length(); j ++)
                query[j] = tolower(query[j]);

            if (map.count(query)) {
                res.push_back(map[query]);
                continue;
            }
            
            for (int j = 0; j < query.length(); j ++)
                if (query[j] == 'a' || query[j] == 'e' || query[j] == 'i' || query[j] == 'o' || query[j] == 'u')
                    query[j] = '_';
            if (map_v.count(query)) {
                res.push_back(map_v[query]);
                continue;
            }
            res.push_back("");
        }
        return res;
    }
};

Leetcode969. Pancake Sorting

Given an array of integers arr, sort the array by performing a series of pancake flips.

In one pancake flip we do the following steps:

  • Choose an integer k where 1 <= k <= arr.length.
  • Reverse the sub-array arr[1…k].

For example, if arr = [3,2,1,4] and we performed a pancake flip choosing k = 3, we reverse the sub-array [3,2,1], so arr = [1,2,3,4] after the pancake flip at k = 3.

Return the k-values corresponding to a sequence of pancake flips that sort arr. Any valid answer that sorts the array within 10 * arr.length flips will be judged as correct.

Example 1:

1
2
3
4
5
6
7
8
9
Input: arr = [3,2,4,1]
Output: [4,2,4,3]
Explanation:
We perform 4 pancake flips, with k values 4, 2, 4, and 3.
Starting state: arr = [3, 2, 4, 1]
After 1st flip (k = 4): arr = [1, 4, 2, 3]
After 2nd flip (k = 2): arr = [4, 1, 2, 3]
After 3rd flip (k = 4): arr = [3, 2, 1, 4]
After 4th flip (k = 3): arr = [1, 2, 3, 4], which is sorted.

Notice that we return an array of the chosen k values of the pancake flips.

Example 2:

1
2
3
Input: arr = [1,2,3]
Output: []
Explanation: The input is already sorted, so there is no need to flip anything.

Note that other answers, such as [3, 3], would also be accepted.

Constraints:

  • 1 <= arr.length <= 100
  • 1 <= arr[i] <= arr.length
  • All integers in arr are unique (i.e. arr is a permutation of the integers from 1 to arr.length).

这道题给了长度为n的数组，由1到n的组成，顺序是打乱的。现在说我们可以任意翻转前k个数字，k的范围是1到n，问怎么个翻转法能将数组翻成有序的。题目说并不限定具体的翻法，只要在 10*n 的次数内翻成有序的都是可以的，任你随意翻，就算有无效的步骤也无所谓。题目中给的例子1其实挺迷惑的，因为并不知道为啥要那样翻，也没有一个固定的翻法，所以可能会误导大家。必须要自己想出一个固定的翻法，这样才能应对所有的情况。每次先将数组中最大数字找出来，然后将最大数字翻转到首位置，然后翻转整个数组，这样最大数字就跑到最后去了。然后将最后面的最大数字去掉，这样又重现一样的情况，重复同样的步骤，直到数组只剩一个数字1为止，在过程中就把每次要翻转的位置都记录到结果 res 中就可以了，注意这里 C++ 的翻转函数 reverse 的结束位置是开区间，很容易出错，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> pancakeSort(vector<int>& arr) {
        vector<int> res;
        for (int i = arr.size(), j; i > 0; --i) {
            for (j = 0; arr[j] != i; ++j);
            reverse(arr.begin(), arr.begin() + j + 1);
            res.push_back(j + 1);
            reverse(arr.begin(), arr.begin() + i);
            res.push_back(i);
        }
        return res;
    }
};

Leetcode970. Powerful Integers

Given two positive integers x and y, an integer is powerful if it is equal to x^i + y^j for some integers i >= 0 and j >= 0. Return a list of all powerful integers that have value less than or equal to bound.

You may return the answer in any order. In your answer, each value should occur at most once.

Example 1:

1
2
3
4
5
6
7
8
9
10
Input: x = 2, y = 3, bound = 10
Output: [2,3,4,5,7,9,10]
Explanation: 
2 = 2^0 + 3^0
3 = 2^1 + 3^0
4 = 2^0 + 3^1
5 = 2^1 + 3^1
7 = 2^2 + 3^1
9 = 2^3 + 3^0
10 = 2^0 + 3^2

Example 2:
1
2
Input: x = 3, y = 5, bound = 15
Output: [2,4,6,8,10,14]

方法很简单，如果x/y等于1，那么幂值只会是1；如果x/y 大于1，由于 bound <= 10^6，幂的最大值是20(pow(2,20) > 10^6)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
	public:
    vector<int> powerfulIntegers(int x, int y, int bound) {
        set<int> res;
        long temp;
        int x_max = x > 1 ? 20 : 1;
        int y_max = y > 1 ? 20 : 1;
        for(int i = 0 ; i < x_max && pow(x, i) <= bound; i ++)
            for(int j = 0 ; j < y_max && pow(y, j) <= bound; j ++) {
                temp = pow(x, i) + pow(y, j);
                if(temp <= bound) 
                    res.insert(temp);
            }
        return vector<int>(res.begin(), res.end());
    }
};

Leetcode971. Flip Binary Tree To Match Preorder Traversal

Given a binary tree with N nodes, each node has a different value from {1, …, N}.

A node in this binary tree can be flipped by swapping the left child and the right child of that node.

Consider the sequence of N values reported by a preorder traversal starting from the root. Call such a sequence of N values the voyage of the tree.

(Recall that a preorder traversal of a node means we report the current node’s value, then preorder-traverse the left child, then preorder-traverse the right child.)

Our goal is to flip the least number of nodes in the tree so that the voyage of the tree matches the voyage we are given.

If we can do so, then return a list of the values of all nodes flipped. You may return the answer in any order.

If we cannot do so, then return the list [-1].

Example 1:

1
2
Input: root = [1,2], voyage = [2,1]
Output: [-1]

Example 2:
1
2
Input: root = [1,2,3], voyage = [1,3,2]
Output: [1]

Example 3:
1
2
Input: root = [1,2,3], voyage = [1,2,3]
Output: []

最少翻转哪些节点，能使得二叉树的前序遍历变成voyage.

其实这个题不难，因为题目就说了是前序遍历，所以做法肯定还是前序遍历。我刚开始一直想不通的地方在于，题目又是返回[-1]，又是正常返回，没想好怎么做区分。其实做法就是递归函数不仅要修改res数组，还要返回表示能不能构成题目条件的bool变量。

看到二叉树的题，很大可能就需要递归，所以直接先写出dfs函数，然后再慢慢向里面填东西。

我们定义的dfs函数意义是，我们能不能通过翻转（或者不翻转）该root节点的左右子树，得到对应v。如果能，返回true，否则返回false。

首先在递归函数中，我们对root节点进行判断，如果root不存在，这种情况不应该认为是题目输入错误，而是应该认为已经遍历到最底部了，这个时候相当于root = [], voyage = []，所以返回true；在先序遍历的时候，root节点是第一个要被遍历到的节点，如果不和voyage[0]相等，直接返回false;

这个题目的难点在于是否需要翻转一个节点的左右孩子。判断的方法其实是简单的：如果voyage第二个元素等于root的左孩子，那么说明不用翻转，直接递归调用左右孩子；否则如果voyage的第二个元素等于root的右孩子，那么还要注意一下，在左孩子存在的情况下，我们需要翻转当前的节点左右孩子。

翻转是什么概念呢？这里并没有直接交换，而是把当前遍历到的位置使用遍历i保存起来，这样voyage[i]就表示当前遍历到哪个位置了。所以dfs调用两个孩子的顺序很讲究，它体现了先序遍历先解决哪个树的问题，也就是完成了逻辑上的交换左右孩子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
	public:
    int i = 0;
    vector<int> ans;
    
    bool dfs(TreeNode* root, vector<int>& voyage) {
        if(!root) 
            return true;
        if(root->val != voyage[i++])
            return false;
        if(root->left && root->left->val == voyage[i])
            return dfs(root->left, voyage) && dfs(root->right, voyage);
        else if(root->right && root->right->val == voyage[i]) {
            if(root->left)
                ans.push_back(root->val);
            return dfs(root->right, voyage) && dfs(root->left, voyage);
        }
        return !root->left && !root->right;
    }
    
    vector<int> flipMatchVoyage(TreeNode* root, vector<int>& voyage) {
        if(dfs(root, voyage))
            return ans;
        return {-1};
    }
};

Leetcode973. K Closest Points to Origin

We have a list of points on the plane. Find the K closest points to the origin (0, 0).

(Here, the distance between two points on a plane is the Euclidean distance.)

You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in.)

Example 1:

1
2
3
4
5
6
7
Input: points = [[1,3],[-2,2]], K = 1
Output: [[-2,2]]
Explanation:
The distance between (1, 3) and the origin is sqrt(10).
The distance between (-2, 2) and the origin is sqrt(8).
Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
We only want the closest K = 1 points from the origin, so the answer is just [[-2,2]].

Example 2:

1
2
3
Input: points = [[3,3],[5,-1],[-2,4]], K = 2
Output: [[3,3],[-2,4]]
(The answer [[-2,4],[3,3]] would also be accepted.)

Note:

  • 1 <= K <= points.length <= 10000
  • -10000 < points[i][0] < 10000
  • -10000 < points[i][1] < 10000

这道题给了平面上的一系列的点，让求最接近原点的K个点。基本上没有什么难度，无非就是要知道点与点之间的距离该如何求。一种比较直接的方法就是给这个二维数组排序，自定义排序方法，按照离原点的距离从小到大排序，注意这里我们并不需要求出具体的距离值，只要知道互相的大小关系即可，所以并不需要开方。排好序之后，返回前k个点即可，参见代码如下：

1
2
3
4
5
6
7
8
9
class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int K) {
        sort(points.begin(), points.end(), [](vector<int>& a, vector<int>& b) {
            return a[0] * a[0] + a[1] * a[1] < b[0] * b[0] + b[1] * b[1];
        });
        return vector<vector<int>>(points.begin(), points.begin() + K);
    }
};

下面这种解法是使用最大堆 Max Heap 来做的，在 C++ 中就是用优先队列来做，这里维护一个大小为k的最大堆，里面放一个 pair 对儿，由距离原点的距离，和该点在原数组中的下标组成，这样优先队列就可以按照到原点的距离排队了，距离大的就在队首。这样每当个数超过k个了之后，就将队首的元素移除即可，最后把剩下的k个点存入结果 res 中即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int K) {
        vector<vector<int>> res;
        priority_queue<pair<int, int>> pq;
        for (int i = 0; i < points.size(); ++i) {
            int t = points[i][0] * points[i][0] + points[i][1] * points[i][1];
            pq.push({t, i});
            if (pq.size() > K) pq.pop();
        }
        while (!pq.empty()) {
            auto t = pq.top(); pq.pop();
            res.push_back(points[t.second]);
        }
        return res;
    }
};

借鉴快速排序的思想：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    
    int comp(vector<int> p1, vector<int> p2) {
        return p1[0] * p1[0] + p1[1] * p1[1] - p2[0] * p2[0] - p2[1] * p2[1];
    }
    
    int helper(vector<vector<int>>& points, int l, int r) {
        vector<int> priot = points[l];
        while(l < r) {
            while(l < r && comp(points[r], priot) >= 0) r --;
            points[l] = points[r];
            while(l < r && comp(points[l], priot) <= 0) l ++;
            points[r] = points[l];
        }
        points[l] = priot;
        return l;
    }
    
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        vector<vector<int>> res;
        int l = 0, r = points.size()-1;
        while(l <= r) {
            int mid = helper(points, l, r);
            if (mid == k)
                break;
            else if (mid > k)
                r = mid-1;
            else
                l = mid+1;
        }
        for (int i = 0; i < k; i ++)
            res.push_back(points[i]);
        return res;
    }
};

Leetcode976. Largest Perimeter Triangle

Given an array A of positive lengths, return the largest perimeter of a triangle with non-zero area, formed from 3 of these lengths.

If it is impossible to form any triangle of non-zero area, return 0.

Example 1:

1
2
Input: [2,1,2]
Output: 5

Example 2:
1
2
Input: [1,2,1]
Output: 0

Example 3:
1
2
Input: [3,2,3,4]
Output: 10

Example 4:
1
2
Input: [3,6,2,3]
Output: 8

三角形的条件：两边之和>第三边。

若要构成最大的三角形周长，只需要对数组排序，一直取出最大的三个值作为三角形的边，符合条件即可返回。

证明：若数组A为自然顺序，A[N]>=A[N-1]+A[N-2]，则A[N]>=A[N-1]+A[N-3]，A[N]与后面的数字更不可能构成三角形，可以直接排除。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
	public:
    int largestPerimeter(vector<int>& A) {
        sort(A.begin(), A.end());
        for(int i = A.size() - 1; i >= 2; i --) {
            if(A[i - 2] + A[i - 1] > A[i])
                return A[i - 2] + A[i - 1] + A[i];
        }
        return 0;
    }
};

Leetcode977. Squares of a Sorted Array

Given an array of integers A sorted in non-decreasing order, return an array of the squares of each number, also in sorted non-decreasing order.

Example 1:

1
2
Input: [-4,-1,0,3,10]
Output: [0,1,9,16,100]

Example 2:
1
2
Input: [-7,-3,2,3,11]
Output: [4,9,9,49,121]

Note:

  • 1 <= A.length <= 10000
  • -10000 <= A[i] <= 10000
  • A is sorted in non-decreasing order.

给一个vector，有正有负，输出排序之后的平方数组。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        vector<int> res(A.size());
        int l = 0, r = A.size()-1, p = A.size() - 1;
        while(l <= r) {
            res[p--] = pow(A[abs(A[l]) > abs(A[r]) ? l++ : r--],2);
        }
        
        return res;
    }
};

另一种方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        vector<int> res(A.size());
        int i = 0, j = 0, k = 0;
        while(i < A.size() && A[i] < 0)
            i ++;
        j = i - 1;
        while(j >= 0 && i < A.size()){
            res[k++] = pow(A[abs(A[i]) < abs(A[j]) ? i ++ : j --], 2);
        }
        
        while(j>=0)
            res[k++]=pow(A[j--],2);
        while(i<A.size())
            res[k++]=pow(A[i++],2);
        
        return res;
    }
};

Leetcode978. Longest Turbulent Subarray

A subarray A[i], A[i+1], …, A[j] of A is said to be turbulent if and only if:

  • For i <= k < j, A[k] > A[k+1] when k is odd, and A[k] < A[k+1] when k is even;
  • OR, for i <= k < j, A[k] > A[k+1] when k is even, and A[k] < A[k+1] when k is odd.

That is, the subarray is turbulent if the comparison sign flips between each adjacent pair of elements in the subarray.

Return the length of a maximum size turbulent subarray of A.

Example 1:

1
2
3
Input: [9,4,2,10,7,8,8,1,9]
Output: 5
Explanation: (A[1] > A[2] < A[3] > A[4] < A[5])

Example 2:
1
2
Input: [4,8,12,16]
Output: 2

Example 3:
1
2
Input: [100]
Output: 1

隐藏很深的dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
	public:
    int maxTurbulenceSize(vector<int>& A) {
        int sizee = A.size();
        int res = 1;
        vector<int> up(sizee, 1);
        vector<int> down(sizee, 1);
        
        for(int i = 1; i < sizee; i ++) {
            if(A[i] > A[i - 1])
                up[i] = down[i - 1] + 1;
            if(A[i] < A[i - 1])
                down[i] = up[i - 1] + 1;
            res = max(res, max(up[i], down[i]));
        }
        return res;
    }
};

首先预处理一下，记录数组中数字变化趋势，1增加-1减少0不变，然后得到一个新的数组，为了省空间我直接在原来数组进行操作的，也可以开辟个新的数组。然后比较相邻数变化即可，若相邻数字乘积为负，则说明满足湍流数组性质，累加记录其长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
	public:
    int maxTurbulenceSize(vector<int>& A) {
        int sizee = A.size();
        int res = 0;
        int count = 2;
        for(int i = 1; i < sizee; i ++) {
            if(A[i] > A[i - 1])
                A[i-1] = 1;
            else if(A[i] < A[i + 1])
                A[i-1] = -1;
            else 
                A[i-1] = 0;
        }
        for(int i = 1; i < sizee - 1; i ++) {
            while(i < sizee - 1 && A[i] * A[i-1] < 0) {
                count ++;
                i ++;
            }
            res = max(res, count);
            count = 2;
        }
        return res;
    }
};

Leetcode979. Distribute Coins in Binary Tree

Given the root of a binary tree with N nodes, each node in the tree has node.val coins, and there are N coins total.

In one move, we may choose two adjacent nodes and move one coin from one node to another. (The move may be from parent to child, or from child to parent.)

Return the number of moves required to make every node have exactly one coin.

Example 1:

Input: [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

Input: [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.

Example 3:

Input: [1,0,2]
Output: 2

Example 4:

Input: [1,0,0,null,3]
Output: 4

Note:

1<= N <= 100
0 <= node.val <= N

给你一个二叉树，对于每个节点的val，每次只能往父亲或者儿子移动1，最后使得所有节点值都为1，求最小的移动次数。

思路：从叶子到根寻找，对于每个节点，只能剩下一个。多了的值肯定要全给父亲，少的值全问父亲要，统计一下就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
	public:
    int ans=0;
    int distributeCoins(TreeNode* root) {
        dfs(root);
        return ans;
    }
    int dfs(TreeNode* root){
        if(root==NULL)
            return 0;
        int left = dfs(root->left);
        int right = dfs(root->right);
        
        ans += abs(left) + abs(right);
        return root->val -1 + left + right ;
    }
};

Leetcode980. Unique Paths III

On a 2-dimensional grid, there are 4 types of squares:

1 represents the starting square. There is exactly one starting square.
2 represents the ending square. There is exactly one ending square.
0 represents empty squares we can walk over.
-1 represents obstacles that we cannot walk over.
Return the number of 4-directional walks from the starting square to the ending square, that walk over every non-obstacle square exactly once.

Example 1:

1
2
3
4
5
Input: [[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
Output: 2
Explanation: We have the following two paths: 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

Example 2:
1
2
3
4
5
6
7
Input: [[1,0,0,0],[0,0,0,0],[0,0,0,2]]
Output: 4
Explanation: We have the following four paths: 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

Example 3:
1
2
3
4
5
Input: [[0,1],[2,0]]
Output: 0
Explanation: 
There is no path that walks over every empty square exactly once.
Note that the starting and ending square can be anywhere in the grid.

Note:

1 <= grid.length * grid[0].length <= 20

给了一个二维矩阵，1代表起点，2代表终点，0代表可以走的格子，-1代表障碍物。求从起点到终点，把所有的可以走的格子都遍历一遍，所有可能的不同路径数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    vector<pair<int, int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    int uniquePathsIII(vector<vector<int>>& grid) {
        int M=grid.size();
        int zerosize=0,res=0;
        int N=grid[0].size();
        for(int i=0;i<M;i++)
            for(int j=0;j<N;j++)
                if(grid[i][j]==0)
                    zerosize++;
        for(int i=0;i<M;i++)
            for(int j=0;j<N;j++)
                if(grid[i][j]==1)
                    dfs(grid,i,j,0,zerosize,res);
        return res;
    }
    
    void dfs(vector<vector<int>>& grid, int x, int y, int pathcount, int zerocount, int& res){
        if(grid[x][y]==2 && zerocount == pathcount ){
            res++;
        }
        int M=grid.size();
        int N=grid[0].size();
        
        int pre=grid[x][y];
        if(pre==0)
            pathcount++;
        grid[x][y]=-1;
        for (auto d : dirs) {
            int nx = x + d.first;
            int ny = y + d.second;
            if (nx < 0 || nx >= M || ny < 0 || ny >= N || grid[nx][ny] == -1)
                continue;
            dfs(grid, nx, ny, pathcount, zerocount, res);
        }
        grid[x][y]=pre;

    }
    
};

Leetcode981. Time Based Key-Value Store

Create a timebased key-value store class TimeMap, that supports two operations.

  • set(string key, string value, int timestamp):Stores the key and value, along with the given timestamp.
  • get(string key, int timestamp)
    • Returns a value such that set(key, value, timestamp_prev) was called previously, with timestamp_prev <= timestamp.
    • If there are multiple such values, it returns the one with the largest timestamp_prev.
    • If there are no values, it returns the empty string (“”).

Example 1:

1
2
3
4
5
6
7
8
9
10
Input: inputs = ["TimeMap","set","get","get","set","get","get"], inputs = [[],["foo","bar",1],["foo",1],["foo",3],["foo","bar2",4],["foo",4],["foo",5]]
Output: [null,null,"bar","bar",null,"bar2","bar2"]
Explanation:   
TimeMap kv;   
kv.set("foo", "bar", 1); // store the key "foo" and value "bar" along with timestamp = 1   
kv.get("foo", 1);  // output "bar"   
kv.get("foo", 3); // output "bar" since there is no value corresponding to foo at timestamp 3 and timestamp 2, then the only value is at timestamp 1 ie "bar"   
kv.set("foo", "bar2", 4);   
kv.get("foo", 4); // output "bar2"   
kv.get("foo", 5); //output "bar2"

这个题太麻烦了，没有耐心做了，只看了看，本来想用很好的方法，比如二分实现一下，但是发现这种简单粗暴的方法竟然也能过，就算了……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class TimeMap {
private:
  unordered_map<string, map<int, string>> mp;
  vector<int> tvec;
public:
  /** Initialize your data structure here. */
  TimeMap() {}

  void set(string key, string value, int timestamp) {
      mp[key][timestamp] = value;
    }

	string get(string key, int timestamp) {
		if(!mp.count(key)) 
			return "";
		if(mp[key].count(timestamp)) 
			return mp[key][timestamp];
    	for(auto it = mp[key].rbegin(); it != mp[key].rend(); it++) {
    		if(it->first > timestamp) 
				continue;
        	else 
				return it->second;
		}
    return "";
	}
};

Leetcode983. Minimum Cost For Tickets

In a country popular for train travel, you have planned some train travelling one year in advance. The days of the year that you will travel is given as an array days. Each day is an integer from 1 to 365.

Train tickets are sold in 3 different ways:

  • a 1-day pass is sold for costs[0] dollars;
  • a 7-day pass is sold for costs[1] dollars;
  • a 30-day pass is sold for costs[2] dollars.

The passes allow that many days of consecutive travel. For example, if we get a 7-day pass on day 2, then we can travel for 7 days: day 2, 3, 4, 5, 6, 7, and 8.

Return the minimum number of dollars you need to travel every day in the given list of days.

Example 1:

1
2
3
4
5
6
7
8
Input: days = [1,4,6,7,8,20], costs = [2,7,15]
Output: 11
Explanation: 
For example, here is one way to buy passes that lets you travel your travel plan:
On day 1, you bought a 1-day pass for costs[0] = $2, which covered day 1.
On day 3, you bought a 7-day pass for costs[1] = $7, which covered days 3, 4, ..., 9.
On day 20, you bought a 1-day pass for costs[0] = $2, which covered day 20.
In total you spent $11 and covered all the days of your travel.

Example 2:
1
2
3
4
5
6
7
Input: days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15]
Output: 17
Explanation: 
For example, here is one way to buy passes that lets you travel your travel plan:
On day 1, you bought a 30-day pass for costs[2] = $15 which covered days 1, 2, ..., 30.
On day 31, you bought a 1-day pass for costs[0] = $2 which covered day 31.
In total you spent $17 and covered all the days of your travel.

Note:

  • 1 <= days.length <= 365
  • 1 <= days[i] <= 365
  • days is in strictly increasing order.
  • costs.length == 3
  • 1 <= costs[i] <= 1000

days数组中存储的是该年中去旅游的日期（范围为1到365之间的数字），costs数组大小为3，存储的是1天，7天和30天火车票的价格。我们需要做一个方案选择合适的购票方案达到旅游days天最省钱的目的。

算法描述

采用动态规划进行解决，假设现在是第days[i]天，我们在该天出行旅游需要选择买票方案，现在我们有三种方案：第一，购买一天的通行票，当天出行，花费就是第days[i-1]天的花费加上一天的通行票价；第二，购买七天的通行票，而七天的通行票可以在连续的七天之内使用，所以花费是第days[i-7]天的花费加上七天的通行票价（即从第days[i-8]天到days[i]天的花费都包含在这七天的通行票中）；第三，购买三十天的通行票，同理，花费是days[i-30]天加上三十天的通行票价。然后我们在这三种方案中选择最实惠的。最后，在实现代码中注意数组越界的问题。

使用dp[j]代表着我们旅行到i天为止需要的最少旅行价格，递推公式为：

  • dp[j] = dp[j-1] （第j天不用旅行）
  • dp[j] = min(dp[j-1] + costs[0], dp[j-7] + costs[1], dp[j-30] + costs[2]) （第j天需要旅行）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
	public:
    int mincostTickets(vector<int>& days, vector<int>& costs) {
        if(days.size() == 0)
            return 0;
        int dp[366] = {0};
        for(int i = 1; i < 366; i ++) {
            if(find(days.begin(), days.end(), i) == days.end() )
                dp[i] = dp[i - 1];
            else {
                dp[i] = min(dp[i-1] + costs[0], min(dp[max(0, i-7)]+costs[1], dp[max(0, i-30)]+costs[2]));
            }
        }
        return dp[365];
    }
};

Leetcode984. String Without AAA or BBB

Given two integers A and B, return any string S such that:

  • S has length A + B and contains exactly A ‘a’ letters, and exactly B ‘b’ letters;
  • The substring ‘aaa’ does not occur in S;
  • The substring ‘bbb’ does not occur in S.

Example 1:

1
2
3
Input: A = 1, B = 2
Output: "abb"
Explanation: "abb", "bab" and "bba" are all correct answers.

Example 2:
1
2
Input: A = 4, B = 1
Output: "aabaa"

使用贪心，先选较多的然后再选较少的字母。主要是看两个字母哪个比较多，较多的哪个放到A上，然后判断A和B是否大于0，或者A是否大于B。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
	public:
    string strWithout3a3b(int A, int B) {
        char a = 'a', b = 'b';
        int temp2;
        string res = "";
        if(A < B) {
            a = 'b';
            b = 'a';
            temp2 = A;
            A = B;
            B = temp2;
        }
        while(A>0 || B>0) {
            if(A > 0) {
                res += a;
                A --;
            }
            if(A > B) {
                res += a;
                A --;
            }
            if(B > 0) {
                res += b;
                B --;
            }
        }
        return res;
    }
};

Leetcode985. Sum of Even Numbers After Queries

We have an array A of integers, and an array queries of queries.

For the i-th query val = queries[i][0], index = queries[i][1], we add val to A[index]. Then, the answer to the i-th query is the sum of the even values of A.

(Here, the given index = queries[i][1] is a 0-based index, and each query permanently modifies the array A.)

Return the answer to all queries. Your answer array should have answer[i] as the answer to the i-th query.

Example 1:

1
2
3
4
5
6
7
8
Input: A = [1,2,3,4], queries = [[1,0],[-3,1],[-4,0],[2,3]]
Output: [8,6,2,4]
Explanation: 
	At the beginning, the array is [1,2,3,4].
	After adding 1 to A[0], the array is [2,2,3,4], and the sum of even values is 2 + 2 + 4 = 8.
	After adding -3 to A[1], the array is [2,-1,3,4], and the sum of even values is 2 + 4 = 6.
	After adding -4 to A[0], the array is [-2,-1,3,4], and the sum of even values is -2 + 4 = 2.
	After adding 2 to A[3], the array is [-2,-1,3,6], and the sum of even values is -2 + 6 = 4.

题意比较曲折，就是在queries中的每个pair，某个位置加上一个数，在计算A数组中所有偶数的和。下边的代码会超时：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
	public:
    vector<int> sumEvenAfterQueries(vector<int>& A, vector<vector<int>>& queries) {
        vector<int> res;
        int size = queries.size(), val, index, sum;
        for(int i = 0; i < size; i ++) {
            sum = 0;
            val = queries[i][0];
            index = queries[i][1];
            A[index] += val;
            for(int j = 0; j < A.size(); j ++)
                sum += (A[j]%2 ? 0 : A[j]);
            res.push_back(sum);
        }
        return res;
    }
};

应首先计算出所有的偶数和，再根据运算之后的结果进行计算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
	public:
    vector<int> sumEvenAfterQueries(vector<int>& A, vector<vector<int>>& queries) {
        vector<int> res;
        int size = queries.size(), val, index, sum = 0;
        for(int i = 0; i < A.size(); i ++)
            sum += (A[i]%2 ? 0 : A[i]);
        for(int i = 0; i < size; i ++) {
            val = queries[i][0];
            index = queries[i][1];
            if(A[index]%2 == 0)
                sum -= A[index];
            A[index] += val;
            if(A[index]%2 == 0)
                sum += A[index];
            res.push_back(sum);
        }
        return res;
    }
};

Leetcode986. Interval List Intersections

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b. The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
	public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& A, vector<vector<int>>& B) {
        if(A.size() == 0 || B.size() == 0)
            return vector<vector<int>>{};
        int sizea = A.size(), sizeb = B.size();
        int l, r;
        vector<vector<int>> res;
        for(int i = 0, j = 0; i < sizea && j < sizeb;) {
            l = max(A[i][0], B[j][0]);
            r = min(A[i][1], B[j][1]);
            if(l <= r) 
                res.push_back({l, r});
            if(r == A[i][1])
                i ++;
            else j ++;
        }
        return res;
    }
};

贪心，由于排好序了，直接双指针扫，思路和归并排序合并比较类似，注意往后移动的条件是尾部，因为一个矩形的结束条件是尾部比完了，不能写成是头部

Leetcode987. Vertical Order Traversal of a Binary Tree

Given a binary tree, return the vertical order traversal of its nodes values.

For each node at position (X, Y), its left and right children respectively will be at positions (X-1, Y-1) and (X+1, Y-1).

Running a vertical line from X = -infinity to X = +infinity, whenever the vertical line touches some nodes, we report the values of the nodes in order from top to bottom (decreasing Y coordinates).

If two nodes have the same position, then the value of the node that is reported first is the value that is smaller.

Return an list of non-empty reports in order of X coordinate. Every report will have a list of values of nodes.

Example 1:

1
2
3
4
5
6
7
8
Input: [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Explanation: 
Without loss of generality, we can assume the root node is at position (0, 0):
Then, the node with value 9 occurs at position (-1, -1);
The nodes with values 3 and 15 occur at positions (0, 0) and (0, -2);
The node with value 20 occurs at position (1, -1);
The node with value 7 occurs at position (2, -2).

Example 2:
1
2
3
4
5
Input: [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation: 
The node with value 5 and the node with value 6 have the same position according to the given scheme.
However, in the report "[1,5,6]", the node value of 5 comes first since 5 is smaller than 6.

Note:

  • The tree will have between 1 and 1000 nodes.
  • Each node s value will be between 0 and 1000.

要求把相同X的节点位置放在一起，并且要求结果中节点的存放是从上到下的。如果两个节点的坐标相同，那么value小的节点排列在前面。通过维护一个队列，我们从上到下依次遍历每个节点，给每个节点设置好了坐标。这个队列存储的是个三元组（TreeNode*,int x,int y）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
	public:
    struct dat{
        TreeNode* root;
        int x, y;
    };

    vector<vector<int>> verticalTraversal(TreeNode* root) {
        queue<struct dat> q;
        struct dat te = {root, 0, 0};
        q.push(te);
        map<int, vector<pair<int, int>>> node;
        while(!q.empty()) {
            struct dat temp = q.front();
            q.pop();
            node[temp.x].push_back(make_pair(-temp.y, temp.root->val));
            if(temp.root->left)
                q.push({temp.root->left, temp.x - 1, temp.y - 1});
            if(temp.root->right)
                q.push({temp.root->right, temp.x + 1, temp.y - 1});
        }
        vector<vector<int>> res;
        for(auto it : node) {
            sort(it.second.begin(), it.second.end());
            vector<int> tempp;
            for(auto i : it.second)
                tempp.push_back(i.second);
            res.push_back(tempp);
        }
        return res;
    }
};

Leetcode988. Smallest String Starting From Leaf

Given the root of a binary tree, each node has a value from 0 to 25 representing the letters ‘a’ to ‘z’: a value of 0 represents ‘a’, a value of 1 represents ‘b’, and so on.

Find the lexicographically smallest string that starts at a leaf of this tree and ends at the root.

(As a reminder, any shorter prefix of a string is lexicographically smaller: for example, “ab” is lexicographically smaller than “aba”. A leaf of a node is a node that has no children.)

Example 1:

1
2
Input: [0,1,2,3,4,3,4]
Output: "dba"

Example 2:
1
2
Input: [25,1,3,1,3,0,2]
Output: "adz"

Example 3:
1
2
Input: [2,2,1,null,1,0,null,0]
Output: "abc"

这个数组代表一个树，图就不上了，从叶子节点开始找到一个最小的字符串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
	public:
    
    string result = "zzzzzzzzzz";
    void bianli(TreeNode* root, string cur) {
        if(root->left == NULL && root->right == NULL) {
            cur = (char)((root->val) + 'a')+cur;
            result = result < cur ? result : cur;
            return;
        }
        if(root->left != NULL) {
            bianli(root->left, (char)(root->val+'a')+cur);
        }
        if(root->right != NULL) {
            bianli(root->right, (char)(root->val+'a')+cur);
        }
    }
    
    string smallestFromLeaf(TreeNode* root) {
        bianli(root, "");
        return result;
    }
};

Leetcode989. Add to Array-Form of Integer

For a non-negative integer X, the array-form of X is an array of its digits in left to right order. For example, if X = 1231, then the array form is [1,2,3,1].

Given the array-form A of a non-negative integer X, return the array-form of the integer X+K.

Example 1:

1
2
3
Input: A = [1,2,0,0], K = 34
Output: [1,2,3,4]
Explanation: 1200 + 34 = 1234

Example 2:
1
2
3
Input: A = [2,7,4], K = 181
Output: [4,5,5]
Explanation: 274 + 181 = 455

Example 3:
1
2
3
Input: A = [2,1,5], K = 806
Output: [1,0,2,1]
Explanation: 215 + 806 = 1021

Example 4:
1
2
3
Input: A = [9,9,9,9,9,9,9,9,9,9], K = 1
Output: [1,0,0,0,0,0,0,0,0,0,0]
Explanation: 9999999999 + 1 = 10000000000

Note：

  • 1 <= A.length <= 10000
  • 0 <= A[i] <= 9
  • 0 <= K <= 10000
  • If A.length > 1, then A[0] != 0

大概意思是一个数组代表一个数，再给一个整数K，返回结果的各位数组成的数组，注意进位，我的做法很麻烦，需要两次反转。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> addToArrayForm(vector<int>& A, int K) {
        vector<int> result;
        int L=K;
        reverse(A.begin(), A.end());
        for(int i = 0; i < A.size(); i++){
            A[i] = A[i] + L;
            L = A[i]/10;
            A[i]=A[i]%10;
        }
        while(L>0) {
            A.push_back(L%10);
            L = L/10;
        }
        reverse(A.begin(), A.end());
        return A;
    }
};

从数组最右边开始，逐位相加，用carry记录进位，每一次取和的最右一位存入链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public List<Integer> addToArrayForm(int[] A, int K) {
        int len = A.length;
        int carry = 0;
        List<Integer> list = new ArrayList<Integer>();
        for(int i = len - 1; i > -1; i--){
            int sum = carry + A[i] + K % 10;
            list.add(sum % 10);
            carry = sum / 10;
            K /= 10;
        }
        carry += K;
        while(carry != 0){
            list.add(carry % 10);
            carry /= 10;
        }
        Collections.reverse(list);
        return list;
    }
}

Leetcode990. Satisfiability of Equality Equations

Given an array equations of strings that represent relationships between variables, each string equations[i] has length 4 and takes one of two different forms: “a==b” or “a!=b”. Here, a and b are lowercase letters (not necessarily different) that represent one-letter variable names.

Return true if and only if it is possible to assign integers to variable names so as to satisfy all the given equations.

Example 1:

1
2
3
Input: ["a==b","b!=a"]
Output: false
Explanation: If we assign say, a = 1 and b = 1, then the first equation is satisfied, but not the second.  There is no way to assign the variables to satisfy both equations.

Example 2:
1
2
3
Input: ["b==a","a==b"]
Output: true
Explanation: We could assign a = 1 and b = 1 to satisfy both equations.

Example 3:
1
2
Input: ["a==b","b==c","a==c"]
Output: true

Example 4:
1
2
Input: ["a==b","b!=c","c==a"]
Output: false

Example 5:
1
2
Input: ["c==c","b==d","x!=z"]
Output: true

Note:

  • 1 <= equations.length <= 500
  • equations[i].length == 4
  • equations[i][0] and equations[i][3] are lowercase letters
  • equations[i][1] is either ‘=’ or ‘!’
  • equations[i][2] is ‘=’

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一：”a==b”或 “a!=b”。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

这个问题一看就是并查集问题，所以直接使用并查集就过了。将所有相等的元素构成一个集合中，然后判断不相等的元素是不是相同根即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int arr[26];
    int find(int x) {
        return arr[x]==x?x:find(arr[x]);
    }
    void uni(int x, int y) {
        arr[find(y)]=find(x);
    }
    bool equationsPossible(vector<string>& equations) {
        for(int i=0;i<26;i++)
            arr[i]=i;
        for(int i=0;i<equations.size();i++){
            if(equations[i][1]=='=') {
                uni(equations[i][0]-'a', equations[i][3]-'a');
            }
        }
        for(int i=0;i<equations.size();i++){ 
            if(equations[i][1]=='!' && find(equations[i][0]-'a')==find(equations[i][3]-'a')) {
                return false;
            }
        }
        return true;
    }
};

Leetcode991. Broken Calculator

On a broken calculator that has a number showing on its display, we can perform two operations:

  • Double: Multiply the number on the display by 2, or;
  • Decrement: Subtract 1 from the number on the display.

Initially, the calculator is displaying the number X.

Return the minimum number of operations needed to display the number Y.

Example 1:

1
2
3
Input: X = 2, Y = 3
Output: 2
Explanation: Use double operation and then decrement operation {2 -> 4 -> 3}.

Example 2:

1
2
3
Input: X = 5, Y = 8
Output: 2
Explanation: Use decrement and then double {5 -> 4 -> 8}.

Example 3:

1
2
3
Input: X = 3, Y = 10
Output: 3
Explanation:  Use double, decrement and double {3 -> 6 -> 5 -> 10}.

Example 4:

1
2
3
Input: X = 1024, Y = 1
Output: 1023
Explanation: Use decrement operations 1023 times.

Note:

  • 1 <= X <= 10^9
  • 1 <= Y <= 10^9

这道题说是有一个坏了的计算器，其实就显示一个数字X，现在我们有两种操作，一种乘以2操作，一种是减1操作，问最少需要多少次操作才能得到目标数字Y。好，现在来分析，由于X和Y的大小关系并不确定，最简单的当然是X和Y相等，就不需要另外的操作了。当X大于Y时，由于都是正数，肯定就不能再乘2了，所以此时直接就可以返回 X-Y。比较复杂的情况就是Y大于X的情况，此时X既可以减1，又可以乘以2，但是仔细想想，我们的最终目的应该是要减小Y，直至其小于等于X，就可以直接得到结果。这里X乘以2的效果就相当于Y除以2，操作数都一样，但是Y除以2时还要看Y的奇偶性，如果Y是偶数，那么 OK，可以直接除以2，若是奇数，需要将其变为偶数，由于X可以减1，等价过来就是Y加1，所以思路就有了，当Y大于X时进行循环，然后判断Y的奇偶性，若是偶数，直接除以2，若是奇数，则加1，当然此时结果 res 也要对应增加。循环退出后，还要加上 X-Y 的值即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int brokenCalc(int start, int target) {
        int res = 0;
        while(target > start) {
            target = (target % 2) ? (target + 1) : target / 2;
            res ++;
        }
        return res + start - target;
    }
};

若用递归来写就相当的简洁了，可以两行搞定，当然若你够 geek 的话，也可以压缩到一行，参见代码如下：

1
2
3
4
5
6
7
class Solution {
public:
    int brokenCalc(int X, int Y) {
        if (X >= Y) return X - Y;
        return (Y % 2 == 0) ? (1 + brokenCalc(X, Y / 2)) : (1 + brokenCalc(X, Y + 1));
    }
};

Leetcode993. Cousins in Binary Tree

In a binary tree, the root node is at depth 0, and children of each depth k node are at depth k+1.

Two nodes of a binary tree are cousins if they have the same depth, but have different parents. We are given the root of a binary tree with unique values, and the values x and y of two different nodes in the tree. Return true if and only if the nodes corresponding to the values x and y are cousins.

Example 1:

1
2
Input: root = [1,2,3,4], x = 4, y = 3
Output: false

Example 2:
1
2
Input: root = [1,2,3,null,4,null,5], x = 5, y = 4
Output: true

Example 3:
1
2
Input: root = [1,2,3,null,4], x = 2, y = 3
Output: false

求解x，y的深度和父亲结点，如果深度一样，父亲结点不同，就是true；否则，就是false。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
	public:
    
    TreeNode* dfs(TreeNode* root, int x, int depth, int &level) {
        if(root == NULL)
            return NULL;
        if((root->left && root->left->val == x) || (root->right && root->right->val == x)) {
            level = depth;
            return root;
        }
        TreeNode *left = dfs(root->left, x, depth + 1, level);
        if (left) 
            return left;

        TreeNode *right = dfs(root->right, x, depth + 1, level);
        if (right) 
            return right;
        return NULL;
    }
    
    bool isCousins(TreeNode* root, int x, int y) {
        int level_a, level_b;
        TreeNode *xx = dfs(root, x, 0, level_a);
        TreeNode *yy = dfs(root, y, 0, level_b);
        if(xx != yy && level_a == level_b)
            return true;
        return false;
    }
};

Leetcode994. Rotting Oranges

You are given an m x n grid where each cell can have one of three values:

  • 0 representing an empty cell,
  • 1 representing a fresh orange, or
  • 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

1
2
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

1
2
3
Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

1
2
3
Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10
  • grid[i][j] is 0, 1, or 2.

这道题说给的一个 mxn 大小的格子上有些新鲜和腐烂的橘子，每一分钟腐烂的橘子都会传染给其周围四个中的新鲜橘子，使得其也变得腐烂。现在问需要多少分钟可以使得所有的新鲜橘子都变腐烂，无法做到时返回 -1。由于这里新鲜的橘子自己不会变腐烂，只有被周围的腐烂橘子传染才会，所以当新鲜橘子周围不会出现腐烂橘子的时候，那么这个新鲜橘子就不会腐烂，这才会有返回 -1 的情况。这道题就是个典型的广度优先遍历 Breadth First Search，并没有什么太大的难度，先遍历一遍整个二维数组，统计出所有新鲜橘子的个数，并把腐烂的橘子坐标放入一个队列 queue，之后进行 while 循环，循环条件是队列不会空，且 freshLeft 大于0，使用层序遍历的方法，用个 for 循环在内部。每次取出队首元素，遍历其周围四个位置，越界或者不是新鲜橘子都跳过，否则将新鲜橘子标记为腐烂，加入队列中，并且 freshLeft 自减1。每层遍历完成之后，结果 res 自增1，最后返回的时候，若还有新鲜橘子，即 freshLeft 大于0时，返回 -1，否则返回 res 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int orangesRotting(vector<vector<int>>& grid) {
        int res = 0, m = grid.size(), n = grid[0].size(), freshLeft = 0;
        queue<pair<int, int> > q;
        vector<vector<int>> dirs{{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
        for (int i = 0; i < m; i ++)
            for (int j = 0; j < n; j ++) {
                if (grid[i][j] == 1)
                    freshLeft ++;
                else if (grid[i][j] == 2)
                    q.push(make_pair(i, j));
            }
        while(!q.empty() && freshLeft > 0) {
            int size = q.size();
            for (int i = 0; i < size; i ++) {
                int x = q.front().first, y = q.front().second;
                q.pop();
    
                for (int j = 0; j < 4; j ++) {
                    int xx = x + dirs[j][0];
                    int yy = y + dirs[j][1];
                    if (0 > xx || xx >= m || 0 > yy || yy >= n || grid[xx][yy] != 1) 
                        continue;
                    grid[xx][yy] = 2;
                    q.push(make_pair(xx, yy));
                    freshLeft --;
                }
            }
            res ++;
        }
        return freshLeft > 0 ? -1 : res;
    }
};

Leetcode997. Find the Town Judge

In a town, there are N people labelled from 1 to N. There is a rumor that one of these people is secretly the town judge.

If the town judge exists, then:

The town judge trusts nobody.
Everybody (except for the town judge) trusts the town judge.
There is exactly one person that satisfies properties 1 and 2.
You are given trust, an array of pairs trust[i] = [a, b] representing that the person labelled a trusts the person labelled b.

If the town judge exists and can be identified, return the label of the town judge. Otherwise, return -1.

Example 1:

1
2
Input: N = 2, trust = [[1,2]]
Output: 2

Example 2:
1
2
Input: N = 3, trust = [[1,3],[2,3]]
Output: 3

Example 3:
1
2
Input: N = 3, trust = [[1,3],[2,3],[3,1]]
Output: -1

Example 4:
1
2
Input: N = 3, trust = [[1,2],[2,3]]
Output: -1

Example 5:
1
2
Input: N = 4, trust = [[1,3],[1,4],[2,3],[2,4],[4,3]]
Output: 3

在一个小镇里，按从 1 到 N 标记了 N 个人。传言称，这些人中有一个是小镇上的秘密法官。如果小镇的法官真的存在，那么：小镇的法官不相信任何人。每个人（除了小镇法官外）都信任小镇的法官。只有一个人同时满足属性 1 和属性 2 。给定数组 trust，该数组由信任对 trust[i] = [a, b] 组成，表示标记为 a 的人信任标记为 b 的人。如果小镇存在秘密法官并且可以确定他的身份，请返回该法官的标记。否则，返回 -1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
	public:
    int findJudge(int N, vector<vector<int>>& trust) {
        int in[1005] = {0}, out[1005] = {0};
        for(int i = 0; i < trust.size(); i ++) {
            in[trust[i][1]] ++;
            out[trust[i][0]] = -1;
        }
        for(int i = 1; i <= N; i ++) {
            if(out[i] == 0 && in[i] == N - 1)
                return i;
        }
        return -1;
    }
};

Leetcode998. Maximum Binary Tree II

We are given the root node of a maximum tree: a tree where every node has a value greater than any other value in its subtree.
Just as in the previous problem, the given tree was constructed from an list A (root = Construct(A)) recursively with the following Construct(A) routine:

  • If A is empty, return null.
  • Otherwise, let A[i] be the largest element of A. Create a root node with value A[i].
  • The left child of root will be Construct([A[0], A[1], …, A[i-1]])
  • The right child of root will be Construct([A[i+1], A[i+2], …, A[A.length - 1]])
  • Return root.

Note that we were not given A directly, only a root node root = Construct(A).

Suppose B is a copy of A with the value val appended to it. It is guaranteed that B has unique values.

Return Construct(B).

Example 1:

1
2
3
Input: root = [4,1,3,null,null,2], val = 5
Output: [5,4,null,1,3,null,null,2]
Explanation: A = [1,4,2,3], B = [1,4,2,3,5]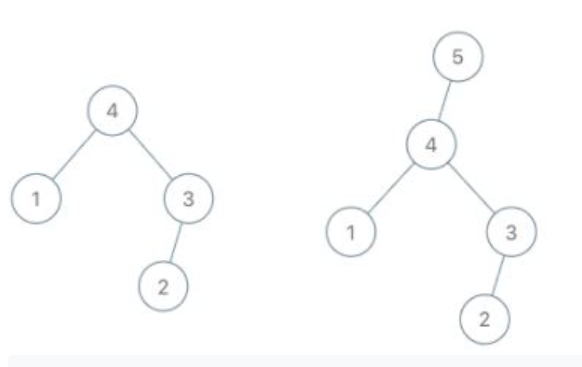

Example 2:

1
2
3
Input: root = [5,2,4,null,1], val = 3
Output: [5,2,4,null,1,null,3]
Explanation: A = [2,1,5,4], B = [2,1,5,4,3]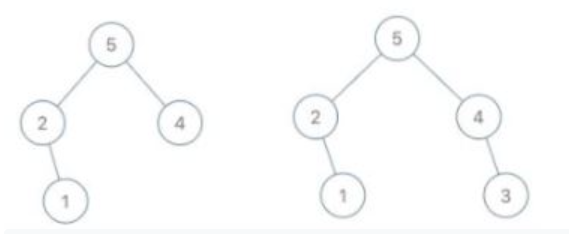

Example 3:

1
2
3
Input: root = [5,2,3,null,1], val = 4
Output: [5,2,4,null,1,3]
Explanation: A = [2,1,5,3], B = [2,1,5,3,4]

Note:

  • 1 <= B.length <= 100

和上一题654相比，这道题没有给max binary tree的原始数组nums，而是已经从654建好的tree root。那么已知新的数组是nums后面再加一个val，要返回modify过的新max binary tree。那么分为三种情况讨论，也就是example给出的三种：

  1. val > root ->val，新数字将成为新的根节点，root被连接到左边；
  2. val < root -> val，那么要遍历寻找该插入的位置，因为顺序问题，我们不考虑向左子树插入，只向右子树方向递归寻找这个再一次使val > root -> val满足的位置。如果没有找到，需要将新节点连成最后一个max的右子树；
  3. 如果找到了这样一个节点parent，那么它的右子树将被连接到新节点的左子树，而新节点被连到parent的右子树。
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    TreeNode* insertIntoMaxTree(TreeNode* root, int val) {
        TreeNode* node = new TreeNode(val);
        if (!root || root -> val < val)  {
            node -> left = root;
            return node;
        }
        root -> right = insertIntoMaxTree(root -> right, val);
        return root;
    }
};

Leetcode999. Available Captures for Rook

On an 8 x 8 chessboard, there is one white rook. There also may be empty squares, white bishops, and black pawns. These are given as characters ‘R’, ‘.’, ‘B’, and ‘p’ respectively. Uppercase characters represent white pieces, and lowercase characters represent black pieces.

The rook moves as in the rules of Chess: it chooses one of four cardinal directions (north, east, west, and south), then moves in that direction until it chooses to stop, reaches the edge of the board, or captures an opposite colored pawn by moving to the same square it occupies. Also, rooks cannot move into the same square as other friendly bishops.

Return the number of pawns the rook can capture in one move.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
Input: 
[[".",".",".",".",".",".",".","."],
 [".",".",".","p",".",".",".","."],
 [".",".",".","R",".",".",".","p"],
 [".",".",".",".",".",".",".","."],
 [".",".",".",".",".",".",".","."],
 [".",".",".","p",".",".",".","."],
 [".",".",".",".",".",".",".","."],
 [".",".",".",".",".",".",".","."]]
Output: 3
Explanation: 
In this example the rook is able to capture all the pawns.

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
Input: [
 [".",".",".",".",".",".",".","."],
 [".","p","p","p","p","p",".","."],
 [".","p","p","B","p","p",".","."],
 [".","p","B","R","B","p",".","."],
 [".","p","p","B","p","p",".","."],
 [".","p","p","p","p","p",".","."],
 [".",".",".",".",".",".",".","."],
 [".",".",".",".",".",".",".","."]]
Output: 0
Explanation: 
Bishops are blocking the rook to capture any pawn.

Example 3:

1
2
3
4
5
6
7
8
9
10
11
12
Input: [
 [".",".",".",".",".",".",".","."],
 [".",".",".","p",".",".",".","."],
 [".",".",".","p",".",".",".","."],
 ["p","p",".","R",".","p","B","."],
 [".",".",".",".",".",".",".","."],
 [".",".",".","B",".",".",".","."],
 [".",".",".","p",".",".",".","."],
 [".",".",".",".",".",".",".","."]]
Output: 3
Explanation: 
The rook can capture the pawns at positions b5, d6 and f5.

Note:

  1. board.length == board[i].length == 8
  2. board[i][j] is either ‘R’, ‘.’, ‘B’, or ‘p’
  3. There is exactly one cell with board[i][j] == ‘R’

非常无聊，数格子就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
class Solution {
public:
    int numRookCaptures(vector<vector<char>>& board) {
        int x,y;
        int res=0;
        bool bBlack;
        for (int row = 0; row < 8; row++) 
            for (int col = 0; col < 8; col++) 
                if (board[row][col] == 'R' ||
                    board[row][col] == 'r') {
                    x = row;
                    y = col;
                    if (board[row][col] == 'R') {
                        bBlack = false;
                    }
                    else {
                        bBlack = true;
                    }
                    break;
                }
        
        for(int j=x-1;j>=0;j--){
            if(board[j][y]=='.')
                continue;
            if(board[j][y]=='P' && bBlack==true){
                res++;
                break;
            }
            else if(board[j][y]=='p' && bBlack==false){
                res++;
                break;
            }
            else
                break;
        }
        for(int j=x+1;j<8;j++){
            if(board[j][y]=='.')
                continue;
            if(board[j][y]=='P' && bBlack==true){
                res++;
                break;
            }
            else if(board[j][y]=='p' && bBlack==false){
                res++;
                break;
            }
            else
                break;            
        }
        for(int j=y-1;j>=0;j--){
            if(board[x][j]=='.')
                continue;
            if(board[x][j]=='P' && bBlack==true){
                res++;
                break;
            }
            else if(board[x][j]=='p' && bBlack==false){
                res++;
                break;
            }
            else
                break;            
        }
        for(int j=y+1;j<8;j++){
            if(board[x][j]=='.')
                continue;
            if(board[x][j]=='P' && bBlack==true){
                res++;
                break;
            }
            else if(board[x][j]=='p' && bBlack==false){
                res++;
                break;
            }
            else
                break;
        }        
        return res;
    }
};