Cannon算法和Stencil计算

————————————————
版权声明：本文为CSDN博主「zongy17」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_43614211/article/details/122105195
————————————————

Cannon和fox算法

Cannon算法：

输入：两个N ∗ N的矩阵A、 B，P个处理器。

输出：若P是完全平方数且N % P = 0，则计算C = A ∗ B并输出。

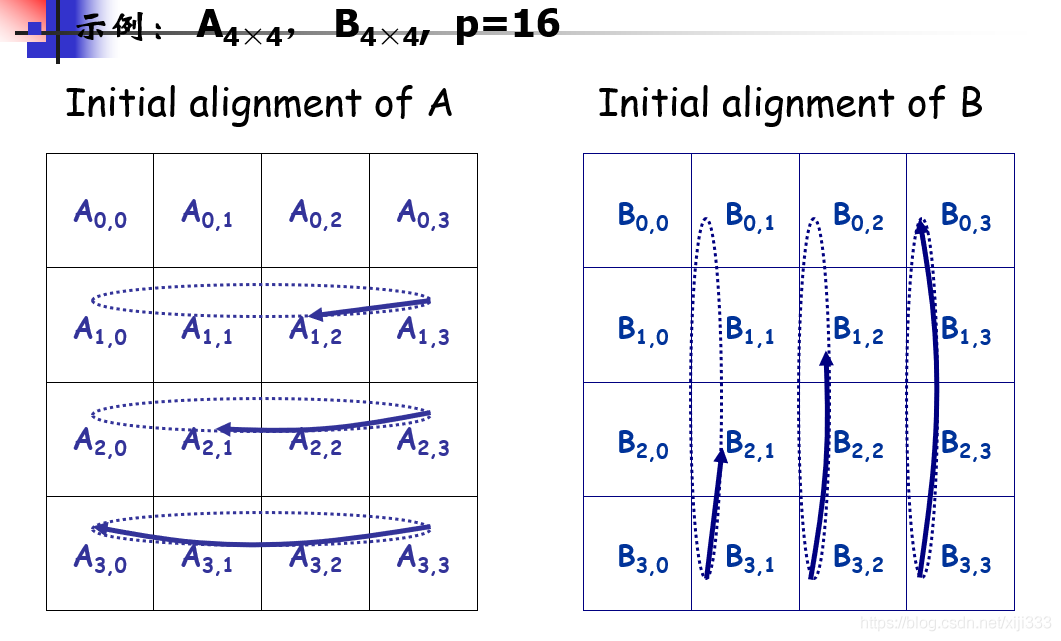
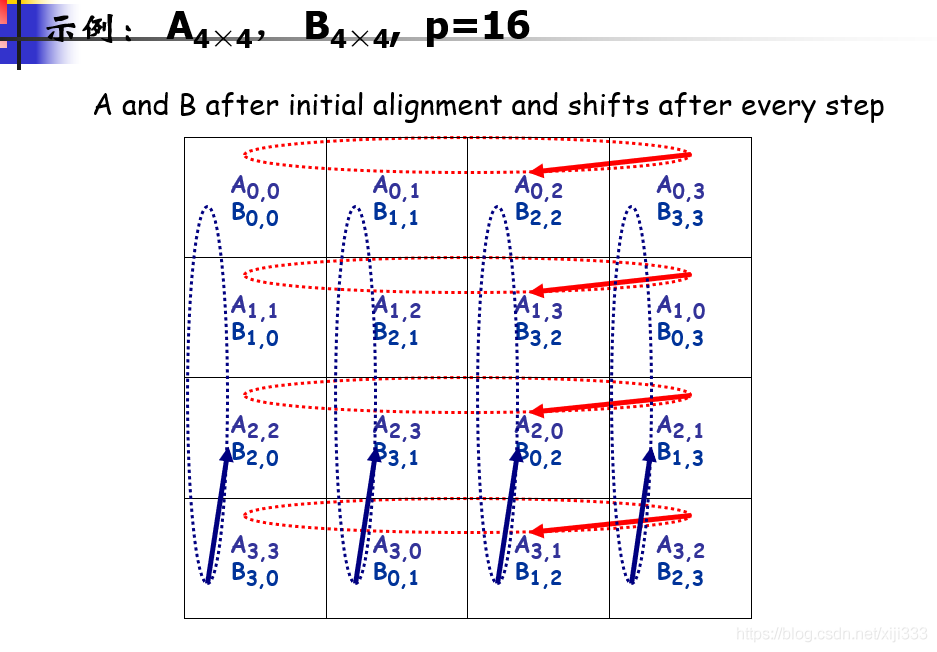
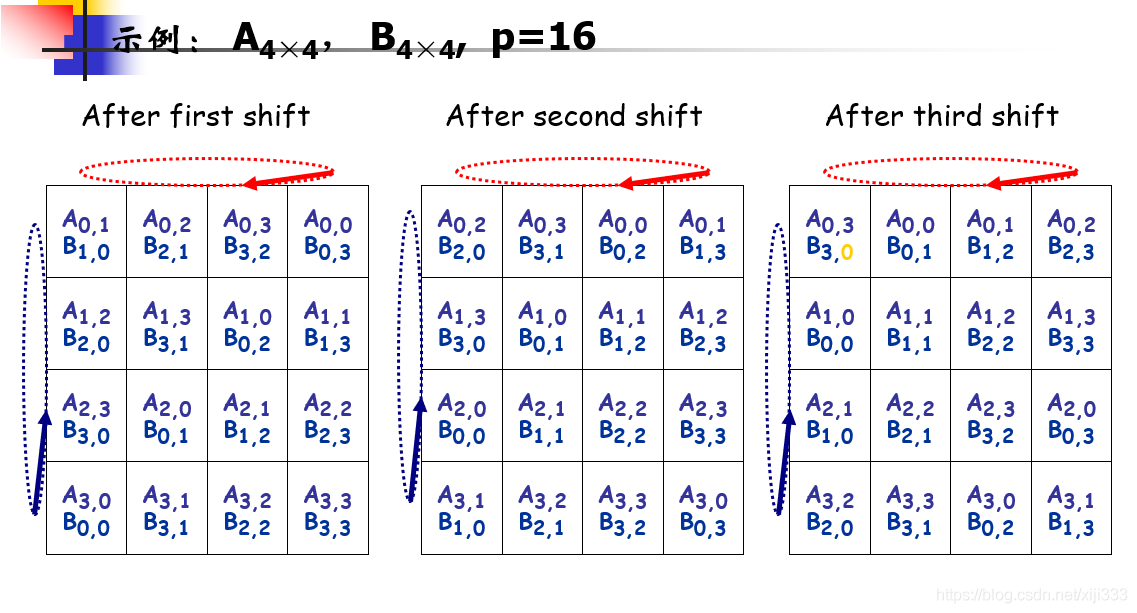
算法思想：将N ∗ N的矩阵分割成P块，即每行每列均有✔P个分块矩阵，那么每个分块的行列都等于N / ✔P。将这些分块分给P个处理器，即处理器 Pij 管理分块Aij、Bij，并计算对应分块Cij的结果。初始时将分块Aij循环左移i步，分块Bij循环上移j步。接下来是运算过程，计算Aij ∗ Bij并将结果放置到Cij中，计算完成后Aij循环左移一步，Bij循环上移一步，重复这个过程✔P次即可计算出最终的Cij，然后由根处理器收集结果即可。

#include <iostream>
#include <cstdio>
#include <mpi.h>
#include <cstdlib>
#include <cstring>
#include <ctime>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;

const int n = 5;	//n是矩阵大小

int MatrixA[n][n], MatrixB[n][n], MatrixC[n][n];	//三个矩阵 已知A B 计算C=A*B
int block, blocknum;	//每个分块的大小(一行有多少元素) blocknum=block*block
int numprocs, sqrnumprocs;	//前者为处理器的个数 后者为其根号
int move_size;	//=blocknum*sizeof(int) 用于memcpy memset等函数

int* blockA, * blockB, * blockC, * tmpa, * tmpb;	//存储 分块矩阵 以及传输数据所需要的缓冲区
int myid, row, col;	//处理器ID 把整个矩阵划分成若干个分块矩阵分给其它处理器 则该处理器处理第row行 第clo列的分块矩阵

inline void init_AB()//初始化矩阵 A B
{
	srand(time(0));
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			MatrixA[i][j] = rand() % 10;
			MatrixB[i][j] = rand() % 10;
		}
	}
}

inline void send_block_AB()
{
	int rowmin, rowmax, colmin, colmax;	//记录分块矩阵的范围
	for (int i = 0; i < numprocs; i++)
	{
		rowmin = (i / sqrnumprocs) * block;
		rowmax = rowmin + block;
		colmin = (i % sqrnumprocs) * block;
		colmax = colmin + block;
		for (int j = rowmin; j < rowmax; j++)
		{
			for (int k = colmin; k < colmax; k++)
			{
				int idx = (j - rowmin) * block + k - colmin;	//由于tmp是一维数组 所以要计算当前元素对应的下标
				tmpa[idx] = MatrixA[j][k];
				tmpb[idx] = MatrixB[j][k];
			}
		}
		if (!i)	//0号处理器
		{
			memcpy(blockA, tmpa, move_size);
			memcpy(blockB, tmpb, move_size);
		}
		else
		{		//发送分块矩阵 A B
			MPI_Send(tmpa, blocknum, MPI_INT, i, 1, MPI_COMM_WORLD);
			MPI_Send(tmpb, blocknum, MPI_INT, i, 2, MPI_COMM_WORLD);
		}
	}
}

inline int getidx(int row, int col)	//通过 分块矩阵的 行row 列col 得到管理它的 处理器ID
{
	//row=id/sqrnumprocs col=id%sqrnumprocs
	return ((row + sqrnumprocs) % sqrnumprocs) * sqrnumprocs + (col + sqrnumprocs) % sqrnumprocs;
}

inline void init_move()	//初始时的移动操作 A中分块(i,j)左移i步 B中分块(i,j)上移j步
{
	MPI_Status s;
	//发送并接受对应的分块
	MPI_Sendrecv(blockA, blocknum, MPI_INT, getidx(row, col - row), 1, tmpa, blocknum, MPI_INT, getidx(row, col + row), 1, MPI_COMM_WORLD, &s);
	MPI_Sendrecv(blockB, blocknum, MPI_INT, getidx(row - col, col), 2, tmpb, blocknum, MPI_INT, getidx(row + col, col), 2, MPI_COMM_WORLD, &s);
	//拷贝
	memcpy(blockA, tmpa, move_size);
	memcpy(blockB, tmpb, move_size);
}

inline void cal()	//计算过程
{
	MPI_Status s;
	for (int times = 0; times < sqrnumprocs; times++)	//sqrnumprocs次 乘法和累加
	{
		for (int i = 0; i < block; i++)	//c[i][j]=a[i][k]*b[k][j]
		{								//c[i][j]=blockC[i * block + j]
			for (int j = 0; j < block; j++)
			{
				int sum = blockC[i * block + j];
				for (int k = 0; k < block; k++)
					sum += blockA[i * block + k] * blockB[k * block + j];
				blockC[i * block + j] = sum;
			}
		}	//每个分块计算完毕后
		//A中分块左移1步 B中分块上移1步
		MPI_Sendrecv(blockA, blocknum, MPI_INT, getidx(row, col - 1), 1, tmpa, blocknum, MPI_INT, getidx(row, col + 1), 1, MPI_COMM_WORLD, &s);
		MPI_Sendrecv(blockB, blocknum, MPI_INT, getidx(row - 1, col), 2, tmpb, blocknum, MPI_INT, getidx(row + 1, col), 2, MPI_COMM_WORLD, &s);
		//拷贝
		memcpy(blockA, tmpa, move_size);
		memcpy(blockB, tmpb, move_size);
	}
}

inline void getans()	//处理器0 从其余处理器处得到分块矩阵的结果并合并
{
	MPI_Status s;
	int rowmin, rowmax, colmin, colmax;
	//处理器0 可直接得到
	for (int i = 0; i < block; i++)
		for (int j = 0; j < block; j++)
			MatrixC[i][j] = blockC[i * block + j];
	//其余的需要 接收
	for (int i = 1; i < numprocs; i++)
	{
		MPI_Recv(blockC, blocknum, MPI_INT, i, 1, MPI_COMM_WORLD, &s);
		rowmin = (i / sqrnumprocs) * block;	//首行坐标
		rowmax = rowmin + block;	//最后一行的坐标
		colmin = (i % sqrnumprocs) * block;	//首列坐标
		colmax = colmin + block;	//最后一列的坐标
		for (int j = rowmin; j < rowmax; j++)
			for (int k = colmin; k < colmax; k++)
				MatrixC[j][k] = blockC[(j - rowmin) * block + k - colmin];
	}
}

inline void print_matrix(int ans[][n])	//输出矩阵
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
			printf("%-5d", ans[i][j]);
		printf("\n");
	}
	printf("\n");
}

int main(int argc, char* argv[])
{
	MPI_Init(&argc, &argv);
	MPI_Comm_size(MPI_COMM_WORLD, &numprocs);	//个数
	MPI_Comm_rank(MPI_COMM_WORLD, &myid);		//ID

	clock_t start = clock();	//开始时间

	sqrnumprocs = sqrt(numprocs);
	if (sqrnumprocs * sqrnumprocs != numprocs || n % sqrnumprocs)
	{
		if (myid == 0)
		{
			if (n % sqrnumprocs == 0)
				cout << "处理器个数应该为完全平方数！\n";
			else
				cout << "sqrnumprocs必须整除矩阵大小n!\n";
		}
		MPI_Finalize();
		return 0;
	}
	block = n/sqrnumprocs;	//分块大小
	blocknum = block * block;	//每个分块的元素总数
	move_size = blocknum * sizeof(int);
	row = myid / sqrnumprocs;		//计算自己处理的分块矩阵的 坐标
	col = myid % sqrnumprocs;
	blockA = new int[blocknum];	//分配空间
	blockB = new int[blocknum];
	blockC = new int[blocknum];
	tmpa = new int[blocknum];
	tmpb = new int[blocknum];
	memset(blockC, 0, move_size);	//初始化c
	if (!myid)	//0号处理器
	{
		init_AB();	//初始化矩阵A B
		send_block_AB();	//计算分块矩阵 并将其发送给其余处理器
	}
	else
	{	//接受0号发过来的 分块矩阵
		MPI_Status s;
		MPI_Recv(blockA, blocknum, MPI_INT, 0, 1, MPI_COMM_WORLD, &s);
		MPI_Recv(blockB, blocknum, MPI_INT, 0, 2, MPI_COMM_WORLD, &s);
	}
	init_move();	//初始时分块矩阵的移动
	cal();	//计算过程
	if (myid == 0)
	{
		getans();
		cout << "矩阵A为:\n";
		print_matrix(MatrixA);
		cout << "矩阵B为:\n";
		print_matrix(MatrixB);
		cout << "矩阵C=A*B为(cannon乘法):\n";
		print_matrix(MatrixC);
		clock_t end = clock();	//结束时间
		cout << "Cannon乘法耗时: " << end - start << "\n";
	}
	else
	{
		MPI_Send(blockC, blocknum, MPI_INT, 0, 1, MPI_COMM_WORLD);
	}

	delete[] blockA;
	delete[] blockB;
	delete[] blockC;
	delete[] tmpa;
	delete[] tmpb;
	MPI_Barrier(MPI_COMM_WORLD);
	MPI_Finalize();
	return 0;
}
————————————————
版权声明：本文为CSDN博主「csu_xiji」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/xiji333/article/details/106713440

Fox算法：

输入、输出、环境都同Cannon算法。

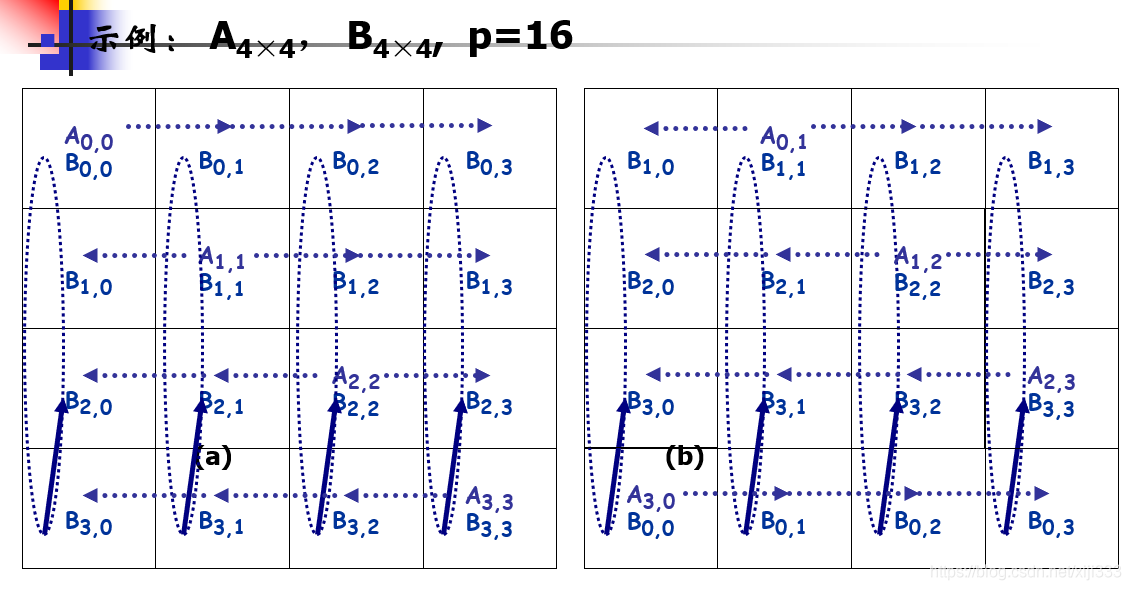
算法思想：分块部分的处理和Cannon算法是一样的。在分完块后，Aii向所在行的其他处理器进行一到多播送，然后处理器将收到的分块A与自己的B块进行乘加运算，计算完成之后自己的分块A保持不变，分块B循环上移一步，如果Aij是上次第i行播送的块，本次选择A[i, j + 1 % ✔P]向所在行的其它处理器进行一到多播送，然后进行乘加运算……进行✔P次乘加运算后即可得到所有的Cij，由根处理器收集结果即可。

#include <iostream>
#include <cstdio>
#include <mpi.h>
#include <cstdlib>
#include <cstring>
#include <ctime>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;

const int n = 1e3;	//n是矩阵大小

int MatrixA[n][n], MatrixB[n][n], MatrixC[n][n];	//三个矩阵 已知A B 计算C=A*B
int block, blocknum;	//每个分块的大小(一行有多少元素) blocknum=block*block
int numprocs, sqrnumprocs;	//前者为处理器的个数 后者为其根号
int move_size;	//=blocknum*sizeof(int) 用于memcpy memset等函数

int* blockA, * blockB, * blockC, * tmpa, * tmpb;	//存储 分块矩阵 以及传输数据所需要的缓冲区
int myid, row, col;	//处理器ID 把整个矩阵划分成若干个分块矩阵分给其它处理器 则该处理器处理第row行 第clo列的分块矩阵

inline void init_AB()//初始化矩阵 A B
{
	srand(time(0));
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			MatrixA[i][j] = rand() % 10;
			MatrixB[i][j] = rand() % 10;
		}
	}
}

inline void send_block_AB()
{
	int rowmin, rowmax, colmin, colmax;	//记录分块矩阵的范围
	for (int i = 0; i < numprocs; i++)
	{
		rowmin = (i / sqrnumprocs) * block;
		rowmax = rowmin + block;
		colmin = (i % sqrnumprocs) * block;
		colmax = colmin + block;
		for (int j = rowmin; j < rowmax; j++)
		{
			for (int k = colmin; k < colmax; k++)
			{
				int idx = (j - rowmin) * block + k - colmin;	//由于tmp是一维数组 所以要计算当前元素对应的下标
				tmpa[idx] = MatrixA[j][k];
				tmpb[idx] = MatrixB[j][k];
			}
		}
		if (!i)	//0号处理器
		{
			memcpy(blockA, tmpa, move_size);
			memcpy(blockB, tmpb, move_size);
		}
		else
		{		//发送分块矩阵 A B
			MPI_Send(tmpa, blocknum, MPI_INT, i, 1, MPI_COMM_WORLD);
			MPI_Send(tmpb, blocknum, MPI_INT, i, 2, MPI_COMM_WORLD);
		}
	}
}

inline int getidx(int row, int col)	//通过 分块矩阵的 行row 列col 得到管理它的 处理器ID
{
	//row=id/sqrnumprocs col=id%sqrnumprocs
	return ((row + sqrnumprocs) % sqrnumprocs) * sqrnumprocs + (col + sqrnumprocs) % sqrnumprocs;
}

inline void cal()	//计算过程
{
	MPI_Status s;
	int send_col_idx = row;	//在分块矩阵的视图上看 初始时 需要发送分块矩阵(row,send_col_idx)
	int idxmin, idxmax;	//记录 需要接收分块的 处理器的id范围
	for (int times = 0; times < sqrnumprocs; times++)	//sqrnumprocs次 乘法和累加
	{
		//该处理器处理的分块的坐标为 (row,col)
		//所以需要从 处理器 getidx(row,send_idx[row]) 处得到分块A 然后进行乘法累加
		if (col == send_col_idx)
		{
			idxmin = getidx(row, 0);
			idxmax = getidx(row, sqrnumprocs - 1);
			for (int i = idxmin; i <= idxmax; i++)
			{
				if (i == myid)	//自己就没必要发送了
					continue;
				MPI_Send(blockA, blocknum, MPI_INT, i, 1, MPI_COMM_WORLD);//发送
			}
			memcpy(tmpa, blockA, move_size);	//直接拷贝到目标位置
		}
		else	//接收分块
		{
			MPI_Recv(tmpa, blocknum, MPI_INT, getidx(row, send_col_idx), 1, MPI_COMM_WORLD, &s);
		}
		send_col_idx = (send_col_idx + 1) % sqrnumprocs;	//递增列号

		for (int i = 0; i < block; i++)	//c[i][j]=a[i][k]*b[k][j]
		{								//c[i][j]=blockC[i * block + j]
			for (int j = 0; j < block; j++)
			{
				int sum = blockC[i * block + j];
				for (int k = 0; k < block; k++)
					sum += tmpa[i * block + k] * blockB[k * block + j];
				blockC[i * block + j] = sum;
			}
		}	//每个分块计算完毕后
		//A中分块保持不动 B中分块上移1步
		MPI_Sendrecv(blockB, blocknum, MPI_INT, getidx(row - 1, col), 2, tmpb, blocknum, MPI_INT, getidx(row + 1, col), 2, MPI_COMM_WORLD, &s);
		//拷贝
		memcpy(blockB, tmpb, move_size);
	}
}

inline void getans()	//处理器0 从其余处理器处得到分块矩阵的结果并合并
{
	MPI_Status s;
	int rowmin, rowmax, colmin, colmax;
	//处理器0 可直接得到
	for (int i = 0; i < block; i++)
		for (int j = 0; j < block; j++)
			MatrixC[i][j] = blockC[i * block + j];
	//其余的需要 接收
	for (int i = 1; i < numprocs; i++)
	{
		MPI_Recv(blockC, blocknum, MPI_INT, i, 1, MPI_COMM_WORLD, &s);
		rowmin = (i / sqrnumprocs) * block;	//首行坐标
		rowmax = rowmin + block;	//最后一行的坐标
		colmin = (i % sqrnumprocs) * block;	//首列坐标
		colmax = colmin + block;	//最后一列的坐标
		for (int j = rowmin; j < rowmax; j++)
			for (int k = colmin; k < colmax; k++)
				MatrixC[j][k] = blockC[(j - rowmin) * block + k - colmin];
	}
}

inline void print_matrix(int ans[][n])	//输出矩阵
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
			printf("%-5d", ans[i][j]);
		printf("\n");
	}
	printf("\n");
}

int main(int argc, char* argv[])
{
	MPI_Init(&argc, &argv);
	MPI_Comm_size(MPI_COMM_WORLD, &numprocs);	//个数
	MPI_Comm_rank(MPI_COMM_WORLD, &myid);		//ID

	clock_t start = clock();	//开始时间

	sqrnumprocs = sqrt(numprocs);
	if (sqrnumprocs * sqrnumprocs != numprocs || n % sqrnumprocs)
	{
		if (myid == 0)
		{
			if (n % sqrnumprocs == 0)
				cout << "处理器个数应该为完全平方数！\n";
			else
				cout << "sqrnumprocs必须整除矩阵大小n!\n";
		}
		MPI_Finalize();
		return 0;
	}
	block = n/sqrnumprocs;	//分块大小
	blocknum = block * block;	//每个分块的元素总数
	move_size = blocknum * sizeof(int);
	row = myid / sqrnumprocs;		//计算自己处理的分块矩阵的 坐标
	col = myid % sqrnumprocs;
	blockA = new int[blocknum];	//分配空间
	blockB = new int[blocknum];
	blockC = new int[blocknum];
	tmpa = new int[blocknum];
	tmpb = new int[blocknum];
	memset(blockC, 0, move_size);	//初始化c
	if (!myid)	//0号处理器
	{
		init_AB();	//初始化矩阵A B
		send_block_AB();	//计算分块矩阵 并将其发送给其余处理器
	}
	else
	{	//接受0号发过来的 分块矩阵
		MPI_Status s;
		MPI_Recv(blockA, blocknum, MPI_INT, 0, 1, MPI_COMM_WORLD, &s);
		MPI_Recv(blockB, blocknum, MPI_INT, 0, 2, MPI_COMM_WORLD, &s);
	}
	cal();	//计算过程
	if (myid == 0)
	{
		getans();
		//cout << "矩阵A为:\n";
		//print_matrix(MatrixA);
		//cout << "矩阵B为:\n";
		//print_matrix(MatrixB);
		//cout << "矩阵C=A*B为:\n";
		//print_matrix(MatrixC);
		clock_t end = clock();	//结束时间
		cout << "Fox乘法耗时: " << end - start << "\n";
	}
	else
	{
		MPI_Send(blockC, blocknum, MPI_INT, 0, 1, MPI_COMM_WORLD);
	}

	delete[] blockA;
	delete[] blockB;
	delete[] blockC;
	delete[] tmpa;
	delete[] tmpb;
	MPI_Barrier(MPI_COMM_WORLD);
	MPI_Finalize();
	return 0;
}
————————————————
版权声明：本文为CSDN博主「csu_xiji」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/xiji333/article/details/106713440

稀疏矩阵

串行优化

作业提供的稀疏矩阵格式为常见的CSR存储格式。最简单的naive写法，可不做预处理，简单地对每一行进行遍历，如下所示。

void spmv(dist_matrix_t *mat, const data_t* x, data_t* y) {
    int m = mat->global_m;
    index_t *r_pos = mat->r_pos;
    index_t *c_idx = mat->c_idx;
    data_t *values = mat->values;
    for (int i = 0; i < m; ++i) {
        int p, begin = r_pos[i], end = r_pos[i+1];
        data_t s = 0;
        for(p = begin; p < end; ++p) {
            int j = c_idx[p];
            s += values[p] * x[j];
        }
        y[i] = s;
    }
}

向量化编译选项

对于大部分代码，都可以首先“无脑”地加上自动向量化的编译选项，看看效果如何。-O3 -fomit-frame-pointer -march=armv8-a -ffast-math的编译选项加上后，效果还是相当明显的。

循环展开

对于串行程序优化，循环展开是常用的方法。将最内层的p循环按步长为4展开，这种写法（下图中所有注释对应成一套）实际上跟用intrinsics的向量化指令（下图中没有注释的对应成一套，arm v8架构的neon intrinsics指令）是效果等价的。

void spmv(dist_matrix_t * mat, const data_t * x, data_t* y) {
    int m = mat->global_m;
    index_t *r_pos = mat->r_pos;
    for (int i = 0; i < m; ++i) {
        int cnt = r_pos[i+1] - r_pos[i];
        // data_t s0 = 0, s1 = 0, s2 = 0, s3 = 0;
        float32x4_t temp, matrix, vector; temp = vdupq_n_f32(0.0); data_t s0 = 0;
        
        int p, max_4p = cnt & (~3);
        data_t * values = mat->values + r_pos[i];
        index_t * c_idx = mat->c_idx + r_pos[i];
        for (p = 0; p < max_4p; p += 4) {
            int j0 = c_idx[p  ];
            int j1 = c_idx[p+1];
            int j2 = c_idx[p+2];
            int j3 = c_idx[p+3];
            // s0 += values[p  ] * x[j0];
            // s1 += values[p+1] * x[j1];
            // s2 += values[p+2] * x[j2];
            // s3 += values[p+3] * x[j3];
            matrix = vld1q_f32(values + p);
            vector = vld1q_lane_f32(x + j0, vector, 0);
            vector = vld1q_lane_f32(x + j1, vector, 1);
            vector = vld1q_lane_f32(x + j2, vector, 2);
            vector = vld1q_lane_f32(x + j3, vector, 3);
            temp   = vmlaq_f32(temp, matrix, vector);
        }
        for (; p < cnt; p++) {
            int j0 = c_idx[p];
            s0 += values[p] * x[j0];
        }
        // y[i] = s0 + s1 + s2 + s3;
        y[i] = s0 + vgetq_lane_f32(temp, 0) + vgetq_lane_f32(temp, 1) + vgetq_lane_f32(temp, 2) + vgetq_lane_f32(temp, 3);
    }
}

其实理论上来说，稀疏矩阵计算应该是memory bound的类型，循环展开这种提高SIMD效率的优化应该是起不到什么作用的。但在这里大部分算例效果有提升，小部分算例没什么效果甚至有一点倒退。除了上述两者，还尝试了内存对齐、消除指针别名等常用方法，但用在此处后发现并没有什么明显的效果。

CSRL格式

本部分详细介绍可以参见刘芳芳、杨超等的文章。CSRL格式适用于具有局部性特征的矩阵，通过对该格式的SpMV进行向量化，使A和x的访问和计算都可以采用SIMD intrinsics来完成，提高了访问速度，进而提高性能。

CSRL格式相对于CSR格式的主要改进在于：对稀疏矩阵中列下标连续的非零元段，存储首个非零元的列下标及段长度。

因此需要四个数组（ 其中矩阵A是mxn矩阵，有nnz个非零元，有nzseg个非零元段）：

• val[nnz]：记录每个非零元的值
• jas[nnz]：记录每个非零元段的首个非零元所在的列下标
• jan[nnz]：记录每个非零元段的段长度
• ptr[m+1]：记录每行的第一个非零元段的索引，其中ptr[m]=nzseg+1

分块COO格式

COO格式是更为简单直接的格式，对于每个非零元直接存储其行索引、列索引和值，即一个三元组（r_idx, c_idx, values）。虽然看起来比CSR格式要多存许多行索引，但它对于高度稀疏的矩阵而言是有利的。最极端地，对于只有一个非零元的稀疏矩阵，COO格式只需要3个数，而CSR格式需要m+1+2个数（m为矩阵行数）。所以COO格式对于分块后的小矩阵存储较为有利。

更有利的是，当分拆成小矩阵后，小矩阵的维度可能小于65536（uint16_t可覆盖）甚至256（uint8_t可覆盖），则可以使用更低精度的无符号数来存储行索引和列索引（小矩阵内部的索引），需要计算时再加上该小矩阵的偏移量（小矩阵在原矩阵中相对于(0,0)的位置）即可，由此可以节省内存带宽，提高性能。

基于OpenMP并行改写

OpenMP的并行非常直观，直接在对矩阵行的遍历上按行做任务划分和并行。如下图所示，实验发现dynamic的调度策略会非常慢。这大概是因为每一行的非零元不算很多，每个线程很快完成一行的计算，然后根据work-stealing的策略，又向调度方申请新的任务，如此频繁的询问、调度带来较大开销。因此尽可能放大并行任务的粒度（调整chunk值）。经过简单调试，static的策略性能最好。

void spmv(dist_matrix_t *mat, const data_t* x, data_t* y) {
    int m = mat->global_m;
    index_t *r_pos = mat->r_pos;
    #pragma omp parallel for schedule(static)
    for (int i = 0; i < m; ++i) {
        int cnt = r_pos[i+1] - r_pos[i];
        data_t s0 = 0, s1 = 0, s2 = 0, s3 = 0;
        int p, max_4p = cnt & (~3);
        data_t * values = mat->values + r_pos[i];
        index_t * c_idx = mat->c_idx + r_pos[i];
        for (p = 0; p < max_4p; p += 4) {
            int j0 = c_idx[p  ];
            int j1 = c_idx[p+1];
            int j2 = c_idx[p+2];
            int j3 = c_idx[p+3];
            s0 += values[p  ] * x[j0];
            s1 += values[p+1] * x[j1];
            s2 += values[p+2] * x[j2];
            s3 += values[p+3] * x[j3];
        }
        for (; p < cnt; p++) {
            int j0 = c_idx[p];
            s0 += values[p] * x[j0];
        }
        y[i] = s0 + s1 + s2 + s3;
    }
}

但即使如此，（在后面与MPI的对比中可见）基于OpenMP并行的效果非常差。大概的原因来自两方面：上述的线程在并行区内启动、调度和销毁的开销；以及线程-线程之间的伪共享。虽然对于向量y的伪共享，已经通过尽可能大的任务粒度、先存局部变量s0,s1,s2,s3最后再写y[i]的措施降低了，但总还是有些影响。

基于MPI并行改写

基于MPI的并行首先要考虑负载均衡的任务划分。由于划分必须要静态的，所以还像OpenMP一样以行来做动态的任务分配（你分几行，我分几行，如此往复）显然是不行的。必须要有合理的负载分配方式。

平均分配矩阵各行显然是不行的，因为可能有的行非零元多，有的行少。因此可用非零元个数来做依据，尽量使每个进程分到的那些行所包括的非零元个数尽可能相近。所以在创建分布式矩阵和向量前，首先要由进程0统计矩阵的非零元信息，做出一个尽可能“公平”的划分。如下图所示。

虽然有一个理论上公平的均摊任务量avg_workload，但实际上不可能总是切得这么精准，使得满足avg_workload的划分刚好落在行与行之间。如果每次总是向下取整（即做得比avg_workload少一点，则最后的那个进程会累积下特别多的任务，导致负载极度不均衡。而如果每次总是向上取整（即做得比avg_workload多一点，则最后的几个进程可能会无任务可做，全程空等，但这总比前者要好得多。为了获得更合理的划分，这里采用均匀随机的方法，即进程按照进程号奇偶，交替地多做一点和少做一点。使得不至于最后有不少的进程无任务可做。

MPI_Bcast(&mat.global_m,   1, MPI_INT, 0, MPI_COMM_WORLD);
MPI_Bcast(&mat.global_nnz, 1, MPI_INT, 0, MPI_COMM_WORLD);
if (p_id == 0) {// 进程0负责记录和分配各个进程计算的范围
    p_ibeg      = (uint32_t*)malloc(sizeof(uint32_t) * p_num);
    p_local_m   = (uint32_t*)malloc(sizeof(uint32_t) * p_num);
    p_local_nnz = (uint32_t*)malloc(sizeof(uint32_t) * p_num);
    assert(mat.r_pos[mat.global_m] == mat.global_nnz);
    int avg_workload = mat.global_nnz / p_num;// 尽可能平均分
    int ptr_last, ptr_curr = 0;
    bool shrink = false;
    for (int p = 0; p < p_num; p++) {
        // p_ibeg[p] = (p > 0) ? (--ptr_curr) : ptr_curr;
        p_ibeg[p] = ptr_curr;
        ptr_last = ptr_curr;
        while (ptr_curr <= mat.global_m &&  mat.r_pos[ptr_curr] - mat.r_pos[ptr_last] < avg_workload) 
            ptr_curr++;
        if (ptr_curr <= mat.global_m) {
            // 如果ptr_curr还落在有效的范围内
            // 此时ptr_curr减一则会比avg_workload小，但直接用avg_workload就会比avg_workload大
            // 因此均匀随机地取
            if (shrink == true)
                ptr_curr--;
            shrink = !shrink;
        } else {// 后面的进程不再有工作了
            for (int remain_p = p+1; remain_p < p_num; remain_p++) 
                p_ibeg[remain_p] = mat.global_m;
            break;
        }
    }
    for (int p = 0; p < p_num; p++) {// 确定每个进程负责计算的局部范围local_m，和实际有的
        if (p != p_num - 1) {
            p_local_m[p]   = p_ibeg[p+1]            - p_ibeg[p];
            p_local_nnz[p] = mat.r_pos[p_ibeg[p+1]] - mat.r_pos[p_ibeg[p]];
        } else {// p_num - 1
            p_local_m[p]   = mat.global_m            - p_ibeg[p];
            p_local_nnz[p] = mat.r_pos[mat.global_m] - mat.r_pos[p_ibeg[p]];
        }
        // printf("p_id: %d, row_beg: %d, work_nnz: %d\n", p, p_ibeg[p], p_local_nnz[p]);
    }
    // 0号进程负责计算的区域
    mat.local_ibeg = 0;
    mat.local_m = p_local_m[0];
    mat.local_nnz = p_local_nnz[0];
    // 告诉其它进程负责计算的区域
    for (int p = 1; p < p_num; p++) {
        MPI_Send(&p_ibeg[p]     , 1, MPI_INT, p,  10, MPI_COMM_WORLD);// tag =  10
        MPI_Send(&p_local_m[p]  , 1, MPI_INT, p, 110, MPI_COMM_WORLD);// tag = 110
        MPI_Send(&p_local_nnz[p], 1, MPI_INT, p, 210, MPI_COMM_WORLD);// tag = 210
        MPI_Send(&mat.global_m  , 1, MPI_INT, p, 310, MPI_COMM_WORLD);// tag = 310
        MPI_Send(&mat.global_nnz, 1, MPI_INT, p, 410, MPI_COMM_WORLD);// tag = 410
    }
} 

而其它进程接收到0号进程的任务分配后，按照各自的需求来开辟分布式矩阵和向量的内存空间。注意这里向量x仍然是全局的，而向量y可以是局部的。

...
else {// 其它进程负责接收
    MPI_Recv(&mat.local_ibeg, 1, MPI_INT, 0,  10, MPI_COMM_WORLD, &status);// tag =  10
    MPI_Recv(&mat.local_m   , 1, MPI_INT, 0, 110, MPI_COMM_WORLD, &status);// tag = 110
    MPI_Recv(&mat.local_nnz , 1, MPI_INT, 0, 210, MPI_COMM_WORLD, &status);// tag = 210
    MPI_Recv(&mat.global_m  , 1, MPI_INT, 0, 310, MPI_COMM_WORLD, &status);// tag = 310
    MPI_Recv(&mat.global_nnz, 1, MPI_INT, 0, 410, MPI_COMM_WORLD, &status);// tag = 410
    // 分配矩阵内存空间
    mat.r_pos = (index_t*)malloc(sizeof(index_t) * (mat.local_m + 1));// 按照行数+1分配正向表的r_pos空间
    mat.c_idx = (index_t*)malloc(sizeof(index_t) * mat.local_nnz);// 按照整个矩阵的非零元数目分配非零元的列序号的存储空间
    mat.values = (data_t*)malloc(sizeof(data_t)  * mat.local_nnz);// 按照整个矩阵的非零元数目分配非零元的数据的存储空间
    // 分配向量内存空间：注意！右端向量x仍然是全局的！只是结果向量是只开一部分
    x = (data_t*)malloc(sizeof(data_t) * mat.global_m);
    y = (data_t*)malloc(sizeof(data_t) * mat.local_m);
}

在开辟好内存空间后，由进程0（因为只有它读入了文件中的数据）向其它进程分发数据。此处需要注意因为对矩阵的行做了划分（前面进程的数据相当于抛弃掉了），各个进程记录每行数据存储位置的r_pos需要做一个偏移。

if (p_id == 0) {
    for (int p = 1; p < p_num; p++) {
        // printf(" Sending for %d\n", p);
        MPI_Send(&mat.r_pos[p_ibeg[p]]            , p_local_m[p]  , MPI_UNSIGNED, p,  10, MPI_COMM_WORLD);
        MPI_Send(&mat.c_idx[mat.r_pos[p_ibeg[p]]] , p_local_nnz[p], MPI_UNSIGNED, p, 110, MPI_COMM_WORLD);
        MPI_Send(&mat.values[mat.r_pos[p_ibeg[p]]], p_local_nnz[p], MPI_DATA,     p, 210, MPI_COMM_WORLD);
        // MPI_Send(&x[p_ibeg[p]]                    , p_local_m[p]  , MPI_DATA,     p, 310, MPI_COMM_WORLD);
        MPI_Send(&x[0]                            , mat.global_m  , MPI_DATA,     p, 310, MPI_COMM_WORLD);
    }
} else {
    MPI_Recv(&mat.r_pos[0],  mat.local_m  , MPI_UNSIGNED, 0,  10, MPI_COMM_WORLD, &status);
    MPI_Recv(&mat.c_idx[0],  mat.local_nnz, MPI_UNSIGNED, 0, 110, MPI_COMM_WORLD, &status);
    MPI_Recv(&mat.values[0], mat.local_nnz, MPI_DATA,     0, 210, MPI_COMM_WORLD, &status);
    MPI_Recv(&x[0],          mat.global_m , MPI_DATA,     0, 310, MPI_COMM_WORLD, &status);
    // 其他进程的数据得到之后需要做个偏移！！！
    uint32_t r_pos_0 = mat.r_pos[0];
    for (uint32_t i = 0; i < mat.local_m; i++)
        mat.r_pos[i] -= r_pos_0;
    mat.r_pos[mat.local_m] = mat.local_nnz;// r_pos的最后一个元素指向末尾
}

CSR混合CSRL格式

如前所述，CSRL格式在nzseg/nnz值很小时，性能远胜于CSR格式。但大部分情况下，CSR仍占优。因此在此采用两者混合的格式。注意到在划分为进行分布式数组后，相当于每一个进程都在做一个local_mxglobal_m的矩阵和global_m的向量的乘法，所以它们可以独立地使用CSRL格式，从预处理到计算都是互不干扰的。

这样的好处的优化更能“包裹”住原问题的一些奇性。比如，某个矩阵某些行很稠密、元素连成一片，很适合于CSRL格式；但也有很多行很稀疏，更适合于CSR格式。如果不做行划分，它最后只有一个nzseg/nnz值，做和不做CSRL格式的优化都是一锤子买卖，总会亏欠另一方。而行划分之后，相当于有了#procs个nzseg/nnz值，可以各自局部地决定是否要做CSRL格式的优化，具备了一点“自适应性”。这也是MPI划分相比OpenMP要更优胜的地方。在这里决定是否做CSRL格式优化的nzseg/nnz阈值为0.3，小于0.3则该进程转换成CSRL格式，否则不动。

GPU版本（单卡）

GPU版本的SpMV优化的参考资料远比CPU的丰富。作业也只要求做CPU或GPU中一种，因此这里文字介绍较为简单。各种方法的原理是类似的，采用尽可能紧致的存储格式，节省带宽，提高访存效率，然后再考虑SIMD效率。

naive版本的算法非常直接，对矩阵做一维行划分，每一个cuda thread负责矩阵一行的计算。如下图所示。

__global__ void spmv_naive_kernel(int m, const uint32_t *r_pos, \
    const uint32_t *c_idx, const data_t *values, const data_t *x, data_t *y) {
    int i = blockIdx.x * blockDim.x + threadIdx.x;
    if(i < m) {
        int p, begin = r_pos[i], end = r_pos[i+1];
        data_t s = y[i];
        for(p = begin; p < end; ++p) {
            int j = c_idx[p];
            s += values[p] * x[j];
        }
        y[i] = s;
    }
}
void spmv(dist_matrix_t *mat, const data_t* x, data_t* y) {
    int m = mat->global_m;
    dim3 grid_size (ceiling(m, 512), 1, 1);
    dim3 block_size (512, 1, 1);
    spmv_naive_kernel<<<grid_size, block_size>>>(m, \
        mat->gpu_r_pos, mat->gpu_c_idx, mat->gpu_values, x, y);
}

稠密矩阵

编译选项

对于naïve版本的代码，如下所示，不妨先“无脑”地加上-O3 -fomit-frame-pointer -march=armv8-a -ffast-math等编译选项来让编译器尽可能提供些自动向量化的效果。

void square_sgemm (int n, float* A, float* B, float* C) {
  /* For each row i of A */
  for (int i = 0; i < n; ++i)
    /* For each column j of B */
    for (int j = 0; j < n; ++j)  {
      /* Compute C(i,j) */
      float cij = C[i+j*n];
      for( int k = 0; k < n; k++ )
        cij += A[i+k*n] * B[k+j*n];
      C[i+j*n] = cij;
  }
}

仅仅是如此，在不同规模的算例上性能就已经有2~10倍的提升，n每逢4的倍数便有显著的性能下降，这是cache thrashing导致的。可做半定量分析：课程集群L1 cache为64B/line，4路组相联，256个组，可知地址低6位为Offset，中间8位为Index，高位为Tag。N-way set associativity只是提供了conflict miss时的“容错性”，因此不失一般性，假定为direct-mapped来分析。地址每隔2^14B就会拥有相同的Index而被映射到同一个set上，对于单精度浮点数而言就是4096个数，因此当n满足(n*m)%4096==0时（m=1,2,…,n-1），就会在一轮k维的循环中产生cache conflict miss，m就是冲突发生时两个B元素相隔的行数。因此冲突频率随n增大而增大，当n≥4096时，就是每两次相邻的对B元素读取都会造成冲突。

循环变换

注意到在naïve的代码中，由于矩阵采用列主序的存储方式，因此先行后列的方式来计算C中元素的值，虽然对B元素访存是连续的，但对于C和A矩阵的访存都是不利的。尤其在循环最内维的k维，A[i+k*n]是大跨步跳跃式访存。

因此可以采用对i和j维的循环交换，来发掘数据复用的空间局部性。代码如下所示。

void square_sgemm (int n, float* A, float* B, float* C) {
  for (int j = 0; j < n; j++){
    for (int i = 0; i < n; i++){
      register float b = B[j*n + i];
      for (int p = 0; p < n; p++)
        C[j*n+p] += A[i*n+p] * b;
    }
  }
}

相当于按列主序遍历B中元素，对于其中的每个元素b，找到它对应有贡献的C和A中的元素所在的列，进行乘加计算。最内维的p维循环对A和C都是连续的，可以有效利用向量化。由于更改循环后，在整轮最内维的p循环中，b的元素是固定不变的寄存器变量，因此不再出现步骤一中的cache conflict miss，反而是矩阵规模n每逢4的倍数就比相邻的有提升，这是因为n为4的倍数能刚好被向量化指令覆盖，而不会多出额外的数据需要标量运算。

消除指针别名

消除指针别名告诉编译器修改指针指向的内存内容只能经过该指针之手，使编译器有更大优化空间。主要方法是给函数形参中的指针添加__restrict__关键字。其它局部的指针变量在定义时也可用此修饰。

循环展开

将循环展开，同时做多列的乘加操作，即取同行不同列的B矩阵元素b0, b1, b2, b3，均与相同的A列做乘法后加到不同的C列上。代码如下所示，需要注意处理余下不足4的列。。

int j, i, p;
for ( j = 0; j < ((n)&(~3)); j+=4)//for each colum j of B
  for ( i = 0; i < n; i++){//for each row i of B
    register float b0 = B(i,j);
    register float b1 = B(i,j+1);
    register float b2 = B(i,j+2);
    register float b3 = B(i,j+3);
    for ( p = 0; p < n; p++){
      C(p,j  ) += A(p,i) * b0;
      C(p,j+1) += A(p,i) * b1;
      C(p,j+2) += A(p,i) * b2;
      C(p,j+3) += A(p,i) * b3;
    }
  }
for ( ; j < n; j++)//for each remaining colum j of B
  for ( i = 0; i < n; i++){//for each row i of B
    register float b0 = B(i,j);
    for ( p = 0; p < n; p++)
      C(p,j  ) += A(p,i  ) * b0;
  }

实验效果显示选4列为一批做乘加效果较好，而大于4列则效果开始下降。循环展开常见的是对最内层做，优势在于循环开销（如终止条件上的分支和计数器变量的更新）的减少。至于为什么要在最外层循环做展开（而不是最内层循环），需要从访存优化的角度来看。对比上一节《循环变换》中最内层循环只有一句C[jn+p] += A[in+p] b;，展开后此处最内层循环有四句C(p,j ) += A(p,i) b0;。注意，改写后，A(p,i)只需要载入寄存器一次，就能服务于C(p,j )，C(p,j+1)，C(p,j+2)，C(p,j+3)等的计算；而原来，相同的A[in+p]值需要为每个C[jn+p]加载一次。因此，外层循环的展开将矩阵A元素加载次数减少了nb倍（nb为循环展开的项数，这里是4）。

内存对齐和简单Blocking

利用分块技术提高计算访存比获得更高的性能是常用的优化手段。从之前的代码来看，有三层循环（从外到内依次是j -> i -> p），因此可以在这3个维度上采取分块，分别设为SET_J_BLOCK_SIZE, SET_I_BLOCK_SIZE, SET_P_BLOCK_SIZE。越内维访存越连续，因此设的分块大小更大。此处同时配合内存对齐的手段，是因为对于每一个分块矩阵的乘法，单独将A和B拷贝到一块对齐的连续的内存A_local和B_local中，计算结果存到同样对齐的连续的C_local中。一个好处是A_local和B_local矩阵在拷贝时已经预热，放进了CPU的cache里；另一个好处是在真正计算时，读取和存储都是连续的，提高了cache效率。将一块realMxrealN大小的矩阵拷贝到setMxsetN大小的内存中的代码如下所示。

float C_local[SET_P_BLOCK_SIZE*SET_J_BLOCK_SIZE] __attribute__((aligned(64)));
float A_local[SET_P_BLOCK_SIZE*SET_I_BLOCK_SIZE] __attribute__((aligned(64)));
float B_local[SET_I_BLOCK_SIZE*SET_J_BLOCK_SIZE] __attribute__((aligned(64)));
static void copy_into_MxN_nopadding(int n, int realM, int realN, int setM, \
      const float* __restrict__ array, float* __restrict__ array_local) {
  for (int local_col = 0; local_col < realN; local_col++){
    for (int local_row = 0; local_row < realM; local_row++)
      array_local[local_row] = array[local_row];
    array_local += setM;
    array += n;
  }
}

整体的计算逻辑如下所示，仅做了一级分块，其中计算部分类似前面步骤四中的j以步长4为单位做循环。区别在于分块后为减低寻址开销，每个分块用局部的指针 xxx_local_ptr指示当前计算的位置。拷贝分块矩阵的函数copy_into_MxN_nopadding与步骤六中的函数copy_PxI_nopadding()几乎一样。为了寻找这组最优的分块，可以通过编一个简单的Shell脚本，设置环境变量来指定各维度的分块，然后在Makefile里根据环境变量定义宏，再编译和运行。

void square_sgemm (int n, float* __restrict__ A, float* __restrict__ B, float* __restrict__ C) {

  for (int j_block = 0; j_block < n; j_block += SET_J_BLOCK_SIZE){//对于B而言的水平划分
    int REAL_J_BLOCK_SIZE = min(SET_J_BLOCK_SIZE, n - j_block);
    for (int i_block = 0; i_block < n; i_block += SET_I_BLOCK_SIZE){//对于B而言的垂直划分
      int REAL_I_BLOCK_SIZE = min(SET_I_BLOCK_SIZE, n - i_block);

      copy_into_MxN_nopadding(n, REAL_I_BLOCK_SIZE, REAL_J_BLOCK_SIZE, SET_I_BLOCK_SIZE,\
                              B + j_block*n + i_block, B_local);

      for (int p_block = 0; p_block < n; p_block += SET_P_BLOCK_SIZE) {
        int REAL_P_BLOCK_SIZE = min(SET_P_BLOCK_SIZE, n - p_block);

        copy_into_MxN_nopadding(n, REAL_P_BLOCK_SIZE, REAL_I_BLOCK_SIZE, SET_P_BLOCK_SIZE,\
                                A + i_block*n + p_block, A_local);

        // local_C清零
        float * C_local_ptr = C_local;
        for (int j = 0; j < REAL_J_BLOCK_SIZE; j++){//拷贝的时候是部分
          for (int p = 0; p < REAL_P_BLOCK_SIZE; p++)
            C_local_ptr[p] = 0.0;
          C_local_ptr += SET_P_BLOCK_SIZE;//而指针前进的时候是全步长！
        }

        // 计算
        float * B_local_ptr = B_local;
        float * A_local_ptr = A_local;
        C_local_ptr = C_local;
        int j;
        for ( j = 0; j < ((REAL_J_BLOCK_SIZE)&(~3)); j+=4){//计算的时候是部分
          for (int i = 0; i < REAL_I_BLOCK_SIZE; i++){
            register float b0 = B_local_ptr[i];
            register float b1 = B_local_ptr[SET_I_BLOCK_SIZE + i];
            register float b2 = B_local_ptr[2*SET_I_BLOCK_SIZE + i];
            register float b3 = B_local_ptr[3*SET_I_BLOCK_SIZE + i];
            for (int p = 0; p < REAL_P_BLOCK_SIZE; p++){
              C_local_ptr[p] += A_local_ptr[p] * b0;
              C_local_ptr[SET_P_BLOCK_SIZE + p] += A_local_ptr[p] * b1;
              C_local_ptr[2*SET_P_BLOCK_SIZE + p] += A_local_ptr[p] * b2;
              C_local_ptr[3*SET_P_BLOCK_SIZE + p] += A_local_ptr[p] * b3;
            }
            A_local_ptr += SET_P_BLOCK_SIZE;//而指针前进的时候是全步长！
          }
          A_local_ptr = A_local;//A重新归位
          B_local_ptr += 4*SET_I_BLOCK_SIZE;
          C_local_ptr += 4*SET_P_BLOCK_SIZE;
        }
        for ( ; j < REAL_J_BLOCK_SIZE; j++){//计算的时候是部分
          for (int i = 0; i < REAL_I_BLOCK_SIZE; i++){
            register float b0 = B_local_ptr[i];
            for (int p = 0; p < REAL_P_BLOCK_SIZE; p++){
              C_local_ptr[p] += A_local_ptr[p] * b0;
            }
            A_local_ptr += SET_P_BLOCK_SIZE;//而指针前进的时候是全步长！
          }
          A_local_ptr = A_local;//A重新归位
          B_local_ptr += SET_I_BLOCK_SIZE;
          C_local_ptr += SET_P_BLOCK_SIZE;
        }

        // 计算完拷贝回去
        C += j_block*n + p_block;
        C_local_ptr = C_local;
        for (int j = 0; j < REAL_J_BLOCK_SIZE; j++){//拷贝的时候是部分
          for (int p = 0; p < REAL_P_BLOCK_SIZE; p++)
            C[p] += C_local_ptr[p];
          C += n;
          C_local_ptr += SET_P_BLOCK_SIZE;//而指针前进的时候是全步长！
        }
        C -= (j_block+REAL_J_BLOCK_SIZE)*n + p_block;
      }
    }
  }
}

两级Blocking+转置重组

为了更细致的优化，可以做二级分块，在原有基础上，在拷贝出来的对齐且连续的A_local和B_local内做进一步的分块，每次计算一个KERNEL_SIZE_ROW x KERNEL_SIZE_COL大小的矩阵乘法。需要说明的是，此部分二级分块的内容参考了Github上的代码，改写融入到原有一级分块的框架中。由于使用了arm neon的intrinsics，每次一次性对A_local和C_local内的4个浮点数操作，故在此处拷贝A和B时使用padding 0来补齐原矩阵分块无法填满A_local和B_local的地方。下图在一级分块中调用二级分块的矩阵乘法subblock_sgemm()函数。类似地，下图的二级分块的乘法调用最内核的sgemm_kernel()完成固定大小的KERNEL_SIZE的小矩阵乘法。此处设置KERNEL_SIZE_ROW = KERNEL_SIZE_COL=8.

static void subblock_sgemm(int n, int REAL_P_BLOCK_SIZE, int REAL_J_BLOCK_SIZE, \
                           int REAL_I_BLOCK_SIZE, float * C) {
  for (int subj = 0; subj < REAL_J_BLOCK_SIZE; subj += KERNEL_SIZE_COL) {
    int subj_block_size = min(KERNEL_SIZE_COL, REAL_J_BLOCK_SIZE - subj);

    for (int subp = 0; subp < REAL_P_BLOCK_SIZE; subp += KERNEL_SIZE_ROW) {
      int subp_block_size = min(KERNEL_SIZE_ROW, REAL_P_BLOCK_SIZE - subp);

      float * const restrict C_ptr = C + subj*n + subp;
      if (subp_block_size==KERNEL_SIZE_ROW && subj_block_size==KERNEL_SIZE_COL)
        sgemm_kernel(REAL_I_BLOCK_SIZE, A_local + subp*REAL_I_BLOCK_SIZE, \
                     B_local + subj*REAL_I_BLOCK_SIZE, C_ptr, 1, n);
      else{
        sgemm_kernel(REAL_I_BLOCK_SIZE, A_local + subp*REAL_I_BLOCK_SIZE, \
                     B_local + subj*REAL_I_BLOCK_SIZE, C_buffer, 0, KERNEL_SIZE_ROW);
        for (int j = 0; j < subj_block_size; j++)
          for (int i = 0; i < subp_block_size; i++)
            C_ptr[n*j + i] += C_buffer[j*KERNEL_SIZE_ROW + i];
      }
    }
  }
}

void square_sgemm(int n, float* __restrict__ A, float* __restrict__ B, float* __restrict__ C) {
  for (int j_block = 0; j_block < n; j_block += SET_J_BLOCK_SIZE){//对于B而言的水平划分
    int REAL_J_BLOCK_SIZE = min(SET_J_BLOCK_SIZE, n - j_block);

    for (int i_block = 0; i_block < n; i_block += SET_I_BLOCK_SIZE){//对于B而言的垂直划分
      int REAL_I_BLOCK_SIZE = min(SET_I_BLOCK_SIZE, n - i_block);
      // 拷贝并转置B的子块到local_B
      copy_transpose_B_into_IxJ(n, REAL_I_BLOCK_SIZE, REAL_J_BLOCK_SIZE,\
                                B + j_block*n + i_block, B_local);
      for (int p_block = 0; p_block < n; p_block += SET_P_BLOCK_SIZE) {
        int REAL_P_BLOCK_SIZE = min(SET_P_BLOCK_SIZE, n - p_block);
        // 拷贝A的子块到local_A
        copy_A_into_PxI(n, REAL_P_BLOCK_SIZE, REAL_I_BLOCK_SIZE, A + i_block*n + p_block, A_local);
        // 子块的乘法
        subblock_sgemm(n, REAL_P_BLOCK_SIZE, REAL_J_BLOCK_SIZE, REAL_I_BLOCK_SIZE, &C(p_block, j_block));
      }
    }
  }
}

在内核函数sgemm_kernel中，利用CPU提供的128bits定长寄存器，通过intrinsics指令完成SIMD操作。基本逻辑是

• 从小分块内存加载到定长寄存器
• 乘加操作得到结果
• 结果从寄存器存储回小分块内存
• 拷回C矩阵或为补齐而设的缓冲区中

static void sgemm_kernel(int REAL_I_BLOCK_SIZE, const float* __restrict__ a, const float* \
    __restrict__ b, float* __restrict__ CorCBuffer, int C_direct, int row_CorCBuffer) {

  float32x4_t c00 = {0}, c01 = {0}, c02 = {0}, c03 = {0};
  float32x4_t c04 = {0}, c05 = {0}, c06 = {0}, c07 = {0};
  float32x4_t c40 = {0}, c41 = {0}, c42 = {0}, c43 = {0};
  float32x4_t c44 = {0}, c45 = {0}, c46 = {0}, c47 = {0};
  for (int l = 0; l < REAL_I_BLOCK_SIZE; l++) {
    float32x4_t value_a0 = vld1q_f32(a + KERNEL_SIZE_ROW*l    );
    float32x4_t value_a4 = vld1q_f32(a + KERNEL_SIZE_ROW*l + 4);
    float32x4_t value_b0 = vld1q_f32(b + KERNEL_SIZE_COL*l    );
    float32x4_t value_b4 = vld1q_f32(b + KERNEL_SIZE_COL*l + 4);
    c00 = vmlaq_laneq_f32(c00, value_a0, value_b0, 0);
    c01 = vmlaq_laneq_f32(c01, value_a0, value_b0, 1);
    c02 = vmlaq_laneq_f32(c02, value_a0, value_b0, 2);
    c03 = vmlaq_laneq_f32(c03, value_a0, value_b0, 3);
    c04 = vmlaq_laneq_f32(c04, value_a0, value_b4, 0);
    c05 = vmlaq_laneq_f32(c05, value_a0, value_b4, 1);
    c06 = vmlaq_laneq_f32(c06, value_a0, value_b4, 2);
    c07 = vmlaq_laneq_f32(c07, value_a0, value_b4, 3);
    c40 = vmlaq_laneq_f32(c40, value_a4, value_b0, 0);
    c41 = vmlaq_laneq_f32(c41, value_a4, value_b0, 1);
    c42 = vmlaq_laneq_f32(c42, value_a4, value_b0, 2);
    c43 = vmlaq_laneq_f32(c43, value_a4, value_b0, 3);
    c44 = vmlaq_laneq_f32(c44, value_a4, value_b4, 0);
    c45 = vmlaq_laneq_f32(c45, value_a4, value_b4, 1);
    c46 = vmlaq_laneq_f32(c46, value_a4, value_b4, 2);
    c47 = vmlaq_laneq_f32(c47, value_a4, value_b4, 3);
  }
  // 存到临时变量
  vst1q_f32(tmp     , c00);
  vst1q_f32(tmp + 4 , c40);
  vst1q_f32(tmp + 8 , c01);
  vst1q_f32(tmp + 12, c41);
  vst1q_f32(tmp + 16, c02);
  vst1q_f32(tmp + 20, c42);
  vst1q_f32(tmp + 24, c03);
  vst1q_f32(tmp + 28, c43);
  vst1q_f32(tmp + 32, c04);
  vst1q_f32(tmp + 36, c44);
  vst1q_f32(tmp + 40, c05);
  vst1q_f32(tmp + 44, c45);
  vst1q_f32(tmp + 48, c06);
  vst1q_f32(tmp + 52, c46);
  vst1q_f32(tmp + 56, c07);
  vst1q_f32(tmp + 60, c47);
  // 拷贝回矩阵C或缓冲区
  if (C_direct == 0){
    for (int j = 0; j < KERNEL_SIZE_COL; j++)
      for (int i = 0; i < KERNEL_SIZE_ROW; i++)
        CorCBuffer[j*row_CorCBuffer + i] = 0.0;
  }
  for (int j = 0; j < KERNEL_SIZE_COL; j++)
    for (int i = 0; i < KERNEL_SIZE_ROW; i++)
      CorCBuffer[j*row_CorCBuffer + i] += tmp[j*KERNEL_SIZE_ROW + i];
}

值得一提的是，原作者在这里拷贝A和B矩阵时，使元素位置重组，设计得很精妙，使得后续计算时对B_local的访存与A_local保持一致的pattern，连续高效。这部分较为难懂，按个人理解，计算逻辑的示意图如下。下图中setX即为上文提到的SET_X_BLOCK_SIZE，realX即为REAL_X_BLOCK_SIZE，而KernelRow和KernelCol分别为KERNEL_SIZE_ROW和KERNEL_SIZE_COL。

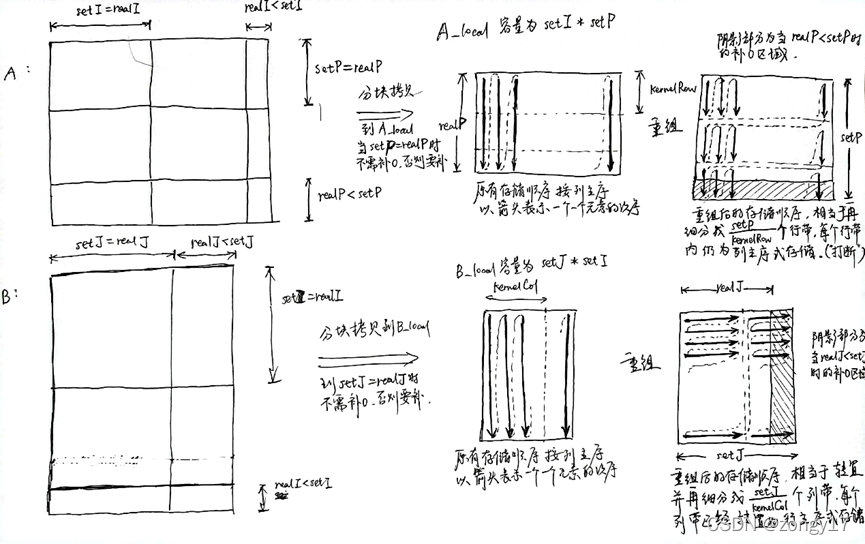
拷贝并重组存储顺序的代码如下。

static void copy_PxI_nopadding(int n, int REAL_I_BLOCK_SIZE, \
            const float* __restrict__ A, float* __restrict__ A_local) {
  for (int local_col = 0; local_col < REAL_I_BLOCK_SIZE; local_col++){
    for (int local_row = 0; local_row < KERNEL_SIZE_ROW; local_row++)
      A_local[local_row] = A(local_row, 0);//相当于把原A中一个块在内存中离散的数据拷贝成A_local中连续的一大片
    A_local += KERNEL_SIZE_ROW;
    A += n;
  }
}
static void copy_A_into_PxI(int n, int REAL_P_BLOCK_SIZE, int REAL_I_BLOCK_SIZE, \
                      const float* __restrict__ A, float* __restrict__ A_local) {
  int part = REAL_P_BLOCK_SIZE / KERNEL_SIZE_ROW;
  int remain_rows = REAL_P_BLOCK_SIZE % KERNEL_SIZE_ROW;
  for (int pa = 0; pa < part; pa++){
    copy_PxI_nopadding(n, REAL_I_BLOCK_SIZE, A, A_local);
    A_local += KERNEL_SIZE_ROW * REAL_I_BLOCK_SIZE;
    A += KERNEL_SIZE_ROW;//指针指向下一个块
  }
  if (remain_rows > 0) {//余下还有
    for (int local_col = 0; local_col < REAL_I_BLOCK_SIZE; local_col++){
      for (int local_row = 0; local_row < remain_rows; local_row++)
        A_local[local_row] = A(local_row, 0);
      for (int local_row = remain_rows; local_row < KERNEL_SIZE_ROW; local_row++)
        A_local[local_row] = 0.0;
      A_local += KERNEL_SIZE_ROW;
      A += n;
    }
  }
}

static void copy_transpose_IxJ_nopadding(int n, int REAL_I_BLOCK_SIZE, \
            const float* __restrict__ B, float* __restrict__ B_local) {
  for (int local_col = 0; local_col < REAL_I_BLOCK_SIZE; local_col++){
    for (int local_row = 0; local_row < KERNEL_SIZE_COL; local_row++)
      B_local[local_row] = B(0, local_row);
    B_local += KERNEL_SIZE_COL;
    B += 1;
  }
}
static void copy_transpose_B_into_IxJ(int n, int REAL_I_BLOCK_SIZE, int REAL_J_BLOCK_SIZE,\
                               const float* __restrict__ B, float* __restrict__ B_local) {
  int part = REAL_J_BLOCK_SIZE / KERNEL_SIZE_COL;
  int remain_cols = REAL_J_BLOCK_SIZE % KERNEL_SIZE_COL;
  for (int pa = 0; pa < part; pa++){
    copy_transpose_IxJ_nopadding(n, REAL_I_BLOCK_SIZE, B, B_local);
    B_local += KERNEL_SIZE_COL * REAL_I_BLOCK_SIZE;
    B += KERNEL_SIZE_COL * n;
  }
  if (remain_cols > 0) {
    for (int local_col = 0; local_col < REAL_I_BLOCK_SIZE; local_col++) {
      for (int local_row = 0; local_row < remain_cols; local_row++)
        B_local[local_row] = B(0, local_row);
      for (int local_row = remain_cols; local_row < KERNEL_SIZE_COL; local_row++)
        B_local[local_row] = 0.0;
      B_local += KERNEL_SIZE_COL;
      B += 1;
    }
  }
}

https://github.com/zongy17/sgemm-serial

Cannon算法

简介

算法流程图

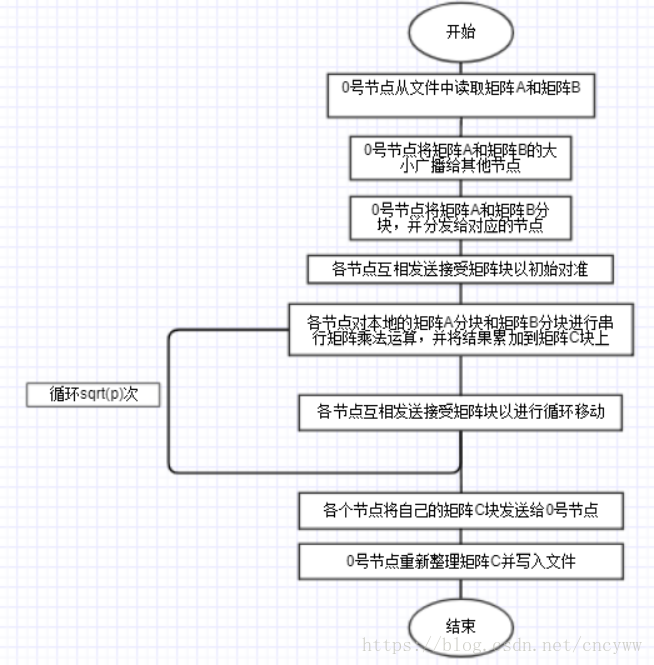
算法设计方法和模式

任务划分

根据矩阵乘法公式中的累加计算的可分离性，将参与计算的两个矩阵分解成p个小矩阵块(共有p个计算节点)，每个节点只进行局部的小矩阵乘法，最终计算结束后将局部的小结果矩阵发送回Master节点。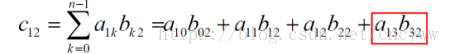

通讯分析

由于算法在下发任务和收集结果的时候采用了主从模式，所以使用了Master-Worker的全局通讯，该部分通讯由于发送方只有一个0号线程，所以无法并行执行，只能串行执行。同时，在迭代进行小矩阵运算时，各计算节点之间也需要交换矩阵，进行了结构化通讯。该部分通讯由于通讯的局部特性，可以并行执行，能够提高效率。

任务组合

每个节点负责一个小矩阵的串行计算，同时负责小矩阵之间的通讯传递。

处理器映射

由于任务的划分个数等于处理器个数，所以在组合任务的同时完成了处理器映射。

Cannon算法采用了主从模式的同时也采用了分而治之的模式。一方面，0号线程作为Master，负责矩阵A和矩阵B以及矩阵C的I/O，也负责小矩阵的分发和结果的聚集。而其他节点作为Worker进行本地的小矩阵串行乘法计算。另一方面，Cannon算法将两个大矩阵的乘法运算分解为若干各小矩阵的乘法运算，最终计算结束后，将计算结果聚集回来，也采用了分而治之的思想。cannon算法不仅实现了矩阵乘法运算的并行化，也减少了分块矩阵乘法的局部存储量，节省了节点的内存开销。

算法复杂度

设计算的是一个n*n的矩阵乘一个n*n的矩阵，共有p个节点，那么Cannon算法的时间复杂度计算如下：

矩阵乘加的时间由于采用了并行化，所以所需时间为： n^3 / p

若不考虑节点延迟时间，设节点之间通讯的启动时间为ti，传输每个数字的时间为tw，则在两个节点间传输一个子矩阵的时间是：ti + n^2*tw / p

所以节点之间传输子矩阵所需的时间为：2*sqrt(p)*(ti + n^2*tw / p)

综上，cannon算法总的所需时间为：2*sqrt(p)*(ti + n^2*tw / p) + n^3 / p

时间复杂度：O(n^3 / p)
空间复杂度：O(n^2)

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#include<mpi.h>
#include<pthread.h>
#include<math.h>
#include<cstring>
int myrank, p;

// Compute C = A*B. A is a n1*n2 matrix. B is a n2*n3 matrix.
void matmul(double* A, double* B, double* C, int n1, int n2, int n3)//做矩阵乘法，结果累加到C矩阵中(需要保证C矩阵初始化过)
{
  int i,j,k;
  //简单的串行矩阵乘法
  for (i = 0; i < n1; i++) {
    for (j = 0; j < n3; j++) {
      for (k = 0; k < n2; k++) {
        C[i*n3+j]+=A[i*n2+k]*B[k*n3+j];
      } 
    }
  } 
}


int setup(int argc,char**argv,double** fstreama,double** fstreamb,int* dim)
{
	FILE* fha;
	FILE* fhb;
	int n1,n2,n3;
	int re=1;
	if (!(fha = fopen(argv[1], "r"))) //打开存储A矩阵的文件
	{
		printf("Can't open file %s, Errno=%d\n", argv[1], 1);//打开失败输出信息
		return -1;
	}
	if(fread(&n1,sizeof(int),1,fha)==0)//读取矩阵的行数
	{
		printf("fread error1!\n");
		return -1;
	}
	if(fread(&n2,sizeof(int),1,fha)==0)//读取矩阵的列数
	{
		printf("fread error2!\n");
		return -1;
	}
	*fstreama = (double *) malloc (n1*n2*sizeof(double));//为矩阵申请内存
	if(fread(*fstreama,sizeof(double),n1*n2,fha)==0)//读取矩阵内容
	{
		printf("fread error3!\n");
		return -1;
	}
	
	fclose(fha);//关闭矩阵文件
	
	if (!(fhb = fopen(argv[2], "r"))) //打开存储A矩阵的文件
	{
		printf("Can't open file %s, Errno=%d\n", argv[2], 2);//打开失败输出信息
		return -1;
	}
	if(fread(&n2,sizeof(int),1,fhb)==0)//读取矩阵的行数
	{
		printf("fread error4!\n");
		return -1;
	}
	if(fread(&n3,sizeof(int),1,fhb)==0)//读取矩阵的列数
	{
		printf("fread error5!\n");
		return -1;
	}
	*fstreamb = (double *) malloc (n2*n3*sizeof(double));//为矩阵申请内存
	if(fread(*fstreamb,sizeof(double),n2*n3,fhb)==0)//读取矩阵内容
	{
		printf("fread error6!\n");
		return -1;
	}
	
	fclose(fhb);//关闭矩阵文件	
	dim[0] = n1;//返回矩阵的大小参数
	dim[1] = n2;//返回矩阵的大小参数
	dim[2] = n3;//返回矩阵的大小参数
	return 0;
}

void scatter_matrix(double* matrixbuf, int rows, int cols, double* local_matrix, int rootp)//将矩阵划分为小矩阵块并分发到各个节点
{
	int row, column, i, j, count;
	int maxrows_block = (rows + rootp - 1)/rootp;//小A矩阵块行数的最大值
	int maxcols_block = (cols + rootp - 1)/rootp;//小矩阵块列数的最大值
	double * matrixbuf2 = NULL;//用来格式化原矩阵的缓冲区
	MPI_Status status;//返回通信的状态
	
	if(myrank == 0)//0号线程
	{
		if(!(matrixbuf2 = (double *)malloc(maxcols_block*maxrows_block*rootp*rootp*sizeof(double))))//为缓冲区申请内存
		{
			printf("Memory allocation failed\n");
		}
		//将矩阵转化为按块连续存放的形式，方便分发每块小矩阵，同时对于边界没有对齐的小矩阵，补零对齐，方便计算
		count = 0;
		for (i = 0; i < rootp; i++){
			for (j = 0; j < rootp; j++){
				if(i!=(rootp-1)&&j==(rootp-1))//特殊处理除了最后一行以外的最后一列
				{
					for (row = 0; row < maxrows_block; row++){
						for (column = 0; column < maxcols_block; column++){
							if((j * maxcols_block + column)>=cols)//补零对齐
							{
								matrixbuf2[count] = 0;
							}else{
								matrixbuf2[count] = matrixbuf[(i * maxrows_block + row ) * cols +j * maxcols_block + column];
							}
							count++;
						}
					}
				}else if(i==(rootp-1)&&j!=(rootp-1))//特殊处理除了最后一列以外的最后一行
				{
					for (row = 0; row < maxrows_block; row++){
						for (column = 0; column < maxcols_block; column++){
							if((i * maxrows_block + row)>=rows)//补零对齐
							{
								matrixbuf2[count] = 0;
							}else{
								matrixbuf2[count] = matrixbuf[(i * maxrows_block + row)*cols + j * maxcols_block + column];
							}
							count++;
						}
					}
				}else if(i==(rootp-1)&&j==(rootp-1))//特殊处理最后一列最后一行的那个块
				{
					for (row = 0; row < maxrows_block; row++){
						for (column = 0; column < maxcols_block; column++){
							if(((j * maxcols_block + column)>=cols) || ((i * maxrows_block + row)>=rows))//补零对齐
							{
								matrixbuf2[count] = 0;
							}else{
								matrixbuf2[count] = matrixbuf[(i * maxrows_block + row) * cols + j * maxcols_block + column];
							}
							count++;
						}
					}
				}else{//普通的块
					for (row = 0; row < maxrows_block; row++){
						for (column = 0; column < maxcols_block; column++){
							matrixbuf2[count] = matrixbuf[(i * maxrows_block + row)*cols + j * maxcols_block + column];
							count++;
						}
					}
				}
			}
		}
		if(count!=maxcols_block*maxrows_block*rootp*rootp)//检查是否出错
		{
			printf("scatter_matrix error!\n");
			return ;
		}
		//将属于本地的那个块留下来
		for(i = 0; i < maxrows_block*maxcols_block; i++)
		{
			local_matrix[i] = matrixbuf2[i];
		}
		//分发其他块到对应的线程
		for(i = 1; i < rootp*rootp; i++)
		{
			MPI_Send((matrixbuf2 + (i * maxcols_block * maxrows_block)), maxcols_block * maxrows_block, MPI_DOUBLE, i, 0, MPI_COMM_WORLD);
		}		
	} else {//非0号线程
		MPI_Recv(local_matrix, maxcols_block * maxrows_block , MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status);//非零线程接受0线程发送的小矩阵块
	}
	if(matrixbuf2!=NULL){//释放缓冲区
		free(matrixbuf2);
	}
	return;
}
//A and bufA : n1_block*n2_block;  B and bufB : n2_block*n3_block
//进行cannon算法，各个节点在本地进行矩阵乘法，并交换矩阵块，进行循环，直到计算完毕
void cannon(double* A, double* bufA, double* B, double* bufB, double* C, int n1_block, int n2_block, int n3_block, int rootp)
{
	MPI_Request send_a_req, send_b_req;
	MPI_Status send_a_status, send_b_status, recv_a_status, recv_b_status;
	int cycle_count;
	int rank_next_a,rank_next_b;
	int rank_last_a,rank_last_b;
	int curRowP,curColP,i,j;
	int tag=0;//表示当前正确数据再A中还是bufA中，0表示在A中，1表示在bufA中
	//先初始化各个块，即A_ij循环左移i步，B_ij循环上移j步，C_ij初始化为零
	
	//初始化矩阵C，值全部设为0
	for(i=0;i<n1_block;i++)
	{
		for(j=0;j<n3_block;j++)
		{
			C[i*n3_block+j] = 0;
		}
	}

	//循环传播小矩阵
	curRowP = myrank/rootp;//当前节点所在行
	curColP = myrank%rootp;//当前节点所在列
	
	//获得左移i步后的节点号
	if((curColP-curRowP)<0)
	{
		rank_next_a = myrank+rootp-curRowP;
	}else{
		rank_next_a = myrank-curRowP;
	}
	
	
	//获得上移j步后的节点号
	if((curRowP-curColP)<0)
	{
		rank_next_b = myrank -curColP*rootp + rootp*rootp;
	}else{
		rank_next_b = myrank -curColP*rootp;
	}
	
	//获得接受左移i步的节点号
	if((curColP+curRowP)>=rootp)
	{
		rank_last_a = myrank+curRowP-rootp;
	}else{
		rank_last_a = myrank+curRowP;
	}
	
	
	//获得接受上移j步的节点号
	if((curRowP+curColP)>=rootp)
	{
		rank_last_b = myrank + curColP*rootp - rootp*rootp;
	}else{
		rank_last_b = myrank + curColP*rootp;
	}
	
	//非阻塞发送矩阵，如果不需要移动，则直接本地memcpy
	if(rank_next_a!=myrank)
	{
		MPI_Isend(A, n1_block*n2_block, MPI_DOUBLE, rank_next_a, 0, MPI_COMM_WORLD, &send_a_req);//非阻塞发送矩阵A，避免死锁
	}else
	{
		memcpy(bufA, A, n1_block*n2_block*sizeof(double));//本地直接memcpy
	}
	if(rank_next_b!=myrank)
	{
		MPI_Isend(B, n2_block*n3_block, MPI_DOUBLE, rank_next_b, 0, MPI_COMM_WORLD, &send_b_req);//非阻塞发送矩阵B，避免死锁
	}else
	{
		memcpy(bufB, B, n2_block*n3_block*sizeof(double));//本地直接memcpy
	}
	
	//阻塞接受矩阵
	if(rank_last_a!=myrank)
	{
		MPI_Recv(bufA, n1_block*n2_block, MPI_DOUBLE, rank_last_a, 0, MPI_COMM_WORLD, &recv_a_status);//阻塞接受矩阵A
	}
	if(rank_last_b!=myrank)
	{
		MPI_Recv(bufB, n2_block*n3_block, MPI_DOUBLE, rank_last_b, 0, MPI_COMM_WORLD, &recv_b_status);//阻塞接受矩阵B
	}

	//阻塞等待发送矩阵结束
	if(rank_next_a!=myrank)
	{
		MPI_Wait(&send_a_req, &send_a_status);//阻塞发送矩阵A到结束
	}
	if(rank_next_b!=myrank)
	{
		MPI_Wait(&send_b_req, &send_b_status);//阻塞发送矩阵B到结束
	}
	
	MPI_Barrier(MPI_COMM_WORLD);//同步
	tag=1;
	if(myrank%rootp==0)//第一列的节点
	{
		rank_next_a = myrank+rootp-1;
	}else{
		rank_next_a = myrank-1;
	}
	
	if(myrank/rootp==0)//第一行的节点
	{
		rank_next_b = myrank+rootp*(rootp-1);
	}else{
		rank_next_b = myrank - rootp;
	}
	
	if(myrank%rootp==(rootp-1))//最后一列的节点
	{
		rank_last_a = myrank-rootp+1;
	}else{
		rank_last_a = myrank+1;
	}
	
	if(myrank/rootp==(rootp-1))//最后一行的节点
	{
		rank_last_b = myrank-rootp*(rootp-1);
	}else{
		rank_last_b = myrank + rootp;
	}
	//循环，每次做当前块的乘加运算，并使得A_ij循环左移1步，B_ij循环上移1步
	for(cycle_count = 0; cycle_count < rootp; cycle_count++)
	{
		if(tag==1)//数据在bufA中
		{
			matmul(bufA, bufB, C, n1_block, n2_block, n3_block);//做当前节点的矩阵乘法
			//循环传播小矩阵
			MPI_Isend(bufA, n1_block*n2_block, MPI_DOUBLE, rank_next_a, 0, MPI_COMM_WORLD, &send_a_req);//非阻塞发送矩阵A，避免死锁
            		MPI_Isend(bufB, n2_block*n3_block, MPI_DOUBLE, rank_next_b, 0, MPI_COMM_WORLD, &send_b_req);//非阻塞发送矩阵B，避免死锁

            		MPI_Recv(A, n1_block*n2_block, MPI_DOUBLE, rank_last_a, 0, MPI_COMM_WORLD, &recv_a_status);//阻塞接受矩阵A
            		MPI_Recv(B, n2_block*n3_block, MPI_DOUBLE, rank_last_b, 0, MPI_COMM_WORLD, &recv_b_status);//阻塞接受矩阵B

            		MPI_Wait(&send_a_req, &send_a_status);//阻塞发送矩阵A到结束
            		MPI_Wait(&send_b_req, &send_b_status);//阻塞发送矩阵B到结束
			tag = 0;
		}else{//数据在A中
			matmul(A, B, C, n1_block, n2_block, n3_block);//做当前节点的矩阵乘法
			//循环传播小矩阵
			MPI_Isend(A, n1_block*n2_block, MPI_DOUBLE, rank_next_a, 0, MPI_COMM_WORLD, &send_a_req);//非阻塞发送矩阵A，避免死锁
            		MPI_Isend(B, n2_block*n3_block, MPI_DOUBLE, rank_next_b, 0, MPI_COMM_WORLD, &send_b_req);//非阻塞发送矩阵B，避免死锁

            		MPI_Recv(bufA, n1_block*n2_block, MPI_DOUBLE, rank_last_a, 0, MPI_COMM_WORLD, &recv_a_status);//阻塞接受矩阵A
            		MPI_Recv(bufB, n2_block*n3_block, MPI_DOUBLE, rank_last_b, 0, MPI_COMM_WORLD, &recv_b_status);//阻塞接受矩阵B

            		MPI_Wait(&send_a_req, &send_a_status);//阻塞发送矩阵A到结束
            		MPI_Wait(&send_b_req, &send_b_status);//阻塞发送矩阵B到结束
			tag = 1;
		}
		MPI_Barrier(MPI_COMM_WORLD);//同步
	}
	return;
}

//gather_matrix((double*)(fstreamc + sizeof(int)*2), n1, n3, C, rootp);
//将各个节点的小矩阵C收集到0号节点
void gather_matrix(double* matrixCbuf, int rows, int cols, double* local_C, int rootp, int rows_block_pad, int cols_block_pad)
{
	int curRow, curCol, i, j, curP;
	MPI_Status status;
	double * matrixC_pad = NULL;//有零填充的矩阵C
	if(myrank == 0) {//0号线程 
		if(!(matrixC_pad = (double *)malloc(rows_block_pad*cols_block_pad*rootp*rootp*sizeof(double))))//为缓冲区申请内存
		{
			printf("Memory allocation failed\n");
		}
		//将本地计算结果直接复制过来
		for(i = 0; i < rows_block_pad * cols_block_pad; i++){
			matrixC_pad[i] = local_C[i];
		}
		//接受其他非0线程的计算结果
		for(i = 1; i < rootp*rootp; i++){
			MPI_Recv(matrixC_pad + (i * rows_block_pad * cols_block_pad), rows_block_pad * cols_block_pad, MPI_DOUBLE, i, 0,MPI_COMM_WORLD, &status);
		}
		
		//重新整理矩阵C，除去零填充，并且重新整理顺序
		for(i=0;i<rows;i++)
		{
			for(j=0;j<cols;j++)
			{
				curP = (i/rows_block_pad)*rootp+(j/cols_block_pad);//属于第几个节点，从0开始
				curRow = i%rows_block_pad;//属于小矩阵的第几行
				curCol = j%cols_block_pad;//属于小矩真的第几列
				matrixCbuf[i * cols + j] = matrixC_pad[curP * rows_block_pad * cols_block_pad +curRow*cols_block_pad+curCol];
			}
		}		
	} else {//非0号线程
		MPI_Send(local_C,rows_block_pad * cols_block_pad, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);//给0号线程发送计算结果
	}
	if(matrixC_pad!=NULL)
	{
		free(matrixC_pad);//释放缓冲区
	}
	return ;
}
int main(int argc, char** argv)
{
	double elapsed_time;
	// Suppose A:n1xn2, B:n2xn3. n1~n3 are read from input files
	int n1, n2, n3,rootp;
	// Buffers for matrix A, B, C. Because A, B will be shifted, so they each have two buffers
	double *A, *B, *C, *bufA, *bufB;
	// On proc 0, buffers to cache matrix files of A, B and C
	double *fstreama, *fstreamb;
	char *fstreamc;
	MPI_Init(&argc, &argv);
	MPI_Comm_rank(MPI_COMM_WORLD, &myrank);
	MPI_Comm_size(MPI_COMM_WORLD, &p);
	rootp = sqrt(p);
	if (p != rootp*rootp) {
		printf("Processor number must be a square!\n");
	}
	// On proc 0, preprocess the command line, read in files for A, B and
	// put their sizes in dim[].
	int dim[3];
	if (myrank == 0) {//0号线程负责从文件中读取矩阵A和B以及他们的大小信息
		if (setup(argc, argv, &fstreama, &fstreamb, dim)!=0) {
			MPI_Finalize(); // Something error during preprocessing
			exit(-1);
		}
	}
	MPI_Bcast(dim, 3, MPI_INT, 0, MPI_COMM_WORLD);//0号线程将A和B矩阵的size广播给所有线程
	n1 = dim[0];//A： n1*n2
	n2 = dim[1];//B:  n2*n3
	n3 = dim[2];

	// Allocate memories for A, B, C, bufA and bufB.
	// Suppose an m*n matrix is 2D block-distributed on a rootp*rootp processor grid.
	// If rootp doesn't divide m or n, then submatrixes won't have the same size.
	// Because we will shift A, B, so we allocate memories according to the max
	// rows and cols of A and B.
	//因为有可能rootp不能整除n1,n2,n3,所以在申请内存的时候考虑最大的块的大小
	int maxrows_a = (n1 + rootp - 1)/rootp;//A矩阵块行数的最大值
	int maxcols_a = (n2 + rootp - 1)/rootp;//A矩阵块列数的最大值
	int maxrows_b = maxcols_a;//B矩阵块行数的最大值
	int maxcols_b = (n3 + rootp - 1)/rootp;//B矩阵块列数的最大值
	int bufA_size = sizeof(double)*maxrows_a*maxcols_a;//大小为一个A矩阵块的大小
	int bufB_size = sizeof(double)*maxrows_b*maxcols_b;//大小为一个B矩阵块的大小
	int bufC_size = sizeof(double)*maxrows_a*maxcols_b;//大小为一个C矩阵块的大小
	char* buf;
	int i;
	if(!(buf = (char *)malloc(bufA_size*2 + bufB_size*2 + bufC_size)))//申请两个A矩阵块，两个B矩阵块，和一个C矩阵块
	{
		printf("Memory allocation failed\n");
	}
	//或者以下4个缓存区的指针位置
	A = (double*)buf;
	bufA = (double*) (buf + bufA_size);
	B = (double*) (buf + bufA_size*2);
	bufB = (double*) (buf + bufA_size*2 + bufB_size);
	C = (double*) (buf + bufA_size*2 + bufB_size*2);
	// Proc 0 scatters A, B to other procs in a 2D block distribution fashion
	scatter_matrix((double*)fstreama, n1, n2, A, rootp);//0号线程分发A矩阵块到各个线程
	MPI_Barrier(MPI_COMM_WORLD);//同步
	scatter_matrix((double*)fstreamb, n2, n3, B, rootp);//0号线程分发B矩阵块到各个线程
	MPI_Barrier(MPI_COMM_WORLD);//同步
	elapsed_time = MPI_Wtime();//记录计算开始的时间戳
	// Compute C=A*B by Cannon algorithm
	cannon(A, bufA, B, bufB, C, maxrows_a,maxcols_a,maxcols_b, rootp);
	MPI_Barrier(MPI_COMM_WORLD);//同步
	elapsed_time = MPI_Wtime() - elapsed_time;//记录计算所用的时间
	// Proc 0 gathers C from other procs and write it out
	FILE* fhc;
	int fsizec = sizeof(int)*2 + sizeof(double)*n1*n3;//存储C矩阵以及两个大小参数的空间大小
	if(myrank == 0)
	{
		if (!(fhc = fopen(argv[3], "w"))) //打开输出C矩阵的文件
		{
			printf("Can't open file %s, Errno=%d\n", argv[3], 3);//打开失败输出信息
			MPI_Finalize();
		}
		fstreamc = (char *)malloc(fsizec);//申请存储矩阵C的内存空间
		((int*)fstreamc)[0] = n1;//记录矩阵C的行数
		((int*)fstreamc)[1] = n3;//记录矩阵C的列数
	}
	gather_matrix((double*)(fstreamc + sizeof(int)*2), n1, n3, C, rootp, maxrows_a, maxcols_b);//聚集计算结果，其他线程将自己的C矩阵块发送给线程0
	MPI_Barrier(MPI_COMM_WORLD); // Make sure proc 0 read all it needs
	if(myrank == 0)
	{
		printf("Cannon algrithm: multiply a %dx%d with a %dx%d, use %.2f(s)\n",n1, n2, n2, n3, elapsed_time);
		fwrite(fstreamc, sizeof(char), fsizec, fhc);//线程0将矩阵C写入文件
		fclose(fhc);//关闭文件
		free(fstreama);//释放内存
		free(fstreamb);//释放内存
		free(fstreamc);//释放内存
	}
	free(buf);//释放存储小矩阵块的内存空间
	MPI_Finalize();
	return 0;
}

Stencil计算

串行程序优化

对于naïve版本的代码，不妨先“无脑”地加上-O3 -fomit-frame-pointer -march=armv8-a -ffast-math等编译选项来让编译器尽可能提供些自动向量化的效果。仅仅是如此，在不同规模的算例上性能就已经有3~5倍的提升，如下图中的VEC图例所示。

再修改benchmark.c内容对开辟的内存加上内存对齐的声明，如下图中ALIGNED图例所示，并无什么变化。从StackOverflow上了解到分配内存时使用的MPI_Alloc_mem函数（在一些实现中）可能已经做了内存对齐，故效果没有提升也合理。

进一步根据Gabriel Rivera等人写的Tiling Optimizations for 3D Scientific Computations，实行分块策略。按照Tiling的方法，逻辑和伪代码如左图所示，在固定的的x-y分区上逐层向上计算，每次先将该x-y分区内的Stencil计算完毕，再移动至下一个x-y分区，目的是每次换层的时候只需将3层a0中的一层替换出L1 cache，在有限的cache容量内尽量提高数据的可复用性。经过简单实验，得到最优的分块大小为X XX=256, Y YY=8。

除此以外，还可利用指针定位读写的位置，避免计算指标INDEX(…)时相互类似的大量计算。如下图所示

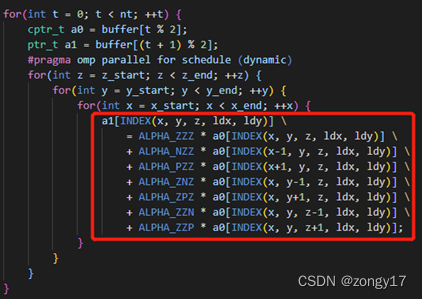
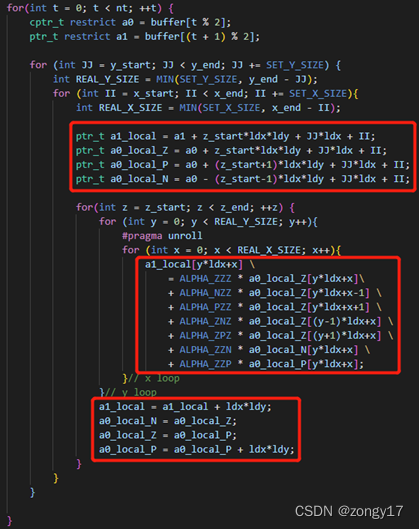
MPI并行

MPI并行模型使用分离的地址空间，因此每个进程做的计算互不干扰，主要需考虑通信带来的开销。由于有3个维度，对进程进行计算任务划分时有多种选择，因此首先从一维划分开始考虑。综合考虑实现复杂性和性能表现，使用MPI的Subarray type来组织和管理halo区的通信。说明，为使负载均衡，以下所有的划分都力求每个进程负责计算的区域大小相等，因此不能整除算例规模的划分方式不予考虑。在跨节点测试时，性能有一定波动，结果取多次测试中的最高值。此部分测试文件见mpi-benchmark.sh和mpi-test.sh文件。

一维z轴划分

将z轴等距划分给n p npnp个进程，每个进程负责n x ∗ n y ∗ ( n z / n p ) nxny(nz/np)nx∗ny∗(nz/np)的任务量。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <mpi.h>
const char* version_name = "A mpi version with 1D partition in z";
#include "common.h"

#ifndef SET_Y_SIZE
#define SET_Y_SIZE 8
#endif
#ifndef SET_X_SIZE
#define SET_X_SIZE 256
#endif
#define MIN(a,b) ((a) < (b) ? (a) : (b))

MPI_Comm cart_comm;
int up_ngb, down_ngb;// z小的为down
MPI_Datatype up_send_subarray, up_recv_subarray;
MPI_Datatype down_send_subarray, down_recv_subarray;
MPI_Status status;

// #define useINDEX

// 创建分布式网格：可以根据7点或27点类型做不同的划分
void create_dist_grid(dist_grid_info_t *grid_info, int stencil_type) {
    // 一维划分 沿z轴切
    if (grid_info->p_id == 0)
        printf(" 1D partition: num_proc_z: %d\n", grid_info->p_num);
    grid_info->local_size_x = grid_info->global_size_x;
    grid_info->local_size_y = grid_info->global_size_y;
    if(grid_info->global_size_z % grid_info->p_num != 0) {
        if (grid_info->p_id == 0)
            printf(" Error: %d cannot divide %d!\n", grid_info->global_size_z, grid_info->p_num);
        MPI_Abort(MPI_COMM_WORLD, 1);
    }
    grid_info->local_size_z = grid_info->global_size_z / grid_info->p_num;

    grid_info->offset_x = 0;
    grid_info->offset_y = 0;
    grid_info->offset_z = grid_info->local_size_z * grid_info->p_id;
    grid_info->halo_size_x = 1;
    grid_info->halo_size_y = 1;
    grid_info->halo_size_z = 1;

    // printf("pid: %d    global: %d %d %d    local : %d %d %d    offset: %d %d %d\n", grid_info->p_id,\
    //     grid_info->global_size_z, grid_info->global_size_y, grid_info->global_size_x,\
    //     grid_info->local_size_z, grid_info->local_size_y, grid_info->local_size_x,\
    //     grid_info->offset_z, grid_info->offset_y, grid_info->offset_x);

    // 创建通信的拓扑
    int dims[1] = {grid_info->p_num};
    int periods = 0;
    MPI_Cart_create(MPI_COMM_WORLD, 1, dims, &periods, 0, &cart_comm);
    MPI_Cart_shift(cart_comm, 0, 1, &down_ngb, &up_ngb);
    // printf("pid: %d    down: %d    up: %d\n", grid_info->p_id, down_ngb, up_ngb);

    // 创建subarray
    int size[3] = { grid_info->local_size_z + 2*grid_info->halo_size_z,\
                    grid_info->local_size_y + 2*grid_info->halo_size_y,\
                    grid_info->local_size_x + 2*grid_info->halo_size_x};
    int subsize[3] = {  grid_info->halo_size_z, \
                        grid_info->local_size_y + 2*grid_info->halo_size_y,\
                        grid_info->local_size_x + 2*grid_info->halo_size_x}; 
    int start[3];
    // send to down_ngb
    start[0] = grid_info->halo_size_z; start[1] = 0; start[2] = 0;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &down_send_subarray);
    MPI_Type_commit(&down_send_subarray);
    // printf("pid: %d    down_send start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);

    // recv from down_ngb
    start[0] = 0; start[1] = 0; start[2] = 0;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &down_recv_subarray);
    MPI_Type_commit(&down_recv_subarray);
    // printf("pid: %d    down_recv start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);

    // send to up_ngb
    start[0] = grid_info->local_size_z; start[1] = 0; start[2] = 0;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &up_send_subarray);
    MPI_Type_commit(&up_send_subarray);
    // printf("pid: %d      up_send start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);

    // recv from up_ngb
    start[0] = grid_info->local_size_z + grid_info->halo_size_z; start[1] = 0; start[2] = 0;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &up_recv_subarray);
    MPI_Type_commit(&up_recv_subarray);
    // printf("pid: %d      up_recv start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);
}

void destroy_dist_grid(dist_grid_info_t *grid_info) {
    for (int i = 1; i <= 8; i++) {
        if (send_subarray[i] != MPI_DATATYPE_NULL) 
            MPI_Type_free(&send_subarray[i]);
        if (recv_subarray[i] != MPI_DATATYPE_NULL)
            MPI_Type_free(&recv_subarray[i]);
    }
}

ptr_t stencil_7(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt, double * calc_time, double * comm_time) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;
    double t_last, t_curr;

    for(int t = 0; t < nt; ++t) {
        cptr_t a0 = buffer[t % 2];
        ptr_t a1 = buffer[(t + 1) % 2];

        // 通信同步(要让a0的边界是对的值！)
        t_curr = MPI_Wtime();
        MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, grid_info->p_id ^ down_ngb,\
                     a0, 1,   up_recv_subarray,   up_ngb, grid_info->p_id ^ up_ngb  , cart_comm, &status);
        MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, grid_info->p_id ^ up_ngb  ,\
                     a0, 1, down_recv_subarray, down_ngb, grid_info->p_id ^ down_ngb, cart_comm, &status);
        // MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, 10,\
        //              a0, 1,   up_recv_subarray,   up_ngb, 10, cart_comm, &status);
        // MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, 11,\
        //              a0, 1, down_recv_subarray, down_ngb, 11, cart_comm, &status);
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *comm_time += t_curr - t_last;
        
        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);
    
                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {  
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x]\
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x];

                        }// x loop
                    }// y loop
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z loop
            }
        }
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *calc_time += t_curr - t_last;
    }
    return buffer[nt % 2];
}


ptr_t stencil_27(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt, double * calc_time, double * comm_time) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;
    double t_last, t_curr;

    for(int t = 0; t < nt; ++t) {
        cptr_t restrict a0 = buffer[t % 2];
        ptr_t restrict a1 = buffer[(t + 1) % 2];

        // 通信同步(要让a0的边界是对的值！)
        t_curr = MPI_Wtime();
        MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, grid_info->p_id ^ down_ngb,\
                     a0, 1,   up_recv_subarray,   up_ngb, grid_info->p_id ^ up_ngb  , cart_comm, &status);
        MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, grid_info->p_id ^ up_ngb  ,\
                     a0, 1, down_recv_subarray, down_ngb, grid_info->p_id ^ down_ngb, cart_comm, &status);
        // MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, 10,\
        //              a0, 1,   up_recv_subarray,   up_ngb, 10, cart_comm, &status);
        // MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, 11,\
        //              a0, 1, down_recv_subarray, down_ngb, 11, cart_comm, &status);
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *comm_time += t_curr - t_last;

        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);

                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x] \
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x] \
                                + ALPHA_NNZ * a0_local_Z[(y-1)*ldx+x-1] \
                                + ALPHA_PNZ * a0_local_Z[(y-1)*ldx+x+1] \
                                + ALPHA_NPZ * a0_local_Z[(y+1)*ldx+x-1] \
                                + ALPHA_PPZ * a0_local_Z[(y+1)*ldx+x+1] \
                                + ALPHA_NZN * a0_local_N[y*ldx+x-1] \
                                + ALPHA_PZN * a0_local_N[y*ldx+x+1] \
                                + ALPHA_NZP * a0_local_P[y*ldx+x-1] \
                                + ALPHA_PZP * a0_local_P[y*ldx+x+1] \
                                + ALPHA_ZNN * a0_local_N[(y-1)*ldx+x] \
                                + ALPHA_ZPN * a0_local_N[(y+1)*ldx+x] \
                                + ALPHA_ZNP * a0_local_P[(y-1)*ldx+x] \
                                + ALPHA_ZPP * a0_local_P[(y+1)*ldx+x] \
                                + ALPHA_NNN * a0_local_N[(y-1)*ldx+x-1] \
                                + ALPHA_PNN * a0_local_N[(y-1)*ldx+x+1] \
                                + ALPHA_NPN * a0_local_N[(y+1)*ldx+x-1] \
                                + ALPHA_PPN * a0_local_N[(y+1)*ldx+x+1] \
                                + ALPHA_NNP * a0_local_P[(y-1)*ldx+x-1] \
                                + ALPHA_PNP * a0_local_P[(y-1)*ldx+x+1] \
                                + ALPHA_NPP * a0_local_P[(y+1)*ldx+x-1] \
                                + ALPHA_PPP * a0_local_P[(y+1)*ldx+x+1];
                        }// x
                    }// y
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z
            }
        }
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *calc_time += t_curr - t_last;
    }
    return buffer[nt % 2];
}

一维y轴划分

将y轴等距划分给n p npnp个进程，每个进程负责n x ∗ ( n y / n p ) ∗ n z nx(ny/np)nznx∗(ny/np)∗nz的任务量。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <mpi.h>
const char* version_name = "A mpi version with 1D partition in y";
#include "common.h"

#ifndef SET_Y_SIZE
#define SET_Y_SIZE 8
#endif
#ifndef SET_X_SIZE
#define SET_X_SIZE 256
#endif
#define MIN(a,b) ((a) < (b) ? (a) : (b))

MPI_Comm cart_comm;
int up_ngb, down_ngb;// y小的为down
MPI_Datatype up_send_subarray, up_recv_subarray;
MPI_Datatype down_send_subarray, down_recv_subarray;
MPI_Status status;

// #define useINDEX

// 创建分布式网格：可以根据7点或27点类型做不同的划分
void create_dist_grid(dist_grid_info_t *grid_info, int stencil_type) {
    // 一维划分 沿y轴切
    if (grid_info->p_id == 0)
        printf(" 1D partition: num_proc_y: %d\n", grid_info->p_num);
    grid_info->local_size_x = grid_info->global_size_x;
    if(grid_info->global_size_y % grid_info->p_num != 0) {
        if (grid_info->p_id == 0)
            printf(" Error: %d cannot divide %d!\n", grid_info->global_size_y, grid_info->p_num);
        MPI_Abort(MPI_COMM_WORLD, 1);
    }
    grid_info->local_size_y = grid_info->global_size_y / grid_info->p_num;
    grid_info->local_size_z = grid_info->global_size_z;

    grid_info->offset_x = 0;
    grid_info->offset_y = grid_info->local_size_y * grid_info->p_id;
    grid_info->offset_z = 0;
    grid_info->halo_size_x = 1;
    grid_info->halo_size_y = 1;
    grid_info->halo_size_z = 1;

    // printf("pid: %d    global: %d %d %d    local : %d %d %d    offset: %d %d %d\n", grid_info->p_id,\
    //     grid_info->global_size_z, grid_info->global_size_y, grid_info->global_size_x,\
    //     grid_info->local_size_z, grid_info->local_size_y, grid_info->local_size_x,\
    //     grid_info->offset_z, grid_info->offset_y, grid_info->offset_x);

    // 创建通信的拓扑
    int dims[1] = {grid_info->p_num};
    int periods = 0;
    MPI_Cart_create(MPI_COMM_WORLD, 1, dims, &periods, 0, &cart_comm);
    MPI_Cart_shift(cart_comm, 0, 1, &down_ngb, &up_ngb);
    // printf("pid: %d    down: %d    up: %d\n", grid_info->p_id, down_ngb, up_ngb);

    // 创建subarray
    int size[3] = { grid_info->local_size_z + 2*grid_info->halo_size_z,\
                    grid_info->local_size_y + 2*grid_info->halo_size_y,\
                    grid_info->local_size_x + 2*grid_info->halo_size_x};
    int subsize[3] = {  grid_info->local_size_z + 2*grid_info->halo_size_z,\
                        grid_info->halo_size_y, \
                        grid_info->local_size_x + 2*grid_info->halo_size_x}; 
    int start[3];
    // send to down_ngb
    start[0] = 0; start[1] = grid_info->halo_size_y; start[2] = 0;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &down_send_subarray);
    MPI_Type_commit(&down_send_subarray);
    // printf("pid: %d    down_send start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);

    // recv from down_ngb
    start[0] = 0; start[1] = 0; start[2] = 0;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &down_recv_subarray);
    MPI_Type_commit(&down_recv_subarray);
    // printf("pid: %d    down_recv start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);

    // send to up_ngb
    start[0] = 0; start[1] = grid_info->local_size_y; start[2] = 0;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &up_send_subarray);
    MPI_Type_commit(&up_send_subarray);
    // printf("pid: %d      up_send start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);

    // recv from up_ngb
    start[0] = 0; start[1] = grid_info->local_size_y + grid_info->halo_size_y; start[2] = 0;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &up_recv_subarray);
    MPI_Type_commit(&up_recv_subarray);
    // printf("pid: %d      up_recv start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);
}

void destroy_dist_grid(dist_grid_info_t *grid_info) {
    for (int i = 1; i <= 8; i++) {
        if (send_subarray[i] != MPI_DATATYPE_NULL) 
            MPI_Type_free(&send_subarray[i]);
        if (recv_subarray[i] != MPI_DATATYPE_NULL)
            MPI_Type_free(&recv_subarray[i]);
    }
}

ptr_t stencil_7(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt, double * calc_time, double * comm_time) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;
    double t_last, t_curr;

    for(int t = 0; t < nt; ++t) {
        cptr_t a0 = buffer[t % 2];
        ptr_t a1 = buffer[(t + 1) % 2];

        // 通信同步(要让a0的边界是对的值！)
        t_curr = MPI_Wtime();
        MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, grid_info->p_id ^ down_ngb,\
                     a0, 1,   up_recv_subarray,   up_ngb, grid_info->p_id ^ up_ngb  , cart_comm, &status);
        MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, grid_info->p_id ^ up_ngb  ,\
                     a0, 1, down_recv_subarray, down_ngb, grid_info->p_id ^ down_ngb, cart_comm, &status);
        // MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, 10,\
        //              a0, 1,   up_recv_subarray,   up_ngb, 10, cart_comm, &status);
        // MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, 11,\
        //              a0, 1, down_recv_subarray, down_ngb, 11, cart_comm, &status);
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *comm_time += t_curr - t_last;

        
        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);
    
                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {  
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x]\
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x];

                        }// x loop
                    }// y loop
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z loop
            }
        }
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *calc_time += t_curr - t_last;
    }
    return buffer[nt % 2];
}


ptr_t stencil_27(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt, double * calc_time, double * comm_time) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;
    double t_last, t_curr;

    for(int t = 0; t < nt; ++t) {
        cptr_t restrict a0 = buffer[t % 2];
        ptr_t restrict a1 = buffer[(t + 1) % 2];

        // 通信同步(要让a0的边界是对的值！)
        t_curr = MPI_Wtime();
        MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, grid_info->p_id ^ down_ngb,\
                     a0, 1,   up_recv_subarray,   up_ngb, grid_info->p_id ^ up_ngb  , cart_comm, &status);
        MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, grid_info->p_id ^ up_ngb  ,\
                     a0, 1, down_recv_subarray, down_ngb, grid_info->p_id ^ down_ngb, cart_comm, &status);
        // MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, 10,\
        //              a0, 1,   up_recv_subarray,   up_ngb, 10, cart_comm, &status);
        // MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, 11,\
        //              a0, 1, down_recv_subarray, down_ngb, 11, cart_comm, &status);
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *comm_time += t_curr - t_last;

        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);

                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x] \
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x] \
                                + ALPHA_NNZ * a0_local_Z[(y-1)*ldx+x-1] \
                                + ALPHA_PNZ * a0_local_Z[(y-1)*ldx+x+1] \
                                + ALPHA_NPZ * a0_local_Z[(y+1)*ldx+x-1] \
                                + ALPHA_PPZ * a0_local_Z[(y+1)*ldx+x+1] \
                                + ALPHA_NZN * a0_local_N[y*ldx+x-1] \
                                + ALPHA_PZN * a0_local_N[y*ldx+x+1] \
                                + ALPHA_NZP * a0_local_P[y*ldx+x-1] \
                                + ALPHA_PZP * a0_local_P[y*ldx+x+1] \
                                + ALPHA_ZNN * a0_local_N[(y-1)*ldx+x] \
                                + ALPHA_ZPN * a0_local_N[(y+1)*ldx+x] \
                                + ALPHA_ZNP * a0_local_P[(y-1)*ldx+x] \
                                + ALPHA_ZPP * a0_local_P[(y+1)*ldx+x] \
                                + ALPHA_NNN * a0_local_N[(y-1)*ldx+x-1] \
                                + ALPHA_PNN * a0_local_N[(y-1)*ldx+x+1] \
                                + ALPHA_NPN * a0_local_N[(y+1)*ldx+x-1] \
                                + ALPHA_PPN * a0_local_N[(y+1)*ldx+x+1] \
                                + ALPHA_NNP * a0_local_P[(y-1)*ldx+x-1] \
                                + ALPHA_PNP * a0_local_P[(y-1)*ldx+x+1] \
                                + ALPHA_NPP * a0_local_P[(y+1)*ldx+x-1] \
                                + ALPHA_PPP * a0_local_P[(y+1)*ldx+x+1];
                        }// x
                    }// y
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z
            }
        }
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *calc_time += t_curr - t_last;
    }
    return buffer[nt % 2];
}

一维x轴划分

将x轴等距划分给n p npnp个进程，每个进程负责( n x / n p ) ∗ n y ∗ n z (nx/np)nynz(nx/np)∗ny∗nz的任务量。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <mpi.h>
const char* version_name ="A mpi version with 1D partition in x";
#include "common.h"

#ifndef SET_Y_SIZE
#define SET_Y_SIZE 8
#endif
#ifndef SET_X_SIZE
#define SET_X_SIZE 256
#endif
#define MIN(a,b) ((a) < (b) ? (a) : (b))

MPI_Comm cart_comm;
int up_ngb, down_ngb;// y小的为down
MPI_Datatype up_send_subarray, up_recv_subarray;
MPI_Datatype down_send_subarray, down_recv_subarray;
MPI_Status status;

// #define useINDEX

// 创建分布式网格：可以根据7点或27点类型做不同的划分
void create_dist_grid(dist_grid_info_t *grid_info, int stencil_type) {
    // 一维划分 沿x轴切
    if(grid_info->global_size_x % grid_info->p_num != 0) {
        if (grid_info->p_id == 0)
            printf(" Error: %d cannot divide %d!\n", grid_info->global_size_x, grid_info->p_num);
        MPI_Abort(MPI_COMM_WORLD, 1);
    }
    grid_info->local_size_x = grid_info->global_size_x / grid_info->p_num;
    grid_info->local_size_y = grid_info->global_size_y;
    grid_info->local_size_z = grid_info->global_size_z;

    grid_info->offset_x = grid_info->local_size_x * grid_info->p_id;
    grid_info->offset_y = 0;
    grid_info->offset_z = 0;
    grid_info->halo_size_x = 1;
    grid_info->halo_size_y = 1;
    grid_info->halo_size_z = 1;

    // printf("pid: %d    global: %d %d %d    local : %d %d %d    offset: %d %d %d\n", grid_info->p_id,\
    //     grid_info->global_size_z, grid_info->global_size_y, grid_info->global_size_x,\
    //     grid_info->local_size_z, grid_info->local_size_y, grid_info->local_size_x,\
    //     grid_info->offset_z, grid_info->offset_y, grid_info->offset_x);

    // 创建通信的拓扑
    int dims[1] = {grid_info->p_num};
    int periods = 0;
    MPI_Cart_create(MPI_COMM_WORLD, 1, dims, &periods, 0, &cart_comm);
    MPI_Cart_shift(cart_comm, 0, 1, &down_ngb, &up_ngb);
    // printf("pid: %d    down: %d    up: %d\n", grid_info->p_id, down_ngb, up_ngb);

    // 创建subarray
    int size[3] = { grid_info->local_size_z + 2*grid_info->halo_size_z,\
                    grid_info->local_size_y + 2*grid_info->halo_size_y,\
                    grid_info->local_size_x + 2*grid_info->halo_size_x};
    int subsize[3] = {  grid_info->local_size_z + 2*grid_info->halo_size_z,\
                        grid_info->local_size_y + 2*grid_info->halo_size_y,\
                        grid_info->halo_size_x}; 
    int start[3];
    // send to down_ngb
    start[0] = 0; start[1] = 0; start[2] = grid_info->halo_size_x; 
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &down_send_subarray);
    MPI_Type_commit(&down_send_subarray);
    // printf("pid: %d    down_send start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);

    // recv from down_ngb
    start[0] = 0; start[1] = 0; start[2] = 0;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &down_recv_subarray);
    MPI_Type_commit(&down_recv_subarray);
    // printf("pid: %d    down_recv start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);

    // send to up_ngb
    start[0] = 0; start[1] = 0; start[2] = grid_info->local_size_x; 
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &up_send_subarray);
    MPI_Type_commit(&up_send_subarray);
    // printf("pid: %d      up_send start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);

    // recv from up_ngb
    start[0] = 0; start[1] = 0; start[2] = grid_info->local_size_x + grid_info->halo_size_x;
    MPI_Type_create_subarray(3, size, subsize, start, MPI_ORDER_C, DATA_TYPE, &up_recv_subarray);
    MPI_Type_commit(&up_recv_subarray);
    // printf("pid: %d      up_recv start: %d %d %d\n", grid_info->p_id, start[0], start[1], start[2]);
}

void destroy_dist_grid(dist_grid_info_t *grid_info) {
    for (int i = 1; i <= 8; i++) {
        if (send_subarray[i] != MPI_DATATYPE_NULL) 
            MPI_Type_free(&send_subarray[i]);
        if (recv_subarray[i] != MPI_DATATYPE_NULL)
            MPI_Type_free(&recv_subarray[i]);
    }
}

ptr_t stencil_7(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;

    for(int t = 0; t < nt; ++t) {
        cptr_t a0 = buffer[t % 2];
        ptr_t a1 = buffer[(t + 1) % 2];

        // 通信同步(要让a0的边界是对的值！)
        MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, grid_info->p_id ^ down_ngb,\
                     a0, 1,   up_recv_subarray,   up_ngb, grid_info->p_id ^ up_ngb  , cart_comm, &status);
        MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, grid_info->p_id ^ up_ngb  ,\
                     a0, 1, down_recv_subarray, down_ngb, grid_info->p_id ^ down_ngb, cart_comm, &status);
        // MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, 10,\
        //              a0, 1,   up_recv_subarray,   up_ngb, 10, cart_comm, &status);
        // MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, 11,\
        //              a0, 1, down_recv_subarray, down_ngb, 11, cart_comm, &status);

        
        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);
    
                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {  
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x]\
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x];

                        }// x loop
                    }// y loop
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z loop
            }
        }
    }
    return buffer[nt % 2];
}


ptr_t stencil_27(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;
    for(int t = 0; t < nt; ++t) {
        cptr_t restrict a0 = buffer[t % 2];
        ptr_t restrict a1 = buffer[(t + 1) % 2];

        // 通信同步(要让a0的边界是对的值！)
        MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, grid_info->p_id ^ down_ngb,\
                     a0, 1,   up_recv_subarray,   up_ngb, grid_info->p_id ^ up_ngb  , cart_comm, &status);
        MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, grid_info->p_id ^ up_ngb  ,\
                     a0, 1, down_recv_subarray, down_ngb, grid_info->p_id ^ down_ngb, cart_comm, &status);
        // MPI_Sendrecv(a0, 1, down_send_subarray, down_ngb, 10,\
        //              a0, 1,   up_recv_subarray,   up_ngb, 10, cart_comm, &status);
        // MPI_Sendrecv(a0, 1,   up_send_subarray,   up_ngb, 11,\
        //              a0, 1, down_recv_subarray, down_ngb, 11, cart_comm, &status);

        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);

                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x] \
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x] \
                                + ALPHA_NNZ * a0_local_Z[(y-1)*ldx+x-1] \
                                + ALPHA_PNZ * a0_local_Z[(y-1)*ldx+x+1] \
                                + ALPHA_NPZ * a0_local_Z[(y+1)*ldx+x-1] \
                                + ALPHA_PPZ * a0_local_Z[(y+1)*ldx+x+1] \
                                + ALPHA_NZN * a0_local_N[y*ldx+x-1] \
                                + ALPHA_PZN * a0_local_N[y*ldx+x+1] \
                                + ALPHA_NZP * a0_local_P[y*ldx+x-1] \
                                + ALPHA_PZP * a0_local_P[y*ldx+x+1] \
                                + ALPHA_ZNN * a0_local_N[(y-1)*ldx+x] \
                                + ALPHA_ZPN * a0_local_N[(y+1)*ldx+x] \
                                + ALPHA_ZNP * a0_local_P[(y-1)*ldx+x] \
                                + ALPHA_ZPP * a0_local_P[(y+1)*ldx+x] \
                                + ALPHA_NNN * a0_local_N[(y-1)*ldx+x-1] \
                                + ALPHA_PNN * a0_local_N[(y-1)*ldx+x+1] \
                                + ALPHA_NPN * a0_local_N[(y+1)*ldx+x-1] \
                                + ALPHA_PPN * a0_local_N[(y+1)*ldx+x+1] \
                                + ALPHA_NNP * a0_local_P[(y-1)*ldx+x-1] \
                                + ALPHA_PNP * a0_local_P[(y-1)*ldx+x+1] \
                                + ALPHA_NPP * a0_local_P[(y+1)*ldx+x-1] \
                                + ALPHA_PPP * a0_local_P[(y+1)*ldx+x+1];
                        }// x
                    }// y
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z
            }
        }
    }
    return buffer[nt % 2];
}

二维zy轴划分

综合上述一维划分的结果，在二维划分时考虑采用z和y轴联合划分。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <mpi.h>
const char* version_name = "A mpi version with 2D partition in z & y";
#include "common.h"

#ifndef SET_Y_SIZE
#define SET_Y_SIZE 8
#endif
#ifndef SET_X_SIZE
#define SET_X_SIZE 256
#endif
#define MIN(a,b) ((a) < (b) ? (a) : (b))
#define MAX(a,b) ((a) > (b) ? (a) : (b))

MPI_Comm cart_comm;
int cart_ids[2];
//     6      2      5
// y(1)
//  ^  3      0      1
//  |
//  |  7      4      8
//  ------> z (0)
int oppo_idx[9] = {0, 3, 4, 1, 2, 7, 8, 5, 6};
int ngbs[9];
MPI_Datatype send_subarray[9], recv_subarray[9];
MPI_Status status;

// 创建分布式网格：可以根据7点或27点类型做不同的划分
void create_dist_grid(dist_grid_info_t *grid_info, int stencil_type) {
    // 二维划分 沿zy轴切
    int sqr_root = 1;
    int num_proc_y, num_proc_z;
    while (sqr_root*sqr_root < grid_info->p_num) sqr_root++;

    if (sqr_root*sqr_root == grid_info->p_num) {
        num_proc_z = num_proc_y = sqr_root;
    } else {
        int tmp = 1;
        while (grid_info->p_num%tmp==0 && grid_info->p_num/tmp>tmp) tmp *= 2;
        num_proc_z = grid_info->p_num / tmp;//跳出while时tmp>sqrt(p_num)
        num_proc_y = tmp;
        // num_proc_z = tmp;
        // num_proc_y = grid_info->p_num / tmp;
    }
    if (grid_info->p_id == 0)
        printf(" 2D partition: num_proc_y: %d, num_proc_z:%d\n", num_proc_y, num_proc_z);
    // x轴不切
    grid_info->local_size_x = grid_info->global_size_x;
    // y轴
    if (grid_info->global_size_y % num_proc_y != 0) {
        if (grid_info->p_id == 0)
            printf(" Error: %d cannot divide %d!\n", grid_info->global_size_y, num_proc_y);
        MPI_Abort(MPI_COMM_WORLD, 1);
    }
    grid_info->local_size_y = grid_info->global_size_y / num_proc_y;
    // z轴
    if (grid_info->global_size_z % num_proc_z != 0) {
        if (grid_info->p_id == 0)
            printf(" Error: %d cannot divide %d!\n", grid_info->global_size_z, num_proc_z);
        MPI_Abort(MPI_COMM_WORLD, 1);
    }
    grid_info->local_size_z = grid_info->global_size_z / num_proc_z;

    // printf("pid: %d    global: %d %d %d    local : %d %d %d    offset: %d %d %d\n", grid_info->p_id,\
    //     grid_info->global_size_z, grid_info->global_size_y, grid_info->global_size_x,\
    //     grid_info->local_size_z, grid_info->local_size_y, grid_info->local_size_x,\
    //     grid_info->offset_z, grid_info->offset_y, grid_info->offset_x);

    // 创建通信的拓扑
    ngbs[0] = grid_info->p_id;
    int dims[2] = {num_proc_z, num_proc_y};
    int periods[2] = {0, 0};
    MPI_Cart_create(MPI_COMM_WORLD, 2, dims, &periods, 0, &cart_comm);
    MPI_Cart_shift(cart_comm, 0, 1, &ngbs[3], &ngbs[1]);
    MPI_Cart_shift(cart_comm, 1, 1, &ngbs[4], &ngbs[2]);

    int dist_y = 1;
    if (ngbs[1]==MPI_PROC_NULL || ngbs[2]==MPI_PROC_NULL) ngbs[5] = MPI_PROC_NULL;
    else ngbs[5] = ngbs[1] + dist_y; 
    if (ngbs[1]==MPI_PROC_NULL || ngbs[4]==MPI_PROC_NULL) ngbs[8] = MPI_PROC_NULL;
    else ngbs[8] = ngbs[1] - dist_y; 
    if (ngbs[2]==MPI_PROC_NULL || ngbs[3]==MPI_PROC_NULL) ngbs[6] = MPI_PROC_NULL;
    else ngbs[6] = ngbs[3] + dist_y;
    if (ngbs[3]==MPI_PROC_NULL || ngbs[4]==MPI_PROC_NULL) ngbs[7] = MPI_PROC_NULL;
    else ngbs[7] = ngbs[3] - dist_y; 

    MPI_Cart_coords(cart_comm, grid_info->p_id, 2, &cart_ids);

    grid_info->offset_x = 0;
    grid_info->offset_y = grid_info->local_size_y * cart_ids[1];
    grid_info->offset_z = grid_info->local_size_z * cart_ids[0];
    grid_info->halo_size_x = 1;
    grid_info->halo_size_y = 1;
    grid_info->halo_size_z = 1;

    // printf("pid: %d    cart_id[0]: %d    cart_id[1]: %d\n %d %d %d %d %d %d %d %d %d\n offset_y:%d    offset_z:%d\n", grid_info->p_id, cart_ids[0], cart_ids[1],\
    //     ngbs[0],ngbs[1],ngbs[2],ngbs[3],ngbs[4],ngbs[5],ngbs[6],ngbs[7],ngbs[8], grid_info->offset_y, grid_info->offset_z);


    // 创建subarray
    int size[3] = { grid_info->local_size_z + 2*grid_info->halo_size_z,\
                    grid_info->local_size_y + 2*grid_info->halo_size_y,\
                    grid_info->local_size_x + 2*grid_info->halo_size_x};
    int subsize[3], send_start[3], recv_start[3];
    for (int i = 1; i <= 8; i++) {
        switch (i) {
        case 1:
            subsize[0] = grid_info->halo_size_z;
            subsize[1] = grid_info->local_size_y;// 注意是local_size 不带halo_width
            break;
        case 2:
            subsize[0] = grid_info->local_size_z;
            subsize[1] = grid_info->halo_size_y;
            break;
        case 3:
            subsize[0] = grid_info->halo_size_z;
            subsize[1] = grid_info->local_size_y;
            break;
        case 4:
            subsize[0] = grid_info->local_size_z;
            subsize[1] = grid_info->halo_size_y;
            break;
        default:// 5,6,7,8
            subsize[0] = grid_info->halo_size_z;
            subsize[1] = grid_info->halo_size_y;
            break;
        }
        subsize[2] = grid_info->local_size_x + 2*grid_info->halo_size_x;

        switch (i) {
        case 1:// up_z
            send_start[0] = grid_info->local_size_z;                          send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = grid_info->local_size_z + grid_info->halo_size_z; recv_start[1] = grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 3:// down_z
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = 0;                      recv_start[1] = grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 2:// up_y
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->local_size_y;                          send_start[2] = 0;
            recv_start[0] = grid_info->halo_size_z; recv_start[1] = grid_info->local_size_y + grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 4:// down_y
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = grid_info->halo_size_z; recv_start[1] = 0;                      recv_start[2] = 0;
            break;
        case 5:// up_z_up_y
            send_start[0] = grid_info->local_size_z;                          send_start[1] = grid_info->local_size_y;                          send_start[2] = 0;
            recv_start[0] = grid_info->local_size_z + grid_info->halo_size_z; recv_start[1] = grid_info->local_size_y + grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 6:// down_z_up_y
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->local_size_y;                          send_start[2] = 0;
            recv_start[0] = 0;                      recv_start[1] = grid_info->local_size_y + grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 7:// down_z_down_y
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = 0;                      recv_start[1] = 0;                      recv_start[2] = 0;
            break;
        case 8:// up_z_down_y
            send_start[0] = grid_info->local_size_z;                          send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = grid_info->local_size_z + grid_info->halo_size_z; recv_start[1] = 0;                      recv_start[2] = 0;
            break;
        default:
            break;
        }
        MPI_Type_create_subarray(3, size, subsize, send_start, MPI_ORDER_C, DATA_TYPE, &send_subarray[i]);
        MPI_Type_commit(&send_subarray[i]);
        MPI_Type_create_subarray(3, size, subsize, recv_start, MPI_ORDER_C, DATA_TYPE, &recv_subarray[i]);
        MPI_Type_commit(&recv_subarray[i]);
    }
}

void destroy_dist_grid(dist_grid_info_t *grid_info) {
    for (int i = 1; i <= 8; i++) {
        if (send_subarray[i] != MPI_DATATYPE_NULL) 
            MPI_Type_free(&send_subarray[i]);
        if (recv_subarray[i] != MPI_DATATYPE_NULL)
            MPI_Type_free(&recv_subarray[i]);
    }
}

ptr_t stencil_7(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt, double * calc_time, double * comm_time) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;
    double t_last, t_curr;

    for(int t = 0; t < nt; ++t) {
        cptr_t a0 = buffer[t % 2];
        ptr_t a1 = buffer[(t + 1) % 2];

        // 通信同步(要让a0的边界是对的值！)
        t_curr = MPI_Wtime();
        for (int i = 1; i <= 4; i++) {// 7点stencil只需要通信4个
            int oppo = oppo_idx[i];
            MPI_Sendrecv(a0, 1, send_subarray[i]   , ngbs[i]   , grid_info->p_id ^ ngbs[i]   ,\
                         a0, 1, recv_subarray[oppo], ngbs[oppo], grid_info->p_id ^ ngbs[oppo], cart_comm, &status);
        }
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *comm_time += t_curr - t_last;
        
        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);
    
                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {  
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x]\
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x];

                        }// x loop
                    }// y loop
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z loop
            }
        }
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *calc_time += t_curr - t_last;
    }
    return buffer[nt % 2];
}


ptr_t stencil_27(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt, double * calc_time, double * comm_time) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;
    double t_last, t_curr;

    for(int t = 0; t < nt; ++t) {
        cptr_t restrict a0 = buffer[t % 2];
        ptr_t restrict a1 = buffer[(t + 1) % 2];

        // 通信同步(要让a0的边界是对的值！)
        t_curr = MPI_Wtime();
        for (int i = 1; i <= 8; i++) {// 27点stencil需要通信8个
            int oppo = oppo_idx[i];
            MPI_Sendrecv(a0, 1, send_subarray[i]   , ngbs[i]   , grid_info->p_id ^ ngbs[i]   ,\
                         a0, 1, recv_subarray[oppo], ngbs[oppo], grid_info->p_id ^ ngbs[oppo], cart_comm, &status);
        }
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *comm_time += t_curr - t_last;

        t_last = MPI_Wtime();
        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);

                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x] \
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x] \
                                + ALPHA_NNZ * a0_local_Z[(y-1)*ldx+x-1] \
                                + ALPHA_PNZ * a0_local_Z[(y-1)*ldx+x+1] \
                                + ALPHA_NPZ * a0_local_Z[(y+1)*ldx+x-1] \
                                + ALPHA_PPZ * a0_local_Z[(y+1)*ldx+x+1] \
                                + ALPHA_NZN * a0_local_N[y*ldx+x-1] \
                                + ALPHA_PZN * a0_local_N[y*ldx+x+1] \
                                + ALPHA_NZP * a0_local_P[y*ldx+x-1] \
                                + ALPHA_PZP * a0_local_P[y*ldx+x+1] \
                                + ALPHA_ZNN * a0_local_N[(y-1)*ldx+x] \
                                + ALPHA_ZPN * a0_local_N[(y+1)*ldx+x] \
                                + ALPHA_ZNP * a0_local_P[(y-1)*ldx+x] \
                                + ALPHA_ZPP * a0_local_P[(y+1)*ldx+x] \
                                + ALPHA_NNN * a0_local_N[(y-1)*ldx+x-1] \
                                + ALPHA_PNN * a0_local_N[(y-1)*ldx+x+1] \
                                + ALPHA_NPN * a0_local_N[(y+1)*ldx+x-1] \
                                + ALPHA_PPN * a0_local_N[(y+1)*ldx+x+1] \
                                + ALPHA_NNP * a0_local_P[(y-1)*ldx+x-1] \
                                + ALPHA_PNP * a0_local_P[(y-1)*ldx+x+1] \
                                + ALPHA_NPP * a0_local_P[(y+1)*ldx+x-1] \
                                + ALPHA_PPP * a0_local_P[(y+1)*ldx+x+1];
                        }// x
                    }// y
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z
            }
        }
        t_last = t_curr;
        t_curr = MPI_Wtime();
        *calc_time += t_curr - t_last;
    }
    return buffer[nt % 2];
}

计算通信重叠和非阻塞通信

基于上一节的二维zy轴划分，考虑计算通信重叠的实现，即每个进程先算自己的内halo区（邻居进程的外halo区），然后用非阻塞通信将内halo区数据通信。在此通信过程中，各进程计算自己真正的内部区域（不与其他进程有依赖关系的区域）。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <mpi.h>
const char* version_name = "A mpi comp-comm overlapped";
#include "common.h"

#ifndef SET_Y_SIZE
#define SET_Y_SIZE 8
#endif
#ifndef SET_X_SIZE
#define SET_X_SIZE 256
#endif
#define MIN(a,b) ((a) < (b) ? (a) : (b))
#define MAX(a,b) ((a) > (b) ? (a) : (b))

MPI_Comm cart_comm;
int cart_ids[2];
//     6      2      5
// y(1)
//  ^  3      0      1
//  |
//  |  7      4      8
//  ------> z (0)
int oppo_idx[9] = {0, 3, 4, 1, 2, 7, 8, 5, 6};
int ngbs[9];
MPI_Datatype send_subarray[9], recv_subarray[9];

static int ih_z_beg[9], ih_z_end[9], ih_y_beg[9], ih_y_end[9];

// 创建分布式网格：可以根据7点或27点类型做不同的划分
void create_dist_grid(dist_grid_info_t *grid_info, int stencil_type) {
    // 二维划分 沿zy轴切
    int sqr_root = 1;
    int num_proc_y, num_proc_z;
    while (sqr_root*sqr_root < grid_info->p_num) sqr_root++;

    if (sqr_root*sqr_root == grid_info->p_num) {
        num_proc_z = num_proc_y = sqr_root;
    } else {
        int tmp = 1;
        while (grid_info->p_num%tmp==0 && grid_info->p_num/tmp>tmp) tmp *= 2;
        num_proc_z = grid_info->p_num / tmp;//跳出while时tmp>sqrt(p_num)
        num_proc_y = tmp;
        // num_proc_z = tmp;
        // num_proc_y = grid_info->p_num / tmp;
    }
    if (grid_info->p_id == 0)
        printf(" 2D partition: num_proc_y: %d, num_proc_z:%d\n", num_proc_y, num_proc_z);
    // x轴不切
    grid_info->local_size_x = grid_info->global_size_x;
    // y轴
    if (grid_info->global_size_y % num_proc_y != 0) {
        if (grid_info->p_id == 0)
            printf(" Error: %d cannot divide %d!\n", grid_info->global_size_y, num_proc_y);
        MPI_Abort(MPI_COMM_WORLD, 1);
    }
    grid_info->local_size_y = grid_info->global_size_y / num_proc_y;
    // z轴
    if (grid_info->global_size_z % num_proc_z != 0) {
        if (grid_info->p_id == 0)
            printf(" Error: %d cannot divide %d!\n", grid_info->global_size_z, num_proc_z);
        MPI_Abort(MPI_COMM_WORLD, 1);
    }
    grid_info->local_size_z = grid_info->global_size_z / num_proc_z;

    // printf("pid: %d    global: %d %d %d    local : %d %d %d    offset: %d %d %d\n", grid_info->p_id,\
    //     grid_info->global_size_z, grid_info->global_size_y, grid_info->global_size_x,\
    //     grid_info->local_size_z, grid_info->local_size_y, grid_info->local_size_x,\
    //     grid_info->offset_z, grid_info->offset_y, grid_info->offset_x);

    // 创建通信的拓扑
    ngbs[0] = grid_info->p_id;
    int dims[2] = {num_proc_z, num_proc_y};
    int periods[2] = {0, 0};
    MPI_Cart_create(MPI_COMM_WORLD, 2, dims, &periods, 0, &cart_comm);
    MPI_Cart_shift(cart_comm, 0, 1, &ngbs[3], &ngbs[1]);
    MPI_Cart_shift(cart_comm, 1, 1, &ngbs[4], &ngbs[2]);

    int dist_y = 1;
    if (ngbs[1]==MPI_PROC_NULL || ngbs[2]==MPI_PROC_NULL) ngbs[5] = MPI_PROC_NULL;
    else ngbs[5] = ngbs[1] + dist_y; 
    if (ngbs[1]==MPI_PROC_NULL || ngbs[4]==MPI_PROC_NULL) ngbs[8] = MPI_PROC_NULL;
    else ngbs[8] = ngbs[1] - dist_y; 
    if (ngbs[2]==MPI_PROC_NULL || ngbs[3]==MPI_PROC_NULL) ngbs[6] = MPI_PROC_NULL;
    else ngbs[6] = ngbs[3] + dist_y;
    if (ngbs[3]==MPI_PROC_NULL || ngbs[4]==MPI_PROC_NULL) ngbs[7] = MPI_PROC_NULL;
    else ngbs[7] = ngbs[3] - dist_y; 

    MPI_Cart_coords(cart_comm, grid_info->p_id, 2, &cart_ids);

    grid_info->offset_x = 0;
    grid_info->offset_y = grid_info->local_size_y * cart_ids[1];
    grid_info->offset_z = grid_info->local_size_z * cart_ids[0];
    grid_info->halo_size_x = 1;
    grid_info->halo_size_y = 1;
    grid_info->halo_size_z = 1;

    // printf("pid: %d    cart_id[0]: %d    cart_id[1]: %d\n %d %d %d %d %d %d %d %d %d\n offset_y:%d    offset_z:%d\n", grid_info->p_id, cart_ids[0], cart_ids[1],\
    //     ngbs[0],ngbs[1],ngbs[2],ngbs[3],ngbs[4],ngbs[5],ngbs[6],ngbs[7],ngbs[8], grid_info->offset_y, grid_info->offset_z);


    // 创建subarray
    int size[3] = { grid_info->local_size_z + 2*grid_info->halo_size_z,\
                    grid_info->local_size_y + 2*grid_info->halo_size_y,\
                    grid_info->local_size_x + 2*grid_info->halo_size_x};
    int subsize[3], send_start[3], recv_start[3];
    for (int i = 1; i <= 8; i++) {
        switch (i) {
        case 1:
            subsize[0] = grid_info->halo_size_z;
            subsize[1] = grid_info->local_size_y;// 注意是local_size 不带halo_width
            break;
        case 2:
            subsize[0] = grid_info->local_size_z;
            subsize[1] = grid_info->halo_size_y;
            break;
        case 3:
            subsize[0] = grid_info->halo_size_z;
            subsize[1] = grid_info->local_size_y;
            break;
        case 4:
            subsize[0] = grid_info->local_size_z;
            subsize[1] = grid_info->halo_size_y;
            break;
        default:// 5,6,7,8
            subsize[0] = grid_info->halo_size_z;
            subsize[1] = grid_info->halo_size_y;
            break;
        }
        subsize[2] = grid_info->local_size_x + 2*grid_info->halo_size_x;

        switch (i) {
        case 1:// up_z
            send_start[0] = grid_info->local_size_z;                          send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = grid_info->local_size_z + grid_info->halo_size_z; recv_start[1] = grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 3:// down_z
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = 0;                      recv_start[1] = grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 2:// up_y
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->local_size_y;                          send_start[2] = 0;
            recv_start[0] = grid_info->halo_size_z; recv_start[1] = grid_info->local_size_y + grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 4:// down_y
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = grid_info->halo_size_z; recv_start[1] = 0;                      recv_start[2] = 0;
            break;
        case 5:// up_z_up_y
            send_start[0] = grid_info->local_size_z;                          send_start[1] = grid_info->local_size_y;                          send_start[2] = 0;
            recv_start[0] = grid_info->local_size_z + grid_info->halo_size_z; recv_start[1] = grid_info->local_size_y + grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 6:// down_z_up_y
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->local_size_y;                          send_start[2] = 0;
            recv_start[0] = 0;                      recv_start[1] = grid_info->local_size_y + grid_info->halo_size_y; recv_start[2] = 0;
            break;
        case 7:// down_z_down_y
            send_start[0] = grid_info->halo_size_z; send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = 0;                      recv_start[1] = 0;                      recv_start[2] = 0;
            break;
        case 8:// up_z_down_y
            send_start[0] = grid_info->local_size_z;                          send_start[1] = grid_info->halo_size_y; send_start[2] = 0;
            recv_start[0] = grid_info->local_size_z + grid_info->halo_size_z; recv_start[1] = 0;                      recv_start[2] = 0;
            break;
        default:
            break;
        }
        MPI_Type_create_subarray(3, size, subsize, send_start, MPI_ORDER_C, DATA_TYPE, &send_subarray[i]);
        MPI_Type_commit(&send_subarray[i]);
        MPI_Type_create_subarray(3, size, subsize, recv_start, MPI_ORDER_C, DATA_TYPE, &recv_subarray[i]);
        MPI_Type_commit(&recv_subarray[i]);
    }

    // 记录计算通信重叠部分的内halo区(注意这是内halo！)
    for (int dir = 1; dir <= 4; dir++) {
        //
        //   ----------------------------
        //   |         2          |     |
        //   |--------------------|     |
        //   |     |              |     |
        //   |     |              |  1  |
        //   |     |              |     |
        // y |  3  |              |     |
        // ^ |     |              |     |
        // | |     |--------------------|
        // | |     |          4         |
        // | ----------------------------
        // O----> z
        switch (dir) {
        case 1:
            ih_z_beg[dir] = grid_info->local_size_z;
            ih_z_end[dir] = grid_info->halo_size_z + grid_info->local_size_z;
            ih_y_beg[dir] = grid_info->halo_size_y * 2;
            ih_y_end[dir] = grid_info->halo_size_y + grid_info->local_size_y;
            break;
        case 2:
            ih_z_beg[dir] = grid_info->halo_size_z;
            ih_z_end[dir] = grid_info->local_size_z;
            ih_y_beg[dir] = grid_info->local_size_y;
            ih_y_end[dir] = ih_y_beg[dir] + grid_info->halo_size_y;
            break;
        case 3:
            ih_z_beg[dir] = grid_info->halo_size_z;
            ih_z_end[dir] = grid_info->halo_size_z * 2;
            ih_y_beg[dir] = grid_info->halo_size_y;
            ih_y_end[dir] = grid_info->local_size_y;
            break;
        case 4:
            ih_z_beg[dir] = grid_info->halo_size_z * 2;
            ih_z_end[dir] = grid_info->halo_size_z + grid_info->local_size_z;
            ih_y_beg[dir] = grid_info->halo_size_y;
            ih_y_end[dir] = grid_info->halo_size_y * 2;
            break;
        default:
            break;
        }
        // printf("pid %d, dir %d, %d %d %d %d\n", grid_info->p_id, dir, ih_z_beg[dir], ih_z_end[dir], ih_y_beg[dir], ih_y_end[dir]);
    }
    
}

void destroy_dist_grid(dist_grid_info_t *grid_info) {
    for (int i = 1; i <= 8; i++) {
        if (send_subarray[i] != MPI_DATATYPE_NULL) 
            MPI_Type_free(&send_subarray[i]);
        if (recv_subarray[i] != MPI_DATATYPE_NULL)
            MPI_Type_free(&recv_subarray[i]);
    }
}

ptr_t stencil_7(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt, double * calc_time, double * comm_time) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;
    MPI_Request req_send[4], req_recv[4];
    MPI_Status status[4];

    // for boundary conditions
    for (int i = 1; i <= 4; i++) {// 7点stencil只需要通信4个
        int oppo = oppo_idx[i];
        MPI_Sendrecv(buffer[0], 1, send_subarray[i]   , ngbs[i]   , grid_info->p_id ^ ngbs[i]   ,\
                     buffer[0], 1, recv_subarray[oppo], ngbs[oppo], grid_info->p_id ^ ngbs[oppo], cart_comm, &status[i-1]);
    }

    // y_start += grid_info->halo_size_y; y_end -= grid_info->halo_size_y;
    // z_start += grid_info->halo_size_z; z_end -= grid_info->halo_size_z;

    for(int t = 0; t < nt; ++t) {
        cptr_t a0 = buffer[t % 2];
        ptr_t a1 = buffer[(t + 1) % 2];

        // 先计算内halo区
        for (int dir = 1; dir <= 4; dir++) {
            ptr_t a1_local = a1 + ih_z_beg[dir]*ldx*ldy + ih_y_beg[dir]*ldx;
            cptr_t a0_local_Z = a0 + (a1_local - a1);
            cptr_t a0_local_P = a0_local_Z + ldy*ldx;
            cptr_t a0_local_N = a0_local_Z - ldy*ldx;
            int yy_end = ih_y_end[dir]-ih_y_beg[dir];
            for (int z = ih_z_beg[dir]; z < ih_z_end[dir]; z++){
                for (int y = 0; y < yy_end; y++)
                    for (int x = x_start; x < x_end; x++)
                        a1_local[y*ldx+x] \
                            = ALPHA_ZZZ * a0_local_Z[y*ldx+x]\
                            + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                            + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                            + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                            + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                            + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                            + ALPHA_ZZP * a0_local_P[y*ldx+x];
                a1_local = a1_local + ldx*ldy;
                a0_local_N = a0_local_Z;
                a0_local_Z = a0_local_P;
                a0_local_P = a0_local_P + ldx*ldy;
            }
        }
        // 隐藏非阻塞通信
        for (int dir = 1; dir <= 4; dir++) {
            int oppo = oppo_idx[dir];
            MPI_Isend(a1, 1, send_subarray[dir],  ngbs[dir],  grid_info->p_id ^ ngbs[dir],  cart_comm, &req_send[dir-1]);
            MPI_Irecv(a1, 1, recv_subarray[oppo], ngbs[oppo], grid_info->p_id ^ ngbs[oppo], cart_comm, &req_recv[oppo-1]);
        }

        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);

                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {  
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x]\
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x];

                        }// x loop
                    }// y loop
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z loop
            }
        }

        MPI_Waitall(4, req_recv, status);
        MPI_Waitall(4, req_send, status);
    }

    return buffer[nt % 2];
}


ptr_t stencil_27(ptr_t grid, ptr_t aux, const dist_grid_info_t *grid_info, int nt, double * calc_time, double * comm_time) {
    ptr_t buffer[2] = {grid, aux};
    int x_start = grid_info->halo_size_x, x_end = grid_info->local_size_x + grid_info->halo_size_x;
    int y_start = grid_info->halo_size_y, y_end = grid_info->local_size_y + grid_info->halo_size_y;
    int z_start = grid_info->halo_size_z, z_end = grid_info->local_size_z + grid_info->halo_size_z;
    int ldx = grid_info->local_size_x + 2 * grid_info->halo_size_x;
    int ldy = grid_info->local_size_y + 2 * grid_info->halo_size_y;
    int ldz = grid_info->local_size_z + 2 * grid_info->halo_size_z;
    MPI_Request req_send[8], req_recv[8];
    MPI_Status status[8];

    // for boundary conditions
    for (int i = 1; i <= 8; i++) {// 27点stencil需要通信8个
        int oppo = oppo_idx[i];
        MPI_Sendrecv(buffer[0], 1, send_subarray[i]   , ngbs[i]   , grid_info->p_id ^ ngbs[i]   ,\
                     buffer[0], 1, recv_subarray[oppo], ngbs[oppo], grid_info->p_id ^ ngbs[oppo], cart_comm, &status[i-1]);
    }

    // 刨去外周一圈，导致对不齐（或者别的原因？），速度骤降，比重新再多算一遍外周还慢得多！！！
    // y_start += grid_info->halo_size_y; y_end -= grid_info->halo_size_y;
    // z_start += grid_info->halo_size_z; z_end -= grid_info->halo_size_z;

    for(int t = 0; t < nt; ++t) {
        cptr_t a0 = buffer[t % 2];
        ptr_t a1 = buffer[(t + 1) % 2];

        // 先计算内halo区
        for (int dir = 1; dir <= 4; dir++) {
            ptr_t a1_local = a1 + ih_z_beg[dir]*ldx*ldy + ih_y_beg[dir]*ldx;
            cptr_t a0_local_Z = a0 + (a1_local - a1);
            cptr_t a0_local_P = a0_local_Z + ldy*ldx;
            cptr_t a0_local_N = a0_local_Z - ldy*ldx;
            int yy_end = ih_y_end[dir]-ih_y_beg[dir];

            for (int z = ih_z_beg[dir]; z < ih_z_end[dir]; z++){
                for (int y = 0; y < yy_end; y++)
                    for (int x = x_start; x < x_end; x++)
                        a1_local[y*ldx+x] \
                            = ALPHA_ZZZ * a0_local_Z[y*ldx+x] \
                            + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                            + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                            + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                            + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                            + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                            + ALPHA_ZZP * a0_local_P[y*ldx+x] \
                            + ALPHA_NNZ * a0_local_Z[(y-1)*ldx+x-1] \
                            + ALPHA_PNZ * a0_local_Z[(y-1)*ldx+x+1] \
                            + ALPHA_NPZ * a0_local_Z[(y+1)*ldx+x-1] \
                            + ALPHA_PPZ * a0_local_Z[(y+1)*ldx+x+1] \
                            + ALPHA_NZN * a0_local_N[y*ldx+x-1] \
                            + ALPHA_PZN * a0_local_N[y*ldx+x+1] \
                            + ALPHA_NZP * a0_local_P[y*ldx+x-1] \
                            + ALPHA_PZP * a0_local_P[y*ldx+x+1] \
                            + ALPHA_ZNN * a0_local_N[(y-1)*ldx+x] \
                            + ALPHA_ZPN * a0_local_N[(y+1)*ldx+x] \
                            + ALPHA_ZNP * a0_local_P[(y-1)*ldx+x] \
                            + ALPHA_ZPP * a0_local_P[(y+1)*ldx+x] \
                            + ALPHA_NNN * a0_local_N[(y-1)*ldx+x-1] \
                            + ALPHA_PNN * a0_local_N[(y-1)*ldx+x+1] \
                            + ALPHA_NPN * a0_local_N[(y+1)*ldx+x-1] \
                            + ALPHA_PPN * a0_local_N[(y+1)*ldx+x+1] \
                            + ALPHA_NNP * a0_local_P[(y-1)*ldx+x-1] \
                            + ALPHA_PNP * a0_local_P[(y-1)*ldx+x+1] \
                            + ALPHA_NPP * a0_local_P[(y+1)*ldx+x-1] \
                            + ALPHA_PPP * a0_local_P[(y+1)*ldx+x+1];
                a1_local = a1_local + ldx*ldy;
                a0_local_N = a0_local_Z;
                a0_local_Z = a0_local_P;
                a0_local_P = a0_local_P + ldx*ldy;
            }
        }
        // 隐藏非阻塞通信
        for (int dir = 1; dir <= 8; dir++) {
            int oppo = oppo_idx[dir];
            MPI_Isend(a1, 1, send_subarray[dir],  ngbs[dir],  grid_info->p_id ^ ngbs[dir],  cart_comm, &req_send[dir-1]);
            MPI_Irecv(a1, 1, recv_subarray[oppo], ngbs[oppo], grid_info->p_id ^ ngbs[oppo], cart_comm, &req_recv[oppo-1]);
        }
        
        for (int JJ = y_start; JJ < y_end; JJ += SET_Y_SIZE) {
            for (int II = x_start; II < x_end; II += SET_X_SIZE){
                int REAL_Y_SIZE = MIN(SET_Y_SIZE, y_end - JJ);
                int REAL_X_SIZE = MIN(SET_X_SIZE, x_end - II);

                ptr_t a1_local = a1 + z_start*ldx*ldy + JJ*ldx + II;
                cptr_t a0_local_Z = a0 + (a1_local - a1);
                cptr_t a0_local_P = a0_local_Z + ldy*ldx;
                cptr_t a0_local_N = a0_local_Z - ldy*ldx;

                for(int z = z_start; z < z_end; ++z) {
                    for(int y = 0; y < REAL_Y_SIZE; y++) {
                        #pragma unroll
                        for(int x = 0; x < REAL_X_SIZE; x++) {
                            a1_local[y*ldx+x] \
                                = ALPHA_ZZZ * a0_local_Z[y*ldx+x] \
                                + ALPHA_NZZ * a0_local_Z[y*ldx+x-1] \
                                + ALPHA_PZZ * a0_local_Z[y*ldx+x+1] \
                                + ALPHA_ZNZ * a0_local_Z[(y-1)*ldx+x] \
                                + ALPHA_ZPZ * a0_local_Z[(y+1)*ldx+x] \
                                + ALPHA_ZZN * a0_local_N[y*ldx+x] \
                                + ALPHA_ZZP * a0_local_P[y*ldx+x] \
                                + ALPHA_NNZ * a0_local_Z[(y-1)*ldx+x-1] \
                                + ALPHA_PNZ * a0_local_Z[(y-1)*ldx+x+1] \
                                + ALPHA_NPZ * a0_local_Z[(y+1)*ldx+x-1] \
                                + ALPHA_PPZ * a0_local_Z[(y+1)*ldx+x+1] \
                                + ALPHA_NZN * a0_local_N[y*ldx+x-1] \
                                + ALPHA_PZN * a0_local_N[y*ldx+x+1] \
                                + ALPHA_NZP * a0_local_P[y*ldx+x-1] \
                                + ALPHA_PZP * a0_local_P[y*ldx+x+1] \
                                + ALPHA_ZNN * a0_local_N[(y-1)*ldx+x] \
                                + ALPHA_ZPN * a0_local_N[(y+1)*ldx+x] \
                                + ALPHA_ZNP * a0_local_P[(y-1)*ldx+x] \
                                + ALPHA_ZPP * a0_local_P[(y+1)*ldx+x] \
                                + ALPHA_NNN * a0_local_N[(y-1)*ldx+x-1] \
                                + ALPHA_PNN * a0_local_N[(y-1)*ldx+x+1] \
                                + ALPHA_NPN * a0_local_N[(y+1)*ldx+x-1] \
                                + ALPHA_PPN * a0_local_N[(y+1)*ldx+x+1] \
                                + ALPHA_NNP * a0_local_P[(y-1)*ldx+x-1] \
                                + ALPHA_PNP * a0_local_P[(y-1)*ldx+x+1] \
                                + ALPHA_NPP * a0_local_P[(y+1)*ldx+x-1] \
                                + ALPHA_PPP * a0_local_P[(y+1)*ldx+x+1];
                        }// x
                    }// y
                    a1_local = a1_local + ldx*ldy;
                    a0_local_N = a0_local_Z;
                    a0_local_Z = a0_local_P;
                    a0_local_P = a0_local_P + ldx*ldy;
                }// z
            }
        }

        MPI_Waitall(8, req_recv, status);
        MPI_Waitall(8, req_send, status);
    }
    return buffer[nt % 2];
}

值得一提的是，当使用8个节点（1024核）时，会出现执行程序非常慢，甚至有时提交任务太久没执行完而被作业系统杀掉的情况。但执行后输出的结果却显示时间仍然只是零点几秒，这大概是由于MPI-IO读取数据时非常耗时。具体原因我没有深究，但由于等待时间实在太久，所以只进行了test.sh中的测试，即跑了16个时间步的循环。而跨节点时本来性能就会有较大波动。

实际上，应用计算通信重叠会导致在某些并行度下性能有较明显的下降。这可能是因为刨去内halo区剩下的区域并不能对齐，导致后续在计算真正的内部区域时，会有更长的计算时间。所以在此只是尝试了一下，后续的优化没有应用计算通信重叠。

节点内进程映射优化

经过进程映射的优化（进程尽可能均匀散布于整个节点，核与核之间距离尽可能远）可以得到单节点内（进程数较小时）更高的可扩展性！这有两个原因。

一方面是L1和L2 cache是各个cpu独有的，而L3 cache整个numa-region内的32个核共享。MPI程序是分离的地址空间，一个进程计算时所需访存的地址肯定与别的进程不一样，不怕伪共享，反而是多个进程共用一个numa-region内的核时会导致L3 cache共用而产生的capacity miss或conflict miss增多！所以应尽量让进程分布距离远一些，避免过度聚集而致共享的L3 cache过热（在进程数较少时可以独享或尽可能多占L3 cache），使整个节点的负载均衡。

另一方面，我认为更重要的是，内存总线一般是几个核共用一条的（具体的排线方式不同机器有差异，只是一般情况），比如在该节点128核内，0-3核（核组0），4-7核（核组1）等是以核组为单位共享内存总线的。所以当进程分布得更散落时，有利于提高机器的内存带宽利用率。这对于stencil这种memory-bounded、严重吃带宽的程序而言，应该是相比于cache更重要的因素。

该映射优化可以通过计算给定进程数np时均匀分布于整个节点的步长stride，和mpirun的命令行参数--map-by slot:PE=$stride --bind-to core来实现，可见mpi-benchmark.sh文件和mpi-test.sh文件。

#!/usr/bin/env bash
#SBATCH --nodes=1
#BATCH --ntasks-per-node=1

if [ "$#" -ne 3 ]; then
  echo "Usage: $0 <executable> <number of nodes> <number of processes per node> " >&2
  exit 1
fi

export DAPL_DBG_TYPE=0
stride=$[128 / $3]

DATAPATH=/storage/readonly/stencil_data

salloc -N $2 --exclusive --ntasks-per-node $3 mpirun --map-by slot:PE=$stride --bind-to core --report-bindings $1 7 256 256 256 16 ${DATAPATH}/stencil_data_256x256x256 ${DATAPATH}/stencil_answer_7_256x256x256_16steps
salloc -N $2 --exclusive --ntasks-per-node $3 mpirun --map-by slot:PE=$stride --bind-to core --report-bindings $1 7 384 384 384 16  ${DATAPATH}/stencil_data_384x384x384 ${DATAPATH}/stencil_answer_7_384x384x384_16steps
salloc -N $2 --exclusive --ntasks-per-node $3 mpirun --map-by slot:PE=$stride --bind-to core --report-bindings $1 7 512 512 512 16  ${DATAPATH}/stencil_data_512x512x512 ${DATAPATH}/stencil_answer_7_512x512x512_16steps
salloc -N $2 --exclusive --ntasks-per-node $3 mpirun --map-by slot:PE=$stride --bind-to core --report-bindings $1 27 256 256 256 16  ${DATAPATH}/stencil_data_256x256x256 ${DATAPATH}/stencil_answer_27_256x256x256_16steps
salloc -N $2 --exclusive --ntasks-per-node $3 mpirun --map-by slot:PE=$stride --bind-to core --report-bindings $1 27 384 384 384 16  ${DATAPATH}/stencil_data_384x384x384 ${DATAPATH}/stencil_answer_27_384x384x384_16steps
salloc -N $2 --exclusive --ntasks-per-node $3 mpirun --map-by slot:PE=$stride --bind-to core --report-bindings $1 27 512 512 512 16  ${DATAPATH}/stencil_data_512x512x512 ${DATAPATH}/stencil_answer_27_512x512x512_16steps