单处理器计算(一)
翻自:《Introduction to High Performance Scientific Computing》-Victor Eijkhout
了解计算机体系结构对于编写高效、科学的代码具有十分重要的作用。两段基于不同处理器架构编写的代码,其计算结果可能相同,但速度差异可能从几个百分点到几个数量级之间不等。显然,仅仅把算法放到计算机上是不够的,计算机架构也是至关重要的内容。
有些问题可以在单个中央处理单元(CPU)上解决,而有些问题则需要由多个处理器组成的并行计算机解决。我们将在下一章详细介绍并行计算机,但即便是使用并行计算机处理,也需要首先了解单个CPU的情况。
在该部分,我们将重点关注CPU及其内存系统内部发生的事情。首先讨论指令如何执行,研究处理器核心中的运算;最后,由于内存访问通常比处理器执行指令要慢得多,因此我们将重点关注内存、处理器以及处理器内部的数据移动情况;“flops(每秒浮点操作数)计数”作为预测代码性能的时代已经一去不复返了。这种差异实际上是一个不断增长的趋势,所以随着时间的推移,处理内存流量的问题变得越来越重要,而非逐渐销声匿迹。
这一章中,我们将对CPU设计是如何影响性能的,以及如何编写优化性能的代码等问题有一个清晰的认识。想学习更多细节,请参阅关于PC架构的在线书籍[114],以及关于计算机架构的标准工作,Hennesey和Patterson[97]。
冯·诺依曼架构
虽然各类计算机在处理器细节上存在很多不同,但也有许多相似之处。总的看来,它们都采用了「冯·诺伊曼架构」(von Neumann architectures)。该架构主要包含:存储程序和数据的内存,以及一个在“获取、执行、存储周期”中对数据进行操作的指令处理单元。
注释 1: 具有指定指令序列的模型也称为「控制流」(control flow),与「数据流」(data flow)相对应。
由于指令和数据共同存储在一个处理器中,这使得冯·诺依曼架构区别于早期或一些其他特殊用途的硬接线当代处理器,能够允许修改或生成其他程序。这给我们提供了编辑器和编译器:计算机可以将程序视为数据进行处理。
注释 2: 存储程序的概念允许一个正在运行的程序修改其源代码。然而,人们很快就意识到这将导致代码变得难以维护,因此在实际中很少见到。
本书将不会讨论编译器将高级语言翻译成机器指令的过程,而是讨论如何编写高质量的程序以确保底层运行的效率。
在科学计算中,我们通常只关注数据在程序执行期间如何移动,而非程序代码具体如何。大多数应用中,程序与数据似乎是分开存储的。与高级语言不同,处理器执行的机器指令通常会指定操作的名称,操作数和结果的位置。这些位置不是表示为内存位置,而是表示为「寄存器」(registers)位置:即在CPU中被称作内存的一小部分。
注释 3: 我们很少分析到内存的架构,尽管它们已经存在。20世纪80年代的Cyber 205超级计算机可以同时有三个数据流,两个从内存到处理器,一个从处理器到内存。这样的架构只有在内存能够跟上处理器速度的情况下才可行,而现在已经不是这样了。
下面是一个简单的C语言例子:
1 | void store(double *a, double *b, double *c) { |
及其X86汇编输出,由gcc -O2 -S -o - store.c得到:
1 | .text |
(程序演示的为64位系统输出;32位系统可以添加-m64指令输出)
这段程序的指令有:
- 从内存加载到寄存器;
- 执行加法操作;
- 将结果写回内存。
每条指令的处理如下:
- 指令获取:根据「程序计数器」(program counter)的指示将下一条指令装入进程。此处我们不考虑这是如何发生以及从哪里发生的问题。
- 指令解码:处理器检查指令以确定操作和操作数。
- 内存获取:必要时,数据将从内存取到寄存器中。
- 执行:执行操作,从寄存器读取数据并将数据写回寄存器。
数组的情况稍微复杂一些:加载(或存储)的元素被确定为数组的基址后会加上一个偏移量。
在某种程度上,现代CPU在程序员看来就像冯·诺伊曼机器,但也有各种例外。首先,虽然内存看起来为随机寻址,但在实际中存在着「局部性」(locality)的概念:一旦一个数据项被加载,相邻的项将更有效地加载,而重新加载初始项也会更快。
简单数据加载的另一个复杂之处是,当前的CPU同时操作多条指令,这些指令被称为“「正在执行」(in flight)”,这意味着它们处于不同的完成阶段。当然,与这些同步指令一起,它们的输入和输出也以重叠的方式在内存和处理器之间移动。这是超标量CPU体系结构的基本思想,也被称为「指令级并行」(Instruction Level Parallelism,ILP)。因此,虽然每个指令可能需要几个时钟周期才能完成,但处理器可以在合适的情况下每个周期完成一条指令;在某些情况下,每个周期可以完成多条指令。
CPU的处理速度处在千兆赫级(G),意味着处理器的速度是决定计算机性能的主要因素。速度虽然与性能紧密联系,但实际情况却更为复杂:一些算法被CPU所限制,此时进程的速度是最重要的制约;另外一些算法受到内存的限制,总线速度和缓存大小等方面是影响该问题的关键。
在科学计算中,第二种情况相当显著,因此在本章中,我们将大量关注将数据从内存转移到处理器的过程,而对实际处理器的关注相对较少。
当代处理器
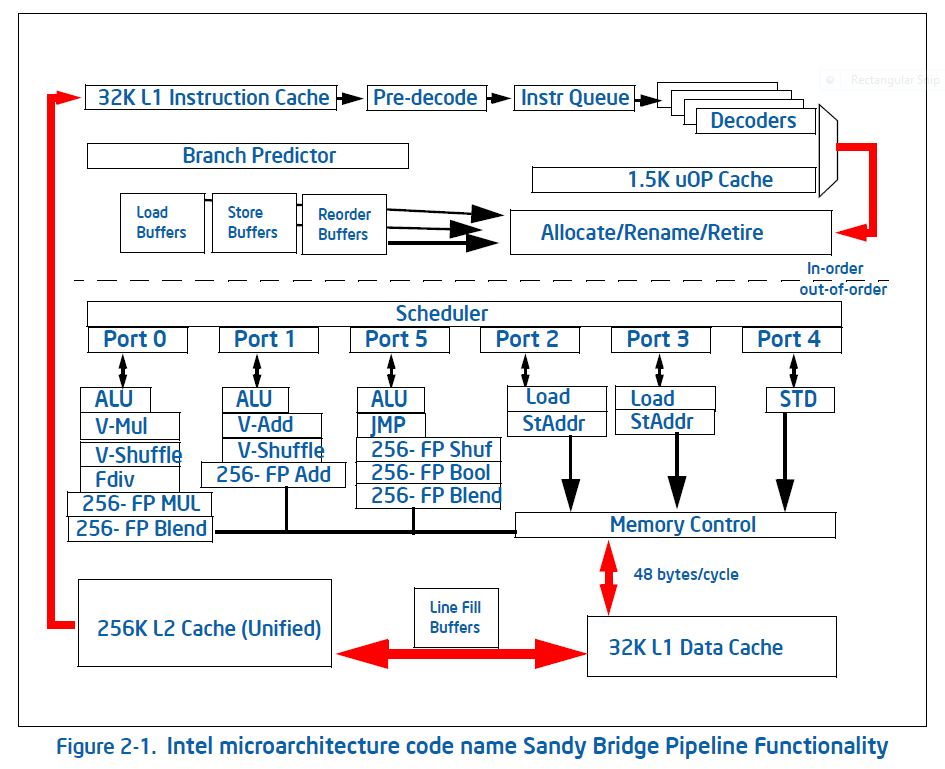
当代处理器极为复杂,在这一节中,我们将简短地介绍一下其组成部分。下图是Intel Sandy Bridge处理器的芯片图。这种芯片大约一英寸大小,包含近十亿个晶体管。

处理核心
冯·诺依曼模型中只有一个执行指令的实体。自21世纪初以来,这种情况并没有显著的增长。上图所示的Sandy Bridge有8个核,每个核都是执行指令流的独立单元。在本章中,我们将主要讨论单个核心的各个方面;第1.4节将讨论多核的集成方面。
指令处理
冯·诺伊曼模型也是不现实的,因为它假设所有的指令都严格按照顺序执行。在过去的二十年中,处理器越来越多地使用了无序指令处理,即指令可以按照不同于用户程序指定的顺序进行处理。当然,处理器只有在不影响执行结果的情况下才允许对指令重新排序!
在图1.2中,你可以看到与指令处理有关的各种单元:这种聪明的做法实际上要花费相当多的能源及大量的晶体管。正因如此,包括第一代英特尔Xeon Phi协处理器,Knights Corner在内的处理器都采取了使用顺序指令处理的策略。然而,在下一代Knights Landing中,这种做法却由于性能不佳而被淘汰。
浮点单元
在科学计算中,我们最感兴趣的是处理器如何处理浮点数据。而并非整数或布尔值的运算。因此,核心在处理数值数据方面具有相当的复杂性。
例如,过去的处理器只有一个「浮点单元」(FPU),而现在的它们有多个且能够同时执行的浮点单元。
例如,加法和乘法通常是分开的;如果编译器可以找到独立的加法和乘法操作,就可以同时调度它们从而使处理器的性能翻倍。在某些情况下,一个处理器会有多个加法或乘法单元。
另一种提高性能的方法是使用「乘加混合运算」(Fused Multiply-Add,FMA)单元,它可以在与单独的加法或乘法相同的时间内执行指令$x \leftarrow ax +b$。配合流水线操作,这意味着处理器在每个时钟周期内有几个浮点运算的渐近速度。
顺便说一句,很少有用除法当制约因素的算法。在现代CPU中,除法操作的优化程度远不及加法和乘法。除法操作可能需要10或20个时钟周期,而CPU可以有多个加法和/或乘法单元(渐进地)使之每个周期都可以产生一个结果。下表为多个处理器架构的浮点能力(每个核心),以及8个操作数的DAXPY周期数
| 处理器 | 年份 | 加/乘/乘加混合 单元(个数$\times$宽度) | daxpy cycles(arith vs load/store) |
|---|---|---|---|
| MIPS R10000 | 1996 | $1\times 1+1\times 1+0$ | 8/24 |
| Alpha EV5 | 1996 | $1\times 1+1\times 1+0$ | 8/12 |
| IBM Power5 | 2004 | $0+0+2\times 1$ | 4/12 |
| AMD Bulldozer | 2011 | $2\times 2+2\times 2+0$ | 2/4 |
| Intel Sandy Bridge | 2012 | $1\times 4+1\times 4+0$ | 2/4 |
| Intel Haswell | 2014 | $0+0+2\times 4$ | 1/2 |
流水线
处理器的浮点加乘单元是流水线式的,其效果是独立的操作流可以以每个时钟周期一个结果的渐近速度执行。流水线背后的思想如下:假设一个操作由若干个简单操作组成,并且每个子操作在处理器中都有独立的硬件。如果我们现在有多个操作要执行,我们可以通过让所有的子操作同步执行来获得加速:每个操作将其结果交给下一个操作,并接受前一个操作的输入。
注释4 这与排队救火的过程非常类似,是一种收缩算法。
例如,加法指令可以包含以下组件:
- 指令解码,包括查找操作数的位置。
- 将操作数复制到寄存器中(数据获取)。
- 调整指数;加法$.35 \times10^{-1} + .6 \times 10^{−2}$变成$.35 \times 10^{-1} + .06 \times 10^{−1}$。
- 执行尾数的加法,在这个例子中是$.41$。
- 将结果归一化,在本例中为$.41 \times 10^{−1}$。(本例中归一化并未执行任何操作,$.3 \times 100 + .8 \times 100$和$.35 \times 10^{−3} +(−.34)\times 10^{−3}$做了很大的调整)
这些部分通常被称为流水线的“「深度」(stages)”或“「阶段」(segments)”。
如果按照顺序执行,上文中每个组件设计为1个时钟周期,则整个过程需要6个时钟周期。然而,如果每个操作都有自己对应的硬件,我们就可以在少于12个周期内执行两个操作:
- 第一个操作执行解码;
- 第一个操作获取数据,同时第二个操作执行解码;
- 同时执行第一操作的第三阶段和第二操作的第二阶段;
- 以此类推。
可以看到,第一个操作仍然需要6个时钟周期,但第二个操作只需再延后一个周期就能同时完成。
对流水线获得的加速做一个正式的分析:在传统的浮点单元上,产生$n$个结果需要花费时间为 $t(n)=n\ell\tau$,其中$\ell$是状态个数,而$\tau$是时钟周期。结果产生的速率是$t(n)/n$的倒数:$r_{serial}\equiv(\ell \tau)^{-1}$
另一方面,对于流水线的浮点单元,时间是$t(n)=[s+l+n-1]t$其中$s$是设置成本;第一次执行时必须要经历一个完整的串行阶段,但在此后,处理器将在每个周期获得更多的收益。可以记作公式
表示线性时间,加上偏移量。流水线示意图描述如下:
练习1.1 请对比传统FPU和流水线FPU的速度差异。证明结果速率依赖于$n$:给出$r(n)$和$r_\infty = \lim\limits_{n\rightarrow \infty}r(n)$的公式。在非流水线情况下$r$的加速极限是什么样?它需要多长时间才能接近极限情况?注意到$n=n_{1/2}$,可以得到$r(n)=r_\infty/2$,这通常被用做$n_{1/2}$的定义。
由于向量处理器同时处理多个指令,因此这些指令必须是独立且相互之间没有依赖关系的。$∀_i:a_i\leftarrow b_i + c_i$有独立的加法运算;$\forall_i:a_{i+1}\leftarrow a_ib_i+c_i$将一次迭代$(a_i)$的结果输入到下一次迭代的输入$(a_{i+1}=…)$,所以这些操作并非独立。
与传统的CPU相比,流水线处理器可以将操作速度提高4、5甚至6倍。在上世纪80年代,当第一台向量计算机成功上市时,这样的加速效率十分常见。现在,CPU可以有20个阶段的流水线,是否意味着它们的速度非常快?这个问题有点复杂。芯片设计者不断提高主频,流水线部分不再能够在一个周期内完成他们的工作,所以他们进一步分裂。有时甚至有一些时间片段什么也没有发生:但这段时间是又是必须的,以确保数据可以及时传输到芯片的不同部分。
人们能从流水线CPU得到的改进是有限的,为了追求更高的性能,计算机科学家们尝试了几种不同的流水线设计。例如,Cyber 205有单独的加法和乘法流水线,可以将一个流水线输入另一个流水线,而无需先将数据返回内存。像 $∀_i: a_i\leftarrow b_i + c·d_i$这样的操作被称为“「链接三元组」(linked triads)”(因为到内存的路径数量,一个输入操作数必须是标量)。
练习1.2 分析链接三元组的加速和$n_{1/2}$。
另一种提高性能的方法是使用多个相同的流水线。NEC SX系列完善了这种设计。例如,有4条流水线时,$∀_i:a_i\leftarrow b_i +c_i$操作将对模块4进行拆分,以便第一条流水线对索引$i = 4·j$操作,第二条流水线对索引$i = 4·j + 1$操作,以此类推。
练习1.3 分析具有多个并行操作流水线处理器的速度提升情况和$n_{1/2}$。也就是说,假设有$p$个执行相同指令的独立流水线,每条流水线都可以处理的操作数流。
(你可能想知道我们为什么在这里提到一些相当老的计算机:真正的流水线超级计算机已经不存在了。在美国,Cray X1是该系列的最后一款,而在日本,只有NEC还在生产。然而,现在CPU的功能单元是流水线的,所以这个概念仍然很重要。)
练习1.4 如下操作
1 | for (i) { |
不能由流水线处理,因为在操作的一次迭代的输入和前一次迭代的输出之间存在依赖关系。但是,我们可以将循环转换为数学上等价的循环,并且可能更有效地计算。导出一个表达式,该表达式从$x[i]$中计算$x[i+2]$而不涉及$x[i+1]$。这就是所谓的「递归加倍」(recursive doubling)。假设有足够的临时存储空间。参考如下:
- 做初步计算;
- 计算$x[i],x[i+2],x[i+4],…$,并从这些中
- 计算缺失项$x[i+1],x[i+3],…$
通过给出$T_0(n)$和$T_s(n)$的计算公式,分析了该格式的有效性。你能想到为什么初步计算在某些情况下可能不那么重要吗?
收缩计算
上面描述的流水线操作是「收缩算法」(systolic algorithm)的一种情况。在20世纪80年代和90年代,有研究使用流水线算法并构建特殊硬件——「脉动阵列」 (systolic arrays)来实现它们[125]。这也与「现场可编程门阵列」(Field-Programmable Gate Arrays,FPGA)的计算连接,其中脉动阵列是由软件定义的。
峰值性能
现代CPU由于流水线的存在,时钟速度和峰值性能之间存在着较为简单的关系。由于每个FPU可以在一个周期内产生一个结果,所以峰值性能是时钟速度乘以独立FPU的数量。浮点运算性能的衡量标准是“「每秒浮点运算」(floating point operations per second)”,缩写为flops。考虑到现在计算机的速度,你会经常听到浮点运算被表示为“gigaflops”:$10^9$次浮点运算的倍数。
8位,16位,32位,64位
处理器的特征通常是可以处理多大的数据块。这可以联系到
- 处理器和内存之间路径的宽度:一个64位的浮点数是否可以在一个周期内加载,还是分块到达处理器。
- 内存的寻址方式:如果地址被限制为16位,只有64,000字节可以被识别。早期的PC有一个复杂的方案,用段来解决这个限制:用段号和段内的偏移量来指定一个地址。
- 单个寄存器中的数值位数,特别是用于操作数据地址的整数寄存器的大小;参见前一点。(浮点寄存器通常更大,例如在x86体系结构中是80位。)这也对应于处理器可以同时操作的数据块的大小。
- 浮点数的大小:如果CPU的算术单元被设计成有效地乘8字节数(“双精度”;见3.2.2节),那么一半大小的数字(“单精度”)有时可以以更高的效率处理,而对于更大的数字(“四倍精度”),则需要一些复杂的方案。例如,一个四精度的数字可以由两个双精度的数字来模拟,指数之间有一个固定的差异。
这些测量值不一定相同。例如,原来的奔腾处理器有64位数据总线,但有一个32位处理器。另一方面,摩托罗拉68000处理器(最初的苹果Macintosh)有一个32位CPU,但16位的数据总线。
第一个英特尔微处理器4004是一个4位处理器,它可以处理4位的数据块。如今,64位处理器正在成为标准。
缓存(Caches):芯片上的内存
计算机内存的大部分是在与处理器分离的芯片中。然而,通常有少量的片上内存(通常是几兆字节),这些被称为「高速缓存」(cache)。后面我们将会详细解释。
图形、控制器、专用硬件
“消费型”和“服务器型”处理器之间的一个区别是,消费型芯片在处理器芯片上花了相当大的空间用于图形处理。手机和平板电脑的处理器甚至可以有专门的安全电路或mp3播放电路。处理器的其他部分专门用于与内存或I/O子系统通信。我们将不在本书中讨论这些方面。
超标量处理和指令级并行性
在冯·诺伊曼模型中,处理器通过控制流进行操作:指令之间线性地或通过分支相互跟踪,而不考虑它们涉及哪些数据。随着处理器变得越来越强大,一次可以执行多条指令,就有必要切换到数据流模型。这种超标量处理器分析多个指令以找到数据相关性,并行执行彼此不依赖的指令。
这个概念也被称为「指令级并行」(Instruction Level Parallelism,ILP),它被各种机制推动:
- 多发射(multiple-issue):独立指令可同时启动;
- 流水线(pipelining):上文提到,算术单元可以在不同的完成阶段处理多个操作;
- 分支预测和推测执行(branch prediction and speculative execution):编译器可以“预测”条件指令的值是否为真,然后相应地执行这些指令;
- 无序执行(out-of-order execution):如果指令之间不相互依赖,并且执行效率更高,则指令可以重新排列;
- 预取(prefetching):数据可以在实际遇到任何需要它的指令之前被推测地请求(这将在后面进一步讨论)。
在上面我们看到了浮点操作上下文中的流水线操作。事实上,不仅是浮点运算,当代处理器的整个CPU都是流水线的,任何类型的指令都将尽快被放入指令流水线中。注意,这个流水线不再局限于相同的指令:现在,流水线的概念被概括为同时 “在执行 “的任何指令流。
随着主频的增加,处理器流水线的长度也在增加,以使分段在更短的时间内可被执行。可以看到,更长的流水线有着更大的$n_{1/2}$,因此需要更多的独立指令来使流水线以充分的效率运行。当达到指令级并行性的极限时,使流水线变长(或者称为“更深”)将不再有好处。因此,芯片设计者们通常转向多核架构以更高效地利用芯片上的晶体管。
这些较长的流水线的第二个问题是:如果代码到达一个分支点(一个条件或循环中的测试),就不清楚要执行的下一条指令是什么。在该点上,流水线就会会停止。例如,CPU总是假设测试结果是正确的,因此采取了「分支预测执行」(speculative execution)。如果代码随后接受了另一个分支(这称为分支错误预测),则必须刷新流水线并重新启动。执行流中产生的延迟称为「分支惩罚」(branch penalty)。
内存层次结构
冯·诺伊曼体系结构中,数据立即从内存加载到处理器,并在处理器中进行操作。然而这是不现实的,因为这一过程中会有「访存墙」(memory wall)[204]的存在:内存速度过慢,无法和处理器速度相匹配。具体来说,单次加载可能需要1000个周期,而处理器每个周期可以执行若干个操作。(在长时间等待加载之后,下一个加载可能会更快,但对处理器来说仍然太慢)
实际上,在FPU和内存之间会有不同的存储器级别:寄存器和缓存,一起称为「存储器层级结构」(memory hierarchy)。它们可以更快速地从内存中读取一些最近使用的数据以缓解访存墙的问题。当然,这是在数据被多次使用的前提下。这类「数据复用」(data reuse)问题将在后面进行更详细的讨论。
寄存器和缓存都在不同程度上比内存快;寄存器的速度越快,其存储量就越小。寄存器的大小和速度之间的矛盾产生了一个有趣的博弈,我们将随后讨论这些问题。
接下来,我们将讨论内存层次结构的各部分并分析其在执行过程所需的理论基础。
总线
在计算机中,将数据从处理器移动到CPU、磁盘控制器或屏幕的线路被称为「总线」(busses)。对我们来说最重要的是连接CPU和内存的「前端总线」(Front-Side Bus,FSB)。在当前较为流行的架构中,这被称为“「北桥」(north bridge)”,与连接外部设备(除了图形控制器)的“「南桥」(south bridge)”相对。
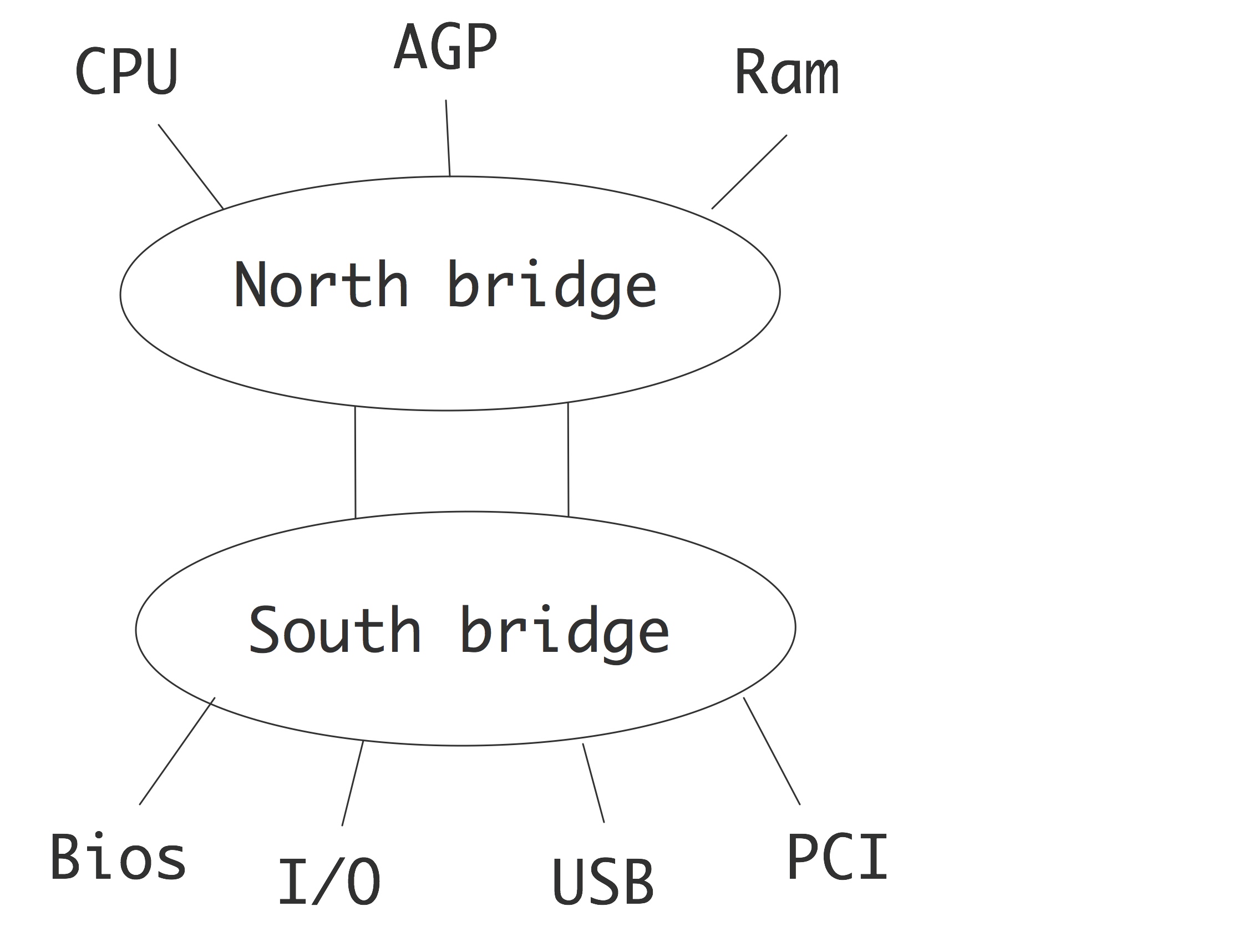
总线通常比处理器的速度慢,其时钟频率作为CPU时钟频率的一部分,数值上略高于1GHz,这也正是引入缓存的原因之一;事实上,一个处理器可以在每个时钟周期中消耗大量数据项。除了频率之外,总线的带宽也由每个时钟周期可移动的比特数决定。在目前的体系结构中,这通常是64或128。我们现在将更详细地讨论这个问题。
延迟和带宽
寄存器中访问数据几乎是瞬时的,而将数据从内存加载到寄存器是进行任何操作之前的一个必要步骤,加载的过程会导致大量的延迟,下面我们将细化这一过程。
有两个重要的概念来描述数据的移动:「延迟和带宽」(latency and bandwidth)。这里的假设是,请求一组数据会引起初始延迟;如果这一项是该组数据的第一个项,则通常是连续的内存地址范围,而该组数据的其余部分将以一个固定的时间周期不再延迟到达。
「延迟」:为处理器发出内存项请求到内存项实际到达之间的延迟。我们可以区分不同的延迟,比如从内存到缓存的传输,缓存到寄存器的传输,或者将它们总结为内存和处理器之间的延迟。延迟是以(纳米)秒或时钟周期来衡量的。如果处理器按照在汇编代码中的顺序去执行指令,则在从内存中提取数据时经常会停止;这也被称为「内存延迟」(memory stall)。低延迟非常重要。在实际中,许多处理器都有指令的“无序执行”情况,即允许它们在等待所请求的数据时执行其他操作。程序员可以考虑这一点,并以一种实现延迟隐藏的方式编写代码;「图形处理单元」(GPU)可以在线程之间快速切换,以实现延迟隐藏。
「带宽」:为克服初始延迟后,数据到达目的地的速率。带宽以字节(千字节k、兆字节m、千兆字节g)/秒或每个时钟周期来衡量。两个存储层之间的带宽通常是通道的周期速度(总线速度)和总线宽度的乘积:总线时钟的每个周期中可以同时发送的比特数。
延迟和带宽的概念通常结合在一个公式中,表示消息从开始到结束所花费的时间: $T(n)=\alpha+\beta n$
其中$\alpha$是延迟,$\beta$是带宽的倒数:即每字节所用的时间。
通常,距离处理器越远,延迟就越长,带宽就越低。因此我们希望处理器尽量使用缓存中的数据而非内存,例如考虑向量加法
1 | for(i) |
每次迭代执行一个浮点操作,现代CPU可以通过流水线技术在一个时钟周期内完成这一操作。但是,每次迭代都需要加载两个数字并写入一个数字,总共需要24字节的内存流量(实际上,$a[i]$在写入之前就被加载了,所以每次迭代有4次内存访问,总共32字节)。典型的内存带宽数字(参见图1.5)远远没有接近24(或32)字节每周期。这意味着,在没有缓存的情况下,算法性能可能受到内存性能的限制。当然,缓存不会加速每一个操作,但这对我们的例子并没有影响。我们将会在1.7节中讨论高效利用缓存的编程策略。
当我们讨论从一个处理器向另一个处理器发送数据时,延迟和带宽的概念也会出现在并行计算机中。
寄存器
每个处理器内部都有少量类似内存的结构:「寄存器」(registers)或「寄存器堆」(registers file)。寄存器是处理器实际操作的对象:例如
1 | a := b + c |
实际过程为
- 将b的值从内存中装入寄存器,
- 将c的值从内存中装入另一个寄存器,
- 计算和并将其写入另一个寄存器,然后
- 将计算后的总和写回a的内存位置。
查看汇编代码(例如编译器的输出)就可以看到显式的加载、计算和存储指令。
像加或乘这样的计算指令只能在寄存器上操作。例如,在汇编语言中我们会看到如下指令
1 | addl %eax %edx |
它将一个寄存器的内容添加到另一个寄存器。正如在这个示例指令中看到的,与内存地址相反,寄存器没有编号,而是具有在汇编指令中引用的不同名称。通常,一个处理器有16或32个浮点寄存器;英特尔安腾(Intel Itanium)的128个浮点寄存器是例外。
寄存器具有高带宽和低延迟,因为它们是处理器的一部分。可以将进出寄存器的数据移动看作是瞬时的。
在本章中,我们会发现从内存中读取数据的时间开销较大。因此,尽可能将数据留在寄存器中是一种简单的优化策略。例如,如果上面的计算后面跟着一个语句
1 | a := b + c |
a的计算值就可以留在寄存器中。编译器通常会帮助我们完成这种优化:编译器不会生成存储和重新加载a的指令。我们就称a停留在寄存器中。
将值保存在寄存器中通常是为了避免重新计算新的变量。例如,在
1 | t1 = sin(alpha) * x + cos(alpha) * y; |
正弦和余弦值可能会保留在寄存器中。我们可以通过显式地引入临时数量来帮助编译器:
1 | s = sin(alpha); c = cos(alpha); |
当然,寄存器的数量是有限制的;试图在寄存器中保留太多的变量被称为「寄存器漫溢」(register spill),这会降低代码的性能。
如果变量出现在内部循环中,那么将该变量保存在寄存器中尤为重要。在计算
1 | for i = 1, length |
中,变量c可能会被编译器保存在寄存器中,而在
1 | for k =1, nevctors |
最好是显式地引入一个临时变量来保存$c[k]$。在C语言中,你可以通过将变量声明为寄存器变量来提示编译器将变量保存在寄存器中:
1 | register double t; |
译者注:声明寄存器格式并不能完全使变量存储在寄存器中,这仅仅起到提示寄存器的作用,如果想完全控制寄存器的执行,则需要编写汇编代码。
缓存
在包含指令即时输入和输出数据的寄存器和大量数据可以长期存放的内存之间,有各种级别的高速缓冲存储器,它们比内存具有更低的延迟和更高的带宽,并将数据保存一段时间。
数据从内存通过高速缓存到达寄存器的好处是,如果一组数据在第一次使用后不久就要被复用,由于它仍然在缓存中,因此访问的速度比从内存中引入数据要快得多。
从历史的角度来看,存储器层次结构的概念早在1946年就已经被讨论过了[25],当时提出的原因是内存技术发展较为缓慢。
示例
例如,假设一个变量$x$被使用了两次,它的两次使用间隔较大,以至于会留在寄存器中:
1 | ... = ... x ..... //执行x的指令 |
汇编代码为:
- 将$x$从内存加载到寄存器中,并对其进行操作;
- 执行中间的指令;
- 将$x$从内存加载到寄存器中,并对其进行操作;
使用缓存,汇编代码保持不变,但内存系统的实际行为现在变成:
- 将$x$从内存加载到缓存中,并从缓存加载到寄存器中,执行操作;
- 执行中间其他的指令;
- 从内存中请求$x$,但由于它仍然在缓存中,因此直接从缓存中加载,继续操作。
由于从缓存加载比从主存加载要快,因此计算速度将会更快。缓存的容量较小,所以数值不能无限期地保存在那里。我们将在下面的讨论中看到它的含义。
缓存和寄存器之间有一个重要的区别:虽然数据是通过显式的汇编指令移入寄存器的,但从内存到缓存的移动完全是由硬件完成的。因此,缓存的使用和重用不在程序员的直接控制范围之内。稍后,特别是在1.6.2和1.7节中,我们将看到如何间接影响缓存的使用。
缓存标签
上面没有提及在缓存中找到某个项的机制,但每个缓存位置都有一个标记,以便我们有足够多的信息来找到某个缓存项与内存的映射。
缓存级别、速度和大小
缓存通常被称为“level 1”和“level 2”(简称L1和L2)缓存;有些处理器可能有L3缓存。L1和L2缓存位于处理器的芯片上;L3缓存则在芯片外部。L1缓存的容量很小,通常在16Kbyte左右。相比之下,第2级(如果有,则是第3级)缓存容量则较大,最多可达几兆字节,但速度也随之下降。与可扩展的内存不同,缓存的大小是固定的。如果某个版本的处理器芯片上附带了一个较大的缓存,那么它的价格通常相当昂贵。
某些操作所需的数据在传送到处理器的过程中被复制到不同的缓存中。如果在一些指令之后,又需要一个数据项,计算机会首先在L1缓存中搜索它;如果没有找到,就在L2缓存中搜索;如果没有找到,就从内存中加载。在缓存中找到数据称为「缓存命中」(cache hit),没有找到数据则称为「缓存失效」(cache miss)。
图1.5展示了缓存层次结构的基本情况,本例是针对Intel Sandy Bridge芯片:缓存越接近FPU,其速度越快,容量越小。
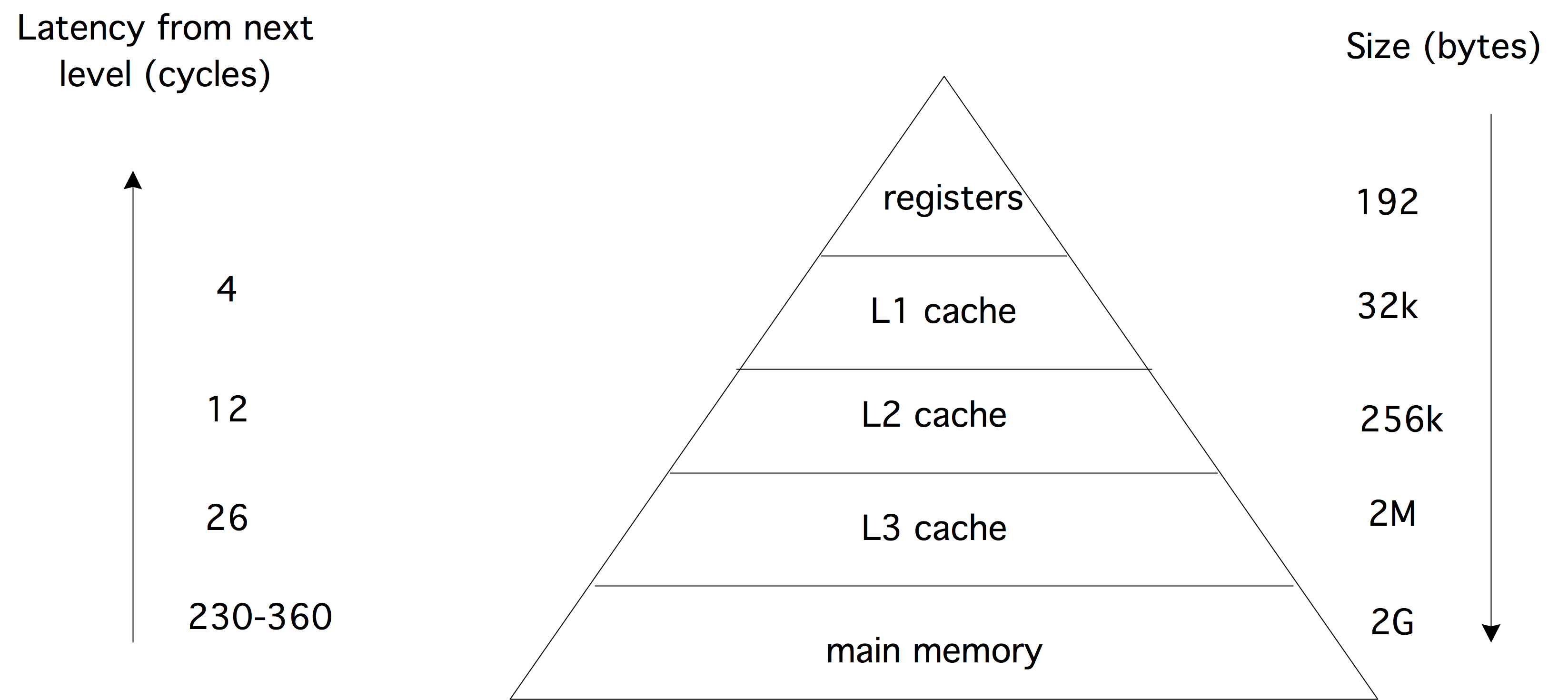
- 从寄存器加载数据是如此之快,以致于它不会成为阻碍算法执行速度的限制。另一方面,寄存器的数量很少。每个核心有16个通用寄存器和16个SIMD寄存器。
- L1缓存很小,但是每个周期保持了32字节的带宽,即4个双精度数。这足以为两个操作分别加载两个操作数,但请注意,内核实际上每个周期可以执行4个操作。因此,为了达到峰值速度,某些操作数需要留在寄存器中:通常,L1带宽足以满足大约一半的峰值性能。
- L2和L3缓存的带宽名义上与L1相同。然而,部分带宽将在缓存一致性问题上浪费。
- 主内存访问带宽大于100个周期,带宽为4.5字节/周期,约为L1带宽的1/7。然而,这个带宽是由一个处理器芯片的多个核心共享的,因此有效的带宽是这个数字的一个小数。大多数集群每个节点也有多个「插槽」(socket,即处理器芯片),通常是2或4个,因此一些带宽花费在维持缓存一致性上(参见1.4节),再次减少了每个芯片的可用带宽。
在L1上,指令和数据有单独的缓存;L2和L3的缓存则同时包含数据和指令。
可以看到,越来越大的缓存无法足够快地向处理器提供数据。因此,有必要以这样一种方式编码,即数据尽可能地保存在最高缓存级别。我们将在本章的其余部分详细讨论这个问题。
练习 1.5 L1缓存比L2缓存小,如果有L3缓存,则L2要比L3小。给出一个实际的和理论上的原因。
缓存失效的类型
缓存失效有三种类型。
正如在上面的例子中看到的,第一次引用数据时,总是会导致缓存丢失,这被称为「强制失效」(compulsory miss),因为这些是不可避免的。这是否意味着在第一次需要数据项时,我们要一直等待它?不一定:第1.3.5节解释了硬件如何通过预测下一步需要什么数据来帮助你。
下一种类型的缓存丢失是由于工作集的大小造成的:「容量失效」(capacity miss)是由于数据被覆盖,因为缓存不能包含所有问题数据(第1.3.4.6节讨论了处理器如何决定要覆盖哪些数据)。如果你想要避免这种类型的失误,需要将问题划分为足够小的块,以便数据可以在缓存中停留相当长的时间。当然,这是在假设数据项被多次操作的前提下,所以把数据项保存在缓存中是有意义的;这将在第1.6.1节中讨论。
最后,由于一个数据项被映射到与另一个相同的缓存位置而导致的「冲突失效」(conflict miss),而这两个数据项仍然是计算所需要的,并且可能有更好的候选者需要被驱逐。这将在1.3.4.10节中讨论。
在多核上下文中还有另外一种类型的缓存丢失:「无效失效」(invalidation miss)。如果缓存中的某个项因为另一个内核改变了相应内存地址的值而失效,就会发生这种情况。内核将不得不重新加载这个地址。
复用是关键
一个或多个缓存的存在并不能立即保证高性能:这在很大程度上取决于代码的内存访问模式,以及如何充分利用缓存。第一次引用一个项时,它被从内存复制到缓存,并通过处理器的寄存器。缓存的存在并没有以任何方式减少延迟和带宽。当同一项第二次被引用时,它可能在缓存中被找到,因此在延迟和带宽方面的成本大大降低:缓存比主存有更短的延迟和更高的带宽。
我们的结论是,首先,算法必须有数据复用的机会。如果每个数据项只被使用一次(就像除了两个向量之外),不存在复用,则缓存的存在在很大程度上是无关紧要的。只有当缓存中的项被多次引用时,代码才会从缓存增加的带宽和减少的延迟中受益;详细的讨论请参见1.6.1节。例如,矩阵向量乘法$𝑦=𝐴𝑥$,其中$𝑥$的每个元素都在$𝑛$操作中使用,其中$𝑛$是矩阵维数。
其次,算法理论上可能有复用的机会,但需要以较为明显的复用方式进行编码。我们将在1.6.2节中解决这些问题。后者尤其重要。
有些问题很小,可以完全放在缓存中,至少在L3缓存中是这样。这是在进行「基准测试」(benchmarking)时需要注意的一点,因为它对处理器性能的描述过于乐观。
替换策略
高速缓存和寄存器中的数据仅由硬件决定,而非由程序员控制。同样地,当缓存或寄存器中的数据在一段时间内没有被引用,并且其他数据需要放在那里时,系统就会决定什么时候覆盖这些数据。下面,我们将详细介绍缓存如何做到这一点,但在整合一个总体原则,一个「最近最少使用」(Least Recently Used,LRU)替换:如果缓存已满,需要放入新数据,最近最少使用的数据从缓存中刷新,这意味着它是覆盖在新项目,因此不再访问。LRU是目前最常见的替换策略;其他的策略还有:「先进先出」(First In First Out,FIFO)或「随机替换」。
练习 1.6 LRU替换策略与直接映射缓存和关联缓存有什么关系?
练习 1.7 描绘一个简单的场景,并给出一些(伪)代码,以论证LRU比FIFO更适合作为替代策略。
缓存线
在内存和高速缓存之间或多个高速缓存之间的数据移动不是用单个字节,甚至字来完成的。相反,移动数据的最小单位称为「高速缓存线」(cache line),有时也称为「高速缓存块」(cache block)。一个典型的缓存行是64或128字节长,在科学计算中意味着8或16个双精度浮点数。移动到L2缓存的数据的缓存线大小可能比移动到L1缓存的数据大。
高速缓存线的第一个设计初衷是便于实际应用:它简化了所涉及的电路。由于许多代码显示出空间局部性,缓存线的存在有着非同寻常的意义。1.6.2章。
反之,我们现在需要利用数据的局部性编写高质量代码,因为任何内存访问都需要传输几个字符(参见1.7.4节中的一些例子)。在加载缓存线后,我们希望尽可能地使用一同加载进来的其他数据以实现高效利用资源,因为同一缓存线上的内容访实际上是自由且方便的。这种现象在通过「跨步访问」(stride access)数组的代码中是十分常见的:以规则的时间间隔读取或写入元素。
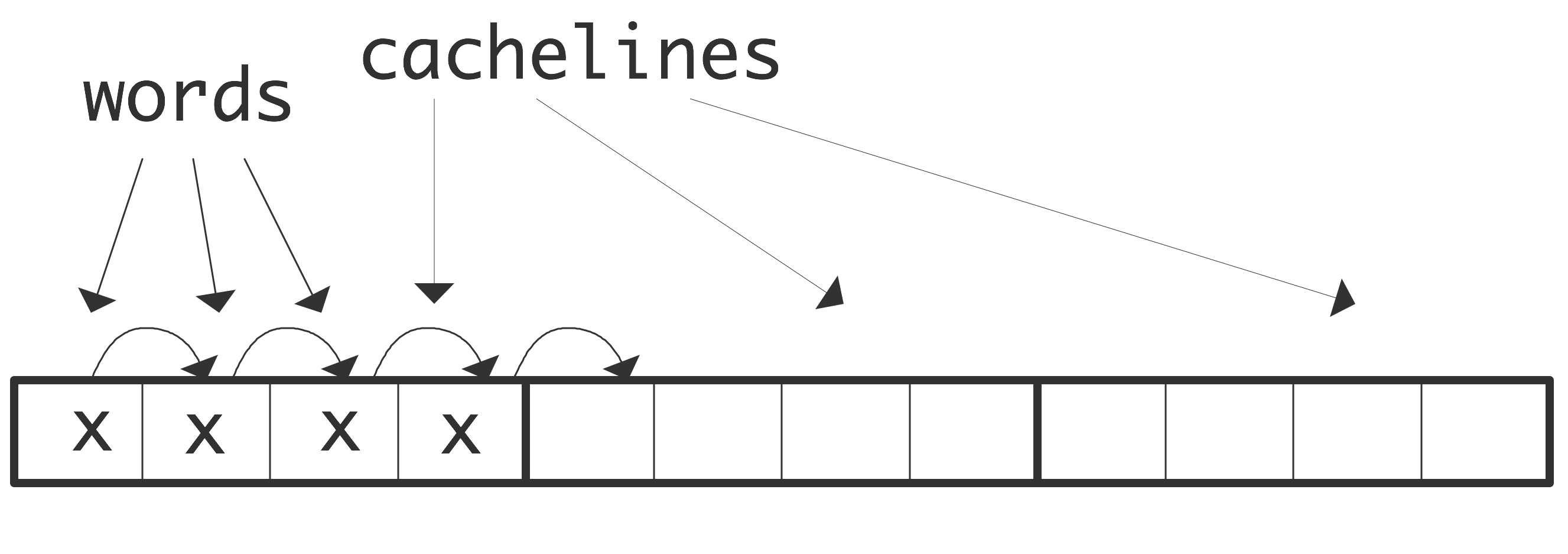
Stride 1 连续访问数组中的元素:
1 | for (i=0; i<N; i++) |
让我们用一个例子来说明:每个缓存线上有4个字。请求第一个元素将包含它的整个缓存线加载到缓存中。然后,对第2、3和4个元素的请求可以从缓存中得到满足,这意味着实现了高带宽和低延迟。
Stride 2 跨步访问数组中的元素:
1 | for (i=1; i<N; i+=stride) |
意味着在每个缓存线中只有某些元素被使用。我们用Stride = 3来说明这一点:第一个元素加载一个缓存线,该也包含第二个元素。然而,第三个元素在下一个缓存上,因此加载它会引起主内存的延迟和带宽。第四个元素也是如此。加载四个元素现在需要加载三条缓存线而不是一条,这意味着三分之二的可用带宽被浪费了。(如果没有注意到常规访问模式的硬件机制,并先发制人地加载进一步的缓存线,第二种情况也会导致三倍于第一种情况的延迟;见1.3.5)

有些应用程序自然会导致大于1的进步,例如,只访问一个复数数组的实数部分(关于复数实际实现的一些注释,请参阅3.7.6节)。另外,使用递归加倍的方法通常具有非单位步长的代码结构
1 | for (i=0; i<N/2; i++) |
在这个关于缓存线的讨论中,我们隐式地假设缓存线的开头也是一个单词的开头,不管是整数还是浮点数。实际情况中往往并非如此:一个8字节的浮点数可以放置在两个缓存线之间的边界上。可以想象,这将极大程度上影响程序性能。第37.1.3节讨论了实际中处理缓存线边界对齐的方法。
缓存映射
越接近FPU的缓存速度越快,其容量也更小。但即便最大的缓存也比内存容量小的多。在第1.3.4.6节中,我们已经讨论了如何做出保留哪些元素和替换哪些元素的决定。
现在我们将讨论缓存映射的问题,也就是“如果一个条目被放在缓存中,它会被放在哪里”的问题。这个问题通常是通过将项目的(主存)地址映射到缓存中的地址来解决的,这就导致了“如果两个项目映射到同一个地址会怎么样”的问题。
直接映射缓存
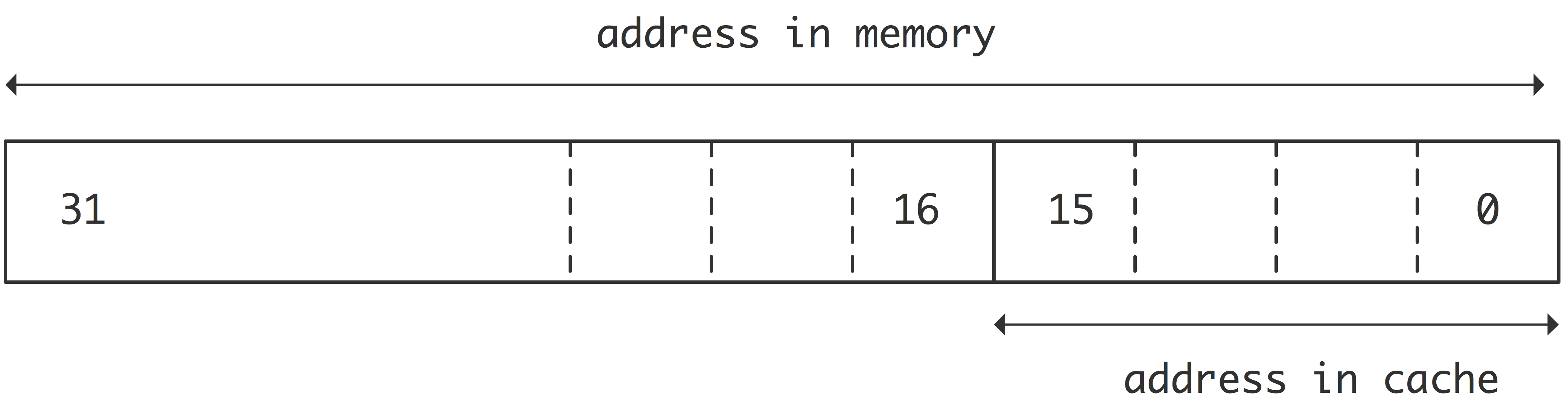
最简单的缓存映射策略是「直接映射」(direct mapping)。假设内存地址是32位长,因此它们可以寻址4G字节;进一步假设缓存有8K个字,也就是64K字节,需要16位来寻址。直接映射从每个内存地址取最后(“最低有效”)16位,并使用这些作为缓存中的数据项的地址;参见图1.8。
直接映射的效率非常高,因为它的地址计算速度非常快,导致了较低的延迟,但在实际应用中存在一个问题。如果两个被8K字分隔的条目被寻址,它们将被映射到相同的缓存位置,这将使某些计算效率低下。例子:
1 | double A[3][8192]; |
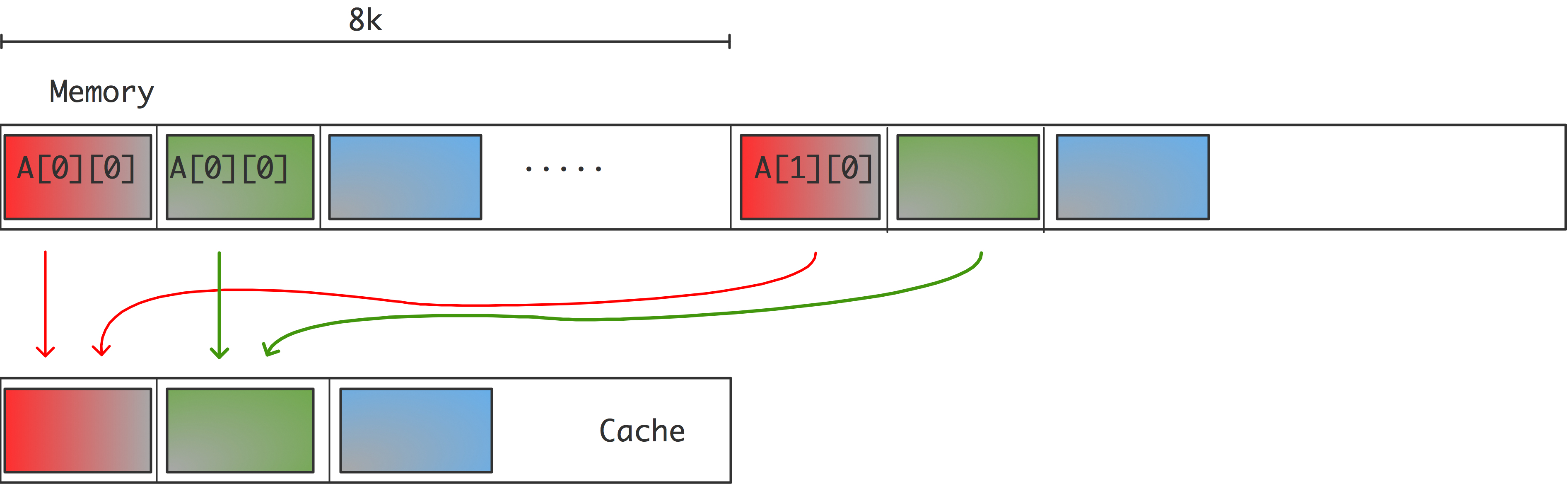
或在Fortran中:
1 | real*8 A(8192,3); |
此处,$[0] [i]$,$[1] [i]$和$[2] [i]$ (或者$a(i,1)$,$a(i,2)$,$a(i,3)$)的位置对于每个$i$来说是8K的,所以它们地址的最后16位是相同的,因此它们将被映射到缓存中的相同位置;参见图1.9。
现在,循环的执行情况将如下:
- $a [0] [0]$处的数据被带入高速缓存和寄存器中,这产生了一定的延时。和这个元素一起,整个高速缓存行被转移。
- 在$[1] [0]$处的数据被带入缓存(和寄存器中),连同其整个缓存行,以一些延迟为代价。由于这个缓存行和第一个缓存行被映射到相同的位置,所以第一个缓存行被覆盖。
- 为了写入输出,包含$a[2] [0]$的缓存行被带入内存。这又被映射到同一位置,导致刚刚加载的$a[1] [0]$的缓存行被刷新。
- 在下一次迭代中,需要$a[0] [1]$,它和$a[0] [0]$在同一个缓存行。然而,这个缓存行已经被刷新了,所以它需要从主内存或更深的缓存层中被重新带入。在这样做的时候,它覆盖了保存$a[2] [0]$的缓存行。
- $a[1] [1]$的情况类似:它在$a[1] [0]$的缓存行上,不幸的是,它已经被上一步覆盖了。
如果一个缓存行有四个字,我们可以看到,循环的每四次迭代都涉及到八个$a$元素的传输的元素,而如果不是因为缓存冲突,两个元素就足够了。
练习 1.8 在直接映射高速缓存的例子中,从内存到高速缓存的映射是通过使用32位内存地址的最后16位作为高速缓存地址完成的。如果使用前16位(”最有意义的”)作为缓冲区地址,那么这个例子中的问题就会消失。为什么在一般情况下这不是一个好的解决方案?
注释5:到目前为止,我们一直假装缓存是基于虚拟内存地址的。实际上,缓存是基于内存中数据的物理地址,这取决于将虚拟地址映射到内存页的算法。
关联式缓存
如果任何数据项目都可以进入任何缓存位置,那么上一节中概述的缓存冲突问题就会得到解决。在这种情况下,除了缓存被填满之外,不会有任何冲突,在这种情况下,缓存替换策略(第1.3.4.6节)会刷新数据,为新来的项目腾出空间。这样的缓存被称为「全关联映射」(fully associative mapping)的,虽然它看起来是最好的,但它的构建成本很高,而且在使用中比直接映射的缓存慢得多。
正因如此,最常见的解决方案是建立一个「k-路关联缓存」($𝑘$-way associative mapping),其中$𝑘$至少是两个。在这种情况下,一个数据项可以进入任何一个$𝑘$缓存位置。代码必须要有$𝑘+1$路冲突,才会像上面的例子那样过早地刷新数据。在这个例子中,$𝑘=2$的值就足够了,但在实践中经常会遇到更高的值。图1.10展示了一个直接映射的和一个三向关联的缓冲区的内存地址与缓冲区位置的映射情况。两个缓冲区都有12个元素,但是它们的使用方式不同。直接映射的高速缓存(左边)在内存地址0和12之间会有冲突,但是在三向关联高速缓存中,这两个地址可以被映射到三个元素中的任何一个。

作为一个实际的例子,英特尔Woodcrest处理器有一个32K字节的L1缓存,它是8路设置的关联性,缓存行大小为64字节,L2缓存为4M字节,是8路设置的关联性,缓存行大小为64字节。另一方面,AMD Barcelona芯片的L1缓存是2路关联,L2缓存是8路关联。更高路关联性显然是可取的,但是会使处理器变得更慢,因为确定一个地址是否已经在缓存中变得更加复杂。由于这个原因,在速度最重要的地方,L1高速缓存的关联性通常比L2低。
练习 1.9 用你喜欢的语言写一个小型的高速缓存模拟器。假设一个有32个条目的$k$方式的同构缓存和一个16位地址的架构。对$𝑘=1, 2, 4, …$进行以下实验。
让$k$模拟高速缓存的关联性。
写下从16位内存地址到32/𝑘缓存地址的转换。
生成32个随机机器地址,并模拟将其存储在缓存中。
由于高速缓存有32个条目,最佳情况下这32个地址都可以存储在高速缓存中。这种情况实际发生的几率很小,往往一个地址的数据会在另一个地址与之冲突时被驱逐出缓存(意味着它被覆盖)。记录在模拟结束时,32个地址中,有多少地址被实际存储在缓存中。将步骤3做100次,并绘制结果;给出中位数和平均值,以及标准偏差。观察一下,增加关联性可以提高存储地址的数量。其极限行为是什么?(为了获得奖励,请做一个正式的统计分析)
缓存内存与普通内存的对比
那么,缓冲存储器有什么特别之处;为什么我们不把它的技术用于所有的存储器?
缓存通常由静态随机存取存储器(SRAM)组成,它比用于主存储器的动态随机存取存储器(DRAM)更快,但也更昂贵,每一位需要5-6个晶体管,而不是一个,而且耗电量更大。
加载与存储
在上述描述中,在程序中访问的所有数据都需要在使用这些数据的指令执行之前被移入高速缓存。这对读取的数据和写入的数据都适用。然而,已经写入的数据,如果不再需要(在一定的合理时间内),就没有理由留在缓存中,可能会产生冲突或驱逐仍然可以重复使用的数据。出于这个原因,编译器通常支持流式存储:一个纯粹输出的连续数据流将被直接写入内存,而不被缓存。
预取流
在传统的冯·诺依曼模型中(第1.1节),每条指令都包含其操作数的位置,所以实现这种模型的CPU会对每个新的操作数进行单独请求。在实践中,往往后续的数据项在内存中是相邻的或有规律的间隔。内存系统可以通过查看高速缓存的数据模式来检测这种数据模式,并请求「预取数据流」(prefetch data stream);
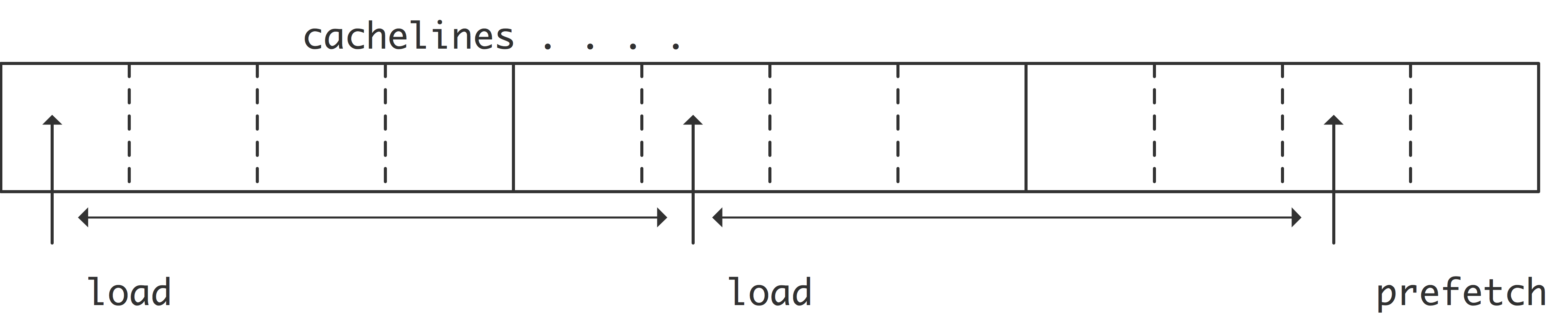
在最简单的形式下,CPU会检测到来自两个连续的高速缓存行的连续加载,并自动发出对接下来的高速缓存行的请求。如果代码对第三条高速缓存线发出实际请求,这个过程可以重复或扩展。由于这些高速缓存行现在是在需要提前从内存中取出,所以预取有可能消除除前几个数据项之外的所有延迟。
现在我们需要重新审视一下缓存失效的概念。从性能的角度来看,我们只对缓存失效的停顿感兴趣,也就是说,在这种情况下,计算必须等待数据被带入。不在缓存中的数据,但在其他指令还在处理的时候可以被带入,这不是一个问题。如果 “L1缺失 “被理解为只是 “缺失时的停顿”,那么术语 “L1缓存重新填充 “被用来描述所有的缓存线负载,无论处理器是否在它们上面停顿。
由于预取是由硬件控制的,所以它也被描述为「硬件预取」(hardware prefetch)。预取流有时可以从软件中控制,例如通过「源语」(intrinsic)。
由程序员引入预取是对一些因素的谨慎平衡[94]。其中最重要的是预取距离:从预取开始到需要数据时的周期数。在实践中,这通常是一个循环的迭代次数:预取指令请求未来迭代的数据。
并发和内存传输
在关于内存层次的讨论中,我们提出了一个观点:内存比处理器慢。如果这还不够糟糕的话,利用内存提供的所有带宽甚至不是小事。换句话说,如果你不仔细编程,你会得到比你根据可用带宽所期望的更少的性能。让我们来分析一下。
内存系统的带宽通常为每周期一个以上的浮点数,所以你需要每周期发出那么多请求来利用可用的带宽。即使在零延迟的情况下也是如此;由于存在延迟,数据从内存中出来并被处理需要一段时间。因此,任何基于第一个数据的计算而请求的数据都必须在延迟至少等于内存延迟的情况下请求。
为了充分利用带宽,在任何时候都必须有相当于带宽乘以延迟的数据量在运行。由于这些数据必须是独立的,我们得到了 「Little 定律」[147]。
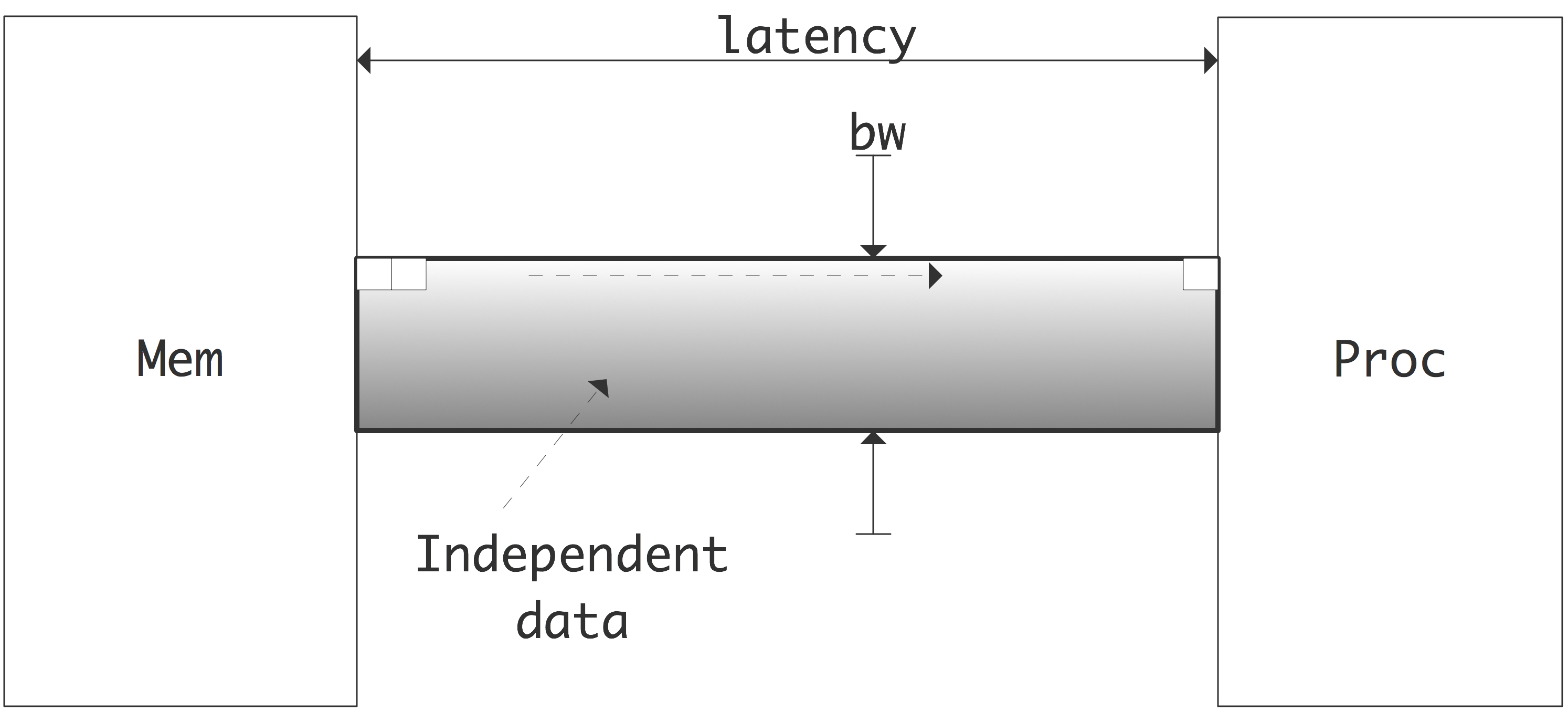
这在图1.12中得到了说明。维护这种并发性的问题并不是程序没有这种并发性,而是程序要让编译器和运行时系统识别它。例如,如果一个循环遍历了一个长的数组,编译器就不会发出大量的内存请求。预取机制(1.3.5节)会提前发出一些内存请求,但通常不够。因此,为了使用可用的带宽,多个数据流需要同时进行。因此,我们也可以将 「Little 定律」表述为
内存bank
上面,我们讨论了与带宽有关的问题。你看到内存,以及在较小程度上的缓存,其带宽低于处理器可以最大限度地吸收的带宽。这种情况实际上比上面的讨论看起来还要糟糕。由于这个原因,内存通常被分为交错的内存组:在四个内存组中,字0、4、8…在0组,字1、5、9…在1组,依此类推。
假设我们现在按顺序访问内存,那么这样的4路交错式内存可以维持4倍于单个内存组的带宽。不幸的是,按跨度2访问将使带宽减半,而更大的跨度则更糟糕。如果两个连续的操作访问同一个内存bank,我们就会说到内存bank冲突[7]。在实践中,内存库的数量会更多,因此,小跨度的内存访问仍然会有完整的广告带宽。例如,Cray-1有16个banks,而Cray-2有1024个。
练习 1.10 证明在有质数的bank时,任何达到该质数的跨步都是无冲突的。你认为为什么这个解决方案没有在实际的内存架构中被采用?
在现代处理器中,DRAM仍然有bank,但由于有缓存的存在,其影响较小。然而,GPU有内存组,没有缓存,所以它们遭受了与老式超级计算机相同的一些问题。
练习 1.11 对一个数组的元素进行求和的递归加倍算法是
1 | for (s=2; s<2*n; s*=2) |
分析该算法的bank冲突。假设$𝑛=2^p$,bank有$2^k$元素,其中$𝑘 < 𝑝$。同时考虑到这是一个并行算法,内循环的所有迭代都是独立的,因此可以同时进行。另外,我们可以使用递归减半法
1 | for (s=(n+1)/2; s>1; s/=2) |
再次分析,bank的混乱情况。这种算法更好吗?在并行情况下呢?
缓存存储器也可以使用bank。例如,AMD巴塞罗那芯片的L1缓存中的缓存线是16个字,分为两个8个字的交错库。这意味着对高速缓存线的元素进行顺序访问是有效的,但串联访问的性能就会下降。
TLB、页和虚拟内存
一个程序的所有数据可能不会同时出现在内存中。这种情况可能由于一些原因而发生:
- 计算机为多个用户服务,所以内存并不专门用于任何一个用户。
- 计算机正在运行多个程序,这些程序加起来需要的内存超过了物理上可用的内存。
- 一个单一的程序所使用的数据可能超过可用的内存。
基于这些原因,计算机使用虚拟内存:如果需要的内存比可用的多,某些内存块会被写入磁盘。实际上,磁盘充当了真实内存的延伸。这意味着一个数据块可以出现在内存的任何地方,事实上,如果它被换入和换出,它可以在不同时间出现在不同位置。交换不是作用于单个内存位置,而是作用于内存页:连续的内存块,大小从几千字节到几兆字节。(在早期的操作系统中,将内存移至磁盘是程序员的责任。互相替换的内存页被称为覆盖层)
由于这个原因,我们需要一个从程序使用的内存地址到内存中实际地址的翻译机制,而且这种翻译必须是动态的。一个程序有一个 “逻辑数据空间”(通常从地址0开始),是编译后的代码中使用的地址,在程序执行过程中需要将其翻译成实际的内存地址。出于这个原因,有一个页表,指定哪些内存页包含哪些逻辑页。
大页
在非常不规则的应用中,例如数据库,页表会变得非常大,因为更多或更少的随机数据被带入内存。然而,有时这些页面显示出某种程度的集群,这意味着如果页面大小更大,需要的页面数量将大大减少。由于这个原因,操作系统可以支持大的页面,通常大小为2Mb左右。(有时会使用’巨大的页面’;例如,英特尔Knights Landing有Gigabyte页面)
大页面的好处取决于应用:如果小页面没有足够的集群,使用大页面可能会使内存过早地被大页面的未使用部分填满。
TLB
然而,通过查找该表进行地址转换是很慢的,所以CPU有一个「转译后备缓冲器」(Translation Look-aside Buffer,TLB)。TLB是一个经常使用的页表项的缓存:它为一些页提供快速的地址转换。如果一个程序需要一个内存位置,就会查询TLB,看这个位置是否真的在TLB所记忆的页面上。如果是这样,逻辑地址就被翻译成物理地址;这是一个非常快速的过程。在TLB中没有记住该页的情况被称为TLB缺失,然后查询页面查找表,如果有必要,将需要的页面带入内存。TLB是(有时是完全)关联的(1.3.4.10节),使用LRU策略(1.3.4.6节)。
一个典型的TLB有64到512个条目。如果一个程序按顺序访问数据,它通常只在几个页面之间交替进行,而且不会出现TLB缺失。另一方面,一个访问许多随机内存位置的程序可能会因为这种错过而出现速度下降。目前正在使用的页面集被称为 “工作集”。
第1.7.5节和附录37.5讨论了一些简单的代码来说明TLB的行为。
[这个故事有一些复杂的情况。例如,通常有一个以上的TLB。第一个与L2缓存相关,第二个与L1相关。在AMD Opteron中,L1 TLB有48个条目,并且是完全(48路)关联的,而L2 TLB有512个条目,但只是4路关联的。这意味着实际上可能存在TLB冲突。在上面的讨论中,我们只谈到了L2 TLB。之所以能与L2缓存而不是主内存相关联,是因为从内存到L2缓存的转换是确定性的]。
使用大页也可以减少潜在的TLB缺失次数,因为可以减少工作页的集合。
单处理器计算(二)
多核架构
近年来,传统的处理器芯片设计已经达到了性能的极限。主要由于
- 主频已经不能再增加,因为这会增大功耗,使芯片发热过大;见1.8.1节。
- 从代码中提取更多的指令级并行(ILP)变得困难,要么是由于编译器的限制,要么是由于内在可用的并行量有限,要么是由于分支预测使之无法实现(见1.2.5节)。
从单个处理器芯片中获得更高的利用率的方法之一是,从进一步完善单个处理器的策略,转向将芯片划分为多个处理 “核心”。这些独立的内核可以在不相关的任务上工作,或者通过引入数据的并行性(第2.3.1节),以更高的整体效率协作完成一个共同的任务[163]。
注释6 另一个解决方案是英特尔的超线程,它可以让一个处理器混合几个指令流的指令。这方面的好处在很大程度上取决于具体情况。然而,这种机制在GPU中也得到了很好的利用,见2.9.3节。讨论见2.6.1.9节。
这就解决了上述两个问题:
- 两个主频较低的内核可以拥有与主频较高的单个处理器相同的吞吐量;因此,多个内核的能效更高。
- 指令级并行现在被明确的任务并行化所取代,由程序员管理。
虽然第一代多核CPU只是在同一个芯片上的两个处理器,但后来的几代CPU都加入了L3或L2缓存,在两个处理器核心之间共享;见图1.13。
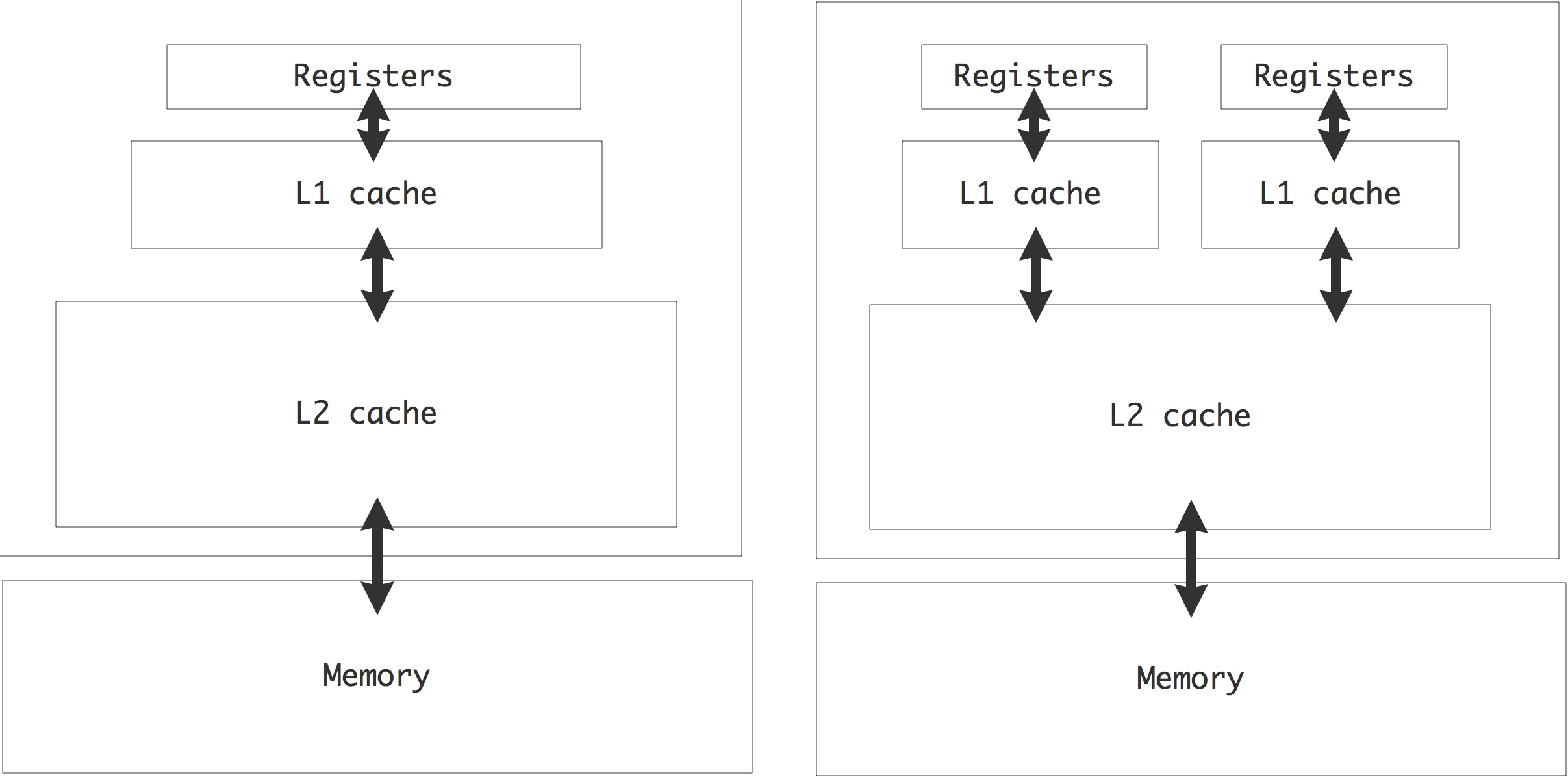
L3或L2缓存,在两个处理器内核之间共享;见图1.13,这种设计使内核能够有效地联合处理同一问题。内核仍然会有自己的L1高速缓存。
而这些独立的高速缓存造成了高速缓存的一致性问题;见下面1.4.1节。
我们注意到,”处理器 “这个词现在是模糊的:它可以指芯片,也可以指芯片上的处理器核心。由于这个原因,我们大多谈论的是整个芯片的「插槽」(socket)和包含一个算术和逻辑单元并有自己的寄存器的部分的核心(core)。目前,具有4或6个内核的CPU很常见,甚至在笔记本电脑中也是如此,英特尔和AMD正在销售12个内核的芯片。核心数量在未来可能会上升。英特尔已经展示了一个80核的原型,它被开发成48核的 “单芯片云计算机”,如图1.14所示。这个芯片的结构有24个双核 “瓦片”,通过一个二维网状网络连接。只有某些瓦片与内存控制器相连,其他的瓦片除了通过片上网络外,无法到达内存。
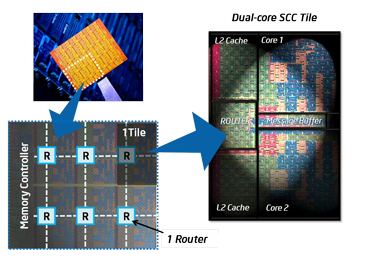
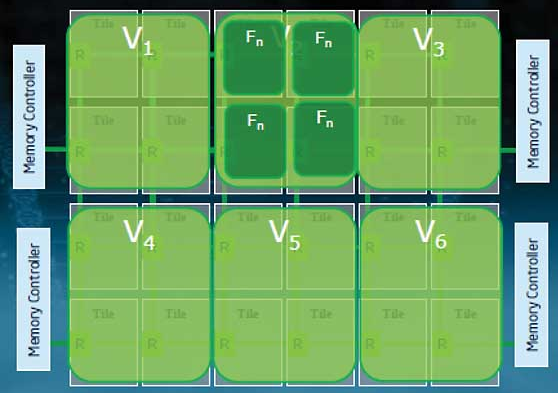
通过这种共享和私有缓存的混合,多核处理器的编程模型正在成为共享和分布式内存的混合体。
核心(Core):各个内核都有自己的私有L1缓存,这是一种分布式内存。上面提到的英特尔80核原型,其核心以分布式内存的方式进行通信。
插槽(Socket):在一个插座上,通常有一个共享的二级缓存,这是内核的共享内存。
节点(Node):在一个 “节点 “或主板上可以有多个插座,访问同一个共享内存。
网络(Network):需要分布式内存编程(见下一章)来让节点进行通信。
从历史上看,多核结构在多处理器共享内存设计中已有先例(第2.4.1节),如Sequent Symmetry和Alliant FX/8。从概念上讲,程序模型是相同的,但现在的技术允许将多处理器板缩小到多核芯片上。
缓存一致性
在并行处理中,如果一个以上的处理器拥有同一个数据项的副本,就有可能发生冲突失效。确保所有的缓存数据都是主内存的准确副本,这个问题被称为「缓存一致性」(cache coherence):如果一个处理器改变了它的副本,则另一个副本也需要更新。
在分布式内存架构中,数据集通常在处理器上被不连续地分割,所以只有在用户知道的情况下才会出现数据的冲突副本,而处理这个问题则是由用户决定的。共享内存的情况更微妙:由于进程访问相同的主内存,似乎冲突实际上是不可能的。然而,处理器通常有一些私有缓存,包含来自内存的数据副本,所以冲突失效的副本可能发生。这种情况特别出现在多核设计中。
假设两个核在它们的(私有)L1高速缓存中有一个相同数据的副本,其中一个修改了它的副本。现在另一个核心的缓存数据不再是其对应的准确副本:处理器将使该项目副本失效,事实上也是其整个缓存线失效。当该进程需要再次访问该项目时,它需要重新加载该缓存线。另一种方法是,任何改变数据的内核都要将该缓存线发送给其他内核。这个策略的开销可能更大,因为其他内核不可能有一个缓存线的副本。
这个更新或废止缓存线的过程被称为「维护缓存一致性」(maintaining cache coherence),它是在处理器的一个非常低的层次上完成的,不需要程序员参与。(这使得更新内存位置成为一个原子操作;关于这一点,请看2.6.1.5节)。然而,这将减慢计算速度,并且浪费了核心的带宽,而这些带宽本来是可以用来加载或存储操作数的。
缓存行相对于主存中的数据项的状态通常被描述为以下几种情况之一。
Scratch:缓存行不包含该项目副本。
Valid:缓存行是主内存中数据的正确拷贝。
Reserved:缓存行是该数据的唯一副本。
- Dirty:缓存行已被修改,但尚未写回主内存。
- Invalid:缓存线上的数据在其他处理器上也存在(它没有被保留),并且另一个进程修改了它的数据副本。
一个更简单的变体是修改后的共享无效(MSI)一致性协议,在一个给定的核心上,一个缓存线可以处于以下状态。
- Modified:缓存线已经被修改,需要写到备份仓库。这个写法可以在行被驱逐时进行,也可以立即进行,取决于回写策略。
- Shared:该行至少存在于一个缓存中且未被修改。
- Invalid:该行在当前缓存中不存在,或者它存在但在另一个缓存中的副本已被修改。
这些状态控制着高速缓存线在内存和高速缓存之间的移动。例如,假设一个核对一个缓存线进行读取,而这个缓存线在该核上是无效的。然后,它可以从内存中加载它,或者从另一个高速缓存中获取它,这可能更快。(找出一个行是否存在于另一个缓冲区(状态为M或S)被称为「监听」(snooping);另一种方法是维护「标签目录」(tag directory;见下文)。如果该行是共享的,现在可以简单地复制;如果它在另一个高速缓存中处于M状态,该核心首先需要把它写回内存。
练习 1.12 考虑两个处理器,内存中的一个数据项 $x$,以及这两个处理器的私有缓存中的缓存线$x_1,x_2$,这两个缓存线被映射到这两个处理器。描述在两个处理器上读写 $x_1$ 和 $x_2$ 的状态之间的转换。同时指出哪些行为会导致内存带宽被使用。(这个过渡列表是一个有限状态自动机(FSA),见第19节)。
MSI协议的变种增加了一个 “独占 “或 “拥有 “状态,以提高工作效率。
缓存一致性的解决方案
有两种实现缓存一致性的基本机制:「监听」(snooping)和基于「标签目录」(tag directory)的方案。
在监听机制中,任何对数据的请求都会被发送到所有的缓冲区,如果数据存在于任何地方,就会被返回;否则就会从内存中检索。这个方案的一个变形为,一个核心 “监听 “所有的总线流量,这样当另一个核心修改它的拷贝时,它就可以使自己的缓存线拷贝失效或更新。缓存失效比更新的代价要小,因为它是一个位操作,而更新涉及到复制整个高速缓存线。
练习 1.13 什么条件下更新才是更优方案?写一个简单的缓存模拟器来评估这个问题。
由于监听通常涉及到向所有核心广播信息,所以它的规模不能超过最少的核心数量。一个可以更好地扩展的解决方案是使用一个标签目录:一个中央目录,它包含了一些缓存中存在的数据的信息,以及具体在哪个缓存中。对于拥有大量内核的处理器(如英特尔Xeon Phi),该目录可以分布在各个内核上。
伪共享
如果内核访问不同的项目,就可能会出现缓存一致性问题。例如,
1 | double x,y; |
可能会在内存中紧挨着分配 $x$ 和 $y$,所以它们很有可能落在同一个缓存线上。现在,如果一个核心更新 $x$,另一个更新 $y$,这个缓存线就会在核心之间不断移动。这就是所谓的「伪共享」(false sharing)。
最常见的错误共享情况发生在线程更新一个数组的连续位置时。例如,在下面的OpenMP片段中,所有线程都在更新自己在部分结果数组中的位置。
1 | local_results = new double[num_threads]; |
虽然没有实际的竞争条件(如果线程都更新global_result变量就会有),但这段代码的性能会很低,因为带有local_result数组的缓存线会不断被废止。
标签目录
在具有分布式但连贯的缓存的多核处理器中(如英特尔Xeon Phi),标签目录本身也可以是分布式的。这增加了缓存查找的延迟。
在多核芯片上进行计算
多核处理器可以通过各种方式提高性能。首先,在桌面情况下,多个内核实际上可以运行多个程序。更重要的是,我们可以利用并行性来加快单个代码的执行速度。这可以通过两种不同的方式实现。
MPI库(2.6.3.3节)通常用于通过网络连接的处理器之间的通信。然而,它也可以在单个多核处理器中使用:然后通过共享内存拷贝实现MPI调用。
另外,我们可以使用共享内存和共享缓存,并使用线程系统,如OpenMP(第2.6.2节)进行编程。这种模式的优点是并行性可以更加动态,因为运行时系统可以在程序运行过程中设置和改变线程和内核之间的对应关系。
我们将比较详细地讨论多核芯片上线性代数操作的调度;第6.12节。
TLB shootdown
第1.3.8.2节解释了TLB是如何用于缓存从逻辑地址,也就是逻辑页到物理页的转换。TLB是插槽内存单元的一部分,所以在多插槽设计中,一个插槽上的进程有可能改变页面映射,这使得其他插槽的映射不正确。
解决这个问题的一个办法叫做TLB shootdown:改变映射的进程会产生一个处理器间中断,从而导致其他处理器重建他们的TLB。
节点架构和插槽
在前面的章节中,我们已经通过内存层次结构,访问了寄存器和各种缓存级别,以及它们可以被私有或共享的程度。在内存层次结构的最底层是所有内核共享的内存。它的范围从低级别的笔记本电脑的几千兆字节到一些超级计算机中心的几兆字节。


虽然这个内存是在所有核心之间共享的,但它有一些结构。这源于一个事实,即集群节点可以有一个以上的插槽,即处理器芯片。节点上的共享内存通常分布在直接连接到一个特定插槽的库中。例如,图1.15显示了TACC Ranger集群超级计算机(已停产)的四插槽节点和TACC Stampede集群超级计算机的两插槽节点,后者包含一个英特尔至强Phi协处理器。在这两个设计中,你可以清楚地看到直接连接到插槽上的内存芯片。
这是一个「非一致内存访问」(Non-Uniform Memory Access,NUMA)架构的例子:对于在某个核心上运行的进程,连接到其插槽上的内存比连接到另一个插座上的内存访问速度略快。
这方面的一个结果就是First-touch现象。动态分配的内存在第一次被写入之前实际上并没有被分配。现在考虑下面的OpenMP(2.6.2节)代码。
1 | double *array = (double*)malloc(N*sizeof(double)); |
由于First-touch,数组被完全分配到插槽的主线程内存上。在随后的并行循环中,其他插槽的核心将对它们操作的内存有较慢的访问。
这里的解决方案是将初始化循环也做成并行的,即使其中的工作量几乎可以忽略不计。
局部性和数据复用
算法的执行不仅包含计算操作,也包含数据传输部分,事实上,数据传输可能是影响算法效率的主要因素。由于缓存和寄存器的存在,数据传输量可以通过编程的方式最小化,使数据尽可能地留在处理器附近。这部分是一个巧妙编程的问题,但我们也可以看看理论上的问题:算法是否一开始就允许这样做。
事实证明,在科学计算中,数据往往主要与在某种意义上靠近的数据互动,这将导致数据的局部性;1.6.2节。通常这种局部性来自于应用的性质,就像第四章看到的PDEs的情况。在其他情况下,如分子动力学(第7章),没有这种内在的局部性,因为所有的粒子都与其他粒子相互作用,为了获得高性能,需要相当的编程技巧。
数据复用和计算密度
在前面的章节中,我们了解到处理器的设计有些不平衡:加载数据比执行实际操作要慢。这种不平衡对于主存储器来说是很大的,而对于各种高速缓存级别来说则较小。因此,我们有动力将数据保存在高速缓存中,并尽可能地保持数据的复用量。
当然,我们首先需要确定计算是否允许数据被重复使用。为此,我们定义了一个算法的计算密度如下。
- 如果$n$是一个算法所操作的数据项的数量,而$f(n)$是它所需要的操作的数量,那么算术强度就是$f(n)/n$。
(我们可以用浮点数或字节来衡量数据项。后者使我们更容易强度与处理器的硬件规格相关联)
计算密度也与延迟隐藏有关:即你可以减轻计算活动背后的数据加载对性能的负面影响的概念。要做到这一点,你需要比数据加载更多的计算来使这种隐藏有效。而这正是计算强度的定义:每一个字节/字/数字加载的高比率操作。
示例:向量操作
考虑到向量加法
这涉及到三次内存访问(两次加载和一次存储)和每次迭代的一次操作,给出的算术强度为1/3。axpy(表示 “$a$乘以 $x$ 加 $y$ “)操作
有两个操作,但内存访问的数量相同,因为 $a$ 的一次性负载被摊销了。因此,它比简单的加法更有效率,重用率为2/3。因此,它比简单的加法更有效,重用率为2/3。
内积计算
在结构上类似于axpy操作,每次迭代涉及一个乘法和加法,涉及两个向量和一个标量。然而,现在只有两个加载操作,因为 $s$ 可以保存在寄存器中,只在循环结束时写回内存。这里的重用是1。
示例:矩阵操作
考虑矩阵乘法
这涉及 $3𝑛^2$ 个数据项和 $2𝑛^3$ 个运算,属于高阶运算。算术强度为 $O(n)$,每个数据项将被使用𝑂(𝑛)次。这意味着,通过适当的编程,这种操作有可能通过将数据保存在快速缓存中来克服带宽/时钟速度的差距。
练习 1.14 根据上述定义,矩阵-矩阵乘积作为一种操作,显然具有数据重用性。矩阵-矩阵乘积显然具有数据复用。请你论证一下,这种复用并不是自然形成的,是什么决定了初始算法中国呢缓存是否对数据进行复用?
[在这次讨论中,我们只关心某个特定实现的操作数,而不是数学操作。例如,有一些方法可以在少于$O(n^3)$的操作中执行矩阵-矩阵乘法和高斯消除算法[189, 167]。然而,这需要不同的实现方式,在内存访问和重用方面有自己的分析]。
矩阵与矩阵乘积是LINPACK基准[51]的核心;见2.11.4节。如果将其作为评价计算机从能的标准则结果可能较为乐观:矩阵与矩阵的乘积是一个具有大量数据复用的操作,因此这对内存带宽并不敏感,对于并行计算及而言,这对网络通信也并不敏感。通常情况下,计算机在Linpack基准测试中会达到其峰值性能的60-90%,而其他测试标准得到的数值则可能较低。
Roofline模型
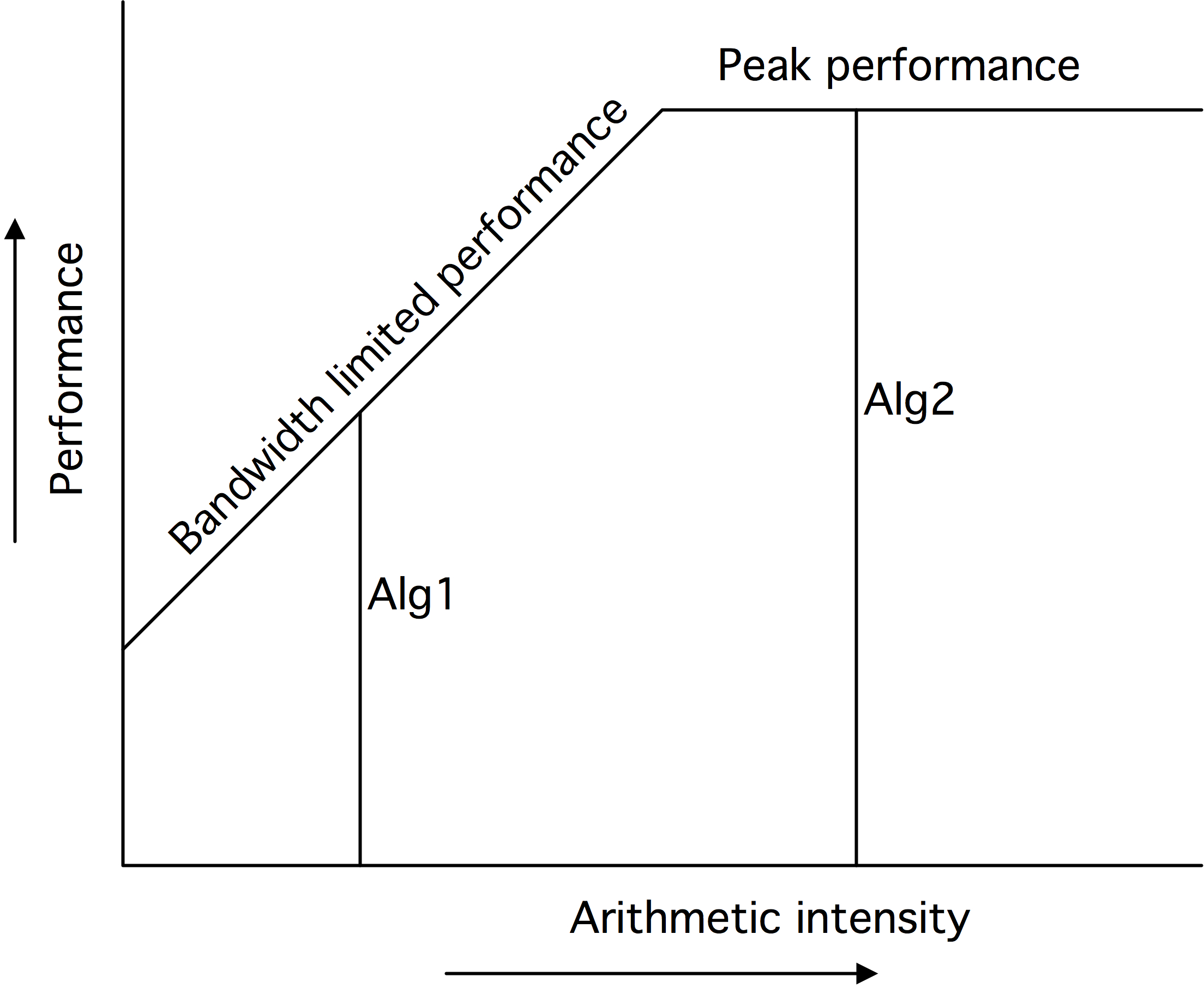
有一种平价计算及性能的理想模型,就是所谓的「屋脊线」(roofline model)模型[202],该模型指出:性能受两个因素的制约,如图1.16的第一个图所示。
图中顶部的横线所表示的峰值性能是对性能的绝对约束3,只有在CPU的各个方面(流水线、多个浮点单元)都完美使用的情况下才能达到。这个数字的计算纯粹是基于CPU的特性和时钟周期;假定内存带宽不是一个限制因素。
每秒的操作数受限于带宽、绝对数和计算密度的乘积。
这是由图中的线性增长线所描述的。
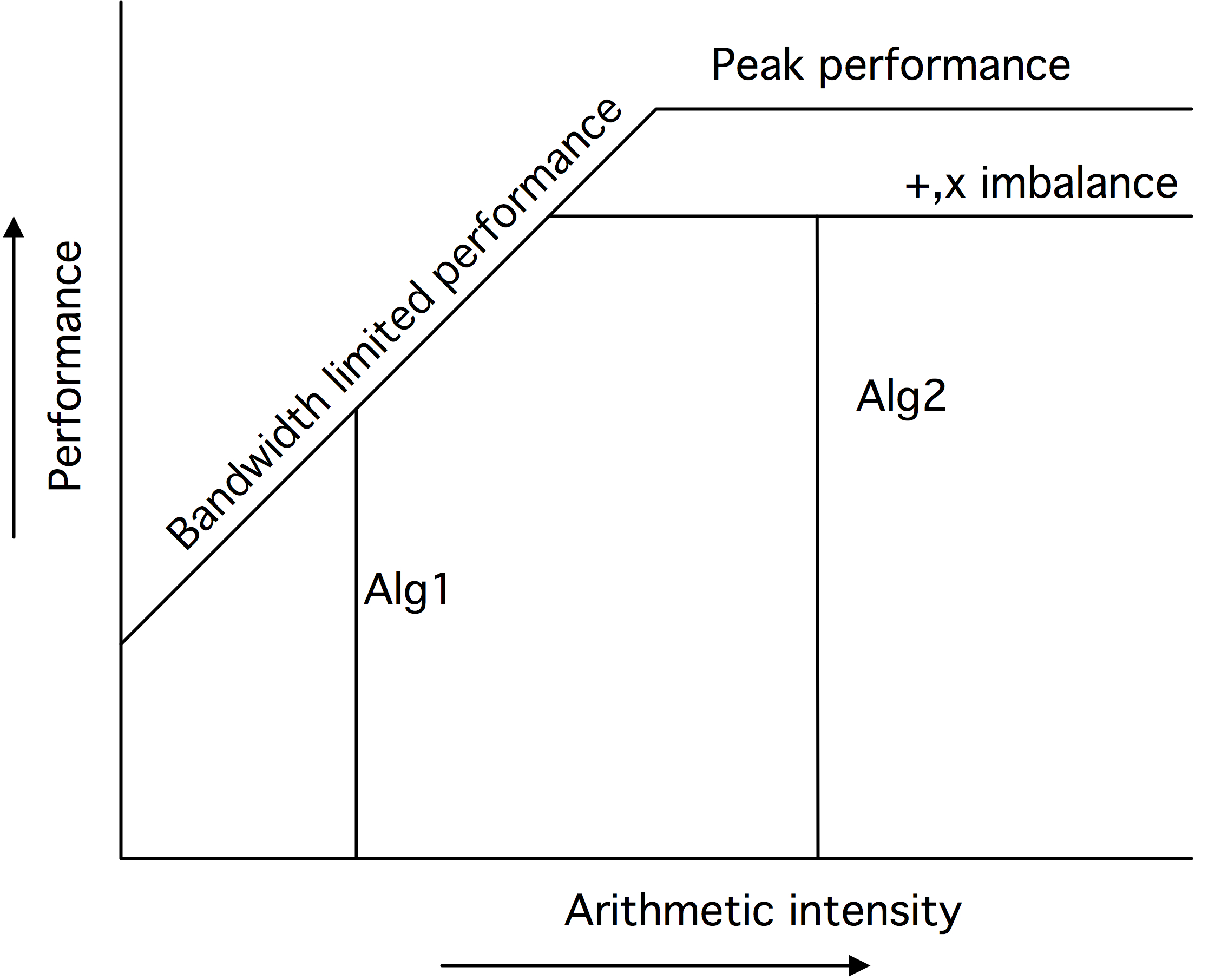
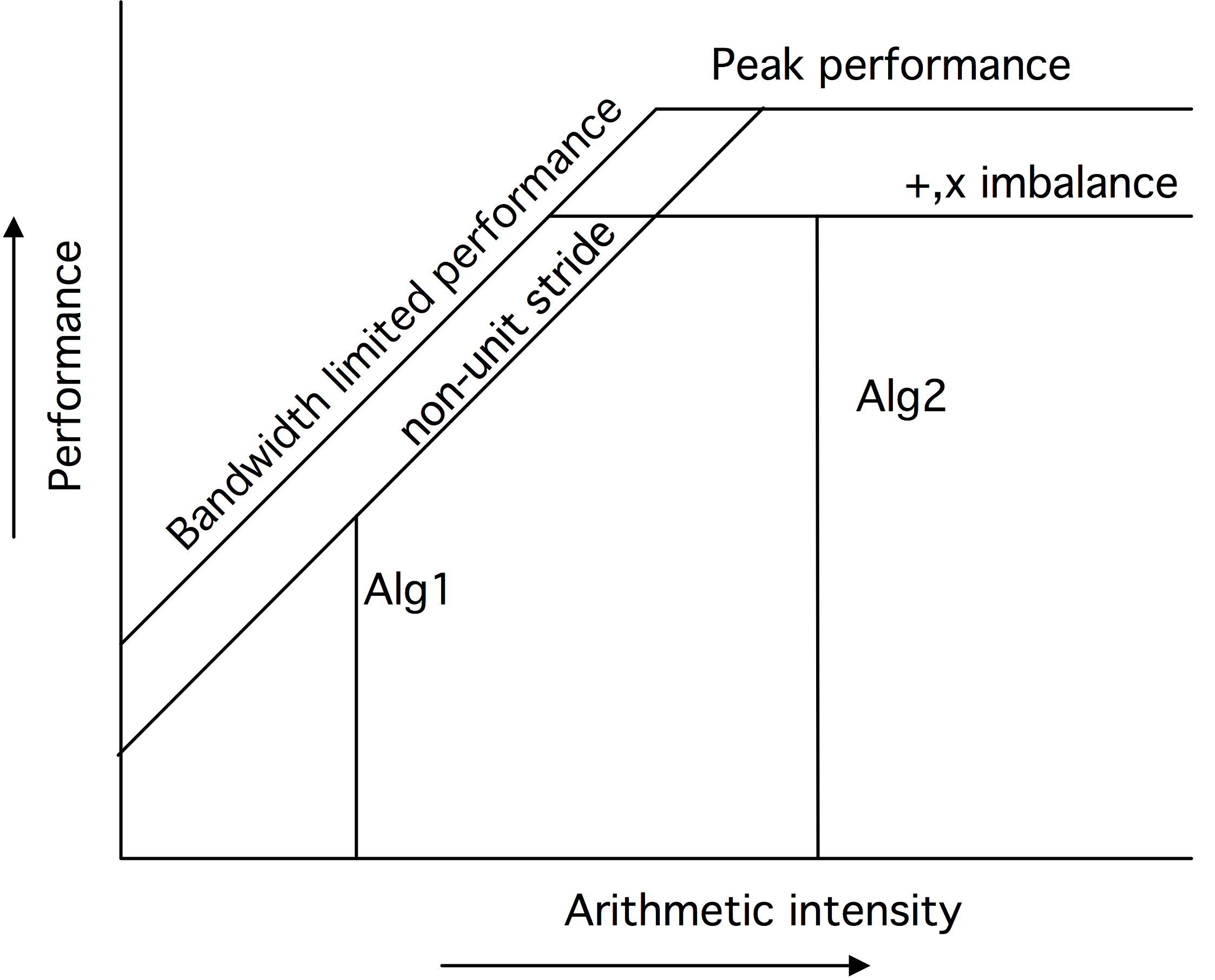
Roofline模型优雅地指出了影响性能的因素。例如,如果一个算法没有使用全部的SIMD宽度,这种不平衡会降低可达到的峰值。图1.16中的第二张图显示了降低上限的各种因素。还有各种降低可用带宽的因素,比如不完善的数据隐藏。这在第三张图中由倾斜的屋顶线的降低表示。
对于一个给定的计算密度,其性能是由其垂直线与Roofline相交的位置决定的。如果这是在水平部分,那么该计算被称为受「计算约束」(compute-bound):性能由处理器的特性决定,而带宽不是问题。另一方面,如果这条垂直线与屋顶的倾斜部分相交,那么计算被称为受「带宽约束」(bandwidth-bound):性能由内存子系统决定,处理器的全部能力没有被使用。
练习 1.15 如何确定一个给定的程序内核是受到带宽约束还是计算约束的?
局部性
由于从缓存中读取数据的时间开销要小于从内存中读取,我们当然希望以这种方式进行编码,进而使缓存中的数据最大程度上得到复用。虽然缓存中的数据不受程序员的控制,甚至编写汇编语言也无法控制(在Cell处理器和一些GPU中,低级别的内存访问可以由程序员控制),但在大多数CPU中,知道缓存的行为,明确什么数据在缓存中,并在一定程度上控制它,还是有可能的。
这里的两个关键概念是「时间局部性」(temporal locality)和「空间局部性」(spatial locality)。时间局部性是最容易解释的:即数据使用一次后短时间内再次被使用。由于大多数缓存使用LRU替换策略,如果在两次引用之间被引用的数据少于缓存的大小,那么该元素仍然会存在缓存之中,进而实现快速访问。而对于其他的替换策略,例如随机替换,则不能保证同样结果。
时间局部性
下面为时间局部性的例子,考虑重复使用一个长向量:
1 | for (loop=0; loop<10; loop++) { |
$x$ 的每个元素将被使用10次,但是如果向量(加上其他被访问的数据)超过了缓存的大小,每个元素将在下一次使用前被刷新。因此,$x[i]$ 的使用并没有表现出时间局部性:再次使用时的时间间隔太远,使得数据无法停留在缓存中。
如果计算的结构允许我们交换循环。
1 | for (i=0; i<N; i++) { |
$x$ 的元素现在被反复使用,因此更有可能留在缓存中。这个重新排列的代码在使用 $x[i]$ 时显示了更好的时间局部性。
空间局部性
空间局部性的概念要稍微复杂一些。如果一个程序引用的内存与它已经引用过的内存 “接近”,那么这个程序就被认为具有空间局部性。经典的冯·诺依曼架构中只有一个处理器和内存,此时空间局部性并不突出,因为内存中的一个地址可以像其他地址一样被快速检索。然而,在一个有缓存的现代CPU中,情况就不同了。上面我们已经看到了两个空间局部性的例子。
由于数据是以缓存线而不是单独的字或字节为单位移动的,因此以这样的方式进行编码,因此使缓存线所有的元素都得到应用是有所裨益的,在下列循环中
1
2
3for (i=0; i<N*s; i+=s){
... x[i] ...
}空间局部性体现为函数所进行的跨步递减$s$。
设 $S$ 为缓存线的大小,那么当 $s$ 的范围从$1 …. S$,每个缓存线使用的元素数就会从S下降到1。相对来说,这增加了循环中的内存流量花销:如果$s=1$,我们为每个元素加载$1/S$的缓存线;如果$s=S$,我们为每个元素加载一个缓存线。这个效果在1.7.4节中得到了证明。
第二个值得注意的空间局部性的例子是TLB(1.3.8.2节)。如果一个程序引用的元素距离很近,它们很可能在同一个内存页上,通过TLB的地址转换会很迅速。另一方面,如果一个程序引用了许多不同的元素,它也将引用许多不同的页。由此产生的TLB缺失是时间花销十分庞大;另见1.7.5节。
练习 1.16 请考虑以下对 $n$ 数字 $x[i]$ 进行求和的算法的伪码,其中 $n$ 是2的倍数。
1 | for s=2,4,8,...,n/2,n: |
分析该算法的空间和时间局部性,并将其与标准算法进行对比
1 | sum = 0 |
练习 1.17 考虑以下代码,并假设nvectors相比于缓存很小,而长度很大。
1 | for (k=0; k<nvectors; k++) |
以下概念与该代码的性能有什么关系。
- 复用(Reuse)
- 缓存尺寸(Cache size)
- 关联性(Associativity)
下面这段交换了循环的代码的性能是更好还是更差,为什么?
1 | for (i=0; i<length; i++) |
局部性示例
让我们看一个实际的例子。矩阵与矩阵的乘法 $C \leftarrow A ·B $可以用几种方法计算。我们比较两种实现方式,假设所有的矩阵都是按行存储的,且缓存大小不足以存储整个行或列。
1 | for i=1..n |
1 | for i=1..n |
这些实现如图1所示。 第一个实现构建了 $(i, j)$ 元素
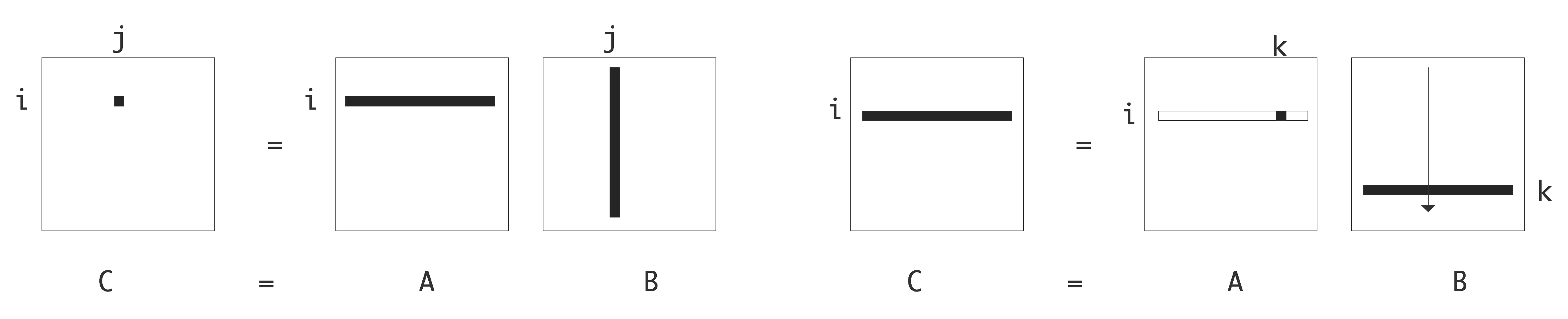
$A$ 的一行与 $B$ 的一列的内积来更新 $C$,在第二行中,$B$ 的一行是通过对 $A$ 的元素进行缩放来更新。$A$ 的元素来更新 $B$ 的行数。
我们的第一个观察结果是,这两种实现都确实计算了 $C \leftarrow C + A ·B$,并且它们都花费了大约 $2n^3$ 的操作。然而,它们的内存行为,包括空间和时间的局部性是非常不同的。
$c[i,j]$ :在第一个实现中,$c[i,j]$在内部迭代中是不变的,这构成了时间局部性,所以它可以被保存在寄存器中。因此,$C$ 的每个元素将只被加载和存储一次。
在第二个实现中,$c[i,j]$ 将在每个内部迭代中被加载和存储。特别是,这意味着现在有 $𝑛^3$ 次存储操作,比第一次实现多了$n$。
$a[i,k]$:在这两种实现中,$a[i,k]$元素都是按行访问的,所以有很好的空间局部性,因为每个加载的缓存线都会被完全使用。在第二个实现中,$a[i,k]$在内循环中是不变的,这构成了时间局部性;它可以被保存在寄存器中。因此,在第二种情况下,$A$只被加载一次,而在第一种情况下则是$n$次。
$b[k,j]$:这两种实现方式在访问矩阵 $B$ 的方式上有很大不同。首先,$b[k,j]$ 从来都是不变的,所以它不会被保存在寄存器中,而且 $B$ 在两种情况下都会产生 $𝑛^3$ 的内存负载。但是,访问模式不同。
在第二种情况下,$b[k,j]$ 是按行访问的,所以有很好的空间局部性性:缓存线在被加载后将被完全利用。
在第一种实现中,$b[k,j]$ 是通过列访问的。由于矩阵的行存储,一个缓存线包含了一个行的一部分,所以每加载一个缓存线,只有一个元素被用于列的遍历。这意味着第一个实现对 $B$ 的加载量要比缓存线长度的系数大。也有可能是TLB的影响。
请注意,我们并没有对这些实现的代码性能做任何绝对的预测,甚至也没有对它们的运行时间做相对比较。这种预测是很难做到的。然而,上面的讨论指出了与广泛的经典CPU相关的问题。
练习 1.18 乘积 $C \leftarrow A ⋅B$ 的实现算法较多。请考虑以下情况。
1 | for k=1..n: |
分析矩阵 $C$ 的内存流量,并表明它比上面给出的两种算法更糟糕。
核心局部性
上述空间和时间局部性的概念主要是程序的属性,尽管诸如高速缓存线长度和高速缓存大小这样的硬件属性在分析局部性的数量方面发挥了作用。还有第三种类型的局部性与硬件有更密切的联系:「核心局部性」(core locality)。
如果空间上或时间上接近的写访问是在同一个核心或处理单元上进行的,那么代码的执行就会表现出核心局部性。这里的问题是缓存一致性的问题,两个核心在他们的本地存储中都有某个缓存线的副本。如果它们都从该缓存中读取,那就没有问题了。但是,如果他们中的一个对它进行了写操作,一致性协议就会把这个缓存线复制到另一个核心的本地存储中。这需要占用宝贵的内存带宽,所以要避免这种情况。
核心局部性不仅仅是一个程序的属性,而且在很大程度上也是程序的并行执行方式。
单处理器计算(三)
高性能编程策略
在本节中,我们将简要介绍不同的编程方式如何影响代码的性能。想要了解更多,见Goedeker和Hoisie的书[78]。
本章中所有的性能结果都是在TACC Ranger集群的AMD Opteron处理器上获得的[173]。
峰值性能
厂家出于营销的目的,定义了CPU的“峰值速度”。由于一个流水线上的浮点单元可以渐进地在每个周期产生一个结果,我们可以把理论上的「峰值性能」(peak performance)定义为时钟速度(以每秒ticks为单位)、浮点单元数量和核心数量的乘积。该峰值速度在实际中是无法实现的,很少有代码能接近它。Linpack基准是衡量接近峰值的评判标准之一;该基准的并行版本作为”top 500”的评分标准。
流水线
在前文中,我们了解到现代CPU中的浮点运算单元是以流水线形式进行的,流水线需要一些独立的操作才能有效地运行。典型的可流水线操作是向量加法;不能流水线操作的一个例子是计算内积和:
1 | for (i=0; i<N; i++) |
$s$ 既被读又被写,使得加法流水线中止。启用流水线的一个方法是循环展开
1 | for (i = 0; i < N/2-1; i ++) { |
现在,在累积之间有两个独立的乘法。通过一点索引优化,这就变成了
1 | for (i = 0; i < N/2-1; i ++) { |
关于这段代码的第一个观察点是,我们隐式地使用了加法的结合律和交换律:虽然同样的量被加起来,但它们现在实际上是以不同的顺序加起来的。正如你将在后面的内容看到的,在计算机运算中,这并不能保证得到完全相同的结果。
在进一步的优化中,我们将每条指令的加法和乘法部分分离开来。希望在积累等待乘法结果的时候,中间的指令能让处理器忙起来,实际上是增加了每秒的操作数。
1 | for (i = 0; i < N/2-1; i ++) { |
最后,我们意识到,我们可以将加法从乘法中移开的最远距离是将它放在下一次迭代的乘法前面
1 | for (i = 0; i < N/2-1; i ++) { |
当然,我们可以将循环展开超过2层。虽然我们期望因为更长的流水线操作序列而提高性能,但大量的循环展开需要大量的寄存器。对寄存器的要求超过了CPU所拥有的数量,这就是所谓的「寄存器漫溢」(register spill),将降低程序性能。
另一个需要注意的问题是,操作的总数不太可能被展开因子所除。这就需要在循环之后进行清理代码,以考虑到最后的迭代。因此,展开的代码比直接的代码更难写,人们已经写了一些工具来自动执行这种源到源的转换。
表1.2中给出了内积循环展开操作的周期时间,最多为六次。请注意,在展开层数达到4时,时间并没有显示展示出单调的性质。这种变化是由于各种与内存有关的因素造成的。
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 6794 | 507 | 340 | 359 | 334 | 528 |
内积操作的周期时间,最多展开六次。
缓存尺寸
上面我们了解到,从L1移动数据可以比从L2移动数据有更低的延迟和更高的带宽,而L2又比L3或内存快。这很容易用重复访问相同数据的代码来证明
1 | for (i=0; i<NRUNS; i++) |
如果尺寸参数允许数组填入缓存,那么操作会相对较快。随着数据集大小的增长,它的一部分将从L1缓存中转移至其他部分,所以操作的速度将由L2缓存的延迟和带宽决定。这可以从图1.18中看出。每个操作的平均周期数与数据集大小的关系图如下:
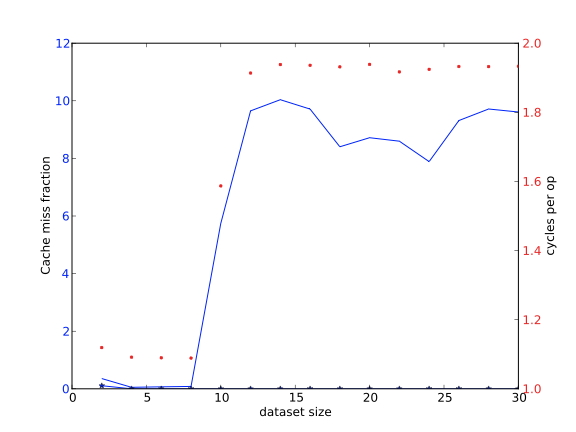
练习 1.19 试论证:如果有一个足够大规模的问题和LRU替换策略(第1.3.4.6节),基本上L1中的所有数据都会在外循环的每次迭代中被替换。你能不能写一个例子,让一些L1的数据保持不变?
通常情况下,可以通过安排操作来将数据保留在L1缓存中。例如,在我们的例子中,我们可以编写
1 | for (b=0; b<size/l1size; b++) { |
假设L1大小与数据集大小平均分配。这种策略被称为「缓存模块化」(cache blocking)或「缓存复用模块化」(blocking for cache reuse)。
在下面的循环中,针对不同的缓存大小值,测量每个周期的内存访问次数。如果观察到时间与缓冲区大小无关,请让编译器生成一个优化报告。对于英特尔的编译器使用-qopt-report
1 | for (int irepeat=0; irepeat<how_many_repeats; irepeat++) { |
论证发生了什么。你能找到防止循环交换的方法吗?
练习 1.21 为了得到模块化的代码,$j$的循环被分割成一个块的循环和一个块元素的内循环;然后i的外循环被替换成块的循环。在这个特殊的例子中,你也可以简单地交换i和j的循环。为什么这不是最佳性能?
注释 7 模块化的代码可能会改变表达式的评估顺序。由于浮点运算不是关联性的,所以模块化不是编译器允许进行的转换。
缓存线与跨步访问
由于数据是以连续的块状形式从内存转移到缓存中的,称为「缓存线」(cache line),没有利用缓存线中所有数据的代码要付出带宽的代价。这可以从一个简单的代码中看出来
1 | for (i=0,n=0; i<L1WORDS; i++,n+=stride) |
此处执行的是固定操作数。但随着跨度的增加,我们预计运行时间也会增加,这在图1.19中得到了证实。
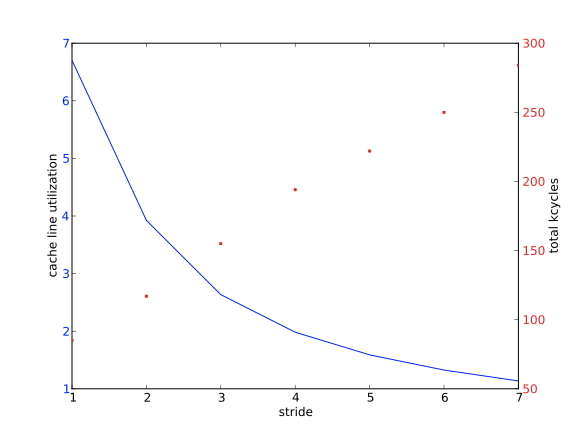
图中还显示了高速缓存线的复用率在下降,定义为向量元素的数量除以L1失误的数量。
下表为:在Frontera的56个核心上,每个核心的数据量为3.2M,每次操作的时间(纳秒)是跨度的函数。
| stride | nsec/word 56 cores, 3M |
56 cores, .3M | 28 cores, 3M |
|---|---|---|---|
| 1 | 7.268 | 1.368 | 1.841 |
| 2 | 13.716 | 1.313 | 2.051 |
| 3 | 20.597 | 1.319 | 2.852 |
| 4 | 27.524 | 1.316 | 3.259 |
| 5 | 34.004 | 1.329 | 3.895 |
| 6 | 40.582 | 1.333 | 4.479 |
| 7 | 47.366 | 1.331 | 5.233 |
| 8 | 53.863 | 1.346 | 5.773 |
滞后的影响可以通过处理器的带宽和缓存行为来缓解。考虑在TACC的Frontera集群的英特尔Cascadelake处理器上的一些运行情况(每个插槽28个核,双插槽,每个节点总共56个核)。我们测量了一个简单的流媒体内核的每操作时间,使用递增的步长。上表在第二栏中报告了每个操作时间确实随着步长的增加而线性上升。
然而,这是对一个溢出二级缓存的数据集而言的。如果我们让这个运行包含在二级缓存中,就像第三列中报告的那样,这种增加就会消失,因为有足够的带宽可以从二级缓存中全速流式传输数据。
TLB
正如前面文章所解释的,转译后备缓冲器(TLB)维护着一个经常使用的内存页及其位置的小列表;寻址位于这些页上的数据比不在其中的数据快得多。因此,人们希望以这样的方式编写代码,使访问的页数保持在低水平。 考虑以两种不同的方式遍历一个二维数组的元素的代码。
1 |
|
结果(源代码见附录37.5)绘制在图1.21和1.20中。
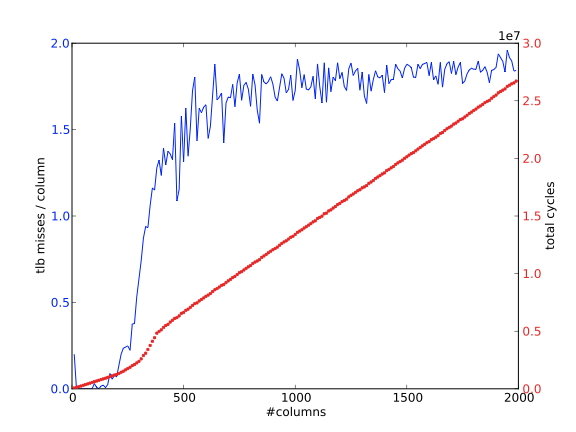
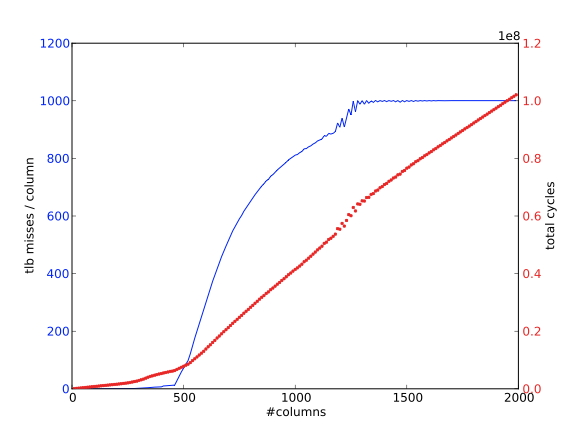
每列的TLB缺失次数与列数的函数关系;数组的逐列遍历
使用 $m=1000$ 意味着,在AMD Opteron上有512个双倍的页面,我们每列大约需要两个页面。我们运行这个例子,绘制 “TLB缺失 “的数量,也就是说,一个页面被引用的次数没有被记录在TLB中。
- 在最初的遍历中,这确实是发生的情况。在我们接触到一个元素,并且TLB记录了它所在的页面后,该页面上的所有其他元素随后被使用,所以没有进一步的TLB缺失发生。图1.20显示,随着𝑛的增加,每列的TLB缺失次数大约为2次。
- 在第二次遍历中,我们为第一行的每一个元素接触一个新的页面。第二行的元素将在这些页面上,因此,只要列的数量少于TLB条目的数量,这些页面仍将被记录在TLB中。随着列数的增加,TLB的数量也在增加,最终每个元素的访问都会有一个TLB缺失。图1.21显示,在列数足够多的情况下,每列的TLB缺失次数等于每列的元素数。
缓存关联性
有许多算法是通过对一个问题的递归划分来工作的,例如快速傅里叶变换(FFT)算法。因此,这类算法的代码经常在长度为2的幂的向量上操作。不幸的是,这可能会与CPU的某些架构特征产生冲突,其中许多涉及到2的幂。
每列的TLB缺失次数与列数的函数关系;数组的按列遍历
在前面,我们看到了将少量向量相加的操作是如何进行的
对于直接映射的缓冲区或具有关联性的集合关联缓冲区是一个问题。
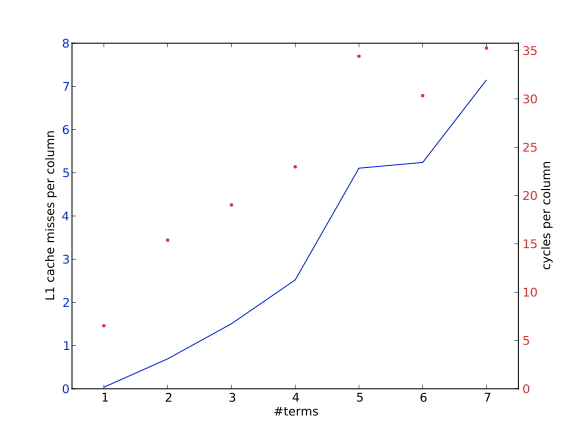
我们以AMD Opteron为例,它有一个64K字节的L1高速缓存,而且是双向设置的关联性。由于设置了关联性,该缓存可以处理两个地址被映射到同一个缓存位置,但不能处理三个或更多。因此,我们让向量的大小 $n=4096$ 个双倍数,我们测量了让 $m=1, 2, ….$ 的缓存缺失和周期的影响。
首先,我们注意到我们是按顺序使用向量的,因此,在一个有8个双倍数的缓存线中,我们最好能看到1/8倍于向量数量𝑚的缓存丢失率。相反,在图1.22中,我们看到了一个与𝑚成正比的速率,这意味着确实有缓存行被立即驱逐。这里的例外是𝑚=1的情况,双向关联性允许两个向量的缓存线留在缓存中。
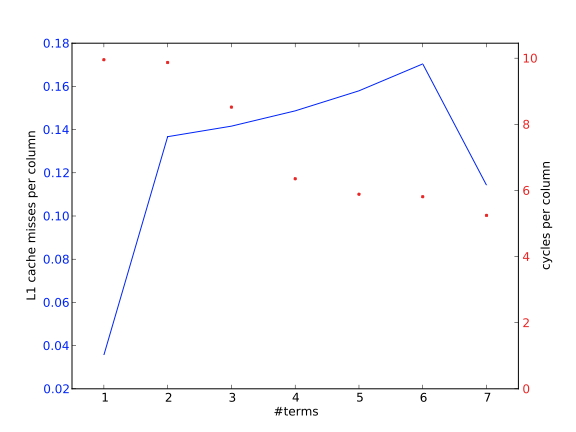
对比图1.23,我们使用了一个稍长的向量长度,所以具有相同$j$的位置不再被映射到同一个缓存位置。因此,我们看到的缓存缺失率约为1/8,而周期数较少,相当于完全重复使用了缓存线。
有两点需要注意的是:由于处理器会使用预取流,所以缓存缺失数实际上比理论预测的要低。其次,在图1.23中,我们看到时间随着 $m$ 的增加而减少;这可能是由于负载和存储操作之间逐渐形成了有利的平衡。由于各种原因,存储操作比负载的开销更大。
L1高速缓存的缺失次数和每个$j$列累积的周期数,向量长度为4096
L1缓存丢失的次数和每个𝑗列累积的周期数,向量长度4096+8
循环嵌套
如果代码中有两层独立的循环嵌套,我们可以自由选择将哪个循环设置为外循环。
练习 1.22 给出一个可以交换与不能交换的双层循环例子,可以的话请使用本书中的实际案例。
「C与Fortran的比较」:如果我们的循环使用了一个二维数组的 $(i, j)$ 索引,对于Fortran来说,通常最好让 $i$ 索引在内,而对于C语言, $j$索引最好在内部。
练习 1.23 试给出两种理由说明这对性能更加。
上述内容并不是一条硬性规定,决定循环的因素有许多,例如:循环的大小和其他等。在矩阵与向量乘积中,改变循环的顺序会改变输入和输出向量的使用方式。
并行模式:如果我们使用OpenMP优化循环,我们通常希望令外部循环次数比内部要多,因为短的内循环有助于编译器向量化操作;如果使用的是GPU优化,则尽量将大循环放在内部,并行工作的单元不应该有分支或循环。
另一方面,如果你的目标是GPU,你希望大循环是内循环。并行工作的单元不应该有分支或循环。
循环分块
在某些情况下,可以通过将一个循环分解成两个嵌套的循环来提高性能:一个是用于迭代空间中的块的外循环,一个是穿过块的内循环。这就是所谓的「循环分块」(loop tiling):(短的)内循环为块,其许多连续的实例构成了迭代空间。
例如
1 | for (i=0; i<n; i++) |
变为
1 | bs = ... /* the blocksize */ |
对于单一循环而言,这可能不会产生任何影响,但在某些情况下就可能会产生影响。例如,如果一个数组被重复使用,但它太大,无法装入缓存。
1 | for (n=0; n<10; n++) |
那么循环分块可能会导致一种情况,即数组被划分为适合缓存的块
1 | bs = ... /* the blocksize */ |
由于这个原因,循环叠加也被称为「缓存模块化」(cache blocking)。块的大小取决于在循环体中访问多少数据;理想情况下,我们会尽量使数据在L1缓存中得到重用,但也有可能为L2重用进行模块化。当然,L2重用的性能不会像L1重用那样高。
分析一下这个例子。 $x$什么时候被带入缓存,什么时候被重新使用,什么时候被刷新?在这个例子中,所需的缓冲区大小是多少?重写这个例子,用一个常数
1 |
下面观察矩阵转置 $A \leftarrow Bt$ 。通常情况下,我们会遍历输入和输出矩阵。
1 | // regular.c |
使用模块化,这就变成了
1 | // blocked.c |
与上面的例子不同,输入和输出的每个元素只被触及一次,所以没有直接的重复使用。然而,缓存线是可以重复使用的。
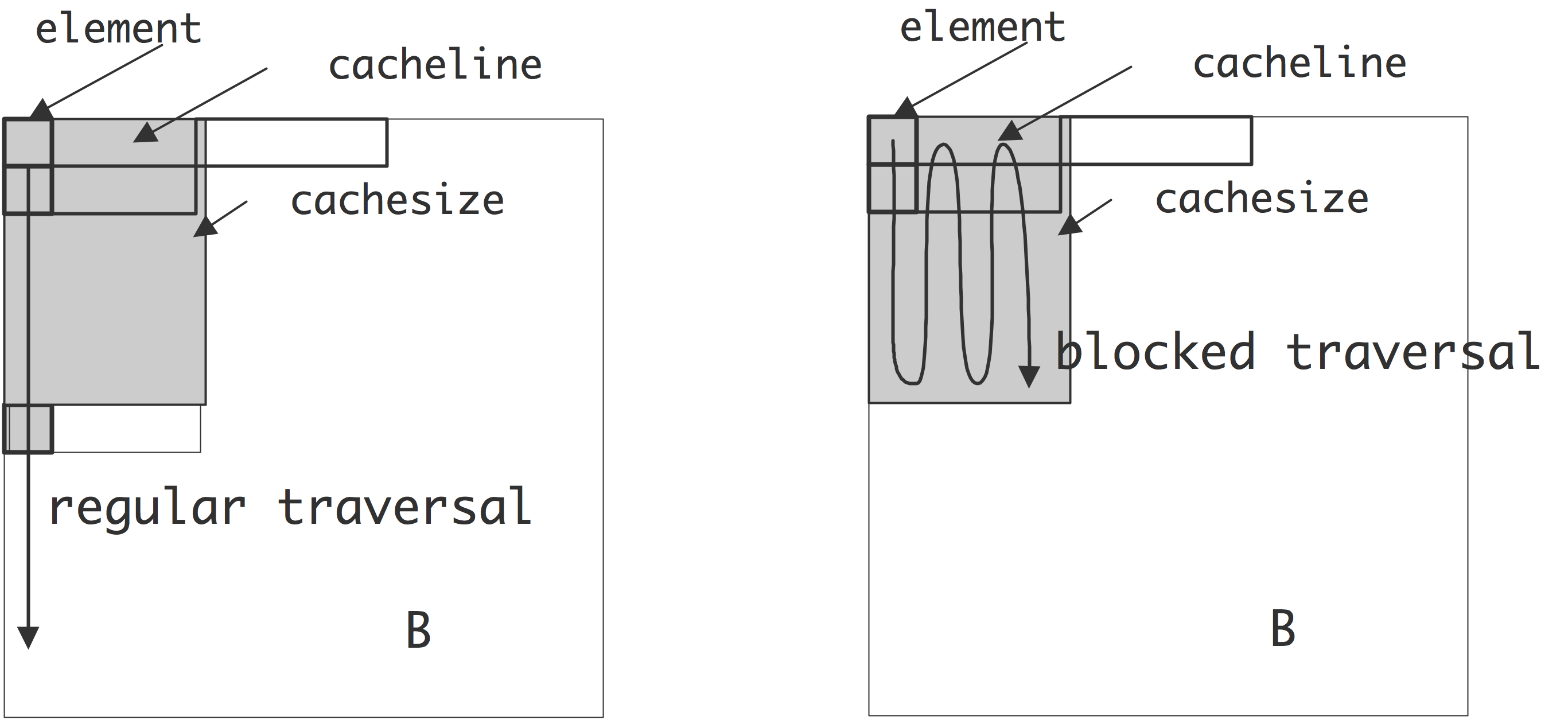
图1.24显示了其中一个矩阵是如何以与它的存储顺序不同的顺序被遍历的,比如说按列存储,而按行存储。这样做的结果是,每个元素的加载都会传输一个缓存线,其中只有一个元素会被立即使用。在常规的遍历中,这种缓存线流很快就溢出了缓存,而且没有重复使用。然而,在模块化遍历中,在需要这些行的下一个元素之前,只有少量的缓存行被遍历了。因此,缓存线是可以重复使用的,也就是空间局部性。
通过模块化获得性能的最重要的例子是矩阵,矩阵积,循环展开。前面,我们研究了矩阵与矩阵的乘法,得出的结论是在高速缓存中可以保留的数据很少。通过循环展开可以改善这种情况。例如,这个乘法的标准写法是
1 | for i=1..n |
只能通过优化使 $c[i,j]$ 保持在寄存器中。
1 | for i=1..n |
假设 $a$ 是按行存储的,使用循环平铺法,我们可以将 $a[i,:]$ 的部分内容保留在缓存中。
1 | for kk=1..n/bs |
优化策略
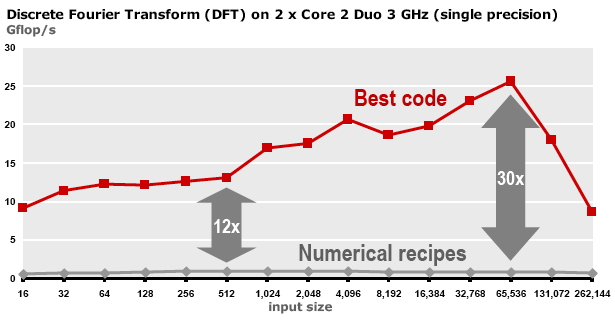
离散傅里叶变换的初始和优化后的性能对比
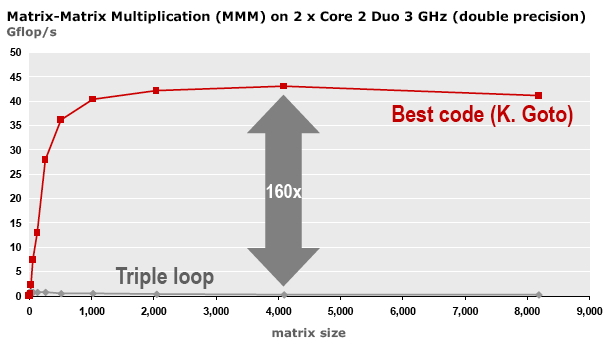
矩阵与矩阵乘积的初始实现和优化后的性能对比
图1.25和1.26显示,一个操作的原始实现(有时称为 “参考实现”)和优化实现的性能之间可能存在很大的差异。然而,优化并没有套路可循。由于使用模块化,循环展开后的操作是正常深度的2倍,矩阵与矩阵乘积变成了深度为6的循环;最佳的模块大小也取决于具体的目标架构等因素。
我们提出以下参考
- 编译器无法提取接近最佳性能的东西。
- 有一些自动调整项目,用于自动生成根据架构进行调整的实现。这种方法可以是适度的,也可以是非常成功的。这些项目中最著名的是用于Blas内核的Atlas[199]和用于变换的Spiral[172]。
缓存感知和缓存无关编程
区别于寄存器和内存可以在(汇编)代码中寻址,缓存的使用是隐式的。即便在汇编语言中程序员也不能显式地将某个数据加载到某个缓冲区。
然而,仍然存在“「缓存感知」(cache aware)”的方式进行编程。若一段代码的复用操作数小于缓冲区大小,这些数据经过第一次访问后将在第二次访问时暂时停留在缓存中;另一方面,若数据量超过了缓存的大小,那么在访问的过程中,它将部分或全部被冲出缓存。
我们可以通过实验来证明这个现象。用一个非常精确的计数器:
1 | for (x=0; x<NX; x++) |
将花费$N$的线性时间,直到$a$填满缓存的时候。一个更容易理解的方法是计算归一化的时间,基本上是每次执行内循环的时间。
1 | t = time(); |
归一化的时间将是恒定的,直到阵列$a$填满缓存,然后增加,最终再次持平。(见1.7.3节的详细讨论)解释是,只要 $a[0]…a[N-1]$ 适合在L1缓存中,内循环就会使用L1缓存中的数据。访问的速度由L1缓存的延迟和带宽决定。当数据量的增长超过L1缓存的大小时,部分或全部的数据将从L1缓存中刷出,而性能将由L2缓存的特性决定。让数据量进一步增长,性能将再次下降到由主内存的带宽决定的线性行为。
如果知道高速缓存的大小,在如上的情况下,就有可能安排算法来最佳地使用高速缓存。但是,每个处理器的缓存大小是不同的,所以这使得我们的代码不能移植,或者至少其高性能不能移植。另外,对多级缓存模块化也很复杂。由于这些原因,有些人主张采用「缓存无关编程」(cache oblivious programming)[70]。
缓存无关编程可以被描述为一种自动使用所有级别的缓存层次的编程方式。这通常是通过使用「分治」(divide-and-conquer)的策略来实现的,也就是对问题进行递归细分。
缓存无关编程的一个简单例子是矩阵转置操作 $B \leftarrow At$。首先我们观察到,两个矩阵的每个元素都被访问一次,所以唯一的重用是在缓存线的利用上。如果两个矩阵都是按行存储的,我们按行遍历 $B$,那么 $A$ 是按列遍历的,每访问一个元素就加载一条缓存线。如果行数乘以每条缓存线的元素数超过了缓存容量,那么在重新使用之前,行将被更新。
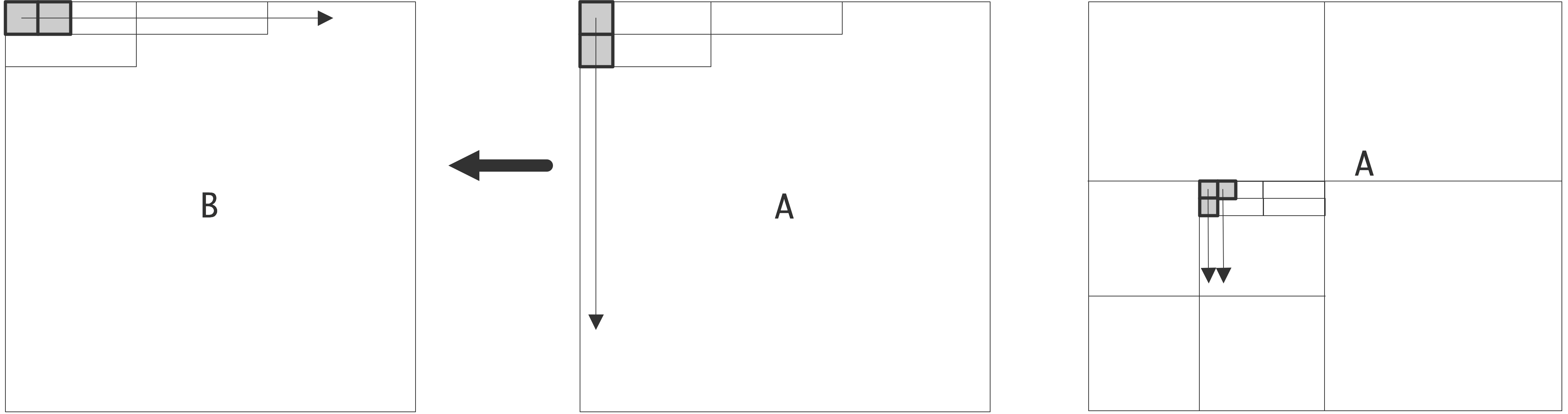
矩阵转置操作,源矩阵的简单和递归遍历
在缓存无关的实现中,我们将$A$和$B$划分为2$\times$2的块矩阵,并递归计算$B_{11} \leftarrow A_{11}^t, B_{12} \leftarrow A_{21}^t$ 等等,见上图。在递归的某一点上,块$A_{ij}$现在将小到足以容纳在缓存中,并且$A$的缓存线将被完全使用。因此,这个算法比简单的算法提高了一个系数,等于缓存线的大小。
缓存遗忘的策略通常可以产生改进,但它不一定是最佳的。在矩阵与矩阵乘积中,它比朴素的算法有所改进,但是它还不如一个明确设计为优化使用缓存的算法[85]。
参见第6.8.4节关于模版计算中的此类技术的讨论。
矩阵与向量乘积的案例研究
考虑如下的矩阵向量乘积:
这涉及到对$n^2+2n$数据项的 $2n^2$操作,所以重用率为𝑂(1):内存访问和操作的顺序相同。然而,我们注意到,这里涉及到一个双循环,而且$x,y$向量只有一个索引,所以其中的每个元素都被多次使用。
利用这种理论上的再利用并非易事。在
1 | /* variant 1*/ |
元素$y[i]$ 似乎被重复使用。然而,这里给出的语句会在每次内存迭代中把$y[i]$写入内存,我们必须把循环写成:
1 | /* variant 2 */ |
以保证重复使用。这个变体使用了$2n^2$的负载和$n$的存储。
这个代码片段只是明确地利用了$y$的重复使用。如果缓冲区太小,不能容纳整个向量$x$和$a$的一列,$x$的每个元素仍然在每个外层迭代中被重复加载。将循环反转为
1 | /* variant 3 */ |
暴露了$x$的重复使用,特别是如果我们把它写成:
1 | /* variant 3 */ |
此外,我们现在有$2n^2+n$的负载,与variant 2相当,但有$n^2$的存储,这是一个更高的顺序。
我们有可能重复使用$𝑥$和$𝑦$,但这需要更复杂的编程。这里的关键是将循环分成若干块。比如说
1 | for (i=0; i<M; i+=2){ |
这也被称为「循环展开」(loop unrolling),或「Strip mining」。循环展开的层数由可用寄存器的数量决定。
拓展探究
功率消耗
高性能计算机的另一个重要话题是其功耗。在这里,我们需要区分单个处理器芯片的功耗和一个完整的集群的功耗。
随着芯片上组件数量的增加,其功耗也会增加。幸运的是,在一个反作用的趋势下,芯片特征的小型化同时也在减少必要的功率。假设特征尺寸$\lambda$(想想看:导线的直径)按比例缩小到$s\lambda$,其中$s<1$。为了保持晶体管中的电场不变,通道的长度和宽度、氧化物厚度、基质浓度密度和工作电压都按相同的因素进行缩放。
缩放属性的推导
「恒电场按比例缩小」(constant field scaling)或Dennard缩放的特性[18, 44]是对电路微型化时的特性的理想情况描述。一个重要的结果是,当芯片特征变小时,功率密度保持不变,而频率同时增加。从电路理论中得出的基本属性是,如果我们将特征尺寸缩小$s$。
| 属性 | 情况 |
|---|---|
| Feature size | ~s |
| Voltage | ~s |
| Current | ~s |
| Frequency | ~s |
则可以推导:
而由于电路的总尺寸也随着 $ s^2$ 的减少而减少,功率密度不变。因此,在一个点路上放置更多的晶体管也可能从根本上不改变冷却问题。
这一结果可以被认为是「摩尔定律」(Moore’s law)背后的驱动力,摩尔定律指出,处理其中的晶体管数量每18个月翻一番。一个程序所需的与频率有关的部分功率来自于对电路电容的充电和放电,因此
| 状态 | 公式 |
|---|---|
| 充电 | q = CV |
| 工作 | W=qV=$CV^2$ |
| 功率 | W/time = WF = CV^2F |
这一分析可以用来证明引入多核处理器的合理性。
多核
在2010年左右,元件的微型化几乎已经停滞不前了,因为降低电压已经达到了峰值。频率也不能扩大,因为这将提高芯片的发热量,导致芯片的发热量过大,下图给出了一种戏剧化的例子。说明了一个芯片所产生的热量,如果采用单核结构:
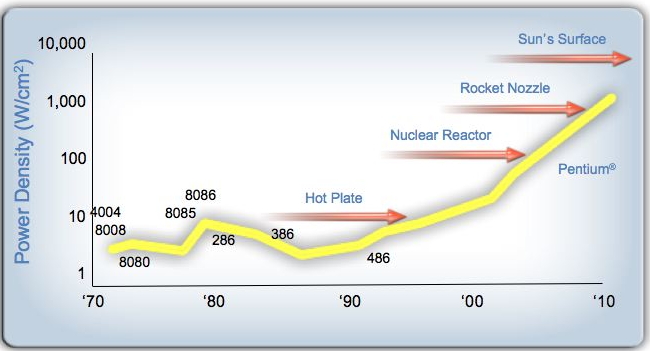
如果趋势继续下去,CPU的预计散热量情况 - (由Pat Helsinger提供)
处理器的趋势仍在继续。
一个结论是:计算机设计正在面临一道「功率墙」(power wall),单核的复杂性不能再增加了(所以我们不能再增加ILP和流水线深度),提高性能的唯一途径是增加明确可见的并行性。这一发展导致了当前一带多核处理器的出现。这也是GPU以其简化的处理设计并因此降低能耗而具有吸引力的原因。回顾上述共识,讲一个处理器与两个频率为一般的处理器进行比较,这应该具有相同的计算能力,对吗?由于我们降低了频率,如果我们保持相同的工业技术,我们可以降低电压。
理想情况下,两个处理器核心的总电功率为:
在实际中,电容会上升到2以上,而电压则不可能完全下降2,所以更可能是$P_{multi}\approx 0.4 \times P$ 当然,集成方面的问题在实践中要复杂一些[19];重要的结论是,现在为了降低功率(或者反过来说,为了在保持功率不变的情况下进一步提高性能),我们现在必须开始并行编程。
计算机总功率
并行计算机的总功率由每个处理器的功率和全部的处理机器数量决定。目前,这通常是几兆瓦。根据上述推理,增加处理器数量所需的功率增加已经不能被更多的高能效处理器所消耗,所以当并行计算机从petascale(2008年IBM的 Roadrunner达到)到预计的exascale时,功率正在成为压倒一切的考虑因素。
在最近几代的处理器中,功率正在成为压倒一切的考虑因素,并且在不可能的地方产生影响。例如:「单指令多数据」(Single Instruction Multiple Data,SIMD)设计是由解码的功率成本决定的。
操作系统影响
HPC从业人员通常不怎么担心操作系统(OS)。然而,有时可以感觉到操作系统的存在进而影响到性能。其原因是「周期性中断」(periodic interrupt),即操作系统每秒中断当前进程100次以上,以让另一个进程或系统守护进程拥有一个时间片。
如果只运行一个程序,我们不希望出现开销和抖动,以及进程运行时间的不可预测性,这就引入了一个问题。因此,已经存在的计算机基本上不需要有操作系统来提高性能。
周期性中断有进一步的负面影响。例如,它污染了高速缓存和TLB。作为抖动的细微影响,它降低了依赖线程间障碍的代码的性能,比如经常发生在OpenMP中。
特别是在金融应用中,非常严格的同步是很重要的,我们采用了一种Linux内核模式,周期性定时器每秒只跳动一次,而不是数百次。这就是所谓的tickless内核。
复习题
判断真假,若为假则请你给出解释
练习 1.25 判断
1 | for (i=0; i<N; i++) |
对a和b中的每个元素都遍历一次,所以每个元素都会有一次缓存丢失。
练习 1.26 请举例说明3路关联缓存会有冲突,但4路缓存不会有冲突的代码片段。
练习 1.27 考虑用一个$N\times N$的矩阵向量积。在执行这个操作时,需要多大的缓存容量才会出现强制性的缓存丢失?你的答案取决于操作的实现方式:分别回答矩阵的行和列的遍历,你可以假设矩阵总是按行存储。
并行计算
规模最大且运算能力最强的计算机通常被称为 “超级计算机”。在过去的二十年里,超级计算机的概念无一例外地指向拥有多个CPU且可同时处理一个问题的机器——并行计算机。
我们很难精确定义并行的概念,因为它在不同的层面上有着不同的含义。在上一章中,同一个CPU内部可以有若干条指令同时“执行”,这是所谓的「指令级并行」(instruction-level parallelism,ILP)。指令级并行并不在用户的控制范围内,而是由编译器和CPU共同决定。另一种并行的概念为多个处理器同时处理一条以上的指令,每个处理器都在自己所在的电路板上,这种并行可以由用户显式地调度。
这一章中,我们将分析这种更明确的并行类型,支持它的硬件,使其成为可能的编程,以及分析它的概念。
引言
在科学计算中,我们常常需要处理大量且有规律的操作。有没有一种并行计算机可以加快这项工作?假设我们需要执行$n$步操作,且每一步操作在单处理器上需要花费的时间为$t$,那么使用$p$个处理器,我们能否在$t/p$的时间内完成这些工作?
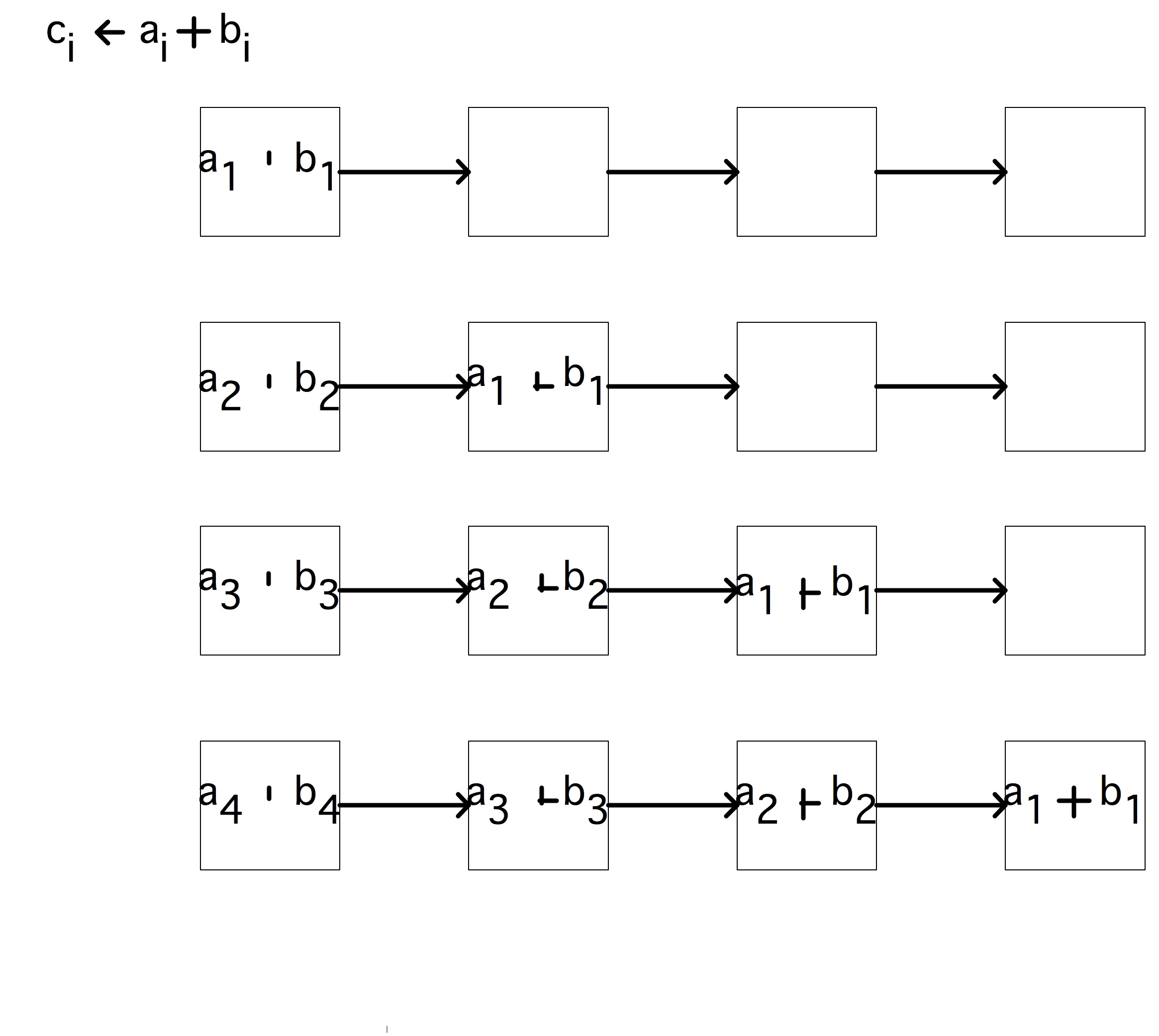
让我们先从一个简单的例子开始。假设需要将两个长度为$n$的向量相加:
1 | for (i=0; i<n; i++) |
最多可以用$n$个处理器来完成。下图所示中,每个处理器都存储一个a,b,c,且各自执行单一指令:a=b+c。
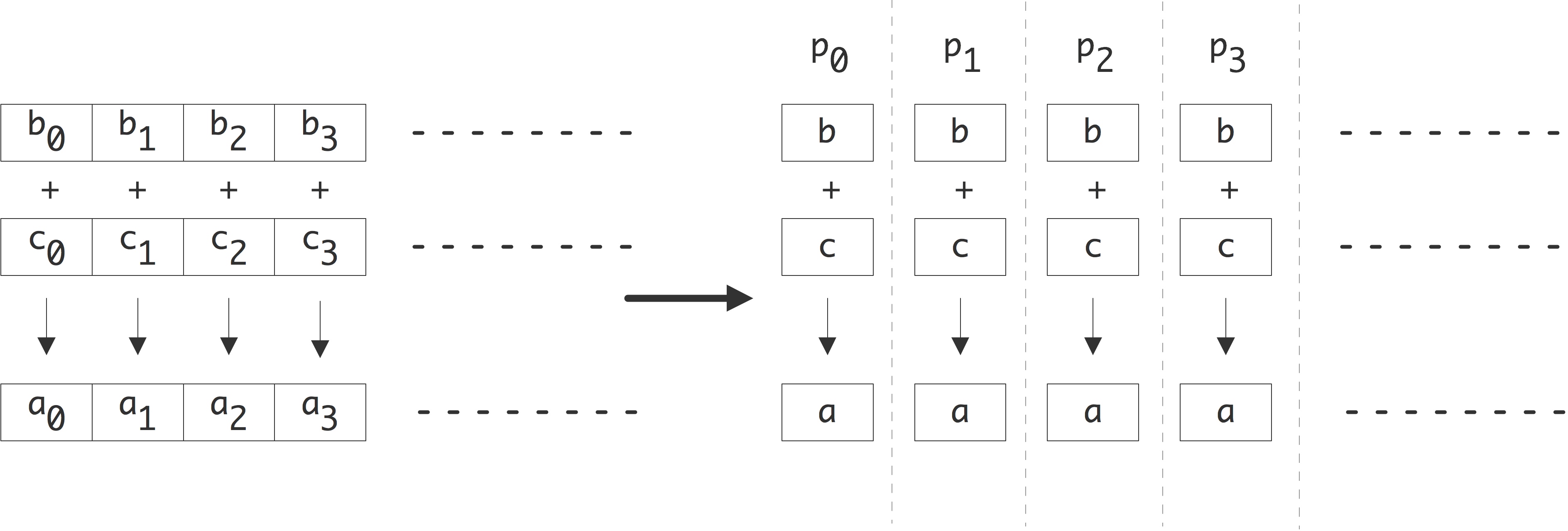
一般情况下,每个处理器执行的指令类似于
1 | for (i=my_low; i<my_high; i++) |
程序执行的时间随着处理器数量的增加而线性减少。若定义每步操作为单位时间,原始算法耗时$n$,而在$p$个处理器上的并行执行需要的时间为$n/p$,并行后的速度是原来的$p$倍。
输入一个向量而得到一个标量的操作通常称为规约(reduction)
下面我们考虑对向量内各元素求和,假设每个处理器只包含一个数组中的元素,顺序执行:
1 | s = 0; |
这段代码的并行情况并不明显,但如果我们将循环改写成:
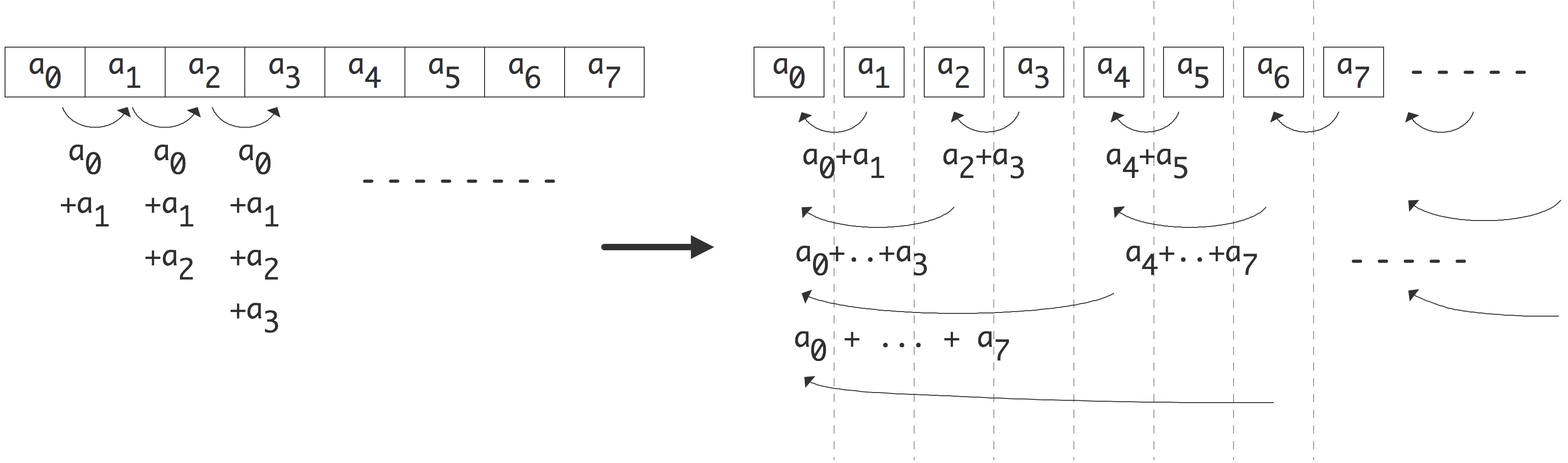
1 | for (s=2; s<2*n; s*=2) |
则可以找到相应的方法将其并行化:外循环的每一次迭代现在都是一个可以由$n/s$处理器并行完成的循环。由于外循环将经过 $log_2n$次迭代,我们可以看到新算法的运行时间缩短为$n/p⋅log_2n$。并行算法的速度比原来快了 $p/log_2n$倍。
从这两个简单的例子中可以看到并行计算的一些特点:
算法被稍加改写后可以成为并行算法。
并行算法并不一定能达到理想加速效果。
此外,第一种情况下每个处理器的$x_i, y_i$都在本地存储,这不会造成额外的时间开销;但在第二种情况下,处理器之间需要进行数据通信,这又会造成大量的开销。
下面我们讨论通信。我们可以把上图右半部分的并行算法变成一个树状图,把输入定义为树的节点,将所有的加和操作视为内部节点,总和作为根节点。如果一个节点是另一个节点的(部分)和的输入,则有一条从一个节点到另一个节点的边。在这个树状图中,可同时计算的元素放置在同一层级;每一级有时被称为「超步计算」(superstep)。垂直排列的节点意味着计算是在同一处理器上完成的,从一个处理器到另一个处理器的箭头对应着一次通信。树状图中的排列顺序并非唯一。如果节点在一个超步或水平层级上重新排列,就会出现不同的通信模式。
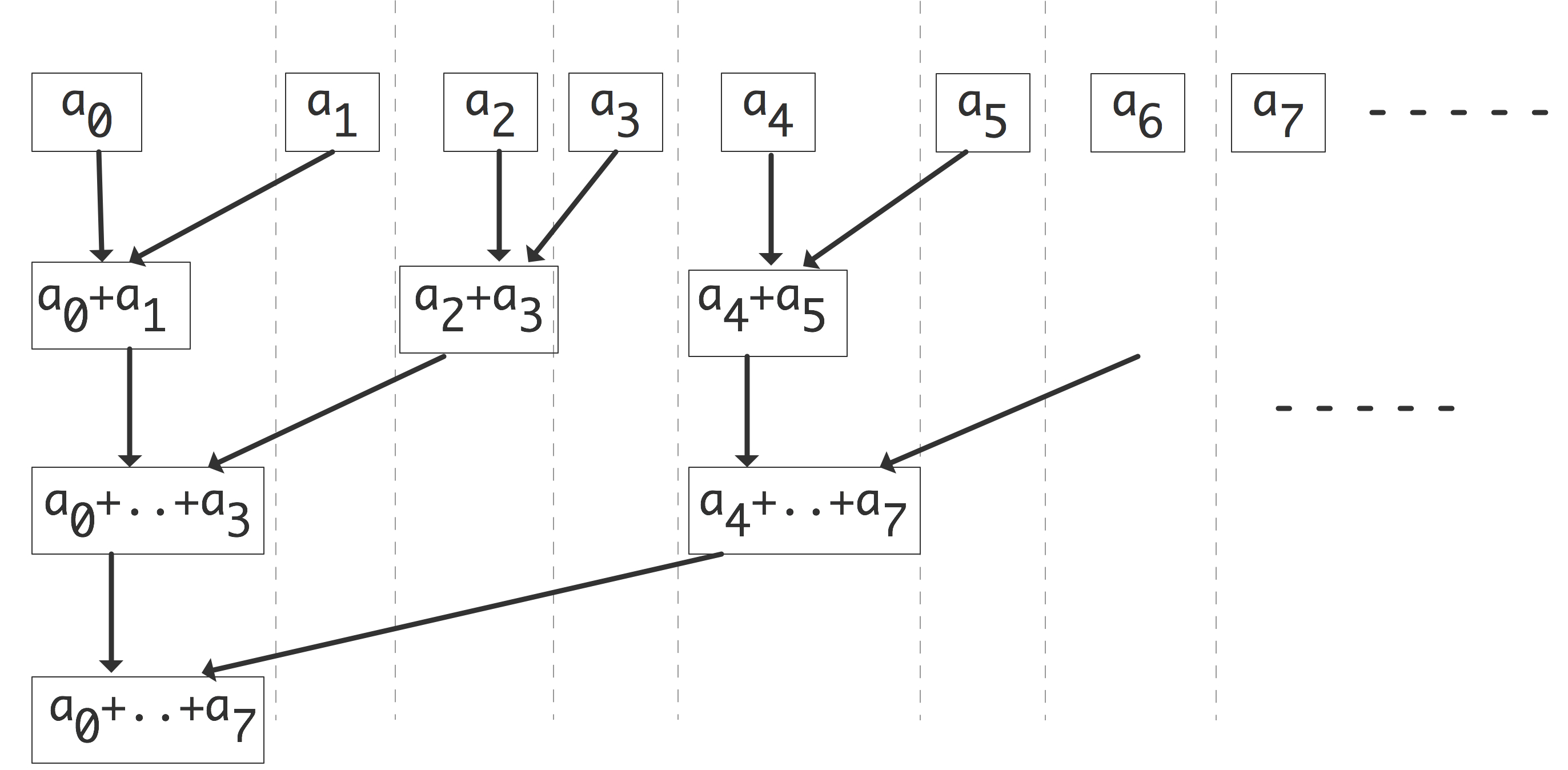
练习 2.1 考虑将超步内的节点放在随机处理器上。表明如果没有两个节点出现在同一个处理器上,那么最多只能进行两倍于图中的通信数量。
练习 2.2 你能画出在每个处理器上留下总和结果的计算图吗?有一种解决方案需要两倍的超步,也有一种解决方案需要相同的数量。在这两种情况下,图不再是一棵树,而是一个更普遍的「有向无环图」(Directed Acyclic Graph,DAG)。
处理器之间通常通过网络连接,由于网络之间传输数据需要时间,我们引入处理器之间距离的概念。在上文树状图中,处理器的排列是线性的,这与它们在排序中的等级有关。如果网络只连接一个处理器和它的邻节点,外循环的每一次迭代都会增加通信的距离。
练习 2.3 假设一个加法操作需要一个单位时间,而把一个数字从一个处理器移到另一个处理器也需要同样的单位时间。证明通信时间等于计算时间。
现在假设从处理器$p$发送一个数字到$p \pm k$需要时间$k$。说明现在并行算法的执行时间与顺序时间是一样的。求和的例子做了一个不现实的假设,即每个处理器最初只存储一个向量元素:实际上我们会有$p < n$,每个处理器都会存储一些向量元素。明显的策略是给每个处理器一个连续的元素序列,但有时明显的策略并不是最好的。
练习 2.4 考虑用4个处理器对8个元素求和的情况。表明图2.3中的一些边不再对应于实际通信。现在考虑用4个处理器对16个元素进行求和。这次通信边的数量是多少?
这些关于算法适应性、效率和通信的问题,对所有的并行计算都是至关重要的。在本章中,我们将以各种形式回到这些问题上。
功能性并行与数据级并行
从上面的介绍中,我们可以将并行概念定义为:在程序的执行过程中寻找独立的操作。这些独立的操作往往其执行逻辑相同,只是用于不同的数据项。我们把这种情况称为「数据级并行」(data parallelism):同一操作被并行地应用于许多数据元素,这在科学计算中是十分常见的。并行性往往源于这样一个事实:一个数据集(向量、矩阵、图……)被分散到许多处理器上,每个处理器都在处理其数据的一部分。
如果是单指令操作,传统上多采用数据级并行;如果是在子程序下处理,则通常称为「任务并行」(task parallelism)。
我们一定可以找到这样一种场景,使得指令之间相互独立且无依赖关系。一般情况下,编译器根据指令级并行来分析、运行代码:一条独立的指令可以被赋予给一个独立的浮点单元,也可以在优化寄存器时被重新排列。(同样参考2.5.2节)。
指令级并行是功能性并行的一种情况;功能并行可以通过连接相互独立的子程序来获得。在更高层次上,功能并行可以通过包含独立的子程序来获得,通常称为任务并行;见2.5.3节。
功能性并行的一些例子是蒙特卡洛模拟,以及其他穿越参数化搜索空间的算法。一个参数化的搜索空间,如布尔可满足性问题。
算法中的并行性与代码中的并行性
有时程序可以直接并行化处理,例如上文讨论的向量加法;有时我们很难找到简易的并行策略,例如在6.10.2节中将要讨论线性递归;而有些情况下,代码看起来可能没办法并行,但我们可以从理论上进行并行化处理。
练习 2.5 回答下列有关双循环$i,j$的问题。
1 | for i in [1:N]: |
1 | for i in [1:N]: |
- 内循环的迭代是否独立,也就是说,它们是否可以同时执行?
- 外循环的迭代是否独立?
- 如果$x[1,1]$是已知的,说明$x[2,1]$和$x[1,2]$可以独立计算。
- 这是否让你对并行化策略有了一个想法?
我们将在第6.10.1节讨论这个难题的解决方案。总的来说,第6章的全部内容都将是关于科学计算算法中内在的并行性数量。
理论概念
使用并行计算机有两个重要原因:获得更多的内存或者获得更高的性能。用更多的内存的原因很容易解释,因为总内存是各个内存的总和;而并行计算机的速度则较难描述。本节将对采用并行架构后的措施和理论速度进行拓展讨论。
定义
加速比和效率
对比同一个程序在单处理器上运行的时间与$p$个处理器上的运行时间可以得到加速比,设$T_1$是在单个处理器上的执行时间,$T_p$是在$p$个处理器上的运行时间,则加速比为$S_p=T_1/T_p$(有时$T_1$被定义为 “在单个处理器上解决问题的最短时间”,这允许在单个处理器上使用不同于并行的算法)。 在理想情况下,$T_p=T_1/p$,但在实际中往往难以达到,因此$S_p\leqslant p$。为了衡量我们离理想的加速有多远,我们引入了效率$E_p = S_p/p$。显然,$0<E_p≤1$。
上面的定义会产生一个问题:某个需要并行解决的问题由于规模太大,无法在任何一个单独的处理器上运行;反之,将单处理器上的问题拆解在多处理器上,由于每个处理器上的数据非常少,因此可能会得到一个十分扭曲的结果。下面我们将讨论更现实的速度提升措施。
有各种原因导致实际速度低于𝑝。首先,使用多个处理器意味着额外的通信开销;其次,如果处理器并未分配到完全相同的工作量,则会产生一部分的闲置,就会造成「负载不均衡」(load unbalance),再次降低实际速度;最后,代码运行可能依赖其原有顺序。
处理器之间的通信是效率损失的一个重要来源。显然,一个不用通信就能解决的问题是非常有效的。这类问题实际上由许多完全独立的计算组成被称为「高度并行」(embarrassingly parallel),它们拥有接近完美的加速比和效率。
练习 2.6 加速比大于处理器数量被称为「超线性加速」(superlinear speedup)。请给出一个理论上的论据,为什么这种情况不会发生。
在实践中,超线性加速可能发生。例如,假设一个问题太大,无法装入内存,一个处理器只能通过交换数据到磁盘来解决。如果同一个问题适合在两个处理器的内存中解决,那么速度的提升很可能大于2,因为磁盘交换不再发生。拥有更少或更局部的数据也可以改善代码的缓存行为。
代价最优
在达不到理想加速比的情况下,我们可以将理想加速比与实际加速之间的差异定义为「额外开销」(overhead):
我们也可以把它解释为在单个处理器上模拟并行算法,与实际的最佳串行算法之间的差异。
我们以后会看到两种不同类型的开销。
并行算法可以与串行算法有本质上的不同。例如,排序算法的复杂度为$O(nlogn)$,但并行双调排序(8.6 节)的复杂度为$O(nlog^2n)$。
并行算法可以有来自于过程或并行化的开销,比如发送消息的成本。我们在6.2.2节中分析了矩阵与向量乘积中的通信开销。
如果一个并行算法与串行算法达到了数量级差距,那么该算法就被称为「代价最优」(cost-optimal)。
练习 2.7 上面的额外开销定义隐含地假定开销是不可并行的。在上述两个例子的背景下讨论这个假设。
渐近论
如果我们忽略一些限制,比如处理器的数量,或者它们之间的互连的物理特性,我们可以就推导出关于并行计算效率极限的理论结果。本节将简要介绍这些结果,并讨论它们与现实中高性能计算的联系。
例如,考虑矩阵与矩阵乘法$𝐶=𝐴𝐵$,它需要$2𝑁$步操作,其中$𝑁$是矩阵规模的大小。由于对$𝐶$元素的操作之间没有依赖性,我们可以并行地执行。如果我们有$𝑁^2$处理器,我们可以将每个处理器分配给$𝐶$中的$(𝑖,𝑗)$坐标,并让它在$2𝑁$时间内计算$c_{ij}$。因此,这个并行操作的效率为1,是最优的。
练习 2.8 证明这个算法忽略了关于内存的严重问题。
如果矩阵被保存在共享内存中,那么从每个内存位置同时读多少次?内存位置进行多少次读取?
如果处理器将输入和输出都保存在本地存储器中,那么有多少重复?
将𝑁数字$\{𝑥\}_{i=1…N}$相加,可以在对数𝑁时间内由𝑁/2个处理器完成。作为一个简单的例子,考虑$n$数之和:$𝑠 = \sum_{i=1}^n a_i$。如果我们有$n/2$个处理器,我们可以计算:
- 定义$s_i^{(0)} = a_i$
- 迭代$j=1,…,log_2n$:
- 计算$n/2^j$ 部分和$s_{i}^{(j)}=s_{2 i}^{(j-1)}+s_{2 i+1}^{(j-1)}$
我们看到,$n/2$ 个处理器在 $log_2n$的时间内总共完成了$n$的操作(应该如此)。这个并行方案的效率是$𝑂(1/ log_2 n)$,是一个缓慢下降的$n$的函数。
练习 2.9 请指出,使用刚才的并行加法方案,用$𝑁^3/2$个处理器在对数$log_2N$时间内完成两个矩阵的相乘所得的效率是多少?
现在,我们可以提出一个合理的理论问题
如果我们有无限多的处理器,矩阵与矩阵乘法的最低时间复杂度是多少?
是否有更快的算法仍然具有𝑂(1)的效率?
这类问题已经被前人研究过了(例如,见[100]),但它们对高性能计算没有什么影响。
对这些理论界线的第一个反对意见是,它们隐含地假定了某种形式的共享内存。事实上,这种算法模型被称为「PRAM模型」(Parallel Random Access Machine),是「RAM模型」(Random Access Machine)在共享内存系统上的扩展。该模型假设所有处理器共享一个连续的内存空间。此外,模型还允许同一位置上同时进行多个访问。这在实际应用中,特别是在扩大问题规模和处理器数量的情况下是不可能的。对PRAM模型的另一个反对意见是,即使在单个处理器上,它也忽略了内存的层次结构;1.3节。
但是,即使我们把分布式内存考虑在内,这个结果仍然是不现实的。上述求和算法确实可以在分布式内存中不变地工作,只是我们必须考虑随着进一步迭代,活跃处理器之间的距离会增加。如果处理器是由一个线性数组连接起来的,那么活跃处理器之间的 “跳跃 “次数就会增加一倍,渐进地,迭代的计算时间也会随之增加。总的执行时间变为𝑛/2,考虑到我们在问题上投入了这么多处理器,这个结果显然令人感到失望。
如果处理器是以超立方体拓扑结构连接的呢(2.7.5节)?不难看出,求和算法确实可以在$log_2n$的时间内完成。然而,当$𝑛\rightarrow \infty$时,我们能否建立一个由$n$节点组成的超立方体序列,并保持两个连接的通信时间不变?由于通信时间取决于延迟,而延迟部分取决于总线的长度,所以我们必须担心最近的邻居之间的物理距离。
这里的关键问题是,超立方体(𝑛维的物体)是否可以被嵌入到三维空间中,同时保持连接的邻居之间的距离(以米计算)不变。很容易看出,3维网格可以任意放大,同时保持总线的单位长度,但对于超立方体来说,这个问题并不明确。在这里,导线的长度可能会随着$n$的增加而增加,这就与电子的有限速度相抵触。
我们草拟了一个证明(详见[65]),即在我们的三维世界和有限的光速下,对于$𝑛$处理器上的问题,无论互连方式如何,速度都被限制在$\sqrt[4]{n}$。该论点如下。考虑一个涉及在一个处理器上收集最终结果的操作。假设每个处理器占用一个单位体积的空间,在单位时间内产生一个结果,并且在单位时间内可以发送一个数据项。那么,在一定的时间内,最多只有半径为$t$的球中的处理器,即$𝑂(𝑡^3)$处理器可以对最终结果做出贡献;所有其他处理器都离得太远。那么,在时间$T$内,能够对最终结果做出贡献的操作数$\int_{0}^{T} t^{3} d t=O\left(T^{4}\right)$.在时间$T$内,这意味着,最大的可实现的速度提升是串行时间的四次方根。
最后,”如果我们有无限多的处理器怎么办 “这个问题本身并不现实,但请先不要急着将它抛弃,我们在后面提出弱可扩展性问题时还会讨论它(第2.2.5节)。”如果我们让问题的大小和处理器的数量成比例增长怎么办”。这个问题是合理的,因为它与购买更多的处理器是否可以运行更大的问题,以及如果可以的话,有什么 “好处 “等非常实际的考虑相一致。
阿姆达尔定律
无法达到理想加速比的一个原因是,部分代码依赖固有顺序执行。假设有5%的代码必须串行执行,那么这部分的时间将不会随着处理器的数量增加而减少。因此,对该代码的提速被限制在20的系数。这种现象被称为「阿姆达尔定律」(Amdahl’s Law)[4],下面我们将对其进行表述。
令$F_s$分别为代码的串行部分,$F_p$为代码的并行部分(更严格地说法应该为:”可并行 “部分)。那么$F_p + F_s = 1$。在$p$个处理器上的并行执行时间$T_p$是串行执行的部分$T_1F_s$和可并行化的部分$T_1F_p/P$之和。
随着处理器数量的增加,当$𝑃 \rightarrow \infty $时,现有的并行执行时间已经接近代码的串行部分的时间。$T_P\downarrow T_1F_s$。我们的结论是,加速受限于$S_P \leqslant 1/F_s$,效率是一个递减函数$E \sim 1/P$。
代码的串行部分可以由I/O操作等内容组成。然而,并行的代码中也有一些部分实际上是串行的。考虑一个执行单个循环的程序,其中的所有迭代都可以独立计算。显然,这段代码没有提供任何的并行化障碍。然而,通过将循环分割成许多部分(每个处理器一个),每个处理器现在必须处理循环开销:计算边界和完成测试。只要有处理器,这种开销就会被复制很多次。实际上,循环开销是代码的一个串行部分。
练习 2.10 我们来做一个具体的例子。假设一段代码的执行需要1秒,可并行部分在单个处理器上需要1000秒。如果该代码在100个处理器上执行,其速度和效率是多少?对于500个处理器来说,速度和效率又是多少?请保留最多两位有效数字。
练习 2.11 调查阿姆达尔定律的含义:如果处理器的数量$P$增加,代码的并行部分必须如何增加才能保持固定的效率?
有通信开销的阿姆达尔定律
尽管阿姆达尔定律十分准确的指出了并行后速度的提升情况,但由于通信开销的存在,实际的性能相比于理论性能仍有所降低。让我们细化一下方程(2.1)的模型(见[137, p. 367])。
其中$T_c$是一个固定的通信时间。为了评估这种通信开销的影响,我们假设代码是完全可并行的,即$F_p=1$。可以发现:
为了使之接近$p$,我们需要$T_c<<T_1/p$或$p<<T_1/T_c$。换句话说,处理器的数量增长不应超过标量执行时间和通信开销的比例。
古斯塔法森定律
阿姆达尔定律认为只增加处理器数量并不会对并行加速结果有明显的提升。其隐含假设是:越来越多的处理器上执行同一个固定计算。然而在实际中情况并非如此:通常有一种方法可以扩大问题的规模(在第四章中我们将学习 “离散化 “的概念),人们根据可用处理器的数量来调整问题规模的大小。
一个更现实的假设是,有一个独立于问题大小的顺序部分,以及可以任意复制的并行部分。为了正式说明这一点,让我们从并行程序的执行时开始:
现在我们有两种可能的$T_1$的定义。首先是在$T$中设置$p=1$得到的$T_1$(说服自己这实际上与$T_p$相同)。然而,我们需要的是$T_1$,它描述的是完成并行程序所有操作的时间。(见图2.4)。
这给我们提供了一个加速比
从这个公式我们可以看出。
加速仍以𝑝为界。
…它仍是一个正数。
对于一个给定的𝑝,它又是顺序分数的一个递减函数。
练习 2.12 重写方程(2.3),用$p$和$F_p$表示速度的提高。效率$E_p$的渐近行为是什么?
与阿姆达尔定律一样,如果我们把通信开销包括在内,我们可以研究古斯塔法森定律的行为。让我们回到一个完全可并行问题的方程(2.2),并将其近似为
现在,在问题逐渐放大的假设下,$T_c,T_1$成为$p$的函数。我们看到,如果$T_1(p)\sim pT_c(p)$,我们得到的线性加速是远离1的恒定分数。一般来说,我们不能进一步进行这种分析;在6.2.2节,你会看到一个例子的详细分析。
阿姆达尔定律和混合结构
上文我们已经认识了分布式和共享内存式的混合结构,这导致阿姆达尔定律的一种新型变式:
假设我们有$p$节点,每个节点有$c$核,$F_p$描述了使用$𝑐$路线程并行的代码的比例。我们假设整个代码在$p$节点上是完全并行的。理想的速度是$p_c$,理想的并行运行时间是$T_1/(pc)$,但实际运行时间是
练习 2.13 证明加速$T_1/T_p$,$c$可以用$p/F_s$近似。
在最初的阿姆达尔定律中,提速被顺序部分限制在一个固定的数字$1/F_s$,在混合结构中,它被任务并行部分限制在$p/F_s$。
关键路径和布伦特定理
上面关于加速和效率的定义,以及对阿姆达尔定律和古斯塔法森定律的讨论都隐含了一个假设,即并行工作可以被任意细分。正如你在第2.1节的求和例子中所看到的,然而事实情况并不总是这样:操作之间可能存在依赖关系,这限制了可以采用的并行量。
我们将「关键路径」(critical path)定义为最长度的依赖关系链(可能是非唯一的),这个长度有时被称为「跨度」(span)。由于关键路径上的任务需要一个接一个地执行,关键路径的长度是并行执行时间的一个下限。
为了使这些概念准确,我们定义了以下概念。
定义 1
- $T_1$:计算在单个处理器上花费的时间
- $T_p$:计算在$p$处理器上花费的时间
- $T_\infty$:如果有无限的处理器,计算所需的时间。
- $P_\infty$:$T_p=T_\infty$的$p$值。
有了这些概念,我们可以将算法的「平均并行度」(average parallelism)定义为$T_1/T_\infty$,而关键路径的长度为$T_\infty$。
现在我们将通过展示一个任务及其依赖关系的图来进行一些说明。为了简单起见,我们假设每个节点是一个单位时间的任务。
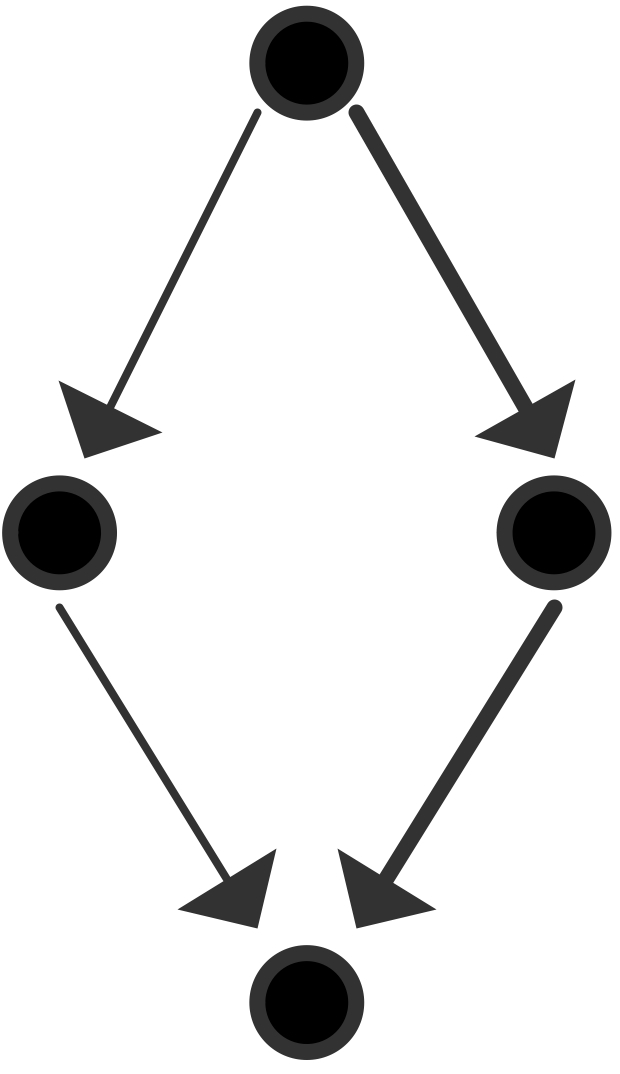
可以使用的最大处理器数量为3,平均并行度为9/5;效率最大的是$p=2$。
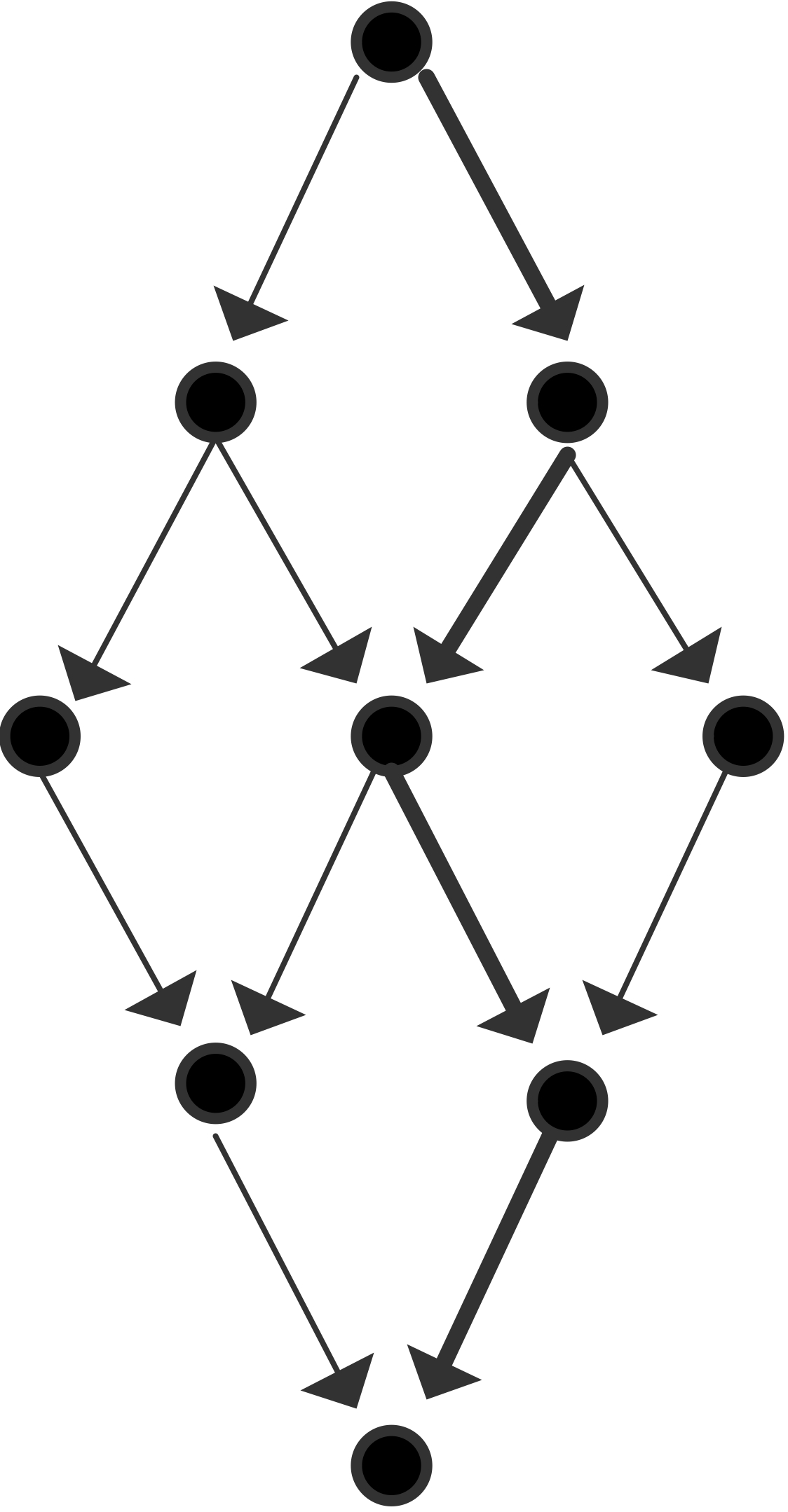
可以使用的最大处理器数量是4,这也是平均并行度;图中说明了一个效率为$\equiv 1$的$P=3$的并行化。
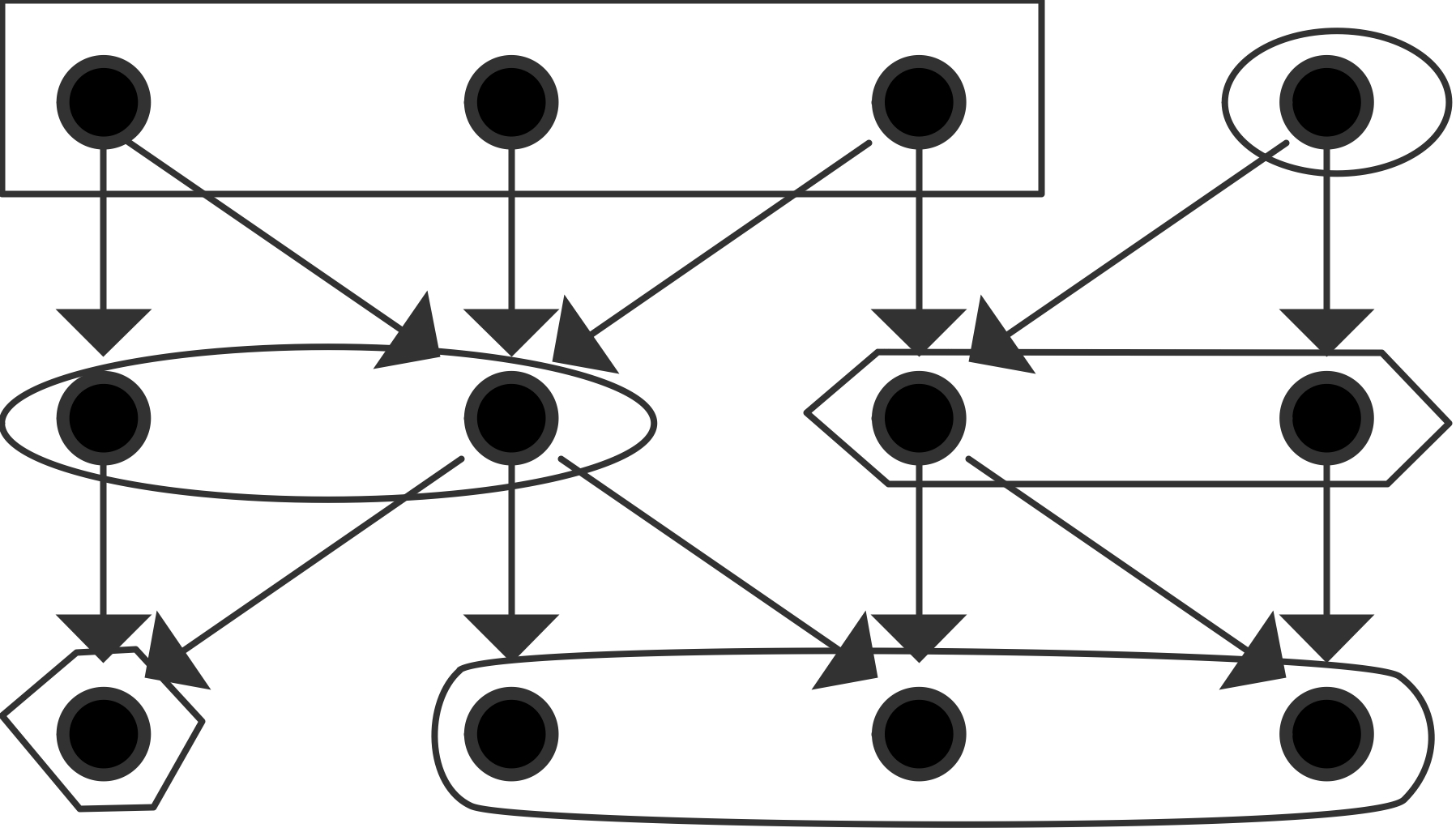
根据这些例子,你可能会发现有两种极端情况:如果每个任务都恰好依赖于其他任务,你会得到一个依赖链。
- 如果每个任务都精确地依赖于其他任务,你会得到一个依赖链,并且对于任何$T_p= T_1$。
- 另一方面,如果所有的任务都是独立的(并且$p$除以它们的数量),你会得到$T_p = T_1/p$,对于任何$p$。
- 在一个比上一个稍微不那么琐碎的情况下,考虑关键路径的长度为$m$,在这些$m$的每一步中,有$p-1$个独立的任务,或者至少:只依赖于前一步的任务。这样,每一个$m$步骤中都会有完美的并行性,我们可以表达为$T_p=T_1/T_p=m +(T_1-m)/p$。
最后这句话实际上在一般情况下是成立的。这被称为 “「布伦特定理」(Brent’s Theorem)”。
命题 1:设$m$为任务总数,$p$为处理器数量,$t$为关键路径的长度。那么计算可以在
证明:将计算分成几步,使$i+1$各步中的任务相互独立,而只依赖于步骤$i$。设步骤中的任务数为$s_i$ ,则该步骤的时间为$\lceil \frac{s_i}{p}\rceil$ 。将其相加得出
练习 2.14 考虑一棵深度为$d$的树,即有$2^d - 1$的节点,以及一个搜索$\max_\limits{n \in \text { nodes }} f(n)$。
假设所有的节点都需要被访问:我们对它们的值没有任何了解或排序。分析在$p$处理器上的并行运行时间,你可以假设$p=2q$,其中$q<d$。这与你从布伦特定理和阿姆达尔定律得到的数字有什么关系?
可扩展性
上文说过,使用越来越多数量的处理器处理一个给定的问题是没有意义的:每个节点上的处理器都没有足够有效地运行。在实践中,并行计算的用户要么选择与问题规模相匹配的处理器数量,要么在相应增加的处理器数量上解决一系列越来越大的问题。在这两种情况下,都很难谈及速度提升。因此我们使用了「可扩展性」(scalability)的概念。
我们区分了两种类型的可扩展性。所谓的「强可扩展性」(strong scalability)实际上与上面讨论的加速相同。我们说,如果一个程序在越来越多的处理器上进行分割,它显示出完美或接近完美的速度,也就是说,执行时间随着处理器数量的增加而线性下降,那么这个程序就显示出强大的可伸缩性。在效率方面,我们可以将其描述为。
通常情况下,人们会遇到类似 “这个问题可以扩展到500个处理器 “的说法,这意味着在500个处理器以下,速度不会明显低于最佳状态。这个问题不一定要在一个处理器上解决:通常使用一个较小的数字,如64个处理器,作为判断可扩展性的基线。
更有趣的是,「弱可扩展性」(weak scalability)是一个定义更模糊的术语。它描述了执行的行为,当问题的大小和处理器的数量都在增长时,但每个处理器的数据量却保持不变。由于操作数和数据量之间的关系可能很复杂,所以诸如加速等措施很难报告。如果这种关系是线性的,可以说每个处理器的数据量保持不变,并报告说随着处理器数量的增加,并行执行时间是不变的。(你能想到工作和数据之间的关系是线性的应用吗?哪里不是呢?)
练习 2.15 我们可以将强扩展性表述为运行时间与处理器数量成反比。
证明在对数图上,也就是将运行时间的对数与处理器数量的对数相比较,你会得到一条斜率为-1的直线。你能提出一种处理不可并行部分的方法吗,也就是说,运行时间$t=c_1+c_2/p$?
练习 2.16 假设你正在研究一个代码的弱可扩展性。在运行了几种规模和相应数量的进程之后,你发现在每一种情况下,翻转率都是大致相同的。论证该代码确实是弱可扩展的。
练习 2.17 在上面的讨论中,我们总是隐含地比较一个串行算法和该算法的并行形式。然而,在第2.2.1节中,我们注意到,有时提速被定义为一个并行算法与同一问题的最佳顺序算法的比较。考虑到这一点,请将运行时间为$(\log𝑛)^2$的并行排序算法(例如双调排序;第8节)与运行时间为$n\log n$的最佳串行算法进行比较。
证明在$n=p$的弱可扩展情况下,速度提升为$p/ \log p$。证明在强可扩展情况下,加速是$n$的一个递减函数。
注释 8 一则历史轶事.
Message: 1023110, 88 lines
Posted: 5:34pm EST, Mon Nov 25/85, imported: ….
Subject: Challenge from Alan Karp
To: Numerical-Analysis, … From GOLUB@SU-SCORE.ARPA
I have just returned from the Second SIAM Conference on Parallel Processing for Scientific Computing in Norfolk, Virginia. There I heard about 1,000 processor systems, 4,000 processor systems, and even a proposed 1,000,000 processor system. Since I wonder if such systems are the best way to do general purpose, scientific computing, I am making the following offer. I will pay $100 to the first person to demonstrate a speedup of at least 200 on a general purpose, MIMD computer used for scientific computing.
This offer will be withdrawn at 11:59
PM on 31 December 1995.
这一点通过扩大问题的规模得到了满足。
等效性
在上述弱可扩展性的定义中,我们指出,在问题规模$N$和处理器数量$P$之间的某种关系下,效率将保持不变。我们可以使之精确化,并将等效率曲线定义为$𝑁$,$𝑃$之间的关系,使效率恒定[86]。
可扩展性到底是什么意思?
在工业界的说法中,”可扩展性 “一词有时被应用于架构或整个计算机系统。
可扩展的计算机是由少量的基本部件设计而成的,没有单一的瓶颈部件,因此计算机可以在其设计的扩展范围内逐步扩展,为一组明确定义的可扩展的应用提供线性递增的性能。通用可扩展计算机提供广泛的处理、内存大小和I/O资源。可扩展性是指可扩展计算机的性能增量是线性的程度”[11]。
在科学计算中,可扩展性是一个算法的属性,以及它在一个架构上的并行化方式,特别是注意到数据的分布方式。在第6.2.2节中,你会发现对矩阵与向量乘积操作的分析:按块行分布的矩阵原来是不可扩展的,但按子矩阵分布的二维是可以的。
缩放模拟
在大多数关于弱扩展的讨论中,我们都假设工作量和存储量是线性关系,这并不总是如此。例如,对于$N^2$的数据,矩阵-矩阵乘积的操作复杂度为$N^3$。如果线性地增加处理器的数量,并保持每个进程的数据不变,工作可能会随着功率的增加而上升。
如果模拟随时间变化的PDEs,也会有类似的效果。(这里,总功是每个时间步骤的功和时间步骤数的乘积。这两个数字是相关的;在第4.1.2节中,你看到时间步长有一定的最小尺寸,是空间离散化的一个函数。因此,时间步数将随着每个时间步数的工作上升而上升。
在本节中,我们不是从算法运行的角度来研究可扩展性,而是研究模拟时间$S$和运行时间$T$是恒定的情况,我们看看这对我们需要的内存量有何影响。这相当于我们有一个模拟,在一定的运行时间内模拟了一定量的现实世界的时间;现在你买了一台更大的计算机,你想知道在相同的运行时间和保持相同的模拟时间内,你能解决多大的问题。换句话说,如果你能在一天内计算出两天的天气预报,你不希望当你买了更大的电脑后,它开始花费三天时间。
让 $m$为每个处理器的内存$P$为处理器的数量,得出
如果𝑑是问题的空间维数,通常是2或3,我们可以得到
为了稳定起见,这将时间步长$\Delta t$限制为
(注意到第四章没有讨论双曲的情况)在模拟时间$S$的情况下,我们发现
如果我们假设各个时间步骤是完全可并行的,也就是说,我们使用显式方法,或带有最优求解器的隐式方法,我们发现运行时间为
令$T/S=C$,则
也就是说,每个处理器的内存量随着处理器数量的增加而减少。(最后一句话中缺少的步骤是什么?)
进一步分析这个结果,我们发现
代入𝑀=𝑃𝑚,我们最终发现
也就是说,我们可以使用的每个处理器的内存会随着处理器数量的高次方而减少。
其他的缩放措施
上面的阿姆达尔定律是以在一个处理器上的执行时间来表述的。在许多实际情况下,这是不现实的,因为并行执行的问题对任何一个处理器来说都太大了。一些公式的处理给了我们在某种程度上等同的数量,但不依赖于这个单处理器的数量[159]。
首先,将定义$S_p(n)=\frac{T_1(n)}{T_p(n)}$应用于强可扩展,我们发现$T_1(n)/n$是每次操作的串行时间。它的倒数$n/T_1(n)$可以称为串行计算率,表示为$R_1(n)$。同样可以定义 “并行计算率”
我们发现
在强可扩展中,$R_1(n)$将是一个常数,所以我们做一个加速的对数图,纯粹是基于测量$T_p(n)$。
并发;异步和分布式计算
即使在非并行的计算机上,也有一个同时执行多个进程的问题。操作系统通常有一个时间切片的概念,在这个概念中,所有活动的进程都被赋予CPU的指令,在一小段时间内轮流执行。通过这种方式,串行可以模拟一个并行机器;当然,这种做法效率较低。
然而,即使不运行并行程序,时间切片也是有用的。操作系统会有一些独立的进程(例如编辑器,收到的邮件,等等),它们都需要保持活跃,或多或少地运行。这种独立进程的困难在于,它们有时需要访问相同的资源。两个进程都需要相同的两个资源,而每个进程都得到一个,这被称为「死锁」(deadlock)。资源争夺的一个著名的形式化被称为「哲学家进餐」(dining philosophers)问题。
研究这种独立进程的领域有多种说法,如「并发性」(concurrency)、「异步计算」(asynchronous computing)或「分布式计算」(distributed computing)。并发这一术语描述了我们正在处理同时活动的任务,它们的行动之间没有时间串行。分布式计算这一术语来源于数据库系统等应用,在这些应用中,多个独立的客户需要访问一个共享数据库。
本书将不多讨论这个话题。第2.6.1节讨论了支持时间切片的线程机制;在现代多核处理器上,线程可以用来实现共享内存并行计算。
《Communicating Sequential Processes》一书对并发进程之间的交互进行了分析[109]。其他作者使用拓扑结构来分析异步计算[103]。
并行计算机架构
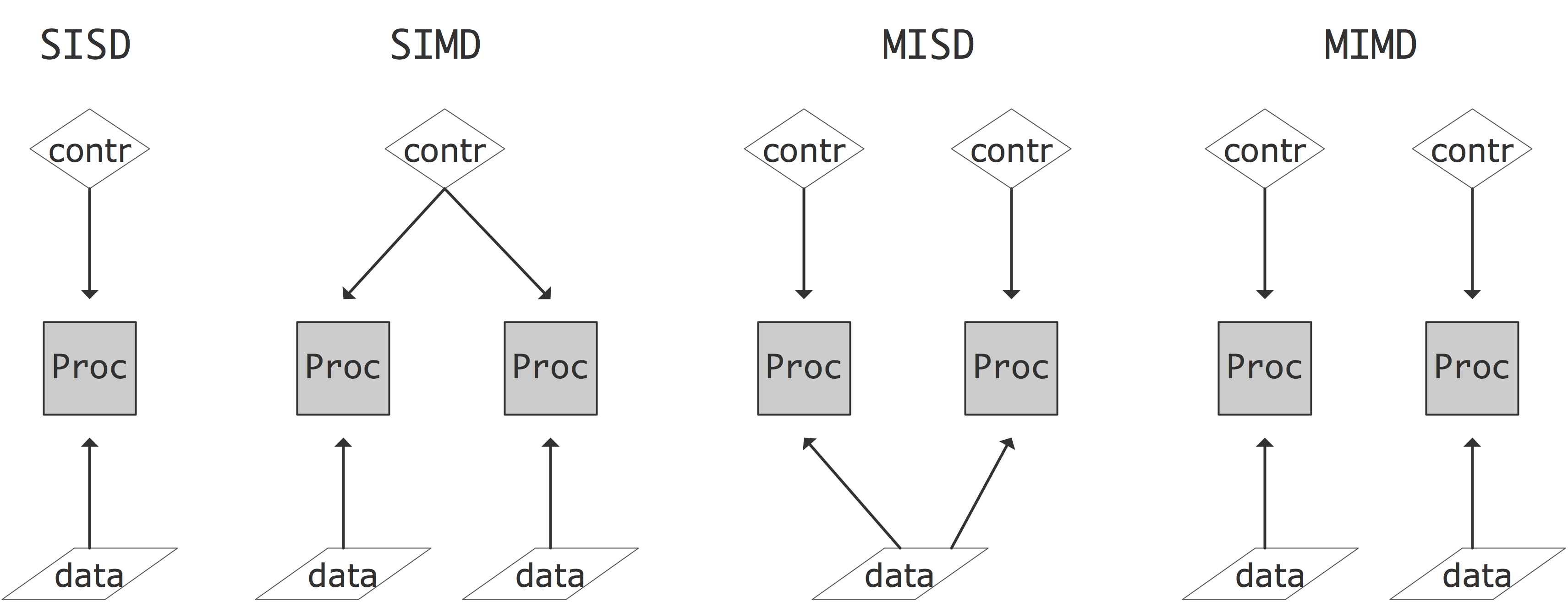
相当一段时间以来,超级计算机都是某种并行计算机,即允许同时执行多个指令或指令序列的架构。福林(Flynn)[66]提出了一种描述这种架构的各种形式的方法。Flynn的分类法通过数据流和控制流是共享的还是独立的来描述结构。结果有以下四种类型(也见图2.5)。
- 「单指令单数据」(Single Instruction Single Data,SISD):这是传统的CPU结构:在任何时候只有一条指令被执行,对一个数据项进行操作。
- 「单指令多数据」(Single Instruction Multiple Data,SIMD):在这种计算机类型中,可以有多个处理器,每个处理器对自己的数据项进行操作,但它们都在对该数据项执行相同的指令。向量计算机(2.3.1.1节)通常也被定性为SIMD。
- 「多指令单数据」(Multiple Instruction Single Data,MISD):目前还没有符合这种描述的架构;人们可以说,安全关键应用的冗余计算就是MISD的一个例子。
- 「多指令多数据」(Multiple Instruction Multiple Data,MIMD):这里有多个CPU对多个数据项进行操作,每个都执行独立的指令。目前大多数并行计算机都属于这种类型。
现在我们将更详细地讨论SIMD和MIMD架构。
SIMD
SIMD类型的并行计算机同时对一些数据项进行相同的操作。这种计算机的CPU的设计可以相当简单,因为算术单元不需要单独的逻辑和指令解码单元:所有的CPU都是锁步执行相同的操作。这使得SIMD计算机在对数组的操作上表现出色,如
1 | for (i=0; i<N; i++) a[i] = b[i]+c[i]; |
而且,由于这个原因,它们也经常被称为「阵列处理器」(array processors)。科学代码通常可以写得很好,使很大一部分时间花在阵列操作上。
另一方面,有些操作不能在阵列处理器上有效执行。例如,评估递归的若干项$x_{i+1}=ax_i+b_i$涉及许多加法和乘法,但它们是交替进行的,因此每次只能处理一种类型的操作。这里没有同时作为加法或乘法输入的数字阵列。
为了允许对数据的不同部分进行不同的指令流,处理器会有一个 “屏蔽位”,可以被设置来阻止指令的执行。在代码中,这通常看起来像
1 | while(x>0) { |
将相同的操作同时应用于一些数据项的编程模型,被称为「数据并行」(data parallelism)。
这种数组操作可以在物理模拟中出现,但另一个重要来源是图形应用。对于这种应用,阵列处理器中的处理器可能比PC中的处理器弱得多:通常它们实际上是位处理器,一次只能对一个位进行操作。按照这种思路,ICL在20世纪80年代有4096个处理器的DAP[115],固特异在20世纪70年代制造了一个16K处理器的MPP[10]。
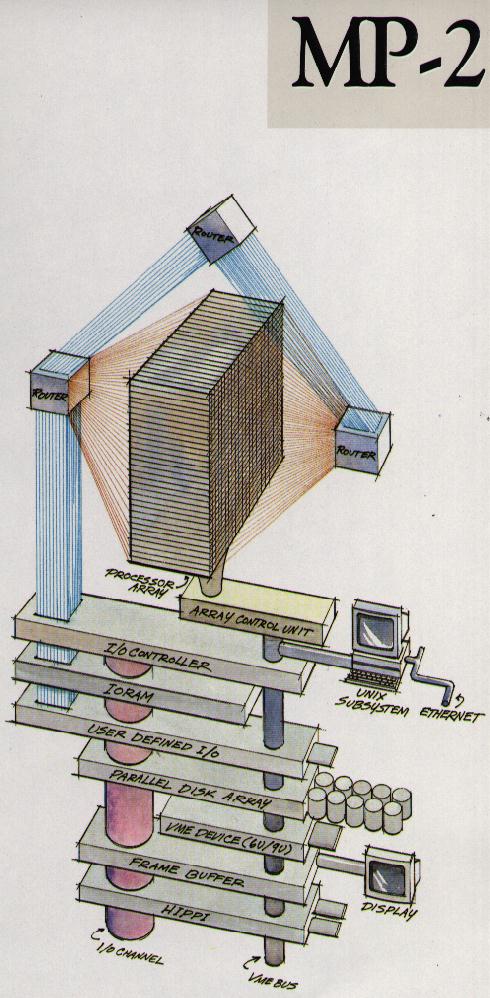
后来,连接机(CM-1、CM-2、CM-5)相当流行。虽然第一台连接机有位处理器(16个到一个芯片),但后来的型号有能够进行浮点运算的传统处理器,并不是真正的SIMD架构。所有这些都是基于超立方体互连网络;见2.7.5节。另一家拥有商业上成功的阵列处理器的制造商是MasPar;图2.6说明了该架构。你可以清楚地看到一个方形阵列处理器的单一控制单元,加上一个做全局操作的网络。
基于阵列处理的超级计算机已经不存在了,但是SIMD的概念以各种形式存在着。例如,GPU是基于SIMD的,通过其CUDA编程语言强制执行。另外,英特尔Xeon Phi有一个强大的SIMD组件。早期的设计SIMD架构的初衷是尽量减少必要的晶体管数量,而这些现代协处理器则是考虑到电源功率。与浮点运算相比,处理指令(称为指令问题)在时间、能源和所需的芯片地产方面实际上是昂贵的。因此,使用 SIMD 是在后两项措施上节约成本的一种方式。
流水线
许多计算机都是基于向量处理器或流水线处理器的设计。第一批商业上成功的超级计算机,Cray-1和Cyber205都属于这种类型。近来,Cray-X1和NEC SX系列都采用了向量流水线。在TOP 500 中领先3年的 “地球模拟器 “计算机[178],就是基于NEC SX处理器的。
虽然基于流水线处理器的超级计算机明显是少数,但流水线现在在作为集群基础的超标量CPU中是主流。一个典型的CPU有流水线的浮点单元,通常有独立的加法和乘法单元。
然而,现代超标量CPU的流水线与更老式的向量单元的流水线有一些重要区别。这些向量计算机中的流水线单元并不是CPU中的集成浮点单元,而是可以更好地看作是附属于本身具有浮点单元的CPU的向量单元。向量单元有矢量寄存器,其长度一般为64个浮点数;通常没有 “向量缓存”。向量单元的逻辑也比较简单,通常可以通过明确的向量指令来寻址。另一方面,超标量CPU完全集成在CPU中,面向利用非结构化代码中的数据流。
CPU和GPU中的真SIMD
真正的SIMD阵列处理可以在现代CPU和GPU中找到,在这两种情况下,都是受到图形应用中需要的并行性的启发。
英特尔和AMD的现代CPU,以及PowerPC芯片,都有向量指令,可以同时执行一个操作的多个实例。在英特尔处理器上,这被称为「SIMD流扩展」(Streaming Extensions,SSE)或「高级矢量扩展」(Advanced Vector Extensions,AVX)。这些扩展最初是用于图形处理的,在这种情况下,往往需要对大量的像素进行相同的操作。通常情况下,数据必须是总共128位,这可以分为两个64位实数,四个32位实数,或更多更小的块,如4位。
AVX指令是基于高达512位宽的SIMD,也就是说,可以同时处理8个浮点数。就像单次浮点运算对寄存器中的数据进行操作一样(第1.3.3节),向量运算使用「向量寄存器」(vector registers)。向量寄存器中的位置有时被称为「SIMD流水线」(SIMD lanes)。
SIMD的使用主要是出于功耗的考虑。解码指令实际上比执行指令更耗电,所以SIMD并行是一种节省功耗的方法。
目前的编译器可以自动生成SSE或AVX指令;有时用户也可以插入pragmas,例如英特尔的编译器。
1 | void func(float *restrict c, float *restrict a, float *restrict b, int n) |
这些扩展的使用通常要求数据与缓存行边界对齐(第1.3.4.7节),所以有一些特殊的allocate和free调用可以返回对齐的内存。
OpenMP的第4版还有指示SIMD并行性的指令。
更大规模的阵列处理可以在GPU中找到。一个GPU包含大量的简单处理器,通常以32个一组的形式排列。每个处理器组只限于执行相同的指令。因此,这是SIMD处理的真正例子。进一步的讨论,见2.9.3节。
MIMD/SPMD计算机
到目前为止,现在最常见的并行计算机结构被称为多指令多数据(MIMD):处理器执行多条可能不同的指令,每条指令都在自己的数据上。说指令不同并不意味着处理器实际上运行不同的程序:这些机器大多以「单程序多数据」(Single Program Multiple Data,SPMD)模式运行,即程序员在并行处理器上启动同一个可执行文件。由于可执行程序的不同实例可以通过条件语句采取不同的路径,或执行不同数量的循环迭代,它们一般不会像SIMD机器上那样完全同步。如果这种不同步是由于处理器处理不同数量的数据造成的,那就叫做「负载不均衡」(load unbalance,),它是导致速度不完美的一个主要原因;见2.10节。
MIMD计算机有很大的多样性。其中一些方面涉及到内存的组织方式,以及连接处理器的网络。除了这些硬件方面,这些机器还有不同的编程方式。我们将在下面看到所有这些方面。现在的许多机器被称为「集群」(clusters)。它们可以由定制的或商品的处理器组成(如果它们由PC组成,运行Linux,并通过以太网连接,它们被称为Beowulf集群[93]);由于处理器是独立的,它们是MIMD或SPMD模型的例子。
不同类型的内存访问
在介绍中,我们将并行计算机定义为多个处理器共同处理同一问题的设置。除了最简单的情况,这意味着这些处理器需要访问一个联合的
数据池。在上一章中,你看到了即使是在单个处理器上,内存也很难跟上处理器的需求。对于并行机器来说,可能有几个处理器想要访问同一个内存位置,这个问题变得更加糟糕。我们可以通过它们在协调多个进程对联合数据池的多次访问问题上所采取的方法来描述并行机器。
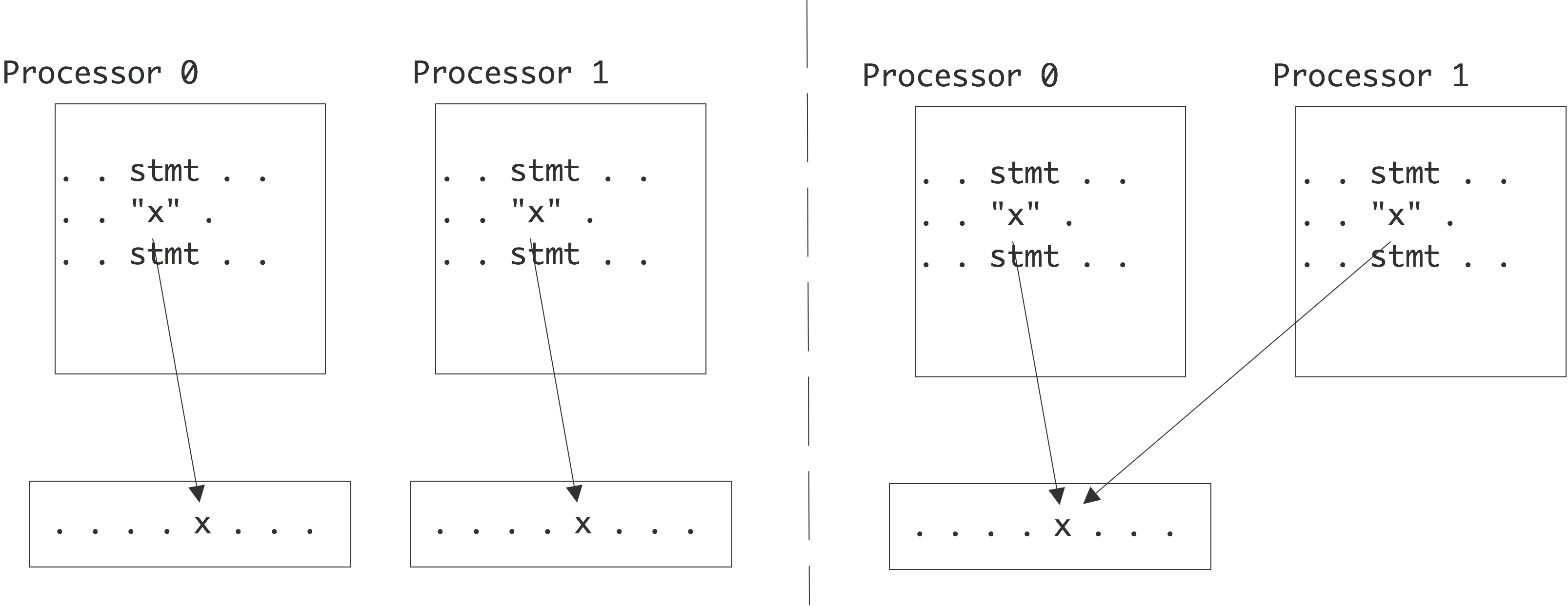
这里的主要区别在于「分布式内存」(distributed memory)和「共享内存」(shared memory)之间的区别。在分布式内存中,每个处理器有自己的物理内存,更重要的是有自己的地址空间。因此,如果两个处理器引用一个变量$x$,他们会访问自己本地内存中的一个变量。另一方面,在共享内存中,所有处理器都访问相同的内存;我们也说它们有一个「共享地址空间」(shared address space)。因此,如果两个处理器都引用一个变量$x$,它们就会访问同一个内存位置。
对称多核处理器:统一内存访问
如果任何处理器都可以访问任何内存位置,并行编程就相当简单。由于这个原因,制造商有很大的动力来制造架构,使处理器看不到一个内存位置和另一个内存位置之间的区别:每个处理器都可以访问任何内存位置,而且访问时间没有区别。这被称为「统一内存访问」(Uniform Memory Access,UMA),基于这一原则的架构的编程模型通常被称为「对称多处理」(Symmetric Multi Processing,SMP)。
有几种方法可以实现SMP架构。目前的台式电脑可以有几个处理器通过一条内存总线访问一个共享的内存;例如,苹果公司在市场上销售一种带有2个六核处理器的机型。处理器之间共享的内存总线只适用于少量的处理器;对于更多的处理器,可以使用连接多个处理器和多个内存bank的横梁。
在多核处理器上,有一种不同类型的统一内存访问:各核通常有一个共享的高速缓存,通常是L3或L2高速缓存。
非统一内存访问
基于共享内存的UMA方法显然只限于少量的处理器。十字架网络是可以扩展的,所以它们似乎是最好的选择。然而,在实践中,人们将具有本地内存的处理器放在一个具有交换网络的配置中。这导致了一种情况,即一个处理器可以快速访问自己的内存,而其他处理器的内存则较慢。这就是所谓的NUMA的一种情况:一种使用物理分布式内存的策略,放弃统一的访问时间,但保持逻辑上的共享地址空间:每个处理器仍然可以访问任何内存位置。
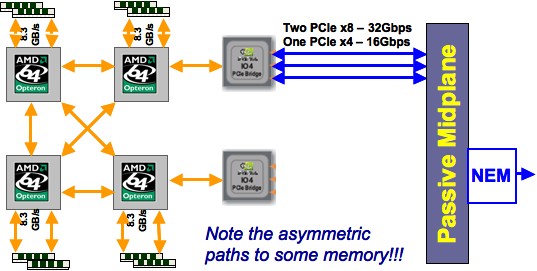
上图说明了TACC Ranger集群的四插槽主板的NUMA情况。每个芯片都有自己的内存(8Gb),但是主板的行为就像处理器可以访问一个32Gb的共享池。很明显,访问另一个处理器的内存比访问本地内存要慢。此外,请注意,每个处理器有三个连接,可以用来访问其他内存,但最右边的两个芯片使用一个连接来连接网络。这意味着访问对方的内存只能通过一个中间处理器进行,减缓了传输速度,并占用了该处理器的连接。
虽然NUMA方法对程序员来说很方便,但它为系统提供了一些挑战。想象一下,两个不同的处理器在其本地(缓存)内存中都有一个内存位置的副本。如果一个处理器改变了这个位置的内容,这个变化必须被传播到其他处理器上。如果两个处理器都试图改变一个内存位置的内容,程序的行为会变得不确定。
保持一个内存位置的副本同步被称为「缓存一致性」(cache coherence)(详见1.4.1节);使用这种方法的多处理器系统有时被称为 “缓存一致性的NUMA “或ccNUMA架构。
将NUMA发挥到极致,有可能有一个软件层,使网络连接的处理器看起来在共享内存上运行。这被称为「分布式共享内存」(distributed shared memory)或「虚拟共享内存」(virtual shared memory)。在这种方法中,管理程序提供了一个共享内存API,通过翻译系统调用到分布式内存管理。这种共享内存API可以被Linux内核所利用,它可以支持4096个线程。
在目前的供应商中,只有SGI(UV系列)和Cray(XE6)的市场产品具有大规模的NUMA。两者都对分区全局地址空间(PGAS)语言提供了强有力的支持;见2.6.5节。有一些厂商,如ScaleMP,为普通集群上的分布式共享内存提供了软件解决方案。
逻辑上和物理上的分布式内存
对内存访问问题最极端的解决方案是提供不仅在物理上,而且在逻辑上也是分布式的内存:处理器有自己的地址空间,不能直接看到其他处理器的内存。这种方法通常被称为 “分布式内存”,但这个术语是不明显的,因为我们必须分别考虑内存是否是分布式的和是否是分布式的问题。请注意,NUMA也有物理上的分布式内存;它的分布式性质对于程序员来说并不明显。
在逻辑和物理的分布式内存中,一个处理器与另一个处理器交换信息的唯一方式是通过网络明确传递信息。你将在2.6.3.3节中看到更多关于这方面的内容。
这种类型的架构有一个显著的优势,即它可以扩展到大量的处理器:IBM蓝色基因已经建立了超过20万个处理器。另一方面,这也是最难编程的一种并行系统。
存在上述类型之间的各种混合体。事实上,大多数现代集群会有NUMA节点,但节点之间是分布式内存网络。
并行计算(二)
并行计算中的粒度
一个程序有多少并行度?事实上,大部分指令都可以并行执行,但我们要考虑并行后的代价:并行后程序是否变得简单?以及并行后加速效率是否明显等问题。
本节的讨论主要是在概念层面上进行的;后面将详细介绍如何对并行进行实际编程。
数据并行化
对于有简单主体循环的程序来说,遍历大数据集的操作相当常见。
1 | for (i=0; i<1000000; i++) |
这样的代码被认为是「数据并行」(data parallelism)或「细粒度并行」(fine-grained parallelism)的一个实例。如果我们有和数组元素一样多的处理器,那么并行后的代码将非常简单:每个处理器将在其本地数据上执行
1 | a = 2*b |
如果代码主要由数组的循环组成,它可以在所有处理器锁步的情况下有效执行。基于这种思想设计的并行架构早已存在,事实上处理器只能以锁步方式工作。这种数组上的完全并行操作出现在计算机图形学中,图像的每个像素都被独立处理。因此,GPU的并行就是基于数据并行的。
继续上面的例子,考虑以下操作
在数据并行机器上,可以实现为
其中shiftleft/right指令导致一个数据项被发送到数字较低或较高为1的处理器。 为了使第二个例子有效,有必要使每个处理器能够与其近邻快速通信,并使第一个和最后一个处理器彼此通信。
在各种情况下,如图形中的 “模糊 “操作,对二维数据的操作是有意义的。
因此,处理器必须能够将数据移动到二维网格中的相邻处。
指令级并行
在ILP中,并行性仍然是在单个指令的层面上,但这些指令不一定是相似的。例如,在
这两个赋值是独立的,因此可以同时执行。编译器可以帮助我们处理这种并行。事实上,识别ILP对于从现代超标量CPU中获得良好的性能至关重要。
任务并行
数据和指令级并行的另一种应用为「任务并行」(task parallelism),是指可以并行执行的整个子程序。例如,在树形数据结构中的搜索可以按以下方式实现。
1 | if optimal (root) then |
这个例子中的搜索任务是不同步的,而且任务数量也不固定。在实际应用中,任务过多并不是一个很好的策略,因为处理器只在一个任务上工作时其效率才最高。上面的例子可以略加改写为:
1 | while there are tasks left do |
(之前的两个伪代码之间有一个微妙的区别。在第一个代码中,任务是自我调度的:每个任务都会衍生出两个新的任务。第二个代码是一个Manager-Worker Paradigm的例子:一个贯穿整个程序执行过程的中心任务负责派生和分配节点任务。)
与数据并行不同,该方案中数据对处理器的分配不是事先确定的。因此,这种并行模式最适合于线程编程,例如通过OpenMP库的并行。下面考虑另一个高度任务并行的例子:
在最简单的情况下,一个有限元网格是覆盖二维物体的三角形的集合。由于应该避免过于尖锐的角度,「Delauney网格细化」(Delauney mesh refinement)过程可以选择某些三角形,用形状更好的三角形取代它们。图2.9说明了这一点:黑色的三角形违反了一些角度条件,所以要么它们自己被细分,要么它们与一些相邻的三角形(呈现为灰色)连接,然后共同被重新细分。
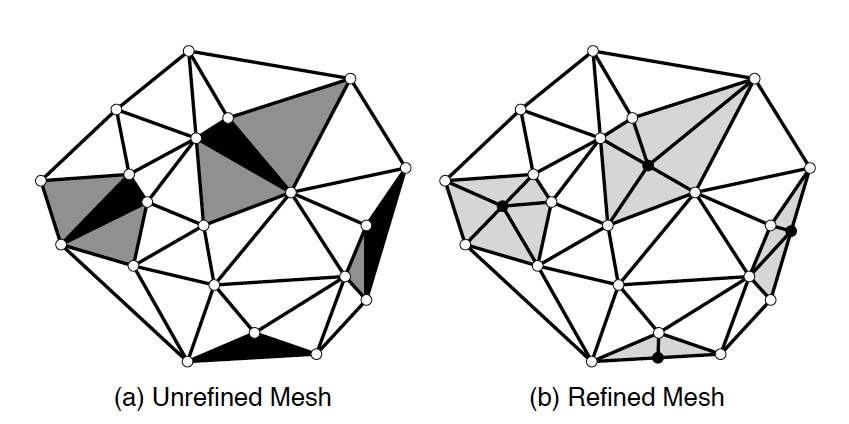
伪代码参考如下。
1 | Mesh m = /* read in initial mesh */ |
很明显,该算法是由一个必须在所有进程之间共享的工作列表(或任务队列)数据结构驱动的。再加上动态分配数据给进程,这意味着这种不规则的并行性适合于共享内存编程,而在分布式内存中则较难做到。
高度并行
单处理器的计算通常需要在众多不同的输入上进行。如果计算的数据不存在相关依赖,且不需要任何特定情况,则被称为「高度并行」(embarrassingly parallel)或「便捷并行」(conveniently parallel)计算。这种并行可以发生在几个层面。在诸如计算Mandelbrot set或评估国际象棋游戏中的棋子的例子中,一个子程序级别的计算被调用了许多参数值。在一个更粗略的层面上,可能是一个简单的程序需要对许多输入进行运行。在这种情况下,整体计算被称为「参数扫描」(parameter sweep)。
中粒度的数据并行化
上述数据并行假定了有与数据元素同样多的处理器。在实际中,处理器内存通常会很大,且处理的数据数量要远远大于处理器数量。因此,数组被分组到子数组的处理器上。伪代码如下
1 | my_lower_bound = // some processor-dependent number |
这种模式有数据并行的特点,因为在大量的数据项上执行的操作是相同的。它也可以被看作是任务并行,因为每个处理器执行的代码部分较大,而且不一定对同等大小的数据块进行操作。
任务粒度
在前面的小节中,我们考虑了寻找并行工作的不同层次,或者说划分工作的不同方式,以便找到并行性。还有另一种方法:我们将并行方案的「粒度」(granularity)定义为一个处理元素在不得不与其他处理元素进行通信或同步之前可以执行的工作量(或任务大小)。
在ILP中,我们处理的是非常细粒度的并行,就像一条指令或几条指令一样。在真正的任务并行中,颗粒度要粗得多。
有趣的是,我们可以自行选择数据并行中的任务大小。SIMD机器上,我们选择的是单指令粒度,但操作可以被分为中等大小的任务。因此,在处理器数量和总问题规模之间的适当平衡下,数据并行的操作可以在分布式内存集群上执行。
练习 2.18 讨论为一个数据并行操作选择合适的粒度,如在二维网格上进行平均化。表明存在一个表面到体积的效应:通信量比计算量低一阶。这意味着,即使通信比计算慢得多,增加任务量仍然会得到一个平衡的执行。
如果试图加大任务规模以减小通信开销,则会导致另一个问题:集合操作时可能会有不同运行时间的任务,导致负载不均衡。一种解决办法是使用过度分解:创建比处理元素更多的任务,并将多个任务分配给一个处理器(或动态分配任务)以平衡不规则的运行时间。这就是所谓的「动态调度」(dynamic scheduling)。
并行编程
并行编程比串行编程更复杂。虽然对于后者来说,大多数编程语言的操作原理是相似的(除了一些例外,如函数式语言或逻辑语言),但有多种方法来处理并行问题。让我们来探讨一下其中的一些概念和实际问题。
并行编程的策略有多种。我们很难做出一个能自动将串行程序转变为并行程序的编译器。除了弄清楚哪些操作是独立的问题之外,最主要的问题是,在并行环境中定位数据的问题是非常困难的。编译器需要考虑整个代码,而不是一次一个子程序。
较为有效的方法是:用户编写串行程序,同时给出哪些计算可以并行化或数据改如何分配的指示。明确指出操作的并行性是在OpenMP中进行的;指出数据分布并将并行性留给编译器和运行时是PGAS语言的基础。这种方法在共享内存中效果最好。
到目前为止最难的并行编程方式,同时也是实际中效果最好的并行方式,就是把一切留给程序员,让程序员管理一切。这种方法在分布式内存编程的情况下是必要的。
线程并行
我们将简要介绍一下 “线程”。为了解释什么是「线程」(thread),我们首先需要从技术上了解什么是「进程」(process)。一个unix进程对应于对应于单个程序的执行。因此,它在内存中拥有
程序代码,以机器语言指令的形式存在。
「堆」(heap),包含malloc创建的数组。
「栈」(stack),包含快速变化的信息,如「程序计数器」(program counter,PC),它显示了当前正在执行的结构。堆栈中包含快速变化的信息,如表明当前正在执行的程序计数器,以及具有本地范围的数据项,以及计算的中间结果。
这个过程可以有多个线程;这些线程的相似之处在于它们看到相同的程序代码和堆,但它们有自己的栈。因此,一个线程是通过进程执行的一个独立 “股”。
进程可以属于不同的用户,或者是一个用户并发运行的不同程序,因此它们有自己的数据空间。另一方面,线程是一个进程的一部分,因此它们共享进程堆。线程可以有一些私有数据,例如通过拥有自己的数据栈,但它们的主要特征是它们可以在相同的数据上进行协作。
叉形连接机制
线程是动态的,它们可以在程序执行过程中被创建。(这与MPI模型不同,在MPI模型中,每个处理器运行一个进程,它们都是在同一时间创建和销毁的)。当程序启动后,处于活跃状态的线程称为「主线程」(main thread),其他线程通过主线程「生成」(thread spawning)创建,主线程需等待其完成,称为「生成-汇合模型」(fork-join)。从同一个线程生成出来并同时活动的一组线程被称为「线程组」(thread team)。
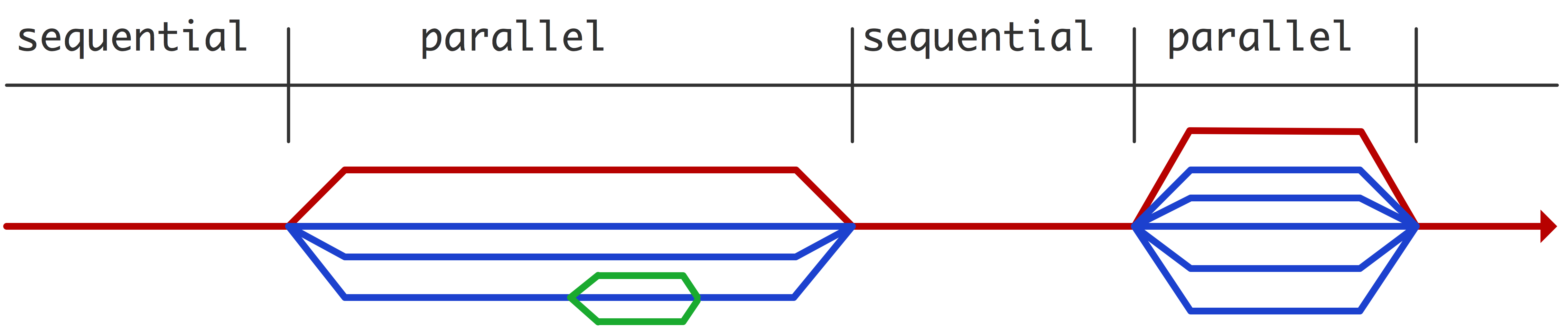
线程的硬件支持
上面所描述的线程是一种软件结构。在并行计算机出现之前,线程是可能的;例如,它们被用来处理操作系统中的独立活动。在没有并行硬件的情况下,操作系统将通过多任务或时间切片来处理线程:每个线程将定期使用CPU的一小部分时间。(从技术上讲,Linux内核通过任务的概念来处理进程和线程;任务被保存在一个列表中,并定期被激活或取消)
这可以导致更高的处理器利用率,因为一个线程的指令可以在另一个线程等待数据时被处理。(在传统的CPU上,线程之间的切换是有些耗费精力的(超线程机制是个例外),但在GPU上则不然,事实上,它们需要许多线程才能达到高性能)。
在现代多核处理器上,有一种明显的支持线程的方法:每个核有一个线程,可以有效地使用硬件的并行执行。共享内存允许线程看到相同的数据,但这也会导致问题。
线程实例
下面的例子,严格来说是在Unix上运行,在Windows上是行不通的,它清楚地说明了fork-join的模型。它使用pthreads库来生成一些任务,这些任务都会更新一个全局计数器。由于线程共享相同的内存空间,它们确实看到并更新相同的内存位置。
1 |
|
事实上,这段代码给出了正确的结果,但这是一个巧合:它之所以发生,只是因为更新变量比创建线程要快得多。(在多核处理器上,出错的机会将大大增加)。如果人为地增加更新的时间,我们将不再得到正确的结果。
1 | void adder() { |
现在所有的线程都读出了sum的值,等待一段时间(估计是在计算什么),然后再更新。
这可以通过在应该是 “互斥 “的代码区域上设置一个锁来解决。
1 | pthread_mutex_t lock; |
锁定和解锁命令保证了没有两个线程可以干扰对方的更新。关于pthreads的更多信息,请参见例如https://computing.llnl.gov/tutorials/pthreads。
上下文
在上面的例子和它的sleep命令版本中,我们忽略了一个事实,即有两种类型的数据参与其中。首先,变量s是在线程生成部分之外创建的。因此,这个变量是「共享」(shared)的。另一方面,变量t是在每个生成的线程中创建一次的。我们称其为「私有」(private)数据。
一个线程可以访问的所有数据的总和被称为其「上下文」(context)。它包含了私有和共享数据,以及线程正在进行的计算的临时结果。(还包含程序计数器和堆栈指针。如果现在不知道这些是什么,请不用担心)
创建的线程比处理器的内核多是很有可能的,所以处理器可能需要在不同线程的执行之间进行切换。这就是所谓的「上下文切换」(context switch)。
普通的CPU进行上下文切换会造成时间开销,所以只有在线程工作的粒度足够高时,我们才会这样执行。下面几种情况则较为常见
- 有硬件支持多线程的CPU,通过「超线程」(hyperthreading)或Intel Xeon Phi来实现
- GPU,它实际上依赖于快速上下文切换。
- 某些其他 “奇特 “的架构,如Cray XMT。
竞争条件、线程安全和原子操作
共享内存使程序员的工作变得简单,因为每个处理器都可以访问所有的数据:处理器之间不需要明确的数据通信。另一方面,多个进程/处理器也可以写到同一个变量,这是潜在问题的来源。
假设两个进程都试图递增一个整数变量I。
进程1:I=I+2
进程2:I=I+3
如果该变量是一个由独立进程计算的累加,这是一个合法的活动。这两个更新的结果取决于处理器读取和写入变量的顺序。
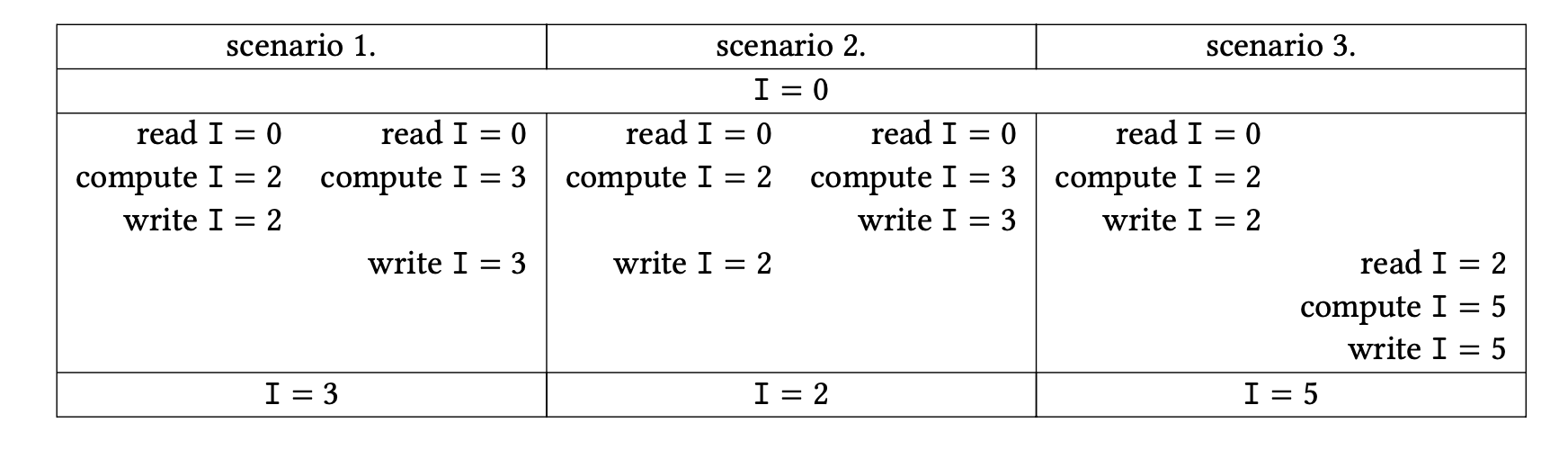
图2.12说明了三种情况。这种情况下,最终结果取决于哪个线程先执行,被称为「竞争条件」(race condition)或「数据竞争」(data race)。一个正式的定义是:如果有两个语句$S_1$,$S_2$,数据竞争为
- 两个语句之间不存在因果关系
- 都是访问一个位置$L$;并且
- 至少有一个访问是写操作。
这种冲突性更新的一个非常实际的例子是内积计算。
1 | for (i=0; i<1000; i++) |
这里的乘积是真正独立的,所以我们可以选择让循环迭代并行进行,例如由它们自己的线程进行。然而,所有的线程都需要更新同一个变量的总和。
无论是串行执行还是线程执行,代码的行为都是一样的,这叫做「线程安全」(thread safe)。从上面的例子可以看出,缺乏线程安全通常是由于对共享数据的处理。这意味着程序越是使用本地数据,它是线程安全的机会就越大。不幸的是,有时线程需要写到共享/全局数据,例如,当程序进行「规约」(reduction)时。
解决这个问题的方法基本上有两种。一种是,我们将共享变量的这种更新宣布为代码的「临界区」(critical section)。这意味着临界区的指令(在内积的例子中,”从内存中读取和,更新,写回内存”)一次只能由一个线程来执行。特别是,它们需要完全由一个线程执行,然后其他线程才能启动它们,所以上面的模糊问题不会出现。当然,上述代码片段非常常见,以至于像OpenMP这样的系统有专门的机制来处理它,把它声明为一个减少操作。
例如,临界区可以通过信号机制[47]来实现。在每个临界区的周围,会有两个原子操作控制着一个信号灯,即一个信号柱。第一个遇到信号灯的进程将降低信号灯,并开始执行临界区。其他进程看到已经降低的信号灯,并等待。当第一个进程完成临界区时,它执行第二条指令,提高信号灯,允许其中一个等待的进程进入临界区。
解决共享数据的共同访问的另一种方法是在某些内存区域设置一个临时「锁」(lock)。如果对临界区的共同执行是可能的,例如,如果它实现了对数据库或哈希表的写入,那么这种解决方案可能是比较好的。在这种情况下,一个进程进入临界区将阻止任何其他进程写入数据,即使他们可能是写入不同的位置;那么锁定被访问的特定数据项是一个更好的解决方案。
锁的问题是,它们通常存在于操作系统层面。这意味着它们的速度相对较慢。由于我们希望上述内积循环的迭代能以浮点单元的速度执行,或者至少以内存总线的速度执行,所以这是不可接受的。
这方面的一个实现是「事务内存」(transactional memory),硬件本身支持原子操作;这个术语来自于数据库事务,它有一个类似的完整性问题。在交易型内存中,一个进程将执行正常的内存更新,除非处理器检测到与另一个进程的更新有冲突。在这种情况下,更新(”事务”)被取消并重新尝试,一个处理器锁定内存,另一个处理器等待锁定。这是一个优雅的解决方案;然而,取消事务可能会带来一定的「流水线冲洗」(pipeline flushing)和缓存线失效的代价。
内存模型和串行一致性
上面提到的竞争条件现象意味着一些程序的结果可能是非确定性的,这取决于指令的执行顺序。还有一个因素在起作用,它被称为处理器和/或语言使用的「内存模型」(memory model)[2]。内存模型控制一个线程或内核的活动如何被其他线程或内核看到。
例如,考虑
初始:A=B=0;,然后
进程1:A=1;x=B。
进程2:B=1;y=A。
如上所述,我们有三种情况,我们通过给出一个全局性的语句序列来描述这些情况。
| 场景 1. | 场景 2. | 场景 3. |
|---|---|---|
| $A\leftarrow 1$ | $A\leftarrow 1$ | $B\leftarrow 1$ |
| $x\leftarrow B$ | $B\leftarrow 1$ | $y\leftarrow A$ |
| $B\leftarrow 1$ | $x\leftarrow B$ | $A\leftarrow 1$ |
| $y\leftarrow A$ | $y\leftarrow A$ | $x\leftarrow B$ |
| $x=0, y=1$ | $x=1, y=1$ | $x=1, y=0$ |
(在第二种情况下,语句1,2和3,4都可以颠倒过来,但结果不会改变。)
这三种不同的结果可以被描述为是由尊重局部排序的状态要素的全局排序来计算的。这被称为「串行一致性」(sequential consistency):并行的结果与顺序执行是一致的,该顺序执行将并行计算交错进行,尊重它们的本地语句排序。
保持串行一致性的代价是很昂贵的:它意味着对一个变量的任何改变都需要立即在所有其他线程上可见,或者对一个线程上的变量的任何访问都需要咨询所有其他线程。
在一个「松弛内存模型」(relaxed memory model)中,有可能会得到一个不符合顺序的结果。假设在上面的例子中,编译器决定对两个进程的语句重新排序,因为读写是独立的。实际上,我们得到了第四种情况。
| 场景 4. |
|---|
| $x\leftarrow B$ |
| $y\leftarrow A$ |
| $A\leftarrow 1$ |
| $B\leftarrow 1$ |
| $x=0, y=0$ |
导致结果$𝑥=0$,$𝑦=0$,这在上面的串行一致模型下是不可能的。(有寻找这种依赖关系的算法[127])。串行一致意味着
1 | integet n |
效果应该与下述相同
1 | n=0 |
有了串行一致性,就不再需要声明原子操作或临界区;然而,这对模型的实现提出了强烈的要求,所以可能导致代码的低效。
亲和性
线程编程非常灵活,可以根据需要有效地创建并行性。然而,本书的很大一部分内容是关于科学计算中数据移动的重要性,在线程编程中不能忽视这一方面。
在多核处理器的背景下,任何线程都可以被安排到任何核上,这没有什么直接的问题。然而,如果你关心的是高性能,这种灵活性会带来意想不到的代价。你想让某些线程只在某些核心上运行,有各种原因。由于操作系统允许迁移线程,可能你只是想让线程留在原地。
- 如果一个线程迁移到不同的核心,而该核心有自己的缓存,你就会失去原来的缓存内容,不必要的内存转移就会发生。
- 如果一个线程迁移了,没有什么可以阻止操作系统把两个线程放在一个核心上,而让另一个核心完全不使用。这显然导致了不太完美的速度提升,即使线程的数量等于核心的数量。
我们称亲和性为「线程亲和性」(thread affinity)或「进程亲和性」(process affinity)与核心之间的映射。亲和性通常表示为一个掩码:对允许一个线程运行的位置的描述。例如,考虑一个双插槽的节点,每个插槽有四个核心。有了两个线程和插槽的亲和力,我们就有了以下的「关联掩码」(affinity mask)。
| thread | socket 0 | socket 1 |
|---|---|---|
| 0 | 0-1-2-3 | |
| 1 | 4-5-6-7 |
对于核心亲和性,面具取决于亲和力类型。典型的策略是 “接近 “和 “扩散”。在亲和关系密切的情况下,掩码可以是
| thread | socket 0 | socket 1 |
|---|---|---|
| 0 | 0 | |
| 1 | 1 |
在同一个插槽上有两个线程意味着它们可能共享一个二级缓存,所以如果它们共享数据,这种策略是合适的。
另一方面,随着「亲和性扩散」(spread affinity),线程被进一步分开。
| thread | socket 0 | socket 1 |
|---|---|---|
| 0 | 0 | |
| 1 | 4 |
这种策略对于带宽受限的应用来说更好,因为现在每个线程都拥有一个插槽的带宽,而不是在 “关闭 “的情况下不得不分享它。
如果分配了所有的内核,关闭和分散策略会导致不同的安排。
| socket 0 | socket 1 |
|---|---|
| 0-1-2-3 | |
| 4-5-6-7 |
相对于
| socket 0 | socket 1 |
|---|---|
| 0-2-4-6 | |
| 1-3-5-7 |
亲和性也可以被认为是一种将执行与数据绑定的策略。
考虑一下这段代码:
1 | for (i=0; i<ndata; i++) // this loop will be done by threads |
第一个循环,通过访问𝑥的元素,将内存带入高速缓存或页表。第二个循环以同样的顺序访问元素,所以为了性能,固定的亲和性是正确的决定。
在其他情况下,固定的映射不是正确的解决方案。
1 | for (i=0; i<ndata; i++) // produces loop |
在这第二个例子中,要么程序必须被改造,要么程序员必须实际维护一个任务队列。
- 第一次接触:从 “把执行放在数据所在的地方 “的角度来考虑亲和性是很自然的。然而,在实践中,相反的观点有时是有意义的。例如,图2.8显示了一个集群节点的共享内存实际上是如何分布的。因此,一个线程可以连接到一个插槽,但数据可以由操作系统分配到任何一个插槽上。操作系统经常使用的机制被称为first-touch策略。
- 当程序分配数据时,操作系统实际上并不创建数据。
- 相反,数据的内存区域是在线程第一次访问它时创建的。
- 因此,第一个接触该区域的线程实际上导致数据被分配到其插槽的内存中。
练习 2.19 用下面的代码解释一下这个问题。
1 | // serial initialization |
关于内存策略的深入讨论,见[134]。
Cilk Plus
还有其他基于线程的编程模型存在。例如,英特尔Cilk Plus(http://www.cilkplus.org/)是一套C/C++的扩展,程序员可以用它创建线程。
1 | //串行代码 |
1 | //Clik 代码 |
在这个例子中,变量rst被两个可能独立的线程更新。这种更新的语义,也就是如何解决同时写入等冲突的精确定义,是由串行一致性定义的;见2.6.1.6节。
超线程与多线程的比较
在上面的例子中,你看到在一个程序运行过程中产生的线程基本上都是执行相同的代码,并且可以访问相同的数据。因此,在硬件层面上,一个线程是由少量的局部变量唯一决定的,比如它在代码中的位置(程序计数器)和它所参与的当前计算的中间结果。
超线程是英特尔的一项技术,让多个线程真正同时使用处理器,这样处理器的一部分将得到最佳利用。
如果一个处理器在执行一个线程和另一个线程之间切换,它将保存一个线程的本地信息,并加载另一个线程的信息。与运行整个程序相比这样做的成本并不高,但与单条指令的成本相比可能很昂贵。因此,超线程不一定能带来性能的提高。
某些架构有对多线程的支持。这意味着硬件实际上对多个线程的本地信息有明确的存储,而且线程之间的切换可以非常快。GPU和英特尔Xeon Phi架构就是这种情况,每个内核可以支持多达四个线程。
OpenMP
OpenMP是对编程语言C和Fortran的一个扩展。它的主要并行方法是循环的并行执行:基于「编译器指令」(compiler directives),预处理器可以安排循环迭代的并行执行。
由于OpenMP是基于线程的,它的特点是「动态并行」(dynamic parallelism):在代码的一个部分和另一个部分之间,并行运行的执行流的数量可以变化。并行性是通过创建并行区域来声明的,例如表明一个循环嵌套的所有迭代都是独立的,然后运行时系统将使用任何可用的资源。
OpenMP不是一种语言,而是对现有的C和Fortran语言的一种扩展。它主要通过在源代码中插入指令来操作,由编译器进行解释。与MPI不同,它也有少量的库调用,但这些不是重点。最后,还有一个运行时系统来管理并行的执行。
与MPI相比,OpenMP的一个重要优势在于它的可编程性:可以从一个串行代码开始,通过「增量并行化」(incremental parallelization)来改造它。相比之下,将串行代码转化为分布式内存MPI程序是一个全有或全无的事情。
许多编译器,如gcc或Intel编译器,支持OpenMP扩展。在Fortran中,OpenMP指令被放在注释语句中;在C中,它们被放在#pragma CPP指令中,用来表示编译器特定的扩展。因此,对于不支持OpenMP的编译器来说,OpenMP代码看起来仍然像合法的C或Fortran语句。程序需要链接到OpenMP运行库,其行为可以通过环境变量来控制。
关于OpenMP的更多信息,见[31]和http://openmp.org/wp/。
OpenMP示例
OpenMP使用的最简单的例子是并行循环。
1 |
|
很明显,所有的迭代都可以独立执行,并且以任何顺序执行。然后,pragma CPP指令将这个事实传达给编译器。
有些循环在概念上是完全并行的,但在实现上不是。
1 | for (i=0; i<ProblemSize; i++) { |
这里看起来好像每个迭代都在向一个共享变量t写和读。然而,t实际上是一个临时变量,是每个迭代的局部。应该是可并行的代码,但由于这样的结构而不能并行,这被称为非线程安全。
OpenMP指出,临时变量对每个迭代都是私有的,如下所示。
1 |
|
如果一个标量确实是共享的,OpenMP有各种机制来处理这个问题。例如,共享变量通常出现在规约操作中。
1 | s = 0; |
正如上面所看到的,串行代码可以较为轻易地并行化。
迭代到线程的分配是由运行时系统完成的,但用户可以指导这种分配。我们主要关注迭代次数多于线程的情况:如果有$P$个线程和$N$个迭代,并且$N > P$,如何将迭代$i$分配给线程?
最简单的分配是使用「Round-robin任务调度」(round-robin task scheduling, a static scheduling),这是一种静态的调度策略,线程$p$获得迭代$p\times (N/P), …, (p + 1) \times (N/P) - 1$。这样做的好处是,如果一些数据在迭代之间被重复使用,它将留在执行该线程的处理器的数据缓存中。另一方面,如果迭代涉及的工作量不同,进程可能会遭受静态调度的负载不均衡。在这种情况下,动态调度策略的效果会更好,每个线程在完成当前迭代后就开始对下一个未处理的迭代进行工作。
我们可以用schedule关键字来控制OpenMP对循环迭代的调度,它的值包括静态和动态。也可以指出一个chunksize,它可以控制一起分配给线程的迭代块的大小。如果省略了chunksize,OpenMP将把迭代分成和线程数量一样多的块。
练习2.20 假设有$t$个线程,代码为
1 | for (i=0; i<N; i++) { |
如果指定chunksize为1,那么迭代0、𝑡、2𝑡……进入第一个线程,1、1+𝑡、1+2𝑡……进入第二个线程,依此类推。讨论一下为什么从性能的角度看这是一个糟糕的策略。提示:查一下「伪共享」(false sharing)的定义。什么是一个好的chunksize?
通过消息传递的分布式内存编程
虽然OpenMP程序和使用其他共享内存范式编写的程序看起来仍然非常像串行程序,但对于消息传递代码来说,情况并非如此。在我们详细讨论消息传递接口(MPI)库之前,我们先来看看并行代码编写方式的这种转变。
分布式编程中的全局视野与局部视野
在观察者看来,一个并行算法与它的实际编程方式之间可能存在明显的差异。考虑这样的情况:我们有一个处理器$\{P_i\}_{i=0…p-1}$的数组,每个处理器包含数组𝑥和𝑦中的一个元素,并且$P_i$计算
这方面的全局描述可以是
每个处理器$𝑃_𝑖$(最后一个除外)都将其$𝑃_𝑖$元素发送给$𝑃_{𝑖+1}$。
除了第一个之外,每个$𝑃_𝑖$处理器都从他们的邻居$𝑃_{𝑖-1}$那里收到一个$𝑥$元素,并且
他们将其添加到自己的$𝑦$元素中。
然而,在一般情况下,我们不能用这些全局术语来编码。在SPMD模型中,每个处理器执行相同的代码,而整体算法是这些单独行为的结果。本地程序只能访问本地数据—其他一切都需要用发送和接收操作来沟通—而且处理器知道自己的编号。
一种可能的写法是
- 如果是第0个处理器,什么都不做;否则从左边接收一个元素,增加一个𝑥元素。
- 如果是最后一个处理器,什么都不做。否则,将我的𝑦元素发送到右边。
首先,我们看一下发送和接收是所谓的「阻塞通信」(blocking communication)的情况:发送指令在实际收到发送的项目之前不会结束,而接收指令则等待相应的发送。这意味着处理器之间的发送和接收必须被仔细配对。现在我们将看到,这可能导致在通往高效代码的路上出现各种问题。
图2.13展示了上述解决方案,我们展示了描述本地处理器代码的局部时间线,以及由此产生的全局行为。你可以看到,处理器不是在同一时间工作的:我们得到的是序列化的执行。
如果我们把发送和接收操作倒过来呢?
- 如果不是最后一个处理器,就把我的𝑥元素发送到右边。
- 如果不是第一个处理器,从左边接收一个𝑥元素,并将其添加到𝑦元素中。
向右边发送数据的算法的局部和结果的全局视野:
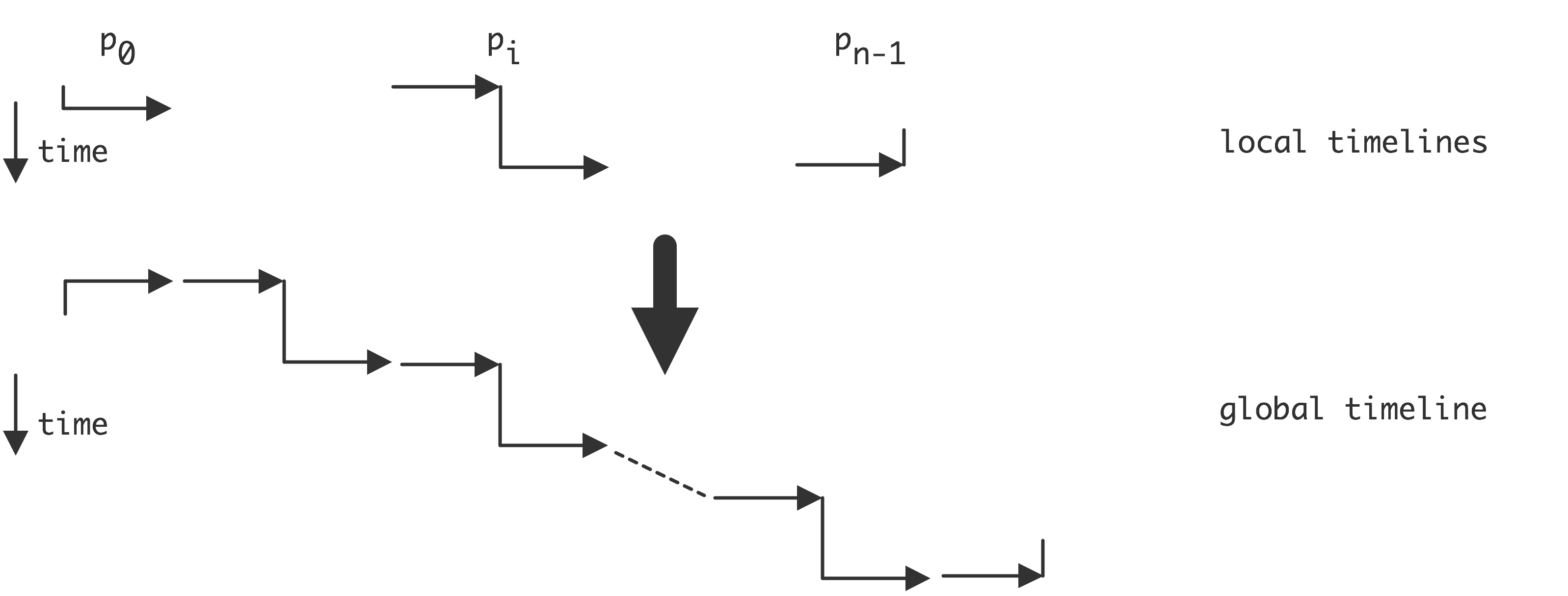
向右边发送数据的算法的局部和结果的全局视野:
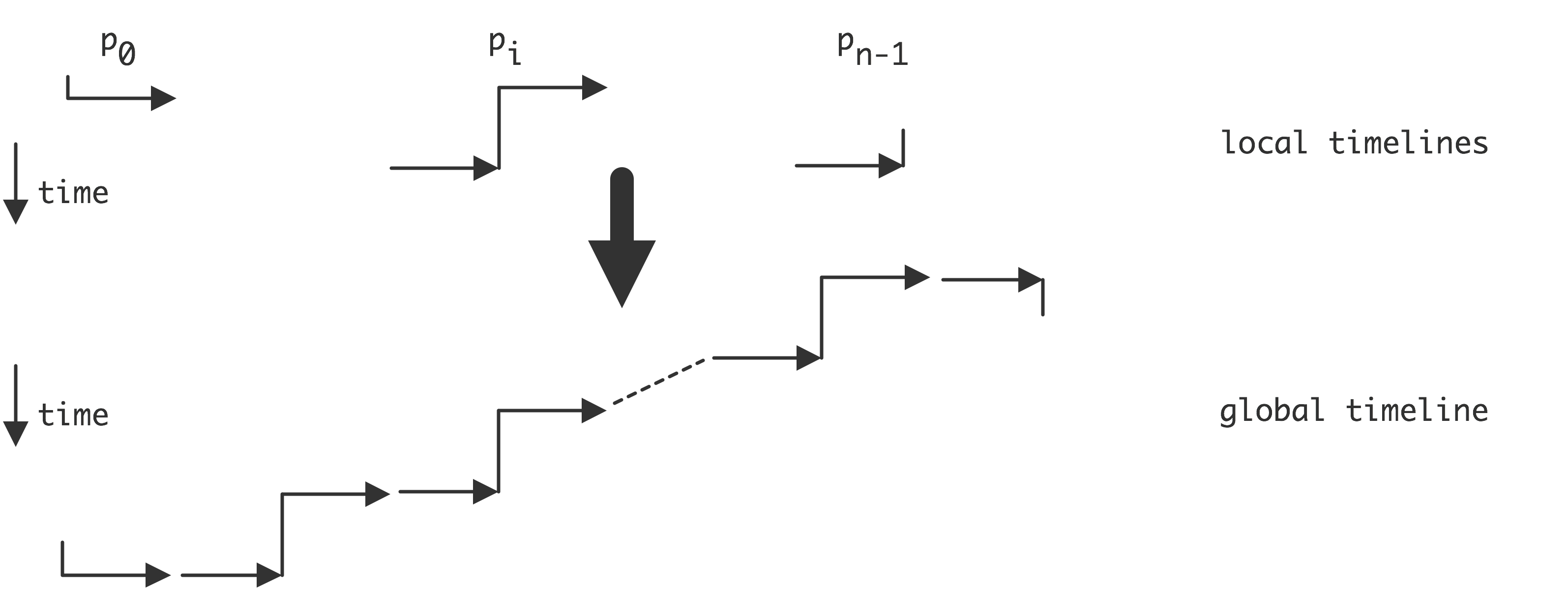
向右边发送数据的算法的局部和结果的全局视图:
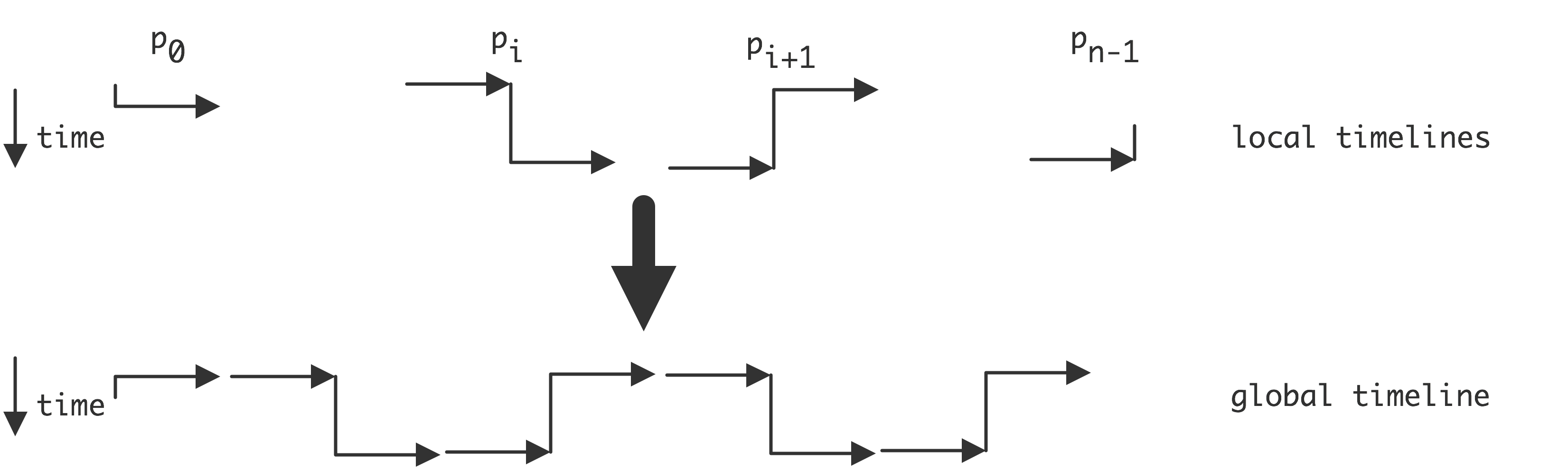
图2.14说明了这一点,你可以看到我们再次得到一个序列化的执行,只不过现在处理器是从右到左激活的。
如果方程2.5中的算法是循环的:
问题会更加严重。现在,最后一个处理器无法开始接收,因为它被阻止向0号处理器发送𝑥𝑛-1。这种情况下,程序无法进展,因为每个处理器都在等待另一个处理器,这被称为「死锁」(deadlock)。
获得高效代码的解决方案是使尽可能多的通信同时发生。毕竟,在算法中没有串行的依赖性。因此,我们对算法的编程如下
- 奇数处理器,先发后收。
- 偶数处理器,先收后发。
图2.15说明了这一点,我们看到现在的执行是并行的。
练习 2.21 再看一下图2.3中的并行规约。其基本动作是 - 接收来自邻居的数据
- 将其添加到自己的数据中
- 将结果发送出去。
正如在图中看到的,至少有一个处理器不发送数据,其他的处理器在发送结果之前可能会做不同次数的接收。编写节点代码,使SPMD程序实现分布式规约。提示:用二进制写每个处理器的编号。该算法使用的步骤数等于该位串的长度。
- 假设一个处理器收到一条消息,用步数表示到该消息的原点的距离。
- 每个处理器最多发送一条消息。用二进制处理器编号来表示发生这种情况的步骤。
阻塞和非阻塞通信
阻断指令的原因是为了防止网络中的数据积累。如果一条发送指令在相应的接收指令开始之前完成,网络将不得不在这段时间内将数据储存在某个地方。考虑一个简单的例子:
1 | buffer = ... ; // 生成一些数据 |
在第一次发送后,我们开始覆盖缓冲区。如果其中的数据还没有被收到,那么第一组数值就必须在网络的某个地方被缓冲,这是不现实的。通过发送操作的阻断,数据会一直留在发送方的缓冲区中,直到它被保证复制到接收方的缓冲区。
解决由阻塞指令引起的顺序化或死锁问题的一个方法是使用「非阻塞通信」(non-blocking communication)指令,其中包括明确的数据缓冲区。使用非阻塞式发送指令,用户需要为每次发送分配一个缓冲区,并检查何时可以安全地覆盖缓冲区。
1 | buffer0 = ... ; // data for processor 0 |
MPI库
如果说OpenMP是对共享内存进行编程的方式,那么消息传递接口(MPI)[184]则是对分布式内存进行编程的标准解决方案。MPI(’Message Passing Interface’)是一个库接口的规范,用于在不共享数据的进程之间移动数据。MPI例程可以大致分为以下几类。
- 进程管理。这包括查询并行环境和构建处理器的子集。
- 点对点通信。这是一组调用,其中两个进程进行交互。这些大多是发送和接收调用的变种。
- 集体调用。在这些程序中,所有的处理器(或整个指定的子集)都参与其中。例如,「广播」(broadcast)调用,一个处理器与其他所有处理器分享它的数据,或者收集调用,一个处理器从所有参与的处理器收集数据。
让我们考虑如何在MPI4中对OpenMP的例子进行编码。首先,我们不再分配
1 | double a[ProblemSize]; |
而是分配
1 | double a[LocalProblemSize]; |
其中,局部尺寸大约是全局尺寸的$1/P$部分。(实际的考虑决定了是让这个分布尽可能的均匀,还是在某种程度上有偏向)
并行循环是琐碎的并行,唯一的区别是它现在只对一部分数组进行操作。
1 | for (i=0; i<LocalProblemSize; i++) { |
然而,如果循环涉及基于迭代数的计算,我们需要将其映射到全局值。
1 | for (i=0; i<LocalProblemSize; i++) { |
(我们将假设每个进程都以某种方式计算了LocalProblemSize和MyFirstVariable的值)。 本地变量现在自动成为本地变量,因为每个进程都有自己的实例。
1 | for (i=0; i<LocalProblemSize; i++) { |
然而,共享变量更难实现。由于每个进程都有自己的数据,因此必须明确地组装本地计算。
1 | for (i=0; i<LocalProblemSize; i++) { |
“规约”操作将所有的本地值s汇总到一个变量globals中,该变量在每个处理器上都收到一个相同的值。这就是所谓的「集合操作」(collective operation)。
让我们把这个例子变得稍微复杂些
1 | for (i=0; i<ProblemSize; i++) { |
如果有共享内存,我们可以写出以下的并行代码。
1 | for (i=0; i<LocalProblemSize; i++) { |
为了将其转化为有效的分布式内存代码,首先我们要说明,对于i==0 (bleft)和i==LocalProblemSize-1 (bright),bleft和bright需要从不同的处理器获得。我们通过与我们的左邻右舍处理器进行交换操作来做到这一点。
1 | // get bfromleft and bfromright from neighbor processors, then |
获得邻居值的方法如下。首先,我们需要询问我们的处理器编号,这样我们就可以与编号高一低一的处理器开始通信。
1 | MPI_Comm_rank(MPI_COMM_WORLD,&myTaskID); |
这段代码仍有两个问题。首先,sendrecv操作需要对第一个和最后一个处理器进行异常处理。这可以通过以下方式优雅地完成。
1 | MPI_Comm_rank(MPI_COMM_WORLD,&myTaskID); |
练习 2.22 这段代码还存在一个问题:没有考虑到原版、全局的边界条件。请给出解决这个问题的代码。
如果不同的进程需要采取不同的行动,例如,如果一个进程需要向另一个进程发送数据,MPI就会变得复杂。这里的问题是每个进程执行的是同一个可执行文件,所以它需要包含发送和接收指令,根据进程的等级来执行。
1 | if (myTaskID==0) { |
阻塞
尽管MPI有时被称为 “并行编程的汇编语言”,因为它被认为是困难的和明确的,但它并不是那么难学,大量使用它的科学代码就证明了这一点。使MPI使用起来有些复杂的主要问题是缓冲区管理和阻塞语义。
这些问题是相关的,源于这样一个事实:理想情况下,数据不应该同时出现在两个地方。让我们简单考虑一下如果处理器1向处理器2发送数据会发生什么。最安全的策略是处理器1执行发送指令,然后等待处理器2确认数据被成功接收。这意味着处理器1被暂时阻断,直到处理器2实际执行其接收指令,并且数据已经通过网络。这是MPI_Send和MPI_Recv调用的标准行为,据说是使用「阻塞通信」(blocking communication)。
另外,处理器1可以把它的数据放在一个缓冲区里,告诉系统确保它在某个时间点被发送出去,然后再检查缓冲区是否可以重新使用。这第二种策略被称为「非阻塞通信」(non-blocking communication),它需要使用一个临时缓冲区。
集合操作
在上面的例子中,你看到了MPI_Allreduce调用,它计算了一个全局和,并将结果留在每个处理器上。还有一个本地版本MPI_Reduce,它只在一个处理器上计算结果。这些调用是集体操作或集合体的例子。集合运算有
- 「规约」(reduction) : 每个处理器都有一个数据项,这些数据项需要用加法、乘法、最大或最小操作进行算术组合。其结果可以留在一个处理器上,也可以留在所有处理器上,在这种情况下,我们称之为allreduce操作。
- 「广播」(broadcast):一个处理器有一个数据项,所有处理器都需要接收。
- 「收集」(gather):每个处理器都有一个数据项,这些数据项需要被收集到一个数组中,而不需要通过加法等操作将其合并。其结果可以留在一个处理器上,也可以留在所有处理器上,在这种情况下,我们称其为allgather。
- 「散发」(scatter):一个处理器有一个数据项的数组,每个处理器接收该数组的一个片段。
- 「全局」(all-to-all):每个处理器都有一个项目数组,将被分散到所有其他处理器。
集合操作是阻塞的,尽管MPI 3.0(目前只是一个草案)将有非阻塞的集合操作。我们将在第6.1节详细分析集体操作的成本。
非阻塞通信
传统的计算机程序中,指令执行的方式取决于处理器中正在进行的操作,而在并行程序中,情况则较为复杂。一个简单发送操作,例如发送某个缓冲区的数据会导致程序执行停止,直至该缓冲区被另一个处理器安全发送和接收时结束。这种操作被称为「非本地操作」(non-local operation ),因为它依赖于其他进程的行动;这也被称为「阻塞通信」(blocking communication)操作,因为执行将停止以等待某个事件的发生。
阻塞操作的缺点是它们可能导致死锁。在消息传递的上下文中表现为:一个进程正在等待一个从未发生的事件;例如,它可能正在等待接收一个消息,而该消息的发送者正在等待其他事情。如果两个进程互相等待,或者更普遍的情况是,如果你有一个进程的循环,每个进程都在等待循环中的下一个进程,就会发生死锁。例如
1 | if ( /* 为处理器 0 */ ) |
这里的块接收会导致死锁。即使没有死锁,处理器在等待时并没有执行任何操作,也会使其产生大量闲置时间。其优点是可以明确缓冲区何时可以被重用:在操作完成后,可以保证数据在另一端被安全地接收。
可以通过使用非阻塞通信操作来避免阻塞行为,但代价是使缓冲区语义复杂化。一个非阻塞的发送(MPI_Isend)声明需要发送一个数据缓冲区,但随后并不等待相应的接收完成。有第二个操作MPI_Wait,它实际上会阻塞,直到接收完成。这种发送和阻塞的解耦的好处是,现在有可能进行写入。
1 | MPI_ISend(somebuffer,&handle); // 开始发送,且 |
运气好的话,本地操作所花的时间比通信的时间多,这样就完全消除了通信时间。
除了非阻塞的发送,还有非阻塞的接收。一个典型的例子如下:
1 | MPI_ISend(sendbuffer,&sendhandle); |
练习 2.23 再看一下方程(2.6),给出使用非阻塞发送和接收解决问题的伪代码。与阻塞式解决方案相比,这个代码的缺点是什么?
三种版本的MPI对比
第一个MPI标准[164]有一些明显的遗漏,这些遗漏包括在MPI 2标准[91]中。其中之一是关于并行输入/输出:没有为多个进程访问同一个文件提供设施,即使底层硬件允许这样做。一个单独的项目MPI-I/O现在已经被纳入MPI-2标准。我们将在本书中讨论并行I/O。
MPI中缺少的第二个设施是进程管理,尽管它在MPI之前的PVM[50, 73]中就已经存在了:没有办法创建新的进程并让它们成为并行运行的一部分。最后,MPI-2支持单边通信:一个进程将数据放入另一个进程的内存中,而接收进程不做实际接收指令。我们将在下面的2.6.3.8节进行简短的讨论。
在MPI-3中,该标准获得了一些新的特性,如非阻塞集合体、邻接集合体和剖析接口。单边机制也得到了更新。
单边通信
MPI编写匹配发送和接收指令的方式并不理想。首先,它要求程序员两次给出相同的数据描述,一次发送,一次接收调用。其次,如果要避免死锁,它需要对通信进行相当精确的协调;如果使用异步调用的替代方法,程序将会十分繁琐,且需要程序管理大量的缓冲区。最后,它要求接收处理器知道要等待多少个传入的消息,这在不规则的应用中可能很棘手。如果有可能从另一个处理器中提取数据,或者反过来把数据放在另一个处理器上,而不需要另一个处理器明确参与,过程就会轻松很多。
一些硬件上存在的远程直接内存访问(RDMA)支持进一步鼓励了这种编程风格。一个早期的例子是Cray T3E。如今,通过在MPI-2库中的整合,单边通信被广泛使用;2.6.3.7节。
让我们简单看一下MPI-2中的单边通信,以数组值的平均化为例:
MPI并行代码为
1 | // 做一些转换 |
转换要完成的任务很清楚:a_local变量需要在等级较高的处理器上成为左边的变量,而在等级较低的处理器上成为右边的变量。
首先,处理器需要明确声明哪些内存区域可用于单边传输,即所谓的 “窗口”。在这个例子中,这包括处理器上的a_local、左边和右边变量。
1 | MPI_Win_create(&a_local,...,&data_window); |
该代码现在有两个选择:可以将数据推送出去
1 | target = my_tid-1; |
或将其拉入
1 | data_window = a_local; |
如果Put和Get调用是阻塞的,上述代码将具有正确的语义;见2.6.3.4节。然而,单边通信的部分吸引力在于它使通信的表达更加容易,为此,我们假设了一个非阻塞语义。
非阻塞的单边调用的问题是,有必要明确地确保通信成功完成。例如,如果一个处理器在另一个处理器上做了一个单边的put操作,另一个处理器就没有办法检查数据是否已经到达,或者是否已经开始传输。因此,有必要在程序中插入一个全局屏障,每个包都有自己的实现。在MPI-2中,相关调用是MPI_Win_fence例程。这些屏障实际上是将程序的执行分为超骤;见2.6.8节。
另一种形式的单边通信在Charm++包中使用;见2.6.7节。
混合共享/分布式内存计算
现代架构通常是共享和分布式内存的混合体。例如,一个集群在节点层面上是分布式的,但节点上的插槽和内核为共享内存。再往上一层,每个插槽可以有一个共享的L3缓存,但有独立的L2和L1缓存。直观地说,共享和分布式编程技术的混合似乎很清楚,可以提供与架构最匹配的代码。在这一节中,我们将讨论这种混合编程模型,并讨论其功效。
一个常见的集群设置使用分布式内存节点,每个节点包含几个彼此之间共享内存的插槽。这建议使用MPI在节点之间进行通信(节点间通信),使用OpenMP在节点上进行并行化(节点内通信)。在实践中,这实现了以下几点
- 在每个节点上启动一个MPI进程(而不是每个核心一个)。
- 这一个MPI进程然后使用OpenMP(或其他线程协议)来产生尽可能多的线程,这些线程在节点上有独立的套接字或核心。
- 然后,OpenMP线程可以访问节点的共享内存。
另一种方法是在每个核或插槽上有一个MPI进程,通过消息传递进行通信,甚至可以看到进程之相同的共享内存。
注释 9:由于亲和性的原因,我们希望每个插槽启动一个MPI进程,而不是每个节点。这并没有实质性地改变上述论点。
这种混合策略听起来是个好主意,但事实上却很复杂。
尽管MPI进程之间消息传递看起来比共享内存的通信开销更大,但当MPI的优化版本检测进程在同一个节点时,就会采取时间开销更小的数据拷贝以代替通信。不使用MPI的唯一理由是:每个进程都有自己的数据空间,这会因为每个进程都要为缓冲区和被复制的数据分配空间而造成内存开销。
线程更加灵活:如果代码的某一部分需要每个进程有更多的内存,那么OpenMP方法可以限制这一部分的线程数量。另一方面,对线程的灵活处理会产生一定的操作系统开销,而MPI的固定进程是没有这种开销的。
共享内存编程在概念上很简单,但也会有意想不到的性能隐患。例如,现在两个进程的性能可能会因为需要维持缓存一致性和虚假共享而受到阻碍。
另一方面,混合方法提供了一些优势,因为它捆绑了消息。例如,如果一个节点上的两个MPI进程分别向另一个节点上的两个进程发送消息,就会有四条消息;在混合模型中,这些消息将被捆绑成一条消息。
练习 2.24 分析上面最后一项的讨论。假设两个节点之间的带宽只够一次维持一条消息。与纯分布式模型相比,混合模型的成本节约是多少?提示:分别考虑频带宽度和延时。
这种MPI进程的捆绑可能有一个更深层次的技术原因的优势。为了支持握手协议,每个MPI进程需要为每个其他进程提供少量的缓冲空间。在进程数量较多的情况下,这可能是一个限制,因此在英特尔Xeon Phi等高核数处理器上,捆绑是有吸引力的。
MPI库中明确指出了其支持的线程类型:是否完全支持多线程、是否所有的MPI调用都必须来自一个线程或一次一个线程,或者在从线程进行MPI调用时是否有完全的自由。
并行语言
缓解并行编程困难的一个方法是设计出对并行性提供明确支持的语言。下面列举了一些方法:
一些语言反映了科学计算中的许多操作是数据并行的(第2.5.1节)。诸如高性能Fortran(HPF)(第2.6.5.3节)等语言有一个数组语法,其中数组的加法等操作可以表示为$A=B+C$。这种语法简化了编程,但更重要的是,它在一个抽象的层次上指定了操作,这样下层就可以对如何处理并行作出具体决定。然而,HPF中表达的数据并行只是最简单的一种,即数据包含在常规数组中。不规则的数据并行比较困难;Chapel语言(第2.6.5.5节)试图解决这个问题。
并行语言中的另一个概念,不一定与前者正交,是分区全局地址空间(PGAS)模型:只有一个地址空间(与MPI模型不同),但这个地址空间是分区的,每个分区与线程或进程有亲和力。因此,这个模型包含了SMP和分布式共享内存。一种典型的PGAS语言,统一并行C(UPC),允许你编写程序,在大多数情况下看起来像普通的C代码。然而,通过指出主要阵列在处理器上的分布方式,程序可以被并行执行。
讨论
并行语言有希望使并行编程变得更容易,因为它们使通信操作看起来像简单的复制或算术操作。然而,通过这样做,它们邀请用户编写可能并不高效的代码,例如,通过诱导许多小信息。
作为一个例子,考虑将数组a,b在处理器上进行水平分割,并进行移位(见图2.16)。
1 | for (i=0; i<N; i++) |
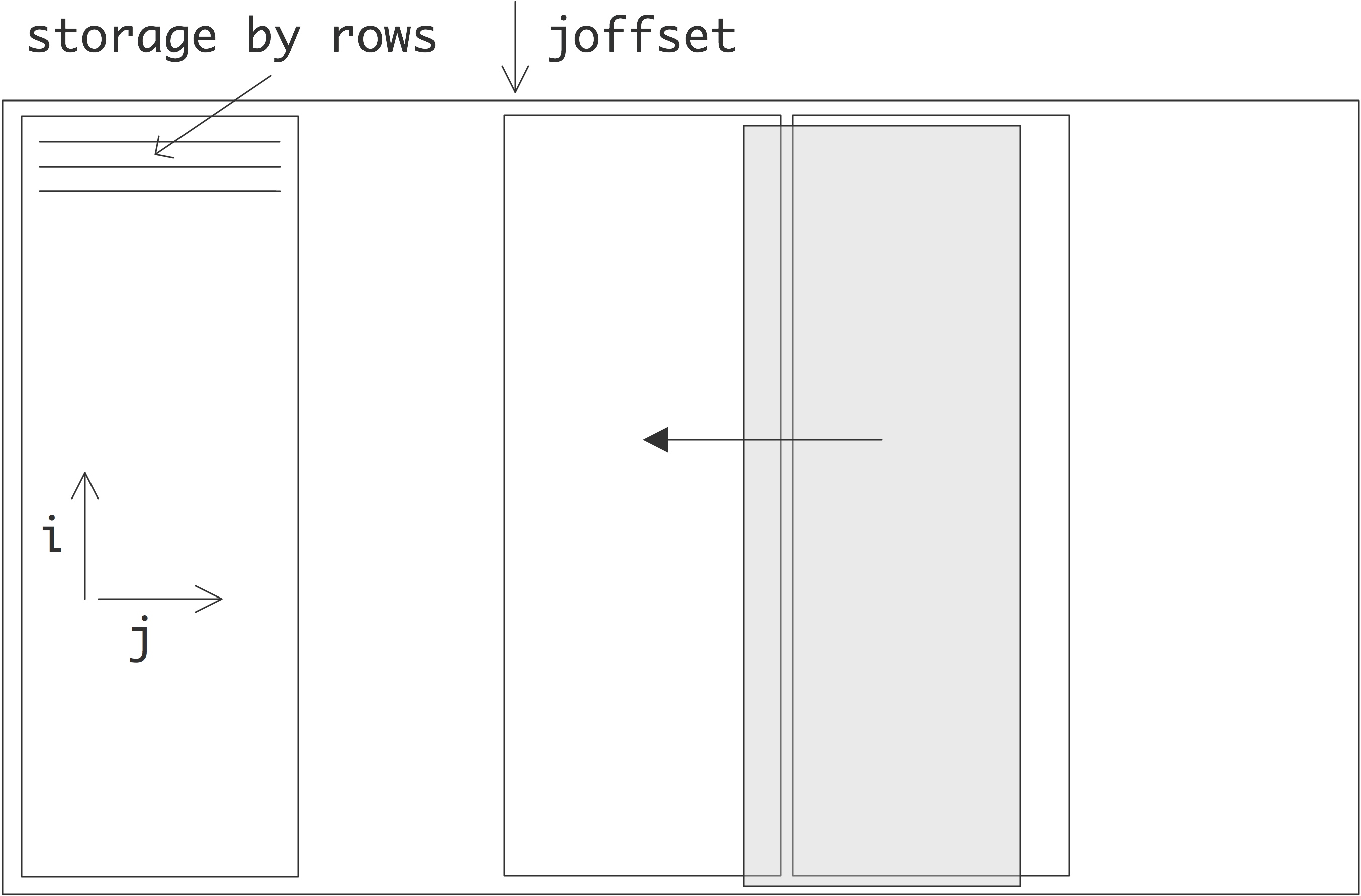
如果这段代码在共享内存机器上执行,它将是高效的,但在分布式情况下的天真翻译将在$i$循环的每个迭代中传达一个数字。显然,这些都可以结合在一个缓冲区的发送/接收操作中,但编译器通常无法进行这种转换。因此,用户被迫,实际上,重新实现了需要在MPI实现中完成的阻塞。
1 | for (i=0; i<N; i++) |
另一方面,某些机器通过全局内存硬件支持直接内存拷贝。在这种情况下,PGAS语言可以比显式消息传递更有效率,即使是物理分布式内存。
Unified Parallel C
统一并行C(UPC)[191]是C语言的一个扩展。它的主要并行来源是数据并行,编译器发现了数组上操作的独立性,并将其分配给不同的处理器。该语言有一个扩展的数组声明,允许用户指定数组是按块划分,还是以轮流方式划分。
下面的UPC程序执行了一个向量与向量加法。
1 | //vect_add.c |
同样的程序有一个明确的并行循环结构
1 | //vect_add.c |
在含义上与UPC相当,但基于Java而不是C。
High Performance Fortran
高性能Fortran5(HPF)是Fortran90的一个扩展,具有支持并行计算的结构,由高性能Fortran论坛(HPFF)发布。HPFF由莱斯大学的Ken Kennedy召集并担任主席。HPF报告的第一个版本发表于1993年。
在Fortran 90引入的数组语法的基础上,HPF使用数据并行计算模型来支持将单个数组计算的工作分散到多个处理器上。这使得在SIMD和MIMD风格的架构上都能有效地实现。HPF的特点包括。
新的Fortran语句,如FORALL,以及创建PURE(无副作用)程序的能力。
使用编译器指令来推荐阵列数据的分布。
用于与非HPF并行程序接口的外在程序接口,如那些使用消息传递。
额外的库例程,包括环境查询、并行前缀/后缀(例如,’扫描’)、数据散射和排序操作。
Fortran 95整合了几个HPF功能。虽然一些供应商在20世纪90年代确实将HPF纳入了他们的编译器中,但有些方面被证明是难以实现的,而且用途值得怀疑。从那时起,大多数供应商和用户都转向了基于OpenMP的并行处理。然而,HPF仍然有影响。例如,为即将到来的Fortran-2008标准提出的BIT数据类型包含了许多直接来自HPF的新的内在函数。
Co-array Fortran
Co-array Fortran(CAF)是Fortran 95/2003语言的一个扩展。支持并行的主要机制是对数组声明语法的扩展,其中一个额外的维度表示并行分布。例如,在
1 | Real,dimension(100),codimension[*] :: X |
数组X,Y在每个处理器上有100个元素。数组Z的行为就像可用的处理器在一个三维网格上,其中两边是指定的,第三边可以调整以适应可用的处理器。
现在处理器之间的通信是通过沿着描述处理器网格的(共)维度的拷贝来完成的。Fortran 2008的标准包括共同数组。
Chapel
Chapel[30]是一种新的并行编程语言6,由Cray公司开发,是DARPA领导的高生产率计算系统计划(HPCS)的一部分。Chapel旨在提高高端计算机用户的生产效率,同时也是一个可移植的并行编程模型,可用于商品集群或桌面多核系统。Chapel致力于极大地提高大规模并行计算机的亲和力,同时匹配或击败当前编程模型(如MPI)的性能和可移植性。
Chapel通过对数据并行、任务并行、并发和嵌套并行的高级抽象支持多线程执行模型。Chapel的locale类型使用户能够指定并重新确定数据和任务在目标架构上的位置,以便对位置进行调整。Chapel支持具有用户定义实现的全局视图数据聚合,允许以自然方式表达对分布式数据结构的操作。与许多以前的高级并行语言相比,Chapel是围绕多分辨率哲学设计的,允许用户最初编写非常抽象的代码,然后逐步增加细节,直到他们接近机器的需要。Chapel通过面向对象的设计、类型推理和通用编程的功能,支持代码重用和快速原型设计。
Chapel是根据第一原则设计的,而不是通过扩展现有的语言。它是一种im-perative块状结构的语言,旨在使C、C++、Fortran、Java、Perl、Matlab和其他流行语言的用户易于学习。虽然Chapel建立在许多以前的语言的概念和语法上,但它的并行功能最直接地受到ZPL、高性能Fortran(HPF)和Cray MTA对C和Fortran的扩展的影响。
下面是Chapel中的向量与向量加法:
1 | const BlockDist= newBlock1D(bbox=[1..m], tasksPerLocale=...); |
Fortress
Fortress[67]是由Sun Microsystems开发的一种编程语言。Fortress7的目的是通过几种方式使平行主义更容易操作。首先,并行性是默认的。这是为了推动工具设计、库设计和程序员技能向并行化方向发展。第二,语言被设计成对并行更友好。不鼓励副作用,因为副作用需要同步化以避免错误。Fortress提供了事务,这样程序员就不会面临确定锁定顺序的任务,或者调整他们的锁定代码,以便有足够的正确性,但又不至于妨碍性能。Fortress的循环结构,连同库,把 “迭代 “变成了内部;而不是循环指定如何访问数据,数据结构指定如何运行循环,聚合数据结构被设计成可以有效地安排并行执行的大型部分。Fortress还包括来自其他语言的功能,旨在普遍地帮助提高生产力—测试代码和方法,与被测试的代码相联系;合同,可以在代码运行时选择检查;以及属性,可能运行成本太高,但可以反馈给定理验证器或模型检查器。此外,Fortress还包括安全的语言特性,如检查数组边界、类型检查和垃圾收集,这些在Java中已经被证明是有用的。Fortress的语法被设计为尽可能地类似于数学语法,因此任何人在解决其规范中的数学问题时,都可以写出一个与原始规范明显相关的程序。
X10
X10是一种实验性的新语言,目前正在IBM与学术伙伴合作开发。X10工作是DARPA高生产率计算机系统计划中的IBM PERCS项目(生产性易使用的可靠计算机系统)的一部分。PERCS项目专注于硬件-软件联合设计方法,以整合芯片技术、架构、操作系统、编译器、编程语言和编程工具方面的进展,提供新的可适应、可扩展的系统,在2010年之前将并行应用的开发效率提高一个数量级。
X10旨在通过开发新的编程模型,结合集成到Eclipse中的一套新的工具和新的实现技术,在可管理的运行环境中提供优化的可扩展的并行性,为提高生产率作出贡献。X10是一种类型安全的、现代的、并行的、面向对象的分布式语言,旨在让Java(TM)程序员能够使用。它的目标是未来的低端和高端系统,其节点由多核SMP芯片构成,具有非统一的内存层次,并以可扩展的集群配置互连。作为分区全局地址空间(PGAS)语言家族中的一员,X10强调以地方的形式明确地重新定义位置;体现在async、future、foreach和attach con-结构中的轻量级活动;用于终止检测(finish)和分阶段计算(clocks)的结构;使用无锁同步(原子块);以及对全局数组和数据结构进行操作。
Linda
现在应该很清楚了,数据的处理是迄今为止并行编程最重要的方面,远比算法方面的考虑更重要。编程系统Linda[74, 75],也被称为协调语言,旨在明确地解决数据处理问题。琳达不是一种语言,但是可以,而且已经被纳入其他语言。
琳达的基本概念是元组空间:通过给数据添加一个标签,将其添加到一个全局可访问的信息池中。然后,进程通过标签值来检索数据,而不需要知道是哪个进程将数据添加到元组空间中的。
Linda主要针对的是与高性能计算(HPC)不同的计算模型:它解决的是异步通信进程的需求。然而,它已经被用于科学计算[45]。例如,在热方程的并行模拟中(第4.3节),处理器可以将他们的数据写入元组空间,而相邻的进程可以检索他们的鬼魂重区,而不必知道它的出处。因此,Linda成为实现单边通信的一种方式。
The Global Arrays library
The Global Arrays library(http://www.emsl.pnl.gov/docs/global/)是另一个单边通信的例子,事实上它早于MPI。这个库的主要数据结构是笛卡尔积数组8,分布在相同或更低维度的处理器网格上。通过库的调用,任何处理器都可以通过放或取的操作访问阵列中的任何子砖。这些操作是非集体的。与任何单边协议一样,屏障同步是必要的,以确保发送/接收的完成。
基于操作系统的方法
可以设计一个具有共享地址空间的架构,并让数据移动由操作系统处理。Kendall Square计算机[124]有一个名为 “全缓存 “的架构,其中没有数据与任何处理器直接相关。相反,所有的数据都被认为是缓存在一个处理器上,并根据需要通过网络移动,就像数据从主内存移动到普通CPU的缓存中一样。这个想法类似于目前SGI架构中的NUMA支持。
活跃通信
MPI范式(第2.6.3.3节)传统上是基于双侧操作的:每个数据传输都需要一个明确的发送和接收操作。这种方法对于相对简单的代码来说效果很好,但是对于复杂的问题来说,就很难协调所有的数据移动。简化的方法之一是使用「活跃通信」(active message)。这在Charm++[119]包中被使用。
通过主动消息,一个处理器可以向另一个处理器发送数据,而不需要第二个处理器做明确的接收操作。相反,接收者声明处理传入数据的代码,用客观方向的说法是 “方法”,而发送处理器则用它想发送的数据调用这个方法。由于发送处理器实际上是激活了另一个处理器上的代码,这也被称为「远程调用」(remote method invocation)。这种方法的一个很大的优点是,通信和编译的重叠变得更容易实现。
作为一个例子,考虑用一个三对角矩阵进行矩阵与向量乘法
关于这个问题在PDEs中的起源,见4.2.2节的解释。假设每个处理器正好有一个索引$i$,MPI代码可以是这样的。
1 |
|
有了活跃通信,这看起来就像
1 | void incorporate_neighbor_data(x) { |
批量同步并行
MPI库(2.6.3.3节)可以带来非常高效的代码。这样做的代价是,程序员需要非常详细地说明通信的内容。在光谱的另一端,PGAS语言(第2.6.5节)对程序员的要求很低,但却没有带来多少性能回报。一种试图找到中间地带的方法是「批量同步并行」(Bulk Synchronous Parallel,BSP)模型[192, 183]。在这里,程序员需要写出通信,但不是它们的顺序。
BSP模型将程序排列成一个超步的序列,每个步骤都以一个障碍物同步结束。在一个超步中开始的通信都是异步的,并依靠屏障来完成。这使得编程更容易,并消除了死锁的可能性。
此外,所有通信都是单边通信类型。
练习 2.25 考虑2.1节中的并行求和例子。论证BSP的实现需要$\log_2n$超步。
由于其通过障碍物完成超级步骤的处理器的同步,BSP模型可以对并行算法做一个简单的成本分析。
BSP模型的另一个方面是它对问题的「过度分解」(overdecomposition),即把多个进程分配给每个处理器,以及「随机放置」(random placement)数据和任务。这是以统计学的论点为依据的,表明它可以补救负载的不均衡。如果有$𝑝$个处理器,如果在一个超步中进行了$𝑝$次远程访问,那么很可能有些处理器会收到$\log𝑝/\log \log 𝑝$次访问,而其他处理器则没有收到。因此,负载不均衡的问题会随着处理器数量的增加而变得更加严重。另一方面,如果有$𝑝\log p$的访问,例如因为每个处理器上有$\log 𝑝$的进程,最大的访问次数是$3\log 𝑝$,而且概率很大。这意味着负载平衡是在一个完美的恒定系数内。
BSP模型是在BSPlib[107]中实现的。其他系统可以说是类似BSP的,因为它们使用了超步的概念;例如,谷歌的Pregel[150]。
数据依赖
如果两个语句引用了相同的数据项,我们就说这些状态之间存在着「数据依赖」(data dependency)关系。这种依赖关系限制了语句的执行可以被重新安排的程度。对这一主题的研究可追溯到20世纪60年代,当时处理器可以不按串行执行语句以提高吞吐量。语句的重新排序受到了限制,因为执行必须遵守程序的「串行语义」(program order):结果必须像语句严格按照它们在程序中出现的串行执行一样。
语句排序以及因此而产生的数据依赖性的问题,以几种方式出现:
- 并行化编译器必须对资源进行分析,以确定允许哪些转换。
- 如果你用OpenMP指令并行化一个顺序代码,你必须自己进行这样的分析。
这里有两种需要进行这种分析的活动:
当一个循环被并行化时,迭代不再按其程序顺序执行,所以我们必须检查依赖关系。
引入任务是指程序的某些部分可以按照与顺序执行不同的顺序执行。
依赖性分析的最简单的情况是检测循环迭代是否可以独立执行。如果一个数据项在两个不同的迭代中被读取,迭代当然是独立的,但是如果同一个项目在一个迭代中被读取,在另一个迭代中被写入,或者在两个不同的迭代中被写入,我们需要做进一步分析。
数据依赖性的分析可以由编译器来执行,但是编译器必须采取一种保守的方法。这意味着迭代可能是独立的,但不能被编译器所识别。因此,OpenMP把这个责任转移给了程序员。
现在,我们将详细讨论数据依赖的细节。
数据依赖类型
这三种类型的依赖关系是
- 「流依赖」(flow dependencies),或 “读后写”。
「反依赖」(anti dependencies),即 “读后写”;以及
「输出依赖」(output dependencies),即 “写完再写”。
这些依赖关系可以在标量代码中进行研究,事实上编译器也是这样做的,以确定语句是否可以重新排列,但是我们将主要关注它们在循环中的出现,因为在科学计算中很多工作都出现在这里。
- 流依赖:如果读和写发生在同一个循环迭代中,那么流量依赖,或者说读-写,就不是一个问题。
1 | for (i=0; i<N; i++) { |
另一方面,如果读取发生在后来的迭代中,就没有简单的方法来并行化或向量化循环。
1 | for (i=0; i<N; i++) { |
这通常需要重写代码。
练习 2.26 考虑如下代码
1 | for (i=0; i<N; i++) { |
其中f()和g()表示没有进一步依赖x或i的算术表达式。
- 反依赖性:反依赖性或读后写的最简单情况是减少。
1 | for(i=0; i<N; i++){ |
这可以通过明确声明循环是一个减法来处理,或者使用6.1.2节中的任何其他策略。
如果读和写是在一个数组上,情况就更复杂了。这个片段中的迭代
1 | for (i=0; i<N; i++) { |
不能像这样以任意顺序执行。然而,从概念上讲,这并不存在依赖性。我们可以通过引入一个临时数组来解决这个问题。
1 | for (i=0; i<N; i++) |
这是一个编译器不太可能执行的转换的例子,因为它可能会大大影响程序的内存需求。因此,这就留给了程序员。
- 输出依赖:输出依赖或写后依赖的情况本身不会发生:如果一个变量被依次写了两次,中间没有读,那么第一次写可以被删除而不改变程序的意义。因此,这种情况会减少为流动依赖。
其他的输出依赖也可以被移除。在下面的代码中,t可以被声明为私有,从而消除了依赖性。
1 | for (i=0; i<N; i++) { |
如果想要t的最终值,可以在OpenMP中使用lastprivate。
嵌套循环的并行化
在上述例子中,如果在一个循环的迭代$𝑖$中出现了不同的指数,如$𝑖$和$𝑖+1$,那么数据的依赖性就是非实质性的。反之,循环如
1 | for (int i=0; i<N; i++) |
是简单的并行化。然而,嵌套的循环则需要更多的思考。OpenMP有一个 “折叠 “指令,用于诸如以下的循环
1 | for (int i=0; i<M; i++) |
这里,整个$i$,$j$迭代空间是并行的。这是怎么回事?
1 | for (n = 0; n < NN; n++) |
练习 2.27 对这个循环做一个重用分析。假设a,b,c不能一起放进缓存。现在假设c和b的一行可以放入缓存,并且还有一点空间。你能找到一个能使性能大大提高的循环交换吗?写一个测试来证实这一点。
分析这个循环嵌套的并行性,你会发现j循环是一个减法,而n循环有流量依赖:每个a[i]在每个n次迭代中被更新。结论是,你只能合理地并行化$i$环路。
练习 2.28 这个并行性分析与练习2.27中的循环交换有什么关系?交换后的循环是否仍然是可并行的?
如果你会说OpenMP,请通过编写将a的元素相加的代码来确认你的答案,无论交换和引入OpenMP并行性,你都应该得到同样的答案。
并行程序设计
很久以前,人们认为编译器和运行时系统的某种神奇组合可以将现有的顺序程序转化为并行程序。这种希望早已破灭,所以现在的并行程序从一开始就被写成了并行程序。当然,有不同类型的并行性,它们对你如何设计你的并行程序都有各自的影响。在这一节中,我们将简要地探讨其中的一些问题。
并行数据结构
并行程序设计中的一个问题是使用数组结构(Array-Of-Structures,AOS)与结构化数组(Structure-Of-Arrays,SOA)。在正常的程序设计中,我们经常定义一个结构
1 | struct { int number; double xcoord,ycoord; } _Node; |
而如果需要许多这样的结构,我们就创建一个这样的结构数组。
1 | Node *nodes = (Node*) malloc( n_nodes*sizeof(struct _Node) ); |
这就是AOS的设计。
现在,假设我们想将一个操作并行化
1 | void shift(Node the_point,Vector by) { |
这是在一个循环中完成的
1 | for (i=0; i<n_nodes; i++) { |
这段代码具有MPI编程的正确结构(2.6.3.3节),每个处理器都有自己的本地节点数组。这个循环也很容易用OpenMP并行化(第2.6.2节)。
然而,在20世纪80年代,人们意识到AOS的设计并不适合向量计算机,因此不得不对代码进行大幅重写。在这种情况下,我们的操作数需要是连续的,所以代码必须采用SOA设计。
1 | node_numbers = (int*) malloc( n_nodes*sizeof(int) ); |
而将迭代
1 | for (i=0; i<n_nodes; i++) { |
最初的SOA设计最适合于分布式内存编程吗,这意味着在向量计算机时代的10年后,每个人都必须为集群重新编写他们的代码。当然,如今随着SIMD宽度的增加,我们也需要部分地回到AOS的设计。(在英特尔的ispc项目中,有一些实验性的软件支持这种转变,http: //ispc.github.io/,它将SPMD代码翻译成SIMD)。
延迟隐蔽性
处理器之间的通信通常很慢,比单个处理器上的内存数据传输要慢,而且比对数据的操作要慢得多。因此在设计一个并行程序时,最好考虑到网络流量与 “有用 “操作的相对数量。每个处理器必须有足够的工作来抵消通信。
应对通信相对缓慢的另一种方法是安排程序,使通信实际发生在一些计算正在进行的时候。这被称为通信的「重叠计算」(overlapping computation with communication)或「延迟隐藏」(latency hiding)。
例如,考虑矩阵与向量乘积$𝑦=𝐴$的并行执行。假设向量是分布式的,那么每个处理器$𝑝$都会执行
由于$𝑥$也是分布式的,我们可以将其写为
这个方案如图2.17所示。我们现在可以按以下方式进行。
- 开始转移$𝑥$的非本地元素。
- 在数据传输过程中,对$𝑥$的本地元素进行操作。
- 确保传输完成。
- 对$𝑥$的非本地元素进行操作。
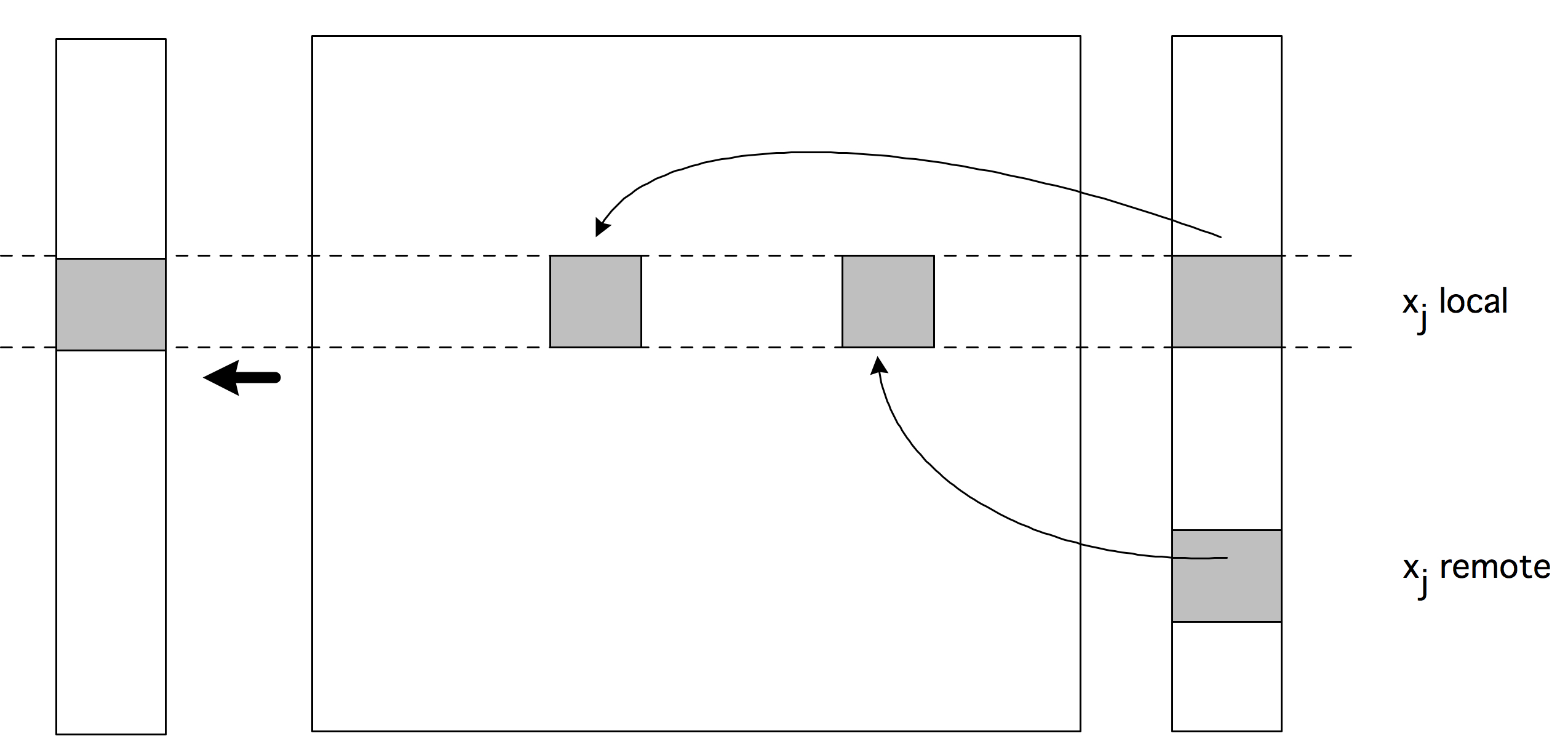
练习 2.29 你能从计算和通信的重叠中获得多少好处?提示:考虑计算耗时为零且只有通信的边界情况,以及相反的情况。现在考虑一般情况。
当然,这种情况的前提是有软件和硬件对这种重叠的支持。MPI允许这样做(见2.6.3.6节),通过所谓的异步通信或非阻塞通信例程。这并不立即意味着重叠将实际发生,因为硬件支持是一个完全独立的问题。
拓扑
如果一些处理器一起工作在一个任务上,他们很可能需要交流数据。由于这个原因,需要有一种方法使数据从任何一个处理器到其他处理器。在本节中,我们将讨论一些可能的方案来连接并行机器中的处理器。这种方案被称为(处理器)「拓扑」(topology)。
为了明确这里的问题,请考虑两个不能 “扩展 “的简单方案。
以太网是一种连接方案,网络上的所有机器都在一条电缆上(见下文注释)。如果一台机器在电线上放了一个信号来发送信息,而另一台机器也想发送信息,那么后者将检测到唯一可用的通信通道被占用,它将等待一段时间后再重新进行发送操作。在以太网上接收数据是很简单的:信息包含了目标接收者的地址,所以一个处理器只需要检查电线上的信号是否是为它准备的。
这个方案的问题应该很清楚。通信通道的容量是有限的,所以当更多的处理器连接到它时,每个处理器可用的容量将下降。由于解决冲突的方案,信息开始前的平均延迟也会增加。
在完全连接的配置中,每个处理器都有一条与其他处理器通信的线路。
其他处理器。这种方案是完美的,因为消息可以在最短的时间内发送,而且两个消息永远不会互相干扰。一个处理器可以发送的数据量不再是处理器数量的递减函数;事实上,它是一个递增函数,如果网络控制器可以处理,一个处理器甚至可以同时进行多次通信。
当然,这个方案的问题是,一个处理器的网络接口的设计不再是固定的:随着更多的处理器被添加到并行机器上,网络接口得到更多的连接线。网络控制器也同样变得更加复杂,机器的成本增加速度超过了处理器数量的线性增长。
注释 10 以上对以太网的描述是对原始设计的描述。随着交换机的使用,特别是在HPC的背景下,这种描述已经不再真正适用。
最初人们认为,信息碰撞意味着以太网将不如其他解决方案,如IBM的令牌环网,它明确地防止碰撞。需要相当复杂的统计分析来证明,以太网的工作原理比朴素预期好得多。
在本节中,我们将看到一些可以增加到大量处理器的方案。
图论
互联并行计算机中的处理器的网络可以方便地用一些基本的图论概念来描述。我们用一个图来描述并行机器,每个处理器都是一个节点,如果两个节点之间有直接的联系,那么这两个节点就是相连的。(我们假设连接是对称的,所以网络是一个无向图)
下面分析图的两个重要概念。
首先,图中一个节点的程度是它所连接的其他节点的数量。节点代表处理器,边代表导线,很明显,高度不仅是计算效率所希望的,而且从工程的角度来看也是昂贵的。我们假设所有处理器都有相同的度。
其次,从一个处理器到另一个处理器的信息,通过一个或多个中间节点,很可能在节点之间路径的每个阶段产生一些延迟。由于这个原因,图的直径很重要。直径被定义为任何两个节点之间的最大最短距离,包括链接的数量。
如果$𝑑$是直径,如果在一条线上发送一个信息需要单位时间,这意味着一个信息总是在最多$𝑑$时间内到达。
练习 2.30 找出处理器的数量、它们的程度和连接图的直径之间的关系。
除了 “一个消息从处理器A到处理器B需要多长时间 “的问题外,我们还经常担心两个同时进行的消息之间的冲突:是否存在两个同时进行的消息需要使用同一网络链接的可能性?在图 2.18 中,我们说明了如果每个处理器$𝑝_𝑖$在$i < n/2$ 的情况下向$𝑝_{i+n/2}$ 发送消息会发生什么:会有$n/2$ 的消息试图通过$p_{n/2-1}$ 和$p_n$之间的线路。这种冲突被称为「拥堵」(congestion)或「争夺」(contention)。显然,一台并行计算机的链接越多,发生拥堵的机会就越小。
描述拥堵可能性的一个精确方法是看「二分宽度」(bisection width)。这被定义为将处理器图分割成两个非连接图所必须移除的最小链接数。例如,考虑处理器连接成一个线性阵列,即处理器$P_𝑖$与$P_{i-1}$和$P_{i+1}$连接。在这种情况下,分界线宽度为1。
二分宽度𝑤描述了在一台并行计算机中可以保证有多少信息同时进行。证明:采取𝑤发送和𝑤接收处理器。这样定义的𝑤路径是不相交的:如果不相交,我们只需去除𝑤-1个链接就可以把处理器分成两组。
当然,在实践中,超过$w$条信息可以同时进行。例如,在一个线性阵列中,$w=1$,如果所有的通信都是在邻居之间,如果一个处理器在任何时候都只能发送或接收,而不能同时发送和接收,则可以同时发送和接收𝑃/2条信息。如果处理器可以同时发送和接收,那么网络中可以有𝑃个信息正在进行。
二分宽度也描述了网络中的「冗余度」(redundancy):如果一个或多个连接出现故障,信息是否仍能从发送方找到接收方?
虽然二分宽度是一种表示导线数量的措施,但实际上我们关心的是通过导线的容量。这里的相关概念是「二分带宽」(bisection bandwidth):横跨分节宽度的带宽,是分节宽度与导线容量(以每秒比特为单位)的乘积。二分带宽可以被认为是衡量任意一半处理器与另一半处理器进行通信所能达到的带宽。二分带宽是一个比有时引用的总带宽更现实的衡量标准,它被定义为每个处理器都在发送时的总数据率:处理器的数量乘以连接的带宽乘以一个处理器可以执行的同时发送的数量。这可能是一个相当高的数字,而且它通常不能代表实际应用中实现的通信速率。
总线
我们考虑的第一个互连设计是让所有的处理器位于同一内存总线上。这种设计将所有处理器直接连接到同一个内存池,因此它提供了一个UMA或SMP模型。
使用总线的主要缺点是可扩展性有限,因为每次只有一个处理器可以进行内存访问。为了克服这个问题,我们需要假设处理器的速度比内存慢,或者处理器有缓存或其他本地内存来操作。在后一种情况下,通过让处理器监听总线上的所有内存流量,维持缓存一致性是很容易的,这个过程被称为「监听」(snooping)。
线性阵列和环状网络
连接多个处理器的一个简单方法是将它们连接成一个「线性阵列」(linear array):每个处理器都有一个编号$i$,处理器$P_i$与$P_{i-1}$和$P_{i+1}$相连。第一个和最后一个处理器是可能的例外情况:如果它们相互连接,我们称该架构为环状网络(ring network)。
这个方案要求每个处理器有两个网络连接,所以设计相当简单。
练习2.31 线性阵列的二分宽度是什么?环状网络的二分宽度是什么?
练习2.32 由于线性数组的连接有限,你可能必须对并行算法进行巧妙的编程。例如,考虑一个 “广播 “操作:处理器0有一个数据项需要发送给其他每个处理器。
我们做了以下简化的假设。
一个处理器可以同时发送任意数量的信息。
但一条线一次只能携带一条信息;然而。
任何两个处理器之间的通信都需要单位时间,不管它们之间有多少个处理器。
在一个「全连接」(fully connected)的网络或一个「星型」(star)网络中,你可以很容易地写出:
1 | for 𝑖 = 1 ... 𝑁 − 1: |
假设一个处理器可以发送多个消息,即操作是一步到位的。现在考虑一个线性阵列。说明即使有这种无限的发送能力,上述算法也会因为拥堵而遇到麻烦。
请你尝试找到一个更好的方法来组织发送操作。提示:假装你的处理器是以二叉树的形式连接的。假设有$𝑁=2^n-1$个处理器。证明广播可以在对数$N$个阶段内完成,并且处理器只需要能够同时发送一条信息即可。
这个练习是一个将 “逻辑 “通信模式嵌入物理模式的例子。
二维和三维阵列、环面
一种流行的并行计算机设计是将处理器组织在一个二维或三维的「笛卡尔网状」(Cartesian mesh)网络中。这意味着每个处理器都有一个坐标$(i, j)$或$(i, j, k)$,并且它在所有坐标方向上都与邻居相连。处理器的设计还是相当简单的:网络连接的数量(连接图的度数)是网络的空间维数(2或3)的两倍。
拥有二维或三维网络是一个相当自然的想法,因为我们周围的世界是三维的,而且计算机经常被用来模拟现实生活的现象。如果我们暂时接受物理模型需要近邻型通信(我们将在第4.2.3节看到这种情况),那么网状计算机是运行物理模拟的自然候选者。
练习2.33 $n \times n \times n$处理器的三维立方体的直径是多少?二分宽度是多少?如果增加环绕环状的连接,会有什么变化?
练习 2.34 你的并行计算机的处理器被组织成一个二维网格。芯片制造商推出了一种具有相同时钟速度的新芯片,它是双核的,而不是单核的,而且可以装在现有的插槽上。批评以下论点:”每秒钟可以完成的工作量(不涉及通信)增加了一倍;由于网络保持不变,二分带宽也保持不变,所以我可以合理地期望我的新机器变得两倍快”。
基于网格的设计通常有所谓的环绕或环形连接,它连接二维网格的左右两边,以及顶部和底部。这在图2.19中有所说明。
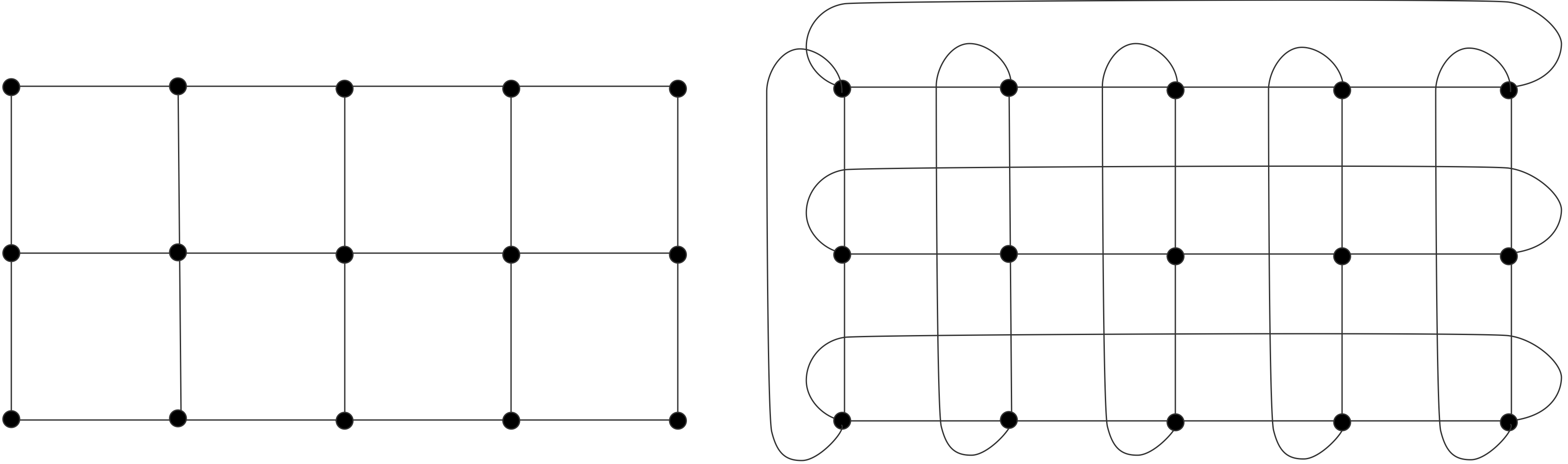
一些计算机设计声称是高维度的网格,例如5D,但这里并不是所有的维度都是平等的。例如,一个3D网格,其中每个节点是一个四插槽四核,可以被认为是一个5D网格。然而,最后两个维度是完全相连的。
超立方体
上面我们根据近邻通信的普遍性,对网状组织处理器的适用性做了一个挥手的论证。然而,有时会发生在随机处理器之间的发送和接收。这方面的一个例子就是上面提到的广播。由于这个原因,它希望有一个比网状网络直径小的网络。另一方面,我们希望避免全连接网络的复杂设计。
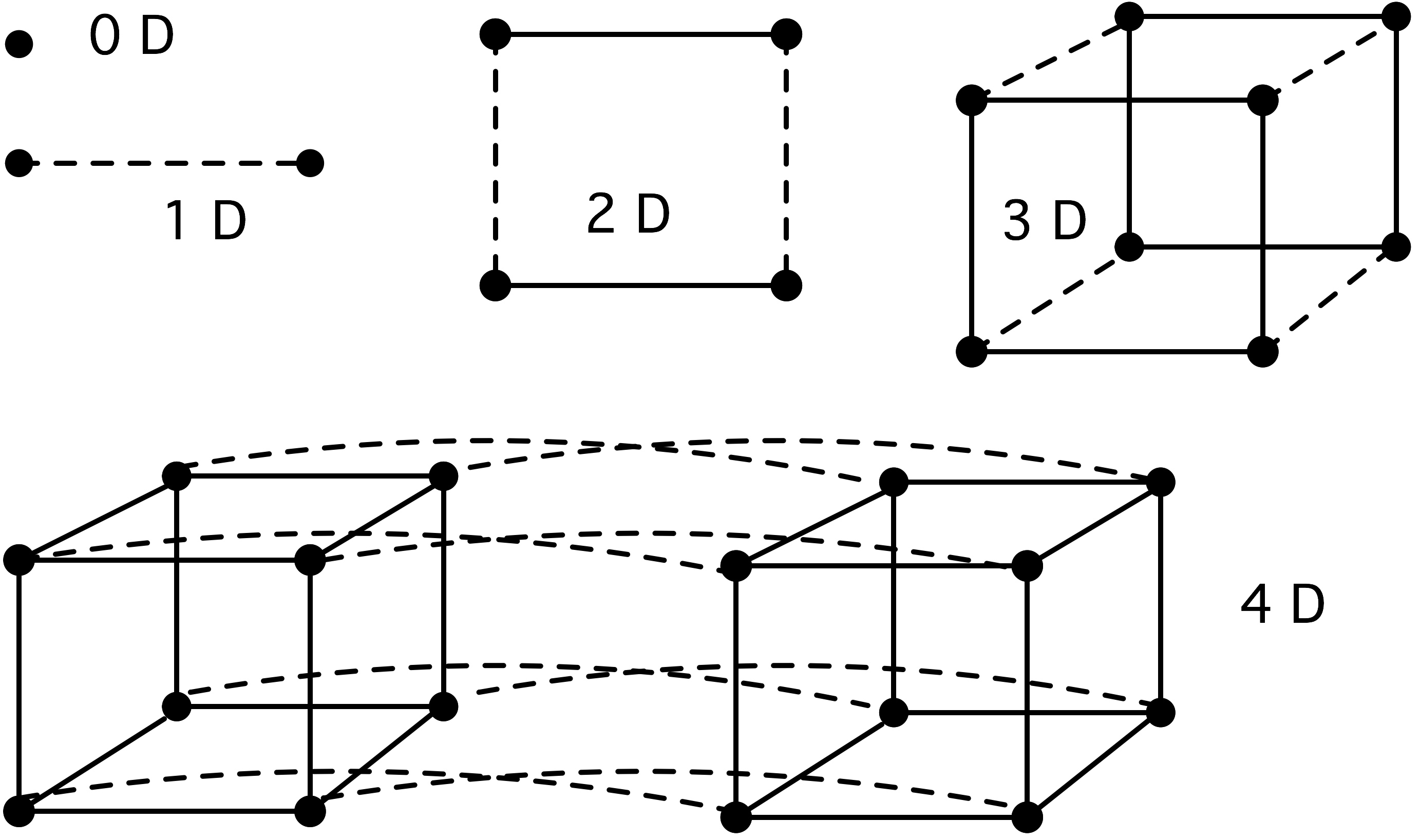
一种不错的解决方案是「超立方体」(hypercube)设计。一个$n$维的超立方体计算机有$2^n$个处理器,每个处理器在每个维度上都与另一个处理器相连;见图2.21。
一个简单的描述方法是给每个处理器一个由$𝑑$位组成的地址:我们给超立方体的每个节点一个数字,这个数字是描述它在立方体中的位置的比特模式;见图 2.20。
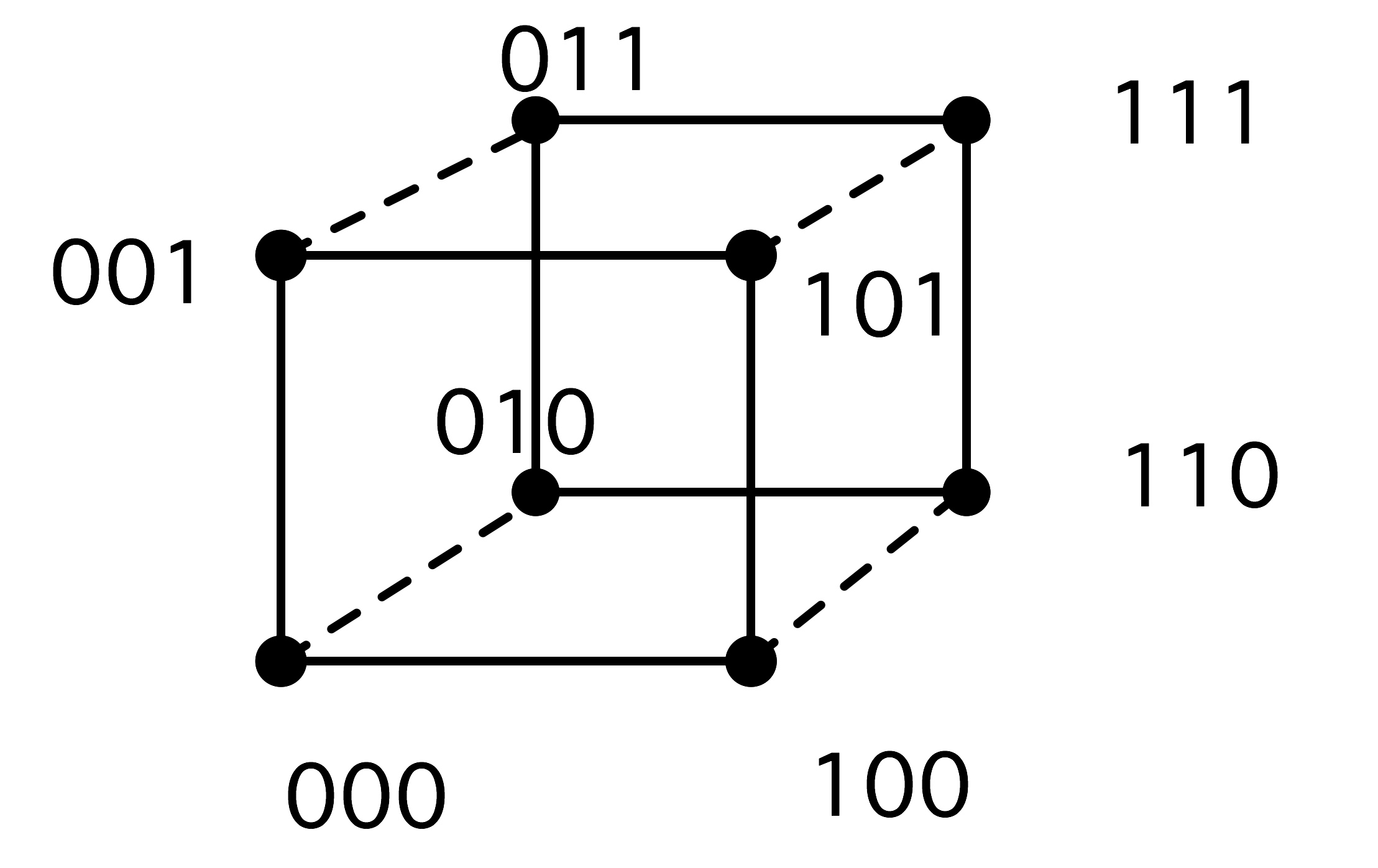
有了这个编号方案,一个处理器就会与其他所有地址正好相差一位的处理器连接起来。这意味着,与网格不同的是,一个处理器的邻居的号码并不是相差1或$\sqrt P$,而是相差1,2,4,8,….。
超立方体设计的最大优点是直径小,通过网络的流量容量大。
练习2.35 超立方体的直径是多少?二分宽度是多少?
该方案的一个缺点是,处理器的设计取决于机器的总尺寸。在实践中,处理器会被设计成可能的最大连接数,而购买较小机器的人就会为未使用的容量买单。另一个缺点是,扩展一台给定的机器只能通过加倍来实现:$2^p$以外的其他尺寸是不可能的。
练习2.36 考虑第2.1节中的并行求和例子,并给出在超立方体上并行实现的执行时间。证明在超立方体上的执行可以达到该例子的理论速度(最多一个系数)。在超立方体中嵌入网格上面我们提出了一个论点,即网格连接的处理器是许多物理现象建模应用的合理选择。超立方体看起来不像网格,但它们有足够的连接,可以通过忽略某些连接来简单地假装成网格。
比方说,我们想要一个一维数组的结构:我们想要有编号的处理器,这样处理器𝑖可以直接向𝑖 - 1和𝑖 + 1发送数据。我们不能像图2.20中那样使用明显的节点编号。例如,节点1与节点0直接相连,但与节点2的距离为2。节点3在一个环中的右邻,节点4,甚至在这个超立方体中的最大距离为3。显然,我们需要以某种方式对节点重新编号。
我们将展示的是,有可能在超立方体中行走,精确地触摸每个角落,这相当于在超立方体中嵌入一个一维网格。

这里的基本概念是一个(二进制反映的)「格雷编码」(Gray code)[87]。这是一种将二进制数$0…2^{𝑑-1}$排序为$𝑔_0,…𝑔_{2𝑑-1}$的方法,即$𝑔_𝑖$和$𝑔_{𝑖+1}$只相差一个比特。显然,普通的二进制数并不满足这一点:1和2的二进制表示已经有两个比特的差异。为什么格雷编码能帮助我们?因为$𝑔_𝑖$和$𝑔_{𝑖+1}$只相差一位,这意味着它们是超立方体中直接相连的节点数。
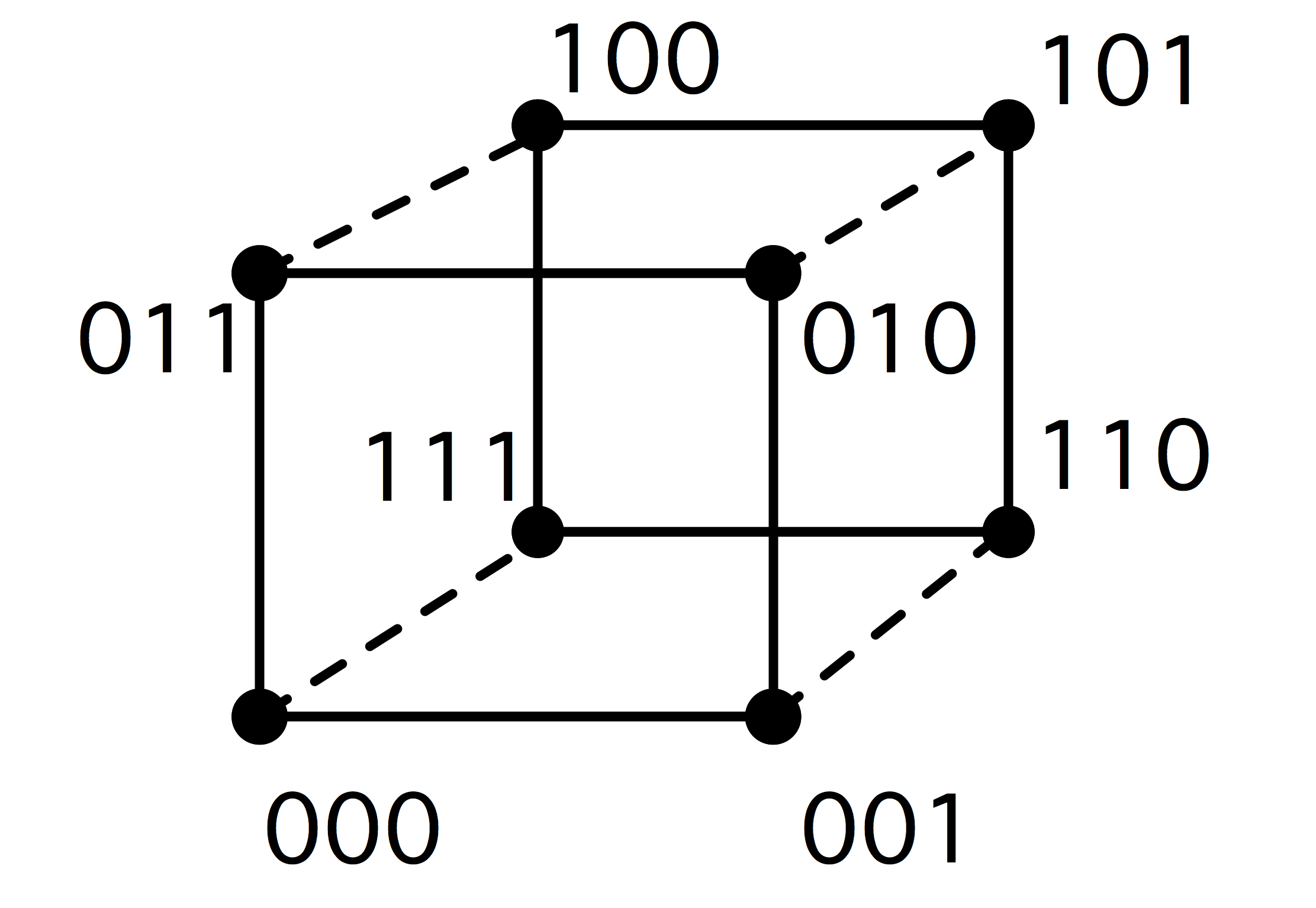
图2.22说明了如何构建一个格雷编码。这个过程是递归的,可以正式描述为 “将立方体分为两个子立方体,对一个子立方体进行编号,交叉到另一个子立方体,并按照第一个子立方体的相反顺序对其节点进行编号”。二维立方体的结果如图2.23所示。
由于格雷编码为我们提供了一种将一维 “网状 “嵌入超立方体的方法,我们现在可以继续往上做。
练习2.37 显示如何将一个$2^{2d}$节点的正方形网格嵌入到一个超立方体中,方法是将两个2𝑑节点的立方体嵌入的比特模式相加。你如何容纳一个$2^{d_1+d_2}$节点的网格?一个由$2^{d_1+d_2+d_3}$个节点组成的三维网格?
交换机网络
上面我们简要地讨论了完全连接的处理器。然而,通过在所有处理器之间制作大量的总线来进行连接是不切实际的。然而,还有另一种可能性,即通过将所有处理器连接到一个「交换机」(switch)或「交换机网络」(switch network)。一些流行的网络设计是「交叉开关」(Cross bar)、「蝶形交换」(butterfly exchange)和「胖树」(fat tree.)。
交换机网络是由交换元件组成的,每个交换元件都有少量(最多十几个)的入站和出站链接。通过将所有的处理器连接到一些交换元件上,并有多个交换阶段,那么就有可能通过网络的路径连接任何两个处理器。
交叉开关
最简单的开关网络是一个交叉开关,由$𝑛$水平线和垂直线组成,每个交叉点上都有一个开关元件,决定这些线是否连接在一起;见图2.24。如果我们把横线指定为输入,竖线指定为输出,这显然是让$𝑛$输入映射到$𝑛$输出的一种方式。每一个输入和输出的组合(有时称为 “排列组合”)都是允许的。
这种类型的网络的一个优点是,没有任何连接可以阻挡另一个连接。主要的缺点是开关元素的数量是$n^2$,是处理器数量$n$的一个快速增长的函数。
蝶形交换
蝶形交换网络是由小型交换元件构成的,它们有多个阶段:随着处理器数量的增加,阶段的数量也随之增加。图2.25显示了连接2、4和8个处理器的蝶形网络,每个处理器有一个本地存储器。(另外,你可以把所有的处理器放在网络的一边,而把所有的存储器放在另一边)。
正如在图2.26中所示,蝶形交换允许几个处理器模拟访问内存。而且,它们的访问时间是相同的,所以交换网络是实现UMA结构的一种方式;见2.4.1节。有一台基于Butterfly交换网络的计算机是BBN Butterfly(http://en.wikipedia.org/wiki/BBN_Butterfly)。在2.7.7.1节中,我们将看到这些想法是如何在一个实际的集群中实现的。
练习 2.38 对于简单的交叉开关和蝶形交换,随着处理器数量的增加网络需要扩展。给出两种情况下连接$𝑛$处理器和存储器所需的导线数量(某种单位长度)和交换元件的数量。一个数据包从存储器到处理器所需的时间,用穿越单位长度的导线和穿越开关元件的时间表示是多少?
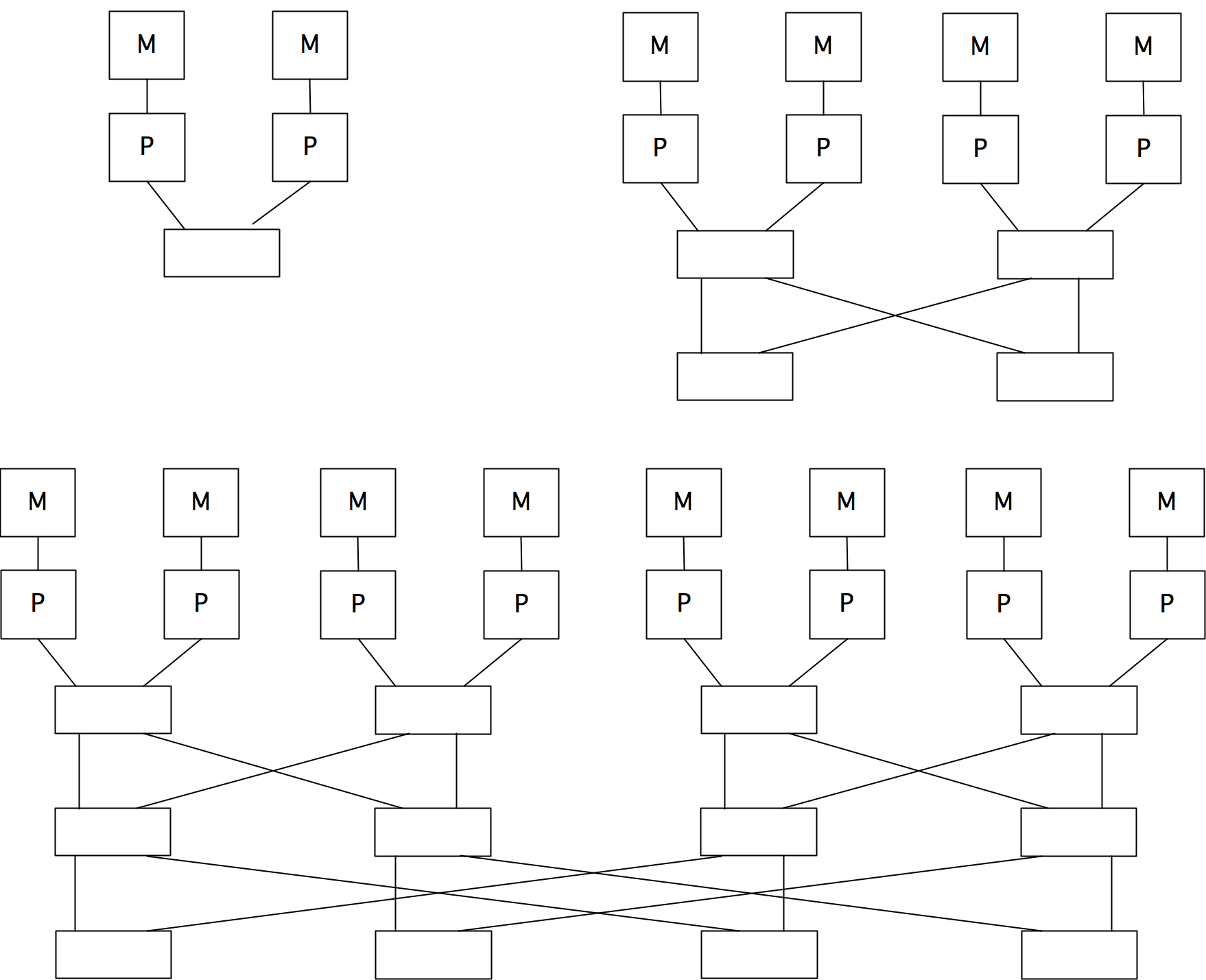
通过蝶形交换网络的数据包路由是基于考虑目的地地址的位数来完成的。在第𝑖层,考虑第𝑖个数字;如果是1,则选择开关的左出口,如果是0,则选择右出口。这在图2.27中有所说明。如果我们把存储器连接到处理器上,如图2.26所示,我们只需要两个比特(到最后一个开关),但还需要三个比特来描述反向路线。
胖树
如果我们像树一样连接交换节点,那么在靠近根部的地方就会出现很大的拥堵问题,因为只有两根线连接到根注。假设我们有一棵$𝑘$级树,所以有$2^𝑘$个叶子节点。如果左边子树上的所有叶子节点都试图与右边子树上的节点通信,我们就有$2{𝑘-1}$条信息通过一条线进入根部,同样也通过一条线出去。胖树是一个树状网络,每一级都有相同的总带宽,这样就不会出现这种拥堵问题:根部实际上会有$2^{𝑘-1}$条进线和出线连接[88]。图2.28在左边显示了这种结构;右边显示了Stampede集群的一个机柜,机柜的上半部和下半部有一个叶子开关。
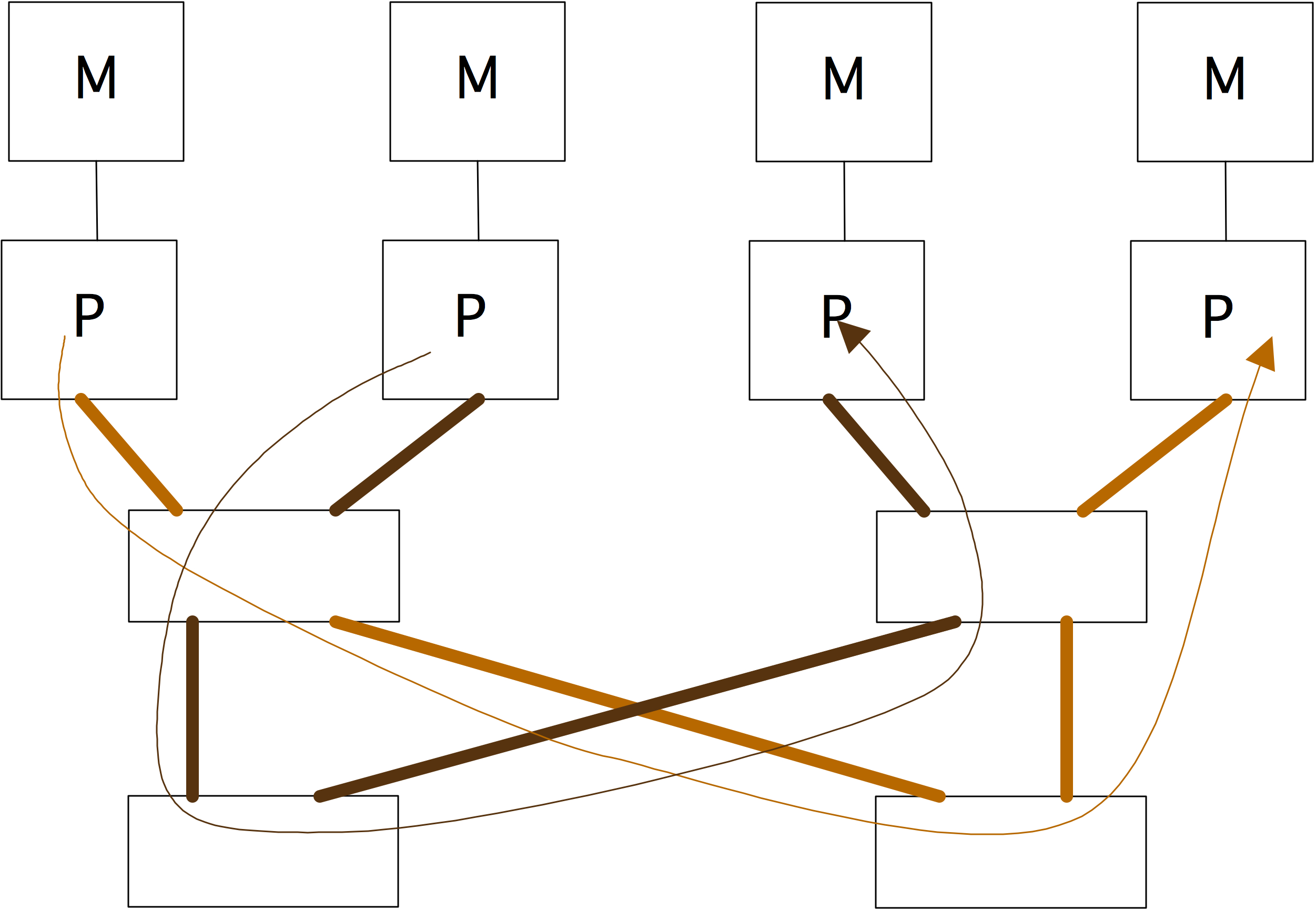
第一个成功的基于胖树的计算机结构是连接机CM5。
在胖树中,就像在其他交换网络中一样,每个信息都带有自己的路由信息。由于在胖树中,选择仅限于上升一级,或者切换到当前级别的其他子树上,因此一条信息需要携带的路由信息的位数与级别相同,对于$𝑛$处理器来说是$\log_2𝑛$。
练习 2.39 证明胖子树的分叉宽度是$𝑃/2$,其中$𝑃$是亲子叶子节点的数量。提示:说明只有一种方法可以将胖树连接的处理器集合分割成两个连接的子集。
[142]中对胖树的理论阐述表明,胖树在某种意义上是最优的:它可以像任何其他需要相同空间来构建的网络一样快速传递信息(最多对数因素)。这个说法的基本假设是,离根更近的开关必须连接更多的线,因此需要更多的组件,相应地也就更大。这个论点虽然在理论上很有趣,但没有实际意义,因为网络的物理尺寸在目前最大的使用胖树互连的计算机中几乎没有起到作用。例如,在德克萨斯大学奥斯汀分校的TACC Frontera集群中,只有6个核心交换机(即容纳胖树最高层的机柜),连接91个处理器机柜。
如上图所示,胖树的建设成本很高,因为每下一级都必须设计一个新的、更大的交换机。因此,在实践中,一个具有胖子树特征的网络是由简单的开关元件构成的;见图2.29。这个网络的带宽和路由可能性与胖树相当。路由算法会稍微复杂一些:在胖树中,一个数据包只能以一种方式上升,但在这里,一个数据包必须知道要路由到两个较高的交换机中的哪个。
这种类型的交换网络是Clos网络的一种情况[34]。
超额订购和争夺
在实践中,胖树网络不使用2进2出的元件,而是使用20进20出的开关。这使得网络中的层数有可能被限制在3或4个。(顶层交换机被称为脊柱卡)。
在这种情况下,网络分析的一个额外的复杂因素是超额订购的可能性。网卡中的端口可以配置为输入或输出,而只有总数是固定的。因此,一个40端口的交换机可以被配置为20进20出,或者21进19出,等等。当然,如果所有连接到交换机的21个节点同时发送,19个出端口将限制带宽。
还有一个问题。让我们考虑建立一个小型集群,交换机配置为有$𝑝$入端口和$w$出端口,这意味着我们有$𝑝+𝑤$端口交换机。图2.30描述了两个这样的开关,总共连接了$2^𝑝$个节点。如果一个节点通过交换机发送数据,它对$𝑤$条可用导线的选择由目标节点决定。这就是所谓的输出路由。
显然,我们只能期望$𝑤$个节点能够在有信息碰撞的情况下进行发送,因为这就是交换机之间可用导线的数量。然而,对于许多$𝑤$目标的选择,无论如何都会有对导线的争夺。这就是生日悖论的一个例子。
练习 2.40 考虑上述架构,$p$个节点通过切换间的$w$线发送。编一个模拟代码,其中$p$个节点中的$w’\leqslant w$向一个随机选择的目标节点发送一个信息。作为$w’$、$w$、$p$的函数,碰撞的概率是多少?找到一种方法来制表或绘制数据。
作为反馈,请给出简单情况下$w’ = 2$的统计分析。
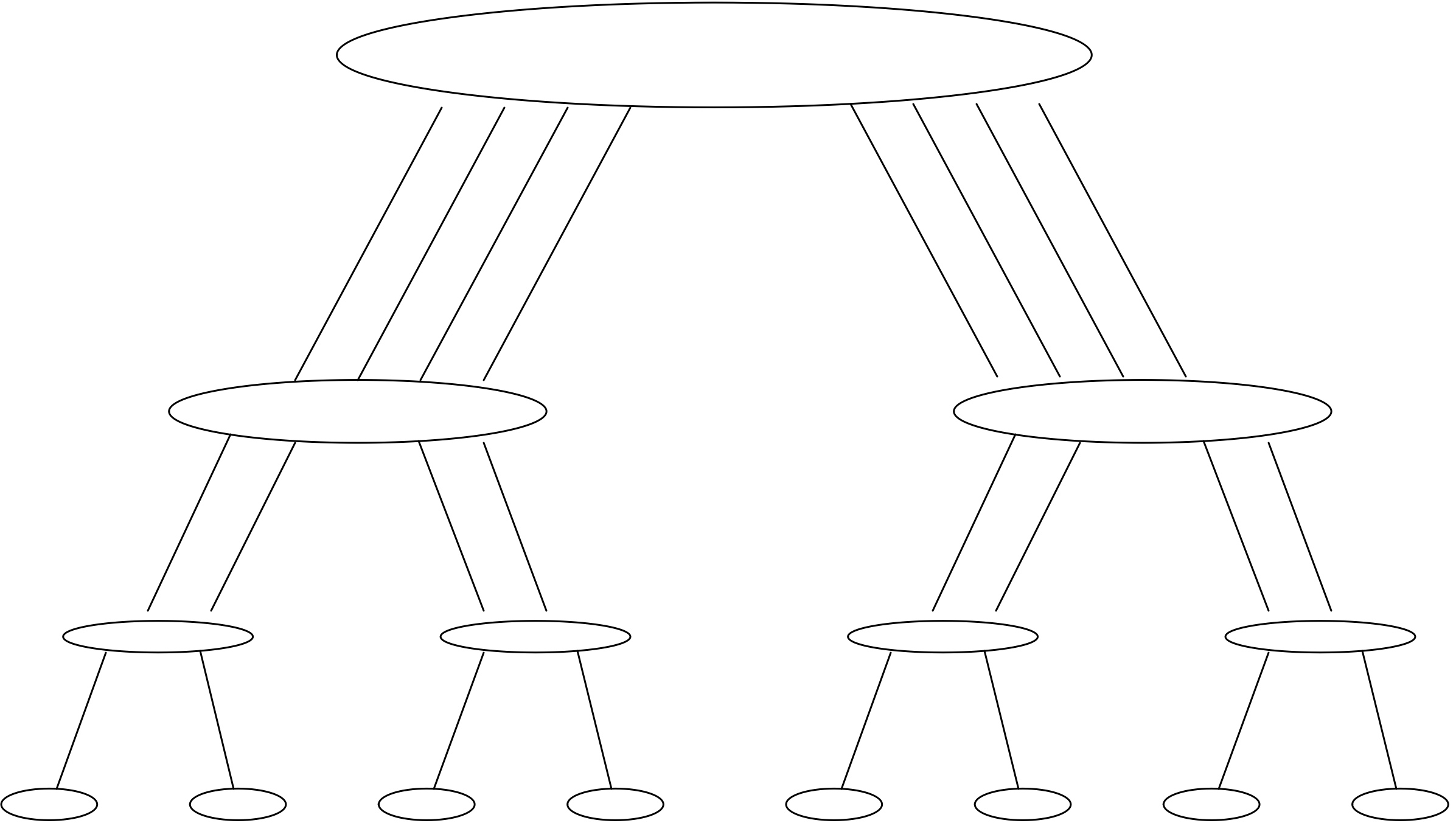


集群网络
上面的讨论有些抽象,但在现实生活中的集群中,你可以实际看到网络设计的体现。例如,肥大的树形集群网络会有一个中央机柜,对应树形中的最高层。图2.31显示了TACC Ranger(已不再使用)和Stampede集群的交换机。在第二张图片中可以看出,实际上有多个冗余的胖树网络。
另一方面,像IBM BlueGene这样基于环状网络的集群,看起来将是一个相同机柜的集合,因为每个机柜都包含网络的一个相同部分;见图2.32。
案例研究: Stampede
作为实践中联网的一个例子,让我们考虑一下德克萨斯高级计算机中心的Stampede集群,它是一个多根多级的胖树。
每个机架由2个机箱组成,每个机箱有20个节点。
每个机箱都有一个叶子开关,它是一个内部的横杆,使机箱中的节点之间有完美的连接性。
叶子交换机有36个端口,其中20个连接到节点,16个向外。这种超额订阅意味着最多只有16个节点在机箱外通信时可以拥有完美的带宽。
- 有8个中心交换机,作为8个独立的胖树根发挥作用。每个机箱通过两个连接到每个中央交换机的 “叶卡”,正好占用了16个出站端口。
- 每个中心交换机有18个针卡,每个针卡有36个端口,每个端口连接到不同的叶卡。
- 每台中央交换机有36个叶卡,18个端口连接到叶子交换机,18个端口连接到脊柱卡。这意味着我们可以支持648个机箱,其中640个被实际使用。
网络中的一个优化是,与同一叶卡的两个连接进行通信,没有较高树级的延迟。这意味着,一个机箱中的16个节点和另一个机箱中的16个节点可以有完美的连接。
然而,对于静态路由,如Infiniband中使用的路由,有一个与每个目的地相关的固定端口。(目的地到端口的这种映射在每个交换机的路由表中)。 因此,对于20个可能的目的地中的16个节点的某些子集,将有完美的带宽,但其他子集将看到两个目的地的流量通过同一个端口。
案例研究:Cray Dragonfly网络
Cray的蜻蜓网络是一个有趣的实际妥协。上面我们说过,一个完全连接的网络将太过昂贵,无法扩大规模。然而,如果数量保持有限的话,拥有一个完全连接的处理器集合是可能的。蜻蜓设计使用小的完全连接的组,然后将这些组组成一个完全连接的图。
这引入了一个明显的不对称性,因为一个组内的处理器拥有更大的带宽,而组与组之间则没有。然而,由于动态路由,信息可以采取非最小路径,通过其他组进行路由。这可以缓解争夺问题。


带宽和延迟
上面所说的发送信息可以被认为是一个单位时间的操作,当然是不现实的。一个大的信息比一个短的信息需要更长的时间来传输。有两个概念可以对传输过程进行更现实的描述;我们已经在1.3.2节中看到了在处理器的缓存层之间传输数据的情况。
- 延迟 在两个处理器之间建立通信需要花费大量时间,这与信息大小无关。这所花费的时间被称为信息的延时。造成这种延迟的原因有很多。
- 两个处理器进行 “握手”,以确保收件人已经准备好,并且有适当的缓冲空间来接收信息。
- 信息需要由发送方进行编码传输,并由接收方进行解码。
- 实际传输可能需要时间:并行计算机通常足够大,即使在光速下,信息的第一个字节也需要数百个周期来穿越两个处理器之间的距离。
- 带宽 在两个处理器之间的传输开始后,主要的数字是每秒可通过通道的字节数。这就是所谓的带宽。带宽通常可由信道速率(物理链路可传送比特的速率)和信道宽度(链路中物理线的数量)决定。信道宽度通常是16的倍数,通常为64或128。这也可以表示为,一个通道可以同时发送一个或两个8字节的字。

带宽和延迟被正式定义为
为一个$n$字节的信息的传输时间。这里,$\alpha$是延迟,$\beta$是每字节的时间,也就是带宽的倒数。有时我们会考虑涉及通信的数据传输,例如在集体操作的情况下;见6.1节。然后我们将传输时间公式扩展为
其中$\gamma$是每次操作的时间,也就是计算率的倒数。
也可以将这个公式细化为
其中$𝑝$是所穿越的网络 “「跳」(hops)”。然而,在大多数网络中,$\delta$的值远远低于$\alpha$的值,所以我们在这里将忽略它。另外,在胖树网络中,跳数是$\log𝑃$的数量级,其中$𝑃$是处理器的总数,所以它无论如何都不可能很大。
并行计算中的局部性
在第1.6.2节中,你发现了关于单处理器计算中的位置性概念的讨论。并行计算中的位置性概念包括所有这些以及更多的层次。
- 核心之间:私有缓存 现代处理器上的核心有私有相干缓存。这意味着你似乎不必担心位置性问题,因为无论数据在哪个缓存中都可以访问。然而,维持一致性需要花费带宽,所以最好是保持访问的本地化。
- 内核之间:共享高速缓存 内核之间共享的高速缓存是一个不需要担心位置性的地方:这是处理核心之间真正对称的内存。
- 在插槽之间:节点(或主板)上的插槽在程序员看来是共享内存的,但这实际上是NUMA访问(2.4.2节),因为内存与特定的插槽相关。
- 通过网络结构:有些网络有明显的位置效应。你在第2.7.1节中看到了一个简单的例子,一般来说,很明显,任何网格型网络都会有利于 “附近 “处理器之间的通信。基于胖树的网络似乎不存在这样的争论问题,但是层次引起了不同形式的定位性。比节点上的局域性高一级,小群的节点通常由一个叶子开关连接,它可以防止数据进入中央开关。
并行计算(三)
多线程架构
当代CPU架构模式很大程度上取决于:机器从内存中获取数据要远比处理这些数据要慢得多。因此,由更快更小的存储器组成的层次结构试图通过靠近处理单元以缓解内存的长延迟和低带宽。此外,在处理单元中进行指令级并行也有助于隐藏延迟、充分利用带宽。
然而,寻找指令级并行属于编译器的工作范畴,该处可执行空间有限;另一方面,科学计算中的代码往往更加适合数据并行,这对于编译器来说较为困难但对程序员说却显而易见。能否让程序员明确地指出这种并行性?并让处理器使用它?
前面我们看到SIMD架构可以以明确的数据并行方式进行编程。如果我们有大量的数据并行,但没有那么多的处理单元该怎么办?在这种情况下,我们可以把指令并行变成线程并行,让多个线程在每个处理单元上执行。每当一个线程因为未完成的内存请求而停滞不前时,处理器可以切换到另一个线程,因为所有必要的输入都是可用的。这就是所谓的「多线程」(multi-threading)。虽然这听起来像是一种防止处理器等待内存的方法,但也可以被看作是一种保持内存最大限度被占用的方法。
练习 2.41 把内存的长延迟和有限的带宽看作是两个独立的问题,多线程是否同时解决了这两个问题?
这里的问题是,大多数CPU并不擅长在线程之间快速切换。上下文切换(在一个线程和另一个线程之间切换)需要大量的周期,与等待主内存的数据相当。在所谓的「多线程架构」(Multi-Threaded Architecture,MTA)中,上下文切换是非常有效的,有时只需要一个周期,这使得一个处理器可以同时在许多线程上工作。
多线程的概念在Tera Computer MTA机器中得到了探索,该机器演变成了目前的Cray XMT9。
MTA的另一个例子是GPU,其中处理器作为SIMD单元工作,同时本身也是多线程的。
GPU与协处理器
当前,CPU在处理各种计算中都参与了一定程度的作用,也就是说,如果限制处理器处理的功能,有可能提高其专注效率,或降低其功耗。因此我们试图在主机进程中加入一个辅助处理器如,英特尔的8086芯片,为第一代的IBM PC提供动力;可以添加一个数字协处理器,即80287,这种处理器在超越函数方面非常有效,而且它还采用了SIMD技术;使用独立的图形功能也很流行,导致了X86处理器的SSE指令,以及独立的GPU单元被连接到PCI-X总线。
进一步的例子是使用数字信号处理(DSP)指令的协处理器,以及可以重新配置以适应特定需求的FPGA板。早期的阵列处理器,如ICL DAP也是协处理器。
在本节中,我们将简要介绍这一理念的一些现代化身,特别是GPU。
追溯历史
协处理器可以用两种不同的方式进行编程:有时它是无缝集成的,某些指令在协处理器中自动执行,而不是在 “主 “处理器上执行。另一方面,也有可能需要明确调用协处理器功能,甚至有可能将协处理器功能与主机功能重叠。从效率的角度看,后一种情况可能听起来很有吸引力,但它提出了一个严重的编程问题。程序员现在需要确定两个工作流:一个用于主机处理器,一个用于协处理器。
采用协处理器的并行机器有:
- 英特尔Paragon(1993)每个节点有两个处理器,一个用于通信,另一个用于计算。这些处理器实际上是相同的,即英特尔i860英特尔i860处理器。在后来的修订中,有可能将数据和函数指针传递给通信处理器。
- 洛斯阿拉莫斯的IBM Roadrunner是第一台达到PetaFlop的机器。(葡萄计算机更早达到了这一点,但那是一台用于分子动力学计算的特殊用途机器)。它通过使用Cell协处理器达到了这个速度。顺便说一下,Cell处理器实质上是索尼Playstation3的引擎,再次显示了超级计算机的商品化。
- 中国的 “天河一号 “在2010年登上了Top500榜单,由于使用了NVidia GPU,达到了约2.5PetaFlop。
- 天河二号和TACC Stampede集群使用英特尔Xeon Phi协处理器。
Roadrunner和Tianhe-1A是协处理器的例子,它们非常强大,需要独立于主机CPU进行明确编程。例如,在天河-1A的GPU上运行的代码是用CUDA编程并单独编译的。
在这两种情况下,由于协处理器不能直接通过网络交流,可编程性问题进一步加剧。要把数据从一个协处理器发送到另一个协处理器,必须先传到一个主处理器,再从那里通过网络传到另一个主处理器,然后才移到目标协处理器。
瓶颈问题
协处理器通常有自己的内存,英特尔Xeon Phi可以独立运行程序,但更多时候存在如何访问主处理器内存的问题。一个流行的解决方案是通过PCI总线连接协处理器。这样访问主机内存的速度比主机处理器的直接连接要慢。例如,Intel Xeon Phi 的带宽为512位宽,每秒5.5GT(我们将在第二部分讨论这个 “GT”),而它与主机内存的连接为5.0GT/s,但只有16位宽。
GT测量 我们习惯于看到以千兆位/秒为单位的带宽。对于PCI总线,人们经常看到GT测量。这代表了千兆传输,它衡量了总线在零和一之间改变状态的速度。通常情况下,每个状态转换都对应一个比特,但总线必须提供自己的时钟信息,如果你发送一个相同的比特流,时钟会被混淆。因此,为了防止这种情况,通常将每8位编码为10位。然而,这意味着有效带宽比理论数字要低,在这种情况下是4/5的系数。
由于制造商喜欢讨论事情的积极一面,因此他们报告的数字会更高。
GPU计算
图形处理单元(Graphics Processing Unit,GPU),有时也称为「通用图形处理单元」(General Purpose Graphics Processing Unit,GPGPU),是一种特殊用途的处理器,是为快速图形处理而设计的。然而,由于为图形所做的操作是一种算术形式,GPU已经逐渐发展出对非图形计算也很有用的设计。GPU的一般设计是由 “图形流水线 “激发的:在数据并行的形式下,对许多数据元素进行相同的操作,并且许多这样的数据并行块可以在同一时间激活。
CPU的基本限制也适用于GPU:对内存的访问会产生很长的延迟。在CPU中解决这个问题的方法是引入各级缓存;在GPU中则采取不同的方法。GPU关注的是吞吐量计算,以高平均速率提供大量数据,而不是尽可能快地提供任何单一结果。这是通过支持许多线程=并在它们之间快速切换而实现的。当一个线程在等待内存中的数据时,另一个已经拥有数据的线程可以继续进行计算。
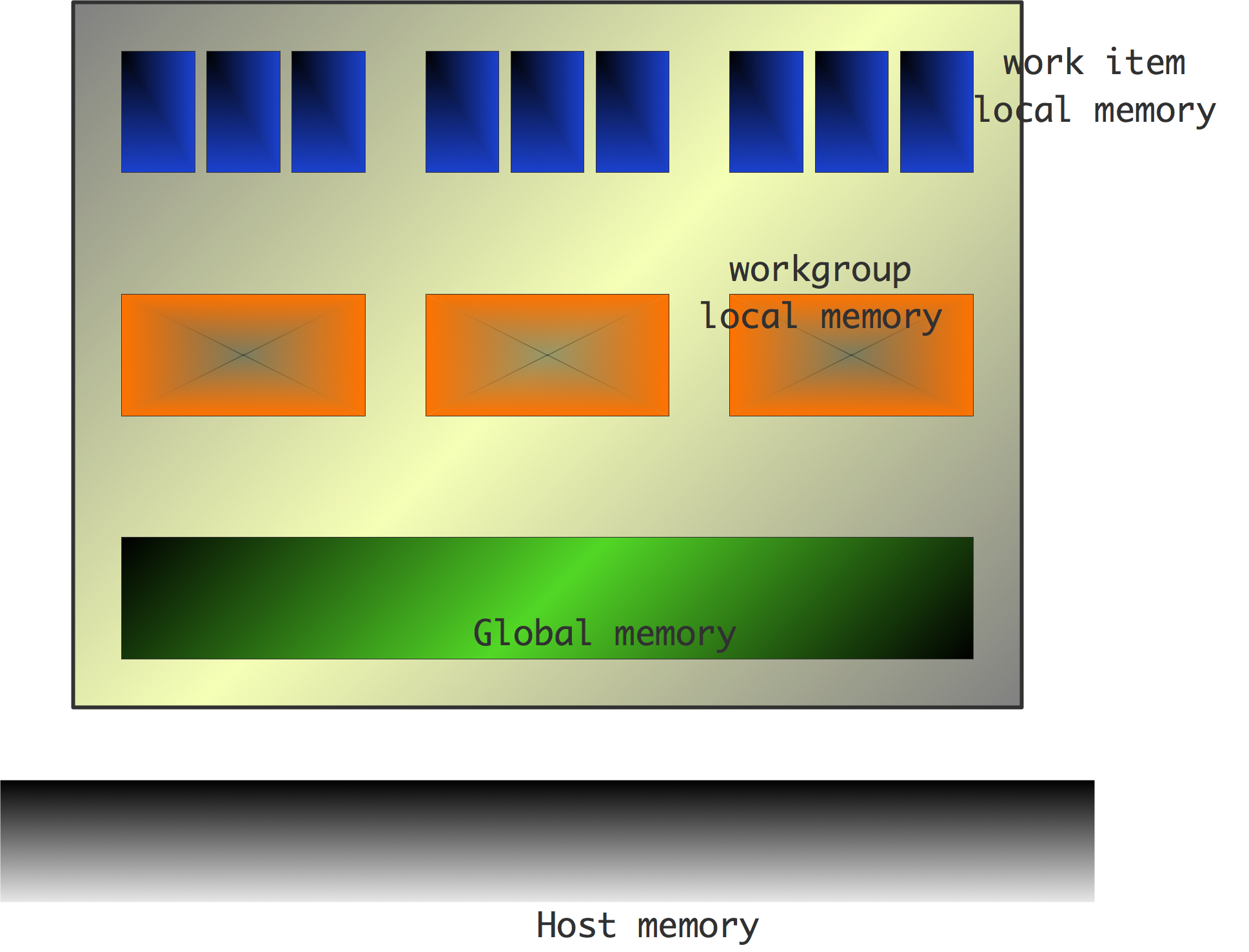
用内核进行SIMD型编程
当前的GPU的一个架构中结合了SIMD和SPMD并行性。线程并非完全独立,而是在线程块中排列,所有的线程块中执行相同的指令以实现SIMD。也有可能将同一指令流(CUDA术语中的 “内核”)安排在一个以上的线程块上。在这种情况下,线程块可以不同步,这有点类似于SPMD上下文中的进程。然而,由于我们在这里处理的是线程,而不是进程,所以使用了「单指令多线程」(Single Instruction Multiple Thread,SIMT)这一术语。
这种软件设计在硬件中很明显;例如,NVidia GPU有16-30个流式多处理器(SMs),一个SMs由8个流式处理器(SPs)组成,对应于处理器内核;见图2.34。SPs以真正的SIMD方式行动。GPU中的内核数量通常比传统的多核处理器要多,但内核的数量却更加有限。因此,这里使用了多核这个术语。
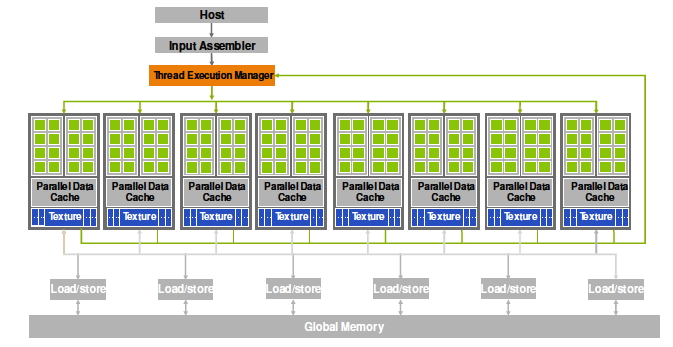
GPU的SIMD(即数据并行)性质在CUDA启动进程的方式中变得很明显。内核,即一个将在GPU上执行的函数,在𝑚𝑛核上启动。
1 | KernelProc<< m,n >>(args) |
执行内核的𝑚𝑛内核的集合被称为「网格」(grid),它的结构为𝑚线程块,每个线程块有𝑛线程。一个线程块最多可以有512个线程。
回顾一下,线程共享一个地址空间,所以它们需要一种方法来识别每个线程将对哪一部分数据进行操作。为此,线程中的区块用𝑥 , 𝑦坐标编号,而区块中的线程用𝑥 , 𝑦 , 𝑧坐标编号。每个线程都知道自己在块中的坐标,以及其块在网格中的坐标。
我们用一个向量加法的例子来说明这一点。
1 | // 每个线程执行一次加法 |
这显示了GPU的SIMD性质:每个线程都在执行相同的标量程序,只是在不同的数据上执行。
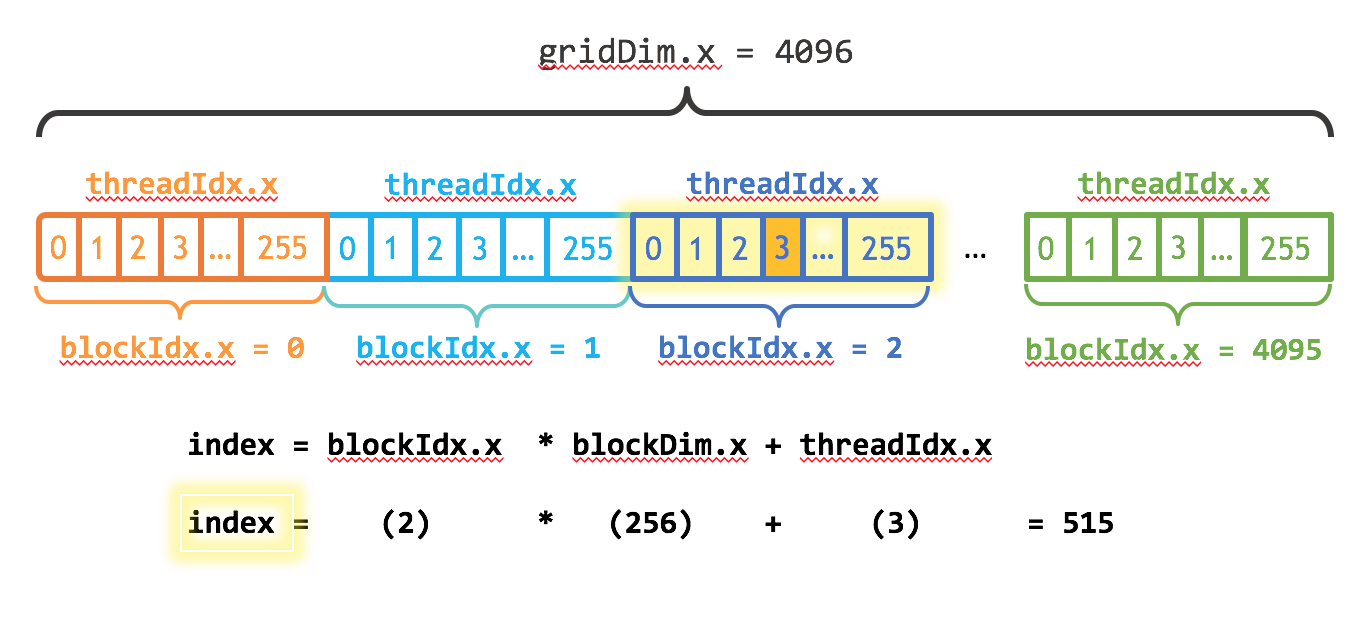
线程块中的线程是真正的数据并行:如果有一个条件,使一些线程走真分支,其他线程走假分支,那么一个分支将首先被执行,另一个分支的所有线程都被停止。随后,而不是同时,另一个分支上的线程将执行他们的代码。这可能会引起严重的性能损失。
GPU依赖于大量的数据并行性和快速上下文切换的能力。这意味着它们将在有大量数据并行的图形和科学应用中茁壮成长。然而,它们不太可能在 “商业应用 “和操作系统中表现良好,因为那里的并行性是指令级并行性(ILP)类型,通常是有限的。
GPU与CPU的对比
这些是GPU和普通CPU之间的一些区别。
- 截至2010年底,GPU是附加的处理器,例如通过PCI-X总线,所以它们操作的任何数据都必须从CPU传输。由于这种传输的内存带宽很低,至少比GPU的内存带宽低10倍,因此必须在GPU上做足够的工作来克服这种开销。
- 由于GPU是图形处理器,所以它强调的是单精度浮点运算的metic。为了适应科学计算界,对双精度的支持正在增加,但双精度速度通常是单精度翻转率的一半。这种差异可能会在未来几代中得到解决。
- CPU被优化为处理单一的指令流,这些指令可能具有很强的异质性;而GPU是明确为数据并行化而制造的,在传统代码上表现很差。
- CPU是为了处理一个线程,或最多是少量的线程。GPU需要大量的线程,远远大于计算核心的数量,才能有效地执行。
GPU的预期收益
GPU在实现高性能、高成本效益方面已经迅速获得了声誉。关于用最小的努力将代码移植到CUDA上的故事比比皆是,由此带来的速度提升有时达到400倍。GPU真的是如此神奇的机器吗?原有的代码是否编程不当?如果GPU这么厉害,为什么我们不把它用于所有的事情呢?
事实有几个方面。
首先,GPU并不像普通CPU那样具有通用性。GPU非常擅长做数据并行计算,而CUDA则擅长优雅地表达这种细粒度的并行性。换句话说,GPU适用于某种类型的计算,而对许多其他类型的计算则不适合。
相反,普通的CPU不一定擅长数据并行化。除非代码写得非常仔细,否则性能会从最佳状态下降,大约有以下几个因素:
- 除非使用明确的并行结构指令,否则编译后的代码将永远使用可用内核中的一个,例如4个。
- 如果指令没有流水线,那么浮点流水线的延迟又会增加4个系数。
- 如果内核有独立的加法和乘法管线,如果不同时使用,又会增加2个因素。
- 如果不使用SIMD寄存器,就会在峰值性能方面增加更多的减慢。
- 编写计算内核的最佳CPU实现往往需要使用汇编程序,而直接的CUDA代码将以相对较少的努力实现高性能,当然,前提是计算有足够的数据并行性。
英特尔Xeon Phi
英特尔Xeon Phi,也被其架构设计称为多集成核心(MIC),是一种专门为数值计算设计的设计。最初的设计,即Knight’s Corner是一个协处理器,而第二次迭代,即Knight’s Landing是自带主机的。
作为一个协处理器,Xeon Phi与GPU既有区别又有相似之处。
- 两者都是通过PCI-X总线连接,这意味着设备上的操作在启动时有相当的延迟。
- Xeon Phi有通用的内核,因此它可以运行整个程序;而GPU只在有限的范围内具有这种功能(见2.9.3.1节)。
- Xeon Phi接受普通的C代码。
- 两种架构都需要大量的SIMD式并行,在Xeon Phi的情况下,因为有8字宽的AVX指令。
- 两种设备都是通过加载主机程序来工作,或者可以通过加载主机程序来工作。
负载均衡
在本章的大部分内容中,我们都假设的是一个问题可以被完美分配到各个处理器上,即一个处理器总是在进行有效的工作且只会因为通信延迟而空闲。然而在实际中,处理器的空闲可能因为其正在等待消息,而发送处理器甚至还没有达到其代码中的发送指令。这种情况下,一个处理器在工作,另一个处理器在闲置,被描述为负载不均衡(load unbalance):一个处理器闲置没有内在的原因,如果我们以不同的方式分配工作负载,它本来可以工作。
在处理器有太多的工作和没有足够的工作之间存在着不对称性:有一个处理器提前完成任务,比有一个超负荷的处理器使所有其他处理器都在等待它要好。
练习 2.42 将这个概念精确化。假设一个并行任务在所有处理器上都需要时间1,但只有一个处理器。
假设$0<\alpha<1$,而一个并行任务花费的时间是$1+\alpha$,那么速度提升和效率与处理器数量的关系是什么?在Amdahl和Gustafsson的意义上考虑这个问题(2.2.3节)。
如果一个处理器需要时间$1-\alpha$,请回答同样的问题。
负载均衡的代价往往是昂贵的,因为它需要移动大量的数据。例如,第6.5节有一个分析表明,在稀疏矩阵与向量乘积过程中的数据交换比存储在处理器上的数据要低一阶。然而,我们不会去研究移动的实际成本:我们在这里主要关注的是均衡工作均衡,以及保留原始负载分布中的任何位置性。
负载均衡与数据分配
工作和数据之间存在着双重性:在许多应用中,数据的分布意味着工作的分布,反之亦然。如果一个应用程序更新一个大的数组,数组的每个元素通常 “生活 “在一个唯一确定的处理器上,该处理器负责该元素的所有更新。这种策略被称为拥有者计算(owner computes)。
因此,数据和工作之间存在着直接的关系,相应地,数据分配和负载均衡也是相辅相成的。例如,在第6.2节中,我们将谈论数据分布如何影响效率,但这立即转化为对负载分布的关注。
- 负载需要被均匀地分配。这通常可以通过均匀地分配数据来实现,但有时这种关系并不是线性的。
- 任务需要被放置,以尽量减少它们之间的流量。在矩阵-向量乘法的情况下,这意味着二维分布要优于一维分布;关于空间填充曲线的讨论也是类似的动机。
作为数据分布如何影响负载均衡的一个简单例子,考虑一个线性数组,其中每个点经历相同的计算,每个计算需要相同的时间。如果数组的长度$𝑁$,完全可以被处理器的数量$𝑝$所分割,那么工作就完全均匀分布。如果数据不能平均分割,我们首先将$⌊N/p⌋$点分配给每个处理器,剩下的$N- p⌊N/p⌋$点分配给最后几个处理器。
练习 2.43 在最坏的情况下,处理器的工作将变得多么不均衡?将这个方案与将$⌈N/p⌉$点分配给所有处理器的方案进行比较,除了一个处理器得到的点数较少;见上面的练习。
将剩余的$r=N-p⌊N/p⌋$分摊到$𝑟$处理器上比一个更好。这可以通过给第一个或最后一个𝑟处理器提供一个额外的数据点来实现。这可以通过给进程$𝑝$分配范围来实现
虽然这个方案是很均衡的,但例如计算一个给定的点属于哪个处理器是很棘手的。下面的方案使这种计算更容易:让$f(i)=⌊iN/p⌋$,那么处理器𝑖得到的点$f(i)$直到$f(i + 1)$。
练习 2.44 证明$⌊N/p⌋ ≤ f(i + 1) - f(i) \leqslant ⌈N/p⌉$。
根据这个方案,拥有索引𝑖的处理器是$⌊(p(i + 1) - 1)/N ⌋$。
负载调度
有些情况下,负载可以比较自由的进行分配,可以通过负载调度实现负载均衡。例如在共享内存的背景下,所有处理器都可以访问所有的数据。在这种情况下,我们可以考虑使用预先确定的工作分配给处理器的静态调度(static scheduling),或在执行期间确定分配的动态调度(dynamic scheduling)之间的区别。
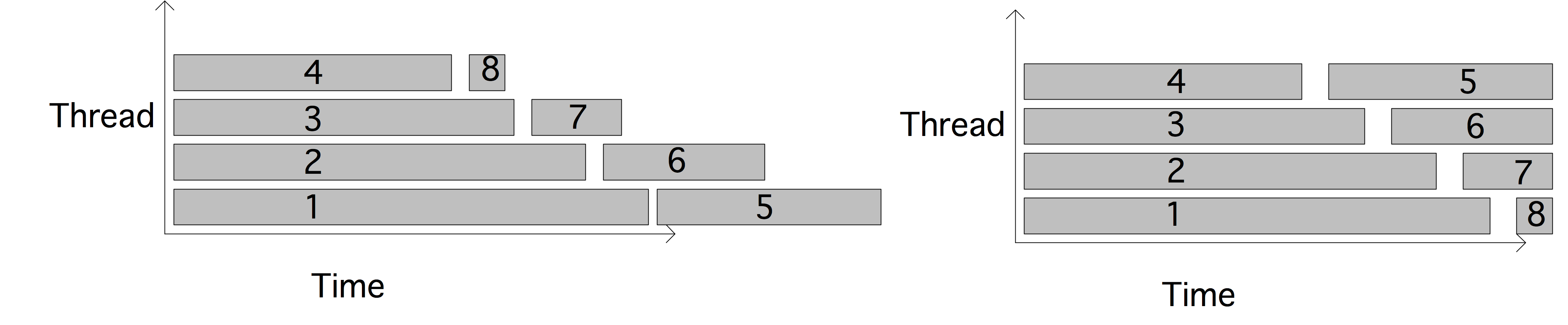
为了说明动态调度的优点,考虑在4个线程上调度8个运行时间递减的任务(图2.36)。在静态调度中,第一个线程得到任务1和4,第二个线程得到2和5,依此类推。在动态调度中,任何完成其任务的线程都会得到下一个任务。在这个特定的例子中,这显然给出了一个更好的运行时间。另一方面,动态调度可能会有更高的开销。
独立任务的负载均衡
在其他情况下,工作负荷不是由数据直接决定的。如果有一个待完成的工作池,而每个工作项目的处理时间不容易从其描述中计算出来,就会发生这种情况。在这种情况下,我们可能希望在给流程分配工作时有一些灵活性。
让我们首先考虑这样一种情况:一项工作可以被划分为不相通的独立任务。一个例子是计算Mandelbrot集图片的像素,其中每个像素都是根据一个不依赖于周围像素的数学函数来设置的。如果我们能够预测绘制图片的任意部分所需的时间,我们就可以对工作进行完美的划分,并将其分配给处理器。这就是所谓的「静态负载均衡」(static load balancing)。
更现实的是,我们无法完美地预测工作的某一部分的运行时间,于是我们采用了「过度分解」(overdecomposition)工作的方法:我们将工作分成比处理器数量更多的任务。然后,这些任务被分配到一个「工作池」(work pool)中,每当处理器完成一项工作,就从工作池中抽取下一项工作。这就是所谓的「动态负载均衡」(dynamic load balancing)。许多图形和组合问题都可以用这种方式来解决。
有结果表明,随机分配任务到处理器在统计学上接近于最优[122],但这忽略了科学计算中的任务通常是频繁交流的方面。
练习2.45 假设你有任务$\{T_i\}_{i=1,…,N}$,运行时间为$𝑡_𝑖$,处理器数量不限。查阅2.2.4节中的Brent定理,并从中推导出任务的最快执行方案可以被描述为:有一个处理器只执行具有最大$𝑡_𝑖$值的任务。(这个练习受到了[170]的启发)。
负载均衡是图论问题
接下来,让我们考虑一个并行的工作,其中各部分都有通信。在这种情况下,我们需要均衡标量工作负载和通信。
一个并行计算可以被表述为一个图(见附录18的图论介绍),其中处理器是顶点,如果两个顶点的处理器需要在某个点上进行通信,那么这两个顶点之间就有一条边。这样的图通常是由被解决的问题的基本图衍生出来的。作为一个例子,考虑矩阵-向量乘积$y=Ax$,其中$A$是一个稀疏的矩阵,详细地看一下正在计算$y_i$的处理器,对于一些$𝑖$。$y_i \leftarrow y_{i} + A_{ij}x_j$意味着这个处理器将需要$x_j$的值,所以,如果这个变量在不同的处理器上,它需要被送过去。
我们可以将其标准化。让向量$x$和$y$不相连地分布在处理器上,并唯一地定义$P(i)$为拥有索引$i$的处理器。如果存在一个非零的元素$a_{ij}$,且$P= P(i)$,$Q = P(j)$,那么就有一条边$(P,Q)$。在结构对称矩阵的情况下,这个图是无定向的,即$a_{ij} \neq 0\Leftrightarrow a_{ij}\neq 0$。
指数在处理器上的分布现在给了我们顶点和边的权重:一个处理器有一个顶点权重,即它所拥有的指数数量;一条边$(P,Q)$有一个权重,即需要从$Q$发送到𝑃的向量成分的数量,如上所述。
现在可以将负载均衡问题表述如下。
找到一个分区$\mathbb{P} = \cup_𝑖\mathbb{P}_i$,这样顶点权重的变化最小,同时边缘权重也尽可能的低。
顶点权重的变化最小化意味着所有处理器的工作量大致相同。保持边缘权重低意味着通信量低。这两个目标不需要同时满足:可能会有一些折衷。
练习 2.46 考虑极限情况,即处理器的速度是无限的,处理器之间的带宽也是无限的。剩下的决定运行时间的唯一因素是什么?你现在需要解决什么图形问题来找到最佳的负载均衡?稀疏矩阵的什么属性给出了最坏情况下的行为?
一个有趣的负载均衡方法来自谱图理论:如果$𝐴𝐺$是无向图的邻接矩阵,$𝐷_𝐺-𝐴_𝐺$是「拉普拉斯矩阵」(graph Laplacian),那么通往最小特征值0的特征向量$u_1$是正的,而通往下一个特征值的特征向量$u_2$是与它正交。因此,$u_2$必须有交替符号的元素;进一步分析表明,有正符号的元素和负符号的元素是相连的。这就导致了图形的自然分割。
负载重分配
在某些应用中,最初的载荷分布是明确的,但后来需要调整。一个典型的例子是在有限元方法(FEM)代码中,载荷可以通过物理域的划分来分配。如果后来领域的离散化发生了变化,负载就必须重新或重新分配。在接下来的小节中,我们将看到旨在保持局部性的负载均衡和再均衡的技术。
扩散负载均衡
在许多实际情况下,我们可以将处理器图与我们的问题联系起来:任何一对进程之间都有一个顶点,通过点对点通信直接互动。因此,在负载均衡中使用这个图似乎是一个很自然的想法,只把负载从一个处理器转移到图中的邻居那里。这就是扩散式负载均衡的想法[37, 112]。虽然该图在本质上不是有向的,但为了负载均衡,我们在边上放上任意的方向。负载均衡的描述如下。
设$l$是进程$i$的负载,$\tau (j)$是边$j\rightarrow i$上负载的转移。那么
虽然我们只是用了一个$i, j$的边数,但在实践中,我们把边数线性化了。然后我们得到一个系统
其中,
$A$是一个大小为$|N|\times |E|$的矩阵,描述了连接到方节点的各条边,其元素值等于$\pm1$,取决于
$T$是转移的向量,大小为$|E|$;和
- $\bar{L}$是负荷偏差向量,表明每个节点比平均负荷高出/低出多少。
在线性处理器阵列的情况下,这个矩阵是欠确定的,边比处理器少,但在大多数情况下,系统将是超确定的,边比进程多。因此,我们要解决
由于$A^tA$和$AA^t$是非正定的,我们可以通过放松来解决大约,只需要局部知识。当然, 这种松弛的收敛速度很慢, 全局性的方法, 如Conjugate Gradients (CG), 会更快[112].
用空间填充曲线实现负载均衡
在前面的章节中,我们考虑了负载均衡的两个方面:确保所有的处理器都有大致相等的工作量,以及让分布反映问题的结构,以便将通信控制在合理范围内。我们可以这样表述第二点,当分布在并行机器上时,试图保持问题的局部性:空间中靠近的点很可能会发生交互,所以它们应该在同一个处理器上,或者至少是一个不太远的处理器。
努力保持位置性显然不是正确的策略。在BSP中,有一个统计学上的论点,即随机放置将提供一个良好的负载均衡以及通信均衡。
练习 2.47 考虑将进程分配给处理器,问题的结构是每个进程只与最近的邻居通信,并让处理器在一个二维网格中排序。如果我们对进程网格进行明显的分配,就不会有争执。现在写一个程序,将进程分配给随机的处理器,并评估会有多少争用。
在上一节中,你看到了图划分技术是如何帮助实现第二点,即保持问题的局部性。在本节中,你将看到一种不同的技术,它对初始负载分配和后续的负载再均衡都有吸引力。在后一种情况下,一个处理器的工作可能会增加或减少,需要将一些负载转移到不同的处理器。
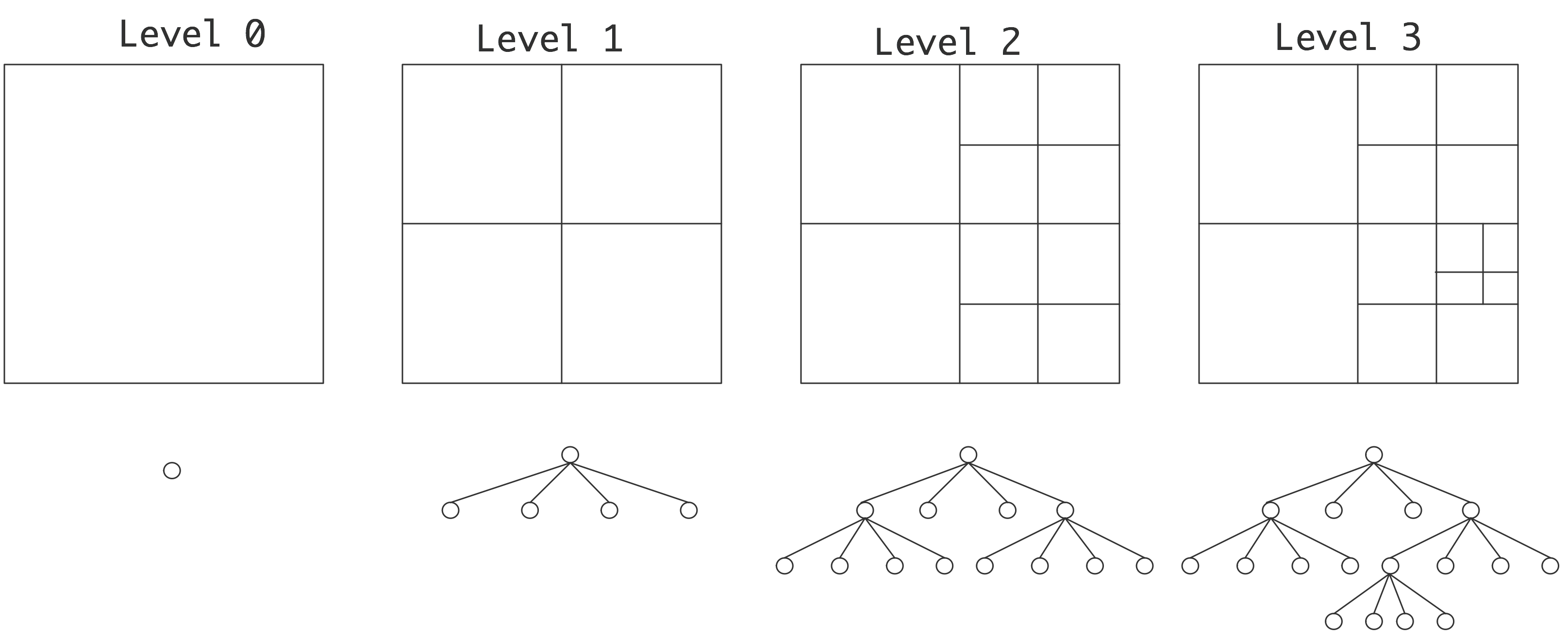
例如,有些问题是自适应细化的 。这在图2.37中得到了说明。如果我们跟踪这些细化水平,问题就会得到一个树状结构,其中的叶子包含所有的工作。负载均衡变成了在处理器上划分树叶的问题;图2.38。现在我们观察到,这个问题有一定的局部性:任何非叶子节点的子树在物理上都很接近,所以它们之间可能会有通信。
- 可能会有更多的子域出现在处理器上;为了尽量减少处理器之间的通信,我们希望每个处理器都包含一个简单连接的子域组。此外,我们希望每个处理器所覆盖的域的一部分是 “紧凑 “的,即它具有低长宽比和低表面体积比。
- 当一个子域被进一步细分时,其处理器的部分负载可能需要转移到另一个处理器。这个负载重新分配的过程应该保持位置性。
为了满足这些要求,我们使用空间填充曲线(SFC)。负载均衡树的空间填充曲线(SFC)如图2.39所示。我们不会对SFC进行正式的讨论;相反,我们将让图2.40代表一个定义:SFC是一个递归定义的曲线,每个子域都接触一次12
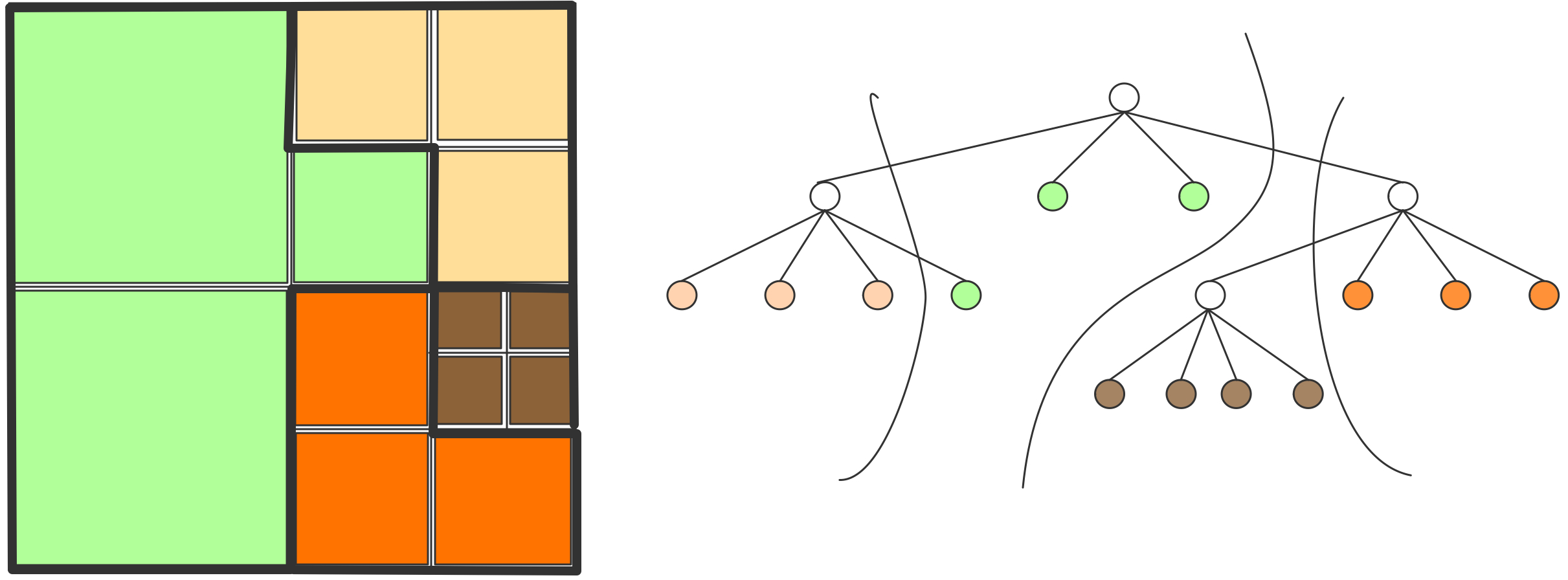
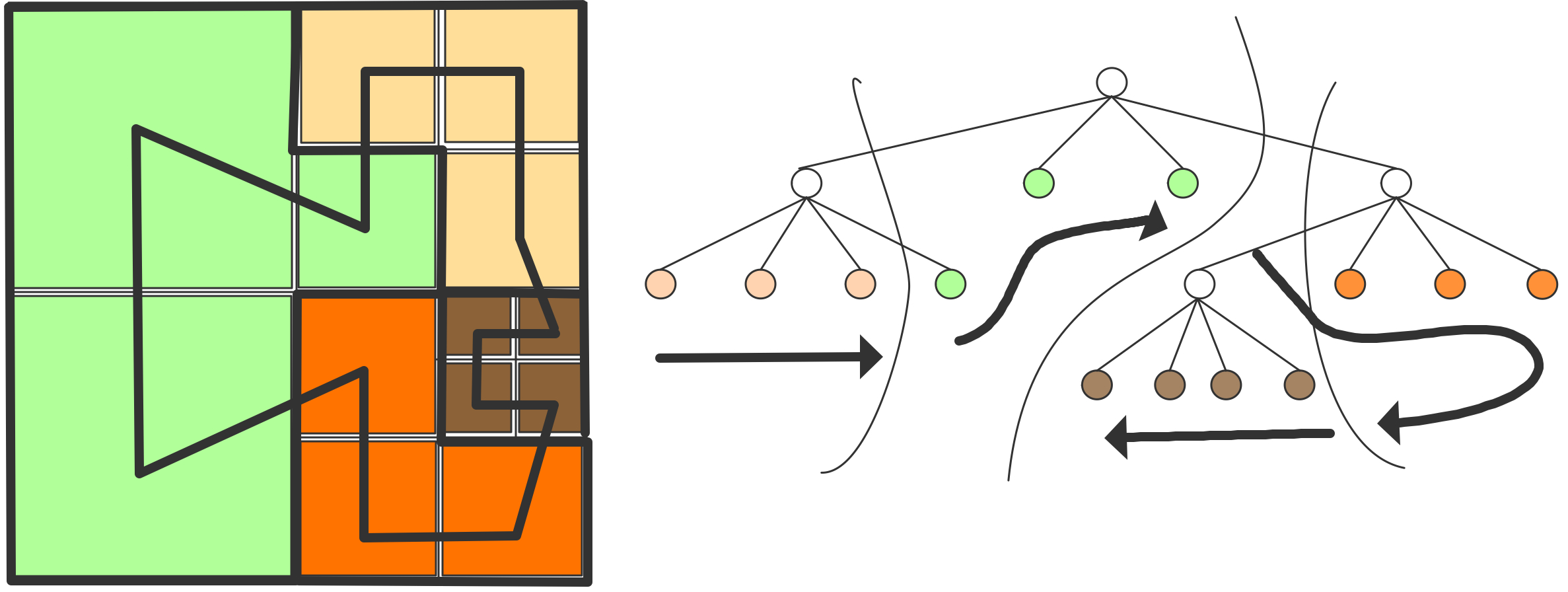
SFC的特性是,在物理上相近的领域元素在曲线上也会相近,所以如果我们将SFC映射到处理器的线性排序上,我们将保留问题的局部性。
更重要的是,如果领域再细化一个层次,我们就可以相应地细化曲线。然后,负载可以被重新分配到曲线上的相邻处理器上,而我们仍然会保留位置性。
(空间填充曲线(SFCs)在N体问题中的使用在[198]和[187]中讨论过)。
其他话题
分布式计算、网格计算、云计算
在本节中,我们将对云计算等术语以及早先的一个术语分布式计算进行简短的了解。这些都是与科学意义上的并行计算有关系的概念,但它们在某些基本方面是不同的。
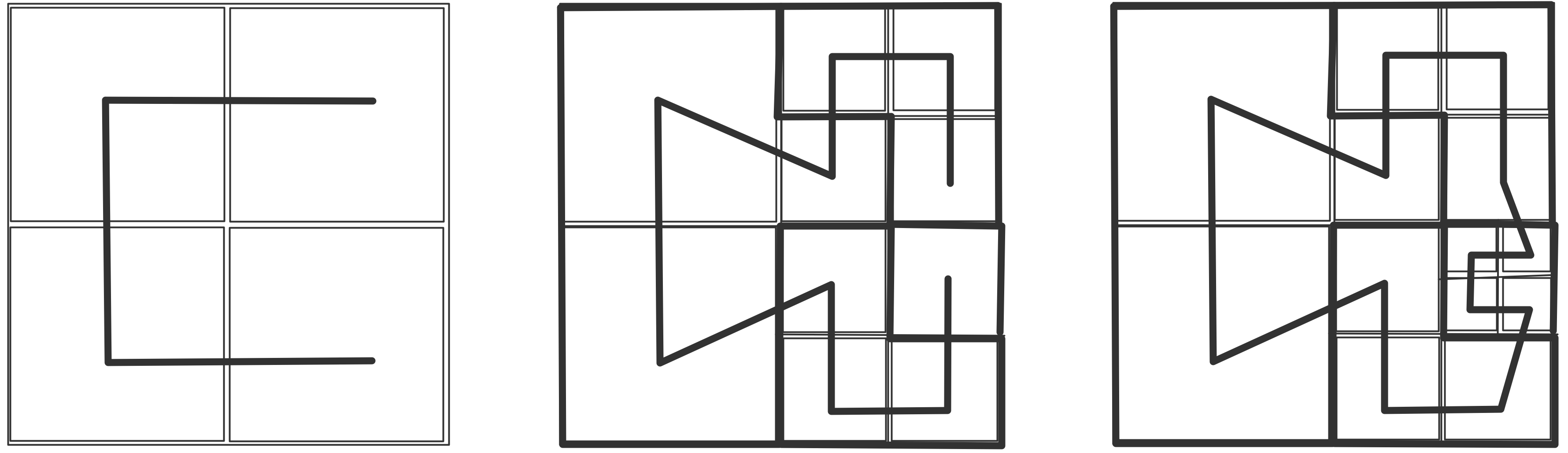
分布式计算可以追溯到来自大型数据库服务器,如航空公司的预订系统,它必须被许多旅行社同时访问。对于足够大的数据库访问量,单台服务器是不够的,因此发明了「远程过程调用」(remote procedure call)的机制,中央服务器将调用不同(远程)机器上的代码(有关的过程)。远程调用可能涉及数据的传输,数据可能已经在远程机器上,或者有一些机制使两台机器的数据保持同步。这就产生了「存储区域网络」(Storage Area Network,SAN)。比分布式数据库系统晚了一代,网络服务器不得不处理同样的问题,即许多人同时访问必须表现得像一个单一的服务器。
我们已经看到了分布式计算和高性能并行计算之间的一个巨大区别。科学计算需要并行性,因为单一的模拟对一台机器来说变得太大或者太慢;上面描述的商业应用涉及许多用户针对一个大数据集执行小程序(即数据库或网络查询)。对于科学需要,并行机器的处理器(集群中的节点)必须有一个非常快的连接;对于商业需要,只要中央数据集保持一致,就不需要这样的网络。
在高性能计算和商业计算中,服务器都必须保持可用和运行,但在分布式计算中,在如何实现这一点上有相当大的自由度。对于一个连接到数据库等服务的用户来说,由哪个实际的服务器来执行他们的请求并不重要。因此,分布式计算可以利用虚拟化:一个虚拟服务器可以在任何硬件上生成。
可以在远程服务器和电网之间做一个类比,前者在需要的地方提供计算能力,后者在需要的地方提供电力。这导致了网格计算或实用计算的出现,美国国家科学基金会拥有的Teragrid就是一个例子。网格计算最初是作为一种连接计算机的方式,通过「局域网」(Local Area Network,LAN)或「广域网」(Wide Area Network,WAN),通常是互联网连接起来。这些机器本身可以是平行的,而且通常由不同的机构拥有。最近,它被视为一种通过网络共享资源的方式,包括数据集、软件资源和科学仪器。
实用计算作为一种提供服务的方式的概念,你从上述分布式计算的描述中认识到,随着谷歌的搜索引擎成为主流,它为整个互联网建立了索引。另一个例子是安卓手机的GPS功能,它结合了地理信息系统、GPS和混搭数据。Google的收集和处理数据的计算模型已经在MapReduce[40]中正式化。它结合了数据并行方面(”地图 “部分)和中央积累部分(”规约”)。两者都不涉及科学计算中常见的紧密耦合的邻居间通信。一个用于MapReduce计算的开源框架为Hadoop[95]。亚马逊提供了一个商业的Hadoop服务。
即使不涉及大型数据集,由远程计算机为用户需求服务的概念也很有吸引力,因为它免除了用户在其本地机器上维护软件的需要。因此,Google Docs提供了各种 “办公 “应用程序,用户无需实际安装任何软件。这种想法有时被称为软件即服务(SAS),用户连接到一个 “应用服务器”,并通过一个客户端(如网络浏览器)访问它。在谷歌文档的情况下,不再有一个大型的中央数据集,而是每个用户与他们自己的数据互动,这些数据在谷歌的服务器上维护。这当然有一个很大的好处,那就是用户可以从任何可以使用网络浏览器的地方获得数据。
SAS的概念与早期技术有一些联系。例如,在大型机和工作站时代之后,所谓的瘦客户机想法曾短暂流行。在这里,用户将拥有一个工作站而不是一个终端,但却可以在一个中央服务器上存储的数据上工作。沿着这种思路的一个产品是Sun公司的Sun Ray(大约在1999年),用户依靠一张智能卡在一个任意的、无状态的工作站上建立他们的本地环境。
使用场景
按需提供服务的模式对企业很有吸引力,这些企业越来越多地使用云服务。它的优点是不需要最初的货币和时间投资,也不需要对设备的类型和大小做出决定。目前,云服务主要集中在数据库和办公应用上,但具有高性能互连的科学云正在开发中。
以下是对云资源使用场景的大致分类13。
- 扩展。在这里,云资源被用作一个平台,可以根据用户需求进行扩展。这可以被认为是平台即服务(PAS):云提供软件和开发平台,免除了用户的管理和维护。
我们可以区分两种情况:如果用户正在运行单个作业并积极等待。如果用户正在运行单个作业并积极等待输出,可以增加资源以减少这些作业的等待时间(能力测试)。另一方面,如果用户正在向一个队列提交作业,并且任何特定作业的完成时间并不重要(能力组合),资源可以随着队列的增长而增加。在HPC应用中,用户可以将云资源视为一个集群;这属于基础设施即服务(IAS):云服务是一个计算平台,允许在操作系统层面进行定制。 - 多租户。在这里,同一个软件被提供给多个用户,让每个人都有机会进行个性化定制。这属于软件即服务(SAS):软件按需提供;客户不购买软件,只为其使用付费。
- 批量处理。这是上述扩展方案之一的有限版本:用户有大量的数据需要以批处理模式进行处理。然后,云就成为一个批处理者。这种模式是MapReduce计算的良好候选者;2.11.3节。
- 存储。大多数云供应商都提供数据库服务,这些模式都是为了让用户不需要维护自己的数据库,就像缩放和批量处理模式让用户不需要担心维护集群硬件一样。
- 同步化。这种模式在商业用户应用中很受欢迎。Netflix和亚马逊的Kindle允许用户消费在线内容(分别是流媒体电影和电子书);暂停内容后,他们可以从任何其他平台恢复。苹果公司最近的iCloud为办公应用中的数据提供了同步,但与Google Docs不同的是,这些应用不是 “在云中”,而是在用户机器上。
第一个可以公开访问的云是亚马逊的弹性计算云(EC2),于2006年推出。EC2提供各种不同的计算平台和存储设施。现在有一百多家公司提供基于云的服务,远远超出了最初的计算机出租的概念。
从计算机科学的角度来看,云计算的基础设施可能是有趣的,涉及到分布式文件系统、调度、虚拟化和确保高可靠性的机制。
一个有趣的项目,结合了网格和云计算的各个方面,是加拿大天文研究高级网络[179]。在这里,大量的中央数据集被提供给天文学家,就像在一个网格中一样,同时还有计算资源,以类似云的方式对其进行分析。有趣的是,云资源甚至采取了用户可配置的虚拟集群的形式。
角色定位
综上所述,14 我们有三种云计算服务模式。
软件即服务:消费者运行供应商的应用程序,通常通过浏览器等客户端;消费者不安装或管理软件。谷歌文档就是一个很好的例子。
平台即服务:向消费者提供的服务是运行由消费者开发的应用程序的能力,消费者不管理所涉及的处理平台或数据存储。
基础设施即服务:供应商向消费者提供运行软件的能力,并管理存储和网络。消费者可以负责操作系统的选择和网络组件,如防火墙。
这些可以按以下方式部署。
私有云:云基础设施由一个组织管理,供其独家使用。
公共云:云基础设施由广大客户群管理使用。我们还可以定义混合模式,如社区云。
那么,云计算的特点是。
按需和自我服务:消费者可以快速请求服务和改变服务水平,而不需要与提供者进行人工互动。
快速弹性:在消费者看来,存储或计算能力的数量是无限的,只受预算的限制。请求额外的设施是快速的,在某些情况下是自动的。
资源池:虚拟化机制使云看起来像一个单一的实体,而不考虑其底层基础设施。在某些情况下,云会记住用户访问的 “状态”;例如,亚马逊的Kindle书籍允许人们在个人电脑和智能手机上阅读同一本书;云存储的书籍 “记住 “读者离开的地方,而不管平台如何。
网络访问:云可以通过各种网络机制使用,从网络浏览器到专用门户。
测量服务:云服务通常是 “计量 “的,消费者为计算时间、存储和带宽付费。
能力与容量计算
大型并行计算机可以以两种不同的方式使用。在后面的章节中,你将看到科学问题是如何几乎可以任意扩大规模的。这意味着,随着对精度或规模的需求越来越大,需要越来越大的计算机。使用整台机器来解决一个问题,只以解决问题的时间作为衡量成功的标准,这被称为能力计算。
另一方面,许多问题需要比整台超级计算机更少的时间来解决,所以通常一个计算中心会设置一台机器,让它为连续的用户问题服务,每个问题都比整台机器小。在这种模式下,衡量成功的标准是单位成本的持续性能。这就是所谓的容量计算,它需要一个精细调整的作业调度策略。
一个流行的方案是公平分享调度,它试图在用户之间,而不是在进程之间平均分配资源。这意味着,如果一个用户最近有作业,它将降低该用户的优先级,它将给短的或小的作业以更高的优先级。这个原则的调度器的例子是SGE和Slurm。
作业可以有依赖性,这使得调度更加困难。事实上,在许多现实条件下,调度问题是NP-complete的,所以在实践中会使用启发式方法。这个话题虽然有趣,但在本书中没有进一步讨论。
MapReduce
MapReduce[40]是一种用于某些并行操作的编程模型。它的一个显著特点是使用函数式编程来实现。MapReduce模型处理以下形式的编译。
对于所有可用的数据,选择满足某种标准的项目。
并为它们发出一个键值对。这就是映射阶段。
可以选择有一个组合/排序阶段,将所有与相同键值有关的对归为一组。
然后对键进行全局还原,产生一个或多个相应的值。这
这是还原阶段。
现在我们将举几个使用MapReduce的例子,并介绍支撑MapReduce抽象的函数式编程模型。
MapReduce模型的表达能力
MapReduce模型的减少部分使其成为计算数据集全局统计数据的主要候选者。一个例子是计算一组词在一些文档中出现的次数。被映射的函数知道这组词,并为每个文档输出一对文档名称和一个包含词的出现次数的列表。然后,减法对出现次数进行分量级的求和。
MapReduce的组合阶段使得数据转换成为可能。一个例子是 “反向网络链接图”:map函数为在名为 “源 “的页面中发现的每个目标URL链接输出目标-源对。reduce函数将与一个给定的目标URL相关的所有源URL的列表连接起来,并排放出目标列表(source)对。
一个不太明显的例子是用MapReduce计算PageRank(第9.4节)。在这里,我们利用PageRank的计算依赖于分布式稀疏矩阵-向量乘积的事实。每个网页对应于网页矩阵𝑊的一列;给定一个在网页$p$上的概率$j$,然后该网页可以计算出图元$⟨i, w_{ij}p_j⟩$。然后MapReduce的组合阶段将$(W p)_{i}=\sum_{j} w_{i j} p_{j}$。
数据库操作可以用MapReduce来实现,但由于它的延迟比较大,不太可能与独立的数据库竞争,因为独立的数据库是为快速处理单个查询而优化的,而不是批量统计。
第8.5.1节中考虑了用MapReduce进行排序。
其他应用见http://horicky.blogspot.com/2010/08/designing-algorithmis-for-map-reduce.html。
MapReduce软件
谷歌对MapReduce的实现是以Hadoop的名义发布的。虽然它适合谷歌的单阶段读取和处理数据的模式,但对许多其他用户来说,它有相当大的缺点。
Hadoop会在每个MapReduce周期后将所有数据冲回磁盘,所以对于需要超过一个周期的操作来说,文件系统和带宽需求太大。
在计算中心环境中,用户的数据不是连续在线的,将数据加载到Hadoop文件系统(HDFS)所需要的时间很可能会压倒实际分析。
由于这些原因,进一步的项目,如Apache Spark(https://spark.apache.org/)提供了数据的缓存。
执行问题
在分布式系统上实现MapReduce有一个有趣的问题:键-值对中的键集是动态确定的。例如,在上面的 “字数 “类型的应用中,我们并不是先验地知道字数的集合。因此,我们并不清楚应该将键值对发送给哪个还原器进程。
例如,我们可以使用一个哈希函数来确定这一点。由于每个进程都使用相同的函数,所以不存在分歧。这就留下了一个问题,即一个进程不知道要接收多少个带有键值对的消息。这个问题的解决方案在第6.5.6节中描述过。
函数式编程
映射和规约操作很容易在任何类型的并行架构上实现,使用线程和消息传递的组合。然而,在开发这个模型的谷歌公司,传统的并行性没有吸引力,原因有二。首先,处理器在计算过程中可能会出现故障,所以传统的并行模式必须要用容错机制来加强。其次,计算硬件可能已经有了负荷,所以部分计算可能需要迁移,而且一般来说,任务之间的任何类型的同步都会非常困难。
MapReduce是一种从并行计算的这些细节中抽象出来的方法,即通过采用函数式编程模型。在这样的模型中,唯一的操作是对一个函数的评估,应用于一些参数,其中参数本身就是一个函数应用的结果,而计算的结果又被作为另一个函数应用的参数。特别是,在严格的函数模型中,没有变量,所以没有静态数据。
一个函数应用,用Lisp风格写成(f a b)(意思是函数f被应用于参数a和b),然后通过收集输入,从它们所在的地方到评估函数f的处理器,来执行。
1 | (map f (some list of arguments)) |
而结果是一个将f应用于输入列表的函数结果列表。所有并行的细节和保证计算成功完成的所有细节都由map函数处理。现在我们只缺少还原阶段,它也同样简单。
1 | (reduce g (map f (the list of inputs))) |
reduce函数接收一个输入列表并对其进行还原。
这种函数模型的吸引力在于函数不能有副作用:因为它们只能产生一个输出结果,不能改变环境,因此不存在多个任务访问相同数据的协调问题。
因此,对于处理大量数据的程序员来说,MapReduce是一个有用的抽象。当然,在实现层面上,MapReduce软件使用了熟悉的概念,如分解数据空间、保存工作列表、将任务分配给处理器、重试失败的操作等等。
异构计算
你现在已经看到了几种计算模型:单核、共享内存多核、分布式内存集群、GPU。这些模型的共同点是,如果有一个以上的指令流处于活动状态,所有的指令流都是可以互换的。关于GPU,我们需要细化这一说法:GPU上的所有指令流都是可互换的。然而,GPU并不是一个独立的设备,而是可以被认为是主机处理器的一个协处理器。
如果我们想让主机执行有用的工作,而协处理器处于活动状态,我们现在有两个不同的指令流或指令流类型。这种情况被称为异构计算。在GPU的情况下,这些指令流的编程机制甚至略有不同—为GPU使用CUDA,但情况不必如此:英特尔许多集成核心(MIC)架构是用普通C语言编程的。
计算机中的运算
科学计算等领域中常见的数字类型有:整数(或整型)$\cdots$,-2,-1,0,1,2,$\cdots$ 实数 0,1,-1.5,2/3,$\sqrt 2$,log 10,$\cdots$,以及复数 $1+2i$,$\sqrt3-\sqrt5i, \cdots$, 计算机硬件的组织方式是只给一定的空间来表示每个数字,是「字节」(bytes)的倍数,每个字节包含8「位」(bits)。典型的数值是整数为4字节,实数为4或8字节,复数为8或16字节。
由于内存空间有限,计算机并不能存储所有范围的数字。整数中计算机只能存储一个范围(Python等语言有任意大的整数,但这没有硬件支持);而在实数里,甚至不能存储一个范围,因为任意区间[a,b]都包含无限多的数字。任何实数的代表都会导致存储的数字之间存在间隔。计算机中的计算被称为「有限精度的运算」(finite precision arithmetic)。由于许多结果是无法表示的,任何导致这种数字的运算都必须通过发出错误或近似的结果来处理。在本章中,我们将研究这种对数值计算的 “真实 “结果的近似的影响。
关于详细的讨论,请参见Overton的书[165];在网上很容易找到Goldberg的文章[80]。关于算法中舍入误差分析的广泛讨论,见Higham [106] 和Wilkinson [201] 的书。
位运算
计算机的最底层是以「位」(bits)来存储和表示的。比特,是 “二进制数字 “的简称,分为0和1。使用比特我们就可以用二进制表达数字。
其中的下标表示数字的进制。
存储器的下一个组织层次是「字节」(bytes):一个字节由8位组成,因此可以代表0-255的数值。
练习 3.1 使用位操作来测试一个数字是奇数还是偶数。你能多想几种方法吗?
整数
科学计算绝大多数情况都是在实数上的运算。除了密码学等应用,对整数的计算很少增加到任意多的位数。也有一些应用,如 “「粒子模型」(particle-in-cell)”,可以用位操作来实现。然而,整数在索引计算中仍有经验。
整数通常以16、32或64位存储,16位越来越少,64位则越来越多。这种增长的主要原因不是计算性质的变化,而是因为整数被用于数组索引。数据集的增长(特别是在并行计算中),需要更大的索引。例如,在32位中可以存储从0到 $2^{32}- 1 \approx 4⋅10^9$的数字。换句话说,一个32位的索引可以解决4GB的内存。直到最近,这对大多数用途来说已经足够了;如今,对更大的数据集的需求使得64位索引成为必要。
我们对数组进行索引时只需要正整数。当然,在一般的整数计算中,我们也需要容纳负整数。现在我们将讨论几种实现负整数的策略。我们的初衷是,正负整数的算术应该和正整数一样简单:我们用于比较和操作比特串的电路应该可以用于(有符号)整数。
有几种实现负整数的方法。其中最简单的是保留一位作为符号位(sign bit),用剩下的31位(或15位或63位;从现在开始,我们将以32位为标准)位来存储绝对大小。通过比较,我们将把比特串的直接解释称为「无符号整数」(unsigned integers)。
| 比特串 | 00⋯0 … 01⋯1 | 10⋯0 … 11⋯1 |
|---|---|---|
| 解释为无符号int | 0 … $2^{31}-1$ | $2^{31}…2^{32}-1$ |
| 解释为有符号整数 | 0 … $2^{31}-1$ | $-0…(2^{31}-1)$ |
这种方案有一些缺点,其中之一是同时存在正数和负数0。这意味着对平等的测试变得更加复杂,而不是简单地作为一个位串来测试平等。更重要的是,在比特串的后半部分,作为有符号的整数的解释减少了,向右走了。这意味着对大于的测试变得复杂;同时,将一个正数加到一个负数上,现在必须与将其加到一个正数上区别对待。
另一个解决方案是将无符号数$n$解释为$n-B$,其中$B$是某个合理的基数,例如 $2^{31}$。
| 比特串 | 00⋯0 … 01⋯1 | 10⋯0 … 11⋯1 |
|---|---|---|
| 解释为无符号int | $0 … 2^{31}-1$ | $2^{31}…2^{32}-1$ |
| 解释为移位的int | $-2^{31}…-1$ | $0…2^{31}-1$ |
这种移位方案不存在$\pm$0的问题,数字的排序也是一致的。然而,如果我们通过对代表$n$的位串进行操作来计算$n-n$,我们并没有得到零的位串。
为了保证这种理想的行为,我们改用正负数旋转数线,将零的模式放回零处。
由此产生的方案,也就是最常用的方案,被称为「二进制补码」(2’s complement)。使用这种方案,整数的表示方法正式定义如下。
定义2:设$n$是一个整数,则其二进制$\beta(n)$是个非负整数定义如下:
如果$0\leqslant n\leqslant 2^{31}-1$,则使用正常的$n$比特模式,即
对于$-2^{31} \leqslant n \leqslant -1$,$n$是由$2^{32} - |n|$的比特模式表示。
我们用$\eta=\beta-1$来表示接受一个比特模式并解释为整数的反函数。
下表显示了比特串与它们作为二进制整数的解释之间的对应关系。
| 比特串$n$ | 00…0 … 01…1 | 10…0 … 11…1 |
|---|---|---|
| 解释为无符号int | $0 …2^{31}-1$ | $2^{31} … 2^{32}-1$ |
| 解释$\beta(n)$为二进制整数 | $0 …2^{31}-1$ | $-2^{31} … -1$ |
值得注意的是:
- 正整数和负整数的比特模式之间没有重叠,特别是,只有一个零的模式。
- 正数的前导位是零,而负数的前导位是1。这使得前导位就像一个符号位;但是请注意上面的讨论
- 如果你有一个正数𝑛,你可以通过翻转所有的位,然后加1来得到-𝑛。
练习 3.2 对于负数的原始方案和二进制补码方案,给出比较测试 $m < n$的伪码,其中 $m$ 和 $n$是整数。请注意区分$m、n$为正数、零数或负数的所有情况。
整数溢出
两个相同符号的数字相加,或两个任意符号的数字相乘,都可能导致结果过大或过小而无法表示。这就是所谓的「溢出」(overflow)。下面以一个例子进行讨论:
练习 3.3 调查一下当你进行这样的计算时会发生什么。如果你试图明确写下一个不可表示的数字,例如在一个赋值语句中,编译器会如何提示?
如果使用C语言,我们可能得到一个有意义的结果,这是因为在有符号数的情况下,C标准下并没有定义溢出行为。
二进制加法
让我们考虑对二进制整数做一些简单的算术。我们首先假设我们拥有能处理无符号整数的硬件。我们的目标是看到我们可以用这个硬件对有符号的整数进行计算,就像用二进制表示一样。
我们考虑$m+n$的计算,其中$m,n$是可表示的数字。
我们区分了不同的情况。
简单的情况是 $0 < m, n$。在这种情况下,我们进行正常的加法运算,只要结果保持在$2^{31}$以下,我们就能得到正确的结果。如果结果是$2^{31}$或更多,我们就会出现整数溢出,对此我们无能为力。
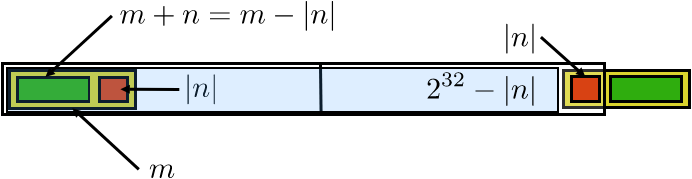
当$m>0,n<0$,并且$m+n>0$.那么$\beta(m)=m$和$\beta(n)=2^{32}-|n|$,所以无符号加法就变成
由于$m - |n|>0$,这个结果$>2^{32}$。(见图 3.1)然而,我们观察到这基本上是$m + n$的第 33 位被设置。如果我们忽略这个溢出的位,我们就会得到正确的结果。
当$m>0, n<0$但$m+n<0$,那么
因为$|n|-m>0$,所以得到
二进制减法
在上面的练习3.2中,我们探索了两个整数的比较。现在让我们来探讨一下如何实现两个补码的减法。考虑$0\leqslant m\leqslant 2^{31}-1$和$1\leqslant n\leqslant 2^{31}$,让我们看看在计算$m-n$时会发生什么。
假设我们有一个无符号32位数加减法的算法。我们能不能用它来减去两个补码的整数?我们先观察一下,整数减法$m-n$变成无符号加法$m+(2^{32}-n)$。
当$m<|n|$时,$m-n$为负数且$1\leqslant |m-n|\leqslant 2^{31}$,那么$m-n$的比特形式为
现在,$2^{32}-(n-m)=m+(2^{32}-n)$,所以我们可以通过将$m$和$-n$的位型相加作为无符号整数来计算$m-n$的二进制码。
当$m>n$,我们注意到$m+(2^{32}-n)=2^{32}+m-n$。由于$m-n>0$,这个数>232,因此不是一个合法的负数表示。然而,如果我们将这个数字存储在33位,我们会发现它是正确的结果$m-n$,加上33位的一个比特。因此,通过执行无符号加法,并忽略溢出位,我们再次得到正确的结果。
在这两种情况下,我们的结论是,我们可以通过将代表$m$和$-n$的无符号数相加,并忽略溢出的情况,来执行减法$m-n$。
其他操作
有些操作在二进制中非常简单:乘以2相当于将所有位向左移动一个,而除以2相当于向右移动一位。至少,无符号整数是这样的。
练习 3.4 当你使用位移在二进制码中乘以或除以2时,是否有额外的复杂情况?
在C语言中,左移操作是<<,右移是>>,因此
1 | i<<3 |
相当于乘以8。
基于二进制的十进制编码
十进制在科学计算中并不重要,但在金融领域却十分有用,因为设计货币的计算绝对要精确。二进制并不擅长使用十进制转换,因为像1/10这样的数字在二进制中是重复的分数。由于尾数的位数有限,这意味着1/10这个数字不能用二进制精确表示。由于这个原因,二进制的十进制编码方案被用于老式的IBM主机,事实上,在IEEE 754[113]的修订中也被标准化了;另见3.3.7节。
在BCD方案中,一个或多个十进制数字被编码为若干比特。最简单的方案是将数字0 … 9的四个比特。这样做的好处是,一个BCD数字中每个数字都很容易被识别;它的缺点是,大约有1/3的比特被浪费了,因为4个比特可以编码0 … 15. 更有效的编码方法是将0 … 999的10个比特,原则上可以存储数字$0 … 10^{23}$. 虽然这样做的效率很高,因为浪费的位数很少,但是识别这样一个数字中的各个位数需要一些解码。由于这个原因,BCD算术需要处理器的硬件支持,现在很少有这种支持;一个例子是IBM Power架构,从IBM Power6开始。
用于计算机算术的其他数基
已经有一些关于三元运算的实验(见http://en.wikipedia.org/wiki/Ternary_computer和http://www.computer-museum.ru/english/setun.htm),但是,没有实际的硬件存在。
实数
在这一节中,我们将研究实数如何在计算机中表示,以及各种方案的局限性。下一节将探讨这对涉及计算机数字的算术的影响。
它们不是真正的实数
在数学科学中,我们通常用实数工作,所以假装计算机也能这样做是很方便的。然而,由于计算机中的数字只有有限的比特数,大多数实数都不能被准确表示。事实上,甚至许多分数也不能准确表示,因为它们会重复;例如,1/3=0.333…,这在十进制或二进制中都不能表示。附录37.6中给出了这方面的一个说明。
练习 3.5 一些编程语言允许你在写循环时不仅使用整数,还可以使用实数作为 “计数器”。解释一下为什么这是个坏主意。提示:何时达到上界?
一个分数是否重复取决于数字系统。(在二进制计算机中,这意味着像1/10这样的分数是重复的,而在十进制算术中,这些分数的位数是有限的。由于小数运算在金融计算中很重要,所以有些人关心这种算术的准确性;关于对此做了什么,见3.2.4.1节。
练习3.6 显示每个二进制分数,即形式为$1.01010111001_2$的数字,都可以精确地表示为一个终止的十进制分数。不是每个十进制分数都能表示为二进制分数的原因是什么?
实数的表示
实数的存储方式类似于所谓的 “科学符号”,即一个数字用一个显数和一个指数表示,例如$6.022⋅10^{23}$,它的显数是6022,第一个数字后有一个「小数点」(radix point),指数是23。这个数字代表
我们引入一个基数,一个小的整数,在前面的例子中是10,在计算机数字中是2,用它来写数字,作为$t$项的和。
其中的组成部分是
「符号位」(sign bit):存储数字是正数还是负数的一个位。
$\beta$是数字系统的基数。
$0 \leqslant d_i \leqslant \beta - 1$ 尾数或显数的位数 - 小数点的位置(小数的小数点)被隐含地假定为小数。小数点的位置被隐含地假定为紧随第一位的位置。
$t$是尾数的长度。
$e\in [L,U]$指数;通常$L<0<U$和$L\approx -U$。
注意,整数有一个明确的符号位;指数的符号处理方式不同。出于效率的考虑,$e$不是一个有符号的数字;相反,它被认为是一个超过某个最小值的无符号数字。例如,数字0的比特模式被解释为$e = L$。
案例
让我们看一下浮点表示法的一些具体例子。对于人类来说,基数10是最合理的选择,但计算机是二进制的,所以基数2占据主导地位。老式的IBM大型机将比特分组,使之成为基数16的表示法。
其中,单精度和双精度格式是迄今为止最常见的。我们将在第3.3.7节和进一步讨论这些问题。
限制:溢出和下溢
由于我们只用有限的比特来存储浮点数,所以不是所有的数字都能被表示出来。那些不能被表示的数字分为两类:那些太大或太小(在某种意义上)的数字,以及那些落在空白处的数字。
第二类是计算结果必须经过四舍五入或截断才能表示,这是舍入误差分析领域的基础。我们将在下面的章节中详细研究这个问题。
数字过大或过小有以下几种情况。溢出 我们可以存储的最大的数字,其每个数字都等于$\beta$。
| unit | fractional | exponent | |
|---|---|---|---|
| position | 0 | 1 … t-1 | |
| digit | $\beta -1$ | $\beta-1 … \beta -1$ | |
| value | 1 | $\beta^{-1}…\beta^{-(t-1)}$ |
加起来就是
而最小的数字(即最负数)是$-(\beta - \beta^{-(t-1)})$;任何大于前者或小于后者的情况都会导致溢出。大于前者或小于后者都会导致「溢出」(overflow)的情况发生。
下溢最接近零的数字是$\beta-(t-1)⋅L$。如果计算结果小于该值(绝对值),就会导致一种叫做「下溢」(underflow)的情况。。
只有少数实数可以被精确表示,这一事实是舍入误差分析领域的基础。我们将在下面的章节中详细研究这个问题。
溢出或下溢的发生意味着你的计算将从这一点上 “出错”。溢出将使计算在本应是非零的地方以零进行;溢出被表示为Inf,简称 “无限”。
练习 3.7 对于实数$x,y$,$g=\sqrt{(x^2+y^2/2)}$满足
所以,如果𝑥和𝑦是可表示的。如果你用上述公式计算𝑔,会出现什么问题?你能想到一个更好的方法吗?
用Inf计算在某种程度上是可能的:将这些数量中的两个相加又会得到Inf。然而,减去它们会得到NaN:”不是一个数字”。
在这些情况下,计算都不会结束:处理器会继续,除非你告诉它不这样做。这个 “否则 “是指你告诉编译器产生一个「中断」(interrupt),用一个错误信息来停止计算。见3.6.5节。
归一化和非归一化的数字
浮点数的一般定义,方程式(3.1),给我们留下了一个问题,即数字有不止一种表示方法。例如,$.5\times 10^2=.05\times 10^3$。由于这将使计算机运算变得不必要的复杂,例如在测试数字是否相等时,我们使用规范化的浮点数。如果一个数字的第一个数字是非零的,那么这个数字就是归一化的。这意味着尾数部分是
在二进制数的情况下,一个实际的含义是,第一个数字总是1,所以我们不需要明确地存储它。在IEEE 754标准中,这意味着每个浮点数的形式为
而只有数字$d_1d_2…d_t$被存储。
这个方案的另一个含义是,我们必须修改下溢的定义(见上面3.3.3节):任何小于$1⋅\beta L$的数字现在都会导致下溢。试图计算一个绝对值小于该值的数,有时会通过使用非正常化的浮点数来处理,这个过程被称为「渐进式下溢」(gradual underflow)。在这种情况下,指数的一个特殊值表明该数字不再被规范化。在IEEE标准算术的情况下,这是通过一个零指数域来实现的。
然而,这通常比用普通的浮点数计算要慢几十或几百倍。在写这篇文章的时候,只有IBM Power6有硬件支持渐进式下溢。
表示性误差
让我们考虑一个在计算机的数字系统中无法表示的实数。
一个不可表示的数字可以通过普通四舍五入、向上或向下四舍五入或截断来近似表示。这意味着,一个机器数$x$是它周围的所有$x$的代表。在尾数为$t$的情况下,这是与$x$不同的数字的区间,在$t+1$个数字中。对于尾数部分,我们得到。
如果𝑥是一个数字,$\tilde{x}$它在计算机中的表示,我们称$x-\tilde{x}$为「表示性误差」(representation error)或「绝对表示误差」(absolute representation error),$(x-\tilde{x})/x$为「相对表示误差」(relative representation error)。通常情况下,我们对误差的符号不感兴趣。所以我们可以将误差和相对误差分别应用于$|𝑥-\tilde{x}|$和$|\frac{\tilde{x}-x}{x}|$。
通常,我们只对误差的界限感兴趣。如果$\epsilon$是对误差的约束,我们将写成
对于相对误差,我们注意到
让我们考虑一个十进制算术的例子,即$\beta=10$,并且有一个3位数的尾数:$t=3$。数字$x=1.256$,其表示方法取决于我们是四舍五入还是截断。$\tilde{x}_{round} = 1.26$, $\tilde{x}_{truncate} = 1.25$。误差在第四位:如果$\varepsilon =x-\tilde{x}$那么$|\varepsilon| < \beta^{-(t-1)}$。
练习3.8 本例中的数字没有指数部分。如果有的话,其误差和相对误差是多少?
练习3.9 如上所述,在二进制运算中,单位数总是1。这对表示错误有什么影响?
机器精度
通常我们只对表示误差的数量级感兴趣,我们将写$\tilde{x}=x(1+\varepsilon)$,其中$|\epsilon| \leqslant \beta-t$。这个最大的相对误差被称为「机器精度」(machine precision)(有时也称为machine epsilon),典型的数值是。
机器精度可以用另一种方式定义:$\epsilon$是可以加到1上的最小的数字,这样$1+\epsilon$的表示方法与1不同。一个小例子表明,对齐指数可以转移一个太小的操作数,这样它在加法运算中就被有效地忽略。
另一种方法是,在加法$x+y$中,如果$x$和$y$的比例过大,结果将与$x$相同。
机器精度是计算可达到的最大精度:如果要求单精度超过6位或更多位数的精度,或者双精度超过15位,是没有意义的。
练习3.10 写一个小程序,计算机器的$\epsilon$值。如果你把编译器的优化级别设置得低或高,有什么区别吗?
练习3.11 数字$e\approx 2.72$,自然对数的基数,有多种定义。其中一个是
写一个单精度程序,尝试用这种方式计算$e$。评估上界$n=10^k$的表达式,$k=1, …. , 10$. 解释一下大$n$的输出。对误差的行为进行评论。
IEEE 754的浮点数标准
几十年前,像尾数的长度和操作的四舍五入行为等问题在不同的计算机制造商之间,甚至在同一制造商的不同型号之间可能会有所不同。从代码的可移植性和结果的可重复性来看,这显然是一个坏情况。IEEE 754标准对这一切进行了编纂,例如,规定单精度和双精度算术的尾数为24和53位,使用符号位、指数、尾数的存储序列,见图3.2。图中列出了单精度标准中所有可能的位模式的含义。
注释 11 754标准的全称是’IEEE二进制浮点运算标准(AN- SI/IEEE Std 754-1985)’。它也与IEC 559:’微处理器系统的二进制浮点算术’相同,被ISO/IEC/IEEE 60559:2011所取代。
IEEE 754是二进制算术的标准;还有一个标准,IEEE 854,允许十进制算术。
注释 12 令人瞩目的是,在场的这么多硬件人士在知道p754有多难的情况下,都同意它应该对整个社区有益。如果它能鼓励浮点软件的生产,缓解可靠软件的开发,就能为大家的硬件创造一个更大的市场。这种利他主义的程度是如此惊人,以至于MATLAB的创建者Cleve Moler博士曾经建议外国游客不要错过该国最令人敬畏的两大景观:大峡谷和IEEE p754的会议。W. Kahan,http://www.cs.berkeley.edu/~wkahan/ieee754status/754story.html。
该标准还宣布四舍五入行为是正确的四舍五入:一个操作的结果应该是精确结果的四舍五入版本。关于四舍五入(和截断)对数字计算的影响,下面会有更多的介绍。
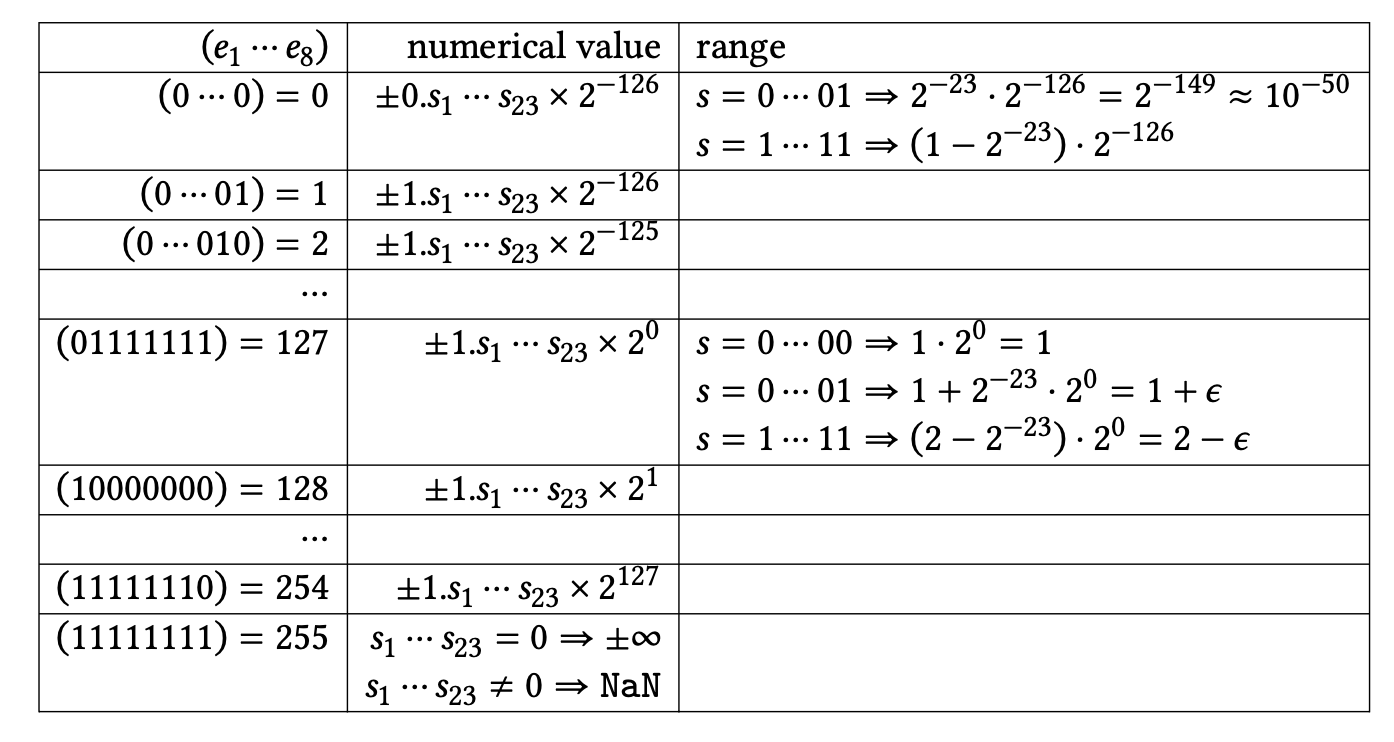
在上面,我们已经看到了溢出和下溢的现象,也就是导致不可表示的数字的操作。还有一种特殊情况需要处理:如果程序要求进行非法运算,如$\sqrt{-4}$,应该返回什么结果?IEEE 754标准对此有两个特殊量。Inf和NaN代表 “无穷大 “和 “不是一个数字”。Inf是指溢出或除以0的结果,not-a-number是指,例如,从infinity中减去infinity的结果。如果NaN出现在一个表达式中,整个表达式将评估为该值。用Inf计算的规则要复杂一些[80]。
图3.3给出了IEEE 754单精度中所有位模式的含义清单。从上面可以看出,对于归一化的数字,第一个非零位是1,它不被存储,所以位模式$d_1d_2 … d_t$被解释为$1.d_1d_2 … d_t$ 。
练习 3.12 每个程序员都会犯这样的错误:将一个实数存储在一个整数中,或者反过来存储。例如,如果你调用一个函数的方式与它的定义不同,就会发生这种情况。
1 | void a(double x) {....} |
当在函数中打印x时会发生什么?考虑一个小整数的比特模式,并使用图3.3中的表格将其解释为一个浮点数。解释一下,它将是一个未归一化的数字。
如今,几乎所有的处理器都遵守了IEEE 754标准。早期的NVidia Tesla GPU在单精度方面不符合标准。这样做的理由是,单精度更可能用于图形,在那里,准确的合规性不太重要。对于许多科学计算,双精度是必要的,因为计算的精度会随着问题大小或运行时间的增加而变差。这对于第四章中的那种计算来说是正确的,但对于其他的计算,如格子玻尔兹曼法(LBM),则不是这样。
浮点数异常
各种各样的操作可能会给出一个无法表示为浮点数的结果。这种情况被称为异常(exception),我们说提出了一个异常。结果取决于错误的类型,而计算则正常进行。(可以让程序中断:第3.6.6节)。
Not-a-Number
以下情况处理器将表示为NaN(’不是一个数字’)的结果。
- 两个无穷大相减,注意两个无穷大相加仍为无穷大
- 0乘以无穷大
- 0除以0或无穷大除以无穷大
- $\sqrt x$当$x<0$时
- 比较 $x < y$ 或 $x > y$ 时,其中任意一个数为$NaN$
由于处理器可以继续对这样的数字进行计算,所以它被称为「安静的NaN」(quiet NaN)。相比之下,一些NaN数量可以导致处理器产生一个中断或异常。这被称为「信号型NaN」(signalling NaN)。
信号NaN是有用途的。例如,你可以用这样一个值来填充分配的内存,以表明它在计算中是未初始化的。任何使用这样一个值的行为都是一个程序错误,并会引起一个异常。
2008年修订的IEEE 754建议使用NaN的最有效位作为is_quiet位来区分安静和信号NaN。
关于GNU编译器中对Nan的处理,请参见https://www.gnu.org/software/libc/manual/html_node/Infinity-and-NaN.html。
除以零
除以0的结果是Inf。如果一个结果不能作为一个有限的数字来表示,就会引发这个异常。
下溢
如果一个数字太小,不能被表示,就会出现这个异常。
不精确
如果出现不精确的结果,例如平方根,就会引发这个异常,如果没有被困住,就会出现溢出。
舍入误差分析
过大或过小的数字无法表示,导致溢出和下溢,是不正常的:通常可以安排计算,使这种情况不会发生。相比之下,计算机数字之间的计算结果(甚至像一个简单的加法)无法表示的情况是非常普遍的。因此,看一个算法的实现,我们需要分析这种小错误在计算中传播的影响。这就是通常所说的「舍入误差分析」(round-off error analysis)。
正确的舍入
3.3.7节中提到的IEEE 754标准,不仅声明了浮点数的存储方式,还给出了加、减、乘、除等运算的准确性标准。该标准中的算术模型是正确的四舍五入模型:一个操作的结果应该像遵循以下程序一样。
计算出运算的确切结果,无论这是否可以表示。
然后将这个结果四舍五入到最接近的计算机数字。
简而言之:一个操作的结果的表示就是该操作的四舍五入的准确结果。(当然,在两次操作之后,它不再需要坚持计算的结果是精确结果的四舍五入版本)。
如果这句话听起来微不足道或不言而喻,请考虑以减法为例。在尾数为两位的十进制数制中,计算结果为$1.0 - 9.4 ⋅ 10^{-1} = 1.0 - 0.94 = 0.06 = 0.6 ⋅ 10^{-2}$。请注意,在一个中间步骤中,尾数.094出现了,它比我们为我们的数字系统声明的两个数字多了一个数字。这个额外的数字被称为「警戒位」(guard digit)。
如果没有警戒位,这个运算将以$1.0-9.4⋅10^{-1}$的形式进行,其中$9.4⋅10^{-1}$将被四舍五入为0.9,最终结果为0.1,这几乎是正确结果的两倍。
练习 3.13 考虑$1.0-9.5⋅10^{-1}$的计算,并再次假设数字被四舍五入以适应两位数的尾数。为什么这个计算在某种程度上比刚才的例子要差很多?
一个警戒位不足以保证正确的舍入。一项我们在此不做转载的分析表明,需要额外的三个比特[79]。
多重添加操作
2008年,IEEE 754标准进行了修订,以包括融合乘加(FMA)操作的行为,也就是说,操作形式为
这种操作有两方面的动机。
首先,FMA有可能比单独的乘法和加法更精确,因为它可以对中间结果使用更高的精度,例如使用80位的扩展精度格式;3.7.3节。
这里的标准定义了正确的四舍五入,即这种组合计算的结果应该是四舍五入后的正确结果。这种操作的原始实现将涉及两次舍入:一次在乘法之后,一次在加法之后3。
练习3.14 你能想出一个例子,说明对FMA进行正确的舍入比对乘法和加法分别进行舍入更准确吗?提示:让c项的符号与a*b相反,并尝试在减法中强制取消。
其次,FMA指令是一种获得更高性能的方法:通过流水线,我们可以在每个周期内获得两个操作。因此,一个FMA单元比单独的加法和乘法单元更便宜。幸运的是,FMA在实际计算中经常出现。
练习3.15 你能想到一些以FMA运算为特征的线性代数运算吗?参见1.2.1.2节,了解FMA在处理器中的历史应用。
加法
两个浮点数的加法是通过几个步骤完成的。首先,指数被对齐:两个数字中较小的数字被写成与较大的数字具有相同的指数。然后再加上尾数。最后,对结果进行调整,使其再次成为一个标准化的数字。
作为一个例子,考虑$1.00+2.00×10^{-2}$。对准指数,这就变成了1.00+0.02=1.02,这个结果不需要最后调整。我们注意到这个计算是精确的,但是和$1.00+2.55×10^{-2}$有同样的结果,这里的计算显然是不精确的:精确的结果是1.0255,它不能用三位数的尾数来表示。
在$6.15\times 10^1+3.98\times 10^1=10.13\times 101=1.013\times 10^2\rightarrow 1.01\times 10^2$的例子中,我们看到在加上尾数后,需要对指数进行调整。误差又来自于对不适合尾数的结果的第一个数字的截断或四舍五入:如果$x$是真实的和,$\tilde{x}$是计算的和,那么$\tilde{x}=x(1+\varepsilon)$ 其中,3位尾数$|\varepsilon|<10^{-3}$。
形式上,让我们考虑计算$s=x_1+x_2$,我们假设数字$i$表示为$\tilde{x}_i= x_i(1 + \varepsilon_i)$。那么和$s$就表示为
在所有$\epsilon_i$都很小且大小大致相等,并且$𝑥_𝑖>0$的假设下,我们看到相对误差在加法下被加上了。
乘法
浮点乘法,就像加法一样,包括几个步骤。为了使两个数字$m_1\times \beta^{e_1}$和$m_2\times\beta^{e_2}$相乘,需要采取以下步骤。
- 指数相加:$e \leftarrow e_1 + e_2$。
- 尾数相乘: $m \leftarrow m_1 \times m_2$。
- 尾数被归一化,指数也相应调整。
例如:$1.23·10^0 ×5.67⋅10^1 =0.69741⋅10^1→6.9741⋅10^0→6.97⋅10^0$。
练习 3.16 分析乘法的相对误差。
减法
减法的表现与加法非常不同。在加法中,误差是相加的,只是逐步增加整体的舍入误差,而减法则有可能在一次操作中大大增加误差。
例如,考虑尾数为3位的减法:$1.24 - 1.23 = 0.01 → 1.00⋅ 10^{-2}$。虽然结果是准确的,但它只有一个有效数字4 。为了了解这一点,可以考虑这样的情况:第一个操作数1.24实际上是一个四舍五入的计算结果,其结果应该是1.235。在这种情况下,减法的结果应该是$5.00 ⋅ 10^{-3}$,也就是说,存在100%的误差,尽管输入的相对误差是可以预期的小。显然,涉及这一减法结果的后续操作也将是不准确的。我们的结论是,减去几乎相等的数字可能是造成数字四舍五入的原因。
这个例子有一些微妙之处。几乎相等的数字的减法是准确的,而且我们有IEEE算术的正确舍入行为。尽管如此,单一运算的正确性并不意味着包含它的运算序列会是准确的。虽然加法的例子只显示了数字精度的适度下降,但这个例子中的取消会产生灾难性的影响。你会在第3.5.1节看到一个例子。
练习3.17 考虑迭代
这个函数是否有一个固定点,$x_0\equiv f(x_0)$,或者是否有一个循环$x_1=f(x_0),x_0\equiv x_2=f(x_1)$等等?现在对这个函数进行编码。是否有可能重现固定点?不同的起始点$x_0$会发生什么。你能解释一下吗?
关联性
处理浮点数的方式的另一个影响是对运算的「关联性」(associativity),如求和。虽然求和在数学上是关联性的,但在计算机运算中却不再是这样。
让我们考虑一个简单的例子,说明这如何由浮点数的舍入行为引起。让浮点数存储为尾数的一个数字,指数的一个数字,以及一个保护数字;现在考虑4+6+7的计算。从左到右的计算结果是:
另一方面,从右到左的评估给出了。
结论是,对中间结果进行四舍五入和截断的顺序是有区别的。你还可以观察到,从较小的数字开始会得到更准确的结果。在3.5.2节中,你会看到这个原理的一个更详细的例子。
练习 3.18 上面的例子使用了四舍五入。你能在算术系统中想出一个使用截断的类似例子吗?
通常情况下,表达式的求值顺序是由编程语言的定义决定的,或者至少是由编译器决定的。在第3.5.5节中,我们将看到在并行计算中,关联性不是那么唯一地确定。
舍入误差的例子
从上面的介绍中,读者可能会得到这样的印象:舍入误差只在特殊情况下才会导致严重的问题。在这一节中,我们将讨论一些非常实际的例子,在这些例子中,计算机算术的不精确性在计算结果中变得非常明显。这些将是相当简单的例子;更复杂的例子存在于本书的范围之外,例如矩阵反演的不稳定性。有兴趣的读者可以参考[201,106]。
取消:”abc模式”。
作为一个实际的例子,考虑二次方程$ax^2+bx+c=0$,其解$x=\frac{-b \pm \sqrt {b^2-4ac}}{2a}$。假设$b>0$且$b^2>>4ac$,则$\sqrt{b^2-4ac}\approx b$,’+’解将是不准确的。在这种情况下,最好计算$x_-= -b-\sqrt{b^2-4ac}$并使用$𝑥_+ - x_- =c/a$。
练习 3.19 探索计算的根基
通过 “教科书 “的方法,并如上所述。
- 这些根是什么?
- 为什么 “教科书 “方法把一个小的根计算为零?
- 两种方法计算的函数值是多少?相对误差?
练习3.20 写一个程序来计算一元二次方程的根,包括 “教科书 “上的方法和上面描述的方法。
- 让$b=-1$,$a=-c$,$4ac\downarrow 0$,逐步取较小的$a$和$c$值。
- 打印出计算出的根,使用稳定计算的根,以及计算出的根中的$f(x)= ax^2 + bx + c$的值。
现在,假设你不太关心根的实际值:你想确保在计算的根中,残差$f(x)$很小。让$x^∗$ 是准确的根,那么
现在分别研究$a \downarrow 0$,$c = -1$ 和 $a = -1$,$ c \downarrow 0$ 的情况,你能解释其中的区别吗?
练习 3.21 考虑函数
证明它们在精确算术中是相同的;但是。
证明$f$可以表现出取消,而$g$则没有这个问题。
编写代码以显示$f$和$g$之间的差异。你可能需要使用较大的$x$的值。
从𝑥和机器精度的角度来分析取消的情况。当$\sqrt{x+1}$和$\sqrt{x}$的距离小于$\varepsilon$?这时会发生什么?(为了更精确的分析,当它们之间相差$\sqrt \varepsilon$,又是如何表现出来的?)
𝑦=𝑓(𝑥)的反函数是
把这个添加到你的代码中。这是否说明了计算的准确性?
请确保在单精度和双精度下测试你的代码。如果你会用python,可以试试bigfloat包。
总结系列
前面的例子是关于防止一次操作中出现大的舍入误差。这个例子表明,即使是逐渐积累的舍入误差也可以用不同的方法来处理。
考虑总和$\sum_{n=1}^{10000}\frac{1}{n^2} = 1.644834$,假设我们使用的是单精度,这对大多数计算机上意味着机器精度为 $10^{-7}$. 这个例子的问题在于,无论是项之间的比率,还是项与部分和的比率,都在不断增加。在 3.3.6 节中,我们注意到过大的比率会导致加法的一个操作数被忽略。
如果我们按照给出的序列对数列进行求和,我们会发现第一项是 1,所以所有的部分和($\sum^N_{n=1}$,其中$N < 10000$)至少是 1。这意味着任何 $1/n^2 < 10^{-7}$ 的项都会被忽略,因为它小于机器精度。具体来说,最后7000个项被忽略,计算出的总和是1.644725。前4位数字是正确的。
然而,如果我们以相反的顺序评估和,我们会得到单精度的精确结果。我们仍然是把小量加到大量上,但现在的比例永远不会像一比$\epsilon$那样糟糕,所以小的数字永远不会被忽略。要看到这一点,请考虑两个项的比率随后的项。
由于我们只对105项求和,而且机器的精度是10-7,所以在加法1/𝑛2+1/(𝑛-1)2中,第二项不会像我们从大到小求和时那样被完全忽略。
练习 3.22 在我们的推理中还缺少一个步骤。我们已经表明,在加两个后续项时,较小的一项不会被忽略。然而,在计算过程中,我们对序列中的下一个项添加了部分和。说明这不会使情况恶化。
这里的教训是,单调(或接近单调)的数列应该从小到大相加,因为如果要加的量的大小比较接近,误差就最小。请注意,这与减法的情况相反,涉及类似数量的操作会导致较大的误差。这意味着,如果一个应用要求对数列进行加减运算,而我们预先知道哪些项是正数,哪些项是负数,那么相应地重新安排算法可能会有收获。
练习3.23 正弦函数定义为
下面是两个计算这个和的代码片段(假设给定了$x$和$n$个项)。
1 | double term = x, sum = term; |
1 | double term = x, sum = term; |
- 解释一下,如果你计算$x>1$的大量项会发生什么。
- 对于大量的术语,这两种代码是否有意义?
- 是否有可能从最小的项开始对其进行求和?
- 你能提出其他方案来改进sin(𝑥)的计算吗?
不稳定的算法
现在我们将考虑一个例子,在这个例子中,我们可以直接论证该算法无法应对因不准确表示的实数而引起的问题。
考虑递归$y_n=\int^1_0\frac{x^n}{x-5}dx=\frac{1}{n}-5y_{n-1}$,它是单调递减的;第一个项可以计算为 $y_0 = ln6 - ln5$。
以小数点后3位数进行计算,我们得到。
我们看到,计算出来的结果很快就不只是不准确,而且实际上是毫无意义的。我们可以分析一下为什么会出现这种情况。
如果我们将$n$在第$n$步中的误差$\varepsilon_n$定义为:
那么
于是$\varepsilon_n \geqslant 5\varepsilon_{n-1}$. 这种计算所产生的误差呈现指数式增长。
线性系统求解
有时我们甚至可以在不指定使用何种算法的情况下对问题的数值精度做出说明。假设我们想解决一个线性系统,也就是说,我们有一个$n\times n$矩阵和一个大小为$n$的向量$b$,我们想计算出使$Ax=b$的向量。(由于向量𝑏将是某种计算或测量的结果,我们实际上是在处理一个向量$\tilde{b}$,它是理想𝑏的某种扰动。
扰动向量$\Delta b$可以是机器精度的数量级,如果它仅仅来自于代表误差。
扰动向量$\Delta b$可以是机器精度的数量级,如果它仅仅来自于代表误差,或者它可以更大,这取决于产生$\tilde{b}$的计算。
我们现在要问的是$x$的精确值与计算值之间的关系,前者是通过对$A$和$b$进行精确计算得到的,而后者是通过对$A$和$\tilde{b}$进行计算得到的。(在讨论中我们将假设𝐴本身是精确的,但这是一种简化)。
写作$\tilde{x}=x+\Delta x$,我们的计算结果现在是
或者
由于$Ax = b$,我们得到$A\Delta x = \Delta b$。由此,我们可以得到(详见附录13)。
$|A||A^{-1}|$的数量被称为矩阵的条件数。边界(3.2)说的是,任何右手边的扰动都会导致解决方案的扰动,该扰动最多只能大于矩阵的条件数$A$。请注意,这并不是说𝑥的扰动必须接近这个大小,但我们不能排除这个可能性,而且在某些情况下,确实可以达到这个界限。
假设$b$是精确到机器精度的,并且$A$的条件数是$10^4$。边界(3.2)通常被解释为:$x$的最后4位数字是不可靠的,或者说,计算 “失去了4位数字的准确性”。
方程(3.2)也可以解释为:当我们解决一个线性系统$ Ax = b$时,我们得到一个近似解$x + \Delta x$,这是一个扰动系统$A(x + \Delta x) = b+ \Delta b$的精确解。解中的扰动可以与系统中的扰动相关,这一事实可以通过说该算法表现出逆向稳定性来表达。
线性代数算法的精度分析本身就是一个研究领域;例如,见Higham的书[106]。
并行计算中的舍入误差
正如我们在第3.4.5节中所讨论的,以及你在上面的数列求和的例子中所看到的,计算机算术中的加法不是关联的。一个类似的事实也适用于乘法。这对并行计算来说有一个有趣的结论:计算在并行处理器上的分布方式会影响结果。
作为一个简单的例子,考虑计算总数 $a+b+c+d$。在单个处理器上,普通执行对应于以下关联性。
另一方面,将这个计算分散到两个处理器上,其中处理器0有$a$,$b$,处理器1有$c$,$d$,相当于
推而广之,我们看到,在不同数量的处理器上,规约操作很可能会得到不同的结果。(MPI标准规定,在同一组处理器上运行的两个程序应该得到相同的结果)。有可能规避这个问题,用对所有处理器的集合操作来代替还原操作,然后再进行局部规约。然而,这增加了处理器的内存需求。
对于并行求和问题,还有一个有趣的解决方案。如果我们用4000比特的尾数来存储浮点数,就不需要指数,这样存储的数字的所有计算都是精确的,因为它们是定点计算的一种形式[129, 128]。虽然用这样的数字做整个应用是非常浪费的,但只为偶尔的内积计算保留这种方案可能是解决可重复性问题的办法。
编程语言中的计算机运算
不同的语言有不同的方法来声明整数和浮点数。这里我们研究一些问题。
Fortran
在Fortran中,变量声明可以采取各种形式。例如,一个类型标识符有可能声明存储一个变量所需的字节数integer2, real8。这种方法的一个优点是容易与其他语言或MPI库互操作。
通常情况下,可以只用INTEGER、REAL来写代码,用编译器标志来表示整数和实数的字节数大小。
更复杂的、现代版本的Fortran可以指出一个浮点数需要有多少位的精度。
1 | integer, parameter :: k9 = selected_real_kind(9) |
kind 值通常为4,8,16,但这取决于编译器。
C99和Fortran2003 最近的C语言和Fortran语言的标准包含了C/Fortran in-teroperability标准,它可以用来声明一种语言的类型,使其与另一种语言的某种类型兼容。
C
在C语言中,常用的类型标识符并不对应于一个标准的长度。对于整数来说,有short int、int、long int,而对于浮点float来说,有double。sizeof()操作符给出了用于存储一个数据类型的字节数。
C整数的数值范围在limit.h中定义,通常给出一个上限或下限。例如,INT_MAX被定义为32767或更大。
浮点类型在float.h中指定。
C语言中存在指定的存储类型:常数如int64_t是由stdint.h中的typedef定义的。
常数NAN是在math.h中声明的。对于检查一个值是否为NaN,可以使用isan()。
Printing bit patterns
1 | // printbits.c |
用作:
1 | // bits.c |
C++
C++语言有以下浮点类型。
float:这通常是作为IEEE 754 32位浮点数实现的。
double:定义为至少和浮点数一样精确,通常实现为IEEE 754的64位浮点数。
long double:这也被定义为至少和double一样精确。在一些架构上,它可以是80位的扩展精度,在其他架构上则是全128位的精度。处理器通常通过软件和硬件功能的结合来实现后者,所以性能会比前两种类型低很多。
边界
你仍然可以使用C头的limit.h或 climits,但最好使用std::numeric_limits,它在类型上是模板化的。比如说
1 | std::numerical_limits<int>.max(); |
有以下几种功能。
- std::numeric_limits
::max() for the largest number. - std::numeric_limits
::min() for the smallest normalized positive number. - std::numeric_limits
::lowest() for the most negative number. - std::numeric_limits
::epsilon() for machine epsilon. - std::numeric_limits
::denorm_min() for smallest subnormal. (See also std::numeric_limits ::has_denorm.) - std::nextafter(x,y)
例外的情况
定义的例外情况。
FE_DIVBYZERO pole error occurred in an earlier floating-point operation.
FE_INEXACT inexact result: rounding was necessary to store the result of an earlier floating-point operation.
FE_INVALID domain error occurred in an earlier floating-point operation.
FE_OVERFLOW the result of the earlier floating-point operation was too large to be representable.
FE_UNDERFLOW the result of the earlier floating-point operation was subnormal with a loss of
precision.
FE_ALL_EXCEPT bitwise OR of all supported floating-point exceptions .
用法:
1 | std::feclearexcept(FE_ALL_EXCEPT); |
在C++中,std::numeric_limits
同一模块还有 infinity() 和 signaling_NaN()。
对于检查一个值是否为NaN,可以使用C++中cmath的std::isan()。请进一步参阅http://en.cppreference.com/w/cpp/numeric/math/nan。
例外情况
IEEE 754标准和C++语言都定义了一个例外的概念,这两个概念是相互不同的。754例外是指 “没有适合每个合理应用的结果 “的操作的发生。这不一定能转化为语言定义的异常。
打印位元模式
1 | // bitprint.cxx |
程序设计中的舍入行为
从上面的讨论中可以看出,一些对数学实数成立的简单说法在浮点数上并不成立。例如,在浮点运算中
这意味着编译器不能在不影响取舍行为的情况下进行某些优化。在一些代码中,这种轻微的差异是可以被容忍的,例如,因为方法有内置的保护措施。例如,第5.5节的静止迭代方法就能抑制任何引入的错误。
另一方面,如果程序员在编写代码时考虑到了舍入行为,那么编译器就没有这样的自由了。这在上面的练习3.10中有所暗示。我们用价值安全的概念来描述编译器被允许如何改变计算的解释。在最严格的情况下,编译器是不允许做任何影响计算结果的改变的。
编译器通常有一个选项,控制是否允许优化,以改变数值行为。对于英特尔的编译器,它是-fp-model=….。另一方面,像-Ofast这样的选项只是为了提高性能,可能会严重影响数值行为。对于Gnu编译器来说,完全符合754标准的选项是-frounding-math,而-ffast-math则允许以性能为导向的编译器转换,这违反了754和/或语言标准。
如果你关心结果的可重复性,这些问题也很重要。如果一个代码被两个不同的编译器编译,用相同的输入运行时,应该有相同的输出?如果一个代码在两个不同的处理器配置上并行运行?这些问题是非常微妙的。在第一种情况下,人们有时会坚持位数的可重复性,而在第二种情况下,只要结果保持 “科学 “上的等价,一些差异是允许的。当然,这个概念是很难做到严格的。
下面是在考虑编译器对代码行为和重现性的影响时的一些相关问题。
重新关联 在编译器对计算所做的改变中,最重要的是重新关联,即把𝑎 + 𝑏 + 𝑐归为𝑎 + (𝑏 + 𝑐)的技术术语。C语言标准和C++语言标准规定了对没有括号的表达式进行严格的从左到右的评估,所以重新关联实际上是标准所不允许的。Fortran语言标准没有这样的规定,但是编译器必须尊重小括号所暗示的评估顺序。
重新关联的一个常见来源是循环解卷;见第1.7.2节。在严格的值安全条件下,编译器在如何展开循环方面受到限制,这对性能有影响。循环解卷的数量,以及是否进行解卷,都取决于编译器的优化水平、编译器的选择和目标平台。
重新关联的一个更微妙的来源是并行执行;见3.5.5节。这意味着代码的输出在不同的并行配置上的两次运行之间不需要严格的重现。
常量表达式 在编译时计算常量表达式是一种常见的编译器优化。例如,在
1 | floaat one = 1, ; |
编译器将赋值改为$x = y+3$。然而,这违反了上面的重新关联规则,而且它忽略了任何动态设置的四舍五入行为。
表达式评估 在评估表达式$a+(b+c)$时,处理器会产生一个中间结果为$b+c$,这个结果没有分配给任何变量。许多处理器能够分配一个更高的中间结果精度。编译器可以有一个标志来决定是否使用这种设施。
浮点单元的行为 四舍五入行为(截断与四舍五入)和渐进下溢的处理可由库函数或编译器选项控制。
库函数 IEEE 754标准只规定了简单的操作;目前还没有处理正弦或对数函数的标准。因此,它们的实现可能是一个变化的来源。
更多的讨论,见[144]。
改变舍入行为
IEEE 754标准还声明,一个处理器应该能够在普通四舍五入、向上或向下四舍五入(有时分别表述为 “向正无穷大 “和 “向负无穷大”)或截断之间切换其四舍五入行为。在C99中,这个API包含在fenv.h中(或者对于C++ cfenv)。
1 |
|
在Fortran2003中,函数IEEE_SET_ROUNDING_MODE在IEEE_ARITHMETIC模块中可用。设置四舍五入行为可以作为一种快速测试算法稳定性的方法:如果结果在两种不同的四舍五入策略之间有明显的变化,那么该算法很可能不稳定。
如果结果在两种不同的四舍五入策略之间有明显的变化,那么该算法可能是不稳定的。
捕捉异常情况
异常这个词有几种含义。
浮点异常是指 “无效数字 “的发生,比如通过溢出或除以零(见3.3.8.1节)。
如果发生任何类型的意外事件,编程语言可以 “抛出异常”,也就是中断正常的程序控制流程。
溢出时的行为也可以被设置为产生一个异常。在C语言中,你可以用一个库调用来指定。
1 |
|
编译器特定行为
捕获异常有时可以由编译器指定。例如,gcc编译器可以通过标志-ffpe-trap=list来捕获异常;见https://gcc.gnu.org/onlinedocs/gfortran/Debugging-Options.html。
更多关于浮点运算的内容
Kahan的总结
3.4.5节中的例子让我们看到了计算机算术的一些问题:四舍五入会导致结果相当错误,而且非常依赖于评估顺序。有一些算法试图弥补这些问题,特别是在加法的情况下。我们简单讨论一下以William Kahan命名的Kahan求和法[117],它是补偿求和算法的一个例子。
练习3.24 通过3.4.5节中的例子,增加最后一项3;即在该例子的条件下计算4+6+7+3和6+7+4+3。表明当17被四舍五入为20时,修正值正好是3的下限,或者当14被四舍五入为10时,修正值是4的过限;在这两种情况下,都能计算出20的正确结果。
其他计算机运算系统
有人提出了其他系统来处理计算机上的不精确算术问题。一个解决方案是扩展精度算术,即以比平常更多的比特存储数字。这方面的一个常见用途是计算向量的内积:在内部以扩展精度进行累加,但以普通浮点数返回。另外,还有一些库,如GMPlib [77],允许以更高的精度进行任何计算。
另一个解决计算机算术不精确问题的方法是 “区间算术”[114],即对每个计算都保持区间界限。虽然这种方法已经研究了相当长的时间,但除了通过专门的库[21]外,它并没有实际使用。
扩展精度
在制定IEEE 754标准时,人们设想处理器可以有一系列的精度。在实践中,只有单精度和双精度的定义被使用。然而,有一个扩展精度的例子仍然存在。英特尔处理器有80位寄存器用于存储中间结果。(这可以追溯到英特尔80287协处理器。)这种策略在FMA指令和内积的积累中是有意义的。
这些80位寄存器有一个奇怪的结构,有一个显著的整数位,可以产生不是任何定义数字的有效表示的位模式[171]。
降低精度
你可以问 “双精度是否总是比单精度有好处”,答案并不总是 “是”,而是:”这取决于”。
迭代细化中的低精度
在迭代线性系统求解中(第5.5节,精度是由计算残差的精度决定的,而不是由求解步骤的精度决定的。因此,人们可以在降低精度的情况下进行操作,如应用预处理程序(第5.5.6节)[1]。这是一种迭代细化的形式;见5.5.6节。
深度学习中的低精度
IEEE 754-2008有一个二进制16半精度格式的定义,它有一个5位指数和11位尾数。
在深度学习(DL)中,表达值的范围比精确的值更重要。(这与传统的科学应用相反,在传统的科学应用中,接近的数值需要重新解决)。这导致了bfloat16 “大脑浮点 “格式的定义 https://en.wikipedia.org/wiki/Bfloat16_floating-point_format 这是一种16位的浮点格式。它使用8位作为指数,7位作为尾数。这意味着它与IEEE单精度格式共享相同的指数范围;见图3.4。
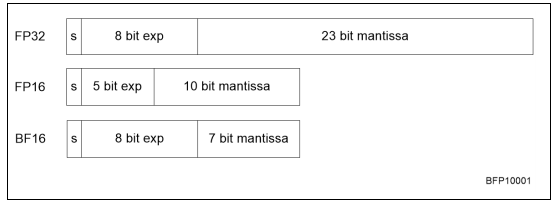
- 由于bfloat16和fp32的前两个字节结构相同,通过截断第三和第四字节,可以从fp32的数字中得出bfloat16的数字。然而,在实践中,四舍五入可能会得到更好的结果。
- 相反,将一个bloat16转换成fp32只需要在最后两个字节中填充0。
bfloat16的有限精度可能足以代表DL应用中的数量,但为了不失去更多的精度,我们设想FMA硬件在内部使用32位数:两个bfloat16数字的乘积是一个常规的32位数。为了计算内积(作为DL中矩阵-矩阵乘法的一部分),我们需要一个FMA单元,如图3.5所示。

- 基于Intel Knights Landing的Intel Knights Mill支持降低精度。
- 英特尔Cooper Lake实现了bfloat16格式[35]。
甚至在[46]中讨论了进一步减少到8位。
定点运算
一个定点数(比这里更深入的讨论,见[206])可以表示为⟨𝑁 , 𝐹 ⟩ 其中$𝑁 \geqslant \beta_0$是整数部分,$𝐹 < 1$是小数部分。另一种说法是,定点数字是以$𝑁+𝐹$位数存储的整数,在第一个$𝑁$位数后隐含小数点。
固定点计算可能会溢出,没有可能调整指数。考虑乘法$⟨𝑁_1,𝐹_1⟩\times⟨𝑁_2,F_2⟩$,其中$𝑁_1\geqslant \beta^{𝑛_1}$,$𝑁_2\geqslant \beta^{𝑛_2}$。如果$𝑛_1+𝑛_2$超过了整数部分的可用位置数,则溢出。(非正式地,乘积的位数是操作数的位数之和)。这意味着在使用定点运算的程序中,如果要进行乘法运算,需要有一定数量的前导零位,这就降低了数字的准确性。这也意味着程序员必须更努力地思考计算问题,以保证不会发生溢出,并在合理范围内保持数字的准确性。
那么,人们为什么要使用定点数字呢?其中一个重要的应用是嵌入式低功耗设备,比如电池供电的数字温度计。由于定点计算与整数计算基本相同,因此不需要浮点运算单元,从而降低了芯片尺寸,减少了对功耗的需求。另外,许多早期的视频游戏系统的处理器要么没有浮点单元,要么整数单元比浮点单元快得多。在这两种情况下,使用整数单元将非整数计算变成定点计算,是实现高吞吐量的关键。
另一个仍然使用定点运算的领域是信号处理。在现代CPU中,整数和浮点运算的速度基本相同,但它们之间的转换相对较慢。现在,如果正弦函数是通过查表实现的,这意味着在sin(sin 𝑥 )中,一个函数的输出被用来索引下一个函数的应用。显然,以定点方式输出正弦函数就不需要在实数和整数之间进行转换,这就简化了所需的芯片逻辑,并加快了计算速度。
复数
有些编程语言将复数作为一种内置的数据类型,有些则不是,还有一些则介于两者之间。例如,在Fortran中你可以声明
1 | COMPLEX z1,z2, z(32) |
一个复数由一对实数组成,分为实部和虚部,在内存中相邻分配。第一个声明用8个字节来存储REAL *4的数字,第二个声明用REAL*8来存储实部和虚部。(另外,第二行使用DOUBLE COMPLEX或在Fortran90中使用COMPLEX(KIND=2))。
相比之下,C语言没有直接的复数,但是C99和C++都有一个复数.h头文件。
complex.h头文件。这就像Fortran中定义复数一样,定义为两个实数。
像这样存储一个复数是很容易的,但有时在计算上并不是最好的解决方案。当我们研究复数的数组时,这就变得很明显了。如果一个计算经常完全依赖于对复数实部(或虚部)的访问,那么在复数数组中跨步,就会有一个跨步二,这是很不利的(见1.3.4.7节)。在这种情况下,最好为实部分配一个数组,为虚部分配另一个数组。
练习 3.25 假设复数数组是以Fortran方式存储的。分析对数组相乘的内存访问模式,即$\forall_i ∶ c_i \leftarrow a_i ⋅ b_i$,其中a(), b(), c()是复数的数组。
练习 3.26 说明复数上的$n\times n$线性系统$Ax=b$可以写成实数上的$2n\times 2n$系统。提示:将矩阵和向量分成实部和虚部。论证复数数组的实部和虚部分开存储的效率。
结论
在计算机上进行的计算无一例外地存在着数字错误。有些时候错误的原因是计算机运算的不完善:如果我们能用实际的实数进行计算,就不会有问题。(仍然会有数据的测量误差和数值方法中的近似问题;见下一章)。然而,如果我们接受四舍五入作为生活中的一个事实,那么各种观察就会成立。
从稳定性的角度来看,数学上的等价运算不需要表现得完全一样;见 “abc公式 “的例子。
即使是相同计算的重新排列也不会有相同的表现;请看求和的例子。
因此,必须分析计算机算法的舍入行为:舍入是否作为问题参数的一个缓慢增长的函数而增加,比如被演算的项的数量,或者有可能出现更糟糕的行为?我们不会在本书中进一步详细讨论这些问题。
复习题
练习 3.27 判断真假
在这一章中,我们将研究常微分方程(ODEs)和偏微分方程(PDEs)的数值解。这些方程在物理学中常用来描述一些现象,如飞机周围的空气流动,或桥梁在各种压力下的弯曲。虽然这些方程通常相当简单,但从它们中得到具体的数字(”如果有一百辆汽车在上面,这座桥会下垂多少”)则比较复杂,往往需要大型计算机来产生所需的结果。这里我们将描述将ODEs和PDEs转化为可计算问题的技术。
我们将首先介绍「初值问题」(IVPs),它描述了随着时间变换的过程。此处我们仅考虑常微分方程:只依赖于时间的标量函数。接下来,我们将研究描述空间过程的「边界值问题」(BVPs)。边界值问题通常涉及到多个空间变量,因此我们可以得到偏微分方程。
最后,我们将考虑 “热方程”,这是一个「初始边界值问题」(IBVP),它同时具有IVP和BVP的特点:它描述了热量在一个物理物体(如杆)上的传播。初始值描述了初始温度,而边界值给出了杆两端的规定温度。
我们在这一章的目的是展示一类重要的计算问题的起源。因此,我们不会去讨论解的存在性、唯一性或条件的理论问题。关于这一点,见[99]或任何专门讨论ODE或PDE的书。为了便于分析,我们还将假设所有涉及的函数都存在任意高阶导数,并且处处光滑。
初值问题
许多物理现象随着时间的推移而变化,物理学定律给出了对变化的描述,而非数值本身的描述。例如,牛顿第二定律
是一个关于点质量的位置变化的公式:表示为
它指出,加速度线性地取决于施加在质量上的力。对于质量的位置,可以通过分析得出一个封闭式的描述$𝑥(𝑡)=…$,但在许多情况下需要某种形式的近似或数值计算。这也被称为 “数值积分“。
牛顿第二定律是一个常微分方程,因为它表述了变量关于时间变化的函数。此外,牛顿第二定律也是一个初值问题,因为它给定了初始条件随着时间变化的情况。该方程是二阶的,如果我们引入向量,则可以通过引入双分量向量$u$,结合位置$x$和速度$x’$将上述方程降为一阶微分方程:
以$u$表示的牛顿方程就变成了
为了简单起见,在本课程中我们将只考虑标量方程;那么我们的参考方程是
方程允许过程有明确的时间依赖性,但一般来说,我们只考虑没有这种明确依赖性的方程,即所谓的 “自治(autonomous) “ODE,其形式为
其中右手边并不明确地依赖于$t$。
注释 13 非自治ODE可以转化为自治ODE,所以这并不是什么限制。如果$u=u(t)$是一个标量函数,并且$f=f(t, u)$,我们定义$u_2(t)= t$,并考虑等同的自治系统$\left(\begin{array}{l}
u^{\prime} \\
u_{2}^{\prime}
\end{array}\right)=\left(\begin{array}{c}
f\left(u_{2}, u\right) \\
1
\end{array}\right)$
通常情况下,在某个起点(通常选择$𝑡=0$)的初始值是给定的:$𝑢(0)=𝑢_0$,对于某个值$𝑢_0$,我们对$𝑢$随着$𝑡\rightarrow \infty$的行为感兴趣。举例来说,$f(x)=x$给出的方程是:$𝑢′(𝑡)= 𝑢(𝑡)$。这是一个简单的人口增长模型:该方程指出,增长速度等于人口规模。对于某些$f$的选择,方程(4.2)可以用分析法解决,但我们不会考虑这个问题。相反,我们只考虑数值解和这个过程的准确性。
在数值方法中,我们考虑用离散大小的时间步长来近似解决连续的时间依赖过程。由于这引入了一定量的误差,我们将分析在每个时间步长中引入的误差,以及这些误差是如何叠加成一个整体误差的。在某些情况下,限制全局误差的需要会对数值方案施加限制。
误差和稳定性
由于机器运算会产生不精确性,我们希望尽量避免因为初始值的小扰动而造成的干扰。因此,如果与不同初值$𝑢_0$相关的解在$t\rightarrow\infty$时相互收敛,我们将称微分方程为 「稳定」的。
稳定性的一个充分标准是
证明:设 $u^$为$f$ 零点,即:$f(u^)=0$,则常函数$u(t)\equiv u^*$为 $u’=f(u)$的一个解,即所谓的“平衡解”。平衡状态下,微小的扰动是不会影响系统的稳定性的。例如:设 $u$ 是PDE的一个解,写作 $u(t)= u^∗ + \eta(t)$,那么我们有
忽略二阶项,存在一个解:
这意味着,如果$f^′(x) < 0$,扰动将被阻尼,如果$f^′(x) > 0$,扰动将被放大。
我们经常会提到简单的例子$f(u)=-\lambda u$,其解$u(t)=u_{0} e^{-\lambda t}$。如果$\lambda>0$,这个问题是稳定的。
有限差分近似法:欧拉显式和隐式方法
为了数值解决这个问题,我们通过研究有限时间/空间步长,将连续问题变成离散问题。假设所有的函数都足够平滑,一个简单的泰勒级数展开就可以得到。
这就得到了$u’$
如果所有的导数都是有界的,我们可以用一个$O(\Delta t^2)$来近似高阶导数的无限之和。或者,你可以证明这个和等于$\Delta t^{2} u^{\prime \prime}(t+\alpha \Delta t)$ 当$0<\alpha<1$ 。我们看到,我们可以通过有限差分来近似微分算子,其误差是已知的,其数量级是时间步长的函数。
将其代入 $u′ = f(t, u)$,得到
或者
注释 14 前面的两个方程是数学上的等式,不应该被理解为对一个给定的函数$u′$进行计算的方法。回顾前面的讨论,你可以看到这样的公式对于小$\Delta t$来说很快就会被取消。关于数值微分的进一步讨论超出了本书的范围,请参见任意一本标准的数值分析教科书。
我们现在使用上述方程来推导一个数值方案:在$t_0=0,t_{k+1}=t_k+\Delta t=\cdots=(k+1)\Delta t$的情况下,我们得到一个差分方程
为$u_k$量,我们希望$u_k$将是对$u(t_k)$的良好近似。这就是所谓的 “显式欧拉 “或 “欧拉正向 “方法。
从微分方程到差分方程的过程通常被称为离散化(discretization),因为我们只在离散的点集中计算函数值。计算的数值本身仍然是实值的。另一种说法是:如果我们计算$𝑘$个时间步长,就可以在有限的二维空间$\mathbb{R}^k$中找到数值解。原问题的解是在$\mathbb{R}\rightarrow \mathbb{R}$的函数空间中找到的。
在上面,我们用一个算子逼近另一个算子,这样做的时候,当$\Delta t \downarrow 0$时,截断误差为$O(\Delta t)$(见附录14对这个数量级的符号的更正式介绍)。这并不意味着差分方程计算出的解就接近于真解。为此,还需要进行一些分析。
我们从分析 “局部误差 “开始:如果假设计算出的解在$𝑘$步骤是精确的,即$𝑢_𝑘=𝑢(𝑡_𝑘)$,那么$𝑘+1$步时将会出现怎样的错误? 我们有
和
于是
这表明,在每一步中,我们的误差为$O(\Delta t^2)$。如果我们假设这些误差可以相加,我们发现全局误差为
由于全局误差在$\Delta t$中是一阶的,我们称之为 “一阶方法”。需要注意的是,这个误差(衡量真实解和计算解之间的距离)与截距误差(即算子的近似误差)是同阶的$O(\Delta t)$。
欧拉显式方法的稳定性
考虑IVP $u′ = f(t,u)$ 对于 $t \geqslant 0$, 其中$f(t,u)= -\lambda u$,给出初始值$u(0) = u_0$。存在一个精确的解,即$u(t)=u_0e^{-\lambda t}$。从上面的讨论中可知这个问题是稳定的,也就是说,如果$\lambda >0$,解的小扰动最终会被抑制。现在我们将研究数值解的表现是否与精确解相同,也就是说,数值解是否也收敛于零。
这个问题的欧拉正向或显式欧拉方案是
为了稳定,我们要求$u_k\rightarrow 0$,因为$k\rightarrow \infty$。这就相当于
我们看到,数值求解方案的稳定性取决于$\Delta t$的值:只有当$\Delta t$足够小时,该方案才是稳定的。为此,我们称显式欧拉方法为条件稳定的。请注意,微分方程的稳定性和数值方案的稳定性是两个不同的问题。如果$\lambda >0$,连续问题是稳定的;数值问题有一个额外的条件,取决于所用的离散化方案。
请注意,我们刚刚进行的稳定性分析是专门针对微分方程$u′=-\lambda u$的。如果你要处理的是不同的IVP,你必须进行单独的分析。一般情况下,显式方法通常会给出条件稳定性。
欧拉隐式方法
刚才的显式方法很容易计算,但条件稳定性是一个潜在的问题。它可能意味着时间步骤的数量将是一个限制性因素。有一个替代显式方法的方法,不会受到同样的限制。
与其扩展$u(t + \Delta t)$,不如考虑以下对$u(t - \Delta t)$的扩展
这意味着
如前所述,我们取方程$u’(t)=f(t, u(t))$,用差分公式近似计算$u′(t)$。
我们再次定义固定点$𝑡_𝑘=𝑘𝑡$,并定义一个数值方案:
其中$u_k$是$u(t_k)$的近似值。
与显式方案的一个重要区别是,$u_{k+1}$现在也出现在方程的右侧。也就是说,$u_{k+1}$的计算现在是隐含的。例如,让$f(t,u)=-u^3$,那么$u_{k+1}=u_k-\Delta tu^3_{k+1}$。换句话说,$u_{k+1}$是方程$\Delta tx=u_k$的解。这是一个非线性方程,通常可以用牛顿法求解。
隐式欧拉方法的稳定性
让我们再看看这个例子$f(t, u(t))=-\lambda u$。用隐式方法计算,可以得到
那么
如果$\lambda>0$,这是一个稳定方程的条件,我们发现,对于所有的$u_k$和$\Delta t$的值,$\lambda \rightarrow 0$。这种方法被称为无条件稳定。与显式方法相比,隐式方法的一个优势显然是稳定性:可以采取较大的时间步长而不用担心非物理行为。当然,大的时间步长会使收敛到稳定状态(见附录15.4)变慢,但至少不会出现发散。
另一方面,隐式方法更加复杂。正如你在上面看到的,它们可能涉及到在每个时间步长中需要解决的非线性系统。在$u$是矢量值的情况下,比如下面讨论的热方程,我们会发现隐式方法需要解决一个方程组。
练习 4.1 分析以下IVP $𝑢′(x) = f(x)$ 方案的准确性和计算性。
相当于把欧拉显式和隐式方案加在一起。我们不需要分析这个方案的稳定性。
练习4.2 考虑初值问题 $y′(t) = y(t)(1-y)$。请注意,$y\equiv 0$和$y\equiv 1$是解决方案。这些被称为 “平衡解”。
一个解决方案是稳定的,如果扰动 “收敛到解决方案”,意味着对于$\varepsilon$足够小。
并且
这就要求,例如
0是一个稳定的解决方案吗?1是吗?
考虑显式方法
用于计算微分方程的数值解。说明
编写一个小程序来研究在不同的$\Delta t$的选择下数值解的行为。在你提交的作业中包括程序清单和一些运行的情况。
通过运行你的程序,你发现数值解会出现振荡。请对$\Delta t$提出一个条件,使数值解呈单调性。只要说明$y_k<1\Rightarrow y_{k+1}<1$,以及$y_k>1\Rightarrow y_{k+1}>1$即可。
现在考虑隐式方法
并说明$y_{k+1}$可以从$y_k$计算出来。编写一个程序,并研究在不同的$\Delta t$选择下的数值解的行为。
显示出对所有$\Delta t$的选择,隐式方案的数值解都是单调的。
边界值问题
在上一节中,我们看到了初值问题,它模拟的是随时间变化的现象。现在我们将转向边界值问题,一般来说,边界值问题在时间上是静止的,但它描述的是与位置有关的现象。例如,桥梁在负载下的形状,或窗玻璃中的热量分布,因为外面的温度与里面的不同。
二阶一维BVP的一般形式是
但这里我们只考虑简单的形式
在一个空间维度上,或
在两个空间维度上。这里,$\delta \Omega$是域$\Omega$的边界。由于我们在边界上规定了$u$的值,这样的问题被称为边界值问题(Boundary Value Problem,BVP)。
注释 15 边界条件可以更普遍,涉及区间端点上的导数。这里我们只看Dirichlet边界条件,它规定了域的边界上的函数值。
一般性PDE理论
有几种类型的PDE,每种都有不同的数学特性。最重要的属性是影响区域:如果我们对问题进行修补,使解决方案在一个点上发生变化,那么还有哪些点会受到影响。
双曲方程
PDEs的形式为
$A,B$的符号相反。这样的方程描述的是波,或更一般的对流现象,是保守的,不倾向于稳定状态。
直观地说,在任何一点上改变波浪方程的解,只会改变未来的某些点,因为波有一个传播速度,使得一个点不可能影响到空间上太远的近期的点。这种类型的PDE将不会在本书中讨论。
抛物线方程
PDEs的形式为
并且它们描述了类似于扩散的现象;这些现象往往趋于稳定状态。描述它们的最好方法是考虑在空间和时间的每一点上的解决方案受到空间的每一点上的某个有限区域的影响。
注释 16 这导致了一个限制IBVP时间的条件,即所谓的Courant-Friedrichs-Lewy条件http://en.wikipedia.org/wiki/Courant-Friedrichs-Lewy_condition。它描述了这样一个概念:在精确问题中,$u(x, t)$取决于$ u(x′, t-\Delta t)$的数值范围;数值方法的时间步长必须小到足以让数值解考虑到所有这些点。
热方程是抛物线类型的标准例子。
椭圆方程
PDEs的形式为
其中$A,B>0$;它们通常描述已经达到稳定状态的过程,例如抛物线问题中的$𝑡 \rightarrow \infty$。它们的特点是所有的点都相互影响。这些方程经常描述结构力学中的现象,如梁或膜。直观地讲,压下膜上的任何一点都会改变其他每一点的高度,无论多么微小。泊松方程(4.2.2节)是这种类型的标准例子。
一维空间的泊松方程
算子$\Delta$
是二阶微分算子,方程(4.7)是二阶PDE。具体来说,问题是
被称为泊松方程(Poisson equation),定义在单位平方上。二阶PDEs相当常见,它们描述了流体和热流以及结构力学中的许多现象。
首先,为了简单起见,我们考虑一维泊松方程
下面我们考虑的是二维的情况;然后扩展到三维的情况。
为了找到一个数值方案,我们像以前一样使用泰勒级数,用$𝑢(𝑥+h)$和$u(x-h)$来表示。
$u$及其在$x$的导数。设$h>0$,则
以及
我们现在的目标是对$u’’(x)$进行近似。我们看到,这些方程中的$u’$项在加法下会被抵消,剩下$2u(x)$。
于是
那么,上述数值方案的基础是观察
这表明我们可以用一个差分算子来近似微分算子,在$h\downarrow 0$时有一个$O(h^2)$。截断误差为$h\downarrow 0$。
为了得出一种数值方法,我们将区间[0, 1]划分为等距的点。$x_k=k_h$ 其中$h=1/(n+1),k=0 … n + 1$. 有了这些,有限差分(FD)公式(4.9)导致了一个形成方程组的数值方案。
这种使用FD公式近似解决PDE的过程被称为有限差分法(Finite Difference Method,FDM)。
对于大多数的$k$值,这个方程将$u_k$未知数与$u_{k-1}$和$u_{k+1}$的未知数联系起来。例外情况是$k=1$和$k=n$。在这种情况下,我们记得$u_0$和$u_{n+1}$是已知的边界条件,我们把左边是未知数,右边是已知量的方程写为
我们现在可以将这些方程总结为$u_k ,k = 1 … n- 1$的矩阵方程。
其形式为$Au=f$,$A$为完全已知矩阵,$f$为完全已知向量,$u$为未知向量。请注意,右边的向量在第一个和最后一个位置有问题的边界值。这意味着,如果你想用不同的边界条件解决同一个微分方程,只有向量$f$会发生变化。
练习 4.3 $u(0)= u_0$这种类型的条件被称为狄利克雷边界条件。在物理学上,这相当于,例如,知道一个棒端点的温度。其他边界条件也存在。如果我们对流体流动进行建模,并且已知$x=0$时的流出率,那么为导数指定一个值,$u’(0)=u_0’$,而不是为函数值指定一个值,是合适的。这就是所谓的诺伊曼边界条件。诺伊曼边界条件 $u’(0) = u_0’$ 可以通过以下方式来模拟
证明与狄利克雷边界条件的情况不同,这影响了线性系统的矩阵。
证明在两端都有诺伊曼边界条件会产生一个奇异矩阵,因此线性系统没有唯一的解。(提示:猜测特征值为零的向量)。
在物理学上这是有意义的。例如,在一个弹性问题中,狄利克雷边界条件说明杆子被夹在一定的高度;诺伊曼边界条件只说明它在端点的角度,这使得它的高度无法确定。
让我们列举一些$𝐴$的属性,你会发现这些属性与解决此类方程组有关。
矩阵非常稀疏:非零元素的百分比很低,零元素不是随机分布的,而是位于主对角线周围的一个带状结构中。在一般情况下,我们称之为带状矩阵(banded matrix),而在这个特定情况下称之为三对角矩阵(tridiagonal matrix)。带状结构是典型的PDEs,但不同应用中的稀疏矩阵可能不太规则。
矩阵非对称。这一特性并不涉及由BVP分解而来的所有矩阵,但如果没有奇数阶(指第一、第三、第五……)导数,例如$u_x,u_{xxx},u_{xy}$。
矩阵元素在每个对角线上是恒定的,也就是说,在每一组点$\{(𝑖,𝑗)∶𝑖 - 𝑗 = 𝑐\}$,对于某个𝑐。这只对非常简单的问题是正确的。如果微分方程$\frac{d}{d x}\left(a(x) \frac{d}{d x} u(x)\right)$。如果我们在区间内设置h变量,它也不再成立,例如,因为我们想更详细地模拟左端点周围的行为。
矩阵元素符合以下符号模式:对角线元素是正的,而非对角线元素是非正的。这一属性取决于所使用的数字方案,但它通常是真实的。连同下面的确定性属性,这被称为$M-$矩阵。关于这些矩阵有一整套数学理论[12]。
矩阵是正定的:$x^tAx>0$,适用于所有非零向量$x$。如果仔细选择数值方案,这一属性将从原始连续问题中继承下来。虽然这一点的用途目前看来并不明确,但以后你会看到取决于它的线性系统的求解方法。
严格地说,方程的解很简单:$u=A^{-1}f$。然而,计算$A^{-1}$并不是找到$u$的最好方法。正如刚才所观察到的,矩阵$A$只有$3N$个非零元素可以存储。另一方面,它的逆矩阵则没有一个非零元素。虽然我们不会证明这一点,但这种说法对大多数稀疏矩阵都是成立的。因此,我们希望以一种不需要储存$O(n^2)$的方式来解决$Au=f$。
练习 4.4 你将如何解决这个三对角方程组?证明系数矩阵的LU因子化给出了双对角矩阵形式的因子:它们有一个非零对角线和正好一个非零子对角线或超对角线。解决三对角方程组的总操作数是多少?一个向量与这样的矩阵相乘的运算次数是多少?这种关系并不典型!
二维空间的泊松方程
上面的一维BVP在很多方面是不典型的,特别是与由此产生的线性代数问题有关。在本节中,我们将研究二维泊松问题。你会看到,它构成了一维问题的非微观概括。三维的情况与二维的情况非常相似,所以我们将不讨论它。
上面的一维问题有一个函数$u=u(x)$,现在变成了二维的$u=u(x,y)$。那么我们感兴趣的二维问题就是
其中边界上的数值是给定的。我们通过在$x$和$y$方向上应用方程得到我们的离散方程
或者说,合起来看
令 $h=1/(n+1)$,定义$x_i=ih$,$y_j=jh$;让$u_{ij}$是对$u(x_i,y_j)$的近似,那么我们的离散方程为
我们现在有$n\times n$未知数$u_{ij}$。为了像以前一样将其转化为一个线性系统,我们需要将它们放在一个线性排序中,我们通过定义$I = I_{ij} = j+ i\times n$来实现。这被称为字典序(lexicographic ordering),因为它将坐标$(i, j)$当作字符串来排序。
使用这个排序,我们可以得到$N=n^2$的方程
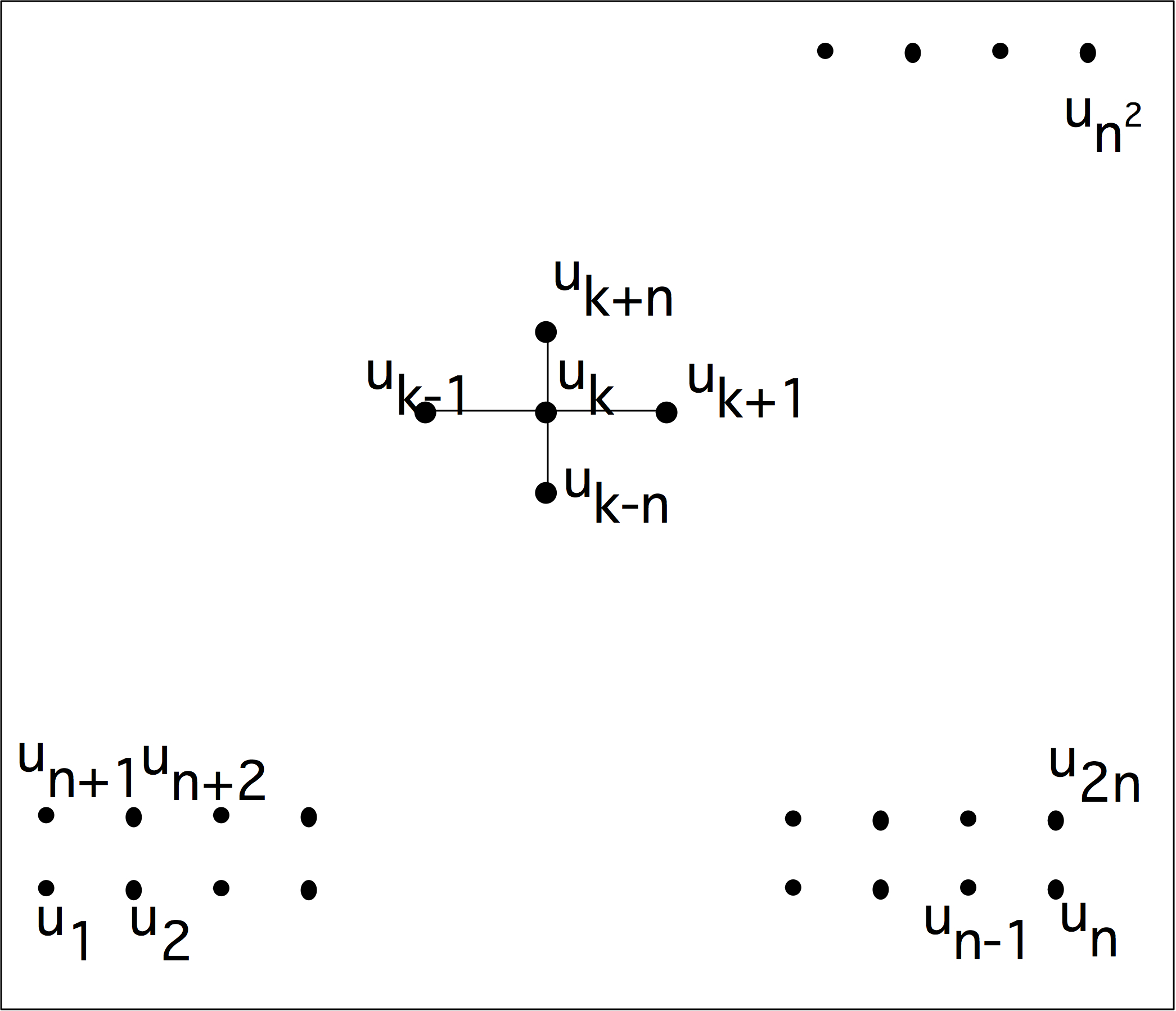
而线性系统看起来像
矩阵的大小为$N\times N$,其中$N=n^2$。与一维的情况一样,我们看到BVP会产生一个稀疏的矩阵。
以矩阵形式考虑这个线性方程组似乎是很自然的事情。然而,以明确未知数的二维联系的方式呈现这些方程可能更有洞察力。为此,图4.1展示了领域中的变量,以及方程如何通过有限差分模板将它们联系起来。从现在开始,在制作这样的领域图片时,我们将只使用变量的索引,而省略 “$u$ “标识符。
方程矩阵和一维的情况一样是带状的,但是和一维的情况不同,带状的内部有零点。因为该矩阵有五个非零对角线,所以被称为五对角线结构。
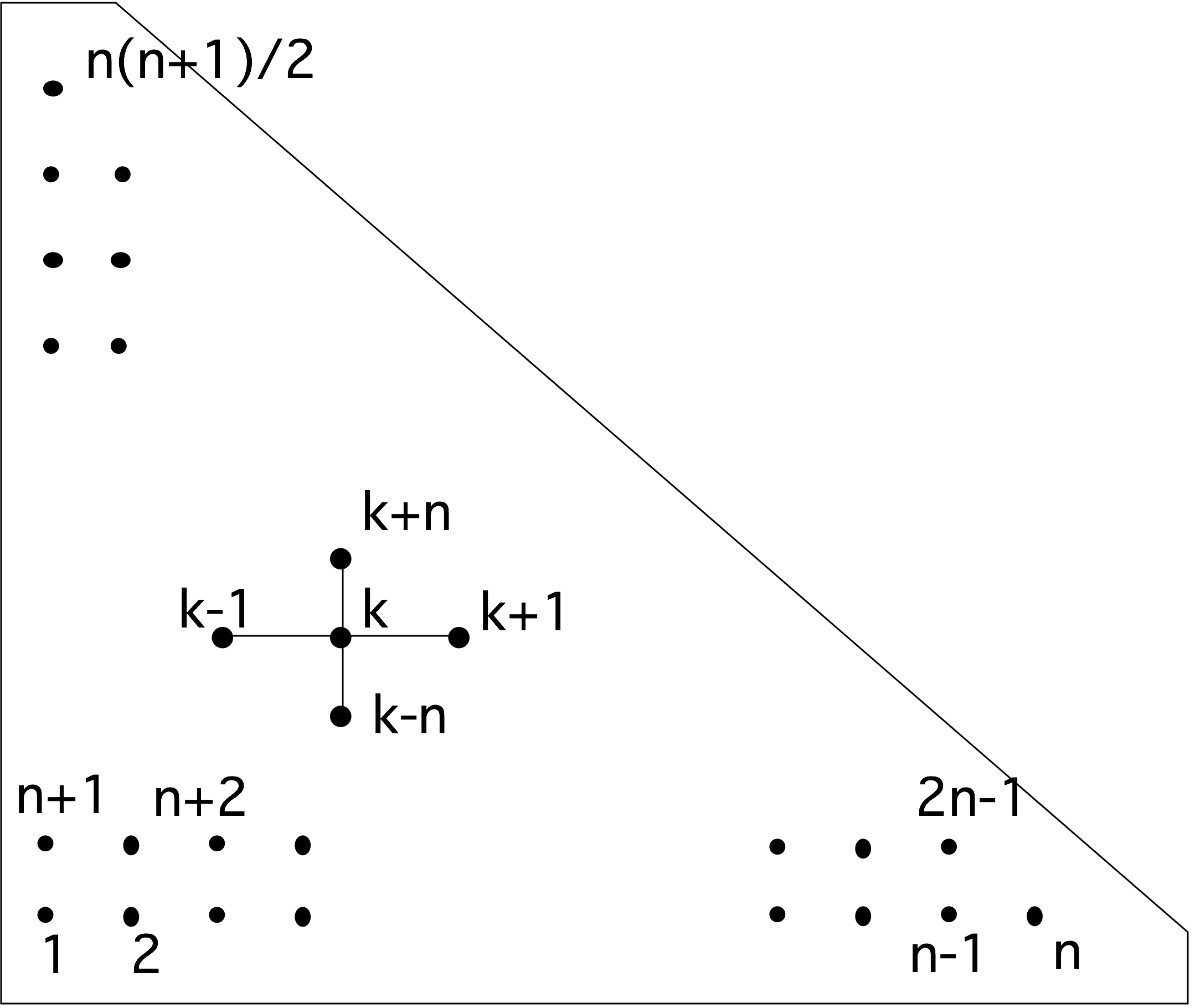
你也可以在矩阵上放一个块状结构,把在域的一行中的未知数组合起来。这被称为分块矩阵(block matrix),在块的层面上,它有一个三对角的矩阵结构,所以我们称之为分块三对角矩阵(block tridiagonal matrix)。请注意,对角线块本身是三对角的;非对角线块是减去单位矩阵的。
这个矩阵和上面的一维例子一样,有恒定的对角线,但这又是由于问题的简单性质造成的。在实际问题中,这不会是真的。也就是说,这样的 “恒定系数 “问题是有的,当它们在矩形域上时,有非常有效的方法来解决线性系统,其时间复杂性为$N\log N$。
练习 4.5 矩阵的块状结构,所有的对角线块都有相同的大小,这是因为我们在方形域上定义了我们的BVP。画出方程离散化所产生的矩阵结构,同样是中心差分,但这次是定义在一个三角形域上;见图4.2。说明同样有一个块状三对角矩阵结构,但现在块的大小不一。提示:先画出一个小例子。对于$n=4$,你应该得到一个$10\times 10$的矩阵,其块结构为$4\times 4$。
对于更加不规则的域,矩阵结构也将是不规则的。
有规律的块状结构也是由我们决定将未知数按行和列排序造成的。这被称为自然排序或词法排序;其他各种排序也是可能的。一种常见的未知数排序方式是红黑排序或棋盘排序,这对并行计算有好处。这将在第6.7节讨论。
关于BVP的分析方面还有更多要说的(例如,解有多平滑,它是如何取决于边界条件的),但这些问题超出了本课程的范围。这里我们只关注矩阵的数值方面。在线性代数一章中,特别是第5.4和5.5节,我们将讨论从BVP中求解线性系统。
stencils 差分
离散化通常被表述为应用stencils差分
到函数$u$。给定一个物理域,我们将stencils应用于该域中的每一个点,得出该点的方程。图 4.1 说明了一个由$n\times n$点组成的正方形域的情况。将此图与上述方程联系起来,你会发现同一条线上的连接产生了主对角线和第一条上下对角线;与下一条线和上一条线的连接则成为非对角线块的非零点。
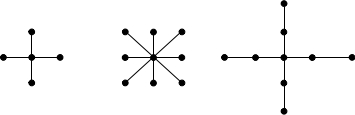
这种特殊的模版通常被称为 “五点星 “或五点模版。还有其他不同的网板;其中一些网板的结构在图4.3中得到描述。只有水平或垂直方向连接的网板被称为 “星形网板”,而有交叉连接的网板(如图4.3中的第二种)则被称为 “星形网板”。
练习 4.6 考虑图4.3中的第三个模版,用于正方形域上的BVP。如果我们再次将变量按行和列排序,所得到的矩阵的稀疏性结构是什么样子的?
除了五点星形之外,还可以使用其他stencils来达到更高的精度,例如,给出一个$O(h^4)$的截断误差。它们还可以用于上面讨论的微分方程以外的其他微分方程。例如,不难看出,对于方程$u_x+u_{yyy}=f$,我们需要一个同时包含$x$ ,$𝑦\pm h$和$x$ ,$𝑦\pm 2h$连接的钢网,如图中的第三个钢网。相反,使用5点stencils,没有系数值的情况下,四阶问题的离散化小于$O(1)$截断误差。
虽然到目前为止讨论的是二维问题,但对于诸如$-u_x- u_y - u_z= f$这样的方程,它可以被推广到更高维。例如,5点stencils的直接泛化,在三维空间中变成了7点stencils。
其他离散化技术
在上面,我们用有限差分法来寻找微分方程的数值解。还有其他各种技术,事实上,在边界值问题的情况下,它们通常比有限差分更受欢迎。最流行的方法是有限元法和有限体积法。尤其是有限元方法很有吸引力,因为它比有限差分更容易处理不规则的形状,而且它更适合于近似误差分析。然而,在这里讨论的简单问题上,它给出的线性系统与FD方法相似甚至相同,所以我们将讨论限制在有限差分上,因为我们主要关注的是线性系统的计算方面。
初始边界值问题
现在我们将继续讨论初始边界值问题(IBVP),正如你可能从名字中推断的那样,它结合了IVP和BVP的各个方面。在这里,我们将把自己限制在一个空间维度。
我们考虑的问题是棒材中的热传导问题,其中$T(x,t)$描述了在时间上$x$的温度,对于$x\in [a,b],t>0$。所谓的热方程(见附录15对一般的PDE,特别是热方程的快速介绍)是
其中
初始条件$T(x,0) = T_0(x)$ 描述初始温度分布。
边界条件$T(a,t)=T_a(t)$,$T(b,t)=T_b(t)$描述棒的末端,例如可以固定在一个已知温度的物体上。
杆的材料由一个参数$\alpha >0$来模拟,即热扩散率,它描述了热量在材料中扩散的速度。
强迫函数$q(x, t)$描述了外部应用的加热,作为时间和地点的函数。
IBVP和BVP之间有一个简单的联系:如果边界函数$T_a$和$T_b$是常数,并且$q$不依赖于时间,只依赖于位置,那么直观地说,$T$将收敛到一个稳定状态。这方面的方程式是$-\alpha u’’(x)=q$。
离散化
现在我们将空间和时间都离散化,即$x_{j+1}=x_j+\Delta x_{k+1}=t_k+\Delta t$,边界条件$x_0=a$,$x_n=b$,并且$t_0=0$。 我们写出$T_{jk}$的数值解,$x=x_j$,$t=t_k$;运气好的话,这将近似于精确解$T(x_j,t_k)$。
对于空间离散化,我们使用中心差分公式
对于时间离散化,我们可以使用前面中的任何一种方案。我们将再次研究显式和隐式方案,对所产生的稳定性有类似的结论。
显式方案
通过明确的时间步进,我们将时间导数近似为
将此与空间的中心差异结合起来,我们现在有
我们将其改写为
在图4.4中,我们将其呈现为一个差分stencils。这表示每个点的函数值是由前一个时间层次上的点的组合决定的。
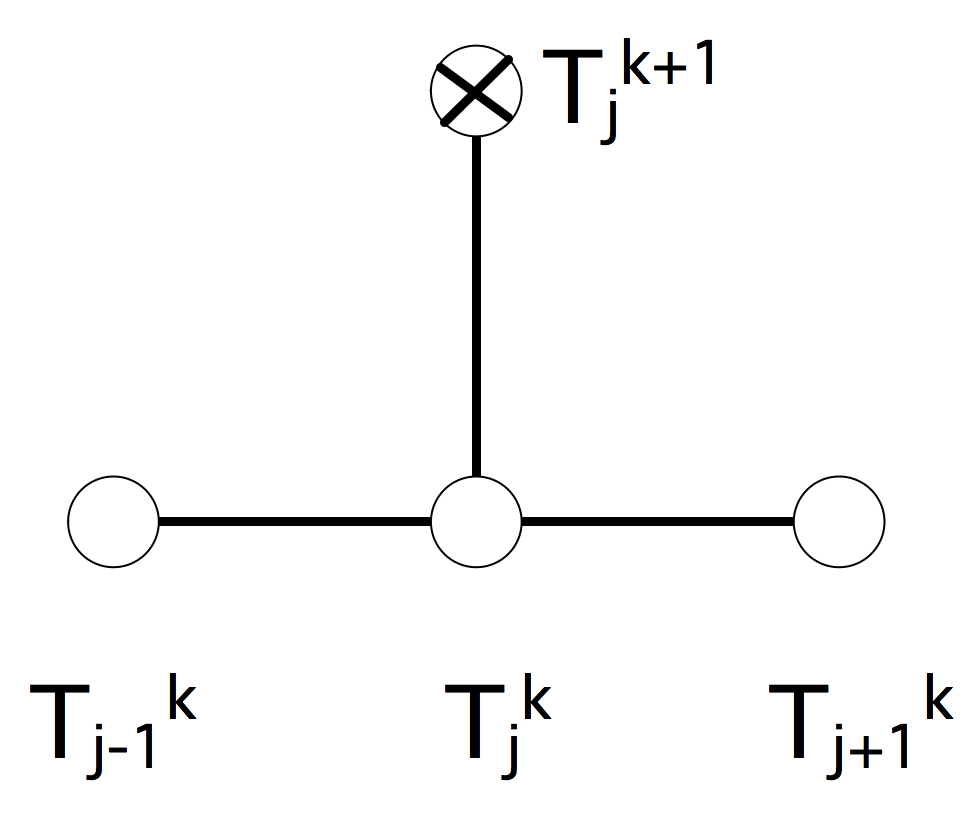
将给定的$k$和所有$j$值的方程组用矢量形式概括为
其中
这里的重要观察是,从$T_{k+1}$得出向量$T_k$的主要计算是一个简单的矩阵-向量乘法。
其中$A= I- \frac{\alpha \Delta t}{\Delta x^2}K$。这是第一个迹象,表明稀疏矩阵-向量乘积是一个重要的操作。使用显式方法的实际计算机程序通常不形成矩阵,而是评估方程。然而,为了分析的目的,线性代数公式是更有见地的。
在后面的章节中,我们将考虑操作的并行执行。现在,我们注意到显式方案是琐碎的并行的:每个点都可以只用周围几个点的信息进行更新。
隐式方案
在上述方程中,我们让$T_{k+1}$从$T_k$定义。我们可以通过从$T_{k-1}$定义$T_k$来扭转这一局面,正如我们在第4.1.2.2节中对IVP所做的那样。对于时间离散化,这就得到
整个热力方程的隐式时间步长离散化,在$t_{k+1}$中进行评估,现在变成了。
或者
图4.5将其渲染成一个模版;这表达了当前时间层上的每一个点都会影响到下一层的点的组合。我们再一次用矢量的形式来写这个。
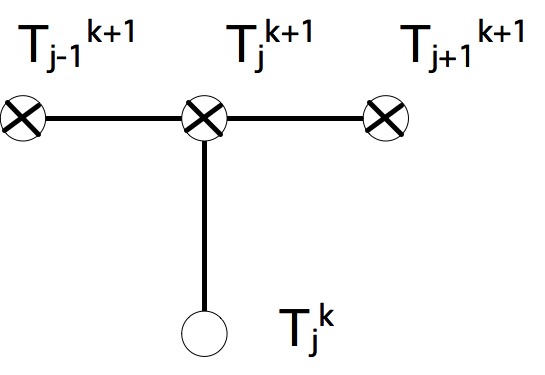
与显式方法相比,在显式方法中,矩阵-向量乘法就足够了,从$𝑇^{𝑘+1}$推导出的向量$𝑇^𝑘$现在涉及一个线性系统解决方案。
其中$A= I+ \frac{\alpha \Delta t}{\Delta x^2}K$ 一个比矩阵-向量乘法更难的操作。在这种情况下,不可能像上面那样,直接评估方程(4.21)。使用隐式方法的代码实际上形成了系数矩阵,并以此来解决线性方程组。解决线性系统将是第5章和第6章的重点。
与显式方案相比,我们现在没有明显的并行化策略。线性系统的并行求解将在第6.6节及以后的章节中占据我们的位置。
练习4.7 证明隐式方法的一个时间步骤的flop数与显式方法的一个时间步骤的flop数是相同的。(这只适用于一个空间维度的问题)。至少给出一个论据,说明为什么我们认为隐式方法在计算上 “更难”。
我们在这里使用的数值方案是时间上的一阶和空间上的二阶:截断误差为$O(\Delta t+ \Delta x^2)$。也可以通过使用时间上的中心差分来使用一个时间上的二阶方案。另外,见练习4.8。
稳定性分析
现在我们在一个简单的情况下分析显式和隐式方案的稳定性。让$q\equiv 0$,并假设$T_j^k=\beta^ke^{i\ell x_j}$,对于某些$\ell$。这一假设在直觉上是站得住脚的:由于微分方程没有 “混合 “$x$和$t$的坐标,我们推测解决方案将是$T(x,t) = v(x) ⋅ \omega (t)$ 的单独解决方案的乘积。
唯一有意义的解发生在$c_1, c_2 < 0$,在这种情况下我们发现。
其中我们用$c=\ell \pi$代替,以考虑到边界条件。
如果对这种形式的解决方案的假设成立,我们需要$|\beta |<1$的稳定性。将推测的$T_{j}^k$形式代入显式方案,可以得到
为了保持稳定,我们需要$|\beta|<1$:
- $\beta<1 \Leftrightarrow 2 \frac{\alpha \Delta t}{\Delta x^{2}}(\cos (\ell \Delta x)-1)<0$ : this is true for any $\ell$ and any choice of $\Delta x, \Delta t$.
- $\beta>-1 \Leftrightarrow 2 \frac{\alpha \Delta t}{\Delta x^{2}}(\cos (\ell \Delta x)-1)>-2:$ this is true for all $\ell$ only if $2 \frac{\alpha \Delta t}{\Delta x^{2}}<1$, that is $\Delta t<\frac{\Delta x^{2}}{2 \alpha}$
后一个条件对允许的时间步长提出了很大的限制:时间步长必须足够小,方法才能稳定。这与IVP的显式方法的稳定性分析类似;然而,现在时间步长也与空间离散化有关。这意味着,如果我们决定需要更多的空间精度,并将空间离散化$\Delta x$减半,时间步数将乘以4。
现在让我们考虑隐式方案的稳定性。将解的形式$T_j^k=\beta^ke^{i\ell x_j}$替换到数值方案中,可以得到
除去$e^{i\ell x_j}\beta^{k+1}$,可得
由于$1-\cos l\Delta x\in (0,2)$,分母严格>1。因此,无论l的值如何,也无论$\Delta x$和$\Delta t$的选择如何,条件$|\beta|<1$总是被满足的:该方法总是稳定的。
练习 4.8 我们在这里考虑的方案是时间上的一阶和空间上的二阶:它们的离散化顺序是$O(\Delta t)+ O(\Delta x^2)$。推导出由显式和隐式方案平均化得到的Crank-Nicolson方法,说明它是不稳定的,并且在时间上是二阶的。
数值线性代数
在第四章中,我们了解了偏微分方程的数值解法是如何产生线性代数的问题。在前向欧拉法的情况下是一个矩阵与向量乘法,较为简单;而在后向欧拉方法下是一个线性方程组的解,较为复杂。解决线性系统将是本章的重点;此处我们将不讨论需要解决特征值问题。
你可能已经学过一种解线性方程组的简单算法:消除未知数,也叫「高斯消元法」(Gaussian elimination)。这种方法仍然可以使用,但我们需要对其效率进行一些仔细的讨论。还有其他一些算法即所谓的迭代求解法,它们通过逐步逼近线性系统的解来进行,这也是我们要讨论的内容。
由于PDE的背景,我们只考虑方形和非星形的线性系统。矩形系统,特别是超定系统,在最优化理论的数值分析中也有重要的应用。然而,在本书中我们不会涉及这些。
关于数值线性代数的标准著作是Golub和Van Loan的《矩阵计算》[83]。它包括算法、误差分析和计算细节。Heath的《科学计算》涵盖了科学计算中出现的最常见的计算类型;这本书有许多优秀的练习和实践项目。
消除未知数
下面我们将系统地讲述高斯消元法。
注释 17 我们可以通过高斯-若尔当(Gauss Jordan)方法,乘以逆矩阵$A^{-1}:x \leftarrow A^{-1}x$,来求解方程,但出于数字精度的考虑,本书不讨论这种方法。
本章的讨论主线是各种算法的效率。即便你学会了高斯消元法,也可能从未在大于$4\times 4$的矩阵上使用这种方法。在PDE求解中出现的线性系统可能要大几千倍,计算它们需要操作数以及内存是十分重要的。
正确选择算法对效率而言十分重要。克拉默法则(Cramer’s rule)指出:线性方程组的解可以用一个相当简单的公式表示,即行列式。尽管它在数学上很优雅,但对我们来说却并不实用。
如果给定了一个矩阵$𝐴$和一个向量$𝑏$,想要求解$𝐴𝑥=𝑏$的解,则$|A|$的行列式:
对于任何矩阵$M$,行列式被递归定义为
其中$M[1,i]$表示从$M$中删除第1行和第$i$列而得到的矩阵。计算一个$n$阶行列式要计算$n$次$n-1$阶行列式。每一次都需要$n-1$个大小为$n-2$的行列式,所以行列式的计算所需操作是矩阵大小的阶乘。在本章的后面,我们会用其他合理的方法解决线性方程组。
现在让我们看一下用消除未知数的方法解线性方程的一个简单例子。考虑以下线性方程组
我们从第二和第三个方程中消除$x_1$,方法是
- 将第二个方程减去第一个方程$\times 2$;
- 将第三个方程减去第一个方程$\times 1/2$。
这样,线性方程组就变成了
最后,我们通过将第二个方程乘以3,在第三个方程中将其减去,消除三式中的$x_2$。
现在我们可以根据上一个方程求出$x_3=9/4$。将其代入第二个方程,我们得到$-4x_2=-6-2x_2=-21/2$,所以$x_2=21/8$。最后,从第一个方程中,$6x_1=16+2x_2-2x_3=16+21/4-9/2=76/4$,所以$x_1=19/6$。
我们可以通过省略$x_i$系数来写得更紧凑。将
记为
那么消元的过程为
在上面的例子中,矩阵系数可以是任何实数(或复数)系数。我们可以重复上面的过程求解任何线性方程组,但有一个例外。数字6、-4、-4,最后处在矩阵的对角线上,这些非零数字被称为主元(pivots)。
练习 5.1 线性方程组
与我们刚才在公式中研究的相同,除了(2,2)元素。确认你在第二步中得到一个零主元。
第一个主元是原矩阵的一个元素;正如你在前面的练习中所看到的,如果不消元,就无法找到其他主元。没有简单的方法可以预测零主元。
如果一个主元被证明是零,所有的计算都不会丢失:我们总是可以交换两个矩阵行;这就是所谓的主元。不难发现(你可以在任何一本初级线性代数教科书中找到),对于一个非奇异矩阵,总有一个行的交换可以将一个非零元素放在主元的位置。
练习 5.2 假设我们想交换方程中方程组的矩阵第2行和第3行。还需要做哪些调整以确保仍然能计算出正确的解?通过交换第2行和第3行,继续求解上一个练习的解,并检查你得到的答案是否正确。
练习 5.3 再看一下练习5.1。不交换第2和第3行,而要交换第2和第3列。就线性方程组而言,这意味着什么?继续求解该系统;检查你是否得到与之前相同的解。
一般来说,在浮点数和四舍五入的情况下,在计算过程中,一个矩阵元素不太可能完全变成零。另外,在PDE背景下,对角线通常是不为零的。这是否意味着主元运算在实践中没有必要?答案是否定的:从数值稳定性的角度来看,主元是可取的。在下一节,你将看到一个例子来说明这个事实。
线性代数在计算机运算中的应用
本章的大部分内容都可以通过数学运算求解,然而由于计算机的精度有限,我们需要设计将舍入误差降到最小的算法。对数值线性代数的算法需要进行严格而全面的误差分析,然而,这超出了本课程的范围。计算机算术中的计算误差分析是威尔金森的经典《代数过程中的舍入误差》[201]和海姆最近的《数值算法的准确性和稳定性》[106]的重点。
本书将注重计算机运算过程中出现的经典例子:将说明为何在LU分解中主元方法不仅仅是理论手段,此外,我们将给出两个由于计算机算术的有限精度而导致的特征值计算中的问题的例子。
消除过程中的舍弃控制
上面我们看到,如果在消除该行和列的过程中,对角线上出现了一个零元素,那么行间交换(’主元’)是必要的。现在我们讨论如果主元元素不是零,但接近零会发生什么。
考虑线性方程组
其中的解决方案是$𝑥=(1, 1)^𝑡$。使用(1, 1)元素清除第一列的剩余部分,可以得到。
现在我们可以解决$x_2$,并从它得到$x_1$。
如果$\epsilon$较小,如$\epsilon <\epsilon_{mach}$,则右侧的1+𝜖替换为1:线性方程组改写为
但解$(1, 1)^𝑡$仍将满足机器运算。接下来,$1/\epsilon $将非常大,所以消除后的右手边第二部分将是$2-\frac{1}{\epsilon}=-1/\epsilon$,并且(2,2)矩阵中的元素是$-1/\epsilon$而不是$1-1/\epsilon$。
首先求解$x_2$,然后求解$x_1$,我们得到。
所以$x_2$是正确的,但$x_1$是完全错误的。
注释 18 在这个例子中,计算机运算中的数字与精确运算中的数字偏差不大。然而,结果却可能是大错特错。对这种现象的分析见[99]的第一章。
如果我们按照上述方法进行透视,会发生什么?我们交换矩阵的行,得到
交换矩阵的行,得到
现在得到的是,无论$\epsilon$的大小如何。
在这个例子中,我们使用了一个非常小的$\epsilon $值;更精细的分析表明,即使$\epsilon$值大于机器精度,主元交换仍然是有意义的。一般的经验法则是。始终进行换行,使当前列中最大的剩余元素进入主元位置。在第4章中,你看到了在某些实际应用中出现的矩阵;可以证明,对它们来说主元是没有必要的;见练习5.13。
上面讨论的主元也被称为部分主元(partial pivoting),因为它只基于行的交换。另一个选择是完全主元(full pivoting),即结合行和列的交换,找到剩余子块中最大的元素,作为主元。最后,对角线主元将同样的交换应用于行和列。(这相当于对问题的未知数进行重新编号)。这意味着主元只在对角线上被搜索到。从现在开始,我们将只考虑部分主元的问题。
舍入对特征值计算的影响
考虑矩阵
其中$\epsilon_{mach} < |\epsilon| < \sqrt{\epsilon_{mach}}$,其特征值为$1 + \epsilon $和$1 - \epsilon$。如果我们用计算机运算来计算它的特征多项式
我们发现一个双重特征值1。请注意,准确的特征值是可以用工作精度来表达的;是算法导致了错误。显然,使用特征多项式并不是计算特征值的正确方法,即使在行为良好的对称正定矩阵中也是如此。
一个非对称的例子:让$A$为大小为20的矩阵
由于这是一个三角矩阵,其特征值是对角线元素。如果我们通过设置$A_{20,1}=10^{-6}$来扰动这个矩阵,我们发现特征值的扰动要比元素的扰动大得多。
另外,有几个计算出来的特征值有虚数的成分,而准确的特征值没有这个成分。
LU分解
到目前为止,我们已经在解决单一线性方程组的背景下研究了消除未知数的问题。假设我们需要解决一个以上的具有相同矩阵的系统,但有不同的右手边。例如,如果在隐式欧拉方法中采取多个时间步骤,就会发生这种情况。我们能否利用第一个系统中所做的工作来使后面的内容更加容易解决?
答案是肯定的。我们可以将求解过程分为只涉及矩阵的部分和专门针对右手边的部分。如果有一系列的系统需要解决,我们只需要做一次第一部分,幸运的是,这甚至是我们需要做的主要工作。
让我们再看一个例子:
在消除的过程中,我们把第二行减去$2\times $第一行,第三行减去$1/2\times$第一行。说服你自己,这种合并行的做法可以通过从左边的$A$乘以
这是与对角线下第一列中的消除系数相同的。消除变量的第一步相当于将系统$Ax=b$转换为$L_1Ax=L_1b$。
在下一步,你从第三行减去3$\times $第二行。让你自己相信,这相当于将当前的矩阵$L_1A$左乘以
这是与对角线下第一列中的消除系数相同的。消除变量的第一步相当于将系统$Ax=b$转换为$L_2L_1Ax=L_2L_1b$。并且$L_2L_1A$是 “上三角 “形式。如果我们定义$U = L_2L_1A$, 那么$A= L_1^{-1}L_2^{-1}U$。计算诸如$L^{-1}$这样的矩阵有多难?很容易,事实证明是这样。
我们提出以下意见:
同样地
甚至更显著的
即$L_1^{-1}L_2^{-1}$包含$L^{-1}$的非对角线元素,$L^{-1}$不变,它们又包含消除系数。(这是Householder反射器的一个特殊情况,见13.6)。
练习 5.4 证明类似的声明是成立的,即使在对角线之上有元素存在。
如果定义$L=L_1^{-1}L_2^{-1}$,现在有$A=LU$;这被称为$LU$因子化。我们看到,对角线以下的$L$系数是消除过程中所用系数的负数。更好的是,$L$的第一列可以在消除$A$的第一列时写出来,所以$L$和$U$的计算可以在没有额外存储的情况下完成,至少我们可以承受失去$𝐴$。
算法
让我们把$LU$因式分解算法写成正式代码
1 | ⟨𝐿𝑈 factorization⟩: |
或者说,把所有东西放在一起。
1 | ⟨𝐿𝑈 factorization⟩: |
这是呈现$LU$因子化的最常见方式。然而,也存在其他计算相同结果的方法。像$LU$因子化这样的算法可以用几种方式进行编码,这些方式在数学上是等价的,但它们有不同的计算行为。这个问题,在密集矩阵的背景下,是van de Geijn和Quintana的《矩阵计算编程的科学》[193]的重点。
Cholesky因式分解
一个对称矩阵的$LU$因式分解并不能得到相互转置的$L$和$U$:$L$在对角线上有1,而$U$有主元。然而,我们可以对对称矩阵$A$进行因式分解,其形式为$A=LL^t$。这样做的好处是,因式分解所占用的空间与原始矩阵相同,即$n(n+1)/2$个元素。如果运气好的话,我们可以像在$LU$情况下一样,用因子化覆盖矩阵。
我们通过归纳推理来推导出这个算法。让我们把$A=LL^t$写成块状。
则$\ell_{11}^2=a_{11}$,由此得到$\ell_{11}$。我们还发现$\ell_{11}(L^t)_{1j} = \ell_{j1} = a_{1j}$,所以我们可以计算出整个$L$的第一列。最后,$A_{22} = L_{22}L^t_{22} + \ell_{12}\ell^t_{12}$,所以
这表明$L_{22}$是更新的$A_{22}$块的Cholesky因子。递归后,现在定义了该算法。
唯一性
我们时常需要分析不同的计算方式是否会导致相同的结果,这被称为结果的“唯一性”:如果计算结果唯一,那么不论我们使用何种软件库,都不会改变计算的有效性。
下面我们分析LU因式分解的唯一性。$LU$因式分解算法的定义是:给定一个非奇异矩阵$A$,它将给出一个下三角矩阵$L$和上三角矩阵$U$,使得$A= LU$。上述计算$LU$因式分解的算法是确定的(它不包含 “取任何满足…的行 “的指令),所以给定相同的输入,它将总是计算相同的输出。然而,其他的算法也是可能的,所以我们需要担心他们是否会得到相同的结果。
我们假设$A=L_1U_1=L_2U_2$,其中$L1、L2$为下三角,$U_1、U_2$为上三角。那么,$L^{-1}L=UU^{-1}$。 在这个等式中,左手边是下三角矩阵的乘积,而右手边只包含上三角矩阵。
练习 5.5 证明下三角矩阵的乘积是下三角,而上三角矩阵的乘积是上三角。对于非奇异三角形矩阵的倒数,类似的说法是否成立?
积$L^{-1}L$显然既是下三角又是上三角,所以它一定是对角线的。我们称它为$D$,那么$L_1=L_2D$,$U_2=D_1$。结论是,𝐿𝑈因式分解不是唯一的,但它是唯一的 “直到对角线缩放”。
练习 5.6 第5.3.1节中的算法产生了一个下三角因子$L$,其对角线上有1。证明这个额外的条件使得因式分解是唯一的。
练习 5.7 证明另一个条件,即$U$的对角线上有1,也足以实现因式分解的唯一性。
由于我们可以要求$L$或$U$中的单位对角线,你可能想知道是否有可能两者都有。(我们可以这样做:假设$A=LU$,其中$L$和$U$是非星形下三角和上三角,但没有以任何方式归一化。请写出
经过重命名,我们现在有一个因式分解
其中$D$是一个包含主元的对角线矩阵。
练习 5.8 证明你也可以将因式分解的形式定为$A= (D+L)D^{-1}(D+ U )$ 。这个$D$与前面的有什么关系?
练习 5.9 这样考虑一个三对角矩阵的因式分解。$L$和$U$与$A$的三角部分有什么关系?推导出$D$和$D_A$之间的关系,并说明这是产生主元的方程。
主元
在上面的因式分解例子中,我们为了保证非零主元的存在,或者为了数值的稳定性,需要进行主元化,也就是交换行。现在我们将把透视纳入$LU$因式分解。
首先,行交换可以用矩阵乘法来描述。令
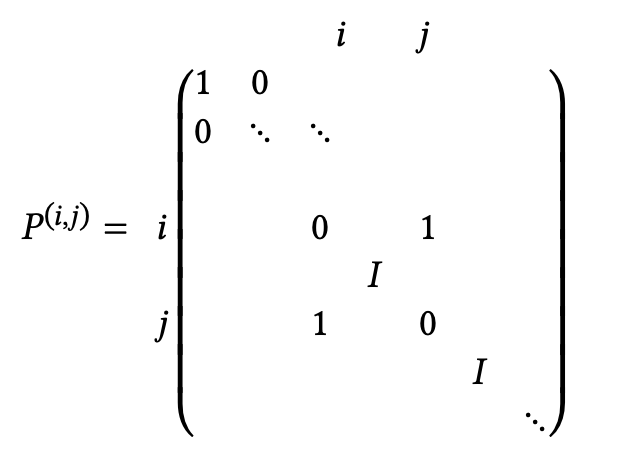
那么$P^{(i,j)}A$是交换了行$i$和$j$的矩阵$A$。由于我们可能要在因式分解过程的每次迭代中进行透视,我们引入一个序列$p(·)$,其中$p(i)$是与第𝑖行交换的第𝑗行的值。简写为$P^{(i)}\equiv P^{(i,p(i))}$。
练习 5.10 证明$P^{(i)}$是其自身的逆。
现在可以将部分主元的因式分解过程描述为:
- 让$A^{(i)}$为矩阵,列$1 … i- 1$被消除,并应用部分主元以获得$(i, i)$位置上的所需元素。
- 让$\ell^{(i)}$为第$i$个消除步骤中的乘数向量。(也就是说,这一步的消除矩阵$L_i$是身份加$\ell(i)$的第$i$列)。
- 让$P^{(i+1)}(j\geqslant i+1)$是为下一个消除步骤做部分透视的矩阵,如上所述。
- 那么$A^{(i+1)} = P^{(i+1)}L_iA^{(i)}$。
这样,我们就得到了一个因式分解的形式
此时我们无法写出$ A= LU$:而是写出
练习 5.11 回顾前面的内容,从性能角度看,分块算法通常是可取的。为什么方程(5.5)中的 “$LU$因子化与交错主元矩阵 “对性能来说是个坏消息?
幸运的是,方程(5.5)可以被简化:$P$和$L$矩阵 “几乎相通”。我们通过一个例子来证明这一点:$P^{(2)}L_1=\tilde{L_1}𝑃^{(2)}$,其中$\tilde{L}_1$非常接近于$L_1$。
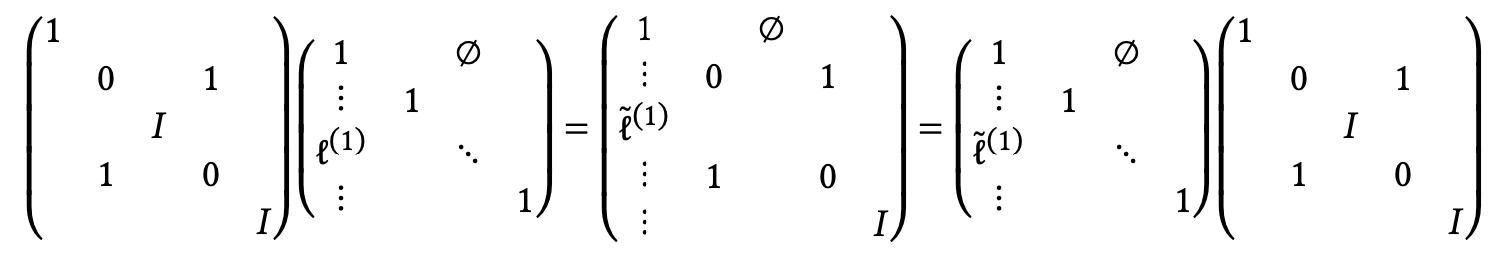
其中$\tilde{\ell}^{(1)}$与$\ell^{(1)}$相同,只是元素$i$和$p(i)$被调换了。你现在可以说服自己,同样$P^{(2)}$等也可以 “拉过 “$L_1$。
因此,我们得到
这意味着我们可以像以前一样再次形成一个矩阵$L$,只是每次我们进行主元时,我们需要更新已经计算过的$L$的列。
练习 5.12 如果我们把方程写成$PA= LU$,得到$A= P^{-1}LU$。是否能得出一个用$P$ 表示的 $P^{-1}$?提示:每个$P^{(i)}$都是对称的,而且是它自己的逆数;见上面的练习。
练习 5.13 早些时候,我们看到二维BVP产生了某种矩阵。我们在没有证明的情况下指出,对于这些矩阵不需要主元。现在我们可以正式证明这一点,重点放在对角线支配的关键属性上。
假设矩阵$A$满足$\forall j\neq i: a_{ij} \leqslant 0$,表明该矩阵是对角域的,即存在向量$u, v \geqslant 0$(意味着每个分量都是非负的),使得$Au = v$。 证明在消除一个变量后,对于剩余的矩阵$\tilde{A}$又有向量$\tilde{u},\tilde{v} \geqslant 0$,使得$\tilde{A}\tilde{u} =\tilde{v}$。 现在完成论证,如果$A$是对称的、对角线主导的,(部分)主元是不必要的。(实际上可以证明,主元对于任何对称正定(SPD)矩阵都是不必要的,对角线主导是比SPD-性更强的条件)。
解决系统问题
现有一个因式分解$A = LU$,我们可以用它来解决线性系统$Ax= LUx =b$。如果我们引入一个临时向量$y= Ux$,那么我们可以看到这需要两个步骤。
第一部分,$Ly = b$被称为 “下三角解”,因为它涉及下三角矩阵$L$。
在第一行,你看到$y_1=b_1$.然后,在第二行$\ell_{21}y_1+y_2=b_2$,所以$y_2=b_2-\ell_{21}y_1$。你可以想象这如何继续:在每$i$行,你可以从以前的$y$值计算$y_i$。
由于我们以递增的方式计算$y_i$,这也被称为正向替换、正向求解或正向扫瞄。
求解过程的后半部分,即上三角求解、后向替换或后向扫描,从$Ux=y$中计算出$x$。
现在我们看一下最后一行,它立即告诉我们$x_n=u^{-1}_{nn}y_n$。由此可见,最后一行说明了$u_{n-1n-1}x_{n-1}+u_{n-1n}x_n=y_{n-1}$,从而得出$x_{n-1}=u^{-1}_{n-1n-1}(y_{n-1}u{_{n-1n}x_n})$。更一般地,我们可以计算
对$i$的数值递减。
练习 5.14 在回扫中,你必须用数字$𝑢_𝑖$进行除法。如果其中任何一个是零,这是不可能的。把这个问题与上面的讨论联系起来。
复杂度
在本章的开头,我们指出,并不是每一种解决线性系统的方法都需要相同数量的操作。因此,让我们仔细研究一下复杂度1,也就是在解决线性系统时使用LU因子化的操作数与问题大小的函数关系。
首先,我们看一下从$LUx = b$(”解决线性系统”)计算$x$,因为我们已经有了因子化$A= LU$。把下三角和上三角部分放在一起看,会发现与所有对角线外的元素(即元素$\ell_{ij}$或$u_{ij}$与$i\neq j$)进行了乘法。 此外,上三角解涉及到对$u_i$元素的除法。 现在,除法运算通常比乘法运算昂贵得多,所以在这种情况下,我们会计算出$1/u_i$的值,并将其存储起来。
练习 5.15 请看一下因式分解算法,并论证存储主元的倒数并不增加计算的复杂性。
总结一下会发现,在一个大小为$n\times n$的系统中,我们要进行$n^2$的乘法运算和大致相同数量的加法运算。这表明,给定一个因式分解,解决一个线性系统的复杂度与简单的矩阵-向量乘法相同,也就是说,给定$A$和$x$的计算复杂度。
构建$LU$因式分解的复杂度,计算起来就比较麻烦了。你可以看到,在$k$第三步发生了两件事:乘数的计算和行的更新。有$𝑛 - 𝑘$个乘数需要计算,每个乘数都涉及一个除数。除法之后,更新需要$(n-k)^2$次加法和乘法。如果我们暂时不考虑除法的问题。因为它们的数量较少,我们发现$LU$因子化需要$\sum_{k=1}^{n-1}2(n-k)^2$次运算。如果我们顺序给这个和中的项编号,我们会发现
由于可以通过积分来近似求和,我们发现这是$2/3n^3$加上一些低阶项。这比解决线性系统要高一阶:随着系统规模的增长,构建$LU$因子化的成本完全占据了主导地位。
当然,算法分析还有比运算计数更重要的内容。虽然解线性系统的复杂度与矩阵-向量乘法相同,但这两种操作的性质非常不同。一个很大的区别是,因式分解和前向/后向求解都涉及递归,所以它们不容易并行化。关于这一点,我们将在后面详细说明。
分块算法
通常,矩阵有一个自然的块状结构,比如二维BVP的情况。许多线性代数操作可以用这些块来表述。与传统的矩阵标量观点相比,这可能有几个好处。例如,它可以改善缓存阻塞;它也有利于在多核架构上调度线性代数算法。
对于分块算法,我们把矩阵写成
其中$M, N$是块的大小,即用子块表示的大小。通常情况下。
我们选择的块是:$M = N$,对角线块为正方形。作为一个简单的例子,考虑矩阵-向量乘积$y= Ax$,以块的形式表示。
为了说明区块算法的计算结果与旧的标量算法相同,我们看一下一个分支$Y_{i_k}$,也就是第$i$块的$k$个标量分量。首先。
于是
是$a$的第$i$个区块行的第$k$行与整个$X$的积。
一个更有趣的算法是$LU$因子化的分块版。算法就变成了
1 | ⟨𝐿𝑈 factorization⟩: |
该算法与之前的算法有很大的不同,即除以$a_{kk}$的方法被一个乘以$A^{-1}_{kk}$。另外,$U$因子现在在对角线上有支点块,而不是支点元素。所以$U$只是 “块状上三角形”,而不是严格的上三角形。
练习 5.16 我们想表明,这里的块状算法再次计算出与标量算法相同的结果。通过明确查看计算的元素来做到这一点是很麻烦的,所以我们采取另一种方法。首先,回顾一下第5.3.3节,$LU$面化是唯一的:如果$A=L_1U_1=L_2U_2$且$L_1、L_2$有单位斜线,那么$L_1=L_2$。$U_1 = U_2$
接下来,考虑计算$A^{-1}_{kk}$的问题。证明这可以通过以下方式完成:首先计算$A_{kk}$的$LU$因子化。现在用它来证明,块状$LU$因子化可以给出严格意义上的三角形的$L$和$U$因子。$LU$因式分解的唯一性就证明了块算法可以计算出标量结果。
稀疏矩阵
BVP(和IBVP)的离散化可能会引起稀疏矩阵的出现。由于这样的矩阵有$N^2$个元素,但只有$O(N)$个非零元素,将其存储为二维数组将是对空间的极大浪费。此外,我们希望避免对零元素进行操作。
在本节中,我们将探讨稀疏矩阵的有效存储方案,以及使用稀疏存储时熟悉的线性代数操作的形式。
稀疏矩阵的存储
稀疏矩阵没有明确定义,只要当矩阵中的零元素多到需要专门存储时,该矩阵即为稀疏矩阵(sparse matrix)。
我们将在此简要讨论最流行的稀疏矩阵的存储方案。由于矩阵不再是作为一个简单的2维数组来存储,使用这种存储方案的算法也需要重写。
带状存储和对角线存储
带状稀疏矩阵的非零元素正好位于一些子对角线上。对于这样的矩阵,可以采用专门的存储方案。
以一维BVP的矩阵为例。它的元素位于三个子对角线上:主对角线和第一个超对角线和子对角线。在带状存储中,我们只将包含非零点的带状存储在内存中。对于这样一个矩阵,最经济的存储方案是连续存储 $2n-2$ 的元素。然而,由于各种原因,浪费一些存储位置会更方便,如图 5.1 所示。
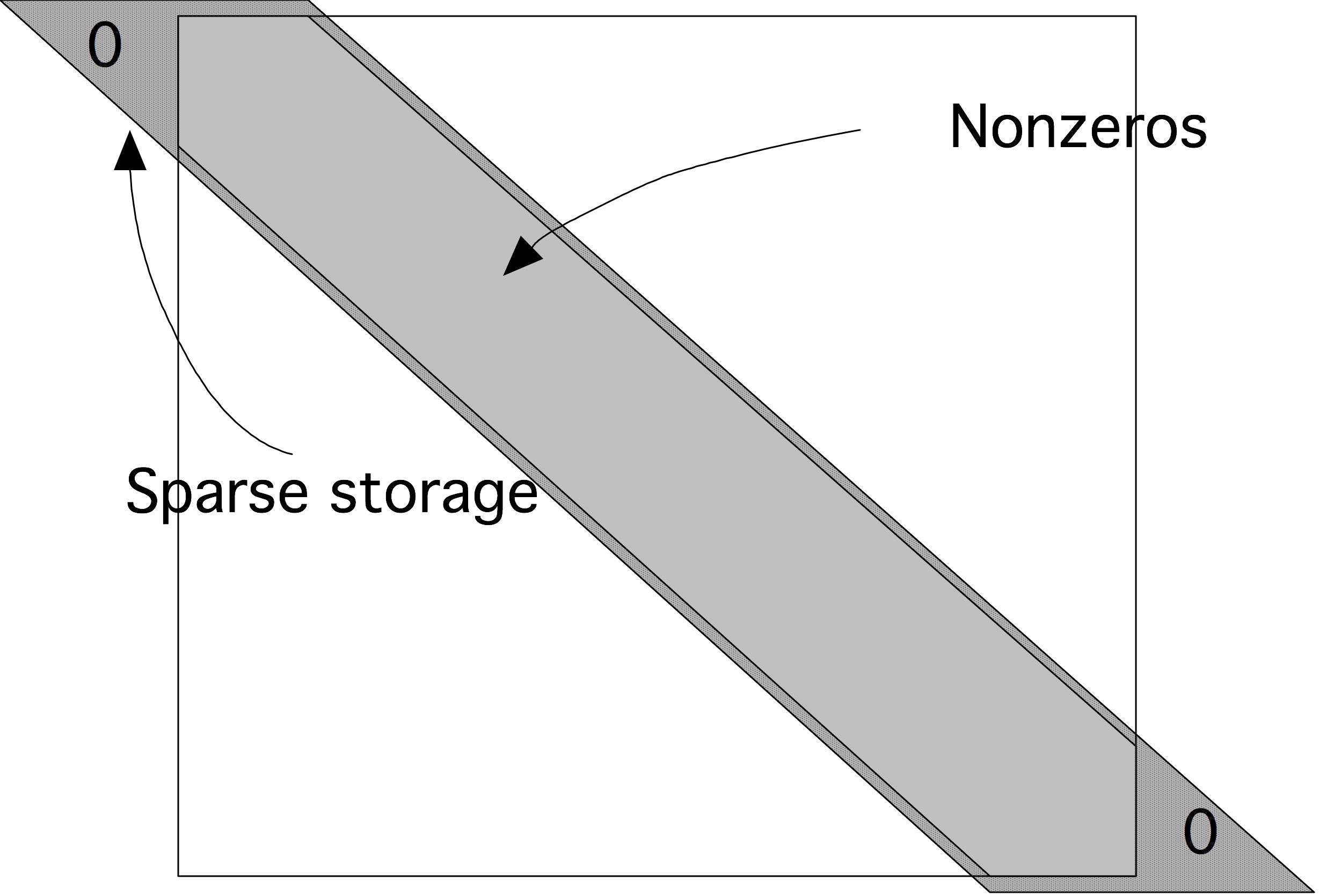
因此,对于一个大小为$n\times n$,矩阵带宽为$p$的矩阵,我们需要一个大小为$n\times p$的矩形数组来存储矩阵。那么,矩阵将被存储为
其中星星表示不对应矩阵元素的数组元素:它们是图5.1中左上和右下的三角形。
当然,现在我们要想知道阵列元素$A(i,j)$和矩阵元素$𝐴_{𝑖𝑗}$之间的转换。这在Fortran语言中是最容易做到的。如果我们将数组分配为
1 | dimension A(n,-1:1) |
那么主对角线$A_i$就被储存在$A(*,0)$中。例如,$A(1,0) \sim A_{11}$。在矩阵$A$的同一行的下一个位置,$A(1,1) \sim A_{12}$。很容易看出,我们一起有这样的转换
练习 5.17 什么是反向转换,也就是说,矩阵元素$A_{ij}$对应于哪个数组位置$A(?,?)$?
练习 5.18 如果你是一个C语言程序员,请推导出矩阵元素$A_{ij}$与数组元素$A[i][j]$之间的转换。
如果我们将这种将矩阵存储为$N\times p$数组的方案应用于二维BVP的矩阵,就会变得很浪费,因为我们会存储许多存在于带内的零。因此,在对角线存储或对角线存储中,我们通过只存储非零对角线来完善这一方案:如果矩阵有$p$个非零对角线,我们需要一个$n\times p$数组。对于方程的矩阵,这意味着。
当然,我们需要一个额外的整数阵来告诉我们这些非零对角线的位置。
练习 5.19 对于$d=1, 2, 3$空间维度的中心差分矩阵,作为$N$阶的带宽是多少?离散化参数$h$的阶数是多少?
在前面的例子中,矩阵在主对角线上下有相同数量的非零对角线。在一般情况下,这不一定是真的。为此,我们引入了以下概念
- 左半带宽度(left halfbandwidth):如果$A$的左半带宽度为$p$,那么$A_{ij} = 0$,因为$i> j + p$,和
- 右半带宽度(right halfbandwidth):如果$A$的右半带宽度为$p$,那么$A_{ij}=0$,因为$j>i+p$。如果左边和右边的半带宽度相同,我们就直接指半带宽度。
对角线存储的操作
对稀疏矩阵最重要的操作是矩阵-向量乘积。对于一个按对角线存储的矩阵,如上所述,仍然可以使用转换公式(5.9)进行普通的ROWISE或Lumnwise乘积;事实上,这就是Lapack带状程序的工作方式。然而,在带宽较小的情况下,这样做的向量长度较短,循环开销相对较高,所以效率不高。有可能做得比这好得多。
如果我们看一下矩阵元素在矩阵-向量乘积中是如何使用的,我们会发现主对角线被用作
第一个超对角线被用作
第一条对角线为
换句话说,整个矩阵-向量乘积只需执行三个长度为$n$(或$n-1$)的向量运算,而不是长度为3(或2)的$n$内积。
1 | for diag = -diag_left, diag_right |
练习 5.20 写一个程序,通过对角线计算$y \leftarrow A^tx$。用你喜欢的语言来实现它,并在一个随机矩阵上测试它。
练习 5.21 如果矩阵在带内是密集的,上述代码片段是有效的。例如,二维BVP的矩阵就不是这种情况。写出只使用非零对角线的矩阵-向量乘积的代码。
练习 5.22 矩阵相乘比矩阵与向量相乘更难。如果矩阵$A$的左半带宽度为$p_A,q_Q$,而矩阵$B$的左半带宽度为$p_B,q_B$, $C=AB
$的左半带宽度为多少? 假设已经为$C$分配了一个足够大的数组,请写一个程序来计算$C \leftarrow AB$。
压缩行存储
如果我们有一个不具有简单带状结构的稀疏矩阵,或者非零对角线的数量变得不切实际,我们可以使用更通用的压缩行存储(Compressed Row Storage,CRS)方案。顾名思义,这个方案是基于压缩所有的行,消除零值;见图5.2。由于这失去了非零最初来自哪一列的信息,我们必须明确地存储这些信息。考虑一个稀疏矩阵的例子。
在压缩了所有的行之后,我们将所有的非零点存储在一个单一的实数数组中。列的索引也同样存储在一个整数数组中,我们存储指向列开始位置的指针。使用基于0的索引,这就得到了。
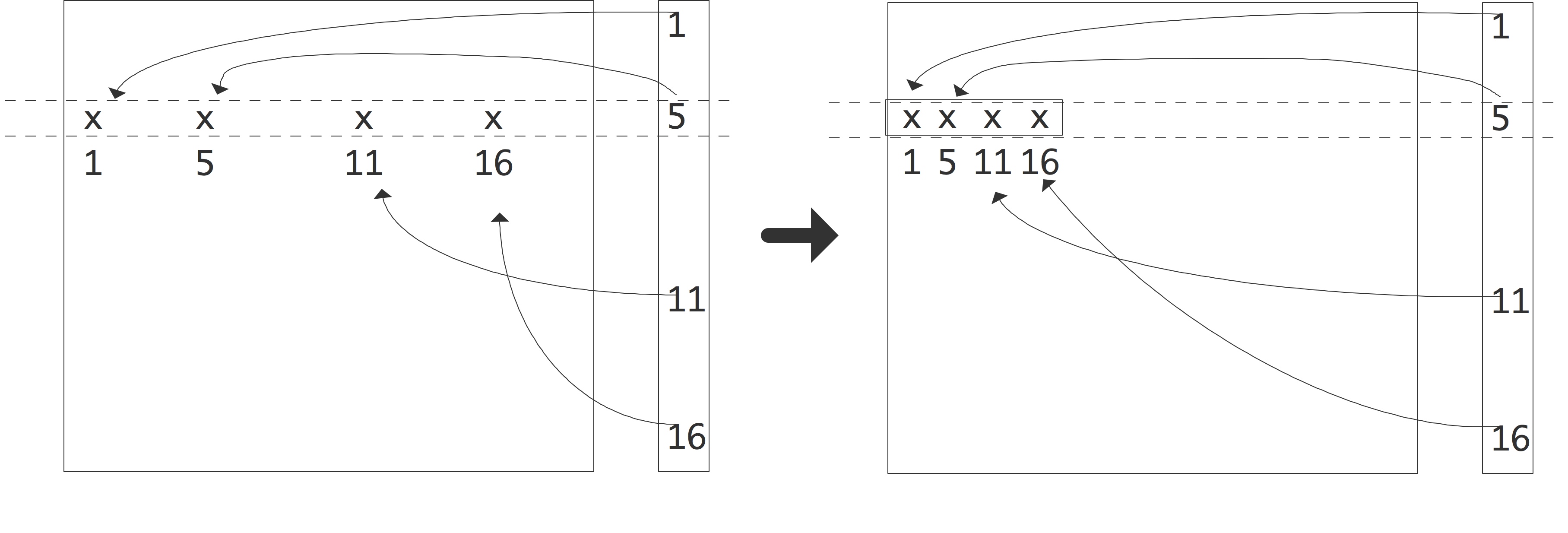
CRS的一个简单变体是压缩列存储(CCS),其中列中的元素被连续存储。这也被称为Harwell-Boeing矩阵格式[55]。你可能会遇到的另一种存储方案是坐标存储,其中矩阵被存储为三联体列表$
关于压缩行存储的算法
在这一节中,我们将看一下一些算法在CRS中的形式。首先我们考虑稀疏矩阵-向量乘积的实现。
1 | for (row=0; row<nrows; row++) { |
标准的矩阵-向量乘积算法$y=Ax$,其中每一行$A_{i∗}$与输入向量$x$进行内积。然而,请注意,内循环不再以列号为索引,而是以要找到该列号的位置为索引。这个额外的步骤被称为间接寻址。
练习 5.23 比较密集矩阵-向量乘积(按行执行)和刚才给出的稀疏乘积的数据位置性。说明对于一般的稀疏矩阵来说,在处理输入向量$x$时的空间局部性已经消失了。是否有一些矩阵结构,我们仍然可以期待一些空间局部性?
现在,如果我们想计算乘积$y=A^tx$呢?在这种情况下,我们需要$A^t$的行,或者说,相当于$A$的列。找到$A$的任意列是很难的,需要大量的搜索,所以可能认为这个算法也相应地难以计算。幸运的是,这并不是真的。
如果我们将标准算法中的$i$和$j$循环交换为$y=Ax$,我们可以得到
使用第二种算法来计算$A^tx$的乘积。
练习 5.24 写出转置积$y=A^tx$的代码,其中$A$是以CRS格式存储。写一个简单的测试程序,确认你的代码计算正确。
练习 5.25 如果需要同时访问行和列呢?实现一种算法,测试以CRS格式存储的矩阵是否对称。提示:保留一个指针数组,每行一个,用来记录在该行的进展情况。
练习 5.26 到目前为止所描述的操作是相当简单的,因为它们从未改变过矩阵的稀疏结构。如上所述,CRS格式并不允许在矩阵中添加新的非零点,但做一个允许添加的扩展并不难。
让数字$p_i, i = 1 … n$,描述第$i$行中非零点的数量。设计一个对CRS的扩展,使每一行都有$q$额外元素的空间。实施这个方案并进行测试:构造一个第$i$行有$p_i$个非零点的矩阵,在添加新元素之前和之后检查矩阵-向量乘积的正确性,每行最多有$q$个元素。
现在假设矩阵中的非零点总数不会超过𝑞𝑛。修改你的代码,使其能够处理从空矩阵开始,并逐渐在随机位置添加非零点。再次,检查正确性。
我们将在第6.5.5节在共享内存并行的背景下重新审视转置积算法。
稀疏矩阵和图论
许多关于稀疏矩阵的论点都可以用图论来表述。为了了解为什么可以这样做,考虑一个大小为$n$的矩阵$A$,并观察到我们可以通过$V={1,…,n}$定义一个图$⟨E,V⟩$,$E=\{(i,j)∶a_{ij} \neq 0\}$。 这被称为矩阵的邻接图。 为简单起见,我们假设$A$有一个非零的对角线。 如果有必要,我们可以给这个图附加权重,定义为$w_{ij}= a_{ij}$。 然后,该图被表示为$⟨E,V,W⟩$。 (如果你不熟悉图论的基本知识,请看附录18)。 图的属性现在与矩阵属性相对应;例如,图的度数是每行的最大非零数,不包括对角线元素。 再比如,如果矩阵的图形是一个无向图,这意味着$a_{ij}\neq 0 \Leftrightarrow a_{ij} \neq 0$。 我们称这样的矩阵为结构对称:它不是真正意义上的对称,即$\forall_{ij}∶ a_{ij} = a_{ij}$ ,但上三角的每个非零都对应于下三角的一个,反之亦然。
变换下的图的特性
考虑矩阵图的一个好处是,图的性质并不取决于我们如何对节点进行排序,也就是说,它们在矩阵的变化下是不变的。
练习 5.27 让我们来看看,当矩阵的图形$G=⟨V,E,W⟩$的节点被重新编号后会发生什么。作为一个简单的例子,我们对节点进行反向编号;也就是说,以$n$为节点数,我们将节点$i$映射为$n+1-i$。相应地,我们发现一个新的图$G’=⟨V,E’,W’⟩$ 其中
这种重新编号对与$G′$相对应的矩阵$A’$意味着什么?如果你交换两个节点上的标签$i, j$,对矩阵$A$有什么影响?
注释 19 有些属性在变异中保持不变。说服自己变异不会改变矩阵的特征值。
有些图的特性很难从矩阵的稀疏模式中看出来,但从图中更容易推导出来。
练习 5.28 让$A$是大小为$n$的一维BVP的三对角矩阵,$n$为奇数。$A$的图形是什么样子的?请考虑将节点按以下顺序排列所产生的变化。
矩阵的疏散模式是什么样子的?
现在取这个矩阵,将最接近矩阵 “中间 “的对角线元素归零:让
描述一下这对$A$的图形有什么影响。这样的图被称为可约图(reducible)。现在应用前面练习中的置换法,画出所产生的稀疏模式。请注意,现在图形的可还原性更难从稀疏模式中读出。
稀疏矩阵的LU因子化
一维BVP导致了一个具有三对角系数矩阵的线性系统。如果我们做一步高斯消除,唯一需要消除的元素是在第二行。
有两个重要的观察结果:一个是这个消除步骤并没有将任何零元素变为非零。另一个观察结果是,剩下要消除的那部分矩阵又是三对角的。归纳起来,在消除过程中,没有零元素变为非零:$L+U$的稀疏模式与$A$相同,因此因式分解所需的存储空间与矩阵的相同。
不幸的是,三对角矩阵的情况并不典型,我们很快就会看到二维问题的情况。但首先我们将把第5.4.2节关于图论的讨论扩展到因子化。
稀疏LU因子化的图论
在讨论稀疏矩阵的LU因子化时,图论往往是有用的。让我们研究一下消除第一个未知数(或扫除第一列)在图论方面意味着什么。我们假设是一个结构对称的矩阵。
我们认为消除一个未知数是一个过程,它将一个图$G=⟨V, E⟩$变成一个图$G’=⟨V’, E’⟩$。这些图形之间的关系首先是一个顶点,比如说$k$,已经从顶点中被移除。$k \notin V’,V’\cup{k}=V$ 。
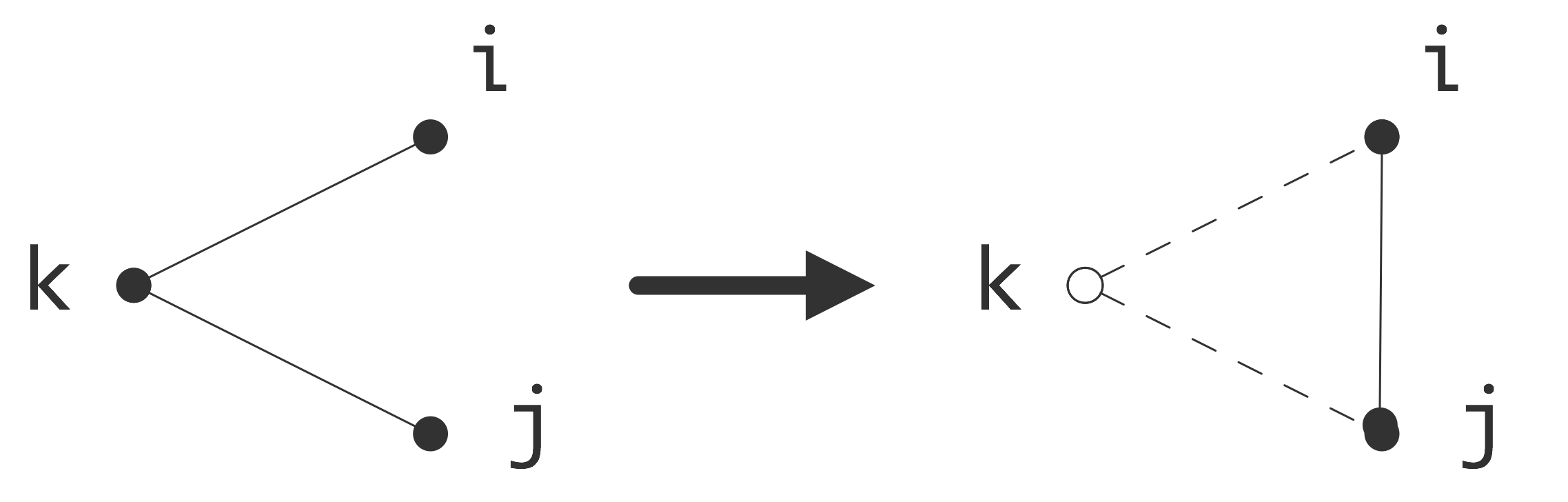
$E$和$E′$之间的关系更为复杂。在高斯消除算法中,消除变量$k$的结果是:声明
对所有$i, j \neq k$执行。 如果$a_{ij}$最初$\neq 0$,即$(i,j)\in E$,那么$a_{ij}$的值只是被改变。 如果原矩阵中的$a_{ij}=0$,即$(i, j)\notin E$,在消除$k$未知数后,会有一个非零元素,称为补入元素。
这在图5.3中有所说明。
综上所述,消除一个未知数可以得到一个少了一个顶点的图,并且对所有$i、j$都有边,这样在$i$或$j$与被消除的变量$k$之间有边。图5.4给出了一个小矩阵上的完整说明。
练习 5.29 回到练习5.28。使用图形参数来确定奇数变量被消除后的稀疏模式。
练习 5.30 证明上述关于消除单一变量的论证的一般化。设$I\subset V$是任意一个顶点集合,设$J$是连接到$I$的顶点。
现在表明,消除$I$中的变量会导致一个图$⟨V′,E′⟩$,其中$J$中的所有节点在剩余的图中是相连的,如果它们之间有一条路径通过$I$。
填充
现在我们回到二维问题的矩阵因式分解上。我们把这种大小为$N\times N$的矩阵写成块维度为$n$的块矩阵,每个块的大小为$n$。(复习问题:这些块从何而来?) 现在,在第一个消除步骤中,我们需要将两个元素归零,即$a_{21}$和$_{n+1,1}$。
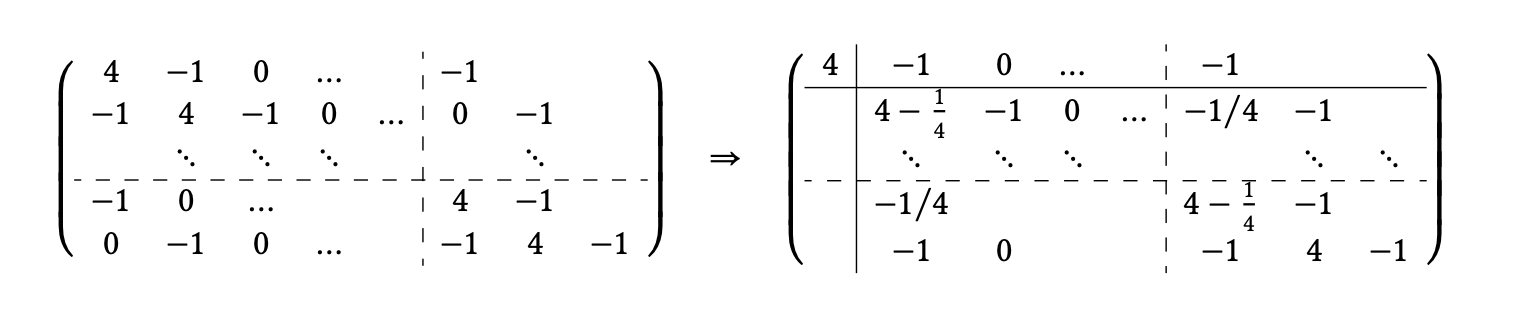
你看,消除$a_{21}$和$a_{n+1,1}$会导致两个填充元素的出现:在原矩阵中,$a_{2,n+1}$和$a_{n+1,2}$为零,但在修改后的矩阵中,这些位置是非零的。我们将填充位置定义为$(i,j)$,其中$a_{ij}=0$,但是$(L+U)_{ij}\neq 0$。 很明显,在因式分解过程中,矩阵被填满了。 只要有一点想象力,你也可以看到,在第一个对角线块之外的带子中的每个元素都会填满。 然而,使用第5.4.3.1节的图形方法,可以很容易地将所产生的填充连接可视化。 在图5.5中,对2d BVP例子的图进行了说明。 (第一行的每个变量被消除后,都会在下一个变量和第二行之间以及第二行的变量之间建立联系。 归纳起来,你会发现在第一行被消除后,第二行是完全连接的。 (将此与练习5.30联系起来。)
练习 5.31 完成这个论证。 第二行的变量是完全相连的,这对矩阵结构意味着什么? 在图中画出第二行的第一个变量被消除后的情况。
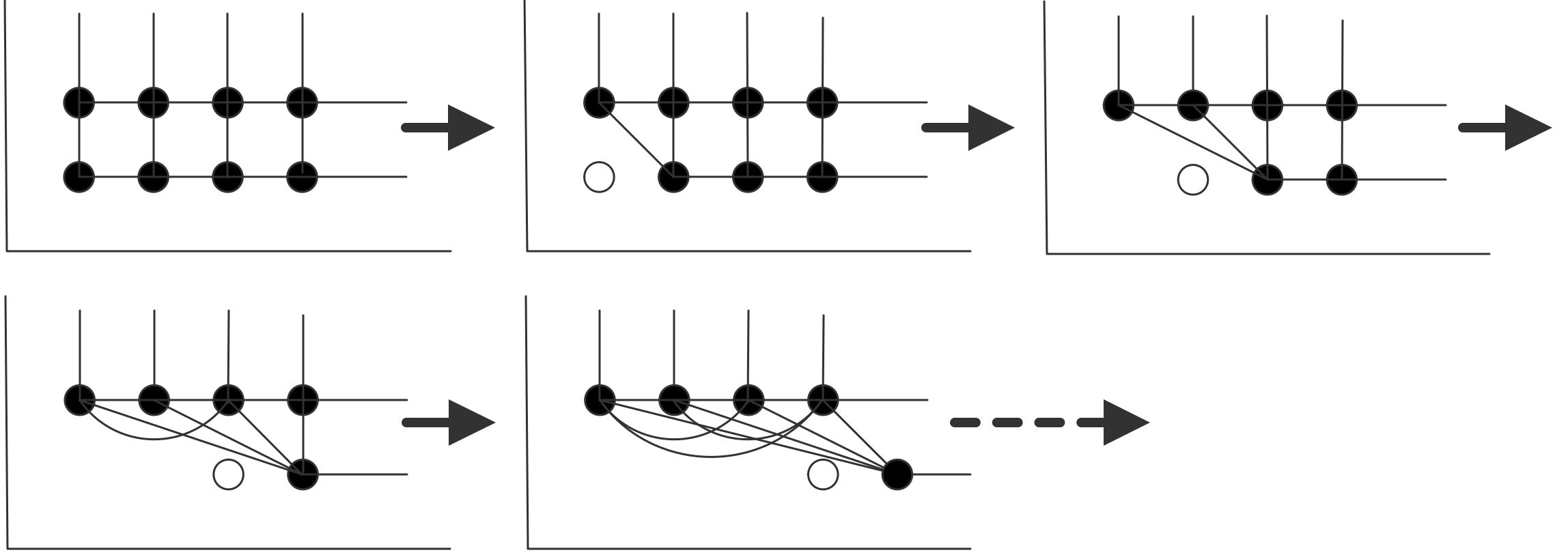
练习 5.32 用于密集线性代数的LAPACK软件有一个$LU$因子化程序,可以用因子覆盖输入矩阵。上面你看到了这是可能的,因为$L$的列正是随着$A$的列被消除而产生的。如果矩阵是以稀疏格式存储的,为什么这样的算法是不可能的?
填充估计
在上面的例子中,你看到稀疏矩阵的因式分解所占用的空间可能比矩阵本身要大得多,但仍比存储整个矩阵维度大小的正方形数组要小。现在我们将给出因式分解的空间复杂度的一些界限,也就是执行因式分解算法所需的空间量。
练习 5.33 证明以下陈述。
- 假设矩阵$A$有一个半带宽$p$,也就是说,如果$|i - j| > p$,则$a_{ij} = 0$。表明在无主元的因式分解后,$L+U$具有相同的半带宽度。
- 证明在经过部分主元的因式分解后,$L$的左半带宽为$p$,而$U$的右半带宽为$2p$。
- 假设没有透视,表明填空可以有如下特征:考虑行$i$。让$j_{min}$是第$i$行中最左边的非零点,即在$j<j_{min}$时,$a_{ij}=0$。那么,在$j_{min}$列左边的第$i$行中就不会有填充物。同样地,如果$i_{min}$是第$j$列中最上面的非零值,那么在第$j$列中就不会有高于$i_{min}$行的填充。给定一个稀疏矩阵,现在很容易分配足够的存储来适应一个没有主元的因式分解:这被称为天际线存储。
练习 5.34 考虑矩阵
前面已经证明,执行𝐿𝑈因式分解的任何填充都只限于包含原始矩阵元素的带。在这种情况下,不存在填充。归纳地证明这一点。
看一下邻接图。(这种图有个名字,叫什么?) 你能根据这个图给出一个没有填充的证明吗?
练习5.33表明,我们可以为带状矩阵的因式分解分配足够的存储空间。
对于带宽为𝑝的矩阵的因式分解,有一个大小为$N\times p$的阵列就可以了。
矩阵的一半带宽$p$和一半带宽$q$的部分主元的因素化。可以用$N\times (p+2q+1)$来描述。
可以根据具体的矩阵来构建足以存储因子化的Askylin配置文件矩阵。
我们可以将这个估计应用于二维BVP的矩阵,第4.2.3节。
练习 5.35 证明在方程(4.16)中,原始矩阵有 $O(N) = O(n^2)$非零元素,$O(N^2) = O(n^4)$元素,而因子化有 $O(nN) = O(n^3) = O(N^{3/2})$ 非零。
这些估计表明,一个𝐿𝑈因式分解所需的存储量可能比𝐴所需的更多,而且这个差别不是一个常数,而是与矩阵大小有关。在没有证明的情况下,我们指出,到目前为止你所看到的那种稀疏矩阵的求逆数是完全密集的,所以存储它们需要更多的时间。这是解决线性系统$Ax=y$的一个重要原因,在实践中不是通过计算$A^{-1}$和随后乘以$x=A^{-1}y$来完成。(数值稳定性是不这样做的另一个原因)。事实上,即使是因式分解也会占用很多空间,这是考虑迭代方法的一个原因,我们将在第5.5节中进行。
上面,你看到一个大小为$n\times n$的密集矩阵的因式分解需要$O(n^3)$操作。对于稀疏矩阵来说,这又是怎么回事呢?让我们考虑一个半带宽度为$p$的矩阵的情况,并假设原始矩阵在该带内是密集的。主元元素$a_{11}$用于将第一列中的$p$元素归零,对于每一个第一行的元素都要加到该行,涉及到$p$乘法和加法。总而言之,我们发现操作的数量大致为
加上或减去低阶项。
练习 5.36 对于二维BVP的矩阵来说,初始密集带的假设并不成立。为什么上述估计仍然成立,直到一些低阶项?
在上面的练习5.33中,你得出了一个易于应用的填充量的估计。然而,这可能是一个相当高的估计。我们希望能以比实际因式分解更少的工作量来计算或估计填充的数量。现在我们将勾勒出一种算法,用于寻找$L+U$中非零点的确切数量,其成本与这个数字呈线性关系。我们将在(结构上)对称的情况下这样做。关键的观察是以下几点。假设列𝑖在对角线下有一个以上的非零。
在第$i$步中消除$a_{ki}$会导致更新$a_{kj}$,如果最初$a_{kj}=0$,则会有一个填充元素。然而,我们可以推断出这个非零值的存在:消除$a_{ji}$会导致位置$(j,k)$的填充元素,而且我们知道结构对称性被保留了。换句话说,如果我们只计算非零点,那么只需看看消除$(j, i)$位置的影响,或者一般来说,消除主元下方的第一个非零点的影响。按照这个论点,我们只需要在每一个主元的一行中记录非零点,整个过程的复杂性与因式分解中的非零点数量成线性关系。
减少填充
矩阵的图形属性,如度数和直径,在对变量重新编号时是不变的。其他属性,如因子化过程中的填充,会受到重新编号的影响。事实上,值得研究的是,是否有可能通过对矩阵图的节点重新编号来减少填充量,或者说,通过对线性系统进行置换来减少填充量。
练习 5.37 考虑 “箭头 “矩阵,只在第一行和第二列以及对角线上有非零点。
假设任何加法都不为零,那么矩阵中和因式分解中的非零数是多少?你能找到一个问题的变量的对称排列,使新的矩阵没有填充物吗?
这个例子并不典型,但是通过对矩阵进行巧妙的置换,有时确实可以改善填充估计(例如见第6.8.1节)。即使这样,作为一项规则,声明也是成立的,稀疏矩阵的𝐿𝑈因式分解比矩阵本身需要的空间大得多。这也是下一节中迭代方法的激励因素之一。
Fill-in reducing orderings
一些矩阵的特性在对称排列下是不变的。
练习 5.38 在线性代数课上,你通常会研究矩阵的特性,以及它们在基数变化下是否不变,特别是在单元基的变换下。
证明对称互换是一种特殊的基础变化。说出一些矩阵
属性在单数变换下不会改变。
其他属性则不然:在上一节中,你看到填空量就是其中之一。因此,你可能会想知道什么是最好的排序,以减少给定矩阵的因式分解的填充量。这个问题在实践中是难以解决的,但存在各种启发式方法。其中一些启发式方法也可以从并行的角度进行论证;事实上,嵌套剖分的排序将只在关于并行的6.8.1节中讨论。在这里,我们简要地展示一下其他两个启发式方法,它们比并行性的需求更早。
首先,我们看一下Cuthill-McKee排序,它直接将填充矩阵的带宽降到最低。由于填充量可以用带宽来约束,我们希望这样一个减少带宽的排序也能减少填充量。
其次,我们将考虑最小度数排序,其目的是更直接地减少填充量。
Cuthill-McKee排序 Cuthill-McKee排序[36]是一种减少带宽的排序,它通过对变量进行水平集排序来实现。它考虑了矩阵的邻接图,并按以下步骤进行。
取一个任意的节点,称其为 “零级”。
给定一个级别$n$,将所有连接到级别𝑛的节点,以及尚未进入级别的节点,分配到级别$n+1$。
对于所谓的 “反向Cuthill-McKee排序”,请将各层的编号倒过来。
练习 5.39 证明根据Cuthill-McKee排序对矩阵进行置换有一个块状三对角结构。
我们将在第6.10.1节中考虑并行性时重新审视这个算法。当然,我们可以想知道带宽可以减少到什么程度。
练习 5.40 一个图的直径被定义为两个节点之间的最大最短距离。
- 论证在二维椭圆问题的图中,这个直径是$O(N^{1/2})$。
- 用带宽来表示节点1和$N$之间的路径长度。
- 认为这给出了直径的下限,并使用指针对带宽进行了下限边界。
最小程度排序 另一个排序的动机是观察到填充量与节点的程度有关。
练习 5.41 证明消除一个度数为𝑑的节点会导致最多 2𝑑的填充元素 所谓最小度数排序的过程如下。
找到具有最低度数的节点。
- 剔除该节点,并更新其余节点的学位信息。
从第一步开始,用更新的矩阵图重复。
练习 5.42 指出上述两种方法的区别。这两种方法都是基于对矩阵图的检查;然而,最小度数方法在使用的数据结构上需要更大的灵活性。解释一下原因并详细讨论两个方面。
迭代法
高斯消除法,即使用𝐿𝑈因式分解法,是一种寻找线性系统解的简单方法,但正如我们在上面看到的,在那种来自离散化PDE的问题中,它可以产生大量的填充。在这一节中,我们将研究一种完全不同的方法,即迭代求解,即通过一连串的逼近来找到系统的解。
这个计算方案看起来,非常粗略,就像。
这里的重要特征是,没有任何系统是用原始系数矩阵解决的;相反,每一次迭代都涉及到矩阵-向量乘法或一个更简单系统的解决。因此,我们用一个重复的更简单、更便宜的操作取代了一个复杂的操作,即构造一个𝐿𝑈因式分解并用它来解决一个系统。这使得迭代方法更容易编码,并有可能更有效率。
让我们考虑一个简单的例子来激励迭代方法的精确定义。假设我们想解决系统
其解为(2,1,1)。假设你知道(例如,从物理学的角度考虑),这么做的分量是大致相同的大小。观察对角线的主导大小,然后,决定
可能是一个很好的近似值。这有一个解决方案(2.1,9/7,8/6)。显然,解决一个只涉及原系统对角线的系统既容易做到,而且,至少在这种情况下,相当准确。
有解(2.1,7.95/7,5.9/6)。解三角形系统比对角线系统更费事一些,但仍比计算𝐿𝑈因式分解容易得多。另外,我们在寻找这个近似解的过程中没有产生任何填充物。
因此我们看到,有一些容易计算的方法可以合理地接近解决方案。我们能否以某种方式重复这个技巧呢?
更抽象地表述一下,我们所做的是不求解$Ax=b$,而是求解$L\tilde{x}=b$。现在将$\Delta x$定义为与真解的距离:$\tilde{x}=x+\Delta x$。这样,$A\Delta x=A\tilde{x}-b \equiv r$,其中$r$是残差。接下来我们再次求解$L\widetilde{\Delta x} = r$,并更新$x = x - \widetilde{\Delta x}$。
在这种情况下,我们每次迭代得到两个小数,这并不典型。
现在很清楚为什么迭代方法会有吸引力。如上图所示,通过高斯消除法解决一个系统需要进行$O(n^3)$运算。如果矩阵是密集的,则上述方案中的单次迭代需要$O(n^2)$操作,对于稀疏矩阵,可能需要低至$O(n)$操作。如果迭代次数少,这就使得迭代方法具有竞争力。
练习 5.43 当比较迭代法和直接法时,运算次数不是唯一相关的指标。概述一些与两种情况下的代码效率有关的问题。同时比较解决一个线性系统和解决多个线性系统的情况。
抽象介绍
现在是时候对上述例子的迭代方案做一个正式介绍了。假设我们想解决$Ax = b$,而直接求解的成本太高,但乘以𝐴是可行的。再假设我们有一个矩阵$K \approx A$,这样就可以廉价地求出 $Ax = b$ 。
我们不求解$Ax=b$,而是求解$Kx=b$,并定义$x_0$为解决方案:$Kx_0=b$。这就给我们留下了一个误差$e_0=x_0-x$,对此我们有一个公式$A(x_0-e_0)=b$或$Ae_0=A_0-b$。我们把$r_0\equiv Ax_0-b$残差;然后误差满足$Ae_0=r_0$。
如果我们能从$Ae_0 = r_0$的方程中解出误差,我们就完成了:然后找到真正的解决方案。然而,由于上次用$A$求解的成本太高,我们这次也不能这样做。
所以我们近似地确定误差修正。我们求解$K\tilde{e}_0 = r_0$,并设定$x_1 ∶= x_0 - \tilde{e}_0$;故事可以继续进行,$e_1=x_1-x$,$r_1=Ax_1-b$,$K\tilde{e}_1=r_1$,$x_2=x_1-\tilde{e}_1$,等等。
那么,迭代方案就是
1 | Let 𝑥0 be given |
我们把基本方案称为
一个固定的迭代。它是静止的,因为每次更新都是以相同的方式进行的,不依赖于迭代数。这种方案的分析很简单,但不幸的是适用性有限。
关于迭代方案,我们有几个问题需要回答。
- 这个方案是否总能带我们找到解决方案?- 如果这个方案收敛了,有多快?
- 我们何时停止迭代?
- 我们如何选择$K$?
现在我们将对这些问题给予一些关注,尽管全面的讨论超出了本书的范围。
收敛性和误差分析
我们从迭代方案是否收敛,以及收敛速度如何的问题开始。考虑一个迭代步骤。
归纳起来,我们发现$r_n=(I-AK^{-1})^nr_0$,所以如果所有的特征值都满足$|\lambda(I-AK^{-1})|<12$,那么$r_n\downarrow 0$。最后这句话给了我们一个收敛的条件,即把$K$与$A$联系起来,以及一个几何收敛率。
如果$K$足够接近的话,我们可以得到一个收敛的条件。
练习 5.44 为$e_n$推导一个类似的归纳关系。
通过计算实际的特征值,很难确定是否满足条件$|\lambda (I- AK^{-1})| < 1$。然而,有时格什哥林定理(附录13.5)给了我们足够的信息。
练习 5.45 考虑我们从二维BVP离散化中得到的方程(4.16)的矩阵$A$。设$K$为包含$A$的对角线的矩阵,即$k_i = a_i$和$k_{ij}= 0$,对于$i\neq j$。 使用格什哥林定理证明$|\lambda (I-AK^{-1})| < 1$。 这个练习中的论证很难推广到更复杂的$K$的选择,例如你将在下面看到。 这里我们只说对于某些矩阵$A$,这些$K$的选择将总是导致收敛,其速度随着矩阵大小的增加而减少。 除了说明对于$M$矩阵(见第4.2.2节),这些迭代方法会收敛外,我们将不做详细说明。 关于静止迭代方法收敛理论的更多细节,见[195]。
计算形式
在上面第5.5.1节中,我们将静止迭代推导为一个涉及到乘以$A$和解$K$的过程。然而,在某些情况下,更简单的实现是可能的。考虑一下这样的情况:$A = K- N$ ,并且我们知道 $K$ 和 $N$ 。然后,我们将$Ax=b$写为
我们观察到,满足(5.13)的𝑥是迭代的一个固定点。
很容易看出,这是一个静止的迭代。
这就是方程(5.11)的基本形式。收敛准则$|\lambda (I-AK^{-1})|<1$(见上文)现在简化为$|\lambda (NK^{-1})|<1$。
让我们考虑一些特殊情况。首先,让$K=DA$,即包含$A$的对角线部分的矩阵:$k_i=a_i$和$k_{ij}=0$,对于所有$i\neq j$。同样地,$n_i =0$和 $n_{ij}=-a_{ij}$对于所有$i\neq j$。
这就是所谓的雅可比方法。迭代方案$Kx^{(n+1)} = Nx^{(n)} + b$ 现在变为
1 | for 𝑡 = 1, ... until convergence, do: |
(考虑到除法的成本相对较高,第1.2节,我们实际上会明确地存储$a^{-1}$的数量,并以乘法代替除法)。
这就要求我们为当前迭代$x^{(t)}$准备一个向量,为下一个向量$x^{(t+1)}$准备一个临时$u$。最简单的写法可能是。
1 | for 𝑡 = 1, ... until convergence, do: for 𝑖 = 1 ... 𝑛: |
对于一个简单的一维问题,如图5.6所示:在每个$x_i$点上,两个相邻点的值与当前值相结合,产生一个新值。由于所有$x_i$点的计算都是独立的,这可以在并行计算机上并行完成。
但是,你可能会想,在总和$\sum_{j\neq i} a_{ij}x_j$为什么不使用已经计算过的$x^{(t+1)}$的值? 就向量$x^(t)$而言,这意味着

1 | for 𝑘 = 1, ... until convergence, do: |
令人惊讶的是,该方法的实现比雅可比方法更简单。
1 | for 𝑡 = 1, ... until convergence, do: |
如果你把这写成一个矩阵方程,你会发现新计算的元素$x^(t+1)$与$D_A+L_A$的元素相乘,而旧的元素$x_j$被$U_A$所取代,得到
这被称为Gauss-Seidel方法。

对于一维的情况,高斯-塞德尔方法如图5.7所示;每一个$x_i$点仍然结合其邻居的值,但现在左边的值实际上是来自下一个外迭代。
最后,我们可以在Gauss-Seidel方案中插入一个阻尼参数,从而得到Successive Over- Relaxation(SOR)方法。
1 | for 𝑡 = 1, ... until convergence, do: |
令人惊讶的是,对于看起来像插值的东西,该方法实际上在$\omega\in (0,2)$的范围内对$\omega $起作用,最佳值大于1[96]。计算最佳的$\omega$并不简单。
该方法的收敛性
我们对两个问题感兴趣:首先,迭代方法是否完全收敛,如果是的话,速度如何。这些问题背后的理论远远超出了本书的范围。上面我们说过,对于$M$矩阵来说,收敛通常是可以保证的;至于收敛速度,通常只有在模型情况下才能进行全面分析。对于来自BVP的矩阵,如第4.2.3节所述,我们不需要证明,就说系数矩阵的最小特征值是$O(h^2)$。那么,上面得出的几何收敛比$|\lambda(I-AK^{-1})|$可以证明如下。
- 对于雅可比方法,该比率为$1 - O(h^2)$。
- 对于高斯-赛德尔迭代,它也是$1-O(h^2)$,但该方法的收敛速度是两倍。
- 对于SOR方法,最佳$\Omega$可以将收敛系数提高到$1 - O(h)$。
雅可比与高斯-塞德尔和并行性的对比
以上,我们主要是从数学的角度看雅可比、高斯-赛德尔和SOR方法。然而,这种考虑在很大程度上被现代计算机上的并行化问题所取代。
首先,我们观察到雅可比方法的一次迭代中的所有计算都是完全独立的,所以它们可以简单地被矢量化或并行完成。高斯-赛德尔法则不同(从现在开始我们忽略SOR,因为它与高斯-赛德尔法的区别仅在于阻尼参数):由于一次迭代的$x_i$点的计算现在是独立的,这种类型的迭代不是简单的矢量化或在并行计算机上实现。
在许多情况下,这两种方法被认为是被CG或广义最小残差(GMRES)方法所取代的(第5.5.11和5.5.13节)。雅可比方法有时被用作这些方法的预处理。高斯-赛德尔方法仍然很流行的一个地方是作为一个多网格平滑器。在这种情况下,经常通过使用变量的红黑排序来找到并行性。
关于这些问题的进一步讨论可以在第6.7节找到。
𝐾的选择
上面的收敛和误差分析表明,$K$越接近$A$,收敛就越快。在最初的例子中,我们已经看到$K$的对角线和下三角的选择。我们可以通过让$A = D_A + L_A + U_A$来正式描述这些,即把$A$分成对角线、下三角、上三角部分。下面是一些方法及其传统名称。
- 理查德森迭代法:$K = \alpha I$。
- 雅可比方法:$K = D_A$(对角线部分)。
- 高斯-塞德尔方法:$K=D_A+L_A$(下三角,包括对角线)
- SOR法:$K=\omega^{-1}D_A+L_{A}$
- 对称SOR(SSOR)法:$K =(D_A+L_A)D_A^{-1}(D_A+U_A)$。
- 在迭代细化中,我们让$K=LU$是$A$的真正因子化。在精确算术中,求解系统$LUx=y$可以得到精确解,所以在迭代方法中使用$K=LU$会在一步之后得到收敛。在实践中,舍入误差会使解不精确,所以人们有时会迭代几步以获得更高的精度。
练习 5.46 假设是密集系统,几步迭代细化的额外成本是多少?
练习 5.47 线性系统$Ax=b$的雅可比迭代定义为
其中𝐾是𝐴的对角线。证明你可以转换这个线性系统(也就是说,找到一个不同的系数矩阵和右手边的向量,仍然有相同的解),这样你就可以计算相同的𝑥𝑖向量,但是𝐾 = 𝐼,身份矩阵。
这种策略在存储和操作数方面有什么影响?如果𝐴是一个稀疏的矩阵,是否有特殊的影响?
假设𝐴是对称的。请举一个简单的例子,说明𝐾-1𝐴不一定是对称的。你能想出一个不同的系统变换,使系数矩阵的对称性得到保留,并具有与上述变换相同的优点吗?你可以假设该矩阵有正对角线元素。
练习 5.48 证明上一练习的变换也可以用于高斯-赛德尔方法。给出几个理由,为什么这不是一个好主意。
注释 20 静态迭代可以看作是不精确的牛顿方法的一种形式,每次迭代都使用相同的导数逆的近似值。标准的函数分析结果[120]说明了这种近似值可以偏离精确的逆值多远。
一个特殊的情况是迭代细化,牛顿方法应该在一个步骤内收敛,但实际上由于计算机运算中的舍入,需要多个步骤。只要函数(或残差)的计算足够精确,牛顿方法就会收敛,这一事实可以通过以较低的精度进行$LU$解来加以利用,从而获得更高的性能[1]。
选择预处理矩阵$K$有许多不同的方法。其中有一些是按常规定义的,比如下面讨论的不完全因式分解。其他的选择则是受到差分方程的启发。例如,如果算子是
那么矩阵$K$可由算子导出
对于一些选择的$\tilde{a},\tilde{b}$。第二组方程被称为可分离问题,并且有快速解算器,意思是它们具有$O(N\log N)$的时间复杂性;见[200]。
构建$K$的不完全$LU$因子化
我们简单提一下$K$的另一个选择,这是受高斯消除法的启发。和高斯消除法一样,我们让$K=LU$,但现在我们使用不完全$LU$($ILU$)分解法。记住,常规的$LU$因式分解是昂贵的,因为有填充现象。在不完全因式分解中,我们人为地限制了填入的情况。
如果我们把高斯消除法写成
1 | for k,i,j: |
我们通过以下方式定义一个不完整的变体
1 | for k,i,j: |
- 得到的因式分解不再是精确的:$LU\approx A$,所以它被称为不完全$LU(ILU)$因式分解。
- $ILU$因式分解比完全因式分解占用的空间要小得多:$L+U$的稀疏程度与$A$相同。
上述算法被称为 “ILU(0)”,其中的 “0 “指的是在不完全因式分解过程中绝对不允许填入。其他允许有限数量的填充的方案也存在。关于这个方法可以说得更多;我们只想说,对于$M$矩阵,这个方案通常会给出一个收敛的方法[154]。
练习 5.49 矩阵-向量乘积的运算次数与用ILU因式分解解系统的运算次数如何比较?
你已经看到,稀疏矩阵的完全因式分解可能需要更高的存储量(因式分解需要3/2,而矩阵需要𝑁),但是不完全因式分解需要𝑂(𝑁),就像矩阵一样。因此,我们可能会惊讶地发现,误差矩阵𝑅 = 𝐴 - 𝐿𝑈不是密集的,而是本身是稀疏的。
练习 5.50 设𝐴是泊松方程的矩阵,𝐿𝑈是不完全因式分解,𝑅 = 𝐴 - 𝐿𝑈 。证明𝑅是一个双对角矩阵。
考虑到𝑅是由那些在分解过程中被忽略的元素组成的。它们在矩阵中的位置是什么?
或者,写出乘积𝐿𝑈的稀疏性模式,并与𝐴的稀疏性模式进行比较。
构建预处理程序的成本
在热方程的例子中(第4.3节),你看到每个时间步骤都涉及到解决一个线性系统。作为一个重要的实际结果,解决线性系统的任何设置成本,如构建预处理程序,将在要解决的系统序列中摊销。类似的论点在非线性方程的背景下也是成立的,我们将不讨论这个问题。非线性方程是通过迭代过程(如牛顿方法)来解决的,它的多维形式导致了一连串的线性系统。尽管这些系统有不同的系数矩阵,但通过重复使用牛顿步骤的预处理程序,又可以摊销设置成本。
并行调节器
构建和使用一个预调节器是许多考虑因素的平衡行为:一个更准确的预调节器会导致在更少的迭代中收敛,但这些迭代可能更昂贵;此外,一个更准确的预调节器的构建成本可能更高。在并行情况下,这种情况甚至更加复杂,因为某些预处理程序一开始就不是非常并行的。因此,我们可能会接受一个并行的预处理程序,但它的迭代次数比串行预处理程序要少。更多的讨论请见第6.7节。
停止测试
我们需要解决的下一个问题是何时停止迭代。上面我们看到,误差以几何级数递减,所以很明显,我们永远不会精确地达到解决方案,即使这在计算机运算中是可能的。既然我们只有这种相对收敛的行为,那么我们怎么知道什么时候已经足够接近了呢?
我们希望误差$e_i = x - x_i$ 很小,但是测量这个误差是不可能的。上面我们观察到,$Ae_i = r_i$,所以
如果我们对$A$的特征值有所了解,这就给了我们一个误差的约束。($A$的准则是只有对称性$A$的最大特征值。一般来说,我们在这里需要奇异值)。另一种可能性是监测计算出的解决方案的变化。如果这些变化很小。
我们也可以得出结论,我们已经接近解决了。
练习 5.51 证明迭代数之间的距离和到真解的距离之间的分析关系。如果你的方程中含有常数,它们可以在理论上或实践中确定吗?
练习 5.52 编写一个简单的程序来试验线性系统的解法。从一维BVP中获取矩阵(使用有效的存储方案),并使用选择$K = D_A$的迭代方法编程。对残差和迭代间的距离进行停止测试的实验。迭代次数如何取决于矩阵的大小?
改变矩阵结构,使某一数量加入对角线,即在原矩阵中加入$\alpha I$。当$\alpha >0$时会发生什么?当$\alpha <0$时会发生什么?你能找到行为改变的数值吗?该值是否取决于矩阵的大小?
一般多项式迭代法的理论
上面,你看到了$x_{i+1}=x_i-K^{-1}r_i$ 的迭代方法,现在我们将看到更一般形式的迭代方法。
也就是说,使用所有以前的残差来更新迭代。有人可能会问,”为什么不引入一个额外的参数而写成$x_{i+1} = \alpha_i x_i + …?$”这里我们给出一个简短的论证,即前一种方案描述了一大类方法。事实上,目前作者并不知道有哪些方法不属于这个方案。
在给定近似解$\tilde{x}$的情况下,我们将残差定义为$ \tilde{r} = A\tilde{x} - b$。在这个一般性讨论中,我们将系统的预设条件定为$K^{-1}Ax=K^{-1}b$。(见第5.5.6节,我们讨论了线性系统的转换。) 初始猜测$x$的相应残差为
我们发现,
现在,Cayley-Hamilton定理指出,对于每一个$A$,都存在一个多项式$\phi (x)$(特征多项式),以便
我们观察到,我们可以把这个多项式$\phi $写为
其中$\pi $是另一个多项式。将此应用于$K^{-1}A$,我们有
所以$x=\tilde{x}+\pi (K^{-1}A)\tilde{r}$。现在,如果我们让$x_0=\tilde{x}$,那么$\tilde{r}=K^{-1}r_0$,得到的公式是
这个方程提出了一个迭代方案:如果我们能找到一系列度数为𝑖的多项式$\pi(i)$来近似$\pi$,它将给我们一串迭代的结果
最终达到真解。基于这种在迭代过程中对多项式的使用,这种方法被称为多项式迭代法。
练习 5.53 静止的迭代方法是多项式方法吗?你能与霍纳法则建立联系吗?
将方程(5.15)乘以$A$,两边减去$b$,得到
其中$\tilde{\pi}^{(i)}(x)=x\pi^{(i)}(x)$。这就立即得到了
其中$\hat{\pi}(i)$是一个度数为𝑖的多项式,$\hat{\pi}(i)(0)=1$。这个声明可以作为迭代方法收敛理论的基础。然而,这已经超出了本书的范围。
让我们看一下方程(5.16)的几个实例。对于$i = 1$,我们有
对于某些值$\alpha_i, \beta_i$。对于$i = 2$
对于不同的值$\alpha_i$。但我们已经确定$AK_{0}^{-1}$是$r_1, r_0$的组合,所以现在我们可以得出
而且很清楚如何归纳证明
将其代入(5.15),最后得到
很容易看出,方案(5.14)的形式是(5.18),反过来的含义也是成立的。综上所述,迭代方法的基础是一个方案,其中迭代数被迄今为止计算的所有残差所更新。
与静止迭代(第5.5.1节)相比,在静止迭代中,迭代数只从最后的残差中更新,而且系数保持不变。
我们可以对$\alpha_{ij}$系数说得更多。如果我们用方程(5.19)乘以$A$,再从两边减去$b$,我们会发现
让我们暂时考虑一下这个方程。如果我们有一个起始残差$r_0$,下一个残差的计算方法是
由此我们得到$AK^{-1}r_0=\alpha_{00}^{-1}(r_1-r_0)$,所以对于下一个残差。
我们看到,我们可以把$AK^{-1}r_1$表示为总和$r_2\beta_2 + r_1\beta_1 + r_0\beta_0$,并且$\sum_i \beta_i = 0$。推而广之,我们发现(与上述不同的$\alpha_{ij}$):
而我们有$\gamma_{i+1,i}=\sum_{j\leqslant i}\gamma_{ji}$。
我们可以把这最后一个方程写成$AK^{-1}R = RH$ 其中
其中,$H$是一个所谓的海森堡矩阵:它是上三角加一个下对角线。我们还注意到,$H$每一列中的元素之和为零。
由于同一性$\gamma_{i+1,i}=\sum_{j\leqslant i}\gamma_{ji}$,我们可以从$b$方程的两边减去$r_{i+1}$并 “除以$A$”,得到
这为我们提供了迭代方法的一般形式。
这种形式适用于许多迭代方法,包括你在上面看到的静止迭代方法。在接下来的章节中,你将看到𝛾𝑖𝑗系数是如何从残差的正交条件中得出的。
通过正交进行迭代
上面描述的静止方法(第5.5.1节)已经以某种形式存在了很长时间了。高斯在给一个学生的信中描述了一些变体。它们在1950年杨的论文[208]中得到完善;最后的参考资料可能是瓦尔加[195]的书。这些方法现在很少被使用,除了在多网格平滑器的专门背景下,这个主题在本课程中没有讨论。
几乎在同一时间,基于正交化的方法领域由两个人[136, 104]拉开了序幕,尽管他们花了几十年时间才找到广泛的适用性。(进一步的历史,见[81])。
其基本思想如下。
如果你能使所有的残差相互正交,并且矩阵的尺寸为$n$,那么经过$n$的迭代,你就已经收敛了:不可能有一个$n+1$的残差与之前所有的残差正交并且不为零。由于零残差意味着相应的迭代就是解,所以我们得出结论,经过$n$的迭代,我们已经掌握了真正的解。
随着当代应用所产生的矩阵的大小,这种推理已经不再适用:在计算上,迭代𝑛次是不现实的。此外,四舍五入可能会破坏解决方案的任何准确性。然而,后来人们意识到[175],在对称正定(SPD)矩阵的情况下,这种方法是一种现实的选择。当时的推理是。
残差序列跨越了一系列维度增加的子空间,通过正交,新的残差被投射到这些空间上。这意味着它们的尺寸会越来越小。
这在图5.8中有所说明。在本节中,你将看到正交迭代的基本思想。这里介绍的方法只具有理论意义;接下来你将看到共轭梯度(CG)和广义最小残差(GMRES)方法,它们是许多现实生活应用的基础。
现在让我们采取基本方案(5.21)并对残差进行正交。我们使用$K^{-1}$内积来代替正常内积。
并且我们将强制残差为$K^{-1}$-正交。
这被称为全正交法(FOM)方案。
1 | Let 𝑟0 be given |
你可能认识到其中的Gram-Schmidt正交化(见附录13.2的解释):在每次迭代中,$r_{i+1}$最初被设置为$AK^{-1}r_i$,并对$r_j$进行正交,$j\leqslant i$。
我们可以使用修改后的Gram-Schmidt,将算法改写为。
1 | Let 𝑟0 be given For 𝑖 ≥ 0: |
这两个版本的FOM算法在精确算术中是等价的,但在实际情况中却有两个不同。
状况下有两个不同之处。
- 修改后的Gram-Schmidt方法在数值上更加稳定。
- 未修改的方法允许你同时计算所有内积。我们在下面的6.6节中讨论
我们将在下文第6.6节讨论这个问题。即使FOM算法在实践中没有被使用,这些计算上的考虑也会延续到下面的GMRES方法中。
迭代方法的耦合递归形式
上面,你看到了生成迭代和搜索方向的一般方程(5.21)。这个方程通常被分割为
$x_i$迭代的更新,来自单一搜索方向。
且
从目前已知的残差中构建搜索方向。
不难看出,我们也可以通过归纳法来定义
而这最后一种形式是在实践中使用的一种。
迭代依赖系数的选择通常是为了让残差满足各种正交性条件。例如,可以选择让方法通过让残差正交来定义$(r_i^tr_j=0\text{ if } i \neq j)$,或者$A$正交$(r_i^tAr_j=0 \text{ if } i\neq j )$ 这种方法的收敛速度比静止迭代快得多,或者对更多的矩阵和预处理程序类型都能收敛。 下面我们将看到两种这样的方法;然而,它们的分析超出了本课程的范围。
共轭梯度的方法
在本节中,我们将推导出共轭梯度(CG)方法,它是FOM算法的一个具体实现。特别是,在SPD矩阵𝐴的情况下,它具有令人愉快的计算特性。CG方法的基本形式是上述的耦合递归公式,系数的定义是要求残差序列$r_0, r_1, r_2, …$满足
我们首先推导出非对称系统的CG方法,然后说明它在对称情况下是如何简化的。(这里的方法取自[60])。基本方程是
其中第一个和第三个方程在上面已经介绍过了,第二个方程可以通过第一个方程乘以𝐴找到(检查一下!)。
现在我们将通过归纳法推导出这个方法中的系数。实质上,我们假设我们有当前的残差$r_{cur}$,一个待计算的残差$r_{new}$,和一个已知的残差$R_{old}$的集合。我们不使用下标 “old, cur, new”,而使用以下惯例。
$x_1, r_1, p_1$是当前迭代数、残差和搜索方向。请注意,这里的下标1并不表示迭代数。
$x_2, r_2, p_2$是我们将要计算的迭代数、残差和搜索方向。同样,下标不等于迭代数。
$X_0, R_0, P_0$是所有以前的迭代、残差和搜索方向捆绑在一起的一个向量块。
就这些数量而言,更新方程为
其中$\delta_1,v_{12}$是标量,$u_{02}$是一个向量,长度为当前迭代前的次数。现在我们从残差的正交性推导出$\delta_1,v_{12},u_{02}$。具体来说,残差在$K^{-1}$内积下必须是正交的:我们希望有
结合这些关系,我们可以得到,比如说。
或缩写为$RJ=APD$,$P(I-U)=R$其中$J$是具有同一对角线和减去同一对角线的矩阵。然后我们观察到
$R^tK^{-1}R$是对角线,表达了残差的正交性。
结合$R{-1}R$是对角线和$P(I-U)=R$,可以得出$R^tP=R^tK^{-1}R(I-U)^{-1}$。我们 现在我们可以推断,$(I-U)^{-1}$是上对角线,所以$R^tP$是上三角形。这告诉我们 诸如$r_2^t p_1$等量是零。
结合$R$和$P$的关系,我们首先得到的是
这告诉我们,$R^t K^{-t}AP$ 是下对角线。在此方程中展开$R$,可以得到
这里$D$和$R^tK^{-1}R$是对角线,$(I-U)^{-t}$和$J$是下三角形,所以$P^tAP$是下三角形。
这告诉我们,$P_0^t Ap_2 = 0$,$p_1^tAp_2 = 0$。
将𝑃0𝑡 𝐴, 𝑝1𝑡 𝐴与方程(5.23)中的𝑝2定义相乘,得到
如果$A$是对称的,$P^tAP$是下三角(见上文)和对称的,所以它实际上是对角的。另外,$R^tK^-{t}AP$是下对角线,所以,利用$A=A^t$,$P^{t}AK^{-1}R$是上对角线。由于$P^tAK^{-1}R=P^tAP(I-U)$,我们得出结论:$I-U$是上二角的,所以,只有在对称情况下,$u_{02}=0$。
关于这个推导的一些看法。
- 严格地说,我们在这里只证明了必要的关系。可以证明,这些也是充分的。
有一些不同的公式可以计算出相同的向量,在精确的算术中。例如,很容易推导出$p_1^t r_1 = r_1^t r_1$,所以可以将其代入刚才的公式中。图5.9给出了CG方法的典型实现方式。
在第3次迭代中,计算$P_0^tAr_2$(需要用于$u_{02}$)需要用到𝑘内积。首先,内积在并行情况下是很不利的。其次,这要求我们无限期地存储所有搜索方向。这第二点意味着工作和存储都随着迭代次数的增加而上升。与此相反,在静止迭代方案中,存储仅限于矩阵和几个向量,而每次迭代的工作量是一样的。
- 刚才提出的反对意见在对称情况下消失了。由于$u_{02}$为零,对$P_0$的依赖消失了,只剩下对$p_1$的依赖。因此,存储是恒定的,每次迭代的工作量也是恒定的。可以证明每次迭代的内积数只有两个。
练习 5.54 对CG方法的一次迭代中的各种操作做一个翻转计数。假设𝐴是一个五点模版的矩阵,预处理器𝑀是𝐴的不完全因式分解(5.5.6.1节)。让𝑁为矩阵大小。
从最小化推导出
上述CG方法的推导在文献中并不常见。典型的推导是从一个具有对称正定(SPD)矩阵$A$的最小化问题开始。
如果我们接受函数𝑓有一个最小值的事实,这是由正定性得出的,我们通过计算导数找到最小值
然后问:f ‘(𝑥) = 0在哪?
练习 5.55 推导上面的导数公式。(提示:将导数的定义写成$\lim_{h\downarrow 0} …$)注意,这要求$A$是对称的。

对于迭代方法的推导,我们指出,迭代的𝑥以一定的步长$\delta_i$更新。沿着一个搜索方向$p_i$更新。
最佳步长
然后推导出沿着$x_i+ \delta\delta p_i$ 的函数$f$的最小化。
从残差中构建搜索方向是通过归纳证明的,即要求残差是正交的。一个典型的证明,见[5]。
GMRES
在上面关于CG方法的讨论中,指出残差的正交性需要存储所有的残差,以及第$k$次迭代中的𝑘内部积。不幸的是,可以证明CG方法的工作节省,就所有的实际情况而言,在SPD矩阵之外无法找到[62]。
GMRES方法是这种完全正交化方案的一个流行实现。为了将计算成本控制在一定范围内,它通常被实现为一种重启的方法。也就是说,只保留一定数量(比如$k=$5或20)的残差,每迭代$k$次,方法就会重新启动。
还有一些方法没有GMRES那样不断增长的存储需求,例如QMR [69] 和 BiCGstab [194]。尽管根据上面的评论,这些方法不能对残差进行正交,但在实践中仍然具有吸引力。
复杂性
高斯消除法的效率相当容易评估:一个系统的因式分解和求解,确定性地需要$\frac{1}{3}n^3$的操作。对于一个迭代方法来说,运算次数是每个迭代的运算次数与迭代次数的乘积。虽然每个单独的迭代都很容易分析,但没有好的理论来预测迭代次数。(事实上,一个迭代方法甚至可能一开始就不收敛。)此外,高斯消除法的编码方式可以有相当多的缓存重用,使算法在计算机峰值速度的相当大比例下运行。另一方面,迭代方法在每秒钟的运算量上要慢得多。
所有这些考虑使得迭代方法在线性系统求解中的应用介于工艺和黑色艺术之间。在实践中,人们做了相当多的实验来决定迭代方法是否会有回报,如果有的话,哪种方法更可取。
特征值法
在本章中,我们到目前为止只限于线性系统的求解。特征值问题是线性代数应用的另一个重要类别,但它们的兴趣更多地在于数学而不是计算本身。我们对所涉及的计算类型做一个简要的概述。
幂法
幂法(power method)是一个简单的迭代过程:给定一个矩阵𝐴和一个任意的起始矢量𝑣,反复计算
向量 “$v$ “很快就成为与绝对值最大的特征值相对应的特征向量大小,因此$|Av|/|v|$成为该最大特征值的近似值。
对$A^{-1}$的应用被称为反迭代(inverse iteration),它可以得到绝对值最小的特征值的反值。
功率法的另一个变种是移位逆向迭代,它可以用来寻找内部特征值。如果$\sigma$接近一个内部特征值,那么对$A - \sigma I$的反迭代将找到该内部特征值。
正交迭代法
不同特征值的特征向量是正交的,这一事实可以被利用。例如,在找到一个特征向量后,可以在与之正交的子空间中进行迭代。另一个选择是在一个向量块上进行迭代,并在每次幂法迭代后对这个块进行正交。这将产生与区块大小一样多的显性特征值。重新启动的Arnoldi方法[141]是这种方案的一个例子。
全光谱法
刚才讨论的迭代方案只产生局部的特征值。其他方法是计算矩阵的全谱。其中最流行的是QR方法。
并行执行
基于Lanczos的方案比QR方法更容易并行化;讨论见[13]。
延伸阅读
迭代方法是一个非常深入的领域。作为对所涉及问题的实际介绍,你可以阅读 “模板书”[9],在http://netlib.org/templates/。对于更深入的理论处理,请看Saad的书[176],其第一版可以在http://www-users.cs.umn. edu/~saad/books.html下载。
高性能线性代数(一)
在本节中,我们将讨论与并行计算机上的线性代数有关的一些问题。假设处理器的数量是有限的,而且相对于处理器的数量,问题数据总是很大。我们将关注处理器之间通信网络的物理方面问题。
我们将分析各种线性代数操作,包括迭代方法,以及它们在具有有限带宽和有限连接的网络中的行为。本章最后将对由于并行执行而产生的算法中的复杂问题进行各种简短的评论。
集合
集合运算在线性代数运算中起着重要的作用。事实上,操作的可扩展性可以取决于这些集合运算的成本,你将在下面看到。在此,我们对其基本思想做一个简短的讨论;详情请见[28]。
在计算集体操作的成本时,三个架构常数足以给出下限。$\alpha$,发送单个消息的时间;$\beta$,发送数据的时间的倒数(见1.3.2节);以及$\gamma$,执行算术运算的时间的倒数。因此,发送$n$数据项需要时间$\alpha+\beta n $。我们进一步假设,一个处理器一次只能发送一条信息。我们对处理器的连接性不做任何假设;因此,这里得出的下限将适用于广泛的架构。
上述架构模型的主要含义是,在算法的每一步中,活动处理器的数量只能增加一倍。例如,要做一个广播,首先处理器0向1发送,然后0和1可以向2和3发送,然后0-3向4-7发送,等等。这种信息的级联被称为处理器网络的最小生成树(minimum spanning tree),由此可见,任何集体算法都有至少$\alpha \log_2p$与累计延迟有关的成本。
广播
向𝑝处理器广播至少需要$\lceil \log_2p\rceil$步,总延迟为$\lceil \log_2p\rceil \alpha$。由于要发送$n$元素,这至少会增加所有元素离开发送处理器的时间$n\beta $,所以总成本下限为
我们可以用下面的方法来说明生成树的方法。
(在$t=1$时,$p_0$发送至$p_1$;在$t=2$时,$p_0,p_1$发送至$p_2,p_3$) 这个算法的$\log_2 \alpha$项正确,但是处理器0重复发送整个向量。所以带宽成本为$\log_2⋅n\beta $。如果$n$较小,则延迟成本占主导地位,因此我们可以将其描述为一个短向量集合操作(short vector collective operation)。下面的算法将广播实现为散点算法和桶状旅算法的结合。首先是散射:
需要$p-1$条大小为$N/p$的信息,总时间为
然后,桶队算法(bucket brigade algorithm)让每个处理器在每一步都处于活动状态,接受部分信息(除了第一步),并将其传递给下一个处理器。
每个部分信息被发送$p - 1$次,所以这个阶段的复杂度也是
现在的复杂度变成了
在延迟方面并不理想,但如果$n$较大,则是一种较好的算法,使之成为一种长向量集合操作(long vector collective operation)。
规约
在规约操作中,每个处理器都有$n$数据元素,一个处理器需要将它们进行元素组合,例如计算$n$的和或积。
通过在时间上向后运行广播,我们看到规约操作的通信下限同样为$\lceil \log_2p\rceil \alpha+n\beta $。缩减操作也涉及到计算,按顺序计算总时间为$(p-1)\gamma n$中的每个项目都在$p$处理器上被缩减。由于这些操作有可能被并行化,因此计算的下限$\frac{(p-1)}{p}\gamma n$,总共有
我们举例说明生成树算法,使用符号$x^{(j)}_i$表示最初在处理器$j$上的数据项$i$,而$x_i$表示处理器$j…k$的项目之和。
在时间$t = 1$时,处理器$p_0$、$p_2$从$p_1$、$p_3$接收,在时间$t= 2$时,$p_0$从$p_2$接收。和上面的广播一样,这个算法没有达到下限;相反,它的复杂度为
对于短向量,$\alpha$项占主导地位,所以这个算法就足够了。对于长向量,可以如上所述,使用其他算法[28]。
长向量的减少可以用一个桶状旅,然后用一个聚集来完成。复杂度同上,只是桶队执行部分规约,时间为$\gamma (p-1)N/p$。聚会不进行任何进一步的操作。
Allreduce
Allreduce操作在每个处理器上对𝑛元素进行同样的元素规约计算,但是将结果留在每个处理器上,而不是仅仅留在生成树的根部。这可以实现为先规约后广播的方式,但是存在更聪明的算法。
值得注意的是,Allreduce的成本下限与简单规约的成本下限几乎相同:因为在规约过程中,并不是所有的处理器都在同一时间活动,我们假设额外的工作可以被完美地分散。这意味着,延迟和计算量的下限保持不变。对于带宽,我们的理由如下:为了使通信完全并行化,$\frac{p-1}{p}n$项目必须到达和离开每个处理器。因此,我们有一个总时间为
Allgather
在对𝑛元素的聚集操作中,每个处理器都有$n/p$元素,一个处理器将它们全部收集起来,而不像规约操作那样将它们合并。Allgather计算的是同样的集合,但将结果留在所有处理器上。
我们再次假设有多个目标的集合是同时活动的。由于每个处理器都会生成一个最小生成树,因此我们有$\log_2p \alpha$延迟;由于每个处理器从$p-1$个处理器接收$n/p$元素,因此有$(p-1)\times (n/p)\beta$带宽成本。那么,通过allgather构建一个长度为$n$的向量的总成本是
我们对此进行说明。
在时间$t = 1$时,邻居$p_0$,$p_1$和同样的𝑝2,𝑝3之间有一个交换;在$t = 2$时,$p_0$,$p_2$和同样的$p_1,p_3$之间有两个距离的交换。
Reduce-scatter
在reduce-scatter操作中,每个处理器都有$n$元素,并对它们进行$n$方式的规约。与reduce或allreduce不同的是,结果会被分解,并像散点操作那样进行分配。
形式上,处理器𝑖有一个项目$x^{(i)}$,它需要$\sum_jx_i^{(j)}$。我们可以通过做大小$p$的缩减来实现,在一个处理器上收集向量$(\sum_ix_0^{(i)}, \sum_ix_1^{(i)},…)$,并将结果散布出去。然而,有可能在所谓的双向交换算法中结合这些操作。
reduce-scatter可以被认为是一个反向的allgather运行,加上算术,所以成本是
并行密集型矩阵-向量乘积
在本节中,我们将详细讨论并行密集矩阵-向量乘积的性能尤其是可扩展性。首先,我们将考虑一个简单的案例,并在一定程度上详细讨论并行性方面。
实现块状行的情况
在设计一个算法的并行版本时,人们常常通过对相关对象进行数据分解来进行。在矩阵-向量运算的情况下,例如乘积$y=Ax$,我们可以选择从向量分解开始,并探索其对如何分解矩阵的影响,或者从矩阵开始,并从它推导出向量分解。在这种情况下,似乎很自然地从分解矩阵开始,而不是从分解矢量开始,因为它很可能具有更大的计算意义。我们现在有两个选择。
我们对矩阵进行一维分解,将其分割成块状行或块状列,并将其中的每一个—或每一组—分配给一个处理器。
或者,我们可以进行二维分解,将一个或多个一般子矩阵分配给每个处理器。
我们首先考虑以块行的方式进行分解。考虑一个处理器$p$和它所拥有的行的索引集合$I_p$,并让$i \in I_p$是分配给这个处理器的行。行中的元素$i$被用于操作
我们现在推理:
如果处理器$p$拥有所有$x_j$的值,那么矩阵-向量乘积就可以简单地执行,完成后,处理器拥有正确的值$y_j\in I_p$。
这意味着每个处理器都需要有一个$x$的副本,这是很浪费的。同时,这也提出了数据完整性的问题:你需要确保每个处理器都有正确的$x$的值。
在某些实际应用中(例如你之前看到的迭代方法),矩阵-向量乘积的输出直接或间接地成为下一个矩阵-向量操作的输入。对于计算$x、Ax、A^2x、….$ 的功率法来说,情况当然是这样的。由于我们的操作开始时每个处理器拥有整个$x$,但结束时它只拥有$Ax$的局部部分,所以我们有一个不匹配。
- 也许我们应该假设每个处理器在操作开始时只拥有$x$的局部部分,也就是那些$i \in I_p$的$x$,这样,算法的开始状态和结束状态是一样的。这意味着我们必须改变算法,包括一些通信,使每个处理器能够获得那些$x_i \notin I_p$的值。

练习 6.1 对矩阵被分解成块列的情况进行类似的推理。像上面一样,详细描述并行算法,但不要给出伪代码。
现在让我们来看看通信的细节:我们将考虑一个固定的处理器$p$,并考虑它执行的操作和需要的通信。根据上述分析,在执行语句$y_i = \sum_j a_{ij}x_j$时,我们必须知道$j$值属于哪个处理器。为了确认这一点,我们写道
如果$j \in I_p$,指令$y_i \leftarrow y_i + a_{ij}x_j$只涉及已经属于处理器的量。因此,让我们集中讨论$j\notin I_p$的情况。 如果我们可以直接写出这样的语句就好了
1 | y(i) = y(i) + a(i,j)*x(j) |
而一些下层将自动把$x^{(j)}$从它所存储的任何处理器转移到本地寄存器。(2.6.5节的PGAS语言旨在做到这一点,但它们的效率远不能保证)。图6.1给出了一个基于这种乐观的并行性观点的实现。
这种 “局部 “方法的直接问题是会有太多的通信发生。
- 如果矩阵$A$是密集的,那么每一行$i \in I_p$都需要一次元素$x_j$,因此每一行$i \in I_p$都将被取走一次。
- 对于每个处理器$q\neq p$,将有(很大)数量的元素$x_j \in I_q$ 需要从处理器$q$转移到$p$。 在不同的信息中做这些,而不是一次批量传输,是非常浪费的。


对于共享内存来说,这些问题并不是什么大问题,但在分布式内存的背景下,最好采取缓冲的方式。
我们不需要交流𝑥的各个元素,而是为每个处理器$B_{pq}\neq p$使用一个本地缓冲区,我们从$q$收集需要在$p$上执行乘法的元素。 (见图6.2的说明。)图6.3给出了并行算法。 除了防止一个元素被取走超过一次之外,这也将许多小的消息合并成一个大的消息,这通常更有效率;回顾我们在2.7.8节中对带宽和延迟的讨论。
练习 6.2 给出使用非阻塞操作的矩阵-向量乘积的伪码(第2.6.3.6节) 上面我们说过,在每个处理器上都有一份整个𝑥的副本,这是对空间的浪费。
这里隐含的论点是,一般来说,我们不希望本地存储是处理器数量的函数:理想情况下,它应该只是本地数据的函数。 (这与弱缩放有关;第2.2.5节。) 你看,由于通信方面的考虑,我们实际上已经决定,每个处理器存储整个输入向量是不可避免的,或者至少是最好的。 这种空间和时间效率之间的权衡在并行编程中相当普遍。 对于密集的矩阵-向量乘积,我们实际上可以为这种开销辩护,因为向量存储的顺序比矩阵存储的顺序要低,所以我们的过度分配比例很小。 下面(第6.5节),我们将看到,对于稀疏矩阵-向量乘积,开销会小很多。
我们很容易看到,如果允许我们忽略通信时间,那么上面描述的并行密集矩阵-向量乘积就有完美的加速。 在接下来的几节中,你会发现如果我们考虑到通信,上面的块行实现并不是最佳的。 对于可扩展性,我们需要一个二维分解。 我们先来讨论一下集合体。
密集矩阵-向量乘积的可扩展性
在本节中,我们将对$y \leftarrow Ax$的并行计算进行全面分析,其中$x,y \in \mathbb{R}^n$和$A\in \mathbb{R}^{n \times n}$。我们将假设使用$p$节点,但我们对它们的连接性不做任何假设。我们将看到,矩阵的分布方式对算法的缩放有很大的影响;原始研究见[101, 180, 188],各种缩放形式的定义见2.2.5节。
矩阵-向量乘积,按行划分
划分
其中,$A_i\in \mathbb{R}^{m_i\times n}$且$x_i,y_i\in \mathbb{R}^{m_i}$,$\sum_{i=0}^{p-1}m_i=n$和$m_i\approx n/p$。我们将首先假设$A_i, x_i y_i$和最初被分配的$P_i$。
计算的特点是,每个处理器需要整个向量$x$,但只拥有其中的$n/p$部分。因此,我们对$x$进行了一次全集。之后,处理器可以执行本地产品$y_i \leftarrow A_ix$;此后不需要进一步的通信。
那么,一个对$y = Ax$进行成本计算的算法就可以通过以下方式得到
成本分析:算法的总成本约为。
由于顺序成本为$T_1(n)=2n^2\gamma $,所以速度提升为
和并行效率,由
乐观的观点:现在,如果我们固定$p$,并让$n$变得很大
因此,如果能使问题足够大,最终的并行效率几乎是完美的。然而,这是以无限内存为前提的,所以这种分析并不实用。
悲观的观点:在强可扩展性分析中,我们固定$n$,让$p$变大,以得到
因此,最终并行效率变得几乎不存在了。
现实主义者的观点 在一个更现实的观点中,我们随着数据量的增加而增加处理器的数量。这被称为弱可扩展性,它使可用于存储问题的内存量与$p$成线性比例。
让$M$等于可以存储在单个节点的内存中的浮点数。那么总内存由$Mp$给出。让$n_{max}(p)$等于在$p$节点的总内存中可以存储的最大问题大小。那么,如果所有内存都可以用于矩阵。
现在的问题是,对于可以存储在$p$节点上的最大问题,其并行效率如何。
现在,如果分析一下当节点数量变得很大时发生了什么,就会发现
因此,这种矩阵-向量乘法的并行算法并没有规模。
如果你仔细看一下这个效率表达式,你会发现主要问题是表达式中的$1/\sqrt{p}$部分。这个条款涉及到一个系数$\beta$,如果你跟着推导往后看,你会发现它来自处理器之间发送数据的时间。非正式地说,这可以被描述为消息大小太大,使问题可扩展。事实上,无论处理器的数量如何,消息大小都是恒定的$𝑛$。
另外,一个现实主义者意识到,完成一个计算的时间是有限的,$T_{max}$。在最好的情况下,即通信开销为零的情况下,我们能在$T_{max}$时间内解决的最大问题为
因此
那么,对于可以在$T_max$时间内解决的最大问题,该算法所达到的并行效率为
而当节点数变多时,其并行效率接近
同样,随着处理器数量的增加和执行时间的上限,效率也无法维持。
我们也可以计算出这个操作的等效率曲线,即$n$,$p$之间的关系,对于这个关系,效率保持不变(见 2.2.5.1 节)。如果我们将上述效率简化为 $E(n,p)=\frac{2\gamma}{\beta} \frac{n}{p}$,则$E\equiv c$相当于$n=O(p)$,因此
因此,为了保持效率,我们需要相当快地增加每个处理器的内存。这是有道理的,因为这淡化了通信的重要性。
矩阵-向量乘积,按列划分
划分
其中 $A_{j} \in \mathbb{R}^{n \times n_{j}}$, $x_{j}, y_{j} \in \mathbb{R}^{n_{j}}$ 在$\sum_{j=0}^{p-1} n_{j}=n$,$ n_{j} \approx n / p$.
我们将首先假设$A_j$、$x_j$和$y_j$最初被分配给$P_j$(但现在$A_i$是一个列块)。在这种按列计算的算法中,处理器𝑖可以计算长度$n$向量$A_ix_i$,而不需要事先沟通。然后,这些部分结果必须被加在一起
每个处理器$i$将其结果的一部分$(A_ix_i)_j$分散到处理器$j$中。然后,接收的处理器进行规约,将所有这些片段相加。
然后,有成本的算法由以下方式给出。
成本分析 算法的总成本约为。
请注意,这与成本𝑇 1D-row(𝑛)是相同的,只是将𝛽替换为(𝛽 + 𝛾)。不难看出关于可扩展性的结论是相同的。
二维划分
下面,划分
其中,$A_{i j} \in \mathbb{R}^{n_{i} \times n_{j}}$ ,$x_{i}, y_{i} \in \mathbb{R}^{n_{i}}$,$\sum_{i=0}^{p-1} n_{i}=N$, $n_{i} \approx N / \sqrt{P}$ .
我们将以$r\times c$网格的形式来看待节点,其中$P=rc$,并以$p_{ij}$的形式来看待,其中$i=0, …, r-1$和$j=0, … , c- 1$. 图6.4,对于3×4处理器网格上的12×12矩阵,说明了数据对节点的分配,其中$i, j$ “单元 “显示了$p_{ij}$拥有的矩阵和向量元素。
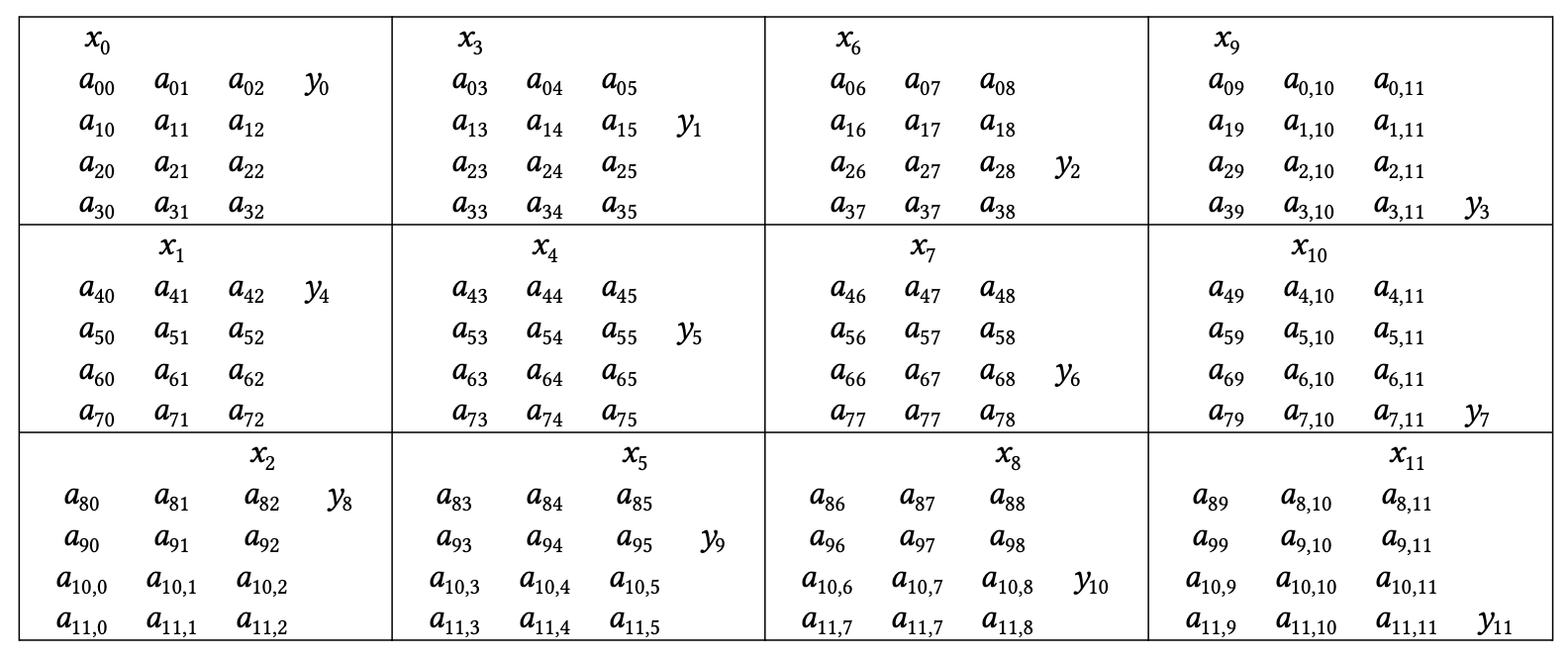
换句话说,$p_{ij}$拥有矩阵块$A_j$以及$x$和$y$的一部分。这使得以下算法成为可能
算法:
由于$x_j$分布在第𝑗列,该算法首先在每个处理器$p_{ij}$上通过处理器列内的allgather收集$x_j$。
每个处理器$p_{ij}$然后计算$y_{ij}=A_{ij}x_j$ 。这不涉及进一步的沟通。
然后,通过将每个处理器行中的碎片$y_i$收集起来,形成$y_i$,然后将其分布在处理器行中,从而得到结果$y_i$。这两个操作实际上是结合在一起的形成一个规约散射。
如果$r=c$,我们可以在处理器上对$y$数据进行转置,这样它就可以作为后续矩阵向量乘法的输入随后的矩阵-向量乘积。另一方面,如果我们正在计算$AA^tx$,那么$y$现在可以正确地分配给$A^t$乘积。
算法 带有成本分析的算法是
成本分析 算法的总成本约为。
现在我们将进行简化,即$r=c=\sqrt{p}$,所以
由于顺序成本为$T_1(n)=2n^2\gamma$,所以速度提升为
和并行效率,由
我们再次提出一个问题,对于可以存储在$p$的最大问题,其并行效率是多少?节点的最大问题的并行效率是多少。
以至于
然而,$\log_2p$随$p$的增长非常缓慢,因此被认为很像一个常数。在这种情况下,$E_p^{\sqrt{p}\times \sqrt{p}}(n_{max}(p))$下降的速度非常慢,而且该算法被认为是可扩展的,以满足实际需要。
请注意,当$r=p$时,二维算法成为 “按行划分 “的算法,而当$c=p$时,则成为 “按列划分 “的算法。不难看出,只要$r/c$保持不变,当$r=c$时,2D算法在上述分析的意义上是可扩展的。
练习 6.3 计算这个操作的等效率曲线。
并行LU因子化
矩阵-向量和矩阵-乘积在某种意义上是很容易并行化的。输出的元素都可以独立地以任何顺序计算,所以我们在算法的并行化方面有很多自由度。这对于计算LU因子化或用因子化的矩阵求解线性系统来说并不成立。
解决一个三角形系统
三角系统$y=L^{-1}x$ (其中$L$为下三角)的解是一个矩阵-向量运算,因此它与矩阵-向量乘积有其𝑂(𝑁2)的共同复杂性。然而,与乘积运算不同的是,这个求解过程包含了输出元素之间的递推关系。
这意味着并行化并非易事。在稀疏矩阵的情况下,可能会有特殊的策略;见6.10节。在这里,我们将对一般的稠密情况做一些评论。
为了简单起见,我们假设通信不需要时间,而且所有的算术运算都需要相同的单位时间。首先,我们考虑按行分布的矩阵,也就是说,处理器$p$存储的元素$\ell_{p*}$。有了这个,我们可以把三角解法实现为:
- 处理器1解决了$t_1=\ell_{11}^{-1}x_1$,并将其值发送给下一个处理器。
- 一般来说,处理器$p$得到的值是$y_1,…,y_{p-1}$来自处理器$p-1$,并计算出$y_p$。
- 然后每个处理器$p$将$y_1,…,y_p$发送给$p + 1$。
练习 6.4 证明这个算法需要时间$2N^2$,就像顺序算法一样。
这个算法中,每个处理器以流水线的方式将所有计算过的𝑦𝑖值传递给它的后继者。然而,这意味着处理器$p$在最后一刻才收到$y_1$,而这个值在第一步已经被计算出来了。我们可以以这样的方式来制定解决算法,使计算的元素尽快被提供出来。
- 处理器1解决$y_1$,并将其发送给所有后来的处理器。
- 一般来说,处理器$p$会等待值为$y_q$的个别消息,因为$q<p$。
- 然后,处理器$p$计算$y_p$,并将其发送给处理器$q$,而$q > p$。
在通信时间可以忽略不计的假设下,这个算法可以快很多。对于在$p>1$的所有处理器都同时收到$y_1$,并能同时计算$\ell_{p1}y_1$。
练习 6.5 说明如果我们不考虑通信,这个算法变体需要的时间是$O(N)$。如果我们将通信纳入成本,那么成本是多少?
练习 6.6 现在考虑按列分布的矩阵:处理器$𝑝$p储存$\ell_{*p}$ 。概述这种分布下的三角解算法,并说明并行解的时间是$O(N)$。
因式分解,密集型情况
对并行密集$LU$分解的可扩展性的全面分析是相当复杂的,所以我们将声明,无需进一步证明,正如在矩阵-向量的情况下,需要一个二维分布。然而,我们可以发现一个进一步的复杂情况。由于任何类型的因式分解3都是通过矩阵进行的,处理器在部分时间内是不活动的。
练习 6.7 考虑有规律的右看高斯消除法
1 | for k=1..n |
分析运行时间、加速和效率与$N$的函数关系,如果我们假设有一个一维分布,并且有足够的处理器为每个处理器存储一列。表明提速是有限的。也对二维分解进行这种分析,每个处理器存储一个元素。
由于这个原因,使用了过度分解,矩阵被分成比处理器数量更多的块,每个处理器存储几个不相邻的子矩阵。我们在图6.5中说明了这一点,我们将一个矩阵的四个块列划分给两个处理器:每个处理器在一个连续的内存块中存储两个非连续的矩阵列。
接下来,我们在图6.6中说明,在不知道处理器存储了矩阵的非连续部分的情况下,可以对这样的矩阵进行矩阵-向量乘积。只需要输入的向量也是循环分布的。
练习6.8. 现在考虑一个4×4的矩阵和一个2×2的处理器网格。矩阵的行和列都是循环分布的。说明只要输入分布正确,如何使用连续的矩阵存储来进行矩阵-向量乘积。输出是如何分布的?说明比起一维例子的规约,需要更多的通信。
具体来说,在$P<N$处理器的情况下,为简单起见,假设$N=cP$,我们让处理器0存储行0,c,2c,3c,…;处理器1存储行1,c+1,2c+1,…等。这个方案可以概括为二维分布,如果$N=c_1P_1=c_2P_2$和$P=P_1P_2$。这被称为二维循环分布。这个方案可以进一步扩展,考虑块的行和列(块的大小较小),将块的行0,c,2c,….,分配给处理器0。
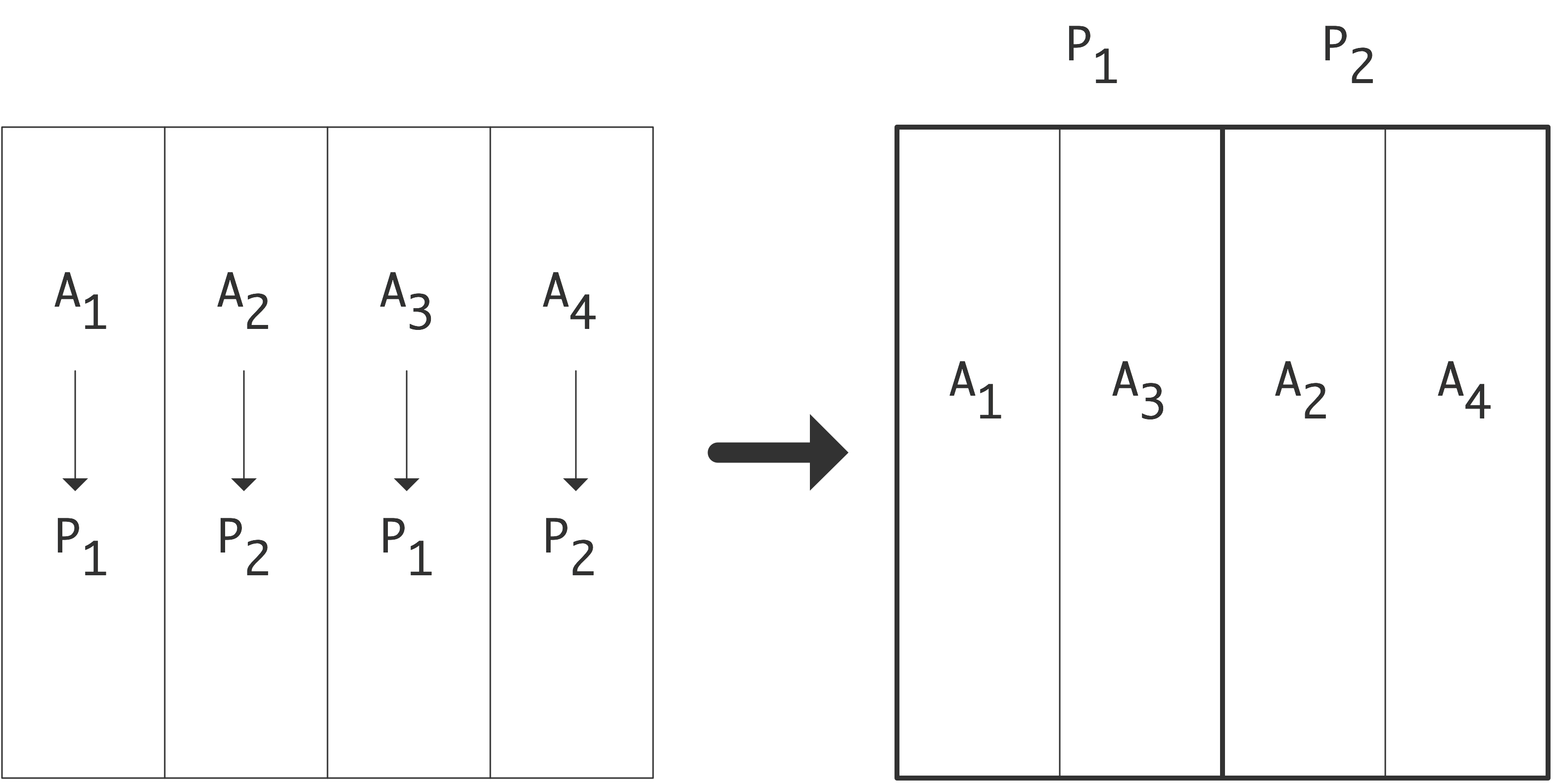
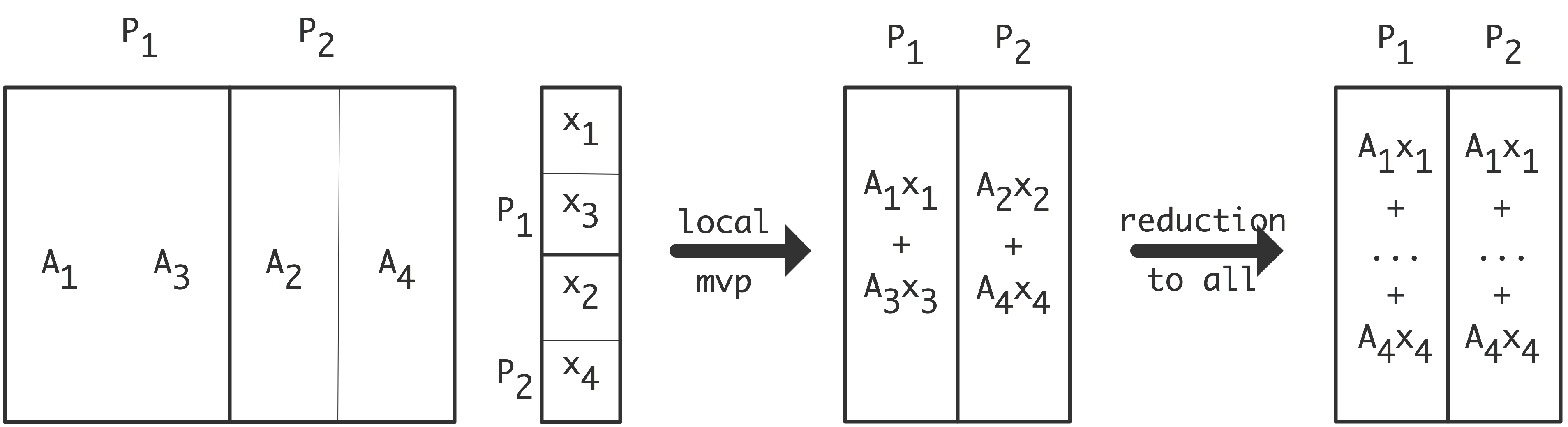
练习 6.9 考虑一个正方形$n\times n$矩阵,以及一个正方形$p\times p$处理器网格,其中$p$除以$n$无余。考虑上述的过度分解,并对$n=6$,$p=2$的特定情况下的矩阵元素分配做一个草图。也就是说,画一个$n\times n$表,其中位置$(i, j)$包含存储相应矩阵元素的处理器编号。同时,为每个处理器制作一个表格,描述局部到全局的映射,即给出局部矩阵中元素的全局$(i, j)$坐标。(你会发现使用零基编号可以方便地完成这项任务。现在写出$i,j$ 的函数$P,Q,I,J$,描述全局到局部的映射,即矩阵元素$a_{ij}$被存储在处理器$(P(i, j), Q(i, j))$的$(I(i,j),J(i,j))$位置上 。
因式分解,稀疏情况
稀疏矩阵$LU$因式分解是一个众所周知的难题。任何类型的因式分解都涉及到顺序部分,这使得它从一开始就不是简单的事情。为了了解稀疏情况下的问题,假设你按顺序处理矩阵的行。密集情况下,每行有足够多的元素,可以在那里衍生出并行性,但是在稀疏情况下,这个数字可能非常低。
解决这个问题的方法是认识到我们对因式分解本身不感兴趣,而是我们可以用它来解决一个线性系统。由于对矩阵进行置换可以得到相同的解,也许本身就是置换过的,所以我们可以探索具有更高平行度的置换。
矩阵排序的话题已经在第5.4.3.5节中出现了,其动机是填空式规约。我们将在下面考虑具有有利的并行性的排序:第6.8.1节中的嵌套剖析,以及第6.8.2节中的多色排序。
矩阵-矩阵乘积
矩阵三乘法$C\leftarrow A·B$(或$C\leftarrow A·B+\gamma C$,如基本线性代数子程序(BLAS)中使用的那样)有一个简单的并行结构。假设所有大小为$N\times N$的正方形矩阵
- $N^3$内积$a_{ik}b_{kj}$可以分别被独立计算,之后
- $N^2$个元素$c_{ij}$是通过独立的求和规约形成的,每个求和规约的时间为对数$\log_2N$。
然而,更有趣的是数据移动的问题。
- 在$N^3$个操作的$O(N^2)$元素上,有相当多的机会进行数据重用(第1.6.1节)。我们将在第6.4.1节探讨 “Goto算法”。
- 根据矩阵的遍历方式,TLB的重用也需要被考虑(第1.3.8.2节)。
- 矩阵-矩阵乘积的分布式内存版本尤其棘手。假设$A$、$B$、$C$都分布在一个处理器网格上,$A$的元素必须通过一个处理器行,而$B$的元素必须通过一个处理器列。我们在下面讨论 “坎农算法 “和外积法。
转到矩阵-矩阵乘积
在第1.6.1节中,我们认为矩阵的矩阵乘积(或BLAS术语中的dgemm)有大量可能的数据重用:在$O(n^3)$数据上有$O(n^2)$操作。现在我们将考虑一个实现,由于Kazushige Goto [85],它确实达到了接近峰值的性能。
矩阵-矩阵算法有三个循环,每个循环我们都可以屏蔽,从而得到一个六路的嵌套循环。由于输出元素上没有递归,所有产生的循环交换都是合法的。结合这个事实,循环阻塞引入了三个阻塞参数,你会发现潜在实现的数量是巨大的。这里我们介绍了支撑Goto实现的全局推理;详细讨论见所引用的论文。
我们首先将乘积$C\leftarrow A\cdot B$ (或者根据Blas标准,$C\leftarrow C+ A\cdot B$)写成一个低秩更新序列。
为4,通过积累。
1 | // compute C[i,*] : |
见图6.9。现在这个算法被调整了。
- 我们需要足够的寄存器来处理$C[i,]$、$A[i,k]$和$B[k,]$。在目前的处理器上,这意味着我们要积累四个$C$元素。
- $C$的这些元素被积累起来,所以它们停留在寄存器中,唯一的数据转移是对$A$和$B$元素的加载;没有存储!这就是为什么我们要把这些元素放在寄存器中。
- 元素$A[i,k]$和$B[k,*]$来自L1。
- 由于相同的$A$块被用于许多连续的$B$片断,我们希望它保持常驻;我们选择$A$的块大小,让它保持在二级缓存中。
- 为了防止TLB问题,$A$被按行存储。如果我们一开始就用(Fortran)列为主的方式存储矩阵,这意味着我们必须进行复制。由于复制的复杂程度较低,这个成本是可以摊销的。
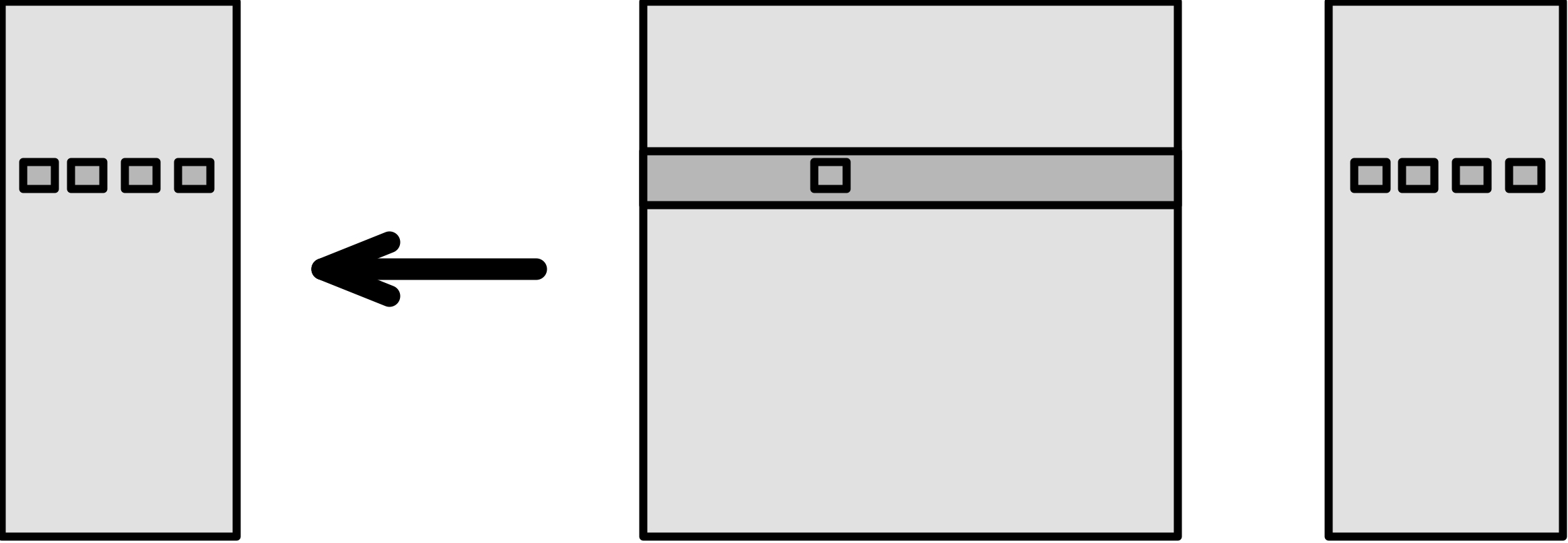
这种算法可以在专门的硬件中实现,如谷歌的TPU[84],具有很大的能源效率。
坎农的分布式内存矩阵-矩阵乘积算法
在第6.4.1节中,我们考虑了单处理器矩阵-矩阵乘法的高性能实现。现在我们将简要地考虑这一操作的分布式内存版本。(值得注意的是,这并不是基于第6.2节的矩阵-向量乘积算法的泛化)。
这种操作的一种算法被称为坎农算法。它是一个正方形的处理器网格,处理器$(i,j)$逐渐积累$(i,j)$块 $C_{i,j}=\sum_kA_{i,k}B_{k,j}$;见图6.10。
如果你从左上角开始,你会看到处理器(0,0)同时拥有$A_{00}$和$B_{00}$,所以它可以立即开始做一个局部乘法。处理器(0,1)有$A_{01}$和$B_{01}$,它们不需要在一起,但是如果我们把$B$的第二列向上旋转一个位置,处理器(0,1)将有$A_{01}$,$B_{11}$,这两个确实需要被乘以。同样地,我们将$B$的第三列向上旋转两个位置,这样(0,2)就有$A_{02}$,$B_{22}$。
这个故事在第二行是如何进行的呢?处理器(1,0)有$A_{10}$,$B_{10}$,它们不需要在一起。如果我们将第二行的$A$向左旋转一个位置,它就包含了$A_{11},B_{10}$,这些是部分内积所需要的。而现在处理器(1,1)有$A_{11},B_{11}$。
如果我们继续这个故事,我们从一个矩阵$A$开始,其中的行已经被向左旋转,而𝐵的列已经被向上旋转。在这个设置中,处理器$(i,j)$包含$A_{i,i+j}$和$B_{i+j,j}$,其中加法是按矩阵大小调制的。这意味着每个处理器都可以从做局部积开始。
现在我们观察到,$C_{ij}=\sum_k A_{ik}B_{kj}$意味着下一个局部积项来自于将𝑘增加1。$A$,$B$的相应元素可以通过旋转行和列的另一个位置移入处理器。

分布式矩阵-矩阵乘积的外积法
坎农的算法因需要一个正方形处理器网格的要求而受到影响。外积法更为普遍。它是基于矩阵-矩阵乘积计算的以下安排。
1 | for ( k ) |
也就是说,对于每个$k$,我们取$A$的一列和$B$的一行,并计算秩-1矩阵(或 “外积”)$A_{,k}\cdot B_{k,}$。然后我们对$k$求和。
看一下这个算法的结构,我们注意到在步骤$k$中,每一列$j$收到$A_{,k}$,每一行$i$收到$B_{,k}$。换句话说,$A_{,k}$的元素通过他们的行广播,而$B_{,k}$的元素则通过他们的行广播。
使用MPI库,这些同步广播是通过为每一行和每一列设置一个子通信器来实现的。
稀疏的矩阵-向量乘积
在通过迭代方法求解线性系统时(见第5.5节),矩阵-向量乘积在计算上是一个重要的内核,因为它在每次可能的数百次迭代中都要执行。在本节中,我们先看一下矩阵-向量乘积在单处理器上的性能;多处理器的情况将在第6.5节中得到关注。
单处理器的稀疏矩阵-向量乘积
在迭代方法的背景下,我们并不太担心密集矩阵-向量乘积的问题,因为人们通常不会对密集矩阵进行迭代。在我们处理块状矩阵的情况下,请参考第1.7.11节对密集积的分析。稀疏乘积就比较麻烦了,因为大部分的分析并不适用。
稀疏矩阵-向量乘积中的数据重用 按行执行的密集矩阵-向量乘积和CRS稀疏乘积(第5.4.1.4节)之间有一些相似之处。在这两种情况下,所有的矩阵元素都是按顺序使用的,所以任何加载的缓存线都被充分利用了。然而,CRS的乘积至少在以下方面要差一些。
- 间接寻址需要加载一个整数向量的元素。这意味着在相同数量的操作中,稀疏产品有更多的内存流量。
- 源向量的元素不是按顺序加载的,实际上它们可以按随机的顺序加载。这意味着包含源元素的缓存线可能不会被完全利用。另外,内存子系统的预取逻辑(1.3.5节)在这里也不能提供帮助。
由于这些原因,一个由稀疏矩阵-向量乘积主导计算的应用很可能以处理器峰值性能的$\approx$5%运行。
如果矩阵的结构在某种意义上是有规律的,那么就有可能提高这一性能。其中一种情况是,我们处理的是一个完全由小型密集块组成的块状矩阵。这至少会导致索引信息量的减少:如果矩阵由2×2块组成,我们会得到整数数据传输量的4倍减少。
练习 6.10 再给出两个理由,说明这个策略有可能提高性能。提示:缓存线,和重用。
这样的矩阵细分可能会带来2倍的性能提升。假设有这样的改进,即使矩阵不是一个完美的块状矩阵,我们也可以采用这种策略:如果每个2×2的块都包含一个零元素,我们仍然可以得到1.5倍的性能改进[197, 26]。
稀疏乘积中的矢量化 在其他情况下,带宽和重用并不是最主要的问题。
- 在旧的矢量计算机上,如旧的Craymachine,内存对处理器来说是足够快的,但矢量化是最重要的。这对稀疏矩阵来说是个问题,因为矩阵行中的零数,以及因此的矢量长度,通常都很低。
- 在GPU上,内存带宽相当高,但有必要找到大量相同的操作。矩阵可以被独立处理,但由于行可能是不等长的,这不是一个合适的并行性来源。
由于这些原因,稀疏矩阵的对角线存储方案的一个变种最近又出现了复兴。这里的观察是,如果你按行数对矩阵的行进行排序,你会得到少量的行块;每个行块都会相当大,而且每个行块中的元素数量都是一样的。
具有这种结构的矩阵对矢量架构来说是很好的[38]。在这种情况下,乘积是通过对角线计算的。
练习 6.11 写出这种情况的伪代码。行的排序是如何改善情况的?
这种排序的存储方案也解决了我们在GPU上注意到的问题[20]。在这种情况下,我们传统的CRS产品算法,我们的并行量等于一个块中的行数。
当然,还有一个复杂的问题,就是我们已经对矩阵进行了置换:输入和输出的向量也需要进行相应的置换。如果乘积操作是迭代方法的一部分,在每次迭代中来回进行这种置换可能会否定任何性能上的提高。相反,我们可以对整个线性系统进行置换,并对置换后的系统进行迭代。
练习 6.12 你能想出这样做的原因吗?为什么不可行呢?
并行稀疏矩阵-向量乘积
在第5.4节中,你看到了关于稀疏矩阵的第一次讨论,仅限于在单个处理器上使用。现在我们将讨论并行性问题。
密集矩阵-向量乘积,正如你在上面看到的,需要每个处理器与其他处理器通信,并有一个基本与全局向量大小相同的本地缓冲区。在稀疏的情况下,需要的缓冲区空间要少得多,通信也要少。让我们分析一下这种情况。我们将假设矩阵是按块行分布的,其中处理器$p$拥有索引在某个集合$I_p$的矩阵行。
行$y_i = y_i +a_{ij}x_j$现在必须考虑到,$a_{ij}$可以是零。特别是,我们需要考虑,对于某些对$i \in I_p$,$j\notin I_p$不需要通信。 为每个$i\in I_p$声明一个稀疏模式集
我们的乘法指令变为
如果我们想避免如上所述的小消息的泛滥,我们把所有的通信合并成每个处理器的一个消息。定义
现在的算法是:
- 将所有必要的非处理器元素$x_j\in S_p$收集到一个缓冲区。
- 执行矩阵-向量乘积,从本地存储中读取$x$的所有元素。
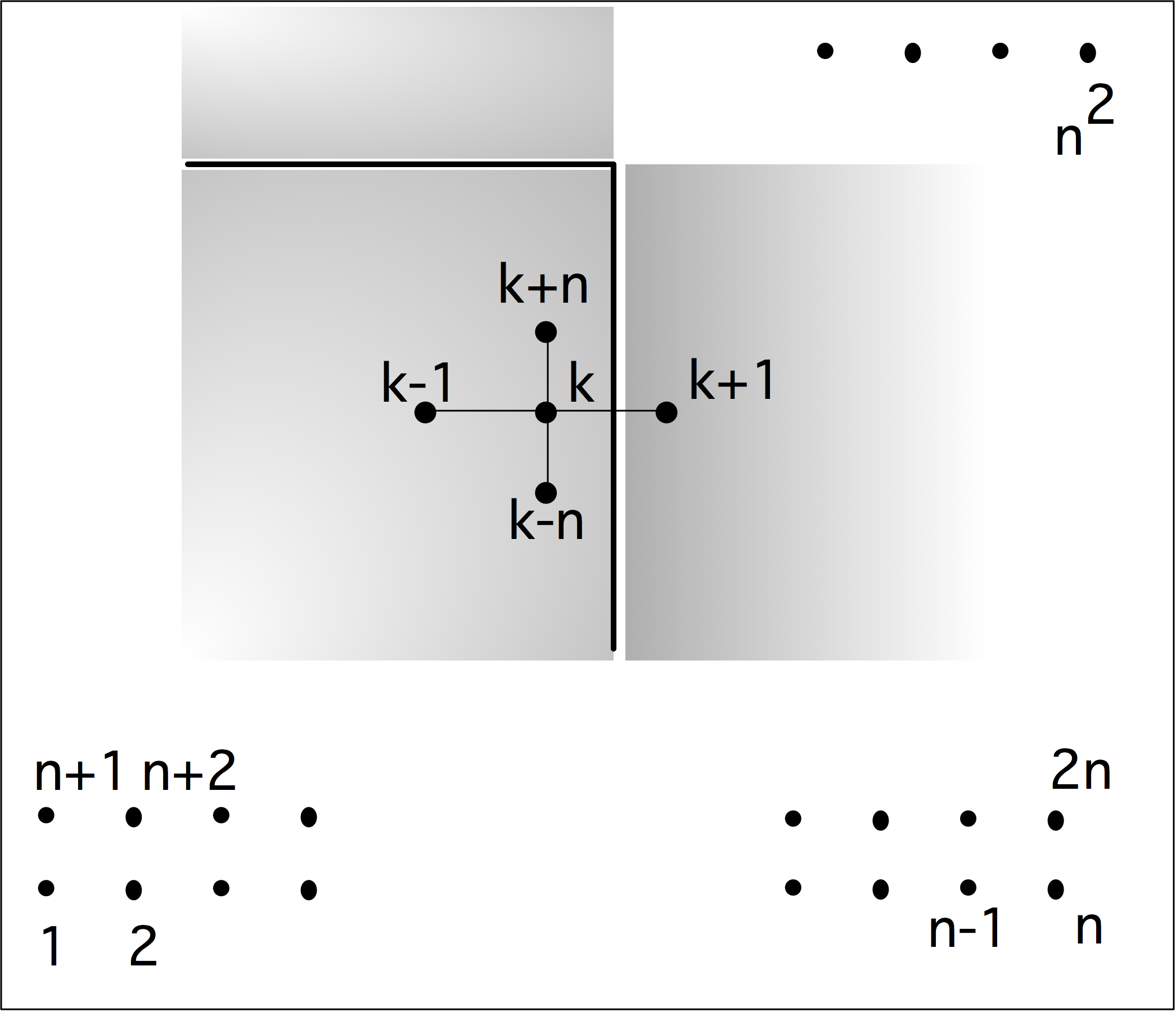
这整个分析当然也适用于密集型矩阵。如果我们考虑到稀疏矩阵的来源。让我们从一个简单的案例开始。
回顾一下图4.1,它说明了一个最简单的域(一个正方形)上的离散边界值问题,现在让我们来并行化它。我们通过分割域来做到这一点;每个处理器得到与其子域对应的矩阵行。图6.11显示了处理器之间的联系:元素$a_{ij}$与$i\in I_p, j\notin I_p$现在是模版的 “腿”,伸向处理器边界之外。 所有这些$j$的集合,正式定义为
被称为处理器的幽灵域;见图6.12。
练习 6.13 证明域的一维划分会导致矩阵被划分为块行,但域的二维划分则不会。你可以抽象地做到这一点,也可以举例说明:取一个4×4的域(给出一个大小为16的矩阵),并将其分割到4个处理器上。一维域的划分相当于给每个处理器一个行的域,而二维的划分则给每个处理器一个2×2的子域。画出这两种情况的矩阵。
练习 6.14 图6.13描述了一个大小为$N$的稀疏矩阵,半带宽度$n=\sqrt{N}$。也就是说。
我们在$p$处理器上对该矩阵进行一维分布,其中$p = n = \sqrt{N}$ 。通过计算效率与处理器数量的关系,表明使用该方案的矩阵-向量乘积是弱可扩展的
为什么这个方案不是真正的弱缩放,就像它通常定义的那样?
关于并行稀疏矩阵-向量乘积的一个关键观察是,对于每个处理器,它所涉及的其他处理器的数量是严格限制的。这对操作的效率有影响。
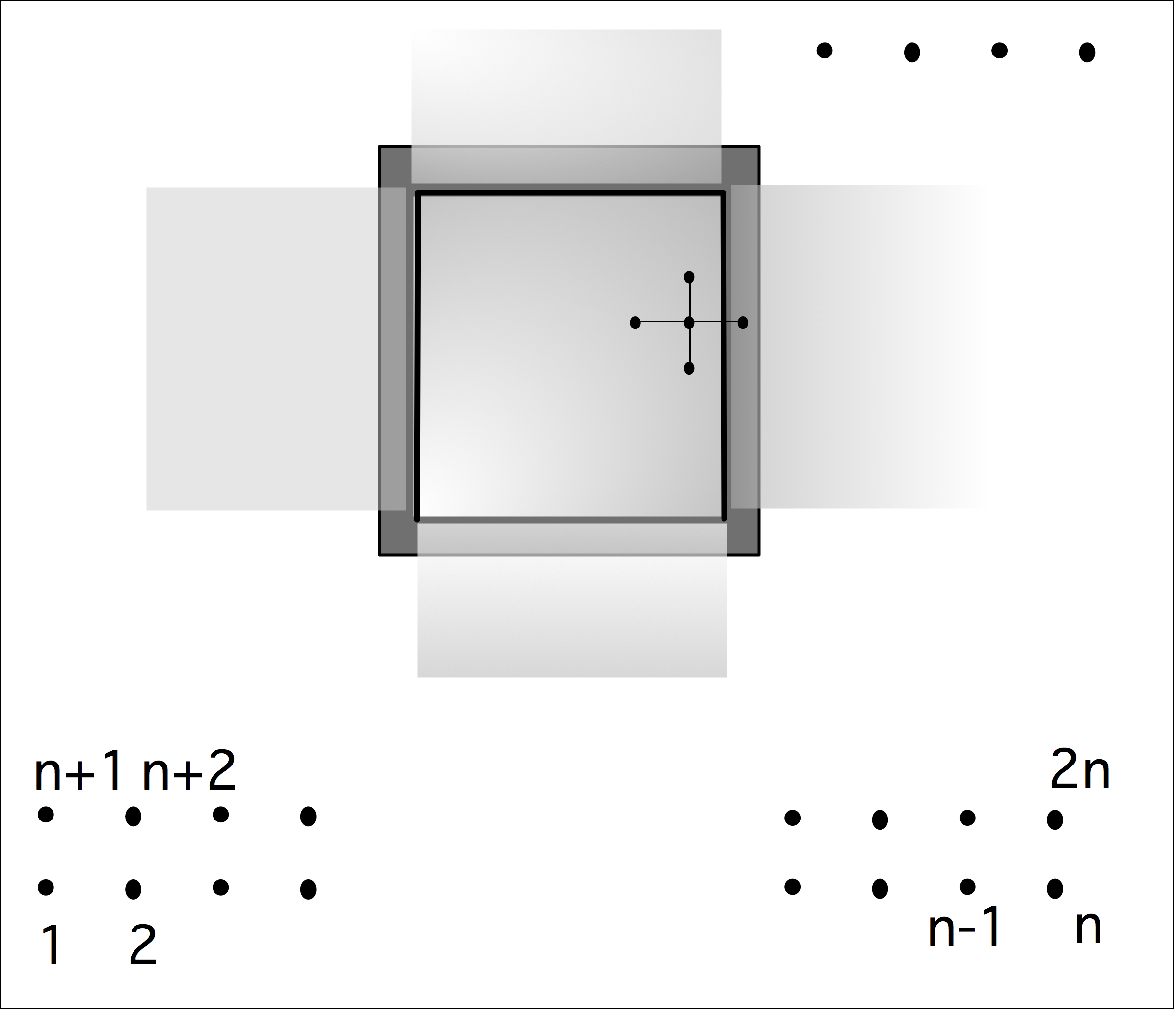
稀疏矩阵-向量乘积的并行效率
在密集矩阵-向量乘积的情况下(第6.2.2节),将矩阵按(块)行划分到处理器上并没有导致一个可扩展的算法。部分原因是每个处理器需要与之通信的邻居数量增加。图6.11显示,对于5-5点模版的矩阵,这个数量限制为4个。
练习 6.15 取一个正方形域和图6.11中的处理器的变量分区。对于图4.3中的盒子模版,一个处理器需要与之通信的最大邻居数是多少?在三个空间维度上,如果使用7点中心差分模版,那么邻居的数量是多少?
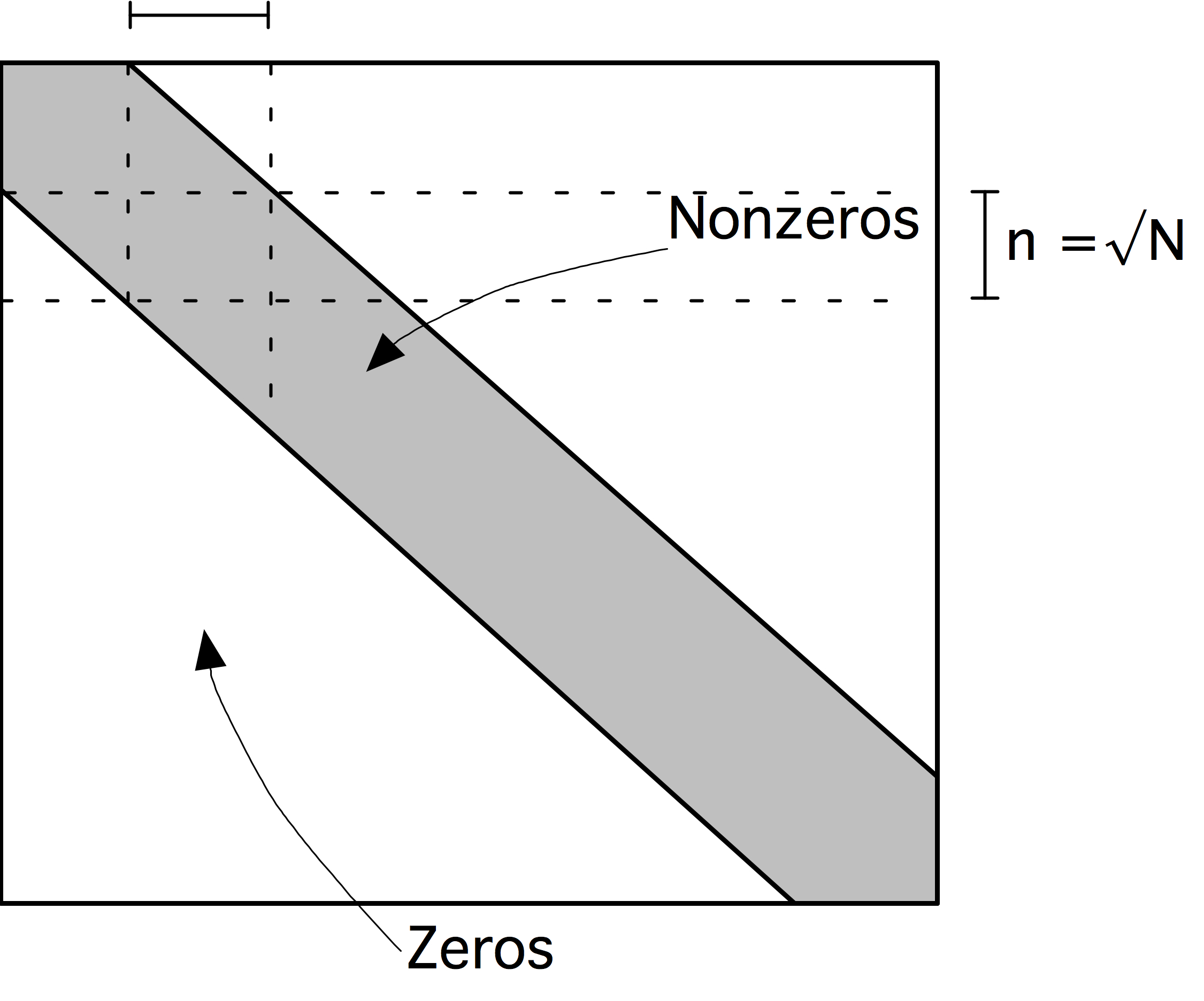
如果我们超越方形域而进入更复杂的物理对象,那么每个处理器只与几个邻居进行通信的观察就保持不变。如果一个处理器收到一个或多或少连续的子域,其邻居的数量将是有限的。这意味着即使在复杂的问题中,每个处理器也只能与少量的其他处理器通信。与密集情况相比,每个处理器不得不从其他每个处理器那里接收数据。很明显,稀疏的情况对互连网络要友好得多。(对于大型系统来说,这也是比较常见的事实,如果你准备购买一台新的并行计算机,可能会影响到对安装网络的选择)。
对于方形域,我们可以使这个论点正式化。让单位域$[0, 1]^2$在$\sqrt{P}$网格中的$P$处理器上进行划分,$\sqrt{P}\times \sqrt{P}$。从图6.11可以看出,每个处理器最多只能与四个邻居进行通信。让每个处理器的工作量为$w$,与每个邻居的通信时间为$c$。那么在单个处理器上执行总工作的时间是$T_1=Pw$,而并行时间是$T_p=w+4c$,给出的速度为
练习 6.16 将$c$和$w$表示为$N$和$P$的函数,并说明在问题的弱标度下,速度的提高是渐近最优的。
练习 6.17 在这个练习中,你将分析一个假设的、但现实的并行机器的并行稀疏矩阵-向量乘积。让机器参数具有以下特点(见第1.3.2节)。
网络延迟:$\alpha=1\mu s=10^{-6}s$。
网络带宽:1𝐺𝑏/𝑠对应于$\beta=10^{-9}$。
计算率。每核运算率为1𝐺flops意味着$\gamma=10^9$。这个数字看起来很低,但请注意,矩阵-向量乘积的重用率低于矩阵-矩阵乘积,后者可以达到接近峰值的性能,而且稀疏矩阵-向量乘积的带宽约束更大。我们进行了渐进式分析和推导具体数字的结合。
我们假设一个有$10^4$个单核处理器的集群4。我们将其应用于大小为$N=25\cdot 10^{10}$的五点模版矩阵。这意味着每个处理器存储$5\cdot 8\cdot N/p=10^{9}$字节。如果矩阵来自一个正方形领域的问题,这意味着该领域的大小为$n\times n$,$n=\sqrt{N}=5\cdot 10^{5}$。
情况1:我们不是划分矩阵,而是划分域,我们首先通过大小为$n\times (n/p)$的水平板块进行划分。论证通信复杂度为 $2(\alpha+ n\beta)$,计算复杂度为$10\cdot n\cdot (n/p)$ 。证明所产生的计算量比通信量多出50倍。
情况2:我们将领域划分为大小为$(n/\sqrt{p})\times (n/\sqrt{p})$的斑块。内存和计算时间与之前相同。推导出通信时间,并表明它比之前的时间要好50倍。
论证第一种情况不具有弱扩展性:在假设$N/p$是恒定的情况下,效率会下降。(证明速度仍然随着$\sqrt{p}$的增加而渐进地上升。论证第二种情况确实是弱扩展的。
一个处理器只与几个邻居连接的论点是基于科学计算的性质。这对FDM和FEM方法来说是真实的。在边界元素法(BEM)的情况下,任何子域都需要与它周围半径为𝑟的所有东西进行通信。随着处理器数量的增加,每个处理器的邻居数量也会增加。
练习 6.18 请对BEM算法的速度和效率进行正式分析。再假设每个处理器的单位工作量为$w$,每个邻居的通信时间为$c$。由于邻居的概念现在是基于物理距离,而不是基于图形属性,所以邻居的数量会增加。对于这种情况,给出$T_1$、$T_p$、$S_p$、$E_p$。
还有一些情况,稀疏矩阵需要与密集矩阵类似地处理。例如,谷歌的PageRank算法(见第9.4节)的核心是重复操作$x\leftarrow A$,$A$是一个稀疏矩阵,如果网页$j$链接到页面$i$,$A\neq 0$;见第9.4节。 这使得$A$是一个非常稀疏的矩阵,没有明显的结构,所以每个处理器都很可能与其他处理器进行交流。
稀疏矩阵-向量乘积的记忆行为
在1.7.11节中,你看到了在单个处理器上对密集情况下的稀疏矩阵-向量乘积的分析。有些分析可以立即延续到稀疏情况下,比如每个矩阵元素只使用一次,性能受处理器和内存之间的带宽限制。
关于输入和输出向量的重用,如果矩阵是按行存储的,比如CRS格式(第5.4.1.3节),对输出向量的访问将被限制为每行写一次。另一方面,用于获得输入向量的重用的循环解卷技巧不能在这里应用。结合两个迭代的代码如下。
1 | for (i=0; i<M; i+=2) { |
这里的问题是,如果$a_{ij}$为非零,就不能保证$a_{i+1,j}$为非零。稀疏模式的不规则性使得优化矩阵-向量乘积变得困难。通过识别矩阵中的小密块部分,可以实现适度的改进[26, 43, 196]。
在GPU上,稀疏的矩阵-向量乘积也受到内存带宽的限制。现在编程更难了,因为GPU必须在数据并行模式下工作,有许多活动线程。
如果我们考虑到稀疏矩阵-向量乘积通常出现的背景,一个有趣的优化就成为可能。这个操作最常见的用途是在线性系统的迭代求解方法中(第5.5节),在那里它被应用于同一个矩阵,可能有数百次迭代。因此,我们可以考虑将矩阵存储在GPU上,只为每个乘积操作复制输入和输出向量。
转置积
在第5.4.1.3节中,你看到正则和转置矩阵-向量乘积的代码都被限制在循环顺序上,其中矩阵的行被遍历。(在第1.6.2节中,你看到了关于循环顺序变化的计算效果的讨论;在这种情况下,我们被存储格式限制在行的遍历上)。
在这一节中,我们将简要地看一下并行转置积。与按行划分矩阵并进行转置乘积相当,我们看一下按列存储和划分的矩阵并进行常规乘积。
列间乘积的算法可以给出:。
在共享内存和分布式内存中,我们都将外迭代分布在处理器上。那么问题来了,每个外部迭代都会更新整个输出向量。这是一个问题:在共享内存中,它导致了对输出位置的多次写入,而在分布式内存中,它需要通信,目前还不清楚。
解决这个问题的一个方法是为每个进程分配一个私有的输出向量$y^{(p)}$。
之后,我们对$y\leftarrow \sum_p y^{(p)}$进行求和。
稀疏矩阵-向量乘积的设置
密集的矩阵-向量乘积依赖于集合体(见第6.2节),而稀疏的情况则使用点对点的通信,也就是说,每个处理器只向几个邻居发送信息,并从几个邻居那里接收信息。这对于来自PDE的稀疏矩阵类型是有意义的,正如你在第4.2.3节中看到的,PDE有明确的结构。然而,有些稀疏矩阵是如此的随机,以至于你基本上不得不使用密集技术;见第9.5节。
然而,发送和接收之间存在着不对称性。对于一个处理器来说,要找出它将从哪些其他处理器那里接收信息是相当容易的。
练习 6.19 假设矩阵是按块行划分给处理器的;见图6.2的说明。还假设每个处理器都知道其他处理器存储了哪些行。(你将如何实现这一知识?)勾勒出一个算法,通过这个算法,处理器可以发现它将从谁那里接收;这个算法本身不应该涉及任何通信。发现向谁发送则更难。
练习 6.20 论证一下,在结构对称矩阵的情况下,这很容易。$a_{ij}\neq 0\Leftrightarrow a_{ji} \neq 0$。在一般情况下,原则上可以要求一个处理器向任何其他处理器发送,所以简单的算法是如下所示。
每个处理器都会列出它所需要的非本地指数的清单。根据上述假设,它知道其他每个处理器拥有的指数范围,然后决定从哪些邻居那里获得哪些指数。
每个处理器向它的每个邻居发送一个指数列表;这个列表对大多数邻居来说都是空的,但我们不能省略发送它。
然后,每个处理器从所有其他处理器那里收到这些列表,并制定出要发送的指数列表。你会注意到,尽管矩阵-向量乘积过程中的通信只涉及每个处理器的几个邻居,给出的成本是处理器数量的𝑂(1),但设置涉及所有对所有的通信,其时间复杂性为$O(\alpha P)$
如果一个处理器只有几个邻居,上述算法是浪费的。理想情况下,你希望空间和运行时间与邻居的数量成正比。如果我们知道预计有多少消息,我们可以在设置中带来接收时间。这个数字是可以找到的。
每个进程都会产生一个长度为$P$的数组,如果进程需要来自处理器𝑖的任何数据,则ereneed[i]为1,否则为0。
在这个数组上的一个reduce-scatter集体,用一个sum运算符,然后在每个处理器上留下一个数字,表示有多少处理器需要它的数据。
该处理器可以执行那么多的接收调用。reduce-scatter调用的时间复杂度为$\alpha \log P+\beta P$,与之前的算法相同,但可能比例常数较低。通过一些复杂的技巧,设置所需的时间和空间可以减少到$O(\log P)$[63,110]。
迭代方法的计算问题
所有的迭代方法都有以下操作。
- 矩阵-向量乘积;这在第5.4节讨论了顺序情况,在第6.5节讨论了平行情况。在并行情况下,FEM矩阵的构造有一个复杂的问题,我们将在第6.6.2节讨论。
- 预处理矩阵$K$的构造$\approx A$,以及系统的解$Kx=y$。这在第5.5.6节的顺序情况下讨论过。下面我们将在第6.7节中讨论并行性问题。
- 一些向量操作(包括内积,一般来说)。这些将在接下来讨论。
向量操作
在一个典型的迭代方法中,有两种类型的向量运算:向量加法和内积。
练习 6.21 考虑第5.5.11节的CG方法,图5.9,应用于二维BVP的矩阵;公式(4.16),首先考虑无条件的情况$M=I$。证明在矩阵-向量乘积和向量运算中进行的浮点运算数量大致相等。用矩阵大小$N$表示一切,忽略低阶项。如果矩阵每行有20个非零点,这种平衡会是怎样的?
接下来,研究一下5.5.9节中FOM方案的矢量和矩阵操作之间的这种平衡。由于向量操作的数量取决于迭代,考虑前50次迭代,计算在向量更新和内积与矩阵-向量乘积中进行了多少浮点操作。矩阵需要有多少个非零点才能使这些数量相等?
练习 6.22 翻牌计数并不是全部的事实。对于在单个处理器上执行的迭代方法中的向量和矩阵操作的效率,你能说什么?
向量加法
向量加法的典型形式是$x\leftarrow \alpha y$或$x\leftarrow \alpha+y$。如果我们假设所有的向量都以相同的方式分布,这个操作就是完全平行的。
内积
内积是向量操作,但它们在计算上比更新更有趣,因为它们涉及通信。
当我们计算一个内积时,很可能每个处理器都需要接收计算的值。我们使用以下算法。
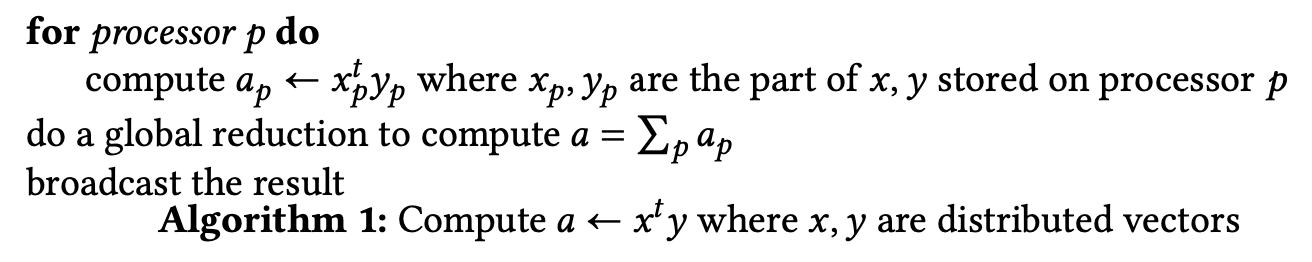
规约和广播(可以加入到Allreduce中)结合了所有处理器的数据,所以它们的通信时间随着处理器的数量而增加。这使得内积有可能成为一个昂贵的操作,人们提出了一些方法来减少它们对迭代方法性能的影响。
练习 6.23 迭代方法通常用于稀疏矩阵。在这种情况下,你可以认为内积中涉及的通信对整体性能的影响可能比矩阵-向量乘积中的通信更大。作为处理器数量的函数,矩阵-向量乘和内积的复杂性是什么?
下面是一些已经采取的方法。
- CG方法每次迭代都有两个相互依赖的内部产品。有可能重写该方法,使其计算相同的迭代结果(至少在精确算术中),但使每次迭代的两个内积可以合并。见[32, 39, 156, 205]。
- 也许可以将内积计算与其他并行计算重叠[41]。
- 在GMRES方法中,使用经典的Gram-Schmidt(GS)方法需要的独立内积要比修改后的GS方法少得多,但它的稳定性较差。人们已经研究了决定何时允许使用经典GS方法的策略[138]。
由于计算机算术不是关联性的,当同一计算在两个不同的处理器配置下执行时,内积是导致结果不同的主要原因。在第3.5.5节中,我们勾画了一个解决方案。
有限元矩阵构造
有限元导致了并行计算中一个有趣的问题。为此,我们需要勾勒出这种方法工作的基本轮廓。有限元的名称来自于这样一个事实:建模的物理对象被划分为小的二维或三维形状,即元素,如二维的三角形和正方形,或三维的金字塔和砖块。在每一个元素上,我们要建模的函数被假定为多项式,通常是低度的,如线性或双线性。
关键的事实是,一个矩阵元素$a_{ij}$是所有包含变量𝑖和𝑗的元素的计算之和,特别是某些积分。
每个元素的计算都有许多共同的部分,所以很自然地把每个元素𝑒唯一地分配给一个处理器$P$,然后由它来计算所有的贡献 𝑎(𝑒)。在图6.14中,元素2被分配给处理器0,元素4被分配给处理器1。
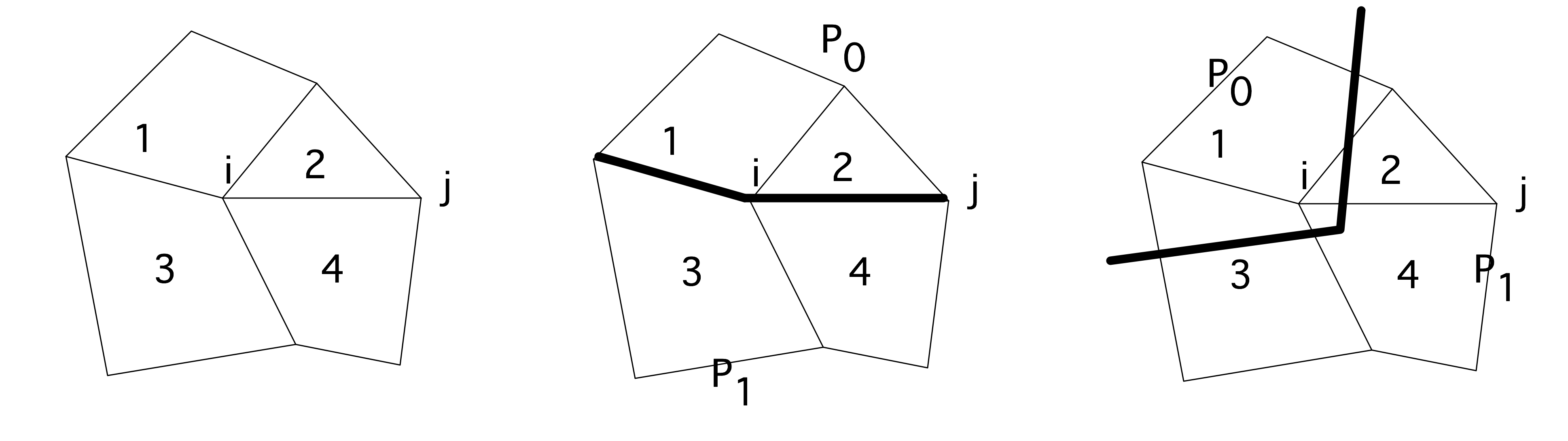
现在考虑变量$i$和$j$以及矩阵元素$a_{ij}$。它被构建为域元素2和4的计算之和,这些元素被分配给不同的处理器。因此,无论什么处理器的行$i$被分配到,至少有一个处理器必须传达它对矩阵元素$a_{ij}$的贡献。
显然,不可能对元素$P_e$和变量$P_i$进行分配,从而使$P_e$对所有$i\in e$都能完全计算系数$a_{ij}$。换句话说,如果我们在本地计算贡献,需要有一定量的通信来集合某些矩阵元素。由于这个原因,现代线性代数库如PETSc允许任何处理器设置任何矩阵元素。
迭代方法性能的一个简单模型
上面我们已经说过,迭代方法很少有机会进行数据重用,因此它们被描述为带宽约束型算法。这使得我们可以对迭代方法的浮点性能做出简单的预测。由于迭代方法的迭代次数很难预测,这里的性能是指单次迭代的性能。与线性系统的直接方法不同(例如见第6.8.1节),解的次数很难事先确定。
首先,我们认为我们可以把自己限制在稀疏矩阵向量乘积的性能上:这个操作所花费的时间比向量操作多得多。此外,大多数预调节器的计算结构与矩阵-向量乘积相当相似。
然后让我们考虑CRS矩阵-向量乘积的性能。
首先我们观察到,矩阵元素和列索引的数组没有重复使用,所以加载它们的性能完全由可用带宽决定。缓存和完美流只是隐藏了延迟,但并没有改善带宽。对于矩阵元素与输入矢量元素的每一次乘法,我们加载一个浮点数字和一个整数。根据指数是32位还是64位,这意味着每次乘法都要加载12或16个字节。
对结果向量的存储要求并不重要:每个矩阵行的输出向量只写一次。
输入向量在带宽计算中可以忽略不计。乍一看,你会认为对输入向量的间接索引或多或少是随机的,因此很昂贵。然而,让我们从矩阵-向量乘积的算子角度出发,考虑矩阵所来自的PDE的空间域;见4.2.3节。我们现在看到,看似随机的索引实际上是被紧密地组合在一起的向量元素。这意味着这些向量元素很可能存在于L3缓存中,因此可以用比主存数据更高的带宽(例如,至少5倍的带宽)来访问。
对于稀疏矩阵-向量乘积的并行性能,我们认为在PDE背景下,每个处理器只与几个邻居进行通信。此外,从表面到体积的论证表明,信息量比节点上的计算量要低一阶。
总之,我们得出结论,稀疏矩阵向量乘积的一个非常简单的模型,从而也是整个迭代求解器的模型,包括测量有效带宽和计算每12或16字节加载一次加法和一次乘法操作的性能。
高性能线性代数(二)
并行预处理程序
上面(第5.5.6节,特别是5.5.6.1节)我们看到了$K$的几种不同选择。在本节中,我们将开始讨论并行化策略。讨论将在接下来的章节中继续详细进行。
雅克比预处理
雅可比方法(5.5.3节)使用𝐴的对角线作为预处理。应用这个方法是尽可能的平行:声明$y\leftarrow K^{-1}x$独立地缩放输入向量的每个元素。不幸的是,使用雅可比预处理器对迭代次数的改进是相当有限的。因此,我们需要考虑更复杂的方法,如ILU。与雅可比预处理程序不同的是,并行化并不简单。
与ILU并行的麻烦
上面我们看到,从计算的角度来看,应用ILU预处理(第5.5.6.1节)与做矩阵-向量乘积一样昂贵。如果我们在并行计算机上运行我们的迭代方法,这就不再是真的了。
乍一看,这些操作很相似。矩阵-向量乘积$y=Ax$看起来像
1 | for i=1..n |
并行时,这看起来像
1 | for i=myfirstrow..mylastrow |
假设一个处理器拥有它所需要的𝐴和𝑥的所有元素的本地副本,那么这个操作就是完全并行的:每个处理器都可以立即开始工作,如果工作负荷大致相等,它们都会在同一时间完成。然后,矩阵-向量乘积的总时间除以处理器的数量,使速度或多或少得到了提高。
现在考虑正向解$Lx=y$,例如在ILU预处理程序的背景下。
1 | for i=1..n |
我们可以简单地编写并行代码。
1 | for i=myfirstrow..mylastrow |
但现在出现了一个问题。我们不能再说 “假设一个处理器拥有右手边所有东西的本地拷贝”,因为向量𝑥同时出现在左手边和右手边。虽然矩阵-向量乘积原则上在矩阵行上是完全并行的,但这个三角解代码是递归的,因此是顺序的。
在并行计算的背景下,这意味着,第二个处理器要启动,需要等待第一个处理器计算的𝑥的某些组件。显然,在第一个处理器完成之前,第二个处理器不能启动,第三个处理器必须等待第二个处理器,以此类推。令人失望的结论是,在并行中,任何时候都只有一个处理器处于活动状态,总时间与顺序算法相同。在密集矩阵的情况下,这实际上不是一个大问题,因为在处理单行的操作中可以找到并行性(见第6.12节),但是在稀疏的情况下,这意味着我们不能使用不完整的因式分解,而需要重新设计。
在接下来的几个小节中,我们将看到不同的策略来寻找能有效地并行执行的前置条件器。
块状雅可比方法
人们提出了各种方法来弥补三角形解法的顺序性。例如,我们可以简单地让处理器忽略那些应该来自其他处理器的𝑥的成分。
1 | for i=myfirstrow..mylastrow |
这在数学上并不等同于顺序算法(从技术上讲,它被称为以ILU为局部解的块状雅可比方法),但由于我们只是在寻找一个近似值$K\approx A$,这只是一个稍微粗糙的近似。
练习 6.24 以你上面写的高斯-赛德尔代码为例,模拟一次并行运行。增加(模拟的)处理器数量的效果如何?
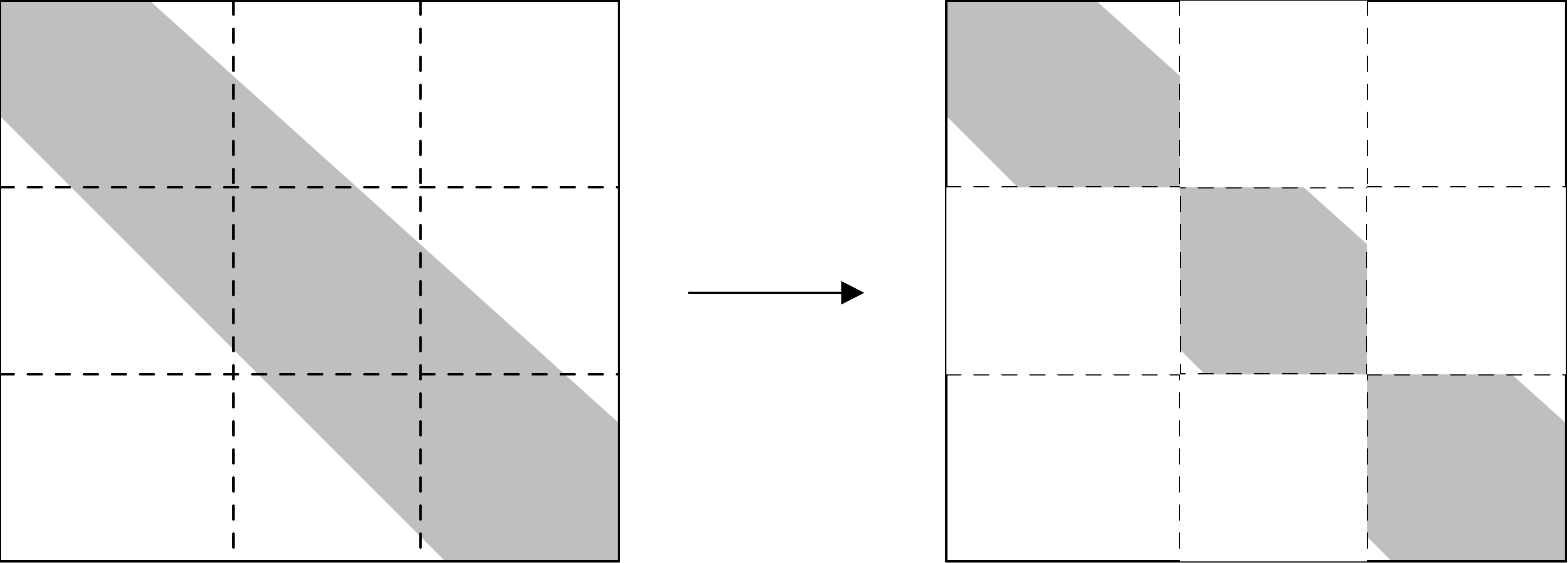
块方法背后的想法可以通过图片来理解,见图6.15。实际上,我们通过忽略处理器之间的所有连接,得到了一个ILU的矩阵。由于在BVP中,所有的点都是相互影响的(见第4.2.1节),如果在顺序计算机上执行,使用连接较少的预调节器将增加迭代的次数。然而,块状方法是并行的,正如我们上面所观察到的,顺序预处理器在并行情况下效率很低,所以我们容忍了这种迭代次数的增加。
并行ILU
块状雅可比预处理通过解耦领域部分进行操作。虽然这可能会产生一种高度并行的方法,但它可能会比真正的ILU预处理程序产生更多的迭代次数。(可以从理论上论证这种解耦降低了迭代方法的效率;见第4.2.1节)。幸运的是,有可能出现一个并行的ILU方法。由于我们需要即将到来的关于变量重新排序的材料,我们把这个讨论推迟到6.8.2.3节。
排序策略和并行性
在前文中,我们已经提到了一个事实,即解决线性方程组本身就是一个递归活动。对于密集系统来说,与递归长度相比,操作的数量足够多,因此寻找并行性是相当直接的。另一方面,稀疏系统则需要更多的复杂性。在这一节中,我们将研究一些重新排列方程的策略(或者说,等同于排列矩阵),这将增加可用的并行性。
这些策略都可以被认为是高斯消除法的变种。通过对它们进行不完全变体(见第5.5.6.1节),所有这些策略也适用于构建迭代求解方法的前置条件。
嵌套剖析
上面,你已经看到了几个在域中对变量进行排序的例子,而不是用列举式排序。在本节中,你将看到嵌套剖析排序,它最初被设计为一种减少填充的方法。然而,它在并行计算的背景下也是有利的。

嵌套剖析是一个递归的过程,用于确定在一个工作中的未知数的非线性排序。在第一步中,计算域被分割成两部分,在它们之间有一个分隔带;见图6.16。准确地说,这个分隔带足够宽,以至于左右子域之间没有任何联系。由此产生的矩阵𝐴DD具有3×3的结构,对应于域的三个分界。由于子域Ω和Ω不相连,子矩阵𝐴DD和𝐴DD为零。
这种用分离器划分域的过程也被称为域分解或子结构,尽管这个名字也与所产生的矩阵的数学分析有关[14]。在这个矩形域的例子中,找到一个分隔符当然是微不足道的。然而,对于我们从BVP中得到的方程类型,通常可以有效地找到任何域的分离器[146];另见18.6.2节。
现在让我们考虑这个矩阵的𝐿𝑈因式分解。如果我们用3×3块状结构来分解它,我们可以得到
其中
这里的重要事实是
- 贡献$A_{31}A^{-1}_{11}A_{13}$和$A_{32}A_{22}^{-1}A_{23}$可以同时计算,所以因式分解在很大程度上是并行的;并且
- 在前向和后向求解中,解的第1和第2部分都可以同时计算,所以求解过程也基本上是并行的。第三块不能以并行方式处理,所以这在算法中引入了一个顺序的部分。算法。我们还需要仔细研究一下$S_{33}$的结构。
练习 6.25 在第5.4.3.1节中,你看到了LU因子化和图论之间的联系:消除一个节点会导致图中的该节点被删除,但会增加某些新的连接。证明在消除前两组变量后,分离器上剩余矩阵的图将是完全连接的。结果是,在消除了第1和第2块中的所有变量后,我们剩下的矩阵$S_{33}$是完全密集的,大小为$n\times n$。
引入分离器后,我们得到了一个双向平行的因式分解。现在我们重复这个过程:我们在第 1 和第 2 块内放置一个分隔符(见图 6.17),这样就得到了以下矩阵结构。
(注意与第5.4.3.4节中的 “箭头 “矩阵的相似性,并回顾一下这导致较低填充的论点)。这个的LU因子化是。
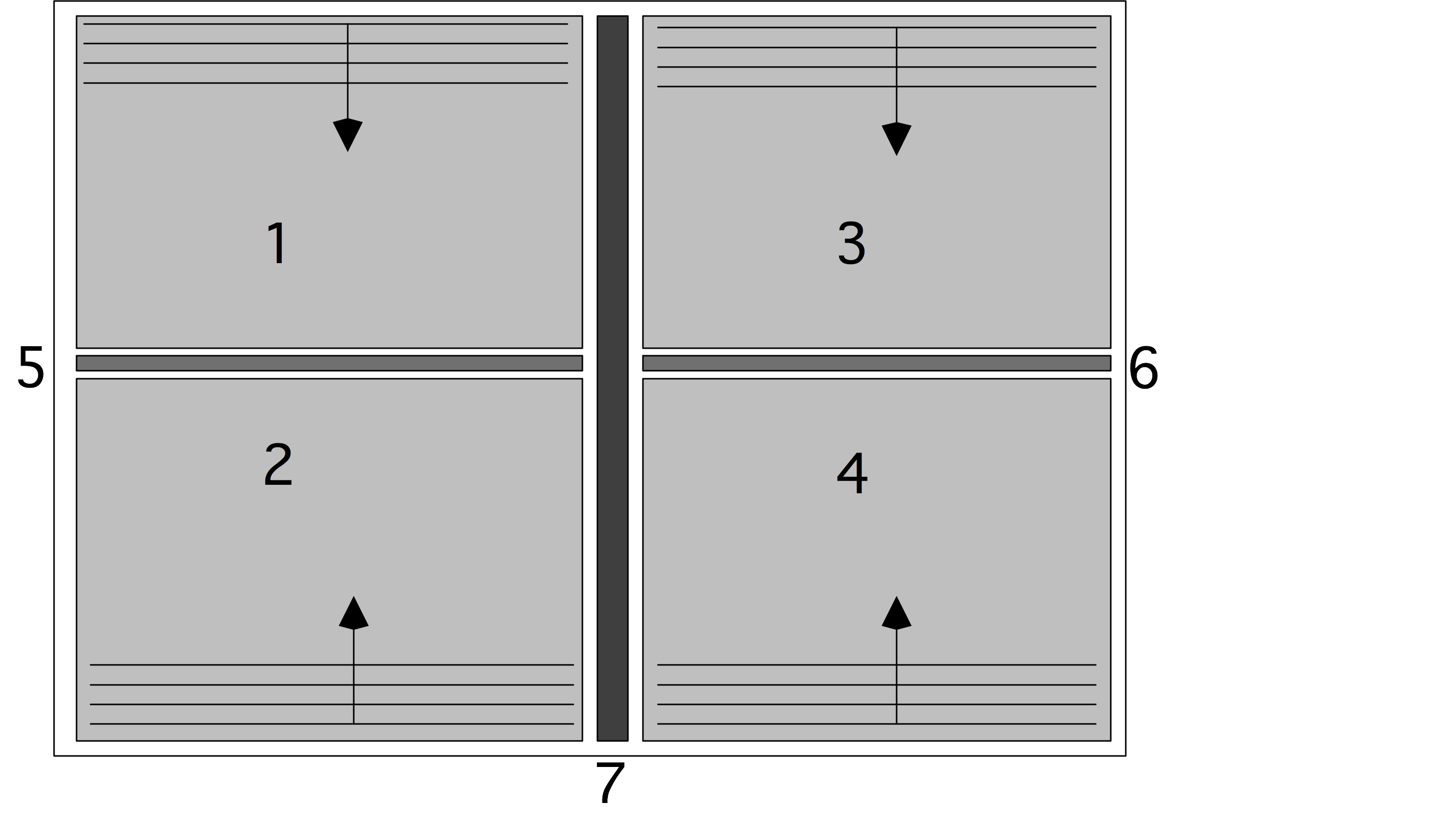
其中
现在构建因式分解的过程如下。
- 对于$i=1,2,3,4$,块$A_{ii}$被并行因式化;同样,对于$i=1,2,3,4$,$A_{5i}A_{ii}^{-1}A_{i5}$,对于$𝑖=3,4$,$A_{6i}A_{ii}^{-1}A_{i6}$,$i=1,2,3,4$,$A_{7i}A_{ii}^{-1}A_{i7}$可以被并行构建。
- 形成舒尔补码$S_5, S_6$,并随后进行并行派生,对$i = 5, 6$的贡献 $A_{7i}S_i^{-1}A_{17}$ 也是并行构建。
- 舒尔补码$S_7$被形成并被分解。
与上述推理类似,我们得出结论:在消除了第1,2,3,4块后,更新的矩阵$S_5$, $S_6$是大小为$n/2$的密集,在消除了第5,6块后,舒尔补码$S_7$是大小为$n$的密集。
练习 6.26 证明用𝐴DD求解一个系统与构建上述因式分解有类似的并行性。
为了便于以后参考,我们将把集合1和2称为彼此的兄弟姐妹,同样,3和4也称为兄弟姐妹。集合5是1和2的父,6是3和4的父;5和6是兄弟姐妹,7是5和6的父。
域的分解
在图6.17中,我们通过一个递归过程将领域分成四种方式。这就引出了我们对嵌套剖分的讨论。也可以立即将一个域分割成任意数量的条状,或者分割成子域的网格。只要分离器足够宽,这将给出一个具有许多独立子域的矩阵结构。在上面的讨论中,LU因子化的特点是
- 在因式分解和𝐿, 𝑈求解中,对子域进行并行处理,并且
- 要在分离器结构上求解的系统。

练习 6.27 二维BVP的矩阵有一个块状三对角结构。将该域分为四条,即使用三个分离器(见图6.18)。注意这些分离器在原始矩阵中是不耦合的。现在勾勒出所得到的系统的稀疏性结构,即分离器是消除子域的。说明该系统是块状三对角的。
在我们到目前为止讨论的所有领域分割方案中,我们使用的领域都是矩形的,或者说是 “砖 “形的,在两个维度以上。所有这些论点都适用于二维或三维的更一般的域,但是像寻找分离器这样的事情变得更加困难[145],而这对于平行情况来说更是如此。参见第18.6.2节对这个话题的一些介绍。
复杂度
嵌套剖析法重复上述过程,直到子域变得非常小。对于理论分析来说,我们一直在分割,直到我们有大小为1×1的子域,但在实践中,我们可以停止在32这样的大小,并使用一个有效的密集求解器来分解和反转块。
为了推导出算法的复杂度,我们再看一下图6.17,可以看到复杂度论证,一个完整的递归嵌套分解所需要的总空间是以下的总和
- 在一个大小为$n$的分离器上的一个密集矩阵,加上
- 大小为$n/2$的分离器上的两个密集矩阵之和。
- 需要$3/2n^2$的空间和$5/12n^3$的时间。
- 上述两项在四个大小为$(n/2)\times (n/2)$的子域上重复。
观察到$n=\sqrt{N}$,这就意味着
显然,我们现在的因式分解在很大程度上是平行的,而且是在$O(N \log N)$空间中完成的,而不是在$O(N^{3/2})$(见5.4.3.3节)。因式分解时间也从$O(N^2)$下降到$O(N^{3/2})$。
不幸的是,这种空间节省只发生在二维空间:在三维空间中,我们需要
- 一个$n$大小的分离器,占用$(n\times n)^2 =N^{4/3}$空间和$1/3\cdot(n\times n)^3=1/3\cdot N^2$时间。
- 两个大小为$n\times n/2$的分离器,占用$N^{3/2}/2$空间和$1/3\cdot N^2/4$时间。
- 四个大小为$n/2 \times n/2$ 的分离器,需要$N^{ 3/2}/4$ 的空间和 $1/3\cdot N^{2}/16$的时间。
- 加起来就是$7/4N^{3/2}$空间和$21/16N^2/3$时间。
- 在下一级,有8个子域贡献这些条款,$n\rightarrow n/2$,因此$N\rightarrow N/8$。
这使得总空间
以及总的时间
我们不再有二维情况下的巨大节省。一个更复杂的分析表明,对于二维的一般问题,阶次的改进是成立的,而三维一般有更高的复杂度[145]。
并行性
嵌套剖析法显然引入了大量的并行性,我们可以将其描述为任务并行性(第2.5.3节):与每个分离器相关的是对其矩阵进行因式分解的任务,随后是对其变量进行线性系统求解的任务。然而,这些任务并不是独立的:在图6.17中,域7上的因式分解必须等待5和6,而且它们必须等待1,2,3,4。因此,我们的任务以树的形式存在依赖关系:每个分离器矩阵只有在其子矩阵被因子化后才能被因子化。
将这些任务映射到处理器上并非易事。首先,如果我们处理的是共享内存,我们可以使用一个简单的任务队列。
1 | Queue ← {} |
这里的主要问题是,在某些时候,我们的处理器会多于任务,从而导致负载不平衡。这个问题由于最后的任务也是最重要的,而变得更加严重,因为分离器的大小从一层到另一层是双倍的。(回顾一下,密集矩阵的因式分解工作随着大小的三次方而增加!) 因此,对于较大的分离器,我们必须从任务并行转为中粒度并行,即处理器合作对一个块进行因子化。
有了分布式内存,我们现在可以用一个简单的任务队列来解决并行问题,因为这将涉及移动大量的数据。(但请记住,工作是矩阵大小的高次方,这一次对我们有利,使通信相对便宜)。那么解决方案就是使用某种形式的域分解。在图6.17中,我们可以有四个处理器,与块1、2、3、4相关联。然后,处理器1和2将协商哪一个因素是第5块(类似地,处理器3和4和第6块),或者它们都可以冗余地做这个。
预处理
与所有的因式分解一样,通过使因式分解不完整,可以将嵌套剖分法变成一个预处理程序。(关于不完全因式分解的基本思想,见5.5.6.1节)。然而,这里的因式分解完全是用块矩阵来表述的,除以枢轴元素就变成了一个反转或与枢轴块矩阵的系统解。我们将不进一步讨论这个问题,详情见文献[6, 57, 157]。

变量的重新排序和着色:独立集
在稀疏矩阵中可以通过使用图形着色(第18.3节)实现并行化。由于 “颜色 “被定义为只与其他颜色相连的点,根据定义它们是相互独立的,因此可以被并行处理。这导致我们采取了以下策略。
- 将问题的邻接图分解成少量独立的集合,称为 “颜色”。
- 用与颜色数量相等的顺序步骤来解决这个问题;在每个步骤中,都会有大量的可独立处理的点。
红黑相间的颜色
我们从一个简单的例子开始,我们考虑一个三对角矩阵$A$。方程$Ax=b$看起来像
我们观察到,$x_i$直接取决于$x_{i-1}$和$x_{i+1}$,但不取决于$x_{i-2}$或$x_{i+1}$。因此,让我们看看,如果我们把指数排列起来,把每一个其他的组成部分放在一起会发生什么。
图形上,我们把$1, … n$,并将它们涂成红色和黑色(图 6.19),然后我们将它们进行置换,先取所有红色的点,然后取所有黑色的点。相应地,经过置换的矩阵看起来如下。
有了这个经过处理的$A$,高斯-塞德尔矩阵$D_A + L_A$看起来像是
这能给我们带来什么?好吧,让我们拼出一个系统的解决方案$Lx=y$。
显然,该算法有三个阶段,每个阶段在一半的域点上是平行的。这在图6.20中得到了说明。理论上,我们可以容纳的处理器数量是域点数量的一半,但实际上每个处理器都会有一个子域。现在你可以在图6.21中看到这如何导致一个非常适度的通信量:每个处理器最多发送两个红点的数据给它的邻居。
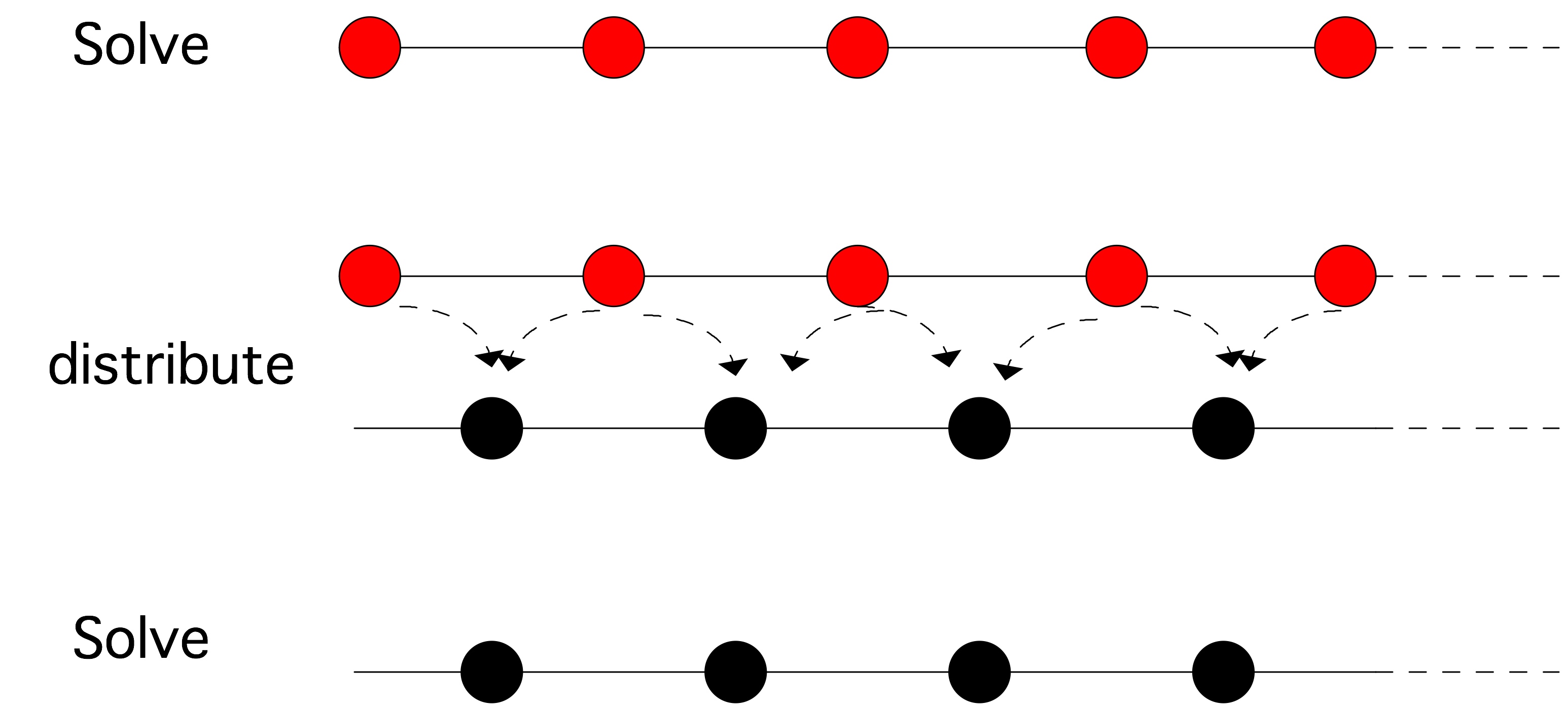
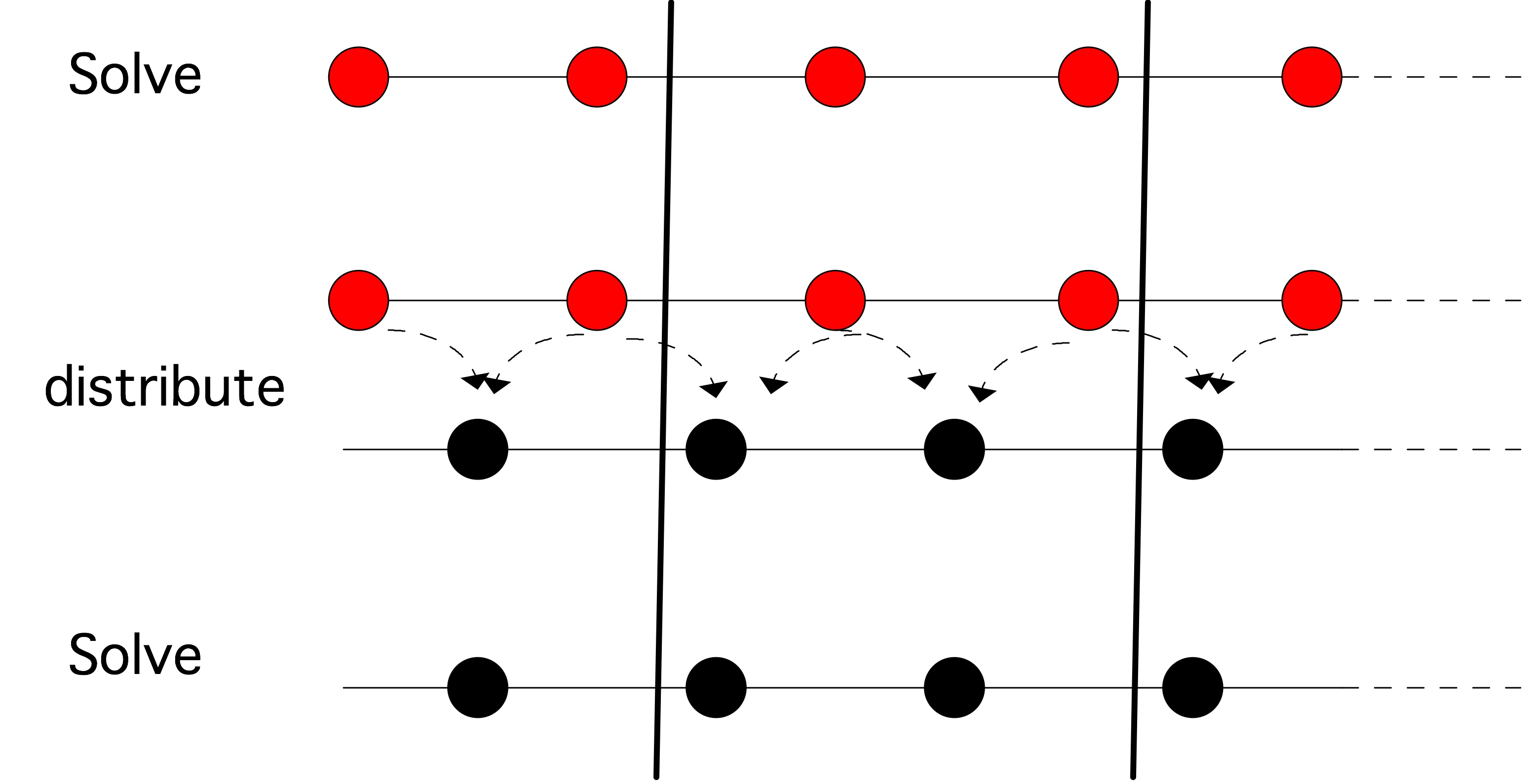
练习 6.28 论证这里的邻接图是一个二边形图。我们看到,这样的图(以及一般的彩色图)与并行性有关。你还能指出非并行处理器的性能优势吗?
红黑排序也可以应用于二维问题。让我们对点$(i, j)$应用红黑排序,其中$1\leqslant i, j\leqslant n$。在这里,我们首先对第一行的奇数点(1,1),(3,1),(5,1),……,然后对第二行的偶数点(2,2),(4,2),(6,2),……,第三行的奇数点进行连续编号,依此类推。这样对域中一半的点进行编号后,我们继续对第一行的偶数点、第二行的奇数点进行编号,依此类推。正如你在图6.22中看到的,现在红色的点只与黑色的点相连,反之亦然。用图论的术语来说,你已经找到了一个有两种颜色的矩阵图的着色(这个概念的定义见附录18)。
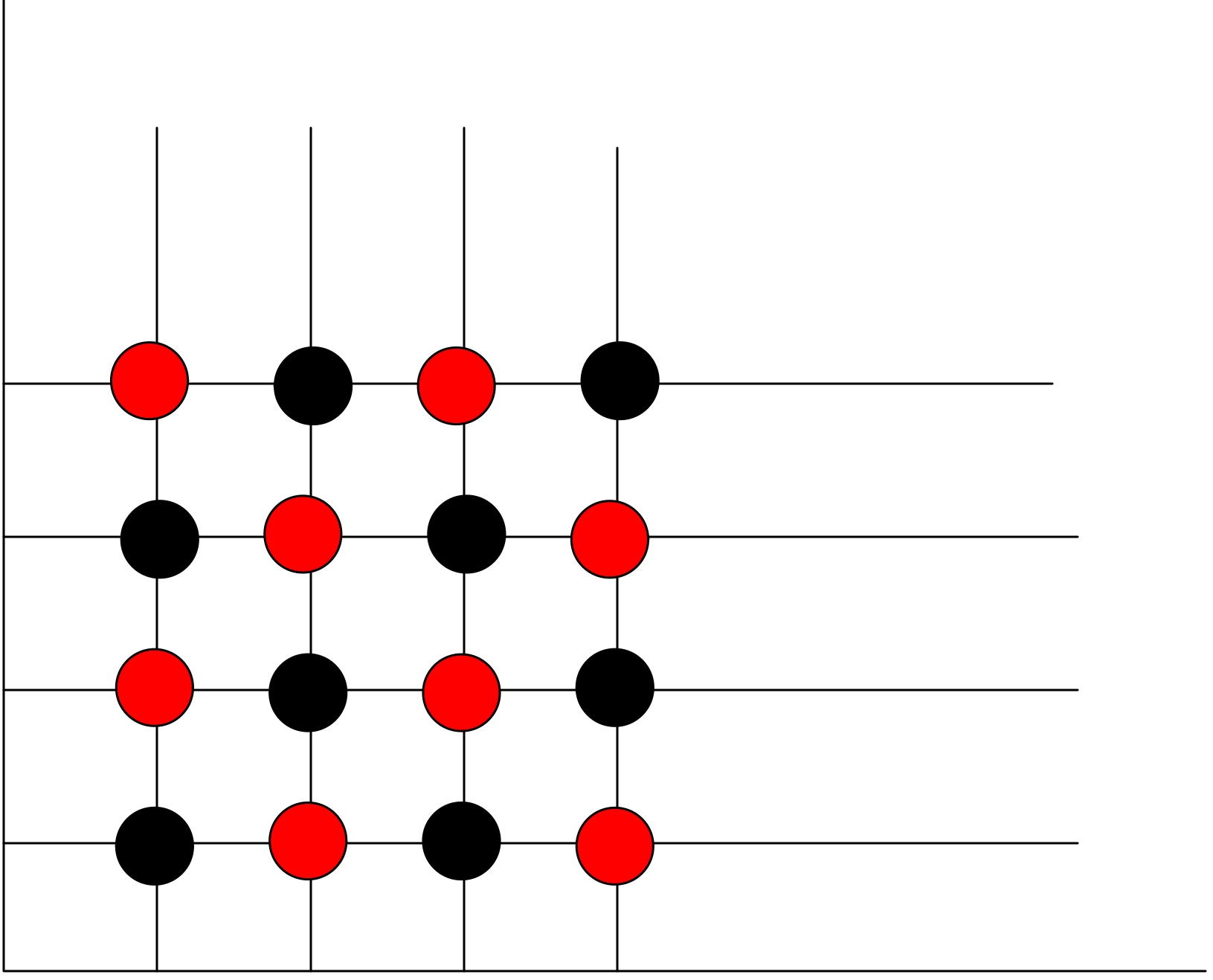
练习 6.29 对二维BVP(4.12)应用红黑排序。画出所产生的矩阵结构。
红黑排序是图形着色(有时称为多重着色)的一个简单例子。在简单的情况下,如我们在第4.2.3节中考虑的单位正方形域或其扩展到三维,邻接图的色数很容易确定;在不太规则的情况下,则比较困难。
练习6.30。你看到了未知数的红黑排序加上有规律的五点星形模版给出了两个变量子集,它们之间没有联系,也就是说,它们形成了矩阵图的双着色。如果节点由图4.3中的第二个模版连接,你能找到一个着色吗?
一般性着色
对于稀疏矩阵的图形所需的颜色数量有一个简单的约束:颜色的数量最多为$d+1$,其中$d$是图形的度数。为了说明我们可以用$d+1$种颜色来给学位为$d$的图形着色,考虑一个学位为$d$的节点。无论它的邻居是如何着色的,在$d+1$种可用的颜色中总有一种未使用的颜色。
练习 6.31 考虑一个稀疏矩阵,该图可以用$d$种颜色来着色。首先列举第一种颜色的未知数,然后列举第二种颜色的未知数,依此类推,对矩阵进行排列。你能说说所产生的排列矩阵的稀疏性模式是什么?
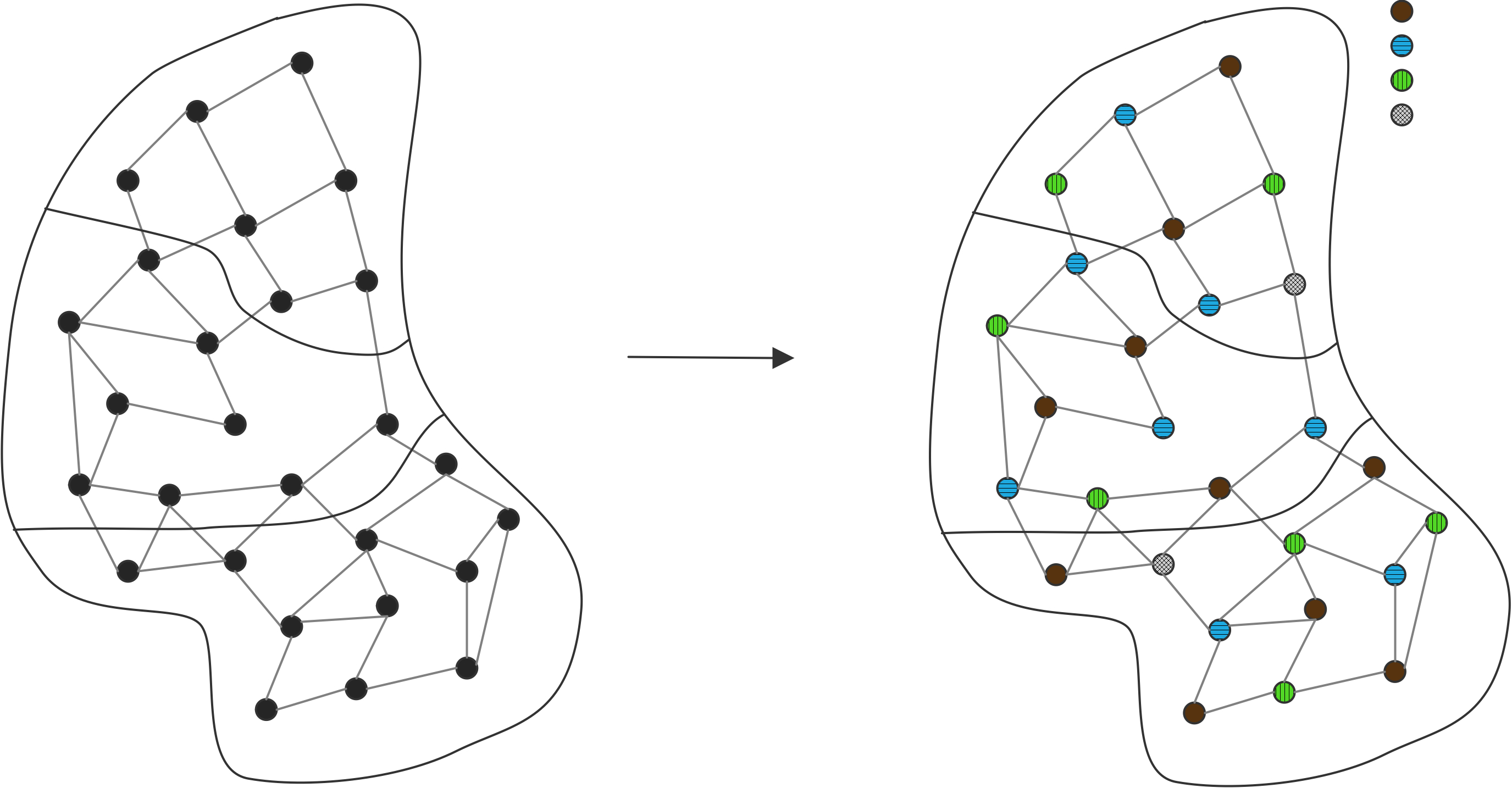
如果你在寻找线性系统的直接解,你可以在消除一种颜色后剩下的矩阵上重复着色和置换的过程。在三对角矩阵的情况下,你看到这个剩余的矩阵又是三对角的,所以很清楚如何继续这个过程。这就是所谓的递归翻倍法。如果矩阵不是三对角的,而是块状三对角的,这个操作可以在块上进行。
多色并行ILU
在第6.8.2节中,你看到了图形着色和包络的结合。让$P$是将相似颜色的变量组合在一起的置换,那么$\tilde{A}=P^tAP$是一个具有如下结构的矩阵。
- $\tilde{A}$具有块状结构,其块数与$A$的头顶相接图中的颜色数相等;并且
- 每个对角线块是一个对角线矩阵。
现在,如果你正在进行迭代系统求解,并且你正在寻找一个并行的预处理程序,你可以使用这个对角的矩阵。考虑到用包络系统来解决$Ly=x$。我们将通常的算法(第5.3.5节)写为
练习 6.32 证明当从自然排序的ILU因式分解到颜色稀释排序的ILU因式分解时,解决系统$LUx=y$的翻转数保持不变(最高阶项)。
这些着色对我们有什么好处?求解仍然是顺序的……嗯,的确,颜色的外循环是顺序的,但是一种颜色的所有点都是相互独立的,所以它们可以在同一时间被求解。因此,如果我们使用普通的域划分,并结合多色彩(见图6.23),处理器在所有的色彩阶段都是活跃的;见图6.24。好吧,如果你仔细看一下这个图,你会发现在最后一个颜色中,有一个处理器没有活动。在每个处理器有大量节点的情况下,这不太可能发生,但可能有一些负载不平衡。
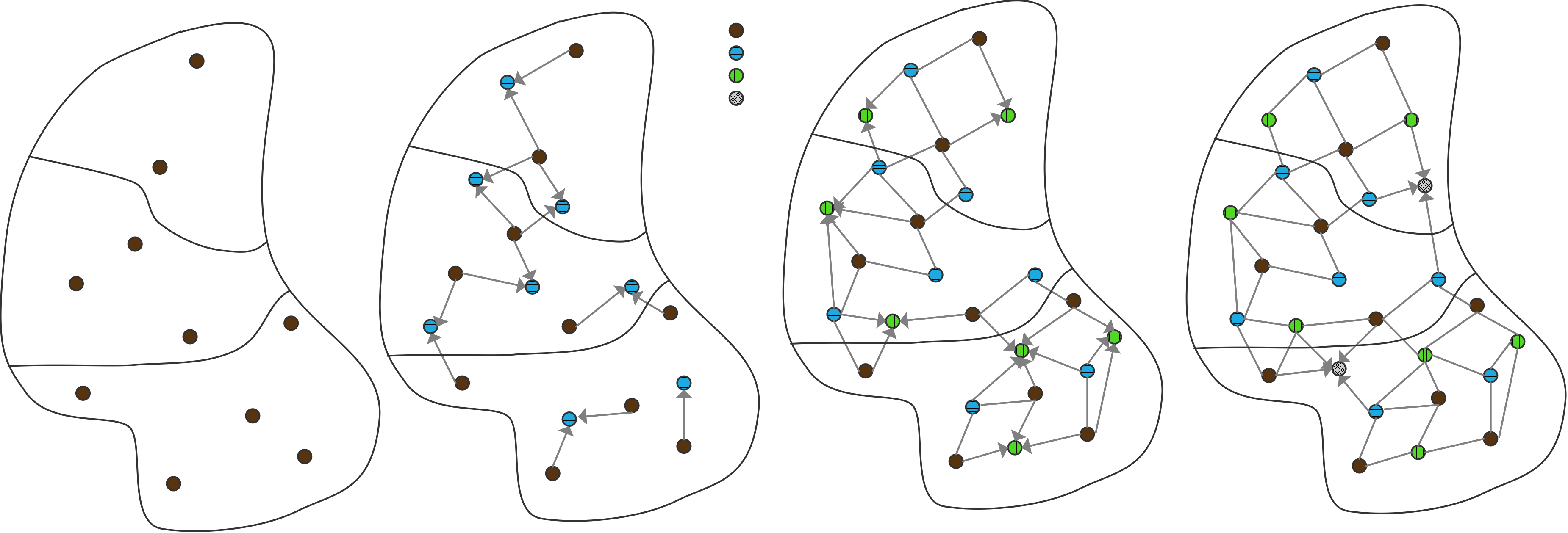
剩下的一个问题是如何并行地生成多色。寻找最佳颜色数是NP-hard。拯救我们的是,我们不一定需要最佳数量,因为我们反正是在做不完全因式分解。(甚至有一种观点认为,使用稍大的颜色数量可以减少迭代的次数)。
[116, 149]发现了一种优雅的并行寻找多色的算法。
- 给每个变量分配一个随机值。
- 找到比所有相邻变量的随机值更高的变量;也就是颜色1。
- 然后找到比所有非1色的邻居有更高随机值的变量。这就是颜色2。
- 反复进行,直到所有的点都被染上颜色。
不规则迭代空间
在显式时间步进的背景下或作为稀疏矩阵-向量乘积,应用计算模版是并行的。然而,在实践中,分割迭代空间可能并非易事。如果迭代空间是直角坐标砖,这很容易,即使是嵌套式的并行。然而,在对称的情况下,要做到均匀的负载分布就比较困难。一个典型的迭代空间看起来像。
1 | for (i=0; i<N; i++) |
在某些情况下(见[22]),界限可能更加复杂,如j=i+i%2或k<max(i+j,N)。在这种情况下,可以做以下工作。
- 循环被遍历,以计算内迭代的总数;这将被分成许多部分,因为有进程。
- 循环被遍历以找到每个过程的开始和结束的$i$、$j$、$k$值。
- 然后重写循环代码,使其能够在这样一个$i,jk$子范围内运行。
缓存效率的排序
模板操作的性能通常相当低。这些操作没有明显的缓存重用;通常它们类似于流操作,从内存中获取长的数据流并只使用一次。如果只做一次模版评估,那就完了。然而,通常我们会做很多这样的更新,我们可以应用类似于1.7.8节中描述的循环叠加的技术。


如果我们考虑到模版的形状,我们可以做得比普通平铺更好。图6.25显示了(左)我们如何首先计算一个包含缓存的时空梯形。然后(右)我们计算另一个建立在第一个梯形上的包含缓存的梯形[71]。
解除PDE线性系统的并行性
PDEs的数值求解是一项重要的活动,所要求的精度往往使其成为并行处理的主要候选者。如果我们想知道我们能做到多大程度的并行,特别是可以达到什么样的速度,我们需要区分问题的各个方面。
首先,我们可以问问题中是否存在任何内在的并行性。在全局层面上,通常不会有这种情况(如果问题的一部分完全不耦合,那么它们将是独立的问题,对吗?)但在较小的层面上,可能存在并行性。
例如,看一下时间相关的问题,参考第4.2.1节,我们可以说每一个下一个时间步骤当然都依赖于上一个时间步骤,但不是下一个时间步骤的每一个单独的点都依赖于上一个步骤的每一个点:有一个影响区域。因此,有可能对问题域进行分区并获得并行性。
操作员拆分
在某些情况下,有必要通过一个二维或三维阵列的所有方向进行隐式计算。例如,在第4.3节中,你看到了热方程的隐式解是如何产生重复系统的
在没有证明的情况下,我们指出,与时间有关的问题也可以通过以下方式解决
为合适的𝛽。这个方案不会在每个单独的时间步长上计算出相同的值,但它会收敛到相同的稳定状态。该方案也可以作为BVP情况下的一个预处理程序。
这种方法有相当大的优势,主要体现在运算次数上:原始系统的求解要么是对矩阵进行因式分解,产生填充,要么是通过迭代求解。
练习 6.33 分析这些方法的相对优点,给出大致的运算次数。考虑$\alpha$对$t$有依赖性和没有依赖性的情况。同时讨论各种操作的预期速度.
当我们考虑(6.3)的并行解时,会出现进一步的优势。注意我们有一个二维的变量集$u$,但是算子$I+d^2u/dx^2$只连接$u_{ij},u_{ij-1},u_{ij+1}$。也就是说,每一行对应的𝑖值都可以被独立处理。因此,这两个算子都可以用一个一维分割域来完全并行地解决。另一方面,(6.2)中系统的求解具有有限的并行性。
不幸的是,有一个严重的问题:$x$方向的算子需要在一个方向上对域进行分割,而𝑦方向的算子则需要在另一个方向上进行分割。通常采取的解决方案是在两个解之间对$u_{ij}$值矩阵进行转置,以便同一处理器的分解可以处理这两个问题。这种转置可能会占用每个时间步骤的大量处理时间。
练习 6.34. 讨论使用$P=p\times p$处理器的网格对域进行二维分解的优点和问题。你能提出一个方法来改善这些问题吗?加快这些计算的一个方法是用显式操作代替隐式求解;见6.10.3节。
并行性和隐式操作
在关于IBVP的讨论中(第4.1.2.2节),你看到从数值稳定性的角度来看,隐式运算有很大的优势。然而,你也看到,它们使基于简单操作(如矩阵-向量乘积)的方法与基于更复杂的线性系统求解的方法之间的区别。当你开始并行计算时,隐式方法会有更多的问题。
练习 6.35 设𝐴为矩阵
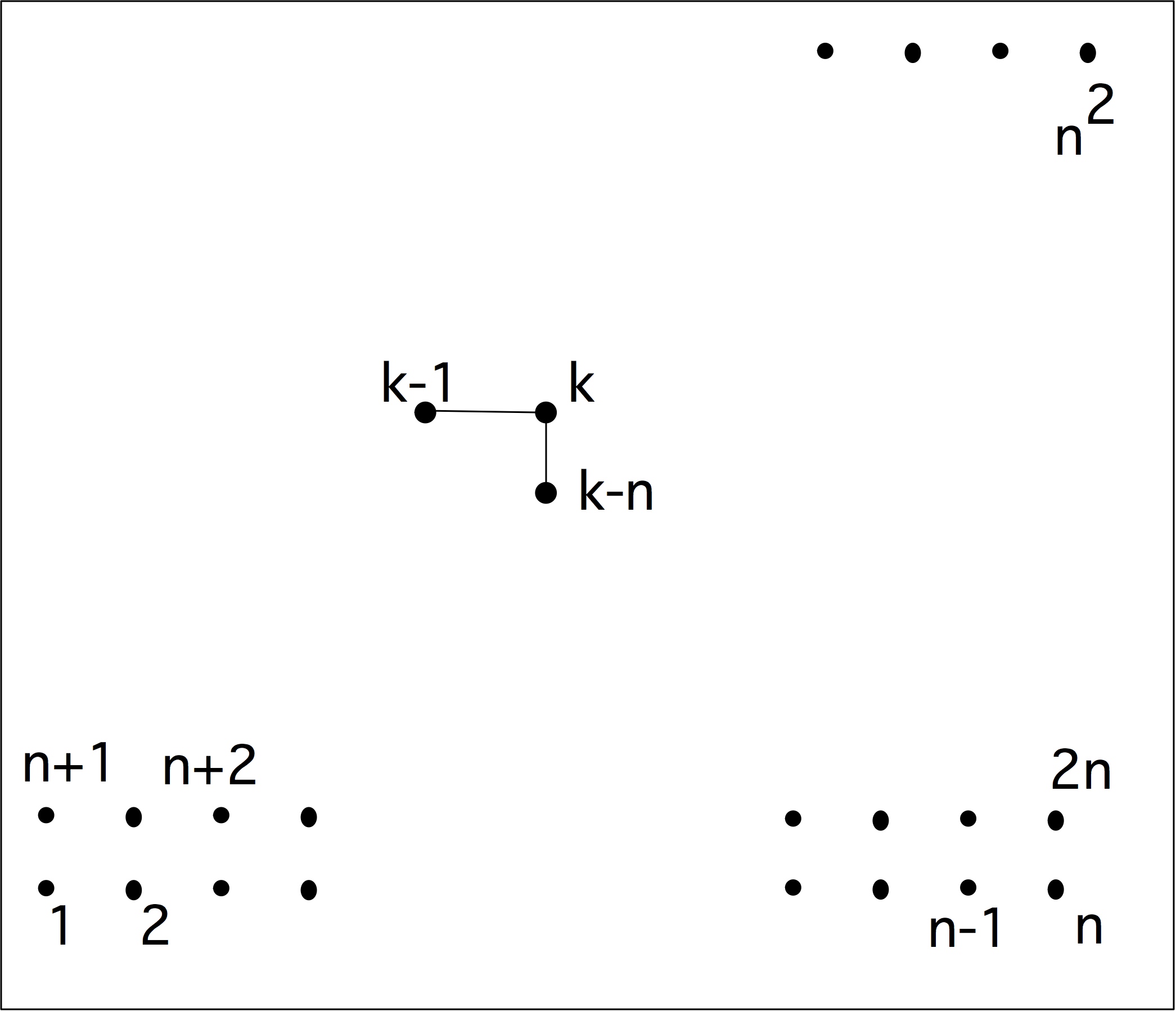
证明矩阵向量乘积$y\leftarrow Ax$ 和系统解决方案$x\leftarrow A^{-1}y$ ,通过解决三角系统$Ax=y$,而不是通过反转 $A$ 得到,具有相同的操作数。 现在考虑将乘积$y\leftarrow Ax$ 并行化。假设我们有$n$处理器,每个处理器$i$存储$x$和$A$的第$i$行。证明除了第一个处理器外,任何一个处理器都可以在没有闲置时间的情况下计算出𝐴𝑥的结果。
三角形系统$Ax=y$的解也可以这样做吗?显示出直接的实现方式是每个处理器在计算过程中都有$(n-1)/n$的空闲时间。现在我们将看到一些处理这个固有的顺序部分的方法。
波峰
上面,你看到解决一个大小为$N$的下三角系统,其顺序时间复杂度为$N$步。在实践中,事情往往没有那么糟糕。像解三角系统这样的隐式算法本身就是顺序的,但步骤数可能比一开始看到的少。
练习 6.36 再看一下单位面积上的二维BVP的矩阵,用中心差分法进行离散。如果我们按对角线排列未知数,请推导出矩阵结构。对于区块的大小和区块本身的结构,你能说什么?
让我们再看一下图4.1,它描述了二维BVP的有限差分模版。图6.26是下三角因子的模版的相应图片。这描述了下三角解过程的顺序性$x\leftarrow L^{-1}y$ 。
换句话说,如果点$k$的左边(即变量$k-1$)和下面(变量$k-n$)的邻居是已知的,就可以找到它的值。
下方(变量$k-n$)是已知的。
反过来,我们可以看到,如果我们知道$x_1$,我们不仅可以找到$x_2$,还可以找到$x_{n+1}$。在下一步,我们可以确定$x_3$、$x_{n+2}$和$x_{2n+1}$。继续这样下去,我们可以通过波阵来解决$x$:每个波阵上的$x$的值都是独立的,所以它们可以在同一个顺序步骤中被平行解决。
练习 6.37 完成这个论证。我们可以使用的最大处理器数量是多少,顺序步骤的数量是多少?最终的效率是多少?
当然,你不需要使用实际的并行处理来利用这种并行性。相反,你可以使用一个矢量处理器、矢量指令或GPU[148]。
在第5.4.3.5节中,你看到了用于减少矩阵填充的Cuthill-McKee排序。我们可以对这个算法进行如下修改,以得到波阵。
- 取一个任意的节点,并称其为 “零级”。
- 对于第$n+1$级,找到与第$n$相连的点,这些点本身并不相连。
- 对于所谓的 “反向Cuthill-McKee排序”,将层次的编号倒过来。
练习 6.38 这个算法并不完全正确。问题出在哪里,你如何纠正?证明所产生的变换矩阵不再是三对角的,但可能仍有一个带状结构。
递推式翻倍
递归$y_{i+1}=a_iy_i+b_i$, 例如在解双线性方程组时出现的情况(见练习4.4), 似乎是内在的顺序性。然而,你已经在练习1.4中看到,以一些初步操作为代价,计算是可以并行化的。
首先,从(6.4)中获取一般的双线性矩阵,并将其扩展为规范化的形式。
我们把它写成$A=I+B$。
练习 6.39 说明可以通过与对角线矩阵相乘来实现对归一化形式的缩放。解决系统$(I+B)x=y$对解决$Ax=y$有什么帮助?以两种不同的方式求解该系统的运算量是多少?
现在我们做一些看起来像高斯消除的事情,只是我们不从第一行开始,而是从第二行开始。(如果你对矩阵$I+B$进行高斯消除或LU分解,会发生什么?) 我们用第二行来消除$b_{32}$。
我们把它写成$L^{(2)}A=A^{(2)}$。我们还计算了$L^{(2)}y=y^{(2)}$,因此$A^{(2)}x=y^{(2)}$与$Ax=y$有相同的解。解决转换后的系统让我们得到了一点好处:在我们计算了$x_1$之后,$x_2$和$x_3$可以被并行计算。
现在我们重复这个消除过程,用第四行来消除$b_{54}$,第六行来消除$b_{76}$,等等。最后的结果是,总结所有$L(i))$矩阵。
我们把它写成$L(I+B)=C$,而解决$(I+B)x=y$现在变成了$C=L^{-1}y$。
这个最终结果需要仔细研究。
- 首先,计算$y=L^{-1}y$很简单。(弄清楚细节,有多少并行性可用?)
- 解决$Cx=y’$仍然是顺序的,但它不再需要$n$步骤:从$x_1$我们可以得到$x_3$,从那里我们得到$x_5$,等等。换句话说,$x$的奇数部分之间只存在顺序关系。
- $x$的偶数部分并不相互依赖,而只依赖奇数部分。$x_2$来自$x_1$,$x_4$来自$x_3$,依此类推。一旦奇数部分被计算出来,这一步就是完全并行的。
我们可以自行描述奇数部分的顺序解法。
其中$c_{i+1i}=-b_{2n+1,2n}b_{2n.2n-1}$。换句话说,我们已经将一个大小为$n$的顺序问题简化为一个大小为同类的顺序问题和一个大小为$n/2$的并行问题。现在我们可以递归地重复这个过程,将原来的问题还原为一连串的并行操作,每一个都是前者的一半大小。
通过递归加倍计算所有部分和的过程也被称为并行前缀操作。这里我们使用前缀和,但在抽象的情况下,它可以应用于任何关联运算符。
通过显性操作逼近隐性操作,系列扩展
如上所述,隐式运算在实践中是有问题的,有各种原因允许用另一种实际上更有利的方法来代替隐式运算。
- 只要我们遵守显式方法的步长限制,用显式方法代替隐式方法(第4.3节)同样是合法的。
- 在迭代方法中修补预处理程序(第5.5.8节)是允许的,因为它只会影响收敛速度,而不会影响方法收敛到的解。你已经在块状雅可比方法中看到了这个一般想法的一个例子;6.7.3节。在本节的其余部分,你将看到预处理程序中的递归,即隐式操作,如何被显式操作所取代,从而带来各种计算优势。
求解线性系统是隐式运算的一个很好的例子,由于这归结为求解两个三角形系统,让我们来看看如何找到替代求解下三角系统的计算方法。如果𝑈是上三角且非 Singular,我们让𝐷是𝑈的对角线,我们写成𝑈 = 𝐷(𝐼 - 𝐵) 其中𝐵是一个对角线为零的上三角矩阵,也称为严格上三角矩阵;我们说𝐼 - 𝐵是一个单位上三角矩阵。
练习 6.40 设$A=LU$是一个LU分解,其中$L$的对角线上有1。说明如何解决$Ax=b$的问题,只涉及单位上下三角系统的解决。证明在系统求解过程中不需要除法。
我们现在感兴趣的操作是解决系统$(I-B)x=y$。我们观察到
和$B^n=0$,其中$n$是矩阵的大小(检查这个!),所以我们可以通过以下方法精确求解$(I-B)x=y$。
当然,我们希望避免明确计算幂$B^𝑘$,所以我们观察到
诸如此类。由此产生的评估$\sum_{k=0}^{n-1}B^ky$的算法被称为霍纳规则,你看它避免了计算矩阵幂$B^k$。
练习 6.41 假设$I - B$是二对角线。证明上述计算需要$n(n+1)$操作。通过三角解法计算$(I-B)x=y$的操作数是多少?
我们现在已经把隐式运算变成了显式运算,但不幸的是,这种运算的次数很高。然而,在实际情况下,我们可以截断矩阵的功率之和。
练习 6.42 设$A$为三对角矩阵
4.2.2节中的一维BVP。
回顾5.3.4节中对角线支配的定义。这个矩阵是对角线主导的吗?
证明该矩阵的LU因子化中的枢轴(无枢轴)满足递归。提示:说明经过$n$消除步骤($n\geqslant 0$)后,剩余的矩阵看起来像
并说明$d_{n+1}$与$d_n$之间的关系。
证明序列$n\mapsto d_n$是递减的,并推导出其极限值。
- 写出以$L$和$U$为单位的$d_n$枢轴的系数。
- $L$和$U$因子是对角线主导的吗?
上述练习意味着(注意,我们实际上并没有证明!),对于来自BVP的矩阵,我们发现$B^k \downarrow 0$,在元素大小和规范方面都是如此。这意味着我们可以用诸如$(I-B)x=y$的方法来近似地计算$(I+B)y$或者$x=(I+B+B^2)y$。这样做仍然比直接三角解法有更多的操作数,但至少在两个方面有计算上的优势。
- 显式算法有更好的流水线行为。
- 正如你所看到的,隐式算法在并行时有问题;显式算法更容易并行化。
当然,这种近似可能对整个数值算法的稳定性有进一步的影响。
练习 6.43 描述霍纳法则的并行性方面;方程(6.6)。
网格更新
第四章的结论之一是,时间相关问题的显式方法在计算上比隐式方法容易。例如,它们通常涉及矩阵-向量乘积而不是系统解,而且显式操作的并行化相当简单:矩阵-向量乘积的每个结果值都可以独立计算。这并不意味着还有其他值得一提的计算方面。
由于我们处理的是稀疏矩阵,源于一些计算模版,我们从操作者的角度出发。在图6.11和6.12中,你看到了在域的每一点上应用模版是如何引起处理器之间的某些关系的:为了在一个处理器上评估矩阵-向量乘积$y\leftarrow A$,该处理器需要获得其幽灵区域的$x$的值。在合理的假设下,在处理器上划分领域,涉及的信息数量将相当少。
练习 6.44 推理一下,在有限元或有限元分析的背景下,当$h\downarrow 0$时,信息的数量是$O(1)$。
在第1.6.1节中,你看到矩阵-向量乘积几乎没有数据重用,尽管计算有一定的位置性;在第5.4.1.4节中指出,稀疏矩阵-向量乘积的位置性更差,因为稀疏性必须有索引方案。这意味着稀疏乘积在很大程度上是一种受带宽限制的算法。
只看一个单一的乘积,我们对此没有什么办法。然而,我们经常连续做一些这样的乘积,例如作为一个随时间变化的过程的步骤。在这种情况下,可能会对操作进行重新安排,以减少对带宽的需求。作为一个简单的例子,可以考虑
并假设集合$\{x(n)\}$太大,无法装入缓存。这是一个模型,例如,在一个空间维度上热方程的显式$i$方案;4.3.1.1节。从原理上讲。
在普通计算中,我们先计算所有$x(n+1)$,然后再计算所有$x(n+2)$,在$n+1$级别的中间值产生后会从缓存中刷掉,然后再作为$n+2$级别数量的输入带回缓存中。
然而,如果我们计算的不是一个,而是两个迭代,中间值可能会留在缓存中。考虑到$x(n+2)$:它需要$x(n+1)$、$x(n+1)$,而后者又需要$x(n)$、…, $x(n)$。
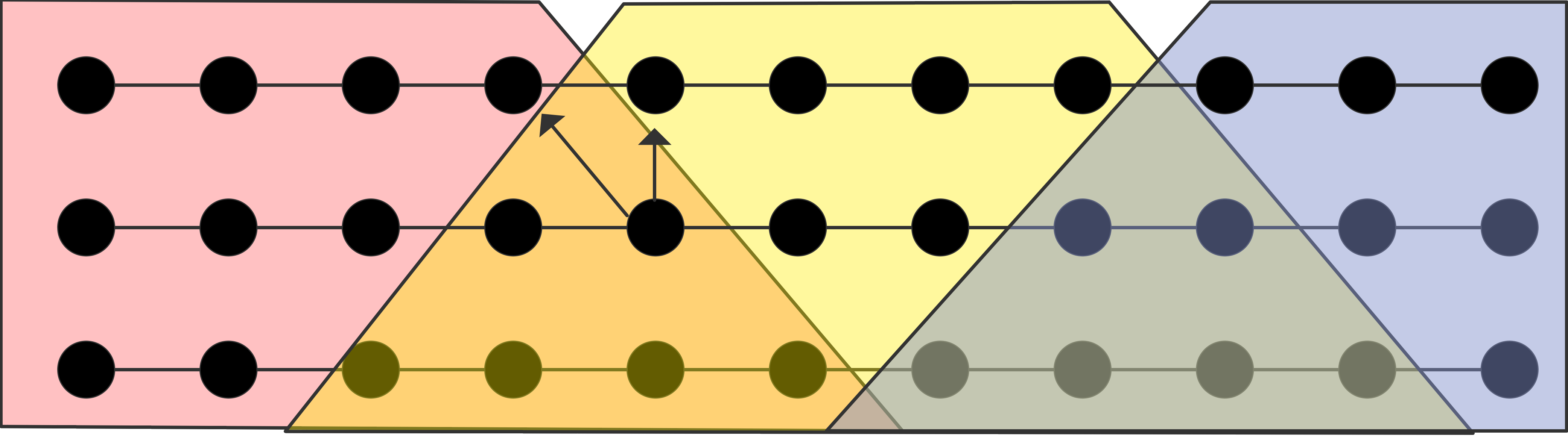
现在假设我们对中间结果不感兴趣,而只对最后的迭代感兴趣。图 6.27 是一个简单的例子。第一个处理器计算了$n+2$层的4个点。为此,它需要从$n+1$层计算5个点,而这些点也需要从$n$层的6个点中计算出来。我们看到,一个进程显然需要收集一个宽度为2的重影区域,而常规的单步更新只需要一个。第一个处理器计算的一个点是$x(n+2)$,它需要$x(n+1)$。这个点也需要用于计算$x(n+2)$,属于第二个处理器。
最简单的解决方法是让中间层的这种点冗余计算,在需要它的两个区块的计算中,在两个不同的处理器上进行。
练习 6.45 你能想到一个点会被两个以上的处理器冗余计算的情况吗?
我们可以对这种按块计算多个更新步骤的方案给出几种解释。
- 首先,如上所述,用一个处理器进行计算可以增加locality:如果一个彩色块中的所有点(见图)都适合于缓存,我们就可以重复使用中间的点。
- 其次,如果我们把它看作是分布式内存计算的化学反应,它减少了信息流量。通常,对于每一个更新步骤,处理器都需要交换他们的边界数据。如果我们接受一些多余的重复工作,我们现在可以消除中间层的数据交换。通信的减少通常会超过工作的增加。
练习 6.46 讨论一下在多核计算中使用这种策略的情况。有哪些节省?有哪些潜在的隐患?
分析
让我们分析一下我们刚刚勾画的算法。如同方程(6.7),我们把自己限制在一个一维的点集和一个三点的函数。描述这个问题的参数是这样的。
$N$是要更新的点的数量,$M$表示更新步骤的数量。因此,我们进行$MN$函数评估。
$\alpha, \beta, \gamma$是描述延迟、单点传输时间和操作时间(这里认为是$f$评价)的通常参数。
$b$是我们挡在一起的步骤数。
每个光环通信由$b$点组成,我们这样做$\sqrt{N}/b$多次。所做的工作包括$MN /p$局部更新,再加上由于晕轮而产生的冗余工作。后者包括$b^2/2$个操作,在处理器域的左边和右边都进行。
将所有这些条款加在一起,我们发现成本为
我们观察到,$\alpha M/b+\gamma Mb$的开销是与$p$无关的。
练习 6.47 计算$b$的最优值,并指出它只取决于结构参数$\alphaa, \beta,\gamma$而不取决于问题参数。
沟通和工作最小化战略
我们可以通过将计算与通信重叠来使这个算法更有效率。如图6.28所示,每个处理器从通信其光环开始,并将此通信与可在本地完成的通信部分重叠。然后,依赖于光环的值将被最后计算。
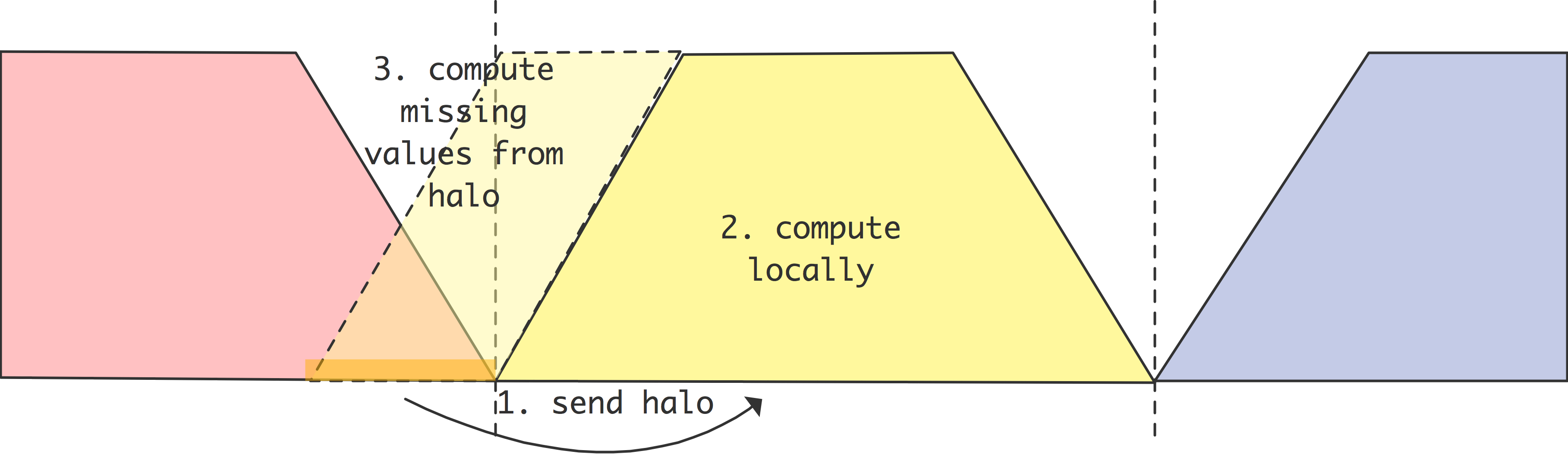
练习 6.48 这样组织你的代码(重点是’代码’!)有什么大的实际问题?
如果每个处理器的点数足够大,那么相对于计算来说,通信量就很低,你可以把$b$拿得相当大。然而,这些网格更新大多用于迭代方法,如CG方法(第5.5.11节),在这种情况下,对舍入的考虑使你不能把$b$拿得太大[32]。
练习 6.49 在点被组织成二维网格的情况下,通过对非重叠算法的复杂性分析。假设每个点的更新涉及四个邻居,每个坐标方向上有两个邻居。
上述算法的进一步细化是可能的。图6.29说明有可能使用一个使用不同时间步骤的不同点的晕区。这种算法(见[42])减少了冗余的计算量。然而,现在需要先计算交流的光环值,所以这需要将本地交流分成两个阶段。
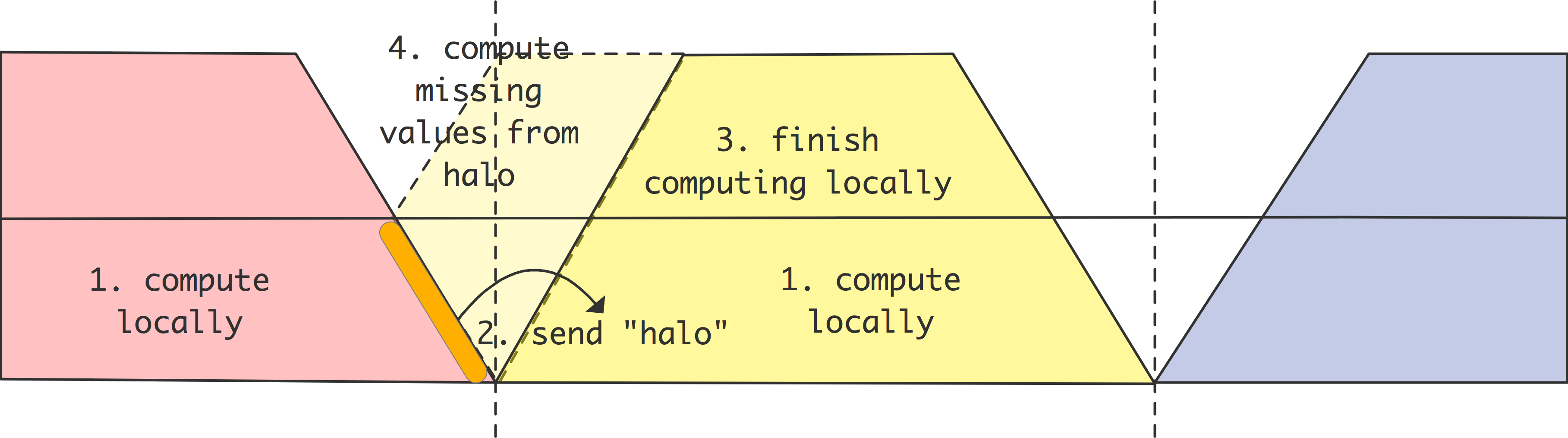
多核架构上的块状算法
在第5.3.7节中,你看到某些线性代数算法可以用子矩阵来表述。这个观点对于在共享内存架构(如目前的多核处理器)上高效执行线性代数操作是有益的。
作为一个例子,让我们考虑Cholesky因式分解,它计算$A=LL^t$为一个对称的正定矩阵。
正定矩阵$A$;另见5.3.2节。递归地,我们可以将该算法描述如下。
其中 $\tilde{A}_{21}=A_{21} L_{11}^{-t}, A_{11}=L_{11} L_{11}^{t}$
在实践中,区块实现被应用于一个分区
其中𝑘是当前块行的索引,对于所有索引$<k$,因式分解已经完成。因式分解的写法如下,用Blas的名字表示操作。
并行性能的关键是对指数$>k$进行分区,并以这些块为单位编写算法。
该算法现在得到了一个额外的内循环级别。
现在很明显,该算法具有很好的并行性:每个l环的迭代都可以独立处理。然而,这些循环在外层$k$-循环的每一次迭代中都会变短,所以我们能容纳多少个处理器并不直接。此外,没有必要保留上述算法的操作顺序。例如,在
因式分解$L_2L_2^t=A_{22}$可以开始,即使剩下的$k = 1$迭代仍未完成。因此,比起我们仅仅对内循环进行并行化,可能存在着更多的并行性。
在这种情况下,处理并行性的最好方法是将算法的控制流观点(其中操作顺序是规定的)转变为数据流观点。在后者中,只有数据的依赖性被指出,而且任何服从这些依赖性的操作顺序都是允许的。(从技术上讲,我们放弃了任务的程序顺序,代之以部分排序5) 。表示算法的数据流的最好方法是构建一个任务的有向无环图(DAG)(见第18节关于图的简要教程)。如果任务𝑗使用了任务$i$的输出,我们就在图中添加一条边$(i, j)$。
练习 6.50 在2.6.1.6节中,你学到了顺序一致性的概念:一个线程化的并行代码程序在并行执行时应该给出与顺序执行时相同的结果。我们刚刚说过,基于DAG的算法可以自由地以任何服从图节点的部分顺序来执行任务。讨论一下在这种情况下,顺序一致性是否是一个问题。
在我们的例子中,我们通过为每个内部迭代制定一个顶点任务来构造一个DAG。图6.30显示了4×4块的矩阵的所有任务的DAG。这个图是通过模拟上面的Cholesky算法构建的。
练习 6.51 这个图的直径是多少?识别出位于决定直径的路径上的任务。这些任务在该算法中的意义是什么?这条路径被称为关键路径。它的长度决定了并行计算的执行时间,即使有无限多的处理器可用。
练习 6.52 假设有$T$个任务,都需要一个单位时间来执行,并假设我们有$p$个处理器。理论上执行该算法的最小时间是多少?现在修改这个公式以考虑到关键路径;称其长度为$C$。
在执行任务的过程中,一个DAG可以有几个观察点。
- 如果有一个以上的更新被加载到锁上,那么让这些更新由同一个进程来计算,可能会更有优势。这样可以简化维护缓存一致性的工作。
- 如果数据被使用并随后被修改,那么在修改开始之前必须完成使用。如果这两个动作是在不同的处理器上进行的,这甚至可能是真的,因为内存子系统通常会保持缓存一致性,所以修改会影响正在读取数据的进程。这种情况可以通过在主内存中有一个数据的拷贝来补救,给读取数据的进程保留一个数据(见1.4.1节)。