CS267 并行计算应用课程笔记

Posted on 2021-12-17 Edited on 2021-12-26

https://sites.google.com/lbl.gov/cs267-spr2020/

lecture 2

单处理器上大部分性能被浪费，主要是因为数据迁移时间太久。

编译器管理内存和寄存器，进行寄存器分配，决定什么时候load/store，什么时候重用。编译器通过图染色的方式决定寄存器重用。

编译器的优化：

循环展开、合并、重排
删除死代码
指令重排来实现指令流水、提高寄存器重用
代码强度降低，比如把乘法变成移位

多级cache：
- 片上cache更快，但是更小。
- 更大的cache有延迟，硬件需要更长的时间来检查地址，更多关联度也会延长时间
- 可以利用第四级cache作为被置换出的cache的cache

其他的cache包括：寄存器，TLB等。

处理内存延迟：
- 在小而快的内存中保存数据并重用
- 将一整块数据存入内存并使用
- 程序利用向量化实现一条指令进行多次读或写
- 程序预取或者延迟写

blocking或者tiling是提高cache性能的好办法，使用分治将问题分割到适合cache的大小。

SSE、SSE2：适合16bytes的类型，比如4个float、2个double或者16个byte。可以并行执行加、乘。但是需要对齐，连续。

矩阵是2维数组，在存储上需要根据cache的特性存储，Fortran是列优先，对cache不友好。采用分块的方法进行并行化，存在理论上的最优化分块方法。这种算法就需要在递归时适当地切割。

func C = RMM(A, B, n)
    if n = 1
        C = A * B
    else {
        C11 = RMM(A11, B11, n/2) + RMM(A12, B21, n/2);
        C12 = RMM(A11, B12, n/2) + RMM(A12, B22, n/2);
        C21 = RMM(A21, B11, n/2) + RMM(A22, B21, n/2);
        C22 = RMM(A21, B12, n/2) + RMM(A22, B22, n/2);
    }
    return

递归的数据分布，可以提高数据局部性，最小化内存延迟，例如画Z字的方式，或者看“cache oblivious algorithm”。好处是可以在任何cache大小下实现较好的性能，不好的是计算index很困难。

删除假的依赖，比如使用局部变量，进行指令重排：

1 2	a[i] = b[i] + c; a[i+1] = b[i+1] * d;

可能会有假的数据依赖，借助局部变量改成

float f1 = b[i];
float f2 = b[i+1];

a[i] = f1 + c;
a[i+1] = f2 * d;

或者对频繁使用的变量进行预先加载，使寄存器中保持有变量。

循环展开促进指令级并行，提高流水线性能，或者向量化。

再设计数据结构时注意cache局部性，比如多使用struct。

strassen’s矩阵乘法，将8次乘+4次加优化到7次乘+18次加，能做到O(n^2.81)：

Let M = | m11 m12| = |a11 a12| |b11 b12|
        | m21 m22|   |a21 a22| |b21 b22|

Let p1 = (a12 - a22) * (b21 + b22)
    p2 = (a11 + a22) * (b11 + b22)
    p3 = (a11 - a21) * (b11 + b12)
    p4 = (a11 + a12) * b22
    p5 = a11 * (b12 - b22)
    p6 = a22 * (b21 - b11)
    p7 = (a21 + a22) * b11

Then m11 = p1 + p2 - p4 + p6
     m12 = p4 + p5
     m21 = p6 + p7
     m22 = p2 - p3 + p5 - p7

其他一些矩阵矩阵乘算法：

世界纪录是O(n^2.37548)
2.37548 reduced to 2.37293
- Virginia Vassilevska Williams, UC Berkeley & Stanford, 2011
2.37293 reduced to 2.37286
- Francois Le Gall, 2014
大概能做到O(n^2+e)
- Cohn, Umans, Kleinberg, 2003

CNN在计算什么？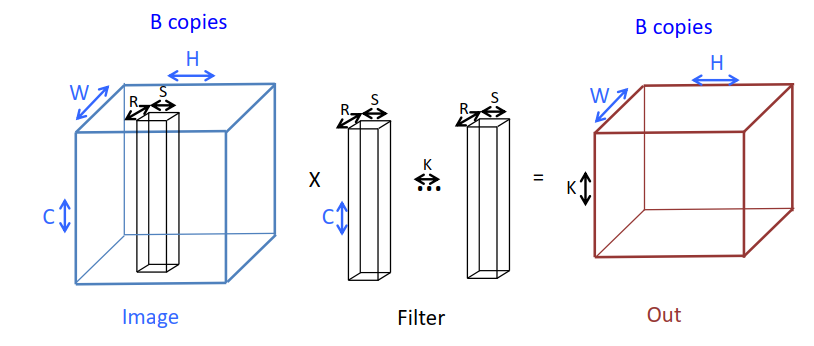

1
2
3

for k=1:K, for h=1:H, for w=1:W, for r=1:R,
    for s=1:S, for c=1:C, for b=1:B
        Out(k, h, w, b) += Image(r+w, s+h, c, b) * Filter( k, r, s, c )

lecture 3

几种并行的模型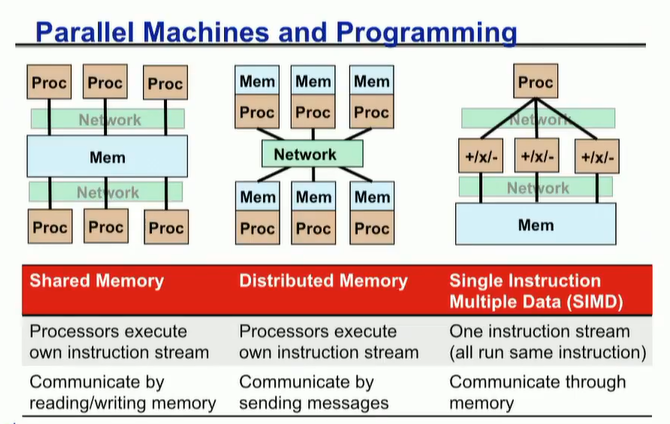

如何并行化下边的程序，每一个y依赖于前一个：

1
2
3

y[0] = 0;
for i = 1 : n
    y[i] = y[i-1] + x[i];

这个图应该是以树形计算前缀和的示意图，最上边是原始数组，中间是逐次计算两两和，最下边是最终结果。

lecture 4

SIMD：数据并行的语言非常成功，不规则的数据（稀疏矩阵乘向量）比较适配，但是不规则的计算（分治、递归等）不太行。

共享内存多处理器时代，出现了一些共享内存模型，POSIX Threads、OpenMP等

集群时代，出现了MPI。

每个线程有一些私有变量，如本地栈。也有一些共享的变量，如通过malloc的变量，静态变量等。线程通过读写共享变量实现数据通信。

pthreads是POSIX线程接口，用来创建和同步线程，但是没有对通信的显示支持，因为共享内存是隐式的。pthread_join意思是等待，直到线程结束。创建线程的开销是不能被忽略的，因为涉及了系统调用。

int pthread_create(pthread_t*, const pthread_attr_t*, void *(*)(void*), void*);

int main() {
    pthread_t threads[16];
    int tn;
    for (tn = 0; tn < 16; tn ++)
        pthread_create(&threads[tn], NULL, function, NULL);
    for (tn = 0; tn < 16; tn ++)
        pthread_join(threads[tn], NULL);
    return 0;
}

数据竞争即为各个线程竞争同一个变量。

mutexes是互斥锁。当线程需要访问一个变量时，需要加锁。信号量允许k个线程同时访问资源，适用于有限个资源的时候。

pthread_mutex_t amutex = PTHREAD_MUTEX_INITIALIZER;
// or pthread_mitex_init(&amutex, NULL);

int pthread_mutex_lock(amutex);
int pthread_mutex_unlock(amutex);

POSIX线程基于OS，可以被多种语言使用，但是创建线程的开销大，数据竞争的bug也有很多。

openmp有C/C++和Fortran的接口：

预处理指令
库函数
环境变量

它是一个方便的线程级内存共享编程工具，允许把程序分成穿兴趣和并行区，而不是纯线程。也不需要进行栈的管理，提供了同步命令。

最经常用的OpenMP命令如下：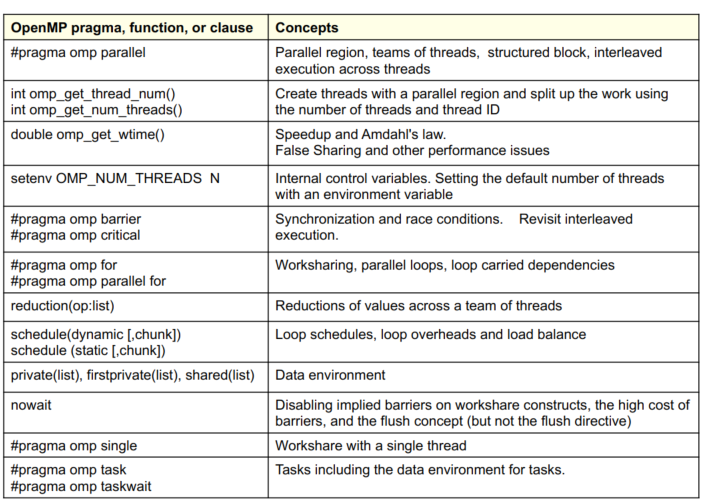

OpenMP的基本语法：

#pragma omp construct [clause [clause]...]

#pragma omp parallel private(x) 
{
}

#include <omp.h>

OpenMP使用的是fork-join模型，主线程派生一系列线程，等待子线程结束后继续执行，遇到需要多线程的代码块时再fork线程。

double A[1000];
omp_set_num_threads(4);
#pragma omp parallel
{
    int id = omp_get_thread_num();
    pooh(id, A);
}

各个线程共享A数组，但是每个线程都有一个id变量。

可以通过omp_get_thread_num请求创建多少个线程，但不是你要创建多少线程就是多少线程，一旦请求了一个数量的线程数并创建，系统就不会减少这个数量。

static long num_steps = 100000;
double step;
int main()
{
    double pi, sum = 0.0;
    step = 1.0/(double)num_steps;

    #pragma omp parallel
    {
        int i, id, nthreads;
        double x;
        id = omp_get_thread_num();
        nthrds = omp_get_num_threads();
        if (id == 0)
            nthreads = nthrds;
        for (i = id; i < num_steps; i += nthrds) {
            x = (i+0.5) / step;
            sum[id] += 4 / (1.0 + x*x);
        }
    }
    for (i = 0; i < nthreads; i ++)
        pi += step * sum[i];
}

每个处理器有自己的多级cache，多处理器系统中存在cache一致性问题。内存中的一个数字被放到处理器P1的cache中，又被放到P2的cache中，如果P1修改了数字，P2是不知道的，这样就不一致了。写回策略中，数据被写回是取决于什么时候，被哪个处理器写回的。

使用cache一致性协议来写回，但是在多处理器中并不具有可扩展性。

内存总线是一个广播的机制，cache中保存着它们存在哪个地址，cache控制器监控着总线上的所有cache事务，一个事务是一个相关的事务，如果涉及的cache行在本地处理器的cache中。

如果独立的数据元素碰巧位于同一个缓存行上，每次更新都会导致缓存行在线程之间“来回晃动”……这称为“假共享”。

如果将标量提升到数组以支持创建 SPMD 程序，则数组元素在内存中是连续的，因此共享缓存行导致可扩展性较差。解决方案：填充数组，以便您使用的元素位于不同的缓存行上。

同步用于施加顺序约束并保护对共享数据的访问，包括：

互斥区
barrier

被互斥区包裹起来的部分每次只能有一个线程访问，barrier是直到所有线程都到这个barrier了才一起往下执行。

for循环可以被并行化，其中的i是默认私有的，各个线程等到for循环完成后再一起执行：

#pragma omp parallel
{
    #pragma omp for
    for (i = 0; i < N; i ++) {

    }
}

schedule命令决定了任务怎么映射到每个进程。有static和dynamic两种，static是静态的，在编译时决定；dynamic会动态调度或者从任务队列中分配，在执行过程中决定。

reduction即规约，进行最大、最小、平均等操作。每一个列表中的变量会被复制到每个线程，并初始化，对局部变量进行操作，局部变量再规约到主线程。

1	#pragma omp parallel for reduction (+:ave)

因为barrier很耗时，而for循环结束之前都会有一个默认的barrier，所以可以在for循环之前使用nowait实现不barrier。

可以针对不同变量选择不同的共享策略，比如：shared、private(为变量创建一个本地拷贝，且不初始化，且原来的全局变量不变)、firstprivate。

#pragma omp parallel for private(tmp)
int tmp = 0;
for (int j = 0; j < 1000; j ++)
    tmp += j;
printf("%d\n", tmp); // tmp为0

default(none)强制您为出现在范围内的变量定义存储属性……如果失败，编译器会报错。可以将default子句放在parallel 和parallel + workshare 结构上。j和y没有规定存储策略，编译器会报错。

#pragma omp parallel for default(none) reduction(*:x)
for (i = 0; i < N; i ++)
    for (j = 0; j < 3; j ++)
        x += foobar(i, j, y);

tasks是一系列独立的work，由执行代码和计算的数据组成，线程被分配执行每个task的工作。

下例中组成一个task的二叉树，直到一个task之前的所有task被完成，这个task才能被完成。

int fib(int n) {
    int x, y;
    if (n < 2) return n;

#pragma omp task shared(x);
    x = fib(n-1);
#pragma omp task shared(y);
    y = fib(n-2);
#pragma omp taskwait;
    return x+y;
}

int main()
{
    int NM = 5000;

    #pragma omp parallel
    {
        #pragma omp single
        fib(NM);
    }
}

single表示这个代码块只能被一个线程执行，这个代码块之后有一个默认的barrier。

flush操作

定义一个序列点，在该点线程强制执行一致的内存视图。
对于其他线程可见并与刷新操作（flush-set）相关联的变量
- 编译器不能在刷新周围进行刷新集的加载/存储：
- 该线程之前对flush-set 的所有读/写都已完成
- 没有发生此线程对刷新集的后续读/写
- 刷新集中的变量从临时存储移动到共享内存。
- 刷新后刷新集中变量的读取从共享内存加载

lecture 5

使用性能模型或工具，以预测架构的性能。需要假定运行时间与需要的运算、数据移动的次数相关，其中，数据移动的次数更相关，因为需要理解cache的行为。

串行机器在访问内存时会遇到延迟，而并行机器在同步、点对点通信、规约时会遇到延迟，所以可以使用算法的依赖链进行分类。

数据移动复杂性

假设运行时间与访问（或移动）的数据量相关
易于计算访问的数据量……计数数组访问
移动的数据更加复杂，因为它需要了解缓存行为……

计算深度

多核处理器甚至单核都依赖于并行性
一些算法有一些固有的串行路径
深度是最长的依赖链
考虑在无限数量的处理器上运行而没有OMP、通信或循环开销

在分布式内存中，通过在处理器之间发送消息来进行通信。消息传递时间可能受到几个组件的限制……

开销（发送/接收消息的 CPU 时间）
延迟（时间消息在网络中；可以隐藏）
消息吞吐量（发送小消息的速率……消息/秒）
带宽（可以发送大消息的速率 GBytes/s）

我们算法的分布式内存版本可以根据 N 和 P（#processors）由这些部分不同地描述

可以用多种方法建模性能，前三个是roofline模型，中间两个是LogCAche模型，后三个是LogGPa模型：

浮点数操作：Flop/s
cache数据操作：GB/s
DRAM数据操作：GB/s
总线数据移动：PCIe带宽
Depth：OMP嵌套深度
MPI数据大小：带宽
MPI发送/等待比例：网络延迟

很多模型都追踪延迟来预测性能，延迟隐藏衍生出多种方法，例如乱序执行（硬件发现并行性），硬件预取（硬件自动家在数据），大规模线程并行（独立的线程提高并行）。

roofline模型是基于吞吐的模型，追踪比例而不是时间。

DRAM的roofline：人们可以希望永远达到峰值性能（FLOP/s），然而，有限的局部性（重用）和带宽限制了性能。我们假定：

理想化的处理器/缓存
冷启动（DRAM 中的数据）

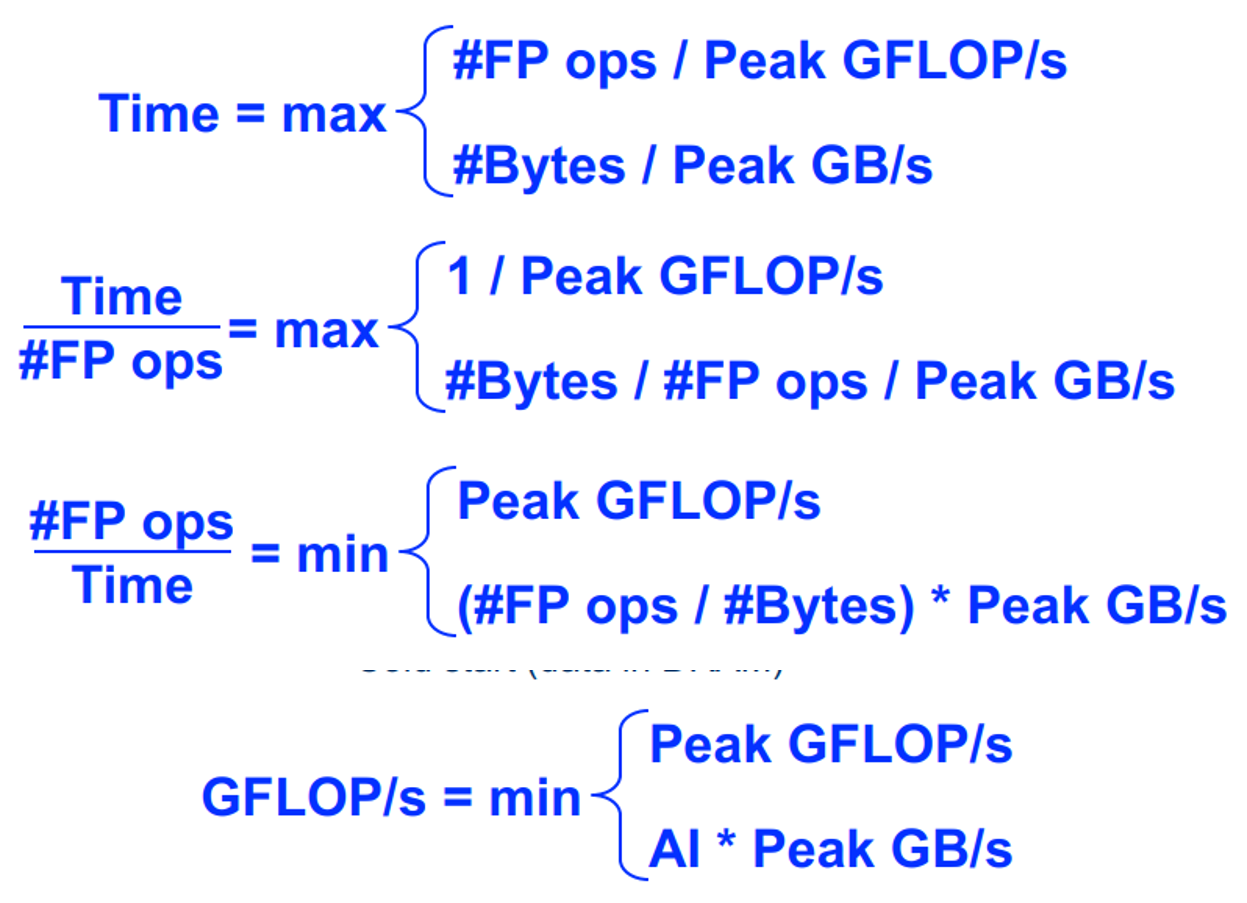
Arithmetic Intensity (AI) = Flops / Bytes (as presented to DRAM )

Roofline 中最重要的概念是算术强度

数据局部性的度量（数据重用）
执行的总Flops与移动的总字节数的比率
对于 DRAM Roofline…
- 进出 DRAM 的总字节数，包括所有缓存和预取器效果
- 可能与总加载/存储（请求的字节数）有很大不同
- 等于持续 GFLOP/s 与持续 GB/s 的比率

使用算术强度作为 x 轴绘制roofline边界，对数刻度使画图变得容易，根据摩尔定律推断性能等……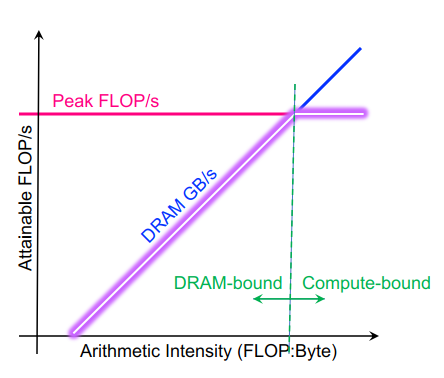

一般的机器现在都是5-10flops每个字节，40-80flops每个double。对于以下计算：

1
2
3

#pragma omp parallel for
for (int i = 0; i < N; i ++)
    z[i] = x[i] + alpha*y[i];

每次迭代2个flops，传送24个bytes（读x[i]，y[i]，写z[i]）AI = 0.083。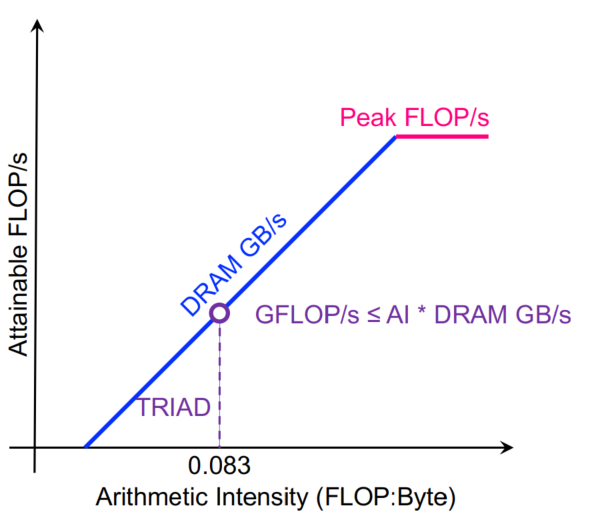

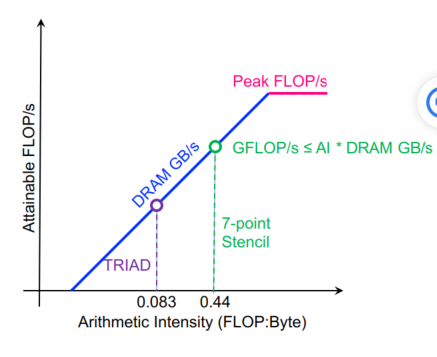
每次循环7flops，每个点8次内存访问，除了一次读和1次写，cache都能搞定，AI=7/16=0.44

#pragma omp parallel for
for(k=1;k<dim+1;k++){
    for(j=1;j<dim+1;j++){
        for(i=1;i<dim+1;i++){
            new[k][j][i] = -6.0*old[k ][j ][i ]
                + old[k ][j ][i-1]
                + old[k ][j ][i+1]
                + old[k ][j-1][i ]
                + old[k ][j+1][i ]
                + old[k-1][j ][i ]
                + old[k+1][j ][i ];
}}}

分层roofline

处理器具有多级内存/缓存
- 寄存器
- L1、L2、L3 缓存
- MCDRAM/HBM（KNL/GPU 设备内存）
- DDR（主存储器）
- NVRAM（非易失性存储器）
应用程序在每个级别都有局部性
独特的数据移动意味着独特的AI
此外，每个级别都有独特的峰值和持续带宽

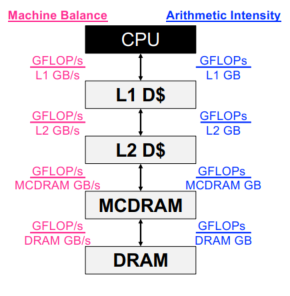
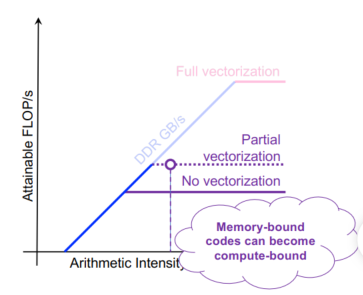
片内并行性：我们假设一个可以获得高flops的运算，也有高局部性。实际上，我们必须……

向量化循环（每条指令 16 个触发器）
使用特殊说明（例如 FMA）
确保 FP 指令在指令组合中占主导地位
使用所有内核和插槽
大多数处理器利用某种形式的 SIMD 或向量。
- KNL 使用 512b 向量 (8x64b)
- GPU 使用 32 线程扭曲 (32x64b)
实际上，应用程序是标量和向量指令的混合体。
- 性能是 SIMD 和无 SIMD 之间的加权平均值
- 有一个基于这个加权平均值的隐含上限

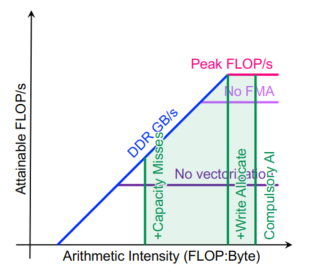
我们可以仅使用强制缓存未命中来绑定 AI

但是，写分配缓存会降低 AI
缓存容量未命中可能会造成巨大损失
计算墙转换成内存墙

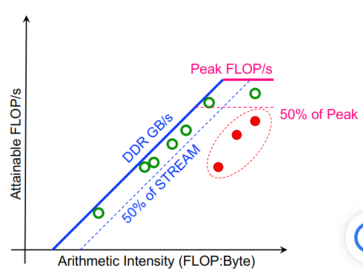
由于计算与内存交互影响，flops可能不能作为优化的依据，所以就可以把AI排序，将这些部分的性能与机器扩展性/容量进行比较。roofline附近的内核正在充分利用计算资源

内核可能具有低性能 (GFLOP/s)，但可以很好地利用机器
内核可以具有高性能 (GFLOP/s)，但不能很好地利用机器

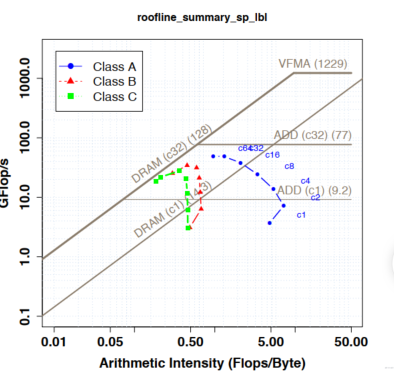
AI（数据移动）因线程并发性和问题大小而异

大问题（绿色和红色）每个线程移动更多数据，最终耗尽缓存容量
由此导致的 AI 下降意味着它们迅速达到带宽上限并降级。
较小的问题会减少 AI，但不要达到带宽上限

现在CPU采用多种方法来增加浮点效率。比如使用fused multiply add来使乘法和加法在同一个流水线中，使用向量指令。

三种方法来提高性能：增加片上性能（比如让编译器进行向量化），增加内存带宽（NUMA），最小化数据移动。

如何构建roofline？要创建 Roofline 模型，我们必须执行基准测试……

持续的flops
- 双精度/单精度/半精度
- 有和没有 FMA（例如编译器标志）
- 有和没有 SIMD（例如编译器标志）
持续带宽
- 在每个级别的内存/缓存之间进行测量
- 迭代各种大小的工作集并识别平台
- 识别带宽不对称（读：写比率）
基准测试必须运行足够长的时间以观察

衡量应用程序 AI 和性能

要使用 Roofline 来描述执行的特征，我们需要……
- 时间
- flops（=> flops/时间）
- 每级内存之间的数据移动（=> FLOPs / GB’s）
我们可以查看完整的应用程序……
- 粗粒度，平均 30 分钟
- 遗漏了很多细节和瓶颈
或者我们可以查看单个循环嵌套……
- 需要逐个循环地进行自动检测
- 此外，我们可能应该逐核区分数据移动或flops

我们如何计算 FLOP？

手动计数
- 遍历每个循环嵌套并计算 FP 操作的数量
- 最适合确定性循环边界
- 或按迭代次数参数化（运行时记录）
- 不可扩展
性能计数器
- 之前/之后读取计数器
- 更准确
- 低开销 (<%) == 可以运行完整的 MPI 应用程序
- 可以检测负载不平衡
- 需要特权访问
- 需要手动检测（+开销）或完整的应用程序表征
- 差的counter得到的数据=垃圾
- 可能无法区分 FMADD 和 FADD
- 没有深入了解特殊流水线
二进制指令测试器
- 在运行时自动检查装配
- 最准确
- 可以按类别/类型统计指令
- 可以检测负载不平衡
- 可以包括来自非 FP 指令的效果
- 自动应用于多个循环嵌套
- 大于10 倍的开销

我们如何衡量数据移动？

手动计数
- 遍历每个循环嵌套并估计将移动多少字节
- 使用缓存的健壮模型
- 最适合从 DRAM 流的简单循环
- 对于复杂的缓存不适用
- 不可扩展
性能计数器
- 之前/之后读取计数器
- 适用于全层级（L2、DRAM）
- 更准确
- 低开销 (<%) == 可以运行完整的 MPI 应用程序
- 可以检测负载不平衡
- 需要特权访问
- 需要手动检测（+开销）或完整的应用程序表征
缓存模拟
- 构建一个由内存地址驱动的全缓存模拟器
- 适用于全层级和多核
- 可以检测负载不平衡
- 自动应用于多个循环嵌套
- 忽略了预取器
- 大于 10 倍的开销

工具：Intel Advisor

lecture 6

并行化和数据局部性都对性能很重要，因为数据迁移是很费劲的。很多对象是独立于其他对象来操作的，更多的是依赖于与之相邻的对象，其依赖关系很简单。

同时讲了一些计算域剖分的问题，减少通信的同时实现局部性。

并行图计算：如果两个进程的图相连，则需要交互，他的数据结构与一般的图算法不一样，将图剖分到各个节点上，平均分布实现均衡，同时最小化节点之间边的关系减少通信。

粒子系统模拟需要实现每个粒子受到的作用和对其他粒子的作用，这就需要通信，通常是对整个区域进行剖分，区域之间进行halo交换。第一个挑战就是在处理区域边界上的粒子碰撞，第二个挑战是如果粒子成簇状分布的话会不均衡，为了减少不均衡，对空间也采取不均衡划分，采用k-d树的形式对粒子进行划分。

远域强迫指的是每个进程都跟其他进程的粒子进行作用，采用循环的方式进行数据通信，最中每个进程得到所有其他进程的数据。如果使用树形剖分的话，将每一簇粒子看成一个整体，降低复杂度。

假定ODE是x(t) = f(x) = A * x(t)，A是一个稀疏矩阵，显式方法可以转化成一个近似的稀疏矩阵乘，隐式方法可以转化成一个线性方程。另外还有直接方法，做LU分解，迭代方法（Jacobi、Successive over-relaxation、Conjugate Gradient）等。

稀疏矩阵向量乘：稀疏矩阵可以只保存非0元，CSR方法是最简单的方法，对稀疏矩阵m*n，一个指针数组有m个元素，每个元素代表着第i行所有元素的起始位置。val数组和ind数组保存着实际的元素。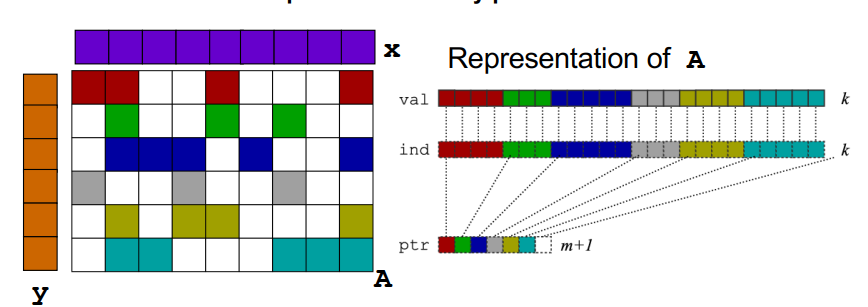

1
2
3

for each row i
    for k = ptr[i] to ptr[i+1]-1 do
        y[i] = y[i] + val[k] * x[ind[k]];

如果要并行化，需要知道，哪个进程拥有y[i]、x[i]、A[i,j]，和哪个进程应该计算最终的y[i] = sum(from 1 to n) A[i,j] * x[j]。

首先将下标1到n进行剖分，对于进程k，它存储了每一个下标i的y[i]、x[i]、A[i,...]，同时计算了y[i] = (row i of A) * x，这里需要通信了。

能否将矩阵重排，使所有非零元素都在对角块上？这样所有运算都可以在本地完成。重排的目标

平衡负载（如何测量负载？）。
- 大约相等数量的非零值（不一定是行）
平衡存储（每个处理器存储多少？）。
- 大约相等数量的非零值
尽量减少通信
- 最小化对角块外的非零值
- 相关优化标准是移动对角线附近的非零值
改进寄存器和缓存重用
- 在小的垂直块中将非零值分组以便源 (x) 元素加载到缓存或寄存器中可以重用（时间局部性）
- 在小的水平块中分组非零值，以便靠近源 (x)中的元素可以命中cache（空间局部性）
其他算法出于其他原因对行/列重新排序
- 在高斯消元后减少矩阵中的非零值
- 提高数值稳定性

图的并行化和矩阵并行化类似。

自适应网格加密：并行化基于patches。

非结构网格的挑战：

如何首先生成它们
- 从对象的几何描述开始
- 三角化
- 3D 更难！
如何划分它们
- ParMetis，一个并行图分区器
如何设计迭代求解器
- PETSc，一种用于科学计算的便携式可扩展工具包
- Prometheus，一个用于有限元问题的多重网格求解器
如何设计直接求解器
- SuperLU，并行稀疏高斯消除

lecture 7

CPU中有取指、解码、ALU、运行上下文、乱序控制逻辑、指令预测、数据预取、cache等模块。第一个优化的方法是取消让单指令流跑得更快的部分，只剩下取指、解码、ALU运行上下文模块，多个线程共享指令流。第二个方法，让多个ALU共享取指令部分，共享部分运行上下文。

如果遇到了分支，那么不是所有的ALU都运行相同的分支，会遇到暂停，通过切换来隐藏延迟。

使用许多精简的内核并行运行；
核心打包大量 ALU；
通过交错执行来避免延迟停滞；
- 当一组停滞时，切换到工作准备就绪的另一组

SIMD单指令流多数据流架构充分使用了数据并行，并行暴露于用户和编译器。SIMD的发展如下：
MMS（8*8 bit int） —> SSE（4*32 bit FP） —> SSE2（2*64 bit FP） —> SSE3（hroizontal ops） —> SSSE3 —> SSE4.1 —> SSE4.2 —> AVX（8*32 bit FP） —> AVX+FMA（3 operand） —> AVX2（256 bit int ops） —> AVX-512（512 bit）

GPU使用的是单指令流多线程（SIMT），每个线程有自己的寄存器组，且可能执行不同的流程，单指令流可以在多个地址上执行。

低占用率会大大降低性能。
控制流分散会大大降低性能。
同步选项非常有限

CUDA是用于SIMT的模型，具有可扩展性。

block有id，每个块内共享内存，可以是1、2、3维；block内有thread，thread有自己的寄存器和私有内存，可以是1、2、3维。2/3维只是组织方式，通过一维手段同样可以达到2/3维的效果。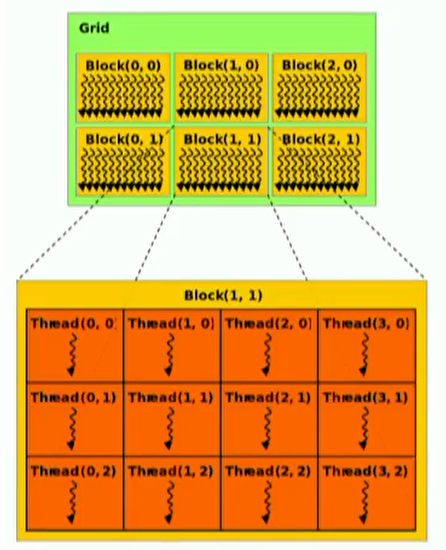

CUDA的线程是独立运行的，有他自己的程序计数器（PC）、变量寄存器、处理器状态位等，不会内定如何调度。线程可能会被映射到GPU上，成为物理线程；也可能在多核CPU下，1 block=1个物理线程，成为虚拟线程。

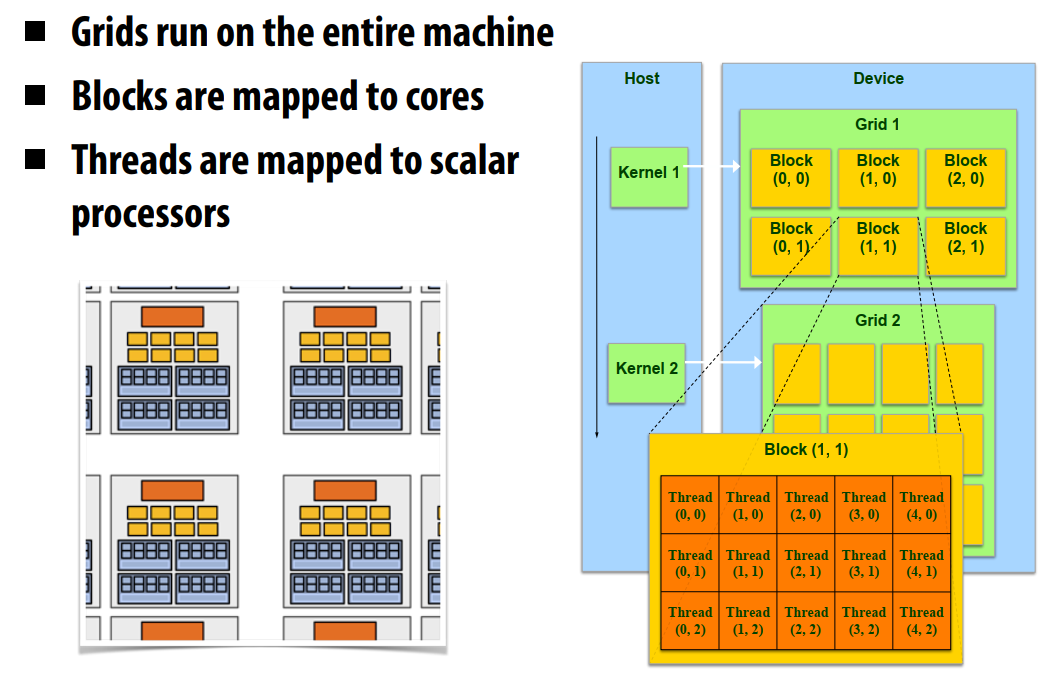
CUDA支持：

线程并行
- 每线程都是独立运行的
数据并行
任务并行
- 不同block是独立的
- 独立的核运行不同的流

线程被分到不同的block中，同一个block中的线程可以合作，不同block的线程不能合作。不同的block之间可以协调但是不能同步，容易死锁；可以进行多种交互。

在GPU上为数据分配空间
创建CPU上的数据
数据复制到GPU上
调用kernel程序来运行GPU
结果数据从GPU拷贝到CPU
释放GPU的空间
释放CPU的空间

三种不同的函数：

__device__ float DFunc()运行在Device上，只能从Device上调用
__global__ void kernel()运行在Device上，只能从host上调用，只能返回void
__host__ float HFunc()运行在host上，只能从host上调用

简单的调用：

// CUDA Kernel function to add the elements
// of two arrays on the GPU
__global__
void add(float *a, float *b, float *c)
{
    int i = blockId.x * blockDim.x + threadId.x;
    c[i] = a[i] + b[i];
}

int main()
{
    // Run N/256 blocks of 256 threads each
    vecAdd<<<N/256, 256>>>(d_a, d_b, d_c);
}

数据管理：

#define N 256*1024

int main()
{
    float *h_a = malloc(sizeof(float) * N);
    float *h_b = malloc(sizeof(float) * N);
    float *h_c = malloc(sizeof(float) * N);

    float *d_a, *d_b, *d_c;
    cudaMalloc(&d_a, sizeof(float) * N);
    cudaMalloc(&d_b, sizeof(float) * N);
    cudaMalloc(&d_c, sizeof(float) * N);

    cudaMemcpy(d_a, h_a, sizeof(float) * N);
    cudaMemcpy(d_b, h_b, sizeof(float) * N);

    vecAdd<<<cell(N/256), 256>>>(d_a, d_b, d_c);
    cudaMemcpy(h_c, d_c, sizeof(float) * N, cudaMemcpyDeviceToHost);
}

CUDA程序一般都要求具有大量并行性，同时局部性也很重要，因为GPU没有能够隐藏延迟的硬件。

每个线程和block都有自己专属的私有内存，而各个kernel之间有共享的全局内存。

同步：

一个block中的线程可能会互相同步
block可以通过原子内存操作来协调运行
- 例如通过一个共享的自增队列指针
互相依赖的kernel可能有隐式的barrier

访问同一个内存地址会造成冲突，变成顺序的访问。连续的32位字被分配给连续的地址。对全局内存也会有这种问题，从Fermi架构开始，全局内存地址会被hash，从而全局地址冲突不会再发生。

每一个load指令都会带来一系列对齐且连续的内存，称为页。硬件自动将从一个warp的不同线程发出的请求合并到同一个page。

以下代码启动256个线程计算数组和。

#include <iostream>
#include <math.h>
// GPU function to add the elements of two arrays
__global__
void add(int n, float *x, float *y)
{
    int index = threadIdx.x;
    int stride = blockDim.x;
    for (int i = index; i < n; i += stride)
        y[i] = x[i] + y[i];
}
int main(void)
{
    int N = 1<<20; // 1M elements
    float *x, *y;
    cudaMallocManaged(&x, N*sizeof(float));
    cudaMallocManaged(&y, N*sizeof(float));
    // initialize x and y arrays on the host
    for (int i = 0; i < N; i++) {
        x[i] = 1.0f;
        y[i] = 2.0f;
    }
    // Run kernel on 1M elements on the GPU
    add<<<1, 256>>>(N, x, y);
    cudaDeviceSynchronize();
    // … for space, remove error checking/free
    return 0;
}

如果想用更多的线程的话：

__global__
void add(int n, float *x, float *y)
{
    int index = blockIdx.x * blockDim.x + threadIdx.x;
    int stride = blockDim.x * gridDim.x;
    for (int i = index; i < n; i += stride)
        y[i] = x[i] + y[i];
}

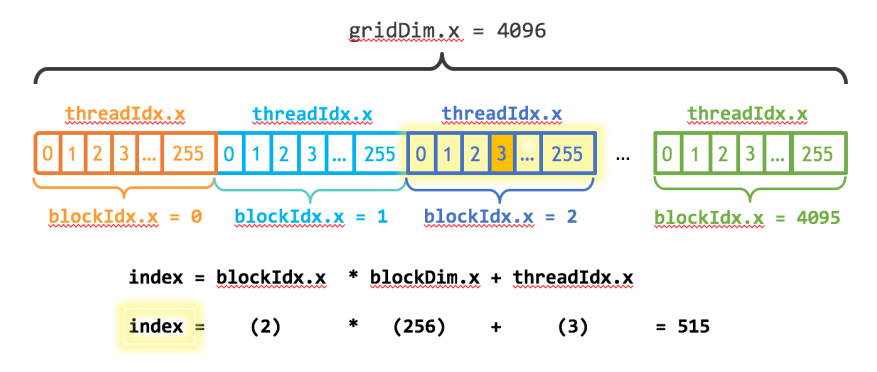
更多指的是numBlocks * blockSize：

1
2
3

int blockSize = 256;
int numBlocks = (N + blockSize - 1) / blockSize;
add<<<numBlocks, blockSize>>>(N, x, y);

lecture 9

互联网络的特性：

直径：给定一对节点之间最短路径的最大值（在所有节点对上）。
延迟：多久能到达一个节点，即发送和接收时间之间的延迟
- 不同体系结构的延迟往往差异很大
- 供应商经常报告硬件延迟（连线时间）
- 应用程序程序员关心软件延迟（用户程序到用户程序）
- 观察结果：
  - 网络设计的延迟相差1-2个数量级
  - 源/目标成本下的软件/硬件开销占主导地位（1s-10s usecs）
  - 硬件延迟随距离变化（每跳10s-100s纳秒），但与开销相比较小
  - 延迟是包含许多小消息的程序的关键
带宽：单位时间内能传输多少数据
- 对大消息的传输很重要
对分带宽：将网络分成相同两部分的最小切割上的带宽
- 对所有进程都需要和其他进程通信的算法很重要

设计网络的参数：

拓扑结构
- crossbar、ring、2-D、3-D、超立方、树形、
- butterfly
  - 真正的超立方体展开版本。
  - d维蝶形具有（d+1）2d“交换节点”（不要与处理器混淆，即n=2d）
  - 发明蝴蝶是因为超立方体需要随着网络变大而增加交换机基数；当时禁止
  - 直径=log n。等分带宽=n
  - 无路径多样性：对抗性流量不好
- 参见高等计算机体系结构课程
路由算法
- all east-west then all north-south
发送策略
- circuit：对整个信息使用全部链路
- packet：信息拆分成单独的消息发送
流量控制
- 消息暂时存储在buffer中、数据重新路由等

dragonflies：

利用光互连（在机房机柜之间）和电气网络（机柜内部）之间的成本和性能差距
- 光纤（光纤）更昂贵，但较长时带宽更高
- 电力（铜）网络更便宜，短路时更快
在层次结构中组合：
- 使用全对全链路将多个组连接在一起，即每个组至少有一个直接连接到其他组的链路。
- 每个组内的拓扑可以是任何拓扑。
使用随机路由算法
结果：程序员可以（通常）忽略拓扑，获得良好的性能
在虚拟化动态环境中非常重要
缺点：性能可变

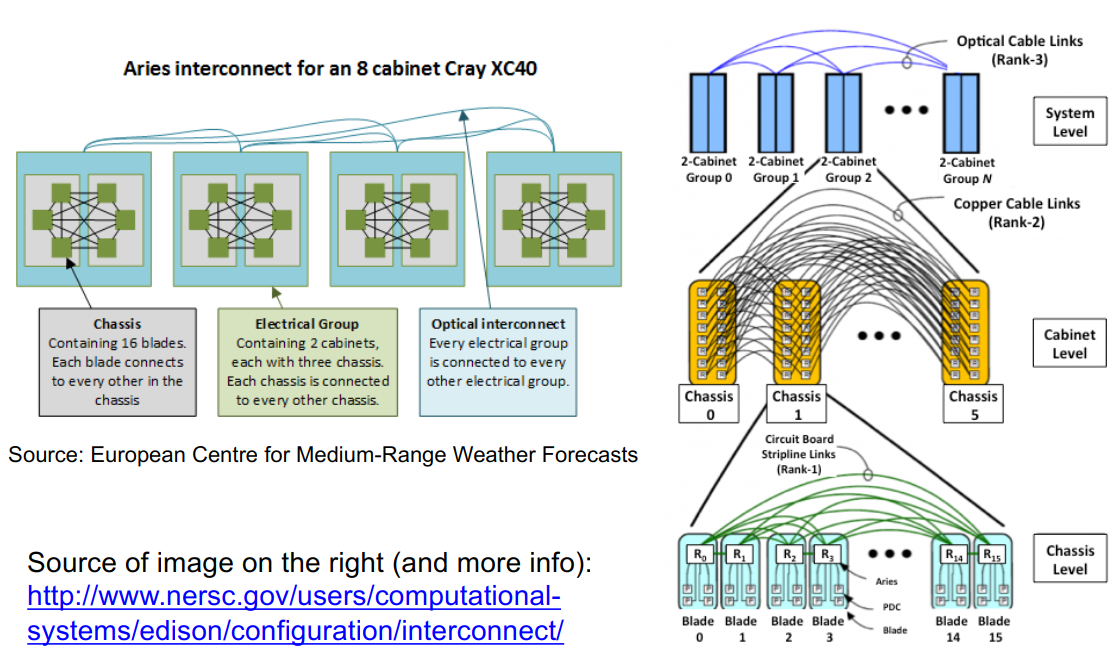
在负载平衡的情况下，最小路由工作得很好，在大量的流量模式中可能会造成灾难性的后果。

随机化思想：对于路由器Rs上的每个数据包，并发送至另一组Rd中的路由器，首先将其路由到中间组。

发送消息的时间大概是：T = latency+n*cost_per_word = latency + n / bandwidth，也叫做Time = α + n * β。通常α远大于β。一个长消息比多个短消息更划算，同时需要较大的计算-通信比。

MPI：进程可以被分组，每个消息必须以一个上下文发送/接收。一个分组+上下文共同组成一个通信域。

MPI消息数据可以用一个（地址，数量，类型）三元组描述，有如下类型：

预先定义的语言相关类型
某类型的连续数组
一个数据块
一些块数据
随机类型的数据

MPI消息发送时会跟上一个用户定义的tag，来协助识别消息。

只有mpi_send时等待完成，或者mpi_send后返回，recv时在某个时间段等待，才能避免创建buffer。

MPI非阻塞操作返回request

MPI_Request request;
MPI_Status status;

MPI_Isend(start, count, datatype, dest, tag, comm, &request);
MPI_Irecv(start, count, datatype, dest, tag, comm, &request);
MPI_Wait(&request, &status);

可以通过测试来等待：

1	MPI_Test(&request, &flag, &status);

在未完成通信时访问缓冲区是未定义的

可以同时等待多个：

1
2
3

MPI_Waitall(count, array_of_requests,array_of_statuses)
MPI_Waitany(count, array_of_requests, &index, &status)
MPI_Waitsome(count, array_of_requests, array_of indices, array_of_statuses)

MPI提供多种发送消息的模式：

同步模式（MPI_Ssend）：在匹配的接收开始之前，发送不会完成。（不安全程序死锁。）
缓冲模式（MPI_Bsend）：用户向系统提供一个缓冲区供其使用。用户分配足够的内存使不安全的程序安全。
就绪模式（MPI_Rsend）：用户保证已发布匹配的接收。
- 允许访问快速协议
- 如果匹配接收未发布，则未定义行为

集合操作：包括broadcast、gather/scatter，allgather、alltoall、reduce、scan。

MXX是一个MPI的库，基于MPI在交换不规则数据的时候以下的几种复杂操作：

交换不规则数据时麻烦
- 交换数量
- 拷贝数据
- 分配空间
- 交换实际数据
创建派生的非PDO类型
将用户定义函数映射给MPI

而MXX只要如下：

// lets take some pairs and find the one with the max second element
std::pair<int, double> v = ...;
std::pair<int, double> min_pair = mxx::allreduce(v, [](const std::pair<int, double>& x, const std::pair<int, double>& y) {
    return x.second > y.second ? x : y;
});

SUMMA：可扩展矩阵乘法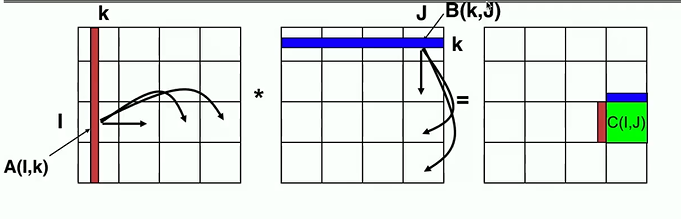

C(I, J) = C(I, J) + ∑k(A(I, k) * B(k, J))，其中I，J代表一个进程所有的行列，k是单独的一行或列，或者一块。

对于每个k（0和n-1之间），

部分K行的所有者沿其进程列广播该行
部分K列的所有者沿其进程行广播该列

完整算法：

在每个进程P(i, j)：
    对于k=0…n-1
        在第i行中广播A（A_i）的第k列
        在第j列中广播B（B_j）的第k行
        C += 外积（a_i，b_j）

如果是P^(1/2)*P^(1/2)剖分：

For k=0 to n/b-1
    for all i = 1 to P^(1/2)
        owner of A[i,k] broadcasts it to whole processor row (using binary tree)
    for all j = 1 to P^(1/2)
        owner of B[k,j] broadcasts it to whole processor column (using bin. tree)
    Receive A[i,k] into Acol
    Receive B[k,j] into Brow
    C_myproc = C_myproc + Acol * Brow

void SUMMA(double *mA, double *mB, double *mc, int p_c)
{
    int row_color = rank / p_c; // p_c = sqrt(p) for simplicity
    MPI_Comm row_comm;
    MPI_Comm_split(MPI_COMM_WORLD, row_color, rank, &row_comm);
    int col_color = rank % p_c;
    MPI_Comm col_comm;
    MPI_Comm_split(MPI_COMM_WORLD, col_color, rank, &col_comm);
    for (int k = 0; k < p_c; ++k) {
        if (col_color == k) memcpy(Atemp, mA, size);
        if (row_color == k) memcpy(Btemp, mB, size);
        MPI_Bcast(Atemp, size, MPI_DOUBLE, k, row_comm);
        MPI_Bcast(Btemp, size, MPI_DOUBLE, k, col_comm);
        SimpleDGEMM(Atemp, Btemp, mc, N/p, N/p, N/p);
    }
}

int MPI_Comm_split(MPI_Comm Comm, int color, int key, MPI_Comm* newcomm)中MPI的内部算法：

使用MPI_Allgather从每个进程获取颜色和键
统计相同颜色的进程数；创建一个具有这么多进程的通信器。如果此进程将MPI_UNDEFINED为颜色，请创建一个具有单个成员的进程。
使用键对列组进行排序

颜色：控制newcomm的分配
键：控制newcomm内的rank分配

MPI内建的集合操作：

MPI_MAX：Maximum
MPI_MIN：Minimum
MPI_PROD：Product
MPI_SUM：Sum
MPI_LAND：Logical and
MPI_LOR：Logical or
MPI_LXOR：Logical exclusive or
MPI_BAND：Binary and
MPI_BOR：Binary or
MPI_BXOR：Binary exclusive or
MPI_MAXLOC：Maximum and location
MPI_MINLOC：Minimum and location

集合操作实现的示例：MPI_AllReduce

所有进程必须接收相同的结果向量；
必须按照规范顺序m0 + m1 + … + mp-1进行归约（如果操作不是可交换的）；
对于结果向量的所有元素，不严格要求使用相同的规约顺序和括号，但应努力做到这一点。

复杂度下界：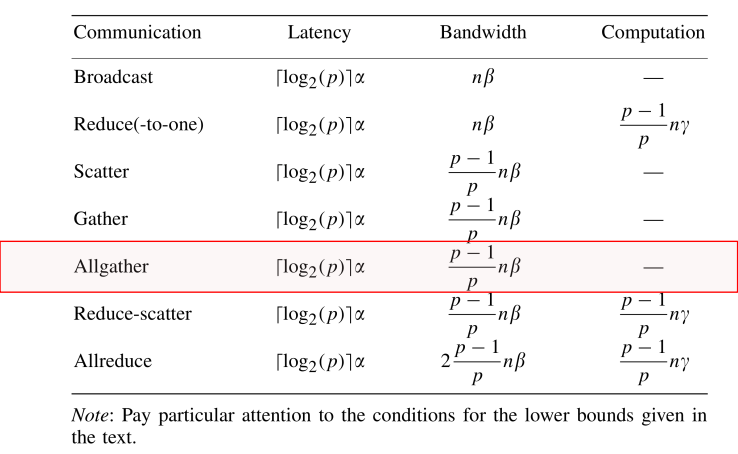

MPI_AllGather有几种实现：

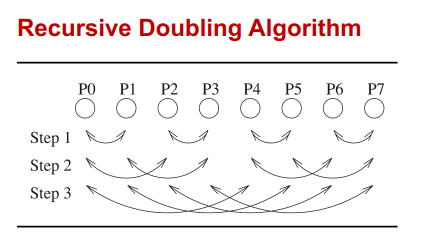
环算法：在0时刻，发送你自己的数据；在t时刻，把你在t-1时刻收到的数据发给你右边，从你左边接收新的数据；利用了带宽，但是有很高的延迟。在数据很大的时候使用，反而比下边的算法快很多，减少数据拷贝，降低通信次数，且只跟邻居通信。
递归算法：在t时刻，进程i与进程i+2^t交换现有的所有数据，形成通信树结构。
bruck算法；在t时刻，进程i从i+2^t接受所有的数据，发送它自己所有的数据给i+2^t。该过程在lg(p)次后结束，在最后一次，仅收发最上边（p-2^(lg(p))）个数据。同时需要租后进行顺序调整。

SUMMA in MPI

void SUMMA(double *mA, double *mB, double *mc, int p_c)
{
    int row_color = rank / p_c; // p_c = sqrt(p) for simplicity
    MPI_Comm row_comm;
    MPI_Comm_split(MPI_COMM_WORLD, row_color, rank, &row_comm);
    int col_color = rank % p_c;
    MPI_Comm col_comm;
    MPI_Comm_split(MPI_COMM_WORLD, col_color, rank, &col_comm);
    double *mA1, *mA2, *mB1, *mB2;
    colsplit(mA, mA1, mA2); // split mA by the middle column
    rowsplit(mB, mB1, mB2); // split mA by the middle row
    if (col_color == 0) memcpy(Atemp1, mA1, size)
    if (row_color == 0) memcpy(Btemp1, mB1, size);
    MPI_Request reqs1[2];
    MPI_Request reqs2[2];
    MPI_Ibcast(Atemp1, size, MPI_DOUBLE, k, row_comm, &reqs1[0]);
    MPI_Ibcast(Btemp1, size, MPI_DOUBLE, k, col_comm, &reqs1[1]);
    for (int k = 0; k < p_c-1; ++ k) {
        if (col_color == k) memcpy(Atemp2, mA2, size);
        if (row_color == k) memcpy(Btemp2, mB2, size);
        MPI_Ibcast(Atemp2,size,MPI_DOUBLE,k,row_comm,&reqs2[0]);
        MPI_Ibcast(Btemp2,size,MPI_DOUBLE,k,col_comm,&reqs2[1]);
        MPI_Waitall(reqs1, MPI_STATUS_IGNORE);
        SimpleDGEMM (Atemp1, Btemp1, mC, N/p, N/p, N/p);
        if (col_color == k) memcpy(Atemp1, mA1, size);
        if (row_color == k) memcpy(Btemp1, mB1, size);
        MPI_Ibcast(Atemp1,size,MPI_DOUBLE,k,row_comm,&reqs1[0]);
        MPI_Ibcast(Btemp1,size,MPI_DOUBLE,k,col_comm,&reqs1[1]);
        MPI_Waitall(reqs2, MPI_STATUS_IGNORE);
        SimpleDGEMM (Atemp2, Btemp2, mC, N/p, N/p, N/p);
    }

    if (col_color == p-1) memcpy(Atemp2, mA2, size);
    if (row_color == p-1) memcpy(Btemp2, mB2, size);
    MPI_Ibcast(Atemp2,size,MPI_DOUBLE,k,row_comm,&reqs2[0]);
    MPI_Ibcast(Btemp2,size,MPI_DOUBLE,k,col_comm,&reqs2[1]);
    MPI_Waitall(reqs1, MPI_STATUS_IGNORE);
    SimpleDGEMM (Atemp1, Btemp1, mC, N/p, N/p, N/p);
    MPI_Waitall(reqs2, MPI_STATUS_IGNORE);
    SimpleDGEMM (Atemp2, Btemp2, mC, N/p, N/p, N/p);
}

MPI描述进程之间的并行性（使用单独的地址空间）Thread并行性在进程内提供共享内存模型

OpenMP和pthread是常见的模型
OpenMP为循环级并行提供了方便的功能。线程由编译器根据用户指令创建和管理。
pthread提供了更复杂、更动态的方法。Thread由用户显式创建和管理。

在仅MPI编程中，每个MPI进程都有一个程序计数器。在MPI+线程混合编程中，可以同时执行多个线程。所有线程共享所有MPI对象（通讯器、请求）。MPI实施可能需要采取措施确保MPI堆栈的状态一致。

MPI的四个线程安全级别：MPI定义了四个线程安全级别

MPI_THREAD_SINGLE：应用程序中只存在一个线程
MPI_THREAD_FUNNELED：多线程，但只有主线程进行MPI调用（调用MPI_Init_thread的调用）
MPI_THREAD_SERIALIZED：多线程，但一次只能有一个线程进行MPI调用
MPI_THREAD_MULTIPLE：多线程，任何线程都可以在任何时候（有一些限制以避免竞争）

MPI定义了MPI_Init的替代方案：MPI_Init_thread(requested, provided)
- 应用程序给出了它所需要的级别；MPI实现提供了它所支持的级别

MPI_THREAD_SINGLE时没有线程

int main(int argc, char ** argv)
{
    int buf[100];
    MPI_Init(&argc, &argv);
    for (i = 0; i < 100; i++)
        compute(buf[i]);
    /* Do MPI stuff */
    MPI_Finalize();
    return 0;
}

MPI_THREAD_FUNNELED时所有MPI调用都是主线程在调用，在OpenMP并行区域外。

int main(int argc, char ** argv)
{
    int buf[100], provided;
    MPI_Init_thread(&argc, &argv, MPI_THREAD_FUNNELED, &provided);
    if (provided < MPI_THREAD_FUNNELED)
        MPI_Abort(MPI_COMM_WORLD, 1);
    
    #pragma omp parallel for
    for (i = 0; i < 100; i++)
        compute(buf[i]);
    /* Do MPI stuff */
    MPI_Finalize();
    return 0;
}

MPI_THREAD_SERIALIZED一次只能有一个线程调用MPI函数，这被critical regions保证。

int main(int argc, char ** argv)
{
    int buf[100], provided;
    MPI_Init_thread(&argc, &argv, MPI_THREAD_SERIALIZED, &provided);
    if (provided < MPI_THREAD_SERIALIZED)
        MPI_Abort(MPI_COMM_WORLD, 1);
    #pragma omp parallel for
    for (i = 0; i < 100; i++) {
        compute(buf[i]);
        #pragma omp critical
        /* Do MPI stuff */
    }
    MPI_Finalize();
    return 0;
}

MPI_THREAD_MULTIPLE任何线程都可以随时进行MPI调用（不受限制）

int main(int argc, char ** argv)
{
    int buf[100], provided;
    MPI_Init_thread(&argc, &argv, MPI_THREAD_MULTIPLE, &provided);
    if (provided < MPI_THREAD_MULTIPLE)
        MPI_Abort(MPI_COMM_WORLD, 1);
    #pragma omp parallel for
    for (i = 0; i < 100; i++) {
        compute(buf[i]);
        /* Do MPI stuff */
    }
    MPI_Finalize();
    return 0;
}

实现不需要支持高于MPI_THREAD_SINGLE的级别；也就是说，实现不需要是线程安全的。

调用MPI_Init（而不是MPI_Init_thread）的程序应假定只支持MPI_THREAD_SINGLE。不调用MPI_Init_thread的线程化MPI程序是不正确的程序。

MPI_THREAD_MULTIPLE的约定

排序：当多个线程同时进行MPI调用时，结果将是，调用在某些情况下按某些顺序执行
在每个线程内维护顺序
用户必须确保在同一个comm上进行集体操作，窗口或文件句柄在线程之间的顺序正确
- 例如，不能在一个线程上调用广播，在另一个线程上调用reduce
当线程处于同一位置时，用户有责任防止冲突MPI调用
- 例如，从一个线程访问信息对象并将其从另一线程释放。
阻塞：阻塞MPI调用将只阻塞调用线程，不会阻止其他线程运行或执行MPI

一个正确的例子：

1
2
3

              Proc 0            Proc 1
Thread1   MPI_Recv(src=1)   MPI_Recv(src=0)
Thread2   MPI_Send(dst=1)   MPI_Send(dst=0)

一个不正确的例子：

1
2
3

              Proc 0            Proc 1
Thread1  MPI_Bcast(comm)   MPI_Bcast(comm)
Thread2  MPI_Barrier(comm)   MPI_Barrier(comm)

P0和P1可以有不同的Bcast和Barrier顺序

在这里，用户必须使用某种类型的同步，以确保线程1或线程2在两个进程上都首先得到调度，否则Bcast可能与同一comm上的Barrier匹配，这在MPI中是不允许的。

单边通信模型的基本思想是将数据移动与进程同步解耦

应能够在不要求远程进程同步的情况下移动数据
每个进程向其他进程公开其内存的一部分
其他进程可以直接读取或写入该内存
创建公共内存
- 默认情况下，进程使用的任何内存都是只有本地可访问
- 分配内存后，用户必须进行显式MPI调用，以将内存区域声明为可远程访问
  - 远程可访问内存的MPI术语是一个“窗口”
  - 一组进程共同创建一个“窗口”
- 一旦内存区域被声明为可远程访问，窗口中的所有进程都可以向该内存读/写数据，而无需与目标进程显式同步
窗口创建存在四种模式
- MPI_WIN_CREATE：您已经有一个分配的缓冲区，您希望远程访问该缓冲区
- MPI_WIN_ALLOCATE：您希望创建一个缓冲区并直接使其可远程访问
- MPI_WIN_CREATE_DYNAMIC：您还没有缓冲区，但将来会有缓冲区，且您可能希望在窗口中动态添加/删除缓冲区
- MPI_WIN_ALLOCATE_SHARED：您希望同一节点上的多个进程共享一个缓冲区

MPI_WIN_ALLOCATE：在RMA窗口中创建一个远端可访问的内存区域

1
2
3

int MPI_Win_allocate(MPI_Aint size, int disp_unit,
    MPI_Info info, MPI_Comm comm, void *baseptr,
    MPI_Win *win)

int main(int argc, char ** argv)
{
    int *a; MPI_Win win;
    MPI_Init(&argc, &argv);
    /* collectively create remote accessible memory in a window */
    MPI_Win_allocate(1000*sizeof(int), sizeof(int), MPI_INFO_NULL, MPI_COMM_WORLD, &a, &win);
    /* Array ‘a’ is now accessible from all processes in MPI_COMM_WORLD */
    MPI_Win_free(&win);
    MPI_Finalize(); 
    return 0;
}

MPI提供了在远程可访问内存区域中读取、写入和原子修改数据的能力：

MPI_PUT
MPI_GET
MPI_ACCUMULATE
MPI_GET_ACCUMULATE
MPI_COMPARE_AND_SWAP
MPI_FETCH_AND_OP

RMA同步模型

RMA数据访问模型
- 何时允许进程读取/写入远程可访问内存？
- 进程X写入的数据何时可供进程Y读取？
- RMA同步模型定义了这些语义
MPI提供的三种同步模型：
- Fence（主动目标）
- 启动后完全等待（通用活动目标）
- 锁定/解锁（被动目标）
数据访问发生在“epochs”内
- 访问时间：包含一组由源进程发出的操作
- 曝光时间：允许远程进程更新目标窗口
- epochs定义了顺序和完成语义
- 同步模型提供了建立epochs的机制

被动目标同步

开始/结束被动模式
- 目标进程不进行相应的MPI调用
- 可以启动多个被动目标事件到不同的进程
- 不允许同一进程的并发（影响线程）
锁
- 共享：其他使用共享的进程可以同时访问
- 独占：没有其他进程可以同时访问

共享内存和消息传递各有优缺点，共享内存更容易并行，容易竞争，且更容易陷入假共享之类的；消息传递需要做更多的工作，但是不容易死锁，具有很高的扩展性。

全局地址空间中，线程可以直接读写远端数据，给通信实现提供了方便。因此需要一种方式来命名全局空间。（以下使用UPC方式）

1 2	shared int *p = upc_malloc(4); shared int a[12];

如果需要单边通信：

1 2	a[i] = ...; p = ...; upc_mem_put(...); ... = a[i]; ... = p; upc_mem_get(...);

lecture 11

PGAS编程的目标

应用：不规则代码的方便编程
- 图
- 哈希表
- 稀疏矩阵
- 自适应（分层）网格
机器：在计算机上显示最佳可用性能
- 小消息的低延迟
- 即使对于中等大小的消息，带宽也很高
- 高注入速率（消息数/秒）
- 最小化软件开销并匹配硬件

UPC++与MPI类似，也是SPMD程序，使用GASNet库通信。

#include <upcxx/upcxx.hpp>
#include <iostream>
using namespace std;
int main(int argc, char *argv[])
{
    upcxx::init();
    cout << "Hello from " << upcxx::rank_me() << endl;
    upcxx::finalize();
    return 0;
}

用UPC++计算π如下：

int main(int argc, char **argv) {
    upcxx::init();
    int hits, trials = 0;
    double pi;

    if (argc != 2) trials = 1000000;
    else trials = atoi(argv[1]);

    generator.seed(upcxx::rank_me()*17);

    for (int i=0; i < trials; i++) hits += hit();
    pi = 4.0*hits/trials;
    cout << "PI estimated to " << pi << endl;
    upcxx::finalize();
}

一般的C++变量和对象在每个线程的私有内存空间分配。共享空间的变量需要用new_显式分配，用delete_释放，共享内存可以被远端进程访问：

1	global_ptr<int> gptr = new_<int>(rank_me());

如果需要广播：

1 2	global_ptr<int> gptr = broadcast(new_<int>(24),0).wait();

future类型的变量有一个状态位，标志是否准备好，等待future类型就绪使用户可以实现异步操作。

future<T> f1 = rget(gptr1); // asynchronous op
future<T> f2 = rget(gptr2);
bool ready = f1.ready(); // non-blocking poll
if !ready … // unrelated work...
T t = f1.wait(); // waits if not ready

单边通信如下，同时支持不连续内存数据：

1 2	future<T> rget(global_ptr<T> src); future<> rput(T val, global_ptr<T> dst);

同步操作：

Barrier: block until all other threads arrive
barrier();
Asynchronous barriers

future<> f =
    barrier_async(); // this thread is ready for barrier
// do computation unrelated to barrier
wait(f); // wait for others to be ready

UPC++有一部分集合操作，都是异步的

template <typename T> future <T>
broadcast (T && value , intrank_t root);

template <typename T> future <T>
broadcast (T * buffer, std::size_t count,
intrank_t sender);

template <typename T, typename BinaryOp>
future <T> reduce_all (T && value, BinaryOp &&op);

远端过程调用：

1 2	future<R> rpc(intrank_t r, F func, Args&&... args);

在进程r执行func(args...)并返回结果，R是返回类型。

int hits = 0;
int main(int argc, char **argv) {
    init();
    int trials = atoi(argv[1]);
    int my_trials = (trials+rank_me())/rank_n();
    generator.seed(rank_me()*17);
    for (int i=0; i < my_trials; i++) {
        rpc(0, [](int hit) { hits += hit; }, hit()).wait();
    }
    barrier();
    if (rank_me() == 0)
        cout << "PI estimated to " << 4.0*hits/trials;
    finalize();
}

lecture 12

mapreduce模型：

每条记录是一个（key, value）
map：(K[in], V[in]) --> list(K[inter], V[inter])
reduce：(K[inter], list(V[inter])) --> list(K[out], V[out])

MapReduce着眼于更高级的数据并行，自动进行数据通信等，关注容错。

lecture 13

BLAS(1)：对于向量的15个操作，对O(1)的数据做O(1)的操作。对于y = a * x + y这种需要2n的计算和3n的读写的操作，计算强度为2/3，读写更多，且不能向量化，所以出现了BLAS(2)，主要针对矩阵-向量对进行25种操作，对O(2)的数据做O(2)的操作。BLAS(3)，主要针对矩阵-矩阵对进行9种操作，对O(2)的数据做O(3)的操作，计算强度为(2n^3)/(4n^2)=n/2。LAPACK在BLAS是并行的时候才并行。

为什么要避免通信：

在DRAM间移动数据很费时；
算法运行时间由:
- flops * time_per_flop
- words moved / bandwidth
- messages * latency
- 组成，后两项是通信时间
- latency是最久的
需要将线性代数组织起来以免通信

blocked matrix multiply：C = A*B。将A、B和C切分成b*b，再分到每个进程，当b=1时退化成原始的矩阵乘。总共需要(n/b)^3 * 4b^2 = 4 * n^3 / b次读写，当(3*b^2)=cache时最小化。

对于矩阵乘的n^3算法，

串行算法，且缓存为M
- 数据从主存中移动的下界为W (n^3 / M^(1/2) )
- 假定使用分块或者cache敏感的算法
P个进程的并行算法
- M是每个进程的内存
- 数据从主存中移动的下界为W((n^3/p) / M^(1/2) )
- 如果M = 3n^2/p (每个矩阵的一份拷贝之和)，下界为W (n^2 /p^(1/2) )

算法的目标：

尽量减少移动的数据
尽量减少发送的信息
- 需要新的数据结构
多个内存层次结构中最小化用量
当矩阵适合最快的内存时，运算/通信最少

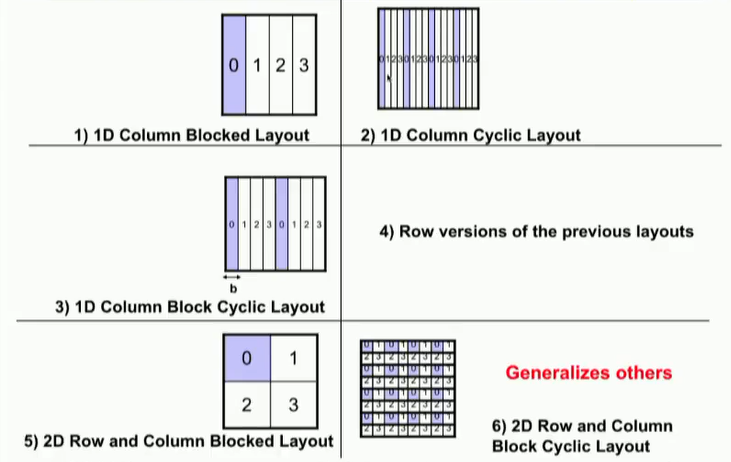
多种不同的矩阵剖分方法：

1D剖分
1D循环剖分
1D列块循环
对应1D的行剖分
2D剖分
2D循环剖分

并行矩阵-向量乘：计算y = y + A * x，使用1D行剖分，A(i)是n/p个进程i拥有的行，x(i)和y(i)类似，也是进程i拥有的数据。

对于每个进程：广播x(i)，计算y(i)=A(i)*x。整个算法使用了y(i) = y(i) + A(i) * x = y(i) + ∑(j) A(i,j)*x(j)。

如果使用列剖分，减少了x的广播，但是增加了一步规约操作。2D块剖分使用了广播和规约，但都是对一个进程子集，通信开销会小一些。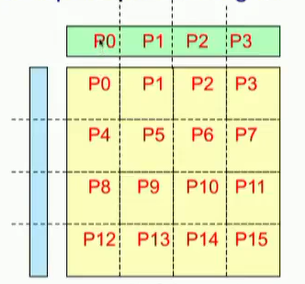

并行矩阵乘法：使用1D剖分且没有广播：

C(myproc) = C(myproc) + A(myproc)*B(myproc,myproc)
for i = 0 to p-1
    for j = 0 to p-1 except i
        if (myproc == i) send A(i) to processor j
        if (myproc == j)
            receive A(i) from processor i
            C(myproc) = C(myproc) + A(i)*B(i,myproc)
        barrier

Cost of inner loop:

computation: 2*n*(n/p)^2 = 2*n^3/p^2
communication: a + b*n^2 /p

Running time = (p*(p-1) + 1)*computation + p*(p-1)*communication = 2*n^3 + p^2*a + p*n^2*b

缺点是每次迭代只有一对进程是活跃的，只有i进程在计算。

改进：相邻的进程对可以同时通信：

Copy A(myproc) into Tmp
C(myproc) = C(myproc) + Tmp*B(myproc , myproc)
for j = 1 to p-1
Send Tmp to processor myproc+1 mod p
Receive Tmp from processor myproc-1 mod p
C(myproc) = C(myproc) + Tmp*B( myproc-j mod p , myproc)

可能需要双倍的buffer
代码中没有考虑可能的死锁
Time of inner loop = 2*(a + b*n^2/p) + 2*n*(n/p)^2
Total Time = 2*n* (n/p)^2 + (p-1) * Time of inner loop = 2*n^3/p + 2*p*a + 2*b*n^2

A(myproc)必须得发给每一个进程，最少开销(p-1)*cost of sending n*(n/p) words

并行效率 = 2*n^3 / (p * Total Time) = 1/(1 + a * p^2/(2*n^3) + b * p/(2*n) ) = 1/ (1 + O(p/n))，当n/p增加时负责度降低。

如果是2.5D矩阵乘：各个进程拥有cn^2 / P数据，总共数据组织成(P/c)^(1/2) * (P/c)^(1/2) * c网格。最开始进程P(i,j,0)拥有A(i,j)和B(i,j)，每一个数组大小为n(c/P)^(1/2)*n(c/P)^(1/2)。

进程P(i,j,0)广播A(i,j)和B(i,j)给P(i,j,k)
k阶的进程执行SUMMA
在k方向上对结果∑(m) A(i,m)*B(m,j)规约，所以P(i,j,0)拥有了C(i,j)。

为了求解Ax=b，进行高斯消去。

… for each column i
… zero it out below the diagonal by adding multiples of row i to later rows
for i = 1 to n-1
    … for each row j below row i
    A(j,i) = A(j,i) / A(i,i);
    for j = i+1 to n
        for k = i+1 to n
            A(j,k) = A(j,k) - A(j,i) * A(i,k)

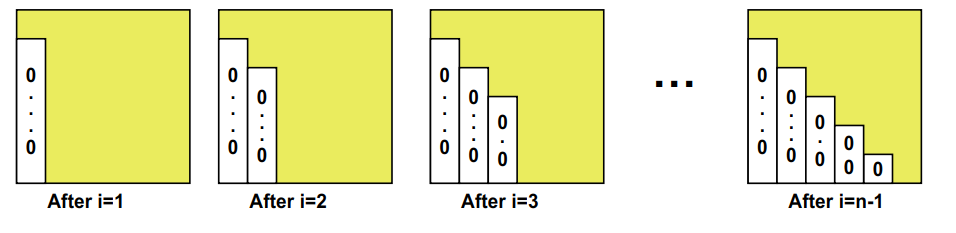
高斯消去实际上也是求了一个LU分解，A=L*U，在求解方程A*x=b时

使用高斯消去分解A=L*U
求解L*y=b
求解U*x=y
因此A*x = (L*U)*x = L*(U*x) = L*y = b

当矩阵A比较小或者有0时，可能会得到错误的结果。因此需要交换把A(i,i)变成一列里最大的，GEPP（Gaussian Elimination with Partial Pivoting）。

for i = 1 to n-1
    find and record k where |A(k,i)| = max{i ≤ j ≤ n} |A(j,i)|
    … i.e. largest entry in rest of column i
    if |A(k,i)| = 0
        exit with a warning that A is singular, or nearly so
    elseif k ≠ i
        swap rows i and k of A
    end if
    A(i+1:n,i) = A(i+1:n,i) / A(i,i) … each |quotient| ≤ 1
    A(i+1:n,i+1:n) = A(i+1:n , i+1:n ) - A(i+1:n , i) * A(i , i+1:n)

以上算法计算A=P*L*U，这是数值上很稳定的。

分块用于计算矩阵乘法，但是在这里由于数据依赖更多很难分块。使用“delayed updates”，将多个连续矩阵的更新保存到跟踪矩阵，之后在一个BLAS3（matmul）操作中同时应用多个更新。

首先要选择一个适当的“b”，这个b应该足够小，使包含b列的子矩阵能够满足cache的大小需要，同时应该足够大以使算法更快。

for ib = 1 to n-1 step b … Process matrix b columns at a time
    end = ib + b-1 … Point to end of block of b columns
    apply BLAS2 version of GEPP to get A(ib:n , ib:end) = P' * L' * U'
    … let LL denote the strict lower triangular part of A(ib:end , ib:end) + I
    A(ib:end , end+1:n) = LL^(-1) * A(ib:end , end+1:n) … update next b rows of U
    A(end+1:n , end+1:n ) = A(end+1:n , end+1:n ) - A(end+1:n , ib:end) * A(ib:end , end+1:n)
        … apply delayed updates with single matrix-multiply
        … with inner dimension b

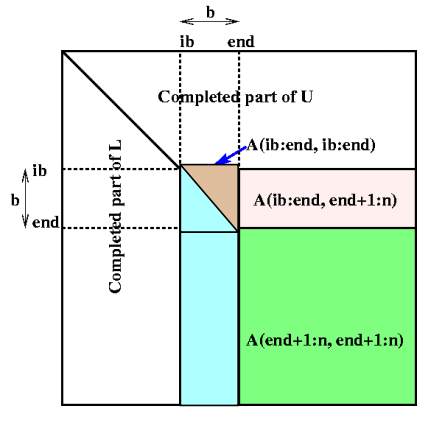
白色部分已经完成，只对中间部分处理。中间的小矩形为LL。贴上代码：

      SUBROUTINE SGETRF( M, N, A, LDA, IPIV, INFO )
!
!     .. Scalar Arguments ..
!     INTEGER            INFO, LDA, M, N
!     ..
!     .. Array Arguments ..
!     INTEGER            IPIV( * )
!     REAL               A( LDA, * )
!     ..
!
!  Purpose
!  =======
!
!  SGETRF computes an LU factorization of a general M-by-N matrix A
!  using partial pivoting with row interchanges.
!
!  The factorization has the form
!     A = P * L * U
!  where P is a permutation matrix, L is lower triangular with unit
!  diagonal elements (lower trapezoidal if m > n), and U is upper
!  triangular (upper trapezoidal if m < n).
!
!  This is the right-looking Level 3 BLAS version of the algorithm.
!
!  Arguments
!  =========
!
!  M       (input) INTEGER
!          The number of rows of the matrix A.  M >= 0.
!
!  N       (input) INTEGER
!          The number of columns of the matrix A.  N >= 0.
!
!  A       (input/output) REAL array, dimension (LDA,N)
!          On entry, the M-by-N matrix to be factored.
!          On exit, the factors L and U from the factorization
!          A = P*L*U; the unit diagonal elements of L are not stored.
!
!  LDA     (input) INTEGER
!          The leading dimension of the array A.  LDA >= max(1,M).
!
!  IPIV    (output) INTEGER array, dimension (min(M,N))
!          The pivot indices; for 1 <= i <= min(M,N), row i of the
!          matrix was interchanged with row IPIV(i).
!
!  INFO    (output) INTEGER
!          = 0:  successful exit
!          < 0:  if INFO = -i, the i-th argument had an illegal value
!          > 0:  if INFO = i, U(i,i) is exactly zero. The factorization
!                has been completed, but the factor U is exactly
!                singular, and division by zero will occur if it is used
!                to solve a system of equations.
!
!  =====================================================================
!
!     .. Parameters ..
!     REAL               ONE
!     PARAMETER          ( ONE = 1.0E+0 )
!     ..
!     .. Local Scalars ..
!     INTEGER            I, IINFO, J, JB, NB
!     ..
!     .. External Subroutines ..
!     EXTERNAL           SGEMM, SGETF2, SLASWP, STRSM, XERBLA
!     ..
!     .. External Functions ..
!     INTEGER            ILAENV
!     EXTERNAL           ILAENV
!     ..
!     .. Intrinsic Functions ..
!     INTRINSIC          MAX, MIN
!     ..
!     .. Executable Statements ..
!
!     Test the input parameters.
!
      INFO = 0
      IF( M.LT.0 ) THEN
         INFO = -1
      ELSE IF( N.LT.0 ) THEN
         INFO = -2
      ELSE IF( LDA.LT.MAX( 1, M ) ) THEN
         INFO = -4
      END IF
      IF( INFO.NE.0 ) THEN
         CALL XERBLA( 'SGETRF', -INFO )
         RETURN
      END IF
!
!     Quick return if possible
!
      IF( M.EQ.0 .OR. N.EQ.0 )
     $   RETURN
!
!     Determine the block size for this environment.
!
      NB = ILAENV( 1, 'SGETRF', ' ', M, N, -1, -1 )
      IF( NB.LE.1 .OR. NB.GE.MIN( M, N ) ) THEN
!
!        Use unblocked code.
!
         CALL SGETF2( M, N, A, LDA, IPIV, INFO )
      ELSE
!
!        Use blocked code.
!
         DO 20 J = 1, MIN( M, N ), NB
            JB = MIN( MIN( M, N )-J+1, NB )
!
!           Factor diagonal and subdiagonal blocks and test for exact
!           singularity.
!
            CALL SGETF2( M-J+1, JB, A( J, J ), LDA, IPIV( J ), IINFO )
!
!           Adjust INFO and the pivot indices.
!
            IF( INFO.EQ.0 .AND. IINFO.GT.0 )
     $         INFO = IINFO + J - 1
            DO 10 I = J, MIN( M, J+JB-1 )
               IPIV( I ) = J - 1 + IPIV( I )
   10       CONTINUE
!
!           Apply interchanges to columns 1:J-1.
!
            CALL SLASWP( J-1, A, LDA, J, J+JB-1, IPIV, 1 )
!
            IF( J+JB.LE.N ) THEN
!
!              Apply interchanges to columns J+JB:N.
!
               CALL SLASWP( N-J-JB+1, A( 1, J+JB ), LDA, J, J+JB-1,
     $                      IPIV, 1 )
!
!              Compute block row of U.
!
               CALL STRSM( 'Left', 'Lower', 'No transpose', 'Unit', JB,
     $                     N-J-JB+1, ONE, A( J, J ), LDA, A( J, J+JB ),
     $                     LDA )
               IF( J+JB.LE.M ) THEN
!
!                 Update trailing submatrix.
!
                  CALL SGEMM( 'No transpose', 'No transpose', M-J-JB+1,
     $                        N-J-JB+1, JB, -ONE, A( J+JB, J ), LDA,
     $                        A( J, J+JB ), LDA, ONE, A( J+JB, J+JB ),
     $                        LDA )
               END IF
            END IF
   20    CONTINUE
      END IF
      RETURN
!
!     End of SGETRF
!
      END

在二维剖分中进行高斯消去：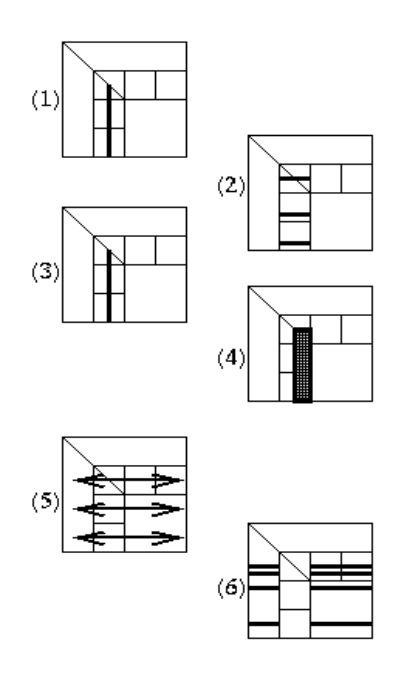

for ib = 1 to n-1 step b
    end = min(ib + b -1, n)
    for i = ib to end
        (1) find pivot row k, column broadcast
        (2) swap rows k and i in block column, broadcast row k
        (3) A(i+1:n, i) = A(i+1:n, i) / A(i,i)
        (4) A(i+1:n, i+1:end) -= A(i+1:n, i)*A(i,1+1:end)
    end for
    (5) broadcast all swap information right and left
    (6) apply all rows swap to other column
    (7) broadcast LL right
    (8) A(ib:end, end+1:n) = LL / A(ib:end, end+1:n)
    (9) broadcast A(ib:end, end+1:n) down
    (10) broadcast A(end+1:n, ib:end) right
    (11) eliminate A(end+1:n, end+1:n)
    // matrix multiply of green = green - blue * pink

lecture 15

compressed sparse row (CSR)存储：

大小为nnz=非零值个数（val）数组
大小为nnz的每个非零值的列索引数组
大小为n=行数的行起始指针数组

其他常用格式（加分块）

压缩稀疏列（CSC）
坐标（COO）：每个非零元素的行+列索引（易于构建）

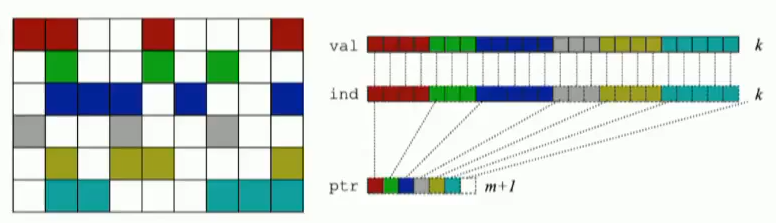
SpMV with CSR算法对y的重用很多，但是对x的重用不足。

1
2
3

for each row i:
    for k = ptr[i] to ptr[i+1] - 1 do
        y[i] = y[i] + val[k] * x[ind[k]]

可能的优化：

把k循环展开，需要知道这一行有多少非零元素
把y[i]挪出for循环
压缩ind[i]，需要知道非零元素出现的规律
重用x，需要很好的非零元素出现规律
cache：需要知道非零元在附近的行
register：需要知道这些非零元存在哪里

SpMV可以利用分块，不需要使用index存储每一个非零元，而是使用1个列序号存储非零r-c块？

Optimizations for SpMV

Register blocking (RB): up to 4x over CSR
Variable block splitting: 2.1x over CSR, 1.8x over RB
Diagonals: 2x over CSR
Reordering to create dense structure + splitting: 2x over CSR
Symmetry: 2.8x over CSR, 2.6x over RB
Cache blocking: 2.8x over CSR
Multiple vectors (SpMM): 7x over CSR
And combinations…

Sparse triangular solve

Hybrid sparse/dense data structure: 1.8x over CSR

SpMV的行并行：对x的访问是随机的，而且没有线程之间的依赖关系，所以没有竞争/锁。剖分的话就根据非零元素的个数进行分割。与列并行相比，都是对y的随机读写，列并行需要同步操作。将行与列结合起来有更多并行性。

优化总结：

NUMA-非统一内存访问
- 将子矩阵固定到分配给它们的核心附近的内存中
预取-值、索引和/或向量
- 对预取距离进行彻底搜索
矩阵压缩-不仅仅是寄存器分块（BCSR）
- 32或16位索引，子矩阵的块坐标格式
缓存阻塞
- 矩阵的2D分区，因此所需的x、y部分适合缓存

分布式SpMV的并行性：

y=A*x，其中A是稀疏矩阵
行并行性（y和A）
- 跨处理器复制x
- 或者只交换必要的元素
- 非零是否聚集在一起，例如，接近对角线？
列并行性（x和A）
- 在所有处理器上设置临时y=[0, …]；
- 更新该信息；并跨处理器添加reduce
p很大和非零一致时的二维并行性
- 将处理器划分为p1 x p2（例如，方形网格）
- 使用混合行和列并行性
- 非零元素聚集时的负载平衡不良

lecture 17

一些机器学习算法与矩阵向量乘相关。隐式的并行是保持整体算法结构（操作序列）完整，并行化各个操作，如将BLAS操作并行化，通常可以获得完全相同的精度（例如，DNN训练中的模型并行性），如果算法的关键路径较长，则可扩展性可能会受到限制。

显式并行化：修改算法以获得更多的并行性，例如算法在单个模块上执行，这些模块的结果稍后可以合并。示例：DNNs中的CA-SVM和数据并行，可以实现显著更好的可扩展性。
训练即更新神经网络的权重。

梯度下降：为了最小化一个函数，以α速率的梯度方向朝相反方向移动，α是步长（也称为学习速率）。用作许多其他机器的优学习方法（示例：NMF）

随机梯度下降SGD，SGD因其“嘈杂”的梯度而避开尖锐的局部极小值。

并行化机会

数据并行性：分发输入（图像、文本、音频等）
- 批处理并行性：将每个完整样本分发到不同的处理器。当人们在文献中提到数据并行时，这就是他们99%的意思
域并行性
- 细分样本并将各部分分发给处理器。一种以前未经探索的并行方法。
模型并行性：分配神经网络（即其权重）

参数服务器中梯度的获取和更新可以同步或异步完成。
两者都有利弊。在异步不可再现的情况下，过度同步会影响性能，并可能会影响收敛

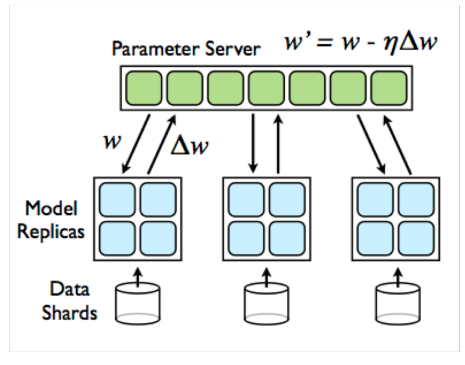
Dean, Jeffrey, et al. “Large scale distributed deep networks.” Advances in neural information processing systems. 2012.

为了避免参数服务器带来的瓶颈，两种方法：全局allreduce参数，或者进程之间两两互相交换参数。

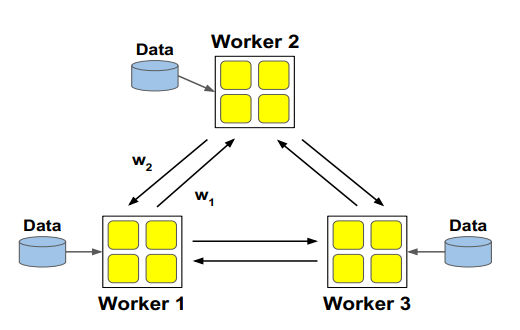
Peter Jin, Forrest Iandola, Kurt Keutzer, “How to scale distributed deep learning?” NIPS ML Sys 201

模型并行性的例子。图中显示了一个五层深度的神经网络，该网络具有独立性，被划分为四台机器（蓝色矩形）。只有跨越分区边界（粗线）的那些才需要它们的状态传输。即使在节点有多条边穿过分区边界的情况下，也会发送到该边界另一侧的计算机一次。

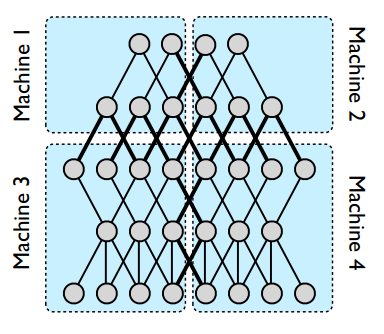
解释1：将神经网络划分到处理器
解释2：并行执行矩阵运算

在每个分区内，各个节点将跨所有可用的CPU核进行并行化。

在反向传播中，误差从最后一层传播到第一层，并且任何两个连续层之间都存在数据依赖性。相比之下，不同层的梯度是相互独立的。激活在前级从左到右传播；错误在反向传播阶段从右向左传播。梯度是使用激活和误差计算的。每个箭头表示数据依赖性。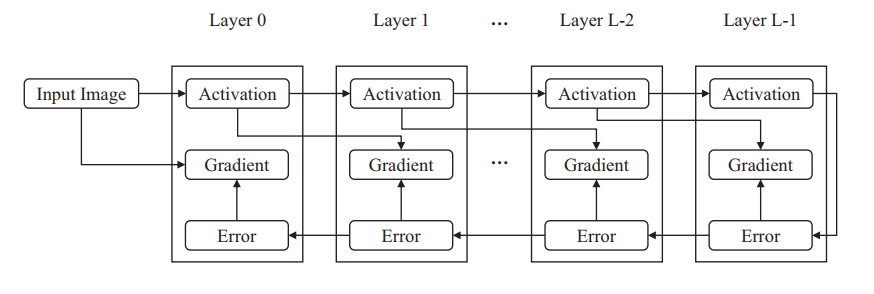

神经网络的SGD训练：如果看成是矩阵乘的话：权重矩阵（N✖M）乘以本层输入（M✖B）=本层输出（N✖B）。

其中权重W会被复制到每个处理器，所以是不会变的。输入和输出会由于数据并行而变得更小，例如，把输入矩阵切分到b=B/p大小

域并行（domain parallel）：总体思路与用于在 HPC 中并行化模板代码的halo区域或ghost区域相同，在卷积之前，交换局部对应halo数据。

在向前和向后传递期间用于光环交换的附加通信

对于激活大小较大的早期层（即卷积层），成本可以忽略不计

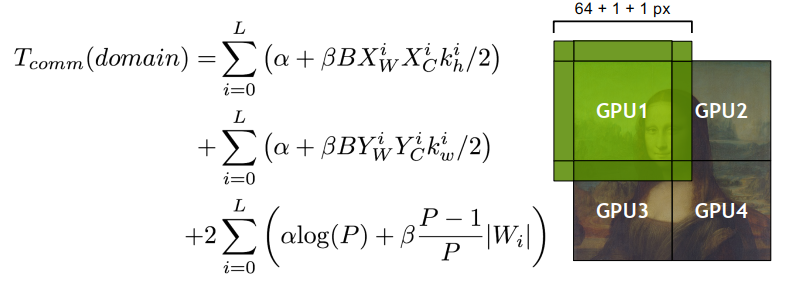
分布式深度学习总结

大batch训练经常导致次优学习
集成并行使用避免通信的算法来扩展可扩展性，而不是增大batch大小
集成并行性将模型和数据（batch和domain）并行性最佳结合起来，并且通常比每个极端都表现得更好。
对全连接层（大参数）使用模型并行，对卷积层（大激活）使用数据并行通常更好

支持向量机：只有支持向量上的分类约束是活动的

导致巨大的二次约束优化 (QP) 问题
特殊算法，例如顺序最小优化 (SMO)，将这个巨大的 QP 分解为更小的（实际上是最小的）QP 子问题。

在特征空间中的计算是耗时的，因为特征空间一般都是高维的。核方法解决这个问题。核方法用任意核函数替换线性模型的点积相似度，该函数计算 x 和 y 之间的相似度：K(x, y): X ✖ X ➡ R。

内核必须是对称的和半正定的。高斯核（即径向基函数）是ML中的事实上的核。K(x, x') = exp(-γ || x - x' ||^2)。我们可以预先计算核（Gram）矩阵，但这太耗时了。

下图中，2D (a) 中的圆形分类边界使用以下变换变为 3D (b) 中的线性边界：φ(x1, x2) = (x1^2, x2^2, 根下2 * x1 *x2)。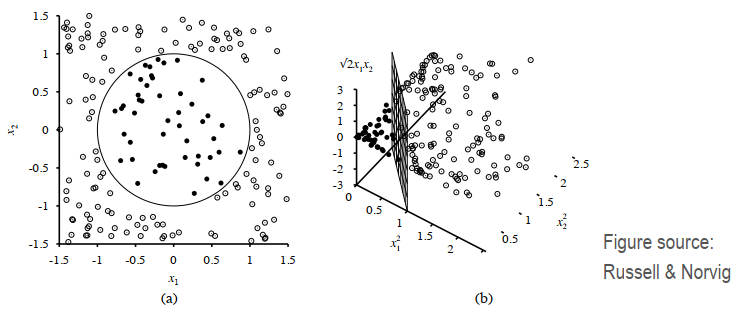

输入数据集是一个n✖d的矩阵，X1、X2、…、Xn都有一个d长度的特征向量。生成一个n✖n的核矩阵，K[i][j] = exp(-r||Xi - Xj||^2)，r是一个正数。计算复杂度O(d*n^2)，内存复杂度O(n^2)，很小的输入会产生很大的核矩阵。357MB的输入(52K✖90) = 2000GB核矩阵。使用SMO（顺序最小优化）

采用迭代法，避免核矩阵
每次迭代使用两行核矩阵
稀疏输入的关键核：稀疏矩阵乘以稀疏向量

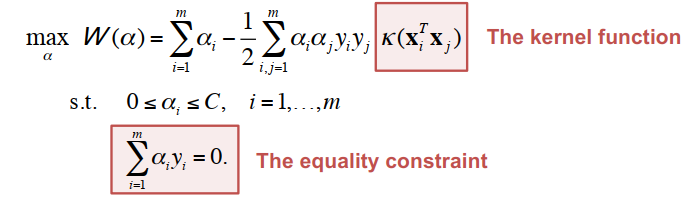
最小可能的优化问题一次涉及“两个”拉格朗日乘子，因为仅仅改变乘数会违反等式约束。

重复直到收敛：

选择一些对 αi 和 αj 进行下一步更新（使用试探法尝试选择这两个，这将使我们能够朝着全局最大值取得最大进展）。
相对于 αi 和 αj 重新优化 W(α)，同时保持所有其他 αk 的固定。

Cascade SVM：数据被分割均匀并由多个SVM处理。逐层去除非支持向量

数据是前一层的支持向量（SV）
将 SV 的参数 αi 传递到下一层以获得更好的启动（热启动）

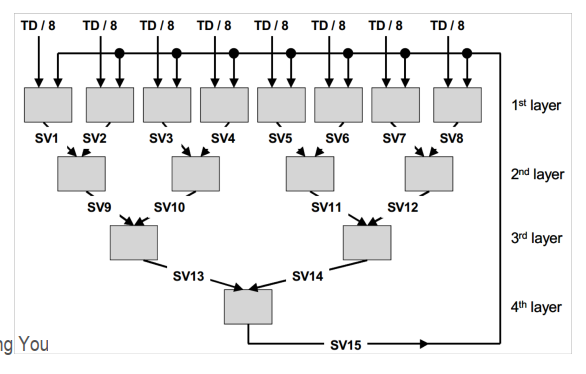
Divide-and-Conquer SVM：全部数据在层与层之间传递；使用内核k-mean实现数据集的分割。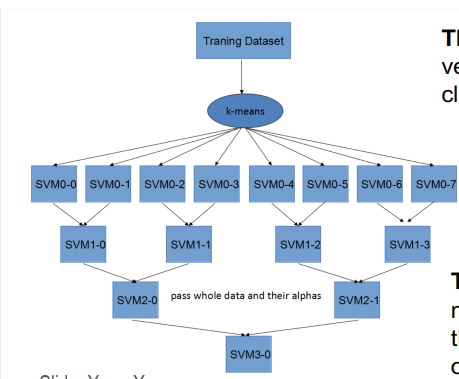

定理1：子问题的支持向量集接近于整个问题的支持向量集
定理2：内核 kmeans 最小化子问题的解与整个问题的解之间的差异

CP-SVM：

divide：K-means将数据划分为P个部分
conquer：欧氏距离选择最佳模型

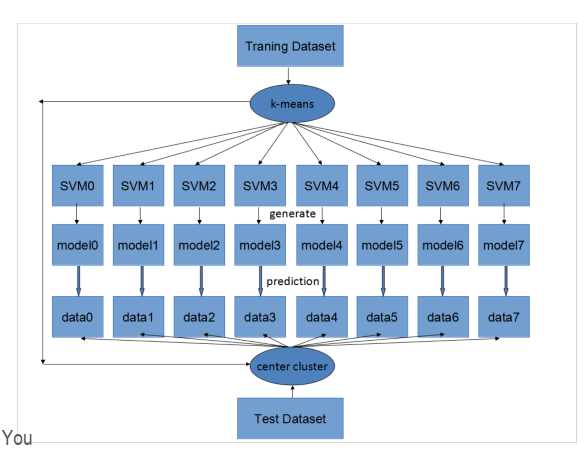
当||Xi - Xj||^2很大时，exp(-r||Xi - Xj||^2)是0。
K-means最大化了数据集之间的欧氏距离
这两个矩阵具有相似的 F 范数
分析假设高斯核：对于给定的样本，只有接近它的支持向量才能对分类产生影响

communication-avoid SVM：设计了一个均衡的聚簇来取代k-means，仍然尽可能近似kmeans的距离分离特性。

非负矩阵分解 (NMF)：min{W≥0, H≥0} f(W, H) = 1/2 || A - WH ||^2。

m✖n矩阵A = m✖k矩阵W * k✖n矩阵H

具有非负约束的降维
“分解”这个名字用词不当。 NMF 只是一个低秩近似，因为精确分解是 NP 难的
NMF 是一系列方法，而不仅仅是一种算法

聚类

基于质心（k 均值、k 中值和变体）
基于流（马尔可夫聚类）
谱方法
基于密度（DBSCAN、OPTICS）
凝聚方法（单链聚类）

通常，正确的方法取决于输入特征并需要一些领域知识。我们将讨论两种并行算法：谱聚类和马尔可夫聚类 (MCL)。

谱聚类

输入：数据点之间的相似性
计算相似度的许多方法，有些是特定领域的：余弦、Jaccard 指数、Pearson 相关性、Spearman’s rho、Bhattacharyya 距离、LOD 分数……
我们可以用图表示数据点之间的关系，通过点之间的相似性对边进行加权

图定义

ε-邻域图
- 确定阈值 ε，如果两点之间的亲和力大于 ε，则加入这条边。
k-最近邻
– 在节点与其 k 个最近邻居之间插入边。
– 每个节点将连接到（至少）k 个节点。
全连接
– 在每对节点之间插入一条边。

谱聚类

图形的最小割确定了数据的最佳分区。
谱聚类：递归分割数据集
- 确定最小割
- 去除边
- 重复直到识别出 k 个集群
问题：识别最小割是NP 难的。
存在使用线性代数的有效近似值，基于拉普拉斯矩阵或图拉普拉斯算子

图拉普拉斯算子

非标准化图拉普拉斯算子：L = D - W
标准化图拉普拉斯算子：
- L(sym) = D^(-1/2) * L * D^(-1/2) = I - D^(-1/2) * W * D^(-1/2)
- L(rw) = D^(-1) * L = I - D^(-1) * W

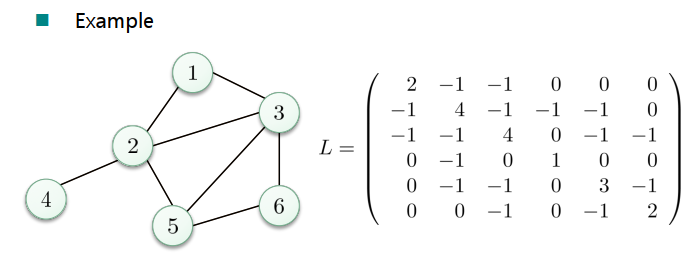
特征值 0 的多重性给出了集群的数量（在这种理想情况下：连接的分量的数量）。
假设真实情况是这种情况的近似。

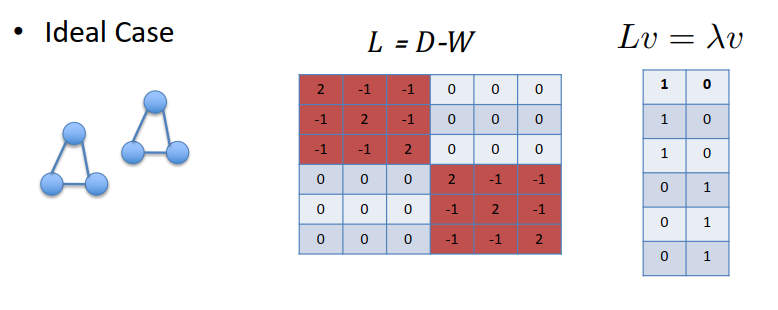
如何计算那些最小的特征向量？

通过 Lanczos 算法实现
- workhorse是稀疏矩阵向量 (SpMV) 乘法
- SpMV 没有/最小化的数据重用，受通信限制
- 为了优化稀疏矩阵向量乘法并最小化其通信，我们绘制分区图（下一讲）
替代算法是可能的
- 幂迭代（power iteration）更廉价但数值不稳定
- LOBPCG（局部优化块预处理共轭梯度，Locally-Optimized Block Preconditioned Conjugate Gradient）使用稀疏矩阵乘以多个向量，由于可能的数据重用，因此具有更有利的性能。
最后，您可能只想调用现有的东西。
- ARPACK 实现反向通信特征求解器：您实现 SpMV，它实现数字外部逻辑
- PARPACK 是它的并行版本，以下代码使用它：https://github.com/openbigdatagroup/pspectraclustering

lecture 18

图分区的定义

给定一个图 G = (N, E, WN, WE)
- N = 节点（或顶点），
- WN = 节点权重
- E = 边
- WE = 边权重
例如：N = {tasks}，WN = {task cost}，E 中的边 (j,k) 表示任务 j 将 WE(j,k) 字节发送到任务 k
选择一个分区 N = N1 U N2 U … U NP 使得
- 每个 Nj 中节点权重的总和大致相同
- 最小化连接所有不同对 Nj 和 Nk 的边的所有边权重之和
例如：平衡工作负载，同时尽量减少通信
- N = N1 U N2 的特例：图二分

稀疏矩阵向量乘法y = y +A*x分割稀疏对称矩阵

… declare A_local, A_remote(1:num_procs), x_local, x_remote, y_local
y_local = y_local + A_local * x_local
for all procs P that need part of x_local
    send(needed part of x_local, P)
for all procs P owning needed part of x_remote
    receive(x_remote, P)
    y_local = y_local + A_remote(P)*x_remote

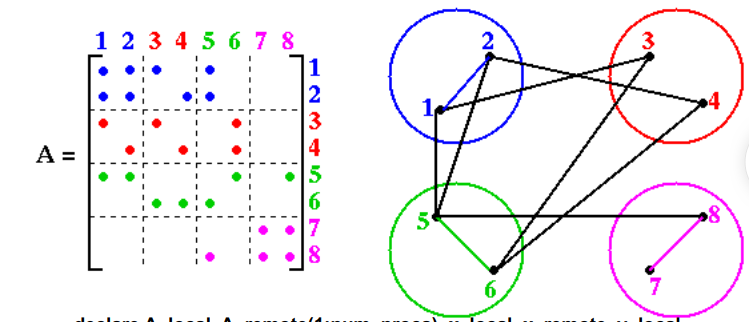
选择最优分区是 NP 完全的

(NP-complete = 我们可以证明它是非确定多项式时间类中其他众所周知的难题)
只有已知的精确算法具有成本 = 指数(n)
我们需要好的启发式方法

第一个启发式：重复图二分法

将 N 分成 2^k 个部分
递归地平分图 k 次
今后主要讨论图二分法

边分隔符与顶点分隔符

边分隔符：如果从 E 中删除 Es，留下 N 的两个大小相等、不相连的分量：N1 和 N2，则 Es（E 的子集）分隔 G
顶点分隔符：如果移除 Ns 和所有的相关边，留下两个大小相等、不连贯的N的组成部分：N1和N2，就说Ns（N 的子集）分割G

从 Es 生成 Ns：选择 Es 中每条边的一个端点
- |Ns| ≤ |Es|
从一个 Ns 生成一个 Es：选取所有在 Ns 上的边
- |Es| ≤ d * |Ns|，其中 d 是图的最大度数
我们会找到边缘或顶点分隔符，因为它们很方便

使用节点坐标（Nodal Coordinates）进行分区

每个节点都有 x,y,z 坐标 ➡ 分区空间
不使用节点坐标（Nodal Coordinates）进行分区
网络文档的稀疏矩阵

节点坐标：惯性分区

对于二维上的图，选择一条分割图的线
- 在 3D 中，选择一个平面，但为了简单起见考虑 2D
选择一条线 L，然后选择一条垂直于它的线 LT，两边各有一半节点

选择一条直线 L 通过这些点。L 由a*(x-xbar)+b*(y-ybar)=0给出，其中a^2+b^2=1；(a,b) 是单位向量垂直于L
将每个点投影到线上。对于每个nj = (xj,yj)，计算沿 L 的坐标Sj = -b*(xj-xbar) + a*(yj-ybar)
计算中位数。让 Sbar = median(S1, …, Sn)
使用中值划分节点。让 Sj < Sbar 的节点在 N1 中，剩余的在 N2 中

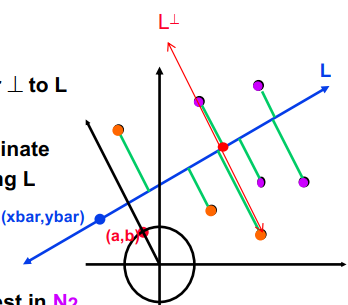
节点坐标：摘要

这些算法的其他变体
算法高效
依赖于节点（主要）连接到空间中最近邻的图
- 算法不依赖于实际边的位置！
当图来自物理模型时很常见
忽略边，但可以用作后续检查边的分区的良好起始
如果图连通性不是空间的，则效果不佳：

图分块的无须坐标系的方法：Kernighan/Lin

取一个初始分区并迭代改进它
- Kernighan/Lin (1970)，开销 = O(|N|^3)
- Fiduccia/Mattheyses (1982)，开销 = O(|E|)，更好，但更复杂
给定 G = (N, E, WE) 和分区 N = A U B，其中 |A| = |B|
- T = cost(A,B) = ∑ {W(e) 其中 e 连接 A 和 B 中的节点}
- 使用|X| = |Y|，查找A的子集X和B的Y
- 如果可以降低成本，请考虑交换 X 和 Y：
  - newA = (A – X) U Y 和 newB = (B – Y) U X
  - newT = cost(newA, newB) < T = cost(A,B)
需要为许多可能的 X 和 Y 有效地计算 newT，选择最小（最佳）

Kernighan/Lin：初步定义

T = cost(A, B), newT = cost(newA, newB)
需要一个有效的newT公式；将使用
- E(a) = A 中 a 的外部开销 = ∑ {W(a,b) for B in b}
- I(a) = A 中 a 的内部成本 = S {W(a,a) for other a’ in A}
- D(a) = A 中 a 的成本 = E(a) - I(a)
- E(b)、I(b) 和 D(b) 对于 B 中的 b 定义类似
考虑交换 X = {a} 和 Y = {b}
- newA = (A - {a}) U {b}
- newB = (B - {b}) U {a}
newT = T - ( D(a) + D(b) - 2*w(a,b) ) ≡ T - gain(a,b)
- gain(a,b) 衡量通过交换 a 和 b 获得的改进
更新公式
- newD(a') = D(a') + 2*w(a',a) - 2*w(a',b)对于 A 中的 a’，a’ ≠ a
- newD(b') = D(b') + 2*w(b',b) - 2*w(b',a)对于 B 中的 b’，b’ ≠ b

红色是第一部分，黑色是第二部分，最开始的切分是随机的，none (8);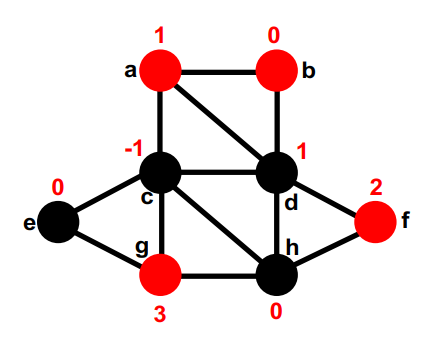

第一部分中最大的gain的是g，把g挪到第二部分，同时计算g的邻居的gain。暂时移动的节点是空心圆。暂时移动节点的gain无关紧要。none (8); g,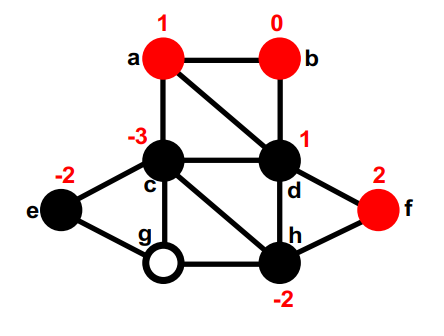

第二部分的gain最大的是d，暂时移动到第一部分，重新计算d的邻居的gain，在这之后，图的切是4。none (8); g, d (4);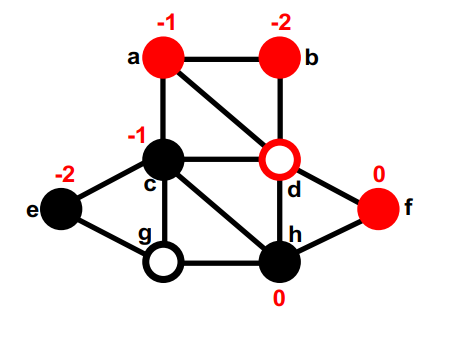

第一部分中没有移动过的最大的gain的是f。暂时移动到第二部分，重新计算它邻居的gain。none (8); g, d (4); f,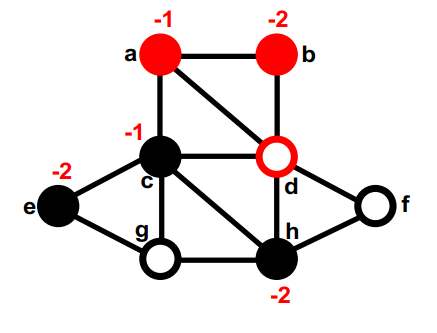

第二部分中没有移动过的最大的gain的是c，暂时移动到第一部分，重新计算c的邻居的gain，这次交换后，这个图的切是5。none (8); g, d (4); f, c (5);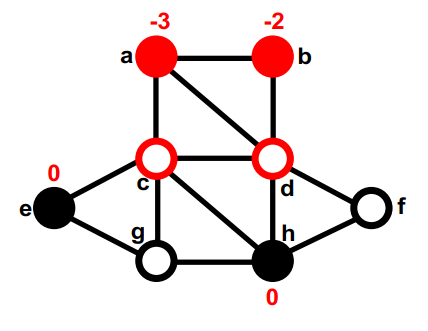

第一部分中没有移动过的最大的gain的是b，暂时移动到第二部分，重新计算b的邻居的gain。none (8); g, d (4); f, c (5); b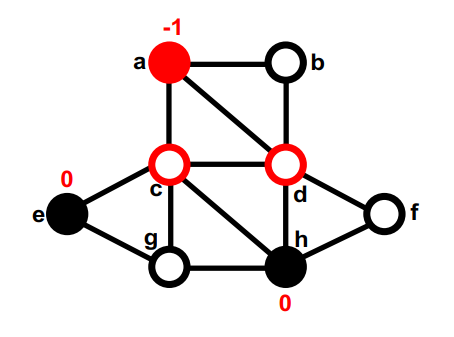

第 2 部分中两个未移动节点之间的最大gain存在联系。我们选择一个（比如e）并暂时将其移至 Part1。它没有未移动的邻居，因此不会重新计算gain。这次交换后，这个图的切是7。none (8); g, d (4); f, c (5); b, e (7);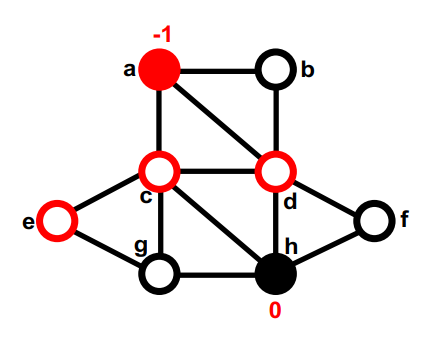

第一部分中没有移动过的最大的gain的是a，暂时移动到第二部分，它没有未移动的邻居，因此不会重新计算gain。none (8); g, d (4); f, c (5); b, e (7); a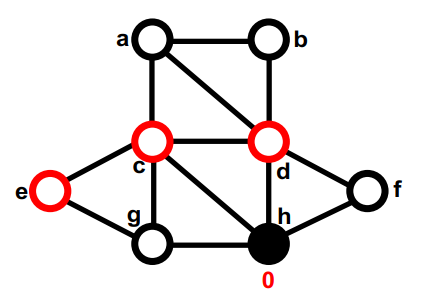

第二部分中没有移动过的最大的gain的是a，暂时移动到第一部分，它没有未移动的邻居，因此不会重新计算gain。最终临时交换后的切大小为 8，和任何动作之前一样。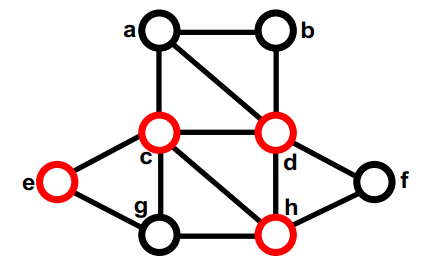

在每个节点都被暂时移动后，我们看到交换 g 和 d 后，最小的切割是 4。我们使该交换永久化并撤消所有后来的临时交换。这是第一个改进步骤的结束。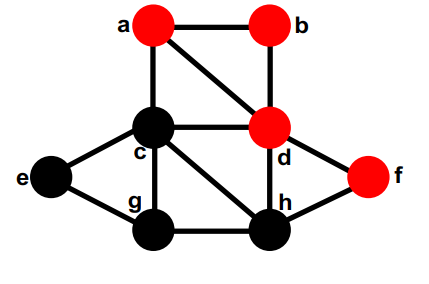

现在我们重新计算gain并从新的最小切4开始进行另一个改进步骤。细节没有显示。第二个改进步骤不改变切大小，所以算法以切为4结束。一般来说，只要切不断变小，我们就会继续进行改进步骤。

Kernighan/Lin 算法

最耗时的线以红色显示，O(n3)
某些gain(k)可能为负，但如果后来的gain很大，则最终gain可能为正
- 可以避免局部最小值，其中切换没有任何帮助
我们重复多少次？
- K/L 在非常小的图 (|N|<=360) 上测试并在 2-4 次扫描后收敛
- 对于（具有理论意义的）随机图，一步收敛的概率似乎下降为 2^(-|N|/30)

多级分区简介

如果我们想对 G(N,E) 进行划分，但它太大而无法有效地进行，我们该怎么办？
- 1. 将 G(N,E) 替换为粗近似 Gc(Nc,Ec)，并划分 Gc
- 1. 使用Gc的分区得到G的粗略分区，然后迭代改进
如果 Gc 仍然太大怎么办？
- 递归应用相同的想法

最大匹配

定义：图 G(N,E) 的匹配是 E 的子集 Em，使得 Em 中没有两条边共享端点
定义：图 G(N,E) 的最大匹配是一个匹配Em，不能添加更多边并保持匹配
一个简单的贪心算法计算最大匹配：

let Em be empty
mark all nodes in N as unmatched
for i = 1 to |N| … visit the nodes in any order
    if i has not been matched
        mark i as matched
        if there is an edge e=(i,j) where j is also unmatched,
            add e to Em
            mark j as matched
        endif
    endif
endfor

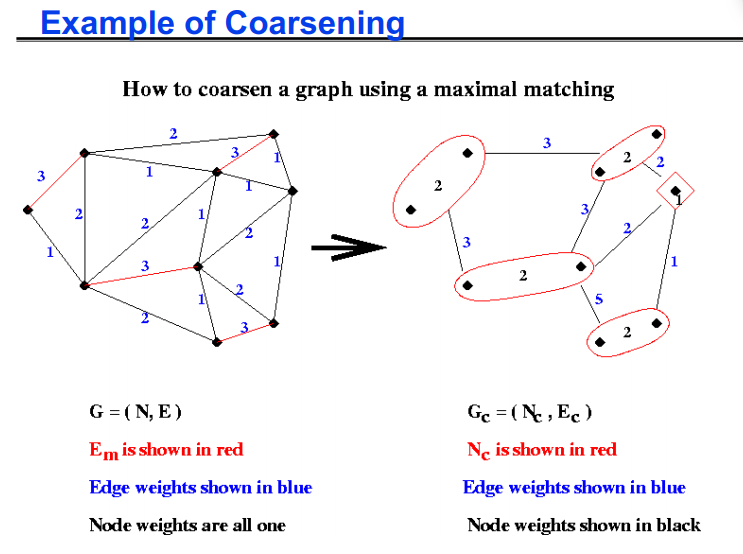
1) 构建G(N, E)的最大匹配Em
for all edges e = (j,k) in Em  2)将匹配的节点折叠成一个节点
    Put node n(e) in Nc 
    W(n(e)) = W(j) + W(k) … gray statements update node/edge weights
for all nodes n in N not incident on an edge in Em 3) 添加不匹配的节点
    Put n in Nc … do not change W(n)
现在 N 中的每个节点 r 都在 Nc 中的唯一节点 n(r) 内

4) 如果两个节点内部的节点在 E 中连接，则在 Nc 中连接两个节点
for all edges e=(j,k) in Em
    for each other edge e'=(j,r) or (k,r) in E
        Put edge ee = (n(e),n(r)) in Ec
        W(ee) = W(e')

如果在 Nc 中有多个边连接两个节点，将它们折叠起来，
    添加边权重

通过稀疏矩阵-矩阵乘进行简化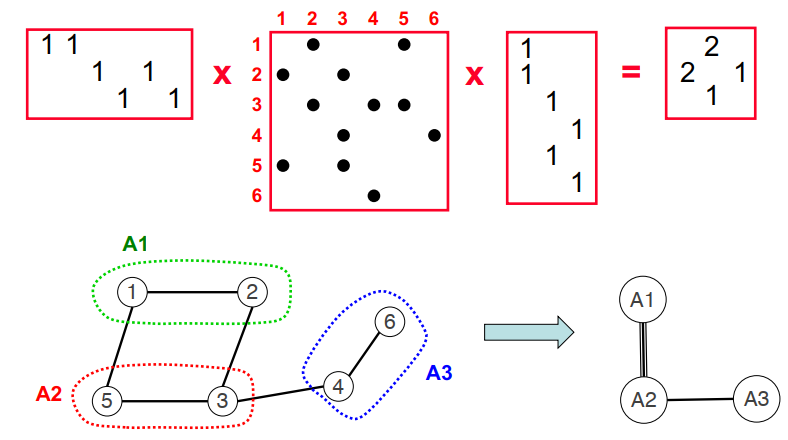

Parallel sparse matrix-matrix multiplication and indexing:
Implementation and experiments. SIAM Journal of Scientific Computing (SISC), 2012

一些实现

Multilevel Kernighan/Lin
- METIS and ParMETIS (glaros.dtc.umn.edu/gkhome/views/metis)
- SCOTCH and PT-SCOTCH (www.labri.fr/perso/pelegrin/scotch/)
Matlab toolbox for geometric and spectral partitioning by Gilbert, Tang, and Li: https://github.com/YingzhouLi/meshpart
Multilevel Spectral Bisection
- S. Barnard and H. Simon, - A fast multilevel implementation of recursive spectral bisection …, 1993
- Chaco (SC’14 Test of Time Award)
Hybrids possible
- Ex: Use Kernighan/Lin to improve a partition from spectral bisection
Recent packages with collection of techniques
- Zoltan (www.cs.sandia.gov/Zoltan)
- KaHIP (http://algo2.iti.kit.edu/kahip/)

超越简单的图划分：将稀疏矩阵表示为超图

edge (vi, vj) ∈ E ➡ y(i) ⬅ y(i) + A(i,j) x(j) and y(j) ⬅ y(j) + A(j,i) x(i)

P1 performs: y(4) ⬅ y(4) + A(4,7) x(7) and y(5) ⬅ y(5) + A(5,7) x(7)

x(7) only needs to be communicated once !

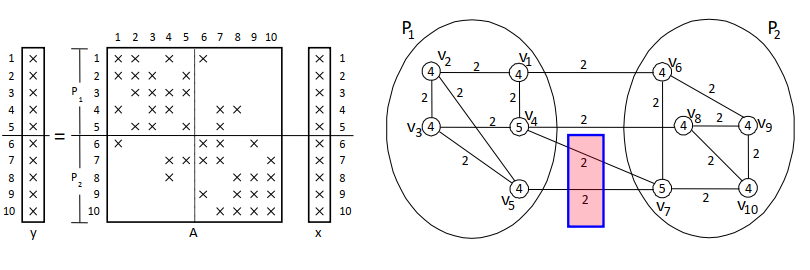
块-行分布的列-网模型
行是顶点，列是网络（超边）

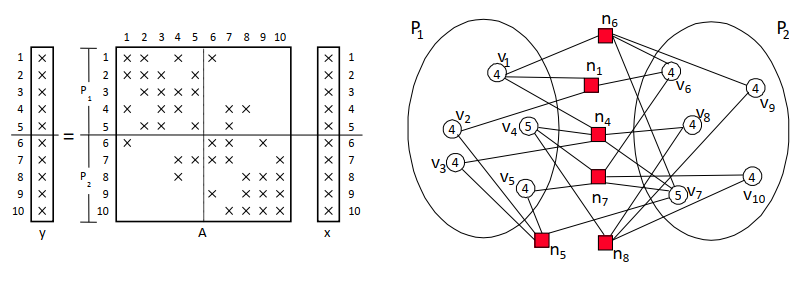
两种不同的2D网格分块方法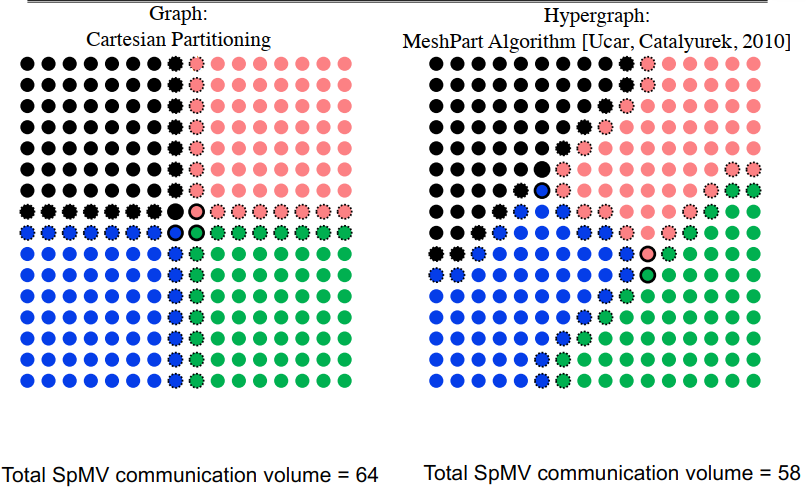

分区质量最重要

当结构在模拟过程中动态变化时，需要动态分区
- 速度可能比质量更重要
- 分区器必须并行快速运行
  - 这里还有一个先有鸡还是先有蛋的问题
- 分区应该是增量的
  - 相对于之前的变化最小
- 不得使用过多内存
最近关于流分区的研究：
- Stanton, I. and Kliot, G., “Streaming graph partitioning for large distributed graphs”. KDD, 2012

lecture 19

这一节中定义了i = sqrt(-1)。

一个有m个元素的向量v的离散傅里叶变换(DFT)为F*v，其中F是一个m*m的矩阵，F(j,k)=ω^(j*k), 0 ≤ j,k ≤ m-1，其中ω=e^(2πi/m)=cos(2π/m)+i*sin(2π/m)，ω是一个复数，它的m次方ω^m=1。例如m=4，则ω=i, ω^2=-1, ω^3=-i, ω^4=1。m*m二维矩阵V的DFT为F*V*F。

快速傅里叶变换主要用在图像处理、信号处理，求解泊松方程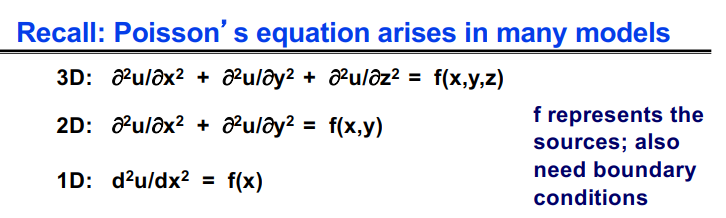

分别在一维二维条件下求解泊松方程：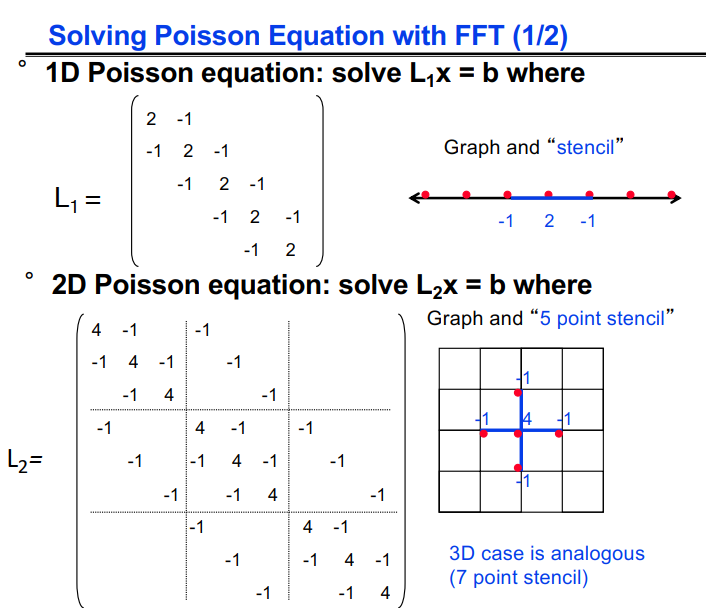

因为L1=F·D·FT，是特征值/特征向量分解，F与FFT很相似，F(j,k)=(2/(n+1))^(1/2) · sin(j k π /(n+1))，D是特征值的对角矩阵，D(j,j)=2(1-cos(j π/(n+1)))。

二维泊松与L1 · X + X · L1 = B类似，

FFT的串行算法：计算m个元素的向量v的FFT(F*v)，(F*v)[j] = ∑(k=0,m-1)(F(j,k)*v(k)) = ∑(k=0,m-1)(ω^(j*k)*v(k)) = ∑(k=0,m-1)((ω^j)^k*v(k)) = V((ω^j))，V是多项式V(x)=∑(k=0,m-1)(x^k * v(k))。

FFT类似在m个点上评估一个m-1阶多项式V(x)。

V可以用分治来计算：V(x)=∑(k=0,m-1)(x^k * v(k))=v[0] + x^2 * v[2] + x^4 * v[4] + ... + x*(v[1] + x^2 * v[3] + x^4 * v[5] + ...) = Veven(x^2) = Vodd(x^2)。

V的阶为m-1，所以Veven和Vodd是m/2-1阶的多项式。

FFT(v, ω, m) … assume m is a power of 2
if m = 1 return v[0]
else
    veven = FFT(v[0:2:m-2], ω^2, m/2)
    vodd = FFT(v[1:2:m-1], ω^2, m/2)
    ω-vec = [ω^0, ω^1, … ω^(m/2-1) ]
    return [Veven + (ω-vec .* Vodd),
            Veven - (ω-vec .* Vodd) ]

Cost: T(m) = 2T(m/2)+O(m) = O(m log m) operations.

FFT的分治算法画图是一个完全二叉树：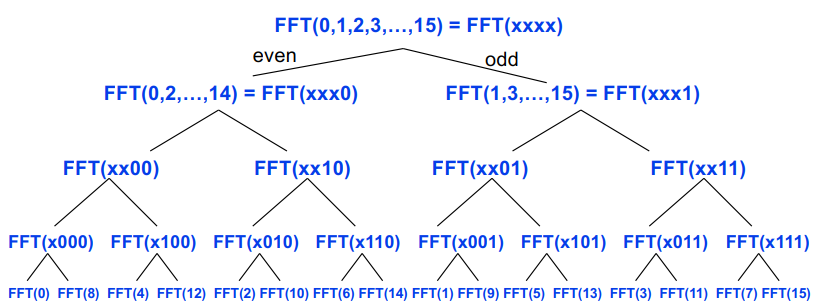

消息发送延迟的来源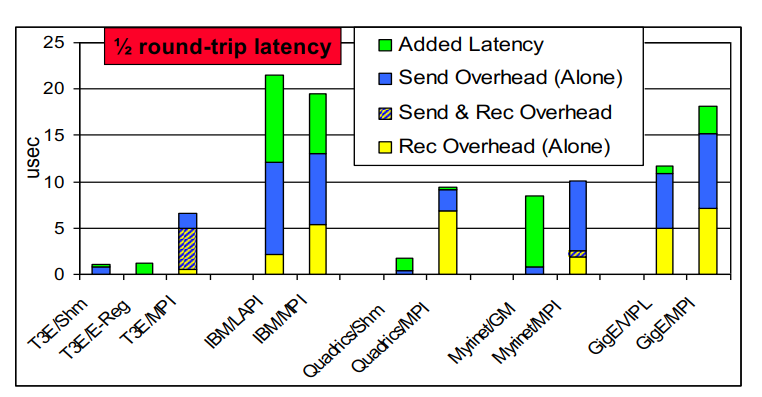

一般地，重叠意味着同时计算和通信，（或与其他通信对象通信，又名流水线）

重叠的潜力是gap和开销之间的差异

如果在整个消息发送过程中 CPU 被占用，则没有潜力
- 例如，没有发送端 DMA
具有 DMA 的机器的潜力随着消息大小的增长而增长（每字节成本由网络处理，即 NIC）
潜力随着网络拥塞量的增加而增长
- 因为差距随着网络变得饱和而增长

对于具有 RDMA 的机器，远程开销为 0，需要良好的软件支持才能利用这一点。

GASNet 提供 put/get 通信，是在网络硬件之上的一层。

一方面：API 中不需要远程 CPU 参与（与 MPI 的主要区别）
- 消息包含远程地址
- 无需与接收匹配
- 无需隐式排序

下图是GASNet和MPI在通信上的差异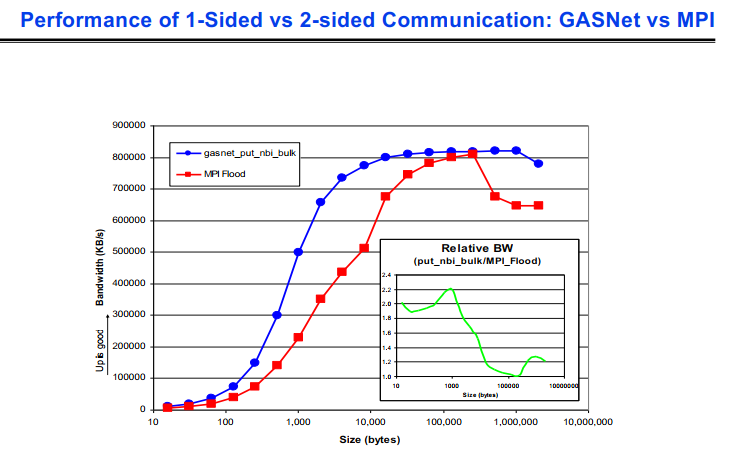

lecture 20

PRAM模型：

理想化的并行共享内存系统模型
无限数量的同步处理器；无同步、通信成本；没有并行开销
EREW（独占读独写）、CREW（并发读独占写）
衡量性能：空间和时间复杂度；操作总数（工作）
优点
- 简单而干净的语义。
- 大多数理论并行算法是使用 PRAM 模型设计的。
- 独立于通信网络拓扑。
缺点
- 不现实，太强大的通信模型。
- 通信成本被忽略。
- 需要同步处理器。
- 没有本地内存。
- 大 O 符号通常具有误导性。

图的表示：压缩稀疏行：缓存高效的邻接表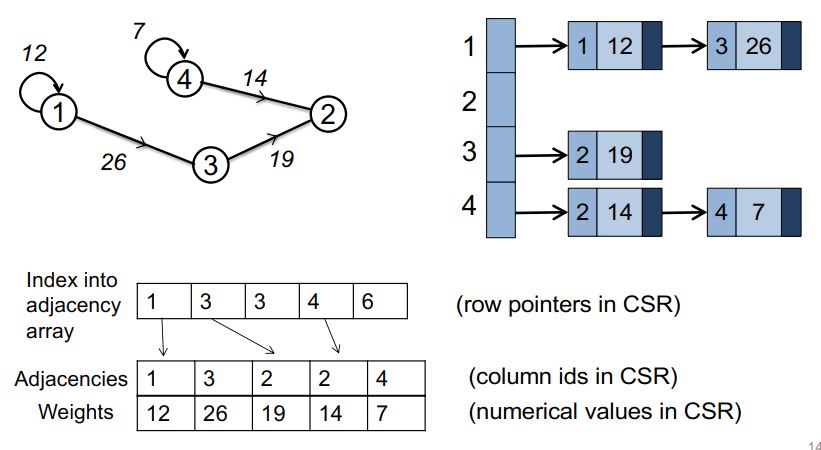

分布式网格表示：

每个处理器存储整个图（“完全复制”）
每个处理器存储 n/p 个顶点以及这些顶点之外的所有邻接（“一维分区”）
如何创建这些“p”顶点分区？
- 图分区算法：递归优化电导（边缘切割/较小分区的大小）
- 随机打乱顶点标识符确保边数/处理器大致相同

二维棋盘表示：

考虑一个逻辑 2D 处理器网格 (pr * pc = p) 和图的矩阵表示
为每个处理器分配一个子矩阵（即子矩阵内的边）

应该是把图的矩阵表示进行分割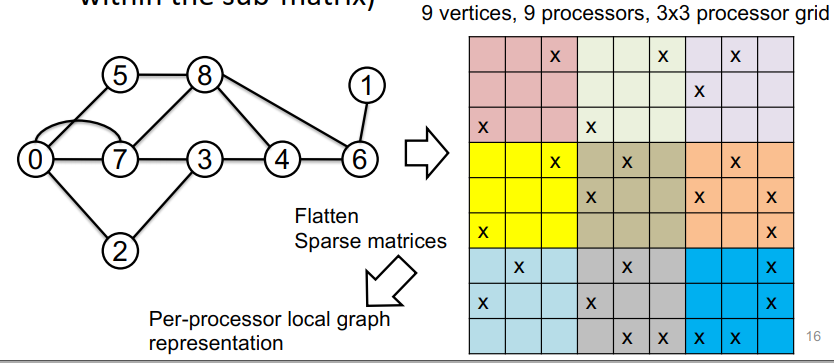

DFS：并行化DFS的复杂度很高，难以并行

procedure DFS(vertex v)
    v.visited = true
    previsit(v)
    for all v s.t. (v, w) ∈ E
        if(!w.visited) DFS(w)
    postvisit(v)

BFS的内存要求：

稀疏图表示：m+n
访问顶点堆栈：n
距离阵列：n

广度优先搜索是其他并行图算法的一个非常重要的构建块，例如（二部）匹配、最大流、（强）连接分量等。

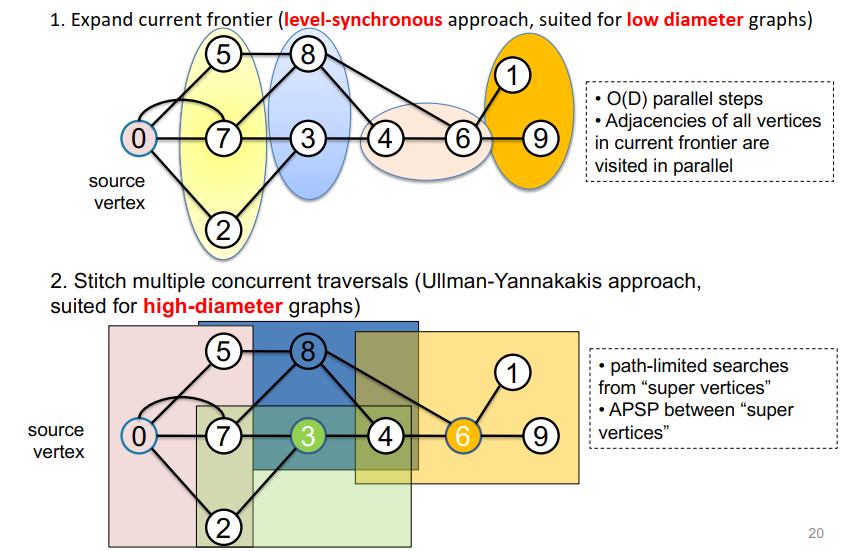
并行化BFS：

扩展当前边界（水平同步方法，适用于小直径图）
- 并行访问当前边界中所有顶点的邻接
拼接多个并发遍历（Ullman-Yannakakis方法，适用于大直径图）

图的矩阵表示A转置为AT。最开始把开始的1点放到parents中，1点的parents是0点。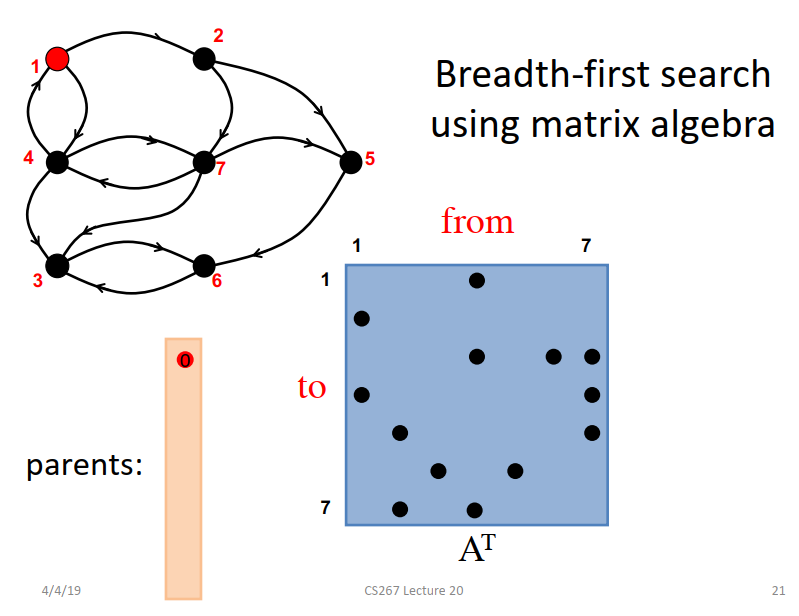

AT乘parents向量得到ATX，得到1的邻接点是2和4，修改parents向量。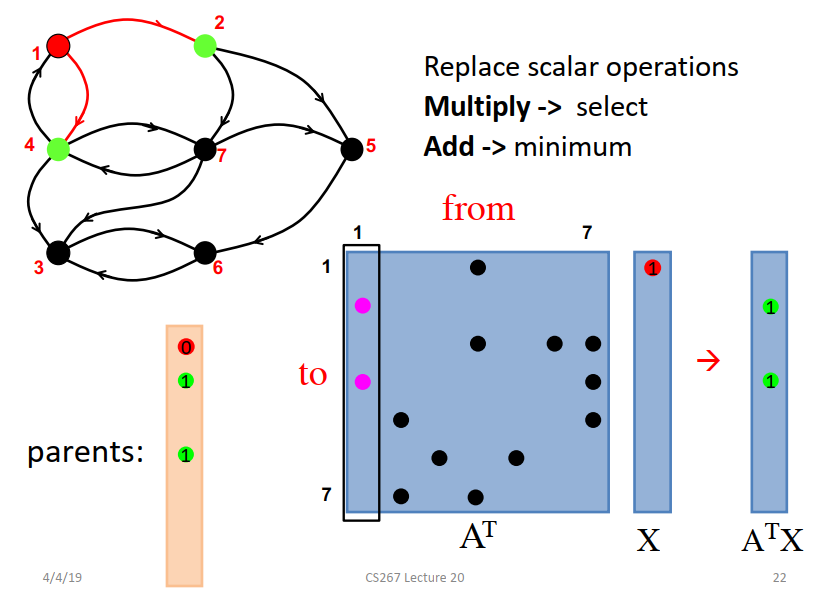

X是上一步求出来的ATX，AT*X得到这一步的邻接点，加入到parent向量中。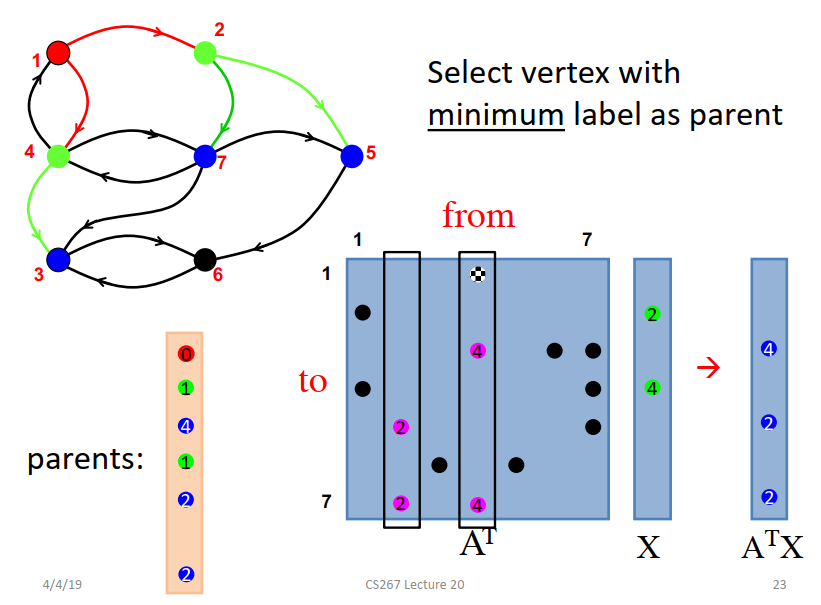

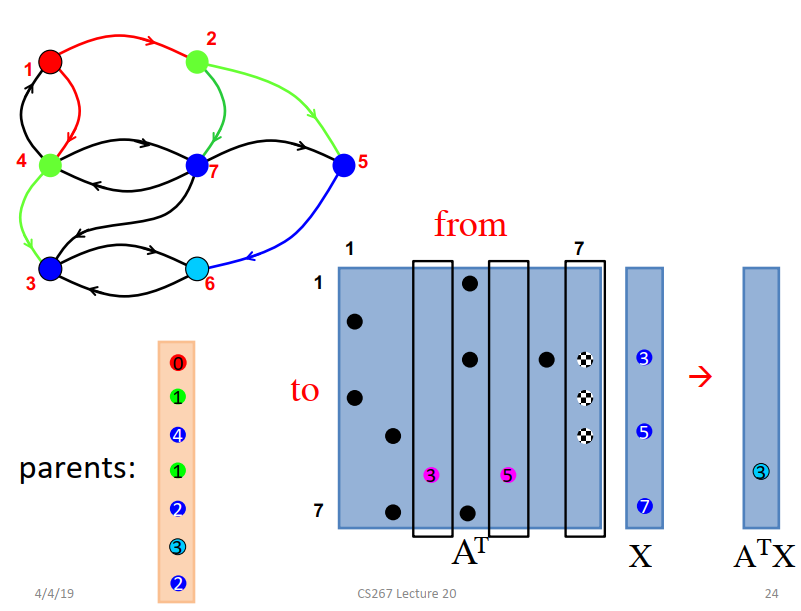
1D Parallel BFS algorithm

查找当前边界邻接的所有者。(计算)
通过all to all交换邻接。(通讯)
更新未访问顶点的distance/parents。(计算)

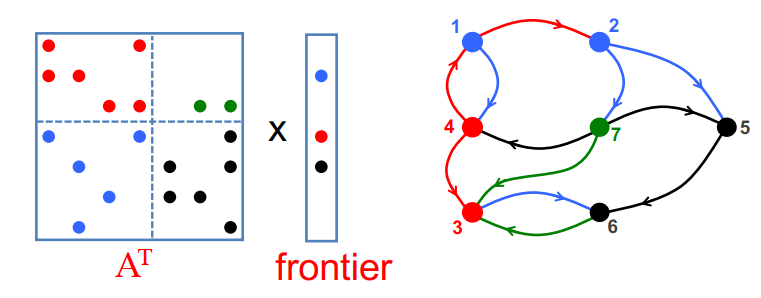
2D Parallel BFS algorithm

在处理器列中收集顶点(通信)
查找当前边界邻接的所有者(计算)
交换处理器行中的邻接(通信)
更新未访问顶点的distance/parents。(计算)

并行单源最短路径（Parallel Single-source Shortest Paths，SSSP）算法

著名的串行算法：
- Bellman-Ford：标签校正-适用于任何图形
- Dijkstra：标签设置–需要非负边权重
没有已知的PRAM算法在次线性时间和O(m+nlogn)下运行
Ullman Yannakakis随机方法
meyer and Sanders，∆ - stepping算法
Chakaravarthy等人，巧妙地结合了∆-stepping和超级计算机规模图上的方向优化（BFS）。

U. Meyer and P.Sanders, ∆ - stepping: a parallelizable shortest path algorithm. Journal of Algorithms 49 (2003)

V. T. Chakaravarthy, F. Checconi, F. Petrini, Y. Sabharwal “Scalable Single Source Shortest Path Algorithms for Massively Parallel Systems ”, IPDPS’14

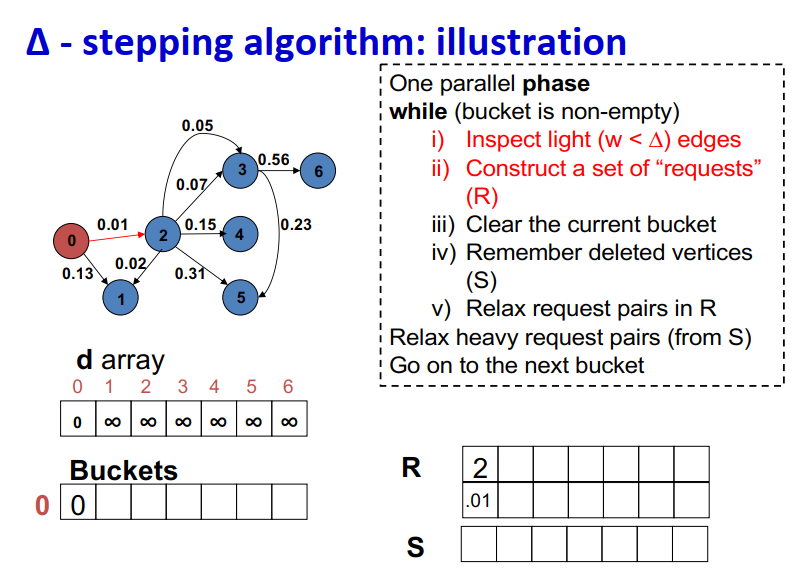
∆ - stepping算法

标签校正算法：可以从未设置的顶点松弛边
“Dijkstra的近似实现”
对于随机边权重[0,1]，在L=从源到任何节点的最大距离处运行，复杂度O(n + m + D·L)
顶点使用宽度∆的桶进行排序
每个桶可以并行处理
基本操作：Relax(e(u, v))
- d(v)=min{d(v)，d(u)+w(u,v)}
∆ < min w(e)：退化为Dijkstra
∆ > max w(e)：退化为Bellman-Ford

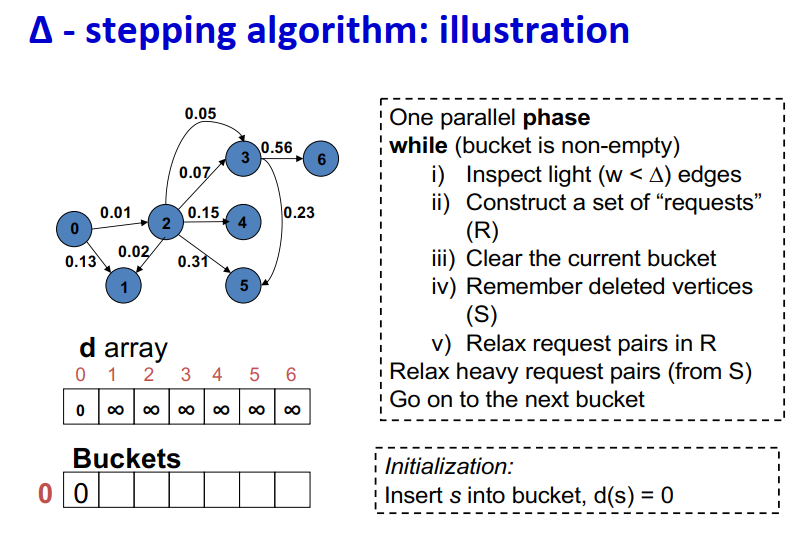
算法说明：

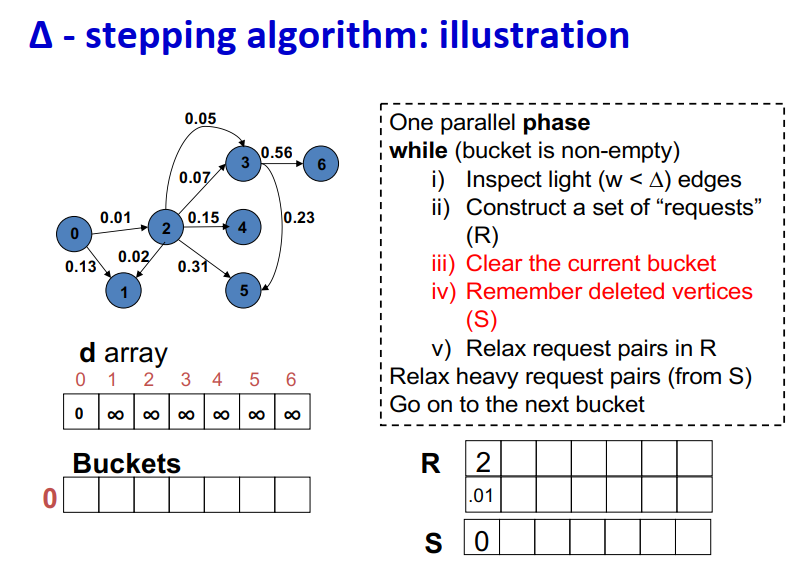
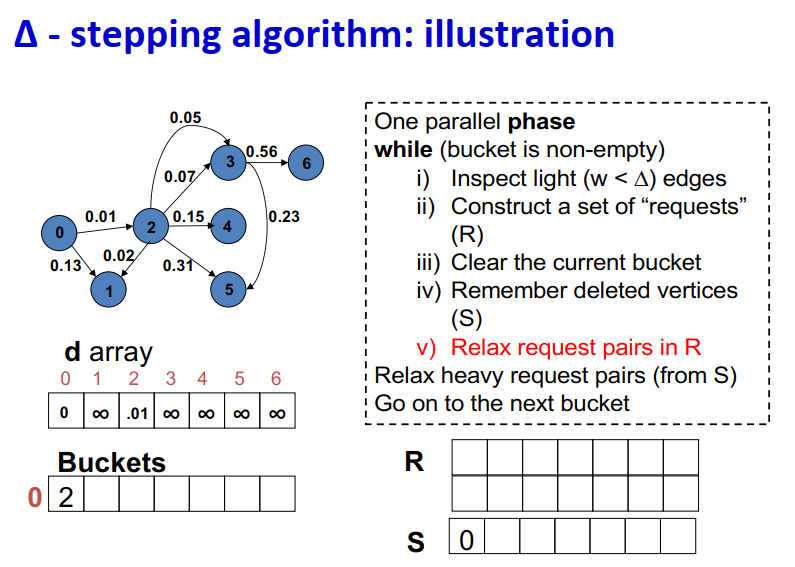
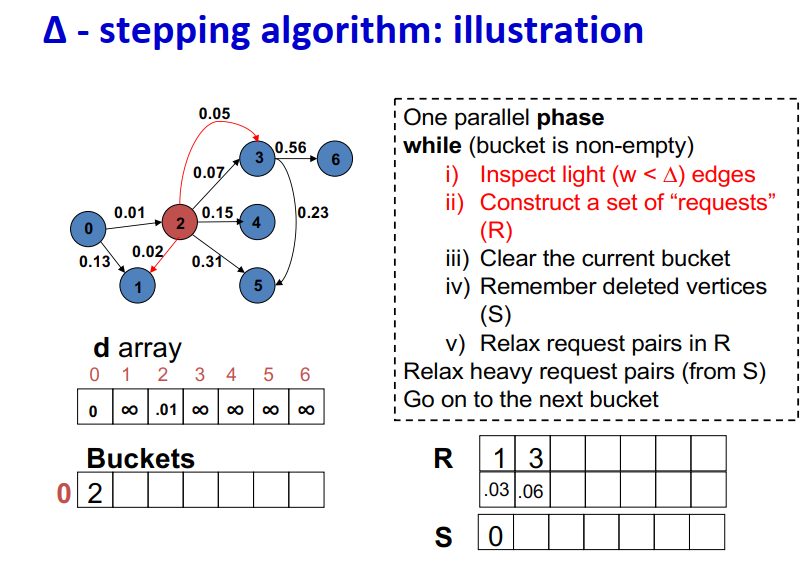
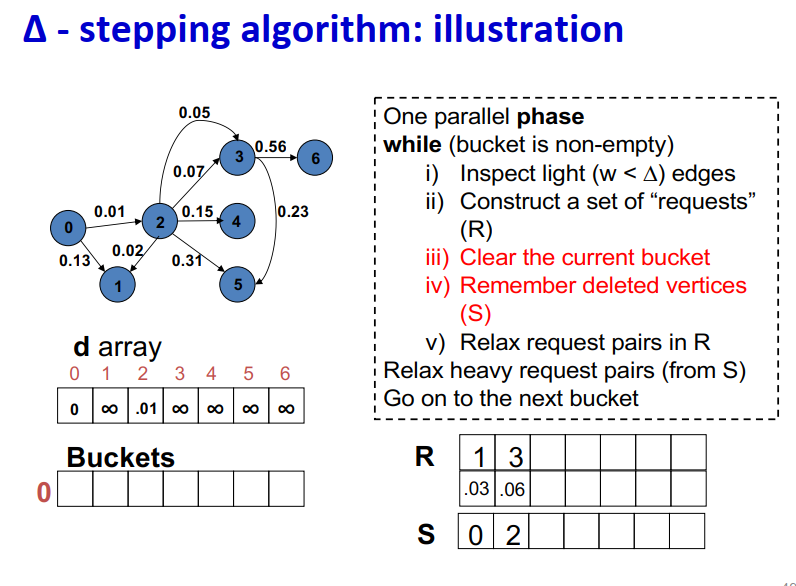
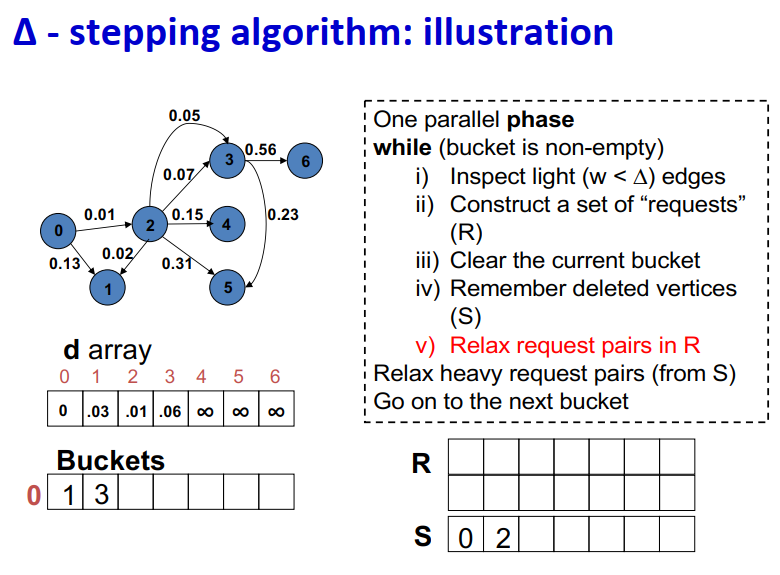
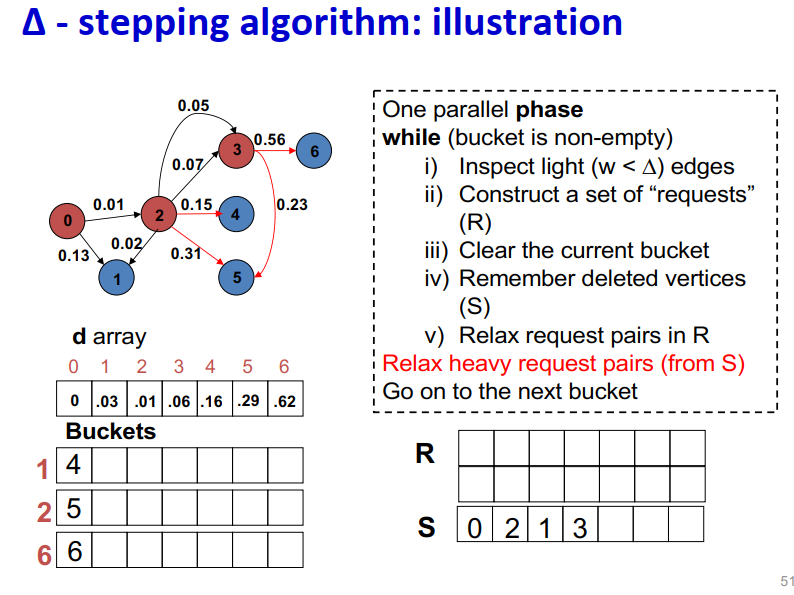
One parallel phase
while (bucket is non-empty)
    i) Inspect light (w < ∆) edges
    ii) Construct a set of “requests” (R)
    iii) Clear the current bucket
    iv) Remember deleted vertices (S)
    v) Relax request pairs in R
Relax heavy request pairs (from S)
Go on to the next bucket

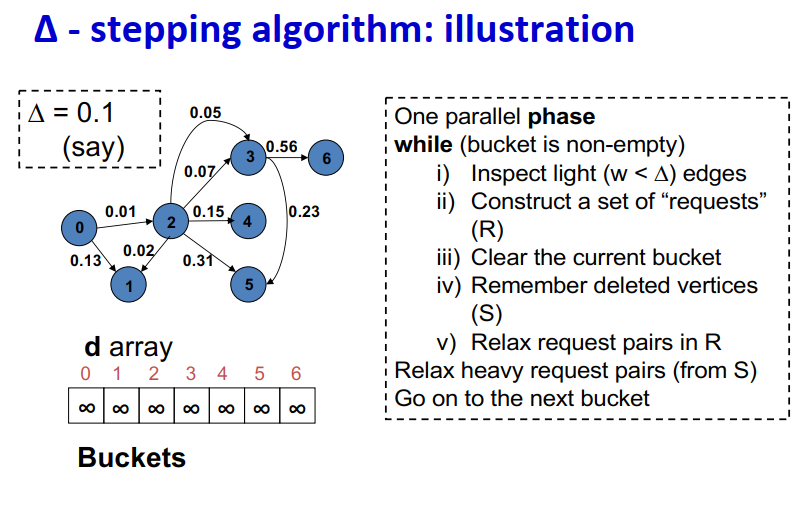
Initialization:

Insert s into bucket, d(s) = 0

最大独立集

顶点V={1,2，…，n}的图
如果S中没有两个顶点是相邻的，则S组顶点是independent的。
如果无法添加另一个顶点并保持独立，则独立集S是maximal的
如果没有其他独立集具有更多顶点，则独立集Smaximum
难以找到最大独立集（NP难）
至少在一个处理器上，找到最大独立集很容易。

红色顶点集S={4，5}是独立的，是maximal的，但不是maximum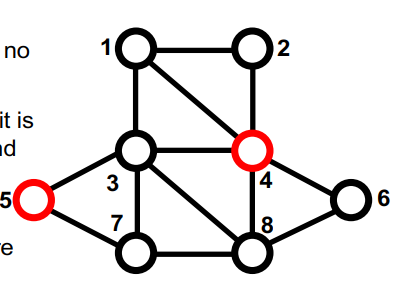

串行的最大独立集算法：

S = empty set;
for vertex v = 1 to n
    if (v has no neighbor in S)
        add v to S

并行随机的最大独立集算法

S = empty set; C = V;
while C is not empty {
    label each v in C with a random r(v);
    for all v in C in parallel {
        if r(v) < min( r(neighbors of v) ) {
            move v from C to S;
            remove neighbors of v from C;
        }
    }
}

M. Luby. “A Simple Parallel Algorithm for the Maximal Independent Set Problem”

Strongly connected components(SCC)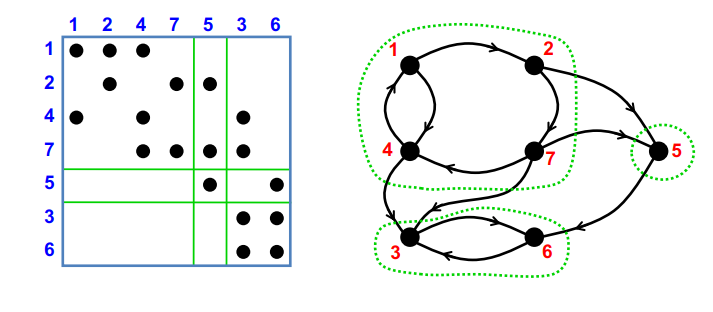

块三角形式的对称置换，通过深度优先搜索在线性时间内找到P。

线性方法：使用DFS，DFS似乎具有内在的顺序性。并行：分而治之和BFS(Fleischer et al.)，最坏情况O(n)，但实际情况良好。

把给定的图分成三个邻接的图，每一个可以递归独立处理。
使用并行BFS

二分图匹配：

匹配：没有公共端点的边的子集M。
| M |=匹配M的基数

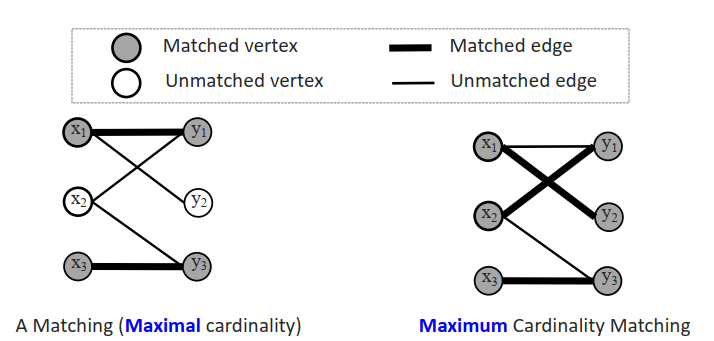
最大基数匹配的单源算法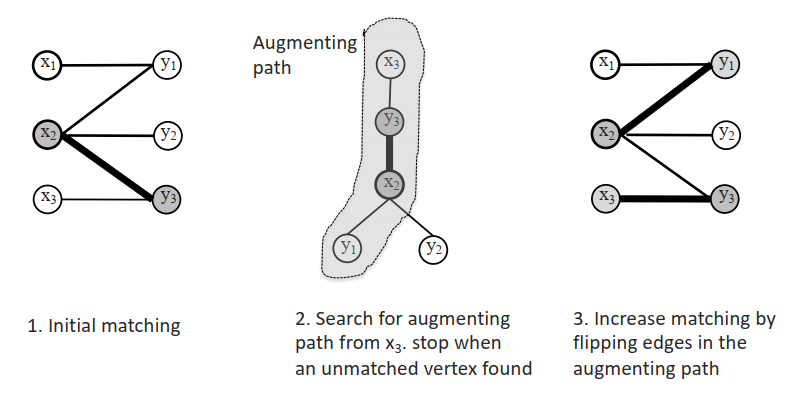

最大基数匹配的多源算法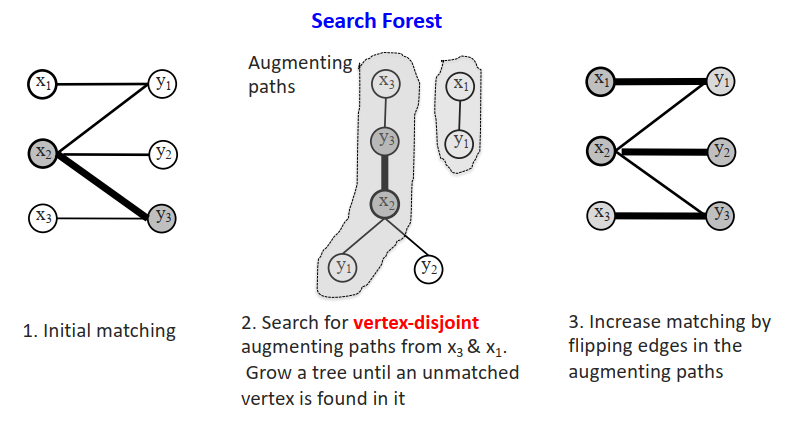

lecture 21

大爆炸宇宙学什么的，没用

lecture 22

云计算和大数据处理

数据编程模型：“数据”并行模型（松散耦合）

限制编程接口
自动处理故障、位置等。

Map-Reduce就是基于这样的模型，每个数据类型都是(key, value)键值对，输入被分到一些节点上，然后结果被reduce到一些节点上

Map：(Kin, Vin) ➡ list(Kinter, Vinter)
Reduce：(Kinter, list(Vinter)) ➡ list(Kout, Vout)

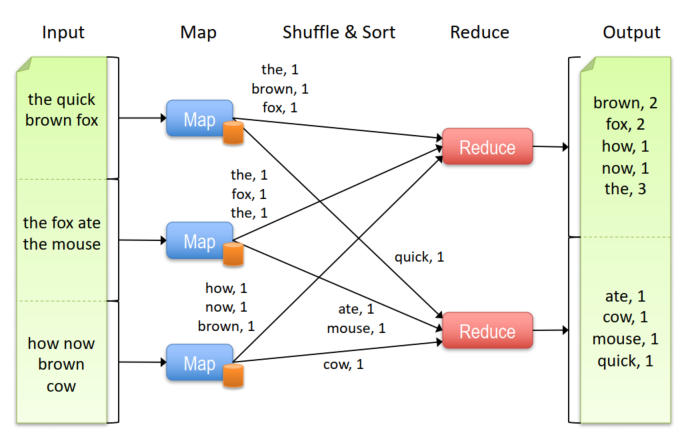
如果一个节点上的作业挂了？

在其他节点上重试这个作业
如果这个作业还是挂掉，结束这个作业

如果节点挂了？在其他节点上重新启动现在的任务

相比于MPI是并行模型，更加细粒度，MapReduce是更高级别的数据级并行，自动进行数据传递。

如果是多步的任务，需要更多的mapper和reducer，比如有21个MR steps的话，就要有21个mapper和21个reducer。因此提出了spark。

spark提供了更简单的API，比MR少5-10倍的代码，内存计算速度更快，也有算子之间的优化。

lecture 23

为什么会有很垃圾的扩展性？

通信开销大
同步开销大
很多进程空闲着（负载不平衡、缺乏并行性等）

如何测试负载不平衡？

很难将负载不平衡与高同步开销分开
基本测量：barrier周围的计时器
- 程序缺乏并行性是固有的负载不平衡——无法通过更好的负载平衡来解决
- 不要性能数据的平均！需要查看所有值或画出直方图
- 特别微妙，如果不是批量同步的话
- 自旋锁可以使同步看起来像是有用的工作
- 不平衡可能由硬件（缓存、动态时钟等）引起

矩阵向量乘：很简单的是稠密乘；比较难的稀疏乘，每一行都有不同的开销，如果提前知道稀疏矩阵的布局，将行按照相同的非零元数分割更好。

任务开销可变性（来自应用程序）

简单：开销相等，数量固定：规则网格、密集矩阵、直接 n 体
困难：任务有不同但可估计的时间，固定数量：自适应和非结构化网格、稀疏矩阵、基于树的 n 体、粒子网格方法
最难：直到执行中期才知道时间或计数：搜索（UTS）、不规则边界、子网格物理、不可预测的机器

请注意，良好的负载平衡无法解决并行性不足的问题。

作业之间的依赖关系：

简单：一组准备好的任务
- 矩阵乘法，域分解（空间循环）
中：任务有已知关系（任务图）
- chain：随着时间的推移循环；迭代方法（外循环）
- tree：分而治之的算法
- graph：直接求解器（密集和稀疏），即 LU、Cholesky…
困难：直到运行时才知道任务结构
- tree：搜索
- graph：离散事件

DFS vs BFS

带有显式堆栈的 DFS——几乎没有并行性
- 将根节点放入栈
- 当栈不为空
  - 将栈顶元素弹出
  - 如果找到了目标就返回
  - 否则将子节点放入栈中
带有显式堆栈的BFS——并行性强
- 将根放入队列（FIFO）
  - 当队列不为空时
  - 移除队列前端
  - 如果找到目标？返回成功
  - 否则将子节点排入队列末尾

分布式任务队列

任务队列对分布式内存的明显扩展是：
- 分布式任务队列（或包），即每个处理器一个
- 空闲处理器可以拉动工作，或者忙碌的处理器推工作
什么时候“分布式”队列是个好主意？
- 分布式内存多处理器
- 通常在共享内存上以避免同步争用
- 任务之间的位置不是（非常）重要
- 事先不知道任务和/或数量的开销
术语旁注：
- 队列：先进先出 (FIFO)
- 堆栈：后进先出 (LIFO)
- 包：任意出局

如何选择发送/接收处理器

基本技术：
- 独立循环（常见bug：都开始看p0）
  - 每个处理器k，保持一个变量targetk
  - 当处理器用完工作时，从 targetk 请求工作
  - 设置 targetk = (targetk +1) mod procs
- 全局循环
  - Proc 0 保持单个可变target变量
  - 当处理器需要工作时，获取target，从target请求工作
  - Proc 0 设置目标 = (target + 1) mod procs
- 随机获取
  - 当处理器需要工作时，随机选择一个处理器并向它请求工作
- 随机推送
  - 当处理器有太多工作（至少两个任务）时，推送任务到随机处理器
终止检测非常重要

随机负载均衡

想要避免共享队列的瓶颈
特别是在分布式内存中（但即使在共享内存中）
所以自调度、Chunked SS、GSS 都不好
使用分布式队列进行共享
如何选择处理器？
- 异步或全局循环
- 随机推送：快速平衡，可能会失去空间局部性
- 随机拉取：缓慢平衡，尽可能保留局部性

Cilk：内建负载均衡的语言

基于扩散的负载均衡

在随机化方案中，机器被处理为全连接。 [Cybenko，1989]
基于扩散的负载平衡将拓扑考虑在内
- 向附近的几个处理器发送一些额外的工作
  - 与附近邻居的平均工作量
  - 与扩散的类比（Jacobi 用于求解泊松方程）
- 局部性优于选择随机处理器
- 负载平衡比随机化慢
- 在创建时必须知道任务的开销
- 任务之间没有依赖关系
参见 Ghosh et al，SPAA96 了解二阶扩散负载平衡算法
- 考虑上次发送的工作量
- 避免一阶方案的一些振荡

DAG调度软件

DAGuE
- 开发库以支持（最初）稠密线性代数
SMPss
- 基于编译器；通过编译指示表达的数据使用；提议在 OpenMP 中；最近添加的 GPU 支持
StarPU (INRIA)
- 基于库； GPU支持；分布式数据管理； Codelets=tasks（映射 CPU、GPU 版本）
OpenMP4.0 / GCC 4.9
- 参见 openmp.org
其他工具（例如，仅限 fork-join 图）
- Cilk、英特尔线程构建块 (TBB)、Microsoft CCR、SuperGlue 和 DuctTEiP

任务通信

静态：常规（或无）
- 网格上的最近邻、密集矩阵、规则网格、FFT、直接 n 体（all-to-all）集合（难以扩展；易于调度）
半静态：可以预先计算通信模式
- 可以预先安排发送/接收对
- 稀疏直接线性代数求解器，例如 LU、Cholesky、AMR、树结构 n 体
动态：随机访问 - 模式事先未知且不会重复
- 搜索、离散事件、稀疏更新、直方图、哈希表

解决方案的范围：一个关键问题是何时知道有关负载平衡问题的某些信息。

静态调度。所有信息都可用于调度算法，该算法在任何实际计算开始之前运行。
- 离线算法，例如图分区、DAG 调度
- 如果信息太多，仍可能使用动态方法
半静态调度。信息可能在程序启动时、每个时间步的开始或其他明确定义的点上是已知的。即使问题是动态的，也可以使用离线算法。
- 例如 Kernighan-Lin，如 Zoltan
动态调度。直到执行中期才知道信息。
- 在线算法——今天的主要话题

动态负载均衡

负载均衡因任务属性而异

任务成本
- 所有任务的成本是否相等？
- 如果没有，成本什么时候知道？
  - 开始前、任务创建时或仅任务结束时
任务依赖
- 所有任务能否以任何顺序运行（包括并行）？
- 如果没有，何时知道相关性？
  - 开始前、任务创建时或仅任务结束时
  - 一项任务可能会提前结束另一项任务（例如搜索）
位置（可能会与负载平衡进行权衡）
- 将某些任务安排在同一处理器（或附近）是否重要？以降低通信成本？
- 什么时候知道有关通信的信息？
如果仅在任务结束时才知道属性
- 统计数据是固定的、缓慢变化的还是突然变化的？

混合并行：作为另一种变体，考虑具有 2 个并行性级别的问题

粗粒度的任务并行性
- 任务多时好，任务少时差
细粒度的数据并行性
- 任务中的并行度高时好，少时差
出现在：
- 自适应网格细化
- 离散事件模拟，例如电路模拟
- 数据库查询处理
- 稀疏矩阵直接求解器
我们如何很好地调度这两种并行？

lecture 24

四叉树

细分平面的数据结构
- 节点可以包含框中心坐标、边长
- 最后还有 CM、总质量等的坐标。
在完整的四叉树中，每个非叶节点有 4 个孩子

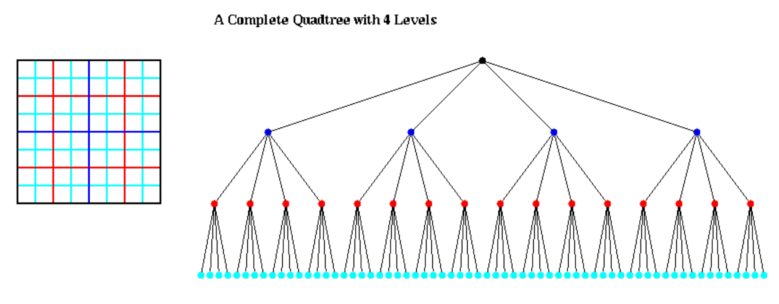
使用四叉树和八叉树

我们所有的算法都从构建一棵树来容纳所有粒子开始
在完整的树中，大多数节点都是空的，浪费空间和时间
Adaptive Quad (Oct) Tree 仅细分粒子所在的空间

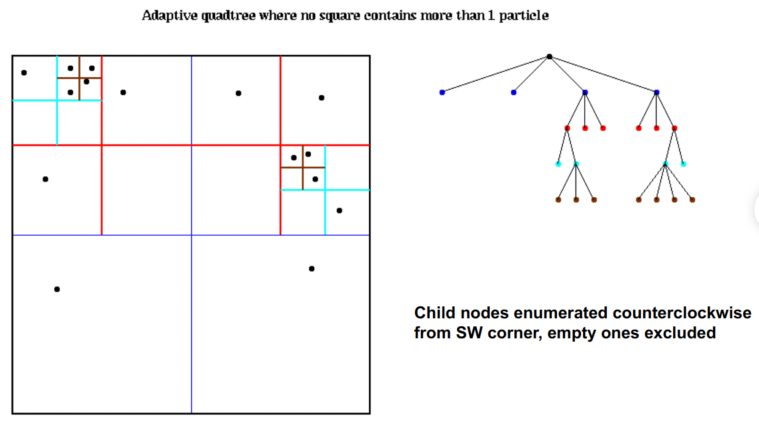
自适应四叉树的开销：

Cost ≤ N * maximum cost of Quad_Tree_Insert
- = O( N * maximum depth of Quad_Tree)
粒子分布平均
- Depth of Quad_Tree = O( log N )
- Cost ≤ O( N * log N )
粒子分布随机
- Depth of Quad_Tree = O( # bits in particle coords ) = O( b )
- Cost ≤ O( b N )

Barnes-Hut Algorithm

N-Body 问题的 O(N log N) 近似算法
使用 QuadTreeBuild 构建四叉树
- 已经描述过，成本 = O( N log N) 或 O(b N)
对于 QuadTree 中的每个节点，计算其包含的所有粒子的 CM 和总质量 (TM)
- 四叉树的后序遍历，成本 = O(N log N) 或 O(b N)
对于每个粒子，遍历四叉树来计算它所受的力，使用距离子平方的CM和TM
- 算法核心
- 开销取决于所需的准确度，但仍为 O(N log N) 或 O(bN)

Step 3 of BH: 计算每个粒子上的力

对于每个节点，可以通过使用节点CM和TM来近似由于节点内部的粒子而对节点外部的粒子施加的力
如果节点离粒子足够远，这将足够准确
对于每个粒子，使用尽可能少的节点来计算力，受精度约束
需要判断一个节点是否离粒子足够远的标准
- D = side length of node
- r = distance from particle to CM of node
- q = user supplied error tolerance < 1
- Use CM and TM to approximate force of node on box if D/r < q

Details of Step 3 of BH

对于每个粒子，遍历四叉树以计算其上的力
for k = 1 to N
- f(k) = TreeForce( k, root )
- 计算由根内所有粒子引起的粒子 k 上的力（k 除外）
function f = TreeForce( k, n )
- 对于节点 n 内的所有粒子（k 除外），计算粒子 k 上的力
- f = 0
- 如果 n 包含一个粒子（不是 k）……直接求值
  - f = 使用直接公式计算的力
- 否则
  - r = 从粒子 k 到粒子在 n 中的 CM 的距离
  - D = size of n
  - if D/r < q … 可以通过 CM 和 TM 来近似
    - 使用 CM 和 TM 近似计算 f
  - else ..需要查看内部节点
    - for all children c of n
    - f = f + TreeForce ( k, c )

lecture 25

元素选择问题：在N个数据中找到第k小个元素，是一些算法的基础部分。快速选择(Hoare方法)类似快排，但是只在一个方向上递归。平均时间O（N），最坏情况O（N2）。

中位数查找 (Blum, Floyd, Pratt, Rivest, Tarjan)：基于quickselect，但保证最坏情况下的线性时间。与并行算法紧密结合。

快速排序的思想，是找出一个中轴（pivot），之后进行左右递归进行排序，关于递归快速排序，C程序算法如下。

void quick_sort(int *arr,int left,int right){
    if(left>right) return;
    int pivot=getPivot();
    quick_sort(arr,left,pivot-1);
    quick_sort(arr,pivot+1,right);
}

关于划分，不同的划分决定快排的效率，下面以lomuto划分和hoare划分来进行讲述思路

lomuto划分思想：lomuto划分主要进行一重循环的遍历，如果比left侧小，则进行交换。然后继续进行寻找中轴。最后交换偏移的数和最左侧数，C程序代码如下。

/**lomuto划分*/
int lomuto_partition(int *arr,int l,int r){
    int p=arr[l];
    int s=l;
    for(int i=l+1;i<=r;i++)
        if(arr[i]<p) {
            s++;
            int tmp=arr[i];
            arr[i]=arr[s];
            arr[s]=tmp;
        }
    int tmp=arr[l];
    arr[l]=arr[s];
    arr[s]=tmp;
    return s;
}

hoare划分思想是先从右侧向左进行寻找，再从左向右进行寻找，如果左边比右边大，则左右进行交换。外侧还有一个嵌套循环，循环终止标志是一重遍历，这种寻找的好处就是，在一次遍历后能基本有序，减少递归的时候产生的比较次数。这也是经典快排中所使用的方法

/**hoare划分*/
int hoare_partition(int *a,int l, int r) {
    int p = a[l];
    int i = l-1;
    int j = r+1 ;
    while (1) {
        do {
            j--;
        }while(a[j]>p);
        do {
            i++;
        }while(a[i] < p);
        if (i < j) {
            int temp = a[i];
            a[i] = a[j];
            a[j] = temp;
        }else
            return j;
    }
}

经典快排实际对hoare划分进行了少许改进，这个temp变量不需要每次找到左右不相等就立即交换，而是，暂时存放，先右边向左找，将左边放在右边，再左边向右找，把右边放左边，最后把初始temp变量放在左值。这样比hoare划分减少少许移动变量次数。

/**经典快排*/
int classic_quick_sort(int *arr,int left,int right){
    int tmp=arr[left];
    while(left<right){
        while(left<right&&arr[right]>=tmp) right--;
        arr[left]=arr[right];
        while(left<right&&arr[left]<=tmp) left++;
        arr[right]=arr[left];
    }
    arr[left]=tmp;
    return left;
}

选择中位数的方法：

将整个列表分成最少N/5个子列表，每个子列表最少5个元素；
对每个子列表排序并找到中位数
对这些子列表中的每个中位数，组织成一个列表M
对M继续上述行为。

最好情况下，递归操作找到中位数，各个元素之间的关系如下，A’中的元素都小于中位数，C’中的元素都大于中位数。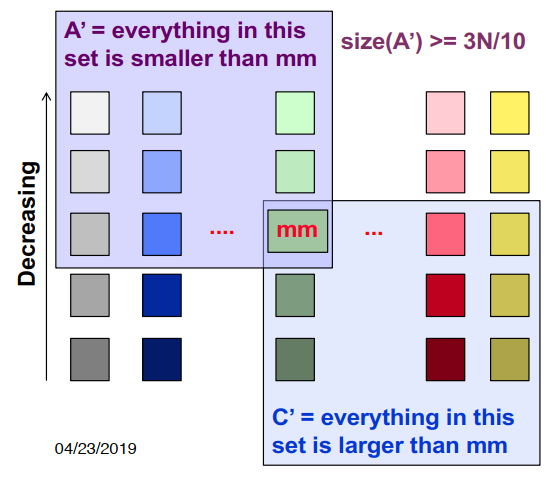

将整个列表划分为三个区域集：A、B、C

A=小于mm的元素集（A’是A的子集）
B=等于mm的元素集
C=大于mm的元素集（C’是C的子集）

SELECT(S, k) // find kth smallest in S
{
    M = DIVIDEANDSORT(S,5); // O(N), M: list of medians
    mm = SELECT(M,|M|/2); // recurse on O(N/5)
    [A,B,C] = PARTITION(S,mm); // O(N)
    if (|A| < k <= |A| + |B|)
        return x;
    else if (k <= |A|), // recurse on O(7N/10)
        return SELECT(A, k)
    else if (if k > |A| + |B|) // recurse on O(7N/10)
        return SELECT(C, k -|A|-|B|)
}

复杂度：T(n) <= T(n/5) + T(7n/10) + O(n)，A不包括C’的成员（C不包括A’的成员）。因为T(n) <= T(9n/10)+O(n)，且nlog109 <= O(n)，所以T(n) = O(n)。

有没有一种并行的算法实现查找中位数？

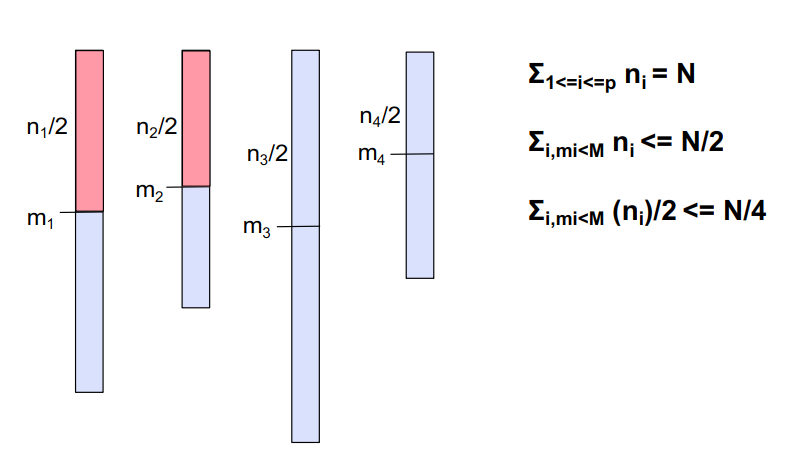
加权中值的中位数

给定p个元素m1, m2 , … , mp 每个元素有正的权重w1 , w2 , … , wp，Σ1<=i<=p wi = 1，加权中值是满足以下条件的元素M，Σi,mi<M wi <= 1/2 and Σi,mi>M wi <= 1/2，就是说找到一个i，使得i前边的元素的权值加起来和i后边的元素的权值加起来都小于等于1/2。

PARALLELSELECT(S, k) // find kth smallest in S
{
    lm = SELECT(S,|S|/2); // find local median
    LMS = MPI_Allgather(lm,0); // exchange medians
    wmm = WeightedMedian(LMS); // redundant computation
    [A,B,C] = PARTITION(S,wmm); // same as in serial
    MPI_Allreduce(size(A), &ls, MPI_SUM); // less than
    MPI_Allreduce(size(B), &eq, MPI_SUM); // equal to
    if (ls < k <= ls + eq) // solution found
        return wmm;
    else if (k <= ls) // recurse on O(3N/4)
        return PARALLELSELECT(A,k)
    else if (if k > ls + eq) // recurse on O(3N/4)
        return PARALLELSELECT( C, k-|A|-|B|)
}

因为Σi,mi<M wi <= 1/2，Σi,mi>M wi <= 1/2，用每个处理器中的元素数替换权重：Σi,mi<M ni <= N/2，Σi,mi>M ni <= N/2。

在处理器i处，小于等于mi的元素至少为ni/2（根据中值定义）。这些元素中有一半也小于M。

因此，小于或等于M的总#元素（在所有处理器中）为N/4
“大于或等于”的大小写是对称的

合并排序

Mergesort是递归排序算法的一个示例。
它基于分而治之的范式
它使用合并操作作为其基本操作（接收两个排序序列并生成单个排序序列）
mergesort的缺点：不是in-place的（使用额外的临时阵列）

template <typename T>
void Merge(T *C, T *A, T *B, int na, int nb) {
    while (na>0 && nb>0) {
        if (*A <= *B) {
            *C++ = *A++; na--;
        } else {
            *C++ = *B++; nb--;
        }
    }
    while (na>0) {
        *C++ = *A++; na--;
    }
    while (nb>0) {
        *C++ = *B++; nb--;
    }
}

template <typename T>
void MergeSort(T *B, T *A, int n) {
    if (n==1) { B[0] = A[0];}
    else {
        T* C = new T[n];
#pragma omp parallel {
    #pragma omp single {
        #pragma omp task
            MergeSort(C, A, n/2);
        #pragma omp task
            MergeSort(C+n/2, A+n/2, n-n/2);
    } 
}
        Merge(B, C, C+n/2, n/2, n-n/2);
        delete[] C;
    } 
}

如果两个数组中要合并的元素总数为n=na+nb，则两个递归合并中较大的一个数组中的元素总数最多为(3/4)n。

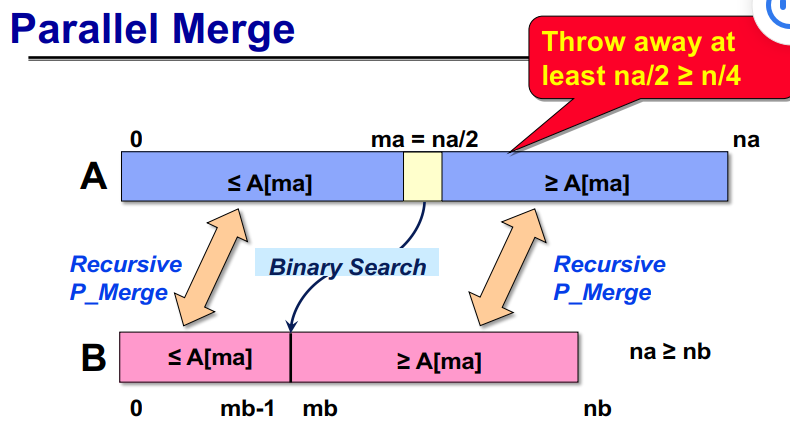
template <typename T>
void P_Merge(T *C, T *A, T *B, int na, int nb) {
    if (na < nb) { P_Merge(C, B, A, nb, na);}
    else if (na==0) { return; }
    else {
        int ma = na/2;
        int mb = BinarySearch(A[ma], B, nb);
        C[ma+mb] = A[ma];
#pragma omp parallel {
    #pragma omp single {
        #pragma omp task
            P_Merge(C, A, B, ma, mb);
        #pragma omp task
            P_Merge(C+ma+mb+1,A+ma+1,B+mb,na-ma-1,nb-mb);
    }
} // implicit taskwait
    }
}

在桶排序中，输入数字的范围[a，b]被划分为m个大小相等的间隔，称为桶。

每个元素都放置在其相应的桶中。
如果数量在范围内均匀划分，则预计bucket的元素数量大致相同。
桶中的元素在本地分类。
该算法的运行时间为Θ(nlog(n/m))。

并行bucket排序

并行桶排序相对简单。我们可以选择m=p。
在这种情况下，每个处理器都有其负责的一系列值。
每个处理器运行其本地array，并将其每个元素分配给相应的处理器。
使用单个all-to-all个性化通信将元素发送到目标处理器。
每个处理器对其接收的所有元素进行排序。
负载不平衡：假设输入元件均匀分布在间隔[a，b]上是不现实的。

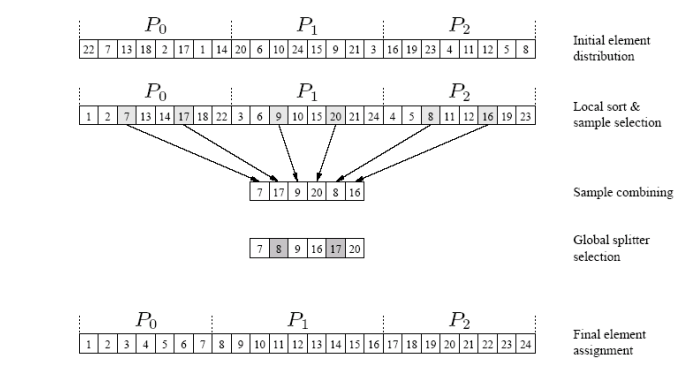
并行采样排序

快速排序的泛化：从1支点到p支点。这是通过选择合适的拆分来实现的。
拆分选择方法将n个元素划分为m个块，每个块的大小为n/m，并使用快速排序对每个块进行排序。
从每个排序块中选择m-1个均匀间隔的样本。
从所有区块中选择的m（m-1）元素代表用于确定铲斗的样本。
该方案保证每个桶中结束的元素数量小于2n/m

并行样本排序：复杂性分析

n/p元素的内部排序需要时间Θ((n/p)log(n/p))，而p–1样本元素的选择需要时间Θ(p)。
all-to-all广播的时间为Θ(p^2)，对p(p–1)样本元素进行内部排序的时间为Θ(p^2log p)，选择p–1等距分离器需要时间Θ(p)。
每个进程可以通过在时间Θ(plog(n/p))中执行p-1二进制搜索，将这些p-1拆分器插入其大小为n/p的本地排序块中。
元素重排时间为O(n/p)