求二进制数中1的个数
问题描述
任意给定一个32位无符号整数n,求n的二进制表示中1的个数,比如n = 5(0101)时,返回2,n = 15(1111)时,返回4
这也是一道比较经典的题目了,相信不少人面试的时候可能遇到过这道题吧,下面介绍了几种方法来实现这道题。
普通法
移位+计数,这种方法的运算次数与输入n最高位1的位置有关,最多循环32次。1
2
3
4
5
6
7
8
9
10
11int BitCount(unsigned int n)
{
unsigned int c =0 ; // 计数器
while (n >0)
{
if((n &1) ==1) // 当前位是1
++c ; // 计数器加1
n >>=1 ; // 移位
}
return c ;
}
一个更精简的版本如下1
2
3
4
5
6
7int BitCount1(unsigned int n)
{
unsigned int c =0 ; // 计数器
for (c =0; n; n >>=1) // 循环移位
c += n &1 ; // 如果当前位是1,则计数器加1
return c ;
}
快速法
这种方法速度比较快,其运算次数与输入n的大小无关,只与n中1的个数有关。如果n的二进制表示中有k个1,那么这个方法只需要循环k次即可。其原理是不断清除n的二进制表示中最右边的1,同时累加计数器,直至n为0,代码如下1
2
3
4
5
6
7
8
9int BitCount2(unsigned int n)
{
unsigned int c =0 ;
for (c =0; n; ++c)
{
n &= (n -1) ; // 清除最低位的1
}
return c ;
}
为什么n &= (n – 1)能清除最右边的1呢?因为从二进制的角度讲,n相当于在n - 1的最低位加上1。举个例子,8(1000)= 7(0111)+ 1(0001),所以8 & 7 = (1000)&(0111)= 0(0000),清除了8最右边的1(其实就是最高位的1,因为8的二进制中只有一个1)。再比如7(0111)= 6(0110)+ 1(0001),所以7 & 6 = (0111)&(0110)= 6(0110),清除了7的二进制表示中最右边的1(也就是最低位的1)。
查表法
动态建表
由于表示在程序运行时动态创建的,所以速度上肯定会慢一些,把这个版本放在这里,有两个原因
- 介绍填表的方法,因为这个方法的确很巧妙。
- 类型转换,这里不能使用传统的强制转换,而是先取地址再转换成对应的指针类型。也是常用的类型转换方法。
1 | int BitCount3(unsigned int n) |
先说一下填表的原理,根据奇偶性来分析,对于任意一个正整数n
- 如果它是偶数,那么n的二进制中1的个数与n/2中1的个数是相同的,比如4和2的二进制中都有一个1,6和3的二进制中都有两个1。为啥?因为n是由n/2左移一位而来,而移位并不会增加1的个数。
- 如果n是奇数,那么n的二进制中1的个数是n/2中1的个数+1,比如7的二进制中有三个1,7/2 = 3的二进制中有两个1。为啥?因为当n是奇数时,n相当于n/2左移一位再加1。
再说一下查表的原理
对于任意一个32位无符号整数,将其分割为4部分,每部分8bit,对于这四个部分分别求出1的个数,再累加起来即可。而8bit对应2^8 = 256种01组合方式,这也是为什么表的大小为256的原因。
注意类型转换的时候,先取到n的地址,然后转换为unsigned char*,这样一个unsigned int(4 bytes)对应四个unsigned char(1 bytes),分别取出来计算即可。举个例子吧,以87654321(十六进制)为例,先写成二进制形式-8bit一组,共四组,以不同颜色区分,这四组中1的个数分别为4,4,3,2,所以一共是13个1,如下面所示。
10000111 01100101 01000011 00100001 = 4 + 4 + 3 + 2 = 13
静态表-4bit
原理和8-bit表相同,详见8-bit表的解释1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18int BitCount4(unsigned int n)
{
unsigned int table[16] =
{
0, 1, 1, 2,
1, 2, 2, 3,
1, 2, 2, 3,
2, 3, 3, 4
} ;
unsigned int count =0 ;
while (n)
{
count += table[n &0xf] ;
n >>=4 ;
}
return count ;
}
静态表-8bit
首先构造一个包含256个元素的表table,table[i]即i中1的个数,这里的i是[0-255]之间任意一个值。然后对于任意一个32bit无符号整数n,我们将其拆分成四个8bit,然后分别求出每个8bit中1的个数,再累加求和即可,这里用移位的方法,每次右移8位,并与0xff相与,取得最低位的8bit,累加后继续移位,如此往复,直到n为0。所以对于任意一个32位整数,需要查表4次。以十进制数2882400018为例,其对应的二进制数为10101011110011011110111100010010,对应的四次查表过程如下:红色表示当前8bit,绿色表示右移后高位补零。
第一次(n & 0xff) 10101011110011011110111100010010
第二次((n >> 8) & 0xff) 00000000101010111100110111101111
第三次((n >> 16) & 0xff)00000000000000001010101111001101
第四次((n >> 24) & 0xff)00000000000000000000000010101011
1 | int BitCount7(unsigned int n) |
当然也可以搞一个16bit的表,或者更极端一点32bit的表,速度将会更快。
平行算法
网上都这么叫,我也这么叫吧,不过话说回来,的确有平行的意味在里面,先看代码,稍后解释
1 | int BitCount4(unsigned int n) |
速度不一定最快,但是想法绝对巧妙。 说一下其中奥妙,其实很简单,先将n写成二进制形式,然后相邻位相加,重复这个过程,直到只剩下一位。
1 | int BitCount5(unsigned int n) |
最喜欢这个,代码太简洁啦,只是有个取模运算,可能速度上慢一些。区区两行代码,就能计算出1的个数,到底有何奥妙呢?为了解释的清楚一点,我尽量多说几句。
第一行代码的作用:先说明一点,以0开头的是8进制数,以0x开头的是十六进制数,上面代码中使用了三个8进制数。
将n的二进制表示写出来,然后每3bit分成一组,求出每一组中1的个数,再表示成二进制的形式。比如n = 50,其二进制表示为110010,分组后是110和010,这两组中1的个数本别是2和3。2对应010,3对应011,所以第一行代码结束后,tmp = 010011,具体是怎么实现的呢?由于每组3bit,所以这3bit对应的十进制数都能表示为2^2 a + 2^1 b + c的形式,也就是4a + 2b + c的形式,这里a,b,c的值为0或1,如果为0表示对应的二进制位上是0,如果为1表示对应的二进制位上是1,所以a + b + c的值也就是4a + 2b + c的二进制数中1的个数了。举个例子,十进制数6(0110)= 4 1 + 2 1 + 0,这里a = 1, b = 1, c = 0, a + b + c = 2,所以6的二进制表示中有两个1。现在的问题是,如何得到a + b + c呢?注意位运算中,右移一位相当于除2,就利用这个性质!
4a + 2b + c 右移一位等于2a + b
4a + 2b + c 右移量位等于a
然后做减法
4a + 2b + c –(2a + b) – a = a + b + c,这就是第一行代码所作的事,明白了吧。
第二行代码的作用:在第一行的基础上,将tmp中相邻的两组中1的个数累加,由于累加到过程中有些组被重复加了一次,所以要舍弃这些多加的部分,这就是&030707070707的作用,又由于最终结果可能大于63,所以要取模。
需要注意的是,经过第一行代码后,从右侧起,每相邻的3bit只有四种可能,即000, 001, 010, 011,为啥呢?因为每3bit中1的个数最多为3。所以下面的加法中不存在进位的问题,因为3 + 3 = 6,不足8,不会产生进位。
tmp + (tmp >> 3)-这句就是是相邻组相加,注意会产生重复相加的部分,比如tmp = 659 = 001 010 010 011时,tmp >> 3 = 000 001 010 010,相加得
001 010 010 011
000 001 010 010
001 011 100 101
011 + 101 = 3 + 5 = 8。(感谢网友Di哈指正。)注意,659只是个中间变量,这个结果不代表659这个数的二进制形式中有8个1。
注意我们想要的只是第二组和最后一组(绿色部分),而第一组和第三组(红色部分)属于重复相加的部分,要消除掉,这就是&030707070707所完成的任务(每隔三位删除三位),最后为什么还要%63呢?因为上面相当于每次计算相连的6bit中1的个数,最多是111111 = 77(八进制)= 63(十进制),所以最后要对63取模。
位标志法
1 | struct _byte |
指令法
使用微软提供的指令,首先要确保你的CPU支持SSE4指令,用Everest和CPU-Z可以查看是否支持。1
2unsigned int n =127 ;
unsigned int bitCount = _mm_popcnt_u32(n) ;
快速幂、快速幂取模
大数模幂运算的缺陷
快速幂取模算法的引入是从大数的小数取模的朴素算法的局限性所提出的,在朴素的方法中我们计算一个数比如5^1003%31是非常消耗我们的计算资源的,在整个计算过程中最麻烦的就是我们的5^1003这个过程
- 缺点1:在我们在之后计算指数的过程中,计算的数字不都拿得增大,非常的占用我们的计算资源(主要是时间,还有空间)
- 缺点2:我们计算的中间过程数字大的恐怖,我们现有的计算机是没有办法记录这么长的数据的,所以说我们必须要想一个更加高效的方法来解决这个问题
快速幂的引入
我们首先从优化的过程开始一步一步优化我们的模幂算法
1.朴素模幂运算过程:1
2
3
4
5#define ans=1
for(int i=1;i<=b;i++)
{
ans*=a;
}
根据我们上面说的,这种算法是非常的无法容忍的,我们在计算的过程中出现的两个缺点在这里都有体现
在这里我们如果要做优化的话,我肥就是每个过程中都加一次模运算,但是我们首先要记住模运算是非常的消耗内存资源的,在计算的次数非常的大的时候,我们是没有办法忍受这种时间耗费的
2.快速幂引入:
在讲解快速幂取模算法之前,我们先将几个必备的知识
1.对于取模运算:(a*b)%c=(a%c)*(b%c)%c,这个是成立的:也是我们实现快速幂的基础。之后我们来看看快速幂的核心本质。
在这里,我们对指数动了一些手脚,核心思想在于:将大数的幂运算拆解成了相对应的乘法运算,利用上面的式子,始终将我们的运算的数据量控制在c的范围以下,这样我们可以客服朴素的算法的缺点二,我们将计算的数据量压缩了很大一部分,当指数非常大的时候这个优化是更加显著的,我们用Python来做一个实验来看看就知道我们优化的效率有多高了
1 | from time import * |
实验结果:1
2
3
4
5
6
7底数:5
指数:1003
模:12
朴素算法结果5
朴素算法耗时:3.289952
快速幂算法结果5
快速幂算法耗时:0.006706
我们现在知道了快速幂取模算法的强大了,我们现在来看核心原理:对于任何一个整数的模幂运算:a^b%c,对于b我们可以拆成二进制的形式:1
b=b0+b1*2+b2*2^2+...+bn*2^n
这里我们的b0对应的是b二进制的第一位,那么我们的a^b运算就可以拆解成1
a^b0*a^b1*2*...*a^(bn*2^n)
对于b来说,二进制位不是0就是1,那么对于bx为0的项我们的计算结果是1就不用考虑了,我们真正想要的其实是b的非0二进制位。那么假设除去了b的0的二进制位之后我们得到的式子是1
a^(bx*2^x)*...*a(bn*2^n)
这里我们再应用我们一开始提到的公式,那么我们的a^b%c运算就可以转化为1
(a^(bx*2^x)%c)*...*(a^(bn*2^n)%c)
这样的话,我们就很接近快速幂的本质了1
(a^(bx*2^x)%c)*...*(a^(bn*2^n)%c)
我们会发现令1
2
3A1=(a^(bx*2^x)%c)
...
An=(a^(bn*2^n)%c)
这样的话,An始终是A(n-1)的平方倍(当然加进去了取模匀速那),依次递推。现在,我们基本的内容都已经了解到了,现在我们来考虑实现它:1
2
3
4
5
6
7
8
9
10
11
12int quick(int a,int b,int c)
{
int ans=1; //记录结果
a=a%c; //预处理,使得a处于c的数据范围之下
while(b!=0)
{
if(b&1) ans=(ans*a)%c; //如果b的二进制位不是0,那么我们的结果是要参与运算的
b>>=1; //二进制的移位操作,相当于每次除以2,用二进制看,就是我们不断的遍历b的二进制位
a=(a*a)%c; //不断的加倍
}
return ans;
}
现在,我们的快速幂已经讲完了。我们来大致的推演一下快速幂取模算法的时间复杂度。首先,我们会观察到,我们每次都是将b的规模缩小了2倍,那么很显然,原本的朴素的时间复杂度是O(n)。快速幂的时间复杂度就是O(logn)无限接近常熟的时间复杂度无疑逼朴素的时间复杂度优秀很多,在数据量越大的时候,者中优化效果越明显。
OJ例题
POJ1995题意:快速幂版题1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42#include"iostream"
#include"cstdio"
#include"cstring"
#include"cstdlib"
using namespace std;
int ans=0;
int a,b;
int c;
int quick(int a,int b,int c)
{
int ans=1;
a=a%c;
while(b!=0)
{
if(b&1) ans=(ans*a)%c;
b>>=1;
a=(a*a)%c;
}
return ans;
}
int main()
{
int for_;
int t;
scanf("%d",&t);
while(t--)
{
ans=0;
scanf("%d%d",&c,&for_);
for(int i=1;i<=for_;i++)
{
scanf("%d%d",&a,&b);
ans=(ans+quick(a,b,c))%c;
}
printf("%d\n",ans);
}
return 0;
}
二叉树
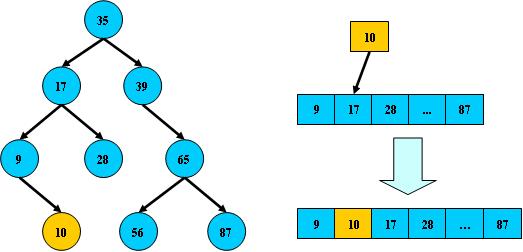
- 所有非叶子结点至多拥有两个儿子(Left和Right);
- 所有结点存储一个关键字;
- 非叶子结点的左指针指向小于其关键字的子树,右指针指向大于其关键字的子树;
二叉树的搜索,从根结点开始,如果查询的关键字与结点的关键字相等,那么就命中;否则,如果查询关键字比结点关键字小,就进入左儿子;如果比结点关键字大,就进入右儿子;如果左儿子或右儿子的指针为空,则报告找不到相应的关键字;如果二叉树的所有非叶子结点的左右子树的结点数目均保持差不多(平衡),那么二叉树的搜索性能逼近二分查找;但它比连续内存空间的二分查找的优点是,改变二叉树结构(插入与删除结点)不需要移动大段的内存数据,甚至通常是常数开销;
但二叉树在经过多次插入与删除后,有可能导致不同的结构: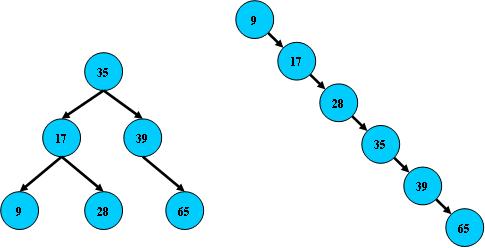
右边也是一个二叉树,但它的搜索性能已经是线性的了;同样的关键字集合有可能导致不同的树结构索引;所以,使用二叉树还要考虑尽可能让二叉树保持左图的结构,和避免右图的结构,也就是所谓的“平衡”问题;实际使用的二叉树都是在原二叉树的基础上加上平衡算法,即“平衡二叉树”;如何保持二叉树结点分布均匀的平衡算法是平衡二叉树的关键;平衡算法是一种在二叉树中插入和删除结点的策略。
1 | class TreeNode{ |
二叉树的题目普遍可以用递归和迭代的方式来解
- 求二叉树的最大深度
1 | int maxDeath(TreeNode node){ |
- 求二叉树的最小深度
1 | int getMinDepth(TreeNode root){ |
- 求二叉树中节点的个数
1 | int numOfTreeNode(TreeNode root){ |
- 求二叉树中叶子节点的个数
1 | int numsOfNoChildNode(TreeNode root){ |
- 求二叉树中第k层节点的个数
1 | int numsOfkLevelTreeNode(TreeNode root,int k){ |
- 判断二叉树是否是平衡二叉树
1 | boolean isBalanced(TreeNode node){ |
- 判断二叉树是否是完全二叉树
1 | boolean isCompleteTreeNode(TreeNode root){ |
- 两个二叉树是否完全相同
1 | boolean isSameTreeNode(TreeNode t1,TreeNode t2){ |
- 两个二叉树是否互为镜像
1 | boolean isMirror(TreeNode t1,TreeNode t2){ |
- 翻转二叉树or镜像二叉树
1 | TreeNode mirrorTreeNode(TreeNode root){ |
- 求两个二叉树的最低公共祖先节点
1 | TreeNode getLastCommonParent(TreeNode root,TreeNode t1,TreeNode t2){ |
- 二叉树的前序遍历
迭代解法
1 | ArrayList<Integer> preOrder(TreeNode root){ |
- 二叉树的中序遍历
1 | ArrayList<Integer> inOrder(TreeNode root){ |
- 二叉树的后序遍历
1 | ArrayList<Integer> postOrder(TreeNode root){ |
- 前序遍历和后序遍历构造二叉树
1 | TreeNode buildTreeNode(int[] preorder,int[] inorder){ |
- 在二叉树中插入节点
1 | TreeNode insertNode(TreeNode root,TreeNode node){ |
- 输入一个二叉树和一个整数,打印出二叉树中节点值的和等于输入整数所有的路径
1 | void findPath(TreeNode r,int i){ |
- 二叉树的搜索区间
给定两个值 k1 和 k2(k1 < k2)和一个二叉查找树的根节点。找到树中所有值在 k1 到 k2 范围内的节点。即打印所有x (k1 <= x <= k2) 其中 x 是二叉查找树的中的节点值。返回所有升序的节点值。
1 | ArrayList<Integer> result; |
- 二叉树的层次遍历
1 | ArrayList<ArrayList<Integer>> levelOrder(TreeNode root){ |
- 二叉树内两个节点的最长距离
二叉树中两个节点的最长距离可能有三种情况:
- 左子树的最大深度+右子树的最大深度为二叉树的最长距离
- 左子树中的最长距离即为二叉树的最长距离
- 右子树种的最长距离即为二叉树的最长距离
因此,递归求解即可
1 | private static class Result{ |
- 不同的二叉树
给出 n,问由 1…n 为节点组成的不同的二叉查找树有多少种?
1 | int numTrees(int n ){ |
- 判断二叉树是否是合法的二叉查找树(BST)
一棵BST定义为:
- 节点的左子树中的值要严格小于该节点的值。
- 节点的右子树中的值要严格大于该节点的值。
- 左右子树也必须是二叉查找树。
一个节点的树也是二叉查找树。
1 | public int lastVal = Integer.MAX_VALUE; |
树转换为二叉树
- 加线。在所有兄弟结点之间加一条连线。
- 去线。树中的每个结点,只保留它与第一个孩子结点的连线,删除它与其它孩子结点之间的连线。
- 层次调整。以树的根节点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。(注意第一个孩子是结点的左孩子,兄弟转换过来的孩子是结点的右孩子)
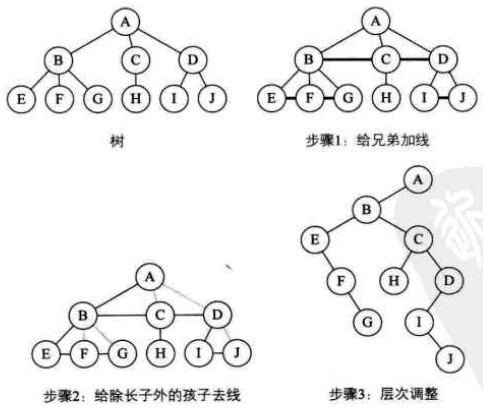
森林转换为二叉树
- 把每棵树转换为二叉树。
- 第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子,用线连接起来。
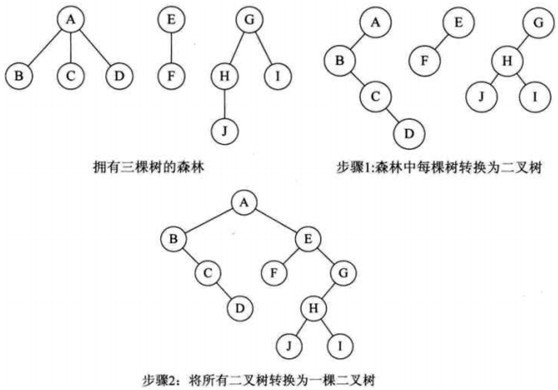
二叉树转换为树
是树转换为二叉树的逆过程。
- 加线。若某结点X的左孩子结点存在,则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点…,都作为结点X的孩子。将结点X与这些右孩子结点用线连接起来。
- 去线。删除原二叉树中所有结点与其右孩子结点的连线。
- 层次调整。
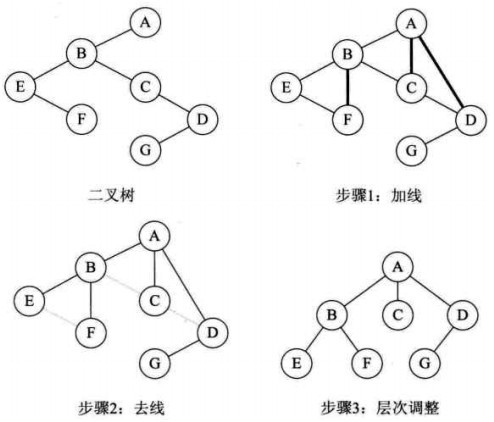
二叉树转换为森林
假如一棵二叉树的根节点有右孩子,则这棵二叉树能够转换为森林,否则将转换为一棵树。
- 从根节点开始,若右孩子存在,则把与右孩子结点的连线删除。再查看分离后的二叉树,若其根节点的右孩子存在,则连线删除…。直到所有这些根节点与右孩子的连线都删除为止。
- 将每棵分离后的二叉树转换为树。
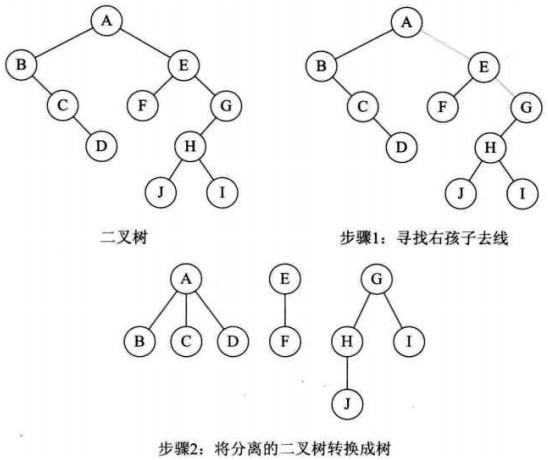
2-3 树
2-3 树的定义如下:
- 2-3 树要么为空要么具有以下性质:
- 对于 2- 节点,和普通的 BST 节点一样,有一个数据域和两个子节点指针,两个子节点要么为空,要么也是一个2-3树,当前节点的数据的值要大于左子树中所有节点的数据,要小于右子树中所有节点的数据。
- 对于 3- 节点,有两个数据域 a 和 b 和三个子节点指针,左子树中所有的节点数据要小于a,中子树中所有节点数据要大于 a 而小于 b ,右子树中所有节点数据要大于 b 。
例如图 2.1 所示的树为一棵 2-3 树: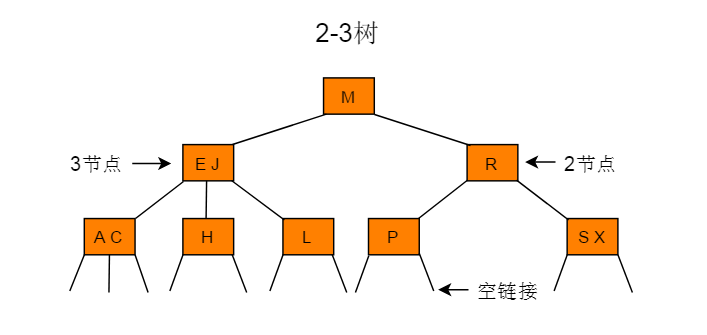
2-3 树性质
性质:
- 对于每一个结点有 1 或者 2 个关键码。
- 当节点有一个关键码的时,节点有 2 个子树。
- 当节点有 2 个关键码时,节点有 3 个子树。
- 所有叶子点都在树的同一层。
2-3树查找
2-3 树的查找类似二叉搜索树的查找过程,根据键值的比较来决定查找的方向。
例如在图 2.1 所示的 2-3 树中查找键为H的节点: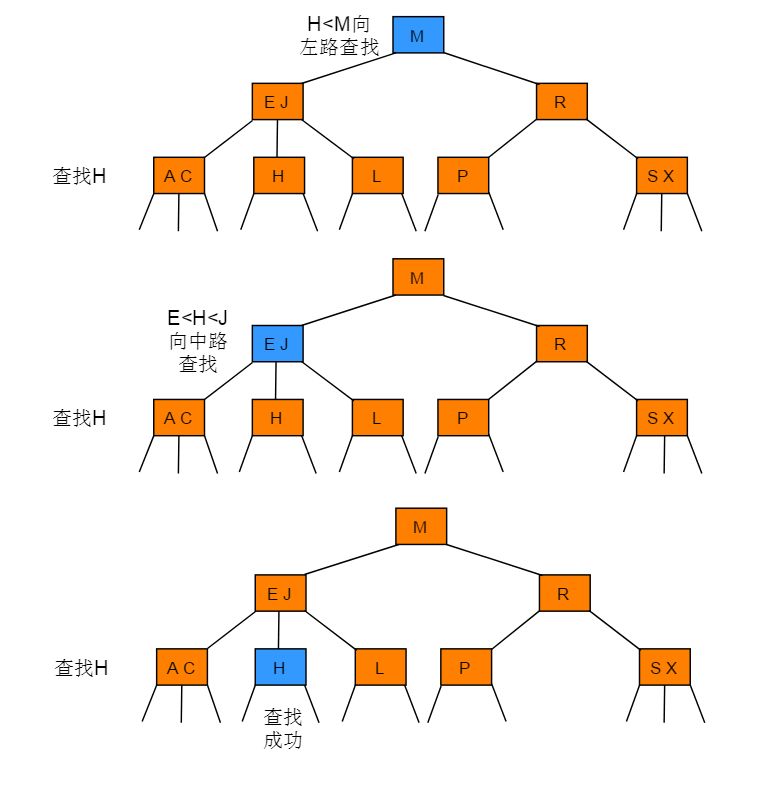
例如在图 2.1 所示的 2-3 树中查找键为 B 的节点: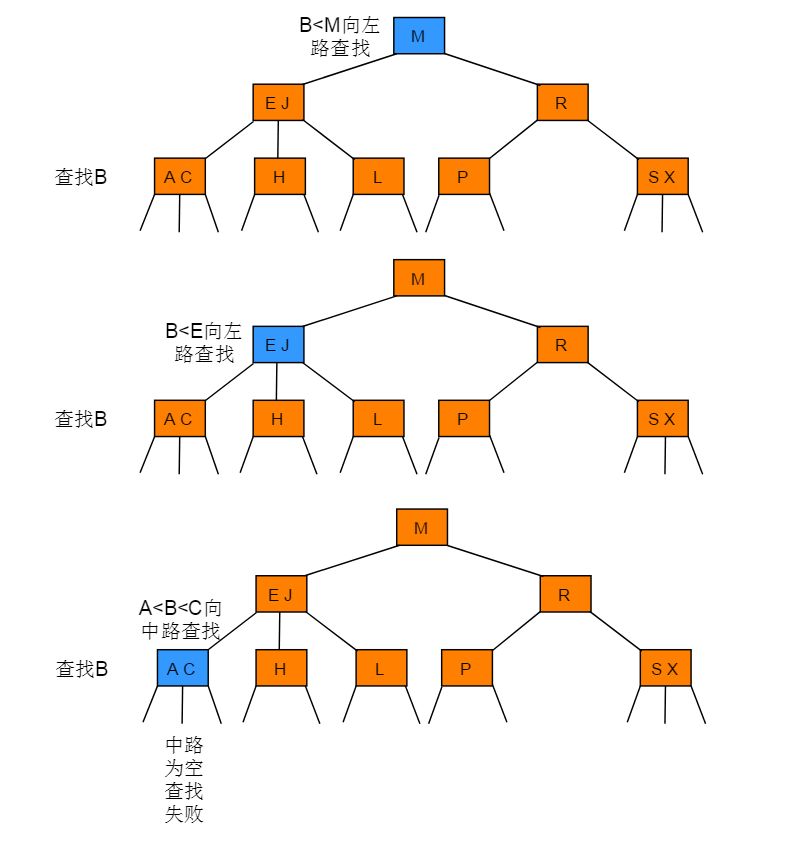
2-3树插入
在树的插入之前需要对带插入的节点进行一次查找操作,若树中已经有此节点则不予插入,若没有查找到此节点则记录未命中查找结束时访问的最后一个节点。
空树的插入最简单,创建一个节点即可,这里不予赘述。
对于非空树插入主要分为 4 种情况:
- 向 2- 节点中插入新节点
- 向一棵只含 3- 节点的树中插入新节点
- 向一个父节点为 2- 节点的 3- 节点中插入新节点
- 向一个父节点为 3- 节点的 3- 节点中插入新节点
向2-节点中插入新节点的操作步骤:如果未命中查找结束于一个 2-节点,直接将 2- 节点替换为一个 3- 节点,并将要插入的键保存在其中。
图解: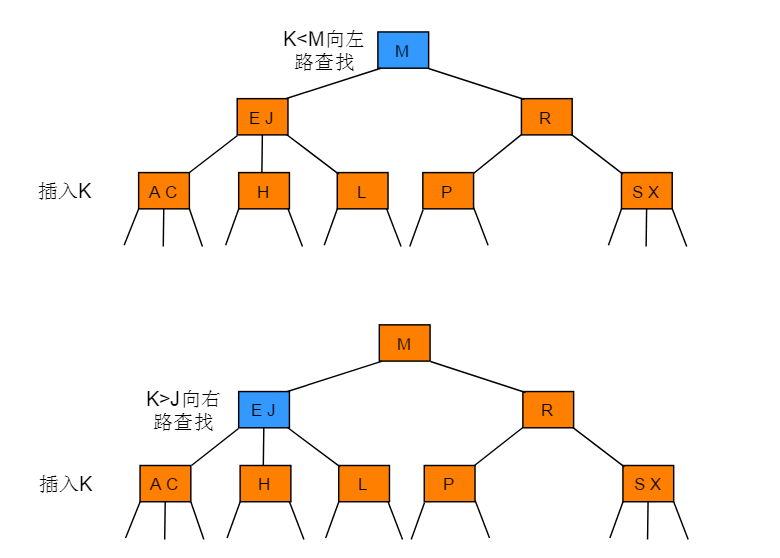
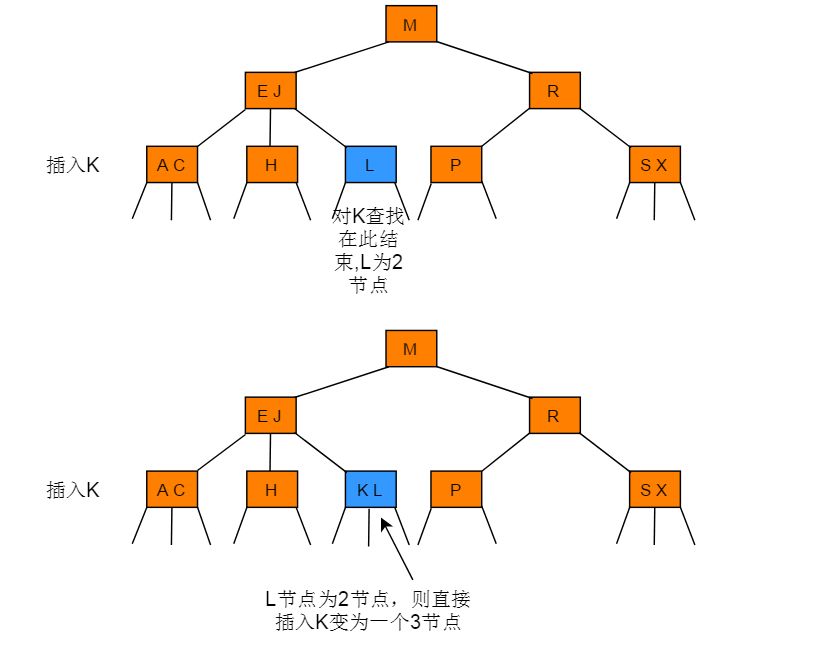
向一棵只含 3- 节点的树中插入新节点的操作步骤:先临时将新键存入唯一的 3- 节点中,使其成为一个 4- 节点,再将它转化为一颗由 3 个 2- 节点组成的 2-3 树,分解后树高会增加 1。
图解: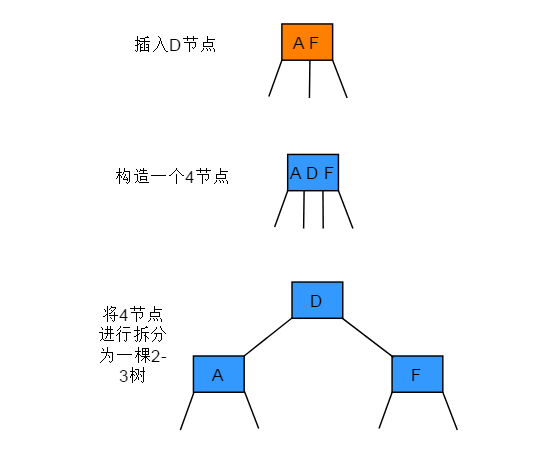
向一个父节点为 2- 节点的 3- 节点中插入新节点的操作步骤:先构造一个临时的 4- 节点并将其分解,分解时将中键移动到父节点中(中键移动后,其父节点中的位置由键的大小确定)
图解: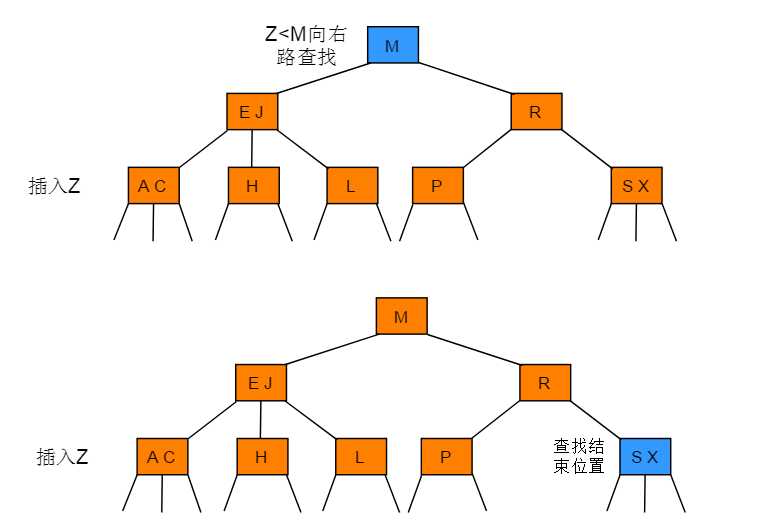
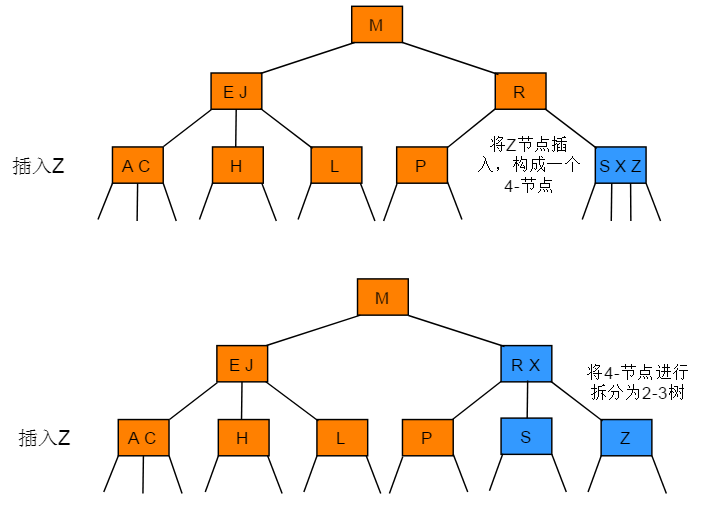
向一个父节点为3-节点的3-节点中插入新节点的操作步骤:插入节点后一直向上分解构造的临时4-节点并将中键移动到更高层双亲节点,直到遇到一个-2节点并将其替换为一个不需要继续分解的3-节点,或是到达树根(3-节点)。
图解: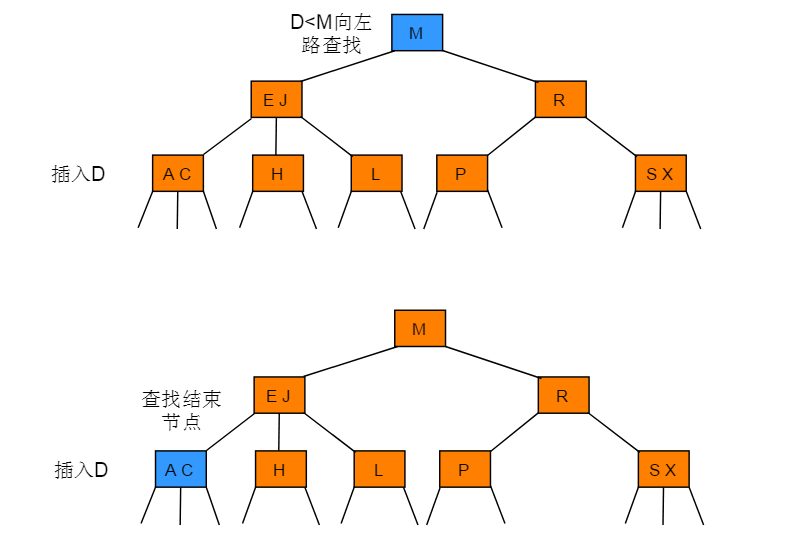
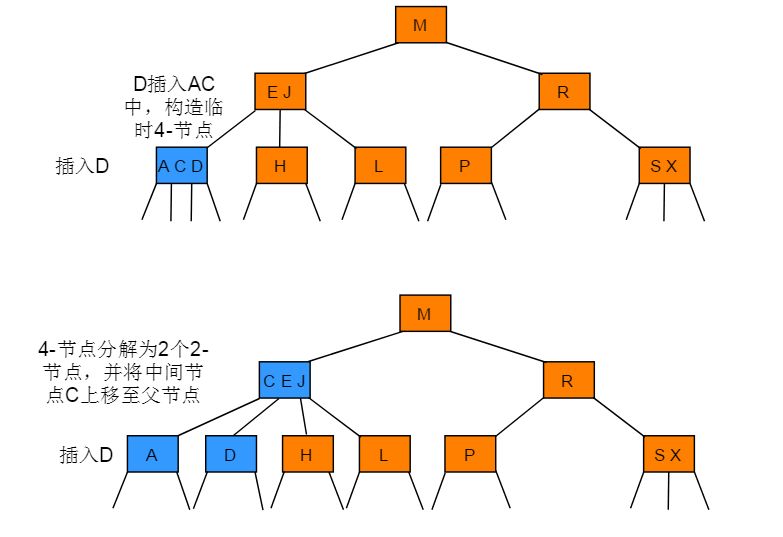
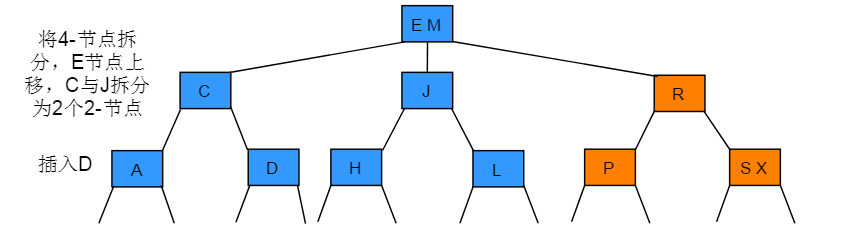
分解根节点
操作步骤:如果从插入节点到根节点的路径上全是3-节点(包含根节点在内),根节点将最终被替换为一个临时的4-节点,将临时的4-节点分解为3个2-节点,分解后树高会增加1。
图解: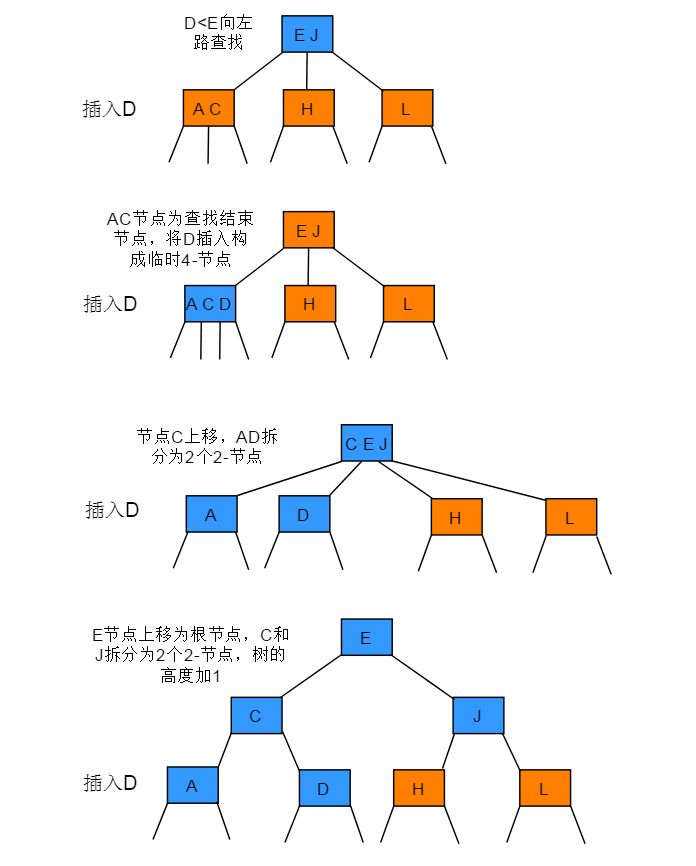
2-3树删除
删除之前,先要对2-3树进行一次命中的查找,查找成功才可以进行删除操作。删除节点大概分为3种情形
- 删除非叶子节点。
- 删除不为2-节点的叶子节点。
- 删除为2-节点的叶子节点。
删除非叶子节点
操作步骤:使用中序遍历下的直接后继节点key来覆盖当前待删除节点key,再删除用来覆盖的后继节点key。
图解: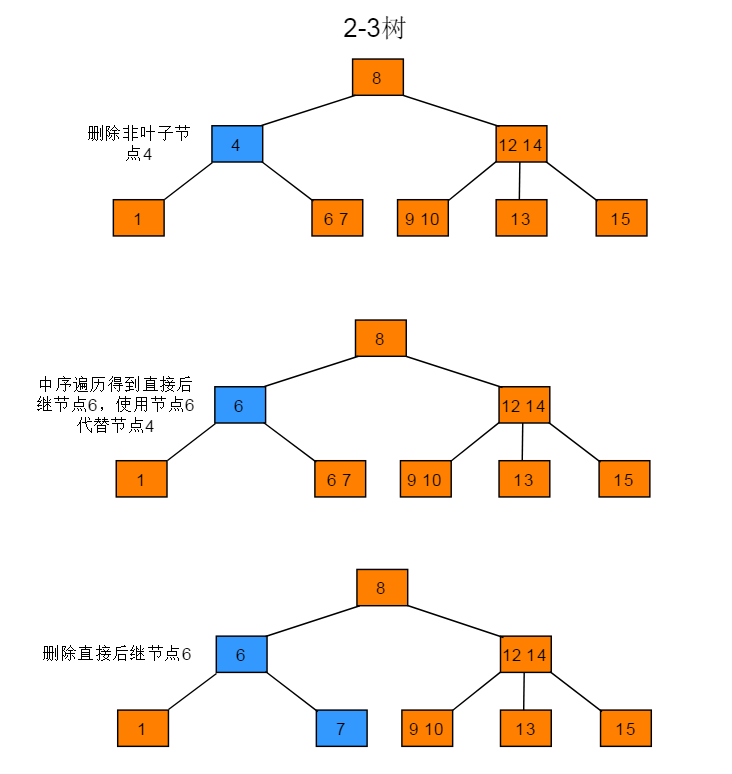
删除不为2-节点的叶子节点操作步骤:删除不为2-节点的叶子节点,直接删除节点即可。**
图解: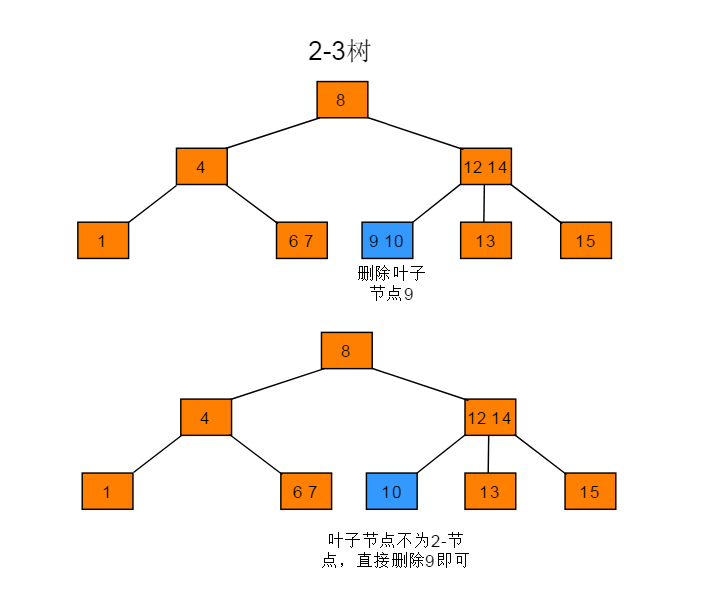
删除为2-节点的叶子节点
删除为2-节点的叶子节点的步骤相对复杂,删除节点后需要做出相应判断,并根据判断结果调整树结构。主要分为四种情形:
删除节点为2-节点,父节点为2-节点,兄弟节点为3-节点的操作步骤:当前待删除节点的父节点是2-节点、兄弟节点是3-节点,将父节点移动到当前待删除节点位置,再将兄弟节点中最接近当前位置的key移动到父节点中。
图解: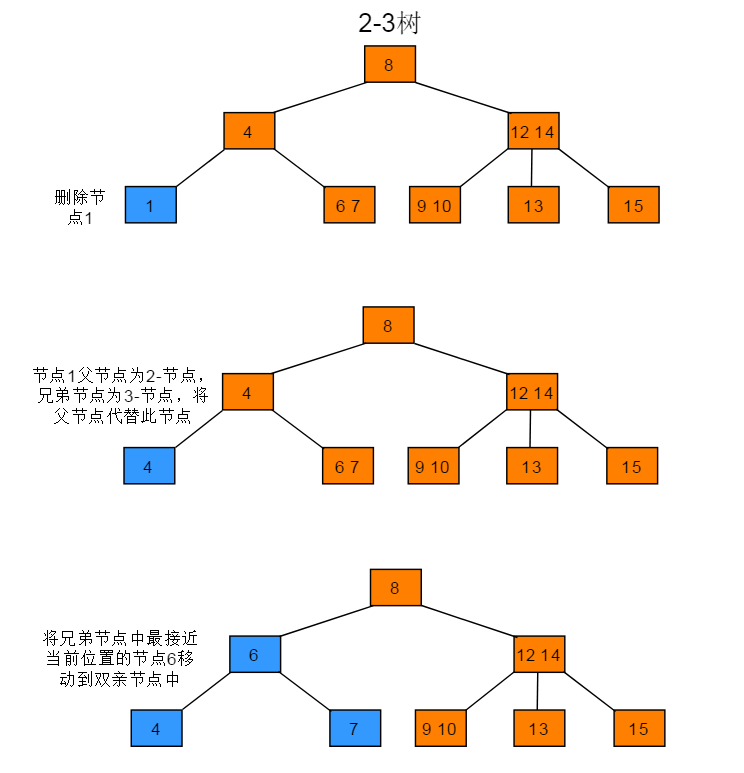
删除节点为2-节点,父节点为2-节点,兄弟节点为2-节点的操作步骤:当前待删除节点的父节点是2-节点、兄弟节点也是2-节点,先通过移动兄弟节点的中序遍历直接后驱到兄弟节点,以使兄弟节点变为3-节点;再进行6.3.1的操作。
图解: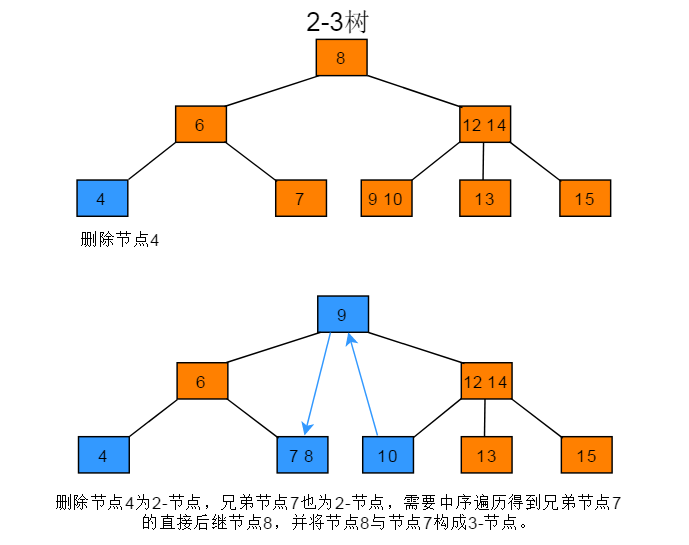
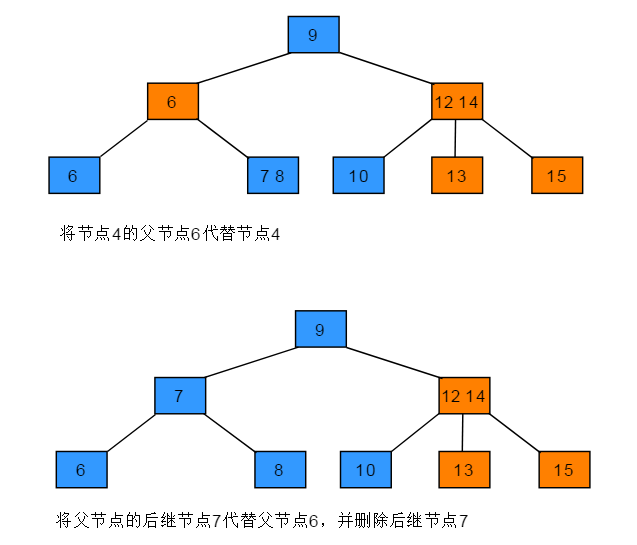
删除节点为2-节点,父节点为3-节点的操作步骤:当前待删除节点的父节点是3-节点,拆分父节点使其成为2-节点,再将再将父节点中最接近的一个拆分key与中孩子合并,将合并后的节点作为当前节点。
图解: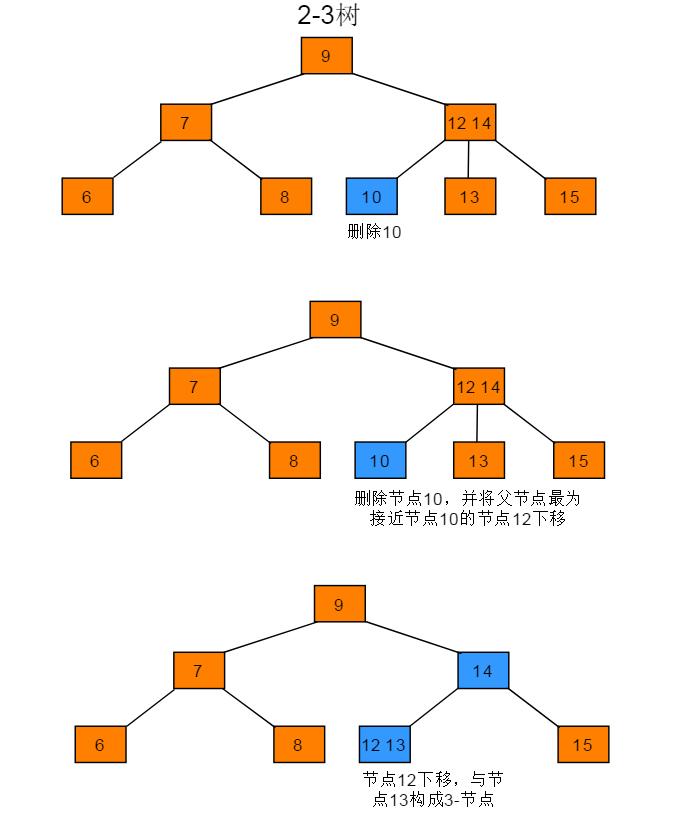
2-3树为满二叉树,删除叶子节点的操作步骤:若2-3树是一颗满二叉树,将2-3树层树减少,并将当前删除节点的兄弟节点合并到父节点中,同时将父节点的所有兄弟节点合并到父节点的父节点中,如果生成了4-节点,再分解4-节点。
图解: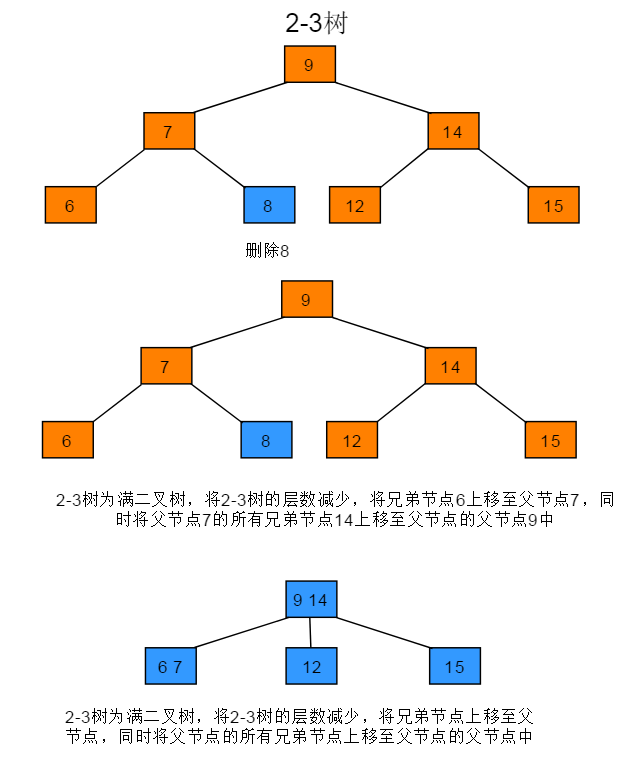
2-3-4树
2-3-4树是对2-3树的概念扩展,包括了4节点的使用。一个4节点中包含小中大三个元素和四个孩子(要么有四个孩子要么没有,不存在其他情况),如果某个4节点有孩子的话,左子树包含小于最小元素的元素;第二子树包含大于最小元素,小于第二元素的元素;第三子树包含大于第二元素,小于最大元素的元素;右子树包含大于最大元素的元素。
总结
先找插入结点,若结点有空(即2-结点),则直接插入。如结点没空(即3-结点),则插入使其临时容纳这个元素,然后分裂此结点,把中间元素移到其父结点中。对父结点亦如此处理。(中键一直往上移,直到找到空位,在此过程中没有空位就先搞个临时的,再分裂。)
2-3树插入算法的根本在于这些变换都是局部的:除了相关的结点和链接之外不必修改或者检查树的其他部分。每次变换中,变更的链接数量不会超过一个很小的常数。所有局部变换都不会影响整棵树的有序性和平衡性。
同时,通过上面树的深度增加的例子,可以看出2-3树和标准二叉树不同,标准的二叉树的的深度是由上到下的增加的,而2-3树的深度生长是由下至上的。
B-树
定义:B-树是一类树,包括B-树、B+树、B*树等,是一棵自平衡的搜索树,它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。
一个 m 阶的B树满足以下条件:
- 每个结点至多拥有m棵子树;
- 根结点至少拥有两颗子树(存在子树的情况下);
- 除了根结点以外,其余每个分支结点至少拥有 m/2 棵子树;
- 所有的叶结点都在同一层上;
- 有 k 棵子树的分支结点则存在 k-1 个关键码,关键码按照递增次序进行排列;
- 关键字数量需要满足ceil(m/2)-1 <= n <= m-1;
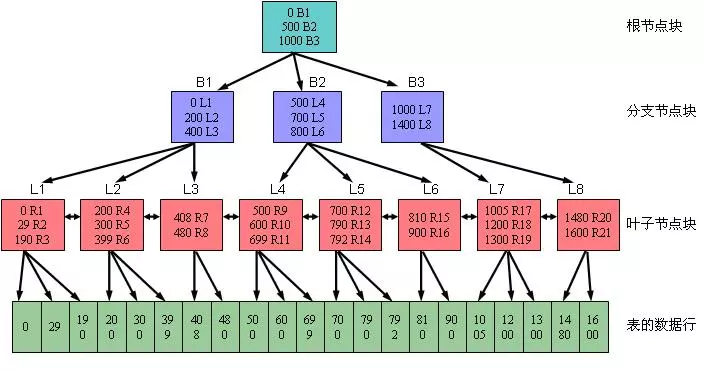
B树上大部分的操作所需要的磁盘存取次数和B树的高度是成正比的,在B树中可以检查多个子结点,由于在一棵树中检查任意一个结点都需要一次磁盘访问,所以B树避免了大量的磁盘访问。
B-树是专门为外部存储器设计的,如磁盘,它对于读取和写入大块数据有良好的性能,所以一般被用在文件系统及数据库中。
定义只需要知道B-树允许每个节点有更多的子节点即可(多叉树)。子节点数量一般在上千,具体数量依赖外部存储器的特性。
先来看看为什么会出现B-树这类数据结构。
传统用来搜索的平衡二叉树有很多,如 AVL 树,红黑树等。这些树在一般情况下查询性能非常好,但当数据非常大的时候它们就无能为力了。原因当数据量非常大时,内存不够用,大部分数据只能存放在磁盘上,只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns,而磁盘在 10 ms 左右。速度相差了近 5 个数量级,磁盘读取时间远远超过了数据在内存中比较的时间。这说明程序大部分时间会阻塞在磁盘 IO 上。那么我们如何提高程序性能?减少磁盘 IO 次数,像 AVL 树,红黑树这类平衡二叉树从设计上无法“迎合”磁盘。
平衡二叉树是通过旋转来保持平衡的,而旋转是对整棵树的操作,若部分加载到内存中则无法完成旋转操作。其次平衡二叉树的高度相对较大为 log n(底数为2),这样逻辑上很近的节点实际可能非常远,无法很好的利用磁盘预读(局部性原理),所以这类平衡二叉树在数据库和文件系统上的选择就被 pass 了。
空间局部性原理:如果一个存储器的某个位置被访问,那么将它附近的位置也会被访问。
我们从“迎合”磁盘的角度来看看B-树的设计。
索引的效率依赖与磁盘 IO 的次数,快速索引需要有效的减少磁盘 IO 次数,如何快速索引呢?索引的原理其实是不断的缩小查找范围,就如我们平时用字典查单词一样,先找首字母缩小范围,再第二个字母等等。平衡二叉树是每次将范围分割为两个区间。为了更快,B-树每次将范围分割为多个区间,区间越多,定位数据越快越精确。那么如果节点为区间范围,每个节点就较大了。所以新建节点时,直接申请页大小的空间(磁盘存储单位是按 block 分的,一般为 512 Byte。磁盘 IO 一次读取若干个 block,我们称为一页,具体大小和操作系统有关,一般为 4 k,8 k或 16 k),计算机内存分配是按页对齐的,这样就实现了一个节点只需要一次 IO。
多叉的好处非常明显,有效的降低了B-树的高度,为底数很大的 log n,底数大小与节点的子节点数目有关,一般一棵B-树的高度在 3 层左右。层数低,每个节点区确定的范围更精确,范围缩小的速度越快(比二叉树深层次的搜索肯定快很多)。上面说了一个节点需要进行一次 IO,那么总 IO 的次数就缩减为了 log n 次。B-树的每个节点是 n 个有序的序列(a1,a2,a3…an),并将该节点的子节点分割成 n+1 个区间来进行索引(X1< a1, a2 < X2 < a3, … , an+1 < Xn < anXn+1 > an)。
点评:B树的每个节点,都是存多个值的,不像二叉树那样,一个节点就一个值,B树把每个节点都给了一点的范围区间,区间更多的情况下,搜索也就更快了,比如:有1-100个数,二叉树一次只能分两个范围,0-50和51-100,而B树,分成4个范围 1-25, 25-50,51-75,76-100一次就能筛选走四分之三的数据。所以作为多叉树的B树是更快的。
插入
新结点一般插在第h层,通过搜索找到对应的结点进行插入,那么根据即将插入的结点的数量又分为下面几种情况。
如果该结点的关键字个数没有到达m-1个,那么直接插入即可;
如果该结点的关键字个数已经到达了m-1个,那么根据B树的性质显然无法满足,需要将其进行分裂。分裂的规则是该结点分成两半,将中间的关键字进行提升,加入到父亲结点中,但是这又可能存在父亲结点也满员的情况,则不得不向上进行回溯,甚至是要对根结点进行分裂,那么整棵树都加了一层。
其过程如下: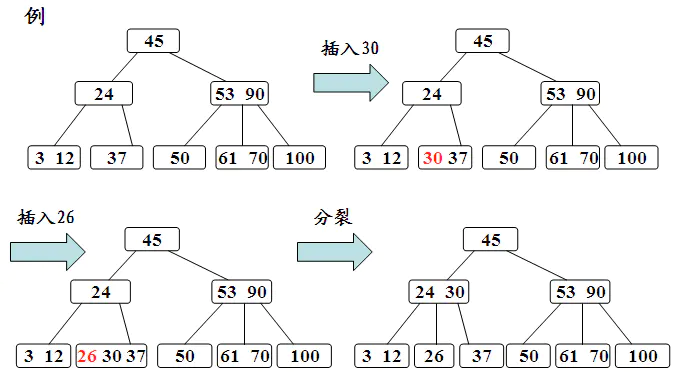
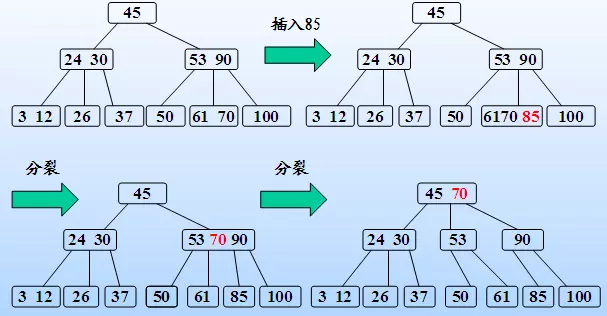
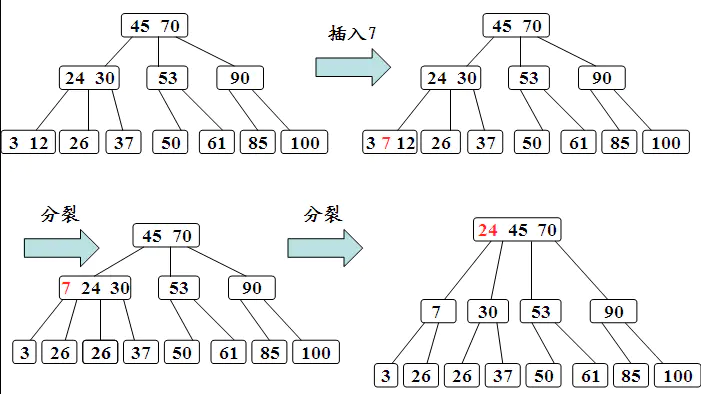
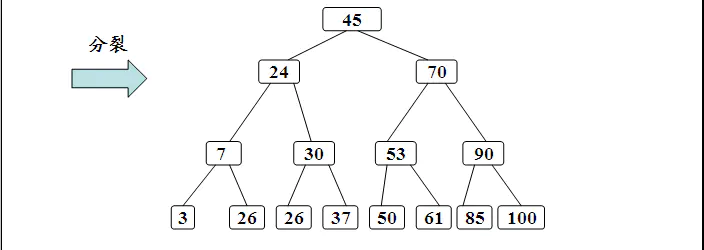
删除
同样的,我们需要先通过搜索找到相应的值,存在则进行删除,需要考虑删除以后的情况,
- 如果该结点拥有关键字数量仍然满足B树性质,则不做任何处理;
- 如果该结点在删除关键字以后不满足B树的性质(关键字没有到达ceil(m/2)-1的数量),则需要向兄弟结点借关键字,这有分为兄弟结点的关键字数量是否足够的情况。
- 如果兄弟结点的关键字足够借给该结点,则过程为将父亲结点的关键字下移,兄弟结点的关键字上移;
- 如果兄弟结点的关键字在借出去以后也无法满足情况,即之前兄弟结点的关键字的数量为ceil(m/2)-1,借的一方的关键字数量为ceil(m/2)-2的情况,那么我们可以将该结点合并到兄弟结点中,合并之后的子结点数量少了一个,则需要将父亲结点的关键字下放,如果父亲结点不满足性质,则向上回溯;
- 其余情况参照BST中的删除。
其过程如下: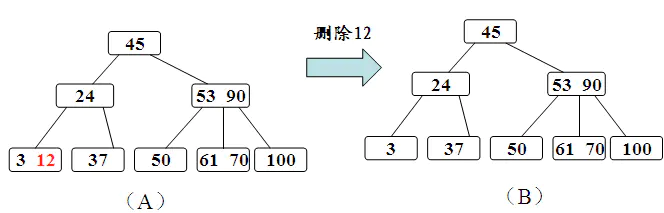
B-树是一种多路搜索树(并不是二叉的):
- 定义任意非叶子结点最多只有M个儿子;且M>2;
- 根结点的儿子数为[2, M];
- 除根结点以外的非叶子结点的儿子数为[M/2, M];
- 每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
- 非叶子结点的关键字个数=指向儿子的指针个数-1;
- 非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
- 非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
- 所有叶子结点位于同一层;
如:(M=3)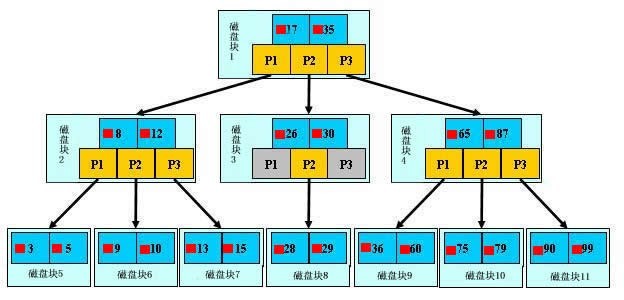
来模拟下查找文件29的过程:
- 根据根结点指针找到文件目录的根磁盘块1,将其中的信息导入内存。【磁盘IO操作1次】
- 此时内存中有两个文件名17,35和三个存储其他磁盘页面地址的数据。根据算法我们发现17<29<35,因此我们找到指针p2。
- 根据p2指针,我们定位到磁盘块3,并将其中的信息导入内存。【磁盘IO操作2次】
- 此时内存中有两个文件名26,30和三个存储其他磁盘页面地址的数据。根据算法我们发现26<29<30,因此我们找到指针p2。
- 根据p2指针,我们定位到磁盘块8,并将其中的信息导入内存。【磁盘IO操作3次】
- 此时内存中有两个文件名28,29。根据算法我们查找到文件29,并定位了该文件内存的磁盘地址。
生成从空树开始,逐个插入关键字。但是由于B-树节点关键字必须大于等于[ceil(m/2)-1],所以每次插入一个关键字不是在树中添加一个叶子结点,而是首先在最底层的某个非终端节点中添加一个“关键字”,该结点的关键字不超过m-1,则插入完成;否则要产生结点的“分裂”,将一半数量的关键字元素分裂到新的其相邻右结点中,中间关键字元素上移到父结点中。
1、咱们通过一个实例来逐步讲解下。插入以下字符字母到一棵空的B 树中(非根结点关键字数小了(小于2个)就合并,大了(超过4个)就分裂):C N G A H E K Q M F W L T Z D P R X Y S,首先,结点空间足够,4个字母插入相同的结点中,如下图: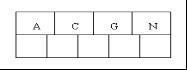
2、当咱们试着插入H时,结点发现空间不够,以致将其分裂成2个结点,移动中间元素G上移到新的根结点中,在实现过程中,咱们把A和C留在当前结点中,而H和N放置新的其右邻居结点中。如下图: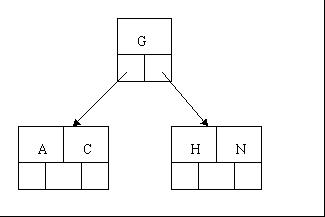
3、当咱们插入E,K,Q时,不需要任何分裂操作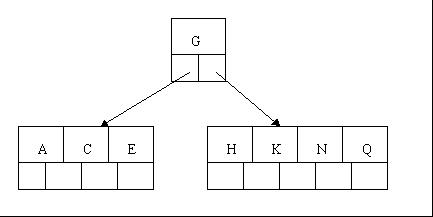
4、插入M需要一次分裂,注意M恰好是中间关键字元素,以致向上移到父节点中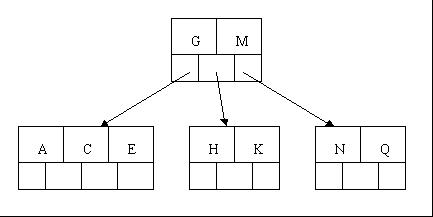
5、插入F,W,L,T不需要任何分裂操作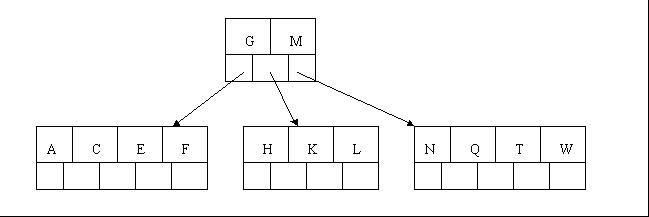
6、插入Z时,最右的叶子结点空间满了,需要进行分裂操作,中间元素T上移到父节点中,注意通过上移中间元素,树最终还是保持平衡,分裂结果的结点存在2个关键字元素。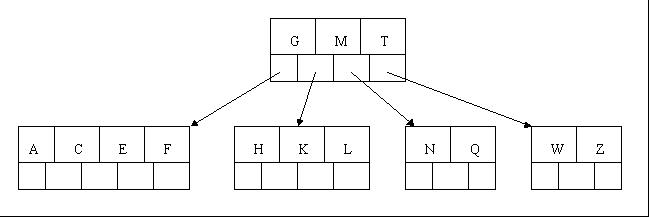
7、插入D时,导致最左边的叶子结点被分裂,D恰好也是中间元素,上移到父节点中,然后字母P,R,X,Y陆续插入不需要任何分裂操作(别忘了,树中至多5个孩子)。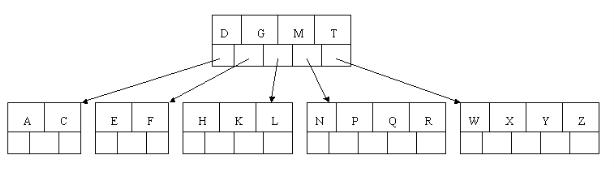
8、最后,当插入S时,含有N,P,Q,R的结点需要分裂,把中间元素Q上移到父节点中,但是情况来了,父节点中空间已经满了,所以也要进行分裂,将父节点中的中间元素M上移到新形成的根结点中,注意以前在父节点中的第三个指针在修改后包括D和G节点中。这样具体插入操作的完成。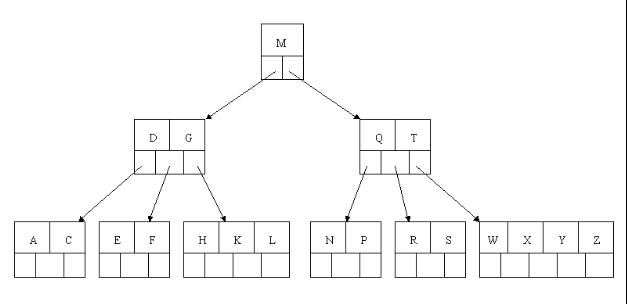
删除操作
首先查找B树中需删除的元素,如果该元素在B树中存在,则将该元素在其结点中进行删除,如果删除该元素后,首先判断该元素是否有左右孩子结点,如果有,则上移孩子结点中的某相近元素到父节点中,然后是移动之后的情况;如果没有,直接删除后,移动之后的情况。
删除元素,移动相应元素之后,如果某结点中元素数目(即关键字数)小于ceil(m/2)-1,则需要看其某相邻兄弟结点是否丰满(结点中元素个数大于ceil(m/2)-1)(还记得第一节中关于B树的第5个特性中的c点么?:c)除根结点之外的结点(包括叶子结点)的关键字的个数n必须满足:(ceil(m / 2)-1) <= n <= m-1。m表示最多含有m个孩子,n表示关键字数。在本小节中举的一颗B树的示例中,关键字数n满足:2<=n<=4),如果丰满,则向父节点借一个元素来满足条件;如果其相邻兄弟都刚脱贫,即借了之后其结点数目小于ceil(m/2)-1,则该结点与其相邻的某一兄弟结点进行“合并”成一个结点,以此来满足条件。那咱们通过下面实例来详细了解吧。
以上述插入操作构造的一棵5阶B树(树中最多含有m(m=5)个孩子,因此关键字数最小为ceil(m / 2)-1=2。还是这句话,关键字数小了(小于2个)就合并,大了(超过4个)就分裂)为例,依次删除H,T,R,E。
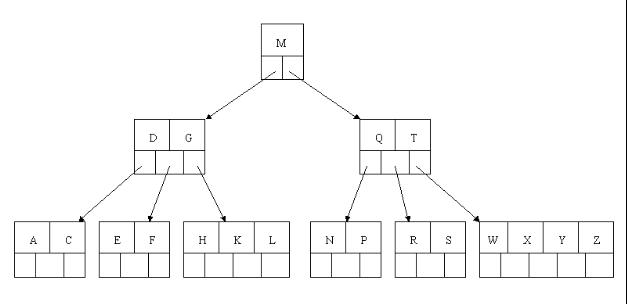
1、首先删除元素H,当然首先查找H,H在一个叶子结点中,且该叶子结点元素数目3大于最小元素数目ceil(m/2)-1=2,则操作很简单,咱们只需要移动K至原来H的位置,移动L至K的位置(也就是结点中删除元素后面的元素向前移动)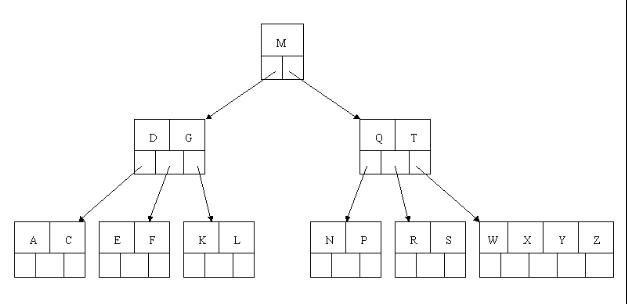
2、下一步,删除T,因为T没有在叶子结点中,而是在中间结点中找到,咱们发现他的继承者W(字母升序的下个元素),将W上移到T的位置,然后将原包含W的孩子结点中的W进行删除,这里恰好删除W后,该孩子结点中元素个数大于2,无需进行合并操作。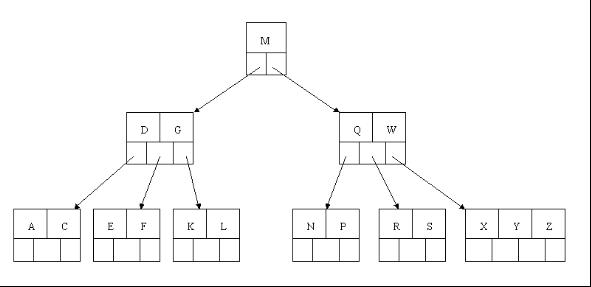
3、下一步删除R,R在叶子结点中,但是该结点中元素数目为2,删除导致只有1个元素,已经小于最小元素数目ceil(5/2)-1=2,而由前面我们已经知道:如果其某个相邻兄弟结点中比较丰满(元素个数大于ceil(5/2)-1=2),则可以向父结点借一个元素,然后将最丰满的相邻兄弟结点中上移最后或最前一个元素到父节点中(有没有看到红黑树中左旋操作的影子?),在这个实例中,右相邻兄弟结点中比较丰满(3个元素大于2),所以先向父节点借一个元素W下移到该叶子结点中,代替原来S的位置,S前移;然后X在相邻右兄弟结点中上移到父结点中,最后在相邻右兄弟结点中删除X,后面元素前移。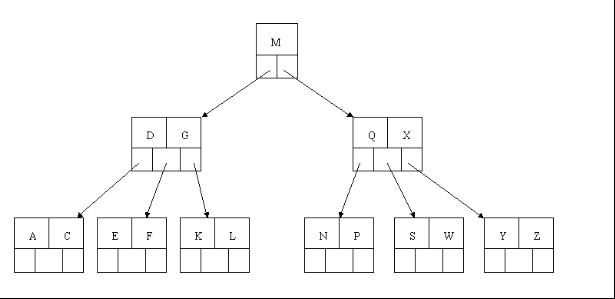
4、最后一步删除E,删除后会导致很多问题,因为E所在的结点数目刚好达标,刚好满足最小元素个数(ceil(5/2)-1=2),而相邻的兄弟结点也是同样的情况,删除一个元素都不能满足条件,所以需要该节点与某相邻兄弟结点进行合并操作;首先移动父结点中的元素(该元素在两个需要合并的两个结点元素之间)下移到其子结点中,然后将这两个结点进行合并成一个结点。所以在该实例中,咱们首先将父节点中的元素D下移到已经删除E而只有F的结点中,然后将含有D和F的结点和含有A,C的相邻兄弟结点进行合并成一个结点。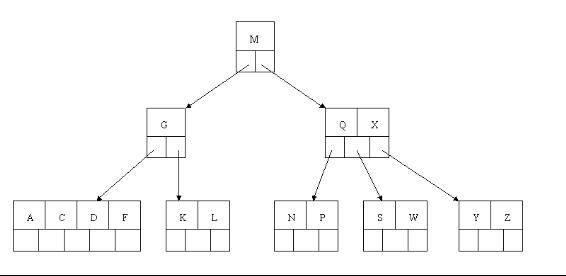
5、也许你认为这样删除操作已经结束了,其实不然,在看看上图,对于这种特殊情况,你立即会发现父节点只包含一个元素G,没达标(因为非根节点包括叶子结点的关键字数n必须满足于2=<n<=4,而此处的n=1),这是不能够接受的。如果这个问题结点的相邻兄弟比较丰满,则可以向父结点借一个元素。假设这时右兄弟结点(含有Q,X)有一个以上的元素(Q右边还有元素),然后咱们将M下移到元素很少的子结点中,将Q上移到M的位置,这时,Q的左子树将变成M的右子树,也就是含有N,P结点被依附在M的右指针上。所以在这个实例中,咱们没有办法去借一个元素,只能与兄弟结点进行合并成一个结点,而根结点中的唯一元素M下移到子结点,这样,树的高度减少一层。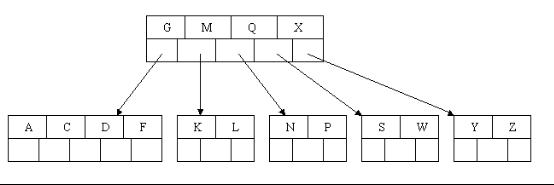
为了进一步详细讨论删除的情况,再举另外一个实例:这里是一棵不同的5序B树,那咱们试着删除C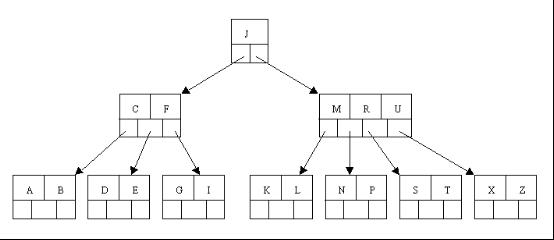
于是将删除元素C的右子结点中的D元素上移到C的位置,但是出现上移元素后,只有一个元素的结点的情况。
又因为含有E的结点,其相邻兄弟结点才刚脱贫(最少元素个数为2),不可能向父节点借元素,所以只能进行合并操作,于是这里将含有A,B的左兄弟结点和含有E的结点进行合并成一个结点。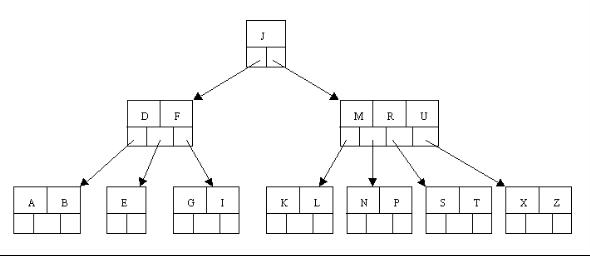
这样又出现只含有一个元素F结点的情况,这时,其相邻的兄弟结点是丰满的(元素个数为3>最小元素个数2),这样就可以想父结点借元素了,把父结点中的J下移到该结点中,相应的如果结点中J后有元素则前移,然后相邻兄弟结点中的第一个元素(或者最后一个元素)上移到父节点中,后面的元素(或者前面的元素)前移(或者后移);注意含有K,L的结点以前依附在M的左边,现在变为依附在J的右边。这样每个结点都满足B树结构性质。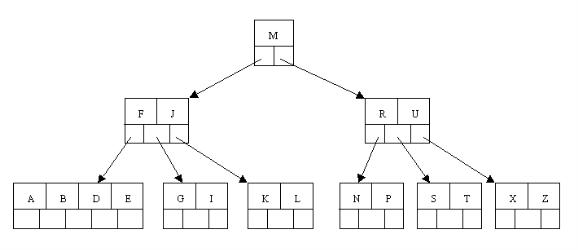
从以上操作可看出:除根结点之外的结点(包括叶子结点)的关键字的个数n满足:(ceil(m / 2)-1) <= n <= m-1,即2<=n<=4。这也佐证了咱们之前的观点。删除操作完。
B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;
B-树的特性:
- 关键字集合分布在整颗树中;
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束;
- 其搜索性能等价于在关键字全集内做一次二分查找;
- 自动层次控制;
由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少利用率,其最底搜索性能为: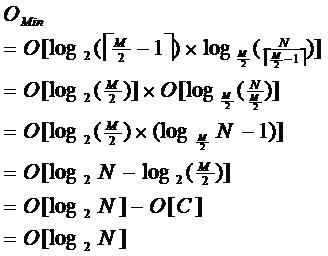
其中,M为设定的非叶子结点最多子树个数,N为关键字总数;所以B-树的性能总是等价于二分查找(与M值无关),也就没有B树平衡的问题;由于M/2的限制,在插入结点时,如果结点已满,需要将结点分裂为两个各占M/2的结点;删除结点时,需将两个不足M/2的兄弟结点合并;
B+树
B+树是B-树的变体,也是一种多路搜索树:
- 其定义基本与B-树同,除了:
- 非叶子结点的子树指针与关键字个数相同;
- 非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
- 为所有叶子结点增加一个链指针;
- 所有关键字都在叶子结点出现;
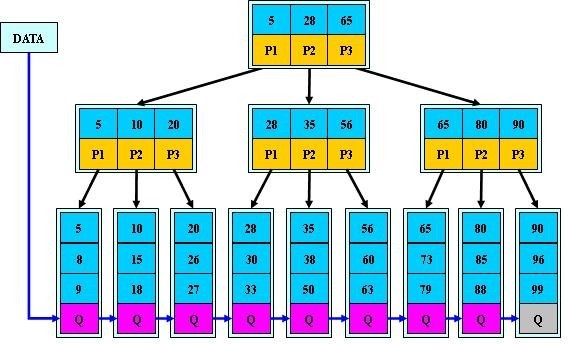
B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找。B+树的主要优点:非终端结点仅仅起高层索引作用,而B树非终端结点的关键字除作子树分界外,本身还是实际记录的有效关键字(含记录指针),因此相同的结点空间,B+树可以设计的阶树比B树大,相同的索引,B+树的索引层数比B树少,因此检索速度比B树快。此外,B+树叶子结点包含完整的索引信息,可以较方便地表示文件的稀疏索引。最后,B+树的检索、插入和删除都在叶子结点进行,比B树相对简单。
B+的特性:
- 所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
- 不可能在非叶子结点命中;
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
- 更适合文件索引系统;
B树和B+树的区别是由于B+树和B具有这不同的存储结构所造成的区别,以一个m阶树为例。
- 关键字的数量不同;B+树中分支结点有m个关键字,其叶子结点也有m个,其关键字只是起到了一个索引的作用,但是B树虽然也有m个子结点,但是其只拥有m-1个关键字。
- 存储的位置不同;B+树中的数据都存储在叶子结点上,也就是其所有叶子结点的数据组合起来就是完整的数据,但是B树的数据存储在每一个结点中,并不仅仅存储在叶子结点上。
- 分支结点的构造不同;B+树的分支结点仅仅存储着关键字信息和儿子的指针(这里的指针指的是磁盘块的偏移量),也就是说内部结点仅仅包含着索引信息。
- 查询不同;B树在找到具体的数值以后,则结束,而B+树则需要通过索引找到叶子结点中的数据才结束,也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径。
B*树
是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;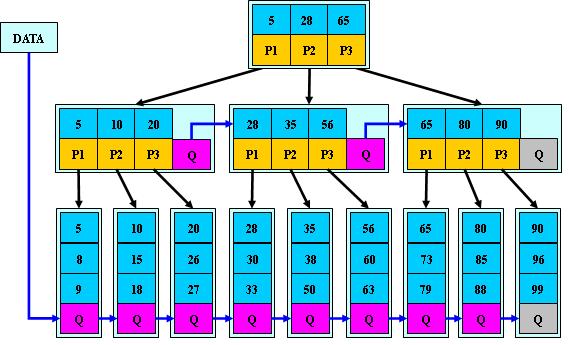
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;
所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
实现
根据B树的特点,我们首先可以写出B树的整体的结构。
B树结构
B树的结构我们定义需要参考规则,我们首先是需要给出保存键值的一个数组,这个数组的大小取决与我们定义的M,然后我们根据规则,可以得到一个保存M+1个子的一个数组,然后当然为了方便访问,parent指针,然后要有一个记录每个节点中键值个数的一个size。
所以定义如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20template <typename K,int M>
struct BTreeNode
{
K _keys[M]; //用来保存键值。
BTreeNode<K, M>* _sub[M + 1]; //用来保存子。
BTreeNode<K, M>* _parent;
size_t _size;
BTreeNode()
:_parent(NULL)
, _size(0)
{
int i = 0;
for ( i = 0; i < M; i++)
{
_keys[i] = K();
_sub[i] = K();
}
_sub[i] = K();
}
};
B树的查找
对于AVL,BST,红黑树,B树这些高级的数据结构而言,查找算法是非常重要的。我们首先确定返回值,对于这种关于key和key-value的数据结构,参考map和set,我们让它返回一个pair的一个结构体。
pair结构体的定义在std中是1
2
3
4
5
6template<typename K,typename V>
struct pair
{
K key;
V value;
}
我们只需要让这个里面的value变为bool值,value返回以后说明的是存不存就可以了。
接下来的思路就是从根节点进行和这个节点当中的每一个key比较,如果=那么就返回找到了,如果小于,那么就到这个节点左面的子节点中找,如果大了,就继续向后面的键值进行查找。如果相等那么就返回。
示例代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43pair <Node*, int> Find(const K &key)
{
Node* cur = _root;
Node* parent = NULL;
while (cur)
{
size_t i = 0;
while (i < cur->_size)
{
//如果小于当前,向后
if (cur->_keys[i] < key)
{
i++;
}
//如果大于,
else if (cur->_keys[i]>key)
{
cur = cur->_sub[i];
parent = cur;
break;
}
//相等,返回这个节点
else
{
return pair<Node *, int>(NULL, -1);
}
}
if (key > cur->_sub[i + 1])
{
cur = cur->_sub[i];
}
//为了防止出现我返回空指针操作,如果是空指针,那么就返回父亲
if (cur != NULL && i == cur->_size)
{
parent = cur;
cur = cur->_sub[i];
}
}
return pair<Node *, int>(parent, 1);
}
B树的插入
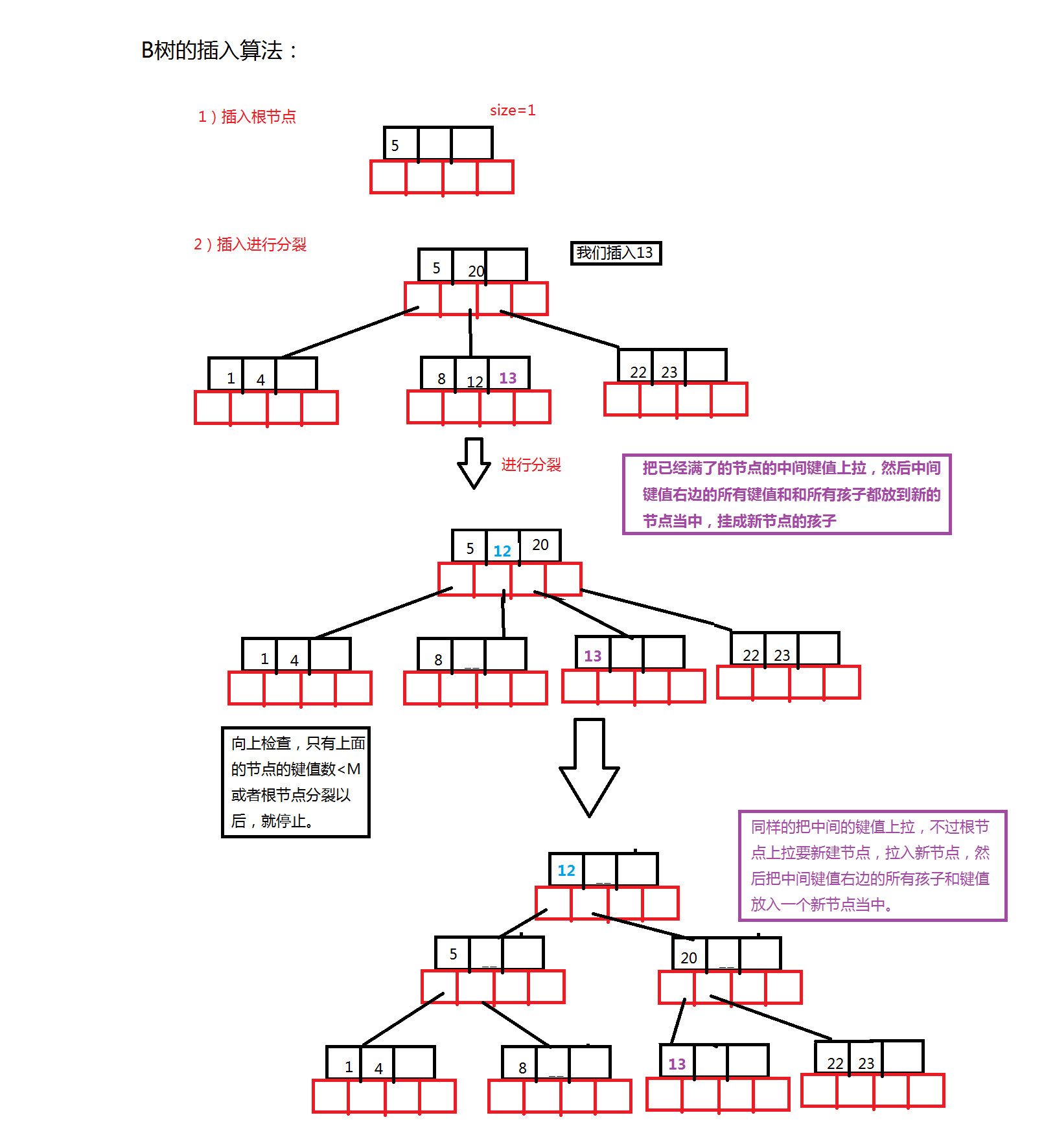
示例代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128bool Insert(const K &key)
{
//首先来考虑空树的情况
if (_root == NULL)
{
//给这个节点中添加key,并且让size++。
_root = new Node;
_root->_keys[0] = key;
_root->_size++;
return true;
}
//使用通用的key-value结构体来保存找到的key所在的节点。
pair<Node*,int > ret=Find(key);
//在这里来看这个节点是否存在,存在就直接return false。
if (ret.second == -1)
{
return false;
}
Node* cur = ret.first;
K newKey = key;
Node *sub = NULL;
//此时表示考虑插入。
while (1)
{
//向cur里面进行插入,如果没满插入,满了就进行分裂。
InsetKey(cur, newKey, sub);
//小于M,这样就可以直接插入
if (cur->_size < M)
{
return true;
}
//如果==M,那么就应该进行分裂
//首先找到中间的节点
size_t mid = cur->_size / 2;
//创建一个节点,用来保存中间节点右边所有的节点和子节点。
Node * tmp = new Node;
size_t j = 0;
//进行移动sub以及所有的子接点。
for (size_t i = mid + 1; i < cur->_size; i++)
{
tmp->_keys[j] = cur->_keys[i];
cur->_keys[i] = K();
cur->_size--;
tmp->_size++;
j++;
}
//移动子串
for (j = 0; j < tmp->_size + 1; j++)
{
tmp->_sub[j] = cur->_sub[mid + 1 + j];
if (tmp->_sub[j])
{
tmp->_sub[j]->_parent = tmp;
}
cur->_sub[mid + 1 + j] = NULL;
}
//进行其他的移动
//分裂的条件就是要么分裂根,要么就是分裂子节点,要么就是所在节点的节点数小于M。
//考虑根分裂,分裂的时候创建节点,然后把中间节点上拉,记得要更改最后的parent
if (cur->_parent == NULL)
{
_root = new Node();
_root->_keys[0] = cur->_keys[mid];
cur->_keys[mid] = K();
cur->_size--;
_root->_size++;
_root->_sub[0] = cur;
cur->_parent = _root;
_root->_sub[1] = tmp;
tmp->_parent = _root;
return true;
}
//分裂如果不是根节点,那么就把mid节点插入到上一层节点中,然后看上一层节点是否要分裂。注意修改cur和sub
else
{
newKey = cur->_keys[mid];
cur->_keys[mid] = K();
cur->_size--;
cur = cur->_parent;
sub = tmp;
sub->_parent = cur;
}
}
}
void InsetKey(Node* cur, const K &key, Node* sub)
{
int i = cur->_size - 1;
while (i>=0)
{
//进行插入
if (key > cur->_keys[i])
{
break;
}
//进行移动
else
{
cur->_keys[i + 1] = cur->_keys[i];
cur->_sub[i + 2] = cur->_sub[i + 1];
}
i--;
}
//进行插入
cur->_keys[i + 1] = key;
//插入子
cur->_sub[i + 2] = sub;
//如果没满,只需要对size++;
if (cur->_size < M)
{
cur->_size++;
}
}
深入浅出分析LSM树
LSM树数据结构定义
LSM树并没有一种固定死的实现方式,更多的是一种将:
“磁盘顺序写” + “多个树(状数据结构)” + “冷热(新老)数据分级” + “定期归并” + “非原地更新”这几种特性统一在一起的思想。
为了方便后续的讲解分析,我们尝试先对LSM树做一个定义。
LSM树的定义:
- LSM树是一个横跨内存和磁盘的,包含多颗”子树”的一个森林。
- LSM树分为Level 0,Level 1,Level 2 … Level n 多颗子树,其中只有Level 0在内存中,其余Level 1-n在磁盘中。
- 内存中的Level 0子树一般采用排序树(红黑树/AVL树)、跳表或者TreeMap等这类有序的数据结构,方便后续顺序写磁盘。
- 磁盘中的Level 1-n子树,本质是数据排好序后顺序写到磁盘上的文件,只是叫做树而已。
- 每一层的子树都有一个阈值大小,达到阈值后会进行合并,合并结果写入下一层。
- 只有内存中数据允许原地更新,磁盘上数据的变更只允许追加写,不做原地更新。
以上6条定义组成了LSM树,如图1所示。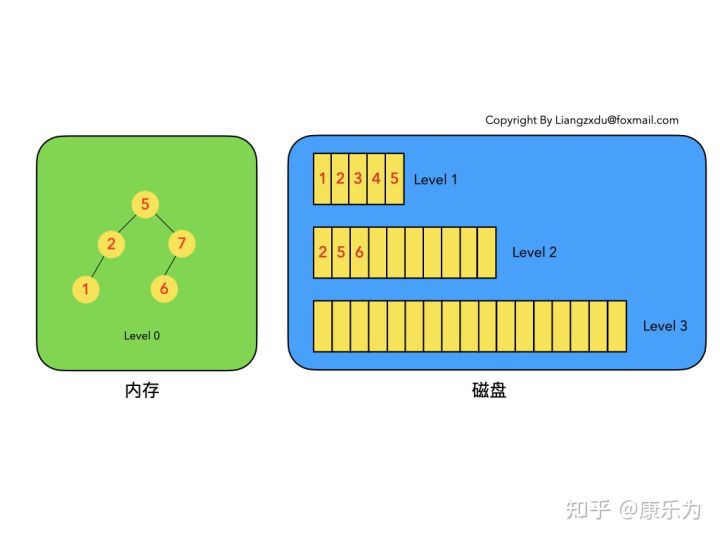
- 图1中分成了左侧绿色的内存部分和右侧蓝色的磁盘部分(定义1)。
- 图1左侧绿色的内存部分只包含Level 0树,右侧蓝色的磁盘部分则包含Level 1-n等多棵”树”(定义2)
- 图1左侧绿色的内存部分中Level 0是一颗二叉排序树(定义3)。注意这里的有序性,该性质决定了LSM树优异的读写性能。
- 图1右侧蓝色的磁盘部分所包含的Level 1到Level n多颗树,虽然叫做“树”,但本质是按数据key排好序后,顺序写在磁盘上的一个个文件(定义4) ,注意这里再次出现了有序性。
- 内存中的Level 0树在达到阈值后,会在内存中遍历排好序的Level 0树并顺序写入磁盘的Level 1。同样的,在磁盘中的Level n(n>0)达到阈值时,则会将Level n层的多个文件进行归并,写入Level n+1层。(定义5)
- 除了内存中的Level 0层做原地更新外,对已写入磁盘上的数据,都采用Append形式的磁盘顺序写,即更新和删除操作并不去修改老数据,只是简单的追加新数据。图1中右侧蓝色的磁盘部分,Level 1和Level 2均包含key为2的数据,同时图1左侧绿色内存中的Level 0树也包含key为2的数据节点。(定义6)
下面我们遵循LSM树的6条定义,通过动图对LSM树的增、删、改、查和归并进行详细分析。
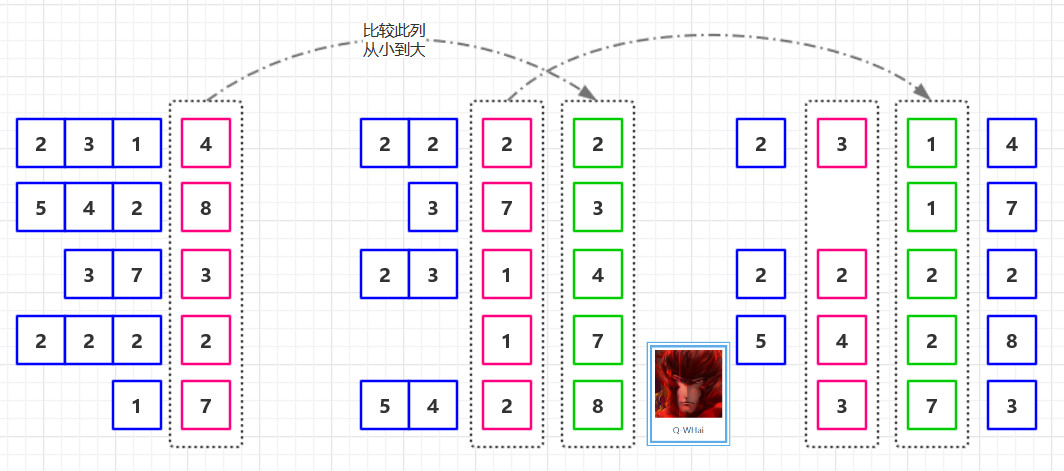
插入操作
LSM树的插入较简单,数据无脑往内存中的Level 0排序树丢即可,并不关心该数据是否已经在内存或磁盘中存在。(已经存在该数据的话,则场景转换成更新操作,详见第四部分)
图2展示了,新数据直接插入Level 0树的过程。
如上图2所示,我们依次插入了key=9、1、6的数据,这三个数据均按照key的大小,插入内存里的Level 0排序树中。该操作复杂度为树高log(n),n是Level 0树的数据量,可见代价很低,能实现极高的写吞吐量。
删除操作
LSM树的删除操作并不是直接删除数据,而是通过一种叫“墓碑标记”的特殊数据来标识数据的删除。
删除操作分为:待删除数据在内存中、待删除数据在磁盘中 和 该数据根本不存在 三种情况。
待删除数据在内存中:
如图3所示,展示了待删除数据在内存中的删除过程。我们不能简单地将Level 0树中的黄色节点2删除,而是应该采用墓碑标记将其覆盖(思考题:为什么不能直接删除而是要用墓碑标记覆盖呢)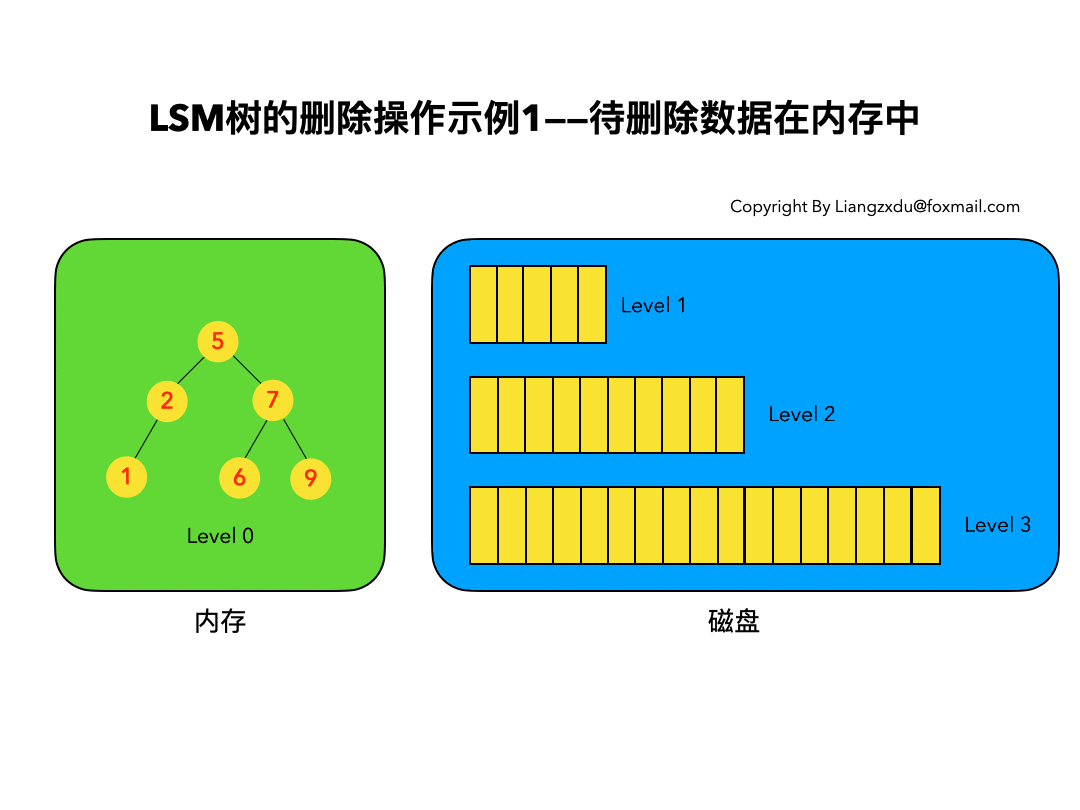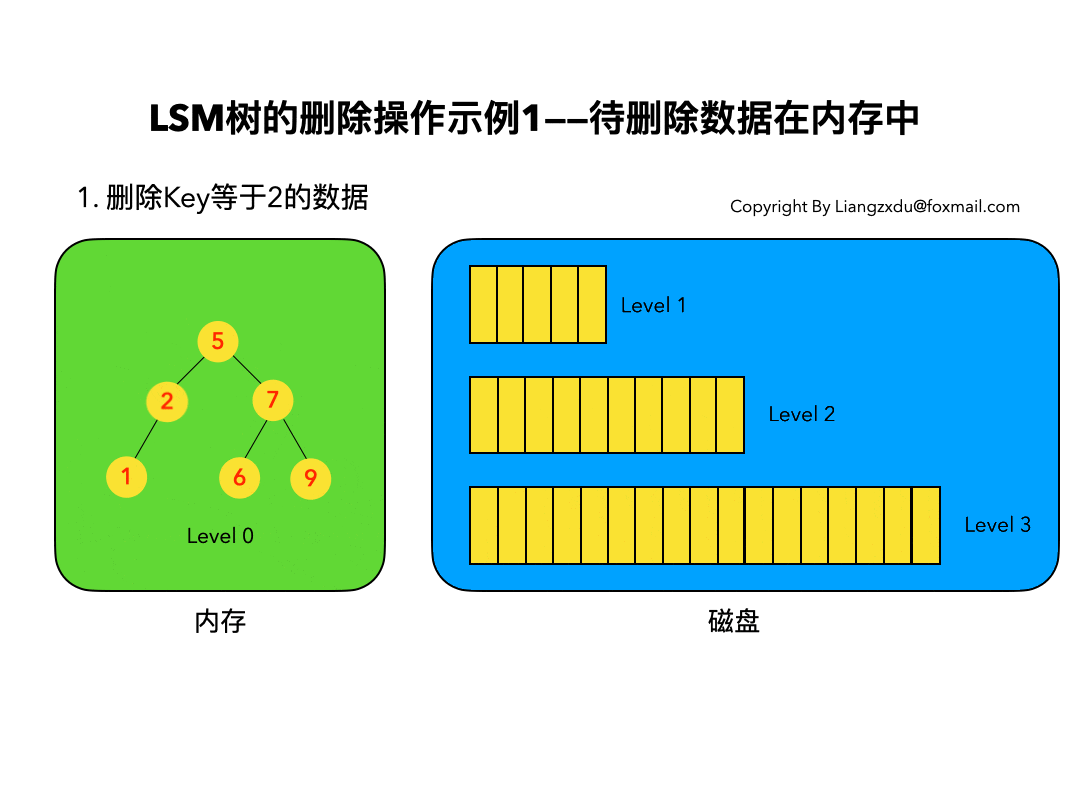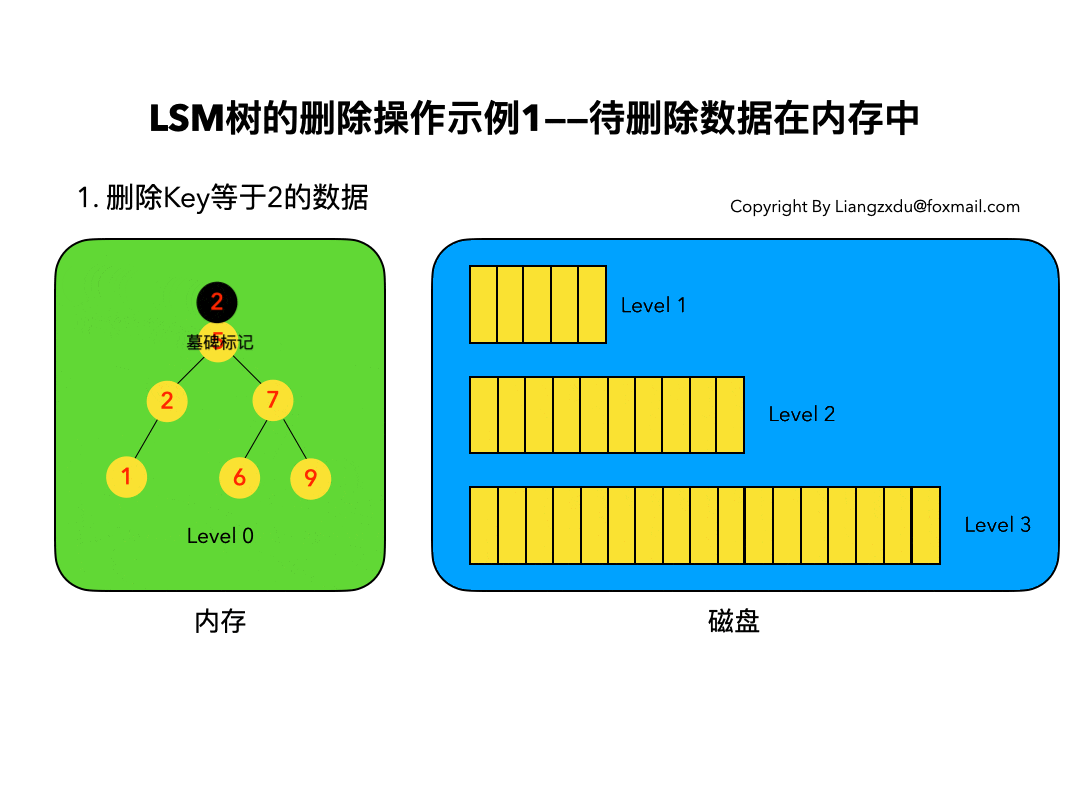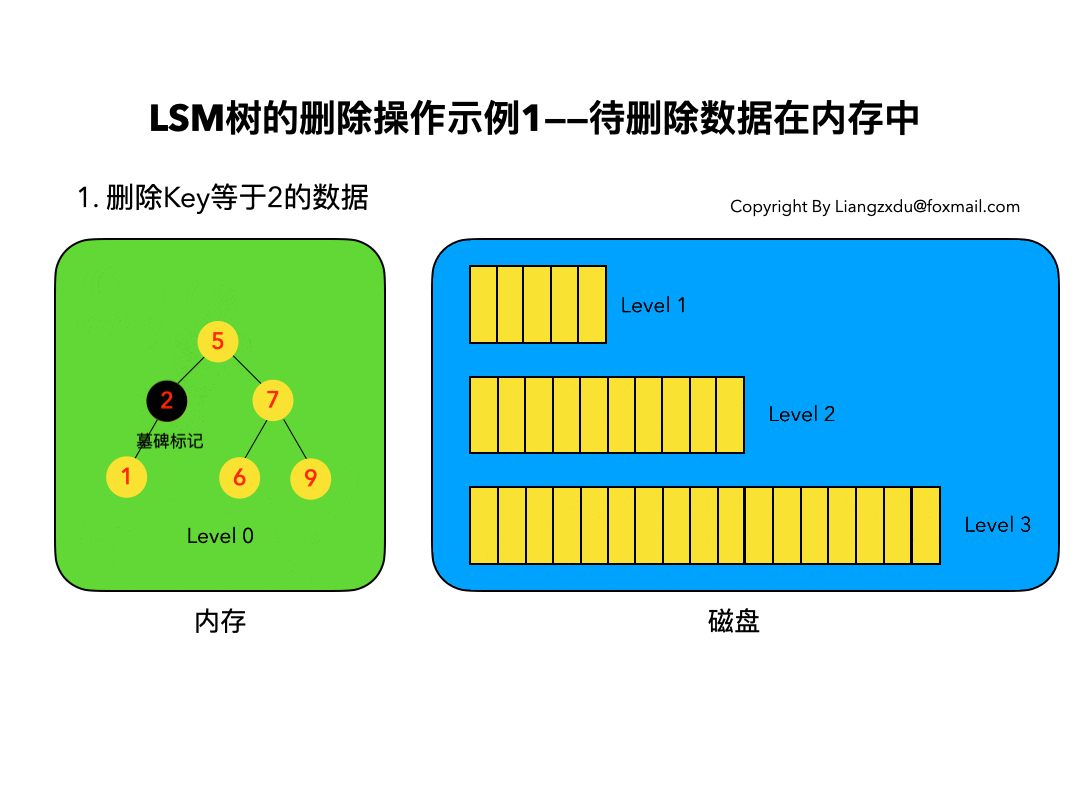
待删除数据在磁盘中
如图4所示,展示了待删除数据在磁盘上时的删除过程。我们并不去修改磁盘上的数据(理都不理它),而是直接向内存中的Level 0树中插入墓碑标记即可。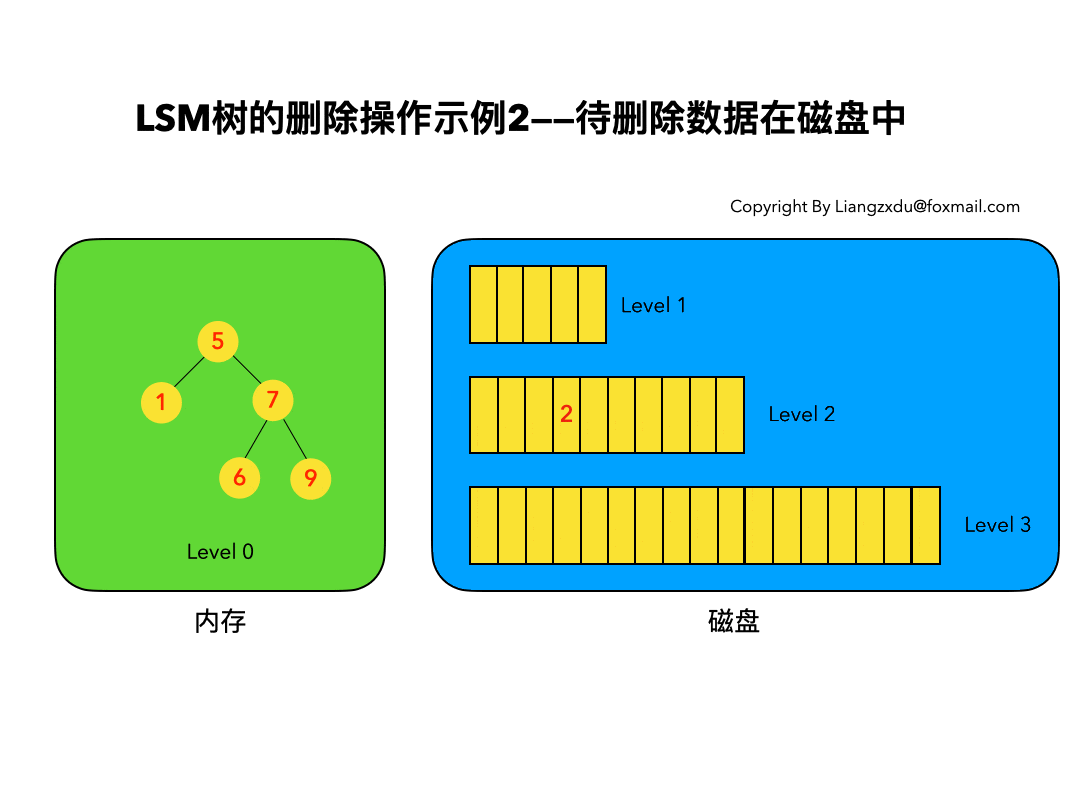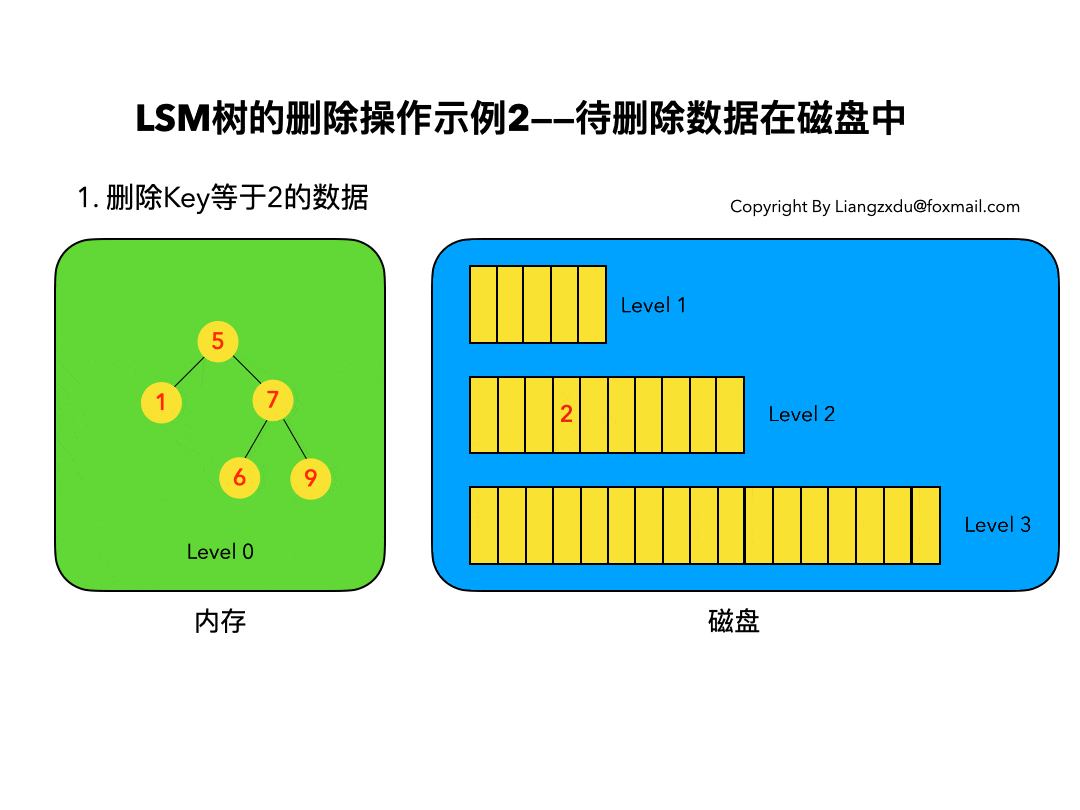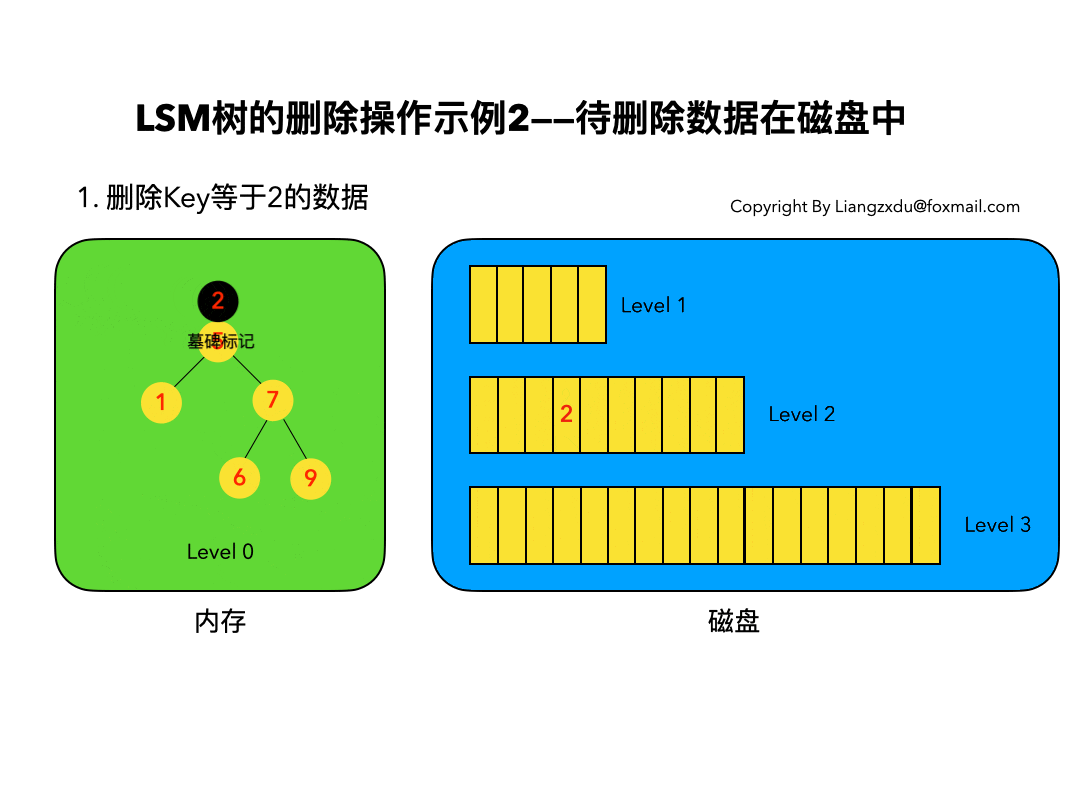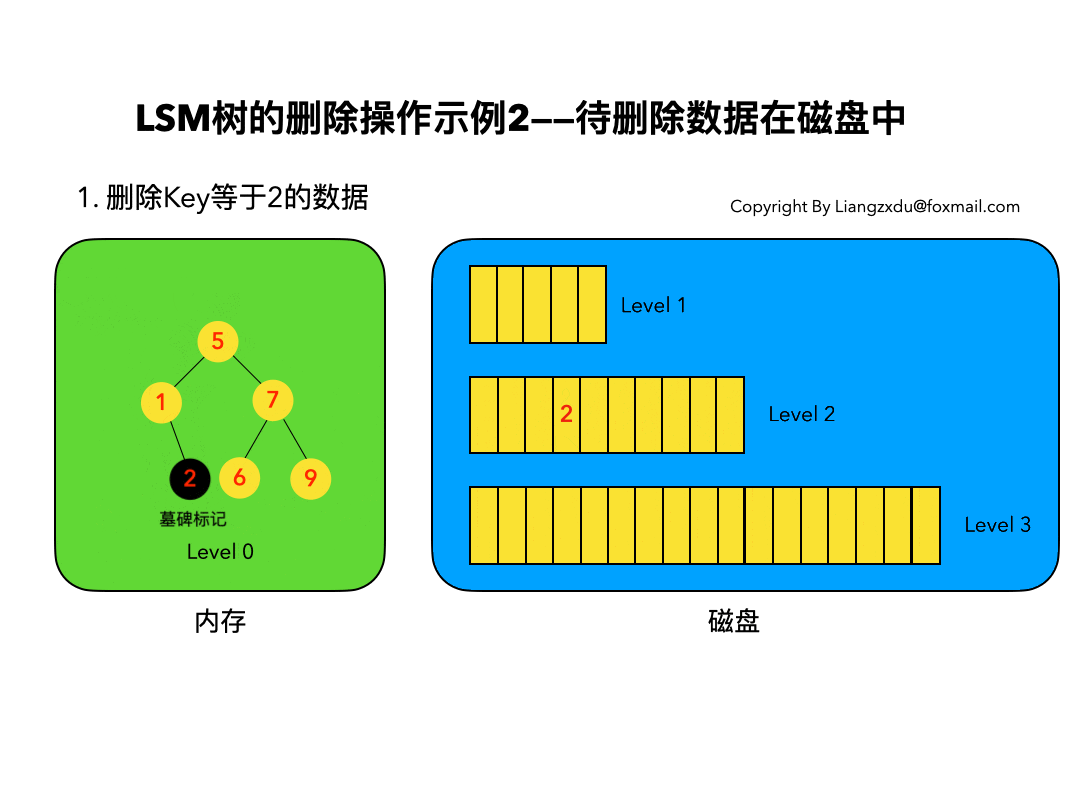
待删除数据根本不存在:
这种情况等价于在内存的Level 0树中新增一条墓碑标记,场景转换为情况3.2的内存中插入墓碑标记操作。
综合看待上述三种情况,发现不论数据有没有、在哪里,删除操作都是等价于向Level 0树中写入墓碑标记。该操作复杂度为树高log(n),代价很低。
修改操作
LSM树的修改操作和删除操作很像,也是分为三种情况:待修改数据在内存中、在磁盘中和 该数据根本不存在。
待修改数据在内存中:
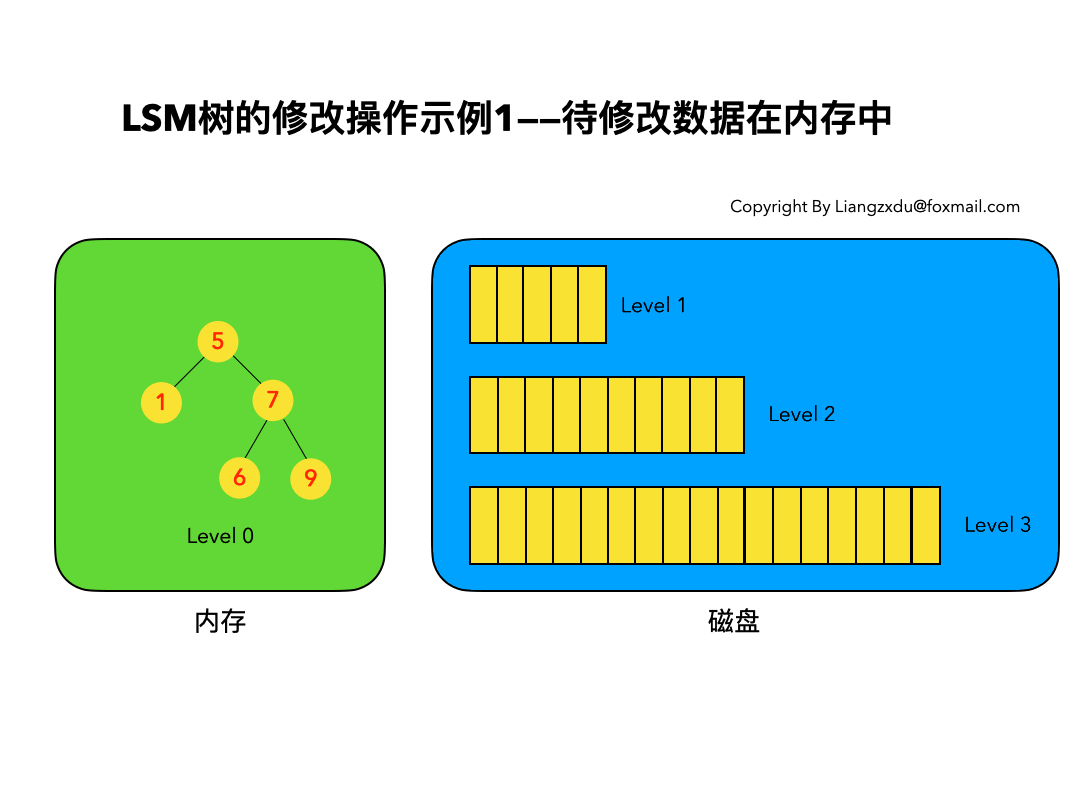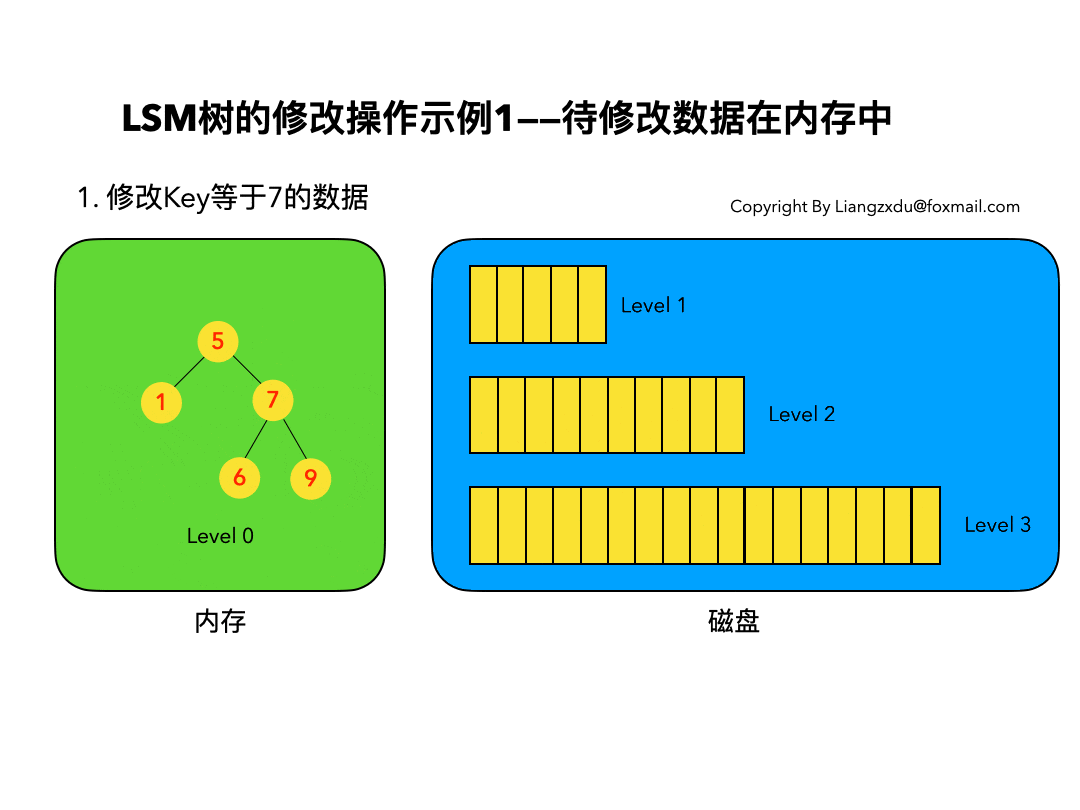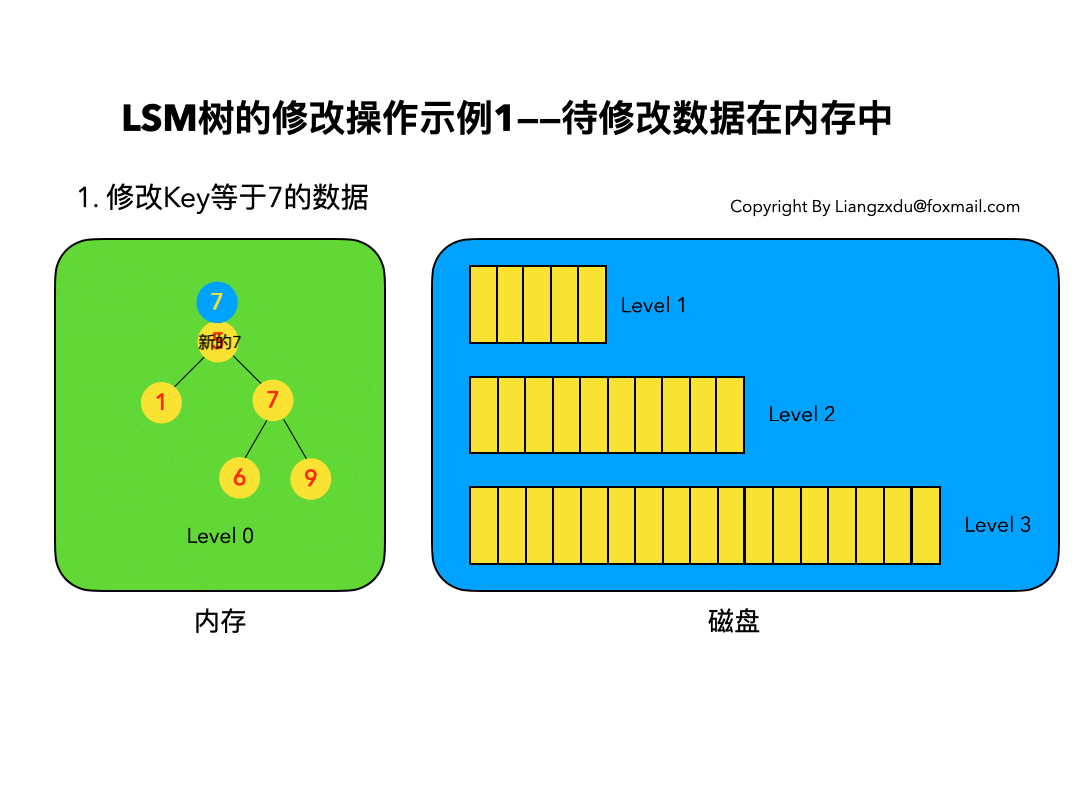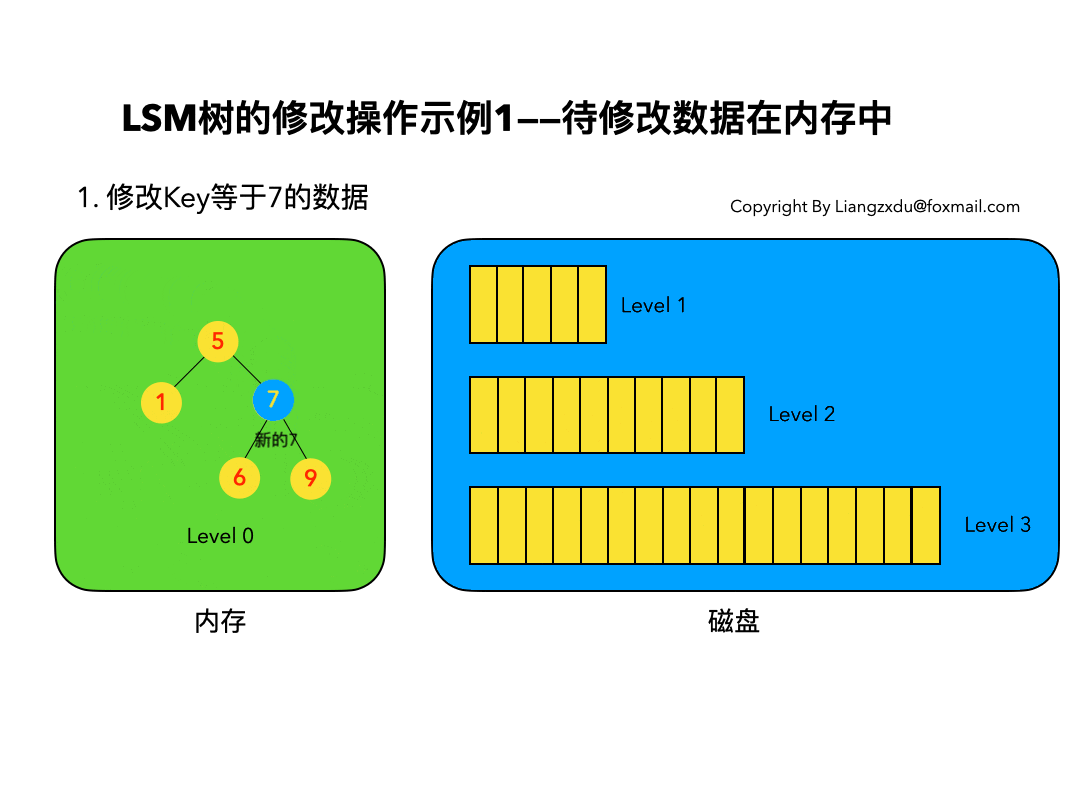
如图5所示,展示了待修改数据在内存中的操作过程。新的蓝色的key=7的数据,直接定位到内存中Level 0树上黄色的老的key=7的位置,将其覆盖即可。
待修改数据在磁盘中:
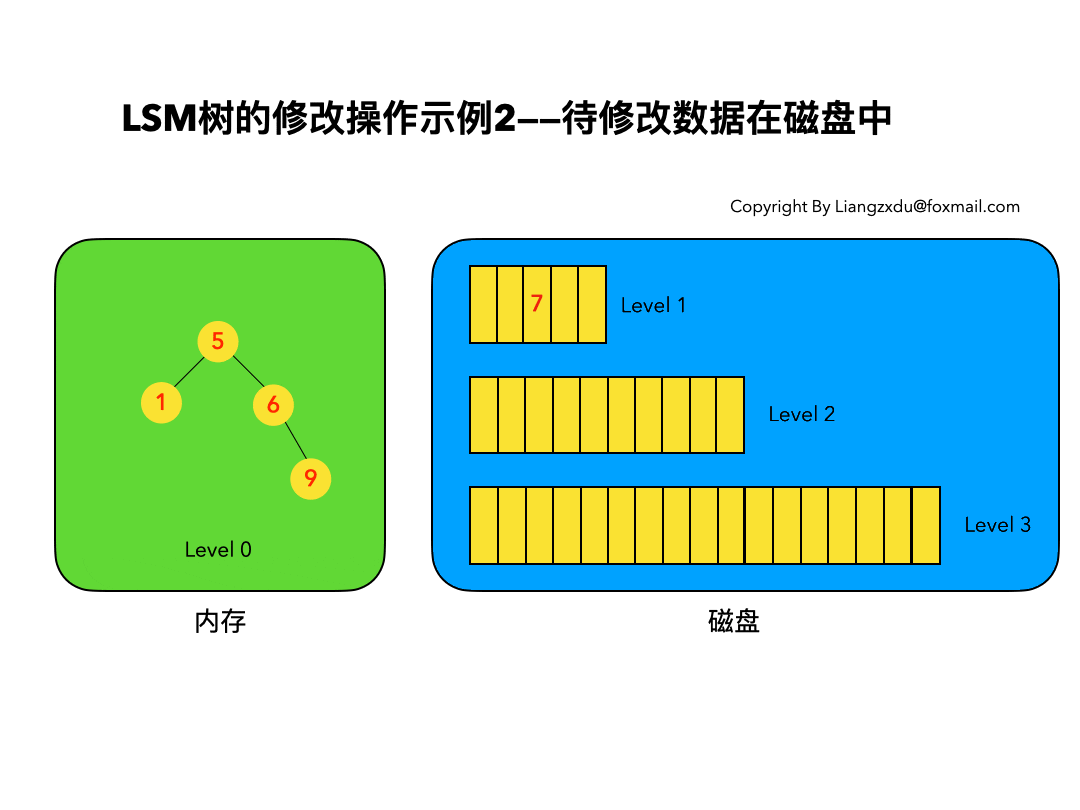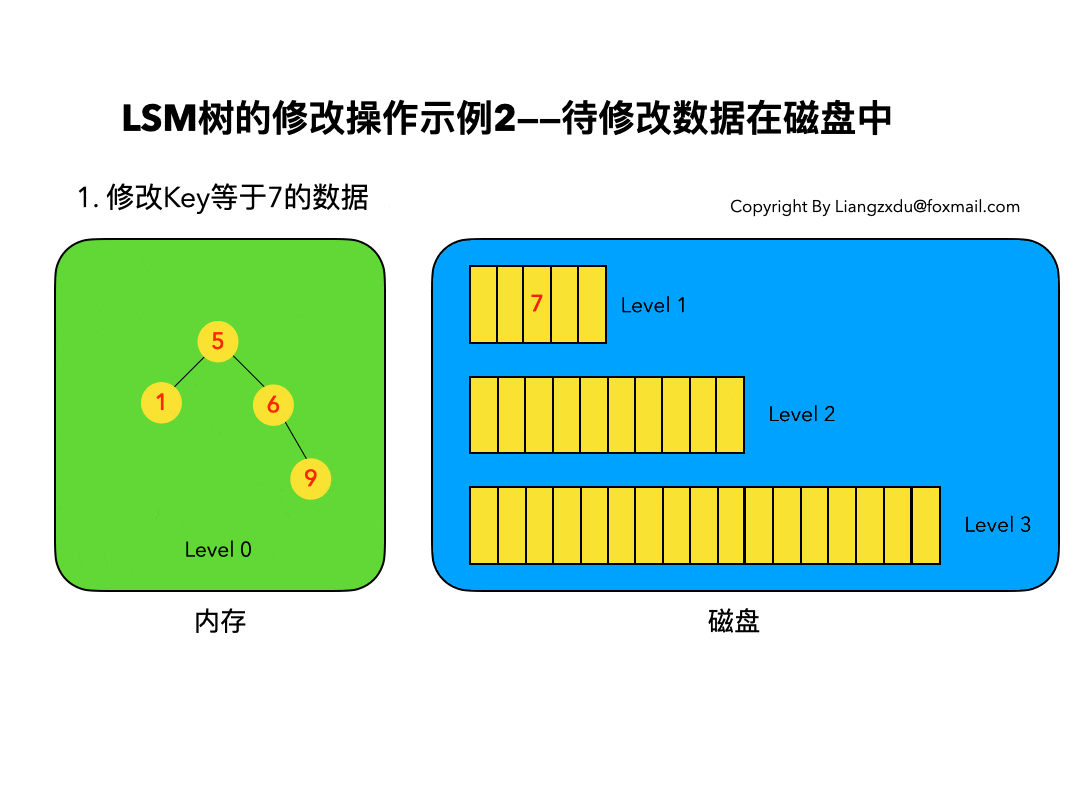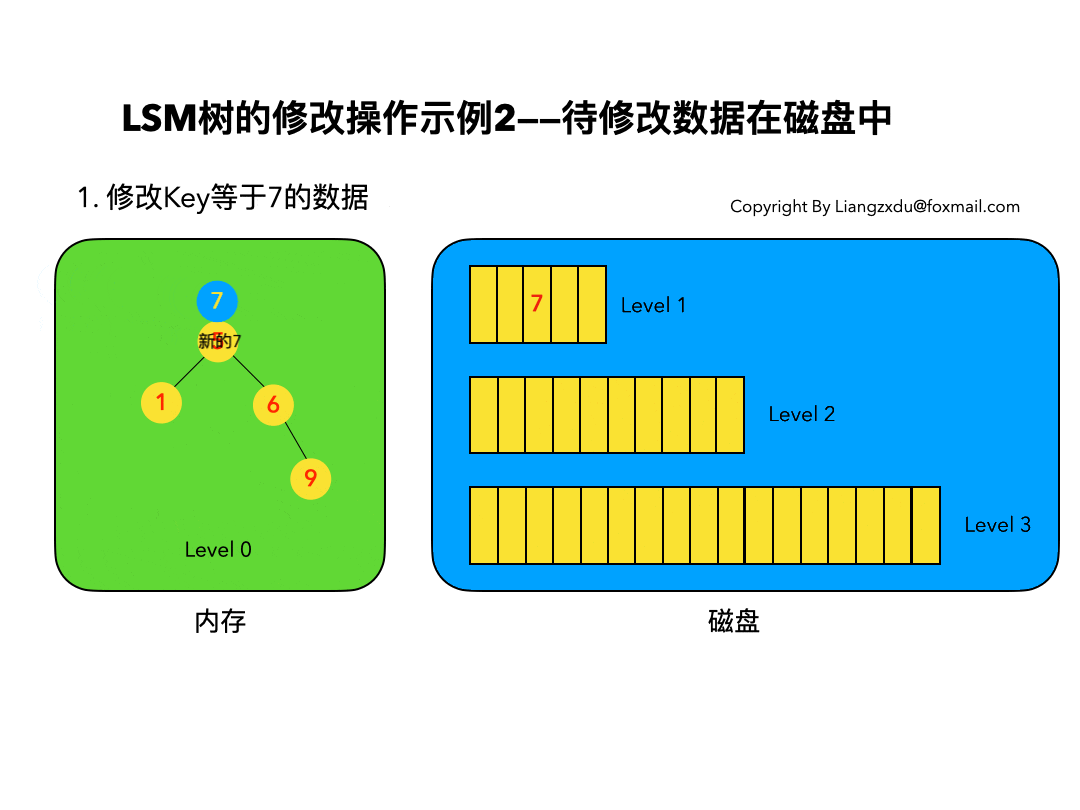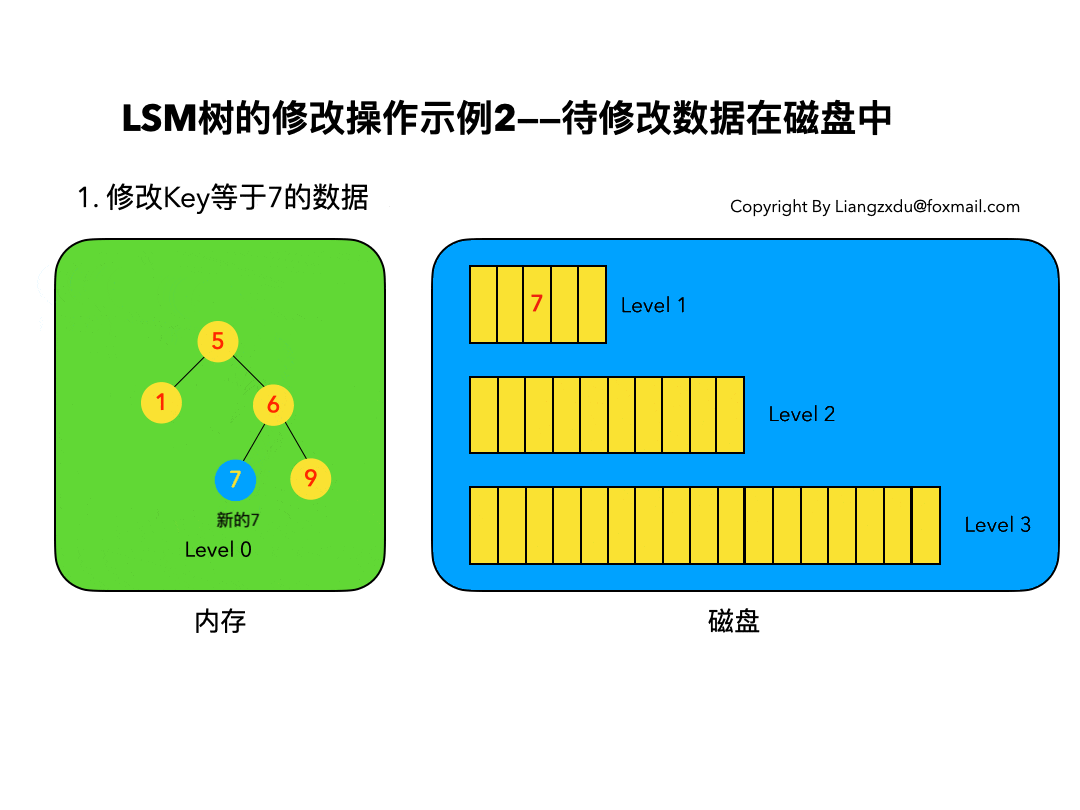
如图6所示,展示了待修改数据在磁盘中的操作过程。LSM树并不会去磁盘中的Level 1树上原地更新老的key=7的数据,而是直接将新的蓝色的节点7插入内存中的Level 0树中。
该数据根本不存在:
此场景等价于情况b,直接向内存中的Level 0树插入新的数据即可。
综上4.1、4.2、4.3三种情况可以看出,修改操作都是对内存中Level 0进行覆盖/新增操作。该操作复杂度为树高log(n),代价很低。
我们会发现,LSM树的增加、删除、修改(这三个都属于写操作)都是在内存中倒腾,完全没涉及到磁盘操作,所以速度飞快,写吞吐量高的离谱。。。
查询操作
LSM树的查询操作会按顺序查找Level 0、Level 1、Level 2 … Level n 每一颗树,一旦匹配便返回目标数据,不再继续查询。该策略保证了查到的一定是目标key最新版本的数据(有点MVCC的感觉)。
我们来分场景分析:依然分为 待查询数据在内存中 和 待查询数据在磁盘中 两种情况。
待查询数据在内存中:
如图7所示,展示了待查询数据在内存中时的查询过程。
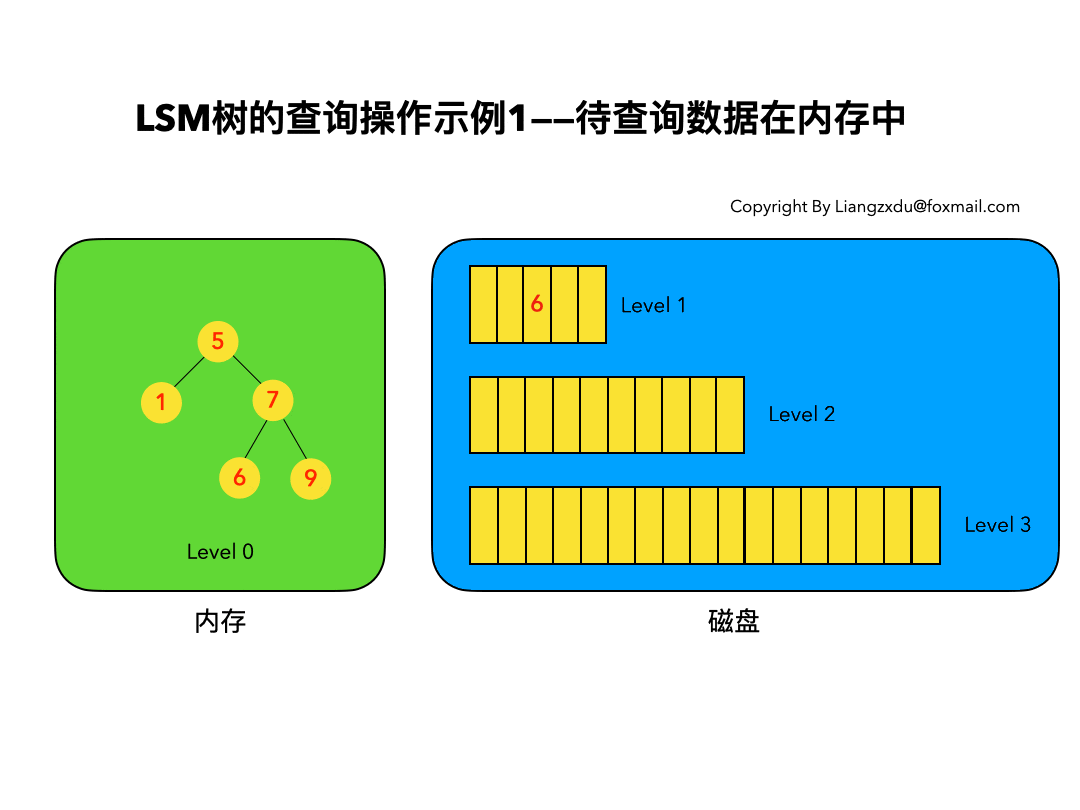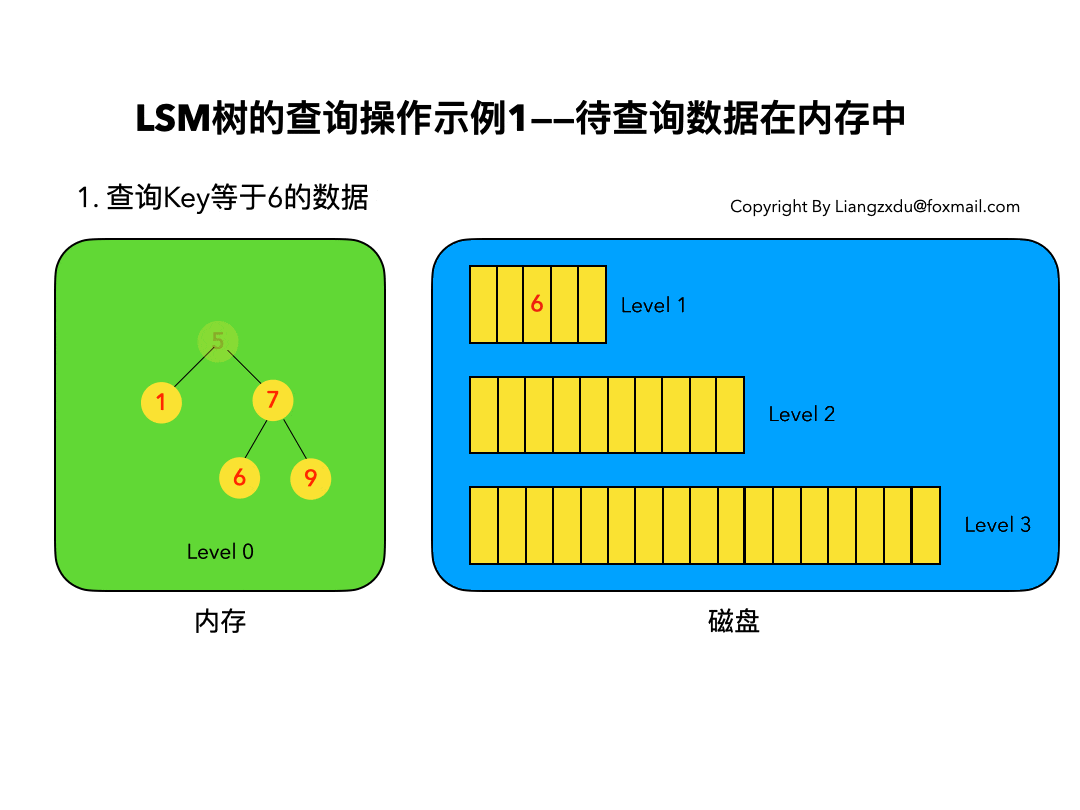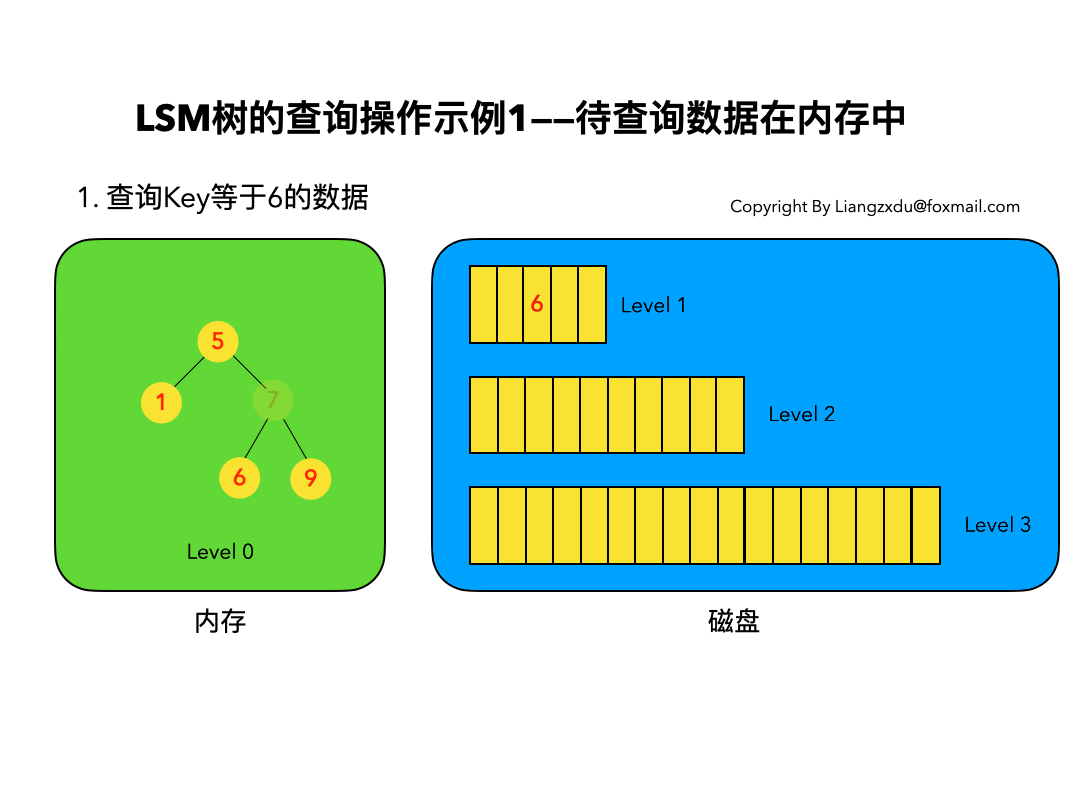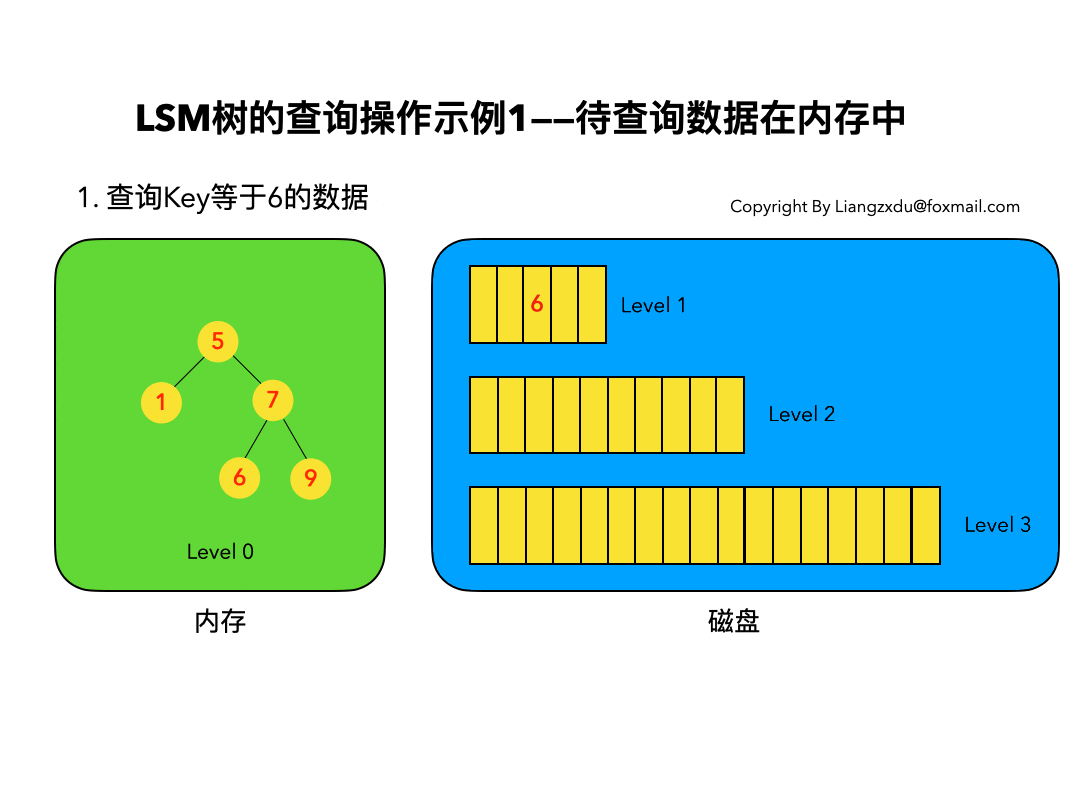
沿着内存中已排好序的Level 0树递归向下比较查询,返回目标节点即可。我们注意到磁盘上的Level 1树中同样包括一个key=6的较老的数据。但LSM树查询的时候会按照Level 0、1、2 … n的顺序查询,一旦查到第一个就返回,因此磁盘上老的key=6的数据没人理它,更不会作为结果被返回。
待查询数据在磁盘中:
如图8所示,展示了待查询数据在磁盘上时的查询过程。
先查询内存中的Level 0树,没查到便查询磁盘中的Level 1树,还是没查到,于是查询磁盘中的Level 2树,匹配后返回key=6的数据。
综合上述两种情况,我们发现,LSM树的查询操作相对来说代价比较高,需要从Level 0到Level n一直顺序查下去。极端情况是LSM树中不存在该数据,则需要把整个库从Level 0到Level n给扫了一遍,然后返回查无此人(可以通过 布隆过滤器 + 建立稀疏索引 来优化查询操作)。代价大于以B/B+树为基本数据结构的传统RDB存储引擎。
合并操作
合并操作是LSM树的核心(毕竟LSM树的名字就叫: 日志结构合并树,直接点名了合并这一操作)
之所以在增、删、改、查这四个基本操作之外还需要合并操作:一是因为内存不是无限大,Level 0树达到阈值时,需要将数据从内存刷到磁盘中,这是合并操作的第一个场景;二是需要对磁盘上达到阈值的顺序文件进行归并,并将归并结果写入下一层,归并过程中会清理重复的数据和被删除的数据(墓碑标记)。我们分别对上述两个场景进行分析:
内存数据写入磁盘的场景:
如图9所示,展示了内存中Level 0树在达到阈值后,归并写入磁盘Level 1树的场景。
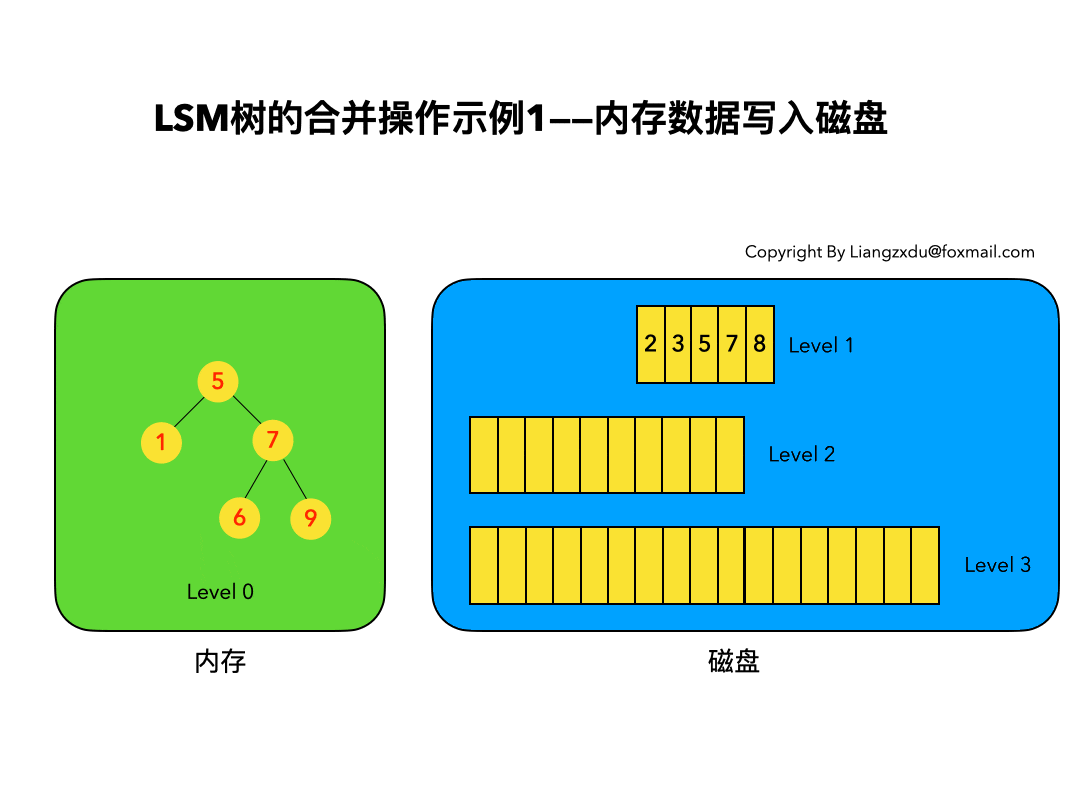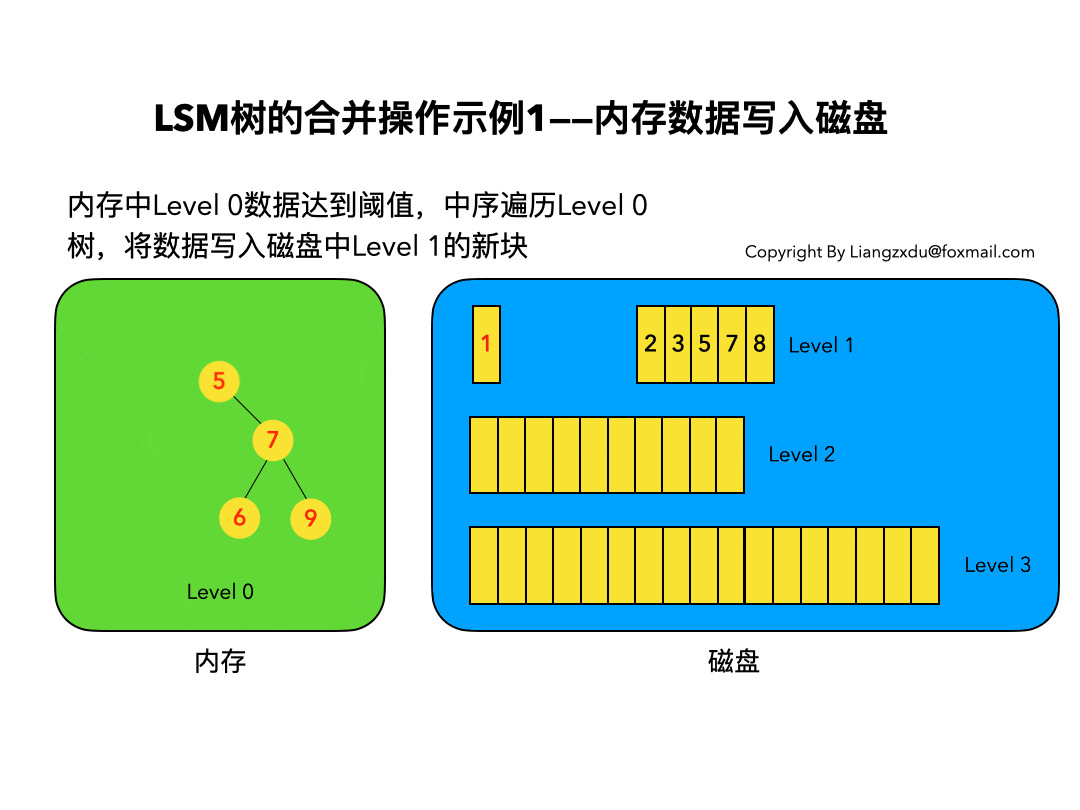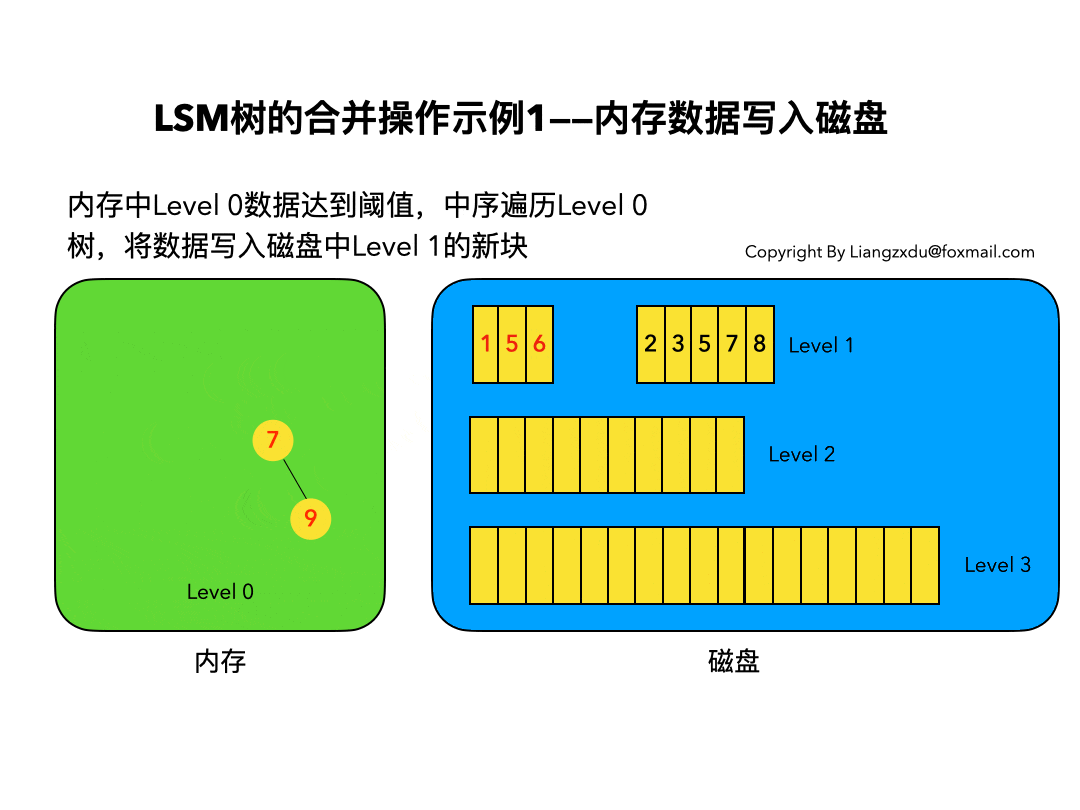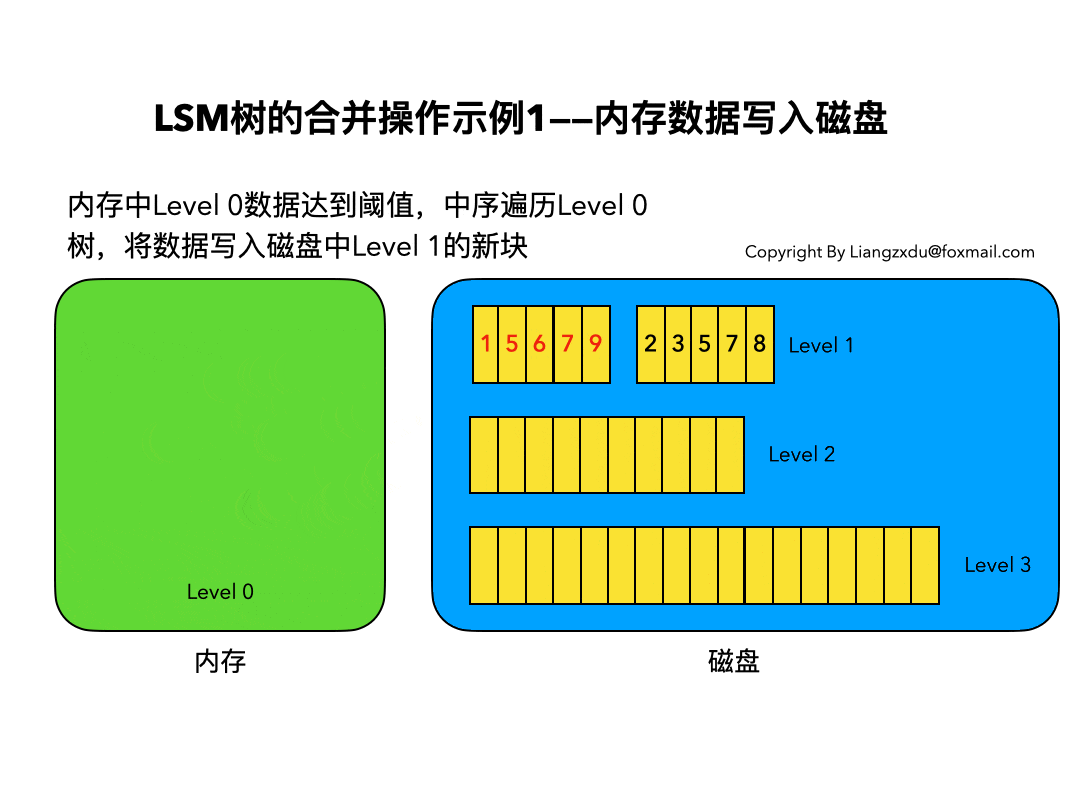
对内存中的Level 0树进行中序遍历,将数据顺序写入磁盘的Level 1层即可,我们可以看到因为Level 0树是已经排好序的,所以写入的Level 1中的新块也是有序的(有序性保证了查询和归并操作的高效)。此时磁盘的Level 1层有两个Block块。
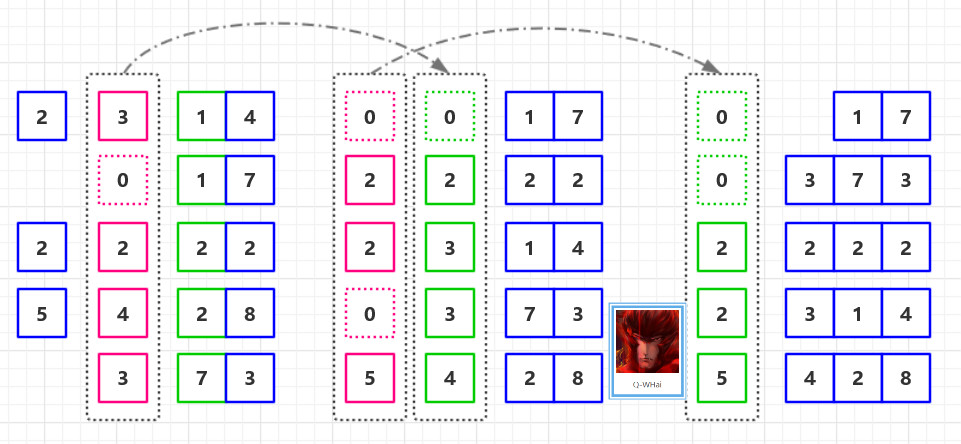
磁盘中多个块的归并:
如图10所示,该图展示了磁盘中Level 1层达到阈值时,对其包含的两个Block块进行归并,并将归并结果写入Level 2层的过程。
我们注意到key=5和key=7的数据同时存在于较老的Block 1和较新的Block 2中。而归并的过程是保留较新的数据,于是我们看到结果中,key=5和7的数据都是红色的(来自于较新的Block2)。
综上我们可以看到,不论是场景6.1还是场景6.2,由于原始数据都是有序的,因此归并的过程只需要对数据集进行一次扫描即可,复杂度为O(n)。
优缺点分析
以上便是对LSM树的增、删、改、查和归并五种核心操作的详细分析。
可以看到LSM树将增、删、改这三种操作都转化为内存insert + 磁盘顺序写(当Level 0满的时候),通过这种方式得到了无与伦比的写吞吐量。
LSM树的查询能力则相对被弱化,相比于B+树的最多3~4次磁盘IO,LSM树则要从Level 0一路查询Level n,极端情况下等于做了全表扫描。(即便做了稀疏索引,也是lg(N0)+lg(N1)+…+lg(Nn)的复杂度,大于B+树的lg(N0+N1+…+Nn)的时间复杂度)。
同时,LSM树只append追加不原地修改的特性引入了归并操作,归并操作涉及到大量的磁盘IO,比较消耗性能,需要合理设置触发该操作的参数。
综上我们可以给出LSM树的优缺点:
优:增、删、改操作飞快,写吞吐量极大。
缺:读操作性能相对被弱化;不擅长区间范围的读操作; 归并操作较耗费资源。
总结
以上是对LSM树基本操作以及优缺点的分析,我们可以据此得出LSM树的设计原则:
- 先内存再磁盘
- 内存原地更新
- 磁盘追加更新
- 归并保留新值
如果说B/B+树的读写性能基本平衡的话,LSM树的设计原则通过舍弃部分读性能,换取了无与伦比的写性能。该数据结构适合用于写吞吐量远远大于读吞吐量的场景,得到了NoSQL届的喜爱和好评。
平衡二叉树详解
二叉搜索树(Binary Sort Tree)
二叉搜索树,又称之为二叉排序树(二叉查找树),它或许是一棵空树,或许是具有以下性质的二叉树:
- 若他的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别是二叉搜索树
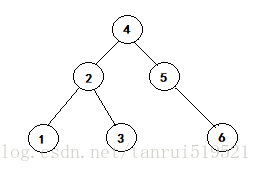
二叉搜索树的这种特性,使得我们在此二叉树上查找某个值就很方便了,从根节点开始,若要寻找的值小于根节点的值,则在左子树上去找,反之则去右子树查找,知道找到与值相同的节点。插入节点也是一样的道理,从根节点出发,所要插入的值,若小于根节点则去左子树寻找该节点所对应的位置,反之去右子树寻找,直到找到该节点合适的位置。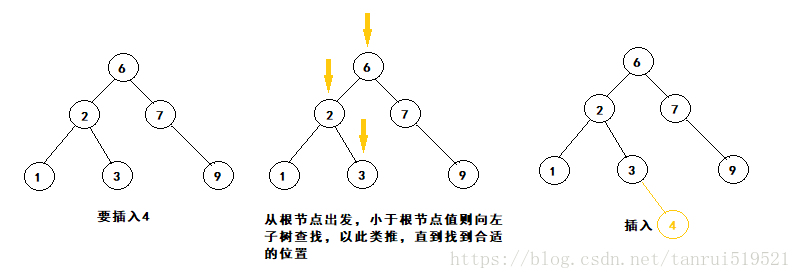
二叉平衡搜索树(AVL)
前面提到了二叉搜索树,我们知道,二叉搜索树的特性便于我们进行查找插入删除等一系列操作,其时间复杂度为O(logn),但是,如果遇见最差的情况,比如以下这棵树:
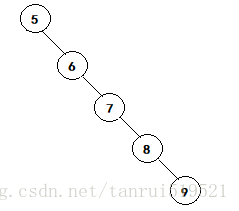
这棵树,说是树,其实它已经退化成链表了,但从概念上来看,它仍是一棵二叉搜索树,只要我们按照逐次增大,如1、2、3、4、5、6的顺序构造一棵二叉搜索树,则形如上图。那么插入的时间复杂度就变成了O(n),导致这种糟糕的情况原因是因为这棵树极其不平衡,右树的重量远大于左树,因此我们提出了叫平衡二叉搜索树的结构,又称之为AVL树,是因为平衡二叉搜索树的发明者为Adel’son-Vel’skii 和Landis二人。
平衡二叉搜索树,它能保持二叉树的高度平衡,尽量降低二叉树的高度,减少树的平均查找长度。
AVL树的性质:
- 左子树与右子树高度之差的绝对值不超过1
- 树的每个左子树和右子树都是AVL树
- 每一个节点都有一个平衡因子(balance factor),任一节点的平衡因子是-1、0、1(每一个节点的平衡因子 = 右子树高度 - 左子树高度)
做到了这点,这棵树看起来就比较平衡了,那么如何生成一棵AVL树呢?算法相对来说复杂,随着新节点的加入,树自动调整自身结构,达到新的平衡状态,这就是我们想要的AVL树。我们先要分析,为什么树会失衡?是由于插入了一个新的元素。
- 当子树的根结点的平衡因子为+1时,它是左倾斜的(left-heavy)。
- 当子树的根结点的平衡因子为 -1时,它是右倾斜的(right-heavy)。
- 一颗子树的根结点的平衡因子就代表该子树的平衡性。
- 保持所有子树几乎都处于平衡状态,AVL树在总体上就能够基本保持平衡。
AVL树的基本查找、插入结点的操作和二叉树的操作一样。但是,当向AVL树中插入一个结点后,还有一些额外的工作要做。首先,必须计算因插入操作对平衡因子带来的改变。其次,如果任何平衡因子变成了+/-2,就必须从这个结点开始往下重新平衡这颗树,这个重新平衡的过程就称为旋转。
在AVL树中,插入一个节点是什么样的过程呢?总结如下:
- AVL树首先是二叉搜索树。我们要根据二叉搜索树的插入节点方式进行插入
- AVL树有判断该树是否平衡的平衡因子,我们要根据平衡因子来对树进行选择调整
具体步骤:
- 判断该树是不是NULL,若为NULL,则直接插入
2· 若不为NULL,找到需要插入节点的位置(用pParent标记双亲,方便插入节点)pCur - 插入节点pCur
- 更新pParent的平衡因子。然后判断该树是否要调整
- 若更新后的pParent平衡因子为0的话,pParent在插入新节点之前只有左孩子或者只有右孩子,此时树的高度不变,该树仍然为AVL
- 若更新后的pParent平衡因子为1或者-1的话,pParent在插入节点前是叶子节点,此时的高度可能发生改变,我们要从pParent节点开始,向上判断调整其祖先节点
- 若平衡因子不满足上面的两种情况,说明该树已经不平衡,需要调整。具体情况见下面,局部调整完后,上面的树已经满足AVL。
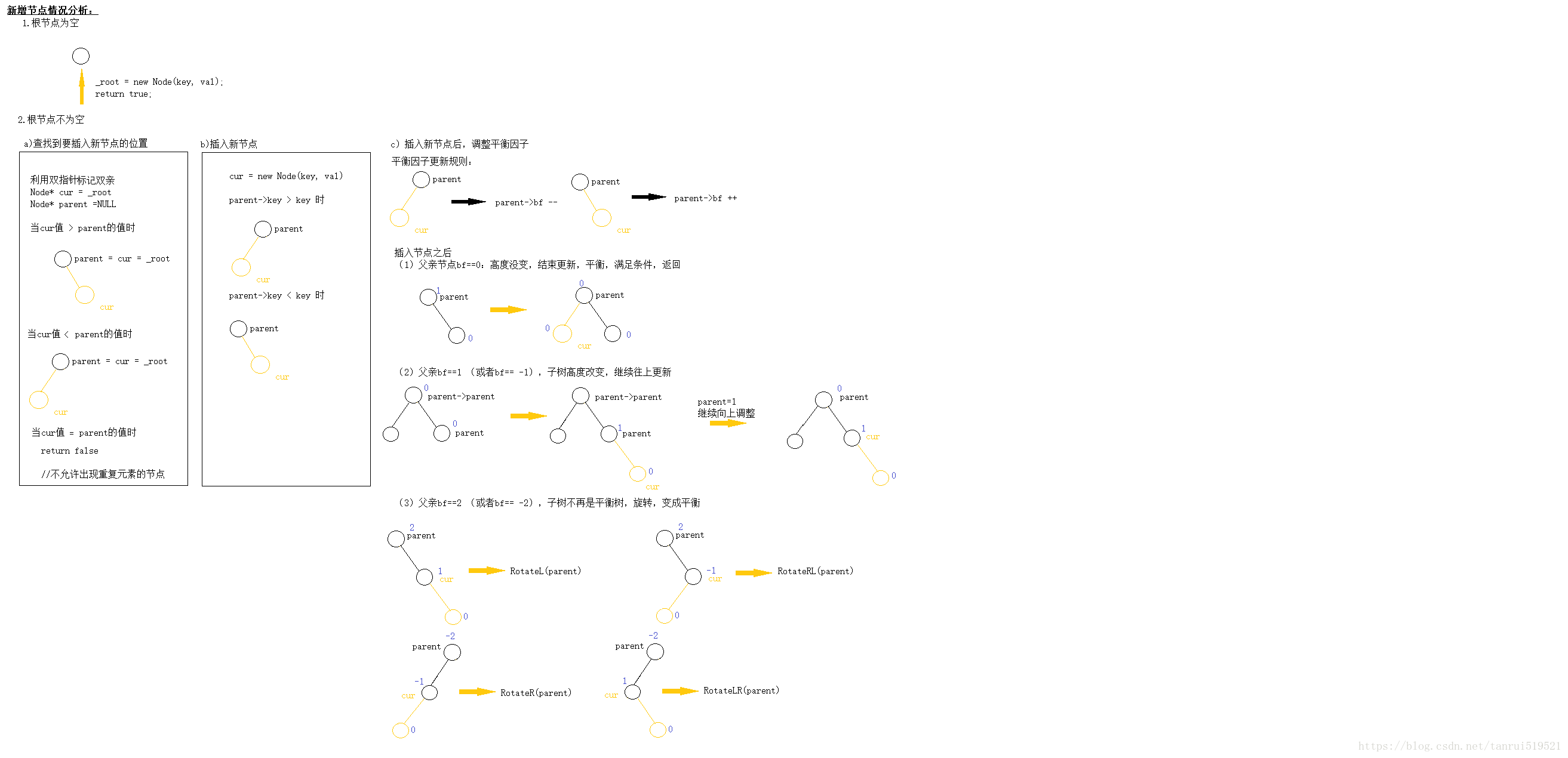
插入节点代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78template <class K, class V>
bool AVLTree<K, V>::AVLInsert(K key, V val)
{
//1.根节点为空,直接插入
if (_root == NULL)
{
_root = new Node(key, val);
return true;
}
//2.根节点不为空
else
{
Node* cur = _root;
Node* parent =NULL;
//a)找到要插入节点的位置
while (cur)
{
parent = cur;
if (cur->_key > key)
cur = cur->_left;
else if (cur->_key < key)
cur = cur->_right;
else
return false; //不允许出现重复元素的节点
}
//b)插入新节点
cur = new Node(key, val);
if (parent->_key > key)
{
parent->_left = cur;
cur->_parent = parent;
}
else
{
parent->_right = cur;
cur->_parent = parent;
}
//c)插入完成后,调整平衡因子
while (parent)
{
if (cur == parent->_left)//插入节点在左子树父节点bf--,反之++
parent->_bf--;
else
parent->_bf++;
//1)插入新节点后,parent->bf==0;说明高度没变,平衡,返回
if (parent->_bf == 0)
break;
//2)插入节点后parent->_bf==-1||parent->_bf==1;说明子树高度改变,则继续向上调整
else if (parent->_bf == -1 || parent->_bf == 1)
{
cur = parent;
parent = parent->_parent;
}
//3)插入节点后parent->_bf==-2||parent->_bf==2;说明已经不平衡,需要旋转
else
{
if (parent->_bf == 2)
{
if (cur->_bf == 1)
RotateL(parent);
else// (cur->_bf == -1)
RotateRL(parent);
}
else//parent->_bf == -2
{
if (cur->_bf == -1)
RotateR(parent);
else// (cur->_bf == 1)
RotateLR(parent);
}
break;
}
}//end while (parent)
return true;
}
}
当树不平衡时,我们需要做出旋转调整,有四种调整方法。以下是节点调平的四种情况。
AVL树的自平衡操作——旋转
AVL树的旋转总体来说分为四种情况:
- 左单旋
- 右单旋
- 左右双旋
- 右左双旋
接下来,我们通过图解来认识这四种节点调平方式
左单旋(逆时针旋转)
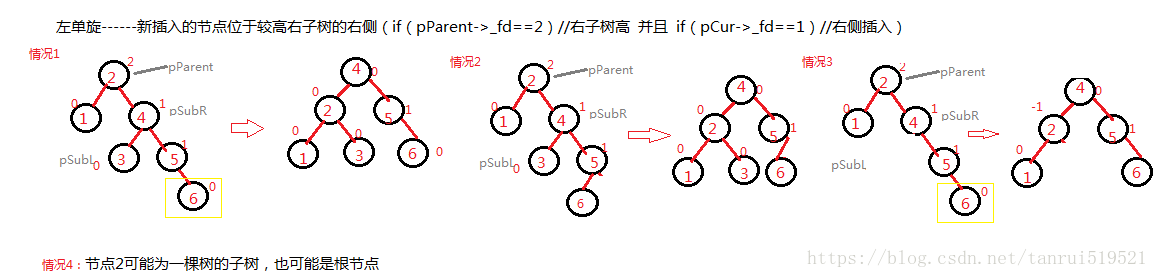
代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29template <class K, class V>
void AVLTree<K, V>::RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* pParent = parent->_parent;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
_root->_parent = NULL;
}
else
{
if (pParent->_left = parent)
pParent->_left = subR;
else
pParent->_right = subR;
subR->_parent = pParent;
}
parent->_bf = subR->_bf = 0;
}
右单旋(顺时针旋转)
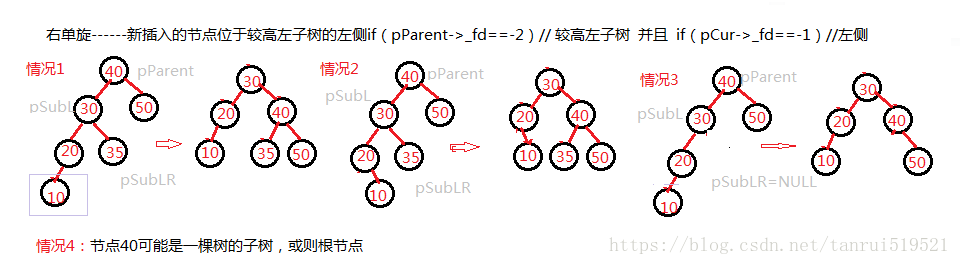
代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35template <class K, class V>
void AVLTree<K, V>::RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* ppNode = parent->_parent;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
subL->_right = parent;
parent->_parent = subL;
if (_root == parent)
{
_root = subL;
subL->_parent = NULL;
}
else
{
if (ppNode->_right == parent)
{
ppNode->_right = subL;
}
else
{
ppNode->_left = subL;
}
subL->_parent = ppNode;
}
subL->_bf = parent->_bf = 0;
}
左右双旋
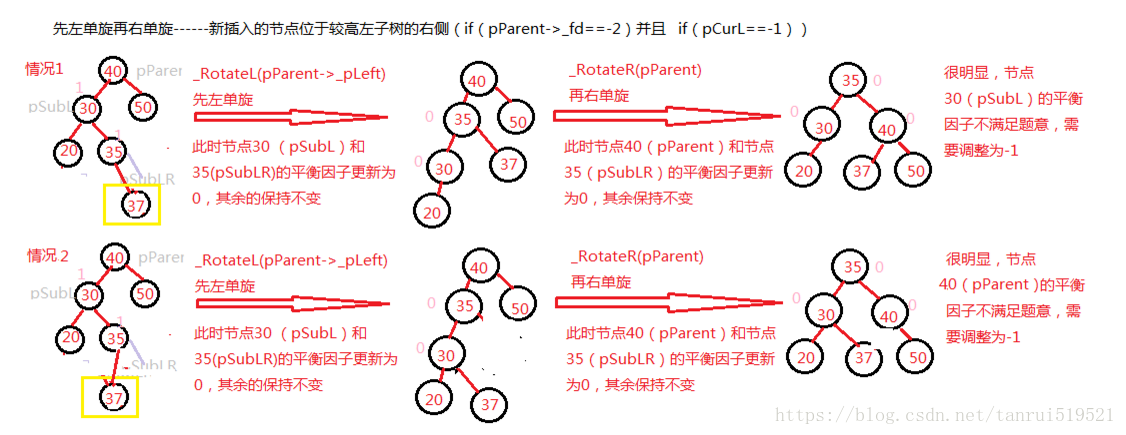
代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31template <class K, class V>
void AVLTree<K, V>::RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 0)
{
subLR->_bf = subL->_bf = parent->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
subLR->_bf = 0;
}
else
{
assert(false);
}
}
右左双旋
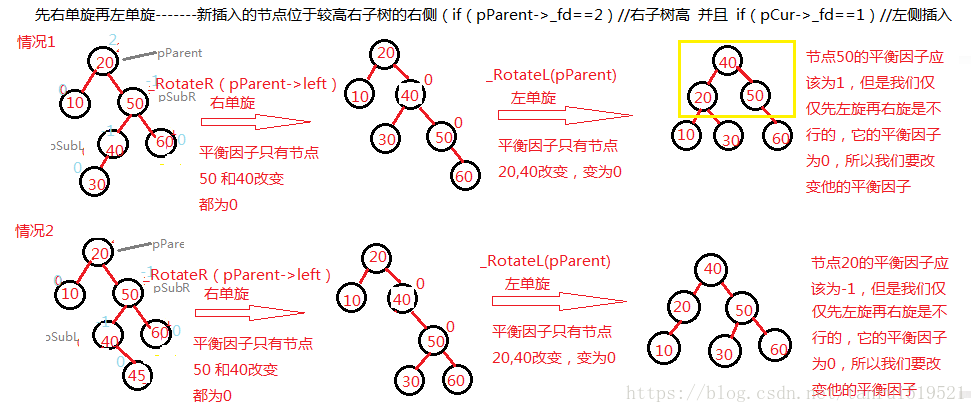
代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31template <class K, class V>
void AVLTree<K, V>::RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
subRL->_bf = subR->_bf = parent->_bf = 0;
}
else if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
subRL->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
平衡因子更新
我们知道AVL树的每一个节点都有一个平衡因子,那么在AVL树插入节点时,其自平衡操作保证了AVL树始终保持平衡状态,但是在每一次插入节点时,都可能会导致节点平衡因子的改变,因此,当插入节点时,我们应当注意平衡因子的更新,这直接关系到之后判断插入节点后的数是否仍为AVL树。
平衡因子更新原则:——平衡因子与节点本身无关,只与其左右子树相关
- 新增节点bf恒为1
- 右子树结点增加,父亲bf ++
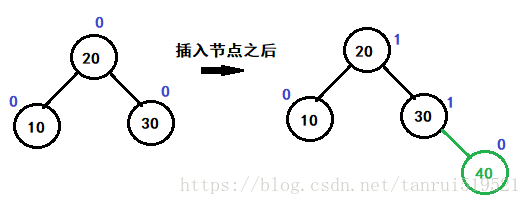
- 左子树结点增加,父亲bf —
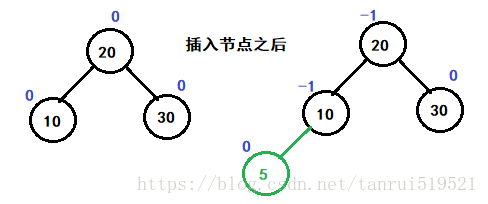
- 若插入节点,更新平衡因子之后
- 父亲节点bf==0:高度没变,结束更新,平衡,满足条件,返回
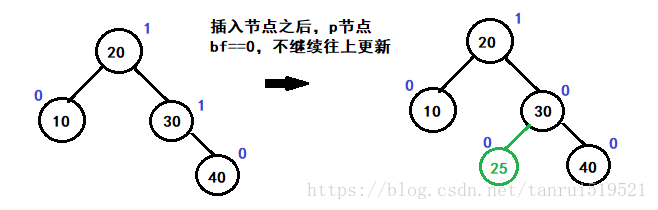
- 父亲bf==1 (或者bf== -1),子树高度改变,继续往上更新
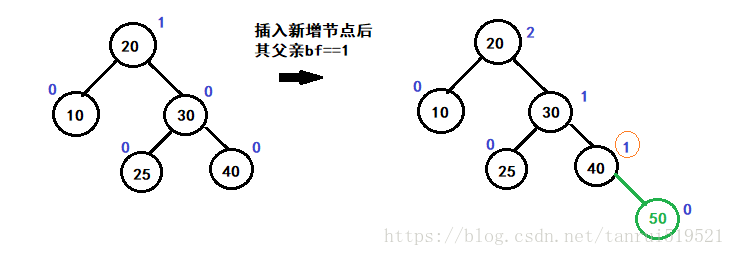
- 父亲bf==2 (或者bf== -2),子树不再是平衡树,旋转,变成平衡
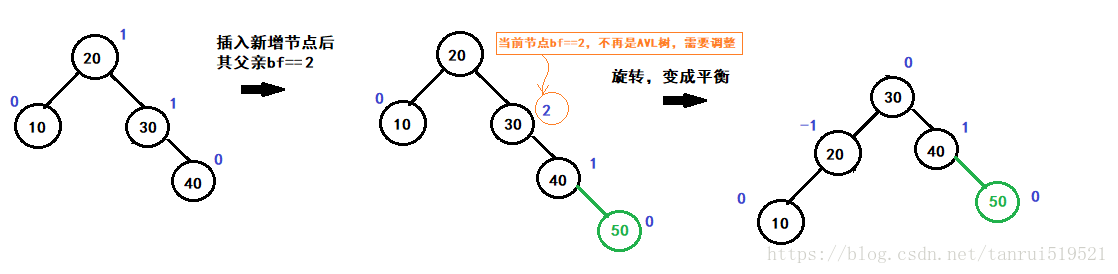
1 |
|
更清晰的一个图
旋转操作用来重新平衡树的某个部分。通过重新安排结点 ,使结点之间的关系始终保持左子结点小于父结点,父结点小于右子结点。使得该树仍然是一颗二叉搜索树。旋转过后,旋转子树中的所有结点的平衡因子都为+1、-1或0。
AVL树的旋转类型有4种, 分别是LL(left-left)旋转、LR(left-right)旋转、RR(right-right)旋转和RL(right-left)旋转。
为方便理解在何时执行哪一种旋转,设x代表刚插入AVL树中的结点,设A为离x最近且平衡因子更改为2的绝对值的祖先。
LL旋转
如下图所示,当x位于A的左子树的左子树上时,执行LL旋转。
设left为A的左子树,要执行LL旋转,将A的左指针指向left的右子结点,left的右指针指向A,将原来指向A的指针指向left。
旋转过后,将A和left的平衡因子都改为0。所有其他结点的平衡因子没有发生变化。
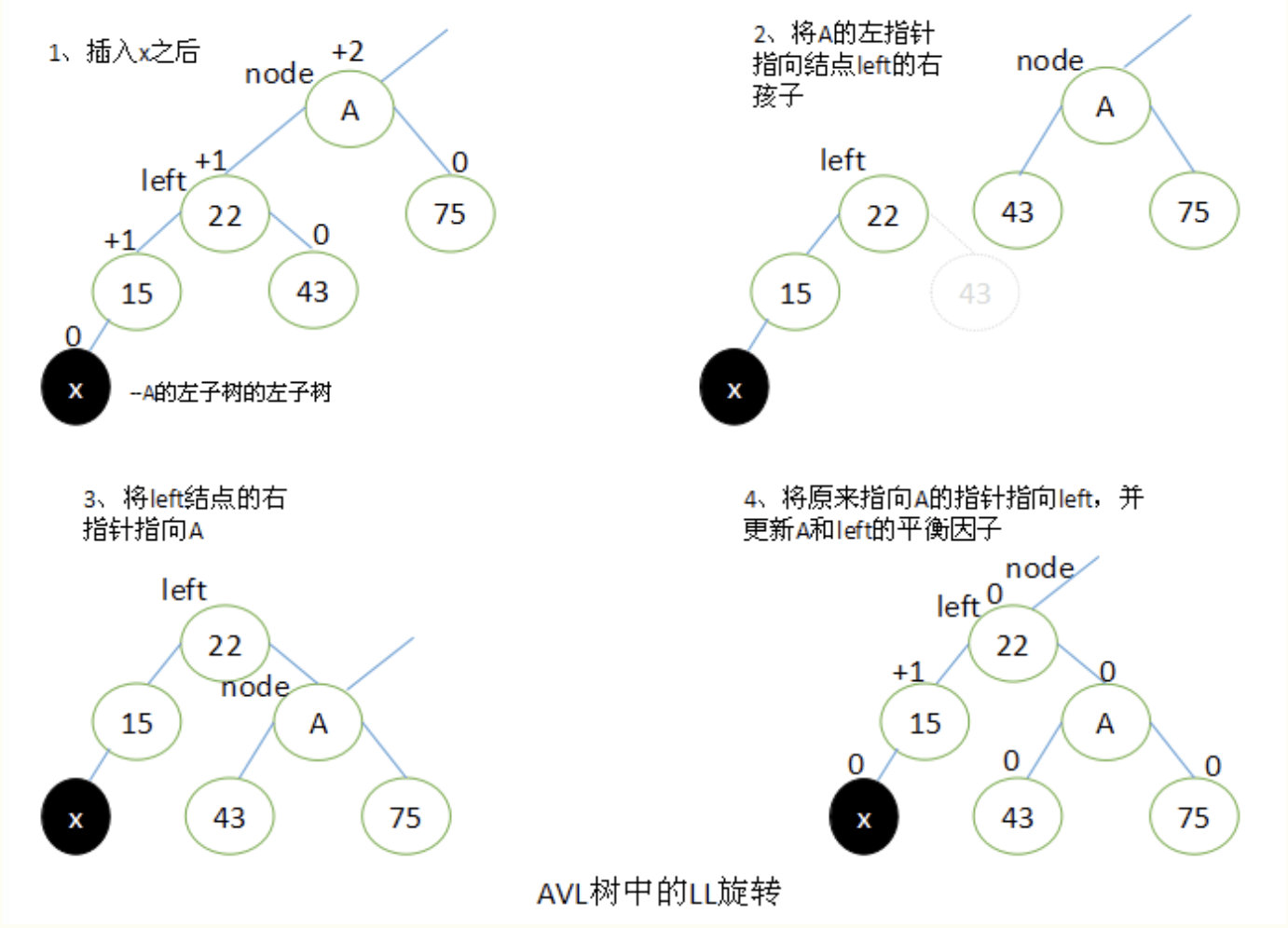
LR旋转
当x位于A的左子树的右子树上时,执行LR旋转。
设left是A的左子结点,并设A的子孙结点grandchild为left的右子结点。
要执行LR旋转,将left的右子结点指向grandchild的左子结点,grandchild的左子结点指向left,A的左子结点指向grandchild的右子结点,再将grandchild的右子结点指向A,最后将原来指向A的指针指向grandchild。
执行LR旋转之后,调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子值。
- 如果grandchild结点的原始平衡因子为+1,就将A的平衡因子设为-1,将left的平衡因子设为0。
- 如果grandchild结点的原始平衡因子为0,就将A和left的平衡因子都设置为0。
- 如果grandchild结点的原始平衡因子为-1,就将A的平衡因子设置为0,将left的平衡因子设置为+1。
在所有的情况下,grandchild的新平衡因子都是0。所有其他结点的平衡因子都没有改变。
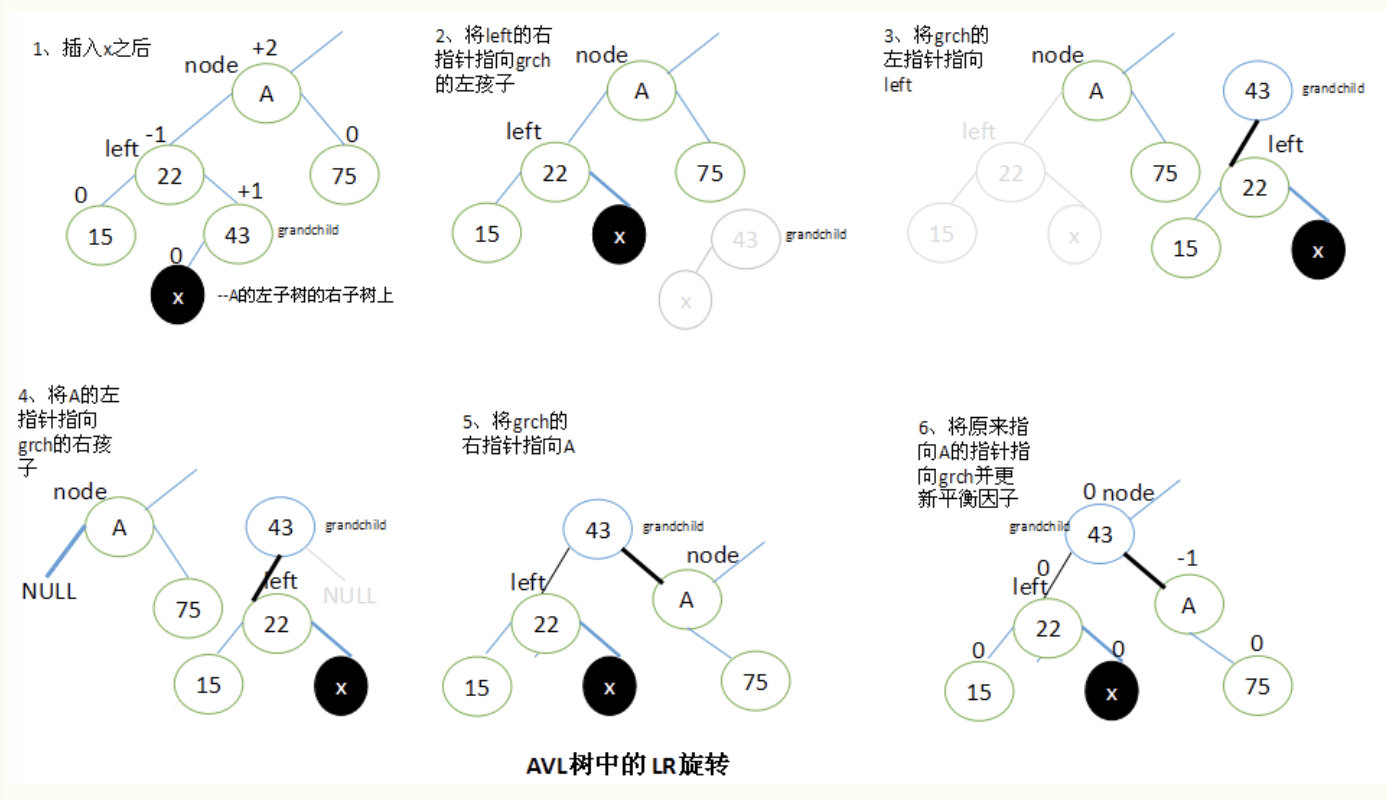
RR旋转
当x位于A的右子树的右子树上时,执行RR旋转。
RR旋转与LL旋转是对称的关系。
设A的右子结点为Right。要执行RR旋转,将A的右指针指向right的左子结点,right的左指针指向A,原来指向A的指针修改为指向right。
完成旋转以后,将A和left的平衡因子都修改为0。所有其他结点的平衡因子都没有改变。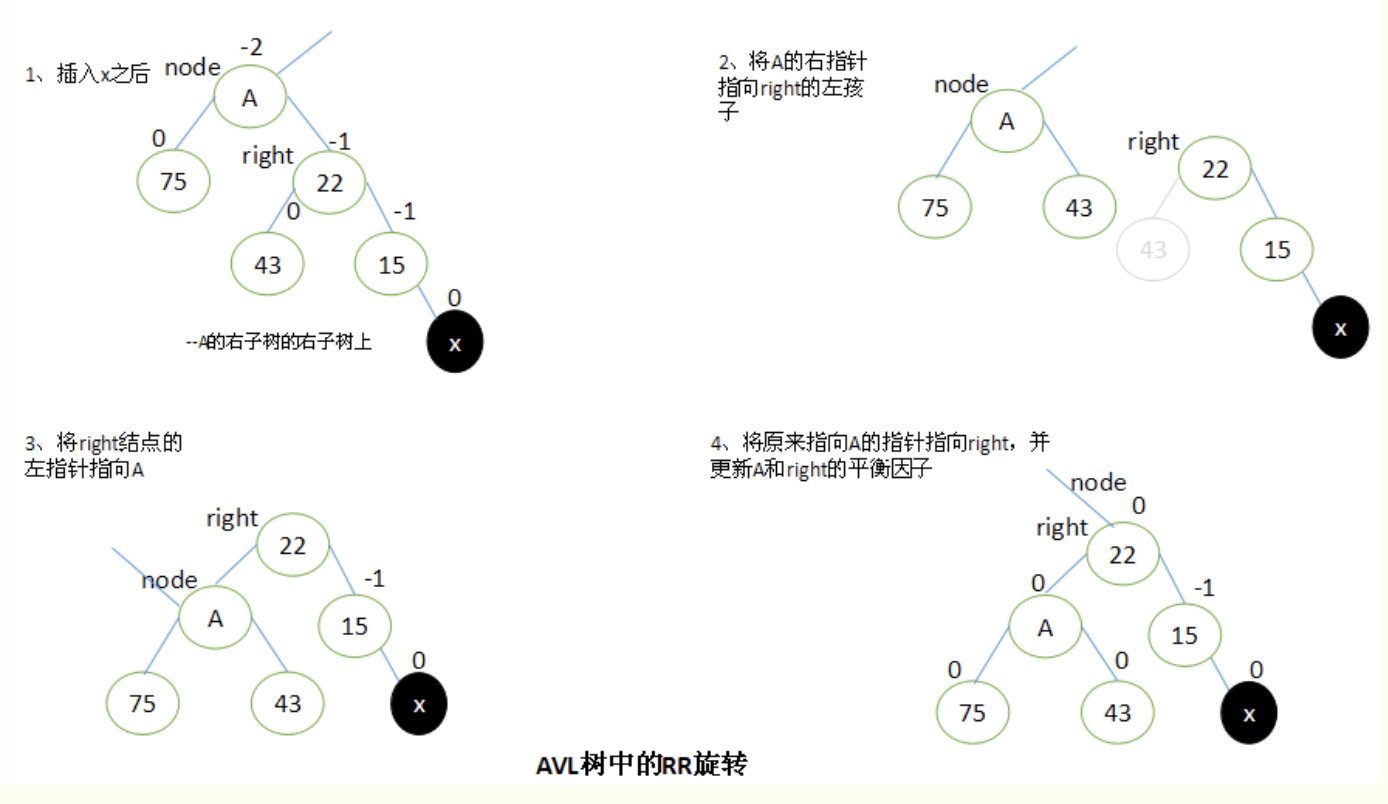
RL旋转
当x位于A的右子树的左子树上时,执行RL旋转。
RL旋转与LR旋转是对称的关系。
设A的右子结点为right,right的左子结点为grandchild。要执行RL旋转,将right结点的左子结点指向grandchild的右子结点,将grandchild的右子结点指向right,将A的右子结点指向grandchild的左子结点,将grandchild的左子结点指向A,最后将原来指向A的指针指向grandchild。
执行RL旋转以后,调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子。这里也有三种情况需要考虑:
- 如果grandchild的原始平衡因子值为+1,将A的平衡因子更新为0,right的更新为-1;
- 如果grandchild的原始平衡因子值为 0,将A和right的平衡因子都更新为0;
- 如果grandchild的原始平衡因子值为-1,将A的平衡因子更新为+1,right的更新为0;
在所有情况中,都将grandchild的新平衡因子设置为0。所有其他结点的平衡因子不发生改变。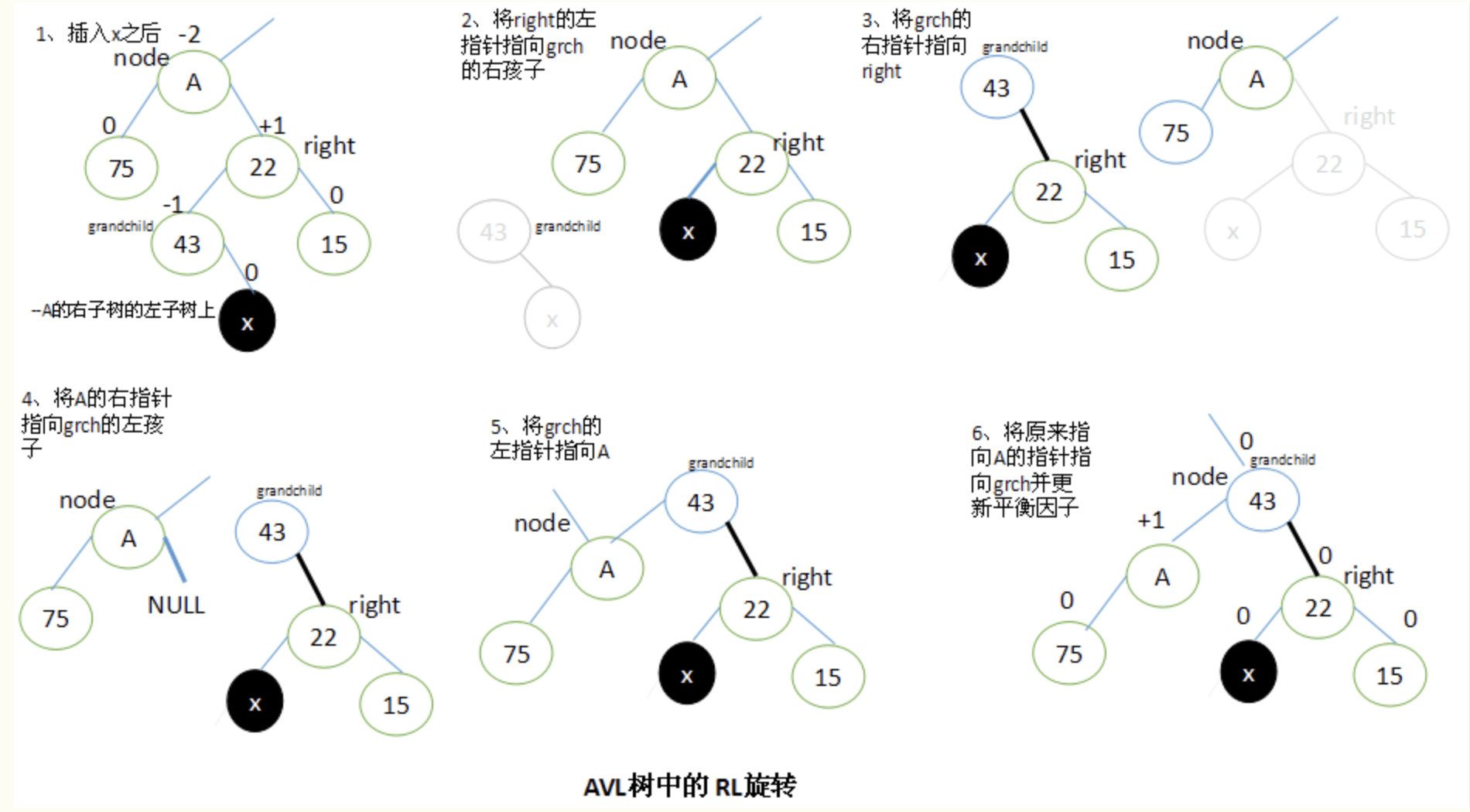
AVL树的删除操作
同插入操作一样,删除结点时也有可能破坏平衡性,这就要求我们删除的时候要进行平衡性调整。
首先在整个二叉树中搜索要删除的结点,如果没搜索到直接返回不作处理,否则执行以下操作:
- 要删除的节点是当前根节点T。
- 如果左右子树都非空。在高度较大的子树中实施删除操作。分两种情况:
- 左子树高度大于右子树高度,将左子树中最大的那个元素赋给当前根节点,然后删除左子树中元素值最大的那个节点。
- 左子树高度小于右子树高度,将右子树中最小的那个元素赋给当前根节点,然后删除右子树中元素值最小的那个节点。
- 如果左右子树中有一个为空,那么直接用那个非空子树或者是NULL替换当前根节点即可。
- 如果左右子树都非空。在高度较大的子树中实施删除操作。分两种情况:
- 要删除的节点元素值小于当前根节点T值,在左子树中进行删除。
- 递归调用,在左子树中实施删除。
- 这个是需要判断当前根节点是否仍然满足平衡条件,
- 如果满足平衡条件,只需要更新当前根节点T的高度信息。
- 否则,需要进行旋转调整:
- 如果T的左子节点的左子树的高度大于T的左子节点的右子树的高度,进行相应的单旋转。否则进行双旋转。
- 要删除的节点元素值大于当前根节点T值,在右子树中进行删除。
1 | 下面给出详细代码实现: |
红黑树详解
转载请标明出处,原文地址:http://blog.csdn.net/hackbuteer1/article/details/7740956
红黑树概述
红黑树和我们以前学过的AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。不过自从红黑树出来后,AVL树就被放到了博物馆里,据说是红黑树有更好的效率,更高的统计性能。这一点在我们了解了红黑树的实现原理后,就会有更加深切的体会。
红黑树和AVL树的区别在于它使用颜色来标识结点的高度,它所追求的是局部平衡而不是AVL树中的非常严格的平衡。学过数据结构的人应该都已经领教过AVL树的复杂,但AVL树的复杂比起红黑树来说简直是小巫见大巫,红黑树才是真正的变态级数据结构。由于STL中的关联式容器默认的底层实现都是红黑树,因此红黑树对于后续学习STL源码还是很重要的,有必要掌握红黑树的实现原理和源码实现。红黑树是AVL树的变种,红黑树通过一些着色法则确保没有一条路径会比其它路径长出两倍,因而达到接近平衡的目的。所谓红黑树,不仅是一个二叉搜索树,而且必须满足以下规则:
- 每个节点不是红色就是黑色。
- 根节点为黑色。
- 如果节点为红色,其子节点必须为黑色。
- 任意一个节点到到NULL(树尾端)的任何路径,所含之黑色节点数必须相同。
上面的这些约束保证了这个树大致上是平衡的,这也决定了红黑树的插入、删除、查询等操作是比较快速的。 根据规则4,新增节点必须为红色;根据规则3,新增节点之父节点必须为黑色。当新增节点根据二叉搜索树的规则到达其插入点时,却未能符合上述条件时,就必须调整颜色并旋转树形,如下图: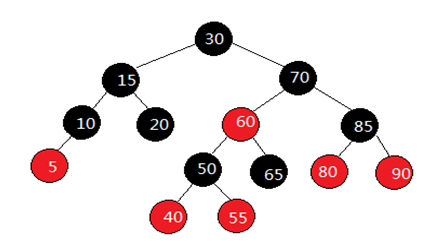
假设我们为上图分别插入节点3、8、35、75,根据二叉搜索树的规则,插入这四个节点后,我们会发现它们都破坏了红黑树的规则,因此我们必须调整树形,也就是旋转树形并改变节点的颜色。
红黑树上结点的插入
在讨论红黑树的插入操作之前必须要明白,任何一个即将插入的新结点的初始颜色都为红色。这一点很容易理解,因为插入黑点会增加某条路径上黑结点的数目,从而导致整棵树黑高度的不平衡。但如果新结点的父结点为红色时(如下图所示),将会违反红黑树的性质:一条路径上不能出现相邻的两个红色结点。这时就需要通过一系列操作来使红黑树保持平衡。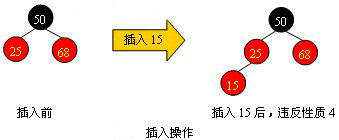
为了清楚地表示插入操作以下在结点中使用“新”字表示一个新插入的结点;使用“父”字表示新插入点的父结点;使用“叔”字表示“父”结点的兄弟结点;使用“祖”字表示“父”结点的父结点。插入操作分为以下几种情况:
黑父
如下图所示,如果新节点的父结点为黑色结点,那么插入一个红点将不会影响红黑树的平衡,此时插入操作完成。红黑树比AVL树优秀的地方之一在于黑父的情况比较常见,从而使红黑树需要旋转的几率相对AVL树来说会少一些。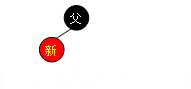
红父
如果新节点的父结点为红色,这时就需要进行一系列操作以保证整棵树红黑性质。如下图所示,由于父结点为红色,此时可以判定,祖父结点必定为黑色。这时需要根据叔父结点的颜色来决定做什么样的操作。青色结点表示颜色未知。由于有可能需要根结点到新点的路径上进行多次旋转操作,而每次进行不平衡判断的起始点(我们可将其视为新点)都不一样。所以我们在此使用一个蓝色箭头指向这个起始点,并称之为判定点。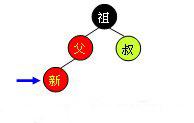
红叔
当叔父结点为红色时,如下图所示,无需进行旋转操作,只要将父和叔结点变为黑色,将祖父结点变为红色即可。但由于祖父结点的父结点有可能为红色,从而违反红黑树性质。此时必须将祖父结点作为新的判定点继续向上(迭代)进行平衡操作。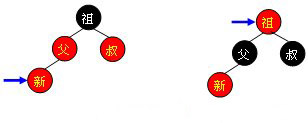
需要注意的是,无论“父节点”在“叔节点”的左边还是右边,无论“新节点”是“父节点”的左孩子还是右孩子,它们的操作都是完全一样的(其实这种情况包括4种,只需调整颜色,不需要旋转树形)。
黑叔
当叔父结点为黑色时,需要进行旋转,以下图示了所有的旋转可能:
Case 1: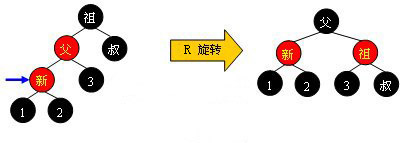
Case 2: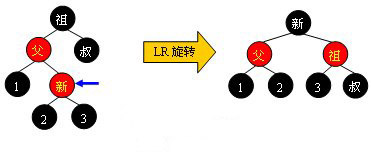
Case 3: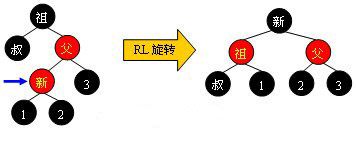
Case 4: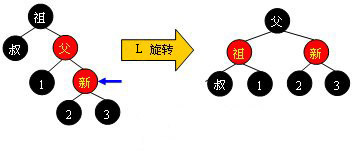
可以观察到,当旋转完成后,新的旋转根全部为黑色,此时不需要再向上回溯进行平衡操作,插入操作完成。需要注意,上面四张图的“叔”、“1”、“2”、“3”结点有可能为黑哨兵结点。
其实红黑树的插入操作不是很难,甚至比AVL树的插入操作还更简单些。红黑树的插入操作源代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160// 元素插入操作 insert_unique()
// 插入新值:节点键值不允许重复,若重复则插入无效
// 注意,返回值是个pair,第一个元素是个红黑树迭代器,指向新增节点
// 第二个元素表示插入成功与否
template<class Key, class Value, class KeyOfValue, class Compare, class Alloc>
pair<typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator, bool>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_unique(const Value &v){
rb_tree_node* y = header; // 根节点root的父节点
rb_tree_node* x = root(); // 从根节点开始
bool comp = true;
while(x != 0) {
y = x;
comp = key_compare(KeyOfValue()(v), key(x)); // v键值小于目前节点之键值?
x = comp ? left(x) : right(x); // 遇“大”则往左,遇“小于或等于”则往右
}
// 离开while循环之后,y所指即插入点之父节点(此时的它必为叶节点)
iterator j = iterator(y); // 令迭代器j指向插入点之父节点y
if(comp) // 如果离开while循环时comp为真(表示遇“大”,将插入于左侧)
{
if(j == begin()) // 如果插入点之父节点为最左节点
return pair<iterator, bool>(_insert(x, y, z), true);
else // 否则(插入点之父节点不为最左节点)
--j; // 调整j,回头准备测试
}
if(key_compare(key(j.node), KeyOfValue()(v) )) // 新键值不与既有节点之键值重复,于是以下执行安插操作
return pair<iterator, bool>(_insert(x, y, z), true);
// 以上,x为新值插入点,y为插入点之父节点,v为新值
// 进行至此,表示新值一定与树中键值重复,那么就不应该插入新值
return pair<iterator, bool>(j, false);
}
// 真正地插入执行程序 _insert()
template<class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename<Key, Value, KeyOfValue, Compare, Alloc>::_insert(base_ptr x_, base_ptr y_, const Value &v)
{ // 参数x_ 为新值插入点,参数y_为插入点之父节点,参数v为新值
link_type x = (link_type) x_;
link_type y = (link_type) y_;
link_type z; // key_compare 是键值大小比较准则。应该会是个function object
if(y == header || x != 0 || key_compare(KeyOfValue()(v), key(y) )) {
z = create_node(v); // 产生一个新节点
left(y) = z; // 这使得当y即为header时,leftmost() = z
if(y == header) {
root() = z;
rightmost() = z;
}
else if(y == leftmost()) // 如果y为最左节点
leftmost() = z; // 维护leftmost(),使它永远指向最左节点
}
else {
z = create_node(v); // 产生一个新节点
right(y) = z; // 令新节点成为插入点之父节点y的右子节点
if(y == rightmost())
rightmost() = z; // 维护rightmost(),使它永远指向最右节点
}
parent(z) = y; // 设定新节点的父节点
left(z) = 0; // 设定新节点的左子节点
right(z) = 0; // 设定新节点的右子节点
// 新节点的颜色将在_rb_tree_rebalance()设定(并调整)
_rb_tree_rebalance(z, header->parent); // 参数一为新增节点,参数二为根节点root
++node_count; // 节点数累加
return iterator(z); // 返回一个迭代器,指向新增节点
}
// 全局函数
// 重新令树形平衡(改变颜色及旋转树形)
// 参数一为新增节点,参数二为根节点root
inline void _rb_tree_rebalance(_rb_tree_node_base* x, _rb_tree_node_base*& root) {
x->color = _rb_tree_red; //新节点必为红
while(x != root && x->parent->color == _rb_tree_red) // 父节点为红
{
if(x->parent == x->parent->parent->left) // 父节点为祖父节点之左子节点
{
_rb_tree_node_base* y = x->parent->parent->right; // 令y为伯父节点
if(y && y->color == _rb_tree_red) // 伯父节点存在,且为红
{
x->parent->color = _rb_tree_black; // 更改父节点为黑色
y->color = _rb_tree_black; // 更改伯父节点为黑色
x->parent->parent->color = _rb_tree_red; // 更改祖父节点为红色
x = x->parent->parent;
}
else // 无伯父节点,或伯父节点为黑色
{
if(x == x->parent->right) // 如果新节点为父节点之右子节点
{
x = x->parent;
_rb_tree_rotate_left(x, root); // 第一个参数为左旋点
}
x->parent->color = _rb_tree_black; // 改变颜色
x->parent->parent->color = _rb_tree_red;
_rb_tree_rotate_right(x->parent->parent, root); // 第一个参数为右旋点
}
}
else // 父节点为祖父节点之右子节点
{
_rb_tree_node_base* y = x->parent->parent->left; // 令y为伯父节点
if(y && y->color == _rb_tree_red) // 有伯父节点,且为红
{
x->parent->color = _rb_tree_black; // 更改父节点为黑色
y->color = _rb_tree_black; // 更改伯父节点为黑色
x->parent->parent->color = _rb_tree_red; // 更改祖父节点为红色
x = x->parent->parent; // 准备继续往上层检查
}
else // 无伯父节点,或伯父节点为黑色
{
if(x == x->parent->left) // 如果新节点为父节点之左子节点
{
x = x->parent;
_rb_tree_rotate_right(x, root); // 第一个参数为右旋点
}
x->parent->color = _rb_tree_black; // 改变颜色
x->parent->parent->color = _rb_tree_red;
_rb_tree_rotate_left(x->parent->parent, root); // 第一个参数为左旋点
}
}
}//while
root->color = _rb_tree_black; // 根节点永远为黑色
}
// 左旋函数
inline void _rb_tree_rotate_left(_rb_tree_node_base* x, _rb_tree_node_base*& root)
{
// x 为旋转点
_rb_tree_node_base* y = x->right; // 令y为旋转点的右子节点
x->right = y->left;
if(y->left != 0)
y->left->parent = x; // 别忘了回马枪设定父节点
y->parent = x->parent;
// 令y完全顶替x的地位(必须将x对其父节点的关系完全接收过来)
if(x == root) // x为根节点
root = y;
else if(x == x->parent->left) // x为其父节点的左子节点
x->parent->left = y;
else // x为其父节点的右子节点
x->parent->right = y;
y->left = x;
x->parent = y;
}
// 右旋函数
inline void _rb_tree_rotate_right(_rb_tree_node_base* x, _rb_tree_node_base*& root)
{
// x 为旋转点
_rb_tree_node_base* y = x->left; // 令y为旋转点的左子节点
x->left = y->right;
if(y->right != 0)
y->right->parent = x; // 别忘了回马枪设定父节点
y->parent = x->parent; // 令y完全顶替x的地位(必须将x对其父节点的关系完全接收过来)
if(x == root)
root = y;
else if(x == x->parent->right) // x为其父节点的右子节点
x->parent->right = y;
else // x为其父节点的左子节点
x->parent->left = y;
y->right = x;
x->parent = y;
}
算法导论书上给出的红黑树的性质如下,跟STL源码剖析书上面的4条性质大同小异。
- 每个结点或是红色的,或是黑色的
- 根节点是黑色的
- 每个叶结点(NIL)是黑色的
- 如果一个节点是红色的,则它的两个儿子都是黑色的。
- 对于每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑色结点。
从红黑树上删除一个节点,可以先用普通二叉搜索树的方法,将节点从红黑树上删除掉,然后再将被破坏的红黑性质进行恢复。我们回忆一下普通二叉树的节点删除方法:Z指向需要删除的节点,Y指向实质结构上被删除的结点,如果Z节点只有一个子节点或没有子节点,那么Y就是指向Z指向的节点。如果Z节点有两个子节点,那么Y指向Z节点的后继节点(其实前趋也是一样的),而Z的后继节点绝对不可能有左子树。因此,仅从结构来看,二叉树上实质被删除的节点最多只可能有一个子树。
现在我们来看红黑性质的恢复过程:如果Y指向的节点是个红色节点,那么直接删除掉Y以后,红黑性质不会被破坏。操作结束。如果Y指向的节点是个黑色节点,那么就有几条红黑性质可能受到破坏了。首先是包含Y节点的所有路径,黑高度都减少了一(第5条被破坏)。其次,如果Y的有红色子节点,Y又有红色的父节点,那么Y被删除后,就出现了两个相邻的红色节点(第4条被破坏)。最后,如果Y指向的是根节点,而Y的子节点又是红色的,那么Y被删除后,根节点就变成红色的了(第2条被破坏)。其中,第5条被破坏是让我们比较难受的。因为这影响到了全局。这样动作就太大太复杂了。而且在这个条件下,进行其它红黑性质的恢复也很困难。
所以我们首先解决这个问题:如果不改变含Y路径的黑高度,那么树的其它部分的黑高度就必须做出相应的变化来适应它。所以,我们想办法恢复原来含Y节点的路径的黑高度。做法就是:无条件的把Y节点的黑色,推到它的子节点X上去。(X可能是NIL节点)。这样,X就可能具有双重黑色,或同时具有红黑两色,也就是第1条性质被破坏了。但第1条性质是比较容易恢复的:
- 如果X是同时具有红黑两色,那么好办,直接把X涂成黑色,就行了。而且这样把所有问题都解决了。因为将X变为黑色,2、4两条如果有问题的话也会得到恢复,算法结束。
- 如果X是双黑色,那么我们希望把这种情况向上推一直推到根节点(调整树结构和颜色,X的指向新的双黑色节点,X不断向上移动),让根节点具双黑色,这时,直接把X的一层黑色去掉就行了(因为根节点被包含在所有的路径上,所以这样做所有路径同时黑高减少一,不会破坏红黑特征)。
下面就具体地分析如何恢复1、2、4三个可能被破坏的红黑特性:我们知道,如果X指向的节点是有红黑两色,或是X是根节点时,只需要简单的对X进行一些改变就行了。要对除X节点外的其它节点进行操作时,必定是这样的情况:X节点是双层黑色,且X有父节点P。由知可知,X必然有兄弟节点W,而且这个W节点必定有两个子节点。(因为这是原树满足红黑条件要求而自然具备的。X为双黑色,那么P的另一个子节点以下一定要有至少两层的节点,否则黑色高度不可能和X路径一致)。所以我们就分析这些节点之间如何变形,把问题限制在比较小的范围内解决。另一个前提是:X在一开始,肯定是树底的叶节点或是NIL节点,所以在递归向上的过程中,每一步都保证下一步进行时,至少X的子树是满足红黑特性的。因此子树的情况就可以认为是已经正确的了,这样,分析就只限制在X节点,X的父节点P和X的兄弟节点W,以及W的两个子节点中。
下面仅仅考虑X原本是黑色的情况即可。在这种情况下,X此时应该具有双重黑色,算法的过程就是将这多出的一重黑色向上移动,直到遇到红节点或者根节点。接着往下分析,会遇到4种情况,实际上是8种,因为其中4种是相互对称的,这可以通过判断X是其父节点的右孩子还是左孩子来区分。下面我们以X是其父节点的左孩子的情况来分析这4种情况,实际上接下来的调整过程,就是要想方设法将经过X的所有路径上的黑色节点个数增加1。
具体分为以下四种情况:(下面针对x是左儿子的情况讨论,右儿子对称)
Case1:X的兄弟W是红色(想办法将其变为黑色)。由于W是红色的,因此其儿子节点和父节点必为黑色,只要将W和其父节点的颜色对换,在对父节点进行一次左旋转,便将W的左子节点放到了X的兄弟节点上,X的兄弟节点变成了黑色,且红黑性质不变。但还不算完,只是暂时将情况1转变成了下面的情况2或3或4。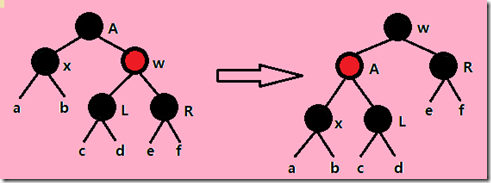
Case2:X的兄弟节点W是黑色的,而且W的两个子节点都是黑色的。此时可以将X的一重黑色和W的黑色同时去掉,而转加给他们的父节点上,这是X就指向它的父节点了,因此此时父节点具有双重颜色了。这一重黑色节点上移。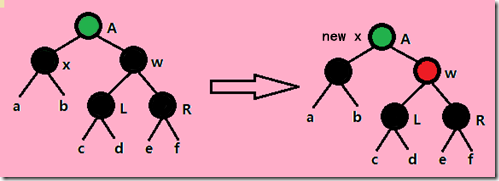
如果父节点原来是红色的,现在又加一层黑色,那么X现在指向的这个节点就是红黑两色的,直接把X(也就是父节点)着为黑色。问题就已经完整解决了。如果父节点现在是双层黑色,那就以父节点为新的X进行向上的下一次的递归。
Case3:X的兄弟节点W是黑色的,而且W的左子节点是红色的,右子节点是黑色的。此时通过交换W和其左子节点的颜色并进行一次向右旋转就可转换成下面的第四种情况。注意,原来L是红色的,所以L的子节点一定是黑色的,所以旋转中L节点的一个子树挂到之后着为红色的W节点上不会破坏红黑性质。变形后黑色高度不变。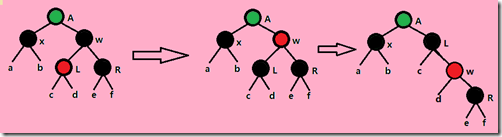
Case4:X的兄弟节点W是黑色的,而且W的右子节点是红色的。这种情况下,做一次左旋,W就处于根的位置,将W保持为原来的根的位置的颜色,同时将W的两个新的儿子节点的颜色变为黑色,去掉X的一重黑色。这样整个问题也就得到了解决。递归结束。(在代码上,为了标识递归结束,我们把X指向根节点)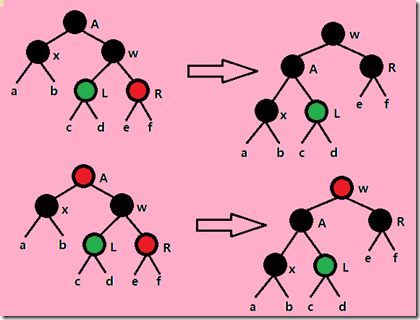
因此,只要按上面四种情况一直递归处理下去,X最终总会指向根结点或一个红色结点,这时我们就可以结束递归并把问题解决了。
以上就是红黑树的节点删除全过程。
总结:如果我们通过上面的情况画出所有的分支图,我们可以得出如下结论
- 插入操作:解决的是 红-红 问题
- 删除操作:解决的是 黑-黑 问题
即你可以从分支图中看出,需要往上遍历的情况为红红(插入),或者为黑黑黑(删除)的情况,如果你认真分析并总结所有的情况后,并坚持下来,红黑树也就没有想象中的那么恐怖了,并且很美妙;
详细的红黑树删除节点的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
using namespace std;
// 定义节点颜色
enum COLOR {
BLACK = 0,
RED
};
// 红黑树节点
typedef struct RB_Tree_Node {
int key;
struct RB_Tree_Node *left;
struct RB_Tree_Node *right;
struct RB_Tree_Node *parent;
unsigned char RB_COLOR;
} RB_Node;
// 红黑树,包含一个指向根节点的指针
typedef struct RBTree {
RB_Node* root;
} *RB_Tree;
// 红黑树的NIL节点
static RB_Tree_Node NIL = {0, 0, 0, 0, BLACK};
void Init_RBTree(RB_Tree pTree) // 初始化一棵红黑树
{
pTree->root = PNIL;
}
// 查找最小键值节点
RB_Node* RBTREE_MIN(RB_Node* pRoot)
{
while (PNIL != pRoot->left)
{
pRoot = pRoot->left;
}
return pRoot;
}
// 查找指定节点的后继节点
RB_Node* RBTREE_SUCCESSOR(RB_Node* pRoot)
{
if (PNIL != pRoot->right)
{
return RBTREE_MIN(pRoot->right);
}
// 节点没有右子树的时候,进入下面的while循环
RB_Node* pParent = pRoot->parent;
while((PNIL != pParent) && (pRoot == pParent->right))
{
pRoot = pParent;
pParent = pRoot->parent;
}
return pParent;
}
// 红黑树的节点删除
RB_Node* Delete(RB_Tree pTree , RB_Node* pDel)
{
RB_Node* rel_delete_point;
if(pDel->left == PNIL || pDel->right == PNIL)
rel_delete_point = pDel;
else
rel_delete_point = RBTREE_SUCCESSOR(pDel);
// 查找后继节点
RB_Node* delete_point_child;
if(rel_delete_point->right != PNIL)
{
delete_point_child = rel_delete_point->right;
}
else if(rel_delete_point->left != PNIL)
{
delete_point_child = rel_delete_point->left;
}
else
{
delete_point_child = PNIL;
}
delete_point_child->parent = rel_delete_point->parent;
if(rel_delete_point->parent == PNIL) // 删除的节点是根节点
{
pTree->root = delete_point_child;
}
else if(rel_delete_point == rel_delete_point->parent->right)
{
rel_delete_point->parent->right = delete_point_child;
}
else
{
rel_delete_point->parent->left = delete_point_child;
}
if(pDel != rel_delete_point)
{
pDel->key = rel_delete_point->key;
}
if(rel_delete_point->RB_COLOR == BLACK)
{
DeleteFixUp(pTree , delete_point_child);
}
return rel_delete_point;
}
/*算法导论上的描述如下:
RB-DELETE-FIXUP(T, x)
1 while x ≠ root[T] and color[x] = BLACK
2 do if x = left[p[x]]
3 then w ← right[p[x]]
4 if color[w] = RED
5 then color[w] ← BLACK Case 1
6 color[p[x]] ← RED Case 1
7 LEFT-ROTATE(T, p[x]) Case 1
8 w ← right[p[x]] Case 1
9 if color[left[w]] = BLACK and color[right[w]] = BLACK
10 then color[w] ← RED Case 2
11 x p[x] Case 2
12 else if color[right[w]] = BLACK
13 then color[left[w]] ← BLACK Case 3
14 color[w] ← RED Case 3
15 RIGHT-ROTATE(T, w) Case 3
16 w ← right[p[x]] Case 3
17 color[w] ← color[p[x]] Case 4
18 color[p[x]] ← BLACK Case 4
19 color[right[w]] ← BLACK Case 4
20 LEFT-ROTATE(T, p[x]) Case 4
21 x ← root[T] Case 4
22 else (same as then clause with "right" and "left" exchanged)
23 color[x] ← BLACK */
//接下来的工作,很简单,即把上述伪代码改写成c++代码即可
void DeleteFixUp(RB_Tree pTree , RB_Node* node)
{
while(node != pTree->root && node->RB_COLOR == BLACK)
{
if(node == node->parent->left)
{
RB_Node* brother = node->parent->right;
if(brother->RB_COLOR==RED) //情况1:x的兄弟w是红色的。
{
brother->RB_COLOR = BLACK;
node->parent->RB_COLOR = RED;
RotateLeft(node->parent);
}
else //情况2:x的兄弟w是黑色的,
{
if(brother->left->RB_COLOR == BLACK && brother->right->RB_COLOR == BLACK) //w的两个孩子都是黑色的
{
brother->RB_COLOR = RED;
node = node->parent;
}
else
{
if(brother->right->RB_COLOR == BLACK) //情况3:x的兄弟w是黑色的,w的右孩子是黑色(w的左孩子是红色)
{
brother->RB_COLOR = RED;
brother->left->RB_COLOR = BLACK;
RotateRight(brother);
brother = node->parent->right; //情况3转换为情况4
} //情况4:x的兄弟w是黑色的,且w的右孩子时红色的
brother->RB_COLOR = node->parent->RB_COLOR;
node->parent->RB_COLOR = BLACK;
brother->right->RB_COLOR = BLACK;
RotateLeft(node->parent);
node = pTree->root;
}//else
}//else
}
else //同上,原理一致,只是遇到左旋改为右旋,遇到右旋改为左旋即可。其它代码不变。
{
RB_Node* brother = node->parent->left;
if(brother->RB_COLOR == RED)
{
brother->RB_COLOR = BLACK;
node->parent->RB_COLOR = RED;
RotateRight(node->parent);
}
else
{
if(brother->left->RB_COLOR==BLACK && brother->right->RB_COLOR == BLACK)
{
brother->RB_COLOR = RED;
node = node->parent;
}
else
{
if(brother->left->RB_COLOR==BLACK)
{
brother->RB_COLOR = RED;
brother->right->RB_COLOR = BLACK;
RotateLeft(brother);
brother = node->parent->left; //情况3转换为情况4
}
brother->RB_COLOR = node->parent->RB_COLOR;
node->parent->RB_COLOR = BLACK;
brother->left->RB_COLOR = BLACK;
RotateRight(node->parent);
node = pTree->root;
}
}
}
}//while
node->RB_COLOR = BLACK; //如果X节点原来为红色,那么直接改为黑色
}
斜堆之图文解析和C语言的实现
概要
本章介绍斜堆。和以往一样,本文会先对斜堆的理论知识进行简单介绍,然后给出C语言的实现。后续再分别给出C++和Java版本的实现;实现的语言虽不同,但是原理如出一辙,选择其中之一进行了解即可。若文章有错误或不足的地方,请不吝指出!
目录
- 斜堆的介绍
- 斜堆的基本操作
- 斜堆的C实现(完整源码)
- 斜堆的C测试程序
转载请注明出处:http://www.cnblogs.com/skywang12345/p/3638493.html
斜堆的介绍
斜堆(Skew heap)也叫自适应堆(self-adjusting heap),它是左倾堆的一个变种。和左倾堆一样,它通常也用于实现优先队列。它的合并操作的时间复杂度也是O(lg n)。
相比于左倾堆,斜堆的节点没有”零距离”这个属性。除此之外,它们斜堆的合并操作也不同。斜堆的合并操作算法如下:
(01) 如果一个空斜堆与一个非空斜堆合并,返回非空斜堆。
(02) 如果两个斜堆都非空,那么比较两个根节点,取较小堆的根节点为新的根节点。将”较小堆的根节点的右孩子”和”较大堆”进行合并。
(03) 合并后,交换新堆根节点的左孩子和右孩子。
第(03)步是斜堆和左倾堆的合并操作差别的关键所在,如果是左倾堆,则合并后要比较左右孩子的零距离大小,若右孩子的零距离 > 左孩子的零距离,则交换左右孩子;最后,在设置根的零距离。
头文件
1 |
|
SkewNode是斜堆对应的节点类。
合并
1 | /* |
merge_skewheap(x, y)的作用是合并x和y这两个斜堆,并返回得到的新堆。merge_skewheap(x, y)是递归实现的。
添加
1 | /* |
insert_skewheap(heap, key)的作用是新建键值为key的结点,并将其插入到斜堆中,并返回堆的根节点。
删除
1 | /* |
delete_skewheap(heap)的作用是删除斜堆的最小节点,并返回删除节点后的斜堆根节点。
斜堆的C实现(完整源码)
斜堆的头文件(skewheap.h)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
typedef int Type;
typedef struct _SkewNode{
Type key; // 关键字(键值)
struct _SkewNode *left; // 左孩子
struct _SkewNode *right; // 右孩子
}SkewNode, *SkewHeap;
// 前序遍历"斜堆"
void preorder_skewheap(SkewHeap heap);
// 中序遍历"斜堆"
void inorder_skewheap(SkewHeap heap);
// 后序遍历"斜堆"
void postorder_skewheap(SkewHeap heap);
// 获取最小值(保存到pval中),成功返回0,失败返回-1。
int skewheap_minimum(SkewHeap heap, int *pval);
// 合并"斜堆x"和"斜堆y",并返回合并后的新树
SkewNode* merge_skewheap(SkewHeap x, SkewHeap y);
// 将结点插入到斜堆中,并返回根节点
SkewNode* insert_skewheap(SkewHeap heap, Type key);
// 删除结点(key为节点的值),并返回根节点
SkewNode* delete_skewheap(SkewHeap heap);
// 销毁斜堆
void destroy_skewheap(SkewHeap heap);
// 打印斜堆
void print_skewheap(SkewHeap heap);
斜堆的实现文件(skewheap.c)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186/**
* C语言实现的斜堆
*
* @author skywang
* @date 2014/03/31
*/
/*
* 前序遍历"斜堆"
*/
void preorder_skewheap(SkewHeap heap)
{
if(heap != NULL)
{
printf("%d ", heap->key);
preorder_skewheap(heap->left);
preorder_skewheap(heap->right);
}
}
/*
* 中序遍历"斜堆"
*/
void inorder_skewheap(SkewHeap heap)
{
if(heap != NULL)
{
inorder_skewheap(heap->left);
printf("%d ", heap->key);
inorder_skewheap(heap->right);
}
}
/*
* 后序遍历"斜堆"
*/
void postorder_skewheap(SkewHeap heap)
{
if(heap != NULL)
{
postorder_skewheap(heap->left);
postorder_skewheap(heap->right);
printf("%d ", heap->key);
}
}
/*
* 交换两个节点的内容
*/
static void swap_skewheap_node(SkewNode *x, SkewNode *y)
{
SkewNode tmp = *x;
*x = *y;
*y = tmp;
}
/*
* 获取最小值
*
* 返回值:
* 成功返回0,失败返回-1
*/
int skewheap_minimum(SkewHeap heap, int *pval)
{
if (heap == NULL)
return -1;
*pval = heap->key;
return 0;
}
/*
* 合并"斜堆x"和"斜堆y"
*
* 返回值:
* 合并得到的树的根节点
*/
SkewNode* merge_skewheap(SkewHeap x, SkewHeap y)
{
if(x == NULL)
return y;
if(y == NULL)
return x;
// 合并x和y时,将x作为合并后的树的根;
// 这里的操作是保证: x的key < y的key
if(x->key > y->key)
swap_skewheap_node(x, y);
// 将x的右孩子和y合并,
// 合并后直接交换x的左右孩子,而不需要像左倾堆一样考虑它们的npl。
SkewNode *tmp = merge_skewheap(x->right, y);
x->right = x->left;
x->left = tmp;
return x;
}
/*
* 新建结点(key),并将其插入到斜堆中
*
* 参数说明:
* heap 斜堆的根结点
* key 插入结点的键值
* 返回值:
* 根节点
*/
SkewNode* insert_skewheap(SkewHeap heap, Type key)
{
SkewNode *node; // 新建结点
// 如果新建结点失败,则返回。
if ((node = (SkewNode *)malloc(sizeof(SkewNode))) == NULL)
return heap;
node->key = key;
node->left = node->right = NULL;
return merge_skewheap(heap, node);
}
/*
* 取出根节点
*
* 返回值:
* 取出根节点后的新树的根节点
*/
SkewNode* delete_skewheap(SkewHeap heap)
{
SkewNode *l = heap->left;
SkewNode *r = heap->right;
// 删除根节点
free(heap);
return merge_skewheap(l, r); // 返回左右子树合并后的新树
}
/*
* 销毁斜堆
*/
void destroy_skewheap(SkewHeap heap)
{
if (heap==NULL)
return ;
if (heap->left != NULL)
destroy_skewheap(heap->left);
if (heap->right != NULL)
destroy_skewheap(heap->right);
free(heap);
}
/*
* 打印"斜堆"
*
* heap -- 斜堆的节点
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
static void skewheap_print(SkewHeap heap, Type key, int direction)
{
if(heap != NULL)
{
if(direction==0) // heap是根节点
printf("%2d is root\n", heap->key);
else // heap是分支节点
printf("%2d is %2d's %6s child\n", heap->key, key, direction==1?"right" : "left");
skewheap_print(heap->left, heap->key, -1);
skewheap_print(heap->right,heap->key, 1);
}
}
void print_skewheap(SkewHeap heap)
{
if (heap != NULL)
skewheap_print(heap, heap->key, 0);
}
斜堆的测试程序(skewheap_test.c)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51/**
* C语言实现的斜堆
*
* @author skywang
* @date 2014/03/31
*/
void main()
{
int i;
int a[]= {10,40,24,30,36,20,12,16};
int b[]= {17,13,11,15,19,21,23};
int alen=LENGTH(a);
int blen=LENGTH(b);
SkewHeap ha,hb;
ha=hb=NULL;
printf("== 斜堆(ha)中依次添加: ");
for(i=0; i<alen; i++)
{
printf("%d ", a[i]);
ha = insert_skewheap(ha, a[i]);
}
printf("\n== 斜堆(ha)的详细信息: \n");
print_skewheap(ha);
printf("\n== 斜堆(hb)中依次添加: ");
for(i=0; i<blen; i++)
{
printf("%d ", b[i]);
hb = insert_skewheap(hb, b[i]);
}
printf("\n== 斜堆(hb)的详细信息: \n");
print_skewheap(hb);
// 将"斜堆hb"合并到"斜堆ha"中。
ha = merge_skewheap(ha, hb);
printf("\n== 合并ha和hb后的详细信息: \n");
print_skewheap(ha);
// 销毁斜堆
destroy_skewheap(ha);
}
左倾堆之图文解析和C语言的实现
概要
本章介绍左倾堆,它和二叉堆一样,都是堆结构中的一员。和以往一样,本文会先对左倾堆的理论知识进行简单介绍,然后给出C语言的实现。后续再分别给出C++和Java版本的实现;实现的语言虽不同,但是原理如出一辙,选择其中之一进行了解即可。若文章有错误或不足的地方,请不吝指出!
目录
- 左倾堆的介绍
- 左倾堆的图文解析
- 左倾堆的C实现(完整源码)
- 左倾堆的C测试程序
转载请注明出处:http://www.cnblogs.com/skywang12345/p/3638327.html
左倾堆的介绍
左倾堆(leftist tree 或 leftist heap),又被成为左偏树、左偏堆,最左堆等。
它和二叉堆一样,都是优先队列实现方式。当优先队列中涉及到”对两个优先队列进行合并”的问题时,二叉堆的效率就无法令人满意了,而本文介绍的左倾堆,则可以很好地解决这类问题。
左倾堆的定义
左倾堆是一棵二叉树,它的节点除了和二叉树的节点一样具有左右子树指针外,还有两个属性:键值和零距离。
(01) 键值的作用是来比较节点的大小,从而对节点进行排序。
(02) 零距离(英文名NPL,即Null Path Length)则是从一个节点到一个”最近的不满节点”的路径长度。不满节点是指该该节点的左右孩子至少有有一个为NULL。叶节点的NPL为0,NULL节点的NPL为-1。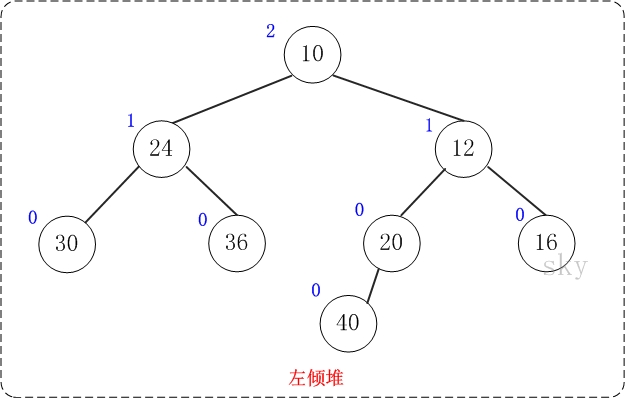
上图是一颗左倾堆,它满足左倾堆的基本性质:
[性质1] 节点的键值小于或等于它的左右子节点的键值。
[性质2] 节点的左孩子的NPL >= 右孩子的NPL。
[性质3] 节点的NPL = 它的右孩子的NPL + 1。
左倾堆,顾名思义,是有点向左倾斜的意思了。它在统计问题、最值问题、模拟问题和贪心问题等问题中有着广泛的应用。此外,斜堆是比左倾堆更为一般的数据结构。当然,今天讨论的是左倾堆,关于斜堆,以后再撰文来表。
前面说过,它能和好的解决”两个优先队列合并”的问题。实际上,左倾堆的合并操作的平摊时间复杂度为O(lg n),而完全二叉堆为O(n)。合并就是左倾树的重点,插入和删除操作都是以合并操作为基础的。插入操作,可以看作两颗左倾树合并;删除操作(移除优先队列中队首元素),则是移除根节点之后再合并剩余的两个左倾树。闲话说到这里,下面开始介绍左倾树的基本方法。
左倾堆的图文解析
合并操作是左倾堆的重点。合并两个左倾堆的基本思想如下:
- 如果一个空左倾堆与一个非空左倾堆合并,返回非空左倾堆。
- 如果两个左倾堆都非空,那么比较两个根节点,取较小堆的根节点为新的根节点。将”较小堆的根节点的右孩子”和”较大堆”进行合并。
- 如果新堆的右孩子的NPL > 左孩子的NPL,则交换左右孩子。
- 设置新堆的根节点的NPL = 右子堆NPL + 1
下面通过图文演示合并以下两个堆的过程。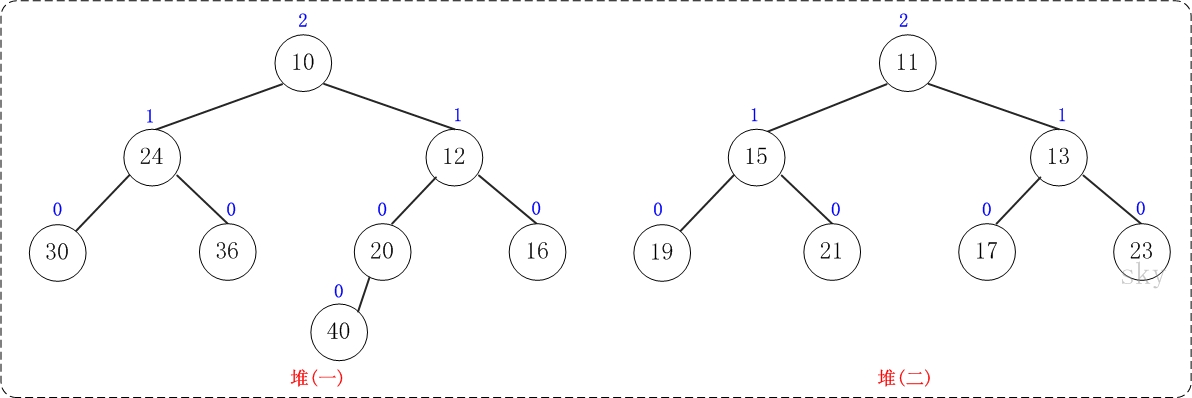
提示:这两个堆的合并过程和测试程序相对应!
第1步:将”较小堆(根为10)的右孩子”和”较大堆(根为11)”进行合并。
合并的结果,相当于将”较大堆”设置”较小堆”的右孩子,如下图所示: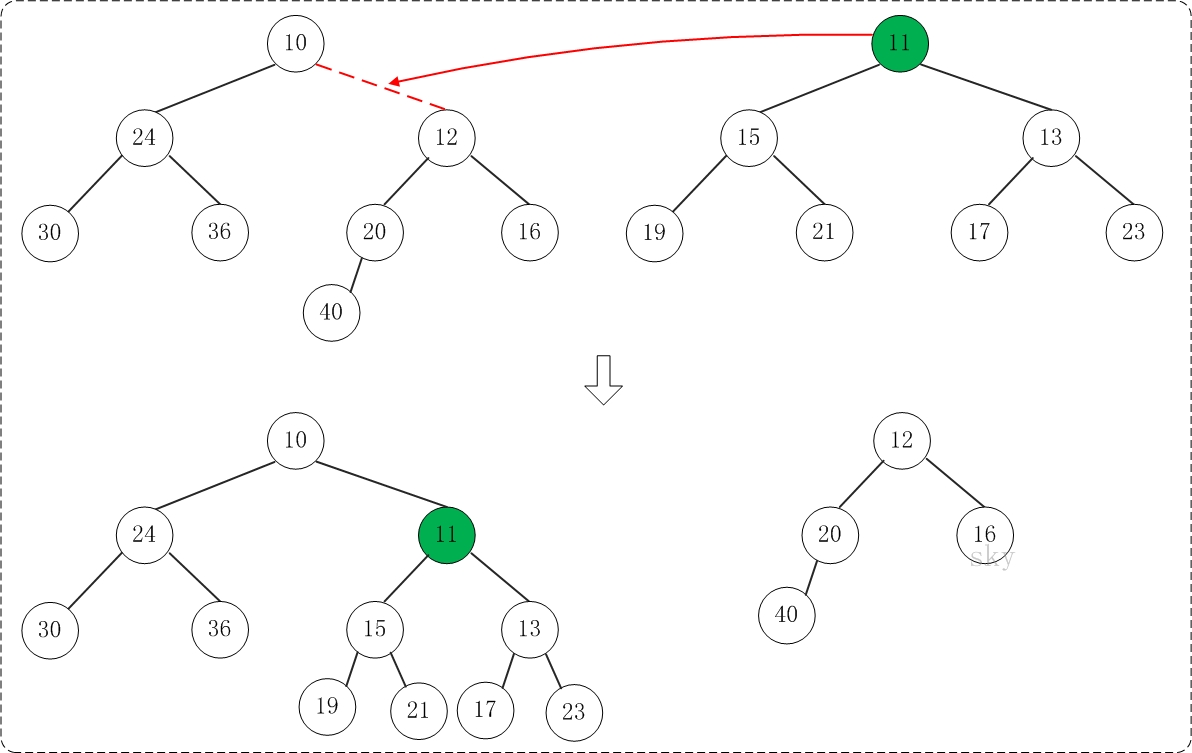
第2步:将上一步得到的”根11的右子树”和”根为12的树”进行合并,得到的结果如下: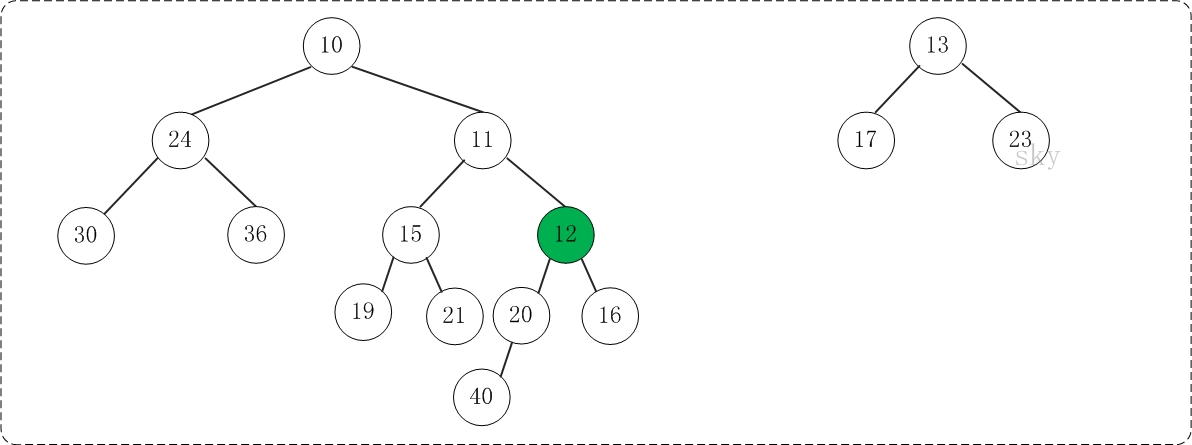
第3步:将上一步得到的”根12的右子树”和”根为13的树”进行合并,得到的结果如下: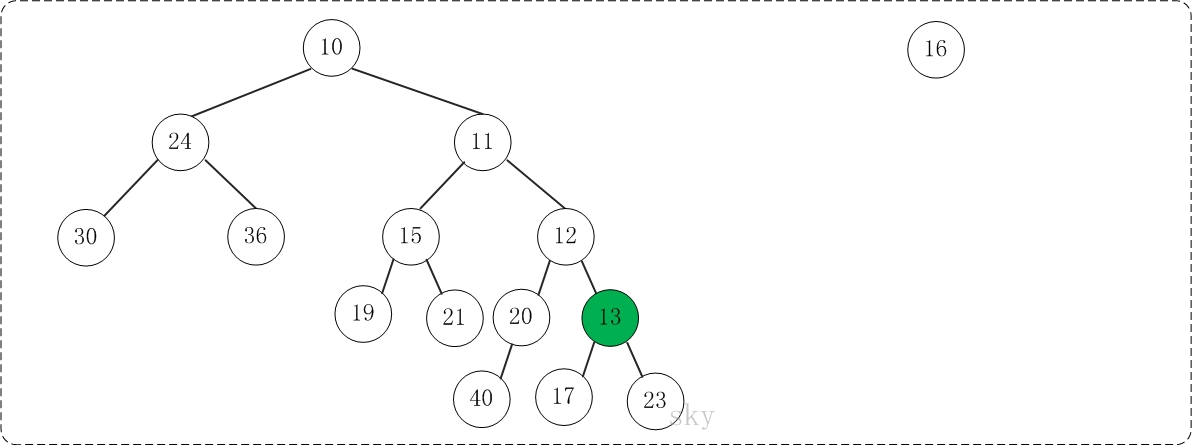
第4步:将上一步得到的”根13的右子树”和”根为16的树”进行合并,得到的结果如下: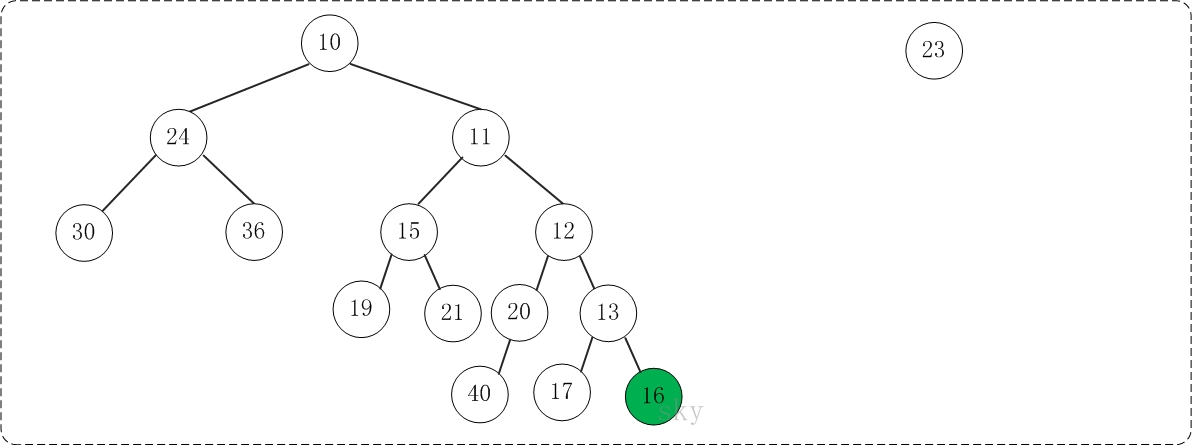
第5步:将上一步得到的”根16的右子树”和”根为23的树”进行合并,得到的结果如下: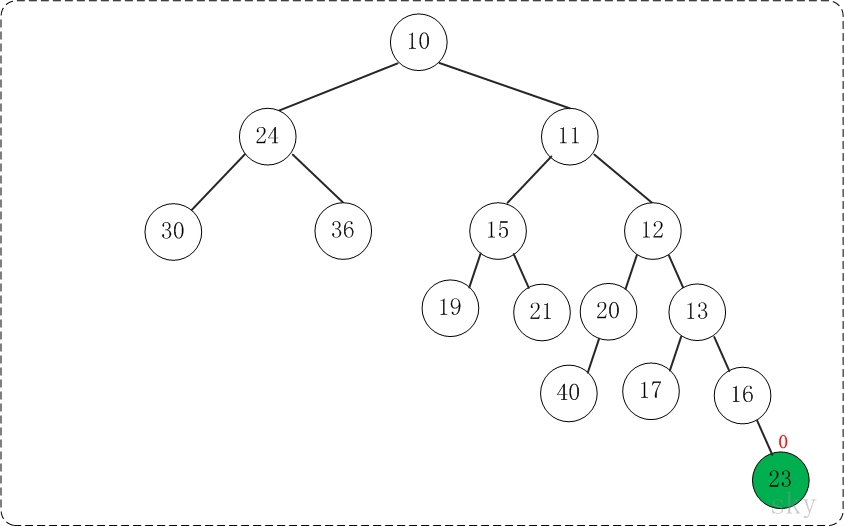
至此,已经成功的将两棵树合并成为一棵树了。接下来,对新生成的树进行调节。
第6步:上一步得到的”树16的右孩子的NPL > 左孩子的NPL”,因此交换左右孩子。得到的结果如下: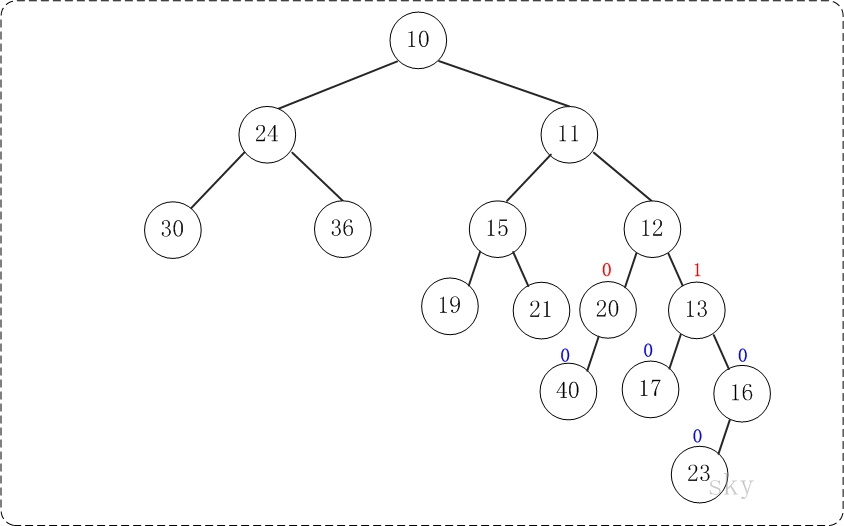
第7步:上一步得到的”树12的右孩子的NPL > 左孩子的NPL”,因此交换左右孩子。得到的结果如下: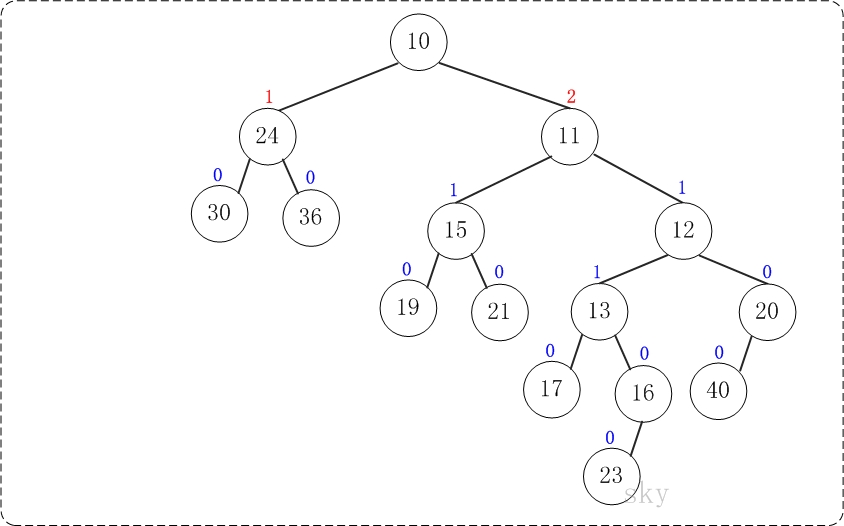
第8步:上一步得到的”树10的右孩子的NPL > 左孩子的NPL”,因此交换左右孩子。得到的结果如下: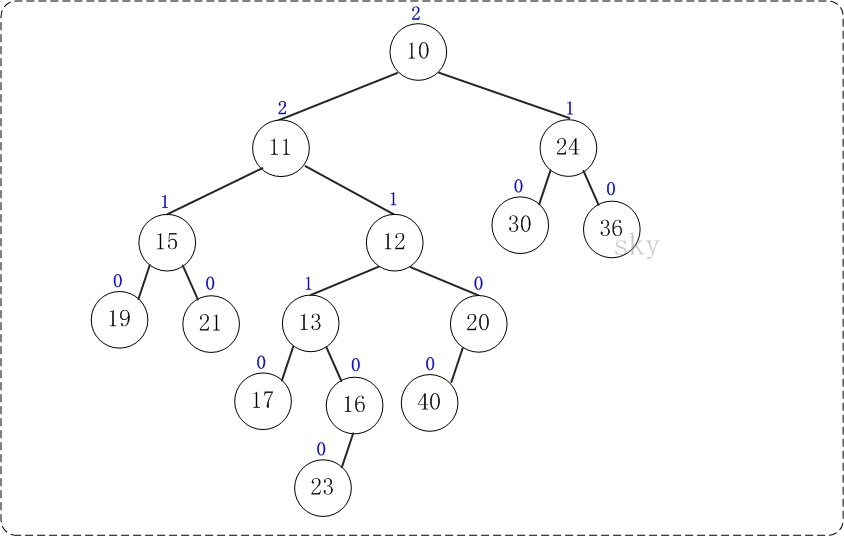
至此,合并完毕。上面就是合并得到的左倾堆!
下面看看左倾堆的基本操作的代码
- 头文件LeftistNode是左倾堆对应的节点类。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
typedef int Type;
typedef struct _LeftistNode{
Type key; // 关键字(键值)
int npl; // 零路经长度(Null Path Length)
struct _LeftistNode *left; // 左孩子
struct _LeftistNode *right; // 右孩子
}LeftistNode, *LeftistHeap;
// 前序遍历"左倾堆"
void preorder_leftist(LeftistHeap heap);
// 中序遍历"左倾堆"
void inorder_leftist(LeftistHeap heap);
// 后序遍历"左倾堆"
void postorder_leftist(LeftistHeap heap);
// 获取最小值(保存到pval中),成功返回0,失败返回-1。
int leftist_minimum(LeftistHeap heap, int *pval);
// 合并"左倾堆x"和"左倾堆y",并返回合并后的新树
LeftistNode* merge_leftist(LeftistHeap x, LeftistHeap y);
// 将结点插入到左倾堆中,并返回根节点
LeftistNode* insert_leftist(LeftistHeap heap, Type key);
// 删除结点(key为节点的值),并返回根节点
LeftistNode* delete_leftist(LeftistHeap heap);
// 销毁左倾堆
void destroy_leftist(LeftistHeap heap);
// 打印左倾堆
void print_leftist(LeftistHeap heap);
- 合并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37/*
* 合并"左倾堆x"和"左倾堆y"
*
* 返回值:
* 合并得到的树的根节点
*/
LeftistNode* merge_leftist(LeftistHeap x, LeftistHeap y)
{
if(x == NULL)
return y;
if(y == NULL)
return x;
// 合并x和y时,将x作为合并后的树的根;
// 这里的操作是保证: x的key < y的key
if(x->key > y->key)
swap_leftist_node(x, y);
// 将x的右孩子和y合并,"合并后的树的根"是x的右孩子。
x->right = merge_leftist(x->right, y);
// 如果"x的左孩子为空" 或者 "x的左孩子的npl<右孩子的npl"
// 则,交换x和y
if(x->left == NULL || x->left->npl < x->right->npl)
{
LeftistNode *tmp = x->left;
x->left = x->right;
x->right = tmp;
}
// 设置合并后的新树(x)的npl
if (x->right == NULL || x->left == NULL)
x->npl = 0;
else
x->npl = (x->left->npl > x->right->npl) ? (x->right->npl + 1) : (x->left->npl + 1);
return x;
}
merge_leftist(x, y)的作用是合并x和y这两个左倾堆,并返回得到的新堆。merge_leftist(x, y)是递归实现的。
添加
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22/*
* 新建结点(key),并将其插入到左倾堆中
*
* 参数说明:
* heap 左倾堆的根结点
* key 插入结点的键值
* 返回值:
* 根节点
*/
LeftistNode* insert_leftist(LeftistHeap heap, Type key)
{
LeftistNode *node; // 新建结点
// 如果新建结点失败,则返回。
if ((node = (LeftistNode *)malloc(sizeof(LeftistNode))) == NULL)
return heap;
node->key = key;
node->npl = 0;
node->left = node->right = NULL;
return merge_leftist(heap, node);
}insert_leftist(heap, key)的作用是新建键值为key的结点,并将其插入到左倾堆中,并返回堆的根节点。
删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19/*
* 取出根节点
*
* 返回值:
* 取出根节点后的新树的根节点
*/
LeftistNode* delete_leftist(LeftistHeap heap)
{
if (heap == NULL)
return NULL;
LeftistNode *l = heap->left;
LeftistNode *r = heap->right;
// 删除根节点
free(heap);
return merge_leftist(l, r); // 返回左右子树合并后的新树
}delete_leftist(heap)的作用是删除左倾堆的最小节点,并返回删除节点后的左倾堆根节点。
左倾堆的头文件(leftist.h)
1 |
|
左倾堆的实现文件(leftist.c)
1 | /** |
左倾堆的测试程序(leftist_test.c)
1 | /** |
左倾堆的C测试程序
左倾堆的测试程序已经包含在它的实现文件(leftist_test.c)中了,这里仅给出它的运行结果:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37== 左倾堆(ha)中依次添加: 10 40 24 30 36 20 12 16
== 左倾堆(ha)的详细信息:
10(2) is root
24(1) is 10's left child
30(0) is 24's left child
36(0) is 24's right child
12(1) is 10's right child
20(0) is 12's left child
40(0) is 20's left child
16(0) is 12's right child
== 左倾堆(hb)中依次添加: 17 13 11 15 19 21 23
== 左倾堆(hb)的详细信息:
11(2) is root
15(1) is 11's left child
19(0) is 15's left child
21(0) is 15's right child
13(1) is 11's right child
17(0) is 13's left child
23(0) is 13's right child
== 合并ha和hb后的详细信息:
10(2) is root
11(2) is 10's left child
15(1) is 11's left child
19(0) is 15's left child
21(0) is 15's right child
12(1) is 11's right child
13(1) is 12's left child
17(0) is 13's left child
16(0) is 13's right child
23(0) is 16's left child
20(0) is 12's right child
40(0) is 20's left child
24(1) is 10's right child
30(0) is 24's left child
36(0) is 24's right child
跳跃表原理
Skip List是在有序链表的基础上进行了扩展,解决了有序链表结构查找特定值困难的问题,查找特定值的时间复杂度为O(logn),他是一种可以代替平衡树的数据结构。下面是skipList的一个介绍,转载来的,源地址:http://kenby.iteye.com/blog/1187303,
什么选择跳表
目前经常使用的平衡数据结构有:B树,红黑树,AVL树,Splay Tree, Treep等。想象一下,给你一张草稿纸,一只笔,一个编辑器,你能立即实现一颗红黑树,或者AVL树出来吗? 很难吧,这需要时间,要考虑很多细节,要参考一堆算法与数据结构之类的树,还要参考网上的代码,相当麻烦。
用跳表吧,跳表是一种随机化的数据结构,目前开源软件 Redis 和 LevelDB 都有用到它,它的效率和红黑树以及 AVL 树不相上下,但跳表的原理相当简单,只要你能熟练操作链表,就能轻松实现一个 SkipList。
有序表的搜索
考虑一个有序表:
从该有序表中搜索元素 < 23, 43, 59 > ,需要比较的次数分别为 < 2, 4, 6 >,总共比较的次数为 2 + 4 + 6 = 12 次。有没有优化的算法吗? 链表是有序的,但不能使用二分查找。类似二叉搜索树,我们把一些节点提取出来,作为索引。得到如下结构: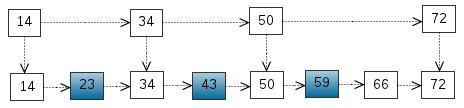
这里我们把 < 14, 34, 50, 72 > 提取出来作为一级索引,这样搜索的时候就可以减少比较次数了。 我们还可以再从一级索引提取一些元素出来,作为二级索引,变成如下结构: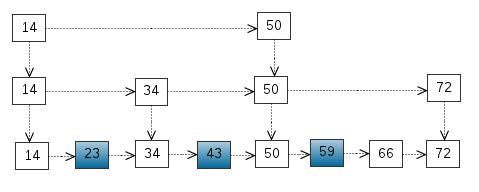
这里元素不多,体现不出优势,如果元素足够多,这种索引结构就能体现出优势来了。
跳表
下面的结构是就是跳表:-1 表示 INT_MIN, 链表的最小值,1 表示 INT_MAX,链表的最大值。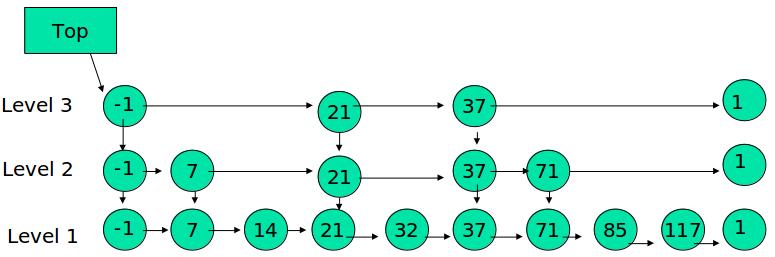
跳表具有如下性质:
- 由很多层结构组成
- 每一层都是一个有序的链表
- 最底层(Level 1)的链表包含所有元素
- 如果一个元素出现在 Level i 的链表中,则它在 Level i 之下的链表也都会出现。
- 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
跳表的搜索
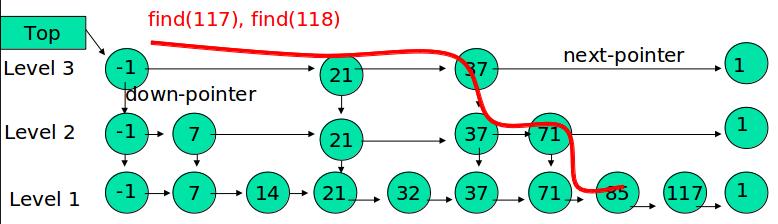
例子:查找元素 117
- 比较 21, 比 21 大,往后面找
- 比较 37, 比 37大,比链表最大值小,从 37 的下面一层开始找
- 比较 71, 比 71 大,比链表最大值小,从 71 的下面一层开始找
- 比较 85, 比 85 大,从后面找
- 比较 117, 等于 117, 找到了节点。
具体的搜索算法如下:1
2
3
4
5
6
7
8
9
10
11
12
13/* 如果存在 x, 返回 x 所在的节点,
* 否则返回 x 的后继节点 */
find(x)
{
p = top;
while (1) {
while (p->next->key < x)
p = p->next;
if (p->down == NULL)
return p->next;
p = p->down;
}
}
跳表的插入
先确定该元素要占据的层数 K(采用丢硬币的方式,这完全是随机的),然后在 Level 1 … Level K 各个层的链表都插入元素。
例子:插入 119, K = 2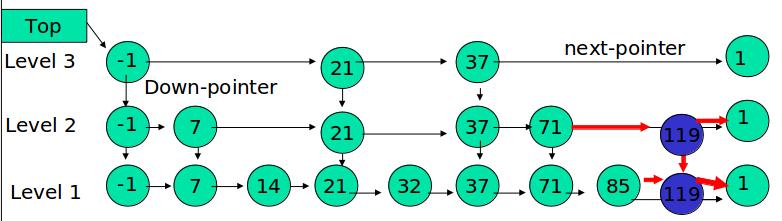
如果 K 大于链表的层数,则要添加新的层。例子:插入 119, K = 4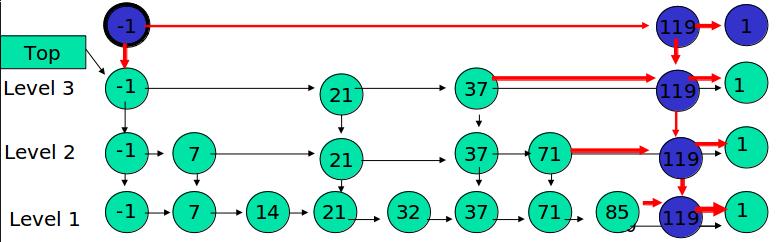
丢硬币决定 K
插入元素的时候,元素所占有的层数完全是随机的,通过一下随机算法产生:1
2
3
4
5
6
7
8
9int random_level()
{
K = 1;
while (random(0,1))
K++;
return K;
}
相当与做一次丢硬币的实验,如果遇到正面,继续丢,遇到反面,则停止,用实验中丢硬币的次数 K 作为元素占有的层数。显然随机变量 K 满足参数为 p = 1/2 的几何分布,K 的期望值 E[K] = 1/p = 2. 就是说,各个元素的层数,期望值是 2 层。
跳表的高度。
n 个元素的跳表,每个元素插入的时候都要做一次实验,用来决定元素占据的层数 K,跳表的高度等于这 n 次实验中产生的最大 K,
跳表的空间复杂度分析
根据上面的分析,每个元素的期望高度为 2, 一个大小为 n 的跳表,其节点数目的期望值是 2n。
跳表的删除
在各个层中找到包含 x 的节点,使用标准的 delete from list 方法删除该节点。
例子:删除 71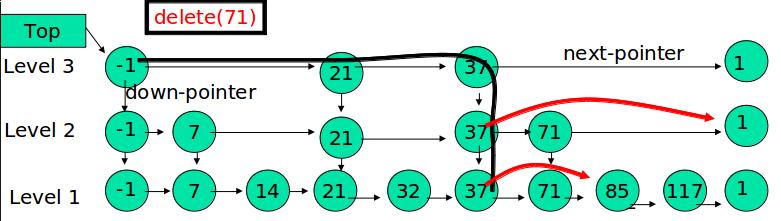
字典树
字典树又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来节约存储空间,最大限度地减少无谓的字符串比较,查询效率比哈希表高。
字典树与字典很相似,当你要查一个单词是不是在字典树中,首先看单词的第一个字母是不是在字典的第一层,如果不在,说明字典树里没有该单词,如果在就在该字母的孩子节点里找是不是有单词的第二个字母,没有说明没有该单词,有的话用同样的方法继续查找.字典树不仅可以用来储存字母,也可以储存数字等其它数据。
Trie的数据结构定义:1
2
3
4
5
6
7
8
typedef struct Trie
{
Trie *next[MAX];
int v; //根据需要变化
};
Trie *root;
next是表示每层有多少种类的数,如果只是小写字母,则26即可,若改为大小写字母,则是52,若再加上数字,则是62了,这里根据题意来确定。
v可以表示一个字典树到此有多少相同前缀的数目,这里根据需要应当学会自由变化。
Trie的查找(最主要的操作):
- 每次从根结点开始一次搜索;
- 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;
- 在相应的子树上,取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
- 迭代过程……
- 在某个结点处,关键词的所有字母已被取出,则读取附在该结点上的信息,即完成查找。
这里给出生成字典树和查找的模版:
生成字典树:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24void createTrie(char *str)
{
int len = strlen(str);
Trie *p = root, *q;
for(int i=0; i<len; ++i)
{
int id = str[i]-'0';
if(p->next[id] == NULL)
{
q = (Trie *)malloc(sizeof(Trie));
q->v = 1; //初始v==1
for(int j=0; j<MAX; ++j)
q->next[j] = NULL;
p->next[id] = q;
p = p->next[id];
}
else
{
p->next[id]->v++;
p = p->next[id];
}
}
p->v = -1; //若为结尾,则将v改成-1表示
}
接下来是查找的过程了:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15int findTrie(char *str)
{
int len = strlen(str);
Trie *p = root;
for(int i=0; i<len; ++i)
{
int id = str[i]-'0';
p = p->next[id];
if(p == NULL) //若为空集,表示不存以此为前缀的串
return 0;
if(p->v == -1) //字符集中已有串是此串的前缀
return -1;
}
return -1; //此串是字符集中某串的前缀
}
对于上述动态字典树,有时会超内存,这是就要记得释放空间了:1
2
3
4
5
6
7
8
9
10
11
12
13int dealTrie(Trie* T)
{
int i;
if(T==NULL)
return 0;
for(i=0;i<MAX;i++)
{
if(T->next[i]!=NULL)
deal(T->next[i]);
}
free(T);
return 0;
}
Trie的删除操作就稍微复杂一些,主要分为以下3种情况:
如果待删除的单词是另一个单词的前缀,只需要把该单词的最后一个节点的 isWord 的改成false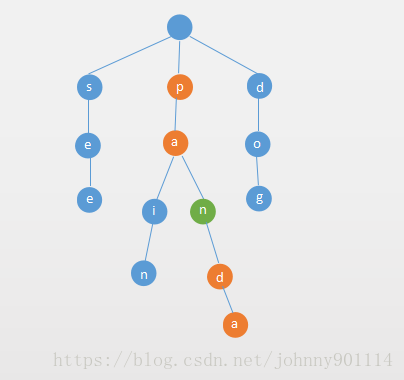
比如Trie中存在 panda 和 pan 这两个单词,删除 pan ,只需要把字符 n 对应的节点的 isWord 改成 false 即可
如果单词的所有字母的都没有多个分支(也就是说该单词所有的字符对应的Node都只有一个子节点),则删除整个单词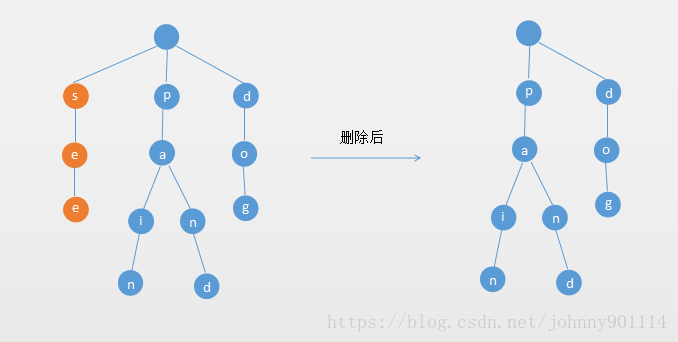
如果单词的除了最后一个字母,其他的字母有多个分支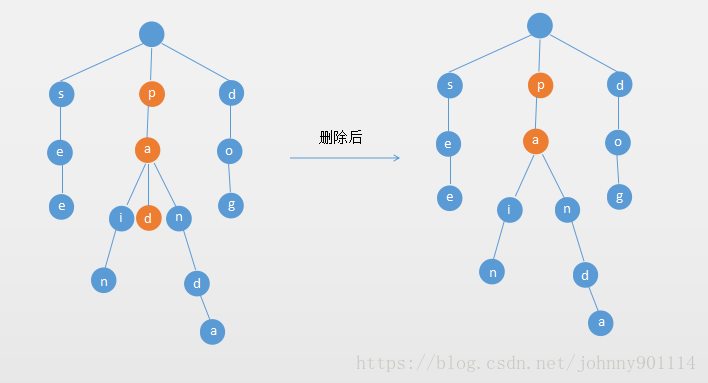
位图(BitMap)索引
案例
有张表名为table的表,由三列组成,分别是姓名、性别和婚姻状况,其中性别只有男和女两项,婚姻状况由已婚、未婚、离婚这三项,该表共有100w个记录。现在有这样的查询: select * from table where Gender=‘男’ and Marital=“未婚”。
| 姓名(Name) | 性别(Gender) | 婚姻状况(Marital) |
|---|---|---|
| 张三 | 男 | 已婚 |
| 李四 | 女 | 已婚 |
| 王五 | 男 | 未婚 |
| 赵六 | 女 | 离婚 |
| 孙七 | 女 | 未婚 |
- 不使用索引
不使用索引时,数据库只能一行行扫描所有记录,然后判断该记录是否满足查询条件。
- B树索引
对于性别,可取值的范围只有’男’,’女’,并且男和女可能各站该表的50%的数据,这时添加B树索引还是需要取出一半的数据, 因此完全没有必要。相反,如果某个字段的取值范围很广,几乎没有重复,比如身份证号,此时使用B树索引较为合适。事实上,当取出的行数据占用表中大部分的数据时,即使添加了B树索引,数据库如oracle、mysql也不会使用B树索引,很有可能还是一行行全部扫描。
位图索引出马
如果用户查询的列的基数非常的小, 即只有的几个固定值,如性别、婚姻状况、行政区等等。要为这些基数值比较小的列建索引,就需要建立位图索引。
对于性别这个列,位图索引形成两个向量,男向量为10100…,向量的每一位表示该行是否是男,如果是则位1,否为0,同理,女向量位01011。
| RowId | 1 | 2 | 3 | 4 | 5 | … |
|---|---|---|---|---|---|---|
| 男 | 1 | 0 | 1 | 0 | 0 | |
| 女 | 0 | 1 | 0 | 1 | 1 |
对于婚姻状况这一列,位图索引生成三个向量,已婚为11000…,未婚为00100…,离婚为00010…。
| RowId | 1 | 2 | 3 | 4 | 5 | … |
|---|---|---|---|---|---|---|
| 已婚 | 1 | 1 | 0 | 0 | 0 | |
| 未婚 | 0 | 0 | 1 | 0 | 1 | |
| 离婚 | 0 | 0 | 0 | 1 | 0 |
当我们使用查询语句“select * from table where Gender=‘男’ and Marital=“未婚”;”的时候 首先取出男向量10100…,然后取出未婚向量00100…,将两个向量做and操作,这时生成新向量00100…,可以发现第三位为1,表示该表的第三行数据就是我们需要查询的结果。
| RowId | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 男 | 1 | 0 | 1 | 0 | 0 |
| 未婚 | 0 | 0 | 1 | 0 | 1 |
| 结果 | 0 | 0 | 1 | 0 | 0 |
位图索引的适用条件
上面讲了,位图索引适合只有几个固定值的列,如性别、婚姻状况、行政区等等,而身份证号这种类型不适合用位图索引。
此外,位图索引适合静态数据,而不适合索引频繁更新的列。举个例子,有这样一个字段busy,记录各个机器的繁忙与否,当机器忙碌时,busy为1,当机器不忙碌时,busy为0。
这个时候有人会说使用位图索引,因为busy只有两个值。好,我们使用位图索引索引busy字段!假设用户A使用update更新某个机器的busy值,比如update table set table.busy=1 where rowid=100;,但还没有commit,而用户B也使用update更新另一个机器的busy值,update table set table.busy=1 where rowid=12; 这个时候用户B怎么也更新不了,需要等待用户A commit。
原因:用户A更新了某个机器的busy值为1,会导致所有busy为1的机器的位图向量发生改变,因此数据库会将busy=1的所有行锁定,只有commit之后才解锁。
源地址:http://www.cnblogs.com/LBSer
Boyer-Moore 字符串匹配算法
在 1977 年,Robert S. Boyer (Stanford Research Institute) 和 J Strother Moore (Xerox Palo Alto Research Center) 共同发表了文章《A Fast String Searching Algorithm》,介绍了一种新的快速字符串匹配算法。这种算法在逻辑上相对于现有的算法有了显著的改进,它对要搜索的字符串进行倒序的字符比较,并且当字符比较不匹配时无需对整个模式串再进行搜索。
Boyer-Moore 算法的主要特点有:
- 对模式字符的比较顺序时从右向左;
- 预处理需要 O(m + σ) 的时间和空间复杂度;
- 匹配阶段需要 O(m × n) 的时间复杂度;
- 匹配阶段在最坏情况下需要 3n 次字符比较;
- 最优复杂度 O(n/m);
在 Naive 算法中,对文本 T 和模式 P 字符串均未做预处理。而在 KMP 算法中则对模式 P 字符串进行了预处理操作,以预先计算模式串中各位置的最长相同前后缀长度的数组。Boyer–Moore 算法同样也是对模式 P 字符串进行预处理。
我们知道,在 Naive 算法中,如果发现模式 P 中的字符与文本 T 中的字符不匹配时,需要将文本 T 的比较位置向后滑动一位,模式 P 的比较位置归 0 并从头开始比较。而 KMP 算法则是根据预处理的结果进行判断以使模式 P 的比较位置可以向后滑动多个位置。Boyer–Moore 算法的预处理过程也是为了达到相同效果。
Boyer–Moore 算法在对模式 P 字符串进行预处理时,将采用两种不同的启发式方法。这两种启发式的预处理方法称为:
- 坏字符(Bad Character Heuristic):当文本 T 中的某个字符跟模式 P 的某个字符不匹配时,我们称文本 T 中的这个失配字符为坏字符。
- 好后缀(Good Suffix Heuristic):当文本 T 中的某个字符跟模式 P 的某个字符不匹配时,我们称文本 T 中的已经匹配的字符串为好后缀。
Boyer–Moore 算法在预处理时,将为两种不同的启发法结果创建不同的数组,分别称为 Bad-Character-Shift(or The Occurrence Shift)和 Good-Suffix-Shift(or Matching Shift)。当进行字符匹配时,如果发现模式 P 中的字符与文本 T 中的字符不匹配时,将比较两种不同启发法所建议的移动位移长度,选择最大的一个值来对模式 P 的比较位置进行滑动。
此外,Naive 算法和 KMP 算法对模式 P 的比较方向是从前向后比较,而 Boyer–Moore 算法的设计则是从后向前比较,即从尾部向头部方向进行比较。
下面,我们将以 J Strother Moore 提供的例子作为示例。1
2Text T : HERE IS A SIMPLE EXAMPLE
Pattern P : EXAMPLE
首先将文本 T 与模式 P 头部对齐,并从尾部开始进行比较。1
2HERE IS A SIMPLE EXAMPLE
EXAMPLE
这样如果尾部的字符不匹配,则前面的字符也就无需比较了,直接跳过。我们看到,”S” 与 “E” 不匹配,我们称文本 T 中的失配字符 “S” 为坏字符(Bad Character)。由于字符 “S” 在模式 “EXAMPLE” 中不存在,则可将搜索位置滑动到 “S” 的后面。1
2HERE IS A SIMPLE EXAMPLE
EXAMPLE
仍然从尾部开始比较,发现 “P” 与 “E” 不匹配,所以 “P” 是坏字符。但此时,”P” 包含在模式 “EXAMPLE” 之中。所以,将模式后移两位,使两个 “P” 对齐。1
2HERE IS A SIMPLE EXAMPLE
EXAMPLE
由此总结坏字符启发法的规则是:1
模式后移位数 = 坏字符在模式中失配的位置 - 坏字符在模式中最后一次出现的位置
坏字符启发法规则中的特殊情况:
- 如果坏字符不存在于模式中,则最后一次出现的位置为 -1。
- 如果坏字符在模式中的位置位于失配位置的右侧,则此启发法不提供任何建议。
以上面示例中坏字符 “P” 为例,它的失配位置为 “E” 的位置 6 (位置从 0 开始),在模式中最后一次出现的位置是 4,则模式后移位数为 6 - 4 = 2 位。模式移动的结果就是使模式中最后出现的 “P” 与文本中的坏字符 “P” 进行对齐。
实际上,前面的坏字符 “S” 出现时,其失配位置为 6,最后一次出现位置为 -1,所以模式后移位数为 6 - (-1) = 7 位。也就是将模式整体移过坏字符。
我们继续上面的过程,仍然从尾部开始比较。仍然从尾部开始比较,发现 “E” 与 “E” 匹配,则继续倒序比较。发现 “L” 与 “L” 匹配,则继续倒序比较。发现 “P” 与 “P” 匹配,则继续倒序比较。发现 “M” 与 “M” 匹配,则继续倒序比较。发现 “I” 与 “A” 不匹配,则 “I” 是坏字符。对于前面已经匹配的字符串 “MPLE”、”PLE”、”LE”、”E”,我们称它们为好后缀(Good Suffix)。1
2HERE IS A SIMPLE EXAMPLE
EXAMPLE
而好后缀启发法的规则是:1
模式后移位数 = 好后缀在模式中的当前位置 - 好后缀在模式中最右出现且前缀字符不同的位置
好后缀在模式中的当前位置以其最后一个字符为准。如果好后缀不存在于模式中,则最右出现的位置为 -1。这样,我们先来找出好后缀在模式中上一次出现的位置。
- “MPLE” : 未出现,最右出现的位置为 -1;
- “PLE” : 未出现在头部,最右出现的位置为 -1;
- “LE” : 未出现在头部,最右出现的位置为 -1;
- “E” : 出现在头部,补充虚拟字符 ‘MPL’E,前缀字符为空,最右出现的位置为 0;
由于只有 “E” 在模式中出现,其当前位置为 6,上一次出现的位置为 0,则依据好后缀启发法规则,模式后移位数为 6 - 0 = 6 位。而如果依据坏字符启发法规则,模式后移位数为 2 - (-1) = 3 位。
Boyer–Moore 算法的特点就在于此,选择上述两种启发法规则计算结果中最大的一个值来对模式 P 的比较位置进行滑动。这里将选择好后缀启发法的计算结果,即将模式向后移 6 位。1
2HERE IS A SIMPLE EXAMPLE
EXAMPLE
此时,仍然从尾部开始比较。发现 “P” 与 “E” 不匹配,则 “P” 是坏字符,则模式后移位数为 6 - 4 = 2 位。1
2HERE IS A SIMPLE EXAMPLE
EXAMPLE
发现 “E” 与 “E” 匹配,则继续倒序比较,直到发现全部匹配,则匹配到的第一个完整的模式 P 被发现。
继续下去则是依据好后缀启示法规则计算好后缀 “E” 的后移位置为 6 - 0 = 6 位,然后继续倒序比较时发现已超出文本 T 的范围,搜索结束。
从上面的示例描述可以看出,Boyer–Moore 算法的精妙之处在于,其通过两种启示规则来计算后移位数,且其计算过程只与模式 P 有关,而与文本 T 无关。因此,在对模式 P 进行预处理时,可预先生成 “坏字符规则之向后位移表” 和 “好后缀规则之向后位移表”,在具体匹配时仅需查表比较两者中最大的位移即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266namespace StringMatching
{
class Program
{
static void Main(string[] args)
{
char[] text1 = "BBC ABCDAB ABCDABCDABDE".ToCharArray();
char[] pattern1 = "ABCDABD".ToCharArray();
int firstShift1;
bool isMatched1 = BoyerMooreStringMatcher.TryMatch(
text1, pattern1, out firstShift1);
Contract.Assert(isMatched1);
Contract.Assert(firstShift1 == 15);
char[] text2 = "ABABDAAAACAAAABCABAB".ToCharArray();
char[] pattern2 = "AAACAAAA".ToCharArray();
int firstShift2;
bool isMatched2 = BoyerMooreStringMatcher.TryMatch(
text2, pattern2, out firstShift2);
Contract.Assert(isMatched2);
Contract.Assert(firstShift2 == 6);
char[] text3 = "ABAAACAAAAAACAAAABCABAAAACAAAAFDLAAACAAAAAACAAAA"
.ToCharArray();
char[] pattern3 = "AAACAAAA".ToCharArray();
int[] shiftIndexes3 = BoyerMooreStringMatcher.MatchAll(text3, pattern3);
Contract.Assert(shiftIndexes3.Length == 5);
Contract.Assert(string.Join(",", shiftIndexes3) == "2,9,22,33,40");
char[] text4 = "GCATCGCAGAGAGTATACAGTACG".ToCharArray();
char[] pattern4 = "GCAGAGAG".ToCharArray();
int firstShift4;
bool isMatched4 = BoyerMooreStringMatcher.TryMatch(
text4, pattern4, out firstShift4);
Contract.Assert(isMatched4);
Contract.Assert(firstShift4 == 5);
char[] text5 = "HERE IS A SIMPLE EXAMPLE AND EXAMPLE OF BM.".ToCharArray();
char[] pattern5 = "EXAMPLE".ToCharArray();
int firstShift5;
bool isMatched5 = BoyerMooreStringMatcher.TryMatch(
text5, pattern5, out firstShift5);
Contract.Assert(isMatched5);
Contract.Assert(firstShift5 == 17);
int[] shiftIndexes5 = BoyerMooreStringMatcher.MatchAll(text5, pattern5);
Contract.Assert(shiftIndexes5.Length == 2);
Contract.Assert(string.Join(",", shiftIndexes5) == "17,29");
Console.WriteLine("Well done!");
Console.ReadKey();
}
}
public class BoyerMooreStringMatcher
{
private static int AlphabetSize = 256;
private static int Max(int a, int b) { return (a > b) ? a : b; }
static int[] PreprocessToBuildBadCharactorHeuristic(char[] pattern)
{
int m = pattern.Length;
int[] badCharactorShifts = new int[AlphabetSize];
for (int i = 0; i < AlphabetSize; i++)
{
//badCharactorShifts[i] = -1;
badCharactorShifts[i] = m;
}
// fill the actual value of last occurrence of a character
for (int i = 0; i < m; i++)
{
//badCharactorShifts[(int)pattern[i]] = i;
badCharactorShifts[(int)pattern[i]] = m - 1 - i;
}
return badCharactorShifts;
}
static int[] PreprocessToBuildGoodSuffixHeuristic(char[] pattern)
{
int m = pattern.Length;
int[] goodSuffixShifts = new int[m];
int[] suffixLengthArray = GetSuffixLengthArray(pattern);
for (int i = 0; i < m; ++i)
{
goodSuffixShifts[i] = m;
}
int j = 0;
for (int i = m - 1; i >= -1; --i)
{
if (i == -1 || suffixLengthArray[i] == i + 1)
{
for (; j < m - 1 - i; ++j)
{
if (goodSuffixShifts[j] == m)
{
goodSuffixShifts[j] = m - 1 - i;
}
}
}
}
for (int i = 0; i < m - 1; ++i)
{
goodSuffixShifts[m - 1 - suffixLengthArray[i]] = m - 1 - i;
}
return goodSuffixShifts;
}
static int[] GetSuffixLengthArray(char[] pattern)
{
int m = pattern.Length;
int[] suffixLengthArray = new int[m];
int f = 0, g = 0, i = 0;
suffixLengthArray[m - 1] = m;
g = m - 1;
for (i = m - 2; i >= 0; --i)
{
if (i > g && suffixLengthArray[i + m - 1 - f] < i - g)
{
suffixLengthArray[i] = suffixLengthArray[i + m - 1 - f];
}
else
{
if (i < g)
{
g = i;
}
f = i;
// find different preceded character suffix
while (g >= 0 && pattern[g] == pattern[g + m - 1 - f])
{
--g;
}
suffixLengthArray[i] = f - g;
}
}
return suffixLengthArray;
}
public static bool TryMatch(char[] text, char[] pattern, out int firstShift)
{
firstShift = -1;
int n = text.Length;
int m = pattern.Length;
int s = 0; // s is shift of the pattern with respect to text
int j = 0;
// fill the bad character and good suffix array by preprocessing
int[] badCharShifts = PreprocessToBuildBadCharactorHeuristic(pattern);
int[] goodSuffixShifts = PreprocessToBuildGoodSuffixHeuristic(pattern);
while (s <= (n - m))
{
// starts matching from the last character of the pattern
j = m - 1;
// keep reducing index j of pattern while characters of
// pattern and text are matching at this shift s
while (j >= 0 && pattern[j] == text[s + j])
{
j--;
}
// if the pattern is present at current shift, then index j
// will become -1 after the above loop
if (j < 0)
{
firstShift = s;
return true;
}
else
{
// shift the pattern so that the bad character in text
// aligns with the last occurrence of it in pattern. the
// max function is used to make sure that we get a positive
// shift. We may get a negative shift if the last occurrence
// of bad character in pattern is on the right side of the
// current character.
//s += Max(1, j - badCharShifts[(int)text[s + j]]);
// now, compare bad char shift and good suffix shift to find best
s += Max(goodSuffixShifts[j], badCharShifts[(int)text[s + j]] - (m - 1) + j);
}
}
return false;
}
public static int[] MatchAll(char[] text, char[] pattern)
{
int n = text.Length;
int m = pattern.Length;
int s = 0; // s is shift of the pattern with respect to text
int j = 0;
int[] shiftIndexes = new int[n - m + 1];
int c = 0;
// fill the bad character and good suffix array by preprocessing
int[] badCharShifts = PreprocessToBuildBadCharactorHeuristic(pattern);
int[] goodSuffixShifts = PreprocessToBuildGoodSuffixHeuristic(pattern);
while (s <= (n - m))
{
// starts matching from the last character of the pattern
j = m - 1;
// keep reducing index j of pattern while characters of
// pattern and text are matching at this shift s
while (j >= 0 && pattern[j] == text[s + j])
{
j--;
}
// if the pattern is present at current shift, then index j
// will become -1 after the above loop
if (j < 0)
{
shiftIndexes[c] = s;
c++;
// shift the pattern so that the next character in text
// aligns with the last occurrence of it in pattern.
// the condition s+m < n is necessary for the case when
// pattern occurs at the end of text
//s += (s + m < n) ? m - badCharShifts[(int)text[s + m]] : 1;
s += goodSuffixShifts[0];
}
else
{
// shift the pattern so that the bad character in text
// aligns with the last occurrence of it in pattern. the
// max function is used to make sure that we get a positive
// shift. We may get a negative shift if the last occurrence
// of bad character in pattern is on the right side of the
// current character.
//s += Max(1, j - badCharShifts[(int)text[s + j]]);
// now, compare bad char shift and good suffix shift to find best
s += Max(goodSuffixShifts[j], badCharShifts[(int)text[s + j]] - (m - 1) + j);
}
}
int[] shifts = new int[c];
for (int y = 0; y < c; y++)
{
shifts[y] = shiftIndexes[y];
}
return shifts;
}
}
}
多阶hash表
原文:https://blog.csdn.net/wm_1991/article/details/52218718
多阶hash表实际上是一个锯齿数组,看起来是这个样子的:
■■■■■■■■■■■■■■■
■■■■■■■■■■■■■
■■■■■■■■■■
■■■■■■
■■■
每一行是一阶,上面的元素个数多,下面的元素个数依次减少。
每一行的元素个数都是素数的。
数组的每个节点用于存储数据的内容,其中,节点的前四个字节用于存储int类型的key或者是hash_code
创建多阶HASH的时候,用户通过参数来指定有多少阶,每一阶最多多少个元素。
那么,下面的每一阶究竟应该选择多少个元素呢?从代码注释上看来,是采用了素数集中原理的算法来查找的。
例如,假设每阶最多1000个元素,一共10阶,则算法选择十个比1000小的最大素数,从大到小排列,以此作为各阶的元素个数。通过素数集中的算法得到的10个素数分别是:997 991 983 977 971 967 953 947 941 937。
可见,虽然是锯齿数组,各层之间的差别并不是很多。
查找过程:
- 先将key在第一阶内取模,看是否是这个元素,如果这个位置为空,直接返回不存在;如果是这个KEY,则返回这个位置。
- 如果这个位置有元素,但是又不是这个key,则说明hash冲突,再到第二阶去找。
- 循环往复。
好处:
- hash冲突的处理非常简单;
- 有多个桶,使得空间利用率很高,你并不需要一个很大的桶来减少冲突。
- 可以考虑动态增长空间,不断加入新的一阶,且对原来的数据没影响。
使用共享内存的多级哈希表的一种实现
在一个服务程序运行的时候,它往往要把数据写入共享内存以便在进城需要重新启动的时候可以直接从共享内存中读取数据,另一方面,在服务进程因某种原因挂掉的时候,共享内存中的数据仍然存在,这样就可以减少带来的损失。关于共享内存的内容请google之,在这里,实现了一种在共享内存中存取数据的hash表,它采用了多级存储求模取余的方法,具体内容请看以下代码:
http://lmlf001.blog.sohu.com/
1 |
|
1 |
|
这段代码作测试的时候发现了一些问题,用gprof查看函数时间的时候发现,getPos函数占用了大部分的执行时间,始主要的性能瓶颈,后来又新设立了一个数组,用来记录每行开始时的位置,性能提高了很多,改动部分的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38template<typename valueType,unsigned long maxLine,int lines>
class hash_shm
{
private:
void *mem; //the start position of the share memory // the mem+memSize space used to storage the runtime data:currentSize
unsigned long memSize; //the size of the share memory
unsigned long modTable[lines]; //modtable,the largest primes
unsigned long modTotal[lines]; //modTotal[i] is the summary of the modTable when x<=i
//used by getPos to improve the performance
...
};
template<typename vT,unsigned long maxLine,int lines>
hash_shm<vT,maxLine,lines>::hash_shm(void *startShm,unsigned long shmSize)
{
...
int i;
for(i=0;i<lines;i++){ //count the maxSize
maxSize+=modTable[i];
if(i!=0)modTotal[i]=modTotal[i-1]+modTable[i-1];
else modTotal[i]=0; //caculate the modTotal
}
...
}
template<typename vT,unsigned long maxLine,int lines>
hash_shm<vT,maxLine,lines>::hash_shm(key_t shm_key)
{ //constructor with get share memory
getMode();
maxSize=0;
for(int i=0;i<lines;i++){
maxSize+=modTable[i];
if(i!=0)modTotal[i]=modTotal[i-1]+modTable[i-1];
else modTotal[i]=0;
}
...
}
1 | template<typename vT,unsigned long maxLine,int lines> |
新增了一个用于遍历的函数foreach1
2
3
4
5
6
7
8
9
10
11
12
13template<typename vT,unsigned long maxLine,int lines>
void hash_shm<vT,maxLine,lines>::foreach(void (*fn)(unsigned long _key,vT &_value))
{
typedef unsigned long u_long;
u_long beg=(u_long)mem;
u_long end=(u_long)mem+sizeof(hash_node)*(modTable[lines-1]+modTotal[lines-1]);
hash_node *p=NULL;
for(u_long pos=beg;pos<end;pos+=sizeof(hash_node))
{
p=(hash_node *)pos;
if(p->key!=0)fn(p->key,p->value);
}
}
为了利于使用新增一个用于查找的函数find,该函数同find(_key)类似,如果找到_key节点,把它赋给_value以返回1
int find(unsigned long _key,vT &_value);
Hash碰撞冲突
我们知道,对象Hash的前提是实现equals()和hashCode()两个方法,那么HashCode()的作用就是保证对象返回唯一hash值,但当两个对象计算值一样时,这就发生了碰撞冲突。如下将介绍如何处理冲突,当然其前提是一致性hash。
开放地址法
开放地执法有一个公式:Hi=(H(key)+di) MOD m i=1,2,…,k(k<=m-1)
其中,m为哈希表的表长。di 是产生冲突的时候的增量序列。如果di值可能为1,2,3,…m-1,称线性探测再散列。
如果di取1,则每次冲突之后,向后移动1个位置.如果di取值可能为1,-1,2,-2,4,-4,9,-9,16,-16,…kk,-kk(k<=m/2),称二次探测再散列。
如果di取值可能为伪随机数列。称伪随机探测再散列。再哈希法
当发生冲突时,使用第二个、第三个、哈希函数计算地址,直到无冲突时。缺点:计算时间增加。
比如上面第一次按照姓首字母进行哈希,如果产生冲突可以按照姓字母首字母第二位进行哈希,再冲突,第三位,直到不冲突为止链地址法(拉链法)
将所有关键字为同义词的记录存储在同一线性链表中。如下: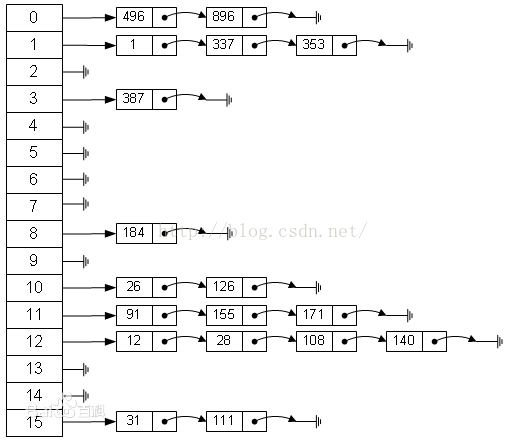
因此这种方法,可以近似的认为是筒子里面套筒子
- 建立一个公共溢出区
假设哈希函数的值域为[0,m-1],则设向量HashTable[0..m-1]为基本表,另外设立存储空间向量OverTable[0..v]用以存储发生冲突的记录。
拉链法的优缺点:
优点:
- 拉链法处理冲突简单,且无堆积现象,即非同义词决不会发生冲突,因此平均查找长度较短;
- 由于拉链法中各链表上的结点空间是动态申请的,故它更适合于造表前无法确定表长的情况;
- 开放定址法为减少冲突,要求装填因子α较小,故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1,且结点较大时,拉链法中增加的指针域可忽略不计,因此节省空间;
- 在用拉链法构造的散列表中,删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。而对开放地址法构造的散列表,删除结点不能简单地将被删结 点的空间置为空,否则将截断在它之后填人散列表的同义词结点的查找路径。这是因为各种开放地址法中,空地址单元(即开放地址)都是查找失败的条件。因此在 用开放地址法处理冲突的散列表上执行删除操作,只能在被删结点上做删除标记,而不能真正删除结点。
缺点:
- 指针需要额外的空间,故当结点规模较小时,开放定址法较为节省空间,而若将节省的指针空间用来扩大散列表的规模,可使装填因子变小,这又减少了开放定址法中的冲突,从而提高平均查找速度。
经典字符串hash函数介绍及性能比较
原文:https://blog.csdn.net/djinglan/article/details/8812934
今天根据自己的理解重新整理了一下几个字符串hash函数,使用了模板,使其支持宽字符串,代码如下:
1 | /// @brief BKDR Hash Function |
我对这些hash的散列质量及效率作了一个简单测试,测试结果如下:
测试1:对100000个由大小写字母与数字随机的ANSI字符串(无重复,每个字符串最大长度不超过64字符)进行散列: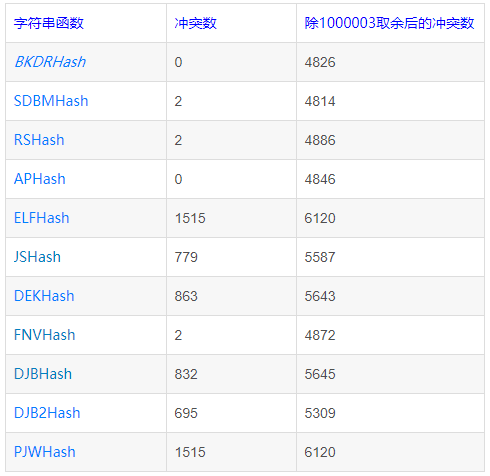
测试2:对100000个由任意UNICODE组成随机字符串(无重复,每个字符串最大长度不超过64字符)进行散列:
测试3:对1000000个随机ANSI字符串(无重复,每个字符串最大长度不超过64字符)进行散列: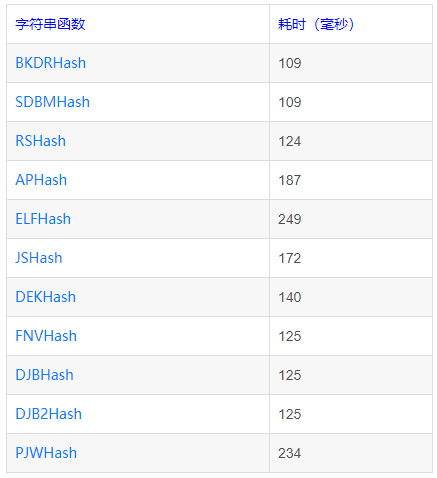
结论:也许是我的样本存在一些特殊性,在对ASCII码字符串进行散列时,PJW与ELF Hash(它们其实是同一种算法)无论是质量还是效率,都相当糟糕;例如:”b5”与“aE”,这两个字符串按照PJW散列出来的hash值就是一样的。 另外,其它几种依靠异或来散列的哈希函数,如:JS/DEK/DJB Hash,在对字母与数字组成的字符串的散列效果也不怎么好。相对而言,还是BKDR与SDBM这类简单的Hash效率与效果更好。
常用的字符串Hash函数还有ELFHash,APHash等等,都是十分简单有效的方法。这些函数使用位运算使得每一个字符都对最后的函数值产生 影响。另外还有以MD5和SHA1为代表的杂凑函数,这些函数几乎不可能找到碰撞。
常用字符串哈希函数有 BKDRHash,APHash,DJBHash,JSHash,RSHash,SDBMHash,PJWHash,ELFHash等等。对于以上几种哈 希函数,我对其进行了一个小小的评测。
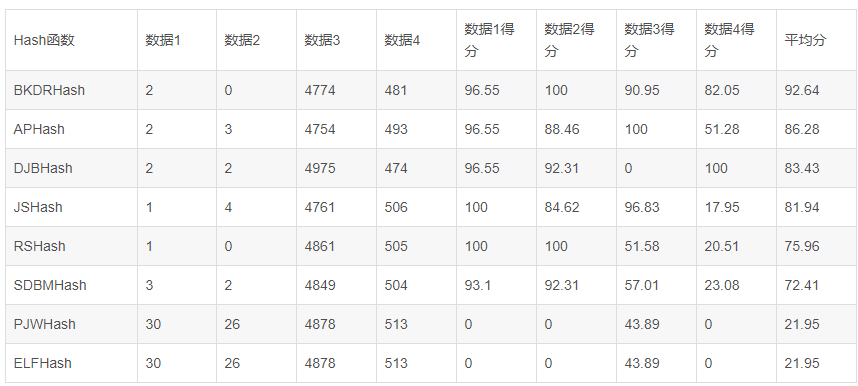
其中数据1为100000个字母和数字组成的随机串哈希冲突个数。数据2为100000个有意义的英文句子哈希冲突个数。数据3为数据1的哈希值与 1000003(大素数)求模后存储到线性表中冲突的个数。数据4为数据1的哈希值与10000019(更大素数)求模后存储到线性表中冲突的个数。
经过比较,得出以上平均得分。平均数为平方平均数。可以发现,BKDRHash无论是在实际效果还是编码实现中,效果都是最突出的。APHash也 是较为优秀的算法。DJBHash,JSHash,RSHash与SDBMHash各有千秋。PJWHash与ELFHash效果最差,但得分相似,其算 法本质是相似的。
Merkle Tree
概念
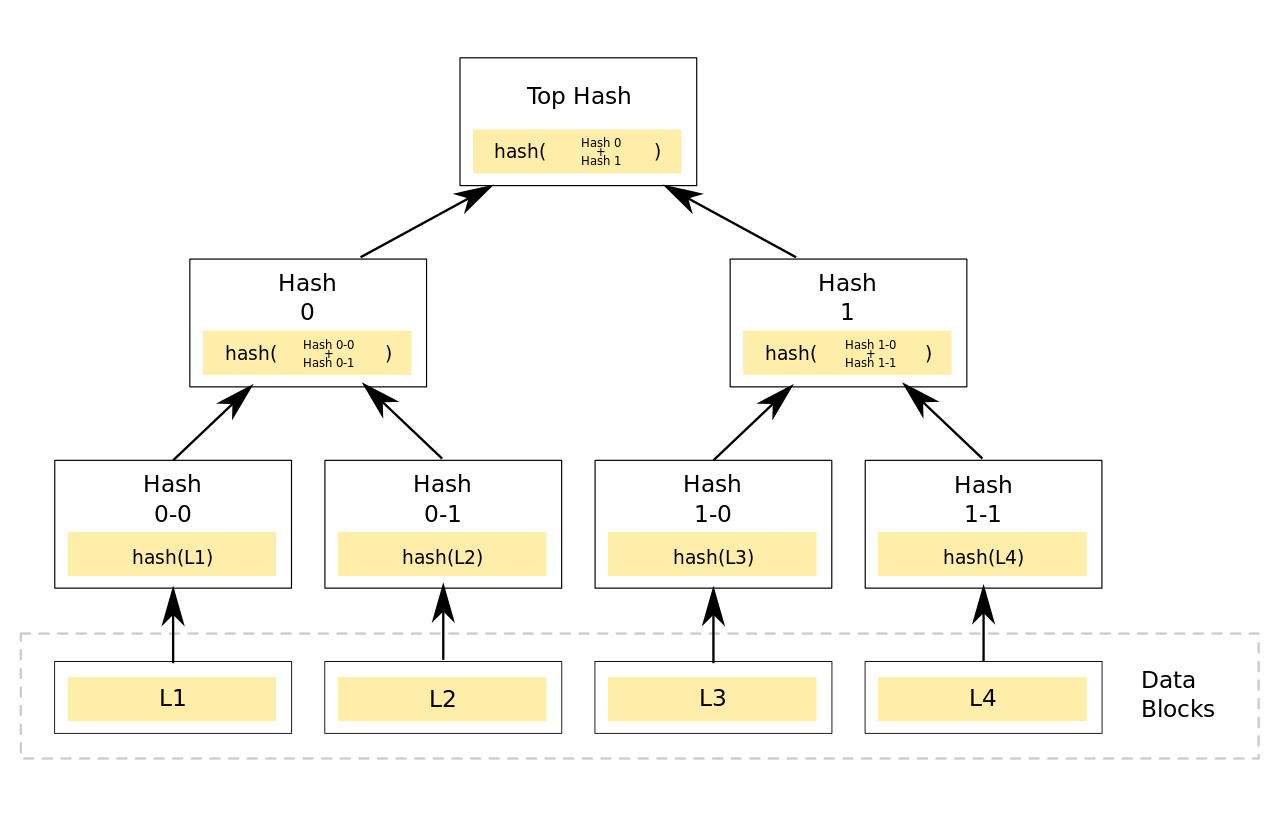
Merkle Tree,通常也被称作Hash Tree,顾名思义,就是存储hash值的一棵树。Merkle树的叶子是数据块(例如,文件或者文件的集合)的hash值。非叶节点是其对应子节点串联字符串的hash。[1]
Hash
Hash是一个把任意长度的数据映射成固定长度数据的函数[2]。例如,对于数据完整性校验,最简单的方法是对整个数据做Hash运算得到固定长度的Hash值,然后把得到的Hash值公布在网上,这样用户下载到数据之后,对数据再次进行Hash运算,比较运算结果和网上公布的Hash值进行比较,如果两个Hash值相等,说明下载的数据没有损坏。可以这样做是因为输入数据的稍微改变就会引起Hash运算结果的面目全非,而且根据Hash值反推原始输入数据的特征是困难的。
如果从一个稳定的服务器进行下载,采用单一Hash是可取的。但如果数据源不稳定,一旦数据损坏,就需要重新下载,这种下载的效率是很低的。
Hash List
在点对点网络中作数据传输的时候,会同时从多个机器上下载数据,而且很多机器可以认为是不稳定或者不可信的。为了校验数据的完整性,更好的办法是把大的文件分割成小的数据块(例如,把分割成2K为单位的数据块)。这样的好处是,如果小块数据在传输过程中损坏了,那么只要重新下载这一快数据就行了,不用重新下载整个文件。
怎么确定小的数据块没有损坏哪?只需要为每个数据块做Hash。BT下载的时候,在下载到真正数据之前,我们会先下载一个Hash列表。那么问题又来了,怎么确定这个Hash列表本事是正确的哪?答案是把每个小块数据的Hash值拼到一起,然后对这个长字符串在作一次Hash运算,这样就得到Hash列表的根Hash(Top Hash or Root Hash)。下载数据的时候,首先从可信的数据源得到正确的根Hash,就可以用它来校验Hash列表了,然后通过校验后的Hash列表校验数据块。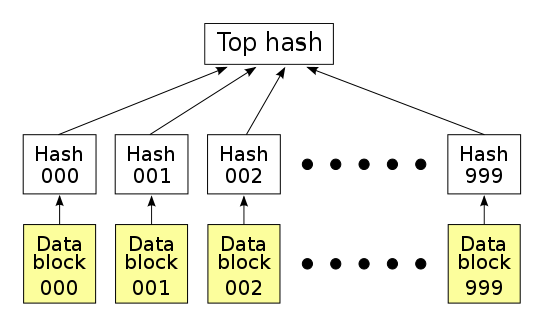
Merkle Tree
Merkle Tree可以看做Hash List的泛化(Hash List可以看作一种特殊的Merkle Tree,即树高为2的多叉Merkle Tree)。
在最底层,和哈希列表一样,我们把数据分成小的数据块,有相应地哈希和它对应。但是往上走,并不是直接去运算根哈希,而是把相邻的两个哈希合并成一个字符串,然后运算这个字符串的哈希,这样每两个哈希就结婚生子,得到了一个”子哈希“。如果最底层的哈希总数是单数,那到最后必然出现一个单身哈希,这种情况就直接对它进行哈希运算,所以也能得到它的子哈希。于是往上推,依然是一样的方式,可以得到数目更少的新一级哈希,最终必然形成一棵倒挂的树,到了树根的这个位置,这一代就剩下一个根哈希了,我们把它叫做 Merkle Root[3]。
在p2p网络下载网络之前,先从可信的源获得文件的Merkle Tree树根。一旦获得了树根,就可以从其他从不可信的源获取Merkle tree。通过可信的树根来检查接受到的Merkle Tree。如果Merkle Tree是损坏的或者虚假的,就从其他源获得另一个Merkle Tree,直到获得一个与可信树根匹配的Merkle Tree。
Merkle Tree和Hash List的主要区别是,可以直接下载并立即验证Merkle Tree的一个分支。因为可以将文件切分成小的数据块,这样如果有一块数据损坏,仅仅重新下载这个数据块就行了。如果文件非常大,那么Merkle tree和Hash list都很到,但是Merkle tree可以一次下载一个分支,然后立即验证这个分支,如果分支验证通过,就可以下载数据了。而Hash list只有下载整个hash list才能验证。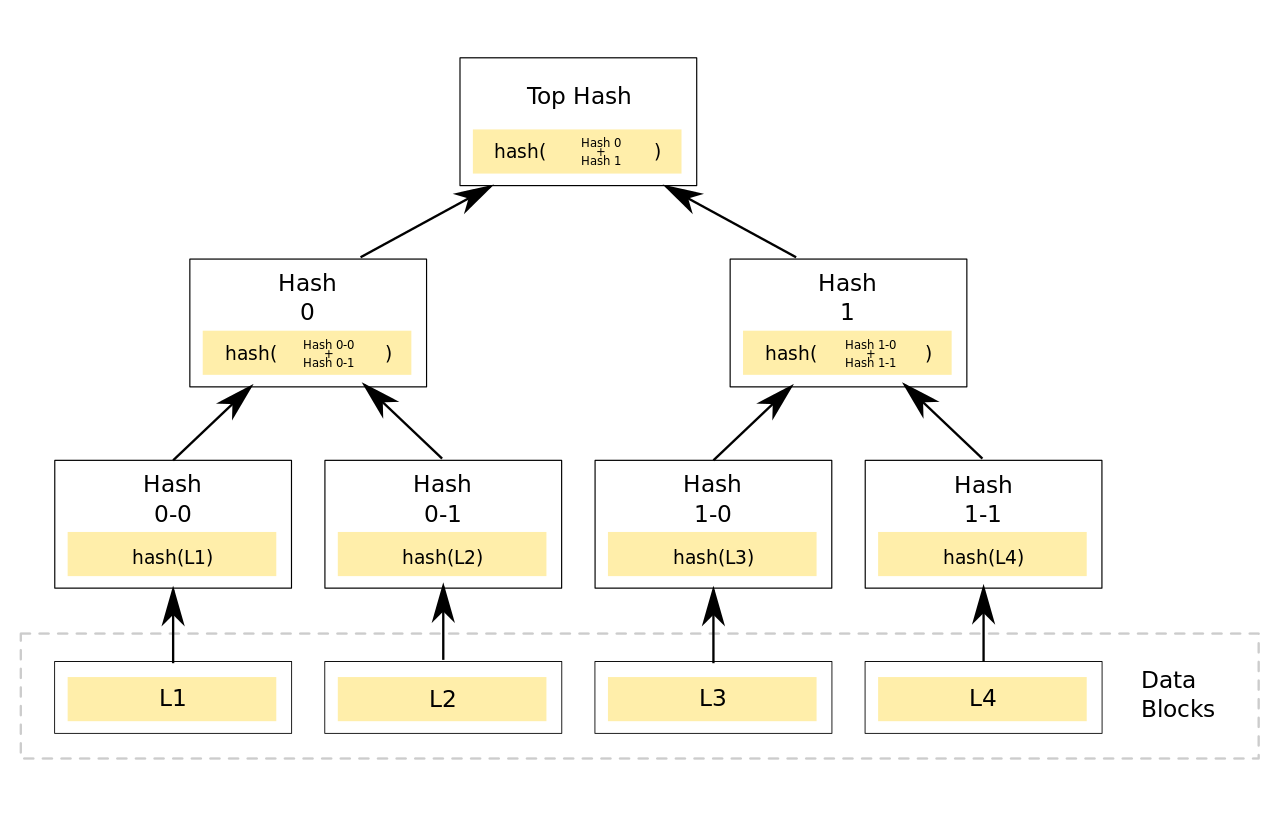
Merkle Tree的特点
MT是一种树,大多数是二叉树,也可以多叉树,无论是几叉树,它都具有树结构的所有特点;
Merkle Tree的叶子节点的value是数据集合的单元数据或者单元数据HASH。
非叶子节点的value是根据它下面所有的叶子节点值,然后按照Hash算法计算而得出的。[4][5]
通常,加密的hash方法像SHA-2和MD5用来做hash。但如果仅仅防止数据不是蓄意的损坏或篡改,可以改用一些安全性低但效率高的校验和算法,如CRC。
Second Preimage Attack: Merkle tree的树根并不表示树的深度,这可能会导致second-preimage attack,即攻击者创建一个具有相同Merkle树根的虚假文档。一个简单的解决方法在Certificate Transparency中定义:当计算叶节点的hash时,在hash数据前加0x00。当计算内部节点是,在前面加0x01。另外一些实现限制hash tree的根,通过在hash值前面加深度前缀。因此,前缀每一步会减少,只有当到达叶子时前缀依然为正,提取的hash链才被定义为有效。
Merkle Tree的操作
创建Merckle Tree
加入最底层有9个数据块。
step1:(红色线)对数据块做hash运算,Node0i = hash(Data0i), i=1,2,…,9
step2: (橙色线)相邻两个hash块串联,然后做hash运算,Node1((i+1)/2) = hash(Node0i+Node0(i+1)), i=1,3,5,7;对于i=9, Node1((i+1)/2) = hash(Node0i)
step3: (黄色线)重复step2
step4:(绿色线)重复step2
step5:(蓝色线)重复step2,生成Merkle Tree Root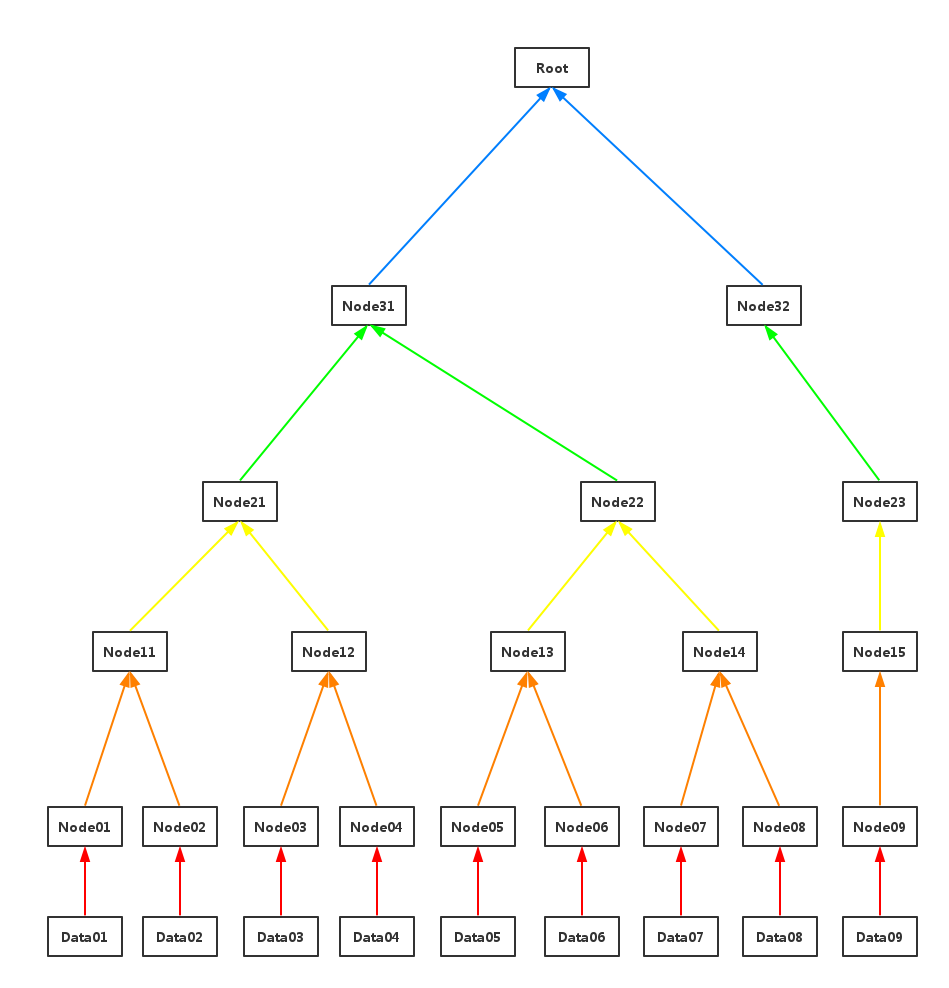
易得,创建Merkle Tree是O(n)复杂度(这里指O(n)次hash运算),n是数据块的大小。得到Merkle Tree的树高是log(n)+1。
检索数据块
为了更好理解,我们假设有A和B两台机器,A需要与B相同目录下有8个文件,文件分别是f1 f2 f3 ….f8。这个时候我们就可以通过Merkle Tree来进行快速比较。假设我们在文件创建的时候每个机器都构建了一个Merkle Tree。具体如下图: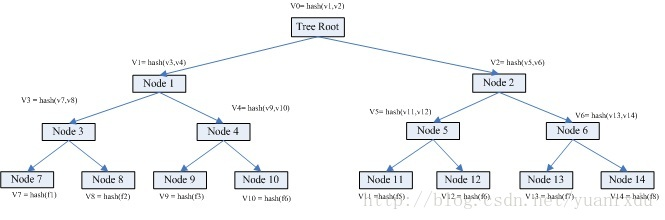
从上图可得知,叶子节点node7的value = hash(f1),是f1文件的HASH;而其父亲节点node3的value = hash(v7, v8),也就是其子节点node7 node8的值得HASH。就是这样表示一个层级运算关系。root节点的value其实是所有叶子节点的value的唯一特征。
假如A上的文件5与B上的不一样。我们怎么通过两个机器的merkle treee信息找到不相同的文件? 这个比较检索过程如下:
Step1. 首先比较v0是否相同,如果不同,检索其孩子node1和node2.
Step2. v1 相同,v2不同。检索node2的孩子node5 node6;
Step3. v5不同,v6相同,检索比较node5的孩子node 11 和node 12
Step4. v11不同,v12相同。node 11为叶子节点,获取其目录信息。
Step5. 检索比较完毕。
以上过程的理论复杂度是Log(N)。过程描述图如下: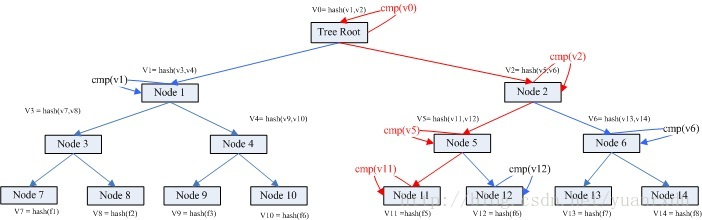
从上图可以得知真个过程可以很快的找到对应的不相同的文件。
更新,插入和删除
虽然网上有很多关于Merkle Tree的资料,但大部分没有涉及Merkle Tree的更新、插入和删除操作,讨论Merkle Tree的检索和遍历的比较多。我也是非常困惑,一种树结构的操作肯定不仅包括查找,也包括更新、插入和删除的啊。后来查到stackexchange上的一个问题,才稍微有点明白,原文见[6]。
对于Merkle Tree数据块的更新操作其实是很简单的,更新完数据块,然后接着更新其到树根路径上的Hash值就可以了,这样不会改变Merkle Tree的结构。但是,插入和删除操作肯定会改变Merkle Tree的结构,如下图,一种插入操作是这样的: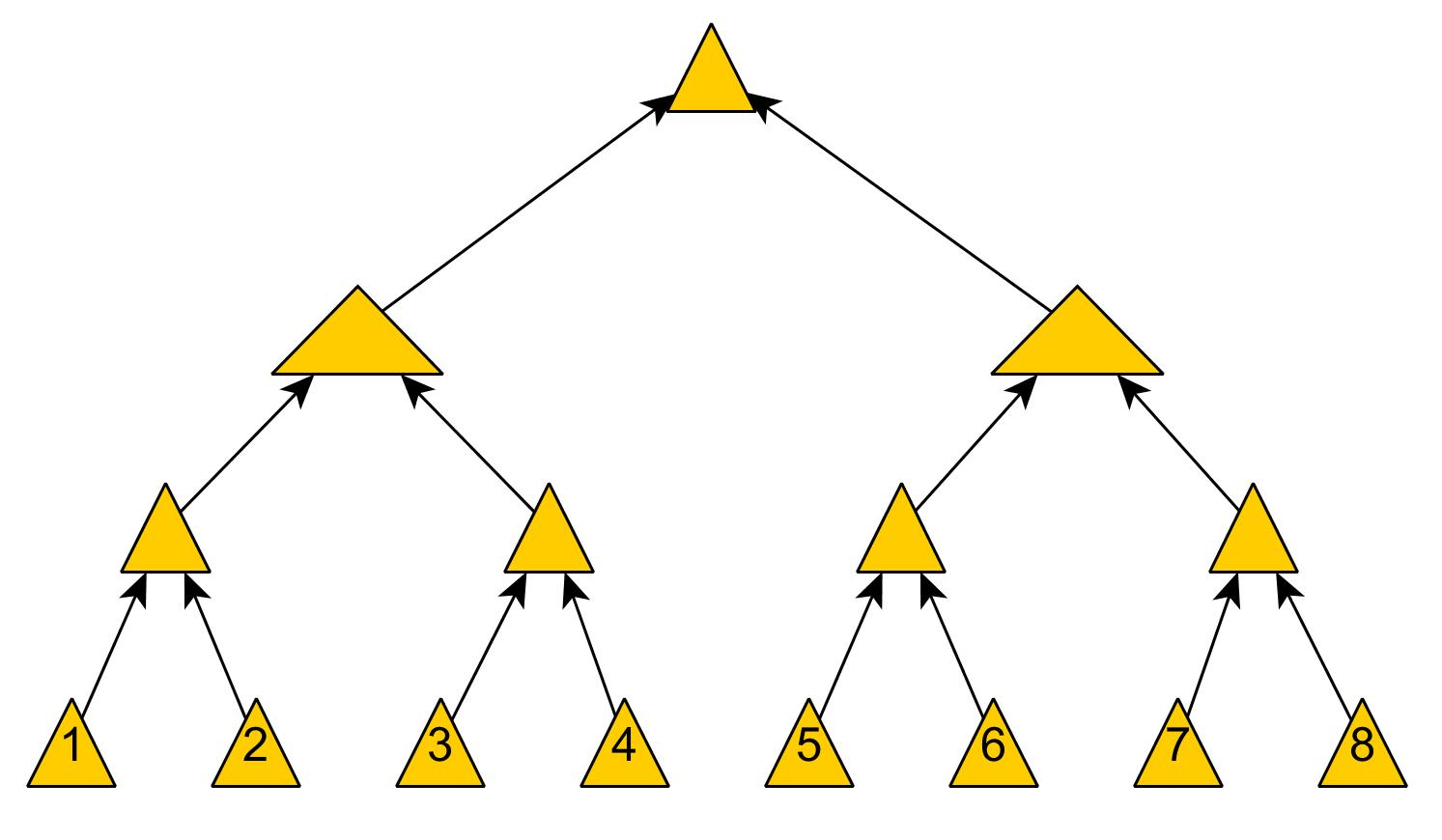
插入数据块0后(考虑数据块的位置),Merkle Tree的结构是这样的: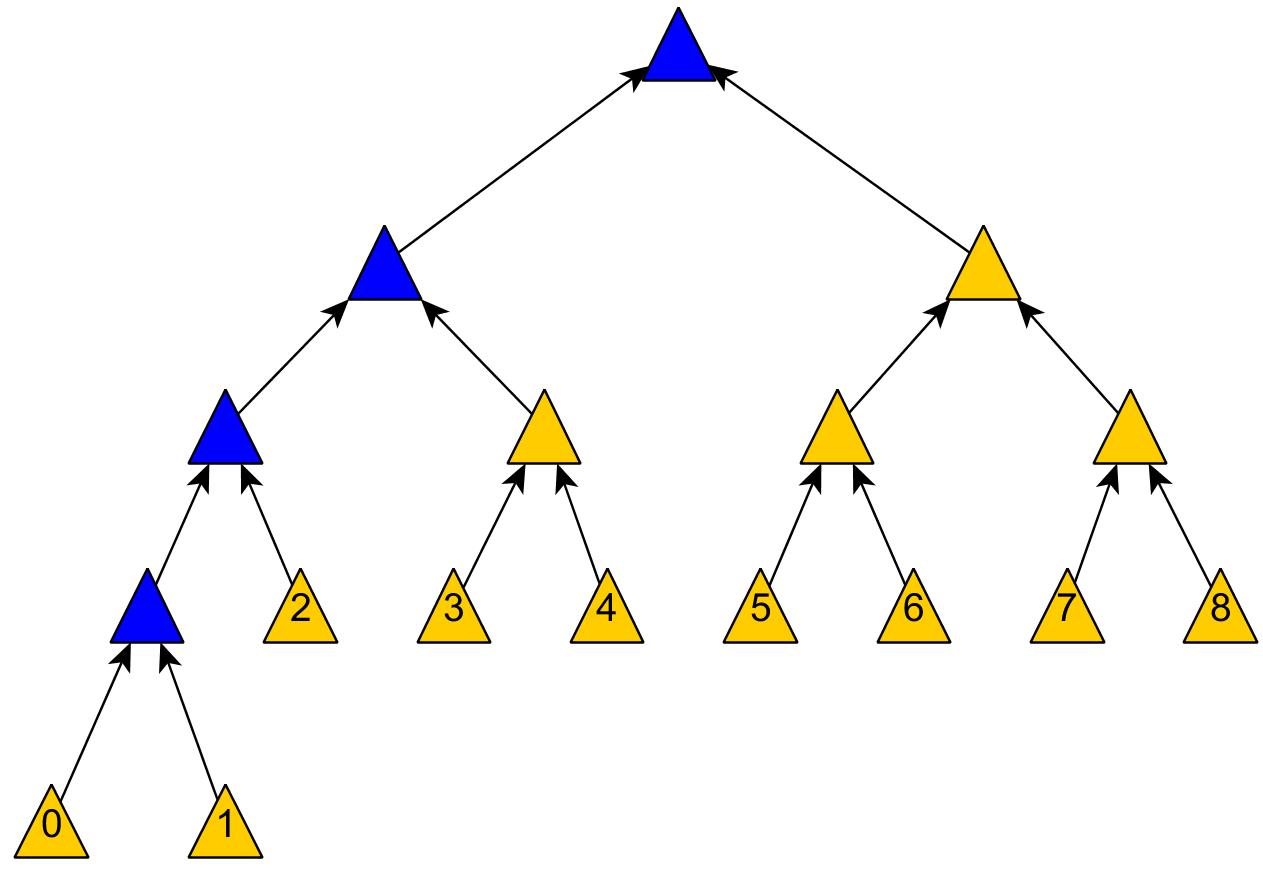
而[6]中的同学在考虑一种插入的算法,满足下面条件:
re-hashing操作的次数控制在log(n)以内
数据块的校验在log(n)+1以内
除非原始树的n是偶数,插入数据后的树没有孤儿,并且如果有孤儿,那么孤儿是最后一个数据块
数据块的顺序保持一致
插入后的Merkle Tree保持平衡
然后上面的插入结果就会变成这样: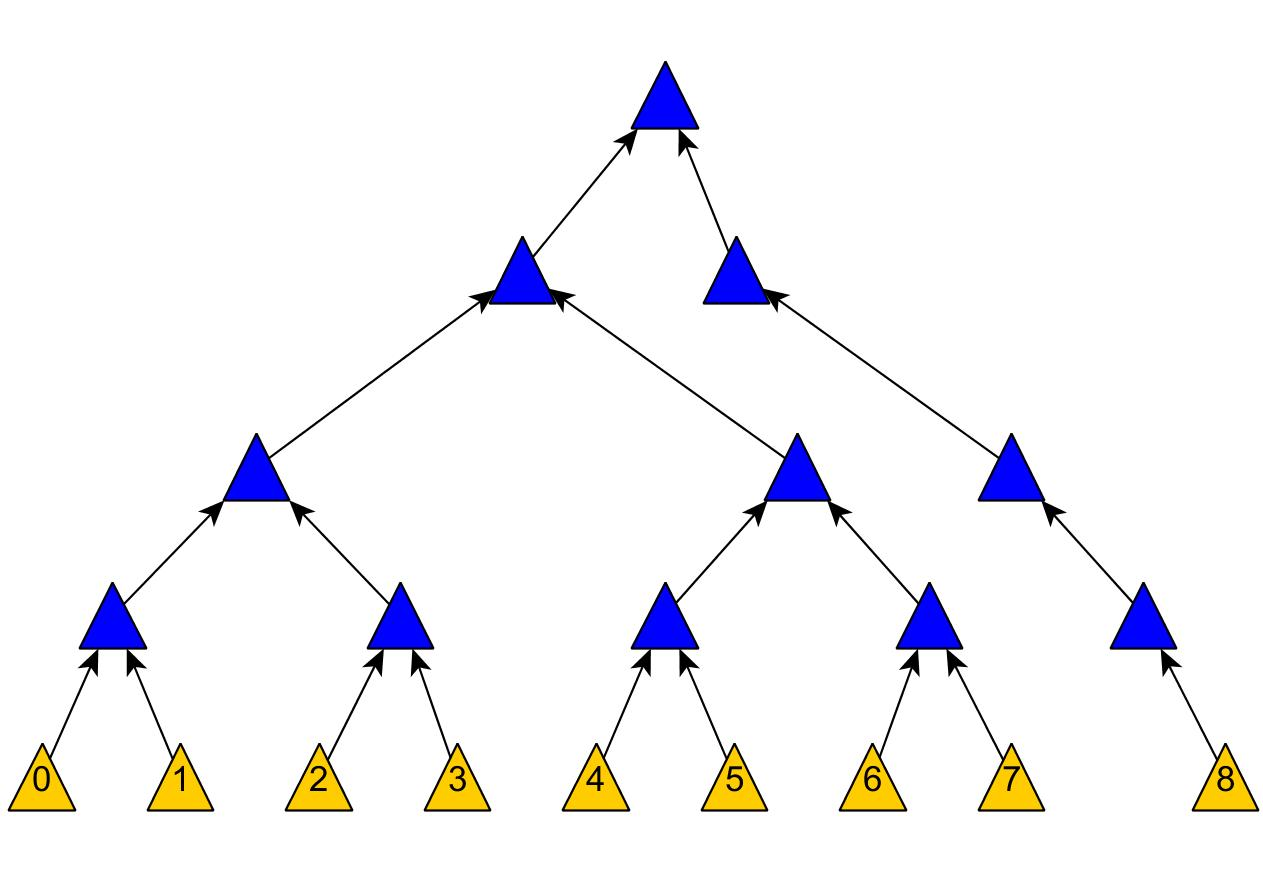
根据[6]中回答者所说,Merkle Tree的插入和删除操作其实是一个工程上的问题,不同问题会有不同的插入方法。如果要确保树是平衡的或者是树高是log(n)的,可以用任何的标准的平衡二叉树的模式,如AVL树,红黑树,伸展树,2-3树等。这些平衡二叉树的更新模式可以在O(lgn)时间内完成插入操作,并且能保证树高是O(lgn)的。那么很容易可以看出更新所有的Merkle Hash可以在O((lgn)2)时间内完成(对于每个节点如要更新从它到树根O(lgn)个节点,而为了满足树高的要求需要更新O(lgn)个节点)。如果仔细分析的话,更新所有的hash实际上可以在O(lgn)时间内完成,因为要改变的所有节点都是相关联的,即他们要不是都在从某个叶节点到树根的一条路径上,或者这种情况相近。
[6]的回答者说实际上Merkle Tree的结构(是否平衡,树高限制多少)在大多数应用中并不重要,而且保持数据块的顺序也在大多数应用中也不需要。因此,可以根据具体应用的情况,设计自己的插入和删除操作。一个通用的Merkle Tree插入删除操作是没有意义的。
Merkle Tree的应用
数字签名
最初Merkle Tree目的是高效的处理Lamport one-time signatures。 每一个Lamport key只能被用来签名一个消息,但是与Merkle tree结合可以来签名多条Merkle。这种方法成为了一种高效的数字签名框架,即Merkle Signature Scheme。
P2P网络
在P2P网络中,Merkle Tree用来确保从其他节点接受的数据块没有损坏且没有被替换,甚至检查其他节点不会欺骗或者发布虚假的块。大家所熟悉的BT下载就是采用了P2P技术来让客户端之间进行数据传输,一来可以加快数据下载速度,二来减轻下载服务器的负担。BT即BitTorrent,是一种中心索引式的P2P文件分分析通信协议[7]。
要进下载必须从中心索引服务器获取一个扩展名为torrent的索引文件(即大家所说的种子),torrent文件包含了要共享文件的信息,包括文件名,大小,文件的Hash信息和一个指向Tracker的URL[8]。Torrent文件中的Hash信息是每一块要下载的文件内容的加密摘要,这些摘要也可运行在下载的时候进行验证。大的torrent文件是Web服务器的瓶颈,而且也不能直接被包含在RSS或gossiped around(用流言传播协议进行传播)。一个相关的问题是大数据块的使用,因为为了保持torrent文件的非常小,那么数据块Hash的数量也得很小,这就意味着每个数据块相对较大。大数据块影响节点之间进行交易的效率,因为只有当大数据块全部下载下来并校验通过后,才能与其他节点进行交易。
就解决上面两个问题是用一个简单的Merkle Tree代替Hash List。设计一个层数足够多的满二叉树,叶节点是数据块的Hash,不足的叶节点用0来代替。上层的节点是其对应孩子节点串联的hash。Hash算法和普通torrent一样采用SHA1。其数据传输过程和第一节中描述的类似。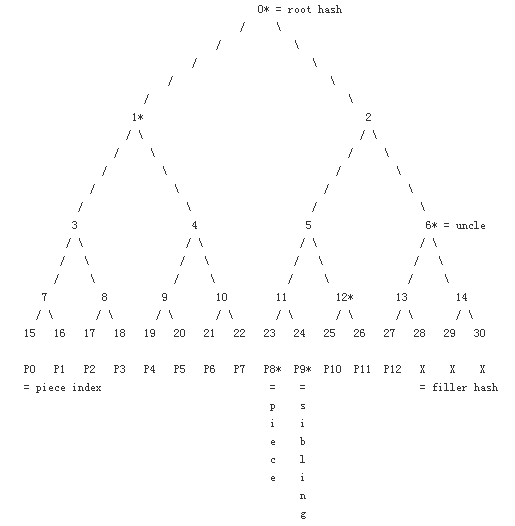
Trusted Computing
可信计算是可信计算组为分布式计算环境中参与节点的计算平台提供端点可信性而提出的。可信计算技术在计算平台的硬件层引入可信平台模块(Trusted Platform,TPM),实际上为计算平台提供了基于硬件的可信根(Root of trust,RoT)。从可信根出发,使用信任链传递机制,可信计算技术可对本地平台的硬件及软件实施逐层的完整性度量,并将度量结果可靠地保存再TPM的平台配置寄存器(Platform configuration register,PCR)中,此后远程计算平台可通过远程验证机制(Remote Attestation)比对本地PCR中度量结果,从而验证本地计算平台的可信性。可信计算技术让分布式应用的参与节点摆脱了对中心服务器的依赖,而直接通过用户机器上的TPM芯片来建立信任,使得创建扩展性更好、可靠性更高、可用性更强的安全分布式应用成为可能[10]。可信计算技术的核心机制是远程验证(remote attestation),分布式应用的参与结点正是通过远程验证机制来建立互信,从而保障应用的安全。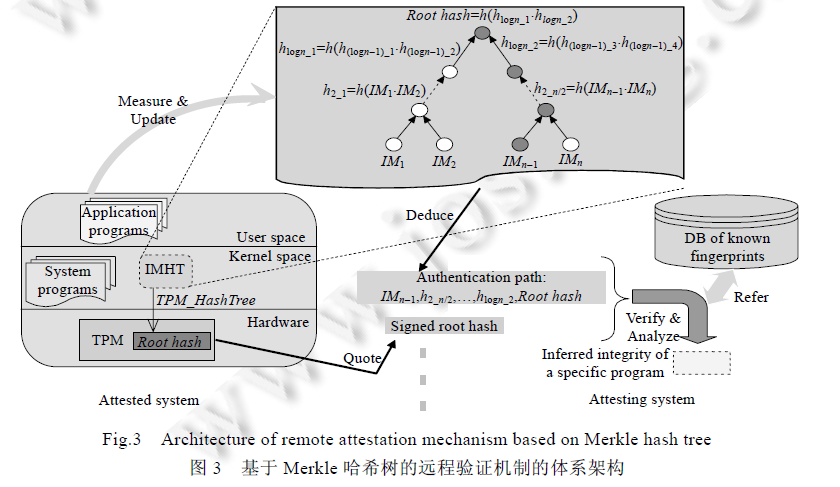
文献[10]提出了一种基于Merkle Tree的远程验证机制,其核心是完整性度量值哈希树。
首先,RAMT 在内核中维护的不再是一张完整性度量值列表(ML),而是一棵完整性度量值哈希树(integrity measurement hash tree,简称IMHT).其中,IMHT的叶子结点存储的数据对象是待验证计算平台上被度量的各种程序的完整性哈希值,而其内部结点则依据Merkle 哈希树的构建规则由子结点的连接的哈希值动态生成。
其次,为了维护IMHT 叶子结点的完整性,RAMT 需要使用TPM 中的一段存储器来保存IMHT 可信根哈希的值。
再次,RAMT 的完整性验证过程基于认证路径(authentication path)实施.认证路径是指IMHT 上从待验证叶子结点到根哈希的路径。
IPFS
IPFS(InterPlanetary File System)是很多NB的互联网技术的综合体,如DHT( Distributed HashTable,分布式哈希表),Git版本控制系统,Bittorrent等。它创建了一个P2P的集群,这个集群允许IPFS对象的交换。全部的IPFS对象形成了一个被称作Merkle DAG的加密认证数据结构。
IPFS对象是一个含有两个域的数据结构:
- Data – 非结构的二进制数据,大小小于256kB
- Links – 一个Link数据结构的数组。IPFS对象通过他们链接到其他对象
Link数据结构包含三个域:
- Name – Link的名字
- Hash – Link链接到对象的Hash
- Size – Link链接到对象的累积大小,包括它的Links
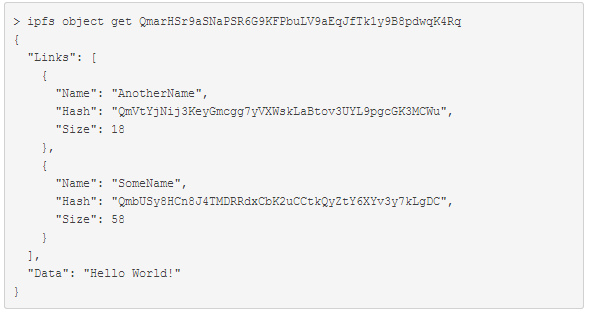
通过Name和Links,IPFS的集合组成了一个Merkle DAG(有向无环图)。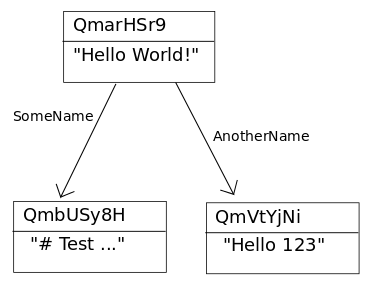
对于小文件(<256kB),是一个没有Links的IPFS对象。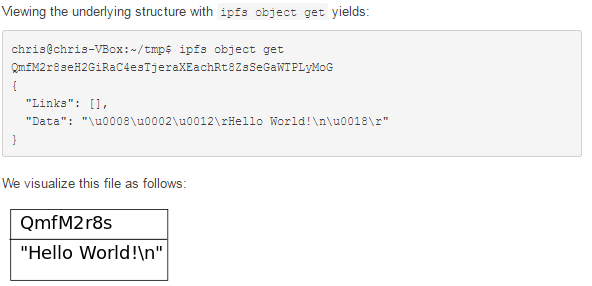
对于大文件,被表示为一个文件块(<256kB)的集合。只有拥有最小的Data的对象来代表这个大文件。这个对象的Links的名字都为空字符串。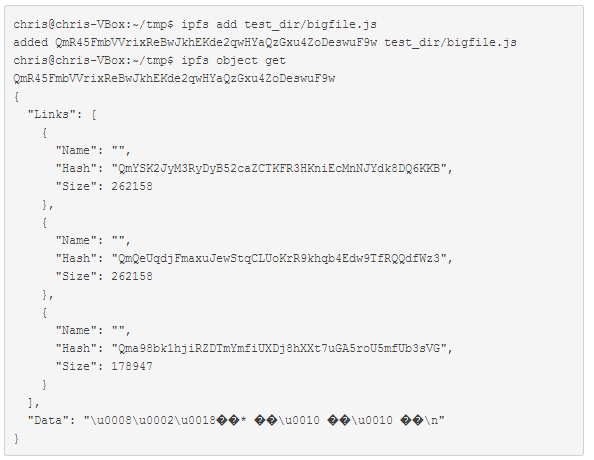
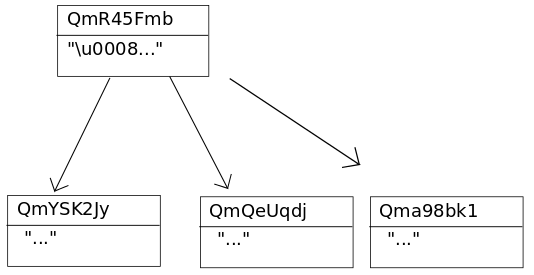
目录结构:目录是没有数据的IPFS对象,它的链接指向其包含的文件和目录。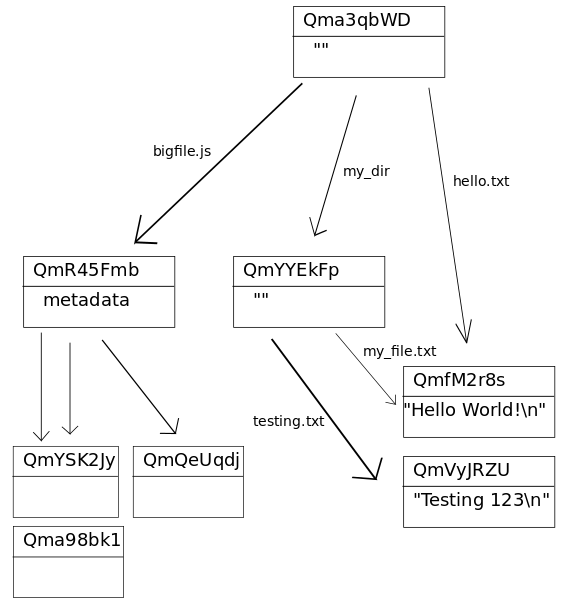
IPFS可以表示Git使用的数据结构,Git commit object。Commit Object主要的特点是他有一个或多个名为’parent0’和‘parent1’等的链接(这些链接指向前一个版本),以及一个名为object的对象(在Git中成为tree)指向引用这个commit的文件系统结构。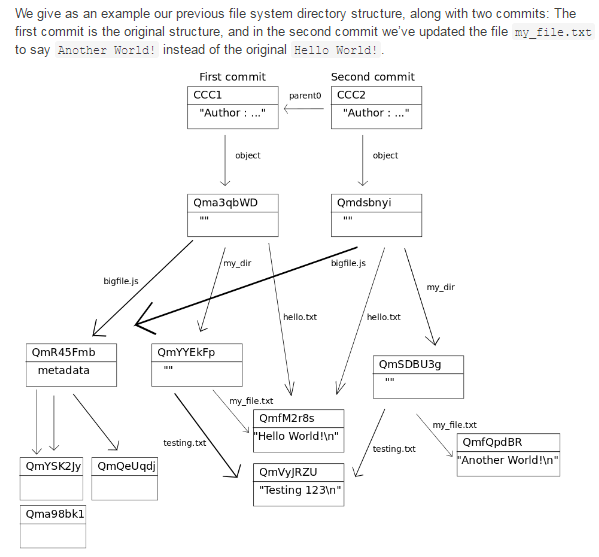
BitCoin和Ethereum
Merkle Proof最早的应用是Bitcoin,它是由中本聪在2009年描述并创建的。Bitcoin的Blockchain利用Merkle proofs来存储每个区块的交易。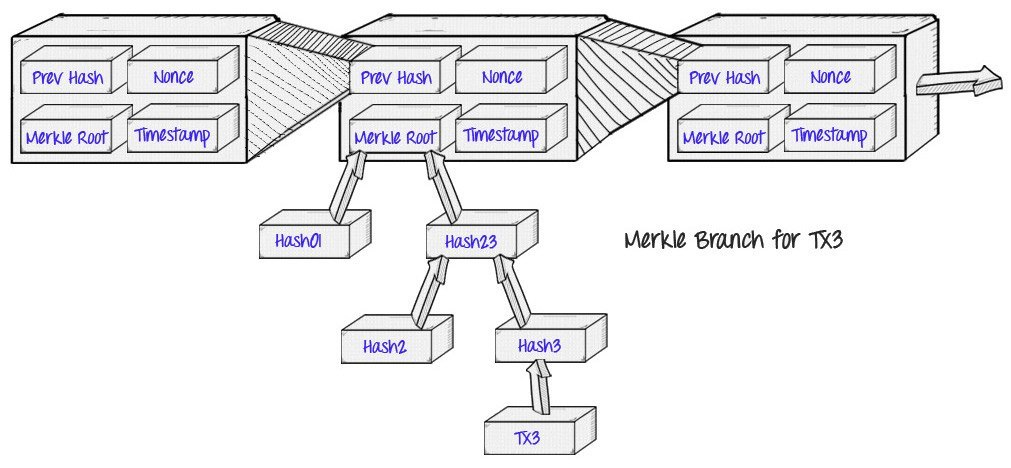
而这样做的好处,也就是中本聪描述到的“简化支付验证”(Simplified Payment Verification,SPV)的概念:一个“轻客户端”(light client)可以仅下载链的区块头即每个区块中的80byte的数据块,仅包含五个元素,而不是下载每一笔交易以及每一个区块:
- 上一区块头的哈希值
- 时间戳
- 挖矿难度值
- 工作量证明随机数(nonce)
- 包含该区块交易的Merkle Tree的根哈希
如果客户端想要确认一个交易的状态,它只需简单的发起一个Merkle proof请求,这个请求显示出这个特定的交易在Merkle trees的一个之中,而且这个Merkle Tree的树根在主链的一个区块头中。
但是Bitcoin的轻客户端有它的局限。一个局限是,尽管它可以证明包含的交易,但是它不能进行涉及当前状态的证明(如数字资产的持有,名称注册,金融合约的状态等)。
Bitcoin如何查询你当前有多少币?一个比特币轻客户端,可以使用一种协议,它涉及查询多个节点,并相信其中至少会有一个节点会通知你,关于你的地址中任何特定的交易支出,而这可以让你实现更多的应用。但对于其他更为复杂的应用而言,这些远远是不够的。一笔交易影响的确切性质(precise nature),可以取决于此前的几笔交易,而这些交易本身则依赖于更为前面的交易,所以最终你可以验证整个链上的每一笔交易。为了解决这个问题,Ethereum的Merkle Tree的概念,会更进一步。
Ethereum的Merkle Proof
每个以太坊区块头不是包括一个Merkle树,而是为三种对象设计的三棵树:
交易Transaction
收据Receipts(本质上是显示每个交易影响的多块数据)
状态State
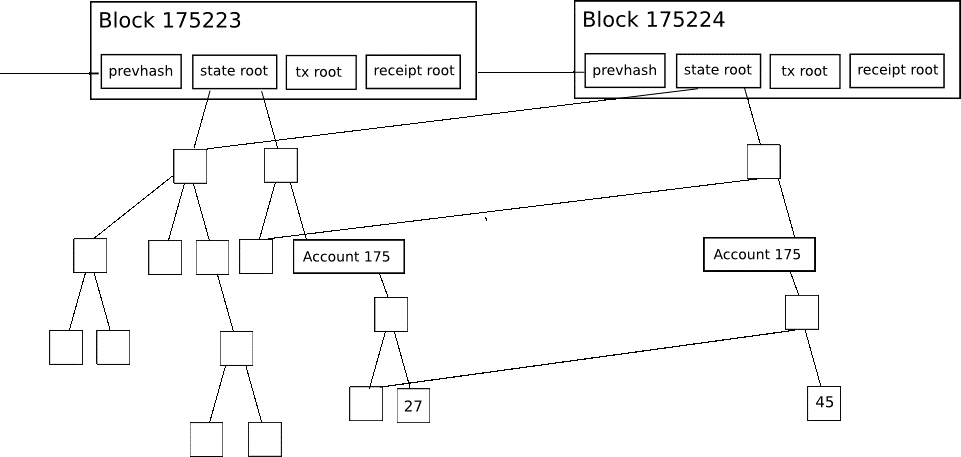
这使得一个非常先进的轻客户端协议成为了可能,它允许轻客户端轻松地进行并核实以下类型的查询答案:
这笔交易被包含在特定的区块中了么?
告诉我这个地址在过去30天中,发出X类型事件的所有实例(例如,一个众筹合约完成了它的目标)
目前我的账户余额是多少?
这个账户是否存在?
假如在这个合约中运行这笔交易,它的输出会是什么?
第一种是由交易树(transaction tree)来处理的;第三和第四种则是由状态树(state tree)负责处理,第二种则由收据树(receipt tree)处理。计算前四个查询任务是相当简单的。服务器简单地找到对象,获取Merkle分支,并通过分支来回复轻客户端。
第五种查询任务同样也是由状态树处理,但它的计算方式会比较复杂。这里,我们需要构建一个Merkle状态转变证明(Merkle state transition proof)。从本质上来讲,这样的证明也就是在说“如果你在根S的状态树上运行交易T,其结果状态树将是根为S’,log为L,输出为O” (“输出”作为存在于以太坊的一种概念,因为每一笔交易都是一个函数调用;它在理论上并不是必要的)。
为了推断这个证明,服务器在本地创建了一个假的区块,将状态设为 S,并在请求这笔交易时假装是一个轻客户端。也就是说,如果请求这笔交易的过程,需要客户端确定一个账户的余额,这个轻客户端(由服务器模拟的)会发出一个余额查询请求。如果需要轻客户端在特点某个合约的存储中查询特定的条目,这个轻客户端就会发出这样的请求。也就是说服务器(通过模拟一个轻客户端)正确回应所有自己的请求,但服务器也会跟踪它所有发回的数据。
然后,服务器从上述的这些请求中把数据合并并把数据以一个证明的方式发送给客户端。
然后,客户端会进行相同的步骤,但会将服务器提供的证明作为一个数据库来使用。如果客户端进行步骤的结果和服务器提供的是一样的话,客户端就接受这个证明。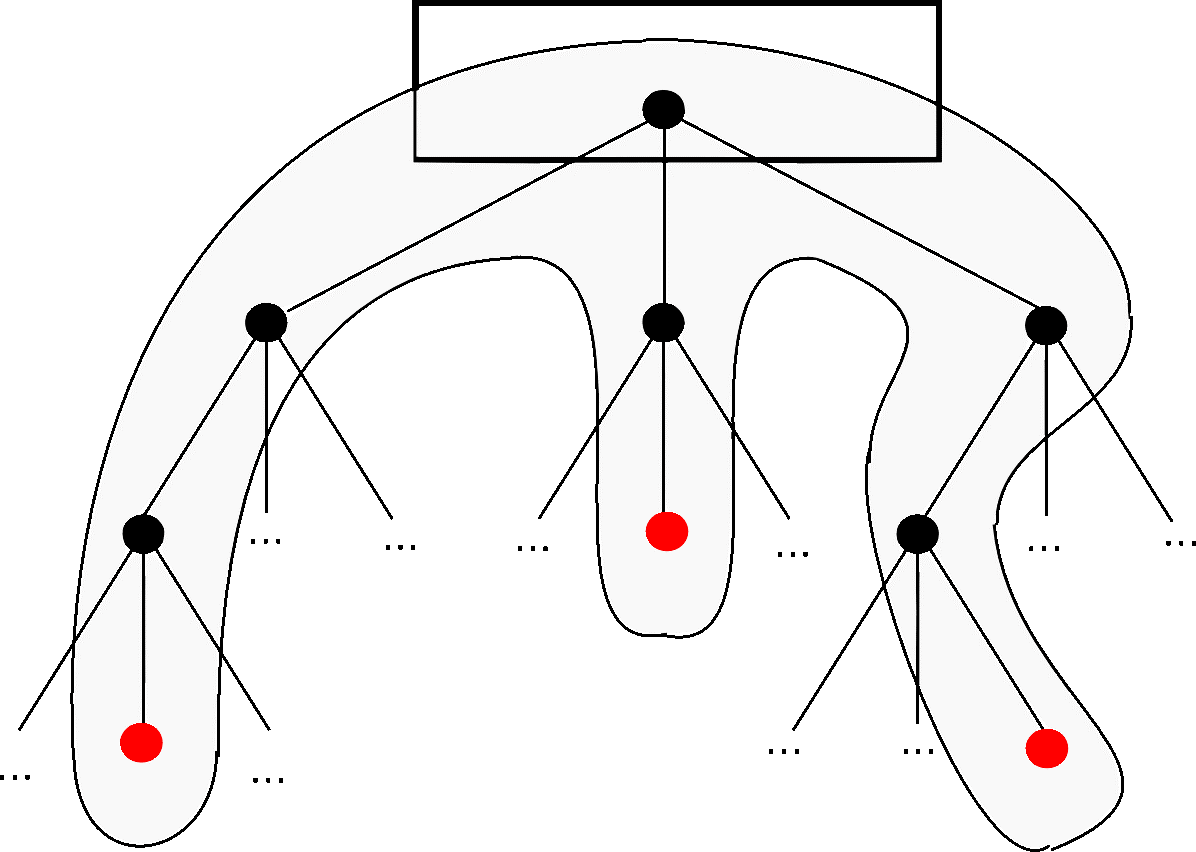
MPT(Merkle Patricia Trees)
前面我们提到,最为简单的一种Merkle Tree大多数情况下都是一棵二叉树。然而,Ethereum所使用的Merkle Tree则更为复杂,我们称之为“梅克尔.帕特里夏树”(Merkle Patricia tree)。
对于验证属于list格式(本质上来讲,它就是一系列前后相连的数据块)的信息而言,二叉Merkle Tree是非常好的数据结构。对于交易树来说,它们也同样是不错的,因为一旦树已经建立,花多少时间来编辑这棵树并不重要,树一旦建立了,它就会永远存在并且不会改变。
但是,对于状态树,情况会更复杂些。以太坊中的状态树基本上包含了一个键值映射,其中的键是地址,而值包括账户的声明、余额、随机数nounce、代码以及每一个账户的存储(其中存储本身就是一颗树)。例如,摩登测试网络(the Morden testnet )的创始状态如下所示: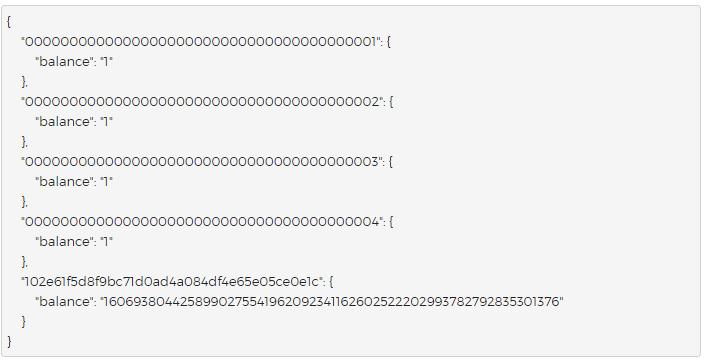
然而,不同于交易历史记录,状态树需要经常地进行更新:账户余额和账户的随机数nonce经常会更变,更重要的是,新的账户会频繁地插入,存储的键( key)也会经常被插入以及删除。我们需要这样的数据结构,它能在一次插入、更新、删除操作后快速计算到树根,而不需要重新计算整个树的Hash。这种数据结构同样得包括两个非常好的第二特征:
树的深度是有限制的,即使考虑攻击者会故意地制造一些交易,使得这颗树尽可能地深。不然,攻击者可以通过操纵树的深度,执行拒绝服务攻击(DOS attack),使得更新变得极其缓慢。
树的根只取决于数据,和其中的更新顺序无关。换个顺序进行更新,甚至重新从头计算树,并不会改变根。
MPT是最接近同时满足上面的性质的的数据结构。MPT的工作原理的最简单的解释是,值通过键来存储,键被编码到搜索树必须要经过的路径中。每个节点有16个孩子,因此路径又16进制的编码决定:例如,键‘dog’的16进制编码是6 4 6 15 6 7,所以从root开始到第六个分支,然后到第四个,再到第六个,再到第十五个,这样依次进行到达树的叶子。
在实践中,当树稀少时也会有一些额外的优化,我们会使过程更为有效,但这是基本的原则。
Leetcode二分查找法小结
二分查找法作为一种常见的查找方法,将原本是线性时间提升到了对数时间范围,大大缩短了搜索时间,具有很大的应用场景,而在 LeetCode 中,要运用二分搜索法来解的题目也有很多,但是实际上二分查找法的查找目标有很多种,而且在细节写法也有一些变化。之前有网友留言希望博主能针对二分查找法的具体写法做个总结,博主由于之前一直很忙,一直拖着没写,为了树立博主言出必行的正面形象,不能再无限制的拖下去了,那么今天就来做个了断吧,总结写起来~ (以下内容均为博主自己的总结,并不权威,权当参考,欢迎各位大神们留言讨论指正)
根据查找的目标不同,博主将二分查找法主要分为以下五类:
第一类: 需查找和目标值完全相等的数
这是最简单的一类,也是我们最开始学二分查找法需要解决的问题,比如我们有数组 [2, 4, 5, 6, 9],target = 6,那么我们可以写出二分查找法的代码如下:
1 | int find(vector<int>& nums, int target) { |
会返回3,也就是 target 的在数组中的位置。注意二分查找法的写法并不唯一,主要可以变动地方有四处:
- 第一处是 right 的初始化,可以写成 nums.size() 或者 nums.size() - 1。
- 第二处是 left 和 right 的关系,可以写成 left < right 或者 left <= right。
- 第三处是更新 right 的赋值,可以写成 right = mid 或者 right = mid - 1。
- 第四处是最后返回值,可以返回 left,right,或 right - 1。
但是这些不同的写法并不能随机的组合,像博主的那种写法,若 right 初始化为了 nums.size(),那么就必须用 left < right,而最后的 right 的赋值必须用 right = mid。但是如果我们 right 初始化为 nums.size() - 1,那么就必须用 left <= right,并且right的赋值要写成 right = mid - 1,不然就会出错。所以博主的建议是选择一套自己喜欢的写法,并且记住,实在不行就带简单的例子来一步一步执行,确定正确的写法也行。
第一类应用实例: Intersection of Two Arrays
第二类: 查找第一个不小于目标值的数,可变形为查找最后一个小于目标值的数
这是比较常见的一类,因为我们要查找的目标值不一定会在数组中出现,也有可能是跟目标值相等的数在数组中并不唯一,而是有多个,那么这种情况下 nums[mid] == target 这条判断语句就没有必要存在。比如在数组 [2, 4, 5, 6, 9] 中查找数字3,就会返回数字4的位置;在数组 [0, 1, 1, 1, 1] 中查找数字1,就会返回第一个数字1的位置。我们可以使用如下代码:
1 | int find(vector<int>& nums, int target) { |
最后我们需要返回的位置就是 right 指针指向的地方。在 C++ 的 STL 中有专门的查找第一个不小于目标值的数的函数 lower_bound,在博主的解法中也会时不时的用到这个函数。但是如果面试的时候人家不让使用内置函数,那么我们只能老老实实写上面这段二分查找的函数。
这一类可以轻松的变形为查找最后一个小于目标值的数,怎么变呢。我们已经找到了第一个不小于目标值的数,那么再往前退一位,返回 right - 1,就是最后一个小于目标值的数。
第二类应用实例:Heaters, Arranging Coins, Valid Perfect Square,Max Sum of Rectangle No Larger Than K,Russian Doll Envelopes
第二类变形应用:Valid Triangle Number
第三类: 查找第一个大于目标值的数,可变形为查找最后一个不大于目标值的数
这一类也比较常见,尤其是查找第一个大于目标值的数,在 C++ 的 STL 也有专门的函数 upper_bound,这里跟上面的那种情况的写法上很相似,只需要添加一个等号,将之前的 nums[mid] < target 变成 nums[mid] <= target,就这一个小小的变化,其实直接就改变了搜索的方向,使得在数组中有很多跟目标值相同的数字存在的情况下,返回最后一个相同的数字的下一个位置。比如在数组 [2, 4, 5, 6, 9] 中查找数字3,还是返回数字4的位置,这跟上面那查找方式返回的结果相同,因为数字4在此数组中既是第一个不小于目标值3的数,也是第一个大于目标值3的数,所以 make sense;在数组 [0, 1, 1, 1, 1] 中查找数字1,就会返回坐标5,通过对比返回的坐标和数组的长度,我们就知道是否存在这样一个大于目标值的数。参见下面的代码:
1 | int find(vector<int>& nums, int target) { |
这一类可以轻松的变形为查找最后一个不大于目标值的数,怎么变呢。我们已经找到了第一个大于目标值的数,那么再往前退一位,返回 right - 1,就是最后一个不大于目标值的数。比如在数组 [0, 1, 1, 1, 1] 中查找数字1,就会返回最后一个数字1的位置4,这在有些情况下是需要这么做的。
第三类应用实例:Kth Smallest Element in a Sorted Matrix
第三类变形应用示例: Sqrt(x)
第四类: 用子函数当作判断关系(通常由 mid 计算得出)
这是最令博主头疼的一类,而且通常情况下都很难。因为这里在二分查找法重要的比较大小的地方使用到了子函数,并不是之前三类中简单的数字大小的比较,比如 Split Array Largest Sum 那道题中的解法一,就是根据是否能分割数组来确定下一步搜索的范围。类似的还有 Guess Number Higher or Lower 这道题,是根据给定函数 guess 的返回值情况来确定搜索的范围。对于这类题目,博主也很无奈,遇到了只能自求多福了。
第四类应用实例:Split Array Largest Sum, Guess Number Higher or Lower,Find K Closest Elements,Find K-th Smallest Pair Distance,Kth Smallest Number in Multiplication Table,Maximum Average Subarray II,Minimize Max Distance to Gas Station,Swim in Rising Water,Koko Eating Bananas,Nth Magical Number
第五类: 其他(通常 target 值不固定)
有些题目不属于上述的四类,但是还是需要用到二分搜索法,比如这道 Find Peak Element,求的是数组的局部峰值。由于是求的峰值,需要跟相邻的数字比较,那么 target 就不是一个固定的值,而且这道题的一定要注意的是 right 的初始化,一定要是 nums.size() - 1,这是由于算出了 mid 后,nums[mid] 要和 nums[mid+1] 比较,如果 right 初始化为 nums.size() 的话,mid+1 可能会越界,从而不能找到正确的值,同时 while 循环的终止条件必须是 left < right,不能有等号。
类似的还有一道 H-Index II,这道题的 target 也不是一个固定值,而是 len-mid,这就很意思了,跟上面的 nums[mid+1] 有异曲同工之妙,target 值都随着 mid 值的变化而变化,这里的right的初始化,一定要是 nums.size() - 1,而 while 循环的终止条件必须是 left <= right,这里又必须要有等号,是不是很头大 -.-!!!
其实仔细分析的话,可以发现其实这跟第四类还是比较相似,相似点是都很难 -.-!!!,第四类中虽然是用子函数来判断关系,但大部分时候 mid 也会作为一个参数带入子函数进行计算,这样实际上最终算出的值还是受 mid 的影响,但是 right 却可以初始化为数组长度,循环条件也可以不带等号,大家可以对比区别一下~
Top-k问题的一些算法
Top K问题是面试时手写代码的常考题,某些场景下的解法与堆排和快排的关系紧密,所以把它放在堆排后面讲。
言归正传,笔者见过关于Top K问题最全的分类总结是在这里(包括海量数据的处理),个人将这些题分成了两类:一类是容易写代码实现的;另一类侧重考察思路的。毫无疑问,后一种比较简单,你只要记住它的应用场景、解决思路,并能在面试的过程中将它顺利地表达出来,便能以不变应万变。前一种,需要手写代码,就必须要掌握一定的技巧,常见的解法有两种,就是前面说过的堆排和快排的变形。
本文主要来看看方便用代码解决的问题。
堆排解法
用堆排来解决Top K的思路很直接。
前面已经说过,堆排利用的大(小)顶堆所有子节点元素都比父节点小(大)的性质来实现的,这里故技重施:既然一个大顶堆的顶是最大的元素,那我们要找最小的K个元素,是不是可以先建立一个包含K个元素的堆,然后遍历集合,如果集合的元素比堆顶元素小(说明它目前应该在K个最小之列),那就用该元素来替换堆顶元素,同时维护该堆的性质,那在遍历结束的时候,堆中包含的K个元素是不是就是我们要找的最小的K个元素?
实现:
在堆排的基础上,稍作了修改,buildHeap和heapify函数都是一样的实现,不难理解。
速记口诀:最小的K个用最大堆,最大的K个用最小堆。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61public class TopK {
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] a = { 1, 17, 3, 4, 5, 6, 7, 16, 9, 10, 11, 12, 13, 14, 15, 8 };
int[] b = topK(a, 4);
for (int i = 0; i < b.length; i++) {
System.out.print(b[i] + ", ");
}
}
public static void heapify(int[] array, int index, int length) {
int left = index * 2 + 1;
int right = index * 2 + 2;
int largest = index;
if (left < length && array[left] > array[index]) {
largest = left;
}
if (right < length && array[right] > array[largest]) {
largest = right;
}
if (index != largest) {
swap(array, largest, index);
heapify(array, largest, length);
}
}
public static void swap(int[] array, int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
}
public static void buildHeap(int[] array) {
int length = array.length;
for (int i = length / 2 - 1; i >= 0; i--) {
heapify(array, i, length);
}
}
public static void setTop(int[] array, int top) {
array[0] = top;
heapify(array, 0, array.length);
}
public static int[] topK(int[] array, int k) {
int[] top = new int[k];
for (int i = 0; i < k; i++) {
top[i] = array[i];
}
//先建堆,然后依次比较剩余元素与堆顶元素的大小,比堆顶小的, 说明它应该在堆中出现,则用它来替换掉堆顶元素,然后沉降。
buildHeap(top);
for (int j = k; j < array.length; j++) {
int temp = top[0];
if (array[j] < temp) {
setTop(top, array[j]);
}
}
return top;
}
}
时间复杂度n*logK
速记:堆排的时间复杂度是n*logn,这里相当于只对前Top K个元素建堆排序,想法不一定对,但一定有助于记忆。
适用场景
实现的过程中,我们先用前K个数建立了一个堆,然后遍历数组来维护这个堆。这种做法带来了三个好处:(1)不会改变数据的输入顺序(按顺序读的);(2)不会占用太多的内存空间(事实上,一次只读入一个数,内存只要求能容纳前K个数即可);(3)由于(2),决定了它特别适合处理海量数据。
这三点,也决定了它最优的适用场景。
快排解法
用快排的思想来解Top K问题,必然要运用到”分治”。
与快排相比,两者唯一的不同是在对”分治”结果的使用上。我们知道,分治函数会返回一个position,在position左边的数都比第position个数小,在position右边的数都比第position大。我们不妨不断调用分治函数,直到它输出的position = K-1,此时position前面的K个数(0到K-1)就是要找的前K个数。
实现:
“分治”还是原来的那个分治,关键是getTopK的逻辑,务必要结合注释理解透彻,自动动手写写。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52public class TopK {
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] array = { 9, 3, 1, 10, 5, 7, 6, 2, 8, 0 };
getTopK(array, 4);
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + ", ");
}
}
// 分治
public static int partition(int[] array, int low, int high) {
if (array != null && low < high) {
int flag = array[low];
while (low < high) {
while (low < high && array[high] >= flag) {
high--;
}
array[low] = array[high];
while (low < high && array[low] <= flag) {
low++;
}
array[high] = array[low];
}
array[low] = flag;
return low;
}
return 0;
}
public static void getTopK(int[] array, int k) {
if (array != null && array.length > 0) {
int low = 0;
int high = array.length - 1;
int index = partition(array, low, high);
//不断调整分治的位置,直到position = k-1
while (index != k - 1) {
//大了,往前调整
if (index > k - 1) {
high = index - 1;
index = partition(array, low, high);
}
//小了,往后调整
if (index < k - 1) {
low = index + 1;
index = partition(array, low, high);
}
}
}
}
}
速记:记住就行,基于partition函数的时间复杂度比较难证明,从来没考过。
适用场景
对照着堆排的解法来看,partition函数会不断地交换元素的位置,所以它肯定会改变数据输入的顺序;既然要交换元素的位置,那么所有元素必须要读到内存空间中,所以它会占用比较大的空间,至少能容纳整个数组;数据越多,占用的空间必然越大,海量数据处理起来相对吃力。
但是,它的时间复杂度很低,意味着数据量不大时,效率极高。
多种不同的排序方法
稳定排序和不稳定排序
首先,排序算法的稳定性大家应该都知道,通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。在简单形式化一下,如果Ai = Aj,Ai原来在位置前,排序后Ai还是要在Aj位置前。
其次,说一下稳定性的好处。排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。另外,如果排序算法稳定,对基于比较的排序算法而言,元素交换的次数可能会少一些(个人感觉,没有证实)。
回到主题,现在分析一下常见的排序算法的稳定性,每个都给出简单的理由。
冒泡排序
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,我想你是不会再无聊地把他们俩交换一下的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
选择排序
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n - 1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法。
第一次从R[0]~R[n-1]中选取最小值,与R[0]交换,第二次从R[1]~R[n-1]中选取最小值,与R[1]交换,….,第i次从R[i-1]~R[n-1]中选取最小值,与R[i-1]交换,…..,第n-1次从R[n-2]~R[n-1]中选取最小值,与R[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。因此它的时间复杂度固定为O(n^2)
插入排序
插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
算法分析:
- 从序列第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,设为待插入元素,在已经排序的元素序列中从后向前扫描,如果该元素(已排序)大于待插入元素,将该元素移到下一位置。
- 重复步骤2,直到找到已排序的元素小于或者等于待排序元素的位置,插入元素
- 重复2,3步骤,完成排序。
快速排序
快速排序有两个方向,左边的i下标一直往右走,当a[i] <= a[center_index],其中center_index是中枢元素的数组下标,一般取为数组第0个元素。而右边的j下标一直往左走,当a[j] > a[center_index]。如果i和j都走不动了,i <= j,交换a[i]和a[j],重复上面的过程,直到i > j。 交换a[j]和a[center_index],完成一趟快速排序。在中枢元素和a[j]交换的时候,很有可能把前面的元素的稳定性打乱,比如序列为5 3 3 4 3 8 9 10 11,现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱,所以快速排序是一个不稳定的排序算法,不稳定发生在中枢元素和a[j]交换的时刻。
归并排序
归并排序是把序列递归地分成短序列,递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的段序列合并成一个有序的长序列,不断合并直到原序列全部排好序。可以发现,在1个或2个元素时,1个元素不会交换,2个元素如果大小相等也没有人故意交换,这不会破坏稳定性。那么,在短的有序序列合并的过程中,稳定是是否受到破坏?没有,合并过程中我们可以保证如果两个当前元素相等时,我们把处在前面的序列的元素保存在结果序列的前面,这样就保证了稳定性。所以,归并排序也是稳定的排序算法。
二路归并排序主旨是“分解”与“归并”
- 分解:
- 将一个数组分成两个数组,分别对两个数组进行排序。
- 循环第一步,直到划分出来的“小数组”只包含一个元素,只有一个元素的数组默认为已经排好序。
- 归并:
- 将两个有序的数组合并到一个大的数组中。
- 从最小的只包含一个元素的数组开始两两合并。此时,合并好的数组也是有序的。
希尔排序(shell)
希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,所以插入排序的元素个数很少,速度很快;当元素基本有序了,步长很小, 插入排序对于有序的序列效率很高。所以,希尔排序的时间复杂度会比O(n^2)好一些。由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
堆排序
我们知道堆的结构是节点i的孩子为2 * i和2 * i + 1节点,大顶堆要求父节点大于等于其2个子节点,小顶堆要求父节点小于等于其2个子节点。在一个长为n 的序列,堆排序的过程是从第n / 2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n / 2 - 1, n / 2 - 2, … 1这些个父节点选择元素时,就会破坏稳定性。有可能第n / 2个父节点交换把后面一个元素交换过去了,而第n / 2 - 1个父节点把后面一个相同的元素没 有交换,那么这2个相同的元素之间的稳定性就被破坏了。所以,堆排序不是稳定的排序算法。
综上,得出结论: 选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法,而冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法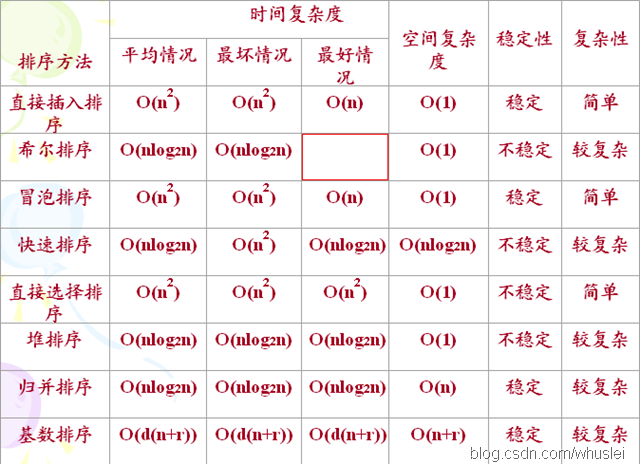
100万个32位整数,如何最快找到中位数。能保证每个数是唯一的,如何实现O(N)算法?
- 内存足够时:快排
- 内存不足时:分桶法:化大为小,把所有数划分到各个小区间,把每个数映射到对应的区间里,对每个区间中数的个数进行计数,数一遍各个区间,看看中位数落在哪个区间,若够小,使用基于内存的算法,否则 继续划分
基数排序
数据背景
在基数排序中,我们不能再只用一位数的序列来列举示例了。一位数的序列对基数排序来说就是一个计数排序。
这里我们列举无序序列 T = [ 2314, 5428, 373, 2222, 17 ]
排序原理
上面说到基数排序不需要进行元素的比较与交换。如果你有一些算法的功底,或者丰富的项目经验,我想你可能已经想到了这可能类似于一些“打表”或是哈希的做法。而计数排序则是打表或是哈希思想最简单的实现。
计数排序
计数排序的核心思想是,构建一个足够大的数组 hashArray[],数组大小需要保证能够把所有元素都包含在这个数组上 。
假设我们有无序序列 T = [ 2314, 5428, 373, 2222, 17 ]
首先初始化数组 hashArray[] 为一个全零数组。当然,在 Java 里,这一步就不需要了,因为默认就是零了。
在对序列 T 进行排序时,只要依次读取序列 T 中的元素,并修改数组 hashArray[] 中把元素值对应位置上的值即可。这一句有一些绕口。打个比方,我们要把 T[0] 映射到 hashArray[] 中,就是 hashArray[T[0]] = 1. 也就是 hashArray[2314] = 1. 如果序列 T 中有两个相同元素,那么在 hashArray 的相应位置上的值就是 2。
下图是计数排序的原理图:
(假设有无序序列:[ 5, 8, 9, 1, 4, 2, 9, 3, 7, 1, 8, 6, 2, 3, 4, 0, 8 ])
基数排序原理图
上面的计数排序只是一个引导,好让你可以循序渐进地了解基数排序。
上面这幅图,或许你已经在其他的博客里见到过。这是一个很好的引导跟说明。在基数排序里,我们需要一个很大的二维数组,二维数组的大小是 (10 * n)。10 代表的是我们每个元素的每一位都有 10 种可能,也就是 10 进制数。在上图中,我们是以每个数的个位来代表这个数,于是,5428 就被填充到了第 8 个桶中了。下次再进行填充的时候,就是以十位进行填充,比如 5428 在此时,就会选择以 2 来代表它。
算法优化
在算法的原理中,我们是以一张二维数组的表来存储这些无序的元素。使用二维数组有一个很明显的不足就是二维数组太过稀疏。数组的利用率为 10%。
在寻求优化的路上,我们想到一种可以压缩空间的方法,且时间复杂度并没有偏离得太厉害。那就是设计了两个辅助数组,一个是 count[],一个是 bucket[]。count 用于记录在某个桶中的最后一个元素的下标,然后再把原数组中的元素计算一下它应该属于哪个“桶”,并修改相应位置的 count 值。直到最大数的最高位也被添加到桶中,或者说,当所有的元素都被被在第 0 个桶中,基数排序就结束了。
优化后的原理图如下:
算法实现
1 | import org.algorithm.array.sort.interf.Sortable; |
基数排序过程图
如果我们的无序是 T = [ 2314, 5428, 373, 2222, 17 ],那么其排序的过程就如下两幅所示。
基数排序过程图-1
基数排序过程图-2
拓扑排序
定义和前置条件
定义:将有向图中的顶点以线性方式进行排序。即对于任何连接自顶点u到顶点v的有向边uv,在最后的排序结果中,顶点u总是在顶点v的前面。
如果这个概念还略显抽象的话,那么不妨考虑一个非常非常经典的例子——选课。我想任何看过数据结构相关书籍的同学都知道它吧。假设我非常想学习一门机器学习的课程,但是在修这么课程之前,我们必须要学习一些基础课程,比如计算机科学概论,C语言程序设计,数据结构,算法等等。那么这个制定选修课程顺序的过程,实际上就是一个拓扑排序的过程,每门课程相当于有向图中的一个顶点,而连接顶点之间的有向边就是课程学习的先后关系。只不过这个过程不是那么复杂,从而很自然的在我们的大脑中完成了。将这个过程以算法的形式描述出来的结果,就是拓扑排序。
那么是不是所有的有向图都能够被拓扑排序呢?显然不是。继续考虑上面的例子,如果告诉你在选修计算机科学概论这门课之前需要你先学习机器学习,你是不是会被弄糊涂?在这种情况下,就无法进行拓扑排序,因为它中间存在互相依赖的关系,从而无法确定谁先谁后。在有向图中,这种情况被描述为存在环路。因此,一个有向图能被拓扑排序的充要条件就是它是一个有向无环图(DAG:Directed Acyclic Graph)。
偏序/全序关系
偏序和全序实际上是离散数学中的概念。这里不打算说太多形式化的定义,形式化的定义教科书上或者上面给的链接中就说的很详细。
还是以上面选课的例子来描述这两个概念。假设我们在学习完了算法这门课后,可以选修机器学习或者计算机图形学。这个或者表示,学习机器学习和计算机图形学这两门课之间没有特定的先后顺序。因此,在我们所有可以选择的课程中,任意两门课程之间的关系要么是确定的(即拥有先后关系),要么是不确定的(即没有先后关系),绝对不存在互相矛盾的关系(即环路)。以上就是偏序的意义,抽象而言,有向图中两个顶点之间不存在环路,至于连通与否,是无所谓的。所以,有向无环图必然是满足偏序关系的。
理解了偏序的概念,那么全序就好办了。所谓全序,就是在偏序的基础之上,有向无环图中的任意一对顶点还需要有明确的关系(反映在图中,就是单向连通的关系,注意不能双向连通,那就成环了)。可见,全序就是偏序的一种特殊情况。回到我们的选课例子中,如果机器学习需要在学习了计算机图形学之后才能学习(可能学的是图形学领域相关的机器学习算法……),那么它们之间也就存在了确定的先后顺序,原本的偏序关系就变成了全序关系。
实际上,很多地方都存在偏序和全序的概念。
比如对若干互不相等的整数进行排序,最后总是能够得到唯一的排序结果(从小到大,下同)。这个结论应该不会有人表示疑问吧:)但是如果我们以偏序/全序的角度来考虑一下这个再自然不过的问题,可能就会有别的体会了。
那么如何用偏序/全序来解释排序结果的唯一性呢?
我们知道不同整数之间的大小关系是确定的,即1总是小于4的,不会有人说1大于或者等于4吧。这就是说,这个序列是满足全序关系的。而对于拥有全序关系的结构(如拥有不同整数的数组),在其线性化(排序)之后的结果必然是唯一的。对于排序的算法,我们评价指标之一是看该排序算法是否稳定,即值相同的元素的排序结果是否和出现的顺序一致。比如,我们说快速排序是不稳定的,这是因为最后的快排结果中相同元素的出现顺序和排序前不一致了。如果用偏序的概念可以这样解释这一现象:相同值的元素之间的关系是无法确定的。因此它们在最终的结果中的出现顺序可以是任意的。而对于诸如插入排序这种稳定性排序,它们对于值相同的元素,还有一个潜在的比较方式,即比较它们的出现顺序,出现靠前的元素大于出现后出现的元素。因此通过这一潜在的比较,将偏序关系转换为了全序关系,从而保证了结果的唯一性。
拓展到拓扑排序中,结果具有唯一性的条件也是其所有顶点之间都具有全序关系。如果没有这一层全序关系,那么拓扑排序的结果也就不是唯一的了。在后面会谈到,如果拓扑排序的结果唯一,那么该拓扑排序的结果同时也代表了一条哈密顿路径。
典型实现算法
Kahn算法
摘一段维基百科上关于Kahn算法的伪码描述:1
2
3
4
5
6
7
8
9
10
11
12
13L← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
remove a node n from S
insert n into L
foreach node m with an edge e from nto m do
remove edge e from thegraph
ifm has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least onecycle)
else
return L (a topologically sortedorder)
不难看出该算法的实现十分直观,关键在于需要维护一个入度为0的顶点的集合:
每次从该集合中取出(没有特殊的取出规则,随机取出也行,使用队列/栈也行,下同)一个顶点,将该顶点放入保存结果的List中。
紧接着循环遍历由该顶点引出的所有边,从图中移除这条边,同时获取该边的另外一个顶点,如果该顶点的入度在减去本条边之后为0,那么也将这个顶点放到入度为0的集合中。然后继续从集合中取出一个顶点…………
当集合为空之后,检查图中是否还存在任何边,如果存在的话,说明图中至少存在一条环路。不存在的话则返回结果List,此List中的顺序就是对图进行拓扑排序的结果。
实现代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69public class KahnTopological
{
private List<Integer> result; // 用来存储结果集
private Queue<Integer> setOfZeroIndegree; // 用来存储入度为0的顶点
private int[] indegrees; // 记录每个顶点当前的入度
private int edges;
private Digraph di;
public KahnTopological(Digraph di)
{
this.di = di;
this.edges = di.getE();
this.indegrees = new int[di.getV()];
this.result = new ArrayList<Integer>();
this.setOfZeroIndegree = new LinkedList<Integer>();
// 对入度为0的集合进行初始化
Iterable<Integer>[] adjs = di.getAdj();
for(int i = 0; i < adjs.length; i++)
{
// 对每一条边 v -> w
for(int w : adjs[i])
{
indegrees[w]++;
}
}
for(int i = 0; i < indegrees.length; i++)
{
if(0 == indegrees[i])
{
setOfZeroIndegree.enqueue(i);
}
}
process();
}
private void process()
{
while(!setOfZeroIndegree.isEmpty())
{
int v = setOfZeroIndegree.dequeue();
// 将当前顶点添加到结果集中
result.add(v);
// 遍历由v引出的所有边
for(int w : di.adj(v))
{
// 将该边从图中移除,通过减少边的数量来表示
edges--;
if(0 == --indegrees[w]) // 如果入度为0,那么加入入度为0的集合
{
setOfZeroIndegree.enqueue(w);
}
}
}
// 如果此时图中还存在边,那么说明图中含有环路
if(0 != edges)
{
throw new IllegalArgumentException("Has Cycle !");
}
}
public Iterable<Integer> getResult()
{
return result;
}
}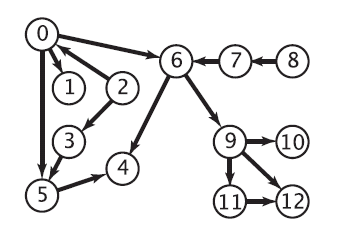
对上图进行拓扑排序的结果:
2->8->0->3->7->1->5->6->9->4->11->10->12
复杂度分析:
- 初始化入度为0的集合需要遍历整张图,检查每个节点和每条边,因此复杂度为O(E+V);
- 然后对该集合进行操作,又需要遍历整张图中的,每条边,复杂度也为O(E+V);
- 因此Kahn算法的复杂度即为O(E+V)。
基于DFS的拓扑排序
除了使用上面直观的Kahn算法之外,还能够借助深度优先遍历来实现拓扑排序。这个时候需要使用到栈结构来记录拓扑排序的结果。
同样摘录一段维基百科上的伪码:1
2
3
4
5
6
7
8
9
10L ← Empty list that will contain the sorted nodes
S ← Set of all nodes with no outgoing edges
for each node n in S do
visit(n)
function visit(node n)
if n has not been visited yet then
mark n as visited
for each node m with an edgefrom m to ndo
visit(m)
add n to L
DFS的实现更加简单直观,使用递归实现。利用DFS实现拓扑排序,实际上只需要添加一行代码,即上面伪码中的最后一行:add n to L。
需要注意的是,将顶点添加到结果List中的时机是在visit方法即将退出之时。
这个算法的实现非常简单,但是要理解的话就相对复杂一点。
关键在于为什么在visit方法的最后将该顶点添加到一个集合中,就能保证这个集合就是拓扑排序的结果呢?
因为添加顶点到集合中的时机是在dfs方法即将退出之时,而dfs方法本身是个递归方法,只要当前顶点还存在边指向其它任何顶点,它就会递归调用dfs方法,而不会退出。因此,退出dfs方法,意味着当前顶点没有指向其它顶点的边了,即当前顶点是一条路径上的最后一个顶点。
下面简单证明一下它的正确性:
考虑任意的边v->w,当调用dfs(v)的时候,有如下三种情况:
- dfs(w)还没有被调用,即w还没有被mark,此时会调用dfs(w),然后当dfs(w)返回之后,dfs(v)才会返回
- dfs(w)已经被调用并返回了,即w已经被mark
- dfs(w)已经被调用但是在此时调用dfs(v)的时候还未返回
需要注意的是,以上第三种情况在拓扑排序的场景下是不可能发生的,因为如果情况3是合法的话,就表示存在一条由w到v的路径。而现在我们的前提条件是由v到w有一条边,这就导致我们的图中存在环路,从而该图就不是一个有向无环图(DAG),而我们已经知道,非有向无环图是不能被拓扑排序的。
那么考虑前两种情况,无论是情况1还是情况2,w都会先于v被添加到结果列表中。所以边v->w总是由结果集中后出现的顶点指向先出现的顶点。为了让结果更自然一些,可以使用栈来作为存储最终结果的数据结构,从而能够保证边v->w总是由结果集中先出现的顶点指向后出现的顶点。
实现代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52public class DirectedDepthFirstOrder
{
// visited数组,DFS实现需要用到
private boolean[] visited;
// 使用栈来保存最后的结果
private Stack<Integer> reversePost;
/**
* Topological Sorting Constructor
*/
public DirectedDepthFirstOrder(Digraph di, boolean detectCycle)
{
// 这里的DirectedDepthFirstCycleDetection是一个用于检测有向图中是否存在环路的类
DirectedDepthFirstCycleDetection detect = new DirectedDepthFirstCycleDetection(
di);
if (detectCycle && detect.hasCycle())
throw new IllegalArgumentException("Has cycle");
this.visited = new boolean[di.getV()];
this.reversePost = new Stack<Integer>();
for (int i = 0; i < di.getV(); i++)
{
if (!visited[i])
{
dfs(di, i);
}
}
}
private void dfs(Digraph di, int v)
{
visited[v] = true;
for (int w : di.adj(v))
{
if (!visited[w])
{
dfs(di, w);
}
}
// 在即将退出dfs方法的时候,将当前顶点添加到结果集中
reversePost.push(v);
}
public Iterable<Integer> getReversePost()
{
return reversePost;
}
}
复杂度分析:
复杂度同DFS一致,即O(E+V)。具体而言,首先需要保证图是有向无环图,判断图是DAG可以使用基于DFS的算法,复杂度为O(E+V),而后面的拓扑排序也是依赖于DFS,复杂度为O(E+V)
还是对上文中的那张有向图进行拓扑排序,只不过这次使用的是基于DFS的算法,结果是:
8->7->2->3->0->6->9->10->11->12->1->5->4
两种实现算法的总结
这两种算法分别使用链表和栈来表示结果集。
对于基于DFS的算法,加入结果集的条件是:顶点的出度为0。这个条件和Kahn算法中入度为0的顶点集合似乎有着异曲同工之妙,这两种算法的思想犹如一枚硬币的两面,看似矛盾,实则不然。一个是从入度的角度来构造结果集,另一个则是从出度的角度来构造。
实现上的一些不同之处:
Kahn算法不需要检测图为DAG,如果图为DAG,那么在出度为0的集合为空之后,图中还存在没有被移除的边,这就说明了图中存在环路。而基于DFS的算法需要首先确定图为DAG,当然也能够做出适当调整,让环路的检测和拓扑排序同时进行,毕竟环路检测也能够在DFS的基础上进行。
二者的复杂度均为O(V+E)。
环路检测和拓扑排序同时进行的实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86public class DirectedDepthFirstTopoWithCircleDetection
{
private boolean[] visited;
// 用于记录dfs方法的调用栈,用于环路检测
private boolean[] onStack;
// 用于当环路存在时构造之
private int[] edgeTo;
private Stack<Integer> reversePost;
private Stack<Integer> cycle;
/**
* Topological Sorting Constructor
*/
public DirectedDepthFirstTopoWithCircleDetection(Digraph di)
{
this.visited = new boolean[di.getV()];
this.onStack = new boolean[di.getV()];
this.edgeTo = new int[di.getV()];
this.reversePost = new Stack<Integer>();
for (int i = 0; i < di.getV(); i++)
{
if (!visited[i])
{
dfs(di, i);
}
}
}
private void dfs(Digraph di, int v)
{
visited[v] = true;
// 在调用dfs方法时,将当前顶点记录到调用栈中
onStack[v] = true;
for (int w : di.adj(v))
{
if(hasCycle())
{
return;
}
if (!visited[w])
{
edgeTo[w] = v;
dfs(di, w);
}
else if(onStack[w])
{
// 当w已经被访问,同时w也存在于调用栈中时,即存在环路
cycle = new Stack<Integer>();
cycle.push(w);
for(int start = v; start != w; start = edgeTo[start])
{
cycle.push(v);
}
cycle.push(w);
}
}
// 在即将退出dfs方法时,将顶点添加到拓扑排序结果集中,同时从调用栈中退出
reversePost.push(v);
onStack[v] = false;
}
private boolean hasCycle()
{
return (null != cycle);
}
public Iterable<Integer> getReversePost()
{
if(!hasCycle())
{
return reversePost;
}
else
{
throw new IllegalArgumentException("Has Cycle: " + getCycle());
}
}
public Iterable<Integer> getCycle()
{
return cycle;
}
}
拓扑排序解的唯一性
哈密顿路径
哈密顿路径是指一条能够对图中所有顶点正好访问一次的路径。本文中只会解释一些哈密顿路径和拓扑排序的关系,至于哈密顿路径的具体定义以及应用,可以参见本文开篇给出的链接。
前面说过,当一个DAG中的任何两个顶点之间都存在可以确定的先后关系时,对该DAG进行拓扑排序的解是唯一的。这是因为它们形成了全序的关系,而对存在全序关系的结构进行线性化之后的结果必然是唯一的(比如对一批整数使用稳定的排序算法进行排序的结果必然就是唯一的)。
需要注意的是,非DAG也是能够含有哈密顿路径的,为了利用拓扑排序来实现判断,所以这里讨论的主要是判断DAG中是否含有哈密顿路径的算法,因此下文中的图指代的都是DAG。
那么知道了哈密顿路径和拓扑排序的关系,我们如何快速检测一张图是否存在哈密顿路径呢?
根据前面的讨论,是否存在哈密顿路径的关键,就是确定图中的顶点是否存在全序的关系,而全序的关键,就是任意一对顶点之间都是能够确定先后关系的。因此,我们能够设计一个算法,用来遍历顶点集中的每一对顶点,然后检查它们之间是否存在先后关系,如果所有的顶点对有先后关系,那么该图的顶点集就存在全序关系,即图中存在哈密顿路径。
但是很显然,这样的算法十分低效。对于大规模的顶点集,是无法应用这种解决方案的。通常一个低效的解决办法,十有八九是因为没有抓住现有问题的一些特征而导致的。因此我们回过头来再看看这个问题,有什么特征使我们没有利用的。还是举对整数进行排序的例子:
比如现在有3, 2, 1三个整数,我们要对它们进行排序,按照之前的思想,我们分别对(1,2),(2,3),(1,3)进行比较,这样需要三次比较,但是我们很清楚,1和3的那次比较实际上是多余的。我们为什么知道这次比较是多余的呢?我认为,是我们下意识的利用了整数比较满足传递性的这一规则。但是计算机是无法下意识的使用传递性的,因此只能通过其它的方式来告诉计算机,有一些比较是不必要的。所以,也就有了相对插入排序,选择排序更加高效的排序算法,比如归并排序,快速排序等,将n2的算法加速到了nlogn。或者是利用了问题的特点,采取了更加独特的解决方案,比如基数排序等。
扯远了一点,回到正题。现在我们没有利用到的就是全序关系中传递性这一规则。如何利用它呢,最简单的想法往往就是最实用的,我们还是选择排序,排序后对每对相邻元素进行检测不就间接利用了传递性这一规则嘛?所以,我们先使用拓扑排序对图中的顶点进行排序。排序后,对每对相邻顶点进行检测,看看是否存在先后关系,如果每对相邻顶点都存在着一致的先后关系(在有向图中,这种先后关系以有向边的形式体现,即查看相邻顶点对之间是否存在有向边)。那么就可以确定该图中存在哈密顿路径了,反之则不存在。
实现代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51/**
* Hamilton Path Detection for DAG
*/
public class DAGHamiltonPath
{
private boolean hamiltonPathPresent;
private Digraph di;
private KahnTopological kts;
// 这里使用Kahn算法进行拓扑排序
public DAGHamiltonPath(Digraph di, KahnTopological kts)
{
this.di = di;
this.kts = kts;
process();
}
private void process()
{
Integer[] topoResult = kts.getResultAsArray();
// 依次检查每一对相邻顶点,如果二者之间没有路径,则不存在哈密顿路径
for(int i = 0; i < topoResult.length - 1; i++)
{
if(!hasPath(topoResult[i], topoResult[i + 1]))
{
hamiltonPathPresent = false;
return;
}
}
hamiltonPathPresent = true;
}
private boolean hasPath(int start, int end)
{
for(int w : di.adj(start))
{
if(w == end)
{
return true;
}
}
return false;
}
public boolean hasHamiltonPath()
{
return hamiltonPathPresent;
}
}