频繁项集的两个算法

Posted on

频繁项集的评估标准

什么样的数据才是频繁项集呢？也许你会说，这还不简单，肉眼一扫，一起出现次数多的数据集就是频繁项集吗！的确，这也没有说错，但是有两个问题，第一是当数据量非常大的时候，我们没法直接肉眼发现频繁项集，这催生了关联规则挖掘的算法，比如Apriori，PrefixSpan，CBA。第二是我们缺乏一个频繁项集的标准。比如10条记录，里面A和B同时出现了三次，那么我们能不能说A和B一起构成频繁项集呢？因此我们需要一个评估频繁项集的标准。

常用的频繁项集的评估标准有支持度，置信度和提升度三个。

支持度就是几个关联的数据在数据集中出现的次数占总数据集的比重。或者说几个数据关联出现的概率。如果我们有两个想分析关联性的数据X和Y，则对应的支持度为:

1
Support(X,Y)=P(XY)=number(XY)/num(AllSamples)

以此类推，如果我们有三个想分析关联性的数据X，Y和Z，则对应的支持度为:

1
Support(X,Y,Z)=P(XYZ)=number(XYZ)/num(AllSamples)

一般来说，支持度高的数据不一定构成频繁项集，但是支持度太低的数据肯定不构成频繁项集。

置信度体现了一个数据出现后，另一个数据出现的概率，或者说数据的条件概率。如果我们有两个想分析关联性的数据X和Y，X对Y的置信度为

1
Confidence(X⇐Y)=P(X|Y)=P(XY)/P(Y)

也可以以此类推到多个数据的关联置信度，比如对于三个数据X，Y，Z，则X对于Y和Z的置信度为：

1
Confidence(X⇐YZ)=P(X|YZ)=P(XYZ)/P(YZ)

举个例子，在购物数据中，纸巾对应鸡爪的置信度为40%，支持度为1%。则意味着在购物数据中，总共有1%的用户既买鸡爪又买纸巾；同时买鸡爪的用户中有40%的用户购买纸巾。

提升度表示含有Y的条件下，同时含有X的概率，与X总体发生的概率之比，即:

1
Lift(X⇐Y)=P(X|Y)/P(X)=Confidence(X⇐Y)/P(X)

提升度体先了X和Y之间的关联关系，提升度大于1则X⇐Y是有效的强关联规则， 提升度小于等于1则X⇐Y是无效的强关联规则 。一个特殊的情况，如果X和Y独立，则有Lift(X⇐Y)=1，因为此时P(X|Y)=P(X)。

一般来说，要选择一个数据集合中的频繁数据集，则需要自定义评估标准。最常用的评估标准是用自定义的支持度，或者是自定义支持度和置信度的一个组合。

Apriori算法

Apriori算法是常用的用于挖掘出数据关联规则的算法，它用来找出数据值中频繁出现的数据集合，找出这些集合的模式有助于我们做一些决策。比如在常见的超市购物数据集，或者电商的网购数据集中，如果我们找到了频繁出现的数据集，那么对于超市，我们可以优化产品的位置摆放，对于电商，我们可以优化商品所在的仓库位置，达到节约成本，增加经济效益的目的。下面我们就对Apriori算法做一个总结。

对于Apriori算法，我们使用支持度来作为我们判断频繁项集的标准。Apriori算法的目标是找到最大的K项频繁集。这里有两层意思，首先，我们要找到符合支持度标准的频繁集。但是这样的频繁集可能有很多。第二层意思就是我们要找到最大个数的频繁集。比如我们找到符合支持度的频繁集AB和ABE，那么我们会抛弃AB，只保留ABE，因为AB是2项频繁集，而ABE是3项频繁集。那么具体的，Apriori算法是如何做到挖掘K项频繁集的呢？

Apriori算法采用了迭代的方法，先搜索出候选1项集及对应的支持度，剪枝去掉低于支持度的1项集，得到频繁1项集。然后对剩下的频繁1项集进行连接，得到候选的频繁2项集，筛选去掉低于支持度的候选频繁2项集，得到真正的频繁二项集，以此类推，迭代下去，直到无法找到频繁k+1项集为止，对应的频繁k项集的集合即为算法的输出结果。

可见这个算法还是很简洁的，第i次的迭代过程包括扫描计算候选频繁i项集的支持度，剪枝得到真正频繁i项集和连接生成候选频繁i+1项集三步。

我们下面这个简单的例子看看：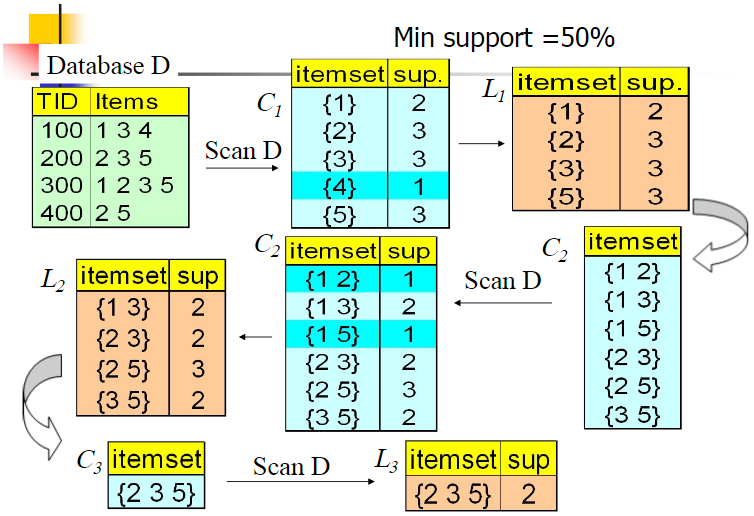

我们的数据集D有4条记录，分别是134，235，1235和25。现在我们用Apriori算法来寻找频繁k项集，最小支持度设置为50%。首先我们生成候选频繁1项集，包括我们所有的5个数据并计算5个数据的支持度，计算完毕后我们进行剪枝，数据4由于支持度只有25%被剪掉。我们最终的频繁1项集为1235，现在我们链接生成候选频繁2项集，包括12，13，15，23，25，35共6组。此时我们的第一轮迭代结束。

进入第二轮迭代，我们扫描数据集计算候选频繁2项集的支持度，接着进行剪枝，由于12和15的支持度只有25%而被筛除，得到真正的频繁2项集，包括13，23，25，35。现在我们链接生成候选频繁3项集，123，135和235共3组，这部分图中没有画出。通过计算候选频繁3项集的支持度，我们发现123和135的支持度均为25%，因此接着被剪枝，最终得到的真正频繁3项集为235一组。由于此时我们无法再进行数据连接，进而得到候选频繁4项集，最终的结果即为频繁3三项集235。

Aprior算法流程

下面我们对Aprior算法流程做一个总结。

  • 输入：数据集合D，支持度阈值α
  • 输出：最大的频繁k项集
  1. 扫描整个数据集，得到所有出现过的数据，作为候选频繁1项集。k=1，频繁0项集为空集。
  2. 挖掘频繁k项集
    1. 扫描数据计算候选频繁k项集的支持度
    2. 去除候选频繁k项集中支持度低于阈值的数据集，得到频繁k项集。如果得到的频繁k项集为空，则直接返回频繁k-1项集的集合作为算法结果，算法结束。如果得到的频繁k项集只有一项，则直接返回频繁k项集的集合作为算法结果，算法结束。
    3. 基于频繁k项集，连接生成候选频繁k+1项集。
  3. 令k=k+1，转入步骤2。

从算法的步骤可以看出，Aprior算法每轮迭代都要扫描数据集，因此在数据集很大，数据种类很多的时候，算法效率很低。

Aprior算法总结

Aprior算法是一个非常经典的频繁项集的挖掘算法，很多算法都是基于Aprior算法而产生的，包括FP-Tree，GSP，CBA等。这些算法利用了Aprior算法的思想，但是对算法做了改进，数据挖掘效率更好一些，因此现在一般很少直接用Aprior算法来挖掘数据了，但是理解Aprior算法是理解其它Aprior类算法的前提，同时算法本身也不复杂，因此值得好好研究一番。

FP Tree

Apriori算法需要多次扫描数据，I/O是很大的瓶颈。为了解决这个问题，FP Tree算法（也称FP Growth算法）采用了一些技巧，无论多少数据，只需要扫描两次数据集，因此提高了算法运行的效率。下面我们就对FP Tree算法做一个总结。

FP Tree数据结构

为了减少I/O次数，FP Tree算法引入了一些数据结构来临时存储数据。这个数据结构包括三部分，如下图所示：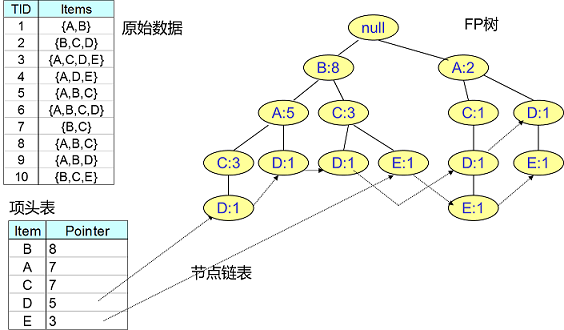

第一部分是一个项头表。里面记录了所有的1项频繁集出现的次数，按照次数降序排列。比如上图中B在所有10组数据中出现了8次，因此排在第一位，这部分好理解。第二部分是FP Tree，它将我们的原始数据集映射到了内存中的一颗FP树，这个FP树比较难理解，它是怎么建立的呢？这个我们后面再讲。第三部分是节点链表。所有项头表里的1项频繁集都是一个节点链表的头，它依次指向FP树中该1项频繁集出现的位置。这样做主要是方便项头表和FP Tree之间的联系查找和更新，也好理解。

项头表的建立

FP树的建立需要首先依赖项头表的建立。首先我们看看怎么建立项头表。

我们第一次扫描数据，得到所有频繁一项集的的计数。然后删除支持度低于阈值的项，将1项频繁集放入项头表，并按照支持度降序排列。接着第二次也是最后一次扫描数据，将读到的原始数据剔除非频繁1项集，并按照支持度降序排列。

上面这段话很抽象，我们用下面这个例子来具体讲解。我们有10条数据，首先第一次扫描数据并对1项集计数，我们发现O，I，L，J，P，M， N都只出现一次，支持度低于20%的阈值，因此他们不会出现在下面的项头表中。剩下的A，C，E，G，B，D，F按照支持度的大小降序排列，组成了我们的项头表。

接着我们第二次扫描数据，对于每条数据剔除非频繁1项集，并按照支持度降序排列。比如数据项ABCEFO，里面O是非频繁1项集，因此被剔除，只剩下了ABCEF。按照支持度的顺序排序，它变成了ACEBF。其他的数据项以此类推。为什么要将原始数据集里的频繁1项数据项进行排序呢？这是为了我们后面的FP树的建立时，可以尽可能的共用祖先节点。

通过两次扫描，项头表已经建立，排序后的数据集也已经得到了，下面我们再看看怎么建立FP树。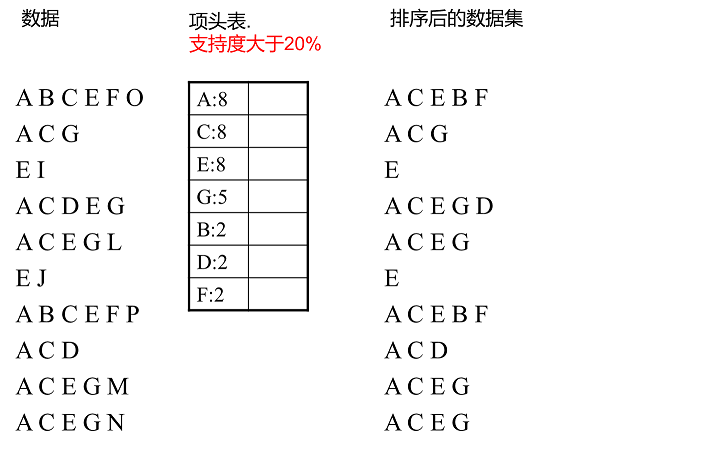

FP Tree的建立

有了项头表和排序后的数据集，我们就可以开始FP树的建立了。开始时FP树没有数据，建立FP树时我们一条条的读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成。

似乎也很抽象，我们还是用第二节的例子来描述。

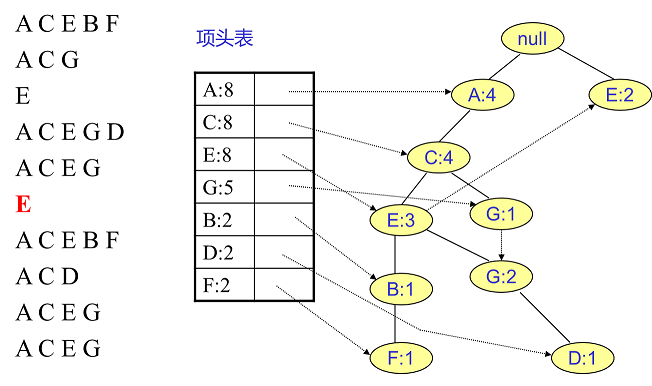
首先，我们插入第一条数据ACEBF，如下图所示。此时FP树没有节点，因此ACEBF是一个独立的路径，所有节点计数为1，项头表通过节点链表链接上对应的新增节点。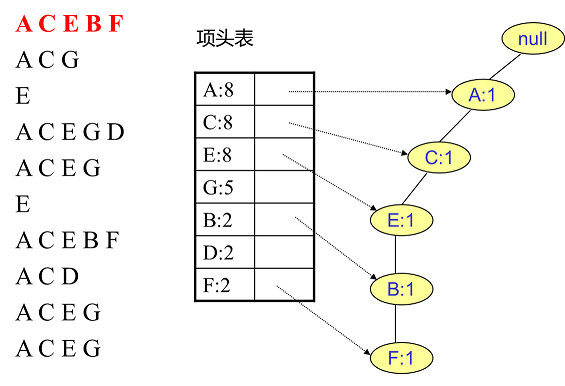

接着我们插入数据ACG，如下图所示。由于ACG和现有的FP树可以有共有的祖先节点序列AC，因此只需要增加一个新节点G，将新节点G的计数记为1。同时A和C的计数加1成为2。当然，对应的G节点的节点链表要更新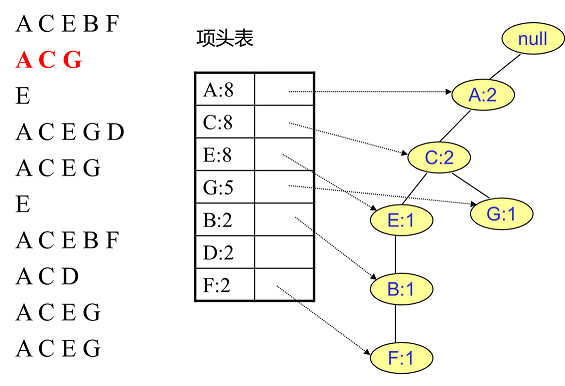

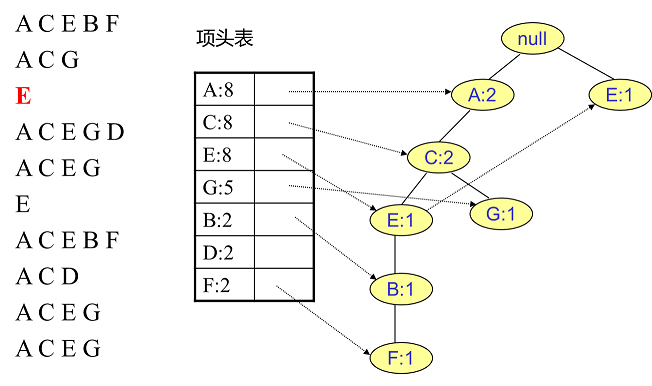
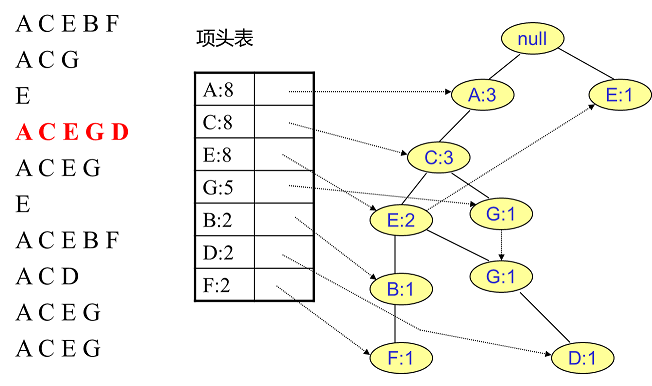
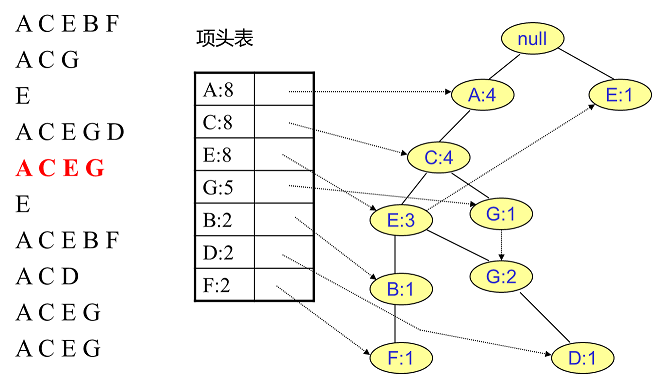
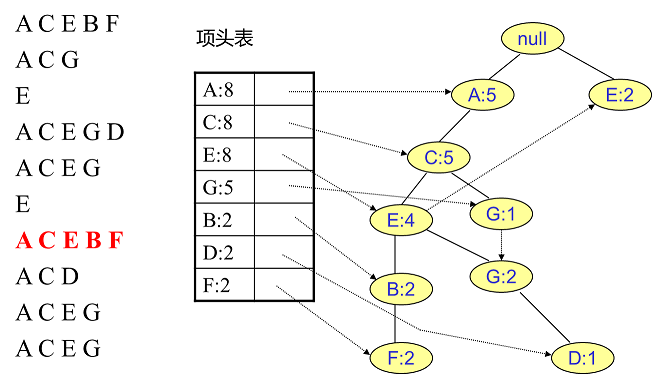
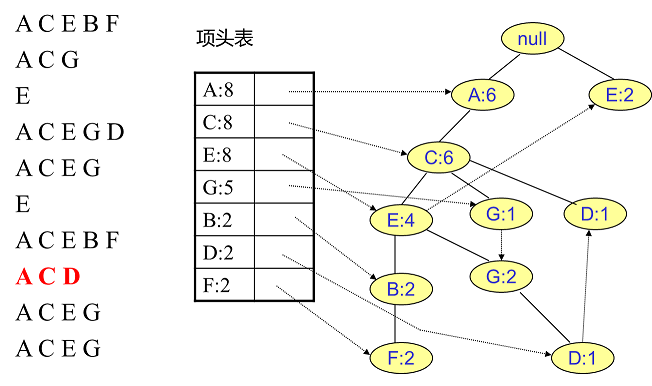
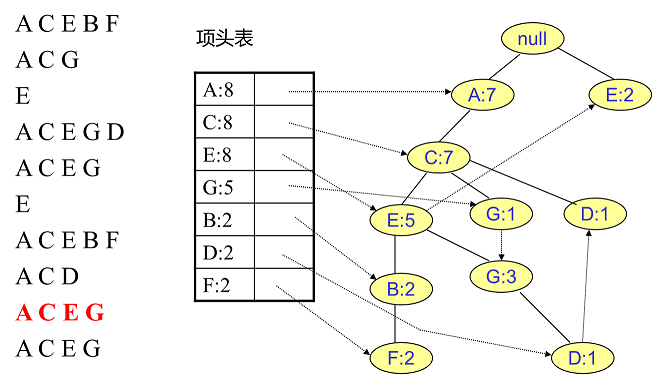
同样的办法可以更新后面8条数据，如下8张图。由于原理类似，这里就不多文字讲解了，大家可以自己去尝试插入并进行理解对比。相信如果大家自己可以独立的插入这10条数据，那么FP树建立的过程就没有什么难度了。








FP Tree的挖掘

下面我们讲如何从FP树里挖掘频繁项集。得到了FP树和项头表以及节点链表，我们首先要从项头表的底部项依次向上挖掘。对于项头表对应于FP树的每一项，我们要找到它的条件模式基。所谓条件模式基是以我们要挖掘的节点作为叶子节点所对应的FP子树。得到这个FP子树，我们将子树中每个节点的的计数设置为叶子节点的计数，并删除计数低于支持度的节点。从这个条件模式基，我们就可以递归挖掘得到频繁项集了。

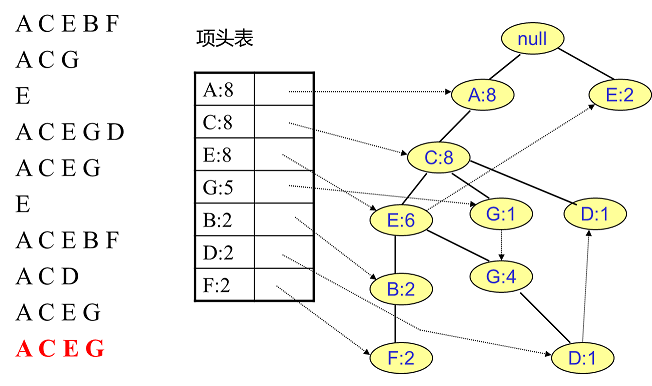
实在太抽象了，之前我看到这也是一团雾水。还是以上面的例子来讲解。我们看看先从最底下的F节点开始，我们先来寻找F节点的条件模式基，由于F在FP树中只有一个节点，因此候选就只有下图左所示的一条路径，对应{A:8,C:8,E:6,B:2,F:2}。我们接着将所有的祖先节点计数设置为叶子节点的计数，即FP子树变成{A:2,C:2,E:2,B:2,F:2}。一般我们的条件模式基可以不写叶子节点，因此最终的F的条件模式基如下图右所示。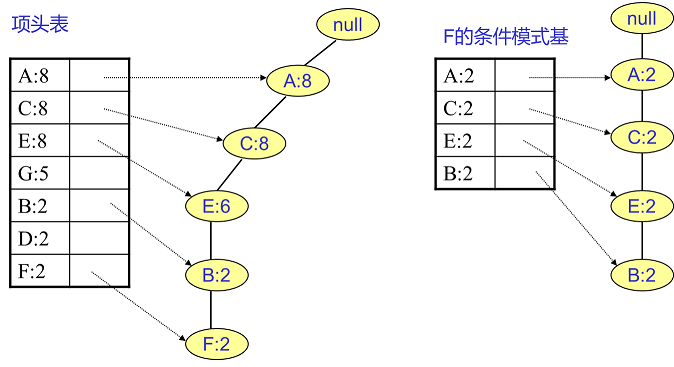

通过它，我们很容易得到F的频繁2项集为{A:2,F:2}，{C:2,F:2}，{E:2,F:2}，{B:2,F:2}。递归合并二项集，得到频繁三项集为{A:2,C:2,F:2}，{A:2,E:2,F:2}，…还有一些频繁三项集，就不写了。当然一直递归下去，最大的频繁项集为频繁5项集，为{A:2,C:2,E:2,B:2,F:2}。

F挖掘完了，我们开始挖掘D节点。D节点比F节点复杂一些，因为它有两个叶子节点，因此首先得到的FP子树如下图左。我们接着将所有的祖先节点计数设置为叶子节点的计数，即变成{A:2,C:2,E:1 G:1,D:1,D:1}此时E节点和G节点由于在条件模式基里面的支持度低于阈值，被我们删除，最终在去除低支持度节点并不包括叶子节点后D的条件模式基为{A:2,C:2}。通过它，我们很容易得到D的频繁2项集为{A:2,D:2}，{C:2,D:2}。递归合并二项集，得到频繁三项集为{A:2,C:2,D:2}。D对应的最大的频繁项集为频繁3项集。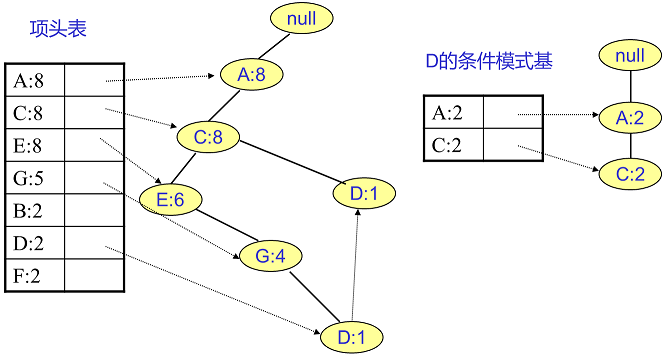

同样的方法可以得到B的条件模式基如下图右边，递归挖掘到B的最大频繁项集为频繁4项集{A:2,C:2,E:2,B:2}。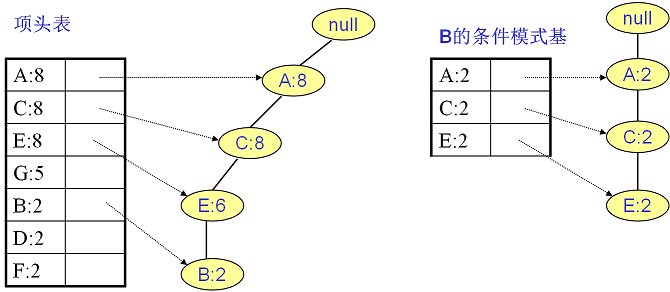

继续挖掘G的频繁项集，挖掘到的G的条件模式基如下图右边，递归挖掘到G的最大频繁项集为频繁4项集{A:5,C:5,E:4,G:4}。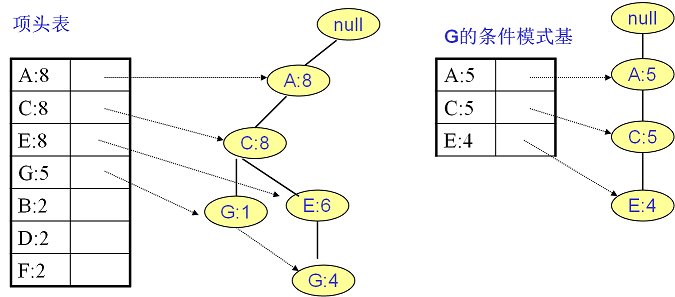

E的条件模式基如下图右边，递归挖掘到E的最大频繁项集为频繁3项集{A:6,C:6,E:6}。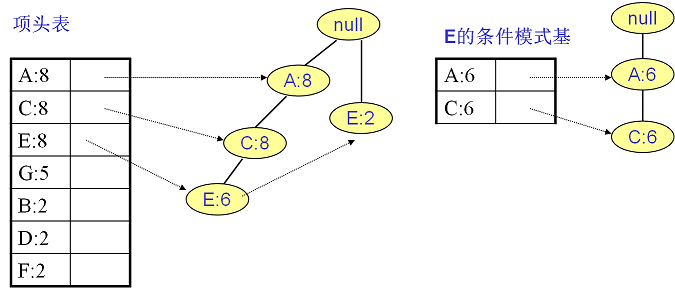

C的条件模式基如下图右边，递归挖掘到C的最大频繁项集为频繁2项集{A:8,C:8}。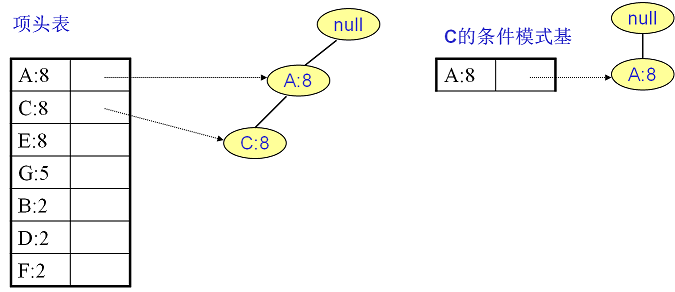

至于A，由于它的条件模式基为空，因此可以不用去挖掘了。

至此我们得到了所有的频繁项集，如果我们只是要最大的频繁K项集，从上面的分析可以看到，最大的频繁项集为5项集。包括{A:2,C:2,E:2,B:2,F:2}。

通过上面的流程，相信大家对FP Tree的挖掘频繁项集的过程也很熟悉了。

FP Tree算法归纳

这里我们对FP Tree算法流程做一个归纳。FP Tree算法包括以下几步：

  1. 扫描数据，得到所有频繁一项集的的计数。然后删除支持度低于阈值的项，将1项频繁集放入项头表，并按照支持度降序排列。
  2. 扫描数据，将读到的原始数据剔除非频繁1项集，并按照支持度降序排列。
  3. 读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成。
  4. 从项头表的底部项依次向上找到项头表项对应的条件模式基。从条件模式基递归挖掘得到项头表项项的频繁项集（可以参见第4节对F的条件模式基的频繁二项集到频繁5五项集的挖掘）。
  5. 如果不限制频繁项集的项数，则返回步骤4所有的频繁项集，否则只返回满足项数要求的频繁项集。

FP tree算法总结

FP Tree算法改进了Apriori算法的I/O瓶颈，巧妙的利用了树结构，这让我们想起了BIRCH聚类，BIRCH聚类也是巧妙的利用了树结构来提高算法运行速度。利用内存数据结构以空间换时间是常用的提高算法运行时间瓶颈的办法。

在实践中，FP Tree算法是可以用于生产环境的关联算法，而Apriori算法则做为先驱，起着关联算法指明灯的作用。除了FP Tree，像GSP，CBA之类的算法都是Apriori派系的。

PrefixSpan算法

前面我们讲到频繁项集挖掘的关联算法Apriori和FP Tree。这两个算法都是挖掘频繁项集的。而今天我们要介绍的PrefixSpan算法也是关联算法，但是它是挖掘频繁序列模式的，因此要解决的问题目标稍有不同。

项集数据和序列数据

首先我们看看项集数据和序列数据有什么不同，如下图所示。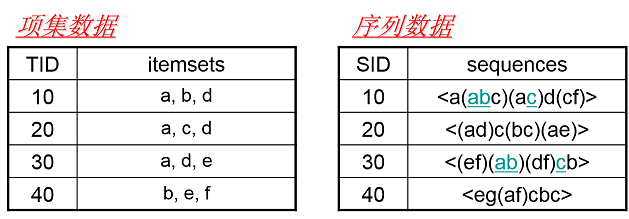

左边的数据集就是项集数据，在Apriori和FP Tree算法中我们也已经看到过了，每个项集数据由若干项组成，这些项没有时间上的先后关系。而右边的序列数据则不一样，它是由若干数据项集组成的序列。比如第一个序列,它由a,abc,ac,d,cf共5个项集数据组成，并且这些项有时间上的先后关系。对于多于一个项的项集我们要加上括号，以便和其他的项集分开。同时由于项集内部是不区分先后顺序的，为了方便数据处理，我们一般将序列数据内所有的项集内部按字母顺序排序。

子序列与频繁序列

了解了序列数据的概念，我们再来看看上面是子序列。子序列和我们数学上的子集的概念很类似，也就是说，如果某个序列A所有的项集在序列B中的项集都可以找到，则A就是B的子序列。当然，如果用严格的数学描述，子序列是这样的：

对于序列A={a1,a2,…an}和序列B={b1,b2,…bm},n≤m，如果存在数字序列1≤j1≤j2≤…≤jn≤m, 满足a1⊆bj1,a2⊆bj2…an⊆bjn，则称A是B的子序列。当然反过来说， B就是A的超序列。

而频繁序列则和我们的频繁项集很类似，也就是频繁出现的子序列。比如对于下图，支持度阈值定义为50%，也就是需要出现两次的子序列才是频繁序列。而子序列<(ab)c>是频繁序列，因为它是图中的第一条数据和第三条序列数据的子序列，对应的位置用蓝色标示。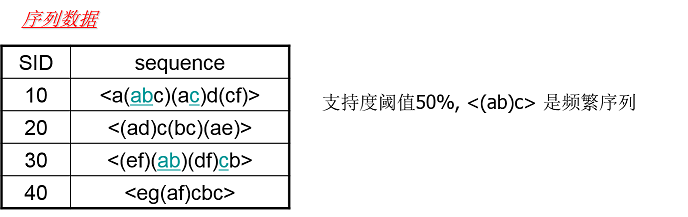

PrefixSpan算法的一些概念

PrefixSpan算法的全称是Prefix-Projected Pattern Growth，即前缀投影的模式挖掘。里面有前缀和投影两个词。那么我们首先看看什么是PrefixSpan算法中的前缀prefix。

在PrefixSpan算法中的前缀prefix通俗意义讲就是序列数据前面部分的子序列。比如对于序列数据B=<a(abc)(ac)d(cf)>，而A=<a(abc)a>,则A是B的前缀。当然B的前缀不止一个，比如<a>，<aa>，<a(ab)>也都是B的前缀。

看了前缀，我们再来看前缀投影，其实前缀投影这儿就是我们的后缀，有前缀就有后缀嘛。前缀加上后缀就可以构成一个我们的序列。下面给出前缀和后缀的例子。对于某一个前缀，序列里前缀后面剩下的子序列即为我们的后缀。如果前缀最后的项是项集的一部分，则用一个“_”来占位表示。

下面这个例子展示了序列<a(abc)(ac)d(cf)>的一些前缀和后缀，还是比较直观的。要注意的是，如果前缀的末尾不是一个完全的项集，则需要加一个占位符。

在PrefixSpan算法中，相同前缀对应的所有后缀的结合我们称为前缀对应的投影数据库。

PrefixSpan算法思想

现在我们来看看PrefixSpan算法的思想，PrefixSpan算法的目标是挖掘出满足最小支持度的频繁序列。那么怎么去挖掘出所有满足要求的频繁序列呢。回忆Aprior算法，它是从频繁1项集出发，一步步的挖掘2项集，直到最大的K项集。PrefixSpan算法也类似，它从长度为1的前缀开始挖掘序列模式，搜索对应的投影数据库得到长度为1的前缀对应的频繁序列，然后递归的挖掘长度为2的前缀所对应的频繁序列，。。。以此类推，一直递归到不能挖掘到更长的前缀挖掘为止。

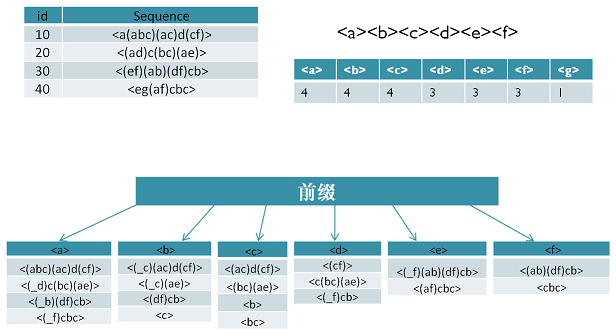
比如对应于我们第二节的例子，支持度阈值为50%。里面长度为1的前缀包括<a>，<b>，<c>，<d>，<e>，<f>，<g>我们需要对这6个前缀分别递归搜索找各个前缀对应的频繁序列。如下图所示，每个前缀对应的后缀也标出来了。由于g只在序列4出现，支持度计数只有1，因此无法继续挖掘。我们的长度为1的频繁序列为<a>，<b>，<c>，<d>，<e>，<f>。去除所有序列中的g，即第4条记录变成<e(af)cbc>。

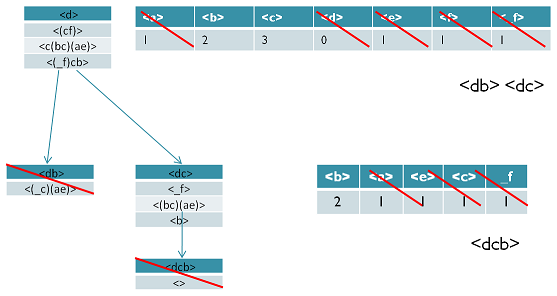
现在我们开始挖掘频繁序列,分别从长度为1的频繁项开始。这里我们以d为例子来递归挖掘，其他的节点递归挖掘方法和D一样。方法如下图，首先我们对ｄ的后缀进行计数，得到{a:1, b:2, c:3, d:0, e:1, f:1，_f:1}。注意f和_f是不一样的，因为前者是在和前缀d不同的项集，而后者是和前缀d同项集。由于此时a,d,e,f,_f都达不到支持度阈值，因此我们递归得到的前缀为d的2项频繁序列为<db>和<dc>。接着我们分别递归db和dc为前缀所对应的投影序列。首先看db前缀，此时对应的投影后缀只有<_c(ae)>，此时_c,a,e支持度均达不到阈值，因此无法找到以db为前缀的频繁序列。现在我们来递归另外一个前缀dc。以dc为前缀的投影序列为<_f>，<(bc)(ae)>，<b>，此时我们进行支持度计数，结果为{b:2, a:1, c:1, e:1, _f:1}，只有b满足支持度阈值，因此我们得到前缀为dc的三项频繁序列为<dcb>。我们继续递归以<dcb>为前缀的频繁序列。由于前缀<dcb>对应的投影序列<(_c)ae>支持度全部不达标，因此不能产生4项频繁序列。至此以d为前缀的频繁序列挖掘结束，产生的频繁序列为<d><db><dc><dcb>。

同样的方法可以得到其他以<a>，<b>，<c>，<e>，<f>为前缀的频繁序列。

PrefixSpan算法流程

下面我们对PrefixSpan算法的流程做一个归纳总结。

  • 输入：序列数据集S和支持度阈值α
  • 输出：所有满足支持度要求的频繁序列集
  1. 找出所有长度为1的前缀和对应的投影数据库
  2. 对长度为1的前缀进行计数，将支持度低于阈值α的前缀对应的项从数据集S删除，同时得到所有的频繁1项序列，i=1.
  3. 对于每个长度为i满足支持度要求的前缀进行递归挖掘：
    1. 找出前缀所对应的投影数据库。如果投影数据库为空，则递归返回。
    2. 统计对应投影数据库中各项的支持度计数。如果所有项的支持度计数都低于阈值α，则递归返回。
    3. 将满足支持度计数的各个单项和当前的前缀进行合并，得到若干新的前缀。
    4. 令i=i+1，前缀为合并单项后的各个前缀，分别递归执行第3步。