第一章:STL概论和版本简介
STL六大组件
- 容器:各种数据结构,如:vector、list、deque、set、map、主要用来存放数据。
- 算法:各种常见算法,如:sort、search、copy、erase
- 迭代器:扮演算法和容器中的中介。迭代器是一种将
operator*、operator->、operator++、operator--等指针相关操作予以重载的class template。所有的容器均有自己独特的迭代器,实现对容器内数据的访问 - 仿函数:行为类似函数,可作为算法的某种策略。仿函数是一种重载了
operator()的class或class template。一般指针函数可视为狭义的仿函数。 - 配接器(adapters): 修饰容器、仿函数、迭代器接口。例如STL提供的queue和stack,虽然看似容器,但是只能算一种容器配接器,因为它们的底部完全借助deque,所有操作都由底层的deque供应。
- 配置器(allocators):负责空间配置和管理,配置器是一个实现了动态空间配置、空间管理、空间释放的class template.
各组件间的关系
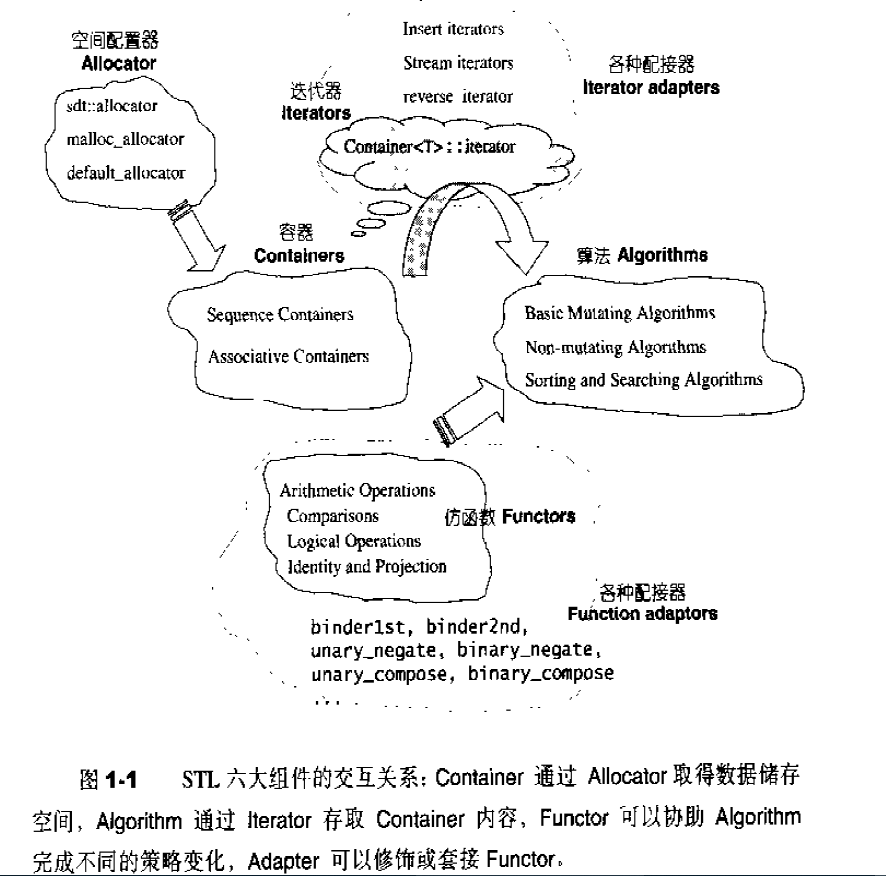
由于STL已成为C++标准程序库的大脉系,因此:目前所有的C++编译器一定支持有一份STL。STL并非以二进制代码面貌出现,而是以源代码面貌供应。某些STL版本同时存在具扩展名和无扩展名的两份文件,例如Visual C++的版本同时具备<vectorr.h>和<vector>。某些STL版本只存在具扩展名的头文件,例如C++ Builder的RaugeWave版本只有<vector.h>。某些STL版本不仅有一线装配,还有二线装配,例如GNU C++的SGI版本不但有一线的<vector.h>和<vector>,还有二线的<stl_vector.h>。
Container通过Allocator取得数据储存空间,Algorithm通过Iterator存取Container内容,Functor可以协助Algorithm完成不同的策略变化,Adapter可以修饰或套接Functor。
SGI STL头文件分布
- C++标准规范下的C头文件:cstdio,csyflib,cstring,…
- C++标准程序库中不属于STL范畴者:stream,string,…
- STL标准头文件(无扩展名):vector,deque,list,map,…
- C++标准定案前,HP所规范的STL头文件:vector.h,deque.h,list.h,…
- SGI STL内部文件(STL真正实现与此):stl_vector.h,stl_deque.h,stl_algo.h,…
不同的编译器对C++语言的支持程度不尽相同。作为一个希望具备广泛移植能力的程序库,SGI STL准备了一个环境组态文件<stl_config.h>,其中定义了许多常量,标示某些组态的成立与否,所有STL头文件都会直接或间接包含这个组态文件,并以条件式写法,让预处理器根据各个常量决定取舍哪一段程序代码,例如: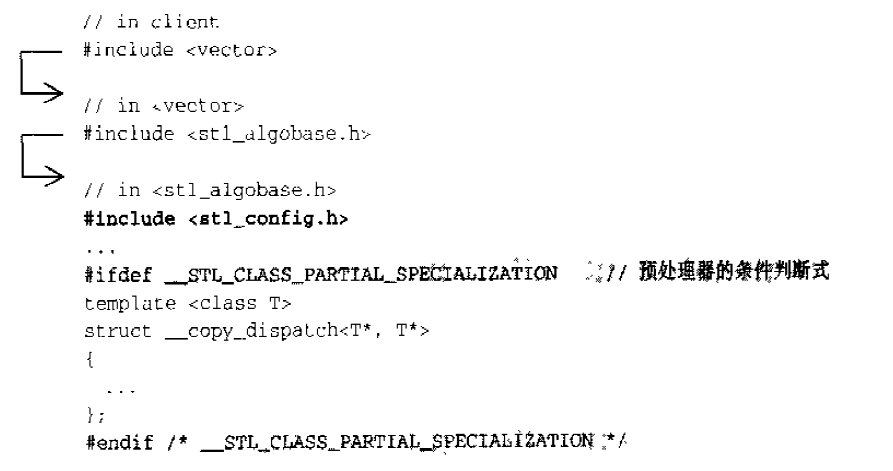
<stl_config.h>文件起始处有一份常量定义说明,针对各家不同的编译器及可能的版本给予常量设定。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246// Filename: stl_config.h
/*
* Copyright (c) 1996-1997
* Silicon Graphics Computer Systems, Inc.
*
* Permission to use, copy, modify, distribute and sell this software
* and its documentation for any purpose is hereby granted without fee,
* provided that the above copyright notice appear in all copies and
* that both that copyright notice and this permission notice appear
* in supporting documentation. Silicon Graphics makes no
* representations about the suitability of this software for any
* purpose. It is provided "as is" without express or implied warranty.
*/
/* NOTE: This is an internal header file, included by other STL headers.
* You should not attempt to use it directly.
*/
// 本配置文件功能表:
// (1) 如果不编译器没有定义bool, true, false则定义
// (2) 如果编译器不支持drand48()函数则定义__STL_NO_DRAND48
// 注: drand48产生双精度的伪随机数, 因为采用了48bit计算, 故名drand48
// (3) 如果编译器不支持static members of template classes(模板类静态成员),
// 则定义__STL_STATIC_TEMPLATE_MEMBER_BUG
// (4) 如果编译器不支持'typename'关键字, 则将'typename'定义为空(null macro)
// (5) 如果编译器支持partial specialization of class templates(模板类偏特化),
// 则定义__STL_CLASS_PARTIAL_SPECIALIZATION
// 参考文献: http://msdn.microsoft.com/en-us/library/9w7t3kf1(v=VS.71).aspx
// (6) 如果编译器支持partial ordering of function templates(模板函数特化优先级),
// 则定义__STL_FUNCTION_TMPL_PARTIAL_ORDER
// 参考资料: http://msdn.microsoft.com/zh-cn/library/zaycz069.aspx
// (7) 如果编译器支持calling a function template by providing its template
// arguments explicitly(显式指定调用模板函数的模板参数)
// 则定义__STL_EXPLICIT_FUNCTION_TMPL_ARGS
// (8) 如果编译器支持template members of classes(类模板成员),
// 则定义__STL_MEMBER_TEMPLATES
// (9) 如果编译器不支持'explicit'关键字, 则将'explicit'定义为空(null macro)
// (10) 如果编译器不能根据前一个模板参数设定后面的默认模板参数,
// 则定义__STL_LIMITED_DEFAULT_TEMPLATES
// (11) 如果编译器处理模板函数的non-type模板参数类型推断有困难,
// 则定义__STL_NON_TYPE_TMPL_PARAM_BUG
// (12) 如果编译器不支持迭代器使用'->'操作符,
// 则定义__SGI_STL_NO_ARROW_OPERATOR
// (13) 如果编译器(在当前编译模式下)支持异常,
// 则定义__STL_USE_EXCEPTIONS
// (14) 如果我们将STL放进命名空间中,
// 则定义__STL_USE_NAMESPACES
// (15) 如果本STL在SGI的编译器上编译, 并且用户没有选择pthreads或者no threads,
// 则默认使用__STL_SGI_THREADS
// 注: POSIX thread 简称为pthread, Posix线程是一个POSIX标准线程.
// (16) 如果本STL在Win32平台的编译器上使用多线程模式编译,
// 则定义__STL_WIN32THREADS
// (17) 适当的定义命名空间相关的宏(__STD, __STL_BEGIN_NAMESPACE, 等)
// (18) 适当的定义异常相关的宏(__STL_TRY, __STL_UNWIND, 等)
// (19) 根据是否定义__STL_ASSERTIONS, 将__stl_assert定义为断言或者空(null macro)
// 如果编译器不提供本STL需要的一些功能,则定义__STL_NEED_XXX
/* glibc pre 2.0 is very buggy. We have to disable thread for it.
It should be upgraded to glibc 2.0 or later. */
// Sun C++ compiler
// _MSC_VER 定义微软编译器的版本
// MS VC++ 10.0 _MSC_VER = 1600
// MS VC++ 9.0 _MSC_VER = 1500
// MS VC++ 8.0 _MSC_VER = 1400
// MS VC++ 7.1 _MSC_VER = 1310
// MS VC++ 7.0 _MSC_VER = 1300
// MS VC++ 6.0 _MSC_VER = 1200
// MS VC++ 5.0 _MSC_VER = 1100
typedef int bool;
// __STL_NO_NAMESPACES is a hook so that users can disable namespaces
// without having to edit library headers.
if (!(expr)) { fprintf(stderr, "%s:%d STL assertion failure: %s\n", \
__FILE__, __LINE__,
// Local Variables:
// mode:C++
// End:
可能困惑的C++语法
stl_config.h中的各种组态(configuration)
组态3__STL_STATIC_TEMPLATE_MEMBER_BUG。如果编译器无法处理static member of template classes(模板类静态成员)就定义
。即对于模板类中,模板类型不同时的静态变量不同。1
2
3
4
5
6
7
8template <typename T>
class test{
public:
static int _data;
}
int test<int>::_data=1;
int test<char>::_data=2;
组态5__STL_CLASS_PARTIAL_SPECIALIZATION。如果编译器支持 partial specialization of class templates(模板类偏特化)就定义。在模板类一般化设计之外(全特化),针对某些template做特殊设计。“所谓的partial specialization的另一个意思是提供另一份template定义式,而其本身仍是templatized”。全特化就是所有的模板都为具体的类。T*特化允许用指针类型匹配的模式(也只能匹配指针类型)。const T*特化允许使用指向const的指针类型匹配(也只能匹配指向const的指针)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23//一般化设计,非特化情况均使用这个
template <class I,class O>
struct test{
test() { cout << "I, O" <<endl; }
};
//特殊化设计1(偏特化1)
template <class T>
struct test <T* ,T*> {
test() { cout << "T* ,T*" << endl; }
};
//特殊化设计2(偏特化2)
template <class T>
struct test <const T* ,T*> {
test() { cout << "const T* ,T*" << endl; }
};
//测试
int main() {
test<int, char> obj1; //I, O
test<int*, int*> obj2; //T*, T*
test<const int*, int*> obj3; //const T*, T*
}
组态6__STL_FUNCTION_TMPL_PARTIAL_ORDER。如果编译器支持partial ordering of function templates或者说partial specialization of function templates就定义。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15template <class T,class Alloc=alloc>
class vec {
public:
void swap(vec<T, Alloc>&) { cout << "swap1()" << endl; }
};
template <class T, class Alloc = alloc>
inline void swap(vec<T, Alloc>& a, vec<T, Alloc>& b) { a.swap(b); }
int main() {
vec<int> a, b;
swap(a, b);
}
组态8__STL_MEMBER_TEMPLATES。如果编译器支持template members of classes(模板类内嵌套模板) 就定义。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class vec {
public:
typedef T value_type;
typedef value_type* iterator;
template<class I>
void insert(iterator position, I first, I last) {
cout << "insert()" << endl;
}
};
int main() {
int ia[5] = { 0,1,2,3,4 };
vec<int> a;
vec<int>::iterator ite;
a.insert(ite, ia, ia + 5);
}
组态10__STL_LIMITED_DEFAULT_TEMPLATES。如果编译器支持一个template参数可以根据前一个template的参数设置就定义。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17template <class T,class Alloc=alloc,size_t BufSiz=0>
class deque {
public:
deque() { cout << deque() << endl; }
};
template <class T,class Sequence=deque<T>>
class stack {
public:
stack() { cout << "Stack" << endl; }
private:
Sequence c;
};
int main() {
stack<int> x;
}
组态11__STL_NON_TYPE_TMPL_PARAM_BUG。测试类模板是否使用非类型模板参数(non-type template parameters) 。当以类型(type)作为模板参数的时候,代码中未决定的是类型;
当以一般的数字(non-type)作为模板参数的时候,代码中待定的内容便是某些数值。使用者这种模板必须要显示指定数值,模板才能实例化。通常它们只能是常数整数(constant integral values )包括枚举,或者是指向外部链接的指针。不能把float,class-type类型的对象,内部链接(internal linkage )对象,作为非类型模板参数。1
2
3
4
5template <class T,class Alloc=alloc,size_t BufSiz=0> //BufSiz即为非类型模板。
class deque {
public:
deque() { cout << deque() << endl; }
};
__STL_NULL_TMPL_ARGS。直接理解为若允许bound friend template(约束模板友元)则定义为 <> ,否则为空。1
friend bool ooperator== __STL_NULL_TMPL_ARGS(const stack&,const stack&);
展开后变成1
friend bool ooperator== <>(const stack&,const stack&);
bound friend template(约束模板友元)即友元类型取决于类被初始化时的类型,但程序必须在类外为友元提供模板定义。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23template <class T,class Sequence=deque<T>>
class stack {
//最标准的写法
friend bool operator== <T>(const stack<T>&, const stack<T>&);
friend bool operator< <T>(const stack<T>&, const stack<T>&);
//参数列表中的<T>实际上可以忽略
friend bool operator== <T>(const stack&, const stack&);
friend bool operator< <T>(const stack&, const stack&);
//当可以从参数中推断出模板类型时,可以改用<>
friend bool operator== <>(const stack&, const stack&);
friend bool operator< <>(const stack&, const stack&);
//下面用法是错误的!
//friend bool operator== (const stack&, const stack&);
//friend bool operator< (const stack&, const stack&);
public:
stack() { cout << "Stack" << endl; }
private:
Sequence c;
};
//定义部分懒得写了,但必须要写!
__STL_TEMPLATE_NULL即template <>显示的模板特化 。1
2
3
4
5
模板特化(class template explicit specialization)即指定一种或多种模板形参的实际值或实际类型,作为特殊情况。(与模板类型偏特化不同!)1
2
3
4
5
6template<class type> struct __type_traits{ ...};//非特化情况均使用这个
__STL_TEMPLATE_NULL struct __type_traits<char> { ... };//特化char情况
template<class Key> struct hash { };//非特化情况均使用这个
__STL_TEMPLATE_NULL struct hash<char> { ... };//特化char情况
__STL_TEMPLATE_NULL struct hash<unsgned char> { ... };//特化unsigned char情况
经展开后:1
2
3
4
5
6template<class type> struct __type_traits{ ...};//非特化情况均使用这个
template<> struct __type_traits<char> { ... };//特化char情况
template<class Key> struct hash { };//非特化情况均使用这个
template<> struct hash<char> { ... };//特化char情况
template<> struct hash<unsgned char> { ... };//特化unsigned char情况
临时对象的产生与应用
刻意制造一些临时对象,在类型名之后直接加一对(),并指定初值,使用时相当于调用该类的临时对象的()操作。常用于仿函数与算法的搭配上。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19template<typename T>
class print {
public:
void operator()(const T& elem) {
cout << elem << " ";
}
};
template<typename T>
class plus{
public:
T operator()(const T& x, const T& y)const { return x + y; }
};
int main() {
vector<int> ai({ 1,2,3,4,5 });
for_each(ai.begin(), ai.end(), print<int>());
int a = 5, b = 3;
print<int>()(plus<int>()(a, b));
}
最后一行便是产生“function template具现体”print<int>的一个临时对象。这个对象将被传入进for_each()中。
静态常量整数成员在class内部直接初始化
如果class内含const static integral data member,那么根据C++规格,我们可以在class之内直接给予初值。所谓integral泛指所有的整数型别(包括浮点数),不单只是指int,下面是一个例子:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
using namespace std;
template <typename T>
class testClass
{
public:
static const double _datai=1.2;
static const long _datal=3L;
static const char _datac='c';
};
int main()
{
cout<<testClass<int>::_datai<<endl;
cout<<testClass<int>::_datal<<endl;
cout<<testClass<int>::_datac<<endl;
}
一般,非const的static数据成员是不能在类的内部初始化,但是,我们可以为静态成员提供const整数类型的类内初始值。
例如,下面的情况会报错:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
using namespace std;
template <typename T>
class testClass
{
public:
static double _datai=1.2;
static const long _datal=3L;
static const char _datac='c';
};
int main()
{
cout<<testClass<int>::_datai<<endl;
cout<<testClass<int>::_datal<<endl;
cout<<testClass<int>::_datac<<endl;
}
如果加了const 或者constexpr之后,就可以在类内进行初始化了。
对于static成员,如果在类的内部提供了一个初值,则成员在类外的定义不能再指定一个初始值了。例如:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
using namespace std;
template <typename T>
class testClass
{
public:
static const double _datai=1.2;
static const long _datal=3L;
static const char _datac='c';
};
template <typename T>
const double testClass<T>::_datai=8.8;
int main()
{
cout<<testClass<int>::_datai<<endl;
cout<<testClass<int>::_datal<<endl;
cout<<testClass<int>::_datac<<endl;
}
下面的情况是允许的,直接在定义的时候提供初始值或者在类内提供初始值之后只在类外定义但不提供初始值。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
using namespace std;
template <typename T>
class testClass
{
public:
static const double _datai;
static const long _datal=3L;
static const char _datac='c';
};
template <typename T>
const double testClass<T>::_datai=8.8;
int main()
{
cout<<testClass<int>::_datai<<endl;
cout<<testClass<int>::_datal<<endl;
cout<<testClass<int>::_datac<<endl;
}
或者1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
using namespace std;
template <typename T>
class testClass
{
public:
static const double _datai=1.2;
static const long _datal=3L;
static const char _datac='c';
};
template <typename T>
const double testClass<T>::_datai;
int main()
{
cout<<testClass<int>::_datai<<endl;
cout<<testClass<int>::_datal<<endl;
cout<<testClass<int>::_datac<<endl;
}
increment/decrement/dereference操作符
increment/dereference操作符在迭代器的实现上占有非常重要的地位,因为任何一个迭代器都必须实现出前进(increment,operator++)和取值(dereference,operator*)功能,前者还分为前置式(prefix)和后置式(Postfix)两种。有写迭代器具备双向移动功能,那么就必须再提供decrement操作符(也分前置式和后置式),下面是一个例子:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
using namespace std;
class INT
{
friend ostream& operator<<(ostream& os,const INT& i);
public:
INT(int i):m_i(i){}
INT& operator++()
{
++(this->m_i);
return *this;
}
const INT operator++(int)
{
INT temp=*this;
++(*this);
return temp;
}
INT& operator--()
{
--(this->m_i);
return *this;
}
const INT operator--(int)
{
INT temp=*this;
--(*this);
return temp;
}
int& operator*() const
{
return (int&)m_i;
}
private:
int m_i;
};
ostream& operator<<(ostream& os,const INT &i)
{
os<<'['<<i.m_i<<']';
return os;
}
int main()
{
INT I(5);
cout<<I++;
cout<<++I;
cout<<I--;
cout<<--I;
cout<<*I;
}
前闭后开区间表示法
任何一个STL算法,都需要获得由一对迭代器(泛型指针)所标示的区间,用以表示操作范围,这一对迭代器所标示的是个所谓的前闭后开区间,以[first,last)表示,也就是说,整个实际范围从first开始,直到last-1.迭代器last所指的是“最后一个元素的下一位置”。这种off by one(偏移一格,或说pass the end)的标示法,带来了很多方便,例如下面两个STL算法的循环设计,就显得干净利落:1
2
3
4
5
6
7
8
9
10
11
12
13
14template<class InputIterator,class T>
InputIterator find(InputIterator first,InputIterator last,const T&value)
{
while(first!=last&&*first!=value) ++first;
return first; //返回迭代器
}
template <class InputIterator,class Function>
Function for_each(InputIterator first,InputIterator last,Function f)
{
for(;first!=last;++first)
f(*first);
return f;
}
function call 操作符
函数调用操作(C++语法中的左右小括号)也可以被重载。
许多STL算法都提供了两个版本,一个用于一般情况(例如排序时以递增方式排列),一个用于特殊情况(例如排序时由使用者指定以何种特殊关系进行排列),像这种情况,需要用户指定某个条件或某个策略,而条件或策略的背后由一整组操作构成,便需要某种特殊的东西来代表这“一整组操作”。
代表“一整组操作“的,当然是函数,过去C语言时代,欲将函数当做参数传递,唯有通过函数指针才能达成,例如:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
using namespace std;
int fcmp(const void* elem1,const void* elem2);
int main()
{
int ia[10]={32,92,67,58,10,4,25,52,59,54};
for(int i=0;i<10;i++)
cout<<ia[i]<<" ";
cout<<endl;
qsort(ia,sizeof(ia)/sizeof(int),sizeof(int),fcmp);
for(int i=0;i<10;i++)
cout<<ia[i]<<" ";
cout<<endl;
}
int fcmp(const void* elem1,const void* elem2)
{
const int *i1=(const int*)elem1;
const int *i2=(const int*)elem2;
if(*i1<*i2)
return -1;
else if(*i1==*i2)
return 0;
else if(*i1>*i2)
return 1;
}
但是函数指针有缺点,最重要的是它无法持有自己的状态(所谓局部状态,local states),也无法达到组件技术中的可适配性(adaptability)——也就是无法再将某些修饰条件加诸于其上面而改变其状态。
为此,STL算法的特殊版本所接受的所谓“条件”或“策略”或“一整组操作”,都以仿函数形式呈现。所谓仿函数(functor)就是使用起来像函数一样的东西。如果你针对么某个class进行operator()重载,它就是一个仿函数,至于要成为一个可配接的仿函数,还需要做一些额外的努力。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//注意,不能使用using namespace std 不然plus和minus会有歧义
using std::cout;
using std::endl;
template <class T>
struct plus
{
T operator()(const T& x,const T& y) const {return x+y;}
};
template <class T>
struct minus
{
T operator()(const T& x,const T& y)const {return x-y;}
};
int main()
{
plus<int> plusObj;
minus<int> minusObj;
cout<<plusObj(3,5)<<endl;
cout<<minusObj(3,5)<<endl;
//注意下面的调用,不要忘记调用默认构造函数的小括号以及函数对象调用参数的小括号
//以下直接产生仿函数的临时对象(第一对小括号),并调用之(第二对小括号)
cout<<plus<int>()(43,50)<<endl;
cout<<minus<int>()(43,50)<<endl;
}
空间配置器
以STL的运用角度而言,空间配置器是最不需要介绍的东西,它总是隐藏在一切组件(更具体地说是指容器,container)的背后,默默工作,默默付出。但若以STL的实现角度而言,第一个需要介绍的就是空间配置器,因为整个STL的操作对象(所有的数据)都存放在容器之内,而容器一定需要配置空间以置放资料。
为什么不说allocator是内存配置器而说它是空间配置器呢?因为空间不一定是内存,空间也可以是磁盘或其它辅助存储介质。是的,你可以一个allocator,直接向硬盘取空间,以下介绍的是SGI STL提供的配置器,配置的对象是内存。
空间配置器的标准接口
根据STL的规范,以下是allocator的必要接口:
allocator::value_typeallocator::pointerallocator::const_pointerallocator::referenceallocator::const_referenceallocator::size_typeallocator::difference_typeallocator::rebind:一个嵌套的class template,class rebind<U>拥有唯一的成员other,那是一个typedef,代表allocator<U>allocator::allocator():default constuctorallocator::allocator(const allocator&):copy constructortemplate<class U>allocator::allocator(const allocator<U>&):泛化的copy constructorallocator::~allocator():destructorpointer allocator::address(reference x)const:返回某个对象的地址,算式a.address(x)等同于&xconst_pointer allocator::address(const_reference x)const:返回某个const对象的地址,算式a.address(x)等同于&xpointer allocator::allocate(size_type n,const void* =0):配置空间,足以存储n个T对象,第二参数是个提示,实际上可能会利用它来增进区域性,或完全忽略之void allocator::deallocate(pointer p,size_type n):归还先前配置的空间size_type allocator::max_size() const:返回可成功分配的最大量void allocator::construct(pointer p,const T& x):等同于new((void*)p) T(x)void allocator::destroy(pointer p):等同于p->~T()
设计一个简单的空间配置器, JJ::allocator
1 |
|
具备次配置力的 SGI 空间配置器
SGI STL的配置器与众不同,它与标准规范不同,其名称是alloc而非allocator。如果要在程序中明白采用SGI配置器,那么应该这样写:1
vector<int, std::alloc> iv; //gcc编译器
配置器名字为alloc,不接受任何参数。标准配置器的名字是allocator,而且可以接受参数。比如VC中写法:1
vector<int, std::allocator<int> > iv; //VC编译器
SGI STL的每一个容器都已经指定了缺省配置其alloc。我们很少需要自己去指定空间配置器。比如vector容器的声明:1
2
3
4template <class T, class Alloc = alloc>
class vector {
//...
}
SGI标准的空间配置器allocator
其实SGI也定义了一个符合部分标准,名为allocator的配置器,但是它自己不使用,也不建议我们使用,主要原因是效率不佳。它只是把C++的操作符::operator new和::operator delete做了一层简单的封装而已。下面仅仅贴出代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
//仅仅是简单的封装了operator new
template <class T>
inline T* allocate(ptrdiff_t size, T*) {
set_new_handler(0);
T* tmp = (T*)(::operator new((size_t)(size * sizeof(T))));
if (tmp == 0) {
cerr << "out of memory" << endl;
exit(1);
}
return tmp;
}
//仅仅是简单的封装了operator::delete
template <class T>
inline void deallocate(T* buffer) {
::operator delete(buffer);
}
template <class T>
class allocator {
public:
typedef T value_type;
typedef T* pointer;
typedef const T* const_pointer;
typedef T& reference;
typedef const T& const_reference;
typedef size_t size_type;
typedef ptrdiff_t difference_type;
pointer allocate(size_type n) {
return ::allocate((difference_type)n, (pointer)0);
}
void deallocate(pointer p) { ::deallocate(p); }
pointer address(reference x) { return (pointer)&x; }
const_pointer const_address(const_reference x) {
return (const_pointer)&x;
}
size_type init_page_size() {
return max(size_type(1), size_type(4096/sizeof(T)));
}
size_type max_size() const {
return max(size_type(1), size_type(UINT_MAX/sizeof(T)));
}
};
// 特化版本
class allocator<void> {
public:
typedef void* pointer;
};
SGI特殊的空间配置器std::alloc
一般而言,我们所习惯的C++内存配置器操作和释放操作时这样的:1
2
3class FOO { ...};
FOO* pf=new FOO; //配置内存,然后构造对象
delete pf; //将对象析构,然后释放内存
这其中的new算式内含两个阶段操作:
- 调用
::operator new配置内存 - 调用
FOO::FOO()构造对象内容
delete算式也内含两个阶段操作:
- 调用
FOO::~FOO()对对象析构 - 调用
::operator delete释放内存
为了精密分工,SGI allocator将两个阶段分开:
内存配置操作由alloc:allocate负责,内存释放由alloc:deallocate负责;对象构造操作由::contructor()负责,对象析构由::destroy()负责。
STL标准告诉我们,配置器定义在头文件<memory>中,它里面又包括两个文件:1
2
内存空间的配置/释放与对象内容的构造/析构,分别落在这两个文件身上。其中<stl_construct.h>定义了两个基本函数:构造用的construct()和析构用的destroy()。
下图显示了其结构: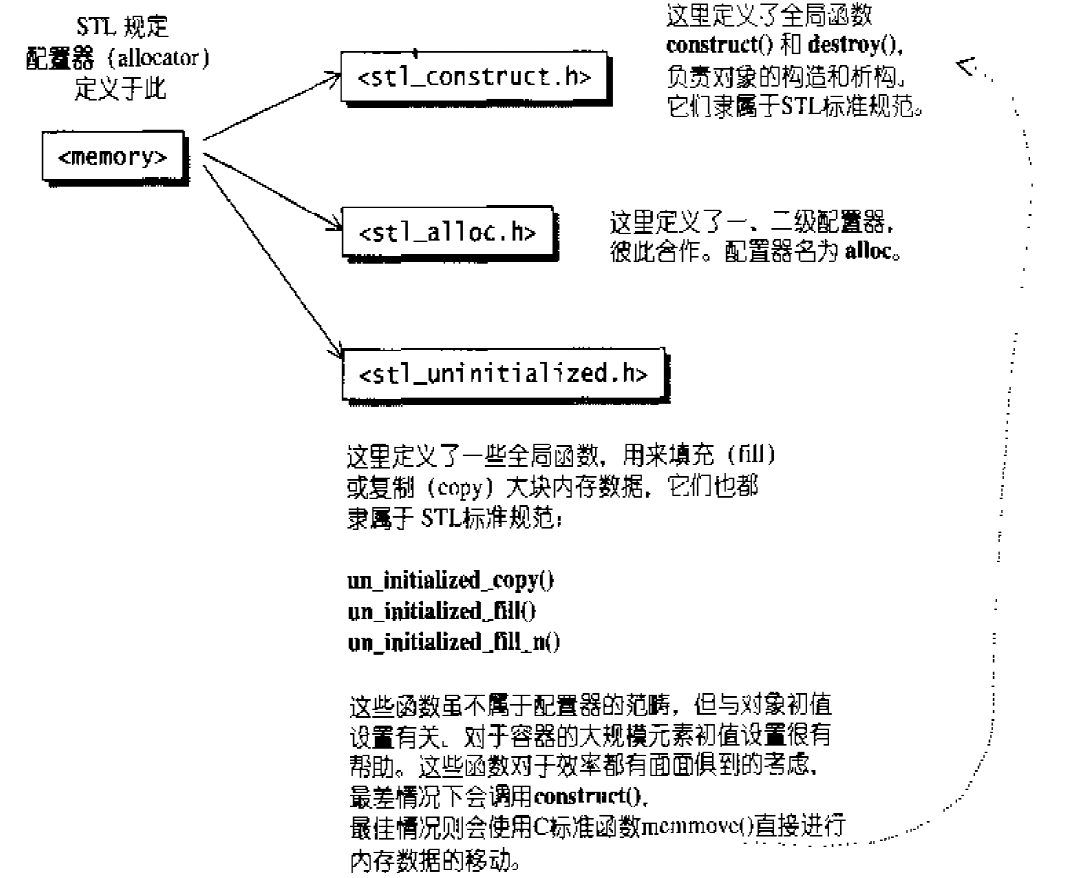
构造函数析构的基本工具:construct()和destroy()
下面是<stl_constuct.h>的部分内容:
函数construct()使用了定位new操作符,其源代码:1
2
3
4template <class T1, class T2>
inline void construct(T1* p, const T2& value) {
new (p) T1(value); // 定为new操作符placement new; 在指针p所指处构造对象
}
函数destroy则有两个版本。
第一个版本较简单,接受一个指针作为参数,直接调用对象的析构函数即可,其源代码:1
2
3
4template <class T>
inline void destroy(T* pointer) {
pointer->~T(); // 调用析构函数
}
第二个版本,其参数接受两个迭代器,将两个迭代器所指范围内的所有对象析构掉。而且,它采用了一种特别的技术:依据元素的型别,判断其是否有trivial destructor(无用的析构函数)进行不同的处理。这也是为了效率考虑。因为如果每个对象的析构函数都是trivial的,那么调用这些毫无作用的析构函数会对效率造成影响。
下面看其源代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26// 以下是 destroy() 第二版本,接受两个迭代器。它会设法找出元素的数值型別,
// 进而利用 __type_traits<> 求取最适当措施。
template <class ForwardIterator>
inline void destroy(ForwardIterator first, ForwardIterator last) {
__destroy(first, last, value_type(first));
}
// 判断元素的数值型別(value type)是否有 trivial destructor,分别调用上面的函数进行不同的处理
template <class ForwardIterator, class T>
inline void __destroy(ForwardIterator first, ForwardIterator last, T*) {
typedef typename __type_traits<T>::has_trivial_destructor trivial_destructor;
__destroy_aux(first, last, trivial_destructor());
}
// 如果元素的数值型別(value type)有 trivial destructor…
template <class ForwardIterator>
inline void __destroy_aux(ForwardIterator, ForwardIterator, __true_type) {}//不调用析构函数
// 如果元素的数值型別(value type)有 non-trivial destructor…
template <class ForwardIterator>
inline void
__destroy_aux(ForwardIterator first, ForwardIterator last, __false_type) {
for ( ; first < last; ++first)
destroy(&*first);//调用析构函数
}
第二版本还针对迭代器为char*和wchar_t*定义了特化版本:1
2inline void destroy(char*, char*) {}
inline void destroy(wchar_t*, wchar_t*) {}
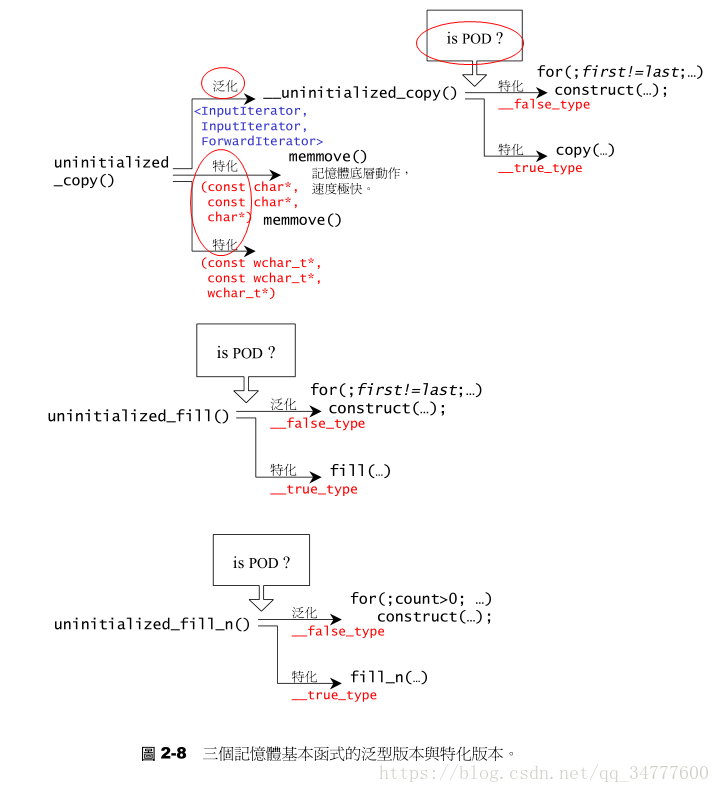
图二显示了这两个函数的结构和功能。他们被包含在头文件stl_construct.h中。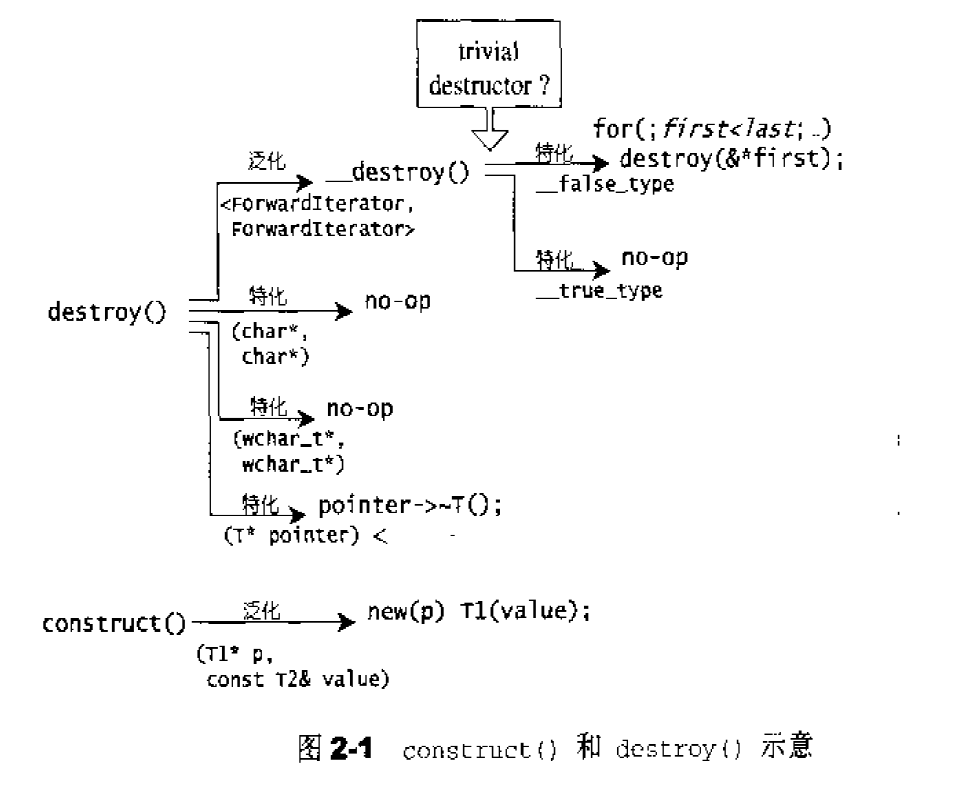
这两个作为构造、析构之用的函数被设计为全局函数,符合STL的规范。此外,STL还规定配置器必须拥有名为construct()和destroy()的两个成员函数。
上述construct()接收一个指针p和一个初值value,该函数的用途就是将初值设定到指针所指的空间上。C++的placement new运算可用来完成这一任务。
destroy()有两个版本,第一版本接受一个指针,准备将该指针所指之物析构掉。这很简单,直接调用该对象的析构函数即可。第二版本接受first和last迭代器,准备将[first,last)范围内的所以对象析构掉。我们不知道这个范围有多大,万一很大,而每个对象的析构函数都无关痛痒(所谓的trivial destructor),那么一次次调用这些无关痛痒的析构函数,对效率是一种伤害。因此,这里先利用value_type()获得迭代器所指对象的型别,再利用_type_traits<T>判断该型别的析构函数是否无关痛痒。若是(_true_type),则什么也不做就结束;若否,(_false_type),这才以循环方式巡访整个范围,并在循环中每经历一个对象就调用一个版本的destroy()。
空间的配置和释放,std::alloc
对象构造前的空间配置和对象析构后的空间释放,由<stl_alloc.h>负责,SGI对此的设计哲学如下:
- 向system heap要求空间
- 考虑多线程状态
- 考虑内存不足时的应变措施
- 考虑过多“小型区块”可能造成的内存碎片问题
C++的内存配置基本操作是::operator new(),内存释放基本操作是::operator delete()。这两个全局函数相当于C的malloc()和free()函数。是的,正是如此,SGI正是以malloc()和free()完成内存的配置和释放。
考虑到小型区块所可能造成的内存碎片问题。SGI设计了双层配置器,第一级配置器直接使用malloc()和free(),第二级配置器则视情况采用不同的策略;当配置区块超过128bytes时,视之为“足够大”,便调用第一级配置器;当配置区块小于128bytes时,视之为“过小”,为了降低额外负担,便采用复杂的memory pool整理方式,而不再求助于第一级配置器。整个设计究竟是开放第一级配置器或是同时开放第二级配置器,取决于_USE_MALLOC是否被定义:1
2
3
4
5
6
7
8
9
...
typedef __malloc_alloc_template<0> malloc_alloc;//令 alloc为第一级配置器
typedef malloc_alloc alloc;
...
//令 alloc 为第二级配置器
typedef __default_alloc_template<__NODE_ALLOCATOR_THREADS, 0> alloc;
其中__malloc_alloc_template就是第一级配置器,__default_alloc_template就是第二级配置器。
无论alloc被定义为第一级或者是第二级配置器,SGI还为它包装一个接口如下,使配置器的接口能够符合STL规格:1
2
3
4
5
6
7
8
9
10
11
12
13template<class T, class Alloc>
class simple_alloc {
public:
static T *allocate(size_t n)
{ return 0 == n? 0 : (T*) Alloc::allocate(n * sizeof (T)); }
static T *allocate(void)
{ return (T*) Alloc::allocate(sizeof (T)); }
static void deallocate(T *p, size_t n)
{ if (0 != n) Alloc::deallocate(p, n * sizeof (T)); }
static void deallocate(T *p)
{ Alloc::deallocate(p, sizeof (T)); }
};
其内部四个成员函数其实都是弹单纯的转调用,调用传递给配置器(可能是第一级也可能是第二级)的成员函数。这个接口使配置器的配置单位从bytes转为个别元素的大小(sizeof(T))。SGI STL容器全都用这个simple_alloc接口。1
2
3
4
5
6
7
8
9
10template <class T, class Alloc = alloc> // 缺省使用alloc为配置器
class vector {
protected:
typedef simple_alloc<value_type, Alloc> data_allocator;
void deallocate() {
if (...)
data_allocator::deallocate(start, end_of_storage - start);
}
};
一、二级配置器的关系如下:
第一级和第二级配置器的包装接口和运用方式如下: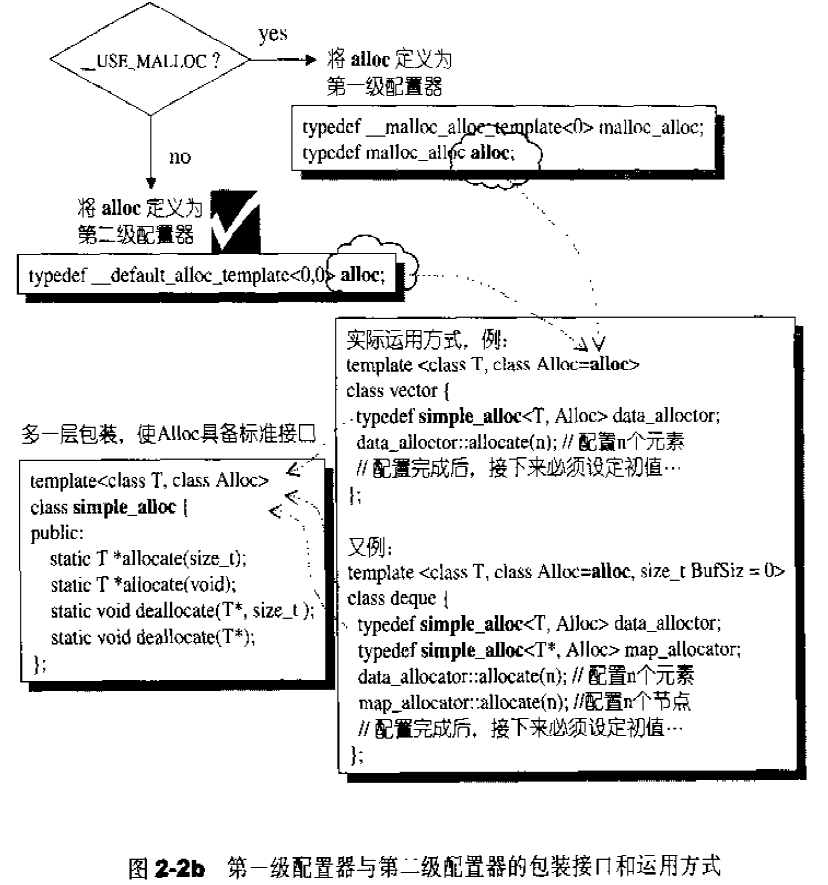
第一级配置器__malloc_alloc_template剖析
首先我们观察第一级配置器:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
// malloc-based allocator. 通常比稍后介绍的 default alloc 速度慢,
//一般而言是 thread-safe,并且对于空间的运用比较高效(efficient)。
//以下是第一级配置器。
//注意,无「template 型别参数」。至于「非型别参数」inst,完全没派上用场。
template <int inst>
class __malloc_alloc_template {
private:
//以下都是函式指标,所代表的函式将用来处理内存不足的情况。
// oom : out of memory.
static void *oom_malloc(size_t);
static void *oom_realloc(void *, size_t);
static void (* __malloc_alloc_oom_handler)();
public:
static void * allocate(size_t n)
{
void *result =malloc(n);//第一级配置器直接使用 malloc()
// 以下,无法满足需求时,改用 oom_malloc()
if (0 == result) result = oom_malloc(n);
return result;
}
static void deallocate(void *p, size_t /* n */)
{
free(p); //第一级配置器直接使用 free()
}
static void * reallocate(void *p, size_t /* old_sz */, size_t new_sz)
{
void * result =realloc(p, new_sz);//第一级配置器直接使用 rea
// 以下,无法满足需求时,改用 oom_realloc()
if (0 == result) result = oom_realloc(p, new_sz);
return result;
}
//以下模拟 C++的 set_new_handler(). 换句话说,你可以透过它,
//指定你自己的 out-of-memory handler
static void (* set_malloc_handler(void (*f)()))()
{
void (* old)() = __malloc_alloc_oom_handler;
__malloc_alloc_oom_handler = f;
return(old);
}
};
// malloc_alloc out-of-memory handling
//初值为 0。有待客端设定。
template <int inst>
void (* __malloc_alloc_template<inst>::__malloc_alloc_oom_handler)() = 0;
template <int inst>
void * __malloc_alloc_template<inst>::oom_malloc(size_t n)
{
void (* my_malloc_handler)();
void *result;
for (;;) {
//不断尝试释放、配置、再释放、再配置…
my_malloc_handler = __malloc_alloc_oom_handler;
if (0 == my_malloc_handler) { __THROW_BAD_ALLOC; }
(*my_malloc_handler)();//呼叫处理例程,企图释放内存。
result = malloc(n); //再次尝试配置内存。
if (result) return(result);
}
}
template <int inst>
void * __malloc_alloc_template<inst>::oom_realloc(void *p, size_t n)
{
void (* my_malloc_handler)();
void *result;
for (;;) { //不断尝试释放、配置、再释放、再配置…
my_malloc_handler = __malloc_alloc_oom_handler;
if (0 == my_malloc_handler) { __THROW_BAD_ALLOC; }
(*my_malloc_handler)();//呼叫处理例程,企图释放内存。
result = realloc(p, n);//再次尝试配置内存。
if (result) return(result);
}
}
//注意,以下直接将参数 inst指定为 0。
typedef __malloc_alloc_template<0> malloc_alloc;
第一级配置器直接使用malloc(),free(),realloc()等C函数执行实际的内存配置、释放、重配置操作,并实现出类似C++ new handler机制。它有独特的out-of-memory内存处理机制:在抛出std::bad_alloc异常之前,调用内存不足处理例程尝试释放空间,如果用户没有定义相应的内存不足处理例程,那么还是会抛出异常。
所谓C++ new handler机制是,你可以要求系统在内存配置要求无法被满足时,调用一个你所指定的函数。换句话说,一旦::operator new无法完成任务,在丢出std::bad_alloc异常状态之前,会先调用由客户端指定的处理例程,该处理例程通常即被称为new-handler。new-handler解决内存不足的做法有特定的模式。
请注意,SGI第一级配置器的allocate()和realloc()都是在调用malloc()和realloc()不成功后,改调用oom_malloc()和oom_realloc()。后两者都有内循环,不断调用“内存不足处理例程”,期望在某次调用之后,获得足够的内存而圆满完成任务。但如果“内存不足处理例程”并未被客户端设定,oom_malloc()和oom_realloc()便老实不客气地调用__THROW_BAD_ALLOC,丢出bad_alloc异常信息,或利用exit(1)硬生生中止程序。
记住,设计“内存不足处理例程”是客端的责任,设定“内存不足处理例程”也是客端的责任。
第二级配置器__default_alloc_template剖析
相比第一级配置器,第二级配置器多了一些机制,避免小额区块造成内存的碎片。不仅仅是碎片的问题,配置时的额外负担也是一个大问题。因为区块越小,额外负担所占的比例就越大。
额外负担是指动态分配内存块的时候,位于其头部的额外信息,包括记录内存块大小的信息以及内存保护区(判断是否越界)。要想了解详细信息,请参考MSVC或者其他malloc实现。
SGI STL第二级配置器具体实现思想如下:
- 如果要分配的区块大于128bytes,则移交给第一级配置器处理。
- 如果要分配的区块小于128bytes,则以内存池管理(memory pool),又称之次层配置(sub-allocation):每次配置一大块内存,并维护对应的自由链表(free-list)。下次若有相同大小的内存需求,则直接从free-list中取。如果有小额区块被释放,则由配置器回收到free-list中——是的,别忘了,配置器除了负责配置,也负责回收。
在第二级配置器中,小额区块内存需求大小都被上调至8的倍数,比如需要分配的大小是30bytes,就自动调整为32bytes。系统中总共维护16个free-lists,各自管理大小为8,16,…,128bytes的小额区块。
为了维护链表,需要额外的指针,为了避免造成另外一种额外的负担,这里采用了一种技术:用union表示链表节点结构:1
2
3
4union obj {
union obj * free_list_link;//指向下一个节点
char client_data[1]; /* The client sees this. */
};
union能够实现一物二用的效果,当节点所指的内存块是空闲块时,obj被视为一个指针,指向另一个节点。当节点已被分配时,被视为一个指针,指向实际区块。
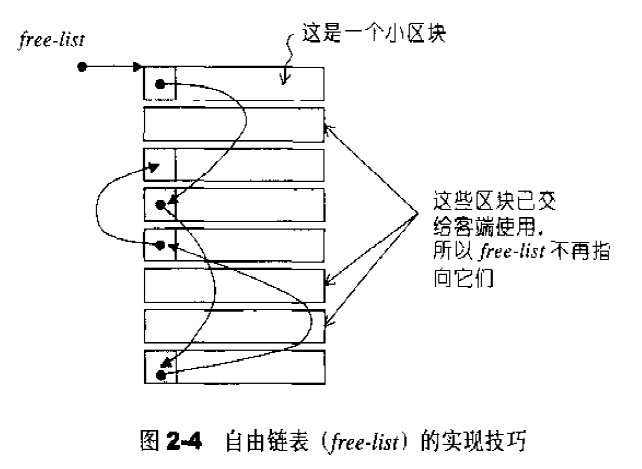
下面是第二级配置器的部分实现内容:1
2
3enum {__ALIGN=8}; //小型区块的上调上界
enum {__MAX_BYTES=128}; //小型区块的上限
enum {__NFREELISTS=__MAX_BYRES/__ALIGN}; //free-lists个数
以下是第二级配置器总体实现代码概览:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65template <bool threads, int inst>
class __default_alloc_template {
private:
// 實際上我們應該使用 static const int x = N
// 來取代 enum { x = N }, 但目前支援該性質的編譯器還不多。
enum {__ALIGN = 8};
enum {__MAX_BYTES = 128};
enum {__NFREELISTS = __MAX_BYTES/__ALIGN};
static size_t ROUND_UP(size_t bytes) {
return (((bytes) + __ALIGN-1) & ~(__ALIGN - 1));
}
__PRIVATE:
union obj {
union obj * free_list_link;
char client_data[1]; /* The client sees this. */
};
private:
static obj * __VOLATILE free_list[];
// Specifying a size results in duplicate def for 4.1
static obj * __VOLATILE free_list[__NFREELISTS];
static size_t FREELIST_INDEX(size_t bytes) {
return (((bytes) + __ALIGN-1)/__ALIGN - 1);
}
// Returns an object of size n, and optionally adds to size n free list.
static void *refill(size_t n);
// Allocates a chunk for nobjs of size "size". nobjs may be reduced
// if it is inconvenient to allocate the requested number.
static char *chunk_alloc(size_t size, int &nobjs);
// Chunk allocation state.
static char *start_free;
static char *end_free;
static size_t heap_size;
/* n must be > 0 */
static void * allocate(size_t n){...}
/* p may not be 0 */
static void deallocate(void *p, size_t n){...}
static void * reallocate(void *p, size_t old_sz, size_t new_sz);
template <bool threads, int inst>
char *__default_alloc_template<threads, inst>::start_free = 0;//内存池起始位置
template <bool threads, int inst>
char *__default_alloc_template<threads, inst>::end_free = 0;//内存池结束位置
template <bool threads, int inst>
size_t __default_alloc_template<threads, inst>::heap_size = 0;
template <bool threads, int inst>
__default_alloc_template<threads, inst>::obj * __VOLATILE
__default_alloc_template<threads, inst> ::free_list[
__NFREELISTS
__default_alloc_template<threads, inst>::__NFREELISTS
] = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, };
空间配置函数allocate()
__default_alloc_template拥有配置器的标准接口函数allocate(),此函数首先判断区块大小,要分配的区块小于128bytes,调用第一级配置器。否则,向对应的free-list寻求帮助。对应的free list有可用的区块,直接拿过来用。如果没有可用的区块,调用函数refill()为`free list重新填充空间。代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 /* n must be > 0 */
static void * allocate(size_t n)
{
obj * __VOLATILE * my_free_list;
obj * __RESTRICT result;
if (n > (size_t) __MAX_BYTES) {
return(malloc_alloc::allocate(n));
}
my_free_list = free_list + FREELIST_INDEX(n);
// Acquire the lock here with a constructor call.
// This ensures that it is released in exit or during stack
// unwinding.
/*REFERENCED*/
lock lock_instance;
result = *my_free_list;
if (result == 0) {
void *r = refill(ROUND_UP(n));
return r;
}
*my_free_list = result -> free_list_link;
return (result);
};
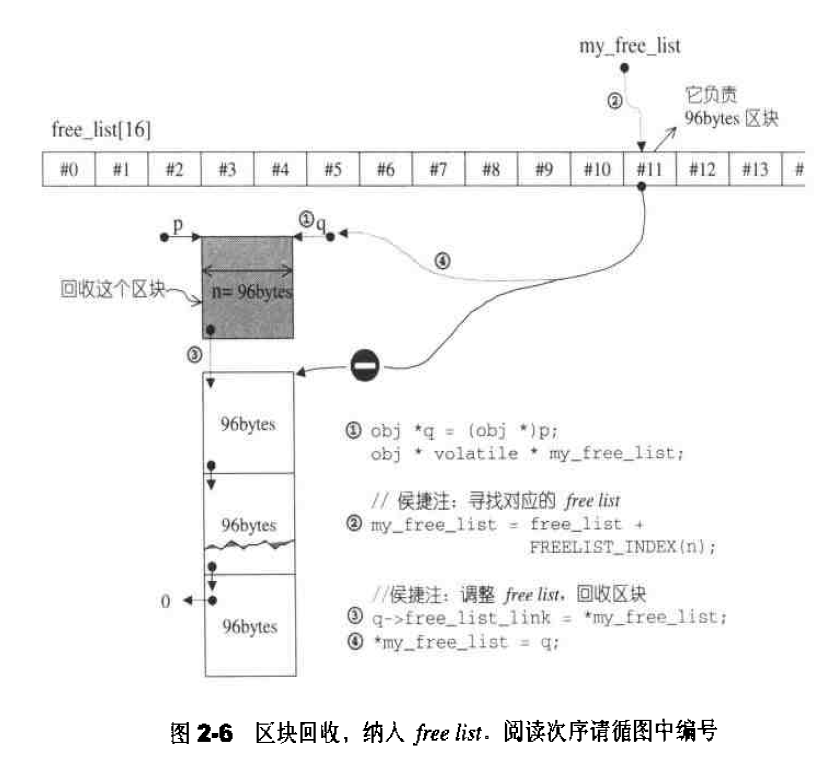
这里需要注意的是,每次都是从对应的free list的头部取出可用的内存块。图示如下:
空间释放函数
身为一个配置器,__default_alloc_template拥有配置器的标准接口函数deallocate(),此函数首先判断区块大小,大于128bytes调用第一级配置器。否则,找出对应的free list,将区块回收。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17// p 不可以为0
static void deallocate(void* p, size_t n)
{
obj *q = (obj *)p;
obj * volatile * my_free_list;
// 大于128就调用一级配置器
if (n > (size_t) __MAX_BYTES) {
malloc_alloc::deallocate(p, n);
return;
}
// 寻找对应的free list
my_free_list = free_list + FREELIST_INDEX(n);
// 调整free list,收回区块
q->free_list_link = *my_free_list;
*my_free_list = q;
}
为free list填充空间
当发现对应的free list没有可用的空闲区块时,就需要调用refill()函数重新填充空间。新的空间将取自于内存池(将经由chunk_alloc()完成)。缺省取得20个新节点(新区块),但万一内存池空间不足,获得的节点数(区块数)可能小于20,内存池的管理后面会讲到。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32/* Returns an object of size n, and optionally adds to size n free list.*/
/* We assume that n is properly aligned. */
/* We hold the allocation lock. */
template <bool threads, int inst>
void* __default_alloc_template<threads, inst>::refill(size_t n)
{
int nobjs = 20;
//调用chunk_alloc(),尝试取得nobjs个区块作为free list的新节点,注意参数nobjs是pass by reference
char * chunk = chunk_alloc(n, nobjs);
obj * __VOLATILE * my_free_list;
obj * result;
obj * current_obj, * next_obj;
int i;
if (1 == nobjs) return(chunk);
my_free_list = free_list + FREELIST_INDEX(n);
/* Build free list in chunk */
result = (obj *)chunk;
*my_free_list = next_obj = (obj *)(chunk + n);
for (i = 1; ; i++) {//将各节点串接起来(注意,索引为0的返回给客端使用)
current_obj = next_obj;
next_obj = (obj *)((char *)next_obj + n);
if (nobjs - 1 == i) {
current_obj -> free_list_link = 0;
break;
} else {
current_obj -> free_list_link = next_obj;
}
}
return(result);
}
内存池
从内存池中取空间供free list使用,是chunk_alloc()的工作。具体实现思想如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
/* We allocate memory in large chunks in order to avoid fragmenting */
/* the malloc heap too much. */
/* We assume that size is properly aligned. */
/* We hold the allocation lock. */
template <bool threads, int inst>
char*
__default_alloc_template<threads, inst>::chunk_alloc(size_t size, int& nobjs)
{
char * result;
size_t total_bytes = size * nobjs;
size_t bytes_left = end_free - start_free;
if (bytes_left >= total_bytes) {
result = start_free;
start_free += total_bytes;
return(result);
} else if (bytes_left >= size) {
nobjs = bytes_left/size;
total_bytes = size * nobjs;
result = start_free;
start_free += total_bytes;
return(result);
} else {
size_t bytes_to_get = 2 * total_bytes + ROUND_UP(heap_size >> 4);//注意此处申请的空间的大小
// Try to make use of the left-over piece.
if (bytes_left > 0) {
obj * __VOLATILE * my_free_list =
free_list + FREELIST_INDEX(bytes_left);
((obj *)start_free) -> free_list_link = *my_free_list;
*my_free_list = (obj *)start_free;
}
start_free = (char *)malloc(bytes_to_get);
if (0 == start_free) {
int i;
obj * __VOLATILE * my_free_list, *p;
// Try to make do with what we have. That can't
// hurt. We do not try smaller requests, since that tends
// to result in disaster on multi-process machines.
for (i = size; i <= __MAX_BYTES; i += __ALIGN) {
my_free_list = free_list + FREELIST_INDEX(i);
p = *my_free_list;
if (0 != p) {
*my_free_list = p -> free_list_link;
start_free = (char *)p;
end_free = start_free + i;
return(chunk_alloc(size, nobjs));
// Any leftover piece will eventually make it to the
// right free list.
}
}
end_free = 0; // In case of exception.
start_free = (char *)malloc_alloc::allocate(bytes_to_get);
// This should either throw an
// exception or remedy the situation. Thus we assume it
// succeeded.
}
heap_size += bytes_to_get;
end_free = start_free + bytes_to_get;
return(chunk_alloc(size, nobjs));
}
}
chunk_alloc()函数以end_free - start_free来判断内存池的数量:
- 内存池剩余空间完全满足20个区块的需求量,则直接取出对应大小的空间。
- 内存池剩余空间不能完全满足20个区块的需求量,但是足够供应一个及一个以上的区块,则取出能够满足条件的区块个数的空间。
- 内存池剩余空间不能满足一个区块的大小,则需要利用
malloc()从heap中配置内存,为内存池注入活水。
举个例子,见图2-7,假设程序一开始,客端就调用chunk_alloc(32,2O),于是malloc()配置40个32 bytes区块,其中第1个交出,另19个交给free_list[3]维护,余20个留给内存池。接下来客端调用chunk_alloc(64,20),此时free_1ist[7]空空如也,必须向内存池要求支持,内存池只够供应(32*20)/M = 10个64 bytes区块,就把这10个区块返回,第1个交给客端、余9个由free_list[7]维护。此时内存池全空,接下来再调用chunk_alloc(96, 20),此时free_list[11]空空如也,必须向内存池要求支持,而内存池此时也是空的,于是以malloc()配置40+n(附加量)个96 bytes区块, 其中第1个交出,另19个交给free_list[11]维护,余20+n(附加量)个区块留给内存池。
万一山穷水尽,整个system heap空问都不够了(以至无法为内存池注入活水源头),malloc()行动失败,chunk_alloc()就四处寻找有无“尚有未用区块,且区块够大”之free lists。找到了就挖一块交出,找不到就调用第一级配置器,第一级配置器其实也是使用malloc()来配置内存,但它有out-of-memory处理机制(类似new-handler机制),或许有机会释放其它的内存拿来此处使用。如果可以,就成功,否则发出bad_alloc异常。
以上便是整个第二级空间配置器的设计。
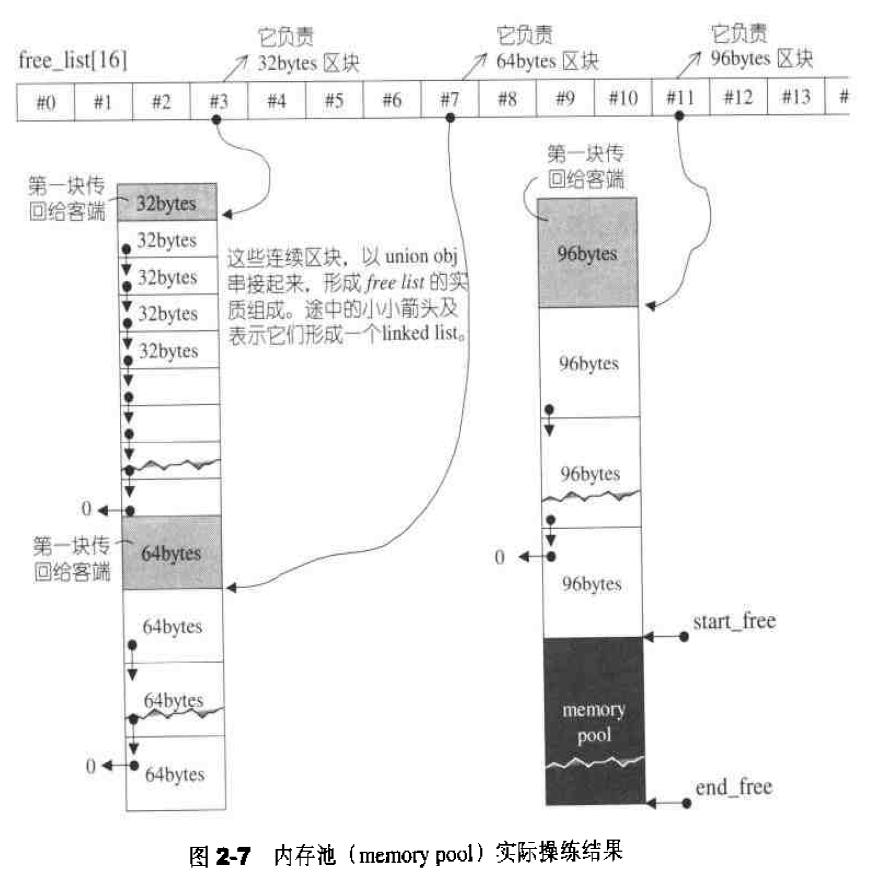
回想一些那个提供配置器标准接口的simple_alloc:1
2
3
4template<class T, class Alloc>
class simple_alloc{
...
};
SGI容器通常以这种方式来使用配置器:1
2
3
4
5
6
7
8
9
10template<class T,class Alloc=alloc> //缺省使用alloc配置器
class vector{
public:
typedef T value_type;
...
protected:
//专属之空间配置器,每次配置一个元素大小
typedef simple_alloc<value_type,Alloc> data_allocator;
...
};
其中第二个template参数所使用的缺省参数alloc,可以是第一级配置器也可以是第二级配置器。不过,SGI STL已经把它设为第二级配置器。
deallocate()
如果需要回收的区块大于128bytes,则调用第一级配置器。如果需要回收的区块小于128bytes,找到对应的free-list,将区块回收。注意是将区块放入free -list的头部。SGI STL源代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 /* p may not be 0 */
static void deallocate(void *p, size_t n)
{
obj *q = (obj *)p;
obj * __VOLATILE * my_free_list;
if (n > (size_t) __MAX_BYTES) {
malloc_alloc::deallocate(p, n);
return;
}
my_free_list = free_list + FREELIST_INDEX(n);
// acquire lock
/*REFERENCED*/
lock lock_instance;
q -> free_list_link = *my_free_list;
*my_free_list = q;
// lock is released here
}
内存基本处理工具
STL定义有五个全局函数,作用于未初始化空间上,这样的功能对于容器的实现很有帮助。前两个函数是用于构造的construct()和用于析构的destroy(),另三个函数是uninitialized_copy(),uninitialized_fill(),uninitialized_fill_n,分别对应于高层次函数copy()、fill()、fill_n()——这些都是STL算法。
uninitialized_copy
1 | template <class InputIterator,class ForwardIterator> |
uninitialized_copy()使我们能够将内存的配置和对象的构造行为分离开来,如果作为输出目的地的[result,result+(last-first))范围内的每一个迭代器都指向为初始化区域,则uninitialized_copy()会使用copy constructor,给身为输入来源之[first,last)范围内的每一个对象产生一份复制品,放进输出范围中。换句话说,针对输入范围内的每一个迭代器i,该函数会调用construct(&*(result+(i-first)),*i),产生*i的复制品,放置于输出范围的相对位置上。
如果你需要实现一个容器,uninitialized_copy()这样的函数会为你带来很大的帮助,因为容器的全区间构造函数通常以两个步骤完成:
- 配置内存块,足以包含范围内的所有元素
- 使用
uninitialized_copy(),在该内存区块上构造元素。
C++标志规格书要求uninitialized_copy()具有“commit or rollback”语意,意思是要么“构造出所有必要的元素”,要么(当有任何一个copy constructor失败时)“不构造任何东西。
uninitialized_fill
1 | template <class ForwardIterator,class T> |
uninitialized_fill()也能够使我们将内存配置与对象的构造行为分离开来。如果[first,last)范围内的每个迭代器都指向未初始化的内存,那么uninitialized_fill()会在该范围内产生x(上式第三个参数)的复制品。换句话说,uninitialized_fill()会针对操作范围内的每个迭代器i,调用construct(&*i,x),在i所指之处产生x的复制品。
与uninitialized_copy()一样,uninitialized_fill()必须具备“commit or rollback”语意,换句话说,它要么产生出所有必要元素,要么不产生任何元素,如果有任何一个copy constructor丢出异常(exception),uninitialized_fill(),必须能够将已产生的所有元素析构掉。
uninitialized_fill_n
1 | template <class ForwardIterator,class Size,class T> |
uninitialized_fill_n()能使我们将内存配置与对象构造行为分离开来,它会为指定范围内的所有元素设定相同的初值。
如果[first,first+n)范围内的每一个迭代器都指向未初始化的内存,那么uninitialized_fill_n()会调用 copy constructor,在该范围内产生x(上式第三个参数——的复制品。也就是说,面对[first,first+n)范围内的每个迭代器i,uninitialized_fill_n()会调用construct(&*i,x),在对应位置产生x的复制品。
uninitialized_fill_n()也具有“commit or rollback”语意:要么产生所有必要的元素,否则就不产生任何元素。如果任何一个copy constructor丢出异常(exception),uninitialized_fill_n()必须析构已产生的所有元素。
以下分别介绍这三个函数的实现法,其中所呈现的iterators(迭代器)、value_type()、_type_traits、_true_type、_false_type、is_POD_type等实现技术,都在后面介绍。
uninitialized_fill_n()
本函数接受三个参数:
- 迭代器first指向欲初始化空间的起始处;n表示欲初始化空间的大小;x表示初值。
1 | template <class ForwardIterator,class Size,class T> |
这个函数的逻辑是,首先萃取出迭代器first的value_type,然后判断是否是POD型别:1
2
3
4
5template <class ForwardIterator, class Size, class T, class T1>
inline ForwardInterator __uninitialized_fill_n(ForwardIterator first, Size n, const T& x, T1*) {
typedef typename __type_traits<T1>::is_POD_type is_POD;
return __uninitialized_fill_n_aux(first, n, x, is_POD());
}
POD意为Plain Old Data,也就是标量型别,或传统的C struct型别,可以用最有效率的初值填写手法,而对non_POD型别采取最保险的做法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17// 如果copy construction等同于assignment,而且destructor是trivial,以下就有效
// 如果是POD型别,执行流程就会转进到以下函数,这借由function template的参数推导机制而得
template <class ForwardIterator,class Size,class T>
inline ForwardInterator __uninitialized_fill_n_aux(ForwardIterator first, Size n, const T& x, __true_type) {
return fill_n(first, n, x);
}
// 如果不是POD型别,就会转进到以下函数,这借由function template的参数推导机制而得
template <class ForwardIterator,class Size,class T>
inline ForwardInterator __uninitialized_fill_n_aux(ForwardIterator first, Size n, const T& x, __false_type) {
ForwardIterator cur = first;
for (; n > 0; --n, ++ cur)
construct(&*cur, x);
return cur;
}
uninitialized_copy()
uninitialized_copy()接受三个函数:
- 迭代器first指向输入端的起始位置
- 迭代器last指向输入端的结束位置
- 迭代器rsult指向输出端(欲初始化空间)的起始处
1 | template <class InputIterator, class ForwardIterator> |
这个函数的逻辑是,首先萃取出迭代器result的value_type,然后判断是否是POD型别:1
2
3
4
5template <class InputIterator, class ForwardIterator, class T>
inline ForwardInterator __uninitialized_copy(InputIterator first, InputIterator last, ForwardIterator result, T*) {
typedef typename __type_traits<T>::is_POD_type is_POD;
return __uninitialized_copy_aux(first, last, result, is_POD());
}
POD可以用最有效率的初值填写手法,而对non_POD型别采取最保险的做法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16// 如果copy construction等同于assignment,而且destructor是trivial,以下就有效
// 如果是POD型别,执行流程就会转进到以下函数,这借由function template的参数推导机制而得
template <class InputIterator, class ForwardIterator>
inline ForwardInterator __uninitialized_copy_aux(InputIterator first, InputIterator last, ForwardIterator result, __true_type) {
return copy(first, last, result);
}
// 如果不是POD型别,就会转进到以下函数,这借由function template的参数推导机制而得
template <class InputIterator, class ForwardIterator>
ForwardInterator __uninitialized_copy_aux(InputIterator first, InputIterator last, ForwardIterator result, __false_type) {
ForwardIterator cur = first;
for (; first != last; ++ first, ++ cur)
construct(&*cur, *first);
return cur;
}
针对char*和wchar_t*两种型别,可以采用最具效率的做法memmove执行复制行为:1
2
3
4
5
6
7
8
9inline char* uninitialized_copy(const char* first, const char* last, char* result) {
memmove(rseult, first, last-first);
return result + (last - first);
}
inline wchar_t* uninitialized_copy(const wchar_t* first, const wchar_t* last, wchar_t* result) {
memmove(rseult, first, sizeof(wchar_t) * (last-first));
return result + (last - first);
}
uninitialized_fill_n()
本函数接受三个参数:
- 迭代器first指向欲初始化空间的起始处;
- 迭代器last指向输出端的结束处;
- x表示初值。
1 | template <class ForwardIterator, class T> |
这个函数的逻辑是,首先萃取出迭代器first的value_type,然后判断是否是POD型别:1
2
3
4
5template <class ForwardIterator, class T, class T1>
inline void __uninitialized_fill(ForwardIterator first, ForwardIterator last, const T& x, T1*) {
typedef typename __type_traits<T1>::is_POD_type is_POD;
return __uninitialized_fill_aux(first, last, x, is_POD());
}
POD意为Plain Old Data,也就是标量型别,或传统的C struct型别,可以用最有效率的初值填写手法,而对non_POD型别采取最保险的做法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16// 如果copy construction等同于assignment,而且destructor是trivial,以下就有效
// 如果是POD型别,执行流程就会转进到以下函数,这借由function template的参数推导机制而得
template <class ForwardIterator, class T>
inline void __uninitialized_fill_aux(ForwardIterator first, ForwardIterator last, const T& x, __true_type) {
fill(first, last, x);
}
// 如果不是POD型别,就会转进到以下函数,这借由function template的参数推导机制而得
template <class ForwardIterator,class Size,class T>
inline void __uninitialized_fill_aux(ForwardIterator first, ForwardIterator last, const T& x, __false_type) {
ForwardIterator cur = first;
for (; cur != last; ++ cur)
construct(&*cur, x);
}
迭代器概念与traits编程技法
迭代器是一种抽象的设计概念,现实程序语言中并没有直接对应于这个概念的实物。
迭代器设计思维——STL关键所在
不论是泛型思维或STL的实际运用,迭代器都扮演这重要的角色。STL的中心思想在于:将数据容器和算法分开,彼此独立设计,最后再以一贴胶着剂将它们撮合在一起。容器和算法的泛型化,从技术的角度来看是并不困难,C++的class template和function templates可分别达成目标。
以下是容器、算法、迭代器的合作展示,以算法find()为例,它接受两个迭代器和一个“搜索目标”:1
2
3
4
5
6
7template <class InputIterator,class T>
InputIterator find(InputIterator first,InputIterator last,const T& value)
{
while(first=!last&&*first!=value)
++first;
return first;
}
只要给出不同的迭代器,find()便能够对不同的容器进行直接操作:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
using namespace std;
int main()
{
const int arraySize=7;
int ia[arraySize]={0,1,2,3,4,5,6};
vector<int> ivect(ia,ia+arraySize);
list<int> ilist(ia,ia+arraySize);
deque<int> ideque(ia,ia+arraySize);
//注意算法和成员方法的区别
vector<int>::iterator it1=find(ivect.begin(),ivect.end(),4);
if(it1!=ivect.end())
cout<<"4 found. "<<*it1<<endl;
else
cout<<"4 not found."<<endl;
list<int>::iterator it2=find(ilist.begin(),ilist.end(),6);
if(it2==ilist.end())
cout<<"6 not found. "<<endl;
else
cout<<"6 found. "<<*it2<<endl;
deque<int>::iterator it3=find(ideque.begin(),ideque.end(),8);
if(it3==ideque.end())
cout<<"8 not found."<<endl;
else
cout<<"8 found. "<<*it3<<endl;
}
从上面的例子看来,迭代器似乎依附于在容器之下,是吗?有没有独立而泛用的迭代器?我们又该如何自行设计特殊的迭代器?
迭代器是一种smart pointer
迭代器是一种行为类似指针的对象,而指针的各种行为中最常见也最重要的便是内容提领(dereference)和成员访问(member access),因此,迭代器最重要的编程工作就是对operator*和operator->进行重载工作。关于这一点,C++标准库有一个auto_ptr可供我们参考。这是一个用来包含原生指针的对象,声名狼藉的内存泄露问题可借此获得解决。auto_ptr用法如下,和原生指针一模一样:1
2
3
4
5
6
7void func()
{
auto_ptr<string> ps(new string("jjhou"));
cout<<*ps<<endl;
cout<<ps->size()<<endl;
//离开前不需要delete,auto_ptr会自动释放内存
}
函数第一行的意思是,以new动态配置一个初值为”jjhou”的string对象,并将所得的结果(一个原生指针)作为auto_ptr<string>对象的初值。注意,auto_ptr尖括号内放的是”原生指针所指对象“的型别,而不是原生指针的型别。
auto_ptr的源代码在头文件<memory>中:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24//file:autoptr.cpp
template<class T>
class auto_ptr{
public:
explicit auto_ptr(T *p=0):pointee(p) {}
template<class U>
auto_ptr(auto_ptr<U>& rhs):pointee(rhs.release()) {}
~auto_ptr() {delete pointee;}
template<class U>
auto_ptr<T>& operator=(auto_ptr<U> &rhs)
{
if(this!=rhs) reset(ths.release());
return *this;
}
T& operator*() const { return *pointee;}
T* operator->() const { return pointee;}
T* get() const {return pointee;}
//...
private:
T *pointee;
};
有了模仿对象,现在我们来为list(链表)设计一个迭代器,假设list及其节点的结构如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
using namespace std;
template<class T>//节点类
class ListItem
{
public:
ListItem(T value):_value(value), _next(NULL){}
T value() {
return _value;
}
void setNext(ListItem<T> *newNode) {
_next = newNode;
}
ListItem* getNext() {
return _next;
}
private:
T _value;
ListItem* _next;
};
//单链表类
template<class T>
class List
{
public:
//...
List():_size(0) {
_front = _end = NULL;
}
void insert_front(T value) {
ListItem<T> *newNode = new ListItem<T>(value);
if(_size == 0) {
_end = _front = newNode;
}
else {
newNode -> setNext(_front);
_front = newNode;
}
_size++;
}
void insert_end(T value) {
ListItem<T> *newNode = new ListItem<T>(value);
if(_size == 0) {
_end = _front = newNode;
}
else {
_end -> setNext(newNode);
_end = _end -> getNext();
}
_size++;
}
void display() {
ListItem<T>* temp = _front;
while(temp != _end -> getNext()) {
printf("%d ", temp -> value());
temp = temp -> getNext();
}
printf("\n");
}
void getSize() {
printf("%d\n", _size);
}
ListItem<T>*front() {
return _front;
}
ListItem<T>*back() {
return _end;
}
private:
ListItem<T>* _end;
ListItem<T>* _front;
long _size;
};
//迭代器类
template<class Item>
struct ListIter
{
Item* ptr;
ListIter(Item* p = 0):ptr(p) {}
Item& operator* () const {return *ptr;}
Item* operator -> () const {return ptr;}
ListIter& operator++() {
ptr = ptr -> getNext();
return *this;
}
ListIter operator++(int) {
ListIter tmp = *this;
++*this;
return tmp;
}
bool operator==(const ListIter& i)const {
return ptr == i.ptr;
}
bool operator!=(const ListIter& i)const {
return ptr != i.ptr;
}
};
ListIter<ListItem<int> > find(ListIter<ListItem<int> > &begin, ListIter<ListItem<int> > &end, int value)
{
ListIter<ListItem<int> > first = begin;
ListIter<ListItem<int> > last = end;
while( first != last -> getNext())
{
if(first -> value() != value)
{
first++;
}
else
{
return first;
}
}
return end -> getNext();
}
并且加上测试程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36int main()
{
List<int> m_ListItor;
for(int i = 0; i < 6; i++)
{
m_ListItor.insert_front(i);
m_ListItor.insert_end(i + 2);
}
m_ListItor.display(); //5 4 3 2 1 0 2 3 4 5 6 7
ListIter<ListItem<int> > begin(m_ListItor.front());
ListIter<ListItem<int> > end(m_ListItor.back());
ListIter<ListItem<int> > iter;
iter = find(begin, end, 3);
if(iter == end -> getNext())
{
printf("%s", "not found");
}
else
{
printf("%d\n", iter -> value());
}
iter = find(begin, end, 8);
if(iter == end -> getNext())
{
printf("%s", "not found");
}
else
{
printf("%d", iter -> value());
}
return 0;
}
以上可以看出,为了完成一个针对List而设计的迭代器,我们必须暴露太多有关于List实现细节,在main函数中制作begin()和end()两个迭代器,我们暴露了ListItem,在ListIter class中为了达成operator++,我们暴露了ListItem的操作函数getNext(),如果不是为了迭代器,ListItem是要完全隐藏起来不曝光的。换句话说只有对ListItem的实现细节特别了解,才能设计出迭代器,既然这无法避免,干脆把迭代器的设计工作交给 List 的设计者,如此一来,所有实现细节反而不被使用者发现,这也是为什么 STL 的每一种容器都有自己专属的迭代器的原因。
迭代器相应型别
在算法运用迭代器的时候,很可能用到起相应型别(即迭代器所指之物的型别),但C++支持sizeof ,并无typeof。可以利用function template的参数推导机制。
- 函数参数的情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
using namespace std;
template <class I,class T>
void func_impl(I iter,T t){
T tmp;//这里解决了问题,T就是迭代器所指之物的类型
//…………
}
template <class I>
void func(I iter){
func_impl(iter,*iter);
}
int main()
{
int i;
func(&i);
}
我们以func()为对外接口,却把实际操作全部置于func_impl()之中。由于func_impl()是一个function template,一旦被调用,编译器会自动进行template参数推导,于是导出型别,顺利解决了问题。迭代器相应型别(associated types)不只是“迭代器所指对象的型别”一种而已。根据经验,最常用的相应型别有五种,然而并非任何情况下任何一种都可利用上述的template参数推导机制来取得,我们需要更全面的解法。
Traits编程技法——STL源代码门钥
迭代器所指对象的型别,称为该迭代器的value type,上述的参数型别推导技巧虽然可用于value,却非全面可用:万一value type必须用于函数的传回值,就束手无策了,毕竟函数的”template参数推导机制”推而导之的只是参数,无法推导函数的返回值类型。
声明内嵌类型是个好主意:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
using namespace std;
template <class T>
class MyIter{
public:
typedef T value_type;
T* ptr;
MyIter(T* p=0):ptr(p){}
T& operator*()const{
return *ptr;
}
};
template <class I>
typename I::value_type//I::value_type编译器不知道代表一个型别或是一个成员函数或是一个数据成员,关键词typename用以告诉编译器这是一个型别
func(I ite){
return *ite;
}
int main(){
MyIter<int> ite(new int(8));
cout<<func(ite);
}
注意,func()的返回类型必须加上关键词,因为是一个template参数,在它被编译器具现化之前,编译器对此一无所悉,换句话说,编译器此时并不知道MyIter<T>::value_type代表的是一个型别或是一个member function或是一个data member。关键词的用意在于告诉编译器这是一个型别,如此才能顺利通过编译。但是并不是所有迭代器都是class,原生指针就不是,如果不是就无法为它定义内嵌型别,但STL(以及整个泛型思维)绝对必须接受原生指针作为一种迭代器,所以上面这样还不够。template partial speciahzation可以做到。
Partial Specialization(偏特化)的意义
如果class template 拥有一个以上的template参数,我们可以针对其中某个(或数个,但非全部)template参数进行特化工作。换句话说,我们可以在泛化设计中提供一个特化版本(也就是将泛化版本中的某些template参数赋予明确的指定)。例如,面对以下这么一个class template:1
2template<typename T>
class C { ... }; // 这个泛化版本允许接受T为任何类型
我们便很容易接受它有一个形式如下的partial specialization1
2template<typename T>
class C<T* { ... }; // 这个泛化版本允许接受T为原生指针的情况
有了这项利器,我们便可以解决前述“内嵌型别”未能解决的问题。先前的问题是,原生指针并非class,因此无法为它们定义内嵌型别。现在,我们可以针对“迭代器之template参数为指针”者,设计特别版的迭代器。
下面这个class template专门用来“萃取”迭代器的特性,而value type正是迭代器的特性之一:1
2
3
4
5
6
7
using namespace std;
template<class T>
struct iterator_traits//traits 意为“特性”
{
typedef typename I::vlue_type value_type;
};
这个所谓的traits,其意义是,如果I定义自己的value type,那么通过这个traits的作用,萃取出来的value_type就是I::value_type。换句话说,如果I定义有自己的value type ,那个func()可以改写成这样:1
2
3
4
5
6template <class T>
typename iteraotr_traits<T>::value_type//这一整行是函数返回值
func(T ite)
{
return *ite;
}
但这除了多了一层间接性,好处是traits可以拥有特化版本。现在,我们令iterator_traites拥有一个partial specializations如下:1
2
3
4
5template<class>
struct iterator_traits<T*>
{
typedef T value_type;
};
于是,原生指针int*虽然不是一种class type ,亦可通过traits取其value type。这就解决了先前的问题。但是注意针对“指向常数对象的指针(pointer-to-const)”,下面这个式子得到什么结果:1
iterator_traits<const int*>::value_type
获得的是const int而非int。我们希望利用这种机制来声明一个暂时变量,使其型别与迭代器的value type相同,而现在,声明一个无法复制的暂时变量,没什么用!因此,如果迭代器是一个pointer-to-const,我们应该设法令其value type为一个non-const型别。只需要另外设计一个特化版本就可以解决问题:1
2
3
4template<class T>
struct iterator_traits<const T*>{//偏特化版—当迭代器是一个pointer-to-const
typedef T value_type;//萃取出来的型别应该是T,而非const T
};
现在,不论面对的是迭代器MyIter,或是原生指针*int或const int*,都可以通过traits取出正确的(我们所期望的)value type。
下图说明了traits所扮演的“特性萃取机”角色,萃取各个迭代器的特性。这里所谓的迭代器特性,指的是迭代器的相应型别。当然,若要这个“特性萃取机”traits嫩够有效运作,每一个迭代器必须遵守约定,自行以内嵌型别定义的方式定义出相应型别。这是一个约定,谁不遵守约定,谁就不能兼容STL这个大家庭。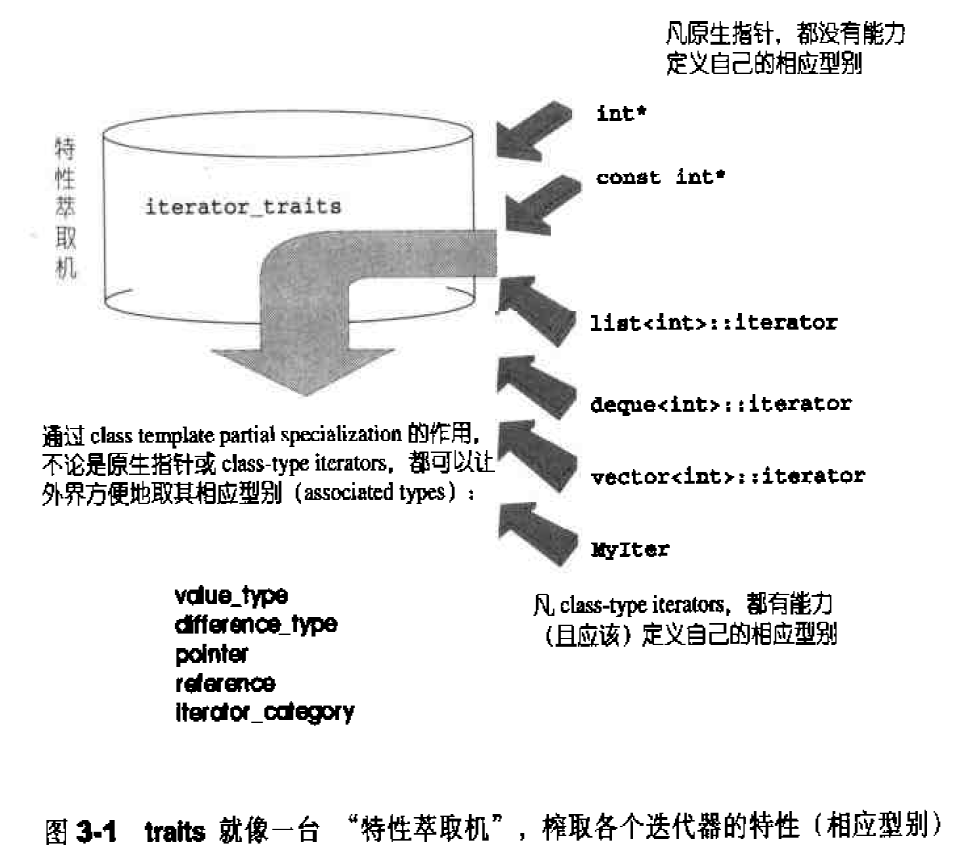
根据经验,最常用到的迭代器相应型别有五种:value type,difference type,pointer,reference,iterator categoly。如果你希望你所开发的容器能与STL水乳交融,一定要为你的容器的迭代器定义这五种相应型别。“特性萃取机”traits会很忠实地将其原汁原味榨取出来:
iterator_traits`必须针对传入的型别为pointer及pointer-to-const者,设计特化版本,稍后数节为你展示如何进行。1
2
3
4
5
6
7temp1ate <class I>
struct itarator_traits {
typedef typename I::iterator_category iterator_category;
typedef typename I::value_type value_type;
typedef typename I::difference_type difference_type;
typedef typename I::pointer pointer;
typedef typename I::reference reference;
迭代器相应型别之一:value type
所谓value type,是指迭代器所指对象的型别。任何一个打算与STL算法有完美搭配的class,都应该定义自己的value type内嵌型别,例如STL中的vector定义:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16template <class T,class Alloc = alloc>
class vector
{
public:
// nested type 定义
typedef T value_type;
typedef value_type* pointer;
typedef const value_type* const_pointer;
typedef value_type* iterator;
typedef const value_type* const_iterator;
typedef value_type& reference;
typedef const value_type& const_reference;
typedef size_t s ize_type;
typedef ptrdiff_t difference_type;
...
};
迭代器相应型别之二:difference type
difference type用来表示两个迭代器之间的距离,因此它也可以用来表示一个容器的最大容量,因为对于连续空间的容器而言,头尾之间的距离就是其最大容量。如果一个泛型算法提供计数功能,例如STL的count(),其传回值就必须使用迭代器的diference type:1
2
3
4
5
6
7
8
9template <class I,class T>
typename iterator_traits<I>::difference_type
count (I first, I last, const T& value){
typename iterator_traits<I>::difference_type n=0;
for(;first!=last;++first)
if(*first == value)
++n;
return n;
}
针对相应型别difference type,traits的如下两个特化版本,以C++内建的ptrdiff_L作为原生指针的difference type:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19template <class I>
struct iterator_traits {
...
typedef typename I::difference_type difference_type;
};
// 针对原生指针偏特化版
template <class T>
struct iterator_traits<T*> {
...
typedef ptrdiff_L difference_type;
};
// 针对原生的pointer-to-const设计的偏特化版
template <class T>
struct iterator_traits<const T*> {
...
typedef ptrdiff_t difference_type;
};
现在,任何时候我们需要任何迭代器I的difference type,可以:1
typename iterator_traits<I>::difference_type;
迭代器相应型别之三:reference type
从“迭代器所指之物的内容是否允许改变”的角度观之,迭代器分为两种:不允许改变“所指对象之内容”者,称为constant iterators,例如const int* pic;允许改变“所指对象之内容”者,称为 mutable iterators,例如int* pi。 当我们对一个 mutable iterators做解引用时,获得的应该是个左值(lvalue) ,可以被赋值。1
2
3
4int* pi = new int(5);
const int* pci = new int(9);
*pi = 7; // 对mutable iterator及逆行操作,获得的是左值,允许赋值
*pci = 1; // 这个操作不被允许,pci是constant iterator,提领pci所得结果是个右值,不能赋值。
在 C++中,函数如果要返回左值,都是以by reference的方式进行,所以当p是个mutable iterators时,如果其value type是T,那么*p的型别不应该是T,应该是T&。将此道理扩充,如果p是一个 constant iterators,其value type是 T,那么*p的型别不应该是const T,而应该是const T&。*p的型别,即所谓的reference type。
迭代器相应型别之四:pointer type
pointers和 references 在C++中有非常密切的关连。 如果“传回一个左值,令它代表p所指之物”是可能的,那么“传回一个左值,令它代表p所指之物的位址”也一定可以。 我们能够传回一个 pointer,指向迭代器所指之物。
这些相应型别已在先前的ListIter class中出现过:1
2Item& operator*() const { return *ptr; }
Item* operator->() const { return ptr; }Item&便是ListIter的reference type而Item*便是其pointer type。
现在把reference type和pointer type这两个相应型别加入traits内:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21template <class I>
struct iterator_traits {
typedef typename I::pointer pointer;
typedef typename I::reference reference;
}
// 针对原生指针偏特化版
template <class T>
struct iterator_traits<T*> {
...
typedef T* pointer;
typedef T& reference;
};
// 针对原生的pointer-to-const设计的偏特化版
template <class T>
struct iterator_traits<const T*> {
...
typedef const T* pointer;
typedef const T& reference;
};
迭代器相应型别之五:iterator_category
最后一个(第五个)迭代器的相应型别会引发较大规模的写代码工程。在那之前,我必须先讨论迭代器的分类。
根据移动特性与施行操作,迭代器被分为五类:
- Input lterator:这种迭代器所指的对象,不允许外界改变。只读(read only)。
- Output terator:唯写(write only)。
- Forward lterator:允许“写入型”算法(例如
replace())在此种迭代器所形成的区间上进行读写操作。 - Bidirectiona lterator:可双向移动。某些算法需要逆向走访某个迭代器区间(例如逆向拷贝某范围内的元素),可以使用Biairectional lterators。
- Random Access lterator:前四种迭代器都只供应一部分指针算术能力(前三种支持
operator++,第四种再加上operator--),第五种则涵盖所有指针算术能力,包括p+n,p-n,p[n],p1-p2,p1<p2。
迭代器的分类与从属关系如下图所示: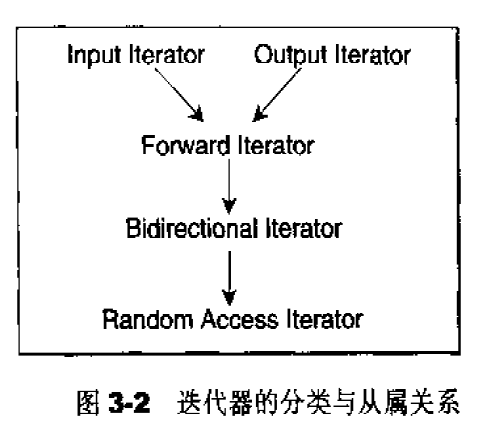
设计算法时,如果可能,我们尽量针对上图中某种迭代器提供一个明确定义,并针对更强化的某种迭代器提供另一定义,这样才能在不同情况下提供最大效率。假设有个算法接受 Forward Iterator,你以 Random Access Iterator 喂给它,也可用,但是可用不一定最佳。
下面以advanced()函数为例,介绍各类迭代器的性能差异。该函数有两个参数,迭代器p和数值n,函数内部将p累进n次,下面有三个定义,一个针对Input iterator,一个针对Bidirectional iterator,另一个针对Random Access iterator。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23template<class InputIterator,class Distance>
void advanced_II(InputIterator& i, Distance n)
{
//单向 逐一前进
while(n--) ++i;
}
template<class BidirectionalIterator, class Distance>
void advanced_BI(BidirectionalIterator& i, Distance n)
{
//双向 逐一前进
if(n>=0)
while(n--) ++i;
else
while(n++) --i;
}
template<class RandomAccessIterator, class Distance>
void advanced_RAI(RandomAccessIterator& i,Distance n)
{
//双向 跳跃前进
i += n;
}
当程序调用advance()时,应该调用哪一份函数定义呢?通常会将三者合一,下面是一种做法:1
2
3
4
5
6
7
8
9
10template <class InputIterator, class Distance>
void advanced(InputIterator& i, Distance n)
{
if(is_random_access_iterator(i))//有待设计
advanced_RAI(i,n);
else if(is_bidirectional_iterator(i))//有待设计
advanced_BI(i,n);
else
advanced_II(i,n);
}
但是上述处理方式,会在程序执行期间才能决定使用哪个处理函数,影响程序效率。最好能够在编译期就选择正确的版本,重载函数机制可以实现该目标。我们可以给advanced()添加第三个参数,即“迭代器类型”这个参数,然后利用traits萃取出迭代器的种类。下面五个classes,即代表五种迭代器类型:1
2
3
4
5struct input_iterator_tag {};
struct output_iterator_tag {};
struct forward_iterator_tag : public input_iterator_tag {};
struct bidirectional_iterator_tag : public forward_iterator_tag {};
struct random_access_iterator_tag : public bidirectional_iterator_tag {};
这些classes只作为标记用,所以不需要任何成员。重新设计__advance(),然后利用第三参数重新定义上面的advance()函数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30template<class InputIterator, class Distance>
inline void __advanced(InputIterator& i, Distance n, input_iterator_tag)
{
//单向 逐一前进
while(n--) ++i;
}
//这是一个单纯的传递调用参数(triv forwarding function) 稍后讨论如何免除之
template<class ForwardIterator,class Distance>
inline void __advanced(ForwardIterator& i, Distance n, forward_iterator_tag)
{
//单纯的进行传递调用
advance(i,n,input_iterator_tag);
}
template<class BidirectionalIterator, class Distance>
inline void __advanced(BidirectionalIterator& i, Distance n, bidirectional_iterator_tag)
{
//双向 逐一前进
if(n>=0)
while(n--) ++i;
else
while(n++) --i;
}
template<class RandomAccessIterator, class Distance>
inline void __advanced(RandomAccessIterator& i, Distance n, random_access_iterator_tag)
{
//双向 跳跃前进
i += n;
}
对外开放的上层接口,调用上述各个重载的__advance()。这一上层接口只需两个参数,当它准备将工作转给上述的__advance()时,才自行加上第三参数:迭代器类型。因此,这个上层函数必须有能力从它所获得的迭代器中推导出其类型——这份工作自然交给traits机制:1
2
3
4
5template<class InputIterator, class Distance>
inline void advanced(InputIterator& i, Distance n)
{
__advance(i,n,iterator_traits<InputIterator>::iterator_categoty());
}
iterator_traits<InputIterator>::iterator_categoty()将产生一个临时对象,其类别应该为前述5个迭代器类型之一。根据这个类别编译器决定调用哪个__advance()重载函数。
任何一个迭代器,其类型永远应该落在“该迭代器所隶属之各种类型中”,最强化的那个。同时,STL算法命名规则:以算法所能接受之最低阶迭代器类型,来为其迭代器型别参数命名,因此advance()中template参数名称为InputIterator。
消除“单纯传递调用的函数”
由于各个迭代器之间存在着继承关系,“传递调用”的行为模式自然存在,即如果不重载Forward Iterators或BidirectionalIterator时,统统都会传递调用InputIterator版的函数。
std::iterator的保证
任何迭代器都应该提供五个内嵌相应类别,以利于traits萃取。STL提供了一个iteratots class如下,如果每个新设计的迭代器都继承自它,则可以保证符合STL规范(即需要提供五个迭代器相应的类型)。1
2
3
4
5
6
7
8
9template <class Category, class T, class Distance = ptrdiff_t,
class Pointer = T*, class Reference = T&>
struct iterator {
typedef Category iterator_category;
typedef T value_type;
typedef Distance difference_type;
typedef Pointer pointer;
typedef Reference reference;
};
iterator class 不含成员,纯粹只是类型定义,所以继承它不会造成任何负担。由于后三个参数都有默认值,新的迭代器只需提供前两个参数即可。
SGI STL的私房菜:__type_traits
traits编程技法很棒,适度弥补了 C++ 语言本身的不足。 STL只对迭代器加以规范,制定出iterator_traits这样的东西。 SGI 把这种技法进一步扩大到迭代器以外的世界,于是有了所谓的__type_traits。
iterator_traits负责萃取迭代器的特性, __type_traits则负责萃取型别(type)的特性。 型别特性是指:这个型别是否具备non-trivial defalt ctor ?是否具备 non-trivial copy ctor?是否具备 non-trivial assignment operator?是否具备 non-trivial dtor?如果答案是否定的,我们在对这个型别进行建构、解构、拷贝、赋值等动作时,就可以采用最有效率的措施,而采用内存直接处理动作如malloc()、memcpy()等等,获得最高效率。这对于大规模而动作频繁的容器,有着显著的效率提升!
type_traits提供了一种机制,允许针对不同的型别属性,在编译时期完成函数派送决定,如果我们事先知道是否有trivial copy constructor,便能够帮助我们确定是否可以使用memcpy()或memmove()。
根据iterator_traits得来的经验,我们希望程序中可以这样运用__type_traits<T>,T代表任意型别:1
2
3
4
5__type_traits<T>::has_trivial_default_constructor
__type_traits<T>::has_trivial_copy_constructor
__type_traits<T>::has_trivial_assignment_operator
__type_traits<T>::has_trivial_destructor
__type_traits<T>::is_POD_type
上述式子应该传回:1
2struct __true_type{};
struct __false_type{};
利用其响应结果进行类型推断。
为了达成上述五个式子,__type_traits应该定义一些typedefs,其值不是_true_type就是_false_type。1
2
3
4
5
6
7
8
9
10template <class type>
struct __type_traits {
typedef __true_type this_dummy_member_must_be_first;
typedef __false_type has_trivial_default_constructor;
typedef __false_type has_trivial_copy_constructor;
typedef __false_type has_trivial_assignment_operator;
typedef __false_type has_trivial_destructor;
typedef __false_type is_POD_type;
};
SGI把所有内嵌型别都定义为_false_type为了定义出最保守的值,然后再针对每一个标量型别(scalar types)设计适当的_type_traits特化版本,这样就解决了问题。上述_type_traits可以接受任何型别的参数,五个typedefs将经由以下管道获得实值:
- 一般具现体(gerera1 instantiation),内含对所有型别都必定有效的保守值。上述各个has_trivial_xxx型别都被定义为
_false_type,就是对所有型别都必定有效的保守值。 - 经过声明的特化版本,例如
<type_traits.h>内对所有C++标量型别(scalar types)提供了对应的特化声明。稍后展示 - 某些编译器会自动为所有型别提供适当的特化版本
以下是<type_traits.h>对所有C++标量类型所定义的__type_traits特化版本:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27__STL_TEMPLATE_NULL struct __type_traits<char> {
typedef __true_type has_trivial_default_constructor;
typedef __true_type has_trivial_copy_constructor;
typedef __true_type has_trivial_assignment_operator;
typedef __true_type has_trivial_destructor;
typedef __true_type is_POD_type;
};
__STL_TEMPLATE_NULL struct __type_traits<int> {
typedef __true_type has_trivial_default_constructor;
typedef __true_type has_trivial_copy_constructor;
typedef __true_type has_trivial_assignment_operator;
typedef __true_type has_trivial_destructor;
typedef __true_type is_POD_type;
};
// 上述还有针对其他数据类型的定义
// 以下针对原生指针设计__type_traits偏特化版本
template <class T>
struct __type_traits<T*> {
typedef __true_type has_trivial_default_constructor;
typedef __true_type has_trivial_copy_constructor;
typedef __true_type has_trivial_assignment_operator;
typedef __true_type has_trivial_destructor;
typedef __true_type is_POD_type;
};
前面第二章提到过的uninitialized_fill_n等函数就在实现中使用了__type_traits机制。1
2
3
4
5template <class ForwardIterator, class Size, class T>
inline ForwardIterator __uninitialized_fill_n(ForwardIterator first, Size n,
const T& x) {
return __uninitialized_fill_n(first, n, x, vaule_type(first));
}
该函数以x为蓝本,自迭代器first开始构造n个元素,首先以value_type()萃取出迭代器first的value_type,再利用__type_traits判断该类型是否为POD类型。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37template <class ForwardIterator, class Size, class T, class T1>
inline ForwardIterator __uninitialized_fill_n(ForwardIterator first, Size n,
const T& x, T1*) {
typedef typename __type_traits<T1>::is_POD_type is_POD;
return __uninitialized_fill_n_aux(first, n, x, is_POD());
}
// 如果不是POD型别 就会派送(dispatch)到这里
template <class ForwardIterator, class Size, class T>
ForwardIterator
__uninitialized_fill_n_aux(ForwardIterator first, Size n,
const T& x, __false_type) {
ForwardIterator cur = first;
__STL_TRY {
for ( ; n > 0; --n, ++cur)
construct(&*cur, x);//需要逐个进行构造
return cur;
}
//如果是POD型别 就会派送到这里 下两行是源文件所附注解
//如果copy construction 等同于 assignment 而且有 trivival destructor
//以下就有效
template <class ForwardIterator, class Size, class T>
inline ForwardIterator
__uninitialized_fill_n_aux(ForwardIterator first, Size n,
const T& x, __true_type) {
return fill_n(first, n, x); //交由高阶函数执行
}
//以下定义于<stl_algobase.h>中的fill_n()
template <class OutputIter, class _Size, class _Tp>
OutputIter fill_n(OutputIter first, Size n, const Tp& value) {
for ( ; n > 0; --n, ++first)
*first = value;
return first;
}
第二个例子是copy()全局函数(泛型算法之一〕,这个函数有非常多的特化〔specialization)与强化(refinement)版本。最基本的想法是这样:1
2
3
4
5
6
7
8
9
10// 拷贝一个数组,其元素为任意型别,视情况采用最有效率的拷贝手段
template <c1ass T> inline void copy(T* source, T* destination, int n) {
copy(source, destination, n, typename __type_traits<T>:::has_trivial_copy_constructor());
}
// 拷贝一个数组,其元素型别拥有non-trivial copy constructors
template <class T> void copy(T* source, T* destination, int n, __false_type) { ... }
// 拷贝一个数组,其元素型别拥有trivial copy constructors
// 可借助memcpy()完成工作
template <class T> void copy(T* source, T* destination, int n, __true_type) { ... }
以上只是针对“函数参数为原生指针”的情况而做的设计。
如果你是SGI STL的用户,你可以在自己的程序中充分运用这个__type_traits,假设我自行定义了一个shape c1ass,__type_traits会对它产生什么效应呢?如果编译器够厉害,__type_traits针对shape萃取出来的每一个特性,其结果将取决于我的Shape是否有trivial default ctor,或triviai copy ctor,或trivial assignment operator, 或trivial dtor而定。但对大部分缺乏这种特异功能的编译器而言,type_traits针对Shape萃取出来的每一个特性都是`false_type,即使shape是个POD型别。这样的结果当然过于保守、但是别无选择,除非我针对shape,自行设计一个__type_traits`特化版本,明白地告诉编译器以下事实(举例):1
2
3
4
5
6
7
8template <class type>
struct __type_traits<Shape> {
typedef __true_type has_trivial_default_constructor;
typedef __false_type has_trivial_copy_constructor;
typedef __false_type has_trivial_assignment_operator;
typedef __false_type has_trivial_destructor;
typedef __false_type is_POD_type;
};
一个简单的判断标准是,如果class内含指针成员,并且对它进行动态内存配置,那么这个class就要实现出自己的non-trival-xxx。
序列式容器
容器的概观与分类
容器,置物之所也。研究数据的特定排列方式,以利于搜寻或排序或其他特殊目的,这一专门学科称为数据结构。几乎可以说,任何特定的数据结构都是为了实现某种特定的算法。
SGI STL的各个容器(本图以内缩方式来表达基层与衍生层的关系)。
这里所谓的衍生,并非派生关系,而是内含关系。例如,heap内含一个vector,priority-queue内含一个heap,stack和queue都内含一个deque,set/map/multiset/multimap都内含一个RB-tree,hash_set/hash_map/hash_multiset/hash_multimap都内含一个hashtabe。
vector概述
vector的数据安排以及操作方式,与array非常相似。两者的唯一差别在于空间的运用的灵活性。array是静态空间,一旦配置了就不能改变;vector的动态空间 ,随着元素的加入,它的内部机制会自行扩充空间以容纳新元素。vector的实现技术,关键在于对其大小的控制以及重新配置时的数据移动效率。
vector的内部定义如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129template <class T, class Alloc = alloc>
class vector {
public:
typedef T value_type;
typedef value_type* pointer;
typedef value_type* iterator;
typedef value_type& reference;
typedef size_t size_type;
typedef ptrdiff_t difference_type;
protected:
typedef simple_alloc<value_type, Alloc> data_allocator; // SGI STL 空间配置器接口
iterator start; // 表示目前使用空间的头
iterator finish; // 表示目前使用空间的尾
iterator end_of_storage; // 表示目前可用空间的尾
void insert_aux(iterator position, const T& x);
void deallocate() { // 释放空间
if (start) data_allocator::deallocate(start, end_of_storage - start);
}
void fill_initialize(size_type n, const T& value) {
start = allocate_and_fill(n, value);
finish = start + n;
end_of_storage = finish;
}
public:
// 各种迭代器
iterator begin() { return start; }
const_iterator begin() const { return start; }
iterator end() { return finish; }
const_iterator end() const { return finish; }
reverse_iterator rbegin() { return reverse_iterator(end()); }
const_reverse_iterator rbegin() const { return const_reverse_iterator(end()); }
reverse_iterator rend() { return reverse_iterator(begin()); }
const_reverse_iterator rend() const { return const_reverse_iterator(begin()); }
// size、max_size、capacity、empty
size_type size() const { return size_type(end() - begin()); }
size_type max_size() const { return size_type(-1) / sizeof(T); }
size_type capacity() const { return size_type(end_of_storage - begin()); }
bool empty() const { return begin() == end(); }
// 重载 []
reference operator[](size_type n) { return *(begin() + n); }
const_reference operator[](size_type n) const { return *(begin() + n); }
// 构造函数,大都调用 fill_initialize
vector() : start(0), finish(0), end_of_storage(0) {}
vector(size_type n, const T& value) { fill_initialize(n, value); }
vector(int n, const T& value) { fill_initialize(n, value); }
vector(long n, const T& value) { fill_initialize(n, value); }
explicit vector(size_type n) { fill_initialize(n, T()); }
// 析构函数
~vector() {
destroy(start, finish);
deallocate();
}
// 首尾元素
reference front() { return *begin(); }
const_reference front() const { return *begin(); }
reference back() { return *(end() - 1); }
const_reference back() const { return *(end() - 1); }
void push_back(const T& x) {
if (finish != end_of_storage) {
construct(finish, x);
++finish;
}
else
insert_aux(end(), x);
}
// 插入操作
iterator insert(iterator position, const T& x) {
size_type n = position - begin();
if (finish != end_of_storage && position == end()) {
construct(finish, x);
++finish;
}
else
insert_aux(position, x);
return begin() + n;
}
// 删除最尾端元素
void pop_back() {
--finish;
destroy(finish);
}
//清除某位置上的元素
iterator erase(iterator position) {
if (position + 1 != end())
copy(position + 1, finish, position); // 后续元素往前移动
--finish;
destroy(finish);
return position;
}
// 清除迭代器所指定的区间的元素
iterator erase(iterator first, iterator last) {
iterator i = copy(last, finish, first);
destroy(i, finish);
finish = finish - (last - first);
return first;
}
// 重新设置 vector 大小,若设置值 new_size 大于当前 size,在尾端插入 x
void resize(size_type new_size, const T& x) {
if (new_size < size())
erase(begin() + new_size, end());
else
insert(end(), new_size - size(), x);
}
void resize(size_type new_size) { resize(new_size, T()); }
void clear() { erase(begin(), end()); }
protected:
// 配置空间并填满内容,其中__STL_TRY、__STL_UNWIND 为异常相关的宏,在 stl_config.h 中定义
iterator allocate_and_fill(size_type n, const T& x) {
iterator result = data_allocator::allocate(n);
__STL_TRY {
uninitialized_fill_n(result, n, x);
return result;
}
__STL_UNWIND(data_allocator::deallocate(result, n));
}
};
vector 的迭代器
vector 维护的是一个连续的线性空间,所以不论其元素型别如何,普通指针都可以作为 vector 的迭代器而满足所有必要条件,因为 vector 迭代器所需要的操作行为,如operator*,operator->,operator++,operator–,operator+,operator-,operator+=,operator-=,普通指针天生就具备。vector 支持随机存取,而普通指针正有这样的能力。所以,vector 提供的是 Random Access Iterators。1
2
3
4
5
6
7
8template <class T, class Alloc = alloc>
class vector
{
public:
typedef T value_type;
typedef value_type* iterator;
...
}
根据定义,如果客户端写出这样的代码:1
2vector<int>::iterator ivite;
vector<Shape>::iterator svite;
ivite 型别就是int*,svite 的型别就是Shape*。
vector数据结构
vector采用线性连续空间的数据结构。它以两个迭代器start和finish分别指向配置的来的连续空间中目前已被使用的范围,并以迭代器end_of_storage指向整块连续空间(含备用空间)的尾端:1
2
3
4
5
6
7
8template<class T,class Alloc = alloc>
class vector{
...
protected :
iterator start ; //表示目前使用空间的头
iterator finish ; // 表示目前使用空间的尾
iterator end_of_storage ; //表示目前可用空间的尾
};
为了降低空间配置时的速度成本,vector 实际配置的大小可能比客户端需求量更大一些,以备将来可能的扩充。这便是容量(capacity)的概念。添加新元素时,如果超出当时的容量,则容量会扩充至两倍,如果两倍容量仍不足,就扩充至足够大的容量。上述容量的扩张必须经历“重新配置、元素移动、释放空间”等过程。vector数据插入过程的示意图如下: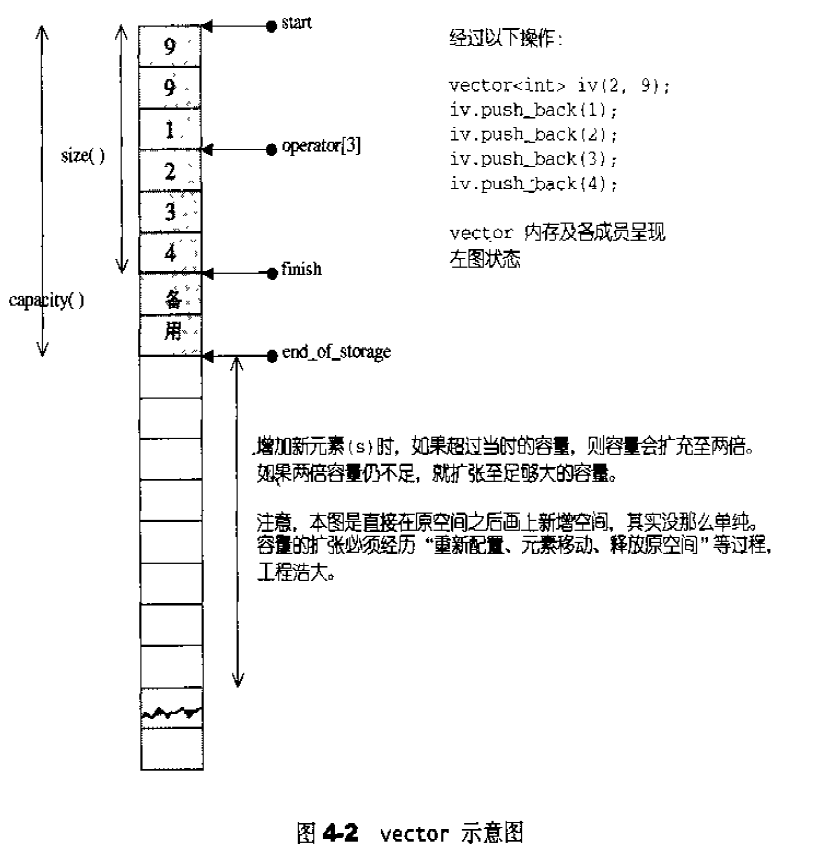
vector构造与内存管理
vector缺省使用alloc作为空间配置器,并据此另外定义了一个data_allocator,为的是更方便以元素大小为配置单位:1
2
3
4
5
6template<class T, class Alloc = alloc>
class vector{
protected:
typedef simple_alloc<value_type,Alloc> data_allocator;
...
}
于是,data_allocator::allocate(n)表示配置n个元素空间。
vector提供许多constructors,其中一个允许我们指定空间大小及初值。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17vector(size_type n, const T& value) {
fill_initialize(n, value);
}
void fill_initialize(n, value) {
start = allocate_and_fill(n, value);
finish = start + n;
end_of_storage = finish;
}
// 配置而后填充
iterator allocate_and_fill(size_type n, const T& x) {
iterator result = data_allocator::allocate(n);
uninitialized_fill_n(result, n, x);
return result;
}
uninitialized_fill_n()会根据第一参数的类型决定使用算法fill_n或反复调用construct()完成任务。
当我们以push_back()将新元素插入vector尾端时,该函数先检查是否还有备用空间,如果有就直接在备用空间上构造元素,并调整迭代器finish,使vector变大。如果没有备用空间,就扩充空间(重新配置、移动数据、释放原空间):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41void push_back(const T& x) {
if (finish != end_of_storage) {
construct(finish, x);
++finish;
}
else
insert_aux(end(), x);
}
template<class T, class Alloc>
void vector<T, Alloc>::insert_aux(iterator position, const T&x){
if (finish != end_of_storage){//还有备用空间
construct(finish, *(finish - 1)); //在备用空间起始处构造一个元素,以vector最后一个元素值为其初值
++finish; //调整finish迭代器
T x_copy = x;
copy_backward(position, finish - 2, finish - 1);
*position = x_copy;
}
else{//没有备用空间
const size_type old_size = size();
const size_type new_size = old_size != 0 ? 2 * old_size : 1;
iterator new_start = data_allocator::allocate(new_size);
iterator new_finish = new_start;
try{
new_finish = uninitialized_copy(start, position, new_start);//将原vector的内容拷贝到新vector
construct(new_finish, x);
++new_finish;
new_finish = uninitialzed_copy(position, finish, new_finish);//将安插点的原内容也拷贝过来
}
catch (excetion e){
destroy(new_start, new_finish);//如果发生异常,析构移动的元素,释放新空间
data_allocator::deallocate(new_start, new_size);
throw;
}//析构并释放原空间
destroy(begin(), end());
deallocator();
start = new_start; //调整迭代器
finish = new_finish;
end_of_storage = new_start + new_size;//调整迭代器
}
}
补充:1
2
3
4
5
6
7
8
9
10
11template<class BidirectionalIterator1, class BidirectionalIterator2>
BidirectionalIterator2 copy_backward ( BidirectionalIterator1 first,
BidirectionalIterator1 last,
BidirectionalIterator2 result);
参数:
first, last
指出被复制的元素的区间范围[first,last).
result
指出复制到目标区间的具体位置[result-(last-first),result)
返回值:
返回一个迭代器,指出已被复制元素区间的起始位置
所谓动态增加大小,并不是在原空间之后接续空间(因为无法包装原空间之后尚有可配置的空间),而是以原大小的两倍另外配置一块较大的空间,然后将原来内容拷贝过来,然后才开始在原内容之后构造新元素,并释放原空间。因此对vector的任何操作,一旦引起空间重新配置,指向原vector的所有迭代器就都失效了。
vector的元素操作
pop_back()实现:1
2
3
4void pop_back(){
--finish; //将尾端标记往前移一格,表示放弃尾端元素
destory(finish); //finish原来指向容器尾部[strat,finish),--后指向最后一个元素,然后析构
}erase()实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16//清除[first,last]中的所有元素
iterator erase(iterator first,iterator last){
iterator i=copy(last,finish,first);
destroy(i,finish);
finish=finish-(last-first);
}
//清除某个位置上的元素
iterator erase(iterator position){
if(position+1!=end())
copoy(position+1,finish,position);
--finish;
destory(finish);
return position;
}
//清除所有元素
void clear() {erase(begin(),end());}
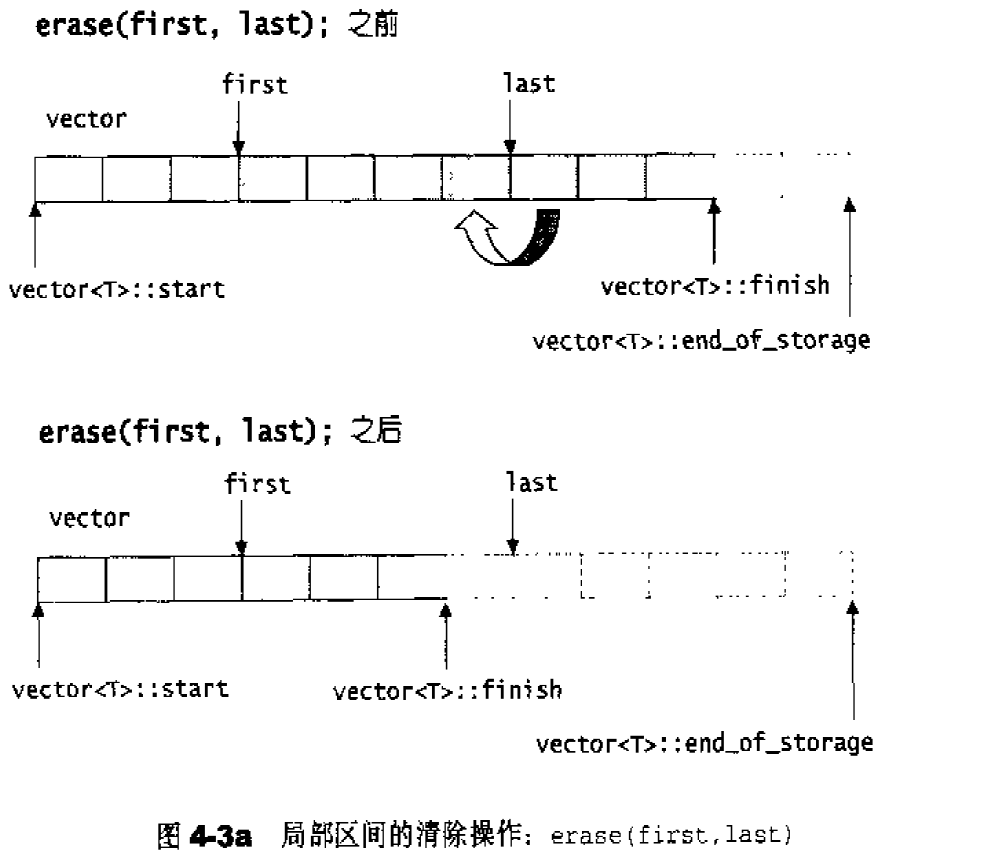
copy()函数具体实现:1
2
3
4
5
6
7
8//InputIterator 版本
template<class InputIterator, class OutputIterator>
inline OutputIterator __copy(InputIterator first, InputIterator last, OutputIterator result, input_iterator_tag){
//如果只是 InputIterator 的话,以迭代器赞同与否,决定循环是否继续、速度慢
for( ; first != last; ++result, ++first)
*result = *first;
return result;
}
即1
2for( ; last != finish; ++first, ++last)
*first = *last; //即将last开始的元素接到first后面
insert()实现,根据备用空间和插入元素的多少分为以下三种情况:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57template <class T, class Alloc>
void vector<T, Alloc>::insert(iterator position, size_type n, const T& x) {
// 当 n != 0 才进行以下所有操作
if (n != 0) {
// 备用空间大于等于新增元素个数
if (size_type(end_of_storage - finish) >= n) {
T x_copy = x;
const size_type elems_after = finish - position;
iterator old_finish = finish;
// 针对插入点后现有元素与新增元素个数的数量采取不同的操作
// 插入点后现有元素个数大于新增元素个数
if (elems_after > n) {
uninitialized_copy(finish - n, finish, finish);
finish += n;
copy_backward(position, old_finish - n, old_finish);
fill(position, position + n, x_copy);
}
// 插入点后现有元素个数小于等于新增元素个数
else {
uninitialized_fill_n(finish, n - elems_after, x_copy);
finish += n - elems_after;
uninitialized_copy(position, old_finish, finish);
finish += elems_after;
fill(position, old_finish, x_copy);
}
}
else {
// 备用空间小于新增元素个数(必须配置额外的内存)
// 首先决定新长度:旧长度的2倍,或者旧长度+新增元素个数
const size_type old_size = size();
const size_type len = old_size + max(old_size, n);
// 配置新的 vector 空间
iterator new_start = data_allocator::allocate(len);
iterator new_finish = new_start;
__STL_TRY {
new_finish = uninitialized_copy(start, position, new_start);
new_finish = uninitialized_fill_n(new_finish, n, x);
new_finish = uninitialized_copy(position, finish, new_finish);
}
catch(...) {
// 如有异常发生,实现 commit or rollback 语义
destroy(new_start, new_finish);
data_allocator::deallocate(new_start, len);
throw;
}
// 清除并释放旧的 vector
destroy(start, finish);
deallocate();
// 调整迭代器
start = new_start;
finish = new_finish;
end_of_storage = new_start + len;
}
}
}
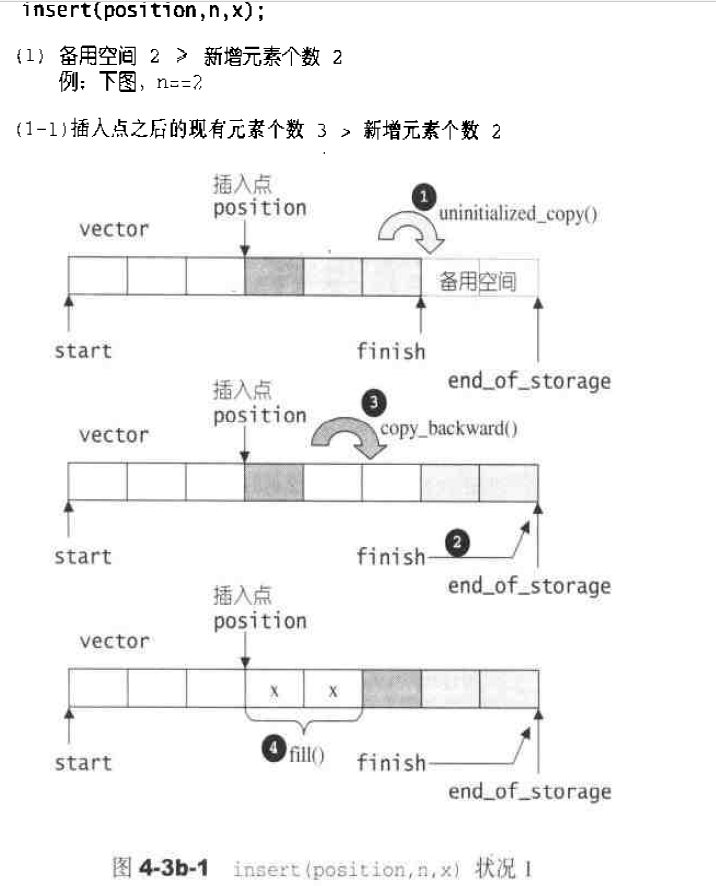
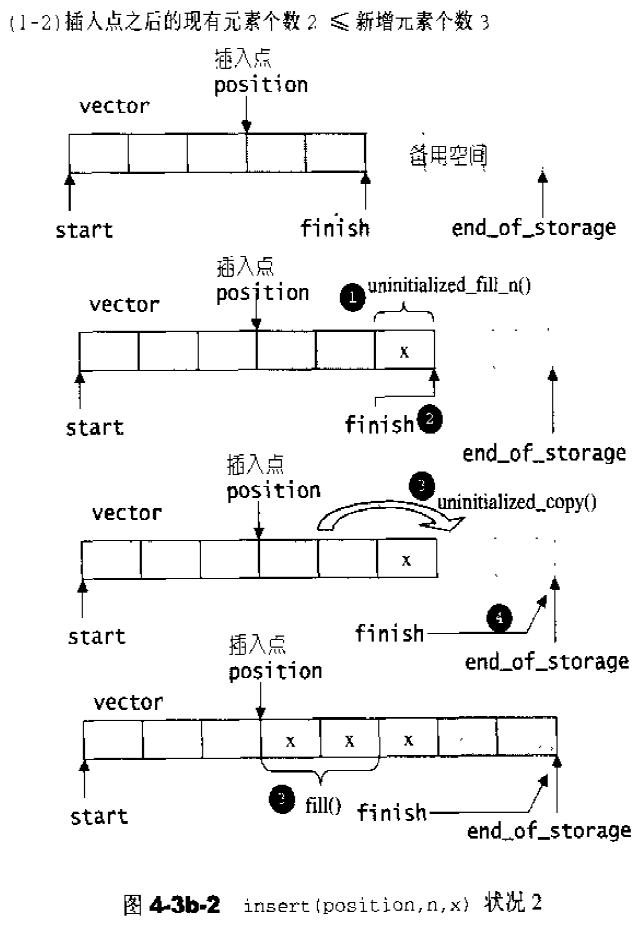
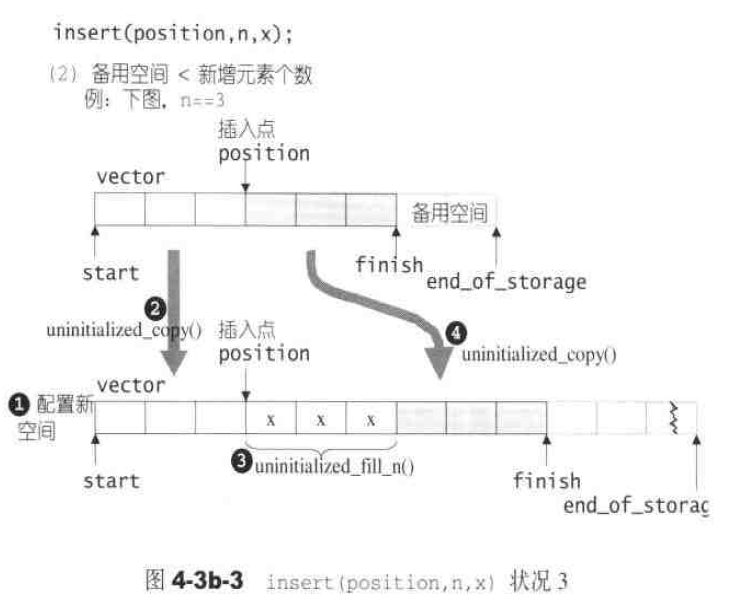
list
list概述
相比于vector的连续线性空间,list显得更为复杂;但list每次插入或删除一个元素时,就将配置或释放一个元素。因此,list对于空间的运用有绝对的精准,一点也不浪费。对于任何位置的插入或元素删除,list永远是常数时间。
list的节点
下面是STL list的节点结构,显然是一个双向链表。1
2
3
4
5
6
7template <class T>
struct __list_node {
typedef void* void_pointer;
void_pointer prev; //型别为void*,其实可设为__list_node<T>*
void_pointer next;
T data;
};
list的迭代器
list中的元素由于都是节点,不保证在存储空间中连续存在。list迭代器必须有能力指向list的节点,并有能力正确递增递减取值存取等操作。其迭代器递增时取用的是下一个节点,递减时取用上一个节点,取值时取的是节点的数据值,成员存取时取用的是节点的成员。
由于list是双向链表,迭代器必须具备前移、后移的能力,因此,list提供的是Bidirectional Iterators;list的插入和接合操作都不会导致原有迭代器失效,但vector的插入可能造成存储空间重新分配,导致原有的迭代器全部失效。甚至list的删除操作也只有指向被删除元素的那个迭代器失效,其他迭代器不受影响。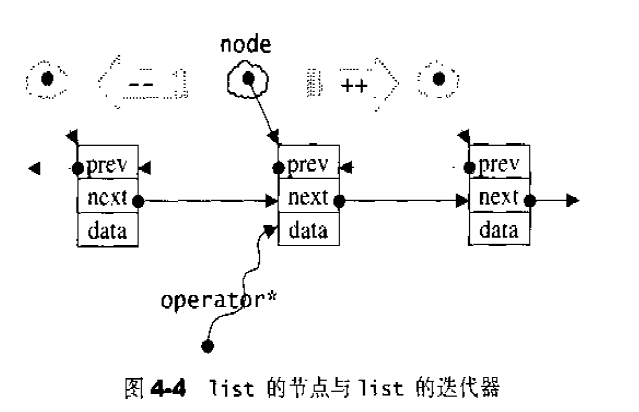
以下是list迭代器的设计:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45template<class T, class Ref, class Ptr>
struct __list_iterator {
typedef __list_iterator<T, P&, T*> iterator;
typedef __list_iterator<T, Ref, Ptr> self;
typedef bidirectionla_iterator_tag iterator_category;
typedef T value_type;
typedef Ptr pointer;
typedef Ref reference;
typedef __list_node<T>* link_type;
typedef size_t size_type;
typedef ptrdiff_t difference_type;
link_type node;
// constrcutor
__list_iterator(link_type x) : node(x) {}
__list_iterator() {}
__list_iterator(const iterator& x) : node(x.node) {}
bool operator==(const self& x) const { return node == x.node; }
bool operator!=(const self& x) const { return node != x.node; }
reference operator*() const { return (*node).data; }
pointer operator->() const { return &(operator*()); }
self& operator++() { //运算符前置++的重载
node = (link_type)((*node).next);
return *this;
}
self operator++(int) { //运算符后置++的重载
self tmp = *this;
++*this;
return tmp;
}
self& operator--() { //运算符前置--的重载
node = (link_type)((*node).prev);
return *this;
}
self operator--(int) { //运算符后置--的重载
self tmp = *this;
--*this;
return tmp;
}
};
list的数据结构
SGI list是一个双向链表,而且是一个环状双向链表:1
2
3
4
5
6
7
8
9template<class T,class Alloc = alloc> //缺省使用alloc为配置器:w
class list{
protected :
typedef __list_node<T> list_node ;
public :
typedef list_node* link_type ;
protected :
link_type node ; //只要一个指针,便可以表示整个环状双向链表
};
如果让指针 node 指向刻意置于尾端的一个空白节点, node 便能符合 STL 对于“前闭后开”区间的要求,成为 last 迭代器。1
2
3
4
5
6
7
8
9
10
11
12
13//取首元素,node是尾端的一个空节点
iterator begin() { return (link_type) ((*node).next); }
//取尾元素的下一个,即node
iterator end() { return node; }
//为空,说明只有node
bool empty() const { return node->next == node; }
size_type size() const {
size_type result = 0;
distance(begin(), end(), result);
return result;
}
reference front() { return *begin(); }
reference back() { return *(--end()); }
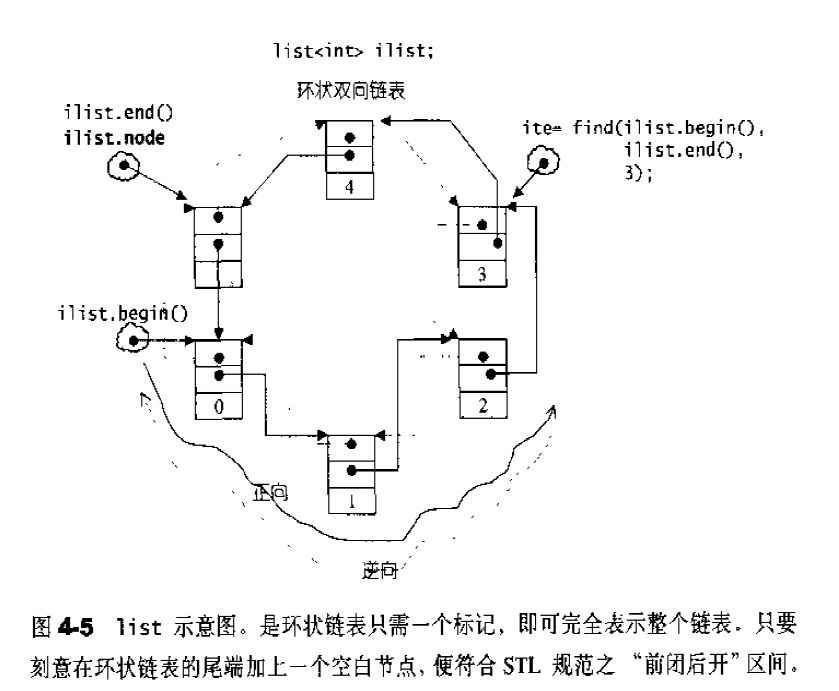
list的构造与内存管理
list采用list_node_allocator来配置节点空间,以下四个函数分别用来配置、释放、构造、销毁一个节点。1
2
3
4
5
6
7
8template<class T,class Alloc = alloc> //缺省使用alloc为配置器:w
class list{
protected :
typedef __list_node<T> list_node ;
//专属之空间配置器,每次配置一个节点大小
typedef simple_alloc<list_node,Alloc> list_node_allocator;
...
};
list_node_allocator(n)表示配置n个节点空间,配置、释放、构造、销毁。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15//配置一个节点
link_type get_node() { return list_node_allocator::allocate(); }
//释放一个节点
void put_node(link_type p) { list_node_deallocator::deallocate(p); }
//产生一个节点,带有元素值
link_type create_node(const T& x) {
link_type p = get_node();
construct(&p->data, x);
return p;
}
//销毁一个节点
void destroy_node(link_type p) {
destroy(&p->data);
put_node(p);
}
list提供了默认的构造函数,使得可以创建一个空list:1
2
3
4
5
6
7
8public:
list() { empty_initialize(); } //默认构造函数
protected:
void empty_initialize() {
node = get_node(); //配置一个节点空间
node->next = node;
node->prev = node;
}
当我们以push_back()将新元素插入list尾端时,此函数内部调用insert(),insert()是一个重载函数,最简单的一种如下:1
2
3
4
5
6
7
8iterator insert(iterator position, const T& x){//在迭代器position所指位置插入一个节点,内容为x
link_type tmp = create_node(x);
tmp->next = position.node;
tmp->prev = position.node->prev;
(link_type(position.node->prev))->next = tmp;
position.node->prev =tmp;
return tmp;
}
当连续插入5个节点之后,list的状态如图,如果希望在list内部的某处插入新节点,首先必须确定插入位置,例如希望在数据为3的节点处插入一个数据值为99的节点,可以:1
2
3ilite = find(li.begin, li.end(), 3);
if (ilite != 0)
il.insert(ilite, 99);
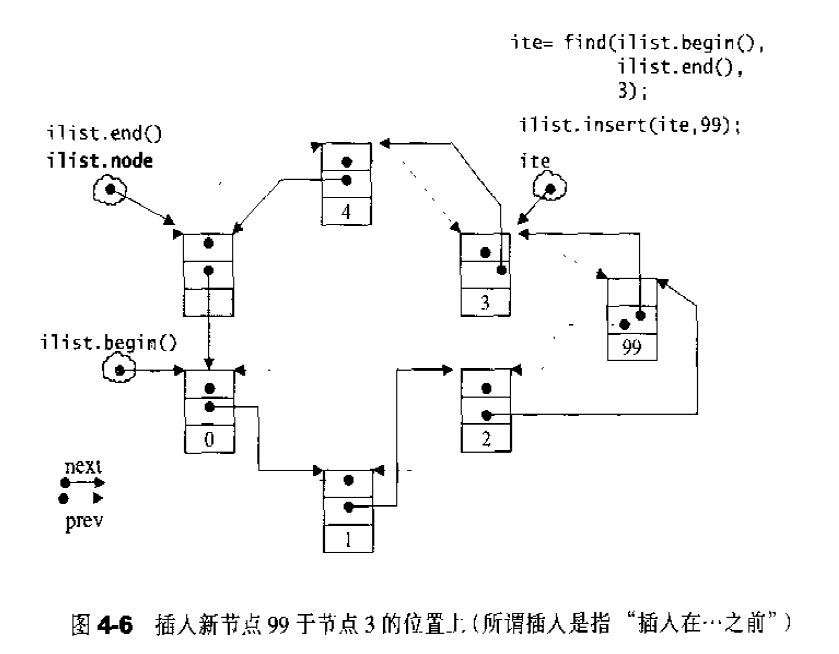
list的元素操作
push_front()函数:将新元素插入于list头端,内部调用insert()函数。1
void push_front(const T&x) { insert(begin(),x); }
push_back()函数:将新元素插入于list尾端,内部调用insert()函数。1
void push_back(const T& x) { insert(end(),x); }
erase()函数:移除迭代器position所指节点。1
2
3
4
5
6
7
8iterator erase(iterator position){
link_type next_node=link_type(position.node->next);
link_type prev_node=link_type(position.node->prev);
prev_node->next=next_node;
next_node->prev=prev_node;
destroy_node(position.node);
return iterator(next_node);
}
pop_front()函数:移除头结点,内部调用erase()函数。1
void pop_front() { erase(begin()); }
pop_back()函数:移除尾结点,内部调用erase()函数。1
2
3
4void pop_back(){
iterator i = end();
erase(--i);
}
clear()函数:清除所有节点:1
2
3
4
5
6
7
8
9
10
11
12
13
14template <class T, class Alloc>
void list<T, Alloc>::clear()
{
link_type cur = (link_type) node->next;//node原来指向list的end,node->next为begin
while (cur != node)
{
link_type tmp = cur;
cur = (link_type) cur->next;
destroy_node(tmp);
}
// 恢复node原始状态
node->next = node;
node->prev = node;
}
remove():将数值为value的所有元素移除1
2
3
4
5
6
7
8
9
10
11
12template <class T, class Alloc>
void list<T, Alloc>::remove(const T& value) {
iterator first = begin();
iterator last = end();
while(first != end) {
iterator next = first;
++ next;
if (*first == value)
erase(first);
first = next;
}
}
transfer()迁移函数:将[ frirst , last ) 内所有元素移动到position之前。1
2
3
4
5
6
7
8
9
10
11void transfer(iterator position, iterator first, iterator last) {
if (position != last) {
(*(link_type((*last.node).prev))).next = position.node; //(1)
(*(link_type((*first.node).prev))).next = last.node; //(2)
(*(link_type((*position.node).prev))).next = first.node;//(3)
link_type tmp = link_type((*position.node).prev); //(4)
(*position.node).prev = (*last.node).prev; //(5)
(*last.node).prev = (*first.node).prev; //(6)
(*first.node).prev = tmp; //(7)
}
}
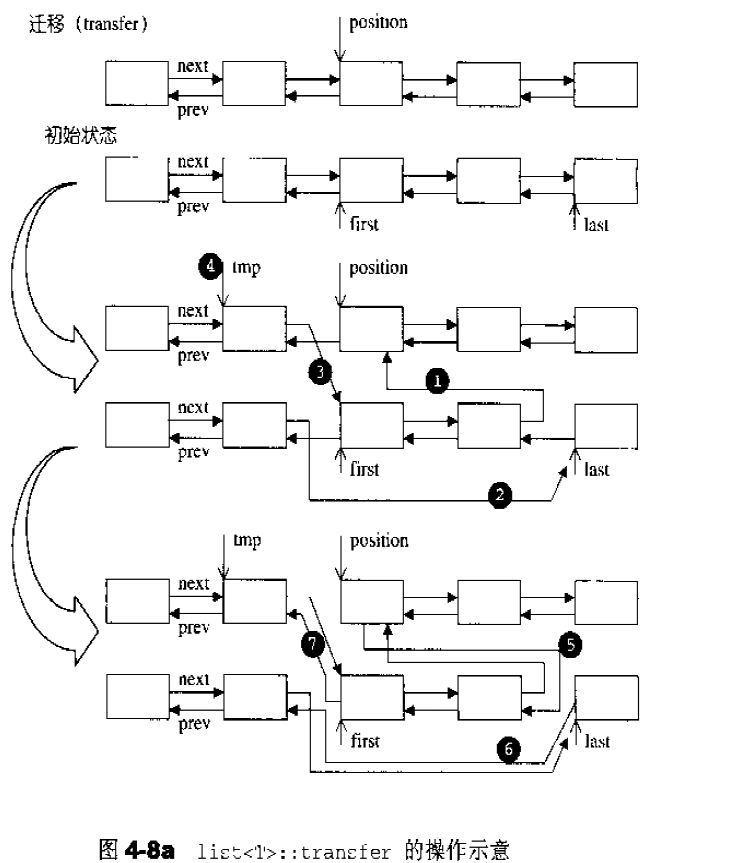
list公开提供的是所谓的接合操作splice,splice结合操作将连续范围的元素从一个list移动到另一个list的某个定点。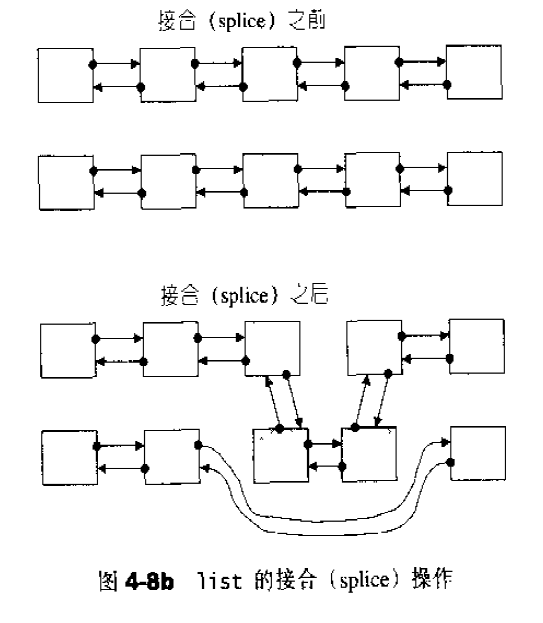
1 | int iv[5] = { 5,6,7,8,9 }; |
以下是merge()、reverse()、sort()的源代码,有了transfer()在手,这些操作都不难完成1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18template<class T, class Alloc>
void list<T, Alloc>::merge(list<T, Alloc>& x) {
iterator first1 = begin();
iterator last1 = end();
iterator first2 = x.begin();
iterator last2 = x.begin();
while(first1 != last1 && first2 != last2)
if (*first2 < *first1) {
iterator next = first2;
transfer(first1, first2, ++next);
first2 = next;
}
else
++first1;
if (first2 != last2)
transfer)last1, first2, last2);
}
reverse()将*this的内容逆向重置1
2
3
4
5
6
7
8
9
10
11
12
13template<class T, class Alloc>
void list<T, Alloc>::reverse() {
// 以下判断,如果是空链表,或仅有一个元素,就不操作
if (node->next == node || size() == 1)
return;
iteratro first = begin();
++first;
while(first != end()) {
iterator old = first;
++ first;
transfer(begin(), old, first);
}
}
list不能使用STL算法sort(),必须使用自己的sort():1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25template <class T, class Alloc>
void list<T, Alloc>::sort() {
// 以下判断,如果是空链表,或仅有一个元素,就不操作
if (node->next == node || size() == 1)
return;
list<T, Alloc> carry;
list<T, Alloc> counter[64];
int fill = 0;
while(!empty()) {
carry.splice(carry.begin(), *this, begin());
int i = 0;
while(i < fill && !counter[i].empty()) {
counter[i].merge(carry);
carry.swap(counter[i++]);
}
carry.swap(counter[i]);
if (i == fill)
++ fill;
}
for (int i = 1; i < fill; i ++)
counter[i].merge(counter[i-1]);
swap(counter[fill-1]);
}
deque
deque(double-ended queue,双端队列)是一种具有队列和栈的性质的数据结构。相比于vector单向开口的连续线性空间而言,deque则是一种双向开口的连续线性空间,可以在头尾两端分别做元素的插入和删除操作。虽然vector从技术层面也可以对头部操作,但是效率极低。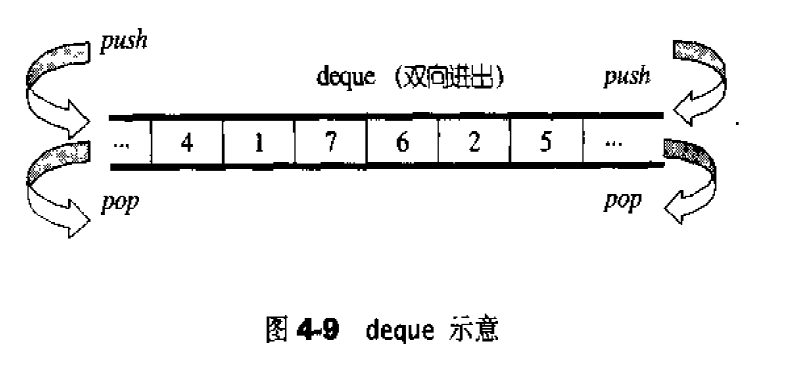
deque与vector的最大差异在于:
- deque可以在常数时间内完成对头部元素的插入或删除操作;
- deque没有容量的概念,它是动态地以分段连续空间组合而成,随时可以增加一段新的空间并链接起来。deque没有必要提供所谓的空间保留reserve功能。
虽然deque也提供Random Access Iterator,但它的迭代器并不是普通指针,其复杂度和vector不同。除非必要我们应该选择vector而不是deque。对deque进行排序操作,为了得到最高效率,可先将deque复制一个vector,将vector排序后再复制回deque。
deque的中控器
deque由一段一段的定量连续空间构成。一旦有必要在dequer前端或尾端增加新空间,便配置一段定量连续空间,串接在整个deque的头端或尾端。deque的最大任务是在这些分段的定量连续空间上,维护其整体连续的假象,并提供随机存取的接口。避开了“重新配置、复制、释放”的轮回,代价则是复杂的迭代器架构。
deque采用一块所谓的map作为主控。这里所谓map是一小块连续空间,其中每个元素(此处称为一个节点,node)都是指针,指向另一段(较大的)连续线性空间,称为缓冲区。缓冲区才是deque的储存空间主体。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16template<class T, class Alloc = alloc, size_t BufSiz = 0>
class deque{
public :
typedef T value_type ;
typedef value_type* pointer ;
...
protected :
//元素的指针的指针(pointer of pointer of T)
typedef pointer* map_pointer ; //其实就是T**
protected :
map_pointer map ; //指向map,map是块连续空间,其内的每个元素
//都是一个指针(称为节点),指向一块缓冲区
size_type map_size ;//map内可容纳多少指针
...
};
map其实是一个T**,所指之物是另一个指针,指向类型为T的一块空间。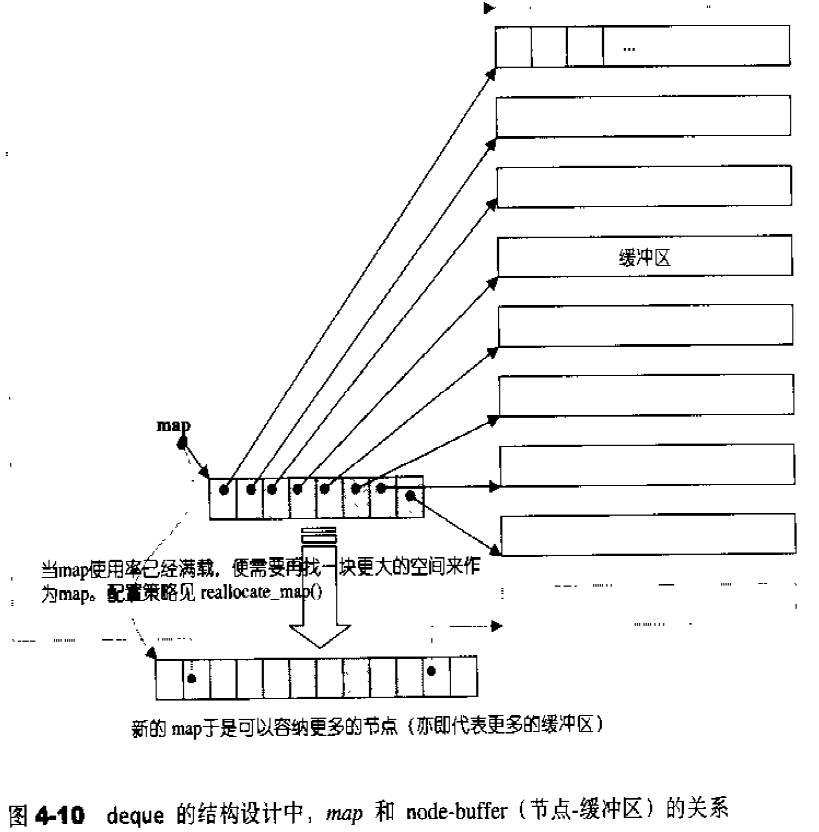
deque的迭代器
deque是分段连续空间,维持“整体连续”假象的任务,落在迭代器的operator++和operator--两个运算子上。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24template<class T, class Ref, class Ptr, size_t BufSiz>
struct __deque_iterator{ //未继承std::iterator
typedef __deque_iterator<T,T&,T*,BufSize> iterator ;
typedef __deque_iterator<T,const T&,const T*,BufSize> const_iterator ;
static size_t buffer_size() {return __deque_buf_size(BufSize,sizeof(T)) ;}
//未继承std::iterator,所以必须自行撰写五个必要的迭代器相应型别
typedef random_access_iterator_tag iterator_category ;
typedef T value_type ;
typedef Ptr pointer ;
typedef Ref reference ;
typedef size_t size_type ;
typedef ptrdiff_t difference_type ;
typedef T** map_pointer ;
typedef __deque_iterator self ;
//保持与容器的联结
T *cut ; //此迭代器所指之缓冲区中的现行(current)元素
T *first ; //此迭代器所指之缓冲区的头
T *last ; //此迭代器所指之缓冲区的尾(含备用空间)
map_pointer node ; //指向管控中心
...
};
其中用来决定缓冲区大小的函数buffer_size()调用__deque_buf_size(),后者是一个全局函数:1
2
3
4
5
6
7
8// 如果n不为0,传回n,表示buffer size由用户定义
// 如果n为0,表示buffer size使用默认值,那么
// 如果sz(元素大小,sizeof(value_type))小于512,传回512/sz
// 如果sz不小于512,传回1
inline size_t __deque_buf_size(size_t n, size_t sz)
{
return n != 0 ? n : (sz < 512 ? size_t(512/sz) : size_t(1));
}
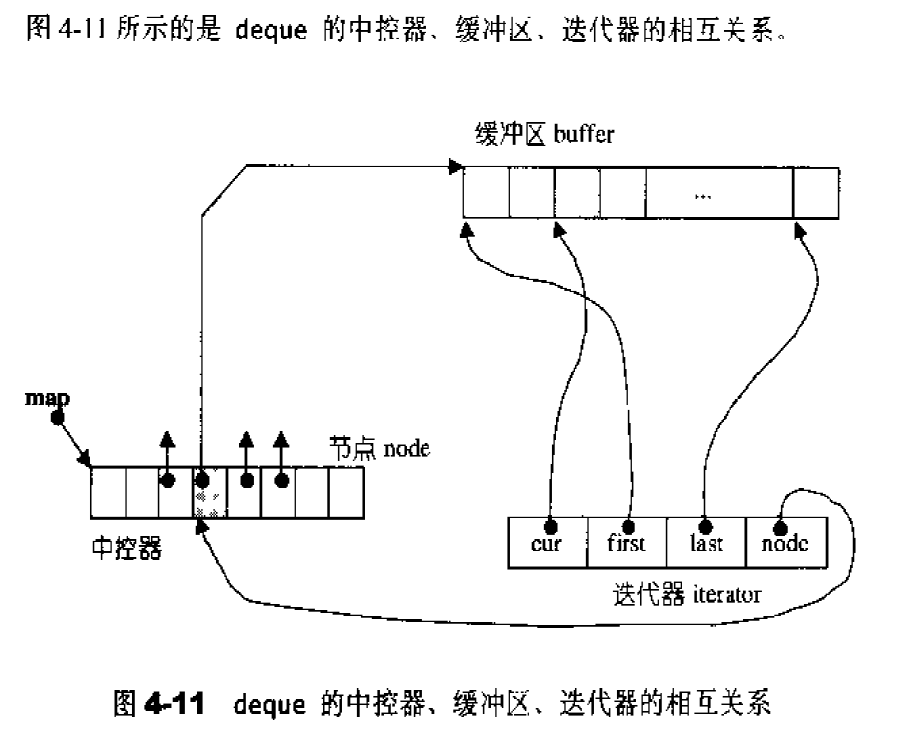
假设现在我们产生1个deque<int>,并令其缓冲区大小为32,于是每个缓冲区可容纳32/sizeof(int)=4个元素:经过某些操作之后,deque拥有20个元素,那么其begin()和end()所传回的两个迭代器应该如图4-12所示。这两个迭代器事实上一直保持在deque内,名为start和finish,稍后在deque数据结构中便可看到。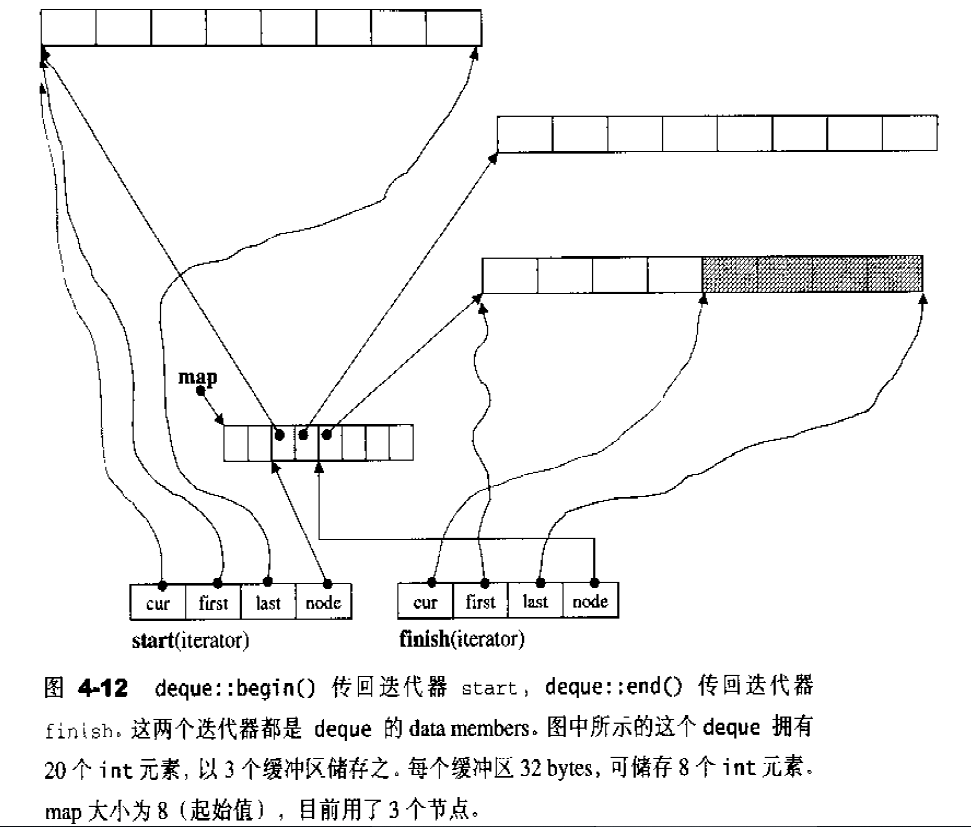
20个元素需要20/8=3个缓冲区,所以map之内运用了三个节点。迭代器start内的cur指针当然指向缓冲区的第一个兀素,迭代器finish内的指针当然指向缓冲区的最后元素(的下一位置)。注意,最后1个缓冲区尚有备用空间。稍后如果有新元素要插入于尾端,可直接拿此备用空间来使用。
下面是deque迭代器的几个关键行为.由于迭代器内对各种指针运算都进行了重载操作,所以各种指针运算如加、减、前进、后退都不能直观视之。其中最关键的就是:一旦行进时遇到缓冲区边缘,要特别当心,视前进或后退而定,可能需要调用set_node()跳一个缓冲区。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86void set_node(map_pointer new_node) {
node = new_node;
first = *new_node;
last = first + difference_type(buffer_size());
}
//以下各个重载运算子是__deque_iterator<>成功运作的关踺
reference operator*() const { return *cur; }
pointer operator->() const { return &(operator*(); }
difference_type operator-(const self& x) const {
return difference_type(buffer_size()) * (node - x.node - 1) + (cur - first) + (x.last - x.cur);
}
self& operator++() {
++ cur; //切换至下一个元素
if (cur == last) { // 如果已达所在缓冲区的尾端
set_node(node + 1); //就切换至下一节点(亦即缓冲区)
cur = first; // 的第一个元素
}
return *this;
}
self operator++(int) {
// 后置式标准写法
self tmp = *this;
++*this;
return tmp;
}
self& operaeor--() {
if (cur == first) { // 如果已达所在缓冲区的头端,
set_node(node - 1); // 就切涣至前一节点(亦即缓冲区)
cur = last; // 的最后一个元素
}
-- cur; //切换至前一个元素
return *this;
}
self operator--(int) {
// 后置标准写法
self tmp = *this;
-- *this;
return tmp;
}
//以下实现随机存取.迭代器可以直接跳跃n个距离
self& operator+=(difference_type n) {
difference_type offset = n + (cur - first);
if (offset >= 0 && offset < difference_type(buffer_size()))
// 目标位置在同一缓冲区内
cur += n;
else {
// 标的位不在同一缓冲区内
difference_type node_offset = offset > 0 ? offset/difference_type(buffer_size()) : -difference_type((-offset-1)/buffer_size()) - 1;
// 切换至正确的节点〈亦即缓冲区)
set_node(node + node_offset);
// 切换至正确的元素
cur = first + (offset - node_offset * difference_type(buffer_size()));
}
return *this;
}
self operator+(difference_type n) const {
self tmp = *this;
return tmp += n; // 调用operator+=
}
self& operator-=(difference_type n) { return *this += -n; }
// 以上利用operator+= 来完成operator-=
self operator-(difference_type n) const {
slef tmp = *this;
return tmp -= n; // 调用operator-=
}
// 以下实现随机存取。迭代器可以直接跳跃n个距离
reference operator[] (difference_type n) const { return *(*this + n); }
// 以上调用operator*, operator+
bool operator== (const self& x) const { return cur == x.cur; }
bool operator!= (const self& x) const { return !(*this == x); }
bool operator< (const self& x) const {
return (node == x.node) ? (cur < x.cur) : (node < x.node);
}
deque的数据结构
deque除了维护一个指向map的指针外,也维护start,finish两个迭代器,分别指向第一缓冲区的第一个元素和最后缓冲区的最后一个元素(的下一个位置)。此外,也必须记住目前的map大小,因为一旦map提供的节点不足,就必须重新配置更大的一块map。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18template<class T, class Alloc = alloc, size_t BufSiz = 0>
class deque{
public :
typedef T value_type ;
typedef value_type* pointer ;
typedef size_t size_type ;
public :
typedef __deque_iterator<T,T&,T*,BufSiz> iterator ;
protected :
//元素的指针的指针(pointer of pointer of T)
typedef pointer* map_pointer ;
protected:
iterator start ; //表现第一节点
iterator finish ; //表现最后一个节点
map_pointer map ; //指向map,map是块连续空间,其每个元素都是个指针,指向一个节点(缓冲区)
size_type map_size ; //map内有多少指针
...
} ;
deque的构造与内存管理
以程序实现来初步了解deque的构造和内存管理:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
using namespace std;
class alloc {
};
int main() {
deque<int, allocator<int>> ideq(20, 9);
//deque<int,alloc,8> ideq(20, 9);//在linux下不支持alloc
cout << "size=" << ideq.size() << endl;
for (int i = 0; i < ideq.size(); ++i)
cout << ideq[i] << ' ';
cout << endl;
for (int i = 0; i < 3; ++i)
ideq.push_back(i);
for (int i = 0; i < ideq.size(); ++i)
cout << ideq[i] << ' ';
cout << endl;
cout << "size=" << ideq.size() << endl;
ideq.push_back(3);
for (int i = 0; i < ideq.size(); ++i)
cout << ideq[i] << ' ';
cout << endl;
cout << "size=" << ideq.size() << endl;
ideq.push_front(99);
for (int i = 0; i < ideq.size(); ++i)
cout << ideq[i] << ' ';
cout << endl;
cout << "size=" << ideq.size() << endl;
ideq.push_front(98);
ideq.push_front(97);
for (int i = 0; i < ideq.size(); ++i)
cout << ideq[i] << ' ';
cout << endl;
cout << "size=" << ideq.size() << endl;
deque<int, allocator<int>>::iterator itr;
itr = find(ideq.begin(), ideq.end(), 99);
cout << *itr << endl;
cout << *(itr._M_cur) << endl;
}
————————————————————————————————————————————————————————————————————————————————
[root@192 4_STL_sequence_container]# ./4_4_5_deque-test
size=20
9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9
9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 0 1 2
size=23
9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 0 1 2 3
size=24
99 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 0 1 2 3
size=25
97 98 99 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 0 1 2 3
size=27
99
99
一开始声明一个deque:1
deque<int, alloc, 32> ideq(20, 9);
其缓冲区为32bytes,并令其保留20个元素空间,每个元素初值为9。现在,deque的情况如图4-12。
deque自行定义了2个专属的空间配置器:1
2
3
4
5protected:
// 每次配置一个元素大小
typedef simple_alloc<value_type, Alloc> data_allocator;
// 每次配置一个指针大小
typedef simple_alloc<pointer, Alloc> map_allocator;
并提供一个constructor:1
2
3
4deque(int n,const value_type& value):start(),finish(),map(0),map_size(0)
{
fill_initialize(n, value);
}
其内调用的fill_initialize()负责产生并安排好deque的结构,并将元素的初值设定妥当。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16template<class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::fill_initialize(size_type n, const value_type& value) {
//负责产生并安排好deque的结构,并将元素的初值设定好
create_map_and_nodes(n); //把deque的结构都安排好
map_pointer cur;
__STL_TRY {
//已经获得空间,为每个节点缓冲区设定初值
for(cur = start.node; cur < finish.node; ++cur) {
uninitialized_fill(*cur, *cur+buffer_size(), value);
}
//最后一个节点的设定稍有不同(尾端可能有备用空间,不必设初值)
uninitialized_fill(finish.first, finish.cur, value);
} catch( ... ) {
...
}
}
其中create_map_and_nodes()负责产生并安排好deque的结构:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30template<class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::creat_map_and_nodes(size_type num_elements)
{ //产生并安排好deque的结构
size_type num_nodes=num_elements/buffer_size()+1;
//一个map要管理几个节点,最少8个,最多是“所需节点数+2”,前后各预留一个,扩充时用
map_size=max(initial_map_size(),num_nodes+2);
map=map_allocator::allocate(map_size);
// 以下令nstart和finish指向map所拥有的全部节点的最中央区段
// 保持在最中央,可使头尾两端的扩充能量一样大,每个节点对应一个缓冲区
map_pointer nstart=map+(map_size-num_nodes)/2;
map_pointer nfinish=nstart+num_nodes-1;
map_pointer cur;
__STL_TRY {
// 为map的每个节点配置缓冲区,所有缓冲区加起来就是deque的可用空间
for(cur=nstart; cur <= nfinish; cur++)
{
*cur=allocate_node();
}
} catch(...) {
...
}
// 为deque内的两个迭代器start和end设置正确内容
start.set_node(nstart);
finish.set_node(nfinish);
start.cur=start.first;
finish.cur=finish.first+num_elements%buffer_size();
}
接下来范例程序为每个元素重新设置值。在尾端插入三个元素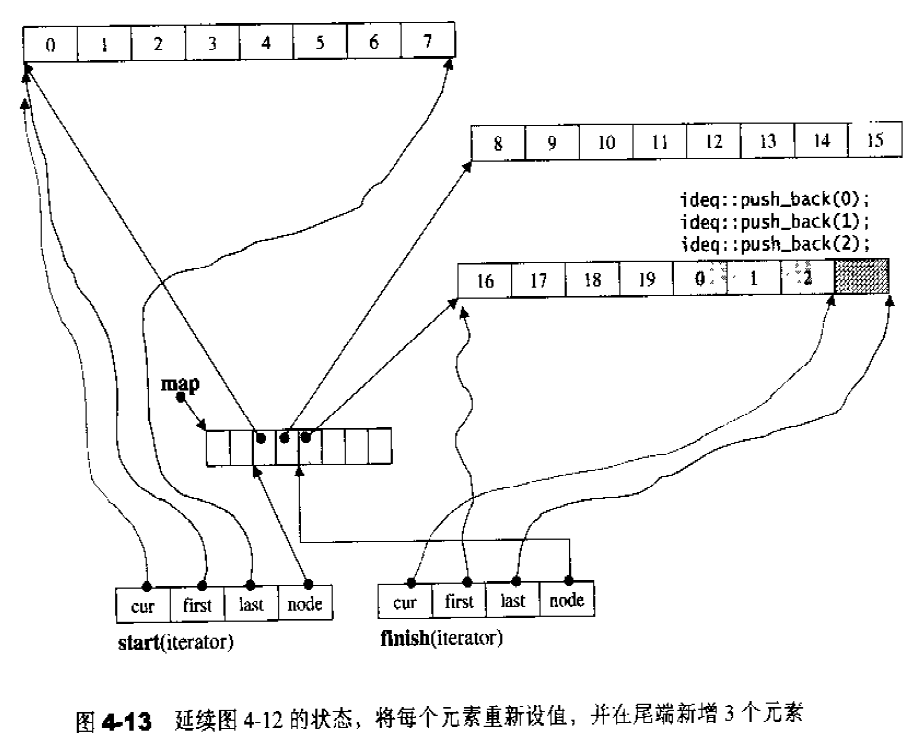
deque的元素操作
1 | void push_back(const value_type &t) |
如果尾端只剩一个元素备用空间,push_back()调用push_back_aux(),先配置一块新的缓冲区,再设妥新元素内容,然后更改迭代器finish状态。1
2
3
4
5
6
7
8
9
10
11
12
13template<class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::push_back_aux(const value_type &t) //只剩最后一个缓冲区的最后一个备用缓冲区
{ //先配置一块新的缓冲区,再设新元素内容,更改迭代器finish的状态
value_type t_copy = t;
reserve_map_at_back(); //若符合某种条件,则必须重换一个map
*(finish.node + 1) = allocate_node(); //配置一新缓冲区
__STL_TRY {
construct(finish.cur, t_copy);
finish.set_node(finish.node + 1);
finish.cur = finish.first;
}
__STL_UNWIND(deallocate_node(*(finish.node + 1)));
}
现在deque的状态如图: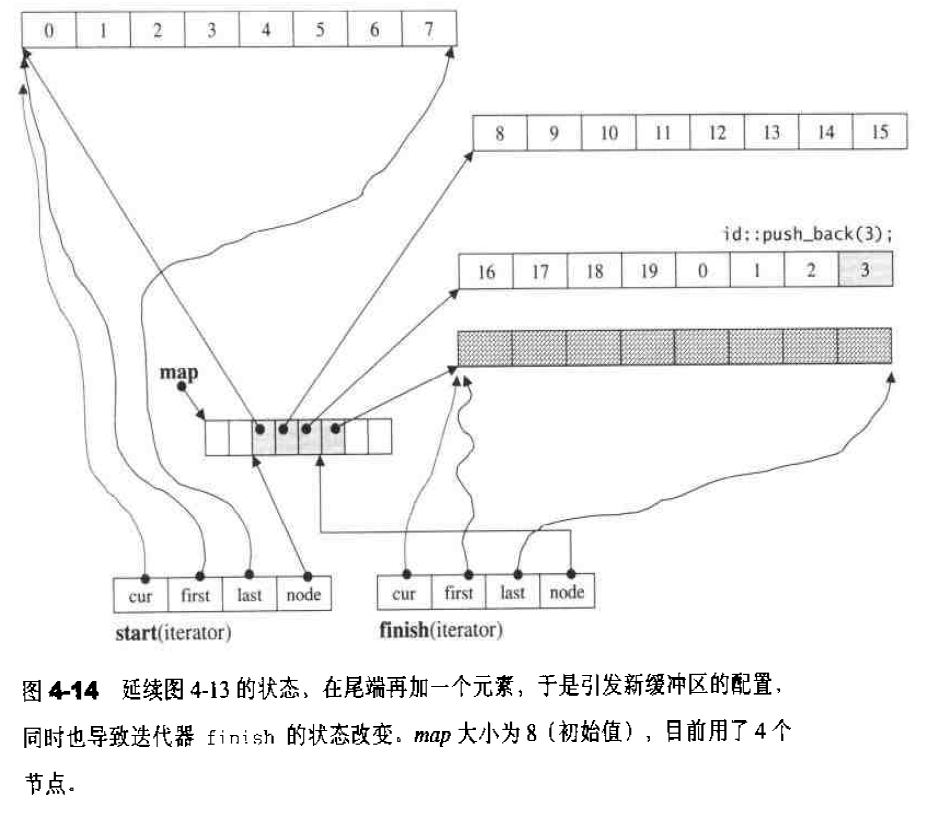
接下来范例程序在deque的前端插入一个新元素:1
ideq.push_front(99);
push_front()的操作如下:1
2
3
4
5
6
7
8
9
10void push_front(const value_type &t)
{
if (start.cur != start.first) { // 第一缓冲区尚有空间
construct(start.cur - 1, t); // 直接在备用空间上构造元素
-- start.cur; // 调整第一缓冲区的使用状态
}
else {
push_front_aux(t);
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18template<class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::push_front_aux(const value_type &t)
{
value_type t_copy = t;
reserve_map_at_front();
*(start.node - 1) = allocate_node();
__STL_TRY {
start.set_node(start.node - 1);
start.cur = start.last - 1;
construct(start.cur, t_copy);
}
catch(...) {
start.set_node(start.node + 1);
start.cur = start.first;
deallocate_node(*(start.node - 1));
throw;
}
}
一开始调用reserve_map_at_front(),判断是否需要扩充map,如果有则付诸行动。后续流程配置了一块新缓冲区,并直接将节点安置在现有的map中,设定新元素,改变迭代器的状态: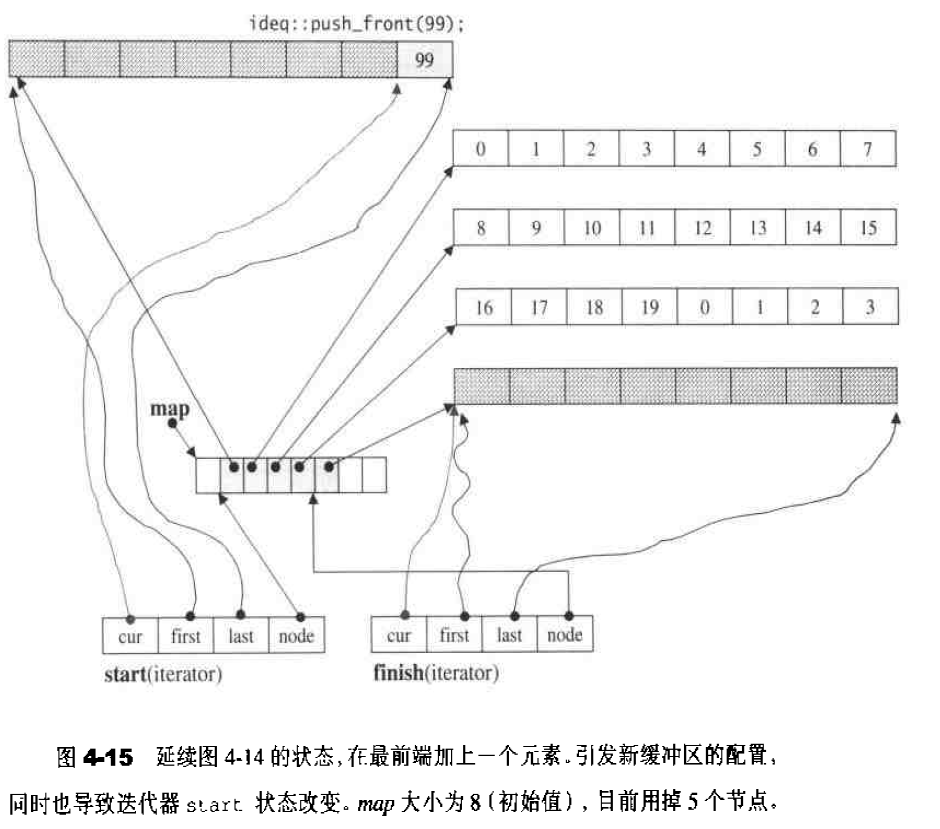
接下来插入两个新的:1
2ideq.push_front(98);
ideq.push_front(97);
这一次,由于第一缓冲区有备用空间,push_front()可以在备用空间上构造新元素: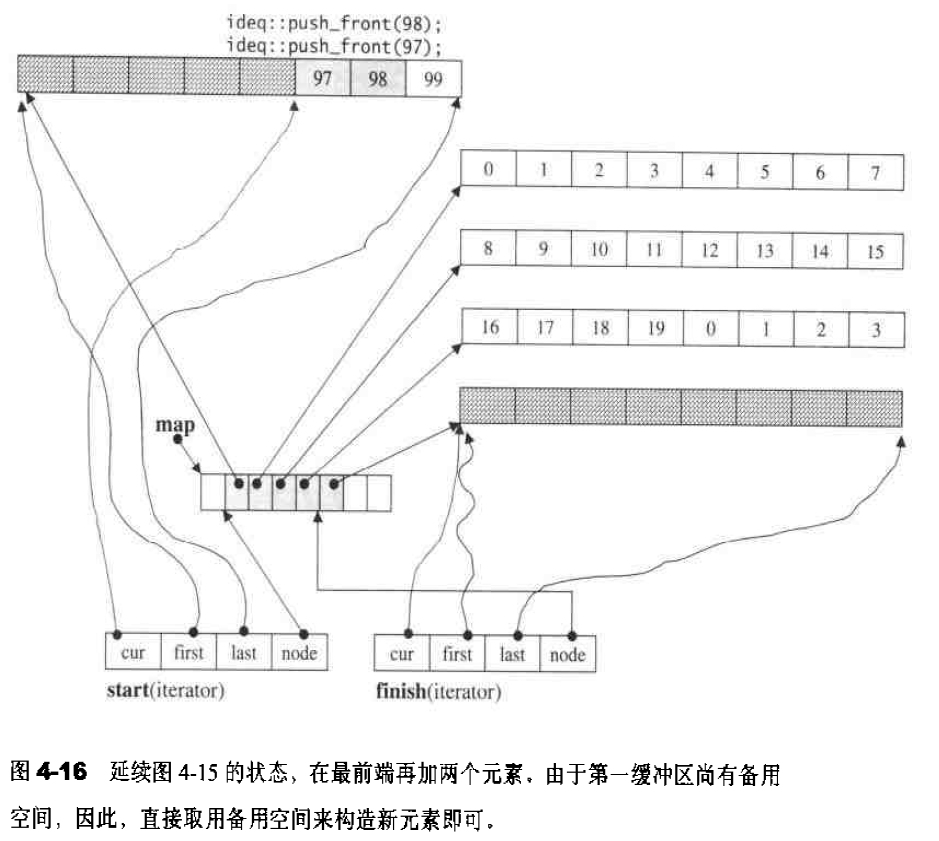
reserve_map_at_back()和reserve_map_at_front()决定map是否需要整治:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16void reserve_map_at_back(size_type nodes_to_add = 1)
{
if (nodes_to_add + 1 > map_size - (finish.node - map)) //map尾端的节点备用空间不足
{
//换一个map(配置更大的,拷贝原来的,释放原来的)
reallocate_map(nodes_to_add, false);
}
}
void reserve_map_at_front(size_type nodes_to_add = 1)
{
if (nodes_to_add > start.node - map)
{
reallocate_map(nodes_to_add, true);
}
}
1 | template<class T, class Alloc, size_t BufSize> |
pop是将元素拿掉:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21void pop_back()
{
if (finish.cur != finish.first)
{
--finish.cur;
destroy(finish.cur); //将最后元素析构,左开右闭
}
else
{
//最后缓冲区没有任何元素
pop_back_aux(); //这里将进行缓冲区的释放工作
}
}
void pop_back_aux()
{ //finish.cur==finish.first 释放该缓冲区
deallocate_node(finish.first); //释放最后一个缓冲区
finish.set_node(finish.node - 1);
finish.cur = finish.last - 1;
destroy(finish.cur); //析构
}
1 | void pop_front() |
clear用来清除整个deque。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21void clear()
{
for (map_pointer node = start.node + 1; node < finish.node; ++node)
{
destory(*node, *node + buffer_size()); //析构元素
data_allocator::deallocate(*node, buffer_size()); //释放内存
}
if (start.node != finish.node) //至少有两个缓冲区
{
destroy(start.cur, start.last);
destroy(finish.first, finish.cur);
//保留头缓冲区
data_allocator::deallocate(finish.first, buffer_size());
}
else
{
destroy(start.cur, finish.cur);
}
finish = start;
}
下面这个例子是clear(),用来清除某个元素:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15// 清除pos所指的元素.pos为清除点
iterator erase(iterator pos) {
iterator next = pos;
++next;
difference_type index = pos - start; // 清除点之前的元素个数
if (index < (size() >> 1)) { // 如果清除点之前的元素比较少,
copy_backward(start, pos, next); // 就移动清除点之前的元素
pop_front(); // 移动完毕,最前一个元素冗余,去除之
}
else { // 清除点之后的元素比较少,
copy(next, finish, pos); // 就移动清除点之后的元素
pop_back(); // 移动完毕,最后一个元素冗余,去除之
}
return start + index;
}
下面这个例子是erase(),用来清除[first, last]区间内的所有元素:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30template<Class T, class Alloc, size_t BufSize>
deque<T, Alloc, BufSize>::eraee(iterator first, iterator last) {
if (first == start && last == finish) {
clear();
return finish;
}
else {
difference_type n = last - first;
difference_type elems_before = first - start;
if (elems_before < (size() - n) / 2) {
copy_backward(start, first, last);
iterator new_start = start + n;
destroy(start, new_start);
// 以下将冗余的缓冲区释放
for(map_pointer cur = start.node; cur < new_start.node; ++cur)
data_allocator::deallocate(*cur, buffer_size());
start = new_start; //设定deque的新起点
}
else {
copy(last, finish, first);
iterator new_finish = finish - n;
destroy(new_finish, finish);
// 以下将冗余的缓冲区释放
for(map_pointer cur = new_finish.node + 1; cur <= finish.node; ++cur)
data_allocator::deallocate(*cur, buffer_size());
finish = new_finish; //设定deque的新尾点
}
return start + elems_before;
}
}
最后一个例子是insert。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44iterator insert(iterator position, const value& x) {
if (position.cur == start.cur) {
push_front(x);
return start;
}
else if (position.cur == finish.cur) {
push_back(x);
iterator tmp = finish;
-- tmp;
return tmp;
}
else {
return insert_aux(position, x);
}
}
template <class T, class Alloc, size_t BufSize>
typename deque<T, Alloc, BufSize>::iterator
deque<T, Alloc, BufSize>::insert_aux(iterator pos, const value_type& x) {
difference_type index = pos - start;
value_type x_copy = x;
if (index < size() / 2) {
push_front(front());
iterator front1 = start;
++ front1;
iterator front2 = front1;
++ front2;
pos = start + index;
iterator pos1 = pos;
++ pos1;
copy(front2, pos1, front1);
}
else {
push_back(back());
iterator back1 = finish;
-- back1;
iterator back2 = back1;
-- back2;
pos = start + index;
copy_backward(pos, back2, back1);
}
*pos = x_copy;
return pos;
}
stack
stack概述
stack是一种先进后出(First In Last Out,FILO)的数据结构,它只有一个出口。stack允许新增元素,移除元素、取得最顶端元素,但不允许有遍历行为。若以deque为底部结构并封闭其头端开口,便轻而易举地形成了一个stack。同时,也可以使用list作为底层实现,它也是具有双向开口的数据结构。由于stack系以底部容器完成其所有工作,而具有这种“修改某物接口,形成另一种风貌”之性质者,称为adapter(配接器)。因此,STL stack往往不被称为container,而被归类为container adapter。
因为stack的所有元素的进出都必须符合“先进后出”的条件,即只有stack顶端的元素,才会被外界取用,所以stack不提供走访功能,也不提供迭代器。
stack 完整定义
SGI STL以deque作为缺省情况下的stack底部结构。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34template<class T, class Sequence = deque<T> >
class stack{
// __STL_NULL_TMPL_ARGS展开为<>
friend bool operator== __STL_NULL_TMPL_ARGS(const stack& , const stack&) ;
friend bool operator< __STL_NULL_TMPL_ARGS(const stack& , const stack&) ;
public :
typedef typename Sequence::value_type value_type ;
typedef typename Sequence::size_type size_type ;
typedef typename Sequence::reference reference ;
typedef typename Sequence::const_reference const_reference ;
protected:
Sequence e ; //底层容器
public :
//以下完全利用Sequence c 的操作,完成stack的操作
bool empty() const {return c.empty() ;}
size_type size() {return c.size();}
reference top() {return c.back();}
const_reference top() const {return c.back();}
//deque是两头可进出,stack是末端进,末端出。
void push(const value_type& x) {c.push_back(x);}
void pop() {c.pop_back();}
};
template <class T, class Sequence>
bool operator==(const stack<T, Sequence>& x, const stack<T, Sequence>& y)
{
return x.c == y.c;
}
template <class T, class Sequence>
bool operator<(const stack<T, Sequence>& x, const stack<T, Sequence>& y)
{
return x.c < y.c;
}
以list作为stack的底部容器
1 |
|
queue
queue概述
queue是一种先进先出(First In First Out,FIFO)的数据结构,它有两个出口。queue允许新增元素、移除元素、从最底端加入元素、取得最顶端元素,但不允许遍历行为,也不提供迭代器。若以deque为底部结构并封闭其头端入口和尾部出口,便轻而易举地形成了一个queue。同时,也可以使用list作为底层实现,它也是具有双向开口的数据结构。因为queue的所有元素的进出都必须符合“先进先出”的条件,queue不提供走访功能,也不提供迭代器。
由于queue系以底部容器完成其所有工作,而具有这种“修改某物接口,形成另一种风貌”之性质者,称为adapter(配接器)。因此,STL queue往往不被称为container,而被归类为container adapter。
queue 完整定义
SGI STL以deque作为缺省情况下的queue底部结构。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36template<class T, class Sequence = deque<T> >
class queue{
// __STL_NULL_TMPL_ARGS展开为<>
friend bool operator== __STL_NULL_TMPL_ARGS(const queue& , const queue&) ;
friend bool operator< __STL_NULL_TMPL_ARGS(const queue& , const queue&) ;
public :
typedef typename Sequence::value_type value_type ;
typedef typename Sequence::size_type size_type ;
typedef typename Sequence::reference reference ;
typedef typename Sequence::const_reference const_reference ;
protected :
Sequence c ; //底层容器
public :
//以下完全利用Sequence c的操作,完成queue的操作
bool empty() const {return c.empty();}
size_type size() const {return c.size();}
reference front() const {return c.front();}
const_reference front() const {return c.front();}
reference back() {return c.back();}
const_reference back() const {return c.back();}
//deque是两头可进出,queue是末端进,前端出。
void push(const value_type &x) {c.push_back(x) ;}
void pop() {c.pop_front();}
};
template <class T, class Sequence>
bool operator==(const queue<T, Sequence>& x, const queue<T, Sequence>& y)
{
return x.c == y.c;
}
template <class T, class Sequence>
bool operator<(const queue<T, Sequence>& x, const queue<T, Sequence>& y)
{
return x.c < y.c;
}
以list作为queue的底部容器
1 |
|
heap概述
heap并不归属于STL容器组件,扮演priority queue的助手,binary max heap适合作为priority queue的底层机制,priority queue允许用户以任意次序将元素推入容器,但是取出是一定是优先权最高(数值最高)的元素先出来。binary heap是一种complete binary tree(完全二叉树),整棵binary tree除了最底层的叶子节点外是填满的,而最底层的叶子节点由左至右不得有空隙。
complete binary tree整棵树内没有任何节点漏洞,这就可以利用array来存储completebinary tree的所有节点,将array的#0元素保留,那么当complete binary tree的某个节点位于array的i处时,其左子节点必位于array的2i处,右子节点必位于array的2i+1处,父节点必位于i/2处。我们需要的是一个array和一组heap算法,array的缺点是无法动态改变大小,以vector代替array是更好的选择。
根据元素排列方式,heap分为max-heap和min-heap两种,前者每个节点的键值都大于或等于其子节点的值,后者每个节点的键值都小于或等于其子节点的值。max-heap中最大值在根节点,min-heap最小值在根节点。底层存储结构为vector或者array。STL 供应的是max-heap。heap的所有元素都必须遵循特别的排列规则,所以heap不提供遍历功能,也不提供迭代器。
heap算法
push_heap算法
push_heap算法:将新加入的元素放在最下层的叶节点,即vector的end()处,还需满足max-heap条件,执行所谓的percolate up(上溯)过程,即不断比较新节点和其父节点,如果键值比父节点大,就父子节点对换位置,最终将其放到合适的位置。举例如下: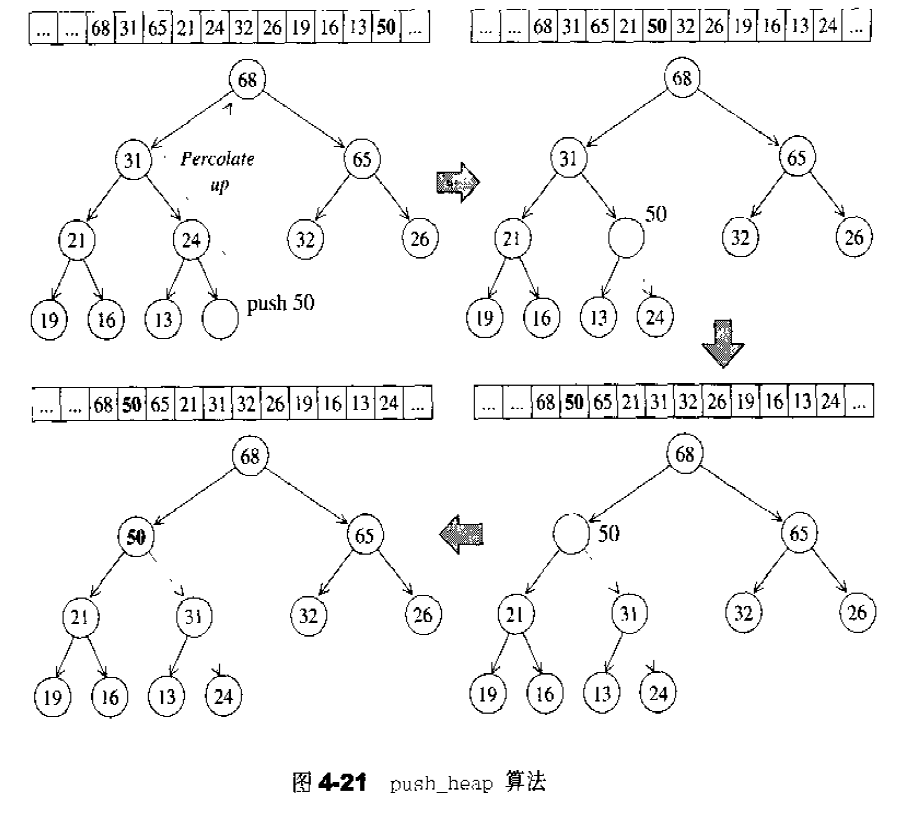
下面是push_heap的实现细节,该函数接受两个迭代器,用来表达一个heap底部容器的头尾,并且新元素已经插入到底部容器的最尾端,如果不符合这两个条件,push_heap的执行结果不可预期。代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23template<class RandomAccessIterator>
inline void push_heap(RandomAccessIterator first,RandomAccessIterator last){
//这个函数被调用时,新元素已经放在底部容器的最尾端
_push_heap_aux(first,last,distance_type(first),value_type(first));
}
template<class RandomAccessIterator,class Distance,class T>
inline void _push_heap_aux(RandomAccessIterator first,RandomAccessIterator last,Distance*,T*)
{_push_heap(first ,Distance((last-first)-1),Distance(0),T(*(last-1)));}
// 一下这组push_back()不允许指定大小比较标准
template<class RandomAccessIterator,class Distance,class T>
void _push_heap(RandomAccessIterator first,Distance holeIndex,Distance topIndex,T value)
{
Distance parent=(holeIndex-1)/2;//找出父节点
while(holeIndex>topIndex&&*(first+parent)<value){
//未到达顶端,父节点小于新值,使用<,所以STL heap是个max_heap。
*(first+holeIndex)=*(first +parent)//父值下移
holeIndex=parent;//调整位置,向上提升至父节点
parent=(holeIndex-1)/2;//找到新的父节点。
}//持续到顶端,或者满足heap的特性就停止了。
*(first+holeIndex)=value;//找到它应该处于的位置,插入操作结束。
}
pop_heap
如图所示的是pop heap算法的实际操演情况。既然身为max-heap,最大值必然在根节点。pop操作取走根节点(其实是移至底部容器vector的最后一个元素)之后,为了满足complete binary tree的条件,必须将最下一层最右边的叶节点拿掉,现在我们的任务是为这个被拿掉的节点找一个适当的位置。
为满足max-heap的条件(每个节点的键值都大于或等于其子节点键值), 我们执行一个所谓的percolate down(下溯)程序:将根节点(最大值被取走后,形成一个“洞”)填人上述那个失去生存空间的叶节点值,再将它拿来和其两个子节点比较键值(key),并与较大子节点对调位置、如此一直下放,直到这个“洞” 的键值大于左右两个子节点,或直到下放至叶节点为止: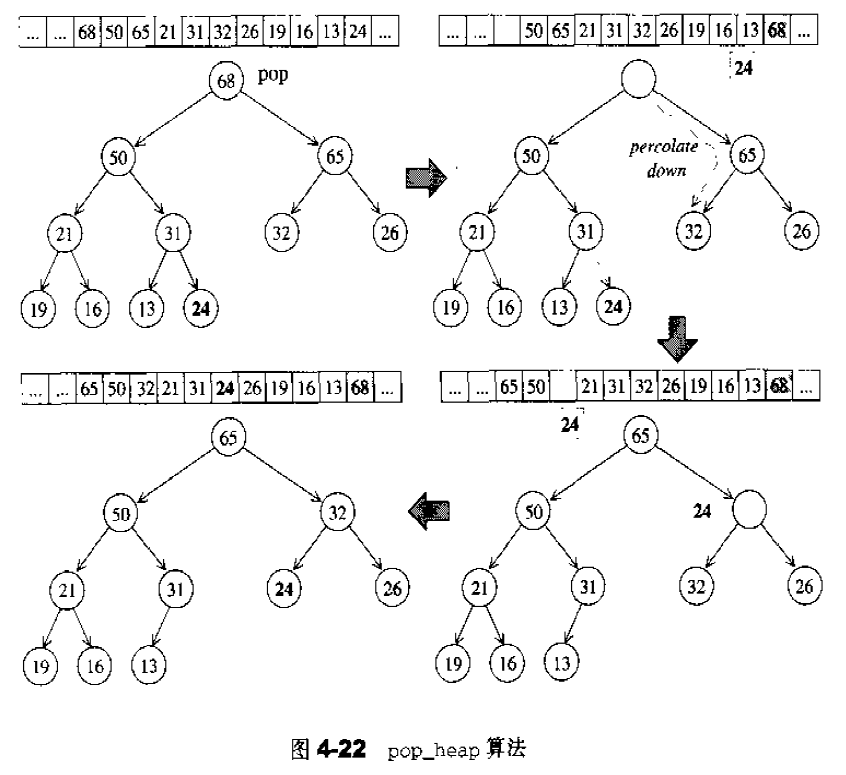
1 | template <class RandomAccessIterator>//提供首尾两个迭代器,否则结果不可预知。 |
注意:pop_heap后,最大元素只是被置于底层容器的最尾部,尚未被取走。如果取值,可用back函数;如果移除,可用pop_back函数。
sort_heap
既然每次pop_heap都将最大值放到vector的末尾,那么如果每次都缩小pop_heap的参数范围(从后向前缩减一个与元素),那么最终得到的vector将是一个递增序列。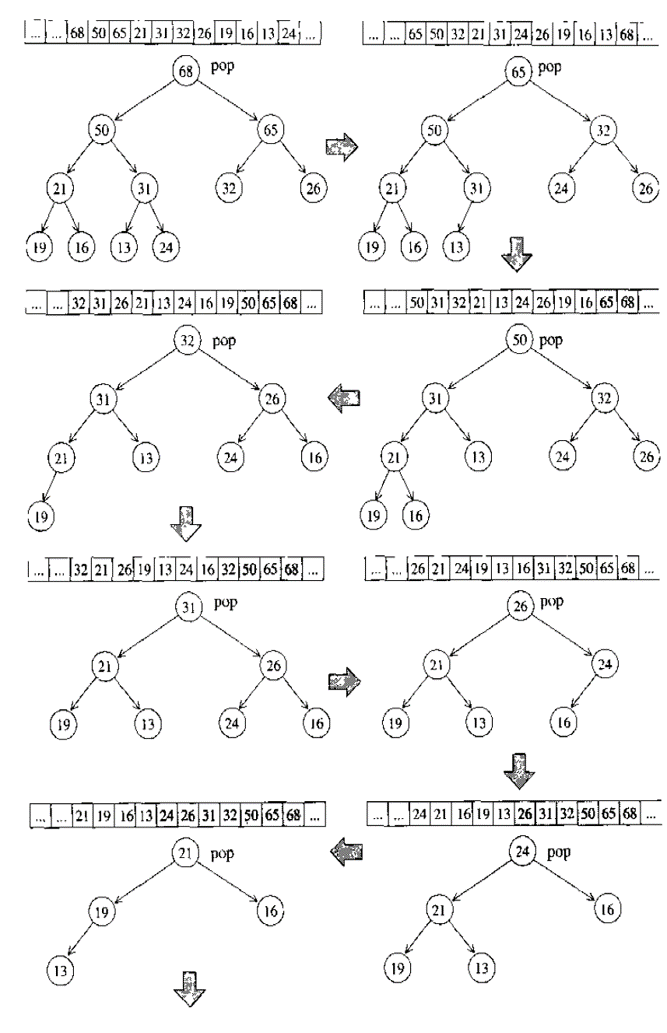
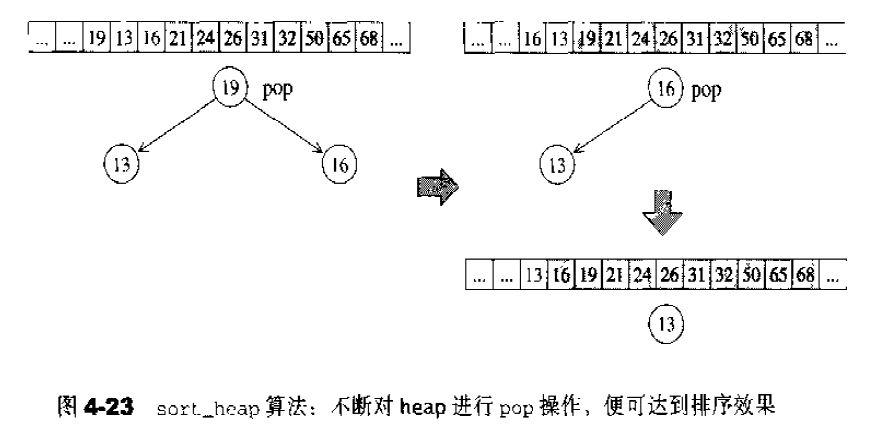
1 | // 以下这个sort_heap()不允许指定「大小比较标准」 |
make_heap
make_heap将一段现有的数据转化成一个heap,代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23// 將 [first,last)排列为一个heap。
template <class RandomAccessIterator>
inline void make_heap(RandomAccessIterator first, RandomAccessIterator last) {
__make_heap(first, last, value_type(first), distance_type(first));
}
// 以下這組 make_heap() 不允許指定「大小比較標準」。
template <class RandomAccessIterator, class T, class Distance>
void __make_heap(RandomAccessIterator first, RandomAccessIterator last, T*,
Distance*) {
if (last - first < 2) return; // 如果長度為 0 或 1,不必重新排列。
Distance len = last - first;
// 找出第一個需要重排的子樹頭部,以 parent 標示出。由於任何葉節點都不需執行
// perlocate down,所以有以下計算。parent 命名不佳,名為 holeIndex 更好。
Distance parent = (len - 2) / 2;//找出第一个有子节点的节点
while (true) {
// 重排以 parent 為首的子樹。len 是為了讓 __adjust_heap() 判斷操作範圍
__adjust_heap(first, parent, len, T(*(first + parent)));//下溯程序
if (parent == 0) return; // 排序到根節點,程序就結束。
parent--; // (重排之子樹的)頭部向前一個節點,迭代过程,排序完一个就接着排序前一个。
}
}
heap测试实例
1 |
|
priority_queue概述
priority_queue是一个拥有权值观念的queue,它允许加入新元素,移除旧元素,审视元素值等功能.只允许在尾部加入元素,并从头部取出元素,除此之外别无其他存取元素的途径。priority_queue缺省情况下是以vector为底层容器,再加上max-heap处理规则,STL priority_queue往往不被归类为Container(容器),而被归类为container adapter。priority_queue的所有元素,进出都有一定规则,只有queue顶端的元素,才有机会被外界取用。它不提供遍历功能,也不提供迭代器。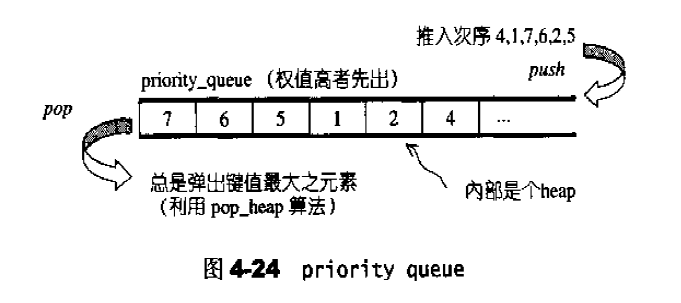
priority_queue 完整定义
priority_queue完全以底部容器为根据,再加上heap处理规则,所以实现很简单,缺省情况下是以vector为底部容器。
1 | template <class T, class Sequence = vector<T>, |
priority_queue测试实例
1 |
|
slist概述
SGI STL另提供一个单向链表slist。slist和list的主要差别在于,前者的迭代器属于单向的Forward Iterator,后者的迭代器属于双向的BidirectionalIterator。slist的功能自然也受到一些限制,不过单向链表所耗用的空间更小,某些操作更快,不失为一种选择。slist和list共同的特点是,插入删除等操作不会造成原有的迭代器失效。
根据STL的习惯,插入操作会将新元素插入于指定位置之前。作为单向链表,slist没有任何方便的方法可以回头定出前一个位置,因此它必须从头找起。为此,slist特别提供了insert_after和erase_after函数供灵活调用。
slist的节点
slist节点和其迭代器的设计,运用了继承关系: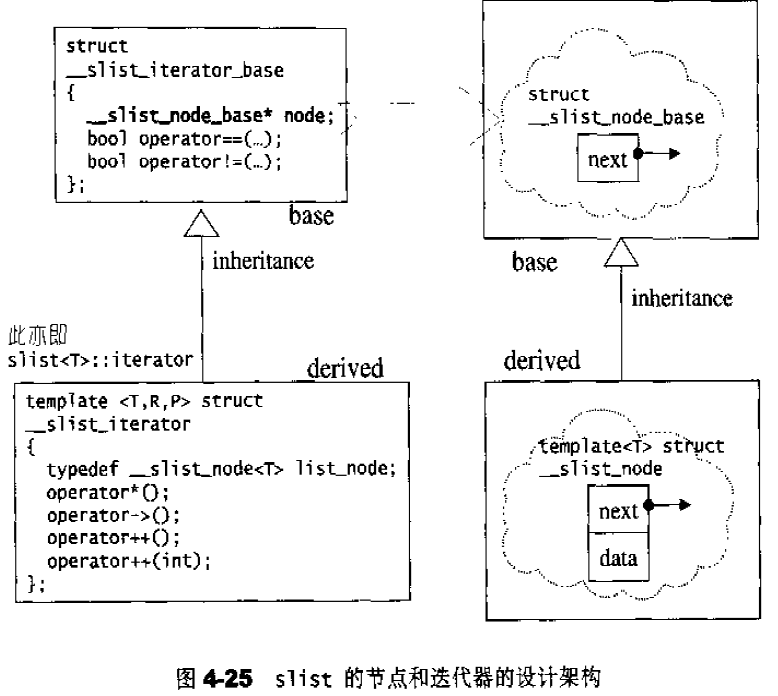
1 | struct __slist_node_base { |
slist的迭代器
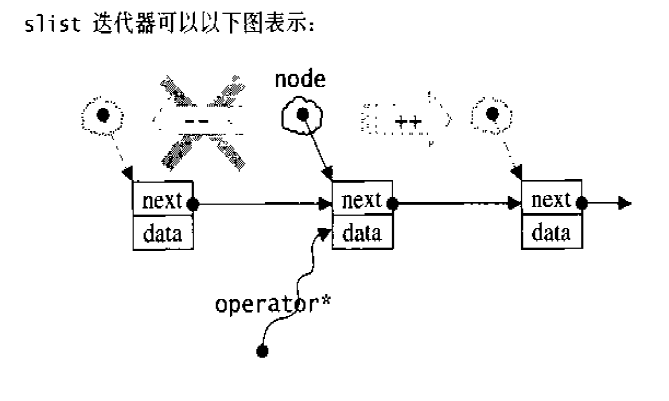
1 | // 单向链表的迭代器基本结构 |
slist的数据结构
1 | template<class T, class Alloc = alloc> |
slist的测试实例
1 | // file: 4slist-test.cpp |
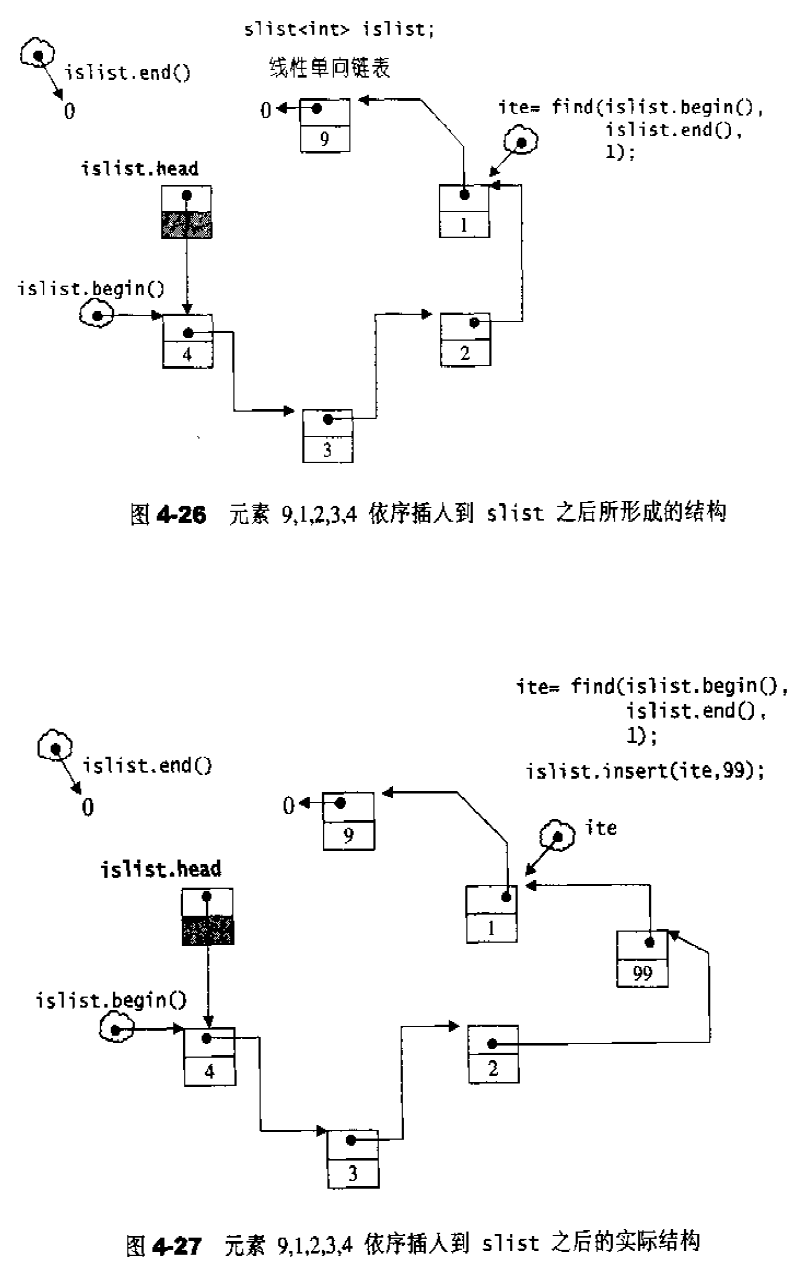
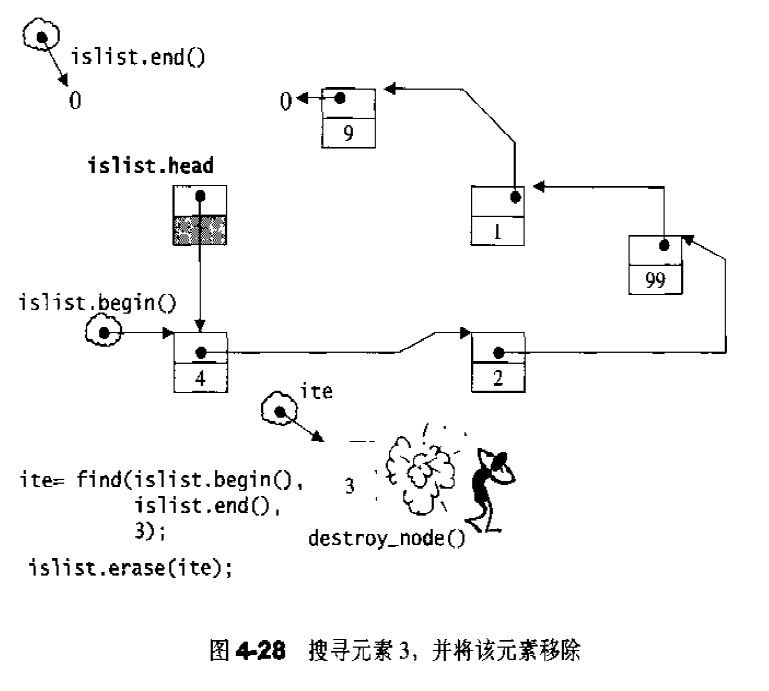
insert
insert函数的实现如下,__slist_previous函数可以根据头节点_M_head和位置节点__pos找到__pos之前的那个节点,然后调用_M_insert_after函数,实际调用__slist_make_link,在__pos-1节点后创建以__x为值的节点:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18islist.insert(ite, 99);
iterator insert(iterator __pos, const value_type& __x) {
return iterator(_M_insert_after(__slist_previous(&this->_M_head,
__pos._M_node),
__x));
}
inline _Slist_node_base* __slist_previous(_Slist_node_base* __head,
const _Slist_node_base* __node)
{
while (__head && __head->_M_next != __node)
__head = __head->_M_next;
return __head;
}
_Node* _M_insert_after(_Node_base* __pos, const value_type& __x) {
return (_Node*) (__slist_make_link(__pos, _M_create_node(__x)));
关联式容器
根据“数据在容器中的排列”特性,容器可概分为序列式(sequence)和关联式(associative)两种。标准的STL关联式容器分为set(集合〕和map(映射表)两大类:以及这两大类的衍生体multi-set(多键集合)和multimap(多键映射表)。这些容器的底层机制均以RB-tree(红黑树)完成。RB-tree也是一个独立容器,但并不开放给外界使用。
RB-tree概述
首先介绍一下基本概念,二叉树:任何节点最多只有两个子节点,这两个子节点分别称为左子节点和右子节点。二叉搜索树:任何节点的键值一定大于其左子树中的每一个节点的键值,小于其右子树中的每一个节点的键值。所谓的RB-tree不仅是二叉搜索树,而且必须满足以下规则:
- 每个节点不是红色就是黑色。
- 根节点为黑色。
- 如果节点为红色,其子节点必须为黑色。
- 任意一个节点到到NULL(树尾端)的任何路径,所含之黑色节点数必须相同。
根据规则4,新增节点必须为红色;根据规则3,新增节点之父节点必须为黑色。当新增节点根据二叉搜索树的规则到达其插入点时,却未能符合上述条件时,就必须调整颜色并旋转树形,如下图: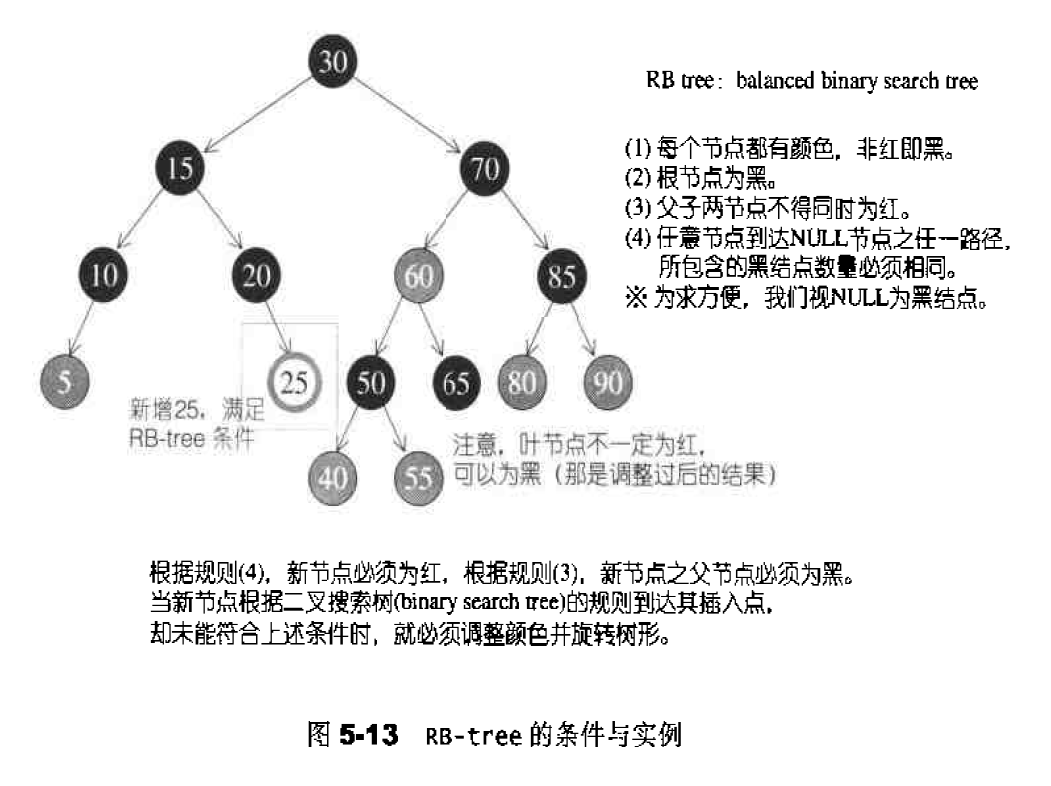
插入节点,会导致不满足RB-tree的规则条件,经历左旋和右旋等操作,使得重新满足规则。
RB-tree节点设计
RB-tree的节点和迭代器都是双层结构,RB-tree迭代器的前进和后退操作,都是调用基础迭代器的increment和decrement实现的。RB-tree的极值通过minimum和maximum可以方便地查找到,1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33typedef bool __rb_tree_color_type;
const __rb_tree_color_type __rb_tree_red = false; // 红色为0
const __rb_tree_color_type __rb_tree_black = true; // 黑色为1
struct __rb_tree_node_base
{
typedef __rb_tree_color_type color_type;
typedef __rb_tree_node_base* base_ptr;
color_type color; // 节点颜色,红色或黑色
base_ptr parent; // 该指针指向其父节点
base_ptr left; // 指向左节点
base_ptr right; // 指向右节点
static base_ptr minimum(base_ptr x)
{
while (x->left != 0) x = x->left; //一直向左走,找到最小值
return x;
}
static base_ptr maximum(base_ptr x)
{
while (x->right != 0) x = x->right; //一直向右走,找到最大值
return x;
}
};
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
typedef __rb_tree_node<Value>* link_type;
Value value_field; //节点值
};
RB-tree的迭代器
为了更大的弹性,RB-tree迭代器实现为两层,下图即为双层节点结构和双层迭代器结构之间的关系,__rb_tree_node继承自__rb_tree_node_base,__rb_tree_iterator继承自__rb_tree_base_iterator。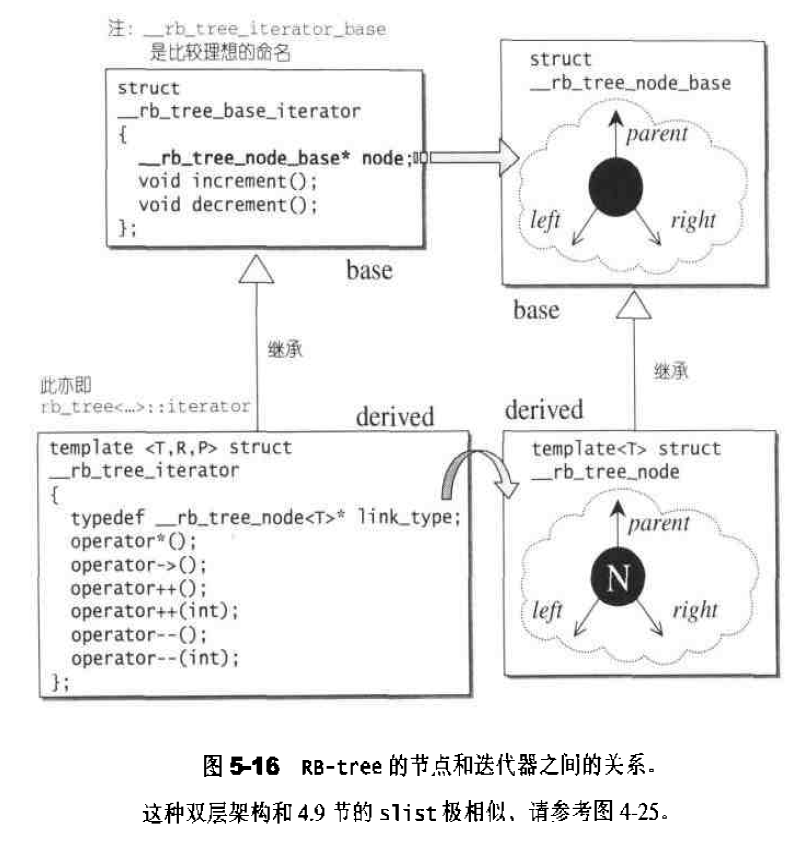
RB-tree迭代器属于双向迭代器,但不具备随机定位能力,其提领操作和成员访问操作与list十分近似,较为特殊的是其前进和后退操作:注意,RB-tree迭代器的前进操作operator()++调用了基层迭代器的increment(),RB-tree迭代器的后退操作operator--()则调用了基层迭代器的decrement()。前进或后退的举止行为完全依据二叉搜索树的节点排列法则,再加上实现上的某些特殊技巧。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92// 基层迭代器
struct __rb_tree_base_iterator
{
typedef __rb_tree_node_base::base_ptr base_ptr;
typedef bidirectional_iterator_tag iterator_category;
typedef ptrdiff_t difference_type;
base_ptr node; //与容器之间生成一个连结关系
void increment()
{
if (node->right != 0) {
node = node->right;
while(node->left != 0)
node = node->left;
}
// 如果有右子节点。状况(1),就向右走。然后一直往左子树走到底,即是解答
else {
// 没有右子节点。状况(2),找出父节点。如果现行节点本身是个右子节点,就一直上溯,直到“不为右子节点”止
base_ptr y = node->parent;
while(node == y->right) {
node = y;
y = y->parent;
}
if (node->right != y)
node = y;
// 若此时的右子节点不等于此时的父节点,状况(3)此时的父节点即为解答。否则此时的node为解答。状况(4)
}
}
// 以下其实可实现于operator--内,因为再无他处会调用此函数了
void decrement()
{
if (node->color == _rb_tree_red && node->parent->parent == node)
node = node->right;
// 如果是红节点、且父节点的父节点等于自己,状况(1)右子节点即为解答
// 以上情况发生于node为header时(亦即node为end()时)
// 注意,header之右子节点即mostright,指向整棵树的max节点
else if (node->left != 0) {
base_ptr y = node->left;
while(y->right != 0)
y = y->right;
node = y;
}
// 如果有左子节点。状况(2)令y指向左子节点。当y有右子节点时,一直往右子节点走到底,最后即为答案
else {
base_ptr y = node->parent;
while (node == y->left) {
node = y;
y = y->parent;
}
node = y;
// 既非根节点,亦无左子节点,状况(3)找出父节点。当现行节点身为左子节点,一直交替往上走,直到现行节点不为左子节点
// 此时之父节点即为答案
}
}
};
template <class Value, class Ref, class Ptr>
struct __rb_tree_iterator : public __rb_tree_base_iterator
{
typedef Value value_type;
typedef Ref reference;
typedef Ptr pointer;
typedef __rb_tree_iterator<Value, Value&, Value*> iterator;
typedef __rb_tree_iterator<Value, const value&, const value*> const_iterator;
typedef __rb_tree_iterator<Value, Ref, Ptr> self;
typedef __rb_tree_node<Value>* link_type;
__rb_tree_iterator(){}
__rb_tree_iterator(link_type x) { node = x; }
__rb_tree_iterator (const iterator& it) { node = it.node; }
reference operator*() const { return link_type(node)->value_field; }
pointer operator->() const { return &(operator*()); }
selt& operator++(){ increment(); return *this; }
self operator++(int) {
self tmp = *this;
increment();
return tmp;
}
self& operator--() {decrement(); return *this; }
self operator--(int) {
self tmp = *this;
decrement();
return *this;
}
};
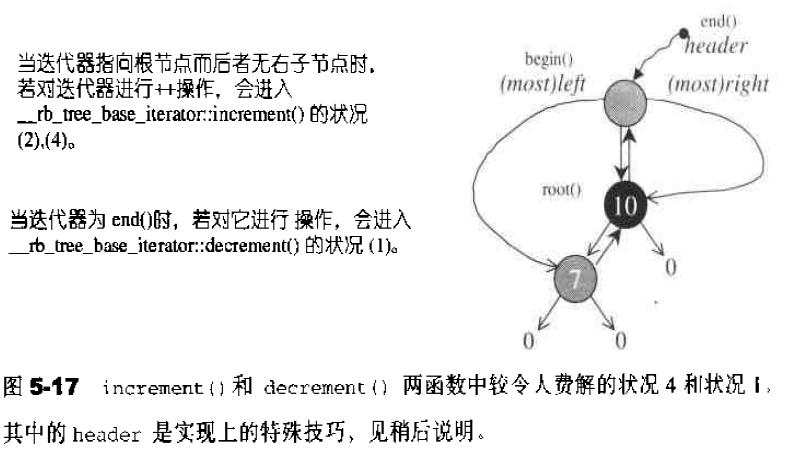
RB-tree数据结构
1 | //stl_tree.h |
RB-tree的构造与内存管理
下面是RB-tree所定义的专属空间配置器rb_tree_node_allocator,每次可恰恰配置一个节点:1
2
3
4
5template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc>
class rb_tree {
protected:
typedef __rb_tree_node<Value> rb_tree_node;
typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator;
rb-tree的构造方式有两种,一种是以现有的rb-tree构造一个新的rb-tree,另一种是构造一个空空如也的新树。1
rb_tree<int, int, identity<int>, less<int> > itree;
然后调用构造函数。1
rb_tree(const Compare& comp = Compare()) : node_count(0), key_compare(comp) { init(); }
其中的init()是一个关键点1
2
3
4
5
6
7
8void init() {
header = get_node(); // 产生一个节点空间,令header指向它
color(header) = __rb_tree_red; // 令 header 尾红色,用來区 header
// 和 root(在 iterator.operator++ 中)
root() = 0;
leftmost() = header; // 令 header 的左孩子为自己。
rightmost() = header; // 令 header 的右孩子为自己。
}
STL为根节点再设计了一个父节点: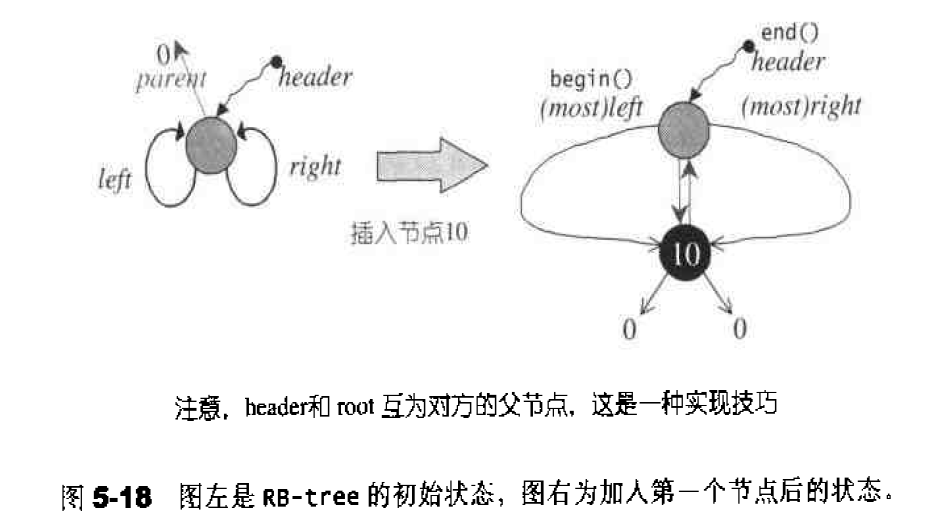
RB-tree的元素操作
RB-tree提供两种插入操作:insert_unique()和insert_equal(),前者标识被插入节点的键值(key)在整棵树中必须独一无二(因此,如果整棵树中已存在相同的键值,插入操作就不会真正进行),后者标识被插入节点的键值在整棵树中可以重复,因此,无论如何插入都会成功(除非空间不足导致配置失败)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
// 安插新值;允许键值重复。返回新插入节点的迭代器
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_equal(const Value& v)
{
link_type y = header;
link_type x = root();
while (x != 0) { // 从根节点开始,向下寻找适当安插位置
y = x;
x = key_compare(KeyOfValue()(v), key(x)) ? left(x) : right(x);
}
return __insert(x, y, v);
}
/*
不允许键值重复,否则安插无效。
返回值是个pair,第一个元素是个RB-tree迭代器,指向新增节点。
第二个元素表示安插是否成功。
*/
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
pair<typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator, bool>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_unique(const Value& v)
{
link_type y = header;
link_type x = root(); //从根节点开始
bool comp = true;
while (x != 0) { // 从根节点开始向下寻找适当安插位置
y = x;
comp = key_compare(KeyOfValue()(v), key(x)); // v 键值小于目前节点的键值?
x = comp ? left(x) : right(x); // 遇「大」往左,遇「小于或等于」往右
}
//离开while循环之后,y所指即为安插点的父节点,x必为叶子节点
iterator j = iterator(y); // 令迭代器j指向安插点之父节点 y
if (comp) //如果离开while循环时comp为真,表示 父节点键值>v ,将安插在左孩子处
if (j == begin()) // 如果j是最左节点
return pair<iterator, bool>(__insert(x, y, v), true);
// 以上,x 为安插点,y 为安插点之父节点,v 为新值。
else // 否则(安插点之父节点不是最左节点)
--j; // 调整 j,回头准备测试...
if (key_compare(key(j.node), KeyOfValue()(v)))
// 小于新值(表示遇「小」,将安插于右侧)
return pair<iterator, bool>(__insert(x, y, v), true);
//若运行到这里,表示键值有重复,不应该插入
return pair<iterator, bool>(j, false);
}
template <class Key, class Val, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::insert_unique(iterator position,
const Val& v) {
if (position.node == header->left) // begin()
if (size() > 0 && key_compare(KeyOfValue()(v), key(position.node)))
return __insert(position.node, position.node, v);
// first argument just needs to be non-null
else
return insert_unique(v).first;
else if (position.node == header) // end()
if (key_compare(key(rightmost()), KeyOfValue()(v)))
return __insert(0, rightmost(), v);
else
return insert_unique(v).first;
else {
iterator before = position;
--before;
if (key_compare(key(before.node), KeyOfValue()(v))
&& key_compare(KeyOfValue()(v), key(position.node)))
if (right(before.node) == 0)
return __insert(0, before.node, v);
else
return __insert(position.node, position.node, v);
// first argument just needs to be non-null
else
return insert_unique(v).first;
}
}
template <class Key, class Val, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::insert_equal(iterator position,
const Val& v) {
if (position.node == header->left) // begin()
if (size() > 0 && key_compare(KeyOfValue()(v), key(position.node)))
return __insert(position.node, position.node, v);
// first argument just needs to be non-null
else
return insert_equal(v);
else if (position.node == header) // end()
if (!key_compare(KeyOfValue()(v), key(rightmost())))
return __insert(0, rightmost(), v);
else
return insert_equal(v);
else {
iterator before = position;
--before;
if (!key_compare(KeyOfValue()(v), key(before.node))
&& !key_compare(key(position.node), KeyOfValue()(v)))
if (right(before.node) == 0)
return __insert(0, before.node, v);
else
return __insert(position.node, position.node, v);
// first argument just needs to be non-null
else
return insert_equal(v);
}
}
真正的插入程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::
__insert(base_ptr x_, base_ptr y_, const Value& v) {
//参数x_为新值安插点,参数y_为安插点之父节点,参数v 为新值
link_type x = (link_type)x_;
link_type y = (link_type)y_;
link_type z;
//key_compare是键值得比较准则,是个函数或函数指针
if (y == header || x != 0 || key_compare(KeyOfValue()(v), key(y))) {
z = create_node(v); // 产生一个新节点
left(y) = z; // 这使得当y为header时,leftmost()=z
if (y == header) {
root() = z;
rightmost() = z;
}
else if (y == leftmost()) // 如果y为最左节点
leftmost() = z; // 维护leftmost(),使它永远指向最左节点
}
else {
z = create_node(v);
right(y) = z; // 令新节点成为安插点之父节点y的右孩子
if (y == rightmost())
rightmost() = z; // 维护rightmost(),使它永远指向最右节点
}
parent(z) = y; // 设定新节点的父节点
left(z) = 0; // 设定新孩子节点的左孩子
right(z) = 0; // 设定新孩子节点的右孩子
// 新节点的颜色将在 __rb_tree_rebalance() 设定并调整
__rb_tree_rebalance(z, header->parent); // 参数一为新增节点,参数二为root
++node_count; // 节点数增加
return iterator(z); // 返回迭代器,指向新增节点
}
set
set的特性是,所有元素都会根据元素的键值自动排序,set的元素不像map那样可以同时拥有实值和键值,set元素的键值就是实值,实值就是键值,且不允许两个元素有相同的键值。set具有以下特点:
- 不能通过set的迭代器改变set的元素,set iterators被定义为底层RB-tree的const_iterators,杜绝写入操作。
- 客户端对set进行元素新增或者删除操作时,操作之前的所有迭代器在操作后都依然有效,被删除的元素的迭代器例外。
STL特别提供了一组set/multiset相关算法,包括交集、联集、差集、对称差集。STL set以RB-tree为底层机制,set的操作几乎都是转调用RB-tree的函数而已。
1 | template <class Key, class Compare = less<Key>, class Alloc = alloc> |
测试程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55// file: 5set-test.cpp
using namespace std;
int main() {
int i;
int ia[5] = {0, 1, 2, 3, 4};
set<int> iset{ia, ia + 5};
cout << "size=" << iset.size() << endl; //size=5
cout << "3 count =" << iset.count(3) << endl; //3 count =1
iset.insert(3);
cout << "size=" << iset.size() << endl; //size=5
cout << "3 count =" << iset.count(3) << endl; //3 count =1
iset.insert(5);
cout << "size=" << iset.size() << endl; //size=6
cout << "5 count =" << iset.count(5) << endl; //5 count =1
iset.erase(1);
cout << "size=" << iset.size() << endl; //size=5
cout << "3 count =" << iset.count(3) << endl; //3 count =1
cout << "1 count =" << iset.count(1) << endl; //1 count =0
set<int>::iterator ite1 = iset.begin();
set<int>::iterator ite2 = iset.end();
for (; ite1 != ite2; ++ite1) {
cout << *ite1; //02345
}
cout << endl;
// 使用STL算法find可以搜索元素,但不推荐
ite1 = find(iset.begin(), iset.end(), 3);
if (ite1 != iset.end())
cout << "3 found" << endl; //3 found
ite1 = find(iset.begin(), iset.end(), 1);
if (ite1 == iset.end())
cout << "1 not found" << endl; //1 not found
// 关联式容器应使用专用的find函数搜索更有效率
ite1 = iset.find(3);
if (ite1 != iset.end())
cout << "3 found" << endl; //3 found
ite1 = iset.find(1);
if (ite1 == iset.end())
cout << "1 not found" << endl; //1 not found
// *ite1 = 9; // 修改失败
}
multiset
multiset的特性及用法和set完全相同,唯一的差别在于它允许键值重复,因为它的插入操作采用的是RB-tree的insert_equal()。测试程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
using namespace std;
int main(){
int ia[] = { 5, 3, 4, 1, 6, 2 };
multiset<int> iset(begin(ia), end(ia));
cout << "size=" << iset.size() << endl; //size=6
cout << "3 count=" << iset.count(3) << endl;//3 count=1
iset.insert(3); //和set区别的地方
cout << "size=" << iset.size() << endl;//size=7
cout << "3 count=" << iset.count(3) << endl;//3 count=2
iset.insert(7);
cout << "size=" << iset.size() << endl;//size=8
cout << "3 count=" << iset.count(3) << endl;//3 count=2
iset.erase(1);
cout << "size=" << iset.size() << endl;//size=7
cout << "1 count=" << iset.count(1) << endl;//1 count=0
set<int>::iterator it;
for (it = iset.begin(); it != iset.end(); ++it)
cout << *it << " "; //2 3 3 4 5 6 7
cout << endl;
it = iset.find(3);
if (it != iset.end())
cout << "3 found" << endl;//3 found
it = iset.find(1);
if (it == iset.end())
cout << "1 not found" << endl;//1 not found
return 0;
}
map概述
map的特性是,所有元素都会根据元素的键值自动排序,map的所有元素都是pair,pair的第一元素是键值,第二元素是实值。map具有以下特点:
- 不能通过map的迭代器改变map的键值,但通过map的迭代器能改变map的实值。因此map的iterators既不是一种const iterators,也不是一种mutable iterators。
- 客户端对map进行元素新增或者删除操作时,操作之前的所有迭代器在操作后都依然有效,被删除的元素的迭代器例外。
- map不允许两个元素拥有相同的键值。
下面是pair的定义1
2
3
4
5
6
7
8
9
10template <class T1, class T2>
struct pair {
typedef T1 first_type;
typedef T2 second_type;
T1 first;
T2 second;
pair() : first(T1()), second(T2()) {}
pair(const T1& a, const T2& b) : first(a), second(b) {}
};
从上可以看出,pair 包含两个类型(可以相同,也可以不相同)的公共元素。
map同set一样,都是关联式容器,内部元素的实值都会根据其键值来进行排序(set 的实值就是键值),所以都不能任意改变元素的键值,但是map可以任意改变元素的实值,我们所有操作的前提以及是否被允许,要看是否会影响到map元素的排序规则。
同样map和multimap 也是以RB-tree 为底层机制,几乎所有的map操作行为,都只是转调用RB-tree的操作行为而已。
set 和 map的内部结构即元素的存储都是RB-tree,set 中,RB-tree的节点内容是单一元素,而map中,节点内容则是一个pair <key,value>。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129class map {
public:
// typedefs:
typedef Key key_type; //键值型别
typedef T data_type; //实值型别
typedef pair<const Key, T> value_type; //元素性别(键值/实值)
typedef Compare key_compare; //键值比较函数
//定义一个函数,其作用就是调用“元素比较函数”
class value_compare
: public binary_function<value_type, value_type, bool> {
friend class map<Key, T, Compare, Alloc>;
protected:
Compare comp;
value_compare(Compare c) : comp(c) {}
public:
//重载
bool operator()(const value_type& x, const value_type& y) const {
return comp(x.first, y.first);
}
};
private:
typedef rb_tree<key_type, value_type,
select1st<value_type>, key_compare, Alloc> rep_type;
rep_type t; // 以RB-tree为底层实现,所有元素(pair)存放在RB-tree节点中
public:
//两种类型的都有,因为map允许用户通过迭代器修改元素的实值
typedef rep_type::pointer pointer;
typedef rep_type::reference reference;
typedef rep_type::const_reference const_reference;
typedef rep_type::iterator iterator;
typedef rep_type::const_iterator const_iterator;
typedef rep_type::reverse_iterator reverse_iterator;
typedef rep_type::const_reverse_iterator const_reverse_iterator;
typedef rep_type::size_type size_type;
typedef rep_type::difference_type difference_type;
// allocation/deallocation
//构造函数
map() : t(Compare()) {}
explicit map(const Compare& comp) : t(comp) {}
/*map一定使用底层RB-tree 的insert_unique()*/
map(const map<Key, T, Compare, Alloc>& x) : t(x.t) {}
map<Key, T, Compare, Alloc>& operator=(const map<Key, T, Compare, Alloc>& x)
{
t = x.t;
return *this;
}
// accessors:
//转调用RB-tree的操作行为
key_compare key_comp() const { return t.key_comp(); }
value_compare value_comp() const { return value_compare(t.key_comp()); }
iterator begin() { return t.begin(); }
const_iterator begin() const { return t.begin(); }
iterator end() { return t.end(); }
const_iterator end() const { return t.end(); }
reverse_iterator rbegin() { return t.rbegin(); }
const_reverse_iterator rbegin() const { return t.rbegin(); }
reverse_iterator rend() { return t.rend(); }
const_reverse_iterator rend() const { return t.rend(); }
bool empty() const { return t.empty(); }
size_type size() const { return t.size(); }
size_type max_size() const { return t.max_size(); }
/*下面这个下标操作符重载函数是的map支持元素的直接存取,索引值是元素的key*/
T& operator[](const key_type& k)
{
return (*((insert(value_type(k, T()))).first)).second;
}
void swap(map<Key, T, Compare, Alloc>& x) { t.swap(x.t); }
// insert/erase
//都是调用底层RB-tree的操作行为
pair<iterator, bool> insert(const value_type& x) { return t.insert_unique(x); }
iterator insert(iterator position, const value_type& x) {
return t.insert_unique(position, x);
}
void erase(iterator position) { t.erase(position); }
size_type erase(const key_type& x) { return t.erase(x); }
void erase(iterator first, iterator last) { t.erase(first, last); }
void clear() { t.clear(); }
// map operations:
/*返回一个迭代器指向键值为key的元素,如果没找到就返回end()*/
iterator find(const key_type& x) { return t.find(x); }
const_iterator find(const key_type& x) const { return t.find(x); }
/*返回键值等于key的元素的个数*/
size_type count(const key_type& x) const { return t.count(x); }
/*返回一个迭代器,指向键值>=key的第一个元素*/
iterator lower_bound(const key_type& x) { return t.lower_bound(x); }
const_iterator lower_bound(const key_type& x) const {
return t.lower_bound(x);
}
/*返回一个迭代器,指向键值>key的第一个元素*/
iterator upper_bound(const key_type& x) { return t.upper_bound(x); }
const_iterator upper_bound(const key_type& x) const {
return t.upper_bound(x);
}
/*返回键值为key的元素的第一个可安插位置和最后一个可安插位置,也就是“键值==key”的元素区间*/
pair<iterator, iterator> equal_range(const key_type& x) {
return t.equal_range(x);
}
pair<const_iterator, const_iterator> equal_range(const key_type& x) const {
return t.equal_range(x);
}
friend bool operator==(const map&, const map&);
friend bool operator<(const map&, const map&);
};
/*运算符重载,几乎有所有的操作行为都是调用RB-tree的操作行为
事实上,包括set在内的关联式容器内部都是以RB-tree方式存放的*/
template <class Key, class T, class Compare, class Alloc>
inline bool operator==(const map<Key, T, Compare, Alloc>& x,
const map<Key, T, Compare, Alloc>& y) {
return x.t == y.t;
}
template <class Key, class T, class Compare, class Alloc>
inline bool operator<(const map<Key, T, Compare, Alloc>& x,
const map<Key, T, Compare, Alloc>& y) {
return x.t < y.t;
}
通常,关联式容器并不提供元素的直接存取,你必须依靠迭代器,不过 map 内部的下标操作符重载函数使得其支持元素的直接存取,看看它是怎么实现的
这是map作为关联式容器特殊的地方(multimap没有哦)
map测试程序
1 |
|
执行结果:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23[root@192 5_STL_associated_container]# ./5_4_map-test
————————————————————插入操作—————————————————
id:1001 name:Jason
id:1002 name:Helen
id:1003 name:Steve
————————————————————取值操作—————————————————
stuMap[1004]:
————————————————————查找操作—————————————————
1001 found name:Jason
1005 not found
————————————————————容量查询—————————————————
stuMap empty state is false
stuMap size is 4
stuMap.count(1008) is 0
————————————————————删除操作—————————————————
before delete
id:1001 name:Jason
id:1002 name:Helen
id:1003 name:Steve
id:1004 name:
after delete
id:1001 name:Jason
id:1003 name:Steve
hashtable
hashtable在插入,删除,搜寻等操作上具有"常数平均时间"的表现,而且这种表现以统计为基础,不依赖输入元素的随机性。(二叉搜索树具有对数平均时间的表现,是建立在输入数据有足够随机性的基础上。)
hash table 可提供对任何有名项的存取操作和删除操作。由于操作对象是有名项,所以hashtable可被视为一种字典结构(dictionary)。举个例子,如果所有元素时16-bits且不带有正负号的整数,范围为0-65535,则可以通过配置一个array拥有65536个元素,对应位置记录元素出现个数,添加A[i]++,删除A[i]—,查找A[i]==0判断。但是进一步,如果所有元素是32-bits,那大小必须是2^32=4GB,那直接分配这么大的空间就不太实际。再进一步,如果元素时字符串,每个字符用7-bits数值(ASCII)表示,这种方法就更不可取了。
为了解决上述问题,引入了hash funtion的概念。hashfuntion可以将某一元素映射为一个“大小可接受之索引”,即大数映射成小数。hashtable通过hashfunction将元素映射到不同的位置,但当不同的元素通过hash function映射到相同位置时,便产生了"碰撞"问题.解决碰撞问题的方法主要有线性探测,二次探测,开链法等.
- 线性探测:当hash function计算出某个元素的插入位置,而该位置的空间已不可用时,循序往下寻找下一个可用位置(到达尾端时绕到头部继续寻找),会产生primary clustering(一次聚集)问题。
- 二次探测:当hash function计算出某个元素的插入位置为H,而该位置的空间已经被占用,就尝试用H+1²、H+2²…,会产生secondary clustering(二次聚集)问题。
- 开链:在每一个表格元素中维护一个list:hash function为我们分配某个list,在那个list上进行元素的插入,删除,搜寻等操作.SGI STL解决碰撞问题的方法就是此方法。
下面以开链法完成hash table的图形表述,hash table 表格内的元素为桶子(bucket),每个bucket都维护一个链表,来解决哈希碰撞,如下所示: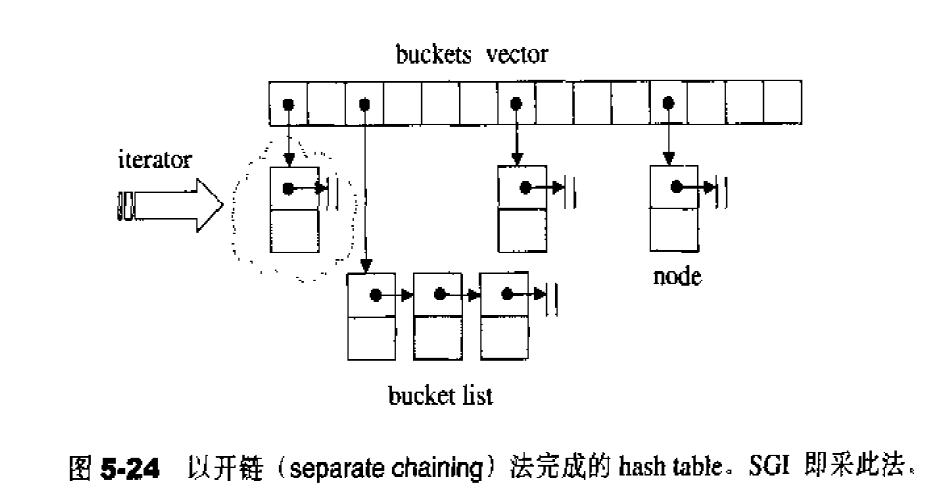
下面看一下 hashtable 的定义:1
2
3
4
5
6template <class Value>
struct __hastabl_node
{
__hastable_node* next;
Value val;
};
以下是hash table的迭代器的定义1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26template <class Value, class Key, class HashFcn,
class ExtractKey, class EqualKey, class Alloc>
struct __hashtable_iterator {
typedef hashtable<Value, Key, HashFcn, ExtractKey, EqualKey, Alloc> hashtable;
typedef __hashtable_iterator<Value, Key, HashFcn, ExtractKey, EqualKey, Alloc> iterator;
typedef __hashtable_const_iterator<Value, Key, HashFcn, ExtractKey, EqualKey, Alloc> const_iterator;
typedef __hashtable_node<Value> node;
typedef forward_iterator_tag iterator_category;
typedef ptrdiff_t difference_type;
typedef size_t size_type;
typedef Value& reference;
typedef Value* pointer;
node* cur; //迭代器目前所指之节点
hashtable* ht; //保持容器的连结关系
...
__hashtable_iterator(node* n, hashtable* tab) : cur(n), ht(tab) {}
__hashtable_iterator() {}
reference operator*() const { return cur->val; }
pointer operator->() const { return &(operator*()); }
iterator& operator++();
iterator operator++(int);
bool operator==(const iterator& it) const { return cur == it.cur; }
bool operator!=(const iterator& it) const { return cur != it.cur; }
};
注意hashtable迭代器必须永远维系着与整个buckets vector的关系,并记录目前所指的节点。其前进操作是首先尝试从目前所指的节点出发,前进一个位置〔节点),由于节点被安置于st内,所以利用节点的next指针即可轻易达成前进操作,如果目前节点正巧是list的尾端,就跳至下一个bucket身上,那正是指向下一个bucket的头部节点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23template <class V, class K, class HF, Class ExK, class EqK, class A>
__hashtable_iteratorc<V, K, HF, ExK, EqK, A>&
__hashtable_iteratorc<V, K, HF, ExK, EqK, A>::operator++()
{
const node* old = cur;
cur = cur->next; //如果存在,就是它。否则进入以下流程
if(!cur) {
//根据元素值,定位出下一个bucket,其起头处就是我们的目的地
size_type bucket = ht->bkt_num(old->val);
while (!cur && ++bucket < ht->buckets.size())
cur = ht->buckets[bucket];
}
return *this;
}
template <class V, class K, class HF, Class ExK, class EqK, class A>
inline __hashtable_iteratorc<V, K, HF, ExK, EqK, A>
__hashtable_iteratorc<V, K, HF, ExK, EqK, A>::operator++(int)
{
iterator tmp = *this;
++*this;
return tmp;
}
hashtable没有逆向操作(operator—())。
hashtable的数据结构
下图是hashtable的定义摘要,其中可见bucket聚合体以vector完成,以利动态扩充:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24template<class Value,class Key, class HashFcn, class ExtractKey, class EqualKey, class Alloc = alloc>
class hashtable;
template< class Value, class Key, class HashFcn, class ExtractKey, class EqualKey, class Alloc>
class hashtable {
public:
typedef HashFcn hasher;
typedef EqualKey key_equal;
typedef size_t size_type;
private:
hasher hash;
key_equal equals;
ExtractKey get_key;
typedef __hashtable_node<Value> node;
typedef simple_alloc<node, Alloc> node_allocator;
vector<node*, Alloc> buckets;
size_type num_elements;
public:
size_type bucket_count() const {return buckets.size(); }
};
虽然开链法不要求表格大小必须为质数,但是SGI STL仍然以质数来设计表格大小。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//表格大小必须为质数,从下述28个质数中取最接近的
static const int __stl_num_primes = 28;
static const unsigned long __stl_prime_list[__stl_num_primes] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473ul, 4294967291ul
};
/* 获取桶的数量 */
inline unsigned long __stl_next_prime(unsigned long n)
{
const unsigned long* first = __stl_prime_list;
const unsigned long* last = __stl_prime_list + __stl_num_primes;
const unsigned long* pos = lower_bound(first, last, n); //>=
return pos == last ? *(last - 1) : *pos;
}
// 总共可以有多少个buckets
size_type max_bucket_count() const
{
return __stl_prime_list(__stl_num_promes - 1);
}
hashtable的构造与内存管理
节点配置函数和节点释放函数:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15node* new_node(const value_type& obj) {
node* n = node_allocator::allocate();
n->next = 0;
__STL_TRY {
construct(&n->val, obj);
return n;
}
__STL_UNWIND(node_allocator::deallocate(n));
}
void delete_node(node* n)
{
destroy(&n->val);
node_allocator::deallocate(n);
}
当我们初始构造一个拥有50个节点的hashtable如下:1
2
3
4
5// <value,key,hash-func,extract-key,equal-key,allocator>
// 注意:hashtable没有提供default constructor
hashtable<int, int, hash<int>, identity<int>, equal_to<int>, alloc> iht(50, hash<int>(), equal_to<int>());
cout<<iht.size()<<endl;
cout<<iht.bucket_count()<<endl;
上述定义调用:1
2
3
4
5
6
7hashtable(size_type n,
const HashFcn& hf,
const EqualKey& eql)
: hash(hf), equals(eql), get_key(ExtractKey()), num_elements(0)
{
initialize_buckets(n);
}
首先初始化三个仿函数,然后调用 initialize_buckets 来初始化hashtable。initialize_buckets 函数定义如下:1
2
3
4
5
6
7void initialize_buckets(size_type n)
{
cost size_type n_buckets = next_size(n);
buckets.reserve(n_buckets);
buckets.insert(buckets.end(), n_buckets, (node*) 0);
num_elements = 0;
}
首先确定 bucket 的数量,然后通过 reserve 初始化,然后再通过 insert 将所有的 bucket 初始化为 NULL。最后将元素个数填为0(其中的 buckets 是一个 vector)。
hashtable 的插入 跟 RB-tree 的插入类似,有两种插入方法 insert_unique 和 insert_equal ,意思也是一样的,insert_unique 不允许有重复值,而 insert_equal 允许有重复值。因为都会用到是否需要重建表格的判断,我们先来整理这一部分:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34template<class V, class K, class HF, class Ex, class Eq, class A>
void hashtable<V, K, HF, Ex, Eq, A>::resize(size_type num_elements_hint)
{
//判断 “表格重建与否” 是拿元素个数和 bucket vector 的大小来比,如果前者大于后者,就重建表格
//所以 每个 bucket list 的最大容量和 bucket vector 的大小相同
const size_type old_n = buckets.size();
if( num_elements_hint > old_n )
{
const size_type n = next_size(num_elements_hint); //next_size 底层调用 __stl_next_prime()
if( n > old_n)
{
vector<node*,A> tmp(n, (node*) 0); //设立新的 buckets
//以下是处理每一个旧的 bucket
for( size_type bucket = 0; bucket < old_n; ++bucket )
{
node* first = buckets[bucket]; //指向节点所对应之串行的起始节点
while( first ) //串行还没结束
{
//找出当前节点应该放在 新buckets 的哪一个位置
size_type new_bucket = bkt_num(first->val, n);
//以下就是对新旧表格的处理,同时还要维护好 first 指针
buckets[bucket] = first->next; // 令旧bucket指向其所对应串行的下一个节点
first->next = tmp[new_bucket]; // 将当前节点插入到新bucket中,成为其对应串行的第一个节点
tmp[new_bucket] = first;
first = buckets[bucket]; // 回到旧bucket所指的待处理串行,准备处理下一个节点
}
buckets.swap( tmp ); //vector::swap 函数,新旧两个buckets对调,对调之后释放tmp内存
}
}
}
}
现在来看一下 insert_unique 函数,需要注意的是插入时,新节点直接插入到链表的头节点,代码如下:1
2
3
4
5pair<iterator, bool> insert_unique(const value_type& obj)
{
resize(num_elements + 1);
return insert_unique_noresize(obj);
}
在不需要重建表格的情况插入新节点,键值不允许重复1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19pair<iterator, bool> insert_unique_noresize(const value_type& obj)
{
const size_type n = bkt_num(obj); //决定 obj 应位于 buckets 的那一个链表中
node* first = buckets[n];
//遍历当前链表,如果发现有相同的键值,就不插入,立刻返回
for( node* cur = first; cur; cur = cur->next)
{
if( equals(get_key(cur->val), get_key(obj)) )
return pair<iterator, bool>(iterator(cur, this), false);
}
//离开以上循环(或根本未进入循环)时,first指向 bucket 所指链表的头节点
node* tmp = new_node(obj); //产生新节点
tmp->next = first;
buckets[n] = tmp; //令新节点为链表的第一个节点
++num_elements; //节点个数累加1
return pair<iterator, bool>( iterator(tmp,this), true);
}
resize()如果有必要就得做表格重建工作:1
2
3
4
5
6
7//(1)令旧bucket指向其所对应之链表的下一个节点(以便迭代处理)
buckets[bucket】 = first->next;
// (2)(3) 将当前节点插人到新bucket内,成为其对应链表的第一个节点
first->next = tmp[new_bucket];
tmp[new_bucket] = first;
// (4) 回到旧bucket所指的待处理链表,准备处理下一个节点
first = buckets[bucket];
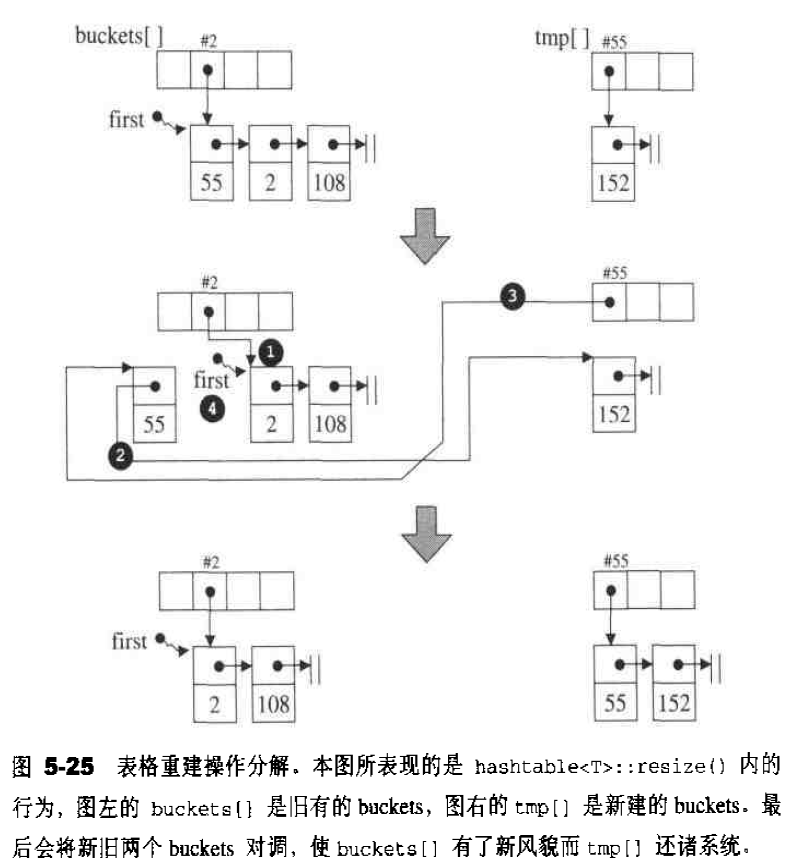
允许重复插入的 insert_equal,需要注意的是插入时,重复节点插入到相同节点的后面,新节点还是插入到链表的头节点,代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33iterator insert_equal(const value_type& obj)
{
resize( num_elements + 1 ); //判断是否 需要重建表格,如需要就扩充
return insert_equal_noresize(obj);
}
template<class V, class K, class HF, class Ex, class Eq, class A>
typename hashtable<V, K, HF, Ex, Eq, A>::iterator
hashtable<V, K, HF, Ex, Eq, A>::insert_equal_noresize(const value_type& obj)
{
const size_type n = bkt_num(obj); //决定 obj 应位于 buckets 的那一个链表中
node* first = buckets[n];
//遍历当前链表,如果发现有相同的键值,就马上插入,立刻返回
for( node* cur = first; cur; cur = cur->next)
{
if( equals(get_key(cur->val), get_key(obj)) )
{
node* tmp = new_node(obj);
tmp->next = cur->next; //新节点插入当前节点位置之后
cur->next = tmp;
++num_elements;
return iterator(tmp, this);
}
}
//运行到这里,表示没有发现重复的键值
node* tmp = new_node(obj); //产生新节点
tmp->next = first;
buckets[n] = tmp; //令新节点为链表的第一个节点
++num_elements; //节点个数累加1
return iterator(tmp, this);
}
删除元素
首先找到指定的bucket,然后从第二个元素开始遍历,如果节点的 key 等于指定的 key,将将其删除。最后再检查第一个元素的 key,如果等于指定的 key,那么就将其删除。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33template <class V, class K, class HF, class Ex, class Eq, class A>
typename hashtable<V, K, HF, Ex, Eq, A>::size_type
hashtable<V, K, HF, Ex, Eq, A>::erase(const key_type& key)
{
const size_type n = bkt_num_key(key);
node* first = buckets[n];
size_type erased = 0;
if (first) {
node* cur = first;
node* next = cur->next;
while (next) {
if (equals(get_key(next->val), key)) {
cur->next = next->next;
delete_node(next);
next = cur->next;
++erased;
--num_elements;
}
else {
cur = next;
next = cur->next;
}
}
if (equals(get_key(first->val), key)) {
buckets[n] = first->next;
delete_node(first);
++erased;
--num_elements;
}
}
return erased;
}
1 | template <class V, class K, class HF, class Ex, class Eq, class A> |
复制操作 copy_from,代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25template <class V, class K, class HF, class Ex, class Eq, class A>
void hashtable<V, K, HF, Ex, Eq, A>::copy_from(const hashtable& ht)
{
//先清除己方的 buckets vector
buckets.clear();
buckets.reserve(ht.buckets.size());
//从己方的 buckets vector 尾端开始,插入 n 个元素,其值为 null 指针
buckets.insert(buckets.end(), ht.buckets.size(), (node*)0);
//真正的执行复制操作
for(size_type i = 0; i < ht.buckets.size(); ++i)
{
if( const node* cur = ht.bucktes[i] )
{
node* copy = new_node(cur->val);
buckets[i] = copy;
for(node* next = cur->next; next; cur = next, next = cur->next)
{
copy->next = new_node(next->val);
copy = copy->next;
}
}
}
}
hash_set
虽然STL只规范复杂度与接口,并不规范实现方法,但STL set多半以RB-tree为底层机制。SGI则是在STL标准规格之外另又提供了一个所谓的hash_set,以hashtable为底层机制。由于hash_set所供应的操作接口, hashtable都提供了,所以几乎所有的hash_set操作行为,都只是转调用hashtable的操作行为而己。
运用set,为的是能够快速搜寻元素。这一点,不论其底层是RB-tree或是hash table、都可以达成任务。但是请注意,RB-tree有自动排序功能而hashtable没有,反应出来的结果就是,set的元素有自动排序功能而hash_set没有。
1 | template<class Value, class HashFcn = hash<Value>, |
hash_map
1 | //class |
hash_multiset
1 | template<class Value, class HashFcn = hash<Value>, |
hash_multimap
1 | template<class Key, class T, class HashFcn = hash<Value>, |
算法
算法概观
算法,问题之解法也。以有限的步骤,解决逻辑或数学上的问题,这一专门科目称为算法。STL 正是将极具复用价值的算法进行封装,包含sort,find,copy等函数。
STL算法总览
表格中凡是不在STL标准规格之列的SGI专属算法,都以*加以标识。


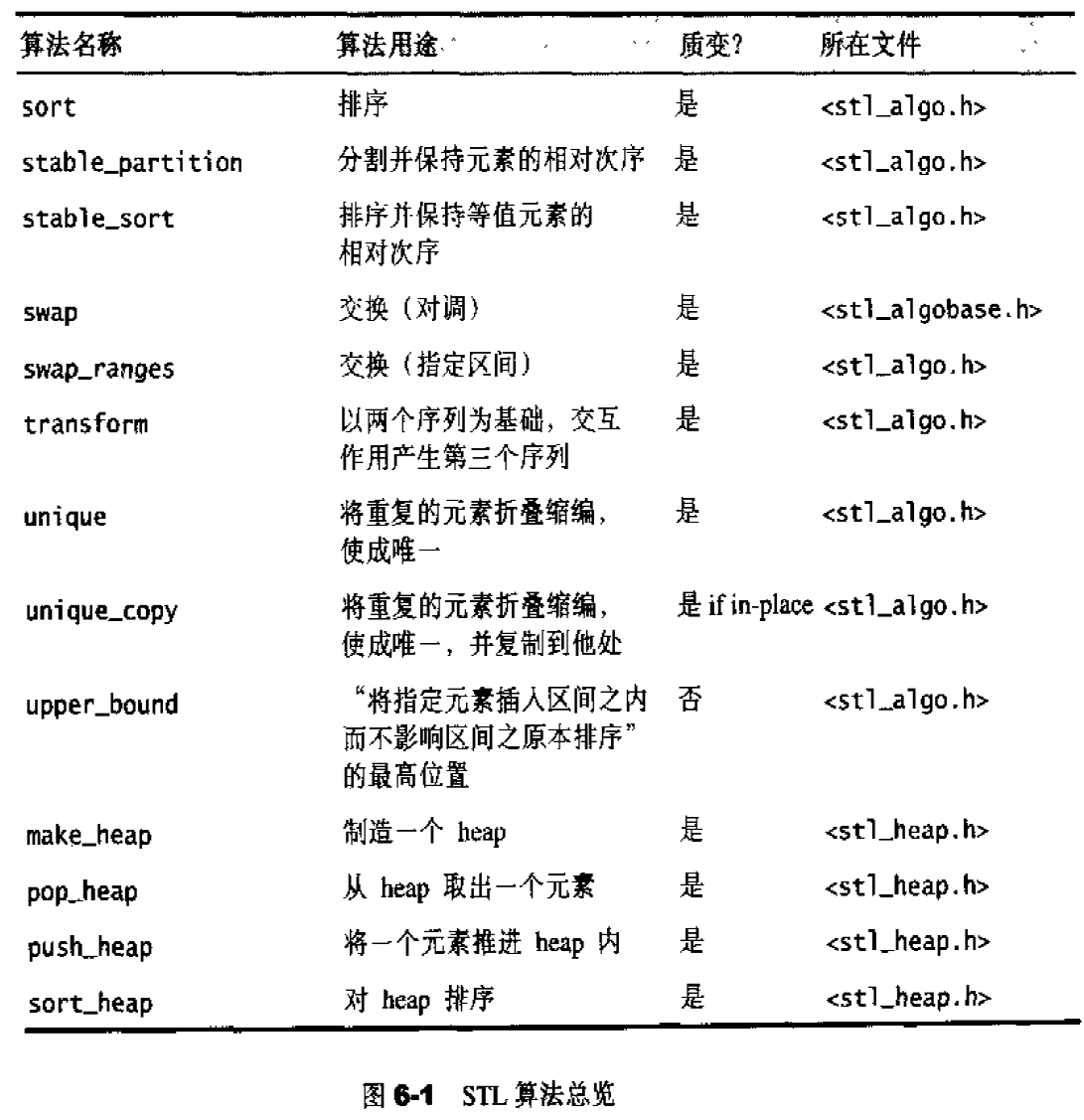
所有的STL算法都作用在迭代器 [first,last) 所标出来的区间上。根据是否改变操作对象的值,可以分为 质变算法(mutating algorithms)和 非质变算法 (nomutating algorithms)。
质变算法,是指运算过程中会更改区间内元素的内容的算法。比如,拷贝(copy),互换(swap),替换(replace),填写(fill),删除(remove),排列组合(permutation),分割(partition),随机重排(random shuffling),排序(sort)等。
非质变算法,是指运算过程中不会更改区间内元素的内容的算法。比如,查找(find),匹配(search),计数(count),巡访(for_each),比较(equal,mismatch),寻找极值(max,min)等。但是在for_each算法上应用一个会改变元素内容的仿函数,所在元素必然会改变:
算法的泛化过程
如何将算法独立于其所处理的数据结构之外,不受数据结构的约束?关键在于,要把操作对象的型别加以抽象化,把操作对象的标示法和区间目标的移动行为抽象化,整个算法也就在一个抽象层面上工作了。整个过程称为算法的泛型化(generalized),简称泛化。
以简单的循序查找为例,编写find()函数,在array中寻找特定值。面对整数array,写出如下程序:1
2
3
4
5
6
7
8
9
10
11
12
13int* find(int* arrayHead, int arraySize, int value)
{
int i=0;
for (; i<arraySize; ++i)
{
if (arrayHead[i] == value)
{
break;
}
}
return &(arrayHead[i]);
}
上述find()函数写法暴露了太多的实现细节(例如arraySize),为了让find()适用于所有类型的容器,其操作应该更抽象化些。让find()接受两个指针作为参数,标示一个操作区间:1
2
3
4
5
6
7int* find(int* begin, int*end, int value)
{
while(begin !=end && *begin != value)
++begin;
return begin;
}
由于find()函数之内并无任何操作是针对特定整数array而发的,所以我们可以把它改成一个template:1
2
3
4
5
6
7
8
9
10template<typename T>
T* find(T* begin, T* end, const T& value)
{
// 注意,以下用到了operator!=, operator*, operator++
while (begin != end && *begin != value)
++begin;
// 注意,以下返回操作用会引发copy行为
return begin;
}
在上述代码中,传入的指针必须支持以下四种操作行为:
- inequality 判断不相等
- dereferencelm 提领
- prefix increment 前置式递增
- copy 复制
上述操作符可以被重载(overload),find()函数就可以从原生(native)指针的思想框框中跳脱出来。我们可以设计一个class,拥有原生指针的行为,这就是迭代器(iterator):1
2
3
4
5
6
7
8template<typename Iterator, typename T>
Iterator find(Iterator begin, Iterator end, const T& value)
{
while(begin != end && *begin != value)
++begin;
return begin;
}
至此,便是完全泛型化的find()函数。
数值算法
C++ STL 的数值算法(Numeric algorithms)是一组对容器元素进行数值计算的模板函数,包括容器元素求和 accumulate 、两序列元素的内积 inner_product 、容器元素的一系列部分元素和 partial_sum 、容器每对相邻元素的差adjacent_difference。其头文件为<numeric>,测试实例如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57// file: 6numeric.cpp
using namespace std;
int main() {
int ia[5] = {1, 2, 3, 4, 5};
vector<int> iv(ia, ia + 5);
// 0+1+2+3...
cout << accumulate(iv.begin(), iv.end(), 0) << endl;
//0是初值,T accumulate(InputIterator first, InputIterator last, T init)
// 0-1-2-3
cout << accumulate(iv.begin(), iv.end(), 0, minus<int>()) << endl;
// 10 + 1*1 + 2*2 + ...
cout << inner_product(iv.begin(), iv.end(), iv.begin(), 10) << endl;
// 10 - 1+1 - 2+2 - ...
cout << inner_product(iv.begin(), iv.end(), iv.begin(), 10,
minus<int>(), plus<int>()) << endl;
// 将迭代器绑定到cout,作为输出用
ostream_iterator<int> oite(cout, " ");
// 1 3 6 10 15 累计和
partial_sum(iv.begin(), iv.end(), oite);
cout << endl;
// 1 -1 -4 -8 -13 累计差
partial_sum(iv.begin(), iv.end(), oite, minus<int>());
cout << endl;
// 1 1 1 1 1 new #n = #n - #n-1
adjacent_difference(iv.begin(), iv.end(), oite);
cout << endl;
// 1 3 5 7 9 new #n = op(#n, #n-1)
adjacent_difference(iv.begin(), iv.end(), oite, plus<int>());
cout << endl;
// mingw c++ 中stl没有power实现
// cout << power(10, 3) << endl;
// cout << power(10, 3, plus<int>()) << endl;
int n = 3;
iota(iv.begin(), iv.end(), n); // 填入n, n+1, n+2
for (int i = 0; i < iv.size(); ++i)
cout << iv[i] << ' ';
return 0;
}
运行结果:1
2
3
4
5
6
7
8
9
10[root@192 6_STL_algorithms] ./6_3_1_numeric
15
-15
65
-20
1 3 6 10 15
1 -1 -4 -8 -13
1 1 1 1 1
1 3 5 7 9
3 4 5 6 7 [
accumlate
1 | /* |
adjacent_differencee
1 | /* |
partial_sum
1 | /* |
power
考虑x^23,可以先从x ->x^2 -> x^4 -> x^8 -> x^16 取result1 = x^16,然后23-16=7。
我们只要计算x^7再与result1相乘就可以得到x^23。对于x^7也可以采用这种方法
取result2 = x^4,然后7-4=3,只要计算x^3再与result2相乘就可以得到x^7。由此可以将x^23写成x^16 x^4 x^2 x,即23=16+4+2+1,而23 = 10111(二进制),所以只要将n化为二进制并由低位到高位依次判断如果第i位为1,则result =x^(2^i)。
此函数可以在相乘O(logN)次内计算x的n次幂,且避免了重复计算。但还可以作进一步的优化,如像48=110000(二进制)这种低位有很多0的数,可以先过滤掉低位的0再进行计算,这样也会提高一些效率。程序如下:
1 | /* |
inner_product
1 | /* |
iota
1 | /* |
基本算法
STL标准中没有区分基本算法或复杂算法,单SGI把常用的一些算法(equal,fill,fill_n,iter_swap,lexicographical_compare,max,min,mismatch,swap,copy,copy_backward,copy_n)定义在<stl_algobase.h>只中,其他算法定义在<stl_algo.h>中。
equal作用:判断[first,last)区间两个元素是否相同,第二个迭代器多出来的元素不予考虑。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17template <class _InputIter1, class _InputIter2>//版本1
inline bool equal(_InputIter1 __first1, _InputIter1 __last1,
_InputIter2 __first2) {
for ( ; __first1 != __last1; ++__first1, ++__first2)//遍历区间[first,last)元素
if (*__first1 != *__first2)//只有有一个不相等返回false
return false;
return true;
}
template <class _InputIter1, class _InputIter2, class _BinaryPredicate>//版本2
inline bool equal(_InputIter1 __first1, _InputIter1 __last1,
_InputIter2 __first2, _BinaryPredicate __binary_pred) {
for ( ; __first1 != __last1; ++__first1, ++__first2)
if (!__binary_pred(*__first1, *__first2))//两个元素执行二元操作符
return false;
return true;
}
fill作用:将指定区间元素改为新值。1
2
3
4
5template <class _ForwardIter, class _Tp>
void fill(_ForwardIter __first, _ForwardIter __last, const _Tp& __value) {
for ( ; __first != __last; ++__first)//遍历整个区间
*__first = __value;//指定新值
}
fill_n作用:将指定区间前n个元素改为新值。1
2
3
4
5
6template <class _OutputIter, class _Size, class _Tp>
_OutputIter fill_n(_OutputIter __first, _Size __n, const _Tp& __value) {
for ( ; __n > 0; --__n, ++__first)
*__first = __value;
return __first;
}
iter_swap作用:将两个迭代器所指对象调换。1
2
3
4
5
6
7
8
9
10
11template <class _ForwardIter1, class _ForwardIter2, class _Tp>
inline void __iter_swap(_ForwardIter1 __a, _ForwardIter2 __b, _Tp*) {
_Tp __tmp = *__a;
*__a = *__b;
*__b = __tmp;
}
template <class _ForwardIter1, class _ForwardIter2>
inline void iter_swap(_ForwardIter1 __a, _ForwardIter2 __b) {
__iter_swap(__a, __b, __VALUE_TYPE(__a));
}iter_swap()是“迭代器之value type派上用场的一个好例子。是的,该函数必须知道迭代器的value type,才能够据此声明一个对象,用来暂时存放迭代器所指对象。为此,上述源代码特别设计了一个双层构造,第一层调用第二层:并多出一个额外的参数value_type(a)。这么一来,第二层就有value type可以用了。乍见之下你可能会对这个额外参数在调用端和接受端的型别感到讶异,调用端是value_type(a),接受端却是T*。只要找出value_type()的定义瞧瞧,就一点也不奇怪了:1
2
3
4template<class Iterator>
inline typename iterator_traits<Iterator>::value_type* value_type(const Iterator&){
return static_cast<typename iterator_traits<Iterator>::value_type*>(0);
}
这种双层构造在SGI STL源代码中十分普遍。其实这并非必要,直接这么写就行:1
2
3
4
5
6template <class ForwardIterator1, class ForwardIterator2>
inline void iter_swap(ForwardIterator1 a, ForwardIterator2 b) {
typename iterator_traits<ForwardIterator1>::value_type tmp = *a;
*a = *b;
*b = tmp;
}
lexicographical_compare作用:以“字典排列方式”对两个序列[first1, last1)和[first2, last2)进行比较。比较操作针对两序列中的对应位置上的元素进行,并持续直到:
- 某组对应元素彼此不相等;
- 同时到达last1和last2(当两序列的大小相同);
- 到达last1或last2(当两序列的大小不同)
当这个函数在对应位置上发现第一组不相等的元素时,有下列几种可能:
- 如果第一序列的元素较小,返回true,否则返回false;
- 如果到达last1而尚未到达last2,返回true;
- 如果到达llast2而尚未到达last1,返回false;
- 如果同时到达last1和last2(换句话说所有元素都匹配),返回false。
1 | // 字典序比较, 非常类似字符串的比较 |
max
去两个对象中的较大值,有两个版本,版本一使用对象类型T所提供的greater-than判断大小,版本二使用仿函数comp判断大小。1
2
3
4
5
6
7
8
9
10
11template <class T>
inline const T& max(const T& a, const T& b)
{
return a < b ? b : a;
}
template <class T, class Compare>
inline const T& max(const T& a, const T& b, Compare comp)
{
return comp(a, b) ? b : a;
}
min
max和min非常简单了, 由于返回的是引用, 因此可以嵌套使用1
2
3
4
5
6
7
8
9
10
11template <class T>
inline const T& min(const T& a, const T& b)
{
return b < a ? b : a;
}
template <class T, class Compare>
inline const T& min(const T& a, const T& b, Compare comp)
{
return comp(b, a) ? b : a;
}
mismatch
用来平行比较两个序列,指出两者之间的第一个不匹配点:返回一对迭代器,分别指向两序列中的不匹配点,如下图,如果两序列的所有对应元素都匹配,返回的便是两序列各自的iast迭代器。缺省情况下是以equality操作符来比较元素。但第二版本允许用户指定比较操作。如果第二序列的元素个数比第一序列多,多出 来的元素忽略不计。如果第几序列的元素个数比第一序列少,会发生未可预期的行为。
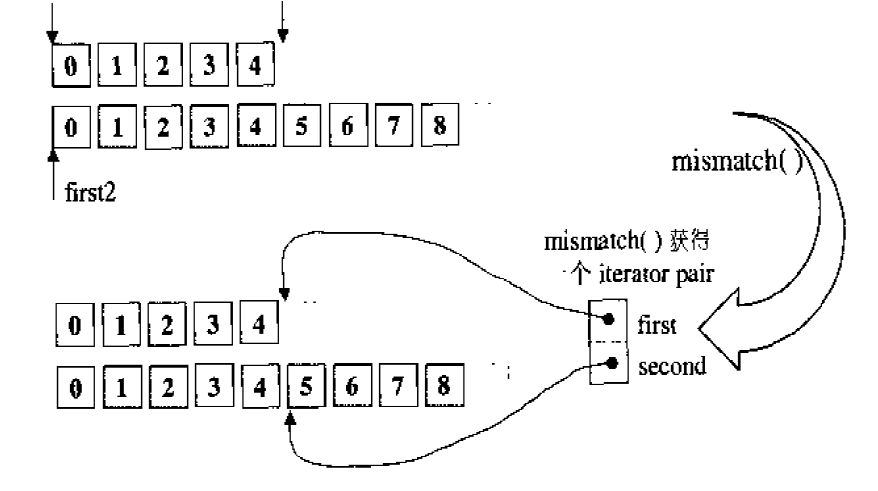
1 | template <class InputIterator1, class InputIterator2> |
swap
交换对调两个对象内容1
2
3
4
5
6
7
8
9//交换a和b的值
//这里采用引用传参
template <class T>
inline void swap(T& a, T& b)
{
T tmp = a;
a = b;
b = tmp;
}
copy
copy()是一个调用频率非常高的函数,所以SGI STL的copy算法用尽各种办法,包括函数重载(function overloading)、型别特性(type traits)、偏特化(partial specialization)编程技巧,无所不用其极地加强效率。下图是整个copy()操作的脉络。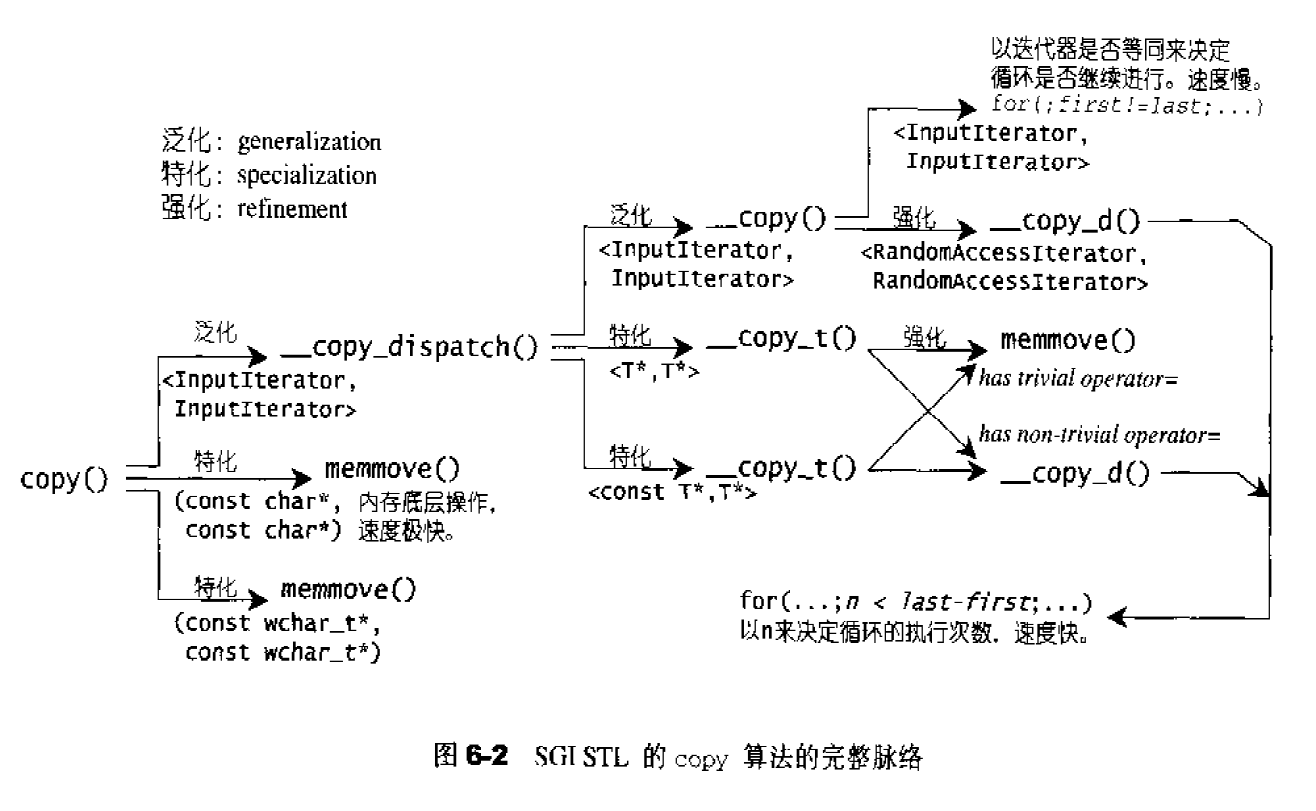
copy算法将输入区间[first, last)内的元素复制到result指向的输出区间内,赋值操作是向前推进的。如果输入区间和输出区间重叠,复制顺序需要多加讨论。当result位于[first, last)之内时,也就是说,如果输出区间的首部与输入区间重叠,copy的结果可能不正确,建议选用copy_backward;如果输出区间的尾部如输入区间重叠,copy_backward的结果可能不正确,建议选用copy。当然,如果两区间完全不重叠,copy和copy_backward都可以选用。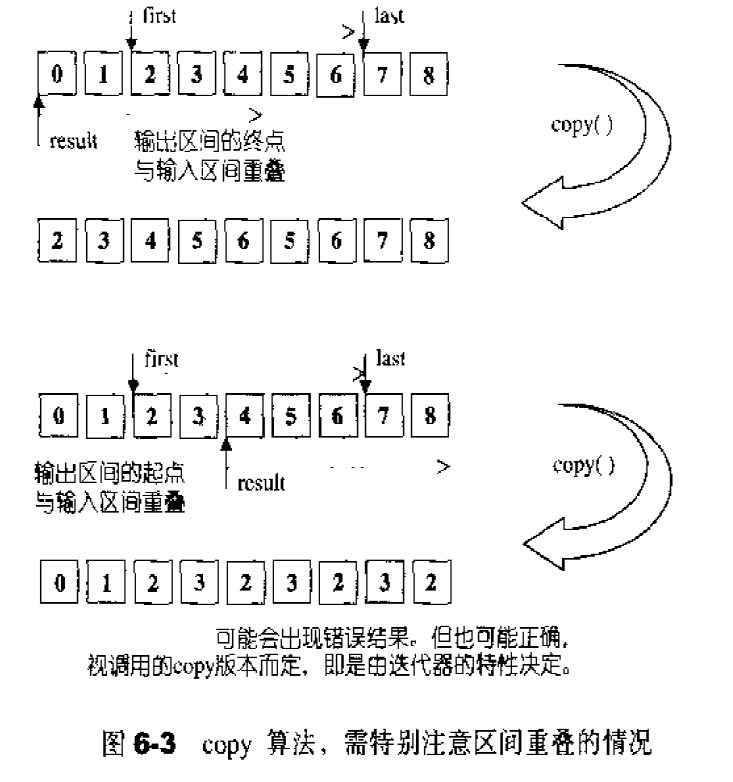
copy算法根据输出迭代器的特性决定是否调用memmove()来执行任务,memmove()会先将整个输入区间的内容复制下来,然后再复制到输入区间。这种情况下,即使输入区间和输出区间有重叠时,copy的结果也是正确的。这也回答了上文中提调的,为什么result位于[first, last)之内时,copy的结果只是“可能不正确”。
copy为输出区间内的元素赋予新值,而不是产生新元素,它不能改变输出区间的长度。换句话说,copy不能用来直接将元素插入到空容器中。如果你想要将元素插入序列之中,要么使用序列容器的insert成员函数,要么使用copy算法并搭配insert_iterator。
下面是copy算法唯三的对外接口,包括一个完全泛化版本和两个重载函数,重载函数针对原生指针const char*和const wchar_t*进行内存直接拷贝操作:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15template <class InputIterator, class OutputIterator>
inline OutputIterator
copy(InputIterator first, InputIterator last, OutputIterator result) {
return __copy_dispatch<InputIterator, OutputIterator>()(first, last, result);
}
inline char* copy(const char* first, const char* last, char* result) {
memmove(result, first, last - first);
return result + (last - first);
}
inline wchar_t* copy(const wchar_t* first, const wchar_t* last, wchar_t* result) {
memmove(result, first, last - first);
return result + (last - first);
}
copy()函数的泛化版本中调用了一个__copy_dispatch()的仿函数,此仿函数有一个完全泛化版本和两个偏特化版本:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18template <class InputIterator, class OutputIterator>
struct __copy_dispatch {
OutputIterator operator(){InputIterator first, InputIterator last, OutputIterator result) {
return __copy(first, last, result, iterator_category(first);
} ;
template <class T>
struct __copy_dispatch<T*, T*> {
T* operator()(T* first, T* last, T* result) {
typedef typename __type_traits<T>::has_trivial_assignment_operator t;
return __copy_t(first, last, result, t());
};
template <class T>
struct __copy_dispatch<const T*, T*> {
T* operator()(T* first, T* last, T* result) {
typedef typename __type_traits<T>::has_trivial_asssignment_operator t;
return __copy_t(first, last, result, t());
};
__copy_dispatch()的完全泛化版本根据迭代器种类的不同,调用不同的__copy(),为的是不同的迭代器使用的循环条件不同,有快慢之别1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22template <class InputIterator, class OutputIterator>
inline OutputIterator __copy(InputIterator first, InputIterator last,
OutputIterator result, input_iterator_tag) {
for( ; first != last; ++first, ++result)
*result = *first;
return result;
}
template <class RandomAccessIterator, class OutputIterator>
inline OutputIterator __copy(RandomAccessIterator first, RandomAccessIterator last,
OutputIterator result, random_access_iterator_tag) {
__return __copy_d(first, last, result, distance_type(first));
}
template <class RandomAccessIterator, class OutputIterator, class Distance>
inline OutputIterator __copy_d(RandomAccessIterator first, RandomAccessIterator last,
OutputIterator result, Distance*) {
// 以n决定循环次数,速度快
for(Distance n = last - first; n > 0; --n, ++result, ++first) {
*result = *first;
return result;
}
这两个偏特化版本是在“参数为原生指针形式”的前提下,利用__type_traits<>编程技巧来探测指针所指向之物是否有trivial assignment operator. 如果指针所指对象拥有trivial assignment operator,则可以通过memmove()进行复制,速度要比利用赋值操作赋快许多。1
2
3
4
5
6
7
8
9template <class T>
inline T* __copy_t(const T* first, const T* last, T* result, __true_type) {
memmove(result, first, sizeof(T) *(last - first);
return result + (last - first);
}
template <class T>
inline T* __copy_t(const T* first, const T* last, T* result, __false_type) {
return __copy_d(first, last, result, (ptrdiff_t *)0);
}
copy_backward
copy_backward()的实现与copy()极为相似,不同是它将[first, last)区间内的每一个元素,以逆行的方向复制到,以result-1为起点,方向同样为逆行的区间上。1
2
3
4
5
6
7
8
9
template <class BidirectionalIterator1, class BidirectionalIterator2>
inline BidirectionalIterator2 __copy_backward(BidirectionalIterator1 first,
BidirectionalIterator1 last,
BidirectionalIterator2 result)
{
while (first != last) *--result = *--last;
return result;
}
这个算法的考虑以及实现的技巧与copy十分类似,其操作示意如图,将[first, last)区间内的每一个元素,以逆行的方向复制到,以result-1为起点,方向同样为逆行的区间上。返回一个迭代器result-(last-first)。copy_backward所接受的迭代器必须是BidirectionIterators才能够“倒行逆施”。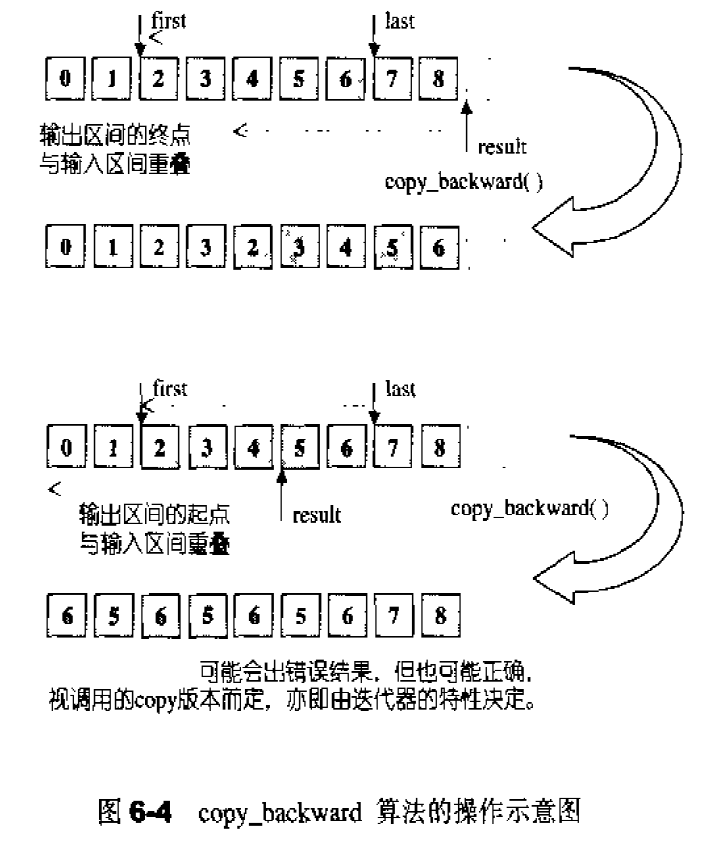
set相关算法
STL提供了4个set相关的算法,分别是并集(union)、交集(intersection)、差集(difference)和对称差集(symmetric difference),这4个算法接受的set必须是有序区间,都至少接受4个参数,分别表示两个set区间。一般而言,set算法前4个参数分别表示两个区间,第五个参数表示存放结果的区间的起始位置。
set_union
求两个集合的并集,能够造出S1 U S2,此集合内含S1或S2内的每一个元素。如果某个值在S1出现n次,在S2出现m次,那么该值在输出区间中会出现max(m, n)次。返回值为一个迭代器,指向输出区间的尾端。是一种稳定操作,输入区间内的每个元素相对顺序都不会改变。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56//并集,求存在于[first1, last1)或存在于[first2, last2)内的所有元素
//注意:输入区间必须是已排序
//版本一,默认是operator<操作的排序方式
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_union(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2,
OutputIterator result) {
//两个区间都尚未到达区间尾端,执行以下操作
while (first1 != last1 && first2 != last2) {
/*在两区间内分别移动迭代器,首先将元素较小者(假设为A区)记录在目标区result,
移动A区迭代器使其前进;同时另一个区的迭代器不变。然后进行一次新的比较,
记录较小值,移动迭代器...直到两区间中有一个到达尾端。
若元素相等, 默认取第一区间元素到目标区result,同时移动两个迭代器.*/
if (*first1 < *first2) {
*result = *first1;
++first1;
}
else if (*first2 < *first1) {
*result = *first2;
++first2;
}
else {
*result = *first1;
++first1;
++first2;
}
++result;
}
/*只要两区间之中有一个区间到达尾端,就结束上面的while循环
以下将尚未到达尾端的区间剩余的元素拷贝到目标区
此刻,[first1, last1)和[first2, last2)至少有一个是空区间*/
return copy(first2, last2, copy(first1, last1, result));
}
//版本二,用户根据仿函数comp指定排序规则
template <class InputIterator1, class InputIterator2, class OutputIterator,class Compare>
OutputIterator set_union(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2,
OutputIterator result, Compare comp) {
while (first1 != last1 && first2 != last2) {
if (comp(*first1, *first2)) {
*result = *first1;
++first1;
}
else if (comp(*first2, *first1)) {
*result = *first2;
++first2;
}
else {
*result = *first1;
++first1;
++first2;
}
++result;
}
return copy(first2, last2, copy(first1, last1, result));
}
图解如下: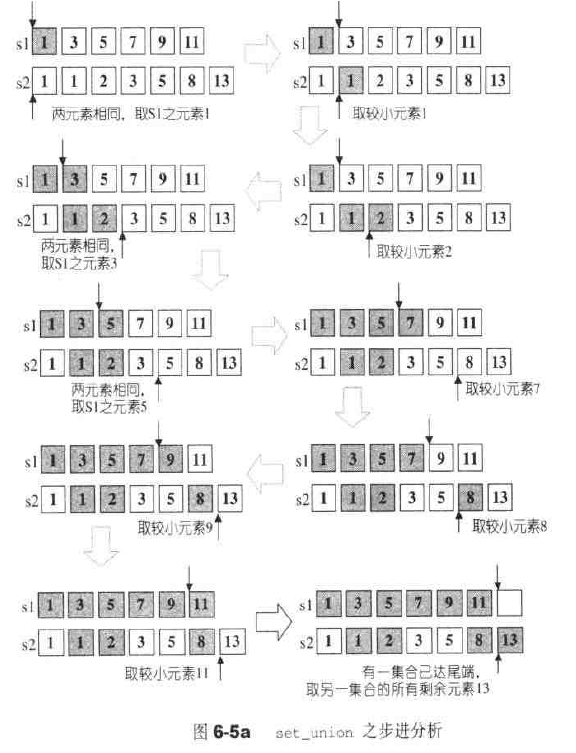
set_intersection
求两个集合的交集,此集合内含同时出现于S1和S2内的每一个元素。如果某个值在S1出现n次,在S2出现m次,那么该值在输出区间中会出现min(m, n)次,并且全部来自S1。
返回值为一个迭代器,指向输出区间的尾端。
是一种稳定操作,输入区间内的每个元素相对顺序都不会改变。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23//交集,求存在于[first1, last1)且存在于[first2, last2)内的所有元素
//注意:输入区间必须是已排序
//版本一,默认是operator<操作的排序方式
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_intersection(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2,
OutputIterator result) {
//若两个区间都尚未到达尾端,则执行以下操作
while (first1 != last1 && first2 != last2)
//在两个区间分别移动迭代器,直到遇到相等元素,记录到目标区
//继续移动迭代器...直到两区间之中有一区到达尾端
if (*first1 < *first2)
++first1;
else if (*first2 < *first1)
++first2;
else {
*result = *first1;
++first1;
++first2;
++result;
}
return result;
}
图解如下: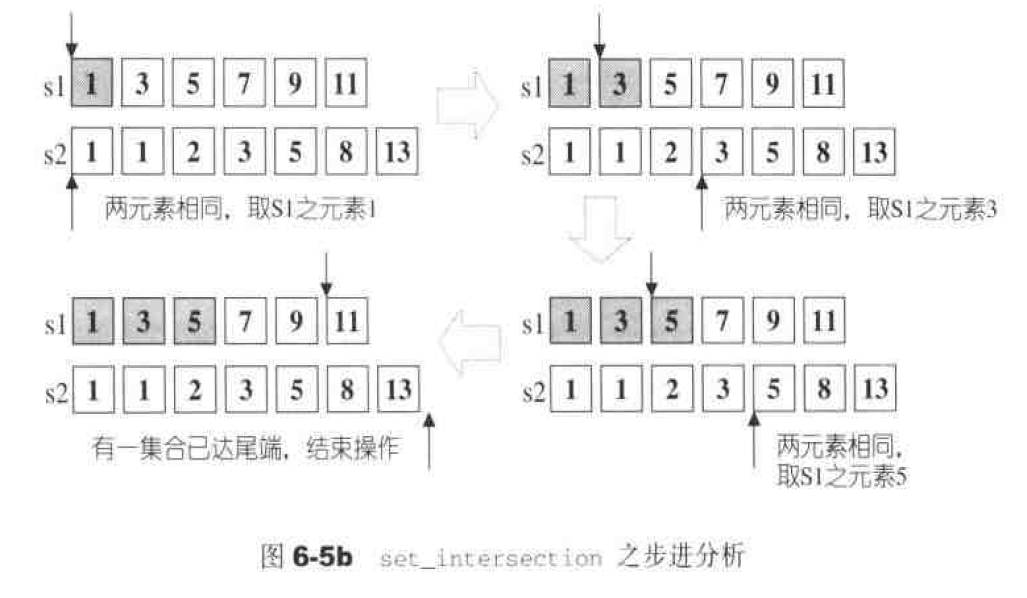
set_difference
求两个集合的差集,此集合内含出现于S1但不出现于S2内的元素。如果某个值在S1出现n次,在S2出现m次,那么该值在输出区间中会出现max(n-m, 0)次,并且全部来自S1。
返回值为一个迭代器,指向输出区间的尾端。
是一种稳定操作,输入区间内的每个元素相对顺序都不会改变。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28//差集,求存在于[first1, last1)且不存在于[first2, last2)内的所有元素
//注意:输入区间必须是已排序
//版本一,默认是operator<操作的排序方式
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_difference(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2,
OutputIterator result) {
//若两个区间都尚未到达尾端,则执行以下操作
while (first1 != last1 && first2 != last2)
/*在两个区间分别移动迭代器,当第一区间元素等于第二区
间元素时,表示两区间共同存在该元素,则同时移动迭代器;
当第一区间元素大于第二区间元素时,就让第二区间迭代器前进;
第一区间元素小于第二区间元素时,把第一区间元素记录到目标区
继续移动迭代器...直到两区间之中有到达尾端*/
if (*first1 < *first2) {
*result = *first1;
++first1;
++result;
}
else if (*first2 < *first1)
++first2;
else {
++first1;
++first2;
}
//把第一区间剩余的元素(若有剩余)复制到目标区
return copy(first1, last1, result);
}
图解如下: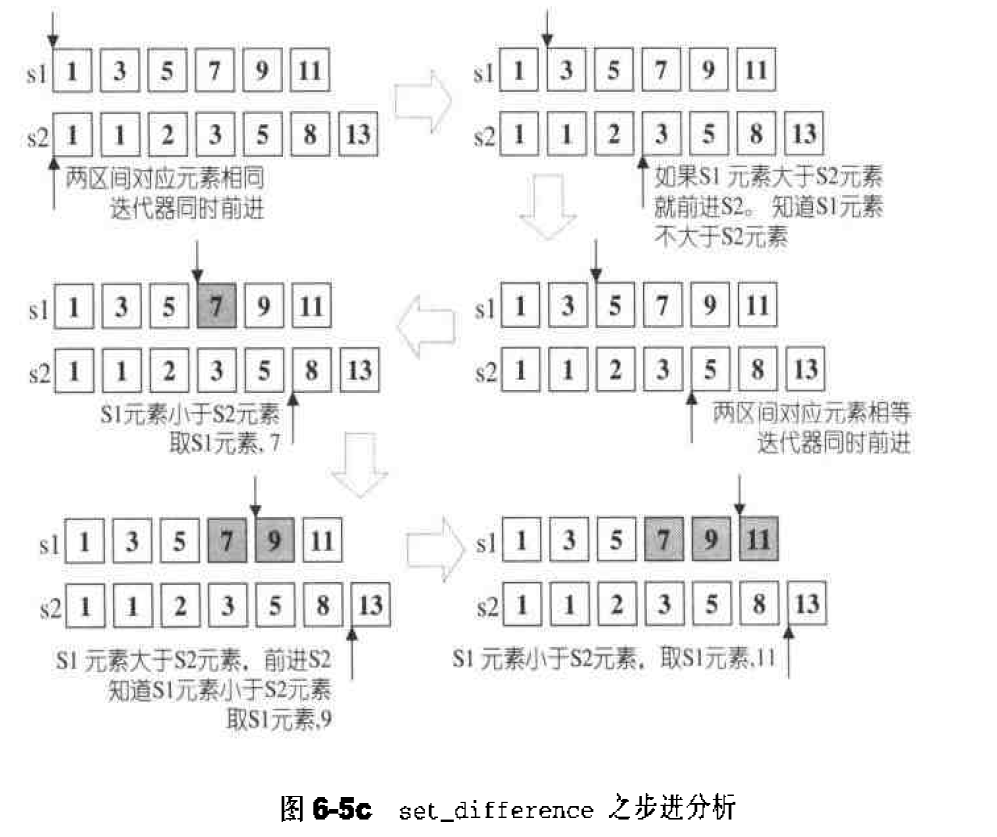
set_symmetric_difference
求两个集合的对称差集(s1-s2)∪(s2-s1),此集合内含出现于S1但不出现于S2内的元素,以及出现于S2但不出现于S1内的每一个元素。如果某个值在S1出现n次,在S2出现m次,那么该值在输出区间中会出现|n-m|次。
返回值为一个迭代器,指向输出区间的尾端。
是一种稳定操作,输入区间内的每个元素相对顺序都不会改变。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31//对称差集,求存在于[first1, last1)但不存在于[first2,
//last2)内的所有元素以及出现在[first2, last2)但不出现在
//[first1, last1)的所有元素
//注意:输入区间必须是已排序
//版本一,默认是operator<操作的排序方式
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_symmetric_difference(InputIterator1 first1,
InputIterator1 last1,
InputIterator2 first2,
InputIterator2 last2,
OutputIterator result) {
//若两个区间都尚未到达尾端,则执行下面的操作
while (first1 != last1 && first2 != last2)
/*在两区间内分别移动迭代器。当两区间内的元素相等,就让两区同时前进;
当两区间内的元素不等,就记录较小值于目标区,并令较小值所在区间前进*/
if (*first1 < *first2) {
*result = *first1;
++first1;
++result;
}
else if (*first2 < *first1) {
*result = *first2;
++first2;
++result;
}
else {
++first1;
++first2;
}
return copy(first2, last2, copy(first1, last1, result));
}
图解如下: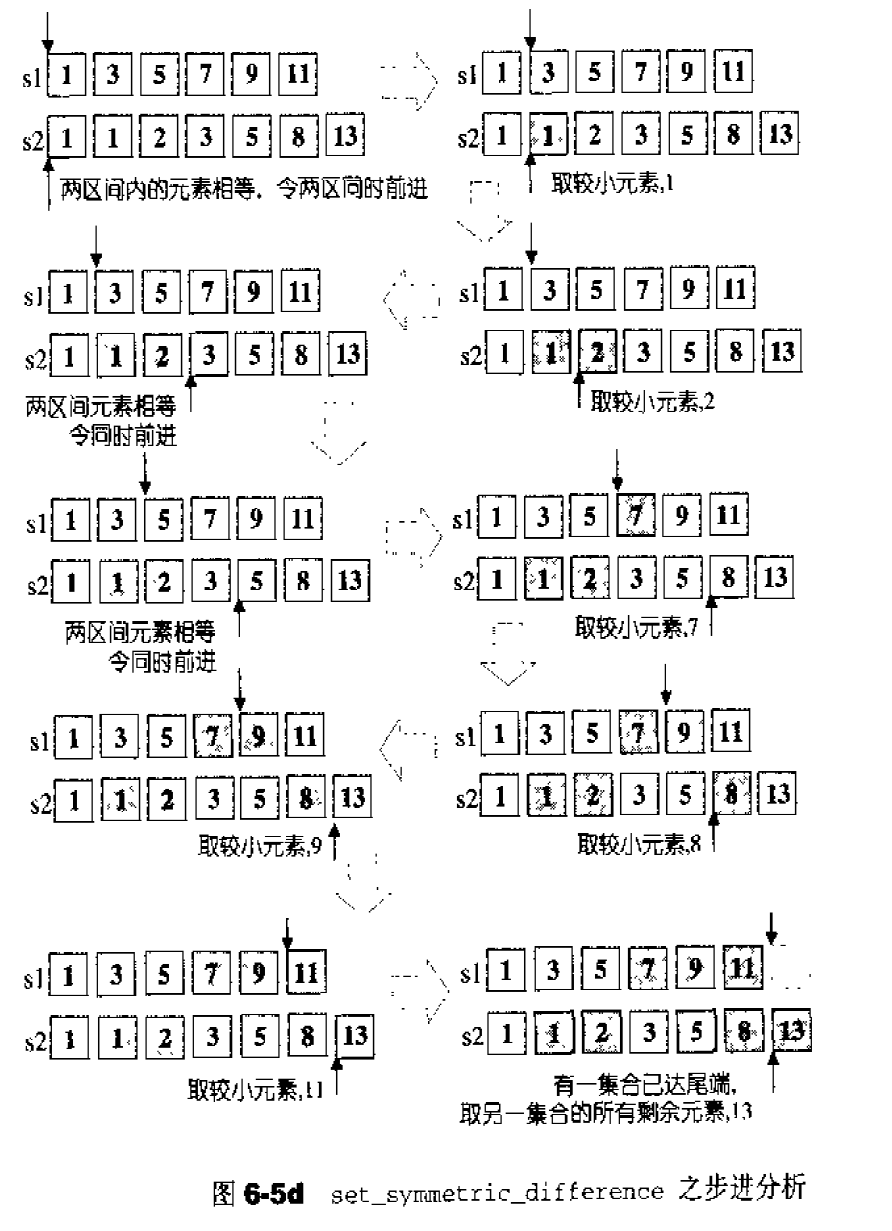
应用实例:
1 |
|
其他算法
单纯的数据处理
测试程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
using namespace std;
// 仿函数
template <class T>
struct display {
void operator() (const T& x) const {
cout << x << ' ';
}
};
// 仿函数,一元谓词
struct even {
bool operator() (int x) const {
return x % 2 ? false : true;
}
};
// 还是一个仿函数
class even_by_two {
public:
int operator() () const {
return _x += 2;
}
private:
static int _x;
};
int even_by_two::_x = 0; // 类内声明类外初始化
int main() {
int ia[] = {0, 1, 2, 3, 4, 5, 6, 6, 6, 7, 8};
vector<int> iv(ia, ia + sizeof(ia) / sizeof(int));
// 找出相邻元素值相等的第一个元素
cout << *adjacent_find(iv.begin(), iv.end()) << endl;
// 找出相邻元素值相等的第一个元素
cout << *adjacent_find(iv.begin(), iv.end(), equal_to<int>()) << endl;
// 找出元素值为6的元素个数
cout << count(iv.begin(), iv.end(), 6) << endl;
// 找出元素值小于7的元素个数
cout << count_if(iv.begin(), iv.end(), bind2nd(less<int>(), 7)) << endl;
// 找出元素值为4的元素所在位置
cout << *find(iv.begin(), iv.end(), 4) << endl;
// 找出元素值大于2的第一个元素所在位置
cout << *find_if(iv.begin(), iv.end(), bind2nd(greater<int>(), 2)) << endl;
// 找出子序列所出现的最后一个位置,加3
vector<int> iv2(ia + 6, ia + 8);
cout << *(find_end(iv.begin(), iv.end(), iv2.begin(), iv2.end()) + 3) << endl;
// 找出子序列所出现的第一个位置,加3
cout << *(find_first_of(iv.begin(), iv.end(), iv2.begin(), iv2.end()) + 3) << endl;
// 迭代iv 每个元素进行display
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
// 以下写法错误,generate的第三个参数是仿函数,本身不得有任何参数
// generate(iv.begin(), iv.end(), bind2nd(plus<int>(), 3)); // error
// 迭代iv2,对每个元素进行even_by_two
generate(iv2.begin(), iv2.end(), even_by_two());
for_each(iv2.begin(), iv2.end(), display<int>());
cout << endl;
// 迭代指定区间,对每个元素进行even_by_two
generate_n(iv2.begin(), 3, even_by_two());
for_each(iv2.begin(), iv2.end(), display<int>());
cout << endl;
// 删除(但不删除)元素6,尾端可能有残余数据(可以使用erase)
remove(iv.begin(), iv.end(), 6);
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
// 删除(但不删除)元素6,结果置于另一区间
vector<int> iv3(12);
remove_copy(iv.begin(), iv.end(), iv3.begin(), 6);
for_each(iv3.begin(), iv3.end(), display<int>());
cout << endl;
// 删除(但不删除)元素6,尾端可能有残余数据
remove_if(iv.begin(), iv.end(), bind2nd(less<int>(), 6));
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
// 删除(但不删除)小于7的元素,结果置于另一区间
remove_copy_if(iv.begin(), iv.end(), iv3.begin(), bind2nd(less<int>(), 7));
for_each(iv3.begin(), iv3.end(), display<int>());
cout << endl;
// 将所有的元素值6,改为元素值3
replace(iv.begin(), iv.end(), 6, 3);
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
// 将所有的元素值3,改为元素值5,结果置于另一区间
replace_copy(iv.begin(), iv.end(), iv3.begin(), 3, 5);
for_each(iv3.begin(), iv3.end(), display<int>());
cout << endl;
// 将所有小于5的元素值,改为元素值2
replace_if(iv.begin(), iv.end(), bind2nd(less<int>(), 5), 2);
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
// 将所有等于8的元素值,改为元素值9,结果置于另一区间
replace_copy_if(iv.begin(), iv.end(), iv3.begin(), bind2nd(equal_to<int>(), 8), 9);
for_each(iv3.begin(), iv3.end(), display<int>());
cout << endl;
// 逆向重排每一个元素
reverse(iv.begin(), iv.end());
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
// 逆向重排每一个元素,结果置于另一区间
reverse_copy(iv.begin(), iv.end(), iv3.begin());
for_each(iv3.begin(), iv3.end(), display<int>());
cout << endl;
// 旋转(互换元素)[first, middle]和[middle, last]
rotate(iv.begin(), iv.begin() + 4, iv.end());
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
// 旋转(互换元素)[first, middle]和[middle, last]
// 结果置于另一区间
rotate_copy(iv.begin(), iv.begin() + 5, iv.end(), iv3.begin());
for_each(iv3.begin(), iv3.end(), display<int>());
cout << endl;
// 查找某个子序列的第一次出现地点
int ia2[3] = {2, 8};
vector<int> iv4(ia2, ia2 + 2);
cout << *search(iv.begin(), iv.end(), iv4.begin(), iv4.end()) << endl;
// 查找连续出现2个8的子序列起点
cout << *search_n(iv.begin(), iv.end(), 2, 8) << endl;
// 查找连续出现3个小于8的子序列起点
cout << *search_n(iv.begin(), iv.end(), 3, 8, less<int>()) << endl;
// 将区间元素互换,第二区间个数不应小于第一区间个数
swap_ranges(iv4.begin(), iv4.end(), iv.begin());
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
for_each(iv4.begin(), iv4.end(), display<int>());
cout << endl;
// 改变区间的值,全部减2,原地搬运
transform(iv.begin(), iv.end(), iv.begin(), bind2nd(minus<int>(), 2));
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
// 改变区间的值,令 第二区间的元素值加到第一区间上
transform(iv.begin(), iv.end(), iv.begin(), iv.begin(), plus<int>());
for_each(iv.begin(), iv.end(), display<int>());
cout << endl;
// *******************************************
vector<int> iv5(ia, ia + sizeof(ia) / sizeof(int));
vector<int> iv6(ia + 4, ia + 8);
vector<int> iv7(15);
for_each(iv5.begin(), iv5.end(), display<int>());
cout << endl;
for_each(iv6.begin(), iv6.end(), display<int>());
cout << endl;
cout << *max_element(iv5.begin(), iv5.end()) << endl;
cout << *min_element(iv5.begin(), iv5.end()) << endl;
// 判断是否iv6内的所有元素都出现于iv5中
cout << includes(iv5.begin(), iv5.end(), iv6.begin(), iv6.end()) << endl;
// 将两个序列合并,必须有序
merge(iv5.begin(), iv5.end(), iv6.begin(), iv6.end(), iv7.begin());
for_each(iv7.begin(), iv7.end(), display<int>());
cout << endl;
// 符合条件的元素放在容器前端,其他放后端
partition(iv7.begin(), iv7.end(), even());
for_each(iv7.begin(), iv7.end(), display<int>());
cout << endl;
// 去除连续重复元素
unique(iv5.begin(), iv5.end());
for_each(iv5.begin(), iv5.end(), display<int>());
cout << endl;
// 去除连续重复元素,结果置于另一区间
unique_copy(iv5.begin(), iv5.end(), iv7.begin());
for_each(iv7.begin(), iv7.end(), display<int>());
cout << endl;
}
adjacent_find
找出第一组满足条件的相邻元素。1
2
3
4
5
6
7
8
9
10template <class ForwardIterator>
ForwardIterator adjacent_find(ForwardIterator first, ForwardIterator last) {
if (first == last) return last;
ForwardIterator next = first;
while(++next != last) {
if (*first == *next) return first;
first = next;
}
return last;
}
count
查找某个元素出现的数目。1
2
3
4
5
6
7template <class InputIterator, class T, class Size>
void count(InputIterator first, InputIterator last, const T& value,
Size& n) {
for ( ; first != last; ++first)
if (*first == value)
++n;
}
count_if
返回仿函数计算结果为true的元素的个数1
2
3
4
5
6
7template <class InputIterator, class Predicate, class Size>
void count_if(InputIterator first, InputIterator last, Predicate pred,
Size& n) {
for ( ; first != last; ++first)
if (pred(*first))
++n;
}
find
查找第一个匹配的元素1
2
3
4
5template <class InputIterator, class T>
InputIterator find(InputIterator first, InputIterator last, const T& value) {
while (first != last && *first != value) ++first;
return first;
}
find_if
查找第一个使仿函数为true的元素。1
2
3
4
5
6template <class InputIterator, class Predicate>
InputIterator find_if(InputIterator first, InputIterator last,
Predicate pred) {
while (first != last && !pred(*first)) ++first;
return first;
}
find_end
在序列一的区间内查找序列二的最后一次出现点。要求完全匹配的序列,即连续出现的序列2。可以利用正向查找,每次向后查找,记录上次找的的位置,最后没有找到了,那么上次找到的位置就是最后一次。也可以利用逆向迭代器从后向前找到第一次出现的位置。上层函数为dispatch function。
1 | template <class ForwardIterator1, class ForwardIterator2> |
这是一种常见的技巧,令函数传递过程中产生迭代器类型的临时对象,再利用编译器的参数推导机制自动调用某个函数:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95template <class ForwardIterator1, class ForwardIterator2>
ForwardIterator1 __find_end(ForwardIterator1 first1, ForwardIterator1 last1,
ForwardIterator2 first2, ForwardIterator2 last2,
forward_iterator_tag, forward_iterator_tag)
{
if (first2 == last2)
return last1;
else {
ForwardIterator1 result = last1;
while (1) {
ForwardIterator1 new_result = search(first1, last1, first2, last2);
if (new_result == last1)
return result;
else {
result = new_result;
first1 = new_result;
++first1;
}
}
}
}
template <class ForwardIterator1, class ForwardIterator2,
class BinaryPredicate>
ForwardIterator1 __find_end(ForwardIterator1 first1, ForwardIterator1 last1,
ForwardIterator2 first2, ForwardIterator2 last2,
forward_iterator_tag, forward_iterator_tag,
BinaryPredicate comp)
{
if (first2 == last2)
return last1;
else {
ForwardIterator1 result = last1;
while (1) {
ForwardIterator1 new_result = search(first1, last1, first2, last2, comp);
if (new_result == last1)
return result;
else {
result = new_result;
first1 = new_result;
++first1;
}
}
}
}
// find_end for bidirectional iterators. Requires partial specialization.
template <class BidirectionalIterator1, class BidirectionalIterator2>
BidirectionalIterator1
__find_end(BidirectionalIterator1 first1, BidirectionalIterator1 last1,
BidirectionalIterator2 first2, BidirectionalIterator2 last2,
bidirectional_iterator_tag, bidirectional_iterator_tag)
{
typedef reverse_iterator<BidirectionalIterator1> reviter1;
typedef reverse_iterator<BidirectionalIterator2> reviter2;
reviter1 rlast1(first1);
reviter2 rlast2(first2);
reviter1 rresult = search(reviter1(last1), rlast1, reviter2(last2), rlast2);
if (rresult == rlast1)
return last1;
else {
BidirectionalIterator1 result = rresult.base();
advance(result, -distance(first2, last2));
return result;
}
}
template <class BidirectionalIterator1, class BidirectionalIterator2,
class BinaryPredicate>
BidirectionalIterator1
__find_end(BidirectionalIterator1 first1, BidirectionalIterator1 last1,
BidirectionalIterator2 first2, BidirectionalIterator2 last2,
bidirectional_iterator_tag, bidirectional_iterator_tag,
BinaryPredicate comp)
{
typedef reverse_iterator<BidirectionalIterator1> reviter1;
typedef reverse_iterator<BidirectionalIterator2> reviter2;
reviter1 rlast1(first1);
reviter2 rlast2(first2);
reviter1 rresult = search(reviter1(last1), rlast1, reviter2(last2), rlast2,
comp);
if (rresult == rlast1)
return last1;
else {
BidirectionalIterator1 result = rresult.base();
advance(result, -distance(first2, last2));
return result;
}
}
find_first of
找到序列2中的任何一个元素在序列一中出现的位置。不需要完全配匹配序列2,任何一个元素出现都可以。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22template <class InputIterator, class ForwardIterator>
InputIterator find_first_of(InputIterator first1, InputIterator last1,
ForwardIterator first2, ForwardIterator last2)
{
for ( ; first1 != last1; ++first1)
for (ForwardIterator iter = first2; iter != last2; ++iter)
if (*first1 == *iter)
return first1;
return last1;
}
template <class InputIterator, class ForwardIterator, class BinaryPredicate>
InputIterator find_first_of(InputIterator first1, InputIterator last1,
ForwardIterator first2, ForwardIterator last2,
BinaryPredicate comp)
{
for ( ; first1 != last1; ++first1)
for (ForwardIterator iter = first2; iter != last2; ++iter)
if (comp(*first1, *iter))
return first1;
return last1;
}
for_each
将仿函数施加于区间内的每个元素之上。不能够改变元素内容,返回值被忽略。可以用于打印元素的值等。1
2
3
4
5
6template <class InputIterator, class Function>
Function for_each(InputIterator first, InputIterator last, Function f) {
for ( ; first != last; ++first)
f(*first);
return f;
}
generate
将仿函数的运算结果赋值给区间内的每一个元素1
2
3
4
5template <class ForwardIterator, class Generator>
void generate(ForwardIterator first, ForwardIterator last, Generator gen) {
for ( ; first != last; ++first)
*first = gen();
}
generate_n
将仿函数的运算结果赋值给迭代器first开始的n个元素上1
2
3
4
5
6template <class OutputIterator, class Size, class Generator>
OutputIterator generate_n(OutputIterator first, Size n, Generator gen) {
for ( ; n > 0; --n, ++first)
*first = gen();
return first;
}
includes
判断序列二S2是否“涵盖于”序列一S1。S1和S2都必须是有序集合:其中的元素都可重复(不必唯一)。所谓涵盖,意思是“S2的每一个元素都出现于S1”。由于判断两个元素是否相等,必须以less或greater运算为依据(当S1元素不小于S2元素且S2元素不小于S1元素,两者即相等;或说当S1元素不大于S2元素且S2元素不大于S1元素,两者即相等),因此配合着两个序列S1和S2的排序方式(递增或递减),includes算法可供用户选择采用less或greater进行两元素的大小比较(comparison)。
换句话说,如果S1和S2是递增排序(以operator<执行比较操作),includes 算法应该这么使用:1
includes(S1.begin(), S1.end(), S2.begin(), S2.end());
这和下一行完全相同:1
includes(S1.begin(), S1.end(), S2.begin(), S2.end(), less<int>());
然而如果S1和S2是递减排序(以operator>执行比较操作),includes算法应该这么使用:1
includes(S1.begin(), S1.end(), S2.begin(), S2.end(), greater<int>());
注意,S1或S2内的元素都可以重复,这种情况下所谓, S1内含一个S2子集合”的定义是:假设某元素在S2出现n次,在S1出现m次。那么如果m < n, 此算法会返回false。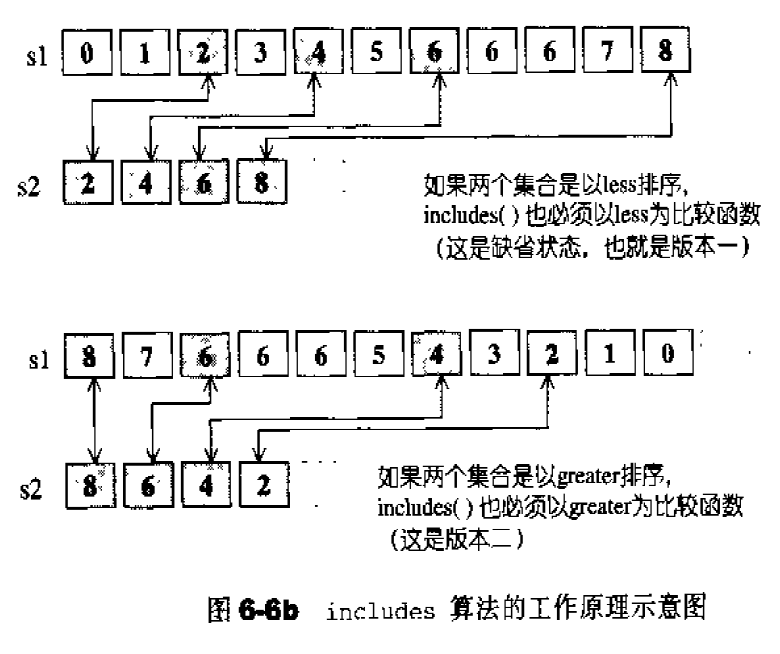
1 | template <class InputIterator1, class InputIterator2> |
max_element
返回区间内最大的元素。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18template <class ForwardIterator>
ForwardIterator max_element(ForwardIterator first, ForwardIterator last) {
if (first == last) return first;
ForwardIterator result = first;
while (++first != last)
if (*result < *first) result = first;
return result;
}
template <class ForwardIterator, class Compare>
ForwardIterator max_element(ForwardIterator first, ForwardIterator last,
Compare comp) {
if (first == last) return first;
ForwardIterator result = first;
while (++first != last)
if (comp(*result, *first)) result = first;
return result;
}
merge
将两个有序序列融合成一个序列,三个序列都是有序的。返回指向结果序列的尾后元素。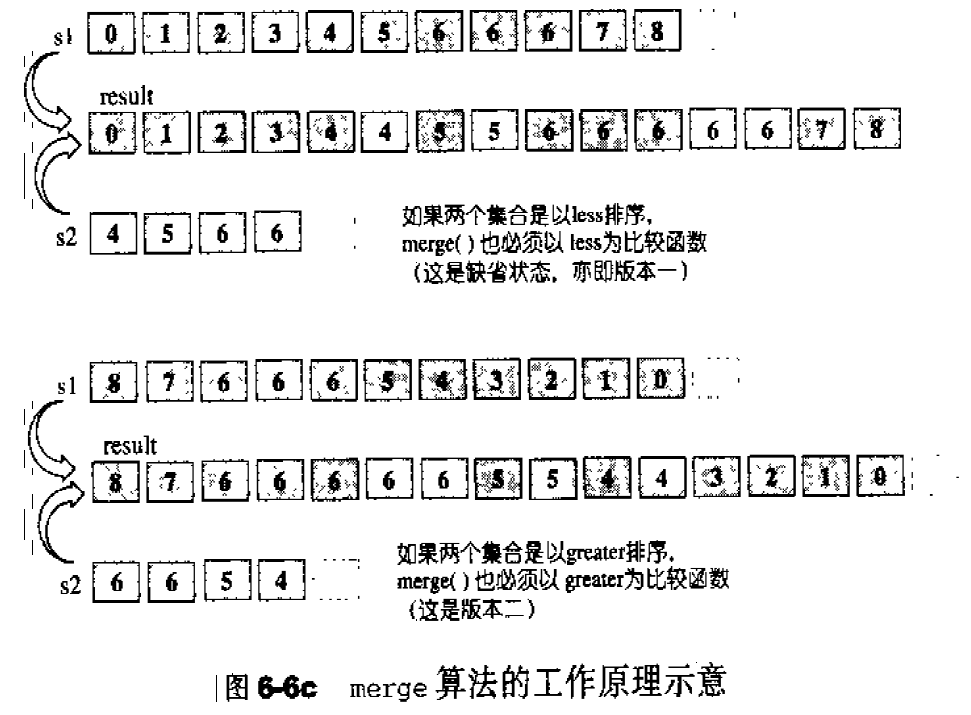
1 |
|
min_element
返回序列中数值最小的元素1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
template <class ForwardIterator>
ForwardIterator min_element(ForwardIterator first, ForwardIterator last) {
if (first == last) return first;
ForwardIterator result = first;
while (++first != last)
if (*first < *result) result = first;
return result;
}
template <class ForwardIterator, class Compare>
ForwardIterator min_element(ForwardIterator first, ForwardIterator last,
Compare comp) {
if (first == last) return first;
ForwardIterator result = first;
while (++first != last)
if (comp(*first, *result)) result = first;
return result;
}
partition
对区间进行重新排列,所有被仿函数判定为true的元素被放倒区间的前端,被判定为false的元素被放到区间的后端。这个算法并不保留元素的原始相对位置。需要保留原始相对位置,应使用stable_partition。算法实现类似于快排,先从前向后找到一个false,再从后向前找到一个true,然后交换。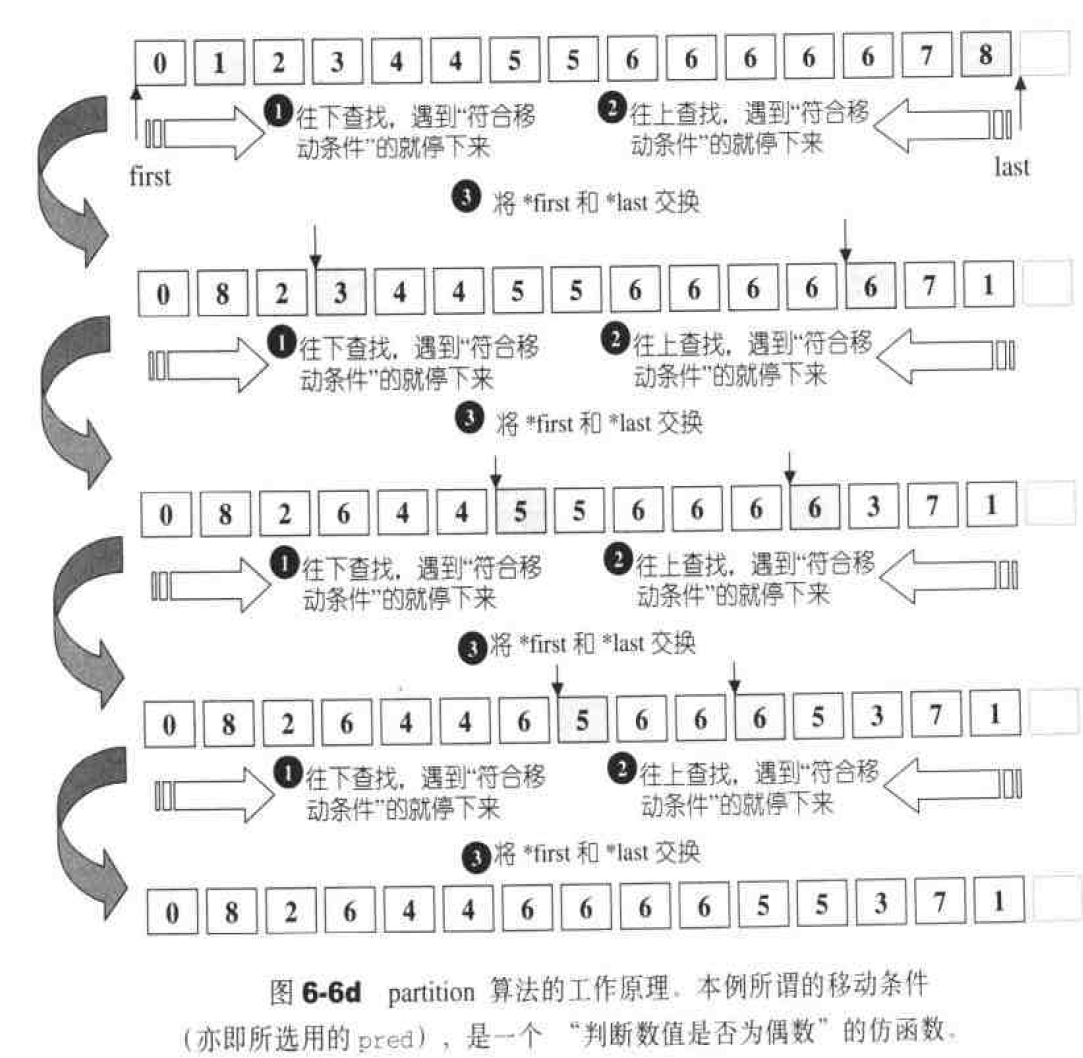
1 | template <class BidirectionalIterator, class Predicate> |
remove
移除区间内与value相等的元素。并不是真正移除,容器大小并未改变。只是将不相等的元素重新赋值到原区间上,所以会在原来有多余的元素。返回在重新整理后的元素的下一位置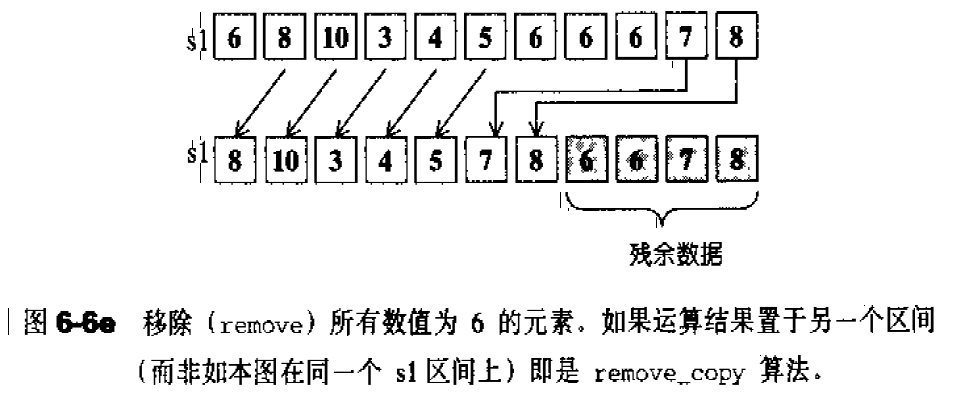
1 | template <class ForwardIterator, class T> |
remove_copy
移除区间内所有与value相等的元素;它并不真正从容器中删除那些元素(换句话说,原容器没有任何改变),而是将结果复制到一个以result标示起始位置的容器身上,新容器可以和原容器重叠,但如果对新容器实际给值时、 超越了旧容器的大小,会产生无法预期的结果。返回值OuputIterator指出被复制的最后元素的下一位置。1
2
3
4
5
6
7
8
9
10template <class InputIterator, class OutputIterator, class T>
OutputIterator remove_copy(InputIterator first, InputIterator last,
OutputIterator result, const T& value) {
for ( ; first != last; ++first)
if (*first != value) {
*result = *first;
++result;
}
return result;
}
remove_if
移除[first, last)区间内所有被仿函数pred核定为true的元素。它并不真正从容器中删除那些元素(换句话说,容器大小并未改变),每一个不符合pred条件的元素都会被轮番赋值给first之后的空间。返回值ForwardIterator标示出重新整理后的最后元素的下一位置,此算法会留有一些残余数据,如果要删除那些残余数据,可将返回的迭代器交给区间所在之容器的erase() member function。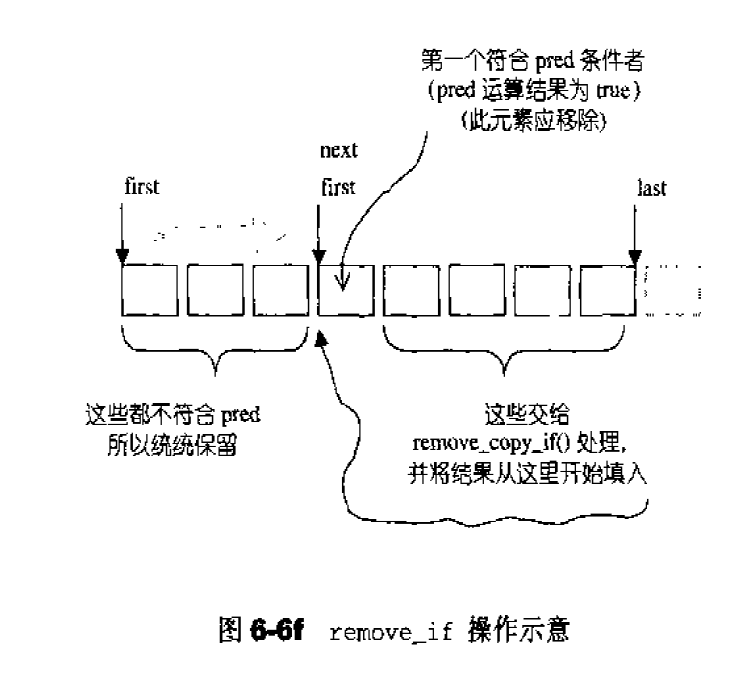
1 | template <class ForwardIterator, class Predicate> |
remove_copy_if
移除区间内所有与value相等的元素;它并不真正从容器中删除那些元素(换句话说,原容器没有任何改变),而是将结果复制到一个以result标示起始位置的容器身上,新容器可以和原容器重叠,但如果对新容器实际给值时、 超越了旧容器的大小,会产生无法预期的结果。1
2
3
4
5
6
7
8
9
10template <class InputIterator, class OutputIterator, class Predicate>
OutputIterator remove_copy_if(InputIterator first, InputIterator last,
OutputIterator result, Predicate pred) {
for ( ; first != last; ++first)
if (!pred(*first)) {
*result = *first;
++result;
}
return result;
}
replace
将区间内的所有元素用新元素取代1
2
3
4
5
6template <class ForwardIterator, class T>
void replace(ForwardIterator first, ForwardIterator last, const T& old_value,
const T& new_value) {
for ( ; first != last; ++first)
if (*first == old_value) *first = new_value;
}
replace_copy
与replace类似,只不过复制到其他容器上。新容器可以与原容器重叠1
2
3
4
5
6
7
8template <class InputIterator, class OutputIterator, class T>
OutputIterator replace_copy(InputIterator first, InputIterator last,
OutputIterator result, const T& old_value,
const T& new_value) {
for ( ; first != last; ++first, ++result)
*result = *first == old_value ? new_value : *first;
return result;
}
replace_if
移除区间内被仿函数判定为true的元素。原理与replace类似。1
2
3
4
5
6template <class ForwardIterator, class Predicate, class T>
void replace_if(ForwardIterator first, ForwardIterator last, Predicate pred,
const T& new_value) {
for ( ; first != last; ++first)
if (pred(*first)) *first = new_value;
}
replace_copy_if
与replace_if类似,但是新序列复制到result所指的区间内。1
2
3
4
5
6
7
8template <class Iterator, class OutputIterator, class Predicate, class T>
OutputIterator replace_copy_if(Iterator first, Iterator last,
OutputIterator result, Predicate pred,
const T& new_value) {
for ( ; first != last; ++first, ++result)
*result = pred(*first) ? new_value : *first;
return result;
}
reverse
将序列的元素在原容器中颠倒重排。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20template <class BidirectionalIterator>
void __reverse(BidirectionalIterator first, BidirectionalIterator last,
bidirectional_iterator_tag) {
while (true)
if (first == last || first == --last)
return;
else
iter_swap(first++, last);
}
template <class RandomAccessIterator>
void __reverse(RandomAccessIterator first, RandomAccessIterator last,
random_access_iterator_tag) {
while (first < last) iter_swap(first++, --last);
}
template <class BidirectionalIterator>
inline void reverse(BidirectionalIterator first, BidirectionalIterator last) {
__reverse(first, last, iterator_category(first));
}
reverse_copy
将序列颠倒重排,将结果置于另一序列1
2
3
4
5
6
7
8
9
10
11template <class BidirectionalIterator, class OutputIterator>
OutputIterator reverse_copy(BidirectionalIterator first,
BidirectionalIterator last,
OutputIterator result) {
while (first != last) {
--last;
*result = *last;
++result;
}
return result;
}
rotate
以middle为中心将序列旋转,middle所指的元素将会变成第一个元素。rotate()可以交换两个长度不同的区间,swap_range()只能交换长度相同的。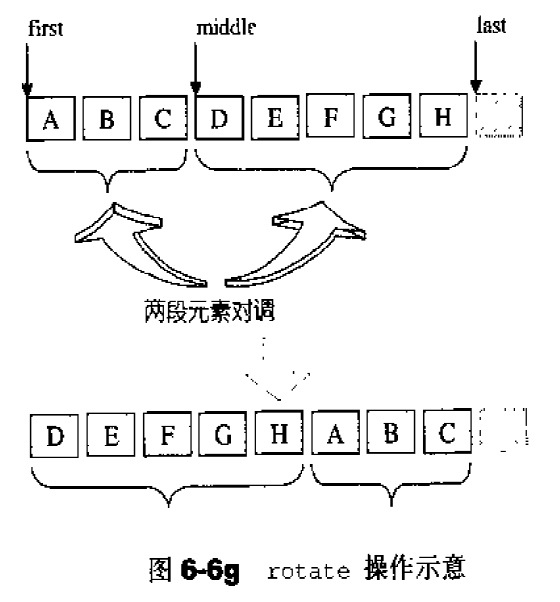
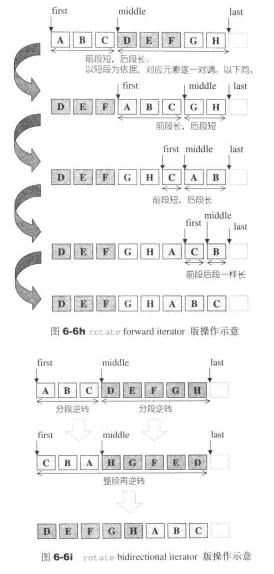
1 | template <class ForwardIterator> |
rotate_copy
和rotate类似,将结果置于另一序列1
2
3
4
5template <class ForwardIterator, class OutputIterator>
OutputIterator rotate_copy(ForwardIterator first, ForwardIterator middle,
ForwardIterator last, OutputIterator result) {
return copy(first, middle, copy(middle, last, result));
}
search
在序列1中查找序列2的首次出现点,序列1中要求序列2完全匹配,不能间隔。不存在就返回last1。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39template <class ForwardIterator1, class ForwardIterator2>
inline ForwardIterator1 search(ForwardIterator1 first1, ForwardIterator1 last1,
ForwardIterator2 first2, ForwardIterator2 last2)
{
return __search(first1, last1, first2, last2, distance_type(first1),
distance_type(first2));
}
template <class ForwardIterator1, class ForwardIterator2,
class BinaryPredicate, class Distance1, class Distance2>
ForwardIterator1 __search(ForwardIterator1 first1, ForwardIterator1 last1,
ForwardIterator2 first2, ForwardIterator2 last2,
BinaryPredicate binary_pred, Distance1*, Distance2*) {
Distance1 d1 = 0;
distance(first1, last1, d1);
Distance2 d2 = 0;
distance(first2, last2, d2);
if (d1 < d2) return last1;
ForwardIterator1 current1 = first1;
ForwardIterator2 current2 = first2;
while (current2 != last2)
if (binary_pred(*current1, *current2)) {
++current1;
++current2;
}
else {
if (d1 == d2)
return last1;
else {
current1 = ++first1;
current2 = first2;
--d1;
}
}
return first1;
}
search_n
和search类似,查找连续n个符合条件的元素形成的子序列。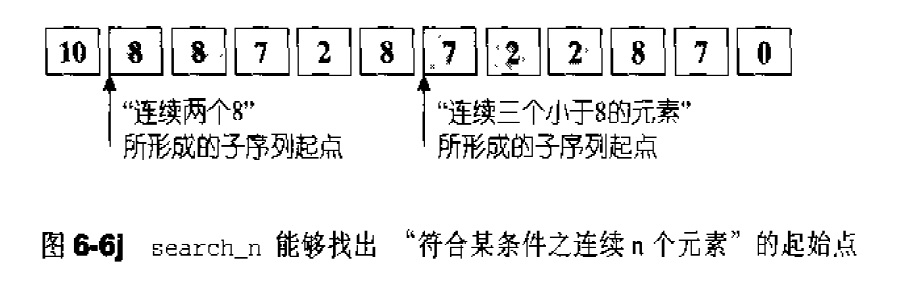
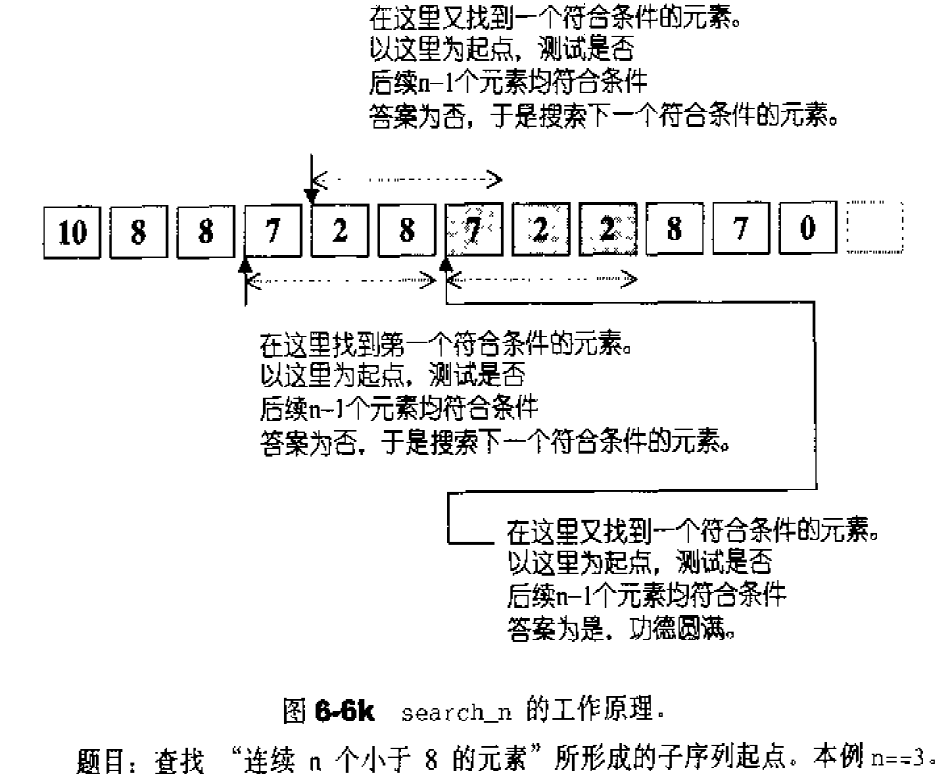
1 | template <class ForwardIterator, class Integer, class T> |
swap_range
将两个长度相同的序列交换。两个序列可以在同一容器,也可在不同容器。如果第一个序列长度小于第二个或者两个序列有重叠,结果不可预期。
返回第二个序列最后一个交换元素的下一位置1
2
3
4
5
6
7template <class ForwardIterator1, class ForwardIterator2>
ForwardIterator2 swap_ranges(ForwardIterator1 first1, ForwardIterator1 last1,
ForwardIterator2 first2) {
for ( ; first1 != last1; ++first1, ++first2)
iter_swap(first1, first2);
return first2;
}
transform
将仿函数作用于每一个元素身上,并以其结果产生出一个新序列1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17template <class InputIterator, class OutputIterator, class UnaryOperation>
OutputIterator transform(InputIterator first, InputIterator last,
OutputIterator result, UnaryOperation op) {
for ( ; first != last; ++first, ++result)
*result = op(*first);
return result;
}
template <class InputIterator1, class InputIterator2, class OutputIterator,
class BinaryOperation>
OutputIterator transform(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, OutputIterator result,
BinaryOperation binary_op) {
for ( ; first1 != last1; ++first1, ++first2, ++result)
*result = binary_op(*first1, *first2);
return result;
}
unique
移除相邻的重复元素。类似于remove,并不是真正移除,而是将不重复的元素重新赋值于区间上。因为区间大小并未改变,所以尾部会有残余数据。算法是稳定的,所有你保留下来的元素其相对位置不变。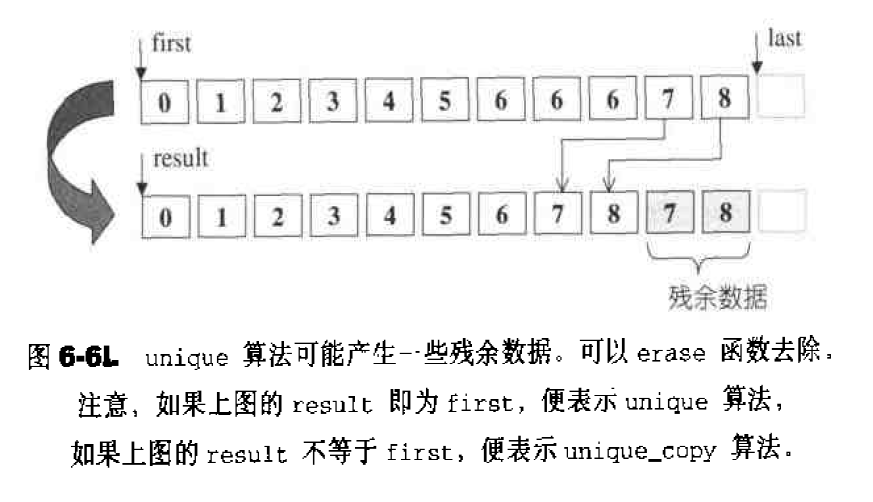
1 | template <class ForwardIterator> |
unique_copy
与unique类似,将结果复制到另一区间。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36template <class InputIterator, class OutputIterator>
inline OutputIterator unique_copy(InputIterator first, InputIterator last,
OutputIterator result) {
if (first == last) return result;
return __unique_copy(first, last, result, iterator_category(result));
}
template <class InputIterator, class ForwardIterator>
ForwardIterator __unique_copy(InputIterator first, InputIterator last,
ForwardIterator result, forward_iterator_tag) {
*result = *first;
while (++first != last)
if (*result != *first) *++result = *first;
return ++result;
}
template <class InputIterator, class OutputIterator>
inline OutputIterator __unique_copy(InputIterator first, InputIterator last,
OutputIterator result,
output_iterator_tag) {
return __unique_copy(first, last, result, value_type(first));
}
template <class InputIterator, class OutputIterator, class T>
OutputIterator __unique_copy(InputIterator first, InputIterator last,
OutputIterator result, T*) {
T value = *first;
*result = value;
while (++first != last)
if (value != *first) {
value = *first;
*++result = value;
}
return ++result;
}
lower_bound
lower_bound 二分查找的一个版本,在已排序区间中查找value。如果区间中有该元素,则返回迭代器,指向第一个该元素。如果没有改元素,则返回一个不小于value的元素。返回值为:在不破坏排序的情况下,可插入value的位置。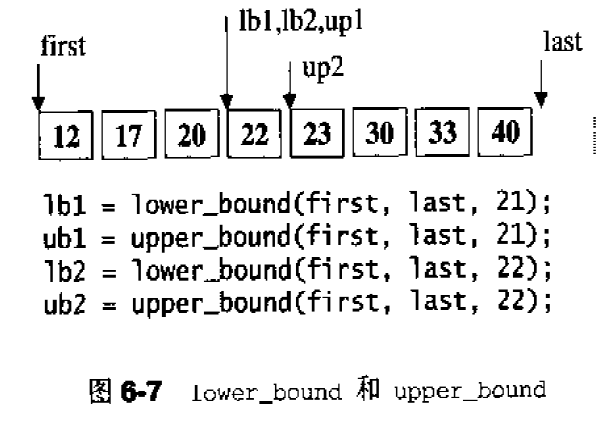
1 | template <class ForwardIterator, class T> |
upper_bound
upper_bound 和上述函数类似,寻找的是符合条件的位置的上限
1 | template <class ForwardIterator, class T> |
binary_search
算法binary_search是一种二分查找法,试图在已排序的[first, last)中寻找元素value。如果[first, last)内有等同于value的元素,便返回true, 否则返回false。
返回单纯的bool或许不能满足你,前面所介绍的lower_bound和upper_bound能够提供额外的信息。事实上binary_search便是利用lower_bound先找出“假设value存在的话,应该出现的位置”。然后再对比该位置上的值是 否为我们所要查找的目标,并返回对比结果。
正式地说,当且仅当(if and only if) [first, last)中存在一个迭代器i使*i < vlaue和value < *i皆不为真,返回true。
函数实现原理如下:在当前序列中,从尾端往前寻找两个相邻元素,前一个记为i,后一个记为ii,并且满足i < ii。然后再从尾端寻找另一个元素j,如果满足i < *j,即将第i个元素与第j个元素对调,并将第ii个元素之后(包括ii)的所有元素颠倒排序,即求出下一个序列了。1
2
3
4
5
6
7
8
9
10
11
12
13
14template <class ForwardIterator, class T>
bool binary_search(ForwardIterator first, ForwardIterator last,
const T& value) {
ForwardIterator i = lower_bound(first, last, value);
return i != last && !(value < *i);
}
template <class ForwardIterator, class T, class Compare>
bool binary_search(ForwardIterator first, ForwardIterator last, const T& value,
Compare comp) {
ForwardIterator i = lower_bound(first, last, value, comp);
return i != last && !comp(value, *i);
}
next_permutation/prev_permutation
STL中提供了2个计算排列组合关系的算法。分别是next_permucation和prev_permutaion。
next_permutation是用来计算下一个(next)字典序排列的组合,而prev_permutation用来计算上一个(prev)字典序的排列组合。
字典排序是指排列组合中,按照大小由小到大的排序,例如123的排列组着,字典排序为123,132,213,231,312,321。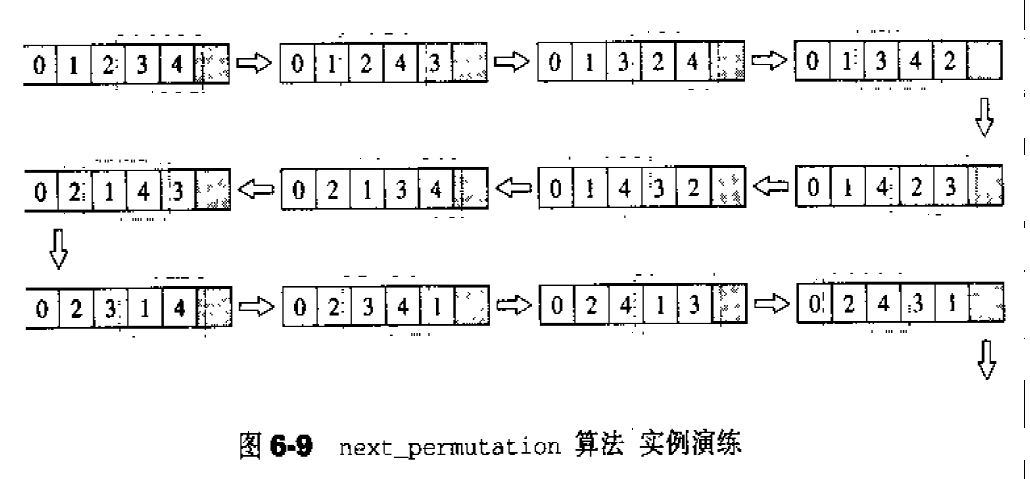
1 | template <class BidirectionalIterator> |
random_shuffle
将区间内的元素随机重排,获得N!种全排列中的任意一种
1 | template <class RandomAccessIterator, class Distance> |
partial_sort/partial_sort_copy
本算法接受一个middle迭代器(位于序列[first, last)之内),然后重新安排[first, last),使序列中的middle-first个最小元素以递增顺序排序, 置于[first, middle)内、其余last-middle个元素安置于[middle, last)中, 不保证有任何特定顺序。
使用sort算法,同样能保证较小的N个元素以递增顺序置于[first, first+N)中,
partial_sort的任务是找出middle-first个最小元素,因此,首先界定出区间[first, middle),并利用make_heap()将它组织成一个 max-heap,然后就可以将[middle, last)中的每一个元素拿来与max-heap的最大值比较(max-heap的最大值就在第一个元素身上,轻松可以获得):如果小于该最大值,则互换位置并保持max-heap状态。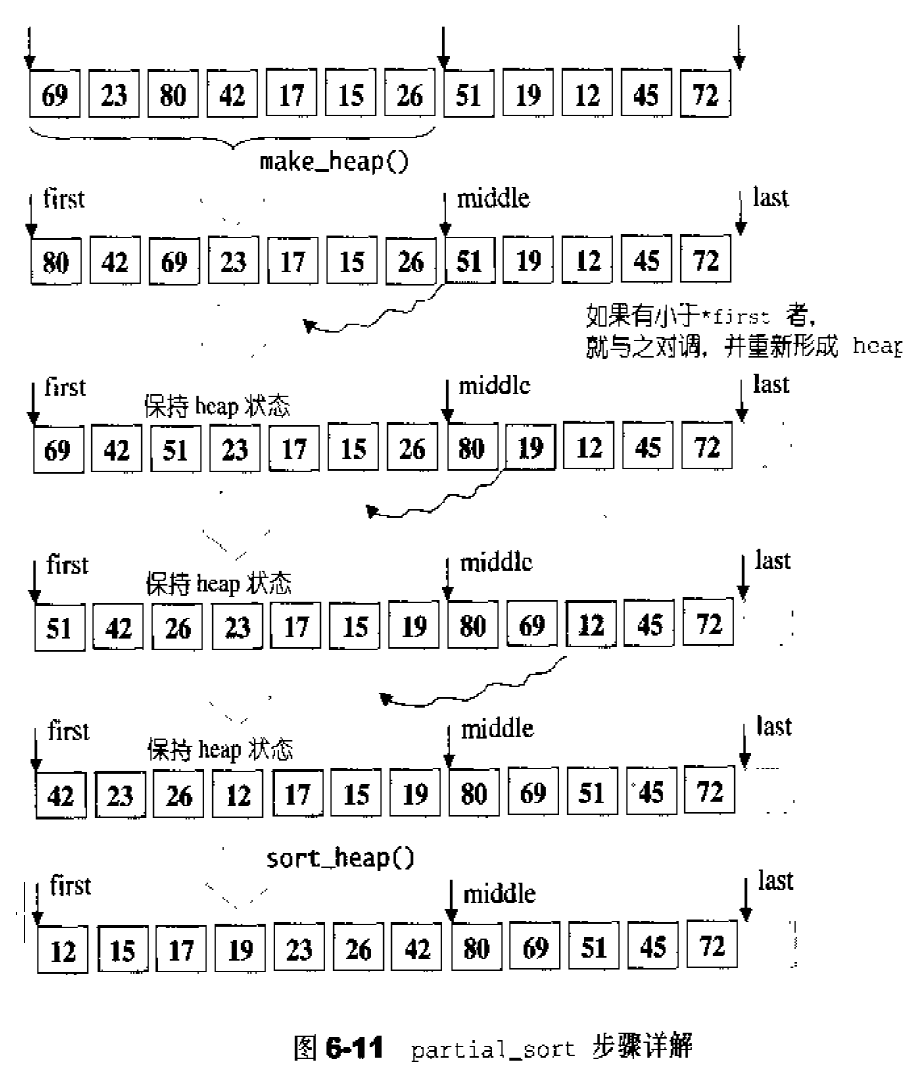
1 | template <class RandomAccessIterator, class T> |
partial_sort有一个姊妹,就是partial_sort_copy,它将(last-first)个最小元素排序后的结果置于(rsult_first, result_last)中。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68template <class InputIterator, class RandomAccessIterator, class Distance,
class T>
RandomAccessIterator __partial_sort_copy(InputIterator first,
InputIterator last,
RandomAccessIterator result_first,
RandomAccessIterator result_last,
Distance*, T*) {
if (result_first == result_last) return result_last;
RandomAccessIterator result_real_last = result_first;
while(first != last && result_real_last != result_last) {
*result_real_last = *first;
++result_real_last;
++first;
}
make_heap(result_first, result_real_last);
while (first != last) {
if (*first < *result_first)
__adjust_heap(result_first, Distance(0),
Distance(result_real_last - result_first), T(*first));
++first;
}
sort_heap(result_first, result_real_last);
return result_real_last;
}
template <class InputIterator, class RandomAccessIterator>
inline RandomAccessIterator
partial_sort_copy(InputIterator first, InputIterator last,
RandomAccessIterator result_first,
RandomAccessIterator result_last) {
return __partial_sort_copy(first, last, result_first, result_last,
distance_type(result_first), value_type(first));
}
template <class InputIterator, class RandomAccessIterator, class Compare,
class Distance, class T>
RandomAccessIterator __partial_sort_copy(InputIterator first,
InputIterator last,
RandomAccessIterator result_first,
RandomAccessIterator result_last,
Compare comp, Distance*, T*) {
if (result_first == result_last) return result_last;
RandomAccessIterator result_real_last = result_first;
while(first != last && result_real_last != result_last) {
*result_real_last = *first;
++result_real_last;
++first;
}
make_heap(result_first, result_real_last, comp);
while (first != last) {
if (comp(*first, *result_first))
__adjust_heap(result_first, Distance(0),
Distance(result_real_last - result_first), T(*first),
comp);
++first;
}
sort_heap(result_first, result_real_last, comp);
return result_real_last;
}
template <class InputIterator, class RandomAccessIterator, class Compare>
inline RandomAccessIterator
partial_sort_copy(InputIterator first, InputIterator last,
RandomAccessIterator result_first,
RandomAccessIterator result_last, Compare comp) {
return __partial_sort_copy(first, last, result_first, result_last, comp,
distance_type(result_first), value_type(first));
}
sort
STL所提供的各式各样算法中,sort()是最复杂最庞大的一个,这个算法接受两个RandomAccessIterator(随机存取迭代器),然后将区间内的所有元素以渐增方式由小到大重新排列,第二个版本则允许用户指定一个仿函数(functor), 作为排序标准。STL的所有关系型容器(associative containers)都拥有自动排序功能(底层结构采用RB - tree),所以不需要用到这个sort算法。至于序列式容器(sequence containers)中的stacks、queue和priority-queue都有特别的出入口,不允许用户对元素排序。剩下vector、 deque和list,前两者的迭代器属于RandormAccessIterators,适合使用sort算法,list的迭代器则属于BidirectionalIterators,不在STL标准之列的slist,其迭代器属于ForwardIterators,都不适合使用sort算法。如果要对list或slist排序,应该使用它们自己提供的member functions sort()。
STL的sort算法,数据量大时采用Quick分段递归排序,一旦分段后的数据量小于某个门槛,为了避免QuickSort的递归调用带来过大的额外负荷,就改用InsertionSort.如果递归层次过深,还会改用HeapSort,以下分别介绍OuickSort和lnsertionSort,然后再整合起来介绍STL sort。
InsertionSort
Insertionsort以双层循环的形式进行,外循环遍历整个序列,每次迭代决定出一个子区间;内循环遍历子区间,将子区间内的每一个“逆转对(inversion)”倒转过来。“逆转对”是指任何两个迭代器i、j,i < j而*i > *j。一旦不存在“逆转对”,序列即排序完毕。这个算法的复杂度为O(N2),说起来并不理想,但是当数据量很少时,却有不错的效果,原因是实现上有一些技巧,而且不像其它较为复杂的排序算法有着诸如递归调用等操作带来的额外负荷。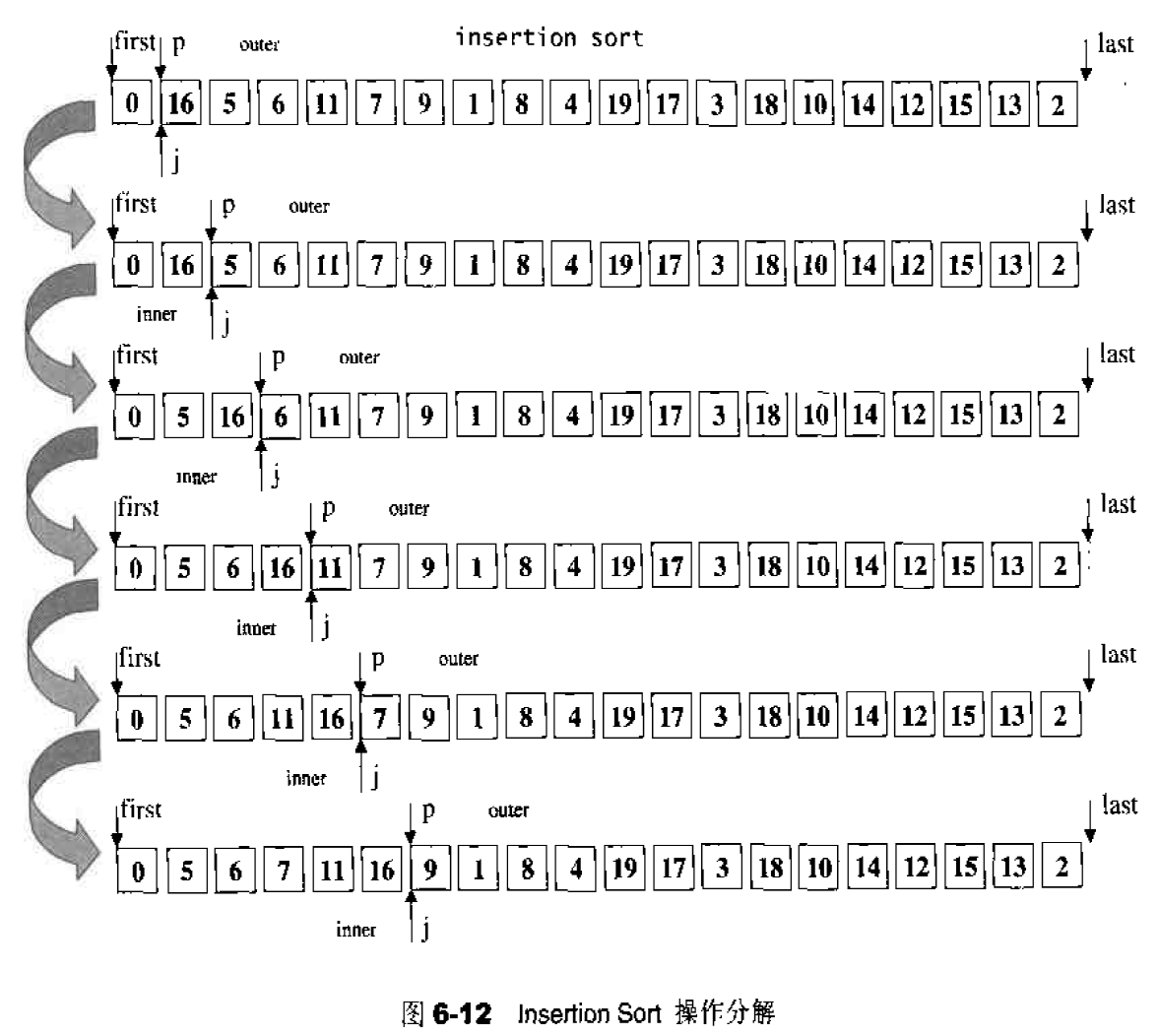
SGISTL的lnsertionsort两个版本,版本一使用以渐增力式排序,也就是说,以operator<为两元素比较的函数,版本二允许用户指定一个仿函数,作为两元素比较的函数。
1 | template <class RandomAccessIterator> |
上述函数之所以命名为unguarded_x是因为,一般的Insertion Sort在内循环原本需要做两次判断,判断是否相邻两元素是“逆转对”;同时也判断循环的行进是否超过边界。但由于上述所示的源代码会导致最小值必然在内循环子区间的最边缘,所以两个判断可合为一个判断,所以称为unguarded。省下一个判断操作,乍见之下无足轻重,但是在大数据量的情况下,影响还是可观的,毕竟这是一 个非常根本的算法核心,在大数据量的情况,执行次数非常惊人。
Quick Sort
如果我们拿Insertion Sort来处理大量数据,其O(N2)的复杂度就令人摇头了。大数据量的情形下有许多更好的排序算法可供选择。正如其名称所昭示,Quick Sort 是目前已知最快的排序法,平均复杂度为O(N logN),最坏情况下将达O(N2),不过IntroSort(极类似median-of-three QuickSort的一种排序算法〕可将最坏情况(分割时产生一个空的子区间)推进到O(N logN)。
快排的步骤:
- 如果s的元素是0或者1,结束
- 取s 中任何一个元素,当做枢纽v
- 将s 分割为l r两部分,使l内的元素都小于等于v,r内的元素都大于v
- 对l,r递归执行快排
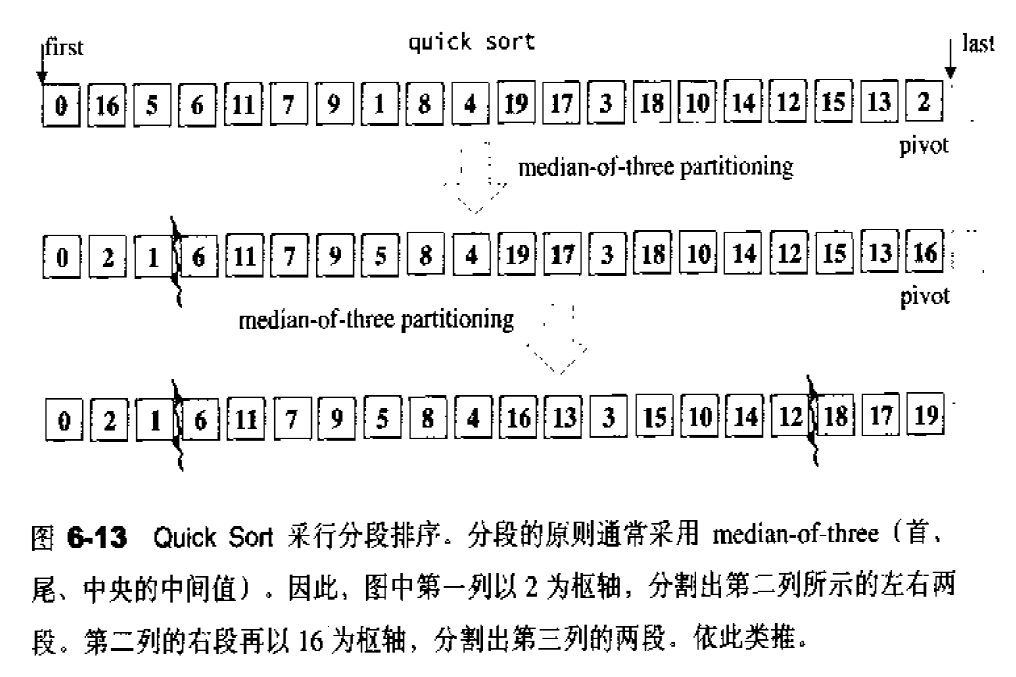
media-of-three partitioning 取头尾中央三个位置的值的中值作为v
1 | template <class T> |
Partitioining(分割)方法不只一种,以下叙述既简单又有良好成效的做法。令头端迭代器first向尾部移动,尾端迭代器last向头部移动。当*first大于或等于枢轴时 就停下来,当*last小于或等于枢轴时也停下来,然后检验两个迭代器是否交错。如果first仍然在左而last仍然在右,就将两者元素互换,然后各自调整一个位置(向中央逼近),再继续进行相同的行为。如果发现两个迭代器交错了,表示整个序列已经调整完毕,以此时的first为轴,将序列分为左右两半,左半部所有元素值都小于或等于枢轴,右半部所有元素值都大于或等于枢轴。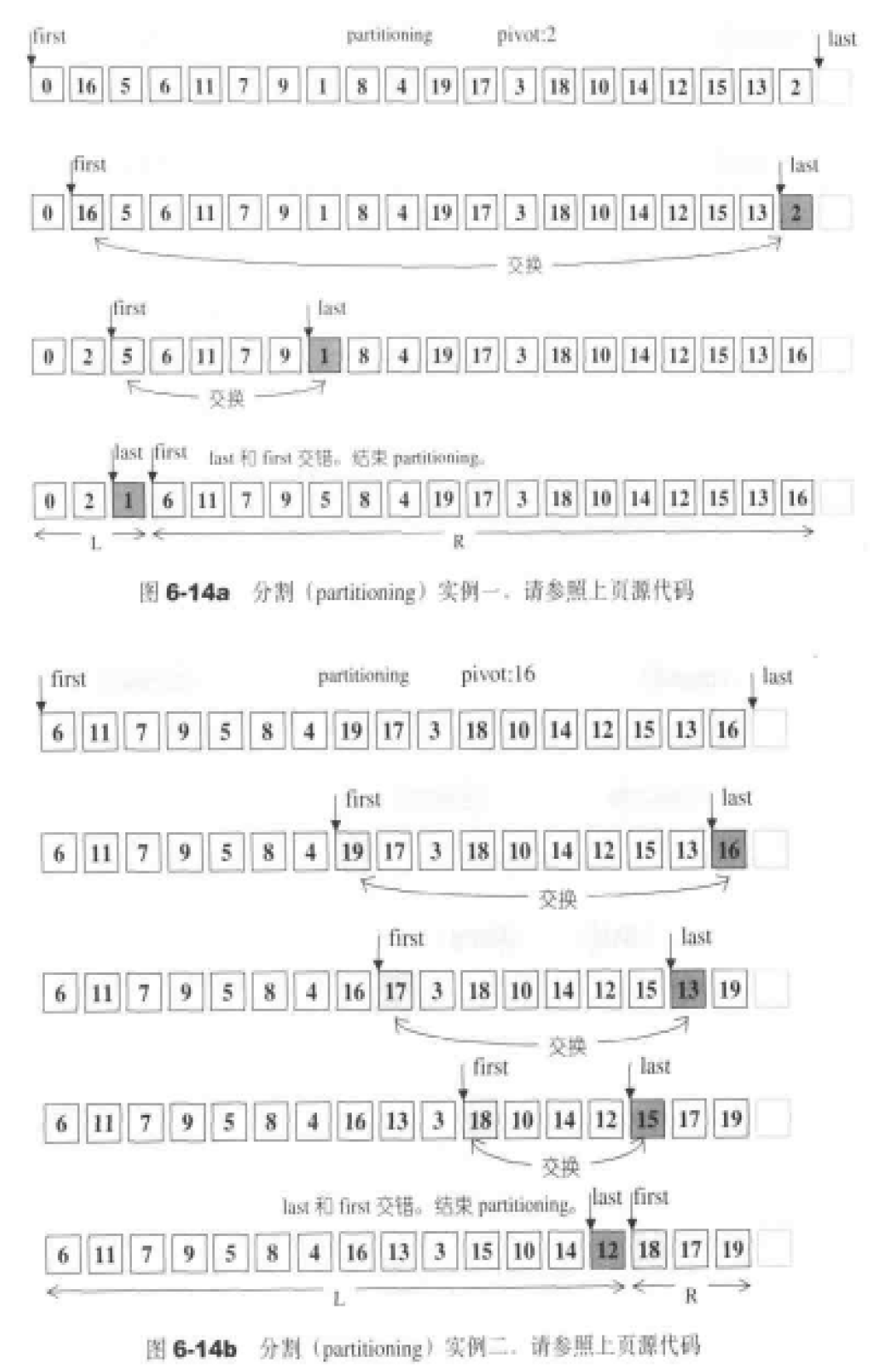
1 | template <class RandomAccessIterator, class T> |
面对一个只有十来个元素的小型序列,使用像Quick Sort这样复杂而需要大量运算的排序法不划算,在小数据量的情况下,甚至简单如Insertion Sort者也可能快过Quick Sort―因为Quick Sort会为了极小的子序 列而产生许多的函数递归调用。鉴于这种情况,适度评估序列的大小,然后决定采用Quick Sort或Insertion Sort是值得采纳的一种优化措施。然而究竟多小的序列才应该断然改用Insertion Sort呢?并无定论,5-2O都可能导致差不多的结果。实际的最佳值因设备而异。
final insertion sort 优化措施永不嫌多,只要我们不是贸然行事。如果我们令某个大小以下的序列滞留在“几近排序但尚未完成”的状态、最后再以一次Insertion Sort将所有这些“几近排序但尚未竞全功”的子序列做一次完整的排序,其效率一般认为会比“将所有子序列彻底排序”更好。这是因为Insertion Sort在面对“几近排序”的序列时、有很好的表现。
introsort:不当的枢轴选择导致Quick Sort恶化为O(N2),Introspective Sorting(内省排序)当分割行为有恶化为二次行为时,能够自我侦测,转而改用Heap Sort。
1 | template <class RandomAccessIterator> |
其中的__lg()用于控制分割恶化的情况。1
2
3
4
5
6template <class Size>
inline Size __lg(Size n) {
Size k;
for (k = 0; n > 1; n >>= 1) ++k;
return k;
}
元素为40个时,__introsort_loop()的最后一个参数为5*2,意思是最多允许10层分割。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36template <class RandomAccessIterator, class T, class Size>
void __introsort_loop(RandomAccessIterator first,
RandomAccessIterator last, T*,
Size depth_limit) {
while (last - first > __stl_threshold) {
if (depth_limit == 0) {
partial_sort(first, last, last);
return;
}
--depth_limit;
RandomAccessIterator cut = __unguarded_partition
(first, last, T(__median(*first, *(first + (last - first)/2),
*(last - 1))));
__introsort_loop(cut, last, value_type(first), depth_limit);
last = cut;
}
}
template <class RandomAccessIterator, class T, class Size, class Compare>
void __introsort_loop(RandomAccessIterator first,
RandomAccessIterator last, T*,
Size depth_limit, Compare comp) {
while (last - first > __stl_threshold) {
if (depth_limit == 0) {
partial_sort(first, last, last, comp);
return;
}
--depth_limit;
RandomAccessIterator cut = __unguarded_partition
(first, last, T(__median(*first, *(first + (last - first)/2),
*(last - 1), comp)), comp);
__introsort_loop(cut, last, value_type(first), depth_limit, comp);
last = cut;
}
}
函数一开始就判断序列大小,__stl_threshold是个全局整型常数,定义如下:1
const int __stl_threshold - 16;
通过元素个数检验之后,再检查分割层次,如果分割层次超过指定值,就改用partition_sort()。都通过了这些检验之后,便进入与Quick Sort完全相同的程序:以median-of-3方法确定枢轴位置,然后调用__unguarded_partition()找出分割点,然后针对左右段落递归进行IntroSort
当__introsort_loop()结束,[first, last)内有多个“元素个数少于16”的子序列,每个子序列都有相当程度的排序,但尚未完全排序(因为元素个数一旦小于__stl_threshold,就被中止进一步的排序操作。回到母函数sort(),再进入final_insertion_sort()。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50template <class RandomAccessIterator>
void __final_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last) {
if (last - first > __stl_threshold) {
__insertion_sort(first, first + __stl_threshold);
__unguarded_insertion_sort(first + __stl_threshold, last);
}
else
__insertion_sort(first, last);
}
template <class RandomAccessIterator, class Compare>
void __final_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last, Compare comp) {
if (last - first > __stl_threshold) {
__insertion_sort(first, first + __stl_threshold, comp);
__unguarded_insertion_sort(first + __stl_threshold, last, comp);
}
else
__insertion_sort(first, last, comp);
}
template <class RandomAccessIterator, class T>
void __unguarded_insertion_sort_aux(RandomAccessIterator first,
RandomAccessIterator last, T*) {
for (RandomAccessIterator i = first; i != last; ++i)
__unguarded_linear_insert(i, T(*i));
}
template <class RandomAccessIterator>
inline void __unguarded_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last) {
__unguarded_insertion_sort_aux(first, last, value_type(first));
}
template <class RandomAccessIterator, class T, class Compare>
void __unguarded_insertion_sort_aux(RandomAccessIterator first,
RandomAccessIterator last,
T*, Compare comp) {
for (RandomAccessIterator i = first; i != last; ++i)
__unguarded_linear_insert(i, T(*i), comp);
}
template <class RandomAccessIterator, class Compare>
inline void __unguarded_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last,
Compare comp) {
__unguarded_insertion_sort_aux(first, last, value_type(first), comp);
}
equal_range
是二分查找法的一个版本,试图在已排序的[first, last)中寻找value,它返回一对迭代器i和j,其中i是在不破坏次序的前提下,value可插人的第一个位置(亦即lower_bound),j则是在不破坏次序的前提下,value可插人的最后一个位置(亦即upper_bound)。因此,[i ,j)内的每个元素都等同于value,而且[i, j)是[fisrt, last)之中符合此一性质的最大子区间。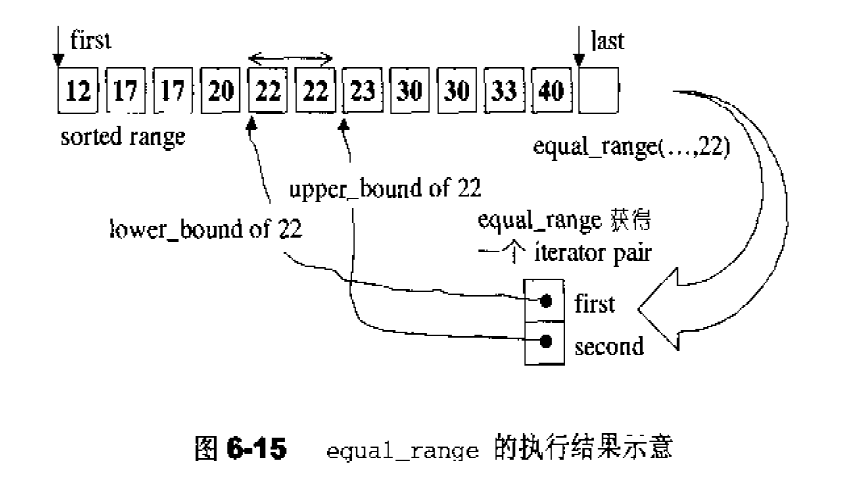
1 | template <class ForwardIterator, class T, class Distance> |
inplace_merge
应用于有序区间,把两个连接在一起且各自有序的序列合并成一个序列,仍保持有序。稳定操作,保持相对次序不变,如果有相同元素,第一个序列的排在前面。内部实现时根据有无缓冲不同处理。
1 | template <class BidirectionalIterator> |
如果有缓冲区的话效率会好很多:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80template <class BidirectionalIterator, class Distance, class Pointer>
void __merge_adaptive(BidirectionalIterator first,
BidirectionalIterator middle,
BidirectionalIterator last, Distance len1, Distance len2,
Pointer buffer, Distance buffer_size) {
if (len1 <= len2 && len1 <= buffer_size) {
Pointer end_buffer = copy(first, middle, buffer);
merge(buffer, end_buffer, middle, last, first);
}
else if (len2 <= buffer_size) {
Pointer end_buffer = copy(middle, last, buffer);
__merge_backward(first, middle, buffer, end_buffer, last);
}
else {
BidirectionalIterator first_cut = first;
BidirectionalIterator second_cut = middle;
Distance len11 = 0;
Distance len22 = 0;
if (len1 > len2) {
len11 = len1 / 2;
advance(first_cut, len11);
second_cut = lower_bound(middle, last, *first_cut);
distance(middle, second_cut, len22);
}
else {
len22 = len2 / 2;
advance(second_cut, len22);
first_cut = upper_bound(first, middle, *second_cut);
distance(first, first_cut, len11);
}
BidirectionalIterator new_middle =
__rotate_adaptive(first_cut, middle, second_cut, len1 - len11,
len22, buffer, buffer_size);
__merge_adaptive(first, first_cut, new_middle, len11, len22, buffer,
buffer_size);
__merge_adaptive(new_middle, second_cut, last, len1 - len11,
len2 - len22, buffer, buffer_size);
}
}
template <class BidirectionalIterator, class Distance, class Pointer,
class Compare>
void __merge_adaptive(BidirectionalIterator first,
BidirectionalIterator middle,
BidirectionalIterator last, Distance len1, Distance len2,
Pointer buffer, Distance buffer_size, Compare comp) {
if (len1 <= len2 && len1 <= buffer_size) {
Pointer end_buffer = copy(first, middle, buffer);
merge(buffer, end_buffer, middle, last, first, comp);
}
else if (len2 <= buffer_size) {
Pointer end_buffer = copy(middle, last, buffer);
__merge_backward(first, middle, buffer, end_buffer, last, comp);
}
else {
BidirectionalIterator first_cut = first;
BidirectionalIterator second_cut = middle;
Distance len11 = 0;
Distance len22 = 0;
if (len1 > len2) {
len11 = len1 / 2;
advance(first_cut, len11);
second_cut = lower_bound(middle, last, *first_cut, comp);
distance(middle, second_cut, len22);
}
else {
len22 = len2 / 2;
advance(second_cut, len22);
first_cut = upper_bound(first, middle, *second_cut, comp);
distance(first, first_cut, len11);
}
BidirectionalIterator new_middle =
__rotate_adaptive(first_cut, middle, second_cut, len1 - len11,
len22, buffer, buffer_size);
__merge_adaptive(first, first_cut, new_middle, len11, len22, buffer,
buffer_size, comp);
__merge_adaptive(new_middle, second_cut, last, len1 - len11,
len2 - len22, buffer, buffer_size, comp);
}
}
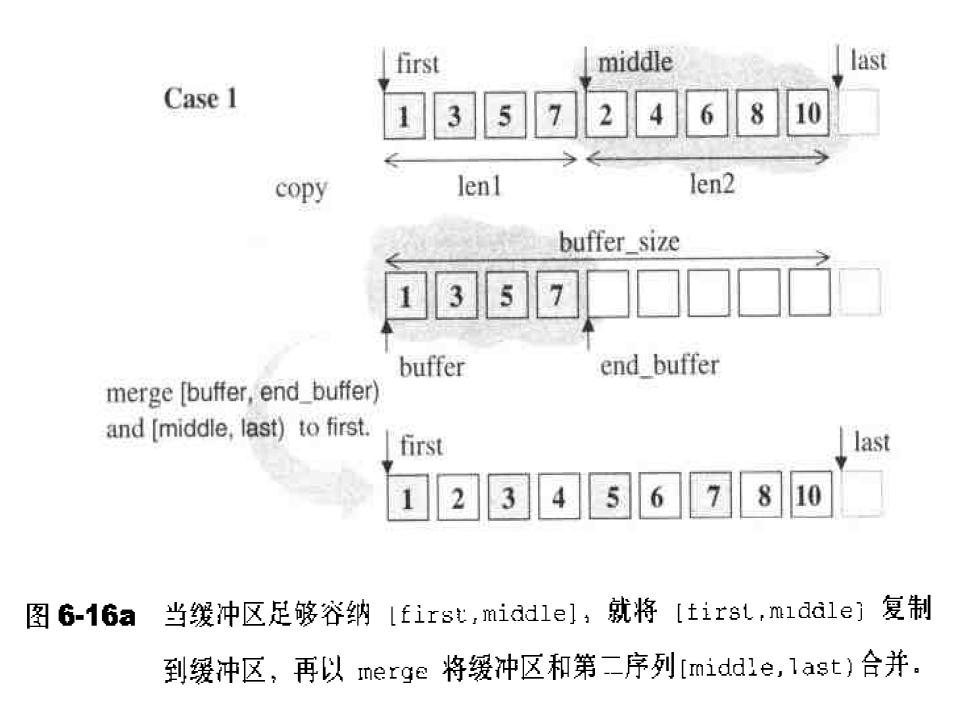
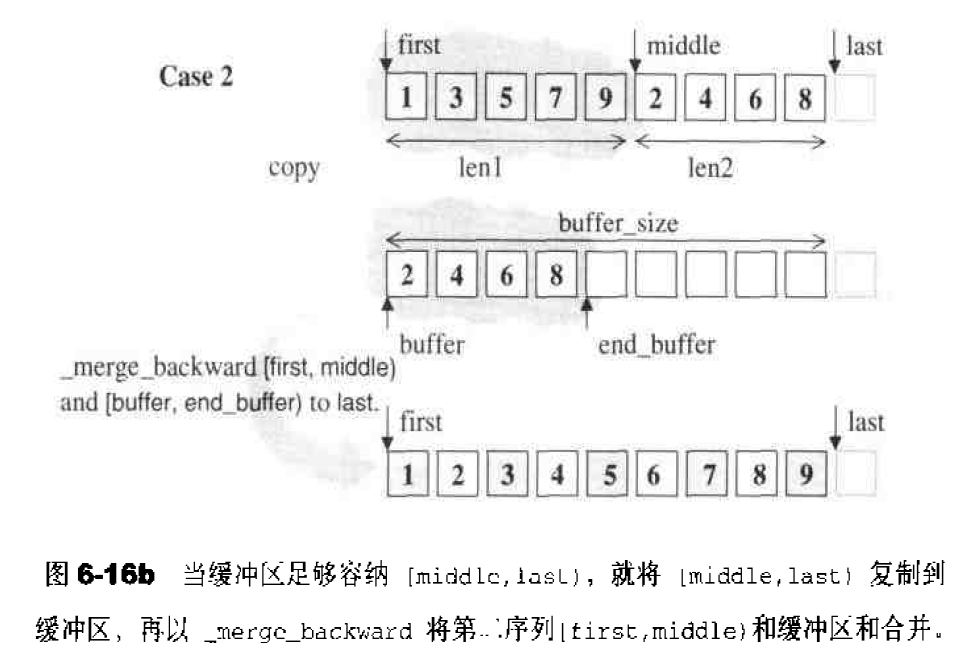
缓冲区不足以容纳一个序列时,以递归分割的方式,让处理长度减半,看能否容纳于缓冲区中。
然后执行旋转操作:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24template <class BidirectionalIterator1, class BidirectionalIterator2,
class Distance>
BidirectionalIterator1 __rotate_adaptive(BidirectionalIterator1 first,
BidirectionalIterator1 middle,
BidirectionalIterator1 last,
Distance len1, Distance len2,
BidirectionalIterator2 buffer,
Distance buffer_size) {
BidirectionalIterator2 buffer_end;
if (len1 > len2 && len2 <= buffer_size) {
buffer_end = copy(middle, last, buffer);
copy_backward(first, middle, last);
return copy(buffer, buffer_end, first);
} else if (len1 <= buffer_size) {
buffer_end = copy(first, middle, buffer);
copy(middle, last, first);
return copy_backward(buffer, buffer_end, last);
} else {
rotate(first, middle, last);
advance(first, len2);
return first;
}
}
nth_element
重新排列区间,使迭代器nth 所指向的元素与整个区间内排序后,同一位置的元素同值。保证nth-last 中没有任何一个元素不大于 first-nth 中的元素
不断用首尾中央三点中值为枢纽之分割法,将序列分割成更小的子序列,如果nth 落入左子序列, 就继续分割左子序列,如果落在右子序列就分割右子序列,最后对小于3的序列进行排序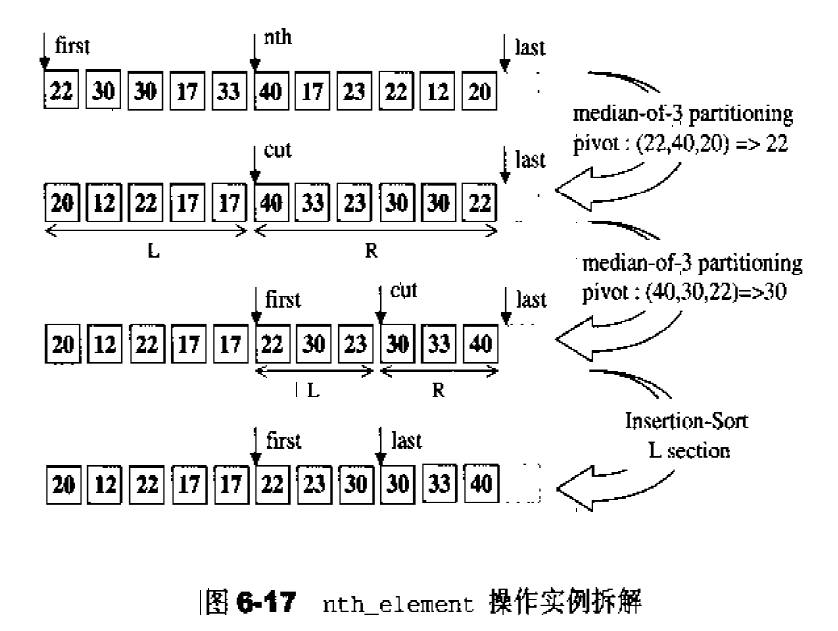
1 | template <class RandomAccessIterator, class T> |
merge_sort
归并排序,需要额外的内存,内存之间的拷贝需要时间,但是实现简单。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35template <class RandomAccessIterator1, class RandomAccessIterator2,
class Distance>
void __merge_sort_loop(RandomAccessIterator1 first,
RandomAccessIterator1 last,
RandomAccessIterator2 result, Distance step_size) {
Distance two_step = 2 * step_size;
while (last - first >= two_step) {
result = merge(first, first + step_size,
first + step_size, first + two_step, result);
first += two_step;
}
step_size = min(Distance(last - first), step_size);
merge(first, first + step_size, first + step_size, last, result);
}
template <class RandomAccessIterator1, class RandomAccessIterator2,
class Distance, class Compare>
void __merge_sort_loop(RandomAccessIterator1 first,
RandomAccessIterator1 last,
RandomAccessIterator2 result, Distance step_size,
Compare comp) {
Distance two_step = 2 * step_size;
while (last - first >= two_step) {
result = merge(first, first + step_size,
first + step_size, first + two_step, result, comp);
first += two_step;
}
step_size = min(Distance(last - first), step_size);
merge(first, first + step_size, first + step_size, last, result, comp);
}
仿函数
仿函数概述
仿函数也叫作函数对象,是一种具有函数特质的对象,调用者可以像函数一样地调用这些对象,被调用者则以对象所定义的function call operator扮演函数的实质角色。就实现观点而言,仿函数其实上就是一个“行为类似函数”的对象。为了“行为类似函数”,其类别定义中必须自定义function call 运算子(operator())。STL中仿函数代替函数指针的原因在于函数指针不能满足STL对抽象性的要求,也不能满足软件积木的要求,函数指针无法与STL其他组件搭配。
STL仿函数的分类,若以操作数的个数划分,可以分为一元和二元仿函数;若以功能划分,可以分为算术运算(Arithmetic)、关系运算(Rational)、逻辑运算(Logical)三大类。其头文件为<functional>。
可配接的关键
STL仿函数应该有能力被函数适配器修饰,就像积木一样串接,然而,为了拥有配接能力,每个仿函数都必须定义自己的associative types(主要用来表示函数参数类型和返回值类型),就想迭代器如果要融入整个STL大家庭,也必须按照规定定义自己的5个相应的类型一样,这些assocaiative type是为了让配接器可以取得仿函数的某些信息,当然,这些associative type都只是一些typedef,所有必要操作在编译器就全部完成了,对程序的执行效率没有任何影响,不会带来额外的负担。
仿函数的相应类型主要用来表现函数参数类型和传回值类型,为了方便起见<stl_functional.h>定义了两个类classes,分别代表一元仿函数和二元仿函数。其中没有任何data members或member functions,唯有一些类型定义,任何仿函数只要依个人需求选择继承其中一个class,便自动拥有了那些相应类型,也自动拥有了配接能力。
unary_function
unary_function用来呈现一元函数的参数类型和返回值类型。1
2
3
4
5
6//STL规定,每一个Adaptable Unary Function都应继承此类别
template <class Arg, class Result>
struct unary_function {
typedef Arg argument_type;
typedef Result result_type;
};
一旦某个仿函数继承了unary_function,其用户便可以这样取得仿函数的参数类型:1
2
3
4
5
6
7
8
9
10
11
12
13
14template <class T>
struct negate : public unary_function<T, T> {
T operator()(const T& x) const { return -x; }
};
// 以下配接器用来表示某个仿函数的逻辑负值
template <class Predicate>
class unary_negate
...
public:
bool operator()(const typename Predicate::argument_type& x) const {
...
}
};
binary_function
binary_function用来呈现二元函数的第一参数型别、第二参数型别及返回值型别。1
2
3
4
5
6
7//STL规定,每一个Adaptable Binary Function都应继承此类别
template <class Arg1, class Arg2, class Result>
struct binary_function {
typedef Arg1 first_argument_type;
typedef Arg2 second_argument_type;
typedef Result result_type;
};
一旦某个仿函数继承了binary_function,其用户便可以这样取得仿函数的参数类型:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17template <class T>
struct plus : public binary_function<T, T, T> {
T operator()(const T& x, const T& y) const { return x+y; }
};
// 以下配接器用来表示某个仿函数的逻辑负值
template <class Operation>
class binder1st
...
protected:
Operation op;
typename Operation::first_argument_type value;
public:
typename Operation::result_type operator()(const typename Operation::second_argument_type& x) const {
...
}
};
算术类仿函数
STL内建算术类仿函数:加法:plus<T>,减法:minus<T>,乘法:multiplies<T>,除法:divides<T>,取模:modulus<T>,取反:negate<T>。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31template <class T>
struct plus : public binary_function<T,T,T> {
T operator()(const T& x, const T& y) const { return x + y; }
};
template <class T>
struct minus : public binary_function<T,T,T> {
T operator()(const T& x, const T& y) const { return x - y; }
};
template <class T>
struct multiplies : public binary_function<T,T,T> {
T operator()(const T& x, const T& y) const { return x * y; }
};
template <class T>
struct divides : public binary_function<T,T,T> {
T operator()(const T& x, const T& y) const { return x / y; }
};
template <class T>
struct modulus : public binary_function<T,T,T>
{
T operator()(const T& x, const T& y) const { return x % y; }
};
template <class T>
struct negate : public unary_function<T,T>
{
T operator()(const T& x) const { return -x; }
};
测试程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
using namespace std;
int main() {
// 产生仿函数实体
plus<int> plusobj;
minus<int> minusobj;
multiplies<int> multipliesobj;
divides<int> dividesobj;
modulus<int> modulusobj;
negate<int> negateobj;
// 使用对象完成函数功能
cout << plusobj(3, 5) << endl; //8
cout << minusobj(3, 5) << endl; //-2
cout << multipliesobj(3, 5) << endl; //15
cout << dividesobj(3, 5) << endl; //0
cout << modulusobj(3, 5) << endl; //3
cout << negateobj(3) << endl; //-3
// 直接使用仿函数的临时对象完成函数功能
cout << plus<int>()(3, 5) << endl;
cout << minus<int>()(3, 5) << endl;
cout << multiplies<int>()(3, 5) << endl;
cout << divides<int>()(3, 5) << endl;
cout << modulus<int>()(3, 5) << endl;
cout << negate<int>()(3) << endl;
return 0;
}
不会这么单纯的使用仿函数,主要用途是搭配STL算法,以下式子表示要以1为基本元素,对vector iv中的每个元素进行乘法操作:1
accumulate(iv.begin(), iv.end(), 1, multiplies<int>());
证同元素(identity element)
所谓“运算op的证同元素(identity element)”,意思是数值A若与该元素做op运算会得到A自己。加法的证同元素为0,因为任何元素加上0仍为自己。乘法的证同元素为1,因为任何元素乘以1仍为自己。
请注意,这些函数并非STL标准规格中的一员。但许多STL实现都有它们:1
2
3
4
5template <class T>
inline T identity_element(plus<T>) { return T(0);} //SGI STL并未实际运用这个函数
template <class T>
inline T identity_element(muitiplies<T>) { return T(1);}
关系运算类仿函数
STL内建关系类仿函数:等于:equal_to<T>,不等于:not_equal_to<T>,大于:greater<T>,大于等于:greater_equal<T>,小于:less<T>,小于等于:less_equal<T>。
1 | template <class T> |
测试程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
using namespace std;
int main() {
// 产生仿函数实体
equal_to<int> equal_to_obj;
not_equal_to<int> not_equal_to_obj;
greater<int> greater_obj;
greater_equal<int> greater_equal_obj;
less<int> less_obj;
less_equal<int> less_equal_obj;
// 使用对象完成函数功能
cout << equal_to_obj(3, 5) << endl; //0
cout << not_equal_to_obj(3, 5) << endl; //1
cout << greater_obj(3, 5) << endl; //0
cout << greater_equal_obj(3, 5) << endl; //0
cout << less_obj(3, 5) << endl; //1
cout << less_equal_obj(3, 5) << endl; //1
// 直接使用仿函数的临时对象完成函数功能
cout << equal_to<int>()(3, 5) << endl;
cout << not_equal_to<int>()(3, 5) << endl;
cout << greater<int>()(3, 5) << endl;
cout << greater_equal<int>()(3, 5) << endl;
cout << less<int>()(3, 5) << endl;
cout << less_equal<int>()(3, 5) << endl;
return 0;
}
不会这么单纯的使用仿函数,主要用途是搭配STL算法,以下式子表示要以递增次序对vector iv排序:1
sort(iv.begin(), iv.end(), greater<int>());
逻辑运算类仿函数
STL内建逻辑类仿函数:逻辑运算And:logical_and<T>,逻辑运算Or:logical_or<T>,逻辑运算Not:logical_not<T>。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17template <class T>
struct logical_and : public binary_function<T,T,bool>
{
bool operator()(const T& x, const T& y) const { return x && y; }
};
template <class T>
struct logical_or : public binary_function<T,T,bool>
{
bool operator()(const T& x, const T& y) const { return x || y; }
};
template <class T>
struct logical_not : public unary_function<T,bool>
{
bool operator()(const T& x) const { return !x; }
};
测试程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
using namespace std;
int main() {
// 产生仿函数实体
logical_and<int> and_obj;
logical_or<int> or_obj;
logical_not<int> not_obj;
// 使用对象完成函数功能
cout << and_obj(true, true) << endl; //1
cout << or_obj(true, false) << endl; //1
cout << not_obj(true) << endl; //0
// 直接使用仿函数的临时对象完成函数功能
cout << logical_and<int>()(true, true) << endl;
cout << logical_or<int>()(true, false) << endl;
cout << logical_not<int>()(true) << endl;
return 0;
}
不会这么单纯的使用仿函数,主要用途是搭配STL算法。
证同、选择、投射
以下介绍的仿函数,都只是将其参数原封不动地传回。其中某些仿函数对传回的参数有刻意的选择,或者刻意的忽略。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47// 证同函数,任何函数经过后不会改变,用于set rb_tree keyOfValue op
// identity is an extensions: it is not part of the standard.
template <class _Tp>
struct _Identity : public unary_function<_Tp,_Tp> {
const _Tp& operator()(const _Tp& __x) const { return __x; }
};
template <class _Tp> struct identity : public _Identity<_Tp> {};
// 选择函数,返回pair第一元素,用于map rb_tree keyOfValue op
// select1st and select2nd are extensions: they are not part of the standard.
template <class _Pair>
struct _Select1st : public unary_function<_Pair, typename _Pair::first_type> {
const typename _Pair::first_type& operator()(const _Pair& __x) const {
return __x.first;
}
};
// 选择函数,返回pair第二元素
template <class _Pair>
struct _Select2nd : public unary_function<_Pair, typename _Pair::second_type>
{
const typename _Pair::second_type& operator()(const _Pair& __x) const {
return __x.second;
}
};
template <class _Pair> struct select1st : public _Select1st<_Pair> {};
template <class _Pair> struct select2nd : public _Select2nd<_Pair> {};
// 传回一个忽略另一个
// project1st and project2nd are extensions: they are not part of the standard
template <class _Arg1, class _Arg2>
struct _Project1st : public binary_function<_Arg1, _Arg2, _Arg1> {
_Arg1 operator()(const _Arg1& __x, const _Arg2&) const { return __x; }
};
template <class _Arg1, class _Arg2>
struct _Project2nd : public binary_function<_Arg1, _Arg2, _Arg2> {
_Arg2 operator()(const _Arg1&, const _Arg2& __y) const { return __y; }
};
template <class _Arg1, class _Arg2>
struct project1st : public _Project1st<_Arg1, _Arg2> {};
template <class _Arg1, class _Arg2>
struct project2nd : public _Project2nd<_Arg1, _Arg2> {};
配接器
配接器(adapters)在 STL 组件的灵活组合运用功能上,扮演着轴承、转换器的角色。Adapter 这个概念,事实上是一种设计模式。《Design Patterns》一书提到 23 个最普及的设计模式,其中对 adapter 样式的定义如下:将一个 class 的接口转换为另一个 class 的接口,使原本因接口不兼容而不能合作的 classes,可以一起运作。
配接器之概观与分类
STL 所提供的各种配接器中,改变容器(containers)接口者,我们称为 container adapter,改变迭代器(iterators)接口者,我们称之为 iterator adapter,改变仿函数(functors)接口者,我们称为 function adapter。
容器配接器
STL 提供的两个容器 queue 和 stack,其实都只不过是一种配接器,底层由deque构成。stack和queue是两个容器配接器,底层默认由deque构成。stack封住了所有的deque对外接口,只开放符合stack原则的几个函数;queue封住了所有的deque对外接口,只开放符合queue原则的几个函数。1
2
3
4
5
6
7
8
9
10
11
12
13template <class T ,class Sequence = deque<T>>
class stack {
protected:
Sequence c ; //底层容器
...
};
template <class T ,class Sequence = deque<T>>
class queue{
protected:
Sequence c ; //底层容器
...
};
迭代器配接器
STL 提供了许多应用于迭代器身上的配接器,包括 insert iterators,reverse iterators,iostream iterators。
insert iterators
insert iterators包括尾端插入的back_insert_iterator,头端插入的front_insert_iterator和可任意位置插入的insert_iterator。主要观念是,每个insert iterators内部都维护有一个容器;容器有自己的迭代器,当客户端对insert iterators做赋值操作时,就在insert iterators中转为对该容器的迭代器做插入操作,其他的迭代器功能则被关闭(例如operator++、operator—、operator*)。
迭代器源码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136// 迭代器配接器,用来将迭代器的赋值操作替换为插入操作
// 从容器尾端插入
template <class _Container>
class back_insert_iterator {
protected:
_Container* container; // 底层容器
public:
typedef _Container container_type;
typedef output_iterator_tag iterator_category; // 注意类型,只写
typedef void value_type;
typedef void difference_type;
typedef void pointer;
typedef void reference;
// 与容器绑定起来
explicit back_insert_iterator(_Container& __x) : container(&__x) {}
back_insert_iterator<_Container>&
operator=(const typename _Container::value_type& __value) {
container->push_back(__value); // 这里是替换成插入操作
return *this;
}
// 以下不起作用,关闭功能
back_insert_iterator<_Container>& operator*() { return *this; }
back_insert_iterator<_Container>& operator++() { return *this; }
back_insert_iterator<_Container>& operator++(int) { return *this; }
};
template <class _Container>
inline output_iterator_tag
iterator_category(const back_insert_iterator<_Container>&)
{
return output_iterator_tag();
}
// 辅助函数
template <class _Container>
inline back_insert_iterator<_Container> back_inserter(_Container& __x) {
return back_insert_iterator<_Container>(__x);
}
// 迭代器配接器,用来将迭代器的赋值操作替换为插入操作
// 从容器头端插入
// 不适用于vector,因为vector没有push_front
template <class _Container>
class front_insert_iterator {
protected:
_Container* container; // 底层容器
public:
typedef _Container container_type;
typedef output_iterator_tag iterator_category; // 注意类型,只写
typedef void value_type;
typedef void difference_type;
typedef void pointer;
typedef void reference;
explicit front_insert_iterator(_Container& __x) : container(&__x) {}
front_insert_iterator<_Container>&
operator=(const typename _Container::value_type& __value) {
container->push_front(__value); // 替换成插入操作
return *this;
}
// 关闭以下功能
front_insert_iterator<_Container>& operator*() { return *this; }
front_insert_iterator<_Container>& operator++() { return *this; }
front_insert_iterator<_Container>& operator++(int) { return *this; }
};
template <class _Container>
inline output_iterator_tag
iterator_category(const front_insert_iterator<_Container>&)
{
return output_iterator_tag();
}
// 辅助函数
template <class _Container>
inline front_insert_iterator<_Container> front_inserter(_Container& __x) {
return front_insert_iterator<_Container>(__x);
}
// 迭代器配接器,用来将迭代器的赋值操作替换为插入操作
// 从容器随机插入
template <class _Container>
class insert_iterator {
protected:
_Container* container; // 底层容器
typename _Container::iterator iter;
public:
typedef _Container container_type;
typedef output_iterator_tag iterator_category; // 类型只写
typedef void value_type;
typedef void difference_type;
typedef void pointer;
typedef void reference;
insert_iterator(_Container& __x, typename _Container::iterator __i)
: container(&__x), iter(__i) {}
insert_iterator<_Container>&
operator=(const typename _Container::value_type& __value) {
iter = container->insert(iter, __value); // 调用insert
++iter; // 使insert iterator永远随其目标贴身移动
return *this;
}
// 关闭功能
insert_iterator<_Container>& operator*() { return *this; }
insert_iterator<_Container>& operator++() { return *this; }
insert_iterator<_Container>& operator++(int) { return *this; }
};
template <class _Container>
inline output_iterator_tag
iterator_category(const insert_iterator<_Container>&)
{
return output_iterator_tag();
}
// 辅助函数
template <class _Container, class _Iterator>
inline
insert_iterator<_Container> inserter(_Container& __x, _Iterator __i)
{
typedef typename _Container::iterator __iter;
return insert_iterator<_Container>(__x, __iter(__i));
}
reverse iterators
reverse iterators将迭代器的移动行为倒转。 当迭代器被逆转,虽然实体位置不变,但逻辑位置必须改变,主要是为了配合迭代器区间的“前闭后开“习惯。
源码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75template <class _Iterator>
class reverse_iterator
{
protected:
_Iterator current;
public:
typedef typename iterator_traits<_Iterator>::iterator_category
iterator_category;
typedef typename iterator_traits<_Iterator>::value_type
value_type;
typedef typename iterator_traits<_Iterator>::difference_type
difference_type;
typedef typename iterator_traits<_Iterator>::pointer
pointer;
typedef typename iterator_traits<_Iterator>::reference
reference;
typedef _Iterator iterator_type;
typedef reverse_iterator<_Iterator> _Self;
public:
reverse_iterator() {}
explicit reverse_iterator(iterator_type __x) : current(__x) {}
reverse_iterator(const _Self& __x) : current(__x.current) {}
template <class _Iter>
reverse_iterator(const reverse_iterator<_Iter>& __x)
: current(__x.base()) {}
iterator_type base() const { return current; }
reference operator*() const {
_Iterator __tmp = current;
return *--__tmp;
}
pointer operator->() const { return &(operator*()); }
_Self& operator++() {
--current;
return *this;
}
_Self operator++(int) {
_Self __tmp = *this;
--current;
return __tmp;
}
_Self& operator--() {
++current;
return *this;
}
_Self operator--(int) {
_Self __tmp = *this;
++current;
return __tmp;
}
_Self operator+(difference_type __n) const {
return _Self(current - __n);
}
_Self& operator+=(difference_type __n) {
current -= __n;
return *this;
}
_Self operator-(difference_type __n) const {
return _Self(current + __n);
}
_Self& operator-=(difference_type __n) {
current += __n;
return *this;
}
reference operator[](difference_type __n) const { return *(*this + __n); }
};
stream iterators
stream iterators可以将迭代器绑定到某个stream对象身上。绑定一个istream object,其实就是在istream iterator内部维护一个istream member,客户端对这个迭代器做的operator++操作,会被导引调用内部所含的那个istream member的输入操作。绑定一个ostream object,就是在ostream iterator内部维护一个ostream member,客户端对这个迭代器做的operator=操作,会被导引调用内部所含的那个ostream member的输出操作。
源码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78template <class _Tp,
class _CharT = char, class _Traits = char_traits<_CharT>,
class _Dist = ptrdiff_t>
class istream_iterator {
public:
typedef _CharT char_type;
typedef _Traits traits_type;
typedef basic_istream<_CharT, _Traits> istream_type;
typedef input_iterator_tag iterator_category;
typedef _Tp value_type;
typedef _Dist difference_type;
typedef const _Tp* pointer;
typedef const _Tp& reference;
istream_iterator() : _M_stream(0), _M_ok(false) {}
istream_iterator(istream_type& __s) : _M_stream(&__s) { _M_read(); }
reference operator*() const { return _M_value; }
pointer operator->() const { return &(operator*()); }
istream_iterator& operator++() {
_M_read();
return *this;
}
istream_iterator operator++(int) {
istream_iterator __tmp = *this;
_M_read();
return __tmp;
}
bool _M_equal(const istream_iterator& __x) const
{ return (_M_ok == __x._M_ok) && (!_M_ok || _M_stream == __x._M_stream); }
private:
istream_type* _M_stream;
_Tp _M_value;
bool _M_ok;
void _M_read() {
_M_ok = (_M_stream && *_M_stream) ? true : false;
if (_M_ok) {
*_M_stream >> _M_value;
_M_ok = *_M_stream ? true : false;
}
}
};
template <class _Tp,
class _CharT = char, class _Traits = char_traits<_CharT> >
class ostream_iterator {
public:
typedef _CharT char_type;
typedef _Traits traits_type;
typedef basic_ostream<_CharT, _Traits> ostream_type;
typedef output_iterator_tag iterator_category;
typedef void value_type;
typedef void difference_type;
typedef void pointer;
typedef void reference;
ostream_iterator(ostream_type& __s) : _M_stream(&__s), _M_string(0) {}
ostream_iterator(ostream_type& __s, const _CharT* __c)
: _M_stream(&__s), _M_string(__c) {}
ostream_iterator<_Tp>& operator=(const _Tp& __value) {
*_M_stream << __value;
if (_M_string) *_M_stream << _M_string;
return *this;
}
ostream_iterator<_Tp>& operator*() { return *this; }
ostream_iterator<_Tp>& operator++() { return *this; }
ostream_iterator<_Tp>& operator++(int) { return *this; }
private:
ostream_type* _M_stream;
const _CharT* _M_string;
};
测试程序
1 |
|
执行结果:1
2
3
4
5
6
7
8[root@192 8_STL_adapter]# ./8_1_2_iterator-adapter
0 1 2 3 4 5
1 0 1 2 3 4 5
1 0 1 2 3 4 5 1
1 0 1 2 3 4 1 5 1
1 5 1 4 3 2 1 0 1
1 2 3 e // 输入数字,停止时可以输入任意字符
1 2 3 1 0 1 2 3 4 1 5 1
function adapter
仿函数配接操作包括绑定(bind)、否定(negate)、组合(compose)、以及对一般函数或成员函数的修饰。仿函数配接器的价值在于,通过它们之间的绑定、组合、修饰能力,几乎可以创造出各种可能的表达式,配合STL算法。例如,我们可能希望找出某个序列中所有不小于12的元素个数。虽然“不小于” 就是“大于或等于”,我们因此可以选择STL内建的仿函数greater_equal。但如果希望完全遵循题目语意(在某些更复杂的情况下,这可能是必要的),坚持找出“不小于”12的元素个数,可以这么做:1
not1(bind2nd(less<int>(), 12))
这个式子将less<int>()的第二参数系结(绑定)为12,再加上否定操作,便形成了“不小于12”的语意,整个凑和成为一个表达式(expression),可与任何 “可接受表达式为参数”之算法搭配。
再举一个例子,假设我们希望对序列中的每一个元素都做某个特殊运算,这个运算的数学表达式为:1
f(g(elem))
其中f和g都是数学函数,那么可以这么写:1
compose(f(x), g(y));
例如我们希望将容器内的每一个元素v进行(v+2)*3的操作,我们可以令f(x)=x*3, g(y)=y+2,并写下这样的式子:1
compose1(bind2nd(multiplies<int>(), 3), bind2nd(plus<int>(), 2));
由于仿函数就是“将function call操作符重载”的一种class,而任何算法接受一个仿函数时,总是在其演算过程中调用该仿函数的operator(),这使得不具备仿函数之形、却有真函数之实的飞一般函数”和“成员函数(member functions)”感到为难。STL又提供了为数众多的配接器,使“一般函数”和“成员函数”得以无缝隙地与其它配接器或算法结合起。
请注意,所有期望获得配接能力的组件,本身都必须是可配接的。换句话说,一元仿函数必须继承自unary_function,二元仿函数必须继承自binary_function,成员函数必须以mem_fun处理过,一般函数必须以ptr_fun处理过。


每一个仿函数配接器内藏了一个member object,其型别等同于它所要配接的对象。
使用场景:
- 对返回值进行逻辑否定:not1,not2
- 对参数进行绑定:bind1st,bind2nd
- 用于函数合成:compose1,compose2
- 用于函数指针:ptr_fun
- 用于成员函数指针:mem_fun,mem_fun_ref
count_if的实例测试程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
using namespace std;
// compose1在mingw中没有,所以把定义搬了过来
template <class _Operation1, class _Operation2>
class unary_compose
: public unary_function<typename _Operation2::argument_type,
typename _Operation1::result_type>
{
protected:
_Operation1 _M_fn1;
_Operation2 _M_fn2;
public:
unary_compose(const _Operation1& __x, const _Operation2& __y)
: _M_fn1(__x), _M_fn2(__y) {}
typename _Operation1::result_type
operator()(const typename _Operation2::argument_type& __x) const {
return _M_fn1(_M_fn2(__x));
}
};
template <class _Operation1, class _Operation2>
inline unary_compose<_Operation1,_Operation2>
compose1(const _Operation1& __fn1, const _Operation2& __fn2)
{
return unary_compose<_Operation1,_Operation2>(__fn1, __fn2);
}
void print(int i) {
cout << i << " ";
}
class Int {
public:
// explicit 只能修改只有一个参数的类构造函数,
// 或是除了第一个参数外其他参数都有默认值的情况
// 表明该构造函数是显示的而非隐式的
// 作用是禁止类构造函数的隐式自动转换
// implicit 表示隐式,类构造函数默认声明为隐式
// google c++规范与effective c++都推荐使用explicit声明
explicit Int(int i) : m_i(i) {}
void print1() const {
cout << "[" << m_i << "]";
}
private:
int m_i;
};
int main() {
// 将outite绑定到cout,每次对outite指派一个元素,就后接一个“ ”
ostream_iterator<int> outite(cout, " ");
int ia[6] = {2, 21, 12, 7, 19, 23};
vector<int> iv(ia, ia + 6);
// 找出不小于12的元素个数
cout << count_if(iv.begin(), iv.end(),
not1(bind2nd(less<int>(), 12)));
cout << endl;
// 令每个元素v执行(v+2)*3然后输往outite
transform(iv.begin(), iv.end(), outite,
compose1(bind2nd(multiplies<int>(), 3),
bind2nd(plus<int>(), 2)));
cout << endl;
// 将所有元素拷贝到outite
copy(iv.begin(), iv.end(), outite);
cout << endl;
// 1. 使用函数指针搭配stl算法
for_each(iv.begin(), iv.end(), print);
cout << endl;
// 2. 以修饰过的一般函数搭配stl算法
for_each(iv.begin(), iv.end(), ptr_fun(print));
cout << endl;
Int t1(3), t2(7), t3(20), t4(14), t5(68);
vector<Int> Iv;
Iv.push_back(t1);
Iv.push_back(t2);
Iv.push_back(t3);
Iv.push_back(t4);
Iv.push_back(t5);
// 3. 以修饰过的成员函数搭配stl算法
for_each(Iv.begin(), Iv.end(), mem_fun_ref(&Int::print1));
return 0;
}
执行结果:1
2
3
4
5
6
7[root@192 8_STL_adapter]# ./8_1_3_functor-adapter
4
12 69 42 27 63 75
2 21 12 7 19 23
2 21 12 7 19 23
2 21 12 7 19 23
[3][7][20][14][68][