Leetcode301 - 400

Posted on

Leetcode301. Remove Invalid Parentheses

Remove the minimum number of invalid parentheses in order to make the input string valid. Return all possible results.

Note: The input string may contain letters other than the parentheses ( and ).

Example 1:

1
2
Input: "()())()"
Output: ["()()()", "(())()"]

Example 2:

1
2
Input: "(a)())()"
Output: ["(a)()()", "(a())()"]

Example 3:

1
2
Input: ")("
Output: [""]

这道题让移除最少的括号使得给定字符串为一个合法的含有括号的字符串，我们从小数学里就有括号，所以应该对合法的含有括号的字符串并不陌生，字符串中的左右括号数应该相同，而且每个右括号左边一定有其对应的左括号，而且题目中给的例子也说明了去除方法不唯一，需要找出所有合法的取法。参考了网上大神的解法，这道题首先可以用 BFS 来解，我把给定字符串排入队中，然后取出检测其是否合法，若合法直接返回，不合法的话，对其进行遍历，对于遇到的左右括号的字符，去掉括号字符生成一个新的字符串，如果这个字符串之前没有遇到过，将其排入队中，用 HashSet 记录一个字符串是否出现过。对队列中的每个元素都进行相同的操作，直到队列为空还没找到合法的字符串的话，那就返回空集，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<string> removeInvalidParentheses(string s) {
        vector<string> res;
        unordered_set<string> visited{{s}};
        queue<string> q{{s}};
        bool found = false;
        while (!q.empty()) {
            string t = q.front(); q.pop();
            if (isValid(t)) {
                res.push_back(t);
                found = true;
            }
            if (found) continue;
            for (int i = 0; i < t.size(); ++i) {
                if (t[i] != '(' && t[i] != ')') continue;
                string str = t.substr(0, i) + t.substr(i + 1);
                if (!visited.count(str)) {
                    q.push(str);
                    visited.insert(str);
                }
            }
        }
        return res;
    }
    bool isValid(string t) {
        int cnt = 0;
        for (int i = 0; i < t.size(); ++i) {
            if (t[i] == '(') ++cnt;
            else if (t[i] == ')' && --cnt < 0) return false;
        }
        return cnt == 0;
    }
};

下面来看一种递归解法，这种解法首先统计了多余的半括号的数量，用 cnt1 表示多余的左括号，cnt2 表示多余的右括号，因为给定字符串左右括号要么一样多，要么左括号多，要么右括号多，也可能左右括号都多，比如 “)(“。所以 cnt1 和 cnt2 要么都为0，要么都大于0，要么一个为0，另一个大于0。好，下面进入递归函数，首先判断，如果当 cnt1 和 cnt2 都为0时，说明此时左右括号个数相等了，调用 isValid 子函数来判断是否正确，正确的话加入结果 res 中并返回即可。否则从 start 开始遍历，这里的变量 start 表示当前递归开始的位置，不需要每次都从头开始，会有大量重复计算。而且对于多个相同的半括号在一起，只删除第一个，比如 “())”，这里有两个右括号，不管删第一个还是删第二个右括号都会得到 “()”，没有区别，所以只用算一次就行了，通过和上一个字符比较，如果不相同，说明是第一个右括号，如果相同则直接跳过。此时来看如果 cnt1 大于0，说明此时左括号多，而如果当前字符正好是左括号的时候，可以删掉当前左括号，继续调用递归，此时 cnt1 的值就应该减1，因为已经删掉了一个左括号。同理，如果 cnt2 大于0，说明此时右括号多，而如果当前字符正好是右括号的时候，可以删掉当前右括号，继续调用递归，此时 cnt2 的值就应该减1，因为已经删掉了一个右括号，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    vector<string> removeInvalidParentheses(string s) {
        vector<string> res;
        int cnt1 = 0, cnt2 = 0;
        for (char c : s) {
            cnt1 += (c == '(');
            if (cnt1 == 0) cnt2 += (c == ')');
            else cnt1 -= (c == ')');
        }
        helper(s, 0, cnt1, cnt2, res);
        return res;
    }
    void helper(string s, int start, int cnt1, int cnt2, vector<string>& res) {
        if (cnt1 == 0 && cnt2 == 0) {
            if (isValid(s)) res.push_back(s);
            return;
        }
        for (int i = start; i < s.size(); ++i) {
            if (i != start && s[i] == s[i - 1]) continue;
            if (cnt1 > 0 && s[i] == '(') {
                helper(s.substr(0, i) + s.substr(i + 1), i, cnt1 - 1, cnt2, res);
            }
            if (cnt2 > 0 && s[i] == ')') {
                helper(s.substr(0, i) + s.substr(i + 1), i, cnt1, cnt2 - 1, res);
            }
        }
    }
    bool isValid(string t) {
        int cnt = 0;
        for (int i = 0; i < t.size(); ++i) {
            if (t[i] == '(') ++cnt;
            else if (t[i] == ')' && --cnt < 0) return false;
        }
        return cnt == 0;
    }
};

下面这种解法由热心网友 fvglty 提供，应该算是一种暴力搜索的方法，并没有太多的技巧在里面，但是思路直接了当，可以作为为面试中最先提出的解法。思路是先将s放到一个 HashSet 中，然后进行该集合 cur 不为空的 while 循环，此时新建另一个集合 next，遍历之前的集合 cur，若某个字符串是合法的括号，直接加到结果 res 中，并且看若 res 不为空，则直接跳过。跳过的部分实际上是去除括号的操作，由于不知道该去掉哪个半括号，所以只要遇到半括号就都去掉，然后加入另一个集合 next 中，这里实际上保存的是下一层的候选者。当前的 cur 遍历完成后，若 res 不为空，则直接返回，因为这是当前层的合法括号，一定是移除数最少的。若 res 为空，则将 next 赋值给 cur，继续循环，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<string> removeInvalidParentheses(string s) {
        vector<string> res;
        unordered_set<string> cur{{s}};
        while (!cur.empty()) {
            unordered_set<string> next;
            for (auto &a : cur) {
                if (isValid(a)) res.push_back(a);
                if (!res.empty()) continue;
                for (int i = 0; i < a.size(); ++i) {
                    if (a[i] != '(' && a[i] != ')') continue;
                    next.insert(a.substr(0, i) + a.substr(i + 1));
                }
            }
            if (!res.empty()) return res;
            cur = next;
        }
        return res;
    }
    bool isValid(string t) {
        int cnt = 0;
        for (int i = 0; i < t.size(); ++i) {
            if (t[i] == '(') ++cnt;
            else if (t[i] == ')' && --cnt < 0) return false;
        }
        return cnt == 0;
    }
};

这种解法的思路是先找到合法字符串的长度，对每段相同字符的序列进行统计，因为每段相同字符序列一定有0个、1个或者多个会被留下来，遍历这些序列，搜索去掉一个序列中的字符是否合法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
class Solution {
public:
    
    vector<pair<char, int> > data;
    vector<string> ret;
    int maxlength;
    
    string gen(vector<pair<char, int>> ans) {
        string str;
        for (const auto& a : ans)
            str += string(a.second, a.first);
        return str;
    }
    
    // cur是当前要枚举哪一块字符串，s是字符串的和，左括号+1，右括号-1
    // len是当前选中的字符数量，len==maxlength
    // s最后应该为0才合法
    void dfs(int cur, int s, int len, vector<pair<char, int>>& ans) {
        if (cur == data.size()) {
            if (!s && len == maxlength)
                ret.push_back(gen(ans));
            return;
        }

        if (data[cur].first != '(' && data[cur].first != ')') {
            if (len + data[cur].second > maxlength)
                return;
            ans.push_back(data[cur]);
            dfs(cur+1, s, len+data[cur].second, ans);
            ans.pop_back();
            return;
        }
        
        ans.push_back(data[cur]);
        for (int i = 0; i <= data[cur].second; i ++) {
            if (data[cur].first == '(') {
                if (len + i <= maxlength) {
                    ans[cur].second = i; // ans
                    dfs(cur+1, s+i, len+i, ans);
                }
            }
            else { // ')'
                if (s >= i && len + i <= maxlength) {
                    ans[cur].second = i;
                    dfs(cur+1, s-i, len+i, ans);
                }
            }
        }
        
        ans.pop_back();
    }
    
    vector<string> removeInvalidParentheses(string str) {
        int cnt = 0, s = 0, r = 0;
        for (int i = 0; i < str.length(); i ++) {
            if (!i || str[i] == str[i-1])
                cnt ++;
            else {
                data.push_back(make_pair(str[i-1], cnt));
                cnt = 1;
            }
            
            if (str[i] == '(')
                s ++;
            else if (str[i] == ')') {
                if (s) s --;
                else r ++;
            }
        }
        data.push_back(make_pair(str.back(), cnt));
        maxlength = str.length() - (s+r);
        
        vector<pair<char, int> > ans;
        dfs(0, 0, 0, ans);
        
        return ret;
    }
};

Leetcode303. Range Sum Query - Immutable

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

Example:

1
2
3
4
5
Given nums = [-2, 0, 3, -5, 2, -1]

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class NumArray {
public:
    vector<int> prefix;
    
    NumArray(vector<int>& nums) {
        prefix.push_back(0);
        for(int i=0;i<nums.size();i++)
        {
            prefix.push_back(prefix[i]+nums[i]);
        }
    }
    
    int sumRange(int i, int j) {
        return prefix[j+1]-prefix[i];
    }
};

Leetcode304. Range Sum Query 2D - Immutable

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Example 1:

1
2
3
4
5
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation

1
2
3
4
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

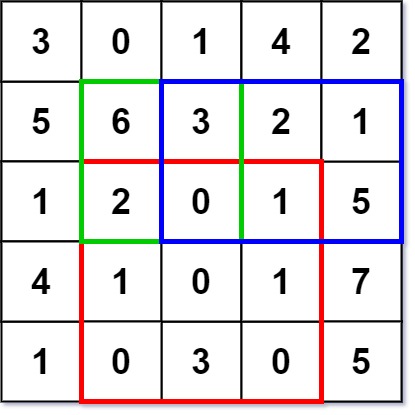
求二维数组中指定左上角和右下角的长方形内所有数字的和。给定的二维数组是不会变的，每次变得是求和的范围。

解题方法：预先求和

这个题肯定是用先把所有的和求出来，然后查找的时候直接计算就行了。我们使用的这个求和矩阵保存的是每个位置到整个矩阵的左上角元素这个矩形的所有元素和。为了方便起见，利用了和DP类似的添加边界的方法，也就是在最左边和最上边添加了全是0的列和行，这样能保证在求和的时候，每个位置的和是左边的和+上边的和+自身-左上元素的和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class NumMatrix {
public:
    vector<vector<int> > dp;
    NumMatrix(vector<vector<int>>& matrix) {
        int width = matrix.size();
        if (width == 0)
            return;
        int height = matrix[0].size();
        
        dp.resize(width+1);
        for (int i = 0; i < dp.size(); i++)
			dp[i].resize(height+1, 0);
        
        for (int i = 1; i <= width; i ++)
            for (int j = 1; j <= height; j ++)
                dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + matrix[i-1][j-1];
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return dp[row2+1][col2+1] + dp[row1+1][col1+1] - dp[row1-1][col2] - dp[row2][col1-1];
    }
};

Leetcode305. Number of Islands II

A 2d grid map of m rows and n columns is initially filled with water. We may perform an addLand operation which turns the water at position (row, col) into a land. Given a list of positions to operate, count the number of islands after each addLand operation. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example:

1
2
Input: m = 3, n = 3, positions = [[0,0], [0,1], [1,2], [2,1]]
Output: [1,1,2,3]

Explanation:

Initially, the 2d grid grid is filled with water. (Assume 0 represents water and 1 represents land).

1
2
3
0 0 0
0 0 0
0 0 0

Operation 1: addLand(0, 0) turns the water at grid[0][0] into a land.

1
2
3
1 0 0
0 0 0   Number of islands = 1
0 0 0

Operation 2: addLand(0, 1) turns the water at grid[0][1] into a land.

1
2
3
1 1 0
0 0 0   Number of islands = 1
0 0 0

Operation 3: addLand(1, 2) turns the water at grid[1][2] into a land.

1
2
3
1 1 0
0 0 1   Number of islands = 2
0 0 0

Operation 4: addLand(2, 1) turns the water at grid[2][1] into a land.

1
2
3
1 1 0
0 0 1   Number of islands = 3
0 1 0

这道题是之前那道 Number of Islands 的拓展，难度增加了不少，因为这次是一个点一个点的增加，每增加一个点，都要统一一下现在总共的岛屿个数，最开始初始化时没有陆地，如下：

1
2
3
0 0 0
0 0 0
0 0 0

假如在(0, 0)的位置增加一个陆地，那么此时岛屿数量为1：
1
2
3
1 0 0
0 0 0
0 0 0

假如再在(0, 2)的位置增加一个陆地，那么此时岛屿数量为2：
1
2
3
1 0 1
0 0 0
0 0 0

假如再在(0, 1)的位置增加一个陆地，那么此时岛屿数量却又变为1：
1
2
3
1 1 1
0 0 0
0 0 0

假如再在(1, 1)的位置增加一个陆地，那么此时岛屿数量仍为1：
1
2
3
1 1 1
0 1 0
0 0 0

为了解决这种陆地之间会合并的情况，最好能够将每个陆地都标记出其属于哪个岛屿，这样就会方便统计岛屿个数。这种群组类问题，很适合使用联合查找 Union Find 来做，又叫并查集 Disjoint Set，一般来说，UF 算法的思路是每个个体先初始化为不同的群组，然后遍历有关联的两个个体，如果发现其 getRoot 函数的返回值不同，则手动将二者加入一个群组，然后总群组数自减1。这里就要分别说一下 root 数组，和 getRoot 函数。两个同群组的个体，通过 getRoot 函数一定会返回相同的值，但是其在 root 数组中的值不一定相同，可以类比成 getRoot 函数返回的是祖先，如果两个人的祖先相同，那么其是属于一个家族的（这里不是指人类共同的祖先哈）。root 可以用数组或者 HashMap 来表示，如果个体是数字的话，那么数组就 OK，如果个体是字符串的话，可能就需要用 HashMap 了。root 数组的初始化可以有两种，可以均初始化为 -1，或者都初始化为不同的数字，博主一般喜欢初始化为不同的数字。getRoot 函数的写法也可用递归或者迭代的方式。

那么具体来看这道题吧，此题跟经典的 UF 使用场景有一点点的区别，因为一般的场景中两个个体之间只有两种关系，属于一个群组或者不属于同一个群组，而这道题里面由于 water 的存在，就多了一种情况，只需要事先检测一下当前位置是不是岛屿就行了，总之问题不大。一般来说 root 数组都是使用一维数组，方便一些，那么这里就可以将二维数组 encode 为一维的，于是需要一个长度为 m*n 的一维数组来标记各个位置属于哪个岛屿，假设每个位置都是一个单独岛屿，岛屿编号可以用其坐标位置表示，但是初始化时将其都赋为 -1，这样方便知道哪些位置尚未变成岛屿。然后开始遍历陆地数组，若某个岛屿位置编码的 root 值不为 -1，说明这是一个重复出现的位置，不需要重新计算了，直接将 cnt 加入结果 res 中。否则将其岛屿编号设置为其坐标位置，然后岛屿计数加1，此时开始遍历其上下左右的位置，遇到越界或者岛屿标号为 -1 的情况直接跳过，现在知道初始化为 -1 的好处了吧，遇到是 water 的地方直接跳过。否则用 getRoot 来查找邻居位置的岛屿编号，同时也用 getRoot 来查找当前点的编号，这一步就是经典的 UF 算法的操作了，因为当前这两个 land 是相邻的，它们是属于一个岛屿，所以其 getRoot 函数的返回值 suppose 应该是相等的，但是如果返回值不同，说明需要合并岛屿，将两个返回值建立关联，并将岛屿计数 cnt 减1。当遍历完当前点的所有邻居时，该合并的都合并完了，将此时的岛屿计数 cnt 存入结果中，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    vector<int> numIslands2(int m, int n, vector<vector<int>>& positions) {
        vector<int> res;
        int cnt = 0;
        vector<int> roots(m * n, -1);
        vector<vector<int>> dirs{{0, -1}, {-1, 0}, {0, 1}, {1, 0}};
        for (auto &pos : positions) {
            int id = n * pos[0] + pos[1];
            if (roots[id] != -1) {
                res.push_back(cnt);
                continue;
            }
            roots[id] = id;
            ++cnt;
            for (auto dir : dirs) {
                int x = pos[0] + dir[0], y = pos[1] + dir[1], cur_id = n * x + y;
                if (x < 0 || x >= m || y < 0 || y >= n || roots[cur_id] == -1) continue;
                int p = findRoot(roots, cur_id), q = findRoot(roots, id);
                if (p != q) {
                    roots[p] = q;
                    --cnt;
                }
            }
            res.push_back(cnt);
        }
        return res;
    }
    int findRoot(vector<int>& roots, int id) {
        return (id == roots[id]) ? id : findRoot(roots, roots[id]);
    }
};

Leetcode306. Additive Number

Additive number is a string whose digits can form additive sequence.

A valid additive sequence should contain at least three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.

Given a string containing only digits ‘0’-‘9’, write a function to determine if it’s an additive number.

Note: Numbers in the additive sequence cannot have leading zeros, so sequence 1, 2, 03 or 1, 02, 3is invalid.

Example 1:

1
2
3
4
Input: "112358"
Output: true 
Explanation: The digits can form an additive sequence: 1, 1, 2, 3, 5, 8. 
             1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8

Example 2:

1
2
3
4
Input: "199100199"
Output: true 
Explanation: The additive sequence is: 1, 99, 100, 199. 
             1 + 99 = 100, 99 + 100 = 199

这道题定义了一种加法数，就是至少含有三个数字，除去前两个数外，每个数字都是前面两个数字的和，题目中给了许多例子，也限定了一些不合法的情况，比如两位数以上不能以0开头等等，让我们来判断一个数是否是加法数。

其实这题可用Brute Force的思想来解，我们让第一个数字先从一位开始，第二个数字从一位，两位，往高位开始搜索，前两个数字确定了，相加得到第三位数字，三个数组排列起来形成一个字符串，和原字符串长度相比，如果小于原长度，那么取出上一次计算的第二个和第三个数，当做新一次计算的前两个数，用相同的方法得到第三个数，再加入当前字符串，再和原字符串长度相比，以此类推，直到当前字符串长度不小于原字符串长度，比较两者是否相同，相同返回true，不相同则继续循环。如果所有情况都遍历完了还是没有返回true，则说明不是Additive Number，返回false，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    bool isAdditiveNumber(string num) {
        for (int i = 1; i < num.size(); ++i) {
            string s1 = num.substr(0, i);
            if (s1.size() > 1 && s1[0] == '0') break;
            for (int j = i + 1; j < num.size(); ++j) {
                string s2 = num.substr(i, j - i);
                long d1 = stol(s1), d2 = stol(s2);
                if ((s2.size() > 1 && s2[0] == '0')) break;
                long next = d1 + d2;
                string nextStr = to_string(next);
                if (nextStr != num.substr(j, nextStr.length())) continue; // optimization here
                string allStr = s1 + s2 + nextStr;
                while (allStr.size() < num.size()) {
                    d1 = d2;
                    d2 = next;
                    next = d1 + d2;
                    nextStr = to_string(next);
                    allStr += nextStr;
                }
                if (allStr == num) return true;
            }
        }
        return false;
    }
};

Leetcode307. Range Sum Query - Mutable

Given an integer array nums , find the sum of the elements between indices i and j ( i ≤ j ), inclusive.

The update(i, val) function modifies nums by updating the element at index i to val.

Example:

1
2
3
4
5
Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8

这道题是之前那道 Range Sum Query - Immutable 的延伸，之前那道题由于数组的内容不会改变，所以我们只需要建立一个累计数组就可以支持快速的计算区间值了，而这道题说数组的内容会改变，如果我们还是用之前的方法建立累计和数组，那么每改变一个数字，之后所有位置的数字都要改变，这样如果有很多更新操作的话，就会十分不高效，估计很难通过吧。But，被 OJ 分分钟打脸， brute force 完全没有问题啊，这年头，装个比不容易啊。直接就用个数组 data 接住 nums，然后要更新就更新，要求区域和，就遍历求区域和，就这样 naive 的方法还能 beat 百分之二十多啊，这不科学啊，参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class NumArray {
public:
    NumArray(vector<int> nums) {
        data = nums;
    }
    
    void update(int i, int val) {
        data[i] = val;
    }
    
    int sumRange(int i, int j) {
        int sum = 0;
        for (int k = i; k <= j; ++k) {
            sum += data[k];
        }
        return sum;
    }
    
private:
    vector<int> data;
};

上面的方法最大的问题，就是求区域和不高效，如果数组很大很大，每次求一个巨型的区间的和，都要一个一个的遍历去累加，累啊～但是一般的累加数组又无法应对这里的 update 操作，随便修改一个数字的话，那么其之后的所有累加和都会发生改变。所以解决方案就是二者折中一下，分块累加，各不干预。就是将原数组分为若干块，怎么分呢，这里就让每个 block 有 sqrt(n) 个数字就可以了，这个基本是让 block 的个数跟每个 blcok 中数字的个数尽可能相同的分割方法。然后我们就需要一个大小跟 block 个数相同的数组，来保存每个 block 的数字之和。在需要更新的时候，我们就先确定要更新的位置在哪个 block 里，然后只更新该 block 的和。而对于求区域和操作，我们还是要分别确定i和j分别属于哪个 block，若属于同一个 block，那么直接遍历累加即可，若属于不同的，则先从i累加到该 blcok 的末尾，然后中间横跨的那些 block 可以直接将和累加，对于j所在的 blcok，则从该 block 的开头遍历累加到j即可，参见代码如下：

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class NumArray {
public:
    NumArray(vector<int> nums) {
        if (nums.empty()) return;
        data = nums;
        double root = sqrt(data.size());
        len = ceil(data.size() / root);
        block.resize(len);
        for (int i = 0; i < data.size(); ++i) {
            block[i / len] += data[i];
        }
    }
    
    void update(int i, int val) {
        int idx = i / len;
        block[idx] += val - data[i];
        data[i] = val;
    }
    
    int sumRange(int i, int j) {
        int sum = 0;
        int start = i / len, end = j / len;
        if (start == end) {
            for (int k = i; k <= j; ++k) {
                sum += data[k];
            }
            return sum;
        }
        for (int k = i; k < (start + 1) * len; ++k) {
            sum += data[k];
        }
        for (int k = start + 1; k < end; ++k) {
            sum += block[k];
        }
        for (int k = end * len; k <= j; ++k) {
            sum += data[k];
        }
        return sum;
    }
    
private:
    int len;
    vector<int> data, block;
};

Leetcode309. Best Time to Buy and Sell Stock with Cooldown

Say you have an array for which the i th element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:

You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)

Example:

1
2
3
prices = [1, 2, 3, 0, 2]
maxProfit = 3
transactions = [buy, sell, cooldown, buy, sell]

这道题加入了一个冷冻期Cooldown之说，就是如果某天卖了股票，那么第二天不能买股票，有一天的冷冻期。此题需要维护三个一维数组buy, sell，和rest。其中：

  • buy[i]表示在第i天之前最后一个操作是买，此时的最大收益。
  • sell[i]表示在第i天之前最后一个操作是卖，此时的最大收益。
  • rest[i]表示在第i天之前最后一个操作是冷冻期，此时的最大收益。

我们写出递推式为：

1
2
3
buy[i]  = max(rest[i-1] - price, buy[i-1]) 
sell[i] = max(buy[i-1] + price, sell[i-1])
rest[i] = max(sell[i-1], buy[i-1], rest[i-1])

上述递推式很好的表示了在买之前有冷冻期，买之前要卖掉之前的股票。一个小技巧是如何保证[buy, rest, buy]的情况不会出现，这是由于buy[i] <= rest[i]， 即rest[i] = max(sell[i-1], rest[i-1])，这保证了[buy, rest, buy]不会出现。

另外，由于冷冻期的存在，我们可以得出rest[i] = sell[i-1]，这样，我们可以将上面三个递推式精简到两个：

1
2
buy[i]  = max(sell[i-2] - price, buy[i-1]) 
sell[i] = max(buy[i-1] + price, sell[i-1])

我们还可以做进一步优化，由于i只依赖于i-1和i-2，所以我们可以在O(1)的空间复杂度完成算法，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int buy = INT_MIN, pre_buy = 0, sell = 0, pre_sell = 0;
        for (int price : prices) {
            pre_buy = buy;
            buy = max(pre_sell - price, pre_buy);
            pre_sell = sell;
            sell = max(pre_buy + price, pre_sell);
        }
        return sell;
    }
};

我自己的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if (len == 0)
            return 0;
        vector<int> buy(len+1, 0), sell(len+1, 0);
        buy[1] = -prices[0];
        for (int i = 2; i < len+1; i ++) {
            buy[i] = max(sell[i-2]-prices[i-1], buy[i-1]);
            sell[i] = max(sell[i-1], buy[i-1]+prices[i-1]);
        }
        return sell[len];
    }
};

Leetcode310. Minimum Height Trees

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs’ root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

1
2
3
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.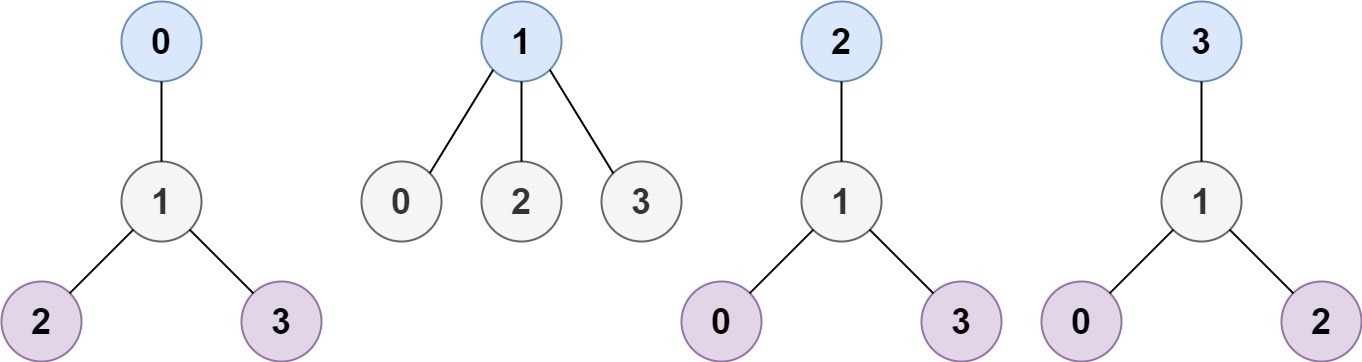

Example 2:

1
2
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]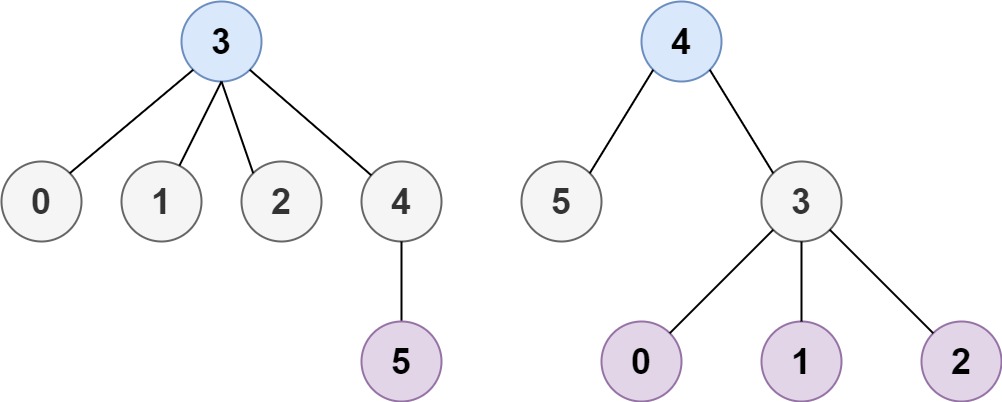

Example 3:

1
2
Input: n = 1, edges = []
Output: [0]

Example 4:

1
2
Input: n = 2, edges = [[0,1]]
Output: [0,1]

大家推崇的方法是一个类似剥洋葱的方法，就是一层一层的褪去叶节点，最后剩下的一个或两个节点就是我们要求的最小高度树的根节点，这种思路非常的巧妙，而且实现起来也不难，跟之前那到课程清单的题一样，我们需要建立一个图g，是一个二维数组，其中g[i]是一个一维数组，保存了i节点可以到达的所有节点。我们开始将所有只有一个连接边的节点(叶节点)都存入到一个队列queue中，然后我们遍历每一个叶节点，通过图来找到和其相连的节点，并且在其相连节点的集合中将该叶节点删去，如果删完后此节点也也变成一个叶节点了，加入队列中，下一轮删除。那么我们删到什么时候呢，当节点数小于等于2时候停止，此时剩下的一个或两个节点就是我们要求的最小高度树的根节点啦，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<pair<int, int> >& edges) {
        if (n == 1) return {0};
        vector<int> res;
        vector<unordered_set<int>> adj(n);
        queue<int> q;
        for (auto edge : edges) {
            adj[edge.first].insert(edge.second);
            adj[edge.second].insert(edge.first);
        }
        for (int i = 0; i < n; ++i) {
            if (adj[i].size() == 1) q.push(i);
        }
        while (n > 2) {
            int size = q.size();
            n -= size;
            for (int i = 0; i < size; ++i) {
                int t = q.front(); q.pop();
                for (auto a : adj[t]) {
                    adj[a].erase(t);
                    if (adj[a].size() == 1) q.push(a);
                }
            }
        }
        while (!q.empty()) {
            res.push_back(q.front()); q.pop();
        }
        return res;
    }
};

Leetcode312. Burst Balloons

Given n balloons, indexed from 0 to n-1. Each balloon is painted with a number on it represented by array nums. You are asked to burst all the balloons. If the you burst balloon iyou will get nums[left] nums[i] nums[right]coins. Here left and right are adjacent indices of i. After the burst, the left and right then becomes adjacent.

Find the maximum coins you can collect by bursting the balloons wisely.

Note:

  • You may imagine nums[-1] = nums[n] = 1. They are not real therefore you can not burst them.
  • 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

Example:

1
2
3
4
Input: [3,1,5,8]
Output: 167 
Explanation: nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
             coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167

这道题提出了一种打气球的游戏，每个气球都对应着一个数字，每次打爆一个气球，得到的金币数是被打爆的气球的数字和其两边的气球上的数字相乘，如果旁边没有气球了，则按1算，以此类推，求能得到的最多金币数。参见题目中给的例子，题意并不难理解。那么大家拿到题后，总是会习惯的先去想一下暴力破解法吧，这道题的暴力搜索将相当的复杂，因为每打爆一个气球，断开的地方又重新挨上，所有剩下的气球又要重新遍历，这使得分治法不能 work，整个的时间复杂度会相当的高，不要指望可以通过 OJ。而对于像这种求极值问题，一般都要考虑用动态规划 Dynamic Programming 来做，维护一个二维动态数组 dp，其中 dp[i][j] 表示打爆区间 [i,j] 中的所有气球能得到的最多金币。题目中说明了边界情况，当气球周围没有气球的时候，旁边的数字按1算，这样可以在原数组两边各填充一个1，方便于计算。这道题的最难点就是找状态转移方程，还是从定义式来看，假如区间只有一个数，比如 dp[i][i]，那么计算起来就很简单，直接乘以周围两个数字即可更新。如果区间里有两个数字，就要算两次了，先打破第一个再打破了第二个，或者先打破第二个再打破第一个，比较两种情况，其中较大值就是该区间的 dp 值。假如区间有三个数呢，比如 dp[1][3]，怎么更新呢？如果先打破第一个，剩下两个怎么办呢，难道还要分别再遍历算一下吗？这样跟暴力搜索的方法有啥区别呢，还要 dp 数组有啥意思。所谓的状态转移，就是假设已知了其他状态，来推导现在的状态，现在是想知道 dp[1][3] 的值，那么如果先打破了气球1，剩下了气球2和3，若之前已经计算了 dp[2][3] 的话，就可以使用其来更新 dp[1][3] 了，就是打破气球1的得分加上 dp[2][3]。那假如先打破气球2呢，只要之前计算了 dp[1][1] 和 dp[3][3]，那么三者加起来就可以更新 dp[1][3]。同理，先打破气球3，就用其得分加上 dp[1][2] 来更新 dp[1][3]。

那么对于有很多数的区间 [i, j]，如何来更新呢？现在是想知道 dp[i][j] 的值，这个区间可能比较大，但是如果知道了所有的小区间的 dp 值，然后聚沙成塔，逐步的就能推出大区间的 dp 值了。还是要遍历这个区间内的每个气球，就用k来遍历吧，k在区间 [i, j] 中，假如第k个气球最后被打爆，那么此时区间 [i, j] 被分成了三部分，[i, k-1]，[k]，和 [k+1, j]，只要之前更新过了 [i, k-1] 和 [k+1, j] 这两个子区间的 dp 值，可以直接用 dp[i][k-1] 和 dp[k+1][j]，那么最后被打爆的第k个气球的得分该怎么算呢，你可能会下意识的说，就乘以周围两个气球被 nums[k-1] nums[k] nums[k+1]，但其实这样是错误的，为啥呢？dp[i][k-1] 的意义是什么呢，是打爆区间 [i, k-1] 内所有的气球后的最大得分，此时第 k-1 个气球已经不能用了，同理，第 k+1 个气球也不能用了，相当于区间 [i, j] 中除了第k个气球，其他的已经爆了，那么周围的气球只能是第 i-1 个，和第 j+1 个了，所以得分应为 nums[i-1] nums[k] nums[j+1]，分析到这里，状态转移方程应该已经跃然纸上了吧，如下所示：

 dp[i][j] = max(dp[i][j], nums[i - 1] * nums[k] * nums[j + 1] + dp[i][k - 1] + dp[k + 1][j])                 ( i ≤ k ≤ j )

有了状态转移方程了，就可以写代码，下面就遇到本题的第二大难点了，区间的遍历顺序。一般来说，遍历所有子区间的顺序都是i从0到n，然后j从i到n，然后得到的 [i, j] 就是子区间。但是这道题用这种遍历顺序就不对，在前面的分析中已经说了，这里需要先更新完所有的小区间，然后才能去更新大区间，而用这种一般的遍历子区间的顺序，会在更新完所有小区间之前就更新了大区间，从而不一定能算出正确的dp值，比如拿题目中的那个例子 [3, 1, 5, 8] 来说，一般的遍历顺序是：

[3] -> [3, 1] -> [3, 1, 5] -> [3, 1, 5, 8] -> [1] -> [1, 5] -> [1, 5, 8] -> [5] -> [5, 8] -> [8]

显然不是我们需要的遍历顺序，正确的顺序应该是先遍历完所有长度为1的区间，再是长度为2的区间，再依次累加长度，直到最后才遍历整个区间：

[3] -> [1] -> [5] -> [8] -> [3, 1] -> [1, 5] -> [5, 8] -> [3, 1, 5] -> [1, 5, 8] -> [3, 1, 5, 8]

这里其实只是更新了 dp 数组的右上三角区域，最终要返回的值存在 dp[1][n] 中，其中n是两端添加1之前数组 nums 的个数。参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxCoins(vector<int>& nums) {
        int n = nums.size();
        nums.insert(nums.begin(), 1);
        nums.push_back(1);
        vector<vector<int>> dp(n + 2, vector<int>(n + 2, 0));
        for (int len = 1; len <= n; ++len) {
            for (int i = 1; i <= n - len + 1; ++i) {
                int j = i + len - 1;
                for (int k = i; k <= j; ++k) {
                    dp[i][j] = max(dp[i][j], nums[i - 1] * nums[k] * nums[j + 1] + dp[i][k - 1] + dp[k + 1][j]);
                }
            }
        }
        return dp[1][n];
    }
};

对于题目中的例子[3, 1, 5, 8]，得到的dp数组如下：

1
2
3
4
5
6
0    0    0    0    0    0
0    3    30   159  167  0
0    0    15   135  159  0
0    0    0    40   48   0
0    0    0    0    40   0
0    0    0    0    0    0

这题还有递归解法，思路都一样，就是写法略有不同，参见代码如下：

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int maxCoins(vector<int>& nums) {
        int n = nums.size();
        nums.insert(nums.begin(), 1);
        nums.push_back(1);
        vector<vector<int>> dp(n + 2, vector<int>(n + 2, 0));
        return burst(nums, dp, 1 , n);
	    }
    int burst(vector<int>& nums, vector<vector<int>>& dp, int i, int j) {
        if (i > j) return 0;
        if (dp[i][j] > 0) return dp[i][j];
        int res = 0;
        for (int k = i; k <= j; ++k) {
            res = max(res, nums[i - 1] * nums[k] * nums[j + 1] + burst(nums, dp, i, k - 1) + burst(nums, dp, k + 1, j));
        }
        dp[i][j] = res;
        return res;
    }
};

Leetcode313. Super Ugly Number

Write a program to find the nth super ugly number.

Super ugly numbers are positive numbers whose all prime factors are in the given prime list primes of sizek. For example, [1, 2, 4, 7, 8, 13, 14, 16, 19, 26, 28, 32] is the sequence of the first 12 super ugly numbers given primes = [2, 7, 13, 19] of size 4.

Note:

  1. 1 is a super ugly number for any given primes.
  2. The given numbers in primes are in ascending order.
  3. 0 < k ≤ 100, 0 < n ≤ 106, 0 < primes[i] < 1000.

这道题让我们求超级丑陋数，是之前那两道Ugly Number 丑陋数和Ugly Number II 丑陋数之二的延伸，质数集合可以任意给定，这就增加了难度。但是本质上和Ugly Number II 丑陋数之二没有什么区别，由于我们不知道质数的个数，我们可以用一个idx数组来保存当前的位置，然后我们从每个子链中取出一个数，找出其中最小值，然后更新idx数组对应位置，注意有可能最小值不止一个，要更新所有最小值的位置，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        vector<int> res(1, 1), idx(primes.size(), 0);
        while (res.size() < n) {
            vector<int> tmp;
            int mn = INT_MAX;
            for (int i = 0; i < primes.size(); ++i) {
                tmp.push_back(res[idx[i]] * primes[i]);
            }
            for (int i = 0; i < primes.size(); ++i) {
                mn = min(mn, tmp[i]);
            }
            for (int i = 0; i < primes.size(); ++i) {
                if (mn == tmp[i]) ++idx[i];
            }
            res.push_back(mn);
        }
        return res.back();
    }
};

Leetcode315. Count of Smaller Numbers After Self

You are given an integer array nums and you have to return a new counts array. The counts array has the property where counts[i] is the number of smaller elements to the right of nums[i].

Example:

1
2
3
4
5
6
7
Input: [5,2,6,1]
Output: [2,1,1,0] 
Explanation:
To the right of 5 there are 2 smaller elements (2 and 1).
To the right of 2 there is only 1 smaller element (1).
To the right of 6 there is 1 smaller element (1).
To the right of 1 there is 0 smaller element.

这道题给定了一个数组，让我们计算每个数字右边所有小于这个数字的个数，目测不能用 brute force，OJ 肯定不答应，那么为了提高运算效率，首先可以使用用二分搜索法，思路是将给定数组从最后一个开始，用二分法插入到一个新的数组，这样新数组就是有序的，那么此时该数字在新数组中的坐标就是原数组中其右边所有较小数字的个数，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// Binary Search
class Solution {
public:
    vector<int> countSmaller(vector<int>& nums) {
        vector<int> t, res(nums.size());
        for (int i = nums.size() - 1; i >= 0; --i) {
            int left = 0, right = t.size();
            while (left < right) {
                int mid = left + (right - left) / 2;
                if (t[mid] >= nums[i]) right = mid;
                else left = mid + 1;
            }
            res[i] = right;
            t.insert(t.begin() + right, nums[i]);
        }
        return res;
    }
};

上面使用二分搜索法是一种插入排序的做法，我们还可以用 C++ 中的 STL 的一些自带的函数，比如求距离 distance，或是求第一个不小于当前数字的函数 lower_bound()，这里利用这两个函数代替了上一种方法中的二分搜索的部分，两种方法的核心思想都是相同的，构造有序数组，找出新加进来的数组在有序数组中对应的位置存入结果中即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
// Insert Sort
class Solution {
public:
    vector<int> countSmaller(vector<int>& nums) {
        vector<int> t, res(nums.size());
        for (int i = nums.size() - 1; i >= 0; --i) {
            int d = distance(t.begin(), lower_bound(t.begin(), t.end(), nums[i]));
            res[i] = d;
            t.insert(t.begin() + d, nums[i]);
        }
        return res;
    }
};

再来看一种利用二分搜索树来解的方法，构造一棵二分搜索树，稍有不同的地方是需要加一个变量 smaller 来记录比当前结点值小的所有结点的个数，每插入一个结点，会判断其和根结点的大小，如果新的结点值小于根结点值，则其会插入到左子树中，此时要增加根结点的 smaller，并继续递归调用左子结点的 insert。如果结点值大于根结点值，则需要递归调用右子结点的 insert 并加上根结点的 smaller，并加1，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// Binary Search Tree
class Solution {
public:
    struct Node {
        int val, smaller;
        Node *left, *right;
        Node(int v, int s) : val(v), smaller(s), left(NULL), right(NULL) {}
    };
    int insert(Node*& root, int val) {
        if (!root) return (root = new Node(val, 0)), 0;
        if (root->val > val) return root->smaller++, insert(root->left, val);
        return insert(root->right, val) + root->smaller + (root->val < val ? 1 : 0);
    }
    vector<int> countSmaller(vector<int>& nums) {
        vector<int> res(nums.size());
        Node *root = NULL;
        for (int i = nums.size() - 1; i >= 0; --i) {
            res[i] = insert(root, nums[i]);
        }
        return res;
    }
};

我们通过一个实例来看看。假设我们有两个已排序的序列等待合并，分别是L = { 8, 12, 16, 22, 100 }和R = { 7, 26, 55, 64, 91 }。一开始我们用指针 lPtr = 0 指向 LL 的头部，rPtr = 0 指向 RR 的头部。记已经合并好的部分为 MM。

1
2
3
L = [8, 12, 16, 22, 100]   R = [7, 26, 55, 64, 91]  M = []
     |                          |
   lPtr                       rPtr

我们发现 lPtr 指向的元素大于 rPtr 指向的元素，于是把 rPtr 指向的元素放入答案，并把 rPtr 后移一位。

1
2
3
L = [8, 12, 16, 22, 100]   R = [7, 26, 55, 64, 91]  M = [7]
     |                              |
    lPtr                          rPtr

接着我们继续合并：
1
2
3
L = [8, 12, 16, 22, 100]   R = [7, 26, 55, 64, 91]  M = [8, 9]
        |                          |
       lPtr                       rPtr

此时 lPtr 比 rPtr 小，把 lPtr 对应的数加入答案。如果我们要统计 88 的右边比 88 小的元素，这里 77 对它做了一次贡献。如果带合并的序列L={8,12,16,22,100}，R={7,7,7,26,55,64,91}，那么一定有一个时刻，lPtr 和 rPtr 分别指向这些对应的位置：

1
2
3
L = [8, 12, 16, 22, 100]   R = [7, 7, 7, 26, 55, 64, 91]  M = [7, 7, 7]
     |                                   |
    lPtr                                rPtr

下一步我们就是把 88 加入 MM 中，此时三个 77 对 88 的右边比 88 小的元素的贡献为 33。以此类推，我们可以一边合并一边计算 RR 的头部到 rPtr 前一个数字对当前 lPtr 指向的数字的贡献。

我们发现用这种「算贡献」的思想在合并的过程中计算逆序对的数量的时候，只在 lPtr 右移的时候计算，是基于这样的事实：当前 lPtr 指向的数字比 rPtr 小，但是比 RR 中 [0 … rPtr - 1] 的其他数字大，[0 … rPtr - 1] 的数字是在 lPtr 右边但是比 lPtr 对应数小的数字，贡献为这些数字的个数。

但是我们又遇到了新的问题，在「并」的过程中 88 的位置一直在发生改变，我们应该把计算的贡献保存到哪里呢？这个时候我们引入一个新的数组，来记录每个数字对应的原数组中的下标，例如：

1
2
    a = [8, 9, 1, 5, 2]
index = [0, 1, 2, 3, 4]

排序的时候原数组和这个下标数组同时变化，则排序后我们得到这样的两个数组：

1
2
    a = [1, 2, 5, 8, 9]
index = [2, 4, 3, 0, 1]

我们用一个数组 ans 来记录贡献。我们对某个元素计算贡献的时候，如果它对应的下标为 p，我们只需要在 ans[p] 上加上贡献即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
public:
    vector<int> res;
    vector<int> idx;
    
    void merge(vector<int>& nums, int l, int r) {
        if (l >= r)
            return;
        int mid = (l + r) >> 1;
        merge(nums, l, mid);
        merge(nums, mid+1, r);
        
        vector<int> tmp(r - l + 1);
        int k = 0, i = l, j = mid+1;
        while(i <= mid && j <= r) {
            if (nums[idx[i]] <= nums[idx[j]]) {
                res[idx[i]] += (j - 1 - mid);
                tmp[k++] = idx[i ++];
            }
            else 
                tmp[k++] = idx[j ++];
        }
        
        while(i <= mid) {
            res[idx[i]] += r - mid;
            tmp[k++] = idx[i++];
        }
        
        while(j <= r)
            tmp[k++] = idx[j++];
        
        for (int i = 0; i < tmp.size(); i ++)
            idx[l+i] = tmp[i];
    }
    
    vector<int> countSmaller(vector<int>& nums) {
        res.assign(nums.size(), 0);    
        idx.assign(nums.size(), 0);
        for (int i = 0; i < nums.size(); i ++)
            idx[i] = i;
        merge(nums, 0, nums.size()-1);
        
        return res;
    }
};

Leetcode316. Remove Duplicate Letters

Given a string s, remove duplicate letters so that every letter appears once and only once. You must make sure your result is the smallest in lexicographical order among all possible results.

Example 1:

1
2
Input: s = "bcabc"
Output: "abc"

Example 2:

1
2
Input: s = "cbacdcbc"
Output: "acdb"

从一组字符串中取字符，使得生成结果中每个字符必须出现一次而且只出现一次，并且要求所得结果是字符串顺序最小的。

这个题的难点在于使得结果是字符串顺序最小。解题思路也是围绕这个展开。

先顺一下思路，首先，每个字符都必须要出现一次，那么当这个字符只有一次机会的时候，必须添加到结果字符串结尾中去，反之，如果这个字符的次数没有降为0，即后面还有机会，那么可以先把优先级高的放进来，把这个字符放到后面再处理。所以，我们可以使用一个栈，有点类似单调递增栈的意思，但其实并不是单调栈。我们的思路就是把还可以放到后面的字符弹出栈，留着以后处理，字符序小的插入到对应的位置。

首先，为了知道每个字符出现了多少次，必须做一次次数统计，这个步骤大家都是知道的。

然后，需要借助一个栈来实现字符串构造的操作。具体操作如下：

从输入字符串中逐个读取字符c，并把c的字符统计减一。

  1. 如果当前字符c已经在栈里面出现，那么跳过。
  2. 如果当前字符c在栈里面，那么：
    1. 如果当前字符c小于栈顶，并且栈顶元素有剩余（后面还能再添加进来），则出栈栈顶，标记栈顶不在栈中。重复该操作直到栈顶元素不满足条件或者栈为空。
    2. 入栈字符c，并且标记c已经在栈中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    string removeDuplicateLetters(string s) {
        string res = "";
        int size = s.length();
        unordered_map<char, int> m;
        unordered_map<char, bool> visited;
        for (int i = 0; i < size; i ++) {
            m[s[i]] ++;
            visited[s[i]] = false;
        }

        for (int i = 0; i < size; i ++) {
            m[s[i]] --;
            if (visited[s[i]])
                continue;
            while(!res.empty() && m[res.back()] > 0 && s[i] < res.back()) {
                visited[res.back()] = false;
                res.pop_back();
            }
            res += s[i];
            visited[s[i]] = true;
        }
        return res;
    }
};

Leetcode318. Maximum Product of Word Lengths

Given a string array words, find the maximum value of length(word[i]) * length(word[j]) where the two words do not share common letters. You may assume that each word will contain only lower case letters. If no such two words exist, return 0.

Example 1:

1
2
3
Given ["abcw", "baz", "foo", "bar", "xtfn", "abcdef"]
Return 16
The two words can be "abcw", "xtfn".

Example 2:

1
2
3
Given ["a", "ab", "abc", "d", "cd", "bcd", "abcd"]
Return 4
The two words can be "ab", "cd".

Example 3:

1
2
3
Given ["a", "aa", "aaa", "aaaa"]
Return 0
No such pair of words.

这道题给我们了一个单词数组，让我们求两个没有相同字母的单词的长度之积的最大值。我开始想的方法是每两个单词先比较，如果没有相同字母，则计算其长度之积，然后每次更新结果就能找到最大值。因为题目中说都是小写字母，那么只有26位，一个整型数int有32位，我们可以用后26位来对应26个字母，若为1，说明该对应位置的字母出现过，那么每个单词的都可由一个int数字表示，两个单词没有共同字母的条件是这两个int数与为0，用这个判断方法可以通过OJ，参见代码如下。注意移位运算符的优先级很低。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int maxProduct(vector<string>& words) {
        int len = words.size();
        vector<int> wordss, lennn;
        for (int i = 0; i < len; i ++) {
            int t = 0;
            for (int j = 0; j < words[i].length(); j ++) {
                t = t | (1 << (words[i][j]-'a'));
            }
            wordss.push_back(t);
            lennn.push_back(words[i].length());
        }
        
        int res = -1;
        for (int i = 0; i < len; i ++)
            for (int j = i + 1; j < len; j ++)
                if ((wordss[i] & wordss[j]) == 0)
                    res = max(res, int(lennn[i] * lennn[j]));
        return res;
    }
};

Leetcode319. Bulb Switcher

There are n bulbs that are initially off. You first turn on all the bulbs. Then, you turn off every second bulb. On the third round, you toggle every third bulb (turning on if it’s off or turning off if it’s on). For the n th round, you only toggle the last bulb. Find how many bulbs are on after n rounds.

Example:

1
2
3
4
5
6
7
8
Given _n_ = 3.   

At first, the three bulbs are [off, off, off].
After first round, the three bulbs are [on, on, on].
After second round, the three bulbs are [on, off, on].
After third round, the three bulbs are [on, off, off].   

So you should return 1, because there is only one bulb is on.

这道题给了我们n个灯泡，第一次打开所有的灯泡，第二次每两个更改灯泡的状态，第三次每三个更改灯泡的状态，以此类推，第n次每n个更改灯泡的状态。让我们求n次后，所有亮的灯泡的个数。此题是CareerCup 6.6 Toggle Lockers 切换锁的状态。

那么我们来看这道题吧，还是先枚举个小例子来分析下，比如只有5个灯泡的情况，’X’表示灭，‘√’表示亮，如下所示：

初始状态： X X X X X

第一次： √ √ √ √ √

第二次： √ X √ X √

第三次： √ X X X √

第四次： √ X X √ √

第五次： √ X X √ X

那么最后我们发现五次遍历后，只有1号和4号灯泡是亮的，而且很巧的是它们都是平方数，是巧合吗，还是其中有什么玄机。我们仔细想想，对于第n个灯泡，只有当次数是n的因子的之后，才能改变灯泡的状态，即n能被当前次数整除，比如当n为36时，它的因数有(1,36), (2,18), (3,12), (4,9), (6,6), 可以看到前四个括号里成对出现的因数各不相同，括号中前面的数改变了灯泡状态，后面的数又变回去了，等于灯泡的状态没有发生变化，只有最后那个(6,6)，在次数6的时候改变了一次状态，没有对应其它的状态能将其变回去了，所以灯泡就一直是点亮状态的。所以所有平方数都有这么一个相等的因数对，即所有平方数的灯泡都将会是点亮的状态。

那么问题就简化为了求1到n之间完全平方数的个数，我们可以用force brute来比较从1开始的完全平方数和n的大小，参见代码如下：

1
2
3
4
5
6
7
8
class Solution {
public:
    int bulbSwitch(int n) {
        int res = 1;
        while (res * res <= n) ++res;
        return res - 1;
    }
};

还有一种方法更简单，我们直接对n开方，在C++里的sqrt函数返回的是一个整型数，这个整型数的平方最接近于n，即为n包含的所有完全平方数的个数，参见代码如下：

1
2
3
4
5
6
class Solution {
public:
    int bulbSwitch(int n) {
        return sqrt(n);
    }
};

Leetcode322. Coin Change

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

Example 1:

1
2
3
Input: coins = [1, 2, 5], amount = 11
Output: 3 
Explanation: 11 = 5 + 5 + 1

Example 2:
1
2
Input: coins = [2], amount = 3
Output: -1

Note:
You may assume that you have an infinite number of each kind of coin.

我们希望既避免重复地计算，又避免无意义的计算（没有答案的子问题）。
生成所有可能的金钱总量就可以避免无意义的计算。
dp[i]表示金钱i对应的最少硬币数。

  • 初始的金钱总量为0，硬币面值为 coins = [1, 2, 5]。
  • 只有一个硬币可以组成的金钱分别为[1, 2, 5]，dp[1]=dp[2]=dp[5]=1
  • 在金钱为1的基础上继续生成[2, 3, 6]，即dp[3]=dp[6]=2，而dp[2]=min(dp[2],dp[1]+1)=1
  • 在金钱为2的基础上生成[3, 4, 7]，即dp[4]=dp[7]=dp[2]+1=2
  • 在金钱为3的基础上生成[4, 5, 8]，即dp[8]=2
  • 依次更新，直到计算到以金钱amount为基础时，结束。

当以某个金钱为基础生成接下来的金钱时，这个金钱对应的最少硬币数已经得到。
通过这种递推的方式可以生成所有的小于amount的有解金钱总量，反证法证明之

  • 假设某个金钱m是有解的，但是并没有被上述的递推过程生成
  • m一定是由{ m-coins[i] | 0 <= i < coins.size() }中某个金钱生成的，这些金钱中一定有某几个（或一个）是有解的，但是也没有被递推过程生成，这样反向推理肯定可以到初始金钱数为0
  • 既然能反推到初始金钱数，那么m一定是有解的。

解题的思想有点类似有向图的宽度优先搜索找最短路径

  • 所有的小于amount的有解金钱总量对应于有向图中的结点
  • m < n ,结点m和n之前有边m -> n当且仅当 m + coins[i] = n
  • 每条边的权值为1，对应于每次硬币数加1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        sort(coins.begin(), coins.end());
        vector<int> dp(amount+1,INT_MAX);
        dp[0]=0;
        for(int i=0;i<amount;i++){
            if(dp[i]==INT_MAX)
                continue;
            for(auto& num: coins){
                if(i+(long long)num>amount) 
                    break;
                dp[i+num] = min(dp[i]+1,dp[i+num]);
            }
        }
        return dp[amount]==INT_MAX?-1:dp[amount];
    }
};

我们维护一个一维动态数组 dp，其中 dp[i] 表示钱数为i时的最小硬币数的找零，注意由于数组是从0开始的，所以要多申请一位，数组大小为 amount+1，这样最终结果就可以保存在 dp[amount] 中了。初始化 dp[0] = 0，因为目标值若为0时，就不需要硬币了。其他值可以初始化是 amount+1，为啥呢？因为最小的硬币是1，所以 amount 最多需要 amount 个硬币，amount+1 也就相当于当前的最大值了，注意这里不能用整型最大值来初始化，因为在后面的状态转移方程有加1的操作，有可能会溢出，除非你先减个1，这样还不如直接用 amount+1 舒服呢。好，接下来就是要找状态转移方程了，没思路？不要紧！回归例子1，假设我取了一个值为5的硬币，那么由于目标值是 11，所以是不是假如我们知道 dp[6]，那么就知道了组成 11 的 dp 值了？所以更新 dp[i] 的方法就是遍历每个硬币，如果遍历到的硬币值小于i值（比如不能用值为5的硬币去更新 dp[3]）时，用 dp[i - coins[j]] + 1 来更新 dp[i]，所以状态转移方程为：

dp[i] = min(dp[i], dp[i - coins[j]] + 1);
其中 coins[j] 为第j个硬币，而 i - coins[j] 为钱数i减去其中一个硬币的值，剩余的钱数在 dp 数组中找到值，然后加1和当前 dp 数组中的值做比较，取较小的那个更新 dp 数组。先来看迭代的写法如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount + 1, amount + 1);
        dp[0] = 0;
        for (int i = 1; i <= amount; ++i) {
            for (int j = 0; j < coins.size(); ++j) {
                if (coins[j] <= i) {
                    dp[i] = min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return (dp[amount] > amount) ? -1 : dp[amount];
    }
};

Leetcode326. Power of Three

Given an integer, write a function to determine if it is a power of three.

Example 1:

1
2
Input: 27
Output: true

Example 2:
1
2
Input: 0
Output: false

Example 3:
1
2
Input: 9
Output: true

Example 4:
1
2
Input: 45
Output: false

这道题让我们判断一个数是不是3的次方数，3的次方数没有显著的特点，最直接的方法就是不停地除以3，看最后的余数是否为1，要注意考虑输入是负数和0的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool isPowerOfThree(int n) {
        if(n == 0)
            return false;
        while(n != 1) {
            if(n % 3 != 0)
                return false;
            n /= 3;
        }
        return true;
    }
};

1
2
3
4
5
6
7
8
9
class Solution {
public:
    bool isPowerOfThree(int n) {
        while (n && n % 3 == 0) {
            n /= 3;
        }
        return n == 1;
    }
};

题目中的Follow up让我们不用循环，那么有一个投机取巧的方法，由于输入是int，正数范围是0-231，在此范围中允许的最大的3的次方数为319=1162261467，那么我们只要看这个数能否被n整除即可，参见代码如下：
1
2
3
4
5
6
class Solution {
public:
    bool isPowerOfThree(int n) {
        return (n > 0 && 1162261467 % n == 0);
    }
};

最后还有一种巧妙的方法，利用对数的换底公式来做，高中学过的换底公式为logab = logcb / logca，那么如果n是3的倍数，则log3n一定是整数，我们利用换底公式可以写为log3n = log10n / log103，注意这里一定要用10为底数，不能用自然数或者2为底数，否则当n=243时会出错，原因请看这个帖子。现在问题就变成了判断log10n / log103是否为整数，在c++中判断数字a是否为整数，我们可以用 a - int(a) == 0 来判断，参见代码如下：
1
2
3
4
5
6
class Solution {
public:
    bool isPowerOfThree(int n) {
        return (n > 0 && int(log10(n) / log10(3)) - log10(n) / log10(3) == 0);
    }
};

Leetcode327. Count of Range Sum

Given an integer array nums, return the number of range sums that lie in [lower, upper] inclusive.
Range sum S(i, j) is defined as the sum of the elements in nums between indices i and j (i ≤ j), inclusive.

Note: A naive algorithm of O ( n 2) is trivial. You MUST do better than that.

Example:

1
2
3
Input: _nums_ = [-2,5,-1], _lower_ = -2, _upper_ = 2,
Output: 3 
Explanation: The three ranges are : [0,0], [2,2], [0,2] and their respective sums are: -2, -1, 2.

这道题给了我们一个数组，又给了一个下限和一个上限，让求有多少个不同的区间使得每个区间的和在给定的上下限之间。类似的区间和的问题一定是要计算累积和数组 sums 的，其中 sum[i] = nums[0] + nums[1] + … + nums[i]，对于某个i来说，只有那些满足 lower <= sum[i] - sum[j] <= upper 的j能形成一个区间 [j, i] 满足题意，目标就是来找到有多少个这样的 j (0 =< j < i) 满足 sum[i] - upper =< sum[j] <= sum[i] - lower，可以用 C++ 中由红黑树实现的 multiset 数据结构可以对其中数据排序，然后用 upperbound 和 lowerbound 来找临界值。lower_bound 是找数组中第一个不小于给定值的数(包括等于情况)，而 upper_bound 是找数组中第一个大于给定值的数，那么两者相减，就是j的个数，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int countRangeSum(vector<int>& nums, int lower, int upper) {
        int res = 0;
        long long sum = 0;
        multiset<long long> sums;
        sums.insert(0);
        for (int i = 0; i < nums.size(); ++i) {
            sum += nums[i];
            res += distance(sums.lower_bound(sum - upper), sums.upper_bound(sum - lower));
            sums.insert(sum);
        }
        return res;
    }        
};

我们再来看一种方法，这种方法的思路和前一种一样，只是没有 STL 的 multiset 和 lower_bound 和 upper_bound 函数，而是使用了 Merge Sort 来解，在混合的过程中，已经给左半边 [start, mid) 和右半边 [mid, end) 排序了。当遍历左半边，对于每个i，需要在右半边找出k和j，使其满足：

j是第一个满足 sums[j] - sums[i] > upper 的下标

k是第一个满足 sums[k] - sums[i] >= lower 的下标

那么在 [lower, upper] 之间的区间的个数是 j - k，同时也需要另一个下标t，用来拷贝所有满足 sums[t] < sums[i] 到一个寄存器 Cache 中以完成混合排序的过程，这个步骤是混合排序的精髓所在，实际上这个寄存器的作用就是将 [start, end) 范围内的数字排好序先存到寄存器中，然后再覆盖原数组对应的位置即可，(注意这里 sums 可能会整型溢出，使用长整型 long 代替)，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int countRangeSum(vector<int>& nums, int lower, int upper) {
        vector<long> sums(nums.size() + 1, 0);
        for (int i = 0; i < nums.size(); ++i) {
            sums[i + 1] = sums[i] + nums[i];
        }
        return countAndMergeSort(sums, 0, sums.size(), lower, upper);
    }
    int countAndMergeSort(vector<long>& sums, int start, int end, int lower, int upper) {
        if (end - start <= 1) return 0;
        int mid = start + (end - start) / 2;
        int cnt = countAndMergeSort(sums, start, mid, lower, upper) + countAndMergeSort(sums, mid, end, lower, upper);
        int j = mid, k = mid, t = mid;
        vector<int> cache(end - start, 0);
        for (int i = start, r = 0; i < mid; ++i, ++r) {
            while (k < end && sums[k] - sums[i] < lower) ++k;
            while (j < end && sums[j] - sums[i] <= upper) ++j;
            while (t < end && sums[t] < sums[i]) cache[r++] = sums[t++];
            cache[r] = sums[i];
            cnt += j - k;
        }
        copy(cache.begin(), cache.begin() + t - start, sums.begin() + start);
        return cnt;
    }
};

Leetcode328. Odd Even Linked List

Given the head of a singly linked list, group all the nodes with odd indices together followed by the nodes with even indices, and return the reordered list.

The first node is considered odd, and the second node is even, and so on.

Note that the relative order inside both the even and odd groups should remain as it was in the input.

You must solve the problem in O(1) extra space complexity and O(n) time complexity.

Example 1:

1
2
Given 1->2->3->4->5->NULL,
return 1->3->5->2->4->NULL.

这道题给了我们一个链表，让我们分开奇偶节点，所有奇节点在前，偶节点在后。我们可以使用两个指针来做，pre指向奇节点，cur指向偶节点，然后把偶节点cur后面的那个奇节点提前到pre的后面，然后pre和cur各自前进一步，此时cur又指向偶节点，pre指向当前奇节点的末尾，以此类推直至把所有的偶节点都提前了即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    ListNode* oddEvenList(ListNode* head) {
        if (head == NULL || head->next == NULL)
            return head;
        ListNode *odd = head, *even = head->next, *p = even;
        while(odd->next && even->next) {
            odd->next = even->next;
            even->next = even->next->next;
            odd = odd->next;
            even = even->next;
        }
        odd->next = p;
        return head;
    }
};

Leetcode329. Longest Increasing Path in a Matrix

Given an integer matrix, find the length of the longest increasing path.

From each cell, you can either move to four directions: left, right, up or down. You may NOT move diagonally or move outside of the boundary (i.e. wrap-around is not allowed).

Example 1:

1
2
3
4
5
6
7
8
Input: nums = 
[
  [9,9,4],
  [6,6,8],
  [2,1,1]
] 
Output: 4 
Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:
1
2
3
4
5
6
7
8
Input: nums = 
[
  [3,4,5],
  [3,2,6],
  [2,2,1]
] 
Output: 4 
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

这道题给我们一个二维数组，让我们求矩阵中最长的递增路径，规定我们只能上下左右行走，不能走斜线或者是超过了边界。那么这道题的解法要用递归和DP来解，用DP的原因是为了提高效率，避免重复运算。我们需要维护一个二维动态数组dp，其中dp[i][j]表示数组中以(i,j)为起点的最长递增路径的长度，初始将dp数组都赋为0，当我们用递归调用时，遇到某个位置(x, y), 如果dp[x][y]不为0的话，我们直接返回dp[x][y]即可，不需要重复计算。我们需要以数组中每个位置都为起点调用递归来做，比较找出最大值。在以一个位置为起点用DFS搜索时，对其四个相邻位置进行判断，如果相邻位置的值大于上一个位置，则对相邻位置继续调用递归，并更新一个最大值，搜素完成后返回即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    int dirs[4][2] = {{0, -1}, {-1, 0}, {0, 1}, {1, 0}};
    int** dp;
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) 
            return 0;
        int res = 1, m = matrix.size(), n = matrix[0].size();
        dp = (int**)malloc(sizeof(int*)*m);
        for(int i=0;i<m;i++){
            dp[i] = (int*)malloc(sizeof(int)*n);
            memset(dp[i],0,n*sizeof(int));
        }
        
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {        
                res = max(res, dfs(matrix, i, j));
            }
        }
        return res;
    }
    
    int dfs(vector<vector<int>>& matrix,int i,int j){
        if (dp[i][j]) 
            return dp[i][j];
        int mx = 1, m = matrix.size(), n = matrix[0].size();
        for(int ii=0;ii<4;ii++){
            int x = i + dirs[ii][0], y = j + dirs[ii][1];
            if (x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] <= matrix[i][j]) 
                continue;
            int len = 1 + dfs(matrix, x, y);
            mx = max(mx, len);
        }
        dp[i][j]=mx;
        return mx;
    }
};

Leetcode331. Verify Preorder Serialization of a Binary Tree

One way to serialize a binary tree is to use preorder traversal. When we encounter a non-null node, we record the node’s value. If it is a null node, we record using a sentinel value such as #.

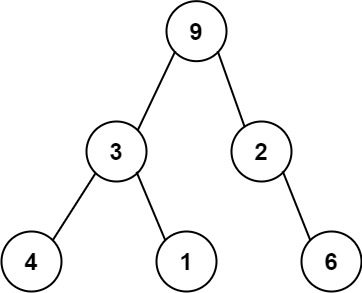
For example, the above binary tree can be serialized to the string “9,3,4,#,#,1,#,#,2,#,6,#,#“, where # represents a null node.

Given a string of comma-separated values preorder, return true if it is a correct preorder traversal serialization of a binary tree.

It is guaranteed that each comma-separated value in the string must be either an integer or a character # representing null pointer.

You may assume that the input format is always valid.

For example, it could never contain two consecutive commas, such as “1,,3”.
Note: You are not allowed to reconstruct the tree.

Example 1:

1
2
Input: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
Output: true

Example 2:

1
2
Input: preorder = "1,#"
Output: false

Example 3:

1
2
Input: preorder = "9,#,#,1"
Output: false

通过二叉树的性质，所有二叉树中Null指针的个数=节点个数+1。因为一棵树要增加一个节点，必然是在null指针的地方增加一个叶子结点，也就是毁掉一个null指针的同时带来两个null指针，意味着每增加一个节点，增加一个null指针。然而最开始一颗空树本来就有一个null指针，因此二叉树中null指针的个数等于节点数+1。从头开始扫描这个字串，如果途中#的个数超了，或者字符串扫描完不满足等式则返回false。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool isValidSerialization(string preorder) {
        int len = preorder.length();
        int i = 0, cnt = 0;
        while(i < len-1) {
            if (preorder[i] == '#') {
                if (cnt == 0)
                    return false;
                cnt --;
                i ++;
            }
            else {
                for(; i < len && preorder[i] != ','; i ++) ;
                cnt ++;
            }
            i ++;
        }
        return cnt == 0 && preorder[len-1] == '#';
    }
};

Leetcode334. Increasing Triplet Subsequence

Given an integer array nums, return true if there exists a triple of indices (i, j, k) such that i < j < k and nums[i] < nums[j] < nums[k]. If no such indices exists, return false.

Example 1:

1
2
3
Input: nums = [1,2,3,4,5]
Output: true
Explanation: Any triplet where i < j < k is valid.

Example 2:

1
2
3
Input: nums = [5,4,3,2,1]
Output: false
Explanation: No triplet exists.

Example 3:

1
2
3
Input: nums = [2,1,5,0,4,6]
Output: true
Explanation: The triplet (3, 4, 5) is valid because nums[3] == 0 < nums[4] == 4 < nums[5] == 6.

dp数组，分别记录当前位置的最大和最小数。时间复杂度O(n)。空间复杂度O（n）.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public boolean increasingTriplet(int[] nums) {
        if(nums.length<3)
            return false;
        int mindp[]=new int[nums.length];
        mindp[0]=nums[0];
        int tempmin=nums[0];
        for(int i=1;i<nums.length;i++){
            tempmin=Math.min(tempmin,nums[i-1]);
            mindp[i]=tempmin;
        }
        int maxdp[]=new int[nums.length];
        maxdp[nums.length-1]=nums[nums.length-1];
        int tempmax=nums[nums.length-1];
        for(int i=nums.length-2;i>=0;i--){
            tempmax=Math.max(tempmax,nums[i+1]);
            maxdp[i]=tempmax;
        }
        for(int i=1;i<nums.length-1;i++){
                if(nums[i]>mindp[i] && nums[i]<maxdp[i])
                    return true;
        }
        return false;
    }
}

找出两个数，分别记录为次小和最小，当一个数 比这两个数都大时，返回true.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public boolean increasingTriplet(int[] nums) {
        int One=Integer.MAX_VALUE,Tow=Integer.MAX_VALUE;
        for(int i=0;i< nums.length;i++){
            if(nums[i]<=One)
                One=nums[i];
            else if(nums[i]<=Tow)
                Tow=nums[i];
            else
                return true;
        }
        return false;
    }
}

Leetcode337. House Robber III

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.

Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police.

Example 1:

1
2
3
Input: root = [3,2,3,null,3,null,1]
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.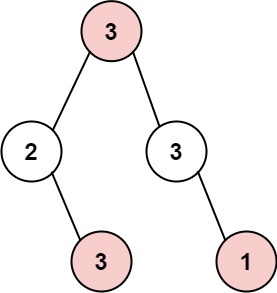

Example 2:

1
2
3
Input: root = [3,4,5,1,3,null,1]
Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.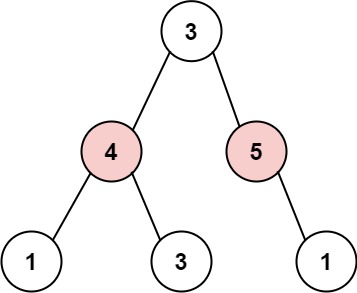

这道题是之前那两道 House Robber II 和 House Robber 的拓展，这个小偷又偷出新花样了，沿着二叉树开始偷，碉堡了，题目中给的例子看似好像是要每隔一个偷一次，但实际上不一定只隔一个，比如如下这个例子：

1
2
3
4
5
6
7
      4
     /
    1
   /
  2
 /
3

如果隔一个偷，那么是 4+2=6，其实最优解应为 4+3=7，隔了两个，所以说纯粹是怎么多怎么来，那么这种问题是很典型的递归问题，可以利用回溯法来做，因为当前的计算需要依赖之前的结果，那么对于某一个节点，如果其左子节点存在，通过递归调用函数，算出不包含左子节点返回的值，同理，如果右子节点存在，算出不包含右子节点返回的值，那么此节点的最大值可能有两种情况，一种是该节点值加上不包含左子节点和右子节点的返回值之和，另一种是左右子节点返回值之和不包含当期节点值，取两者的较大值返回即可，但是这种方法无法通过 OJ，超时了，所以必须优化这种方法，这种方法重复计算了很多地方，比如要完成一个节点的计算，就得一直找左右子节点计算，可以把已经算过的节点用 HashMap 保存起来，以后递归调用的时候，现在 HashMap 里找，如果存在直接返回，如果不存在，等计算出来后，保存到 HashMap 中再返回，这样方便以后再调用，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int rob(TreeNode* root) {
        unordered_map<TreeNode*, int> m;
        return dfs(root, m);
    }
    int dfs(TreeNode *root, unordered_map<TreeNode*, int> &m) {
        if (!root) return 0;
        if (m.count(root)) return m[root];
        int val = 0;
        if (root->left) {
            val += dfs(root->left->left, m) + dfs(root->left->right, m);
        }
        if (root->right) {
            val += dfs(root->right->left, m) + dfs(root->right->right, m);
        }
        val = max(val + root->val, dfs(root->left, m) + dfs(root->right, m));
        m[root] = val;
        return val;
    }
};

下面再来看一种方法，这种方法的递归函数返回一个大小为2的一维数组 res，其中 res[0] 表示不包含当前节点值的最大值，res[1] 表示包含当前值的最大值，那么在遍历某个节点时，首先对其左右子节点调用递归函数，分别得到包含与不包含左子节点值的最大值，和包含于不包含右子节点值的最大值，则当前节点的 res[0] 就是左子节点两种情况的较大值加上右子节点两种情况的较大值，res[1] 就是不包含左子节点值的最大值加上不包含右子节点值的最大值，和当前节点值之和，返回即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> res = dfs(root);
        return max(res[0], res[1]);
    }
    vector<int> dfs(TreeNode *root) {
        if (!root) return vector<int>(2, 0);
        vector<int> left = dfs(root->left);
        vector<int> right = dfs(root->right);
        vector<int> res(2, 0);
        res[0] = max(left[0], left[1]) + max(right[0], right[1]);
        res[1] = left[0] + right[0] + root->val;
        return res;
    }
};

下面这种解法思路和解法二有些类似。这里的 helper 函数返回当前结点为根结点的最大 rob 的钱数，里面的两个参数l和r表示分别从左子结点和右子结点开始 rob，分别能获得的最大钱数。在递归函数里面，如果当前结点不存在，直接返回0。否则对左右子结点分别调用递归函数，得到l和r。另外还得到四个变量，ll和lr表示左子结点的左右子结点的最大 rob 钱数，rl 和 rr 表示右子结点的最大 rob 钱数。那么最后返回的值其实是两部分的值比较，其中一部分的值是当前的结点值加上 ll, lr, rl, 和 rr 这四个值，这不难理解，因为抢了当前的房屋，则左右两个子结点就不能再抢了，但是再下一层的四个子结点都是可以抢的；另一部分是不抢当前房屋，而是抢其左右两个子结点，即 l+r 的值，返回两个部分的值中的较大值即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int rob(TreeNode* root) {
        int l = 0, r = 0;
        return helper(root, l, r);
    }
    int helper(TreeNode* node, int& l, int& r) {
        if (!node) return 0;
        int ll = 0, lr = 0, rl = 0, rr = 0;
        l = helper(node->left, ll, lr);
        r = helper(node->right, rl, rr);
        return max(node->val + ll + lr + rl + rr, l + r);
    }
};

Leetcode338. Counting Bits

Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1’s in their binary representation and return them as an array.

Example 1:

1
2
Input: 2
Output: [0,1,1]

Example 2:
1
2
Input: 5
Output: [0,1,1,2,1,2]

Follow up: It is very easy to come up with a solution with run time O(n*sizeof(integer)). But can you do it in linear time O(n) /possibly in a single pass? Space complexity should be O(n). Can you do it like a boss? Do it without using any builtin function like __builtin_popcount in c++ or in any other language.

从低位入手。‘1’的个数等于除了最低位之外的‘1’的个数加上最低位‘1’的个数，即ret[n] = ret[n>>1] + n%2，具体代码：

1
2
3
4
5
6
7
8
9
class Solution {
public:
    vector<int> countBits(int num) {
        vector<int> ret(num+1, 0);
        for(int i=1; i<=num; ++i)
            ret[i] = ret[i>>1] + i%2;
        return ret;
    }
};

Leetcode 339. Nested List Weight Sum

Given a nested list of integers, return the sum of all integers in the list weighted by their depth. Each element is either an integer, or a list — whose elements may also be integers or other lists.

Example 1:

1
2
3
Input: [[1,1],2,[1,1]]
Output: 10 
Explanation: Four 1's at depth 2, one 2 at depth 1.

Example 2:
1
2
3
Input: [1,[4,[6]]]
Output: 27 
Explanation: One 1 at depth 1, one 4 at depth 2, and one 6 at depth 3; 1 + 4*2 + 6*3 = 27.

这道题定义了一种嵌套链表的结构，链表可以无限往里嵌套，规定每嵌套一层，深度加1，让我们求权重之和，就是每个数字乘以其权重，再求总和。那么我们考虑，由于嵌套层数可以很大，所以我们用深度优先搜索DFS会很简单，每次遇到嵌套的，递归调用函数，一层一层往里算就可以了，我最先想的方法是遍历给的嵌套链表的数组，对于每个嵌套链表的对象，调用getSum函数，并赋深度值1，累加起来返回。在getSum函数中，首先判断其是否为整数，如果是，则返回当前深度乘以整数，如果不是，那么我们再遍历嵌套数组，对每个嵌套链表再调用递归函数，将返回值累加起来返回即可，参见代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int depthSum(vector<NestedInteger>& nestedList) {
        int res = 0;
        for (auto a : nestedList) {
            res += getSum(a, 1);
        }
        return res;
    }
    int getSum(NestedInteger ni, int level) {
        int res = 0;
        if (ni.isInteger()) return level * ni.getInteger();
        for (auto a : ni.getList()) {
            res += getSum(a, level + 1);
        }
        return res;
    }
};

但其实上面的方法可以优化，我们可以把给的那个嵌套链表的一维数组直接当做一个嵌套链表的对象，然后调用递归函数，递归函数的处理方法跟上面一样，只不过用了个三元处理使其看起来更加简洁了一些：
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int depthSum(vector<NestedInteger>& nestedList) {
        return helper(nestedList, 1);
    }
    int helper(vector<NestedInteger>& nl, int depth) {
        int res = 0;
        for (auto a : nl) {
            res += a.isInteger() ? a.getInteger() * depth : helper(a.getList(), depth + 1);
        }
        return res;
    }
};

Leetcode342. Power of Four

Given an integer (signed 32 bits), write a function to check whether it is a power of 4.

Example 1:

1
2
Input: 16
Output: true

Example 2:
1
2
Input: 5
Output: false

这道题让我们判断一个数是否为4的次方数，那么最直接的方法就是不停的除以4，看最终结果是否为1，参见代码如下：
1
2
3
4
5
6
7
8
9
class Solution {
public:
    bool isPowerOfFour(int num) {
        while (num && (num % 4 == 0)) {
            num /= 4;
        }
        return num == 1;
    }
};

还有一种方法是跟 Power of Three 中的解法三一样，使用换底公式来做
1
2
3
4
5
6
class Solution {
public:
    bool isPowerOfFour(int num) {
        return num > 0 && int(log10(num) / log10(4)) - log10(num) / log10(4) == 0;
    }
};

下面这种方法是网上比较流行的一种解法，思路很巧妙，首先根据 Power of Two 中的解法，我们知道 num & (num - 1) 可以用来判断一个数是否为2的次方数，更进一步说，就是二进制表示下，只有最高位是1，那么由于是2的次方数，不一定是4的次方数，比如8，所以我们还要其他的限定条件，我们仔细观察可以发现，4的次方数的最高位的1都是奇数位，那么我们只需与上一个数 (0x55555555) <==> 1010101010101010101010101010101，如果得到的数还是其本身，则可以肯定其为4的次方数：
1
2
3
4
5
6
class Solution {
public:
    bool isPowerOfFour(int num) {
        return num > 0 && !(num & (num - 1)) && (num & 0x55555555) == num;
    }
};

Leetcode343. Integer Break

Given an integer n, break it into the sum of k positive integers, where k >= 2, and maximize the product of those integers.

Return the maximum product you can get.

Example 1:

1
2
3
Input: n = 2
Output: 1
Explanation: 2 = 1 + 1, 1 × 1 = 1.

Example 2:

1
2
3
Input: n = 10
Output: 36
Explanation: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36.

这道题给了我们一个正整数n，让拆分成至少两个正整数之和，使其乘积最大。当前的拆分方法需要用到之前的拆分值，这种重现关系就很适合动态规划 Dynamic Programming 来做，我们使用一个一维数组 dp，其中 dp[i] 表示数字i拆分为至少两个正整数之和的最大乘积，数组大小为 n+1，值均初始化为1，因为正整数的乘积不会小于1。可以从3开始遍历，因为n是从2开始的，而2只能拆分为两个1，乘积还是1。i从3遍历到n，对于每个i，需要遍历所有小于i的数字，因为这些都是潜在的拆分情况，对于任意小于i的数字j，首先计算拆分为两个数字的乘积，即j乘以 i-j，然后是拆分为多个数字的情况，这里就要用到 dp[i-j] 了，这个值表示数字 i-j 任意拆分可得到的最大乘积，再乘以j就是数字i可拆分得到的乘积，取二者的较大值来更新 dp[i]，最后返回 dp[n] 即可，

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n+1, 1);
        for (int i = 3; i <= n; i ++) {
            for (int j = 1; j < i; j ++)
            dp[i] = max(dp[i], max(j*(i-j), dp[i-j] *j)); 
        }
        return dp[n];
    }
};

题目提示中让用 O(n) 的时间复杂度来解题，而且告诉我们找7到 10 之间的规律，那么我们一点一点的来分析：

正整数从1开始，但是1不能拆分成两个正整数之和，所以不能当输入。

那么：

  • 2只能拆成 1+1，所以乘积也为1。
  • 数字3可以拆分成 2+1 或 1+1+1，显然第一种拆分方法乘积大为2。
  • 数字4拆成 2+2，乘积最大，为4。
  • 数字5拆成 3+2，乘积最大，为6。
  • 数字6拆成 3+3，乘积最大，为9。
  • 数字7拆为 3+4，乘积最大，为 12。
  • 数字8拆为 3+3+2，乘积最大，为 18。
  • 数字9拆为 3+3+3，乘积最大，为 27。
  • 数字10拆为 3+3+4，乘积最大，为 36。

….

那么通过观察上面的规律，我们可以看出从5开始，数字都需要先拆出所有的3，一直拆到剩下一个数为2或者4，因为剩4就不用再拆了，拆成两个2和不拆没有意义，而且4不能拆出一个3剩一个1，这样会比拆成 2+2 的乘积小。这样我们就可以写代码了，先预处理n为2和3的情况，然后先将结果 res 初始化为1，然后当n大于4开始循环，结果 res 自乘3，n自减3，根据之前的分析，当跳出循环时，n只能是2或者4，再乘以 res 返回即可：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int integerBreak(int n) {
        if (n == 2 || n == 3) return n - 1;
        int res = 1;
        while (n > 4) {
            res *= 3;
            n -= 3;
        }
        return res * n;
    }
};

直接分别算出能拆出3的个数和最后剩下的余数2或者4，然后直接相乘得到结果，参见代码如下：

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int integerBreak(int n) {
        if (n == 2 || n == 3) return n - 1;
        if (n == 4) return 4;
        n -= 5;
        return (int)pow(3, (n / 3 + 1)) * (n % 3 + 2);
    }
};

Leetcode344. Reverse String

Write a function that reverses a string. The input string is given as an array of characters char[].

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory. You may assume all the characters consist of printable ascii characters.

Example 1:

1
2
Input: ["h","e","l","l","o"]
Output: ["o","l","l","e","h"]

Example 2:
1
2
Input: ["H","a","n","n","a","h"]
Output: ["h","a","n","n","a","H"]

我的解法：
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    void reverseString(vector<char>& s) {
        int l = 0, r = s.size() - 1;
        while(l < r) {
            int temp = s[l];
            s[l] = s[r];
            s[r] = temp;
            l ++;
            r --;
        }
    }
};

Leetcode345. Reverse Vowels of a String

Write a function that takes a string as input and reverse only the vowels of a string.

Example 1:

1
2
Input: "hello"
Output: "holle"

Example 2:
1
2
Input: "leetcode"
Output: "leotcede"

用首尾两个指针，当前后两个字符都是元音字母时交换，并且首指针向后移动，尾指针向前移动，如果只有首指针指的是元音字母而尾指针指的是非元音字母，则尾指针向前移动，否则首指针向后移动。有一些特殊样例，比如“.,”，导致用while会错。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    
    bool isv(char c) {
        return c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u' || 
               c == 'A' || c == 'E' || c == 'I' || c == 'O' || c == 'U';
    }
    
    string reverseVowels(string s) {
        int l = 0, r = s.length() - 1;
        char temp;
        while(l < r) {
            if(isv(s[l]) && isv(s[r])) {
                temp = s[l];
                s[l] = s[r];
                s[r] = temp;
                l ++;
                r --;
            }
            if(!isv(s[l])) l ++;
            if(!isv(s[r])) r --;
        }
        return s;
    }
};

LeetCode346. Moving Average from Data Stream

Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.

Example:

1
2
3
4
5
MovingAverage m = new MovingAverage(3);
m.next(1) = 1
m.next(10) = (1 + 10) / 2
m.next(3) = (1 + 10 + 3) / 3
m.next(5) = (10 + 3 + 5) / 3

这道题定义了一个MovingAverage类，里面可以存固定个数字，然后我们每次读入一个数字，如果加上这个数字后总个数大于限制的个数，那么我们移除最早进入的数字，然后返回更新后的平均数，这种先进先出的特性最适合使用队列queue来做，而且我们还需要一个double型的变量sum来记录当前所有数字之和，这样有新数字进入后，如果没有超出限制个数，则sum加上这个数字，如果超出了，那么sum先减去最早的数字，再加上这个数字，然后返回sum除以queue的个数即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class MovingAverage {
public:
    MovingAverage(int size) {
        this->size = size;
        sum = 0;
    }
    
    double next(int val) {
        if (q.size() >= size) {
            sum -= q.front(); q.pop();
        }
        q.push(val);
        sum += val;
        return sum / q.size();
    }
    
private:
    queue<int> q;
    int size;
    double sum;
};

Leetcode347. Top K Frequent Elements

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order.

Example 1:

1
2
Input: nums = [1,1,1,2,2,3], k = 2
Output: [1,2]

Example 2:

1
2
Input: nums = [1], k = 1
Output: [1]

这道题给了我们一个数组，让统计前k个高频的数字，那么对于这类的统计数字的问题，首先应该考虑用 HashMap 来做，建立数字和其出现次数的映射，然后再按照出现次数进行排序。可以用堆排序来做，使用一个最大堆来按照映射次数从大到小排列，在 C++ 中使用 priority_queue 来实现，默认是最大堆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int, int> m;
        priority_queue<pair<int, int> > q;
        for (int i : nums)
            m[i] ++;
        for(pair<int, int> p : m)
            q.push({p.second, p.first});
        
        vector<int> res;
        for(int i = 0; i < k; i ++) {
            res.push_back(q.top().second);
            q.pop();
        }
        return res;
    }
};

Leetcode349. Intersection of Two Arrays

Given two arrays, write a function to compute their intersection.

Example 1:

1
2
Input: nums1 = [1,2,2,1], nums2 = [2,2]
Output: [2]

Example 2:
1
2
Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
Output: [9,4]

Note:

  • Each element in the result must be unique.
  • The result can be in any order.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        int l1 = nums1.size(), l2 = nums2.size(), mark = 0;
        vector<int> res;
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        for(int i = 0, j = 0; i < l1 && j < l2;) {
            if(nums1[i] < nums2[j])
                i ++;
            else if(nums1[i] > nums2[j])
                j ++;
            else {
                if(res.size() == 0 || mark != nums1[i]) {
                    res.push_back(nums1[i]);
                    mark = nums1[i];
                }
                i ++;
                j ++;
            }
        }
        return res;
    }
};

Leetcode350. Intersection of Two Arrays II

Given two arrays, write a function to compute their intersection.

Example 1:

1
2
Input: nums1 = [1,2,2,1], nums2 = [2,2]
Output: [2,2]

Example 2:
1
2
Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
Output: [4,9]

Note:

  • Each element in the result should appear as many times as it shows in both arrays.
  • The result can be in any order.

跟上一个题一样，只是可以加上重复的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        int l1 = nums1.size(), l2 = nums2.size();
        vector<int> res;
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        for(int i = 0, j = 0; i < l1 && j < l2;) {
            if(nums1[i] < nums2[j])
                i ++;
            else if(nums1[i] > nums2[j])
                j ++;
            else {
                res.push_back(nums1[i]);
                i ++;
                j ++;
            }
        }
        return res;
    }
};

Leetcode354. Russian Doll Envelopes

You have a number of envelopes with widths and heights given as a pair of integers (w, h). One envelope can fit into another if and only if both the width and height of one envelope is greater than the width and height of the other envelope.

What is the maximum number of envelopes can you Russian doll? (put one inside other)

Example:

1
Given envelopes = [[5,4],[6,4],[6,7],[2,3]], the maximum number of envelopes you can Russian doll is 3 ([2,3] => [5,4] => [6,7]).

这道题给了我们一堆大小不一的信封，让我们像套俄罗斯娃娃那样把这些信封都给套起来，这道题实际上是之前那道Longest Increasing Subsequence的具体应用，而且难度增加了，从一维变成了两维，但是万变不离其宗，解法还是一样的，首先来看DP的解法，这是一种brute force的解法，首先要给所有的信封按从小到大排序，首先根据宽度从小到大排，如果宽度相同，那么高度小的再前面，这是STL里面sort的默认排法，所以我们不用写其他的comparator，直接排就可以了，然后我们开始遍历，对于每一个信封，我们都遍历其前面所有的信封，如果当前信封的长和宽都比前面那个信封的大，那么我们更新dp数组，通过dp[i] = max(dp[i], dp[j] + 1)。然后我们每遍历完一个信封，都更新一下结果res，参见代码如下；

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int maxEnvelopes(vector<pair<int, int>>& envelopes) {
        int res = 0, n = envelopes.size();
        vector<int> dp(n, 1);
        sort(envelopes.begin(), envelopes.end());
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                if (envelopes[i].first > envelopes[j].first && envelopes[i].second > envelopes[j].second) {
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
            res = max(res, dp[i]);
        }
        return res;
    }
};

Leetcode355. Design Twitter

Design a simplified version of Twitter where users can post tweets, follow/unfollow another user and is able to see the 10 most recent tweets in the user’s news feed. Your design should support the following methods:

  • postTweet(userId, tweetId) : Compose a new tweet.
  • getNewsFeed(userId) : Retrieve the 10 most recent tweet ids in the user’s news feed. Each item in the news feed must be posted by users who the user followed or by the user herself. Tweets must be ordered from most recent to least recent.
  • follow(followerId, followeeId) : Follower follows a followee.
  • unfollow(followerId, followeeId) : Follower unfollows a followee.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Twitter twitter = new Twitter();

// User 1 posts a new tweet (id = 5).
twitter.postTweet(1, 5);

// User 1's news feed should return a list with 1 tweet id -> [5].
twitter.getNewsFeed(1);

// User 1 follows user 2.
twitter.follow(1, 2);

// User 2 posts a new tweet (id = 6).
twitter.postTweet(2, 6);

// User 1's news feed should return a list with 2 tweet ids -> [6, 5].
// Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.getNewsFeed(1);

// User 1 unfollows user 2.
twitter.unfollow(1, 2);

// User 1's news feed should return a list with 1 tweet id -> [5],
// since user 1 is no longer following user 2.
twitter.getNewsFeed(1);

这道题让我们设计个简单的推特，具有发布消息，获得新鲜事，添加关注和取消关注等功能。我们需要用两个哈希表来做，第一个是建立用户和其所有好友之间的映射，另一个是建立用户和其所有消息之间的映射。由于获得新鲜事是需要按时间顺序排列的，那么我们可以用一个整型变量cnt来模拟时间点，每发一个消息，cnt自增1，那么我们就知道cnt大的是最近发的。那么我们在建立用户和其所有消息之间的映射时，还需要建立每个消息和其时间点cnt之间的映射。这道题的主要难点在于实现getNewsFeed()函数，这个函数获取自己和好友的最近10条消息，我们的做法是用户也添加到自己的好友列表中，然后遍历该用户的所有好友，遍历每个好友的所有消息，维护一个大小为10的哈希表，如果新遍历到的消息比哈希表中最早的消息要晚，那么将这个消息加入，然后删除掉最早的那个消息，这样我们就可以找出最近10条消息了，参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Twitter {
public:
    Twitter() {
        time = 0;
    }
    
    void postTweet(int userId, int tweetId) {
        follow(userId, userId);
        tweets[userId].insert({time++, tweetId});
    }
    
    vector<int> getNewsFeed(int userId) {
        vector<int> res;
        map<int, int> top10;
        for (auto id : friends[userId]) {
            for (auto a : tweets[id]) {
                top10.insert({a.first, a.second});
                if (top10.size() > 10) top10.erase(top10.begin());
            }
        }
        for (auto a : top10) {
            res.insert(res.begin(), a.second);
        }
        return res;
    }
    
    void follow(int followerId, int followeeId) {
        friends[followerId].insert(followeeId);
    }
    
    void unfollow(int followerId, int followeeId) {
        if (followerId != followeeId) {
            friends[followerId].erase(followeeId);
        }
    }
    
private:
    int time;
    unordered_map<int, unordered_set<int>> friends;
    unordered_map<int, map<int, int>> tweets;
};

Leetcode357. Count Numbers with Unique Digits

Given an integer n, return the count of all numbers with unique digits, x, where 0 <= x < 10n.

Example 1:

1
2
3
Input: n = 2
Output: 91
Explanation: The answer should be the total numbers in the range of 0 ≤ x < 100, excluding 11,22,33,44,55,66,77,88,99

Example 2:

1
2
Input: n = 0
Output: 1

题目要求： 找出0到10的n次方中所有unique的数(既该数的所有位数无重复数组)，如123为为unique，122不为unique，因为后两位2重复出现。

其实这个题的思路还是蛮简单的，回想下最简单的排列组合的知识。如找出所有十位unique digits number， 那么我们在十位可取1-9这九个数字，在个位能取除十位的数字外剩下的数字，由于个位可取0，所以个位还是可以取9个数字，则十位数的unique number为9*9 = 81。同理, 所有百位数unique digits number为9*9*8=648，以此类推。

由于此题目要求返回0到10的n次方中所有的unique number个数，因此我们可以分别求出个，十，百…每个位数上分别对应的unique number个数，然后加起来就好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int countNumbersWithUniqueDigits(int n) {
        if (n == 0)
            return 1;
        int res = 10;
        for (int i = 2; i <= n; i ++) {
            int idx = 9;
            int mul = 9;
            int count = i;
            while(count > 1) {
                mul *= idx;
                idx --;
                count --;
            }
            res += mul;
        }
        return res;
    }
};

Leetcode359. Logger Rate Limiter

Design a logger system that receive stream of messages along with its timestamps, each message should be printed if and only if it is not printed in the last 10 seconds.

Given a message and a timestamp (in seconds granularity), return true if the message should be printed in the given timestamp, otherwise returns false.

It is possible that several messages arrive roughly at the same time.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Logger logger = new Logger();

// logging string "foo" at timestamp 1
logger.shouldPrintMessage(1, "foo"); returns true; 

// logging string "bar" at timestamp 2
logger.shouldPrintMessage(2,"bar"); returns true;

// logging string "foo" at timestamp 3
logger.shouldPrintMessage(3,"foo"); returns false;

// logging string "bar" at timestamp 8
logger.shouldPrintMessage(8,"bar"); returns false;

// logging string "foo" at timestamp 10
logger.shouldPrintMessage(10,"foo"); returns false;

// logging string "foo" at timestamp 11
logger.shouldPrintMessage(11,"foo"); returns true;

这道题让我们设计一个记录系统每次接受信息并保存时间戳，然后让我们打印出该消息，前提是最近10秒内没有打印出这个消息。这不是一道难题，我们可以用哈希表来做，建立消息和时间戳之间的映射，如果某个消息不再哈希表表，我们建立其和时间戳的映射，并返回true。如果应经在哈希表里了，我们看当前时间戳是否比哈希表中保存的时间戳大10，如果是，更新哈希表，并返回true，反之返回false，参见代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Logger {
public:
    Logger() {}
    
    bool shouldPrintMessage(int timestamp, string message) {
        if (!m.count(message)) {
            m[message] = timestamp;
            return true;
        } 
        if (timestamp - m[message] >= 10) {
            m[message] = timestamp;
            return true;
        }
        return false;
    }

private:
    unordered_map<string, int> m;
};

Leetcode367. Valid Perfect Square

Given a positive integer num, write a function which returns True if num is a perfect square else False.

Follow up: Do not use any built-in library function such as sqrt.

Example 1:

1
2
Input: num = 16
Output: true

Example 2:
1
2
Input: num = 14
Output: false

给了我们一个数，让我们判断其是否为完全平方数，那么显而易见的是，肯定不能使用 brute force，这样太不高效了，那么最小是能以指数的速度来缩小范围。
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    bool isPerfectSquare(int num) {
        if(num == 1)
            return 1;
        for(int i = 1; i <= num/i; i ++) {
            if(i * i == num)
                return true;
        }
        return false;
    }
};

Leetcode368. Largest Divisible Subset

Given a set of distinct positive integers, find the largest subset such that every pair (S i, Sj) of elements in this subset satisfies: Si % Sj = 0 or Sj % Si = 0.

If there are multiple solutions, return any subset is fine.

Example 1:

1
2
3
nums: [1,2,3]

Result: [1,2] (of course, [1,3] will also be ok)

Example 2:

1
2
3
nums: [1,2,4,8]

Result: [1,2,4,8]

这道题给了我们一个数组，让我们求这样一个子集合，集合中的任意两个数相互取余均为0，而且提示中说明了要使用DP来解。那么我们考虑，较小数对较大数取余一定不为0，那么问题就变成了看较大数能不能整除这个较小数。那么如果数组是无序的，处理起来就比较麻烦，所以我们首先可以先给数组排序，这样我们每次就只要看后面的数字能否整除前面的数字。定义一个动态数组dp，其中dp[i]表示到数字nums[i]位置最大可整除的子集合的长度，还需要一个一维数组parent，来保存上一个能整除的数字的位置，两个整型变量mx和mx_idx分别表示最大子集合的长度和起始数字的位置，我们可以从后往前遍历数组，对于某个数字再遍历到末尾，在这个过程中，如果nums[j]能整除nums[i], 且dp[i] < dp[j] + 1的话，更新dp[i]和parent[i]，如果dp[i]大于mx了，还要更新mx和mx_idx，最后循环结束后，我们来填res数字，根据parent数组来找到每一个数字，参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<int> largestDivisibleSubset(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<int> dp(nums.size(), 0), parent(nums.size(), 0), res;
        int mx = 0, mx_idx = 0;
        for (int i = nums.size() - 1; i >= 0; --i) {
            for (int j = i; j < nums.size(); ++j) {
                if (nums[j] % nums[i] == 0 && dp[i] < dp[j] + 1) {
                    dp[i] = dp[j] + 1;
                    parent[i] = j;
                    if (mx < dp[i]) {
                        mx = dp[i];
                        mx_idx = i;
                    }
                }
            }
        }
        for (int i = 0; i < mx; ++i) {
            res.push_back(nums[mx_idx]);
            mx_idx = parent[mx_idx];
        }
        return res;
    }
};

Leetcode371. Sum of Two Integers

Calculate the sum of two integers a and b, but you are not allowed to use the operator + and -.

Example 1:

1
2
Input: a = 1, b = 2
Output: 3

Example 2:
1
2
Input: a = -2, b = 3
Output: 1

首先，先对数据a，b进行&（与）运算，原因是下面用^（异或）的方法来进行加法会漏掉进位，所以，先对数据进行&运算得到carry，carry中为1的位是会进行进位的位，接下来对数据进行^运算，结果记为add1，实现伪加法，之所以是伪加法，是因为它漏掉了进位。那漏掉的进位怎么办呢？对carry进行左移得到C，C+add1就是两个数据的真正的和。那怎么实现C+add1呢？将add1赋予a，C赋予b,重复以上的操作，直到b等于0。
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int getSum(int a, int b) {
        int c; 
        while(b !=0 ) { 
            c = (unsigned)(a&b) << 1;
            a = a ^ b; 
            b = c;
        }
        return a;
    }
};

Leetcode372. Super Pow

Your task is to calculate a b mod 1337 where a is a positive integer and b is an extremely large positive integer given in the form of an array.

Example1:

1
2
3
4
a = 2
b = [3]

Result: 8

Example2:

1
2
3
4
a = 2
b = [1,0]

Result: 1024

这道题让我们求一个数的很大的次方对1337取余的值，开始一直在想这个1337有什么玄机，为啥突然给这么一个数，感觉很突兀，后来想来想去也没想出来为啥，估计就是怕结果太大无法表示，随便找个数取余吧。那么这道题和之前那道Pow(x, n)的解法很类似，我们都得对半缩小，不同的是后面都要加上对1337取余。由于给定的指数b是一个一维数组的表示方法，我们要是折半缩小处理起来肯定十分不方便，所以我们采用按位来处理，比如223 = (22)10 * 23, 所以我们可以从b的最高位开始，算出个结果存入res，然后到下一位是，res的十次方再乘以a的该位次方再对1337取余，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int superPow(int a, vector<int>& b) {
        long long res = 1;
        for (int i = 0; i < b.size(); ++i) {
            res = pow(res, 10) * pow(a, b[i]) % 1337;
        }
        return res;
    }
    int pow(int x, int n) {
        if (n == 0) return 1;
        if (n == 1) return x % 1337;
        return pow(x % 1337, n / 2) * pow(x % 1337, n - n / 2) % 1337;
    }
};

Leetcode373. Find K Pairs with Smallest Sums

You are given two integer arrays nums1 and nums2 sorted in ascending order and an integer k.

Define a pair (u, v) which consists of one element from the first array and one element from the second array.

Return the k pairs (u1, v1), (u2, v2), …, (uk, vk) with the smallest sums.

Example 1:

1
2
3
Input: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
Output: [[1,2],[1,4],[1,6]]
Explanation: The first 3 pairs are returned from the sequence: [1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]

Example 2:

1
2
3
Input: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
Output: [[1,1],[1,1]]
Explanation: The first 2 pairs are returned from the sequence: [1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]

Example 3:

1
2
3
Input: nums1 = [1,2], nums2 = [3], k = 3
Output: [[1,3],[2,3]]
Explanation: All possible pairs are returned from the sequence: [1,3],[2,3]

Constraints:

  • 1 <= nums1.length, nums2.length <= 104
  • -109 <= nums1[i], nums2[i] <= 109
  • nums1 and nums2 both are sorted in ascending order.
  • 1 <= k <= 1000

这道题给了我们两个数组，让从每个数组中任意取出一个数字来组成不同的数字对，返回前K个和最小的数字对。那么这道题有多种解法，首先来看 brute force 的解法，这种方法从0循环到数组的个数和k之间的较小值，这样做的好处是如果k远小于数组个数时，不需要计算所有的数字对，而是最多计算 k*k 个数字对，然后将其都保存在 res 里，这时候给 res 排序，用自定义的比较器，就是和的比较，然后把比k多出的数字对删掉即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<pair<int, int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
        vector<pair<int, int>> res;
        for (int i = 0; i < min((int)nums1.size(), k); ++i) {
            for (int j = 0; j < min((int)nums2.size(), k); ++j) {
                res.push_back({nums1[i], nums2[j]});
            }
        }
        sort(res.begin(), res.end(), [](pair<int, int> &a, pair<int, int> &b){return a.first + a.second < b.first + b.second;});
        if (res.size() > k) res.erase(res.begin() + k, res.end());
        return res;
    }
};

Leetcode374. Guess Number Higher or Lower

We are playing the Guess Game. The game is as follows:

  • I pick a number from 1 to n. You have to guess which number I picked.
  • Every time you guess wrong, I’ll tell you whether the number is higher or lower.
  • You call a pre-defined API guess(int num) which returns 3 possible results (-1, 1, or 0):
    • -1 : My number is lower
    • 1 : My number is higher
    • 0 : Congrats! You got it!

Example :

1
2
Input: n = 10, pick = 6
Output: 6

二分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int guessNumber(int n) {
        int l = 0, r = n, mid;
        while(l <= r) {
            mid = l + (r - l) / 2;
            if(guess(mid) < 0)
                r = mid - 1;
            else if(guess(mid) > 0)
                l = mid + 1;
            else if(0 == guess(mid))
                return mid;
        }
        return -1;
    }
};

Leetcode375. Guess Number Higher or Lower II

We are playing the Guessing Game. The game will work as follows:

  1. I pick a number between 1 and n.
  2. You guess a number.
  3. If you guess the right number, you win the game.
  4. If you guess the wrong number, then I will tell you whether the number I picked is higher or lower, and you will continue guessing.
  5. Every time you guess a wrong number x, you will pay x dollars. If you run out of money, you lose the game.
    Given a particular n, return the minimum amount of money you need to guarantee a win regardless of what number I pick.

Example 1:

1
2
Input: n = 10
Output: 16

Explanation: The winning strategy is as follows:

  • The range is [1,10]. Guess 7.
    • If this is my number, your total is $0. Otherwise, you pay $7.
    • If my number is higher, the range is [8,10]. Guess 9.
      • If this is my number, your total is $7. Otherwise, you pay $9.
      • If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
      • If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
    • If my number is lower, the range is [1,6]. Guess 3.
      • If this is my number, your total is $7. Otherwise, you pay $3.
      • If my number is higher, the range is [4,6]. Guess 5.
        • If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
        • If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
        • If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
      • If my number is lower, the range is [1,2]. Guess 1.
        • If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
        • If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.

The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.

Example 2:

1
2
Input: n = 1
Output: 0

Explanation: There is only one possible number, so you can guess 1 and not have to pay anything.

Example 3:

1
2
Input: n = 2
Output: 1

Explanation: There are two possible numbers, 1 and 2.

  • Guess 1.
    • If this is my number, your total is $0. Otherwise, you pay $1.
    • If my number is higher, it must be 2. Guess 2. Your total is $1.
      The worst case is that you pay $1.

这道题需要用到 Minimax 极小化极大算法，并且题目中还说明了要用 DP 来做，需要建立一个二维的 dp 数组，其中 dp[i][j] 表示从数字i到j之间猜中任意一个数字最少需要花费的钱数，那么需要遍历每一段区间 [j, i]，维护一个全局最小值 global_min 变量，然后遍历该区间中的每一个数字，计算局部最大值local_max = k + max(dp[j][k - 1], dp[k + 1][i])，这个正好是将该区间在每一个位置都分为两段，然后取当前位置的花费加上左右两段中较大的花费之和为局部最大值，相当于是猜k这个值时的代价。为啥要取两者之间的较大值呢，因为要 cover 所有的情况，就得取最坏的情况。然后更新全局最小值，最后在更新 dp[j][i] 的时候看j和i是否是相邻的，相邻的话赋为j，否则赋为 global_min。这里为啥又要取较小值呢，因为 dp 数组是求的 [j, i] 范围中的最低 cost，比如只有两个数字1和2，那么肯定是猜1的 cost 低。

如果只有一个数字，那么不用猜，cost 为0。如果有两个数字，比如1和2，猜1，即使不对，cost 也比猜2要低。如果有三个数字 1，2，3，那么就先猜2，根据对方的反馈，就可以确定正确的数字，所以 cost 最低为2。如果有四个数字 1，2，3，4，那么情况就有点复杂了，策略是用k来遍历所有的数字，然后再根据k分成的左右两个区间，取其中的较大 cost 加上k。

  • 当k为1时，左区间为空，所以 cost 为0，而右区间 2，3，4，根据之前的分析应该取3，所以整个 cost 就是 1+3=4。
  • 当k为2时，左区间为1，cost 为0，右区间为 3，4，cost 为3，整个 cost 就是 2+3=5。
  • 当k为3时，左区间为 1，2，cost 为1，右区间为4，cost 为0，整个 cost 就是 3+1=4。
  • 当k为4时，左区间 1，2，3，cost 为2，右区间为空，cost 为0，整个 cost 就是 4+2=6。

综上k的所有情况，此时应该取整体 cost 最小的，即4，为最后的答案，这就是极小化极大算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int getMoneyAmount(int n) {
        vector<vector<int>> dp(n+1, vector<int>(n+1, 0));
        
        for (int i = 0; i < n + 1; i++)
            for (int j = 0; j < n + 1; j++)
                if (i != j)
                    dp[i][j] = INT_MAX;
        
        for (int i = 1; i < n; i ++)
            dp[i][i+1] = i;
        
        for(int i = 2; i <= n; i ++) {
            for (int j = i-1; j >= 1; j --) {
                int local, minn = INT_MAX;
                for (int k = j+1; k < i; k ++) {
                    local = max(dp[j][k-1], dp[k+1][i]) + k;
                    minn = min(minn, local);
                }
                dp[j][i] = min(minn, dp[j][i]);
            }
        }
        return dp[1][n];
    }
};

极小极大的定义

Minimax算法 又名极小化极大算法，是一种找出失败的最大可能性中的最小值的算法（即最小化对手的最大得益）。通常以递归形式来实现。

Minimax算法常用于棋类等由两方较量的游戏和程序。该算法是一个零总和算法，即一方要在可选的选项中选择将其优势最大化的选择，另一方则选择令对手 优势最小化的一个，其输赢的总和为0（有点像能量守恒，就像本身两个玩家都有1点，最后输家要将他的1点给赢家，但整体上还是总共有2点）。很多棋类游戏 可以采取此算法，例如tic-tac-toe。

以TIC-TAC-TOE为例

tic-tac-toe就是井字棋。

一般X的玩家先下。设定X玩家的最大利益为正无穷（+∞），O玩家的最大利益为负无穷（-∞），这样我们称X玩家为MAX（因为他总是追求更大的值），成O玩家为MIN（她总是追求更小的值），各自都为争取自己的最大获益而努力。

现在，让我们站在MAX的立场来分析局势（这是必须的，应为你总不能两边倒吧，你喜欢的话也可以选择MIN）。由于MAX是先下的（习惯上X的玩家先下），于是构建出来的博弈树如下(前面两层)：

MAX总是会选择MIN最大获利中的最小值（对MAX最有利），同样MIN也会一样，选择对自己最有利的（即MAX有可能获得的最大值）。有点难理解，其实就是自己得不到也不给你得到这样的意思啦，抢先把对对手有利的位置抢占了。你会看出，这是不断往下深钻的，直到最底层（即叶节点）你才能网上回溯，确定那个是对你最有利的。

具体过程会像是这么一个样子的：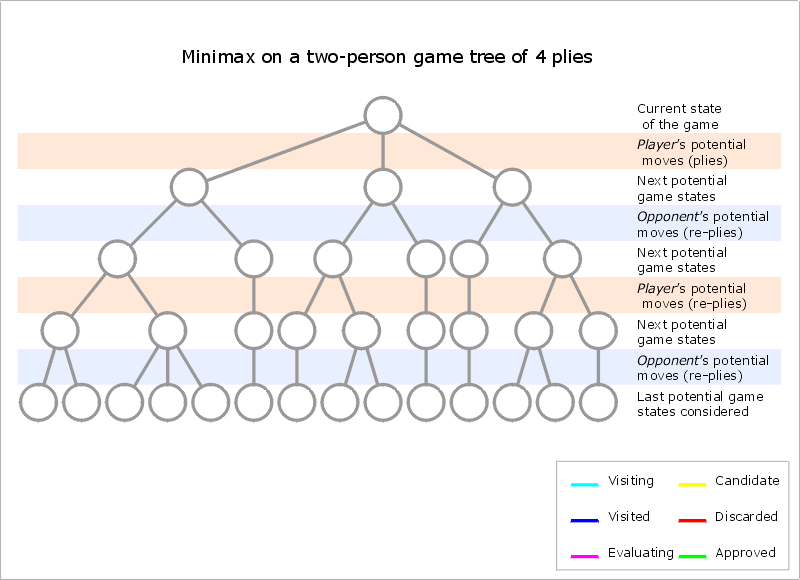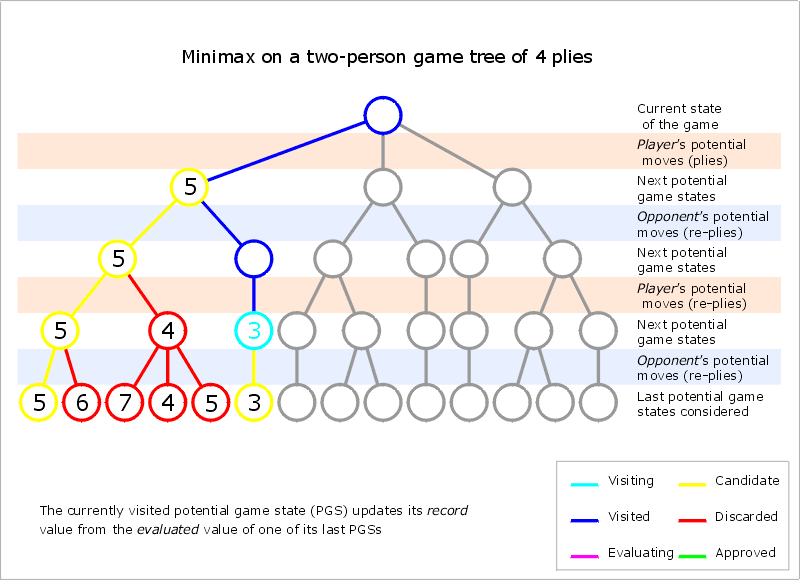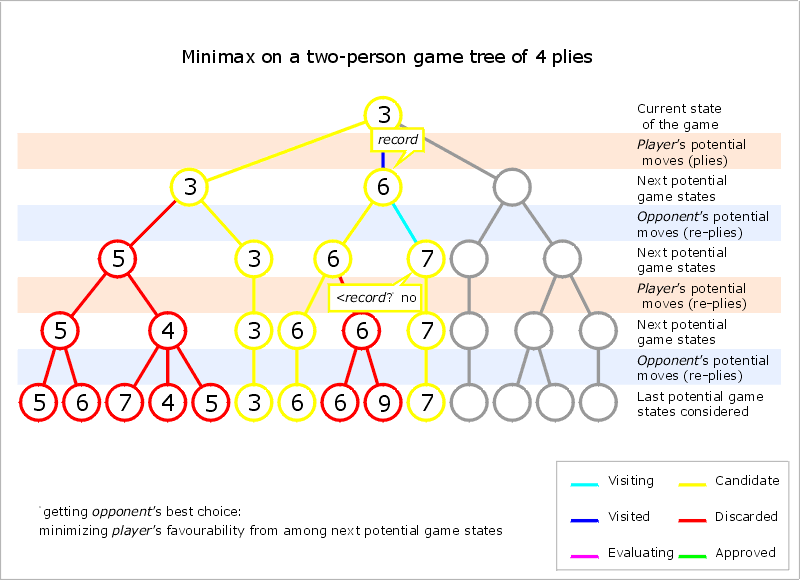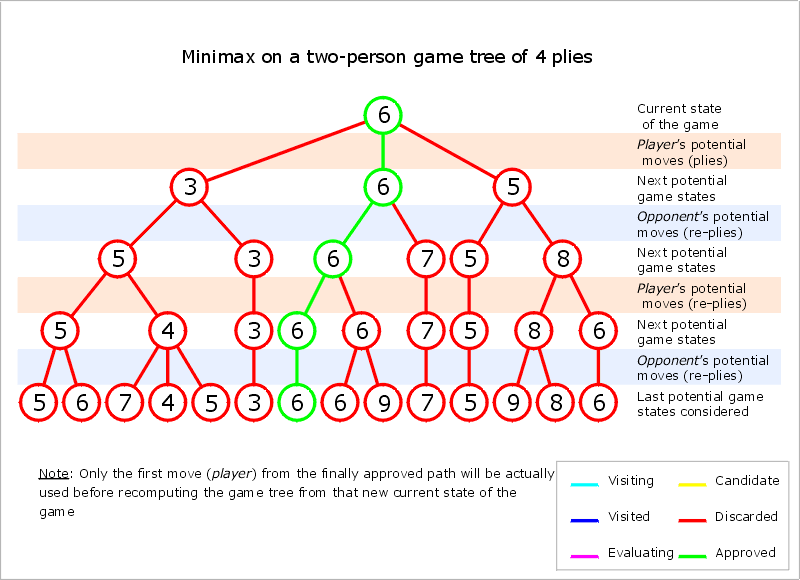

但实际情况下，完全遍历一颗博弈树是不现实的，因为层级的节点数是指数级递增的，完全遍历会很耗时…一般情况下需要限制深钻的层数，在达到限定的层数时就返回一个估算值（通过一个启发式的函数对当前博弈位置进行估值），这样获得的值就不是精确的了（遍历的层数越深越精确，当然和估算函数也有一定关系），但该值依然是足够帮助我们做出决策的。于是，对耗时和精确度需要做一个权衡。一般我们限定其遍历的深度为6（目前多数的象棋游戏也是这么设定的）。

于是，我们站在MAX的角度，评估函数会是这样子的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
static   final   int   INFINITY = 100 ;   // 表示无穷的值  
static   final   int   WIN = +INFINITY ;   // MAX的最大利益为正无穷  
static   final   int   LOSE = -INFINITY ;   // MAX的最小得益（即MIN的最大得益）为负无穷  
static   final   int   DOUBLE_LINK = INFINITY / 2 ;   // 如果同一行、列或对角上连续有两个，赛点  
static   final   int   INPROGRESS = 1 ;   // 仍可继续下（没有胜出或和局）  
static   final   int   DRAW = 0 ;   // 和局  
static   final   int [][] WIN_STATUS =   {  
      { 0, 1, 2 },  
      { 3, 4, 5 },  
      { 6, 7, 8 },  
      { 0, 3, 6 },  
      { 1, 4, 7 },  
      { 2, 5, 8 },  
      { 0, 4, 8 },  
      { 2, 4, 6   }  
};  
/** 
 * 估值函数，提供一个启发式的值，决定了游戏AI的高低 
 */  
public   int   gameState( char []   board )   {  
    int   result = INPROGRESS;  
    boolean   isFull =   true ;  
     
    // is game over?  
    for ( int   pos = 0; pos < 9; pos++) {  
        char chess = board[pos];  
        if ( empty   == chess) {  
            isFull =   false ;  
            break ;  
        }  
    }  
    // is Max win/lose?  
    for   ( int [] status : WIN_STATUS) {  
        char   chess = board[status[0]];  
        if (chess ==   empty ) {  
            break ;  
        }  
         int i = 1;  
         for (; i < status.length; i++) {  
            if (board[status[i]] != chess) {  
                break ;  
            }  
        }  
        if (i == status.length) {  
            result = chess ==   x   ? WIN : LOSE;  
             break ;  
        }  
    }  
    if (result != WIN & result != LOSE) {
        if (isFull) {  
            // is draw  
            result = DRAW;  
        } 
        else {
            // check double link  
            // finds[0]->'x', finds[1]->'o'  
            int [] finds =   new   int [2];  
            for ( int [] status : WIN_STATUS) {  
                char chess =   empty ;  
                boolean hasEmpty =   false ;  
                int count = 0;  
                for ( int   i = 0; i < status.length; i++) {  
                    if (board[status[i]] ==   empty ) {  
                        hasEmpty =   true ;  
                    }
                    else {
                        if (chess ==   empty ) {  
                            chess = board[status[i]];  
                        }  
                        if (board[status[i]] == chess) {  
                            count++;  
                        }  
                    }  
                }
                if (hasEmpty && count > 1) {  
                    if (chess ==   x ) {  
                        finds[0]++;  
                    } else {  
                        finds[1]++;  
                    }
                }  
            }
            // check if two in one line  
            if   (finds[1] > 0) {  
                result = -DOUBLE_LINK;  
            } else   if   (finds[0] > 0) {  
                result = DOUBLE_LINK;  
            }  
        }  
    }  
    return result;  
}

基于这些，一个限定层数的实现是这样的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
/** 
 * 以'x'的角度来考虑的极小极大算法 
 */  
public int minimax( char [] board,   int   depth){  
        int [] bestMoves =   new   int [9];  
        int   index = 0;  
        int   bestValue = - INFINITY ;  
        for ( int   pos=0; pos<9; pos++){
            if (board[pos]== empty ){  
                board[pos] =   x ;  
                    
                int   value = min(board, depth);  
                if (value>bestValue){  
                    bestValue = value;  
                    index = 0;  
                    bestMoves[index] = pos;  
                } else  
                    if (value==bestValue){  
                        index++;  
                        bestMoves[index] = pos;  
                }  
                    
                board[pos] =   empty ;  
            }  
        }  
        if (index>1){  
            index = ( new   Random (System. currentTimeMillis ()).nextInt()>>>1)%index;  
        }  
        return   bestMoves[index];  
}  
/** 
 * 对于'x'，估值越大对其越有利 
 */  
public   int   max( char [] board,   int   depth){  
    int   evalValue =   gameState (board);  
    boolean isGameOver = (evalValue== WIN || evalValue== LOSE || evalValue== DRAW );  
    if (depth==0 || isGameOver){  
        return   evalValue;  
    }  
    
    int   bestValue = - INFINITY ;  
    for ( int   pos=0; pos<9; pos++){  
        if (board[pos]== empty ){  
            // try  
            board[pos] =   x ;  
                
            //   maximixing  
            bestValue = Math. max (bestValue, min(board, depth-1));  
            // reset  
            board[pos] =   empty ;  
        }  
    }  
    return   evalValue;  
}
/** 
 * 对于'o'，估值越小对其越有利 
 */  
public   int   min( char [] board,   int   depth){  
    int   evalValue =   gameState (board);  
    boolean   isGameOver = (evalValue== WIN   || evalValue== LOSE   || evalValue== DRAW );  
    if (depth==0 || isGameOver){  
        return   evalValue;  
    }  
    int   bestValue = + INFINITY ;  
    for ( int   pos=0; pos<9; pos++){  
        if (board[pos]== empty ){  
            // try  
            board[pos] =   o ;  
            //   minimixing  
            bestValue = Math.min(bestValue, max(board, depth-1));  
            // reset  
            board[pos] =   empty ;  
        }  
    }
    return   evalValue;     
}

Alpha-beta剪枝

另外，通过结合Alpha-beta剪枝能进一步优化效率。Alpha-beta剪枝顾名思义就是裁剪掉一些不必要的分支，以减少遍历的节点数。实际上是通过传递两个参数alpha和beta到递归的极小极大函数中，alpha表示了MAX的最坏情况，beta表示了MIN的最坏情况，因此他们的初始值为负无穷和正无穷。在递归的过程中，在轮到MAX的回合，如果极小极大的值比alpha大，则更新alpha；在MIN的回合中，如果极小极大值比beta小，则更新beta。当alpha和beta相交时（即alpha>=beta），这时该节点的所有子节点对于MAX和MIN双方都不会带来好的获益，所以可以忽略掉（裁剪掉）以该节点为父节点的整棵子树。

根据这一定义，可以很轻易地在上面程序的基础上进行改进：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
/** 
 * 以'x'的角度来考虑的极小极大算法 
 */  
public   int   minimax( char [] board,   int   depth){  
    int [] bestMoves =   new   int [9];  
    int   index = 0;  
     
    int   bestValue = - INFINITY ;  
    for ( int   pos=0; pos<9; pos++){  
        if (board[pos]== empty ){  
            board[pos] =   x ;  
              
            int   value = min(board, depth, - INFINITY , + INFINITY );  
            if (value>bestValue){  
                bestValue = value;  
                index = 0;  
                bestMoves[index] = pos;  
            } 
            else if (value==bestValue){  
                index++;  
                bestMoves[index] = pos;  
            } 
            board[pos] =   empty ;  
        }  
      }  
    if (index>1){  
        index = ( new   Random (System. currentTimeMillis ()).nextInt()>>>1)%index;  
    }  
    return   bestMoves[index];  
}  
/** 
 * 对于'x'，估值越大对其越有利 
 */  
public   int   max( char [] board,   int   depth,   int   alpha,   int   beta){  
    int   evalValue =   gameState (board);  
    boolean   isGameOver = (evalValue== WIN   || evalValue== LOSE   || evalValue== DRAW );  
    if (beta<=alpha){  
        return   evalValue;  
    }  
    if (depth==0 || isGameOver){  
        return   evalValue;  
    }
    int   bestValue = - INFINITY ;  
    for ( int   pos=0; pos<9; pos++){  
        if (board[pos]== empty ){
            // try  
            board[pos] =   x ;  
            //   maximixing  
            bestValue = Math. max (bestValue, min(board, depth-1, Math. max (bestValue, alpha), beta));  
            // reset  
            board[pos] =   empty ;  
        }  
    }
    return   evalValue;  
}  
/** 
 * 对于'o'，估值越小对其越有利 
 */  
public   int   min( char [] board,   int   depth,   int   alpha,   int   beta){  
    int   evalValue =   gameState (board);  
    boolean   isGameOver = (evalValue== WIN   || evalValue== LOSE   || evalValue== DRAW );  
    if (alpha>=beta){  
        return   evalValue;  
    }  
    // try  
    if (depth==0 || isGameOver || alpha>=beta){  
        return   evalValue;  
    }  
        
    int   bestValue = + INFINITY ;  
    for ( int   pos=0; pos<9; pos++){  
        if (board[pos]== empty ){  
            // try  
            board[pos] =   o ;  
            //   minimixing  
            bestValue = Math.min(bestValue, max(board, depth-1, alpha, Math.min(bestValue, beta)));  
            // reset  
            board[pos] =   empty ;  
        }
    }
    return   evalValue;  
}

Leetcode376. Wiggle Subsequence

A wiggle sequence is a sequence where the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with one element and a sequence with two non-equal elements are trivially wiggle sequences.

For example, [1, 7, 4, 9, 2, 5] is a wiggle sequence because the differences (6, -3, 5, -7, 3) alternate between positive and negative.
In contrast, [1, 4, 7, 2, 5] and [1, 7, 4, 5, 5] are not wiggle sequences. The first is not because its first two differences are positive, and the second is not because its last difference is zero.
A subsequence is obtained by deleting some elements (possibly zero) from the original sequence, leaving the remaining elements in their original order.

Given an integer array nums, return the length of the longest wiggle subsequence of nums.

Example 1:

1
2
3
Input: nums = [1,7,4,9,2,5]
Output: 6
Explanation: The entire sequence is a wiggle sequence with differences (6, -3, 5, -7, 3).

Example 2:

1
2
3
4
Input: nums = [1,17,5,10,13,15,10,5,16,8]
Output: 7
Explanation: There are several subsequences that achieve this length.
One is [1, 17, 10, 13, 10, 16, 8] with differences (16, -7, 3, -3, 6, -8).

Example 3:

1
2
Input: nums = [1,2,3,4,5,6,7,8,9]
Output: 2

一个整数序列，如果两个相邻元素的差恰好正负交替出现，则该序列被称为摇摆序列。一个小于2个元素的序列直接为摇摆序列。给一个随机序列，求这个序列满足摇摆序列定义的最长子序列的长度。

解法：记录序列中前后两个元素的状态。初始状态为begin，如果后一个元素大于前一个元素，则状态为up，反之状态为down。当状态转换时，摇摆序列的长度加1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        if(nums.size() < 2)
            return nums.size();
        
        int dir = 0, res = 1;
        for (int i = 1; i < nums.size(); i ++) {
            if(nums[i] > nums[i-1]) {
                if (dir == 0 || dir == -1) {
                    res ++;
                    dir = 1;
                }
            }
            else if (nums[i] < nums[i-1]) {
                if (dir == 0 || dir == 1) {
                    res ++;
                    dir = -1;
                }
            }
        }
    	return res; 
    }
};

状态转移方程

  • dp[i][0]=max{dp[j][1]}+1 当nums[i]>nums[j]
  • dp[i][1]=max{dp[j][0]}+1 当nums[i]<nums[j]

其中 0<=j<i

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int len = nums.size();
        if(len < 2)
            return len;
        
        vector<vector<int> > dp(len+1, vector<int>(2, 0));
        dp[0][0] = 1;
        dp[0][1] = 1;
        for (int i = 1; i < len; i ++) {
            int a = INT_MIN;
            int b = INT_MIN;
            for (int k = i-1; k >= 0; k --) {
                if (nums[i] > nums[k])
                    a = max(a, dp[k][0]);
                if (nums[i] < nums[k])
                    b = max(b, dp[k][1]);
            }
            dp[i][1] = a > INT_MIN ? a+1 : 1;
			dp[i][0] = b > INT_MIN ? b+1 : 1;
        }
        
    	return max(dp[len-1][0], dp[len-1][1]); 
    }
};

Leetcode377. Combination Sum IV

Given an array of distinct integers nums and a target integer target, return the number of possible combinations that add up to target.

The answer is guaranteed to fit in a 32-bit integer.

Example 1:

1
2
Input: nums = [1,2,3], target = 4
Output: 7

Explanation:

1
2
3
4
5
6
7
8
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

Note that different sequences are counted as different combinations.

这里需要一个一维数组 dp，其中 dp[i] 表示目标数为i的解的个数，然后从1遍历到 target，对于每一个数i，遍历 nums 数组，如果 i>=x, dp[i] += dp[i - x]。这个也很好理解，比如说对于 [1,2,3] 4，这个例子，当计算 dp[3] 的时候，3可以拆分为 1+x，而x即为 dp[2]，3也可以拆分为 2+x，此时x为 dp[1]，3同样可以拆为 3+x，此时x为 dp[0]，把所有的情况加起来就是组成3的所有情况了。

如果 target 远大于 nums 数组的个数的话，上面的算法可以做适当的优化，先给 nums 数组排个序，然后从1遍历到 target，对于i小于数组中的数字x时，直接 break 掉，因为后面的数更大，其余地方不变，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<int> dp(target+1, 0);
        sort(nums.begin(), nums.end());
        dp[0] = 1;
        for (int i = 1; i < target+1; i ++) {
            for (int ii : nums) {
                if (i < ii)
                    break;
                if (long(dp[i]) + dp[i-ii] > INT_MAX)
                    continue;
                else
                    dp[i] = dp[i] + dp[i - ii];
            }
        }
        return dp[target];
    }
};

中间可能会溢出，超过INT_MAX，需要处理一下，如果超过了INT_MAX以后也就不可能用到了，所以直接continue。

Leetcode378. Kth Smallest Element in a Sorted Matrix

Given an n x n matrix where each of the rows and columns are sorted in ascending order, return the kth smallest element in the matrix.

Note that it is the kth smallest element in the sorted order, not the kth distinct element.

Example 1:

1
2
3
Input: matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
Output: 13
Explanation: The elements in the matrix are [1,5,9,10,11,12,13,13,15], and the 8th smallest number is 13

Example 2:

1
2
Input: matrix = [[-5]], k = 1
Output: -5

输入矩阵matrix，每一行可以看做是一个排序好的数组，可以将这几个小数组排序好之后取第k个数，即可。排序几个已经排序好的数组，可以参考leetcode23。时间复杂度O(klogn)。

因为同时每一列也是排序号的，考虑用二分查找实现。

二分思路

返回值一定在matrix[0][0]到matrix[n-1][n-1]之间。令函数g(x)={matrix中小于等于x的数量}={of(matrix[i][j]<=x)}。g(x)是一个递增的函数，x越大，g(x)越大。返回值是满足g(x)>=k，的最小值。

1
2
3
4
5
6
7
8
9
10
11
12
int kthSmallest(vector<vector<int>>& matrix, int k) {
    int len = matrix.size();
    int left = matrix[0][0], right = matrix[len-1][len-1];
    while(left <= right) {
        int middle = left + (right - left) / 2;
        if (count(matrix, middle, len) >= k)
            right = middle - 1;
        else
            left = middle + 1;
    }
    return left;   
}

计算小于等于middle值的个数

接下来的问题是如何数出< = middle的数量。可以发现一个性质：任取一个数 mid 满足l <= middle <= r，那么矩阵中不大于 mid 的数，肯定全部分布在矩阵的左上角。

我们可以从左下角开始遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private int countSmallerOrEqual(int[][] matrix, int middle, int n){
    int i = n - 1;
    int j = 0;
    int num = 0;
    while(i>=0 && j<n){
        if(matrix[i][j]<=middle){
            num += i+1;
            j++;
        }else{
            i--;
        }
    }
    return num;
}

时间复杂度O(nlog(r−l))。二分查找进行次数为O(log(r-l))，每次操作时间复杂度为 O(n)。

当然我们也可以每次遍历一个子数组，二分查找个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
private int countSmallerOrEqual(int[][] matrix, int middle, int n){
       int num = 0;
       for(int i = 0;i<n;i++){
           int l = 0, r = n-1;
           while(l<=r){
               int m = l + ((r-l)>>1);
               if(matrix[i][m]>middle){
                   r = m - 1;
               }else{
                   l = m + 1;
               }
           }
           if(l>=0){
               num += l;
           }
       } 
       return num;
   }

Leetcode382. Linked List Random Node

Given a singly linked list, return a random node’s value from the linked list. Each node must have the same probability of being chosen.

Example 1:

1
2
3
4
5
Input
["Solution", "getRandom", "getRandom", "getRandom", "getRandom", "getRandom"]
[[[1, 2, 3]], [], [], [], [], []]
Output
[null, 1, 3, 2, 2, 3]

Explanation
1
2
3
4
5
6
7
Solution solution = new Solution([1, 2, 3]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.

这道题给了我们一个链表，让随机返回一个节点，那么最直接的方法就是先统计出链表的长度，然后根据长度随机生成一个位置，然后从开头遍历到这个位置即可。

Leetcode383. Ransom Note

Given an arbitrary ransom note string and another string containing letters from all the magazines, write a function that will return true if the ransom note can be constructed from the magazines ; otherwise, it will return false.

Each letter in the magazine string can only be used once in your ransom note.

Example 1:

1
2
Input: ransomNote = "a", magazine = "b"
Output: false

Example 2:
1
2
Input: ransomNote = "aa", magazine = "ab"
Output: false

Example 3:
1
2
Input: ransomNote = "aa", magazine = "aab"
Output: true

判断给定字符串Ransom 能否由另一字符串magazine中字符中的某些字符组合生成。 显然，统计字符出现次数即可！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        vector<int> re(27, 0), ree(27, 0);
        for(int i = 0; i < magazine.length(); i ++)
            re[magazine[i]-'a'] ++;
        for(int i = 0; i < ransomNote.length(); i ++) {
            re[ransomNote[i]-'a'] --;
            if(re[ransomNote[i]-'a'] < 0)
                return false;
        }
        return true;
    }
};

Leetcode384. Shuffle an Array

Given an integer array nums, design an algorithm to randomly shuffle the array.

Implement the Solution class:

  • Solution(int[] nums) Initializes the object with the integer array nums.
  • int[] reset() Resets the array to its original configuration and returns it.
  • int[] shuffle() Returns a random shuffling of the array.

Example 1:

1
2
3
4
5
Input
["Solution", "shuffle", "reset", "shuffle"]
[[[1, 2, 3]], [], [], []]
Output
[null, [3, 1, 2], [1, 2, 3], [1, 3, 2]]

Explanation
1
2
3
4
Solution solution = new Solution([1, 2, 3]);
solution.shuffle();    // Shuffle the array [1,2,3] and return its result. Any permutation of [1,2,3] must be equally likely to be returned. Example: return [3, 1, 2]
solution.reset();      // Resets the array back to its original configuration [1,2,3]. Return [1, 2, 3]
solution.shuffle();    // Returns the random shuffling of array [1,2,3]. Example: return [1, 3, 2]

我们遍历数组每个位置，每次都随机生成一个坐标位置，然后交换当前遍历位置和随机生成的坐标位置的数字，这样如果数组有n个数字，那么我们也随机交换了n组位置，从而达到了洗牌的目的，这里需要注意的是i + rand() % (res.size() - i)不能写成rand() % res.size()，不是真正的随机分布，应该使用Knuth shuffle算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    Solution(vector<int> nums): v(nums) {}

    /** Resets the array to its original configuration and return it. */
    vector<int> reset() {
        return v;
    }

    /** Returns a random shuffling of the array. */
    vector<int> shuffle() {
        vector<int> res = v;
        for (int i = 0; i < res.size(); ++i) {
            int t = i + rand() % (res.size() - i);
            swap(res[i], res[t]);
        }
        return res;
    }

private:
    vector<int> v;
};

洗牌的正确姿势-Knuth shuffle算法

怎样用计算机模拟出足够随机的洗牌结果，看似很简单，但其实它比给一副乱糟糟的牌排好序可能还更难一些。洗牌问题的描述很简单：即如何通过打乱顺序，让一副扑克牌变成随机的排列，而且每一种可能的排列有相同机会出现。关键点在于“相同机会”，即各种随机排列是等可能的。下面先简单介绍一个常见的错误做法，然后看看如何改进变成Knuth 洗牌算法。

先看看一个很直接的做法（一副牌在这里用一个数组表示）：

对数组从头到尾扫描一遍，扫描过程中，每次都从整个数组随机选一个元素，跟当前扫描到的元素交换位置。

也就是，先拿起第一张牌，把它跟从整副牌里随机挑出的另一张牌（把它叫做随机牌）交换位置（随机牌也可能是第一张牌自己，这个时候就相当于不交换位置）；接着拿起第二张牌，也把它跟随机选出的另一张牌交换位置；一直重复直到把最后一张牌跟随机牌交换位置。

用python实现起来也只有几行：

1
2
3
4
5
def shuffleSort(a):
  N = len(a)
  for i in range(N):
    j = random.randint(0, N-1)
    a[j], a[i] = a[i], a[j]

这样随机交换之后，每种排列出现的可能性会是等概率的吗？看起来好像会，但事实上，经过这样交换，总有一部分排列出现的概率更高一些，这个洗牌过程并没有很公平。

为什么不够公平？要从直觉上能够理解清楚还不是那么容易。我们用一个简单的例子来看看，假设这副牌只有三张，分别是{A，B， C}.

按照前面说的方法，第一轮把第一张牌A跟随机一张牌进行交换，会产生三个等可能的结果：

1
2
3
no change:      {A, B,  C}
swap with B:    {B,  A, C}
swap with C:   {C, B,  A}

第二轮从上述三种排列出发，把第二张牌跟随机的一张牌交换，得到九种（有重复）等可能的排列。第三轮也类似。用树状图表示可以看得直观些。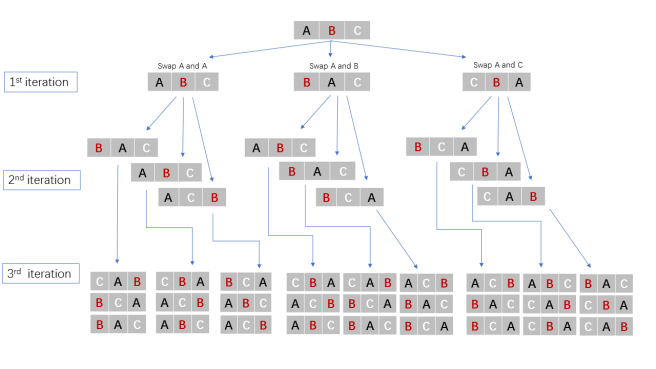

可以看到，最后产生的27个结果里面，{A, B, C}, {C, A, B}, {C, B, A}都出现了4次，而{A, C, B}, {B, A, C}, {B, C, A}都出现了5次。也就是说有些排序出现的可能性是4/27，有些却是5/27. 而且，随着牌数目的增加，这个概率的不均衡会更加严重。

我们重新看看这个方法。A,B,C三张牌的全排列只有6种，但是在这个方法里，一共产生了27个结果（27个分支），它不是6的倍数，怎么都没法给6种排列平均分嘛。所以，要让结果够公平，一个必要条件就是产生的分支是6的整数倍，也就是N!的整数倍。

Knuth洗牌算法

所以牌该怎么洗呢？在上述方法的基础上，做一处修改，就能剪去一些分支，让分支数是N!的整数倍。这就是Knuth洗牌算法。

1
2
3
4
5
def shuffleSort(a):
  N = len(a)
  for i in range(N):
    j = random.randint(0, i)
    a[j], a[i] = a[i], a[j]

唯一修改的就是随机牌j选取的方法，在拿起第i张牌时，只从它前面的牌随机选出j，而不是从整副牌里面随机选取。

Really? 就只是这样吗？

是的。就这么简单。

还是用{A, B, C}这三张牌作为例子看看。

第一轮拿起牌A， 现在随机牌只能是A，经过第一轮之后，其实没有发生变换，还是{A,B,C}; (这一步也可以省略)

第二轮拿起牌B， 从{A，B}里面随机选一张牌跟B交换，会得到两种等可能的结果：

1
2
swap with A: {B, A, C}
no change: {A, B, C}

第三轮从上面两种可能的排列出发，拿起最后一张牌（这里都是C）， 再从所有牌里面随机选一张跟它交换。树状图如下：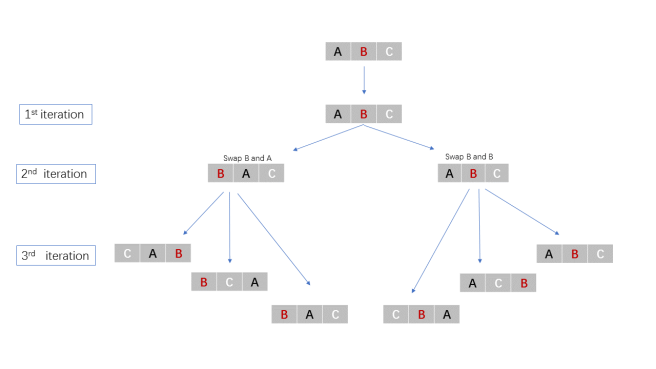

最终得到的结果只有6个，正好是三张牌的所有6种排列结果，每种出现一次。所以，Knuth洗牌算法是公平的。

Leetcode385. Mini Parser

Given a nested list of integers represented as a string, implement a parser to deserialize it.

Each element is either an integer, or a list – whose elements may also be integers or other lists.

Note: You may assume that the string is well-formed:

  • String is non-empty.
  • String does not contain white spaces.
  • String contains only digits 0-9, [, - ,, ].

Example 1:

1
2
3
Given s = "324",

You should return a NestedInteger object which contains a single integer 324.

Example 2:

1
2
3
4
5
6
7
8
Given s = "[123,[456,[789]]]",

Return a NestedInteger object containing a nested list with 2 elements:
1. An integer containing value 123.
2. A nested list containing two elements:
    i.  An integer containing value 456.
    ii. A nested list with one element:
         a. An integer containing value 789.

这道题让我们实现一个迷你解析器用来把一个字符串解析成NestInteger类，关于这个嵌套链表类的题我们之前做过三道，Nested List Weight Sum II，Flatten Nested List Iterator，和Nested List Weight Sum。应该对这个类并不陌生了，我们可以先用递归来做，思路是，首先判断s是否为空，为空直接返回，不为空的话看首字符是否为[，不是的话说明s为一个整数，我们直接返回结果。如果首字符是[，且s长度小于等于2，说明没有内容，直接返回结果。反之如果s长度大于2，我们从i=1开始遍历，我们需要一个变量start来记录某一层的其实位置，用cnt来记录跟其实位置是否为同一深度，cnt=0表示同一深度，由于中间每段都是由逗号隔开，所以当我们判断当cnt为0，且当前字符是逗号或者已经到字符串末尾了，我们把start到当前位置之间的字符串取出来递归调用函数，把返回结果加入res中，然后start更新为i+1。如果遇到[，计数器cnt自增1，若遇到]，计数器cnt自减1。参见代码如下：

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    NestedInteger deserialize(string s) {
        if (s.empty()) return NestedInteger();
        if (s[0] != '[') return NestedInteger(stoi(s));
        if (s.size() <= 2) return NestedInteger();
        NestedInteger res;
        int start = 1, cnt = 0;
        for (int i = 1; i < s.size(); ++i) {
            if (cnt == 0 && (s[i] == ',' || i == s.size() - 1)) {
                res.add(deserialize(s.substr(start, i - start)));
                start = i + 1;
            } else if (s[i] == '[') ++cnt;
            else if (s[i] == ']') --cnt;
        }
        return res;
    }
};

Leetcode386. Lexicographical Numbers

Given an integer n, return all the numbers in the range [1, n] sorted in lexicographical order.

You must write an algorithm that runs in O(n) time and uses O(1) extra space.

Example 1:

1
2
Input: n = 13
Output: [1,10,11,12,13,2,3,4,5,6,7,8,9]

Example 2:

1
2
Input: n = 2
Output: [1,2]

给出一个整数 n ，将 1 到 n 的所有整数按照字典顺序排列。例：给出13，返回[1,10,11,12,13,2,3,4,5,6,7,8,9]。注意：尽量使用少的时间和空间复杂度，输入整数大小可能接近5,000,000。

设数组ans，用来存放最后返回的结果，设temp，表示当前应该存入的数字，初始为1.
按照字典序的规则，尽可能先把位数少的，顺序靠前的先放进去，那么应该先放1，10，100，1000。。。
即if（temp 10 <= n ） temp = 10;
然后当超出上限的时候，退回到上一位，开始每次加1，例如：1001，1002，1003。。。。一直到个位数到9为止，即1009，此时加1变成1100，把最右边连续的 0 去除，即回退到11，然后再开始乘10，再循环加个位，再回退。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> lexicalOrder(int n) {
        vector<int> res(n);
        int temp = 1;
        
        for (int i = 0; i < n; i ++) {
            res[i] = temp;
            if (temp * 10 <= n)
                temp = temp * 10;
            else {
                if (temp >= n)
                    temp /= 10;
                temp ++;
                while(temp % 10 == 0)
                    temp /= 10;
            }
        }
        return res;
    }
};

Leetcode387. First Unique Character in a String

Given a string, find the first non-repeating character in it and return it’s index. If it doesn’t exist, return -1.

Examples:

1
2
s = "leetcode"
return 0.

1
2
s = "loveleetcode",
return 2.

用哈希表建立每个字符和其出现次数的映射，然后按顺序遍历字符串，找到第一个出现次数为1的字符，返回其位置即可。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int firstUniqChar(string s) {
        unordered_map<char, int> m;
        for (char c : s) ++m[c];
        for (int i = 0; i < s.size(); ++i) {
            if(m[s[i]] == 1)
                return i;
        }
        return -1;
    }
};

Leetcode389. Find the Difference

Given two strings s and t which consist of only lowercase letters. String t is generated by random shuffling string s and then add one more letter at a random position. Find the letter that was added in t.

Example:

1
2
3
4
5
6
Input:
s = "abcd"
t = "abcde"
Output: e
Explanation:
'e' is the letter that was added.

一个hash表可以解决, 甚至可以用两个加起来然后异或

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    char findTheDifference(string s, string t) {
        unordered_map<char, int> hash;
        char ans;
        for(auto ch: s) hash[ch]++;
        for(auto ch: t) 
            if(--hash[ch]<0) ans = ch; 
        return ans;
    }
};

Leetcode392. Is Subsequence

Given a string s and a string t, check if s is subsequence of t.

You may assume that there is only lower case English letters in both s and t. t is potentially a very long (length ~= 500,000) string, and s is a short string (<=100).

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, “ace” is a subsequence of “abcde” while “aec” is not).

Example 1:

1
2
s = "abc", t = "ahbgdc"
Return true.

Example 2:

1
2
s = "axc", t = "ahbgdc"
Return false.

Follow up:
If there are lots of incoming S, say S1, S2, … , Sk where k >= 1B, and you want to check one by one to see if T has its subsequence. In this scenario, how would you change your code?

检查一个串是不是另一个串的子串，找两个指针即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool isSubsequence(string s, string t) {
        int ss,tt;
        ss=0;
        tt=0;
        while(ss<s.length() && tt<t.length()){
            if(s[ss]==t[tt]){
                ss++;
                tt++;
            }
            else
                tt++;
        }
        if(ss==s.length()){
            return true;
        }
        else
            return false;
    }
};

我们可以用俩个指针i，j分别指向字符串s，t. 算法描述如下: j指针一直往后走，碰到t[j]==s[i]的时候，说明匹配上了一个，将i++，否则i不加1，当t都走完的时候，这个时候，我们判断一下i指针是否走完了s字符串，如果走完了，说明也匹配上了，如果没有走完，那么就是没有匹配上，中间的过程，i提前等于s.length()的时候，也可以退出！此时的时间复杂度就是扫描一遍t，s串的线性复杂度O(t_len+s_len)。

算法正确性：

我们算法的关键点就在于，当s[i]=t[j]的时候，i和j都需要加1，那么这俩个指针加1的过程是否一定是对的呢？我们可以这样理解，当s=”abc”,t=”ahbgdc”,i=1,j=1的时候，我们只需要判断s后面的子串bc是否是t的子串hbgdc的子集（相当于分解为子问题），如果s的子串bc满足是t的子串hbgdc的子集，我们就返回true，如果不满足，我们就返回false。这样一步一步贪心下去就能保证算法正确性。

下面举一个简单例子走一遍算法帮助理解: s=”abc”, t=“ahbgdc” 首先i，j都为0，分别指向s，t俩个串开头. 第一步，当j=0<t_len=6的时候，进入循环，此时t[0]=a,s[0]=a,俩者相等，那么i,j都1，此时i=1，j=1，i!=(s_len=3),不跳出, j还是小于t_len。 此时t[1]=h ,s[1]=b,它们不相等，那么只有j加1，此时i=1,j=2，i!=3，不跳出. j还是小于t_len=6，此时t[2]=b,s[1]=b,它们相等，那么i,j分别加1，此时i=2，j=3,i!=3不跳出. 那么t[3]=g,s[2]=c,它们不相等，那么之后j加1，此时i=2,j=4，i!=3不跳出. 此时t[4]=d,s[2]=2,它们不相等,此时j加1,i=2,j=5,i!=3不跳出. j还是小于6，t[5]=c,s[2]=c,此时它们相等，i++，i=3，此时等于s_len，res=true，跳出while循环，返回结果为true。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    bool isSubsequence(string s, string t) {
        //俩个指针都往前走
        if(s.length()==0)
            return true;        //空字符串是任何字符串的子串
        int i = 0,j = 0;
        bool res = false;
        int s_len = s.length(),t_len = t.length();
        while(j < t_len)
        {
            if(t[j] == s[i])
            {
                i++;
                if(i==s_len)
                {
                    res = true;
                    break;
                }
            }
            j++;         //无论t[j]是否等于s[i]，j都要加1
        }
        return res;
    }
};

Leetcode393. UTF-8 Validation

A character in UTF8 can be from 1 to 4 bytes long, subjected to the following rules:

For 1-byte character, the first bit is a 0, followed by its unicode code.
For n-bytes character, the first n-bits are all one’s, the n+1 bit is 0, followed by n-1 bytes with most significant 2 bits being 10.
This is how the UTF-8 encoding would work:

1
2
3
4
5
6
7
Char. number range  |        UTF-8 octet sequence
   (hexadecimal)    |              (binary)
--------------------+---------------------------------------------
0000 0000-0000 007F | 0xxxxxxx
0000 0080-0000 07FF | 110xxxxx 10xxxxxx
0000 0800-0000 FFFF | 1110xxxx 10xxxxxx 10xxxxxx
0001 0000-0010 FFFF | 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx

Given an array of integers representing the data, return whether it is a valid utf-8 encoding.

Note:
The input is an array of integers. Only the least significant 8 bits of each integer is used to store the data. This means each integer represents only 1 byte of data.

Example 1: data = [197, 130, 1], which represents the octet sequence: 11000101 10000010 00000001. Return true.It is a valid utf-8 encoding for a 2-bytes character followed by a 1-byte character.

Example 2: data = [235, 140, 4], which represented the octet sequence: 11101011 10001100 00000100. Return false. The first 3 bits are all one’s and the 4th bit is 0 means it is a 3-bytes character. The next byte is a continuation byte which starts with 10 and that’s correct. But the second continuation byte does not start with 10, so it is invalid.

这道题考察我们 UTF-8 编码，这种互联网所采用的通用的编码格式的产生是为了解决ASCII只能表示英文字符的局限性，和统一 Unicode 的实现方式。下面这段摘自维基百科 UTF-8 编码：

对于 UTF-8 编码中的任意字节B，如果B的第一位为0，则B独立的表示一个字符(ASCII 码)；

  • 如果B的第一位为1，第二位为0，则B为一个多字节字符中的一个字节(非 ASCII 字符)；
  • 如果B的前两位为1，第三位为0，则B为两个字节表示的字符中的第一个字节；
  • 如果B的前三位为1，第四位为0，则B为三个字节表示的字符中的第一个字节；
  • 如果B的前四位为1，第五位为0，则B为四个字节表示的字符中的第一个字节；

因此，对 UTF-8 编码中的任意字节，根据第一位，可判断是否为 ASCII 字符；根据前二位，可判断该字节是否为一个字符编码的第一个字节；根据前四位（如果前两位均为1），可确定该字节为字符编码的第一个字节，并且可判断对应的字符由几个字节表示；根据前五位（如果前四位为1），可判断编码是否有错误或数据传输过程中是否有错误。

如果是标识字节，先将其向右平移五位，如果得到 110，则说明后面跟了一个字节，否则向右平移四位，如果得到 1110，则说明后面跟了两个字节，否则向右平移三位，如果得到 11110，则说明后面跟了三个字节，否则向右平移七位，如果为1的话，说明是 10000000 这种情况，不能当标识字节，直接返回 false。在非标识字节中，向右平移六位，如果得到的不是 10，则说明不是以 10 开头的，直接返回 false，否则 cnt 自减1，成功完成遍历返回 true。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    bool validUtf8(vector<int>& data) {
        int cnt = 0;
        for(int i = 0; i < data.size(); i ++) {
            if(cnt == 0) {
                if((data[i] >> 7) == 0)
                    cnt = 0;
                else if((data[i] >> 5) == 0b110)
                    cnt = 1;
                else if((data[i] >> 4) == 0b1110)
                    cnt = 2;
                else if((data[i] >> 3) == 0b11110)
                    cnt = 3;
                else
                    return false;
            }
            else {
                if((data[i] >> 6) != 0b10)
                    return false;
                cnt --;
            }
        }
        return cnt == 0;
    }
};

Leetcode394. Decode String

Given an encoded string, return its decoded string.

The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guaranteed to be a positive integer.

You may assume that the input string is always valid; there are no extra white spaces, square brackets are well-formed, etc.

Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k. For example, there will not be input like 3a or 2[4].

Example 1:

1
2
Input: s = "3[a]2[bc]"
Output: "aaabcbc"

Example 2:

1
2
Input: s = "3[a2[c]]"
Output: "accaccacc"

Example 3:

1
2
Input: s = "2[abc]3[cd]ef"
Output: "abcabccdcdcdef"

这道题让我们把一个按一定规则编码后的字符串解码成其原来的模样，编码的方法很简单，就是把重复的字符串放在一个括号里，把重复的次数放在括号的前面，注意括号里面有可能会嵌套括号，这题可以用递归和迭代两种方法来解，我们首先来看递归的解法，把一个括号中的所有内容看做一个整体，一次递归函数返回一对括号中解码后的字符串。给定的编码字符串实际上只有四种字符，数字，字母，左括号，和右括号。那么我们开始用一个变量i从0开始遍历到字符串的末尾，由于左括号都是跟在数字后面，所以首先遇到的字符只能是数字或者字母，如果是字母，直接存入结果中，如果是数字，循环读入所有的数字，并正确转换，那么下一位非数字的字符一定是左括号，指针右移跳过左括号，对之后的内容调用递归函数求解，注意我们循环的停止条件是遍历到末尾和遇到右括号，由于递归调用的函数返回了子括号里解码后的字符串，而我们之前把次数也已经求出来了，那么循环添加到结果中即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    string decodeString(string s) {
        int i = 0;
        return decode(s, i);
    }
    string decode(string s, int& i) {
        string res = "";
        int n = s.size();
        while (i < n && s[i] != ']') {
            if (s[i] < '0' || s[i] > '9') {
                res += s[i++];
            } else {
                int cnt = 0;
                while (s[i] >= '0' && s[i] <= '9') {
                    cnt = cnt * 10 + s[i++] - '0';
                }
                ++i;
                string t = decode(s, i);
                ++i;
                while (cnt-- > 0) {
                    res += t;
                }
            }
        }
        return res;
    }
};

我们也可以用迭代的方法写出来，当然需要用 stack 来辅助运算，我们用两个 stack，一个用来保存个数，一个用来保存字符串，我们遍历输入字符串，如果遇到数字，我们更新计数变量 cnt；如果遇到左括号，我们把当前 cnt 压入数字栈中，把当前t压入字符串栈中；如果遇到右括号时，我们取出数字栈中顶元素，存入变量k，然后给字符串栈的顶元素循环加上k个t字符串，然后取出顶元素存入字符串t中；如果遇到字母，我们直接加入字符串t中即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    string decodeString(string s) {
        string t = "";
        stack<int> s_num;
        stack<string> s_str;
        int cnt = 0;
        for (int i = 0; i < s.size(); ++i) {
            if (s[i] >= '0' && s[i] <= '9') {
                cnt = 10 * cnt + s[i] - '0';
            } else if (s[i] == '[') {
                s_num.push(cnt);
                s_str.push(t);
                cnt = 0; t.clear();
            } else if (s[i] == ']') {
                int k = s_num.top(); s_num.pop();
                for (int j = 0; j < k; ++j) s_str.top() += t;
	                t = s_str.top(); s_str.pop();
            } else {
                t += s[i];
            }
        }
        return s_str.empty() ? t : s_str.top();
    }
};

我自己的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
public:
    
    bool is_digit(char c) {
        return '0' <= c && c <= '9';
    }
    
    bool is_char(char c) {
        return 'a' <= c && c <= 'z';
    }
    
    string decodeString(string s) {
        stack<int> st1;
        stack<string> st2;
        int len = s.length();
        for (int i = 0; i < len;) {
            if (is_digit(s[i])) {
                int t = 0;
                while(i < len && is_digit(s[i]))
                    t = t*10 + s[i++] - '0';
                st1.push(t);
            }
            else if (s[i] == '[') {
                int t = 0;
                i ++;
                while(i+t < len && is_char(s[i+t])) {
                    t ++;
                }
                st2.push(s.substr(i, t));
                i += t;
            }
            else if (s[i] == ']') {
                string temp;
                int t = st1.top(); st1.pop();
                string te = st2.top(); st2.pop();
                while(t--)
                    temp = temp + te;
                if (!st2.empty()) {te = st2.top(); st2.pop();st2.push(te + temp);}
                else
                    st2.push(temp);
                i ++;
            }
            else {
                string te;
                int t = 0;
                while(i+t < len && is_char(s[i+t])) {
                    t ++;
                }
                if (!st2.empty()) {te = st2.top(); st2.pop();st2.push(te + s.substr(i, t));}
                else
                    st2.push(s.substr(i, t));
                i += t;
            }
        }
        return st2.top();
    }
};

Leetcode395. Longest Substring with At Least K Repeating Characters

Find the length of the longest substring T of a given string (consists of lowercase letters only) such that every character in T appears no less than k times.

Example 1:

1
2
3
4
5
6
7
Input:
s = "aaabb", k = 3

Output:
3

The longest substring is "aaa", as 'a' is repeated 3 times.

Example 2:

1
2
3
4
5
6
7
Input:
s = "ababbc", k = 2

Output:
5

The longest substring is "ababb", as 'a' is repeated 2 times and 'b' is repeated 3 times.

这道题给了我们一个字符串s和一个正整数k，让求一个最大子字符串并且每个字符必须至少出现k次。用 mask 就很好的解决了判断是否出现这个问题，由于字母只有 26 个，而整型 mask 有 32 位，足够用了，每一位代表一个字母，如果为1，表示该字母不够k次，如果为0就表示已经出现了k次。遍历字符串，对于每一个字符，都将其视为起点，然后遍历到末尾，增加 HashMap 中字母的出现次数，如果其小于k，将 mask 的对应位改为1，如果大于等于k，将 mask 对应位改为0。然后看 mask 是否为0，是的话就更新 res 结果，然后把当前满足要求的子字符串的起始位置j保存到 max_idx 中，等内层循环结束后，将外层循环变量i赋值为 max_idx+1，继续循环直至结束，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int longestSubstring(string s, int k) {
        int res = 0, i = 0, n = s.size();
        while (i + k <= n) {
            int m[26] = {0}, mask = 0, max_idx = i;
            for (int j = i; j < n; ++j) {
                int t = s[j] - 'a';
                ++m[t];
                if (m[t] < k) mask |= (1 << t);
                else mask &= (~(1 << t));
                if (mask == 0) {
                    res = max(res, j - i + 1);
                    max_idx = j;
                }
            }
            i = max_idx + 1;
        }
        return res;
    }
};

虽然上面的方法很机智的使用了 mask 了标记某个子串的字母是否都超过了k，但仍然不是很高效，因为遍历了所有的子串，使得时间复杂度到达了平方级。来想想如何进行优化，因为题目中限定了字符串中只有字母，这意味着最多不同的字母数只有 26 个，最后满足题意的子串中的不同字母数一定是在 [1, 26] 的范围，这样就可以遍历这个范围，每次只找不同字母个数为 cnt，且每个字母至少重复k次的子串，来更新最终结果 res。这里让 cnt 从1遍历到 26，对于每个 cnt，都新建一个大小为 26 的数组 charCnt 来记录每个字母的出现次数，使用的思想其实还是滑动窗口 Sliding Window，使用两个变量 start 和 i 来分别标记窗口的左右边界，当右边界小于n时，进行 while 循环，需要一个变量 valid 来表示当前子串是否满足题意，初始化为 true，还需要一个变量 uniqueCnt 来记录子串中不同字母的个数。此时若 s[i] 这个字母在 charCnt 中的出现次数为0，说明遇到新字母了，uniqueCnt 自增1，同时把该字母的映射值加1。此时由于 uniqueCnt 变大了，有可能会超过之前限定了 cnt，所以这里用一个 while 循环，条件是当 uniqueCnt 大于 cnt ，此时应该收缩滑动窗口的左边界，那么对应的左边界上的字母的映射值要自减1，若减完后为0了，则 uniqueCnt 自减1，注意这里一会后加，一会先减的操作，不要搞晕了。当 uniqueCnt 没超过 cnt 的时候，此时还要看当前窗口中的每个字母的出现次数是否都大于等于k，遇到小于k的字母，则直接 valid 标记为 false 即可。最终若 valid 还是 true，则表示滑动窗口内的字符串是符合题意的，用其长度来更新结果 res 即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int longestSubstring(string s, int k) {
        int res = 0, n = s.size();
        for (int cnt = 1; cnt <= 26; ++cnt) {
            int start = 0, i = 0, uniqueCnt = 0;
            vector<int> charCnt(26);
            while (i < n) {
                bool valid = true;
                if (charCnt[s[i++] - 'a']++ == 0) ++uniqueCnt;
                while (uniqueCnt > cnt) {
                    if (--charCnt[s[start++] - 'a'] == 0) --uniqueCnt;
                }
                for (int j = 0; j < 26; ++j) {
                    if (charCnt[j] > 0 && charCnt[j] < k) valid = false;
                }
                if (valid) res = max(res, i - start);
            }
        }    
        return res;
    }
};

下面这种解法用的分治法 Divide and Conquer 的思想，看起来简洁了不少，但是个人感觉比较难想，这里使用了一个变量 max_idx，是用来分割子串的，实现开始统计好了字符串s的每个字母出现的次数，然后再次遍历每个字母，若当前字母的出现次数小于k了，则从开头到前一个字母的范围内的子串可能是满足题意的，还需要对前面的子串进一步调用递归，用返回值来更新当前结果 res，此时变量 ok 标记为 false，表示当前整个字符串s是不符合题意的，因为有字母出现次数小于k，此时 max_idx 更新为 i+1，表示再从新的位置开始找下一个出现次数小于k的字母的位置，可以对新的范围的子串继续调用递归。当 for 循环结束后，若 ok 是 true，说明整个s串都是符合题意的，直接返回n，否则要对 [max_idx, n-1] 范围内的子串再次调用递归，因为这个区间的子串也可能是符合题意的，还是用返回值跟结果 res 比较，谁大就返回谁，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int longestSubstring(string s, int k) {
        int n = s.size(), max_idx = 0, res = 0;
        int m[128] = {0};
        bool ok = true;
        for (char c : s) ++m[c];
        for (int i = 0; i < n; ++i) {
            if (m[s[i]] < k) {
                res = max(res, longestSubstring(s.substr(max_idx, i - max_idx), k));
                ok = false;
                max_idx = i + 1;
            }
        }
        return ok ? n : max(res, longestSubstring(s.substr(max_idx, n - max_idx), k));
    }
};

Leetcode397. Integer Replacement

Given a positive integer n and you can do operations as follow:

  • If n is even, replace n with n /2.
  • If n is odd, you can replace n with either n + 1 or n - 1.

What is the minimum number of replacements needed for n to become 1?

Example 1:

1
2
3
4
5
6
7
8
Input:
8

Output:
3

Explanation:
8 -> 4 -> 2 -> 1

Example 2:

1
2
3
4
5
6
7
8
9
10
Input:
7

Output:
4

Explanation:
7 -> 8 -> 4 -> 2 -> 1
or
7 -> 6 -> 3 -> 2 -> 1

这道题给了我们一个整数n，然后让我们通过变换变为1，如果n是偶数，我们变为n/2，如果是奇数，我们可以变为n+1或n-1，让我们求变为1的最少步骤。那么一看道题的要求，就会感觉应该用递归很合适，我们直接按照规则写出递归即可，注意由于有n+1的操作，所以当n为INT_MAX的时候，就有可能溢出，所以我们可以先将n转为长整型，然后再进行运算，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int integerReplacement(int n) {
        if (n == 1) return 0;
        if (n % 2 == 0) return 1 + integerReplacement(n / 2);
        else {
            long long t = n;
            return 2 + min(integerReplacement((t + 1) / 2), integerReplacement((t - 1) / 2));
        }
    }
};

Leetcode398. Random Pick Index

Given an integer array nums with possible duplicates, randomly output the index of a given target number. You can assume that the given target number must exist in the array.

Implement the Solution class:

  • Solution(int[] nums) Initializes the object with the array nums.
  • int pick(int target) Picks a random index i from nums where nums[i] == target. If there are multiple valid i’s, then each index should have an equal probability of returning.

Example 1:

1
2
3
4
5
Input
["Solution", "pick", "pick", "pick"]
[[[1, 2, 3, 3, 3]], [3], [1], [3]]
Output
[null, 4, 0, 2]

Explanation

1
2
3
4
Solution solution = new Solution([1, 2, 3, 3, 3]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums[0] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.

这道题指明了我们不能用太多的空间，那么省空间的随机方法只有水塘抽样Reservoir Sampling了，LeetCode之前有过两道需要用这种方法的题目Shuffle an Array和Linked List Random Node。那么如果了解了水塘抽样，这道题就不算一道难题了，我们定义两个变量，计数器cnt和返回结果res，我们遍历整个数组，如果数组的值不等于target，直接跳过；如果等于target，计数器加1，然后我们在[0,cnt)范围内随机生成一个数字，如果这个数字是0，我们将res赋值为i即可，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    Solution(vector<int> nums): v(nums) {}
    
    int pick(int target) {
        int cnt = 0, res = -1;
        for (int i = 0; i < v.size(); ++i) {
            if (v[i] != target) continue;
            ++cnt;
            if (rand() % cnt == 0) res = i;
        }
        return res;
    }
private:
    vector<int> v;
};

Leetcode399. Evaluate Division

You are given an array of variable pairs equations and an array of real numbers values, where equations[i] = [Ai, Bi] and values[i] represent the equation Ai / Bi = values[i]. Each Ai or Bi is a string that represents a single variable.

You are also given some queries, where queries[j] = [Cj, Dj] represents the jth query where you must find the answer for Cj / Dj = ?.

Return the answers to all queries. If a single answer cannot be determined, return -1.0.

Note: The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.

Example 1:

1
2
3
4
5
6
Input: equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
Output: [6.00000,0.50000,-1.00000,1.00000,-1.00000]
Explanation: 
Given: a / b = 2.0, b / c = 3.0
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
return: [6.0, 0.5, -1.0, 1.0, -1.0 ]

这道题已知条件中给了一些除法等式，然后给了另外一些除法等式，问我们能不能根据已知条件求出结果，不能求出来的用-1表示。问题本身是很简单的数学问题，但是写代码来自动实现就需要我们用正确的数据结构和算法，通过观察题目中的例子，我们可以看出如果需要分析的除法式的除数和被除数如果其中任意一个没有在已知条件中出现过，那么返回结果-1，所以我们在分析已知条件的时候，可以使用set来记录所有出现过的字符串，然后我们在分析其他除法式的时候，可以使用递归来做。通过分析得出，不能直接由已知条件得到的情况主要有下面三种：

  • 已知: a / b = 2, b / c = 3， 求 a / c
  • 已知: a / c = 2, b / c = 3， 求 a / b
  • 已知: a / b = 2, a / c = 3， 求 b / c

虽然有三种情况，但其实后两种情况都可以转换为第一种情况，对于每个已知条件，我们将其翻转一下也存起来，那么对于对于上面美中情况，就有四个已知条件了：

  • 已知: a / b = 2 ，b / a = 1/2， b / c = 3 ，c / b = 1/3，求 a / c
  • 已知: a / c = 2 ，c / a = 1/2，b / c = 3， c / b = 1/3 ，求 a / b
  • 已知: a / b = 2， b / a = 1/2 ， a / c = 3 ，c / a = 1/3，求 b / c

我们发现，第二种和第三种情况也能转化为第一种情况，只需将上面加粗的两个条件相乘即可。对于每一个需要解析的表达式，我们需要一个HashSet来记录已经访问过的表达式，然后对其调用递归函数。在递归函数中，我们在HashMap中快速查找该表达式，如果跟某一个已知表达式相等，直接返回结果。如果没有的话，那么就需要间接寻找了，我们在HashMap中遍历跟解析式中分子相同的已知条件，跳过之前已经遍历过的，否则就加入visited数组，然后再对其调用递归函数，如果返回值是正数，则乘以当前已知条件的值返回，就类似上面的情况一，相乘以后b就消掉了。如果已知找不到解，最后就返回-1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<double> calcEquation(vector<pair<string, string>> equations, vector<double>& values, vector<pair<string, string>> queries) {
        vector<double> res;
        for (int i = 0; i < equations.size(); ++i) {
            m[equations[i].first][equations[i].second] = values[i];
            m[equations[i].second][equations[i].first] = 1.0 / values[i];
        }
        for (auto query : queries) {
            unordered_set<string> visited;
            double t = helper(query.first, query.second, visited);
            res.push_back((t > 0.0) ? t : -1);
        }
        return res;
    }
    double helper(string up, string down, unordered_set<string>& visited) {
        if (m[up].count(down)) return m[up][down];
        for (auto a : m[up]) {
            if (visited.count(a.first)) continue;
            visited.insert(a.first);
            double t = helper(a.first, down, visited);
            if (t > 0.0) return t * a.second;
        }
        return -1.0;
    }

private:
    unordered_map<string, unordered_map<string, double>> m;
};

Leetcode400. Nth Digit

Given an integer n, return the nth digit of the infinite integer sequence [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …].

Example 1:

1
2
Input: n = 3
Output: 3

Example 2:

1
2
3
Input: n = 11
Output: 0
Explanation: The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.

自然数序列看成一个长字符串，问我们第N位上的数字是什么。那么这道题的关键就是要找出第N位所在的数字，然后可以把数字转为字符串，这样直接可以访问任何一位。那么我们首先来分析自然数序列和其位数的关系，前九个数都是1位的，然后10到99总共90个数字都是两位的，100到999这900个数都是三位的，那么这就很有规律了，我们可以定义个变量cnt，初始化为9，然后每次循环扩大10倍，再用一个变量len记录当前循环区间数字的位数，另外再需要一个变量start用来记录当前循环区间的第一个数字，我们n每次循环都减去len*cnt (区间总位数)，当n落到某一个确定的区间里了，那么(n-1)/len就是目标数字在该区间里的坐标，加上start就是得到了目标数字，然后我们将目标数字start转为字符串，(n-1)%len就是所要求的目标位，最后别忘了考虑int溢出问题，我们干脆把所有变量都申请为长整型的好了，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int findNthDigit(int n) {
        long long digit = 1, start = 1, count = 9;
        while(n > count) {
            n -= count;
            digit += 1;
            start *= 10;
            count = 9 * digit * start;
        }
        int num = start + (n - 1) / digit;
        return (to_string(num))[(n-1)%digit] - '0';
    }
};