Leetcode802. Find Eventual Safe States
We start at some node in a directed graph, and every turn, we walk along a directed edge of the graph. If we reach a terminal node (that is, it has no outgoing directed edges), we stop.
We define a starting node to be safe if we must eventually walk to a terminal node. More specifically, there is a natural number k, so that we must have stopped at a terminal node in less than k steps for any choice of where to walk.
Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.
The directed graph has n nodes with labels from 0 to n - 1, where n is the length of graph. The graph is given in the following form: graph[i] is a list of labels j such that (i, j) is a directed edge of the graph, going from node i to node j.
Example 1:1
2
3
4Illustration of graph
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Explanation: The given graph is shown above.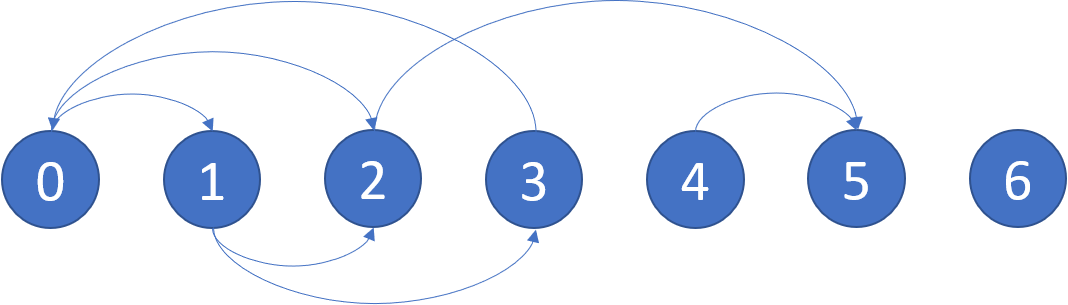
Example 2:1
2Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Output: [4]
深度优先搜索。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public: // -1: unknow, 1: safe, 2: visiting, 3: unsafe
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
int size = graph.size();
vector<int> safe(size, -1);
vector<int> res;
for (int i = 0; i < size; i ++) {
if (helper(graph, safe, i) == 1)
res.push_back(i);
}
return res;
}
int helper(vector<vector<int>>& graph, vector<int>& safe, int cur) {
if (safe[cur] == 2)
return safe[cur] = 3;
if (safe[cur] != -1)
return safe[cur];
safe[cur] = 2;
for (int i = 0; i < graph[cur].size(); i ++)
if (helper(graph, safe, graph[cur][i]) == 3)
return safe[cur] = 3;
return safe[cur] = 1;
}
};
Leetcode804. Unique Morse Code Words
International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows: “a” maps to “.-“, “b” maps to “-…”, “c” maps to “-.-.”, and so on.
For convenience, the full table for the 26 letters of the English alphabet is given below:
[“.-“,”-…”,”-.-.”,”-..”,”.”,”..-.”,”—.”,”….”,”..”,”.—-“,”-.-“,”.-..”,”—“,”-.”,”—-“,”.—.”,”—.-“,”.-.”,”…”,”-“,”..-“,”…-“,”.—“,”-..-“,”-.—“,”—..”]
Now, given a list of words, each word can be written as a concatenation of the Morse code of each letter. For example, “cba” can be written as “-.-..—…”, (which is the concatenation “-.-.” + “-…” + “.-“). We’ll call such a concatenation, the transformation of a word.
Return the number of different transformations among all words we have.
Example:1
2
3
4
5
6
7
8Input: words = ["gin", "zen", "gig", "msg"]
Output: 2
Explanation:
The transformation of each word is:
"gin" -> "--...-."
"zen" -> "--...-."
"gig" -> "--...--."
"msg" -> "--...--."
There are 2 different transformations, “—…-.” and “—…—.”.
Note:
- The length of words will be at most 100.
- Each words[i] will have length in range [1, 12].
- words[i] will only consist of lowercase letters.
1 | class Solution { |
借助set和数组辅助,遍历保存结果,最后统计哈希表的大小
Leetcode806. Number of Lines To Write String
We are to write the letters of a given string S, from left to right into lines. Each line has maximum width 100 units, and if writing a letter would cause the width of the line to exceed 100 units, it is written on the next line. We are given an array widths, an array where widths[0] is the width of ‘a’, widths[1] is the width of ‘b’, …, and widths[25] is the width of ‘z’.
Now answer two questions: how many lines have at least one character from S, and what is the width used by the last such line? Return your answer as an integer list of length 2.
Example :1
2
3
4
5
6
7Input:
widths = [10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10]
S = "abcdefghijklmnopqrstuvwxyz"
Output: [3, 60]
Explanation:
All letters have the same length of 10. To write all 26 letters,
we need two full lines and one line with 60 units.
Example :1
2
3
4
5
6
7
8
9
10Input:
widths = [4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10]
S = "bbbcccdddaaa"
Output: [2, 4]
Explanation:
All letters except 'a' have the same length of 10, and
"bbbcccdddaa" will cover 9 * 10 + 2 * 4 = 98 units.
For the last 'a', it is written on the second line because
there is only 2 units left in the first line.
So the answer is 2 lines, plus 4 units in the second line.
Note:
- The length of S will be in the range [1, 1000].
- S will only contain lowercase letters.
- widths is an array of length 26.
- widths[i] will be in the range of [2, 10].
好坑啊,一个字母还不能拆开放。。。。现在的行长度是cur,如果cur加上当前的字母长度超过100了,则从下一行开始,cur变为当前的字母长度。1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
vector<int> numberOfLines(vector<int>& widths, string S) {
int res=1;
int cur=0;
for(int i=0;i<S.length();i++){
int width = widths[S[i]-'a'];
res = cur + width > 100 ? res+1 : res;
cur = cur + width > 100 ? width : cur+width;
}
return {res,cur};
}
};
Leetcode807. Max Increase to Keep City Skyline
In a 2 dimensional array grid, each value grid[i][j] represents the height of a building located there. We are allowed to increase the height of any number of buildings, by any amount (the amounts can be different for different buildings). Height 0 is considered to be a building as well.
At the end, the “skyline” when viewed from all four directions of the grid, i.e. top, bottom, left, and right, must be the same as the skyline of the original grid. A city’s skyline is the outer contour of the rectangles formed by all the buildings when viewed from a distance. See the following example.
What is the maximum total sum that the height of the buildings can be increased?
Example:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18Input: grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
Output: 35
Explanation:
The grid is:
[ [3, 0, 8, 4],
[2, 4, 5, 7],
[9, 2, 6, 3],
[0, 3, 1, 0] ]
The skyline viewed from top or bottom is: [9, 4, 8, 7]
The skyline viewed from left or right is: [8, 7, 9, 3]
The grid after increasing the height of buildings without affecting skylines is:
gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]
Notes:
- 1 < grid.length = grid[0].length <= 50.
- All heights grid[i][j] are in the range [0, 100].
- All buildings in grid[i][j] occupy the entire grid cell: that is, they are a 1 x 1 x grid[i][j] rectangular prism.
这道题非常简单,首先找到每行每列的最大值,然后每个元素要小于对应的最大值中的小者,比如grid[0][0]要小于topmax[0]和leftmax[0]之中的最小值,grid[0][1]要小于topmax[0]和leftmax[1]之中的最小值。为什么花了这么长时间呢,是因为傻逼了,max数组设成了4爆了。。。煞笔。。。
1 | class Solution { |
Leetcode808. Soup Servings
There are two types of soup: type A and type B. Initially we have N ml of each type of soup. There are four kinds of operations:
- Serve 100 ml of soup A and 0 ml of soup B
- Serve 75 ml of soup A and 25 ml of soup B
- Serve 50 ml of soup A and 50 ml of soup B
- Serve 25 ml of soup A and 75 ml of soup B
When we serve some soup, we give it to someone and we no longer have it. Each turn, we will choose from the four operations with equal probability 0.25. If the remaining volume of soup is not enough to complete the operation, we will serve as much as we can. We stop once we no longer have some quantity of both types of soup.
Note that we do not have the operation where all 100 ml’s of soup B are used first.
Return the probability that soup A will be empty first, plus half the probability that A and B become empty at the same time.
Example:1
2
3
4Input: N = 50
Output: 0.625
Explanation:
If we choose the first two operations, A will become empty first. For the third operation, A and B will become empty at the same time. For the fourth operation, B will become empty first. So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 * (1 + 1 + 0.5 + 0) = 0.625.
Notes:
- 0 <= N <= 10^9.
- Answers within 10^-6 of the true value will be accepted as correct.
自己当初写的代码的思路是对的,但是细节实现上没考虑周全。这里还是参考了网上代码的总结:
我们在这里采用的方法严格来讲是DFS + memorization,也就是需要计算一个子问题的时候,我们首先在表格中查找,看看原来有没有被计算过,如果被计算过,则直接返回结果,否则就再重新计算,并将结果保存在表格中。这样的好处是没必要计算每个子问题,只计算递归过程中用到的子问题。如果我们定义f(a, b)表示有a毫升的A和b毫升的B时符合条件的概率,那么容易知道递推公式就是:f(a, b) = 0.25 * (f(a - 4, b) + f(a - 3, b - 1) + f(a - 2, b - 2) + f(a - 1, b - 3)),其中平凡条件是:
当a < 0 && b < 0时,f(a, b) = 0.5,表示A和B同时用完;
当a <= 0 && b > 0时,f(a, b) = 1.0,表示A先用完;
当a > 0 && b<= 0时,f(a, b) = 0.0,表示B先用完。
所以当遇到这三种情况的时候,我们直接返回对应的平凡值;否则就首先查表,看看原来有没有计算过,如果已经计算过了,就直接返回;否则才开始按照递推公式计算。
1)如果A或者B不足25ml,但是又大于0ml,那么我们需要把它当做完整的25ml来对待。另外,由于A和B serve的最小单位是25ml,所以我们在f(a, b)中约定a和b是25ml的倍数,具体在实现中,我们需要首先对n做n = ceil(N / 25.0)的处理。
2)题目中给出N的范围是[0, 10^9],这是一个特别大的数字了。另外又提到当我们返回的结果与真实误差小于10^6的时候,就算正确。直觉告诉我们,当N趋向于无穷大时,A先被serve完以及A和B同时被serve完的概率会无限接近于1。经过严格计算我们知道当N >= 4800之后,返回的概率值与1的差距就小于10^6了。所以当N >= 4800的时候,我们就直接返回1。如果不这样做的话,就会导致memo需要开辟的内容特别大,引起MLE。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
double soupServings(int N) {
int n = ceil(N / 25.0);
return N >= 4800 ? 1.0 : f(n, n);
}
private:
double f(int a, int b) {
if (a <= 0 && b <= 0) {
return 0.5;
}
if (a <= 0) {
return 1;
}
if (b <= 0) {
return 0;
}
if (memo[a][b] > 0) {
return memo[a][b];
}
memo[a][b] = 0.25 * (f(a - 4, b) + f(a - 3, b - 1) + f(a - 2, b - 2) + f(a - 1, b - 3));
return memo[a][b];
}
double memo[200][200];
};
Leetcode809. Expressive Words
Sometimes people repeat letters to represent extra feeling. For example:1
2"hello" -> "heeellooo"
"hi" -> "hiiii"
In these strings like “heeellooo”, we have groups of adjacent letters that are all the same: “h”, “eee”, “ll”, “ooo”.
You are given a string s and an array of query strings words. A query word is stretchy if it can be made to be equal to s by any number of applications of the following extension operation: choose a group consisting of characters c, and add some number of characters c to the group so that the size of the group is three or more.
For example, starting with “hello”, we could do an extension on the group “o” to get “hellooo”, but we cannot get “helloo” since the group “oo” has a size less than three. Also, we could do another extension like “ll” -> “lllll” to get “helllllooo”. If s = “helllllooo”, then the query word “hello” would be stretchy because of these two extension operations: query = “hello” -> “hellooo” -> “helllllooo” = s.
Return the number of query strings that are stretchy.
Example 1:1
2
3
4
5Input: s = "heeellooo", words = ["hello", "hi", "helo"]
Output: 1
Explanation:
We can extend "e" and "o" in the word "hello" to get "heeellooo".
We can't extend "helo" to get "heeellooo" because the group "ll" is not size 3 or more.
Example 2:1
2Input: s = "zzzzzyyyyy", words = ["zzyy","zy","zyy"]
Output: 3
依次按顺序统计s与各个单词的字母个数,如果相同顺序(连续相等字母算顺序中的一位)的字母不相等,则不符合条件,如果s的字母个数小于3且s与单词的字母个数不等,不符合条件,如果s的字母个数大于等于3且小于单词的字母个数,不符合条件,执行到某个字符串结束,如果没都达到最后,则不符合条件,否则满足条件。Version 2只统计s一次,然后再比对。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
int expressiveWords(string s, vector<string>& words) {
int res = 0;
bool legal = true;
int len = s.length();
for (string word : words) {
int len2 = word.length();
legal = true;
if (len < len2)
continue;
int p1 = 0, p2 = 0;
while (p1 < len && p2 < len2) {
if (s[p1] == word[p2]) {
int t1 = 1, t2 = 1;
while (p1 < len-1 && s[p1] == s[p1+1]) {
t1 ++; p1 ++;
}
while (p2 < len2-1 && word[p2] == word[p2+1]) {
t2 ++; p2 ++;
}
if (t1 == 2 && t1 - t2 == 1)
legal = false;
if ((t1 < 3 && t1 != t2) || t1 < t2)
break;
}
else
break;
p1 ++;
p2 ++;
}
if (p1 == len && p2 == word.size() && legal)
res ++;
}
return res;
}
};
Leetcode811. Subdomain Visit Count
A website domain like “discuss.leetcode.com” consists of various subdomains. At the top level, we have “com”, at the next level, we have “leetcode.com”, and at the lowest level, “discuss.leetcode.com”. When we visit a domain like “discuss.leetcode.com”, we will also visit the parent domains “leetcode.com” and “com” implicitly.
Now, call a “count-paired domain” to be a count (representing the number of visits this domain received), followed by a space, followed by the address. An example of a count-paired domain might be “9001 discuss.leetcode.com”.
We are given a list cpdomains of count-paired domains. We would like a list of count-paired domains, (in the same format as the input, and in any order), that explicitly counts the number of visits to each subdomain.
Example 1:1
2
3
4
5
6Input:
["9001 discuss.leetcode.com"]
Output:
["9001 discuss.leetcode.com", "9001 leetcode.com", "9001 com"]
Explanation:
We only have one website domain: "discuss.leetcode.com". As discussed above, the subdomain "leetcode.com" and "com" will also be visited. So they will all be visited 9001 times.
Example 2:1
2
3
4
5
6Input:
["900 google.mail.com", "50 yahoo.com", "1 intel.mail.com", "5 wiki.org"]
Output:
["901 mail.com","50 yahoo.com","900 google.mail.com","5 wiki.org","5 org","1 intel.mail.com","951 com"]
Explanation:
We will visit "google.mail.com" 900 times, "yahoo.com" 50 times, "intel.mail.com" once and "wiki.org" 5 times. For the subdomains, we will visit "mail.com" 900 + 1 = 901 times, "com" 900 + 50 + 1 = 951 times, and "org" 5 times.
这个题就是非常简单的统计字符串,如果用java和python做的话几分钟就出来了,但是用了原生C++,没有用高级功能,自己手写的一些函数,就当熟悉熟悉了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44class Solution {
public:
vector<string> subdomainVisits(vector<string>& cpdomains) {
vector<string> res;
unordered_map<string,int> m;
for(int i=0;i<cpdomains.size();i++){
int num = 0;
string domain=cpdomains[i];
int domain_len = domain.length();
int j=0;
while(domain[j]!=' ')
j++;
for(int i=0;i<j;i++)
num = num *10 + (domain[i]-'0');
vector<string> temp;
int part_end=j+1;
string tt;
for(int i=j+1;i<domain_len;i++){
if(domain[i]=='.'){
tt = domain.substr(part_end,part_end-i+1);
temp.push_back(tt);
part_end=i+1;
}
}
tt=domain.substr(part_end,domain_len-part_end);
temp.push_back(tt);
for(int i=0;i<temp.size();i++)
if(m.find(temp[i])==m.end()){
m.insert(pair<string,int>(temp[i],num));
}
else
m[temp[i]]+=num;
}
unordered_map<string,int>::iterator it;
for(it=m.begin();it!=m.end();it++){
string ddd = to_string(it->second)+" "+it->first;
res.push_back(ddd);
}
return res;
}
};
贴一下其他解法:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
vector<string> subdomainVisits(vector<string>& cpdomains) {
vector<string> ans;
unordered_map<string, int> domains;
for(string s:cpdomains){
int count = stoi(s.substr(0, s.find(' ')));
domains[s.substr(s.find(' ') + 1)] += count;
domains[s.substr(s.find('.') + 1)] += count;
// try to find the second '.'
string sub = s.substr(s.find('.') + 1);
if(sub.find('.') != -1){
domains[sub.substr(sub.find('.') + 1)] += count;
}
}
for(auto it = domains.begin(); it!= domains.end(); ++it){
ans.push_back(to_string(it->second) + " " + it->first);
}
return ans;
}
};
python版本的:1
2
3
4
5
6
7
8
9
10class Solution(object):
def subdomainVisits(self, cpdomains):
ans = collections.Counter()
for domain in cpdomains:
count, domain = domain.split()
count = int(count)
frags = domain.split('.')
for i in xrange(len(frags)):
ans[".".join(frags[i:])] += count
return ["{} {}".format(ct, dom) for dom, ct in ans.items()]
Leetcode812. Largest Triangle Area
You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.
Example:1
2Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2
Explanation:
The five points are show in the figure below. The red triangle is the largest.
给定包含多个点的集合,从其中取三个点组成三角形,返回能组成的最大三角形的面积。
示例:输入: points = [[0,0],[0,1],[1,0],[0,2],[2,0]] 输出: 2
1 | class Solution { |
Leetcode813. Largest Sum of Averages
We partition a row of numbers A into at most K adjacent (non-empty) groups, then our score is the sum of the average of each group. What is the largest score we can achieve?
Note that our partition must use every number in A, and that scores are not necessarily integers.
Example:1
2
3
4
5
6
7
8Input:
A = [9,1,2,3,9]
K = 3
Output: 20
Explanation:
The best choice is to partition A into [9], [1, 2, 3], [9]. The answer is 9 + (1 + 2 + 3) / 3 + 9 = 20.
We could have also partitioned A into [9, 1], [2], [3, 9], for example.
That partition would lead to a score of 5 + 2 + 6 = 13, which is worse.
Note:
- 1 <= A.length <= 100.
- 1 <= A[i] <= 10000.
- 1 <= K <= A.length.
- Answers within 10^-6 of the correct answer will be accepted as correct.
首先来考虑dp数组的定义,dp数组不把K加进去的话就不知道当前要分几组,这个Hidden Information是解题的关键。这是DP中比较难的一类,有些DP题的隐藏信息藏的更深,不挖出来就无法解题。这道题的dp数组应该是个二维数组,其中dp[i][k]表示范围是[i, n-1]的子数组分成k组的最大得分。那么这里你就会纳闷了,为啥范围是[i, n-1]而不是[0, i],为啥要取后半段呢。由于把[i, n-1]范围内的子数组分成k组,那么suppose我们已经知道了任意范围内分成k-1组的最大分数,这是此类型题目的破题关键所在,要求状态k,一定要先求出所有的状态k-1,那么问题就转换成了从k-1组变成k组,即多分出一组,那么在范围[i, n-1]多分出一组,实际上就是将其分成两部分,一部分是一组,另一部分是k-1组,怎么分,就用一个变量j,遍历范围(i, n-1)中的每一个位置,那么分成的这两部分的分数如何计算呢?第一部分[i, j),由于是一组,那么直接求出平均值即可,另一部分由于是k-1组,由于我们已经知道了所有k-1的情况,可以直接从cache中读出来dp[j][k-1],二者相加即可 avg(i, j) + dp[j][k-1],所以我们可以得出状态转移方程如下:1
dp[i][k] = max(avg(i, n) + max_{j > i} (avg(i, j) + dp[j][k-1]))
这里的avg(i, n)是其可能出现的情况,由于是至多分为k组,所以我们可以不分组,所以直接计算范围[i, n-1]内的平均值,然后用j来遍历区间(i, n-1)中的每一个位置,最终得到的dp[i][k]就即为所求。注意这里我们通过建立累加和数组sums来快速计算某个区间之和。前面提到了dp[i][k]表示的是范围[i, n-1]的子数组分成k组的最大得分,现在想想貌似定义为[0, i]范围内的子数组分成k组的最大得分应该也是可以的,那么此时j就是遍历(0, i)中的每个位置了,好像也没什么不妥的地方,有兴趣的童鞋可以尝试的写一下~
1 | class Solution { |
我们可以对空间进行优化,由于每次的状态k,只跟前一个状态k-1有关,所以我们不需要将所有的状态都保存起来,只需要保存前一个状态的值就行了,那么我们就用一个一维数组就可以了,不断的进行覆盖,从而达到了节省空间的目的,参见代码如下:
1 | class Solution { |
我们也可以是用递归加记忆数组的方式来实现,记忆数组的运作原理和DP十分类似,也是一种cache,将已经计算过的结果保存起来,用的时候直接取即可,避免了大量的重复计算,参见代码如下:
1 | class Solution { |
Leetcode814. Binary Tree Pruning
We are given the head node root of a binary tree, where additionally every node’s value is either a 0 or a 1.
Return the same tree where every subtree (of the given tree) not containing a 1 has been removed.
(Recall that the subtree of a node X is X, plus every node that is a descendant of X.)
Example 1:1
2Input: [1,null,0,0,1]
Output: [1,null,0,null,1]
Explanation:
Only the red nodes satisfy the property “every subtree not containing a 1”.
The diagram on the right represents the answer.
Example 2:1
2Input: [1,0,1,0,0,0,1]
Output: [1,null,1,null,1]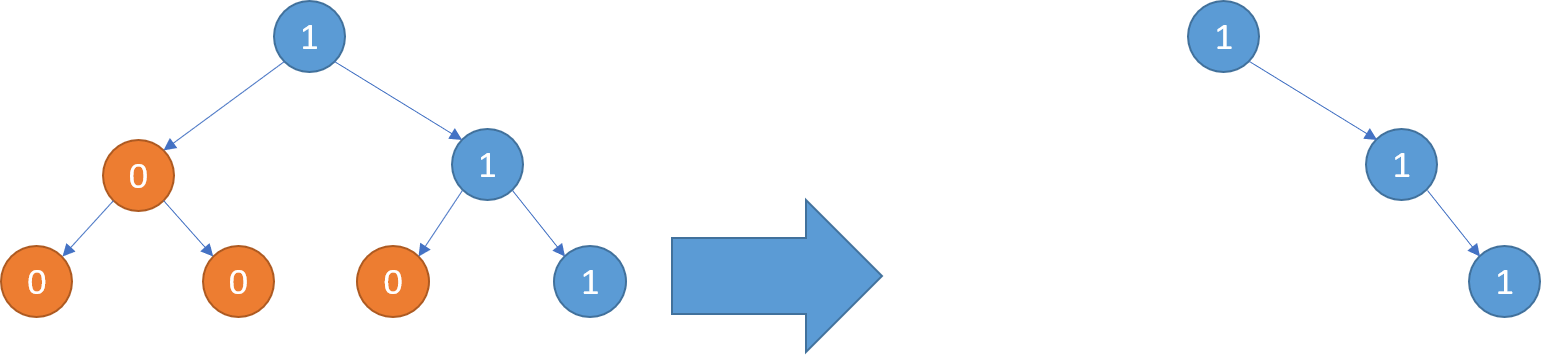
Example 3:1
2Input: [1,1,0,1,1,0,1,0]
Output: [1,1,0,1,1,null,1]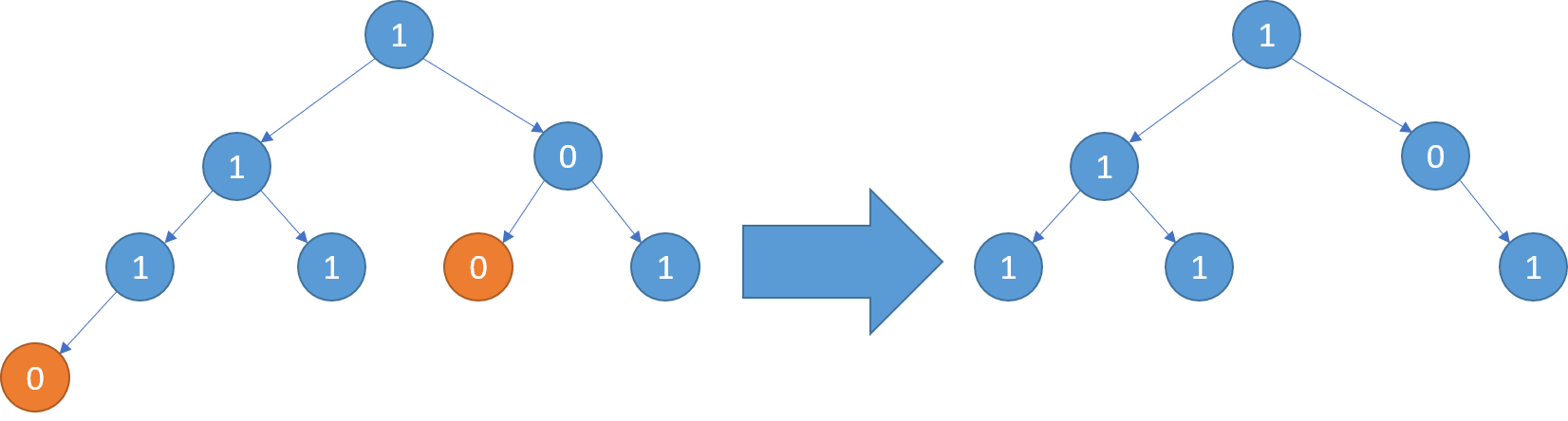
删掉子树里没有1的,返回这棵树。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool dele(TreeNode* root){
if(root == NULL)
return false;
bool a1 = dele(root->left);
bool a2 = dele(root->right);
if(!a1) root->left=NULL;
if(!a2) root->right=NULL;
return root->val==1 || a1 || a2;
}
TreeNode* pruneTree(TreeNode* root) {
return dele(root)?root:NULL;
}
};
Leetcode816. Ambiguous Coordinates
We had some 2-dimensional coordinates, like “(1, 3)” or “(2, 0.5)”. Then, we removed all commas, decimal points, and spaces, and ended up with the string S. Return a list of strings representing all possibilities for what our original coordinates could have been.
Our original representation never had extraneous zeroes, so we never started with numbers like “00”, “0.0”, “0.00”, “1.0”, “001”, “00.01”, or any other number that can be represented with less digits. Also, a decimal point within a number never occurs without at least one digit occuring before it, so we never started with numbers like “.1”.
The final answer list can be returned in any order. Also note that all coordinates in the final answer have exactly one space between them (occurring after the comma.)
Example 1:1
2Input: "(123)"
Output: ["(1, 23)", "(12, 3)", "(1.2, 3)", "(1, 2.3)"]
Example 2:1
2
3
4Input: "(00011)"
Output: ["(0.001, 1)", "(0, 0.011)"]
Explanation:
0.0, 00, 0001 or 00.01 are not allowed.
Example 3:1
2Input: "(0123)"
Output: ["(0, 123)", "(0, 12.3)", "(0, 1.23)", "(0.1, 23)", "(0.1, 2.3)", "(0.12, 3)"]
Example 4:1
2
3
4Input: "(100)"
Output: [(10, 0)]
Explanation:
1.0 is not allowed.
Note:
- 4 <= S.length <= 12.
- S[0] = “(“, S[S.length - 1] = “)”, and the other elements in S are digits.
这道题给了我们一个模糊坐标,括号里面很只有一个数字字符串,没有逗号也没有小数点,让我们自己添加逗号和小数点,让把所有可能的组合都返回。题目中给了很多例子,理解起题意来很容易。这道题的难点是如何合理的拆分,很多拆分是不合法的,题目举了很多不合法的例子,比如 “00”, “0.0”, “0.00”, “1.0”, “001”, “00.01”。那么我们需要归纳出所有不合法的corner case,然后剩下一般情况比如123,我们就按位加小数点即可。那么我们再来看一下那些非法的例子,我们发现一眼望去好多0,不错,0就是trouble maker,首先不能有0开头的长度大于1的整数,比如00, 001。其次,不能有0结尾的小数,比如0.0,0.00,1.0等。还有,小数的整数位上也不能有0开头的长度大于1的整数。那么我们来归纳一下吧,首先如果字符串为空,那么直接返回空集合。然后如果字符串长度大于1,且首尾字符都是0的话,那么不可分,比如 0xxx0,因为整数长度大于1的话不能以0开头,中间也没法加小数点,因为小数最后一位不能是0。如果长度大于1,第一位是0,但最后一位不是0,那我们可以在第一个0后面加个小数点返回,这时就必须要加小数点了,因为长度大于1的整数不能以0开头。再之后,如果最后一位是0,说明不能加小数点,直接把当前值返回即可。最后就是一般情况了,我们先把原数加入结果res,然后遍历中间的每个位置,都加个小数点,所有情况归纳如下:1
2
3
4
5
6if S == “”: return []
if S == “0”: return [S]
if S == “0XXX0”: return []
if S == “0XXX”: return [“0.XXX”]
if S == “XXX0”: return [S]
return [S, “X.XXX”, “XX.XX”, “XXX.X”…]
1 | class Solution { |
Leetcode817. Linked List Components
We are given head, the head node of a linked list containing unique integer values.
We are also given the list G, a subset of the values in the linked list.
Return the number of connected components in G, where two values are connected if they appear consecutively in the linked list.
Example 1:1
2
3
4
5
6Input:
head: 0->1->2->3
G = [0, 1, 3]
Output: 2
Explanation:
0 and 1 are connected, so [0, 1] and [3] are the two connected components.
Example 2:1
2
3
4
5
6Input:
head: 0->1->2->3->4
G = [0, 3, 1, 4]
Output: 2
Explanation:
0 and 1 are connected, 3 and 4 are connected, so [0, 1] and [3, 4] are the two connected components.
Note:
- If N is the length of the linked list given by head, 1 <= N <= 10000.
- The value of each node in the linked list will be in the range [0, N - 1].
- 1 <= G.length <= 10000.
- G is a subset of all values in the linked list.
这道题给了我们一个链表,又给了我们一个结点值数组,里面不一定包括了链表中所有的结点值。让我们返回结点值数组中有多少个相连的组件,因为缺失的结点值会将原链表断开,实际上就是让我们求有多少个相连的子链表,题目中给的例子很好的说明题意。这道题并不需要什么特别高深的技巧,难懂的算法,直接按题目的要求来找就可以了。首先,为了快速的在结点值数组中查找某个结点值是否存在,我们可以将所有的结点值放到一个HashSet中,这样我们就能在常数级的时间复杂度中查找。然后我们就可以来遍历链表了,对于遍历到的每个结点值,我们只有两种情况,在或者不在HashSet中。不在HashSet中的情况比较好办,说明此时断开了,而在HashSet中的结点,有可能是该连续子链表的起始点,或者是中间的某个点,而我们的计数器对该子链表只能自增1,所以我们需要想办法来hanlde这种情况。博主最先想到的办法是先处理不在HashSet中的结点,处理方法就是直接跳到下一个结点。那么对于在HashSet中的结点,我们首先将计数器res自增1,然后再来个循环,将之后所有在集合中的结点都遍历完,这样才不会对同一个子链表多次增加计数器,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int numComponents(ListNode* head, vector<int>& G) {
int res = 0;
unordered_set<int> nodeSet(G.begin(), G.end());
while (head) {
if (!nodeSet.count(head->val)) {
head = head->next;
continue;
}
++res;
while (head && nodeSet.count(head->val)) {
head = head->next;
}
}
return res;
}
};
Leetcode819. Most Common Word
Given a paragraph and a list of banned words, return the most frequent word that is not in the list of banned words. It is guaranteed there is at least one word that isn’t banned, and that the answer is unique.
Words in the list of banned words are given in lowercase, and free of punctuation. Words in the paragraph are not case sensitive. The answer is in lowercase.
Example:1
2
3
4Input:
paragraph = "Bob hit a ball, the hit BALL flew far after it was hit."
banned = ["hit"]
Output: "ball"
Explanation:
“hit” occurs 3 times, but it is a banned word.
“ball” occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as “ball,”),
and that “hit” isn’t the answer even though it occurs more because it is banned.
1 | class Solution { |
1 | class Solution { |
1 | class Solution { |
Leetcode820. Short Encoding of Words
A valid encoding of an array of words is any reference string s and array of indices indices such that:
- words.length == indices.length
- The reference string s ends with the ‘#’ character.
- For each index indices[i], the substring of s starting from indices[i] and up to (but not including) the next ‘#’ character is equal to words[i].
Given an array of words, return the length of the shortest reference string s possible of any valid encoding of words.
Example 1:1
2
3
4
5
6Input: words = ["time", "me", "bell"]
Output: 10
Explanation: A valid encoding would be s = "time#bell#" and indices = [0, 2, 5].
words[0] = "time", the substring of s starting from indices[0] = 0 to the next '#' is underlined in "time#bell#"
words[1] = "me", the substring of s starting from indices[1] = 2 to the next '#' is underlined in "time#bell#"
words[2] = "bell", the substring of s starting from indices[2] = 5 to the next '#' is underlined in "time#bell#"
Example 2:1
2
3Input: words = ["t"]
Output: 2
Explanation: A valid encoding would be s = "t#" and indices = [0].
这道题给了我们一个单词数组,让我们对其编码,不同的单词之间加入#号,每个单词的起点放在一个坐标数组内,终点就是#号,能合并的单词要进行合并,问输入字符串的最短长度。题意不难理解,难点在于如何合并单词,我们观察题目的那个例子,me和time是能够合并的,只要标清楚其实位置,time的起始位置是0,me的起始位置是2,那么根据#号位置的不同就可以顺利的取出me和time。需要注意的是,如果me换成im,或者tim的话,就不能合并了,因为我们是要从起始位置到#号之前所有的字符都要取出来。搞清楚了这一点之后,我们在接着观察,由于me是包含在time中的,所以我们处理的顺序应该是先有time#,然后再看能否包含me,而不是先生成了me#之后再处理time,所以我们可以得出结论,应该先处理长单词,那么就给单词数组按长度排序一下就行,自己重写一个comparator就行。然后我们遍历数组,对于每个单词,我们都在编码字符串查找一下,如果没有的话,直接加上这个单词,再加一个#号,如果有的话,就可以得到出现的位置。比如在time#中查找me,得到found=2,然后我们要验证该单词后面是否紧跟着一个#号,所以我们直接访问found+word.size()这个位置,如果不是#号,说明不能合并,我们还是要加上这个单词和#号。最后返回编码字符串的长度即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int minimumLengthEncoding(vector<string>& words) {
string res = "";
sort(words.begin(), words.end(), [](string &a, string &b){ return a.length() > b.length();});
for (string word : words) {
int t = 0, prev_t = -1;
while((t=res.find(word, t))!=string::npos) {
prev_t = t;
t++;
}
if (prev_t == -1 || res[prev_t + word.length()] != '#')
res += (word + '#');
}
return res.length();
}
};
Leetcode821. Shortest Distance to a Character
Given a string S and a character C, return an array of integers representing the shortest distance from the character C in the string.
Example 1:1
2Input: S = "loveleetcode", C = 'e'
Output: [3, 2, 1, 0, 1, 0, 0, 1, 2, 2, 1, 0]
简单题,这里是对于每个是字符C的位置,然后分别像左右两边扩散,不停是更新距离,这样当所有的字符C的点都扩散完成之后,每个非字符C位置上的数字就是到字符C的最短距离了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
vector<int> shortestToChar(string S, char C) {
int len = S.length();
int signal[len];
vector<int> res(len,INT_MAX);
int i;
for(i=0;i<len;i++){
if(S[i] == C){
res[i]=0;
for(int j=i;j<len;j++)
res[j]=min(res[j],j-i);
for(int j=i;j>=0;j--)
res[j]=min(res[j],i-j);
}
}
return res;
}
};
下面这种方法也是建立距离场的思路,不过更加巧妙一些,只需要正反两次遍历就行。首先进行正向遍历,若当前位置是字符C,那么直接赋0,否则看如果不是首位置,那么当前位置的值等于前一个位置的值加1。这里不用和当前的值进行比较,因为这个算出来的值不会大于初始化的值。然后再进行反向遍历,要从倒数第二个值开始往前遍历,用后一个值加1来更新当前位置的值,此时就要和当前值做比较,取较小的那个,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
vector<int> shortestToChar(string S, char C) {
vector<int> res(S.size(), S.size());
for (int i = 0; i < S.size(); ++i) {
if (S[i] == C) res[i] = 0;
else if (i > 0) res[i] = res[i - 1] + 1;
}
for (int i = (int)S.size() - 2; i >= 0; --i) {
res[i] = min(res[i], res[i + 1] + 1);
}
return res;
}
};
Leetcode822. Card Flipping Game
On a table are N cards, with a positive integer printed on the front and back of each card (possibly different).
We flip any number of cards, and after we choose one card.
If the number X on the back of the chosen card is not on the front of any card, then this number X is good.
What is the smallest number that is good? If no number is good, output 0.
Here, fronts[i] and backs[i] represent the number on the front and back of card i.
A flip swaps the front and back numbers, so the value on the front is now on the back and vice versa.
Example:1
2
3
4Input: fronts = [1,2,4,4,7], backs = [1,3,4,1,3]
Output: 2
Explanation: If we flip the second card, the fronts are [1,3,4,4,7] and the backs are [1,2,4,1,3].
We choose the second card, which has number 2 on the back, and it isn't on the front of any card, so 2 is good.
Note:
- 1 <= fronts.length == backs.length <= 1000.
- 1 <= fronts[i] <= 2000.
- 1 <= backs[i] <= 2000.
给了一些正反都有正数的卡片,可以翻面,让我们找到一个最小的数字,在卡的背面,且要求其他卡正面上均没有这个数字。简而言之,就是要在backs数组找一个最小数字,使其不在fronts数组中。我们想,既然不能在fronts数组中,说明卡片背面的数字肯定跟其正面的数字不相同,否则翻来翻去都是相同的数字,肯定会在fronts数组中。那么我们可以先把正反数字相同的卡片都找出来,将数字放入一个HashSet,也方便我们后面的快速查找。现在其实我们只需要在其他的数字中找到一个最小值即可,因为正反数字不同,就算fronts中其他卡片的正面还有这个最小值,我们可以将那张卡片翻面,使得相同的数字到backs数组,总能使得fronts数组不包含有这个最小值,就像题目中给的例子一样,数字2在第二张卡的背面,就算其他卡面也有数字2,只要其不是正反都是2,我们都可以将2翻到背面去,参见代码如下:
1 | class Solution { |
Leetcode823. Binary Trees With Factors
Given an array of unique integers, each integer is strictly greater than 1.
We make a binary tree using these integers and each number may be used for any number of times.
Each non-leaf node’s value should be equal to the product of the values of it’s children.
How many binary trees can we make? Return the answer modulo 10 ** 9 + 7.
Example 1:1
2
3Input: A = [2, 4]
Output: 3
Explanation: We can make these trees: [2], [4], [4, 2, 2]
Example 2:1
2
3Input: A = [2, 4, 5, 10]
Output: 7
Explanation: We can make these trees: [2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2].
Note:
- 1 <= A.length <= 1000.
- 2 <= A[i] <= 10 ^ 9.
两个难点,定义dp表达式跟推导状态转移方程。怎么简单怎么来呗,我们用一个一维dp数组,其中dp[i]表示值为i的结点做根结点时,能够形成的符合题意的二叉树的个数。这样我们将数组A中每个结点的dp值都累加起来就是最终的结果了。好了,有了定义式,接下来就是最大的难点了,推导状态转移方程。题目中的要求是根结点的值必须是左右子结点值的乘积,那么根结点的dp值一定是跟左右子结点的dp值有关的,是要加上左右子结点的dp值的乘积的,为啥是乘呢,比如有两个球,一个有2种颜色,另一个有3种颜色,问两个球放一起总共能有多少种不同的颜色组合,当然是相乘啦。每个结点的dp值初始化为1,因为就算是当个光杆司令的叶结点,也是符合题意的,所以至少是1。然后就要找其左右两个子结点了,怎么找,有点像 Two Sum 的感觉,先确定一个,然后在HashMap中快速定位另一个,想到了这一层的话,我们的dp定义式就需要做个小修改,之前说的是用一个一维dp数组,现在看来就不太合适了,因为我们需要快速查找某个值,所以这里我们用一个HashMap来定义dp。好,继续,既然要先确定一个结点,由于都是大于1的正数,那么这个结点肯定要比根结点值小,为了遍历方便,我们想把小的放前面,那么我们就需要给数组A排个序,这样就可以遍历之前较小的数字了,那么如何快速定位另一个子结点呢,我们只要用根结点值对遍历值取余,若为0,说明可以整除,然后再在HashMap中查找这个商是否存在,在的话,说明存在这样的两个结点,其结点值之积等于结点A[i],然后我们将这两个结点值之积加到dp[A[i]]中即可,注意还要对超大数取余,防止溢出。最后当所有结点的dp值都更新完成了,将其和算出来返回即可,参见代码如下:
1 | class Solution { |
Leetcode824. Goat Latin
A sentence S is given, composed of words separated by spaces. Each word consists of lowercase and uppercase letters only.
We would like to convert the sentence to “Goat Latin” (a made-up language similar to Pig Latin.)
The rules of Goat Latin are as follows:
- If a word begins with a vowel (a, e, i, o, or u), append “ma” to the end of the word.
For example, the word ‘apple’ becomes ‘applema’. - If a word begins with a consonant (i.e. not a vowel), remove the first letter and append it to the end, then add “ma”.
For example, the word “goat” becomes “oatgma”. - Add one letter ‘a’ to the end of each word per its word index in the sentence, starting with 1.
For example, the first word gets “a” added to the end, the second word gets “aa” added to the end and so on.
Return the final sentence representing the conversion from S to Goat Latin.
Example 1:1
2Input: "I speak Goat Latin"
Output: "Imaa peaksmaaa oatGmaaaa atinLmaaaaa"
Example 2:1
2Input: "The quick brown fox jumped over the lazy dog"
Output: "heTmaa uickqmaaa rownbmaaaa oxfmaaaaa umpedjmaaaaaa overmaaaaaaa hetmaaaaaaaa azylmaaaaaaaaa ogdmaaaaaaaaaa"
Notes:
- S contains only uppercase, lowercase and spaces. Exactly one space between each word.
- 1 <= S.length <= 150.
1 | class Solution { |
1 | class Solution { |
Leetcode825. Friends Of Appropriate Ages
Some people will make friend requests. The list of their ages is given and ages[i] is the age of the ith person.
Person A will NOT friend request person B (B != A) if any of the following conditions are true:
age[B] <= 0.5 * age[A] + 7age[B] > age[A]age[B] > 100 && age[A] < 100
Otherwise, A will friend request B.
Note that if A requests B, B does not necessarily request A. Also, people will not friend request themselves.
How many total friend requests are made?
Example 1:1
2
3Input: [16,16]
Output: 2
Explanation: 2 people friend request each other.
Example 2:1
2
3Input: [16,17,18]
Output: 2
Explanation: Friend requests are made 17 -> 16, 18 -> 17.
Example 3:1
2
3Input: [20,30,100,110,120]
Output:
Explanation: Friend requests are made 110 -> 100, 120 -> 110, 120 -> 100.
Notes:
- 1 <= ages.length <= 20000.
- 1 <= ages[i] <= 120.
这道题是关于好友申请的,说是若A想要加B的好友,下面三个条件一个都不能满足才行:
- B的年龄小于等于A的年龄的一半加7。
- B的年龄大于A的年龄。
- B大于100岁,且A小于100岁。
实际上如果你仔细看条件3,B要是大于100岁,A小于100岁,那么B一定大于A,这就跟条件2重复了。那么由于只能给比自己小的人发送好友请求,那么博主就想到我们可以献给所有人拍个序,然后从后往前遍历,对于每个遍历到的人,再遍历所有比他小的人,这样第二个条件就满足了,前面说了,第三个条件可以不用管了,那么只要看满足第一个条件就可以了,还有要注意的,假如两个人年龄相同,那么满足了前两个条件后,其实是可以互粉的,所以要额外的加1,这样才不会漏掉任何一个好友申请,参见代码如下:
1 | class Solution { |
这个方法会超时。
我们可以来优化一下上面的解法,根据上面的分析,其实题目给的这三个条件可以归纳成一个条件,若A想加B的好友,那么B的年龄必须在 (A*0.5+7, A] 这个范围内,由于区间要有意义的话,A0.5+7 < A 必须成立,解出 A > 14,那么A最小就只能取15了。意思说你不能加小于15岁的好友(青少年成长保护???)。我们的优化思路是对于每一个年龄,我们都只要求出上面那个区间范围内的个数,就是符合题意的。那么既然是求区域和,建立累加数组就是一个很好的选择了,首先我们先建立一个统计数组numInAge,范围是[0, 120],用来统计在各个年龄点上有多少人,然后再建立累加和数组sumInAge。这个都建立好了以后,我们就可以开始遍历,由于之前说了不能加小于15的好友,所以我们从15开始遍历,如果某个年龄点没有人,直接跳过。然后就是统计出 (A*0.5+7, A] 这个范围内有多少人,可以通过累计和数组来快速求的,由于当前时间点的人可以跟这个区间内的所有发好友申请,而当前时间点可能还有多人,所以二者相乘,但由于我们但区间里还包括但当前年龄点本身,所以还要减去当前年龄点上的人数,参见代码如下:
1 | class Solution { |
Leetcode826. Most Profit Assigning Work
You have n jobs and m workers. You are given three arrays: difficulty, profit, and worker where:
difficulty[i]and profit[i] are the difficulty and the profit of the ith job, and worker[j] is the ability of jth worker (i.e., the jth worker can only complete a job with difficulty at most worker[j]).
Every worker can be assigned at most one job, but one job can be completed multiple times.
For example, if three workers attempt the same job that pays $1, then the total profit will be $3. If a worker cannot complete any job, their profit is $0. Return the maximum profit we can achieve after assigning the workers to the jobs.
Example 1:1
2
3Input: difficulty = [2,4,6,8,10], profit = [10,20,30,40,50], worker = [4,5,6,7]
Output: 100
Explanation: Workers are assigned jobs of difficulty [4,4,6,6] and they get a profit of [20,20,30,30] separately.
Example 2:1
2Input: difficulty = [85,47,57], profit = [24,66,99], worker = [40,25,25]
Output: 0
贪心的策略是给每个工人计算在他的能力范围内,他能获得的最大收益,把这样的工作分配给他。
做的方法是先把困难程度和收益压缩排序,然后对工人排序,再对每个工人,通过从左到右的遍历确定其能获得收益最大值。由于工作和工人都已经排好序了,每次只需要从上次停止的位置继续即可,因此各自只需要遍历一次。
你可能会想到,每个工作的收益和其困难程度可能不是正相关的,可能存在某个工作难度小,但是收益反而很大,这种怎么处理呢?其实这也就是这个算法妙的地方,curMax并不是在每个工人查找其满足条件的工作时初始化的,而是在一开始就初始化了,这样一直保持的是所有的工作难度小于工人能力的工作中,能获得的收益最大值。
也就是说在查找满足条件的工作的时候,curMax有可能不更新,其保存的是目前为止的最大。res加的也就是在满足工人能力情况下的最大收益了。
时间复杂度是O(M+N),空间复杂度是O(MN)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int maxProfitAssignment(vector<int>& difficulty, vector<int>& profit, vector<int>& worker) {
int res = 0, curmax = 0, curwork = 0;
int len = difficulty.size();
vector<pair<int, int>> v;
for (int i = 0; i < len; i ++)
v.push_back(make_pair(difficulty[i], profit[i]));
sort(v.begin(), v.end(), [](pair<int, int>& a,pair<int, int>& b){ return a.first < b.first; });
sort(worker.begin(), worker.end());
int j = 0;
for (int i = 0; i < worker.size(); i ++) {
while (j < len) {
if (worker[i] < v[j].first)
break;
curmax = max(curmax, v[j].second);
j ++;
}
res += curmax;
}
return res;
}
};
Leetcode830. Positions of Large Groups
In a string S of lowercase letters, these letters form consecutive groups of the same character. For example, a string like S = “abbxxxxzyy” has the groups “a”, “bb”, “xxxx”, “z” and “yy”.
Call a group large if it has 3 or more characters. We would like the starting and ending positions of every large group. The final answer should be in lexicographic order.
Example 1:1
2
3Input: "abbxxxxzzy"
Output: [[3,6]]
Explanation: "xxxx" is the single large group with starting 3 and ending positions 6.
Example 2:1
2
3Input: "abc"
Output: []
Explanation: We have "a","b" and "c" but no large group.
找到长度大于3的子串。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
vector<vector<int>> largeGroupPositions(string S) {
vector<vector<int>> res;
int len = S.length();
int begin, end;
for(int i = 0; i < len; i ++) {
begin = i;
while(i < len-1 && S[i] == S[i+1])
i ++;
if(i - begin + 1 >= 3)
res.push_back({begin, i});
}
return res;
}
};
Leetcode831. Masking Personal Information
We are given a personal information string S, which may represent either an email address or a phone number.
We would like to mask this personal information according to the following rules:
- Email address:
- We define a name to be a string of length ≥ 2consisting of only lowercase letters a-z or uppercase letters A-Z.
- An email address starts with a name, followed by the symbol ‘@’, followed by a name, followed by the dot ‘.’ and followed by a name.
- All email addresses are guaranteed to be valid and in the format of “name1@name2.name3”.
- To mask an email, all names must be converted to lowercase and all letters between the first and last letter of the first name must be replaced by 5 asterisks ‘*’.
- Phone number:
- A phone number is a string consisting of only the digits 0-9or the characters from the set {‘+’, ‘-‘, ‘(‘, ‘)’, ‘ ‘}. You may assume a phone number contains 10 to 13 digits.
- The last 10 digits make up the local number, while the digits before those make up the country code. Note that the country code is optional. We want to expose only the last 4 digits and mask all other digits.
- The local number should be formatted and masked as
***-***-1111, where 1 represents the exposed digits. - To mask a phone number with country code like
+111 111 111 1111, we write it in the form+***-***-***-1111. The ‘+’ sign and the first ‘-‘ sign before the local number should only exist if there is a country code. For example, a 12 digit phone number mask should start with “+**-“.
Note that extraneous characters like “(“, “)”, “ “, as well as extra dashes or plus signs not part of the above formatting scheme should be removed.
Return the correct “mask” of the information provided.
Example 1:1
2
3
4
5Input: "LeetCode@LeetCode.com"
Output: "l*****e@leetcode.com"
Explanation: All names are converted to lowercase, and the letters between the
first and last letter of the first name is replaced by 5 asterisks.
Therefore, "leetcode" -> "l*****e".
Example 2:1
2
3
4Input: "AB@qq.com"
Output: "a*****b@qq.com"
Explanation: There must be 5 asterisks between the first and last letter
of the first name "ab". Therefore, "ab" -> "a*****b".
Example 3:1
2
3Input: "1(234)567-890"
Output: "***-***-7890"
Explanation: 10 digits in the phone number, which means all digits make up the local number.
Example 4:1
2
3Input: "86-(10)12345678"
Output: "+**-***-***-5678"
Explanation: 12 digits, 2 digits for country code and 10 digits for local number.
这道题让我们给个人信息打码。这里对邮箱和电话分别进行了不同的打码方式,对于邮箱来说,只保留用户名的首尾两个字符,然后中间固定加上五个星号,还有就是所有的字母转小写。对于电话来说,有两种方式,有和没有国家代号,有的话其前面必须有加号,跟后面的区域号用短杠隔开,后面的10个电话号分为三组,个数分别为3,3,4。每组之间还是用短杠隔开,除了最后一组的数字保留之外,其他的都用星号代替。弄清楚了题意,就开始解题吧。既然是字符串的题目,那么肯定要遍历这个字符串了,我们关心的主要是数字和字母,所以要用个变量str来保存遍历到的数字和字母,所以判断,如果是数字或者小写字母的话,直接加入str中,若是大写字母的话,转成小写字母再加入str,如果遇到了 ‘@’ 号,那么表示当前处理的是邮箱,而此时的用户已经全部读入str了,那直接就取出首尾字符,然后中间加五个星号,并再加上 ‘@’ 号存入结果res中,并把str清空。若遇到了点,说明此时是邮箱的后半段,因为题目中限制了用户名中不会有点存在,那么我们将str和点一起加入结果res,并将str清空。当遍历结束时,若此时结果res不为空,说明我们处理的是邮箱,那么返回结果res加上str,因为str中存的是 “com”,还没有来得及加入结果res。若res为空,说明处理的是电话号码,所有的数字都已经加入了str,由于国家代号可能有也可能没有,所以判断一下存入的数字的个数,如果超过10个了,说明有国家代号,那么将超过的部分取出来拼装一下,前面加 ‘+’ 号,后面加短杠。然后再将10位号码的前六位的星号格式加上,并加上最后四个数字即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53class Solution {
public:
char tolower(char c) {
if ('A' <= c && c <= 'Z')
return c + ('a'-'A');
else
return c;
}
string maskPII(string s) {
string t, res = "";
bool is_email = false;
int _size = 0;
int aa = 0, bb = -1;
for (int i = 0; i < s.length(); i ++) {
if ('@' == s[i]) {
is_email = true;
aa = i-1;
}
if ('-' == s[i])
_size ++;
if (_size == 1 && bb == -1 && '-' == s[i])
bb = i;
if ('+' == s[i] || '-' == s[i] || '(' == s[i] || ')' == s[i] || ' ' == s[i])
continue;
t.push_back(tolower(s[i]));
}
if (is_email) {
for (int i = 0; i < t.length(); i ++) {
if (i == 0) {
res += t[i];
res += "*****";
}
else if (i >= aa)
res += t[i];
}
}
else {
int length = t.length();
if (length > 10) {
res += "+";
res += string(length-10, '*');
res += "-";
}
res += "***-***-";
for (int i = length-4; i < length; i ++)
res += t[i];
}
return res;
}
};
Leetcode832. Flipping an Image
Given a binary matrix A, we want to flip the image horizontally, then invert it, and return the resulting image.
To flip an image horizontally means that each row of the image is reversed. For example, flipping [1, 1, 0] horizontally results in [0, 1, 1].
To invert an image means that each 0 is replaced by 1, and each 1 is replaced by 0. For example, inverting [0, 1, 1] results in [1, 0, 0].
Example 1:1
2
3
4Input: [[1,1,0],[1,0,1],[0,0,0]]
Output: [[1,0,0],[0,1,0],[1,1,1]]
Explanation: First reverse each row: [[0,1,1],[1,0,1],[0,0,0]].
Then, invert the image: [[1,0,0],[0,1,0],[1,1,1]]
Example 2:1
2
3
4Input: [[1,1,0,0],[1,0,0,1],[0,1,1,1],[1,0,1,0]]
Output: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
Explanation: First reverse each row: [[0,0,1,1],[1,0,0,1],[1,1,1,0],[0,1,0,1]].
Then invert the image: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
没啥好说的,普通的矩阵操作。
1 | class Solution { |
Leetcode833. Find And Replace in String
To some string S, we will perform some replacement operations that replace groups of letters with new ones (not necessarily the same size).
Each replacement operation has 3 parameters: a starting index i, a source word x and a target word y. The rule is that if x starts at position i in the original string S, then we will replace that occurrence of x with y. If not, we do nothing.
For example, if we have S = “abcd” and we have some replacement operation i = 2, x = “cd”, y = “ffff”, then because “cd” starts at position 2 in the original string S, we will replace it with “ffff”.
Using another example on S = “abcd”, if we have both the replacement operation i = 0, x = “ab”, y = “eee”, as well as another replacement operation i = 2, x = “ec”, y = “ffff”, this second operation does nothing because in the original string S[2] = ‘c’, which doesn’t match x[0] = ‘e’.
All these operations occur simultaneously. It’s guaranteed that there won’t be any overlap in replacement: for example, S = “abc”, indexes = [0, 1], sources = [“ab”,”bc”] is not a valid test case.
Example 1:1
2
3
4Input: S = "abcd", indexes = [0,2], sources = ["a","cd"], targets = ["eee","ffff"]
Output: "eeebffff"
Explanation: "a" starts at index 0 in S, so it's replaced by "eee".
"cd" starts at index 2 in S, so it's replaced by "ffff".
Example 2:1
2
3
4Input: S = "abcd", indexes = [0,2], sources = ["ab","ec"], targets = ["eee","ffff"]
Output: "eeecd"
Explanation: "ab" starts at index 0 in S, so it's replaced by "eee".
"ec" doesn't starts at index 2 in the original S, so we do nothing.
Notes:
- 0 <= indexes.length = sources.length = targets.length <= 100
- 0 < indexes[i] < S.length <= 1000
- All characters in given inputs are lowercase letters.
这道题给了我们一个字符串S,并给了一个坐标数组,还有一个源字符串数组,还有目标字符串数组,意思是若某个坐标位置起,源字符串数组中对应位置的字符串出现了,将其替换为目标字符串。此题的核心操作就两个,查找和替换,需要注意的是,由于替换操作会改变原字符串,但是我们查找始终是基于最初始的S。
首先我们需要给indexes数组排个序,因为可能不是有序的,但是却不能直接排序,这样会丢失和sources,targets数组的对应关系,这很麻烦。所以我们新建了一个保存pair对儿的数组,将indexes数组中的数字跟其位置坐标组成pair对儿,加入新数组v中,然后给这个新数组按从大到小的方式排序。
下面就要开始遍历新数组v了,对于遍历到的pair对儿,取出第一个数字,保存到i,表示S中需要查找的位置,取出第二个数字,然后根据这个位置分别到sources和targets数组中取出源字符串和目标字符串,然后我们在S中的i位置,向后取出和源字符串长度相同的子串,然后比较,若正好和源字符串相等,则将其替换为目标字符串即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
public:
string findReplaceString(string s, vector<int>& indices, vector<string>& sources, vector<string>& targets) {
vector<pair<int, int>> v;
for (int i = 0; i < indices.size(); ++i) {
v.push_back({indices[i], i});
}
sort(v.begin(), v.end());
int len = s.length();
string res = "";
int p1 = 0, p2 = 0, i = 0;
while(i < len && p1 < v.size()) {
int tmp = i, j = 0;
if (i > indices[v[p1].second])
p1 ++;
else if (i == indices[v[p1].second]) {
int len2 = sources[v[p1].second].length();
while(j < len2 && tmp < len) {
if (sources[v[p1].second][j] != s[tmp])
break;
j ++; tmp++;
}
if (j == len2) {
res += targets[v[p1].second];
p1 ++;
i += len2;
}
else
res += s[i++];
}
else if (i < len)
res += s[i++];
}
while(i < len)
res += s[i++];
return res;
}
};
Leetcode835. Image Overlap
You are given two images, img1 and img2, represented as binary, square matrices of size n x n. A binary matrix has only 0s and 1s as values.
We translate one image however we choose by sliding all the 1 bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the overlap by counting the number of positions that have a 1 in both images.
Note also that a translation does not include any kind of rotation. Any 1 bits that are translated outside of the matrix borders are erased.
Return the largest possible overlap.

Example 2:1
2Input: img1 = [[1]], img2 = [[1]]
Output: 1
Example 3:1
2Input: img1 = [[0]], img2 = [[0]]
Output: 0
经过观察
(0,0)->(1,1)->(0,0)-(1,1)=(-1,-1)
(0,1)->(1,2)->(0,1)-(1,2)=(-1,-1)
(1,1)->(2,2)->(1,1)-(2,2)=(-1,-1)
从A对应到B是把整个矩阵的坐标x轴-1, y轴-1;
变相就是在求所有A矩阵1的点到B矩阵1的点的X轴和Y轴距离;
所有坐标的取值范围在(-N—N)之间;
实际上就是把一个一维求距离的easy的题换成了二维的题目;
1 | class Solution { |
Leetcode836. Rectangle Overlap
A rectangle is represented as a list [x1, y1, x2, y2], where (x1, y1) are the coordinates of its bottom-left corner, and (x2, y2) are the coordinates of its top-right corner.
Two rectangles overlap if the area of their intersection is positive. To be clear, two rectangles that only touch at the corner or edges do not overlap.
Given two (axis-aligned) rectangles, return whether they overlap.
Example 1:1
2Input: rec1 = [0,0,2,2], rec2 = [1,1,3,3]
Output: true
Example 2:1
2Input: rec1 = [0,0,1,1], rec2 = [1,0,2,1]
Output: false
这道题让我们求两个矩形是否是重叠,矩形的表示方法是用两个点,左下和右上点来定位的。下面的讲解是参见网友大神jayesch的帖子来的,首先,返璞归真,在玩 2D 之前,先看下 1D 上是如何运作的。对于两条线段,它们相交的话可以是如下情况:1
2
3
4 x3 x4
|--------------|
|--------------|
x1 x2
我们可以直观的看出一些关系: x1 < x3 < x2 && x3 < x2 < x4,可以稍微化简一下:x1 < x4 && x3 < x2。就算是调换个位置:1
2
3
4 x1 x2
|--------------|
|--------------|
x3 x4
还是能得到同样的关系:x3 < x2 && x1 < x4。好,下面我们进军 2D 的世界,实际上 2D 的重叠就是两个方向都同时满足 1D 的重叠条件即可。由于题目中说明了两个矩形的重合面积为正才算 overlap,就是说挨着边的不算重叠,那么两个矩形重叠主要有这四种情况:
1)两个矩形在矩形1的右上角重叠:1
2
3
4
5
6
7 ____________________x4,y4
| |
_______|______x2,y2 |
| |______|____________|
| x3,y3 |
|______________|
x1,y1
满足的条件为:x1 < x4 && x3 < x2 && y1 < y4 && y3 < y2
2)两个矩形在矩形1的左上角重叠:1
2
3
4
5
6
7 ___________________ x4,y4
| |
| _______|____________x2,y2
|___________|_______| |
x3,y3 | |
|___________________|
x1,y1
满足的条件为:x3 < x2 && x1 < x4 && y1 < y4 && y3 < y2
3)两个矩形在矩形1的左下角重叠:1
2
3
4
5
6
7 ____________________x2,y2
| |
_______|______x4,y4 |
| |______|____________|
| x1,y1 |
|______________|
x3,y3
满足的条件为:x3 < x2 && x1 < x4 && y3 < y2 && y1 < y4
4)两个矩形在矩形1的右下角重叠:1
2
3
4
5
6
7 ___________________ x2,y2
| |
| _______|____________x4,y4
|___________|_______| |
x1,y1 | |
|___________________|
x3,y3
满足的条件为:x1 < x4 && x3 < x2 && y3 < y2 && y1 < y4
仔细观察可以发现,上面四种情况的满足条件其实都是相同的,只不过顺序调换了位置,所以我们只要一行就可以解决问题了,碉堡了。。。1
2
3
4class Solution {
public:
bool isRectangleOverlap(vector<int>& rec1, vector<int>& rec2) {
return rec1[0] < rec2[2] && rec2[0] < rec1[2] && rec1[1] < rec2[3] && rec2[1] < rec1[3];
Leetcode838. Push Dominoes
There are N dominoes in a line, and we place each domino vertically upright.
In the beginning, we simultaneously push some of the dominoes either to the left or to the right.
After each second, each domino that is falling to the left pushes the adjacent domino on the left.
Similarly, the dominoes falling to the right push their adjacent dominoes standing on the right.
When a vertical domino has dominoes falling on it from both sides, it stays still due to the balance of the forces.
For the purposes of this question, we will consider that a falling domino expends no additional force to a falling or already fallen domino.
Given a string “S” representing the initial state. S[i] = ‘L’, if the i-th domino has been pushed to the left; S[i] = ‘R’, if the i-th domino has been pushed to the right; S[i] = ‘.’, if the i-th domino has not been pushed.
Return a string representing the final state.
Example 1:1
2Input: ".L.R...LR..L.."
Output: "LL.RR.LLRRLL.."
Example 2:1
2
3Input: "RR.L"
Output: "RR.L"
Explanation: The first domino expends no additional force on the second domino.
Note:
- 0 <= N <= 10^5
- String dominoes contains only ‘L‘, ‘R’ and ‘.’
这道题给我们摆好了一个多米诺骨牌阵列,但是与一般的玩法不同的是,这里没有从一头开始推,而是在很多不同的位置分别往两个方向推,结果是骨牌各自向不同的方向倒下了,而且有的骨牌由于左右两边受力均等,依然屹立不倒,这样的话骨牌就很难受了,能不能让哥安心的倒下去?!生而为骨牌,总是要倒下去啊,就像漫天飞舞的樱花,秒速五厘米的落下,回到最终归宿泥土里。喂,不要给骨牌强行加戏好么!~ 某个位置的骨牌会不会倒,并且朝哪个方向倒,是由左右两边受到的力的大小决定的,那么可以分为下列四种情况:
1)R….R -> RRRRRR
这是当两个向右推的操作连在一起时,那么中间的骨牌毫无悬念的都要向右边倒去。
2)L….L -> LLLLLL
同理,
当两个向左推的操作连在一起时,那么中间的骨牌毫无悬念的都要向左边倒去。
3)L….R -> L….R
当左边界的骨牌向左推,右边界的骨牌向右推,那么中间的骨牌不会收到力,所以依然保持坚挺。
4)R….L -> RRRLLL or R…..L -> RRR.LLL
当左边界的骨牌向右推,右边界的骨牌向左推时,就要看中间的骨牌个数了,若是偶数,那么对半分,若是奇数,那么最中间的骨牌保持站立,其余的对半分。
由于上述四种情况包含了所有的情况,所以我们的目标就是在字符串中找出中间是‘点’的小区间,为了便于我们一次遍历就处理完,我们在dominoes字符串左边加个L,右边加个R,这并不会影响骨牌倒下的情况。我们使用双指针来遍历,其中i初始化为0,j初始化为1,当j指向‘点’时,我们就跳过,目标是i指向小区间的左边界,j指向右边界,然后用 j-i-1 算出中间‘点’的个数,为0表示中间没有点。若此时 i>0,则将左边界加入结果res中。若左右边界相同,那么中间的点都填成左边界,这是上述的情况一和二;若左边界是L,右边界是R,则是上述的情况三,中间还是保持点不变;若左边界是R,右边界是L,则是情况四,那么先加 mid/2 个R,再加 mid%2 个点,最后加 mid/2 个L即可。然后i更新为j,继续循环即可,参见代码如下:
1 | class Solution { |
下面这种解法遍历了两次字符串,第一次遍历是先把R后面的点全变成R,同时累加一个cnt数组,其中cnt[i]表示在dominoes数组中i位置时R连续出现的个数,那么拿题目中的例子1来说,第一次遍历之后,原dominoes数组,修改后的dominoes数组,以及cnt数组分别为:1
2
3.L.R...LR..L..
.L.RRRRLRRRL..
00001230012000
我们可以发现cnt数字记录的是R连续出现的个数,第一次遍历只模拟了所有往右推倒的情况,很明显不是最终答案,因为还需要往左推,那么就要把某些点变成L,已经把某些R变成点或者L,这时我们的cnt数组就非常重要,因为它相当于记录了往右推的force的大小。第二次遍历是从右往左,我们找所有L前面的位置,若其为点,则直接变为L。若其为R,那么也有可能变L,此时就要计算往左的force,通过 cnt[i+1] + 1 获得,然后跟往右的force比较,若此位置往右的force大,说明当前骨牌应该往左倒,更新此时cnt[i]为往左的force。若此时左右force相等了,说明当前骨牌不会向任意一遍倒,改为点即可,最终修改后的dominoes数组和cnt数组分别为:1
2LL.RR.LLRRLL..
10001210011000
1 | class Solution { |
Leetcode840. Magic Squares In Grid
A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.
Given an grid of integers, how many 3 x 3 “magic square” subgrids are there? (Each subgrid is contiguous).
Example 1:1
2
3
4
5
6
7
8
9
10
11
12
13
14Input: [[4,3,8,4],
[9,5,1,9],
[2,7,6,2]]
Output: 1
Explanation:
The following subgrid is a 3 x 3 magic square:
438
951
276
while this one is not:
384
519
762
In total, there is only one magic square inside the given grid.
幻方的特点是,全体数和=3X幻和,幻和=3×中心数。在基本三阶幻方中,幻和=1+2+…+9=45/3=15,所以中心数=5。因此只要从[1,1]开始判断中间数为5,再进一步判断是否为幻方。进一步判断:首先可使用二进制数来判断是否该矩阵是由1~9的组成。再判断通过中心的4组对角值和为10,&& 第一行和第一列和为15。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
public:
bool isMagic(int i, int j, vector<vector<int>>& grid){
int chknum = 0;
for(int a=i-1; a<=i+1; a++){
for(int b=j-1; b<=j+1; b++){
if(grid[a][b]>0 && grid[a][b]<10)
chknum |= 1<<(grid[a][b]-1);
}
}
if(chknum!=0b111111111) return false;
if(grid[i-1][j-1]+grid[i+1][j+1]==10 && grid[i][j-1]+grid[i][j+1]==10 &&
grid[i-1][j]+grid[i+1][j]==10 && grid[i-1][j+1]+grid[i+1][j-1]==10 &&
grid[i-1][j-1]+grid[i-1][j]+grid[i-1][j+1]==15 &&
grid[i-1][j-1]+grid[i][j-1]+grid[i+1][j-1]==15)
return true;
else return false;
}
int numMagicSquaresInside(vector<vector<int>>& grid) {
int N=grid.size();
int res=0;
for(int i=1; i<N-1; i++){
for(int j=1; j<N-1; j++){
if(grid[i][j]==5 && isMagic(i,j,grid)){
res++;
j++;
}
}
}
return res;
}
};
Leetcode841. Keys and Rooms
There are N rooms and you start in room 0. Each room has a distinct number in 0, 1, 2, …, N-1, and each room may have some keys to access the next room.
Formally, each room i has a list of keys rooms[i], and each key rooms[i][j] is an integer in [0, 1, …, N-1] where N = rooms.length. A key rooms[i][j] = v opens the room with number v.
Initially, all the rooms start locked (except for room 0).
You can walk back and forth between rooms freely.
Return true if and only if you can enter every room.
Example 1:1
2
3
4
5
6
7Input: [[1],[2],[3],[]]
Output: true
Explanation:
We start in room 0, and pick up key 1.
We then go to room 1, and pick up key 2.
We then go to room 2, and pick up key 3.
We then go to room 3. Since we were able to go to every room, we return true.
Example 2:1
2
3Input: [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can't enter the room with number 2.
Note:
- 1 <= rooms.length <= 1000
- 0 <= rooms[i].length <= 1000
- The number of keys in all rooms combined is at most 3000.
这道题给了我们一些房间,房间里有一些钥匙,用钥匙可以打开对应的房间,说是起始时在房间0,问最终是否可以打开所有的房间。这不由得让博主想起了惊悚片《万能钥匙》,还真是头皮发麻啊。赶紧扯回来,这是一道典型的有向图的遍历的题,邻接链表都已经建立好了,这里直接遍历就好了,这里先用 BFS 来遍历。使用一个 HashSet 来记录访问过的房间,先把0放进去,然后使用 queue 来辅助遍历,同样将0放入。之后进行典型的 BFS 遍历,取出队首的房间,然后遍历其中的所有钥匙,若该钥匙对应的房间已经遍历过了,直接跳过,否则就将钥匙加入 HashSet。此时看若 HashSet 中的钥匙数已经等于房间总数了,直接返回 true,因为这表示所有房间已经访问过了,否则就将钥匙加入队列继续遍历。最后遍历结束后,就看 HashSet 中的钥匙数是否和房间总数相等即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
unordered_set<int> visited{{0}};
queue<int> q{{0}};
while (!q.empty()) {
int t = q.front(); q.pop();
for (int key : rooms[t]) {
if (visited.count(key)) continue;
visited.insert(key);
if (visited.size() == rooms.size()) return true;
q.push(key);
}
}
return visited.size() == rooms.size();
}
};
我自己的:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
int len = rooms.size();
vector<int> visited(len, 0);
queue<int> q;
q.push(0);
while(!q.empty()) {
int t = q.front();
q.pop();
visited[t] = true;
for (int i = 0; i < rooms[t].size(); i ++) {
if (visited[rooms[t][i]])
continue;
q.push(rooms[t][i]);
}
}
for (int i = 0; i < len; i ++)
if (!visited[i])
return false;
return true;
}
};
Leetcode844. Backspace String Compare
Given two strings S and T, return if they are equal when both are typed into empty text editors. # means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
Example 1:1
2
3Input: S = "ab#c", T = "ad#c"
Output: true
Explanation: Both S and T become "ac".
Example 2:1
2
3Input: S = "ab##", T = "c#d#"
Output: true
Explanation: Both S and T become "".
Example 3:1
2
3Input: S = "a##c", T = "#a#c"
Output: true
Explanation: Both S and T become "c".
Example 4:1
2
3Input: S = "a#c", T = "b"
Output: false
Explanation: S becomes "c" while T becomes "b".
1 | class Solution { |
一种更好的做法:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44class Solution {
public:
bool backspaceCompare(string s, string t) {
int k=0,p=0;
for(int i=0;i<s.size();i++)
{
if(s[i]=='#')
{
k--;
k=max(0,k);
}
else
{
s[k]=s[i];
k++;
}
}
for(int i=0;i<t.size();i++)
{
if(t[i]=='#')
{
p--;
p=max(0,p);
}
else
{
t[p]=t[i];
p++;
}
}
if(k!=p)
return false;
else
{
for(int i=0;i<k;i++)
{
if(s[i]!=t[i])
return false;
}
return true;
}
}
};
Leetcode845. Longest Mountain in Array 数组中最长的山
Let’s call any (contiguous) subarray B (of A) a mountain if the following properties hold:1
B.length >= 3
There exists some 0 < i < B.length - 1 such that B[0] < B[1] < ... B[i-1] < B[i] > B[i+1] > ... > B[B.length - 1]
(Note that B could be any subarray of A, including the entire array A.)
Given an array A of integers, return the length of the longest mountain.
Return 0 if there is no mountain.
Example 1:1
2
3Input: [2,1,4,7,3,2,5]
Output: 5
Explanation: The largest mountain is [1,4,7,3,2] which has length 5.
Example 2:1
2
3Input: [2,2,2]
Output: 0
Explanation: There is no mountain.
Note:
- 0 <= A.length <= 10000
- 0 <= A[i] <= 10000
这道题给了我们一个数组,然后定义了一种像山一样的子数组,就是先递增再递减的子数组,注意这里是强行递增或者递减的,并不存在相等的情况。那么实际上这道题就是让在数组中寻找一个位置,使得以此位置为终点的递增数组和以此位置为起点的递减数组的长度最大。而以某个位置为起点的递减数组,如果反个方向来看,其实就是就该位置为终点的递增数列,那么既然都是求最长的递增数列,我们可以分别用两个 dp 数组 up 和 down,其中up[i]表示以i位置为终点的最长递增数列的个数,down[i]表示以i位置为起点的最长递减数列的个数,这样我们正向更新up数组,反向更新down数组即可。先反向更新好了down之后,在正向更新up数组的同时,也可以更新结果res,当某个位置的up[i]和down[i]均大于0的时候,那么就可以用up[i] + down[i] + 1来更新结果res了,参见代码如下:
1 | class Solution { |
我们可以对空间进行优化,不必使用两个数组来记录所有位置的信息,而是只用两个变量 up 和 down 来分别记录以当前位置为终点的最长递增数列的长度,和以当前位置为终点的最长递减数列的长度。 我们从 i=1 的位置开始遍历,因为山必须要有上坡和下坡,所以 i=0 的位置永远不可能成为 peak。此时再看,如果当前位置跟前面的位置相等了,那么当前位置的 up 和 down 都要重置为0,从当前位置开始找新的山,和之前的应该断开。或者是当 down 不为0,说明此时是在下坡,如果当前位置大于之前的了,突然变上坡了,那么之前的累计也需要重置为0。然后当前位置再进行判断,若大于前一个位置,则是上坡,up 自增1,若小于前一个位置,是下坡,down 自增1。当 up 和 down 同时为正数,则用 up+down+1 来更新结果 res 即可,参见代码如下:
1 | class Solution { |
Leetcode848. Shifting Letters
You are given a string s of lowercase English letters and an integer array shifts of the same length.
Call the shift() of a letter, the next letter in the alphabet, (wrapping around so that ‘z’ becomes ‘a’).
For example, shift(‘a’) = ‘b’, shift(‘t’) = ‘u’, and shift(‘z’) = ‘a’.
Now for each shifts[i] = x, we want to shift the first i + 1 letters of s, x times.
Return the final string after all such shifts to s are applied.
Example 1:1
2
3
4
5
6Input: s = "abc", shifts = [3,5,9]
Output: "rpl"
Explanation: We start with "abc".
After shifting the first 1 letters of s by 3, we have "dbc".
After shifting the first 2 letters of s by 5, we have "igc".
After shifting the first 3 letters of s by 9, we have "rpl", the answer.
Example 2:1
2Input: s = "aaa", shifts = [1,2,3]
Output: "gfd"
题目大意:给定一组反转数,要求你将字母向前翻转(字母范围a~z)(z反转为a)
思路方法:这题用前缀和处理,一次性求出每个字母需要翻转的次数,否则会超时,当然要防止数据溢出,所以要将过程取余。
1 | class Solution { |
Leetcode849. Maximize Distance to Closest Person
In a row of seats, 1 represents a person sitting in that seat, and 0 represents that the seat is empty.
There is at least one empty seat, and at least one person sitting.
Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized.
Return that maximum distance to closest person.
Example 1:1
2
3
4
5
6Input: [1,0,0,0,1,0,1]
Output: 2
Explanation:
If Alex sits in the second open seat (seats[2]), then the closest person has distance 2.
If Alex sits in any other open seat, the closest person has distance 1.
Thus, the maximum distance to the closest person is 2.
Example 2:1
2
3
4
5Input: [1,0,0,0]
Output: 3
Explanation:
If Alex sits in the last seat, the closest person is 3 seats away.
This is the maximum distance possible, so the answer is 3.
Note:
- 1 <= seats.length <= 20000
- seats contains only 0s or 1s, at least one 0, and at least one 1.
这道题给了我们一个只有0和1且长度为n的数组,代表n个座位,其中0表示空座位,1表示有人座。现在说是爱丽丝想找个位置坐下,但是希望能离最近的人越远越好,这个不难理解,就是想左右两边尽量跟人保持距离,让我们求这个距离最近的人的最大距离。来看题目中的例子1,有三个空位连在一起,那么爱丽丝肯定是坐在中间的位置比较好,这样跟左右两边人的距离都是2。例子2有些特别,当空位连到了末尾的时候,这里可以想像成靠墙,那么靠墙坐肯定离最远啦,所以例子2中爱丽丝坐在最右边的位子上距离左边的人距离最远为3。那么不难发现,爱丽丝肯定需要先找出最大的连续空位长度,若连续空位靠着墙了,那么就直接挨着墙坐,若两边都有人,那么就坐到空位的中间位置。如何能快速知道连续空位的长度呢,只要知道了两边人的位置,相减就是中间连续空位的个数。所以博主最先使用的方法是用一个数组来保存所有1的位置,即有人坐的位置,然后用相邻的两个位置相减,就可以得到连续空位的长度。当然,靠墙这种特殊情况要另外处理一下。当把所有1位置存入数组 nums 之后,开始遍历 nums 数组,第一个人的位置有可能不靠墙,那么他的位置坐标就是他左边靠墙的连续空位个数,直接更新结果 res 即可,因为靠墙连续空位的个数就是离右边人的最远距离。然后对于其他的位置,我们减去前一个人的位置坐标,然后除以2,更新结果 res。还有最右边靠墙的情况也要处理一下,就用 n-1 减去最后一个人的位置坐标,然后更新结果 res 即可,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int maxDistToClosest(vector<int>& seats) {
int n = seats.size(), res = 0;
vector<int> nums;
for (int i = 0; i < n; ++i) {
if (seats[i] == 1) nums.push_back(i);
}
for (int i = 0; i < nums.size(); ++i) {
if (i == 0) res = max(res, nums[0]);
else res = max(res, (nums[i] - nums[i - 1]) / 2);
}
if (!nums.empty())
res = max(res, n - 1 - nums.back());
return res;
}
};
我们也可以只用一次遍历,那么就需要在遍历的过程中统计出连续空位的个数,即连续0的个数。那么采用双指针来做,start 指向连续0的起点,初始化为0,i为当前遍历到的位置。遍历 seats 数组,跳过0的位置,当遇到1的时候,此时先判断下 start 的值,若是0的话,表明当前这段连续的空位是靠着墙的,所以要用连续空位的长度 i-start 来直接更新结果 res,否则的话就是两头有人的中间的空位,那么用长度加1除以2来更新结果 res,此时 start 要更新为 i+1,指向下一段连续空位的起始位置。for 循环退出后,还是要处理最右边靠墙的位置,用 n-start 来更新结果 res 即可,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int maxDistToClosest(vector<int>& seats) {
int n = seats.size(), start = 0, res = 0;
for (int i = 0; i < n; ++i) {
if (seats[i] != 1) continue;
if (start == 0) res = max(res, i - start);
else res = max(res, (i - start + 1) / 2);
start = i + 1;
}
res = max(res, n - start);
return res;
}
};
讨论:这道题的一个很好的 follow up 是让我们返回爱丽丝坐下的位置,那么要在结果 res 可以被更新的时候,同时还应该记录下连续空位的起始位置 start,这样有了 start 和 最大距离 res,那么就可以定位出爱丽丝的座位了。
Leetcode851. Loud and Rich
There is a group of n people labeled from 0 to n - 1 where each person has a different amount of money and a different level of quietness.
You are given an array richer where richer[i] = [ai, bi] indicates that ai has more money than bi and an integer array quiet where quiet[i] is the quietness of the ith person. All the given data in richer are logically correct (i.e., the data will not lead you to a situation where x is richer than y and y is richer than x at the same time).
Return an integer array answer where answer[x] = y if y is the least quiet person (that is, the person y with the smallest value of quiet[y]) among all people who definitely have equal to or more money than the person x.
Example 1:1
2
3
4
5
6
7
8
9Input: richer = [[1,0],[2,1],[3,1],[3,7],[4,3],[5,3],[6,3]], quiet = [3,2,5,4,6,1,7,0]
Output: [5,5,2,5,4,5,6,7]
Explanation:
answer[0] = 5.
Person 5 has more money than 3, which has more money than 1, which has more money than 0.
The only person who is quieter (has lower quiet[x]) is person 7, but it is not clear if they have more money than person 0.
answer[7] = 7.
Among all people that definitely have equal to or more money than person 7 (which could be persons 3, 4, 5, 6, or 7), the person who is the quietest (has lower quiet[x]) is person 7.
The other answers can be filled out with similar reasoning.
Example 2:1
2Input: richer = [], quiet = [0]
Output: [0]
有n 个人,编号0 ∼ n − 1 ,它们有两个属性,财富和安静,给定两个数组r和q,r里面的元素都是数对,(a , b)表示a比b财富严格更多,而q qq存的是每个人的安静值。要求返回一个数组c,使得c[i]表示对于编号i的这个人,财富不少于他的所有人里安静值最小的人的编号。题目保证财富比较的传递关系没有环。
思路是记忆化搜索。先建图,将这些人看成若干个点,从财富少的到多的人连一条边,然后从每个点开始DFS。DFS到顶点u uu的时候,先DFS所有u的邻接点,这样就求出了u的邻接点的c值,接着在这些邻接点的c值里找到q值最小的(即找的安静值最小的)即可。可以做记忆化,当某个点的c值已经算出了,则不必重复算。代码如下:
1 | class Solution { |
Leetcode852. Peak Index in a Mountain Array
Let’s call an array A a mountain if the following properties hold:
A.length >= 3
There exists some 0 < i < A.length - 1 such that A[0] < A[1] < … A[i-1] < A[i] > A[i+1] > … > A[A.length - 1]
Given an array that is definitely a mountain, return any i such that A[0] < A[1] < … A[i-1] < A[i] > A[i+1] > … > A[A.length - 1].
Example 1:1
2Input: [0,1,0]
Output: 1
Example 2:1
2Input: [0,2,1,0]
Output: 1
Note:
3 <= A.length <= 10000
0 <= A[i] <= 10^6
A is a mountain, as defined above.
判断一个“山峰”数组的山峰在哪里,本来以为还要判断这个是不是山峰数组的,所以多写了一些,对结果没影响,懒得删了。
1 | class Solution { |
我这个做法不好,可以用二分查找。1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public int peakIndexInMountainArray(int[] A) {
int lo = 0, hi = A.length - 1;
while (lo < hi) {
int mi = lo + (hi - lo) / 2;
if (A[mi] < A[mi + 1])
lo = mi + 1;
else
hi = mi;
}
return lo;
}
Leetcode853. Car Fleet
N cars are going to the same destination along a one lane road. The destination is target miles away.
Each car i has a constant speed speed[i] (in miles per hour), and initial position position[i] miles towards the target along the road.
A car can never pass another car ahead of it, but it can catch up to it, and drive bumper to bumper at the same speed.
The distance between these two cars is ignored - they are assumed to have the same position.
A car fleet is some non-empty set of cars driving at the same position and same speed. Note that a single car is also a car fleet.
If a car catches up to a car fleet right at the destination point, it will still be considered as one car fleet.
How many car fleets will arrive at the destination?
Example 1:1
2
3
4
5
6
7Input: target = 12, position = [10,8,0,5,3], speed = [2,4,1,1,3]
Output: 3
Explanation:
The cars starting at 10 and 8 become a fleet, meeting each other at 12.
The car starting at 0 doesn't catch up to any other car, so it is a fleet by itself.
The cars starting at 5 and 3 become a fleet, meeting each other at 6.
Note that no other cars meet these fleets before the destination, so the answer is 3.
Note:
- 0 <= N <= 10 ^ 4
- 0 < target <= 10 ^ 6
- 0 < speed[i] <= 10 ^ 6
- 0 <= position[i] < target
- All initial positions are different.
这道题说是路上有一系列的车,车在不同的位置,且分别有着不同的速度,但行驶的方向都相同。如果后方的车在到达终点之前追上前面的车了,那么它就会如痴汉般尾随在其后,且速度降至和前面的车相同,可以看作是一个车队,当然,单独的一辆车也可以看作是一个车队,问我们共有多少个车队到达终点。这道题是小学时候的应用题的感觉,什么狗追人啊,人追狗啊之类的。这道题的正确解法的思路其实不太容易想,因为我们很容易把注意力都集中到每辆车,去计算其每个时刻所在的位置,以及跟前面的车相遇的位置,这其实把这道题想复杂了,其实并不需要知道车的相遇位置,只关心是否能组成车队一同经过终点线,那么如何才能知道是否能一起过线呢,最简单的方法就是看时间,假如车B在车A的后面,而车B到终点线的时间小于等于车A,那么就知道车A和B一定会组成车队一起过线。这样的话,就可以从离终点最近的一辆车开始,先算出其撞线的时间,然后再一次遍历身后的车,若后面的车撞线的时间小于等于前面的车的时间,则会组成车队。反之,若大于前面的车的时间,则说明无法追上前面的车,于是自己会形成一个新的车队,且是车头,则结果 res 自增1即可。
思路有了,就可以具体实现了,使用一个 TreeMap 来建立小车位置和其到达终点时间之间的映射,这里的时间使用 double 型,通过终点位置减去当前位置,并除以速度来获得。我们希望能从 position 大的小车开始处理,而 TreeMap 是把小的数字排在前面,这里使用了个小 trick,就是映射的时候使用的是 position 的负数,这样就能先处理原来 position 大的车,从而统计出正确的车队数量,参见代码如下:
1 | class Solution { |
Leetcode855. Exam Room
In an exam room, there are N seats in a single row, numbered 0, 1, 2, …, N-1.
When a student enters the room, they must sit in the seat that maximizes the distance to the closest person. If there are multiple such seats, they sit in the seat with the lowest number. (Also, if no one is in the room, then the student sits at seat number 0.)
Return a class ExamRoom(int N) that exposes two functions: ExamRoom.seat() returning an int representing what seat the student sat in, and ExamRoom.leave(int p) representing that the student in seat number p now leaves the room. It is guaranteed that any calls to ExamRoom.leave(p) have a student sitting in seat p.
Example 1:1
2
3
4
5
6
7
8
9
10Input: ["ExamRoom","seat","seat","seat","seat","leave","seat"], [[10],[],[],[],[],[4],[]]
Output: [null,0,9,4,2,null,5]
Explanation:
ExamRoom(10) -> null
seat() -> 0, no one is in the room, then the student sits at seat number 0.
seat() -> 9, the student sits at the last seat number 9.
seat() -> 4, the student sits at the last seat number 4.
seat() -> 2, the student sits at the last seat number 2.
leave(4) -> null
seat() -> 5, the student sits at the last seat number 5.
Note:
- 1 <= N <= 10^9
- ExamRoom.seat() and ExamRoom.leave() will be called at most 10^4 times across all test cases.
- Calls to ExamRoom.leave(p) are guaranteed to have a student currently sitting in seat number p.
有个考场,每个考生入座的时候都要尽可能的跟左右两边的人距离保持最大,当最大距离相同的时候,考生坐在座位编号较小的那个位置。对于墙的处理跟之前那道是一样的,能靠墙就尽量靠墙,这样肯定离别人最远。
最先想的方法是用一个大小为N的数组来表示所有的座位,初始化为0,表示没有一个人,若有人入座了,则将该位置变为1,离开则变为0,那么对于 leave() 函数就十分简单了,直接将对应位置改为0即可。重点就是 seat() 函数了,采用双指针来做,主要就是找连续的0进行处理,还是要分 start 是否为0的情况,因为空位从墙的位置开始,跟空位在两人之间的处理情况是不同的,若空位从墙开始,肯定是坐墙边,而若是在两人之间,则需要坐在最中间,还要记得更新 start 为下一个空座位。最后在处理末尾空位连到墙的时候,跟之前稍有些不同,因为题目要求当最大距离相同的时候,需要选择座位号小的位置,而当此时 start 为0的时候,说明所有的位置都是空的,那么我们不需要再更新 idx 了,就用其初始值0,表示就坐在第一个位置,是符合题意的。最后别忘了将 idx 位置赋值为1,表示有人坐了。
那么比较直接的改进方法就是去掉那些0,我们只保存有人坐的位置,即所有1的位置。这样省去了遍历0的时间,大大提高了效率,此时我们就可以使用 TreeSet 来保存1的位置,其余部分并不怎么需要改变,在确定了座位 idx 时,将其加入 TreeSet 中。在 leave() 中,直接移除离开人的座位位置即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class ExamRoom {
public:
int n;
set<int> s;
ExamRoom(int N) {
n = N;
}
int seat() {
int start = 0, pos = 0, left = -1, dist = 0;
for (int i : s) {
if (start == 0) {
if (dist < i - start) {
dist = i - start;
pos = 0;
}
}
else {
if (dist < (i - start + 1) / 2) {
dist = (i - start + 1) / 2;
pos = start + dist - 1;
}
}
start = i + 1;
}
if (start > 0 && dist < n - start)
pos = n-1;
s.insert(pos);
return pos;
}
void leave(int p) {
s.erase(p);
}
};
Leetcode856. Score of Parentheses
Given a balanced parentheses string S, compute the score of the string based on the following rule:
()has score 1ABhas score A + B, where A and B are balanced parentheses strings.(A)has score 2 * A, where A is a balanced parentheses string.
Example 1:1
2Input: "()"
Output: 1
Example 2:1
2Input: "(())"
Output: 2
Example 3:1
2Input: "()()"
Output: 2
Example 4:1
2Input: "(()(()))"
Output: 6
Note:
- S is a balanced parentheses string, containing only ( and ).
- 2 <= S.length <= 50
这道题给了我们一个只有括号的字符串,一个简单的括号值1分,并排的括号是分值是相加的关系,包含的括号是乘的关系,每包含一层,都要乘以个2。题目中给的例子很好的说明了题意,博主最先尝试的方法是递归来做,思路是先找出每一个最外层的括号,再对其中间的整体部分调用递归,比如对于 “()(())” 来说,第一个最外边的括号是 “()”,其中间为空,对空串调用递归返回0,但是结果 res 还是加1,这个特殊的处理后面会讲到。第二个最外边的括号是 “(())” 的外层括号,对其中间的 “()” 调用递归,返回1,再乘以2,则得到 “(())” 的值,然后把二者相加,就是最终需要的结果了。找部分合法的括号字符串的方法就是使用一个计数器,遇到左括号,计数器自增1,反之右括号计数器自减1,那么当计数器为0的时候,就是一个合法的字符串了,我们对除去最外层的括号的中间内容调用递归,然后把返回值乘以2,并和1比较,取二者间的较大值加到结果 res 中,这是因为假如中间是空串,那么返回值是0,乘以2还是0,但是 “()” 的分值应该是1,所以累加的时候要跟1做比较。之后记得要更新i都正确的位置,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int scoreOfParentheses(string S) {
int res = 0, n = S.size();
for (int i = 0; i < n; ++i) {
if (S[i] == ')') continue;
int pos = i + 1, cnt = 1;
while (cnt != 0) {
(S[pos++] == '(') ? ++cnt : --cnt;
}
int cur = scoreOfParentheses(S.substr(i + 1, pos - i - 2));
res += max(2 * cur, 1);
i = pos - 1;
}
return res;
}
};
我们也可以使用迭代来做,这里就要借助栈 stack 来做,因为递归在调用的时候,其实也是将当前状态压入栈中,等递归退出后再从栈中取出之前的状态。这里的实现思路是,遍历字符串S,当遇到左括号时,将当前的分数压入栈中,并把当前得分清0,若遇到的是右括号,说明此时已经形成了一个完整的合法的括号字符串了,而且除去外层的括号,内层的得分已经算出来了,就是当前的结果 res,此时就要乘以2,并且要跟1比较,取二者中的较大值,这样操作的原因已经在上面解法的讲解中解释过了。然后还要加上栈顶的值,因为栈顶的值是之前合法括号子串的值,跟当前的是并列关系,所以是相加的操作,最后不要忘了要将栈顶元素移除即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int scoreOfParentheses(string S) {
int res = 0;
stack<int> st;
for (char c : S) {
if (c == '(') {
st.push(res);
res = 0;
} else {
res = st.top() + max(res * 2, 1);
st.pop();
}
}
return res;
}
};
我们可以对空间复杂度进行进一步的优化,并不需要使用栈去保留所有的中间情况,可以只用一个变量 cnt 来记录当前在第几层括号之中,因为本题的括号累加值是有规律的,”()” 是1,因为最中间的括号在0层括号内,2^0 = 1。”(())” 是2,因为最中间的括号在1层括号内,2^1 = 2。”((()))” 是4,因为最中间的括号在2层括号内,2^2 = 4。因此类推,其实只需要统计出最中间那个括号外变有几个括号,就可以直接算出整个多重包含的括号字符串的值,参见代码如下:1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int scoreOfParentheses(string S) {
int res = 0, cnt = 0, n = S.size();
for (int i = 0; i < n; ++i) {
(S[i] == '(') ? ++cnt : --cnt;
if (S[i] == ')' && S[i - 1] == '(') res += (1 << cnt);
}
return res;
}
};
Leetcode858. Mirror Reflection
There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered 0, 1, and 2.
The square room has walls of length p, and a laser ray from the southwest corner first meets the east wall at a distance q from the 0th receptor.
Return the number of the receptor that the ray meets first. (It is guaranteed that the ray will meet a receptor eventually.)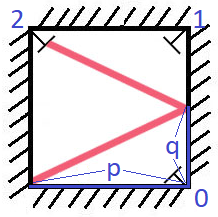
Example 1:1
2
3Input: p = 2, q = 1
Output: 2
Explanation: The ray meets receptor 2 the first time it gets reflected back to the left wall.
题目大意:
存在一个方形空间,如上图所示,一束光从左下角射出,方形空间的四条边都会反射,在0,1,2处存在3个接收器,问,给定方形空间的边长 p 和第一次到达右边界时距离0号接收器的距离,这束光最终会落到哪个接收器上?
解题思路
首先对于给定的p,q,如果我们把这两个数都同时放大N倍,光线的走法结果不会改变,因此,首先要找p,q得最大公约数,使得p,q互质;
然后,当p,q互质时,不可能两个都是偶数,因此分情况,当p为偶数,q为奇数时,光线会一直走右边界的奇数坐标(1,3,5,7….),然后再走左边的偶数坐标,因此最终必定会走到左边界,即2号接收器;若p为奇数,q为偶数,那么光线射到右边界时是偶数坐标,射到左边界时也是偶数坐标,而由于边长p是奇数,因此最终是不会走到左边界或右边界,即不会到接收器1和2,而是经过1,2之间的边界进行反向,然后往下走,而下面只有接收器0,因此最终必定会走到0;若p是奇数,且q也是奇数,那么光线到右边界时是奇数坐标,到左边界时是偶数坐标,因此最终一定走到接收器1。
1 | class Solution { |
Leetcode859. Buddy Strings
Given two strings A and B of lowercase letters, return true if and only if we can swap two letters in A so that the result equals B.
Example 1:1
2Input: A = "ab", B = "ba"
Output: true
Example 2:1
2Input: A = "ab", B = "ab"
Output: false
Example 3:1
2Input: A = "aa", B = "aa"
Output: true
Example 4:1
2Input: A = "aaaaaaabc", B = "aaaaaaacb"
Output: true
Example 5:1
2Input: A = "", B = "aa"
Output: false
Note:
- 0 <= A.length <= 20000
- 0 <= B.length <= 20000
- A and B consist only of lowercase letters.
- 如果两个字符串长度不相等,则返回 false。
- 如果两个字符串有超过两处位置,其对应字符不一致,返回 false。
- 如果仅有两处位置字符不相同,则分别判断这两处位置交换后是否相同。
- 如果仅有一处位置字符不相同,则返回 false。
- 如果没有位置字符不相同,则根据题意,我们不得不找到两处位置交换。如果字符串中有两处位置字符相同,则返回 true;否则返回 false。
1 | class Solution { |
Leetcode860. Lemonade Change
At a lemonade stand, each lemonade costs $5.
Customers are standing in a queue to buy from you, and order one at a time (in the order specified by bills).
Each customer will only buy one lemonade and pay with either a $5, $10, or $20 bill. You must provide the correct change to each customer, so that the net transaction is that the customer pays $5.
Note that you don’t have any change in hand at first.
Return true if and only if you can provide every customer with correct change.
Example 1:1
2Input: [5,5,5,10,20]
Output: true
Explanation:
- From the first 3 customers, we collect three $5 bills in order.
- From the fourth customer, we collect a $10 bill and give back a $5.
- From the fifth customer, we give a $10 bill and a $5 bill.
- Since all customers got correct change, we output true.
Example 2:1
2Input: [5,5,10]
Output: true
Example 3:1
2Input: [10,10]
Output: false
Example 4:1
2Input: [5,5,10,10,20]
Output: false
Explanation:
- From the first two customers in order, we collect two $5 bills.
- For the next two customers in order, we collect a $10 bill and give back a $5 bill.
- For the last customer, we can’t give change of $15 back because we only have two $10 bills.
- Since not every customer received correct change, the answer is false.
Note:
- 0 <= bills.length <= 10000
- bills[i] will be either 5, 10, or 20.
题目大意:卖lemon,5块钱一个,现在有3种面值的钞票分别为10,20,5,开始的时候没有找零的钱,问能否让每个人都有找零。
1 | class Solution { |
Leetcode861. Score After Flipping Matrix
We have a two dimensional matrix A where each value is 0 or 1.
A move consists of choosing any row or column, and toggling each value in that row or column: changing all 0s to 1s, and all 1s to 0s.
After making any number of moves, every row of this matrix is interpreted as a binary number, and the score of the matrix is the sum of these numbers.
Return the highest possible score.
Example 1:1
2
3
4
5Input: [[0,0,1,1],[1,0,1,0],[1,1,0,0]]
Output: 39
Explanation:
Toggled to [[1,1,1,1],[1,0,0,1],[1,1,1,1]].
0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39
Note:
1 <= A.length <= 20
1 <= A[0].length <= 20
A[i][j] is 0 or 1.
思路:对一个只有0和1的二维矩阵,移动是指选择任一行或任一列,将所有的0变成1,所有的1变成0,在作出任意次数的移动后,将该矩阵中的每一行都按照二进制数来解释,输出和的最大值。要注意的是行和列任意次移动,达到最大值。即以求出最优解为目标(可重复移动)。按二进制数来解释,注意数组[0-n]对应二进制“高位-低位”。
首先对行移动求最优解:二进制数,高位的有效值“1”大于后面所有位数之和,举个例子:10000=16 01010=10 00111=7。所以我们需要判断A[i]0是否为“1”,将为“0”的进行移动操作,本行即达到最优。重复每行即为所有行最优
再对列移动求最优解:本题为矩阵,所以同一列的数字在二进制解释中位于相同的位置(2^n),当一列中”1”的数量最大时,结果值最大。即为列最优解,同理求出所有列最优解。
最后计算矩阵的总和,注意从低位(数组尾部开始计算)。
- 若行最高位(数组行首元素)不为“1”,移动行。
- 若列“0”数量多于“1”,移动列。
- 从低位(行数组尾部)开始计算数组行值。
1 | class Solution { |
附上Solution:
Notice that a 1 in the i’th column from the right, contributes 2^i to the score.
Say we are finished toggling the rows in some configuration. Then for each column, (to maximize the score), we’ll toggle the column if it would increase the number of 1s.
We can brute force over every possible way to toggle rows.
Say the matrix has R rows and C columns.
For each state, the transition trans = state ^ (state-1) represents the rows that must be toggled to get into the state of toggled rows represented by (the bits of) state.
We’ll toggle them, and also maintain the correct column sums of the matrix on the side.
Afterwards, we’ll calculate the score. If for example the last column has a column sum of 3, then the score is max(3, R-3), where R-3 represents the score we get from toggling the last column.
In general, the score is increased by max(col_sum, R - col_sum) * (1 << (C-1-c)), where the factor (1 << (C-1-c)) is the power of 2 that each 1 contributes.
Note that this approach may not run in the time allotted.
1 | class Solution { |
Leetcode863. All Nodes Distance K in Binary Tree
Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.
You can return the answer in any order.
Example 1:1
2
3Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.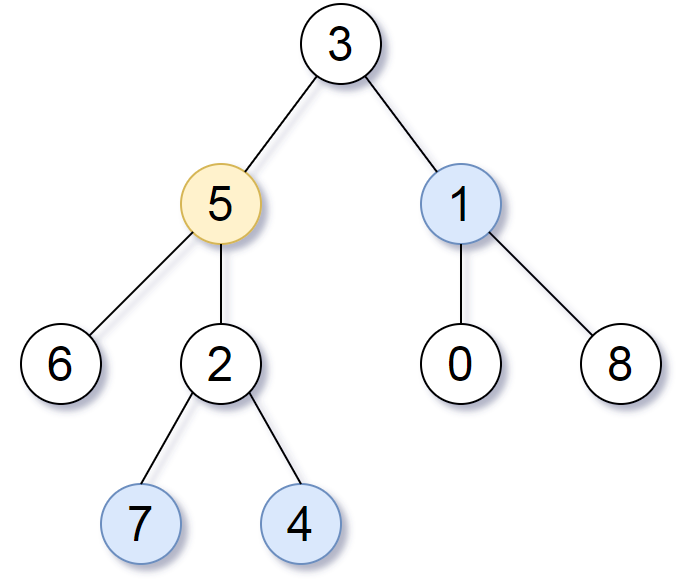
Example 2:1
2Input: root = [1], target = 1, k = 3
Output: []
这道题给了我们一棵二叉树,一个目标结点 target,还有一个整数K,让返回所有跟目标结点 target 相距K的结点。我们知道在子树中寻找距离为K的结点很容易,因为只需要一层一层的向下遍历即可,难点就在于符合题意的结点有可能是祖先结点,或者是在旁边的兄弟子树中,这就比较麻烦了,因为二叉树只有从父结点到子结点的路径,反过来就不行。既然没有,我们就手动创建这样的反向连接即可,这样树的遍历问题就转为了图的遍历(其实树也是一种特殊的图)。建立反向连接就是用一个 HashMap 来来建立每个结点和其父结点之间的映射,使用先序遍历建立好所有的反向连接,然后再开始查找和目标结点距离K的所有结点,这里需要一个 HashSet 来记录所有已经访问过了的结点。
在递归函数中,首先判断当前结点是否已经访问过,是的话直接返回,否则就加入到 visited 中。再判断此时K是否为0,是的话说明当前结点已经是距离目标结点为K的点了,将其加入结果 res 中,然后直接返回。否则分别对当前结点的左右子结点调用递归函数,注意此时带入 K-1,这两步是对子树进行查找。之前说了,还得对父结点,以及兄弟子树进行查找,这是就体现出建立的反向连接 HashMap 的作用了,若当前结点的父结点存在,我们也要对其父结点调用递归函数,并同样带入 K-1,这样就能正确的找到所有满足题意的点了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {
if (!root)
return {};
unordered_map<TreeNode*, TreeNode*> parents;
unordered_set<TreeNode*> visited;
vector<int> res;
build_parent(root, parents);
find_res(target, k, visited, parents, res);
return res;
}
void find_res(TreeNode* root, int k, unordered_set<TreeNode*> visited, unordered_map<TreeNode*, TreeNode*> parents, vector<int>& res) {
if (visited.count(root))
return;
visited.insert(root);
if (k == 0) {
res.push_back(root->val);
return;
}
if (root->left) find_res(root->left, k-1, visited, parents, res);
if (root->right) find_res(root->right, k-1, visited, parents, res);
if (parents[root]) find_res(parents[root], k-1, visited, parents,res);
}
void build_parent(TreeNode* root, unordered_map<TreeNode*, TreeNode*>& parents) {
if (root == NULL)
return ;
if (root->left) parents[root->left] = root;
if (root->right) parents[root->right] = root;
build_parent(root->left, parents);
build_parent(root->right, parents);
}
};
既然是图的遍历,那就也可以使用 BFS 来做,为了方便起见,我们直接建立一个邻接链表,即每个结点最多有三个跟其相连的结点,左右子结点和父结点,使用一个 HashMap 来建立每个结点和其相邻的结点数组之间的映射,这样就几乎完全将其当作图来对待了,建立好邻接链表之后,原来的树的结构都不需要用了。既然是 BFS 进行层序遍历,就要使用队列 queue,还要一个 HashSet 来记录访问过的结点。在 while 循环中,若K为0了,说明当前这层的结点都是符合题意的,就把当前队列中所有的结点加入结果 res,并返回即可。否则就进行层序遍历,取出当前层的每个结点,并在邻接链表中找到和其相邻的结点,若没有访问过,就加入 visited 和 queue 中即可。记得每层遍历完成之后,K要自减1,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public:
vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
if (!root) return {};
vector<int> res;
unordered_map<TreeNode*, vector<TreeNode*>> m;
queue<TreeNode*> q{{target}};
unordered_set<TreeNode*> visited{{target}};
findParent(root, NULL, m);
while (!q.empty()) {
if (K == 0) {
for (int i = q.size(); i > 0; --i) {
res.push_back(q.front()->val); q.pop();
}
return res;
}
for (int i = q.size(); i > 0; --i) {
TreeNode *t = q.front(); q.pop();
for (TreeNode *node : m[t]) {
if (visited.count(node)) continue;
visited.insert(node);
q.push(node);
}
}
--K;
}
return res;
}
void findParent(TreeNode* node, TreeNode* pre, unordered_map<TreeNode*, vector<TreeNode*>>& m) {
if (!node) return;
if (m.count(node)) return;
if (pre) {
m[node].push_back(pre);
m[pre].push_back(node);
}
findParent(node->left, node, m);
findParent(node->right, node, m);
}
};
其实这道题也可以不用 HashMap,不建立邻接链表,直接在递归中完成所有的需求,真正体现了递归的博大精深。在进行递归之前,我们要先判断一个 corner case,那就是当 K==0 时,此时要返回的就是目标结点值本身,可以直接返回。否则就要进行递归了。这里的递归函数跟之前的有所不同,是需要返回值的,这个返回值表示的含义比较复杂,若为0,表示当前结点为空或者当前结点就是距离目标结点为K的点,此时返回值为0,是为了进行剪枝,使得不用对其左右子结点再次进行递归。当目标结点正好是当前结点的时候,递归函数返回值为1,其他的返回值为当前结点离目标结点的距离加1。还需要一个参数 dist,其含义为离目标结点的距离,注意和递归的返回值区别,这里不用加1,且其为0时候不是为了剪枝,而是真不知道离目标结点的距离。
在递归函数中,首先判断若当前结点为空,则直接返回0。然后判断 dist 是否为k,是的话,说目标结点距离当前结点的距离为K,是符合题意的,需要加入结果 res 中,并返回0,注意这里返回0是为了剪枝。否则判断,若当前结点正好就是目标结点,或者已经遍历过了目标结点(表现为 dist 大于0),那么对左右子树分别调用递归函数,并将返回值分别存入 left 和 right 两个变量中。注意此时应带入 dist+1,因为是先序遍历,若目标结点之前被遍历到了,那么说明目标结点肯定不在当前结点的子树中,当前要往子树遍历的话,肯定离目标结点又远了一些,需要加1。若当前结点不是目标结点,也还没见到目标结点时,同样也需要对左右子结点调用递归函数,但此时 dist 不加1,因为不确定目标结点的位置。若 left 或者 right 值等于K,则说明目标结点在子树中,且距离当前结点为K(为啥呢?因为目标结点本身是返回1,所以当左右子结点返回K时,和当前结点距离是K)。接下来判断,若当前结点是目标结点,直接返回1,这个前面解释过了。然后再看 left 和 right 的值是否大于0,若 left 值大于0,说明目标结点在左子树中,我们此时就要对右子结点再调用一次递归,并且 dist 带入 left+1,同理,若 right 值大于0,说明目标结点在右子树中,我们此时就要对左子结点再调用一次递归,并且 dist 带入 right+1。这两步很重要,是之所以能不建立邻接链表的关键所在。若 left 大于0,则返回 left+1,若 right 大于0,则返回 right+1,否则就返回0,参见代码如下:
1 | class Solution { |
Leetcode865. Smallest Subtree with all the Deepest Nodes
Given the root of a binary tree, the depth of each node is the shortest distance to the root.
Return the smallest subtree such that it contains all the deepest nodes in the original tree.
A node is called the deepest if it has the largest depth possible among any node in the entire tree.
The subtree of a node is tree consisting of that node, plus the set of all descendants of that node.
Example 1:1
2
3
4
5Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest nodes of the tree.
Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.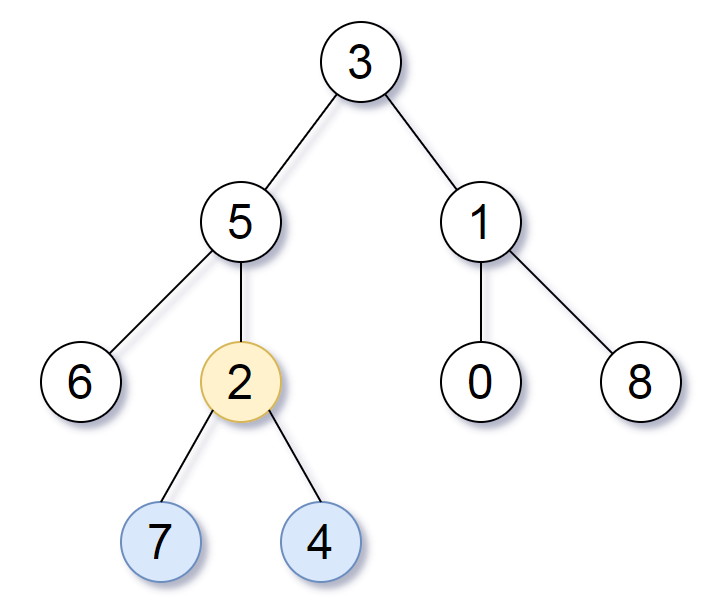
Example 2:1
2
3Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree.
Example 3:1
2
3Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.
题目的意思是:给定一个根为 root 的二叉树,每个结点的深度是它到根的最短距离。如果一个结点在整个树的任意结点之间具有最大的深度,则该结点是最深的。一个结点的子树是该结点加上它的所有后代的集合。
返回能满足“以该结点为根的子树中包含所有最深的结点”这一条件的具有最大深度的结点。
二叉树一般就是递归,思路很直接,代码很简洁,用到pair把深度和root回传。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
return solve(root).second;
}
pair<int, TreeNode*> solve(TreeNode* root) {
if (root == NULL) return make_pair(0, root);
pair<int, TreeNode*> left = solve(root->left);
pair<int, TreeNode*> right = solve(root->right);
if (left.first == right.first) return make_pair(left.first+1, root);
else if (left.first > right.first) return make_pair(left.first+1, left.second);
else return make_pair(right.first+1, right.second);
}
};
Leetcode867. Transpose Matrix
Given a matrix A, return the transpose of A.
The transpose of a matrix is the matrix flipped over it’s main diagonal, switching the row and column indices of the matrix.
Example 1:1
2Input: [[1,2,3],[4,5,6],[7,8,9]]
Output: [[1,4,7],[2,5,8],[3,6,9]]
Example 2:1
2Input: [[1,2,3],[4,5,6]]
Output: [[1,4],[2,5],[3,6]]
Note:
- 1 <= A.length <= 1000
- 1 <= A[0].length <= 1000
Easy题目,矩阵转置基本操作,i,j下标对调1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
vector<vector<int>> transpose(vector<vector<int>>& A) {
int m = A.size(), n = A[0].size();
vector<vector<int>> result(n, vector<int>(m, 0));
for(int i = 0; i < m; i ++)
for(int j = 0; j < n; j ++)
result[j][i] = A[i][j];
return result;
}
};
Leetcode868. Binary Gap
Given a positive integer N, find and return the longest distance between two consecutive 1’s in the binary representation of N.
If there aren’t two consecutive 1’s, return 0.
Example 1:1
2
3
4
5
6
7
8Input: 22
Output: 2
Explanation:
22 in binary is 0b10110.
In the binary representation of 22, there are three ones, and two consecutive pairs of 1's.
The first consecutive pair of 1's have distance 2.
The second consecutive pair of 1's have distance 1.
The answer is the largest of these two distances, which is 2.
Example 2:1
2
3
4Input: 5
Output: 2
Explanation:
5 in binary is 0b101.
Example 3:1
2
3
4Input: 6
Output: 1
Explanation:
6 in binary is 0b110.
Example 4:1
2
3
4
5Input: 8
Output: 0
Explanation:
8 in binary is 0b1000.
There aren't any consecutive pairs of 1's in the binary representation of 8, so we return 0.
找到一个数的二进制表示中最远的两个1的距离。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int binaryGap(int N) {
int res = 0, prev = -1, cur = -1;
int count = 0;
while(N) {
int temp = N & 1;
if(temp == 1) {
prev = cur;
cur = count;
if(prev != -1 && cur != -1)
res = max(res, cur - prev);
}
count ++;
N = N >> 1;
}
return res;
}
};
LeetCode869. Reordered Power of 2
Starting with a positive integer N, we reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return true if and only if we can do this in a way such that the resulting number is a power of 2.
Example 1:1
2Input: 1
Output: true
Example 2:1
2Input: 10
Output: false
Example 3:1
2Input: 16
Output: true
Example 4:1
2Input: 24
Output: false
Example 5:1
2Input: 46
Output: true
Note:
- 1 <= N <= 10^9
这道题说是给了我们一个正整数N,让对各位上的数字进行重新排序,但是要保证最高位上不是0,问能否变为2的指数。刚开始的时候博主理解错了,以为是对N的二进制数的各位进行重排序,但除了2的指数本身,其他数字怎么也组不成2的指数啊,因为2的指数的二进制数只有最高位是1,其余都是0。后来才发现,是让对N的十进制数的各位上的数字进行重排序,比如 N=46,那么换个位置,变成 64,就是2的指数了。搞清了题意后,就可以开始解题了,由于N给定了范围,在 [1, 1e9] 之间,所以其调换位数能组成的二进制数也是有范围的,为 [2^0, 2^30] 之间,这样的话,一个比较直接的解法就是,现将整数N转为字符串,然后对字符串进行排序。然后遍历所有可能的2的指数,将每个2的指数也转为字符串并排序,这样只要某个排序后的字符串跟之前由N生成的字符串相等的话,则表明整数N是符合题意的,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
bool reorderedPowerOf2(int N) {
string str = to_string(N);
sort(str.begin(), str.end());
for (int i = 0; i < 31; ++i) {
string t = to_string(1 << i);
sort(t.begin(), t.end());
if (t == str) return true;
}
return false;
}
};
下面这种方法没有将数字转为字符串并排序,而是使用了另一种比较巧妙的方法来实现类似的功能,是通过对N的每位上的数字都变为10的倍数,并相加,这样相当于将N的各位的上的数字都加码到了10的指数空间,而对于所有的2的指数,进行相同的操作,只要某个加码后的数字跟之前整数N的处理后的数字相同,则说明N是符合题意的。需要注意的是,为了防止整型移除,加码后的数字用长整型来表示即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
bool reorderedPowerOf2(int N) {
long sum = helper(N);
for (int i = 0; i < 31; i++) {
if (helper(1 << i) == sum) return true;
}
return false;
}
long helper(int N) {
long res = 0;
for (; N; N /= 10) res += pow(10, N % 10);
return res;
}
};
Leetcode870. Advantage Shuffle
Given two arrays A and B of equal size, the advantage of A with respect to B is the number of indices i for which A[i] > B[i].
Return any permutation of A that maximizes its advantage with respect to B.
Example 1:1
2Input: A = [2,7,11,15], B = [1,10,4,11]
Output: [2,11,7,15]
Example 2:1
2Input: A = [12,24,8,32], B = [13,25,32,11]
Output: [24,32,8,12]
Note:
- 1 <= A.length = B.length <= 10000
- 0 <= A[i] <= 10^9
- 0 <= B[i] <= 10^9
这道题给了我们两个数组A和B,让对A进行重排序,使得每个对应对位置上A中的数字尽可能的大于B。这不就是大名鼎鼎的田忌赛马么,但想出高招并不是田忌,而是孙膑,就是孙子兵法的作者,但这 credit 好像都给了田忌,让人误以为是田忌的智慧,不禁想起了高富帅重金买科研成果的冠名权的故事。孙子原话是,“今以君之下驷与彼上驷,取君上驷与彼中驷,取君中驷与彼下驷”。就是自己的下马跟人上马比,稳输不用管,上马跟其中马跑,稳赢,中马跟其下马跑,还是稳赢。那我还全马跟其半马跑,能赢否?不过说的,今天博主所在的城市还真有马拉松比赛,而且博主还报了半马,但是由于身不由己的原因无法去跑,实在是可惜,没事,来日方长,总是有机会的。扯了这么久的犊子,赶紧拉回来做题吧。其实这道题的思路还真是田忌赛马的智慧一样,既然要想办法大过B中的数,那么对于B中的每个数(可以看作每匹马),先在A中找刚好大于该数的数字(这就是为啥中马跟其下马比,而不是上马跟其下马比),用太大的数字就浪费了,而如果A中没有比之大的数字,就用A中最小的数字(用下马跟其上马比,不过略有不同的是此时我们没有上马)。就用这种贪婪算法的思路就可以成功解题了,为了方便起见,就是用一个 MultiSet 来做,相当于一个允许重复的 TreeSet,既允许重复又自带排序功能,岂不美哉!那么遍历B中每个数字,在A进行二分搜索第一个大于的数字,这里使用了 STL 自带的 upper_bound 来做,当然想自己写二分也没问题。然后看,若不存在,则将A中最小的数字加到结果 res 中,否则就将第一个大于的数字加入结果 res 中,参见代码如下:
1 | class Solution { |
当两个数组都是有序的时候,我们就能快速的直到各自的最大值与最小值,问题就变得容易很多了。比如可以先从B的最大值开始,这是就看A的最大值能否大过B,能的话,就移动到对应位置,不能的话就用最小值,然后再看B的次大值,这样双指针就可以解决问题。所以可以先给A按从小到大的顺序,对于B的话,不能直接排序,因为这样的话原来的顺序就完全丢失了,所以将B中每个数字和其原始坐标位置组成一个 pair 对儿,加入到一个最大堆中,这样B中的最大值就会最先被取出来,再进行上述的操作,这时候就可以发现保存的原始坐标就发挥用处了,根据其坐标就可以直接更新结果 res 中对应的位置了,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
vector advantageCount(vector& A, vector& B) {
int n = A.size(), left = 0, right = n - 1;
vector<int> res(n);
sort(A.begin(), A.end());
priority_queue<pair<int, int>> q;
for (int i = 0; i < n; ++i)
q.push({B[i], i});
while (!q.empty()) {
int val = q.top().first, idx = q.top().second; q.pop();
if (A[right] > val) res[idx] = A[right--];
else res[idx] = A[left++];
}
return res;
}
};
Leetcode871. Minimum Number of Refueling Stops
A car travels from a starting position to a destination which is target miles east of the starting position.
Along the way, there are gas stations. Each station[i] represents a gas station that is station[i][0] miles east of the starting position, and has station[i][1] liters of gas.
The car starts with an infinite tank of gas, which initially has startFuel liters of fuel in it. It uses 1 liter of gas per 1 mile that it drives.
When the car reaches a gas station, it may stop and refuel, transferring all the gas from the station into the car.
What is the least number of refueling stops the car must make in order to reach its destination? If it cannot reach the destination, return -1.
Note that if the car reaches a gas station with 0 fuel left, the car can still refuel there. If the car reaches the destination with 0 fuel left, it is still considered to have arrived.
Example 1:1
2
3Input: target = 1, startFuel = 1, stations = []
Output: 0
Explanation: We can reach the target without refueling.
Example 2:1
2
3Input: target = 100, startFuel = 1, stations = [[10,100]]
Output: -1
Explanation: We can't reach the target (or even the first gas station).
Example 3:1
2
3
4
5
6
7
8Input: target = 100, startFuel = 10, stations = [[10,60],[20,30],[30,30],[60,40]]
Output: 2
Explanation:
We start with 10 liters of fuel.
We drive to position 10, expending 10 liters of fuel. We refuel from 0 liters to 60 liters of gas.
Then, we drive from position 10 to position 60 (expending 50 liters of fuel),
and refuel from 10 liters to 50 liters of gas. We then drive to and reach the target.
We made 2 refueling stops along the way, so we return 2.
Note:
- 1 <= target, startFuel, stations[i][1] <= 10^9
- 0 <= stations.length <= 500
- 0 < stations[0][0] < stations[1][0] < … < stations[stations.length-1][0] < target
这道题说有一辆小车,需要向东行驶 target 的距离,路上有许多加油站,每个加油站有两个信息,一个是距离起点的距离,另一个是可以加的油量,问我们到达 target 位置最少需要加的油量。我们可以从第三个例子来分析,开始时有 10 升油,可以到达第一个加油站,此时花掉了 10 升,但是可以补充 60 升,当前的油可以到达其他所有的加油站,由于已经开了 10 迈,所以到达后面的加油站的距离分别为 10,20,和 50。若我们到最后一个加油站,那离起始位置就有 60 迈了,再加上此加油站提供的 40 升油,直接就可以到达 100 位置,不用再加油了,所以总共只需要加2次油。由此可以看出来其实我们希望到达尽可能远的加油站的位置,同时最好该加油站中的油也比较多,这样下一次就能到达更远的位置。像这种求极值的问题,十有八九要用动态规划 Dynamic Programming 来做,但是这道题的 dp 定义式并不是直接来定义需要的最少加油站的个数,那样定义的话不太好推导出状态转移方程。正确的定义应该是根据加油次数能到达的最远距离,我们就用一个一维的 dp 数组,其中 dp[i] 表示加了i次油能到达的最远距离,那么最后只要找第一个i值使得 dp[i] 大于等于 target 即可。dp 数组的大小初始化为加油站的个数加1,值均初始化为 startFuel 即可,因为初始的油量能到达的距离是确定的。现在来推导状态转移方程了,遍历每一个加油站,对于每个遍历到的加油站k,需要再次遍历其之前的所有的加油站i,能到达当前加油站k的条件是当前的 dp[i] 值大于等于加油站k距起点的距离,若大于等于的话,我们可以更新 dp[i+1] 为 dp[i]+stations[k][1],这样就可以得到最远能到达的距离。当 dp 数组更新完成后,需要再遍历一遍,找到第一个大于等于 target 的 dp[i] 值,并返回i即可,参见代码如下:
1 | class Solution { |
这道题还有一个标签是 Heap,说明还可以用堆来做,这里是用最大堆。因为之前也分析了,我们关心的是在最小的加油次数下能达到的最远距离,那么每个加油站的油量就是关键因素,可以将所有能到达的加油站根据油量的多少放入最大堆,这样每一次都选择油量最多的加油站去加油,才能尽可能的到达最远的地方(如果骄傲没被现实大海冷冷拍下,又怎会懂得要多努力,才走得到远方。。。打住打住,要唱起来了 ^o^)。这里需要一个变量i来记录当前遍历到的加油站的位置,外层循环的终止条件是 startFuel 小于 target,然后在内部也进行循环,若当前加油站的距离小于等于 startFuel,说明可以到达,则把该加油站油量存入最大堆,这个 while 循环的作用就是把所有当前能到达的加油站的油量都加到最大堆中。这样取出的堆顶元素就是最大的油量,也是我们下一步需要去的地方(最想要去的地方,怎么能在半路就返航?!),假如此时堆为空,则直接返回 -1,表示无法到达 target。否则就把堆顶元素加到 startFuel 上,此时的startFuel 就表示当前能到的最远距离,是不是跟上面的 DP 解法核心思想很类似。由于每次只能去一个加油站,此时结果 res 也自增1,当 startFuel 到达 target 时,结果 res 就是最小的加油次数,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int minRefuelStops(int target, int startFuel, vector<vector>& stations) {
int res = 0, i = 0, n = stations.size();
priority_queue<int> pq;
for (; startFuel < target; ++res) {
while (i < n && stations[i][0] <= startFuel) {
pq.push(stations[i++][1]);
}
if (pq.empty()) return -1;
startFuel += pq.top(); pq.pop();
}
return res;
}
};
Leetcode872. Leaf-Similar Trees
Consider all the leaves of a binary tree. From left to right order, the values of those leaves form a leaf value sequence.
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8). Two binary trees are considered leaf-similar if their leaf value sequence is the same. Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.
题目并不是很难,只不过利用dfs的方法对树进行遍历,并利用vector对叶子节点进行记录,最后再比较两个得到的vector是否相同就可以得到结果了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
public:
bool leafSimilar(TreeNode* root1, TreeNode* root2) {
vector<int> v1, v2;
dfs(root1, v1);
dfs(root2, v2);
return issim(v1, v2);
}
bool issim(vector<int> v1, vector<int> v2) {
if(v1.size() != v2.size())
return false;
for(int i = 0; i < v1.size(); i ++) {
if(v1[i] != v2[i])
return false;
}
return true;
}
void dfs(TreeNode* root, vector<int> &v) {
if(root == NULL)
return;
if(root->left == nullptr && root->right == nullptr)
v.push_back(root->val);
dfs(root->left, v);
dfs(root->right, v);
}
};
Leetcode873. Length of Longest Fibonacci Subsequence
A sequence x1, x2, …, xn is Fibonacci-like if:1
2n >= 3
xi + xi+1 == xi+2 for all i + 2 <= n
Given a strictly increasing array arr of positive integers forming a sequence, return the length of the longest Fibonacci-like subsequence of arr. If one does not exist, return 0.
A subsequence is derived from another sequence arr by deleting any number of elements (including none) from arr, without changing the order of the remaining elements. For example, [3, 5, 8] is a subsequence of [3, 4, 5, 6, 7, 8].
Example 1:1
2
3Input: arr = [1,2,3,4,5,6,7,8]
Output: 5
Explanation: The longest subsequence that is fibonacci-like: [1,2,3,5,8].
Example 2:1
2
3Input: arr = [1,3,7,11,12,14,18]
Output: 3
Explanation: The longest subsequence that is fibonacci-like: [1,11,12], [3,11,14] or [7,11,18].
这道题的 DP 定义式也是难点之一,一般来说,对于子数组子序列的问题,我们都会使用一个二维的 dp 数组,其中dp[i][j]表示范围 [i, j] 内的极值,但是在这道题不行,就算你知道了子区间 [i, j] 内的最长斐波那契数列的长度,还是无法更新其他区间。再回过头来看一下斐波那契数列的定义,从第三个数开始,每个数都是前两个数之和,所以若想增加数列的长度,这个条件一定要一直保持,比如对于数组 [1, 2, 3, 4, 7],在子序列 [1, 2, 3] 中以3结尾的斐氏数列长度为3,虽然 [3, 4, 7] 也可以组成斐氏数列,但是以7结尾的斐氏数列长度更新的时候不能用以3结尾的斐氏数列长度的信息,因为 [1, 2, 3, 4, 7] 不是一个正确的斐氏数列,虽然 1+2=3, 3+4=7,但是 2+3!=4。所以每次只能增加一个长度,而且必须要知道前两个数字,正确的dp[i][j]应该是表示以A[i]和A[j]结尾的斐氏数列的长度。
接下来看该怎么更新 dp 数组,我们还是要确定两个数字,跟之前的解法不同的是,先确定一个数字,然后遍历之前比其小的所有数字,这样A[i]和A[j]两个数字确定了,此时要找一个比A[i]和A[j]都小的数,即A[i]-A[j],若这个数字存在的话,说明斐氏数列存在,因为[A[i]-A[j], A[j], A[i]]是满足斐氏数列要求的。这样状态转移就有了,dp[j][i] = dp[indexOf(A[i]-A[j])][j] + 1,可能看的比较晕,但其实就是A[i]加到了以A[j]和A[i]-A[j]结尾的斐氏数列的后面,使得长度增加了1。不过前提是A[i]-A[j]必须要在原数组中存在,而且还需要知道某个数字在原数组中的坐标,那么就用 HashMap 来建立数字跟其坐标之间的映射。可以事先把所有数字都存在 HashMap 中,也可以在遍历i的时候建立,因为我们只关心位置i之前的数字。这样在算出A[i]-A[j]之后,在 HashMap 查找差值是否存在,不存在的话赋值为 -1。在更新dp[j][i]的时候,我们看A[i]-A[j] < A[j]且 k>=0 是否成立,因为A[i]-A[j]是斐氏数列中最小的数,且其位置k必须要存在才能更新。否则的话更新为2。最后还是要注意,若 res 小于3的时候,要返回0,因为斐波那契数列的最低消费是3个,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int lenLongestFibSubseq(vector<int>& arr) {
int len = arr.size(), res = 0;
vector<vector<int>> dp(len, vector<int>(len, 0));
unordered_map<int, int> m;
for (int i = 0; i < len; i ++)
m[arr[i]] = i;
for (int i = 0; i < len; i ++) {
for (int j = 0; j < i; j ++) {
if (arr[i] - arr[j] < arr[j] && m.count(arr[i]-arr[j]))
dp[j][i] = dp[m[arr[i]-arr[j]]][j] + 1;
else
dp[j][i] = 2;
res = max(res, dp[j][i]);
}
}
return res > 2 ? res : 0;
}
};
Leetcode874. Walking Robot Simulation
A robot on an infinite grid starts at point (0, 0) and faces north. The robot can receive one of three possible types of commands:
- -2: turn left 90 degrees
- -1: turn right 90 degrees
- 1 <= x <= 9: move forward x units
- Some of the grid squares are obstacles.
The i-th obstacle is at grid point (obstacles[i][0], obstacles[i][1])
If the robot would try to move onto them, the robot stays on the previous grid square instead (but still continues following the rest of the route.)
Return the square of the maximum Euclidean distance that the robot will be from the origin.
Example 1:1
2
3Input: commands = [4,-1,3], obstacles = []
Output: 25
Explanation: robot will go to (3, 4)
Example 2:1
2
3Input: commands = [4,-1,4,-2,4], obstacles = [[2,4]]
Output: 65
Explanation: robot will be stuck at (1, 4) before turning left and going to (1, 8)
Note:
- 0 <= commands.length <= 10000
- 0 <= obstacles.length <= 10000
- -30000 <= obstacle[i][0] <= 30000
- -30000 <= obstacle[i][1] <= 30000
- The answer is guaranteed to be less than 2 ^ 31.
把障碍存在一个set里,方便以后查找判断。每次计算目前最大的x^2 + y^2,用一个大小为2的数组来表示X、Y坐标,之后只需要用axis=0来表示X,axis=1来表示Y即可,不需要知道到底是哪个轴。在进行移动的时候,每次只走一格,计算max_square。值得注意的是,max_square的初始值为0,因为如果被障碍遮挡或者根本没有移动指令导致原地不动的情况下,最大值是0。
1 | class Solution { |
Leetcode875. Koko Eating Bananas
Koko loves to eat bananas. There are N piles of bananas, the i-th pile has piles[i] bananas. The guards have gone and will come back in H hours.
Koko can decide her bananas-per-hour eating speed of K. Each hour, she chooses some pile of bananas, and eats K bananas from that pile. If the pile has less than K bananas, she eats all of them instead, and won’t eat any more bananas during this hour.
Koko likes to eat slowly, but still wants to finish eating all the bananas before the guards come back.
Return the minimum integer K such that she can eat all the bananas within Hhours.
Example 1:1
2Input: piles = [3,6,7,11], H = 8
Output: 4
Example 2:1
2Input: piles = [30,11,23,4,20], H = 5
Output: 30
Example 3:1
2Input: piles = [30,11,23,4,20], H = 6
Output: 23
Note:
- 1 <= piles.length <= 10^4
- piles.length <= H <= 10^9
- 1 <= piles[i] <= 10^9
这道题说有一只叫科科的猩猩,非常的喜欢吃香蕉,现在有N堆香蕉,每堆的个数可能不同,科科有H小时的时间来吃。要求是,每个小时内,科科只能选某一堆香蕉开始吃,若科科的吃速固定为K,即便在一小时内科科已经吃完了该堆的香蕉,也不能换堆,直到下一个小时才可以去另一堆吃。为了健康,科科想尽可能的吃慢一些,但同时也想在H小时内吃完所有的N堆香蕉,让我们找出一个最小的吃速K值。那么首先来想,既然每个小时只能吃一堆,总共要在H小时内吃完N堆,那么H一定要大于等于N,不然一定没法吃完N堆,这个条件题目中给了,所以就不用再 check 了。我们想一下K的可能的取值范围,当H无穷大的时候,科科有充足的时间去吃,那么就可以每小时只吃一根,也可以吃完,所以K的最小取值是1。那么当H最小,等于N时,那么一个小时内必须吃完任意一堆,那么K值就应该是香蕉最多的那一堆的个数,题目中限定了不超过 1e9,这就是最大值。所以要求的K值的范围就是 [1, 1e9],固定的范围内查找数字,当然,最暴力的方法就是一个一个的试,凭博主多年与 OJ 抗衡的经验来说,基本可以不用考虑的。那么二分查找法就是不二之选了,我们知道经典的二分查找法,是要求数组有序的,而这里香蕉个数数组又不一定是有序的。这是一个很好的观察,但是要弄清楚到底是什么应该是有序的,要查找的K是吃速,跟香蕉堆的个数并没有直接的关系,而K所在的数组其实应该是 [1, 1e9] 这个数组,其本身就是有序的,所以二分查找没有问题。当求出了 mid 之后,需要统计用该速度吃完所有的香蕉堆所需要的时间,统计的方法就是遍历每堆的香蕉个数,然后算吃完该堆要的时间。比如 K=4,那么假如有3个香蕉,需要1个小时,有4香蕉,还是1个小时,有5个香蕉,就需要两个小时,如果将三种情况融合为一个式子呢,就是用吃速加上香蕉个数减去1,再除以吃速即可,即 (pile+mid-1)/mid,大家可以自行带数字检验,是没有问题的。算出需要的总时间后去跟H比较,若小于H,说明吃的速度慢了,需要加快速度,所以 left 更新为 mid+1,否则 right 更新为 mid,最后返回 right 即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int minEatingSpeed(vector<int>& piles, int H) {
int left = 1, right = 1e9;
while (left < right) {
int mid = left + (right - left) / 2, cnt = 0;
for (int pile : piles) cnt += (pile + mid - 1) / mid;
if (cnt > H) left = mid + 1;
else right = mid;
}
return right;
}
};
Leetcode876. Middle of the Linked List
Given a non-empty, singly linked list with head node head, return a middle node of linked list.
If there are two middle nodes, return the second middle node.
Example 1:1
2
3
4
5Input: [1,2,3,4,5]
Output: Node 3 from this list (Serialization: [3,4,5])
The returned node has value 3. (The judge's serialization of this node is [3,4,5]).
Note that we returned a ListNode object ans, such that:
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, and ans.next.next.next = NULL.
Example 2:1
2
3Input: [1,2,3,4,5,6]
Output: Node 4 from this list (Serialization: [4,5,6])
Since the list has two middle nodes with values 3 and 4, we return the second one.
Note: The number of nodes in the given list will be between 1 and 100.
题目大意:求链表的中间节点。思路:构造两个节点,遍历链接,一个每次走一步,另一个每次走两步,一个遍历完链表,另一个恰好在中间
1 | class Solution { |
久仰大名的快慢指针做法,但是这里有坑,一定要注意while里的判断条件是两个,保证在有奇数个数和偶数个数的链表都不会访问空指针。
Leetcode877. Stone Game
Alex and Lee play a game with piles of stones. There are an even number of piles arranged in a row, and each pile has a positive integer number of stones piles[i].
The objective of the game is to end with the most stones. The total number of stones is odd, so there are no ties.
Alex and Lee take turns, with Alex starting first. Each turn, a player takes the entire pile of stones from either the beginning or the end of the row. This continues until there are no more piles left, at which point the person with the most stones wins.
Assuming Alex and Lee play optimally, return True if and only if Alex wins the game.
Example 1:1
2
3
4
5
6
7
8Input: [5,3,4,5]
Output: true
Explanation:
Alex starts first, and can only take the first 5 or the last 5.
Say he takes the first 5, so that the row becomes [3, 4, 5].
If Lee takes 3, then the board is [4, 5], and Alex takes 5 to win with 10 points.
If Lee takes the last 5, then the board is [3, 4], and Alex takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alex, so we return true.
Note:
- 2 <= piles.length <= 500
- piles.length is even.
- 1 <= piles[i] <= 500
- sum(piles) is odd.
这道题说是有偶数堆的石子,每堆的石子个数可能不同,但石子总数是奇数个。现在 Alex 和 Lee (不应该是 Alice 和 Bob 么??)两个人轮流选石子堆,规则是每次只能选开头和末尾中的一堆,最终获得石子总数多的人获胜。若 Alex 先选,两个人都会一直做最优选择,问我们最终 Alex 是否能获胜。博主最先想到的方法是像 Predict the Winner 中的那样,用个 player 变量来记录当前是哪个玩家在操作,若为0,表示 Alex 在选,那么他只有两种选择,要么拿首堆,要么拿尾堆,两种情况分别调用递归,两个递归函数只要有一个能返回 true,则表示 Alex 可以获胜,还需要用个变量 cur0 来记录当前 Alex 的石子总数。同理,若 Lee 在选,即 player 为1的时候,也是只有两种选择,分别调用递归,两个递归函数只要有一个能返回 true,则表示 Lee 可以获胜,用 cur1 来记录当前 Lee 的石子总数。需要注意的是,当首堆或尾堆被选走了后,我们需要标记,这里就有两种方法,一种是从原 piles 中删除选走的堆(或者是新建一个不包含选走堆的数组),但是这种方法会包括大量的拷贝运算,无法通过 OJ。另一种方法是用两个指针 left 和 right,分别指向首尾的位置。当选取了首堆时,则 left 自增1,若选了尾堆时,则 right 自减1。这样就不用执行删除操作,或是拷贝数组了,大大的提高了运行效率,参见代码如下:
1 | class Solution { |
这道题也可以使用动态规划 Dynamic Programming 来做,由于玩家获胜的规则是拿到的石子数多,那么多的石子数就可以量化为 dp 值。所以我们用一个二维数组,其中dp[i][j]表示在区间[i, j]内 Alex 比 Lee 多拿的石子数,若为正数,说明 Alex 拿得多,若为负数,则表示 Lee 拿得多。则最终只要看dp[0][n-1]的值,若为正数,则 Alex 能获胜。现在就要找状态转移方程了,我们想,在区间[i, j]内要计算 Alex 比 Lee 多拿的石子数,在这个区间内,Alex 只能拿i或者j位置上的石子,那么当 Alex 拿了piles[i]的话,等于 Alex 多了piles[i]个石子,此时区间缩小成了[i+1, j],此时应该 Lee 拿了,此时根据我们以往的 DP 经验,应该调用子区间的 dp 值,没错,但这里dp[i+1][j]表示是在区间[i+1, j]内 Alex 多拿的石子数,但是若区间[i+1, j]内 Lee 先拿的话,其多拿的石子数也应该是dp[i+1][j],因为两个人都要最优化拿,那么dp[i][j]的值其实可以被piles[i] - dp[i+1][j]更新,因为 Alex 拿了piles[i],减去 Lee 多出的dp[i+1][j],就是区间[i, j]中 Alex 多拿的石子数。同理,假如 Alex 先拿piles[j],那么就用piles[j] - dp[i][j-1]来更新dp[i][j],则我们用二者的较大值来更新即可。注意开始的时候要把dp[i][i]都初始化为piles[i],还需要注意的是,这里的更新顺序很重要,是从小区间开始更新1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
bool stoneGame(vector<int>& piles) {
int n = piles.size();
vector<vector<int>> dp(n, vector<int>(n));
for (int i = 0; i < n; ++i) dp[i][i] = piles[i];
for (int len = 1; len < n; ++len) {
for (int i = 0; i < n - len; ++i) {
int j = i + len;
dp[i][j] = max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
}
}
return dp[0][n - 1] > 0;
}
};
其实这道题是一道脑筋急转弯题,跟之前那道 Nim Game 有些像。原因就在于题目中的一个条件,那就是总共有偶数堆,那么就是可以分为堆数相等的两堆,比如我们按奇偶分为两堆。题目还说了石子总数为奇数个,那么分出的这两堆的石子总数一定是不相等的,那么我们只要每次一直取石子总数多的奇数堆或者偶数堆,Alex 就一定可以躺赢,所以最叼的方法就是直接返回 true。
1 | class Solution { |
Leetcode881. Boats to Save People
You are given an array people where people[i] is the weight of the ith person, and an infinite number of boats where each boat can carry a maximum weight of limit. Each boat carries at most two people at the same time, provided the sum of the weight of those people is at most limit.
Return the minimum number of boats to carry every given person.
Example 1:1
2
3Input: people = [1,2], limit = 3
Output: 1
Explanation: 1 boat (1, 2)
Example 2:1
2
3Input: people = [3,2,2,1], limit = 3
Output: 3
Explanation: 3 boats (1, 2), (2) and (3)
Example 3:1
2
3Input: people = [3,5,3,4], limit = 5
Output: 4
Explanation: 4 boats (3), (3), (4), (5)
这道题让我们载人过河,说是每个人的体重不同,每条船承重有个限度 limit(限定了这个载重大于等于最重人的体重),同时要求每条船不能超过两人,问我们将所有人载到对岸最少需要多少条船。从题目中的例子2可以看出,最肥的人有可能一人占一条船,当然如果船的载量够大的话,可能还能挤上一个瘦子,那么最瘦的人是最可能挤上去的,所以策略就是胖子加瘦子的上船组合。那么这就是典型的贪婪算法的适用场景啊,首先要给所有人按体重排个序,从瘦子到胖子,这样我们才能快速的知道当前最重和最轻的人。然后使用双指针,left 指向最瘦的人,right 指向最胖的人,当 left 小于等于 right 的时候,进行 while 循环。在循环中,胖子是一定要上船的,所以 right 自减1是肯定有的,但是还是要看能否再带上一个瘦子,能的话 left 自增1。然后结果 res 一定要自增1,因为每次都要用一条船,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int numRescueBoats(vector<int>& people, int limit) {
int n = people.size(), res = 0;
int left = 0, right = n-1;
sort(people.begin(), people.end());
while(left <= right) {
if (people[left] + people[right] > limit)
right --;
else {
right --;
left ++;
}
res ++;
}
return res;
}
};
Leetcode883. Projection Area of 3D Shapes
On a N N grid, we place some 1 1 * 1 cubes that are axis-aligned with the x, y, and z axes. Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j). Now we view the projection of these cubes onto the xy, yz, and zx planes. A projection is like a shadow, that maps our 3 dimensional figure to a 2 dimensional plane.
Here, we are viewing the “shadow” when looking at the cubes from the top, the front, and the side. Return the total area of all three projections.
Example 1:1
2Input: [[2]]
Output: 5
Example 2: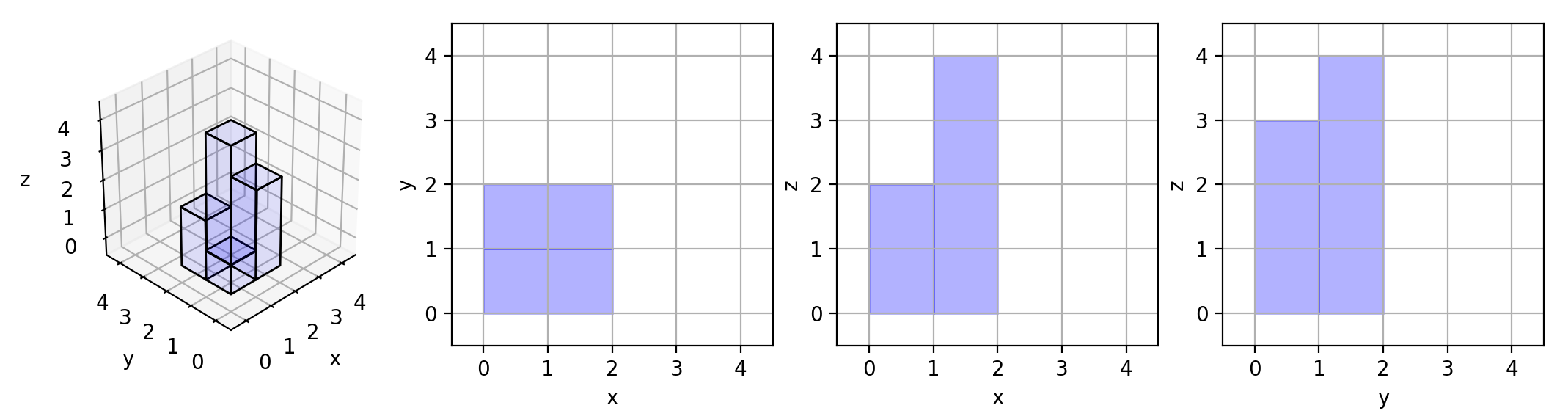
1
2
3
4Input: [[1,2],[3,4]]
Output: 17
Explanation:
Here are the three projections ("shadows") of the shape made with each axis-aligned plane.
Example 3:1
2Input: [[1,0],[0,2]]
Output: 8
Example 4:1
2Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 14
Example 5:1
2Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 21
Note:
- 1 <= grid.length = grid[0].length <= 50
- 0 <= grid[i][j] <= 50
投影题,之前做过类似的,从上往下看的数量是不为零的格子数,从左往右看和从右往左看是每行(或列)最高的,求和。
1 | class Solution { |
1 | class Solution { |
Leetcode884. Uncommon Words from Two Sentences
We are given two sentences A and B. (A sentence is a string of space separated words. Each word consists only of lowercase letters.)
A word is uncommon if it appears exactly once in one of the sentences, and does not appear in the other sentence.
Return a list of all uncommon words.
You may return the list in any order.
Example 1:1
2Input: A = "this apple is sweet", B = "this apple is sour"
Output: ["sweet","sour"]
Example 2:1
2Input: A = "apple apple", B = "banana"
Output: ["banana"]
Note:
- 0 <= A.length <= 200
- 0 <= B.length <= 200
- A and B both contain only spaces and lowercase letters.
把单词合并然后找到只出现过一次的就好。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
vector<string> uncommonFromSentences(string A, string B) {
vector<string> result;
map<string, int> mapp;
string temp;
for(int i = 0; i < A.length(); i ++) {
temp = "";
while(i < A.length() && A[i] != ' ')
temp += A[i++];
cout<<temp<<endl;
if(mapp.find(temp) == mapp.end())
mapp[temp] = 1;
else
mapp[temp] ++;
}
for(int i = 0; i < B.length(); i ++) {
temp = "";
while(i < B.length() && B[i] != ' ')
temp += B[i++];
cout<<temp<<endl;
if(mapp.find(temp) == mapp.end())
mapp[temp] = 1;
else
mapp[temp] ++;
}
for(auto iter = mapp.begin(); iter != mapp.end(); iter ++) {
if(iter->second == 1)
result.push_back(iter->first);
}
return result;
}
};
简洁做法:1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
vector<string> uncommonFromSentences(string A, string B) {
unordered_map<string, int> count;
istringstream iss(A + " " + B);
while (iss >> A) count[A]++;
vector<string> res;
for (auto w: count)
if (w.second == 1)
res.push_back(w.first);
return res;
}
};
Leetcode885. Spiral Matrix III
On a 2 dimensional grid with R rows and C columns, we start at (r0, c0) facing east. Here, the north-west corner of the grid is at the first row and column, and the south-east corner of the grid is at the last row and column. Now, we walk in a clockwise spiral shape to visit every position in this grid.
Whenever we would move outside the boundary of the grid, we continue our walk outside the grid (but may return to the grid boundary later.) Eventually, we reach all R * C spaces of the grid. Return a list of coordinates representing the positions of the grid in the order they were visited.
Example 1:1
2Input: R = 1, C = 4, r0 = 0, c0 = 0
Output: [[0,0],[0,1],[0,2],[0,3]]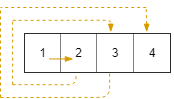
Example 2:1
2Input: R = 5, C = 6, r0 = 1, c0 = 4
Output: [[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]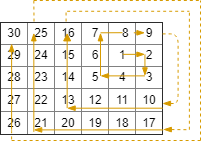
给定起点(r0,c0),螺旋走路,输出经过的点坐标,简单,只是注意细节。按照顺序,先向右走,再向下走,再向左走,再向上走,经观察发现每个方向的步数依次为1,1,2,2,3,3,…,依次类推,按照步骤走即可,发现不在网格内就跳过。
1 | class Solution { |
一个大佬给了三种做法:
这道题给了我们一个二维矩阵,还给了其中一个位置,让从这个位置开始螺旋打印矩阵。首先是打印给定的位置,然后向右走一位,打印出来,再向下方走一位打印,再向左边走两位打印,再向上方走三位打印,以此类推,螺旋打印。那仔细观察,可以发现,刚开始只是走一步,后来步子越来越大,若只看每个方向走的距离,可以得到如下数组 1,1,2,2,3,3…
步长有了,下面就是方向了,由于确定了起始是向右走,那么方向就是 右->下->左->上 这样的循环。方向和步长都分析清楚了,现在就可以尝试进行遍历了。由于最终是会遍历完所有的位置的,那么最后结果 res 里面的位置个数一定是等于 RxC 的,所以循环的条件就是当结果 res 中的位置数小于R*C。我们还需要一个变量 step 表示当前的步长,初始化为1。
在循环中,首先要向右走 step 步,一步一步走,走到一个新的位置上,要进行判断,若当前位置没有越界,才能加入结果 res 中,由于每次都要判断,所以把这部分抽取出来,放到一个子函数中。由于是向右走,每走一步之后,c0 都要自增1。右边走完了之后,再向下方走 step 步,同理,每走一步之后,要将 r0 自增1。再向左边走之前,要将步数增1,不然无法形成正确的螺旋,同理,再完成向上方走 step 步之后,step 要再增1,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
vector<vector<int>> res;
int step = 1;
while (res.size() < R * C) {
for (int i = 0; i < step; ++i) add(R, C, r0, c0++, res);
for (int i = 0; i < step; ++i) add(R, C, r0++, c0, res);
++step;
for (int i = 0; i < step; ++i) add(R, C, r0, c0--, res);
for (int i = 0; i < step; ++i) add(R, C, r0--, c0, res);
++step;
}
return res;
}
void add(int R, int C, int x, int y, vector<vector<int>>& res) {
if (x >= 0 && x < R && y >= 0 && y < C) res.push_back({x, y});
}
};
可以用两个数组 dirX 和 dirY 来控制下一个方向,就像迷宫遍历中的那样,这样只需要一个变量 cur,来分别到 dirX 和 dirY 中取值,初始化为0,表示向右的方向。从螺旋遍历的机制可以看出,每当向右或者向左前进时,步长就要加1,那么我们只要判断当 cur 为0或者2的时候,step 就自增1。由于 cur 初始化为0,所以刚开始 step 就会增1,那么就可以将 step 初始化为0,同时还需要把起始位置提前加入结果 res 中。此时在 while 循环中只需要一个 for 循环即可,朝当前的 cur 方向前进 step 步,r0 加上 dirX[cur],c0 加上 dirY[cur],若没有越界,则加入结果 res 中即可。之后记得 cur 要自增1,为了防止越界,对4取余,就像循环数组一样的操作,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
vector<vector<int>> res{{r0, c0}};
vector<int> dirX{0, 1, 0, -1}, dirY{1, 0, -1, 0};
int step = 0, cur = 0;
while (res.size() < R * C) {
if (cur == 0 || cur == 2) ++step;
for (int i = 0; i < step; ++i) {
r0 += dirX[cur]; c0 += dirY[cur];
if (r0 >= 0 && r0 < R && c0 >= 0 && c0 < C) res.push_back({r0, c0});
}
cur = (cur + 1) % 4;
}
return res;
}
};
我们也可以不使用方向数组,若仔细观察 右->下->左->上 四个方向对应的值 (0, 1) -> (1, 0) -> (0, -1) -> (-1, 0), 实际上,下一个位置的x值是当前的y值,下一个位置的y值是当前的-x值,因为两个方向是相邻的两个方向是垂直的,由向量的叉乘得到 (x, y, 0) × (0, 0, 1) = (y, -x, 0)。所以可以通过当前的x和y值,来计算出下一个位置的值。同理,根据之前的说的步长数组 1,1,2,2,3,3…,可以推出通项公式为 n/2 + 1,这样连步长变量 step 都省了,不过需要统计当前已经遍历的位置的个数,实在想偷懒,也可以用 res.size() 来代替,参见代码如下:
解法三:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
vector<vector<int>> res{{r0, c0}};
int x = 0, y = 1, t = 0;
for (int k = 0; res.size() < R * C; ++k) {
for (int i = 0; i < k / 2 + 1; ++i) {
r0 += x; c0 += y;
if (r0 >= 0 && r0 < R && c0 >= 0 && c0 < C) res.push_back({r0, c0});
}
t = x; x = y; y = -t;
}
return res;
}
};
LeetCode886. Possible Bipartition
Given a set of N people (numbered 1, 2, …, N), we would like to split everyone into two groups of any size.
Each person may dislike some other people, and they should not go into the same group.
Formally, if dislikes[i] = [a, b], it means it is not allowed to put the people numbered a and b into the same group.
Return true if and only if it is possible to split everyone into two groups in this way.
Example 1:1
2
3Input: N = 4, dislikes = [[1,2],[1,3],[2,4]]
Output: true
Explanation: group1 [1,4], group2 [2,3]
Example 2:1
2Input: N = 3, dislikes = [[1,2],[1,3],[2,3]]
Output: false
Example 3:1
2Input: N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
Output: false
Note:
- 1 <= N <= 2000
- 0 <= dislikes.length <= 10000
- 1 <= dislikes[i][j] <= N
- dislikes[i][0] < dislikes[i][1]
- There does not exist i != j for which dislikes[i] == dislikes[j].
这道题又是关于二分图的题,第一次接触的时候是 Is Graph Bipartite?,那道题给的是建好的邻接链表(虽然是用数组实现的),但是本质上和这道题是一样的,同一条边上的两点是不能在同一个集合中的,那么这就相当于本题中的 dislike 的关系,也可以把每个 dislike 看作是一条边,那么两端的两个人不能在同一个集合中。看透了题目的本质后,就不难做了,跟之前的题相比,这里唯一不同的就是邻接链表没有给我们建好,需要自己去建。不管是建邻接链表,还是邻接矩阵都行,反正是要先把图建起来才能遍历。那么这里我们先建立一个邻接矩阵好了,建一个大小为 (N+1) x (N+1) 的二维数组g,其中若 g[i][j] 为1,说明i和j互相不鸟。那么先根据 dislikes 的情况,把二维数组先赋上值,注意这里 g[i][j] 和 g[j][i] 都要更新,因为是互相不鸟,而并不是某一方热脸贴冷屁股。下面就要开始遍历了,还是使用染色法,使用一个一维的 colors 数组,大小为 N+1,初始化是0,由于只有两组,可以用1和 -1 来区分。那么开始遍历图中的结点,对于每个遍历到的结点,如果其还未被染色,还是一张白纸的时候,调用递归函数对其用颜色1进行尝试染色。在递归函数中,现将该结点染色,然后就要遍历所有跟其合不来的人,这里就发现邻接矩阵的好处了吧,不然每次还得遍历 dislikes 数组。由于这里是邻接矩阵,所以只有在其值为1的时候才处理,当找到一个跟其合不来的人,首先检测其染色情况,如果此时两个人颜色相同了,说明已经在一个组里了,这就矛盾了,直接返回 false。如果那个人还是白纸一张,我们尝试用相反的颜色去染他,如果无法成功染色,则返回 false。循环顺序退出后,返回 true,参见代码如下:
1 | class Solution { |
Leetcode888. Fair Candy Swap
Alice and Bob have candy bars of different sizes: A[i] is the size of the i-th bar of candy that Alice has, and B[j] is the size of the j-th bar of candy that Bob has.
Since they are friends, they would like to exchange one candy bar each so that after the exchange, they both have the same total amount of candy. (The total amount of candy a person has is the sum of the sizes of candy bars they have.)
Return an integer array ans where ans[0] is the size of the candy bar that Alice must exchange, and ans[1] is the size of the candy bar that Bob must exchange.
If there are multiple answers, you may return any one of them. It is guaranteed an answer exists.
Example 1:1
2Input: A = [1,1], B = [2,2]
Output: [1,2]
Example 2:1
2Input: A = [1,2], B = [2,3]
Output: [1,2]
Example 3:1
2Input: A = [2], B = [1,3]
Output: [2,3]
Example 4:1
2Input: A = [1,2,5], B = [2,4]
Output: [5,4]
Note:
- 1 <= A.length <= 10000
- 1 <= B.length <= 10000
- 1 <= A[i] <= 100000
- 1 <= B[i] <= 100000
- It is guaranteed that Alice and Bob have different total amounts of candy.
- It is guaranteed there exists an answer.
考虑到最终两个人的糖果总量相等,那么可以计算出最终这个相等的总量是多少。
比如1中的例子,A的总量是8,B的总量是6,那么平均下来每个人应该是7。
那么接下来就要在A中找到一个元素比B中某个元素大1的,逐个对比,可以发现交换5和4就可以达成目标。
其中逐个对比这个部分,难道我们要做一个双重循环吗?也没有必要。
我们先做一个升序排序,接着就是两个指针在A中和B中不断地移动就可以了。
1 | vector<int> fairCandySwap(vector<int>& A, vector<int>& B) |
Leetcode889. Construct Binary Tree from Preorder and Postorder Traversal
Return any binary tree that matches the given preorder and postorder traversals.
Values in the traversals pre and post are distinct positive integers.
Example 1:1
2Input: pre = [1,2,4,5,3,6,7], post = [4,5,2,6,7,3,1]
Output: [1,2,3,4,5,6,7]
Note:
- 1 <= pre.length == post.length <= 30
- pre[] and post[] are both permutations of 1, 2, …, pre.length.
- It is guaranteed an answer exists. If there exists multiple answers, you can return any of them.
这道题给了一棵树的先序遍历和后序遍历的数组,让我们根据这两个数组来重建出原来的二叉树。之前也做过二叉树的先序遍历 Binary Tree Preorder Traversal 和 后序遍历 Binary Tree Postorder Traversal,所以应该对其遍历的顺序并不陌生。其实二叉树最常用的三种遍历方式,先序,中序,和后序遍历,只要知道其中的任意两种遍历得到的数组,就可以重建出原始的二叉树,而且正好都在 LeetCode 中有出现,其他两道分别是 Construct Binary Tree from Inorder and Postorder Traversal 和 Construct Binary Tree from Preorder and Inorder Traversal。如果做过之前两道题,那么这道题就没有什么难度了,若没有的话,可能还是有些 tricky 的,虽然这仅仅只是一道 Medium 的题。
我们知道,先序遍历的顺序是 根->左->右,而后序遍历的顺序是 左->右->根,既然要建立树,那么肯定要从根结点开始创建,然后再创建左右子结点,若你做过很多树相关的题目的话,就会知道大多数都是用递归才做,那么创建的时候也是对左右子结点调用递归来创建。心中有这么个概念就好,可以继续来找这个重复的 pattern。由于先序和后序各自的特点,根结点的位置是固定的,既是先序遍历数组的第一个,又是后序遍历数组的最后一个,而如果给我们的是中序遍历的数组,那么根结点的位置就只能从另一个先序或者后序的数组中来找了,但中序也有中序的好处,其根结点正好分割了左右子树,就不在这里细讲了,还是回到本题吧。知道了根结点的位置后,我们需要分隔左右子树的区间,先序和后序的各个区间表示如下:
- preorder -> [root] [left subtree] [right subtree]
- postorder -> [left subtree] [right substree] [root]
具体到题目中的例子就是:
- preorder -> [1] [2,4,5] [3,6,7]
- postorder -> [4,5,2] [6,7,3] [root]
先序和后序中各自的左子树区间的长度肯定是相等的,但是其数字顺序可能是不同的,但是我们仔细观察的话,可以发现先序左子树区间的第一个数字2,在后序左右子树区间的最后一个位置,而且这个规律对右子树区间同样适用,这是为啥呢,这就要回到各自遍历的顺序了,先序遍历的顺序是 根->左->右,而后序遍历的顺序是 左->右->根,其实这个2就是左子树的根结点,当然会一个在开头,一个在末尾了。发现了这个规律,就可以根据其来定位左右子树区间的位置范围了。既然要拆分数组,那么就有两种方式,一种是真的拆分成小的子数组,另一种是用双指针来指向子区间的开头和末尾。前一种方法无疑会有大量的数组拷贝,不是很高效,所以我们这里采用第二种方法来做。用 preL 和 preR 分别表示左子树区间的开头和结尾位置,postL 和 postR 表示右子树区间的开头和结尾位置,那么若 preL 大于 preR 或者 postL 大于 postR 的时候,说明已经不存在子树区间,直接返回空指针。然后要先新建当前树的根结点,就通过 pre[preL] 取到即可,接下来要找左子树的根结点在 post 中的位置,最简单的方法就是遍历 post 中的区间 [postL, postR],找到其位置 idx,然后根据这个 idx,就可以算出左子树区间长度为 len = (idx-postL)+1,那么 pre 数组中左子树区间为 [preL+1, preL+len],右子树区间为 [preL+1+len, preR],同理,post 数组中左子树区间为 [postL, idx],右子树区间为 [idx+1, postR-1]。知道了这些信息,就可以分别调用递归函数了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
TreeNode* constructFromPrePost(vector<int>& pre, vector<int>& post) {
return helper(pre, 0, (int)pre.size() - 1, post, 0, (int)post.size() - 1);
}
TreeNode* helper(vector<int>& pre, int preL, int preR, vector<int>& post, int postL, int postR) {
if (preL > preR || postL > postR) return nullptr;
TreeNode *node = new TreeNode(pre[preL]);
if (preL == preR) return node;
int idx = -1;
for (idx = postL; idx <= postR; ++idx) {
if (pre[preL + 1] == post[idx]) break;
}
node->left = helper(pre, preL + 1, preL + 1 + (idx - postL), post, postL, idx);
node->right = helper(pre, preL + 1 + (idx - postL) + 1, preR, post, idx + 1, postR - 1);
return node;
}
};
Leetcode890. Find and Replace Pattern
You have a list of words and a pattern, and you want to know which words in words matches the pattern.
A word matches the pattern if there exists a permutation of letters p so that after replacing every letter x in the pattern with p(x), we get the desired word.
(Recall that a permutation of letters is a bijection from letters to letters: every letter maps to another letter, and no two letters map to the same letter.)
Return a list of the words in words that match the given pattern.
You may return the answer in any order.
Example 1:1
2
3
4
5Input: words = ["abc","deq","mee","aqq","dkd","ccc"], pattern = "abb"
Output: ["mee","aqq"]
Explanation: "mee" matches the pattern because there is a permutation {a -> m, b -> e, ...}.
"ccc" does not match the pattern because {a -> c, b -> c, ...} is not a permutation,
since a and b map to the same letter.
Note:
- 1 <= words.length <= 50
- 1 <= pattern.length = words[i].length <= 20
1 | class Solution { |
这个题判断给定的字符串是不是符合pattern串的模式,很简单的题搞复杂了。用了一个map来匹配字符组合,用seen判断这个pattern字符是否出现过,如果出现过就是非法的了。
Leetcode892. Surface Area of 3D Shapes
On a N N grid, we place some 1 1 * 1 cubes.
Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j).
Return the total surface area of the resulting shapes.
Example 1:1
2Input: [[2]]
Output: 10
Example 2:1
2Input: [[1,2],[3,4]]
Output: 34
Example 3:1
2Input: [[1,0],[0,2]]
Output: 16
Example 4:1
2Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 32
Example 5:1
2Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 46
Note:
- 1 <= N <= 50
- 0 <= grid[i][j] <= 50
这道题给了我们一个二维数组 grid,其中 grid[i][j] 表示在位置 (i,j) 上累计的小正方体的个数,实际上就像搭积木一样,由这些小正方体来组成一个三维的物体,这里让我们求这个三维物体的表面积。我们知道每个小正方体的表面积是6,若在同一个位置累加两个,表面积就是10,三个累加到了一起就是14,其实是有规律的,n个小正方体累在一起,表面积是 4n+2。
现在不仅仅是累加在一个小正方体上,而是在 nxn 的区间,累加出一个三维物体。当中间的小方块缺失了之后,实际上缺失的地方会产生出四个新的面,而这四个面是应该算在表面积里的,但是用投影的方法是没法算进去的。无奈只能另辟蹊径,实际上这道题正确的思路是一个位置一个位置的累加表面积,就类似微积分的感觉,前面提到了当n个小正方体累到一起的表面积是 4n+2,而这个n就是每个位置的值 grid[i][j],当你在旁边紧挨着再放一个累加的物体时,二者就会产生重叠,重叠的面数就是二者较矮的那堆正方体的个数再乘以2。
明白了这一点,我们就可以从 (0,0) 位置开始累加,先根据 grid[0][0] 的值算出若仅有该位置的三维物体的表面积,然后向 (0,1) 位置遍历,同样要先根据 grid[0][1] 的值算出若仅有该位置的三维物体的表面积,跟之前 grid[0][0] 的累加,然后再减去遮挡住的面积,通过 min(grid[0][0],grid[0][1])x2 来得到,这样每次可以计算出水平方向的遮挡面积,同时还需要减去竖直方向的遮挡面积 min(grid[i][j],grid[i-1][j])x2,这样才能算出正确的表面积.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int surfaceArea(vector<vector<int>>& grid) {
int n =grid.size(), res = 0;
for(int i = 0 ; i < n; i ++)
for(int j = 0; j < n; j ++) {
if(grid[i][j] > 0) {
res += 4 * grid[i][j] + 2;
if(i > 0) res -= min(grid[i][j], grid[i-1][j]) * 2;
if(j > 0) res -= min(grid[i][j], grid[i][j-1]) * 2;
}
}
return res;
}
};
Leetcode893. Groups of Special-Equivalent Strings
You are given an array A of strings.
A move onto S consists of swapping any two even indexed characters of S, or any two odd indexed characters of S.
Two strings S and T are special-equivalent if after any number of moves onto S, S == T.
For example, S = “zzxy” and T = “xyzz” are special-equivalent because we may make the moves “zzxy” -> “xzzy” -> “xyzz” that swap S[0] and S[2], then S[1] and S[3].
Now, a group of special-equivalent strings from A is a non-empty subset of A such that:
Every pair of strings in the group are special equivalent, and;
The group is the largest size possible (ie., there isn’t a string S not in the group such that S is special equivalent to every string in the group)
Return the number of groups of special-equivalent strings from A.
Example 1:1
2
3
4
5
6Input: ["abcd","cdab","cbad","xyzz","zzxy","zzyx"]
Output: 3
Explanation:
One group is ["abcd", "cdab", "cbad"], since they are all pairwise special equivalent, and none of the other strings are all pairwise special equivalent to these.
The other two groups are ["xyzz", "zzxy"] and ["zzyx"]. Note that in particular, "zzxy" is not special equivalent to "zzyx".
Example 2:1
2Input: ["abc","acb","bac","bca","cab","cba"]
Output: 3
对于一个字符串,假如其偶数位字符之间可以互相交换,且其奇数位字符之间可以互相交换,交换后若能跟另一个字符串相等,则这两个字符串是特殊相等的关系。现在给了我们一个字符串数组,将所有特殊相等的字符串放到一个群组中,问最终能有几个不同的群组。最开始的时候博主没仔细审题,以为是随意交换字母,就直接对每个单词进行排序,然后扔到一个 HashSet 中就行了。后来发现只能是奇偶位上互相交换,于是只能现先将奇偶位上的字母分别抽离出来,然后再进行分别排序,之后再合并起来组成一个新的字符串,再丢到 HashSet 中即可,利用 HashSet 的自动去重复功能,这样最终留下来的就是不同的群组了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int numSpecialEquivGroups(vector<string>& A) {
unordered_set<string> st;
for (string word : A) {
string even, odd;
for (int i = 0; i < word.size(); ++i)
if (i % 2 == 0) even += word[i];
else odd += word[i];
sort(even.begin(), even.end());
sort(odd.begin(), odd.end());
st.insert(even + odd);
}
return st.size();
}
};
Leetcode894. All Possible Full Binary Trees
A full binary tree is a binary tree where each node has exactly 0 or 2 children.
Return a list of all possible full binary trees with N nodes. Each element of the answer is the root node of one possible tree.
Each node of each tree in the answer must have node.val = 0.
You may return the final list of trees in any order.
Example 1:1
2Input: 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
Explanation: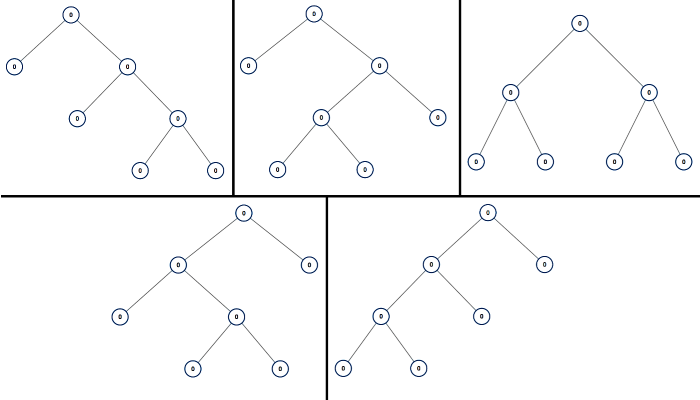
给出了个N,代表一棵二叉树有N个节点,求所能构成的树。
解题方法
所有能构成的树,并且返回的不是数目,而是真正的树。所以一定会把所有的节点都求出来。一般就使用了递归。
这个题中,重点是返回一个列表,也就是说每个能够成的树的根节点都要放到这个列表里。而且当左子树、右子树的节点个数固定的时候,也会出现排列组合的情况,所以使用了两重for循环来完成所有的左右子树的组合。
另外的一个技巧就是,左右子树的个数一定是奇数个。
递归方法,虽然比较慢,但是容易理解,就是组成小的子树,一个个拼接,为啥要减1,是因为一定会有个根节点,先把这个减去再说。
代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
vector<TreeNode*> allPossibleFBT(int N) {
N--;
vector<TreeNode*> res;
if(N==0){
res.push_back(new TreeNode(0));
return res;
}
for (int i = 1; i < N; i += 2) {
for (auto& left : allPossibleFBT(i)) {
for (auto& right : allPossibleFBT(N - i)) {
TreeNode* root = new TreeNode(0);
root->left = left;
root->right = right;
res.push_back(root);
}
}
}
return res;
}
};
Leetcode896. Monotonic Array
An array is monotonic if it is either monotone increasing or monotone decreasing.
An array A is monotone increasing if for all i <= j, A[i] <= A[j]. An array A is monotone decreasing if for all i <= j, A[i] >= A[j].
Return true if and only if the given array A is monotonic.
判断数组是否单调。1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
bool isMonotonic(vector<int>& A) {
bool inc=true, dec=true;
for(int i = 0; i < A.size()-1; i ++) {
if(A[i] > A[i+1]) inc = false;
if(A[i] < A[i+1]) dec = false;
}
return inc || dec;
}
};
Leetcode897. Increasing Order Search Tree
Given a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only 1 right child.
Example 1:
Input: [5,3,6,2,4,null,8,1,null,null,null,7,9]1
2
3
4
5
6
7 5
/ \
3 6
/ \ \
2 4 8
/ / \
1 7 9
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
171
\
2
\
3
\
4
\
5
\
6
\
7
\
8
\
9
Note:
The number of nodes in the given tree will be between 1 and 100.
Each node will have a unique integer value from 0 to 1000.
本题要求把二叉树的结点重新排列,使其成为从小到大只有右孩子的二叉树。考虑使用中序遍历的迭代方法,对每个结点入栈,出栈时先访问左结点,然后中结点,最后把右指针和下一个入栈的结点链接起来。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
TreeNode* increasingBST(TreeNode* root) {
if(root==NULL)
return NULL;
if(!root->left && !root->right)
return root;
stack<TreeNode*> dst;
TreeNode *head = new TreeNode(0), *pre = head;
while(root || !dst.empty()){
while(root){
dst.push(root);
root = root->left;
}
root = dst.top();
dst.pop();
pre->right=root;
pre = pre -> right;
root -> left = NULL;
root=root->right;
}
return head->right;
}
};
然后朴素的中序遍历是这样1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
TreeNode *s=NULL,*p=NULL;
void inorder(TreeNode* root){
if(root){
inorder(root->left);
if(s == NULL) {
s = new TreeNode(root->val);
p = s;
}
else{
TreeNode* temp = new TreeNode(root->val);
s->right = temp;
s = s->right;
}
inorder(root->right);
}
}
TreeNode* increasingBST(TreeNode* root) {
if(root==NULL)
return NULL;
inorder(root);
return p;
}
};
Leetcode900. RLE Iterator
Write an iterator that iterates through a run-length encoded sequence.
The iterator is initialized by RLEIterator(int[] A), where A is a run-length encoding of some sequence. More specifically, for all even i, A[i] tells us the number of times that the non-negative integer value A[i+1] is repeated in the sequence.
The iterator supports one function: next(int n), which exhausts the next n elements (n >= 1) and returns the last element exhausted in this way. If there is no element left to exhaust, next returns -1instead.
For example, we start with A = [3,8,0,9,2,5], which is a run-length encoding of the sequence [8,8,8,5,5]. This is because the sequence can be read as “three eights, zero nines, two fives”.
Example 1:1
2
3
4
5
6
7
8
9
10
11Input: ["RLEIterator","next","next","next","next"], [[[3,8,0,9,2,5]],[2],[1],[1],[2]]
Output: [null,8,8,5,-1]
Explanation:
RLEIterator is initialized with RLEIterator([3,8,0,9,2,5]).
This maps to the sequence [8,8,8,5,5].
RLEIterator.next is then called 4 times:
.next(2) exhausts 2 terms of the sequence, returning 8. The remaining sequence is now [8, 5, 5].
.next(1) exhausts 1 term of the sequence, returning 8. The remaining sequence is now [5, 5].
.next(1) exhausts 1 term of the sequence, returning 5. The remaining sequence is now [5].
.next(2) exhausts 2 terms, returning -1. This is because the first term exhausted was 5, but the second term did not exist. Since the last term exhausted does not exist, we return -1.
Note:
- 0 <= A.length <= 1000
- A.length is an even integer.
- 0 <= A[i] <= 10^9
这道题给了我们一种 Run-Length Encoded 的数组,就是每两个数字组成一个数字对儿,前一个数字表示后面的一个数字重复出现的次数。然后有一个 next 函数,让我们返回数组的第n个数字,题目中给的例子也很好的说明了题意。将每个数字对儿抽离出来,放到一个新的数组中。这样我们就只要遍历这个只有数字对儿的数组,当出现次数是0的时候,直接跳过当前数字对儿。若出现次数大于等于n,那么现将次数减去n,然后再返回该数字。否则用n减去次数,并将次数赋值为0,继续遍历下一个数字对儿。若循环退出了,直接返回 -1 即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class RLEIterator {
public:
vector<pair<int, int>> m;
int pointer_en, pointer_m;
RLEIterator(vector<int>& encoding) {
int len = encoding.size();
pointer_en = 0;
pointer_m = 0;
for (int i = 0; i < len; i += 2)
if (encoding[i] > 0)
m.push_back(make_pair(encoding[i], encoding[i+1]));
}
int next(int n) {
int len = m.size();
while(pointer_m < len) {
if (m[pointer_m].first < n) {
n -= m[pointer_m].first;
pointer_m ++;
}
else {
m[pointer_m].first -= n;
break;
}
}
if (pointer_m < len)
return m[pointer_m].second;
else
return -1;
}
};
其实我们根本不用将数字对儿抽离出来,直接用输入数组的形式就可以,再用一个指针 cur,指向当前数字对儿的次数即可。那么在 next 函数中,我们首先来个 while 循环,判读假如 cur 没有越界,且当n大于当前当次数了,则n减去当前次数,cur 自增2,移动到下一个数字对儿的次数上。当 while 循环结束后,判断若此时 cur 已经越界了,则返回 -1,否则当前次数减去n,并且返回当前数字即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class RLEIterator {
public:
RLEIterator(vector& A): nums(A), cur(0) {}
int next(int n) {
while (cur < nums.size() && n > nums[cur]) {
n -= nums[cur];
cur += 2;
}
if (cur >= nums.size()) return -1;
nums[cur] -= n;
return nums[cur + 1];
}
private:
int cur;
vector nums;
};