Leetcode1002. Find Common Characters
Given an array A of strings made only from lowercase letters, return a list of all characters that show up in all strings within the list (including duplicates). For example, if a character occurs 3 times in all strings but not 4 times, you need to include that character three times in the final answer.
You may return the answer in any order.
Example 1:
Input: [“bella”,”label”,”roller”]
Output: [“e”,”l”,”l”]
Example 2:
Input: [“cool”,”lock”,”cook”]
Output: [“c”,”o”]
Note:
- 1 <= A.length <= 100
- 1 <= A[i].length <= 100
A[i][j]is a lowercase letter
这个打表要二维打表,第一次的时候没有注意,用了一维的,所以错了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
vector<string> commonChars(vector<string>& A) {
string s;
int vis[102][27]={0};
vector<string> res;
for(int i=0;i<A.size();i++){
s = A[i];
for(int j=0;j<A[i].length();j++){
vis[i][s[j]-'a']++;
}
}
// 打表,记下来每个string中每个字母出现的次数
for(int i=0;i<26;i++){
int minn=1000;
for(int j=0;j<A.size();j++)
{
if(vis[j][i]<minn)
minn=vis[j][i];
}
//看这个字母在每个string中出现的最少次数,
for(int j=0;j<minn;j++){
string s1;
s1+=char('a'+i);
res.push_back(s1);
}
}
return res;
}
};
Leetcode1003. Check If Word Is Valid After Substitutions
We are given that the string “abc” is valid.
From any valid string V, we may split V into two pieces X and Y such that X + Y (X concatenated with Y) is equal to V. (X or Y may be empty.) Then, X + “abc” + Y is also valid.
If for example S = “abc”, then examples of valid strings are: “abc”, “aabcbc”, “abcabc”, “abcabcababcc”. Examples of invalid strings are: “abccba”, “ab”, “cababc”, “bac”.
Return true if and only if the given string S is valid.
Example 1:1
2
3
4
5Input: "aabcbc"
Output: true
Explanation:
We start with the valid string "abc".
Then we can insert another "abc" between "a" and "bc", resulting in "a" + "abc" + "bc" which is "aabcbc".
Example 2:1
2
3
4
5Input: "abcabcababcc"
Output: true
Explanation:
"abcabcabc" is valid after consecutive insertings of "abc".
Then we can insert "abc" before the last letter, resulting in "abcabcab" + "abc" + "c" which is "abcabcababcc".
Example 3:1
2Input: "abccba"
Output: false
Example 4:1
2Input: "cababc"
Output: false
Note:
- 1 <= S.length <= 20000
- S[i] is ‘a’, ‘b’, or ‘c’
使用 vector 来模拟栈, 当遍历访问到 c 时, 需要判断 stack 中是否已经有 a 和 b 的存在.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool isValid(string s) {
vector<char> v;
v.resize(20000);
int p = 0;
for (char c : s) {
if (c == 'c') {
if (!(p > 0 && v[p-1] == 'b') || !(p > 1 && v[p-2] == 'a'))
return false;
p -= 2;
}
else {
v[p] = c;
p ++;
}
}
return p == 0;
}
};
1 | class Solution { |
Leetcode1004. Max Consecutive Ones III
Given an array A of 0s and 1s, we may change up to K values from 0 to 1.
Return the length of the longest (contiguous) subarray that contains only 1s.
Example 1:1
2
3
4
5Input: A = [1,1,1,0,0,0,1,1,1,1,0], K = 2
Output: 6
Explanation:
[1,1,1,0,0,1,1,1,1,1,1]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
Example 2:1
2
3
4
5Input: A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
Output: 10
Explanation:
[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
Note:
- 1 <= A.length <= 20000
- 0 <= K <= A.length
- A[i] is 0 or 1
一个由0和1组成的数组,最多反转k个元素,问能够形成的最长的1序列是多长。这个是滑动窗口的题。对数组进行遍历,如果遇到0,就先把它反转,统计被反转的0的个数,如果反转了0之后,发现反转多了,就移动窗口(left++),直到反转的0小于等于k个,再计算窗口的大小。
用个变量 cnt 记录当前将0变为1的个数,在遍历数组的时候,若遇到了0,则 cnt 自增1。若此时 cnt 大于K了,说明该缩小窗口了,用个 while 循环,若左边界为0,移除之后,此时 cnt 应该自减1,left 自增1,每次用窗口大小更新结果 res 即可1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int longestOnes(vector<int>& nums, int k) {
int left = 0;
int cnt = 0, res = 0, len = nums.size();
for(int i = 0; i < len; i ++) {
if (nums[i] == 0)
cnt ++;
while(cnt > k) {
if (nums[left] == 0)
cnt --;
left ++;
}
res = max(res, i - left + 1);
}
return res;
}
};
我们也可以写的更简洁一些,不用 while 循环,但是还是用的滑动窗口的思路,其中i表示左边界,j为右边界。在遍历的时候,若遇到0,则K自减1,若K小于0了,且 A[i] 为0,则K自增1,且i自增1,最后返回窗口的大小即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int longestOnes(vector<int>& A, int K) {
int n = A.size(), i = 0, j = 0;
for (; j < n; ++j) {
if (A[j] == 0) --K;
if (K < 0 && A[i++] == 0) ++K;
}
return j - i;
}
};
Leetcode1005. Maximize Sum Of Array After K Negations
Given an array A of integers, we must modify the array in the following way: we choose an i and replace A[i] with -A[i], and we repeat this process K times in total. (We may choose the same index i multiple times.) Return the largest possible sum of the array after modifying it in this way.
Example 1:1
2
3Input: A = [4,2,3], K = 1
Output: 5
Explanation: Choose indices (1,) and A becomes [4,-2,3].
Example 2:1
2
3Input: A = [3,-1,0,2], K = 3
Output: 6
Explanation: Choose indices (1, 2, 2) and A becomes [3,1,0,2].
Example 3:1
2
3Input: A = [2,-3,-1,5,-4], K = 2
Output: 13
Explanation: Choose indices (1, 4) and A becomes [2,3,-1,5,4].
题目的意思是将A中的数进行取反(正变负,负变正)K次,可以重复对一个元素取反,最后求A中元素总和的最大值。取反可以分为两种情况:当A中都是正数的时候,比如{1,2,4,6},如果K是偶数,那么可以不用进行取反操作,因为负负得正;如果K是奇数,则只需要对最小的数取反一次即可。当A中有正数也有负数的时候,比如{-4,-3,-1,2,5},此时对负数元素进行取反操作,直到当前元素大于0或者K次转换已用完,此时针对K中剩余的转换次数,又可以细分为两种情况:
- K中剩余的转换次数为偶数,即A中元素全是正数,依据负负得正,不用再进行额外的转换了。
- K中剩余的转换次数为奇数,即还需要再将某个元素转换一次,而为了元素总和最大,需要比较当前元素(正数)和前一个元素(负数)的绝对值大小,对较小的元素进行取反。
最后使用一个for循环,计算A中所有元素总和。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int largestSumAfterKNegations(vector<int>& A, int K) {
int b = 0, s = 0, length = A.size();
int i = 0, sum = 0;
sort(A.begin(), A.end());
if(A[0] >= 0) {
if(K % 2)
A[0] = -A[0];
}
else {
i = 0;
while(i < length && A[i] < 0 && K --) {
A[i] = -A[i];
i++;
}
if (K > 0 && K%2 != 0) {
abs(A[i]) < abs(A[i-1]) ? A[i] = -A[i] : A[i-1] = -A[i-1];
}
}
for(i = 0; i < length; i ++)
sum += A[i];
return sum;
}
};
Leetcode1006. Clumsy Factorial
Normally, the factorial of a positive integer n is the product of all positive integers less than or equal to n. For example, factorial(10) = 10 9 8 7 6 5 4 3 2 * 1.
We instead make a clumsy factorial: using the integers in decreasing order, we swap out the multiply operations for a fixed rotation of operations: multiply (*), divide (/), add (+) and subtract (-) in this order.
For example, clumsy(10) = 10 9 / 8 + 7 - 6 5 / 4 + 3 - 2 * 1. However, these operations are still applied using the usual order of operations of arithmetic: we do all multiplication and division steps before any addition or subtraction steps, and multiplication and division steps are processed left to right.
Additionally, the division that we use is floor division such that 10 * 9 / 8 equals 11. This guarantees the result is an integer.
Implement the clumsy function as defined above: given an integer N, it returns the clumsy factorial of N.
Example 1:1
2
3Input: 4
Output: 7
Explanation: 7 = 4 * 3 / 2 + 1
Example 2:1
Input: 10 Output: 12 Explanation: 12 = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1
Note:
- 1 <= N <= 10000
- -2^31 <= answer <= 2^31 - 1 (The answer is guaranteed to fit within a 32-bit integer.)
这道题定义了一种笨拙的阶乘,与正常的连续相乘不同的是,这里按顺序使用乘除加减号来计算,这里要保持乘除的优先级,现在给了一个正整数N,让求这种笨拙的阶乘是多少。由于需要保持乘除的优先级,使得问题变的稍微复杂了一些,否则直接按顺序一个个的计算就好。根据题目中的例子2分析,刚开始的乘和除可以直接计算,紧跟其后的加法,也可以直接累加,但是之后的减号,就不能直接计算,而是要先计算后面的乘和除,所以遇到了减号,是需要特殊处理一下的。
把算式进行分割,注意到算符是循环的,除了第一组是+、*、/、+以外,其他的-、*、/、+,所以用一个临时变量来记下当前组的符号即可,剩下的就按照循环来做。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int clumsy(int n) {
int sum = 0, i = n, j = 0;
while(i > 0) {
int tmp = 1;
if (i != n)
tmp = -1;
for (j = 0; j < 4 && i > 0; j ++) {
if (j == 0) tmp *= (i --);
if (j == 1) tmp *= (i --);
if (j == 2) tmp /= (i --);
if (j == 3) tmp += (i --);
}
sum += tmp;
if (i == 0)
break;
}
return sum;
}
};
其他的做法:用个变量j来循环遍历这个数组,从而知道当前该做什么操作。还需要一个变量 cur 来计算乘和除优先级的计算,初始化为N,此时从 N-1 遍历到1,若遇到乘号,则 cur 直接乘以当前数字,若遇到除号,cur 直接除以当前数字,若遇到加号,可以直接把当前数字加到结果 res 中,若遇到减号,此时需要判断一下,因为只有第一个乘和除后的结果是要加到 res 中的,后面的都是要减去的,所以要判断一下若当前数字等于 N-4 的时候,加上 cur,否者都是减去 cur,然后 cur 更新为当前数字,因为减号的优先级小于乘除,不能立马运算。之后j自增1并对4取余,最终返回的时候也需要做个判断,因为有可能数字比较小,减号还没有出来,且此时的最后面的乘除结果还保存在 cur 中,那么是加是减还需要看N的大小,若小于等于4,则加上 cur,反之则减去 cur,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int clumsy(int N) {
int res = 0, cur = N, j = 0;
vector<char> ops{'*', '/', '+', '-'};
for (int i = N - 1; i >= 1; --i) {
if (ops[j] == '*') {
cur *= i;
} else if (ops[j] == '/') {
cur /= i;
} else if (ops[j] == '+') {
res += i;
} else {
res += (i == N - 4) ? cur : -cur;
cur = i;
}
j = (j + 1) % 4;
}
return res + ((N <= 4) ? cur : -cur);
}
};
再来看一种比较简洁的写法,由于每次遇到减号时,优先级会被改变,而前面的乘除加是可以提前计算的,所以可以每次处理四个数字,即首先处理 N, N-1, N-2, N-3 这四个数字,这里希望每次可以得到乘法计算时的第一个数字,可以通过N - i*4得到,这里需要满足i*4 < N,知道了这个数字,然后可以立马算出乘除的结果,只要其大于等于3。然后需要将乘除之后的结果更新到 res 中,还是需要判断一下,若是第一个乘除的结果,需要加上,后面的都是减去。乘除后面跟的是加号,所以要加上 num-3 这个数字,前提是 num 大于3,参见代码如下:
1 | class Solution { |
Leetcode1007. Minimum Domino Rotations For Equal Row
In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)
We may rotate the ith domino, so that tops[i] and bottoms[i] swap values.
Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.
If it cannot be done, return -1.
Example 1: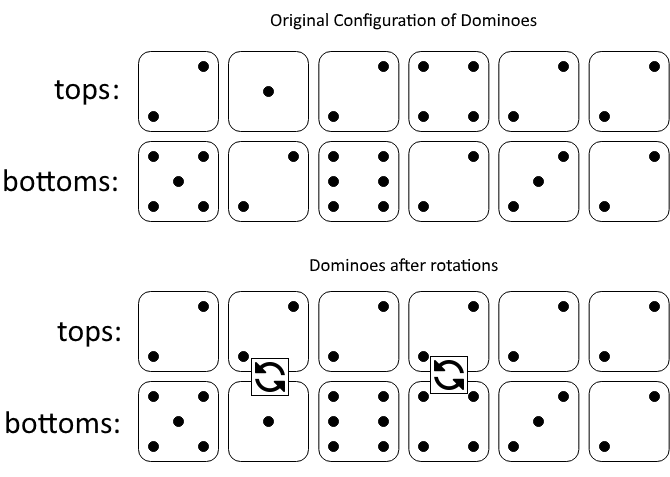
1 | Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2] |
Example 2:1
2
3
4Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
Output: -1
Explanation:
In this case, it is not possible to rotate the dominoes to make one row of values equal.
Constraints:
- 2 <= tops.length <= 2 * 104
- bottoms.length == tops.length
- 1 <= tops[i], bottoms[i] <= 6
这道题说是有长度相等的两个数组A和B,分别表示一排多米诺的上边数字和下边数字,多米诺的个数和数组的长度相同,数字为1到6之间,问最少旋转多少次多米诺,可以使得上边或下边的数字全部相同。例子1中给了图解,很好的帮我们理解题意,实际上出现次数越多的数字越可能就是最终全部相同的数字,所以统计A和B中每个数字出现的次数就变的很重要了,由于A和B中有可能相同位置上的是相同的数字,则不用翻转,要使得同一行变为相同的数字,翻转的地方必须是不同的数字,如何才能知道翻转后可以使同一行完全相同呢?需要某个数字在A中出现的次数加上在B中出现的次数减去A和B中相同位置出现的次数后正好等于数组的长度,这里就需要用三个数组 cntA,cntB,和 same 来分别记录某个数字在A中,B中,A和B相同位置上出现的个数,然后遍历1到6,只要符合上面提到的条件,就可以直接返回数组长度减去该数字在A和B中出现的次数中的较大值。
总结就是:tops中某种大小的个数,加上bottoms中某种大小的个数,减去tops和bottoms里这种大小相同的个数,需要等于总个数,这样才能实现一排相同的。
1 | class Solution { |
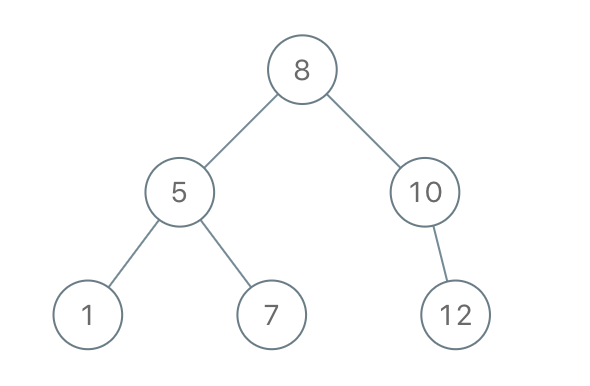
Leetcode1008. Construct Binary Search Tree from Preorder Traversal
Return the root node of a binary search tree that matches the given preorder traversal.
(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)
Example 1:
Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]
1 | class Solution { |
一道简单的中序遍历题竟然做了这么久。。。
Leetcode1009. Complement of Base 10 Integer
Every non-negative integer N has a binary representation. For example, 5 can be represented as “101” in binary, 11 as “1011” in binary, and so on. Note that except for N = 0, there are no leading zeroes in any binary representation.
The complement of a binary representation is the number in binary you get when changing every 1 to a 0 and 0 to a 1. For example, the complement of “101” in binary is “010” in binary.
For a given number N in base-10, return the complement of it’s binary representation as a base-10 integer.
Example 1:1
2
3Input: 5
Output: 2
Explanation: 5 is "101" in binary, with complement "010" in binary, which is 2 in base-10.
Example 2:1
2
3Input: 7
Output: 0
Explanation: 7 is "111" in binary, with complement "000" in binary, which is 0 in base-10.
Example 3:1
2
3Input: 10
Output: 5
Explanation: 10 is "1010" in binary, with complement "0101" in binary, which is 5 in base-10.
将十进制变成二进制然后取反加和1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int bitwiseComplement(int N) {
if(N == 0)
return 1;
if(N == 1)
return 0;
vector<int> re;
while(N) {
re.push_back(N & 1);
N = N >> 1;
}
reverse(re.begin(), re.end());
int res = 0;
for(int i = 0; i < re.size(); i ++) {
res = res * 2 + (~re[i] & 1);
}
return res;
}
};
方法二,利用位运算直接取反。1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int bitwiseComplement(int N) {
int i = 0;
if(!N)
return 1;
while(N > pow(2, i))
i ++;
return (~N) & ((int)pow(2, i) - 1);
}
};
Leetcode1010. Pairs of Songs With Total Durations Divisible by 60
In a list of songs, the i-th song has a duration of time[i] seconds.
Return the number of pairs of songs for which their total duration in seconds is divisible by 60. Formally, we want the number of indices i, j such that i < j with (time[i] + time[j]) % 60 == 0.
Example 1:1
2
3
4
5
6Input: [30,20,150,100,40]
Output: 3
Explanation: Three pairs have a total duration divisible by 60:
(time[0] = 30, time[2] = 150): total duration 180
(time[1] = 20, time[3] = 100): total duration 120
(time[1] = 20, time[4] = 40): total duration 60
Example 2:1
2
3Input: [60,60,60]
Output: 3
Explanation: All three pairs have a total duration of 120, which is divisible by 60.
一开始的思路,是暴力枚举,枚举第一首歌,然后第二首歌是枚举在第一首歌之后的所有情况,判断条件成立就 ans++ 。但这样子的时间复杂度是 O(n^2) 。题目中,数组长度 n<=6e+4,所以时间复杂度是 3.6e+9,这样子会超时。
因此上述暴力枚举的方法行不通。
如果两首歌时间之和要能被60整除,说明余数为0,那么假设第一首歌对60的余数是 a ,那么另一首歌的对60的余数为 60-a 才行。所以我们可以用一个长度为60的数组,下标刚好对应求余后的数,每次找到一个新的歌余数为 a,就看它前面对应余数为 60-a 的有多少首歌,即可以匹配为多少对。最后这首歌的余数对应的下标数组值 ++。
这样解决之后,我们只用遍历一次数组即可,所以时间复杂度是 O(n) ,但是需要了额外的空间开销。1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int numPairsDivisibleBy60(vector<int>& time) {
int length = time.size();
int res = 0;
vector<int> yushu(60, 0);
for(int i = 0; i < length; i ++) {
res += yushu[(60 - time[i]%60)%60];
yushu[ time[i]%60 ] ++;
}
return res;
}
};
Leetcode1011. Capacity To Ship Packages Within D Days
A conveyor belt has packages that must be shipped from one port to another within D days.
The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.
Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within D days.
Example 1:1
2
3
4
5
6
7
8Input: weights = [1,2,3,4,5,6,7,8,9,10], D = 5
Output: 15
Explanation: A ship capacity of 15 is the minimum to ship all the packages in 5 days like this:
1st day: 1, 2, 3, 4, 5
2nd day: 6, 7
3rd day: 8
4th day: 9
5th day: 10
Note that the cargo must be shipped in the order given, so using a ship of capacity 14 and splitting the packages into parts like (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) is not allowed.
Example 2:1
2
3
4
5
6Input: weights = [3,2,2,4,1,4], D = 3
Output: 6
Explanation: A ship capacity of 6 is the minimum to ship all the packages in 3 days like this:
1st day: 3, 2
2nd day: 2, 4
3rd day: 1, 4
Example 3:1
2
3
4
5
6
7Input: weights = [1,2,3,1,1], D = 4
Output: 3
Explanation:
1st day: 1
2nd day: 2
3rd day: 3
4th day: 1, 1
Constraints:
- 1 <= D <= weights.length <= 5 * 104
- 1 <= weights[i] <= 500
这道题说是有一条传送带在运送包裹货物,每个包裹有各自的重量,每天要把若干包裹运送到货轮上,货轮有特定的承载量,要求在给定的D天内将所有货物装上货轮,问船的最小载重量是多少。
首先来分析,由于船的载重量是固定的,而包裹在传送带上又只能按照顺序上传,并不能挑拣,所以一旦加上当前包裹超过了船的载重量,则必须要放弃这个包裹,比较极端的例子就是,假如船的载重量是 50,现在船上已经装了一个重量为1的包裹,而下一个包裹重量是 50,那么这个包裹只能装在下一条船上。知道了这一点后,再来分析一下,船的载重量的范围,先来分析一下最小值,由于所有的包裹都要上船,所以最小的船载重量至少应该是最重的那个包裹,不然上不了船了,而最大的载重量就是包裹的总重量,一条船就能拉走了。所以正确的答案就在这两个边界范围之内,挨个遍历的话实在有些太不高效了。
这里就要祭出二分搜索法了,当算出了中间值 mid 后,利用这个载重量去算需要多少天能运完,然后去和D做比较,如果大于D,说明需要增加载重量,否则减少载重量,最终会终止到正确的结果。具体来看代码,left 初始化为最大的包裹重量,right 初始化为所有的包裹重量总和。然后进行 while 循环,求出 mid,同时使用两个变量 cnt 和 cur,分别用来计算需要的天数,和当前货物的重量,其中 cnt 初始化为1,至少需要一天来运货物。然后遍历所有的包裹重量,每次加到 cur,若此时 cur 大于 mid 了,说明当前包裹不能加了,将 cur 重置为当前包裹重量,为下条船做准备,然后 cnt 自增1。遍历完了之后,判断若 cnt 大于D,则 left 赋值为 mid+1,否则 right 赋值为 mid,最终返回 left 即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
int shipWithinDays(vector<int>& weights, int days) {
int sum = 0, size = weights.size(), max_val = -1, need;
for (int i = 0; i < size; i ++) {
max_val = max(max_val, weights[i]);
sum += weights[i];
}
int left = max_val, right = sum, mid;
while(left < right) {
mid = left + (right - left) / 2;
int cur = 0;
need = 1;
for (int i = 0; i < size; i ++) {
if (cur + weights[i] > mid) {
need ++;
cur = 0;
}
cur += weights[i];
}
if (need > days)
left = mid+1;
else
right = mid;
}
return right;
}
};
Leetcode1013. Partition Array Into Three Parts With Equal Sum
Given an array A of integers, return true if and only if we can partition the array into three non-empty parts with equal sums.
Formally, we can partition the array if we can find indexes i+1 < j with (A[0] + A[1] + … + A[i] == A[i+1] + A[i+2] + … + A[j-1] == A[j] + A[j-1] + … + A[A.length - 1])
Example 1:1
2
3Input: A = [0,2,1,-6,6,-7,9,1,2,0,1]
Output: true
Explanation: 0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
Example 2:1
2Input: A = [0,2,1,-6,6,7,9,-1,2,0,1]
Output: false
Example 3:1
2
3Input: A = [3,3,6,5,-2,2,5,1,-9,4]
Output: true
Explanation: 3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4
1、检查总数是否能被3整除;
2、循环遍历数组A,计算和的一部分;如果找到平均值,则将该部分重置为0,并增加计数器;
3、到最后,如果平均可以看到至少3次,返回true;否则返回假。
注意:如果在数组结束前找到2次平均值(sum / 3),那么剩下的部分也等于平均值。因此,计数器达到3后无需继续。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
bool canThreePartsEqualSum(vector<int>& A) {
int sum = 0, part_sum = 0, i;
for(int i = 0; i < A.size(); i ++)
sum += A[i];
if(sum % 3 != 0)
return false;
sum /= 3;
for(i = 0; i < A.size(); i ++) {
part_sum += A[i];
if(part_sum == sum)
break;
}
for(part_sum = 0, i = i + 1; i < A.size(); i++) {
part_sum += A[i];
if(part_sum == sum)
break;
}
if(i < A.size() - 1)
return true;
return false;
}
};
Leetcode1014. Best Sightseeing Pair
Given an array A of positive integers, A[i] represents the value of the i-th sightseeing spot, and two sightseeing spots i and j have distance j - i between them.
The score of a pair (i < j) of sightseeing spots is (A[i] + A[j] + i - j) : the sum of the values of the sightseeing spots, minus the distance between them.
Return the maximum score of a pair of sightseeing spots.
Example 1:1
2
3Input: [8,1,5,2,6]
Output: 11
Explanation: i = 0, j = 2, A[i] + A[j] + i - j = 8 + 5 + 0 - 2 = 11
Note:
- 2 <= A.length <= 50000
- 1 <= A[i] <= 1000
这道题给了一个正整数的数组A,定义了一种两个数字对儿的记分方式,为A[i] + A[j] + i - j,现在让找出最大的那组的分数。利用加法的分配律,可以得到A[i] + i + A[j] - j,为了使这个表达式最大化,A[i] + i自然是越大越好,这里可以使用一个变量 mx 来记录之前出现过的A[i] + i的最大值,则当前的数字就可以当作数对儿中的另一个数字,其减去当前坐标值再加上 mx 就可以更新结果 res 了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int maxScoreSightseeingPair(vector<int>& values) {
int maxx = INT_MIN, res = INT_MIN;
for (int i = 0; i < values.size(); i ++) {
res = max(res, maxx + values[i] - i);
maxx = max(maxx, values[i] + i);
}
return res;
}
};
Leetcode1015. Smallest Integer Divisible by K
Given a positive integer K, you need to find the length of the smallest positive integer N such that N is divisible by K, and N only contains the digit 1.
Return the length of N. If there is no such N, return -1.
Note: N may not fit in a 64-bit signed integer.
Example 1:1
2
3Input: K = 1
Output: 1
Explanation: The smallest answer is N = 1, which has length 1.
Example 2:1
2
3Input: K = 2
Output: -1
Explanation: There is no such positive integer N divisible by 2.
Example 3:1
2
3Input: K = 3
Output: 3
Explanation: The smallest answer is N = 111, which has length 3.
Constraints:
- 1 <= K <= 105
这道题说是给了一个正整数K,让找到一个长度最短且只由1组成的正整数N,可以整除K,问最短的长度是多少,若没有,则返回 -1。关于整除的一些性质,博主记得小学就应该学过,比如能被2整除的数字必须是偶数,能被3整除的数字各个位加起来必须能被3整除,能被5整除的数字的末尾数字必须是0或者5。由于N都是由1组成的,所以一定不可能整除2或者5,所以只要K中包含2或者5,直接返回 -1。其实有一个定理,若K不能被2或5整除,则一定有一个长度小于等于K且均由1组成的数,可以整除K。这里只要找到那个最短的长度即可。
从1开始检查,每次乘以 10 再加1,就可以得到下一个数字,但是由于K可能很大,则N就会超出整型数的范围,就算是长整型也不一定 hold 的住,所以不能一直变大,而是每次累加后都要对 K 取余,若余数为0,则直接返回当前长度,若不为0,则用余数乘以 10 再加1。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int smallestRepunitDivByK(int k) {
if (k % 2 == 0 || k % 5 == 0)
return -1;
int r = 0;
for (int i = 1; i <= k; i ++) {
r = r * 10 + 1;
if (r % k == 0)
return i;
r = r % k;
}
return -1;
}
};
Leetcode1016. Binary String With Substrings Representing 1 To N
Given a binary string S (a string consisting only of ‘0’ and ‘1’s) and a positive integer N, return true if and only if for every integer X from 1 to N, the binary representation of X is a substring of S.
Example 1:1
2Input: S = "0110", N = 3
Output: true
Example 2:1
2Input: S = "0110", N = 4
Output: false
Note:
- 1 <= S.length <= 1000
- 1 <= N <= 10^9
这道题给了一个二进制的字符串S,和一个正整数N,问从1到N的所有整数的二进制数的字符串是否都是S的子串。
验证从N到1之间所有的数字,先求出其二进制数的字符串,在 C++ 中可以利用 bitset 来做,将其转为字符串即可。由于定义了 32 位的 bitset,转为字符串后可能会有许多 leading zeros,所以首先要移除这些0,通过在字符串中查找第一个1,然后通过取子串的函数就可以去除所有的起始0了。然后在S中查找是否存在这个二进制字符串,若不存在,直接返回 false,遍历完成后返回 true 即可,参见代码如下:
学到了,bitset还可以这么用,转成二进制字符串确实很方便。1
2
3
4
5
6
7
8
9
10class Solution {
public:
bool queryString(string S, int N) {
for (int i = N; i > 0; --i) {
string b = bitset<32>(i).to_string();
if (S.find(b.substr(b.find("1"))) == string::npos) return false;
}
return true;
}
};
Leetcode1017. Convert to Base -2
Given an integer n, return a binary string representing its representation in base -2.
Note that the returned string should not have leading zeros unless the string is “0”.
Example 1:1
2
3Input: n = 2
Output: "110"
Explantion: (-2)2 + (-2)1 = 2
Example 2:1
2
3Input: n = 3
Output: "111"
Explantion: (-2)2 + (-2)1 + (-2)0 = 3
Example 3:1
2
3Input: n = 4
Output: "100"
Explantion: (-2)2 = 4
这道题给了一个十进制的非负数N,让转为以负二进制的数。我们对于十进制数转二进制的数字应该比较熟悉,就是每次N%2或者N&1,然后再将N右移一位,即相当于除以2,直到N为0为止。对于转为负二进制的数字,也是同样的做法,唯一不同的是,每次要除以 -2,即将N右移一位之后,要变为相反数,参见代码如下:1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
string baseNeg2(int N) {
string res;
while (N != 0) {
res = to_string(N & 1) + res;
N = -(N >> 1);
}
return res == "" ? "0" : res;
}
};
由于转二进制数是要对2取余,则转负二进制就要对 -2 取余,然后N要除以 -2,但是有个问题是,取余操作可能会得到负数,但我们希望只得到0或1,这样就需要做些小调整,使其变为正数,变化方法是,余数加2,N加1,证明方法如下所示:1
2
3-1 = (-2) * 0 + (-1)
-1 = (-2) * 0 + (-2) + (-1) - (-2)
-1 = (-2) * (0 + 1) + (-1) - (-2)
先加上一个 -2,再减去一个 -2,合并后就是N加1,余数加2,这样就可以把余数加到结果字符串中了,参见代码如下:
1 | class Solution { |
Leetcode1018. Binary Prefix Divisible By 5
Given an array A of 0s and 1s, consider N_i: the i-th subarray from A[0] to A[i] interpreted as a binary number (from most-significant-bit to least-significant-bit.)
Return a list of booleans answer, where answer[i] is true if and only if N_i is divisible by 5.
Example 1:1
2
3Input: [0,1,1]
Output: [true,false,false]
Explanation: The input numbers in binary are 0, 01, 011; which are 0, 1, and 3 in base-10. Only the first number is divisible by 5, so answer[0] is true.
Example 2:1
2Input: [1,1,1]
Output: [false,false,false]
Example 3:1
2Input: [0,1,1,1,1,1]
Output: [true,false,false,false,true,false]
Example 4:1
2Input: [1,1,1,0,1]
Output: [false,false,false,false,false]
假设当前访问 A[i - 1], 表示的数为 old_number, 那么当访问 A[i] 时, 所表示的数 new_number = old_number * 2 + A[i];
- 如果直接判断 new_number 是否能被 5 整除, 容易出现溢出的问题, 因为按照上面遍历的方式, C++ 只能保存 32-bit 的数据, 但是题目中说明 1 <= A.length <= 30000.
- 我们不需要知道具体的 new_number 数值大小, 而只需要它与 5 的余数;
-发现一个数学公式:(a*b + c) % d = ((a%d)*(b%d) + c%d) % d, 因此new_number % 5可以表示为((old_number % 5) * 2 + A[i]) % 5. - 由第 4 点, 可以将 number % 5 作为一个整体, 更新公式为
a = (a * 2 + A[i]) % 5.
1 | class Solution { |
Leetcode1019. Next Greater Node In Linked List
You are given the head of a linked list with n nodes.
For each node in the list, find the value of the next greater node. That is, for each node, find the value of the first node that is next to it and has a strictly larger value than it.
Return an integer array answer where answer[i] is the value of the next greater node of the ith node (1-indexed). If the ith node does not have a next greater node, set answer[i] = 0.
Example 1:1
2Input: head = [2,1,5]
Output: [5,5,0]
Example 2:1
2Input: head = [2,7,4,3,5]
Output: [7,0,5,5,0]
这道题给了一个链表,让找出每个结点值的下一个较大的结点值,跟之前的 Next Greater Element I,Next Greater Element II,和 Next Greater Element III 很类似,不同的是这里不是数组,而是链表,就稍稍的增加了一些难度,因为链表无法直接根据下标访问元素,在遍历链表之前甚至不知道总共有多少个结点。基本上来说,为了达到线性的时间复杂度,这里需要维护一个单调递减的栈,若当前的数字小于等于栈顶元素,则加入栈,若当前数字大于栈顶元素,非常棒,说明栈顶元素的下一个较大数字找到了,标记上,且把栈顶元素移除,继续判断下一个栈顶元素和当前元素的关系,直到当前数字小于等于栈顶元素为止。通过这种方法,就可以在线性的时间内找出所有数字的下一个较大的数字了。
这里新建两个数组,res 和 nums 分别保存要求的结果和链表的所有结点值,还需要一个栈 st 和一个变量 cnt(记录当前的数组坐标),然后开始遍历链表,首先把当前结点值加入数组 nums,然后开始循环,若栈不空,且当前结点值大于栈顶元素(注意这里单调栈存的并不是结点值,而是该值在 nums 数组中的坐标值,这是为了更好的在结果 res 中定位),此时用该结点值来更新结果 res 中的对应的位置,然后将栈顶元素移除,继续循环直到条件不满足位置。然后把当前的坐标加入栈中,此时还要更新结果 res 的大小,因为由于链表的大小未知,无法直接初始化 res 的大小,当然我们可以在开头的时候先遍历一遍链表,得到结点的个数也是可以的,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
vector<int> nextLargerNodes(ListNode* head) {
vector<int> res;
stack<int> s;
int cnt = 0;
ListNode* cur = head;
while(cur) {
cnt ++;
res.push_back(cur->val);
cur = cur->next;
}
vector<int> res2(cnt, 0);
cnt = 0;
while(head != NULL) {
while (!s.empty() && res[s.top()] < head->val) {
res2[s.top()] = head->val;
s.pop();
}
s.push(cnt);
head = head->next;
cnt ++;
}
return res2;
}
};
这个人写的方法需要经常resize,不一定更快。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
vector<int> nextLargerNodes(ListNode* head) {
vector<int> res, nums;
stack<int> st;
int cnt = 0;
while (head) {
nums.push_back(head->val);
while (!st.empty() && head->val > nums[st.top()]) {
res[st.top()] = head->val;
st.pop();
}
st.push(cnt);
res.resize(++cnt);
head = head->next;
}
return res;
}
};
再看一种方法,首先把链表反转,也是用单调栈的方法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45class Solution {
ListNode* reverseList(ListNode* head)
{
if (head->next == nullptr)
return head;
ListNode* newHead = reverseList(head->next);
head->next->next = head;
head->next = nullptr;
return newHead;
}
public:
vector<int> nextLargerNodes(ListNode* head) {
if (head == nullptr)
return {};
ListNode* revHead = reverseList(head);
ListNode* curr = revHead;
std::vector<int> result;
std::stack<int> st;
while (curr != nullptr)
{
if (st.empty())
{
result.push_back(0);
st.push(curr->val);
curr = curr->next;
}
else
{
while (!st.empty() && curr->val >= st.top())
st.pop();
if (!st.empty())
result.push_back(st.top());
else
result.push_back(0);
st.push(curr->val);
curr = curr->next;
}
}
std::reverse(result.begin(), result.end());
return result;
}
};
Leetcode1020. Number of Enclaves
Given a 2D array A, each cell is 0 (representing sea) or 1 (representing land)
A move consists of walking from one land square 4-directionally to another land square, or off the boundary of the grid.
Return the number of land squares in the grid for which we cannot walk off the boundary of the grid in any number of moves.
Example 1:1
2
3
4Input: [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
Output: 3
Explanation:
There are three 1s that are enclosed by 0s, and one 1 that isn't enclosed because its on the boundary.
Example 2:1
2
3
4Input: [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
Output: 0
Explanation:
All 1s are either on the boundary or can reach the boundary.
Note:
- 1 <= A.length <= 500
- 1 <= A[i].length <= 500
- 0 <= A[i][j] <= 1
- All rows have the same size.
这道题给了一个只有0和1的二维数组A,其中0表示海洋,1表示陆地,每次只能从一块陆地走到和其相连的另一块陆地上,问有多少块陆地可以不用走到边界上。其实这道题就是让找出被0完全包围的1的个数,反过来想,如果有1在边界上,那么和其相连的所有1都是不符合题意的,所以只要以边界上的1为起点,遍历所有和其相连的1,并且标记,则剩下的1一定就是被0完全包围的。遍历的方法可以用 BFS 或者 DFS,先来看 BFS 的解法,使用一个队列 queue,遍历数组A,现将所有1的个数累加到结果 res,然后将边界上的1的坐标加入队列中。然后开始 while 循环,去除队首元素,若越界了,或者对应的值不为1,直接跳过。否则标记当前位置值为0,并且 res 自减1,然后将周围四个位置都排入队列中,最后返回结果 res 即可,参见代码如下:
1 | class Solution { |
用深度优先确实能快一点点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
void dfs(vector<vector<int>>& grid, int i, int j) {
if (i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || grid[i][j] != 1)
return;
grid[i][j] = 0;
dfs(grid, i, j+1);
dfs(grid, i, j-1);
dfs(grid, i+1, j);
dfs(grid, i-1, j);
}
int numEnclaves(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size(), num1 = 0;
for (int i = 0; i < m; i ++) {
if (grid[i][0] == 1)
dfs(grid, i, 0);
if (grid[i][n-1] == 1)
dfs(grid, i, n-1);
}
for (int i = 0; i < n; i ++) {
if (grid[0][i] == 1)
dfs(grid, 0, i);
if (grid[m-1][i] == 1)
dfs(grid, m-1, i);
}
for (int i = 0; i < m; i ++)
for (int j = 0; j < n; j ++)
if (grid[i][j] == 1)
num1 ++;
return num1;
}
};
Leetcode1021. Remove Outermost Parentheses
A valid parentheses string is either empty (“”), “(“ + A + “)”, or A + B, where A and B are valid parentheses strings, and + represents string concatenation. For example, “”, “()”, “(())()”, and “(()(()))” are all valid parentheses strings.
A valid parentheses string S is primitive if it is nonempty, and there does not exist a way to split it into S = A+B, with A and B nonempty valid parentheses strings.
Given a valid parentheses string S, consider its primitive decomposition: S = P_1 + P_2 + … + P_k, where P_i are primitive valid parentheses strings.
Return S after removing the outermost parentheses of every primitive string in the primitive decomposition of S.
Example 1:1
2
3
4
5Input: "(()())(())"
Output: "()()()"
Explanation:
The input string is "(()())(())", with primitive decomposition "(()())" + "(())".
After removing outer parentheses of each part, this is "()()" + "()" = "()()()".
Example 2:1
2
3
4
5Input: "(()())(())(()(()))"
Output: "()()()()(())"
Explanation:
The input string is "(()())(())(()(()))", with primitive decomposition "(()())" + "(())" + "(()(()))".
After removing outer parentheses of each part, this is "()()" + "()" + "()(())" = "()()()()(())".
Example 3:1
2
3
4
5Input: "()()"
Output: ""
Explanation:
The input string is "()()", with primitive decomposition "()" + "()".
After removing outer parentheses of each part, this is "" + "" = "".
Note:
- S.length <= 10000
- S[i] is “(“ or “)”
- S is a valid parentheses string
比较简单,把最外边的一层括号移走,可以用栈,也可以用计数器。如果遇到左括号且栈不空说明这个左括号不是外边的括号,加到结果中,再把这个左括号压栈;如果是右括号,就先弹出栈,再判断如果栈不空则说明这个右括号也不是外边的括号,加到结果中。
不知道为啥我这个这么慢,反正过了就行。
1 | class Solution { |
Leetcode1022. Sum of Root To Leaf Binary Numbers
Given a binary tree, each node has value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit. For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.
For all leaves in the tree, consider the numbers represented by the path from the root to that leaf.
Return the sum of these numbers.
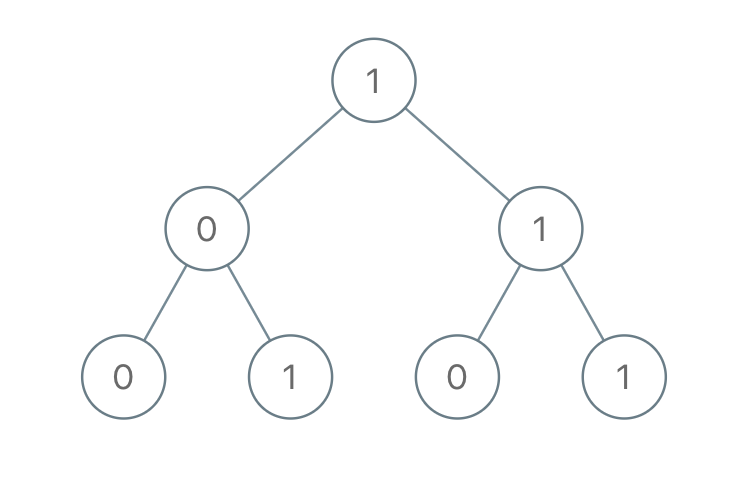
深度优先遍历一波,因为好久没写dsf了,所以特地写一写。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int result;
void dfs(TreeNode* root ,int now){
if(!root->left && !root->right){
result += (now<<1) + root->val;
}
int val = (now<<1) + root->val;
if(root->left)
dfs(root->left, val);
if(root->right)
dfs(root->right, val);
}
int sumRootToLeaf(TreeNode* root) {
result=0;
dfs(root,0);
return result;
}
};
Leetcode1023. Camelcase Matching
A query word matches a given pattern if we can insert lowercase letters to the pattern word so that it equals the query. (We may insert each character at any position, and may insert 0 characters.)
Given a list of queries, and a pattern, return an answer list of booleans, where answer[i] is true if and only if queries[i] matches the pattern.
Example 1:1
2
3
4
5
6Input: queries = ["FooBar","FooBarTest","FootBall","FrameBuffer","ForceFeedBack"], pattern = "FB"
Output: [true,false,true,true,false]
Explanation:
"FooBar" can be generated like this "F" + "oo" + "B" + "ar".
"FootBall" can be generated like this "F" + "oot" + "B" + "all".
"FrameBuffer" can be generated like this "F" + "rame" + "B" + "uffer".
Example 2:1
2
3
4
5Input: queries = ["FooBar","FooBarTest","FootBall","FrameBuffer","ForceFeedBack"], pattern = "FoBa"
Output: [true,false,true,false,false]
Explanation:
"FooBar" can be generated like this "Fo" + "o" + "Ba" + "r".
"FootBall" can be generated like this "Fo" + "ot" + "Ba" + "ll".
Example 3:1
2
3
4Input: queries = ["FooBar","FooBarTest","FootBall","FrameBuffer","ForceFeedBack"], pattern = "FoBaT"
Output: [false,true,false,false,false]
Explanation:
"FooBarTest" can be generated like this "Fo" + "o" + "Ba" + "r" + "T" + "est".
Note:
- 1 <= queries.length <= 100
- 1 <= queries[i].length <= 100
- 1 <= pattern.length <= 100
- All strings consists only of lower and upper case English letters.
给一个字符串和一个模式串,看能不能在模式串里加小写字母来转换成字符串,比较简单。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
vector<bool> camelMatch(vector<string>& queries, string pattern) {
vector<bool> ans;
for(int i=0;i<queries.size();i++){
bool succ=true;
int index=0;
for(int j=0;j<queries[i].size();j++){
while(islower(queries[i][j])&& pattern[index]!=queries[i][j]){
j++;
}
if(pattern[index]==queries[i][j])
index++;
else{
succ=false;
break;
}
}
ans.push_back(succ);
}
return ans;
}
};
我的代码比较慢,可以看看大佬们怎么写的。
Solution 1, Find
For each query, find all letters in pattern left-to-right. If we found all pattern letters, check that the rest of the letters is in the lower case.
对每个查询,从左到右找pattern里的字幕,如果找到了,检查剩余的是否是小写字母。感觉跟我的类似。
For simplicity, we can replace the found pattern letter in query with a lowercase ‘a’.1
2
3
4
5
6
7
8
9
10
11
12
13
14vector<bool> camelMatch(vector<string>& qs, string pattern, vector<bool> res = {}) {
for (auto i = 0; i < qs.size(); ++i) {
for (auto p = -1, j = 0; j < pattern.size(); ++j) {
p = qs[i].find(pattern[j], p + 1);
if (p == string::npos) {
res.push_back(false);
break;
}
qs[i][p] = 'a';
}
if (res.size() <= i) res.push_back(all_of(begin(qs[i]), end(qs[i]), [](char ch) { return islower(ch); }));
}
return res;
}
Solution 2, Simple Scan
Instead of using the find function, we can just check all characters in the query. If a character matches the pattern pointer (pattern[p]), we advance that pointer (++p). Otherwise, we check that the query character is in the lower case.
检查查询的字符串,如果一个字符与pattern[p]匹配了,就继续,如果不匹配,看是不是小些
With this solution, it’s also easer to realize that the complexity is O(n), where n is the total number of query characters.1
2
3
4
5
6
7
8
9
10vector<bool> camelMatch(vector<string>& qs, string pattern, vector<bool> res = {}) {
for (auto i = 0, j = 0, p = 0; i < qs.size(); ++i) {
for (j = 0, p = 0; j < qs[i].size(); ++j) {
if (p < pattern.size() && qs[i][j] == pattern[p]) ++p;
else if (!islower(qs[i][j])) break;
}
res.push_back(j == qs[i].size() && p == pattern.size());
}
return res;
}
Complexity Analysis
- Runtime: O(n), where n is all letters in all queries. We process each letter only once.
- Memory: O(m), where m is the number of queries (to store the result).
- 时间复杂度O(n),空间复杂度O(m)
Leetcode1024. Video Stitching
You are given a series of video clips from a sporting event that lasted T seconds. These video clips can be overlapping with each other and have varied lengths.
Each video clip clips[i] is an interval: it starts at time clips[i][0] and ends at time clips[i][1]. We can cut these clips into segments freely: for example, a clip [0, 7] can be cut into segments [0, 1] + [1, 3] + [3, 7].
Return the minimum number of clips needed so that we can cut the clips into segments that cover the entire sporting event ([0, T]). If the task is impossible, return -1.
寻找最少的可以覆盖[0, T]区间的区间数量,一开始没搞定,看答案搞定的。总体思路就是一开始先排序,并且记下来两个end,一个是当前的end,一个是之前一次的end,如果现在这个小区间的end比之前的pre_end还小,直接不考虑了。我做的时候忽略了这一点,如果不记下来之前的per_end的话,可能有区间是重复的(现在这个小区间如果加进去了,就跟上次加进去的那个小区间有重复的部分或者重合)
Example 1:1
2
3
4
5
6
7Input: clips = [[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]], T = 10
Output: 3
Explanation:
We take the clips [0,2], [8,10], [1,9]; a total of 3 clips.
Then, we can reconstruct the sporting event as follows:
We cut [1,9] into segments [1,2] + [2,8] + [8,9].
Now we have segments [0,2] + [2,8] + [8,10] which cover the sporting event [0, 10].
Example 2:1
2
3
4Input: clips = [[0,1],[1,2]], T = 5
Output: -1
Explanation:
We can't cover [0,5] with only [0,1] and [0,2].
Example 3:1
2
3
4Input: clips = [[0,1],[6,8],[0,2],[5,6],[0,4],[0,3],[6,7],[1,3],[4,7],[1,4],[2,5],[2,6],[3,4],[4,5],[5,7],[6,9]], T = 9
Output: 3
Explanation:
We can take clips [0,4], [4,7], and [6,9].
Example 4:1
2
3
4Input: clips = [[0,4],[2,8]], T = 5
Output: 2
Explanation:
Notice you can have extra video after the event ends.
Note:
1 <= clips.length <= 100
0 <= clips[i][0], clips[i][1] <= 100
0 <= T <= 100
1 | class Solution { |
Leetcode1025. Divisor Game
Alice and Bob take turns playing a game, with Alice starting first.
Initially, there is a number N on the chalkboard. On each player’s turn, that player makes a move consisting of:
Choosing any x with 0 < x < N and N % x == 0.
Replacing the number N on the chalkboard with N - x.
Also, if a player cannot make a move, they lose the game.
Return True if and only if Alice wins the game, assuming both players play optimally.
Example 1:1
2
3Input: 2
Output: true
Explanation: Alice chooses 1, and Bob has no more moves.
Example 2:1
2
3Input: 3
Output: false
Explanation: Alice chooses 1, Bob chooses 1, and Alice has no more moves.
Note:
- 1 <= N <= 1000
两个人玩游戏,给一个数字N,先轮到A走,A选一个数字x使得0 < x < N且N % x == 0,之后N变为N-x,如果谁选不出来x,那就输了,A遇见偶数赢,奇数输。
如果A看见偶数,就选x=1,则N变成奇数,B只能再选一个奇数,又把N变成偶数,由于1是奇数且1没法再选,故A遇见偶数一定赢,反之则输。
1 | class Solution { |
Leetcode1026. Maximum Difference Between Node and Ancestor
Given the root of a binary tree, find the maximum value V for which there exists different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.
(A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.)
Example 1: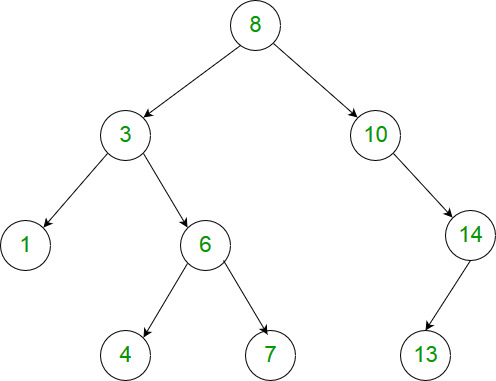
1
2
3
4
5
6
7
8
9Input: [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation:
We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
Note:
- The number of nodes in the tree is between 2 and 5000.
- Each node will have value between 0 and 100000.
给一棵树,找到最大值v,这个v是节点和祖先的值的差的绝对值。dfs里一定要有一个最大一个最小,这样才能算出来绝对值最大的一个,之前考虑只放一个值,没有搞定。
一个dfs1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int val=0;
void dfs(TreeNode* root,int maxval,int minval){
val = max(val, abs(root->val - maxval));
val = max(val, abs(root->val - minval));
maxval = max(maxval, root->val);
minval = min(minval, root->val);
if(root->right) dfs(root->right,maxval,minval);
if(root->left) dfs(root->left,maxval,minval);
}
int maxAncestorDiff(TreeNode* root) {
dfs(root,root->val,root->val);
return val;
}
};
Leetcode1027. Longest Arithmetic Sequence
Given an array A of integers, return the length of the longest arithmetic subsequence in A.
Recall that a subsequence of A is a list A[i_1], A[i_2], …, A[i_k] with 0 <= i_1 < i_2 < … < i_k <= A.length - 1, and that a sequence B is arithmetic if B[i+1] - B[i] are all the same value (for 0 <= i < B.length - 1).
Example 1:1
2
3
4Input: A = [3,6,9,12]
Output: 4
Explanation:
The whole array is an arithmetic sequence with steps of length = 3.
Example 2:1
2
3
4Input: A = [9,4,7,2,10]
Output: 3
Explanation:
The longest arithmetic subsequence is [4,7,10].
Example 3:1
2
3
4Input: A = [20,1,15,3,10,5,8]
Output: 4
Explanation:
The longest arithmetic subsequence is [20,15,10,5].
Constraints:
- 2 <= A.length <= 1000
- 0 <= A[i] <= 500
这道题给了一个数组,让找最长的等差数列的长度,首先来考虑如何定义 DP 数组,最直接的就是用一个一维数组,其中dp[i]表示区间 [0, i] 中的最长等差数列的长度,但是这样定义的话,很难找出状态转移方程。因为有些隐藏信息被我们忽略了,就是等差数列的相等的差值,不同的等差数列的差值可以是不同的,所以不包括这个信息的话将很难更新 dp 值。所以这里就需要一个二维数组,dp[i][j]表示在区间 [0, i] 中的差值为j的最长等差数列的长度减1,这里减1是因为起始的数字并没有被算进去,不过不要紧,最后再加回来就行了。
还有一个需要注意的地方,由于等差数列的差值有可能是负数,而数组的下标不能是负数,所以需要处理一下,题目中限定了数组中的数字范围为0到 500 之间,所以差值的范围就是 -500 到 500 之间,可以给差值加上个 1000,这样差值范围就是 500 到 1500 了,二维 dp 数组的大小可以初始化为 nx2000。更新 dp 值的时候,先遍历一遍数组,对于每个遍历到的数字,再遍历一遍前面的所有数字,算出差值 diff,再加上 1000,然后此时的dp[i][diff]可以赋值为dp[j][diff]+1,然后用这个新的 dp 值来更新结果 res,最后别忘了 res 加1后返回,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int longestArithSeqLength(vector<int>& A) {
int res = 0, n = A.size();
vector<vector<int>> dp(n, vector<int>(2000));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
int diff = A[i] - A[j] + 1000;
dp[i][diff] = dp[j][diff] + 1;
res = max(res, dp[i][diff]);
}
}
return res + 1;
}
};
Leetcode1028. Recover a Tree From Preorder Traversal
We run a preorder depth-first search (DFS) on the root of a binary tree.
At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node. If the depth of a node is D, the depth of its immediate child is D + 1. The depth of the root node is 0.
If a node has only one child, that child is guaranteed to be the left child.
Given the output traversal of this traversal, recover the tree and return its root.
Example 1:1
2Input: traversal = "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]
Example 2:1
2Input: traversal = "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]
Example 3:1
2Input: traversal = "1-401--349---90--88"
Output: [1,401,null,349,88,90]
这道题让我们根据一棵二叉树的先序遍历的结果来重建这棵二叉树。这里为了能够只根据先序遍历的结果来唯一的重建出二叉树,提供了每个结点值的深度,用短杠的个数来表示,根结点的深度为0,前方没有短杠,后面的数字前方只有一个短杠的就是根结点的左右子结点,然后紧跟在一个短杠后面的两个短杠的数字就是根结点左子结点的左子结点,以此类推。
遍历输入字符串,先提取短杠的个数,因为除了根结点之外,所有的深度值都是在结点值前面的,所有用一个 for 循环先提取出短杠的个数 level,然后提取结点值,也是用一个 for 循环,因为结点值可能是个多位数,有了结点值之后我们就可以新建一个结点了。下一步就比较 tricky 了,因为先序遍历跟 DFS 搜索一样有一个回到先前位置的过程,比如例子1中,当我们遍历到结点5的时候,此时是从叶结点4回到了根结点的右子结点5,现在栈中有4个结点,而当前深度为1的结点5是要连到根结点的,所以栈中的无关结点就要移除,需要把结点 2,3,4 都移除,就用一个 while 循环,假如栈中元素个数大于当前的深度 level,就移除栈顶元素。那么此时栈中就只剩根结点了,就可以连接了。此时我们的连接策略是,假如栈顶元素的左子结点为空,则连在左子结点上,否则连在右子结点上,因为题目中说了,假如只有一个子结点,一定是左子结点。然后再把当前结点压入栈即可,字符串遍历结束后,栈中只会留有一个结点(题目中限定了树不为空),就是根结点,直接返回即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
TreeNode* recoverFromPreorder(string S) {
vector<TreeNode*> st;
int i = 0, level = 0, val = 0, n = S.size();
while (i < n) {
for (level = 0; i < n && S[i] == '-'; ++i) {
++level;
}
for (val = 0; i < n && S[i] != '-'; ++i) {
val = 10 * val + (S[i] - '0');
}
TreeNode *node = new TreeNode(val);
while (st.size() > level) st.pop_back();
if (!st.empty()) {
if (!st.back()->left) st.back()->left = node;
else st.back()->right = node;
}
st.push_back(node);
}
return st[0];
}
};
我自己的方法是根据-的数量得到层数,判断这是到第几层了,如果超过了当前的层数,就说明到底了,返回就行。但是不知道为什么很慢。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
TreeNode* dfs(string s, int& cur, int depth) {
if (cur == s.length())
return NULL;
int i = cur, len = s.length();
while(i < len && i < cur+depth) {
if (s[i] != '-')
break;
i ++;
}
if (i != cur+depth)
return NULL;
int val = 0;
while(i < len)
if ('0' <= s[i] && s[i] <= '9')
val = val * 10 + s[i++] - '0';
else
break;
TreeNode* res = new TreeNode(val);
cur = i;
res->left = dfs(s, cur, depth+1);
res->right = dfs(s, cur, depth+1);
return res;
}
TreeNode* recoverFromPreorder(string s) {
int pos = 0;
return dfs(s, pos, 0);
}
};
Leetcode1029. Two City Scheduling
There are 2N people a company is planning to interview. The cost of flying the i-th person to city A is costs[i][0], and the cost of flying the i-th person to city B is costs[i][1].
Return the minimum cost to fly every person to a city such that exactly N people arrive in each city.
Example 1:1
2
3
4
5
6
7Input: [[10,20],[30,200],[400,50],[30,20]]
Output: 110
Explanation:
The first person goes to city A for a cost of 10.
The second person goes to city A for a cost of 30.
The third person goes to city B for a cost of 50.
The fourth person goes to city B for a cost of 20.
The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.
Note:
- 1 <= costs.length <= 100
- It is guaranteed that costs.length is even.
- 1 <= costs[i][0], costs[i][1] <= 1000
公司计划面试 2N 人。第 i 人飞往 A 市的费用为 costs[i][0],飞往 B 市的费用为 costs[i][1]。
返回将每个人都飞到某座城市的最低费用,要求每个城市都有 N 人抵达。
由于人数是偶数个,一半的人去A,一半的人去B,换个角度,每个人要么去A,要么去B。如果他去A比去B的路程短,而且,这个节省的路程比一半的人还多,那么他就去A。所以,以去A和去B的路程差作为Key进行升序排序,前面一半人去A,后面去B。
1 | class Solution { |
Leetcode1030. Matrix Cells in Distance Order
We are given a matrix with R rows and C columns has cells with integer coordinates (r, c), where 0 <= r < R and 0 <= c < C.
Additionally, we are given a cell in that matrix with coordinates (r0, c0).
Return the coordinates of all cells in the matrix, sorted by their distance from (r0, c0) from smallest distance to largest distance. Here, the distance between two cells (r1, c1) and (r2, c2) is the Manhattan distance, |r1 - r2| + |c1 - c2|. (You may return the answer in any order that satisfies this condition.)
Example 1:1
2
3Input: R = 1, C = 2, r0 = 0, c0 = 0
Output: [[0,0],[0,1]]
Explanation: The distances from (r0, c0) to other cells are: [0,1]
Example 2:1
2
3
4Input: R = 2, C = 2, r0 = 0, c0 = 1
Output: [[0,1],[0,0],[1,1],[1,0]]
Explanation: The distances from (r0, c0) to other cells are: [0,1,1,2]
The answer [[0,1],[1,1],[0,0],[1,0]] would also be accepted as correct.
Example 3:1
2
3
4Input: R = 2, C = 3, r0 = 1, c0 = 2
Output: [[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]]
Explanation: The distances from (r0, c0) to other cells are: [0,1,1,2,2,3]
There are other answers that would also be accepted as correct, such as [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]].
Note:
- 1 <= R <= 100
- 1 <= C <= 100
- 0 <= r0 < R
- 0 <= c0 < C
根据与给定的点的顺序排序。
看到一种比较辣鸡的做法,就是先把所有点都加进去,再排序,顺便学习了一个新的写法,如下的lambda表达式:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {
auto comp = [r0,c0](vector<int> &a, vector<int> &b){
return abs(a[0]-r0) + abs(a[1]-c0) < abs(b[0]-r0) + abs(b[1]-c0);
};
vector<vector<int>> res;
for(int i=0;i<R;i++)
for(int j=0;j<C;j++)
res.push_back({i,j});
sort(res.begin(),res.end(),comp);
return res;
}
};
用bfs做也行:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
vector<vector<int> > allCellsDistOrder(int R, int C, int r0, int c0) {
int visit[R][C];
memset(visit,0,sizeof(int)*R*C);
int direction[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
queue< pair<int, int> > qu;
vector< vector<int> > res;
qu.push({r0,c0});
while(!qu.empty()){
pair<int ,int> temp = qu.front();
qu.pop();
int x = temp.first;
int y = temp.second;
if(visit[x][y]==1)
continue;
res.push_back({x,y});
visit[x][y]=1;
for(int i=0;i<4;i++){
int xx = x + direction[i][0];
int yy = y + direction[i][1];
if ( xx>= 0 && xx < R && yy >=0 && yy < C && visit[xx][yy] == 0){
qu.push({xx,yy});
}
}
}
return res;
}
};
更新一种做法:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
static bool comp(vector<int>& a, vector<int>& b) {
return a[2] < b[2];
}
vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {
int k = 0;
vector<vector<int>> v(R*C, vector<int>(3));
for (int i = 0; i < R; i ++) {
for(int j = 0; j < C; j ++) {
v[k][0] = i;
v[k][1] = j;
v[k][2] = abs(i - r0) + abs(j - c0);
k ++;
}
}
sort(v.begin(), v.end(), comp);
for(int kk = 0; kk < R*C; kk ++) {
v[kk].pop_back();
}
return v;
}
};
Leetcode1031. Maximum Sum of Two Non-Overlapping Subarrays
Given an integer array nums and two integers firstLen and secondLen, return the maximum sum of elements in two non-overlapping subarrays with lengths firstLen and secondLen.
The array with length firstLen could occur before or after the array with length secondLen, but they have to be non-overlapping.
A subarray is a contiguous part of an array.
Example 1:1
2
3Input: nums = [0,6,5,2,2,5,1,9,4], firstLen = 1, secondLen = 2
Output: 20
Explanation: One choice of subarrays is [9] with length 1, and [6,5] with length 2.
Example 2:1
2
3Input: nums = [3,8,1,3,2,1,8,9,0], firstLen = 3, secondLen = 2
Output: 29
Explanation: One choice of subarrays is [3,8,1] with length 3, and [8,9] with length 2.
Example 3:1
2
3Input: nums = [2,1,5,6,0,9,5,0,3,8], firstLen = 4, secondLen = 3
Output: 31
Explanation: One choice of subarrays is [5,6,0,9] with length 4, and [3,8] with length 3.
题意:给你一个数组,再给你一个L,M,求在这个数组里面,两个不重合的长度分别为L,M的最的最大和。
思路:先预处理一个dp[i][2],dp[i][0]表示以i为开头,长度为L的值;dp[i][1]表示以i为开头,长度为M的值。再两层for,遍历i,j分别表示两个数组的头,只要两个数组不重合,就是合适的数组。最后求个最大值就好了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int maxSumTwoNoOverlap(vector<int>& nums, int l, int m) {
int n = nums.size(), res = 0;
vector<int> sum(n, 0);
vector<vector<int>> dp(n, vector<int>(2, 0));
for (int i = 0; i < n; i ++) {
for (int j = 0; j < l && i+j < n; j ++)
dp[i][0] += nums[i+j];
for (int j = 0; j < m && i+j < n; j ++)
dp[i][1] += nums[i+j];
}
for (int i = 0; i < n; i ++) {
for (int j = 0; j < n; j ++) {
if (i + l <= j)
res = max(res, dp[i][0]+dp[j][1]);
if (j + m <= i)
res = max(res, dp[i][0]+dp[j][1]);
}
}
return res;
}
};
这道题给了一个非负数组A,还有两个长度L和M,说是要分别找出不重叠且长度分别为L和M的两个子数组,前后顺序无所谓,问两个子数组最大的数字之和是多少。来看论坛上的高分解法吧,首先建立累加和数组,这里可以直接覆盖A数组,然后定义Lmax为在最后M个数字之前的长度为L的子数组的最大数字之和,同理,Mmax表示在最后L个数字之前的长度为M的子数组的最大数字之和。结果res初始化为前 L+M 个数字之和,然后遍历数组,从 L+M 开始遍历,先更新Lmax和Mmax,其中Lmax用A[i - M] - A[i - M - L]来更新,Mmax用A[i - L] - A[i - M - L]来更新。然后取Lmax + A[i] - A[i - M]和Mmax + A[i] - A[i - L]之间的较大值来更新结果 res 即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int maxSumTwoNoOverlap(vector<int>& A, int L, int M) {
for (int i = 1; i < A.size(); ++i) {
A[i] += A[i - 1];
}
int res = A[L + M - 1], Lmax = A[L - 1], Mmax = A[M - 1];
for (int i = L + M; i < A.size(); ++i) {
Lmax = max(Lmax, A[i - M] - A[i - M - L]);
Mmax = max(Mmax, A[i - L] - A[i - M - L]);
res = max(res, max(Lmax + A[i] - A[i - M], Mmax + A[i] - A[i - L]));
}
return res;
}
};
Leetcode1033. Moving Stones Until Consecutive
Three stones are on a number line at positions a, b, and c. Each turn, you pick up a stone at an endpoint (ie., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let’s say the stones are currently at positions x, y, z with x < y < z. You pick up the stone at either position x or position z, and move that stone to an integer position k, with x < k < z and k != y. The game ends when you cannot make any more moves, ie. the stones are in consecutive positions.
When the game ends, what is the minimum and maximum number of moves that you could have made? Return the answer as an length 2 array: answer = [minimum_moves, maximum_moves]
Example 1:1
2
3Input: a = 1, b = 2, c = 5
Output: [1,2]
Explanation: Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
Example 2:1
2
3Input: a = 4, b = 3, c = 2
Output: [0,0]
Explanation: We cannot make any moves.
Example 3:1
2
3Input: a = 3, b = 5, c = 1
Output: [1,2]
Explanation: Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
a,b,c表示三个位置,在三个位置上各有一个石头。现在要移动三个石头中的若干个,每次移动都必须选两端石头的里面的位置,最终使得它们三个放在连续的位置。问最少需要多少次移动,最多需要多少次移动。
如果三个石头本来就连续,则不用移动。例:1,2,3
如果三个石头本来不连续,则:
最少移动次数:
- 有两个石头之间的距离小于等于2,则最少只需要一次移动。例:1,2,4,把4移动到3即可;或者例1,3,5,把5移到2即可。
- 所有石头之间的最小距离>2,则最少需要移动两个石头。例:1,4,7,需要把两个石头移动到另一个的旁边。
最多移动次数:
题目说了,只能像两端石头里面的那些位置上放,所以最多移动的次数就是本来两端石头中间包含的点(并且去掉中间的石头),策略是每次向内移动一步。例:1,3,5,在1和5中间之间共有2个可以放的点(分别为2,4),所以最多只能有max_ - min_ - 2次移动。
1 | class Solution { |
Leetcode1034. Coloring A Border
Given a 2-dimensional grid of integers, each value in the grid represents the color of the grid square at that location.
Two squares belong to the same connected component if and only if they have the same color and are next to each other in any of the 4 directions.
The border of a connected component is all the squares in the connected component that are either 4-directionally adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
Given a square at location (r0, c0) in the grid and a color, color the border of the connected component of that square with the given color, and return the final grid.
Example 1:1
2Input: grid = [[1,1],[1,2]], r0 = 0, c0 = 0, color = 3
Output: [[3, 3], [3, 2]]
Example 2:1
2Input: grid = [[1,2,2],[2,3,2]], r0 = 0, c0 = 1, color = 3
Output: [[1, 3, 3], [2, 3, 3]]
Example 3:1
2Input: grid = [[1,1,1],[1,1,1],[1,1,1]], r0 = 1, c0 = 1, color = 2
Output: [[2, 2, 2], [2, 1, 2], [2, 2, 2]]
Note:
- 1 <= grid.length <= 50
- 1 <= grid[0].length <= 50
- 1 <= grid[i][j] <= 1000
- 0 <= r0 < grid.length
- 0 <= c0 < grid[0].length
- 1 <= color <= 1000
这道题给了一个二维数组 grid,和一个起始位置 (r0, c0),格子里的数字代表不同的颜色,又给了一个新的颜色 color,现在让给起始位置所在的连通区域的边缘填充这种新的颜色。这道题的难点就是如何找出连通区域的边缘,找连通区域并不难,因为有了起始点,可以用 DFS 或者 BFS 来找出所有相连的位置,而边缘位置需要进一步判断,一种情况是当前位置是二维矩阵的边缘,那么其一定也是连通区域的边缘,另一种情况是若四个相邻位置有其他的颜色,则当前位置也一定是边缘。下面先来看 BFS 的解法,主体还是经典的 BFS 写法不变,使用队列 queue,和一个 TreeSet 来记录已经遍历过的位置。将起始位置先放入 queue 和 visited 集合,然后进行 while 循环,取出队首元素,然后判断当前位置是否是二维数组的边缘,是的话直接将颜色更新 color。然后遍历周围四个位置,若越界了或者访问过了直接跳过,然后看若颜色和起始位置的颜色相同,则加入 visited 和 queue,否则将当前位置的颜色更新为 color,因为周围有不同的颜色了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
vector<vector<int>> colorBorder(vector<vector<int>>& grid, int row, int col, int color) {
int m = grid.size(), n = grid[0].size(), ori_color = grid[row][col];
vector<vector<int>> visited(m, vector<int>(n, 0));
vector<vector<int>> dirs{{-1, 0}, {0, 1}, {1, 0}, {0, -1}} ;
queue<int> q;
q.push(row*n + col);
visited[row][col] = 1;
while(!q.empty()) {
int x = q.front() / n;
int y = q.front() % n;
q.pop();
if (x == 0 || x == m-1 || y == 0 || y == n-1)
grid[x][y] = color;
for (int i = 0; i < 4; i ++) {
int xx = x + dirs[i][0];
int yy = y + dirs[i][1];
if (xx < 0 || xx >= m || yy < 0 || yy >= n || visited[xx][yy] == 1)
continue;
if (grid[xx][yy] == ori_color) {
q.push(xx * n + yy);
visited[xx][yy] = 1;
}
else
grid[x][y] = color;
}
}
return grid;
}
};
Leetcode1035. Uncrossed Lines
We write the integers of A and B (in the order they are given) on two separate horizontal lines.
Now, we may draw connecting lines : a straight line connecting two numbers A[i] and B[j] such that:A[i] == B[j];
The line we draw does not intersect any other connecting (non-horizontal) line.
Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.
Return the maximum number of connecting lines we can draw in this way.
Example 1:1
2
3
4Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.
Example 2:1
2Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3
Example 3:1
2Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2
Note:
- 1 <= A.length <= 500
- 1 <= B.length <= 500
- 1 <= A[i], B[i] <= 2000
这道题给了A和B两个数字数组,并且上下并列排放,说是可以用线来连接相同的数字,问最多能连多少根线而且不会发生重叠。首先来想一下,什么情况下两条连线会相交,可以观察下例子1给的图,发现若把4和2分别连上会交叉,这是因为在A数组中是 4,2,而且在B数组中是 2,4,顺序不一样。再来看例子2,分别连 5,1,2 或者 2,1,2,或者 5,2,5 都是可以的,仔细观察,可以发现这些其实就是最长公共子序列 Longest Common Subsequence。使用一个二维数组dp,其中dp[i][j]表示数组A的前i个数字和数组B的前j个数字的最长相同的子序列的数字个数,这里大小初始化为 (m+1)x(n+1),这里的m和n分别是数组A和数组B的长度。接下来就要找状态转移方程了,如何来更新dp[i][j],若二者对应位置的字符相同,表示当前的 LCS 又增加了一位,所以可以用dp[i-1][j-1] + 1来更新dp[i][j]。否则若对应位置的字符不相同,由于是子序列,还可以错位比较,可以分别从数组A或者数组B去掉一个当前数字,那么其dp值就是dp[i-1][j]和dp[i][j-1],取二者中的较大值来更新dp[i][j]即可,最终的结果保存在了dp[m][n]中,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int maxUncrossedLines(vector<int>& A, vector<int>& B) {
int m = A.size(), n = B.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (A[i - 1] == B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
};
Leetcode1037. Valid Boomerang
A boomerang is a set of 3 points that are all distinct and not in a straight line. Given a list of three points in the plane, return whether these points are a boomerang.
Example 1:1
2Input: [[1,1],[2,3],[3,2]]
Output: true
Example 2:1
2Input: [[1,1],[2,2],[3,3]]
Output: false
Note:
points.length == 3
points[i].length == 2
0 <=points[i][j]<= 100
判断三个点是不是互异且不共线的,简单1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
bool isBoomerang(vector<vector<int>>& points) {
for(int i=0;i<points.size();i++)
for(int j=i+1;j<points.size();j++)
if(points[i][0]==points[j][0] && points[i][1]==points[j][1])
return false;
int dx1 = points[1][0] - points[0][0];
int dx2 = points[1][1] - points[0][1];
int dx3 = points[2][0] - points[1][0];
int dx4 = points[2][1] - points[1][1];
if(dx1*dx4-dx2*dx3==0)
return false;
return true;
}
};
Leetcode1038. Binary Search Tree to Greater Sum Tree
Given the root of a binary search tree with distinct values, modify it so that every node has a new value equal to the sum of the values of the original tree that are greater than or equal to node.val.
As a reminder, a binary search tree is a tree that satisfies these constraints:
The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.
Example 1:
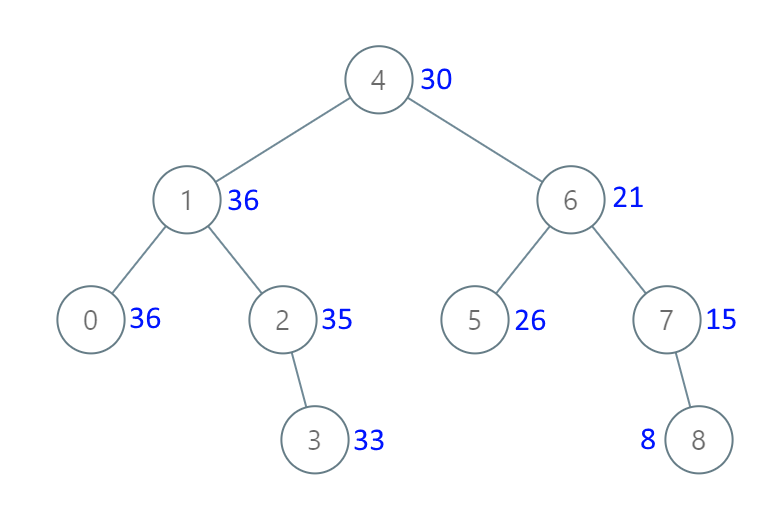
Input: [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
典型的中序遍历,先遍历右子树,再把root赋值,最后看左子树
1 | class Solution { |
Leetcode1039. Minimum Score Triangulation of Polygon
You have a convex n-sided polygon where each vertex has an integer value. You are given an integer array values where values[i] is the value of the ith vertex (i.e., clockwise order).
You will triangulate the polygon into n - 2 triangles. For each triangle, the value of that triangle is the product of the values of its vertices, and the total score of the triangulation is the sum of these values over all n - 2 triangles in the triangulation.
Return the smallest possible total score that you can achieve with some triangulation of the polygon.
Example 1:1
2
3Input: values = [1,2,3]
Output: 6
Explanation: The polygon is already triangulated, and the score of the only triangle is 6.
Example 2:1
2
3
4Input: values = [3,7,4,5]
Output: 144
Explanation: There are two triangulations, with possible scores: 3*7*5 + 4*5*7 = 245, or 3*4*5 + 3*4*7 = 144.
The minimum score is 144.
Example 3:1
2
3Input: values = [1,3,1,4,1,5]
Output: 13
Explanation: The minimum score triangulation has score 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13.
Constraints:
- n == values.length
- 3 <= n <= 50
- 1 <= values[i] <= 100
这道题说有一个N边形,让我们连接不相邻的顶点,从而划分出三角形,最多可以划分出 N-2 个三角形,每划分出一个三角形,得分是三个顶点的乘积,问最小的得分是多少。首先要来定义 DP 数组,这里一维数组肯定是不够用的,因为需要保存区间信息,所以这里用个二维数组,其中dp[i][j]表示从顶点i到顶点j为三角形的一条边,可以组成的所有的三角形的最小得分。接下来推导状态转移方程,由于三角形的一条边已经确定了,接下来就要找另一个顶点的位置,这里需要遍历所有的情况,使用一个变量k,遍历区间 (i, j) 中的所有的顶点,由顶点i,j,和k组成的三角形的得分是A[i] * A[k] * A[j]可以直接算出来,这个三角形将整个区间分割成了两部分,分别是 (i, k) 和 (k, j),这两个区间的最小得分值可以直接从 dp 数组中取得,分别是dp[i][k]和dp[k][j],这样状态转移方程就有了,用dp[i][k] + A[i] * A[k] * A[j] + dp[k][j]来更新dp[i][j],为了防止整型越界,不能直接将 dp 数组都初始化为整型最大值INT_MAX,而是在更新的时候,判断若dp[i][j]为0时,用INT_MAX,否则用其本身值,最终的结果保存在dp[0][n-1]中,参见代码如下:
1 | class Solution { |
再来看一种同样的 DP 解法,和上面的区别是 dp 数组更新的顺序不同,之前说过了更新大区间的 dp 值需要用到小区间的 dp 值,这里是按照区间的大小来更新的,从2更新到n,然后确定区间 (i, j) 的大小为 len,再遍历中间所有的k,状态转移方程还是跟上面一样的。这种更新方法在其他的题目也有用到,最典型的就是那道 Burst Balloons,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int minScoreTriangulation(vector<int>& A) {
int n = A.size();
vector<vector<int>> dp(n, vector<int>(n));
for (int len = 2; len < n; ++len) {
for (int i = 0; i + len < n; ++i) {
int j = i + len;
dp[i][j] = INT_MAX;
for (int k = i + 1; k < j; ++k) {
dp[i][j] = min(dp[i][j], dp[i][k] + A[i] * A[k] * A[j] + dp[k][j]);
}
}
}
return dp[0][n - 1];
}
};
Leetcode1041. Robot Bounded In Circle
On an infinite plane, a robot initially stands at (0, 0) and faces north. The robot can receive one of three instructions:
- “G”: go straight 1 unit;
- “L”: turn 90 degrees to the left;
- “R”: turn 90 degrees to the right.
The robot performs the instructions given in order, and repeats them forever.
Return true if and only if there exists a circle in the plane such that the robot never leaves the circle.
Example 1:1
2
3
4Input: instructions = "GGLLGG"
Output: true
Explanation: The robot moves from (0,0) to (0,2), turns 180 degrees, and then returns to (0,0).
When repeating these instructions, the robot remains in the circle of radius 2 centered at the origin.
Example 2:1
2
3Input: instructions = "GG"
Output: false
Explanation: The robot moves north indefinitely.
Example 3:1
2
3Input: instructions = "GL"
Output: true
Explanation: The robot moves from (0, 0) -> (0, 1) -> (-1, 1) -> (-1, 0) -> (0, 0) -> ...
Constraints:
- 1 <= instructions.length <= 100
- instructions[i] is ‘G’, ‘L’ or, ‘R’.
这道题说是在一个无限大的区域,有个机器人初始化站在原点 (0, 0) 的位置,面朝北方。该机器人有三种指令可以执行,G表示朝当前方向前进一步,L表示向左转 90 度,R表示向右转 90 度,现在给了一些连续的这样的指令,若一直重复的按顺序循环执行下去,问机器人是否会在一个固定的圆圈路径中循环。首先我们需要执行一遍所有的指令,然后根据最后的状态(包括位置和朝向)来分析机器人是否之后会一直走循环路线。若执行过一遍所有指令之后机器人还在原点上,则一定是在一个圆圈路径上(即便是机器人可能就没移动过,一个点也可以看作是圆圈路径)。若机器人偏离了起始位置,只要看此时机器人的朝向,只要不是向北,则其最终一定会回到起点。
知道了最终状态和循环路径的关系,现在就是如何执行这些指令了。也不难,用一个变量表示当前的方向,0表示北,1为东,2为南,3为西,按这个顺序写出偏移量数组 dirs,就是在迷宫遍历的时候经常用到的那个数组。然后记录当前位置 cur,初始化为 (0, 0),然后就可以执行指令了,若遇到G指令,根据 idx 从 dirs 数组中取出偏移量加到 cur 上即可。若遇到L指令,idx 是要减1的,为了避免负数,先加上个4,再减1,再对4取余。同理,若遇到R指令,idx 加1之后对4取余。最后判断若还在原点,或者朝向不为北的时候,返回 true 即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
bool isRobotBounded(string instructions) {
vector<vector<int>> dirs{{0, 1}, {-1, 0}, {0, -1}, {1, 0}};
int xx = 0, yy = 0;
int direction = 0;
for (int i = 0; i < instructions.size(); i ++) {
if (instructions[i] == 'G') {
xx += dirs[direction][0];
yy += dirs[direction][1];
}
else if (instructions[i] == 'L')
direction = (direction + 1 ) % 4;
else if (instructions[i] == 'R')
direction = (direction + 4 - 1) % 4;
}
return (xx == 0 && yy == 0) || direction != 0;
}
};
Leetcode1042. Flower Planting With No Adjacent
You have N gardens, labelled 1 to N. In each garden, you want to plant one of 4 types of flowers. paths[i] = [x, y] describes the existence of a bidirectional path from garden x to garden y. Also, there is no garden that has more than 3 paths coming into or leaving it.
Your task is to choose a flower type for each garden such that, for any two gardens connected by a path, they have different types of flowers.
Return any such a choice as an array answer, where answer[i] is the type of flower planted in the (i+1)-th garden. The flower types are denoted 1, 2, 3, or 4. It is guaranteed an answer exists.
Example 1:1
2Input: N = 3, paths = [[1,2],[2,3],[3,1]]
Output: [1,2,3]
Example 2:1
2Input: N = 4, paths = [[1,2],[3,4]]
Output: [1,2,1,2]
Example 3:1
2Input: N = 4, paths = [[1,2],[2,3],[3,4],[4,1],[1,3],[2,4]]
Output: [1,2,3,4]
Note:
- 1 <= N <= 10000
- 0 <= paths.size <= 20000
- No garden has 4 or more paths coming into or leaving it.
- It is guaranteed an answer exists.
有 N 个花园,按从 1 到 N 标记。在每个花园中,你打算种下四种花之一。 paths[i] = [x, y] 描述了花园 x 到花园 y 的双向路径。另外,没有花园有 3 条以上的路径可以进入或者离开。你需要为每个花园选择一种花,使得通过路径相连的任何两个花园中的花的种类互不相同。以数组形式返回选择的方案作为答案 answer,其中 answer[i] 为在第 (i+1) 个花园中种植的花的种类。花的种类用 1, 2, 3, 4 表示。保证存在答案。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
vector<int> gardenNoAdj(int N, vector<vector<int>>& paths) {
vector<int> res(N, 0);
vector<vector<int>> graph(N);
for(int i = 0 ; i < paths.size(); i ++) {
graph[paths[i][0]-1].push_back(paths[i][1]-1);
graph[paths[i][1]-1].push_back(paths[i][0]-1);
}
for (int i = 0; i < N; ++i) {
int mask = 0;
for (const auto& j : graph[i])
mask |= (1 << res[j]);
for (int c = 1; c <= 4 && res[i] == 0; ++c)
if (!(mask & (1 << c))) res[i] = c;
}
return res;
}
};
Leetcode1043. Partition Array for Maximum Sum
Given an integer array arr, you should partition the array into (contiguous) subarrays of length at most k. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return the largest sum of the given array after partitioning.
Example 1:1
2
3Input: arr = [1,15,7,9,2,5,10], k = 3
Output: 84
Explanation: arr becomes [15,15,15,9,10,10,10]
Example 2:1
2Input: arr = [1,4,1,5,7,3,6,1,9,9,3], k = 4
Output: 83
Example 3:1
2Input: arr = [1], k = 1
Output: 1
Constraints:
- 1 <= arr.length <= 500
- 0 <= arr[i] <= 109
- 1 <= k <= arr.length
这道题给了一个数组 arr,和一个正整数k,说是将数组分成若干个长度不超过k的子数组,分割后的子数组所有的数字都变成该子数组中的最大值,让求分割后的所有子数组数字之和。由于分割的子数组长度不固定,用暴力搜索的话将会有很多很多种情况,不出意外的话会超时。对于这种玩子数组,又是求极值的题,刷题老司机们应该立马就能想到用动态规划 Dynamic Programming 来做。先来定义 dp 数组,先从最简单的考虑,使用一个一维的 dp 数组,其中dp[i]就表示分割数组中的前i个数字组成的数组可以得到的最大的数字之和。下面来考虑状态转移方程怎么求,对于dp[i]来说,若把最后k个数字分割出来,那么前i个数字就被分成了两个部分,前 i-k 个数字,其数字之和可以直接由dp[i-k]来取得,后面的k个数字,则需要求出其中最大的数字,然后乘以k,用这两部分之和来更新dp[i]即可。由于题目中说了分割的长度不超过k,那么就是说小于k的也是可以的,则需要遍历 [1, k] 区间所有的长度,均进行分割。接下来看代码,建立一个大小为 n+1 的 dp 数组,然后i从1遍历到n,此时新建一个变量 curMax 记录当前的最大值,然后用j从1遍历到k,同时要保证 i-j 是大于等于0的,因为需要前半部分存在,实际上这是从第i个数字开始往前找j个数字,然后记录其中最大的数字 curMax,并且不断用dp[i-j] + curMax * j来更新dp[i]即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int maxSumAfterPartitioning(vector<int>& arr, int k) {
int n = arr.size();
vector<int> dp(n + 1);
for (int i = 1; i <= n; ++i) {
int curMax = 0;
for (int j = 1; j <= k && i - j >= 0; ++j) {
curMax = max(curMax, arr[i - j]);
dp[i] = max(dp[i], dp[i - j] + curMax * j);
}
}
return dp[n];
}
};
Leetcode1046. Last Stone Weight
We have a collection of stones, each stone has a positive integer weight.
Each turn, we choose the two heaviest stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:
- If x == y, both stones are totally destroyed;
- If x != y, the stone of weight x is totally destroyed, and the stone of weight y has new weight y-x.
- At the end, there is at most 1 stone left. Return the weight of this stone (or 0 if there are no stones left.)
Example 1:1
2
3
4
5
6
7Input: [2,7,4,1,8,1]
Output: 1
Explanation:
We combine 7 and 8 to get 1 so the array converts to [2,4,1,1,1] then,
we combine 2 and 4 to get 2 so the array converts to [2,1,1,1] then,
we combine 2 and 1 to get 1 so the array converts to [1,1,1] then,
we combine 1 and 1 to get 0 so the array converts to [1] then that's the value of last stone.
堆排序解法,主要是看看人家的堆排序怎么写。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50class Solution {
public:
int lastStoneWeight(vector<int>& stones) {
int p, q;
if(stones.size() == 1)
return stones[0];
while(stones.size() >= 2) {
heapsort(stones);
p = stones.back(); stones.pop_back();
q = stones.back(); stones.pop_back();
int diff = p - q;
if(diff) stones.push_back(diff);
}
if(stones.empty())
return 0;
return stones[0];
}
void heapsort(vector<int>& stones) {
if(stones.size() <= 1) return;
build_heap(stones);
int heap_size = stones.size();
while(heap_size >= 2) {
swap(stones[0], stones[heap_size - 1]);
heap_size --;
max_heapify(stones, 0, heap_size);
}
}
void build_heap(vector<int>& stones) {
for(int i=stones.size()/2; i>=0; i--){
max_heapify(stones, i, stones.size());
}
}
void max_heapify(vector<int>& stones, int i, int heap_size){
int large = i;
if(2*i+1<heap_size && stones[i]<stones[2*i+1]) large = 2*i+1;
if(2*i+2<heap_size && stones[large]<stones[2*i+2]) large = 2*i+2;
if(large != i){
swap(stones[i], stones[large]);
max_heapify(stones, large, heap_size);
}
}
void swap(int &a, int &b){
int temp;
temp = a; a = b; b = temp;
}
};
Leetcode1047. Remove All Adjacent Duplicates In String
Given a string S of lowercase letters, a duplicate removal consists of choosing two adjacent and equal letters, and removing them.
We repeatedly make duplicate removals on S until we no longer can.
Return the final string after all such duplicate removals have been made. It is guaranteed the answer is unique.
Example 1:1
2
3
4Input: "abbaca"
Output: "ca"
Explanation:
For example, in "abbaca" we could remove "bb" since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca", of which only "aa" is possible, so the final string is "ca".
Note:
- 1 <= S.length <= 20000
- S consists only of English lowercase letters.
借用了栈的思想,但是这么做会超内存。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
string removeDuplicates(string S) {
stack<char> st;
for(int i=S.length()-1;i>=0;i--){
if(!st.empty() && st.top()==S[i]){
st.pop();
continue;
}
else
st.push(S[i]);
}
string res;
while(!st.empty()){
res = res + st.top();
st.pop();
}
return res;
}
};
借鉴了大佬的做法:1
2
3
4
5
6
7
8
9string removeDuplicates(string S) {
string res = "";
for (char& c : S)
if (res.size() && c == res.back())
res.pop_back();
else
res.push_back(c);
return res;
}
1 | class Solution { |
这里a.size()是返回字符数量,a.back()返回最后一个字符,pop_back和push_back和vector一样了。
把我自己的超时的代码改了一下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
string removeDuplicates(string S) {
string res="";
int len = 0;
int S_len = S.size();
for(int i=0;i<S_len;i++){
if( len>0 && res[len-1]==S[i]){
res.pop_back();
len--;
}
else{
res += S[i];
len++;
}
}
return res;
}
};
Leetcode1048. Longest String Chain
Given a list of words, each word consists of English lowercase letters.
Let’s say word1 is a predecessor of word2 if and only if we can add exactly one letter anywhere in word1 to make it equal to word2. For example, “abc” is a predecessor of “abac”.
A word chain is a sequence of words [word_1, word_2, …, word_k] with k >= 1, where word_1 is a predecessor of word_2, word_2 is a predecessor of word_3, and so on.
Return the longest possible length of a word chain with words chosen from the given list of words.
Example 1:1
2
3Input: words = ["a","b","ba","bca","bda","bdca"]
Output: 4
Explanation: One of the longest word chain is "a","ba","bda","bdca".
Example 2:1
2Input: words = ["xbc","pcxbcf","xb","cxbc","pcxbc"]
Output: 5
Constraints:
- 1 <= words.length <= 1000
- 1 <= words[i].length <= 16
- words[i] only consists of English lowercase letters.
这道题给了一个单词数组,定义了一种前任关系,说是假如在 word1 中任意位置加上一个字符,能变成 word2 的话,那么 word1 就是 word2 的前任,实际上 word1 就是 word2 的一个子序列。现在问在整个数组中最长的前任链有多长,暴力搜索的话会有很多种情况,会产生大量的重复计算,所以会超时。这种玩数组求极值的题十有八九都是用动态规划 Dynamic Programming 来做的,这道题其实跟之前那道 Longest Arithmetic Subsequence 求最长的等差数列的思路是很像的。首先来定义 dp 数组,这里用一个一维的数组就行了,其中 dp[i] 表示 [0, i] 区间的单词的最长的前任链。下面来推导状态转移方程,对于当前位置的单词,需要遍历前面所有的单词,这里需要先给单词按长度排个序,因为只有长度小1的单词才有可能是前任,所以只需要遍历之前所有长度正好小1的单词,若是前任关系,则用其 dp 值加1来更新当前 dp 值即可。判断前任关系可以放到一个子数组中来做,其实就是检测是否是子序列,没啥太大的难度,参见代码如下:
1 | class Solution { |
论坛上的高分解法在检验是否是前任时用了一种更好的方法,不是检测子序列,而是将当前的单词,按顺序每次去掉一个字符,然后看剩下的字符串是否在之前出现过,是的话就说明有前任,用其 dp 值加1来更新当前 dp 值,这是一种更巧妙且简便的方法。这里由于要快速判断前任是否存在,所以不是用的 dp 数组,而是用了个 HashMap,对于每个遍历到的单词,按顺序移除掉每个字符,若剩余的部分在 HashMap 中,则更新 dp 值和结果 res,参见代码如下:
1 | class Solution { |
Leetcode1049. Last Stone Weight II
You are given an array of integers stones where stones[i] is the weight of the ith stone.
We are playing a game with the stones. On each turn, we choose any two stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:
If x == y, both stones are destroyed, and
If x != y, the stone of weight x is destroyed, and the stone of weight y has new weight y - x.
At the end of the game, there is at most one stone left.
Return the smallest possible weight of the left stone. If there are no stones left, return 0.
Example 1:1
2
3
4
5
6
7Input: stones = [2,7,4,1,8,1]
Output: 1
Explanation:
We can combine 2 and 4 to get 2, so the array converts to [2,7,1,8,1] then,
we can combine 7 and 8 to get 1, so the array converts to [2,1,1,1] then,
we can combine 2 and 1 to get 1, so the array converts to [1,1,1] then,
we can combine 1 and 1 to get 0, so the array converts to [1], then that's the optimal value.
Example 2:1
2Input: stones = [31,26,33,21,40]
Output: 5
Example 3:1
2Input: stones = [1,2]
Output: 1
Constraints:
- 1 <= stones.length <= 30
- 1 <= stones[i] <= 100
这道题是之前那道 Last Stone Weight 的拓展,之前那道题说是每次取两个最大的进行碰撞,问最后剩下的重量。而这里是可以任意取两个石头进行碰撞,并且需要最后剩余的重量最小,这种玩数组求极值的题十有八九都是用动态规划 Dynamic Programming 来做的。首先来考虑 dp 数组该如何定义,若是直接用 dp[i] 来表示区间 [0, i] 内的石头碰撞后剩余的最小重量,状态转移方程将十分难推导,因为石子是任意选的,当前的 dp 值和之前的没有太大的联系。这里需要重新考虑 dp 数组的定义,这道题的解法其实挺难想的,需要转换一下思维,虽说是求碰撞后剩余的重量,但实际上可以看成是要将石子分为两堆,且尽可能让二者的重量之和最接近。若分为的两堆重量相等,则相互碰撞后最终将直接湮灭,剩余为0;若不相等,则剩余的重量就是两堆石子的重量之差。这道题给的数据范围是石子个数不超过 30 个,每个的重量不超过 100,这样的话总共的石子重量不超过 3000,分为两堆的话,每堆的重量不超过 1500。我们应该将 dp[i] 定义为数组中的石子是否能组成重量为i的一堆,数组大小设为 1501 即可,且 dp[0] 初始化为 true。这里的状态转移的思路跟之前那道 Coin Change 是很相似的,遍历每个石头,累加当前石头重量到 sum,然后从 1500 和 sum 中的较小值开始遍历(因为每堆的总重量不超过 1500),且i要大于 stone,小于当前石头的i不需要更新,由于当前的石头重量 stone 知道了,那么假如 i-stone 的 dp 值为 true 的话,则 dp[i] 也一定为 true。更新完成之后,从 sum/2 开始遍历,假如其 dp 值为 true,则用总重量 sum 减去当前重量的2倍,就是二堆石头重量的差值了,也就是碰撞后的剩余重量了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
vector<bool> dp(1501);
dp[0] = true;
int sum = 0;
for (int stone : stones) {
sum += stone;
for (int i = min(1500, sum); i >= stone; --i) {
dp[i] = dp[i] || dp[i - stone];
}
}
for (int i = sum / 2; i >= 0; --i) {
if (dp[i]) return sum - 2 * i;
}
return 0;
}
};
Leetcode1051. Height Checker
Students are asked to stand in non-decreasing order of heights for an annual photo.
Return the minimum number of students not standing in the right positions. (This is the number of students that must move in order for all students to be standing in non-decreasing order of height.)
Example 1:1
2Input: [1,1,4,2,1,3]
Output: 3
Explanation:
Students with heights 4, 3 and the last 1 are not standing in the right positions.
Note:
- 1 <= heights.length <= 100
- 1 <= heights[i] <= 100
看上去比较简单的题,找到没有按照顺序排列的数,想用一种不需要排序的方法来做,但是失败了,因为如果其他数字有序,只有一个无序,是要移动很多的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
/*int heightChecker(vector<int>& heights) {
int res=0;
for(int i=1;i<heights.size()-1;i++){
if(!(heights[i]>=heights[i-1] && heights[i]<=heights[i+1]))
res++;
}
return res;
}
*/
int heightChecker(vector<int>& h) {
int res = 0
vector<int> s = h;
sort(begin(s), end(s));
for (auto i = 0; i < h.size(); ++i)
res += h[i] != s[i];
return res;
}
};
Leetcode1052. Grumpy Bookstore Owner
Today, the bookstore owner has a store open for customers.length minutes. Every minute, some number of customers (customers[i]) enter the store, and all those customers leave after the end of that minute.
On some minutes, the bookstore owner is grumpy. If the bookstore owner is grumpy on the i-th minute, grumpy[i] = 1, otherwise grumpy[i] = 0. When the bookstore owner is grumpy, the customers of that minute are not satisfied, otherwise they are satisfied.
The bookstore owner knows a secret technique to keep themselves not grumpy for X minutes straight, but can only use it once.
Return the maximum number of customers that can be satisfied throughout the day.
Example 1:1
2
3
4Input: customers = [1,0,1,2,1,1,7,5], grumpy = [0,1,0,1,0,1,0,1], X = 3
Output: 16
Explanation: The bookstore owner keeps themselves not grumpy for the last 3 minutes.
The maximum number of customers that can be satisfied = 1 + 1 + 1 + 1 + 7 + 5 = 16.
Note:
- 1 <= X <= customers.length == grumpy.length <= 20000
- 0 <= customers[i] <= 1000
- 0 <= grumpy[i] <= 1
滑动窗口. 统计在大小为 X 的窗口中, 有多少顾客刚好处在店主脾气不好的时刻, 即grumpy[i] == 1。其中grumpy[i] == 0对应的顾客始终是满意的, 使用 base 来统计. 而对于那些grumpy[i] == 1的顾客, 只有在他们刚好在滑动窗口中, 才能满意, 用 new_satisfied 统计在滑动窗口中新满意的顾客, 在窗口滑动过程中使用 max_satisfied 来记录最大值. 最后返回 base + max_satisfied.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int maxSatisfied(vector<int>& customers, vector<int>& grumpy, int minutes) {
int res = 0, len = grumpy.size();
int sat = 0, new_sat = 0, max_sat = 0;
for (int i = 0; i < len; i ++) {
if (grumpy[i] == 0)
sat += customers[i];
else
new_sat += customers[i];
if (i >= minutes)
new_sat -= (customers[i-minutes] * grumpy[i-minutes]);
max_sat = max(max_sat, new_sat);
}
return sat + max_sat;
}
};
Leetcode1053. Previous Permutation With One Swap
Given an array of positive integers arr (not necessarily distinct), return the lexicographically largest permutation that is smaller than arr, that can be made with exactly one swap (A swap exchanges the positions of two numbers arr[i] and arr[j]). If it cannot be done, then return the same array.
Example 1:1
2
3Input: arr = [3,2,1]
Output: [3,1,2]
Explanation: Swapping 2 and 1.
Example 2:1
2
3Input: arr = [1,1,5]
Output: [1,1,5]
Explanation: This is already the smallest permutation.
Example 3:1
2
3Input: arr = [1,9,4,6,7]
Output: [1,7,4,6,9]
Explanation: Swapping 9 and 7.
Example 4:1
2
3Input: arr = [3,1,1,3]
Output: [1,3,1,3]
Explanation: Swapping 1 and 3.
Constraints:
- 1 <= arr.length <= 104
- 1 <= arr[i] <= 104
这道题给了一个正整数的数组,说是让任意交换两个数字,使得变成字母顺序最大的一种全排列,但是需要小于原先的排列,若无法得到这样的全排列(说明当前已经是最小的全排列),则返回原数组。通过分析题目中给的例子不难理解题意,根据例子2来看,若给定的数组就是升序排列的,则无法得到更小的全排列,说明只有遇到降序的位置的时候,才有可能进行交换。但是假如有多个可以下降的地方呢,比如例子1,3到2下降,2到1下降,这里是需要交换2和1的,所以最好是从后往前检验,遇到前一个数字比当前数字大的情况时,前一个数字必定是交换方之一,而当前数字并不是。比如例子3,数字4的前面是9,正确结果是9和7交换,所以还要从4往后遍历一下,找到一个仅次于9的数字交换才行,而且数字相同的话,取坐标较小的那个,比如例子4就是这种情况。
首先从后往前遍历,假如当前数字大于等于前一个数字,直接跳过,否则说明需要交换的。从当前位置再向后遍历一遍,找到第一个仅次于拐点的数字交换即可,注意下面的代码虽然嵌套了两个 for 循环,其实是线性的时间复杂度,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
vector<int> prevPermOpt1(vector<int>& arr) {
int n = arr.size(), mx = 0, idx = -1;
for (int i = n - 1; i > 0; --i) {
if (arr[i] >= arr[i - 1]) continue;
for (int j = i; j < n; ++j) {
if (arr[j] < arr[i - 1] && mx < arr[j]) {
mx = arr[j];
idx = j;
}
}
swap(arr[i - 1], arr[idx]);
break;
}
return arr;
}
};
Leetcode1054. Distant Barcodes
In a warehouse, there is a row of barcodes, where the ith barcode is barcodes[i].
Rearrange the barcodes so that no two adjacent barcodes are equal. You may return any answer, and it is guaranteed an answer exists.
Example 1:1
2Input: barcodes = [1,1,1,2,2,2]
Output: [2,1,2,1,2,1]
Example 2:1
2Input: barcodes = [1,1,1,1,2,2,3,3]
Output: [1,3,1,3,1,2,1,2]
Constraints:
- 1 <= barcodes.length <= 10000
- 1 <= barcodes[i] <= 10000
这道题说在一个仓库,有一排条形码,这里用数字表示,现在让给数字重新排序,使得相邻的数字不相同,并且说了一定会有合理的答案。意思就是说最多的重复个数不会超过数组长度的一半,否则一定会有相邻的重复数字。那么来分析一下题目,既然是为了避免重复数字被排在相邻的位置,肯定是要优先关注出现次数多的数字,因为它们更有可能出现在相邻的位置。这道题是可以用贪婪算法来做的,每次取出出现次数最多的两个数字,将其先排列起来,然后再取下一对出现次数最多的两个数字,以此类推直至排完整个数组。这里为了快速知道出现次数最多的数字,可以使用优先队列来做,里面放一个 pair 对儿,由频率和数字组成,这样优先队列就可以根据频率由高到低来自动排序了。统计频率的话就使用一个 HashMap,然后将频率和数字组成的 pair 对儿加入优先队列。进行 while 循环,条件是队列中的 pair 对儿至少两个,这样才能每次取出两个,将其加入结果 res 中,然后其频率分别减1,只要没减到0,就都加回优先队列中。最后可能队列还有一个剩余,有的话将数字加入结果 res 中即可,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<int> rearrangeBarcodes(vector<int>& barcodes) {
vector<int> res;
priority_queue<pair<int, int>> pq;
unordered_map<int, int> numCnt;
for (int num : barcodes) ++numCnt[num];
for (auto &a : numCnt) {
pq.push({a.second, a.first});
}
while (pq.size() > 1) {
auto a = pq.top(); pq.pop();
auto b = pq.top(); pq.pop();
res.push_back(a.second);
res.push_back(b.second);
if (--a.first > 0) pq.push(a);
if (--b.first > 0) pq.push(b);
}
if (!pq.empty())
res.push_back(pq.top().second);
return res;
}
};
论坛上的高分解法貌似没有用到优先队列,不过整个思路还是大体相同的,还是用 HashMap 来统计频率,这里将组成的频率和数字的 pair 对儿放到一个数组中,然后给数组按照从大到小的顺序来排列。接下里就要填充 res 数组了,方法是先填偶数坐标的位置,将频率最大的数字分别填进去,当偶数坐标填完了之后,再填奇数坐标的位置,这样保证不会有相连的重复数字。使用一个变量 pos,表示当前要填的坐标,初始化为0,之后来遍历这个频率和数字的 pair 对儿,从高到低,先填充所有偶数,若 pos 大于数组长度了,则切换为填充奇数即可,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
vector<int> rearrangeBarcodes(vector<int>& barcodes) {
int n = barcodes.size(), pos = 0;
vector<int> res(n);
vector<pair<int, int>> vec;
unordered_map<int, int> numCnt;
for (int num : barcodes) ++numCnt[num];
for (auto &a : numCnt) {
vec.push_back({a.second, a.first});
}
sort(vec.rbegin(), vec.rend());
for (auto &a : vec) {
for (int i = 0; i < a.first; ++i, pos += 2) {
if (pos >= n) pos = 1;
res[pos] = a.second;
}
}
return res;
}
};
Leetcode1055. Shortest Way to Form String
From any string, we can form a subsequence of that string by deleting some number of characters (possibly no deletions).
Given two strings source and target, return the minimum number of subsequences of source such that their concatenation equals target. If the task is impossible, return -1.
Example 1:1
2
3Input: source = "abc", target = "abcbc"
Output: 2
Explanation: The target "abcbc" can be formed by "abc" and "bc", which are subsequences of source "abc".
Example 2:1
2
3Input: source = "abc", target = "acdbc"
Output: -1
Explanation: The target string cannot be constructed from the subsequences of source string due to the character "d" in target string.
Example 3:1
2
3Input: source = "xyz", target = "xzyxz"
Output: 3
Explanation: The target string can be constructed as follows "xz" + "y" + "xz".
Constraints:
- Both the source and target strings consist of only lowercase English letters from “a”-“z”.
- The lengths of source and target string are between 1 and 1000.
这道题说我们可以通过删除某些位置上的字母从而形成一个新的字符串,现在给了两个字符串 source 和 target,问最少需要删除多个字母,可以把 source 字母串拼接成为 target。注意这里的 target 字符串可能会远长于 source,所以需要多个 source 字符串 concatenate 到一起,然后再进行删除字母。对于 target 中的每个字母,都需要在 source 中匹配到,所以最外层循环肯定是遍历 target 中的每个字母,可以使用一个指针j,初始化赋值为0,接下来就要在 source 中匹配这个 target[j],所以需要遍历一下 source 字符串,如果匹配上了 target[j],则j自增1,继续匹配下一个,当循环退出后,此时有一种情况需要考虑,就是对于这个 target[j] 字母,整个 source 字符串都无法匹配,说明 target 中存在 source 中没有的字母,这种情况下是要返回 -1 的,如何判定这种情况呢?当然可以在最开始把 source 中所有的字母放到一个 HashSet 中,然后对于 target 中每个字母都检测看是否在集合中。但这里可以使用更简便的方法,就是在遍历 source 之前,用另一个变量 pre 记录当前j的位置,然后当遍历完 source 之后,若j没有变化,则说明有其他字母存在,直接返回 -1 即可,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int shortestWay(string source, string target) {
int res = 0, j = 0, m = source.size(), n = target.size();
while (j < n) {
int pre = j;
for (int i = 0; i < m; ++i) {
if (j < n && source[i] == target[j]) ++j;
}
if (j == pre) return -1;
++res;
}
return res;
}
};
下面这种方法思路和上面基本一样,就是没有直接去遍历 source 数组,而是使用了 STL 的 find 函数。开始还是要遍历 target 字符串,对于每个字母,首先在 source 中调用 find 函数查找一下,假如找不到,直接返回 -1。有的话,就从 pos+1 位置开始再次查找该字母,且其位置赋值为 pos,注意这里 pos+1 的原因是因为其初始化为了 -1,需要从0开始找,或者 pos 已经赋值为上一个匹配位置了,所以要从下一个位置开始查找。假如 pos 为 -1 了,说明当前剩余字母中无法匹配了,需要新的一轮循环,此时将 res 自增1,并将 pos 赋值为新的 source 串中的第一个匹配位置,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int shortestWay(string source, string target) {
int res = 1, pos = -1, n = target.size();
for (int i = 0; i < n; ++i) {
if (source.find(target[i]) == -1) return -1;
pos = source.find(target[i], pos + 1);
if (pos == -1) {
++res;
pos = source.find(target[i]);
}
}
return res;
}
};
Leetcode1056. Confusing Number
Given a number N, return true if and only if it is a confusing number , which satisfies the following condition:
We can rotate digits by 180 degrees to form new digits. When 0, 1, 6, 8, 9 are rotated 180 degrees, they become 0, 1, 9, 8, 6 respectively. When 2, 3, 4, 5 and 7 are rotated 180 degrees, they become invalid. A confusing number is a number that when rotated 180 degrees becomes a different number with each digit valid.
Example 1:1
2
3
4Input: 6
Output: true
Explanation:
We get `9` after rotating `6`, `9` is a valid number and `9!=6`.
Example 2:1
2
3
4Input: 89
Output: true
Explanation:
We get `68` after rotating `89`, `86` is a valid number and `86!=89`.
Example 3:1
2
3
4Input: 11
Output: false
Explanation:
We get `11` after rotating `11`, `11` is a valid number but the value remains the same, thus `11` is not a confusing number.
Example 4:1
2
3
4Input: 25
Output: false
Explanation:
We get an invalid number after rotating `25`.
Note:
- 0 <= N <= 10^9
- After the rotation we can ignore leading zeros, for example if after rotation we have 0008 then this number is considered as just 8.
这道题定义了一种迷惑数,将数字翻转 180 度,其中 0, 1, 8 旋转后保持不变,6变成9,9变成6,数字 2, 3, 4, 5, 和 7 旋转后变为非法数字。若能将某个数翻转后成为一个合法的新的数,就说这个数是迷惑数。这道题的难度并不大,就是考察的是遍历整数各个位上的数字,使用一个 while 循环,然后用 mod10 取出当前最低位上的数字,将不合法的数字放入一个 HashSet 中,这样直接在 HashSet 中查找一下当前数字是否存在,存在直接返回 false。不存在的话,则要进行翻转,因为只有6和9两个数字翻转后会得到不同的数字,所以单独判断一下,然后将当前数字拼到 num 的最低位即可,最终拼成的 num 就是原数字 N 的翻转,最后别忘了比较一下是否相同,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
bool confusingNumber(int N) {
int num = 0, oldN = N;
unordered_set<int> invalid{{2, 3, 4, 5, 7}};
while (N > 0) {
int digit = N % 10;
if (invalid.count(digit)) return false;
if (digit == 6) digit = 9;
else if (digit == 9) digit = 6;
num = num * 10 + digit;
N /= 10;
}
return num != oldN;
}
};
这也可以用一个 HashMap 来建立所有的数字映射,然后还是用一个变量 oldN 来记录原来的数字,然后遍历N上的每一位数字,若其不在 HashMap 中,说明有数字无法翻转,直接返回 false,否则就把翻转后的数字加入 res,最后只要看 res 和 oldN 是否相等即可,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
bool confusingNumber(int N) {
unordered_map<int, int> m{{0, 0}, {1, 1}, {6, 9}, {8, 8}, {9, 6}};
long oldN = N, res = 0;
while (N > 0) {
if (!m.count(N % 10)) return false;
res = res * 10 + m[N % 10];
N /= 10;
}
return res != oldN;
}
};
下面来看一种双指针的解法,这里先用一个数组 rotate 来按位记录每个数字翻转后得到的数字,用 -1 来表示非法情况,然后将数字 N 转为字符串,用两个指针 left 和 right 分别指向开头和末尾。用 while 循环进行遍历,假如此时 left 和 right 中有任何一个指向的数字翻转后是非法,直接返回 false。然后看 left 指向的数字翻转后跟 right 指向的数字是否相同,若不同,则将 res 标记为 true,然后移动 left 和 right 指针,最终返回 res 即可,参见代码如下:
解法三:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
bool confusingNumber(int N) {
bool res = false;
vector<int> rotate{0, 1, -1, -1, -1, -1, 9, -1, 8, 6};
string str = to_string(N);
int n = str.size(), left = 0, right = n - 1;
while (left <= right) {
if (rotate[str[left] - '0'] == -1 || rotate[str[right] - '0'] == -1) return false;
if (rotate[str[left] - '0'] != (str[right] - '0')) res = true;
++left; --right;
}
return res;
}
};
Leetcode1057. Campus Bikes
On a campus represented as a 2D grid, there are N workers and M bikes, with N <= M. Each worker and bike is a 2D coordinate on this grid.
Our goal is to assign a bike to each worker. Among the available bikes and workers, we choose the (worker, bike) pair with the shortest Manhattan distance between each other, and assign the bike to that worker. (If there are multiple (worker, bike) pairs with the same shortest Manhattan distance, we choose the pair with the smallest worker index; if there are multiple ways to do that, we choose the pair with the smallest bike index). We repeat this process until there are no available workers.
The Manhattan distance between two points p1 and p2 is Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|.
Return a vector ans of length N, where ans[i] is the index (0-indexed) of the bike that the i-th worker is assigned to.
Example 1:1
2
3
4Input: workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]]
Output: [1,0]
Explanation:
Worker 1 grabs Bike 0 as they are closest (without ties), and Worker 0 is assigned Bike 1. So the output is [1, 0].
Example 2:1
2
3
4Input: workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]]
Output: [0,2,1]
Explanation:
Worker 0 grabs Bike 0 at first. Worker 1 and Worker 2 share the same distance to Bike 2, thus Worker 1 is assigned to Bike 2, and Worker 2 will take Bike 1. So the output is [0,2,1].
Note:
- 0 <= workers[i][j], bikes[i][j] < 1000
- All worker and bike locations are distinct.
- 1 <= workers.length <= bikes.length <= 1000
这道题用一个二维数组来表示一个校园坐标,上面有一些人和共享单车,人的数量不多余单车的数量,现在要让每一个人都分配一辆单车,人和单车的距离是用曼哈顿距离表示的。这里的分配方法其实是有一些 confuse 的,并不是每个人要拿离其距离最近的单车,也不是每辆单车要分配给距离其最近的人,而是要从所有的 单车-人 对儿中先挑出距离最短的一对儿,然后再挑出距离第二短的组合,以此类推,直到所有的人都被分配到单车了为止。这样的话就需要求出每一对人车距离,将所有的人车距离,和对应的人和车的标号都存到一个二维数组中。然后对这个二维数组进行排序,这里需要重写排序规则,将人车距离小的排前面,假如距离相等,则将人标号小的放前面,假如人的标号也相同,则就将车标号小的放前面。对人车距离数组排好序之后,此时需要两个数组来分别标记每个人被分配的车标号,和每个车的主人标号。现在从最小的人车距离开始取,若此时的人和车都没有分配,则进行分配,遍历完所有的人车距离之后,最终的结果就存在了标记每个人分配的车标号的数组中,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
vector<int> assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {
int m = workers.size(), n = bikes.size();
vector<int> assignedWorker(m, -1), assignedBike(n, -1);
vector<vector<int>> dist;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int d = abs(workers[i][0] - bikes[j][0]) + abs(workers[i][1] - bikes[j][1]);
dist.push_back({d, i, j});
}
}
sort(dist.begin(), dist.end(), [](vector<int>& a, vector<int>& b) {
return a[0] < b[0] || (a[0] == b[0] && a[1] < b[1]) || (a[0] == b[0] && a[1] == b[1] && a[2] < b[2]);
});
for (auto &a : dist) {
if (assignedWorker[a[1]] == -1 && assignedBike[a[2]] == -1) {
assignedWorker[a[1]] = a[2];
assignedBike[a[2]] = a[1];
}
}
return assignedWorker;
}
};
上面的解法虽然可以通过 OJ,但是并不是很高效,应该是排序的部分拖慢了速度。其实这道题的范围是有限的,因为车和人的坐标是有限的,最大的人车距离也不会超过 2000,那么利用桶排序来做就是个不错的选择,只需要 2001 个桶就行了,桶中放的是 pair 对儿,其中 buckets[i] 表示距离是i的人和车的标号组成的 pair 对儿。这样当计算出每个人车距离后,将其放入对应的桶中即可,就自动排好了序。然后开始遍历每个桶,由于每个桶中可能不止放了一个 pair 对儿,所以需要遍历每个桶中所有的组合,然后的操作就和上面的相同了,若此时的人和车都没有分配,则进行分配,遍历完所有的人车距离之后,最终的结果就存在了标记每个人分配的车标号的数组中,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<int> assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {
int m = workers.size(), n = bikes.size();
vector<int> assignedWorker(m, -1), assignedBike(n, -1);
vector<vector<pair<int, int>>> buckets(2001);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int dist = abs(workers[i][0] - bikes[j][0]) + abs(workers[i][1] - bikes[j][1]);
buckets[dist].push_back({i, j});
}
}
for (int dist = 0; dist <= 2000; ++dist) {
for (int k = 0; k < buckets[dist].size(); ++k) {
if (assignedWorker[buckets[dist][k].first] == -1 && assignedBike[buckets[dist][k].second] == -1) {
assignedWorker[buckets[dist][k].first] = buckets[dist][k].second;
assignedBike[buckets[dist][k].second] = buckets[dist][k].first;
}
}
}
return assignedWorker;
}
};
Leetcode1058. Minimize Rounding Error to Meet Target
Given an array of prices [p1,p2…,pn] and a target, round each price pi to Roundi(pi) so that the rounded array [Round1(p1),Round2(p2)…,Roundn(pn)] sums to the given target. Each operation Roundi(pi) could be either Floor(pi) or Ceil(pi).
Return the string “-1” if the rounded array is impossible to sum to target. Otherwise, return the smallest rounding error, which is defined as Σ |Roundi(pi) - (pi)| for i from 1 to n, as a string with three places after the decimal.
Example 1:1
2
3
4Input: prices = [“0.700”,”2.800”,”4.900”], target = 8
Output: “1.000”
Explanation:
Use Floor, Ceil and Ceil operations to get (0.7 - 0) + (3 - 2.8) + (5 - 4.9) = 0.7 + 0.2 + 0.1 = 1.0 .
Example 2:1
2
3
4Input: prices = [“1.500”,”2.500”,”3.500”], target = 10
Output: “-1”
Explanation:
It is impossible to meet the target.
Note:
- 1 <= prices.length <= 500.
- Each string of prices prices[i] represents a real number which is between 0 and 1000 and has exactly 3 decimal places.
target is between 0 and 1000000.
如果一个数字是一个整数, 那么我们只能取floor,不能取ceil。这相当于一个无法调整的数字,否则就是一个可调整的数字。我们把所有可调整的数字的小数部分放入一个priority queue中,把priority queue的size记为pqsize。
然后我们先判断什么情况下无法得到target:
- 如果取最小的可能的和,那么所有数字都要取floor。如果这个和仍然比target大,或者比target-pqsize小,那么就说明无论如何也不可能得到target。这样我们就返回 “-1”
- 若满足上述条件,我们一定可以取到满足题目条件的和。我们需要知道调整多少个数字,即把floor操作变成ceil操作。需要调整的数字个数等于target-pqsize。
- 为了的达到最小的rounding error,对于每个调整的操作,我们希望它们小数尽可能大,这可以由之前的priority queue得到。取那个数字的ceil。最后把所有不需要调整的小数也加上,就是最小的rounding error了。
- 注意最后返回字符串是,需要做些特殊处理,只保留最后3位小数即可。
1 | class Solution { |
Leetcode1059. 从始点到终点的所有路径
给定有向图的边 edges,以及该图的始点 source 和目标终点 destination,确定从始点 source 出发的所有路径是否最终结束于目标终点 destination,即:
- 从始点 source 到目标终点 destination 存在至少一条路径
- 如果存在从始点 source 到没有出边的节点的路径,则该节点就是路径终点。
- 从始点source到目标终点 destination 可能路径数是有限数字
- 当从始点 source 出发的所有路径都可以到达目标终点 destination 时返回 true,否则返回 false。
1 | 输入:n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2 |
1 | 输入:n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3 |
1 | 输入:n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3 |
简单dfs,搜索时不能搜索到非end的断头路或者有end在中间的路。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution{
public:
bool leadToDestination(int n,std::vector<std::vector<int>>& edge,int start,int end){
std::vector<std::vector<int>> m(m);
std::vector<bool> visited(n,false);
for(auto e:edge){
m[e[0]].push_back(e[1]);
}
if(!m[end].empty()){
return false;
}
return DFS(m,visited,start,end);
}
bool DFS(std::vector<std::vector<int>>& m,std::vector<bool>& visitd,int cur,int end){
if(!m[cur].size()==0&&cur!=end){
return false;
}
for(auto next:m[cur]){
if(visitd[next]){
return false;
}
visitd[next]=true;
if(!DFS(m,visitd,cur,end)){
return false;
}
visitd[next]=false;
}
}
};
Leetcode1060. Missing Element in Sorted Array
Given a sorted array A of unique numbers, find the K-th missing number starting from the leftmost number of the array.
Example 1:1
2
3
4Input: A = [4,7,9,10], K = 1
Output: 5
Explanation:
The first missing number is 5.
Example 2:1
2
3
4Input: A = [4,7,9,10], K = 3
Output: 8
Explanation:
The missing numbers are [5,6,8,...], hence the third missing number is 8.
Example 3:1
2
3
4Input: A = [1,2,4], K = 3
Output: 6
Explanation:
The missing numbers are [3,5,6,7,...], hence the third missing number is 6.
Note:
- 1 <= A.length <= 50000
- 1 <= A[i] <= 1e7
- 1 <= K <= 1e8
给出一个有序数组 A,数组中的每个数字都是 独一无二的,找出从数组最左边开始的第 K 个缺失数字。
拿到这个题之后,看了下Note中取值范围都比较大,因此如果想一个数字一个数字去判断的话肯定会超时。所以需要使用一个点小技巧,即跳过不需要判断的数字。直接计算出每两个相邻数字之间能满足多少个,从而更新k。
先对nums排序。然后开始遍历,计算nums相邻两个元素之间的数字数即nums[i] - pre - 1个,是否可以满足需要的k。如果能满足,那么直接找出要返回的数字pre+k。如果不能满足,把k去掉已能满足的数字nums[i] - pre - 1。最后如果所有的nums数字都已经用完,但是还不能满足k,则需要返回nums[nums.size() - 1] + k。
1 | class Solution { |
Leetcode1061. 按字典序排列最小的等效字符串
给出长度相同的两个字符串:A 和 B,其中 A[i] 和 B[i] 是一组等价字符。举个例子,如果 A = “abc” 且 B = “cde”,那么就有 ‘a’ == ‘c’, ‘b’ == ‘d’, ‘c’ == ‘e’。
等价字符遵循任何等价关系的一般规则:
- 自反性:’a’ == ‘a’
- 对称性:’a’ == ‘b’ 则必定有 ‘b’ == ‘a’
- 传递性:’a’ == ‘b’ 且 ‘b’ == ‘c’ 就表明 ‘a’ == ‘c’
例如,A 和 B 的等价信息和之前的例子一样,那么 S = “eed”, “acd” 或 “aab”,这三个字符串都是等价的,而 “aab” 是 S 的按字典序最小的等价字符串。利用 A 和 B 的等价信息,找出并返回 S 的按字典序排列最小的等价字符串。
示例 1:1
2
3
4
5输入:A = "parker", B = "morris", S = "parser"
输出:"makkek"
解释:根据 A 和 B 中的等价信息,
我们可以将这些字符分为 [m,p], [a,o], [k,r,s], [e,i] 共 4 组。
每组中的字符都是等价的,并按字典序排列。所以答案是 "makkek"。
示例 2:1
2
3
4
5输入:A = "hello", B = "world", S = "hold"
输出:"hdld"
解释:根据 A 和 B 中的等价信息,
我们可以将这些字符分为 [h,w], [d,e,o], [l,r] 共 3 组。
所以只有 S 中的第二个字符 'o' 变成 'd',最后答案为 "hdld"。
示例 3:1
2
3
4
5输入:A = "leetcode", B = "programs", S = "sourcecode"
输出:"aauaaaaada"
解释:我们可以把 A 和 B 中的等价字符分为
[a,o,e,r,s,c], [l,p], [g,t] 和 [d,m] 共 4 组,
因此 S 中除了 'u' 和 'd' 之外的所有字母都转化成了 'a',最后答案为 "aauaaaaada"。
并查集merge的时候,让祖先字符更小的作为代表1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class dsu
{
vector<int> f;
public:
dsu(int n)
{
f.resize(n);
for(int i = 0; i < n; ++i)
f[i] = i;
}
void merge(int a, int b)
{
int fa = find(a), fb = find(b);
if(fa > fb)//字母小的当代表,关键点
f[fa] = fb;
else
f[fb] = fa;
}
int find(int a)
{
int origin = a;
while(a != f[a])
a = f[a];
return f[origin] = a;
}
};
class Solution {
public:
string smallestEquivalentString(string A, string B, string S) {
dsu u(26);
for(int i = 0; i < A.size(); ++i)
u.merge(A[i]-'a', B[i]-'a');
for(int i = 0; i < S.size(); ++i)
S[i] = u.find(S[i]-'a')+'a';
return S;
}
};
Leetcode1062. Longest Repeating Substring
Given a string S, find out the length of the longest repeating substring(s). Return 0 if no repeating substring exists.
Example 1:1
2
3Input: “abcd”
Output: 0
Explanation: There is no repeating substring.
Example 2:1
2
3Input: “abbaba”
Output: 2
Explanation: The longest repeating substrings are “ab” and “ba”, each of which occurs twice.
Example 3:1
2
3Input: “aabcaabdaab”
Output: 3
Explanation: The longest repeating substring is “aab”, which occurs 3 times.
Example 4:1
2
3Input: “aaaaa”
Output: 4
Explanation: The longest repeating substring is “aaaa”, which occurs twice.
Constraints:
- The string S consists of only lowercase English letters from ‘a’ - ‘z’.
- 1 <= S.length <= 1500
解题思路:这题我们采用动态规划的方法。我们先定义dp[i][j]为分别以第i个字符和第j个字符结尾的substring有相同共同后缀的最大长度。因此,我们也要求i>j。我们注意到,当S[i] != S[j],那么dp[i][j] = 0,否则dp[i][j] = dp[i-1][j-1] + 1。这就是我们的状态转移方程。1
2dp[i][j] = dp[i-1][j-1] + 1 ----------- S[i] == S[j]
dp[i][j] = 0 -------------------------- S[i] != S[j]
我们更新dp[i][j]的最大值,就可以得到最后的答案。
1 | class Solution { |
复杂度分析
- N是字符串的长度。
- 时间复杂度: O(N^2)
- 空间复杂度: O(N^2)
Leetcode 1064. Fixed Point
Given an array A of distinct integers sorted in ascending order, return the smallest index i that satisfies A[i] == i. Return -1 if no such i exists.
Example 1:1
2
3
4Input: [-10,-5,0,3,7]
Output: 3
Explanation:
For the given array, A[0] = -10, A[1] = -5, A[2] = 0, A[3] = 3, thus the output is 3.
Example 2:1
2
3
4Input: [0,2,5,8,17]
Output: 0
Explanation:
A[0] = 0, thus the output is 0.
Example 3:1
2
3
4Input: [-10,-5,3,4,7,9]
Output: -1
Explanation:
There is no such i that A[i] = i, thus the output is -1.
Note:
- 1 <= A.length < 10^4
- -10^9 <= A[i] <= 10^9
因为给出的是一个排序的array,而index也是自然从0到n-1的排序数组,因此本题采用二分法来查找A[i] == i的index。当i < A[i],我们往左边查找,当i >= A[i]时, 我们往右边查找。需要注意的因为要求最小的index,我们更新右端点时,需要i >= A[i]。如果是最大的index, 则应该是i > A[i]。
1 | class Solution { |
Leetcode1065. Index Pairs of a String
Given a text string and words (a list of strings), return all index pairs [i, j] so that the substring text[i]…text[j] is in the list of words.
Example 1:1
2Input: text = “thestoryofleetcodeandme”, words = [“story”,”fleet”,”leetcode”]
Output: [[3,7],[9,13],[10,17]]
Example 2:1
2
3
4Input: text = “ababa”, words = [“aba”,”ab”]
Output: [[0,1],[0,2],[2,3],[2,4]]
Explanation:
Notice that matches can overlap, see “aba” is found in [0,2] and [2,4].
Note:
- All strings contains only lowercase English letters.
- It’s guaranteed that all strings in words are different.
- 1 <= text.length <= 100
- 1 <= words.length <= 20
- 1 <= words[i].length <= 50
Return the pairs [i,j] in sorted order (i.e. sort them by their first coordinate in case of ties sort them by their second coordinate).
这道题可以直接用string find函数来做,但是需要分析一下时间复杂度。取决于具体的函数实现,比如CPP的find函数没有用KMP实现,所以最坏的情况复杂度是O(M N),这样带入本题,时间复杂度是`O(M sum(len(word)))。其中M是text的长度,sum(len(word))`是words中word的长度之和。
如果用字典树Trie来实现,则当M < sum(len(word))时,时间复杂度可以优化。首先建立基于words的字典树trie,然后在text中以每一个位置i为起点向后遍历,并判断往后每一个位置j是否在字典树中,若在则加入要返回的结果rets中。
1 | struct Trie { |
Leetcode1071. Greatest Common Divisor of Strings
For strings S and T, we say “T divides S” if and only if S = T + … + T (T concatenated with itself 1 or more times)
Return the largest string X such that X divides str1 and X divides str2.
Example 1:1
2Input: str1 = "ABCABC", str2 = "ABC"
Output: "ABC"
Example 2:1
2Input: str1 = "ABABAB", str2 = "ABAB"
Output: "AB"
Example 3:1
2Input: str1 = "LEET", str2 = "CODE"
Output: ""
最长公共重复子串重复若干次之后能分别得到str1和str2,那么最明显地,该子串的长度一定是str1和str2长度的公因数。看了一下字符串的长度最多只有1000,所以我们完全可以对长度进行遍历,判断每个公因数是不是构成最长公共重复子串。因为要找最长的,所以找到最长之后,直接返回即可。时间复杂度O(N^2)。外部循环找到公因数,时间复杂度O(N);内部要创建新的字符串和原先的字符串进行比较,时间复杂度也是O(N)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
string gen(string str, int i) {
string res;
while (i--) {
res += str;
}
return res;
}
string gcdOfStrings(string str1, string str2) {
int l1 = str1.length(), l2 = str2.length();
int length = min(l1, l2);
string res;
for(int i = length; i > 0; i --) {
if(l1 % i == 0 && l2 % i == 0) {
int t1 = l1 / i;
int t2 = l2 / i;
string gcd = str1.substr(0, i);
string s1 = gen(gcd, t1);
string s2 = gen(gcd, t2);
if ((s1 == str1) && (s2 == str2)) {
res = gcd;
break;
}
}
}
return res;
}
};
题目要求 X 能除尽 str1 且 X 能除尽 str2,且 X 为最长。那么可以理解为 str1 由 m 个 X 连接而成, str2 由 n 个 X 连接而成。由此可知 str1 + str2 由 m + n 个 X 拼接而成,而且 str1 + str2 与 str2 + str1 在值上是相等的。然后此题就转化为了求最大公约数。str1 和 str2 长度的最大公约数,就是所求 X 的长度。
辗转相除法是递归算法,一句话概括这个算法就是:两个整数的最大公约数,等于其中较小的数 和两数相除余数 的最大公约数。比如 10 和 25,25 除以 10 商 2 余 5,那么 10 和 25 的最大公约数,等同于 10 和 5 的最大公约数。
1 | class Solution { |
Leetcode1072. Flip Columns For Maximum Number of Equal Rows
You are given an m x n binary matrix matrix.
You can choose any number of columns in the matrix and flip every cell in that column (i.e., Change the value of the cell from 0 to 1 or vice versa).
Return the maximum number of rows that have all values equal after some number of flips.
Example 1:1
2
3Input: matrix = [[0,1],[1,1]]
Output: 1
Explanation: After flipping no values, 1 row has all values equal.
Example 2:1
2
3Input: matrix = [[0,1],[1,0]]
Output: 2
Explanation: After flipping values in the first column, both rows have equal values.
Example 3:1
2
3Input: matrix = [[0,0,0],[0,0,1],[1,1,0]]
Output: 2
Explanation: After flipping values in the first two columns, the last two rows have equal values.
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 300
- matrix[i][j] is either 0 or 1.
其实按照列翻转没有什么用,把0开头的或者1开头的,选一种,全部翻转,用哈希表计数,找到最多出现的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
int maxEqualRowsAfterFlips(vector<vector<int>>& matrix) {
unordered_map<string, int> m;
for (auto& mat : matrix) {
int length = mat.size();
string str(length, ' ');
if (mat[0] == 0){
for(int i = 0; i < length; i ++) {
mat[i] ^= 1;
str[i] = mat[i] == 1 ? '1': '0';
}
}
else {
for(int i = 0; i < length; i ++) {
str[i] = mat[i] == 1 ? '1' : '0';
}
}
m[str] ++;
}
int res = 0;
for (auto it = m.begin(); it != m.end(); it ++)
res = max(res, it->second);
return res;
}
};
Leetcode1073. Adding Two Negabinary Numbers
Given two numbers arr1 and arr2 in base -2, return the result of adding them together.
Each number is given in array format: as an array of 0s and 1s, from most significant bit to least significant bit. For example, arr = [1,1,0,1] represents the number (-2)^3 + (-2)^2 + (-2)^0 = -3. A number arr in array, format is also guaranteed to have no leading zeros: either arr == [0] or arr[0] == 1.
Return the result of adding arr1 and arr2 in the same format: as an array of 0s and 1s with no leading zeros.
Example 1:1
2
3Input: arr1 = [1,1,1,1,1], arr2 = [1,0,1]
Output: [1,0,0,0,0]
Explanation: arr1 represents 11, arr2 represents 5, the output represents 16.
Example 2:1
2Input: arr1 = [0], arr2 = [0]
Output: [0]
Example 3:1
2Input: arr1 = [0], arr2 = [1]
Output: [1]
Constraints:
- 1 <= arr1.length, arr2.length <= 1000
- arr1[i] and arr2[i] are 0 or 1
- arr1 and arr2 have no leading zeros
这道题说是有两个负二进制数是用数组来表示的,现在让返回它们相加后的结果,还是放在数组中来表示。这道题其实利用的方法跟那道很像,都是一位一位的处理的,直接加到结果 res 数组中的。这里使用两个指针i和j,分别指向数组 arr1 和 arr2 的末尾,然后用个变量 carry 表示进位,当i大于等于0时,carry 加上i指向的数字,并且i自减1,同理,当j大于等于0时,carry 加上j指向的数字,并且j自减1。由于数组中当每位上只能放一个数字,所以让 carry ‘与’上1,并加入到结果 res 数组后。然后需要再填充更高一位上的数字,对于二进制来说,直接右移1位即可,这里由于是负二进制,所以右移1位之后再取负。之后要移除所有的 leading zeros,因为这里高位是加到了 res 的后面,所以要去除末尾的零,使用个 while 去除。最后别忘了将 res 翻转一下返回即可,参见代码如下:
1 | class Solution { |
Leetcode1078. Occurrences After Bigram
Given words first and second, consider occurrences in some text of the form “first second third”, where second comes immediately after first, and third comes immediately after second.
For each such occurrence, add “third” to the answer, and return the answer.
Example 1:1
2Input: text = "alice is a good girl she is a good student", first = "a", second = "good"
Output: ["girl","student"]
Example 2:1
2Input: text = "we will we will rock you", first = "we", second = "will"
Output: ["we","rock"]
Note:
- 1 <= text.length <= 1000
- text consists of space separated words, where each word consists of lowercase English letters.
- 1 <= first.length, second.length <= 10
- first and second consist of lowercase English letters.
第一种是先split,然后对比,运行时间较长但是内存占用小:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
vector<string> split(string text){
vector<string> res;
int begin=0;
string temp="";
for(int i=0;i<text.length();i++){
if(text[i]==' '){
res.push_back(temp);
temp="";
}
else{
temp = temp + text[i];
}
}
res.push_back(temp);
return res;
}
vector<string> findOcurrences(string text, string first, string second) {
int n;
vector<string> res;
vector<string> split_string = split(text);
for(int i=0;i<split_string.size()-2;i++){
if(split_string[i]==first && split_string[i+1]==second)
res.push_back(split_string[i+2]);
}
return res;
}
};
人家有的大佬是用了流做的:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
vector<string> findOcurrences(string text, string first, string second) {
vector<string>rst;
stringstream ss(text);
string s1,s2,cand;
ss>>s1>>s2;
while(ss>>cand){
if(s1==first && s2==second)rst.push_back(cand);
s1=s2;
s2=cand;
}
return rst;
}
};
Leetcode1079. Letter Tile Possibilities
You have a set of tiles, where each tile has one letter tiles[i] printed on it. Return the number of possible non-empty sequences of letters you can make.
Example 1:1
2
3Input: "AAB"
Output: 8
Explanation: The possible sequences are "A", "B", "AA", "AB", "BA", "AAB", "ABA", "BAA".
Example 2:1
2Input: "AAABBC"
Output: 188
Note:
- 1 <= tiles.length <= 7
- tiles consists of uppercase English letters.
求一个字符串的所有子串。第一想法优先使用全排列,即深度优先,但有一个核心问题:子串怎么办?全排列无法解决,子串的检索问题,这是我一开始苦思而不得解的地方。
解法一:
这是本题区别于普通全排列中,最隐蔽而又最有趣的一个点:字符串的全排列出来了,那字符串的所有不同子串,还会远吗?答案就是,全排列字符串的所有前缀子串里!检索全排列的全部不同子串(包含全排列本身),即为所求。
解法二:
因为问题的规模在7个字符内,解法一在时间和内存上均可接受。但当问题规模快速扩大时,基于解法一,如何优化?优化核心是,首先将字符串排序(排序大法好),一旦发生不同字符间的交换,则自字符串起始位置至交换发生的位置为前缀的子串,均发生变化!
1 | class Solution { |
Leetcode1080. Insufficient Nodes in Root to Leaf Paths
Given the root of a binary tree, consider all root to leaf paths: paths from the root to any leaf. (A leaf is a node with no children.)
A node is insufficient if every such root to leaf path intersecting this node has sum strictly less than limit.
Delete all insufficient nodes simultaneously, and return the root of the resulting binary tree.
Example 1:1
2Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
Output: [1,2,3,4,null,null,7,8,9,null,14]
Example 2:1
2Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
Output: [5,4,8,11,null,17,4,7,null,null,null,5]
Example 3:1
2Input: root = [1,2,-3,-5,null,4,null], limit = -1
Output: [1,null,-3,4]
Note:
- The given tree will have between 1 and 5000 nodes.
- -10^5 <= node.val <= 10^5
- -10^9 <= limit <= 10^9
这道题定义了一种不足结点,就是说经过该结点的所有根到叶路径之和的都小于给定的 limit,现在让去除所有的这样的不足结点,返回剩下的结点组成的二叉树。这题好就好在给的例子都配了图,能够很好的帮助我们理解题意,给的例子很好的覆盖了大多数的情况,博主能想到的唯一没有覆盖的情况就是可能根结点也是不足结点,这样的话有可能会返回空树。这里首先处理一下 corner case,即根结点是叶结点的情况,这样只需要看根结点值是否小于 limit,是的话直接返回空指针,因为此时的根结点是个不足结点,需要被移除,否则直接返回根结点。一个比较快速的判断是否是叶结点的方法是看其左右子结点是否相等,因为只有均为空的时候才会相等。若根结点不为叶结点,且其左子结点存在的话,就对其左子结点调用递归,此时的 limit 需要减去根结点值,将返回的结点赋值给左子结点。同理,若其右子结点存在的话,就对其右子结点调用递归,此时的 limit 需要减去根结点值,将返回的结点赋值给右子结点。最后还需要判断一下,若此时的左右子结点都被赋值为空了,则当前结点也需要被移除,因为经过其左右子结点的根到叶路径就是经过该结点的所有路径,若其和均小于 limit,则当前结点也需要被移除,参见代码如下:
1 | class Solution { |
Leetcode1081. Smallest Subsequence of Distinct Characters
Given a string s, return the lexicographically smallest subsequence of s that contains all the distinct characters of s exactly once.
Example 1:1
2Input: s = "bcabc"
Output: "abc"
Example 2:1
2Input: s = "cbacdcbc"
Output: "acdb"
找出字典序最小的子序列。一次遍历,维护一个stack,存一个降序排列的堆,堆底是最小值,如果是之前出现过的字符,则跳过;否则遇到当前字符字典序小于之前最大值,并且最大值之后还会出现,那么就pop掉,直到之前的stack没有值或者比当前小。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
string smallestSubsequence(string s) {
string res;
stack<int> st;
int* record = (int*)malloc(sizeof(int)*128);
int* visited = (int*)malloc(sizeof(int)*128);
for (int i = 0; i < 128; i ++) {
record[i] = 0;
visited[i] = 0;
}
for (char c : s)
record[c] ++;
for (char c : s) {
-- record[c];
if (visited[c])
continue;
while(!st.empty() && st.top() > c && record[st.top()] > 0) {
visited[st.top()] = 0;
st.pop();
}
st.push(c);
visited[c] = 1;
}
while(!st.empty()) {
res += (char)(st.top());
st.pop();
}
reverse(res.begin(), res.end());
return res;
}
};
这道题实际上需要用单调栈的思路来做,首先需要统计每个字母出现的次数,这里可以使用一个大小为 128 的数组 cnt 来表示,还需要一个数组 visited 来记录某个字母是否出现过。先遍历一遍字符串,统计每个字母出现的次数到 cnt 中。再遍历一遍给定的字符串,对于遍历到的字母,在 cnt 数组中减去一个,然后看该字母是否已经在 visited 数组中出现过,是的话直接跳过。否则需要进行一个 while 循环,这里的操作实际上是为了确保得到的结果是字母顺序最小的,若当前字母小于结果 res 中的最后一个字母,且该最后的字母在 cnt 中还存在,说明之后还会遇到这个字母,则可以在 res 中先去掉这个字母,以保证字母顺序最小,并且 visited 数组中标记为0,表示未访问。这里是尽可能的将 res 打造成单调递增的,但如果后面没有这个字母了,就不能移除,所以说并不能保证一定是单调递增的,但可以保证得到的结果是字母顺序最小的。while 循环退出后,将该字母加到结果 res 后,并且 visited 标记为1。这里还有个小 trick,结果 res 在初始化给个0,这样就不用判空了,而且0是小于所有字母的,不会影响这个逻辑,最后返回的时候去掉首位0就行了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
string smallestSubsequence(string s) {
string res = "0";
vector<int> cnt(128), visited(128);
for (char c : s) ++cnt[c];
for (char c : s) {
--cnt[c];
if (visited[c]) continue;
while (c < res.back() && cnt[res.back()]) {
visited[res.back()] = 0;
res.pop_back();
}
res += c;
visited[c] = 1;
}
return res.substr(1);
}
};
Leetcode1089. Duplicate Zeros
Given a fixed length array arr of integers, duplicate each occurrence of zero, shifting the remaining elements to the right. Note that elements beyond the length of the original array are not written. Do the above modifications to the input array in place, do not return anything from your function.
Example 1:1
2
3Input: [1,0,2,3,0,4,5,0]
Output: null
Explanation: After calling your function, the input array is modified to: [1,0,0,2,3,0,0,4]
Example 2:1
2
3Input: [1,2,3]
Output: null
Explanation: After calling your function, the input array is modified to: [1,2,3]
双指针也许是本题的最优解法。具体思路是维护一个快指针和一个慢指针。快指针是遇到0就多进一步。这样遍历一遍数据后,快指针和慢指针会有一个差值。这个差值就是需要填充0的个数。
接下来,我们需要从后向前遍历数组。如果慢指针指向的元素不为0,则把快指针指向的元素替换为慢指针指向的元素;如果慢指针指向的元素为0,则把快指针和快指针之前指向的元素替换为0。
你可能会发现对于不同的数组,第一遍遍历之后fast指针的值是不一样的。区别在于数组末尾是否为0,如果末尾为0,则fast指针的值(数组索引)为数组长度+1。如果末尾不是0,则fast指针的值是数组长度。其实数组最后一位是0的话,其实是不用复制这个值的。因此从后向前遍历的时候需要判断fast指针的值是否小于n,这样就可以把数组末尾为0的时候就不会复制了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int n = arr.size();
int slow = 0, fast = 0;
while(fast < n) {
if(arr[slow] == 0)
fast ++;
fast ++;
slow ++;
}
fast --;
slow --;
while(slow >= 0) {
if(fast < n)
arr[fast] = arr[slow];
if(arr[slow] == 0)
arr[--fast] = arr[slow];
fast --;
slow --;
}
}
};
Leetcode1090. Largest Values From Labels
We have a set of items: the i-th item has value values[i] and label labels[i].
Then, we choose a subset S of these items, such that:
- |S| <= num_wanted
- For every label L, the number of items in S with label L is <= use_limit.
Return the largest possible sum of the subset S.
Example 1:1
2
3Input: values = [5,4,3,2,1], labels = [1,1,2,2,3], `num_wanted` = 3, use_limit = 1
Output: 9
Explanation: The subset chosen is the first, third, and fifth item.
Example 2:1
2
3Input: values = [5,4,3,2,1], labels = [1,3,3,3,2], `num_wanted` = 3, use_limit = 2
Output: 12
Explanation: The subset chosen is the first, second, and third item.
Example 3:1
2
3Input: values = [9,8,8,7,6], labels = [0,0,0,1,1], `num_wanted` = 3, use_limit = 1
Output: 16
Explanation: The subset chosen is the first and fourth item.
Example 4:1
2
3Input: values = [9,8,8,7,6], labels = [0,0,0,1,1], `num_wanted` = 3, use_limit = 2
Output: 24
Explanation: The subset chosen is the first, second, and fourth item.
Note:
- 1 <= values.length == labels.length <= 20000
- 0 <= values[i], labels[i] <= 20000
- 1 <= num_wanted, use_limit <= values.length
这道题说是给了一堆物品,每个物品有不同的价值和标签,分别放在 values 和 labels 数组中,现在让选不超过 num_wanted 个物品,且每个标签类别的物品不超过 use_limit,问能得到的最大价值是多少。说实话这道题博主研究了好久才弄懂题意,而且主要是看例子分析出来的,看了看踩比赞多,估计许多人跟博主一样吧。这道题可以用贪婪算法来做,因为需要尽可能的选价值高的物品,但同时要兼顾到物品的标签种类。所以可以将价值和标签种类组成一个 pair 对儿,放到一个优先队列中,这样就可以按照价值从高到低进行排列了。同时,由于每个种类的物品不能超过 use_limit 个,所以需要统计每个种类被使用了多少次,可以用一个 HashMap 来建立标签和其使用次数之间的映射。先遍历一遍所有物品,将价值和标签组成 pair 对儿加入优先队列中。然后进行循环,条件是 num_wanted 大于0,且队列不为空,此时取出队顶元素,将其标签映射值加1,若此时仍小于 use_limit,说明当前物品可以入选,将其价值加到 res 中,并且 num_wanted 自减1即可,参见代码如下:
1 | class Solution { |
Leetcode1091. Shortest Path in Binary Matrix
Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.
A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:
- All the visited cells of the path are 0.
- All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).
- The length of a clear path is the number of visited cells of this path.
Example 1:1
2Input: grid = [[0,1],[1,0]]
Output: 2
Example 2:1
2Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4
Example 3:1
2Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1
Constraints:
- n == grid.length
- n == grid[i].length
- 1 <= n <= 100
- grid[i][j] is 0 or 1
这道题给了一个 nxn 的二维数组,里面都是0和1,让找出一条从左上角到右下角的干净路径,所谓的干净路径就是均由0组成,并且定义了相邻的位置是八个方向,不仅仅是通常的上下左右。例子中还给了图帮助理解,但是也有一丢丢的误导,博主最开始以为只需要往右,下,和右下三个方向走就行了,其实并不一定,任何方向都是可能的,说白了还是一道迷宫遍历的问题。既然是迷宫遍历求最少步数,那么广度优先遍历 Breadth-First Search 就是不二之选了,还是使用一个队列 queue 来做,初识时将 (0, 0) 放进去,再用一个 TreeSet 来标记访问过的位置。注意这里的方向数组要用到八个方向,while 循环中用的还是经典的层序遍历的写法,就是经典的写法,没有啥特殊的地方,博主感觉已经写了无数次了,在进行这一切之前,先判断一下起始点,若为1,直接返回 -1 即可,参见代码如下:
1 | class Solution { |
Leetcode1093. Statistics from a Large Sample
You are given a large sample of integers in the range [0, 255]. Since the sample is so large, it is represented by an array count where count[k] is the number of times that k appears in the sample.
Calculate the following statistics:
- minimum: The minimum element in the sample.
- maximum: The maximum element in the sample.
- mean: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
- median:
- If the sample has an odd number of elements, then the median is the middle element once the sample is sorted.
- If the sample has an even number of elements, then the median is the average of the two middle elements once the sample is sorted.
- mode: The number that appears the most in the sample. It is guaranteed to be unique.
Return the statistics of the sample as an array of floating-point numbers [minimum, maximum, mean, median, mode]. Answers within 10-5 of the actual answer will be accepted.
Example 1:1
2
3
4
5
6
7Input: count = [0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
Output: [1.00000,3.00000,2.37500,2.50000,3.00000]
Explanation: The sample represented by count is [1,2,2,2,3,3,3,3].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
Example 2:1
2
3
4
5
6
7Input: count = [0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
Output: [1.00000,4.00000,2.18182,2.00000,1.00000]
Explanation: The sample represented by count is [1,1,1,1,2,2,2,3,3,4,4].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
Constraints:
- count.length == 256
- 0 <= count[i] <= 109
- 1 <= sum(count) <= 109
- The mode of the sample that count represents is unique.
这道题说是有很多在0到 255 中的整数,由于重复的数字太多了,所以这里采用的是统计每个数字出现的个数的方式,用数组 count 来表示,其中 count[i] 表示数字i出现的次数。现在让统计原始数组中的最大值,最小值,平均值,中位数,和众数。这里面的最大最小值很好求,最小值就是 count 数组中第一个不为0的位置,最大值就是 count 数组中最后一个不为0的位置。最小值 mn 初始化为 256,在遍历 count 数组的过程中,遇到不为0的数字时,若此时 mn 为 256,则更新为坐标i。最大值 mx 直接每次更新为值不为0的坐标i即可。平均值也好求,只要求出所有的数字之和,跟数字的个数相除就行了,注意由于数字之和可能很大,需要用 double 来表示。众数也不难求,只要找出 count 数组中的最大值,则其坐标就是众数。比较难就是中位数了,由于数组的个数可奇可偶,中位数的求法不同,这里为了统一,采用一个小 trick,比如数组 1,2,3 和 1,2,3,4,可以用坐标为 (n-1)/2 和 n/2 的两个数字求平均值得到,对于长度为奇数的数组,这两个坐标表示的是相同的数字。这里由于是统计数组,所以要找的两个位置是 (cnt+1)/2 和 (cnt+2)/2,其中 cnt 是所有数字的个数。再次遍历 count 数组,使用 cur 来累计当前经过的数字个数,若 cur 小于 first,且 cur 加上 count[i] 大于等于 first,说明当前数字i即为所求,加上其的一半到 median。同理,若 cur 小于 second,cur 加上 count[i] 大于等于 second,说明当前数字i即为所求,加上其的一半到 median 即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<double> sampleStats(vector<int>& count) {
double mn = 256, mx = 0, mean = 0, median = 0, sum = 0;
int cnt = 0, mode = 0;
for (int i = 0; i < count.size(); ++i) {
if (count[i] == 0) continue;
if (mn == 256) mn = i;
mx = i;
sum += (double)i * count[i];
cnt += count[i];
if (count[i] > count[mode]) mode = i;
}
mean = sum / cnt;
int first = (cnt + 1) / 2, second = (cnt + 2) / 2, cur = 0;
for (int i = 0; i < count.size(); ++i) {
if (cur < first && cur + count[i] >= first) median += i / 2.0;
if (cur < second && cur + count[i] >= second) median += i / 2.0;
cur += count[i];
}
return {mn, mx, sum / cnt, median, (double)mode};
}
};
Leetcode1094. Car Pooling
You are driving a vehicle that has capacity empty seats initially available for passengers. The vehicle only drives east (ie. it cannot turn around and drive west.)
Given a list of trips, trip[i] = [num_passengers, start_location, end_location] contains information about the i-th trip: the number of passengers that must be picked up, and the locations to pick them up and drop them off. The locations are given as the number of kilometers due east from your vehicle’s initial location.
Return true if and only if it is possible to pick up and drop off all passengers for all the given trips.
Example 1:1
2Input: trips = [[2,1,5],[3,3,7]], capacity = 4
Output: false
Example 2:1
2Input: trips = [[2,1,5],[3,3,7]], capacity = 5
Output: true
Example 3:1
2Input: trips = [[2,1,5],[3,5,7]], capacity = 3
Output: true
Example 4:1
2Input: trips = [[3,2,7],[3,7,9],[8,3,9]], capacity = 11
Output: true
Constraints:
- trips.length <= 1000
- trips[i].length == 3
- 1 <= trips[i][0] <= 100
- 0 <= trips[i][1] < trips[i][2] <= 1000
- 1 <= capacity <= 100000
这道题说的是拼车的那些事儿,给了一个数组,里面是很多三元对儿,分别包含乘客个数,上车时间和下车时间,还给了一个变量 capacity,说是任何时候的乘客总数不超过 capacity 的话,返回 true,否则就返回 false。这道题其实跟之前的 Meeting Rooms II 是一样,只不过那道题是求需要的房间的总个数,而这里是限定了乘客的总数,问是否会超载。使用的解题思想都是一样的,主要是需要将上车时间点和下车时间点拆分开,然后按时间顺序排列在同一条时间轴上,上车的时候就加上这些人数,下车的时候就减去这些人数。若某个时间点上的总人数超过了限定值,就直接返回 false 就行了,这里博主没有用 TreeMap,而是直接都放到一个数组中,然后对该数组按时间点进行排序,再遍历排序后的数组,进行累加元素之和即可,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool carPooling(vector<vector<int>>& trips, int capacity) {
int cur = 0;
vector<vector<int>> data;
for (auto trip : trips) {
data.push_back({trip[1], trip[0]});
data.push_back({trip[2], -trip[0]});
}
sort(data.begin(), data.end());
for (auto &a : data) {
cur += a[1];
if (cur > capacity) return false;
}
return true;
}
};
接下来看一种更加高效的解法,并不用进行排序,那个太耗时了。题目限定了时间点不会超过 1000,所以这里就建立一个大小为 1001 的 cnt 数组,然后遍历 trips 数组,将对应的上车时间点加上乘客人数,下车时间点减去乘客人数,这样的话就相当于排序完成了,有点计数排序的感觉。之后再遍历这个 cnt 数组,累加当前的值,只要超过 capacity 了,就返回 false,否则最终返回 true 即可,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
bool carPooling(vector<vector<int>>& trips, int capacity) {
int cur = 0;
vector<int> cnt(1001);
for (auto &trip : trips) {
cnt[trip[1]] += trip[0];
cnt[trip[2]] -= trip[0];
}
for (int i = 1; i <= 1000; ++i) {
cur += cnt[i];
if (cur > capacity) return false;
}
return true;
}
};