Leetcode605. Can Place Flowers
Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die.
Given a flowerbed (represented as an array containing 0 and 1, where 0 means empty and 1 means not empty), and a number n, return if n new flowers can be planted in it without violating the no-adjacent-flowers rule.
Example 1:1
2Input: flowerbed = [1,0,0,0,1], n = 1
Output: True
Example 2:1
2Input: flowerbed = [1,0,0,0,1], n = 2
Output: False
逐次的添加新的到数组中,然后统计最大可承受的数量。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
int ans = 0;
for(int i = 0; i < flowerbed.size(); i ++) {
if(flowerbed[i] == 0)
if(i-1 >= 0 && flowerbed[i-1] == 0 || i==0)
if(i+1 < flowerbed.size() && flowerbed[i+1] == 0 || i == flowerbed.size()-1) {
flowerbed[i] = 1;
ans ++;
}
}
cout << ans <<endl;
return ans >= n;
}
};
Leetcode606. Construct String from Binary Tree
You need to construct a string consists of parenthesis and integers from a binary tree with the preorder traversing way.
The null node needs to be represented by empty parenthesis pair “()”. And you need to omit all the empty parenthesis pairs that don’t affect the one-to-one mapping relationship between the string and the original binary tree.
Example 1:1
2
3
4
5
6
7
8
9
10
11
12Input: Binary tree: [1,2,3,4]
1
/ \
2 3
/
4
Output: "1(2(4))(3)"
Explanation: Originallay it needs to be "1(2(4)())(3()())",
but you need to omit all the unnecessary empty parenthesis pairs.
And it will be "1(2(4))(3)".
Example 2:1
2
3
4
5
6
7
8
9
10Input: Binary tree: [1,2,3,null,4]
1
/ \
2 3
\
4
Output: "1(2()(4))(3)"
Explanation: Almost the same as the first example,
except we can't omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
string tree2str(TreeNode* t) {
if(t == NULL)
return "";
if(!t->left && !t->right)
return to_string(t->val);
if (t->left != NULL && t->right == NULL) {
return to_string(t->val) + "(" + tree2str(t->left) + ")";
}
if (t->left == NULL && t->right != NULL) {
return to_string(t->val) + "()" + "(" + tree2str(t->right) + ")";
}
return to_string(t->val) + "(" + tree2str(t->left) + ")" + "(" + tree2str(t->right) + ")";
}
};
Leetcode609. Find Duplicate File in System
Given a list of directory info including directory path, and all the files with contents in this directory, you need to find out all the groups of duplicate files in the file system in terms of their paths.
A group of duplicate files consists of at least two files that have exactly the same content.
A single directory info string in the input list has the following format:
“root/d1/d2/…/dm f1.txt(f1_content) f2.txt(f2_content) … fn.txt(fn_content)”
It means there are n files (f1.txt, f2.txt … fn.txt with content f1_content, f2_content … fn_content, respectively) in directory root/d1/d2/…/dm. Note that n >= 1 and m >= 0. If m = 0, it means the directory is just the root directory.
The output is a list of group of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
“directory_path/file_name.txt”
Example 1:1
2
3
4Input:
["root/a 1.txt(abcd) 2.txt(efgh)", "root/c 3.txt(abcd)", "root/c/d 4.txt(efgh)", "root 4.txt(efgh)"]
Output:
[["root/a/2.txt","root/c/d/4.txt","root/4.txt"],["root/a/1.txt","root/c/3.txt"]]
这道题给了我们一堆字符串数组,每个字符串中包含了文件路径,文件名称和内容,让我们找到重复的文件,这里只要文件内容相同即可,不用管文件名是否相同,而且返回结果中要带上文件的路径。博主个人感觉这实际上应该算是字符串操作的题目,因为思路上并不是很难想,就是要处理字符串,把路径,文件名,和文件内容从一个字符串中拆出来,我们这里建立一个文件内容和文件路径加文件名组成的数组的映射,因为会有多个文件有相同的内容,所以我们要用数组。然后把分离出的路径和文件名拼接到一起,最后我们只要看哪些映射的数组元素个数多于1个的,就说明有重复文件,我们把整个数组加入结果res中。这么麻烦的题不值得浪费时间。参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
vector<vector<string>> findDuplicate(vector<string>& paths) {
vector<vector<string>> res;
unordered_map<string, vector<string>> m;
for (string path : paths) {
istringstream is(path);
string pre = "", t = "";
is >> pre;
while (is >> t) {
int idx = t.find_last_of('(');
string dir = pre + "/" + t.substr(0, idx);
string content = t.substr(idx + 1, t.size() - idx - 2);
m[content].push_back(dir);
}
}
for (auto a : m) {
if (a.second.size() > 1)res.push_back(a.second);
}
return res;
}
};
Leetcode611. Valid Triangle Number
Given an array consists of non-negative integers, your task is to count the number of triplets chosen from the array that can make triangles if we take them as side lengths of a triangle.
Example 1:1
2
3
4
5
6
7Input: [2,2,3,4]
Output: 3
Explanation:
Valid combinations are:
2,3,4 (using the first 2)
2,3,4 (using the second 2)
2,2,3
Note:
- The length of the given array won’t exceed 1000.
- The integers in the given array are in the range of [0, 1000].
这道题给了我们一堆数字,问我们能组成多少个正确的三角形,我们初中就知道三角形的性质,任意两条边之和要大于第三边。那么问题其实就变成了找出所有这样的三个数字,使得任意两个数字之和都大于第三个数字。那么可以转变一下,三个数字中如果较小的两个数字之和大于第三个数字,那么任意两个数字之和都大于第三个数字,这很好证明,因为第三个数字是最大的,所以它加上任意一个数肯定大于另一个数。先确定前两个数,将这两个数之和sum作为目标值,然后用二分查找法来快速确定第一个小于目标值的数,我们找到这个临界值,那么这之前一直到j的位置之间的数都满足题意,直接加起来即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int triangleNumber(vector<int>& nums) {
int res = 0, n = nums.size();
sort(nums.begin(), nums.end());
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
int sum = nums[i] + nums[j], left = j + 1, right = n;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < sum) left = mid + 1;
else right = mid;
}
res += right - 1 - j;
}
}
return res;
}
};
其实还有更进一步优化的方法,思路是排序之后,从数字末尾开始往前遍历,将left指向首数字,将right之前遍历到的数字的前面一个数字,然后如果left小于right就进行循环,循环里面判断如果left指向的数加上right指向的数大于当前的数字的话,那么right到left之间的数字都可以组成三角形,这是为啥呢,相当于此时确定了i和right的位置,可以将left向右移到right的位置,中间经过的数都大于left指向的数,所以都能组成三角形。加完之后,right自减一,即向左移动一位。如果left和right指向的数字之和不大于nums[i],那么left自增1,即向右移动一位,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int triangleNumber(vector<int>& nums) {
int res = 0, n = nums.size();
sort(nums.begin(), nums.end());
for (int i = n - 1; i >= 2; --i) {
int left = 0, right = i - 1;
while (left < right) {
if (nums[left] + nums[right] > nums[i]) {
res += right - left;
--right;
} else {
++left;
}
}
}
return res;
}
};
Leetcode617. Merge Two Binary Trees
Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not.
You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.
Example 1:1
2
3
4
5
6
7
8
9
10
11
12
13
14Input:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
Output:
Merged tree:
3
/ \
4 5
/ \ \
5 4 7
把两棵树合并,比较简单,递归即可。
1 | class Solution { |
Leetcode620. Not Boring Movies
X city opened a new cinema, many people would like to go to this cinema. The cinema also gives out a poster indicating the movies’ ratings and descriptions.
Please write a SQL query to output movies with an odd numbered ID and a description that is not ‘boring’. Order the result by rating.
For example, table cinema:1
2
3
4
5
6
7
8
9+---------+-----------+--------------+-----------+
| id | movie | description | rating |
+---------+-----------+--------------+-----------+
| 1 | War | great 3D | 8.9 |
| 2 | Science | fiction | 8.5 |
| 3 | irish | boring | 6.2 |
| 4 | Ice song | Fantacy | 8.6 |
| 5 | House card| Interesting| 9.1 |
+---------+-----------+--------------+-----------+
For the example above, the output should be:1
2
3
4
5
6+---------+-----------+--------------+-----------+
| id | movie | description | rating |
+---------+-----------+--------------+-----------+
| 5 | House card| Interesting| 9.1 |
| 1 | War | great 3D | 8.9 |
+---------+-----------+--------------+-----------+1
SELECT id, movie, description, rating from cinema where (id%2) != 0 AND (description != "boring") ORDER BY rating DESC;
Leetcode621. Task Scheduler
Given a char array representing tasks CPU need to do. It contains capital letters A to Z where different letters represent different tasks.Tasks could be done without original order. Each task could be done in one interval. For each interval, CPU could finish one task or just be idle.
However, there is a non-negative cooling interval n that means between two same tasks, there must be at least n intervals that CPU are doing different tasks or just be idle.
You need to return the least number of intervals the CPU will take to finish all the given tasks.
Example 1:1
2
3Input: tasks = ['A','A','A','B','B','B'], n = 2
Output: 8
Explanation: A -> B -> idle -> A -> B -> idle -> A -> B.
Note:
- The number of tasks is in the range [1, 10000].
- The integer n is in the range [0, 100].
这道题让我们安排CPU的任务,规定在两个相同任务之间至少隔n个时间点。说实话,刚开始博主并没有完全理解题目的意思,后来看了大神们的解法才悟出个道理来。由于题目中规定了两个相同任务之间至少隔n个时间点,那么我们首先应该处理的出现次数最多的那个任务,先确定好这些高频任务,然后再来安排那些低频任务。如果任务F的出现频率最高,为k次,那么我们用n个空位将每两个F分隔开,然后我们按顺序加入其他低频的任务,来看一个例子:
AAAABBBEEFFGG 3
我们发现任务A出现了4次,频率最高,于是我们在每个A中间加入三个空位,如下:
A—-A—-A—-A
AB—AB—AB—A (加入B)
ABE-ABE-AB—A (加入E)
ABEFABE-ABF-A (加入F,每次尽可能填满或者是均匀填充)
ABEFABEGABFGA (加入G)
再来看一个例子:
ACCCEEE 2
我们发现任务C和E都出现了三次,那么我们就将CE看作一个整体,在中间加入一个位置即可:
CE-CE-CE
CEACE-CE (加入A)
注意最后面那个idle不能省略,不然就不满足相同两个任务之间要隔2个时间点了。
这道题好在没有让我们输出任务安排结果,而只是问所需的时间总长,那么我们就想个方法来快速计算出所需时间总长即可。我们仔细观察上面两个例子可以发现,都分成了(mx - 1)块,再加上最后面的字母,其中mx为最大出现次数。比如例子1中,A出现了4次,所以有A—模块出现了3次,再加上最后的A,每个模块的长度为4。例子2中,CE-出现了2次,再加上最后的CE,每个模块长度为3。我们可以发现,模块的次数为任务最大次数减1,模块的长度为n+1,最后加上的字母个数为出现次数最多的任务,可能有多个并列。这样三个部分都搞清楚了,写起来就不难了,我们统计每个大写字母出现的次数,然后排序,这样出现次数最多的字母就到了末尾,然后我们向前遍历,找出出现次数一样多的任务个数,就可以迅速求出总时间长了,下面这段代码可能最不好理解的可能就是最后一句了,那么我们特别来讲解一下。先看括号中的第二部分,前面分析说了mx是出现的最大次数,mx-1是可以分为的块数,n+1是每块中的个数,而后面的 25-i 是还需要补全的个数,用之前的例子来说明:
AAAABBBEEFFGG 3
A出现了4次,最多,mx=4,那么可以分为mx-1=3块,如下:
A—A—A—
每块有n+1=4个,最后还要加上末尾的一个A,也就是25-24=1个任务,最终结果为13:
ABEFABEGABFGA
再来看另一个例子:
ACCCEEE 2
C和E都出现了3次,最多,mx=3,那么可以分为mx-1=2块,如下:
CE-CE-
每块有n+1=3个,最后还要加上末尾的一个CE,也就是25-23=2个任务,最终结果为8:
CEACE-CE
好,那么此时你可能会有疑问,为啥还要跟原任务个数len相比,取较大值呢?我们再来看一个例子:
AAABBB 0
A和B都出现了3次,最多,mx=3,那么可以分为mx-1=2块,如下:
ABAB
每块有n+1=1个?你会发现有问题,这里明明每块有两个啊,为啥这里算出来n+1=1呢,因为给的n=0,这有没有矛盾呢,没有!因为n表示相同的任务间需要间隔的个数,那么既然这里为0了,说明相同的任务可以放在一起,这里就没有任何限制了,我们只需要执行完所有的任务就可以了,所以我们最终的返回结果一定不能小于任务的总个数len的,这就是要对比取较大值的原因了。
参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int leastInterval(vector<char>& tasks, int n) {
vector<int> cnt(26, 0);
for (char task : tasks) {
++cnt[task - 'A'];
}
sort(cnt.begin(), cnt.end());
int i = 25, mx = cnt[25], len = tasks.size();
while (i >= 0 && cnt[i] == mx) --i;
return max(len, (mx - 1) * (n + 1) + 25 - i);
}
};
Leetcode622. Design Circular Queue
Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle. It is also called “Ring Buffer”.
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Implementation the MyCircularQueue class:
MyCircularQueue(k)Initializes the object with the size of the queue to be k.int Front()Gets the front item from the queue. If the queue is empty, return -1.int Rear()Gets the last item from the queue. If the queue is empty, return -1.boolean enQueue(int value)Inserts an element into the circular queue. Return true if the operation is successful.boolean deQueue()Deletes an element from the circular queue. Return true if the operation is successful.boolean isEmpty()Checks whether the circular queue is empty or not.boolean isFull()Checks whether the circular queue is full or not.
手写循环队列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49class MyCircularQueue {
public:
int size, head, tail, cnt;
vector<int> v;
MyCircularQueue(int k) {
size = k;
cnt = 0;
v.resize(k);
head = tail = 0;
}
bool enQueue(int value) {
if (isFull())
return false;
v[tail] = value;
tail = (tail+1) % size;
cnt ++;
return true;
}
bool deQueue() {
if (isEmpty())
return false;
cnt --;
head = (head+1) % size;
return true;
}
int Front() {
if (isEmpty())
return -1;
return v[head];
}
int Rear() {
if (isEmpty())
return -1;
return v[(tail+size-1) % size];
}
bool isEmpty() {
return cnt == 0;
}
bool isFull() {
return cnt == size;
}
};
Leetcode623. Add One Row to Tree
Given the root of a binary tree and two integers val and depth, add a row of nodes with value val at the given depth depth.
Note that the root node is at depth 1.
The adding rule is:
- Given the integer depth, for each not null tree node cur at the depth depth - 1, create two tree nodes with value val as cur’s left subtree root and right subtree root.
- cur’s original left subtree should be the left subtree of the new left subtree root.
- cur’s original right subtree should be the right subtree of the new right subtree root.
- If depth == 1 that means there is no depth depth - 1 at all, then create a tree node with value val as the new root of the whole original tree, and the original tree is the new root’s left subtree.
Example 1:1
2Input: root = [4,2,6,3,1,5], val = 1, depth = 2
Output: [4,1,1,2,null,null,6,3,1,5]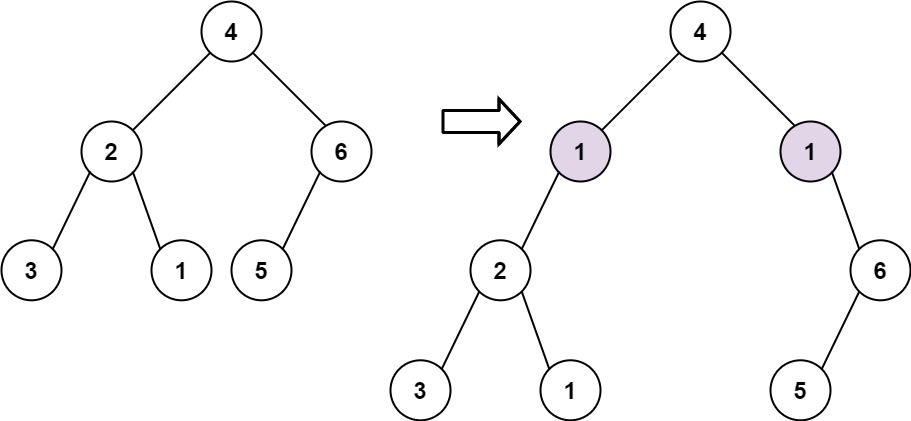
Example 2:1
2Input: root = [4,2,null,3,1], val = 1, depth = 3
Output: [4,2,null,1,1,3,null,null,1]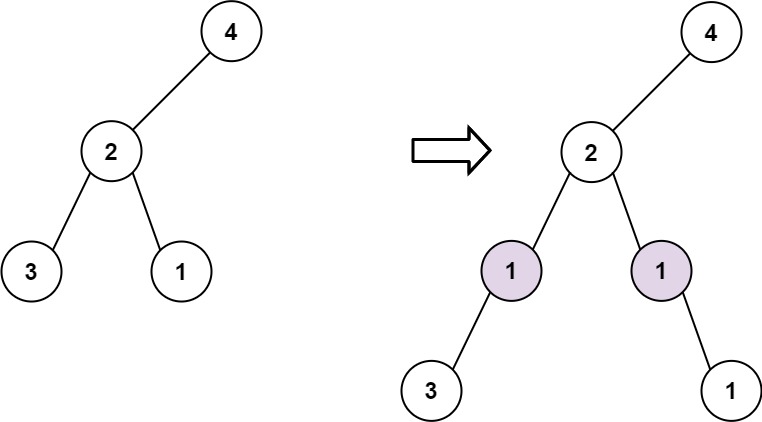
这道题让我们给二叉树增加一行,给了需要增加的值,还有需要增加的位置深度,题目中给的例子也比较能清晰的说明问题。但是漏了一种情况,那就是当d=1时,这该怎么加?这时候就需要替换根结点了。其他情况的处理方法都一样,每遍历完一层,d自减1,当d==1时,需要对于当前层的每一个结点,先用临时变量保存其原有的左右子结点,然后新建值为v的左右子结点,将原有的左子结点连到新建的左子结点的左子结点上,将原有的右子结点连到新建的右子结点的右子结点。如果d不为1,那么就是层序遍历原有的排入队列操作,记得当检测到d为0时,直接返回,因为添加操作已经完成,没有必要遍历完剩下的结点,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public:
TreeNode* addOneRow(TreeNode* root, int val, int depth) {
if (depth == 1)
return new TreeNode(val, root, NULL);
queue<TreeNode*> q;
int cur_dep = 1;
q.push(root);
while(!q.empty()) {
vector<TreeNode*> v;
v.clear();
int size = q.size();
while(size --) {
TreeNode* tmp = q.front();
v.push_back(tmp);
q.pop();
}
int i = 0;
size = v.size();
if (depth == cur_dep + 1) {
for (i = 0; i < size; i++) {
v[i]->left = new TreeNode(val, v[i]->left, NULL);
v[i]->right = new TreeNode(val, NULL, v[i]->right);
}
return root;
}
i = 0;
size = v.size();
while(i < size) {
if (v[i]->left) q.push(v[i]->left);
if (v[i]->right) q.push(v[i]->right);
i ++;
}
cur_dep ++;
}
return root;
}
};
Leetcode626. Exchange Seats
Mary is a teacher in a middle school and she has a table seat storing students’ names and their corresponding seat ids.
The column id is continuous increment.
Mary wants to change seats for the adjacent students.
Can you write a SQL query to output the result for Mary?1
2
3
4
5
6
7
8
9+---------+---------+
| id | student |
+---------+---------+
| 1 | Abbot |
| 2 | Doris |
| 3 | Emerson |
| 4 | Green |
| 5 | Jeames |
+---------+---------+
For the sample input, the output is:1
2
3
4
5
6
7
8
9+---------+---------+
| id | student |
+---------+---------+
| 1 | Doris |
| 2 | Abbot |
| 3 | Green |
| 4 | Emerson |
| 5 | Jeames |
+---------+---------+
Note: If the number of students is odd, there is no need to change the last one’s seat.
交换相邻的两个学生的位置。IF语句及SELECT子句使用,如下所示:1
2# Write your MySQL query statement below
SELECT IF(id%2 = 0, id-1, IF (id = (SELECT COUNT(*) FROM seat), id, id + 1)) as id , student from seat ORDER BY id;
Leetcode628. Maximum Product of Three Numbers
Given an integer array, find three numbers whose product is maximum and output the maximum product.
Example 1:1
2Input: [1,2,3]
Output: 6
Example 2:1
2Input: [1,2,3,4]
Output: 24
先排序,然后找最大的三个数,或者最大的一个数和最小的两个数,看哪个乘积大。1
2
3
4
5
6
7
8class Solution {
public:
int maximumProduct(vector<int>& nums) {
sort(nums.begin(), nums.end());
int len = nums.size() - 1;
return max(nums[len] * nums[len-1] * nums[len-2], nums[len] * nums[0] * nums[1]);
}
};
Leetcode630. Course Schedule III
There are n different online courses numbered from 1 to n. Each course has some duration(course length) tand closed on dth day. A course should be taken continuously for t days and must be finished before or on the dth day. You will start at the 1st day.
Given n online courses represented by pairs (t,d), your task is to find the maximal number of courses that can be taken.
Example:1
2Input: [[100, 200], [200, 1300], [1000, 1250], [2000, 3200]]
Output: 3
Explanation:
- There’re totally 4 courses, but you can take 3 courses at most:
- First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day.
- Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day.
- Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day.
- The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.
Note:
- The integer 1 <= d, t, n <= 10,000.
- You can’t take two courses simultaneously.
这道题给了我们许多课程,每个课程有两个参数,第一个是课程的持续时间,第二个是课程的最晚结束日期,让我们求最多能上多少门课。这道题给的提示是用贪婪算法,那么我们首先给课程排个序,按照结束时间的顺序来排序,我们维护一个当前的时间,初始化为0,再建立一个优先数组,然后我们遍历每个课程,对于每一个遍历到的课程,当前时间加上该课程的持续时间,然后将该持续时间放入优先数组中,然后我们判断如果当前时间大于课程的结束时间,说明这门课程无法被完成,我们并不是直接减去当前课程的持续时间,而是取出优先数组的顶元素,即用时最长的一门课,这也make sense,因为我们的目标是尽可能的多上课,既然非要去掉一门课,那肯定是去掉耗时最长的课,这样省下来的时间说不定能多上几门课呢,最后返回优先队列中元素的个数就是能完成的课程总数啦,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
static bool comp(vector<int>& a, vector<int>& b) {
return a[1] < b[1];
}
int scheduleCourse(vector<vector<int>>& courses) {
int res = 0, cur = 0;
priority_queue<int> q;
sort(courses.begin(), courses.end(), comp);
for (vector<int> a : courses) {
cur += a[0];
q.push(a[0]);
if (cur > a[1]) {
cur -= q.top();
q.pop();
}
}
return q.size();
}
};
Leetcode632. Smallest Range Covering Elements from K Lists
You have k lists of sorted integers in ascending order. Find the smallest range that includes at least one number from each of the k lists.
We define the range [a,b] is smaller than range [c,d] if b-a < d-c or a < c if b-a == d-c.
Example 1:1
2
3
4
5
6Input:[[4,10,15,24,26], [0,9,12,20], [5,18,22,30]]
Output: [20,24]
Explanation:
List 1: [4, 10, 15, 24,26], 24 is in range [20,24].
List 2: [0, 9, 12, 20], 20 is in range [20,24].
List 3: [5, 18, 22, 30], 22 is in range [20,24].
Note:
- The given list may contain duplicates, so ascending order means >= here.
- 1 <= k <= 3500
- -105 <= value of elements <= 105.
- For Java users, please note that the input type has been changed to List
- . And after you reset the code template, you’ll see this point.
这道题给了我们一些数组,都是排好序的,让求一个最小的范围,使得这个范围内至少会包括每个数组中的一个数字。虽然每个数组都是有序的,但是考虑到他们之间的数字差距可能很大,所以最好还是合并成一个数组统一处理比较好,但是合并成一个大数组还需要保留其原属数组的序号,所以大数组中存pair对,同时保存数字和原数组的序号。然后重新按照数字大小进行排序,这样问题实际上就转换成了求一个最小窗口,使其能够同时包括所有数组中的至少一个数字。这不就变成了那道 Minimum Window Substring。所以说啊,这些题目都是换汤不换药的,总能变成我们见过的类型。这里用两个指针 left 和 right 来确定滑动窗口的范围,还要用一个 HashMap 来建立每个数组与其数组中数字出现的个数之间的映射,变量 cnt 表示当前窗口中的数字覆盖了几个数组,diff 为窗口的大小,让 right 向右滑动,然后判断如果 right 指向的数字所在数组没有被覆盖到,cnt 自增1,然后 HashMap 中对应的数组出现次数自增1,然后循环判断如果 cnt 此时为k(数组的个数)且 left 不大于 right,那么用当前窗口的范围来更新结果,然后此时想缩小窗口,通过将 left 向右移,移动之前需要减小 HashMap 中的映射值,因为去除了数字,如果此时映射值为0了,说明有个数组无法覆盖到了,cnt 就要自减1。这样遍历后就能得到最小的范围了,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
vector<int> smallestRange(vector<vector<int>>& nums) {
vector<int> res;
vector<pair<int, int>> v;
unordered_map<int, int> m;
for (int i = 0; i < nums.size(); ++i) {
for (int num : nums[i]) {
v.push_back({num, i});
}
}
sort(v.begin(), v.end());
int left = 0, n = v.size(), k = nums.size(), cnt = 0, diff = INT_MAX;
for (int right = 0; right < n; ++right) {
if (m[v[right].second] == 0) ++cnt;
++m[v[right].second];
while (cnt == k && left <= right) {
if (diff > v[right].first - v[left].first) {
diff = v[right].first - v[left].first;
res = {v[left].first, v[right].first};
}
if (--m[v[left].second] == 0) --cnt;
++left;
}
}
return res;
}
};
这道题还有一种使用 priority_queue 来做的,优先队列默认情况是最大堆,但是这道题我们需要使用最小堆,重新写一下 comparator 就行了。解题的主要思路很上面的解法很相似,只是具体的数据结构的使用上略有不同,这 curMax 表示当前遇到的最大数字,用一个 idx 数组表示每个 list 中遍历到的位置,然后优先队列里面放一个pair,是数字和其所属list组成的对儿。遍历所有的list,将每个 list 的首元素和该 list 序号组成 pair 放入队列中,然后 idx 数组中每个位置都赋值为1,因为0的位置已经放入队列了,所以指针向后移一个位置,还要更新当前最大值 curMax。此时 queue 中是每个 list 各有一个数字,由于是最小堆,所以最小的数字就在队首,再加上最大值 curMax,就可以初始化结果 res 了。然后进行循环,注意这里循环的条件不是队列不为空,而是当某个 list 的数字遍历完了就结束循环,因为范围要 cover 每个 list 至少一个数字。所以 while 循环条件即是队首数字所在的 list 的遍历位置小于该 list 的总个数,在循环中,取出队首数字所在的 list 序号t,然后将该 list 中下一个位置的数字和该 list 序号t组成 pair,加入队列中,然后用这个数字更新 curMax,同时 idx 中t对应的位置也自增1。现在来更新结果 res,如果结果 res 中两数之差大于 curMax 和队首数字之差,则更新结果 res,参见代码如下:
1 | class Solution { |
Leetcode633. Sum of Square Numbers
Given a non-negative integer c, your task is to decide whether there’re two integers a and b such that a2 + b2 = c.
Example 1:1
2
3Input: 5
Output: True
Explanation: 1 * 1 + 2 * 2 = 5
Example 2:1
2Input: 3
Output: False
判断一个数是不是两个数的平方之和,不要用加法,容易溢出,要用减法判断。1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
bool judgeSquareSum(int c) {
int len = sqrt(c);
for(int i = 0; i <= len; i ++) {
int remain = c - i*i;
int rr = sqrt(remain);
if(rr * rr == remain)
return true;
}
return false;
}
};
Leetcode636. Exclusive Time of Functions
On a single-threaded CPU, we execute a program containing n functions. Each function has a unique ID between 0 and n-1.
Function calls are stored in a call stack: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is the current function being executed. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list logs, where logs[i] represents the ith log message formatted as a string “{function_id}:{“start” | “end”}:{timestamp}”. For example, “0:start:3” means a function call with function ID 0 started at the beginning of timestamp 3, and “1:end:2” means a function call with function ID 1 ended at the end of timestamp 2. Note that a function can be called multiple times, possibly recursively.
A function’s exclusive time is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for 2 time units and another call executing for 1 time unit, the exclusive time is 2 + 1 = 3.
Return the exclusive time of each function in an array, where the value at the ith index represents the exclusive time for the function with ID i.
Example 1:1
2Input: n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"]
Output: [3,4]
Explanation:
- Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
- Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
- Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
- So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
Example 2:1
2Input: n = 1, logs = ["0:start:0","0:start:2","0:end:5","0:start:6","0:end:6","0:end:7"]
Output: [8]
Explanation:
- Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
- Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
- Function 0 (initial call) resumes execution then immediately calls itself again.
- Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
- Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
- So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
Example 3:1
2Input: n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:6","1:end:6","0:end:7"]
Output: [7,1]
Explanation:
- Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
- Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
- Function 0 (initial call) resumes execution then immediately calls function 1.
- Function 1 starts at the beginning of time 6, executes 1 units of time, and ends at the end of time 6.
- Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
- So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
Example 4:1
2Input: n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:7","1:end:7","0:end:8"]
Output: [8,1]
Example 5:1
2Input: n = 1, logs = ["0:start:0","0:end:0"]
Output: [1]
这道题让我们函数的运行的时间。一个函数调用其他函数的时候自身也在运行,这样的话用栈stack就比较合适了,函数开启了就压入栈,结束了就出栈,不会有函数被漏掉。这样的我们可以遍历每个log,然后把三部分分开,函数idx,类型type,时间点time。如果此时栈不空,说明之前肯定有函数在跑,那么不管当前是start还是end,之前函数时间都得增加,增加的值为time - preTime,这里的preTime是上一个时间点。然后我们更新preTime为当前时间点time。然后我们判断log的类型,如果是start,我们将当前函数压入栈;如果是end,那么我们将栈顶元素取出,对其加1秒,并且preTime也要加1秒,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38class Solution {
public:
vector<int> exclusiveTime(int n, vector<string>& logs) {
vector<int> res(n, 0);
int cur = 0, pre = 0;
stack<int> ss;
for (string s : logs) {
int len = s.length();
int p = 0, id = 0, time = 0, type;
while(p < len) {
while(s[p] != ':')
id = id * 10 + s[p++] - '0';
p ++;
if (s[p] == 's')
type = 1;
else
type = 0;
while(p < len && s[p++] != ':');
while(p < len)
time = time * 10 + s[p++] - '0';
if (!ss.empty()) {
res[ss.top()] += (time - pre);
}
pre = time;
if (type == 1) {
ss.push(id);
}
else {
int i = ss.top();
ss.pop();
res[i] ++;
pre ++;
}
}
}
return res;
}
};
Leetcode637. Average of Levels in Binary Tree
Given a non-empty binary tree, return the average value of the nodes on each level in the form of an array.
Example 1:1
2
3
4
5
6
7
8
9Input:
3
/ \
9 20
/ \
15 7
Output: [3, 14.5, 11]
Explanation:
The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11. Hence return [3, 14.5, 11].
层次遍历计算平均值。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
queue<TreeNode*> q;
vector<double> res;
q.push(root);
int counter;
while(!q.empty()) {
vector<TreeNode*> vec;
double sum = 0;
int n = q.size();
while(n--) {
TreeNode* temp = q.front();
sum += temp->val;
vec.push_back(temp);
q.pop();
if(temp->left) q.push(temp->left);
if(temp->right) q.push(temp->right);
}
sum = (double)sum / vec.size();
res.push_back(sum);
}
return res;
}
};
Leetcode638. Shopping Offers
In LeetCode Store, there are some kinds of items to sell. Each item has a price.
However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.
You are given the each item’s price, a set of special offers, and the number we need to buy for each item. The job is to output the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers.
Each special offer is represented in the form of an array, the last number represents the price you need to pay for this special offer, other numbers represents how many specific items you could get if you buy this offer.
You could use any of special offers as many times as you want.
Example 1:1
2
3
4
5
6
7Input: [2,5], [[3,0,5],[1,2,10]], [3,2]
Output: 14
Explanation:
There are two kinds of items, A and B. Their prices are $2 and $5 respectively.
In special offer 1, you can pay $5 for 3A and 0B
In special offer 2, you can pay $10 for 1A and 2B.
You need to buy 3A and 2B, so you may pay $10 for 1A and 2B (special offer #2), and $4 for 2A.
Example 2:1
2
3
4
5
6
7Input: [2,3,4], [[1,1,0,4],[2,2,1,9]], [1,2,1]
Output: 11
Explanation:
The price of A is $2, and $3 for B, $4 for C.
You may pay $4 for 1A and 1B, and $9 for 2A ,2B and 1C.
You need to buy 1A ,2B and 1C, so you may pay $4 for 1A and 1B (special offer #1), and $3 for 1B, $4 for 1C.
You cannot add more items, though only $9 for 2A ,2B and 1C.
Note:
- There are at most 6 kinds of items, 100 special offers.
- For each item, you need to buy at most 6 of them.
- You are not allowed to buy more items than you want, even if that would lower the overall price.
这道题说有一些商品,各自有不同的价格,然后给我们了一些优惠券,可以在优惠的价格买各种商品若干个,要求我们每个商品要买特定的个数,问我们使用优惠券能少花多少钱,注意优惠券可以重复使用,而且商品不能多买。那么我们可以先求出不使用任何商品需要花的钱数作为结果res的初始值,然后我们遍历每一个优惠券,定义一个变量isValid表示当前优惠券可以使用,然后遍历每一个商品,如果某个商品需要的个数小于优惠券中提供的个数,说明当前优惠券不可用,isValid标记为false。如果遍历完了发现isValid还为true的话,表明该优惠券可用,我们可以更新结果res,对剩余的needs调用递归并且加上使用该优惠券需要付的钱数。最后别忘了恢复needs的状态,主要是dfs。参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int shoppingOffers(vector<int>& price, vector<vector<int>>& specials, vector<int>& needs) {
int len = price.size();
int res = 0;
for (int i = 0; i < len; i ++)
res += (price[i] * needs[i]);
for (auto special : specials) {
bool isvalid = true;
for (int i = 0; i < len; i ++) {
if (needs[i] < special[i])
isvalid = false;
needs[i] -= special[i];
}
if (isvalid)
res = min(res, shoppingOffers(price, specials, needs) + special.back());
for (int i = 0; i < len; i ++) {
needs[i] += special[i];
}
}
return res;
}
};
Leetcode639. Decode Ways II
A message containing letters from A-Z is being encoded to numbers using the following mapping way:1
2
3
4'A' -> 1
'B' -> 2
...
'Z' -> 26
Beyond that, now the encoded string can also contain the character ‘*’, which can be treated as one of the numbers from 1 to 9.
Given the encoded message containing digits and the character ‘*’, return the total number of ways to decode it.
Also, since the answer may be very large, you should return the output mod 109 + 7.
Example 1:1
2
3Input: "*"
Output: 9
Explanation: The encoded message can be decoded to the string: "A", "B", "C", "D", "E", "F", "G", "H", "I".
Example 2:1
2Input: "1*"
Output: 9 + 9 = 18
Note:
- The length of the input string will fit in range [1, 105].
- The input string will only contain the character ‘*’ and digits ‘0’ - ‘9’.
这道解码的题是之前那道Decode Ways的拓展,难度提高了不少,引入了星号,可以代表1到9之间的任意数字,是不是有点外卡匹配的感觉。有了星号以后,整个题就变得异常的复杂,所以结果才让我们对一个很大的数求余,避免溢出。这道题的难点就是要分情况种类太多,一定要全部理通顺才行。我们还是用DP来做,建立一个一维dp数组,其中dp[i]表示前i个字符的解码方法等个数,长度为字符串的长度加1。将dp[0]初始化为1,然后我们判断,如果字符串第一个字符是0,那么直接返回0,如果是*,则dp[1]初始化为9,否则初始化为1。下面就来计算一般情况下的dp[i]了,我们从i=2开始遍历,由于要分的情况种类太多,我们先选一个大分支,就是当前遍历到的字符s[i-1],只有三种情况,要么是0,要么是1到9的数字,要么是星号。我们一个一个来分析:
首先来看s[i-1]为0的情况,这种情况相对来说比较简单,因为0不能单独拆开,只能跟前面的数字一起,而且前面的数字只能是1或2,其他的直接返回0即可。那么当前面的数字是1或2的时候,dp[i]的种类数就跟dp[i-2]相等,可以参见之前那道Decode Ways的讲解,因为后两数无法单独拆分开,就无法产生新的解码方法,所以只保持住原来的拆分数量就不错了;如果前面的数是星号的时候,那么前面的数可以为1或者2,这样就相等于两倍的dp[i-2];如果前面的数也为0,直接返回0即可。
再来看s[i-1]为1到9之间的数字的情况,首先搞清楚当前数字是可以单独拆分出来的,那么dp[i]至少是等于dp[i-1]的,不会拖后腿,还要看其能不能和前面的数字组成两位数进一步增加解码方法。那么就要分情况讨论前面一个数字的种类,如果当前数字可以跟前面的数字组成一个小于等于26的两位数的话,dp[i]还需要加上dp[i-2];如果前面的数字为星号的话,那么要看当前的数字是否小于等于6,如果是小于等于6,那么前面的数字就可以是1或者2了,此时dp[i]需要加上两倍的dp[i-2],如果大于6,那么前面的数字只能是1,所以dp[i]只能加上dp[i-2]。
最后来看s[i-1]为星号的情况,如果当前数字为星号,那么就创造9种可以单独拆分的方法,所以那么dp[i]至少是等于9倍的dp[i-1],还要看其能不能和前面的数字组成两位数进一步增加解码方法。那么就要分情况讨论前面一个数字的种类,如果前面的数字是1,那么当前的9种情况都可以跟前面的数字组成两位数,所以dp[i]需要加上9倍的dp[i-2];如果前面的数字是2,那么只有小于等于6的6种情况都可以跟前面的数字组成两位数,所以dp[i]需要加上6倍的dp[i-2];如果前面的数字是星号,那么就是上面两种情况的总和,dp[i]需要加上15倍的dp[i-2]。
每次算完dp[i]别忘了对超大数取余,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
int numDecodings(string s) {
int n = s.size(), M = 1e9 + 7;
vector<long> dp(n + 1, 0);
dp[0] = 1;
if (s[0] == '0') return 0;
dp[1] = (s[0] == '*') ? 9 : 1;
for (int i = 2; i <= n; ++i) {
if (s[i - 1] == '0') {
if (s[i - 2] == '1' || s[i - 2] == '2') {
dp[i] += dp[i - 2];
} else if (s[i - 2] == '*') {
dp[i] += 2 * dp[i - 2];
} else {
return 0;
}
} else if (s[i - 1] >= '1' && s[i - 1] <= '9') {
dp[i] += dp[i - 1];
if (s[i - 2] == '1' || (s[i - 2] == '2' && s[i - 1] <= '6')) {
dp[i] += dp[i - 2];
} else if (s[i - 2] == '*') {
dp[i] += (s[i - 1] <= '6') ? (2 * dp[i - 2]) : dp[i - 2];
}
} else { // s[i - 1] == '*'
dp[i] += 9 * dp[i - 1];
if (s[i - 2] == '1') dp[i] += 9 * dp[i - 2];
else if (s[i - 2] == '2') dp[i] += 6 * dp[i - 2];
else if (s[i - 2] == '*') dp[i] += 15 * dp[i - 2];
}
dp[i] %= M;
}
return dp[n];
}
};
下面这种解法是论坛上排名最高的解法,常数级的空间复杂度,写法非常简洁,思路也巨牛逼,博主是无论如何也想不出来的,只能继续当搬运工了。这里定义了一系列的变量e0, e1, e2, f0, f1, f2。其中:
- e0表示当前可以获得的解码的次数,当前数字可以为任意数 (也就是上面解法中的dp[i])
- e1表示当前可以获得的解码的次数,当前数字为1
- e2表示当前可以获得的解码的次数,当前数字为2
- f0, f1, f2分别为处理完当前字符c的e0, e1, e2的值
那么下面我们来进行分类讨论,当c为星号的时候,f0的值就是9e0 + 9e1 + 6*e2,这个应该不难理解了,可以参考上面解法中的讲解,这里的e0就相当于dp[i-1],e1和e2相当于两种不同情况的dp[i-2],此时f1和f2都赋值为e0,因为要和后面的数字组成两位数的话,不会增加新的解码方法,所以解码总数跟之前的一样,为e0, 即dp[i-1]。
当c不为星号的时候,如果c不为0,则f0首先应该加上e0。然后不管c为何值,e1都需要加上,总能和前面的1组成两位数;如果c小于等于6,可以和前面的2组成两位数,可以加上e2。然后我们更新f1和f2,如果c为1,则f1为e0;如果c为2,则f2为e0。
最后别忘了将f0,f1,f2赋值给e0,e1,e2,其中f0需要对超大数取余,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int numDecodings(string s) {
long e0 = 1, e1 = 0, e2 = 0, f0, f1, f2, M = 1e9 + 7;
for (char c : s) {
if (c == '*') {
f0 = 9 * e0 + 9 * e1 + 6 * e2;
f1 = e0;
f2 = e0;
} else {
f0 = (c > '0') * e0 + e1 + (c <= '6') * e2;
f1 = (c == '1') * e0;
f2 = (c == '2') * e0;
}
e0 = f0 % M;
e1 = f1;
e2 = f2;
}
return e0;
}
};
Leetcode640. Solve the Equation
Solve a given equation and return the value of ‘x’ in the form of a string “x=#value”. The equation contains only ‘+’, ‘-‘ operation, the variable ‘x’ and its coefficient. You should return “No solution” if there is no solution for the equation, or “Infinite solutions” if there are infinite solutions for the equation.
If there is exactly one solution for the equation, we ensure that the value of ‘x’ is an integer.
Example 1:1
2Input: equation = "x+5-3+x=6+x-2"
Output: "x=2"
Example 2:1
2Input: equation = "x=x"
Output: "Infinite solutions"
Example 3:1
2Input: equation = "2x=x"
Output: "x=0"
Example 4:1
2Input: equation = "2x+3x-6x=x+2"
Output: "x=-1"
Example 5:1
2Input: equation = "x=x+2"
Output: "No solution"
这道题给了我们一个用字符串表示的方程式,让我们求出x的解,根据例子可知,还包括x有无穷多个解和x没有解的情况。解一元一次方程没什么难度,难点在于处理字符串,如何将x的系数合并起来,将常数合并起来,化简成ax=b的形式来求解。博主最开始的思路是先找到等号,然后左右两部分分开处理。由于要化成ax=b的格式,所以左半部分对于x的系数都是加,右半部分对于x的系数都是减。同理,左半部分对于常数是减,右半部分对于常数是加。
那么我们就开始处理字符串了,我们定义一个符号变量sign,初始化为1,数字变量num,初始化为-1,后面会提到为啥不能初始化为0。我们遍历每一个字符,如果遇到了符号位,我们看num的值,如果num是-1的话,说明是初始值,没有更新过,我们将其赋值为0;反之,如果不是-1,说明num已经更新过了,我们乘上当前的正负符号值sign。这是为了区分”-3”和”3+3”这种两种情况,遇到-3种的符号时,我们还不需要加到b中,所以num此时必须为0,而遇到3+3中的加号时,此时num已经为3了,我们要把前面的3加到b中。
遇到数字的时候,我们还是要看num的值,如果是初始值,那么就将其赋值为0,然后计算数字的时候要先给num乘10,再加上当前的数字。这样做的原因是常数不一定都是个位数字,有可能是两位数或者三位数,这样做才能正确的读入数字。我们在遇到数字的时候并不更新a或者b,我们只在遇到符号位或者x的时候才更新。这样如果最后一位是数字的话就会产生问题,所以我们要在字符串的末尾加上一个+号,这样确保了末尾数字会被处理。
遇到x的时候比较tricky,因为可能是x, 0x, -x这几种情况,我们还是首先要看num的值是否为初始值-1,如果是的话,那么就可能是x或-x这种情况,我们此时将num赋值为sign;如果num不是-1,说明num已经被更新了,可能是0x, -3x等等,所以我们要将num赋值为num*sign。这里应该就明白了为啥不能将num初始化为0了,因为一旦初始化为0了,就没法区分x和0x这两种情况了。
那么我们算完了a和b,得到了ax=b的等式,下面的步骤就很简单了,只要分情况讨论得出正确的返回结果即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
string solveEquation(string equation) {
int a = 0, b = 0;
auto found = equation.find("=");
helper(equation.substr(0, found), true, a, b);
helper(equation.substr(found + 1), false, a, b);
if (a == 0 && a == b) return "Infinite solutions";
if (a == 0 && a != b) return "No solution";
return "x=" + to_string(b / a);
}
void helper(string e, bool isLeft, int& a, int& b) {
int sign = 1, num = -1;
e += "+";
for (int i = 0; i < e.size(); ++i) {
if (e[i] == '-' || e[i] == '+') {
num = (num == -1) ? 0 : (num * sign);
b += isLeft ? -num : num;
num = -1;
sign = (e[i] == '+') ? 1 : -1;
} else if (e[i] >= '0' && e[i] <= '9') {
if (num == -1) num = 0;
num = num * 10 + e[i] - '0';
} else if (e[i] == 'x') {
num = (num == -1) ? sign : (num * sign);
a += isLeft ? num : -num;
num = -1;
}
}
}
};
以下是我的:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62class Solution {
public:
void helper(string e, int &i, int &x_l, int &l, bool isright) {
int len = e.length();
int num, flag;
if (isright)
i ++;
while(i < len && (isright || e[i] != '=')) {
num = 0;
flag = 1;
if (e[i] == '-') {
flag = -1;
i++;
}
else if (e[i] == '+') {
flag = 1;
i ++;
}
else if (e[i] == 'x') {
x_l ++;
i ++;
}
int or_i = i;
while(i < len && '0' <= e[i] && e[i] <= '9')
num = num * 10 + e[i++] - '0';
num *= flag;
if (num == 0 && flag == -1)
num = -1;
if (num != 0 && e[i] == 'x' || or_i != i && e[i] == 'x') {
x_l += num;
i ++;
}
else {
l += num;
}
}
}
string solveEquation(string e) {
int len = e.length(), i = 0;
int x_l = 0, x_r = 0;
int l = 0, r = 0;
int num, flag;
helper(e, i, x_l, l, false);
helper(e, i, x_r, r, true);
if (l - r == 0 && x_l - x_r == 0)
return "Infinite solutions";
else if (x_l - x_r == 0 && l - r != 0)
return "No solution";
else if (l - r == 0 && x_l - x_r != 0)
return "x=0";
else {
x_l -= x_r;
r -= l;
return "x="+to_string(r/x_l);
}
return "";
}
};
Leetcode641. Design Circular Deque
Design your implementation of the circular double-ended queue (deque).
Your implementation should support following operations:
MyCircularDeque(k): Constructor, set the size of the deque to be k.insertFront(): Adds an item at the front of Deque. Return true if the operation is successful.insertLast(): Adds an item at the rear of Deque. Return true if the operation is successful.deleteFront(): Deletes an item from the front of Deque. Return true if the operation is successful.deleteLast(): Deletes an item from the rear of Deque. Return true if the operation is successful.getFront(): Gets the front item from the Deque. If the deque is empty, return -1.getRear(): Gets the last item from Deque. If the deque is empty, return -1.isEmpty(): Checks whether Deque is empty or not.isFull(): Checks whether Deque is full or not.
Example:1
2
3
4
5
6
7
8
9
10MyCircularDeque circularDeque = new MycircularDeque(3); // set the size to be 3
circularDeque.insertLast(1); // return true
circularDeque.insertLast(2); // return true
circularDeque.insertFront(3); // return true
circularDeque.insertFront(4); // return false, the queue is full
circularDeque.getRear(); // return 2
circularDeque.isFull(); // return true
circularDeque.deleteLast(); // return true
circularDeque.insertFront(4); // return true
circularDeque.getFront(); // return 4
Note:
- All values will be in the range of [0, 1000].
- The number of operations will be in the range of [1, 1000].
- Please do not use the built-in Deque library.
就像前一道题中的分析的一样,上面的解法并不是本题真正想要考察的内容,我们要用上环形Circular的性质,我们除了使用size来记录环形队列的最大长度之外,还要使用三个变量,head,tail,cnt,分别来记录队首位置,队尾位置,和当前队列中数字的个数,这里我们将head初始化为k-1,tail初始化为0。还是从简单的做起,判空就看当前个数cnt是否为0,判满就看当前个数cnt是否等于size。接下来取首尾元素,先进行判空,然后根据head和tail分别向后和向前移动一位取即可,记得使用上循环数组的性质,要对size取余。再来看删除末尾函数,先进行判空,然后tail向前移动一位,使用循环数组的操作,然后cnt自减1。同理,删除开头函数,先进行判空,队首位置head要向后移动一位,同样进行加1之后对长度取余的操作,然后cnt自减1。再来看插入末尾函数,先进行判满,然后将新的数字加到当前的tail位置,tail移动到下一位,为了避免越界,我们使用环形数组的经典操作,加1之后对长度取余,然后cnt自增1即可。同样,插入开头函数,先进行判满,然后将新的数字加到当前的head位置,head移动到前一位,然后cnt自增1,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76class MyCircularDeque {
public:
vector<int> v;
int size, head, tail, cnt;
/** Initialize your data structure here. Set the size of the deque to be k. */
MyCircularDeque(int k) {
size = k;
head = k-1;
tail = 0;
cnt = 0;
v.resize(k);
}
/** Adds an item at the front of Deque. Return true if the operation is successful. */
bool insertFront(int value) {
if (isFull())
return false;
v[head] = value;
head = (head-1+size) % size;
cnt ++;
return true;
}
/** Adds an item at the rear of Deque. Return true if the operation is successful. */
bool insertLast(int value) {
if (isFull())
return false;
v[tail] = value;
tail = (tail + 1) % size;
cnt ++;
return true;
}
/** Deletes an item from the front of Deque. Return true if the operation is successful. */
bool deleteFront() {
if (isEmpty())
return false;
head = (head + 1) % size;
cnt --;
return true;
}
/** Deletes an item from the rear of Deque. Return true if the operation is successful. */
bool deleteLast() {
if (isEmpty())
return false;
tail = (tail - 1 + size) % size;
cnt --;
return true;
}
/** Get the front item from the deque. */
int getFront() {
if (isEmpty())
return -1;
return v[(head+1)%size];
}
/** Get the last item from the deque. */
int getRear() {
if (isEmpty())
return -1;
return v[(tail-1+size)%size];
}
/** Checks whether the circular deque is empty or not. */
bool isEmpty() {
return cnt == 0;
}
/** Checks whether the circular deque is full or not. */
bool isFull() {
return cnt == size;
}
};
Leetcode643. Maximum Average Subarray I
Given an array consisting of n integers, find the contiguous subarray of given length k that has the maximum average value. And you need to output the maximum average value.
Example 1:1
2
3Input: [1,12,-5,-6,50,3], k = 4
Output: 12.75
Explanation: Maximum average is (12-5-6+50)/4 = 51/4 = 12.75
Note:
- 1 <= k <= n <= 30,000.
- Elements of the given array will be in the range [-10,000, 10,000].
1 | class Solution { |
Leetcode645. Set Mismatch
The set S originally contains numbers from 1 to n. But unfortunately, due to the data error, one of the numbers in the set got duplicated to another number in the set, which results in repetition of one number and loss of another number.
Given an array nums representing the data status of this set after the error. Your task is to firstly find the number occurs twice and then find the number that is missing. Return them in the form of an array.
Example 1:1
2Input: nums = [1,2,2,4]
Output: [2,3]
1 | class Solution { |
Leetcode646. Maximum Length of Pair Chain
You are given an array of n pairs pairs where pairs[i] = [lefti, righti] and lefti < righti.
A pair p2 = [c, d] follows a pair p1 = [a, b] if b < c. A chain of pairs can be formed in this fashion.
Return the length longest chain which can be formed.
You do not need to use up all the given intervals. You can select pairs in any order.
Example 1:1
2
3Input: pairs = [[1,2],[2,3],[3,4]]
Output: 2
Explanation: The longest chain is [1,2] -> [3,4].
Example 2:1
2
3Input: pairs = [[1,2],[7,8],[4,5]]
Output: 3
Explanation: The longest chain is [1,2] -> [4,5] -> [7,8].
这道题给了我们一些链对,规定了如果后面链对的首元素大于前链对的末元素,那么这两个链对就可以链起来,问我们最大能链多少个。那么我们想,由于规定了链对的首元素一定小于尾元素,我们需要比较的是某个链表的首元素和另一个链表的尾元素之间的关系,如果整个链对数组是无序的,那么就很麻烦,所以我们需要做的是首先对链对数组进行排序,按链对的尾元素进行排序,小的放前面。这样我们就可以利用Greedy算法进行求解了。我们可以用一个栈,先将第一个链对压入栈,然后对于后面遍历到的每一个链对,我们看其首元素是否大于栈顶链对的尾元素,如果大于的话,就将当前链对压入栈,这样最后我们返回栈中元素的个数即可,用一个变量对栈进行优化。参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
static bool comp(vector<int> &a, vector<int> &b) {
return a[1] < b[1];
}
int findLongestChain(vector<vector<int>>& pairs) {
sort(pairs.begin(), pairs.end(), comp);
stack<vector<int> > s;
int tail = INT_MIN, res = 0;
for (auto p : pairs) {
if (tail < p[0]) {
tail = p[1];
res ++;
}
}
return res;
}
};
Leetcode647. Palindromic Substrings
Given a string, your task is to count how many palindromic substrings in this string.
The substrings with different start indexes or end indexes are counted as different substrings even they consist of same characters.
Example 1:1
2
3Input: "abc"
Output: 3
Explanation: Three palindromic strings: "a", "b", "c".
Example 2:1
2
3Input: "aaa"
Output: 6
Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".
Note:
- The input string length won’t exceed 1000.
这道题给了一个字符串,让我们计算有多少个回文子字符串。以字符串中的每一个字符都当作回文串中间的位置,然后向两边扩散,每当成功匹配两个左右两个字符,结果 res 自增1,然后再比较下一对。注意回文字符串有奇数和偶数两种形式,如果是奇数长度,那么i位置就是中间那个字符的位置,所以左右两遍都从i开始遍历;如果是偶数长度的,那么i是最中间两个字符的左边那个,右边那个就是 i+1,这样就能 cover 所有的情况啦,而且都是不同的回文子字符串,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int countSubstrings(string s) {
if (s.empty()) return 0;
int n = s.size(), res = 0;
for (int i = 0; i < n; ++i) {
helper(s, i, i, res);
helper(s, i, i + 1, res);
}
return res;
}
void helper(string s, int i, int j, int& res) {
while (i >= 0 && j < s.size() && s[i] == s[j]) {
--i; ++j; ++res;
}
}
};
将dp[i][j]定义成子字符串[i, j]是否是回文串就行了,然后i从 n-1 往0遍历,j从i往 n-1 遍历,然后看s[i]和s[j]是否相等,这时候需要留意一下,有了s[i]和s[j]相等这个条件后,i和j的位置关系很重要,如果i和j相等了,则dp[i][j]肯定是 true;如果i和j是相邻的,那么dp[i][j]也是 true;如果i和j中间只有一个字符,那么dp[i][j]还是 true;如果中间有多余一个字符存在,则需要看dp[i+1][j-1]是否为 true,若为 true,那么dp[i][j]就是 true。赋值dp[i][j]后,如果其为 true,结果res自增1,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int countSubstrings(string s) {
int n = s.size(), res = 0;
vector<vector<bool>> dp(n, vector<bool>(n));
for (int i = n - 1; i >= 0; --i) {
for (int j = i; j < n; ++j) {
dp[i][j] = (s[i] == s[j]) && (j - i <= 2 || dp[i + 1][j - 1]);
if (dp[i][j]) ++res;
}
}
return res;
}
};
Leetcode648. Replace Words
In English, we have a concept called root, which can be followed by some other words to form another longer word - let’s call this word successor. For example, the root an, followed by other, which can form another word another.
Now, given a dictionary consisting of many roots and a sentence. You need to replace all the successor in the sentence with the root forming it. If a successor has many roots can form it, replace it with the root with the shortest length.
You need to output the sentence after the replacement.
Example 1:1
2Input: dictionary = ["cat","bat","rat"], sentence = "the cattle was rattled by the battery"
Output: "the cat was rat by the bat"
Example 2:1
2Input: dictionary = ["a","b","c"], sentence = "aadsfasf absbs bbab cadsfafs"
Output: "a a b c"
Example 3:1
2Input: dictionary = ["a", "aa", "aaa", "aaaa"], sentence = "a aa a aaaa aaa aaa aaa aaaaaa bbb baba ababa"
Output: "a a a a a a a a bbb baba a"
Example 4:1
2Input: dictionary = ["catt","cat","bat","rat"], sentence = "the cattle was rattled by the battery"
Output: "the cat was rat by the bat"
Example 5:1
2Input: dictionary = ["ac","ab"], sentence = "it is abnormal that this solution is accepted"
Output: "it is ab that this solution is ac"
Note:
- The input will only have lower-case letters.
- 1 <= dict words number <= 1000
- 1 <= sentence words number <= 1000
- 1 <= root length <= 100
- 1 <= sentence words length <= 1000
这道题给了我们一个前缀字典,又给了一个句子,让我们将句子中较长的单词换成其前缀(如果在前缀字典中存在的话)。我们对于句子中的一个长单词如何找前缀呢,是不是可以根据第一个字母来快速定位呢,比如cattle这个单词的首字母是c,那么我们在前缀字典中找所有开头是c的前缀,为了方便查找,我们将首字母相同的前缀都放到同一个数组中,总共需要26个数组,所以我们可以定义一个二维数组来装这些前缀。还有,我们希望短前缀在长前缀的前面,因为题目中要求用最短的前缀来替换单词,所以我们可以先按单词的长度来给所有的前缀排序,然后再依次加入对应的数组中,这样就可以保证短的前缀在前面。
下面我们就要来遍历句子中的每一个单词了,由于C++中没有split函数,所以我们就采用字符串流来提取每一个单词,对于遍历到的单词,我们根据其首字母查找对应数组中所有以该首字母开始的前缀,然后直接用substr函数来提取单词中和前缀长度相同的子字符串来跟前缀比较,如果二者相等,说明可以用前缀来替换单词,然后break掉for循环。别忘了单词之前还要加上空格,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
string replaceWords(vector<string>& dict, string sentence) {
string res = "", t = "";
vector<vector<string>> v(26);
istringstream is(sentence);
sort(dict.begin(), dict.end(), [](string &a, string &b) {return a.size() < b.size();});
for (string word : dict) {
v[word[0] - 'a'].push_back(word);
}
while (is >> t) {
for (string word : v[t[0] - 'a']) {
if (t.substr(0, word.size()) == word) {
t = word;
break;
}
}
res += t + " ";
}
res.pop_back();
return res;
}
};
我们要做的就是把所有的前缀都放到前缀树里面,而且在前缀的最后一个结点的地方将标示isWord设为true,表示从根节点到当前结点是一个前缀,然后我们在遍历单词中的每一个字母,我们都在前缀树查找,如果当前字母对应的结点的表示isWord是true,我们就返回这个前缀,如果当前字母对应的结点在前缀树中不存在,我们就返回原单词。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57class Solution {
public:
class Trie {
public:
bool isword;
Trie* t[26];
Trie() : isword(false) {
for(int i = 0; i < 26; i ++)
t[i] = NULL;
}
};
string replaceWords(vector<string>& dictionary, string sentence) {
string res = "";
Trie *root = new Trie();
for (int i = 0; i < dictionary.size(); i ++)
insert(root, dictionary[i]);
int i = 0, len = sentence.length();
while (i < len) {
res += find(root, sentence, i);
while(i < len && sentence[i] != ' ')
i ++;
i ++;
if (i < len)
res += ' ';
}
return res;
}
void insert(Trie *root, string s) {
for (char c : s) {
if (root->t[c - 'a'] == NULL) {
root->t[c - 'a'] = new Trie();
}
root = root->t[c - 'a'];
}
root->isword = true;
}
string find(Trie *root, string s, int& i) {
int len = s.length();
string t = "";
while(i < len && s[i] != ' ') {
root = root->t[s[i] - 'a'];
if (root == NULL)
break;
t += s[i ++];
if (root->isword)
return t;
}
while (i < len && s[i] != ' ') {
t += s[i++];
}
return t;
}
};
Leetcode649. Dota2 Senate
In the world of Dota2, there are two parties: the Radiant and the Dire.
The Dota2 senate consists of senators coming from two parties. Now the senate wants to make a decision about a change in the Dota2 game. The voting for this change is a round-based procedure. In each round, each senator can exercise one of the two rights:
- Ban one senator’s right: A senator can make another senator lose all his rights in this and all the following rounds.
- Announce the victory: If this senator found the senators who still have rights to vote are all from the same party, he can announce the victory and make the decision about the change in the game.
Given a string representing each senator’s party belonging. The character ‘R’ and ‘D’ represent the Radiant party and the Dire party respectively. Then if there are n senators, the size of the given string will be n.
The round-based procedure starts from the first senator to the last senator in the given order. This procedure will last until the end of voting. All the senators who have lost their rights will be skipped during the procedure.
Suppose every senator is smart enough and will play the best strategy for his own party, you need to predict which party will finally announce the victory and make the change in the Dota2 game. The output should be Radiant or Dire.
Example 1:1
2
3
4
5Input: "RD"
Output: "Radiant"
Explanation: The first senator comes from Radiant and he can just ban the next senator's right in the round 1.
And the second senator can't exercise any rights any more since his right has been banned.
And in the round 2, the first senator can just announce the victory since he is the only guy in the senate who can vote.
Example 2:1
2
3
4
5
6
7Input: "RDD"
Output: "Dire"
Explanation:
The first senator comes from Radiant and he can just ban the next senator's right in the round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And the third senator comes from Dire and he can ban the first senator's right in the round 1.
And in the round 2, the third senator can just announce the victory since he is the only guy in the senate who can vote.
这道题模拟了刀塔类游戏开始之前的BP过程,两个阵营按顺序Ban掉对方的英雄,看最后谁剩下来了,就返回哪个阵营。我们可以用两个队列queue,把各自阵营的位置存入不同的队列里面,然后进行循环,每次从两个队列各取一个位置出来,看其大小关系,小的那个说明在前面,就可以把后面的那个Ban掉,所以我们要把小的那个位置要加回队列里面,但是不能直接加原位置,因为下一轮才能再轮到他来Ban,所以我们要加上一个n,再排入队列。这样当某个队列为空时,推出循环,我们返回不为空的那个阵营,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
string predictPartyVictory(string senate) {
int n = senate.size();
queue<int> q1, q2;
for (int i = 0; i < n; ++i) {
(senate[i] == 'R') ? q1.push(i) : q2.push(i);
}
while (!q1.empty() && !q2.empty()) {
int i = q1.front(); q1.pop();
int j = q2.front(); q2.pop();
(i < j) ? q1.push(i + n) : q2.push(j + n);
}
return (q1.size() > q2.size()) ? "Radiant" : "Dire";
}
};
Leetcode650. 2 Keys Keyboard
Initially on a notepad only one character ‘A’ is present. You can perform two operations on this notepad for each step:
- Copy All: You can copy all the characters present on the notepad (partial copy is not allowed).
- Paste: You can paste the characters which are copied last time.
Given a number n. You have to get exactly n ‘A’ on the notepad by performing the minimum number of steps permitted. Output the minimum number of steps to get n ‘A’.
Example 1:1
2
3
4
5
6
7Input: 3
Output: 3
Explanation:
Intitally, we have one character 'A'.
In step 1, we use Copy All operation.
In step 2, we use Paste operation to get 'AA'.
In step 3, we use Paste operation to get 'AAA'.
这道题就是给了复制和粘贴这两个按键,然后给了一个A,目标时利用这两个键来打印出n个A,注意复制的时候时全部复制,不能选择部分来复制,然后复制和粘贴都算操作步骤,问打印出n个A需要多少步操作。
当n = 1时,已经有一个A了,不需要其他操作,返回0
当n = 2时,需要复制一次,粘贴一次,返回2
当n = 3时,需要复制一次,粘贴两次,返回3
当n = 4时,这就有两种做法,一种是需要复制一次,粘贴三次,共4步,另一种是先复制一次,粘贴一次,得到 AA,然后再复制一次,粘贴一次,得到 AAAA,两种方法都是返回4
当n = 5时,需要复制一次,粘贴四次,返回5
当n = 6时,需要复制一次,粘贴两次,得到 AAA,再复制一次,粘贴一次,得到 AAAAAA,共5步,返回5
通过分析上面这6个简单的例子,已经可以总结出一些规律了,首先对于任意一个n(除了1以外),最差的情况就是用n步,不会再多于n步,但是有可能是会小于n步的,比如 n=6 时,就只用了5步,仔细分析一下,发现时先拼成了 AAA,再复制粘贴成了 AAAAAA。那么什么情况下可以利用这种方法来减少步骤呢,分析发现,小模块的长度必须要能整除n,这样才能拆分。对于 n=6,我们其实还可先拼出 AA,然后再复制一次,粘贴两次,得到的还是5。分析到这里,解题的思路应该比较清晰了,找出n的所有因子,然后这个因子可以当作模块的个数,再算出模块的长度 n/i,调用递归,加上模块的个数i来更新结果 res 即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int minSteps(int n) {
if (n == 1) return 0;
int res = n;
for (int i = n - 1; i > 1; --i) {
if (n % i == 0) {
res = min(res, minSteps(n / i) + i);
}
}
return res;
}
};
下面这种方法是用 DP 来做的,我们可以看出来,其实就是上面递归解法的迭代形式,思路没有任何区别,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int minSteps(int n) {
vector<int> dp(n + 1, 0);
for (int i = 2; i <= n; ++i) {
dp[i] = i;
for (int j = i - 1; j > 1; --j) {
if (i % j == 0) {
dp[i] = min(dp[i], dp[j] + i / j);
}
}
}
return dp[n];
}
};
Leetcode652. Find Duplicate Subtrees
Given a binary tree, return all duplicate subtrees. For each kind of duplicate subtrees, you only need to return the root node of any oneof them.
Two trees are duplicate if they have the same structure with same node values.
Example 1:1
2
3
4
5
6
7 1
/ \
2 3
/ / \
4 2 4
/
4
The following are two duplicate subtrees:1
2
3 2
/
4
and1
4
Therefore, you need to return above trees’ root in the form of a list.
这道题让我们寻找重复树,建立序列化跟其出现次数的映射,这样如果我们得到某个结点的序列化字符串,而该字符串正好出现的次数为1,说明之前已经有一个重复树了,我们将当前结点存入结果res,这样保证了多个重复树只会存入一个结点,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
vector<TreeNode*> res;
unordered_map<string, int> m;
helper(root, m, res);
return res;
}
string helper(TreeNode* root, unordered_map<string, int>& m, vector<TreeNode*>& res) {
if (!root)
return "#";
string str = to_string(root->val) + ',' + helper(root->left, m, res) + ',' + helper(root->right, m, res);
if (m[str] == 1)
res.push_back(root);
m[str] ++;
return str;
}
};
Leetcode653. Two Sum IV - Input is a BST
Given a Binary Search Tree and a target number, return true if there exist two elements in the BST such that their sum is equal to the given target.
Example 1:1
2
3
4
5
6
7
8
9Input:
5
/ \
3 6
/ \ \
2 4 7
Target = 9
Output: True
Example 2:1
2
3
4
5
6
7
8
9Input:
5
/ \
3 6
/ \ \
2 4 7
Target = 28
Output: False
这道题又是一道2sum的变种题。只要是两数之和的题,一定要记得先尝试用HashSet来做,这道题只不过是把数组变成了一棵二叉树而已,换汤不换药,我们遍历二叉树就行,然后用一个HashSet,在递归函数函数中,如果node为空,返回false。如果k减去当前结点值在HashSet中存在,直接返回true;否则就将当前结点值加入HashSet,然后对左右子结点分别调用递归函数并且或起来返回即可。本来想用双指针的,但是不好办,要考虑的情况太多。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
bool dfs(TreeNode* root, unordered_set<int> &mp, int k) {
if(!root)
return false;
if(mp.count(k - root->val))
return true;
mp.insert(root->val);
return dfs(root->left, mp, k) || dfs(root->right, mp, k);
}
bool findTarget(TreeNode* root, int k) {
unordered_set<int> mp;
return dfs(root, mp, k);
}
};
Leetcode654. Maximum Binary Tree
Given an integer array with no duplicates. A maximum tree building on this array is defined as follow:
The root is the maximum number in the array.
The left subtree is the maximum tree constructed from left part subarray divided by the maximum number.
The right subtree is the maximum tree constructed from right part subarray divided by the maximum number.
Construct the maximum tree by the given array and output the root node of this tree.
Example 1:1
2
3
4
5
6
7
8
9
10Input: [3,2,1,6,0,5]
Output: return the tree root node representing the following tree:
6
/ \
3 5
\ /
2 0
\
1
Note:
The size of the given array will be in the range [1,1000].
这个题比较奇怪,其实不太懂题意,主要是给一个数组,把数组建立成一个树,找到最大的数作为root,然后递归建立,大概是这个意思。
1 | class Solution { |
Leetcode655. Print Binary Tree
Print a binary tree in an m*n 2D string array following these rules:
The row number m should be equal to the height of the given binary tree.
The column number n should always be an odd number.
The root node’s value (in string format) should be put in the exactly middle of the first row it can be put. The column and the row where the root node belongs will separate the rest space into two parts (left-bottom part and right-bottom part). You should print the left subtree in the left-bottom part and print the right subtree in the right-bottom part. The left-bottom part and the right-bottom part should have the same size. Even if one subtree is none while the other is not, you don’t need to print anything for the none subtree but still need to leave the space as large as that for the other subtree. However, if two subtrees are none, then you don’t need to leave space for both of them.
Each unused space should contain an empty string “”.
Print the subtrees following the same rules.
Example 1:1
2
3
4
5
6
7Input:
1
/
2
Output:
[["", "1", ""],
["2", "", ""]]
Example 2:1
2
3
4
5
6
7
8
9
10Input:
1
/ \
2 3
\
4
Output:
[["", "", "", "1", "", "", ""],
["", "2", "", "", "", "3", ""],
["", "", "4", "", "", "", ""]]
Example 3:1
2
3
4
5
6
7
8
9
10
11
12
13Input:
1
/ \
2 5
/
3
/
4
Output:
[["", "", "", "", "", "", "", "1", "", "", "", "", "", "", ""]
["", "", "", "2", "", "", "", "", "", "", "", "5", "", "", ""]
["", "3", "", "", "", "", "", "", "", "", "", "", "", "", ""]
["4", "", "", "", "", "", "", "", "", "", "", "", "", "", ""]]
Note: The height of binary tree is in the range of [1, 10].
这道题给了我们一棵二叉树,让我们以数组的形式打印出来。数组每一行的宽度是二叉树的最底层数所能有的最多结点数,存在的结点需要填入到正确的位置上。那么这道题我们就应该首先要确定返回数组的宽度,由于宽度跟数组的深度有关,所以我们首先应该算出二叉树的最大深度,直接写一个子函数返回这个最大深度,从而计算出宽度。下面就是要遍历二叉树从而在数组中加入结点值。我们先来看第一行,由于根结点只有一个,所以第一行只需要插入一个数字,不管这一行多少个位置,我们都是在最中间的位置插入结点值。下面来看第二行,我们仔细观察可以发现,如果我们将这一行分为左右两部分,那么插入的位置还是在每一部分的中间位置,这样我们只要能确定分成的部分的左右边界位置,就知道插入结点的位置了,所以应该是使用分治法的思路。在递归函数中,如果当前node不存在或者当前深度超过了最大深度直接返回,否则就给中间位置赋值为结点值,然后对于左子结点,范围是左边界到中间位置,调用递归函数,注意当前深度加1;同理对于右子结点,范围是中间位置加1到右边界,调用递归函数,注意当前深度加1,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
vector<vector<string>> printTree(TreeNode* root) {
int h = getHeight(root), w = pow(2, h) - 1;
vector<vector<string>> res(h, vector<string>(w, ""));
helper(root, 0, w - 1, 0, h, res);
return res;
}
void helper(TreeNode* node, int i, int j, int curH, int height, vector<vector<string>>& res) {
if (!node || curH == height) return;
res[curH][(i + j) / 2] = to_string(node->val);
helper(node->left, i, (i + j) / 2, curH + 1, height, res);
helper(node->right, (i + j) / 2 + 1, j, curH + 1, height, res);
}
int getHeight(TreeNode* node) {
if (!node) return 0;
return 1 + max(getHeight(node->left), getHeight(node->right));
}
};
Leetcode657. Robot Return to Origin
There is a robot starting at position (0, 0), the origin, on a 2D plane. Given a sequence of its moves, judge if this robot ends up at (0, 0) after it completes its moves.
The move sequence is represented by a string, and the character moves[i] represents its ith move. Valid moves are R (right), L (left), U (up), and D (down). If the robot returns to the origin after it finishes all of its moves, return true. Otherwise, return false.
Note: The way that the robot is “facing” is irrelevant. “R” will always make the robot move to the right once, “L” will always make it move left, etc. Also, assume that the magnitude of the robot’s movement is the same for each move.
Example 1:1
2
3Input: "UD"
Output: true
Explanation: The robot moves up once, and then down once. All moves have the same magnitude, so it ended up at the origin where it started. Therefore, we return true.
Example 2:1
2
3Input: "LL"
Output: false
Explanation: The robot moves left twice. It ends up two "moves" to the left of the origin. We return false because it is not at the origin at the end of its moves.
一个序列,判断‘L’和‘R’是不是个数相等,‘U’和‘D’是不是个数相等。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
bool judgeCircle(string moves) {
int ud=0,lr=0;
for(int i=0;i<moves.length();i++){
if(moves[i]=='U') ud++;
else if(moves[i]=='D') ud--;
else if(moves[i]=='L') lr++;
else if(moves[i]=='R') lr--;
}
if(ud==0 && lr==0)
return true;
else
return false;
}
};
Leetcode658. Find K Closest Elements
Given a sorted array, two integers k and x, find the k closest elements to x in the array. The result should also be sorted in ascending order. If there is a tie, the smaller elements are always preferred.
Example 1:1
2Input: [1,2,3,4,5], k=4, x=3
Output: [1,2,3,4]
Example 2:1
2Input: [1,2,3,4,5], k=4, x=-1
Output: [1,2,3,4]
Note:
- The value k is positive and will always be smaller than the length of the sorted array.
- Length of the given array is positive and will not exceed 104
- Absolute value of elements in the array and x will not exceed 104
这道题给我们了一个数组,还有两个变量k和x。让找数组中离x最近的k个元素,而且说明了数组是有序的,如果两个数字距离x相等的话,取较小的那个。从给定的例子可以分析出x不一定是数组中的数字,由于数组是有序的,所以最后返回的k个元素也一定是有序的,那么其实就是返回了原数组的一个长度为k的子数组,转化一下,实际上相当于在长度为n的数组中去掉 n-k 个数字,而且去掉的顺序肯定是从两头开始去,因为距离x最远的数字肯定在首尾出现。那么问题就变的明朗了,每次比较首尾两个数字跟x的距离,将距离大的那个数字删除,直到剩余的数组长度为k为止,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
vector<int> findClosestElements(vector<int>& arr, int k, int x) {
int len = arr.size(), l = 0, r = len-1;
while(r - l + 1 > k) {
if (x - arr[l] < arr[r] - x)
r --;
else if (x - arr[l] > arr[r] - x)
l ++;
else {
if (arr[l] < arr[r])
r --;
else
l ++;
}
}
vector<int> res;
for (int i = l; i <= r; i ++)
res.push_back(arr[i]);
return res;
}
};
下面这种解法是论坛上的高分解法,用到了二分搜索法。其实博主最开始用的方法并不是帖子中的这两个方法,虽然也是用的二分搜索法,但博主搜的是第一个不小于x的数,然后同时向左右两个方向遍历,每次取和x距离最小的数加入结果 res 中,直到取满k个为止。但是下面这种方法更加巧妙一些,二分法的判定条件做了一些改变,就可以直接找到要返回的k的数字的子数组的起始位置,感觉非常的神奇。每次比较的是 mid 位置和x的距离跟 mid+k 跟x的距离,以这两者的大小关系来确定二分法折半的方向,最后找到最近距离子数组的起始位置,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
vector<int> findClosestElements(vector<int>& arr, int k, int x) {
int left = 0, right = arr.size() - k;
while (left < right) {
int mid = left + (right - left) / 2;
if (x - arr[mid] > arr[mid + k] - x) left = mid + 1;
else right = mid;
}
return vector<int>(arr.begin() + left, arr.begin() + left + k);
}
};
Leetcode659. Split Array into Consecutive Subsequences
You are given an integer array sorted in ascending order (may contain duplicates), you need to split them into several subsequences, where each subsequences consist of at least 3 consecutive integers. Return whether you can make such a split.
Example 1:1
2
3
4
5
6Input: [1,2,3,3,4,5]
Output: True
Explanation:
You can split them into two consecutive subsequences :
1, 2, 3
3, 4, 5
Example 2:1
2
3
4
5
6Input: [1,2,3,3,4,4,5,5]
Output: True
Explanation:
You can split them into two consecutive subsequences :
1, 2, 3, 4, 5
3, 4, 5
Example 3:1
2Input: [1,2,3,4,4,5]
Output: False
这道题让将数组分割成多个连续递增的子序列,注意这里可能会产生歧义,实际上应该是分割成一个或多个连续递增的子序列,因为 [1,2,3,4,5] 也是正确的解。这道题就用贪婪解法就可以了,使用两个 HashMap,第一个 HashMap 用来建立数字和其出现次数之间的映射 freq,第二个用来建立可以加在某个连续子序列后的数字与其可以出现的次数之间的映射 need。对于第二个 HashMap,举个例子来说,就是假如有个连牌,比如对于数字1,此时检测数字2和3是否存在,若存在的话,表明有连牌 [1,2,3] 存在,由于后面可以加上4,组成更长的连牌,所以不管此时牌里有没有4,都可以建立 4->1 的映射,表明此时需要一个4。这样首先遍历一遍数组,统计每个数字出现的频率,然后开始遍历数组,对于每个遍历到的数字,首先看其当前出现的次数,如果为0,则继续循环;如果 need 中存在这个数字的非0映射,那么表示当前的数字可以加到某个连的末尾,将当前数字在 need 中的映射值自减1,然后将下一个连续数字的映射值加1,因为当 [1,2,3] 连上4后变成 [1,2,3,4] 之后,就可以连上5了,说明此时还需要一个5;如果不能连到其他子序列后面,则来看其是否可以成为新的子序列的起点,可以通过看后面两个数字的映射值是否大于0,都大于0的话,说明可以组成3连儿,于是将后面两个数字的映射值都自减1,还有由于组成了3连儿,在 need 中将末尾的下一位数字的映射值自增1;如果上面情况都不满足,说明该数字是单牌,只能划单儿,直接返回 false。最后别忘了将当前数字的 freq 映射值自减1。退出 for 循环后返回 true,参见代码如下:
1 | class Solution { |
Leetcode661. Image Smoother
Given a 2D integer matrix M representing the gray scale of an image, you need to design a smoother to make the gray scale of each cell becomes the average gray scale (rounding down) of all the 8 surrounding cells and itself. If a cell has less than 8 surrounding cells, then use as many as you can.
Example 1:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15Input:
[[1,1,1],
[1,0,1],
[1,1,1]]
Output:
[[0, 0, 0],
[0, 0, 0],
[0, 0, 0]]
Explanation:
For the point (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the point (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
Note:
The value in the given matrix is in the range of [0, 255].
The length and width of the given matrix are in the range of [1, 150].
假设一个二维整数矩阵M代表图像的灰度,你需要设计一个更平滑的方法,使每个单元格的灰度范围变成所有8个周围单元格的平均灰度(四舍五入)。如果一个单元格的周围单元格少于8个,那么就尽可能多地使用。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int getval(vector<vector<int>>& M, int ii, int jj) {
int sum = 0;
int count = 0;
for(int i = ii-1; i <= ii+1; i ++)
for(int j = jj-1; j <= jj+1; j ++)
if(i >= 0 && j >= 0 && i < M.size() && j < M[0].size()) {
count ++;
sum += M[i][j];
}
return sum / count;
}
vector<vector<int>> imageSmoother(vector<vector<int>>& M) {
int m = M.size(), n = M[0].size();
vector<vector<int>> res(m, vector(n, 0));
for(int i = 0; i < m; i ++)
for(int j = 0; j < n; j ++)
res[i][j] = getval(M, i, j);
return res;
}
};
Leetcode662. Maximum Width of Binary Tree
Given a binary tree, write a function to get the maximum width of the given tree. The width of a tree is the maximum width among all levels. The binary tree has the same structure as a full binary tree, but some nodes are null.
The width of one level is defined as the length between the end-nodes (the leftmost and right most non-null nodes in the level, where the null nodes between the end-nodes are also counted into the length calculation.
Example 1:1
2
3
4
5
6
7
8
9Input:
1
/ \
3 2
/ \ \
5 3 9
Output: 4
Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).
Example 2:1
2
3
4
5
6
7
8Input:
1
/
3
/ \
5 3
Output: 2
Explanation: The maximum width existing in the third level with the length 2 (5,3).
Example 3:1
2
3
4
5
6
7
8
9Input:
1
/ \
3 2
/
5
Output: 2
Explanation: The maximum width existing in the second level with the length 2 (3,2).
Example 4:1
2
3
4
5
6
7
8
9
10
11Input:
1
/ \
3 2
/ \
5 9
/ \
6 7
Output: 8
Explanation:The maximum width existing in the fourth level with the length 8 (6,null,null,null,null,null,null,7).
这道题让我们求二叉树的最大宽度,根据题目中的描述可知,这里的最大宽度不是满树的时候的最大宽度,如果是那样的话,肯定是最后一层的结点数最多。这里的最大宽度应该是两个存在的结点中间可容纳的总的结点个数,中间的结点可以为空。那么其实只要我们知道了每一层中最左边和最右边的结点的位置,我们就可以算出这一层的宽度了。所以这道题的关键就是要记录每一层中最左边结点的位置,我们知道对于一棵完美二叉树,如果根结点是深度1,那么每一层的结点数就是2*n-1,那么每个结点的位置就是[1, 2*n-1]中的一个,假设某个结点的位置是i,那么其左右子结点的位置可以直接算出来,为2*i和2*i+1。这里使用了队列 queue 来辅助运算,queue 里存的是一个 pair,结点和其当前位置,在进入新一层的循环时,首先要判断该层是否只有1个结点,是的话重置结点坐标位置,再将首结点的位置保存出来当作最左位置,然后对于遍历到的结点,都更新右结点的位置,遍历一层的结点后来计算宽度更新结果 res,注意防止溢出,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
if (!root)
return 0;
queue<pair<TreeNode*, int>> q;
q.push({root, 1});
int res = 0;
while(!q.empty()) {
int cnt = q.size();
int left = q.front().second, right = left;
int maxx = q.back().second;
for (int i = 0; i < cnt; i ++) {
TreeNode* tmp = q.front().first;
right = q.front().second;
q.pop();
if (tmp->left) q.push({tmp->left, right*2-maxx});
if (tmp->right) q.push({tmp->right, right*2+1-maxx});
}
res = max(res, right - left + 1);
}
return res;
}
};
Leetcode664. Strange Printer
There is a strange printer with the following two special requirements:
The printer can only print a sequence of the same character each time.
At each turn, the printer can print new characters starting from and ending at any places, and will cover the original existing characters.
Given a string consists of lower English letters only, your job is to count the minimum number of turns the printer needed in order to print it.
Example 1:1
2
3Input: "aaabbb"
Output: 2
Explanation: Print "aaa" first and then print "bbb".
Example 2:1
2
3Input: "aba"
Output: 2
Explanation: Print "aaa" first and then print "b" from the second place of the string, which will cover the existing character 'a'.
这道题说有一种奇怪的打印机每次只能打印一排相同的字符,然后可以在任意起点和终点位置之间打印新的字符,用来覆盖原有的字符。现在给了我们一个新的字符串,问我们需要几次可以正确的打印出来。题目中给了两个非常简单的例子,主要是帮助我们理解的。博主最开始想的方法是一种类似贪婪算法,先是找出出现次数最多的字符,然后算需要多少次变换能将所有其他字符都变成那个出现最多次的字符,结果fail了。然后又试了一种类似剥洋葱的方法,从首尾都分别找连续相同的字符,如果首尾字符相同,则两部分一起移去,否则就移去连续相同个数多的子序列。
二维dp数组中dp[i][j]表示打印出字符串[i, j]范围内字符的最小步数,难点就是找递推公式啦。遇到乍看去没啥思路的题,博主一般会先从简单的例子开始,看能不能分析出规律,从而找到解题的线索。首先如果只有一个字符,比如字符串是”a”的话,那么直接一次打印出来就行了。如果字符串是”ab”的话,那么我们要么先打印出”aa”,再改成”ab”,或者先打印出”bb”,再改成”ab”。同理,如果字符串是”abc”的话,就需要三次打印。那么一个很明显的特征是,如果没有重复的字符,打印的次数就是字符的个数。燃鹅这题的难点就是要处理有相同字符的情况,比如字符串是”aba”的时候,我们先打”aaa”的话,两步就搞定了,如果先打”bbb”的话,就需要三步。我们再来看一个字符串”abcb”,我们知道需要需要三步,我们看如果把这个字符串分成两个部分”a”和”bcb”,它们分别的步数是1和2,加起来的3是整个的步数。而对于字符串”abba”,如果分成”a”和”bba”,它们分别的步数也是1和2,但是总步数却是2。这是因为分出的”a”和”bba”中的最后一个字符相同。对于字符串”abbac”,因为位置0上的a和位置3上的a相同,那么整个字符串的步数相当于”bb”和”ac”的步数之和,为3。那么分析到这,是不是有点眉目了?我们关心的是字符相等的地方,对于[i, j]范围的字符,我们从i+1位置上的字符开始遍历到j,如果和i位置上的字符相等,我们就以此位置为界,将[i+1, j]范围内的字符拆为两个部分,将二者的dp值加起来,和原dp值相比,取较小的那个。所以我们的递推式如下:1
dp[i][j] = min(dp[i][j], dp[i + 1][k - 1] + dp[k][j] (s[k] == s[i] and i + 1 <= k <= j)
要注意一些初始化的值,dp[i][i]是1,因为一个字符嘛,打印1次,还是就是在遍历k之前,dp[i][j]初始化为 1 + dp[i + 1][j],为啥呢,可以看成在[i + 1, j]的范围上多加了一个s[i]字符,最坏的情况就是加上的是一个不曾出现过的字符,步数顶多加1步,注意我们的i是从后往前遍历的,当然你可以从前往后遍历,参数对应好就行了,参见代码如下:
1 | class Solution { |
理解了上面的DP的方法,那么也可以用递归的形式来写,记忆数组memo就相当于dp数组,整个思路完全一样,参见代码如下:
1 | class Solution { |
Leetcode665. Non-decreasing Array
Given an array nums with n integers, your task is to check if it could become non-decreasing by modifying at most 1 element.
We define an array is non-decreasing if nums[i] <= nums[i + 1] holds for every i (0-based) such that (0 <= i <= n - 2).
Example 1:1
2
3Input: nums = [4,2,3]
Output: true
Explanation: You could modify the first 4 to 1 to get a non-decreasing array.
Example 2:1
2
3Input: nums = [4,2,1]
Output: false
Explanation: You can't get a non-decreasing array by modify at most one element.
这道题给了我们一个数组,说我们最多有1次修改某个数字的机会,问能不能将数组变为非递减数组。题目中给的例子太少,不能覆盖所有情况,我们再来看下面三个例子:
- 4,2,3
- -1,4,2,3
- 2,3,3,2,4
我们通过分析上面三个例子可以发现,当我们发现后面的数字小于前面的数字产生冲突后,有时候需要修改前面较大的数字(比如前两个例子需要修改4),有时候却要修改后面较小的那个数字(比如前第三个例子需要修改2),那么有什么内在规律吗?是有的,判断修改那个数字其实跟再前面一个数的大小有关系,首先如果再前面的数不存在,比如例子1,4前面没有数字了,我们直接修改前面的数字为当前的数字2即可。而当再前面的数字存在,并且小于当前数时,比如例子2,-1小于2,我们还是需要修改前面的数字4为当前数字2;如果再前面的数大于当前数,比如例子3,3大于2,我们需要修改当前数2为前面的数3。这是修改的情况,由于我们只有一次修改的机会,所以用一个变量cnt,初始化为1,修改数字后cnt自减1,当下次再需要修改时,如果cnt已经为0了,直接返回false。遍历结束后返回true,1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool checkPossibility(vector<int>& nums) {
bool res = true;
int count = 1;
for(int i = 1; i < nums.size(); i ++)
if(nums[i-1] > nums[i]) {
if(!count) {
return false;
}
if (i == 1 || nums[i] >= nums[i - 2])
nums[i-1] = nums[i];
else
nums[i] = nums[i-1];
count --;
}
return true;
}
};
Leetcode667. Beautiful Arrangement II
Given two integers n and k, you need to construct a list which contains n different positive integers ranging from 1 to n and obeys the following requirement:
Suppose this list is [a1, a2, a3, … , an], then the list [|a1 - a2|, |a2 - a3|, |a3 - a4|, … , |an-1 - an|] has exactly k distinct integers.
If there are multiple answers, print any of them.
Example 1:1
2
3Input: n = 3, k = 1
Output: [1, 2, 3]
Explanation: The [1, 2, 3] has three different positive integers ranging from 1 to 3, and the [1, 1] has exactly 1 distinct integer: 1.
Example 2:1
2
3Input: n = 3, k = 2
Output: [1, 3, 2]
Explanation: The [1, 3, 2] has three different positive integers ranging from 1 to 3, and the [2, 1] has exactly 2 distinct integers: 1 and 2.
Note:
- The n and k are in the range 1 <= k < n <= 104.
这道题给我们了一个数字n和一个数字k,让找出一种排列方式,使得1到n组成的数组中相邻两个数的差的绝对值正好有k种。给了k和n的关系为k<n。那么我们首先来考虑,是否这种条件关系下,是否已定存在这种优美排列呢,我们用一个例子来分析,比如说当n=8,我们有数组:
1, 2, 3, 4, 5, 6, 7, 8
当我们这样有序排列的话,相邻两数的差的绝对值为1。我们想差的绝对值最大能为多少,应该是把1和8放到一起,为7。那么为了尽可能的产生不同的差的绝对值,我们在8后面需要放一个小数字,比如2,这样会产生差的绝对值6,同理,后面再跟一个大数,比如7,产生差的绝对值5,以此类推,我们得到下列数组:
1, 8, 2, 7, 3, 6, 4, 5
其差的绝对值为:7,6,5,4,3,2,1
共有7种,所以我们知道k最大为n-1,所以这样的排列一定会存在。我们的策略是,先按照这种最小最大数相邻的方法排列,每排一个,k自减1,当k减到1的时候,后面的排列方法只要按照生序的方法排列,就不会产生不同的差的绝对值,这种算法的时间复杂度是O(n),属于比较高效的那种。我们使用两个指针,初始时分别指向1和n,然后分别从i和j取数加入结果res,每取一个数字k自减1,直到k减到1的时候,开始按升序取后面的数字,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
vector<int> constructArray(int n, int k) {
vector<int> res;
int i = 1, j = n;
while (i <= j) {
if (k > 1) res.push_back(k-- % 2 ? i++ : j--);
else res.push_back(i++);
}
return res;
}
};
Leetcode669. Trim a Binary Search Tree
Given a binary search tree and the lowest and highest boundaries as L and R, trim the tree so that all its elements lies in [L, R] (R >= L). You might need to change the root of the tree, so the result should return the new root of the trimmed binary search tree.
Example 1:1
2
3
4
5
6
7
8
9
10
11
12Input:
1
/ \
0 2
L = 1
R = 2
Output:
1
\
2
Example 2:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18Input:
3
/ \
0 4
\
2
/
1
L = 1
R = 3
Output:
3
/
2
/
1
修剪一棵二叉搜索树,给定一个区间[L, R],剪掉value值不在该区间内的节点。由于这是一棵二次搜索树,它或者是一棵空树,或者是具有下列性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树。
所以会出现以下三种情况:
- 当前节点的值 < L,当前节点的左子树的值都是小于当前节点的值,所以都要减掉,我们只需要继续修剪当前节点的右子树。
- 当前节点的值 > R,当前节点的右子树的值都是大于当前节点的值,所以也要全部减掉,我们只需要继续修剪当前节点的左子树。
- L <= 当前节点的值 <= R,需要修剪他的左子树和右子树。
1 | class Solution { |
Leetcode670. Maximum Swap
You are given an integer num. You can swap two digits at most once to get the maximum valued number.
Return the maximum valued number you can get.
Example 1:1
2
3Input: num = 2736
Output: 7236
Explanation: Swap the number 2 and the number 7.
Example 2:1
2
3Input: num = 9973
Output: 9973
Explanation: No swap.
这道题给了一个数字,我们有一次机会可以置换该数字中的任意两位,让返回置换后的最大值,当然如果当前数字就是最大值,也可以选择不置换,直接返回原数。由于希望置换后的数字最大,那么肯定最好的高位上的小数字和低位上的大数字进行置换,比如例子1。而如果高位上的都是大数字,像例子2那样,很有可能就不需要置换。所以需要找到每个数字右边的最大数字(包括其自身),这样再从高位像低位遍历,如果某一位上的数字小于其右边的最大数字,说明需要调换,由于最大数字可能不止出现一次,这里希望能跟较低位的数字置换,这样置换后的数字最大,所以就从低位向高位遍历来找那个最大的数字,找到后进行调换即可。比如对于 1993 这个数:
1 9 9 3
9 9 1 3
我们建立好数组后,从头遍历原数字,发现1比9小,于是从末尾往前找9,找到后一置换,就得到了 9913。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
public:
int maximumSwap(int num) {
vector<int> r;
int o_num = num;
while(num > 0) {
r.push_back(num%10);
num /= 10;
}
int len = r.size(), i, j;
vector<int> max_num(len, -1);
for (i = len-1; i >= 0; i --) {
for (j = i; j >= 0; j --) {
max_num[i] = max(max_num[i], r[j]);
}
}
for (i = len-1; i >= 0; i --) {
if (max_num[i] > r[i])
break;
}
if (i == -1)
return o_num;
for (j = 0; j < len; j ++ )
if (r[j] == max_num[i])
break;
swap(r[i], r[j]);
int res = 0;
for (i = len-1; i >= 0; i --)
res = res * 10 + r[i];
return res;
}
};
Leetcode671. Second Minimum Node In a Binary Tree
Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes. More formally, the property root.val = min(root.left.val, root.right.val) always holds.
Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.
If no such second minimum value exists, output -1 instead.
Example 1:1
2
3
4
5
6
7
8
9Input:
2
/ \
2 5
/ \
5 7
Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.
Example 2:1
2
3
4
5
6
7Input:
2
/ \
2 2
Output: -1
Explanation: The smallest value is 2, but there isn't any second smallest value.
本来想用两个最小值来记录,但是很麻烦,还是先遍历再用set去重吧1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int findSecondMinimumValue(TreeNode* root) {
set<int> s;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()) {
TreeNode* temp = q.front();
q.pop();
s.insert(temp->val);
if(temp->left)
q.push(temp->left);
if(temp->right)
q.push(temp->right);
}
auto it = s.begin();
it++;
if(it == s.end())
return -1;
return *it;
}
};
Leetcode672. Bulb Switcher II
There is a room with n lights which are turned on initially and 4 buttons on the wall. After performing exactly m unknown operations towards buttons, you need to return how many different kinds of status of the n lights could be.
Suppose n lights are labeled as number [1, 2, 3 …, n], function of these 4 buttons are given below:
- Flip all the lights.
- Flip lights with even numbers.
- Flip lights with odd numbers.
- Flip lights with (3k + 1) numbers, k = 0, 1, 2, …
Example 1:1
2
3Input: n = 1, m = 1.
Output: 2
Explanation: Status can be: [on], [off]
Example 2:1
2
3Input: n = 2, m = 1.
Output: 3
Explanation: Status can be: [on, off], [off, on], [off, off]
Example 3:1
2
3Input: n = 3, m = 1.
Output: 4
Explanation: Status can be: [off, on, off], [on, off, on], [off, off, off], [off, on, on].
Note: n and m both fit in range [0, 1000].
这道题是之前那道Bulb Switcher的拓展,但是关灯的方式改变了。现在有四种关灯方法,全关,关偶数灯,关奇数灯,关3k+1的灯。现在给我们n盏灯,允许m步操作,问我们总共能组成多少种不同的状态。博主开始想,题目没有让列出所有的情况,而只是让返回总个数。那么博主觉得应该不能用递归的暴力破解来做,一般都是用DP来做啊。可是想了半天也没想出递推公式,只得作罢。只好去参考大神们的做法,发现这道题的结果并不会是一个超大数,最多情况只有8种。转念一想,也是,如果结果是一个超大数,一般都会对一个超大数10e7来取余,而这道题并没有,所以是一个很大的hint,只不过博主没有get到。博主应该多列几种情况的,说不定就能找出规律。下面先来看一种暴力解法,首先我们先做一个小小的优化,我们来分析四种情况:
第一种情况: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 ,…
第二种情况:1, 2 ,3, 4 ,5, 6 ,7, 8 ,9, 10 ,11, 12 ,13, 14 ,15,…
第三种情况: 1 ,2, 3 ,4, 5 ,6, 7 ,8, 9 ,10, 11 ,12, 13 ,14, 15 ,…
第四种情况: 1 ,2,3, 4 ,5,6, 7 ,8,9, 10 ,11,12, 13 ,14,15,…
通过观察上面的数组,我们可以发现以6个为1组,都是重复的pattern,那么实际上我们可以把重复的pattern去掉而且并不会影响结果。如果n大于6,我们则对其取余再加上6,新的n跟使用原来的n会得到同样的结果,但这样降低了我们的计算量。
下面我们先来生成n个1,这里1表示灯亮,0表示灯灭,然后我们需要一个set来记录已经存在的状态,用一个queue来辅助我们的BFS运算。我们需要循环m次,因为要操作m次,每次开始循环之前,先统计出此时queue中数字的个数len,然后进行len次循环,这就像二叉树中的层序遍历,必须上一层的结点全部遍历完了才能进入下一层,当然,在每一层开始前,我们都需要情况集合s,这样每个操作之间才不会互相干扰。然后在每层的数字循环中,我们取出队首状态,然后分别调用四种方法,突然感觉,这很像迷宫遍历问题,上下左右四个方向,周围四个状态算出来,我们将不再集合set中的状态加入queue和集合set。当m次操作遍历完成后,队列queue中状态的个数即为所求,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49class Solution {
public:
int flipLights(int n, int m) {
n = (n <= 6) ? n : (n % 6 + 6);
int start = (1 << n) - 1;
unordered_set<int> s;
queue<int> q{{start}};
for (int i = 0; i < m; ++i) {
int len = q.size();
s.clear();
for (int k = 0; k < len; ++k) {
int t = q.front(); q.pop();
vector<int> next{flipAll(t, n), flipEven(t, n), flipOdd(t, n), flip3k1(t, n)};
for (int num : next) {
if (s.count(num)) continue;
q.push(num);
s.insert(num);
}
}
}
return q.size();
}
int flipAll(int t, int n) {
int x = (1 << n) - 1;
return t ^ x;
}
int flipEven(int t, int n) {
for (int i = 0; i < n; i += 2) {
t ^= (1 << i);
}
return t;
}
int flipOdd(int t, int n) {
for (int i = 1; i < n; i += 2) {
t ^= (1 << i);
}
return t;
}
int flip3k1(int t, int n) {
for (int i = 0; i < n; i += 3) {
t ^= (1 << i);
}
return t;
}
};
上面那个方法虽然正确,但是有些复杂了,由于这道题最多只有8中情况,所以很适合分情况来讨论:
- 当m和n其中有任意一个数是0时,返回1
- 当n = 1时只有两种情况,0和1
- 当n = 2时,这时候要看m的次数,如果m = 1,那么有三种状态 00,01,10
- 当m > 1时,那么有四种状态,00,01,10,11
- 当m = 1时,此时n至少为3,那么我们有四种状态,000,010,101,011
- 当m = 2时,此时n至少为3,我们有七种状态:111,101,010,100,000,001,110
- 当m > 2时,此时n至少为3,我们有八种状态:111,101,010,100,000,001,110,011
1 | class Solution { |
Leetcode673. Number of Longest Increasing Subsequence
Given an unsorted array of integers, find the number of longest increasing subsequence.
Example 1:1
2
3Input: [1,3,5,4,7]
Output: 2
Explanation: The two longest increasing subsequence are [1, 3, 4, 7] and [1, 3, 5, 7].
Example 2:1
2
3Input: [2,2,2,2,2]
Output: 5
Explanation: The length of longest continuous increasing subsequence is 1, and there are 5 subsequences' length is 1, so output 5.
Note: Length of the given array will be not exceed 2000 and the answer is guaranteed to be fit in 32-bit signed int.
这道题给了我们一个数组,让求最长递增序列的个数。这里用len[i]表示以nums[i]为结尾的递推序列的长度,用cnt[i]表示以nums[i]为结尾的递推序列的个数,初始化都赋值为1,只要有数字,那么至少都是1。然后遍历数组,对于每个遍历到的数字nums[i],再遍历其之前的所有数字nums[j],当nums[i]小于等于nums[j]时,不做任何处理,因为不是递增序列。反之,则判断len[i]和len[j]的关系,如果len[i]等于len[j] + 1,说明nums[i]这个数字可以加在以nums[j]结尾的递增序列后面,并且以nums[j]结尾的递增序列个数可以直接加到以nums[i]结尾的递增序列个数上。如果len[i]小于len[j] + 1,说明找到了一条长度更长的递增序列,那么此时将len[i]更新为len[j]+1,并且原本的递增序列都不能用了,直接用cnt[j]来代替。在更新完len[i]和cnt[i]之后,要更新 mx 和结果 res,如果 mx 等于 len[i],则把cnt[i]加到结果 res 之上;如果 mx 小于len[i],则更新 mx 为len[i],更新结果 res 为cnt[i],参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int findNumberOfLIS(vector<int>& nums) {
int res = 0, mx = 0, n = nums.size();
vector<int> len(n, 1), cnt(n, 1);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
if (nums[i] <= nums[j]) continue;
if (len[i] == len[j] + 1) cnt[i] += cnt[j];
else if (len[i] < len[j] + 1) {
len[i] = len[j] + 1;
cnt[i] = cnt[j];
}
}
if (mx == len[i]) res += cnt[i];
else if (mx < len[i]) {
mx = len[i];
res = cnt[i];
}
}
return res;
}
};
Leetcode674. Longest Continuous Increasing Subsequence
Given an unsorted array of integers, find the length of longest continuous increasing subsequence (subarray).
Example 1:1
2
3
4Input: [1,3,5,4,7]
Output: 3
Explanation: The longest continuous increasing subsequence is [1,3,5], its length is 3.
Even though [1,3,5,7] is also an increasing subsequence, it's not a continuous one where 5 and 7 are separated by 4.
Example 2:1
2
3Input: [2,2,2,2,2]
Output: 1
Explanation: The longest continuous increasing subsequence is [2], its length is 1.
找一个最长递增子串1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
if(nums.size() == 0)
return 0;
int res = 0, cur = 1;
for(int i = 1; i < nums.size(); i ++) {
if(nums[i] > nums[i-1])
cur ++;
else {
res = max(res, cur);
cur = 1;
}
}
return max(res, cur);
}
};
Leetcode676. Implement Magic Dictionary
Implement a magic directory with buildDict, and search methods.
For the method buildDict, you’ll be given a list of non-repetitive words to build a dictionary.
For the method search, you’ll be given a word, and judge whether if you modify exactly one character into another character in this word, the modified word is in the dictionary you just built.
Example 1:1
2
3
4
5Input: buildDict(["hello", "leetcode"]), Output: Null
Input: search("hello"), Output: False
Input: search("hhllo"), Output: True
Input: search("hell"), Output: False
Input: search("leetcoded"), Output: False
这道题让我们设计一种神奇字典的数据结构,里面有一些单词,实现的功能是当我们搜索一个单词,只有存在和这个单词只有一个位置上的字符不相同的才能返回true,否则就返回false,注意完全相同也是返回false,必须要有一个字符不同。博主首先想到了One Edit Distance那道题,只不过这道题的两个单词之间长度必须相等。所以只需检测和要搜索单词长度一样的单词即可,所以我们用的数据结构就是根据单词的长度来分,把长度相同相同的单词放到一起,这样就可以减少搜索量。那么对于和要搜索单词进行比较的单词,由于已经保证了长度相等,我们直接进行逐个字符比较即可,用cnt表示不同字符的个数,初始化为0。如果当前遍历到的字符相等,则continue;如果当前遍历到的字符不相同,并且此时cnt已经为1了,则break,否则cnt就自增1。退出循环后,我们检测是否所有字符都比较完了且cnt为1,是的话则返回true,否则就是跟下一个词比较。如果所有词都比较完了,则返回false,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class MagicDictionary {
public:
/** Initialize your data structure here. */
MagicDictionary() {}
/** Build a dictionary through a list of words */
void buildDict(vector<string> dict) {
for (string word : dict) {
m[word.size()].push_back(word);
}
}
/** Returns if there is any word in the trie that equals to the given word after modifying exactly one character */
bool search(string word) {
for (string str : m[word.size()]) {
int cnt = 0, i = 0;
for (; i < word.size(); ++i) {
if (word[i] == str[i]) continue;
if (word[i] != str[i] && cnt == 1) break;
++cnt;
}
if (i == word.size() && cnt == 1) return true;
}
return false;
}
private:
unordered_map<int, vector<string>> m;
};
下面这种解法实际上是用到了前缀树中的search的思路,但是我们又没有整个用到prefix tree,博主感觉那样写法略复杂,其实我们只需要借鉴一下search方法就行了。我们首先将所有的单词都放到一个集合中,然后在search函数中,我们遍历要搜索的单词的每个字符,然后把每个字符都用a-z中的字符替换一下,形成一个新词,当然遇到本身要跳过。然后在集合中看是否存在,存在的话就返回true。记得换完一圈字符后要换回去,不然就不满足只改变一个字符的条件了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class MagicDictionary {
public:
/** Initialize your data structure here. */
MagicDictionary() {}
/** Build a dictionary through a list of words */
void buildDict(vector<string> dict) {
for (string word : dict) s.insert(word);
}
/** Returns if there is any word in the trie that equals to the given word after modifying exactly one character */
bool search(string word) {
for (int i = 0; i < word.size(); ++i) {
char t = word[i];
for (char c = 'a'; c <= 'z'; ++c) {
if (c == t) continue;
word[i] = c;
if (s.count(word)) return true;
}
word[i] = t;
}
return false;
}
private:
unordered_set<string> s;
};
Leetcode677. Map Sum Pairs
Implement a MapSum class with insert, and sum methods.
For the method insert, you’ll be given a pair of (string, integer). The string represents the key and the integer represents the value. If the key already existed, then the original key-value pair will be overridden to the new one.
For the method sum, you’ll be given a string representing the prefix, and you need to return the sum of all the pairs’ value whose key starts with the prefix.
Example 1:1
2
3
4Input: insert("apple", 3), Output: Null
Input: sum("ap"), Output: 3
Input: insert("app", 2), Output: Null
Input: sum("ap"), Output: 5
这道题让我们实现一个MapSum类,里面有两个方法,insert和sum,其中inser就是插入一个键值对,而sum方法比较特别,是在找一个前缀,需要将所有有此前缀的单词的值累加起来返回。使用map来代替前缀树啦。博主开始想到的方法是建立前缀和一个pair之间的映射,这里的pair的第一个值表示该词的值,第二个值表示将该词作为前缀的所有词的累加值,那么我们的sum函数就异常的简单了,直接将pair中的两个值相加即可。关键就是要在insert中把数据结构建好,构建的方法也不难,首先我们suppose原本这个key是有值的,我们更新的时候只需要加上它的差值即可,就算key不存在默认就是0,算差值也没问题。然后我们将first值更新为val,然后就是遍历其所有的前缀了,给每个前缀的second都加上diff即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class MapSum {
public:
/** Initialize your data structure here. */
MapSum() {}
void insert(string key, int val) {
int diff = val - m[key].first, n = key.size();
m[key].first = val;
for (int i = n - 1; i > 0; --i) {
m[key.substr(0, i)].second += diff;
}
}
int sum(string prefix) {
return m[prefix].first + m[prefix].second;
}
private:
unordered_map<string, pair<int, int>> m;
};
下面这种方法用的是带排序的map,insert就是把单词加入map。在map里会按照字母顺序自动排序,然后在sum函数里,我们根据prefix来用二分查找快速定位到第一个不小于prefix的位置,然后向后遍历,向后遍历的都是以prefix为前缀的单词,如果我们发现某个单词不是以prefix为前缀了,直接break;否则就累加其val值,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class MapSum {
public:
/** Initialize your data structure here. */
MapSum() {}
void insert(string key, int val) {
m[key] = val;
}
int sum(string prefix) {
int res = 0, n = prefix.size();
for (auto it = m.lower_bound(prefix); it != m.end(); ++it) {
if (it->first.substr(0, n) != prefix) break;
res += it->second;
}
return res;
}
private:
map<string, int> m;
};
自己写的基于字典树的:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57class Trie {
public:
Trie* child[26];
bool isword;
int number;
Trie() {
for (int i = 0; i < 26; i ++)
child[i] = NULL;
isword = false;
number = 0;
}
};
class MapSum {
public:
Trie * root;
/** Initialize your data structure here. */
MapSum() {
root = new Trie();
}
void insert(string key, int val) {
Trie *cur = root;
for (char c : key) {
if (cur->child[c-'a'] == NULL)
cur->child[c-'a'] = new Trie();
cur = cur->child[c-'a'];
}
cur->isword = true;
cur->number = val;
}
int sum(string prefix) {
Trie *cur = root;
int sum = 0;
for (char c : prefix) {
cur = cur->child[c-'a'];
if (!cur)
break;
}
queue<Trie*> q;
if (cur)
q.push(cur);
while(!q.empty()) {
Trie* t = q.front();
q.pop();
if (t->number != 0)
sum += t->number;
for (int i = 0; i < 26; i ++) {
if (t->child[i])
q.push(t->child[i]);
}
}
return sum;
}
};
Leetcode678. Valid Parenthesis String
Given a string containing only three types of characters: ‘(‘, ‘)’ and ‘*’, write a function to check whether this string is valid. We define the validity of a string by these rules:
- Any left parenthesis ‘(‘ must have a corresponding right parenthesis ‘)’.
- Any right parenthesis ‘)’ must have a corresponding left parenthesis ‘(‘.
- Left parenthesis ‘(‘ must go before the corresponding right parenthesis ‘)’.
- ‘*’ could be treated as a single right parenthesis ‘)’ or a single left parenthesis ‘(‘ or an empty string.
- An empty string is also valid.
Example 1:1
2Input: "()"
Output: True
Example 2:1
2Input: "(*)"
Output: True
Example 3:1
2Input: "(*))"
Output: True
Note: The string size will be in the range [1, 100].
这道题让我们验证括号字符串,由于星号的存在,这道题就变的复杂了,由于星号可以当括号用,所以当遇到右括号时,就算此时变量为0,也可以用星号来当左括号使用。那么星号什么时候都能当括号来用吗,我们来看两个例子*)和(,在第一种情况下,星号可以当左括号来用,而在第二种情况下,无论星号当左括号,右括号,还是空,(都是不对的。当然这种情况只限于星号和左括号之间的位置关系,而只要星号在右括号前面,就一定可以消掉右括号。那么我们使用两个stack,分别存放左括号和星号的位置,遍历字符串,当遇到星号时,压入星号栈star,当遇到左括号时,压入左括号栈left,当遇到右括号时,此时如果left和star均为空时,直接返回false;如果left不为空,则pop一个左括号来抵消当前的右括号;否则从star中取出一个星号当作左括号来抵消右括号。当循环结束后,我们希望left中没有多余的左括号,就算有,我们可以尝试着用星号来抵消,当star和left均不为空时,进行循环,如果left的栈顶左括号的位置在star的栈顶星号的右边,那么就组成了*(模式,直接返回false;否则就说明星号可以抵消左括号,各自pop一个元素。最终退出循环后我们看left中是否还有多余的左括号,没有就返回true,否则false,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool checkValidString(string s) {
stack<int> left, star;
for (int i = 0; i < s.size(); ++i) {
if (s[i] == '*') star.push(i);
else if (s[i] == '(') left.push(i);
else {
if (left.empty() && star.empty()) return false;
if (!left.empty()) left.pop();
else star.pop();
}
}
while (!left.empty() && !star.empty()) {
if (left.top() > star.top()) return false;
left.pop(); star.pop();
}
return left.empty();
}
};
既然星号可以当左括号和右括号,那么我们就正反各遍历一次,正向遍历的时候,我们把星号都当成左括号,此时用经典的验证括号的方法,即遇左括号计数器加1,遇右括号则自减1,如果中间某个时刻计数器小于0了,直接返回false。如果最终计数器等于0了,我们直接返回true,因为此时我们把星号都当作了左括号,可以跟所有的右括号抵消。而此时就算计数器大于0了,我们暂时不能返回false,因为有可能多余的左括号是星号变的,星号也可以表示空,所以有可能不多,我们还需要反向q一下,哦不,是反向遍历一下,这是我们将所有的星号当作右括号,遇右括号计数器加1,遇左括号则自减1,如果中间某个时刻计数器小于0了,直接返回false。遍历结束后直接返回true,这是为啥呢?此时计数器有两种情况,要么为0,要么大于0。为0不用说,肯定是true,为啥大于0也是true呢?因为之前正向遍历的时候,我们的左括号多了,我们之前说过了,多余的左括号可能是星号变的,也可能是本身就多的左括号。本身就多的左括号这种情况会在反向遍历时被检测出来,如果没有检测出来,说明多余的左括号一定是星号变的。而这些星号在反向遍历时又变做了右括号,最终导致了右括号有剩余,所以当这些星号都当作空的时候,左右括号都是对应的,即是合法的。你可能会有疑问,右括号本身不会多么,其实不会的,如果多的话,会在正向遍历中被检测出来,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
bool checkValidString(string s) {
int left = 0, right = 0, n = s.size();
for (int i = 0; i < n; ++i) {
if (s[i] == '(' || s[i] == '*') ++left;
else --left;
if (left < 0) return false;
}
if (left == 0) return true;
for (int i = n - 1; i >= 0; --i) {
if (s[i] == ')' || s[i] == '*') ++right;
else --right;
if (right < 0) return false;
}
return true;
}
};
下面这种方法是用递归来写的,思路特别的简单直接,感觉应该属于暴力破解法。使用了变量cnt来记录左括号的个数,变量start表示当前开始遍历的位置,那么在递归函数中,首先判断如果cnt小于0,直接返回false。否则进行从start开始的遍历,如果当前字符为左括号,cnt自增1;如果为右括号,若cnt此时小于等于0,返回false,否则cnt自减1;如果为星号,我们同时递归三种情况,分别是当星号为空,左括号,或右括号,只要有一种情况返回true,那么就是true了。如果循环退出后,若cnt为0,返回true,否则false,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool checkValidString(string s) {
return helper(s, 0, 0);
}
bool helper(string s, int start, int cnt) {
if (cnt < 0) return false;
for (int i = start; i < s.size(); ++i) {
if (s[i] == '(') {
++cnt;
} else if (s[i] == ')') {
if (cnt <= 0) return false;
--cnt;
} else {
return helper(s, i + 1, cnt) || helper(s, i + 1, cnt + 1) || helper(s, i + 1, cnt - 1);
}
}
return cnt == 0;
}
};
Leetcode679. 24 Game
You have 4 cards each containing a number from 1 to 9. You need to judge whether they could operated through *, /, +, -, (, )to get the value of 24.
Example 1:1
2
3Input: [4, 1, 8, 7]
Output: True
Explanation: (8-4) * (7-1) = 24
Example 2:1
2Input: [1, 2, 1, 2]
Output: False
Note:
- The division operator / represents real division, not integer division. For example, 4 / (1 - 2/3) = 12.
- Every operation done is between two numbers. In particular, we cannot use - as a unary operator. For example, with [1, 1, 1, 1] as input, the expression -1 - 1 - 1 - 1 is not allowed.
- You cannot concatenate numbers together. For example, if the input is [1, 2, 1, 2], we cannot write this as 12 + 12.
这道题就是经典的24点游戏了,记得小时候经常玩这个游戏,就是每个人发四张牌,看谁最快能算出24,这完全是脑力大比拼啊,不是拼的牌技。玩的多了,就会摸出一些套路来,比如尽量去凑2和12,3和8,4和6等等,但是对于一些特殊的case,比如 [1, 5, 5, 5] 这种,正确的解法是 5 * (5 - 1 / 5),一般人都会去试加减乘,和能整除的除法,而像这种带小数的确实很难想到,但是程序计算就没问题,可以遍历所有的情况,这也是这道题的实际意义所在吧。那么既然是要遍历所有的情况,我们应该隐约感觉到应该是要使用递归来做的。我们想,任意的两个数字之间都可能进行加减乘除,其中加法和乘法对于两个数字的前后顺序没有影响,但是减法和除法是有影响的,而且做除法的时候还要另外保证除数不能为零。我们要遍历任意两个数字,然后对于这两个数字,尝试各种加减乘除后得到一个新数字,将这个新数字加到原数组中,记得原来的两个数要移除掉,然后调用递归函数进行计算,我们可以发现每次调用递归函数后,数组都减少一个数字,那么当减少到只剩一个数字了,就是最后的计算结果,所以我们在递归函数开始时判断,如果数组只有一个数字,且为24,说明可以算出24,结果res赋值为true返回。这里我们的结果res是一个全局的变量,如果已经为true了,就没必要再进行运算了,所以第一行应该是判断结果res,为true就直接返回了。我们遍历任意两个数字,分别用p和q来取出,然后进行两者的各种加减乘除的运算,将结果保存进数组临时数组t,记得要判断除数不为零。然后将原数组nums中的p和q移除,遍历临时数组t中的数字,将其加入数组nums,然后调用递归函数,记得完成后要移除数字,恢复状态,这是递归解法很重要的一点。最后还要把p和q再加回原数组nums,这也是还原状态,参见代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
bool judgePoint24(vector<int>& nums) {
bool res = false;
double eps = 0.001;
vector<double> arr(nums.begin(), nums.end());
helper(arr, eps, res);
return res;
}
void helper(vector<double>& nums, double eps, bool& res) {
if (res) return;
if (nums.size() == 1) {
if (abs(nums[0] - 24) < eps) res = true;
return;
}
for (int i = 0; i < nums.size(); ++i) {
for (int j = 0; j < i; ++j) {
double p = nums[i], q = nums[j];
vector<double> t{p + q, p - q, q - p, p * q};
if (p > eps) t.push_back(q / p);
if (q > eps) t.push_back(p / q);
nums.erase(nums.begin() + i);
nums.erase(nums.begin() + j);
for (double d : t) {
nums.push_back(d);
helper(nums, eps, res);
nums.pop_back();
}
nums.insert(nums.begin() + j, q);
nums.insert(nums.begin() + i, p);
}
}
}
};
来看一种很不同的递归写法,这里将加减乘除操作符放到了一个数组ops中。并且没有用全局变量res,而是让递归函数带有bool型返回值。在递归函数中,还是要先看nums数组的长度,如果为1了,说明已经计算完成,直接看结果是否为0就行了。然后遍历任意两个数字,注意这里的i和j都分别从0到了数组长度,而上面解法的j是从0到i,这是因为上面解法将p - q, q - p, q / q, q / p都分别列出来了,而这里仅仅是nums[i] - nums[j], nums[i] / nums[j],所以i和j要交换位置,但是为了避免加法和乘法的重复计算,我们可以做个判断,还有别忘记了除数不为零的判断,i和j不能相同的判断。我们建立一个临时数组t,将非i和j位置的数字都加入t,然后遍历操作符数组ops,每次取出一个操作符,然后将nums[i]和nums[j]的计算结果加入t,调用递归函数,如果递归函数返回true了,那么就直接返回true。否则移除刚加入的结果,还原t的状态,参见代码如下:
解法二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
bool judgePoint24(vector<int>& nums) {
double eps = 0.001;
vector<char> ops{'+', '-', '*', '/'};
vector<double> arr(nums.begin(), nums.end());
return helper(arr, ops, eps);
}
bool helper(vector<double>& nums, vector<char>& ops, double eps) {
if (nums.size() == 1) return abs(nums[0] - 24) < eps;
for (int i = 0; i < nums.size(); ++i) {
for (int j = 0; j < nums.size(); ++j) {
if (i == j) continue;
vector<double> t;
for (int k = 0; k < nums.size(); ++k) {
if (k != i && k != j) t.push_back(nums[k]);
}
for (char op : ops) {
if ((op == '+' || op == '*') && i > j) continue;
if (op == '/' && nums[j] < eps) continue;
switch(op) {
case '+': t.push_back(nums[i] + nums[j]); break;
case '-': t.push_back(nums[i] - nums[j]); break;
case '*': t.push_back(nums[i] * nums[j]); break;
case '/': t.push_back(nums[i] / nums[j]); break;
}
if (helper(t, ops, eps)) return true;
t.pop_back();
}
}
}
return false;
}
};
Leetcode680. Valid Palindrome II
Given a non-empty string s, you may delete at most one character. Judge whether you can make it a palindrome.
Example 1:1
2Input: "aba"
Output: True
Example 2:1
2
3Input: "abca"
Output: True
Explanation: You could delete the character 'c'.
首先,对于这样的回文判断,一次遍历肯定是必不可少的。如果没有多出的字符,只需要从两端向中间依次进行判断即可。
但是现在是有多出的字符,因此,要么前面多出一个字符,要么后面多出一个字符。这两种情况是不确定的,因此需要分别来进行判断。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool validPalindrome(string s) {
int left = 0, right = s.length()-1;
while(left < right) {
if(s[left] == s[right]) {
left ++;
right --;
}
else {
int left1 = left+1, right1 = right;
int left2 = left, right2 = right-1;
while(left1 < right1 && s[left1] == s[right1]) left1++, right1--;
while(left2 < right2 && s[left2] == s[right2]) left2++, right2--;
return left1 >= right1 || left2 >= right2;
}
}
return true;
}
};
Leetcode682. Baseball Game
You’re now a baseball game point recorder.
Given a list of strings, each string can be one of the 4 following types:
- Integer (one round’s score): Directly represents the number of points you get in this round.
- “+” (one round’s score): Represents that the points you get in this round are the sum of the last two valid round’s points.
- “D” (one round’s score): Represents that the points you get in this round are the doubled data of the last valid round’s points.
- “C” (an operation, which isn’t a round’s score): Represents the last valid round’s points you get were invalid and should be removed.
Each round’s operation is permanent and could have an impact on the round before and the round after.
You need to return the sum of the points you could get in all the rounds.
Example 1:1
2
3
4
5
6
7
8Input: ["5","2","C","D","+"]
Output: 30
Explanation:
Round 1: You could get 5 points. The sum is: 5.
Round 2: You could get 2 points. The sum is: 7.
Operation 1: The round 2's data was invalid. The sum is: 5.
Round 3: You could get 10 points (the round 2's data has been removed). The sum is: 15.
Round 4: You could get 5 + 10 = 15 points. The sum is: 30.
Example 2:1
2
3
4
5
6
7
8
9
10
11Input: ["5","-2","4","C","D","9","+","+"]
Output: 27
Explanation:
Round 1: You could get 5 points. The sum is: 5.
Round 2: You could get -2 points. The sum is: 3.
Round 3: You could get 4 points. The sum is: 7.
Operation 1: The round 3's data is invalid. The sum is: 3.
Round 4: You could get -4 points (the round 3's data has been removed). The sum is: -1.
Round 5: You could get 9 points. The sum is: 8.
Round 6: You could get -4 + 9 = 5 points. The sum is 13.
Round 7: You could get 9 + 5 = 14 points. The sum is 27.
简单模拟。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
int calPoints(vector<string>& ops) {
vector<int> res(ops.size());
int pointer = 0;
for(int i = 0; i < ops.size(); i ++) {
if(ops[i] == "C") {
pointer --;
}
else if(ops[i] == "D") {
res[pointer] = res[pointer-1]*2;
pointer++;
}
else if(ops[i] == "+") {
res[pointer] = res[pointer-1]+res[pointer-2];
pointer++;
}
else {
res[pointer] = stoi(ops[i]);
pointer++;
}
}
int sum = 0;
for(int i = 0;i < pointer; i ++)
sum += res[i];
return sum;
}
};
大佬做法:1
2
3
4
5
6
7
8
9int calPoints(char ** ops, int opsSize){
int p[1000] = { 0 }, r = 0, t = 0;
for (int i = 0 ; i < opsSize ; i++)
*ops[i] == '+' ? r ? p[r] = p[r - 1], r > 1 ? p[r] += p[r - 2] : 0, t += p[r++] : 0 :
*ops[i] == 'D' ? r ? t += p[r] = p[r - 1] * 2, r++ : 0 :
*ops[i] == 'C' ? r ? t -= p[--r] : 0 :
(t += p[r++] = atoi(ops[i]));
return t;
}
Leetcode684. Redundant Connection
In this problem, a tree is an undirected graph that is connected and has no cycles.
The given input is a graph that started as a tree with N nodes (with distinct values 1, 2, …, N), with one additional edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.
The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] with u < v, that represents an undirected edge connecting nodes u and v.
Return an edge that can be removed so that the resulting graph is a tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array. The answer edge [u, v] should be in the same format, with u < v.
Example 1:1
2
3
4
5
6Input: [[1,2], [1,3], [2,3]]
Output: [2,3]
Explanation: The given undirected graph will be like this:
1
/ \
2 - 3
Example 2:1
2
3
4
5
6Input: [[1,2], [2,3], [3,4], [1,4], [1,5]]
Output: [1,4]
Explanation: The given undirected graph will be like this:
5 - 1 - 2
| |
4 - 3
Note:
- The size of the input 2D-array will be between 3 and 1000.
- Every integer represented in the 2D-array will be between 1 and N, where N is the size of the input array.
这道题给我们了一个无向图,让删掉组成环的最后一条边用并查集做即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
vector<int> root(2001, -1);
for (auto edge : edges) {
int x = find(root, edge[0]), y = find(root, edge[1]);
if (x == y) return edge;
root[x] = y;
}
return {};
}
int find(vector<int>& root, int i) {
while (root[i] != -1) {
i = root[i];
}
return i;
}
};
Leetcode686. Repeated String Match
Given two strings A and B, find the minimum number of times A has to be repeated such that B is a substring of it. If no such solution, return -1.
For example, with A = “abcd” and B = “cdabcdab”.
Return 3, because by repeating A three times (“abcdabcdabcd”), B is a substring of it; and B is not a substring of A repeated two times (“abcdabcd”).
Note:
The length of A and B will be between 1 and 10000.
这道题题意清晰,解决题目的关键在于把可能的情况想清楚。
本题分为三种情况处理:
- A比B短,这是最容易想到的情况,比如A为“abc”,B为“bcab”,我们要重复1次,使得A的长度大于等于B。接着猜判断B能不能在A中找到,这时我们用find函数即可。还有另一种情况,A重复完之后刚好长度等于B,但是我们有时能找到B,有时还要再重复一次才能找到B。比如A为“abc”,B为“abcabc”,这种就是重复1次,长度刚好等于B,能找到B的情况。比如A为“abc”,B为“bcabca”,这种就是重复1次,长度刚好等于B,但不能找到B的情况,要再重复1次。
- A比B长,有两种情况,第一种就是刚好能找到,不用重复。比如A为“abcdefg”,B为“bcd”。另一种是找不到,要再重复一次,比如A为“abcdefg”,B为“efga”,要再重复一次才能找到。
- A和B一样长,同样两种情况,第一种就是刚好能找到,A==B。另一种就是要再重复一次,比如A为“abcdefg”,B为“efgabcd”,要再重复一次才能找到。
综上所述,我们使得A的长度大于等于B,如果这个时候能找到B,那么ok,返回重复的次数。如果不能找到B,那么再重复一次A,如果重复之后能找到,那么返回新的重复的次数。如果还是找不到,我们认为当A的长度大于等于B的时候,这时候可能还会找不到B,但如果再重复一次A,重复之后还是找不到B,那么就是不可能通过重复A来找到B的,返回-1。
1 | class Solution { |
Leetcode687. Longest Univalue Path
Given a binary tree, find the length of the longest path where each node in the path has the same value. This path may or may not pass through the root.
The length of path between two nodes is represented by the number of edges between them.
Example 1:1
2
3
4
5
6
7Input:
5
/ \
4 5
/ \ \
1 1 5
Output: 2
Example 2:1
2
3
4
5
6
7Input:
1
/ \
4 5
/ \ \
4 4 5
Output: 2
Note: The given binary tree has not more than 10000 nodes. The height of the tree is not more than 1000.
要求的是最长的路径,所以就不可以往回走,只能是两个节点的路径,那这个路径就可以表示为一个根结点到左边的最长路径+到右边最长路径,简单的对每一个根结点往左往右递归求解就好。
对每一个结点,以其作为根结点,对左右分别dfs求得从当前节点出发左边最长和右边最长的值,然后加起来和max对比,如果大于max则替换max。然后返回上一层,返回上一层的数要为左边或右边的最大值,而不是相加值,因为对于父节点为根结点的话只能往左或者往右寻找最长路径,而不能先去左边然后去右边然后返回。
1 | class Solution { |
Leetcode690. Employee Importance
You are given a data structure of employee information, which includes the employee’s unique id, his importance value and his direct subordinates’ id.
For example, employee 1 is the leader of employee 2, and employee 2 is the leader of employee 3. They have importance value 15, 10 and 5, respectively. Then employee 1 has a data structure like [1, 15, [2]], and employee 2 has [2, 10, [3]], and employee 3 has [3, 5, []]. Note that although employee 3 is also a subordinate of employee 1, the relationship is not direct.
Now given the employee information of a company, and an employee id, you need to return the total importance value of this employee and all his subordinates.
Example 1:1
2
3
4Input: [[1, 5, [2, 3]], [2, 3, []], [3, 3, []]], 1
Output: 11
Explanation:
Employee 1 has importance value 5, and he has two direct subordinates: employee 2 and employee 3. They both have importance value 3. So the total importance value of employee 1 is 5 + 3 + 3 = 11.
超级麻烦的一道题,就模拟呗……1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30/*
// Definition for Employee.
class Employee {
public:
int id;
int importance;
vector<int> subordinates;
};
*/
class Solution {
public:
int getImportance(vector<Employee*> employees, int id) {
int total = 0;
vector<int> subids;
for (Employee* employee : employees)
{
if (employee->id == id)
{
total += employee->importance;
subids = employee->subordinates;
break;
}
}
if (subids.size() == 0) return total;
for (int subid : subids)
total += getImportance(employees, subid);
return total;
}
};
};
Leetcode692. Top K Frequent Words
Given a non-empty list of words, return the k most frequent elements.
Your answer should be sorted by frequency from highest to lowest. If two words have the same frequency, then the word with the lower alphabetical order comes first.
Example 1:1
2
3
4Input: ["i", "love", "leetcode", "i", "love", "coding"], k = 2
Output: ["i", "love"]
Explanation: "i" and "love" are the two most frequent words.
Note that "i" comes before "love" due to a lower alphabetical order.
Example 2:1
2
3
4Input: ["the", "day", "is", "sunny", "the", "the", "the", "sunny", "is", "is"], k = 4
Output: ["the", "is", "sunny", "day"]
Explanation: "the", "is", "sunny" and "day" are the four most frequent words,
with the number of occurrence being 4, 3, 2 and 1 respectively.
这道题让我们求前K个高频词,跟之前那道题 Top K Frequent Elements 极其类似,换了个数据类型就又是一道新题。唯一的不同就是之前那道题对于出现频率相同的数字,没有顺序要求。而这道题对于出现频率相同的单词,需要按照字母顺序来排。但是解法都一样,还是用最小堆和桶排序的方法。首先来看最小堆的方法,思路是先建立每个单词和其出现次数之间的映射,然后把单词和频率的pair放进最小堆,如果没有相同频率的单词排序要求,我们完全可以让频率当作pair的第一项,这样priority_queue默认是以pair的第一项为key进行从大到小的排序,而当第一项相等时,又会以第二项由大到小进行排序,这样第一项的排序方式就与题目要求的相同频率的单词要按字母顺序排列不相符,当然我们可以在存入结果res时对相同频率的词进行重新排序处理,也可以对priority_queue的排序机制进行自定义,这里我们采用第二种方法,我们自定义排序机制,我们让a.second > b.second,让小频率的词在第一位,然后当a.second == b.second时,我们让a.first < b.first,这是让字母顺序大的排在前面(这里博主需要强调一点的是,priority_queue的排序机制的写法和vector的sort的排序机制的写法正好顺序相反,同样的写法,用在sort里面就是频率小的在前面,不信的话可以自己试一下)。定义好最小堆后,我们首先统计单词的出现频率,然后组成pair排序最小堆之中,我们只保存k个pair,超过了就把队首的pair移除队列,最后我们把单词放入结果res中即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
vector<string> topKFrequent(vector<string>& words, int k) {
vector<string> res(k);
unordered_map<string, int> freq;
auto cmp = [](pair<string, int>& a, pair<string, int>& b) {
return a.second > b.second || (a.second == b.second && a.first < b.first);
};
priority_queue<pair<string, int>, vector<pair<string, int>>, decltype(cmp) > q(cmp);
for (auto word : words) ++freq[word];
for (auto f : freq) {
q.push(f);
if (q.size() > k) q.pop();
}
for (int i = res.size() - 1; i >= 0; --i) {
res[i] = q.top().first; q.pop();
}
return res;
}
};
下面这种解法还是一种堆排序的思路,这里我们用map,来建立次数和出现该次数所有单词的集合set之间的映射,这里也利用了set能自动排序的特性,当然我们还是需要首先建立每个单词和其出现次数的映射,然后将其组成pair放入map种,map是从小到大排序的,这样我们从最后面取pair,就是次数最大的,每次取出一层中所有的单词,如果此时的k大于该层的单词个数,就将整层的单词加入结果res中,否则就取前K个就行了,取完要更更新K值,如果K小于等于0了,就break掉,返回结果res即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
vector<string> topKFrequent(vector<string>& words, int k) {
vector<string> res;
unordered_map<string, int> freq;
map<int, set<string>> m;
for (string word : words) ++freq[word];
for (auto a : freq) {
m[a.second].insert(a.first);
}
for (auto it = m.rbegin(); it != m.rend(); ++it) {
if (k <= 0) break;
auto t = it->second;
vector<string> v(t.begin(), t.end());
if (k >= t.size()) {
res.insert(res.end(), v.begin(), v.end());
} else {
res.insert(res.end(), v.begin(), v.begin() + k);
}
k -= t.size();
}
return res;
}
};
Leetcode693. Binary Number with Alternating Bits
Given a positive integer, check whether it has alternating bits: namely, if two adjacent bits will always have different values.
Example 1:1
2
3
4Input: 5
Output: True
Explanation:
The binary representation of 5 is: 101
Example 2:1
2
3
4Input: 7
Output: False
Explanation:
The binary representation of 7 is: 111.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
bool hasAlternatingBits(int n) {
int flag = 0;
int prev = n & 1;
n = n >> 1;
while(n) {
int temp = n & 1;
if(prev == temp)
return false;
prev = temp;
n = n >> 1;
}
return true;
}
};
Leetcode695. Max Area of Island
Given a non-empty 2D array grid of 0’s and 1’s, an island is a group of 1‘s (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
Find the maximum area of an island in the given 2D array. (If there is no island, the maximum area is 0.)
Example 1:1
2
3
4
5
6
7
8
9
10[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Given the above grid, return 6. Note the answer is not 11, because the island must be connected 4-directionally.
Example 2:1
2
3[[0,0,0,0,0,0,0,0]]
Given the above grid, return 0.
Note: The length of each dimension in the given grid does not exceed 50.
这道题需要统计出每个岛的大小,再来更新结果res。先用递归来做,遍历grid,当遇到为1的点,我们调用递归函数,在递归函数中,我们首先判断i和j是否越界,还有grid[i][j]是否为1,我们没有用visited数组,而是直接修改了grid数组,遍历过的标记为-1。如果合法,那么cnt自增1,并且更新结果res,然后对其周围四个相邻位置分别调用递归函数即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
vector<vector<int>> dirs{{0,-1},{-1,0},{0,1},{1,0}};
int maxAreaOfIsland(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size(), res = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] != 1) continue;
int cnt = 0;
helper(grid, i, j, cnt, res);
}
}
return res;
}
void helper(vector<vector<int>>& grid, int i, int j, int& cnt, int& res) {
int m = grid.size(), n = grid[0].size();
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] <= 0) return;
res = max(res, ++cnt);
grid[i][j] *= -1;
for (auto dir : dirs) {
helper(grid, i + dir[0], j + dir[1], cnt, res);
}
}
};
Leetcode696. Count Binary Substrings
Give a string s, count the number of non-empty (contiguous) substrings that have the same number of 0’s and 1’s, and all the 0’s and all the 1’s in these substrings are grouped consecutively.
Substrings that occur multiple times are counted the number of times they occur.
Notice that some of these substrings repeat and are counted the number of times they occur.
Also, “00110011” is not a valid substring because all the 0’s (and 1’s) are not grouped together.
Example 1:1
2
3Input: "00110011"
Output: 6
Explanation: There are 6 substrings that have equal number of consecutive 1's and 0's: "0011", "01", "1100", "10", "0011", and "01".
Example 2:1
2
3Input: "10101"
Output: 4
Explanation: There are 4 substrings: "10", "01", "10", "01" that have equal number of consecutive 1's and 0's.
Note:
- s.length will be between 1 and 50,000.
- s will only consist of “0” or “1” characters.
从例子00110011来看,在第一个1出现时,preLength为2,即前面有两个相等的字符00,此时01可以满足条件,当第二个1出现时,此时0011可以满足条件,在遇到下一个0时,将currLength的次数置为1,preLength为2,此时0前面有连个连续的1,可以组成10满足条件,遇到下一个0时currLength的次数置为2,此时可以满足条件,依此类推..。用两个变量preLength(当前字符前连续的相同字符的个数),currLength(当前字符连续个数),当preLength>=preLength,则满足条件的结果加1。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int countBinarySubstrings(string s) {
int res = 0, prev = 0, cur = 1;
for(int i = 1; i < s.length(); i ++) {
if(s[i-1] == s[i])
cur ++;
else {
prev = cur;
cur = 1;
}
if(prev>=cur)
res ++;
}
return res;
}
};
Leetcode697. Degree of an Array
Given a non-empty array of non-negative integers nums, the degree of this array is defined as the maximum frequency of any one of its elements.
Your task is to find the smallest possible length of a (contiguous) subarray of nums, that has the same degree as nums.
Example 1:1
2
3
4
5
6
7Input: [1, 2, 2, 3, 1]
Output: 2
Explanation:
The input array has a degree of 2 because both elements 1 and 2 appear twice.
Of the subarrays that have the same degree:
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
The shortest length is 2. So return 2.
Example 2:1
2Input: [1,2,2,3,1,4,2]
Output: 6
定义数组的度为某个或某些数字出现最多的次数,要我们找最短的子数组使其和原数组拥有相同的度。那么我们肯定需要统计每个数字出现的次数,就要用哈希表来建立每个数字和其出现次数之间的映射。由于我们要求包含原度的最小长度的子数组,那么最好的情况就是子数组的首位数字都是统计度的数字,即出现最多的数字。那么我们肯定要知道该数字的第一次出现的位置和最后一次出现的位置,由于我们开始不知道哪些数字会出现最多次,所以我们统计所有数字的首尾出现位置,那么我们再用一个哈希表,建立每个数字和其首尾出现的位置。我们用变量degree来表示数组的度。好,现在我们遍历原数组,累加当前数字出现的次数,当某个数字是第一次出现,那么我们用当前位置的来更新该数字出现的首尾位置,否则只更新尾位置。每遍历一个数,我们都更新一下degree。当遍历完成后,我们已经有了数组的度,还有每个数字首尾出现的位置,下面就来找出现次数为degree的数组,然后计算其首尾位置差加1就是candidate数组的长度,由于出现次数为degree的数字不一定只有一个,我们遍历所有的,找出其中最小的即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int findShortestSubArray(vector<int>& nums) {
unordered_map<int, int> mp;
unordered_map<int, pair<int, int>> mpp;
int maxx = -1;
for(int i = 0; i < nums.size(); i ++) {
if(mp[nums[i]] == 0)
mpp[nums[i]] = {i, i};
else
mpp[nums[i]].second = i;
mp[nums[i]] ++;
maxx = max(maxx, mp[nums[i]]);
}
int res = 9999999;
for(auto it = mp.begin(); it != mp.end(); it ++) {
if(it->second == maxx) {
res = min(res, mpp[it->first].second - mpp[it->first].first + 1);
}
}
return res;
}
};
记录下每个元素的出现次数和出现的首尾坐标。然后根据首尾坐标计算长度。
Leetcode698. Partition to K Equal Sum Subsets
Given an array of integers nums and a positive integer k, find whether it’s possible to divide this array into knon-empty subsets whose sums are all equal.
Example 1:1
2
3Input: nums = [4, 3, 2, 3, 5, 2, 1], k = 4
Output: True
Explanation: It's possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.
Note:
- 1 <= k <= len(nums) <= 16.
- 0 < nums[i] < 10000.
这道题给了我们一个数组nums和一个数字k,问我们该数字能不能分成k个非空子集合,使得每个子集合的和相同。给了k的范围是[1,16],而且数组中的数字都是正数。这跟之前那道 Partition Equal Subset Sum 很类似,但是那道题只让分成两个子集合,所以问题可以转换为是否存在和为整个数组和的一半的子集合,可以用dp来做。但是这道题让求k个和相同的,感觉无法用dp来做,因为就算找出了一个,其余的也需要验证。这道题我们可以用递归来做,首先我们还是求出数组的所有数字之和sum,首先判断sum是否能整除k,不能整除的话直接返回false。然后需要一个visited数组来记录哪些数组已经被选中了,然后调用递归函数,我们的目标是组k个子集合,是的每个子集合之和为target = sum/k。我们还需要变量start,表示从数组的某个位置开始查找,curSum为当前子集合之和,在递归函数中,如果k=1,说明此时只需要组一个子集合,那么当前的就是了,直接返回true。如果curSum等于target了,那么我们再次调用递归,此时传入k-1,start和curSum都重置为0,因为我们当前又找到了一个和为target的子集合,要开始继续找下一个。否则的话就从start开始遍历数组,如果当前数字已经访问过了则直接跳过,否则标记为已访问。然后调用递归函数,k保持不变,因为还在累加当前的子集合,start传入i+1,curSum传入curSum+nums[i],因为要累加当前的数字,如果递归函数返回true了,则直接返回true。否则就将当前数字重置为未访问的状态继续遍历,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool canPartitionKSubsets(vector<int>& nums, int k) {
int sum = accumulate(nums.begin(), nums.end(), 0);
if (sum % k != 0) return false;
vector<bool> visited(nums.size(), false);
return helper(nums, k, sum / k, 0, 0, visited);
}
bool helper(vector<int>& nums, int k, int target, int start, int curSum, vector<bool>& visited) {
if (k == 1) return true;
if (curSum == target) return helper(nums, k - 1, target, 0, 0, visited);
for (int i = start; i < nums.size(); ++i) {
if (visited[i]) continue;
visited[i] = true;
if (helper(nums, k, target, i + 1, curSum + nums[i], visited)) return true;
visited[i] = false;
}
return false;
}
};
我们也可以对上面的解法进行一些优化,比如先给数组按从大到小的顺序排个序,然后在递归函数中,我们可以直接判断,如果curSum大于target了,直接返回false,因为题目中限定了都是正数,并且我们也给数组排序了,后面的数字只能更大,这个剪枝操作大大的提高了运行速度。
Leetcode700. Search in a Binary Search Tree
Given the root node of a binary search tree (BST) and a value. You need to find the node in the BST that the node’s value equals the given value. Return the subtree rooted with that node. If such node doesn’t exist, you should return NULL.
For example,
Given the tree:1
2
3
4
5 4
/ \
2 7
/ \
1 3
And the value to search: 2
You should return this subtree:1
2
3 2
/ \
1 3
In the example above, if we want to search the value 5, since there is no node with value 5, we should return NULL.
Note that an empty tree is represented by NULL, therefore you would see the expected output (serialized tree format) as [], not null.
给一棵树,查找对应value的子树。
1 | class Solution { |