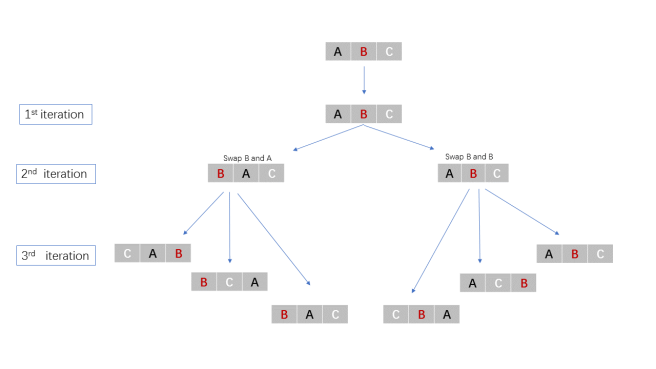
Leetcode401. Binary Watch
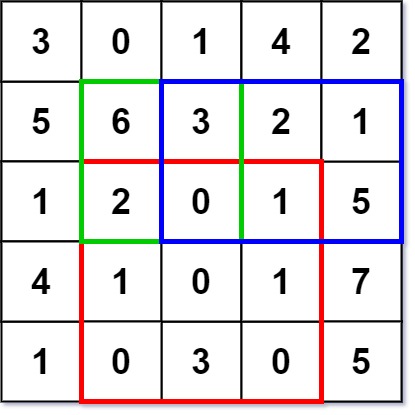
A binary watch has 4 LEDs on the top which represent the hours (0-11), and the 6 LEDs on the bottom represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
Given a non-negative integer n which represents the number of LEDs that are currently on, return all possible times the watch could represent.
Example:1
2Input: n = 1
Return: ["1:00", "2:00", "4:00", "8:00", "0:01", "0:02", "0:04", "0:08", "0:16", "0:32"]
Note:
- The order of output does not matter.
- The hour must not contain a leading zero, for example “01:00” is not valid, it should be “1:00”.
- The minute must be consist of two digits and may contain a leading zero, for example “10:2” is not valid, it should be “10:02”.
首先先明白二进制手表的含义,把1,2,4,8转化为四位的二进制就是0001, 0010, 0100,1000, 9点时亮1和8,是1001。分钟数也是同理。
其次表示小时的数值只有0-11,表示分钟的数值只有0-59。先分别对小时跟分钟的数值进行预处理,按照包含而二进制中包含1的个数分开保存小时数值的字符串跟分钟数值的字符串。
用bitset可以方便地记下来每个数字有几个二进制1,这样可以简单地做出来。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
vector<string> readBinaryWatch(int num) {
vector<string> res;
for(int i = 0; i < 12; i ++) {
bitset<4> h(i);
for(int j = 0; j < 60; j ++) {
bitset<6> m(j);
if(h.count() + m.count() == num)
res.push_back(to_string(i) + (j < 10? ":0": ":") + to_string(j));
}
}
return res;
}
};
基本还是一道DFS的题目,分别在小时和分钟上做DFS,给定几个灯亮,然后把这些亮的灯枚举分给小时和分钟.需要注意的是剪枝,即小时必须小于12,分钟小于60。然后将小时和分钟组合即可.还有一个需要注意的是如果分钟只有1位数,还要补0.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
void DFS(int len, int k, int curIndex, int val, vector<int>& vec)
{
if(k==0 && len==4 && val < 12) vec.push_back(val);
if(k==0 && len==6 && val < 60) vec.push_back(val);
if(curIndex == len || k == 0) return;
DFS(len, k, curIndex+1, val, vec);
val += pow(2, curIndex), k--, curIndex++;
DFS(len, k, curIndex, val, vec);
}
vector<string> readBinaryWatch(int num) {
vector<string> ans;
for(int i = max(0, num-6); i <= min(4, num); i++)
{
vector<int> vec1, vec2;
DFS(4, i, 0, 0, vec1), DFS(6, num-i, 0, 0, vec2);
for(auto val1: vec1)
for(auto val2: vec2)
{
string str = (to_string(val2).size()==1?"0":"") + to_string(val2);
ans.push_back(to_string(val1)+":"+ str);
}
}
return ans;
}
};
Leetcode402. Remove K Digits
Given string num representing a non-negative integer num, and an integer k, return the smallest possible integer after removing k digits from num.
Example 1:1
2
3Input: num = "1432219", k = 3
Output: "1219"
Explanation: Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
Example 2:1
2
3Input: num = "10200", k = 1
Output: "200"
Explanation: Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
Example 3:1
2
3Input: num = "10", k = 2
Output: "0"
Explanation: Remove all the digits from the number and it is left with nothing which is 0.
这道题让我们将给定的数字去掉k位,要使得留下来的数字最小。
首先来考虑,若数字是递增的话,比如 1234,那么肯定是要从最后面移除最大的数字。若是乱序的时候,比如 1324,若只移除一个数字,移除谁呢?这个例子比较简单,我们一眼可以看出是移除3,变成 124 是最小。这里我们维护一个递增栈,只要发现当前的数字小于栈顶元素的话,就将栈顶元素移除,比如点那个遍历到2的时候,栈里面有1和3,此时2小于栈顶元素3,那么将3移除即可。为何一定要移除栈顶元素呢,后面说不定有更大的数字呢?这是因为此时栈顶元素在高位上,就算后面的数字再大,也是在低位上,我们只有将高位上的数字尽可能的变小,才能使整个剩下的数字尽可能的小。
我们开始遍历给定数字 num 的每一位,对于当前遍历到的数字c,进行如下 while 循环,如果 res 不为空,且k大于0,且 res 的最后一位大于c,那么应该将 res 的最后一位移去,且k自减1。当跳出 while 循环后,我们将c加入 res 中,最后将 res 的大小重设为 n-k。根据题目中的描述,可能会出现 “0200” 这样不符合要求的情况,所以我们用一个 while 循环来去掉前面的所有0,然后返回时判断是否为空,为空则返回 “0”。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
string removeKdigits(string num, int k) {
string res = "";
int len = num.length();
for (int i = 0; i < len; i ++) {
while (k > 0 && res.length() > 0 && num[i] < res.back()) {
res.pop_back();
k --;
}
if (res.length() > 0 || num[i] != '0')
res += num[i];
}
while(res.size() > 0 && k--)
res.pop_back();
return res.empty() ? "0" : res;
}
};
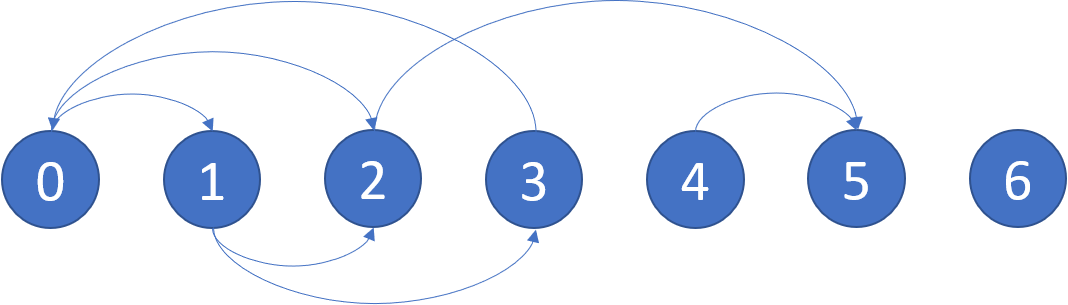
Leetcode403. Frog Jump
A frog is crossing a river. The river is divided into x units and at each unit there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of stones’ positions (in units) in sorted ascending order, determine if the frog is able to cross the river by landing on the last stone. Initially, the frog is on the first stone and assume the first jump must be 1 unit.
If the frog’s last jump was k units, then its next jump must be either k - 1, k , or k + 1 units. Note that the frog can only jump in the forward direction.
Note:
- The number of stones is ≥ 2 and is < 1,100.
- Each stone’s position will be a non-negative integer < 231.
- The first stone’s position is always 0.
Example 1:1
2
3
4
5
6
7
8
9
10
11[0,1,3,5,6,8,12,17]
There are a total of 8 stones.
The first stone at the 0th unit, second stone at the 1st unit,
third stone at the 3rd unit, and so on...
The last stone at the 17th unit.
Return true. The frog can jump to the last stone by jumping
1 unit to the 2nd stone, then 2 units to the 3rd stone, then
2 units to the 4th stone, then 3 units to the 6th stone,
4 units to the 7th stone, and 5 units to the 8th stone.
Example 2:1
2
3
4[0,1,2,3,4,8,9,11]
Return false. There is no way to jump to the last stone as
the gap between the 5th and 6th stone is too large.
题目中说青蛙如果上一次跳了k距离,那么下一次只能跳 k-1, k, 或 k+1 的距离,那么青蛙跳到某个石头上可能有多种跳法,由于这道题只是让判断青蛙是否能跳到最后一个石头上,并没有让返回所有的路径,这样就降低了一些难度。我们可以用递归来做,这里维护一个 HashMap,建立青蛙在 pos 位置和拥有 jump 跳跃能力时是否能跳到对岸。为了能用一个变量同时表示 pos 和 jump,可以将jump左移很多位并或上 pos,由于题目中对于位置大小有限制,所以不会产生冲突。首先判断 pos 是否已经到最后一个石头了,是的话直接返回 true;然后看当前这种情况是否已经出现在 HashMap 中,是的话直接从 HashMap 中取结果。如果没有,就遍历余下的所有石头,对于遍历到的石头,计算到当前石头的距离dist,如果距离小于 jump-1,接着遍历下一块石头;如果 dist 大于 jump+1,说明无法跳到下一块石头,m[key] 赋值为 false,并返回 false;如果在青蛙能跳到的范围中,调用递归函数,以新位置i为 pos,距离 dist 为 jump,如果返回 true 了,给 m[key] 赋值为 true,并返回 true。如果结束遍历给 m[key] 赋值为 false,并返回 false,参加代码如下:
解法一:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
bool canCross(vector<int>& stones) {
unordered_map<int, bool> m;
return helper(stones, 0, 0, m);
}
bool helper(vector<int>& stones, int pos, int jump, unordered_map<int, bool>& m) {
int n = stones.size(), key = pos | jump << 11;
if (pos >= n - 1) return true;
if (m.count(key)) return m[key];
for (int i = pos + 1; i < n; ++i) {
int dist = stones[i] - stones[pos];
if (dist < jump - 1) continue;
if (dist > jump + 1) return m[key] = false;
if (helper(stones, i, dist, m)) return m[key] = true;
}
return m[key] = false;
}
};
我们也可以用迭代的方法来解,用一个 HashMap 来建立每个石头和在该位置上能跳的距离之间的映射,建立一个一维 dp 数组,其中 dp[i] 表示在位置为i的石头青蛙的弹跳力(只有青蛙能跳到该石头上,dp[i] 才大于0),由于题目中规定了第一个石头上青蛙跳的距离必须是1,为了跟后面的统一,对青蛙在第一块石头上的弹跳力初始化为0(虽然为0,但是由于题目上说青蛙最远能到其弹跳力+1的距离,所以仍然可以到达第二块石头)。这里用变量k表示当前石头,然后开始遍历剩余的石头,对于遍历到的石头i,来找到刚好能跳到i上的石头k,如果i和k的距离大于青蛙在k上的弹跳力+1,则说明青蛙在k上到不了i,则k自增1。从k遍历到i,如果青蛙能从中间某个石头上跳到i上,更新石头i上的弹跳力和最大弹跳力。这样当循环完成后,只要检查最后一个石头上青蛙的最大弹跳力是否大于0即可,参见代码如下:
1 | class Solution { |
Leetcode404. Sum of Left Leaves
Find the sum of all left leaves in a given binary tree.
Example:1
2
3
4
5
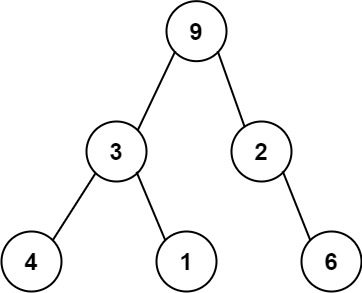
6 3
/ \
9 20
/ \
15 7
There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.
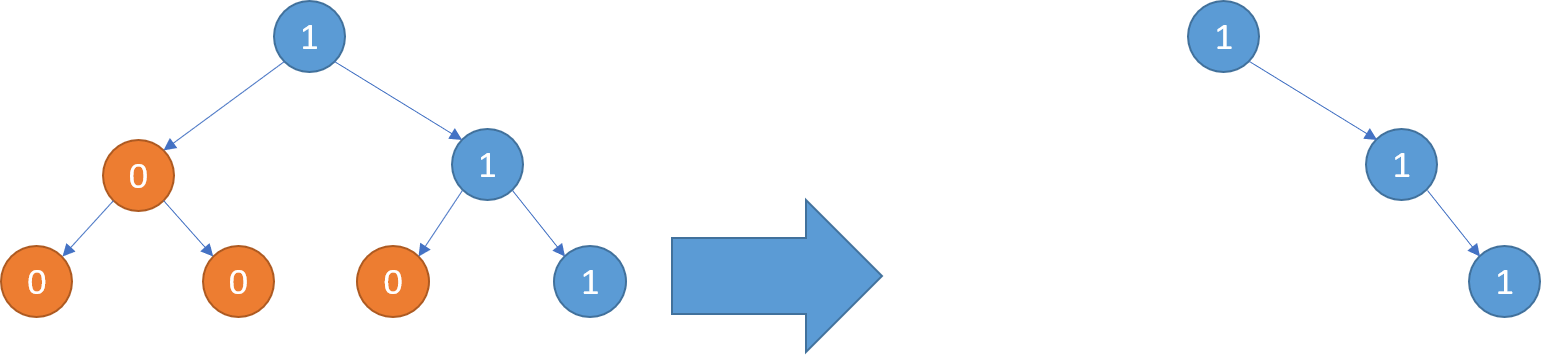
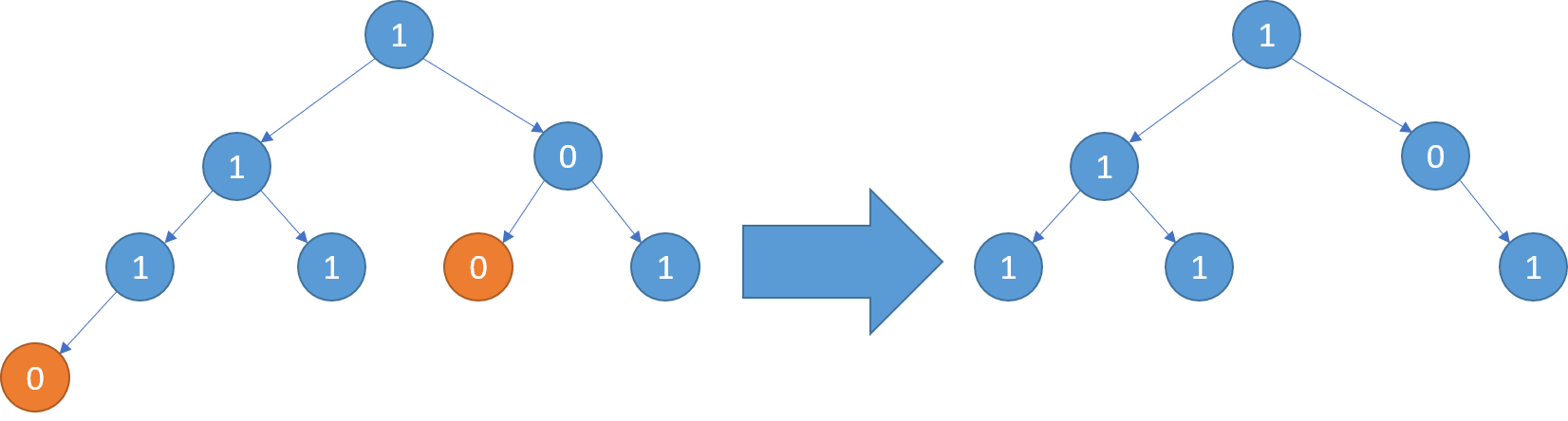
求二叉树的所有左叶子节点的和,判断是不是左叶子节点,加到对列中。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if(!root)
return 0;
if(!root->left && !root->right)
return 0;
queue<TreeNode*> q;
int res = 0;
q.push(root);
while(!q.empty()) {
TreeNode* temp = q.front();
q.pop();
if(temp->left)
q.push(temp->left);
if(temp->right && (temp->right->left || temp->right->right))
q.push(temp->right);
if(!temp->left && !temp->right)
res += temp->val;
}
return res;
}
};
Leetcode405. Convert a Number to Hexadecimal
Given an integer, write an algorithm to convert it to hexadecimal. For negative integer, two’s complement method is used.
Note:
- All letters in hexadecimal (a-f) must be in lowercase.
- The hexadecimal string must not contain extra leading 0s. If the number is zero, it is represented by a single zero character ‘0’; otherwise, the first character in the hexadecimal string will not be the zero character.
- The given number is guaranteed to fit within the range of a 32-bit signed integer.
- You must not use any method provided by the library which converts/formats the number to hex directly.
Example 1:1
2Input: 26
Output: "1a"
Example 2:1
2Input: -1
Output: "ffffffff"
十进制转十六进制,简单。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
string toHex(int num) {
string res = "";
if(num == 0)
return "0";
char digits[] = {'0','1','2','3','4','5','6','7','8','9','a','b','c','d','e','f'};
if(num < 0) {
num = abs(num);
num = ~num + 1;
}
int count = 8;
while(count --) {
int temp = 15 & num;
num = num >> 4;
res = digits[temp] + res;
if(num == 0)
break;
cout << digits[temp] << " " << num << endl;
}
return res;
}
};
Leetcode406. Queue Reconstruction by Height
You are given an array of people, people, which are the attributes of some people in a queue (not necessarily in order). Each people[i] = [hi, ki] represents the ith person of height hi with exactly ki other people in front who have a height greater than or equal to hi.
Reconstruct and return the queue that is represented by the input array people. The returned queue should be formatted as an array queue, where queue[j] = [hj, kj] is the attributes of the jth person in the queue (queue[0] is the person at the front of the queue).
Example 1:1
2Input: people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
Output: [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
Explanation:
- Person 0 has height 5 with no other people taller or the same height in front.
- Person 1 has height 7 with no other people taller or the same height in front.
- Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
- Person 3 has height 6 with one person taller or the same height in front, which is person 1.
- Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
- Person 5 has height 7 with one person taller or the same height in front, which is person 1.
- Hence [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] is the reconstructed queue.
这道题给了我们一个队列,队列中的每个元素是一个 pair,分别为身高和前面身高不低于当前身高的人的个数,让我们重新排列队列,使得每个 pair 的第二个参数都满足题意。首先来看一种超级简洁的方法,给队列先排个序,按照身高高的排前面,如果身高相同,则第二个数小的排前面。然后新建一个空的数组,遍历之前排好序的数组,然后根据每个元素的第二个数字,将其插入到 res 数组中对应的位置,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort(people.begin(), people.end(), [](vector<int>& a, vector<int>& b) {
return a[0] > b[0] || (a[0] == b[0] && a[1] < b[1]);
});
vector<vector<int>> res;
for (auto a : people) {
res.insert(res.begin() + a[1], a);
}
return res;
}
};
Leetcode407. Trapping Rain Water II
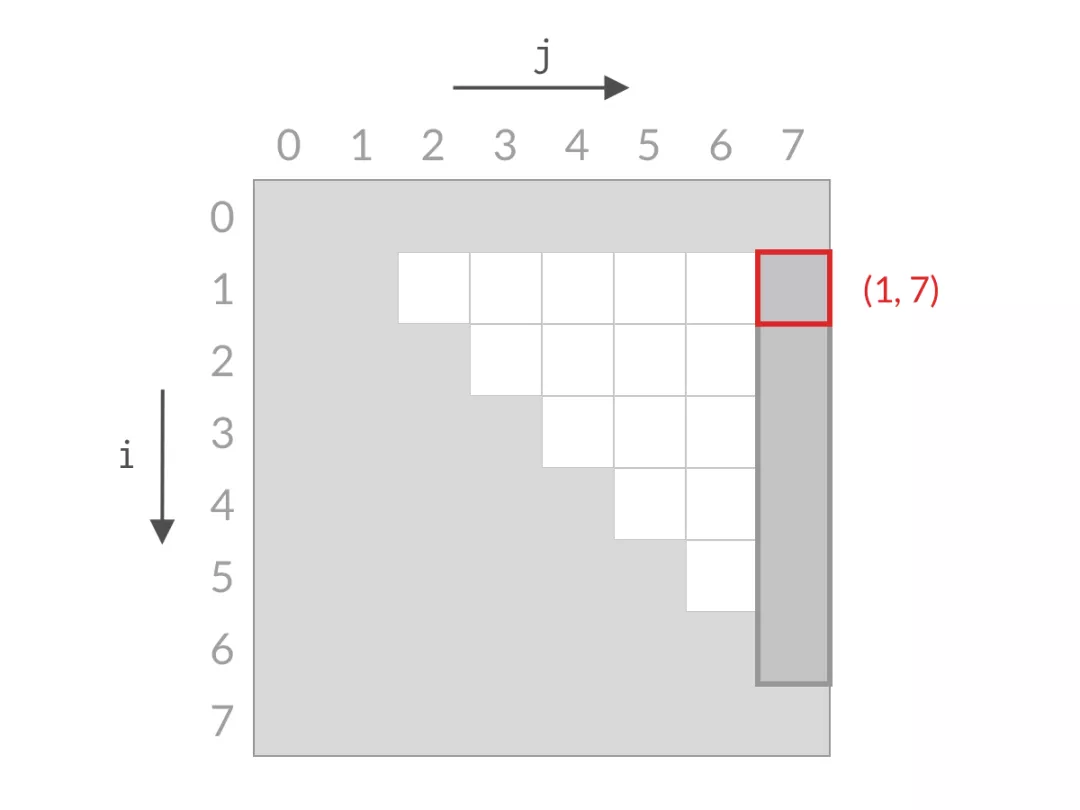
Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.
Example 1:1
2
3
4
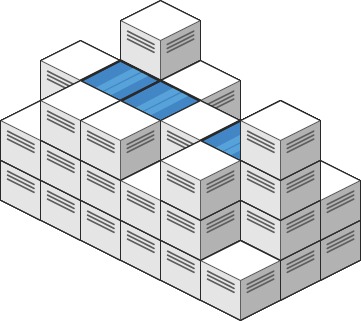
5Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small pounds 1 and 3 units trapped.
The total volume of water trapped is 4.
Example 2:1
2Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10
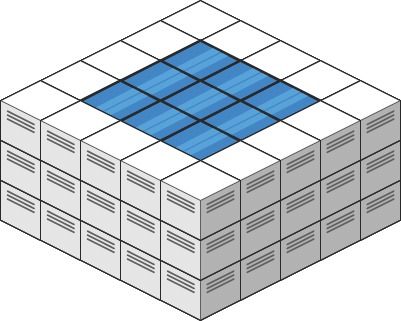
这道三维的,我们需要用 BFS 来做,解法思路很巧妙,下面我们就以题目中的例子来进行分析讲解,多图预警,手机流量党慎入:
首先我们应该能分析出,能装水的底面肯定不能在边界上,因为边界上的点无法封闭,那么所有边界上的点都可以加入 queue,当作 BFS 的启动点,同时我们需要一个二维数组来标记访问过的点,访问过的点我们用红色来表示,那么如下图所示:
我们再想想,怎么样可以成功的装进去水呢,是不是周围的高度都应该比当前的高度高,形成一个凹槽才能装水,而且装水量取决于周围最小的那个高度,有点像木桶原理的感觉,那么为了模拟这种方法,我们采用模拟海平面上升的方法来做,我们维护一个海平面高度 mx,初始化为最小值,从1开始往上升,那么我们 BFS 遍历的时候就需要从高度最小的格子开始遍历,那么我们的 queue 就不能使用普通队列了,而是使用优先级队列,将高度小的放在队首,最先取出,这样我们就可以遍历高度为1的三个格子,用绿色标记出来了,如下图所示:
如上图所示,向周围 BFS 搜索的条件是不能越界,且周围格子未被访问,那么可以看出上面的第一个和最后一个绿格子无法进一步搜索,只有第一行中间那个绿格子可以搜索,其周围有一个灰格子未被访问过,将其加入优先队列 queue 中,然后标记为红色,如下图所示:
那么优先队列 queue 中高度为1的格子遍历完了,此时海平面上升1,变为2,此时我们遍历优先队列 queue 中高度为2的格子,有3个,如下图绿色标记所示:
我们发现这三个绿格子周围的格子均已被访问过了,所以不做任何操作,海平面继续上升,变为3,遍历所有高度为3的格子,如下图绿色标记所示:
由于我们没有特别声明高度相同的格子在优先队列 queue 中的顺序,所以应该是随机的,其实谁先遍历到都一样,对结果没啥影响,我们就假设第一行的两个绿格子先遍历到,那么那么周围各有一个灰格子可以遍历,这两个灰格子比海平面低了,可以存水了,把存水量算出来加入结果 res 中,如下图所示:
上图中这两个遍历到的蓝格子会被加入优先队列 queue 中,由于它们的高度小,所以下一次从优先队列 queue 中取格子时,它们会被优先遍历到,那么左边的那个蓝格子进行BFS搜索,就会遍历到其左边的那个灰格子,由于其高度小于海平面,也可以存水,将存水量算出来加入结果 res 中,如下图所示:
等两个绿格子遍历结束了,它们会被标记为红色,蓝格子遍历会先被标记红色,然后加入优先队列 queue 中,由于其周围格子全变成红色了,所有不会有任何操作,如下图所示:
此时所有的格子都标记为红色了,海平面继续上升,继续遍历完优先队列 queue 中的格子,不过已经不会对结果有任何影响了,因为所有的格子都已经访问过了,此时等循环结束后返回res即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
int trapRainWater(vector<vector<int>>& heights) {
if (heights.size() == 0)
return 0;
int m = heights.size(), n = heights[0].size(), res = 0;
vector<vector<bool> > visited(m, vector<bool>(n, false));
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
vector<vector<int>> dir{{0,-1},{-1,0},{0,1},{1,0}};
for (int i = 0; i < m; i ++)
for (int j = 0; j < n; j ++)
if (i == 0 || i == m-1 || j == 0 || j == n-1) {
q.push({heights[i][j], i*n+j});
visited[i][j] = true;
}
int max_height = 0;
while(!q.empty()) {
pair<int, int> t = q.top();
q.pop();
int h = t.first, r = t.second / n, c = t.second % n;
max_height = max(max_height, h);
for (int i = 0; i < 4; i ++) {
int x = r + dir[i][0];
int y = c + dir[i][1];
if (x < 0 || x >= m || y < 0 || y >= n || visited[x][y])
continue;
visited[x][y] = true;
if (heights[x][y] < max_height)
res = res + (max_height - heights[x][y]);
q.push({heights[x][y], x*n+y});
}
}
return res;
}
};
Leetcode409. Longest Palindrome
Given a string which consists of lowercase or uppercase letters, find the length of the longest palindromes that can be built with those letters.
This is case sensitive, for example “Aa” is not considered a palindrome here.
Note:
Assume the length of given string will not exceed 1,010.
Example:1
2
3
4Input: "abccccdd"
Output: 7
Explanation:
One longest palindrome that can be built is "dccaccd", whose length is 7.
先统计每个字母的个数,然后如果这个字母是偶数个的话,可以放到回文里,如果是奇数的话,先放进去个数减一个,然后如果现在回文长度是偶数,那还可以加一个。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int longestPalindrome(string s) {
int ch[128] = {0};
for(char c : s)
ch[c]++;
int ans = 0;
for(int i : ch) {
ans += (i / 2 * 2);
if(ans % 2== 0 && i % 2 == 1)
ans ++;
}
return ans;
}
};
Leetcode410. Split Array Largest Sum
Given an array which consists of non-negative integers and an integer m , you can split the array into m non-empty continuous subarrays. Write an algorithm to minimize the largest sum among these m subarrays.
Note: Given m satisfies the following constraint: 1 ≤ m ≤ length(nums) ≤ 14,000.
Examples:1
2
3
4
5
6Input:
nums = [7,2,5,10,8]
m = 2
Output:
18
Explanation:
- There are four ways to split nums into two subarrays.
- The best way is to split it into [7,2,5] and [10,8],
- where the largest sum among the two subarrays is only 18.
这道题给了我们一个非负数的数组 nums 和一个整数m,让把数组分割成m个非空的连续子数组,让最小化m个子数组中的最大值。
首先来分析,如果m和数组 nums 的个数相等,那么每个数组都是一个子数组,所以返回 nums 中最大的数字即可,如果m为1,那么整个 nums 数组就是一个子数组,返回 nums 所有数字之和,所以对于其他有效的m值,返回的值必定在上面两个值之间,所以可以用二分搜索法来做。用一个例子来分析,nums = [1, 2, 3, 4, 5], m = 3,将 left 设为数组中的最大值5,right 设为数字之和 15,然后算出中间数为 10,接下来要做的是找出和最大且小于等于 10 的子数组的个数,[1, 2, 3, 4], [5],可以看到无法分为3组,说明 mid 偏大,所以让 right=mid,然后再次进行二分查找,算出 mid=7,再次找出和最大且小于等于7的子数组的个数,[1,2,3], [4], [5],成功的找出了三组,说明 mid 还可以进一步降低,让 right=mid,再次进行二分查找,算出 mid=6,再次找出和最大且小于等于6的子数组的个数,[1,2,3], [4], [5],成功的找出了三组,尝试着继续降低 mid,让 right=mid,再次进行二分查找,算出 mid=5,再次找出和最大且小于等于5的子数组的个数,[1,2], [3], [4], [5],发现有4组,此时的 mid 太小了,应该增大 mid,让 left=mid+1,此时 left=6,right=6,循环退出了,返回 right 即可,参见代码如下:
1 | class Solution { |
上面的解法相对来说比较难想,在热心网友 perthblank 的提醒下,再来看一种 DP 的解法,相对来说,这种方法应该更容易理解一些。建立一个二维数组 dp,其中 dp[i][j] 表示将数组中前j个数字分成i组所能得到的最小的各个子数组中最大值,初始化为整型最大值,如果无法分为i组,那么还是保持为整型最大值。为了能快速的算出子数组之和,还是要建立累计和数组,难点就是在于推导状态转移方程了。
来分析一下,如果前j个数字要分成i组,那么i的范围是什么,由于只有j个数字,如果每个数字都是单独的一组,那么最多有j组;如果将整个数组看为一个整体,那么最少有1组,所以i的范围是[1, j],所以要遍历这中间所有的情况,假如中间任意一个位置k,dp[i-1][k] 表示数组中前k个数字分成 i-1 组所能得到的最小的各个子数组中最大值,而 sums[j]-sums[k] 就是后面的数字之和,取二者之间的较大值,然后和 dp[i][j] 原有值进行对比,更新 dp[i][j] 为二者之中的较小值,这样k在 [1, j] 的范围内扫过一遍,dp[i][j] 就能更新到最小值,最终返回 dp[m][n] 即可,博主认为这道题所用的思想应该是之前那道题 Reverse Pairs 中解法二中总结的分割重现关系 (Partition Recurrence Relation),由此看来很多问题的本质都是一样,但是披上华丽的外衣,难免会让人有些眼花缭乱了,参见代码如下:
1 | class Solution { |
Leetcode412. Fizz Buzz
Write a program that outputs the string representation of numbers from 1 to n.
But for multiples of three it should output “Fizz” instead of the number and for the multiples of five output “Buzz”. For numbers which are multiples of both three and five output “FizzBuzz”.
Example:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19n = 15,
Return:
[
"1",
"2",
"Fizz",
"4",
"Buzz",
"Fizz",
"7",
"8",
"Fizz",
"Buzz",
"11",
"Fizz",
"13",
"14",
"FizzBuzz"
]
太简单了浪费时间。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
vector<string> fizzBuzz(int n) {
vector<string> res;
if(n == 0)
return res;
for(int i = 0; i < n; i ++)
{
if((i + 1) % 3 == 0 && (i + 1) % 5 == 0)
res.push_back("FizzBuzz");
else if((i + 1) % 3 == 0)
res.push_back("Fizz");
else if((i + 1) % 5 == 0)
res.push_back("Buzz");
else
res.push_back(to_string(i + 1));
}
return res;
}
};
Leetcode413. Arithmetic Slices
An integer array is called arithmetic if it consists of at least three elements and if the difference between any two consecutive elements is the same.
For example, [1,3,5,7,9], [7,7,7,7], and [3,-1,-5,-9] are arithmetic sequences. Given an integer array nums, return the number of arithmetic subarrays of nums.
A subarray is a contiguous subsequence of the array.
Example 1:1
2
3Input: nums = [1,2,3,4]
Output: 3
Explanation: We have 3 arithmetic slices in nums: [1, 2, 3], [2, 3, 4] and [1,2,3,4] itself.
Example 2:1
2Input: nums = [1]
Output: 0
这道题让我们算一种算数切片,说白了就是找等差数列,限定了等差数列的长度至少为3,那么[1,2,3,4]含有3个长度至少为3的算数切片,我们再来看[1,2,3,4,5]有多少个呢:
len = 3: [1,2,3], [2,3,4], [3,4,5]
len = 4: [1,2,3,4], [2,3,4,5]
len = 5: [1,2,3,4,5]
那么我们可以归纳出规律,长度为n的等差数列有1个,长度为n-1的等差数列有2个,… ,长度为3的等差数列有 n-2 个,那么总共就是 1 + 2 + 3 + … + n-2 ,此时就要祭出高斯求和公式了,长度为n的等差数列中含有长度至少为3的算数切片的个数为(n-1)(n-2)/2,那么题目就变成了找原数组中等差数列的长度,然后带入公式去算个数即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int numberOfArithmeticSlices(vector<int>& A) {
int res = 0, len = 2, n = A.size();
for (int i = 2; i < n; ++i) {
if (A[i] - A[i - 1] == A[i - 1] - A[i - 2]) {
++len;
} else {
if (len > 2) res += (len - 1) * (len - 2) * 0.5;
len = 2;
}
}
if (len > 2) res += (len - 1) * (len - 2) * 0.5;
return res;
}
};
Leetcode414. Third Maximum Number
Given a non-empty array of integers, return the third maximum number in this array. If it does not exist, return the maximum number. The time complexity must be in O(n).
Example 1:1
2
3Input: [3, 2, 1]
Output: 1
Explanation: The third maximum is 1.
Example 2:1
2
3Input: [1, 2]
Output: 2
Explanation: The third maximum does not exist, so the maximum (2) is returned instead.
Example 3:1
2
3
4Input: [2, 2, 3, 1]
Output: 1
Explanation: Note that the third maximum here means the third maximum distinct number.
Both numbers with value 2 are both considered as second maximum.
遍历数组,通过跟三个变量(max, mid, min)的比较,来交换它们之间数字。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
int thirdMax(vector<int>& nums) {
long min = LONG_MIN, mid = LONG_MIN, max = LONG_MIN;
int count = 0;
for(int i = 0; i < nums.size(); i ++) {
if(nums[i] == max || nums[i] == mid)
continue;
if(nums[i] > max) {
min = mid;
mid = max;
max = nums[i];
count ++;
}
else if(nums[i] > mid) {
min = mid;
mid = nums[i];
count ++;
}
else if(nums[i] >= min) {
min = nums[i];
count ++;
}
}
if(count >= 3)
return min;
else return max;
}
};
Leetcode415. Add Strings
Given two non-negative integers num1 and num2 represented as string, return the sum of num1 and num2.
Note:
- The length of both num1 and num2 is < 5100.
- Both num1 and num2 contains only digits 0-9.
- Both num1 and num2 does not contain any leading zero.
- You must not use any built-in BigInteger library or convert the inputs to integer directly.
简单模拟,做的及其纠结。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
public:
string addStrings(string nums1, string nums2) {
if(nums1.length() < nums2.length()) {
string temp = nums1;
nums1 = nums2;
nums2 = temp;
}
int i, j;
for(i = nums1.length()-1, j = nums2.length()-1; i >= 0 && j >= 0; i --, j --) {
nums1[i] = nums1[i] + nums2[j] - 48;
if(nums1[i] > 57) {
if(i == 0)
break;
nums1[i] -= 10;
nums1[i - 1] = nums1[i - 1] + 1;
}
}
if(i < 0) {
i ++;
if(nums1[i] > 57) {
nums1[i] -= 10;
if(i == 0)
nums1 = "1" + nums1;
else
nums1[i - 1] ++;
}
}
else {
while(i >= 0 && nums1[i] > 57) {
nums1[i] -= 10;
if(i == 0)
nums1 = "1" + nums1;
else
nums1[i - 1] ++;
i --;
}
}
return nums1;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public:
string addStrings(string num1, string num2) {
// computing lengths of both strings
int num1length = num1.length() - 1;
int num2length = num2.length()- 1;
// solution string
string sol = "";
// remainder for when summing two numbers
int remainder = 0;
// while both strings haven't been consumed
while (num1length >= 0 || num2length >= 0) {
// get current characters of iteration
int current_num1 = (num1length >= 0) ? num1.at(num1length) - '0' : 0;
int current_num2 = (num2length >= 0) ? num2.at(num2length) - '0' : 0;
// appending sum and remainder from previous to solution string
int sum = current_num1 + current_num2 + remainder;
sol = std::to_string(sum % 10) + sol;
// determining whether there's a remainder for next sum
remainder = (sum > 9) ? 1 : 0;
// decrementing for next addition
num1length--;
num2length--;
}
// append final remainder if there is one
sol = (remainder == 1) ? std::to_string(1) + sol : sol;
return sol;
}
};
Leetcode416. Partition Equal Subset Sum
Given a non-empty array nums containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.
Example 1:1
2
3Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].
Example 2:1
2
3Input: nums = [1,2,3,5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.
这道题给了我们一个数组,问这个数组能不能分成两个非空子集合,使得两个子集合的元素之和相同。那么想,原数组所有数字和一定是偶数,不然根本无法拆成两个和相同的子集合,只需要算出原数组的数字之和,然后除以2,就是 target,那么问题就转换为能不能找到一个非空子集合,使得其数字之和为 target。开始博主想的是遍历所有子集合,算和,但是这种方法无法通过 OJ 的大数据集合。于是乎,动态规划 Dynamic Programming 就是不二之选。定义一个一维的 dp 数组,其中 dp[i] 表示原数组是否可以取出若干个数字,其和为i。那么最后只需要返回 dp[target] 就行了。
初始化 dp[0] 为 true,由于题目中限制了所有数字为正数,就不用担心会出现和为0或者负数的情况。关键问题就是要找出状态转移方程了,需要遍历原数组中的数字,对于遍历到的每个数字 nums[i],需要更新 dp 数组,既然最终目标是想知道 dp[target] 的 boolean 值,就要想办法用数组中的数字去凑出 target,因为都是正数,所以只会越加越大,加上 nums[i] 就有可能会组成区间 [nums[i], target] 中的某个值,那么对于这个区间中的任意一个数字j,如果 dp[j - nums[i]] 为 true 的话,说明现在已经可以组成 j-nums[i] 这个数字了,再加上 nums[i],就可以组成数字j了,那么 dp[j] 就一定为 true。如果之前 dp[j] 已经为 true 了,当然还要保持 true,所以还要 ‘或’ 上自身,于是状态转移方程如下:1
dp[j] = dp[j] || dp[j - nums[i]] (nums[i] <= j <= target)
有了状态转移方程,就可以写出代码了,这里需要特别注意的是,第二个 for 循环一定要从 target 遍历到 nums[i],而不能反过来,想想为什么呢?因为如果从 nums[i] 遍历到 target 的话,假如 nums[i]=1 的话,那么 [1, target] 中所有的 dp 值都是 true,因为 dp[0] 是 true,dp[1] 会或上 dp[0],为 true,dp[2] 会或上 dp[1],为 true,依此类推,完全使的 dp 数组失效了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = accumulate(nums.begin(), nums.end(), 0), target = sum >> 1;
if (sum & 1) return false;
vector<bool> dp(target + 1, false);
dp[0] = true;
for (int num : nums) {
for (int i = target; i >= num; --i) {
dp[i] = dp[i] || dp[i - num];
}
}
return dp[target];
}
};
Leetcode417. Pacific Atlantic Water Flow
There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island’s left and top edges, and the Atlantic Ocean touches the island’s right and bottom edges.
The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).
The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell’s height is less than or equal to the current cell’s height. Water can flow from any cell adjacent to an ocean into the ocean.
Return a 2D list of grid coordinates result where result[i] = [ri, ci] denotes that rain water can flow from cell (ri, ci) to both the Pacific and Atlantic oceans.
Example 1:1
2Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]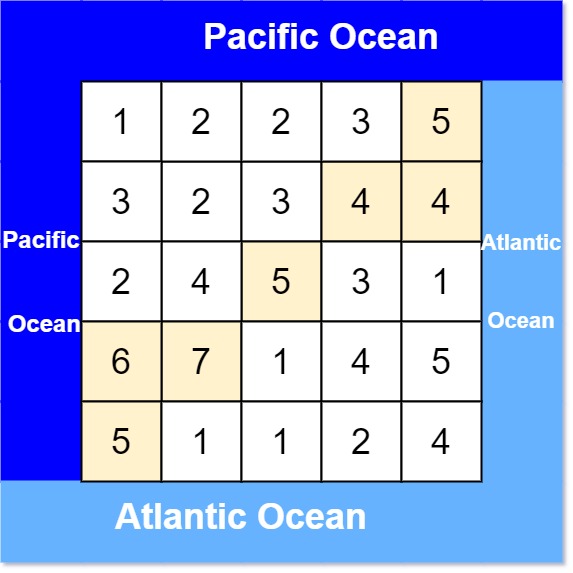
Example 2:1
2Input: heights = [[2,1],[1,2]]
Output: [[0,0],[0,1],[1,0],[1,1]]
上面一条边和左边一条边代表的是太平洋,右边一条边和下边一条边代表的是大西洋。现在告诉你水往低处流,问哪些位置的水能同时流进太平洋和大西洋?
直接DFS求解。一般来说DFS需要有固定的起点,但是对于这个题,四条边界的每个位置都算作起点。
使用两个二维数组,分别记录每个位置的点能不能到达太平洋和大西洋。然后对4条边界进行遍历,看这些以这些边为起点能不能所有的地方。注意了,因为是从边界向中间去寻找,所以,这个时候是新的点要比当前的点海拔高才行。
最坏情况下的时间复杂度是O((M+N)*MN),空间复杂度是O(MN)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45class Solution {
public:
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
int m = heights.size();
if (m == 0)
return {};
int n = heights[0].size();
vector<vector<int>> res;
vector<vector<bool>> p_flags(m, vector<bool>(n ,false));
vector<vector<bool>> a_flags(m, vector<bool>(n ,false));
for (int i = 0; i < m; i ++) {
dfs(heights, p_flags, i, 0);
dfs(heights, a_flags, i, n-1);
}
for (int i = 0; i < n; i ++) {
dfs(heights, p_flags, 0, i);
dfs(heights, a_flags, m-1, i);
}
for (int i = 0; i < m; i ++)
for (int j = 0; j < n; j ++)
if (p_flags[i][j] && a_flags[i][j]) {
vector<int> t;
t.push_back(i);
t.push_back(j);
res.push_back(t);
}
return res;
}
void dfs(vector<vector<int>>& heights, vector<vector<bool>>& flags, int i, int j) {
int m = heights.size(), n = heights[0].size();
vector<pair<int, int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
flags[i][j] = true;
for (int ii = 0; ii < 4; ii ++) {
int x = i + dirs[ii].first;
int y = j + dirs[ii].second;
if (x >= 0 && x < m && y >= 0 && y < n && !flags[x][y] && heights[x][y] >= heights[i][j]) {
flags[x][y] = true;
dfs(heights, flags, x, y);
}
}
}
};
Leetcode419. Battleships in a Board
Given an 2D board, count how many battleships are in it. The battleships are represented with ‘X’s, empty slots are represented with ‘.’s. You may assume the following rules:
You receive a valid board, made of only battleships or empty slots.
Battleships can only be placed horizontally or vertically. In other words, they can only be made of the shape 1xN (1 row, N columns) or Nx1 (N rows, 1 column), where N can be of any size.
At least one horizontal or vertical cell separates between two battleships - there are no adjacent battleships.
Example:1
2
3X..X
...X
...X
In the above board there are 2 battleships.
Invalid Example:1
2
3...X
XXXX
...X
This is an invalid board that you will not receive - as battleships will always have a cell separating between them.
Follow up:
Could you do it in one-pass, using only O(1) extra memory and without modifying the value of the board?
利用最简单的方法找有多少个X块,这里用的遍历很方便。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int countBattleships(vector<vector<char>>& board) {
int x = board.size();
int y = board[0].size();
int res=0;
for(int i=0;i<x;i++)
for(int j=0;j<y;j++)
if(board[i][j]=='X'){
if(j<y-1 && board[i][j+1]=='X') continue;
if(i<x-1 && board[i+1][j]=='X') continue;
res++;
}
return res;
}
};
Leetcode421. Maximum XOR of Two Numbers in an Array
Given an integer array nums, return the maximum result of nums[i] XOR nums[j], where 0 <= i <= j < n.
Example 1:1
2
3Input: nums = [3,10,5,25,2,8]
Output: 28
Explanation: The maximum result is 5 XOR 25 = 28.
Example 2:1
2Input: nums = [14,70,53,83,49,91,36,80,92,51,66,70]
Output: 127
Constraints:
- 1 <= nums.length <= 2 * 105
- 0 <= nums[i] <= 231 - 1
这个是求一个数组中任意两个元素的最大异或值,我们就要让最高位尽可能的不同,使用字典树解决这个问题。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class Solution {
public:
struct Node {
int son[2];
Node() {
son[0] = son[1] = -1;
}
};
vector<Node> nodes;
int findMaximumXOR(vector<int>& a) {
// 让异或的结果最高位尽可能大
// 从高位到低位考虑,ai当前这个位为0,那希望aj当前位为1
// 用前缀树
if (a.size() == 0)
return 0;
nodes.push_back({});
insert(a.back());
int ret = 0;
for (int i = a.size()-2; i >= 0; i --) {
int ans = query(a[i]);
ret = max(ret, ans);
insert(a[i]);
}
return ret;
}
void insert(int a) {
int id = 0;
for (int i = 31; i >= 0; i --) {
int t = (a >> i) & 1;
if (nodes[id].son[t] == -1) {
nodes.push_back({});
nodes[id].son[t] = nodes.size()-1;
}
id = nodes[id].son[t];
}
}
int query(int x) {
int ret = 0;
int id = 0;
for (int i = 31; i >= 0; i --) {
int b = (x >> i) & 1;
int b2 = b ^ 1;
if (nodes[id].son[b2] != -1) {
id = nodes[id].son[b2];
ret |= (1 << i);
}
else {
id = nodes[id].son[b];
}
}
return ret;
}
};
Leetcode423. Reconstruct Original Digits from English
Given a non-empty string containing an out-of-order English representation of digits 0-9, output the digits in ascending order.
Note:
- Input contains only lowercase English letters.
- Input is guaranteed to be valid and can be transformed to its original digits. That means invalid inputs such as “abc” or “zerone” are not permitted.
- Input length is less than 50,000.
Example 1:1
2Input: "owoztneoer"
Output: "012"
Example 2:1
2Input: "fviefuro"
Output: "45"
这道题给了我们一串英文字符串,是由表示数字的英文单词组成的,不过字符顺序是打乱的,让我们重建出数字。那么这道题的思路是先要统计出各个字符出现的次数,然后算出每个单词出现的次数,然后就可以重建了。由于题目中限定了输入的字符串一定是有效的,那么不会出现无法成功重建的情况,这里需要用个trick。
我们仔细观察这些表示数字的单词”zero”, “one”, “two”, “three”, “four”, “five”, “six”, “seven”, “eight”, “nine”,我们可以发现有些的单词的字符是独一无二的,比如z,只出现在zero中,还有w,u,x,g这四个单词,分别只出现在two,four,six,eight中,那么这五个数字的个数就可以被确定了,由于含有o的单词有zero,two,four,one,其中前三个都被确定了,那么one的个数也就知道了;由于含有h的单词有eight,three,其中eight个数已知,那么three的个数就知道了;由于含有f的单词有four,five,其中four个数已知,那么five的个数就知道了;由于含有s的单词有six,seven,其中six个数已知,那么seven的个数就知道了;由于含有i的单词有six,eight,five,nine,其中前三个都被确定了,那么nine的个数就知道了。
知道了这些问题就变的容易多了,我们按这个顺序”zero”, “two”, “four”, “six”, “eight”, “one”, “three”, “five”, “seven”, “nine”就能找出所有的个数了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
string originalDigits(string s) {
string res = "";
vector<string> words{"zero", "two", "four", "six", "eight", "one", "three", "five", "seven", "nine"};
vector<int> nums{0, 2, 4, 6, 8, 1, 3, 5, 7, 9}, counts(26, 0);
vector<char> chars{'z', 'w', 'u', 'x', 'g', 'o', 'h', 'f', 's', 'i'};
for (char c : s) ++counts[c - 'a'];
for (int i = 0; i < 10; ++i) {
int cnt = counts[chars[i] - 'a'];
for (int j = 0; j < words[i].size(); ++j) {
counts[words[i][j] - 'a'] -= cnt;
}
while (cnt--) res += (nums[i] + '0');
}
sort(res.begin(), res.end());
return res;
}
};
Leetcode424. Longest Repeating Character Replacement
Given a string that consists of only uppercase English letters, you can replace any letter in the string with another letter at most k times. Find the length of a longest substring containing all repeating letters you can get after performing the above operations.
Note:
Both the string’s length and k will not exceed 10 4.
Example 1:1
2
3
4
5
6
7
8Input:
s = "ABAB", k = 2
Output:
4
Explanation:
Replace the two 'A's with two 'B's or vice versa.
Example 2:1
2
3
4
5
6
7
8
9Input:
s = "AABABBA", k = 1
Output:
4
Explanation:
Replace the one 'A' in the middle with 'B' and form "AABBBBA".
The substring "BBBB" has the longest repeating letters, which is 4.
这道题给我们了一个字符串,说我们有k次随意置换任意字符的机会,让我们找出最长的重复字符的字符串。我们首先来想,如果没有k的限制,让我们求把字符串变成只有一个字符重复的字符串需要的最小置换次数,那么就是字符串的总长度减去出现次数最多的字符的个数。如果加上k的限制,我们其实就是求满足 (子字符串的长度减去出现次数最多的字符个数)<=k 的最大子字符串长度即可,搞清了这一点,我们也就应该知道怎么用滑动窗口来解了吧。我们用一个变量 start 记录滑动窗口左边界,初始化为0,然后遍历字符串,每次累加出现字符的个数,然后更新出现最多字符的个数,然后我们判断当前滑动窗口是否满足之前说的那个条件,如果不满足,我们就把滑动窗口左边界向右移动一个,并注意去掉的字符要在 counts 里减一,直到满足条件,我们更新结果 res 即可。需要注意的是,当滑动窗口的左边界向右移动了后,窗口内的相同字母的最大个数貌似可能会改变啊,为啥这里不用更新 maxCnt 呢?这是个好问题,原因是此题让求的是最长的重复子串,maxCnt 相当于卡了一个窗口大小,我们并不希望窗口变小,虽然窗口在滑动,但是之前是出现过跟窗口大小相同的符合题意的子串,缩小窗口没有意义,并不会使结果 res 变大,所以我们才不更新 maxCnt 的,参见代码如下:
1 | class Solution { |
Leetcode427. Construct Quad Tree
Given a n * n matrix grid of 0’s and 1’s only. We want to represent the grid with a Quad-Tree.
Return the root of the Quad-Tree representing the grid.
Notice that you can assign the value of a node to True or False when isLeaf is False, and both are accepted in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
val: True if the node represents a grid of 1’s or False if the node represents a grid of 0’s.isLeaf: True if the node is leaf node on the tree or False if the node has the four children.
1 | class Node { |
We can construct a Quad-Tree from a two-dimensional area using the following steps:
If the current grid has the same value (i.e all 1’s or all 0’s) set isLeaf True and set val to the value of the grid and set the four children to Null and stop.
Example 1:1
2
3
4
5
6Input: grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
Output: [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
Explanation: All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below: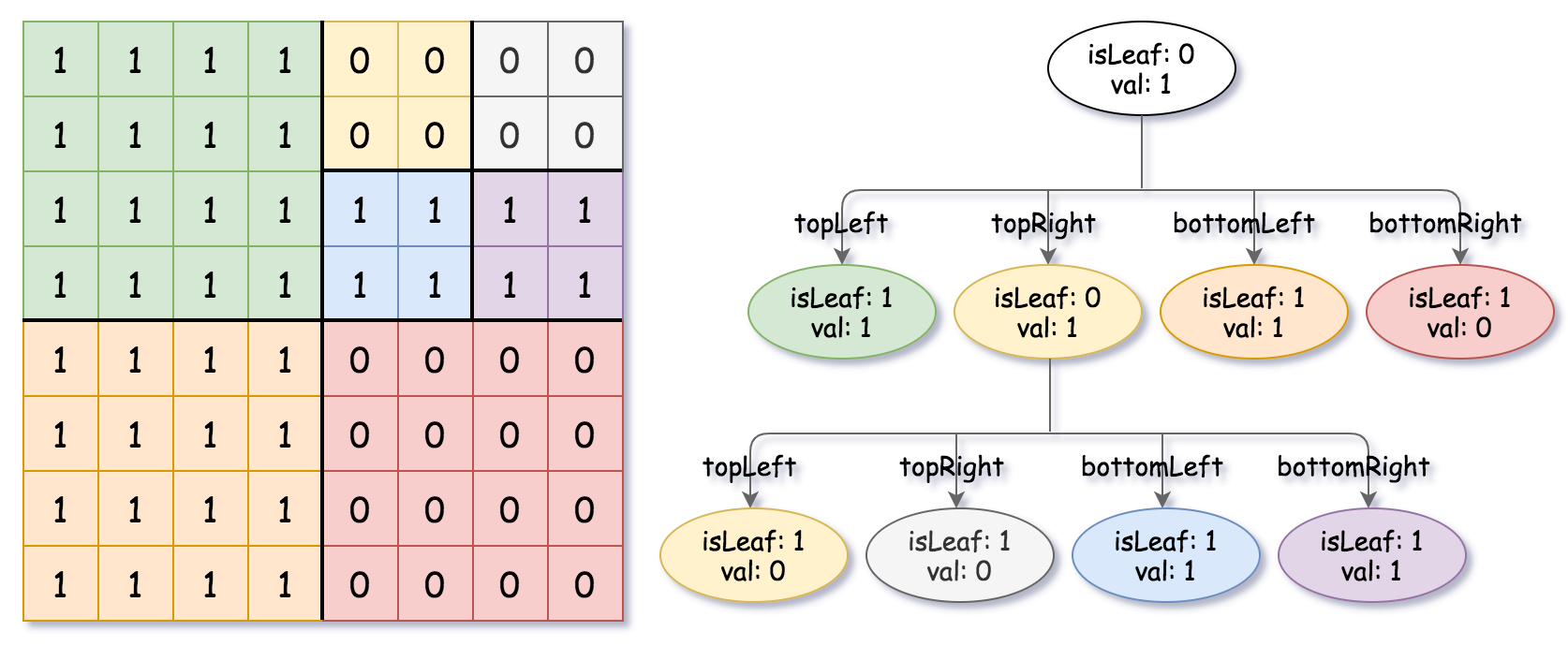
这道题让我们根据一个二维数组来建立一棵四叉树,首先整个数组被分成了四等份,左上,左下,和右下部分内的值均相同,那么他们都是一个叶结点,而右上只有再四等分一下,才能使各自部分内的值相同,所以其就不是叶结点,而四等分后的每个区间才是叶结点。题目中限定了N的值一定是2的指数,就是说其如果可分的话,一定可以四等分,而之前说了,只有区间内的值不同时,才需要四等分,否则整体就当作一个叶结点。所以我们需要check四等分区间内的值是否相同,当然,我们可以将二维数组拆分为四个二维数组,但是那样可能不太高效,而且还占用额外空间,一个比较好的选择是用坐标变量来控制等分数组的范围,我们只需要一个起始点坐标,和区间的长度,就可以精确定位一个区间了。
比如说对于例子中的整个二维数组数组来说,知道起始点坐标 (0, 0),还有长度8,就知道表示的是哪个区间。我们可以遍历这个区间上的其他所有的点,跟起点对比,只要有任何点跟起点不相同,则说明该区间是可分的,因为我们前面说了,只有一个区间上所有的值均相同,才能当作一个叶结点。只要有不同,就表示可以四分,那么我们就新建一个结点,这里的左上,左下,右上,和右下四个子结点就需要用过调用递归函数来实现了,实现原理都一样。
对于非叶结点,结点值可以是true或者false都没问题。如果某个区间上所有值均相同,那么就生成一个叶结点,结点值就跟区间值相同,isLeaf是true,四个子结点均为NULL即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
Node* construct(vector<vector<int>>& grid) {
return build(grid, 0, 0, grid.size()-1, grid.size()-1);
}
Node* build(vector<vector<int>>& grid, int r0, int c0, int r1, int c1) {
if (r0 > r1 || c0 > c1)
return NULL;
bool isleaf = true;
int val = grid[r0][c0];
for (int i = r0; i <= r1; i ++)
for (int j = c0; j <= c1; j ++)
if (grid[i][j] != val) {
isleaf = false;
break;
}
if (isleaf)
return new Node(val == 1, true, NULL, NULL, NULL, NULL);
int mid1 = (r0+r1) / 2, mid2 = (c0+c1) / 2;
return new Node(false, false,
build(grid, r0, c0, mid1, mid2),
build(grid, r0, mid2+1, mid1, c1),
build(grid, mid1+1, c0, r1, mid2),
build(grid, mid1+1, mid2+1, r1, c1));
}
};
Leetcode429. N-ary Tree Level Order Traversal
Given an n-ary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).
Note:
- The depth of the tree is at most 1000.
- The total number of nodes is at most 5000.
这道题给了我们一棵N叉树,让我们对其进行层序遍历。虽说现在每一个结点可能有很多个子结点,但其实处理的思路的都是一样的。子结点放到了一个children数组中,我们访问的时候只要遍历数组就行了。先来看迭代的写法,用到了队列queue来辅助,首先判断root是否为空,为空直接返回空数组,否则加入queue中。然后遍历queue,这里用的trick就是,要加个for循环,要将当前queue中的结点的个数统计下来,因为再加入下一层的结点时,queue的结点个数会增加,而在加入下一层结点之前,当前queue中的结点个数全都属于一层,所以我们要把层与层区分开来,将同一层的结点都放到一个数组out中,之后再放入结果res中,这种层序遍历的思想在迷宫遍历找最短路径的时候应用的也很多,是个必须要掌握的方法呢,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
if (!root) return {};
vector<vector<int>> res;
queue<Node*> q{{root}};
while (!q.empty()) {
vector<int> out;
for (int i = q.size(); i > 0; --i) {
auto t = q.front(); q.pop();
out.push_back(t->val);
if (!t->children.empty()) {
for (auto a : t->children) q.push(a);
}
}
res.push_back(out);
}
return res;
}
};
Leetcode430. Flatten a Multilevel Doubly Linked List
You are given a doubly linked list which in addition to the next and previous pointers, it could have a child pointer, which may or may not point to a separate doubly linked list. These child lists may have one or more children of their own, and so on, to produce a multilevel data structure, as shown in the example below.
Flatten the list so that all the nodes appear in a single-level, doubly linked list. You are given the head of the first level of the list.
Example 1:1
2Input: head = [1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]
Output: [1,2,3,7,8,11,12,9,10,4,5,6]
Explanation: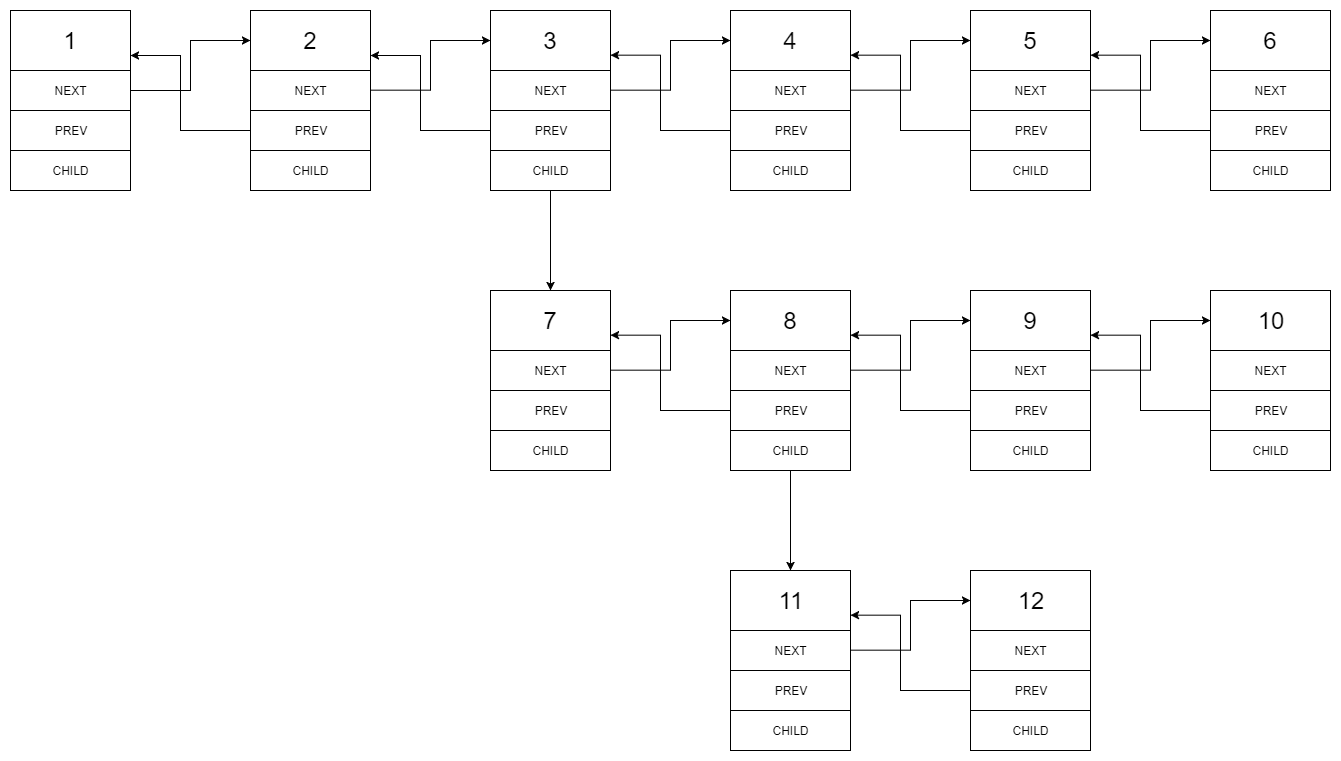
The multilevel linked list in the input is as follows:
Example 2:1
2Input: head = [1,2,null,3]
Output: [1,3,2]
Explanation:1
2
3
4
5The input multilevel linked list is as follows:
1---2---NULL
|
3---NULL
这道题给了一个多层的双向链表,让我们压平成为一层的双向链表,题目中给了形象的图例,不难理解题意。根据题目中给的例子,我们可以看出如果某个结点有下一层双向链表,那么下一层双向链表中的结点就要先加入进去,如果下一层链表中某个结点还有下一层,那么还是优先加入下一层的结点,整个加入的机制是DFS的,就是有岔路先走岔路,走到没路了后再返回,这就是深度优先遍历的机制。好,那么既然是DFS,肯定优先考虑递归啦。方法有了,再来看具体怎么递归。由于给定的多层链表本身就是双向的,所以我们只需要把下一层的结点移到第一层即可,那么没有子结点的结点就保持原状,不作处理。只有对于那些有子结点的,我们需要做一些处理,由于子结点链接的双向链表要加到后面,所以当前结点之后要断开,再断开之前,我们用变量 next 指向下一个链表,然后对子结点调用递归函数,我们 suppose 返回的结点已经压平了,那么就只有一层,就相当于要把这一层的结点加到断开的地方,所以需要知道这层的最后一个结点的位置,我们用一个变量 last,来遍历到压平的这一层的末结点。现在就可以开始链接了,首先把子结点链到 cur 的 next,然后把反向指针 prev 也链上。此时 cur 的子结点 child 可以清空,然后压平的这一层的末节点 last 链上之前保存的 next 结点,如果 next 非空,那么链上反向结点 prev。这些操作完成后,我们就已经将压平的这一层完整的加入了之前层断开的地方,继续在之前层往下遍历即可,参见代码如下:
1 | class Solution { |
Leetcode433. Minimum Genetic Mutation
A gene string can be represented by an 8-character long string, with choices from ‘A’, ‘C’, ‘G’, and ‘T’.
Suppose we need to investigate a mutation from a gene string start to a gene string end where one mutation is defined as one single character changed in the gene string.
For example, “AACCGGTT” —> “AACCGGTA” is one mutation. There is also a gene bank bank that records all the valid gene mutations. A gene must be in bank to make it a valid gene string.
Given the two gene strings start and end and the gene bank bank, return the minimum number of mutations needed to mutate from start to end. If there is no such a mutation, return -1.
Note that the starting point is assumed to be valid, so it might not be included in the bank.
Example 1:1
2Input: start = "AACCGGTT", end = "AACCGGTA", bank = ["AACCGGTA"]
Output: 1
Example 2:1
2Input: start = "AACCGGTT", end = "AAACGGTA", bank = ["AACCGGTA","AACCGCTA","AAACGGTA"]
Output: 2
Example 3:1
2Input: start = "AAAAACCC", end = "AACCCCCC", bank = ["AAAACCCC","AAACCCCC","AACCCCCC"]
Output: 3
先建立bank数组的距离场,这里距离就是两个字符串之间不同字符的个数。然后以start字符串为起点,向周围距离为1的点扩散,采用BFS搜索,每扩散一层,level自加1,当扩散到end字符串时,返回当前level即可。注意我们要把start字符串也加入bank中,而且此时我们也知道start的坐标位置,bank的最后一个位置,然后在建立距离场的时候,调用一个count子函数,用来统计输入的两个字符串之间不同字符的个数,注意dist[i][j]和dist[j][i]是相同,所以我们只用算一次就行了。然后我们进行BFS搜索,用一个visited集合来保存遍历过的字符串,注意检测距离的时候,dist[i][j]和dist[j][i]只要有一个是1,就可以了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42class Solution {
public:
int minMutation(string start, string end, vector<string>& bank) {
if (bank.empty())
return -1;
bank.push_back(start);
int res = 0, len = bank.size();
queue<int> q;
vector<vector<int> > dist(len, vector<int>(len, 0));
vector<int> visited(len, 0);
for (int i = 0; i < len; i ++)
for (int j = i+1; j < len; j ++)
dist[i][j] = cal_dist(bank[i], bank[j]);
q.push(len-1);
while(!q.empty()) {
res ++;
int size = q.size();
for (int i = 0; i < size; i ++) {
int t = q.front();
q.pop();
visited[t] = true;
for (int j = 0; j < len; j ++) {
if ((dist[t][j] != 1 && dist[j][t] != 1) || visited[j])
continue;
q.push(j);
if (bank[j] == end)
return res;
}
}
}
return -1;
}
int cal_dist(string a, string b) {
int cnt = 0, len = a.length();
for (int i = 0; i < len; i ++)
if (a[i] != b[i])
cnt ++;
return cnt;
}
};
Leetcode434. Number of Segments in a String
Count the number of segments in a string, where a segment is defined to be a contiguous sequence of non-space characters.
Please note that the string does not contain any non-printable characters.
Example:1
2Input: "Hello, my name is John"
Output: 5
判断一个句子中有几个段。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int countSegments(string s) {
int res = 0;
if(s == "" || s == " ")
return 0;
for(int i = 0; i < s.length(); i ++) {
if(s[i] != ' ')
res ++;
while(i < s.length() && s[i] != ' ')
i ++;
}
return res;
}
};
有一种简单做法:1
2
3
4
5
6
7
8int countSegments(string s) {
stringstream ss(s);
string word;
int count = 0;
while (ss >> word)
count++;
return count;
}
Leetcode435. Non-overlapping Intervals
Given an array of intervals intervals where intervals[i] = [starti, endi], return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Example 1:1
2
3Input: intervals = [[1,2],[2,3],[3,4],[1,3]]
Output: 1
Explanation: [1,3] can be removed and the rest of the intervals are non-overlapping.
Example 2:1
2
3Input: intervals = [[1,2],[1,2],[1,2]]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of the intervals non-overlapping.
这道题给了我们一堆区间,让求需要至少移除多少个区间才能使剩下的区间没有重叠,那么首先要给区间排序,根据每个区间的 start 来做升序排序,然后开始要查找重叠区间,判断方法是看如果前一个区间的 end 大于后一个区间的 start,那么一定是重复区间,此时结果 res 自增1,我们需要删除一个,那么此时究竟该删哪一个呢,为了保证总体去掉的区间数最小,我们去掉那个 end 值较大的区间,而在代码中,我们并没有真正的删掉某一个区间,而是用一个变量 last 指向上一个需要比较的区间,我们将 last 指向 end 值较小的那个区间;如果两个区间没有重叠,那么此时 last 指向当前区间,继续进行下一次遍历,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
int res = 0, begin = 0, end = 0;
sort(intervals.begin(), intervals.end());
begin = intervals[0][0], end = intervals[0][1];
for (int i = 1; i < intervals.size(); i ++) {
if (end > intervals[i][0]) {
res ++;
if (end > intervals[i][1])
end = intervals[i][1];
}
else
end = intervals[i][1];
}
return res;
}
};
Leetcode436. Find Right Interval
You are given an array of intervals, where intervals[i] = [starti, endi] and each starti is unique.
The right interval for an interval i is an interval j such that startj >= endi and startj is minimized.
Return an array of right interval indices for each interval i. If no right interval exists for interval i, then put -1 at index i.
Example 1:1
2
3Input: intervals = [[1,2]]
Output: [-1]
Explanation: There is only one interval in the collection, so it outputs -1.
Example 2:1
2
3
4
5Input: intervals = [[3,4],[2,3],[1,2]]
Output: [-1,0,1]
Explanation: There is no right interval for [3,4].
The right interval for [2,3] is [3,4] since start0 = 3 is the smallest start that is >= end1 = 3.
The right interval for [1,2] is [2,3] since start1 = 2 is the smallest start that is >= end2 = 2.
Example 3:1
2
3
4Input: intervals = [[1,4],[2,3],[3,4]]
Output: [-1,2,-1]
Explanation: There is no right interval for [1,4] and [3,4].
The right interval for [2,3] is [3,4] since start2 = 3 is the smallest start that is >= end1 = 3.
这道题给了我们一堆区间,让我们找每个区间的最近右区间,要保证右区间的 start 要大于等于当前区间的 end,由于区间的顺序不能变,所以我们不能给区间排序,我们需要建立区间的 start 和该区间位置之间的映射,由于题目中限定了每个区间的 start 都不同,所以不用担心一对多的情况出现。然后我们把所有的区间的 start 都放到一个数组中,并对这个数组进行降序排序,那么 start 值大的就在数组前面。然后我们遍历区间集合,对于每个区间,我们在数组中找第一个小于当前区间的 end 值的位置,如果数组中第一个数就小于当前区间的 end,那么说明该区间不存在右区间,结果 res 中加入-1;如果找到了第一个小于当前区间 end 的位置,那么往前推一个就是第一个大于等于当前区间 end 的 start,我们在 HashMap 中找到该区间的坐标加入结果 res 中即可,参见代码如下:(下边改进为二分搜索,速度快了十几倍)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
vector<int> findRightInterval(vector<vector<int>>& intervals) {
unordered_map<int, int> map;
vector<int> start;
for (int i = 0; i < intervals.size(); i ++) {
map[intervals[i][0]] = i;
start.push_back(intervals[i][0]);
}
sort(start.begin(), start.end());
vector<int> ress;
int len = intervals.size();
for (int i = 0; i < len; i ++) {
int low = 0, high = len-1, mid;
int best = -1;
while(low <= high) {
mid = low + (high-low) / 2;
if (start[mid] < intervals[i][1])
low = mid+1;
else {
best = map[start[mid]];
high = mid-1;
}
}
ress.push_back(best);
}
return ress;
}
};
Leetcode437. Path Sum III
You are given a binary tree in which each node contains an integer value. Find the number of paths that sum to a given value. The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes).
The tree has no more than 1,000 nodes and the values are in the range -1,000,000 to 1,000,000.
Example:1
2
3
4
5
6
7
8
9
10
11
12root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
Return 3. The paths that sum to 8 are:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
这道题让我们求二叉树的路径的和等于一个给定值,说明了这条路径不必要从根节点开始,可以是中间的任意一段,而且二叉树的节点值也是有正有负。那么可以用递归来做,相当于先序遍历二叉树,对于每一个节点都有记录了一条从根节点到当前节点到路径,同时用一个变量 curSum 记录路径节点总和,然后看 curSum 和 sum 是否相等,相等的话结果 res 加1,不等的话继续查看子路径和有没有满足题意的,做法就是每次去掉一个节点,看路径和是否等于给定值,注意最后必须留一个节点,不能全去掉了,因为如果全去掉了,路径之和为0,而如果给定值刚好为0的话就会有问题。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
int ans = 0;
void dfs(TreeNode* root, vector<TreeNode*>& out, int sum, int cur) {
if(root == NULL)
return;
cur += root->val;
if (cur == sum) ++ans;
out.push_back(root);
int t = cur;
for(int i = 0; i < out.size() - 1; i ++) {
t = t - out[i]->val;
if (t == sum)
++ans;
}
dfs(root->left, out, sum, cur);
dfs(root->right, out, sum, cur);
out.pop_back();
}
int pathSum(TreeNode* root, int sum) {
vector<TreeNode*> out;
dfs(root, out, sum, 0);
return ans;
}
};
Leetcode438. Find All Anagrams in a String
Given two strings s and p, return an array of all the start indices of p’s anagrams in s. You may return the answer in any order.
Example 1:1
2
3
4
5Input: s = "cbaebabacd", p = "abc"
Output: [0,6]
Explanation:
The substring with start index = 0 is "cba", which is an anagram of "abc".
The substring with start index = 6 is "bac", which is an anagram of "abc".
Example 2:1
2
3
4
5
6Input: s = "abab", p = "ab"
Output: [0,1,2]
Explanation:
The substring with start index = 0 is "ab", which is an anagram of "ab".
The substring with start index = 1 is "ba", which is an anagram of "ab".
The substring with start index = 2 is "ab", which is an anagram of "ab".
这道题给了我们两个字符串s和p,让在s中找字符串p的所有变位次的位置,所谓变位次就是字符种类个数均相同但是顺序可以不同的两个词,那么肯定首先就要统计字符串p中字符出现的次数,然后从s的开头开始,每次找p字符串长度个字符,来验证字符个数是否相同,如果不相同出现了直接 break,如果一直都相同了,则将起始位置加入结果 res 中,参见代码如下:(不用unordered_map而是用vector会更快!)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
vector<int> findAnagrams(string s, string p) {
unordered_map<char, int> map, maps;
vector<int> res;
int lens = s.length(), lenp = p.length();
for (int i = 0; i < 26; i ++) {
map['a' + i] = 0;
maps['a' + i] = 0;
}
for (int i = 0; i < lenp; i ++) {
map[p[i]] ++;
}
if (lenp > lens)
return {};
for (int i = 0; i < lenp-1; i ++)
maps[s[i]] ++;
for (int i = lenp-1; i < lens; i ++) {
maps[s[i]] ++;
int j = 0;
for(j = 0; j < 26; j ++)
if (maps['a' + j] != map['a' + j])
break;
if (j == 26)
res.push_back(i-lenp+1);
maps[s[i-lenp+1]] --;
}
return res;
}
};
Leetcode441. Arranging Coins
You have a total of n coins that you want to form in a staircase shape, where every k-th row must have exactly k coins.
Given n, find the total number of full staircase rows that can be formed. n is a non-negative integer and fits within the range of a 32-bit signed integer.
Example 1:1
2
3
4
5
6
7n = 5
The coins can form the following rows:
¤
¤ ¤
¤ ¤
Because the 3rd row is incomplete, we return 2.
Example 2:1
2
3
4
5
6
7
8
9n = 8
The coins can form the following rows:
¤
¤ ¤
¤ ¤ ¤
¤ ¤
Because the 4th row is incomplete, we return 3.
直接遍历即可,从1开始,如果剩下是数不能构成一行则返回。注意要先判断剩下的数是否满足,而不是累加以后再判断,这样可能会导致溢出。1
2
3
4
5
6
7
8
9
10int arrangeCoins(int n) {
int i = 1, ans = n;
if(n == 1)
return 1;
while(ans >= i) {
ans -= i;
i ++;
}
return i-1;
}
前 i 行完整的硬币数量为i * (i + 1) / 2 ,前 i+1 行则为(i + 2) * (i + 1) / 2。所以(i + 1)*i / 2 ≤ n < (i + 2) * (i + 1) / 2,所以sqrt(2n + 0.25) - 1.5 < n ≤ sqrt(2n + 0.25) - 0.5。1
2
3
4int arrangeCoins(int n)
{
return (int)(sqrt(2 * (double)n + 0.25) - 0.5);
}
Leetcode442. Find All Duplicates in an Array
Given an integer array nums of length n where all the integers of nums are in the range [1, n] and each integer appears once or twice, return an array of all the integers that appears twice.
You must write an algorithm that runs in O(n) time and uses only constant extra space.
Example 1:1
2Input: nums = [4,3,2,7,8,2,3,1]
Output: [2,3]
Example 2:1
2Input: nums = [1,1,2]
Output: [1]
Example 3:1
2Input: nums = [1]
Output: []
这类问题的一个重要条件就是1 ≤ a[i] ≤ n (n = size of array),不然很难在O(1)空间和O(n)时间内完成。首先来看一种正负替换的方法,这类问题的核心是就是找nums[i]和nums[nums[i] - 1]的关系,我们的做法是,对于每个nums[i],我们将其对应的nums[nums[i] - 1]取相反数,如果其已经是负数了,说明之前存在过,我们将其加入结果res中即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
vector<int> findDuplicates(vector<int>& nums) {
vector<int> res;
for (int i = 0; i < nums.size(); ++i) {
int idx = abs(nums[i]) - 1;
if (nums[idx] < 0) res.push_back(idx + 1);
nums[idx] = -nums[idx];
}
return res;
}
};
本题使用Set的数据结构对数组进行遍历,找到出现两次的元素。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
vector<int> findDuplicates(vector<int>& nums) {
vector<int> res;
set<int> s;
unordered_map<int, bool> flags;
for (int n : nums) {
if (!s.count(n))
s.insert(n);
else
res.push_back(n);
}
return res;
}
};
Leetcode443. String Compression
Given an array of characters, compress it in-place. The length after compression must always be smaller than or equal to the original array. Every element of the array should be a character (not int) of length 1. After you are done modifying the input array in-place, return the new length of the array.
Follow up:
Could you solve it using only O(1) extra space?
Example 1:1
2
3
4
5
6
7
8Input:
["a","a","b","b","c","c","c"]
Output:
Return 6, and the first 6 characters of the input array should be: ["a","2","b","2","c","3"]
Explanation:
"aa" is replaced by "a2". "bb" is replaced by "b2". "ccc" is replaced by "c3".
Example 2:1
2
3
4
5
6
7
8Input:
["a"]
Output:
Return 1, and the first 1 characters of the input array should be: ["a"]
Explanation:
Nothing is replaced.
Example 3:1
2
3
4
5
6
7
8
9Input:
["a","b","b","b","b","b","b","b","b","b","b","b","b"]
Output:
Return 4, and the first 4 characters of the input array should be: ["a","b","1","2"].
Explanation:
Since the character "a" does not repeat, it is not compressed. "bbbbbbbbbbbb" is replaced by "b12".
Notice each digit has it's own entry in the array.
字符串压缩,坑很多,如果是只有一个字符的话就不用压缩,否则的话把字符和字符的数量都加到vector中,还要原地修改。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
int compress(vector<char>& chars) {
int ans = 0;
char c = chars[0], cc = c;
int cur = 1, pointer = 0;
string nums;
for(int i = 1; i < chars.size(); i ++) {
if(chars[i] != c) {
cout << c << " " << cur << endl;
chars[pointer++] = c;
nums = to_string(cur);
if(cur == 1) {
c = chars[i];
continue;
}
for(int i = 0; i < nums.length(); i ++) {
chars[pointer++] = nums[i];
}
cur = 1;
c = chars[i];
}
else
cur ++;
}
chars[pointer++] = c;
if(cur == 1) {
return pointer;
}
nums = to_string(cur);
for(int i = 0; i < nums.length(); i ++) {
chars[pointer++] = nums[i];
}
return pointer;
}
};
Leetcode445. Add Two Numbers II
You are given two non-empty linked lists representing two non-negative integers. The most significant digit comes first and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example 1:1
2Input: l1 = [7,2,4,3], l2 = [5,6,4]
Output: [7,8,0,7]
Example 2:1
2Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [8,0,7]
Example 3:1
2Input: l1 = [0], l2 = [0]
Output: [0]
由于加法需要从最低位开始运算,而最低位在链表末尾,链表只能从前往后遍历,没法取到前面的元素,那怎么办呢?我们可以利用栈来保存所有的元素,然后利用栈的后进先出的特点就可以从后往前取数字了,我们首先遍历两个链表,将所有数字分别压入两个栈s1和s2中,我们建立一个值为0的res节点,然后开始循环,如果栈不为空,则将栈顶数字加入sum中,然后将res节点值赋为sum%10,然后新建一个进位节点head,赋值为sum/10,如果没有进位,那么就是0,然后我们head后面连上res,将res指向head,这样循环退出后,我们只要看res的值是否为0,为0返回res->next,不为0则返回res即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
stack<int> s1, s2;
ListNode *head = l1;
while(head) {
s1.push(head->val);
head = head->next;
}
head = l2;
while(head) {
s2.push(head->val);
head = head->next;
}
head = NULL;
int sum = 0;
while(!s1.empty() || !s2.empty()) {
if (!s1.empty()) {
sum += s1.top();
s1.pop();
}
if (!s2.empty()) {
sum += s2.top();
s2.pop();
}
head = new ListNode(sum%10, head);
sum /= 10;
}
if (sum > 0)
head = new ListNode(sum, head);
return head;
}
};
Leetcode447. Number of Boomerangs
Given n points in the plane that are all pairwise distinct, a “boomerang” is a tuple of points (i, j, k) such that the distance between i and j equals the distance between i and k (the order of the tuple matters).
Find the number of boomerangs. You may assume that n will be at most 500 and coordinates of points are all in the range [-10000, 10000] (inclusive).
Example:1
2
3Input: [[0,0],[1,0],[2,0]]
Output: 2
Explanation: The two boomerangs are [[1,0],[0,0],[2,0]] and [[1,0],[2,0],[0,0]]
给定 n 个两两各不相同的平面上的点,一个 “回旋镖” 是一个元组(tuple)的点(i,j,k),并且 i 和 j 的距离等于 i 和 k之间的距离(考虑顺序)。找出回旋镖的个数。你可以假设 n 不大于500,点的坐标范围在[-10000, 10000](包括边界)。
抓住两组点 (x1,y1)、(x2,y2) 和 (x1,y1)、(x3,y3) 之间的距离相等这个信息:distance = sqrt{(x1-x2)^2+(y1-y2)^2} = sqrt{(x1-x3)^2+(y1-y3)^2}
按照这种相等的距离,我们可以给所有点进行分类,相同距离的这些点(假设n个)可以构成一个排列组合中的排列:n*(n-1)个回旋镖。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int numberOfBoomerangs(vector<vector<int>>& points) {
int ans = 0;
unordered_map<int, int> hash;
for(int i=0;i<points.size();i++){
for(int j=0;j<points.size();j++){
hash[pow(points[i][0]-points[j][0],2)+pow(points[i][1]-points[j][1],2)] += 1;
}
for(auto d:hash){
ans += d.second*(d.second-1);
}
hash.clear();
}
return ans;
}
};
Leetcode448. Find All Numbers Disappeared in an Array
Given an array of integers where 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once. Find all the elements of [1, n] inclusive that do not appear in this array. Could you do it without extra space and in O(n) runtime? You may assume the returned list does not count as extra space.
Example:1
2
3
4
5Input:
[4,3,2,7,8,2,3,1]
Output:
[5,6]
这道题让我们找出数组中所有消失的数,将nums[i]置换到其对应的位置nums[nums[i]-1]上去,比如对于没有缺失项的正确的顺序应该是[1, 2, 3, 4, 5, 6, 7, 8],而我们现在却是[4,3,2,7,8,2,3,1],我们需要把数字移动到正确的位置上去,比如第一个4就应该和7先交换个位置,以此类推,最后得到的顺序应该是[1, 2, 3, 4, 3, 2, 7, 8],我们最后在对应位置检验,如果nums[i]和i+1不等,那么我们将i+1存入结果res中即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> res;
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] != nums[nums[i] - 1]) {
swap(nums[i], nums[nums[i] - 1]);
--i;
}
}
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] != i + 1) {
res.push_back(i + 1);
}
}
return res;
}
};
Leetcode449. Serialize and Deserialize BST
Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary search tree. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
The encoded string should be as compact as possible.
Example 1:1
2Input: root = [2,1,3]
Output: [2,1,3]
Example 2:1
2Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range [0, 104].
- 0 <= Node.val <= 104
- The input tree is guaranteed to be a binary search tree.
用队列来做,比较慢,但是很原生且具有通用性:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
string res = "";
if (root == NULL)
return "";
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* temp = q.front();
q.pop();
if (temp) {
res += to_string(temp->val) + " ";
q.push(temp->left);
q.push(temp->right);
}
else
res += "# ";
}
return res;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if (data == "")
return NULL;
int pos = 0;
TreeNode *root = new TreeNode(get_num(data, pos));
pos ++;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()) {
TreeNode* temp = q.front();
q.pop();
if (data[pos] == '#') {
temp->left = NULL;
pos ++;
}
else {
temp->left = new TreeNode(get_num(data, pos));
q.push(temp->left);
}
pos ++;
if (data[pos] == '#') {
temp->right = NULL;
pos ++;
}
else {
temp->right = new TreeNode(get_num(data, pos));
q.push(temp->right);
}
pos ++;
}
return root;
}
int get_num(string data, int& pos) {
int res = 0;
while(data[pos] != ' ')
res = res * 10 + data[pos++] - '0';
return res;
}
};
层序遍历的非递归解法略微复杂一些,我们需要借助queue来做,本质是BFS算法,也不是很难理解,就是BFS算法的常规套路稍作修改即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
if (!root) return "";
ostringstream os;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode *t = q.front(); q.pop();
if (t) {
os << t->val << " ";
q.push(t->left);
q.push(t->right);
} else {
os << "# ";
}
}
return os.str();
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if (data.empty()) return NULL;
istringstream is(data);
queue<TreeNode*> q;
string val = "";
is >> val;
TreeNode *res = new TreeNode(stoi(val)), *cur = res;
q.push(cur);
while (!q.empty()) {
TreeNode *t = q.front(); q.pop();
if (!(is >> val)) break;
if (val != "#") {
cur = new TreeNode(stoi(val));
q.push(cur);
t->left = cur;
}
if (!(is >> val)) break;
if (val != "#") {
cur = new TreeNode(stoi(val));
q.push(cur);
t->right = cur;
}
}
return res;
}
};
Leetcode450. Delete Node in a BST
Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.
Basically, the deletion can be divided into two stages:
Search for a node to remove.
If the node is found, delete the node.
Follow up: Can you solve it with time complexity O(height of tree)?
Example 1:1
2
3
4
5Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.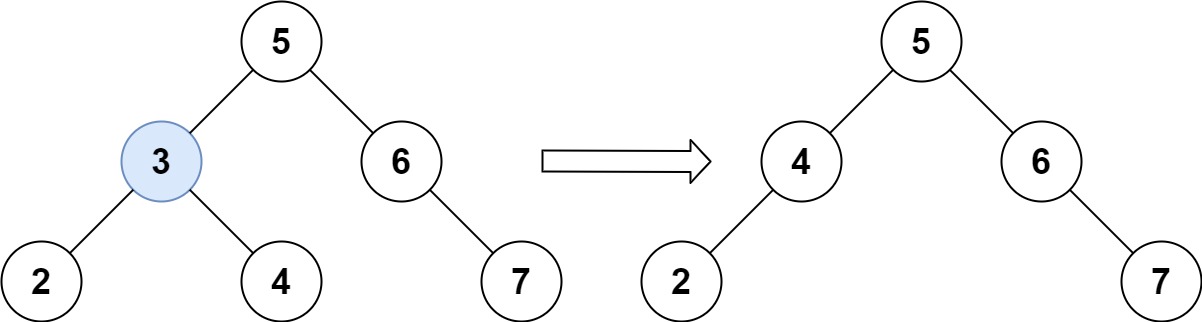
这道题让我们删除二叉搜索树中的一个节点,难点在于删除完结点并补上那个结点的位置后还应该是一棵二叉搜索树。被删除掉的结点位置,不一定是由其的左右子结点补上,比如下面这棵树:1
2
3
4
5
6
7 7
/ \
4 8
/ \
2 6
\ /
3 5
如果要删除结点4,那么应该将结点5补到4的位置,这样才能保证还是 BST,那么结果是如下这棵树:1
2
3
4
5
6
7 7
/ \
5 8
/ \
2 6
\
3
先来看一种递归的解法,首先判断根节点是否为空。由于 BST 的左<根<右的性质,使得可以快速定位到要删除的结点,对于当前结点值不等于 key 的情况,根据大小关系对其左右子结点分别调用递归函数。若当前结点就是要删除的结点,先判断若有一个子结点不存在,就将 root 指向另一个结点,如果左右子结点都不存在,那么 root 就赋值为空了,也正确。难点就在于处理左右子结点都存在的情况,需要在右子树找到最小值,即右子树中最左下方的结点,然后将该最小值赋值给 root,然后再在右子树中调用递归函数来删除这个值最小的结点,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (!root)
return NULL;
if (root->val > key)
root->left = deleteNode(root->left, key);
else if (root->val < key)
root->right = deleteNode(root->right, key);
else {
if (!root->left || !root->right)
root = root->left ? root->left : root->right;
else {
TreeNode* cur = root->right;
while(cur->left)
cur = cur->left;
root->val = cur->val;
root->right = deleteNode(root->right, cur->val);
}
}
return root;
}
};
Leetcode451. Sort Characters By Frequency
Given a string s, sort it in decreasing order based on the frequency of characters, and return the sorted string.
Example 1:1
2
3
4Input: s = "tree"
Output: "eert"
Explanation: 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr" is also a valid answer.
Example 2:1
2
3
4Input: s = "cccaaa"
Output: "aaaccc"
Explanation: Both 'c' and 'a' appear three times, so "aaaccc" is also a valid answer.
Note that "cacaca" is incorrect, as the same characters must be together.
Example 3:1
2
3
4Input: s = "Aabb"
Output: "bbAa"
Explanation: "bbaA" is also a valid answer, but "Aabb" is incorrect.
Note that 'A' and 'a' are treated as two different characters.
竟然还要区分大小写,还要排序,那map等结构就不能用了,直接用数组。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
static bool comp(pair<char, int>& a, pair<char, int>& b) {
return a.second > b.second || a.second == b.second && a.first < b.first;
}
string frequencySort(string s) {
int count[256] = {0};
for (char c : s)
count[c] ++;
sort(s.begin(), s.end(), [&](char a, char b){
return count[a] > count[b] || count[a] == count[b] && a < b;
});
return s;
}
};
Leetcode452. Minimum Number of Arrows to Burst Balloons
There are a number of spherical balloons spread in two-dimensional space. For each balloon, provided input is the start and end coordinates of the horizontal diameter. Since it’s horizontal, y-coordinates don’t matter and hence the x-coordinates of start and end of the diameter suffice. Start is always smaller than end. There will be at most 104 balloons.
An arrow can be shot up exactly vertically from different points along the x-axis. A balloon with xstart and xend bursts by an arrow shot at x if xstart ≤ x ≤ xend. There is no limit to the number of arrows that can be shot. An arrow once shot keeps travelling up infinitely. The problem is to find the minimum number of arrows that must be shot to burst all balloons.
Example 1:1
2
3Input: points = [[10,16],[2,8],[1,6],[7,12]]
Output: 2
Explanation: One way is to shoot one arrow for example at x = 6 (bursting the balloons [2,8] and [1,6]) and another arrow at x = 11 (bursting the other two balloons).
Example 2:1
2Input: points = [[1,2],[3,4],[5,6],[7,8]]
Output: 4
Example 3:1
2Input: points = [[1,2],[2,3],[3,4],[4,5]]
Output: 2
这道题给了我们一堆大小不等的气球,用区间范围来表示气球的大小,可能会有重叠区间。然后我们用最少的箭数来将所有的气球打爆。那么这道题是典型的用贪婪算法来做的题,因为局部最优解就等于全局最优解,我们首先给区间排序,我们不用特意去写排序比较函数,因为默认的对于pair的排序,就是按第一个数字升序排列,如果第一个数字相同,那么按第二个数字升序排列,这个就是我们需要的顺序,所以直接用即可。然后我们将res初始化为1,因为气球数量不为0,所以怎么也得先来一发啊,然后这一箭能覆盖的最远位置就是第一个气球的结束点,用变量end来表示。然后我们开始遍历剩下的气球,如果当前气球的开始点小于等于end,说明跟之前的气球有重合,之前那一箭也可以照顾到当前的气球,此时我们要更新end的位置,end更新为两个气球结束点之间较小的那个,这也是当前气球和之前气球的重合点,然后继续看后面的气球;如果某个气球的起始点大于end了,说明前面的箭无法覆盖到当前的气球,那么就得再来一发,既然又来了一发,那么我们此时就要把end设为当前气球的结束点了,这样贪婪算法遍历结束后就能得到最少的箭数了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
static bool comp(vector<int>& a, vector<int>& b) {
return a[0] < b[0];
}
int findMinArrowShots(vector<vector<int>>& points) {
sort(points.begin(), points.end(), comp);
int res = 1, end = points[0][1];
for (int i = 1; i < points.size(); i ++) {
if (end >= points[i][0])
end = min(end, points[i][1]);
else {
res ++;
end = points[i][1];
}
}
return res;
}
};
Leetcode453. Minimum Moves to Equal Array Elements
Given a non-empty integer array of size n, find the minimum number of moves required to make all array elements equal, where a move is incrementing n - 1 elements by 1.
Example:1
2
3
4
5
6
7
8
9Input:
[1,2,3]
Output:
3
Explanation:
Only three moves are needed (remember each move increments two elements):
[1,2,3] => [2,3,3] => [3,4,3] => [4,4,4]
这道题给了我们一个长度为n的数组,说是每次可以对 n-1 个数字同时加1,问最少需要多少次这样的操作才能让数组中所有的数字相等。那么想,为了快速的缩小差距,该选择哪些数字加1呢,不难看出每次需要给除了数组最大值的所有数字加1,这样能快速的到达平衡状态。但是这道题如果老老实实的每次找出最大值,然后给其他数字加1,再判断是否平衡,思路是正确,但是 OJ 不答应。正确的解法相当的巧妙,需要换一个角度来看问题,其实给 n-1 个数字加1,效果等同于给那个未被选中的数字减1,比如数组 [1,2,3],给除去最大值的其他数字加1,变为 [2,3,3],全体减1,并不影响数字间相对差异,变为 [1,2,2],这个结果其实就是原始数组的最大值3自减1,那么问题也可能转化为,将所有数字都减小到最小值,这样难度就大大降低了,只要先找到最小值,然后累加每个数跟最小值之间的差值即可。1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int minMoves(vector<int>& nums) {
int minn = INT_MAX, res = 0;
for(int i : nums)
minn = min(minn, i);
for(int i : nums)
res += (i - minn);
return res;
}
};
Leetcode454. 4Sum II
Given four integer arrays nums1, nums2, nums3, and nums4 all of length n, return the number of tuples (i, j, k, l) such that:
- 0 <= i, j, k, l < n
- nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
Example 1:1
2Input: nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
Output: 2
Explanation: The two tuples are:
- (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
- (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0
这道题是之前那道 4Sum 的延伸,让我们在四个数组中各取一个数字,使其和为0。如果把A和B的两两之和都求出来,在 HashMap 中建立两数之和跟其出现次数之间的映射,那么再遍历C和D中任意两个数之和,只要看哈希表存不存在这两数之和的相反数就行了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
int n = nums1.size();
unordered_map<int, int> mab, mcd;
for (int i = 0; i < n; i ++)
for (int j = 0; j < n; j ++) {
mab[nums1[i]+nums2[j]] ++;
}
int res = 0;
for (int i = 0; i < n; i ++)
for (int j = 0; j < n; j ++) {
res += mab[-nums3[i]-nums4[j]];
}
return res;
}
};
用两个 HashMap 分别记录 AB 和 CB 的两两之和出现次数,然后遍历其中一个 HashMap,并在另一个 HashMap 中找和的相反数出现的次数,更方便,但更慢。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
int n = nums1.size();
unordered_map<int, int> mab, mcd;
for (int i = 0; i < n; i ++)
for (int j = 0; j < n; j ++) {
mab[nums1[i]+nums2[j]] ++;
mcd[nums3[i]+nums4[j]] ++;
}
int res = 0;
for (auto i : mab)
res += (i.second * mcd[-i.first]);
return res;
}
};
1 | class Solution { |
Leetcode455. Assign Cookies
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie. Each child i has a greed factor gi, which is the minimum size of a cookie that the child will be content with; and each cookie j has a size sj. If sj >= gi, we can assign the cookie j to the child i, and the child i will be content. Your goal is to maximize the number of your content children and output the maximum number.
Note:
You may assume the greed factor is always positive.
You cannot assign more than one cookie to one child.
Example 1:1
2
3
4
5Input: [1,2,3], [1,1]
Output: 1
Explanation: You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
Example 2:1
2
3
4
5Input: [1,2], [1,2,3]
Output: 2
Explanation: You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
有一堆饼干和一堆孩子,每个饼干大小为s[j],每个孩子想要的大小为g[i],求这堆饼干能满足至多多少个孩子?
很容易想到,每个孩子尽量拿到和他想要的大小差距最小的饼干,就能保证不会“浪费”大块饼干。因此把g和s排序后,把最相邻的饼干分给刚刚好满足的孩子,就能得到最大的满足数量了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int count = 0;
for(int i = 0, j = 0; i < g.size() && j < s.size(); j ++){
if(s[j] >= g[i]) {
count ++;
i ++;
}
}
return count;
}
};
Leetcode456. 132 Pattern
Given an array of n integers nums, a 132 pattern is a subsequence of three integers nums[i], nums[j] and nums[k] such that i < j < k and nums[i] < nums[k] < nums[j].
Return true if there is a 132 pattern in nums, otherwise, return false.
Example 1:1
2
3Input: nums = [1,2,3,4]
Output: false
Explanation: There is no 132 pattern in the sequence.
Example 2:1
2
3Input: nums = [3,1,4,2]
Output: true
Explanation: There is a 132 pattern in the sequence: [1, 4, 2].
Example 3:1
2
3Input: nums = [-1,3,2,0]
Output: true
Explanation: There are three 132 patterns in the sequence: [-1, 3, 2], [-1, 3, 0] and [-1, 2, 0].
思路是维护一个栈和一个变量 third,其中 third 就是第三个数字,也是 pattern 132 中的2,初始化为整型最小值,栈里面按顺序放所有大于 third 的数字,也是 pattern 132 中的3,那么在遍历的时候,如果当前数字小于 third,即 pattern 132 中的1找到了,直接返回 true 即可,因为已经找到了,注意应该从后往前遍历数组。如果当前数字大于栈顶元素,那么将栈顶数字取出,赋值给 third,然后将该数字压入栈,这样保证了栈里的元素仍然都是大于 third 的,想要的顺序依旧存在,进一步来说,栈里存放的都是可以维持坐标 second > third 的 second 值,其中的任何一个值都是大于当前的 third 值,如果有更大的值进来,那就等于形成了一个更优的 second > third 的这样一个组合,并且这时弹出的 third 值比以前的 third 值更大,为什么要保证 third 值更大,因为这样才可以更容易的满足当前的值 first 比 third 值小这个条件,举个例子来说吧,比如 [2, 4, 2, 3, 5],由于是从后往前遍历,所以后三个数都不会进入 while 循环,那么栈中的数字为 5, 3, 2(其中2为栈顶元素),此时 third 还是整型最小,那么当遍历到4的时候,终于4大于栈顶元素2了,那么 third 赋值为2,且2出栈。此时继续 while 循环,因为4还是大于新栈顶元素3,此时 third 赋值为3,且3出栈。现在栈顶元素是5,那么 while 循环结束,将4压入栈。下一个数字2,小于 third,则找到符合要求的序列 [2, 4, 3],参见代码如下:
1 | class Solution { |
Leetcode459. Repeated Substring Pattern
Given a non-empty string check if it can be constructed by taking a substring of it and appending multiple copies of the substring together. You may assume the given string consists of lowercase English letters only and its length will not exceed 10000.
Example 1:1
2
3Input: "abab"
Output: True
Explanation: It's the substring "ab" twice.
Example 2:1
2Input: "aba"
Output: False
Example 3:1
2
3Input: "abcabcabcabc"
Output: True
Explanation: It's the substring "abc" four times. (And the substring "abcabc" twice.)
传统方法,挨个子字符串对比1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
bool repeatedSubstringPattern(string s) {
string temp;
int length = s.length();
for(int i = 1; i <= length/2; i ++) {
if(length % i)
continue;
temp = s.substr(0, i);
temp = gen(temp, length/i);
if(temp == s)
return true;
}
return false;
}
string gen(string temp, int i) {
string ans = "";
while(i--)
ans += temp;
return ans;
}
};
另一种做法,用dp。维护的一位数组dp[i]表示,到位置i-1为止的重复字符串的字符个数,不包括被重复的那个字符串,什么意思呢,我们举个例子,比如”abcabc”的dp数组为[0 0 0 0 1 2 3],dp数组长度要比原字符串长度多一个。那么我们看最后一个位置数字为3,就表示重复的字符串的字符数有3个。如果是”abcabcabc”,那么dp数组为[0 0 0 0 1 2 3 4 5 6],我们发现最后一个数字为6,那么表示重复的字符串为“abcabc”,有6个字符。那么怎么通过最后一个数字来知道原字符串是否由重复的子字符串组成的呢,首先当然是最后一个数字不能为0,而且还要满足dp[n] % (n - dp[n]) == 0才行,因为n - dp[n]是一个子字符串的长度,那么重复字符串的长度和肯定是一个子字符串的整数倍。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool repeatedSubstringPattern(string s) {
int n = s.length();
vector<int> dp(n+1, 0);
int i = 1, j = 0;
while(i < n) {
if(s[i] == s[j])
dp[++i] = ++j;
else if(j == 0)
i ++;
else
j = dp[j];
}
return dp[n] && (dp[n] % (n - dp[n]) == 0);
}
};
Leetcode461. Hamming Distance
The Hamming distance between two integers is the number of positions at which the corresponding bits are different. Given two integers x and y, calculate the Hamming distance.
Note:
0 ≤ x, y < 231.
Example:1
2
3
4
5
6
7Input: x = 1, y = 4
Output: 2
Explanation:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
求两个数的海明距离,就是判断其二进制有多少不一样的位1
2
3
4
5
6
7
8
9
10class Solution {
public:
int hammingDistance(int x, int y) {
int temp = x ^ y;
int res=0;
for(int i=temp;i>0;i=i>>1)
if(i&1) res++;
return res;
}
};
Leetcode462. Minimum Moves to Equal Array Elements II
Given an integer array nums of size n, return the minimum number of moves required to make all array elements equal.
In one move, you can increment or decrement an element of the array by 1.
Test cases are designed so that the answer will fit in a 32-bit integer.
Example 1:1
2
3
4
5Input: nums = [1,2,3]
Output: 2
Explanation:
Only two moves are needed (remember each move increments or decrements one element):
[1,2,3] => [2,2,3] => [2,2,2]
Example 2:1
2Input: nums = [1,10,2,9]
Output: 16
这道题每次对任意一个数字加1或者减1,让我们用最少的次数让数组所有值相等。首先给数组排序,最终需要变成的相等的数字就是中间的数,如果数组有奇数个,那么就是最中间的那个数字;如果是偶数个,那么就是中间两个数的区间中的任意一个数字。而两端的数字变成中间的一个数字需要的步数实际上就是两端数字的距离。参见代码如下:1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int minMoves2(vector<int>& nums) {
int res = 0, i = 0, j = (int)nums.size() - 1;
sort(nums.begin(), nums.end());
while (i < j) {
res += nums[j--] - nums[i++];
}
return res;
}
};
既然有了上面的分析,我们知道实际上最后相等的数字就是数组的最中间的那个数字,那么我们在给数组排序后,直接利用坐标定位到中间的数字,然后算数组中每个数组与其的差的绝对值累加即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int minMoves2(vector<int>& nums) {
sort(nums.begin(), nums.end());
int res = 0, mid = nums[nums.size() / 2];
for (int num : nums) {
res += abs(num - mid);
}
return res;
}
};
上面的两种方法都给整个数组排序了,时间复杂度是O(nlgn),其实我们并不需要给所有的数字排序,我们只关系最中间的数字,那么这个stl中自带的函数nth_element就可以完美的发挥其作用了,我们只要给出我们想要数字的位置,它就能在O(n)的时间内返回正确的数字,然后算数组中每个数组与其的差的绝对值累加即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int minMoves2(vector<int>& nums) {
int res = 0, n = nums.size(), mid = n / 2;
nth_element(nums.begin(), nums.begin() + mid, nums.end());
for (int i = 0; i < n; ++i) {
res += abs(nums[i] - nums[mid]);
}
return res;
}
};
Leetcode463. Island Perimeter
You are given a map in form of a two-dimensional integer grid where 1 represents land and 0 represents water.
Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn’t have “lakes” (water inside that isn’t connected to the water around the island). One cell is a square with side length 1. The grid is rectangular, width and height don’t exceed 100. Determine the perimeter of the island.
Example:1
2
3
4
5
6
7Input:
[[0,1,0,0],
[1,1,1,0],
[0,1,0,0],
[1,1,0,0]]
Output: 16
Explanation: The perimeter is the 16 yellow stripes in the image below:
看一共有几条边,对每个格子进行遍历。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int islandPerimeter(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int ans = 0, temp;
for(int i = 0; i < m; i ++) {
for(int j = 0; j < n; j ++) {
if(!grid[i][j])
continue;
temp = 0;
if(j == 0 || (j > 0 && !grid[i][j-1])) temp ++;
if(j == n-1 || (j < n-1 && !grid[i][j+1])) temp ++;
if(i == 0 || (i > 0 && !grid[i-1][j])) temp ++;
if(i == m-1 || (i < m-1 && !grid[i+1][j])) temp ++;
ans += temp;
}
}
return ans;
}
};
Leetcode464. Can I Win
In the “100 game,” two players take turns adding, to a running total, any integer from 1..10. The player who first causes the running total to reach or exceed 100 wins.
What if we change the game so that players cannot re-use integers?
For example, two players might take turns drawing from a common pool of numbers of 1..15 without replacement until they reach a total >= 100.
Given an integer maxChoosableInteger and another integer desiredTotal, determine if the first player to move can force a win, assuming both players play optimally.
You can always assume that maxChoosableInteger will not be larger than 20 and desiredTotal will not be larger than 300.
Example1
2
3
4
5
6
7
8
9
10
11
12
13Input:
maxChoosableInteger = 10
desiredTotal = 11
Output:
false
Explanation:
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
这道题给了我们一堆数字,然后两个人,每人每次选一个数字,看数字总数谁先到给定值,有点像之前那道 Nim Game,但是比那题难度大。我刚开始想肯定说用递归啊,结果写完发现 TLE 了,后来发现我们必须要优化效率,使用 HashMap 来记录已经计算过的结果。我们首先来看如果给定的数字范围大于等于目标值的话,直接返回 true。如果给定的数字总和小于目标值的话,说明谁也没法赢,返回 false。然后我们进入递归函数,首先我们查找当前情况是否在 HashMap 中存在,有的话直接返回即可。我们使用一个整型数按位来记录数组中的某个数字是否使用过,我们遍历所有数字,将该数字对应的 mask 算出来,如果其和 used 相与为0的话,说明该数字没有使用过,我们看如果此时的目标值小于等于当前数字,说明已经赢了,或者调用递归函数,如果返回 false,说明也是第一个人赢了。为啥呢,因为当前已经选过数字了,此时就该对第二个人调用递归函数,只有返回的结果是 false,我们才能赢,所以此时我们 true,并返回 true。如果遍历完所有数字,标记 false,并返回 false,参见代码如下:
1 | class Solution { |
Leetcode467. Unique Substrings in Wraparound String
Consider the string s to be the infinite wraparound string of “abcdefghijklmnopqrstuvwxyz”, so s will look like this: “…zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd….”.
Now we have another string p. Your job is to find out how many unique non-empty substrings of p are present in s. In particular, your input is the string p and you need to output the number of different non-empty substrings of p in the string s.
Note: p consists of only lowercase English letters and the size of p might be over 10000.
Example 1:1
2
3
4Input: "a"
Output: 1
Explanation: Only the substring "a" of string "a" is in the string s.
Example 2:1
2
3Input: "cac"
Output: 2
Explanation: There are two substrings "a", "c" of string "cac" in the string s.
Example 3:1
2
3Input: "zab"
Output: 6
Explanation: There are six substrings "z", "a", "b", "za", "ab", "zab" of string "zab" in the string s.
这道题说有一个无限长的封装字符串,然后又给了我们另一个字符串p,问我们p有多少非空子字符串在封装字符串中。我们通过观察题目中的例子可以发现,由于封装字符串是26个字符按顺序无限循环组成的,那么满足题意的p的子字符串要么是单一的字符,要么是按字母顺序的子字符串。这道题遍历p的所有子字符串会TLE,因为如果p很大的话,子字符串很多,会有大量的满足题意的重复子字符串,必须要用到trick,而所谓技巧就是一般来说你想不到的方法。我们看abcd这个字符串,以d结尾的子字符串有abcd, bcd, cd, d,那么我们可以发现bcd或者cd这些以d结尾的字符串的子字符串都包含在abcd中,那么我们知道以某个字符结束的最大字符串包含其他以该字符结束的字符串的所有子字符串,说起来很拗口,但是理解了我上面举的例子就行。那么题目就可以转换为分别求出以每个字符(a-z)为结束字符的最长连续字符串就行了,我们用一个数组cnt记录下来,最后在求出数组cnt的所有数字之和就是我们要的结果啦,参见代码如下:
1 | class Solution { |
Leetcode468. Validate IP Address
Given a string IP, return “IPv4” if IP is a valid IPv4 address, “IPv6” if IP is a valid IPv6 address or “Neither” if IP is not a correct IP of any type.
A valid IPv4 address is an IP in the form “x1.x2.x3.x4” where 0 <= xi <= 255 and xi cannot contain leading zeros. For example, “192.168.1.1” and “192.168.1.0” are valid IPv4 addresses but “192.168.01.1”, while “192.168.1.00” and “192.168@1.1” are invalid IPv4 addresses.
A valid IPv6 address is an IP in the form “x1:x2:x3:x4:x5:x6:x7:x8” where:
- 1 <= xi.length <= 4
- xi is a hexadecimal string which may contain digits, lower-case English letter (‘a’ to ‘f’) and upper-case English letters (‘A’ to ‘F’).
- Leading zeros are allowed in xi.
For example, “2001:0db8:85a3:0000:0000:8a2e:0370:7334” and “2001:db8:85a3:0:0:8A2E:0370:7334” are valid IPv6 addresses, while “2001:0db8:85a3::8A2E:037j:7334” and “02001:0db8:85a3:0000:0000:8a2e:0370:7334” are invalid IPv6 addresses.
Example 1:1
2
3Input: IP = "172.16.254.1"
Output: "IPv4"
Explanation: This is a valid IPv4 address, return "IPv4".
Example 2:1
2
3Input: IP = "2001:0db8:85a3:0:0:8A2E:0370:7334"
Output: "IPv6"
Explanation: This is a valid IPv6 address, return "IPv6".
Example 3:1
2
3Input: IP = "256.256.256.256"
Output: "Neither"
Explanation: This is neither a IPv4 address nor a IPv6 address.
Example 4:1
2Input: IP = "2001:0db8:85a3:0:0:8A2E:0370:7334:"
Output: "Neither"
巨难搞,就跟判断一个数是不是合法一样。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75class Solution {
public:
bool is_number(char c) {
return ('0' <= c && c <= '9');
}
bool is_char(char c) {
return ('A' <= c && c <= 'F') || ('a' <= c && c <= 'f');
}
string validIPAddress(string IP) {
if (isv4(IP))
return "IPv4";
else if (isv6(IP))
return "IPv6";
else
return "Neither";
}
bool isv4(string IP) {
int len = IP.length();
int num_points = 0, number = 0;
bool is_begin = true;
for (int i = 0; i < len; i ++) {
if (number > 255)
return false;
else if (IP[i] == '.') {
num_points ++;
number = 0;
if (is_begin)
return false;
is_begin = true;
}
else if (!is_number(IP[i]))
return false;
else {
if (i < len-1 && is_begin && IP[i+1] != '.' && IP[i] == '0')
return false;
is_begin = false;
if (i > 0 && IP[i] == '0' && IP[i-1] == 0)
return false;
number = number * 10 + IP[i] - '0';
}
}
if (number > 255 || num_points != 3 || IP[len-1] == '.')
return false;
return true;
}
bool isv6(string IP) {
int len = IP.length();
int num_points = 0, number = 0, sum = 0;
bool is_begin = true;
for (int i = 0; i < len; i ++) {
if (IP[i] == ':') {
if (number > 4)
return false;
num_points ++;
number = 0;
if (is_begin)
return false;
is_begin = true;
}
else {
is_begin = false;
if (!(is_number(IP[i]) || is_char(IP[i])) )
return false;
number ++;
}
}
if (num_points != 7 || number > 4 || IP[len-1] == ':')
return false;
return true;
}
};
内存占用最小的提交:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
static auto _ = [] () {ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);return 0;}();
class Solution
{
public:
string validIPAddress(string const& IP)
{
bool isV6 = IP.find(':') != string::npos;
if (isV6) { // Try to parse ipv6
int count = 0, segments = 0;
auto isValidHex = [](char c) {
return isdigit(c) ||
('a' <= c && c <= 'f') ||
('A' <= c && c <= 'F');
};
int ptr = -1, size = IP.size();
while (ptr < size && segments < 8) {
++ptr; // skip leading ':'
while (ptr < size && IP[ptr] != ':')
if (isValidHex(IP[ptr]))
++ptr, ++count;
else
return "Neither";
if (count == 0 || count > 4)
return "Neither";
else
count = 0,
++segments;
}
if (ptr == IP.size() && segments == 8)
return "IPv6";
else
return "Neither";
}
else { // Try to parse ipv4
int segments = 0, number = 0, count = 0;
int ptr = -1, size = IP.size();
while (ptr < size && segments < 4) {
++ptr; // skip initial dot
if (ptr < size && IP[ptr] == '0') {
++segments;
++ptr;
if (ptr == size || IP[ptr] == '.')
continue;
else
return "Neither";
}
while (ptr < size && IP[ptr] != '.')
if (number < 250 && isdigit(IP[ptr])) {
++count;
number *= 10;
number += IP[ptr] - '0';
++ptr;
}
else {
return "Neither";
}
if (1 <= count && count <= 4 && 1 <= number && number <= 255) {
count = 0;
number = 0;
++segments;
}
else {
return "Neither";
}
}
if (ptr == IP.size() && segments == 4)
return "IPv4";
else
return "Neither";
}
return "Neither";
}
};
Leetcode470. Implement Rand10() Using Rand7()
Given the API rand7() that generates a uniform random integer in the range [1, 7], write a function rand10() that generates a uniform random integer in the range [1, 10]. You can only call the API rand7(), and you shouldn’t call any other API. Please do not use a language’s built-in random API.
Each test case will have one internal argument n, the number of times that your implemented function rand10() will be called while testing. Note that this is not an argument passed to rand10().
Follow up:
- What is the expected value for the number of calls to rand7() function?
- Could you minimize the number of calls to rand7()?
Example 1:1
2Input: n = 1
Output: [2]
Example 2:1
2Input: n = 2
Output: [2,8]
Example 3:1
2Input: n = 3
Output: [3,8,10]
这道题给了我们一个随机生成 [1, 7] 内数字的函数rand7(),需要利用其来生成一个能随机生成 [1, 10] 内数字的函数rand10(),注意这里的随机生成的意思是等概率生成范围内的数字。这是一道很有意思的题目,由于rand7()只能生成1到7之间的数字,所以 8,9,10 这三个没法生成,那么怎么办?
大多数人可能第一个想法就是,再用一个呗,然后把两次的结果加起来,范围不就扩大了么,扩大成了 [2, 14] 之间,然后如果再减去1,范围不就是 [1, 13] 了么。想法不错,但是有个问题,这个范围内的每个数字生成的概率不是都相等的,为啥这么说呢,我们来举个简单的例子看下,就比如说rand2(),我们知道其可以生成两个数字1和2,且每个的概率都是 1/2。那么对于(rand2() - 1) +rand2()``呢,看一下:1
2
3
4
5rand2() - 1 + rand()2 = ?
1 1 1
1 2 2
2 1 2
2 2 3
我们发现,生成数字范围 [1, 3] 之间的数字并不是等概率大,其中2出现的概率为 1/2,1和3分别为 1/4。这就不随机了。问题出在哪里了呢,如果直接相加,不同组合可能会产生相同的数字,比如 1+2 和 2+1 都是3。所以需要给第一个rand2()升一个维度,让其乘上一个数字,再相加。比如对于(rand2() - 1) * 2 +rand2()``,如下:1
2
3
4
5(rand2() - 1) * 2 + rand()2 = ?
1 1 1
1 2 2
2 1 3
2 2 4
这时右边生成的 1,2,3,4 就是等概率出现的了。这样就通过使用rand2(),来生成rand4()了。那么反过来想一下,可以通过rand4()来生成rand2(),其实更加简单,我们只需通过rand4() % 2 + 1即可,如下:1
2
3
4
5rand4() % 2 + 1 = ?
1 2
2 1
3 2
4 1
同理,我们也可以通过rand6()来生成rand2(),我们只需通过rand6() % 2 + 1即可,如下:1
2
3
4
5
6
7rand6() % 2 + 1 = ?
1 2
2 1
3 2
4 1
5 2
6 1
所以,回到这道题,我们可以先凑出rand10*N(),然后再通过rand10*N() % 10 + 1来获得rand10()。那么,只需要将rand7()转化为rand10*N()即可,根据前面的讲解,我们转化也必须要保持等概率,那么就可以变化为(rand7() - 1) * 7 + rand7(),就转为了rand49()。但是 49 不是 10 的倍数,不过 49 包括好几个 10 的倍数,比如 40,30,20,10 等。这里,我们需要把rand49()转为rand40(),需要用到拒绝采样Rejection Sampling。这种采样方法就是随机到需要的数字就接受,不是需要的就拒绝,并重新采样,这样还能保持等概率。
当用 rand49()生成一个 [1, 49] 范围内的随机数,如果其在 [1, 40] 范围内,我们就将其转为rand10()范围内的数字,直接对 10 去余并加1,返回即可。如果不是,则继续循环即可,参见代码如下:1
2
3
4
5
6
7
8
9class Solution {
public:
int rand10() {
while (true) {
int num = (rand7() - 1) * 7 + rand7();
if (num <= 40) return num % 10 + 1;
}
}
};
我们可以不用 while 循环,而采用调用递归函数。1
2
3
4
5
6
7class Solution {
public:
int rand10() {
int num = (rand7() - 1) * 7 + rand7();
return (num <= 40) ? (num % 10 + 1) : rand10();
}
};
Leetcode472. Concatenated Words
Given an array of strings words (without duplicates), return all the concatenated words in the given list of words.
A concatenated word is defined as a string that is comprised entirely of at least two shorter words in the given array.
Example 1:1
2
3
4
5Input: words = ["cat","cats","catsdogcats","dog","dogcatsdog","hippopotamuses","rat","ratcatdogcat"]
Output: ["catsdogcats","dogcatsdog","ratcatdogcat"]
Explanation: "catsdogcats" can be concatenated by "cats", "dog" and "cats";
"dogcatsdog" can be concatenated by "dog", "cats" and "dog";
"ratcatdogcat" can be concatenated by "rat", "cat", "dog" and "cat".
Example 2:1
2Input: words = ["cat","dog","catdog"]
Output: ["catdog"]
这道题给了一个由单词组成的数组,某些单词是可能由其他的单词组成的,让我们找出所有这样的单词。我们首先把所有单词都放到一个unordered_set中,这样可以快速找到某个单词是否在数组中存在。对于当前要判断的单词,我们先将其从set中删去,然后调用之前的Word Break的解法。如果是可以拆分,那么我们就存入结果res中,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {
if (words.size() == 0)
return {};
vector<string> res;
unordered_set<string> dict(words.begin(), words.end());
for (int i = 0; i < words.size(); i ++) {
dict.erase(words[i]);
int len = words[i].size();
vector<bool> flag(len+1, false);
flag[0] = true;
for (int j = 0; j <= len; j ++)
for (int k = 0; k < j; k ++)
if (flag[k] && dict.count(words[i].substr(k, j-k))) {
flag[j] = true;
break;
}
if (flag[len])
res.push_back(words[i]);
dict.insert(words[i]);
}
return res;
}
};
Leetcode473. Matchsticks to Square
Remember the story of Little Match Girl? By now, you know exactly what matchsticks the little match girl has, please find out a way you can make one square by using up all those matchsticks. You should not break any stick, but you can link them up, and each matchstick must be used exactly one time.
Your input will be several matchsticks the girl has, represented with their stick length. Your output will either be true or false, to represent whether you could make one square using all the matchsticks the little match girl has.
Example 1:1
2
3Input: [1,1,2,2,2]
Output: true
Explanation: You can form a square with length 2, one side of the square came two sticks with length 1.
Example 2:1
2
3Input: [3,3,3,3,4]
Output: false
Explanation: You cannot find a way to form a square with all the matchsticks.
Note:
- The length sum of the given matchsticks is in the range of 0 to 10^9.
- The length of the given matchstick array will not exceed 15.
这道题让我们用数组中的数字来摆出一个正方形。这道题实际上是让我们将一个数组分成四个和相等的子数组。可以用优化过的递归来解,递归的方法基本上等于brute force。先给数组从大到小的顺序排序,这样大的数字先加,如果超过target了,就直接跳过了后面的再次调用递归的操作,效率会提高不少。我们建立一个长度为4的数组sums来保存每个边的长度和,我们希望每条边都等于target,数组总和的四分之一。然后我们遍历sums中的每条边,我们判断如果加上数组中的当前数字大于target,那么我们跳过,如果没有,我们就加上这个数字,然后对数组中下一个位置调用递归,如果返回为真,我们返回true,否则我们再从sums中对应位置将这个数字减去继续循环,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
bool makesquare(vector<int>& nums) {
if (nums.empty() || nums.size() < 4) return false;
int sum = accumulate(nums.begin(), nums.end(), 0);
if (sum % 4 != 0) return false;
vector<int> sums(4, 0);
sort(nums.rbegin(), nums.rend());
return helper(nums, sums, 0, sum / 4);
}
bool helper(vector<int>& nums, vector<int>& sums, int pos, int target) {
if (pos >= nums.size()) {
return sums[0] == target && sums[1] == target && sums[2] == target;
}
for (int i = 0; i < 4; ++i) {
if (sums[i] + nums[pos] > target) continue;
sums[i] += nums[pos];
if (helper(nums, sums, pos + 1, target)) return true;
sums[i] -= nums[pos];
}
return false;
}
};
Leetcode474. Ones and Zeroes
In the computer world, use restricted resource you have to generate maximum benefit is what we always want to pursue.
For now, suppose you are a dominator of m 0s and n 1s respectively. On the other hand, there is an array with strings consisting of only 0s and 1s.
Now your task is to find the maximum number of strings that you can form with given m 0s and n 1s. Each 0 and 1 can be used at most once.
Note:
- The given numbers of 0s and 1s will both not exceed 100
- The size of given string array won’t exceed 600.
Example 1:1
2
3Input: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
Output: 4
Explanation: This are totally 4 strings can be formed by the using of 5 0s and 3 1s, which are “10,”0001”,”1”,”0”
Example 2:1
2
3Input: Array = {"10", "0", "1"}, m = 1, n = 1
Output: 2
Explanation: You could form "10", but then you'd have nothing left. Better form "0" and "1".
这道题是一道典型的应用DP来解的题,我们需要建立一个二维的DP数组,其中dp[i][j]表示有i个0和j个1时能组成的最多字符串的个数,而对于当前遍历到的字符串,我们统计出其中0和1的个数为zeros和ones,然后dp[i - zeros][j - ones]表示当前的i和j减去zeros和ones之前能拼成字符串的个数,那么加上当前的zeros和ones就是当前dp[i][j]可以达到的个数,我们跟其原有数值对比取较大值即可,所以递推式如下:1
dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1);
有了递推式,我们就可以很容易的写出代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (string str : strs) {
int zeros = 0, ones = 0;
for (char c : str) (c == '0') ? ++zeros : ++ones;
for (int i = m; i >= zeros; --i) {
for (int j = n; j >= ones; --j) {
dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1);
}
}
}
return dp[m][n];
}
};
Leetcode475. Heaters
Winter is coming! Your first job during the contest is to design a standard heater with fixed warm radius to warm all the houses.
Now, you are given positions of houses and heaters on a horizontal line, find out minimum radius of heaters so that all houses could be covered by those heaters.
So, your input will be the positions of houses and heaters seperately, and your expected output will be the minimum radius standard of heaters.
Note:
- Numbers of houses and heaters you are given are non-negative and will not exceed 25000.
- Positions of houses and heaters you are given are non-negative and will not exceed 10^9.
- As long as a house is in the heaters’ warm radius range, it can be warmed.
- All the heaters follow your radius standard and the warm radius will the same.
Example 1:1
2
3Input: [1,2,3],[2]
Output: 1
Explanation: The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
Example 2:1
2
3Input: [1,2,3,4],[1,4]
Output: 1
Explanation: The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
思路:
- 先对houses和heaters排序,result记录全局最小温暖半径,temp记录当前house的最小温暖半径。
- 依次为每个house查找最小的温暖半径(显然,每个house的最小半径只需考虑其左边最近的heaters和右边最近的heaters)。
- 对每一个house先查找位置不小于其位置的第一个heater,其位置为j。
- 若未找到,则当前house的最小温暖半径由左边最近的heaters决定。
- 若第一个heater的位置就不小于当前house的位置,则当前house的最小温暖半径由右边最近的heaters决定。
- 若找到的位置不小于当前house位置的第一个heater的位置大于当前house位置(若等于,则当前house的最小温暖半径等于0),则当前house的最小温暖半径是其与左边最近的heaters的距离和其与右边最近的heaters的距离的较小值。
- 若当前house的最小温暖半径大于全局result,则更新result。
1 | class Solution { |
Leetcode476. Number Complement
Given a positive integer num, output its complement number. The complement strategy is to flip the bits of its binary representation.
Example 1:1
2
3Input: num = 5
Output: 2
Explanation: The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
Example 2:1
2
3Input: num = 1
Output: 0
Explanation: The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
给定一个正整数,对该数的二进制表示形式,从最高位的1开始向后按位取反。如果我们能知道该数最高位的1所在的位置,就可以构造一个长度和该数据所占位置一样长的一个掩码mask,然后概述和mask进行异或即可。例如:5的二进制是101,我们的构造的掩码为mask=111,两者异或则为010,即是所要的结果。1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int findComplement(int num) {
long mask = 1, temp = num;
while(temp > 0) {
mask = mask << 1;
temp = temp >> 1;
}
return num^(mask-1);
}
};
Leetcode477. Total Hamming Distance
The Hamming distance between two integers is the number of positions at which the corresponding bits are different.
Given an integer array nums, return the sum of Hamming distances between all the pairs of the integers in nums.
Example 1:1
2
3
4
5
6Input: nums = [4,14,2]
Output: 6
Explanation: In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
Example 2:1
2Input: nums = [4,14,4]
Output: 4
这道题是之前那道 Hamming Distance 的拓展,由于有之前那道题的经验,我们知道需要用异或来求每个位上的情况,那么需要来找出某种规律来,比如看下面这个例子,4,14,2 和1:
4: 0 1 0 0
14: 1 1 1 0
2: 0 0 1 0
1: 0 0 0 1
先看最后一列,有三个0和一个1,那么它们之间相互的汉明距离就是3,即1和其他三个0分别的距离累加,然后在看第三列,累加汉明距离为4,因为每个1都会跟两个0产生两个汉明距离,同理第二列也是4,第一列是3。仔细观察累计汉明距离和0跟1的个数,可以发现其实就是0的个数乘以1的个数,发现了这个重要的规律,那么整道题就迎刃而解了,只要统计出每一位的1的个数即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int totalHammingDistance(vector<int>& nums) {
int res = 0, n = nums.size();
for (int i = 0; i < 32; ++i) {
int cnt = 0;
for (int num : nums) {
if (num & (1 << i)) ++cnt;
}
res += cnt * (n - cnt);
}
return res;
}
};
Leetcode478. Generate Random Point in a Circle
Given the radius and x-y positions of the center of a circle, write a function randPoint which generates a uniform random point in the circle.
Note:
- input and output values are in floating-point.
- radius and x-y position of the center of the circle is passed into the class constructor.
- a point on the circumference of the circle is considered to be in the circle.
- randPoint returns a size 2 array containing x-position and y-position of the random point, in that order.
Example 1:1
2
3
4Input:
["Solution","randPoint","randPoint","randPoint"]
[[1,0,0],[],[],[]]
Output: [null,[-0.72939,-0.65505],[-0.78502,-0.28626],[-0.83119,-0.19803]]
Example 2:1
2
3
4Input:
["Solution","randPoint","randPoint","randPoint"]
[[10,5,-7.5],[],[],[]]
Output: [null,[11.52438,-8.33273],[2.46992,-16.21705],[11.13430,-12.42337]]
Explanation of Input Syntax:
- The input is two lists: the subroutines called and their arguments. Solution’s constructor has three arguments, the radius, x-position of the center, and y-position of the center of the circle. randPoint has no arguments. Arguments are always wrapped with a list, even if there aren’t any.
这道题给了我们一个圆,包括中点位置和半径,让随机生成圆中的任意一个点。这里说明了圆上也当作是圆中,而且这里的随机意味着要等概率。
圆的方程表示为(x - a) ^ 2 + (y - b) ^ 2 = r ^ 2,这里的(a, b)是圆心位置,r为半径。那么如何生成圆中的任意位置呢,如果用这种方式来生成,先随机出一个x,随机出y的时候还要考虑其是否在圆中间,比较麻烦。继续回到高中时代,模糊的记忆中飘来了三个字,极坐标。是的,圆还可以用极坐标的形式来表示,只需随机出一个角度 theta,再随机出一个小于半径的长度,这样就可以得到圆中的坐标位置了。
先来生成 theta吧,由于一圈是 360 度,即 2pi,所以随机出一个 [0, 1] 中的小数,再乘以 2pi,就可以了。然后就是随机小于半径的长度,这里有个问题需要注意一下,这里并不是直接随机出一个 [0, 1] 中的小数再乘以半径r,而是要对随机出的 [0, 1] 中的小数取个平方根再乘以半径r。这是为啥呢,简单来说,是为了保证等概率。如果不用平方根的话,那么表示圆的时候(len * cos(theta)) ^ 2 + (len * sin(theta) ^ 2,这里就相当于对随机出的 [0, 1] 中的小数平方了,那么其就不是等概率的了,因为两个小于1的小数相乘了,其会更加靠近0,这就是为啥要平方一下的原因。最后在求点位置的时候要加上圆心的偏移即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
Solution(double radius, double x_center, double y_center) {
r = radius; centerX = x_center; centerY = y_center;
}
vector<double> randPoint() {
double theta = 2 * M_PI * ((double)rand() / RAND_MAX);
double len = sqrt((double)rand() / RAND_MAX) * r;
return {centerX + len * cos(theta), centerY + len * sin(theta)};
}
private:
double r, centerX, centerY;
};
这其实就是拒绝采样的经典应用,在一个正方形中有均匀分布的点,随机出其内切圆中的一个点,那么就是随机出x和y之后,然后算其平方和,如果小于等于r平方,说明其在圆内,可以返回其坐标,记得加上圆心偏移,否则重新进行采样。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
Solution(double radius, double x_center, double y_center) {
r = radius; centerX = x_center; centerY = y_center;
}
vector<double> randPoint() {
while (true) {
double x = (2 * (double)rand() / RAND_MAX - 1.0) * r;
double y = (2 * (double)rand() / RAND_MAX - 1.0) * r;
if (x * x + y * y <= r * r) return {centerX + x, centerY + y};
}
}
private:
double r, centerX, centerY;
};
480. Sliding Window Median
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.
Examples:
[2,3,4] , the median is 3
[2,3], the median is (2 + 3) / 2 = 2.5
Given an array nums , there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Your job is to output the median array for each window in the original array.
For example,
Given nums = [1,3,-1,-3,5,3,6,7], and k = 3.1
2
3
4
5
6
7
8Window position Median
--------------- -----
[1 3 -1] -3 5 3 6 7 1
1 [3 -1 -3] 5 3 6 7 -1
1 3 [-1 -3 5] 3 6 7 -1
1 3 -1 [-3 5 3] 6 7 3
1 3 -1 -3 [5 3 6] 7 5
1 3 -1 -3 5 [3 6 7] 6
Therefore, return the median sliding window as [1,-1,-1,3,5,6].
Note:
- You may assume k is always valid, ie: 1 ≤ k ≤ input array’s size for non-empty array.
这道题给了我们一个数组,还是滑动窗口的大小,让我们求滑动窗口的中位数。我想起来之前也有一道滑动窗口的题Sliding Window Maximum,于是想套用那道题的方法,可以用deque怎么也做不出,因为求中位数并不是像求最大值那样只操作deque的首尾元素。后来看到了史蒂芬大神的方法,原来是要用一个multiset集合,和一个指向最中间元素的iterator。我们首先将数组的前k个数组加入集合中,由于multiset自带排序功能,所以我们通过k/2能快速的找到指向最中间的数字的迭代器mid,如果k为奇数,那么mid指向的数字就是中位数;如果k为偶数,那么mid指向的数跟前面那个数求平均值就是中位数。当我们添加新的数字到集合中,multiset会根据新数字的大小加到正确的位置,然后我们看如果这个新加入的数字比之前的mid指向的数小,那么中位数肯定被拉低了,所以mid往前移动一个,再看如果要删掉的数小于等于mid指向的数(注意这里加等号是因为要删的数可能就是mid指向的数),则mid向后移动一个。然后我们将滑动窗口最左边的数删掉,我们不能直接根据值来用erase来删数字,因为这样有可能删掉多个相同的数字,而是应该用lower_bound来找到第一个不小于目标值的数,通过iterator来删掉确定的一个数字,参见代码如下:
1 | class Solution { |
假定窗口里已经排序了,前半部分是x,后半部分是y,用multiset能自动排序。两个集合的size顶多相差1。
a[i-k]在x中,从x中删除;若不在x中则从y中删除。x中的最大值挪到y中成为最小值。维护x.size()-y.size()=1。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72class Solution {
public:
double calc(const multiset<int>& x, const multiset<int>& y, int k) {
if (k & 1) return *x.rbegin();
return (1.0 * *x.rbegin() + *y.begin()) / 2.0;
}
void remove(multiset<int>& x, multiset<int>& y, int val) {
if (x.count(val)) {
x.erase(x.find(val));
if (x.size() < y.size() && y.size()) {
int v = *y.begin();
x.insert(v);
y.erase(y.find(v));
}
return;
}
y.erase(y.find(val));
if (x.size() - y.size() > 1) {
int v = *x.rbegin();
x.erase(x.find(v));
y.insert(v);
}
}
void add(multiset<int>& x, multiset<int>& y, int val) {
if (x.empty() || val < *x.rbegin()) {
x.insert(val);
if (x.size() - y.size() > 1) {
int v = *x.rbegin();
x.erase(x.find(v));
y.insert(v);
}
return;
}
y.insert(val);
if (y.size() > x.size()) {
int v = *y.begin();
y.erase(y.find(v));
x.insert(v);
}
}
vector<double> medianSlidingWindow(vector<int>& a, int k) {
int n = a.size();
multiset<int> x, y;
// k 个元素
for (int i = 0 ; i < k; i ++)
x.insert(a[i]);
for (int i = 0; i < k/2; i ++) {
int val = *x.rbegin();
x.erase(x.find(val));
y.insert(val);
}
vector<double> res;
res.push_back(calc(x, y, k));
for (int l = 1, r = k; r < n; l ++, r ++) {
// 先删除a[l-1],这是上一个窗口的最小元素
remove(x, y, a[l-1]);
add(x, y, a[r]);
res.push_back(calc(x, y, k));
}
return res;
}
};
上面的方法用到了很多STL内置的函数,比如next,lower_bound啥的,下面我们来看一种不使用这些函数的解法。这种解法跟Find Median from Data Stream那题的解法很类似,都是维护了small和large两个堆,分别保存有序数组的左半段和右半段的数字,保持small的长度大于等于large的长度。我们开始遍历数组nums,如果i>=k,说明此时滑动窗口已经满k个了,再滑动就要删掉最左值了,我们分别在small和large中查找最左值,有的话就删掉。然后处理增加数字的情况(分两种情况:1.如果small的长度小于large的长度,再看如果large是空或者新加的数小于等于large的首元素,我们把此数加入small中。否则就把large的首元素移出并加入small中,然后把新数字加入large。2.如果small的长度大于large,再看如果新数字大于small的尾元素,那么新数字加入large中,否则就把small的尾元素移出并加入large中,把新数字加入small中)。最后我们再计算中位数并加入结果res中,根据k的奇偶性来分别处理,参见代码如下:
1 | class Solution { |
Leetcode481. Magical String
A magical string S consists of only ‘1’ and ‘2’ and obeys the following rules:
The string S is magical because concatenating the number of contiguous occurrences of characters ‘1’ and ‘2’ generates the string S itself.
The first few elements of string S is the following: S = “1221121221221121122……”
If we group the consecutive ‘1’s and ‘2’s in S, it will be:1
1 22 11 2 1 22 1 22 11 2 11 22 ……
and the occurrences of ‘1’s or ‘2’s in each group are:1
1 2 2 1 1 2 1 2 2 1 2 2 ……
You can see that the occurrence sequence above is the S itself.
Given an integer N as input, return the number of ‘1’s in the first N number in the magical string S.
Note: N will not exceed 100,000.
Example 1:1
2
3Input: 6
Output: 3
Explanation: The first 6 elements of magical string S is "12211" and it contains three 1's, so return 3.
这道题介绍了一种神奇字符串,只由1和2组成,通过计数1组和2组的个数,又能生成相同的字符串。而让我们求前n个数字中1的个数。让我们按规律生成这个神奇字符串,只有生成了字符串的前n个字符,才能统计出1的个数。其实这道题的难点就是在于找到规律来生成字符串。
根据第三个数字2开始往后生成数字,此时生成两个1,然后根据第四个数字1,生成一个2,再根据第五个数字1,生成一个1,以此类推,生成的数字1或2可能通过异或3来交替生成,在生成的过程中同时统计1的个数即可,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int magicalString(int n) {
if (n <= 0) return 0;
if (n <= 3) return 1;
int res = 1, head = 2, tail = 3, num = 1;
vector<int> v{1, 2, 2};
while (tail < n) {
for (int i = 0; i < v[head]; ++i) {
v.push_back(num);
if (num == 1 && tail < n) ++res;
++tail;
}
num ^= 3;
++head;
}
return res;
}
}
Leetcode482. License Key Formatting
You are given a license key represented as a string S which consists only alphanumeric character and dashes. The string is separated into N+1 groups by N dashes.
Given a number K, we would want to reformat the strings such that each group contains exactly K characters, except for the first group which could be shorter than K, but still must contain at least one character. Furthermore, there must be a dash inserted between two groups and all lowercase letters should be converted to uppercase.
Given a non-empty string S and a number K, format the string according to the rules described above.
Example 1:1
2
3
4Input: S = "5F3Z-2e-9-w", K = 4
Output: "5F3Z-2E9W"
Explanation: The string S has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
Example 2:1
2
3Input: S = "2-5g-3-J", K = 2
Output: "2-5G-3J"
Explanation: The string S has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
Note:
- The length of string S will not exceed 12,000, and K is a positive integer.
- String S consists only of alphanumerical characters (a-z and/or A-Z and/or 0-9) and dashes(-).
- String S is non-empty.
繁琐的字符串拼接题。。。。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
string licenseKeyFormatting(string S, int K) {
string tmp, res;
for (int i = S.size() - 1; i >= 0; i--) {
if(S[i] == '-')
continue;
tmp = (char) toupper(S[i]) + tmp;
if(tmp.length() == K) {
res.insert(0, "-" + tmp);
tmp.clear();
}
}
if (tmp.empty() && !res.empty()) return res.substr(1);
res = tmp + res;
return res;
}
};
Leetcode485. Max Consecutive Ones
Given a binary array, find the maximum number of consecutive 1s in this array.
Example 1:1
2
3
4Input: [1,1,0,1,1,1]
Output: 3
Explanation: The first two digits or the last three digits are consecutive 1s.
The maximum number of consecutive 1s is 3.
计算最长的连续11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int findMaxConsecutiveOnes(vector<int>& nums) {
int res = 0, count = 0;;
for(int i = 0; i < nums.size(); i ++) {
if(nums[i] == 0) {
res = count > res ? count : res;
count = 0;
}
else
count ++;
}
res = count > res ? count : res;
return res;
}
};
Leetcode486. Predict the Winner
Given an array of scores that are non-negative integers. Player 1 picks one of the numbers from either end of the array followed by the player 2 and then player 1 and so on. Each time a player picks a number, that number will not be available for the next player. This continues until all the scores have been chosen. The player with the maximum score wins.
Given an array of scores, predict whether player 1 is the winner. You can assume each player plays to maximize his score.
Example 1:1
2
3
4
5
6Input: [1, 5, 2]
Output: False
Explanation: Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return False.
Example 2:1
2
3
4Input: [1, 5, 233, 7]
Output: True
Explanation: Player 1 first chooses 1. Then player 2 have to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
Note:
- 1 <= length of the array <= 20.
- Any scores in the given array are non-negative integers and will not exceed 10,000,000.
- If the scores of both players are equal, then player 1 is still the winner.
这道题给了一个小游戏,有一个数组,两个玩家轮流取数,说明了只能从开头或结尾取,问我们第一个玩家能赢吗。而且当前玩家赢返回 true 的条件就是递归调用下一个玩家输返回 false。这里需要一个变量来标记当前是第几个玩家,还需要两个变量来分别记录两个玩家的当前数字和,在递归函数里面,如果当前数组为空了,直接比较两个玩家的当前得分即可,如果数组中只有一个数字了,根据玩家标识来将这个数字加给某个玩家并进行比较总得分。如果数组有多个数字,分别生成两个新数组,一个是去掉首元素,一个是去掉尾元素,然后根据玩家标识分别调用不同的递归,只要下一个玩家两种情况中任意一种返回 false 了,那么当前玩家就可以赢了,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool PredictTheWinner(vector<int>& nums) {
return canWin(nums, 0, 0, 1);
}
bool canWin(vector<int> nums, int sum1, int sum2, int player) {
if (nums.empty()) return sum1 >= sum2;
if (nums.size() == 1) {
if (player == 1) return sum1 + nums[0] >= sum2;
else if (player == 2) return sum2 + nums[0] > sum1;
}
vector<int> va = vector<int>(nums.begin() + 1, nums.end());
vector<int> vb = vector<int>(nums.begin(), nums.end() - 1);
if (player == 1) {
return !canWin(va, sum1 + nums[0], sum2, 2) || !canWin(vb, sum1 + nums.back(), sum2, 2);
} else if (player == 2) {
return !canWin(va, sum1, sum2 + nums[0], 1) || !canWin(vb, sum1, sum2 + nums.back(), 1);
}
}
};
两人依次拿,如果Player1赢,则Player1拿的>Player2拿的。我们把Player1拿的视为”+”,把Player2拿的视为”-“,如果最后结果大于等于0则Player1赢。
因此对于递归来说,beg ~ end的结果为max(nums[beg] - partition(beg + 1, end), nums[end] - partition(beg, end + 1));对于非递归来说DP[beg][end]表示即为beg ~ end所取的值的大小(最终与零比较)。
总结:
- 该问题没有直接比较一个选手所拿元素的和值,而是把问题转换为两个选手所拿元素的差值。这一点很巧妙,是关键的一步。
- 找出递推表达式:
max(nums[beg] - partition(beg + 1, end), nums[end] - partition(beg, end + 1)) - 通过递推表达式构造递归算法是比较简单的。但是要构造一个非递归的算法难度较大。对于非递归算法,首先在dp中赋初始值,这是我们解题的第一步。在这个问题中,我们使用一个二位的数组dp来表示nums数组中任意开始和结束位置两人结果的差值。
初始的时候,我们仅仅知道对角线上的值。dp[i][i] = nums[i]。
接下来既然是求任意的开始和结束,对于二维数组,那肯定是一个双层的循环。通过dp中已知的元素和动态规划的递推表达式,我们就可以构造出我们的需要的结果。非递归的方式是从小问题到大问题的过程。1
2
3
4
5
6
7
8
9
10public class Solution {
public boolean PredictTheWinner(int[] nums) {
return helper(nums, 0, nums.length-1) >= 0;
}
public int helper(int[] nums, int start, int end) {
if(start == end) return nums[start];
else return Math.max(nums[start]-helper(nums, start+1, end), nums[end]-helper(nums, start, end-1));
}
}
【java代码——递归2(保存中间状态)】1
2
3
4
5
6
7
8
9
10
11
12
13public class Solution {
public boolean PredictTheWinner(int[] nums) {
return helper(nums, 0, nums.length-1, new Integer[nums.length][nums.length]) >= 0;
}
public int helper(int[] nums, int start, int end, Integer[][] dp) {
if(dp[start][end] == null) {
if(start == end) return nums[start];
else return Math.max(nums[start]-helper(nums, start+1,end, dp), nums[end]-helper(nums, start,end-1, dp));
}
return dp[start][end];
}
}
Leetcode488. 祖玛游戏
你正在参与祖玛游戏的一个变种。
在这个祖玛游戏变体中,桌面上有 一排 彩球,每个球的颜色可能是:红色 ‘R’、黄色 ‘Y’、蓝色 ‘B’、绿色 ‘G’ 或白色 ‘W’ 。你的手中也有一些彩球。
你的目标是 清空 桌面上所有的球。每一回合:
从你手上的彩球中选出 任意一颗 ,然后将其插入桌面上那一排球中:两球之间或这一排球的任一端。
接着,如果有出现 三个或者三个以上 且 颜色相同 的球相连的话,就把它们移除掉。
如果这种移除操作同样导致出现三个或者三个以上且颜色相同的球相连,则可以继续移除这些球,直到不再满足移除条件。
如果桌面上所有球都被移除,则认为你赢得本场游戏。
重复这个过程,直到你赢了游戏或者手中没有更多的球。
给你一个字符串 board ,表示桌面上最开始的那排球。另给你一个字符串 hand ,表示手里的彩球。请你按上述操作步骤移除掉桌上所有球,计算并返回所需的 最少 球数。如果不能移除桌上所有的球,返回 -1 。
示例 1:1
2
3
4
5
6输入:board = "WRRBBW", hand = "RB"
输出:-1
解释:无法移除桌面上的所有球。可以得到的最好局面是:
- 插入一个 'R' ,使桌面变为 WRRRBBW 。WRRRBBW -> WBBW
- 插入一个 'B' ,使桌面变为 WBBBW 。WBBBW -> WW
桌面上还剩着球,没有其他球可以插入。
示例 2:1
2
3
4
5
6输入:board = "WWRRBBWW", hand = "WRBRW"
输出:2
解释:要想清空桌面上的球,可以按下述步骤:
- 插入一个 'R' ,使桌面变为 WWRRRBBWW 。WWRRRBBWW -> WWBBWW
- 插入一个 'B' ,使桌面变为 WWBBBWW 。WWBBBWW -> WWWW -> empty
只需从手中出 2 个球就可以清空桌面。
示例 3:1
2
3
4
5
6输入:board = "G", hand = "GGGGG"
输出:2
解释:要想清空桌面上的球,可以按下述步骤:
- 插入一个 'G' ,使桌面变为 GG 。
- 插入一个 'G' ,使桌面变为 GGG 。GGG -> empty
只需从手中出 2 个球就可以清空桌面。
示例 4:1
2
3
4
5
6
7输入:board = "RBYYBBRRB", hand = "YRBGB"
输出:3
解释:要想清空桌面上的球,可以按下述步骤:
- 插入一个 'Y' ,使桌面变为 RBYYYBBRRB 。RBYYYBBRRB -> RBBBRRB -> RRRB -> B
- 插入一个 'B' ,使桌面变为 BB 。
- 插入一个 'B' ,使桌面变为 BBB 。BBB -> empty
只需从手中出 3 个球就可以清空桌面。
根据题目要求,桌面上最多有 1616 个球,手中最多有 55 个球;我们可以以任意顺序在 55 个回合中使用手中的球;在每个回合中,我们可以选择将手中的球插入到桌面上任意两球之间或这一排球的任意一端。
因为插入球的颜色和位置的选择是多样的,选择的影响也可能在多次消除操作之后才能体现出来,所以通过贪心方法根据当前情况很难做出全局最优的决策。实际每次插入一个新的小球时,并不保证插入后一定可以消除,因此我们需要搜索和遍历所有可能的插入方法,找到最小的插入次数。比如以下测试用例:
桌面上的球为 RRWWRRBBRR,手中的球为 WB,如果我们按照贪心法每次插入进行消除就会出现无法完全消除。因此,我们使用广度优先搜索来解决这道题。即对状态空间进行枚举,通过穷尽所有的可能来找到最优解,并使用剪枝的方法来优化搜索过程。
为什么使用广度优先搜索?
我们不妨规定,每一种不同的桌面上球的情况和手中球的情况的组合都是一种不同的状态。对于相同的状态,其清空桌面上球所需的回合数总是相同的;而不同的插入球的顺序,也可能得到相同的状态。因此,如果使用深度优先搜索,则需要使用记忆化搜索,以避免重复计算相同的状态。
因为只需要找出需要回合数最少的方案,因此使用广度优先搜索可以得到可以消除桌面上所有球的方案时就直接返回结果,而不需要继续遍历更多需要回合数更多的方案。而广度优先搜索虽然需要在队列中存储较多的状态,但是因为使用深度优先搜索也需要存储这些状态及这些状态对应的结果,因此使用广度优先搜索并不会需要更多的空间。
在算法的实现中,我们可以通过以下方法来实现广度优先:
使用队列来维护需要处理的状态队列,使用哈希集合存储已经访问过的状态。每一次取出队列中的队头状态,考虑其中所有可以插入球的方案,如果新方案还没有被访问过,则将新方案添加到队列的队尾。
下面,我们考虑剪枝条件:
第 1 个剪枝条件:手中颜色相同的球每次选择时只需要考虑其中一个即可
如果手中有颜色相同的球,那么插入这些球中的哪一个都没有区别。因此,手中颜色相同的球,我们只需要考虑其中一个即可。在具体的实现中,我们可以先将手中的球排序,如果当前遍历的球的颜色和上一个遍历的球的颜色相同,则跳过当前遍历的球。
第 2 个剪枝条件:只在连续相同颜色的球的开头位置或者结尾位置插入新的颜色相同的球
如果桌面上有一个红球,那么在其左侧和右侧插入一个新的红球没有区别;同理,如果桌面上有 2 个连续的红球,那么在其左侧、中间和右侧插入一个新的红球没有区别。因此,如果新插入的球和桌面上某组连续颜色相同的球(也可以是 1 个)的颜色相同,我们只需要考虑在其左侧插入新球的情况即可。在具体的实现中,如果新插入的球和插入位置左侧的球的颜色相同,则跳过这个位置。
第 3 个剪枝条件:只考虑放置新球后有可能得到更优解的位置
考虑插入新球的颜色与插入位置周围球的颜色的情况,在已经根据第 2 个剪枝条件剪枝后,还可能出现如下三种情况:插入新球与插入位置右侧的球颜色相同;插入新球与插入位置两侧的球颜色均不相同,且插入位置两侧的球的颜色不同;插入新球与插入位置两侧的球颜色均不相同,且插入位置两侧的球的颜色相同。
对于「插入新球与插入位置右侧的球颜色相同」的情况,这种操作可能可以构成连续三个相同颜色的球实现消除,是有可能得到更优解的。读者可以结合以下例子理解。
例如:桌面上的球为 WWRRBBWW,手中的球为 WWRB,答案为 2。
操作方法如下:WWRRBBWW -> WW(R)RRBBWW -> WWBBWW -> WW(B)BBWW -> WWWW “”。
对于「插入新球与插入位置两侧的球颜色均不相同,且插入位置两侧的球的颜色不同」的情况,这种操作可以将连续相同颜色的球拆分到不同的组合中消除,也是有可能得到更优解的。读者可以结合以下例子理解。
例如:桌面上的球为 RRWWRRBBRR,手中的球为 WB,答案为 2。
操作方法如下:RRWWRRBBRR→RRWWRRBBR(W)R→RRWWRR(B)BBRWR→RRWWRRRWR→RRWWWR→RRR→””。
对于「插入新球与插入位置两侧的球颜色均不相同,且插入位置两侧的球的颜色相同」的情况,这种操作并不能对消除顺序产生任何影响。如插入位置旁边的球可以消除的话,那么这种插入方法与直接将新球插入到与之颜色相同的球的旁边没有区别。因此,这种操作不能得到比「插入新球与插入位置右侧的球颜色相同」更好的情况,得到更优解。读者可以结合以下例子理解。
例如:桌面上的球为 WWRRBBWW,手中的球为 WWRB,答案为 2。
操作方法如下:WWRRBBWW→WWRRBB(R)WW→WWRRB(B)BRWW→WWRRRWW→WWWW→””。
细节
题目规定了如果在消除操作后,如果导致出现了新的连续三个或者三个以上颜色相同的球,则继续消除这些球,直到不再满足消除条件,实际消除时我们可以利用栈的特性,每次遇到连续可以消除的球时,我们就将其从栈中弹出。在实现中,我们可以在遍历桌面上的球时,使用列表维护遍历过的每种球的颜色和连续数量,从而通过一次遍历消除连续三个或者三个以上颜色相同的球。具体地:
使用 visited_ball 维护遍历过的每种球的颜色和连续数量,设其中最后一个颜色 last_color,其连续数量为last_num;遍历桌面上的球,设当前遍历到的球为cur_ball,其颜色为cur_color。
- 首先,判断:如果visited_ball 不为空,且cur_color 与last_color 不同,则判断:如果last_num 大于等于 3,则从visited_ball 中移除last_color 和last_num。
- 接着,判断:如果visited_ball 为空,或cur_color 与last_color 不同,则向visited_ball 添加cur_color 及连续数量 1;
- 否则,累加last_num。
- 最后,根据列表中维护的每种球的颜色和连续数量,重新构造桌面上的球的组合即可。
1 | struct State { |
Leetcode491. Increasing Subsequences
Given an integer array nums, return all the different possible increasing subsequences of the given array with at least two elements. You may return the answer in any order.
The given array may contain duplicates, and two equal integers should also be considered a special case of increasing sequence.
Example 1:1
2Input: nums = [4,6,7,7]
Output: [[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
Example 2:1
2Input: nums = [4,4,3,2,1]
Output: [[4,4]]
这道题让我们找出所有的递增子序列,应该不难想到,这题肯定是要先找出所有的子序列,从中找出递增的。首先来看一种迭代的解法,对于重复项的处理,最偷懒的方法是使用 TreeSet,利用其自动去处重复项的机制,然后最后返回时再转回 vector 即可。由于是找递增序列,所以需要对递归函数做一些修改,首先题目中说明了递增序列数字至少两个,所以只有子序列个数大于等于2时,才加入结果。然后就是要递增,如果之前的数字大于当前的数字,那么跳过这种情况,继续循环,参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
vector<vector<int>> findSubsequences(vector<int>& nums) {
set<vector<int>> res;
vector<int> s;
helper(nums, 0, s, res);
return vector(res.begin(), res.end());
}
void helper(vector<int>& nums, int i, vector<int> s, set<vector<int>>& res) {
if (s.size() > 1)
res.insert(s);
for (; i < nums.size(); i ++) {
if (!s.empty() && s.back() > nums[i])
continue;
s.push_back(nums[i]);
helper(nums, i+1, s, res);
s.pop_back();
}
}
};
Leetcode492. Construct the Rectangle
For a web developer, it is very important to know how to design a web page’s size. So, given a specific rectangular web page’s area, your job by now is to design a rectangular web page, whose length L and width W satisfy the following requirements:
- The area of the rectangular web page you designed must equal to the given target area.
- The width W should not be larger than the length L, which means L >= W.
- The difference between length L and width W should be as small as possible.
You need to output the length L and the width W of the web page you designed in sequence.
Example:1
2
3
4Input: 4
Output: [2, 2]
Explanation: The target area is 4, and all the possible ways to construct it are [1,4], [2,2], [4,1].
But according to requirement 2, [1,4] is illegal; according to requirement 3, [4,1] is not optimal compared to [2,2]. So the length L is 2, and the width W is 2.
构造矩形,并不断比较长宽差,差距最小的保留输出1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
vector<int> constructRectangle(int area) {
int ii = sqrt(area);
vector<int> res;
res.push_back(1);
res.push_back(area);
for(int i = 1; i <= ii; i ++) {
int temp = area / i;
if(temp * i == area) {
if(abs(res[0]-res[1]) > abs(temp - i)) {
res[0] = i;
res[1] = temp;
}
}
}
if(res[0] < res[1]) {
int temp = res[0];
res[0] = res[1];
res[1] = temp;
}
return res;
}
};
Leetcode493. Reverse Pairs
Given an array nums, we call (i, j) an important reverse pair if i < j and nums[i] > 2*nums[j].
You need to return the number of important reverse pairs in the given array.
Example1:1
2Input: [1,3,2,3,1]
Output: 2
Example2:1
2Input: [2,4,3,5,1]
Output: 3
Note:
- The length of the given array will not exceed 50,000.
- All the numbers in the input array are in the range of 32-bit integer.
一种方法叫分割重现关系 (Partition Recurrence Relation),用式子表示是 T(i, j) = T(i, m) + T(m+1, j) + C。这里的C就是处理合并两个部分的子问题,那么用文字来描述就是“已知翻转对的两个数字分别在子数组 nums[i, m] 和 nums[m+1, j] 之中,求满足要求的翻转对的个数”,这里翻转对的两个条件中的顺序条件已经满足,就只需要找到满足大小关系的的数对即可。如果两个子数组是有序的,那么我们可以用双指针的方法在线性时间内就可以统计出符合题意的翻转对的个数。要想办法产生有序的子数组,那么这就和 MergeSort 的核心思想完美匹配了。我们知道混合排序就是不断的将数组对半拆分成子数组,拆到最小的数组后开始排序,然后一层一层的返回,最后原数组也是有序的了。这里我们在混合排序的递归函数中,对有序的两个子数组进行统计翻转对的个数,区间 [left, mid] 和 [mid+1, right] 内的翻转对儿个数就被分别统计出来了,此时还要统计翻转对儿的两个数字分别在两个区间中的情况,那么i遍历 [left, mid] 区间所有的数字,j则从 mid+1 开始检测,假如 nums[i] 大于 nums[j] 的二倍,则这两个数字就是翻转对,此时j再自增1,直到不满足这个条件停止,则j增加的个数就是符合题意的翻转对的个数,所以用当前的j减去其初始值 mid+1 即为所求,然后再逐层返回
1 | class Solution { |
Leetcode494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-‘ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-‘ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:1
2
3
4
5
6
7
8输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:1
2输入:nums = [1], target = 1
输出:1
这道题给了我们一个数组,和一个目标值,让给数组中每个数字加上正号或负号,然后求和要和目标值相等,求有多少中不同的情况。那么对于这种求多种情况的问题,博主最想到的方法使用递归来做。从第一个数字,调用递归函数,在递归函数中,分别对目标值进行加上当前数字调用递归,和减去当前数字调用递归,这样会涵盖所有情况,并且当所有数字遍历完成后,若目标值为0了,则结果 res 自增1,参见代码如下:
1 | class Solution { |
我们对上面的递归方法进行优化,使用 memo 数组来记录中间值,这样可以避免重复运算,参见代码如下:
1 | class Solution { |
Leetcode495. Teemo Attacking
Our hero Teemo is attacking an enemy Ashe with poison attacks! When Teemo attacks Ashe, Ashe gets poisoned for a exactly duration seconds. More formally, an attack at second t will mean Ashe is poisoned during the inclusive time interval [t, t + duration - 1]. If Teemo attacks again before the poison effect ends, the timer for it is reset, and the poison effect will end duration seconds after the new attack.
You are given a non-decreasing integer array timeSeries, where timeSeries[i] denotes that Teemo attacks Ashe at second timeSeries[i], and an integer duration.
Return the total number of seconds that Ashe is poisoned.
Example 1:1
2
3
4
5
6Input: timeSeries = [1,4], duration = 2
Output: 4
Explanation: Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 4, Teemo attacks, and Ashe is poisoned for seconds 4 and 5.
Ashe is poisoned for seconds 1, 2, 4, and 5, which is 4 seconds in total.
Example 2:1
2
3
4
5
6Input: timeSeries = [1,2], duration = 2
Output: 3
Explanation: Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 2 however, Teemo attacks again and resets the poison timer. Ashe is poisoned for seconds 2 and 3.
Ashe is poisoned for seconds 1, 2, and 3, which is 3 seconds in total.
直接使用贪心算法,比较相邻两个时间点的时间差,如果小于duration,就加上这个差,如果大于或等于,就加上duration即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int findPoisonedDuration(vector<int>& timeSeries, int duration) {
int last = -1, res = 0;
for (int i = 0; i < timeSeries.size(); i ++) {
if (timeSeries[i] <= last) {
if (timeSeries[i] + duration > last) {
res = res + (timeSeries[i] + duration - last -1);
last = timeSeries[i] + duration - 1;
}
}
else {
res += duration;
last = timeSeries[i] + duration - 1;
}
}
return res;
}
};
Leetcode496. Next Greater Element I
You are given two arrays (without duplicates) nums1 and nums2 where nums1’s elements are subset of nums2. Find all the next greater numbers for nums1’s elements in the corresponding places of nums2.
The Next Greater Number of a number x in nums1 is the first greater number to its right in nums2. If it does not exist, output -1 for this number.
Example 1:1
2
3
4
5
6Input: nums1 = [4,1,2], nums2 = [1,3,4,2].
Output: [-1,3,-1]
Explanation:
For number 4 in the first array, you cannot find the next greater number for it in the second array, so output -1.
For number 1 in the first array, the next greater number for it in the second array is 3.
For number 2 in the first array, there is no next greater number for it in the second array, so output -1.
Example 2:1
2
3
4
5Input: nums1 = [2,4], nums2 = [1,2,3,4].
Output: [3,-1]
Explanation:
For number 2 in the first array, the next greater number for it in the second array is 3.
For number 4 in the first array, there is no next greater number for it in the second array, so output -1.
在num2中找到num1的每个元素,然后从这个元素往后找一个比它大的数,用标志位控制即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
vector<int> res;
int first = nums1.size(), second = nums2.size();
int i, j;
bool find;
for(i = 0; i < first; i ++){
find = false;
for(j = 0; j < second; j ++) {
if(nums1[i] == nums2[j])
find = true;
if(find && nums1[i] < nums2[j])
break;
}
if(j == second)
res.push_back(-1);
else
res.push_back(nums2[j]);
}
return res;
}
};
Leetcode498. Diagonal Traverse
Given an m x n matrix mat, return an array of all the elements of the array in a diagonal order.
Example 1:1
2Input: mat = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,4,7,5,3,6,8,9]
Example 2:1
2Input: mat = [[1,2],[3,4]]
Output: [1,2,3,4]
这道题给了我们一个mxn大小的数组,让我们进行对角线遍历,先向右上,然后左下,再右上,以此类推直至遍历完整个数组,题目中的例子和图示也能很好的帮我们理解。由于移动的方向不再是水平或竖直方向,而是对角线方向,那么每移动一次,横纵坐标都要变化,向右上移动的话要坐标加上[-1, 1],向左下移动的话要坐标加上[1, -1],那么难点在于我们如何处理越界情况,越界后遍历的方向怎么变换。向右上和左下两个对角线方向遍历的时候都会有越界的可能,但是除了左下角和右上角的位置越界需要改变两个坐标之外,其余的越界只需要改变一个。那么我们就先判断要同时改变两个坐标的越界情况,即在右上角和左下角的位置。如果在右上角位置还要往右上走时,那么要移动到它下面的位置的,那么如果col超过了n-1的范围,那么col重置为n-1,并且row自增2,然后改变遍历的方向。同理如果row超过了m-1的范围,那么row重置为m-1,并且col自增2,然后改变遍历的方向。然后我们再来判断一般的越界情况,如果row小于0,那么row重置0,然后改变遍历的方向。同理如果col小于0,那么col重置0,然后改变遍历的方向。参见代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
if (mat.empty() || mat[0].empty())
return {};
int x = 0, y = 0, dir = 0;
vector<int> res;
vector<vector<int>> dirs{{-1,1}, {1,-1}};
int m = mat.size(), n = mat[0].size(), size = m*n;
for (int i = 0; i < size; i ++) {
res.push_back(mat[x][y]);
x += dirs[dir][0];
y += dirs[dir][1];
if (x >= m) { x = m - 1; y += 2; dir = 1 - dir; }
if (y >= n) { y = n - 1; x += 2; dir = 1 - dir; }
if (x < 0) { x = 0; dir = 1 - dir; }
if (y < 0) { y = 0; dir = 1 - dir; }
}
return res;
}
};
Leetcode500. Keyboard Row
Given a List of words, return the words that can be typed using letters of alphabet on only one row’s of American keyboard like the image below.
Example:1
2Input: ["Hello", "Alaska", "Dad", "Peace"]
Output: ["Alaska", "Dad"]
给出n个字符串,从而判断每个字符串中的字符石头来自美式键盘上的同一行,若来自同一行,返回该string。过程将键盘上的每行字符存储到相应的vector或者数组中,然后循环Input中的每个string,并且循环string中的每个char,从而进行比较。
1 | class Solution { |